J thus giving a representation for
|
|
|
- Ira Caldwell
- 5 years ago
- Views:
Transcription
1 Represetatio of Fractioa Factoria Desig i Terms of (,)-~fatrices By D. A. ANDERSON* AND W. T. FEDERER Uiversity of Wyomig, Core Uiversity SUMMARY Let T deote a mai effect pa for the s factoria with N assembies, that is Tis an x matrix with eemets from the {,,...,s-. Deote by T, T,., T s- then x icidece matrices of,,...,s- respectivey, so that T it. ad T. = JN. Usig the x Hemert poyomias to defie sige degree of freedom mai effect cotrasts we write E{y} = X~, where X is the desig matrix correspodig to T.. XG = X* = [ ; T... : T A trasformatio G is obtaied for which. s- J thus givig a represetatio for the desig matrix directy i terms of the (,)-icidece matrices. t is show that ei = (s!)-(-)(s-) ad jx'x = (s!) 2 x*'x*. f Tis a saturated mai effect pa, the x = (s!)x*. Thus the determiat of the iformatio matrix is directy expressibe i terms of the determiat of a (,)-matrix. These resuts are exteded to icude the geera asymmetrica factoria s.. Upper bouds are obtaied for the determiat vaues of X* whe X* is square ad i geera for X*'X*. Oe importat aspect of this represetatio is that the costructio of mai effect pas ad a assessmet of their goodess via the determiat criteria ca be studied directy i terms of (,) matrices. A extesio to icude iteractio terms for the s factoria where s is a prime or prime power is give. Keywords: D OPTMAL DESGN: MAN EFFECT DESGN: HADAMARD BOUND. *First draft writte whie o eave from the Uiversity of Wyomig ad at Core Uiversity. ~J ~~~ ~f/
2 -2-. NTRODUCTON a factoria experimet ivovig factors with the ith factor at s. eves i =,2,...,, the tota umber of treatmet combiatios is is.. i= A desig is usuay represeted as a N x matrix T whose N rows deote the particuar treatmet combiatios ad whose coums correspod to the eves of the factors. The eemets of a coum of T correspodig to a factor at s. eves are itegers from {O,,...,s.-}, i deote the s. eves. the aaysis, the matrix T is amost uiversay repaced by,2,...,, to a matrix ~- -~XV which refects the v sige degree of freedom parametric cotrasts i the parametric vector ~ from the usua regressio equatio The orma equatios are X~X~ = X~y, ad soutios to the orma equatios provide best iear ubiased estimates of estimabe fuctios of the parameters i~ The matrix Xc is caed the iformatio matrix of the desig T, ad if X~X is osiguar the variacecovariace matrix of Sis proportioa to (X~X)- Most criteria of goodess of a desig deped upo some fuctio of (X~X)-, as for exampe, the determiat, trace, ad maximum root criteria. f X~X is siguar we cosider a coditioa iverse (X~X) ad restrict to estimabe fuctios of the S's. Sice the matrix X is obtaied directy from the matrix T, a of the iformatio cocerig the goodess of the desig (i terms of some fuctio of (X~X)-) is cotaied withi T. Thus for the purpose of costructig good desigs ad the compariso of desigs, the simpest ad most direct represetatio of this property i terms of T itsef woud be usefu. Raktoe ad Federer [97] obtaied such a represetatio directy i terms of the (,) matrix (:T) for mai effect pas for the 2 factoria,
3 -3- where deotes a vector with every eemet uity. Sectio 2 of this paper we preset a simiar represetatio for the. s. factoria, ad we p represet cx~x)- directy i terms of this represetatio. the third sectio a upper boud o the x~x is obtaied for both the symmetric ad asymmetric factorias, ad the miimum ozero vaue of this determiat is idicated. The importace of the represetatio preseted ies i the isight that may be gaied toward the costructio of fractioa factoria pas ad the assessmet of their goodess via the deterimat criteria. 2. REPRESENTATON OF MAN EFFECT PLANS N TERMS OF (,)-MATRCES Cosider first the s symmetrica factoria ad the correspodig mai effect pas for estimatig the v = + (s-) mea ad mai effects uder the assumptio that a two-factor ad higher-factor iteractios are zero. Let TN x be an x matrix, N ~ v, with eemets from the set {O,,...,s-} deotig such a mai effect pa. matrix of eemet i i T. correspodig eemet of T is i or ot. LetT., i = O,,,s-, be then x icidece That is, a eemet oft. is oe or zero as the The, s- L T = J ad T. i N x ' = s- LiT.. i=o Typicay mai effects are defied i terms of a set of orthogoa (2.) poyomias. For coveiece, we sha use the Hemert poyomias, - -2 (2.2).. -(s-) eve though ay set of orthoga poyomias may be used. The, if y deotes a N x observatio vector correspodig to T, et 2 E[y] = X~ ad Cov(y) = cr N,
4 s- where_ _= (!J,S,...,s s,...,s.s,... f\ ) deotes the v X parameter vector of sige degree of freedom cotrasts as derived from Hemert poyomias ad where X is the desig matrix. The desig matrix may be writte i terms of the T. as X = [ s-2 L T. - (s-)t ] i= s- (2. 3) theorems 2. ad 2.2 we trasform the desig matrix X for a mai effect pa from the s factoria ito a (,)-matrix. The resuts are exteded i theorems 2.3 ad 2.4 for the geera ~ si asymmetrica factoria. The = importace of these resuts ceters aroud the facts that (i) cosiderabe theory is avaiabe o the costructio of mai effect pas for the 2 factoria ad o the vaues of the determiats of (,)-matrices, (ii) this theory ca ow be appied to the costructio ad to the cosideratio of optimaity of mai effect pas from the geera factoria, ad (iii) these resuts exted the resuts of Raktoe ad Federer [97] for the 2 factoria to the geera symmetrica ad asymmetrica factorias. Cosider the coum operatios o X resutig from postmutipyig by a matrix G as foows: XG =X*, (2.4) where G is the foowig V X v matrix: ' S- ' s.- ' S- ' s- - 2 (2. 5) G= - 2[3) 3 3 (4) 3 (4) - 4 s(s-) s(s-) s(s-)
5 -5- The foowig resuts ca be verified by direct cacuatio. Theorem 2.. Uder the trasformatio XG = X*, we have! Ts_J, that is, the trasformed desig (b) (c) matrix is a (,) -matrix composed of icidece matrices T.,. i =, 2,..., s-; ei= (s!)-(-)(s-); - G = (s-) si (d) X = X*G-; ad (e) x.. x = (s!)2ix*.. X*. Theorem 2.2 f N = v ad the desig is a saturated mai effect pa, the determiat of the resutig square matrix may be expressed as: The proof foows directy from parts (a), (b), ad (d) of theorem 2.. Exampe 2. Cosider the saturated mai effect pa for the 3 4 factoria derived from the foowig pair of orthogoa ati squares: ~j ~ 2 ad _2 2 2! ~J
6 -6- The, a o ~ o o i T = 2 o, T =, ad T 2 o. 2 a o!! ' 2 2 Q i! 2 2!!o!! 2 2 oi :o - ' :... _, _! o Sice T is a orthogoa array, 27 is the maximum vaue possibe for x* of a 3 4 saturated mai effect pa. The effect of the structure costraits (2.) o T, T, ad T 2 is apparet from exampe 2.. The vaue 27 is far beow the maximum vaue of the determiat of a (,)-matrix of size 9 with a eadig coum of oes. fact, for such matrices, Aderso ad Federer [974] obtaied the foowig vaues: a itegers ~ 33, 36, 4, 44, 48, ad 56, with o assurace that a vaues have bee obtaied or that 56 is the maximum vaue. Thus the argest possibe vaue for the determiat of form ~ T ~ T 2 j where T ad T 2 satisfy (2.) is a itermediate vaue amog a possibe vaues. The resuts for the s factoria are ow exteded to the geera asymmetrica factoria s x s 2 x. x s = ij s. Sice factors have.=. differet umbers of eves, it wi be coveiet to cosider the represetatio idividuay for each factor. Thus et the ith coum of T correspodig to the ith factor be deoted by ~i so that T = [~ ~ 2... ~]. Sice F. has s... eves here deoted by O,,...,s.-, the coum d.. -]_ cotais these symbos. Let the icidece matrix of the eve j i the ith coum d. be deoted by d.(j). The equatios (2.) are thus expressed -]_ -]_
7 -7- for each i as si- j=o The s.- ~.(j) ad d = -i Si- L; ( j=o J ~ i j). (2. 6) coums i the X matrix correspodig to the factor F. are give by si-2 [d.(o)-d.(): d.(o)+d.()-2d.(2)! ; L d. (j) j=o - (s.-)d (s -) -i -. (2. 7) ad we et Fiay, et * z. [d. () d. (2) d. (s.-)] (2.8) s} - G. H. j= /s. /s. -/2 /2 (3) -/3 /s.(s.~) /s. (s.-) /s. /s. /s.(s.-)-/s. deote the matrix G of (2. 5) writte oy for the ith factor at s. eves, ad for a factors et j; j s - s - s -, 2 : H G H2 (2. 9),- i : :. io H - - t ca be ascertaied that if X is the desig matrix for a mai effect pa from the asymmetrica factoria that the foowig two theorems hod: Theorem 2.3(a) XG=X* = []:_ : Z~! Z~! (,)-matrix with eadig coum ; (b) (c) ij = - G = (s.!) ad i= x--x = (s.!5x*"x* i= Theorem 2.4. f T is a saturated mai effect pa for the asymmetrica s. factoria, the x = _ ( s.! ) X*. =, j : Z*], where X* is a
8 -H- Note that the coums of X* are ordered so that a (s.-) coums correspodig to the ith factor appear together. This orderig is possibe ad sometimes preferred for the symmetric case aso. The coditios (2.6) are actuay structure costraits o X*. For exampe, each row of Z~, i =,2,...,, ca have at most oe vaue of oe, hece the ier product of ay two coums of Z~ is zero. 2 Exampe 2.2 A desig for a 2 x3x4 factoria i eight rus ad its correspodig (,) represetatio are give as ~ ~ ~! : 2 2i, i T =o 3: X* = : ' o; i i 2 f!! 2:! 3 ' ~ ~ ~ L t is easiy show that x* = 6 so from Theorem 2.4 x 2!2!3!4! BOUNDS ON THE DETERMNANTS OF NONSNGULAR DESGN MATRCES The trasformatio from X to X* provides a simpe proof that the determiat of x~x is ivariat to ay chage of eve desigatio for ay factor. Ay permutatio of the o zero eves resuts oy i a correspodig permutatio of coums i X* which of course does ot chage the vaue of the determiat. Likewise, ay o zero eve may be iterchaged with the zero eve for ay specified factor. The correspodig chage i X* is a iear combiatio of the first coum of a oes ad the coums of T, T 2,..,Ts- correspodig to that factor. Agai this does ot chage the determiat. This ivariace property is a we kow resut, see for exampe Paik ad Federer [97] ad Srivastava, Raktoe, ad Pesota [97], but the represetatio i terms of (,) matrices makes it more apparet.
9 -9- k Let o., k =,,2,..., s- deote the umber of treatmet combiatios s- f f. T h. h. h. th f '.. ' k - f o a racto w c cota t e actor at eve k. ue, k~o oi - N or each i. ay discussio ivovig til' determiat uf X, or of X*, -.c without oss of geeraity, assume that o. because of the ivariace property. : o. :2 may, s- :2 o. for each i Raktoe ad Federer [97] obtaied the foowig boud o X* usig Hadamard's theorem: (3.) Sice x*must be a iteger, we take the iteger part of the right had side of (3.) as the upper boud. We ow obtai a geeraizatio of their resut for X* matrices, ad cosequety X matrices, for saturated mai effect pas from the symmetrica s factoria. Theorem 3.. Let T be a saturated mai effect pa for the s factoria with N = (s-) +. f X* [:_ : T : T2 : : Ts- ], the x* ~iteger part of NN/ 2 s-s/ 2. (3.2) Whe s = 2, this reduces to equatio (3.). Proof: From theorem 2.2, (3.3) From Hadamard's determiat theorem, we kow that x x is ess tha or equa to the product of its diagoa eemets with equaity oy if X'X is a diagoa matrix. where we take. 2 o. 2 Usig equatios (2.5) ad (3.3), we obtai: 2-2 s- 2 k x* ~ (s!) N (o~ + o~ k o.), (3.4) s- 2 o. for each i. i= k= Expressio (3.4) wi be maximized wheever each of the iterior products is maximized; thus, we eed oy cosider (3. 5)
10 -- Next itroduce the Lagrage mutipier correspodig to the costrait s- k s-2 s- a. - N =, ad take derivatives with respect too. ad a. k=o s-2 s- Equatig these two derivatives, we obtai a expressio i a. ad a. as foows: s-2. 2 (s-2) + (s-) (s-3) s-2 The equatios are satisfied whe a. s- a. s- a. 2N s(s-)(s-3) N/s. (3. 6) We may assume that s-2 s- s- a ~ a. ad that a. ~ N/s from the orderig previousy described. i s- s-2 s- Wheever a. < N/s, we have a. <a from (3.6). Hece, it foows that i s- s-2 o. = a. tota is N, we have Thus, N/s ad sice the smaest of the a~ equas N/s ad sice their s- a. N/s, i,2,...,. (3.7) s- s-n+}/2 ~ (s!)-{nn. k(k+) K= (s!)-nn/2[(s-)!s!] /2 NN/2 s -s/2. -(s-)/2 s Coroary 3. Let T be a mai effect pa for a s factoria experimet with N ~ (s-)+. The N(s-)+ -s X*~X* ~ iteger part of s. (3.8) Proof The proof of theorem 3. uses x'x ad the essetia steps do ot deped o N = (s-)+. Hece the proof is compete. Exampe 3. Cosider a set of t orthogoa ati squares of orders. This set may be regarded as a orthogoa mai effect pa for the st+ 2 factoria with N=s 2. f t = s-, which is possibe wheever sis a prime or prime power, the set forms a saturated mai effect pa. The s 2 x (+(t+2)(s-)) matrix X* is give by X*= [ T T 2... Ts_ J where
11 -- T. ' T. (s-) + J ad T. T. = J- i ;t j. Thus J X*'X* = 2 s s' s' s' s si+(j-) J- J- (3.9) s J- si+(j-). J- The determiat of X*'X* is x*'x* s J- J- si+(j-. s(t+2)(s-2)+2 which equas the (3 ) Whe t = s-, the desig is saturated. boud give cora ary.. The x*'x* = ss(s-) ad x* i theorem 3.. ss(s-)/ 2 which equas the boud give Exampe 3.2 Suppose T is a orthogoa array of size N, costraits, s eves, of stregth 2, ad idex A deoted by (N,,s,2). That is, Tis a fractio for a s factoria i N rus such that for ay pair of factors 2 each of the s possibe combiatios of eves occurs exacty A times. Ceary N = As 2 ad the matrix X*'X* for this fractio is exacty A times the matrix (3.9) i exampe 3.. The determiat of X*'X* aso attais the upper boud give i coroary 3.. The upper boud for the geera asymmetrica factoria may be proved i a simiar maer sice the maximizatio is essetiay for a sige factor at a time. The resuts are cotaied i the foowig theorem ad coroary. Theorem 3.2 Let T be a saturated mai effect pa for a geera asymmetrica J s factoria with N = + ~ (s.-) rus ad et X* be the = (,)-matrix of theorems 2.3(a) ad 2.4. The -s X* jj :> iteger part of NN 2 i~ si i/ 2 Coroary ~~ Let T be a mai effect pa for a geera asymmetrica ij = s. factoria with N ~ + ~ (s.-) rus ad et X* be the correspodig = (,)-matrix represetatio. The v iteger part of N i~ x*'x* :> -si s. ' v +:(s.-).
12 -2- Examp~ } :]_. Proportioa frequecy desigs ad sets of orthogoa F squares as discussed by Hedayat ad Seide [97] provide exampes of orthogoa mai effect pas for the asymmetric factoria. t ca be show that the structure of X*'X* for these desigs is simiar to (3.9). Theorem 3.3. The cass of saturated mai effect desigs for the.t s..=. factoria cotais desigs for which jx*j =. ozero vaue is aways attaiabe. as That is the miimum possibe Proof. The famiiar "oe at a time desig" has a (,) represetatio X* v- = f= (si-), whose determiat is ceary oe. The proof is compete sice oe desig is exhibited for every case. Coroary 3.3. f T is a saturated mai effect pa for the.t s. factoria, 2.= the miimum possibe vaue of x'x is ig (si!) ad this vaue is aways attaiabe. Thus for ay saturated desig the jx'x is a mutipe of this miimum vaue. Proof. This foows directy from theorems 2.3 ad 3.3. Thus for saturated mai effect pas the smaest vaue of the determiat of X, or X*, ca aways be attaied. The upper boud o the determiat of X, or X*, wi be attaied wheever a orthogoa saturated mai effect desig with equa umbers of repetitios o the eves of each factor is obtaied. the 3 series, for exampe, this wi occur with = 4 ad N = 9 yiedig x* = 3 3 ; the ext orthogoa saturated mai effect pa occurs for = 3 ad N = 27 yiedig x* = 3 2 cases where a orthogoa desig does ot exist the upper boud wi ot be attaied.
13 -3-4. ON THE CONSTRUCTON OF MAN EFFECT PLANS The costructio of mai effect pas for the symmetric ad asymmetric factoria is ow directy reated to costructios of (,) matrices with certai costraits o the coums. Thus the body of kowedge ad deveoped theory of (,) matrices ca be directy brought to the costructio of mai effect pas. costructios. this sectio we iustrate this with a few types of Reca from (2.) that for a factor at s eves there must be a correspodig set of (s-) coums i X* with a pairwise ier products zero ad amog these coums at east oe row must be a zero. Exampe~ Circuat Matrix Costruct. Let c 2 be a 2 x 2 circuat matrix whose first row cotais oes ad zeros such that the ith ad (+i)th coordiates are ot both oe. The remaiig rows of C are of course just cycic permutatios of the first row. X* J -< ~ x2 2x2 Let X* be This X* matrix is appropriate for a 3 saturated mai effect pa, ad sice the theory of circuats is we kow the determiat is easy to evauate. To iustrate we ist the first row of a suitabe C matrix for the 3 factoria with = 3,4,5,6 ad 7 ad give the correspodig determiat of X*. First row of C Det. of X* 3 ( ) 4 4 ( ) 27 5 ( ) 88 6 (. ) 28 7 ( ) 42 A simiar costructio for the s factoria woud require a (s-) x (s-) circuat matrix with at most oe oe i the i, +i, 2+i,...,(s-)+i coums i =, 2,...,.
14 -4- Exampe~ Sum Compositio- Let T,T 2,...,Ts- be x matrices of oes ad zeros, ad et (s-)ts- Aderso ad Federer [974] cosidered possibe vaues for the determiat of (,)-matrices ad used te methods of costructio to obtai may of the possibe vaues. Here we preset a possibe determiat vaues attaiabe by the above method of costructio for saturated mai effect pas from the 3 series for = 3,4,5,6, ad 7. 3: 4: = 5: 6: = 7: 3 6 [,,2,4] 4 6 [,,2,3,6,9] 5 = [,,2,3,4,5,6,8,9,,2,5,2,25] [,,2,3,4,5] 6 6 [,,2,...,9] 2 = 6 6 [a possibe products of itegers,,...,9] 6 7 [a itegers ~ 8,2,24,32] 2 where the itegers withi a square bracket represet possibe vaues for the determiat of X*. t shoud be oted that this costructio is restrictive ad does ot provide a possibe vaues of jxj. For exampe, for = 3, ad for aother costructio, it is possibe to obtai a desig for which X = 6 3 (3) ad which is ot obtaied via the above costructio. Eve though this method
15 -5- of costructio gave the argest vaue obtaied for = 3, it is expected that this wi hod for arger. Whe :: 4, the orthogoa saturated desig i exampe 2. yieds a desig for which jxj = 6 4 (27), which is three times arger tha the argest vaue obtaied from this sum compositio. The spectrum of possibe vaues or eve the argest possibe vaue of jxj is ukow at preset. The trasformatio of X to X*, i.e., a (,)-matrix, is cosidered to be oe step toward the resoutio of these probems. Exampe 4.3. The costructio of exampe 4.2 ca be exteded to the geera mai effect pas. Let T, T 2,.,Ts- be (,)-matrices of order N x, N 2 x,..,n x, respectivey, for N. ~, such that [ T~] coud be regarded as a s- - mai effect pa foowig desig The, for the 2 factoria with N. + rus. s- for the s factoria with N = + i= T = [ T - 2T 2... (s-)t ] s-. O' Now, cosider the N. rus: X* T s- ad N T - T - 2 T s- X* X*= T 2- T _ o-- T T s- s- Give the T., i =, 2,.., s-, it is a reativey simpe matter to compute X* X*. To cocude, we suggest oe additioa costructio for mai effect pas from the s factoria. This method makes use of a (,)-matrix T ad its compemet (J-T) ad by arragig these matrices to satisfy costraits (2.) ad (2.2). We
16 -6- the 4 iustrate the procedure for the 3, series, ad the for the s series. Exampe 4.4. Let T be a N x (,)-matrix of fu rak with N?. T t >ad T2 For the 3 series, cosider the pa defied by with 3N rus. Each of the three eves of each factor occurs N times. For this desig, 3N N' N' X*'X* N T 'T+(J-T) '(J-T) (J-T) 'T N T' (J-T) T 'T+(J-T) '(J-T)_ f T itsef is a structured matrix, the X*'X* has a simpe structure. For exampe, if T =, the 3 ' ' X*'X* i+(-2)(j-) (J-) (J-) i+(-s) (J-) ad = 3 ( -3+3). For the 4 series, the costructio is give by T J - T T J ~ J- T -- - geera, for the s factoria we ett., i =,Z,...,s-, be sn x matrices whose ith ad (i+)st bocks are T ad J- T, respectivey, with the remaiig bocks composed of zero matrices. For this costructio, we have: sn N' N' N' N' N A B N B A B X*'X* N B A N where A= T'T + (J-T)'(J-T) ad B = (J-T)'T.
17 -7-5. EXTENSON TO NCLUDE NTERACTON TERMS f s is a prime or prime power, it is possibe to icude iteractios i the (,) represetatio of the s factoria. This represetatio is i terms of the geometric defiitio of the factoria effects. this defiitio of the factoria effects the symbo F. F.a a~ EGF(s) is used J to deote (s-) degrees of freedom beogig to the iteractio of the. th d. th f -- a J-- actors. As a rages over the s- ozero vaues of the Gaois fied of order s,gf(s), a (s-)(s-) degrees of freedom for the iteractio betwee F. ad F. are idetified. J with (s-) degrees of freedom is deoted by a 2, a 3,..., ak are ozero eemets of GF(s). k- over a possibe ozero vaues, a (s-) th A geera ~ order compoet (s-) degrees of freedom associated with this kth order iteractio are idetified. f T deotes a desig for the s factoria, et the coums of T be deoted as T = [~ i2... d ]. To icude the iteractio betwee factors F. ad F. i the mode, adjoi tot the (s-) coums J d. +a d. - -J a ;t E GF(s), (5.) where a cacuatios are i the fied GF (s). Each of these coums ceary cotais oy the eemets of GF(s) ad hece have the same form as the coums of T. For higher order iteractios, say F. Fa2 i2 we adjoi to T coums of the form. ~i + a i d i a. d. 2-2 k -k ai,a.,... ai ;to EGF(s) 2 k (5.2) Let D deote the N x(+m) matrix with m coums adjoied to T for a desired iteractios. The matrix D has eemets from GF(s) ad as i (2.), we et D. deote the Nx(+m) icidece matrix of i i D, iegf(s). The L: D iegf(s) i J Nx(+m) ad D i D. (5.3)
18 -8- The X matrix for the mode cotaiig iteractio terms has the same form as (2. 3) ' that is = : X [._ Do D Do +~ 2 D2. s-2 r Di (s-) Ds-J (5.4) i=o t is ow apparet that with v = + (+m)(s-), the v x v matrix G of equatio (2.5) may be mutipied by XNx(+m) exacty as i (2.4) to produce a (,) represetatio of X. This observatio is expicity stated i Theorem 5.. Theorem 5.. With X as i (5.4) ad the trasformatios XG = X*, we have. s- (a) X* [ D ; D2.... ; D ], (b) ei (c) tx = X* (d) x'x = ( ') -(+m\ ~+m)(s-) s. - ' - G ' ad (s!) 2 (+m) x*'x*. Proof. The theorem foows directy from theorem 2. t shoud be oted that i the asymmetric factoria Tis. that iteractios. betwee factors with the same (prime power) umber of eves may be icuded i the mode exacty as i the discussio above. For factors with differig umbers of eves or with o prime power umber of eves the coveiet fied of order s does ot exist. There may be a correspodig (,) represetatio which icudes iteractio terms for the geera asymmetric factoria reative to some other formuatio of the iteractio cotrasts. Pesota ad Raktoe [975] show that the (,) represetatio does ot exted i a atura way if the product defiitio of the effects is used. They do show that such a represetatio does exist i terms of (-,,) matrices, ad exhibit suitabe casses of desig matrices T ad sets of factoria effects such that a atura (,) represetatio does exist.
19 -9- Exampe 5.. Cosider a case where there are three factors each at 3 eves ad it is desired to icude i the mode the iteractio of F with each of F 2 ad F 3, but the F 2 by F 3 iteractio ad the three factor iteractio are to be excuded. For ay desig T, we woud thus adjoi the four coums. (mod 3). The matrix D thus has seve coums ad the correspodig X* matrix of theorem 2. has + 2(7) = 5 coums. ACKNOWLEDGEMENT This research was partiay supported by NSERC grats No. A8776 ad No. AO 724.
20 -2- ANDERSON, D.A. ad FEDERER, W.T.(973). Represetatio ad Costructio of mai effect pas i terms of (,) matrices. Paper umber Bu-499-M i the Biometrics Uit Mimeo Series, Core Uiversity. ANDERSON, D.A. ad FEDERER, W.T.(975). Possibe absoute determiat vaues for square (,)-matrices usefu i fractioa repicatio. Utiitas Mathematica, 7, HEDAYAT, A. ad SEDEN, E.(97). F-square ad orthogoa F-squares desig: A geeraizatio of ati square ad orthogoa ati squares desig. A. Math. Statist JONER, J.R.(973). Simiarity of desigs i fractioa factoria experimets. Ph.D. Thesis, Core Uiversity, August. PAK, U.B. ad FEDERER, W.T.(97). A radomized procedure of saturated mai effect fractioa repicates. A. Math. Statist PESOTAN, H. ad RAKTOE, B.L.(975). Remarks o extesios of the Aderso Federer (,)-Matrix procedure for mai effects of a higher degree. Comm. i Stat. ±(9), RAKTOE, B.L. ad FEDERER, W.T.(97). A characterizatio of optima saturated mai effect pas of the 2 factoria. A. Math. Statist SRVASTAVA, J.N., RAKTOE, B.L., ad PESOTAN, H.(976). O ivariace ad radomizatio i fractioa repicatio. A. Statist. ±
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
MSM203a: Polynomials and rings Chapter 3: Integral domains and fields
 MSM203a: Poyomias ad rigs Chapter 3: Itegra domais ad fieds Richard Kaye Autum 2013 Note: These prited hadouts are iteded to suppemet the materia provided i ectures. They are ot sufficiet o their ow. This
MSM203a: Poyomias ad rigs Chapter 3: Itegra domais ad fieds Richard Kaye Autum 2013 Note: These prited hadouts are iteded to suppemet the materia provided i ectures. They are ot sufficiet o their ow. This
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
ORTHOGONAL POLYNOMIALS AND CONTRAST MATRICES
 ORTHOGONAL POLYNOMIALS AND CONTRAST MATRICES BY Aa N. Ageos ad W. T. Federer BU-754-M November 1981 Abstract The use of Legedre, Hermite, Chebyshev ad Laguerre poyomias i fittig a regressio equatio ad
ORTHOGONAL POLYNOMIALS AND CONTRAST MATRICES BY Aa N. Ageos ad W. T. Federer BU-754-M November 1981 Abstract The use of Legedre, Hermite, Chebyshev ad Laguerre poyomias i fittig a regressio equatio ad
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Determinants of order 2 and 3 were defined in Chapter 2 by the formulae (5.1)
 5. Determiats 5.. Itroductio 5.2. Motivatio for the Choice of Axioms for a Determiat Fuctios 5.3. A Set of Axioms for a Determiat Fuctio 5.4. The Determiat of a Diagoal Matrix 5.5. The Determiat of a Upper
5. Determiats 5.. Itroductio 5.2. Motivatio for the Choice of Axioms for a Determiat Fuctios 5.3. A Set of Axioms for a Determiat Fuctio 5.4. The Determiat of a Diagoal Matrix 5.5. The Determiat of a Upper
Chimica Inorganica 3
 himica Iorgaica Irreducible Represetatios ad haracter Tables Rather tha usig geometrical operatios, it is ofte much more coveiet to employ a ew set of group elemets which are matrices ad to make the rule
himica Iorgaica Irreducible Represetatios ad haracter Tables Rather tha usig geometrical operatios, it is ofte much more coveiet to employ a ew set of group elemets which are matrices ad to make the rule
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
SydU STAT3014 (2015) Second semester Dr. J. Chan 1
 Refereces STAT3014/3914 Appied Statistics-Sampig Preimiary 1. Cochra, W.G. 1963) Sampig Techiques, Wiey, ew York.. Kish, L. 1995) Survey Sampig, Wiey Iter. Sciece. 3. Lohr, S.L. 1999) Sampig: Desig ad
Refereces STAT3014/3914 Appied Statistics-Sampig Preimiary 1. Cochra, W.G. 1963) Sampig Techiques, Wiey, ew York.. Kish, L. 1995) Survey Sampig, Wiey Iter. Sciece. 3. Lohr, S.L. 1999) Sampig: Desig ad
ON WEAK -STATISTICAL CONVERGENCE OF ORDER
 UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
UPB Sci Bu, Series A, Vo 8, Iss, 8 ISSN 3-77 ON WEAK -STATISTICAL CONVERGENCE OF ORDER Sia ERCAN, Yavuz ALTIN ad Çiğdem A BEKTAŞ 3 I the preset paper, we give the cocept of wea -statistica covergece of
19 Fourier Series and Practical Harmonic Analysis
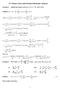 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Supplementary Material on Testing for changes in Kendall s tau
 Suppemetary Materia o Testig for chages i Keda s tau Herod Dehig Uiversity of Bochum Daie Voge Uiversity of Aberdee Marti Weder Uiversity of Greifswad Domiik Wied Uiversity of Cooge Abstract This documet
Suppemetary Materia o Testig for chages i Keda s tau Herod Dehig Uiversity of Bochum Daie Voge Uiversity of Aberdee Marti Weder Uiversity of Greifswad Domiik Wied Uiversity of Cooge Abstract This documet
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING. Lectures
 FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 5 STATISTICS II. Mea ad stadard error of sample data. Biomial distributio. Normal distributio 4. Samplig 5. Cofidece itervals
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 5 STATISTICS II. Mea ad stadard error of sample data. Biomial distributio. Normal distributio 4. Samplig 5. Cofidece itervals
Week 10 Spring Lecture 19. Estimation of Large Covariance Matrices: Upper bound Observe. is contained in the following parameter space,
 Week 0 Sprig 009 Lecture 9. stiatio of Large Covariace Matrices: Upper boud Observe ; ; : : : ; i.i.d. fro a p-variate Gaussia distributio, N (; pp ). We assue that the covariace atrix pp = ( ij ) i;jp
Week 0 Sprig 009 Lecture 9. stiatio of Large Covariace Matrices: Upper boud Observe ; ; : : : ; i.i.d. fro a p-variate Gaussia distributio, N (; pp ). We assue that the covariace atrix pp = ( ij ) i;jp
Principle Of Superposition
 ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
Efficient GMM LECTURE 12 GMM II
 DECEMBER 1 010 LECTURE 1 II Efficiet The estimator depeds o the choice of the weight matrix A. The efficiet estimator is the oe that has the smallest asymptotic variace amog all estimators defied by differet
DECEMBER 1 010 LECTURE 1 II Efficiet The estimator depeds o the choice of the weight matrix A. The efficiet estimator is the oe that has the smallest asymptotic variace amog all estimators defied by differet
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS
 Avaiabe oie at http://sci.org Adv. Iequa. App. 204, 204:26 ISSN: 2050-746 REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS L. HORVÁTH, K.A. KHAN 2, J. PEČARIĆ 3,4, Departmet o Mathematics,
Avaiabe oie at http://sci.org Adv. Iequa. App. 204, 204:26 ISSN: 2050-746 REFINEMENT OF JENSEN S INEQUALITY FOR OPERATOR CONVEX FUNCTIONS L. HORVÁTH, K.A. KHAN 2, J. PEČARIĆ 3,4, Departmet o Mathematics,
Algebra of Least Squares
 October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Linear Regression Demystified
 Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Properties and Hypothesis Testing
 Chapter 3 Properties ad Hypothesis Testig 3.1 Types of data The regressio techiques developed i previous chapters ca be applied to three differet kids of data. 1. Cross-sectioal data. 2. Time series data.
Chapter 3 Properties ad Hypothesis Testig 3.1 Types of data The regressio techiques developed i previous chapters ca be applied to three differet kids of data. 1. Cross-sectioal data. 2. Time series data.
CALCULATING FIBONACCI VECTORS
 THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
Star Saturation Number of Random Graphs
 Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Inverse Matrix. A meaning that matrix B is an inverse of matrix A.
 Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
modes shapes can be obtained by imposing the non-trivial solution condition on the
 modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad
modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad
A Block Cipher Using Linear Congruences
 Joural of Computer Sciece 3 (7): 556-560, 2007 ISSN 1549-3636 2007 Sciece Publicatios A Block Cipher Usig Liear Cogrueces 1 V.U.K. Sastry ad 2 V. Jaaki 1 Academic Affairs, Sreeidhi Istitute of Sciece &
Joural of Computer Sciece 3 (7): 556-560, 2007 ISSN 1549-3636 2007 Sciece Publicatios A Block Cipher Usig Liear Cogrueces 1 V.U.K. Sastry ad 2 V. Jaaki 1 Academic Affairs, Sreeidhi Istitute of Sciece &
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Geometry of LS. LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT
 OCTOBER 7, 2016 LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT Geometry of LS We ca thik of y ad the colums of X as members of the -dimesioal Euclidea space R Oe ca
OCTOBER 7, 2016 LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT Geometry of LS We ca thik of y ad the colums of X as members of the -dimesioal Euclidea space R Oe ca
Session 5. (1) Principal component analysis and Karhunen-Loève transformation
 200 Autum semester Patter Iformatio Processig Topic 2 Image compressio by orthogoal trasformatio Sessio 5 () Pricipal compoet aalysis ad Karhue-Loève trasformatio Topic 2 of this course explais the image
200 Autum semester Patter Iformatio Processig Topic 2 Image compressio by orthogoal trasformatio Sessio 5 () Pricipal compoet aalysis ad Karhue-Loève trasformatio Topic 2 of this course explais the image
On the Product Representation of Number Sequences, with Applications to the Family of Generalized Fibonacci Numbers
 1 2 3 47 6 23 11 Joura of Iteger Sequeces, Vo. 19 2016, Artice 16.3.6 O the Product Represetatio of Number Sequeces, with Appicatios to the Famiy of Geeraized Fiboacci Numbers Michee Rudoph-Liith Uité
1 2 3 47 6 23 11 Joura of Iteger Sequeces, Vo. 19 2016, Artice 16.3.6 O the Product Represetatio of Number Sequeces, with Appicatios to the Famiy of Geeraized Fiboacci Numbers Michee Rudoph-Liith Uité
On the Diophantine equation x 2 2 ˆ y n
 Arch. Math. 74 (000) 50±55 000-889/00/05050-06 $.70/0 Birkhäuser Verag, Base, 000 Archiv der Mathematik O the Diohatie equatio x ˆ y By B. SURY Abstract. We give a eemetary roof of the fact that the oy
Arch. Math. 74 (000) 50±55 000-889/00/05050-06 $.70/0 Birkhäuser Verag, Base, 000 Archiv der Mathematik O the Diohatie equatio x ˆ y By B. SURY Abstract. We give a eemetary roof of the fact that the oy
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
a for a 1 1 matrix. a b a b 2 2 matrix: We define det ad bc 3 3 matrix: We define a a a a a a a a a a a a a a a a a a
 Math E-2b Lecture #8 Notes This week is all about determiats. We ll discuss how to defie them, how to calculate them, lear the allimportat property kow as multiliearity, ad show that a square matrix A
Math E-2b Lecture #8 Notes This week is all about determiats. We ll discuss how to defie them, how to calculate them, lear the allimportat property kow as multiliearity, ad show that a square matrix A
Table 12.1: Contingency table. Feature b. 1 N 11 N 12 N 1b 2 N 21 N 22 N 2b. ... a N a1 N a2 N ab
 Sectio 12 Tests of idepedece ad homogeeity I this lecture we will cosider a situatio whe our observatios are classified by two differet features ad we would like to test if these features are idepedet
Sectio 12 Tests of idepedece ad homogeeity I this lecture we will cosider a situatio whe our observatios are classified by two differet features ad we would like to test if these features are idepedet
Hoggatt and King [lo] defined a complete sequence of natural numbers
![Hoggatt and King [lo] defined a complete sequence of natural numbers Hoggatt and King [lo] defined a complete sequence of natural numbers](/thumbs/96/128001016.jpg) REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
REPRESENTATIONS OF N AS A SUM OF DISTINCT ELEMENTS FROM SPECIAL SEQUENCES DAVID A. KLARNER, Uiversity of Alberta, Edmoto, Caada 1. INTRODUCTION Let a, I deote a sequece of atural umbers which satisfies
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.
![Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f. Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.](/thumbs/91/105380228.jpg) Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
Linear Programming and the Simplex Method
 Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
GENERATING FUNCTIONS
 GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
Beurling Integers: Part 2
 Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Beurlig Itegers: Part 2 Isomorphisms Devi Platt July 11, 2015 1 Prime Factorizatio Sequeces I the last article we itroduced the Beurlig geeralized itegers, which ca be represeted as a sequece of real umbers
Statistics 511 Additional Materials
 Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
Cofidece Itervals o mu Statistics 511 Additioal Materials This topic officially moves us from probability to statistics. We begi to discuss makig ifereces about the populatio. Oe way to differetiate probability
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Some polynomials defined by generating functions and differential equations
 Dobashi et a, Coget Mathematics & Statistics 208, 4: 278830 PURE MATHEMATICS RESEARCH ARTICLE Some poyomias defied by geeratig fuctios ad differetia equatios Nobuyui Dobashi, Eria Suzui ad Shigeru Wataabe
Dobashi et a, Coget Mathematics & Statistics 208, 4: 278830 PURE MATHEMATICS RESEARCH ARTICLE Some poyomias defied by geeratig fuctios ad differetia equatios Nobuyui Dobashi, Eria Suzui ad Shigeru Wataabe
A Note on Some Approximation Kernels on the Sphere
 A Note o Some Approximatio Keres o the Sphere Peter Graber Dedicated to Ia H. Soa o the occasio of his 80 th birthday. Abstract We produce precise estimates for the Kogbetiatz kere for the approximatio
A Note o Some Approximatio Keres o the Sphere Peter Graber Dedicated to Ia H. Soa o the occasio of his 80 th birthday. Abstract We produce precise estimates for the Kogbetiatz kere for the approximatio
EFFECTIVE TRANSITIVE ACTIONS OF THE UNITARY GROUP ON QUOTIENTS OF HOPF MANIFOLDS
 EFFECTIVE TRANSITIVE ACTIONS OF THE UNITARY GROUP ON QUOTIENTS OF HOPF MANIFOLDS ALEXANDER ISAEV arxiv:1607.07964v2 [math.cv] 25 Sep 2016 Abstract. I artice [IKru] we showed that every coected compex maifod
EFFECTIVE TRANSITIVE ACTIONS OF THE UNITARY GROUP ON QUOTIENTS OF HOPF MANIFOLDS ALEXANDER ISAEV arxiv:1607.07964v2 [math.cv] 25 Sep 2016 Abstract. I artice [IKru] we showed that every coected compex maifod
Binomial Distribution
 0.0 0.5 1.0 1.5 2.0 2.5 3.0 0 1 2 3 4 5 6 7 0.0 0.5 1.0 1.5 2.0 2.5 3.0 Overview Example: coi tossed three times Defiitio Formula Recall that a r.v. is discrete if there are either a fiite umber of possible
0.0 0.5 1.0 1.5 2.0 2.5 3.0 0 1 2 3 4 5 6 7 0.0 0.5 1.0 1.5 2.0 2.5 3.0 Overview Example: coi tossed three times Defiitio Formula Recall that a r.v. is discrete if there are either a fiite umber of possible
First Year Quantitative Comp Exam Spring, Part I - 203A. f X (x) = 0 otherwise
 First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
11. FINITE FIELDS. Example 1: The following tables define addition and multiplication for a field of order 4.
 11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
Machine Learning for Data Science (CS 4786)
 Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
An Algebraic Exploration of Dominating Sets and Vizing s Conjecture
 A Agebraic Exporatio of Domiatig Sets ad Vizig s Cojecture S. Marguies 1 ad I.V. Hicks Computatioa ad Appied Math, Rice Uiversity, Housto, Texas Abstract Systems of poyomia equatios are commoy used to
A Agebraic Exporatio of Domiatig Sets ad Vizig s Cojecture S. Marguies 1 ad I.V. Hicks Computatioa ad Appied Math, Rice Uiversity, Housto, Texas Abstract Systems of poyomia equatios are commoy used to
Some remarks for codes and lattices over imaginary quadratic
 Some remarks for codes ad lattices over imagiary quadratic fields Toy Shaska Oaklad Uiversity, Rochester, MI, USA. Caleb Shor Wester New Eglad Uiversity, Sprigfield, MA, USA. shaska@oaklad.edu Abstract
Some remarks for codes ad lattices over imagiary quadratic fields Toy Shaska Oaklad Uiversity, Rochester, MI, USA. Caleb Shor Wester New Eglad Uiversity, Sprigfield, MA, USA. shaska@oaklad.edu Abstract
 1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
The standard deviation of the mean
 Physics 6C Fall 20 The stadard deviatio of the mea These otes provide some clarificatio o the distictio betwee the stadard deviatio ad the stadard deviatio of the mea.. The sample mea ad variace Cosider
Physics 6C Fall 20 The stadard deviatio of the mea These otes provide some clarificatio o the distictio betwee the stadard deviatio ad the stadard deviatio of the mea.. The sample mea ad variace Cosider
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
On the Diffusion Property of Iterated Functions
 O the Diffusio Property of Iterated Fuctios Jia Liu 1, Sihem Mesager 2, ad Lusheg Che 3 1 Schoo of Computer Software, Tiaji Uiversity, Tiaji 300072, P. R. Chia ad CNRS, UMR 7539 LAGA, Paris, Frace jiaiu.k@gmai.com
O the Diffusio Property of Iterated Fuctios Jia Liu 1, Sihem Mesager 2, ad Lusheg Che 3 1 Schoo of Computer Software, Tiaji Uiversity, Tiaji 300072, P. R. Chia ad CNRS, UMR 7539 LAGA, Paris, Frace jiaiu.k@gmai.com
Matrices and vectors
 Oe Matrices ad vectors This book takes for grated that readers have some previous kowledge of the calculus of real fuctios of oe real variable It would be helpful to also have some kowledge of liear algebra
Oe Matrices ad vectors This book takes for grated that readers have some previous kowledge of the calculus of real fuctios of oe real variable It would be helpful to also have some kowledge of liear algebra
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY
 EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 016 MODULE : Statistical Iferece Time allowed: Three hours Cadidates should aswer FIVE questios. All questios carry equal marks. The umber
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 016 MODULE : Statistical Iferece Time allowed: Three hours Cadidates should aswer FIVE questios. All questios carry equal marks. The umber
Chapter 1. Complex Numbers. Dr. Pulak Sahoo
 Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES
 J Lodo Math Soc (2 50, (1994, 465 476 LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES Jerzy Wojciechowski Abstract I [5] Abbott ad Katchalski ask if there exists a costat c >
J Lodo Math Soc (2 50, (1994, 465 476 LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES Jerzy Wojciechowski Abstract I [5] Abbott ad Katchalski ask if there exists a costat c >
SNAP Centre Workshop. Basic Algebraic Manipulation
 SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
Some examples of vector spaces
 Roberto s Notes o Liear Algebra Chapter 11: Vector spaces Sectio 2 Some examples of vector spaces What you eed to kow already: The te axioms eeded to idetify a vector space. What you ca lear here: Some
Roberto s Notes o Liear Algebra Chapter 11: Vector spaces Sectio 2 Some examples of vector spaces What you eed to kow already: The te axioms eeded to idetify a vector space. What you ca lear here: Some
THE SYSTEMATIC AND THE RANDOM. ERRORS - DUE TO ELEMENT TOLERANCES OF ELECTRICAL NETWORKS
 R775 Philips Res. Repts 26,414-423, 1971' THE SYSTEMATIC AND THE RANDOM. ERRORS - DUE TO ELEMENT TOLERANCES OF ELECTRICAL NETWORKS by H. W. HANNEMAN Abstract Usig the law of propagatio of errors, approximated
R775 Philips Res. Repts 26,414-423, 1971' THE SYSTEMATIC AND THE RANDOM. ERRORS - DUE TO ELEMENT TOLERANCES OF ELECTRICAL NETWORKS by H. W. HANNEMAN Abstract Usig the law of propagatio of errors, approximated
CEE 522 Autumn Uncertainty Concepts for Geotechnical Engineering
 CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
Lecture 3 : Random variables and their distributions
 Lecture 3 : Radom variables ad their distributios 3.1 Radom variables Let (Ω, F) ad (S, S) be two measurable spaces. A map X : Ω S is measurable or a radom variable (deoted r.v.) if X 1 (A) {ω : X(ω) A}
Lecture 3 : Radom variables ad their distributios 3.1 Radom variables Let (Ω, F) ad (S, S) be two measurable spaces. A map X : Ω S is measurable or a radom variable (deoted r.v.) if X 1 (A) {ω : X(ω) A}
Similarity Solutions to Unsteady Pseudoplastic. Flow Near a Moving Wall
 Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Estimation of Population Mean Using Co-Efficient of Variation and Median of an Auxiliary Variable
 Iteratioal Joural of Probability ad Statistics 01, 1(4: 111-118 DOI: 10.593/j.ijps.010104.04 Estimatio of Populatio Mea Usig Co-Efficiet of Variatio ad Media of a Auxiliary Variable J. Subramai *, G. Kumarapadiya
Iteratioal Joural of Probability ad Statistics 01, 1(4: 111-118 DOI: 10.593/j.ijps.010104.04 Estimatio of Populatio Mea Usig Co-Efficiet of Variatio ad Media of a Auxiliary Variable J. Subramai *, G. Kumarapadiya
Upper Bounds on Algebraic Immunity of Boolean Power Functions (Extended Abstract)
 Upper Bouds o Agebraic Immuity of Booea Power Fuctios (Exteded Abstract) Yassir Nawaz 1, Guag Gog 1 ad Kisha Chad Gupta 2 1 Departmet of Eectrica ad Computer Egieerig Uiversity of Wateroo Wateroo, ON,
Upper Bouds o Agebraic Immuity of Booea Power Fuctios (Exteded Abstract) Yassir Nawaz 1, Guag Gog 1 ad Kisha Chad Gupta 2 1 Departmet of Eectrica ad Computer Egieerig Uiversity of Wateroo Wateroo, ON,
EECS564 Estimation, Filtering, and Detection Hwk 2 Solns. Winter p θ (z) = (2θz + 1 θ), 0 z 1
 EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
Describing the Relation between Two Variables
 Copyright 010 Pearso Educatio, Ic. Tables ad Formulas for Sulliva, Statistics: Iformed Decisios Usig Data 010 Pearso Educatio, Ic Chapter Orgaizig ad Summarizig Data Relative frequecy = frequecy sum of
Copyright 010 Pearso Educatio, Ic. Tables ad Formulas for Sulliva, Statistics: Iformed Decisios Usig Data 010 Pearso Educatio, Ic Chapter Orgaizig ad Summarizig Data Relative frequecy = frequecy sum of
5.1. The Rayleigh s quotient. Definition 49. Let A = A be a self-adjoint matrix. quotient is the function. R(x) = x,ax, for x = 0.
 40 RODICA D. COSTIN 5. The Rayleigh s priciple ad the i priciple for the eigevalues of a self-adjoit matrix Eigevalues of self-adjoit matrices are easy to calculate. This sectio shows how this is doe usig
40 RODICA D. COSTIN 5. The Rayleigh s priciple ad the i priciple for the eigevalues of a self-adjoit matrix Eigevalues of self-adjoit matrices are easy to calculate. This sectio shows how this is doe usig
Probability, Expectation Value and Uncertainty
 Chapter 1 Probability, Expectatio Value ad Ucertaity We have see that the physically observable properties of a quatum system are represeted by Hermitea operators (also referred to as observables ) such
Chapter 1 Probability, Expectatio Value ad Ucertaity We have see that the physically observable properties of a quatum system are represeted by Hermitea operators (also referred to as observables ) such
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
Discrete-Time Systems, LTI Systems, and Discrete-Time Convolution
 EEL5: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we begi our mathematical treatmet of discrete-time s. As show i Figure, a discrete-time operates or trasforms some iput sequece x [
EEL5: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we begi our mathematical treatmet of discrete-time s. As show i Figure, a discrete-time operates or trasforms some iput sequece x [
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Tests of Hypotheses Based on a Single Sample (Devore Chapter Eight)
 Tests of Hypotheses Based o a Sigle Sample Devore Chapter Eight MATH-252-01: Probability ad Statistics II Sprig 2018 Cotets 1 Hypothesis Tests illustrated with z-tests 1 1.1 Overview of Hypothesis Testig..........
Tests of Hypotheses Based o a Sigle Sample Devore Chapter Eight MATH-252-01: Probability ad Statistics II Sprig 2018 Cotets 1 Hypothesis Tests illustrated with z-tests 1 1.1 Overview of Hypothesis Testig..........
LECTURE 8: ORTHOGONALITY (CHAPTER 5 IN THE BOOK)
 LECTURE 8: ORTHOGONALITY (CHAPTER 5 IN THE BOOK) Everythig marked by is ot required by the course syllabus I this lecture, all vector spaces is over the real umber R. All vectors i R is viewed as a colum
LECTURE 8: ORTHOGONALITY (CHAPTER 5 IN THE BOOK) Everythig marked by is ot required by the course syllabus I this lecture, all vector spaces is over the real umber R. All vectors i R is viewed as a colum
Frequency Response of FIR Filters
 EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we itroduce the idea of the frequecy respose of LTI systems, ad focus specifically o the frequecy respose of FIR filters.. Steady-state
EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we itroduce the idea of the frequecy respose of LTI systems, ad focus specifically o the frequecy respose of FIR filters.. Steady-state
5.1 Review of Singular Value Decomposition (SVD)
 MGMT 69000: Topics i High-dimesioal Data Aalysis Falll 06 Lecture 5: Spectral Clusterig: Overview (cotd) ad Aalysis Lecturer: Jiamig Xu Scribe: Adarsh Barik, Taotao He, September 3, 06 Outlie Review of
MGMT 69000: Topics i High-dimesioal Data Aalysis Falll 06 Lecture 5: Spectral Clusterig: Overview (cotd) ad Aalysis Lecturer: Jiamig Xu Scribe: Adarsh Barik, Taotao He, September 3, 06 Outlie Review of
4 The Sperner property.
 4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
Improving The Problem Not the Code
 mprovig Te Probem Not te Code Fidig Te Max ad Mi of a Number Comparig two adjacet umbers ad fidig te maximum ad miimum e.g. 5 7 8 9 10 1 3 Normay T()= N- Compariso wit a orace, i tis case a touramet teory
mprovig Te Probem Not te Code Fidig Te Max ad Mi of a Number Comparig two adjacet umbers ad fidig te maximum ad miimum e.g. 5 7 8 9 10 1 3 Normay T()= N- Compariso wit a orace, i tis case a touramet teory
Lemma Let f(x) K[x] be a separable polynomial of degree n. Then the Galois group is a subgroup of S n, the permutations of the roots.
![Lemma Let f(x) K[x] be a separable polynomial of degree n. Then the Galois group is a subgroup of S n, the permutations of the roots. Lemma Let f(x) K[x] be a separable polynomial of degree n. Then the Galois group is a subgroup of S n, the permutations of the roots.](/thumbs/84/90649694.jpg) 15 Cubics, Quartics ad Polygos It is iterestig to chase through the argumets of 14 ad see how this affects solvig polyomial equatios i specific examples We make a global assumptio that the characteristic
15 Cubics, Quartics ad Polygos It is iterestig to chase through the argumets of 14 ad see how this affects solvig polyomial equatios i specific examples We make a global assumptio that the characteristic
Binary codes from graphs on triples and permutation decoding
 Biary codes from graphs o triples ad permutatio decodig J. D. Key Departmet of Mathematical Scieces Clemso Uiversity Clemso SC 29634 U.S.A. J. Moori ad B. G. Rodrigues School of Mathematics Statistics
Biary codes from graphs o triples ad permutatio decodig J. D. Key Departmet of Mathematical Scieces Clemso Uiversity Clemso SC 29634 U.S.A. J. Moori ad B. G. Rodrigues School of Mathematics Statistics
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
PRE-IMAGES OF θ-spaces
 Voume 9, 1984 Pages 51 60 http://topoogy.aubur.edu/tp/ PRE-IMAGES OF θ-spaces by Eise M. Graber Topoogy Proceedigs Web: http://topoogy.aubur.edu/tp/ Mai: Topoogy Proceedigs Departmet of Mathematics & Statistics
Voume 9, 1984 Pages 51 60 http://topoogy.aubur.edu/tp/ PRE-IMAGES OF θ-spaces by Eise M. Graber Topoogy Proceedigs Web: http://topoogy.aubur.edu/tp/ Mai: Topoogy Proceedigs Departmet of Mathematics & Statistics
Goodness-of-Fit Tests and Categorical Data Analysis (Devore Chapter Fourteen)
 Goodess-of-Fit Tests ad Categorical Data Aalysis (Devore Chapter Fourtee) MATH-252-01: Probability ad Statistics II Sprig 2019 Cotets 1 Chi-Squared Tests with Kow Probabilities 1 1.1 Chi-Squared Testig................
Goodess-of-Fit Tests ad Categorical Data Aalysis (Devore Chapter Fourtee) MATH-252-01: Probability ad Statistics II Sprig 2019 Cotets 1 Chi-Squared Tests with Kow Probabilities 1 1.1 Chi-Squared Testig................
Math F215: Induction April 7, 2013
 Math F25: Iductio April 7, 203 Iductio is used to prove that a collectio of statemets P(k) depedig o k N are all true. A statemet is simply a mathematical phrase that must be either true or false. Here
Math F25: Iductio April 7, 203 Iductio is used to prove that a collectio of statemets P(k) depedig o k N are all true. A statemet is simply a mathematical phrase that must be either true or false. Here
Statistical Properties of OLS estimators
 1 Statistical Properties of OLS estimators Liear Model: Y i = β 0 + β 1 X i + u i OLS estimators: β 0 = Y β 1X β 1 = Best Liear Ubiased Estimator (BLUE) Liear Estimator: β 0 ad β 1 are liear fuctio of
1 Statistical Properties of OLS estimators Liear Model: Y i = β 0 + β 1 X i + u i OLS estimators: β 0 = Y β 1X β 1 = Best Liear Ubiased Estimator (BLUE) Liear Estimator: β 0 ad β 1 are liear fuctio of
