modes shapes can be obtained by imposing the non-trivial solution condition on the
|
|
|
- Primrose Gordon
- 6 years ago
- Views:
Transcription
1 modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad their state-space represetatio are derived uder distributed vertica oadig coditio. The rest of this chapter is orgaized as foows: Sectios 3. presets the moda aaysis ad forced vibratio formuatio of EB beam with mutipe cross-sectioa discotiuities; Sectios 3.3 icudes the case study of a beam with two step discotiuities i the cross-sectio, to umericay ad graphicay demostrate the effects of discotiuities; ad fiay, Sectio 3.4 presets the cocudig remarks. 3.. Euer-Beroui (EB Beam with Mutipe Stepped Discotiuities Cosider a iitiay straight o-uiform EB beam of egth L, with variabe cross sectio A = A(x, variabe stiffess E = E(x, ad variabe momet of iertia I = I(x. Let x [ 0, L] ad t [ 0, be the spatia ad time variabes, respectivey. The goverig equatio for trasverse vibratio of beam with variabe mass per uit egth m(x ad dampig coefficiet of c(x subjected to a vertica time varyig distributed oad P(x,t is a fourth-order PDE expressed as: wxt (, wxt (, wxt (, ExIx ( ( cx ( mx ( Pxt (, = x x t t (3. with w(x,t beig the trasversa dispacemet fuctio. I order to obtai atura frequecies ad eigefuctios (mode shapes of system, the eigevaue probem 45
2 associated with the trasversa vibratio of beam is obtaied by appyig free ad udamped coditios to Eq. (3. as foows: wxt (, wxt (, ExIx ( ( mx ( = x x t (3. Let s assume that the soutio of Eq. (3. is separabe i time ad space domais, wxt (, = φ( xqt ( (3.3 where φ ( x deotes the spatia mode shape fuctio ad q(t represets the geeraized time-depedet coordiate. Substitutig Eq. (3.3 ito Eq. (3., the eigevaue equatio ca be writte i the foowig form of separated time ad space equatios: ( ExIx ( ( / ( mx ( φ( x = qt ( / qt ( = ω d d φ x (3.4 where ω is a costat parameter. The mode shapes are obtaied by sovig the spatia part of Eq. (3.4 writte as: d d φ( x ExIx ( ( mx ( ( x = ω φ (3.5 For a beam with parametric discotiuities (e.g., jump i the momet of iertia or mass distributio Eq. (3.5 caot be soved usig covetioa approaches. A aterative method is to partitio the beam ito uiform segmets betwee ay two successive stepped poits ad appy the cotiuity coditios at these poits. Therefore, the o-uiform beam is coverted to a set of uiform segmets costraied through the cotiuity coditios. The ext sectio discusses this techique i detai ad proposes a 46
3 framework for dyamic aaysis of fexibe beams with jumped cross-sectioa cofiguratio Moda Aaysis of Stepped EB Beam Figure 3. iustrates a straight EB beam with arbitrary boudary coditios ad jumped discotiuities i its spatia spa. The beam cosidered i this study has a uiform cross-sectio at each segmet. Hece, Eq. (3.5 ca be divided ito uiform equatios expressed as: d φ ( x = < < = (3.6 4 ( EI ω m ( 4 φ x, - x ;,,3,..., ; 0 = 0 where φ ( x, (EI, ad m are mode shapes, fexura stiffess, ad mass per uit egth of beam at the th segmet, respectivey *. Let, 4 m = ω (3.7 ( EI Eq. (3.6 ca be rewritte i a more recogizabe form 4 d φ ( x 4 φ( 0 4 x = (3.8 with the foowig geera soutio φ ( x = A si x B cos x C sih x D cosh x (3.9 * ( deotes the mode shape or parameter vaue for the th cross-sectio, whie ( (r, which wi be used ater i the dissertatio, deotes the mode shape or parameter vaue of the r th mode; though, ω r which represets the r th atura frequecy is a exceptio. 47
4 where A, B, C ad D are the costats of itegratio determied by suitabe boudary ad cotiuity coditios. It is to be oted that ay covetioa boudary coditios ca be appied to the beam; however, without the oss of geeraity, the camped-free coditios are chose here for the boudaries. Appyig the camped coditio at x = 0 requires: dφ (0 φ (0 = = 0 (3.0 Substitutig Eq. (3.0 ito Eq. (3.9 yieds: B D =0 ad A C =0 (3. O the other had, the cotiuity coditios for dispacemet, sope, bedig momet, ad shear force of beam at discotiuity ocatios are give by: φ = φ ( (3. ( d φ ( d ( = φ (3.3 ( EI d φ ( = ( EI d φ ( (3.4 ( EI d 3 φ ( 3 = ( EI d 3 φ ( 3 (3.5 q q d φ( d φ( x q q x=. 48
5 49 Figure 3.. EB beam cofiguratio with jumped discotiuities. Ideed, these coditios are appied at the boudaries of adjacet segmets to satisfy the cotiuity ad equiibrium coditios immediatey before ad after stepped poits. Appyig coditios (3.-(3.5 to Eq. (3.9 resuts i: D C B A D C B A cosh sih cos si cosh sih cos si = (3.6 sih cosh si cos ( sih cosh si cos ( D C B A D C B A = (3.7 cosh sih cos si ( cosh sih cos si ( D C B A D C B A = γ (3.8 sih cosh si cos ( sih cosh si cos ( 3 D C B A D C B A = γ (3.9 where ( ( = EI EI γ. Fiay, the free boudary coditio at x = L= requires:
6 d 3 φ ( d φ ( = 3 = 0 (3.0 Substitutig Eq. (3.0 ito Eq. (3.9 yieds: ( A si B cos C sih D cosh = 0 (3. 3 ( A cos B si C cosh D sih = 0 (3. ote that s are fuctios of beam atura frequecy with a expicit expressio give i Eq. (3.7. Sice the atura frequecy is idepedet of segmets idices ad is cosidered for the etire egth of beam, s of differet segmets ca be iterreated i terms of a sige parameter usig Eq. (3.7: = α (3.3 where ote that α = ad thus, =. /4 m ( EI = m ( EI α (3.4 Eqs. (3., (3. ad (3. derived from boudary coditios whie Eqs. (3.6-(3.9 are obtaied from the cotiuity coditios form the characteristics matrix equatio as: J P = 0 ( where J is the characteristics matrix ad P is the vector of mode shape coefficiets P = (3.6 T [ A B C D A B C D A B C D ] 4 50
7 Matrix J is costructed based o three sets of equatios. The first two rows ad ast two rows represet the boudary coditios at x = 0 ad x = L, respectivey, ad the midde part of matrix demostrates the cotiuity coditios at the siguarity poits. Matrix J ca be divided ito three parts as: J [ J] [ J ] [ J ] 4 = 4( (3.7 where J = (3.8 represets the camed boudary coditio at x = 0 give by Eq. (3., J 8 ( [ J ] ( 0 [ J ] 4 8 = 0 4( 4 ( [ J ] 4 8 4( 4 (3.9 icudes the cotiuity coditios give by Eqs. (3.6-(3.9 at (- poits of discotiuity with J siα cosα sihα coshα α cosα α siα α coshα α sihα ( = γα siα γα cosα γα sihα γα coshα γα cosα γα siα γα coshα γ α 3 sih α 5
8 α α α siα cosα α cosα siα α sihα si α α cosα α sihα α coshα cosα α siα α coshα α sihα coshα α coshα sihα 4 8 ad (3.30 J 0 0 α siα α cosα α sihα α coshα 3 = α cosα α siα α coshα α sihα 4 (3.3 represets the free boudary coditio at x = L give by Eqs. (3. ad (3.. I order to obtai a o-trivia soutio for Eq. (3.5 ad fid the atura frequecies ad mode shapes, the determiat of matrix J must be set to zero det [ J( ] = 0 (3.3 Sice this matrix is a fuctio of oy parameter ( 0,, its determiat ca be umericay evauated for its zero vaues by cotiuousy varyig parameter with a reasoaby sma step size withi a rage of iterest startig from, but excudig zero. The vaues of which satisfy Eq. (3.3 ead to cacuatio of atura frequecies usig a modified versio of Eq. (3.7 as foows: ( EI ( EI ω = = (3.33 ( ( ( r 4 ( r 4 r m m 5
9 where ( r s are soutios for Eq. (3.3 ad ω r is the correspodig r th atura frequecy. Sice the determiat of matrix J has bee set to zero for the seected vaues of, the mode shape coefficiets A to D are ieary depedet. I order to obtai uique soutio for these coefficiets, orthoormaity betwee mode shapes ca be utiized. For the covetioa boudary coditios cosidered here, this coditio is stated as: ( r ( s ( r mx ( φ ( x φ ( x = δ rs or mx ( ( φ ( x = ( ( where δrs is the Kroecker deta fuctio, ad φ r ( x is the r th mode shape of beam expressed as: ( r ( r ( r ( r ( r ( r ( r ( r ( r φ ( x = A si x B cos x C sih x D cosh, 0 x ( r ( r ( r ( r ( r ( r ( r ( r ( r ( ( x A si x B cos x C sih x D cosh x, r φ = < x φ ( x = φ ( x = A si x B cos ( ( ( ( < (3.35 ( r ( r ( r ( r ( r x C r sih r r cosh r x D x, x The obtaied mode shapes ad atura frequecies are used to derive the ODE of motio for a beam uder distributed dyamic excitatio as wi be discussed ext Forced Motio Aaysis of Stepped EB Beam Usig expasio theorem for the beam vibratio aaysis, the expressio for the trasverse dispacemet becomes: ( r ( r (, φ ( ( wxt = xq t (3.36 r= 53
10 where q ( r ( t is the geeraized time-depedet coordiate for the r th mode. Substitutig Eq. (3.36 ito PDE of motio Eq. (3. yieds: ( r= ( r d d φ x ( r ( r ( r ( r ( r E( x I( x q ( t c( x φ ( x q ( t m( x φ ( x q ( t = P( x, t (3.37 To safey take the term E(xI(x out of the bracket for the beam with mutipe discotiuities, Eq. (3.37 is mutipied by s th ( s mode shape, φ ( x, ad is itegrated over the beam egth: 0 r= ( r d d φ ( x ( s ( r ( r ( s ( r ExI ( ( x φ ( xq ( t cx ( φ ( x φ ( xq ( t m x x x q t = P x t x = 0 ( r ( s ( r ( s ( φ ( φ ( ( (, φ ( 0 (3.38 Reca Eq. (3.6 which ca be modified to 4 ( r d φ ( x ( r ( EI = ω ( 4 rmφ x (3.39 Usig Eq. (3.39 ad dividig the spatia itegra ito uiform segmets, oe ca write: ExIx ( ( ( xq ( t = ( EI ( xq ( t = ( r 4 ( r d d φ ( x ( s ( r d φ ( x ( s ( r 4 φ φ = 0 m ( x ( xq ( t = q ( t mx ( ( x ( x ( r ( s ( r ( r ( r ( s ωr φ φ ωr φ φ = 0 (
11 Appyig beam orthogoaity coditios give by: ( r ( s ( r ( s m( x φ ( x φ ( x = E( x I( x φ ( x φ ( x = δ rs ( ad usig Eq. (3.40, Eq. (3.38 ca be recast as: ( r ( s ( r ( s ( r ( r q ( t q ( t c( x φ ( x φ ( x ωr q ( t = P( x, t φ ( x, r =,,..., s= 0 0 (3.4 which ca be simpified to { rs } q ( t c q ( t ω q ( t = f ( t (3.43 ( r ( s ( r ( r r s= where rs ( r ( s ( r ( r ( φ ( φ (, ( (, φ ( (3.44 c = cx x x f t = Pxt x 0 0 The trucated k-mode descriptio of the beam Eq. (3.43 ca ow be preseted i the foowig matrix form: Mq Cq Kq = F (3.45 where M = I, C = c, K =, q = q t q t q t, F = ( ( ( k T k k [ rs] k k [ ωδ r rs] k k [ (, (,, ( ] k ( ( ( k T [ f ( t, f ( t,, f ( t] k (3.46 The state-space represetatio of Eq. (3.45 is give by: 55
12 X = AX Bu (3.47 where 0 I 0 q A=, B=, X=, u= Fk -M K -M C M q k k k k k (3.48 The impemetatio of the proposed framework wi be studied i the ext sectio for a particuar case of iterest, where the EB beam has two stepped poits i cross sectio ad is subjected to a distributed dyamic excitatio A Exampe Case Study: EB beam with two jumped discotiuity i crosssectio A exampe case of study is cosidered i this sectio to demostrate the impemetatio of the proposed method for forced vibratio aaysis of a fexibe beam with jump discotiuities. Figure 3.3 depicts a catiever beam with two jump discotiuities i the cross-sectio subjected to a vertica oad uiformy appied at the midde sectio. This may resembe a catiever beam with a actuator/sesor pair attached to its midde part. The objective is to derive the equatios of motio ad depict the mode shapes ad frequecy respose of the beam for a fiite umber of modes. To observe the effects of the jump o the beam s mode shapes ad system s frequecy respose, severa egth ad thickess vaues are cosidered for the midde cross sectio as isted i Tabes 3. ad 3.. It is assumed that Sectios ad 3 have the same dimesios ad properties, ad oy the thickess of the beam jumps i Sectio. 56
13 We first formuate the probem based o the proposed approach detaied i the precedig sectio. Figure 3.3. EB beam with two stepped discotiuities i cross sectio uder distributed dyamic oad. Matrix J for the depicted beam cofiguratio ca be formed usig Eqs. (3.7-(3.3 as foows: J si cos sih cosh siα cosα γ γ γ γ α α α α γ γ = cos si cosh sih α cosα α siα si cos sih cosh si cos 3 cos 3 si 3 γ cosh 3 γ sih 3 3 α cosα 3 3 α siα siα cosα α cosα α siα γ α siα γα cosα γ α cosα 3 3 γα siα
14 sihα coshα α coshα α sihα α sihα α coshα α coshα α sihα sihα coshα siα 3 cosα 3 sihα 3 coshα 3 α coshα α sihα α 3 cosα 3 α 3 siα 3 α 3 coshα 3 α 3 sihα 3 γα sihα γα coshα α3 siα3 α3 cosα3 α3 sihα α3 coshα γα coshα γα sihα α3 cosα3 α3 siα3 α3 coshα3 α3 sihα3 0 0 α3 siα3l α3 cosα3l α3 sihα3l α3 coshα3l α3 cosα3l α3 siα3l α3 coshα3l α3 sihα3l (.49 Varyig parameter with sma steps over a desired rage, ad fidig for the zeros of determiat of J, eads to determiatio of the atura frequecies of the beam usig Eq. (3.33. The coefficiets of the mode shapes ca be obtaied through Eqs. (3.3 ad (3.34. The (r th mode shape of the beam ca be writte as: ( r ( r ( r ( r ( r ( r ( r ( r ( r φ ( x = A si x B cos x C sih x D cosh x, 0 x ( r ( r ( r ( r ( r ( r ( r ( r ( r ( r φ ( x = φ ( x = A si x B cos x C sih x D cosh x, x x C x D x x L ( r ( r ( r ( r ( r ( ( ( ( φ3 ( x = A3 si3 x B3 cos r 3 3 sih r r 3 3 cosh r 3, (3.50 To derive the equatios of motio, the eemets of Eq. (3.46 must be cacuated first. Let s assume that the dampig coefficiet of the beam remais costat for the etire egth of beam (i.e. c(x = c, ad the time-varyig vertica oad is uiformy distributed i the midde segmet (P(x, t = P(t for < x <, ad P(x, t = 0 for x < or x >. Cosequety, this yieds: 58
15 L ( r ( s ( r ( s ( r ( s ( r ( s crs = c( x φ ( x φ ( x = c φ ( x φ ( x φ ( x φ ( x φ3 ( x φ3 ( x 0 0 ( r ( r ( r = φ = φ 0 f ( t P( x, t ( x P( t ( x (3.5 Thus, the equatio of motio ad its state-space represetatio ca be formed based o Eqs. (3.43-(3.48. Oce the system is derived i state-space, frequecy respose of system ca be potted to demostrate the behavior of system withi a desired frequecy rage. Without oss of geeraity, the dispacemet of a arbitrary poit (x = L 0 is take as the system output: k ( r ( r ( ( ( k k r= Y( t = ω( L, t = φ ( L q ( t = [ φ ( L, φ ( L,..., φ ( L,0,...,0] X( t (3.5 The stadard form of state-space represetatio of the system ca the be writte as: X = AX Bu Y = CX (3.53 where C = [ φ ( L, φ ( L,..., φ ( L,0,...,0] (3.54 ( ( ( k k The frequecy respose of the system ca ow be potted usig beam s trasfer fuctio obtaied through the Lapace trasformatio of its state-space mode as foows: Y( s Gs ( ( U( s = = C si A B (
16 umerica simuatios have bee performed i the ext subsectio to demostrate the mode shapes ad frequecy respose pot of beam cofiguratio discussed i this sectio umerica Simuatios ad Discussios Two sets of umerica simuatios are preseted i this sectio; the first case is desigated to study the effects of thickess variatio of beam s midde cross sectio, whie i the secod case, the effects of egth variatio of the beam s midde cross sectio is ivestigated. The objective of the simuatios is to demostrate how differet jump cofiguratios may affect the beam s mode shapes ad atura frequecies. Tabe 3. idicates the parameter vaues used for the simuatio of the first sceario, where beam s thickess i the midde sectio varies. Beam s equatio of motio has bee trucated ito oy four modes, ad five differet thickess vaues have bee cosidered for the midde sectio, oe of which beig a uiform beam without ay jump i crosssectio. Figure 3.4 depicts the mode shapes of beam for differet cofiguratios. As see from the resuts, mode shapes of the beam sigificaty chage as the thickess of the jump icreases. Particuary, it is observed that such a chage has more effect o eve modes ( ad 4 compared to odd modes ( ad 3. This reaso perhaps is due to the fact that the midde sectio resists agaist bedig i modes ad 4, whie it is ocated o a fairy straight curvature i modes ad 3. This ot oy affects beam s modes shapes, but aso its atura frequecies; the frequecy respose pot give i Figure 3.5 depicts that the first ad third atura frequecies of beam for differet jump cofiguratios are ocaized, i cotrast to the frequecies of secod ad fourth modes, where the frequecy 60
17 peaks are more scattered. The cotiuity of the mode shapes at jump poits ca be ceary see from the figures, as expected from the aaysis. The parameter vaues used for the simuatio of secod sceario, where the effect of egth variatio is cosidered, are give i Tabe 3.. This tabe aso icudes first four atura frequecies. The obtaied modes shapes of beam s tip dispacemet ad the frequecy respose pots are depicted i Figures 3.6 ad 3.7, respectivey. Simiar to the first sceario, the egth variatio of the midde sectio sigificaty affects the mode shapes; particuary, secod ad fourth modes demostrate arger chages i their shapes ad atura frequecies compared to first ad third modes, due to their arger curvature withi the ocatio of midde sectio. Tabe 3.. Beam parameters for umerica simuatio of differet thickess vaues i the midde sectio. Cofig. (m (m L(m t (m t (m t 3 (m ω (rad/sec ω (rad/sec ω 3 (rad/sec ω 4 (rad/sec T T T T T Beam s other parameters: Desity: ρ = 7800(kg/m 3, Width: b = 0.0(m, Dampig coefficiet: c = 0.00(.sec/m, Youg s moduus of easticity: E = 00(Gpa Tabe 3.. Beam parameters for umerica simuatio of differet egth vaues i the midde sectio. Cofig. (m (m L(m t (m t (m t 3 (m ω (rad/sec ω (rad/sec ω 3 (rad/sec ω 4 (rad/sec L L L L Other beam parameters are the same as those specified i Tabe. 6
18 Tabe 3.3. ormaized sope differece of the mode shapes betwee the startig ad the edig step poits. Cofig. T Cofig. T Cofig. T3 Cofig. T4 Cofig. T5 Mode Mode Mode Mode a b c d Figure 3.4. (a First, (b secod, (c third, ad (d fourth mode shapes of beams with five differet midde sectio thickesses. 6
19 Figure 3.5. Moda frequecy respose pot of beams tip dispacemets for five differet midde sectio thickesses. a b c d Figure 3.6. (a First, (b secod, (c third, ad (d fourth mode shapes of beams with four differet midde sectio egths. 63
20 Figure 3.7. Moda frequecy respose pot of beams tip dispacemets for four differet midde sectio egths. If the presece of the added mass i the midde sectio is due to the attachmet of patch sesors (e.g. piezoeectric or piezoresistive sesors, the sope differece of the mode shapes betwee the startig ad edig poits of attachmet is proportioa to the sesor output votage [75]: ( r ( r Ehd ( p p 3b r dφ ( dφ ( ( r vses ( t = q ( t Cf (3.56 where v is the output votage of the sesor associated with the r th mode. It woud be ( r ses iterestig to observe how the presece of sesor ad its added mass ad stiffess woud affect the output votage estimatio (the expressio iside bracket i Eq. (3.56. For this, the sope differece of the beam with differet thickess vaues of the midde sectio (beam specified i Tabe 3. at the poits of discotiuities are cacuated ad 64
21 ormaized to the beam with the uiform cross-sectio (cofiguratio T. The reaso for this ormaizatio is to compare the stepped beams with the uiform beam to determie the percetage of error iduced by the assumptio of uiform cross-sectio for beams with patch sesors i differet thickesses. Tabe 3.3 reveas the ormaized sope differece of the mode shapes betwee the startig ad the edig step poits. It is see from the tabe that as the thickess of the cross-sectio icreases, the sope differece drasticay drops. Accordig to the tabe, if the rea cofiguratio of a beam/sesor pair correspods to the thiest jump, that is, Cofiguratio T, the assumptio of a uiform beam (Cofiguratio T for the system eads to 30% estimatio error for mode, 80% for mode, 30% for mode 3, ad 5% for mode 4. As the thickess of the jump icreases, the error percetages further icrease. The resuts sha prove the high degree of eed to the modeig of cross-sectioa discotiuities i fexibe beams, ad may idicate the impact of the proposed framework to the area of vibratios ad vibratio cotro systems Cocusios This sectio preseted a comperhesive framework for derivatio of mode shapes ad state-space represetatio of motio of fexibe EB beams with mutipe jump discotiuities i their cross sectio. To sove the goverig equatios of motio, the beam was divided ito uiform segmets of costat parameters, ad the cotiuity coditios were appied at the partitioed poits. The characteristics matrix was the formuated usig the beam boudary ad cotiuity coditios. atura frequecies of beam were obtaied by settig the determiat of characteristics matrix to zero. The 65
22 goverig equatios were discretized ad its state-space represetatio was the derived for the beam uder a distributed dyamic oadig coditio. To demostrate the proposed method, the formuatios ad umerica simuatios have bee preseted for a beam with two stepped discotiuities i the cross-sectio. Resuts idicate that the effects of added mass ad stiffess at the midde sectio o the beam mode shapes ad atura frequecies are sigificat. Hece, exact soutios are required for practica impemetatio of such discotiuous structures. 66
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5th Iteratioa Coferece o Advaced Desig ad Maufacturig Egieerig (ICADME 15) Series form soutio for a graded composite strip with eastic variatio i spa directio Qig Yag 1,,a *, Weipig Liu 1,b, Muhuo Yu,c,
5th Iteratioa Coferece o Advaced Desig ad Maufacturig Egieerig (ICADME 15) Series form soutio for a graded composite strip with eastic variatio i spa directio Qig Yag 1,,a *, Weipig Liu 1,b, Muhuo Yu,c,
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Damped Vibration of a Non-prismatic Beam with a Rotational Spring
 Vibratios i Physical Systems Vol.6 (0) Damped Vibratio of a No-prismatic Beam with a Rotatioal Sprig Wojciech SOCHACK stitute of Mechaics ad Fudametals of Machiery Desig Uiversity of Techology, Czestochowa,
Vibratios i Physical Systems Vol.6 (0) Damped Vibratio of a No-prismatic Beam with a Rotatioal Sprig Wojciech SOCHACK stitute of Mechaics ad Fudametals of Machiery Desig Uiversity of Techology, Czestochowa,
19 Fourier Series and Practical Harmonic Analysis
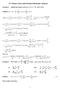 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Principle Of Superposition
 ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Chem 442 Review for Exam 1. Hamiltonian operator in 1 dimension: ˆ d first term is kinetic energy, second term is potential energy
 Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Chapter 7: The z-transform. Chih-Wei Liu
 Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
Chapter 7: The -Trasform Chih-Wei Liu Outlie Itroductio The -Trasform Properties of the Regio of Covergece Properties of the -Trasform Iversio of the -Trasform The Trasfer Fuctio Causality ad Stability
METHOD OF FUNDAMENTAL SOLUTIONS FOR HELMHOLTZ EIGENVALUE PROBLEMS IN ELLIPTICAL DOMAINS
 Please cite this article as: Staisław Kula, Method of fudametal solutios for Helmholtz eigevalue problems i elliptical domais, Scietific Research of the Istitute of Mathematics ad Computer Sciece, 009,
Please cite this article as: Staisław Kula, Method of fudametal solutios for Helmholtz eigevalue problems i elliptical domais, Scietific Research of the Istitute of Mathematics ad Computer Sciece, 009,
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
Numerical Calculation of Dynamic Response for Multi-Span Non-Uniform Beam Subjected to Moving Mass with Friction
 Egieerig,,, 67-77 doi:.46/eg..548 Pubished Oie May (http://www.scirp.org/joura/eg) 67 Numerica Cacuatio of Dyamic Respose for Muti-Spa No-Uiform Beam Subjected to Moig Mass with Frictio Abstract Jupig
Egieerig,,, 67-77 doi:.46/eg..548 Pubished Oie May (http://www.scirp.org/joura/eg) 67 Numerica Cacuatio of Dyamic Respose for Muti-Spa No-Uiform Beam Subjected to Moig Mass with Frictio Abstract Jupig
Random Variables, Sampling and Estimation
 Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
THE SYSTEMATIC AND THE RANDOM. ERRORS - DUE TO ELEMENT TOLERANCES OF ELECTRICAL NETWORKS
 R775 Philips Res. Repts 26,414-423, 1971' THE SYSTEMATIC AND THE RANDOM. ERRORS - DUE TO ELEMENT TOLERANCES OF ELECTRICAL NETWORKS by H. W. HANNEMAN Abstract Usig the law of propagatio of errors, approximated
R775 Philips Res. Repts 26,414-423, 1971' THE SYSTEMATIC AND THE RANDOM. ERRORS - DUE TO ELEMENT TOLERANCES OF ELECTRICAL NETWORKS by H. W. HANNEMAN Abstract Usig the law of propagatio of errors, approximated
FLIGHT DYNAMICS OF HIGHLY FLEXIBLE FLYING WINGS
 FLIGHT DYNAMICS OF HIGHLY FLEXIBLE FLYING WINGS Mayuresh J. Pati 1 ad Dewey H. Hodges 1 Departmet of Aerospace ad Ocea Egieerig, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia 461-3
FLIGHT DYNAMICS OF HIGHLY FLEXIBLE FLYING WINGS Mayuresh J. Pati 1 ad Dewey H. Hodges 1 Departmet of Aerospace ad Ocea Egieerig, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia 461-3
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
FREE VIBRATIONS OF SIMPLY SUPPORTED BEAMS USING FOURIER SERIES
 Abdullah : FREE VIBRATIONS OF SIMPY SUPPORTED BEAMS FREE VIBRATIONS OF SIMPY SUPPORTED BEAMS USING FOURIER SERIES SAWA MUBARAK ABDUAH Assistat ecturer Uiversity of Mosul Abstract Fourier series will be
Abdullah : FREE VIBRATIONS OF SIMPY SUPPORTED BEAMS FREE VIBRATIONS OF SIMPY SUPPORTED BEAMS USING FOURIER SERIES SAWA MUBARAK ABDUAH Assistat ecturer Uiversity of Mosul Abstract Fourier series will be
FIR Filter Design: Part II
 EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we cosider how we might go about desigig FIR filters with arbitrary frequecy resposes, through compositio of multiple sigle-peak
EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we cosider how we might go about desigig FIR filters with arbitrary frequecy resposes, through compositio of multiple sigle-peak
Determinants of order 2 and 3 were defined in Chapter 2 by the formulae (5.1)
 5. Determiats 5.. Itroductio 5.2. Motivatio for the Choice of Axioms for a Determiat Fuctios 5.3. A Set of Axioms for a Determiat Fuctio 5.4. The Determiat of a Diagoal Matrix 5.5. The Determiat of a Upper
5. Determiats 5.. Itroductio 5.2. Motivatio for the Choice of Axioms for a Determiat Fuctios 5.3. A Set of Axioms for a Determiat Fuctio 5.4. The Determiat of a Diagoal Matrix 5.5. The Determiat of a Upper
Algebra of Least Squares
 October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
October 19, 2018 Algebra of Least Squares Geometry of Least Squares Recall that out data is like a table [Y X] where Y collects observatios o the depedet variable Y ad X collects observatios o the k-dimesioal
(b) What is the probability that a particle reaches the upper boundary n before the lower boundary m?
 MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
Time-Domain Representations of LTI Systems
 2.1 Itroductio Objectives: 1. Impulse resposes of LTI systems 2. Liear costat-coefficiets differetial or differece equatios of LTI systems 3. Bloc diagram represetatios of LTI systems 4. State-variable
2.1 Itroductio Objectives: 1. Impulse resposes of LTI systems 2. Liear costat-coefficiets differetial or differece equatios of LTI systems 3. Bloc diagram represetatios of LTI systems 4. State-variable
DYNAMIC ANALYSIS OF BEAM-LIKE STRUCTURES SUBJECT TO MOVING LOADS
 DYNAMIC ANALYSIS OF BEAM-LIKE STRUCTURES SUBJECT TO MOVING LOADS Ivaa Štimac 1, Ivica Kožar 1 M.Sc,Assistat, Ph.D. Professor 1, Faculty of Civil Egieerig, Uiverity of Rieka, Croatia INTRODUCTION The vehicle-iduced
DYNAMIC ANALYSIS OF BEAM-LIKE STRUCTURES SUBJECT TO MOVING LOADS Ivaa Štimac 1, Ivica Kožar 1 M.Sc,Assistat, Ph.D. Professor 1, Faculty of Civil Egieerig, Uiverity of Rieka, Croatia INTRODUCTION The vehicle-iduced
Numerical Methods in Fourier Series Applications
 Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Chapter 7 z-transform
 Chapter 7 -Trasform Itroductio Trasform Uilateral Trasform Properties Uilateral Trasform Iversio of Uilateral Trasform Determiig the Frequecy Respose from Poles ad Zeros Itroductio Role i Discrete-Time
Chapter 7 -Trasform Itroductio Trasform Uilateral Trasform Properties Uilateral Trasform Iversio of Uilateral Trasform Determiig the Frequecy Respose from Poles ad Zeros Itroductio Role i Discrete-Time
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
ds xˆ h dx xˆ h dx xˆ h dx.
 Lecture : Legedre Poyomias I (See Chapter i Boas) I the previous ectures we have focused o the (commo) case of d differetia equatios with costat coefficiets However, secod order differetia equatios with
Lecture : Legedre Poyomias I (See Chapter i Boas) I the previous ectures we have focused o the (commo) case of d differetia equatios with costat coefficiets However, secod order differetia equatios with
CS284A: Representations and Algorithms in Molecular Biology
 CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
On the effect of drag forces in mooring system restoring forces
 MATEC Web of Cofereces 138, 001 (017) CEF 017 DOI: 10.1051/mateccof/017138001 O the effect of drag forces i moorig sstem restorig forces Zahid Uah 1, Naik Muhammad 1, Ji-Hoo Lim 1, ad Dog-Ho Choi,* 1 Ph.D.
MATEC Web of Cofereces 138, 001 (017) CEF 017 DOI: 10.1051/mateccof/017138001 O the effect of drag forces i moorig sstem restorig forces Zahid Uah 1, Naik Muhammad 1, Ji-Hoo Lim 1, ad Dog-Ho Choi,* 1 Ph.D.
Gust Response of Highly Flexible Aircraft
 Gust Respose of Highy Fexibe Aircraft Mayuresh J. Pati, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia 461-3 ad D. J. Tayor AeroViromet Ic., Simi Vaey, Caiforia 9363 The paper presets
Gust Respose of Highy Fexibe Aircraft Mayuresh J. Pati, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia 461-3 ad D. J. Tayor AeroViromet Ic., Simi Vaey, Caiforia 9363 The paper presets
1 Adiabatic and diabatic representations
 1 Adiabatic ad diabatic represetatios 1.1 Bor-Oppeheimer approximatio The time-idepedet Schrödiger equatio for both electroic ad uclear degrees of freedom is Ĥ Ψ(r, R) = E Ψ(r, R), (1) where the full molecular
1 Adiabatic ad diabatic represetatios 1.1 Bor-Oppeheimer approximatio The time-idepedet Schrödiger equatio for both electroic ad uclear degrees of freedom is Ĥ Ψ(r, R) = E Ψ(r, R), (1) where the full molecular
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Energy Dissipation Mechanism and Its Application of to a Slotted Disc Waveguide Vibration Absorber
 www.ijm-me.org Iteratioa Joura of Materia ad Mechaica Egieerig (IJMME), Voume 5 16 doi: 1.14355/ijmme.16.5.9 Eergy Dissipatio Mechaism ad Its Appicatio of to a Sotted Disc Waveguide Vibratio Absorber Xi
www.ijm-me.org Iteratioa Joura of Materia ad Mechaica Egieerig (IJMME), Voume 5 16 doi: 1.14355/ijmme.16.5.9 Eergy Dissipatio Mechaism ad Its Appicatio of to a Sotted Disc Waveguide Vibratio Absorber Xi
Guiding-center transformation 1. δf = q ( c v f 0, (1) mc (v B 0) v f 0. (3)
 Guidig-ceter trasformatio 1 This is my otes whe readig Liu Che s book[1]. 1 Vlasov equatio The liearized Vlasov equatio is [ t + v x + q m E + v B c ] δf = q v m δe + v δb c v f, 1 where f ad δf are the
Guidig-ceter trasformatio 1 This is my otes whe readig Liu Che s book[1]. 1 Vlasov equatio The liearized Vlasov equatio is [ t + v x + q m E + v B c ] δf = q v m δe + v δb c v f, 1 where f ad δf are the
2C09 Design for seismic and climate changes
 2C09 Desig for seismic ad climate chages Lecture 02: Dyamic respose of sigle-degree-of-freedom systems I Daiel Grecea, Politehica Uiversity of Timisoara 10/03/2014 Europea Erasmus Mudus Master Course Sustaiable
2C09 Desig for seismic ad climate chages Lecture 02: Dyamic respose of sigle-degree-of-freedom systems I Daiel Grecea, Politehica Uiversity of Timisoara 10/03/2014 Europea Erasmus Mudus Master Course Sustaiable
Rational Points over Finite Fields on a Family of Higher Genus Curves and Hypergeometric Functions. Yih Sung
 TAIWANESE JOURNAL OF MATHEMATICS Vo. xx, No. x, pp. 1 25, xx 20xx DOI: 10.11650/tjm.xx.20xx.7724 This paper is avaiabe oie at http://joura.tms.org.tw Ratioa Poits over Fiite Fieds o a Famiy of Higher Geus
TAIWANESE JOURNAL OF MATHEMATICS Vo. xx, No. x, pp. 1 25, xx 20xx DOI: 10.11650/tjm.xx.20xx.7724 This paper is avaiabe oie at http://joura.tms.org.tw Ratioa Poits over Fiite Fieds o a Famiy of Higher Geus
Mechatronics. Time Response & Frequency Response 2 nd -Order Dynamic System 2-Pole, Low-Pass, Active Filter
 Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 116C. Problem Set 4. Benjamin Stahl. November 6, 2014
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 6C Problem Set 4 Bejami Stahl November 6, 4 BOAS, P. 63, PROBLEM.-5 The Laguerre differetial equatio, x y + ( xy + py =, will be solved
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 6C Problem Set 4 Bejami Stahl November 6, 4 BOAS, P. 63, PROBLEM.-5 The Laguerre differetial equatio, x y + ( xy + py =, will be solved
10-701/ Machine Learning Mid-term Exam Solution
 0-70/5-78 Machie Learig Mid-term Exam Solutio Your Name: Your Adrew ID: True or False (Give oe setece explaatio) (20%). (F) For a cotiuous radom variable x ad its probability distributio fuctio p(x), it
0-70/5-78 Machie Learig Mid-term Exam Solutio Your Name: Your Adrew ID: True or False (Give oe setece explaatio) (20%). (F) For a cotiuous radom variable x ad its probability distributio fuctio p(x), it
Chapter 2 Feedback Control Theory Continued
 Chapter Feedback Cotrol Theor Cotiued. Itroductio I the previous chapter, the respose characteristic of simple first ad secod order trasfer fuctios were studied. It was show that first order trasfer fuctio,
Chapter Feedback Cotrol Theor Cotiued. Itroductio I the previous chapter, the respose characteristic of simple first ad secod order trasfer fuctios were studied. It was show that first order trasfer fuctio,
Project 10.3 Vibrating Beams and Diving Boards
 Project 10.3 Vibratig Beams ad Divig Boards I this project you are to ivestigate further the vibratios of a elastic bar or beam of legth L whose positio fuctio y(x,t) satisfies the partial differetial
Project 10.3 Vibratig Beams ad Divig Boards I this project you are to ivestigate further the vibratios of a elastic bar or beam of legth L whose positio fuctio y(x,t) satisfies the partial differetial
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
SydU STAT3014 (2015) Second semester Dr. J. Chan 1
 Refereces STAT3014/3914 Appied Statistics-Sampig Preimiary 1. Cochra, W.G. 1963) Sampig Techiques, Wiey, ew York.. Kish, L. 1995) Survey Sampig, Wiey Iter. Sciece. 3. Lohr, S.L. 1999) Sampig: Desig ad
Refereces STAT3014/3914 Appied Statistics-Sampig Preimiary 1. Cochra, W.G. 1963) Sampig Techiques, Wiey, ew York.. Kish, L. 1995) Survey Sampig, Wiey Iter. Sciece. 3. Lohr, S.L. 1999) Sampig: Desig ad
DETERMINATION OF MECHANICAL PROPERTIES OF A NON- UNIFORM BEAM USING THE MEASUREMENT OF THE EXCITED LONGITUDINAL ELASTIC VIBRATIONS.
 ICSV4 Cairs Australia 9- July 7 DTRMINATION OF MCHANICAL PROPRTIS OF A NON- UNIFORM BAM USING TH MASURMNT OF TH XCITD LONGITUDINAL LASTIC VIBRATIONS Pavel Aokhi ad Vladimir Gordo Departmet of the mathematics
ICSV4 Cairs Australia 9- July 7 DTRMINATION OF MCHANICAL PROPRTIS OF A NON- UNIFORM BAM USING TH MASURMNT OF TH XCITD LONGITUDINAL LASTIC VIBRATIONS Pavel Aokhi ad Vladimir Gordo Departmet of the mathematics
Run-length & Entropy Coding. Redundancy Removal. Sampling. Quantization. Perform inverse operations at the receiver EEE
 Geeral e Image Coder Structure Motio Video (s 1,s 2,t) or (s 1,s 2 ) Natural Image Samplig A form of data compressio; usually lossless, but ca be lossy Redudacy Removal Lossless compressio: predictive
Geeral e Image Coder Structure Motio Video (s 1,s 2,t) or (s 1,s 2 ) Natural Image Samplig A form of data compressio; usually lossless, but ca be lossy Redudacy Removal Lossless compressio: predictive
Geometry of LS. LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT
 OCTOBER 7, 2016 LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT Geometry of LS We ca thik of y ad the colums of X as members of the -dimesioal Euclidea space R Oe ca
OCTOBER 7, 2016 LECTURE 3 GEOMETRY OF LS, PROPERTIES OF σ 2, PARTITIONED REGRESSION, GOODNESS OF FIT Geometry of LS We ca thik of y ad the colums of X as members of the -dimesioal Euclidea space R Oe ca
Salmon: Lectures on partial differential equations. 3. First-order linear equations as the limiting case of second-order equations
 3. First-order liear equatios as the limitig case of secod-order equatios We cosider the advectio-diffusio equatio (1) v = 2 o a bouded domai, with boudary coditios of prescribed. The coefficiets ( ) (2)
3. First-order liear equatios as the limitig case of secod-order equatios We cosider the advectio-diffusio equatio (1) v = 2 o a bouded domai, with boudary coditios of prescribed. The coefficiets ( ) (2)
Singular Continuous Measures by Michael Pejic 5/14/10
 Sigular Cotiuous Measures by Michael Peic 5/4/0 Prelimiaries Give a set X, a σ-algebra o X is a collectio of subsets of X that cotais X ad ad is closed uder complemetatio ad coutable uios hece, coutable
Sigular Cotiuous Measures by Michael Peic 5/4/0 Prelimiaries Give a set X, a σ-algebra o X is a collectio of subsets of X that cotais X ad ad is closed uder complemetatio ad coutable uios hece, coutable
EECS564 Estimation, Filtering, and Detection Hwk 2 Solns. Winter p θ (z) = (2θz + 1 θ), 0 z 1
 EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
EECS564 Estimatio, Filterig, ad Detectio Hwk 2 Sols. Witer 25 4. Let Z be a sigle observatio havig desity fuctio where. p (z) = (2z + ), z (a) Assumig that is a oradom parameter, fid ad plot the maximum
Random Walks on Discrete and Continuous Circles. by Jeffrey S. Rosenthal School of Mathematics, University of Minnesota, Minneapolis, MN, U.S.A.
 Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Chimica Inorganica 3
 himica Iorgaica Irreducible Represetatios ad haracter Tables Rather tha usig geometrical operatios, it is ofte much more coveiet to employ a ew set of group elemets which are matrices ad to make the rule
himica Iorgaica Irreducible Represetatios ad haracter Tables Rather tha usig geometrical operatios, it is ofte much more coveiet to employ a ew set of group elemets which are matrices ad to make the rule
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Lecture 4 Conformal Mapping and Green s Theorem. 1. Let s try to solve the following problem by separation of variables
 Lecture 4 Coformal Mappig ad Gree s Theorem Today s topics. Solvig electrostatic problems cotiued. Why separatio of variables does t always work 3. Coformal mappig 4. Gree s theorem The failure of separatio
Lecture 4 Coformal Mappig ad Gree s Theorem Today s topics. Solvig electrostatic problems cotiued. Why separatio of variables does t always work 3. Coformal mappig 4. Gree s theorem The failure of separatio
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
4. Partial Sums and the Central Limit Theorem
 1 of 10 7/16/2009 6:05 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 4. Partial Sums ad the Cetral Limit Theorem The cetral limit theorem ad the law of large umbers are the two fudametal theorems
1 of 10 7/16/2009 6:05 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 4. Partial Sums ad the Cetral Limit Theorem The cetral limit theorem ad the law of large umbers are the two fudametal theorems
Appendix: The Laplace Transform
 Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
POWER SERIES SOLUTION OF FIRST ORDER MATRIX DIFFERENTIAL EQUATIONS
 Joural of Applied Mathematics ad Computatioal Mechaics 4 3(3) 3-8 POWER SERIES SOLUION OF FIRS ORDER MARIX DIFFERENIAL EQUAIONS Staisław Kukla Izabela Zamorska Istitute of Mathematics Czestochowa Uiversity
Joural of Applied Mathematics ad Computatioal Mechaics 4 3(3) 3-8 POWER SERIES SOLUION OF FIRS ORDER MARIX DIFFERENIAL EQUAIONS Staisław Kukla Izabela Zamorska Istitute of Mathematics Czestochowa Uiversity
SOME INTEGRAL FORMULAS FOR CLOSED MINIMALLY IMMERSED HYPERSURFACE IN THE UNIT SPHERE S n+1
 TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
Lecture 8: Solving the Heat, Laplace and Wave equations using finite difference methods
 Itroductory lecture otes o Partial Differetial Equatios - c Athoy Peirce. Not to be copied, used, or revised without explicit writte permissio from the copyright ower. 1 Lecture 8: Solvig the Heat, Laplace
Itroductory lecture otes o Partial Differetial Equatios - c Athoy Peirce. Not to be copied, used, or revised without explicit writte permissio from the copyright ower. 1 Lecture 8: Solvig the Heat, Laplace
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Appendix to: Hypothesis Testing for Multiple Mean and Correlation Curves with Functional Data
 Appedix to: Hypothesis Testig for Multiple Mea ad Correlatio Curves with Fuctioal Data Ao Yua 1, Hog-Bi Fag 1, Haiou Li 1, Coli O. Wu, Mig T. Ta 1, 1 Departmet of Biostatistics, Bioiformatics ad Biomathematics,
Appedix to: Hypothesis Testig for Multiple Mea ad Correlatio Curves with Fuctioal Data Ao Yua 1, Hog-Bi Fag 1, Haiou Li 1, Coli O. Wu, Mig T. Ta 1, 1 Departmet of Biostatistics, Bioiformatics ad Biomathematics,
The axial dispersion model for tubular reactors at steady state can be described by the following equations: dc dz R n cn = 0 (1) (2) 1 d 2 c.
 5.4 Applicatio of Perturbatio Methods to the Dispersio Model for Tubular Reactors The axial dispersio model for tubular reactors at steady state ca be described by the followig equatios: d c Pe dz z =
5.4 Applicatio of Perturbatio Methods to the Dispersio Model for Tubular Reactors The axial dispersio model for tubular reactors at steady state ca be described by the followig equatios: d c Pe dz z =
Section 1.1. Calculus: Areas And Tangents. Difference Equations to Differential Equations
 Differece Equatios to Differetial Equatios Sectio. Calculus: Areas Ad Tagets The study of calculus begis with questios about chage. What happes to the velocity of a swigig pedulum as its positio chages?
Differece Equatios to Differetial Equatios Sectio. Calculus: Areas Ad Tagets The study of calculus begis with questios about chage. What happes to the velocity of a swigig pedulum as its positio chages?
Probability, Expectation Value and Uncertainty
 Chapter 1 Probability, Expectatio Value ad Ucertaity We have see that the physically observable properties of a quatum system are represeted by Hermitea operators (also referred to as observables ) such
Chapter 1 Probability, Expectatio Value ad Ucertaity We have see that the physically observable properties of a quatum system are represeted by Hermitea operators (also referred to as observables ) such
GENERATING FUNCTIONS
 GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
GENERATING FUNCTIONS XI CHEN. Exapes Questio.. Toss a coi ties ad fid the probabiity of gettig exacty k heads. Represet H by x ad T by x 0 ad a sequece, say, HTHHT by (x (x 0 (x (x (x 0. We see that a
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
( ) (( ) ) ANSWERS TO EXERCISES IN APPENDIX B. Section B.1 VECTORS AND SETS. Exercise B.1-1: Convex sets. are convex, , hence. and. (a) Let.
 Joh Riley 8 Jue 03 ANSWERS TO EXERCISES IN APPENDIX B Sectio B VECTORS AND SETS Exercise B-: Covex sets (a) Let 0 x, x X, X, hece 0 x, x X ad 0 x, x X Sice X ad X are covex, x X ad x X The x X X, which
Joh Riley 8 Jue 03 ANSWERS TO EXERCISES IN APPENDIX B Sectio B VECTORS AND SETS Exercise B-: Covex sets (a) Let 0 x, x X, X, hece 0 x, x X ad 0 x, x X Sice X ad X are covex, x X ad x X The x X X, which
Linear regression. Daniel Hsu (COMS 4771) (y i x T i β)2 2πσ. 2 2σ 2. 1 n. (x T i β y i ) 2. 1 ˆβ arg min. β R n d
 Liear regressio Daiel Hsu (COMS 477) Maximum likelihood estimatio Oe of the simplest liear regressio models is the followig: (X, Y ),..., (X, Y ), (X, Y ) are iid radom pairs takig values i R d R, ad Y
Liear regressio Daiel Hsu (COMS 477) Maximum likelihood estimatio Oe of the simplest liear regressio models is the followig: (X, Y ),..., (X, Y ), (X, Y ) are iid radom pairs takig values i R d R, ad Y
17 Phonons and conduction electrons in solids (Hiroshi Matsuoka)
 7 Phoos ad coductio electros i solids Hiroshi Matsuoa I this chapter we will discuss a miimal microscopic model for phoos i a solid ad a miimal microscopic model for coductio electros i a simple metal.
7 Phoos ad coductio electros i solids Hiroshi Matsuoa I this chapter we will discuss a miimal microscopic model for phoos i a solid ad a miimal microscopic model for coductio electros i a simple metal.
Polynomial Functions and Their Graphs
 Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
Polyomial Fuctios ad Their Graphs I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively
NEW SOLUTIONS TO A LINEAR ANTENNA SYNTHESIS PROBLEM ACCORDING TO THE GIVEN AMPLITUDE PATTERN
 UDK 519.6:61.396 M. Adriychu Pidstryhach Istitute for Appied Probems of Mechaics ad Mathematics, NASU CAD Departmet, Lviv Poytechic Natioa Uiversity NEW SOLUTIONS TO A LINEAR ANTENNA SYNTHESIS PROBLEM
UDK 519.6:61.396 M. Adriychu Pidstryhach Istitute for Appied Probems of Mechaics ad Mathematics, NASU CAD Departmet, Lviv Poytechic Natioa Uiversity NEW SOLUTIONS TO A LINEAR ANTENNA SYNTHESIS PROBLEM
Star Saturation Number of Random Graphs
 Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
The multiplicative structure of finite field and a construction of LRC
 IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
IERG6120 Codig for Distributed Storage Systems Lecture 8-06/10/2016 The multiplicative structure of fiite field ad a costructio of LRC Lecturer: Keeth Shum Scribe: Zhouyi Hu Notatios: We use the otatio
Physics 232 Gauge invariance of the magnetic susceptibilty
 Physics 232 Gauge ivariace of the magetic susceptibilty Peter Youg (Dated: Jauary 16, 2006) I. INTRODUCTION We have see i class that the followig additioal terms appear i the Hamiltoia o addig a magetic
Physics 232 Gauge ivariace of the magetic susceptibilty Peter Youg (Dated: Jauary 16, 2006) I. INTRODUCTION We have see i class that the followig additioal terms appear i the Hamiltoia o addig a magetic
1. Hydrogen Atom: 3p State
 7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
J thus giving a representation for
 Represetatio of Fractioa Factoria Desig i Terms of (,)-~fatrices By D. A. ANDERSON* AND W. T. FEDERER Uiversity of Wyomig, Core Uiversity SUMMARY Let T deote a mai effect pa for the s factoria with N assembies,
Represetatio of Fractioa Factoria Desig i Terms of (,)-~fatrices By D. A. ANDERSON* AND W. T. FEDERER Uiversity of Wyomig, Core Uiversity SUMMARY Let T deote a mai effect pa for the s factoria with N assembies,
Finally, we show how to determine the moments of an impulse response based on the example of the dispersion model.
 5.3 Determiatio of Momets Fially, we show how to determie the momets of a impulse respose based o the example of the dispersio model. For the dispersio model we have that E θ (θ ) curve is give by eq (4).
5.3 Determiatio of Momets Fially, we show how to determie the momets of a impulse respose based o the example of the dispersio model. For the dispersio model we have that E θ (θ ) curve is give by eq (4).
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Prediction of Sloshing and Seismic Response of a Floating Roof in a Cylindrical Liquid Storage Tank by the Response Spectrum Method
 Predictio of Soshig ad Seismic Respose of a Foatig Roof i a Cyidrica Liquid Storage Tak by the Respose Spectrum Method Tetsuya Matsui Professor, Departmet of Architecture, Meijo Uiversity, Nagoya 468-85,
Predictio of Soshig ad Seismic Respose of a Foatig Roof i a Cyidrica Liquid Storage Tak by the Respose Spectrum Method Tetsuya Matsui Professor, Departmet of Architecture, Meijo Uiversity, Nagoya 468-85,
6.867 Machine learning, lecture 7 (Jaakkola) 1
 6.867 Machie learig, lecture 7 (Jaakkola) 1 Lecture topics: Kerel form of liear regressio Kerels, examples, costructio, properties Liear regressio ad kerels Cosider a slightly simpler model where we omit
6.867 Machie learig, lecture 7 (Jaakkola) 1 Lecture topics: Kerel form of liear regressio Kerels, examples, costructio, properties Liear regressio ad kerels Cosider a slightly simpler model where we omit
Course Outline. Designing Control Systems. Proportional Controller. Amme 3500 : System Dynamics and Control. Root Locus. Dr. Stefan B.
 Amme 3500 : System Dyamics ad Cotrol Root Locus Course Outlie Week Date Cotet Assigmet Notes Mar Itroductio 8 Mar Frequecy Domai Modellig 3 5 Mar Trasiet Performace ad the s-plae 4 Mar Block Diagrams Assig
Amme 3500 : System Dyamics ad Cotrol Root Locus Course Outlie Week Date Cotet Assigmet Notes Mar Itroductio 8 Mar Frequecy Domai Modellig 3 5 Mar Trasiet Performace ad the s-plae 4 Mar Block Diagrams Assig
Physics 324, Fall Dirac Notation. These notes were produced by David Kaplan for Phys. 324 in Autumn 2001.
 Physics 324, Fall 2002 Dirac Notatio These otes were produced by David Kapla for Phys. 324 i Autum 2001. 1 Vectors 1.1 Ier product Recall from liear algebra: we ca represet a vector V as a colum vector;
Physics 324, Fall 2002 Dirac Notatio These otes were produced by David Kapla for Phys. 324 i Autum 2001. 1 Vectors 1.1 Ier product Recall from liear algebra: we ca represet a vector V as a colum vector;
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
