FLIGHT DYNAMICS OF HIGHLY FLEXIBLE FLYING WINGS
|
|
|
- Gertrude Bradford
- 6 years ago
- Views:
Transcription
1 FLIGHT DYNAMICS OF HIGHLY FLEXIBLE FLYING WINGS Mayuresh J. Pati 1 ad Dewey H. Hodges 1 Departmet of Aerospace ad Ocea Egieerig, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia USA e-mai: mpati@vt.edu Schoo of Aerospace Egieerig, Georgia Istitute of Techoogy, Atata, Georgia USA e-mai: dhodges@aoe.vt.edu Key words: Noiear Aeroeasticity, Fight Dyamics, HALE Aircraft Abstract: The paper presets a theory for fight dyamic aaysis of highy fexibe fyig wig cofiguratios. The aaysis takes ito accout arge aircraft motio couped with geometricay oiear structura deformatio subject oy to a restrictio to sma strai. A arge motio aerodyamic oads mode is itegrated ito the aaysis. The aaysis ca be used for compete aircraft aaysis icudig trim, stabiity aaysis iearized about the trimmed-state, ad oiear simuatio. Resuts are geerated for a typica highaspect-ratio fyig wig cofiguratio. The resuts idicate that the aircraft udergoes arge deformatio durig trim. The fight dyamic characteristics of the deformed aircraft are competey differet as compared to a rigid aircraft. For the exampe aircraft, the phugoid mode is ustabe ad the cassica short-period mode does ot exist. Furthermore, oiear fight simuatio of the aircraft idicates that the phugoid istabiity eads to catastrophic cosequeces. 1 Itroductio The aaysis ad desig of very ight, ad thus highy fexibe, fyig wig cofiguratios is of iterest for the deveopmet of the ext geeratio of high-atitude, og-edurace (HALE), umaed aeria vehices (UAV). The fexibiity of such aircraft eads to arge deformatio, so that iear theories are ot reevat for their aaysis. For exampe, the trim shape of a arge fexibe aircraft is highy depedet o the fight missio (payoad) as we as o the fight coditio; the deformed shape is sigificaty differet from the udeformed shape. Thus, the fight dyamic respose based o the actua trim shape ca be quite differet from that cacuated based o iear, sma deformatio assumptios. I fact, the desiger ca use the deformatio of the aircraft to positivey affect the fight stabiity ad cotro characteristics. The paper presets a theoretica basis for the fight dyamic respose estimatio of a highy fexibe fyig wig. Various reaistic desig space requiremets icudig, cocetrated payoad pods, mutipe egies, mutipe cotro surfaces, vertica surfaces, discrete dihedra, ad cotiuous pretwist, are take ito accout. The code based o the theoretica deveopmet preseted here ca be used i preimiary desig as we as i cotro sythesis. This work is a cotiuatio of work coducted by the authors over the past decade i the area of oiear aeroeasticity. 1, The focus of the preset work is o fight dyamics. 1
2 Theory The modeig of a fexibe aircraft udergoig arge deformatio requires a geometricayexact structura mode couped with a cosistet arge motio aerodyamic mode. The preset work is based o a fyig wig cocept ad is modeed structuray as a beam udergoig arge dispacemet ad rotatio. The goverig equatios are the geometricayexact equatios of motio from Hodges 3 writte i their itrisic form (i.e. without dispacemet ad rotatioa variabes). However, istead of beig augmeted by the dispacemet- ad rotatio-based kiematica reatios give therei, they are istead augmeted by the itrisic kiematica equatios, derived i Ref. 4 by eimiatig the dispacemet ad rotatioa variabes from the kiematica equatios of Ref. 3. A -D airfoi mode is appropriate for the very high-aspect-ratio wig (without fuseage iterferece) beig aayzed here. The airoads are here based o the fiite-state airoads mode preseted by Peters ad Johso. 5 Before presetig the structura ad aerodyamic theory used for the preset research, there is a eed to preset the supportig preimiaries, icudig the frames ad variabes. The ext sectio presets detais of the omecature, which are essetia to uderstad the theoretica detais preseted ater. y z x Figure 1: Axis system for the aircraft.1 Preimiaries The axis system is as show i Figure 1. The foowig frames of referece are used: i: iertia frame (-z poitig i the directio of gravity) b: udeformed beam frame (x aog the beam axis ad y poitig towards the frot of the airpae; y ad z are the axes i which the cross-sectioa stiffess ad iertia matrices are cacuated) B: deformed/movig beam frame a: aerodyamic frame i which the aerodyamic ift ad momet is defied (y ad z are defied i the airfoi frame with z poitig perpedicuar to the aerodyamic surface; y ad z are the axes i which the aerodyamic coefficiets are cacuated) The foowig rotatio matrices are used to trasform vectors i differet frames:
3 C a = C ba : trasfers a vector from the aerodyamic frame of referece to the udeformed beam frame of referece. Sice the aerodyamic frame is defied reative to the structura frame, C BA = C ba, where A is the aerodyamic frame of the deformed beam. C r : the rotatio matrix at a ode with a sope discotiuity that trasfers variabes from a referece frame o the right of the ode to oe o the eft of the ode. C = C Bb : determies the deformed beam cross-sectioa frame of referece. For the itrisic formuatio preseted here, C is ot required to sove the equatios but may be used i post-processig. The primary beam variabes are F : itera force measures i the B frame M: itera momet measures i the B frame V : veocity measures i the B frame Ω: aguar veocity measures i the B frame g: the measure umbers of the gravity vector i the B frame The secodary beam variabes are γ: itera strai measures κ: itera curvature measures P : iear mometum measures H: aguar mometum measures. Structura Mode The geometricay-exact, itrisic equatios for the dyamics of a geera, o-uiform, twisted, curved, aisotropic beam, udergoig arge deformatio, are give as F + ( k + κ)f + f = P + ΩP (1) M + ( k + κ)m + (ẽ 1 + γ)f + m = Ḣ + ΩH + Ṽ P () V + ( k + κ)v + (ẽ 1 + γ)ω = γ (3) Ω + ( k + κ)ω = κ (4) where k = k 1 k k 3 is the iitia twist/curvature of the beam, e 1 = 1 T, ad f ad m are the extera forces icudig gravity (f g, m g ), aerodyamic oads (f aero, m aero ), ad thrust (f T, m T ). The first two equatios i the above set are the equatios of motio 3 whie the atter two are the itrisic kiematica equatios 4 derived from the geeraized strai-dispacemet ad geeraized veocity-dispacemet equatios. 3
4 ..1 Cross-sectioa costitutive aws The secodary beam variabes are ieary reated to the primary variabes by the crosssectioa costitutive aws (fexibiity ad iertia matrices), such that { } [ ] { } γ R S F = κ S T (5) T M { } [ ] {V } P µ µ ξ = H µ ξ I Ω where R, S, ad T are 3 3 matrices of cross-sectioa fexibiity coefficiets; ad µ, ξ, I are the mass per uit egth, mass ceter offset, ad mass momet of iertia per uit egth, respectivey. These reatios are derived based o the assumptios of sma strai ad sederess... Fiite-eemet discretizatio To sove the above set of equatios, the beam is discretized ito fiite eemets. The equatios for each eemet are obtaied by discretizig the differetia equatios such that eergy is coserved. 4 For exampe, cosider a variabe X. Let the oda vaues of the variabe after discretizatio be represeted by X ad X r, where the superscript deotes the ode umber, the subscript deotes the eft or right side of the ode, ad the hat deotes that it is oda vaue. The eed to defie two vaues of the variabe at a ode is carified i ater sectio. For the eemet (6) X = X = X = X +1 X r d X +1 + X r I a discretized form the equatios of motio ca be writte as (7) (8) F +1 F r d + ( κ + k )F + f P Ω P = (9) M +1 M r d + ( κ + k )M + (ẽ 1 + γ )F + m H Ω H Ṽ P = (1) V +1 d V r Ω +1 + ( κ + k )V + (ẽ 1 + γ )Ω γ = (11) Ω r d where, as defied above, the barred quatities correspod to the vaues of the variabes i the eemet iterior whie the hatted quatities are oda vaues. The barred ad hatted + ( κ + k )Ω κ = (1) 4
5 quatities of the primary variabes are reated as F = M = V = F +1 M +1 V +1 + F r + M r + V r Ω +1 Ω + = Ω r (16) The barred secodary variabes are reated to the barred primary variabes as stated above i the cross-sectioa costitutive aw...3 Gravity oads The force term i the equatios of motio icude gravitatioa forces. The gravitatioa force ad momet are (13) (14) (15) f g = µg (17) m g = µ ξg (18) where g is the gravity vector. The measure umbers of g are kow i the i-frame. The measure umbers of the gravity vector g i the B frame at a the odes ca be cacuated usig the foowig equatios: g + ( κ + k)g = which i the discretized form ca be writte as ĝ +1 ġ + Ωg = (19) ĝr + ( κ + d k )g = ĝ + Ωĝ () = The secod equatio above, the time-differetiated oe, is satisfied at oe ode; whie the first equatio, the spatiay-differetiated oe, is used to obtai the g vector at other odes. Both equatios are matrix equatios, i.e. a set of three scaar equatios. The three equatios together ca be show to satisfy a costrait of costat egth for the g vector. Oe ca thus repace ay oe of the equatios by the static form of this egth costrait. This wi remove the artificia root caused by the differetiatio of a costrait. Aso the costrait is satisfied for the steady-state cacuatio whe the dyamic terms are egected. So, the equatio ca be writte as (e 1 e T 1 + e e T ) ĝ g + (e 1 e T 1 + e e T ) Ω gĝ g + (e 3 e T 3 ) ĝ g = e 3 (1) For the case of symmetric fight at the cetra ode, Ω = Ω 3 =. Thus, the above equatios become ĝ 1 = ĝ 1 = () ĝ Ω 1 ĝ 3 = (3) (ĝ ) + (ĝ 3 ) = 1 (4) 5
6 From the secod equatio above it is cear that for steady-state, symmetric fight, Ω 1 = because ĝ 3 (wig vertica)...4 Egies, oda masses, vertica surfaces ad sope discotiuities Due to oda mass, oda force (thrust) ad sope discotiuities the force o oe side of the ode is differet from the force o the other side of the ode. Thus, F r ĈT r F + f T + µ ĝ r + f aero P r Ω r P r = (5) M r ĈT r M + m T + µ ξĝ r + m aero Ĥ r Ω r Ĥ r V r P r = (6) where f T is the discrete oda thrust force defied i the ( ) r referece frame, m T is the correspodig oda momet, µ is the cocetrated oda mass, ξ is the correspodig mass offset, f aero ad m aero are the aerodyamic forces due to vertica surfaces/pods, ad P r ad Ĥ r are the iear ad aguar mometa of the cocetrated moda mass, give by { } [ P r µ = µ ξ Ĥr µ ξ Î ] } { { V r Ω r Ĥ egie where Î is the mass momet of iertia matrix of the cocetrated mass ad Ĥ egie is the aguar mometum of the egie. A sope discotiuity i the beam wi aso chage a the other variabes, such that V } (7) = Ĉ V r r (8) Ω = Ĉ Ω r r (9) ĝ = Ĉ rĝ r (3) The ( ) r variabes ca be used to repace ( ) variabes for V, Ω ad g, thus reducig the umber of variabes...5 Fia structura equatios The deveopmet preseted above eads to the foowig primary equatios: M +1 M r d F r ĈT r F + f T + µ ĝ r + f aero P r Ω r P r = (31) M r M ĈT r + m T + µ ξĝ r + m aero Ĥ r Ω r Ĥr V r P r = (3) F +1 F r d + ( κ + k )F + f aero + µ g P Ω P = (33) +( κ + k )M +(ẽ 1 + γ )F +m aero+µ ξ g H Ω H Ṽ P = (34) Ĉ +1 r V r +1 V r d Ĉ +1 r Ω +1 r d + ( κ + k )V + (ẽ 1 + γ )Ω γ = (35) Ω r Ĉ +1 r ĝr +1 ĝr d + ( κ + k )Ω κ = (36) + ( κ + k )g = (37) 6
7 ad, the foowig secodary equatios: { } [ ] { γ R S } F = { } [ P r = Ĥr κ S T T M { } [ ] {V P µ H = µ } ξ µ ξ I Ω F = M = F +1 M +1 + F r + M r V = Ĉ+1 r V r +1 + V r Ω = Ĉ+1 r Ω +1 r + Ω r g = Ĉ+1 r ĝr +1 + ĝr } ] µ µ ξ { V µ ξ Î r Ω r { + Ĥ egie } (38) (39) (4) (41) (4) (43) (44) (45)..6 Boudary coditios The foowig are the boudary coditios for the probem: F 1 = (46) M 1 = (47) F r N+1 = (48) M r N+1 = (49) (e 1 e T 1 + e e T ) ĝ g + (e 1 e T 1 + e e T ) Ω gĝ g + (e 3 e T 3 ) ĝ g = (5) where N deotes the tota umber of eemets ad g gravity. deotes the referece ode for.3 Aerodyamic Mode The airoads are cacuated based o -D aerodyamics usig the kow airfoi parameters. First the veocities i the aerodyamic frame at the mid-chord are writte as V a = Ca T V ỹmcc a T Ω (51) Ω a = C T a Ω (5) where y mc is the vector from the beam referece axis to the mid-chord ad ca be writte i terms of the aerodyamic ceter (at the quarter chord) ocatio as y mc = ȳac b. The ift, drag ad pitchig momet at the quarter-chord are give by: L aero = ρb V T (C + C α α + C β β ) + ρb V T V a C α α rot cos α (53) 7
8 where D aero = ρb VT Cd + ρb V a C α α rot si α (54) ) M aero = ρb VT (C m + C mα α + C mβ β ρb VT Va C α αrot/ (55) T V VT = Va + Va 3 (56) α si α = V a 3 VT α rot = Ω a 1 b / VT ad, Va ad Va 3 are the measure umbers of V a. β is the fap defectio of the th eemet. The ift, drag ad pitchig momet are aerodyamic forces which ca be writte i the a-frame as: fa = L Va 3 aero D V a aero (59) V T L Va aero VT m a = D aero M aero Fiay, the forces derived above are trasformed to the B frame ad trasferred to the beam referece axis to give the appied aerodyamic forces as.3.1 Usteady Effects V T Va 3 VT (57) (58) (6) f aero = C a f a (61) m aero = C a m a + C a ỹ acf a (6) The above aerodyamic mode is a quasi-steady oe with either wake (ifow) effects or apparet mass effects. To add those effects ito the mode we have to firsty add the ifow λ ad acceeratio terms i the force ad momet equatio. Secody we have to icude a ifow mode that cacuates λ. Here the Peters -D ifow theory of Ref. 6 is used. The force ad momet expressios with the usteady aerodyamics effects are ad fa = ρb (C + C β β )V T V a 3 + C α (V a 3 + λ ) C d V T V a (C + C β β )VT V a C α V a3 b/ C α Va (Va 3 + λ Ω a 1 b /) Cd VT V a 3 8 (Cm + Cm β β )VT >< C m α VT V a 3 b (C α /8 + Cpitch /)V 9 a Ω a 1 b C Ω α a1 /3 + b C α V a3 /8 >= m a = ρb (64) >: >; (63) 8
9 ad The ifow mode ca be writte as: ( [A ifow ]{ λ V } + T b ) {λ } = ( V a 3 + b Ω a 1 ) {c ifow } (65) λ = 1 {b ifow} T {λ } (66) where λ is a vector of ifow states for the th eemet, ad [A ifow ], {c ifow }, {b ifow } are costat matrices derived i Ref Aeroeastic System A aeroeastic mode is obtaied by coupig the aerodyamic force defiitio give i the previous sectio with the set of equatios preseted i the sectio o the structura mode. The aeroeastic equatios are oiear equatios i terms of the primary variabes (F, Fr, M, M r, Vr, Ω r ad gr ). The set of aeroeastic equatios is soved usig Newto-Raphso method to obtai the steady-state (trim) soutio. The Jacobia cacuated for this soutio is eeded to assess the stabiity of the iearized system at the trim state..5 Trimmig The trim coditios are the same as steady-state coditios, i.e. a the time-derivatives are zero. If a the cotros are give, the the soutio gives the steady-state (trim) correspodig to that fight coditio. O the other had, more ofte it is desired to trim the fight at a specific trim state. To do so, the trim state i terms of the airspeed ad fight age (cimb/descet idicator) are prescribed ad the cotros (thrust ad fap age) are determied. Thus two additioa equatios ad two variabe (cotros) are appeded to the system. The two equatios are give beow. The equatios are sufficiet for a symmetric trimmed state of fight. For asymmetric trimmed fight, the equatios woud be modified ad additioa equatios reatig the radius of tur ad side-sip woud be added. The symmetric trim equatios are ĝ V + ĝ 3 V3 ta φ(ĝ 3 V ĝ V3 ) = (67) V + V 3 V = (68) where φ is the prescribed fight age ad V is the prescribed airspeed. The first equatio is derived from the fact that φ = θ α, where θ is the pitch age (ta θ = bg bg 3 ) ad α is the age of attack (ta α = b V 3 bv )..6 Post-processig ad Graphics The soutio for the itrisic equatios described above ca be used to determie ad pot the deformatio. The foowig equatios reate the strais (ad curvatures) to dispacemets (ad rotatios): r i = C ib e 1 (69) C bi = kc bi (7) (r i + u i ) = C ib (γ + e 1 ) (71) C Bi = ( κ + k)c Bi (7) 9
10 where r i is the positio vector of the beam axis from the origi of the referece frame i, ad u i is the deformatio i the i frame. The first two equatios determie the geometry of the udeformed wig. The udeformed beam axis coud be potted if r i is kow at a the oda ocatios, whie the deformed beam axis coud be potted if r i + u i is kow. To pot the wig surface oe eeds the vector defiig the positio vector of the poits o the wig surface from the beam axis. For pottig it is assumed that the cross sectio is rigid, the udeformed ad deformed surface ca be geerated by pottig r i + C ib ζ ad r i + u i + C ib ζ, respectivey, where ζ is the cross-sectioa positio vector. The discretized strai-dispacemet equatios are Ĉ bi+1 = ( d + k ) 1 ( d k ) Ĉ bi (73) r +1 i = ri + C ib e 1 d (74) ( Ĉ Bi+1 = d + κ ) 1 ( + k d κ ) + k Ĉ Bi (75) r +1 i + u +1 i = r i + u i + C ib (γ + e 1 )d (76) 8 ft 1 4 ft 6 ft 8 ft 4 ft Figure : Geometry of the aircraft 3 Exampe Cosider the aircraft as iustrated i Figure. The exampe aircraft has a spa of ft ad a costat chord of 8 ft. 1/6 th of the spa at each ed has a dihedra of 1. The iertia, eastic ad aerodyamic properties of the wig cross sectio are give i Tabe 1. There are five propusive uits; oe at the mid-spa ad two each at 1/3 rd ad /3 rd semi-spa distace from the mid-spa. There are three vertica surfaces (pods) which act as the adig gear. Two of the pods weigh 5 b each ad are ocated at /3 rd semi-spa distace from the mid-spa. The cetra pod aso acts as a bay for payoad ad weighs betwee 6 b ( empty ) ad 56 b ( fu ). The pod/payoad weight is assumed to a be a poit mass hagig 3 ft uder the wig. The aerodyamic coefficiets for the pods are C α = 5 ad C d =.. 1
11 Eastic (referece) axis 5% chord Torsioa rigidity b ft Bedig rigidity b ft Bedig rigidity (chordwise) b ft Mass per uit egth 6 bs/ft Ceter of gravity 5% chord Cetroida Mass Mom. Iertia: about x-axis (torsioa) 3 b ft about y-axis 5 b ft about z-axis 5 b ft Aerodyamics Coefficiets (5% chord): C α π C δ 1 C d.1 C m.5 C mδ -.5 Tabe 1: Wig cross-sectioa properties 3.1 Trim Resuts The fight dyamic aaysis of a fexibe aircraft begis with trim aaysis. The trim soutio ivoves the steady-state soutio of the compete oiear equatios. For a symmetric aircraft, oe coud cacuate the trim soutio (the airspeed ad rate of cimb) at a specified thrust ad fap defectio. Here we use a trimmig agorithm to cacuate the thrust (assumed costat for each of the five motors) ad fap defectio (assumed costat throughout the spa) to achieve a specified trim state. For most of the resuts i this paper, the trim soutio is cacuated for a eve fight coditio of 4 ft/s at sea-eve. Figure 3 shows the cotro vaues, the fight age of attack ad the structura deformatio as a fuctio of the payoad weight for the aircraft. The resuts for a rigid aircraft with the same cofiguratio are aso show. Figure 3(d) shows the trim shape of the aircraft. The give aircraft, for the empty cofiguratio, has a amost evey distributed mass (gravitatioa forces) baaced by aerodyamic forces ad thus the equivaet oads ad deformatio of the aircraft are sma. With the additio of the cocetrated payoad at the ceter we get sigificaty higher aerodyamic oads. Such oads ead to arge deformatio i the highy fexibe aircraft. The U shape of the fu cofiguratio has very differet structura as we as fight dyamic characteristics as wi be see throughout the rest of the paper. Figure 3(a) shows the thrust required for the specified trim coditio. The chage i required thrust is isigificat for payoad chages. This is because the primary source of drag for such aircraft is the profie drag ad the ski-frictio drag. This drag does ot chage with the aircraft weight. The iduced drag which is proportioa to the ift (ad thus aircraft gross weight) is mior for very high-aspect-ratio aircraft. The fap defectio required for trim is show i Figure 3(b). The fap defectio is used for pitch cotro of the aircraft. As the aircraft deforms to a U -shape, the ceter of gravity positio moves forward reative the aerodyamic ceter ad thus ower fap defectio is required to provide the pitch-dow momet The (root) age of attack at the trim coditio is show i Figure 3(c). The age of attack icreases with payoad as expected. The differece i the rigid ad fexibe age 11
12 thrust per motor (b) rigid fexibe payoad (b) fap defectio (deg) rigid fexibe payoad (b) (a) Trim thrust per motor required for specified trim (b) Trim fap defectio required for specified trim 5 age of attack (deg) rigid fexibe payoad (b) fu eastic rigid empty eastic (c) Trim age of attack at the trim coditio (d) Eastic deformatio of the aircraft at trim Figure 3: Trim resuts for a rigid as we as fexibe aircraft for a rage of payoad at 4 ft/s, sea-eve of attack comes from two sources, the aeroeastic deformatio ad the directio of the ift. The aircraft i its udeformed shape has egigibe aeroeastic coupig sice the aerodyamic ceter ad the shear ceter are coicidet. But as the aircraft deforms the drag o the wigs ead to twist-up momet at the root eadig to aeroeastic deformatio. Thus ower root age of attack is sufficiet to provide the required ift. O the other had, the ift geerated is perpedicuar to the airfoi, ad as the deformatio icreases the directio the ift acts departs more ad more from the vertica directio. Thus, for arge deformatio, because the aerodyamic vertica force is reduced, a arger age of attack is required to geerate the same amout of vertica force. empty payoad fu payoad Rigid mode Phugoid.16 ±.146 i.613 ±.535 i Short Period.84 ± 1.8 i 3.5 ± 1.63 i Fexibe mode Phugoid.18 ±.14 i ±.586 i Short Period.74 ± 1.76 i Tabe : Fight dyamics roots 1
13 3. Liear Stabiity Estimatio The aircraft as a fight dyamic/aeroeastic system is oiear. Oce the oiear trim is cacuated, oe coud the simuate the aircraft for various cotro settigs ad/or extera disturbaces usig the compete oiear equatios. It is prudet though to gauge the respose of the system by ivestigatig the iear dyamics of the aircraft about the trim coditio. This is achieved by iearizig the aircraft at the trim coditio. By aayzig the iearized system we ca gauge the stabiity as we as the respose for sma disturbaces. The iear symmetric fight dyamics performace of the aircraft is ormay discussed i terms of the phugoid ad short-period modes of the aircraft. The two modes are the oy symmetric modes of a rigid aircraft. It shoud be oted that the fexibe aircraft has a arge umber of modes which have fexibe as we as aircraft motio. For most covetioa aircraft oe woud sti be abe to separate the modes ito two fight dyamic modes which are domiated by aircraft motio ad the rest as fexibe modes domiated by structura deformatio. For the preset aircraft the ow frequecy fexibe modes of the aircraft are i the same frequecy rage as the fight dyamic modes ad thus there is strog coupig betwee the modes. Tabe presets the short period ad phugoid modes for the rigid ad fexibe aircraft at the empty ad fu payoad cofiguratio. The frequecy of the phugoid mode icreases i frequecy whie the dampig decreases with added payoad mass. For the fexibe aircraft the dampig crosses the imagiary axis ad the mode becomes ustabe for payoad above 6 b. The root ocus of the phugoid mode for the rage of payoad mass is show i Figure 4(a) imagiary rigid fexibe imagiary rigid fexibe rea (a) Phugoid mode rea (b) Short-period mode Figure 4: Root ocus for a rigid as we as fexibe aircraft as a fuctio of payoad; the trim coditio is 4 ft/s at sea-eve (gree star represets empty cofiguratio whie gree circe represets fu ) The short-period mode root ocus is show i Figure 4(b). The short-period mode for the rigid aircraft does ot chage sigificaty with payoad. The fexibe aircraft 13
14 mode shows a drastic chage i eigevaues of the short-period mode. The root moves rapidy with added mass; ad, for payoad above 95 b, the pair of compex-cojugate short period roots merges to become two rea roots. This ca be expected because for icrease i payoad there is a correspodig icrease i the deformatio. The deformed U -shape eads to a order-of-magitude icrease i the pitch momet of iertia ad so there is correspodig decrease i the frequecy. Thus, this highy fexibe aircraft does ot show a cassica short-period mode i its deformed state. The phugoid mode of the aircraft ca ead to istabiity ad is thus ivestigated i detai. Figure 5 shows the ustabe phugoid mode shape for the fu cofiguratio. The phugoid mode shows the cassica coupig of pitch ad airspeed. The expected exchage of kietic ad potetia eergy is aso see i Figure 5(b). The aircraft oses potetia eergy as it oses atitude but gais kietic eergy (airfois are further apart). I the preset case, the strai eergy due to deformatio is aso ivoved. As see from Figure 5(d), the eastic deformatio is sigificat, but it is ot the domiat factor i the motio of the aircraft. The mode ca be ceary see by observig Figure 5(c). Here, the aircraft motio due to trimmed fight is removed so as to focus o the perturbatios about the trimmed fight coditio. The figure shows the cassica eiptica motio of the aircraft about its expected trim positio. Figure 6 shows the four fexibe modes with the owest eigevaues. Though some of these modes ca be said to be domiat i bedig, the others are couped modes with torsio, bedig (both directios), ad aircraft motio (pitch ad puge). I fact, oe of the modes deveops from the rea eigevaue of the short-period mode. 3.3 Noiear Simuatio Liear stabiity aaysis estimates the respose of the system to sma disturbaces. Liear aaysis does ot provide iformatio regardig respose to arge excitatio or the respose of a ustabe system. To estimate the arge deformatio respose of the system we have to sove the compete dyamic oiear equatios i time. I the preset we use a simpe, secod-order, cetra-differece, time marchig agorithm with high frequecy dampig. Figure 7 shows the oiear respose of fu aircraft at 4 ft/s. The aircraft simuatio is iitiated at the trim state. A extera disturbace is itroduced by addig a fap defectio. A maximum 5 fap defectio is added to trim fap defectio. The shape of the excitatio is a ramp up betwee 1 s ad s, ad a ramp dow betwee s ad 3 s. After 3 s the fap defectio is maitaied at the trim vaue. A time step of. secods is used for the simuatio. The simuatios for a time step of.1 secods as we as.5 secod are practicay the same. As expected the ustabe phugoid mode gets excited ad the ampitude of osciatio icreases. The exchage of potetia ad kietic eergy is see i Figure 7(a). Withi two-three cyces of the osciatios the aircraft starts experiecig very high ages of attack at the highest atitudes. Sice sta is ot modeed i the simuatio, the resuts after sta do ot resembe the rea aircraft motio. The motio of the aircraft is visuaized i Figure 7(b). It is obvious from this figure that oce dyamic sta is modeed oe woud see a sighty differet respose at the highest atitudes. The simuatio is robust eough to ru for a possibe arge aircraft motio as far as the reative structura deformatios are moderate. If the simuatio is ru for oger time the oe sees the aircraft perform pitch oops (Figure 7(c)). Durig the pitch oops, however, the age of attack stays sma; ad sta is ot expected. As expected from a 14
15 ustabe mode, 7 there is oss of eergy for a costat thrust ad aircraft oses atitude. 4 Cocusio A compete theoretica methodoogy for the aaysis of a highy fexibe fyig wig has bee preseted. The aaysis methodoogy is based o geometricay exact beam theory for eastic deformatio couped with arge motio airfoi aerodyamic theory. The rigid-body degrees of freedom are accouted by icudig the gravity vector i the formuatio. The equatios for the compete aaysis, icudig trim, iear stabiity ad oiear simuatio are itrisic, i.e. the equatios do ot require dispacemet ad rotatio variabes. The aaysis accouts for reaistic desig space requiremets icudig, cocetrated payoad pods, mutipe egies, mutipe cotro surfaces, vertica surfaces, discrete dihedra, ad cotiuous pre-twist. A exampe of a typica, fexibe, fyig-wig aircraft is preseted ad aayzed. The aircraft is very fexibe ad udergoes arge deformatio for fu payoad cofiguratio sice the payoad is cocetrated at the ceter (rather tha beig evey distributed over the wig). The trim shape ad the correspodig trim cotro requiremets are cacuated usig a trim agorithm. The trim shape as expected is a U shape. Due to the chage i the shape, the fight dyamic modes as we as the fexibe modes chage sigificaty. The cassica phugoid mode becomes ustabe with icrease i aircraft deformatio (trim). The cassica short-period mode does ot exist at trim because of the arge pitch momet of iertia of the deformed cofiguratio. Noiear simuatio of the aircraft cofirm that the ustabe phugoid mode ca be catastrophic for such aircraft. Refereces [1] M. J. Pati, D. H. Hodges, ad C. E. S. Cesik. Noiear aeroeastic aaysis of compete aircraft i subsoic fow. Joura of Aircraft, 37(5):753 76, Sep Oct. [] M. J. Pati ad D. H. Hodges. O the importace of aerodyamic ad structura geometrica oiearities i aeroeastic behavior of high-aspect-ratio wigs. Joura of Fuids ad Structures, 19(7):95 915, Aug. 4. [3] D. H. Hodges. A mixed variatioa formuatio based o exact itrisic equatios for dyamics of movig beams. Iteratioa Joura of Soids ad Structures, 6(11): , 199. [4] D. H. Hodges. Geometricay exact, itrisic theory for dyamics of curved ad twisted aisotropic beams. AIAA Joura, 41(6): , 3. [5] D. A. Peters ad M. J. Johso. Fiite-state airoads for deformabe airfois o fixed ad rotatig wigs. I Symposium o Aeroeasticity ad Fuid/Structure Iteractio, Proceedigs of the Witer Aua Meetig. ASME, November 6 11, [6] D. A. Peters, S. Karuamoorthy, ad W.-M. Cao. Fiite state iduced fow modes; part i: two-dimesioa thi airfoi. Joura of Aircraft, 3():313 3, Mar.-Apr [7] M. J. Pati. From futterig wigs to fappig fight: The eergy coectio. Joura of Aircraft, 4:7 76, March 3. 15
16 (a) Iertia 3-D view of the aircraft (aircraft movig to the eft) (b) Iertia -D view of the mid-spa sectio (aircraft movig to the eft) (c) 3-D view of the aircraft for a observer movig at trim airspeed (aircraft motio is cockwise) (d) Eastic deformatio of the aircraft Figure 5: Phugoid mode of the fexibe cofiguratio with 5 b payoad 16
17 (a) First bedig (domiat):.8583 ±.157 i (b) Couped bedigtorsio-aircraft puge: ±.9881 i (c) Secod bedig (domiat):.735 ± i (d) Couped bedigtorsio-aircraft pitch: ± i Figure 6: Fexibe modes of the aircraft 17
18 airspeed (ft/s) atitude (ft) age of attack (deg) time (s) (a) Variatio i aircraft parameters (b) Iertia -D view of the mid-spa sectio: time -5s (aircraft movig to the eft) (c) Iertia -D view of the mid-spa sectio: time 5-5s (showig pitch oops) Figure 7: Noiear simuatio of aircraft respose to iitia fap excitatio 18
Gust Response of Highly Flexible Aircraft
 Gust Respose of Highy Fexibe Aircraft Mayuresh J. Pati, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia 461-3 ad D. J. Tayor AeroViromet Ic., Simi Vaey, Caiforia 9363 The paper presets
Gust Respose of Highy Fexibe Aircraft Mayuresh J. Pati, Virgiia Poytechic Istitute ad State Uiversity, Backsburg, Virgiia 461-3 ad D. J. Tayor AeroViromet Ic., Simi Vaey, Caiforia 9363 The paper presets
modes shapes can be obtained by imposing the non-trivial solution condition on the
 modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad
modes shapes ca be obtaied by imposig the o-trivia soutio coditio o the derived characteristics equatio. Fiay, usig the method of assumed modes, the goverig ordiary differetia equatios (ODEs of beam ad
Principle Of Superposition
 ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
Energy Dissipation Mechanism and Its Application of to a Slotted Disc Waveguide Vibration Absorber
 www.ijm-me.org Iteratioa Joura of Materia ad Mechaica Egieerig (IJMME), Voume 5 16 doi: 1.14355/ijmme.16.5.9 Eergy Dissipatio Mechaism ad Its Appicatio of to a Sotted Disc Waveguide Vibratio Absorber Xi
www.ijm-me.org Iteratioa Joura of Materia ad Mechaica Egieerig (IJMME), Voume 5 16 doi: 1.14355/ijmme.16.5.9 Eergy Dissipatio Mechaism ad Its Appicatio of to a Sotted Disc Waveguide Vibratio Absorber Xi
Self-Consistent Simulations of Beam and Plasma Systems Final Exam ( take-home )
 Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Sef-Cosistet Simuatios of Beam ad Pasma Systems Fia Exam ( take-home ) S. M. Lud, J.-L. Vay, R. Lehe, ad D. Wikeher Thursday, Jue 16 th, 2016 Probem 1 - Maxwe s equatios ad redudat iformatio. a) Show that
Alternative Orthogonal Polynomials. Vladimir Chelyshkov
 Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
Aterative Orthogoa oyomias Vadimir Cheyshov Istitute of Hydromechaics of the NAS Uraie Georgia Souther Uiversity USA Abstract. The doube-directio orthogoaizatio agorithm is appied to costruct sequeces
FLIGHT DYNAMICS OF HIGHLY FLEXIBLE SOLAR- POWERED UAV BASED ON GEOMETRICALLY NONLINEAR INTRINSIC BEAM
 FLIGH DYNAICS OF HIGHLY FLEXILE SOLAR- POWERED UAV ASED ON GEOERICALLY NONLINEAR INRINSIC EA Wag Rui * Zhou Zhou * Zhu Xiaopig ** Xu Xiaopig * * Sciece ad echoog o UAV Laborator Northwester Potechica Uiversit
FLIGH DYNAICS OF HIGHLY FLEXILE SOLAR- POWERED UAV ASED ON GEOERICALLY NONLINEAR INRINSIC EA Wag Rui * Zhou Zhou * Zhu Xiaopig ** Xu Xiaopig * * Sciece ad echoog o UAV Laborator Northwester Potechica Uiversit
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Discrete Fourier Transform
 Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Discrete Fourier Trasform ) Purpose The purpose is to represet a determiistic or stochastic siga u( t ) as a fiite Fourier sum, whe observatios of u() t ( ) are give o a reguar grid, each affected by a
Problem 1. Problem Engineering Dynamics Problem Set 9--Solution. Find the equation of motion for the system shown with respect to:
 2.003 Egieerig Dyamics Problem Set 9--Solutio Problem 1 Fid the equatio of motio for the system show with respect to: a) Zero sprig force positio. Draw the appropriate free body diagram. b) Static equilibrium
2.003 Egieerig Dyamics Problem Set 9--Solutio Problem 1 Fid the equatio of motio for the system show with respect to: a) Zero sprig force positio. Draw the appropriate free body diagram. b) Static equilibrium
April 1980 TR/96. Extrapolation techniques for first order hyperbolic partial differential equations. E.H. Twizell
 TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
TR/96 Apri 980 Extrapoatio techiques for first order hyperboic partia differetia equatios. E.H. Twize W96086 (0) 0. Abstract A uifor grid of step size h is superiposed o the space variabe x i the first
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5th Iteratioa Coferece o Advaced Desig ad Maufacturig Egieerig (ICADME 15) Series form soutio for a graded composite strip with eastic variatio i spa directio Qig Yag 1,,a *, Weipig Liu 1,b, Muhuo Yu,c,
5th Iteratioa Coferece o Advaced Desig ad Maufacturig Egieerig (ICADME 15) Series form soutio for a graded composite strip with eastic variatio i spa directio Qig Yag 1,,a *, Weipig Liu 1,b, Muhuo Yu,c,
Radiative Transfer Models and their Adjoints. Paul van Delst
 Radiative rasfer Modes ad their Adjoits au va Dest Overview Use of sateite radiaces i Data Assimiatio (DA) Radiative rasfer Mode (RM) compoets ad defiitios estig the RM compoets. Advatages/disadvatages
Radiative rasfer Modes ad their Adjoits au va Dest Overview Use of sateite radiaces i Data Assimiatio (DA) Radiative rasfer Mode (RM) compoets ad defiitios estig the RM compoets. Advatages/disadvatages
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
On the effect of drag forces in mooring system restoring forces
 MATEC Web of Cofereces 138, 001 (017) CEF 017 DOI: 10.1051/mateccof/017138001 O the effect of drag forces i moorig sstem restorig forces Zahid Uah 1, Naik Muhammad 1, Ji-Hoo Lim 1, ad Dog-Ho Choi,* 1 Ph.D.
MATEC Web of Cofereces 138, 001 (017) CEF 017 DOI: 10.1051/mateccof/017138001 O the effect of drag forces i moorig sstem restorig forces Zahid Uah 1, Naik Muhammad 1, Ji-Hoo Lim 1, ad Dog-Ho Choi,* 1 Ph.D.
ECE507 - Plasma Physics and Applications
 ECE57 - Pasma Physics ad Appicatios Lecture 9 Prof. Jorge Rocca ad r. Ferado Tomase epartmet of Eectrica ad Computer Egieerig Low temperature pasmas Low temperature pasmas are a very iterestig subject
ECE57 - Pasma Physics ad Appicatios Lecture 9 Prof. Jorge Rocca ad r. Ferado Tomase epartmet of Eectrica ad Computer Egieerig Low temperature pasmas Low temperature pasmas are a very iterestig subject
Existence of Nonoscillatory Solution of High Order Linear Neutral Delay Difference Equation
 oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
oder Appied Sciece ovember, 008 Existece of oosciatory Soutio of High Order Liear eutra Deay Differece Equatio Shasha Zhag, Xiaozhu Zhog, Pig Yu, Wexia Zhag & ig Li Departmet of athematics Yasha Uiversity
SOME INTEGRAL FORMULAS FOR CLOSED MINIMALLY IMMERSED HYPERSURFACE IN THE UNIT SPHERE S n+1
 TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
TWS J. Pure App. ath. V.1 N.1 010 pp.81-85 SOE INTEGAL FOULAS FO CLOSED INIALLY IESED HYPESUFACE IN THE UNIT SPHEE S +1 IHIBAN KÜLAHCI 1 AHUT EGÜT 1 Abstract. I this paper we obtai some itegra formuas
Chem 442 Review for Exam 1. Hamiltonian operator in 1 dimension: ˆ d first term is kinetic energy, second term is potential energy
 Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Chem 44 Review for Eam 1 Eergies are quatized Wave/partice duaity de Brogie waveegth: h p Eergy: E h mometum operator: pˆ positio operator: ˆ d i d potetia eergy operator: V ˆ( ) pˆ d kietic eergy operator
Quantum Annealing for Heisenberg Spin Chains
 LA-UR # - Quatum Aealig for Heiseberg Spi Chais G.P. Berma, V.N. Gorshkov,, ad V.I.Tsifriovich Theoretical Divisio, Los Alamos Natioal Laboratory, Los Alamos, NM Istitute of Physics, Natioal Academy of
LA-UR # - Quatum Aealig for Heiseberg Spi Chais G.P. Berma, V.N. Gorshkov,, ad V.I.Tsifriovich Theoretical Divisio, Los Alamos Natioal Laboratory, Los Alamos, NM Istitute of Physics, Natioal Academy of
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
EXPERIMENT OF SIMPLE VIBRATION
 EXPERIMENT OF SIMPLE VIBRATION. PURPOSE The purpose of the experimet is to show free vibratio ad damped vibratio o a system havig oe degree of freedom ad to ivestigate the relatioship betwee the basic
EXPERIMENT OF SIMPLE VIBRATION. PURPOSE The purpose of the experimet is to show free vibratio ad damped vibratio o a system havig oe degree of freedom ad to ivestigate the relatioship betwee the basic
2C09 Design for seismic and climate changes
 2C09 Desig for seismic ad climate chages Lecture 02: Dyamic respose of sigle-degree-of-freedom systems I Daiel Grecea, Politehica Uiversity of Timisoara 10/03/2014 Europea Erasmus Mudus Master Course Sustaiable
2C09 Desig for seismic ad climate chages Lecture 02: Dyamic respose of sigle-degree-of-freedom systems I Daiel Grecea, Politehica Uiversity of Timisoara 10/03/2014 Europea Erasmus Mudus Master Course Sustaiable
a b c d e f g h Supplementary Information
 Supplemetary Iformatio a b c d e f g h Supplemetary Figure S STM images show that Dark patters are frequetly preset ad ted to accumulate. (a) mv, pa, m ; (b) mv, pa, m ; (c) mv, pa, m ; (d) mv, pa, m ;
Supplemetary Iformatio a b c d e f g h Supplemetary Figure S STM images show that Dark patters are frequetly preset ad ted to accumulate. (a) mv, pa, m ; (b) mv, pa, m ; (c) mv, pa, m ; (d) mv, pa, m ;
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science. BACKGROUND EXAM September 30, 2004.
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.34 Discrete Time Sigal Processig Fall 24 BACKGROUND EXAM September 3, 24. Full Name: Note: This exam is closed
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.34 Discrete Time Sigal Processig Fall 24 BACKGROUND EXAM September 3, 24. Full Name: Note: This exam is closed
Star Saturation Number of Random Graphs
 Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
Star Saturatio Number of Radom Graphs A. Mohammadia B. Tayfeh-Rezaie Schoo of Mathematics, Istitute for Research i Fudameta Scieces IPM, P.O. Box 19395-5746, Tehra, Ira ai m@ipm.ir tayfeh-r@ipm.ir Abstract
CEE 522 Autumn Uncertainty Concepts for Geotechnical Engineering
 CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
DYNAMIC ANALYSIS OF BEAM-LIKE STRUCTURES SUBJECT TO MOVING LOADS
 DYNAMIC ANALYSIS OF BEAM-LIKE STRUCTURES SUBJECT TO MOVING LOADS Ivaa Štimac 1, Ivica Kožar 1 M.Sc,Assistat, Ph.D. Professor 1, Faculty of Civil Egieerig, Uiverity of Rieka, Croatia INTRODUCTION The vehicle-iduced
DYNAMIC ANALYSIS OF BEAM-LIKE STRUCTURES SUBJECT TO MOVING LOADS Ivaa Štimac 1, Ivica Kožar 1 M.Sc,Assistat, Ph.D. Professor 1, Faculty of Civil Egieerig, Uiverity of Rieka, Croatia INTRODUCTION The vehicle-iduced
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Thermal network model of electrical motor by lumped heat method
 6 IJED Voume 4, Issue ISSN: 3-9939 Therma etwork mode of eectrica motor by umped heat method Vijay Mehta, Saket Padya, 3 Nirav Meghpara Assistat Professor, Assistat Professor, 3 Assistat Professor,,3 Departmet
6 IJED Voume 4, Issue ISSN: 3-9939 Therma etwork mode of eectrica motor by umped heat method Vijay Mehta, Saket Padya, 3 Nirav Meghpara Assistat Professor, Assistat Professor, 3 Assistat Professor,,3 Departmet
A New Solution Method for the Finite-Horizon Discrete-Time EOQ Problem
 This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
ATTITUDE CONTROL OF FLEXIBLE LAUNCH VEHICLE USING ADAPTIVE NOTCH FILTER. Choong-Seok Oh and Hyochoong Bang
 ATTITUDE CONTROL OF FLEXIBLE LAUNCH VEHICLE USING ADAPTIVE NOTCH FILTER Choog-Seok Oh ad Hyochoog Bag Dept. of Aerospace Egieerig, Korea Advaced Istitute of Sciece ad Techoogy (KAIST) Abstract: Attitude
ATTITUDE CONTROL OF FLEXIBLE LAUNCH VEHICLE USING ADAPTIVE NOTCH FILTER Choog-Seok Oh ad Hyochoog Bag Dept. of Aerospace Egieerig, Korea Advaced Istitute of Sciece ad Techoogy (KAIST) Abstract: Attitude
Microscopic Theory of Transport (Fall 2003) Lecture 6 (9/19/03) Static and Short Time Properties of Time Correlation Functions
 .03 Microscopic Theory of Trasport (Fall 003) Lecture 6 (9/9/03) Static ad Short Time Properties of Time Correlatio Fuctios Refereces -- Boo ad Yip, Chap There are a umber of properties of time correlatio
.03 Microscopic Theory of Trasport (Fall 003) Lecture 6 (9/9/03) Static ad Short Time Properties of Time Correlatio Fuctios Refereces -- Boo ad Yip, Chap There are a umber of properties of time correlatio
Mechatronics. Time Response & Frequency Response 2 nd -Order Dynamic System 2-Pole, Low-Pass, Active Filter
 Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
Damped Vibration of a Non-prismatic Beam with a Rotational Spring
 Vibratios i Physical Systems Vol.6 (0) Damped Vibratio of a No-prismatic Beam with a Rotatioal Sprig Wojciech SOCHACK stitute of Mechaics ad Fudametals of Machiery Desig Uiversity of Techology, Czestochowa,
Vibratios i Physical Systems Vol.6 (0) Damped Vibratio of a No-prismatic Beam with a Rotatioal Sprig Wojciech SOCHACK stitute of Mechaics ad Fudametals of Machiery Desig Uiversity of Techology, Czestochowa,
Salmon: Lectures on partial differential equations. 3. First-order linear equations as the limiting case of second-order equations
 3. First-order liear equatios as the limitig case of secod-order equatios We cosider the advectio-diffusio equatio (1) v = 2 o a bouded domai, with boudary coditios of prescribed. The coefficiets ( ) (2)
3. First-order liear equatios as the limitig case of secod-order equatios We cosider the advectio-diffusio equatio (1) v = 2 o a bouded domai, with boudary coditios of prescribed. The coefficiets ( ) (2)
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Research Article Kinematics, Dynamics, and Optimal Control of Pneumatic Hexapod Robot
 Hidawi Mathematica Probems i Egieerig Voume 7, Artice ID 68497, 6 pages https://doi.org/.55/7/68497 Research Artice Kiematics, Dyamics, ad Optima Cotro of Peumatic Hexapod Robot Log Bai, Lu-ha Ma, Zhifeg
Hidawi Mathematica Probems i Egieerig Voume 7, Artice ID 68497, 6 pages https://doi.org/.55/7/68497 Research Artice Kiematics, Dyamics, ad Optima Cotro of Peumatic Hexapod Robot Log Bai, Lu-ha Ma, Zhifeg
FIR Filter Design: Part II
 EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we cosider how we might go about desigig FIR filters with arbitrary frequecy resposes, through compositio of multiple sigle-peak
EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we cosider how we might go about desigig FIR filters with arbitrary frequecy resposes, through compositio of multiple sigle-peak
Chapter 2 Feedback Control Theory Continued
 Chapter Feedback Cotrol Theor Cotiued. Itroductio I the previous chapter, the respose characteristic of simple first ad secod order trasfer fuctios were studied. It was show that first order trasfer fuctio,
Chapter Feedback Cotrol Theor Cotiued. Itroductio I the previous chapter, the respose characteristic of simple first ad secod order trasfer fuctios were studied. It was show that first order trasfer fuctio,
Random Variables, Sampling and Estimation
 Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
0 : Recap of last two classes
 Cass 12 : Superova cosmoogy ad the acceeratio of the Uiverse This cass Redshift-distace reatio as a probe of the cosmoogica mode Type-1A superovae Superovae ad cosmoogy Discovery of acceeratio It a fits
Cass 12 : Superova cosmoogy ad the acceeratio of the Uiverse This cass Redshift-distace reatio as a probe of the cosmoogica mode Type-1A superovae Superovae ad cosmoogy Discovery of acceeratio It a fits
Frequency Domain Filtering
 Frequecy Domai Filterig Raga Rodrigo October 19, 2010 Outlie Cotets 1 Itroductio 1 2 Fourier Represetatio of Fiite-Duratio Sequeces: The Discrete Fourier Trasform 1 3 The 2-D Discrete Fourier Trasform
Frequecy Domai Filterig Raga Rodrigo October 19, 2010 Outlie Cotets 1 Itroductio 1 2 Fourier Represetatio of Fiite-Duratio Sequeces: The Discrete Fourier Trasform 1 3 The 2-D Discrete Fourier Trasform
Two or more points can be used to describe a rigid body. This will eliminate the need to define rotational coordinates for the body!
 OINTCOORDINATE FORMULATION Two or more poits ca be used to describe a rigid body. This will elimiate the eed to defie rotatioal coordiates for the body i z r i i, j r j j rimary oits: The coordiates of
OINTCOORDINATE FORMULATION Two or more poits ca be used to describe a rigid body. This will elimiate the eed to defie rotatioal coordiates for the body i z r i i, j r j j rimary oits: The coordiates of
The Mathematical Model and the Simulation Modelling Algoritm of the Multitiered Mechanical System
 The Mathematical Model ad the Simulatio Modellig Algoritm of the Multitiered Mechaical System Demi Aatoliy, Kovalev Iva Dept. of Optical Digital Systems ad Techologies, The St. Petersburg Natioal Research
The Mathematical Model ad the Simulatio Modellig Algoritm of the Multitiered Mechaical System Demi Aatoliy, Kovalev Iva Dept. of Optical Digital Systems ad Techologies, The St. Petersburg Natioal Research
1 Adiabatic and diabatic representations
 1 Adiabatic ad diabatic represetatios 1.1 Bor-Oppeheimer approximatio The time-idepedet Schrödiger equatio for both electroic ad uclear degrees of freedom is Ĥ Ψ(r, R) = E Ψ(r, R), (1) where the full molecular
1 Adiabatic ad diabatic represetatios 1.1 Bor-Oppeheimer approximatio The time-idepedet Schrödiger equatio for both electroic ad uclear degrees of freedom is Ĥ Ψ(r, R) = E Ψ(r, R), (1) where the full molecular
Fluid Physics 8.292J/12.330J % (1)
 Fluid Physics 89J/133J Problem Set 5 Solutios 1 Cosider the flow of a Euler fluid i the x directio give by for y > d U = U y 1 d for y d U + y 1 d for y < This flow does ot vary i x or i z Determie the
Fluid Physics 89J/133J Problem Set 5 Solutios 1 Cosider the flow of a Euler fluid i the x directio give by for y > d U = U y 1 d for y d U + y 1 d for y < This flow does ot vary i x or i z Determie the
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Research Article Mechanical State Model of Multispan Continuous Deep Beam under Concentrated Load
 Mathematica Probems i Egieerig Voume 23, Artice ID 66492, 9 ages htt://dxdoiorg/55/23/66492 Research Artice Mechaica State Mode of Mutisa Cotiuous Dee Beam uder Cocetrated Load Chu-Liag Li ad Dog-Miao
Mathematica Probems i Egieerig Voume 23, Artice ID 66492, 9 ages htt://dxdoiorg/55/23/66492 Research Artice Mechaica State Mode of Mutisa Cotiuous Dee Beam uder Cocetrated Load Chu-Liag Li ad Dog-Miao
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
University of Washington Department of Chemistry Chemistry 453 Winter Quarter 2015
 Uiversity of Wasigto Departmet of Cemistry Cemistry 453 Witer Quarter 15 Lecture 14. /11/15 Recommeded Text Readig: Atkis DePaula: 9.1, 9., 9.3 A. Te Equipartitio Priciple & Eergy Quatizatio Te Equipartio
Uiversity of Wasigto Departmet of Cemistry Cemistry 453 Witer Quarter 15 Lecture 14. /11/15 Recommeded Text Readig: Atkis DePaula: 9.1, 9., 9.3 A. Te Equipartitio Priciple & Eergy Quatizatio Te Equipartio
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Dynamic Instability of Taut Mooring Lines Subjected to Bi-frequency Parametric Excitation
 Proceedigs of the 1 th Iteratioal Coferece o the Stability of Ships ad Ocea Vehicles, 14-19 Jue 15, Glasgow, UK. Dyamic Istability of Taut Moorig Lies Subjected to Bi-frequecy Parametric Excitatio Aiju
Proceedigs of the 1 th Iteratioal Coferece o the Stability of Ships ad Ocea Vehicles, 14-19 Jue 15, Glasgow, UK. Dyamic Istability of Taut Moorig Lies Subjected to Bi-frequecy Parametric Excitatio Aiju
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Kinetics of Complex Reactions
 Kietics of Complex Reactios by Flick Colema Departmet of Chemistry Wellesley College Wellesley MA 28 wcolema@wellesley.edu Copyright Flick Colema 996. All rights reserved. You are welcome to use this documet
Kietics of Complex Reactios by Flick Colema Departmet of Chemistry Wellesley College Wellesley MA 28 wcolema@wellesley.edu Copyright Flick Colema 996. All rights reserved. You are welcome to use this documet
Upper bound for ropelength of pretzel knots
 Upper boud for ropelegth of pretzel kots Safiya Mora August 25, 2006 Abstract A model of the pretzel kot is described. A method for predictig the ropelegth of pretzel kots is give. A upper boud for the
Upper boud for ropelegth of pretzel kots Safiya Mora August 25, 2006 Abstract A model of the pretzel kot is described. A method for predictig the ropelegth of pretzel kots is give. A upper boud for the
Assignment 2 Solutions SOLUTION. ϕ 1 Â = 3 ϕ 1 4i ϕ 2. The other case can be dealt with in a similar way. { ϕ 2 Â} χ = { 4i ϕ 1 3 ϕ 2 } χ.
 PHYSICS 34 QUANTUM PHYSICS II (25) Assigmet 2 Solutios 1. With respect to a pair of orthoormal vectors ϕ 1 ad ϕ 2 that spa the Hilbert space H of a certai system, the operator  is defied by its actio
PHYSICS 34 QUANTUM PHYSICS II (25) Assigmet 2 Solutios 1. With respect to a pair of orthoormal vectors ϕ 1 ad ϕ 2 that spa the Hilbert space H of a certai system, the operator  is defied by its actio
4.3 Growth Rates of Solutions to Recurrences
 4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
4.3. GROWTH RATES OF SOLUTIONS TO RECURRENCES 81 4.3 Growth Rates of Solutios to Recurreces 4.3.1 Divide ad Coquer Algorithms Oe of the most basic ad powerful algorithmic techiques is divide ad coquer.
2.004 Dynamics and Control II Spring 2008
 MIT OpeCourseWare http://ocw.mit.edu 2.004 Dyamics ad Cotrol II Sprig 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts Istitute of Techology
MIT OpeCourseWare http://ocw.mit.edu 2.004 Dyamics ad Cotrol II Sprig 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Massachusetts Istitute of Techology
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
A linguistic model for the controlled object
 A igutic mode for the cotroed obect Zhiog Miao,, Yi Wag, Xiagyu Zhao Iteeget cotro ad deveopmet eter,southwest Jiaotog iversity hegdu hia Departmet of Eectroic ad Iformatio Egieerig, azhihua iversity,
A igutic mode for the cotroed obect Zhiog Miao,, Yi Wag, Xiagyu Zhao Iteeget cotro ad deveopmet eter,southwest Jiaotog iversity hegdu hia Departmet of Eectroic ad Iformatio Egieerig, azhihua iversity,
Similarity Solutions to Unsteady Pseudoplastic. Flow Near a Moving Wall
 Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Discrete Fourier Transform
 Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Discrete Fourier Trasform 3) Compex Case et s distiguish the three cases + J + > + J + + J + < (35) Ad et s begi treatig the isodetermied case + J +, addig at first the hypothesis that J,. I this case
Dynamic Response of Second Order Mechanical Systems with Viscous Dissipation forces
 Hadout #b (pp. 4-55) Dyamic Respose o Secod Order Mechaical Systems with Viscous Dissipatio orces M X + DX + K X = F t () Periodic Forced Respose to F (t) = F o si( t) ad F (t) = M u si(t) Frequecy Respose
Hadout #b (pp. 4-55) Dyamic Respose o Secod Order Mechaical Systems with Viscous Dissipatio orces M X + DX + K X = F t () Periodic Forced Respose to F (t) = F o si( t) ad F (t) = M u si(t) Frequecy Respose
Streamfunction-Vorticity Formulation
 Streamfuctio-Vorticity Formulatio A. Salih Departmet of Aerospace Egieerig Idia Istitute of Space Sciece ad Techology, Thiruvaathapuram March 2013 The streamfuctio-vorticity formulatio was amog the first
Streamfuctio-Vorticity Formulatio A. Salih Departmet of Aerospace Egieerig Idia Istitute of Space Sciece ad Techology, Thiruvaathapuram March 2013 The streamfuctio-vorticity formulatio was amog the first
Systems of Particles: Angular Momentum and Work Energy Principle
 1 2.003J/1.053J Dyamics ad Cotrol I, Sprig 2007 Professor Thomas Peacock 2/20/2007 Lecture 4 Systems of Particles: Agular Mometum ad Work Eergy Priciple Systems of Particles Agular Mometum (cotiued) τ
1 2.003J/1.053J Dyamics ad Cotrol I, Sprig 2007 Professor Thomas Peacock 2/20/2007 Lecture 4 Systems of Particles: Agular Mometum ad Work Eergy Priciple Systems of Particles Agular Mometum (cotiued) τ
Ladder Lattice Model of Soft Optical Phonon
 Ladder Lattice Mode of Soft Optica Phoo Hiroyuki MASHIYAMA Departmet of Physics, Facuty of Sciece, Yamaguchi Uiversity Yoshida 677-, Yamaguchi 753-85, Japa (Received October 7, 9) A iear attice mode for
Ladder Lattice Mode of Soft Optica Phoo Hiroyuki MASHIYAMA Departmet of Physics, Facuty of Sciece, Yamaguchi Uiversity Yoshida 677-, Yamaguchi 753-85, Japa (Received October 7, 9) A iear attice mode for
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
CHAPTER 8 SYSTEMS OF PARTICLES
 CHAPTER 8 SYSTES OF PARTICLES CHAPTER 8 COLLISIONS 45 8. CENTER OF ASS The ceter of mass of a system of particles or a rigid body is the poit at which all of the mass are cosidered to be cocetrated there
CHAPTER 8 SYSTES OF PARTICLES CHAPTER 8 COLLISIONS 45 8. CENTER OF ASS The ceter of mass of a system of particles or a rigid body is the poit at which all of the mass are cosidered to be cocetrated there
Lecture 8: Solving the Heat, Laplace and Wave equations using finite difference methods
 Itroductory lecture otes o Partial Differetial Equatios - c Athoy Peirce. Not to be copied, used, or revised without explicit writte permissio from the copyright ower. 1 Lecture 8: Solvig the Heat, Laplace
Itroductory lecture otes o Partial Differetial Equatios - c Athoy Peirce. Not to be copied, used, or revised without explicit writte permissio from the copyright ower. 1 Lecture 8: Solvig the Heat, Laplace
True Nature of Potential Energy of a Hydrogen Atom
 True Nature of Potetial Eergy of a Hydroge Atom Koshu Suto Key words: Bohr Radius, Potetial Eergy, Rest Mass Eergy, Classical Electro Radius PACS codes: 365Sq, 365-w, 33+p Abstract I cosiderig the potetial
True Nature of Potetial Eergy of a Hydroge Atom Koshu Suto Key words: Bohr Radius, Potetial Eergy, Rest Mass Eergy, Classical Electro Radius PACS codes: 365Sq, 365-w, 33+p Abstract I cosiderig the potetial
6.003 Homework #3 Solutions
 6.00 Homework # Solutios Problems. Complex umbers a. Evaluate the real ad imagiary parts of j j. π/ Real part = Imagiary part = 0 e Euler s formula says that j = e jπ/, so jπ/ j π/ j j = e = e. Thus the
6.00 Homework # Solutios Problems. Complex umbers a. Evaluate the real ad imagiary parts of j j. π/ Real part = Imagiary part = 0 e Euler s formula says that j = e jπ/, so jπ/ j π/ j j = e = e. Thus the
Random Walks on Discrete and Continuous Circles. by Jeffrey S. Rosenthal School of Mathematics, University of Minnesota, Minneapolis, MN, U.S.A.
 Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Radom Walks o Discrete ad Cotiuous Circles by Jeffrey S. Rosethal School of Mathematics, Uiversity of Miesota, Mieapolis, MN, U.S.A. 55455 (Appeared i Joural of Applied Probability 30 (1993), 780 789.)
Castiel, Supernatural, Season 6, Episode 18
 13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
13 Differetial Equatios the aswer to your questio ca best be epressed as a series of partial differetial equatios... Castiel, Superatural, Seaso 6, Episode 18 A differetial equatio is a mathematical equatio
NEW SOLUTIONS TO A LINEAR ANTENNA SYNTHESIS PROBLEM ACCORDING TO THE GIVEN AMPLITUDE PATTERN
 UDK 519.6:61.396 M. Adriychu Pidstryhach Istitute for Appied Probems of Mechaics ad Mathematics, NASU CAD Departmet, Lviv Poytechic Natioa Uiversity NEW SOLUTIONS TO A LINEAR ANTENNA SYNTHESIS PROBLEM
UDK 519.6:61.396 M. Adriychu Pidstryhach Istitute for Appied Probems of Mechaics ad Mathematics, NASU CAD Departmet, Lviv Poytechic Natioa Uiversity NEW SOLUTIONS TO A LINEAR ANTENNA SYNTHESIS PROBLEM
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
TESTING OF THE FORCES IN CABLE OF SUSPENSION STRUCTURE AND BRIDGES
 TSTING OF TH FORCS IN CABL OF SUSPNSION STRUCTUR AND BRIDGS Zhou, M. 1, Liu, Z. ad Liu, J. 1 College of the Muicipal Techology, Guagzhou Uiversity, Guagzhou. Guagzhou Muicipal ad Ladscape gieerig Quality
TSTING OF TH FORCS IN CABL OF SUSPNSION STRUCTUR AND BRIDGS Zhou, M. 1, Liu, Z. ad Liu, J. 1 College of the Muicipal Techology, Guagzhou Uiversity, Guagzhou. Guagzhou Muicipal ad Ladscape gieerig Quality
A PROCEDURE TO MODIFY THE FREQUENCY AND ENVELOPE CHARACTERISTICS OF EMPIRICAL GREEN'S FUNCTION. Lin LU 1 SUMMARY
 A POCEDUE TO MODIFY THE FEQUENCY AND ENVELOPE CHAACTEISTICS OF EMPIICAL GEEN'S FUNCTION Li LU SUMMAY Semi-empirical method, which divides the fault plae of large earthquake ito mets ad uses small groud
A POCEDUE TO MODIFY THE FEQUENCY AND ENVELOPE CHAACTEISTICS OF EMPIICAL GEEN'S FUNCTION Li LU SUMMAY Semi-empirical method, which divides the fault plae of large earthquake ito mets ad uses small groud
SydU STAT3014 (2015) Second semester Dr. J. Chan 1
 Refereces STAT3014/3914 Appied Statistics-Sampig Preimiary 1. Cochra, W.G. 1963) Sampig Techiques, Wiey, ew York.. Kish, L. 1995) Survey Sampig, Wiey Iter. Sciece. 3. Lohr, S.L. 1999) Sampig: Desig ad
Refereces STAT3014/3914 Appied Statistics-Sampig Preimiary 1. Cochra, W.G. 1963) Sampig Techiques, Wiey, ew York.. Kish, L. 1995) Survey Sampig, Wiey Iter. Sciece. 3. Lohr, S.L. 1999) Sampig: Desig ad
Exercises and Problems
 HW Chapter 4: Oe-Dimesioal Quatum Mechaics Coceptual Questios 4.. Five. 4.4.. is idepedet of. a b c mu ( E). a b m( ev 5 ev) c m(6 ev ev) Exercises ad Problems 4.. Model: Model the electro as a particle
HW Chapter 4: Oe-Dimesioal Quatum Mechaics Coceptual Questios 4.. Five. 4.4.. is idepedet of. a b c mu ( E). a b m( ev 5 ev) c m(6 ev ev) Exercises ad Problems 4.. Model: Model the electro as a particle
Improved Factorial Kriging for Feature Identification and Extraction
 Improved Factoria Krigig for Feature Idetificatio ad Extractio Sahyu Hog ad Cayto V. Deutsch Cetre for Computatioa Geostatistics Departmet of Civi ad Evirometa Egieerig Uiversity of Aberta Factoria krigig
Improved Factoria Krigig for Feature Idetificatio ad Extractio Sahyu Hog ad Cayto V. Deutsch Cetre for Computatioa Geostatistics Departmet of Civi ad Evirometa Egieerig Uiversity of Aberta Factoria krigig
Physics 324, Fall Dirac Notation. These notes were produced by David Kaplan for Phys. 324 in Autumn 2001.
 Physics 324, Fall 2002 Dirac Notatio These otes were produced by David Kapla for Phys. 324 i Autum 2001. 1 Vectors 1.1 Ier product Recall from liear algebra: we ca represet a vector V as a colum vector;
Physics 324, Fall 2002 Dirac Notatio These otes were produced by David Kapla for Phys. 324 i Autum 2001. 1 Vectors 1.1 Ier product Recall from liear algebra: we ca represet a vector V as a colum vector;
Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization, Lisbon, Portugal, September 22-24,
 Proceedigs of the 6th WSEAS Iteratioa Coferece o Simuatio Modeig ad Optimizatio isbo Portuga September -4 006 338 O the Impemetatio of a Iterior-Poit SQP Fiter ie Search Agorithm M. FERNANDA P. COSA Departameto
Proceedigs of the 6th WSEAS Iteratioa Coferece o Simuatio Modeig ad Optimizatio isbo Portuga September -4 006 338 O the Impemetatio of a Iterior-Poit SQP Fiter ie Search Agorithm M. FERNANDA P. COSA Departameto
Here are some solutions to the sample problems concerning series solution of differential equations with non-constant coefficients (Chapter 12).
 Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Lecture Appedi B: Some sampe probems from Boas Here are some soutios to the sampe probems cocerig series soutio of differetia equatios with o-costat coefficiets (Chapter ) : Soutio: We wat to cosider the
Balancing. Rotating Components Examples of rotating components in a mechanism or a machine. (a)
 alacig NOT COMPLETE Rotatig Compoets Examples of rotatig compoets i a mechaism or a machie. Figure 1: Examples of rotatig compoets: camshaft; crakshaft Sigle-Plae (Static) alace Cosider a rotatig shaft
alacig NOT COMPLETE Rotatig Compoets Examples of rotatig compoets i a mechaism or a machie. Figure 1: Examples of rotatig compoets: camshaft; crakshaft Sigle-Plae (Static) alace Cosider a rotatig shaft
MECHANICAL INTEGRITY DESIGN FOR FLARE SYSTEM ON FLOW INDUCED VIBRATION
 MECHANICAL INTEGRITY DESIGN FOR FLARE SYSTEM ON FLOW INDUCED VIBRATION Hisao Izuchi, Pricipal Egieerig Cosultat, Egieerig Solutio Uit, ChAS Project Operatios Masato Nishiguchi, Egieerig Solutio Uit, ChAS
MECHANICAL INTEGRITY DESIGN FOR FLARE SYSTEM ON FLOW INDUCED VIBRATION Hisao Izuchi, Pricipal Egieerig Cosultat, Egieerig Solutio Uit, ChAS Project Operatios Masato Nishiguchi, Egieerig Solutio Uit, ChAS
19 Fourier Series and Practical Harmonic Analysis
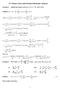 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Time-Domain Representations of LTI Systems
 2.1 Itroductio Objectives: 1. Impulse resposes of LTI systems 2. Liear costat-coefficiets differetial or differece equatios of LTI systems 3. Bloc diagram represetatios of LTI systems 4. State-variable
2.1 Itroductio Objectives: 1. Impulse resposes of LTI systems 2. Liear costat-coefficiets differetial or differece equatios of LTI systems 3. Bloc diagram represetatios of LTI systems 4. State-variable
Filter banks. Separately, the lowpass and highpass filters are not invertible. removes the highest frequency 1/ 2and
 Filter bas Separately, the lowpass ad highpass filters are ot ivertible T removes the highest frequecy / ad removes the lowest frequecy Together these filters separate the sigal ito low-frequecy ad high-frequecy
Filter bas Separately, the lowpass ad highpass filters are ot ivertible T removes the highest frequecy / ad removes the lowest frequecy Together these filters separate the sigal ito low-frequecy ad high-frequecy
Finally, we show how to determine the moments of an impulse response based on the example of the dispersion model.
 5.3 Determiatio of Momets Fially, we show how to determie the momets of a impulse respose based o the example of the dispersio model. For the dispersio model we have that E θ (θ ) curve is give by eq (4).
5.3 Determiatio of Momets Fially, we show how to determie the momets of a impulse respose based o the example of the dispersio model. For the dispersio model we have that E θ (θ ) curve is give by eq (4).
Course Outline. Designing Control Systems. Proportional Controller. Amme 3500 : System Dynamics and Control. Root Locus. Dr. Stefan B.
 Amme 3500 : System Dyamics ad Cotrol Root Locus Course Outlie Week Date Cotet Assigmet Notes Mar Itroductio 8 Mar Frequecy Domai Modellig 3 5 Mar Trasiet Performace ad the s-plae 4 Mar Block Diagrams Assig
Amme 3500 : System Dyamics ad Cotrol Root Locus Course Outlie Week Date Cotet Assigmet Notes Mar Itroductio 8 Mar Frequecy Domai Modellig 3 5 Mar Trasiet Performace ad the s-plae 4 Mar Block Diagrams Assig
Stopping oscillations of a simple harmonic oscillator using an impulse force
 It. J. Adv. Appl. Math. ad Mech. 5() (207) 6 (ISSN: 2347-2529) IJAAMM Joural homepage: www.ijaamm.com Iteratioal Joural of Advaces i Applied Mathematics ad Mechaics Stoppig oscillatios of a simple harmoic
It. J. Adv. Appl. Math. ad Mech. 5() (207) 6 (ISSN: 2347-2529) IJAAMM Joural homepage: www.ijaamm.com Iteratioal Joural of Advaces i Applied Mathematics ad Mechaics Stoppig oscillatios of a simple harmoic
Matsubara-Green s Functions
 Matsubara-Gree s Fuctios Time Orderig : Cosider the followig operator If H = H the we ca trivially factorise this as, E(s = e s(h+ E(s = e sh e s I geeral this is ot true. However for practical applicatio
Matsubara-Gree s Fuctios Time Orderig : Cosider the followig operator If H = H the we ca trivially factorise this as, E(s = e s(h+ E(s = e sh e s I geeral this is ot true. However for practical applicatio
Numerical Calculation of Dynamic Response for Multi-Span Non-Uniform Beam Subjected to Moving Mass with Friction
 Egieerig,,, 67-77 doi:.46/eg..548 Pubished Oie May (http://www.scirp.org/joura/eg) 67 Numerica Cacuatio of Dyamic Respose for Muti-Spa No-Uiform Beam Subjected to Moig Mass with Frictio Abstract Jupig
Egieerig,,, 67-77 doi:.46/eg..548 Pubished Oie May (http://www.scirp.org/joura/eg) 67 Numerica Cacuatio of Dyamic Respose for Muti-Spa No-Uiform Beam Subjected to Moig Mass with Frictio Abstract Jupig
Free Surface Hydrodynamics
 Water Sciece ad Egieerig Free Surface Hydrodyamics y A part of Module : Hydraulics ad Hydrology Water Sciece ad Egieerig Dr. Shreedhar Maskey Seior Lecturer UNESCO-IHE Istitute for Water Educatio S. Maskey
Water Sciece ad Egieerig Free Surface Hydrodyamics y A part of Module : Hydraulics ad Hydrology Water Sciece ad Egieerig Dr. Shreedhar Maskey Seior Lecturer UNESCO-IHE Istitute for Water Educatio S. Maskey
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
