Universal Hyperbolic Geometry, Sydpoints and Finite Fields: A Projective and Algebraic Alternative
|
|
|
- Nicholas O’Neal’
- 5 years ago
- Views:
Transcription
1 Artile Universl Hyperboli Geoetry, Sydpoints nd Finite Fields: A Projetive nd Algebri Alterntive Norn J. Wildberger Shool of thetis nd Sttistis, University of New South Wles, Sydney 05, Austrli; n.wildberger@unsw.edu.u; Tel.: Reeived: 6 Otober 07; Aepted: 6 eeber 07; Published: Jnury 08 Abstrt: Universl hyperboli geoetry gives purely lgebri pproh to the subjet tht onnets nturlly with Einstein s speil theory of reltivity. In this pper, we give n overview of soe spets of this theory relting to tringle geoetry nd in prtiulr the rerkble new nlogues of idpoints lled sydpoints. We lso disuss how the generlity llows us to onsider hyperboli geoetry over generl fields, in prtiulr over finite fields. Keywords: rtionl trigonoetry; universl hyperboli geoetry; sydpoints; finite fields. Two Fous Questions nd Projetive/Algebri ook t Hyperboli Geoetry While physiists hve long pondered the question of the physil nture of the ontinuu, thetiins hve struggled to siilrly understnd the orresponding thetil struture. In the lst dede, we hve seen the eergene of rtionl trigonoetry [,] s vible lterntive to trditionl geoetry, built not over ontinuu of rel nubers, but rther lgebrilly over generl field, so lso over the rtionl nubers, or over finite fields. Universl hyperboli geoetry (UHG) extends this understnding to the projetive setting, yielding new nd broder pproh to the yley Klein frework (see []) for the rerkble geoetry disovered now lost two enturies go by Bolyi, Guss nd obhevsky s in [4 6]. See lso [7,8] for the lssil nd odern use of projetive etril strutures in geoetry. In this pper, we will give n outline of this new pproh, whih onnets nturlly to the reltivisti geoetry of orentz, Einstein nd inkowski nd lso llows us to onsider hyperboli geoetries over generl fields, inluding finite fields. To void tehnilities nd ke the subjet essible to wider udiene, inluding physiists, we i to desribe things both geoetrilly in projetive visul fshion, s well s lgebrilly in liner lgebri setting.. The Polrity of oni isovered by Apollonius We ugent the projetive plne, whih we y regrd s two-diensionl ffine plne nd line t infinity, with fixed oni. This oni is lled the bsolute in yley Klein geoetry. In this universl hyperboli geoetry (UHG), developed in [9 ], we tke it to be irle, typilly in blue, nd ll it the null irle. The polrity ssoited with oni ws investigted by Apollonius nd gives dulity between points nd lines A = in the spe, whih we lso write s = A. Given point, onsider ny two lines through, whih eet the oni t two points eh s in Figure. The other two digonl points of this yli qudrilterl defines the dul line A. Rerkbly, this onstrution does not depend on the hoie of lines through, s Apollonius relized. Universe 08, 4, ; doi:0.90/universe
2 Universe 08, 4, of 0 When pprohes the oni, the dul A pprohes the tngent to the oni t tht point. If b lies on A =, then it turns out tht lies on B = b. A b K Figure. The dul of point is line = A. Fro this dulity, we y define the perpendiulrity, whih lies t the ore of hyperboli geoetry. Two points re perpendiulr when one lies on the dul of the other, nd siilrly two lines re perpendiulr when one psses through the dul of the other. We tret points nd lines syetrilly! Hyperboli geoetry is then the study of those spets of projetive geoetry tht re deterined by the fixed oni, with isoetries just those projetive trnsfortions, whih fix the null irle. This turns out to be essentilly the reltivisti group O (, ), with oeffiients in the bse field, s we shll see. However, to desribe the tul etril struture, we ove beyond the usul hyperboli distne nd ngle found in the lssil theory of Bolyi, Guss nd obhevsky; rther, we eploy hyperboli nlogues of the qudrne nd spred of rtionl trigonoetry.. Null Points, ines nd ight ones Null points re perpendiulr to theselves; these re the points lying on the originl null irle, suh s α nd β in Figure. Null lines re lso perpendiulr to theselves; these re just duls of null points or the tngents to the null irle, s shown in Figure. In lssil hyperboli geoetry, only the interior of the irle is usully onsidered, nd the bsolute irle is onsidered to be infinitely fr wy. Here, we re interested in the entire projetive plne, inluding lso the null oni itself nd its exterior, inluding tully points t infinity. A= b Figure. Null points nd null lines on the null oni. This orresponds to onsidering + reltivisti spe projetively: with the null oni orresponding to the light one; points inside the null oni to tie-like diretions; nd points outside the null oni to spe-like diretions. ike the physiist, we regrd the entire spe s of priry interest, not just the interior of our light one, even if this is our initil orienttion!
3 Universe 08, 4, of 0 The usul geoetry of speil reltivity in + diensions, in vetor spe with inner produt: (x, y, z ) (x, y, z ) = x x + y y z z () when looked t projetively, gives us UHG, with the null one x + y z = 0. The usul hyperboloid of two sheets x + y z =, the top sheet of whih lssilly orresponds to the hyperboli plne, is Riennin sub-nifold of the orentzin three-diensionl spe. This vrint of Euliden struture holds in the interior of the null oni, but outside, we re in de Sitter-type spe s represented by the hyperboloid of one sheet x + y z =. This kind of universl hyperboli geoetry is no longer hoogeneous, s points outside the null oni behve differently fro points inside the oni, nd indeed over ore generl fields, the distintion between these two types of points is onsiderbly ore subtle. 4. Tringle nd ul To see, the iportne nd usefulness of onsidering both interior nd exterior points, let us look t tringle with sides the lines,,, nd its dul tringle l l l, with sides A, A nd A. These two tringles ply now syetril role: the duls of the points,, re the lines A, A, A, while the duls of the points l, l, l re the lines,,. The dul tringle plys nturl role in estblishing the existene of n orthoenter of generl tringle, whih is vlid theore in this for of hyperboli geoetry, lthough it is not in lssil hyperboli geoetry! In Figure, we see the three ltitudes of the tringle deterined by lines fro verties to dul verties, eeting t the orthoenter h. The reson tht this does not work in generl in lssil hyperboli geoetry is tht the eeting of the three ltitudes y well be outside the null oni even if ll three points of the tringle re inside, nd so it is invisible to the geoetry of Bolyi, Guss nd obhevsky! Sine this nedotlly ws one of Einstein s fvourite geoetry theores, it is definitely worthwhile hving it s prt of the piture. In ft, siilr disussion y be hd for the iruenter. This is ll prt of the rih nd ostly new subjet of hyperboli tringle geoetry; see for exple [,,4], whih reently hs lso been extended to inlude qudrilterl geoetry in [5]. A l l A h A l Figure. The dul tringle nd the orthoenter h. 5. Qudrne y Be efined Algebrilly In lssil hyperboli geoetry, the etril struture is introdued using differentil geoetry in the ontext of Riennin etris on sooth nifolds. In the ore projetive sitution, s in [6], the notions of projetive qudrne nd projetive spred n be introdued using the fundentl ide of ross-rtio of four points on line, s ppreited lso by [7].
4 Universe 08, 4, 4 of 0 If four olliner points hve projetive oordintes, b, nd d, whih n be either fro the given field or possibly hve the vlue infinity ( ), then their ross-rtio y be defined s: (, b :, d) ( ) (d b) ( b) (d ). Now, given two points nd in the hyperboli plne, they hve dul lines A nd A, whih eet the line in the onjugte points: b A ( ) nd b A ( ) giving four olliner points,, b nd b. Then, the (projetive) qudrne between nd is the ross-rtio: q (, ) (, b :, b ). In Figure 4, we see n exple of exterior nd interior, to ephsize the se tht this etril notion pplies very generlly to ll non-null points. B ( ) b A= B A = b Figure 4. onjugte points ke ross-rtio. efine the spred between lines dully, so tht: S (A, A ) q (, ). In this wy, the reltion between the points nd lines etrilly is opletely syetri. There is nturl onnetion with the usul lssil etril notions in the Beltri Klein odel (see [5]) when we restrit to interior points (inside the light one or null oni) nd lines tht eet lso t interior points; in these ses: 6. The Algebri Approh q (, ) = sinh (d (, )) nd S (, ) = sin (θ (, )). ue to the odern filirity with liner lgebr, it y be useful to refre the projetive setup bove using hoogeneous oordintes, where we follow: [9]. In three-diensionl vetor spe of row vetors (x, y, z), we y define (hyperboli) point [x : y : z] to be one-diensionl subspe through non-zero vetor (x, y, z). This orresponds to the plnr point [ x z, y z ] if z = 0. A (hyperboli) line (l : : n) y be defined to be two-diensionl subspe with eqution lx + y nz = 0. The inidene between these points nd lines is tht the point [x : y : z] lies on the line (l : : n), or equivlently psses through, preisely when: lx + y nz = 0.
5 Universe 08, 4, 5 of 0 In trix ters, this is the reltion: ( ) 0 0 l x y z 0 0 = n The point [x : y : z] is then dul to the line (l : : n) preisely when: x : y : z = l : : n. In this se, we write = or =. This lgebri struture ensures tht these definitions work over generl field. The etril struture oes bout fro the syetri biliner for () of Einstein, orentz nd inkowski of the bient three-diensionl spe. It y be used to define reltion between one-diensionl subspes s follows: the qudrne between points [x : y : z ] nd [x : y : z ] is: (x q (, ) x + y y z z ) ( x + y ) ( z x + y. ) z ully, the spred between lines (l : : n ) nd (l : : n ) is: S (, ) (l l + n n ) ( l + ) ( n l +. ) n For three points, nd, the three qudrnes will be: q = q (, ) q = q (, ) q = q (, ) nd for three lines, nd, the three spreds will be: 7. The in Trigonoetri ws of UHG S = S (, ) S = S (, ) S = S (, ). Here re the in trigonoetri lws in the subjet, estblished first in [9]. We begin with essentilly the one-diensionl situtions: Theore (Triple qud forul). If, nd re olliner points, then: ( ) (q + q + q ) = q + q + q + 4q q q. Theore (Triple spred forul). If, nd re onurrent lines, then: ( ) (S + S + S ) = S + S + S + 4S S S. Now, for the qudrnes nd spreds of tringle s in Figure 5:
6 Universe 08, 4, 6 of 0 S q S q q S Figure 5. Qudrne nd spreds in hyperboli tringle. Theore (Pythgors). If nd re perpendiulr lines, then: q = q + q q q. Theore 4 (Pythgors dul). If nd re perpendiulr points, then: S = S + S S S. Theore 5 (Spred lw). Theore 6 (Spred dul lw). S q = S q = S q. q S = q S = q S. Theore 7 (ross lw). Theore 8 (ross dul lw). (q q S (q + q + q ) + ) = 4 ( q ) ( q ) ( q ). (S S q (S + S + S ) + ) = 4 ( S ) ( S ) ( S ). There re three syetril fors of Pythgors s theore, the ross lw nd their duls, obtined by rotting indies. These vrious lws reple the trnsendentl hyperboli Pythgors theore, the sine lw nd osine lw of both kinds. They work over generl field, both inside nd outside the null irle, nd tully even with ore generl biliner fors. They re rgubly ore nturl nd onvenient for physiists. The quntity: A q q S = q q S = q q S is the qudre of the tringle nd is soewht nlogous to the hyperboli re of the tringle, but it is deidedly of different hrter. It is big step to ke the trnsition fro trnsendentl to purely lgebri onepts here: oputtions n tully now be exhibited opletely nd lerly. 8. irles, idpoints nd iruenters A hyperboli irle with entre nd qudrne k is the lous of points x, whih stisfy q (, x) = k. This is oni, whih inludes wht in the lssil literture re lled equi-distnt urves in the se of n externl entre. A idpoint of side is point lying on the line tht stisfies q (, ) = q (, ). idpoints exist preisely when q (, ) is squre in the field. There re in generl two idpoints
7 Universe 08, 4, 7 of 0 if they exist t ll, nd they re perpendiulr. A idline is the dul of idpoint, or equivlently line through idpoint perpendiulr to the line joining the two originl points; in other words, the hyperboli version of perpendiulr bisetor. The following is illustrted in Figure 6. Theore 9 (iruenters). Assue tht the six idpoints of tringle exist. Then, they re olliner three t tie, lying on four distint irulines. The six idlines of re onurrent three t tie, eeting t four distint iruenters tht re dul to the irulines. The iruenters re the entres of in generl four hyperboli irles tht pss through the points of the tringle. Figure 6. iruenters nd irulines of tringle. 9. Sydpoints Augent idpoints While idpoints hve been studied sine the erly dys of the subjet, n iportnt relted notion ws only introdued very reently in []. A sydpoint of side is point s lying on tht stisfies q(, s) = q(, s). Sydpoints exist preisely when q (, ) is squre in the field. There re in generl two sydpoints, if they exist t ll, but they re not perpendiulr. A onstrution of sydpoints r nd s of b y be dedued fro Figure 7. l w s r n b z k x y Figure 7. onstrution of sydpoints.
8 Universe 08, 4, 8 of 0 First onstrut = (b), then the idpoints nd n of nd then use the null points x nd y lying on b s shown. Sydpoints work with idpoints to extend tringle geoetry to tringles with verties both inside nd outside the null oni. In Figure 8, we see entroids g nd irulines of suh tringle. For the rerkble onnetion of the iruenters to irles through the three points, see []. g s g s g s s Figure 8. entroids nd irulines of tringle. 0. Sydpoints nd the Prbol In [8,9], we defined the hyperboli prbol P 0 to be the lous of point p 0 (tully oni) stisfying: q(p 0, f ) + q(p 0, f ) = for fixed points f, f lled the foi. Equivlently: q (p 0, f ) = q (p 0, F ) or q (p 0, f ) = q (p 0, F ), where F f, F f re the diretries. Note tht the qudrne between point nd line is defined in ters of the perpendiulr trnsversl. Suh prbol is shown in red in Figure 9. V V f f b v b f b f v B F B F B F B P0 Figure 9. A prbol with foi f nd f. In generl, if we tke duls of the tngents of oni, we get dul oni. It turns out tht the dul of prbol P 0 is nother prbol: the twin prbol P 0 whose foi f, f re the sydpoints of
9 Universe 08, 4, 9 of 0 the originl foi pir f, f, shown in ornge in Figure 0. Therefore, sydpoints pper proinently in the geoetry of the prbol! f b F p0 P0 f f v b b v f 0 P F b F p0 P 0 V F P0 V Figure 0. The twin prbol with foi f nd f.. UHG over Finite Fields n idpoints nd sydpoints exist together? The onditions tht q (, b) is squre nd q (, b) is squre re not siultneously stisfied over our usul nuber syste, or over field F p where p od 4. However, in the se of F p where p od 4, then is squre, so both idpoints nd sydpoints n exist together. This is n entirely new spet of hyperboli geoetry tht is invisible to us usully. However, how n we visulize UHG over finite field? Fortuntely, new nd powerful progr being developed by ihel Reynolds t University of New South Wles (UNSW) Sydney oplishes extly this. This progr will hopefully be vilble for publi use in the ner future. In ft, hyperboli geoetry over finite fields hs been onsidered previously; see [0,]. With UHG, we get novel pproh tht unifies ll these geoetries over rbitrry fields, so freeing us fro the reline on prtiulr ideology with respet to the ontinuu. onflits of Interest: The uthors delre no onflits of interest. Abbrevitions The following bbrevitions re used in this nusript: UHG Referenes Universl hyperboli geoetry. Wildberger, N.J. ivine Proportions: Rtionl Trigonoetry to Universl Geoetry; Wild Egg Books: Sydney, Austrli, Wildberger, N.J. Affine nd Projetive Universl Geoetry. rxiv 006, rxiv:th/ Busenn, H.; Kelly, P.J. Projetive Geoetry nd Projetive etris; over Publitions: New York, NY, USA, 006; originlly published by Adei Press: New York, NY, USA, oolidge, J.. The Eleents of Non-Euliden Geoetry; Oxford lrendon Press: Oxford, UK, Greenberg,.J. Euliden nd Non-Euliden Geoetries: evelopent nd History, 4th ed.; W. H. Freen nd o.: Sn Frniso, A, USA, Rsy, A.; Rihtyer, R.. Introdution to Hyperboli Geoetry; Springer: New York, NY, USA, Bhnn, F. Aufbu der Geoetrie us de Spiegelungsbegriff; Springer: New York, NY, USA, 97.
10 Universe 08, 4, 0 of 0 8. olnár, E.; Prok, I.; Sziri, J. On xil hoogeneous -geoetries nd their visuliztion. Universe 07,, Wildberger, N.J. Universl Hyperboli Geoetry I: Trigonoetry. Geo. edi. 0, 6, Wildberger, N.J. Universl Hyperboli Geoetry II: A pitoril overview. KoG 00, 4, 4.. Wildberger, N.J. Universl Hyperboli Geoetry III: First steps in projetive tringle geoetry. KoG 0, 5, Wildberger, N.J.; Alkhldi, A. Universl Hyperboli Geoetry IV: Sydpoints nd Twin iruirles. KoG 0, 6, Ungr, A.A. Hyperboli trigonoetry in the Einstein reltivisti veloity odel of hyperboli geoetry. oput. th. Appl. 000, 40,. 4. Ungr, A. Hyperboli Tringle enters: The Speil Reltivisti Approh; Springer: New York, NY, USA, Blefri, S.; Wildberger, N.J. Qudrngle entroids in universl hyperboli geoetry. KoG 07, 0, Onishhik, A..; Sulnke, R. Projetive nd yley-klein Geoetries; Springer: New York, NY, USA, Bruner, H. Geoetrie Projektiver Räue I, II; Bibliogrphishes Institut: nnhei, Gerny, Alkhldi, A.; Wildberger, N.J. The Prbol in Universl Hyperboli Geoetry I. KoG 0, 7, Alkhldi, A.; Wildberger, N.J. The Prbol in Universl Hyperboli Geoetry II: nonil points nd the Y-oni. J. Geo. Grph. 06, 0,. 0. Angel, J. Finite upper hlf plnes over finite fields. Finite Fields Appl. 996,, Soto-Andrde, J. Geoetril Gel fnd odels, tensor quotients, nd Weil representtions. Pro. Syp. Pure th. 987, 47, by the uthors. iensee PI, Bsel, Switzerlnd. This rtile is n open ess rtile distributed under the ters nd onditions of the retive oons Attribution ( BY) liense (
The Relationship between the Nine-Point Circle, the Circumscribed Circle and the Inscribed Circle of Archimedes Triangle Yuporn Rimcholakarn
 Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
The Legacy of Pythagoras Theorem
 Prol Volue 39, Issue 1(2003) The Legy of Pythgors Theore Peter G.rown 1 When sked wht thetil result they reeer fro High Shool, the verge person would proly reply with Pythgors Theore. In ny right tringle,
Prol Volue 39, Issue 1(2003) The Legy of Pythgors Theore Peter G.rown 1 When sked wht thetil result they reeer fro High Shool, the verge person would proly reply with Pythgors Theore. In ny right tringle,
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
Electromagnetism Notes, NYU Spring 2018
 Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
The Inspherical Gergonne Center of a Tetrahedron
 Journl for Geometry nd Grphis Volume 8 (2004), No. 1, 23 32. The Inspheril Gergonne Center of Tetrhedron Mowffq Hjj 1, Peter Wlker 2 1 Deprtment of Mthemtis, Yrmouk University Irbid, Jordn emil: mhjj@yu.edu.jo
Journl for Geometry nd Grphis Volume 8 (2004), No. 1, 23 32. The Inspheril Gergonne Center of Tetrhedron Mowffq Hjj 1, Peter Wlker 2 1 Deprtment of Mthemtis, Yrmouk University Irbid, Jordn emil: mhjj@yu.edu.jo
Learning Objectives of Module 2 (Algebra and Calculus) Notes:
 67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
Properties of Different Types of Lorentz Transformations
 merin Journl of Mthemtis nd ttistis 03 3(3: 05-3 DOI: 0593/jjms03030303 roperties of Different Types of Lorentz Trnsformtions tikur Rhmn izid * Md hh lm Deprtment of usiness dministrtion Leding niversity
merin Journl of Mthemtis nd ttistis 03 3(3: 05-3 DOI: 0593/jjms03030303 roperties of Different Types of Lorentz Trnsformtions tikur Rhmn izid * Md hh lm Deprtment of usiness dministrtion Leding niversity
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Chapter17. Congruence and transformations. Contents: A Transformations B Congruent figures C Congruent triangles D Proof using congruence
 hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
Solutions to Assignment 1
 MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Lecture Summaries for Multivariable Integral Calculus M52B
 These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
ON AN INEQUALITY FOR THE MEDIANS OF A TRIANGLE
 Journl of Siene nd Arts Yer, No. (9), pp. 7-6, OIGINAL PAPE ON AN INEQUALITY FO THE MEDIANS OF A TIANGLE JIAN LIU Mnusript reeived:.5.; Aepted pper:.5.; Pulished online: 5.6.. Astrt. In this pper, we give
Journl of Siene nd Arts Yer, No. (9), pp. 7-6, OIGINAL PAPE ON AN INEQUALITY FO THE MEDIANS OF A TIANGLE JIAN LIU Mnusript reeived:.5.; Aepted pper:.5.; Pulished online: 5.6.. Astrt. In this pper, we give
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Pre-Lie algebras, rooted trees and related algebraic structures
 Pre-Lie lgers, rooted trees nd relted lgeri strutures Mrh 23, 2004 Definition 1 A pre-lie lger is vetor spe W with mp : W W W suh tht (x y) z x (y z) = (x z) y x (z y). (1) Exmple 2 All ssoitive lgers
Pre-Lie lgers, rooted trees nd relted lgeri strutures Mrh 23, 2004 Definition 1 A pre-lie lger is vetor spe W with mp : W W W suh tht (x y) z x (y z) = (x z) y x (z y). (1) Exmple 2 All ssoitive lgers
Figure 1. The left-handed and right-handed trefoils
 The Knot Group A knot is n emedding of the irle into R 3 (or S 3 ), k : S 1 R 3. We shll ssume our knots re tme, mening the emedding n e extended to solid torus, K : S 1 D 2 R 3. The imge is lled tuulr
The Knot Group A knot is n emedding of the irle into R 3 (or S 3 ), k : S 1 R 3. We shll ssume our knots re tme, mening the emedding n e extended to solid torus, K : S 1 D 2 R 3. The imge is lled tuulr
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mathematics 10 Page 1 of 5 Properties of Triangle s and Quadrilaterals. Isosceles Triangle. - 2 sides and 2 corresponding.
 Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
SOME NEW HERMITE-HADAMARD TYPE INEQUALITIES FOR FUNCTIONS WHOSE HIGHER ORDER PARTIAL DERIVATIVES ARE CO-ORDINATED s-convex
 Krgujev Journl of Mthetis Volue 38 4, Pges 5 46 SOME NEW HERMITE-HADAMARD TYPE INEQUALITIES FOR FUNCTIONS WHOSE HIGHER ORDER PARTIAL DERIVATIVES ARE CO-ORDINATED s-convex MUHAMMAD AMER LATIF Abstrt In
Krgujev Journl of Mthetis Volue 38 4, Pges 5 46 SOME NEW HERMITE-HADAMARD TYPE INEQUALITIES FOR FUNCTIONS WHOSE HIGHER ORDER PARTIAL DERIVATIVES ARE CO-ORDINATED s-convex MUHAMMAD AMER LATIF Abstrt In
A Survey on Optical Orthogonal Codes
 A urvey on Optil Orthogonl Codes Mohd M. Ale-Krldni Optil orthogonl odes (OOC) defined by lehi [1] nd Chung, lehi, nd Wei [] re fily of (0,1) seuenes with desired utoorreltion nd ross-orreltion properties
A urvey on Optil Orthogonl Codes Mohd M. Ale-Krldni Optil orthogonl odes (OOC) defined by lehi [1] nd Chung, lehi, nd Wei [] re fily of (0,1) seuenes with desired utoorreltion nd ross-orreltion properties
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Two Triads of Congruent Circles from Reflections
 Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
SOME NEW HERMITE-HADAMARD TYPE INEQUALITIES FOR FUNCTIONS WHOSE HIGHER ORDER PARTIAL DERIVATIVES ARE CO-ORDINATED CONVEX
 FACTA UNIVERSITATIS (NIŠ) Ser. Mth. Inor. Vol. 7 No 3 (), 3 336 SOME NEW HERMITE-HADAMARD TYPE INEQUALITIES FOR FUNCTIONS WHOSE HIGHER ORDER PARTIAL DERIVATIVES ARE CO-ORDINATED CONVEX Muhd Aer Lti nd
FACTA UNIVERSITATIS (NIŠ) Ser. Mth. Inor. Vol. 7 No 3 (), 3 336 SOME NEW HERMITE-HADAMARD TYPE INEQUALITIES FOR FUNCTIONS WHOSE HIGHER ORDER PARTIAL DERIVATIVES ARE CO-ORDINATED CONVEX Muhd Aer Lti nd
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
An Introduction to Trigonometry
 n Introduction to Trigonoetry First of ll, let s check out the right ngled tringle below. The LETTERS, B & C indicte the ngles nd the letters, b & c indicte the sides. c b It is iportnt to note tht side
n Introduction to Trigonoetry First of ll, let s check out the right ngled tringle below. The LETTERS, B & C indicte the ngles nd the letters, b & c indicte the sides. c b It is iportnt to note tht side
On the Scale factor of the Universe and Redshift.
 On the Sle ftor of the Universe nd Redshift. J. M. unter. john@grvity.uk.om ABSTRACT It is proposed tht there hs been longstnding misunderstnding of the reltionship between sle ftor of the universe nd
On the Sle ftor of the Universe nd Redshift. J. M. unter. john@grvity.uk.om ABSTRACT It is proposed tht there hs been longstnding misunderstnding of the reltionship between sle ftor of the universe nd
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Is there an easy way to find examples of such triples? Why yes! Just look at an ordinary multiplication table to find them!
 PUSHING PYTHAGORAS 009 Jmes Tnton A triple of integers ( bc,, ) is clled Pythgoren triple if exmple, some clssic triples re ( 3,4,5 ), ( 5,1,13 ), ( ) fond of ( 0,1,9 ) nd ( 119,10,169 ). + b = c. For
PUSHING PYTHAGORAS 009 Jmes Tnton A triple of integers ( bc,, ) is clled Pythgoren triple if exmple, some clssic triples re ( 3,4,5 ), ( 5,1,13 ), ( ) fond of ( 0,1,9 ) nd ( 119,10,169 ). + b = c. For
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
SCIENTIFIC-PROFESSIONAL JOURNAL OF CROATIAN SOCIETY FOR GEOMETRY AND GRAPHICS No. 14. (2010) ISSN
 CIENTIFIC-PROFEIONAL JOURNAL OF CROATIAN OCIETY FOR GEOMETRY AND GRAPHIC No. 4. (00) IN -6 Offiil pulition of the Crotin oiety for Geometry nd Grphis pulishes sientifi nd professionl ppers from the fields
CIENTIFIC-PROFEIONAL JOURNAL OF CROATIAN OCIETY FOR GEOMETRY AND GRAPHIC No. 4. (00) IN -6 Offiil pulition of the Crotin oiety for Geometry nd Grphis pulishes sientifi nd professionl ppers from the fields
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
The Intouch Triangle and the OI-line
 Forum Geometriorum Volume 4 004 15 134. FORUM GEOM ISSN 1534-1178 The Intouh Tringle nd the OI-line Eri Dnneel Abtrt. We prove ome intereting reult relting the intouh tringle nd the OI line of tringle.
Forum Geometriorum Volume 4 004 15 134. FORUM GEOM ISSN 1534-1178 The Intouh Tringle nd the OI-line Eri Dnneel Abtrt. We prove ome intereting reult relting the intouh tringle nd the OI line of tringle.
03. Early Greeks & Aristotle
 03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Vibration with more (than one) degrees of freedom (DOF) a) longitudinal vibration with 3 DOF. b) rotational (torsional) vibration with 3 DOF
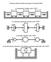 irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY
 UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We estblish soe uniqueness results ner 0 for ordinry differentil equtions of the
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We estblish soe uniqueness results ner 0 for ordinry differentil equtions of the
Modified Farey Trees and Pythagorean Triples
 Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Modified Frey Trees d Pythgore Triples By Shi-ihi Kty Deprtet of Mthetil Siees, Fulty of Itegrted Arts d Siees, The Uiversity of Tokushi, Tokushi 0-0, JAPAN e-il ddress : kty@istokushi-ujp Abstrt I 6,
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
OXFORD H i g h e r E d u c a t i o n Oxford University Press, All rights reserved.
 Renshw: Mths for Econoics nswers to dditionl exercises Exercise.. Given: nd B 5 Find: () + B + B 7 8 (b) (c) (d) (e) B B B + B T B (where 8 B 6 B 6 8 B + B T denotes the trnspose of ) T 8 B 5 (f) (g) B
Renshw: Mths for Econoics nswers to dditionl exercises Exercise.. Given: nd B 5 Find: () + B + B 7 8 (b) (c) (d) (e) B B B + B T B (where 8 B 6 B 6 8 B + B T denotes the trnspose of ) T 8 B 5 (f) (g) B
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Hyers-Ulam stability of Pielou logistic difference equation
 vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
f (x)dx = f(b) f(a). a b f (x)dx is the limit of sums
 Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P. (a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg) Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Electromagnetic-Power-based Modal Classification, Modal Expansion, and Modal Decomposition for Perfect Electric Conductors
 LIAN: EM-BASED MODAL CLASSIFICATION EXANSION AND DECOMOSITION FOR EC 1 Eletromgneti-ower-bsed Modl Clssifition Modl Expnsion nd Modl Deomposition for erfet Eletri Condutors Renzun Lin Abstrt Trditionlly
LIAN: EM-BASED MODAL CLASSIFICATION EXANSION AND DECOMOSITION FOR EC 1 Eletromgneti-ower-bsed Modl Clssifition Modl Expnsion nd Modl Deomposition for erfet Eletri Condutors Renzun Lin Abstrt Trditionlly
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Global alignment. Genome Rearrangements Finding preserved genes. Lecture 18
 Computt onl Biology Leture 18 Genome Rerrngements Finding preserved genes We hve seen before how to rerrnge genome to obtin nother one bsed on: Reversls Knowledge of preserved bloks (or genes) Now we re
Computt onl Biology Leture 18 Genome Rerrngements Finding preserved genes We hve seen before how to rerrnge genome to obtin nother one bsed on: Reversls Knowledge of preserved bloks (or genes) Now we re
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
ILLUSTRATING THE EXTENSION OF A SPECIAL PROPERTY OF CUBIC POLYNOMIALS TO NTH DEGREE POLYNOMIALS
 ILLUSTRATING THE EXTENSION OF A SPECIAL PROPERTY OF CUBIC POLYNOMIALS TO NTH DEGREE POLYNOMIALS Dvid Miller West Virgini University P.O. BOX 6310 30 Armstrong Hll Morgntown, WV 6506 millerd@mth.wvu.edu
ILLUSTRATING THE EXTENSION OF A SPECIAL PROPERTY OF CUBIC POLYNOMIALS TO NTH DEGREE POLYNOMIALS Dvid Miller West Virgini University P.O. BOX 6310 30 Armstrong Hll Morgntown, WV 6506 millerd@mth.wvu.edu
Relations between a dual unit vector and Frenet vectors of a dual curve
 Kuwit J. Si. 4 () pp. 59-69, 6 Burk Şhiner *, Mehmet Önder Dept. of Mthemtis, Mnis Cell Byr University, Murdiye, Mnis, 454, Turkey * Corresponding uthor: burk.shiner@bu.edu.tr Abstrt In this pper, we generlize
Kuwit J. Si. 4 () pp. 59-69, 6 Burk Şhiner *, Mehmet Önder Dept. of Mthemtis, Mnis Cell Byr University, Murdiye, Mnis, 454, Turkey * Corresponding uthor: burk.shiner@bu.edu.tr Abstrt In this pper, we generlize
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Vectors. Chapter14. Syllabus reference: 4.1, 4.2, 4.5 Contents:
 hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Planck constant estimation using constant period relativistic symmetric oscillator
 Plnk onstnt estition using onstnt period reltivisti syetri osilltor J. Br-Sgi * Applied Phys. Div. Soreq NRC, Yvne 818, Isrel. The eletrogneti wve quntu-energy depends only on its frequeny, not on the
Plnk onstnt estition using onstnt period reltivisti syetri osilltor J. Br-Sgi * Applied Phys. Div. Soreq NRC, Yvne 818, Isrel. The eletrogneti wve quntu-energy depends only on its frequeny, not on the
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Exponents and Powers
 EXPONENTS AND POWERS 9 Exponents nd Powers CHAPTER. Introduction Do you know? Mss of erth is 5,970,000,000,000, 000, 000, 000, 000 kg. We hve lredy lernt in erlier clss how to write such lrge nubers ore
EXPONENTS AND POWERS 9 Exponents nd Powers CHAPTER. Introduction Do you know? Mss of erth is 5,970,000,000,000, 000, 000, 000, 000 kg. We hve lredy lernt in erlier clss how to write such lrge nubers ore
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
Chapter 2. Vectors. 2.1 Vectors Scalars and Vectors
 Chpter 2 Vectors 2.1 Vectors 2.1.1 Sclrs nd Vectors A vector is quntity hving both mgnitude nd direction. Emples of vector quntities re velocity, force nd position. One cn represent vector in n-dimensionl
Chpter 2 Vectors 2.1 Vectors 2.1.1 Sclrs nd Vectors A vector is quntity hving both mgnitude nd direction. Emples of vector quntities re velocity, force nd position. One cn represent vector in n-dimensionl
Section 3.6. Definite Integrals
 The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
PHYS 601 HW3 Solution
 3.1 Norl force using Lgrnge ultiplier Using the center of the hoop s origin, we will describe the position of the prticle with conventionl polr coordintes. The Lgrngin is therefore L = 1 2 ṙ2 + 1 2 r2
3.1 Norl force using Lgrnge ultiplier Using the center of the hoop s origin, we will describe the position of the prticle with conventionl polr coordintes. The Lgrngin is therefore L = 1 2 ṙ2 + 1 2 r2
Algebra. Trigonometry. area of a triangle is 1 2
 Algebr Algebr is the foundtion of lulus The bsi ide behind lgebr is rewriting equtions nd simplifying expressions; this inludes suh things s ftoring, FOILing (ie, (+b)(+d) = +d+b+bd), dding frtions (remember
Algebr Algebr is the foundtion of lulus The bsi ide behind lgebr is rewriting equtions nd simplifying expressions; this inludes suh things s ftoring, FOILing (ie, (+b)(+d) = +d+b+bd), dding frtions (remember
Bisimulation, Games & Hennessy Milner logic
 Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Final Exam Review. [Top Bottom]dx =
![Final Exam Review. [Top Bottom]dx = Final Exam Review. [Top Bottom]dx =](/thumbs/90/103300886.jpg) Finl Exm Review Are Between Curves See 7.1 exmples 1, 2, 4, 5 nd exerises 1-33 (odd) The re of the region bounded by the urves y = f(x), y = g(x), nd the lines x = nd x = b, where f nd g re ontinuous nd
Finl Exm Review Are Between Curves See 7.1 exmples 1, 2, 4, 5 nd exerises 1-33 (odd) The re of the region bounded by the urves y = f(x), y = g(x), nd the lines x = nd x = b, where f nd g re ontinuous nd
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
