Planck constant estimation using constant period relativistic symmetric oscillator
|
|
|
- Grace Charity Adams
- 5 years ago
- Views:
Transcription
1 Plnk onstnt estition using onstnt period reltivisti syetri osilltor J. Br-Sgi * Applied Phys. Div. Soreq NRC, Yvne 818, Isrel. The eletrogneti wve quntu-energy depends only on its frequeny, not on the eitting syste s rdition power. The proportionlity onstnt between the frequeny nd the quntuenergy of the eletrogneti wve, the Plnk s onstnt is in the essene of quntu ehnis. This onstnt is known experientlly but till now there ws no lue for lulting its vlue on theoretil bsis. In the present work ethodology for lulting lower bound for Plnk s onstnt is presented, bsed on siple priniples. In order to get resonble good lower bound it is neessry to hve odel of reltivisti osilltor whose period is independent of its energy nd whih effiiently rdites eletrogneti energy. It is highly desired tht the thetis involved is siple enough to enble good insight into the results. Suh odel n lso be used for other investigtions, nd therefore, in this work potentil tht onserves the vibrtion period of syetri osilltors t reltivisti veloities is found nd nlyzed. The eletrilly hrged syste of onstnt period is used to lulte lower bound H of the Plnk s onstnt h. The vlue of H is sller thn h by ftor very lose to 3. The explntion of this ftor lso explins the vlue of Plnk s onstnt. Fro this vlue the fine struture onstnt vlue is lulted nd new interprettion of this onstnt obtined. PACS nuber(s): 14.7.Bh, 3.65.Sq, , 3.3.+p I. INTRODUCTION At the beginning of the th entury when the quntiztion of eletrogneti (EM) energy ws disovered, there were no theoretil tools to estite the vlue of Plnk s onstnt; onstnt tht reltes the energy of EM qunt to the frequeny of the eletrogneti wves. Lter it ws believed tht this is bsi onstnt so there ws no point to investigte its vlue theoretilly. There is need for n iproved odel to resonble estite Plnk s onstnt. This odel will reple the hroni osilltor odel. The siple hroni osilltor (SHO) is frequently used to explin different spets of physil phenoen. The siple nlytil solutions of the perti- * E-il ddress: j.br-sgi@fiuu.o
2 nent differentil equtions, both in the lssil nd quntu ehnis fres, ke this syste speil.the one diensionl (1D) SHO hs in ddition unique property nely, t non reltivisti veloities it hs onstnt period, independently of its energy. When 1D SHO is eletrilly hrged, its rdition frequeny is the se s the osilltions frequeny both ording to lssil eletrognetis nd quntu ehnil theories. A two diensionl (D) syetri SHO exhibits ore interesting properties, while retining the sipliity of single frequeny of osilltion nd rdition. It is well known tht t high energies, when reltivisti effets re iportnt the osilltion period is not onstnt [1]. It is energy dependent. The potentil for 1D osilltor tht ensures the onstnt period, independently of energy, t reltivisti veloities hs been lulted []. However the ext potentil ws not desribed by n nlyti expression. The first objetive of the present work is to find the potentil tht ensures onstnt period in the irulr ode of vibrtion (Syetri Constnt Period Potentil - SCPP) t reltivisti veloities. In this work, the potentil is expressed in losed-for. At reltivisti veloities, D eletrilly hrged syste is expeted to rdite its energy ore effiiently thn the 1D syste. For the generl ellipti odes of vibrtion there is need to fit potentil for eh vlue of eentriity. In this pper generl for for n pproxite potentil with one preter is presented. The vlue of this preter y be found nd n be heked for ury in the future. I hope tht the present work provides the thetil tools tht will help to enhne our understnding of reltivisti lssil ehnis nd reltivisti quntu ehnis. The otivtion for this study is the ttept to understnd the EM quntu-energy, i.e., the photon energy. This understnding strts with the siple observtion tht ording to lssil wve theory, In order tht EM rdition will hve defined frequeny within soe ury, it needs to be rditing t lest during one yle. Plnk s interprettion of blk body rdition [3] inludes the odel where the rdition is produed by eleentry systes, presubly eleentry hroni osilltors, with qunt of energy independent of the osilltors energy, despite the ft tht the rdition power inreses with the osilltors energy growth. The frequeny is one of the bsi properties of the photon; property tht deterines its energy. The obined result is tht t ny frequeny the EM quntu-energy ust be lrger thn the ount tht ny eleentry syste of onstnt period 1 n produe in one yle. At very high syste s energies, new hnnels, in ddition to the EM rdition, re opened for the relese of energy. Suh proesses of energy relese will liit the EM rdition of n osilltor. A high energy osilltor is nturlly in the reltivisti veloities doin. In order to get lower bound for the energy quntu we need n eleentry syste with onstnt period tht rdites energy effiiently. For this purpose syetri onstnt period osilltor (SCPO) is seleted. A odel of prtile hving ss nd eleentry eletri hrge of n eletron e is used s the oving oponent of the SCPO. A opetitive energy relese proess is pir retion. Above the required energy of this proess y be doinnt. Only under the energy of we n be ertin tht n isolted hrged SCPO will eit its vilble energy s EM wves. 1 For rditing syste of onstnt period, the independene of its rdited EM quntu-energy fro the syste s energy follows fro the ft tht the EM quntu-energy only depends upon its frequeny, whih is onstnt.
3 The rdition power of the hrged SCPO t energy equls will be lulted. Clulting the energy rdited in one period of osilltion t tht power gives lower bound for the EM quntu E H. Here ν is the rdition frequeny nd H is lulted ftor. Copring this result with the experientl vlue of Plnk s onstnt yields surprisingly siple reltion h 3H. The error in this reltion is.14%. Although there is no theoretil explntion for this ftor of 3, it y be explined in the future. Considering this reltion s n expression for h in ters of H llows the lultion of the fine struture onstnt (within the se reltive error). This onstnt is inversely proportionl to the squre of the referene norlized elertion derived fro the SCPO odel t energy of. In the rosopi world the EM quntu-energy is desribed s inute ount of energy. For n eleentry syste of oleulr size, this is tully huge ount of energy tht nnot be rdited during single period of osilltion. Atully, ording to lssil eletrodynis lws in usul ses there is need for thousnds of periods of osilltions in order to produe one quntu. The quntu ehnil equivlent is the verge witing tie (or dey tie) until photon is reted, the se tie tht this nuber of osilltions tkes. The present work gives n intuitive explntion for the gnitude of the EM quntu. II. THE RELATIVISTIC SYMMETRIC CONSTANT PERIOD POTENTIAL For irulr otion the potentil tht ensures onstnt period T should openste for the entrifugl potentil (relted to the entrifugl fore); tht is the se potentil with opposite sign. Suh reltivisti entrifugl potentil is lredy known [4]. The derivtion for this potentil is repeted here in order to hve interedite results. In unifor irulr otion the tngentil veloity v nd rdius of rottion r re relted to the period T nd ngulr veloity ording to T r. ( 1) v This reltion is used to express the veloity of prtile rotting with ngulr veloity s funtion of the rdius r v r ( r ). ( ) In the irulr otion the reltivisti proper (or intrinsi) entripetl elertion is v r r, ( 3) r r
4 where r is rdil unit vetor nd 1/ 1 s funtion of r. Inserting () r yields the proper elertion r/ r. ( 4) r 1 r / The fore tht genertes this proper elertion t ny r, for given period T is ording to Newton s seond lw: The potentil is found by integrtion r F r. ( 5) 1 r/ F r.5 ln 1 ( 6) V d q 1 ln q 1. 1 q Here diensionless vrible q r r T is used in order to siplify expressions. This onstnt-period potentil is generliztion of the SHO into the reltivisti regie in two or three diensions. There is no dvntge of working in 3 diensions, therefore in the present work we will restrit to the two diensionl frework. The onstny of the period for ny plitude (nd therefore for ny energy), is only gurnteed for irulr otion. A. Properties of the syetri potentil of onstnt period A grph of the potentil, in units of the rest ss energy, s funtion of norlized distne is shown in figure 1.
5 FIG. 1. A ut of the SCPP through the origin in units of rest ss energy. q r / T 1. Centrl region As r tends to zero, the potentil tends to behve s the usul syetri hroni osilltor V r x y r. Edge region 1 1. There is potentil singulrity t r T. It posts brrier tht prevents irultion of prtile on n orbit of iruferene longer thn T. B. Coprison with the one diensionl se The 1D osilltor of onstnt period ext potentil [] is not given nlytilly. Anlytil pproxitions re vilble; none of the re of logrithi for. The derived fore of one of the pproxitions is however siilr to the fore of SCPP: F liner x 4x 1 T 5 4. ( 7) C. Approxite reltivisti onstnt period potentil for ellipti otion This fore given by eq. (7) nd the fore derived in the present work n be written in ters of oon ellipse nottion using the eentriity preter nd the ellipse relted iruferene
6 of unit jor xis L( ) 4 ( ). The funtion is the oplete ellipti integrl of the seond kind [8]. It tkes the for Here xx yy F ellipse. ( 8) n( ) L( ) y 1 x T 1 xnd yre orthogonl unit vetors in the xy plne. For irulr orbit, Ln,,,1 nd for liner trjetory, Ln, 1,4,5 4. It is expeted tht for generl ellipse se the vlue of the exponent n n be expressed s funtion of the eentriity. At non reltivisti veloities, proper initil onditions re enough to ke the prtile enter into desired elliptil pth nd to osillte in the right period T. At the extree reltivisti se the prtile will stik to the elliptil singulrity line nd oplish round trip t period of L( ) / T. A proper hoie of the exponent n( ) will give good fit for the interedite veloities. III. OSCILLATOR PROPERTIES When prtile is osillting under the influene of the SCPP, it follows trjetory in the XY plne ording to its initil onditions. A. The nonreltivisti liit In the nonreltivisti liit ( E ) ll orbits of vibrtion will sty in the entrl region of the potentil nd will hve the se period of osilltions independent of energy or eentriity. B. The super-reltivisti liit In the super-reltivisti liit ( E ) the trjetory will be very lose to the line of singulrity. For irulr otion s initil onditionr, v : 1) r v, ) r v, the orbits re of onstnt period. In the next setions we will refer only to suh orbits. Devition of the Initil onditions fro these two rules leds to distorted trjetory tht is usully not periodi (not losed urve). Though for speil ses the trjetory is periodi. The period is thn energy dependent. See ppendix for lultion nd exples.
7 IV. ENERGY VERSUS VELOCITY AND RADIATION LIMIT A reltivisti prtile rotting in the SCPP possess totl vilble (not inluding rest ss) energy of 1 1 E 1 ln(1 ). 1 ( 9) Here we use the reltion found in eq. (), q. In the next setion the rdition of eletrilly hrged SCPO will be onsidered. Theoretilly, there is no obvious liit for the EM power it n rdite. The liit for the rdition ppers when opetitor energy relese proess exists. Suh proess is retion of prtiles pirs. Tht is when the energy of the SCPO rehes the level of. To be preise we ssue tht the prtile osillting under the influene of the SCPP is n eletron, nd the retion is of eletron-positron pir. Using eqution (9) the veloity of the SCPO t tht ritil energy of is deterined ording to ln(1 ). ( 1) The resulted vlue is A. Mxiu rdited energy t one yle The power rdited by elerting prtile, with n eleentry eletri hrge, e, is ording to Lror forul [5] e P, 3 6 ( 11) where is the prtile s elertion. The extension to reltivisti veloities [6] is de by substituting the proper elertion for [7]. The revolving prtile s proper elertion is given in eq. (3) where the rdius of revolution is onneted to the veloity ording to eq. (). It is useful to norlize the elertion of the prtile by the ngulr veloity nd the speed of light to get diensionless quntity. The definition nd expression for the present se ording to equtions (, 3) re def (1 ) (1 ). ( 1) Cobining equtions (11, 3, nd 1), the rdition power of the syste tkes the for
8 v e, 3 r ( 13) r e P 6 6 where 1 T is the osilltion frequeny. The energy E 1 rdited during one osilltion is just this power ultiplied by the period tie T. The result is (usingt 1) e E1 PT. ( 14) 3 In order to find the xiu rdited energy per period tht the hrged SCPO n eit one should substitute the liiting veloity vlue for pir retion to get norlized elertion. The xiu rdited energy is then E 1, e H. ( 15) 3 We introdued the onstnt H defined by the eqution bove. The vlue of this onstnt is H J s The energy E1, is lower bound to the EM quntu-energy: E h H. H is therefore lower bound for the Plnk onstnt h H. ( 16) The vlue of H is very lose to the vlue of Plnk s onstnt, this is n interesting issue to look t ore losely. This is done in setion V. B. Coprison with the one diensionl se Using the pproxite potentil, relted to the fore given by eq. (7), of the one diensionl osilltor of onstnt period (1DCPO) nd its equtions of otion [], it is stright forwrd to l- ulte its rdition when eletrilly hrged. When the osilltor s energy equls the rdited energy per yle is bout.6 ties less thn the energy rdited by the SCPO t se onditions. This result is not very intuitive. At non reltivisti veloities the effiienies (defined s the rdited energy per yle nd per syste s energy) of the two systes (1DCPO nd
9 SCPO) re identil. The rdition of reltivisti linerly elerting hrge gets ftor of 6 [7]. This provides the one diensionl se with n extr ftor opred to the irulr se [see eqution (13)]. The rdition is, therefore enhned by reltivisti effets. The ft is tht 1DCPO t high energies exhibits sw-tooth profile of position versus tie; so tht long ost of its trjetory there is lost no elertion. High elertion is obtined only t the turning points where the veloity (nd therefore ) is not high. Fro this oprison one n dedue tht diensionlity is iportnt onerning rdition effiieny, t reltivisti veloities. V. THE MATCHING FACTOR AND INTERPRETATIONS Nuerilly, to good pproxition, one n write h H. ( 17) 3 The ury of the reltion is.14%. Suh reltion is puzzling: On one hnd it n be identl, on the other hnd, s 3 is for exple, the digonl of unit ube; it y be sign tht there is hidden physil reltion. A. Vlues of fundentl onstnts Soe interesting onlusions ould be drwn for the fine struture onstnt α, if we onsidering H not only s the lower bound for h, but lso fix the reltion: h 3 H, nd leve it s n investigtion issue to explin it. Then, using eq. (15), we find: nd being e h, ( 18) 3 when inserting the expression for h one gets e, ( 19) h
10 3. ( ) 4 Here is the norlized elertion lulted ording to eqution (1) using the liiting veloity of the SCPO; with energy suffiient for pir retion [see vlue bellow eqution (1)]. It is usul to onsider the inverse vlue, for whih one gets: The vlue of is in greeent with the experientl vlue, within the se error, s in the vlue of h lulted ording to eq. (18), of.14%. The reltive errors re of the order of whih is eptble if good physil explntion to the ftor of B. Interprettion of lph 3 is vilble. The fine struture onstnt is thought by ny physiists to be even ore fundentl quntity thn the Plnk s onstnt, in quntu ehnis in generl nd espeilly in quntu eletrodynis. This diensionless quntity is first used in the lultion of reltivisti orretions to toi energy levels together with the spin-orbit oupling [9]. Fro the result of the present work it is obvious tht origin lies in the reltivity theory, i.e., the reltivisti onnetion between ss nd energy. Its tul vlue is deterined by the physis of rdition s result of elertion, ording to the lws of EM theory. To illustrte the ening of eq. () nd the norlized elertion tht ppers there let s ke use of it. The rte of photons prodution A by n eleentry osillting hrge ording to lssil eletrognetis is just the power eitted by the hrge divided by the EM quntu-energy of the se frequeny. Introduing norlized elertion ording to the definition in eqution (1), A beoes The ngle brkets denote tie verge. P e 1 4 A. ( 1) h h Inserting the vlue of α ording to eq. () into eq. (1) one n write the photon prodution rte s 1 A 3. ()
11 The quntity ppers in eqution () s referene vlue for the verge norlized is esure for how elertion of eleentry rditing systes. The rtio of to fst the syste eits photons on sle of to 1. ACKNOWLAGMENT The uthor grteful to Dr. Aos Sorgen (Universidd de Belgrno, Buenos Aires, Argentin) for his gret help in the revision of this pper nd to Asso. Prof. Ido Brslvsky (Ohio University, Athens, OH) for his enourgeent. APPENDIX The fore derived fro the SCPP tht ts on the prtile ording to Newton s lws in the inertil oordinte syste oving instntneously with the prtile is Bold letters designte vetors. ' F r. The elertion is divided into two oponents: one is prllel to the prtile veloity v, nd the other is perpendiulr to it )A1( ' ' v v v ' ' '. )A( The elertion trnsfortion to the oordinte syste tthed to the enter of rottion with fixed orienttion is ording to speil reltivity rules [1] 3 ' '. )A3( The veloity nd position re then lulted in Crtesin oordintes, using [, ], x y d vi i i x, y dt d ri v. i dt )A4(
12 We prefored nueril oputer integrtion of the set of equtions A1-A4 for different initil onditions. All oputtions were done for 1, nd T 1nd the results re nlyzed in the following setions. A. Super-reltivisti se Clultion ws de for initil veloity,.995, x y, with different initil lotions. When the initil lotion does not use irulr otion the prtile usully bounes between different points on the enlosing irulr brrier of potentil singulrity (See setion II.A.) long lines tht re lost stright, without losing loop. In ertin ses polygonl shpe is fored. Two exples, one for tringle nd seond for squre re shown in figure together with the irle resulting fro proper initil onditions. The periods of these 3 trjetories re different nd they re surized in tble I. FIG.. Clulted periodi trjetories in the super-reltivisti (.995 ) region on the xy plne. The third xis is the tie xis. Initil onditions re given in tble I. TABLE I. Periodi trjetories initil onditions nd resulted periods nd shpes. Initil onditions outoe No. x. y / x, Period shpe irle squre tringle Rounded tringle
13 B. Interedite to high energies At oderte reltivisti veloities, the non irulr trjetories re rounded. Fro bout.7 nd up, by fitting the vlue of the initil perpendiulr rdius, we find t lest one periodi trjetory in ddition to the irulr one. Suh periodi rounded tringle is shown in figure 3. The initil onditions nd the period for this se re surized in the lst row of tble I. FIG. 3. A lulted periodi trjetory in the interedite energy region (.75 ), on the xy plne. C. Low to interedite energies At very low nonreltivisti energies the usul ellipti trjetories re obtined, ll with the se period nd different shpes ording to their initil onditions. As the energy inreses the elliptil trjetories strt to show preession effets, typil to reltivisti orbits.. This effet inreses with inresing energy until it is no longer possible, in the generl se to hve defined period (unless initil onditions ensure irulr orbit). One exple of suh trjetory is shown in Figure 4 together with irle resulting fro the se vlue for x.
14 FIG. 4 Clulted trjetories on the xy plne for ses where.4,. 1) r Results in preessing ellipse. ) r,. /,.4 / Results in irle. D. Liner trjetories In ddition to the entioned trjetories, there re liner trjetories resulting fro the initil onditions r or r β. The period of suh trjetories hnges with energy, nd in the superreltivisti liit we get: T T 1. T Here is the low energy period of osilltion. The grph of the period s funtion of the initil veloity, for the se r is shown in figure 5. FIG. 5. Liner osilltions period versus initil veloity (initil position t the origin).
15 Referenes [1] H. Goldstein, Clssil Mehnis, nd edition (Edison-Wesley, Reding, MA, 1981), p. 34. [] Jung-Hoo Ki, Seung-Woo Lee, Hns Mssen nd Hi-Woong Lee, Phys. Rev. A, Vol. 53, No. 5, 991 (1996). [3] Mx Plnk, Annlen der Physik, vol. 1, no 4. April, 719. (19). [4] Moses Fynogold, Speil reltivity nd how it works, WILEY-VCH Verlg GBH & Co. KGA., Weinhei. Chp. 13, p. 68 (8). [5] J. Lror, Phils. Mg. 44, 94 (1897). [6] O. Heviside, Nture 67, 6 (19). [7] J. D. Jkson, Clssil eletrodynis, 3rd edition, John Wiley & sons, In. 111 River Street, Hoboken, NJ, p. 667 (1999). [8] L. M. Milne-Thoson, Hndbook of Mthetil Funtions with Foruls, Grphs, nd Mthetil Tbles, 1th edition, edited by Milton Abrowitz nd Irene A. Stegun, Dover, New York, p. 587 (197). [9] Dvid J. Griffiths, Introdution to quntu Mehnis, Prentie Hll, Upper Sddle River, New Jersey 7458 (1994), Chp 6.3. p. 35. [1] Ref. [7], p. 569 (1999).
Electromagnetism Notes, NYU Spring 2018
 Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Solutions to Assignment 1
 MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
a) Read over steps (1)- (4) below and sketch the path of the cycle on a P V plot on the graph below. Label all appropriate points.
 Prole 3: Crnot Cyle of n Idel Gs In this prole, the strting pressure P nd volue of n idel gs in stte, re given he rtio R = / > of the volues of the sttes nd is given Finlly onstnt γ = 5/3 is given You
Prole 3: Crnot Cyle of n Idel Gs In this prole, the strting pressure P nd volue of n idel gs in stte, re given he rtio R = / > of the volues of the sttes nd is given Finlly onstnt γ = 5/3 is given You
PHYS 601 HW3 Solution
 3.1 Norl force using Lgrnge ultiplier Using the center of the hoop s origin, we will describe the position of the prticle with conventionl polr coordintes. The Lgrngin is therefore L = 1 2 ṙ2 + 1 2 r2
3.1 Norl force using Lgrnge ultiplier Using the center of the hoop s origin, we will describe the position of the prticle with conventionl polr coordintes. The Lgrngin is therefore L = 1 2 ṙ2 + 1 2 r2
PHY 5246: Theoretical Dynamics, Fall Assignment # 5, Solutions. θ = l mr 2 = l
 PHY 546: Theoreticl Dynics, Fll 15 Assignent # 5, Solutions 1 Grded Probles Proble 1 (1.) Using the eqution of the orbit or force lw d ( 1 dθ r)+ 1 r = r F(r), (1) l with r(θ) = ke αθ one finds fro which
PHY 546: Theoreticl Dynics, Fll 15 Assignent # 5, Solutions 1 Grded Probles Proble 1 (1.) Using the eqution of the orbit or force lw d ( 1 dθ r)+ 1 r = r F(r), (1) l with r(θ) = ke αθ one finds fro which
Vibration with more (than one) degrees of freedom (DOF) a) longitudinal vibration with 3 DOF. b) rotational (torsional) vibration with 3 DOF
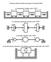 irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
MATH Final Review
 MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
University of Sioux Falls. MAT204/205 Calculus I/II
 University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Lecture Summaries for Multivariable Integral Calculus M52B
 These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
The Emission-Absorption of Energy analyzed by Quantum-Relativity. Abstract
 The mission-absorption of nergy nlyzed by Quntum-Reltivity Alfred Bennun* & Néstor Ledesm** Abstrt The uslity horizon llows progressive quntifition, from n initil nk prtile, whih yields its energy s blk
The mission-absorption of nergy nlyzed by Quntum-Reltivity Alfred Bennun* & Néstor Ledesm** Abstrt The uslity horizon llows progressive quntifition, from n initil nk prtile, whih yields its energy s blk
f (x)dx = f(b) f(a). a b f (x)dx is the limit of sums
 Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
The Atwood Machine OBJECTIVE INTRODUCTION APPARATUS THEORY
 The Atwood Mchine OBJECTIVE To derive the ening of Newton's second lw of otion s it pplies to the Atwood chine. To explin how ss iblnce cn led to the ccelertion of the syste. To deterine the ccelertion
The Atwood Mchine OBJECTIVE To derive the ening of Newton's second lw of otion s it pplies to the Atwood chine. To explin how ss iblnce cn led to the ccelertion of the syste. To deterine the ccelertion
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Problems set # 3 Physics 169 February 24, 2015
 Prof. Anhordoqui Problems set # 3 Physis 169 Februry 4, 015 1. A point hrge q is loted t the enter of uniform ring hving liner hrge density λ nd rdius, s shown in Fig. 1. Determine the totl eletri flux
Prof. Anhordoqui Problems set # 3 Physis 169 Februry 4, 015 1. A point hrge q is loted t the enter of uniform ring hving liner hrge density λ nd rdius, s shown in Fig. 1. Determine the totl eletri flux
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
ECE 330 POWER CIRCUITS AND ELECTROMECHANICS LECTURE 17 FORCES OF ELECTRIC ORIGIN ENERGY APPROACH(1)
 ECE 330 POWER CIRCUITS AND ELECTROMECHANICS LECTURE 17 FORCES OF ELECTRIC ORIGIN ENERGY APPROACH(1) Aknowledgent-These hndouts nd leture notes given in lss re bsed on teril fro Prof. Peter Suer s ECE 330
ECE 330 POWER CIRCUITS AND ELECTROMECHANICS LECTURE 17 FORCES OF ELECTRIC ORIGIN ENERGY APPROACH(1) Aknowledgent-These hndouts nd leture notes given in lss re bsed on teril fro Prof. Peter Suer s ECE 330
Section 3.6. Definite Integrals
 The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx
![Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx](/thumbs/79/79316452.jpg) Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
7-1: Zero and Negative Exponents
 7-: Zero nd Negtive Exponents Objective: To siplify expressions involving zero nd negtive exponents Wr Up:.. ( ).. 7.. Investigting Zero nd Negtive Exponents: Coplete the tble. Write non-integers s frctions
7-: Zero nd Negtive Exponents Objective: To siplify expressions involving zero nd negtive exponents Wr Up:.. ( ).. 7.. Investigting Zero nd Negtive Exponents: Coplete the tble. Write non-integers s frctions
On the Scale factor of the Universe and Redshift.
 On the Sle ftor of the Universe nd Redshift. J. M. unter. john@grvity.uk.om ABSTRACT It is proposed tht there hs been longstnding misunderstnding of the reltionship between sle ftor of the universe nd
On the Sle ftor of the Universe nd Redshift. J. M. unter. john@grvity.uk.om ABSTRACT It is proposed tht there hs been longstnding misunderstnding of the reltionship between sle ftor of the universe nd
Vortex-induced vibrations of structures
 Struturl Engineers World Congress 7, Noeber -7, 7. Bnglore, Indi. Vortex-indued ibrtions of strutures Send Ole Hnsen ABSTRACT Vortex-indued ibrtions y our on slender strutures suh s hineys, towers nd bridge
Struturl Engineers World Congress 7, Noeber -7, 7. Bnglore, Indi. Vortex-indued ibrtions of strutures Send Ole Hnsen ABSTRACT Vortex-indued ibrtions y our on slender strutures suh s hineys, towers nd bridge
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
( ) as a fraction. Determine location of the highest
 AB/ Clulus Exm Review Sheet Solutions A Prelulus Type prolems A1 A A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f( x) Set funtion equl to Ftor or use qudrti eqution if qudrti Grph to
AB/ Clulus Exm Review Sheet Solutions A Prelulus Type prolems A1 A A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f( x) Set funtion equl to Ftor or use qudrti eqution if qudrti Grph to
The Spring. Consider a spring, which we apply a force F A to either stretch it or compress it
 The Spring Consider spring, which we pply force F A to either stretch it or copress it F A - unstretched -F A 0 F A k k is the spring constnt, units of N/, different for different terils, nuber of coils
The Spring Consider spring, which we pply force F A to either stretch it or copress it F A - unstretched -F A 0 F A k k is the spring constnt, units of N/, different for different terils, nuber of coils
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Learning Objectives of Module 2 (Algebra and Calculus) Notes:
 67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
Line Integrals and Entire Functions
 Line Integrls nd Entire Funtions Defining n Integrl for omplex Vlued Funtions In the following setions, our min gol is to show tht every entire funtion n be represented s n everywhere onvergent power series
Line Integrls nd Entire Funtions Defining n Integrl for omplex Vlued Funtions In the following setions, our min gol is to show tht every entire funtion n be represented s n everywhere onvergent power series
Chapter17. Congruence and transformations. Contents: A Transformations B Congruent figures C Congruent triangles D Proof using congruence
 hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
hpter17 ongruene nd trnsfortions ontents: Trnsfortions ongruent figures ongruent tringles Proof using ongruene 352 ONGRUENE N TRNSFORMTIONS (hpter 17) Opening prole Jne ut two tringulr slies of heeseke,
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY
 UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We estblish soe uniqueness results ner 0 for ordinry differentil equtions of the
UNIQUENESS THEOREMS FOR ORDINARY DIFFERENTIAL EQUATIONS WITH HÖLDER CONTINUITY YIFEI PAN, MEI WANG, AND YU YAN ABSTRACT We estblish soe uniqueness results ner 0 for ordinry differentil equtions of the
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P. (a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg) Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Contact Analysis on Large Negative Clearance Four-point Contact Ball Bearing
 Avilble online t www.sciencedirect.co rocedi ngineering 7 0 74 78 The Second SR Conference on ngineering Modelling nd Siultion CMS 0 Contct Anlysis on Lrge Negtive Clernce Four-point Contct Bll Bering
Avilble online t www.sciencedirect.co rocedi ngineering 7 0 74 78 The Second SR Conference on ngineering Modelling nd Siultion CMS 0 Contct Anlysis on Lrge Negtive Clernce Four-point Contct Bll Bering
The Relationship between the Nine-Point Circle, the Circumscribed Circle and the Inscribed Circle of Archimedes Triangle Yuporn Rimcholakarn
 Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
For the flux through a surface: Ch.24 Gauss s Law In last chapter, to calculate electric filede at a give location: q For point charges: K i r 2 ˆr
 Ch.24 Guss s Lw In lst hpter, to lulte eletri filed t give lotion: q For point hrges: K i e r 2 ˆr i dq For ontinuous hrge distributions: K e r 2 ˆr However, for mny situtions with symmetri hrge distribution,
Ch.24 Guss s Lw In lst hpter, to lulte eletri filed t give lotion: q For point hrges: K i e r 2 ˆr i dq For ontinuous hrge distributions: K e r 2 ˆr However, for mny situtions with symmetri hrge distribution,
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
1.2. Linear Variable Coefficient Equations. y + b "! = a y + b " Remark: The case b = 0 and a non-constant can be solved with the same idea as above.
 1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 This diagram represents the energy change that occurs when a d electron in a transition metal ion is excited by visible light.
 1 This igrm represents the energy hnge tht ours when eletron in trnsition metl ion is exite y visile light. Give the eqution tht reltes the energy hnge ΔE to the Plnk onstnt, h, n the frequeny, v, of the
1 This igrm represents the energy hnge tht ours when eletron in trnsition metl ion is exite y visile light. Give the eqution tht reltes the energy hnge ΔE to the Plnk onstnt, h, n the frequeny, v, of the
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
Hyperbolic Velocity Model
 Interntionl Journl of Geosienes 0 4 74-745 doi:046/ijg044067 Pulished Online June 0 (http://wwwsirporg/journl/ijg) Hyperoli eloity odel Igor Rvve Zvi Koren Prdig Geophysil Herzliy Isrel Eil: igorrvve@pdgo
Interntionl Journl of Geosienes 0 4 74-745 doi:046/ijg044067 Pulished Online June 0 (http://wwwsirporg/journl/ijg) Hyperoli eloity odel Igor Rvve Zvi Koren Prdig Geophysil Herzliy Isrel Eil: igorrvve@pdgo
16z z q. q( B) Max{2 z z z z B} r z r z r z r z B. John Riley 19 October Econ 401A: Microeconomic Theory. Homework 2 Answers
 John Riley 9 Otober 6 Eon 4A: Miroeonomi Theory Homework Answers Constnt returns to sle prodution funtion () If (,, q) S then 6 q () 4 We need to show tht (,, q) S 6( ) ( ) ( q) q [ q ] 4 4 4 4 4 4 Appeling
John Riley 9 Otober 6 Eon 4A: Miroeonomi Theory Homework Answers Constnt returns to sle prodution funtion () If (,, q) S then 6 q () 4 We need to show tht (,, q) S 6( ) ( ) ( q) q [ q ] 4 4 4 4 4 4 Appeling
A Survey on Optical Orthogonal Codes
 A urvey on Optil Orthogonl Codes Mohd M. Ale-Krldni Optil orthogonl odes (OOC) defined by lehi [1] nd Chung, lehi, nd Wei [] re fily of (0,1) seuenes with desired utoorreltion nd ross-orreltion properties
A urvey on Optil Orthogonl Codes Mohd M. Ale-Krldni Optil orthogonl odes (OOC) defined by lehi [1] nd Chung, lehi, nd Wei [] re fily of (0,1) seuenes with desired utoorreltion nd ross-orreltion properties
ON AN INEQUALITY FOR THE MEDIANS OF A TRIANGLE
 Journl of Siene nd Arts Yer, No. (9), pp. 7-6, OIGINAL PAPE ON AN INEQUALITY FO THE MEDIANS OF A TIANGLE JIAN LIU Mnusript reeived:.5.; Aepted pper:.5.; Pulished online: 5.6.. Astrt. In this pper, we give
Journl of Siene nd Arts Yer, No. (9), pp. 7-6, OIGINAL PAPE ON AN INEQUALITY FO THE MEDIANS OF A TIANGLE JIAN LIU Mnusript reeived:.5.; Aepted pper:.5.; Pulished online: 5.6.. Astrt. In this pper, we give
We divide the interval [a, b] into subintervals of equal length x = b a n
![We divide the interval [a, b] into subintervals of equal length x = b a n We divide the interval [a, b] into subintervals of equal length x = b a n](/thumbs/80/80533932.jpg) Arc Length Given curve C defined by function f(x), we wnt to find the length of this curve between nd b. We do this by using process similr to wht we did in defining the Riemnn Sum of definite integrl:
Arc Length Given curve C defined by function f(x), we wnt to find the length of this curve between nd b. We do this by using process similr to wht we did in defining the Riemnn Sum of definite integrl:
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
, g. Exercise 1. Generator polynomials of a convolutional code, given in binary form, are g. Solution 1.
 Exerise Genertor polynomils of onvolutionl ode, given in binry form, re g, g j g. ) Sketh the enoding iruit. b) Sketh the stte digrm. ) Find the trnsfer funtion T. d) Wht is the minimum free distne of
Exerise Genertor polynomils of onvolutionl ode, given in binry form, re g, g j g. ) Sketh the enoding iruit. b) Sketh the stte digrm. ) Find the trnsfer funtion T. d) Wht is the minimum free distne of
Physics 505 Homework No. 11 Solutions S11-1
 Physis 55 Homework No 11 s S11-1 1 This problem is from the My, 24 Prelims Hydrogen moleule Consider the neutrl hydrogen moleule, H 2 Write down the Hmiltonin keeping only the kineti energy terms nd the
Physis 55 Homework No 11 s S11-1 1 This problem is from the My, 24 Prelims Hydrogen moleule Consider the neutrl hydrogen moleule, H 2 Write down the Hmiltonin keeping only the kineti energy terms nd the
AP CALCULUS Test #6: Unit #6 Basic Integration and Applications
 AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret
AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret
Discussion Question 1A P212, Week 1 P211 Review: 2-D Motion with Uniform Force
 Discussion Question 1A P1, Week 1 P11 Review: -D otion with Unifor Force The thetics nd phsics of the proble below re siilr to probles ou will encounter in P1, where the force is due to the ction of n
Discussion Question 1A P1, Week 1 P11 Review: -D otion with Unifor Force The thetics nd phsics of the proble below re siilr to probles ou will encounter in P1, where the force is due to the ction of n
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Exponents and Powers
 EXPONENTS AND POWERS 9 Exponents nd Powers CHAPTER. Introduction Do you know? Mss of erth is 5,970,000,000,000, 000, 000, 000, 000 kg. We hve lredy lernt in erlier clss how to write such lrge nubers ore
EXPONENTS AND POWERS 9 Exponents nd Powers CHAPTER. Introduction Do you know? Mss of erth is 5,970,000,000,000, 000, 000, 000, 000 kg. We hve lredy lernt in erlier clss how to write such lrge nubers ore
(h+ ) = 0, (3.1) s = s 0, (3.2)
 Chpter 3 Nozzle Flow Qusistedy idel gs flow in pipes For the lrge vlues of the Reynolds number typilly found in nozzles, the flow is idel. For stedy opertion with negligible body fores the energy nd momentum
Chpter 3 Nozzle Flow Qusistedy idel gs flow in pipes For the lrge vlues of the Reynolds number typilly found in nozzles, the flow is idel. For stedy opertion with negligible body fores the energy nd momentum
Equations from the Millennium Theory of Inertia and Gravity. Copyright 2004 Joseph A. Rybczyk
 Equtions fo the illenniu heoy of Ineti nd vity Copyight 004 Joseph A. Rybzyk ollowing is oplete list of ll of the equtions used o deived in the illenniu heoy of Ineti nd vity. o ese of efeene the equtions
Equtions fo the illenniu heoy of Ineti nd vity Copyight 004 Joseph A. Rybzyk ollowing is oplete list of ll of the equtions used o deived in the illenniu heoy of Ineti nd vity. o ese of efeene the equtions
Discussion Introduction P212, Week 1 The Scientist s Sixth Sense. Knowing what the answer will look like before you start.
 Discussion Introduction P1, Week 1 The Scientist s Sith Sense As scientist or engineer, uch of your job will be perforing clcultions, nd using clcultions perfored by others. You ll be doing plenty of tht
Discussion Introduction P1, Week 1 The Scientist s Sith Sense As scientist or engineer, uch of your job will be perforing clcultions, nd using clcultions perfored by others. You ll be doing plenty of tht
SOLUTIONS TO CONCEPTS CHAPTER 10
 SOLUTIONS TO CONCEPTS CHPTE 0. 0 0 ; 00 rev/s ; ; 00 rd/s 0 t t (00 )/4 50 rd /s or 5 rev/s 0 t + / t 8 50 400 rd 50 rd/s or 5 rev/s s 400 rd.. 00 ; t 5 sec / t 00 / 5 8 5 40 rd/s 0 rev/s 8 rd/s 4 rev/s
SOLUTIONS TO CONCEPTS CHPTE 0. 0 0 ; 00 rev/s ; ; 00 rd/s 0 t t (00 )/4 50 rd /s or 5 rev/s 0 t + / t 8 50 400 rd 50 rd/s or 5 rev/s s 400 rd.. 00 ; t 5 sec / t 00 / 5 8 5 40 rd/s 0 rev/s 8 rd/s 4 rev/s
PHYS 705: Classical Mechanics. Small Oscillations: Example A Linear Triatomic Molecule
 PHYS 75: Clssicl echnics Sll Oscilltions: Exple A Liner Tritoic olecule A Liner Tritoic olecule x b b x x3 x Experientlly, one ight be interested in the rdition resulted fro the intrinsic oscilltion odes
PHYS 75: Clssicl echnics Sll Oscilltions: Exple A Liner Tritoic olecule A Liner Tritoic olecule x b b x x3 x Experientlly, one ight be interested in the rdition resulted fro the intrinsic oscilltion odes
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
CHAPTER 5 Newton s Laws of Motion
 CHAPTER 5 Newton s Lws of Motion We ve been lerning kinetics; describing otion without understnding wht the cuse of the otion ws. Now we re going to lern dynics!! Nno otor 103 PHYS - 1 Isc Newton (1642-1727)
CHAPTER 5 Newton s Lws of Motion We ve been lerning kinetics; describing otion without understnding wht the cuse of the otion ws. Now we re going to lern dynics!! Nno otor 103 PHYS - 1 Isc Newton (1642-1727)
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
8 THREE PHASE A.C. CIRCUITS
 8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
r = cos θ + 1. dt ) dt. (1)
 MTHE 7 Proble Set 5 Solutions (A Crdioid). Let C be the closed curve in R whose polr coordintes (r, θ) stisfy () Sketch the curve C. r = cos θ +. (b) Find pretriztion t (r(t), θ(t)), t [, b], of C in polr
MTHE 7 Proble Set 5 Solutions (A Crdioid). Let C be the closed curve in R whose polr coordintes (r, θ) stisfy () Sketch the curve C. r = cos θ +. (b) Find pretriztion t (r(t), θ(t)), t [, b], of C in polr
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Electromagnetic-Power-based Modal Classification, Modal Expansion, and Modal Decomposition for Perfect Electric Conductors
 LIAN: EM-BASED MODAL CLASSIFICATION EXANSION AND DECOMOSITION FOR EC 1 Eletromgneti-ower-bsed Modl Clssifition Modl Expnsion nd Modl Deomposition for erfet Eletri Condutors Renzun Lin Abstrt Trditionlly
LIAN: EM-BASED MODAL CLASSIFICATION EXANSION AND DECOMOSITION FOR EC 1 Eletromgneti-ower-bsed Modl Clssifition Modl Expnsion nd Modl Deomposition for erfet Eletri Condutors Renzun Lin Abstrt Trditionlly
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Parabola and Catenary Equations for Conductor Height Calculation
 ELECTROTEHNICĂ, ELECTRONICĂ, AUTOMATICĂ, 6 (), nr. 3 9 Prbol nd Ctenr Equtions for Condutor Height Clultion Alen HATIBOVIC Abstrt This pper presents new equtions for ondutor height lultion bsed on the
ELECTROTEHNICĂ, ELECTRONICĂ, AUTOMATICĂ, 6 (), nr. 3 9 Prbol nd Ctenr Equtions for Condutor Height Clultion Alen HATIBOVIC Abstrt This pper presents new equtions for ondutor height lultion bsed on the
Topological Properties of the Braid Stirring Pattern
 Originl Pper Form, 0, 7, 0 Topologil Properties of the Brid Stirring Pttern Yoshihiro Ymguhi Teikyo Heisei University, Ihihr, Chib 90-070, Jpn E-mil ddress: hosfrtl@icloud.om (Reeived June 7, 0; Aepted
Originl Pper Form, 0, 7, 0 Topologil Properties of the Brid Stirring Pttern Yoshihiro Ymguhi Teikyo Heisei University, Ihihr, Chib 90-070, Jpn E-mil ddress: hosfrtl@icloud.om (Reeived June 7, 0; Aepted
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
KINEMATICS OF RIGID BODIES
 KINEMTICS OF RIGID ODIES Introduction In rigid body kinemtics, e use the reltionships governing the displcement, velocity nd ccelertion, but must lso ccount for the rottionl motion of the body. Description
KINEMTICS OF RIGID ODIES Introduction In rigid body kinemtics, e use the reltionships governing the displcement, velocity nd ccelertion, but must lso ccount for the rottionl motion of the body. Description
Forces on curved surfaces Buoyant force Stability of floating and submerged bodies
 Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Eigenvectors and Eigenvalues
 MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
#6A&B Magnetic Field Mapping
 #6A& Mgnetic Field Mpping Gol y performing this lb experiment, you will: 1. use mgnetic field mesurement technique bsed on Frdy s Lw (see the previous experiment),. study the mgnetic fields generted by
#6A& Mgnetic Field Mpping Gol y performing this lb experiment, you will: 1. use mgnetic field mesurement technique bsed on Frdy s Lw (see the previous experiment),. study the mgnetic fields generted by
Arrow s Impossibility Theorem
 Rep Fun Gme Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Fun Gme Properties Arrow s Theorem Leture Overview 1 Rep 2 Fun Gme 3 Properties
Rep Fun Gme Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Fun Gme Properties Arrow s Theorem Leture Overview 1 Rep 2 Fun Gme 3 Properties
Properties of Different Types of Lorentz Transformations
 merin Journl of Mthemtis nd ttistis 03 3(3: 05-3 DOI: 0593/jjms03030303 roperties of Different Types of Lorentz Trnsformtions tikur Rhmn izid * Md hh lm Deprtment of usiness dministrtion Leding niversity
merin Journl of Mthemtis nd ttistis 03 3(3: 05-3 DOI: 0593/jjms03030303 roperties of Different Types of Lorentz Trnsformtions tikur Rhmn izid * Md hh lm Deprtment of usiness dministrtion Leding niversity
21.1 Using Formulae Construct and Use Simple Formulae Revision of Negative Numbers Substitution into Formulae
 MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
