The Inspherical Gergonne Center of a Tetrahedron
|
|
|
- Dulcie Blankenship
- 5 years ago
- Views:
Transcription
1 Journl for Geometry nd Grphis Volume 8 (2004), No. 1, The Inspheril Gergonne Center of Tetrhedron Mowffq Hjj 1, Peter Wlker 2 1 Deprtment of Mthemtis, Yrmouk University Irbid, Jordn emil: mhjj@yu.edu.jo 2 Deprtment of Mthemtis nd Sttistis, Amerin University of Shrjh P.O. Box 26666, Shrjh, United Arb Emirtes emil: peterw@us..e Abstrt. With the trditionl definition of the Gergonne enter of tringle in mind, it is nturl to onsider, for given tetrhedron, the intersetion of the evins tht join the verties to the points where the insphere touhes the fes. However, these evins re onurrent for the limited lss of wht we ll inspheril tetrhedr. Another pproh is to note tht the evins through ny point inside tringle divide the sides into 6 segments, nd tht the Gergonne enter is hrterized by the requirement tht every two segments shring vertex re equl. Similrly, the evins through ny point inside tetrhedron divide the fes into 12 subtringles, nd one my define the Gergonne enter s the point for whih every two subtringles tht shre n edge re equl in re. This ws done by the uthors in [8], where the existene nd uniquenes of suh point is estblished. It turns out tht tetrhedr whose Gergonne enter hs the stronger property tht every two subtringles tht shre n edge re ongruent (resp. skew-ongruent) re preisely the inspheril (resp. equifil) ones. This is proved in Setion 4. In Setions 2 nd 3, we give hrteriztion of the inspheril tetrhedr nd we outline method for onstruting them. Key Words: Bryentri oordintes, Cev s theorem, Gergonne point, Fermt- Torrielli point, isoseles or equifil tetrhedron, isogonl tetrhedron. MSC 2000: 51M04, 51M20, 52B10 1. Introdution nd terminology The Gergonne enter of tringle ABC is defined to be the point of intersetion of the evins AA, BB, nd CC, where A, B, nd C re the points where the inirle touhes the sides ISSN /$ Heldermnn Verlg
2 24 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron BC, CA, nd AB, respetively, s in Fig. 1. Suh evins re onurrent by Cev s Theorem sine A, B, C n be equivlently defined by the lgebri reltions AB = AC, BC = BA, CA = CB, where XY denotes the length of the line segment XY. It is then quite nturl to onsider the point of intersetion (if ny) of the evins AA, BB, CC, nd DD of tetrhedron ABCD, where A, B, C, nd D re the points where the insphere touhes the fes. We shll see tht suh evins re onurrent for limited lss of tetrhedr nd we shll desribe suh lss. We ll the resulting enter (when it exists) the inspheril Gergonne enter, or simply the inspheril enter to distinguish it from the Gergonne enter defined in [8], nd we shll ll tetrhedron with n inspheril enter n inspheril tetrhedron. The reltion between these two enters is disussed in Setion 4. A C C. B. B B A Figure 1: C Throughout the rest of this rtile, the term tetrhedron stnds for non-degenerte tetrhedron. An equifil or isoseless tetrhedron is tetrhedron whose fes re ongruent, or equivlently hve the sme re; see [10, Chpter 9, pges 90 97], [12, Theorem 4.4, pge 156], [2, Cor. 307, pge 108] or [7]. If A 1 A 2 A 3 is tetrhedron, then by its j-th fe we shll men the fe opposite to the j-th vertex A j. Two edges of tetrhedron will be lled opposite if they hve no vertex in ommon. Two tringles ABC nd A B C re lled ongruent if there is n isometry tht rries A, B, nd C to A, B, nd C in the sme order. Finlly, we ll two n-tuples (x 1,..., x n ) nd (y 1,..., y n ) equivlent, nd we write (x 1,..., x n ) (y 1,..., y n ) if one of them is positive multiple of the other. Thus two n- tuples (x 1,..., x n ) nd (y 1,..., y n ) re bryentri oordintes of the sme point if nd only if they re equivlent. 2. A hrteriztion of inspheril tetrhedr In Theorem 1 below, we prove tht tetrhedron is inspheril if nd only if its insphere touhes the fes t their Fermt-Torrielli points. However, to see how lrge the lss of suh tetrhedr is nd to desribe how they n be onstruted, stronger nd more tehnil sttement is needed nd is provided by Theorem 2. For ese of referene nd to be self-ontined, we strt with two firly well-known lemms. The first desribes the Fermt-Torrielli point of tringle nd the seond is threedimensionl version of Cev s Theorem. Both will be used freely.
3 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron 25 Lemm 1. Let ABC be non-degenerte tringle. Then there exists unique point F whose distnes from the verties hve minimum sum. If the ngles of ABC re less thn 120 eh, then F is interior nd is hrterized by the equi-ngulr property AF B = BF C = CF A = 120. Otherwise, F is the vertex tht holds the lrgest ngle. In ll ses, F is lled the Fermt-Torrielli point of ABC. Proof. See [6], or [1] nd [13] for higher-dimensionl versions. Lemm 2. Let T = A 1 A 2 A 3 be tetrhedron nd let D j, 1 j 4, be point on its j-th fe. Then the evins A j D j, 1 j 4, re onurrent if nd only if there exist M 1, M 2, M 3 nd M 4 suh tht for ll rrngements (i, j, k, t) of {1, 2, 3, 4}, (M i, M j, M k ) re bryentri oordintes of D t reltive to A i A j A k. In this se, (M 1, M 2, M 3, M 4 ) re bryentri oordintes of the point of onurrene reltive to A 1 A 2 A 3. Proof. See [14]. Theorem 1. Let A 1 A 2 A 3 be tetrhedron nd let D j, 1 j 4, be the point where the insphere touhes the j-th fe. Then the evins A j D j, 1 j 4, re onurrent if nd only if D j, 1 j 4, is the Fermt-Torrielli point of the j-th fe. A 1 α d d α β γ γ β α β γ A 3 b b b α β γ d A 2 Figure 2: Proof. Following the rgument in [10, pge 93], we first note tht the line segments A 1 D 2, A 1 D 3, nd A 1 D 4 hve equl lengths sine they re tngent lines to the sme sphere from the sme point A 1. We denote their ommon length by, nd we define b,, d similrly. This is shown in Fig. 3 where our tetrhedron is flttened. It follows tht the tringles A 1 A 2 D 3
4 26 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron nd A 1 A 2 D 4 re ongruent nd hene A 1 D 3 A 2 = A 1 D 4 A 2. We denote the mesure of this ngle by γ, nd we define α, β, α, β, γ similrly, s in Fig. 2. The equtions α + β + γ = α + β + γ = α + β + γ = α + β + γ = 360 (1) led immeditely to the onlusion α = α, β = β, γ = γ. (2) Now ssume tht the evins A j D j, 1 j 4, re onurrent. If (M 1, M 2, M 3, M 4 ) re bryentri oordintes of their point of intersetion reltive to A 1 A 2 A 3, then by Lemm 2, (M 1, M 2, M 3 ) re bryentri oordintes of D 4 reltive to A 1 A 2 A 3. Thus (b sin α, sin β, b sin γ) (M 1, M 2, M 3 ) (bd sin β, d sin α, b sin γ) (M 1, M 2, M 4 ). Therefore b sin α sin β = bd sin β d sin α ( = M ) 1 M 2 nd hene α = β. Similrly, α = γ nd therefore α = β = γ = 120. Hene D 1 is the Fermt-Torrielli point of the fe A 1 A 2 A 3. Similrly for the other fes. Thus if our evins re onurrent, then the D j s re the Fermt-Torrielli points of the fes. A 1 D 2 D 3 D 4 A 3 b D 1 A 2 Figure 3:
5 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron 27 Conversely, suppose tht the D j s re the Fermt-Torrielli points of the fes. It is ler tht the bryentri oordintes of D 4 with respet to A 1 A 2 A 3 re ( 1 (b sin 120, sin 120, b sin 120 ), 1 b, 1 ). Similr sttements hold for the other D j s. Lemm 2 now implies tht the evins A j D j re onurrent (nd tht they onur t the point whose bryentri oordintes reltive to A 1 A 2 A 3 re (1/, 1/b, 1/, 1/d)). 3. Constrution of generl inspheril nd non-inspheril tetrhedr Theorem 1 desribes how to onstrut non-inspheril tetrhedron. Strt with ny tringle ABC nd ny point P inside ABC tht is different from the Fermt-Torrielli point of ABC. Ple smll sphere S so tht it touhes the plne of ABC t P nd drw three plnes through the sides of ABC tht re tngent to S. If D is the point where these three plnes interset, then ABCD would be non-inspheril tetrhedron. To ensure tht these plnes interset within the hlfspe of the plne of ABC whih ontins S, we tke the rdius of S suffiiently smll. For exmple, it is suffiient (but by no mens neessry) to tke the rdius of S to be less thn eh of the distnes of P from the sides of ABC. On the other hnd, to desribe how to onstrut inspheril tetrhedr, we need the following theorem, whih will lso be needed in proving Theorem 4. X A 1 X y D 2 Z D 3 z D 4 A 3 Y b x Z D 1 Y A 2 Figure 4: Theorem 2. Let A 1 A 2 A 3 be tetrhedron whose fes hve interior Fermt-Torrielli points D 1, D 2, D 3 nd D 4. If A i D j = A i D k = A i D t for ll rrngements (i, j, k, t) of {1, 2, 3, 4}, then our tetrhedron is inspheril.
6 28 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron Proof. Let denote the ommon length of the line segments A 1 D 2, A 1 D 3, nd A 1 D 4, nd define b,, d similrly, s shown in Fig. 4. Let I be the inenter nd r the inrdius of our tetrhedron, nd let I j be the orthogonl projetion of I on the j-th fe. To prove tht I j = D j for ll j, it is suffiient by symmetry to prove tht I 4 = D 4. Equivlently, it is suffiient to prove tht the distnes from I 4 to A 1, A 2, nd A 3 re, b, nd, respetively. Agin, it is suffiient by symmetry to prove tht I 4 A 1 =, or equivlently α 2 r 2 = 2, (3) where α = IA 1. Without loss of generlity, we my ssume tht I is the origin. To omplish this, we note tht ll the elements of our tetrhedron n be omputed in terms of, b,, nd d. We find r (in terms of, b,, d) by first finding the lengths of the edges (using the Lw of Cosines), then the res F j of the fes nd the volume V of the tetrhedron, nd then using the formul V = (r/3)(f 1 +F 2 +F 3 +F 4 ). Then we find α = A 1 by solving system of 10 liner equtions in the unknowns A i A j, i j. We then hek tht (3) is indeed stisfied. We find it more onvenient to denote the lengths of the edges by x, X,... s shown in Fig. 4. Thus we hve x = b b, y = , z = 2 + b 2 + b, X = 2 + d 2 + d, Y = b 2 + d 2 + bd, Z = 2 + d 2 + d. (4) The re F j of the j-th fe is given by F j = ( 3/4)f j, where f 1 = b + d + db, f 2 = + d + d, f 3 = b + bd + d, f 4 = b + b +. (5) The volume V of the tetrhedron is given by 144V 2 = (xx + yy + zz)(x + X + y + Y + z + Z) (xyz + xy Z + XyZ + XY z) = 2(x 2 X + X 2 x + y 2 Y + Y 2 y + z 2 Z + Z 2 z). (6) Using (4), this simplifies into where Sine 16V 2 = bds, (7) S = b + b + + d + bd + d = f 1 + f 2 + f 3 + f 4. (8) 2 V = r 3 (F 1 + F 2 + F 3 + F 4 ) = r 3 it follows tht From (7) nd (9), it follows tht 3 4 (f 1 + f 2 + f 3 + f 4 ) = r (2S) = r 3 6 S, 16V 2 = 4r2 S 2. (9) 3 r 2 = 3bd 4S. (10)
7 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron 29 It remins to ompute the distnes from the inenter I to the verties. The bryentri oordintes of I with respet to A 1 A 2 A 3 re (f 1, f 2, f 3, f 4 ). Therefore I = 0 = f 1 A 1 + f 2 A 2 + f 3 A 3 + f 4. Tking the slr produt with eh A j, nd letting A ij = A i A j, we obtin the first four liner equtions represented by (11) below. Next, every edge gives rise to n eqution in the mnner tht z = A 2 A 3 2 = (A 2 A 3 ) (A 2 A 3 ) = A 22 + A 33 2A 23. The six equtions thus obtined re the lst 6 equtions of the system (11). The system f f 2 f 3 f A f f f 3 f 4 0 A f f 1 0 f 2 0 f 4 A f f 1 0 f 2 f A A 13 = x y A 14 z A 23 X A 24 Y A 34 Z hs unique solution. Using (4) nd (5), we obtin the vlues of the A ij in terms of, b,, nd d. In prtiulr, we obtin α 2 = A 11 = 2 + 3bd 4S. This together with (10) implies tht α 2 r 2 proof. (11) = 2, s desired in (3), nd ompletes the Theorem 2 bove desribes ompletely how to onstrut generl inspheril tetrhedron. We drw three vetors OA 1, OA 2, nd OA 3 tht mke n ngle of 120 with eh other nd tht hve rbitrry lengths, b, nd (see Fig. 5). In other words, we tke tringle A 1 A 2 A 3 with Fermt-Torrielli point O. By vlley-folding long the edges of A 1 A 2 A 3, we rete three more tringles B 1 A 2 A 3, A 1 B 2 A 3, nd A 1 A 2 B 3 tht re identil with A 1 A 2 A 3. Let O 1, O 2, nd O 3 be the Fermt-Torrielli points of these tringles, respetively. For eh j, tke point C j on the line segments O j B j in suh wy tht O 1 C 1, O 2 C 2, nd O 3 C 3 hve the sme length, d sy. Now, we ut long the edges A 1 C 2, C 2 A 3, A 3 C 1, C 1 A 2, A 2 C 3, nd C 3 A 1 nd we vlley-fold long the sides of A 1 A 2 A 3 until the points C 1, C 2, nd C 3 oinide nd oupy the sme position, sy. The resulting tetrhedron A 1 A 2 A 3 stisfies the onditions of Theorem 2, nd thus is inspheril. It is quite legitimte to question the lim, impliitly mde bove, tht totlly rbitrry positive numbers, b,, d do give rise to fesible tetrhedron. After ll, very similr sitution ws met when onstruting n equifil tetrhedron. Trying to get the verties of given tringle to oinide nd oupy the sme position by vlley-folding long the three segments tht join, two by two, the mid-points of the sides, one soon disovers tht this is possible only if the given tringle is ute-ngled. Theorem 3 below ssures us tht the onstrution desribed in the previous prgrph is vlid for ll hoies of positive, b,, d. Its proof mkes use of the following lemm.
8 30 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron Lemm 3. Let x, y, z, X, Y, Z be given positive numbers. Then there exists tetrhedron suh tht the lengths of the sides of one of its fes re x, y, z nd the lengths of the opposite sides re X, Y, Z, respetively, if nd only if the right hnd side of (6) is positive nd ll the relevnt tringle inequlities pertining to the six fes re stisfied. Proof. See [9] or [3]. Theorem 3. Let 1, 2, 3, 4 be rbitrry positive numbers. Then there exists tetrhedron A 1 A 2 A 3 whose fes hve interior Fermt-Torrielli points D 1, D 2, D 3, D 4, suh tht A i D j = A i D k = A i D t = i for ll rrngements (i, j, k, t) of {1, 2, 3, 4}. C 2 B 2 A 1 O 2 C 3 B 3 O 3 O A 3 O 1 B 1 A 2 C 1 Figure 5: Proof. Let 1, 2, 3, 4 be renmed s, b,, d nd let x, X,... be defined s in (4). In view of the onstrution exhibited in Fig. 5, nd in view of Lemm 3, we need only show tht the right hnd side of (6) is positive. This holds sine the right hnd side of (6) simplifies into the positive quntity bds given in (7). 4. Reltion to other Gergonne enters We end this note by disussing possible lterntive definitions of the Gergonne enter. Observe tht ny evins A 1 D 1, A 2 D 2, nd A 3 D 3 of tringle A 1 A 2 A 3 divide the sides into six segments A i D j, i j, nd tht these evins meet t the Gergonne enter if nd only if ny two of these segments tht shre vertex re equl, or equivlently A i D j = A i D k for every rrngement (i, j, k) of {1, 2, 3}. Similrly, ny evins A 1 D 1, A 2 D 2, A 3 D 3, nd D 4 of tetrhedron A 1 A 2 A 3 divide the fes into 12 tringles A i A j D k, i, j, k re pirwise distint. In [8], it ws proved tht there
9 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron 31 exist unique onurrent evins suh tht the twelve tringles into whih they divide the fes hve the property tht ny two whih shre n edge hve equl re, or equivlently A i A j D s nd A i A j D t hve the sme re for every rrngement (i, j, s, t) of {1, 2, 3, 4}. (12) The bove disussion shows tht the inspheril enter is obtined by repling (12) with the stronger requirement tht A i A j D s nd A i A j D t re ongruent for every rrngement (i, j, s, t) of {1, 2, 3, 4}. (13) This shows in prtiulr tht if the inspheril enter exists, then it is the Gergonne enter itself. Thus in sense, the two pprohes to defining the Gergonne enter of tetrhedron led to the sme enter. Also, ny referene to the insphere is mde obsolete in view of (13). It is nturl to lso investigte the result of repling (13) by the similr ondition A i A j D s nd A j A i D t re ongruent for every rrngement (i, j, s, t) of {1, 2, 3, 4} (14) nd to see whether this skew-ongruene ondition, too, is equivlent to some nturl geometri requirement. The next theorem provides the nswer. Theorem 4. Let T = A 1 A 2 A 3 be tetrhedron nd let A j D j, 1 j 4, be the unique onurrent evins (gurnteed in [8]) tht stisfy (12). Then (13) holds if nd only if T is inspheril (in whih se the D j s re the Fermt-Torrielli points of the fes), nd (14) holds if nd only if T is equifil (in whih se the D j s re the entroids of the fes.) Proof. If (13) holds, then the first prgrph in the proof of Theorem 1 shows tht the D j s re the Fermt-Torrielli points of the fes. By Theorem 2, T is inspheril. Conversely, if T is inspheril, then the Fermt-Torrielli points stisfy (13) nd hene (12). By their uniqueness, the D j s re the Fermt-Torrielli points nd hene they stisfy (13). If (14) holds, then letting, b, nd α, α,... be s shown in Fig. 2, we see tht (1) holds nd leds to the onlusion (2). Thus the fes of T re ongruent nd T is equifil. Conversely, if T is equifil, then the entroids of the fes stisfy (12). By their uniqueness, the D j s re the entroids nd hene they stisfy (14). Epilogue nd knowledgments After writing this rtile, it me to our ttention tht the problem of hrterizing inspheril tetrhedr ws onsidered by Edwin Koźniewski nd Rent A. Górsk in [11], where n lterntive hrteriztion is hieved. We re grteful to E. Koźniewski for sending us opy of [11] nd for drwing our ttention to the ft tht our Theorem 1 is lredy known to Aleksey Zslvsky s nnouned in [15]. We re lso grteful to Zslvsky for writing nd telling us tht the mteril in [15] will pper (in Russin) in the Mrh 2004 issue of Mthemtiheskoe Prosveshenije nd tht the ontents re ontributions by sholrs D. Kosov (Mosow), M. Isev (Brnul) nd V. Filimonov (Ekterinburg). Lter, we found out tht Theorem 1 is more thn one entury old, s implied by Footnote 1 of [4, pge 373], where the term isogonl is used to men inspheril. The sme footnote sttes tht the three ngles subtended by the sides of fe of tetrhedron t the point where the insphere touhes tht fe re the sme for ll fes. Thus if the insphere of tetrhedron touhes fe ABC t X, then the mesures of the three ngles AXB, BXC, nd CXA
10 32 M. Hjj, P. Wlker: The Inspheril Gergonne Center of Tetrhedron re independent of tht prtiulr fe. This beutiful, yet obsure, theorem is lso stted in [5, 2nd prgrph, pge 174], nd it lerly implies tht the ondition, in Theorem 1, tht ll points of ontt of the insphere of ABCD with the fes re the Fermt-Torrielli points of the respetive fes is equivlent to the seemingly weker ondition tht one of these points is. The first-nmed uthor is supported by reserh grnt from Yrmouk University nd would like to express his thnks for tht grnt. The uthors re lso grteful to Aymn Hjj for drwing the figures nd to the editors for onverting them into PostSript. Referenes [1] S. Abu-Symeh, M. Hjj: On the Fermt-Torrielli points of tetrhedr (nd higher dimensionl simplexes). Mth. Mg. 70, (1997). [2] N. Altshiller-Court: Modern Pure Solid Geometry. Chelse Publishing Co., N.Y [3] L.M. Blumenthl: A budget of urios metri. Amer. Mth. Monthly 66, (1959). [4] B.H. Brown: A theorem on isogonl tetrhedr. Amer. Mth. Monthly 31, (1924). [5] J.L. Coolidge: Some unsolved problems in solid geometry. Amer. Mth. Monthly 30, (1923). [6] M. Hjj: An dvned lulus pproh to finding the Fermt point. Mth. Mg. 67, (1994). [7] M. Hjj: A vetor proof of theorem of Bng. Amer. Mth. Monthly 108, (2001). [8] M. Hjj, P. Wlker: The Gergonne nd Ngel enters of tetrhedron. J. Geom. 75, (2002). [9] F. Herzog: Completely tetrhedrl sextuples. Amer. Mth. Monthly 66, (1959). [10] R. Honsberger: Mthemtil Gems II. Dolini Mthemtil Expositions No. 2, Mthemtil Assoition of Ameri, Wshington, DC, [11] E. Koźniewski, R.A. Górsk: Gergonne nd Ngel points for simplies in the n- dimensionl spe. J. Geometry Grphis 4, (2000). [12] Y.S. Kupitz, H. Mrtini: The Fermt-Torrielli point nd isoseles tetrhedr. J. Geom. 49, (1994). [13] Y.S. Kupitz, H. Mrtini: Geometri spets of the generlized Fermt-Torrielli problem. Intuitive Geometry, Bolyi Soiety Mth. Studies 6, (1997). [14] S. Lndy: A generliztion of Cev s theorem to higher dimensions. Amer. Mth. Monthly 95, (1988). [15] A. Zslvsky: Comprtive Geometry in the Tringle nd the Tetrhedron. Reeived November 30, 2003; finl form July 19, 2004
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Two Triads of Congruent Circles from Reflections
 Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Section 3.6. Definite Integrals
 The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
The Intouch Triangle and the OI-line
 Forum Geometriorum Volume 4 004 15 134. FORUM GEOM ISSN 1534-1178 The Intouh Tringle nd the OI-line Eri Dnneel Abtrt. We prove ome intereting reult relting the intouh tringle nd the OI line of tringle.
Forum Geometriorum Volume 4 004 15 134. FORUM GEOM ISSN 1534-1178 The Intouh Tringle nd the OI-line Eri Dnneel Abtrt. We prove ome intereting reult relting the intouh tringle nd the OI line of tringle.
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
#A42 INTEGERS 11 (2011) ON THE CONDITIONED BINOMIAL COEFFICIENTS
 #A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
#A42 INTEGERS 11 (2011 ON THE CONDITIONED BINOMIAL COEFFICIENTS Liqun To Shool of Mthemtil Sienes, Luoyng Norml University, Luoyng, Chin lqto@lynuedun Reeived: 12/24/10, Revised: 5/11/11, Aepted: 5/16/11,
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
Co-ordinated s-convex Function in the First Sense with Some Hadamard-Type Inequalities
 Int. J. Contemp. Mth. Sienes, Vol. 3, 008, no. 3, 557-567 Co-ordinted s-convex Funtion in the First Sense with Some Hdmrd-Type Inequlities Mohmmd Alomri nd Mslin Drus Shool o Mthemtil Sienes Fulty o Siene
Int. J. Contemp. Mth. Sienes, Vol. 3, 008, no. 3, 557-567 Co-ordinted s-convex Funtion in the First Sense with Some Hdmrd-Type Inequlities Mohmmd Alomri nd Mslin Drus Shool o Mthemtil Sienes Fulty o Siene
Solutions to Assignment 1
 MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
SOME COPLANAR POINTS IN TETRAHEDRON
 Journl of Pure n Applie Mthemtis: Avnes n Applitions Volume 16, Numer 2, 2016, Pges 109-114 Aville t http://sientifivnes.o.in DOI: http://x.oi.org/10.18642/jpm_7100121752 SOME COPLANAR POINTS IN TETRAHEDRON
Journl of Pure n Applie Mthemtis: Avnes n Applitions Volume 16, Numer 2, 2016, Pges 109-114 Aville t http://sientifivnes.o.in DOI: http://x.oi.org/10.18642/jpm_7100121752 SOME COPLANAR POINTS IN TETRAHEDRON
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Hyers-Ulam stability of Pielou logistic difference equation
 vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
vilble online t wwwisr-publitionsom/jns J Nonliner Si ppl, 0 (207, 35 322 Reserh rtile Journl Homepge: wwwtjnsom - wwwisr-publitionsom/jns Hyers-Ulm stbility of Pielou logisti differene eqution Soon-Mo
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
arxiv: v1 [math.ca] 21 Aug 2018
![arxiv: v1 [math.ca] 21 Aug 2018 arxiv: v1 [math.ca] 21 Aug 2018](/thumbs/84/89276688.jpg) rxiv:1808.07159v1 [mth.ca] 1 Aug 018 Clulus on Dul Rel Numbers Keqin Liu Deprtment of Mthemtis The University of British Columbi Vnouver, BC Cnd, V6T 1Z Augest, 018 Abstrt We present the bsi theory of
rxiv:1808.07159v1 [mth.ca] 1 Aug 018 Clulus on Dul Rel Numbers Keqin Liu Deprtment of Mthemtis The University of British Columbi Vnouver, BC Cnd, V6T 1Z Augest, 018 Abstrt We present the bsi theory of
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
More Properties of the Riemann Integral
 More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
More Properties of the Riemnn Integrl Jmes K. Peterson Deprtment of Biologil Sienes nd Deprtment of Mthemtil Sienes Clemson University Februry 15, 2018 Outline More Riemnn Integrl Properties The Fundmentl
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Electromagnetism Notes, NYU Spring 2018
 Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
f (x)dx = f(b) f(a). a b f (x)dx is the limit of sums
 Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Properties of Different Types of Lorentz Transformations
 merin Journl of Mthemtis nd ttistis 03 3(3: 05-3 DOI: 0593/jjms03030303 roperties of Different Types of Lorentz Trnsformtions tikur Rhmn izid * Md hh lm Deprtment of usiness dministrtion Leding niversity
merin Journl of Mthemtis nd ttistis 03 3(3: 05-3 DOI: 0593/jjms03030303 roperties of Different Types of Lorentz Trnsformtions tikur Rhmn izid * Md hh lm Deprtment of usiness dministrtion Leding niversity
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
16z z q. q( B) Max{2 z z z z B} r z r z r z r z B. John Riley 19 October Econ 401A: Microeconomic Theory. Homework 2 Answers
 John Riley 9 Otober 6 Eon 4A: Miroeonomi Theory Homework Answers Constnt returns to sle prodution funtion () If (,, q) S then 6 q () 4 We need to show tht (,, q) S 6( ) ( ) ( q) q [ q ] 4 4 4 4 4 4 Appeling
John Riley 9 Otober 6 Eon 4A: Miroeonomi Theory Homework Answers Constnt returns to sle prodution funtion () If (,, q) S then 6 q () 4 We need to show tht (,, q) S 6( ) ( ) ( q) q [ q ] 4 4 4 4 4 4 Appeling
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
Linearly Similar Polynomials
 Linerly Similr Polynomils rthur Holshouser 3600 Bullrd St. Chrlotte, NC, US Hrold Reiter Deprtment of Mthemticl Sciences University of North Crolin Chrlotte, Chrlotte, NC 28223, US hbreiter@uncc.edu stndrd
Linerly Similr Polynomils rthur Holshouser 3600 Bullrd St. Chrlotte, NC, US Hrold Reiter Deprtment of Mthemticl Sciences University of North Crolin Chrlotte, Chrlotte, NC 28223, US hbreiter@uncc.edu stndrd
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
The Riemann-Stieltjes Integral
 Chpter 6 The Riemnn-Stieltjes Integrl 6.1. Definition nd Eistene of the Integrl Definition 6.1. Let, b R nd < b. ( A prtition P of intervl [, b] is finite set of points P = { 0, 1,..., n } suh tht = 0
Chpter 6 The Riemnn-Stieltjes Integrl 6.1. Definition nd Eistene of the Integrl Definition 6.1. Let, b R nd < b. ( A prtition P of intervl [, b] is finite set of points P = { 0, 1,..., n } suh tht = 0
42nd International Mathematical Olympiad
 nd Interntionl Mthemticl Olympid Wshington, DC, United Sttes of Americ July 8 9, 001 Problems Ech problem is worth seven points. Problem 1 Let ABC be n cute-ngled tringle with circumcentre O. Let P on
nd Interntionl Mthemticl Olympid Wshington, DC, United Sttes of Americ July 8 9, 001 Problems Ech problem is worth seven points. Problem 1 Let ABC be n cute-ngled tringle with circumcentre O. Let P on
Technische Universität München Winter term 2009/10 I7 Prof. J. Esparza / J. Křetínský / M. Luttenberger 11. Februar Solution
 Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
= x x 2 = 25 2
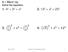 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Well Centered Spherical Quadrangles
 Beiträge zur Algebr und Geometrie Contributions to Algebr nd Geometry Volume 44 (003), No, 539-549 Well Centered Sphericl Qudrngles An M d Azevedo Bred 1 Altino F Sntos Deprtment of Mthemtics, University
Beiträge zur Algebr und Geometrie Contributions to Algebr nd Geometry Volume 44 (003), No, 539-549 Well Centered Sphericl Qudrngles An M d Azevedo Bred 1 Altino F Sntos Deprtment of Mthemtics, University
Duality # Second iteration for HW problem. Recall our LP example problem we have been working on, in equality form, is given below.
 Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
SEMI-EXCIRCLE OF QUADRILATERAL
 JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
JP Journl of Mthemtil Sienes Volume 5, Issue &, 05, Pges - 05 Ishn Pulishing House This pper is ville online t http://wwwiphsiom SEMI-EXCIRCLE OF QUADRILATERAL MASHADI, SRI GEMAWATI, HASRIATI AND HESY
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
Bisimulation, Games & Hennessy Milner logic
 Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Bisimultion, Gmes & Hennessy Milner logi Leture 1 of Modelli Mtemtii dei Proessi Conorrenti Pweł Soboiński Univeristy of Southmpton, UK Bisimultion, Gmes & Hennessy Milner logi p.1/32 Clssil lnguge theory
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P. (a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg) Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
2. Topic: Summation of Series (Mathematical Induction) When n = 1, L.H.S. = S 1 = u 1 = 3 R.H.S. = 1 (1)(1+1)(4+5) = 3
 GCE A Level Otober/November 008 Suggested Solutions Mthemtis H (970/0) version. MATHEMATICS (H) Pper Suggested Solutions. Topi: Definite Integrls From the digrm: Are A = y dx = x Are B = x dy = y dy dx
GCE A Level Otober/November 008 Suggested Solutions Mthemtis H (970/0) version. MATHEMATICS (H) Pper Suggested Solutions. Topi: Definite Integrls From the digrm: Are A = y dx = x Are B = x dy = y dy dx
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Vectors. Chapter14. Syllabus reference: 4.1, 4.2, 4.5 Contents:
 hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
HW3, Math 307. CSUF. Spring 2007.
 HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.
![T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions. T b a(f) [f ] +. P b a(f) = Conclude that if f is in AC then it is the difference of two monotone absolutely continuous functions.](/thumbs/78/77085178.jpg) Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
Rel Vribles, Fll 2014 Problem set 5 Solution suggestions Exerise 1. Let f be bsolutely ontinuous on [, b] Show tht nd T b (f) P b (f) f (x) dx [f ] +. Conlude tht if f is in AC then it is the differene
MAA 4212 Improper Integrals
 Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
Notes by Dvid Groisser, Copyright c 1995; revised 2002, 2009, 2014 MAA 4212 Improper Integrls The Riemnn integrl, while perfectly well-defined, is too restrictive for mny purposes; there re functions which
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
The Relationship between the Nine-Point Circle, the Circumscribed Circle and the Inscribed Circle of Archimedes Triangle Yuporn Rimcholakarn
 Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
Integral points on the rational curve
 Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
Line Integrals. Chapter Definition
 hpter 2 Line Integrls 2.1 Definition When we re integrting function of one vrible, we integrte long n intervl on one of the xes. We now generlize this ide by integrting long ny curve in the xy-plne. It
hpter 2 Line Integrls 2.1 Definition When we re integrting function of one vrible, we integrte long n intervl on one of the xes. We now generlize this ide by integrting long ny curve in the xy-plne. It
Lecture 3. Limits of Functions and Continuity
 Lecture 3 Limits of Functions nd Continuity Audrey Terrs April 26, 21 1 Limits of Functions Notes I m skipping the lst section of Chpter 6 of Lng; the section bout open nd closed sets We cn probbly live
Lecture 3 Limits of Functions nd Continuity Audrey Terrs April 26, 21 1 Limits of Functions Notes I m skipping the lst section of Chpter 6 of Lng; the section bout open nd closed sets We cn probbly live
