Ellipses. The second type of conic is called an ellipse.
|
|
|
- Beryl Mason
- 5 years ago
- Views:
Transcription
1 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d d Fous Fous d + d is onstnt. There re numer of prts of n ellipse tht should e noted:
2 overte verte mjor is Fous enter Fous verte minor is overte The midpoint etween the foi is the enter. The line segment through the foi, with endpoints on the ellipses, is the mjor is. The endpoints of the mjor is re the verties of the ellipse. The line segment through the enter nd perpendiulr to the mjor is, with endpoints on the ellipse, is the minor is. The endpoints of the minor is re the overties of the ellipse.
3 There re 3 distnes tht re importnt when studying n ellipse. Fous Fous Fous Fous is lwys the longest length nd is lwys the fol length 3
4 Stndrd Eqution of n Ellipse The stndrd form of the eqution of n ellipse entered t (h, k), with mjor is of length, minor is of length, where 0 < <, is ) ( ) ( k y h Mjor is is horizontl ) ( ) ( k y h Mjor is is vertil The foi lie on the mjor is, units from the enter, with. If the enter is t the origin (0, 0), the eqution tkes one of the following forms. y Mjor is is horizontl y Mjor is is vertil
5 Emple: Find the enter, verties, nd foi of the ellipse given y 9 + y = 36. Solution: First divide through y 36 to get the orret form. y 9 Rememering tht the lrger numer on the ottom orresponds to, we n see tht: so 9 so 3 Using, we n find. 3 The enter of the ellipse is (0, 0). From tht point: We go 3 units up nd down for the verties: (0,3), (0,-3) We go units right nd left for overties: (, 0), (-, 0) We go units up nd down for the foi: (0, ), (0,- )
6 - - Emple: Find the stndrd form of the eqution of the ellipse entered t the origin with mjor is of length 0 nd foi t (±3, 0). Solution: If the mjor is is 0, we know tht =. If the foi re t (±3, 0), we know tht = 3. Solve for
7 Sine the foi lwys lie on the mjor is, we know tht the mjor is is horizontl. Tht tells us tht goes under the term. Sine it is entered t the origin, we hve: y 6 y - - 7
8 Emple: Find the stndrd form of the eqution of the ellipse with foi (0, 0) nd (0, ) with mjor is of length of 8. Solution: If the mjor is is 8, we know tht =. If the foi re t (0, 0) nd (0, ), we know tht is hlf the distne etween them so =. Solve for. 3 Sine the foi lwys lie on the mjor is, we know tht the mjor is is vertil. Tht tells us tht goes under the y term. The enter is hlf wy etween the foi, so the enter must e (0, ). Thus we hve ( 0) ( y ) 6 8
9 y - - Emple: Sketh the grph of y 6 8y 9 0. Solution: You need to omplete the squre with the -terms nd the y-terms. y 6 8y 9 0 *Get the onstnt on the other side nd group the -terms together nd the y-terms terms, putting in lnks on oth sides of the eqution. 9
10 ( 6 ) (y 8y ) 9 *Before ompleting the squre, pull the out of the y group. ( 6 ) ( y y ) 9 *Complete the squres. ( 6 9) ( y y ) 9 9 *Rememer to dd () on the right for the y group. ( 3) ( y ) *Beuse we need on the right, divide through y. ( 3) ( y ) ( 3) ( y enter: (-3, ) mjor is: horizontl nd = minor is: vertil nd = ) 0
11 y - - Emple: Find the enter, verties, nd foi of the ellipse 6 9y 96 36y 36 0 Solution: Put the eqution in stndrd form y ompleting the squres.
12 6 (6 6( 6( 6( 3) 6( 3) ( 3) 9 9y y ) ) 9( y 6 9) 9( y 9( y ( y ) 6 ) (9y 9( y ) y 36 36y y enter: (3, -) mjor is: vertil nd = minor is: horizontl nd = 3 0 ) ) ) Find the foi y first finding The foi re 7 units ove nd elow the enter, so the oordintes would e (3, -+ 7 ) nd (3, -- 7 ).
13 y - - Eentriity To mesure the ovlness of n ellipse, we use the onept of eentriity. Definition of Eentriity The eentriity e of n ellipse is given y the rtio e 3
14 *Note: Beuse is lwys greter thn, the frtion will lwys e etween 0 nd. When is lose to, tht mens the foi re lose the the verties nd the frtion is lose to. When is muh smller thn, tht mens the foi re lose to the enter nd the frtion is smll.
15 Emple: Find the eentriity of the ellipse ) ( 9 ) ( y Solution: Find. 6 3 The eentriity is e Emple: Find the eentriity of the ellipse 7) ( ) ( y so e e e
16 Applition Emple: A pssgewy in house is to hve stright sides nd semielliptilly-rhed top. The stright sides re feet tll nd the pssgewy is 7 feet tll t its enter nd 6 feet wide. Where should the foi e loted to mke the templte for the rh? 6 = 3 nd =. Find The foi should e pled.36 feet to the right nd left of the enter of the semiellipse. 6
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Algebra II Notes Unit Ten: Conic Sections
 Syllus Ojective: 10.1 The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting
Syllus Ojective: 10.1 The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
CONIC SECTIONS. Chapter 11
 CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
I. Equations of a Circle a. At the origin center= r= b. Standard from: center= r=
 11.: Circle & Ellipse I cn Write the eqution of circle given specific informtion Grph circle in coordinte plne. Grph n ellipse nd determine ll criticl informtion. Write the eqution of n ellipse from rel
11.: Circle & Ellipse I cn Write the eqution of circle given specific informtion Grph circle in coordinte plne. Grph n ellipse nd determine ll criticl informtion. Write the eqution of n ellipse from rel
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
8.2: CIRCLES AND ELLIPSES
 8.: CIRCLES AND ELLIPSES GEOMETRY OF AN ELLIPSE Geometry of n Ellipse Definition: An ellipse is the set of ll points in plne whose distnce from two fixed points in the plne hve constnt sum. Voculry The
8.: CIRCLES AND ELLIPSES GEOMETRY OF AN ELLIPSE Geometry of n Ellipse Definition: An ellipse is the set of ll points in plne whose distnce from two fixed points in the plne hve constnt sum. Voculry The
Chapter 6 Continuous Random Variables and Distributions
 Chpter 6 Continuous Rndom Vriles nd Distriutions Mny economic nd usiness mesures such s sles investment consumption nd cost cn hve the continuous numericl vlues so tht they cn not e represented y discrete
Chpter 6 Continuous Rndom Vriles nd Distriutions Mny economic nd usiness mesures such s sles investment consumption nd cost cn hve the continuous numericl vlues so tht they cn not e represented y discrete
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
SIMPLE NONLINEAR GRAPHS
 S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Section 7.1 Area of a Region Between Two Curves
 Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
This enables us to also express rational numbers other than natural numbers, for example:
 Overview Study Mteril Business Mthemtis 05-06 Alger The Rel Numers The si numers re,,3,4, these numers re nturl numers nd lso lled positive integers. The positive integers, together with the negtive integers
Overview Study Mteril Business Mthemtis 05-06 Alger The Rel Numers The si numers re,,3,4, these numers re nturl numers nd lso lled positive integers. The positive integers, together with the negtive integers
K 7. Quadratic Equations. 1. Rewrite these polynomials in the form ax 2 + bx + c = 0. Identify the values of a, b and c:
 Qudrti Equtions The Null Ftor Lw Let's sy there re two numers nd. If # = then = or = (or oth re ) This mens tht if the produt of two epressions is zero, then t lest one of the epressions must e equl to
Qudrti Equtions The Null Ftor Lw Let's sy there re two numers nd. If # = then = or = (or oth re ) This mens tht if the produt of two epressions is zero, then t lest one of the epressions must e equl to
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
P 1 (x 1, y 1 ) is given by,.
 MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
MA00 Clculus nd Bsic Liner Alger I Chpter Coordinte Geometr nd Conic Sections Review In the rectngulr/crtesin coordintes sstem, we descrie the loction of points using coordintes. P (, ) P(, ) O The distnce
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
10.2 The Ellipse and the Hyperbola
 CHAPTER 0 Conic Sections Solve. 97. Two surveors need to find the distnce cross lke. The plce reference pole t point A in the digrm. Point B is meters est nd meter north of the reference point A. Point
CHAPTER 0 Conic Sections Solve. 97. Two surveors need to find the distnce cross lke. The plce reference pole t point A in the digrm. Point B is meters est nd meter north of the reference point A. Point
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
= x x 2 = 25 2
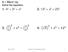 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Scientific notation is a way of expressing really big numbers or really small numbers.
 Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Chapter 1: Fundamentals
 Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Chapter 1: Logarithmic functions and indices
 Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chapters Five Notes SN AA U1C5
 Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P. (a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg) Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
BEGINNING ALGEBRA (ALGEBRA I)
 /0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
/0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
Lesson 1: Quadratic Equations
 Lesson 1: Qudrtic Equtions Qudrtic Eqution: The qudrtic eqution in form is. In this section, we will review 4 methods of qudrtic equtions, nd when it is most to use ech method. 1. 3.. 4. Method 1: Fctoring
Lesson 1: Qudrtic Equtions Qudrtic Eqution: The qudrtic eqution in form is. In this section, we will review 4 methods of qudrtic equtions, nd when it is most to use ech method. 1. 3.. 4. Method 1: Fctoring
Exam 1 Formula Sheet. du a2 u du = arcsin + C du a 2 + u 2 du = du u u 2 a 2 du =
 [rsin(u)] = u x [ros(u)] = u x u [rtn(u)] = + x [rot(u)] = u + x [rse(u)] = u x x [rs(u)] = u x x Exm Formul Sheet tn(u) u = ln os(u) + C ot(u) u = ln sin(u) + C se(u) u = ln se(u) + tn(u) + C s(u) u =
[rsin(u)] = u x [ros(u)] = u x u [rtn(u)] = + x [rot(u)] = u + x [rse(u)] = u x x [rs(u)] = u x x Exm Formul Sheet tn(u) u = ln os(u) + C ot(u) u = ln sin(u) + C se(u) u = ln se(u) + tn(u) + C s(u) u =
k ) and directrix x = h p is A focal chord is a line segment which passes through the focus of a parabola and has endpoints on the parabola.
 Stndrd Eqution of Prol with vertex ( h, k ) nd directrix y = k p is ( x h) p ( y k ) = 4. Verticl xis of symmetry Stndrd Eqution of Prol with vertex ( h, k ) nd directrix x = h p is ( y k ) p( x h) = 4.
Stndrd Eqution of Prol with vertex ( h, k ) nd directrix y = k p is ( x h) p ( y k ) = 4. Verticl xis of symmetry Stndrd Eqution of Prol with vertex ( h, k ) nd directrix x = h p is ( y k ) p( x h) = 4.
A quick overview of the four conic sections in rectangular coordinates is presented below.
 MAT 6H Rectngulr Equtions of Conics A quick overview of the four conic sections in rectngulr coordintes is presented elow.. Circles Skipped covered in previous lger course.. Prols Definition A prol is
MAT 6H Rectngulr Equtions of Conics A quick overview of the four conic sections in rectngulr coordintes is presented elow.. Circles Skipped covered in previous lger course.. Prols Definition A prol is
ES.182A Topic 32 Notes Jeremy Orloff
 ES.8A Topic 3 Notes Jerem Orloff 3 Polr coordintes nd double integrls 3. Polr Coordintes (, ) = (r cos(θ), r sin(θ)) r θ Stndrd,, r, θ tringle Polr coordintes re just stndrd trigonometric reltions. In
ES.8A Topic 3 Notes Jerem Orloff 3 Polr coordintes nd double integrls 3. Polr Coordintes (, ) = (r cos(θ), r sin(θ)) r θ Stndrd,, r, θ tringle Polr coordintes re just stndrd trigonometric reltions. In
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Integration. antidifferentiation
 9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
QUADRATIC EQUATION EXERCISE - 01 CHECK YOUR GRASP
 QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
8.6 The Hyperbola. and F 2. is a constant. P F 2. P =k The two fixed points, F 1. , are called the foci of the hyperbola. The line segments F 1
 8. The Hperol Some ships nvigte using rdio nvigtion sstem clled LORAN, which is n cronm for LOng RAnge Nvigtion. A ship receives rdio signls from pirs of trnsmitting sttions tht send signls t the sme time.
8. The Hperol Some ships nvigte using rdio nvigtion sstem clled LORAN, which is n cronm for LOng RAnge Nvigtion. A ship receives rdio signls from pirs of trnsmitting sttions tht send signls t the sme time.
KEY CONCEPTS. satisfies the differential equation da. = 0. Note : If F (x) is any integral of f (x) then, x a
 KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
KEY CONCEPTS THINGS TO REMEMBER :. The re ounded y the curve y = f(), the -is nd the ordintes t = & = is given y, A = f () d = y d.. If the re is elow the is then A is negtive. The convention is to consider
/ 3, then (A) 3(a 2 m 2 + b 2 ) = 4c 2 (B) 3(a 2 + b 2 m 2 ) = 4c 2 (C) a 2 m 2 + b 2 = 4c 2 (D) a 2 + b 2 m 2 = 4c 2
 SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
SET I. If the locus of the point of intersection of perpendiculr tngents to the ellipse x circle with centre t (0, 0), then the rdius of the circle would e + / ( ) is. There re exctl two points on the
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Plotting Ordered Pairs Using Integers
 SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Mathematics 10 Page 1 of 5 Properties of Triangle s and Quadrilaterals. Isosceles Triangle. - 2 sides and 2 corresponding.
 Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
GEOMETRY OF THE CIRCLE TANGENTS & SECANTS
 Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Calculus AB. For a function f(x), the derivative would be f '(
 lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
SECTION 9-4 Translation of Axes
 9-4 Trnsltion of Aes 639 Rdiotelescope For the receiving ntenn shown in the figure, the common focus F is locted 120 feet bove the verte of the prbol, nd focus F (for the hperbol) is 20 feet bove the verte.
9-4 Trnsltion of Aes 639 Rdiotelescope For the receiving ntenn shown in the figure, the common focus F is locted 120 feet bove the verte of the prbol, nd focus F (for the hperbol) is 20 feet bove the verte.
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
Introduction. Definition of Hyperbola
 Section 10.4 Hperbols 751 10.4 HYPERBOLAS Wht ou should lern Write equtions of hperbols in stndrd form. Find smptotes of nd grph hperbols. Use properties of hperbols to solve rel-life problems. Clssif
Section 10.4 Hperbols 751 10.4 HYPERBOLAS Wht ou should lern Write equtions of hperbols in stndrd form. Find smptotes of nd grph hperbols. Use properties of hperbols to solve rel-life problems. Clssif
Answers for Lesson 3-1, pp Exercises
 Answers for Lesson -, pp. Eercises * ) PQ * ) PS * ) PS * ) PS * ) SR * ) QR * ) QR * ) QR. nd with trnsversl ; lt. int. '. nd with trnsversl ; lt. int. '. nd with trnsversl ; sme-side int. '. nd with
Answers for Lesson -, pp. Eercises * ) PQ * ) PS * ) PS * ) PS * ) SR * ) QR * ) QR * ) QR. nd with trnsversl ; lt. int. '. nd with trnsversl ; lt. int. '. nd with trnsversl ; sme-side int. '. nd with
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS
 QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
