Dynamics of Distant Moons of Asteroids
|
|
|
- Marian McGee
- 5 years ago
- Views:
Transcription
1 ICARUS 128, (1997) ARTICLE NO. IS Dynamics of Distant Moons of Asteroids Douglas P. Hamilton Astronomy Department, University of Maryland, College Park, Maryland and Alexander V. Krivov Astronomical Institute, St. Petersburg University, St. Petersburg, Russia Received October 7, 1996; revised March 24, 1997 solar perturbations dominate. Since the detailed mass distribution We introduce a new analytic method for treating the orbital within the asteroid is relatively unimportant in motions of objects about asteroids and planets. For an asteroid this regime, orbits about one asteroid are similar to those following a circular path around the Sun, we rewrite Jacobi s about another as long as the eccentricities of the asteroidal integral of the motion in terms of the orbital elements relative orbits do not differ greatly. to the asteroid. This procedure is similar to the derivation of In this paper, we investigate two distinct types of or- Tisserand s Constant, but here we make the approximation bits prograde and retrograde in which the Sun, asterthat the satellite is bound to the asteroid rather than far from it. In addition, we retain high order terms that Tisserand ig- oid, and asteroidal satellite all move within a fixed plane. nored and make no assumptions about the relative masses of Prograde orbits are those for which the angular momentum the asteroid and its satellite. We then average our expression vectors of the satellite s motion about the asteroid and the over one circuit of the binary asteroid about its center of mass asteroid s motion around the Sun are parallel; for retro- and obtain the Generalized Tisserand Constant. We use the grade orbits, these vectors are antiparallel. Several numeri- Generalized Tisserand Constant to elucidate properties of dis- cal studies have focused on the differences between protant orbits and test our predictions against numerical integra- grade and retrograde orbits and found the latter are more tions. In particular, we show analytically that planar prograde stable than the former (for historical references, consult orbits are elongated along the Sun asteroid line, that planar retrograde orbits extend furthest perpendicular to the Sun Szebehely 1978; for more recent work see, e.g. Innanen asteroid line, and that retrograde orbits are more stable than 1979, Huang and Innanen 1983, Zhang and Innanen 1988, prograde ones. Our formalism can be extended (i) to three Chauvineau and Mignard 1990a, 1990b, and Hamilton and dimensions and (ii) to apply to faint dusty rings around planets Burns 1991). Approximate analytic escape criteria have by including the effects of planetary oblateness, radiation pres- been derived, most of which follow from considerations sure, and the electromagnetic force from a rotating dipolar of the Jacobi constant (e.g. Szebehely 1978, and Markellos magnetic field Academic Press and Roy 1981) or equating forces in a rotating frame (e.g. King 1962, Innanen 1979). Interestingly, all previous estimates 1. INTRODUCTION which made use of the Jacobi constant show that, with increasing orbital size, retrograde orbits are energetically able to escape before prograde orbits despite the fact The unexpected discovery of Dactyl, a moon with radius 0.75 km orbiting the asteroid Ida, suggests that binary that retrograde orbits are numerically observed to be more asteroids may be quite common and has led to renewed stable. Here we resolve this apparent paradox by deriving interest in the orbital dynamics of asteroidal satellites. Sevand using it to show analytically that prograde orbits are a Generalized Tisserand Constant from Jacobi s Integral, eral recent studies have investigated orbits of a test mass near an irregular, rotating asteroid where a highly nonnot indeed less stable than retrograde orbits. Our purpose is spherical gravity field determines orbital motions (Geissler to derive a highly accurate orbital theory (e.g. Brown et al. 1995, Scheeres 1994, Scheeres et al. 1996). Here we and Shook 1933, Murray and Harper 1993), but rather to instead focus on relatively distant orbits where the influence elucidate the differences between prograde and retrograde of an asteroid s asymmetric gravity field is small and orbits about asteroids and planets with a simple analytical /97 $25.00 Copyright 1997 by Academic Press All rights of reproduction in any form reserved.
2 242 HAMILTON AND KRIVOV argument. In the next sections, we first derive the General- appears in Eq. (2)), which is an excellent approximation ized Tisserand Constant and then use it to investigate basic as long as the comet is far from the planet. For the current properties of distant orbits. application to distant circumasteroidal orbits, however, gravity from both the Sun and the asteroid is important 2. GENERALIZED TISSERAND CONSTANT and, moreover, that of the asteroid dominates. We must, therefore, extend Tisserand s Constant by including both The three body problem of celestial mechanics, for which asteroidal and solar gravity. no general analytic solution exists, has been extensively This is accomplished by first transforming Jacobi s intestudied and classified into several subproblems. One of gral from Sun-centered to asteroid-centered coordinates these, the restricted three body problem, concerns the mo- (e.g., Chauvineau and Mignard 1990a, Hamilton and Burns tion of an (assumed massless) particle in the gravitational 1991) since the asteroid s gravity is the dominant force. fields of two massive objects. The two large objects are We simplify the integral by taking only the first-order peruninfluenced by the massless particle and hence move turbation term due to solar gravity, the so-called tidal along Keplerian orbits; these orbits are circles in the circu- term rather than the full expression. This step is Hill s lar restricted three body problem. Although there is no approximation; it assumes that the asteroid satellite disgeneral solution for the circular restricted three body prob- tance is much less than the asteroid Sun distance which lem either, an integral of the motion known as Jacobi s is an excellent approximation for all bound asteroidal satelintegral or Jacobi s constant does exist. Jacobi s integral lites. Hill s approximation also assumes that one mass (the is normally written as a function of the coordinates (x cm, Sun) is large compared to the other two (the binary astery cm ) of the massless body measured in a reference frame oid), while the circular restricted approximation assumes with its origin at the center of mass of the system (nearly that one mass (the asteroidal satellite) is small compared the center of the Sun for the Sun asteroid system which we to the other two (the Sun and the asteroid); these approxiconsider) and rotating with the constant angular velocity n mations are independent cases of the full three body probof the circular orbits. In this frame, Jacobi s integral has lem (e.g. Hénon and Petit 1986). As we are using Hill s the form (Danby 1988): approximation, the following results apply to binary asteroids with arbitrary mass ratios; in particular, the satellite s mass need not be small compared to the asteroid s. Trans- C 2GM 2GM n 2 (x 2 cm y 2 cm) v 2 cm, (1) r r forming Jacobi s integral, we find (Hamilton and Burns 1991) that where G is the gravitational constant, M and M are the solar and asteroidal masses, and r and r are the distances from the third body to the Sun and to the asteroid, respectively. C 2GM n 2 (3x 2 z 2 ) v 2, r (3) The coordinate x cm is measured along the Sun asteroid line, the coordinate y cm is perpendicular to this where n (GM /R 3 ) 1/2 is the mean motion of the asteroid line and in the plane of the asteroid s orbit, and v cm is the about the Sun. The quantities x, z, v, and C/2 are the speed of the massless object in the rotating reference coordinate along the Sun asteroid line, the vertical coordiframe. The total orbital energy measured in the rotating nate, the speed, and the orbital energy, respectively all frame is given by C /2, where C is Jacobi s constant. If measured in the rotating asteroid centered reference the coordinates of the massless body are eliminated in frame. This expression is accurate to first order in r/r (cf. favor of its orbital elements one obtains, after assuming Eq. (1)). M M and large r, Tisserand s Constant, Next, we convert the asteroid-centered Jacobi integral into orbital elements relative to the asteroid. The first and last terms are simple to convert and yield a result which 2 C GM 2n 2 R a 1/2 a R (1 e 2 ) 1/2 cos(i ). (2) is only slightly different from Eq. (2), Here a, e, i are the heliocentric semimajor axis, eccentricity, and inclination of the massless body, respectively, C GM a 2nn a 2 (1 e 2 ) 1/2 cos(i) n 2 (3x 2 r 2 ), (4) and R is the Sun asteroid distance. Tisserand originally considered the Sun Jupiter comet problem and applied where n (GM/a 3 ) 1/2 is the mean motion of the satellite Eq. (2) to identify comets which had suffered gravitational around the asteroid, and a, e, i are the semimajor axis, interactions with Jupiter. Tisserand s Constant includes the effects of solar gravity on the assumed massless comet but ignores the gravity of Jupiter (note that only the solar mass eccentricity, and inclination of the circumasteroidal orbit. The first two terms of Eq. (4) are much larger than the final term for strongly bound orbits but inclusion of the
3 DISTANT MOONS OF ASTEROIDS 243 final term, which contains the solar tidal perturbations on vation is particularly enlightening, however, because (i) it circumasteroidal orbits, extends the zone of validity of the connects Eq. (6) to the well-known Jacobi integral of the Tisserand Constant to more distant orbits. Unfortunately, circular restricted three-body problem, and (ii) it demonstrates the solar tidal term is more difficult to transform into orbital unambiguously that Eq. (6) may be generalized to elements; its conversion yields an expression with 12 three dimensions. terms which not only are functions of the semimajor axis The three-dimensional version of Eq. (6) can be further a, eccentricity e, and inclination i, as Tisserand s Constant generalized by the inclusion of additional time-independent (Eq. (2)) is, but also are functions of the longitudes of the forces that can be derived from potentials including ascending node, pericenter ϖ, and the satellite l as well planetary oblateness and solar radiation pressure (Hamilton (six variables in all). To reduce the complexity of this result, and Krivov 1996). Electromagnetic forces on a charged we make two simplifying assumptions. First, we limit our ring particle orbiting in a spinning dipolar magnetic field study to planar orbits, which eliminates the dependence cannot be included for three-dimensional orbits but, for on i and, and second, we average our expression over planar orbits, Hamilton and Krivov (1996) found an effective one circuit of the satellite around the asteroid, which eliminates electromagnetic energy which, when added to Eq. the dependence on l. The result is the Generalized (6), reproduces the correct equations of motion. Tisserand Constant: 3. PROGRADE AND RETROGRADE ORBITS C GM 3.1. Distant Orbits a 2nn a 2 (1 e 2 ) 1/2 a2 n 2 2 (5) The validity of the Generalized Tisserand Constant may 3a2 e 2 n 2 [1 5 cos(2 )], be tested by performing numerical integrations of asteroi- 4 dal satellites and monitoring the constant H as calculated from Eq. (6). We use a simple Bulirsch-Stoer routine and where the plus sign corresponds to prograde orbits (i numerically solve Newton s F ma in a frame centered 0) and the minus sign to retrograde orbits (i 180 ), and on the asteroid. As expected, H is well conserved for orbits is the angle between the Sun and the orbit s pericenter close to the asteroid (which are nearly Keplerian). For as seen from the asteroid. more distant orbits, solar perturbations are stronger, orbit- When orbit-averaging, however, we make the implicit averaging yields poorer results, and H is less well conassumption that the changes to a Keplerian orbit due to served. Nevertheless, even for very distant orbits H reperturbations are small over one orbital period. This ap- mains nearly constant and is still a useful quantity. We proximation is the most restrictive of all those made so demonstrate this with several example orbits started with far; it introduces errors which are greatest for orbits most a r H (this corresponds to 64(R/1 AU)( /2.0 g distant from the asteroid (where the solar gravity is a large cm 3 ) 1/3 asteroid radii or about 1.5 times the lunar distance perturbation). In addition, orbit-averaging results in a for Earth-centered orbits), eccentricities between 0.0 and purely secular expression mean motion resonances be- 0.8, and 0. Here r H (M/3M ) 1/3 R is the radius of tween the satellite and asteroid orbital periods, which are the Hill sphere. The orbits, which are plotted in Fig. 1, are important for some distant orbits (e.g. Jupiter s Sinope, not far from the numerically determined prograde stability Saha and Tremaine 1993), are ignored by our method. limit at 0.49r H (Hamilton and Burns 1991). Finally, Eq. (5) need not remain constant all along an orbit, Rather than showing plots of H versus time for the orbits only its average is conserved from one orbit to the next. of Fig. 1, we take advantage of the fact that H can be easily Since the orbit-averaging procedure also yields the result plotted as a function of the two variables e and. In Fig. a const (e.g. Hamilton 1993), our two approximations 2, we show contours of constant H for orbits with a reduce the number of variables from six to only two: e and r H as calculated from Eq. (6). In addition, we trans-. Combining the constants C, GM/a, and a 2 n 2 /2 into a late the (x, y) pairs of Fig. 1 into (e, ) pairs and overplot single constant H and dividing through by 2nn a 2,wefi- them on each panel of Fig. 2. In this way, we can compare nally obtain: numerical integrations directly to theory. The numerically determined orbits of Fig. 2 are elongated as predicted by the contours, but have nonzero width due to variations of H (1 e 2 ) 1/2 3n e 2 8n [1 5 cos(2 )], (6) H over one orbital period. This indicates that the orbitaveraging approximation is not especially good for such where again the plus sign corresponds to prograde orbits distant orbits. Furthermore, the orbits with eccentricities and the minus sign to retrograde orbits. The prograde 0.7 and 0.8 are more elongated than predicted which indicates version of this expression was first derived by Hamilton that our method is less accurate for these highly and Krivov (1996) using another method. The present deri- eccentric orbits. Orbits with large eccentricities reach
4 244 HAMILTON AND KRIVOV FIG. 1. Nine prograde orbits started at pericenter with a r H, eccentricities between 0.0 and 0.8, and 0; here r H (M/3M ) 1/3 R is the Hill radius. The orbits are plotted in a rotating frame centered on the asteroid (solid circle, not to scale), so the Sun is always located along the positive x-axis. The length and width of each box is 1.0r H. Note that the zones swept out by the orbits are elongated along the Sun asteroid line. each of the level curves. Since the eccentricity is maximum at 0 and (Fig. 2), the eccentricity varies with a period of one half an asteroid year. This result is in agreement with perturbation theory, e.g. Goldreich et al. (1989), and with numerical integrations, e.g. Hamilton and Burns (1991), Benner and McKinnon (1995a). Figures 3 and 4 are the retrograde equivalents of Figs. 1 and 2. Although the initial satellite asteroid separation is the same in all four figures, several interesting differences between the prograde and retrograde plots are immediately apparent. First, the retrograde orbits and curves of constant H are extended perpendicular to the Sun-asteroid line rather than parallel to it. The different orientation of the prograde and retrograde level curves of H follows from the change of sign in Eq. (6), and Fig. 4 shows that this perpendicular extension is a general property of the entire family of retrograde orbits with a r H. Furthermore, a careful inspection of Figs. 2 and 4 shows that the level curves are less elongated for retrograde orbits than for prograde ones; this property is also apparent in the greater distances from the asteroid where the larger solar perturbations cause our averaging method to be less valid. Nevertheless, it is a triumph for the method that it successfully predicts the shape and orientation of these distant orbits. From the level curves of Fig. 2, we can also predict the shape and orientation of the orbits in space (cf. Fig. 1). Each orbit reaches its maximum eccentricity, and also its most distant and closest points to the asteroid, when 0or. Thus the level curves of Fig. 2 correctly predict that orbits will be stretched toward and away from the Sun in Fig. 1. The level curves also imply that the entire family of prograde orbits with a r H will be elongated along the Sun asteroid line since any initial condition in the (e, ) plane should closely follow one of the oval curves in the clockwise direction (see Fig. 2). This is a powerful statement: Fig. 2 predicts the shape of all orbits with a r H, regardless of the starting eccentricity e, solar angle, and position along the elliptical orbit l. Finally, while Eq. (6) gives the exact shape of the level curves of Fig. 2, it provides no information about the time it takes a satellite to complete one circuit around a given level curve. For weakly perturbed orbits, however, the angle between the Sun and orbital pericenter,, varies primarily due to the motion of the Sun. Hence it takes about one asteroidal year for a satellite to travel around FIG. 2. Lines of constant H for prograde orbits from Eq. (6) (oval curves) plotted in polar coordinates h e cos( ) and k e sin( ) for the conditions of Fig. 1. Curves correspond to initial conditions e 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0 with 0 the outer circles indicate e 1. For each panel, the orbit from the corresponding panel of Fig. 1 was translated into (e, ) coordinates and plotted as points over the lines of constant H. The agreement between theory (ovals) and the numerically calculated orbits is good, but not perfect. Nevertheless, in all cases the curves are broadest along the horizontal axis which indicates the orbits are most eccentric when 0or ; i.e., these orbits extend furthest from the asteroid in the solar and antisolar directions in agreement with Fig. 1.
5 DISTANT MOONS OF ASTEROIDS 245 FIG. 3. Nine retrograde orbits started at pericenter with a r H, eccentricities between 0.0 and 0.8, and 0. As in Fig. 1, the orbits are plotted in rotating coordinates with the Sun along the positive x-axis, the asteroid is marked with a solid circle, and the size of the box is 1.0r H. Note that, in contrast to Fig. 1, the retrograde orbits are most extended perpendicular to the Sun asteroid line. The particle in the final graph collided with the asteroid after a short time. because our orbit-averaged approximation assumes bound, nearly Keplerian orbits. Using Eq. (6) to study the bound escape transition pushes the theory beyond its design specifications but, surprisingly, the level curves of Fig. 6 still provide useful information for these very distant orbits. For instance, note the gradual transformation of phase space with increasing distance in Fig. 6. The curves start out nearly circular in the upper left graph, indicating that the orbital eccentricities of not-so-distant prograde orbits do not change much. Level curves for more distant orbits are increasingly flattened along the Sun asteroid line and finally, for orbits distant enough to escape, the prograde phase space begins to show a figure-eight topology. These results predict that all bound prograde orbits, regardless of their size, are extended along the Sun asteroid line with the distortion increasing for larger orbits. Furthermore, when escape does occur, it occurs along the Sun asteroid line where tidal forces are greatest and where Eq. (6) predicts that prograde orbits are most elongated. The change in topology of the phase portraits in Fig. 6 is also quite interesting. The oval topology for near-asteroid actual orbits displayed in Figs. 1 and 3. This shape difference between prograde and retrograde orbits stems from the interplay between the -dependent and the -independent parts of the second term of Eq. (6); in the vertical directions of Figs. 2 and 4, these terms compete, while in the horizontal directions they reinforce one another Very Distant Orbits All of these differences between prograde and retrograde orbits can be more clearly seen when the initial starting distance from the asteroid is varied. Figures 5 and 6 show prograde orbits similar to Figs. 1 and 2, except that we vary the orbital size rather than the eccentricity from panel to panel. All prograde orbits in Fig. 5 are started on initially circular paths; these orbits become progressively more perturbed as the initial distance is increased until escape from the asteroid inevitably occurs. Low-energy escape from circumasteroidal space always occurs near one of the Lagrange points located along the Sun asteroid line at a r H (Hamilton and Burns 1991); in Fig. 5, the four escape orbits all slip past L 1, the Lagrange point between the asteroid and the Sun, on their way to heliocentric space. The phase curves of Fig. 6, by contrast, predict that all prograde orbits remain bound since the level curves all close. In fact, Eq. (6) can never directly predict escape FIG. 4. Lines of constant H (selected as in Fig. 2) for retrograde orbits from Eq. (6) (oval curves) plotted in polar coordinates h e cos( ) and k e sin( ) for the conditions of Fig. 3. The orbits were overplotted in the same manner as in Fig. 2. The agreement between theory (ovals) and the orbits is significantly better than in Fig. 2, but differences are still noticeable. In all cases the curves are broadest along the vertical axis which indicates the orbits are most eccentric when /2 or 3 /2; these orbits extend furthest from the asteroid in directions perpendicular to the Sun asteroid line in agreement with Fig. 3.
6 246 HAMILTON AND KRIVOV FIG. 5. Nine different-sized prograde orbits started with e 0.0 from the positive x-axis. Coordinates and symbols are as in Fig. 1. In the first four panels, the satellite is bound, in panel 8 it crashes into the asteroid, and in the remaining panels it escapes. Note that bound orbits are stretched in along the Sun asteroid line (x-axis) and that escape always occurs along this line. indications that the underlying figure-eight topology is a good approximation to reality. First, if we interpret the predictions of the bottom row of Fig. 6 s graphs literally, initially circular orbits should increase their eccentricities to the point where impacts with the asteroid are possible. While most distant orbits are stripped away from the asteroid before an impact occurs, the orbit in the eighth graph of Fig. 5 does intersect the asteroid as predicted; in fact, this hypothetical satellite strikes the asteroid from roughly the anti-sun direction, one of the two possibilities predicted by Fig. 6. Second, consider the fourth panel of Figs. 5 and 6 which shows an interesting orbit which always keeps its pericenter away from the Sun. This type of librating orbit is exactly what is predicted to exist in the lefthand lobe of one of the figure-eights of Fig. 6, although it appears slightly earlier than our theory predicts. Support for this interpretation comes from work by Hénon (1969) who studied periodic orbits in Hill s problem. Working with prograde orbits, Hénon (1969) found a bifurcation of a stable nearly-circular periodic orbit (his critical orbit g1) into a symmetric pair of stable elongated periodic orbits (members of his family g ) and an unstable periodic orbit (a member of his family g). We identify our topology change with Hénon s bifurcation of simple periodic orbits orbits has an equilibrium point at e 0, which corresponds to an unperturbed circular orbit (first graph in Figs. 5 and 6). Taken literally, Eq. (6) predicts that orbits with e 0 should be unperturbed; in reality, short-period oscillations ignored in the orbit-averaging process cause orbits to evolve somewhat, but eccentricities do remain small as predicted (top three graphs of Figs. 5 and 6). The figureeight topology, by contrast, has three equilibrium points 2 maxima and a saddle at e 0 (Hamilton and Krivov 1996). Orbits starting with e 0 are not stable, but rather evolve rapidly so that they are extended along the Sun asteroid line; i.e. these orbits change from relatively safe circular orbits to elongated ones which are subject to strong destabilizing tidal perturbations. It is perhaps not surprising that orbits begin to escape at just about the point where the single equilibrium point at e 0 bifurcates into three. By considering the derivatives of Eq. (6), we find that the prograde change of topology occurs at A 3n / 4n 1/6 (Hamilton and Krivov 1996), which can be written as a 0.53r H, while numerical simulations show that initially circular orbits escape when launched at distances outside about 0.49r H (Hamilton and Burns 1991). We should be very careful to avoid overinterpreting the predictions of the figure-eight phase space after all, this topology occurs only for very distant orbits which are not well governed by Eq. (6). Nevertheless, there are several FIG. 6. Phase plots: lines of constant H for the prograde orbits of Fig. 5 (cf. Fig. 2). Curves correspond to initial conditions e 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0 with 0 and 180. Note the change in topology between the fourth and fifth graphs, roughly coincident with where escape first occurs in Fig. 5. In each panel, the initially circular orbit from Fig. 5 is converted into h e cos( ) and k e sin( ) coordinates and overplotted.
7 DISTANT MOONS OF ASTEROIDS 247 FIG. 7. Nine different-sized retrograde orbits started with e 0.0 from the positive x-axis. Coordinates and symbols are as in Fig. 1, and starting distances are as in Fig. 5. All orbits are bound and extended perpendicular to the Sun asteroid line. Note that this extension is more pronounced for larger orbits. (in our approximation, all orbits are simple periodic!). Hénon s bifurcation occurs at a 0.45r H, which agrees well with our numerical results for the librating orbit of Figs. 5 and 6. The discrepancy between this value and our prediction of 0.53r H illustrates the errors inherent in applying our orbit-averaged approach to distant orbits, and is the price that one pays for simplicity! Figure 7 shows initially circular retrograde orbits started at the same distances as the prograde orbits in Fig. 5; Fig. 8 is the phase-portrait counterpart. All of the retrograde orbits in Fig. 7 are bound and stretched perpendicular to the Sun asteroid line as predicted by the contours of Fig. 8. Furthermore, as with prograde orbits, the distortions increase with distance from the asteroid until finally retrograde orbits become perturbed enough to escape at about a r H. Thus Fig. 8 predicts that all retrograde orbits, regardless of a, e,, and l, are elongated perpendicular to the Sun asteroid line. Increasing distortions in these directions are consistent with the limiting epicyclic motion in the rotating frame: i.e. for extremely distant retrograde orbits, the asteroid s gravity is unimportant and motion in the rotating frame occurs along a 2 : 1 ellipse centered on the asteroid and elongated perpendicular to the Sun asteroid line (Hamilton and Burns 1991). The 2 : 1 ellipse is a member of a retrograde family of periodic orbits, all of which are elongated perpendicular to the Sun asteroid line and all of which are stable (Hénon 1969). As with prograde orbits, we calculate the point at which the retrograde change of topology occurs (A 1/4 or a 0.69r H ) and compare it to the numerically determined escape distance of a r H. The discrepancy between these values is large, and it appears that the figure-eight topology is not a good indicator of instability for retrograde orbits. In fact, Hénon (1969) finds that his retrograde family of periodic orbits, family f, experiences no bifurcation, hence it is likely that the topology change that we find is an artifact of the averaging process. These conclusions are supported by the two largest orbits of Figs. 7 and 8, which do not extend as far from the asteroid as their level curves predict. Our secular orbit-averaged theory predicts that all prograde orbits are elongated along the Sun asteroid line while all retrograde orbits are extended in the perpendicular directions. This conclusion is consistent with the fact that the majority of simple periodic orbits studied by Hénon (1969) are stable when they are elongated in the directions that we predict in this work. In addition, Hénon s unstable periodic orbits are almost alway elongated in directions opposite to our predictions. In comparing Figs. 5 8, note that, for each distance, the prograde curves are more elongated than their retrograde counterparts as we noticed for the a r H examples in Figs This too, is a general property of distant orbits. Another difference between prograde and retrograde is that while the pre- FIG. 8. Phase plots: lines of constant H for the retrograde orbits of Fig. 7 (cf. Fig. 4). Note the change in topology between the sixth and seventh graphs. In each panel, the initially circular orbit from Fig. 7 is converted into h e cos( ) and k e sin( ) coordinates and overplotted.
8 248 HAMILTON AND KRIVOV dicted topology of phase space changes from ovals to fig- these orbits, respectively. In Figs. 2, 4, 6 and 8, the Coriolis ure-eights for both types of orbits, the transformation occurs acceleration causes satellites to move along the curves of closer to the asteroid for prograde orbits than for constant H in such a way that retrograde satellites complete retrograde ones. one cycle faster than prograde orbits do. This gives pro- These differences between prograde and retrograde or- grade orbits more time to built up greater deviations from bits, all of which follow from the Generalized Tisserand the prediction of Eq. (6) than retrograde orbits as seen in Constant, support the notion that retrograde orbits should Figs. 2, 4, 6, and 8. Hence the Coriolis acceleration, like the be more stable that prograde ones. Prograde orbits are Generalized Tisserand Constant, causes prograde orbits to elongated in the dangerous toward-sun and away-from- be less stable than retrograde ones (Hamilton and Burns Sun directions where the solar tidal forces are strongest, 1991). It is the omission of Coriolis effects that limits the while retrograde orbits are extended in the perpendicular accuracy of all escape criteria derived from the Jacobi directions. In addition, the change in topology from ovals Constant, including our change-of-topology criterion dis- to figure-eights occurs earlier for prograde than for retro- cussed in the last paragraph. grade orbits. If we use topology change as an approximate criterion for escape, we obtain analytic results (stability 4. SUMMARY for initially circular prograde orbits with a 0.53r H and for initially circular retrograde orbits with a 0.69r H ) In this short paper, we have derived an accurate asteroidcentered which, while not in impressive agreement with numerical (or planet-centered) version of Tisserand s Conwhich, results, are superior to all others attained to date. In fact, stant and applied it to planar prograde and retrograde these results are the only ones based on the Jacobi Constant orbits around asteroids moving on circular paths around that correctly predict that prograde orbits are less the Sun. Our method is most applicable to distant orbits stable than retrograde ones. There are several caveats, which are far enough from the asteroid that the effects of however. Our naive change-of-topology criterion ignores its asymmetric gravity field may be ignored, but close the orientation of the figure-eight in phase space and includes enough that the orbits are only weakly perturbed by solar errors introduced in the averaging process. It also gravity. The method also proves to be a useful guide for assumes that the change in the phase space topology corresponds the more distant strongly perturbed orbits studied here. to a real change in orbital dynamics, which although Simple analytical arguments based on the Generalized Tis- true for prograde orbits, appears not to be the case for serand Constant show that all prograde orbits are extended retrograde ones. For these reasons, and because the effects along the Sun-asteroid line and that all retrograde orbits of the Coriolis acceleration are not include in the Generalized are elongated at right angles to this line, with the magnitude Tisserand Constant as discussed below, the stability of the distortion increasing for more distant orbits. More limits predicted by this method should not be taken too seriously. careful reasoning, using the Generalized Tisserand Con- stant, knowledge of the form of the tidal acceleration field, Another major difference between prograde and retrograde and of the direction of the Coriolis acceleration (whose orbits is that, at a given distance, the retrograde effects are not included in Eq. (6)) shows that retrograde orbits (Figs. 4 and 8) clearly fit the predictions of Eq. (6) orbits are more stable that prograde ones. much better than do the prograde orbits (Figs. 2 and 6). Our approach can be extended to three dimensions, but This indicates that our assumptions, in particular the orbitaveraged the resulting expression is somewhat unwieldy. Neverthe- approximation, are better for retrograde orbits. less, a three-dimensional version of Eq. (6) may provide Since the Generalized Tisserand Constant predicts that explanations for additional properties of distant orbits, all orbits are bound, its validity must break down before such as the propensity for objects on highly inclined orbits satellites can actually escape; hence prograde orbits are to strike the central asteroid (Hamilton and Burns 1991, able to escape earlier than retrograde ones. This difference 1992). A spectacular example of the instability of highly cannot be understood with the Generalized Tisserand Constant; inclined orbits is given by Lidov (1961, 1963) who showed it follows rather from the Coriolis acceleration in that if the Moon had a circular i 90 orbit, it would strike the rotating frame as pointed out by Hamilton and Burns the Earth in just over six years! Comet Shoemaker Levy (1991). The effects of the Coriolis acceleration are not 9, a temporary highly inclined satellite of Jupiter which included in Eq. (6), which is the energy integral in a frame struck the planet in 1994, provides another dramatic exam- rotating with the mean motion of the asteroid around the ple (Benner and McKinnon 1995b). As with the planar Sun. Since the Coriolis acceleration is always perpendicular prograde and retrograde orbits studied here, however, the to the satellite s velocity vector, it cannot affect the energy most interesting effects occur when the orbit-averaging integral. The Coriolis acceleration points inward for retrograde approximation begins to break down; in such cases the orbits and outward for prograde orbits (Hamilton Generalized Tisserand Constant must be applied with and Burns 1991) which tends to stabilize and destabilize caution.
9 DISTANT MOONS OF ASTEROIDS 249 ACKNOWLEDGMENTS Hamilton, D. P., and A. V. Krivov Circumplanetary dust dynamics: Effects of solar gravity, radiation pressure, planetary oblateness, and We thank Prasenjit Saha and Dan Scheeres for their detailed and electromagnetism. Icarus 123, helpful reviews of this work. Hénon, M Numerical exploration of the restricted problem, V. Astron. Astrophys. 1, Hénon, M., and J. M. Petit Series expansions for encounter-type REFERENCES solutions of Hill s problem. Celest. Mech. 38, Benner, L. A. M., and W. B. McKinnon 1995a. Orbital behavior of Huang, T.-Y., and K. A. Innanen The gravitational escape/capture captured satellites: The effect of solar gravity on Triton s postcapture of planetary satellites. Astron. J. 88, orbit. Icarus 114, Innanen, K. A The limiting radii of direct and retrograde satellite Benner, L. A. M., and W. B. McKinnon 1995b. On the orbital evolution orbits, with applications to the solar system and to stellar systems. Astron. J. 84, and origin of Comet Shoemaker Levy 9. Icarus 118, King, I The structure of star clusters. I. An empirical density law. Brown, E. W., and C. A. Shook Planetary Theory. Cambridge Univ. Astron. J. 67, Press, Cambridge, UK. Lidov, M. L Evolution of orbits of artificial planetary satellites Chauvineau, B., and F. Mignard 1990a. Dynamics of binary asteroids perturbed by gravity of external bodies. In Artificial Earth Satellites, I Hill s case. Icarus 83, Issue 8. [In Russian] Chauvineau, B., and F. Mignard 1990b. Dynamics of binary asteroids Lidov, M. L On the approximate analysis of orbital evolution of II Jovian perturbations. Icarus 87, artificial satellites. In Problems of Motion of Artificial Celestial Bodies. Danby, J. M. A Fundamentals of Celestial Mechanics, 2nd ed. Academy of Sciences of USSR, Moscow. [in Russian] Willmann Bell, Richmond, VA. Markellos, V. V., and A. E. Roy Hill stability of satellite orbits. Geissler, P., J.-M. Petit, D. Durda, R. Greenberg, W. Bottke, M. Nolan, Celest. Mech. 23, and J. Moore Erosion and ejecta reaccretion on 243 Ida and its Murray, C. D., and D. Harper Expansion of the Planetary Disturbing moon. Icarus 120, Goldreich, P., N. Murray, P. Y. Longaretti, and D. Banfield Neptune s story. Science, 245, Scheeres, D. J Dynamics about uniformly rotating tri-axial ellip- Hamilton, D. P Motion of dust in a planetary magnetosphere: Orbit-averaged equations for oblateness, electromagnetic, and radiation forces with application to Saturn s E ring. Icarus 101, ; soids. Icarus 110, Erratum. Icarus 103, 161. Hamilton, D. P., and J. A. Burns Orbital stability zones about asteroids. Icarus 92, Hamilton, D. P., and J. A. Burns Orbital stability zones about asteroids II. The destabilizing effects of eccentric orbits and of solar radiation. Icarus 96, Function to Eighth Order in the Individual Orbital Elements, QMW Math Notes No. 15. Queen Mary and Westfield College, London. Saha, P., and S. Tremaine The orbits of the retrograde jovian satellites. Icarus 106, Scheeres, D. J., S. J. Ostro, R. S. Hudson, and R. A. Werner Orbits close to Asteroid 4769 Castalia, Icarus 121, Szebehely, V Stability of artificial and natural satellites. Celest. Mech. 18, Zhang, S. P., and K. A. Innanen The stable region of satellites of large asteroids. Icarus 75,
A REGION VOID OF IRREGULAR SATELLITES AROUND JUPITER
 The Astronomical Journal, 136:909 918, 2008 September c 2008. The American Astronomical Society. All rights reserved. Printed in the U.S.A. doi:10.1088/0004-6256/136/3/909 A REGION VOID OF IRREGULAR SATELLITES
The Astronomical Journal, 136:909 918, 2008 September c 2008. The American Astronomical Society. All rights reserved. Printed in the U.S.A. doi:10.1088/0004-6256/136/3/909 A REGION VOID OF IRREGULAR SATELLITES
Astronomy 241: Review Questions #2 Distributed: November 7, 2013
 Astronomy 241: Review Questions #2 Distributed: November 7, 2013 Review the questions below, and be prepared to discuss them in class. For each question, list (a) the general topic, and (b) the key laws
Astronomy 241: Review Questions #2 Distributed: November 7, 2013 Review the questions below, and be prepared to discuss them in class. For each question, list (a) the general topic, and (b) the key laws
Lecture 13. Gravity in the Solar System
 Lecture 13 Gravity in the Solar System Guiding Questions 1. How was the heliocentric model established? What are monumental steps in the history of the heliocentric model? 2. How do Kepler s three laws
Lecture 13 Gravity in the Solar System Guiding Questions 1. How was the heliocentric model established? What are monumental steps in the history of the heliocentric model? 2. How do Kepler s three laws
Kozai-Lidov oscillations
 Kozai-Lidov oscillations Kozai (1962 - asteroids); Lidov (1962 - artificial satellites) arise most simply in restricted three-body problem (two massive bodies on a Kepler orbit + a test particle) e.g.,
Kozai-Lidov oscillations Kozai (1962 - asteroids); Lidov (1962 - artificial satellites) arise most simply in restricted three-body problem (two massive bodies on a Kepler orbit + a test particle) e.g.,
Gravitation and the Motion of the Planets
 Gravitation and the Motion of the Planets 1 Guiding Questions 1. How did ancient astronomers explain the motions of the planets? 2. Why did Copernicus think that the Earth and the other planets go around
Gravitation and the Motion of the Planets 1 Guiding Questions 1. How did ancient astronomers explain the motions of the planets? 2. Why did Copernicus think that the Earth and the other planets go around
Gravitation and the Waltz of the Planets
 Gravitation and the Waltz of the Planets Chapter Four Guiding Questions 1. How did ancient astronomers explain the motions of the planets? 2. Why did Copernicus think that the Earth and the other planets
Gravitation and the Waltz of the Planets Chapter Four Guiding Questions 1. How did ancient astronomers explain the motions of the planets? 2. Why did Copernicus think that the Earth and the other planets
Gravitation and the Waltz of the Planets. Chapter Four
 Gravitation and the Waltz of the Planets Chapter Four Guiding Questions 1. How did ancient astronomers explain the motions of the planets? 2. Why did Copernicus think that the Earth and the other planets
Gravitation and the Waltz of the Planets Chapter Four Guiding Questions 1. How did ancient astronomers explain the motions of the planets? 2. Why did Copernicus think that the Earth and the other planets
Kepler, Newton, and laws of motion
 Kepler, Newton, and laws of motion First: A Little History Geocentric vs. heliocentric model for solar system (sec. 2.2-2.4)! The only history in this course is this progression: Aristotle (~350 BC) Ptolemy
Kepler, Newton, and laws of motion First: A Little History Geocentric vs. heliocentric model for solar system (sec. 2.2-2.4)! The only history in this course is this progression: Aristotle (~350 BC) Ptolemy
Dynamical properties of the Solar System. Second Kepler s Law. Dynamics of planetary orbits. ν: true anomaly
 First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
First Kepler s Law The secondary body moves in an elliptical orbit, with the primary body at the focus Valid for bound orbits with E < 0 The conservation of the total energy E yields a constant semi-major
PADEU. Pulsating zero velocity surfaces and capture in the elliptic restricted three-body problem. 1 Introduction
 PADEU PADEU 15, 221 (2005) ISBN 963 463 557 c Published by the Astron. Dept. of the Eötvös Univ. Pulsating zero velocity surfaces and capture in the elliptic restricted three-body problem F. Szenkovits
PADEU PADEU 15, 221 (2005) ISBN 963 463 557 c Published by the Astron. Dept. of the Eötvös Univ. Pulsating zero velocity surfaces and capture in the elliptic restricted three-body problem F. Szenkovits
Gravity: Motivation An initial theory describing the nature of the gravitational force by Newton is a product of the resolution of the
 Gravity: Motivation An initial theory describing the nature of the gravitational force by Newton is a product of the resolution of the Geocentric-Heliocentric debate (Brahe s data and Kepler s analysis)
Gravity: Motivation An initial theory describing the nature of the gravitational force by Newton is a product of the resolution of the Geocentric-Heliocentric debate (Brahe s data and Kepler s analysis)
AST111, Lecture 1b. Measurements of bodies in the solar system (overview continued) Orbital elements
 AST111, Lecture 1b Measurements of bodies in the solar system (overview continued) Orbital elements Planetary properties (continued): Measuring Mass The orbital period of a moon about a planet depends
AST111, Lecture 1b Measurements of bodies in the solar system (overview continued) Orbital elements Planetary properties (continued): Measuring Mass The orbital period of a moon about a planet depends
1 The Solar System. 1.1 a journey into our galaxy
 1 The Solar System Though Pluto, and the far-flung depths of the Solar System, is the focus of this book, it is essential that Pluto is placed in the context of the planetary system that it inhabits our
1 The Solar System Though Pluto, and the far-flung depths of the Solar System, is the focus of this book, it is essential that Pluto is placed in the context of the planetary system that it inhabits our
arxiv: v1 [astro-ph.ep] 3 Apr 2018
![arxiv: v1 [astro-ph.ep] 3 Apr 2018 arxiv: v1 [astro-ph.ep] 3 Apr 2018](/thumbs/94/120341164.jpg) Astronomy& Astrophysics manuscript no. zanardi_ c ESO 28 September 2, 28 The role of the general relativity on icy body reservoirs under the effects of an inner eccentric Jupiter M. Zanardi, 2, G. C. de
Astronomy& Astrophysics manuscript no. zanardi_ c ESO 28 September 2, 28 The role of the general relativity on icy body reservoirs under the effects of an inner eccentric Jupiter M. Zanardi, 2, G. C. de
An Introduction to Celestial Mechanics
 An Introduction to Celestial Mechanics This accessible text on classical celestial mechanics the principles governing the motions of bodies in the solar system provides a clear and concise treatment of
An Introduction to Celestial Mechanics This accessible text on classical celestial mechanics the principles governing the motions of bodies in the solar system provides a clear and concise treatment of
THE PLANE OF THE KUIPER BELT
 The Astronomical Journal, 127:2418 2423, 2004 April # 2004. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE PLANE OF THE KUIPER BELT Michael E. Brown Division of Geological
The Astronomical Journal, 127:2418 2423, 2004 April # 2004. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE PLANE OF THE KUIPER BELT Michael E. Brown Division of Geological
Tides and Lagrange Points
 Ast111, Lecture 3a Tides and Lagrange Points Arial view of Tidal surge in Alaska (S. Sharnoff) Tides Tidal disruption Lagrange Points Tadpole Orbits and Trojans Tidal Bulges Tides Tidal Force The force
Ast111, Lecture 3a Tides and Lagrange Points Arial view of Tidal surge in Alaska (S. Sharnoff) Tides Tidal disruption Lagrange Points Tadpole Orbits and Trojans Tidal Bulges Tides Tidal Force The force
D. A system of assumptions and principles applicable to a wide range of phenomena that has been repeatedly verified
 ASTRONOMY 1 EXAM 1 Name Identify Terms - Matching (20 @ 1 point each = 20 pts.) 1 Solar System G 7. aphelion N 14. eccentricity M 2. Planet E 8. apparent visual magnitude R 15. empirical Q 3. Star P 9.
ASTRONOMY 1 EXAM 1 Name Identify Terms - Matching (20 @ 1 point each = 20 pts.) 1 Solar System G 7. aphelion N 14. eccentricity M 2. Planet E 8. apparent visual magnitude R 15. empirical Q 3. Star P 9.
Resonance and chaos ASTRONOMY AND ASTROPHYSICS. II. Exterior resonances and asymmetric libration
 Astron. Astrophys. 328, 399 48 (1997) ASTRONOMY AND ASTROPHYSICS Resonance and chaos II. Exterior resonances and asymmetric libration O.C. Winter 1,2 and C.D. Murray 2 1 Grupo de Dinâmica Orbital e Planetologia,
Astron. Astrophys. 328, 399 48 (1997) ASTRONOMY AND ASTROPHYSICS Resonance and chaos II. Exterior resonances and asymmetric libration O.C. Winter 1,2 and C.D. Murray 2 1 Grupo de Dinâmica Orbital e Planetologia,
Astronomy Section 2 Solar System Test
 is really cool! 1. The diagram below shows one model of a portion of the universe. Astronomy Section 2 Solar System Test 4. Which arrangement of the Sun, the Moon, and Earth results in the highest high
is really cool! 1. The diagram below shows one model of a portion of the universe. Astronomy Section 2 Solar System Test 4. Which arrangement of the Sun, the Moon, and Earth results in the highest high
Most of the time during full and new phases, the Moon lies above or below the Sun in the sky.
 6/16 Eclipses: We don t have eclipses every month because the plane of the Moon s orbit about the Earth is different from the plane the ecliptic, the Earth s orbital plane about the Sun. The planes of
6/16 Eclipses: We don t have eclipses every month because the plane of the Moon s orbit about the Earth is different from the plane the ecliptic, the Earth s orbital plane about the Sun. The planes of
Introduction To Modern Astronomy I
 ASTR 111 003 Fall 2006 Lecture 03 Sep. 18, 2006 Introduction To Modern Astronomy I Introducing Astronomy (chap. 1-6) Planets and Moons (chap. 7-17) Ch1: Astronomy and the Universe Ch2: Knowing the Heavens
ASTR 111 003 Fall 2006 Lecture 03 Sep. 18, 2006 Introduction To Modern Astronomy I Introducing Astronomy (chap. 1-6) Planets and Moons (chap. 7-17) Ch1: Astronomy and the Universe Ch2: Knowing the Heavens
Satellite Communications
 Satellite Communications Lecture (3) Chapter 2.1 1 Gravitational Force Newton s 2nd Law: r r F = m a Newton s Law Of Universal Gravitation (assuming point masses or spheres): Putting these together: r
Satellite Communications Lecture (3) Chapter 2.1 1 Gravitational Force Newton s 2nd Law: r r F = m a Newton s Law Of Universal Gravitation (assuming point masses or spheres): Putting these together: r
AST Section 2: Test 1
 AST1002 - Section 2: Test 1 Date: 10/06/2009 Name: Equations: c = λ f, λ peak = Question 1: A star with a declination of +40.0 degrees will be 1. east of the vernal equinox. 2. west of the vernal equinox.
AST1002 - Section 2: Test 1 Date: 10/06/2009 Name: Equations: c = λ f, λ peak = Question 1: A star with a declination of +40.0 degrees will be 1. east of the vernal equinox. 2. west of the vernal equinox.
Orbital Stability Regions for Hypothetical Natural Satellites
 Orbital Stability Regions for Hypothetical Natural Satellites By Samantha RIEGER, 1) Daniel SCHEERES, 1) 1) Ann and H.J. Smead Department of Aerospace Engineering Sciences, University of Colorado Boulder,
Orbital Stability Regions for Hypothetical Natural Satellites By Samantha RIEGER, 1) Daniel SCHEERES, 1) 1) Ann and H.J. Smead Department of Aerospace Engineering Sciences, University of Colorado Boulder,
October 19, NOTES Solar System Data Table.notebook. Which page in the ESRT???? million km million. average.
 Celestial Object: Naturally occurring object that exists in space. NOT spacecraft or man-made satellites Which page in the ESRT???? Mean = average Units = million km How can we find this using the Solar
Celestial Object: Naturally occurring object that exists in space. NOT spacecraft or man-made satellites Which page in the ESRT???? Mean = average Units = million km How can we find this using the Solar
Periodic Orbits in Rotating Second Degree and Order Gravity Fields
 Chin. J. Astron. Astrophys. Vol. 8 (28), No. 1, 18 118 (http://www.chjaa.org) Chinese Journal of Astronomy and Astrophysics Periodic Orbits in Rotating Second Degree and Order Gravity Fields Wei-Duo Hu
Chin. J. Astron. Astrophys. Vol. 8 (28), No. 1, 18 118 (http://www.chjaa.org) Chinese Journal of Astronomy and Astrophysics Periodic Orbits in Rotating Second Degree and Order Gravity Fields Wei-Duo Hu
Phys 214. Planets and Life
 Phys 214. Planets and Life Dr. Cristina Buzea Department of Physics Room 259 E-mail: cristi@physics.queensu.ca (Please use PHYS214 in e-mail subject) Lecture 28. Search for life on jovian moons. March
Phys 214. Planets and Life Dr. Cristina Buzea Department of Physics Room 259 E-mail: cristi@physics.queensu.ca (Please use PHYS214 in e-mail subject) Lecture 28. Search for life on jovian moons. March
The Restricted 3-Body Problem
 The Restricted 3-Body Problem John Bremseth and John Grasel 12/10/2010 Abstract Though the 3-body problem is difficult to solve, it can be modeled if one mass is so small that its effect on the other two
The Restricted 3-Body Problem John Bremseth and John Grasel 12/10/2010 Abstract Though the 3-body problem is difficult to solve, it can be modeled if one mass is so small that its effect on the other two
Useful Formulas and Values
 Name Test 1 Planetary and Stellar Astronomy 2017 (Last, First) The exam has 20 multiple choice questions (3 points each) and 8 short answer questions (5 points each). This is a closed-book, closed-notes
Name Test 1 Planetary and Stellar Astronomy 2017 (Last, First) The exam has 20 multiple choice questions (3 points each) and 8 short answer questions (5 points each). This is a closed-book, closed-notes
as the orbits of distant planetoids are expected to be randomized over billions of year by the gravity of the four giant planets.
 Dynamics of Extreme Outer Solar System Objects Principle investigators/supervisors: Denis Gaidashev (Matematiska Institution); Erik Zackrisson (Institutionen fo r fysik och astronomi) 1. Purpose and aims
Dynamics of Extreme Outer Solar System Objects Principle investigators/supervisors: Denis Gaidashev (Matematiska Institution); Erik Zackrisson (Institutionen fo r fysik och astronomi) 1. Purpose and aims
ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS
 ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS A1.1. Kepler s laws Johannes Kepler (1571-1630) discovered the laws of orbital motion, now called Kepler's laws.
ANNEX 1. DEFINITION OF ORBITAL PARAMETERS AND IMPORTANT CONCEPTS OF CELESTIAL MECHANICS A1.1. Kepler s laws Johannes Kepler (1571-1630) discovered the laws of orbital motion, now called Kepler's laws.
Celestial mechanics and dynamics. Topics to be covered. The Two-Body problem. Solar System and Planetary Astronomy Astro 9601
 Celestial mechanics and dynamics Solar System and Planetary Astronomy Astro 9601 1 Topics to be covered The two-body problem (.1) The three-body problem (.) Perturbations and resonances (.3) Long-term
Celestial mechanics and dynamics Solar System and Planetary Astronomy Astro 9601 1 Topics to be covered The two-body problem (.1) The three-body problem (.) Perturbations and resonances (.3) Long-term
Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws
 Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws Craig Lage New York University - Department of Physics craig.lage@nyu.edu February 24, 2014 1 / 21 Tycho Brahe s Equatorial
Observational Astronomy - Lecture 4 Orbits, Motions, Kepler s and Newton s Laws Craig Lage New York University - Department of Physics craig.lage@nyu.edu February 24, 2014 1 / 21 Tycho Brahe s Equatorial
Celestial mechanics and dynamics. Solar System and Planetary Astronomy Astro 9601
 Celestial mechanics and dynamics Solar System and Planetary Astronomy Astro 9601 1 Topics to be covered The two-body problem (2.1) The three-body problem (2.2) Perturbations ti and resonances (2.3) Long-term
Celestial mechanics and dynamics Solar System and Planetary Astronomy Astro 9601 1 Topics to be covered The two-body problem (2.1) The three-body problem (2.2) Perturbations ti and resonances (2.3) Long-term
WILLIAM I. NEWMAN, UCLA PHILIP W. SHARP, U. OF AUCKLAND BRUCE G. BILLS, JPL
 CATASTROPHIC METEORITE 1 IMPACTS ON EARTH WILLIAM I. NEWMAN, UCLA PHILIP W. SHARP, U. OF AUCKLAND BRUCE G. BILLS, JPL Solar system with different scales for distance and for size: presents role of giant
CATASTROPHIC METEORITE 1 IMPACTS ON EARTH WILLIAM I. NEWMAN, UCLA PHILIP W. SHARP, U. OF AUCKLAND BRUCE G. BILLS, JPL Solar system with different scales for distance and for size: presents role of giant
AS3010: Introduction to Space Technology
 AS3010: Introduction to Space Technology L E C T U R E S 8-9 Part B, Lectures 8-9 23 March, 2017 C O N T E N T S In this lecture, we will look at factors that cause an orbit to change over time orbital
AS3010: Introduction to Space Technology L E C T U R E S 8-9 Part B, Lectures 8-9 23 March, 2017 C O N T E N T S In this lecture, we will look at factors that cause an orbit to change over time orbital
Today. Planetary Motion. Tycho Brahe s Observations. Kepler s Laws Laws of Motion. Laws of Motion
 Today Planetary Motion Tycho Brahe s Observations Kepler s Laws Laws of Motion Laws of Motion In 1633 the Catholic Church ordered Galileo to recant his claim that Earth orbits the Sun. His book on the
Today Planetary Motion Tycho Brahe s Observations Kepler s Laws Laws of Motion Laws of Motion In 1633 the Catholic Church ordered Galileo to recant his claim that Earth orbits the Sun. His book on the
Planetary system dynamics. Planetary migration Kozai resonance Apsidal resonance and secular theories Mean motion resonances Gravitational scattering
 Planetary system dynamics Planetary migration Kozai resonance Apsidal resonance and secular theories Mean motion resonances Gravitational scattering How should the planets of a typical planetary system
Planetary system dynamics Planetary migration Kozai resonance Apsidal resonance and secular theories Mean motion resonances Gravitational scattering How should the planets of a typical planetary system
INVESTIGATION OF ORBITAL EVOLUTION OF INTERPLANETARY DUST PARTICLES ORIGINATING FROM KUIPER BELT AND ASTEROID BELT OBJECTS
 INVESTIGATION OF ORBITAL EVOLUTION OF INTERPLANETARY DUST PARTICLES ORIGINATING FROM KUIPER BELT AND ASTEROID BELT OBJECTS 1 PALAK DHARSANDIA, 2 DR. JAYESH PABARI, 3 DR. CHARMY PATEL 1 Research Scholar,
INVESTIGATION OF ORBITAL EVOLUTION OF INTERPLANETARY DUST PARTICLES ORIGINATING FROM KUIPER BELT AND ASTEROID BELT OBJECTS 1 PALAK DHARSANDIA, 2 DR. JAYESH PABARI, 3 DR. CHARMY PATEL 1 Research Scholar,
Clicker Question: Clicker Question: Clicker Question:
 Test results Last day to drop without a grade is Feb 29 Grades posted in cabinet and online F D C B A In which direction would the Earth move if the Sun s gravitational force were suddenly removed from
Test results Last day to drop without a grade is Feb 29 Grades posted in cabinet and online F D C B A In which direction would the Earth move if the Sun s gravitational force were suddenly removed from
Tenuous ring formation by the capture of interplanetary dust at Saturn
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 110,, doi:10.1029/2004ja010577, 2005 Tenuous ring formation by the capture of interplanetary dust at Saturn C. J. Mitchell, 1 J. E. Colwell, and M. Horányi 1 Laboratory
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 110,, doi:10.1029/2004ja010577, 2005 Tenuous ring formation by the capture of interplanetary dust at Saturn C. J. Mitchell, 1 J. E. Colwell, and M. Horányi 1 Laboratory
Joseph Castro Mentor: Nader Haghighipour
 ON THE POSSIBILITY OF ADDITIONAL PLANETS IN THE γ CEPHEI BINARY-PLANETARY SYSTEM Joseph Castro Mentor: Nader Haghighipour ABSTRACT Results of the simulations of the dynamical stability of additional hypothetical
ON THE POSSIBILITY OF ADDITIONAL PLANETS IN THE γ CEPHEI BINARY-PLANETARY SYSTEM Joseph Castro Mentor: Nader Haghighipour ABSTRACT Results of the simulations of the dynamical stability of additional hypothetical
Celestial mechanics and dynamics. Topics to be covered
 Celestial mechanics and dynamics Solar System and Planetary Astronomy Astro 9601 1 Topics to be covered The two-body problem (2.1) The three-body problem (2.2) Perturbations and resonances (2.3) Long-term
Celestial mechanics and dynamics Solar System and Planetary Astronomy Astro 9601 1 Topics to be covered The two-body problem (2.1) The three-body problem (2.2) Perturbations and resonances (2.3) Long-term
Gravity and the Orbits of Planets
 Gravity and the Orbits of Planets 1. Gravity Galileo Newton Earth s Gravity Mass v. Weight Einstein and General Relativity Round and irregular shaped objects 2. Orbits and Kepler s Laws ESO Galileo, Gravity,
Gravity and the Orbits of Planets 1. Gravity Galileo Newton Earth s Gravity Mass v. Weight Einstein and General Relativity Round and irregular shaped objects 2. Orbits and Kepler s Laws ESO Galileo, Gravity,
Identifying Safe Zones for Planetary Satellite Orbiters
 AIAA/AAS Astrodynamics Specialist Conference and Exhibit 16-19 August 2004, Providence, Rhode Island AIAA 2004-4862 Identifying Safe Zones for Planetary Satellite Orbiters M.E. Paskowitz and D.J. Scheeres
AIAA/AAS Astrodynamics Specialist Conference and Exhibit 16-19 August 2004, Providence, Rhode Island AIAA 2004-4862 Identifying Safe Zones for Planetary Satellite Orbiters M.E. Paskowitz and D.J. Scheeres
Lecture 25: The Outer Planets
 Lecture 25: The Outer Planets Neptune Uranus Pluto/Charon Uranus and three moons Neptune and two moons 1 The Outer Planets Uranus Discovered by William Herschel in 1781, who realized that this extended
Lecture 25: The Outer Planets Neptune Uranus Pluto/Charon Uranus and three moons Neptune and two moons 1 The Outer Planets Uranus Discovered by William Herschel in 1781, who realized that this extended
Gravitation & Kepler s Laws
 Gravitation & Kepler s Laws What causes YOU to be pulled down to the surface of the earth? THE EARTH.or more specifically the EARTH S MASS. Anything that has MASS has a gravitational pull towards it. F
Gravitation & Kepler s Laws What causes YOU to be pulled down to the surface of the earth? THE EARTH.or more specifically the EARTH S MASS. Anything that has MASS has a gravitational pull towards it. F
AP Physics QUIZ Gravitation
 AP Physics QUIZ Gravitation Name: 1. If F1 is the magnitude of the force exerted by the Earth on a satellite in orbit about the Earth and F2 is the magnitude of the force exerted by the satellite on the
AP Physics QUIZ Gravitation Name: 1. If F1 is the magnitude of the force exerted by the Earth on a satellite in orbit about the Earth and F2 is the magnitude of the force exerted by the satellite on the
ABSTACT KUIPER BINARY OBJECT FORMATION
 KUIPER BINARY OBJECT FORMATION R. C. Nazzario, K Orr, C. Covington, D. Kagan, and T. W. Hyde Center for Astrophysics, Space Physics and Engineering Research, Baylor University, Waco, TX 76798-7310, USA,
KUIPER BINARY OBJECT FORMATION R. C. Nazzario, K Orr, C. Covington, D. Kagan, and T. W. Hyde Center for Astrophysics, Space Physics and Engineering Research, Baylor University, Waco, TX 76798-7310, USA,
Astronomy 1140 Quiz 4 Review
 Astronomy 1140 Quiz 4 Review Anil Pradhan November 16, 2017 I Jupiter 1. How do Jupiter s mass, size, day and year compare to Earth s? Mass: 318 Earth masses (or about 1/1000th the mass of the Sun). Radius:
Astronomy 1140 Quiz 4 Review Anil Pradhan November 16, 2017 I Jupiter 1. How do Jupiter s mass, size, day and year compare to Earth s? Mass: 318 Earth masses (or about 1/1000th the mass of the Sun). Radius:
9.2 - Our Solar System
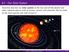 9.2 - Our Solar System Scientists describe our solar system as the Sun and all the planets and other celestial objects, such as moons, comets, and asteroids, that are held by the Sun s gravity and orbit
9.2 - Our Solar System Scientists describe our solar system as the Sun and all the planets and other celestial objects, such as moons, comets, and asteroids, that are held by the Sun s gravity and orbit
Patterns in the Solar System (Chapter 18)
 GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
astronomy A planet was viewed from Earth for several hours. The diagrams below represent the appearance of the planet at four different times.
 astronomy 2008 1. A planet was viewed from Earth for several hours. The diagrams below represent the appearance of the planet at four different times. 5. If the distance between the Earth and the Sun were
astronomy 2008 1. A planet was viewed from Earth for several hours. The diagrams below represent the appearance of the planet at four different times. 5. If the distance between the Earth and the Sun were
The stability of planets in the Alpha Centauri system
 The stability of planets in the Alpha Centauri system Paul A. Wiegert 1, Matt Holman 2 1 Department of Astronomy, University of Toronto, Toronto, Canada 2 Canadian Institute for Theoretical Astrophysics,
The stability of planets in the Alpha Centauri system Paul A. Wiegert 1, Matt Holman 2 1 Department of Astronomy, University of Toronto, Toronto, Canada 2 Canadian Institute for Theoretical Astrophysics,
Restricted three body problems in the Solar System: simulations
 Author:. Facultat de Física, Universitat de Barcelona, Diagonal 645, 0808 Barcelona, Spain. Advisor: Antoni Benseny i Ardiaca. Facultat de Matemàtiques, Universitat de Barcelona, Gran Via de les Corts
Author:. Facultat de Física, Universitat de Barcelona, Diagonal 645, 0808 Barcelona, Spain. Advisor: Antoni Benseny i Ardiaca. Facultat de Matemàtiques, Universitat de Barcelona, Gran Via de les Corts
orbits Moon, Planets Spacecrafts Calculating the and by Dr. Shiu-Sing TONG
 A Science Enrichment Programme for Secondary 3-4 Students : Teaching and Learning Resources the and Spacecrafts orbits Moon, Planets Calculating the 171 of by Dr. Shiu-Sing TONG 172 Calculating the orbits
A Science Enrichment Programme for Secondary 3-4 Students : Teaching and Learning Resources the and Spacecrafts orbits Moon, Planets Calculating the 171 of by Dr. Shiu-Sing TONG 172 Calculating the orbits
Learning Objectives. one night? Over the course of several nights? How do true motion and retrograde motion differ?
 Kepler s Laws Learning Objectives! Do the planets move east or west over the course of one night? Over the course of several nights? How do true motion and retrograde motion differ?! What are geocentric
Kepler s Laws Learning Objectives! Do the planets move east or west over the course of one night? Over the course of several nights? How do true motion and retrograde motion differ?! What are geocentric
Chapter 14 Satellite Motion
 1 Academic Physics Mechanics Chapter 14 Satellite Motion The Mechanical Universe Kepler's Three Laws (Episode 21) The Kepler Problem (Episode 22) Energy and Eccentricity (Episode 23) Navigating in Space
1 Academic Physics Mechanics Chapter 14 Satellite Motion The Mechanical Universe Kepler's Three Laws (Episode 21) The Kepler Problem (Episode 22) Energy and Eccentricity (Episode 23) Navigating in Space
Physical Science 1 Chapter 16 INTRODUCTION. Astronomy is the study of the universe, which includes all matter, energy, space and time.
 INTRODUCTION Astronomy is the study of the universe, which includes all matter, energy, space and time. Although the universe is vast and almost beyond imagination, much is known about its make-up and
INTRODUCTION Astronomy is the study of the universe, which includes all matter, energy, space and time. Although the universe is vast and almost beyond imagination, much is known about its make-up and
Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION
 Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION CHAPTER 4 The Solar System Lecture Presentation 4.0 What can be seen with the naked eye? Early astronomers knew about the Sun, Moon, stars, Mercury,
Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION CHAPTER 4 The Solar System Lecture Presentation 4.0 What can be seen with the naked eye? Early astronomers knew about the Sun, Moon, stars, Mercury,
Resonance Capture. Alice Quillen. University of Rochester. Isaac Newton Institute Dec 2009
 Resonance Capture Alice Quillen University of Rochester Isaac Newton Institute Dec 2009 This Talk Resonance Capture extension to nonadiabatic regime Astrophysical settings: Dust spiraling inward via radiation
Resonance Capture Alice Quillen University of Rochester Isaac Newton Institute Dec 2009 This Talk Resonance Capture extension to nonadiabatic regime Astrophysical settings: Dust spiraling inward via radiation
Three objects; 2+1 problem
 Three objects; 2+1 problem Having conquered the two-body problem, we now set our sights on more objects. In principle, we can treat the gravitational interactions of any number of objects by simply adding
Three objects; 2+1 problem Having conquered the two-body problem, we now set our sights on more objects. In principle, we can treat the gravitational interactions of any number of objects by simply adding
VISUAL PHYSICS ONLINE
 VISUAL PHYSICS ONLINE EXCEL SIMULATION MOTION OF SATELLITES DOWNLOAD the MS EXCEL program PA50satellite.xlsx and view the worksheet Display as shown in the figure below. One of the most important questions
VISUAL PHYSICS ONLINE EXCEL SIMULATION MOTION OF SATELLITES DOWNLOAD the MS EXCEL program PA50satellite.xlsx and view the worksheet Display as shown in the figure below. One of the most important questions
Eccentricity pumping of a planet on an inclined orbit by a disc
 Mon. Not. R. Astron. Soc. 44, 49 414 21) doi:1.1111/j.1365-2966.21.16295.x Eccentricity pumping of a planet on an inclined orbit by a disc Caroline Terquem 1,2 and Aikel Ajmia 1 1 Institut d Astrophysique
Mon. Not. R. Astron. Soc. 44, 49 414 21) doi:1.1111/j.1365-2966.21.16295.x Eccentricity pumping of a planet on an inclined orbit by a disc Caroline Terquem 1,2 and Aikel Ajmia 1 1 Institut d Astrophysique
18. Kepler as a young man became the assistant to A) Nicolaus Copernicus. B) Ptolemy. C) Tycho Brahe. D) Sir Isaac Newton.
 Name: Date: 1. The word planet is derived from a Greek term meaning A) bright nighttime object. B) astrological sign. C) wanderer. D) nontwinkling star. 2. The planets that were known before the telescope
Name: Date: 1. The word planet is derived from a Greek term meaning A) bright nighttime object. B) astrological sign. C) wanderer. D) nontwinkling star. 2. The planets that were known before the telescope
CHAPTER 8 PLANETARY MOTIONS
 1 CHAPTER 8 PLANETARY MOTIONS 8.1 Introduction The word planet means wanderer (πλάνητες αστέρες wandering stars); in contrast to the fixed stars, the planets wander around on the celestial sphere, sometimes
1 CHAPTER 8 PLANETARY MOTIONS 8.1 Introduction The word planet means wanderer (πλάνητες αστέρες wandering stars); in contrast to the fixed stars, the planets wander around on the celestial sphere, sometimes
Exoplanets: a dynamic field
 Exoplanets: a dynamic field Alexander James Mustill Amy Bonsor, Melvyn B. Davies, Boris Gänsicke, Anders Johansen, Dimitri Veras, Eva Villaver The (transiting) exoplanet population Solar System Hot Jupiters:
Exoplanets: a dynamic field Alexander James Mustill Amy Bonsor, Melvyn B. Davies, Boris Gänsicke, Anders Johansen, Dimitri Veras, Eva Villaver The (transiting) exoplanet population Solar System Hot Jupiters:
Cosmic Microwave Background Radiation
 Base your answers to questions 1 and 2 on the passage below and on your knowledge of Earth Science. Cosmic Microwave Background Radiation In the 1920s, Edwin Hubble's discovery of a pattern in the red
Base your answers to questions 1 and 2 on the passage below and on your knowledge of Earth Science. Cosmic Microwave Background Radiation In the 1920s, Edwin Hubble's discovery of a pattern in the red
A Kozai-resonating Earth quasi-satellite
 MNRASL 437, L85 L89 (2014) Advance Access publication 2013 November 13 doi:10.1093/mnrasl/slt147 A Kozai-resonating Earth quasi-satellite M. Connors Athabasca University Observatories, Athabasca AB T9S
MNRASL 437, L85 L89 (2014) Advance Access publication 2013 November 13 doi:10.1093/mnrasl/slt147 A Kozai-resonating Earth quasi-satellite M. Connors Athabasca University Observatories, Athabasca AB T9S
Physics Mechanics Lecture 30 Gravitational Energy
 Physics 170 - Mechanics Lecture 30 Gravitational Energy Gravitational Potential Energy Gravitational potential energy of an object of mass m a distance r from the Earth s center: Gravitational Potential
Physics 170 - Mechanics Lecture 30 Gravitational Energy Gravitational Potential Energy Gravitational potential energy of an object of mass m a distance r from the Earth s center: Gravitational Potential
Lecture Outlines. Chapter 15. Astronomy Today 7th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 15 Astronomy Today 7th Edition Chaisson/McMillan Chapter 15 The Formation of Planetary Systems Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Terrestrial and Jovian Planets
Lecture Outlines Chapter 15 Astronomy Today 7th Edition Chaisson/McMillan Chapter 15 The Formation of Planetary Systems Units of Chapter 15 15.1 Modeling Planet Formation 15.2 Terrestrial and Jovian Planets
Today. Planetary Motion. Tycho Brahe s Observations. Kepler s Laws of Planetary Motion. Laws of Motion. in physics
 Planetary Motion Today Tycho Brahe s Observations Kepler s Laws of Planetary Motion Laws of Motion in physics Page from 1640 text in the KSL rare book collection That the Earth may be a Planet the seeming
Planetary Motion Today Tycho Brahe s Observations Kepler s Laws of Planetary Motion Laws of Motion in physics Page from 1640 text in the KSL rare book collection That the Earth may be a Planet the seeming
Regular n-gon as a model of discrete gravitational system. Rosaev A.E. OAO NPC NEDRA, Jaroslavl Russia,
 Regular n-gon as a model of discrete gravitational system Rosaev A.E. OAO NPC NEDRA, Jaroslavl Russia, E-mail: hegem@mail.ru Introduction A system of N points, each having mass m, forming a planar regular
Regular n-gon as a model of discrete gravitational system Rosaev A.E. OAO NPC NEDRA, Jaroslavl Russia, E-mail: hegem@mail.ru Introduction A system of N points, each having mass m, forming a planar regular
Lesson 9. Luis Anchordoqui. Physics 168. Tuesday, October 24, 17
 Lesson 9 Physics 168 1 Static Equilibrium 2 Conditions for Equilibrium An object with forces acting on it but that is not moving is said to be in equilibrium 3 Conditions for Equilibrium (cont d) First
Lesson 9 Physics 168 1 Static Equilibrium 2 Conditions for Equilibrium An object with forces acting on it but that is not moving is said to be in equilibrium 3 Conditions for Equilibrium (cont d) First
cosmogony geocentric heliocentric How the Greeks modeled the heavens
 Cosmogony A cosmogony is theory about ones place in the universe. A geocentric cosmogony is a theory that proposes Earth to be at the center of the universe. A heliocentric cosmogony is a theory that proposes
Cosmogony A cosmogony is theory about ones place in the universe. A geocentric cosmogony is a theory that proposes Earth to be at the center of the universe. A heliocentric cosmogony is a theory that proposes
ISIMA lectures on celestial mechanics. 3
 ISIMA lectures on celestial mechanics. 3 Scott Tremaine, Institute for Advanced Study July 2014 1. The stability of planetary systems To understand the formation and evolution of exoplanet systems, we
ISIMA lectures on celestial mechanics. 3 Scott Tremaine, Institute for Advanced Study July 2014 1. The stability of planetary systems To understand the formation and evolution of exoplanet systems, we
Chapter 13. Universal Gravitation
 Chapter 13 Universal Gravitation Planetary Motion A large amount of data had been collected by 1687. There was no clear understanding of the forces related to these motions. Isaac Newton provided the answer.
Chapter 13 Universal Gravitation Planetary Motion A large amount of data had been collected by 1687. There was no clear understanding of the forces related to these motions. Isaac Newton provided the answer.
Radial Acceleration. recall, the direction of the instantaneous velocity vector is tangential to the trajectory
 Radial Acceleration recall, the direction of the instantaneous velocity vector is tangential to the trajectory 1 Radial Acceleration recall, the direction of the instantaneous velocity vector is tangential
Radial Acceleration recall, the direction of the instantaneous velocity vector is tangential to the trajectory 1 Radial Acceleration recall, the direction of the instantaneous velocity vector is tangential
Name Period Date Earth and Space Science. Solar System Review
 Name Period Date Earth and Space Science Solar System Review 1. is the spinning a planetary object on its axis. 2. is the backward motion of planets. 3. The is a unit less number between 0 and 1 that describes
Name Period Date Earth and Space Science Solar System Review 1. is the spinning a planetary object on its axis. 2. is the backward motion of planets. 3. The is a unit less number between 0 and 1 that describes
Black Holes. Jan Gutowski. King s College London
 Black Holes Jan Gutowski King s College London A Very Brief History John Michell and Pierre Simon de Laplace calculated (1784, 1796) that light emitted radially from a sphere of radius R and mass M would
Black Holes Jan Gutowski King s College London A Very Brief History John Michell and Pierre Simon de Laplace calculated (1784, 1796) that light emitted radially from a sphere of radius R and mass M would
Extending the Patched-Conic Approximation to the Restricted Four-Body Problem
 Monografías de la Real Academia de Ciencias de Zaragoza 3, 133 146, (6). Extending the Patched-Conic Approximation to the Restricted Four-Body Problem Thomas R. Reppert Department of Aerospace and Ocean
Monografías de la Real Academia de Ciencias de Zaragoza 3, 133 146, (6). Extending the Patched-Conic Approximation to the Restricted Four-Body Problem Thomas R. Reppert Department of Aerospace and Ocean
Hill's Approximation in the Three-Body Problem
 Progress of Theoretical Physics Supplement No. 96, 1988 167 Chapter 15 Hill's Approximation in the Three-Body Problem Kiyoshi N AKAZA W A and Shigeru IDA* Department of Applied Physics, T.okyo Institute
Progress of Theoretical Physics Supplement No. 96, 1988 167 Chapter 15 Hill's Approximation in the Three-Body Problem Kiyoshi N AKAZA W A and Shigeru IDA* Department of Applied Physics, T.okyo Institute
The Heliocentric Model of Copernicus
 Celestial Mechanics The Heliocentric Model of Copernicus Sun at the center and planets (including Earth) orbiting along circles. inferior planets - planets closer to Sun than Earth - Mercury, Venus superior
Celestial Mechanics The Heliocentric Model of Copernicus Sun at the center and planets (including Earth) orbiting along circles. inferior planets - planets closer to Sun than Earth - Mercury, Venus superior
Coriolis Effect - the apparent curved paths of projectiles, winds, and ocean currents
 Regents Earth Science Unit 5: Astronomy Models of the Universe Earliest models of the universe were based on the idea that the Sun, Moon, and planets all orbit the Earth models needed to explain how the
Regents Earth Science Unit 5: Astronomy Models of the Universe Earliest models of the universe were based on the idea that the Sun, Moon, and planets all orbit the Earth models needed to explain how the
lightyears observable universe astronomical unit po- laris perihelion Milky Way
 1 Chapter 1 Astronomical distances are so large we typically measure distances in lightyears: the distance light can travel in one year, or 9.46 10 12 km or 9, 600, 000, 000, 000 km. Looking into the sky
1 Chapter 1 Astronomical distances are so large we typically measure distances in lightyears: the distance light can travel in one year, or 9.46 10 12 km or 9, 600, 000, 000, 000 km. Looking into the sky
What is it like? When did it form? How did it form. The Solar System. Fall, 2005 Astronomy 110 1
 What is it like? When did it form? How did it form The Solar System Fall, 2005 Astronomy 110 1 Fall, 2005 Astronomy 110 2 The planets all orbit the sun in the same direction. The Sun spins in the same
What is it like? When did it form? How did it form The Solar System Fall, 2005 Astronomy 110 1 Fall, 2005 Astronomy 110 2 The planets all orbit the sun in the same direction. The Sun spins in the same
ORBITAL CHARACTERISTICS DUE TO THE THREE DIMENSIONAL SWING-BY IN THE SUN-JUPITER SYSTEM
 ORBITAL CHARACTERISTICS DUE TO THE THREE DIMENSIONAL SWING-BY IN THE SUN-JUPITER SYSTEM JORGE K. S. FORMIGA 1,2 and ANTONIO F B A PRADO 2 National Institute for Space Research -INPE 1 Technology Faculty-FATEC-SJC
ORBITAL CHARACTERISTICS DUE TO THE THREE DIMENSIONAL SWING-BY IN THE SUN-JUPITER SYSTEM JORGE K. S. FORMIGA 1,2 and ANTONIO F B A PRADO 2 National Institute for Space Research -INPE 1 Technology Faculty-FATEC-SJC
Orbital Evolution in Extra-solar systems
 Orbital Evolution in Extra-solar systems George Voyatzis Section of Astronomy, Astrophysics and Mechanics, Department of Physics, Aristotle University of Thessaloniki, Greece. Abstract Nowadays, extra-solar
Orbital Evolution in Extra-solar systems George Voyatzis Section of Astronomy, Astrophysics and Mechanics, Department of Physics, Aristotle University of Thessaloniki, Greece. Abstract Nowadays, extra-solar
Astronomy Unit Notes Name:
 Astronomy Unit Notes Name: (DO NOT LOSE!) To help with the planets order 1 My = M 2 V = Venus 3 Eager = E 4 M = Mars 5 Just = J 6 Served = Saturn 7 Us = Uranus 8 N = N 1 Orbit: The path (usually elliptical)
Astronomy Unit Notes Name: (DO NOT LOSE!) To help with the planets order 1 My = M 2 V = Venus 3 Eager = E 4 M = Mars 5 Just = J 6 Served = Saturn 7 Us = Uranus 8 N = N 1 Orbit: The path (usually elliptical)
9/12/2010. The Four Fundamental Forces of Nature. 1. Gravity 2. Electromagnetism 3. The Strong Nuclear Force 4. The Weak Nuclear Force
 The Four Fundamental Forces of Nature 1. Gravity 2. Electromagnetism 3. The Strong Nuclear Force 4. The Weak Nuclear Force The Universe is made of matter Gravity the force of attraction between matter
The Four Fundamental Forces of Nature 1. Gravity 2. Electromagnetism 3. The Strong Nuclear Force 4. The Weak Nuclear Force The Universe is made of matter Gravity the force of attraction between matter
Lecture Outlines. Chapter 6. Astronomy Today 7th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 6 Astronomy Today 7th Edition Chaisson/McMillan Chapter 6 The Solar System Units of Chapter 6 6.1 An Inventory of the Solar System 6.2 Measuring the Planets 6.3 The Overall Layout
Lecture Outlines Chapter 6 Astronomy Today 7th Edition Chaisson/McMillan Chapter 6 The Solar System Units of Chapter 6 6.1 An Inventory of the Solar System 6.2 Measuring the Planets 6.3 The Overall Layout
ASTRONOMY CURRICULUM Unit 1: Introduction to Astronomy
 Chariho Regional School District - Science Curriculum September, 2016 ASTRONOMY CURRICULUM Unit 1: Introduction to Astronomy OVERVIEW Summary Students will be introduced to the overarching concept of astronomy.
Chariho Regional School District - Science Curriculum September, 2016 ASTRONOMY CURRICULUM Unit 1: Introduction to Astronomy OVERVIEW Summary Students will be introduced to the overarching concept of astronomy.
Orbital resonances in the inner neptunian system I. The 2:1 Proteus Larissa mean-motion resonance
 Icarus 188 (2007) 386 399 www.elsevier.com/locate/icarus Orbital resonances in the inner neptunian system I. The 2:1 Proteus arissa mean-motion resonance Ke Zhang, Douglas P. Hamilton Department of Astronomy,
Icarus 188 (2007) 386 399 www.elsevier.com/locate/icarus Orbital resonances in the inner neptunian system I. The 2:1 Proteus arissa mean-motion resonance Ke Zhang, Douglas P. Hamilton Department of Astronomy,
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter 4 - Group Homework Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) Density is defined as A) mass times weight. B) mass per unit volume.
Chapter 4 - Group Homework Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) Density is defined as A) mass times weight. B) mass per unit volume.
What is a Satellite? A satellite is an object that orbits another object. Ex. Radio satellite, moons, planets
 Planetary Orbit Planetary Orbits What shape do planets APPEAR to orbit the sun? Planets APPEAR to orbit in a circle. What shape do the planets orbit the sun??? Each planet Orbits the Sun in an ellipse
Planetary Orbit Planetary Orbits What shape do planets APPEAR to orbit the sun? Planets APPEAR to orbit in a circle. What shape do the planets orbit the sun??? Each planet Orbits the Sun in an ellipse
EXTENDING NACOZY S APPROACH TO CORRECT ALL ORBITAL ELEMENTS FOR EACH OF MULTIPLE BODIES
 The Astrophysical Journal, 687:1294Y1302, 2008 November 10 # 2008. The American Astronomical Society. All rights reserved. Printed in U.S.A. EXTENDING NACOZY S APPROACH TO CORRECT ALL ORBITAL ELEMENTS
The Astrophysical Journal, 687:1294Y1302, 2008 November 10 # 2008. The American Astronomical Society. All rights reserved. Printed in U.S.A. EXTENDING NACOZY S APPROACH TO CORRECT ALL ORBITAL ELEMENTS
Theory of mean motion resonances.
 Theory of mean motion resonances. Mean motion resonances are ubiquitous in space. They can be found between planets and asteroids, planets and rings in gaseous disks or satellites and planetary rings.
Theory of mean motion resonances. Mean motion resonances are ubiquitous in space. They can be found between planets and asteroids, planets and rings in gaseous disks or satellites and planetary rings.
The Solar Nebula Theory. This lecture will help you understand: Conceptual Integrated Science. Chapter 28 THE SOLAR SYSTEM
 This lecture will help you understand: Hewitt/Lyons/Suchocki/Yeh Conceptual Integrated Science Chapter 28 THE SOLAR SYSTEM Overview of the Solar System The Nebular Theory The Sun Asteroids, Comets, and
This lecture will help you understand: Hewitt/Lyons/Suchocki/Yeh Conceptual Integrated Science Chapter 28 THE SOLAR SYSTEM Overview of the Solar System The Nebular Theory The Sun Asteroids, Comets, and
PHYS 155 Introductory Astronomy
 PHYS 155 Introductory Astronomy - observing sessions: Sunday Thursday, 9pm, weather permitting http://www.phys.uconn.edu/observatory - Exam - Tuesday March 20, - Review Monday 6:30-9pm, PB 38 Marek Krasnansky
PHYS 155 Introductory Astronomy - observing sessions: Sunday Thursday, 9pm, weather permitting http://www.phys.uconn.edu/observatory - Exam - Tuesday March 20, - Review Monday 6:30-9pm, PB 38 Marek Krasnansky
