A sharp Blaschke Santaló inequality for α-concave functions
|
|
|
- Janis Merritt
- 5 years ago
- Views:
Transcription
1 Noname manuscript No will be inserted b the editor) A sharp Blaschke Santaló inequalit for α-concave functions Liran Rotem the date of receipt and acceptance should be inserted later Abstract We define a new transform on α-concave functions which we call the - transform Using this new transform we prove a sharp Blaschke-Santaló inequalit for α-concave functions and characterize the equalit case This extends the known functional Blaschke-Santaló inequalit of Artstein-Avidan Klartag and Milman and strengthens a result of Bobkov Finall we prove that the -transform is a dualit transform when restricted to its image However this transform is neither surjective nor injective on the entire class of α-concave functions Kewords Blaschke-Santaló inequalit convexit α-concavit log-concavit Mathematics Subject Classification 200) 52A40 26B25 Blaschke Santaló tpe inequalities We begin b recalling the classic Blaschke-Santaló inequalit A convex bod in R n is compact convex set with non-empt interior Such a convex bod K is called smmetric if K = K We will denote b K the Lebesgue) volume of K Finall we define the polar bod of K to be K = {x R n : x for all K} where is the standard scalar product on R n Polarit is a basic notion in convex geometr It is eas to see that if K is smmetric convex bod then so is K The map K K satisfies two fundamental properties: It is order reversing: If K K 2 then K K 2 2 It is an involution: For ever smmetric convex bod K we have K = K ) L Rotem School of Mathematical Sciences Tel Aviv Universit Ramat Aviv Tel Aviv Israel liranro@posttauacil
2 2 Liran Rotem These two properties sa that polarit is a dualit transform see eg [2]) The volume of K is related to the volume of K b the Blaschke-Santaló inequalit Theorem Blaschke Santaló) Assume K R n is a smmetric convex bod Then K K D 2 where D R n is the unit Euclidean ball Furthermore we have an equalit if and onl if K is an ellipsoid This theorem was proven b Blaschke in dimensions 2 and 3 and Santaló extended the result to arbitrar dimensions There exists a version of the inequalit for nonsmmetric bodies but for simplicit we will onl deal with the smmetric case The generalized statement proofs and further references can be found eg in [2] In [] Artstein-Avidan Klartag and Milman prove a functional extension of the Blaschke-Santaló inequalit To explain their result and put it in perspective we will need to define α-concave functions: Definition Fix α We sa that a function f : R n [0 ) is α-concave if f is supported on some convex set Ω and for ever x Ω and 0 λ we have f λx + λ)) [λfx) α + λ) f) α ] α We will alwas assume that f is upper semicontinuous and that max fx) = f0) = x Rn this last condition is sometimes known as saing that f is geometric) The class of all such α-concave functions will be denoted b C α R n ) Remember that f : R n [0 ) is called upper semicontinuous if its upper level sets {x R n : fx) t} are closed for all t 0 α-concave functions were first defined b Avriel [5]) and were studied b Borell [8][9]) and b Brascamp and Lieb [0]) In the case α = we understand the definition in the limiting sense as f λx + λ)) max {fx) f)} This just means that f is constant on its support so functions in C R n ) are indicator functions of convex sets which b our assumptions must also be closed and contain the origin If we further assume that f C R n ) satisf 0 < f < then f must be the indicator function of a convex bod and we can identif these functions with the convex bodies themselves If α < α 2 then C α R n ) C α2 R n ) This means that we can think of ever class of functions C α R n ) as extending the class of convex bodies Originall this was done for the class C 0 R n ) of log-concave functions Again we interpret Definition in the limiting sense and sa that a function f : R n [0 ) is log-concave if f λx + λ)) fx) λ f) λ for ever x R n and 0 λ
3 A sharp Blaschke Santaló inequalit for α-concave functions 3 Man definitions and theorems of convex geometr were generalized to the class of log-concave functions Except the usual aspiration for generalit the developed theor helped to prove new deep theorems in convexit and asmptotic geometric analsis For a surve of such results and their importance see [6] One of the first results in this new direction was the functional Santaló theorem In order to state it we will begin with a convenient definition: Definition 2 For ever f C 0 R n ) we define f = exp L log f)) C 0 R n ) where L is the Legendre transform defined b Lϕ) x) = sup R n x ϕ)) This definition just means that if f = e ϕ for a convex function ϕ then f = e Lϕ It turns out that the map f f is a dualit transform on C 0 R n ) and we have the following theorem: Theorem 2 Assume f C 0 R n ) is even and 0 < f < Then f 2 f G) = 2π) n where Gx) = e x 2 2 Equalit occurs if and onl if f = G T for an invertible linear map T : R n R n This inequalit in the even case is originall due to Ball [6]) In [] Artstein- Avidan Klartag and Milman present this result as a Blaschke Santaló tpe inequalit extend the result to the non-even case and characterize the equalit case As a side note let us mention that given our current knowledge the form of Theorem 2 is somewhat surprising Following a series of works b Artstein- Avidan and Milman we now understand that even though the map f f is a dualit transform it is not the correct extension of the classic notion of polarit see [3]) The correct extension is another dualit transform usuall denoted f f which is based on the so-called A-transform Hence we expect the functional Blaschke Santaló inequalit to bound an expression of the form f f ) which is not what we see in Theorem 2 In fact a sharp upper bound on ) is not known even though an asmptotic result was recentl found b Artstein-Avidan and Slomka [4]) The goal of this paper is to discuss Blaschke-Santaló inequalities for α-concave functions for values of α different from 0 The case α > 0 was resolved alread in [] so we will assume from now on that α 0 The following definition appeared in [7]:
4 4 Liran Rotem Definition 3 Assume < α < 0 The convex base of a function f C α R n ) is base α f = f α α Put differentl ϕ = base α f is the unique convex function such that f = + ϕ ) Here and after we use the parameter = α As α 0 and 0 it is often less confusing to use instead of α In the limiting case α = 0 we define base 0 f) = log f Using the notion of a convex base we can extend Definition 2 to the general case: Definition 4 The dual of a function f C α R n ) is the function f C α R n ) defined b relation base α f ) = L base α f)) Note that the operation depends on α Remember that if f C α R n ) then f C α R n ) for all α < α Thinking of f as an element in C α R n ) will ield a different f than thinking about f as function in C α R n ) Therefore strictl speaking we should use a notation like f α However this notation is extremel cumbersome so we will use the simpler notation f and keep in mind the implicit dependence on α We can now state what appears to be the natural extension of Theorem 2 to the α-concave case: Theorem 3 Fix n < α 0 For ever even function f C α R n ) such that 0 < f < we have ) 2 f f H α 2) where H α x) = ) + x 2 2 Cα R n ) This theorem was proven b Bobkov [7]) using a general result b Fradelizi and Meer []) which we will cite in the next section as Theorem 5 The condition α > n is necessar because the function H α is no longer integrable for α n In fact it is not hard to check that H α Hα as α n so it is not possible to find a finite upper bound for f f whenever α n Notice that as α 0 the functions H α converge to the Gaussian G and we obtain Theorem 2 as a special case of Theorem 3 Surprisingl as was alread observed b Bobkov Theorem 3 is not sharp when α < 0 Given the previousl described results it is ver natural to expect an equalit in 2) when f = H α However an explicit et tedious) calculation shows that Hαx) < H α x) for all x 0 so ) 2 H α Hα < H α
5 A sharp Blaschke Santaló inequalit for α-concave functions 5 In fact there exists a unique function G α C α R n ) such that G α = G α and this function is ) G α x) = + x 2 2 Notice that in the limiting case α 0 we have H 0 = G 0 = G but for other values of α these functions are quite different Inspired b Theorems and 2 it ma seem reasonable to conjecture that f ) 2 f G α for all even f C α R n ) Such an inequalit if true will obviousl be sharp Unfortunatel this inequalit is false for α < 0 As one possible counterexample take f = D the indicator function of the ball In this case f = + x ) and a direct computation of the integrals show that this is indeed a counterexample if the dimension n is large enough compared to For concreteness it is enough to take n = for all large enough ) 2 In the next sections we will show the reason inequalit 2) is not sharp is that the transform is not the correct extension of polarit to use in the functional Blaschke-Santaló inequalit In section 2 we will define a new transform on C α R n ) which we call -transform We will then use this -transform to prove a sharp version of Theorem 3 Finall in section 3 we will discuss further properties of which are not directl related to the Blaschke-Santaló inequalit and give a geometric interpretation of this transform 2 A new transform on α-concave functions In [] Artstein-Avidan Klartag and Milman obtain Theorem 2 as the limit of Blaschke-Santaló tpe inequalities for α-concave functions α 0 Let us warn the reader that [] uses a slightl different notation than the one used in this paper: an α-concave function in this paper is the same as a α -concave function in [] and vice versa Inspired b the transforms in [] we define the following: Definition 5 For f C α R n ) we define f x) = inf f) + x ) = sup [f) + x ) ] where the infimum is taken over all points R n such that f) > 0 and x > Like the transform the transform also depends on α so in principle we should write f α Nonetheless we opt for the simpler notation f Let us begin b checking that f C α R n ):
6 6 Liran Rotem Proposition For ever f C α R n ) we have f C α R n ) If f is even so is f Proof For a fixed R n with f) > 0 the function ) f x) = f) + x if x > otherwise is upper semicontinuous and α-concave except the fact it can attain the value + which we usuall exclude from the definition) Now we can write f x) = inf f x) : f)>0 so f is α-concave as the infimum of a famil of α-concave functions Similarl f is upper semicontinuous as the infimum of a famil of upper semicontinuous functions For ever x R n we have Additionall f x) = inf f 0) = inf f) + x f) + 0 ) ) ) = f0) + x0 + = inf f) = sup f) = and we see that f is geometric Hence we have f C α R n ) like we wanted Finall if f is even then f x) = inf = inf so f is even as well f) + x f) + x ) = inf ) = f x) f ) + x Our main goal in this section is to prove the following theorem: Theorem 4 Fix n < α 0 For ever even f C α R n ) such that 0 < f < we have ) 2 f f H α with equalit if and onl if f = H α T for an invertible linear transformation T : R n R n ) Here we have H α x) = + x 2 2 just like in Theorem 3 of Bobkov For α n one cannot hope for a finite upper bound on the product f f This can be seen b choosing f = H α and considering the following proposition: )
7 A sharp Blaschke Santaló inequalit for α-concave functions 7 Proposition 2 H α = H α and H α is the onl function with this propert Proof First we calculate H α explicitl and show that H α = H α B definition H αx) = [ sup H α ) + = sup + 2 ) ] x ) 2 + ) x }{{} ) Notice that if we take a vector and rotate it to have the same direction as x we can onl increase the expression ) Hence H αx) = = sup λ>0 sup λ>0 ) + λx λ x 2 + λ2 x 2 ) 2 2 x λx ) It is now an exercise in calculus to differentiate and check that the supremum is actuall a maximum which is obtained for λ = Hence H αx) = + x 2 + x 2 ) 2 2 = ) + x 2 2 = Hα x) which is what we needed to show Now assume that f C α R n ) is an function such that f = f For ever x R n with fx) > 0 we have fx) = f x) = inf f) + x ) fx) + x 2 so multipling b fx) and taking a square root we get fx) H α x) If fx) = 0 then fx) H α x) holds triviall so the inequalit is true for all x R n It is obvious from the definition that is order reversing so we ma appl it on both sides and obtain so f = H α like we wanted f = f H α = H α Theorem 4 like Theorem 3 will follow from a general result of Fradelizi and Meer []) We state their result here: )
8 8 Liran Rotem Theorem 5 Let f f 2 : R n R + and ρ : R + R + be measurable functions such that f x)f 2 ) ρ 2 x ) for ever x R n such that x > 0 If additionall f is even then f 2 f 2 ρ x )dx) 2 Assume further that ρ is continuous Then equalit will occur if and onl if: ρs)ρt) ρ st) for ever s t 0 2 If n 2 then either ρ0) > 0 or ρ 0 3 There exists a positive definite matrix T and a constant d > 0 such that almost everwhere f x) = d ρ T x 2) f 2 x) = T d ρ x 2) Let us use this result to prove Theorem 4: Proof Proof of Theorem 4) Define a function ρ : R + R + b ρt) = + t ) /2 Fix x R n with x > 0 If fx) = 0 then obviousl fx)f ) ρ 2 x ) If on the other hand fx) > 0 then fx) f ) = inf z = + fx) fz) x ) + z + ) = ρ 2 x ) fx) fx) + x ) From Theorem 5 we conclude that indeed 2 f f ρ x )dx) 2 = H α ) 2 Next we analze the equalit case From Theorem 5 we see that a necessar condition to have equalit is fx) = d ρ T x 2) = d H α T x) for a constant d > 0 and a linear map T : R n R n which we ma take to be positive definite if we want) Since f C α R n ) we know that so we must have f = H α T = f0) = d H α 0) = d = d
9 A sharp Blaschke Santaló inequalit for α-concave functions 9 To see that this condition is also sufficient notice that for ever f C α R n ) and ever invertible linear map T we have f T ) x) = [ sup ft ) + ) ] x = T ) ) x = sup f) + sup f) x T ) + = f T ) x ) Using a simple change of variables and Proposition 2 we get that if f = H α T then f f = H α T ) Hα T ) ) so we are done = dett ) det T ) ) ) 2 H α Hα = H α Remark For simplicit Theorem 4 is onl stated for even functions Fradelizi and Meer also proved in [] a generalization of Theorem 5 for non-even functions which can be used to extend Theorem 4 to the non-even case The proof remains essentiall the same so we leave the details to the interested reader To conclude this section let us compare Theorem 4 with Theorem 3 We have the following proposition: Proposition 3 For ever f C α R n ) we have f f Proof Denote ϕ = base α f) We need to prove that for ever x R n we have f x) f x) which is equivalent to inf + x + ϕ) Choose a sequence { n } such that ) inf + + x n ) f x) + ϕ n) ) x ϕ) We claim it is alwas possible to choose this sequence in such a wa that x n ϕ n ) 0 for ever n Indeed we know that f x) If f x) < we will automaticall have x n > ϕ n ) 0 for large enough n If f x) = just take n = 0 for all n For ever two numbers B A 0 we have + B + A + B A
10 0 Liran Rotem as one easil checks Appling this to B = x n and A = ϕ n) we see that + x n ) + x ) n ϕ n ) f x) + ϕ n) for all n Sending n we see that f x) f x) like we wanted This means that for ever value of α Theorem 3 follows from Theorem 4 When α 0 the transforms and coincide so both theorems reduce to same result - Theorem 2 3 Further properties of -transform In this section we will discuss further properties of the new -transform : C α R n ) C α R n ) for α < 0 We alread used the simple fact that is order reversing: if f g C α R n ) and f g pointwise) then f g Surprisingl however is not a dualit transform as it is not an involution One simple wa of verifing the last assertion is b computing a few examples: Example Let K be a convex bod containing the origin Remember that the gauge function of K is defined b { x } x K = inf r > 0 : r K Let us denote b K the indicator function of K Then a simple calculation gives K = K = + x ) K and [ + x ) ] { } K = min x K In particular we see that K K for ever α < 0 equivalentl for ever < ) In order to prove more delicate properties of the -transform we will need to examine it from a different point view Denote b Cvx 0 R n ) the class of all convex functions ϕ : R n [0 ] such that ϕ is lower semicontinuous and ϕ0) = 0 The map base α : C α R n ) Cvx 0 R n ) from Definition 3 is easil seen to be an order reversing bijection Hence if we wish to understand the -transform it is enough to stud its conjugate T α : Cvx 0 R n ) Cvx 0 R n ) which is defined b T α = base α base α The transform T α can be written down explicitl: Proposition 4 For ever ϕ Cvx 0 R n ) and ever x R n we have x ϕ) x ϕ) T α ϕ) x) = sup = sup 3) R n αϕ) R n + ϕ) )
11 A sharp Blaschke Santaló inequalit for α-concave functions In particular we see that T 0 = L is the Legendre transform This also follows from the fact that on C 0 R n ) the -transform and the -transform coincide Proof Let us use equation 3) as the definition of T α and check that under this definition we reall have ) T α = base α base α This is of course the same as base ) α Tα = base ) α Plugging in all of the definitions we need to prove that for ever ϕ Cvx 0 R n ) and ever x R n + sup ) ) x ϕ) + x = inf + ϕ) ) + ϕ) and checking this equalit involves nothing more than simple algebra Interestingl the transforms T α were introduced and studied b Milman around 970 for ver different applications in functional analsis see [3] [5] for the original papers in Russian and section 33 of the surve [4] for a partial translation to English The remark in the end of section 3 of [] is also relevant but inaccurate) The onl result we will need from these works is the following geometric characterization of T α : Fix a function ϕ Cvx 0 R n ) We will use ϕ to construct a function ρ : R n R [0 ] in the following wa: first we define ρ x ) = + ϕx) Next we extend ρ b requiring it to be -homoegeneous Hence for ever x R n and t 0 we define ) t x ρ x t) = ρ )) = t + ϕ x t = t + t ) x t ϕ t The values of ρ on the hperplane t = 0 are not so important but for concreteness we will define ρx 0) = lim t 0 + ρx t) the limit exists b the convexit of ϕ) The function ρ is -homoegeneous b construction but in general it will not be a norm on R n+ since there is no reason for ρ to be convex Nonetheless we can define the dual norm ρ x + ts x t) = sup s) R ρ s) n+ which is alwas a proper norm on R n+ Now if we restrict ourselves back to the hperplane t = a direct calculation gives ρ x ) = + T αϕ) x) which shows the relation between the transform T α and the classic notion of dualit Using this construction we can prove several properties of the -transform Specificall we have:
12 2 Liran Rotem Theorem 6 Fix < α < 0 and let : C α R n ) C α R n ) be the -transform Then: For ever f C α R n ) we have f f 2 For ever f C α R n ) we have f = f In other words is a dualit transform on its image 3 is neither injective nor surjective Theorem 6 is an immediate corollar of the following proposition establishing the same properties for the transform T α : Proposition 5 Fix < α < 0 and let T α : Cvx 0 R n ) Cvx 0 R n ) be the transform defined above Then: For ever ϕ Cvx 0 R n ) we have T 2 α ϕ ϕ 2 For ever ϕ Cvx 0 R n ) we have T 3 α ϕ = T α ϕ In other words T α is a dualit transform on its image 3 T α is neither injective nor surjective Proof Fix ϕ Cvx 0 R n ) and let ρ : R n+ [0 ] we defined as above It is well known that if ρ is an -homogenous function which is not necessaril convex then ρ ρ In particular + T 2 α ϕ ) x) = ρ x ) ρx ) = + ϕx) which proves ) Since ρ is alread a norm we must have ρ = ρ ) = ρ Restricting again to the hperplane t = we see that T 3 α ϕ = T α ϕ which proves 2) Next we prove 3) and begin b showing that T α is not surjective If ϕ is in the image of T α then the above discussion implies that the corresponding ρ must be a norm on R n+ In particular ρ must be comparable to the Euclidean norm ie there exists a constant C > 0 such that Therefore ρx t) C x t) = C x 2 + t 2 ϕx) = ρ x ) C ) x 2 + C x + and we see that ever function ϕ in the image of T α must grow at most linearl In particular the function ϕx) = x 2 is not in the image of T α so T α is not surjective Finall we will show that T α is also not injective Take an ϕ Cvx 0 R n ) which is not in the image of T α Then T α T 2 α ϕ ) = T 3 α ϕ = T α ϕ even though T 2 α ϕ ϕ This shows that T α is not injective and the proof is complete
13 A sharp Blaschke Santaló inequalit for α-concave functions 3 References Shiri Artstein-Avidan Bo az Klartag and Vitali Milman The Santaló point of a function and a functional form of the Santaló inequalit Mathematika 5-2):33 Februar Shiri Artstein-Avidan and Vitali Milman A characterization of the concept of dualit Electronic Research Announcements in Mathematical Sciences 4: Shiri Artstein-Avidan and Vitali Milman Hidden structures in the class of convex functions and a new dualit transform Journal of the European Mathematical Societ 34): Shiri Artstein-Avidan and Boaz Slomka A note on Santaló inequalit for the polarit transform and its reverse arxiv: Mordecai Avriel r-convex functions Mathematical Programming 2): Februar Keith Ball Isometric problems in l p and sections of convex sets PhD thesis Universit of Cambridge Serge G Bobkov Convex bodies and norms associated to convex measures Probabilit Theor and Related Fields 47-2): March Christer Borell Convex measures on locall convex spaces Arkiv för matematik 2-2): December Christer Borell Convex set functions in d-space Periodica Mathematica Hungarica 62): Herm J Brascamp and Elliott H Lieb On extensions of the Brunn-Minkowski and Prékopa-Leindler theorems including inequalities for log concave functions and with an application to the diffusion equation Journal of Functional Analsis 224): August 976 Matthieu Fradelizi and Mathieu Meer Some functional forms of Blaschke-Santaló inequalit Mathematische Zeitschrift 2562): December Mathieu Meer and Alain Pajor On the Blaschke-Santaló inequalit Archiv der Mathematik 55):82 93 Jul Vitali Milman A certain transformation of convex functions and a dualit of the and δ characteristics of a B-space Doklad Akademii Nauk SSSR 87: Vitali Milman Geometric theor of Banach spaces part II: Geometr of the unit sphere Russian Mathematical Surves 266):79 63 December 97 5 Vitali Milman Dualit of certain geometric characteristics of a Banach space Teorija Funkcii Funkcionalni Analiz i ih Prilozenija 8: Vitali Milman Geometrization of probabilit In Mikhail Kapranov Sergi Kolada Yuri Ivanovich Manin Pieter Moree and Leonid Potagailo editors Geometr and Dnamics of Groups and Spaces volume 265 of Progress in Mathematics pages Birkhäuser Basel Liran Rotem Support functions and mean width for α-concave functions Advances in Mathematics 243:68 86 August 203
Characterization of Self-Polar Convex Functions
 Characterization of Self-Polar Convex Functions Liran Rotem School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel Abstract In a work by Artstein-Avidan and Milman the concept of
Characterization of Self-Polar Convex Functions Liran Rotem School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel Abstract In a work by Artstein-Avidan and Milman the concept of
On isotropicity with respect to a measure
 On isotropicity with respect to a measure Liran Rotem Abstract A body is said to be isoptropic with respect to a measure µ if the function θ x, θ dµ(x) is constant on the unit sphere. In this note, we
On isotropicity with respect to a measure Liran Rotem Abstract A body is said to be isoptropic with respect to a measure µ if the function θ x, θ dµ(x) is constant on the unit sphere. In this note, we
Mixed volumes and mixed integrals
 Snapshots of modern mathematics from Oberwolfach xx/xxxx Mixed volumes and mixed integrals Liran Rotem In recent years, analytic and probabilistic tools proved themselves to be very useful in the study
Snapshots of modern mathematics from Oberwolfach xx/xxxx Mixed volumes and mixed integrals Liran Rotem In recent years, analytic and probabilistic tools proved themselves to be very useful in the study
Tensor products in Riesz space theory
 Tensor products in Riesz space theor Jan van Waaij Master thesis defended on Jul 16, 2013 Thesis advisors dr. O.W. van Gaans dr. M.F.E. de Jeu Mathematical Institute, Universit of Leiden CONTENTS 2 Contents
Tensor products in Riesz space theor Jan van Waaij Master thesis defended on Jul 16, 2013 Thesis advisors dr. O.W. van Gaans dr. M.F.E. de Jeu Mathematical Institute, Universit of Leiden CONTENTS 2 Contents
QUADRATIC AND CONVEX MINIMAX CLASSIFICATION PROBLEMS
 Journal of the Operations Research Societ of Japan 008, Vol. 51, No., 191-01 QUADRATIC AND CONVEX MINIMAX CLASSIFICATION PROBLEMS Tomonari Kitahara Shinji Mizuno Kazuhide Nakata Toko Institute of Technolog
Journal of the Operations Research Societ of Japan 008, Vol. 51, No., 191-01 QUADRATIC AND CONVEX MINIMAX CLASSIFICATION PROBLEMS Tomonari Kitahara Shinji Mizuno Kazuhide Nakata Toko Institute of Technolog
Hidden structures in the class of convex functions and a new duality transform
 J. Eur. Math. Soc. 13, 975 1004 c European Mathematical Society 2011 DOI 10.4171/JEMS/273 Shiri Artstein-Avidan Vitali Milman Hidden structures in the class of convex functions and a new duality transform
J. Eur. Math. Soc. 13, 975 1004 c European Mathematical Society 2011 DOI 10.4171/JEMS/273 Shiri Artstein-Avidan Vitali Milman Hidden structures in the class of convex functions and a new duality transform
A. Derivation of regularized ERM duality
 A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
The Concept of Duality in Convexity Theory
 The Concept of Duality in Convexity Theory S. Artstein-Avidan and V.D. Milman Tel Aviv University Cortona, 2007 A. Let Cvx(R n ) denote the family of all lower-semi-continuous convex functions {f : R n
The Concept of Duality in Convexity Theory S. Artstein-Avidan and V.D. Milman Tel Aviv University Cortona, 2007 A. Let Cvx(R n ) denote the family of all lower-semi-continuous convex functions {f : R n
4. Product measure spaces and the Lebesgue integral in R n.
 4 M. M. PELOSO 4. Product measure spaces and the Lebesgue integral in R n. Our current goal is to define the Lebesgue measure on the higher-dimensional eucledean space R n, and to reduce the computations
4 M. M. PELOSO 4. Product measure spaces and the Lebesgue integral in R n. Our current goal is to define the Lebesgue measure on the higher-dimensional eucledean space R n, and to reduce the computations
Notes on Convexity. Roy Radner Stern School, NYU. September 11, 2006
 Notes on Convexit Ro Radner Stern School, NYU September, 2006 Abstract These notes are intended to complement the material in an intermediate microeconomic theor course. In particular, the provide a rigorous
Notes on Convexit Ro Radner Stern School, NYU September, 2006 Abstract These notes are intended to complement the material in an intermediate microeconomic theor course. In particular, the provide a rigorous
Autonomous Equations / Stability of Equilibrium Solutions. y = f (y).
 Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y
![Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y](/thumbs/83/88503328.jpg) Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
On Range and Reflecting Functions About the Line y = mx
 On Range and Reflecting Functions About the Line = m Scott J. Beslin Brian K. Heck Jerem J. Becnel Dept.of Mathematics and Dept. of Mathematics and Dept. of Mathematics and Computer Science Computer Science
On Range and Reflecting Functions About the Line = m Scott J. Beslin Brian K. Heck Jerem J. Becnel Dept.of Mathematics and Dept. of Mathematics and Dept. of Mathematics and Computer Science Computer Science
Irrational constructions in Convex Geometry
 Irrational constructions in Convex Geometry Vitali Milman and Liran Rotem 1 Introduction We begin by quickly recalling some basic definitions from convex geometry. We refer the reader to [0] for more information.
Irrational constructions in Convex Geometry Vitali Milman and Liran Rotem 1 Introduction We begin by quickly recalling some basic definitions from convex geometry. We refer the reader to [0] for more information.
Quantitative stability of the Brunn-Minkowski inequality for sets of equal volume
 Quantitative stabilit of the Brunn-Minkowski inequalit for sets of equal volume Alessio Figalli and David Jerison Abstract We prove a quantitative stabilit result for the Brunn-Minkowski inequalit on sets
Quantitative stabilit of the Brunn-Minkowski inequalit for sets of equal volume Alessio Figalli and David Jerison Abstract We prove a quantitative stabilit result for the Brunn-Minkowski inequalit on sets
Linear programming: Theory
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analsis and Economic Theor Winter 2018 Topic 28: Linear programming: Theor 28.1 The saddlepoint theorem for linear programming The
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analsis and Economic Theor Winter 2018 Topic 28: Linear programming: Theor 28.1 The saddlepoint theorem for linear programming The
Convex Optimization. Convex Analysis - Functions
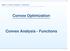 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions
 Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions J. L. Seton This version: 9 Januar 2014 First version: 2 December 2011 Research Report No. 9, 2011,
Nash Equilibrium and the Legendre Transform in Optimal Stopping Games with One Dimensional Diffusions J. L. Seton This version: 9 Januar 2014 First version: 2 December 2011 Research Report No. 9, 2011,
Non-standard constructions in convex geometry: Geometric means of convex bodies
 Non-standard constructions in convex geometry: Geometric means of convex bodies Vitali Milman Liran Rotem Abstract In this note we discuss new constructions of convex bodies By thinking of the polarity
Non-standard constructions in convex geometry: Geometric means of convex bodies Vitali Milman Liran Rotem Abstract In this note we discuss new constructions of convex bodies By thinking of the polarity
Approximation of Continuous Functions
 Approximation of Continuous Functions Francis J. Narcowich October 2014 1 Modulus of Continuit Recall that ever function continuous on a closed interval < a x b < is uniforml continuous: For ever ɛ > 0,
Approximation of Continuous Functions Francis J. Narcowich October 2014 1 Modulus of Continuit Recall that ever function continuous on a closed interval < a x b < is uniforml continuous: For ever ɛ > 0,
2 (Bonus). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
3.0 PROBABILITY, RANDOM VARIABLES AND RANDOM PROCESSES
 3.0 PROBABILITY, RANDOM VARIABLES AND RANDOM PROCESSES 3.1 Introduction In this chapter we will review the concepts of probabilit, rom variables rom processes. We begin b reviewing some of the definitions
3.0 PROBABILITY, RANDOM VARIABLES AND RANDOM PROCESSES 3.1 Introduction In this chapter we will review the concepts of probabilit, rom variables rom processes. We begin b reviewing some of the definitions
In applications, we encounter many constrained optimization problems. Examples Basis pursuit: exact sparse recovery problem
 1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
8. BOOLEAN ALGEBRAS x x
 8. BOOLEAN ALGEBRAS 8.1. Definition of a Boolean Algebra There are man sstems of interest to computing scientists that have a common underling structure. It makes sense to describe such a mathematical
8. BOOLEAN ALGEBRAS 8.1. Definition of a Boolean Algebra There are man sstems of interest to computing scientists that have a common underling structure. It makes sense to describe such a mathematical
Associativity of triangular norms in light of web geometry
 Associativit of triangular norms in light of web geometr Milan Petrík 1,2 Peter Sarkoci 3 1. Institute of Computer Science, Academ of Sciences of the Czech Republic, Prague, Czech Republic 2. Center for
Associativit of triangular norms in light of web geometr Milan Petrík 1,2 Peter Sarkoci 3 1. Institute of Computer Science, Academ of Sciences of the Czech Republic, Prague, Czech Republic 2. Center for
Moment Measures. Bo az Klartag. Tel Aviv University. Talk at the asymptotic geometric analysis seminar. Tel Aviv, May 2013
 Tel Aviv University Talk at the asymptotic geometric analysis seminar Tel Aviv, May 2013 Joint work with Dario Cordero-Erausquin. A bijection We present a correspondence between convex functions and Borel
Tel Aviv University Talk at the asymptotic geometric analysis seminar Tel Aviv, May 2013 Joint work with Dario Cordero-Erausquin. A bijection We present a correspondence between convex functions and Borel
The Entropy Power Inequality and Mrs. Gerber s Lemma for Groups of order 2 n
 The Entrop Power Inequalit and Mrs. Gerber s Lemma for Groups of order 2 n Varun Jog EECS, UC Berkele Berkele, CA-94720 Email: varunjog@eecs.berkele.edu Venkat Anantharam EECS, UC Berkele Berkele, CA-94720
The Entrop Power Inequalit and Mrs. Gerber s Lemma for Groups of order 2 n Varun Jog EECS, UC Berkele Berkele, CA-94720 Email: varunjog@eecs.berkele.edu Venkat Anantharam EECS, UC Berkele Berkele, CA-94720
Orientations of digraphs almost preserving diameter
 Orientations of digraphs almost preserving diameter Gregor Gutin Department of Computer Science Roal Hollowa, Universit of London Egham, Surre TW20 0EX, UK, gutin@dcs.rhbnc.ac.uk Anders Yeo BRICS, Department
Orientations of digraphs almost preserving diameter Gregor Gutin Department of Computer Science Roal Hollowa, Universit of London Egham, Surre TW20 0EX, UK, gutin@dcs.rhbnc.ac.uk Anders Yeo BRICS, Department
Estimates for probabilities of independent events and infinite series
 Estimates for probabilities of independent events and infinite series Jürgen Grahl and Shahar evo September 9, 06 arxiv:609.0894v [math.pr] 8 Sep 06 Abstract This paper deals with finite or infinite sequences
Estimates for probabilities of independent events and infinite series Jürgen Grahl and Shahar evo September 9, 06 arxiv:609.0894v [math.pr] 8 Sep 06 Abstract This paper deals with finite or infinite sequences
You don't have to be a mathematician to have a feel for numbers. John Forbes Nash, Jr.
 Course Title: Real Analsis Course Code: MTH3 Course instructor: Dr. Atiq ur Rehman Class: MSc-II Course URL: www.mathcit.org/atiq/fa5-mth3 You don't have to be a mathematician to have a feel for numbers.
Course Title: Real Analsis Course Code: MTH3 Course instructor: Dr. Atiq ur Rehman Class: MSc-II Course URL: www.mathcit.org/atiq/fa5-mth3 You don't have to be a mathematician to have a feel for numbers.
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
MATH LECTURE NOTES FIRST ORDER SEPARABLE DIFFERENTIAL EQUATIONS OVERVIEW
 MATH 234 - LECTURE NOTES FIRST ORDER SEPARABLE DIFFERENTIAL EQUATIONS OVERVIEW Now will will begin with the process of learning how to solve differential equations. We will learn different techniques for
MATH 234 - LECTURE NOTES FIRST ORDER SEPARABLE DIFFERENTIAL EQUATIONS OVERVIEW Now will will begin with the process of learning how to solve differential equations. We will learn different techniques for
Linear Transformations
 inear Transformations 6 The main objects of stud in an course in linear algebra are linear functions: Definition A function : V! W is linear if V and W are vector spaces and (ru + sv) r(u)+s(v) for all
inear Transformations 6 The main objects of stud in an course in linear algebra are linear functions: Definition A function : V! W is linear if V and W are vector spaces and (ru + sv) r(u)+s(v) for all
Ordinal One-Switch Utility Functions
 Ordinal One-Switch Utilit Functions Ali E. Abbas Universit of Southern California, Los Angeles, California 90089, aliabbas@usc.edu David E. Bell Harvard Business School, Boston, Massachusetts 0163, dbell@hbs.edu
Ordinal One-Switch Utilit Functions Ali E. Abbas Universit of Southern California, Los Angeles, California 90089, aliabbas@usc.edu David E. Bell Harvard Business School, Boston, Massachusetts 0163, dbell@hbs.edu
1 Lesson 1: Brunn Minkowski Inequality
 1 Lesson 1: Brunn Minkowski Inequality A set A R n is called convex if (1 λ)x + λy A for any x, y A and any λ [0, 1]. The Minkowski sum of two sets A, B R n is defined by A + B := {a + b : a A, b B}. One
1 Lesson 1: Brunn Minkowski Inequality A set A R n is called convex if (1 λ)x + λy A for any x, y A and any λ [0, 1]. The Minkowski sum of two sets A, B R n is defined by A + B := {a + b : a A, b B}. One
Math 328 Course Notes
 Math 328 Course Notes Ian Robertson March 3, 2006 3 Properties of C[0, 1]: Sup-norm and Completeness In this chapter we are going to examine the vector space of all continuous functions defined on the
Math 328 Course Notes Ian Robertson March 3, 2006 3 Properties of C[0, 1]: Sup-norm and Completeness In this chapter we are going to examine the vector space of all continuous functions defined on the
1 + x 1/2. b) For what values of k is g a quasi-concave function? For what values of k is g a concave function? Explain your answers.
 Questions and Answers from Econ 0A Final: Fall 008 I have gone to some trouble to explain the answers to all of these questions, because I think that there is much to be learned b working through them
Questions and Answers from Econ 0A Final: Fall 008 I have gone to some trouble to explain the answers to all of these questions, because I think that there is much to be learned b working through them
MAT 1275: Introduction to Mathematical Analysis. Graphs and Simplest Equations for Basic Trigonometric Functions. y=sin( x) Function
 MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS
 Trends in Mathematics Information Center for Mathematical Sciences Volume 6, Number 1, June, 23, Pages 45 49 OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS SANG UK RYU Abstract. We stud the
Trends in Mathematics Information Center for Mathematical Sciences Volume 6, Number 1, June, 23, Pages 45 49 OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS SANG UK RYU Abstract. We stud the
Exercises: Brunn, Minkowski and convex pie
 Lecture 1 Exercises: Brunn, Minkowski and convex pie Consider the following problem: 1.1 Playing a convex pie Consider the following game with two players - you and me. I am cooking a pie, which should
Lecture 1 Exercises: Brunn, Minkowski and convex pie Consider the following problem: 1.1 Playing a convex pie Consider the following game with two players - you and me. I am cooking a pie, which should
3.2 Differentiability; Tangent planes; differentials
 4 Chapter 3 Draft October 23, 2009 3.2 Differentiabilit; Tangent planes; differentials Overview: In this section, differentiabilit is defined in terms of linear approximation. A function is differentiable
4 Chapter 3 Draft October 23, 2009 3.2 Differentiabilit; Tangent planes; differentials Overview: In this section, differentiabilit is defined in terms of linear approximation. A function is differentiable
A set C R n is convex if and only if δ C is convex if and only if. f : R n R is strictly convex if and only if f is convex and the inequality (1.
 ONVEX OPTIMIZATION SUMMARY ANDREW TULLOH 1. Eistence Definition. For R n, define δ as 0 δ () = / (1.1) Note minimizes f over if and onl if minimizes f + δ over R n. Definition. (ii) (i) dom f = R n f()
ONVEX OPTIMIZATION SUMMARY ANDREW TULLOH 1. Eistence Definition. For R n, define δ as 0 δ () = / (1.1) Note minimizes f over if and onl if minimizes f + δ over R n. Definition. (ii) (i) dom f = R n f()
4 Inverse function theorem
 Tel Aviv Universit, 2013/14 Analsis-III,IV 53 4 Inverse function theorem 4a What is the problem................ 53 4b Simple observations before the theorem..... 54 4c The theorem.....................
Tel Aviv Universit, 2013/14 Analsis-III,IV 53 4 Inverse function theorem 4a What is the problem................ 53 4b Simple observations before the theorem..... 54 4c The theorem.....................
Week 3 September 5-7.
 MA322 Weekl topics and quiz preparations Week 3 September 5-7. Topics These are alread partl covered in lectures. We collect the details for convenience.. Solutions of homogeneous equations AX =. 2. Using
MA322 Weekl topics and quiz preparations Week 3 September 5-7. Topics These are alread partl covered in lectures. We collect the details for convenience.. Solutions of homogeneous equations AX =. 2. Using
Marcinkiewicz Interpolation Theorem by Daniel Baczkowski
 1 Introduction Marcinkiewicz Interpolation Theorem b Daniel Baczkowski Let (, µ be a measure space. Let M denote the collection of all extended real valued µ-measurable functions on. Also, let M denote
1 Introduction Marcinkiewicz Interpolation Theorem b Daniel Baczkowski Let (, µ be a measure space. Let M denote the collection of all extended real valued µ-measurable functions on. Also, let M denote
Lecture 4: Exact ODE s
 Lecture 4: Exact ODE s Dr. Michael Doughert Januar 23, 203 Exact equations are first-order ODE s of a particular form, and whose methods of solution rel upon basic facts concerning partial derivatives,
Lecture 4: Exact ODE s Dr. Michael Doughert Januar 23, 203 Exact equations are first-order ODE s of a particular form, and whose methods of solution rel upon basic facts concerning partial derivatives,
Approximately Gaussian marginals and the hyperplane conjecture
 Approximately Gaussian marginals and the hyperplane conjecture Tel-Aviv University Conference on Asymptotic Geometric Analysis, Euler Institute, St. Petersburg, July 2010 Lecture based on a joint work
Approximately Gaussian marginals and the hyperplane conjecture Tel-Aviv University Conference on Asymptotic Geometric Analysis, Euler Institute, St. Petersburg, July 2010 Lecture based on a joint work
Moment Measures. D. Cordero-Erausquin 1 and B. Klartag 2
 Moment Measures D. Cordero-Erausquin 1 and B. Klartag 2 Abstract With any convex function ψ on a finite-dimensional linear space X such that ψ goes to + at infinity, we associate a Borel measure µ on X.
Moment Measures D. Cordero-Erausquin 1 and B. Klartag 2 Abstract With any convex function ψ on a finite-dimensional linear space X such that ψ goes to + at infinity, we associate a Borel measure µ on X.
Lecture 2: Separable Ordinary Differential Equations
 Lecture : Separable Ordinar Differential Equations Dr. Michael Doughert Januar 8, 00 Some Terminolog: ODE s, PDE s, IVP s The differential equations we have looked at so far are called ordinar differential
Lecture : Separable Ordinar Differential Equations Dr. Michael Doughert Januar 8, 00 Some Terminolog: ODE s, PDE s, IVP s The differential equations we have looked at so far are called ordinar differential
Investigating Euler s Method and Differential Equations to Approximate π. Lindsay Crowl August 2, 2001
 Investigating Euler s Metod and Differential Equations to Approximate π Lindsa Crowl August 2, 2001 Tis researc paper focuses on finding a more efficient and accurate wa to approximate π. Suppose tat x
Investigating Euler s Metod and Differential Equations to Approximate π Lindsa Crowl August 2, 2001 Tis researc paper focuses on finding a more efficient and accurate wa to approximate π. Suppose tat x
PICONE S IDENTITY FOR A SYSTEM OF FIRST-ORDER NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS
 Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 143, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu PICONE S IDENTITY
Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 143, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu PICONE S IDENTITY
Inverse Brascamp-Lieb inequalities along the Heat equation
 Inverse Brascamp-Lieb inequalities along the Heat equation Franck Barthe and Dario Cordero-Erausquin October 8, 003 Abstract Adapting Borell s proof of Ehrhard s inequality for general sets, we provide
Inverse Brascamp-Lieb inequalities along the Heat equation Franck Barthe and Dario Cordero-Erausquin October 8, 003 Abstract Adapting Borell s proof of Ehrhard s inequality for general sets, we provide
Chapter 6. Self-Adjusting Data Structures
 Chapter 6 Self-Adjusting Data Structures Chapter 5 describes a data structure that is able to achieve an epected quer time that is proportional to the entrop of the quer distribution. The most interesting
Chapter 6 Self-Adjusting Data Structures Chapter 5 describes a data structure that is able to achieve an epected quer time that is proportional to the entrop of the quer distribution. The most interesting
On John type ellipsoids
 On John type ellipsoids B. Klartag Tel Aviv University Abstract Given an arbitrary convex symmetric body K R n, we construct a natural and non-trivial continuous map u K which associates ellipsoids to
On John type ellipsoids B. Klartag Tel Aviv University Abstract Given an arbitrary convex symmetric body K R n, we construct a natural and non-trivial continuous map u K which associates ellipsoids to
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
Notions such as convergent sequence and Cauchy sequence make sense for any metric space. Convergent Sequences are Cauchy
 Banach Spaces These notes provide an introduction to Banach spaces, which are complete normed vector spaces. For the purposes of these notes, all vector spaces are assumed to be over the real numbers.
Banach Spaces These notes provide an introduction to Banach spaces, which are complete normed vector spaces. For the purposes of these notes, all vector spaces are assumed to be over the real numbers.
d max (P,Q) = max{ x 1 x 2, y 1 y 2 }. Check is it d max a distance function. points in R 2, and let d : R 2 R 2 R denote a
 2 Metric geometr At this level there are two fundamental approaches to the tpe of geometr we are studing. The first, called the snthetic approach, involves deciding what are the important properties of
2 Metric geometr At this level there are two fundamental approaches to the tpe of geometr we are studing. The first, called the snthetic approach, involves deciding what are the important properties of
x y plane is the plane in which the stresses act, yy xy xy Figure 3.5.1: non-zero stress components acting in the x y plane
 3.5 Plane Stress This section is concerned with a special two-dimensional state of stress called plane stress. It is important for two reasons: () it arises in real components (particularl in thin components
3.5 Plane Stress This section is concerned with a special two-dimensional state of stress called plane stress. It is important for two reasons: () it arises in real components (particularl in thin components
Star bodies with completely symmetric sections
 Star bodies with completely symmetric sections Sergii Myroshnychenko, Dmitry Ryabogin, and Christos Saroglou Abstract We say that a star body is completely symmetric if it has centroid at the origin and
Star bodies with completely symmetric sections Sergii Myroshnychenko, Dmitry Ryabogin, and Christos Saroglou Abstract We say that a star body is completely symmetric if it has centroid at the origin and
An example of a convex body without symmetric projections.
 An example of a convex body without symmetric projections. E. D. Gluskin A. E. Litvak N. Tomczak-Jaegermann Abstract Many crucial results of the asymptotic theory of symmetric convex bodies were extended
An example of a convex body without symmetric projections. E. D. Gluskin A. E. Litvak N. Tomczak-Jaegermann Abstract Many crucial results of the asymptotic theory of symmetric convex bodies were extended
High-dimensional distributions with convexity properties
 High-dimensional distributions with convexity properties Bo az Klartag Tel-Aviv University A conference in honor of Charles Fefferman, Princeton, May 2009 High-Dimensional Distributions We are concerned
High-dimensional distributions with convexity properties Bo az Klartag Tel-Aviv University A conference in honor of Charles Fefferman, Princeton, May 2009 High-Dimensional Distributions We are concerned
ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION
 ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION CRISTINA STAMATE Institute of Mathematics 8, Carol I street, Iasi 6600, Romania cstamate@mail.com Abstract: We present the principal properties of the
ABOUT THE WEAK EFFICIENCIES IN VECTOR OPTIMIZATION CRISTINA STAMATE Institute of Mathematics 8, Carol I street, Iasi 6600, Romania cstamate@mail.com Abstract: We present the principal properties of the
Symmetry Arguments and the Role They Play in Using Gauss Law
 Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
MATH 51H Section 4. October 16, Recall what it means for a function between metric spaces to be continuous:
 MATH 51H Section 4 October 16, 2015 1 Continuity Recall what it means for a function between metric spaces to be continuous: Definition. Let (X, d X ), (Y, d Y ) be metric spaces. A function f : X Y is
MATH 51H Section 4 October 16, 2015 1 Continuity Recall what it means for a function between metric spaces to be continuous: Definition. Let (X, d X ), (Y, d Y ) be metric spaces. A function f : X Y is
Continuity of convex functions in normed spaces
 Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
School of Computer and Communication Sciences. Information Theory and Coding Notes on Random Coding December 12, 2003.
 ÉCOLE POLYTECHNIQUE FÉDÉRALE DE LAUSANNE School of Computer and Communication Sciences Handout 8 Information Theor and Coding Notes on Random Coding December 2, 2003 Random Coding In this note we prove
ÉCOLE POLYTECHNIQUE FÉDÉRALE DE LAUSANNE School of Computer and Communication Sciences Handout 8 Information Theor and Coding Notes on Random Coding December 2, 2003 Random Coding In this note we prove
Analysis II Lecture notes
 Analysis II Lecture notes Christoph Thiele (lectures 11,12 by Roland Donninger lecture 22 by Diogo Oliveira e Silva) Summer term 2015 Universität Bonn July 5, 2016 Contents 1 Analysis in several variables
Analysis II Lecture notes Christoph Thiele (lectures 11,12 by Roland Donninger lecture 22 by Diogo Oliveira e Silva) Summer term 2015 Universität Bonn July 5, 2016 Contents 1 Analysis in several variables
Ch 3 Alg 2 Note Sheet.doc 3.1 Graphing Systems of Equations
 Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Invariant monotone vector fields on Riemannian manifolds
 Nonlinear Analsis 70 (2009) 850 86 www.elsevier.com/locate/na Invariant monotone vector fields on Riemannian manifolds A. Barani, M.R. Pouraevali Department of Mathematics, Universit of Isfahan, P.O.Box
Nonlinear Analsis 70 (2009) 850 86 www.elsevier.com/locate/na Invariant monotone vector fields on Riemannian manifolds A. Barani, M.R. Pouraevali Department of Mathematics, Universit of Isfahan, P.O.Box
A Beckman-Quarles type theorem for linear fractional transformations of the extended double plane
 Rose- Hulman Undergraduate Mathematics Journal A Beckman-Quarles tpe theorem for linear fractional transformations of the extended double plane Andrew Jullian Mis a Josh Keilman b Volume 12, No. 2, Fall
Rose- Hulman Undergraduate Mathematics Journal A Beckman-Quarles tpe theorem for linear fractional transformations of the extended double plane Andrew Jullian Mis a Josh Keilman b Volume 12, No. 2, Fall
Functional Analysis Exercise Class
 Functional Analysis Exercise Class Wee November 30 Dec 4: Deadline to hand in the homewor: your exercise class on wee December 7 11 Exercises with solutions Recall that every normed space X can be isometrically
Functional Analysis Exercise Class Wee November 30 Dec 4: Deadline to hand in the homewor: your exercise class on wee December 7 11 Exercises with solutions Recall that every normed space X can be isometrically
6. Linear transformations. Consider the function. f : R 2 R 2 which sends (x, y) (x, y)
 Consider the function 6 Linear transformations f : R 2 R 2 which sends (x, ) (, x) This is an example of a linear transformation Before we get into the definition of a linear transformation, let s investigate
Consider the function 6 Linear transformations f : R 2 R 2 which sends (x, ) (, x) This is an example of a linear transformation Before we get into the definition of a linear transformation, let s investigate
Functional Analysis, Stein-Shakarchi Chapter 1
 Functional Analysis, Stein-Shakarchi Chapter 1 L p spaces and Banach Spaces Yung-Hsiang Huang 018.05.1 Abstract Many problems are cited to my solution files for Folland [4] and Rudin [6] post here. 1 Exercises
Functional Analysis, Stein-Shakarchi Chapter 1 L p spaces and Banach Spaces Yung-Hsiang Huang 018.05.1 Abstract Many problems are cited to my solution files for Folland [4] and Rudin [6] post here. 1 Exercises
Introduction to Topology
 Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Part V. 17 Introduction: What are measures and why measurable sets. Lebesgue Integration Theory
 Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Probabilistic Methods in Asymptotic Geometric Analysis.
 Probabilistic Methods in Asymptotic Geometric Analysis. C. Hugo Jiménez PUC-RIO, Brazil September 21st, 2016. Colmea. RJ 1 Origin 2 Normed Spaces 3 Distribution of volume of high dimensional convex bodies
Probabilistic Methods in Asymptotic Geometric Analysis. C. Hugo Jiménez PUC-RIO, Brazil September 21st, 2016. Colmea. RJ 1 Origin 2 Normed Spaces 3 Distribution of volume of high dimensional convex bodies
Auerbach bases and minimal volume sufficient enlargements
 Auerbach bases and minimal volume sufficient enlargements M. I. Ostrovskii January, 2009 Abstract. Let B Y denote the unit ball of a normed linear space Y. A symmetric, bounded, closed, convex set A in
Auerbach bases and minimal volume sufficient enlargements M. I. Ostrovskii January, 2009 Abstract. Let B Y denote the unit ball of a normed linear space Y. A symmetric, bounded, closed, convex set A in
A glimpse into convex geometry. A glimpse into convex geometry
 A glimpse into convex geometry 5 \ þ ÏŒÆ Two basis reference: 1. Keith Ball, An elementary introduction to modern convex geometry 2. Chuanming Zong, What is known about unit cubes Convex geometry lies
A glimpse into convex geometry 5 \ þ ÏŒÆ Two basis reference: 1. Keith Ball, An elementary introduction to modern convex geometry 2. Chuanming Zong, What is known about unit cubes Convex geometry lies
Isomorphic and almost-isometric problems in high-dimensional convex geometry
 Isomorphic and almost-isometric problems in high-dimensional convex geometry Bo az Klartag Abstract. The classical theorems of high-dimensional convex geometry exhibit a surprising level of regularity
Isomorphic and almost-isometric problems in high-dimensional convex geometry Bo az Klartag Abstract. The classical theorems of high-dimensional convex geometry exhibit a surprising level of regularity
Normed and Banach spaces
 Normed and Banach spaces László Erdős Nov 11, 2006 1 Norms We recall that the norm is a function on a vectorspace V, : V R +, satisfying the following properties x + y x + y cx = c x x = 0 x = 0 We always
Normed and Banach spaces László Erdős Nov 11, 2006 1 Norms We recall that the norm is a function on a vectorspace V, : V R +, satisfying the following properties x + y x + y cx = c x x = 0 x = 0 We always
Chapter 4 Analytic Trigonometry
 Analtic Trigonometr Chapter Analtic Trigonometr Inverse Trigonometric Functions The trigonometric functions act as an operator on the variable (angle, resulting in an output value Suppose this process
Analtic Trigonometr Chapter Analtic Trigonometr Inverse Trigonometric Functions The trigonometric functions act as an operator on the variable (angle, resulting in an output value Suppose this process
Unbounded Convex Semialgebraic Sets as Spectrahedral Shadows
 Unbounded Convex Semialgebraic Sets as Spectrahedral Shadows Shaowei Lin 9 Dec 2010 Abstract Recently, Helton and Nie [3] showed that a compact convex semialgebraic set S is a spectrahedral shadow if the
Unbounded Convex Semialgebraic Sets as Spectrahedral Shadows Shaowei Lin 9 Dec 2010 Abstract Recently, Helton and Nie [3] showed that a compact convex semialgebraic set S is a spectrahedral shadow if the
Math 5052 Measure Theory and Functional Analysis II Homework Assignment 7
 Math 5052 Measure Theory and Functional Analysis II Homework Assignment 7 Prof. Wickerhauser Due Friday, February 5th, 2016 Please do Exercises 3, 6, 14, 16*, 17, 18, 21*, 23*, 24, 27*. Exercises marked
Math 5052 Measure Theory and Functional Analysis II Homework Assignment 7 Prof. Wickerhauser Due Friday, February 5th, 2016 Please do Exercises 3, 6, 14, 16*, 17, 18, 21*, 23*, 24, 27*. Exercises marked
8 Differential Calculus 1 Introduction
 8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
Problem Set 6: Solutions Math 201A: Fall a n x n,
 Problem Set 6: Solutions Math 201A: Fall 2016 Problem 1. Is (x n ) n=0 a Schauder basis of C([0, 1])? No. If f(x) = a n x n, n=0 where the series converges uniformly on [0, 1], then f has a power series
Problem Set 6: Solutions Math 201A: Fall 2016 Problem 1. Is (x n ) n=0 a Schauder basis of C([0, 1])? No. If f(x) = a n x n, n=0 where the series converges uniformly on [0, 1], then f has a power series
MAT389 Fall 2016, Problem Set 2
 MAT389 Fall 2016, Problem Set 2 Circles in the Riemann sphere Recall that the Riemann sphere is defined as the set Let P be the plane defined b Σ = { (a, b, c) R 3 a 2 + b 2 + c 2 = 1 } P = { (a, b, c)
MAT389 Fall 2016, Problem Set 2 Circles in the Riemann sphere Recall that the Riemann sphere is defined as the set Let P be the plane defined b Σ = { (a, b, c) R 3 a 2 + b 2 + c 2 = 1 } P = { (a, b, c)
SECOND-ORDER DIFFERENTIAL EQUATIONS: CONDITIONS OF COMPLETE INTEGRABILITY 1. from Lectures on Integration of Differential Equations
 Applicable Analsis and Discrete Mathematics available online at http://pefmath.etf.bg.ac.u Appl. Anal. Discrete Math. 008, 3 45. doi:0.98/aadm0803e SECOND-ORDER DIFFERENTIAL EQUATIONS: CONDITIONS OF COMPLETE
Applicable Analsis and Discrete Mathematics available online at http://pefmath.etf.bg.ac.u Appl. Anal. Discrete Math. 008, 3 45. doi:0.98/aadm0803e SECOND-ORDER DIFFERENTIAL EQUATIONS: CONDITIONS OF COMPLETE
Metric spaces and metrizability
 1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
Examples of Dual Spaces from Measure Theory
 Chapter 9 Examples of Dual Spaces from Measure Theory We have seen that L (, A, µ) is a Banach space for any measure space (, A, µ). We will extend that concept in the following section to identify an
Chapter 9 Examples of Dual Spaces from Measure Theory We have seen that L (, A, µ) is a Banach space for any measure space (, A, µ). We will extend that concept in the following section to identify an
Research Article On Sharp Triangle Inequalities in Banach Spaces II
 Hindawi Publishing Corporation Journal of Inequalities and Applications Volume 2010, Article ID 323609, 17 pages doi:10.1155/2010/323609 Research Article On Sharp Triangle Inequalities in Banach Spaces
Hindawi Publishing Corporation Journal of Inequalities and Applications Volume 2010, Article ID 323609, 17 pages doi:10.1155/2010/323609 Research Article On Sharp Triangle Inequalities in Banach Spaces
PROBLEMS. (b) (Polarization Identity) Show that in any inner product space
 1 Professor Carl Cowen Math 54600 Fall 09 PROBLEMS 1. (Geometry in Inner Product Spaces) (a) (Parallelogram Law) Show that in any inner product space x + y 2 + x y 2 = 2( x 2 + y 2 ). (b) (Polarization
1 Professor Carl Cowen Math 54600 Fall 09 PROBLEMS 1. (Geometry in Inner Product Spaces) (a) (Parallelogram Law) Show that in any inner product space x + y 2 + x y 2 = 2( x 2 + y 2 ). (b) (Polarization
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Real Analysis Notes. Thomas Goller
 Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem
 56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
56 Chapter 7 Locally convex spaces, the hyperplane separation theorem, and the Krein-Milman theorem Recall that C(X) is not a normed linear space when X is not compact. On the other hand we could use semi
Chapter 1: Banach Spaces
 321 2008 09 Chapter 1: Banach Spaces The main motivation for functional analysis was probably the desire to understand solutions of differential equations. As with other contexts (such as linear algebra
321 2008 09 Chapter 1: Banach Spaces The main motivation for functional analysis was probably the desire to understand solutions of differential equations. As with other contexts (such as linear algebra
Integral Jensen inequality
 Integral Jensen inequality Let us consider a convex set R d, and a convex function f : (, + ]. For any x,..., x n and λ,..., λ n with n λ i =, we have () f( n λ ix i ) n λ if(x i ). For a R d, let δ a
Integral Jensen inequality Let us consider a convex set R d, and a convex function f : (, + ]. For any x,..., x n and λ,..., λ n with n λ i =, we have () f( n λ ix i ) n λ if(x i ). For a R d, let δ a
Blow-up collocation solutions of nonlinear homogeneous Volterra integral equations
 Blow-up collocation solutions of nonlinear homogeneous Volterra integral equations R. Benítez 1,, V. J. Bolós 2, 1 Dpto. Matemáticas, Centro Universitario de Plasencia, Universidad de Extremadura. Avda.
Blow-up collocation solutions of nonlinear homogeneous Volterra integral equations R. Benítez 1,, V. J. Bolós 2, 1 Dpto. Matemáticas, Centro Universitario de Plasencia, Universidad de Extremadura. Avda.
INTRODUCTION TO DIOPHANTINE EQUATIONS
 INTRODUCTION TO DIOPHANTINE EQUATIONS In the earl 20th centur, Thue made an important breakthrough in the stud of diophantine equations. His proof is one of the first eamples of the polnomial method. His
INTRODUCTION TO DIOPHANTINE EQUATIONS In the earl 20th centur, Thue made an important breakthrough in the stud of diophantine equations. His proof is one of the first eamples of the polnomial method. His
Convex Geometry. Otto-von-Guericke Universität Magdeburg. Applications of the Brascamp-Lieb and Barthe inequalities. Exercise 12.
 Applications of the Brascamp-Lieb and Barthe inequalities Exercise 12.1 Show that if m Ker M i {0} then both BL-I) and B-I) hold trivially. Exercise 12.2 Let λ 0, 1) and let f, g, h : R 0 R 0 be measurable
Applications of the Brascamp-Lieb and Barthe inequalities Exercise 12.1 Show that if m Ker M i {0} then both BL-I) and B-I) hold trivially. Exercise 12.2 Let λ 0, 1) and let f, g, h : R 0 R 0 be measurable
Math 209B Homework 2
 Math 29B Homework 2 Edward Burkard Note: All vector spaces are over the field F = R or C 4.6. Two Compactness Theorems. 4. Point Set Topology Exercise 6 The product of countably many sequentally compact
Math 29B Homework 2 Edward Burkard Note: All vector spaces are over the field F = R or C 4.6. Two Compactness Theorems. 4. Point Set Topology Exercise 6 The product of countably many sequentally compact
