SECOND-ORDER DIFFERENTIAL EQUATIONS: CONDITIONS OF COMPLETE INTEGRABILITY 1. from Lectures on Integration of Differential Equations
|
|
|
- Sarah Howard
- 6 years ago
- Views:
Transcription
1 Applicable Analsis and Discrete Mathematics available online at Appl. Anal. Discrete Math. 008, doi:0.98/aadm0803e SECOND-ORDER DIFFERENTIAL EQUATIONS: CONDITIONS OF COMPLETE INTEGRABILITY Vasilij Petrovich Ermakov from Lectures on Integration of Differential Equations Linear second-order equations with variable coefficients can be completel integrated onl in ver rare cases. We consider the most important of them. To begin we prove that, if a particular integral of the equation + Ad + B = 0 is known, then the determination of a complete integral is reduced to a quadrature. Let u be a particular integral of this equation, ie d u + Adu + Bu = 0. We eliminate B from and to obtain 3 u d d u + A u d du = Mathematics Subject Classification. 34A05, 34A34. Kewords and Phrases. Ermakov, integral, complete integrabilit. Translated from Russian b A. O. Harin, under redaction b P. G. L. Leach 3
2 4 Vasilij Petrovich Ermakov A first integral of 3 is u d du = C exp A. When we integrate again, we obtain the complete integral = C u exp A u + C u. An linear differential equation of the second order, videlicet + A d + B = 0, can alwas be reduced b a transformation of the dependent variable to a form in which the first derivative is absent. Explicitl we set = z exp A to obtain d z = 4 A + da B z. We see below that this form makes it eas to discover conditions of integrabilit for differential equations. 3 The majorit of differential equations for which it is possible to find conditions of integrabilit reduce to the form 4 Ax + Bx + C d + Dx + E + F = 0, where the uppercase coefficients are parameters independent of the variables, x and. When we take the nth derivative of 4 and set we obtain z = dn n, 5 Ax + Bx + C d z D+Anx+E+Bx dz + F + An + Dn + An z = 0. Editor s Note: The integral for the second solution is known as Abel s formula.
3 Second-order differential equations: Conditions of complete integrabilit 5 Thus, if an integral of 4 is known, we can find an integral of 5 when n is a natural number. An integral of 4 can alwas be found in the case that F = 0, ie the equation has the form 6 Ax + Bx + C d + Dx + E = 0. We write Dx + E Ax = ϕx. + Bx + C Then we determine an integral of 5 of the form = α exp ϕx + β, where α and β are the arbitrar constants of integration. Consequentl we have proven that, if n is a natural number, then a particular integral of the equation Ax + Bx + C d z dz D + Anx + E + Bx + n D + A + An z = 0 is given b the formula z = dn n exp ϕx. 4 We pass to a more thorough investigation of particular cases. From what we proved above it is evident that the differential equation, 7 x+ax+b d z + n λx+b+n µx+a dz +nn λ µz = 0, is completel integrable if n is a natural number. In the present case λx + b + µx + a ϕx = = λlogx + a + µ logx + b. x + ax + b Hence a particular integral of the equation is given b the formula z = dn n x + a λ x + b µ. We appl the transformation of to 7. When we set z = x + a λ n/ x + b µ n/,
4 6 Vasilij Petrovich Ermakov we reduce 7 to the form x + ax + b d z = n λ When we compare this equation with 4 x + ax + b d = b a x + a + n µ 4 α x + a + a b x + b + λ + µ + z. 4 β x + b + γ, we obtain three algebraic equations the solutions of which are n = ± + 4α b a ± + 4β a b ± + 4γ, λ = ± + 4α b a + 4β a b 8 + 4γ, µ = + 4α b a ± + 4β a b + 4γ. Before each of the roots in these equations either upper or lower sign can be taken so that altogether there are eight solutions which leads to the following result. To find the complete integrabilit conditions of the differential equation 9 decompose the fraction into partial fractions according to = Ax + Bx + C x + a x + b Ax + Bx + C x + ax + b Ax + Bx + C x + ax + b = α x + a + β x + b + γ. The equation can be completel integrated if one of the eight expressions + 4α b a ± + 4β a b ± + 4γ is an odd integer. If this condition be satisfied, a particular integral of 9 is 0 = x + a n λ/ c + b n µ/ dn n a + a λ x + b µ,
5 Second-order differential equations: Conditions of complete integrabilit 7 where n, λ and µ are given b the formulæ 8 in which, naturall, signs should be chosen so that n be a positive integer. If two of the numbers in 0 are odd integers, we can find two independent particular integrals and consequentl the complete integral without the use of quadratures. 5 The conditions of integrabilit found above are not unique. We demonstrate the existence of other conditions. It is eas to verif that the complete integral of the equation t + b a d z dt + t dz dt δ z = 0 is given b the formula C t + δ t + b a + C t δ t + b a. As was proven in 3, the nth derivative of is the complete integral of the equation 3 t + b a d z dz + n + t dt dt + n δ z = 0. The nth derivative of is nothing but the coefficient of u n in the expansion of the expression, 4 C t + u + δ t + b a + C t + u δ t + b a, in increasing powers of u. Under the change of independent variable t x + a equation 3 becomes 5 x + ax + b d z + dz x + b + n + x + a + n δ z = 0. 4 When we substitute for t into 4, we find that the complete integral of 5 is the coefficient of u n in the expansion of the expression 6 C x + a + u + x + b + u x + a + u δ in increasing powers of u. + C x + a + u x + b + u x + a + u δ
6 8 Vasilij Petrovich Ermakov When we take the mth derivative of 5 and set s = d m z/ m, we obtain 7 x + ax + b d s + ds m + x + b + m + n + x + a + m + n δ z = 0. 4 The complete integral of 8 is the mth derivative of the coefficient of u n in the expansion of 6 in increasing powers of u. we obtain We appl the transformation of to 8. When we set s = x + a m+/4 x + b m+n+/4, 8 x + ax + b d = m 4 6 b a x + a + m + n 4 6 a b x + b + δ. 4 If we compare 8 with 9 x + ax + b d α = x + a + β x + b + γ, we make the identifications m = + + 4α b a, m + n = + + 4β a b and δ = + 4γ. Thus 9 is completel integrable if + + 4α b a and + + 4β a b are integers. In this case we obtain the complete integral through multipling x + a m+/4 x + b m n+/4 b the mth derivative of the coefficient of u n in the expansion of 6 in increasing powers of u. We have found that the equation 0 x + ax + b d α = x + a + β x + b + γ, 6
7 Second-order differential equations: Conditions of complete integrabilit 9 can be completel integrated if + + 4α b a and + + 4β a b are whole numbers. To find further conditions for integrabilit we transform the variables of 0 according to x + a b a t + a and z t + a to obtain t + at + b d z dt = γb a t + a + β t + b + α z. b a This equation is of the same form as 0 and hence is completel integrable if + + 4γ and + + 4β a b are whole numbers. With this condition 0 is also integrable. In the same wa we can prove that 0 is also integrable in the case that + + 4γ and are integers. Thus we obtain the result that + + 4α a b The equation x + ax + b d α = x + a + β x + b + γ, in addition to the cases indicated in 4, is completel integrable if two among the three numbers, + + 4α b a, + + 4β and + 4γ, a b are whole numbers. The equation x + ax + bx + c d α = x + a + 7 β x + b + γ x + c
8 30 Vasilij Petrovich Ermakov can be transformed to the form of the equation, 0, examined above b a transformation of variables. When we make the change c ac b 3 x + c = t + a + b c, = z t + a + b c, we obtain 4 t + at + b d z dt = α c at + a + β c bt + b + γ z. c ac b The integrabilit conditions for this equation can be found following the rules given in 4 and 6. Thus we obtain the following result. To find the integrabilit conditions for the differential equation decompose the fraction into partial fractions according to = Ax + Bx + C x + a x + b x + c Ax + Bx + C x + a x + b x + c Ax + Bx + C x + a x + b x + c = α x + a + The equation is completel integrable if 4α + a ba c ± + β x + b + 4β b ab c ± + γ x + c. 4γ c ac b is an odd integer. The equation is completel integrable also in the case when two of the three numbers, + + are whole numbers. 4α a ba c, + + 4β b ab c and + 4γ + c ac b, We now pass to a new form of the equation 5 x + a d z + n µ λx a dz λnz = 0. 8
9 Second-order differential equations: Conditions of complete integrabilit 3 This equation, as was shown in 3, is completel integrable if n is a positive integer. In the present case 6 ϕx = λ + µ = λx + µ logx + a. x + a Therefore a particular integral of 5 is given b the formula 7 z = dn n x + a µ e λx. We appl the transformation of to 5. When we set 8 z = x + a µ n e λx/, 5 becomes 9 d λ = λn + µ + 4 x + a + n µ 4x + a. Comparing this equation with the equation 30 α + = β x + a + we make the identifications n = ± + 4γ ± 3 µ = + 4γ ± λ = ± α. Thus we obtain the result that is completel integrable if = α + β x + a + + 4γ ± γ x + a β α, β α and γ x + a β α is an integer. Given that this condition holds, a particular integral of the equation is 3 = x + a n µ/ λx/ dn e n x + aµ e λx, where n, λ and µ are given b 3.
10 3 Vasilij Petrovich Ermakov 9 The integrabilit condition found in 8 is not unique. Moreover it does not hold in the case that α = 0, ie when the equation has the form d β 33 = x + a + γ x + a. To find the integrabilit condition for this equation we appl the transformation 34 x + a = t + a, = z t + a. Then 33 becomes 35 d z dt = β γ 4t + a z. Equation 35, hence 33, is completel integrable if + 4γ is an odd integer. Thus we obtain = α + β x + a + γ x + a is completel integrable if α = 0 and + 4γ is an odd integer. In addition to the two cases indicated the equation is also completel integrable when α = β = 0, ie, the equation is 36 = γ x + a. The solution of 36 is 37 = C x + a µ + C x + a µ, where µ = + + 4γ. 0 We demonstrate the determination of the integrabilit condition and solution given in 9. It is eas to show that 38 sx = C exp δ x + a + C exp δ x + a
11 Second-order differential equations: Conditions of complete integrabilit 33 is the solution of the equation 39 x + a d s + ds δ s = 0. We differentiate 39 n times and set Then the equation becomes z = dn s n. 40 x + a d z + n + dz δ z = 0. The solution of 40 is given b the formula 4 zx = dn n C exp δ x + a + C exp δ x + a. We appl the transformation of to 4. When we set 4 z = x + a +n/4, we obtain 43 d δ = x + a + n 4 6x + a. On comparison of 43 with 44 d β = x + a + γ x + a we obtain δ = β and n = + + 4γ. For n a positive integer the solution of 43 is +n/4 dn 45 x = x + a n C exp δ x + a + C exp δ x + a. 46 x + b d = α x + b + β x + ax + b + γ x + a
12 34 Vasilij Petrovich Ermakov can be transformed b a change of variables to the form of the equation examined in the three previous sections. When we appl the transformation 47 x + b = a b t + a and = z t + a to 46, we obtain 48 a b d z dt = α + β t + a + γ t + a. The integrabilit conditions for 48 can be found according to the rules developed in the three previous sections. Thus we obtain x + b d = α x + b + β x + ax + b + γ x + a is completel integrable in the following three cases:. if + 4γ a b ± β a b α is an odd integer,. if α = 0 and + + 4γ a b is an integer and 3. if α = β = d = α x + a 4 + β x + a 3 + γ x + a can be transformed b a change of variables to the form of the equation examined in 8, 9 and 0. If we set x + a = t + a and = z t + a,
13 Second-order differential equations: Conditions of complete integrabilit becomes 50 Thus we obtain = d z dt = α + β t + a + γ t + a z. α x + a 4 + β x + a 3 + γ x + a is completel integrable in the following three cases:. if + 4γ ± β α is an odd integer,. if α = 0 and + 4γ is an odd integer and 3. if α = β = 0. 3 The first of the integrabilit conditions given in and the solution of 50 can also be obtained as below. As was shown in 3, the differential equation 5 x + a d z + n λx + a + µ dz + nn λz = 0 is completel integrable if n is an integer. In the present case λ 5 ϕx = x + a µ x + a = λlogx + a + µ x + a. A particular integral of the equation is expressed b the formula 53 zx = dn µ n x + a λ exp. x + a When we appl the transformation of, namel z = x + a λ n/ exp we obtain 54 d = µ x + a, µ µn λ + 4x + a 4 x + a 3 + λ + 4x + a.
14 36 Vasilij Petrovich Ermakov On comparison with 49, namel we obtain n = d = α x + a 4 + β x + a 3 + γ x + a, ± + 4γ ± β, λ = ± + 4γ and µ = ± α. α If n is found to be a positive integer, a particular integral of the equation ma be written as 55 = x + a n λ/ µ d n µ exp x + a n x + a λ exp. x + a 56 4 = αx + βx + γ can be transformed b a change of variables to a particular form of the equation examined in 8. If we set we obtain 57 x + β α = t + a and = zt + a /4, d z α dt = 4αγ β + 4 6αt + a 3 6t + a z. As has been proved in 8, we obtain is completel integrable if is an odd integer. = αx + βx + γ ± 4αγ β 4α α
15 Second-order differential equations: Conditions of complete integrabilit 37 5 The integrabilit condition given in the previous section and the solution can be found as follows. 58 As has been shown in 3, the differential equation d z dz λ + µ λnz = 0 is completel integrable if n is a positive integer. In the case of 58 ϕx = λx + µ = λx + µx. Therefore a particular integral of the equation is given b z = dn n exp λx + µx. When we appl the transformation of, videlicet z = exp λx + µ, we obtain 59 d λ = x + λµx + µ 4 λ + λn. When we compare 59 with 56, videlicet we find that λ = ± α, = αx + βx + γ, µ = ± β and n = ± 4αγ β α 4α. α If n is a positive integer, the solution of 56 is 60 x = exp d n λx + µ expλx n + µx. 6 6 d = α x + a 6 + β x + a 5 + γ x + a 4
16 38 Vasilij Petrovich Ermakov can be transformed to 56 b the change of variables x + a = t and = z t. Specificall we obtain d z dt = αt + βt + γ z. As a consequence of the result of 5 we have d = α x + a 6 + β x + a 5 + γ x + a 4 can be completel integrated if ± 4αγ β 4α α is an integer. 7 All of the differential equations examined thus far can be expressed in terms of a single general formula, videlicet 6 = Ax + Bx + C Dx 3 + Ex + Fx + G. The methods of integration of 6 and its integrabilit conditions essentiall depend upon the roots of the equation 63 Dx 3 + Ex + Fx + G = 0. The sections in which we examined the different particular cases are. 7 when all roots of 63 are different,. when 63 has two roots equal, 3. 6 when 63 has three roots equal, 4. 4 and 6 when D = 0 and the roots of the equation 64 Ex + Fx + G = 0 are unequal,
17 Second-order differential equations: Conditions of complete integrabilit and 3 when D = 0 and the roots of 64 are equal, 6. 8, 9 and 0 when D = E = 0 and 7. 4 and 5 when D = E = F = We can transform the differential equation, Ex + Fx + G d + Hx + K + L = 0, to the standard form b the application of the transformation of, videlicet = z exp Hx + K Ex + Fx + G. Equation 65 becomes 66 d z = Ax + Bx + C Ex + Fx + G which is a particular case of 6 with D = 0. 8 There are man differential equations which can be reduced to the equations examined above b a change of variables. We consider some of them. 67 is transformed to 68 b the transformation = aex + be x + c αe x + β d z dt = 4t + at + bt + c t z αt + β x = log t and = z t. The integrabilit conditions for this equation can be found according to the rules developed in 4, 6, 8, 9, 0, and x d = alog x + b logx + c α log x + β
18 40 Vasilij Petrovich Ermakov is transformed to 70 b the transformation d z dt = 4 + at + bt + c z αt + β x = e t and = z expt/. The integrabilit conditions for 69 can be found according to the rules developed in 8, 9, 0, 4 and 5. 7 cos x d = a sin x + b sinx + c is transformed to 7 b the transformation t d z dt = a t + bt + c z 4 sin x = t and = z t /4. According to the rule developed in 4 7, hence 7, is completel integrable if 4 + a b + c ± 4 + a + b + c ± a is an odd integer. According to the rule developed in 6 this equation is also completel integrable in the case when two of the three numbers a b + c, a + b + c and + a are integers. 73 is transformed to 74 b the transformation = a tan x + b tanx + c t + d z dt = at + bt + c z tan x = t and = z + t /.
19 Second-order differential equations: Conditions of complete integrabilit 4 According to the rule developed in 4 74, hence 73, is completel integrable if + 4a ± a c + ib ± a c ib is an odd integer. 75 Pfaff s equation, ax δ + b x d + cx δ + e x d + fx δ + g = 0, can be transformed to the form 76 ax δ + b x d z = αx δ + βx δ + γ z b using the transformation of. Under the change of variables 77 x = t /δ and z = st δ/δ equation 76 becomes 78 δ d s dt = δ 4t + αt + βt + γ t at + b s. The integrabilit conditions for 78 can be found according to the rules developed in 4, 6, 8, 9, 0, and 3. When we set a = β = γ = 0 and b = in 76, we obtain 79 d z = αxδ z, which is known as Riccati s equation. When we appl the transformation 77, equation 79 becomes δ d s α dt = + δ 4t s. According to the rule developed in 8 we find that Riccati s equation is completel integrable if /δ is an odd integer. 9 Some nonlinear differential equations of the first and second orders are reduced to linear form b a transformation of the dependent variable. The equation 80 d = + A + B is reduced to the linear second-order equation 8 d z A dz + Bz = 0
20 4 Vasilij Petrovich Ermakov under the transformation The more general equation = z dz. 8 d = A + B + C, where A, B and C ma be functions of x, can be reduced to 80 b a change of the independent variable. We set = z A to obtain dz = z + B + da z + AC. A As has been shown above, this equation can be reduced to a linear second-order differential equation. 83 d d + A + B d + C = 0 can be transformed to the form of 8 b a change of the dependent variable. If we set 84 = exp z, we obtain dz = A + z Bz + C. As we have proven above, this equation can be reduced to the linear second-order differential equation. The particular case of 83 with A =, videlicet 85 d d + B d + C = 0, deserves special attention. Equation 85 can alwas be completel integrated since it reduces to the linear first-order equation under the transformation 84. dz + Bz = C
21 Second-order differential equations: Conditions of complete integrabilit 43 0 Some nonlinear differential equations are related to linear second-order differential equations. If an integral of the equation 86 = M is known, one can find an integral of the equation 87 where α is some constant. 88 d z = Mz + α z 3, We eliminate M from 86 and 87 to obtain d dz z d = α z 3. When we multipl both sides of 88 b dz z d, 88 becomes We integrate this to obtain 89 d dz z d = α z dz z d = C α z. d. z If and are two particular integrals of 86, we obtain two first integrals of 87 when we substitute them for in 89. The integrals are dz z d = C α z and dz z d = C α z. On the elimination of dz/ from these two first integrals we obtain the solution of 87. The solution of 87 can also be obtained as follows. From 89 we obtain = dz z d. C α z
22 44 Vasilij Petrovich Ermakov When we divide both sides b, this becomes z = d z. C z α We multipl b C and integrate both sides to obtain 90 C + C 0 = C z α, where C 0 is the second constant of integration. In 90 we have the solution of 87. Instead of it is sufficient to take an particular solution 3 of 86. Conversel, if a particular solution of 87 is known, we can find the complete solution of 86. Since it is sufficient to find particular integrals of 86, we can set C = 0 in 89. Thus we obtain dz z d = ± α z which is variables separable and can be written as d = dz z ± α z. On integration this becomes from which it follows that log = log z ± α z = z exp ± α z. We take the upper and then the lower sign to obtain two particular integrals of 86. The theorem proven in 0 can be generalised as below. If p is some known function of x and f is some other given function, then the solution of the equation 9 p d d p = p f p 3 Editor s Note: In 90 one has a generalisation of Abel s formula for a second solution of a linear second-order differential equation given a particular solution.
23 Second-order differential equations: Conditions of complete integrabilit 45 can be determined b means of quadratures. The multiplication of 9 b p d dp leads to the differential form d p d dp = f d p. p We integrate this to obtain p d dp = ϕ + C, p where ϕz = fzdz. This is the expression for a first integral of 9. We solve for, namel p d dp =, ϕ + C p divide b p and integrate to obtain 9 p + C 0 = d p, ϕ + C p where C 0 is the second constant of integration. Equation 9 represents the complete integral of the equation. In the particular case for which p = x equation 9 takes the form x 3 d = f. x REFERENCES. V. P. Ermakov: Second order differential equations. Conditions of complete integrabilit. Universita Izvestia Kiev, Series III Translator: A. O. Harin Received Jul 9, 008 Redactor: P. G. L. Leach School of Mathematical Sciences, Universit of KwaZulu-Natal, Private Bag X5400 Durban 4000, Republic of South Africa E mail: leachp@ukzn.ac.za and leach@math.aegean.gr
Symmetry Properties of Autonomous Integrating Factors
 Smmetr, Integrabilit and Geometr: Methods and Applications Vol. 1 2005), Paper 024, 12 pages Smmetr Properties of Autonomous Integrating Factors Sibusiso MOYO and P.G.L. LEACH Department of Mathematics,
Smmetr, Integrabilit and Geometr: Methods and Applications Vol. 1 2005), Paper 024, 12 pages Smmetr Properties of Autonomous Integrating Factors Sibusiso MOYO and P.G.L. LEACH Department of Mathematics,
then the substitution z = ax + by + c reduces this equation to the separable one.
 7 Substitutions II Some of the topics in this lecture are optional and will not be tested at the exams. However, for a curious student it should be useful to learn a few extra things about ordinary differential
7 Substitutions II Some of the topics in this lecture are optional and will not be tested at the exams. However, for a curious student it should be useful to learn a few extra things about ordinary differential
First Order Differential Equations f ( x,
 Chapter d dx First Order Differential Equations f ( x, ).1 Linear Equations; Method of Integrating Factors Usuall the general first order linear equations has the form p( t ) g ( t ) (1) where pt () and
Chapter d dx First Order Differential Equations f ( x, ).1 Linear Equations; Method of Integrating Factors Usuall the general first order linear equations has the form p( t ) g ( t ) (1) where pt () and
Higher-order ordinary differential equations
 Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
Higher-order ordinary differential equations 1 A linear ODE of general order n has the form a n (x) dn y dx n +a n 1(x) dn 1 y dx n 1 + +a 1(x) dy dx +a 0(x)y = f(x). If f(x) = 0 then the equation is called
4 Differential Equations
 Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
Advanced Calculus Chapter 4 Differential Equations 65 4 Differential Equations 4.1 Terminology Let U R n, and let y : U R. A differential equation in y is an equation involving y and its (partial) derivatives.
A = (a + 1) 2 = a 2 + 2a + 1
 A = (a + 1) 2 = a 2 + 2a + 1 1 A = ( (a + b) + 1 ) 2 = (a + b) 2 + 2(a + b) + 1 = a 2 + 2ab + b 2 + 2a + 2b + 1 A = ( (a + b) + 1 ) 2 = (a + b) 2 + 2(a + b) + 1 = a 2 + 2ab + b 2 + 2a + 2b + 1 3 A = (
A = (a + 1) 2 = a 2 + 2a + 1 1 A = ( (a + b) + 1 ) 2 = (a + b) 2 + 2(a + b) + 1 = a 2 + 2ab + b 2 + 2a + 2b + 1 A = ( (a + b) + 1 ) 2 = (a + b) 2 + 2(a + b) + 1 = a 2 + 2ab + b 2 + 2a + 2b + 1 3 A = (
Lecture 5: Moment generating functions
 Lecture 5: Moment generating functions Definition 2.3.6. The moment generating function (mgf) of a random variable X is { x e tx f M X (t) = E(e tx X (x) if X has a pmf ) = etx f X (x)dx if X has a pdf
Lecture 5: Moment generating functions Definition 2.3.6. The moment generating function (mgf) of a random variable X is { x e tx f M X (t) = E(e tx X (x) if X has a pmf ) = etx f X (x)dx if X has a pdf
Math 4381 / 6378 Symmetry Analysis
 Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
The Laplace Transform. Background: Improper Integrals
 The Laplace Transform Background: Improper Integrals Recall: Definite Integral: a, b real numbers, a b; f continuous on [a, b] b a f(x) dx 1 Improper integrals: Type I Infinite interval of integration
The Laplace Transform Background: Improper Integrals Recall: Definite Integral: a, b real numbers, a b; f continuous on [a, b] b a f(x) dx 1 Improper integrals: Type I Infinite interval of integration
ENGI 9420 Engineering Analysis Solutions to Additional Exercises
 ENGI 940 Engineering Analsis Solutions to Additional Exercises 0 Fall [Partial differential equations; Chapter 8] The function ux (, ) satisfies u u u + = 0, subject to the x x u x,0 = u x, =. Classif
ENGI 940 Engineering Analsis Solutions to Additional Exercises 0 Fall [Partial differential equations; Chapter 8] The function ux (, ) satisfies u u u + = 0, subject to the x x u x,0 = u x, =. Classif
The Laplace Transform. Background: Improper Integrals
 The Laplace Transform Background: Improper Integrals Recall: Definite Integral: a, b real numbers, a b; f continuous on [a, b] b a f(x) dx 1 Improper integrals: Type I Infinite interval of integration
The Laplace Transform Background: Improper Integrals Recall: Definite Integral: a, b real numbers, a b; f continuous on [a, b] b a f(x) dx 1 Improper integrals: Type I Infinite interval of integration
UCLA Math 135, Winter 2015 Ordinary Differential Equations Review of First-Order Equations from Math 33b
 UCLA Math 35, Winter 205 Ordinar Differential Equations Review of First-Order Equations from Math 33b 9. Special Equations and Substitution C. David Levermore Department of Mathematics Universit of Marland
UCLA Math 35, Winter 205 Ordinar Differential Equations Review of First-Order Equations from Math 33b 9. Special Equations and Substitution C. David Levermore Department of Mathematics Universit of Marland
Math 141: Lecture 11
 Math 141: Lecture 11 The Fundamental Theorem of Calculus and integration methods Bob Hough October 12, 2016 Bob Hough Math 141: Lecture 11 October 12, 2016 1 / 36 First Fundamental Theorem of Calculus
Math 141: Lecture 11 The Fundamental Theorem of Calculus and integration methods Bob Hough October 12, 2016 Bob Hough Math 141: Lecture 11 October 12, 2016 1 / 36 First Fundamental Theorem of Calculus
Figure 1: ET is an oblique-angled diameter
 1 Snopsis b section of Euler s paper ON SOME PROPERTIES OF CONIC SECTIONS THAT ARE SHARED WITH INFINITELY MANY OTHER CURVED LINES (E08) Thomas J Osler and Edward Greve Mathematics Department Rowan Universit
1 Snopsis b section of Euler s paper ON SOME PROPERTIES OF CONIC SECTIONS THAT ARE SHARED WITH INFINITELY MANY OTHER CURVED LINES (E08) Thomas J Osler and Edward Greve Mathematics Department Rowan Universit
The first order quasi-linear PDEs
 Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
Math 3313: Differential Equations Second-order ordinary differential equations
 Math 3313: Differential Equations Second-order ordinary differential equations Thomas W. Carr Department of Mathematics Southern Methodist University Dallas, TX Outline Mass-spring & Newton s 2nd law Properties
Math 3313: Differential Equations Second-order ordinary differential equations Thomas W. Carr Department of Mathematics Southern Methodist University Dallas, TX Outline Mass-spring & Newton s 2nd law Properties
First integrals and reduction of a class of nonlinear higher order ordinary differential equations
 J. Math. Anal. Appl. 287 (2003) 473 486 www.elsevier.com/locate/jmaa First integrals and reduction of a class of nonlinear higher order ordinary differential equations N. Euler a and P.G.L. Leach b, a
J. Math. Anal. Appl. 287 (2003) 473 486 www.elsevier.com/locate/jmaa First integrals and reduction of a class of nonlinear higher order ordinary differential equations N. Euler a and P.G.L. Leach b, a
MATH 2413 TEST ON CHAPTER 4 ANSWER ALL QUESTIONS. TIME 1.5 HRS.
 MATH 1 TEST ON CHAPTER ANSWER ALL QUESTIONS. TIME 1. HRS. M1c Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Use the summation formulas to rewrite the
MATH 1 TEST ON CHAPTER ANSWER ALL QUESTIONS. TIME 1. HRS. M1c Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Use the summation formulas to rewrite the
(x 3)(x + 5) = (x 3)(x 1) = x + 5. sin 2 x e ax bx 1 = 1 2. lim
 SMT Calculus Test Solutions February, x + x 5 Compute x x x + Answer: Solution: Note that x + x 5 x x + x )x + 5) = x )x ) = x + 5 x x + 5 Then x x = + 5 = Compute all real values of b such that, for fx)
SMT Calculus Test Solutions February, x + x 5 Compute x x x + Answer: Solution: Note that x + x 5 x x + x )x + 5) = x )x ) = x + 5 x x + 5 Then x x = + 5 = Compute all real values of b such that, for fx)
MATH 105: PRACTICE PROBLEMS FOR CHAPTER 3: SPRING 2010
 MATH 105: PRACTICE PROBLEMS FOR CHAPTER 3: SPRING 010 INSTRUCTOR: STEVEN MILLER (SJM1@WILLIAMS.EDU Question 1 : Compute the partial derivatives of order 1 order for: (1 f(x, y, z = e x+y cos(x sin(y. Solution:
MATH 105: PRACTICE PROBLEMS FOR CHAPTER 3: SPRING 010 INSTRUCTOR: STEVEN MILLER (SJM1@WILLIAMS.EDU Question 1 : Compute the partial derivatives of order 1 order for: (1 f(x, y, z = e x+y cos(x sin(y. Solution:
NUMERICAL METHODS. x n+1 = 2x n x 2 n. In particular: which of them gives faster convergence, and why? [Work to four decimal places.
 NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
MATH LECTURE NOTES FIRST ORDER SEPARABLE DIFFERENTIAL EQUATIONS OVERVIEW
 MATH 234 - LECTURE NOTES FIRST ORDER SEPARABLE DIFFERENTIAL EQUATIONS OVERVIEW Now will will begin with the process of learning how to solve differential equations. We will learn different techniques for
MATH 234 - LECTURE NOTES FIRST ORDER SEPARABLE DIFFERENTIAL EQUATIONS OVERVIEW Now will will begin with the process of learning how to solve differential equations. We will learn different techniques for
Journal of Mathematical Analysis and Applications. Complete symmetry group and nonlocal symmetries for some two-dimensional evolution equations
 J. Math. Anal. Appl. 357 (2009) 225 231 Contents lists available at ScienceDirect Journal of Mathematical Analysis and Applications www.elsevier.com/locate/jmaa Complete symmetry group and nonlocal symmetries
J. Math. Anal. Appl. 357 (2009) 225 231 Contents lists available at ScienceDirect Journal of Mathematical Analysis and Applications www.elsevier.com/locate/jmaa Complete symmetry group and nonlocal symmetries
Math 106: Review for Exam II - SOLUTIONS
 Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
Math 6: Review for Exam II - SOLUTIONS INTEGRATION TIPS Substitution: usually let u a function that s inside another function, especially if du (possibly off by a multiplying constant) is also present
AS PURE MATHS REVISION NOTES
 AS PURE MATHS REVISION NOTES 1 SURDS A root such as 3 that cannot be written exactly as a fraction is IRRATIONAL An expression that involves irrational roots is in SURD FORM e.g. 2 3 3 + 2 and 3-2 are
AS PURE MATHS REVISION NOTES 1 SURDS A root such as 3 that cannot be written exactly as a fraction is IRRATIONAL An expression that involves irrational roots is in SURD FORM e.g. 2 3 3 + 2 and 3-2 are
2010 Maths. Advanced Higher. Finalised Marking Instructions
 00 Maths Advanced Higher Finalised Marking Instructions Scottish Qualifications Authority 00 The information in this publication may be reproduced to support SQA qualifications only on a noncommercial
00 Maths Advanced Higher Finalised Marking Instructions Scottish Qualifications Authority 00 The information in this publication may be reproduced to support SQA qualifications only on a noncommercial
Asymptotics at regular singular points
 Ma 7, 2011 Asmptotics at regular singular points Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Introduction 1. Examples 2. Regular singular points 3. Regular singular points at infinit
Ma 7, 2011 Asmptotics at regular singular points Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Introduction 1. Examples 2. Regular singular points 3. Regular singular points at infinit
Solution of Additional Exercises for Chapter 4
 1 1. (1) Try V (x) = 1 (x 1 + x ). Solution of Additional Exercises for Chapter 4 V (x) = x 1 ( x 1 + x ) x = x 1 x + x 1 x In the neighborhood of the origin, the term (x 1 + x ) dominates. Hence, the
1 1. (1) Try V (x) = 1 (x 1 + x ). Solution of Additional Exercises for Chapter 4 V (x) = x 1 ( x 1 + x ) x = x 1 x + x 1 x In the neighborhood of the origin, the term (x 1 + x ) dominates. Hence, the
3 Applications of partial differentiation
 Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
Advanced Calculus Chapter 3 Applications of partial differentiation 37 3 Applications of partial differentiation 3.1 Stationary points Higher derivatives Let U R 2 and f : U R. The partial derivatives
DRAFT - Math 102 Lecture Note - Dr. Said Algarni
 Math02 - Term72 - Guides and Exercises - DRAFT 7 Techniques of Integration A summery for the most important integrals that we have learned so far: 7. Integration by Parts The Product Rule states that if
Math02 - Term72 - Guides and Exercises - DRAFT 7 Techniques of Integration A summery for the most important integrals that we have learned so far: 7. Integration by Parts The Product Rule states that if
MATH 312 Section 4.5: Undetermined Coefficients
 MATH 312 Section 4.5: Undetermined Coefficients Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Differential Operators 2 Annihilators 3 Undetermined Coefficients 4 Conclusion ODEs
MATH 312 Section 4.5: Undetermined Coefficients Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Differential Operators 2 Annihilators 3 Undetermined Coefficients 4 Conclusion ODEs
z = 1 2 x 3 4 y + 3 y dt
 Exact First Order Differential Equations This Lecture covers material in Section 2.6. A first order differential equations is exact if it can be written in the form M(x, ) + N(x, ) d dx = 0, where M =
Exact First Order Differential Equations This Lecture covers material in Section 2.6. A first order differential equations is exact if it can be written in the form M(x, ) + N(x, ) d dx = 0, where M =
y = ± x 2 + c. ln y = 2 ln x + 2C sin(x) dx
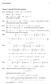 Worked Solutions Chapter 4: Separable First-Order Equations 43 a Factoring out 2, we get 3 sinx)) 2, which is f x)g), ds with f x) 3 sinx) and g) 2 So the equation is separable 43 c x x )2 x )2 f x)g)
Worked Solutions Chapter 4: Separable First-Order Equations 43 a Factoring out 2, we get 3 sinx)) 2, which is f x)g), ds with f x) 3 sinx) and g) 2 So the equation is separable 43 c x x )2 x )2 f x)g)
Decomposition of a recursive family of polynomials
 Decomposition of a recursive family of polynomials Andrej Dujella and Ivica Gusić Abstract We describe decomposition of polynomials f n := f n,b,a defined by f 0 := B, f 1 (x := x, f n+1 (x = xf n (x af
Decomposition of a recursive family of polynomials Andrej Dujella and Ivica Gusić Abstract We describe decomposition of polynomials f n := f n,b,a defined by f 0 := B, f 1 (x := x, f n+1 (x = xf n (x af
The Economy of Complete Symmetry Groups for Linear Higher Dimensional Systems
 Journal of Nonlinear Mathematical Physics Volume 9, Supplement 2 (22), 1 23 Birthday Issue The Economy of Complete Symmetry Groups for Linear Higher Dimensional Systems K ANDRIOPOULOS and P G L LEACH GEODYSYC,
Journal of Nonlinear Mathematical Physics Volume 9, Supplement 2 (22), 1 23 Birthday Issue The Economy of Complete Symmetry Groups for Linear Higher Dimensional Systems K ANDRIOPOULOS and P G L LEACH GEODYSYC,
Calculus II Practice Test Problems for Chapter 7 Page 1 of 6
 Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Calculus II Practice Test Problems for Chapter 7 Page of 6 This is a set of practice test problems for Chapter 7. This is in no way an inclusive set of problems there can be other types of problems on
Section 5.8. Taylor Series
 Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Difference Equations to Differential Equations Section 5.8 Taylor Series In this section we will put together much of the work of Sections 5.-5.7 in the context of a discussion of Taylor series. We begin
Autonomous Equations / Stability of Equilibrium Solutions. y = f (y).
 Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
Worksheet 7, Math 10560
 Worksheet 7, Math 0560 You must show all of your work to receive credit!. Determine whether the following series and sequences converge or diverge, and evaluate if they converge. If they diverge, you must
Worksheet 7, Math 0560 You must show all of your work to receive credit!. Determine whether the following series and sequences converge or diverge, and evaluate if they converge. If they diverge, you must
Math 234. What you should know on day one. August 28, You should be able to use general principles like. x = cos t, y = sin t, 0 t π.
 Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Math 21B - Homework Set 8
 Math B - Homework Set 8 Section 8.:. t cos t dt Let u t, du t dt and v sin t, dv cos t dt Let u t, du dt and v cos t, dv sin t dt t cos t dt u v v du t sin t t sin t dt [ t sin t u v ] v du [ ] t sin t
Math B - Homework Set 8 Section 8.:. t cos t dt Let u t, du t dt and v sin t, dv cos t dt Let u t, du dt and v cos t, dv sin t dt t cos t dt u v v du t sin t t sin t dt [ t sin t u v ] v du [ ] t sin t
COMPLEMENTARY RESULTS TO HEUVERS S CHARACTERIZATION OF LOGARITHMIC FUNCTIONS. Martin Himmel. 1. Introduction
 Annales Mathematicae Silesianae 3 207), 99 06 DOI: 0.55/amsil-207-000 COMPLEMENTARY RESULTS TO HEUVERS S CHARACTERIZATION OF LOGARITHMIC FUNCTIONS Martin Himmel Abstract. Based on a characterization of
Annales Mathematicae Silesianae 3 207), 99 06 DOI: 0.55/amsil-207-000 COMPLEMENTARY RESULTS TO HEUVERS S CHARACTERIZATION OF LOGARITHMIC FUNCTIONS Martin Himmel Abstract. Based on a characterization of
1. First-order ODE s
 18.03 EXERCISES 1. First-order ODE s 1A. Introduction; Separation of Variables 1A-1. Verif that each of the following ODE s has the indicated solutions (c i,a are constants): a) 2 + = 0, = c 1 e x +c 2
18.03 EXERCISES 1. First-order ODE s 1A. Introduction; Separation of Variables 1A-1. Verif that each of the following ODE s has the indicated solutions (c i,a are constants): a) 2 + = 0, = c 1 e x +c 2
PUTNAM PROBLEMS DIFFERENTIAL EQUATIONS. First Order Equations. p(x)dx)) = q(x) exp(
 PUTNAM PROBLEMS DIFFERENTIAL EQUATIONS First Order Equations 1. Linear y + p(x)y = q(x) Muliply through by the integrating factor exp( p(x)) to obtain (y exp( p(x))) = q(x) exp( p(x)). 2. Separation of
PUTNAM PROBLEMS DIFFERENTIAL EQUATIONS First Order Equations 1. Linear y + p(x)y = q(x) Muliply through by the integrating factor exp( p(x)) to obtain (y exp( p(x))) = q(x) exp( p(x)). 2. Separation of
Linearization of Second-Order Ordinary Dif ferential Equations by Generalized Sundman Transformations
 Symmetry, Integrability and Geometry: Methods and Applications SIGMA 6 (2010), 051, 11 pages Linearization of Second-Order Ordinary Dif ferential Equations by Generalized Sundman Transformations Warisa
Symmetry, Integrability and Geometry: Methods and Applications SIGMA 6 (2010), 051, 11 pages Linearization of Second-Order Ordinary Dif ferential Equations by Generalized Sundman Transformations Warisa
Engg. Math. II (Unit-IV) Numerical Analysis
 Dr. Satish Shukla of 33 Engg. Math. II (Unit-IV) Numerical Analysis Syllabus. Interpolation and Curve Fitting: Introduction to Interpolation; Calculus of Finite Differences; Finite Difference and Divided
Dr. Satish Shukla of 33 Engg. Math. II (Unit-IV) Numerical Analysis Syllabus. Interpolation and Curve Fitting: Introduction to Interpolation; Calculus of Finite Differences; Finite Difference and Divided
arxiv:solv-int/ v1 7 Jul 1998
 SCHLESINGER TRANSFORMATIONS FOR LINEARISABLE EQUATIONS arxiv:solv-int/9807003v1 7 Jul 1998 Abstract A. Ramani CPT, Ecole Poltechnique CNRS, UPR 14 91128 Palaiseau, France B. Grammaticos GMPIB, Université
SCHLESINGER TRANSFORMATIONS FOR LINEARISABLE EQUATIONS arxiv:solv-int/9807003v1 7 Jul 1998 Abstract A. Ramani CPT, Ecole Poltechnique CNRS, UPR 14 91128 Palaiseau, France B. Grammaticos GMPIB, Université
Homogeneous Geodesics of Left Invariant Randers Metrics on a Three-Dimensional Lie Group
 Int. J. Contemp. Math. Sciences, Vol. 4, 009, no. 18, 873-881 Homogeneous Geodesics of Left Invariant Randers Metrics on a Three-Dimensional Lie Group Dariush Latifi Department of Mathematics Universit
Int. J. Contemp. Math. Sciences, Vol. 4, 009, no. 18, 873-881 Homogeneous Geodesics of Left Invariant Randers Metrics on a Three-Dimensional Lie Group Dariush Latifi Department of Mathematics Universit
McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II)
 McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II) HIGHER ORDER DIFFERENTIAL EQUATIONS (IV) 1 Introduction (Text: pp. 338-367, Chap.
McGill University Math 325A: Differential Equations LECTURE 12: SOLUTIONS FOR EQUATIONS WITH CONSTANTS COEFFICIENTS (II) HIGHER ORDER DIFFERENTIAL EQUATIONS (IV) 1 Introduction (Text: pp. 338-367, Chap.
For more information visit
 If the integrand is a derivative of a known function, then the corresponding indefinite integral can be directly evaluated. If the integrand is not a derivative of a known function, the integral may be
If the integrand is a derivative of a known function, then the corresponding indefinite integral can be directly evaluated. If the integrand is not a derivative of a known function, the integral may be
EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as
![EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as](/thumbs/85/92409620.jpg) L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
Core Mathematics 3 Algebra
 http://kumarmathsweeblycom/ Core Mathematics 3 Algebra Edited by K V Kumaran Core Maths 3 Algebra Page Algebra fractions C3 The specifications suggest that you should be able to do the following: Simplify
http://kumarmathsweeblycom/ Core Mathematics 3 Algebra Edited by K V Kumaran Core Maths 3 Algebra Page Algebra fractions C3 The specifications suggest that you should be able to do the following: Simplify
Consider an ideal pendulum as shown below. l θ is the angular acceleration θ is the angular velocity
 1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
1 Second Order Ordinary Differential Equations 1.1 The harmonic oscillator Consider an ideal pendulum as shown below. θ l Fr mg l θ is the angular acceleration θ is the angular velocity A point mass m
Mathematics, Algebra, and Geometry
 Mathematics, Algebra, and Geometry by Satya http://www.thesatya.com/ Contents 1 Algebra 1 1.1 Logarithms............................................ 1. Complex numbers........................................
Mathematics, Algebra, and Geometry by Satya http://www.thesatya.com/ Contents 1 Algebra 1 1.1 Logarithms............................................ 1. Complex numbers........................................
x 3y 2z = 6 1.2) 2x 4y 3z = 8 3x + 6y + 8z = 5 x + 3y 2z + 5t = 4 1.5) 2x + 8y z + 9t = 9 3x + 5y 12z + 17t = 7
 Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
Linear Algebra and its Applications-Lab 1 1) Use Gaussian elimination to solve the following systems x 1 + x 2 2x 3 + 4x 4 = 5 1.1) 2x 1 + 2x 2 3x 3 + x 4 = 3 3x 1 + 3x 2 4x 3 2x 4 = 1 x + y + 2z = 4 1.4)
Lecture 4: Exact ODE s
 Lecture 4: Exact ODE s Dr. Michael Doughert Januar 23, 203 Exact equations are first-order ODE s of a particular form, and whose methods of solution rel upon basic facts concerning partial derivatives,
Lecture 4: Exact ODE s Dr. Michael Doughert Januar 23, 203 Exact equations are first-order ODE s of a particular form, and whose methods of solution rel upon basic facts concerning partial derivatives,
Introduction to Differential Equations
 Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Chapter 2 Non-linear Equations
 Chapter 2 Non-linear Equations 2.1 First Examples of Non-linear Ordinary Differential Equations Before describing some general properties of non-linear equations, we find it useful to present some well-known
Chapter 2 Non-linear Equations 2.1 First Examples of Non-linear Ordinary Differential Equations Before describing some general properties of non-linear equations, we find it useful to present some well-known
Random Variables. Random variables. A numerically valued map X of an outcome ω from a sample space Ω to the real line R
 In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures. Dr. Abdulla Eid. College of Science. MATHS 101: Calculus I
 Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Section 5.5 More Integration Formula (The Substitution Method) 2 Lectures College of Science MATHS : Calculus I (University of Bahrain) Integrals / 7 The Substitution Method Idea: To replace a relatively
Existence Theory: Green s Functions
 Chapter 5 Existence Theory: Green s Functions In this chapter we describe a method for constructing a Green s Function The method outlined is formal (not rigorous) When we find a solution to a PDE by constructing
Chapter 5 Existence Theory: Green s Functions In this chapter we describe a method for constructing a Green s Function The method outlined is formal (not rigorous) When we find a solution to a PDE by constructing
1 Arithmetic calculations (calculator is not allowed)
 1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain.
 Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
Chapter 1 Numerical approximation of data : interpolation, least squares method
 Chapter 1 Numerical approximation of data : interpolation, least squares method I. Motivation 1 Approximation of functions Evaluation of a function Which functions (f : R R) can be effectively evaluated
Chapter 1 Numerical approximation of data : interpolation, least squares method I. Motivation 1 Approximation of functions Evaluation of a function Which functions (f : R R) can be effectively evaluated
First-Order ODE: Separable Equations, Exact Equations and Integrating Factor
 First-Order ODE: Separable Equations, Exact Equations and Integrating Factor Department of Mathematics IIT Guwahati REMARK: In the last theorem of the previous lecture, you can change the open interval
First-Order ODE: Separable Equations, Exact Equations and Integrating Factor Department of Mathematics IIT Guwahati REMARK: In the last theorem of the previous lecture, you can change the open interval
Formulas that must be memorized:
 Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Formulas that must be memorized: Position, Velocity, Acceleration Speed is increasing when v(t) and a(t) have the same signs. Speed is decreasing when v(t) and a(t) have different signs. Section I: Limits
Name: Math Homework Set # 5. March 12, 2010
 Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
Name: Math 4567. Homework Set # 5 March 12, 2010 Chapter 3 (page 79, problems 1,2), (page 82, problems 1,2), (page 86, problems 2,3), Chapter 4 (page 93, problems 2,3), (page 98, problems 1,2), (page 102,
Math 226 Calculus Spring 2016 Exam 2V1
 Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 6 Calculus Spring 6 Exam V () (35 Points) Evaluate the following integrals. (a) (7 Points) tan 5 (x) sec 3 (x) dx (b) (8 Points) cos 4 (x) dx Math 6 Calculus Spring 6 Exam V () (Continued) Evaluate
Math 489AB Exercises for Chapter 2 Fall Section 2.3
 Math 489AB Exercises for Chapter 2 Fall 2008 Section 2.3 2.3.3. Let A M n (R). Then the eigenvalues of A are the roots of the characteristic polynomial p A (t). Since A is real, p A (t) is a polynomial
Math 489AB Exercises for Chapter 2 Fall 2008 Section 2.3 2.3.3. Let A M n (R). Then the eigenvalues of A are the roots of the characteristic polynomial p A (t). Since A is real, p A (t) is a polynomial
Math 214 Spring problem set (a) Consider these two first order equations. (I) dy dx = x + 1 dy
 Math 4 Spring 08 problem set. (a) Consider these two first order equations. (I) d d = + d (II) d = Below are four direction fields. Match the differential equations above to their direction fields. Provide
Math 4 Spring 08 problem set. (a) Consider these two first order equations. (I) d d = + d (II) d = Below are four direction fields. Match the differential equations above to their direction fields. Provide
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math 10860, Honors Calculus 2
 Math 10860, Honors Calculus 2 Worksheet/Information sheet on partial fractions March 8 2018 This worksheet (or rather, information sheet with a few questions) takes you through the method of partial fractions
Math 10860, Honors Calculus 2 Worksheet/Information sheet on partial fractions March 8 2018 This worksheet (or rather, information sheet with a few questions) takes you through the method of partial fractions
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Examples: Solving nth Order Equations
 Atoms L. Euler s Theorem The Atom List First Order. Solve 2y + 5y = 0. Examples: Solving nth Order Equations Second Order. Solve y + 2y + y = 0, y + 3y + 2y = 0 and y + 2y + 5y = 0. Third Order. Solve
Atoms L. Euler s Theorem The Atom List First Order. Solve 2y + 5y = 0. Examples: Solving nth Order Equations Second Order. Solve y + 2y + y = 0, y + 3y + 2y = 0 and y + 2y + 5y = 0. Third Order. Solve
Chapter 7: Techniques of Integration
 Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Green s Theorem. Fundamental Theorem for Conservative Vector Fields
 Assignment - Mathematics 4(Model Answer) onservative vector field and Green theorem onservative Vector Fields If F = φ, for some differentiable function φ in a domaind, then we say that F is conservative
Assignment - Mathematics 4(Model Answer) onservative vector field and Green theorem onservative Vector Fields If F = φ, for some differentiable function φ in a domaind, then we say that F is conservative
Assignment 11 Assigned Mon Sept 27
 Assignment Assigned Mon Sept 7 Section 7., Problem 4. x sin x dx = x cos x + x cos x dx ( = x cos x + x sin x ) sin x dx u = x dv = sin x dx du = x dx v = cos x u = x dv = cos x dx du = dx v = sin x =
Assignment Assigned Mon Sept 7 Section 7., Problem 4. x sin x dx = x cos x + x cos x dx ( = x cos x + x sin x ) sin x dx u = x dv = sin x dx du = x dx v = cos x u = x dv = cos x dx du = dx v = sin x =
Math 263 Assignment #3 Solutions. 1. A function z = f(x, y) is called harmonic if it satisfies Laplace s equation:
 Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
PLC Papers. Created For:
 PLC Papers Created For: Algebra and proof 2 Grade 8 Objective: Use algebra to construct proofs Question 1 a) If n is a positive integer explain why the expression 2n + 1 is always an odd number. b) Use
PLC Papers Created For: Algebra and proof 2 Grade 8 Objective: Use algebra to construct proofs Question 1 a) If n is a positive integer explain why the expression 2n + 1 is always an odd number. b) Use
Lecture Notes on. Differential Equations. Emre Sermutlu
 Lecture Notes on Differential Equations Emre Sermutlu ISBN: Copyright Notice: To my wife Nurten and my daughters İlayda and Alara Contents Preface ix 1 First Order ODE 1 1.1 Definitions.............................
Lecture Notes on Differential Equations Emre Sermutlu ISBN: Copyright Notice: To my wife Nurten and my daughters İlayda and Alara Contents Preface ix 1 First Order ODE 1 1.1 Definitions.............................
Section 5.6. Integration By Parts. MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10
 Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
 MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Volumes Math 11 Winter 17 SOLUTIONS 1. (a) i. The axis of smmetr is a horizontal line, so we integrate with respect to x. The
MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Volumes Math 11 Winter 17 SOLUTIONS 1. (a) i. The axis of smmetr is a horizontal line, so we integrate with respect to x. The
LECTURE 16 GAUSS QUADRATURE In general for Newton-Cotes (equispaced interpolation points/ data points/ integration points/ nodes).
 CE 025 - Lecture 6 LECTURE 6 GAUSS QUADRATURE In general for ewton-cotes (equispaced interpolation points/ data points/ integration points/ nodes). x E x S fx dx hw' o f o + w' f + + w' f + E 84 f 0 f
CE 025 - Lecture 6 LECTURE 6 GAUSS QUADRATURE In general for ewton-cotes (equispaced interpolation points/ data points/ integration points/ nodes). x E x S fx dx hw' o f o + w' f + + w' f + E 84 f 0 f
Math 201 Solutions to Assignment 1. 2ydy = x 2 dx. y = C 1 3 x3
 Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 12 Final Exam Review 1
 Math 12 Final Exam Review 1 Part One Calculators are NOT PERMITTED for this part of the exam. 1. a) The sine of angle θ is 1 What are the 2 possible values of θ in the domain 0 θ 2π? 2 b) Draw these angles
Math 12 Final Exam Review 1 Part One Calculators are NOT PERMITTED for this part of the exam. 1. a) The sine of angle θ is 1 What are the 2 possible values of θ in the domain 0 θ 2π? 2 b) Draw these angles
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by Partial Fractions MATH 1700 December 6, 2016 MATH 1700 Partial Fractions December 6, 2016 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 Partial Fractions
Title Integration of Rational Functions by Partial Fractions MATH 1700 December 6, 2016 MATH 1700 Partial Fractions December 6, 2016 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 Partial Fractions
Theoretical Tutorial Session 2
 1 / 36 Theoretical Tutorial Session 2 Xiaoming Song Department of Mathematics Drexel University July 27, 216 Outline 2 / 36 Itô s formula Martingale representation theorem Stochastic differential equations
1 / 36 Theoretical Tutorial Session 2 Xiaoming Song Department of Mathematics Drexel University July 27, 216 Outline 2 / 36 Itô s formula Martingale representation theorem Stochastic differential equations
Engg. Math. I. Unit-I. Differential Calculus
 Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Exact Simulation of Diffusions and Jump Diffusions
 Exact Simulation of Diffusions and Jump Diffusions A work by: Prof. Gareth O. Roberts Dr. Alexandros Beskos Dr. Omiros Papaspiliopoulos Dr. Bruno Casella 28 th May, 2008 Content 1 Exact Algorithm Construction
Exact Simulation of Diffusions and Jump Diffusions A work by: Prof. Gareth O. Roberts Dr. Alexandros Beskos Dr. Omiros Papaspiliopoulos Dr. Bruno Casella 28 th May, 2008 Content 1 Exact Algorithm Construction
Calculus I (Math 241) (In Progress)
 Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
MAS113 Introduction to Probability and Statistics. Proofs of theorems
 MAS113 Introduction to Probability and Statistics Proofs of theorems Theorem 1 De Morgan s Laws) See MAS110 Theorem 2 M1 By definition, B and A \ B are disjoint, and their union is A So, because m is a
MAS113 Introduction to Probability and Statistics Proofs of theorems Theorem 1 De Morgan s Laws) See MAS110 Theorem 2 M1 By definition, B and A \ B are disjoint, and their union is A So, because m is a
Mar 10, Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule: integration 1 / 18
 Calculus with Algebra and Trigonometry II Lecture 14 Undoing the product rule: integration by parts Mar 10, 2015 Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule:
Calculus with Algebra and Trigonometry II Lecture 14 Undoing the product rule: integration by parts Mar 10, 2015 Calculus with Algebra and Trigonometry II Lecture 14Undoing the Marproduct 10, 2015 rule:
MATH 104: INTRODUCTORY ANALYSIS SPRING 2008/09 PROBLEM SET 8 SOLUTIONS
 MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 8 SOLUTIONS. Let f : R R be continuous periodic with period, i.e. f(x + ) = f(x) for all x R. Prove the following: (a) f is bounded above below
MATH 04: INTRODUCTORY ANALYSIS SPRING 008/09 PROBLEM SET 8 SOLUTIONS. Let f : R R be continuous periodic with period, i.e. f(x + ) = f(x) for all x R. Prove the following: (a) f is bounded above below
MATH H53 : Final exam
 MATH H53 : Final exam 11 May, 18 Name: You have 18 minutes to answer the questions. Use of calculators or any electronic items is not permitted. Answer the questions in the space provided. If you run out
MATH H53 : Final exam 11 May, 18 Name: You have 18 minutes to answer the questions. Use of calculators or any electronic items is not permitted. Answer the questions in the space provided. If you run out
Section 3.1 Homework Solutions. 1. y = 5, so dy dx = y = 3x, so dy dx = y = x 12, so dy. dx = 12x11. dx = 12x 13
 Math 122 1. y = 5, so dx = 0 2. y = 3x, so dx = 3 3. y = x 12, so dx = 12x11 4. y = x 12, so dx = 12x 13 5. y = x 4/3, so dx = 4 3 x1/3 6. y = 8t 3, so = 24t2 7. y = 3t 4 2t 2, so = 12t3 4t 8. y = 5x +
Math 122 1. y = 5, so dx = 0 2. y = 3x, so dx = 3 3. y = x 12, so dx = 12x11 4. y = x 12, so dx = 12x 13 5. y = x 4/3, so dx = 4 3 x1/3 6. y = 8t 3, so = 24t2 7. y = 3t 4 2t 2, so = 12t3 4t 8. y = 5x +
Complex Numbers and Exponentials
 omple Numbers and Eponentials Definition and Basic Operations comple number is nothing more than a point in the plane. The sum and product of two comple numbers ( 1, 1 ) and ( 2, 2 ) is defined b ( 1,
omple Numbers and Eponentials Definition and Basic Operations comple number is nothing more than a point in the plane. The sum and product of two comple numbers ( 1, 1 ) and ( 2, 2 ) is defined b ( 1,
Math 152 Take Home Test 1
 Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
