Invariant monotone vector fields on Riemannian manifolds
|
|
|
- Henry Knight
- 5 years ago
- Views:
Transcription
1 Nonlinear Analsis 70 (2009) Invariant monotone vector fields on Riemannian manifolds A. Barani, M.R. Pouraevali Department of Mathematics, Universit of Isfahan, P.O.Box , Isfahan, Iran Received 7 Jul 2007; accepted 25 Februar 2008 Abstract Various concepts of invariant monotone vector fields on Riemannian manifolds are introduced. Some examples of invariant monotone vector fields are given. Several notions of invexities for functions on Riemannian manifolds are defined their relations with invariant monotone vector fields are studied. c 2008 Elsevier Ltd. All rights reserved. Kewords: Generalized invex functions; Monotone vector fields; Invariant monotone vector fields; Riemannian manifolds. Introduction The theor of variational inequalit has proven its applicabilit in man fields of mathematics phsics. On the other h monotonicit has plaed a ver important role in the stud of the existence of solutions of variational inequalit problems. It is also well known that generalized monotonicit is a powerful tool in the stud of the existence the sensitivit analsis of solutions for variational inclusion complementarit problems. The convexit of a real valued function is equivalent to the monotonicit of the corresponding gradient function; see [3,5,9]. The relation between generalized convexit of functions generalized monotone operators has been investigated b man authors; for example see [4,7,6,8]. In the nonsmooth case the relationships between monotonicit convexit of subdifferential operators as an application of the approximate Mean Value Theorem are studied in Section of [4]. In [] Hanson introduced the concept of invexit which was a generalization of convexit. Generalized invexit its relation with generalized invex monotonicit has been investigated in [6,23]. The notion of invariant monotonicit as a generalization of monotonicit was studied in [24]. In general a manifold is not a linear space extensions of concepts techniques from linear spaces to Riemannian manifolds are natural. Rapscák [20] Udriste [22] considered a generalization of convexit called geodesic convexit extended man results of convex analsis optimization theor to Riemannian manifolds. The also studied the monotonicit of the gradient of a geodesic convex function. The interested reader is referred to the books [20,22] references therein. The concept of monotone vector field on Riemannian manifolds which was a generalization of monotone operator was introduced in [5] b Németh. Since then numerous articles have appeared in the literature reflecting further generalizations applications in this categor; for example see [6,0]. Corresponding author. Tel.: ; fax: addresses: barani@math.ui.ac.ir (A. Barani), poura@math.ui.ac.ir (M.R. Pouraevali) X/$ - see front matter c 2008 Elsevier Ltd. All rights reserved. doi:0.06/j.na
2 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) In [7] the notion of invex function on Riemannian manifolds was introduced in [2] invex functions preinvex functions on invex subsets of Riemannian manifolds are studied. In this paper various concepts of generalized invexities for functions on Riemannian manifolds are introduced. Then, invariant monotone vector fields generalized invariant monotone vector fields on Riemannian manifolds are defined their relations with generalized invexities are investigated. The organization of the paper is as follows. In Section 2 some concepts facts from Riemannian geometr are collected. In Section 3 we recall the notion of invexit introduce the concept of strong invexit on Riemannian manifolds. Section 4 is devoted to the notions of monotone invariant monotone vector fields. Then the relation between invexit monotonicit is studied. Finall in Section 5 we introduce pseudoinvexit invariant pseudomonotonicit of functions on Riemannian manifolds. 2. Preliminaries In this section, we recall some definitions known results concerning Riemannian manifolds which will be used throughout the paper. We refer the reader to [2,3] for the stard material of differential geometr. Throughout this paper M is a C smooth manifold modelled on a Hilbert space H, either finite dimensional or infinite dimensional, endowed with a Riemannian metric g p (.,.) on the tangent space T p M = H. Therefore, we have a smooth assignment of an inner product to each tangent space. It is usual to write g p (v, w) = v, w p for all v, w T p M. Thus, M is now a Riemannian manifold. The corresponding norm is denoted b p. Let us recall that the length of a piecewise C curve γ : [a, b] M is defined b L(γ ) := b a γ (t) γ (t) dt. Minimizing this length functional on the set of all piecewise C curves joining p, q M, we obtain a distance function (p, q) d(p, q). Then d is a distance which induces the original topolog on M. Given a manifold M, denote b X(M) the space of all vector fields over M. The metric induces a map f grad f X(M) which associates with each f its gradient via the rule d f, X = d f (X) for each X X(M). On ever Riemannian manifold there exists exactl one covariant derivation called the Levi-Civita connection, denoted b X Y for an vector fields X, Y on M. We also recall that a geodesic is a C smooth path γ whose tangent is parallel along the path γ, that is, γ satisfies the equation dγ (t)/dt dγ (t)/dt = 0. An path γ joining p q in M such that L(γ ) = d(p, q) is a geodesic, it is called a minimal geodesic. The existence theorem for ordinar differential equations implies that for ever v T M there exist an open interval J(v) containing 0 a unique geodesic γ v : J(v) M with dγ (0)/dt = v. This implies that there is an open neighborhood T M of the submanifold M of T M such that for ever v T M the geodesic γ v (t) is defined for t < 2. The exponential mapping exp : T M M is then defined as exp(v) = J v () the restriction of exp to a fiber T p M in T M is denoted b exp p for ever p M. Since (T p M, p ) is a Hilbert space, there is a linear isometric identification between this space its dual (T p M, p ). If γ : [a, b] M is a geodesic then for each t, t 2 [a, b] the Levi-Civita connection induces an isometr P t 2 t,γ : T γ (t )M T γ (t2 )M, the so called parallel translation along γ from γ (t ) to γ (t 2 ). We also recall that a simpl connected complete Riemannian manifold of nonpositive sectional curvature is called a Cartan Hadamard manifold. If f is a differentiable map from manifold M to manifold N, we shall denote b d f x the differential of f at x. 3. Invexit on Riemannian manifolds In this section, motivated b [7], the notion of strong invexit for functions is introduced. Let M be a Riemannian manifold η : M M T M be a function such that for ever x, M, η(x, ) T M. Definition 3.. Let M be a Riemannian manifold f : M R be a differentiable function; then, f is said to be: (i) Invex with respect to η on M if f (x) f () d f (η(x, )) for all x, M. ()
3 852 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) If the inequalit () is strict for x, then f is said to be strictl invex with respect to η. (ii) Strongl invex with respect to η on M if there exists a constant α > 0 such that for ever x, M we have f (x) f () d f (η(x, )) + α η(x, ) 2. Example 3.. Let M be a Riemannian manifold f : M R be a differentiable function such that for ever M, d f 0. Suppose that the function η : M M T M is defined b η(x, ) := ( f (x) f ()) d f 2 d f. Then, for ever x, M we have ( f (x) f ()) d f, η(x, ) = d f, d f 2 d f ( f (x) f ()) = d f 2 d f, d f ( f (x) f ()) = d f 2 d f 2 = f (x) f (). Therefore, f is an invex function with respect to η. The following definitions are introduced in [7]. Definition 3.2. Let M be a Riemannian manifold α x, : [0, ] M be a curve on M such that α x, (0) = α x, () = x. Then, α x, is said to possess the propert (P) with respect to, x M if α x, (s)(t s) = η(α x,(t), α x, (s)), for all s, t [0, ]. Definition 3.3. Let M be a Riemannian manifold. Then, the function η : M M T M is said to be integrable if for ever x, M there exists at least one curve α x, possessing the propert (P) with respect to, x M. For an example of an integrable map η, see [7, p. 305]. Remark 3.. Let M be a Riemannian manifold function η : M M T M be integrable. Then, we have η(x, ) = η(α x, (), α x, (0)) = α x, (0). In the case where α x, is a geodesic, then, η(, α x, (s)) = sα x, (s) = s Ps 0,α x, [α x, (0)] = s Ps 0,α x, [η(x, )] η(α x, (), α x, (s)) = ( s)α x, (s) = ( s)ps 0,α x, [η(x, )]. 4. Monotonicit on Riemannian manifolds Let us recall the definition of a monotone vector field on a Riemannian manifold; see [0,5] for the details. Definition 4.. Let M be a Riemannian manifold X be a vector field on M. Then, X is said to be monotone on M if for ever x, M we have α x, (0), P0,α x, [X (x)] X () 0, where α x, is a geodesic joining x. (2)
4 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) Motivated b Yang et al. [24] we generalize the notion of invariant monotonicit to Riemannian manifolds. Definition 4.2. Let M be a Riemannian manifold X be a vector field on M; then: (i) X is said to be invariant monotone on M with respect to η if for ever x, M one has X (), η(x, ) + X (x), η(, x) x 0. (3) If the inequalit (3) is strict for x, then X is said to be strictl invariant monotone with respect to η. (ii) X is said to be strongl invariant monotone on M with respect to η if there exists an α > 0 such that for ever, x M one has X (), η(x, ) + X (x), η(, x) x α( η(x, ) 2 + η(, x) 2 x ). It should be noted that on ever Cartan Hadamard manifold M each monotone vector field X is an invariant monotone vector field with respect to η(x, ) := exp (x). Indeed, for ever x, M, α x, (t) := exp (t exp (x)), for all t [0, ], is the unique geodesic joining to x α x, (0) := exp (x). B (2) the propert P 0,α x, [exp (x)] = exp () of parallel translation we have x exp Therefore, (x), P0,α x, [X (x)] X () = P0,α x, [exp (x)], X (x) x exp (x), X () exp x (), X (x) x + exp (x), X () 0. = exp x (), X (x) x exp (x), X () 0. (4) Considering η(x, ) = exp (x) for ever x, M, we conclude that X is an invariant monotone vector field on M with respect to η. Despite the above fact, in the following example we show that on ever Cartan Hadamard manifold M there exists a strictl invariant monotone vector field X with respect to an η : M M T M which is not monotone. Example 4.. Let M be a Cartan Hadamard manifold x M. Then, the distance function z d(x, z) is smooth on M \ {x}. We denote the partial derivatives of the function d : M M R b d(x,) d(x,). Suppose that x l := d(x, ) = exp (x) x. If γ (t) := exp (t exp (x)/ exp (x) x) for all t [0, l] is the unique minimizing geodesic joining to x, then, b [, p. 347], we have the following antismmetr properties: [ ] d(x, ) P0,γ l d(x, ) =. (5) On the other h, b [2, p. 08] we have d(x, ) = γ (l), d(x, ) = d(x, ) =. x Since γ (0) = l exp (x), b Eq. (6) we can write d(x, ) = γ (l) = P l 0,γ [γ (0)] (6) (7)
5 854 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) [ ] = P0,γ l l exp (x) = l Pl 0,γ [exp (x)] = l exp x (). (8) Now, we define the function η vector field X; η(x, ) := l exp (x) X () := d(x, ). The vector field X is invariant monotone with respect to η. Indeed, b utilizing (8) we get d(x, ) X (x), η(, x) x =, l exp x () x = l l exp x (), exp x () Similarl, Hence, X (), η(x, ) = l 2. = exp x () 2 x = l 2. X (x), η(, x) x + X (), η(x, ) < 0. We show that the vector field X is not monotone. B (5) (7) we get [ ] γ (0), P,γ 0 [X (x)] X () = γ (0), P,γ 0 d(x, ) = γ (0), P 0,γ = γ (0), P,γ 0 = 2 γ (0), P,γ 0 = 2 P0,γ [γ (0)], x [ d(x, ) [ d(x, ) [ ] d(x, ) d(x, ) d(x, ) d(x, ) = 2, x = 2 d(x, ) 2 x = 2 < 0. ( ] P,γ 0 ] + P,γ 0 x ) d(x, ) [ ] d(x, ) [ ] d(x, ) The following example shows that there exists a strictl invariant monotone vector field on ever Riemannian manifold.
6 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) Example 4.2. Let M be a Riemannian manifold f : M R be a differentiable function such that for ever M, d f 0. Suppose that for ever x, M the function η : M M T M is defined b η(x, ) := 2 d f 2 d f. Then, d f is a strictl invariant monotone vector field with respect to η. Indeed, for ever x, M with x we have d f, η(x, ) = d f, 2 d f 2 d f Similarl, we have = 2 d f 2 d f, d f = 2 d f 2 d f 2 = 2. (9) d f x, η(, x) x = 2. (0) Therefore, d f, η(x, ) + d f x, η(, x) x < 0. Let S be a convex subset of a finite dimensional Cartan Hadamard manifold M x M. Then, there exists a unique point p S (x) such that for each S, d(x, p S (x)) d(x, ). The point p S (x) is called the projection of x onto S; see [9, p. 262]. Now, we give an example of a strictl invariant monotone vector field which is not of gradient tpe. Example 4.3. Let M be a Cartan Hadamard manifold of constant sectional curvature K 0. Suppose that x, M, x, r > 0. Moreover, assume that B x := B(x, r) B := B(, r) are two closed balls such that B x B = φ. Let x := P Bx (x) := P B () be projections of x on B x B, respectivel. Suppose that l := exp x. Let γ (t) := exp (t exp x / exp x ), for all t [0, l], be the normalized geodesic joining to x. Assume that J is a Jacobi field along γ normal to γ w(t) is a parallel field along γ with w(t) γ (t) = γ, w(t) γ (t) = 0 for ever t [0, l]. We define the function η : M M T M b η(x, ) := P 0 l,γ [ w(l)]. We also define the vector field X as follows: X () := P 0 l,γ [J(l)]. B [8, p. 2] we have J(l) = sinh(l K ) w(l). K () B the definitions of X η utilizing () we get X (), η(x, ) = Pl,γ 0 [J(l)], P0 l,γ [ w(l)] = J(l), w(l) x = sinh(l K ) w(l), w(l) K x
7 856 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) = sinh(l K ) K w(l), w(l) x = sinh(l K ) K < 0. Therefore, X (), η(x, ) < 0. Similarl, let l be the length of the normalized geodesic β joining x to defined b β(t) := exp x (t exp x / exp x x ), for all t [0, l ]. Then, we have η(, x) = P 0 l,β [ w (l )], X (x) = P 0 l,β [J (l )]. Hence, b (3) (4) we have X (), η(x, ) < 0. B appling (2) (5) we get X (), η(x, ) + X (), η(x, ) < 0. Therefore, X is strictl invariant monotone with respect to η. (2) (3) (4) (5) Proposition 4.. Let M be a Riemannian manifold f : M R be a differentiable function. If f is (strongl, strictl) invex with respect to η, then d f is (strongl, strictl) invariant monotone with respect to η on M. Proof. We prove onl the result when f is strongl invex. The proofs for other cases are similar. Let f be strongl invex on M x, M. Since f is strongl invex, we have f (x) f () d f (η(x, )) + α η(x, ) 2, f () f (x) d f x (η(, x)) + α η(, x) 2 x. B adding these two inequalities we get 0 d f (η(x, )) + d f x (η(, x)) + α( η(x, ) 2 + η(, x) 2 x ). We need the following proposition from [7]. Proposition 4.2. Let M be a Riemannian manifold f : M R be a differentiable function. Suppose that the function η : M M T M is integrable. Then, f is an invex function on M if onl if g x, (t) = f (α x, (t)) is convex on [0, ] for some α x,. Theorem 4.. Let M be a Riemannian manifold f : M R be a differentiable function. Suppose that the function η : M M T M is integrable. If d f is invariant monotone on M with respect to η, then f is an invex function on M. Proof. Let x, M. Since η is integrable, there exists at least one curve α x, possessing the Propert (P) such that α x, (0) = α x, () = x. If f is not invex on M, then, b Proposition 4.2, f (α x, (t)) is not convex on [0, ]. Hence there exists a λ (0, ) such that f (α x, (λ)) > λf (x) + ( λ) f (),
8 or A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) λ[ f (α x, (λ)) f (x)] > ( λ)[ f (α x, (λ)) f ()]. B the Mean Value Theorem there exist λ, λ 2 (0, ), 0 < λ 2 < λ < λ < λ(λ )d f αx, (λ )(α x, (λ )) + ( λ)λd f αx, (λ 2 )(α x, (λ 2)) > 0. This is equivalent to d f αx, (λ )(α x, (λ )) + d f αx, (λ 2 )(α x, (λ 2)) > 0. B the condition (P) we have Therefore, (λ λ 2 ) η(α x,(λ ), α x, (λ 2 )) = α x, (λ 2), (λ λ 2 ) η(α x,(λ 2 ), α x, (λ )) = α x, (λ ). d f αx, (λ )(η(α x, (λ 2 ), α x, (λ ))) + d f αx, (λ 2 )(η(α x, (λ ), α x, (λ 2 ))) > 0. This contradicts the invariant monotonicit of f. Theorem 4.2. Let M be a Riemannian manifold such that there is a geodesic between ever two points let f : M R be a differentiable function. Suppose that the function η : M M T M is integrable. If d f is strongl invariant monotone on M with respect to η, then f is a strongl invex function on M. Proof. Let x, M. Then, there exists a geodesic α x, : [0, ] M such that α x, (0) =, α x, () = x. Let z =: α x, ( 2 ); then, b the Mean Value Theorem there exist t, t 2 (0, ) such that 0 < t 2 < 2 < t < we have f (x) f (z) = 2 d f u(α x, (t )), (6) f (z) f () = 2 d f v(α x, (t 2)), (7) where u := α x, (t ), v := α x, (t 2 ). Since d f is strongl invariant monotone, then, d f u (η(, u)) + d f (η(u, )) α( η(, u) 2 u + η(u, ) 2 ). (8) Since condition (P) holds, then, b Remark 3. utilizing the parallel translation, we have η(, α x, (t )) = t P t 0,α x, [η(x, )], η(α x, (t ), ) = t η(x, ). B combining (8) (20) we have d f u ( t P t 0,α x, [η(x, )]) + d f (t [η(x, )]) α( t P t 0,α x, [η(x, )] 2 u + t [η(x, )] 2 ). This is equivalent to (9) (20) d f u (P t 0,α x, [η(x, )]) + d f ([η(x, )]) 2t α [η(x, )] 2. (2) Since P t 0,α x, [η(x, )] = α x, (t ) we have 2 d f u(α x, (t )) 2 d f ([η(x, )]) + t α [η(x, )] 2. (22)
9 858 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) In a similar wa we get 2 d f v(α x, (t 2)) 2 d f ([η(x, )]) + t 2 α [η(x, )] 2. (23) From (6), (7), (22) (23) we conclude that f (x) f (z) 2 d f (η(x, )) + t α [η(x, )] 2, f (z) f () 2 d f (η(x, )) + t 2 α [η(x, )] 2. B adding these two inequalities we obtain f (x) f () d f (η(x, )) + α(t + t 2 ) η(x, ) 2 d f (η(x, )) + 2 α η(x, ) 2. Therefore, f is strongl invex. 5. Pseudoinvexit invariant pseudomonotonicit Definition 5.. Let M be a Riemannian manifold f : M R be a differentiable function; then: (i) f is said to be pseudoinvex with respect to η on M if for ever x, M, one has d f (η(x, )) 0 f (x) f (). (ii) f is said to be strictl pseudoinvex with respect to η on M if for ever x, M with x one has d f (η(x, )) 0 f (x) > f (). (iii) f is said to be strongl pseudoinvex with respect to η on M if there exists a constant α > 0 such that for ever x, M, one has d f (η(x, )) 0 f (x) f () + α η(x, ) 2. Definition 5.2. Let M be a Riemannian manifold X be a vector field on M; then: (i) X said to be invariant pseudomonotone on M with respect to η if for ever x, M one has X (x), η(, x) x 0 X (), η(x, ) 0. (ii) X is said to be strictl invariant pseudomonotone on M with respect to η if for ever x, M with x one has X (x), η(, x) x 0 X (), η(x, ) < 0. (iii) X is said to be strongl invariant pseudomonotone on M with respect to η if there exists a constant α > 0 such that for ever x, M one has X (x), η(, x) x 0 X (), η(x, ) α η(x, ) 2. The following theorem is a generalization of Theorem 4. in [24] to Riemannian manifolds. Theorem 5.. Let M be a Riemannian manifold f : M R be a differentiable function. Suppose that the function η : M M T M is integrable. Then, f is strictl pseudoinvex with respect to η on M if onl if d f is strictl invariant pseudomonotone on M with respect to η.
10 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) Proof. Suppose that f is strictl pseudoinvex with respect to η on M. Let x, M, x be such that d f (η(x, )) 0. Then, b the strict pseudoinvexit of f we have f (x) > f (). We need to show that d f x (η(, x)) < 0. Assume that d f x (η(, x)) 0. Again utilizing the strict pseudoinvexit of f with respect to η ields f () f (x), which contradicts (24). Conversel, suppose that d f is strictl invariant pseudomonotone on M. Let x, M, x be such that d f (η(x, )) 0. Since η is integrable, there exists at least one curve α x, possessing the Propert (P) such that α x, (0) = α x, () = x. We need to show that f (x) > f (). Assume f (x) f (), B the Mean Value Theorem there exists λ (0, ) such that (24) (25) (26) f (x) f () = d f αx, (λ)(α x, (λ)). Now, (26) (27) implies that d f αx, (λ)(α x, (λ)) 0. Hence, b the Propert (P) we have d f αx, (λ)(α x, (λ)) = d f α x, (λ) [ ] λ η(, α x,(λ)) (27) = λ d f α x, (λ)[η(, α x, (λ))] 0. Therefore, d f αx, (λ)(η(, α x, (λ))) 0. Since d f is strictl invariant pseudomonotone, from (28) we have d f (η(α x, (λ), )) < 0, b the Propert (P) we conclude that d f (λα x, (0)) = λd f (η(x, )) < 0. Therefore, d f (η(x, )) < 0 which contradicts (25). Hence, f is strictl pseudoinvex with respect to η on M. (28) Theorem 5.2. Let M be a Riemannian manifold such that there is a geodesic between ever two points let f : M R be a differentiable function. Suppose that the function η : M M T M is integrable. If f is strongl invariant pseudomonotone on M with respect to η, then f is strongl pseudoinvex with respect to η on M. Proof. Suppose that d f η((x, )) 0. (29) Let x, M. Then, there exists a geodesic α x, : [0, ] M such that α x, (0) =, α x, () = x. Let z := α x, ( 2 ); then, b the Mean Value Theorem, there exist t, t 2 (0, ) such that 0 < t 2 < 2 < t < f (x) f (z) = 2 d f u(α x, (t )) (30) f (z) f () = 2 d f v(α x, (t 2)), (3)
11 860 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) where u := α x, (t ), v := α x, (t 2 ). B the propert (P) equalities (30) (3) we obtain f (x) f (z) = 2t d f u η((, u)), f (z) f () = 2t 2 d f v η((, v)). The Propert (P) (29) impl that (32) (33) 0 d f (η(x, )) = t d f (η(u, )) = t 2 d f (η(v, )). (34) Since d f is strongl invariant pseudomonotone on M with respect to η, b utilizing (34) Propert (P) we have d f u (η(, u)) α η(, u) 2 u = α t P t 0,α x, [η(x, )] 2 u = αt 2 Pt 0,α x, [η(x, )] 2 u = αt 2 η(x, ) 2, (35) d f v (η(, v)) α η(, v) 2 v = α t P t 2 0,α x, [η(x, )] 2 v = αt 2 Pt 2 0,α x, [η(x, )] 2 v = αt 2 2 η(x, ) 2. Now, from (32) (35) we conclude that f (x) f (z) α 2 t η(x, ) 2. (36) (37) Similarl, b using (33) (36) we have f (z) f () α 2 t 2 η(x, ) 2. (38) B adding (37) (38) we obtain f (x) f () α 2 (t + t 2 ) η(x, ) 2 α 4 η(x, ) 2. Therefore, f is strongl pseudoinvex with respect to η on M. Acknowledgement This research was partiall supported b the Center of Excellence for Mathematics, Universit of Isfahan, Isfahan, Iran. References [] D. Azagra, J. Ferrera, F. López-Mesas, Nonsmooth analsis Hamilton Jacobi equations on Riemannian manifolds, Journal of Functional Analsis 220 (2005) [2] A. Barani, M.R. Pouraevali, Invex sets preinvex functions on Riemannian manifolds, Journal of Mathematical Analsis Applications 328 (2007)
12 A. Barani, M.R. Pouraevali / Nonlinear Analsis 70 (2009) [3] M. Bianchi, S. Schaible, Equilibrium problems under generalized convexit generalized monotonicit, Journal of Global Optimization 30 (2004) [4] R. Correa, A. Jofré, L. Thibault, Characterization of lower semicontinuous convex functions, Proceedings of the American Mathematical Societ 6 (992) [5] J.P. Crouzeix, J.A. Ferl, Criteria for quasiconvexit pseudoconvexit, Mathematical Programming 23 (982) [6] J.X. Da Cruze Neto, O.P. Ferreira, L.R. Lucambio Pérez, Contributions to the stud of monotone vector fields, Acta Mathematica Hungarica 94 (2002) [7] L. Fan, S. Liu, S. Gao, Generalized monotonicit convexit of nondifferentiable functions, Journal of Mathematical Analsis Applications 279 (2003) [8] M.P. do Carmo, Riemannian Geometr, Birkhäuser, 992. [9] O.P. Ferreira, P.R. Oliveira, Proximal point algorithm on Riemannian manifolds, Optimization 5 (2002) [0] O.P. Ferreira, L.R. Lucambio Pérez, S.Z. Németh, Singularities of monotone vector fields an extragradient-tpe algorithm, Journal of Global Optimization 3 (2005) [] M.A. Hanson, On sufficienc of the Kuhn Tucker conditions, Journal of Mathematical Analsis Applications 80 (98) [2] W. Klingenberg, Riemannian Geometr, in: Studies in Mathematics, vol., Walter de Gruter, Berlin, 982. [3] S. Lang, Fundamentals of Differential Geometr, in: Graduate Text in Mathematics, vol. 9, Springer-Verlag, New York, 999. [4] B.S. Mordukhovich, Variational Analsis Generalized Differentiation. I. Basic Theor, Springer-Verlag, Berlin, [5] S.Z. Németh, Monotone vector fields, Publicationes Mathematics 54 (999) [6] R. Pini, C. Singh, Generalized convexit generalized monotonicit, Journal of Information Optimization Sciences 20 (999) [7] R. Pini, Convexit along curves invexit, Optimization 29 (994) [8] J.P. Penot, P.H. Quang, Generalized convexit of functions generalized monotonicit of set-valued maps, Journal of Optimization Theor Applications 92 (997) [9] J.P. Penot, P.H. Sach, Generalized monotonicit of subdifferentials generalized convexit, Journal of Optimization Theor Applications 94 (997) [20] T. Rapscák, Smooth Nonlinear Optimization in R n, Kluwer Academic Publishers, Dordrecht, 997. [2] T. Sakai, Riemannian Geometr, in: Translations of Mathematical Monographs, vol. 49, American Mathematic Societ, 992. [22] C. Udriste, Convex Functions Optimization Methods on Riemannian Manifolds, in: Mathematics its Applications, vol. 297, Kluwer Academic Publishers, 994. [23] X.M. Yang, X.Q. Yang, K.L. Teo, Criteria for generalized invex monotonicities, European Journal of Operational Research 64 (2005) 5 9. [24] X.M. Yang, X.Q. Yang, K.L. Teo, Generalized invexit generalized invariant monotonicit, Journal of Optimization Theor Applications 7 (2003)
Generalized vector equilibrium problems on Hadamard manifolds
 Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 (2016), 1402 1409 Research Article Generalized vector equilibrium problems on Hadamard manifolds Shreyasi Jana a, Chandal Nahak a, Cristiana
Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 (2016), 1402 1409 Research Article Generalized vector equilibrium problems on Hadamard manifolds Shreyasi Jana a, Chandal Nahak a, Cristiana
Monotone Point-to-Set Vector Fields
 Monotone Point-to-Set Vector Fields J.X. da Cruz Neto, O.P.Ferreira and L.R. Lucambio Pérez Dedicated to Prof.Dr. Constantin UDRIŞTE on the occasion of his sixtieth birthday Abstract We introduce the concept
Monotone Point-to-Set Vector Fields J.X. da Cruz Neto, O.P.Ferreira and L.R. Lucambio Pérez Dedicated to Prof.Dr. Constantin UDRIŞTE on the occasion of his sixtieth birthday Abstract We introduce the concept
Generalized monotonicity and convexity for locally Lipschitz functions on Hadamard manifolds
 Generalized monotonicity and convexity for locally Lipschitz functions on Hadamard manifolds A. Barani 1 2 3 4 5 6 7 Abstract. In this paper we establish connections between some concepts of generalized
Generalized monotonicity and convexity for locally Lipschitz functions on Hadamard manifolds A. Barani 1 2 3 4 5 6 7 Abstract. In this paper we establish connections between some concepts of generalized
Weak sharp minima on Riemannian manifolds 1
 1 Chong Li Department of Mathematics Zhejiang University Hangzhou, 310027, P R China cli@zju.edu.cn April. 2010 Outline 1 2 Extensions of some results for optimization problems on Banach spaces 3 4 Some
1 Chong Li Department of Mathematics Zhejiang University Hangzhou, 310027, P R China cli@zju.edu.cn April. 2010 Outline 1 2 Extensions of some results for optimization problems on Banach spaces 3 4 Some
Variational inequalities for set-valued vector fields on Riemannian manifolds
 Variational inequalities for set-valued vector fields on Riemannian manifolds Chong LI Department of Mathematics Zhejiang University Joint with Jen-Chih YAO Chong LI (Zhejiang University) VI on RM 1 /
Variational inequalities for set-valued vector fields on Riemannian manifolds Chong LI Department of Mathematics Zhejiang University Joint with Jen-Chih YAO Chong LI (Zhejiang University) VI on RM 1 /
OPTIMALITY CONDITIONS FOR GLOBAL MINIMA OF NONCONVEX FUNCTIONS ON RIEMANNIAN MANIFOLDS
 OPTIMALITY CONDITIONS FOR GLOBAL MINIMA OF NONCONVEX FUNCTIONS ON RIEMANNIAN MANIFOLDS S. HOSSEINI Abstract. A version of Lagrange multipliers rule for locally Lipschitz functions is presented. Using Lagrange
OPTIMALITY CONDITIONS FOR GLOBAL MINIMA OF NONCONVEX FUNCTIONS ON RIEMANNIAN MANIFOLDS S. HOSSEINI Abstract. A version of Lagrange multipliers rule for locally Lipschitz functions is presented. Using Lagrange
Characterization of lower semicontinuous convex functions on Riemannian manifolds
 Wegelerstraße 6 53115 Bonn Germany phone +49 228 73-3427 fax +49 228 73-7527 www.ins.uni-bonn.de S. Hosseini Characterization of lower semicontinuous convex functions on Riemannian manifolds INS Preprint
Wegelerstraße 6 53115 Bonn Germany phone +49 228 73-3427 fax +49 228 73-7527 www.ins.uni-bonn.de S. Hosseini Characterization of lower semicontinuous convex functions on Riemannian manifolds INS Preprint
Steepest descent method on a Riemannian manifold: the convex case
 Steepest descent method on a Riemannian manifold: the convex case Julien Munier Abstract. In this paper we are interested in the asymptotic behavior of the trajectories of the famous steepest descent evolution
Steepest descent method on a Riemannian manifold: the convex case Julien Munier Abstract. In this paper we are interested in the asymptotic behavior of the trajectories of the famous steepest descent evolution
Two-Step Methods for Variational Inequalities on Hadamard Manifolds
 Appl. Math. Inf. Sci. 9, No. 4, 1863-1867 (2015) 1863 Applied Mathematics & Information Sciences An International Journal http://dx.doi.org/10.12785/amis/090424 Two-Step Methods for Variational Inequalities
Appl. Math. Inf. Sci. 9, No. 4, 1863-1867 (2015) 1863 Applied Mathematics & Information Sciences An International Journal http://dx.doi.org/10.12785/amis/090424 Two-Step Methods for Variational Inequalities
Chapter 3. Riemannian Manifolds - I. The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves
 Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Monotone and Accretive Vector Fields on Riemannian Manifolds
 Monotone and Accretive Vector Fields on Riemannian Manifolds J.H. Wang, 1 G. López, 2 V. Martín-Márquez 3 and C. Li 4 Communicated by J.C. Yao 1 Corresponding author, Department of Applied Mathematics,
Monotone and Accretive Vector Fields on Riemannian Manifolds J.H. Wang, 1 G. López, 2 V. Martín-Márquez 3 and C. Li 4 Communicated by J.C. Yao 1 Corresponding author, Department of Applied Mathematics,
Hopf-Rinow and Hadamard Theorems
 Summersemester 2015 University of Heidelberg Riemannian geometry seminar Hopf-Rinow and Hadamard Theorems by Sven Grützmacher supervised by: Dr. Gye-Seon Lee Prof. Dr. Anna Wienhard Contents Introduction..........................................
Summersemester 2015 University of Heidelberg Riemannian geometry seminar Hopf-Rinow and Hadamard Theorems by Sven Grützmacher supervised by: Dr. Gye-Seon Lee Prof. Dr. Anna Wienhard Contents Introduction..........................................
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
The nonsmooth Newton method on Riemannian manifolds
 The nonsmooth Newton method on Riemannian manifolds C. Lageman, U. Helmke, J.H. Manton 1 Introduction Solving nonlinear equations in Euclidean space is a frequently occurring problem in optimization and
The nonsmooth Newton method on Riemannian manifolds C. Lageman, U. Helmke, J.H. Manton 1 Introduction Solving nonlinear equations in Euclidean space is a frequently occurring problem in optimization and
Journal of Inequalities in Pure and Applied Mathematics
 Journal of Inequalities in Pure and Applied Mathematics http://jipam.vu.edu.au/ Volume 4, Issue 4, Article 67, 2003 ON GENERALIZED MONOTONE MULTIFUNCTIONS WITH APPLICATIONS TO OPTIMALITY CONDITIONS IN
Journal of Inequalities in Pure and Applied Mathematics http://jipam.vu.edu.au/ Volume 4, Issue 4, Article 67, 2003 ON GENERALIZED MONOTONE MULTIFUNCTIONS WITH APPLICATIONS TO OPTIMALITY CONDITIONS IN
Steepest descent method on a Riemannian manifold: the convex case
 Steepest descent method on a Riemannian manifold: the convex case Julien Munier To cite this version: Julien Munier. Steepest descent method on a Riemannian manifold: the convex case. 2006.
Steepest descent method on a Riemannian manifold: the convex case Julien Munier To cite this version: Julien Munier. Steepest descent method on a Riemannian manifold: the convex case. 2006.
2 Preliminaries. is an application P γ,t0,t 1. : T γt0 M T γt1 M given by P γ,t0,t 1
 804 JX DA C NETO, P SANTOS AND S SOUZA where 2 denotes the Euclidean norm We extend the definition of sufficient descent direction for optimization on Riemannian manifolds and we relax that definition
804 JX DA C NETO, P SANTOS AND S SOUZA where 2 denotes the Euclidean norm We extend the definition of sufficient descent direction for optimization on Riemannian manifolds and we relax that definition
Strictly convex functions on complete Finsler manifolds
 Proc. Indian Acad. Sci. (Math. Sci.) Vol. 126, No. 4, November 2016, pp. 623 627. DOI 10.1007/s12044-016-0307-2 Strictly convex functions on complete Finsler manifolds YOE ITOKAWA 1, KATSUHIRO SHIOHAMA
Proc. Indian Acad. Sci. (Math. Sci.) Vol. 126, No. 4, November 2016, pp. 623 627. DOI 10.1007/s12044-016-0307-2 Strictly convex functions on complete Finsler manifolds YOE ITOKAWA 1, KATSUHIRO SHIOHAMA
In applications, we encounter many constrained optimization problems. Examples Basis pursuit: exact sparse recovery problem
 1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
Mathematical Programming Involving (α, ρ)-right upper-dini-derivative Functions
 Filomat 27:5 (2013), 899 908 DOI 10.2298/FIL1305899Y Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Mathematical Programming Involving
Filomat 27:5 (2013), 899 908 DOI 10.2298/FIL1305899Y Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Mathematical Programming Involving
1.4 The Jacobian of a map
 1.4 The Jacobian of a map Derivative of a differentiable map Let F : M n N m be a differentiable map between two C 1 manifolds. Given a point p M we define the derivative of F at p by df p df (p) : T p
1.4 The Jacobian of a map Derivative of a differentiable map Let F : M n N m be a differentiable map between two C 1 manifolds. Given a point p M we define the derivative of F at p by df p df (p) : T p
OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS
 Trends in Mathematics Information Center for Mathematical Sciences Volume 6, Number 1, June, 23, Pages 45 49 OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS SANG UK RYU Abstract. We stud the
Trends in Mathematics Information Center for Mathematical Sciences Volume 6, Number 1, June, 23, Pages 45 49 OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS SANG UK RYU Abstract. We stud the
FIRST ORDER CHARACTERIZATIONS OF PSEUDOCONVEX FUNCTIONS. Vsevolod Ivanov Ivanov
 Serdica Math. J. 27 (2001), 203-218 FIRST ORDER CHARACTERIZATIONS OF PSEUDOCONVEX FUNCTIONS Vsevolod Ivanov Ivanov Communicated by A. L. Dontchev Abstract. First order characterizations of pseudoconvex
Serdica Math. J. 27 (2001), 203-218 FIRST ORDER CHARACTERIZATIONS OF PSEUDOCONVEX FUNCTIONS Vsevolod Ivanov Ivanov Communicated by A. L. Dontchev Abstract. First order characterizations of pseudoconvex
Homogeneous Geodesics of Left Invariant Randers Metrics on a Three-Dimensional Lie Group
 Int. J. Contemp. Math. Sciences, Vol. 4, 009, no. 18, 873-881 Homogeneous Geodesics of Left Invariant Randers Metrics on a Three-Dimensional Lie Group Dariush Latifi Department of Mathematics Universit
Int. J. Contemp. Math. Sciences, Vol. 4, 009, no. 18, 873-881 Homogeneous Geodesics of Left Invariant Randers Metrics on a Three-Dimensional Lie Group Dariush Latifi Department of Mathematics Universit
An inexact subgradient algorithm for Equilibrium Problems
 Volume 30, N. 1, pp. 91 107, 2011 Copyright 2011 SBMAC ISSN 0101-8205 www.scielo.br/cam An inexact subgradient algorithm for Equilibrium Problems PAULO SANTOS 1 and SUSANA SCHEIMBERG 2 1 DM, UFPI, Teresina,
Volume 30, N. 1, pp. 91 107, 2011 Copyright 2011 SBMAC ISSN 0101-8205 www.scielo.br/cam An inexact subgradient algorithm for Equilibrium Problems PAULO SANTOS 1 and SUSANA SCHEIMBERG 2 1 DM, UFPI, Teresina,
OPTIMALITY CONDITIONS AND DUALITY FOR SEMI-INFINITE PROGRAMMING INVOLVING SEMILOCALLY TYPE I-PREINVEX AND RELATED FUNCTIONS
 Commun. Korean Math. Soc. 27 (2012), No. 2, pp. 411 423 http://dx.doi.org/10.4134/ckms.2012.27.2.411 OPTIMALITY CONDITIONS AND DUALITY FOR SEMI-INFINITE PROGRAMMING INVOLVING SEMILOCALLY TYPE I-PREINVEX
Commun. Korean Math. Soc. 27 (2012), No. 2, pp. 411 423 http://dx.doi.org/10.4134/ckms.2012.27.2.411 OPTIMALITY CONDITIONS AND DUALITY FOR SEMI-INFINITE PROGRAMMING INVOLVING SEMILOCALLY TYPE I-PREINVEX
Steepest descent method with a generalized Armijo search for quasiconvex functions on Riemannian manifolds
 J. Math. Anal. Appl. 341 (2008) 467 477 www.elsevier.com/locate/jmaa Steepest descent method with a generalized Armijo search for quasiconvex functions on Riemannian manifolds E.A. Papa Quiroz, E.M. Quispe,
J. Math. Anal. Appl. 341 (2008) 467 477 www.elsevier.com/locate/jmaa Steepest descent method with a generalized Armijo search for quasiconvex functions on Riemannian manifolds E.A. Papa Quiroz, E.M. Quispe,
Application of Harmonic Convexity to Multiobjective Non-linear Programming Problems
 International Journal of Computational Science and Mathematics ISSN 0974-3189 Volume 2, Number 3 (2010), pp 255--266 International Research Publication House http://wwwirphousecom Application of Harmonic
International Journal of Computational Science and Mathematics ISSN 0974-3189 Volume 2, Number 3 (2010), pp 255--266 International Research Publication House http://wwwirphousecom Application of Harmonic
Nondifferentiable Higher Order Symmetric Duality under Invexity/Generalized Invexity
 Filomat 28:8 (2014), 1661 1674 DOI 10.2298/FIL1408661G Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Nondifferentiable Higher
Filomat 28:8 (2014), 1661 1674 DOI 10.2298/FIL1408661G Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Nondifferentiable Higher
Local Convergence Analysis of Proximal Point Method for a Special Class of Nonconvex Functions on Hadamard Manifolds
 Local Convergence Analysis of Proximal Point Method for a Special Class of Nonconvex Functions on Hadamard Manifolds Glaydston de Carvalho Bento Universidade Federal de Goiás Instituto de Matemática e
Local Convergence Analysis of Proximal Point Method for a Special Class of Nonconvex Functions on Hadamard Manifolds Glaydston de Carvalho Bento Universidade Federal de Goiás Instituto de Matemática e
Results from MathSciNet: Mathematical Reviews on the Web c Copyright American Mathematical Society 2000
 2000k:53038 53C23 20F65 53C70 57M07 Bridson, Martin R. (4-OX); Haefliger, André (CH-GENV-SM) Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles
2000k:53038 53C23 20F65 53C70 57M07 Bridson, Martin R. (4-OX); Haefliger, André (CH-GENV-SM) Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles
II. DIFFERENTIABLE MANIFOLDS. Washington Mio CENTER FOR APPLIED VISION AND IMAGING SCIENCES
 II. DIFFERENTIABLE MANIFOLDS Washington Mio Anuj Srivastava and Xiuwen Liu (Illustrations by D. Badlyans) CENTER FOR APPLIED VISION AND IMAGING SCIENCES Florida State University WHY MANIFOLDS? Non-linearity
II. DIFFERENTIABLE MANIFOLDS Washington Mio Anuj Srivastava and Xiuwen Liu (Illustrations by D. Badlyans) CENTER FOR APPLIED VISION AND IMAGING SCIENCES Florida State University WHY MANIFOLDS? Non-linearity
A splitting minimization method on geodesic spaces
 A splitting minimization method on geodesic spaces J.X. Cruz Neto DM, Universidade Federal do Piauí, Teresina, PI 64049-500, BR B.P. Lima DM, Universidade Federal do Piauí, Teresina, PI 64049-500, BR P.A.
A splitting minimization method on geodesic spaces J.X. Cruz Neto DM, Universidade Federal do Piauí, Teresina, PI 64049-500, BR B.P. Lima DM, Universidade Federal do Piauí, Teresina, PI 64049-500, BR P.A.
Applied Mathematics Letters
 Applied Mathematics Letters 25 (2012) 974 979 Contents lists available at SciVerse ScienceDirect Applied Mathematics Letters journal homepage: www.elsevier.com/locate/aml On dual vector equilibrium problems
Applied Mathematics Letters 25 (2012) 974 979 Contents lists available at SciVerse ScienceDirect Applied Mathematics Letters journal homepage: www.elsevier.com/locate/aml On dual vector equilibrium problems
A double projection method for solving variational inequalities without monotonicity
 A double projection method for solving variational inequalities without monotonicity Minglu Ye Yiran He Accepted by Computational Optimization and Applications, DOI: 10.1007/s10589-014-9659-7,Apr 05, 2014
A double projection method for solving variational inequalities without monotonicity Minglu Ye Yiran He Accepted by Computational Optimization and Applications, DOI: 10.1007/s10589-014-9659-7,Apr 05, 2014
AN INTRODUCTION TO EXTREME POINTS AND APPLICATIONS IN ISOMETRIC BANACH SPACE THEORY
 AN INTRODUCTION TO EXTREME POINTS AND APPLICATIONS IN ISOMETRIC BANACH SPACE THEORY AUDREY CURNOCK Abstract. This technical paper is the looking at extreme point structure from an isometric view point,
AN INTRODUCTION TO EXTREME POINTS AND APPLICATIONS IN ISOMETRIC BANACH SPACE THEORY AUDREY CURNOCK Abstract. This technical paper is the looking at extreme point structure from an isometric view point,
SYNGE-WEINSTEIN THEOREMS IN RIEMANNIAN GEOMETRY
 SYNGE-WEINSTEIN THEOREMS IN RIEMANNIAN GEOMETRY AKHIL MATHEW Abstract. We give an exposition of the proof of a few results in global Riemannian geometry due to Synge and Weinstein using variations of the
SYNGE-WEINSTEIN THEOREMS IN RIEMANNIAN GEOMETRY AKHIL MATHEW Abstract. We give an exposition of the proof of a few results in global Riemannian geometry due to Synge and Weinstein using variations of the
arxiv:math/ v1 [math.dg] 24 May 2005
![arxiv:math/ v1 [math.dg] 24 May 2005 arxiv:math/ v1 [math.dg] 24 May 2005](/thumbs/75/72064954.jpg) arxiv:math/0505496v1 [math.dg] 24 May 2005 INF-CONVOLUTION AND REGULARIZATION OF CONVEX FUNCTIONS ON RIEMANNIAN MANIFOLDS OF NONPOSITIVE CURVATURE DANIEL AZAGRA AND JUAN FERRERA Abstract. We show how an
arxiv:math/0505496v1 [math.dg] 24 May 2005 INF-CONVOLUTION AND REGULARIZATION OF CONVEX FUNCTIONS ON RIEMANNIAN MANIFOLDS OF NONPOSITIVE CURVATURE DANIEL AZAGRA AND JUAN FERRERA Abstract. We show how an
Smooth Dynamics 2. Problem Set Nr. 1. Instructor: Submitted by: Prof. Wilkinson Clark Butler. University of Chicago Winter 2013
 Smooth Dynamics 2 Problem Set Nr. 1 University of Chicago Winter 2013 Instructor: Submitted by: Prof. Wilkinson Clark Butler Problem 1 Let M be a Riemannian manifold with metric, and Levi-Civita connection.
Smooth Dynamics 2 Problem Set Nr. 1 University of Chicago Winter 2013 Instructor: Submitted by: Prof. Wilkinson Clark Butler Problem 1 Let M be a Riemannian manifold with metric, and Levi-Civita connection.
How to Reach his Desires: Variational Rationality and the Equilibrium Problem on Hadamard Manifolds
 How to Reach his Desires: Variational Rationality and the Equilibrium Problem on Hadamard Manifolds G. C. Bento J. X. Cruz Neto Soares Jr. P.A. A. Soubeyran June 15, 2015 Abstract In this paper we present
How to Reach his Desires: Variational Rationality and the Equilibrium Problem on Hadamard Manifolds G. C. Bento J. X. Cruz Neto Soares Jr. P.A. A. Soubeyran June 15, 2015 Abstract In this paper we present
A CHARACTERIZATION OF STRICT LOCAL MINIMIZERS OF ORDER ONE FOR STATIC MINMAX PROBLEMS IN THE PARAMETRIC CONSTRAINT CASE
 Journal of Applied Analysis Vol. 6, No. 1 (2000), pp. 139 148 A CHARACTERIZATION OF STRICT LOCAL MINIMIZERS OF ORDER ONE FOR STATIC MINMAX PROBLEMS IN THE PARAMETRIC CONSTRAINT CASE A. W. A. TAHA Received
Journal of Applied Analysis Vol. 6, No. 1 (2000), pp. 139 148 A CHARACTERIZATION OF STRICT LOCAL MINIMIZERS OF ORDER ONE FOR STATIC MINMAX PROBLEMS IN THE PARAMETRIC CONSTRAINT CASE A. W. A. TAHA Received
Local convexity on smooth manifolds 1,2,3. T. Rapcsák 4
 Local convexity on smooth manifolds 1,2,3 T. Rapcsák 4 1 The paper is dedicated to the memory of Guido Stampacchia. 2 The author wishes to thank F. Giannessi for the advice. 3 Research was supported in
Local convexity on smooth manifolds 1,2,3 T. Rapcsák 4 1 The paper is dedicated to the memory of Guido Stampacchia. 2 The author wishes to thank F. Giannessi for the advice. 3 Research was supported in
Journal of Inequalities in Pure and Applied Mathematics
 Journal of Inequalities in Pure and Applied Mathematics MONOTONE TRAJECTORIES OF DYNAMICAL SYSTEMS AND CLARKE S GENERALIZED JACOBIAN GIOVANNI P. CRESPI AND MATTEO ROCCA Université de la Vallée d Aoste
Journal of Inequalities in Pure and Applied Mathematics MONOTONE TRAJECTORIES OF DYNAMICAL SYSTEMS AND CLARKE S GENERALIZED JACOBIAN GIOVANNI P. CRESPI AND MATTEO ROCCA Université de la Vallée d Aoste
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17
 DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
Inertial Game Dynamics
 ... Inertial Game Dynamics R. Laraki P. Mertikopoulos CNRS LAMSADE laboratory CNRS LIG laboratory ADGO'13 Playa Blanca, October 15, 2013 ... Motivation Main Idea: use second order tools to derive efficient
... Inertial Game Dynamics R. Laraki P. Mertikopoulos CNRS LAMSADE laboratory CNRS LIG laboratory ADGO'13 Playa Blanca, October 15, 2013 ... Motivation Main Idea: use second order tools to derive efficient
Relaxed Quasimonotone Operators and Relaxed Quasiconvex Functions
 J Optim Theory Appl (2008) 138: 329 339 DOI 10.1007/s10957-008-9382-6 Relaxed Quasimonotone Operators and Relaxed Quasiconvex Functions M.R. Bai N. Hadjisavvas Published online: 12 April 2008 Springer
J Optim Theory Appl (2008) 138: 329 339 DOI 10.1007/s10957-008-9382-6 Relaxed Quasimonotone Operators and Relaxed Quasiconvex Functions M.R. Bai N. Hadjisavvas Published online: 12 April 2008 Springer
Banach Journal of Mathematical Analysis ISSN: (electronic)
 Banach J Math Anal (009), no, 64 76 Banach Journal of Mathematical Analysis ISSN: 75-8787 (electronic) http://wwwmath-analysisorg ON A GEOMETRIC PROPERTY OF POSITIVE DEFINITE MATRICES CONE MASATOSHI ITO,
Banach J Math Anal (009), no, 64 76 Banach Journal of Mathematical Analysis ISSN: 75-8787 (electronic) http://wwwmath-analysisorg ON A GEOMETRIC PROPERTY OF POSITIVE DEFINITE MATRICES CONE MASATOSHI ITO,
Complete Surfaces of Constant Gaussian Curvature in Euclidean Space R 3.
 Summary of the Thesis in Mathematics by Valentina Monaco Complete Surfaces of Constant Gaussian Curvature in Euclidean Space R 3. Thesis Supervisor Prof. Massimiliano Pontecorvo 19 May, 2011 SUMMARY The
Summary of the Thesis in Mathematics by Valentina Monaco Complete Surfaces of Constant Gaussian Curvature in Euclidean Space R 3. Thesis Supervisor Prof. Massimiliano Pontecorvo 19 May, 2011 SUMMARY The
SOME HERMITE HADAMARD TYPE INEQUALITIES FOR THE PRODUCT OF TWO OPERATOR PREINVEX FUNCTIONS
 Banach J. Math. Anal. 9 15), no., uncorrected galleyproo DOI: 1.1535/bjma/9-- ISSN: 1735-8787 electronic) www.emis.de/journals/bjma/ SOME HERMITE HADAMARD TYPE INEQUALITIES FOR THE PRODUCT OF TWO OPERATOR
Banach J. Math. Anal. 9 15), no., uncorrected galleyproo DOI: 1.1535/bjma/9-- ISSN: 1735-8787 electronic) www.emis.de/journals/bjma/ SOME HERMITE HADAMARD TYPE INEQUALITIES FOR THE PRODUCT OF TWO OPERATOR
Relationships between upper exhausters and the basic subdifferential in variational analysis
 J. Math. Anal. Appl. 334 (2007) 261 272 www.elsevier.com/locate/jmaa Relationships between upper exhausters and the basic subdifferential in variational analysis Vera Roshchina City University of Hong
J. Math. Anal. Appl. 334 (2007) 261 272 www.elsevier.com/locate/jmaa Relationships between upper exhausters and the basic subdifferential in variational analysis Vera Roshchina City University of Hong
About the Convexity of a Special Function on Hadamard Manifolds
 Noname manuscript No. (will be inserted by the editor) About the Convexity of a Special Function on Hadamard Manifolds Cruz Neto J. X. Melo I. D. Sousa P. A. Silva J. P. the date of receipt and acceptance
Noname manuscript No. (will be inserted by the editor) About the Convexity of a Special Function on Hadamard Manifolds Cruz Neto J. X. Melo I. D. Sousa P. A. Silva J. P. the date of receipt and acceptance
CHAPTER 1 PRELIMINARIES
 CHAPTER 1 PRELIMINARIES 1.1 Introduction The aim of this chapter is to give basic concepts, preliminary notions and some results which we shall use in the subsequent chapters of the thesis. 1.2 Differentiable
CHAPTER 1 PRELIMINARIES 1.1 Introduction The aim of this chapter is to give basic concepts, preliminary notions and some results which we shall use in the subsequent chapters of the thesis. 1.2 Differentiable
Notes on the Riemannian Geometry of Lie Groups
 Rose- Hulman Undergraduate Mathematics Journal Notes on the Riemannian Geometry of Lie Groups Michael L. Geis a Volume, Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre
Rose- Hulman Undergraduate Mathematics Journal Notes on the Riemannian Geometry of Lie Groups Michael L. Geis a Volume, Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre
1. Introduction. An optimization problem with value function objective is a problem of the form. F (x, y) subject to y K(x) (1.2)
 OPTIMIZATION PROBLEMS WITH VALUE FUNCTION OBJECTIVES ALAIN B. ZEMKOHO Abstract. The famil of optimization problems with value function objectives includes the minmax programming problem and the bilevel
OPTIMIZATION PROBLEMS WITH VALUE FUNCTION OBJECTIVES ALAIN B. ZEMKOHO Abstract. The famil of optimization problems with value function objectives includes the minmax programming problem and the bilevel
NON POSITIVELY CURVED METRIC IN THE SPACE OF POSITIVE DEFINITE INFINITE MATRICES
 REVISTA DE LA UNIÓN MATEMÁTICA ARGENTINA Volumen 48, Número 1, 2007, Páginas 7 15 NON POSITIVELY CURVED METRIC IN THE SPACE OF POSITIVE DEFINITE INFINITE MATRICES ESTEBAN ANDRUCHOW AND ALEJANDRO VARELA
REVISTA DE LA UNIÓN MATEMÁTICA ARGENTINA Volumen 48, Número 1, 2007, Páginas 7 15 NON POSITIVELY CURVED METRIC IN THE SPACE OF POSITIVE DEFINITE INFINITE MATRICES ESTEBAN ANDRUCHOW AND ALEJANDRO VARELA
GENERALIZED CONVEXITY AND OPTIMALITY CONDITIONS IN SCALAR AND VECTOR OPTIMIZATION
 Chapter 4 GENERALIZED CONVEXITY AND OPTIMALITY CONDITIONS IN SCALAR AND VECTOR OPTIMIZATION Alberto Cambini Department of Statistics and Applied Mathematics University of Pisa, Via Cosmo Ridolfi 10 56124
Chapter 4 GENERALIZED CONVEXITY AND OPTIMALITY CONDITIONS IN SCALAR AND VECTOR OPTIMIZATION Alberto Cambini Department of Statistics and Applied Mathematics University of Pisa, Via Cosmo Ridolfi 10 56124
A sharp Blaschke Santaló inequality for α-concave functions
 Noname manuscript No will be inserted b the editor) A sharp Blaschke Santaló inequalit for α-concave functions Liran Rotem the date of receipt and acceptance should be inserted later Abstract We define
Noname manuscript No will be inserted b the editor) A sharp Blaschke Santaló inequalit for α-concave functions Liran Rotem the date of receipt and acceptance should be inserted later Abstract We define
Associativity of triangular norms in light of web geometry
 Associativit of triangular norms in light of web geometr Milan Petrík 1,2 Peter Sarkoci 3 1. Institute of Computer Science, Academ of Sciences of the Czech Republic, Prague, Czech Republic 2. Center for
Associativit of triangular norms in light of web geometr Milan Petrík 1,2 Peter Sarkoci 3 1. Institute of Computer Science, Academ of Sciences of the Czech Republic, Prague, Czech Republic 2. Center for
SYMPLECTIC MANIFOLDS, GEOMETRIC QUANTIZATION, AND UNITARY REPRESENTATIONS OF LIE GROUPS. 1. Introduction
 SYMPLECTIC MANIFOLDS, GEOMETRIC QUANTIZATION, AND UNITARY REPRESENTATIONS OF LIE GROUPS CRAIG JACKSON 1. Introduction Generally speaking, geometric quantization is a scheme for associating Hilbert spaces
SYMPLECTIC MANIFOLDS, GEOMETRIC QUANTIZATION, AND UNITARY REPRESENTATIONS OF LIE GROUPS CRAIG JACKSON 1. Introduction Generally speaking, geometric quantization is a scheme for associating Hilbert spaces
Chapter 16. Manifolds and Geodesics Manifold Theory. Reading: Osserman [7] Pg , 55, 63-65, Do Carmo [2] Pg ,
![Chapter 16. Manifolds and Geodesics Manifold Theory. Reading: Osserman [7] Pg , 55, 63-65, Do Carmo [2] Pg , Chapter 16. Manifolds and Geodesics Manifold Theory. Reading: Osserman [7] Pg , 55, 63-65, Do Carmo [2] Pg ,](/thumbs/81/84541290.jpg) Chapter 16 Manifolds and Geodesics Reading: Osserman [7] Pg. 43-52, 55, 63-65, Do Carmo [2] Pg. 238-247, 325-335. 16.1 Manifold Theory Let us recall the definition of differentiable manifolds Definition
Chapter 16 Manifolds and Geodesics Reading: Osserman [7] Pg. 43-52, 55, 63-65, Do Carmo [2] Pg. 238-247, 325-335. 16.1 Manifold Theory Let us recall the definition of differentiable manifolds Definition
Euler Characteristic of Two-Dimensional Manifolds
 Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
Euler Characteristic of Two-Dimensional Manifolds M. Hafiz Khusyairi August 2008 In this work we will discuss an important notion from topology, namely Euler Characteristic and we will discuss several
MONOTONE OPERATORS ON BUSEMANN SPACES
 MONOTONE OPERATORS ON BUSEMANN SPACES David Ariza-Ruiz Genaro López-Acedo Universidad de Sevilla Departamento de Análisis Matemático V Workshop in Metric Fixed Point Theory and Applications 15-17 Noviembre,
MONOTONE OPERATORS ON BUSEMANN SPACES David Ariza-Ruiz Genaro López-Acedo Universidad de Sevilla Departamento de Análisis Matemático V Workshop in Metric Fixed Point Theory and Applications 15-17 Noviembre,
The approximation of piecewise linear membership functions and Łukasiewicz operators
 Fuzz Sets and Sstems 54 25 275 286 www.elsevier.com/locate/fss The approimation of piecewise linear membership functions and Łukasiewicz operators József Dombi, Zsolt Gera Universit of Szeged, Institute
Fuzz Sets and Sstems 54 25 275 286 www.elsevier.com/locate/fss The approimation of piecewise linear membership functions and Łukasiewicz operators József Dombi, Zsolt Gera Universit of Szeged, Institute
The best generalised inverse of the linear operator in normed linear space
 Linear Algebra and its Applications 420 (2007) 9 19 www.elsevier.com/locate/laa The best generalised inverse of the linear operator in normed linear space Ping Liu, Yu-wen Wang School of Mathematics and
Linear Algebra and its Applications 420 (2007) 9 19 www.elsevier.com/locate/laa The best generalised inverse of the linear operator in normed linear space Ping Liu, Yu-wen Wang School of Mathematics and
On constraint qualifications with generalized convexity and optimality conditions
 On constraint qualifications with generalized convexity and optimality conditions Manh-Hung Nguyen, Do Van Luu To cite this version: Manh-Hung Nguyen, Do Van Luu. On constraint qualifications with generalized
On constraint qualifications with generalized convexity and optimality conditions Manh-Hung Nguyen, Do Van Luu To cite this version: Manh-Hung Nguyen, Do Van Luu. On constraint qualifications with generalized
A. Derivation of regularized ERM duality
 A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
Solutions to the Hamilton-Jacobi equation as Lagrangian submanifolds
 Solutions to the Hamilton-Jacobi equation as Lagrangian submanifolds Matias Dahl January 2004 1 Introduction In this essay we shall study the following problem: Suppose is a smooth -manifold, is a function,
Solutions to the Hamilton-Jacobi equation as Lagrangian submanifolds Matias Dahl January 2004 1 Introduction In this essay we shall study the following problem: Suppose is a smooth -manifold, is a function,
Marcinkiewicz Interpolation Theorem by Daniel Baczkowski
 1 Introduction Marcinkiewicz Interpolation Theorem b Daniel Baczkowski Let (, µ be a measure space. Let M denote the collection of all extended real valued µ-measurable functions on. Also, let M denote
1 Introduction Marcinkiewicz Interpolation Theorem b Daniel Baczkowski Let (, µ be a measure space. Let M denote the collection of all extended real valued µ-measurable functions on. Also, let M denote
arxiv: v2 [math.oc] 17 Jul 2017
![arxiv: v2 [math.oc] 17 Jul 2017 arxiv: v2 [math.oc] 17 Jul 2017](/thumbs/88/117665218.jpg) Lower semicontinuity of solution mappings for parametric fixed point problems with applications arxiv:1608.03452v2 [math.oc] 17 Jul 2017 Yu Han a and Nan-jing Huang b a. Department of Mathematics, Nanchang
Lower semicontinuity of solution mappings for parametric fixed point problems with applications arxiv:1608.03452v2 [math.oc] 17 Jul 2017 Yu Han a and Nan-jing Huang b a. Department of Mathematics, Nanchang
Characterizations of the solution set for non-essentially quasiconvex programming
 Optimization Letters manuscript No. (will be inserted by the editor) Characterizations of the solution set for non-essentially quasiconvex programming Satoshi Suzuki Daishi Kuroiwa Received: date / Accepted:
Optimization Letters manuscript No. (will be inserted by the editor) Characterizations of the solution set for non-essentially quasiconvex programming Satoshi Suzuki Daishi Kuroiwa Received: date / Accepted:
Convex Optimization. Convex Analysis - Functions
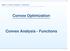 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Nonlinear Analysis 71 (2009) Contents lists available at ScienceDirect. Nonlinear Analysis. journal homepage:
 Nonlinear Analysis 71 2009 2744 2752 Contents lists available at ScienceDirect Nonlinear Analysis journal homepage: www.elsevier.com/locate/na A nonlinear inequality and applications N.S. Hoang A.G. Ramm
Nonlinear Analysis 71 2009 2744 2752 Contents lists available at ScienceDirect Nonlinear Analysis journal homepage: www.elsevier.com/locate/na A nonlinear inequality and applications N.S. Hoang A.G. Ramm
1. Geometry of the unit tangent bundle
 1 1. Geometry of the unit tangent bundle The main reference for this section is [8]. In the following, we consider (M, g) an n-dimensional smooth manifold endowed with a Riemannian metric g. 1.1. Notations
1 1. Geometry of the unit tangent bundle The main reference for this section is [8]. In the following, we consider (M, g) an n-dimensional smooth manifold endowed with a Riemannian metric g. 1.1. Notations
PREISSMAN S THEOREM ALEXANDER GRANT
 PREISSMAN S THEOREM ALEXANDER GRANT Abstract. This paper presents a proof of Preissman s Theorem, a theorem from the study of Riemannian Geometry that imposes restrictions on the fundamental group of compact,
PREISSMAN S THEOREM ALEXANDER GRANT Abstract. This paper presents a proof of Preissman s Theorem, a theorem from the study of Riemannian Geometry that imposes restrictions on the fundamental group of compact,
HIGHER ORDER OPTIMALITY AND DUALITY IN FRACTIONAL VECTOR OPTIMIZATION OVER CONES
 - TAMKANG JOURNAL OF MATHEMATICS Volume 48, Number 3, 273-287, September 2017 doi:10.5556/j.tkjm.48.2017.2311 - - - + + This paper is available online at http://journals.math.tku.edu.tw/index.php/tkjm/pages/view/onlinefirst
- TAMKANG JOURNAL OF MATHEMATICS Volume 48, Number 3, 273-287, September 2017 doi:10.5556/j.tkjm.48.2017.2311 - - - + + This paper is available online at http://journals.math.tku.edu.tw/index.php/tkjm/pages/view/onlinefirst
Some Hermite-Hadamard type integral inequalities for operator AG-preinvex functions
 Acta Univ. Sapientiae, Mathematica, 8, (16 31 33 DOI: 1.1515/ausm-16-1 Some Hermite-Hadamard type integral inequalities or operator AG-preinvex unctions Ali Taghavi Department o Mathematics, Faculty o
Acta Univ. Sapientiae, Mathematica, 8, (16 31 33 DOI: 1.1515/ausm-16-1 Some Hermite-Hadamard type integral inequalities or operator AG-preinvex unctions Ali Taghavi Department o Mathematics, Faculty o
LECTURE 16: CONJUGATE AND CUT POINTS
 LECTURE 16: CONJUGATE AND CUT POINTS 1. Conjugate Points Let (M, g) be Riemannian and γ : [a, b] M a geodesic. Then by definition, exp p ((t a) γ(a)) = γ(t). We know that exp p is a diffeomorphism near
LECTURE 16: CONJUGATE AND CUT POINTS 1. Conjugate Points Let (M, g) be Riemannian and γ : [a, b] M a geodesic. Then by definition, exp p ((t a) γ(a)) = γ(t). We know that exp p is a diffeomorphism near
A LOWER BOUND ON THE SUBRIEMANNIAN DISTANCE FOR HÖLDER DISTRIBUTIONS
 A LOWER BOUND ON THE SUBRIEMANNIAN DISTANCE FOR HÖLDER DISTRIBUTIONS SLOBODAN N. SIMIĆ Abstract. Whereas subriemannian geometry usually deals with smooth horizontal distributions, partially hyperbolic
A LOWER BOUND ON THE SUBRIEMANNIAN DISTANCE FOR HÖLDER DISTRIBUTIONS SLOBODAN N. SIMIĆ Abstract. Whereas subriemannian geometry usually deals with smooth horizontal distributions, partially hyperbolic
New Class of duality models in discrete minmax fractional programming based on second-order univexities
 STATISTICS, OPTIMIZATION AND INFORMATION COMPUTING Stat., Optim. Inf. Comput., Vol. 5, September 017, pp 6 77. Published online in International Academic Press www.iapress.org) New Class of duality models
STATISTICS, OPTIMIZATION AND INFORMATION COMPUTING Stat., Optim. Inf. Comput., Vol. 5, September 017, pp 6 77. Published online in International Academic Press www.iapress.org) New Class of duality models
Optimality, identifiability, and sensitivity
 Noname manuscript No. (will be inserted by the editor) Optimality, identifiability, and sensitivity D. Drusvyatskiy A. S. Lewis Received: date / Accepted: date Abstract Around a solution of an optimization
Noname manuscript No. (will be inserted by the editor) Optimality, identifiability, and sensitivity D. Drusvyatskiy A. S. Lewis Received: date / Accepted: date Abstract Around a solution of an optimization
A generic property of families of Lagrangian systems
 Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 24 (2008), ISSN
 Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 24 (2008), 25 31 www.emis.de/journals ISSN 1786-0091 ON THE RECTILINEAR EXTREMALS OF GEODESICS IN SOL GEOMETRY Abstract. In this paper we deal with
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 24 (2008), 25 31 www.emis.de/journals ISSN 1786-0091 ON THE RECTILINEAR EXTREMALS OF GEODESICS IN SOL GEOMETRY Abstract. In this paper we deal with
DIFFERENTIAL GEOMETRY. LECTURE 12-13,
 DIFFERENTIAL GEOMETRY. LECTURE 12-13, 3.07.08 5. Riemannian metrics. Examples. Connections 5.1. Length of a curve. Let γ : [a, b] R n be a parametried curve. Its length can be calculated as the limit of
DIFFERENTIAL GEOMETRY. LECTURE 12-13, 3.07.08 5. Riemannian metrics. Examples. Connections 5.1. Length of a curve. Let γ : [a, b] R n be a parametried curve. Its length can be calculated as the limit of
Isometries, Local Isometries, Riemannian Coverings and Submersions, Killing Vector Fields
 Chapter 15 Isometries, Local Isometries, Riemannian Coverings and Submersions, Killing Vector Fields The goal of this chapter is to understand the behavior of isometries and local isometries, in particular
Chapter 15 Isometries, Local Isometries, Riemannian Coverings and Submersions, Killing Vector Fields The goal of this chapter is to understand the behavior of isometries and local isometries, in particular
H-convex Riemannian submanifolds
 H-convex Riemannian submanifolds Constantin Udrişte and Teodor Oprea Abstract. Having in mind the well known model of Euclidean convex hypersurfaces [4], [5] and the ideas in [1], many authors defined
H-convex Riemannian submanifolds Constantin Udrişte and Teodor Oprea Abstract. Having in mind the well known model of Euclidean convex hypersurfaces [4], [5] and the ideas in [1], many authors defined
RANDERS METRICS WITH SPECIAL CURVATURE PROPERTIES
 Chen, X. and Shen, Z. Osaka J. Math. 40 (003), 87 101 RANDERS METRICS WITH SPECIAL CURVATURE PROPERTIES XINYUE CHEN* and ZHONGMIN SHEN (Received July 19, 001) 1. Introduction A Finsler metric on a manifold
Chen, X. and Shen, Z. Osaka J. Math. 40 (003), 87 101 RANDERS METRICS WITH SPECIAL CURVATURE PROPERTIES XINYUE CHEN* and ZHONGMIN SHEN (Received July 19, 001) 1. Introduction A Finsler metric on a manifold
A NOTION OF NONPOSITIVE CURVATURE FOR GENERAL METRIC SPACES
 A NOTION OF NONPOSITIVE CURVATURE FOR GENERAL METRIC SPACES MIROSLAV BAČÁK, BOBO HUA, JÜRGEN JOST, MARTIN KELL, AND ARMIN SCHIKORRA Abstract. We introduce a new definition of nonpositive curvature in metric
A NOTION OF NONPOSITIVE CURVATURE FOR GENERAL METRIC SPACES MIROSLAV BAČÁK, BOBO HUA, JÜRGEN JOST, MARTIN KELL, AND ARMIN SCHIKORRA Abstract. We introduce a new definition of nonpositive curvature in metric
Existence Results for Multivalued Semilinear Functional Differential Equations
 E extracta mathematicae Vol. 18, Núm. 1, 1 12 (23) Existence Results for Multivalued Semilinear Functional Differential Equations M. Benchohra, S.K. Ntouyas Department of Mathematics, University of Sidi
E extracta mathematicae Vol. 18, Núm. 1, 1 12 (23) Existence Results for Multivalued Semilinear Functional Differential Equations M. Benchohra, S.K. Ntouyas Department of Mathematics, University of Sidi
5.2 The Levi-Civita Connection on Surfaces. 1 Parallel transport of vector fields on a surface M
 5.2 The Levi-Civita Connection on Surfaces In this section, we define the parallel transport of vector fields on a surface M, and then we introduce the concept of the Levi-Civita connection, which is also
5.2 The Levi-Civita Connection on Surfaces In this section, we define the parallel transport of vector fields on a surface M, and then we introduce the concept of the Levi-Civita connection, which is also
Proximal Point Method for a Class of Bregman Distances on Riemannian Manifolds
 Proximal Point Method for a Class of Bregman Distances on Riemannian Manifolds E. A. Papa Quiroz and P. Roberto Oliveira PESC-COPPE Federal University of Rio de Janeiro Rio de Janeiro, Brazil erik@cos.ufrj.br,
Proximal Point Method for a Class of Bregman Distances on Riemannian Manifolds E. A. Papa Quiroz and P. Roberto Oliveira PESC-COPPE Federal University of Rio de Janeiro Rio de Janeiro, Brazil erik@cos.ufrj.br,
PROJECTIONS ONTO CONES IN BANACH SPACES
 Fixed Point Theory, 19(2018), No. 1,...-... DOI: http://www.math.ubbcluj.ro/ nodeacj/sfptcj.html PROJECTIONS ONTO CONES IN BANACH SPACES A. DOMOKOS AND M.M. MARSH Department of Mathematics and Statistics
Fixed Point Theory, 19(2018), No. 1,...-... DOI: http://www.math.ubbcluj.ro/ nodeacj/sfptcj.html PROJECTIONS ONTO CONES IN BANACH SPACES A. DOMOKOS AND M.M. MARSH Department of Mathematics and Statistics
THE DOUBLE COVER RELATIVE TO A CONVEX DOMAIN AND THE RELATIVE ISOPERIMETRIC INEQUALITY
 J. Aust. Math. Soc. 80 (2006), 375 382 THE DOUBLE COVER RELATIVE TO A CONVEX DOMAIN AND THE RELATIVE ISOPERIMETRIC INEQUALITY JAIGYOUNG CHOE (Received 18 March 2004; revised 16 February 2005) Communicated
J. Aust. Math. Soc. 80 (2006), 375 382 THE DOUBLE COVER RELATIVE TO A CONVEX DOMAIN AND THE RELATIVE ISOPERIMETRIC INEQUALITY JAIGYOUNG CHOE (Received 18 March 2004; revised 16 February 2005) Communicated
Subdifferential representation of convex functions: refinements and applications
 Subdifferential representation of convex functions: refinements and applications Joël Benoist & Aris Daniilidis Abstract Every lower semicontinuous convex function can be represented through its subdifferential
Subdifferential representation of convex functions: refinements and applications Joël Benoist & Aris Daniilidis Abstract Every lower semicontinuous convex function can be represented through its subdifferential
Some aspects of the Geodesic flow
 Some aspects of the Geodesic flow Pablo C. Abstract This is a presentation for Yael s course on Symplectic Geometry. We discuss here the context in which the geodesic flow can be understood using techniques
Some aspects of the Geodesic flow Pablo C. Abstract This is a presentation for Yael s course on Symplectic Geometry. We discuss here the context in which the geodesic flow can be understood using techniques
Loos Symmetric Cones. Jimmie Lawson Louisiana State University. July, 2018
 Louisiana State University July, 2018 Dedication I would like to dedicate this talk to Joachim Hilgert, whose 60th birthday we celebrate at this conference and with whom I researched and wrote a big blue
Louisiana State University July, 2018 Dedication I would like to dedicate this talk to Joachim Hilgert, whose 60th birthday we celebrate at this conference and with whom I researched and wrote a big blue
The uniformly accelerated motion in General Relativity from a geometric point of view. 1. Introduction. Daniel de la Fuente
 XI Encuentro Andaluz de Geometría IMUS (Universidad de Sevilla), 15 de mayo de 2015, págs. 2934 The uniformly accelerated motion in General Relativity from a geometric point of view Daniel de la Fuente
XI Encuentro Andaluz de Geometría IMUS (Universidad de Sevilla), 15 de mayo de 2015, págs. 2934 The uniformly accelerated motion in General Relativity from a geometric point of view Daniel de la Fuente
Research Article Optimality Conditions and Duality in Nonsmooth Multiobjective Programs
 Hindawi Publishing Corporation Journal of Inequalities and Applications Volume 2010, Article ID 939537, 12 pages doi:10.1155/2010/939537 Research Article Optimality Conditions and Duality in Nonsmooth
Hindawi Publishing Corporation Journal of Inequalities and Applications Volume 2010, Article ID 939537, 12 pages doi:10.1155/2010/939537 Research Article Optimality Conditions and Duality in Nonsmooth
A note on the σ-algebra of cylinder sets and all that
 A note on the σ-algebra of cylinder sets and all that José Luis Silva CCM, Univ. da Madeira, P-9000 Funchal Madeira BiBoS, Univ. of Bielefeld, Germany (luis@dragoeiro.uma.pt) September 1999 Abstract In
A note on the σ-algebra of cylinder sets and all that José Luis Silva CCM, Univ. da Madeira, P-9000 Funchal Madeira BiBoS, Univ. of Bielefeld, Germany (luis@dragoeiro.uma.pt) September 1999 Abstract In
The only global contact transformations of order two or more are point transformations
 Journal of Lie Theory Volume 15 (2005) 135 143 c 2005 Heldermann Verlag The only global contact transformations of order two or more are point transformations Ricardo J. Alonso-Blanco and David Blázquez-Sanz
Journal of Lie Theory Volume 15 (2005) 135 143 c 2005 Heldermann Verlag The only global contact transformations of order two or more are point transformations Ricardo J. Alonso-Blanco and David Blázquez-Sanz
SHADOWING PROPERTY FOR INDUCED SET-VALUED DYNAMICAL SYSTEMS OF SOME EXPANSIVE MAPS
 Dynamic Systems and Applications 19 (2010) 405-414 SHADOWING PROPERTY FOR INDUCED SET-VALUED DYNAMICAL SYSTEMS OF SOME EXPANSIVE MAPS YUHU WU 1,2 AND XIAOPING XUE 1 1 Department of Mathematics, Harbin
Dynamic Systems and Applications 19 (2010) 405-414 SHADOWING PROPERTY FOR INDUCED SET-VALUED DYNAMICAL SYSTEMS OF SOME EXPANSIVE MAPS YUHU WU 1,2 AND XIAOPING XUE 1 1 Department of Mathematics, Harbin
