Skyup's Media. Interpolation is the process of finding a function whose graph passes thr
|
|
|
- Marybeth Perry
- 5 years ago
- Views:
Transcription
1 Itpotio is th pocss of fidig fuctio whos gph psss th pimttio, d tis to costuct fuctio which cos fits thos d cuv fittig o gssio sis. Itpotio is spcific cs of cuv fittig, i which th. I foowig subsctio, w discuss th tps of fiit diffcs: fist diffcs
2 spctiv. I g, fist fowd diffcs giv b. Futh scod fowd diffcs dfid s th diffcs of th fist diffcs. i.., cd th fist bckwd diffcs. H,
3 is dfid s
4 Th diffti cofficit of d is dfid s
5 8. fid th vu od
6 Th fist fowd diffc is Fom bov sut, it is obvious tht th fist diffc of poomi o B dfiitio of fowd diffc w hv
7 d fid vus of Obti th fist tm of th sis whos scod d subsqut tms
8 d ssumig th fifth od diffcs to b costt, pov Fid th fuctio whos fist diffc is fo which fifth diffcs costt d
9 Obti th fuctio whos fist diffc is 9
10 Obti th fuctio whos fist diffc is 9 Sic fiv figus kow, ssum th fifth od diffcs figus ukow, w d two qutios to dtmi thm -
11 , w hv dfid
12 Usig Nwto s fowd itpotio fomu,fid th of cic of
13
14 Us Nwto s fowd diffc itpotio fomu to fid. Fist, w fid th umb of studts who got ss th 55 mks.
15 Fom th foowig tb, fid th vu of
16 Us Nwto s fowd fomu to fid i if tb, fid s ccut s th
17 tm. Fid th fist d tth tms of th sis., w hv dfid
18
19 Usig Nwto s bckwd diffc fomu, fid th vu of
20
21 is tbutd bow: Usig th Lgg s itpotio fomu, fid th itpotio cofficits quid to b ccutd. This bou of
22 ,... b giv poits, th th fist dividd diffc fo th gum dfid s is dfid s is dfid s fom th dfiitio of dividd diffcs,w hv
23 Usig th foowig tb fid
24
25 Usig dividd diffc, fid th vu of Fid poomi stisfid b Usig th foowig tb, fid Aso fid fid th vu of App Lgg s fomu to fid Appig Lgg s fomu, fid cubic poomi which ppoim
26 Th cuv fittig pocss fits th qutio of ppoimtig cuvs to th w fid dt. Nvthss, fo giv st of dt, th fittig cuvs of giv tp g N Th cuv of bst fit is tht fo which th sum of squs of th sidu Th mthod of st squs ssums tht th bst-fit cuv of giv b fittd to d th cospodig vu o th fittig th bst fittig of th cuv to th dt.
27 b th stight i to b fittd. Fo th sk of simpicit v suffi ottio to obti th foowig fom of o
28 Hc th fittd stight i is
29 fit th giv dt. Th mimum dfctio. B ms of pu bock, fid i w of th fim
30 Th ppictios of th mthod of st squs cuv fittig usig poomis bif discussd. Th bst fittig cuv Equtig s stight i cs, th fist pti divtivs with spct simpifig, w gt th foowig om qutios (w igod suffi I pticu, fo fittig of pbo
31 Hc th fittd pbo is
32 Hc, th cuv of bst fit is Th pofit of cti comp i th ; fid
33 This is quivt to stight i fittig. Comput This is quivt to stight i fittig. Comput Fid th cuv of fit of th tp Th cuv to b fittd is
34 which is bst fit to th foowig dt ccodig to Th cuv to b fittd is
35
36
37
38 fist od. Covgc with od is cd qudtic covgc shows tht coditio 6. is stifid fo this itv. Now w m pp go
39 . Stop ittio pocss t this stp. Hc fi ppoimtd
40 Th b dfiitio i sctio 6., squc of ppoimtios i bisctio Us th bisctio mthod to fid th idictd oots of th foowig qutios. U
41 Us bisctio Mthod to fid out th positiv oot of coct upto 4 dc
42
43 th sigifict digits usig mthod of fs positio.
44 W m itt th pocss to fi th oot. I g, w m wit
45 shoud b sctd i which th bov is stisfid.
46 Fid ittiv fomu to fid is positiv umb d hc, fid B usig Nwto-Rphso s mthod, fid th oot of
47 gbic sstm of i qutios occu budt i vious fids of s sticit,ctic giig,fuid dmics,ht tsf,stuctu s costt cofficits,th
48 wh th cofficit mti A is giv b,th th sstm is sid to b cosistt d hs soutio. W c fid th sou I this mthod, th cofficit mti A is dcomposd ito mtics L d U.
49 Equtig cofficits d th o simpifictio, w gt
50
51 fom th fist qutio, i..,
52
53
54
55 ,,,
56
57
58
59
60
61
62
63
64 is mimum d fid this vu of Fid th fist d scod divtivs fo th fuctio tbutd bow t A sid i mchi movs og fid stight od. Its distc is miimum? Aso fid this vu of
65 App th bov suts to fid d spcific voum
66 fid fom th foowig tb, th boudd b th cuv d
67 Usig simpso s / u, fid th tim tk b th ptic to tv 6 mt.
68
69 b dividig th itv of itgtio ito 8 qu pts. Hc fid
70
71
72
73
74
75
76
77
78 Cosid th fist od diffti qutio
79 which is quit difficut to itgt. So w stop ou pocss h. W us o fist od ppoimtio. B puttig Cosid th simutous fist od diffti qutio
80
81 , th bov qutio ducs to fist od simutous diffti q
82 , fid th vu of t =. usig Picd s mthod. Giv tht
83 Suppos tht w wish to fid succssiv
84 i fiv stps.
85
86 Stp. Dfi Us th Rug-Kutt fouth od mthod to fid th vu of
87
88 qutio ito sstm of fist
89 Us Rug Kutt mthd to fid
90 Us Rug-Kutt Fouth od fomu to fid sov odi diff. qutio fo fist od. Hc sov 5. Usig Fouth od Rug-Kutt mthod, fid th soutio i
91
92
93
94
95
96
97
98
99
100
101 FOURIER SERIES PERIODIC FUNCTIONS A fuctio f () is sid to hv piod T if fo, f ( T) f ( ), wh T is positiv costt. Th st vu of T> is cd th piod of f (). EXAMPLES W kow tht f () = si = si ( 4 ) = Thfo th fuctio hs piod, 4, 6, tc. Howv, is th st vu d thfo is th piod of f(). Simi cos is piodic fuctio with th piod d t hs piod. DIRICHLET S CONDITIONS A fuctio f () dfid i c c c b pdd s ifiit tigoomtic o sis of th fom cos b si, povidd. f () is w dfid d sig vud, piodic d fiit i (c, c). f () is cotiuous o picwis cotiuous with fiit umb of fiit discotiuitis i (c, c).. f () hs o o fiit umb of mim o miim i (c, c). SOME BASIC TRIGONOMETRIC OBSERVATIONS: (i) cosπ = (-) (ii) siπ = (iii) cos()π= (iv) si()π= (-) EULER S FORMULAS If fuctio f () dfid i (c, c) c b pdd s th ifiit tigoomtic sis o cos b si th c f ( )cos d, c
102 b c f ( )si d, c [Fomus giv bov fo d b cd Eu s fomus fo Foui cofficits] DEFINITION OF FOURIER SERIES Th ifiit tigoomtic sis o cos b si is cd th Foui sis of f () i th itv c c, povidd th cofficits giv b th Eu s fomus. EVEN FUNCTION If f () = () i (-, ) such tht ( ) = (), th f () is sid to b v fuctio of i (-, ). If ( ) f ( ) ( ) i (,) i (, ) Such tht ( ) = ( ) o ( ) = ( ), th f () is sid to b v fuctio of i (-, ). EXAMPLE: = cos, = ODD FUNCTION v fuctios. If f () = () i (-, ) such tht ( ) = - (), th f () is sid to b odd fuctio of i (-, ). If ( ) f ( ) ( ) i (,) i (, ) f () is sid to b odd fuctio of i (-, ). Such tht ( ) = - ( ) o ( ) = - ( ), th EXAMPLE; = si, = odd fuctios. FOURIER SERIES OF EVEN AND ODD FUNCTIONS. Th Foui sis of v fuctio f () i (-, ) cotis o cosi tms (Costt tm icudd), i.. th Foui sis of v fuctio f () i (-, ) is giv b
103 PROBLEMS f () = o cos, wh f ( )cos d.. Th Foui sis of odd fuctio f () i (-, ) cotis o si tms, i.. th Foui sis of odd fuctio f () i (-, ) is giv b f () = b si, wh b f ( )si d.. Fid th Foui sis of piod fo th fuctio f () = ( ) i (, ). Dduc th sum of f () = Soutio: Lt f () = o cos b si i (, ) () d ( )cos o ( si cos si ) ( ) ( ) cos 4 = 4 ( ) d. b d ( )si = Usig ths vus i (), w hv usig Boui s fomu., ( - ) = 4 cos i (, )..() Th quid sis c b obtid b puttig = i th Foui
104 sis i (). = is i (, ) d is poit of cotiuit of th fuctio f () = ( ). Sum th Foui sis i () = f() i.. 4 cos = ( - ) 4 i =. Fid th Foui sis of piod fo th fuctio f () = cos i < <. Soutio: o Lt f () = cos cosd o cos b si... () cos( ) cos( ) d si( ) cos( ). ( ) =, if = cos d si cos 4 b cossi d ( cos) d. si( ) cos( ). ( ) if, 4
105 si( ) si( ) d cos( ) si( ). ( ) =, if b cos si d si d = cos Usig ths vus i (), w gt f() = cos si si 4,,... si. Fid th Foui sis psio of f () = si i (-, ). Soutio: cos( ) si( ). ( ) if Sic f () is dfid i g of gth, w c pd f () i Foui sis of piod. Aso f ( ) = si[(-)] = -si = - f () f () is odd fuctio of i (-, ). Hc Foui sis of f () wi ot coti cosi tms. Lt f () = b si cos cos d si si.(), 5
106 ( ) si Usig ths vus i (), w gt si si ( ) si ( ) si ( ) si si si ( ) si 4. Fid th Foui sis psio of f () = i (, ). Hc obti sis fo cosc Soutio: Though th g (, ) is smmtic bout th oigi, o odd fuctio. o Lt f () = i (, ) th gth of th g is cosd is ith v fuctio cos b si.... () ( ) ( ) ( ) sih ( ) cos si o sih 6
107 b si d si cos ( ) sih ( ) Usig ths vus i (), w gt ( ) ( ) sih sih ( ) sih ( ) si = cos i (, ) Sum of th Foui sis of f ( ) f (), i.., sih ( ) i.., ( ) cosch i.., ( ) cosch HALF-RANGE FOURIER SERIES [Sic = is poit of cotiuit of f()] Th Foui psio of o piodic fuctio f() dfid i th itv (, ) of gth is kow s hf g psio o hf g Foui sis.i pticu hf g psio cotis o cosi tms is kow s hf g Foui cosi sis of f() i th itv (, ).I simi w hf g Foui si sis cotis o si tms. (i) Th hf g cosi sis i (, ) is f () = o cos wh o f ( ) d. f ( )cos d. 7
108 (ii) Th hf g si sis i (, ) is f () = b si, wh b f ( )si d. (iii) Th hf g cosi sis i (, ) is giv b f () = o cos wh o f ( ) d. EXAMPLES f ( )cos d. (iv) Th hf g si sis i (, ) is giv b f () = b si, wh b f ( )si d.. Fid th hf-g (i) cosi sis d (ii) si sis fo f () = i (, ) Soutio: (i) To gt th hf-g cosi sis fo f () i (, ), w shoud giv v i.. put () tsio fo f () i (, ). f = = Now f () is v i (, ). i ( o f () =, ) cos.() f ( )cosd. cosd 8
109 si 4. ( ) 4( ) cos, si o f ( ) d d Th Foui hf-g cosi sis of is giv b ( ) 4 cos i (, ). (ii) To gt th hf-g si sis of f () i (, ), w shoud giv odd tsio fo f () i (-, ). i.. Put () f = - Now f () is odd i (-, ). i (-, ) = - i (-, ) f () = b si.() b f ( )si d ( ), 4, ( ) si d cos si cos if is odd if is v Usig this vu i(), w gt th hf-g si sis of i (, ).. Fid th hf-g si sis of f () = si i (, ). Soutio: W giv odd tsio fo f () i (-, ). i.. w put f () = -si[(-)] = si i (-, ) f () is odd i (-, ) 9
110 Lt ) ( f = si b d b.si si d si si cos cos si si ) (. si ) ( si ) ( si ) ( Usig this vus i (), w gt th hf-g si sis s si. ) ( si si. Fid th hf-g cosi sis of ) ( f = i (, ). Dduc th sum of 5. Soutio: Givig odd tsio fo ) ( f i (-, ), ) ( f is md odd fuctio i (-, ). Lt f() = b si.. () d b si cos v is if odd is if,, 4
111 Usig this vu i (), w gt = ) (, si 4,,5 i Sic th sis whos sum is quid cotis costt mutips of squs of b, w pp Psv s thom. d f b ) ( ,,5 i i 4. Epd ) ( f = - s Foui sis i - < < d usig this sis fid th.m.s. vu of ) ( f i th itv. Soutio: Th Foui sis of ) ( f i (-, -) is giv b () f = o b si cos. () )...( ) ( o o d d f si ) ( cos si cos )cos ( d d f cos cos 4cos.()
112 b f ( )si d cos si d si cos cos cos ( ) b Substitutig (), (), (4) i () w gt cos ( ) 4( ) ( ) f () = cos si W kow tht.m.s. vu of f() i (-, ) is Fom () w gt Fom () w gt Fom (4) w gt ( 4) o b.(5) 4 4 o o...(6) 9 b 4( ) ( ) b Substitutig (6), (7) d (8) i (5) w gt Fid th Foui sis fo f () = Soutio: i. Th Foui sis of f () i (-, ) is giv b f () = Hc show tht 4( ) cos..(7).. (8) Th co-fficits,, b o
113 , ) 4(, o b Psv s thom is , ,. 4 4 ) ( o o i i b d b d f 9., i i.., 5 = 9 4 FOURIER INTEGRAL THEOREM If ) ( f is giv fuctio dfid i (-, ) d stisfis Diicht s coditios, th ) ( )cos ( ) ( d dt t t f f At poit of discotiuit th vu of th itg o th ft of bov qutio is. ) ( ) ( f f EXAMPLES. Epss th fuctio ) ( fo fo f s Foui Itg. Hc vut d cos si d fid th vu of. si d Soutio: W kow tht th Foui Itg fomu fo ) ( f is ) ( )cos ( ) ( d dt t t f f.() H ) (t f = fo t i.., f(t) = i - < t <
114 Equtio () f (t) = fo t f (t) = i t d t f ( ) cos( t ) dt d si ( t ) d si ( ) si ( ) d si ( ) si ( ) d si cos f ( ) d. () This is Foui Itg of th giv fuctio. Fom () w gt Substitutig (4) i () w gt Puttig = w gt si cos d But si cos d = si d [Usig si (AB) si (A-B) = si A cos B] = f ( ).( fo f ( )..(4) fo. Fid th Foui Itg of th fuctio f ( ) Vif th psttio dict t th poit =. Soutio: Th Foui itg of f () is fo fo 4
115 f ( ) f ( t)cos( t ) dt d.() t f ( t)cos( t ) dt.cos( t ) dt t f ( t)cos( t ) dtd cos( t ) dtd cos t si( t d ) f () cos si d. () Puttig = i (), w gt f () d t t t Th vu of th giv fuctio t = is. Hc vifid. FOURIER SINE AND COSINE INTEGRALS Th itg of th fom () f ( ) si f ( t)si t dt d is kow s Foui si itg. Th itg of th fom f ( ) cos f ( t)cos t dt d is kow s Foui cosi itg. PROBLEMS. Usig Foui itg fomu, pov tht b ( b ) ( u u si u du )( u b ) (, b ) 5
116 Soutio: Th psc of si u i th itg suggsts tht th Foui si itg fomu hs b usd. Foui si itg psttio is giv b f ( ) si u f ( t)si ut dt du b t bt si u du si ut dt t si u du u si u du u u si ut u cosut bsi ut u cosut b u u bt b u ( b ) ( u. Usig Foui itg fomu, pov tht cos cos d 4 u si u du )( u b ) Soutio: Th psc of cos i th itg suggsts tht th Foui cosi itg fomu fo cos hs b usd. Foui cosi itg psttio is giv b f ( ) cos f ( t) cos t dt d cos cos d t cost cost dt cos d t cos( ) t cos( ) t dt 6
117 ( ) cos d ( ) ( ) cos d ( ) ( )cos d. 4 t t cos( ) t ( ) si( ) t cos( ) t ( ) si( ) t HARMONIC ANALYSIS Th pocss of fidig th Foui sis fo fuctio giv b umic vu is kow s hmoic sis. I hmoic sis th Foui cofficits o,, d b of th fuctio = f () i (, ) giv b o = [m vu of i (, )] = [m vu of cos i (, )] b = [m vu of si i (, )] (i) Suppos th fuctio f () is dfid i th itv (, ), th its Foui sis is, d ow, f () = o cos b si o = [m vu of i (, )] = b = m vu of cos i (, ) m vu of si i (, ) (ii) If th hf g Foui si sis of f () i (, ) is, f () = b = b si, th m vu of si i (, ) (iii) If th hf g Foui si sis of f () i (, ) is, f () = b si, th 7
118 b = m vu of si i (, ) (iv) If th hf g Foui cosi sis of f () i (, ) is, f () = o cos o, th = [m vu of i (, )] = m vu of cos i (, ) (v) If th hf g Foui cosi sis of f () i (, ) is, f () = o cos, th EXAMPLES o = [m vu of i (, )] = m vu of cos i (, ).. Th foowig tb givs th vitios of piodic fuctio ov piod T. T 6 T f () Show tht f () =.75.7 cos.4 T si, wh T Soutio: H th st vu is m ptitio of th fist thfo w omit tht vu d cosid th miig 6 vus. = 6. Giv....() T T T T T 5T wh tks th vus of,,,,, 6 6 T 5T 6 tks th vus,,, T, 4 5,. (B usig ()) Lt th Foui sis b of th fom f o ) cos b si, () ( wh o, 8
119 cos, si, b = 6 cos si cos si , o b , 6 6 si.456 Substitutig ths vus of o,, d b i (), w gt cos.7 f () =.75.7 cos.4 si. Fid th Foui sis upto th thid hmoic fo th fuctio = f () dfid i (, ) fom th tb 6 6 f () Soutio: W c pss th giv dt i hf g Foui si sis. f ) b si b si b si.....() ( = f() si si si si si si
120 si 6 Now b b si b si Substitutig ths vus i (), w gt f () =.4 si. si.75 si Comput th fist two hmoics of th Foui sis fo f() fom th foowig dt Soutio: H th gth of th itv is. w c pss th giv dt i hf g Foui si sis i.., f () f ) b si b si () ( si si si Now b
121 b si f () = si si 4. Fid th Foui sis s f s th scod hmoic to pst th fuctio giv i th foowig dt. Soutio: 4 5 f () H th gth of th itv is 6 (ot ) i.., = 6 o = Th Foui sis is f o ) cos cos b si b si..() ( cos si cos si Now b b o , 6 6 cos 8. si. cos si 6.9
122 Substitutig ths vus of o,, b, d b i (), w gt f ( ) cos 6. cos. si 6.9 si COMPLEX FORM OF FOURIER SERIES Th qutio of th fom f ( ) c is cd th comp fom o poti fom of th Foui sis of f () i (c, c). Th cofficit c is giv b c c i c f ( ) d i Wh =, th comp fom of Foui sis of f () i (c, c ) tks th fom PROBLEMS i f ( ) c, wh c c c f ( ) i d.. Fid th comp fom of th Foui sis of f () = Soutio: Sic = o =, th comp fom of th Foui sis is f ( ) c c i f ( ) i i d i i d i i i (, ).
123 Usig this vu i (), w gt i i i cos i si. Fid th comp fom of th Foui sis of f () = si i (, ). Soutio: H = o =. i Th comp fom of Foui sis is Usig this vu i (), w gt si f i ( ) c..() c si i 4 i d isi cos i i i (, ). Fid th comp fom of th Foui sis of f () = Soutio: Lt th comp fom of th Foui sis b f ( ) c i i (-, ). c f ( ) i d i d
124 i / d i i i i i ( ) ( ) i i cos isi sih ( ) i sih. i ( ) ( ) Usig this vu i (), w hv ( ) i i sih i (-, ) 4. Fid th comp fom of th Foui sis of f () = cos i (-, ), wh is ith o o itg. Soutio: H = o =. Th comp fom of Foui sis is f i ( ) c.() c cos. i Usig this vu i (), w gt i icos si d i i icos si icos si ( ) si si ( ) cos i i (-, ). 4
125 SHORT QUETIONS. Dtmi th vu of i th Foui sis psio of f ( ) i. As: f ( ) is odd fuctio.. Fid th oot m squ vu of f ( ) i th itv, ) (. As: RMS V of f ( ) i, ) ( is 5 5 d 4 5. Fid th cofficit b 5 of th itv (, ) As: H f ( ) si 5 Foui cosi sis is 4. If o f () = f ( )cos d 5 4 d 5 cos 5 i th Foui cosi sis of th fuctio f ( ) si 5 i cos cos(5 ) cos(5 ) 5 5, wh si 5 cos d si(5 ) si(5 ) d cos, if f ( ) d f ( ) f ( ) fo, fid th sum of th Foui 5, if sis of f () t. As: H is poit of discotiuit. Th sum of th Foui sis is qu to th vg of ight hd d ft hd imit of th giv fuctio t. 5
126 i.., f ( ) f ( ) cos 5 5. Fid b i th psio of f ( ) 49 s Foui sis i (, ). As: Sic b = f ( ) is v fuctio i (, ). 6. If f () is odd fuctio dfid i (-, ) wht th vus of As: = sic f () is odd fuctio. 7. Fid th Foui costts b fo As: Sic b = si i (, ). f ( ) si is v fuctio i (, ). 8. Stt Psv s idtit fo th hf-g cosi psio of f () i (, ). As: wh f ( ) d f ( ) d f ( )cos d 9. Fid th costt tm i th Foui sis psio of f ( ) i (, ). As: = sic f () is odd fuctio i (, ).. Stt Diicht s coditios fo Foui sis. As: (i) f () is dfid d sig vud cpt possib t fiit umb of poits i (, ). (ii) f () is piodic with piod. (iii) f () d f () picwis cotiuous i (, ). Th th Foui sis of f () covgs to 6
127 () f () if is poit of cotiuit (b) f ( ) f ( ) if is poit of discotiuit.. Wht ou m b Hmoic Asis? As: Th pocss of fidig th Foui sis fo fuctio giv b umic vu is kow s hmoic sis. I hmoic sis th Foui cofficits fuctio = f () i (, ) giv b,, d b of th o o = [m vu of i (, )] = [m vu of cos i (, )] b = [m vu of si i (, )]. I th Foui psio of th cofficit of si. As:, f ( ) i (, ). Fid th vu of b,, Sic f () is v fuctio th vu of b =. ( ) I i..,, f ( ) f ( ). Wht is th costt tm d th cofficit of cos, i th Foui psio of f ( ) As: Giv i (-7, 7)? f ( ) f ( ) ( ) f ( ) Th giv fuctio is odd fuctio. Hc d o. 4. Fid Foui si sis fo th fuctio f () = ; < <. As: Th Foui si sis of f ( ) b si.() 7
128 b f ( )si d cos si d b, wh ' ' is v 4, wh ' ' is odd 4 f ( ).si,,5, ( ) 5. If th Foui sis fo th fuctio cos cos4 f ( ) si..5 As: Puttig w gt f ( ) is si f Dfi Root m squ vu of fuctio? Dduc tht As: If fuctio = f () is dfid i (c, c), th d is cd th oot msqu(r.m.s.) vu of i (c, c) d is dotd b. c Thus. d c 7. If f ( ) is pssd s Foui sis i th itv (-, ), to which vu this sis covgs t =. As: Sic = is poit of cotiuit, th Foui sis covgs to th ithmtic m of f () t = - d = c c 8
129 f () f ( ) 4 4 i.., 4 8. If th Foui sis cospodig to f ( ) i th itv (, ) is ( cos b ( b ). si ), As: B usig Psv s idtit, without fidig th vus of,, b fid th vu of 8 ( ). b d 9. Fid th costt tm i th Foui sis cospodig to f ( ) cos pssd i th itv (, ). As: Giv f ( ) cos cos si Now cos d d LONG QUESTIONS. (i) Epss f ( ) si s Foui sis i. (ii) Show tht fo < <, vu of, dduc th vu of si si si. Usig oot m squ p. (i) Fid th Foui sis of piodicit fo f ( ) i < <. (ii) Fid th Foui sis psio of piod fo th fuctio f () which is dfid i (, ) b ms of th tb of vus giv bow. Fid th sis upto th thid hmoic. f ()
130 .(i) Fid th Foui sis of piodicit fo f ( ) fo < <. (ii) Show tht fo < <, 4 cos cos. Dduc tht (i) Fid th Foui sis fo th sis ( )., f ( ). Hc dduc th sum to ifiit of, (ii) Fid th comp fom of Foui sis of f ( ) ( ) i th fom sih i ( ) i ( ) d hc pov tht. sih 5. Obti th hf g cosi sis fo f ( ) i (, ). 6. Fid th Foui sis fo f ( ) cos i th itv (, ). 7. (i) Epdig ( ) s si sis i (, ) show tht. 5 (ii) Fid th Foui sis s f s th scod hmoic to pst th fuctio giv i th foowig dt. 4 5 f () Obti th Foui sis fo f () of piod d dfid s foows L f ( ) L i ( L,) i (, L) Hc dduc tht Obti th hf g cosi sis fo f ( ) i (, ).. (i) Fid th Foui sis of f ( ) (ii) Obti th si sis fo th fuctio i (, ) i (, )
131 i f ( ) i. (i) Fid th Foui sis fo th fuctio i (, ) f ( ) d f ( ) f ( ) fo. i (, ) (ii) Dtmi th Foui sis fo th fuctio, f ( ) ( ),. Obti th Foui sis fo. 6 f ( ) i (, ). Dduc tht. Obti th costt tm d th fist hmoic i th Foui sis psio fo f () wh f () is giv i th foowig tb f () (i) Epss f ( ) si s Foui sis i (, ). (ii) Obti th hf g cosi sis fo 5. Fid th hf g si sis of f ( ) cos i (, ). f ( ) ( ) i th itv < <. 6. (i) Fid th Foui sis psio of f () = i (, ) (ii) Fid th hf-g si sis of f () = si i (, ). 7. Epd f () = - vu of f () i th itv. s Foui sis i - < < d usig this sis fid th.m.s. 8. Th foowig tb givs th vitios of piodic fuctio ov piod T. T 6 T f () T T 5T 6 T Show tht f () =.75.7 cos.4 si, wh T
132 9. Fid th Foui sis up to th thid hmoic fo th fuctio = f () dfid i (, ) fom th tb 6 6 f () (i) Fid th hf-g (i) cosi sis d (ii) si sis fo f () = i (, ) (ii) Fid th comp fom of th Foui sis of f () = cos i (-, ).
133 INTEGRAL TRANSFORM FOURIER TRANSFORMS Th itg tsfom of fuctio f () is dfid b b f ( ). k( s, ) d wh k(s, ) is kow fuctio of s d d it is cd th k of th tsfom. Wh k(s, ) is si o cosi fuctio, w gt tsfoms cd Foui si o cosi tsfoms. COMPLEX FORM OF FOURIER INTEGRALS Th itg of th fom f ( ) i f ( t) i t dt d is kow s Comp fom of Foui Itg. FOURIER TRANSFORMS COMPLEX FOURIER TRANSFORMS Th fuctio F f ( ) ist f ( t). dt is cd th Comp Foui tsfom of f (). INVERSION FORMULA FOR THE COMPLEX FOURIER TRANSFORM is Th fuctio f ( ) F f ( ). ds is cd th ivsio fomu fo th Comp Foui tsfom of F [ f ( )] d it is dotd b F F( f ( )). FOURIER SINE TRANSFORMS Th fuctio F S f ( ) f ( t).si st dt is cd th Foui Si Tsfom of th fuctio f (). Th fuctio f ( ) FS f ( ).si s ds is cd th ivsio fomu fo th Foui si tsfom d it is dotd b F F ( f ( )). S S
134 FOURIER COSINE TRANSFORMS Th fuctio F C f ( ) f ( t).cosst dt is cd th Foui Cosi Tsfom of f (). Th fuctio f ( ) FC f ( ).coss ds is cd th ivsio fomu fo th Foui Cosi Tsfom d it is dotd b F F ( f ( )). PROBLEMS C C. Fid th Foui Tsfom of i f ( ) i si s s cos s Hc pov tht s s 6 cos ds. Soutio: W kow tht th Foui tsfom of f () is giv b F f ( ) f ( ). f ( ).. ( ( is d is is ). d d is d ( ) i s f ( ). ). is is d i s d is ) ( is is is. f ( ). is d is d s is is is s is i s is ( s is is ) ( is is is ) 4 coss s 4 si s s 4 (si s s s coss) B usig ivs Foui Tsfom w gt
135 f ( ). 4 s 4 s (si s (si s 4 s (si s s cos s).(coss s cos s) coss ds 4 s s cos s). (si s is ds i si s) ds s cos s) isi s ds Th scod itg is odd d hc its vus is o. i.., Puttig si s si s scos s f ( ) coss ds s s 4 s cos s si s s cos s coss ds s coss ds f ( ), w gt si s s cos s si s s s 4 6 cos ds f. s cos s s s 4 6 cos ds.. Fid th Foui si tsfom of, (o) si m d. Soutio: Th Foui si tsfom of f() is giv b 4 4, >. Hc vut H = F S f ( ) f ( ).si s d fo > F S.si s d s s Usig ivs Foui si tsfom w gt si b d b b f ( ) F.si s ds s
136 s s. s si s.si s ds s ds i.., i.., f ( ) s s.si s ds s s.si s ds Rpcig b m w gt i.., s.si ms ds s m.si m m i.., d [sic s is dumm vib, w c pc it b ]. Fid th Foui cosi tsfom of. Soutio: W kow tht f ( ) f ( ).coss d F C H f ( ). FC f ( ).coss d Lt f ( ) F( s) Th F C F( s).coss d Difftitig o both sids w..t. w gt, 4
137 5 si. ) ( si ). si (.cos.cos ) ( b b d b s s ds s df d s d s d s s d s ds d ds s df ) (.og ) (.og.. ) ( s s ds s s s F 4. Fid th Foui cosi tsfom of. b Soutio: W kow tht th Foui cosi tsfom of f() is ).cos ( ) ( d s f f F C H f b ) (.cos d s F b b C og ) ( og ) ( og cos.cos s b s b s s F F d s d s b c c b
138 s 5. Fid f (), if its si tsfom is. s Hc dduc tht th ivs si tsfom of. s Soutio: W kow tht th ivs Foui si tsfom of F S f () is giv b H F ( ) F f ( ).si s ds f S f ( s s f ( ) s.si s ds s S ) d f ( ) d d f ( ) d f ( ) s s. (si s) ds.coss s ds s s f ( ) t To fid th ivs Foui si tsfom of : s Put =, i (), w gt f ( ) t ( d ). s cosb d t.coss ds b PROPERTIES. Liit Popt If F(s) d G(s) th Foui tsfom of f () d g () spctiv th F f ( ) b g( ) F( s) b G( s) Poof: 6
139 F[ f ( ) b g( )] f ( ) b g( ) is d f ( ). is d b g( ). is d f ( ). is d b g( ). is d F( s) b G( s). Chg of Sc Popt s If F(s) is th Foui tsfom of f () th F f ( ) F, Poof: F f ( ) Put = Wh d = d f ( ). is d i.., d = d, d, F f ( ) F s f ( ). is d.. Shiftig Popt ( Shiftig i ) f ( ). is If F(s) is th Foui tsfom of f () th F f ( ) F( s) Poof: is F f ( ) f ( ). d i s. d Put Wh - = d = d, d, F f ( ) f ( ). is ( ). d is f ( ). is. d is f ( ). is. d is F( s) 7
140 4. Shiftig i spct of s Poof: If F(s) is th Foui tsfom of f () th F i f ( ) F( s ) F i f ( ) i f ( ) is d i( s ) f ( ). d F( s ) 5. Modutio Thom If F(s) is th Foui tsfom of f () th F f ( ) cos F( s ) F( s ) Poof: F f ( ) cos is f ( ).cos. d F f ( s f ( ). ) is i f ( s ) i i( s ) i( s. f ( ). d. f ( ). ) d f ( ) cos F( s ) F( s ) COROLLARIES ( i) FC f ( ) cos FC ( s ) FC ( s ) ( ii) FC f ( )si FS ( s) FS ( s) ( iii) FS f ( )cos FS ( s ) FS ( s ) ( iv) FS f ( )si FC ( s ) FC ( s ) 6. Cojugt Smmt Popt d f ( s ) f ( s ) Poof: If F(s) is th Foui tsfom of f () th F f ( ) F( s) W kow tht F( s) f ( ). is d 8
141 Tkig comp cojugt o both sids w gt is F( s) f ( ). d Put = - d = -d Wh, d, F( s) f ( ). is ( d) f ( ). is d f ( ). is d F f ( ) 7. Tsfom of Divtivs If F(s) is th Foui tsfom of f () d if f () is cotiuous, f () is picwis cotiuous difftib, f () d f () bsout itgb i (, ) d im f ( ), th F f ( ) is F( s) Poof: B th fist th coditios giv, F f () d F f () ist. F f ( ) f ( ) is f ( ) is d is f ( ) d, isf f ( ), b th giv coditio. is o it gtig b pts. is F( s). Th thom c b tdd s foows. If ( ) f, f, f,, f cotiuous, () f is picwis cotiuous, ( ) bsout itgb i (, ) d f, f, f,, f s f, f, f,, th, f ( ) F f ( ) ( ) ( is) F( s) 8. Divtivs of th Tsfom If F(s) is th Foui tsfom of f () th F. f ( ) ( df( s) i) ds 9
142 Poof: F( s) f ( ) is d df( s) ds d ds f ( ) is d i. f ( ) is d if f ( ) ( df( s) i) ds F. f ( ) Etdig, w gt, F. f ( ) ( i) d F( s) ds DEFINITION f ( u) g( u) du is cd th covoutio poduct o simp th covoutio of th fuctios f () d g () d is dotd b f ( )* g( ). 9. Covoutio Thom If F(s) d G(s) th Foui tsfom of f () d g () spctiv th th Foui tsfom of th covoutio of f() d g() is th poduct of thi Foui tsfoms. i.., F f ( ) * g( ) F( s). G( s) Poof is F f ( ) * g( ) f ( ) * g( ) d g( u) F( s). F( s). G( s) Ivtig, w gt f ( u) g( u) du f ( u) d d du, o chgig th od of it gtio. g( u) ius F( s) du, g( u). ius du is is b th shiftig popt.
143 ) ( * ) ( ) ( ) * ( ) ( ). ( s G F s F F g f s G s F F PROBLEMS. Evut ) )( ( b d usig tsfoms. Soutio: W kow tht th Foui cosi tsfom of.. ) ( s is f Simi th Foui cosi tsfom of.. ) ( b s b is f W kow tht ) ( ). ( ) (. ) ( d g f ds g F f F C C ) ( ) )( (.,. ) ( ) ( ) )( (., ,. ) ( ) ( b b b d i b b b ds ds b s s b i d ds b s b s i b b b. Fid th Foui tsfom of d hc dduc tht (i) dt t t cos (ii) ) ( s s i F Soutio:
144 .. ) ( ) ( ) ( ). ( ) ( d d if if f H d f d f d f f F is is is is is ) ( ) (. d d is is ) ( ) ( ) ( ) ( s F is is is is is is Usig ivsio fomu, w gt ) (. ) ( cos cos si cos. ) ( o f d s s ds s ds s s i s ds s f is. cos dt s t
145 Puttig =, w gt, F. s d coss ds s ( o) cost dt t FINITE FOURIER TRANSFORMS If f () is fuctio dfid i th itv (, ) th th fiit Foui si tsfom of f () i < < is dfid s PROBLEMS F S f ( ) f ( ).si d Th ivs fiit Foui si tsfom of F S f () is f () d is giv b f ( ) F S f ( ) si Th fiit Foui cosi tsfom of f () i < < is dfid s F C f ( ) f ( ).cos d Th ivs fiit Foui cosi tsfom of F C f () is f () d is giv b f ( ) FC () F C f ( ) cos. Fid th fiit Foui si d cosi tsfoms of Soutio: Th fiit Foui si tsfom is f ( ) i < <. H F S f ( ) f ( ) f ( ).si d
146 4 ) ( ) ( cos cos cos si cos.si S d F Th fiit Foui cosi tsfom is C d f f F ).cos ( ) ( H ) ( f C d F cos. ) ( cos si cos si. Fid th fiit Foui si d cosi tsfoms of ) (, ) ( i f. Soutio: Th fiit Foui si tsfom of ) (, ) ( i f is ).si ( ) ( d f f F S H ) (, ) ( i f
147 F S.si d cos si cos ( ). Th fiit Foui cosi tsfom of f ( ) i (, ) is F C f ( ) f ( ).cos d H f ( ) i (, ) F C.cos d si cos cos p ( ). Fid f () if its fiit si tsfom is giv b, p itg d. Soutio: W kow tht th ivs Foui si tsfom is giv b f ( ) p ( ) H F S f () = p F S p Substitutig () i (), w gt ( ) f ( ) p p f ( ) p si p si p ( ) wh p is positiv ( 4 p ) p p si p p cos 4. If f ( p) fid F C f ( p) if < <. ( p ) Soutio: W kow tht F p cos H f ( p) ( p ) C f ( p) FC () F C f ( ) cos 5
148 6 Lt ) ( ) ( p f f F C.cos ) ( cos cos ) ( () ) ( C C p p p f f p f F
149 SHORT QUESTIONS. Stt th Foui itg thom. As: If f () is giv fuctio dfid i (-, ) d f ( ) f ( t) cos ( t ) dt d. Stt th covoutio thom of th Foui tsfom. As: If F(s) d G(s) th Foui tsfom of f () d g () spctiv th th Foui tsfom of th covoutio of f() d g() is th poduct of thi Foui tsfoms. i.., F f ( ) * g( ) F( s). G( s). Wit th Foui tsfom pi. As: F f () d F F( S) Foui tsfom pis. 4. Fid th Foui si tsfom of As: f ( ) f ( ).si s d F S f ) ( ( > )..si s d s s s s si b d 5. If th Foui tsfom of f () is F(s) th pov tht. F f ( ) is F( s) As: F f ( ) is f ( ). d Put - = d = d Wh, d, F f ( ) f ( ). is ( ). d is f ( ). is. d b b is f ( ). is. d is F( s) 6. Stt th Foui tsfoms of th divtivs of fuctio. As: ( ) F f ( ) ( is) F( s) 7. Fid th Foui si tsfom of As: f ) (. 7
150 H F S f ( ) f ( ).si s d fo > s.si s d s s s si b d b b s 8. Pov tht FC f ( ) FC Poof:, f ( ) f ( ).coss d Put Wh F C = d = d, d, F C f ( ) F C s i.., d = d f ( ).cos s d. 9. If F(s) is th Foui tsfom of f () th pov tht Poof: ( F( s) df( s) ds df( s) i) ds i F. f ( ) f ( ) d ds is f ( ). f ( ). Fid th Foui si tsfom of As: f ( ) f ( ).si s d F S d is is f ( ) d d if f ( ) f ( ).cos.si s d s s s F. f ( ). d si b d ( df( s) i) ds b b 8
151 s s. Fid Foui si tsfom of As: f ( ) f ( ).si s d F S.si s d si d,. Fid Foui cosi tsfom of As: F C f ( ) f ( ).si s d f ( ).coss d s s cosb d. If F(s) is th Foui tsfom of f () th FS f ( )cos FS ( s ) FS ( s ) Poof: F S f ( ) cos f ( ).cos.si s. d. f ( ) si( s) si( s) d b F S. f ( )cos F ( s ) F ( s ) S f ( )si( s). d. f ( ).si( s) d. S 4. If F(s) is th Foui tsfom of f () th F f ( ) cos F( s ) F( s ) Poof: F f ( ) cos is f ( ).cos. d 9
152 f ( ). is i i d. f ( ).. i( s ) i( s ) d f ( ). d f ( s ) f ( s ) f ( s ) f ( s ) F f ( ) cos F( s ) F( s ) 5. If F(s) is th Foui tsfom of f () th F f ( ) s F, Poof: F f ( ) is f ( ). d Put = d = d d i.., d = Wh F f ( ), d, F s f ( ). is d. f ( ). i s. d. Fid th Foui Tsfom of i f ( ) i si s Hc pov tht s cos s s cos s 6 ds.
153 . Fid th Foui cosi tsfom of.. Fid th Foui Tsfom of f () if f ( ),, Hc dduc tht si t t 4 dt 4. Evut d ( )( b ) usig tsfoms 5. Fid th Foui tsfom of (i) cost t dt s (ii) F i ( s ) 6. Show tht th Foui tsfom of 7.. Fid th Foui tsfom of f () if Hc dduc tht si d d hc dduc tht si 8. Fid th Foui si tsfom of si, f ( ),. Fid th Foui tsfom of (i) cos d f ( ) is d f ( ),, d hc dduc tht (ii) si d 6 othwis. Stt d pov covoutio thom fo Foui tsfoms. 8. Fid th Foui cosi tsfom of. (i) Fid th Foui cosi tsfom of (ii) Fid th Foui si tsfom of, f ( ),
154 4. Fid Foui si d cosi tsfom of d hc fid th Foui si tsfom of d Foui cosi tsfom of.
155 PARTIAL DIFFERENTIAL EQUATIONS A pti diffti qutio is qutio ivovig fuctio of two o mo vibs d som of its pti divtivs. Thfo pti diffti qutio cotis o dpdt vib d o idpdt vib. so tht f, H wi b tk s th dpdt vib d d th idpdt vib. W wi us th foowig stdd ottios to dot th pti divtivs. p, q,, s, t Th od of pti diffti qutio is tht of th highst od divtiv occuig i it. Fomtio of pti diffti qutio: Th two mthods to fom pti diffti qutio. (i) B imitio of bit costts. Pobms (ii) B imitio of bit fuctios. Fomtio of pti diffti qutio b imitio of bit costts: ()Fom th pti diffti qutio b imitig th bit costts fom b b. Soutio: Giv b b... () H w hv two bit costts & b.
156 Difftitig qutio () pti with spct to d spctiv w gt p () b q. () Substitut () d () i () w gt p q p q, which is th quid pti diffti qutio. () Fom th pti diffti qutio b imitig th bit costts, b, c fom. b c Soutio: W ot tht th umb of costts is mo th th umb of idpdt vib. Hc th od of th sutig qutio wi b mo th. b c... () Difftitig () pti with spct to d th with spct to, w gt p c q b c Difftitig () pti with spct to, p Wh () () ( )..(4) c c Fom () d (4), c Fom (5) d (6), w gt p p (5) (6)., which is th quid pti diffti
157 qutio. () Fid th diffti qutio of sphs of th sm dius c hvig thi ct o th o-p.. Soutio: Th qutio of sph hvig its ct t,,b, tht is o th o -p d hvig its dius qu to c is ( ) ( b) c. () If d b ttd s bit costts, () psts th fmi of sphs hvig th giv popt. Difftitig () pti with spct to d th with spct to, w hv bp () d bq.() Fom (), b.(4) p q Usig (4) i (), b..(5) p Usig (4) d (5) i (), w gt q p p c. i.. p q c p, which is th quid pti diffti qutio. Pobms Fomtio of pti diffti qutio b imitio of bit fuctios: ()Fom th pti diffti qutio b imitig th bit fuctio f fom f b soutio: Giv f b i.. f b ()
158 Difftitig () pti with spct to d th with spct to, w gt wh p q u b f ' u. f ' ub..().() Eimitig f (u) fom () d (), w gt q b p i.. q bp () Fom th pti diffti qutio b imitig th bit fuctio, Soutio: Giv, () Lt u, v Th th giv qutio is of th fom u, v. Th imitio of fom qutio (), w gt, u u v v p p i.. q q q p i. p q i. p q () Fom th pti diffti qutio b imitig th bit fuctio f fom g f Soutio: Giv f g. () 4
159 Difftitig () pti with spct to, p f u. gv..() Wh u d v Difftitig () pti with spct to, u. gv ( ) q f. () Difftitig () pti with spct to d th with spct to, f u. 4 g v9.. (4) s.. (5) d f u. g v.( ) Difftitig () pti with spct to, u. g v. t f.. (6) Eimitig hv u d g v f 4 9 s = t fom (4), (5) d (6) usig dtmits, w i.. 5 5s t o 6 (4) Fom th pti diffti qutio b imitig th bit fuctio fom Soutio: Giv u u....() Wh u Difftitig pti with spct to d, w gt p u ( ) u u ( ) () q u. u..() u. u u u...(4) 5
160 s u u u ( ) (5) t u. u...(6) Fom (4) d (6), w gt i.. t u u = u u = Soutios of pti diffti qutios Cosid th foowig two qutios d b..() f..() Equtio () cotis bit costts d b, but qutio () cotis o o bit fuctio f. If w imit th bit costts d b fom () w gt pti diffti qutio of th fom p q. If w imit th bit fuctio f fom () w gt pti diffti qutio of th fom p q. Thfo fo giv pti diffti qutio w m hv mo th o tp of soutios. Tps of soutios: () A soutio i which th umb of bit costts is qu to th umb of idpdt vibs is cd Compt Itg (o) Compt soutio. (b) I compt itg if w giv pticu vus to th bit costts w gt 6
161 Pticu Itg. (c) Th qutio which dos ot hv bit costts is kow s Sigu Itg. To fid th g itg: Suppos tht,,, p, q f...() is fist od pti diffti qutio whos compt soutio is,,,, b..() Wh d b bit costts. Lt b f Th () bcoms, wh f is bit fuctio.,,,, f.() Difftitig () pti with spct to, w gt. f b.(4) Th imit of btw th two qutios () d (4), wh it ists, is cd th g itg of (). G soutio of pti diffti qutios: Pti diffti qutios, fo which th g soutio c b obtid dict, c b dividd i to th foowig th ctgois. () Equtios tht c b sovd b dict (pti) itgtio. () Lgg s i qutio of th fist od. () Li pti diffti qutios of high od with costt cofficits. Equtios tht c b sovd b dict (pti) itgtio: Pobms: u t ()Sov th qutio cos, t Aso show tht u si, wht. Soutio: u if u wh t d wh. t 7
162 u t Giv: cos, t Itgtig () pti with spct to,.() u t f t t si.() u Wh d t t i (), w gt t Equtio () bcoms u t si t f. Itgtig () pti with spct to t, w gt.() t u si g (4) Usig th giv coditio, m u wh t, w gt o g si g si Usig this vu i (4), th quid pticu soutio of () is u si t t Now im u si im i.. wh t si t t, u si. () Sov th qutio d cos simutous. Soutio: Giv...() cos...() Itgtig () pti with spct to, f..() Difftitig () pti with spct to, f Compig () d (4), w gt...(4) 8
163 f f cos si c......( 5) Thfo th quid soutio is si c, wh c is bit costt. Lgg s i qutio of th fist od: A i pti diffti qutio of th fist od, which is of th fom Pp Qq R wh P, Q, R fuctios of,, is cd Lgg s i qutio. Wokig u to sov ()To sov d P d Q Pp Qq R Pp Qq R, w fom th cospodig subsidi simutous qutios d. R ()Sovig ths qutios, w gt two idpdt soutios u d v b. ()Th th quid g soutio is f u v o u v o v u,. Soutio of th simutous qutios. Mthods of goupig: B goupig two of th tios, it m b possib to gt odi diffti qutio cotiig o two vibs, vthough P;Q;R i g, fuctios of,,. B sovig this qutio, w c gt soutio of th simutous qutios. B this mthod, w m b b to gt two idpdt soutios, b usig difft goupigs. d P d Q d R Mthods of mutipis: If w c fid st of th qutitis,m, which m b costts o fuctios of th vibs,,, such tht P mq R, th th soutio of th simutous qutio is foud out s foows. d P d Q d R d md d P mq R 9
164 Sic P mq R, d md d. If d md d is ct diffti of som fuctio u,,, th w gt du. Itgtig this, w gt d d d u, which is soutio of. P Q R Simi, if w c fid oth st of idpdt mutipis, m,, w c gt oth idpdt soutio v b. Pobms: ()Sov p q. Soutio: Giv: p q. This is of Lgg s tp of PDE wh P, Q, R. d d d Th subsidi qutios. Tkig fist two mmbs d d Itgtig w gt og og og c c i.. u Tkig fist d st mmbs i.. Itgtig w gt d d..() d d. c...() v. Thfo th soutio of th giv PDE is u, v i.., ()Sov th qutio p q. Soutio: Giv: p q. This is of Lgg s tp of PDE wh P, Q, R. d d d Th subsidi qutios..()
165 Usig th mutipis,,, ch tio i ()= d d d. d d d. Itgtig, w gt () Usig th mutipis,,, ch tio i ()= d d. d d d. Itgtig, w gt b () Thfo th g soutio of th giv qutio is, f. ()Show tht th itg sufc of th PDE p q. Which cotis th stight i, is. Soutio: Th subsidi qutios of th giv Lgg s qutio d d d. Usig th mutipis,,,. ch tio i ()= Itgtig, w gt d d d. () d d d. () d d d Usig th mutipis,, -, ch tio i () =. d d d. Itgtig, w gt b () Th quid sufc hs to pss though Usig (4) i () d (), w hv b (4) (5)
166 Eimitig i (5) w gt, b.(6) Substitutig fo d b fom () d () i (6), w gt sufc., which is th qutio of th quid Mthods to sov th fist od No Li pti diffti qutio: Stdd Tp : Equtio of th fom f ( p, q)...() i. th qutio cotis p d q o. Suppos tht b c...() is soutio of th qutio, b p, q b substitut th bov i (), w gt f (, b) o sovig this w c gt b, wh is kow fuctio. Usig this vu of b i (), th compt soutio of th giv pti diffti qutio is c () is compt soutio, To fid th sigu soutio, w hv to imit d c fom c Difftitig th bov with spct to d c, w gt, d =. Th st qutio is bsud. Hc th is o sigu soutio fo th qutio of Tp. Pobms: () Sov p q.
167 Soutio: Giv: p q.() Equtio () is of th fom f ( p, q). Assum b c.() b th soutio of qutio (). Fom () w gt p, q b. () b b.() Substitut () i () w gt This is compt soutio. To fid th g soutio: W put i.. c...(4) c f i (4), wh f is bit fuctio. f (5) Difftitig (5) pti with spct to, w gt f (6) Eimitig btw qutios (5) d (6), w gt th quid g soutio. To fid th sigu soutio: Difftit (4) pti with spct to d c, w gt, =.(which is bsud) so th is o sigu soutio. () Sov p q pq Soutio:
168 Giv: p q pq..() Equtio () is of th fom f ( p, q) Assum b c () b th soutio of qutio (). Fom () w gt p, q b () b b b...() Substitutig () i (), w gt c (4) This is compt soutio. To fid th g soutio: W put c f i (4), w gt f Difftitig (5) pti with spct to, w gt f..(5)..(6) Eimitig btw qutios (5) d (6), w gt th quid g soutio To fid th sigu soutio: Difftitig (4) with spct to d c., d = (which is bsud). So th is o sigu soutio. Stdd Tp : Equtios ot cotiig d picit, i.. qutios of th fom, p, q f.() Fo qutios of this tp,it is kow tht soutio wi b of th fom 4
169 .() Wh is th bit costt d is spcific fuctio to b foud out. Puttig d u, () bcoms u o u d u p. du d u q. du d du d du If () is to b soutio of (), th vus of p d q obtid shoud stisf (). d d i.. f,,..() du du Fom (), w gt d du,.(4) Now (4) is odi diffti qutio, which c b sovd b vib spb mthod. Th soutio of (4), which wi b of th fom g u b o g, b compt soutio of ().,, is th Th g d sigu soutio of () c b foud out b usu mthod. Pobms: ()Sov p q. Soutio: Giv: p q () Equtio () is of th fom f, p, q Assum u wh, u b soutio of (). d u d d p. p.() du du du d u d d q. q () du du du Substitutig qutio () & () i (), w gt d du d du 5
170 d du d du d du B vib spb mthod, d du B itgtig, w gt d du c c k c This is th compt soutio. To fid th g soutio: W put k f i (4), w gt f Difftit (5) pti with spct to, w gt.(4)..(5) f..(6) Eimitig btw qutios (4) d (5), w gt th quid g soutio. To fid th sigu soutio: Difftit (4) pti with spct to d k, w gt 6
171 ..(7) d (which is bsud) So th is o sigu soutio. ()Sov9 q 4 p. Soutio: Giv: 9 q 4 p () Equtio () is of th fom f, p, q Assum u wh, u b soutio of (). d u d d p. p.() du du du d u d d q. q () du du du Substitutig qutio () & () i (), w gt 9 9 d du d du d du d du d du d du 4 Itgtig th bov, w gt d du c u c c 7
172 k This is th compt soutio. To fid th g soutio: W put k f i (4), w gt..(4) f Difftit (5) pti with spct to, w gt..(5) f..(6) Eimitig btw qutios (4) d (5), w gt th quid g soutio. To fid th sigu soutio: Difftit (4) pti with spct to d k, w gt..(7) d (which is bsud) So th is o sigu soutio. Stdd Tp : Equtios of th fom f p g, q,.. () i.. Equtio which do ot coti picit d i which tms cotiig p d c b sptd fom thos cotiig q d. To fid th compt soutio of (), W ssum tht f p g, q,.wh is bit costt. Sovig f, p,w c gt p, d sovig g, q,w c gt q, Now d d d o i.. d, d, d pd qd Itgtig with spct to th cocd vibs, w gt, d, d b.(). Th compt soutio of () is giv b (), which cotis two bit costts d b. Th g d sigu soutio of () c b foud out b usu mthod. 8
173 Pobms: ()Sov pq. Soutio: Giv: pq p..() q Equtio () is of th fom f, p g, q Lt Simi, Assum p q (s) p p.() q q () d pd qd b soutio of () Substitut qutio () d () to th bov, w gt d d d Itgtig th bov w gt, d d c d c k..(4) This is th compt soutio. Th g d sigu soutio of () c b foud out b usu mthod. () Sov p q. Soutio: Giv: p q p q.. () Equtio () is of th fom f, p g, q Lt p q (s) 9
174 p p. () Simi, q q () Assum d pd qd b soutio of () Substitut qutio () d () to th bov, w gt d d d Itgtig th bov w gt, d d d c c This is th compt soutio. c (4) Th g d sigu soutio of () c b foud out b usu mthod. Stdd Tp 4: (Ciut s tp) Th qutio of th fom p q f ( p, q) () is kow s Ciut s qutio. Assum b c () b soutio of ()., b p, q b Substitut th bov i (), w gt b f (, b)..() which is th compt soutio. Pobm: () Sov p q pq Soutio: Giv: p q pq.() Equtio () is Ciut s qutio Lt b c..() b th soutio of ().
175 Put p, q b i (), w gt b b.() which is compt soutio. To fid th g soutio: W put b f i (), w gt f f (4) Difftit (4) pti with spct to, w gt f f f..(5) f Eimitig btw qutios (4) d (5), w gt th quid g soutio To fid sigu soutio, Difftit () pti with spct to, w gt. b b b..(6) Difftit () pti with spct to b, w gt. b..(7) b Mutipig qutio (6) d (7),w gt 4 4 b b q () Sov p q p p
176 q Soutio: Giv: p q p.() p Equtio () is Ciut s qutio Lt b c...() b th soutio of (). Put p, q b i (), w gt b b.() which is th compt soutio. To fid th g soutio: W put b f i (), w gt f f..(4) Difftit (4) pti with spct to, w gt f f f..(5) Eimitig btw qutios (4) d (5), w gt th quid g soutio To fid th sigu soutio: Difftit () pti with spct to, b b b b... (4) Difftit () pti with spct to b,.(5)
177 Substitutig qutio (4) d (5) i qutio (), w gt Equtios ducib to stdd tps-tsfomtios: m m Tp A: Equtios of th fom f p, q o f p, q, Wh m d costts, ch ot qu to. W mk th tsfomtios X Th p Y q. Y d m Y. X m. m P, wh P d X X Q, m Thfo th qutio f p, q qutio. m Th qutio f p, q, qutio. wh Q Y ducs to mp, Q, ducs to mp, Q,, f.which is tp f.which is tp. Pobm: ()Sov p 4 q. Soutio: Giv: p This c b witt s 4 q p q.
178 m Which is of th fom f p, q,, wh m=,=. Put X m ; Y P. p p X X Q. q q Y Y Substitutig i th giv qutio, P q. This is of th fom p, q, Lt Z f X Y f., wh u X Y d d P, Q du du Equtio bcoms, d Sovig fo, du d du d du d og og d du 8 8 du 8 X Y b 8 b is compt soutio. Th g d sigu soutio c b foud out b usu mthod. k k k k Tp B: Equtios of th fom f p, q o f p, q,, Wh k is costt, which is ot qu to -. W mk th tsfomtios Z k. Z d k Th P k p 4
179 Z Q k k p k k Thfo th qutio f p, q qutio. k k Th qutio f p, q,, tp 4 qutio. P Q ducs to f,, which is tp k k P Q ducs to f,,,, which is k k Pobms: 4 ()Sov: q p. 4 Soutio: Giv: q p. Th qutio c b witt s q p Which cotis p d q. Hc w mk th tsfomtio Simi Z P P p q Q Usig ths vus i (), w gt p () Z Q P 9..() As () is qutio cotiig P d Q o, soutio of () wi b of th fom Z b c.() Now P d Q b, obtid fom () stisf qutio () b 9 i.. b 9 Thfo th compt soutio of () is Z 9 c i. compt soutio of () is 9 c Sigu soutio dos ot ist. G soutio is foud out s usu. 5
180 6 Tp C: Equtios of th fom, q p f k k m, wh ;, k m W mk th tsfomtios, k m d Z Y X Th dx d d dz X Z P.. m p k m k. d q k Q k. Thfo th giv qutio ducs to, Q k P k m f This is of tp qutio. Pobm: ()Sov q p Soutio: Giv: q p It c b witt s q p..() which is of th fom q p k k m w mk th tsfomtios, k m d Z Y X i.., d Z Y X Th P d dx X Z dz d p.... p P, Simi, q Q, Usig ths i (),it bcoms
181 P Q () As () cotis o P d Q picit, soutio of th qutio wi b of th fom Z X by c.() Thfo P d Q b, obtid fom () stisf qutio () i.. b b, Thfo th compt soutio of () is Z X Y c Thfo th compt soutio of () is c Sigu soutio dos ot ist. G soutio is foud out s usu. p q Tp D: Equtio of th fom f, B puttig Z Z wh P d Q. X Y Pobms: ()Sov pq. Soutio: Giv: Rwitig (), X og, Y og d Z og th qutio ducs to f P, Q, pq..() p q..() p q As () cotis d, w mk th substitutios X og, Y og d Z og Th P d Z dx... P. dz X d 7
182 i.. p P Simi, q Q Usig ths i (), it bcoms PQ..() which cotis o P d Q picit. A soutio of () is of th fom Z X by c (4) Thfo P d Q b, obtid fom (4) stisf qutio () i.. b o b Thfo th compt soutio of () is Thfo th compt soutio of () is G soutio of () is obtid s usu. Z X Y c og og og c..(5) APPLICATION OF PARTIAL DIFFERENTIAL EQUATIONS I m phsic d giig pobms, w ws sk soutio of th diffti qutios, whth it is odi o pti, which stisfis som spcifid coditios cd th boud coditios. A diffti qutios togth with ths boud coditios is cd boud vu pobm. I this chpt w sh stud som of th most impott pti diffti qutios occuig i giig ppictios. O of th most fudmt commo phom tht foud i tu is th phom of wv motio. Wh sto is doppd i to poud, th sufc of wt is distubd d wvs of dispcmt tv pid outwd. Wh b o tuig fok is stuck, soud wvs popgtd fom th souc of soud. Whtv is th tu of wv phom, whth it is th dispcmt of tight sttchd stig, th dfctio of sttchd mmb, th popgtio of cuts d pottis og ctic tsmissio i, ths titis govd b pti diffti qutio, kow s th Wv Equtio. Vib Spb Soutio of th Wv Equtio t, t X. T t.. () Lt 8
183 b th soutio of th qutio.. () t Wh X is fuctio of o d T t is fuctio of t o. Th d T d XT d X T, Wh T d X Stisf qutio () t dt d i.., XT T X T () X T Th L.H.S of () is fuctio of o d th R.H.S is fuctio of t o. Th qu fo vus of th idpdt vib d t. This is possib o if ch is costt. d X T k, Wh k is costt. X T X kx.. (4) T k T.. (5) Th tu of th soutio of (4) d (5) dpds o th tu of vus of k. Hc th foowig th css is. Cs : k is positiv. Lt k p Th qutio (4) d (5) bcom D p X d D p T d d Wh D d D d dt Th soutios of ths qutios p p X A B d pt pt T C D Cs : k is gtiv. Lt k p Th qutio (4) d (5) bcom D p X d D p T Th soutios of ths qutios X Acos p Bsi p d T C cos pt Dsi pt 9
184 Cs : k. Th qutio (4) d (5) bcom d X d d T d dt Th soutios of ths qutios X A B d T Ct D Sic, t X. T is th soutio of th wv qutio, th th mthmtic possib soutios of th wv qutios p p pt pt t A B C D, (6), t Acos p Bsi pc cos pt Dsi pt. (7), t A B Ct D (8) d Pobms: ()A uifom stig is sttchd d fstd to two poits pt. Motio is sttd b dispcig th stig ito th fom of th cuv (i) k si d (ii) k d th sig it fom this positio t tim t=. Fid th dispcmt of th poit of th stig t distc fom o d t tim t. Soutio: fig. Th dispcmt, tof th poit of th stig t distc fom th ft d t tim t is giv b th qutio (fig.). () t
185 Sic th ds of th stig = d = fid, th do ot udgo dispcmt t tim. Hc, t, fo t. () d, t, fo t. () Sic th stig is sd fom st iiti, tht is, t t=, th iiti vocit of v poit of th stig i th -dictio is o. Hc,, fo.. (4) t Sic th stig is iiti dispcd i to th fom of th cuv f, th coodits,,stisf th qutio f, wh, is th iiti dispcmt of th poit i th -dictio. Hc, f, fo. (5) Wh i (i) d i (ii). Coditios (),(),(4) d (5) coctiv cd boud coditios of th pobm. W hv to gt th soutio of qutio (), th ppopit soutio, cosistt with th vibtio of th stig is, t Acos p Bsi p C cos pt Dsi pt (6) Wh A, B, C, D d p bit costts tht to b foud out b usig th boud coditios. Usig boud coditios () i (6), w hv A C cos pt Dsi pt fo t A Usig boud coditios () i (6), w hv Bsi p C cos pt Dsi pt fo t Bsi p Eith B o si p, t which is migss. If B=, th soutio bcoms, si p p p Wh,, Difftitig both sids of (6) pti with spct to t, w hv, t Bsi p. p C si pt Dcos pt t Wh p Usig boud coditios (4) i (7), w hv Bsi p. p. D fo As B d p, w gt D Usig ths vus of A, p, D i (6), th soutio ducs to t, t BCsi cos, wh,, (7)
186 Tkig BC=k, Eq.() hs ifiit m soutios giv bow. t, t k si cos t, t k si cos t, t k si cos, tc. Sic Eq.() is i, i combitio of th R.H.S mmbs of th bov soutios is th g soutio of Eq.().Thus th most g soutio of Eq.() is t, t ck si cos o t, t si cos.... (8) Wh is t to b foud out. Usig boud coditios (5) i (8), w hv si f, fo (9) If w c pss f() i sis compb with th L.H.S. sis of (9), w c gt th vus of. (i) f k si k si si 4 Usig this fom of f() i (9) d compig ik tms, w gt k k,, Usig ths vus i (8), th quid soutio is k t k t, t si cos si cos 4 4 (ii) k If w pd f() s Foui hf-g si sis i,, tht is i th fom b si it is compb with th L.H.S sis of (9). Thus b f si d, b Eu s fomu k si d
187 k cos si cos k 4 odd is if k v is if, 8, Usig this vu of i (8), th quid soutio is cos si 8, t k t () Sov th o dimsio wv qutio,, t i t giv tht.,,,,,, b d t t t Soutio: Shiftig th oigi to th poit,, w gt Y X Wh Y d X,, th coodits of th poit (, ) with fc to th w sstm of coodit s. Th diffti qutio i th w sstm is,, t X t.. () Th boud coditios bcom, t Y (), t Y... (). t fo, X t Y. (4) d X i X b X i X b X Y,,,.(5) Sic th st boud coditio i th od sstm is i b i b,,, Th quid soutio of qutio () is cos si si 8, t X b t X Y
188 Sicsi, Wh is v itg, th soutio c b witt s 8b X t Y X, t si si cos Wh X, t.,,5, Chgig ov to th od sstm of coodits, th soutio bcoms 8b t, t si si cos,,5 Now si si si cos cos si si cos, Sic is odd. Th quid soutio is 8b t, t si cos cos Wh 8b d,,5,, t t cos cos t.,,5, () A tight sttchd stigs with fid d poits = d =5 is iiti t st i its quiibium positio. If it is sid to vibt b givig ch poit vocit (i) v v si d 5 (ii) v v si cos, 5 5 Fid th dispcmt of poit of th stig t subsqut tim. Soutio: Th dispcmt (, t) of poit of th stig t tim t is giv b t.. () W hv to sov qutio () stisfig th foowig boud coditios., t, fo t () 5, t, fo t.... (),, fo 5 (4) Sic th stig is i its quiibium positio iiti d so th iiti dispcmt of v poit of th stig is o., f, t fo (5) wh f v si 5 Fo (i) d f v si cos, Fo (ii) 5 5 4
189 Th suitb soutio of Eq (), cosistt with th vibtio of th stig, is, t Acos p Bsi pc cos pt Dsi pt... (6) Usig boud coditios () i (6), w hv A C cos pt Dsi pt fo t A Usig boud coditios () i (6), w hv B si 5 p C cos pt Dsi pt fo t Eith B o si5p If w ssum tht B=, w gt tivi soutio. si 5p 5p p 5 Wh,, Usig boud coditios (4) i (6), w hv B si p. C fo 5 As B, w gt C Usig ths vus of A, p, C i (6), th soutio ducs to t, t k si si, ( 7) wh k BD d,, Th most g soutio of Eq.() is t, t si cos (8) Difftitig both sids of (8) pti with spct to t, w hv t, t. si cos t (9) Usig boud coditio (5) i (9), w hv si v. Sic v,, 5 5 t (i) v v si d 5 v si si v si si si Compig ik tms, w gt v v, d , fo,4,5,6 75v 5v, d Usig ths vus i (8), th quid soutio is 5
190 75v 5v t, t si si si si (ii) v v si cos 5 5 v si si 5 5 v si si si Compig ik tms, w gt v v, d, fo,4,5, v 5v, d 4 5 Usig ths vus i (8), th quid soutio is 5v t 5v t, t si si si si (4) A tut stig of gth, fstd t both ds, is distubd fom its positio of quiibium b imptig to ch of its poits iiti vocit of mgitud k. Fid th dispcmt fuctio, t. Soutio: Th dispcmt (, t) of poit of th stig t tim t is giv b t.. () W hv to sov qutio () stisfig th foowig boud coditios., t, fo t (), t, fo t... (),, fo... (4), k, t fo (5) Th suitb soutio of Eq (), cosistt with th vibtio of th stig, is, t Acos p Bsi pc cos pt Dsi pt (6) Usig boud coditios () i (6), w hv A C cos pt Dsi pt fo t A Usig boud coditios () i (6), w hv B si p C cos pt Dsi pt fo t Eith B o si p If w ssum tht B=, w gt tivi soutio. si p p p 6
191 7 Wh,, Usig boud coditios (4) i (6), w hv fo p C B. si As, C gt w B Usig ths vus of A, p, C i (6), th soutio ducs to,,,...(7)..., si si, wh t k t Th most g soutio of Eq.() is cos si, t t. (8) Difftitig both sids of (8) pti with spct to t, w hv cos si., t t t. (9) Usig boud coditio (5) i (9), w hv si, si b fo k Which is Foui hf-g si sis of. k i,. Compig ik tms, w gt fomu s Eu b d f b, si. d k si k 8 cos 4 si cos k 4 4 odd is if k v is if,, 4 4 Usig this vu of i (8), th quid soutio is 4 4 cos si 64, t k t
192 ONE DIMENSIONAL HEAT FLOW VARIABLE SEPARABLE SOLUTIONS OF THE HEAT EQUATION Th o dimsio ht fow qutio is u u t....() Lt u(,t) = X().T(t)....() b soutio of Eq.(), wh X() is fuctio of o d T(t) is fuctio of t o. u u dt d X Th XT d X T, wh T d X, stisf Eq.(). t dt d i.., XT X T i.., X T X T....() Th L.H.S. of () is fuctio of o d th R.H.S is fuctio of t o. Th qu fo vus of idpdt vibs d t. This is possib o if ch is costt. X T k, wh k is costt. X T X kx d T k T... (4) Th tu of th soutios of (4) d (5) dpds o th tu of th vus of k. Hc th foowig th css com ito big. Cs : k is positiv. Lt k p. Th qutios (4) d (5) bcom ( D p ) X d ( D p ) T, wh d d D d D. d dt Th soutios of ths qutios X C p C p d T C p t Cs : k is gtiv. Lt k p. Th qutios (4) d (5) bcom ( D p ) X d ( D p ) T, Th soutios of ths qutios X C cos p C si p d Cs : k= Th qutios (4) d (5) bcom d X dt d d dt Th soutios of ths qutios X C C d T C T C p t Sic u(, t) = X.T is th soutio of Eq.(), th th mthmtic possib soutios of Eq.() u(, t) u(, t) p p p t ( A B )....(6) p t ( Acos p Bsi p)... (7) 8
193 d u(, t) A B... (8) wh C C d C C hv b tk s A d B. PROBLEMS. Fid th tmptu distibutio i homogous b of gth which is isutd t, if th ds kpt t o tmptu d if, iiti, th tmptu is k t th ct of th b d fs uifom to o t its ds. Soutio: Figu 4. psts th gph of th iiti tmptu i th b. k Equtio of OA is d th qutio of AB is k i.., k ( ) Hc k, i u(,) k ( ), i Th tmptu distibutio u(, t) i th b is giv b u u t t...() W hv to sov Eq.() stisfig th foowig boud coditios. u (, t), fo t...() u(, t), fo t... () k, i u(,) k ( ), i... (4) As u(, t) hs to mi fiit wh t, th pop soutio of Eq.() is u(, t) Usig boud coditio () i (5), w hv p t ( Acos p Bsi p).....(5) 9
194 p t A., fo t A = Usig boud coditio () i (5), w hv p t Bsi p., fo t B o si p B = ds to tivi soutio. si p p o p, wh,,, Usig ths vus of A d p i (5), it ducs to u(, t) wh,,, Thfo th most g soutio of Eq.() is u(, t) t Bsi.(6) B si. t Usig boud coditio (4) i (7), w hv B si f ( ) i (, ), wh k, f ( ) k ( ), i i.(7) If th Foui hf-g si sis of f ( ) i (, ) is B si, it is compb with B si. Hc B b k si d 4k cos si 8k si Usig this vu i (7), th quid soutio is 8k t u(, t) si si. 8k u(, t) ( ) ( ) si( ). k ( )si d cos ( ) () t si 4
195 . Sov th o dimsio ht fow qutio u u t stisfig th foowig boud coditios. (i) u (, t), fo t u (ii) (, t), fo t ; d (iii) u(,) cos, Soutio: Th ppopit soutio of th qutio u u t () stisfig th coditio tht u wh t is u(, t) Difftitig () pti w..t., w hv u p t (, t) p( Asi p Bcos p) Usig boud coditio (i) i (), w hv p t ( Acos p Bsi p)....() p t p. B., fo t if p, u(, t) A, Usig boud coditio (ii) i (), w hv....() B = which is migss p t p. Asi p., fo t Eith A = o si p A = ds to tivi soutio. si p p o p, wh,,, Usig ths vus of B d p i (), it ducs to u(, t) wh,,, t Acos...(4) Thfo th most g soutio of Eq.() is u(, t) A cos. t Usig boud coditio (iii) i (5), w hv..(5) A cos cos i (, ) I g, w hv to pd th fuctio i th R.H.S. s Foui hf-g cosi sis i (, ) so tht it m b compd with L.H.S. sis. I this pobm, it is ot css. W c wit cos s ( cos), so tht compiso is possib. 4
196 Thus A cos cos Compig ik tms, w hv A, A, A A A4 Usig ths vus i (5), th quid soutio is 4 t u(, t) cos u u. Sov th qutio stisfig th foowig coditios. t (i) u is fiit wh t. u (ii) wh =, fo vus of t. (iii) u = wh =, fo vus of t. (iv) u u wh t =, fo < <. Soutio: W hv to sov th qutio u u () t stisfig th foowig boud coditios. u (, t), fo t () u(, t) =, fo t...() u(, ) u fo < <.... (4) Sic u is fiit wh t, th pop soutio of Eq.() is u(, t) Difftitig (5) pti w..t., w hv u p t (, t) p( Asi p Bcos p) Usig boud coditio (ii) i (6), w hv p t ( Acos p Bsi p) (5) p. B. p t, fo t if p, u(, t) A,....(6) B = which is migss Usig boud coditio (iii) i (5), w hv p t Acos p., fo t Eith A = o cos p A = ds to tivi soutio. cos p p odd mutip of o ( ) ( ) p, wh,,,. 4
197 Usig ths vus of B d p i (5), it ducs to ( ) () t 4 u(, t) Acos......(7) wh,,,. Thfo th most g soutio of Eq.() is ( ) () t 4 u(, t) A cos......(8) Usig boud coditio (iv) i (8), w hv ( ) A cos. u i (, ).(9) Th sis i th L.H.S of (9) is ot i th fom of th Foui hf-g cosi sis of fuctio i (, ), tht is, cos. Hc, to fid A, w pocd s i th divtio of Eu s fomu fo th Foui cofficits. ( ) Mutipig both sids of (9) b cos d itgtig w..t. btw d, w gt ( ) ( ) A cos d u cos d A. A oth it gs i th L. H. S. vish ( ) ( ) si si u ( ) ( ) ( ) A. u. si ( ) 4u A ( ) ( ) Usig this vu i (8), th quid soutio is 4uo ( ) ( ) u(, t) cos.. ( ) () t 4 Sovd pobms () Fom pti diffti qutio b imitig bit costts d b fom b As: Giv b. () 4
198 p q b p q Substitutig () & () i (), w gt 4 4 () Fom pti diffti qutio b imitig th bit costts d b fom th qutio b cot. As: Giv: b cot.. () Pti difftitig with spct to d w gt p cot.. () b cot q... () () p cot (4) () b q cot.. (5) Substitutig (4) d (5) i () w gt 4 4 p cot q cot cot. p q t. () Fid th compt soutio of th pti diffti qutio p q 4 pq. As: Giv p q 4 pq... () Lt us ssum tht b c () b th soutio of () Pti difftitig with spct to d w gt p.. () q b Substitutig () i () w gt b 4b Fom th bov qutio w gt, 4b 6b 4 b b b 4. (4) Substitutig (5) i () w gt 4 b c b (4) Fid th PDE of ps hvig qu itcpts o th d is. As: Th qutio of such p is b. () 44
199 Pti difftitig () with spct to d w gt p b p b.. () q b q b.. () Fom () d (), w gt p q (5) Fid th soutio of p q. As: Th S.E is d d d Tkig fist two mmbs, w gt d d Itgtig w gt c i. u c Tkig st two mmbs, w gt d d Itgtig w gt c i. v c Th compt soutio is, (6) Fid th sigu itg of th pti diffti qutio p q p q. As: Th compt itg is b b. b b b Thfo 45
200 (7) Sov:. m q p As: m q p Giv.. () Lt us ssum tht c b () b th soutio of () Pti difftitig with spct to d w gt b q p.. () Substitutig () i () w gt m b This is th quid soutio. (8) Fom pti diffti qutio b imitig th bit costts d b fom. b As:. b Giv () Pti difftitig with spct to d w gt.. q b b q p p.. () Substitutig () i () w gt q p q p This is th quid PDE. (9) Fom pti diffti qutio b imitig th bit costts d b fom. b As: Giv b. () q q p b b p Substitutig () & () i (), w gt p q.
201 pq 4 () Fom pti diffti qutio b imit th bit fuctio f fom f. As: Giv : f.. p p f... q q f.. Fom (), w gt p f p Substitutig () i(), w gt.....().....()......() () Obti pti diffti qutio b imitig bit costts d b fom b. As: Giv b. () p p...( ) b q b q Substitutig () & () i (), w gt p q p q () Fid th compt itg of p q pq, wh p, q. As: Lt us ssum tht b c () b th soutio of th giv qutio. Pti difftitig with spct to d w gt p q b.. () Substitutig () i () w gt b b b Substitutig th bov i () w gt 47
202 c This givs th compt itg. () Fid th PDE of th fmi of sphs hvig thi cts o th i ==. As: Th qutio of such sph is Pti difftitig with spct to d w gt p....() q....() Fom (), p....() p Fom (), q....(4) q Fom () d (4), w gt p q p q This is th quid PDE. 48
203 VECTOR CALCULAS UNIT STRUCTURE 5. Objctivs 5. Itoductio 5. Vcto difftitio 5. Vcto opto 5.. Gdit 5.. Gomtic mig of gdit 5.. Divgc 5..4 Sooid fuctio 5..5 Cu 5..6 Itio fid 5.4 Poptis of gdit, divgc d cu 5.5 Lt Us Sum Up 5.6 Uit Ed Ecis 5. OBJECTIVES Aft goig though this uit, ou wi b b to L vcto difftitio. Optos, d, gd d cu. Poptis of optos 5. INTRODUCTION Vcto gb ds with dditio, subtctio d mutipictio of vt. I vcto ccuus w sh stud difftitio of vctos fuctios, gdit, divgc d cu. Vcto: Vcto is phsic qutit which quid mgitud d dictio both. Uit Vcto:
204 Uit Vcto is vcto which hs mgitud. Uit vctos og coodit is i d j, k spctiv. i = j = k = Sc Tip Vcto: Sc tip poduct of th vctos is dfid s. b c o b c. Gomtic mig of b c mius dgs, b d c. is voum of ppipd with cott W hv, b c = b c = c b b c = - b c Vcto Tip Poduct: Vcto tip poduct of b d c is coss poduct of d b b c o coss poduct of b d c b c =. c b. b c b c =. c b b. c Rmk : Vcto tip poduct is ot ssocitiv i g i.. b c b c c i.. Cop Vctos: Th vctos, b d c cop if b c = fo, b, c 5. VECTORS DIFFERENTIATION Lt v b vcto fuctio of sc t. Lt cospodig to th icmt t i t. v b th sm icmt i Th,
205 v v t t - v(t) v = t v t t - v(t) t Tkig imit t w gt, im v = im t t t dv v = im = im v t t - v(t) t v t t - v(t) dt t t t t dv = im dt t v t t - v(t) Fomus of vcto difftitio: t (i) d = k v = k dv k is costt dt dt (ii) (iii) (iv) d du dv u v = dt dt dt d dv du u. v = u. v. dt dt dt d dv du u v = u v dt dt dt (v) If v vi v j vk Th, Not: dv dv dv dv i j k dt dt dt dt If i j k th = = Emp : If t i t t - j t - t k fid d dt d d dt
206 Soutio: t i t t - j t - t k d dt d dt i t j j k Emp : t - k If cos wt b si wt wh w is costt show tht d d = w b d = -w dt dt Soutio: cos wt b si wt (i) d dt cos wt b si wt (ii) d dt cos wt b si wt -w si wt bw cos wt b = w cos wt b w si wt b b = b w cos wt b w si wt b w cos wt si wt b w w Agi difftitig q b b = = - b d dt - w cos wt - b w si wt = -w cos wt b si wt -w fom (i) Emp. Evut th foowig: i) d b c dt ii) d d d dt dt dt
207 Soutio: i) d b c dt d =. b c dt d =. b c b c. dt d dt dc db d =. b c b c. dt dt dt dc db d =. b. c b c. dt dt dt dc db d = b c b c dt dt dt Soutio: ii) d d d dt dt dt d d d d d d d dt dt dt dt dt dt dt = c (Fom Rsut i) d d = dt dt =. d dt d dt Emp 4. Evut th foowig: d Soutio: = b c dt dc d = b b c dt dt dc db d = b b c dt dt dt d = b c dt dc db d = b c b c dt dt dt d d Emp 5. Show tht = dt, wh dt =
208 Soutio : W hv d d dt dt d d - dt dt d d dt dt = L.H.S. = d d dt dt d d dt dt d dt d dt R.H.S Emp 6. If Soutio: = t i t - 5t = t i t j d dt 5t t i 6t j 5t j. Th show tht d dt = k L.H.S. i j k d dt 5t t t t 6t 5t
209 i - j k t 6t - t t 5t 5t 5 5 k 6t 6t 5 5 k R. H. S. Emp 7. If Soutio: mt mt = b. Show tht d mt mt = b...(i) d dt d dt d dt mt mt m - m b m m b mt mt m b mt mt m m Chck ou pogss: du () If = w u d dv = w v dt dt d Show tht u v = w u v dt () If = t i t - t j 7t k Fid d, dt dt d dt = (fom (i)) () If: = t i t j st - k, Fid d d d d,,, dt dt dt dt (4) If t = i cos t j 7si t j Fid d dt t t = (5) Show tht: mgitud of.. d dt = d dt wh = i j k d is
210 5. VECTOR OPERATOR Th vcto diffti opto is dfid s = i j k. 5.. Gdit: Th gdit of sc fuctio is dotd b gd o d is dfid s = i j k. qutit. 5.. Gomtic mig of gdit: Not tht gd is vcto Th gd is vcto ight gd to th sufc, whos qutio is,, = c, wh c is costt. Hc fo = i j k poit o sufc. d = i.. t is ight gs to d d d is o th tgt p to th sufc t P. d Gomtic psts vcto om to th sufc,, = costt. Emp 8: Fid gd, wh Soutio: gd = = i j k = i j k = i j k = i j k Emp 9: If i j k fid gd Soutio:
211 = i j k = Gd = i j k = i j k = i j. k = i j k = i jk gd = Emp : If i j k fid gd Soutio: = i j k = gd = =,, = i j k = i j k = i j k = i j k
212 = i j k =. i j k = = Emp : If fid gd t (, -, ) Soutio: gd = i j k - = i - j - k - = i 6 j - k - = i 6 j - - k At (, -, d ) gd = 6 i j k = 6 i j 4 k = -6 i 6j k Emp : Evut gd Soutio : Gd, wh = i j k = i j k = i. j. k. = i.. j. k. = i j k =
213 Emp : Fid gd Soutio: gd = = i j k Emp 4: Fid gd Soutio: gd og = i j k = i j k = i j k = i j k = i j k = og = i j k (og ) = i (og ) j (og ) k (og ) = i j k = i j k = i j k = = gd og = gd (og ) = gd (og ).. Emp 5: Show tht gd i j k wh
214 Soutio: t = i j k. =. gd. i j k ow i i i i simi j d k k j gd i j k - i j k
215 Chck ou pogss: () If i j k d Show tht: ) gd og b) gd c) gd f () If f = 4 5 Fid gd t (,, -) () Show tht (4) If gd - 5 F,, Fid F t (,, ) (5) Show tht f wh i j k (6) Fid uit vcto om to th sufc t (,, ) [Hit :- Uit vcto om to sufc i.. ] 5.. Divgc: If v (,, ) = vi v j v k c b dfid d difftitd t ch poit (,, ) i gio of spc th divgc of v is dfid s div v =. v
216 = i j k. v i v j v k = v v v Emp 6 If F = i j k, fid F Soutio: div F =. F = i j k. i j k = = = 4 Emp 7 Show tht div = wh = i j k Soutio: div =. F = i j k. i j k = = = Emp 8 Fo = i j k show tht wh div = () Soutio: L.H.S. div =. = i j k. i j k = =
217 = =... = = = = = R.H.S. Emp 9 Evut div wh = i j k Soutio: W hv = i j k div =. = i j k = i j k. = = = = = = -
218 - = = Emp If Soutio: gd F = F 4 F = Fid div (gd F) = i j k 4 4 = i j 4 k div (gd F) =. i j 4 k = 4 = Emp Fid th vu of div vcto d = i j k Soutio: div = i. = i.. = i. = i. i wh is costt = i. i = i i. i = i
219 i Sooid Fuctio: A vcto fuctio F is cd Sooid if div F = t poits of th fuctio Cu: Th cu of vcto poit fuctio F is dfid s cu F F if Fi F j F k. cu F F F = i j k Fi F j F k = i j k F F F F F F F F F = i - j k Th cu of th i vocit of ptic of igid bod is qu to twic th gu vocit of bod. i.. if w = wi w j wk b th gu vocit of ptic of th bod with positio vcto dfid s = i j k th i vocit v = w. Hc cu v v = w i j k = w w w = i w -w j w -w k w -w
220 = i j k w -w w -w w -w = i w w j w -w k w w = w i w j w k = w cu v = w 5..6 Iottio fid: A vcto poit fuctio F is cd iottio if F t poits of th fuctio. Emp Fid cu (cu F ) If Soutio: Cu F = i j k = i - k = F = i - j k t (,, ) cu cu (F) = i j k i j k = i j k = i j k = j At (,, )
221 cu F () j 4 j Emp Fid cu V if Soutio: cu V V i j k V = i j k = i - j k i - - j - k - Emp 4 Evut cu wh if = i j Soutio: Cu = i j k i - j k i - j k k Emp 5 Evut cu Soutio: wh if = i j k = = i j k
222 cu = i j k i j k i k - j i i i j k = i j k Emp 5 If Soutio: cu F i j k F = i j k fid div (cu F ) i - j k i - - j - k - - i - div (cu F) k
223 i j k. - i k - = Emp 7 If F = gd, fid (cu F ). Soutio: F = gd i j k i j k i j (cu F) i j k k i - - j k i - - j - k - i j k 5.4 PROPERTIES OF GRADIENT, DIVERGENCE AND CURL (i) f g = f g (ii). A B =. A. B (iii) A B = A. B
224 Poof: (i) f g i j k f g i f g j f g k f g i f j f k i g j g g f g (ii) Lt A = Ai A j Ak B = B i B j B k. A B. A B i A B j A B k A B A B A B A A A B B B. A. B (ii) Lt A B i j k A B A B A B i A B A B i A B i A B A i i A B B
225 Dictio divtiv Th divtiv of poit fuctio (sc o vcto) i pticu dictio is cd its dictio divtiv og th dictio. Th dictio divtiv of sc poit fuctio φ i giv dictio is th t of chg of φ i th dictio. It is giv b th compot of gdφ i tht dictio. Th dictio divtiv of sc poit fuctio φ (,,) i th dictio of is giv b φ.. Dictio divtiv of φ is mimum i th dictio of Hc th mimum dictio divtiv is φogdφ φ. Uit om vcto to th sufc If φ (,, ) b sc fuctio, th φ (,, ) = c psts A sufc d th uit om vcto to th sufc φ is giv b φ φ Equtio of th tgt p d om to th sufc Suppos is th positio vcto of th poit,, ) O th sufc φ (,, ) = c. If ( = i j k is th positio vcto of poit (,,) o th tgt p to th sufc t, th th qutio of th tgt p to th sufc φ t giv poit o it is giv b. gdφ = If is th positio vcto of poit o th om to th sufc t th poit o it. Th vcto qutio of th om t giv poit o th sufc φ is gdφ = Th Ctsi fom of th om t,, ) o th sufc ( φ (,,) = c is φ = φ o = φ Divgc of vcto If (,, ) is cotiuous difftib vcto poit fuctio i F giv gio of spc, th th divgcs of F is dfid b F. F = divf = i F F j k
226 = F i If = k F j F i F F,th ).( = k F j F i F F div i.., F F F divf = Sooid Vcto A vcto F is sid to b sooid if = F div (i). = F Cu of vcto fuctio If ),, ( F is difftib vcto poit fuctio dfid t ch poit (,, ), th th cu of F is dfid b = F F cu = F k F j F i = F i If = k F j F i F F,th ) ( = k F j F i F F cu F F F k j i F cu = = F F k F F j F F i Cu F is so sid to b ottio F Iottio Vcto A vcto F is cd iottio if Cu = F (i) if = F Sc Potti If F is iottio vcto, th th ists sc fuctio φ Such tht φ = F. Such sc fuctio is cd sc potti of F Poptis of Gdit. If f d g two sc poit fuctio tht ( ) g f g f ± = ± (o) ( ) gdg gdf g f gd ± = ± Soutio: ( ) ( ) g f k j i g f ± = ±
227 = ( ) ( ) ( ) ± ± ± g f k g f j g f i = g k f k g j f j g i f i ± ± ± = ± g k g j g i f k f j f i = g f ±. If f d g two sc poit fuctios th ( ) f g g f fg = (o) ggdf fgdg fg gd = ) ( Soutio: ( ) = fg ( ) fg k j i = ( ) ( ) ( ) fg k fg j fg i = f g g f k f g g f j f g g f i = f k f j f i g g k g j g i f = f g g f. If f d g two sc poit fuctio th g g f f g g f = wh g Soutio: = g f g f k j i = g f i = g g f f g i = g i f f i g g = [ ] g f f g g 4. If = k j i such tht =,pov tht = Soutio: k j i = = k j i
228 = k j i = k j i = k j i = 5. Fid uit om to th sufc 4 = t (,-, ) Soutio: Giv tht = φ ) ( k j i = φ = ( ) ( ) ( ) k j i At (,-, ) ( ) ) (4 (4) 6 8 = k j i φ = k j i = = = φ Uit om to th giv sufc t (,-,) φ φ = k j i = k j i 6. Fid th dictio divtiv of = 4 φ t (,,) i th dictio of k j i Soutio: Giv = 4 φ ) 4 ( k j i = φ = ( ) ( ) ( ) k j i 8 4 At (,, ) = k j i φ Giv: = k j i 6 4 = =
229 = D D.. φ = k j i k j i = [ ] [ ] = 7. Fid th g btw th sufc 5 = d 5 = t (,,) Soutio: Lt = φ d = φ,, = = = φ φ φ,, = = = φ φ φ = k j i φ = k j i ) ( φ At (o,,) = k j 4 φ = k j i 4 φ Cos = = k j i k j φ φ φ φ θ cos = = θ = 4 cos θ = 4 cos 8. Fid th g btw th sufcs og = d = t th poit (,,) Soutio: t og = φ d = φ = = =,, og φ φ φ,, = = = φ φ φ = k k j i ) og ( φ = k j φ
230 Cos = = = φ φ φ φ θ = 6 5 cos θ 9. Fid ( ) Soutio: ( ) = ( ). = ( ) ( ) ( ) k j i = k j i = k j i = = = = = = = = = ( )= k j i = k j i = Sic = u div u u φ φ φ. ( ) = = ( ).. = k j i k j i. = = ( ) ( ) =. = ( )( ) 4. = ( )( ) ( ) [ ] ( ) = =
231 . If = k j i d =.Pov tht is sooid if = d is iottio fo vctos of. Soutio: = k j i div ( ) ( ) ( ) = () Now = Difftitig pti w..to, = = Simi, = = = = Now ( ) ( ) =. =. ( ) = ( ) = Fom () w hv ( ) div = = = ( ) Th vcto is sooid if div = ( ) = = = is sooid o if = - Now k j i cu = = ( ) ( ) i = i
232 = i = ( ) i = Cu ( ) = k j i = Cu ( ) = fo vus of Hc is iottio fo vus of.. Pov tht ( ) ( ) = k j i F 4 si cos is iottio d fid its sc potti Soutio: 4 si cos k j i F cu = = [ ] [ ] [ ] cos cos = k j i F is iottio. To Fid φ such tht φ gd F = ( ) ( ) k j i k j i = φ φ φ 4 si cos Itgtig th qutio pti w..to,, spctiv ), si ( f = φ ), ( 4 si f = φ ), ( f = φ, 4 si C = φ is sc potti. Pov tht ).( ).( = B cu A A cu B B A div Poof : ).( = B A B A div = B A i = B A i B A i = B A i A B i
233 = B A i. A i. B = cu B. A cua. B.Pov tht Soutio: cu cuf = F F cu cuf = F B usig b c =. c b. b c. F. F = ( ) =. F F Pobms bsd o i Itg Emp : If F ( 6) (,,) og th cuv VECTOR INTEGRATION Li, sufc d Voum Itgs = i 4j k Evut F. d fom (,,) to = t =, = t, t Soutio: Th d poits (,, ) d (,, ) Ths poits cospod to t = d t = d = dt, d = t, d = t F. d = ( 6) d 4d d C C 5 7 = ( t 6t ) dt 4t ( tdt) t ( t ) dt 6 9 = ( t 8t 6t ) 9 dt t 4t 6t 7 = ( ) = [( 4 6) ] = 5 C Emp : Show tht F = i j k is cosvtiv vcto fid.
234 Soutio: If F is cosvtiv th = F is cosvtiv vcto fid. i j k Now F = = i j k = F Sufc Itgs Dfiitio: Cosid sufc S. Lt dot th uit outwd om to th sufc S. Lt R b th pojctio of th sufc o th XY p. Lt f b vcto vud dfid i som gio cotiig th sufc S. Th th sufc itg of f is dfid to b Emp ; Evut S S f. f. ds = d. d R. k f. ds wh F = i j k d S is th sufc of th cid = icudd i th fist octt btw th ps = d =. Soutio: Giv φ F = i j k = φ = i j φ = = = 4 4 Th uit om to th sufc = φ φ i j = = i j F. = i j k. i j =
235
236
237
238 (i) (ii) (iii) INTEGRAL THEOREMS Guss s divgc thom Stok s thom G s thom i th p G s Thom Sttmt: If M(,) d N(,) cotiuous fuctios with cotiuous pti divtivs i gio R of th p boudd b simp cosd cuv C, th N M Md d = dd, wh C is th cuv dscibd i th c R positiv dictio.
239 Vif G s thom i p fo th itg ( ) d d tk oud th cic = 4 Soutio: G s thom givs N M Md Nd = dd c R Cosid ( ) d d c M = N = M N =, = N M dd R dd dd ( ) = R R = [A of th cic] = π =. π. 4 = π () Now Md Nd W kow tht th pmtic qutio of th cic = 4 = cosθ = siθ d = siθdθ, d = cosθdθ Md Nd = ( ) d d cosθ 4siθ siθdθ cosθ cosθ d = ( )( ) ( ) θ = cosθ siθ 8si θ 4cos θdθ Wh θ vious fom to π π ( cosθ siθ 4si θ 4) Md Nd = dθ C π cos θ = si θ 4 4 d θ π = ( si θ 6 cos θ ) d θ cos θ si θ = 6θ = π = π.() Fom () d () π c
240 N M Md Nd = dd c R Hc G s Thom is vifid. Emp Usig G s thoms fid th of cic of dius. Soutio: B G s thom w kow tht A cosd b C = d d Th pmtic qutio of cic of dius is = Wh θ π π C A of th cic = cosθ ( cosθ ) siθ ( siθ ) dθ Emp : π = ( cos θ si θ ) dθ π = dθ θ π = π = [ ] Evut [( ) d cosd] c cosθ, = siθ si wh c is th tig with π vtics (,),(,) d ( π,) Soutio: Equtio of OB is = π = π
241 N M B G s thom Md Nd = dd c R M H M = si, = N N = cos, = si [( si ) d cosd] = ( si )dd C R π π I th gio R, vis fom = to d vis fom = to = C π ( si ) d cosd = ( si ) π = [ cos ] dd π π d π π π = cos d π π π = si π 4 π π π = = π 4 π Emp 4 Vif G s thom i th p fo 8 d 4 6d wh C is th boud of th gio dfid ( ) ( ) C b X =, =, = Soutio: W hv to pov tht
242 c N M Md Nd = dd R M = 8, N = 4 6 M N = 6, = 6 B G s thom i th p N M Md Nd = dd c R = ( ) dd = = ( ) 5 d ( ) = 5 Cosid Md Nd = c OA Aog OA, =, vis fom to OA AB Md Nd = 5 = BO d = [ ] = Aog AB, = - d = d d vis fom to. AB STOKE S THEOREM Md Nd = [ 8( ) 4( ) 6( ) ]d ( ) 4( ) 8 = 8 = = 8
243 If S is op sufc boudd b simp cosd cuv C d if vcto fuctio F is cotiuous d hs cotiuous pti divtivs i S d o C, th cu F. ds = F. d wh is th uit vcto om to th c sufc (i) Th sufc itg of th om compot of to th itg of th tgti compot of F tk oud C. Emp Vif Stok s thom fo F ( ) cu F is qu = i j k wh S is th upp hf of th sph = d C is th cicu boud o = p. Soutio: B Stok s thom H =k ( ) c F = i j k cuf = F. d = cuf. ds i j k = i [ ] j( ) k( ) s = k sic C is th cicu boud o = p S = of th cic cu F. ds = S dd = π ( ) = π.() ON =, c O C, = cosθ, = siθ d = si θdθ, d = cosθdθ θ vis fom to π F. d = cuf. ds s
Problem Session (3) for Chapter 4 Signal Modeling
 Pobm Sssio fo Cht Sig Modig Soutios to Pobms....5. d... Fid th Pdé oimtio of scod-od to sig tht is giv by [... ] T i.. d so o. I oth wods usig oimtio of th fom b b b H fid th cofficits b b b d. Soutio
Pobm Sssio fo Cht Sig Modig Soutios to Pobms....5. d... Fid th Pdé oimtio of scod-od to sig tht is giv by [... ] T i.. d so o. I oth wods usig oimtio of th fom b b b H fid th cofficits b b b d. Soutio
New Advanced Higher Mathematics: Formulae
 Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
Vtusolution.in FOURIER SERIES. Dr.A.T.Eswara Professor and Head Department of Mathematics P.E.S.College of Engineering Mandya
 LECTURE NOTES OF ENGINEERING MATHEMATICS III Su Cod: MAT) Vtusoutio.i COURSE CONTENT ) Numric Aysis ) Fourir Sris ) Fourir Trsforms & Z-trsforms ) Prti Diffrti Equtios 5) Lir Agr 6) Ccuus of Vritios Tt
LECTURE NOTES OF ENGINEERING MATHEMATICS III Su Cod: MAT) Vtusoutio.i COURSE CONTENT ) Numric Aysis ) Fourir Sris ) Fourir Trsforms & Z-trsforms ) Prti Diffrti Equtios 5) Lir Agr 6) Ccuus of Vritios Tt
PESIT Bangalore South Campus Hosur road, 1km before Electronic City, Bengaluru -100 Department of Basic Science and Humanities
 P E PESIT Bglo South Cpus Hosu od, k bfo Elctoic Cit, Bgluu -00 Dptt of Bsic Scic d Huitis INTERNAL ASSESSMENT TEST Dt : 0/0/07 Mks: 0 Subjct & Cod : Egiig Mthtics I 5MAT Sc : ALL N of fcult : GVR,GKJ,RR,SV,NHM,DN,KR,
P E PESIT Bglo South Cpus Hosu od, k bfo Elctoic Cit, Bgluu -00 Dptt of Bsic Scic d Huitis INTERNAL ASSESSMENT TEST Dt : 0/0/07 Mks: 0 Subjct & Cod : Egiig Mthtics I 5MAT Sc : ALL N of fcult : GVR,GKJ,RR,SV,NHM,DN,KR,
Chapter 3 Higher Order Linear ODEs
 ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
Classical Theory of Fourier Series : Demystified and Generalised VIVEK V. RANE. The Institute of Science, 15, Madam Cama Road, Mumbai
 Clssil Thoy o Foi Sis : Dmystii Glis VIVEK V RANE Th Istitt o Si 5 Mm Cm Ro Mmbi-4 3 -mil ss : v_v_@yhoooi Abstt : Fo Rim itgbl tio o itvl o poit thi w i Foi Sis t th poit o th itvl big ot how wh th tio
Clssil Thoy o Foi Sis : Dmystii Glis VIVEK V RANE Th Istitt o Si 5 Mm Cm Ro Mmbi-4 3 -mil ss : v_v_@yhoooi Abstt : Fo Rim itgbl tio o itvl o poit thi w i Foi Sis t th poit o th itvl big ot how wh th tio
CBSE , ˆj. cos CBSE_2015_SET-1. SECTION A 1. Given that a 2iˆ ˆj. We need to find. 3. Consider the vector equation of the plane.
 CBSE CBSE SET- SECTION. Gv tht d W d to fd 7 7 Hc, 7 7 7. Lt,. W ow tht.. Thus,. Cosd th vcto quto of th pl.. z. - + z = - + z = Thus th Cts quto of th pl s - + z = Lt d th dstc tw th pot,, - to th pl.
CBSE CBSE SET- SECTION. Gv tht d W d to fd 7 7 Hc, 7 7 7. Lt,. W ow tht.. Thus,. Cosd th vcto quto of th pl.. z. - + z = - + z = Thus th Cts quto of th pl s - + z = Lt d th dstc tw th pot,, - to th pl.
ELEC9721: Digital Signal Processing Theory and Applications
 ELEC97: Digital Sigal Pocssig Thoy ad Applicatios Tutoial ad solutios Not: som of th solutios may hav som typos. Q a Show that oth digital filts giv low hav th sam magitud spos: i [] [ ] m m i i i x c
ELEC97: Digital Sigal Pocssig Thoy ad Applicatios Tutoial ad solutios Not: som of th solutios may hav som typos. Q a Show that oth digital filts giv low hav th sam magitud spos: i [] [ ] m m i i i x c
ASSERTION AND REASON
 ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
Department of Mathematics. Birla Institute of Technology, Mesra, Ranchi MA 2201(Advanced Engg. Mathematics) Session: Tutorial Sheet No.
 Dpm o Mhmics Bi Isi o Tchoog Ms Rchi MA Advcd gg. Mhmics Sssio: 7---- MODUL IV Toi Sh No. --. Rdc h oowig i homogos dii qios io h Sm Liovi om: i. ii. iii. iv. Fid h ig-vs d ig-cios o h oowig Sm Liovi bod
Dpm o Mhmics Bi Isi o Tchoog Ms Rchi MA Advcd gg. Mhmics Sssio: 7---- MODUL IV Toi Sh No. --. Rdc h oowig i homogos dii qios io h Sm Liovi om: i. ii. iii. iv. Fid h ig-vs d ig-cios o h oowig Sm Liovi bod
PhysicsAndMathsTutor.com
 PhysicsAdMthsTuto.com PhysicsAdMthsTuto.com Jue 009 3. Fid the geel solutio of the diffeetil equtio blk d si y ycos si si, d givig you swe i the fom y = f(). (8) 6 *M3544A068* PhysicsAdMthsTuto.com Jue
PhysicsAdMthsTuto.com PhysicsAdMthsTuto.com Jue 009 3. Fid the geel solutio of the diffeetil equtio blk d si y ycos si si, d givig you swe i the fom y = f(). (8) 6 *M3544A068* PhysicsAdMthsTuto.com Jue
PROGRESSION AND SERIES
 INTRODUCTION PROGRESSION AND SERIES A gemet of umbes {,,,,, } ccodig to some well defied ule o set of ules is clled sequece Moe pecisely, we my defie sequece s fuctio whose domi is some subset of set of
INTRODUCTION PROGRESSION AND SERIES A gemet of umbes {,,,,, } ccodig to some well defied ule o set of ules is clled sequece Moe pecisely, we my defie sequece s fuctio whose domi is some subset of set of
DISCRETE-TIME RANDOM PROCESSES
 DISCRT-TIM RNDOM PROCSSS Rado Pocsss Dfiitio; Ma ad vaiac; autocoatio ad autocovaiac; Ratiosip btw ado vaiabs i a sig ado pocss; Coss-covaiac ad coss-coatio of two ado pocsss; Statioa Rado Pocsss Statioait;
DISCRT-TIM RNDOM PROCSSS Rado Pocsss Dfiitio; Ma ad vaiac; autocoatio ad autocovaiac; Ratiosip btw ado vaiabs i a sig ado pocss; Coss-covaiac ad coss-coatio of two ado pocsss; Statioa Rado Pocsss Statioait;
PhysicsAndMathsTutor.com
 PhsicsAMthsTuto.com 6. The hpeol H hs equtio, whee e costts. The lie L hs equtio m c, whee m c e costts. Leve lk () Give tht L H meet, show tht the -cooites of the poits of itesectio e the oots of the
PhsicsAMthsTuto.com 6. The hpeol H hs equtio, whee e costts. The lie L hs equtio m c, whee m c e costts. Leve lk () Give tht L H meet, show tht the -cooites of the poits of itesectio e the oots of the
ENGG 1203 Tutorial. Difference Equations. Find the Pole(s) Finding Equations and Poles
 ENGG 03 Tutoial Systms ad Cotol 9 Apil Laig Obctivs Z tasfom Complx pols Fdbac cotol systms Ac: MIT OCW 60, 6003 Diffc Equatios Cosid th systm pstd by th followig diffc quatio y[ ] x[ ] (5y[ ] 3y[ ]) wh
ENGG 03 Tutoial Systms ad Cotol 9 Apil Laig Obctivs Z tasfom Complx pols Fdbac cotol systms Ac: MIT OCW 60, 6003 Diffc Equatios Cosid th systm pstd by th followig diffc quatio y[ ] x[ ] (5y[ ] 3y[ ]) wh
National Quali cations
 Ntiol Quli ctios AH07 X77/77/ Mthmtics FRIDAY, 5 MAY 9:00 AM :00 NOON Totl mrks 00 Attmpt ALL qustios. You my us clcultor. Full crdit will b giv oly to solutios which coti pproprit workig. Stt th uits
Ntiol Quli ctios AH07 X77/77/ Mthmtics FRIDAY, 5 MAY 9:00 AM :00 NOON Totl mrks 00 Attmpt ALL qustios. You my us clcultor. Full crdit will b giv oly to solutios which coti pproprit workig. Stt th uits
Linear Algebra Existence of the determinant. Expansion according to a row.
 Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Chapter 2 Reciprocal Lattice. An important concept for analyzing periodic structures
 Chpt Rcpocl Lttc A mpott cocpt o lyzg podc stuctus Rsos o toducg cpocl lttc Thoy o cystl dcto o x-ys, utos, d lctos. Wh th dcto mxmum? Wht s th tsty? Abstct study o uctos wth th podcty o Bvs lttc Fou tsomto.
Chpt Rcpocl Lttc A mpott cocpt o lyzg podc stuctus Rsos o toducg cpocl lttc Thoy o cystl dcto o x-ys, utos, d lctos. Wh th dcto mxmum? Wht s th tsty? Abstct study o uctos wth th podcty o Bvs lttc Fou tsomto.
CBSE SAMPLE PAPER SOLUTIONS CLASS-XII MATHS SET-2 CBSE , ˆj. cos. SECTION A 1. Given that a 2iˆ ˆj. We need to find
 BSE SMLE ER SOLUTONS LSS-X MTHS SET- BSE SETON Gv tht d W d to fd 7 7 Hc, 7 7 7 Lt, W ow tht Thus, osd th vcto quto of th pl z - + z = - + z = Thus th ts quto of th pl s - + z = Lt d th dstc tw th pot,,
BSE SMLE ER SOLUTONS LSS-X MTHS SET- BSE SETON Gv tht d W d to fd 7 7 Hc, 7 7 7 Lt, W ow tht Thus, osd th vcto quto of th pl z - + z = - + z = Thus th ts quto of th pl s - + z = Lt d th dstc tw th pot,,
If a is any non zero real or imaginary number and m is the positive integer, then a...
 Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
2011 HSC Mathematics Extension 1 Solutions
 0 HSC Mathmatics Etsio Solutios Qustio, (a) A B 9, (b) : 9, P 5 0, 5 5 7, si cos si d d by th quotit ul si (c) 0 si cos si si cos si 0 0 () I u du d u cos d u.du cos (f) f l Now 0 fo all l l fo all Rag
0 HSC Mathmatics Etsio Solutios Qustio, (a) A B 9, (b) : 9, P 5 0, 5 5 7, si cos si d d by th quotit ul si (c) 0 si cos si si cos si 0 0 () I u du d u cos d u.du cos (f) f l Now 0 fo all l l fo all Rag
BINOMIAL THEOREM SOLUTION. 1. (D) n. = (C 0 + C 1 x +C 2 x C n x n ) (1+ x+ x 2 +.)
 BINOMIAL THEOREM SOLUTION. (D) ( + + +... + ) (+ + +.) The coefficiet of + + + +... + fo. Moeove coefficiet of is + + + +... + if >. So. (B)... e!!!! The equied coefficiet coefficiet of i e -.!...!. (A),
BINOMIAL THEOREM SOLUTION. (D) ( + + +... + ) (+ + +.) The coefficiet of + + + +... + fo. Moeove coefficiet of is + + + +... + if >. So. (B)... e!!!! The equied coefficiet coefficiet of i e -.!...!. (A),
UNIT V: Z-TRANSFORMS AND DIFFERENCE EQUATIONS. Dr. V. Valliammal Department of Applied Mathematics Sri Venkateswara College of Engineering
 UNIT V: -TRANSFORMS AND DIFFERENCE EQUATIONS D. V. Vllimml Deptmet of Applied Mthemtics Si Vektesw College of Egieeig TOPICS:. -Tsfoms Elemet popeties.. Ivese -Tsfom usig ptil fctios d esidues. Covolutio
UNIT V: -TRANSFORMS AND DIFFERENCE EQUATIONS D. V. Vllimml Deptmet of Applied Mthemtics Si Vektesw College of Egieeig TOPICS:. -Tsfoms Elemet popeties.. Ivese -Tsfom usig ptil fctios d esidues. Covolutio
National Quali cations
 PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
GUC (Dr. Hany Hammad)
 Lct # Pl s. Li bdsid s with ifm mplitd distibtis. Gl Csidtis Uifm Bimil Optimm (Dlph-Tchbshff) Cicl s. Pl s ssmig ifm mplitd citti m F m d cs z F d d M COMM Lct # Pl s ssmig ifm mplitd citti F m m m T
Lct # Pl s. Li bdsid s with ifm mplitd distibtis. Gl Csidtis Uifm Bimil Optimm (Dlph-Tchbshff) Cicl s. Pl s ssmig ifm mplitd citti m F m d cs z F d d M COMM Lct # Pl s ssmig ifm mplitd citti F m m m T
Physics 235 Final Examination December 4, 2006 Solutions
 Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
Handout 7. Properties of Bloch States and Electron Statistics in Energy Bands
 Hdout 7 Popts of Bloch Stts d Elcto Sttstcs Eg Bds I ths lctu ou wll l: Popts of Bloch fuctos Podc boud codtos fo Bloch fuctos Dst of stts -spc Elcto occupto sttstcs g bds ECE 407 Spg 009 Fh R Coll Uvst
Hdout 7 Popts of Bloch Stts d Elcto Sttstcs Eg Bds I ths lctu ou wll l: Popts of Bloch fuctos Podc boud codtos fo Bloch fuctos Dst of stts -spc Elcto occupto sttstcs g bds ECE 407 Spg 009 Fh R Coll Uvst
PhysicsAndMathsTutor.com
 PhysicsAMthsTuto.com . M 6 0 7 0 Leve lk 6 () Show tht 7 is eigevlue of the mti M fi the othe two eigevlues of M. (5) () Fi eigevecto coespoig to the eigevlue 7. *M545A068* (4) Questio cotiue Leve lk *M545A078*
PhysicsAMthsTuto.com . M 6 0 7 0 Leve lk 6 () Show tht 7 is eigevlue of the mti M fi the othe two eigevlues of M. (5) () Fi eigevecto coespoig to the eigevlue 7. *M545A068* (4) Questio cotiue Leve lk *M545A078*
Chapter 3 Fourier Series Representation of Periodic Signals
 Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3
![SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3 SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3](/thumbs/89/98215718.jpg) SOLVED EXAMPLES E. If f() E.,,, th f() f() h h LHL RHL, so / / Lim f() quls - (D) Dos ot ist [( h)+] [(+h) + ] f(). LHL E. RHL h h h / h / h / h / h / h / h As.[C] (D) Dos ot ist LHL RHL, so giv it dos
SOLVED EXAMPLES E. If f() E.,,, th f() f() h h LHL RHL, so / / Lim f() quls - (D) Dos ot ist [( h)+] [(+h) + ] f(). LHL E. RHL h h h / h / h / h / h / h / h As.[C] (D) Dos ot ist LHL RHL, so giv it dos
[5 points] (c) Find the charge enclosed by the cylindrical surface of radius ρ 0 = 9 mm and length L = 1 m. [2
![[5 points] (c) Find the charge enclosed by the cylindrical surface of radius ρ 0 = 9 mm and length L = 1 m. [2 [5 points] (c) Find the charge enclosed by the cylindrical surface of radius ρ 0 = 9 mm and length L = 1 m. [2](/thumbs/85/91744669.jpg) STUDENT NAME: STUDENT ID: ELEC ENG FH3: MIDTERM EXAMINATION QUESTION SHEET This emitio is TWO HOURS log. Oe double-sided cib sheet is llowed. You c use the McMste ppoved clculto Csio f99. You c tke y mteil
STUDENT NAME: STUDENT ID: ELEC ENG FH3: MIDTERM EXAMINATION QUESTION SHEET This emitio is TWO HOURS log. Oe double-sided cib sheet is llowed. You c use the McMste ppoved clculto Csio f99. You c tke y mteil
IFYFM002 Further Maths Appendix C Formula Booklet
 Ittol Foudto Y (IFY) IFYFM00 Futh Mths Appd C Fomul Booklt Rltd Documts: IFY Futh Mthmtcs Syllbus 07/8 Cotts Mthmtcs Fomul L Equtos d Mtcs... Qudtc Equtos d Rmd Thom... Boml Epsos, Squcs d Ss... Idcs,
Ittol Foudto Y (IFY) IFYFM00 Futh Mths Appd C Fomul Booklt Rltd Documts: IFY Futh Mthmtcs Syllbus 07/8 Cotts Mthmtcs Fomul L Equtos d Mtcs... Qudtc Equtos d Rmd Thom... Boml Epsos, Squcs d Ss... Idcs,
PhysicsAndMathsTutor.com
 PhysicsAdMthsTuto.com 5. () Show tht d y d PhysicsAdMthsTuto.com Jue 009 4 y = sec = 6sec 4sec. (b) Fid Tylo seies epsio of sec π i scedig powes of 4, up to d 3 π icludig the tem i 4. (6) (4) blk *M3544A08*
PhysicsAdMthsTuto.com 5. () Show tht d y d PhysicsAdMthsTuto.com Jue 009 4 y = sec = 6sec 4sec. (b) Fid Tylo seies epsio of sec π i scedig powes of 4, up to d 3 π icludig the tem i 4. (6) (4) blk *M3544A08*
On Jackson's Theorem
 It. J. Cotm. Math. Scics, Vol. 7, 0, o. 4, 49 54 O Jackso's Thom Ema Sami Bhaya Datmt o Mathmatics, Collg o Educatio Babylo Uivsity, Babil, Iaq mabhaya@yahoo.com Abstact W ov that o a uctio W [, ], 0
It. J. Cotm. Math. Scics, Vol. 7, 0, o. 4, 49 54 O Jackso's Thom Ema Sami Bhaya Datmt o Mathmatics, Collg o Educatio Babylo Uivsity, Babil, Iaq mabhaya@yahoo.com Abstact W ov that o a uctio W [, ], 0
COLLECTION OF SUPPLEMENTARY PROBLEMS CALCULUS II
 COLLECTION OF SUPPLEMENTARY PROBLEMS I. CHAPTER 6 --- Trscdtl Fuctios CALCULUS II A. FROM CALCULUS BY J. STEWART:. ( How is th umbr dfid? ( Wht is pproimt vlu for? (c ) Sktch th grph of th turl potil fuctios.
COLLECTION OF SUPPLEMENTARY PROBLEMS I. CHAPTER 6 --- Trscdtl Fuctios CALCULUS II A. FROM CALCULUS BY J. STEWART:. ( How is th umbr dfid? ( Wht is pproimt vlu for? (c ) Sktch th grph of th turl potil fuctios.
Boyce/DiPrima 9 th ed, Ch 7.6: Complex Eigenvalues
 BocDPm 9 h d Ch 7.6: Compl Egvlus Elm Dffl Equos d Boud Vlu Poblms 9 h do b Wllm E. Boc d Rchd C. DPm 9 b Joh Wl & Sos Ic. W cosd g homogous ssm of fs od l quos wh cos l coffcs d hus h ssm c b w s ' A
BocDPm 9 h d Ch 7.6: Compl Egvlus Elm Dffl Equos d Boud Vlu Poblms 9 h do b Wllm E. Boc d Rchd C. DPm 9 b Joh Wl & Sos Ic. W cosd g homogous ssm of fs od l quos wh cos l coffcs d hus h ssm c b w s ' A
( ) ( ) ( ) 2011 HSC Mathematics Solutions ( 6) ( ) ( ) ( ) π π. αβ = = 2. α β αβ. Question 1. (iii) 1 1 β + (a) (4 sig. fig.
 HS Mathmatics Solutios Qustio.778.78 ( sig. fig.) (b) (c) ( )( + ) + + + + d d (d) l ( ) () 8 6 (f) + + + + ( ) ( ) (iii) β + + α α β αβ 6 (b) si π si π π π +,π π π, (c) y + dy + d 8+ At : y + (,) dy 8(
HS Mathmatics Solutios Qustio.778.78 ( sig. fig.) (b) (c) ( )( + ) + + + + d d (d) l ( ) () 8 6 (f) + + + + ( ) ( ) (iii) β + + α α β αβ 6 (b) si π si π π π +,π π π, (c) y + dy + d 8+ At : y + (,) dy 8(
PhysicsAndMathsTutor.com
 PhysicsAdMthsTuto.com PhysicsAdMthsTuto.com Jue 009 7. () Sketch the gph of y, whee >, showig the coodites of the poits whee the gph meets the es. () Leve lk () Solve, >. (c) Fid the set of vlues of fo
PhysicsAdMthsTuto.com PhysicsAdMthsTuto.com Jue 009 7. () Sketch the gph of y, whee >, showig the coodites of the poits whee the gph meets the es. () Leve lk () Solve, >. (c) Fid the set of vlues of fo
Helping every little saver
 Spt th diffc d cut hw u c fid I c spt thigs! Hlpig v littl sv Hw d u p i? I ch Just pp it f u chs. T fid u lcl ch just visit s.c.uk/ch If u pig i chqu, it c tk ud 4 wkig ds t cl Ov th ph Just cll Tlph
Spt th diffc d cut hw u c fid I c spt thigs! Hlpig v littl sv Hw d u p i? I ch Just pp it f u chs. T fid u lcl ch just visit s.c.uk/ch If u pig i chqu, it c tk ud 4 wkig ds t cl Ov th ph Just cll Tlph
Order Statistics from Exponentiated Gamma. Distribution and Associated Inference
 It J otm Mth Scc Vo 4 9 o 7-9 Od Stttc fom Eottd Gmm Dtto d Aoctd Ifc A I Shw * d R A Bo G og of Edcto PO Bo 369 Jddh 438 Sd A G og of Edcto Dtmt of mthmtc PO Bo 469 Jddh 49 Sd A Atct Od tttc fom ottd
It J otm Mth Scc Vo 4 9 o 7-9 Od Stttc fom Eottd Gmm Dtto d Aoctd Ifc A I Shw * d R A Bo G og of Edcto PO Bo 369 Jddh 438 Sd A G og of Edcto Dtmt of mthmtc PO Bo 469 Jddh 49 Sd A Atct Od tttc fom ottd
19 Fourier Series and Practical Harmonic Analysis
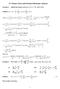 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Quantum Mechanics & Spectroscopy Prof. Jason Goodpaster. Problem Set #2 ANSWER KEY (5 questions, 10 points)
 Chm 5 Problm St # ANSWER KEY 5 qustios, poits Qutum Mchics & Spctroscopy Prof. Jso Goodpstr Du ridy, b. 6 S th lst pgs for possibly usful costts, qutios d itgrls. Ths will lso b icludd o our futur ms..
Chm 5 Problm St # ANSWER KEY 5 qustios, poits Qutum Mchics & Spctroscopy Prof. Jso Goodpstr Du ridy, b. 6 S th lst pgs for possibly usful costts, qutios d itgrls. Ths will lso b icludd o our futur ms..
and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform
![and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform and integrated over all, the result is f ( 0) ] //Fourier transform ] //inverse Fourier transform](/thumbs/90/103666297.jpg) NANO 70-Nots Chapt -Diactd bams Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio. Idal cystals a iiit this, so th will b som iiitis lii about. Usually, th iiit quatity oly ists
NANO 70-Nots Chapt -Diactd bams Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio. Idal cystals a iiit this, so th will b som iiitis lii about. Usually, th iiit quatity oly ists
SULIT 3472/2. Rumus-rumus berikut boleh membantu anda menjawab soalan. Simbol-simbol yang diberi adalah yang biasa digunakan.
 SULT 347/ Rumus-umus eikut oleh memtu d mejw sol. Simol-simol yg diei dlh yg is diguk. LGER. 4c x 5. log m log m log 9. T d. m m m 6. log = log m log 0. S d m m 3. 7. log m log m. S, m m logc 4. 8. log.
SULT 347/ Rumus-umus eikut oleh memtu d mejw sol. Simol-simol yg diei dlh yg is diguk. LGER. 4c x 5. log m log m log 9. T d. m m m 6. log = log m log 0. S d m m 3. 7. log m log m. S, m m logc 4. 8. log.
Integration by Guessing
 Itgrtio y Gussig Th computtios i two stdrd itgrtio tchiqus, Sustitutio d Itgrtio y Prts, c strmlid y th Itgrtio y Gussig pproch. This mthod cosists of thr stps: Guss, Diffrtit to chck th guss, d th Adjust
Itgrtio y Gussig Th computtios i two stdrd itgrtio tchiqus, Sustitutio d Itgrtio y Prts, c strmlid y th Itgrtio y Gussig pproch. This mthod cosists of thr stps: Guss, Diffrtit to chck th guss, d th Adjust
1985 AP Calculus BC: Section I
 985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
Instrumentation for Characterization of Nanomaterials (v11) 11. Crystal Potential
 Istumtatio o Chaactizatio o Naomatials (v). Cystal Pottial Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio om cystal. Idal cystals a iiit this, so th will b som iiitis lii
Istumtatio o Chaactizatio o Naomatials (v). Cystal Pottial Dlta uctio W d som mathmatical tools to dvlop a physical thoy o lcto diactio om cystal. Idal cystals a iiit this, so th will b som iiitis lii
Chapter 2 Infinite Series Page 1 of 11. Chapter 2 : Infinite Series
 Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Time : 1 hr. Test Paper 08 Date 04/01/15 Batch - R Marks : 120
 Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
CHAPTER 5d. SIMULTANEOUS LINEAR EQUATIONS
 CHAPTE 5. SIUTANEOUS INEA EQUATIONS A. J. Crk Schoo of Egirig Dprtmt of Civi Eviromt Egirig by Dr. Ibrhim A. Asskkf Sprig ENCE - Compttio thos i Civi Egirig II Dprtmt of Civi Eviromt Egirig Uivrsity of
CHAPTE 5. SIUTANEOUS INEA EQUATIONS A. J. Crk Schoo of Egirig Dprtmt of Civi Eviromt Egirig by Dr. Ibrhim A. Asskkf Sprig ENCE - Compttio thos i Civi Egirig II Dprtmt of Civi Eviromt Egirig Uivrsity of
PHY 309: QUANTUM MECHANICS I (3 UNITS) COURSE GUIDE
 PHY 9: QUANTUM MECHANICS I UNITS COURSE GUIDE I Qutu Mchics I PHY 9, you t bout th iqucis of Cssic Mchics th ffots by Physicists to ss th shotcoigs o th ptfo of Qutu Mchics. You hv t oo t th thtic foutio
PHY 9: QUANTUM MECHANICS I UNITS COURSE GUIDE I Qutu Mchics I PHY 9, you t bout th iqucis of Cssic Mchics th ffots by Physicists to ss th shotcoigs o th ptfo of Qutu Mchics. You hv t oo t th thtic foutio
Eigenfunction Expansion. For a given function on the internal a x b the eigenfunction expansion of f(x):
 Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
CLASS XI CHAPTER 3. Theorem 1 (sine formula) In any triangle, sides are proportional to the sines of the opposite angles. That is, in a triangle ABC
 CLSS XI ur I CHPTER.6. Proofs d Simpl pplictios of si d cosi formul Lt C b trigl. y gl w m t gl btw t sids d C wic lis btw 0 d 80. T gls d C r similrly dfid. T sids, C d C opposit to t vrtics C, d will
CLSS XI ur I CHPTER.6. Proofs d Simpl pplictios of si d cosi formul Lt C b trigl. y gl w m t gl btw t sids d C wic lis btw 0 d 80. T gls d C r similrly dfid. T sids, C d C opposit to t vrtics C, d will
UNIT I FOURIER SERIES T
 UNIT I FOURIER SERIES PROBLEM : Th urig mom T o h crkh o m gi i giv or ri o vu o h crk g dgr 6 9 5 8 T 5 897 785 599 66 Epd T i ri o i. Souio: L T = i + i + i +, Sic h ir d vu o T r rpd gc o T T i T i
UNIT I FOURIER SERIES PROBLEM : Th urig mom T o h crkh o m gi i giv or ri o vu o h crk g dgr 6 9 5 8 T 5 897 785 599 66 Epd T i ri o i. Souio: L T = i + i + i +, Sic h ir d vu o T r rpd gc o T T i T i
ریاضیات عالی پیشرفته
 ریاضیات عالی پیشرفته Numic Mthods o Enins مدرس دکتر پدرام پیوندی http://www.pdm-pyvndy.com ~ in Aic Equtions ~ Guss Eimintion Chpt 9 http://numicmthods.n.us.du Sovin Systms o Equtions A in qution in n
ریاضیات عالی پیشرفته Numic Mthods o Enins مدرس دکتر پدرام پیوندی http://www.pdm-pyvndy.com ~ in Aic Equtions ~ Guss Eimintion Chpt 9 http://numicmthods.n.us.du Sovin Systms o Equtions A in qution in n
DRAFT. Formulae and Statistical Tables for A-level Mathematics SPECIMEN MATERIAL. First Issued September 2017
 Fist Issued Septembe 07 Fo the ew specifictios fo fist techig fom Septembe 07 SPECIMEN MATERIAL Fomule d Sttisticl Tbles fo A-level Mthemtics AS MATHEMATICS (7356) A-LEVEL MATHEMATICS (7357) AS FURTHER
Fist Issued Septembe 07 Fo the ew specifictios fo fist techig fom Septembe 07 SPECIMEN MATERIAL Fomule d Sttisticl Tbles fo A-level Mthemtics AS MATHEMATICS (7356) A-LEVEL MATHEMATICS (7357) AS FURTHER
Who is this Great Team? Nickname. Strangest Gift/Friend. Hometown. Best Teacher. Hobby. Travel Destination. 8 G People, Places & Possibilities
 Who i thi Gt Tm? Exi Sh th foowing i of infomtion bot of with o tb o tm mt. Yo o not hv to wit n of it own. Yo wi b givn on 5 mint to omih thi tk. Stngt Gift/Fin Niknm Homtown Bt Th Hobb Tv Dtintion Robt
Who i thi Gt Tm? Exi Sh th foowing i of infomtion bot of with o tb o tm mt. Yo o not hv to wit n of it own. Yo wi b givn on 5 mint to omih thi tk. Stngt Gift/Fin Niknm Homtown Bt Th Hobb Tv Dtintion Robt
MA6351-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES. Department of Mathematics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY
 MA635-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES Deprtmet of Mthemtics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY MADURAI 65, Tmildu, Idi Bsic Formule DIFFERENTIATION &INTEGRATION
MA635-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES Deprtmet of Mthemtics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY MADURAI 65, Tmildu, Idi Bsic Formule DIFFERENTIATION &INTEGRATION
PREPARATORY MATHEMATICS FOR ENGINEERS
 CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
The Reign of Grace and Life. Romans 5:12-21 (5:12-14, 17 focus)
 Th Rig of Gc d Lif Rom 5:12-21 (5:12-14, 17 focu) Th Ifluc of O h d ud Adolph H J o ph Smith B i t l m t Fid Idi Gdhi Ci Lu Gu ich N itz y l M d i M ch Nlo h Vig T L M uhmmd B m i o t T Ju Chit w I N h
Th Rig of Gc d Lif Rom 5:12-21 (5:12-14, 17 focu) Th Ifluc of O h d ud Adolph H J o ph Smith B i t l m t Fid Idi Gdhi Ci Lu Gu ich N itz y l M d i M ch Nlo h Vig T L M uhmmd B m i o t T Ju Chit w I N h
Advanced Higher Maths: Formulae
 : Fomule Gee (G): Fomule you bsolutely must memoise i ode to pss Advced Highe mths. Remembe you get o fomul sheet t ll i the em! Ambe (A): You do t hve to memoise these fomule, s it is possible to deive
: Fomule Gee (G): Fomule you bsolutely must memoise i ode to pss Advced Highe mths. Remembe you get o fomul sheet t ll i the em! Ambe (A): You do t hve to memoise these fomule, s it is possible to deive
TWO MARKS WITH ANSWER
 TWO MARKS WITH ANSWER MA65/TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS REGULATION: UNIT I PARTIAL DIFFERENTIAL EQUATIONS Formtio o rti dirti utio Sigur itgr -- Soutio o tdrd t o irt ordr rti dirti utio
TWO MARKS WITH ANSWER MA65/TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS REGULATION: UNIT I PARTIAL DIFFERENTIAL EQUATIONS Formtio o rti dirti utio Sigur itgr -- Soutio o tdrd t o irt ordr rti dirti utio
Generating Function for Partitions with Parts in A.P
 Geetig Fuctio fo Ptitio wi Pt i AP Hum Reddy K # K Jkmm * # Detmet of Memtic Hidu Coege Gutu 50 AP Idi * Detmet of Memtic 8 Mi AECS Lyout B BLOCK Sigd Bgoe 5604 Idi Abtct: I i e we deive e geetig fuctio
Geetig Fuctio fo Ptitio wi Pt i AP Hum Reddy K # K Jkmm * # Detmet of Memtic Hidu Coege Gutu 50 AP Idi * Detmet of Memtic 8 Mi AECS Lyout B BLOCK Sigd Bgoe 5604 Idi Abtct: I i e we deive e geetig fuctio
BRAIN TEASURES INDEFINITE INTEGRATION+DEFINITE INTEGRATION EXERCISE I
 EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
Some Common Fixed Point Theorems for a Pair of Non expansive Mappings in Generalized Exponential Convex Metric Space
 Mish Kumr Mishr D.B.OhU Ktoch It. J. Comp. Tch. Appl. Vol ( 33-37 Som Commo Fi Poit Thorms for Pir of No psiv Mppigs i Grliz Epotil Cov Mtric Spc D.B.Oh Mish Kumr Mishr U Ktoch (Rsrch scholr Drvii Uivrsit
Mish Kumr Mishr D.B.OhU Ktoch It. J. Comp. Tch. Appl. Vol ( 33-37 Som Commo Fi Poit Thorms for Pir of No psiv Mppigs i Grliz Epotil Cov Mtric Spc D.B.Oh Mish Kumr Mishr U Ktoch (Rsrch scholr Drvii Uivrsit
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
82A Engineering Mathematics
 Clss Notes 9: Power Series /) 8A Egieerig Mthetics Secod Order Differetil Equtios Series Solutio Solutio Ato Differetil Equtio =, Hoogeeous =gt), No-hoogeeous Solutio: = c + p Hoogeeous No-hoogeeous Fudetl
Clss Notes 9: Power Series /) 8A Egieerig Mthetics Secod Order Differetil Equtios Series Solutio Solutio Ato Differetil Equtio =, Hoogeeous =gt), No-hoogeeous Solutio: = c + p Hoogeeous No-hoogeeous Fudetl
Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics
 Peso Edecel Level Advced Subsidiy d Advced GCE Mthemtics d Futhe Mthemtics Mthemticl fomule d sttisticl tbles Fo fist cetifictio fom Jue 08 fo: Advced Subsidiy GCE i Mthemtics (8MA0) Advced GCE i Mthemtics
Peso Edecel Level Advced Subsidiy d Advced GCE Mthemtics d Futhe Mthemtics Mthemticl fomule d sttisticl tbles Fo fist cetifictio fom Jue 08 fo: Advced Subsidiy GCE i Mthemtics (8MA0) Advced GCE i Mthemtics
Chapter 11 Solutions ( ) 1. The wavelength of the peak is. 2. The temperature is found with. 3. The power is. 4. a) The power is
 Chapt Solutios. Th wavlgth of th pak is pic 3.898 K T 3.898 K 373K 885 This cospods to ifad adiatio.. Th tpatu is foud with 3.898 K pic T 3 9.898 K 50 T T 5773K 3. Th pow is 4 4 ( 0 ) P σ A T T ( ) ( )
Chapt Solutios. Th wavlgth of th pak is pic 3.898 K T 3.898 K 373K 885 This cospods to ifad adiatio.. Th tpatu is foud with 3.898 K pic T 3 9.898 K 50 T T 5773K 3. Th pow is 4 4 ( 0 ) P σ A T T ( ) ( )
IIT JEE MATHS MATRICES AND DETERMINANTS
 IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
(HELD ON 22nd MAY SUNDAY 2016) MATHEMATICS CODE - 2 [PAPER -2]
![(HELD ON 22nd MAY SUNDAY 2016) MATHEMATICS CODE - 2 [PAPER -2] (HELD ON 22nd MAY SUNDAY 2016) MATHEMATICS CODE - 2 [PAPER -2]](/thumbs/93/113007992.jpg) QUESTION PAPER WITH SOLUTION OF JEE ADVANCED - 6 7. Lt P (HELD ON d MAY SUNDAY 6) FEEL THE POWER OF OUR KNOWLEDGE & EXPERIENCE Our Top clss IITi fculty tm promiss to giv you uthtic swr ky which will b
QUESTION PAPER WITH SOLUTION OF JEE ADVANCED - 6 7. Lt P (HELD ON d MAY SUNDAY 6) FEEL THE POWER OF OUR KNOWLEDGE & EXPERIENCE Our Top clss IITi fculty tm promiss to giv you uthtic swr ky which will b
2. Fourier Series, Fourier Integrals and Fourier Transforms
 Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Time: 2 hours IIT-JEE 2006-MA-1. Section A (Single Option Correct) + is (A) 0 (B) 1 (C) 1 (D) 2. lim (sin x) + x 0. = 1 (using L Hospital s rule).
 IIT-JEE 6-MA- FIITJEE Solutios to IITJEE 6 Mthemtics Time: hours Note: Questio umber to crries (, -) mrks ech, to crries (5, -) mrks ech, to crries (5, -) mrks ech d to crries (6, ) mrks ech.. For >, lim
IIT-JEE 6-MA- FIITJEE Solutios to IITJEE 6 Mthemtics Time: hours Note: Questio umber to crries (, -) mrks ech, to crries (5, -) mrks ech, to crries (5, -) mrks ech d to crries (6, ) mrks ech.. For >, lim
PURE MATHEMATICS A-LEVEL PAPER 1
 -AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
-AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
Advanced Higher Maths: Formulae
 Advced Highe Mths: Fomule Advced Highe Mthemtics Gee (G): Fomule you solutely must memoise i ode to pss Advced Highe mths. Rememe you get o fomul sheet t ll i the em! Ame (A): You do t hve to memoise these
Advced Highe Mths: Fomule Advced Highe Mthemtics Gee (G): Fomule you solutely must memoise i ode to pss Advced Highe mths. Rememe you get o fomul sheet t ll i the em! Ame (A): You do t hve to memoise these
Chapter 6 Perturbation theory
 Ct 6 Ptutio to 6. Ti-iddt odgt tutio to i o tutio sst is giv to fid solutios of λ ' ; : iltoi of si stt : igvlus of : otool igfutios of ; δ ii Rlig-Södig tutio to ' λ..6. ; : gl iltoi ': tutio λ : sll
Ct 6 Ptutio to 6. Ti-iddt odgt tutio to i o tutio sst is giv to fid solutios of λ ' ; : iltoi of si stt : igvlus of : otool igfutios of ; δ ii Rlig-Södig tutio to ' λ..6. ; : gl iltoi ': tutio λ : sll
ALGEBRA. ( ) is a point on the line ( ) + ( ) = + ( ) + + ) + ( Distance Formula The distance d between two points x, y
 ALGEBRA Popeties of Asoute Vue Fo e umes : 0, 0 + + Tige Iequity Popeties of Itege Epoets Ris Assume tt m e positive iteges, tt e oegtive, tt eomitos e ozeo. See Appeies B D fo gps fute isussio. + ( )
ALGEBRA Popeties of Asoute Vue Fo e umes : 0, 0 + + Tige Iequity Popeties of Itege Epoets Ris Assume tt m e positive iteges, tt e oegtive, tt eomitos e ozeo. See Appeies B D fo gps fute isussio. + ( )
EXERCISE - 01 CHECK YOUR GRASP
 DEFNTE NTEGRATON EXERCSE - CHECK YOUR GRASP. ( ) d [ ] d [ ] d d ƒ( ) ƒ '( ) [ ] [ ] 8 5. ( cos )( c)d 8 ( cos )( c)d + 8 ( cos )( c) d 8 ( cos )( c) d sic + cos 8 is lwys posiiv f() d ( > ) ms f() is
DEFNTE NTEGRATON EXERCSE - CHECK YOUR GRASP. ( ) d [ ] d [ ] d d ƒ( ) ƒ '( ) [ ] [ ] 8 5. ( cos )( c)d 8 ( cos )( c)d + 8 ( cos )( c) d 8 ( cos )( c) d sic + cos 8 is lwys posiiv f() d ( > ) ms f() is
February 12 th December 2018
 208 Fbu 2 th Dcb 208 Whgt Fbu Mch M 2* 3 30 Ju Jul Sptb 4* 5 7 9 Octob Novb Dcb 22* 23 Put ou blu bgs out v d. *Collctios d lt du to Public Holid withi tht wk. Rcclig wk is pik Rcclig wk 2 is blu Th stick
208 Fbu 2 th Dcb 208 Whgt Fbu Mch M 2* 3 30 Ju Jul Sptb 4* 5 7 9 Octob Novb Dcb 22* 23 Put ou blu bgs out v d. *Collctios d lt du to Public Holid withi tht wk. Rcclig wk is pik Rcclig wk 2 is blu Th stick
1. (25 points) Use the limit definition of the definite integral and the sum formulas to compute. [1 x + x2
 Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
MA6351 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C
 MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit
MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit
07 - SEQUENCES AND SERIES Page 1 ( Answers at he end of all questions ) b, z = n
 07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
ADORO TE DEVOTE (Godhead Here in Hiding) te, stus bat mas, la te. in so non mor Je nunc. la in. tis. ne, su a. tum. tas: tur: tas: or: ni, ne, o:
 R TE EVTE (dhd H Hdg) L / Mld Kbrd gú s v l m sl c m qu gs v nns V n P P rs l mul m d lud 7 súb Fí cón ví f f dó, cru gs,, j l f c r s m l qum t pr qud ct, us: ns,,,, cs, cut r l sns m / m fí hó sn sí
R TE EVTE (dhd H Hdg) L / Mld Kbrd gú s v l m sl c m qu gs v nns V n P P rs l mul m d lud 7 súb Fí cón ví f f dó, cru gs,, j l f c r s m l qum t pr qud ct, us: ns,,,, cs, cut r l sns m / m fí hó sn sí
CITY UNIVERSITY LONDON
 CITY UNIVERSITY LONDON Eg (Hos) Degree i Civil Egieerig Eg (Hos) Degree i Civil Egieerig with Surveyig Eg (Hos) Degree i Civil Egieerig with Architecture PART EXAMINATION SOLUTIONS ENGINEERING MATHEMATICS
CITY UNIVERSITY LONDON Eg (Hos) Degree i Civil Egieerig Eg (Hos) Degree i Civil Egieerig with Surveyig Eg (Hos) Degree i Civil Egieerig with Architecture PART EXAMINATION SOLUTIONS ENGINEERING MATHEMATICS
n 2 + 3n + 1 4n = n2 + 3n + 1 n n 2 = n + 1
 Ifiite Series Some Tests for Divergece d Covergece Divergece Test: If lim u or if the limit does ot exist, the series diverget. + 3 + 4 + 3 EXAMPLE: Show tht the series diverges. = u = + 3 + 4 + 3 + 3
Ifiite Series Some Tests for Divergece d Covergece Divergece Test: If lim u or if the limit does ot exist, the series diverget. + 3 + 4 + 3 EXAMPLE: Show tht the series diverges. = u = + 3 + 4 + 3 + 3
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
x a y n + b = 1 0<b a, n > 0 (1.1) x 1 - a y = b 0<b a, n > 0 (1.1') b n sin 2 + cos 2 = 1 x n = = cos 2 6 Superellipse (Lamé curve)
 6 Supeellipse (Lmé cuve) 6. Equtios of supeellipse A supeellipse (hoizotlly log) is epessed s follows. Implicit Equtio y + b 0 0 (.) Eplicit Equtio y b - 0 0 (.') Whe 3, b, the supeellipses fo
6 Supeellipse (Lmé cuve) 6. Equtios of supeellipse A supeellipse (hoizotlly log) is epessed s follows. Implicit Equtio y + b 0 0 (.) Eplicit Equtio y b - 0 0 (.') Whe 3, b, the supeellipses fo
C-Curves. An alternative to the use of hyperbolic decline curves S E R A F I M. Prepared by: Serafim Ltd. P. +44 (0)
 An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
Today s topic 2 = Setting up the Hydrogen Atom problem. Schematic of Hydrogen Atom
 Today s topic Sttig up th Hydog Ato pobl Hydog ato pobl & Agula Motu Objctiv: to solv Schödig quatio. st Stp: to dfi th pottial fuctio Schatic of Hydog Ato Coulob s aw - Z 4ε 4ε fo H ato Nuclus Z What
Today s topic Sttig up th Hydog Ato pobl Hydog ato pobl & Agula Motu Objctiv: to solv Schödig quatio. st Stp: to dfi th pottial fuctio Schatic of Hydog Ato Coulob s aw - Z 4ε 4ε fo H ato Nuclus Z What
3.1 Laplace s Equation 3.2 The Method of Images 3.3 Separation of Variables
 Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the
Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the
Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics
 Peso Edecel Level 3 Advced Subsidiy d Advced GCE Mthemtics d Futhe Mthemtics Mthemticl fomule d sttisticl tbles Fo fist cetifictio fom Jue 08 fo: Advced Subsidiy GCE i Mthemtics (8MA0) Advced GCE i Mthemtics
Peso Edecel Level 3 Advced Subsidiy d Advced GCE Mthemtics d Futhe Mthemtics Mthemticl fomule d sttisticl tbles Fo fist cetifictio fom Jue 08 fo: Advced Subsidiy GCE i Mthemtics (8MA0) Advced GCE i Mthemtics
y udv uv y v du 7.1 INTEGRATION BY PARTS
 7. INTEGRATION BY PARTS Ever differetitio rule hs correspodig itegrtio rule. For istce, the Substitutio Rule for itegrtio correspods to the Chi Rule for differetitio. The rule tht correspods to the Product
7. INTEGRATION BY PARTS Ever differetitio rule hs correspodig itegrtio rule. For istce, the Substitutio Rule for itegrtio correspods to the Chi Rule for differetitio. The rule tht correspods to the Product
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
D. Bertsekas and R. Gallager, "Data networks." Q: What are the labels for the x-axis and y-axis of Fig. 4.2?
 pd by J. Succ ECE 543 Octob 22 2002 Outl Slottd Aloh Dft Stblzd Slottd Aloh Uslottd Aloh Splttg Algoths Rfc D. Btsks d R. llg "Dt twoks." Rvw (Slottd Aloh): : Wht th lbls fo th x-xs d y-xs of Fg. 4.2?
pd by J. Succ ECE 543 Octob 22 2002 Outl Slottd Aloh Dft Stblzd Slottd Aloh Uslottd Aloh Splttg Algoths Rfc D. Btsks d R. llg "Dt twoks." Rvw (Slottd Aloh): : Wht th lbls fo th x-xs d y-xs of Fg. 4.2?
Galaxy Photometry. Recalling the relationship between flux and luminosity, Flux = brightness becomes
 Galaxy Photomty Fo galaxis, w masu a sufac flux, that is, th couts i ach pixl. Though calibatio, this is covtd to flux dsity i Jaskys ( Jy -6 W/m/Hz). Fo a galaxy at som distac, d, a pixl of sid D subtds
Galaxy Photomty Fo galaxis, w masu a sufac flux, that is, th couts i ach pixl. Though calibatio, this is covtd to flux dsity i Jaskys ( Jy -6 W/m/Hz). Fo a galaxy at som distac, d, a pixl of sid D subtds
Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics
 Peso Edecel Level Advced Subsidiy d Advced GCE Mthemtics d Futhe Mthemtics Mthemticl fomule d sttisticl tbles Fo fist cetifictio fom Jue 08 fo: Advced Subsidiy GCE i Mthemtics (8MA0) Advced GCE i Mthemtics
Peso Edecel Level Advced Subsidiy d Advced GCE Mthemtics d Futhe Mthemtics Mthemticl fomule d sttisticl tbles Fo fist cetifictio fom Jue 08 fo: Advced Subsidiy GCE i Mthemtics (8MA0) Advced GCE i Mthemtics
Chapter 9 Infinite Series
 Sctio 9. 77. Cotiud d + d + C Ar lim b lim b b b + b b lim + b b lim + b b 6. () d (b) lim b b d (c) Not tht d c b foud by prts: d ( ) ( ) d + C. b Ar b b lim d lim b b b b lim ( b + ). b dy 7. () π dy
Sctio 9. 77. Cotiud d + d + C Ar lim b lim b b b + b b lim + b b lim + b b 6. () d (b) lim b b d (c) Not tht d c b foud by prts: d ( ) ( ) d + C. b Ar b b lim d lim b b b b lim ( b + ). b dy 7. () π dy
ANSWER KEY PHYSICS. Workdone X
 ANSWER KEY PHYSICS 6 6 6 7 7 7 9 9 9 0 0 0 CHEMISTRY 6 6 6 7 7 7 9 9 9 0 0 60 MATHEMATICS 6 66 7 76 6 6 67 7 77 7 6 6 7 7 6 69 7 79 9 6 70 7 0 90 PHYSICS F L l. l A Y l A ;( A R L L A. W = (/ lod etesio
ANSWER KEY PHYSICS 6 6 6 7 7 7 9 9 9 0 0 0 CHEMISTRY 6 6 6 7 7 7 9 9 9 0 0 60 MATHEMATICS 6 66 7 76 6 6 67 7 77 7 6 6 7 7 6 69 7 79 9 6 70 7 0 90 PHYSICS F L l. l A Y l A ;( A R L L A. W = (/ lod etesio
ME 501A Seminar in Engineering Analysis Page 1
 Fobeius ethod pplied to Bessel s Equtio Octobe, 7 Fobeius ethod pplied to Bessel s Equtio L Cetto Mechicl Egieeig 5B Sei i Egieeig lsis Octobe, 7 Outlie Review idte Review lst lectue Powe seies solutios/fobeius
Fobeius ethod pplied to Bessel s Equtio Octobe, 7 Fobeius ethod pplied to Bessel s Equtio L Cetto Mechicl Egieeig 5B Sei i Egieeig lsis Octobe, 7 Outlie Review idte Review lst lectue Powe seies solutios/fobeius
MATH 174: Numerical Analysis. Lecturer: Jomar F. Rabajante 1 st Sem AY
 MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
