Vtusolution.in FOURIER SERIES. Dr.A.T.Eswara Professor and Head Department of Mathematics P.E.S.College of Engineering Mandya
|
|
|
- Ira Lyons
- 5 years ago
- Views:
Transcription
1 LECTURE NOTES OF ENGINEERING MATHEMATICS III Su Cod: MAT) Vtusoutio.i COURSE CONTENT ) Numric Aysis ) Fourir Sris ) Fourir Trsforms & Z-trsforms ) Prti Diffrti Equtios 5) Lir Agr 6) Ccuus of Vritios Tt Book: Highr Egirig Mthmtics y Dr. B.S.Grw 6th Editio ) Kh Puishrs,Nw Dhi Rfrc Book: Advcd Egirig Mthmtics y E. Kryszig 8th Editio ) Joh Wiy & Sos, INC. Nw York DEFINITIONS : FOURIER SERIES Dr.A.T.Eswr Profssor d Hd Dprtmt of Mthmtics P.E.S.Cog of Egirig Mdy -57 A fuctio y = f) is sid to v, if f-) = f). Th grph of th v fuctio is wys symmtric out th y-is. A fuctio y=f) is sid to odd, if f-) = - f). Th grph of th odd fuctio is wys symmtric out th origi. Vtusoutio.i For mp, th fuctio f) = i [-,] is v s f-) = = f) d th fuctio f) = i [-,] is odd s f-) = - = -f). Th grphs of ths fuctios r show ow : Vtusoutio.i
2 Vtusoutio.i Grph of f) = Grph of f) = Not tht th grph of f) = is symmtric out th y-is d th grph of f) = is symmtric out th origi.. If f) is v d g) is odd, th h) = f) g) is odd h) = f) f) is v h) = g) g) is v For mp,. h) = cos is v, sic oth d cos r v fuctios. h) = si is v, sic d si r odd fuctios. h) = si is odd, sic is v d si is odd.. If f) is v, th. If f) is odd, th f ) d f ) d Vtusoutio.i For mp, d f ) d cos d cosd, s cos is v si d, s si is odd Vtusoutio.i
3 PERIODIC FUNCTIONS :- A priodic fuctio hs sic shp which Vtusoutio.i is rptd ovr d ovr gi. Th fudmt rg is th tim or somtims distc) ovr which th sic shp is dfid. Th gth of th fudmt rg is cd th priod. A gr priodic fuctio f) of priod T stisfis th coditio f+t) = f) Hr f) is r-vud fuctio d T is positiv r umr. As cosquc, it foows tht f) = f+t) = f+t) = f+t) =.. = f+t) Thus, f) = f+t), =,,,.. Th fuctio f) = si is priodic of priod sic Si+ ) = si, =,,,.. Th grph of th fuctio is show ow : Not tht th grph of th fuctio tw d is th sm s tht tw d d so o. It my vrifid tht ir comitio of priodic fuctios is so priodic. Vtusoutio.i FOURIER SERIES A Fourir sris of priodic fuctio cosists of sum of si d cosi trms. Sis d cosis r th most fudmt priodic fuctios. Th Fourir sris is md ftr th Frch Mthmtici d Physicist Jcqus Fourir 768 8). Fourir sris hs its ppictio i proms prtiig to Ht coductio, coustics, tc. Th sujct mttr my dividd ito th foowig su topics. Vtusoutio.i
4 FOURIER SERIES Vtusoutio.i Sris with ritrry priod FORMULA FOR FOURIER SERIES Cosidr r-vud fuctio f) which oys th foowig coditios cd Diricht s coditios :. f) is dfid i itrv,+), d f+) = f) so tht f) is priodic fuctio of priod.. f) is cotiuous or hs oy fiit umr of discotiuitis i th itrv,+).. f) hs o or oy fiit umr of mim or miim i th itrv,+). Aso, t Hf-rg sris Comp sris Hrmoic Aysis f ) d f )cos f )si d, d, Vtusoutio.i ),,,... ),,,... ) Th, th ifiit sris cos si ) is cd th Fourir sris of f) i th itrv,+). Aso, th r umrs,,,., d,,. r cd th Fourir cofficits of f). Th formu ), ) d ) r cd Eur s formu. It c provd tht th sum of th sris ) is f) if f) is cotiuous t. Thus w hv f) = cos si. 5) Suppos f) is discotiuous t, th th sum of th sris ) woud f ) f ) whr f + ) d f - ) r th vus of Vtusoutio.i f) immdity to th right d to th ft of f) rspctivy.
5 Prticur Css Cs i) Suppos =. Th f) is dfid ovr Vtusoutio.i th itrv,). Formu ), ), ) rduc to f ) d f )cos f )si d, d,,,... 6) Th th right-hd sid of 5) is th Fourir psio of f) ovr th itrv,). If w st =, th f) is dfid ovr th itrv, ). Formu 6) rduc to Aso, i this cs, 5) coms Cs ii) = f ) d f )cosd, =,,.. 7) f )sid =,,.. f) = cos si Suppos =-. Th f) is dfid ovr th itrv -, ). Formu ), ) ) rduc to f )cos d Vtusoutio.i f ) d 8) =,, 9) f )si d, Th th right-hd sid of 5) is th Fourir psio of f) ovr th itrv -, ). =,, If w st =, th f) is dfid ovr th itrv -, ). Formu 9) rduc to = f ) d Vtusoutio.i
6 f ) cosd, =,,.. ) Vtusoutio.i f ) sid =,,.. Puttig = PARTIAL SUMS i 5), w gt f) = cos si Th Fourir sris givs th ct vu of th fuctio. It uss ifiit umr of trms which is impossi to ccut. Howvr, w c fid th sum through th prti sum S N dfid s foows : N SN ) cos si whr N tks positiv itgr vus. I prticur, th prti sums for N=, r S ) cos si S ) cos si cos si If w drw th grphs of prti sums d compr ths with th grph of th origi fuctio f), it my vrifid tht S N ) pproimts f) for som rg N. Som usfu rsuts :. Th foowig ru cd Broui s grizd ru of itgrtio y prts is usfu i vutig th Fourir cofficits. ' '' uvd uv u v u... Hr u, u v,.. r th succssiv drivtivs of u d Vtusoutio.i v vd, v vd,... W iustrt th ru, through th foowig mps : cos si cos sid d Th foowig itgrs r so usfu : Vtusoutio.i
7 cosd sid cos si Vtusoutio.i si cos. If is itgr, th si =, cos = -), si =, cos = Emps. Oti th Fourir psio of W hv, f) = i - < < f ) d ) d = f )cosd Hr w us itgrtio y prts, so tht si cos ) ) cosd cos si Vtusoutio.i ) )sid Usig th vus of, d i th Fourir psio ) w gt, f ) cos si Vtusoutio.i
8 ) f ) si Vtusoutio.i This is th rquird Fourir psio of th giv fuctio.. Oti th Fourir psio of f)= - i th itrv -, ). Dduc tht Hr, cosch = d ) sih ) sih cosd sid cos si = si cos ) sih = Thus, sih sih f) = For =, =, th sris rducs to sih sih f)= = cos sih si Vtusoutio.i ) ) ) or = sih sih ) Vtusoutio.i
9 sih or = Thus, cosch ) Vtusoutio.i ) This is th dsird dductio.. Oti th Fourir psio of f) = ovr th itrv -, ). Dduc tht... 6 Th fuctio f) is v. Hc = f ) d= or = d = = Itgrtig y prts, w gt ) f ) cosd f ) d f )cosd, sic f)cos is v cosd si cos si Vtusoutio.i Aso, f )sid sic f)si is odd. Thus Vtusoutio.i
10 f ) 6 ) cos Hc, Oti th Fourir psio of, f ), Dduc tht 8 5 Th grph of f) is show ow. Hr, = f ) d=... Hr OA rprsts th i f)=, AB rprsts th i f)= -) d AC rprsts th i =. Not tht th grph is symmtric out th i AC, which i tur is pr to y-is. Hc th fuctio f) is v fuctio. f ) d Vtusoutio.i = d f )cosd cosd Vtusoutio.i f )cosd sic f)cos is v. Vtusoutio.i
11 si cos = Vtusoutio.i ) Aso, f )sid, sic f)si is odd Thus th Fourir sris of f) is For =, w gt or Thus, f ) ) cos f ) ) cos cos ) ) 8 ) or This is th sris s rquird. 5. Oti th Fourir psio of, f) =, Dduc tht 8 5 Hr,... Vtusoutio.i d d ) cosd cosd Vtusoutio.i
12 sid sid Vtusoutio.i ) Fourir sris is ) f) = ) cos si Not tht th poit = is poit of discotiuity of f). Hr f + ) =, f - )=- t =. Hc [ f ) f )] Th Fourir psio of f) t = coms [ ) ] Simpifyig w gt, or 8 [ 5 ) Oti th Fourir sris of f) = - ovr th itrv -,). Th giv fuctio is v, s f-) = f). Aso priod of f) is --)= Hr = = ] f ) d= f ) d ) d Vtusoutio.i = Itgrtig y prts, w gt f )cos f )cos ) d ) d ) cos ) d s f) cos ) is v si ) Vtusoutio.i cos ) ) si )
13 ) Vtusoutio.i f )si ) d =, sic f)si ) is odd. = Th Fourir sris of f) is f) = 7. Oti th Fourir psio of i f) = i Dduc tht 8 ) cos ) 5... Th priod of f) is Aso f-) = f). Hc f) is v Aso, / Vtusoutio.i = / / / / / / / / f ) d d si / f )cos d / f )cos d / ) f ) d Vtusoutio.i cos /
14 f )si Vtusoutio.i d Thus f) = puttig =, w gt f) = ) ) 8 or =... 5 Thus, NOTE cos Hr vrify th vidity of Fourir psio through prti sums y cosidrig mp. W rc tht th Fourir psio of f) = ovr -, ) is ) cos f ) Lt us dfi N ) cos SN ) Th prti sums corrspodig to N =,,..6 S ) S ) r cos cos cos S6 ) cos cos cos cos cos5 cos Th grphs of S, S, S 6 gist th grph of f) = r pottd idividuy d show ow : Vtusoutio.i Vtusoutio.i
15 Vtusoutio.i O compriso, w fid tht th grph of f) = coicids with tht of S 6 ). This vrifis th vidity of Fourir psio for th fuctio cosidrd. Ercis Chck for th vidity of Fourir psio through prti sums og with rvt grphs for othr mps so. HALF-RANGE FOURIER SERIES Th Fourir psio of th priodic fuctio f) of priod my coti oth si d cosi trms. My tim it is rquird to oti th Fourir psio of f) i th itrv,) which is rgrdd s hf itrv. Th dfiitio c tdd to th othr hf i such mr tht th fuctio coms v or odd. This wi rsut i cosi sris or si sris oy. Si sris : Suppos f) = ) is giv i th itrv,). Th w dfi f) = - -) i -,). Hc f) coms odd fuctio i -, ). Th Fourir sris th is Vtusoutio.i f ) si ) whr f )si d Th sris ) is cd hf-rg si sris ovr,). Puttig = i ), w oti th hf-rg Vtusoutio.i si sris of f) ovr, ) giv y
16 f ) si Vtusoutio.i Cosi sris : Lt us dfi f ) f )sid i,)... giv i -,)..i ordr to mk th fuctio v. Th th Fourir sris of f) is giv y f ) cos ) whr, f ) d f )cos Th sris ) is cd hf-rg cosi sris ovr,) Puttig = Emps : i ), w gt d Vtusoutio.i. Epd f) = -) s hf-rg si sris ovr th itrv, ). W hv, f ) whr Itgrtig y prts, w gt f )sid )sid ) f ) d ) cos f )cosd,,,.. Vtusoutio.i
17 Th si sris of f) is f ). Oti th cosi sris of Hr d ) cos si Vtusoutio.i ) si, f ) ovr, ), cosd ) d )cosd Prformig itgrtio y prts d simpifyig, w gt ) cos 8,,6,,... Thus, th Fourir cosi sris is cos cos6 cos f) =... 5 cos Vtusoutio.i. Oti th hf-rg cosi sris of f) = c- i <<c Hr c c ) d c c )cos d c c Itgrtig y prts d simpifyig w gt, c c Vtusoutio.i )
18 c ) Th cosi sris is giv y Vtusoutio.i Ercics: f) = c c ) cos c Oti th Fourir sris of th foowig fuctios ovr th spcifid itrvs :. f) = ovr -, ). f) = + ovr -, ). f) = ovr, ). f) = ovr -, ) ; Dduc tht f) = ovr -, ) ; Dduc tht... 8, 6. f) = ovr -, ), Dduc tht... 8, 7. f) =,, ovr -, ) Dduc tht f) = si ovr ; Dduc tht 9. f) =,, ovr -, ). f) = -) ovr,). f) = ovr -,). f) =, ), Vtusoutio.i Vtusoutio.i
19 Oti th hf-rg si sris of th foowig fuctios ovr th spcifid itrvs :. f) = cos ovr, ). f) = si ovr, ) 5. f) = - ovr, ) Vtusoutio.i Oti th hf-rg cosi sris of th foowig fuctios ovr th spcifid itrvs : 6. f) = ovr, ) 7. f) = si ovr, ) 8. f) = -) ovr,) 9. f) = k, k ), HARMONIC ANALYSIS Th Fourir sris of kow fuctio f) i giv itrv my foud y fidig th Fourir cofficits. Th mthod dscrid cot mpoyd wh f) is ot kow picity, ut dfid through th vus of th fuctio t som quidistt poits. I such cs, th itgrs i Eur s formu cot vutd. Hrmoic ysis is th procss of fidig th Fourir cofficits umricy. To driv th rvt formu for Fourir cofficits i Hrmoic ysis, w mpoy th foowig rsut : Th m vu of cotiuous fuctio f) ovr th itrv,) dotd y [f)] is dfid s f ) f ) d. Th Fourir cofficits dfid through Eur s formu, ), ), ) my rdfid s f ) d f )cos Vtusoutio.i f )si [ f )] d d f )cos f )si Usig ths i 5), w oti th Fourir sris of f). Th trm cos+ si is cd th first hrmoic or fudmt hrmoic, th trm cos+ si is cd th scod hrmoic d so o. Th mpitud of th first hrmoic is hrmoic is d so o. Vtusoutio.i d tht of scod
20 Emps. Fid th first two hrmoics of th Fourir sris of f) giv th foowig t : Vtusoutio.i Vtusoutio.i 5 f) Not tht th vus of y = f) r sprd ovr th itrv d f) = f ) =.. Hc th fuctio is priodic d so w omit th st vu f ) =. W prpr th foowig t to comput th first two hrmoics. y = f) cos cos si si ycos W hv Puttig, =,, w gt f )cos f )si [ ycos] [ ycos] [ y cos] [ ysi] ycos.) 6 6 ycos.) Vtusoutio.i 6 6 s th gth of itrv= = or =.67. ycos ysi. ysi Tot
21 ysi [ ysi ].9 6 Vtusoutio.i ysi [ ysi] Th first two hrmoics r cos+ si d cos+ si. Tht is -.67cos +.9 si) d -.cos.577si). Eprss y s Fourir sris upto th third hrmoic giv th foowig vus : 5 y Th vus of y t =,,,,,5 r giv d hc th itrv of shoud gth of th itrv = 6- = 6, so tht = 6 or =. Th Fourir sris upto th third hrmoic is or y cos si cos si cos < 6. Th si y cos si cos si cos si Put, th y cos si cos si cos si ) W prpr th foowig t usig th giv vus : = y ycos ycos ycos ysi ysi ysi Vtusoutio.i Tot -8.5 Vtusoutio.i
22 Usig ths i ), w gt [ f )] [ Vtusoutio.i y y] ) 6 [ y cos ] 6 8.5).8 [ ysi ].99) 6. [ y cos ] 6.5).5 [ ysi ] 6.598).866 [ y cos ] 8) [ ysi ] y 7,8cos.)si.5cos.866si This is th rquird Fourir sris upto th third hrmoic. Vtusoutio.i.667cos. Th foowig t givs th vritios of priodic currt A ovr priod T : tscs) T/6 T/ T/ T/ 5T/6 T A mp) Show tht thr is costt prt of.75mp. i th currt A d oti th mpitud of th first hrmoic. Not tht th vus of A t t= d t=t r th sm. Hc At) is priodic fuctio of priod T. Lt us dot t. W hv T [ A] Acos t [ Acos ] ) T Asi t [ Asi ] T W prpr th foowig t: Vtusoutio.i
23 t t T A cos si Acos Asi Vtusoutio.i T/ T/ T/ T/ T/ Tot.5..7 Usig th vus of th t i ), w gt A Acos. 6.7 Asi Th Fourir psio upto th first hrmoic is A cos t T si t t.75.7cos.6si T T Th prssio shows tht A hs costt prt.75 i it. Aso th mpitud of th first hrmoic is t T Vtusoutio.i =.77. Vtusoutio.i
24 ASSIGNMENT :. Th dispcmt y of prt of mchism is tutd with corrspodig gur movmt of th crk. Eprss y s Vtusoutio.i Fourir sris upto th third hrmoic y Oti th Fourir sris of y upto th scod hrmoic usig th foowig t : y Oti th costt trm d th cofficits of th first si d cosi trms i th Fourir psio of y s giv i th foowig t : 5 y Fid th Fourir sris of y upto th scod hrmoic from th foowig t : 6 8 Y Oti th first thr cofficits i th Fourir cosi sris for y, whr y is giv i th foowig t : 5 y Vtusoutio.i 6. Th turig momt T is giv for sris of vus of th crk g = 75. Vtusoutio.i
25 Vtusoutio.i T Oti th first four trms i sris of sis to rprst T d ccut T t = 75. Vtusoutio.i Vtusoutio.i
Chapter 3 Fourier Series Representation of Periodic Signals
 Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
ASSERTION AND REASON
 ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
ASSERTION AND REASON Som qustios (Assrtio Rso typ) r giv low. Ech qustio cotis Sttmt (Assrtio) d Sttmt (Rso). Ech qustio hs choics (A), (B), (C) d (D) out of which ONLY ONE is corrct. So slct th corrct
Linear Algebra Existence of the determinant. Expansion according to a row.
 Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
How much air is required by the people in this lecture theatre during this lecture?
 3 NTEGRATON tgrtio is us to swr qustios rltig to Ar Volum Totl qutity such s: Wht is th wig r of Boig 747? How much will this yr projct cost? How much wtr os this rsrvoir hol? How much ir is rquir y th
3 NTEGRATON tgrtio is us to swr qustios rltig to Ar Volum Totl qutity such s: Wht is th wig r of Boig 747? How much will this yr projct cost? How much wtr os this rsrvoir hol? How much ir is rquir y th
SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3
![SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3 SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3](/thumbs/89/98215718.jpg) SOLVED EXAMPLES E. If f() E.,,, th f() f() h h LHL RHL, so / / Lim f() quls - (D) Dos ot ist [( h)+] [(+h) + ] f(). LHL E. RHL h h h / h / h / h / h / h / h As.[C] (D) Dos ot ist LHL RHL, so giv it dos
SOLVED EXAMPLES E. If f() E.,,, th f() f() h h LHL RHL, so / / Lim f() quls - (D) Dos ot ist [( h)+] [(+h) + ] f(). LHL E. RHL h h h / h / h / h / h / h / h As.[C] (D) Dos ot ist LHL RHL, so giv it dos
Integration by Guessing
 Itgrtio y Gussig Th computtios i two stdrd itgrtio tchiqus, Sustitutio d Itgrtio y Prts, c strmlid y th Itgrtio y Gussig pproch. This mthod cosists of thr stps: Guss, Diffrtit to chck th guss, d th Adjust
Itgrtio y Gussig Th computtios i two stdrd itgrtio tchiqus, Sustitutio d Itgrtio y Prts, c strmlid y th Itgrtio y Gussig pproch. This mthod cosists of thr stps: Guss, Diffrtit to chck th guss, d th Adjust
National Quali cations
 Ntiol Quli ctios AH07 X77/77/ Mthmtics FRIDAY, 5 MAY 9:00 AM :00 NOON Totl mrks 00 Attmpt ALL qustios. You my us clcultor. Full crdit will b giv oly to solutios which coti pproprit workig. Stt th uits
Ntiol Quli ctios AH07 X77/77/ Mthmtics FRIDAY, 5 MAY 9:00 AM :00 NOON Totl mrks 00 Attmpt ALL qustios. You my us clcultor. Full crdit will b giv oly to solutios which coti pproprit workig. Stt th uits
COLLECTION OF SUPPLEMENTARY PROBLEMS CALCULUS II
 COLLECTION OF SUPPLEMENTARY PROBLEMS I. CHAPTER 6 --- Trscdtl Fuctios CALCULUS II A. FROM CALCULUS BY J. STEWART:. ( How is th umbr dfid? ( Wht is pproimt vlu for? (c ) Sktch th grph of th turl potil fuctios.
COLLECTION OF SUPPLEMENTARY PROBLEMS I. CHAPTER 6 --- Trscdtl Fuctios CALCULUS II A. FROM CALCULUS BY J. STEWART:. ( How is th umbr dfid? ( Wht is pproimt vlu for? (c ) Sktch th grph of th turl potil fuctios.
National Quali cations
 PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
CHAPTER 5d. SIMULTANEOUS LINEAR EQUATIONS
 CHAPTE 5. SIUTANEOUS INEA EQUATIONS A. J. Crk Schoo of Egirig Dprtmt of Civi Eviromt Egirig by Dr. Ibrhim A. Asskkf Sprig ENCE - Compttio thos i Civi Egirig II Dprtmt of Civi Eviromt Egirig Uivrsity of
CHAPTE 5. SIUTANEOUS INEA EQUATIONS A. J. Crk Schoo of Egirig Dprtmt of Civi Eviromt Egirig by Dr. Ibrhim A. Asskkf Sprig ENCE - Compttio thos i Civi Egirig II Dprtmt of Civi Eviromt Egirig Uivrsity of
Probability & Statistics,
 Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
PURE MATHEMATICS A-LEVEL PAPER 1
 -AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
-AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
page 11 equation (1.2-10c), break the bar over the right side in the middle
 I. Corrctios Lst Updtd: Ju 00 Complx Vrils with Applictios, 3 rd ditio, A. Dvid Wusch First Pritig. A ook ought for My 007 will proly first pritig With Thks to Christi Hos of Swd pg qutio (.-0c), rk th
I. Corrctios Lst Updtd: Ju 00 Complx Vrils with Applictios, 3 rd ditio, A. Dvid Wusch First Pritig. A ook ought for My 007 will proly first pritig With Thks to Christi Hos of Swd pg qutio (.-0c), rk th
[ ] Review. For a discrete-time periodic signal xn with period N, the Fourier series representation is
![[ ] Review. For a discrete-time periodic signal xn with period N, the Fourier series representation is [ ] Review. For a discrete-time periodic signal xn with period N, the Fourier series representation is](/thumbs/95/123561596.jpg) Discrt-tim ourir Trsform Rviw or discrt-tim priodic sigl x with priod, th ourir sris rprsttio is x + < > < > x, Rviw or discrt-tim LTI systm with priodic iput sigl, y H ( ) < > < > x H r rfrrd to s th
Discrt-tim ourir Trsform Rviw or discrt-tim priodic sigl x with priod, th ourir sris rprsttio is x + < > < > x, Rviw or discrt-tim LTI systm with priodic iput sigl, y H ( ) < > < > x H r rfrrd to s th
UNIT I FOURIER SERIES T
 UNIT I FOURIER SERIES PROBLEM : Th urig mom T o h crkh o m gi i giv or ri o vu o h crk g dgr 6 9 5 8 T 5 897 785 599 66 Epd T i ri o i. Souio: L T = i + i + i +, Sic h ir d vu o T r rpd gc o T T i T i
UNIT I FOURIER SERIES PROBLEM : Th urig mom T o h crkh o m gi i giv or ri o vu o h crk g dgr 6 9 5 8 T 5 897 785 599 66 Epd T i ri o i. Souio: L T = i + i + i +, Sic h ir d vu o T r rpd gc o T T i T i
Problem Session (3) for Chapter 4 Signal Modeling
 Pobm Sssio fo Cht Sig Modig Soutios to Pobms....5. d... Fid th Pdé oimtio of scod-od to sig tht is giv by [... ] T i.. d so o. I oth wods usig oimtio of th fom b b b H fid th cofficits b b b d. Soutio
Pobm Sssio fo Cht Sig Modig Soutios to Pobms....5. d... Fid th Pdé oimtio of scod-od to sig tht is giv by [... ] T i.. d so o. I oth wods usig oimtio of th fom b b b H fid th cofficits b b b d. Soutio
ESS 265 Spring Quarter 2005 Time Series Analysis: Some Fundamentals of Spectral Analysis
 ESS 65 Srig Qurtr 5 Tim Sris ysis: Som Fudmts of Sctr ysis Lctur My, 5 Fourir Sris y riodic fuctio ttt whr ωt is th riod c xrssd s Fourir sris t c cos t s si t ω ω t must stisfy th coditio T t dt < y rso
ESS 65 Srig Qurtr 5 Tim Sris ysis: Som Fudmts of Sctr ysis Lctur My, 5 Fourir Sris y riodic fuctio ttt whr ωt is th riod c xrssd s Fourir sris t c cos t s si t ω ω t must stisfy th coditio T t dt < y rso
1985 AP Calculus BC: Section I
 985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
PREPARATORY MATHEMATICS FOR ENGINEERS
 CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
CIVE 690 This qusti ppr csists f 6 pritd pgs, ch f which is idtifid by th Cd Numbr CIVE690 FORMULA SHEET ATTACHED UNIVERSITY OF LEEDS Jury 008 Emiti fr th dgr f BEg/ MEg Civil Egirig PREPARATORY MATHEMATICS
z 1+ 3 z = Π n =1 z f() z = n e - z = ( 1-z) e z e n z z 1- n = ( 1-z/2) 1+ 2n z e 2n e n -1 ( 1-z )/2 e 2n-1 1-2n -1 1 () z
 Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Time : 1 hr. Test Paper 08 Date 04/01/15 Batch - R Marks : 120
 Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Skyup's Media. Interpolation is the process of finding a function whose graph passes thr
 Itpotio is th pocss of fidig fuctio whos gph psss th pimttio, d tis to costuct fuctio which cos fits thos d cuv fittig o gssio sis. Itpotio is spcific cs of cuv fittig, i which th. I foowig subsctio, w
Itpotio is th pocss of fidig fuctio whos gph psss th pimttio, d tis to costuct fuctio which cos fits thos d cuv fittig o gssio sis. Itpotio is spcific cs of cuv fittig, i which th. I foowig subsctio, w
Chapter 2 Infinite Series Page 1 of 11. Chapter 2 : Infinite Series
 Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
(HELD ON 22nd MAY SUNDAY 2016) MATHEMATICS CODE - 2 [PAPER -2]
![(HELD ON 22nd MAY SUNDAY 2016) MATHEMATICS CODE - 2 [PAPER -2] (HELD ON 22nd MAY SUNDAY 2016) MATHEMATICS CODE - 2 [PAPER -2]](/thumbs/93/113007992.jpg) QUESTION PAPER WITH SOLUTION OF JEE ADVANCED - 6 7. Lt P (HELD ON d MAY SUNDAY 6) FEEL THE POWER OF OUR KNOWLEDGE & EXPERIENCE Our Top clss IITi fculty tm promiss to giv you uthtic swr ky which will b
QUESTION PAPER WITH SOLUTION OF JEE ADVANCED - 6 7. Lt P (HELD ON d MAY SUNDAY 6) FEEL THE POWER OF OUR KNOWLEDGE & EXPERIENCE Our Top clss IITi fculty tm promiss to giv you uthtic swr ky which will b
Digital Signal Processing, Fall 2006
 Digital Sigal Procssig, Fall 6 Lctur 9: Th Discrt Fourir Trasfor Zhg-Hua Ta Dpartt of Elctroic Systs Aalborg Uivrsity, Dar zt@o.aau.d Digital Sigal Procssig, I, Zhg-Hua Ta, 6 Cours at a glac MM Discrt-ti
Digital Sigal Procssig, Fall 6 Lctur 9: Th Discrt Fourir Trasfor Zhg-Hua Ta Dpartt of Elctroic Systs Aalborg Uivrsity, Dar zt@o.aau.d Digital Sigal Procssig, I, Zhg-Hua Ta, 6 Cours at a glac MM Discrt-ti
07 - SEQUENCES AND SERIES Page 1 ( Answers at he end of all questions ) b, z = n
 07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
IIT JEE MATHS MATRICES AND DETERMINANTS
 IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
Chapter 9 Infinite Series
 Sctio 9. 77. Cotiud d + d + C Ar lim b lim b b b + b b lim + b b lim + b b 6. () d (b) lim b b d (c) Not tht d c b foud by prts: d ( ) ( ) d + C. b Ar b b lim d lim b b b b lim ( b + ). b dy 7. () π dy
Sctio 9. 77. Cotiud d + d + C Ar lim b lim b b b + b b lim + b b lim + b b 6. () d (b) lim b b d (c) Not tht d c b foud by prts: d ( ) ( ) d + C. b Ar b b lim d lim b b b b lim ( b + ). b dy 7. () π dy
EXERCISE - 01 CHECK YOUR GRASP
 DEFNTE NTEGRATON EXERCSE - CHECK YOUR GRASP. ( ) d [ ] d [ ] d d ƒ( ) ƒ '( ) [ ] [ ] 8 5. ( cos )( c)d 8 ( cos )( c)d + 8 ( cos )( c) d 8 ( cos )( c) d sic + cos 8 is lwys posiiv f() d ( > ) ms f() is
DEFNTE NTEGRATON EXERCSE - CHECK YOUR GRASP. ( ) d [ ] d [ ] d d ƒ( ) ƒ '( ) [ ] [ ] 8 5. ( cos )( c)d 8 ( cos )( c)d + 8 ( cos )( c) d 8 ( cos )( c) d sic + cos 8 is lwys posiiv f() d ( > ) ms f() is
New Advanced Higher Mathematics: Formulae
 Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
Advcd High Mthmtics Nw Advcd High Mthmtics: Fomul G (G): Fomul you must mmois i od to pss Advcd High mths s thy ot o th fomul sht. Am (A): Ths fomul giv o th fomul sht. ut it will still usful fo you to
Q.28 Q.29 Q.30. Q.31 Evaluate: ( log x ) Q.32 Evaluate: ( ) Q.33. Q.34 Evaluate: Q.35 Q.36 Q.37 Q.38 Q.39 Q.40 Q.41 Q.42. Q.43 Evaluate : ( x 2) Q.
 LASS XII Q Evlut : Q sc Evlut c Q Evlut: ( ) Q Evlut: Q5 α Evlut: α Q Evlut: Q7 Evlut: { t (t sc )} / Q8 Evlut : ( )( ) Q9 Evlut: Q0 Evlut: Q Evlut : ( ) ( ) Q Evlut : / ( ) Q Evlut: / ( ) Q Evlut : )
LASS XII Q Evlut : Q sc Evlut c Q Evlut: ( ) Q Evlut: Q5 α Evlut: α Q Evlut: Q7 Evlut: { t (t sc )} / Q8 Evlut : ( )( ) Q9 Evlut: Q0 Evlut: Q Evlut : ( ) ( ) Q Evlut : / ( ) Q Evlut: / ( ) Q Evlut : )
Discrete Fourier Transform (DFT)
 Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Option 3. b) xe dx = and therefore the series is convergent. 12 a) Divergent b) Convergent Proof 15 For. p = 1 1so the series diverges.
 Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
FOURIER ANALYSIS Signals and System Analysis
 FOURIER ANALYSIS Isc Nwo Whi ligh cosiss of sv compos J Bpis Josph Fourir Bor: Mrch 768 i Auxrr, Bourgog, Frc Did: 6 My 83 i Pris, Frc Fourir Sris A priodic sigl of priod T sisfis ft f for ll f f for ll
FOURIER ANALYSIS Isc Nwo Whi ligh cosiss of sv compos J Bpis Josph Fourir Bor: Mrch 768 i Auxrr, Bourgog, Frc Did: 6 My 83 i Pris, Frc Fourir Sris A priodic sigl of priod T sisfis ft f for ll f f for ll
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) Awr: = ( + )(y + ) Diff prtilly w.r.to & y hr p & q y p = (y + ) ;
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) Awr: = ( + )(y + ) Diff prtilly w.r.to & y hr p & q y p = (y + ) ;
Lectures 5-8: Fourier Series
 cturs 5-8: Fourir Sris PHY6 Rfrcs Jord & Smith Ch.6, Bos Ch.7, Kryszig Ch. Som fu jv pplt dmostrtios r vilbl o th wb. Try puttig Fourir sris pplt ito Googl d lookig t th sits from jhu, Flstd d Mths Oli
cturs 5-8: Fourir Sris PHY6 Rfrcs Jord & Smith Ch.6, Bos Ch.7, Kryszig Ch. Som fu jv pplt dmostrtios r vilbl o th wb. Try puttig Fourir sris pplt ito Googl d lookig t th sits from jhu, Flstd d Mths Oli
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) = ( + )(y + ) Diff prtilly w.r.to & y hr p & q p = (y + ) ; q = ( +
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) = ( + )(y + ) Diff prtilly w.r.to & y hr p & q p = (y + ) ; q = ( +
EEE 303: Signals and Linear Systems
 33: Sigls d Lir Sysms Orhogoliy bw wo sigls L us pproim fucio f () by fucio () ovr irvl : f ( ) = c( ); h rror i pproimio is, () = f() c () h rgy of rror sigl ovr h irvl [, ] is, { }{ } = f () c () d =
33: Sigls d Lir Sysms Orhogoliy bw wo sigls L us pproim fucio f () by fucio () ovr irvl : f ( ) = c( ); h rror i pproimio is, () = f() c () h rgy of rror sigl ovr h irvl [, ] is, { }{ } = f () c () d =
Eigenfunction Expansion. For a given function on the internal a x b the eigenfunction expansion of f(x):
 Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
TWO MARKS WITH ANSWER
 TWO MARKS WITH ANSWER MA65/TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS REGULATION: UNIT I PARTIAL DIFFERENTIAL EQUATIONS Formtio o rti dirti utio Sigur itgr -- Soutio o tdrd t o irt ordr rti dirti utio
TWO MARKS WITH ANSWER MA65/TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS REGULATION: UNIT I PARTIAL DIFFERENTIAL EQUATIONS Formtio o rti dirti utio Sigur itgr -- Soutio o tdrd t o irt ordr rti dirti utio
Lectures 2 & 3 - Population ecology mathematics refresher
 Lcturs & - Poultio cology mthmtics rrshr To s th mov ito vloig oultio mols, th olloig mthmtics crisht is suli I i out r mthmtics ttook! Eots logrithms i i q q q q q q ( tims) / c c c c ) ( ) ( Clculus
Lcturs & - Poultio cology mthmtics rrshr To s th mov ito vloig oultio mols, th olloig mthmtics crisht is suli I i out r mthmtics ttook! Eots logrithms i i q q q q q q ( tims) / c c c c ) ( ) ( Clculus
H2 Mathematics Arithmetic & Geometric Series ( )
 H Mathmatics Arithmtic & Gomtric Sris (08 09) Basic Mastry Qustios Arithmtic Progrssio ad Sris. Th rth trm of a squc is 4r 7. (i) Stat th first four trms ad th 0th trm. (ii) Show that th squc is a arithmtic
H Mathmatics Arithmtic & Gomtric Sris (08 09) Basic Mastry Qustios Arithmtic Progrssio ad Sris. Th rth trm of a squc is 4r 7. (i) Stat th first four trms ad th 0th trm. (ii) Show that th squc is a arithmtic
Advanced Engineering Mathematics, K.A. Stroud, Dexter J. Booth Engineering Mathematics, H.K. Dass Higher Engineering Mathematics, Dr. B.S.
 Rfrc: (i) (ii) (iii) Advcd Egirig Mhmic, K.A. Sroud, Dxr J. Booh Egirig Mhmic, H.K. D Highr Egirig Mhmic, Dr. B.S. Grwl Th mhod of m Thi coi of h followig xm wih h giv coribuio o h ol. () Mid-rm xm : 3%
Rfrc: (i) (ii) (iii) Advcd Egirig Mhmic, K.A. Sroud, Dxr J. Booh Egirig Mhmic, H.K. D Highr Egirig Mhmic, Dr. B.S. Grwl Th mhod of m Thi coi of h followig xm wih h giv coribuio o h ol. () Mid-rm xm : 3%
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
CLASS XI CHAPTER 3. Theorem 1 (sine formula) In any triangle, sides are proportional to the sines of the opposite angles. That is, in a triangle ABC
 CLSS XI ur I CHPTER.6. Proofs d Simpl pplictios of si d cosi formul Lt C b trigl. y gl w m t gl btw t sids d C wic lis btw 0 d 80. T gls d C r similrly dfid. T sids, C d C opposit to t vrtics C, d will
CLSS XI ur I CHPTER.6. Proofs d Simpl pplictios of si d cosi formul Lt C b trigl. y gl w m t gl btw t sids d C wic lis btw 0 d 80. T gls d C r similrly dfid. T sids, C d C opposit to t vrtics C, d will
ENGI 3424 Appendix Formulæ Page A-01
 ENGI 344 Appdix Formulæ g A-0 ENGI 344 Egirig Mthmtics ossibilitis or your Formul Shts You my slct itms rom this documt or plcmt o your ormul shts. Howvr, dsigig your ow ormul sht c b vlubl rvisio xrcis
ENGI 344 Appdix Formulæ g A-0 ENGI 344 Egirig Mthmtics ossibilitis or your Formul Shts You my slct itms rom this documt or plcmt o your ormul shts. Howvr, dsigig your ow ormul sht c b vlubl rvisio xrcis
MAT 182: Calculus II Test on Chapter 9: Sequences and Infinite Series Take-Home Portion Solutions
 MAT 8: Clculus II Tst o Chptr 9: qucs d Ifiit ris T-Hom Portio olutios. l l l l 0 0 L'Hôpitl's Rul 0 . Bgi by computig svrl prtil sums to dvlop pttr: 6 7 8 7 6 6 9 9 99 99 Th squc of prtil sums is s follows:,,,,,
MAT 8: Clculus II Tst o Chptr 9: qucs d Ifiit ris T-Hom Portio olutios. l l l l 0 0 L'Hôpitl's Rul 0 . Bgi by computig svrl prtil sums to dvlop pttr: 6 7 8 7 6 6 9 9 99 99 Th squc of prtil sums is s follows:,,,,,
n 2 + 3n + 1 4n = n2 + 3n + 1 n n 2 = n + 1
 Ifiite Series Some Tests for Divergece d Covergece Divergece Test: If lim u or if the limit does ot exist, the series diverget. + 3 + 4 + 3 EXAMPLE: Show tht the series diverges. = u = + 3 + 4 + 3 + 3
Ifiite Series Some Tests for Divergece d Covergece Divergece Test: If lim u or if the limit does ot exist, the series diverget. + 3 + 4 + 3 EXAMPLE: Show tht the series diverges. = u = + 3 + 4 + 3 + 3
Quantum Mechanics & Spectroscopy Prof. Jason Goodpaster. Problem Set #2 ANSWER KEY (5 questions, 10 points)
 Chm 5 Problm St # ANSWER KEY 5 qustios, poits Qutum Mchics & Spctroscopy Prof. Jso Goodpstr Du ridy, b. 6 S th lst pgs for possibly usful costts, qutios d itgrls. Ths will lso b icludd o our futur ms..
Chm 5 Problm St # ANSWER KEY 5 qustios, poits Qutum Mchics & Spctroscopy Prof. Jso Goodpstr Du ridy, b. 6 S th lst pgs for possibly usful costts, qutios d itgrls. Ths will lso b icludd o our futur ms..
Problem Value Score Earned No/Wrong Rec -3 Total
 GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING ECE6 Fall Quiz # Writt Eam Novmr, NAME: Solutio Kys GT Usram: LAST FIRST.g., gtiit Rcitatio Sctio: Circl t dat & tim w your Rcitatio
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING ECE6 Fall Quiz # Writt Eam Novmr, NAME: Solutio Kys GT Usram: LAST FIRST.g., gtiit Rcitatio Sctio: Circl t dat & tim w your Rcitatio
Part B: Transform Methods. Professor E. Ambikairajah UNSW, Australia
 Par B: rasform Mhods Profssor E. Ambikairaah UNSW, Ausralia Chapr : Fourir Rprsaio of Sigal. Fourir Sris. Fourir rasform.3 Ivrs Fourir rasform.4 Propris.4. Frqucy Shif.4. im Shif.4.3 Scalig.4.4 Diffriaio
Par B: rasform Mhods Profssor E. Ambikairaah UNSW, Ausralia Chapr : Fourir Rprsaio of Sigal. Fourir Sris. Fourir rasform.3 Ivrs Fourir rasform.4 Propris.4. Frqucy Shif.4. im Shif.4.3 Scalig.4.4 Diffriaio
The z-transform. Dept. of Electronics Eng. -1- DH26029 Signals and Systems
 0 Th -Trsform Dpt. of Elctroics Eg. -- DH609 Sigls d Systms 0. Th -Trsform Lplc trsform - for cotios tim sigl/systm -trsform - for discrt tim sigl/systm 0. Th -trsform For ipt y H H h with ω rl i.. DTFT
0 Th -Trsform Dpt. of Elctroics Eg. -- DH609 Sigls d Systms 0. Th -Trsform Lplc trsform - for cotios tim sigl/systm -trsform - for discrt tim sigl/systm 0. Th -trsform For ipt y H H h with ω rl i.. DTFT
Engineering Mathematics (21)
 Egieerig Mathematics () Zhag, Xiyu Departmet of Computer Sciece ad Egieerig, Ewha Womas Uiversity, Seoul, Korea zhagy@ewha.ac.kr Fourier Series Sectios.-3 (8 th Editio) Sectios.- (9 th Editio) Fourier
Egieerig Mathematics () Zhag, Xiyu Departmet of Computer Sciece ad Egieerig, Ewha Womas Uiversity, Seoul, Korea zhagy@ewha.ac.kr Fourier Series Sectios.-3 (8 th Editio) Sectios.- (9 th Editio) Fourier
IX. Ordinary Differential Equations
 IX. Orir Diffrtil Equtios A iffrtil qutio is qutio tht iclus t lst o rivtiv of uow fuctio. Ths qutios m iclu th uow fuctio s wll s ow fuctios of th sm vribl. Th rivtiv m b of orr thr m b svrl rivtivs prst.
IX. Orir Diffrtil Equtios A iffrtil qutio is qutio tht iclus t lst o rivtiv of uow fuctio. Ths qutios m iclu th uow fuctio s wll s ow fuctios of th sm vribl. Th rivtiv m b of orr thr m b svrl rivtivs prst.
DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1
![DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1 DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1](/thumbs/79/79094742.jpg) DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
PESIT Bangalore South Campus Hosur road, 1km before Electronic City, Bengaluru -100 Department of Basic Science and Humanities
 P E PESIT Bglo South Cpus Hosu od, k bfo Elctoic Cit, Bgluu -00 Dptt of Bsic Scic d Huitis INTERNAL ASSESSMENT TEST Dt : 0/0/07 Mks: 0 Subjct & Cod : Egiig Mthtics I 5MAT Sc : ALL N of fcult : GVR,GKJ,RR,SV,NHM,DN,KR,
P E PESIT Bglo South Cpus Hosu od, k bfo Elctoic Cit, Bgluu -00 Dptt of Bsic Scic d Huitis INTERNAL ASSESSMENT TEST Dt : 0/0/07 Mks: 0 Subjct & Cod : Egiig Mthtics I 5MAT Sc : ALL N of fcult : GVR,GKJ,RR,SV,NHM,DN,KR,
15/03/1439. Lectures on Signals & systems Engineering
 Lcturs o Sigals & syms Egirig Dsigd ad Prd by Dr. Ayma Elshawy Elsfy Dpt. of Syms & Computr Eg. Al-Azhar Uivrsity Email : aymalshawy@yahoo.com A sigal ca b rprd as a liar combiatio of basic sigals. Th
Lcturs o Sigals & syms Egirig Dsigd ad Prd by Dr. Ayma Elshawy Elsfy Dpt. of Syms & Computr Eg. Al-Azhar Uivrsity Email : aymalshawy@yahoo.com A sigal ca b rprd as a liar combiatio of basic sigals. Th
Discrete Fourier Transform. Nuno Vasconcelos UCSD
 Discrt Fourir Trasform uo Vascoclos UCSD Liar Shift Ivariat (LSI) systms o of th most importat cocpts i liar systms thory is that of a LSI systm Dfiitio: a systm T that maps [ ito y[ is LSI if ad oly if
Discrt Fourir Trasform uo Vascoclos UCSD Liar Shift Ivariat (LSI) systms o of th most importat cocpts i liar systms thory is that of a LSI systm Dfiitio: a systm T that maps [ ito y[ is LSI if ad oly if
NET/JRF, GATE, IIT JAM, JEST, TIFR
 Istitut for NET/JRF, GATE, IIT JAM, JEST, TIFR ad GRE i PHYSICAL SCIENCES Mathmatical Physics JEST-6 Q. Giv th coditio φ, th solutio of th quatio ψ φ φ is giv by k. kφ kφ lφ kφ lφ (a) ψ (b) ψ kφ (c) ψ
Istitut for NET/JRF, GATE, IIT JAM, JEST, TIFR ad GRE i PHYSICAL SCIENCES Mathmatical Physics JEST-6 Q. Giv th coditio φ, th solutio of th quatio ψ φ φ is giv by k. kφ kφ lφ kφ lφ (a) ψ (b) ψ kφ (c) ψ
A Simple Proof that e is Irrational
 Two of th most bautiful ad sigificat umbrs i mathmatics ar π ad. π (approximatly qual to 3.459) rprsts th ratio of th circumfrc of a circl to its diamtr. (approximatly qual to.788) is th bas of th atural
Two of th most bautiful ad sigificat umbrs i mathmatics ar π ad. π (approximatly qual to 3.459) rprsts th ratio of th circumfrc of a circl to its diamtr. (approximatly qual to.788) is th bas of th atural
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
Section 3: Antiderivatives of Formulas
 Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Chapter 5. Chapter 5 125
 Chptr 5 Chptr 5: Itroductio to Digitl Filtrs... 6 5. Itroductio... 6 5.. No rcursiv digitl filtrs FIR... 7 5.. Rcursiv digitl filtr IIR... 8 5. Digitl Filtr Rlistio... 5.. Prlll rlistio... 5.. Cscd rlistio...
Chptr 5 Chptr 5: Itroductio to Digitl Filtrs... 6 5. Itroductio... 6 5.. No rcursiv digitl filtrs FIR... 7 5.. Rcursiv digitl filtr IIR... 8 5. Digitl Filtr Rlistio... 5.. Prlll rlistio... 5.. Cscd rlistio...
19 Fourier Series and Practical Harmonic Analysis
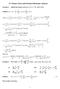 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
10. Joint Moments and Joint Characteristic Functions
 0 Joit Momts ad Joit Charactristic Fctios Followig sctio 6 i this sctio w shall itrodc varios paramtrs to compactly rprst th iformatio cotaid i th joit pdf of two rvs Giv two rvs ad ad a fctio g x y dfi
0 Joit Momts ad Joit Charactristic Fctios Followig sctio 6 i this sctio w shall itrodc varios paramtrs to compactly rprst th iformatio cotaid i th joit pdf of two rvs Giv two rvs ad ad a fctio g x y dfi
Limits Indeterminate Forms and L Hospital s Rule
 Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
MA6351 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C
 MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit
MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit
Some Common Fixed Point Theorems for a Pair of Non expansive Mappings in Generalized Exponential Convex Metric Space
 Mish Kumr Mishr D.B.OhU Ktoch It. J. Comp. Tch. Appl. Vol ( 33-37 Som Commo Fi Poit Thorms for Pir of No psiv Mppigs i Grliz Epotil Cov Mtric Spc D.B.Oh Mish Kumr Mishr U Ktoch (Rsrch scholr Drvii Uivrsit
Mish Kumr Mishr D.B.OhU Ktoch It. J. Comp. Tch. Appl. Vol ( 33-37 Som Commo Fi Poit Thorms for Pir of No psiv Mppigs i Grliz Epotil Cov Mtric Spc D.B.Oh Mish Kumr Mishr U Ktoch (Rsrch scholr Drvii Uivrsit
+ x. x 2x. 12. dx. 24. dx + 1)
 INTEGRATION of FUNCTION of ONE VARIABLE INDEFINITE INTEGRAL Fidig th idfiit itgrals Rductio to basic itgrals, usig th rul f ( ) f ( ) d =... ( ). ( )d. d. d ( ). d. d. d 7. d 8. d 9. d. d. d. d 9. d 9.
INTEGRATION of FUNCTION of ONE VARIABLE INDEFINITE INTEGRAL Fidig th idfiit itgrals Rductio to basic itgrals, usig th rul f ( ) f ( ) d =... ( ). ( )d. d. d ( ). d. d. d 7. d 8. d 9. d. d. d. d 9. d 9.
terms of discrete sequences can only take values that are discrete as opposed to
 Diol Bgyoko () OWER SERIES Diitio Sris lik ( ) r th sm o th trms o discrt sqc. Th trms o discrt sqcs c oly tk vls tht r discrt s opposd to cotios, i.., trms tht r sch tht th mric vls o two cosctivs os
Diol Bgyoko () OWER SERIES Diitio Sris lik ( ) r th sm o th trms o discrt sqc. Th trms o discrt sqcs c oly tk vls tht r discrt s opposd to cotios, i.., trms tht r sch tht th mric vls o two cosctivs os
MATH 174: Numerical Analysis. Lecturer: Jomar F. Rabajante 1 st Sem AY
 MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
STIRLING'S 1 FORMULA AND ITS APPLICATION
 MAT-KOL (Baja Luka) XXIV ()(08) 57-64 http://wwwimviblorg/dmbl/dmblhtm DOI: 075/МК80057A ISSN 0354-6969 (o) ISSN 986-588 (o) STIRLING'S FORMULA AND ITS APPLICATION Šfkt Arslaagić Sarajvo B&H Abstract:
MAT-KOL (Baja Luka) XXIV ()(08) 57-64 http://wwwimviblorg/dmbl/dmblhtm DOI: 075/МК80057A ISSN 0354-6969 (o) ISSN 986-588 (o) STIRLING'S FORMULA AND ITS APPLICATION Šfkt Arslaagić Sarajvo B&H Abstract:
FOURIER SERIES. Series expansions are a ubiquitous tool of science and engineering. The kinds of
 Do Bgyoko () FOURIER SERIES I. INTRODUCTION Srs psos r ubqutous too o scc d grg. Th kds o pso to utz dpd o () th proprts o th uctos to b studd d (b) th proprts or chrctrstcs o th systm udr vstgto. Powr
Do Bgyoko () FOURIER SERIES I. INTRODUCTION Srs psos r ubqutous too o scc d grg. Th kds o pso to utz dpd o () th proprts o th uctos to b studd d (b) th proprts or chrctrstcs o th systm udr vstgto. Powr
Chapter 11.00C Physical Problem for Fast Fourier Transform Civil Engineering
 haptr. Physical Problm for Fast Fourir Trasform ivil Egirig Itroductio I this chaptr, applicatios of FFT algorithms [-5] for solvig ral-lif problms such as computig th dyamical (displacmt rspos [6-7] of
haptr. Physical Problm for Fast Fourir Trasform ivil Egirig Itroductio I this chaptr, applicatios of FFT algorithms [-5] for solvig ral-lif problms such as computig th dyamical (displacmt rspos [6-7] of
BRAIN TEASURES INDEFINITE INTEGRATION+DEFINITE INTEGRATION EXERCISE I
 EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
Chapter Taylor Theorem Revisited
 Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
Name of the Student:
 Egieerig Mthemtics 5 NAME OF THE SUBJECT : Mthemtics I SUBJECT CODE : MA65 MATERIAL NAME : Additiol Prolems MATERIAL CODE : HGAUM REGULATION : R UPDATED ON : M-Jue 5 (Sc the ove QR code for the direct
Egieerig Mthemtics 5 NAME OF THE SUBJECT : Mthemtics I SUBJECT CODE : MA65 MATERIAL NAME : Additiol Prolems MATERIAL CODE : HGAUM REGULATION : R UPDATED ON : M-Jue 5 (Sc the ove QR code for the direct
Options: Calculus. O C.1 PG #2, 3b, 4, 5ace O C.2 PG.24 #1 O D PG.28 #2, 3, 4, 5, 7 O E PG #1, 3, 4, 5 O F PG.
 O C. PG.-3 #, 3b, 4, 5ce O C. PG.4 # Optios: Clculus O D PG.8 #, 3, 4, 5, 7 O E PG.3-33 #, 3, 4, 5 O F PG.36-37 #, 3 O G. PG.4 #c, 3c O G. PG.43 #, O H PG.49 #, 4, 5, 6, 7, 8, 9, 0 O I. PG.53-54 #5, 8
O C. PG.-3 #, 3b, 4, 5ce O C. PG.4 # Optios: Clculus O D PG.8 #, 3, 4, 5, 7 O E PG.3-33 #, 3, 4, 5 O F PG.36-37 #, 3 O G. PG.4 #c, 3c O G. PG.43 #, O H PG.49 #, 4, 5, 6, 7, 8, 9, 0 O I. PG.53-54 #5, 8
Chapter Five. More Dimensions. is simply the set of all ordered n-tuples of real numbers x = ( x 1
 Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
Fourier Series and Applications
 9/7/9 Fourier Series d Applictios Fuctios epsio is doe to uderstd the better i powers o etc. My iportt probles ivolvig prtil dieretil equtios c be solved provided give uctio c be epressed s iiite su o
9/7/9 Fourier Series d Applictios Fuctios epsio is doe to uderstd the better i powers o etc. My iportt probles ivolvig prtil dieretil equtios c be solved provided give uctio c be epressed s iiite su o
Ordinary Differential Equations
 Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
3.1 Laplace s Equation 3.2 The Method of Images 3.3 Separation of Variables
 Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the
Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the
Week 13 Notes: 1) Riemann Sum. Aim: Compute Area Under a Graph. Suppose we want to find out the area of a graph, like the one on the right:
 Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
Week 1 Notes: 1) Riem Sum Aim: Compute Are Uder Grph Suppose we wt to fid out the re of grph, like the oe o the right: We wt to kow the re of the red re. Here re some wys to pproximte the re: We cut the
If a is any non zero real or imaginary number and m is the positive integer, then a...
 Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Idices d Surds.. Defiitio of Idices. If is o ero re or igir uer d is the positive iteger the...... ties. Here is ced the se d the ide power or epoet... Lws of Idices. 0 0 0. where d re rtio uers where
Discrete Fourier Series and Transforms
 Lctur 4 Outi: Discrt Fourir Sris ad Trasforms Aoucmts: H 4 postd, du Tus May 8 at 4:3pm. o at Hs as soutios wi b avaiab immdiaty. Midtrm dtais o t pag H 5 wi b postd Fri May, du foowig Fri (as usua) Rviw
Lctur 4 Outi: Discrt Fourir Sris ad Trasforms Aoucmts: H 4 postd, du Tus May 8 at 4:3pm. o at Hs as soutios wi b avaiab immdiaty. Midtrm dtais o t pag H 5 wi b postd Fri May, du foowig Fri (as usua) Rviw
Chapter 8 Approximation Methods, Hueckel Theory
 Witr 3 Chm 356: Itroductory Qutum Mchics Chptr 8 Approimtio Mthods, ucl Thory... 8 Approimtio Mthods... 8 Th Lir Vritiol Pricipl... mpl Lir Vritios... 3 Chptr 8 Approimtio Mthods, ucl Thory Approimtio
Witr 3 Chm 356: Itroductory Qutum Mchics Chptr 8 Approimtio Mthods, ucl Thory... 8 Approimtio Mthods... 8 Th Lir Vritiol Pricipl... mpl Lir Vritios... 3 Chptr 8 Approimtio Mthods, ucl Thory Approimtio
B. Examples 1. Finite Sums finite sums are an example of Riemann Sums in which each subinterval has the same length and the same x i
 Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Mth 06 Clculus Sec. 5.: The Defiite Itegrl I. Riem Sums A. Def : Give y=f(x):. Let f e defied o closed itervl[,].. Prtitio [,] ito suitervls[x (i-),x i ] of legth Δx i = x i -x (i-). Let P deote the prtitio
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fooling Newton s Method a) Find a formula for the Newton sequence, and verify that it converges to a nonzero of f. A Stirling-like Inequality
 Foolig Nwto s Mthod a Fid a formla for th Nwto sqc, ad vrify that it covrgs to a ozro of f. ( si si + cos 4 4 3 4 8 8 bt f. b Fid a formla for f ( ad dtrmi its bhavior as. f ( cos si + as A Stirlig-li
Foolig Nwto s Mthod a Fid a formla for th Nwto sqc, ad vrify that it covrgs to a ozro of f. ( si si + cos 4 4 3 4 8 8 bt f. b Fid a formla for f ( ad dtrmi its bhavior as. f ( cos si + as A Stirlig-li
Math 3B Midterm Review
 Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 643u Office Hours: R 11:00 m - 1:00 pm Lst updted /15/015 Here re some short otes o Sectios 7.1-7.8 i your ebook. The best idictio of wht
Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 643u Office Hours: R 11:00 m - 1:00 pm Lst updted /15/015 Here re some short otes o Sectios 7.1-7.8 i your ebook. The best idictio of wht
Integration by Parts
 Intgration by Parts Intgration by parts is a tchniqu primarily for valuating intgrals whos intgrand is th product of two functions whr substitution dosn t work. For ampl, sin d or d. Th rul is: u ( ) v'(
Intgration by Parts Intgration by parts is a tchniqu primarily for valuating intgrals whos intgrand is th product of two functions whr substitution dosn t work. For ampl, sin d or d. Th rul is: u ( ) v'(
MA6351-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES. Department of Mathematics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY
 MA635-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES Deprtmet of Mthemtics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY MADURAI 65, Tmildu, Idi Bsic Formule DIFFERENTIATION &INTEGRATION
MA635-TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS SUBJECT NOTES Deprtmet of Mthemtics FATIMA MICHAEL COLLEGE OF ENGINEERING & TECHNOLOGY MADURAI 65, Tmildu, Idi Bsic Formule DIFFERENTIATION &INTEGRATION
(A) 1 (B) 1 + (sin 1) (C) 1 (sin 1) (D) (sin 1) 1 (C) and g be the inverse of f. Then the value of g'(0) is. (C) a. dx (a > 0) is
 [STRAIGHT OBJECTIVE TYPE] l Q. Th vlu of h dfii igrl, cos d is + (si ) (si ) (si ) Q. Th vlu of h dfii igrl si d whr [, ] cos cos Q. Vlu of h dfii igrl ( si Q. L f () = d ( ) cos 7 ( ) )d d g b h ivrs
[STRAIGHT OBJECTIVE TYPE] l Q. Th vlu of h dfii igrl, cos d is + (si ) (si ) (si ) Q. Th vlu of h dfii igrl si d whr [, ] cos cos Q. Vlu of h dfii igrl ( si Q. L f () = d ( ) cos 7 ( ) )d d g b h ivrs
The limit comparison test
 Roerto s Notes o Ifiite Series Chpter : Covergece tests Sectio 4 The limit compriso test Wht you eed to kow lredy: Bsics of series d direct compriso test. Wht you c ler here: Aother compriso test tht does
Roerto s Notes o Ifiite Series Chpter : Covergece tests Sectio 4 The limit compriso test Wht you eed to kow lredy: Bsics of series d direct compriso test. Wht you c ler here: Aother compriso test tht does
[Q. Booklet Number]
![[Q. Booklet Number] [Q. Booklet Number]](/thumbs/82/85468362.jpg) 6 [Q. Booklet Numer] KOLKATA WB- B-J J E E - 9 MATHEMATICS QUESTIONS & ANSWERS. If C is the reflecto of A (, ) i -is d B is the reflectio of C i y-is, the AB is As : Hits : A (,); C (, ) ; B (, ) y A (,
6 [Q. Booklet Numer] KOLKATA WB- B-J J E E - 9 MATHEMATICS QUESTIONS & ANSWERS. If C is the reflecto of A (, ) i -is d B is the reflectio of C i y-is, the AB is As : Hits : A (,); C (, ) ; B (, ) y A (,
Time: 2 hours IIT-JEE 2006-MA-1. Section A (Single Option Correct) + is (A) 0 (B) 1 (C) 1 (D) 2. lim (sin x) + x 0. = 1 (using L Hospital s rule).
 IIT-JEE 6-MA- FIITJEE Solutios to IITJEE 6 Mthemtics Time: hours Note: Questio umber to crries (, -) mrks ech, to crries (5, -) mrks ech, to crries (5, -) mrks ech d to crries (6, ) mrks ech.. For >, lim
IIT-JEE 6-MA- FIITJEE Solutios to IITJEE 6 Mthemtics Time: hours Note: Questio umber to crries (, -) mrks ech, to crries (5, -) mrks ech, to crries (5, -) mrks ech d to crries (6, ) mrks ech.. For >, lim
Emil Olteanu-The plane rotation operator as a matrix function THE PLANE ROTATION OPERATOR AS A MATRIX FUNCTION. by Emil Olteanu
 Emil Oltu-Th pl rottio oprtor s mtri fuctio THE PLNE ROTTON OPERTOR S MTRX UNTON b Emil Oltu bstrct ormlism i mthmtics c offr m simplifictios, but it is istrumt which should b crfull trtd s it c sil crt
Emil Oltu-Th pl rottio oprtor s mtri fuctio THE PLNE ROTTON OPERTOR S MTRX UNTON b Emil Oltu bstrct ormlism i mthmtics c offr m simplifictios, but it is istrumt which should b crfull trtd s it c sil crt
1. (25 points) Use the limit definition of the definite integral and the sum formulas to compute. [1 x + x2
 Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Mth 3, Clculus II Fil Exm Solutios. (5 poits) Use the limit defiitio of the defiite itegrl d the sum formuls to compute 3 x + x. Check your swer by usig the Fudmetl Theorem of Clculus. Solutio: The limit
Part B: Transform Methods. Professor E. Ambikairajah UNSW, Australia
 Part B: Trasform Mthods Chaptr 3: Discrt-Tim Fourir Trasform (DTFT) 3. Discrt Tim Fourir Trasform (DTFT) 3. Proprtis of DTFT 3.3 Discrt Fourir Trasform (DFT) 3.4 Paddig with Zros ad frqucy Rsolutio 3.5
Part B: Trasform Mthods Chaptr 3: Discrt-Tim Fourir Trasform (DTFT) 3. Discrt Tim Fourir Trasform (DTFT) 3. Proprtis of DTFT 3.3 Discrt Fourir Trasform (DFT) 3.4 Paddig with Zros ad frqucy Rsolutio 3.5
