3.1 Laplace s Equation 3.2 The Method of Images 3.3 Separation of Variables
|
|
|
- Peter Sanders
- 5 years ago
- Views:
Transcription
1 Lecture Note #3B Chpter 3. Potetis 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Boudry coditios re very importt to sove the poteti probems Dimesio (D, D, 3D) ectgur, Spheric, The seprtio of vribes c be used to sove the poteti distributios from fixed poteti cofigurtio (rectgur, spheric,...) X Ih Uiversity The Lpce s equtio x y z x, y, z X xy yz z X x Y Y y Z Z z i) whe y ii) whe y iii) whe z iv) whe z b v) s x vi) y,z whe x. r r r r r si si r si The, the fi form of the geer soutio of the equtio for zimuth symmetric probems becomes r, A r P B cos r
2 3.3 Seprtio of ribes ( 변수분리 ) 3.3. Crtesi Coordites [Exmpe 3.3] Let Ih Uiversity x, y X xy y The Lpce s equtio c be expressed s (Soutio) The cofigurtio is idepedet of z, so this is -D probem. The Lpce s equtio becomes x y The boudry coditios : i) whe y X Y Y X x y X Y x Y y Divide the bove equtio by XY. ii) iii) iv) whe y whe x whe x f x gy X k k (3.) (3.) (3.) (3.3)
3 3.3 Seprtio of ribes [Exmpe 3.3] (Soutio) - cotiued () X X x Y Y y k k X x Y y k k X x kx kx x, y X xy y Ae Be C si ky Dcos ky X Y Y y Ae kx Be kx Csi ky Dcos ky (3.7) Now, et us ppy the boudry coditios to the soutio of (x,y). iv) whe x k k, y Ae Be C si ky Dcos ky A iii) whe x kx x, Be D D i) whe y kx ii) whe y x, Be C si k k,, 3, Thus, the geer soutio becomes kx y x, y C' e si where C = BC : proportio costt y, y C' si y (3.9) (3.3) (3.3) Ih Uiversity Fourier sie series 3
4 3.3 Seprtio of ribes [Exmpe 3.3] (Soutio) - cotiued () Eq. (3.3) x si( y/), d the itegrte from to : y ' y C' si si dy ysi ' y dy (3.3) If (y) = t < y < [() = () = ], Thus, the fi form of the geer soutio becomes C' y ' y, si si dy, y ysi dy kx x, y C' e si if if y ' ' C' 4,3,5 (3.33) y ysi dy e x (3.34), if y y C' si cos cos 4 y dy, if y o y si is eve Pge 7 is odd. (3.36) Ih Uiversity 4
5 3.3 Seprtio of ribes [Exmpe 3.3] Eq. (3.36) (Soutio) - cotiued (3) x, y 4,3,5 e x y si = = 5 = = x, y 4,3,5 e x si y t si y sih x (3.37) Thus, the fi form of the geer soutio stisfies the four boudry coditios. Ih Uiversity 5
6 3.3 Seprtio of ribes Two Mjor Properties of the Seprbe Soutios to the Prti Differeti Equtios Competeess A set of fuctios f (y) is compete if fuctio f(y) is ier combitio of them. f y C f y (3.38) Orthogo A set of fuctios is orthogo if the itegr of the product of y two differet members of the set is zero: y y f f' dy for ' (3.39) Ih Uiversity 6
7 f x Mthemtic Iformtio Fourier series For periodic odd fuctio f(x) with period L, the Fourier series of f(x) is expressed s with x x cos b si L L b L t f t cos dt, L L L,,, 3, L t f t si dt, L L L,,, 3, [ef.] G. B. Arfke d H. J. Weber, Mthemtic Methods for Physicists, 5 th Ed., Acdemic Press () pge 873. Trigoometric fuctio six y si x cos y si y cos x cosx y cos x cos y si x si y If x = y, cos x cos x - si x si x si x cos x If x y, x si x dx 4 si bx si b si x si bx dx b b cosx dx si x Ih Uiversity [ef.] I. S. Grdshtey d I. M. yzhik, Tbe of Itegrs, Series, d Products, Acdemic Press (98) pge 39. x Bck 7
8 3.3 Seprtio of ribes ( 변수분리법 ) 3.3. Crtesi Coordites [Exmpe 3.4] Ih Uiversity (Soutio) The cofigurtio is idepedet of z, so this is -D probem. The Lpce s equtio becomes The boudry coditios : X Y Let x, y X xy y Y X x y Divide the bove equtio by XY. The Lpce s equtio c be expressed s X X x k i ) ii ) Y Y y iii ) iv ) k x whe y y whe y whe x b whe x b (3.4) (3.4) (3.4) (3.43) 8
9 3.3 Seprtio of ribes [Exmpe 3.4] Now, et us ppy the boudry coditios to the soutio of (x,y). Ih Uiversity (Soutio) - cotiued () X X x Y Y y k k k X x Ae kx kx x, y X xy y Ae Be C si ky Dcos ky The poteti (x,y) is symmetric with respect to x. x,y x,y i) whe y iii) whe x b X x Y y k b, y C' cosh b si y x, y X Y C' Y A B y where C = AC d D =AD : proportio costts. x y cosh si kx Be kx Csi ky Dcos ky kx kx x, y Ae e C si ky Dcos ky cosh kxc'si ky D'cos ky x, cosh kxc'si D'cos D' x, C'coshkxsik k (3.44) (3.45) (3.46) ii) whe y The poteti (x,y) is symmetric with respect to x, (x,y) stisfies the 3 rd d 4th boudry coditios simuteousy. (3.47) (3.48) 9
10 3.3 Seprtio of ribes [Exmpe 3.4] (Soutio) - cotiued () Eq. (3.47) x si( y/), d the itegrte the equtio over y from to : b y ' y C' cosh si si dy ysi C' b cosh y ' y, si si dy, If (y) = t < y < & () = () =, C y ysi dy ' y if ' if ' C' dy b cosh (3.49) (3.5) y ysi dy (3.5), if is eve. 4, if is odd. b y y ' cosh y si dy cos cos yo Thus, the fi form of the geer soutio becomes, from Eq. (3.48), x, y C' x y cosh si 4,3,5 cosh cosh x b y si (3.5) Ih Uiversity
11 3.3 Seprtio of ribes [Exmpe 3.4] (Soutio) - cotiued (3) x, y 4,3,5 cosh cosh x b y si (3.5) Ih Uiversity x cosh b cosh e x e x cosh x sech cosh x cosh x sech e e x b e e x x e e x x x b
12 3.3. Crtesi Coordites [Exmpe 3.5] 3.3 Seprtio of ribes Let Ih Uiversity (Soutio) x, y, z X xy yz z This is 3-dimesio probem. The Lpce s equtio becomes x y The boudry coditios : i) whe y ii) whe y iii) whe z iv) whe z b v) vi) s x z y,z whe x. Substitutig this ito Eq. (3.53) d divide it by XYZ., the Lpce s equtio c be expressed s X X x Y Y y Z Z z (3.53) (3.54) (3.55) (3.56)
13 [Exmpe 3.5] 3.3 Seprtio of ribes (Soutio) - cotiued () X X X x C Y C k k x k x x Ae Be, k x k x x, y, z X xy yz z Ae Be C si ky Dcos kye si z F cos z Now, et us ppy the boudry coditios to the soutio of (x, y, z). i) whe y, Y y C C C C C C k 3 X x k X, Y y Y, Z C 3 Z 3 k Y, z Z z Z. y Csi ky Dcos ky, v) s x k x, y, z Ae x, y, z D Z A D, (3.57) z Esi z F cos z. (3.58) (3.59) (3.6) iii) ii) iv) whe z x, y, z F whe whe Ih Uiversity y z b k x x, y, z C' e siksiz k x x, y, z b C' e sikysib where C = BCE : proportio costt. m b x, y, z C' e m F k m b x y mz, m si si b (3.6) (3.6) (3.63) (3.64) 3
14 [Exmpe 3.5] 3.3 Seprtio of ribes (Soutio) - cotiued () Eq. (3.64) Let us ppy the st boudry coditios to the soutio of (x, y, z). y,z whe x. vi) / m b x, y, z C' e m x y mz, m si si b y mz b,, m, m x y, z C' si si x y (3.65) (3.66) Eq. (3.66) x si( y/) si(m z/b), d the itegrte the equtio over y from to d over z from to b : b b C' si si dy si si dz x, ysi si m y ' y y ' y, si si dy, if ' if ' mz b b m' z b mz m' z, si si dz b b b, ' y m' z b dy dz (3.67) if m' m if m' m C', m 4 b b x, y y mz si si dy dz b (3.68) Ih Uiversity 4
15 3.3 Seprtio of ribes [Exmpe 3.5] (Soutio) - cotiued (3) If the (x, y) = ( costt poteti) t x =, the soutio becomes Eq. (3.68) C', m 4 b y mz b b si dy si dz (3.68) y y si dy cos, if is eve. cos, if is odd. yo C' m 4 b b, 6 m, m if or m is eve, if d, m re odd. (3.7) (3.7) 6 x y mz e si si m m b, m,3,5 / m b Eq. (3.65) x, y, z (3.7) Ih Uiversity 5
16 3.3. Spheric Coordites 3.3 Seprtio of ribes I the spheric coordites, Lpce s equtio is writte s si r r r r r si r si (3.73) For zimuth symmetric probems, is idepedet of. r r r si si (3.74) Let Ih Uiversity r r, The Lpce s equtio c be expressed s Divide the bove equtio by. r r r r r r r d dr r r r si r si si si d dr (3.75) (3.76) (3.77) 6
17 3.3. Spheric Coordites 3.3 Seprtio of ribes The geer soutio of the equtio B r Ar r - cotiued () d d r dr dr (3.78) [Check whether this soutio stisfies Eq. (3.77) or ot]. Eq. (3.76) si si is writte s d d d si d The soutio of the gur equtio is cos P Legedre poyomis is defied by the odrigues formu: d P!! dx x x si (3.79) : Legedre poyomis i the vribe cos. (3.8) (3.8) Ih Uiversity P 7
18 3.3. Spheric Coordites For =, Eq. (3.79) 3.3 Seprtio of ribes i) Oe soutio of the bove equtio is P cos d d d d si d d d d si d d P cos P cos (3.83) - cotiued () (3.8) ii) Aother possibe soutio of the bove equtio is t (3.84) u t du sec d d u du u cos d d du sec d du d u si Eq. (3.8) si si cos d d d si si d d d si x y si xcos y si ycos x si si si cos si cos d d Ih Uiversity t - t This mes tht this type soutio is ot pproprite. (3.85) 8
19 3.3 Seprtio of ribes 3.3. Spheric Coordites - cotiued (3) Thus, the geer soutio of the equtio for zimuth symmetric probems becomes B r r r Ar P cos, (3.86) The, the fi form of the geer soutio of the equtio for zimuth symmetric probems becomes r, A r P B cos r (3.87) P cos : Legedre poyomis i the vribe cos. Ih Uiversity 9
20 3.3. Spheric Coordites [Exmpe 3.6] 3.3 Seprtio of ribes (Soutio) Eq. (3.87) B r, A r P cos r B r, A P cos ( ) r, A r P cos The boudry coditios :, A P cos Eq. (3.9) x P (cos) si d itegrtig Ih Uiversity A P ' P cos P cos si d P cos si d xp xdx P cos P cos ' ' ', si d, B if ' if ' (3.87) (3.88) (3.89) (3.9) (3.9) (3.9) : orthogo property of the Legedre poyomis
21 3.3 Seprtio of ribes [Exmpe 3.6] (Soutio) - cotiued () Eq. (3.9) ' A ' Thus, A ' P ' cos si d P cos si d (3.93) (3.94) ( ) r, A r P cos : Poteti iside the sphere (3.89) Ih Uiversity
22 Ih Uiversity 3.3 Seprtio of ribes [Exmpe 3.6] (Soutio) - cotiued () If k si, Eq. (3.95) Eq. (3.9) : Eq. (3.96) Eq. (3.89) : k cos P cos cos A r, A r P cos A k k si P P P P cos P cos k r k cos k cos A P cos A P cos P cos P cos P k A, k x y cos xcos y si xsi y cos cos cos cos si cos A cos r P cos cos k si k r si (3.95) (3.96) (3.97) : Poteti iside the sphere
23 3.3. Spheric Coordites [Exmpe 3.7] 3.3 Seprtio of ribes (Soutio) Eq. (3.87) B r, A r P (3.98) cos r A (3.99) B r, A P cos ( ) B (3.) r, P cos r The boudry coditios : B, (3.) P cos Eq. (3.9) x P (cos) si d itegrtig B P P d P d (3.) cos cos si ' cos si ', if ' (3.9) P xp ' xdx P cos P ' cos si d, if ' Ih Uiversity : orthogo property of the Legedre poyomis 3
24 3.3 Seprtio of ribes [Exmpe 3.7] (Soutio) - cotiued () Eq. (3.) B ' ' ' P cos si d ' (3.3) ( ) B P cos si d r, P B cos r : Poteti outside the sphere (3.4) (3.) Ih Uiversity 4
25 3.3. Spheric Coordites [Exmpe 3.8] 3.3 Seprtio of ribes r E E zˆ Ih Uiversity (Soutio) The metic sphere is equipoteti zero poteti. The etire xy pe withi the sphere is t zero poteti. Fr from the sphere, the fied is E E zˆ, d the poteti is The boudry coditios : E z C, B r A P cos i), whe r B A Eq. (3.87) Sice = i the equtori xy pe, C i), whe r ii) E r cos θ, for r B A (3.) (3.) (3.3) (3.4) (3.5) 5
26 3.3 Seprtio of ribes [Exmpe 3.8] (Soutio) - cotiued () Eq. (3.87) B r, A r P cos r Eq. (3.5) Eq. (3.87) : ) E r cos θ, The iduced chrge desity : E E r (3.87) r, A r P cos for r r for r (3.6) ii r, A r P cos Er cos cos E cos r A E, A r P 3 E r cos r Eq. (3.8) Eq. (3.6) : r, r r E r cos E cos, exter fied effect Cotributio from the iduced chrge 3 cos 3 3 r E r Ih Uiversity r 3 cos q E d S ecosed (3.7) (3.8) (3.9) d S E (3.) 6
27 3.3. Spheric Coordites [Exmpe 3.9] 3.3 Seprtio of ribes Ih Uiversity (Soutio) ) Method (Direct itegrtio method) : Eq. (.3) ( ) ) Method (Seprtio of vribes method, 변수분리법 ) : Poteti iside the sphere : Eq. (3.89) Eq. (3.) r r, P cos r Sice the poteti is cotiuous t the she surfce, Eq. (3.) = Eq. (3.3) t r =. Poteti outside the sphere : 4 B r S r r' (3.3) d' (3.) r, A r P cos r A P cos P cos B (3.) (3.4) r 7
28 3.3 Seprtio of ribes [Exmpe 3.9] (Soutio) - cotiued () B A B A (3.5) ( ) Ih Uiversity The rdi derivtive of suffers discotiuity t the surfce: Eq. (.36) Eqs. (3.) & (3.3) Eq. (3.6): Eq. (3.5) Eq. (3.7): B P cos A P cos Eq. (3.8) x P (cos) si d itegrtig (3.6) P cos A P cos P cos si d P cos si d ' ' P r xp xdx P cos P cos ' out r i r ' A, if ' si d, if ' E : orthogo property of the Legedre poyomis E E bove // bove E beow // beow. (3.7) (3.8) (3.9) (3.) 8
29 3.3 Seprtio of ribes [Exmpe 3.9] (Soutio) - cotiued () ' Eq. (3.9) ' A P cos si d ' ' ' (3.) ( ) Eq. (3.) Thus, A P cos si d r, A r P cos r (3.) (3.3) Eqs. (3.3) & (3.5) r r, A P cos r (3.4) Ih Uiversity 9
30 3.3 Seprtio of ribes [Exmpe 3.9] (Soutio) - cotiued (3) If k kpcos, cos (3.5) Eq. (3.) Eq. (3.3) A k k (3.6) P cos si d 3 k 3 r, r cos r (3.7) ( ) Eq. (3.4) Ih Uiversity 3 k 3 r r cos r, (3.8) If () is the iduced chrge o met sphere i exter fied E zˆ so tht k E, The Poteti iside the sphere Eq. (3.7) r E r cos E z r, The Poteti outside the sphere r 3, r E cos r (3.9) Eq. (3.8) (3.3) Eq. (3.9) E from Eq. (3.) E 3 zˆ Eq. (3.9) 3
31 Chpter 3. Potetis Next Css 3. Lpce s Equtio 3. The Method of Imges 3.3 Seprtio of ribes 3.3. Crtesi Coordites 3.3. Spheric coordites 3.4 Mutipoe Expsio Ih Uiversity 3
MA6351 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C
 MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit
MA635 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS L T P C 3 4 OBJECTIVES: To itroduce Fourier series ysis which is cetr to my ppictios i egieerig prt from its use i sovig boudry vue probems? To cquit
0 otherwise. sin( nx)sin( kx) 0 otherwise. cos( nx) sin( kx) dx 0 for all integers n, k.
 . Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
. Computtio of Fourier Series I this sectio, we compute the Fourier coefficiets, f ( x) cos( x) b si( x) d b, i the Fourier series To do this, we eed the followig result o the orthogolity of the trigoometric
Chapter 10 Partial Differential Equations and Fourier Series
 Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
Question 1: The magnetic case
 September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
BRAIN TEASURES INDEFINITE INTEGRATION+DEFINITE INTEGRATION EXERCISE I
 EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
EXERCISE I t Q. d Q. 6 6 cos si Q. Q.6 d d Q. d Q. Itegrte cos t d by the substitutio z = + e d e Q.7 cos. l cos si d d Q. cos si si si si b cos Q.9 d Q. si b cos Q. si( ) si( ) d ( ) Q. d cot d d Q. (si
MAS221 Analysis, Semester 2 Exercises
 MAS22 Alysis, Semester 2 Exercises Srh Whitehouse (Exercises lbelled * my be more demdig.) Chpter Problems: Revisio Questio () Stte the defiitio of covergece of sequece of rel umbers, ( ), to limit. (b)
MAS22 Alysis, Semester 2 Exercises Srh Whitehouse (Exercises lbelled * my be more demdig.) Chpter Problems: Revisio Questio () Stte the defiitio of covergece of sequece of rel umbers, ( ), to limit. (b)
MATH 174: Numerical Analysis. Lecturer: Jomar F. Rabajante 1 st Sem AY
 MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
MATH 74: Numeric Aysis Lecturer: Jomr F. Rbjte st Sem AY - INTERPOLATION THEORY We wt to seect fuctio p from give css of fuctios i such wy tht the grph of y=p psses through fiite set of give dt poits odes.
SCHOOL OF MATHEMATICS AND STATISTICS. Mathematics II (Materials)
 Dt proie: Form Sheet MAS5 SCHOOL OF MATHEMATICS AND STATISTICS Mthemtics II (Mteris) Atm Semester -3 hors Mrks wi e wre or swers to qestios i Sectio A or or est THREE swers to qestios i Sectio. Sectio
Dt proie: Form Sheet MAS5 SCHOOL OF MATHEMATICS AND STATISTICS Mthemtics II (Mteris) Atm Semester -3 hors Mrks wi e wre or swers to qestios i Sectio A or or est THREE swers to qestios i Sectio. Sectio
Math 3B Midterm Review
 Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 643u Office Hours: R 11:00 m - 1:00 pm Lst updted /15/015 Here re some short otes o Sectios 7.1-7.8 i your ebook. The best idictio of wht
Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 643u Office Hours: R 11:00 m - 1:00 pm Lst updted /15/015 Here re some short otes o Sectios 7.1-7.8 i your ebook. The best idictio of wht
5.1 - Areas and Distances
 Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 63u Office Hours: R 9:5 - :5m The midterm will cover the sectios for which you hve received homework d feedbck Sectios.9-6.5 i your book.
Mth 3B Midterm Review Writte by Victori Kl vtkl@mth.ucsb.edu SH 63u Office Hours: R 9:5 - :5m The midterm will cover the sectios for which you hve received homework d feedbck Sectios.9-6.5 i your book.
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Strauss PDEs 2e: Section Exercise 4 Page 1 of 5. u tt = c 2 u xx ru t for 0 < x < l u = 0 at both ends u(x, 0) = φ(x) u t (x, 0) = ψ(x),
 Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
Strauss PDEs e: Sectio 4.1 - Exercise 4 Page 1 of 5 Exercise 4 Cosider waves i a resistat medium that satisfy the probem u tt = c u xx ru t for < x < u = at both eds ux, ) = φx) u t x, ) = ψx), where r
ECE Spring Prof. David R. Jackson ECE Dept. Notes 20
 ECE 6341 Sprig 016 Prof. David R. Jackso ECE Dept. Notes 0 1 Spherical Wave Fuctios Cosider solvig ψ + k ψ = 0 i spherical coordiates z φ θ r y x Spherical Wave Fuctios (cot.) I spherical coordiates we
ECE 6341 Sprig 016 Prof. David R. Jackso ECE Dept. Notes 0 1 Spherical Wave Fuctios Cosider solvig ψ + k ψ = 0 i spherical coordiates z φ θ r y x Spherical Wave Fuctios (cot.) I spherical coordiates we
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES. To a 2π-periodic function f(x) we will associate a trigonometric series. a n cos(nx) + b n sin(nx),
 FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
FOURIER SERIES PART I: DEFINITIONS AND EXAMPLES To -periodic fuctio f() we will ssocite trigoometric series + cos() + b si(), or i terms of the epoetil e i, series of the form c e i. Z For most of the
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 116C. Problem Set 4. Benjamin Stahl. November 6, 2014
 UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 6C Problem Set 4 Bejami Stahl November 6, 4 BOAS, P. 63, PROBLEM.-5 The Laguerre differetial equatio, x y + ( xy + py =, will be solved
UNIVERSITY OF CALIFORNIA - SANTA CRUZ DEPARTMENT OF PHYSICS PHYS 6C Problem Set 4 Bejami Stahl November 6, 4 BOAS, P. 63, PROBLEM.-5 The Laguerre differetial equatio, x y + ( xy + py =, will be solved
Lecture 38 (Trapped Particles) Physics Spring 2018 Douglas Fields
 Lecture 38 (Trpped Prticles) Physics 6-01 Sprig 018 Dougls Fields Free Prticle Solutio Schrödiger s Wve Equtio i 1D If motio is restricted to oe-dimesio, the del opertor just becomes the prtil derivtive
Lecture 38 (Trpped Prticles) Physics 6-01 Sprig 018 Dougls Fields Free Prticle Solutio Schrödiger s Wve Equtio i 1D If motio is restricted to oe-dimesio, the del opertor just becomes the prtil derivtive
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Notes 17 Sturm-Liouville Theory
 ECE 638 Fll 017 Dvid R. Jckso Notes 17 Sturm-Liouville Theory Notes re from D. R. Wilto, Dept. of ECE 1 Secod-Order Lier Differetil Equtios (SOLDE) A SOLDE hs the form d y dy 0 1 p ( x) + p ( x) + p (
ECE 638 Fll 017 Dvid R. Jckso Notes 17 Sturm-Liouville Theory Notes re from D. R. Wilto, Dept. of ECE 1 Secod-Order Lier Differetil Equtios (SOLDE) A SOLDE hs the form d y dy 0 1 p ( x) + p ( x) + p (
UNIVERSITY OF BRISTOL. Examination for the Degrees of B.Sc. and M.Sci. (Level C/4) ANALYSIS 1B, SOLUTIONS MATH (Paper Code MATH-10006)
 UNIVERSITY OF BRISTOL Exmitio for the Degrees of B.Sc. d M.Sci. (Level C/4) ANALYSIS B, SOLUTIONS MATH 6 (Pper Code MATH-6) My/Jue 25, hours 3 miutes This pper cotis two sectios, A d B. Plese use seprte
UNIVERSITY OF BRISTOL Exmitio for the Degrees of B.Sc. d M.Sci. (Level C/4) ANALYSIS B, SOLUTIONS MATH 6 (Pper Code MATH-6) My/Jue 25, hours 3 miutes This pper cotis two sectios, A d B. Plese use seprte
Quantization and Special Functions
 Otocec 6.-9.0.003 Quatizatio ad Special Fuctios Christia B. Lag Ist. f. theoret. Physik Uiversität Graz Cotets st lecture Schrödiger equatio Eigevalue equatios -dimesioal problems Limitatios of Quatum
Otocec 6.-9.0.003 Quatizatio ad Special Fuctios Christia B. Lag Ist. f. theoret. Physik Uiversität Graz Cotets st lecture Schrödiger equatio Eigevalue equatios -dimesioal problems Limitatios of Quatum
sin m a d F m d F m h F dy a dy a D h m h m, D a D a c1cosh c3cos 0
 Q1. The free vibrtio of the plte is give by By ssumig h w w D t, si cos w W x y t B t Substitutig the deflectio ito the goverig equtio yields For the plte give, the mode shpe W hs the form h D W W W si
Q1. The free vibrtio of the plte is give by By ssumig h w w D t, si cos w W x y t B t Substitutig the deflectio ito the goverig equtio yields For the plte give, the mode shpe W hs the form h D W W W si
Calculus II Homework: The Integral Test and Estimation of Sums Page 1
 Clculus II Homework: The Itegrl Test d Estimtio of Sums Pge Questios Emple (The p series) Get upper d lower bouds o the sum for the p series i= /ip with p = 2 if the th prtil sum is used to estimte the
Clculus II Homework: The Itegrl Test d Estimtio of Sums Pge Questios Emple (The p series) Get upper d lower bouds o the sum for the p series i= /ip with p = 2 if the th prtil sum is used to estimte the
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Eigenfunction Expansion. For a given function on the internal a x b the eigenfunction expansion of f(x):
 Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
Eigefuctio Epsio: For give fuctio o the iterl the eigefuctio epsio of f(): f ( ) cmm( ) m 1 Eigefuctio Epsio (Geerlized Fourier Series) To determie c s we multiply oth sides y Φ ()r() d itegrte: f ( )
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
CITY UNIVERSITY LONDON
 CITY UNIVERSITY LONDON Eg (Hos) Degree i Civil Egieerig Eg (Hos) Degree i Civil Egieerig with Surveyig Eg (Hos) Degree i Civil Egieerig with Architecture PART EXAMINATION SOLUTIONS ENGINEERING MATHEMATICS
CITY UNIVERSITY LONDON Eg (Hos) Degree i Civil Egieerig Eg (Hos) Degree i Civil Egieerig with Surveyig Eg (Hos) Degree i Civil Egieerig with Architecture PART EXAMINATION SOLUTIONS ENGINEERING MATHEMATICS
Now we are looking to find a volume of solid S that lies below a surface z = f(x,y) and R= ab, cd,,[a,b] is the interval over
![Now we are looking to find a volume of solid S that lies below a surface z = f(x,y) and R= ab, cd,,[a,b] is the interval over Now we are looking to find a volume of solid S that lies below a surface z = f(x,y) and R= ab, cd,,[a,b] is the interval over](/thumbs/82/86586734.jpg) Multiple Itegratio Double Itegrals, Volume, ad Iterated Itegrals I sigle variable calculus we looked to fid the area uder a curve f(x) bouded by the x- axis over some iterval usig summatios the that led
Multiple Itegratio Double Itegrals, Volume, ad Iterated Itegrals I sigle variable calculus we looked to fid the area uder a curve f(x) bouded by the x- axis over some iterval usig summatios the that led
PhysicsAndMathsTutor.com
 PhysicsAdMthsTutor.com PhysicsAdMthsTutor.com Jue 009 4. Give tht y rsih ( ), > 0, () fid d y d, givig your swer s simplified frctio. () Leve lk () Hece, or otherwise, fid 4 d, 4 [ ( )] givig your swer
PhysicsAdMthsTutor.com PhysicsAdMthsTutor.com Jue 009 4. Give tht y rsih ( ), > 0, () fid d y d, givig your swer s simplified frctio. () Leve lk () Hece, or otherwise, fid 4 d, 4 [ ( )] givig your swer
Name of the Student:
 SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Mthemtics Revisio Guides Itegrtig Trig, Log d Ep Fuctios Pge of MK HOME TUITION Mthemtics Revisio Guides Level: AS / A Level AQA : C Edecel: C OCR: C OCR MEI: C INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
Physics 235 Final Examination December 4, 2006 Solutions
 Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
Physics 35 Fi Emitio Decembe, 6 Soutios.. Fist coside the two u quks. They e idetic spi ½ ptices, so the tot spi c be eithe o. The Pui Picipe equies tht the ove wvefuctio be echge tisymmetic. Sice the
radians A function f ( x ) is called periodic if it is defined for all real x and if there is some positive number P such that:
 Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
Fourier Series. Graph of y Asix ad y Acos x Amplitude A ; period 36 radias. Harmoics y y six is the first harmoic y y six is the th harmoics 3. Periodic fuctio A fuctio f ( x ) is called periodic if it
LECTURE 8: ASYMPTOTICS I
 LECTURE 8: ASYMPTOTICS I We are iterested i the properties of estimators as. Cosider a sequece of radom variables {, X 1}. N. M. Kiefer, Corell Uiversity, Ecoomics 60 1 Defiitio: (Weak covergece) A sequece
LECTURE 8: ASYMPTOTICS I We are iterested i the properties of estimators as. Cosider a sequece of radom variables {, X 1}. N. M. Kiefer, Corell Uiversity, Ecoomics 60 1 Defiitio: (Weak covergece) A sequece
Particle in a Box. and the state function is. In this case, the Hermitian operator. The b.c. restrict us to 0 x a. x A sin for 0 x a, and 0 otherwise
 Prticle i Box We must hve me where = 1,,3 Solvig for E, π h E = = where = 1,,3, m 8m d the stte fuctio is x A si for 0 x, d 0 otherwise x ˆ d KE V. m dx I this cse, the Hermiti opertor 0iside the box The
Prticle i Box We must hve me where = 1,,3 Solvig for E, π h E = = where = 1,,3, m 8m d the stte fuctio is x A si for 0 x, d 0 otherwise x ˆ d KE V. m dx I this cse, the Hermiti opertor 0iside the box The
Schrödinger Equation Via Laplace-Beltrami Operator
 IOSR Jourl of Mthemtics (IOSR-JM) e-issn: 78-578, p-issn: 39-765X. Volume 3, Issue 6 Ver. III (Nov. - Dec. 7), PP 9-95 www.iosrjourls.org Schrödiger Equtio Vi Lplce-Beltrmi Opertor Esi İ Eskitşçioğlu,
IOSR Jourl of Mthemtics (IOSR-JM) e-issn: 78-578, p-issn: 39-765X. Volume 3, Issue 6 Ver. III (Nov. - Dec. 7), PP 9-95 www.iosrjourls.org Schrödiger Equtio Vi Lplce-Beltrmi Opertor Esi İ Eskitşçioğlu,
A second look at separation of variables
 A secod look at separatio of variables Assumed that u(x,t)x(x)t(t) Pluggig this ito the wave, diffusio, or Laplace equatio gave two ODEs The solutios to those ODEs subject to boudary ad iitial coditios
A secod look at separatio of variables Assumed that u(x,t)x(x)t(t) Pluggig this ito the wave, diffusio, or Laplace equatio gave two ODEs The solutios to those ODEs subject to boudary ad iitial coditios
UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION. (2014 Admn. onwards) III Semester. B.Sc. Mathematics CORE COURSE CALCULUS AND ANALYTICAL GEOMETRY
 UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION (0 Adm. owrds) III Semester B.Sc. Mthemtics CORE COURSE CALCULUS AND ANALYTICAL GEOMETRY Questio Bk & Aswer Key. l l () =... 0.00 b) 0 c). l d =... c
UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION (0 Adm. owrds) III Semester B.Sc. Mthemtics CORE COURSE CALCULUS AND ANALYTICAL GEOMETRY Questio Bk & Aswer Key. l l () =... 0.00 b) 0 c). l d =... c
19 Fourier Series and Practical Harmonic Analysis
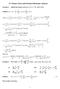 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Assignment 1 : Real Numbers, Sequences. for n 1. Show that (x n ) converges. Further, by observing that x n+2 + x n+1
 Assigmet : Real Numbers, Sequeces. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a upper boud of A for every N. 2. Let y (, ) ad x (, ). Evaluate
Assigmet : Real Numbers, Sequeces. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a upper boud of A for every N. 2. Let y (, ) ad x (, ). Evaluate
Lecture 7: Properties of Random Samples
 Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Chapter 10: The Z-Transform Adapted from: Lecture notes from MIT, Binghamton University Dr. Hamid R. Rabiee Fall 2013
 Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Sigls & Systems Chpter 0: The Z-Trsform Adpted from: Lecture otes from MIT, Bighmto Uiversity Dr. Hmid R. Rbiee Fll 03 Lecture 5 Chpter 0 Lecture 6 Chpter 0 Outlie Itroductio to the -Trsform Properties
Chapter 4 Postulates of Quantum Mechanics
 F 014 Chem 350: Itroductory Qutum Mechics Chpter 4 Postutes of Qutum Mechics... 48 MthChpter C... 48 The Postutes of Qutum Mechics... 50 Properties of Hermiti Opertors... 53 Discussio of Mesuremet... 55
F 014 Chem 350: Itroductory Qutum Mechics Chpter 4 Postutes of Qutum Mechics... 48 MthChpter C... 48 The Postutes of Qutum Mechics... 50 Properties of Hermiti Opertors... 53 Discussio of Mesuremet... 55
PARTIAL DIFFERENTIAL EQUATIONS SEPARATION OF VARIABLES
 Diola Bagayoko (0 PARTAL DFFERENTAL EQUATONS SEPARATON OF ARABLES. troductio As discussed i previous lectures, partial differetial equatios arise whe the depedet variale, i.e., the fuctio, varies with
Diola Bagayoko (0 PARTAL DFFERENTAL EQUATONS SEPARATON OF ARABLES. troductio As discussed i previous lectures, partial differetial equatios arise whe the depedet variale, i.e., the fuctio, varies with
1. Hydrogen Atom: 3p State
 7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
7633A QUANTUM MECHANICS I - solutio set - autum. Hydroge Atom: 3p State Let us assume that a hydroge atom is i a 3p state. Show that the radial part of its wave fuctio is r u 3(r) = 4 8 6 e r 3 r(6 r).
We will begin by supplying the proof to (a).
 (The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce
(The solutios of problem re mostly from Jeffrey Mudrock s HWs) Problem 1. There re three sttemet from Exmple 5.4 i the textbook for which we will supply proofs. The sttemets re the followig: () The spce
Indian Institute of Information Technology, Allahabad. End Semester Examination - Tentative Marking Scheme
 Idia Istitute of Iformatio Techology, Allahabad Ed Semester Examiatio - Tetative Markig Scheme Course Name: Mathematics-I Course Code: SMAT3C MM: 75 Program: B.Tech st year (IT+ECE) ate of Exam:..7 ( st
Idia Istitute of Iformatio Techology, Allahabad Ed Semester Examiatio - Tetative Markig Scheme Course Name: Mathematics-I Course Code: SMAT3C MM: 75 Program: B.Tech st year (IT+ECE) ate of Exam:..7 ( st
Classical Electrodynamics
 A First Look t Qutum Phsics Clssicl Electrodmics Chpter Boudr-Vlue Prolems i Electrosttics: I 11 Clssicl Electrodmics Prof. Y. F. Che Cotets A First Look t Qutum Phsics.1 Poit Chrge i the Presece of Grouded
A First Look t Qutum Phsics Clssicl Electrodmics Chpter Boudr-Vlue Prolems i Electrosttics: I 11 Clssicl Electrodmics Prof. Y. F. Che Cotets A First Look t Qutum Phsics.1 Poit Chrge i the Presece of Grouded
Expected Number of Level Crossings of Legendre Polynomials
 Expected Number of Level Crossigs of Legedre olomials ROUT, LMNAYAK, SMOHANTY, SATTANAIK,NC OJHA,DRKMISHRA Research Scholar, G DEARTMENT OF MATHAMATICS,COLLEGE OF ENGINEERING AND TECHNOLOGY,BHUBANESWAR,ODISHA
Expected Number of Level Crossigs of Legedre olomials ROUT, LMNAYAK, SMOHANTY, SATTANAIK,NC OJHA,DRKMISHRA Research Scholar, G DEARTMENT OF MATHAMATICS,COLLEGE OF ENGINEERING AND TECHNOLOGY,BHUBANESWAR,ODISHA
POWER SERIES R. E. SHOWALTER
 POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
POWER SERIES R. E. SHOWALTER. sequeces We deote by lim = tht the limit of the sequece { } is the umber. By this we me tht for y ε > 0 there is iteger N such tht < ε for ll itegers N. This mkes precise
CHAPTER 2: Boundary-Value Problems in Electrostatics: I. Applications of Green s theorem
 CHAPTER : Boudr-Vlue Problems i Electrosttics: I Applictios of Gree s theorem .6 Gree Fuctio for the Sphere; Geerl Solutio for the Potetil The geerl electrosttic problem (upper figure): ( ) ( ) with b.c.
CHAPTER : Boudr-Vlue Problems i Electrosttics: I Applictios of Gree s theorem .6 Gree Fuctio for the Sphere; Geerl Solutio for the Potetil The geerl electrosttic problem (upper figure): ( ) ( ) with b.c.
y udv uv y v du 7.1 INTEGRATION BY PARTS
 7. INTEGRATION BY PARTS Ever differetitio rule hs correspodig itegrtio rule. For istce, the Substitutio Rule for itegrtio correspods to the Chi Rule for differetitio. The rule tht correspods to the Product
7. INTEGRATION BY PARTS Ever differetitio rule hs correspodig itegrtio rule. For istce, the Substitutio Rule for itegrtio correspods to the Chi Rule for differetitio. The rule tht correspods to the Product
AMS570 Lecture Notes #2
 AMS570 Lecture Notes # Review of Probability (cotiued) Probability distributios. () Biomial distributio Biomial Experimet: ) It cosists of trials ) Each trial results i of possible outcomes, S or F 3)
AMS570 Lecture Notes # Review of Probability (cotiued) Probability distributios. () Biomial distributio Biomial Experimet: ) It cosists of trials ) Each trial results i of possible outcomes, S or F 3)
82A Engineering Mathematics
 Clss Notes 9: Power Series /) 8A Egieerig Mthetics Secod Order Differetil Equtios Series Solutio Solutio Ato Differetil Equtio =, Hoogeeous =gt), No-hoogeeous Solutio: = c + p Hoogeeous No-hoogeeous Fudetl
Clss Notes 9: Power Series /) 8A Egieerig Mthetics Secod Order Differetil Equtios Series Solutio Solutio Ato Differetil Equtio =, Hoogeeous =gt), No-hoogeeous Solutio: = c + p Hoogeeous No-hoogeeous Fudetl
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING
 OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
OLLSCOIL NA héireann, CORCAIGH THE NATIONAL UNIVERSITY OF IRELAND, CORK COLÁISTE NA hollscoile, CORCAIGH UNIVERSITY COLLEGE, CORK SUMMER EXAMINATION 2005 FIRST ENGINEERING MATHEMATICS MA008 Clculus d Lier
Mathematical Statistics - MS
 Paper Specific Istructios. The examiatio is of hours duratio. There are a total of 60 questios carryig 00 marks. The etire paper is divided ito three sectios, A, B ad C. All sectios are compulsory. Questios
Paper Specific Istructios. The examiatio is of hours duratio. There are a total of 60 questios carryig 00 marks. The etire paper is divided ito three sectios, A, B ad C. All sectios are compulsory. Questios
Using Quantum Mechanics in Simple Systems Chapter 15
 /16/17 Qutiztio rises whe the loctio of prticle (here electro) is cofied to dimesiolly smll regio of spce qutum cofiemet. Usig Qutum Mechics i Simple Systems Chpter 15 The simplest system tht c be cosidered
/16/17 Qutiztio rises whe the loctio of prticle (here electro) is cofied to dimesiolly smll regio of spce qutum cofiemet. Usig Qutum Mechics i Simple Systems Chpter 15 The simplest system tht c be cosidered
National Quali cations SPECIMEN ONLY
 AH Ntiol Quli ctios SPECIMEN ONLY SQ/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite workig.
AH Ntiol Quli ctios SPECIMEN ONLY SQ/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite workig.
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
CALCULUS AB SECTION I, Part A Time 60 minutes Number of questions 30 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM.
 AP Calculus AB Portfolio Project Multiple Choice Practice Name: CALCULUS AB SECTION I, Part A Time 60 miutes Number of questios 30 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM. Directios: Solve
AP Calculus AB Portfolio Project Multiple Choice Practice Name: CALCULUS AB SECTION I, Part A Time 60 miutes Number of questios 30 A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAM. Directios: Solve
Lesson 03 Heat Equation with Different BCs
 PDE & Complex Variables P3- esso 3 Heat Equatio with Differet BCs ( ) Physical meaig (SJF ) et u(x, represet the temperature of a thi rod govered by the (coductio) heat equatio: u t =α u xx (3.) where
PDE & Complex Variables P3- esso 3 Heat Equatio with Differet BCs ( ) Physical meaig (SJF ) et u(x, represet the temperature of a thi rod govered by the (coductio) heat equatio: u t =α u xx (3.) where
BC Calculus Path to a Five Problems
 BC Clculus Pth to Five Problems # Topic Completed U -Substitutio Rule Itegrtio by Prts 3 Prtil Frctios 4 Improper Itegrls 5 Arc Legth 6 Euler s Method 7 Logistic Growth 8 Vectors & Prmetrics 9 Polr Grphig
BC Clculus Pth to Five Problems # Topic Completed U -Substitutio Rule Itegrtio by Prts 3 Prtil Frctios 4 Improper Itegrls 5 Arc Legth 6 Euler s Method 7 Logistic Growth 8 Vectors & Prmetrics 9 Polr Grphig
Today in Physics 217: separation of variables IV
 Today i Physics 27: separatio of variables IV Separatio i cylidrical coordiates Exaple of the split cylider (solutio sketched at right) More o orthogoality of trig fuctios ad Fourier s trick V = V V =
Today i Physics 27: separatio of variables IV Separatio i cylidrical coordiates Exaple of the split cylider (solutio sketched at right) More o orthogoality of trig fuctios ad Fourier s trick V = V V =
Informal Notes: Zeno Contours, Parametric Forms, & Integrals. John Gill March August S for a convex set S in the complex plane.
 Iformal Notes: Zeo Cotours Parametric Forms & Itegrals Joh Gill March August 3 Abstract: Elemetary classroom otes o Zeo cotours streamlies pathlies ad itegrals Defiitio: Zeo cotour[] Let gk ( z = z + ηk
Iformal Notes: Zeo Cotours Parametric Forms & Itegrals Joh Gill March August 3 Abstract: Elemetary classroom otes o Zeo cotours streamlies pathlies ad itegrals Defiitio: Zeo cotour[] Let gk ( z = z + ηk
MATH 10550, EXAM 3 SOLUTIONS
 MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION
 School Of Distce Eductio Questio Bk UNIVERSITY OF ALIUT SHOOL OF DISTANE EDUATION B.Sc MATHEMATIS (ORE OURSE SIXTH SEMESTER ( Admissio OMPLEX ANALYSIS Module- I ( A lytic fuctio with costt modulus is :
School Of Distce Eductio Questio Bk UNIVERSITY OF ALIUT SHOOL OF DISTANE EDUATION B.Sc MATHEMATIS (ORE OURSE SIXTH SEMESTER ( Admissio OMPLEX ANALYSIS Module- I ( A lytic fuctio with costt modulus is :
Løsningsførslag i 4M
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Calculus Summary Sheet
 Clculus Summry Sheet Limits Trigoometric Limits: siθ lim θ 0 θ = 1, lim 1 cosθ = 0 θ 0 θ Squeeze Theorem: If f(x) g(x) h(x) if lim f(x) = lim h(x) = L, the lim g(x) = L x x x Ietermite Forms: 0 0,,, 0,
Clculus Summry Sheet Limits Trigoometric Limits: siθ lim θ 0 θ = 1, lim 1 cosθ = 0 θ 0 θ Squeeze Theorem: If f(x) g(x) h(x) if lim f(x) = lim h(x) = L, the lim g(x) = L x x x Ietermite Forms: 0 0,,, 0,
Math 234 Test 1, Tuesday 27 September 2005, 4 pages, 30 points, 75 minutes.
 Math 34 Test 1, Tuesday 7 September 5, 4 pages, 3 poits, 75 miutes. The high score was 9 poits out of 3, achieved by two studets. The class average is 3.5 poits out of 3, or 77.5%, which ordiarily would
Math 34 Test 1, Tuesday 7 September 5, 4 pages, 3 poits, 75 miutes. The high score was 9 poits out of 3, achieved by two studets. The class average is 3.5 poits out of 3, or 77.5%, which ordiarily would
Taylor series expansion of nonlinear integrodifferential equations
 AMERCA JOURAL OF SCEFC AD DUSRAL RESEARCH 2, Sciece Huβ, http://www.scihu.org/ajsr SS: 253-649X doi:.525/jsir.2.2.3.376.38 yor series expsio of oier itegrodiffereti equtios Eke A.. d 2 Jckreece P. C. Deprtet
AMERCA JOURAL OF SCEFC AD DUSRAL RESEARCH 2, Sciece Huβ, http://www.scihu.org/ajsr SS: 253-649X doi:.525/jsir.2.2.3.376.38 yor series expsio of oier itegrodiffereti equtios Eke A.. d 2 Jckreece P. C. Deprtet
Topics in Fourier Analysis-I 1
 Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Topics i Fourier Aaysis-I 1 M.T.Nair Departmet of Mathematics, IIT Madras Cotets 1 Fourier Series 1.1 Motivatio through heat equatio.............................. 1. Fourier Series of -Periodic fuctios...........................
Direction: This test is worth 250 points. You are required to complete this test within 50 minutes.
 Term Test October 3, 003 Name Math 56 Studet Number Directio: This test is worth 50 poits. You are required to complete this test withi 50 miutes. I order to receive full credit, aswer each problem completely
Term Test October 3, 003 Name Math 56 Studet Number Directio: This test is worth 50 poits. You are required to complete this test withi 50 miutes. I order to receive full credit, aswer each problem completely
Numerical Methods in Fourier Series Applications
 Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Numerical Methods i Fourier Series Applicatios Recall that the basic relatios i usig the Trigoometric Fourier Series represetatio were give by f ( x) a o ( a x cos b x si ) () where the Fourier coefficiets
Fourier series. (sine and cosine)( ) ... : w h ere 2 (1 1)
 Fourier series... 3. 4. 5. 6 ( (sie ad osie( ( (... u A si t A si t u A o s t A o s t w h ere (. (.(frequey ( (omplex( i t e os t i si t ( A z A e i t ( ( ( 3 z (Argad.(Argad diagram ( z x iy A (os t i
Fourier series... 3. 4. 5. 6 ( (sie ad osie( ( (... u A si t A si t u A o s t A o s t w h ere (. (.(frequey ( (omplex( i t e os t i si t ( A z A e i t ( ( ( 3 z (Argad.(Argad diagram ( z x iy A (os t i
is continuous at x 2 and g(x) 2. Oil spilled from a ruptured tanker spreads in a circle whose area increases at a
 . Cosider two fuctios f () d g () defied o itervl I cotiig. f () is cotiuous t d g() is discotiuous t. Which of the followig is true bout fuctios f g d f g, the sum d the product of f d g, respectively?
. Cosider two fuctios f () d g () defied o itervl I cotiig. f () is cotiuous t d g() is discotiuous t. Which of the followig is true bout fuctios f g d f g, the sum d the product of f d g, respectively?
National Quali cations AHEXEMPLAR PAPER ONLY
 Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
Ntiol Quli ctios AHEXEMPLAR PAPER ONLY EP/AH/0 Mthemtics Dte Not pplicble Durtio hours Totl mrks 00 Attempt ALL questios. You my use clcultor. Full credit will be give oly to solutios which coti pproprite
lecture 16: Introduction to Least Squares Approximation
 97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
97 lecture 16: Itroductio to Lest Squres Approximtio.4 Lest squres pproximtio The miimx criterio is ituitive objective for pproximtig fuctio. However, i my cses it is more ppelig (for both computtio d
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
IIT JAM Mathematical Statistics (MS) 2006 SECTION A
 IIT JAM Mathematical Statistics (MS) 6 SECTION A. If a > for ad lim a / L >, the which of the followig series is ot coverget? (a) (b) (c) (d) (d) = = a = a = a a + / a lim a a / + = lim a / a / + = lim
IIT JAM Mathematical Statistics (MS) 6 SECTION A. If a > for ad lim a / L >, the which of the followig series is ot coverget? (a) (b) (c) (d) (d) = = a = a = a a + / a lim a a / + = lim a / a / + = lim
Probability for mathematicians INDEPENDENCE TAU
 Probbility for mthemticis INDEPENDENCE TAU 2013 21 Cotets 2 Cetrl limit theorem 21 2 Itroductio............................ 21 2b Covolutio............................ 22 2c The iitil distributio does
Probbility for mthemticis INDEPENDENCE TAU 2013 21 Cotets 2 Cetrl limit theorem 21 2 Itroductio............................ 21 2b Covolutio............................ 22 2c The iitil distributio does
where c is a scaling constant, 0, 0,. r c sinh cos csinh cos cos, csinh cos sin, ccosh sin U csinh sin sin, csinh sin cos,0
 MATH 38:Partial Differetial Equatios Solutios to The Secod Midterm DEGENERATE ELLIPSOID COORDINATES. Problem PROOF: Give csih si cos, y csihsi si, z ccoshcos, where c is a scalig costat,,,. r We compute
MATH 38:Partial Differetial Equatios Solutios to The Secod Midterm DEGENERATE ELLIPSOID COORDINATES. Problem PROOF: Give csih si cos, y csihsi si, z ccoshcos, where c is a scalig costat,,,. r We compute
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,
![SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0, SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,](/thumbs/94/119566625.jpg) 4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
Topic 4 Fourier Series. Today
 Topic 4 Fourier Series Toy Wves with repetig uctios Sigl geertor Clssicl guitr Pio Ech istrumet is plyig sigle ote mile C 6Hz) st hrmoic hrmoic 3 r hrmoic 4 th hrmoic 6Hz 5Hz 783Hz 44Hz A sigle ote will
Topic 4 Fourier Series Toy Wves with repetig uctios Sigl geertor Clssicl guitr Pio Ech istrumet is plyig sigle ote mile C 6Hz) st hrmoic hrmoic 3 r hrmoic 4 th hrmoic 6Hz 5Hz 783Hz 44Hz A sigle ote will
Abstract Vector Spaces. Abstract Vector Spaces
 Astract Vector Spaces The process of astractio is critical i egieerig! Physical Device Data Storage Vector Space MRI machie Optical receiver 0 0 1 0 1 0 0 1 Icreasig astractio 6.1 Astract Vector Spaces
Astract Vector Spaces The process of astractio is critical i egieerig! Physical Device Data Storage Vector Space MRI machie Optical receiver 0 0 1 0 1 0 0 1 Icreasig astractio 6.1 Astract Vector Spaces
( ) k ( ) 1 T n 1 x = xk. Geometric series obtained directly from the definition. = 1 1 x. See also Scalars 9.1 ADV-1: lim n.
 Sclrs-9.0-ADV- Algebric Tricks d Where Tylor Polyomils Come From 207.04.07 A.docx Pge of Algebric tricks ivolvig x. You c use lgebric tricks to simplify workig with the Tylor polyomils of certi fuctios..
Sclrs-9.0-ADV- Algebric Tricks d Where Tylor Polyomils Come From 207.04.07 A.docx Pge of Algebric tricks ivolvig x. You c use lgebric tricks to simplify workig with the Tylor polyomils of certi fuctios..
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
n 3 ln n n ln n is convergent by p-series for p = 2 > 1. n2 Therefore we can apply Limit Comparison Test to determine lutely convergent.
 06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
Lecture 15: Density estimation
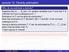 Lecture 15: Desity estimatio Why do we estimate a desity? Suppose that X 1,...,X are i.i.d. radom variables from F ad that F is ukow but has a Lebesgue p.d.f. f. Estimatio of F ca be doe by estimatig f.
Lecture 15: Desity estimatio Why do we estimate a desity? Suppose that X 1,...,X are i.i.d. radom variables from F ad that F is ukow but has a Lebesgue p.d.f. f. Estimatio of F ca be doe by estimatig f.
When dealing with series, n is always a positive integer. Remember at every, sine has a value of zero, which means
 Fourier Series Some Prelimiar Ideas: Odd/Eve Fuctios: Sie is odd, which meas si ( ) si Cosie is eve, which meas cos ( ) cos Secial values of siie a cosie at Whe dealig with series, is alwas a ositive iteger.
Fourier Series Some Prelimiar Ideas: Odd/Eve Fuctios: Sie is odd, which meas si ( ) si Cosie is eve, which meas cos ( ) cos Secial values of siie a cosie at Whe dealig with series, is alwas a ositive iteger.
Chapter 25 Sturm-Liouville problem (II)
 Chpter 5 Sturm-Liouville problem (II Speer: Lug-Sheg Chie Reerece: [] Veerle Ledou, Study o Specil Algorithms or solvig Sturm-Liouville d Schrodiger Equtios. [] 王信華教授, chpter 8, lecture ote o Ordiry Dieretil
Chpter 5 Sturm-Liouville problem (II Speer: Lug-Sheg Chie Reerece: [] Veerle Ledou, Study o Specil Algorithms or solvig Sturm-Liouville d Schrodiger Equtios. [] 王信華教授, chpter 8, lecture ote o Ordiry Dieretil
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
 M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
6. Uniform distribution mod 1
 6. Uiform distributio mod 1 6.1 Uiform distributio ad Weyl s criterio Let x be a seuece of real umbers. We may decompose x as the sum of its iteger part [x ] = sup{m Z m x } (i.e. the largest iteger which
6. Uiform distributio mod 1 6.1 Uiform distributio ad Weyl s criterio Let x be a seuece of real umbers. We may decompose x as the sum of its iteger part [x ] = sup{m Z m x } (i.e. the largest iteger which
PRELIM PROBLEM SOLUTIONS
 PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
MATH2007* Partial Answers to Review Exercises Fall 2004
 MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
MATH27* Partial Aswers to Review Eercises Fall 24 Evaluate each of the followig itegrals:. Let u cos. The du si ad Hece si ( cos 2 )(si ) (u 2 ) du. si u 2 cos 7 u 7 du Please fiish this. 2. We use itegratio
 + {JEE Advace 03} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks: 00. If A (α, β) = (a) A( α, β) = A( α, β) (c) Adj (A ( α, β)) = Sol : We
+ {JEE Advace 03} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks: 00. If A (α, β) = (a) A( α, β) = A( α, β) (c) Adj (A ( α, β)) = Sol : We
EVALUATING DEFINITE INTEGRALS
 Chpter 4 EVALUATING DEFINITE INTEGRALS If the defiite itegrl represets re betwee curve d the x-xis, d if you c fid the re by recogizig the shpe of the regio, the you c evlute the defiite itegrl. Those
Chpter 4 EVALUATING DEFINITE INTEGRALS If the defiite itegrl represets re betwee curve d the x-xis, d if you c fid the re by recogizig the shpe of the regio, the you c evlute the defiite itegrl. Those
is completely general whenever you have waves from two sources interfering. 2
 MAKNG SENSE OF THE EQUATON SHEET terferece & Diffrctio NTERFERENCE r1 r d si. Equtio for pth legth differece. r1 r is completely geerl. Use si oly whe the two sources re fr wy from the observtio poit.
MAKNG SENSE OF THE EQUATON SHEET terferece & Diffrctio NTERFERENCE r1 r d si. Equtio for pth legth differece. r1 r is completely geerl. Use si oly whe the two sources re fr wy from the observtio poit.
