Duality, Statistical Mechanics and Random Matrices. Bielefeld Lectures
|
|
|
- Ariel Hart
- 5 years ago
- Views:
Transcription
1 Duality, Statistical Mechanics and Random Matrices Bielefeld Lectures Tom Spencer Institute for Advanced Study Princeton, NJ August 16, 2016
2 Overview Statistical mechanics motivated by Random Matrix theory Topics: Mean Field models, Phase transitions, Symmetry breaking, Goldstone modes, Infra-red bounds, Mermin-Wagner, Lee-Yang Zeros, SUSY Hyperbolic Sigma model Duality : SUSY Statistical mechanics provides equivalent way to study spectral properties of such disordered quantum systems. Especially useful for analysis of Random Band Matrices.
3 Advantage of Statistical Mechanics Perspective It enables one to get estimates and insights not available by direct analysis. Role of Symmetry and Geometry - transparent. We will see that ordered and disordered phases of lattice spin systems correspond to different spectral types and quantum time evolutions. Wigner Dyson Universality of level spacing can be understood via the study of the saddle manifold.
4 Disadvantages SUSY statistical mechanics is complicated: Spins are 4 by 4 matrices with both commuting and Grassmann variables. Complex measure with oscillations and determinants. For this reason SUSY is often difficult to control analytically. Focus on simple models to illustrate the main ideas
5 Duality and Phase transitions in D 2 Ising model: Disordered T > T c, ordered < T c. Symmetry Z 2. In 2D dual to Grassmann Free Field - Determinant of Dirac. 2D XY dual to 2D Coulomb Gas : plasma phase and dipole phase. Vortices charges. U(1) symmetry. Reinforced Random Walks in 3D strong reinforcement walk is recurrent; weak reinforcement it is transient Dual to SUSY hyperbolic sigma model. Quantum Heisenberg Dual to Random adjacent permutations macroscopic loops - BE condensate, SU(2) symmetry. Anderson Transition in 3D: Localization to delocalization. Dual to SUSY mechanics with U(1, 1 2) Symmetry.
6 Background and History E. Wigner (1955) studied the energy level statistics of a large nucleus. Wigner s brilliant insight: Statistics Energy levels are given by the eigenvalues of a large random matrix - Mean Field model - each matrix element has equal variance. Conjecture: After rescaling, statistical properties of local energy level spacings depend only on symmetry. Universality of Wigner-Dyson Statistics
7 Proof of Universality for Mean Field Models F. J. Dyson, M. Gaudin and M. L. Mehta P. Deift et al; L. Pastur and M. Shcherbina: Invariant ensembles K. Johansson for perturbation of GUE ensembles More Recent work: L. Erdős, B. Schlein and H-T Yau; T. Tao and V. Vu L. Erdős, A. Knowles, H-T Yau, J.Yin (Random Graphs.) Universality of eigenvalue statistics at spectral edges for RBM, W N 5/6, Tracy-Widom (A. Sodin)
8 Gaussian Random Band Matrices: A. GUE: Gaussian Unitary Ensemble, H = H, H ij = 0 H ij H i j = 1 N δ ij δ ji i, j [1, 2,...N] B. RBM: Random Band matrices, H = H, Λ = Large Box H ij = 0, H ij H i j = J ij δ ij δ ji i, j Λ Z d where J ij 0 for i j > W, W = band width. Example: J jk = ( W 2 + 1) 1 (j, k) (2W ) 1 e j k /W. Spectrum H [ 2, 2].
9 Conjectures Beyond Mean Field Theory Fix W 1 and let Λ Z d, Energy in the Bulk Conjecture 1: For D 3 local eigenvalue statistics of Random Band Matrix in large box match those of GUE after scaling. Random Schrödinger version: + λv, v real, random potential, λ 1, local statistics GOE. ID version: If W 2 N = Λ local statistics is GUE. Conjecture 2: In 2D, Localization length e W 2. If N e W 2. Poisson statistics.
10 N! = 0 Simple Examples of Duality e t t N dt = N N+1 e N[s ln s] ds, N N e N 2πN expand about s = 1 0 (t = Ns) P(N) Number of Partitions of N, Hardy - Ramanujan (1918), P(N) = 1 1 2πi m (1 zm ) z N 1 dz 1 4 3N eπ 2N/3 Circle Method in Number Theory.
11 Exercises: Work out corrections to Stirling s formula Why can P(N) be represented as above contour integral? Stationary Phase: Evaluate for large real k > 0: 1 e i k cos(θ) dθ (2πk) 1/2 cos(k π/4) 2π
12 Key Gaussian Integral Identity Let z = (z 1, z 2,..., z N ), z j = x j + iy j x j, y j R If H = H is an N N matrix. det(h E iɛ) 1 = e i z (H E ɛ)z D N z E ɛ = E + i ɛ, ɛ > 0, D N z N j dx j dy j iπ If H is Gaussian of mean 0 then we have e i z Hz H = e 1/2 (z Hz) 2 H = e (z z) 2 /2N GUE
13 GUE Average of det(h E ɛ ) 1 det(h E ɛ ) 1 GUE = e (z z) 2 /2N ie ɛz z D N z e (z z) 2 /2N = 1 2πN e N s2 /2 e i s z z ds Now we can integrate quadratic expression in z z to get 2πN det(h E ɛ ) 1 GUE = Saddle Point: s = E/2 i 1 (E/2) 2 Exercise: Find the asymptotics for E 1.8 e Ns2 /2 (s E ɛ ) N ds
14 Mean field Heisenberg Model Heisenberg spins: s j S 2, j = 1, 2,...N. Magnetic field h R 3, Dual variable x R 3, Z N (β, h) s j S 2 β Temp 1 exp { β N 2N ( s j ) 2 + h s j } Decoupling trick (Hubbard-Stratonovich): exp β N 2N {( s j ) 2 } = ( N 2πβ )3/2 j j N dµ(s j ) e x ( N s j ) e N 2β x2 d 3 x Let F ( x ) = e x s j dµ(s j ) = x 1 sinh x j
15 Z N (β, h) = ( N 2πβ )3/2 Phase transition e N{ln F ( x+h x 2 /2β} d 3 x. When h = 0, Minima of {ln F ( x ) x 2 /2β}: If β 3, x (β) = 0, M(β) = 0 If β > 3, x (β) = r(β)u, r(β) > 0, U S 2, Saddle manifold Second order transition: M(β) = r(β)/β and vanishes continuously as β β c = 3. M 2 (β) 1 N N 2 [ s j ] 2 (β, 0) j
16 Exercises: 1) Prove that for β < 3, {ln F ( x ) x 2 /2β} is a concave function of r = x, F (r) = sinh r r, thus r=0 only saddle point. 2) For GUE 2πN det(h E ɛ ) 1 GUE = Saddle Point: s = E/2 i 1 (E/2) 2 e Ns2 /2 (s E ɛ ) N ds Show that this saddle is correct and analyze the integral by contour deformation. for E 1.8
17 To see the dependence on h expand about the minimum: ln F ( x + h/n ) ln F (r) = 1 N M(β)U h Thus as N, Z N (β, h/n) Z N (β, 0) = e M(β)h U dµ(u) = Mh 1 sinh(m h ) S 2 Formula is valid if we replace s j S 2 by a potential distribution V (s j ) = ((s j ) 2 1) 2, s R 3. The large N limit depends only on the symmetry group and on M(β) - Analogous, to Wigner-Dyson universality!
18 Lattice Spin systems and Lee-Yang Let Λ Z d. For j Λ we consider the spin S j = ±1 Ising; S j = (cos(θ j ), sin(θ j )) XY model; S j S 2 Heisenberg. The partition function Z Λ (β, h) = exp[ βj j,k S j S k + j,k j h S j ] j Λ dµ(s j ) Lee-Yang Theorem If βj j,k 0, then all Zeros of Z Λ (β, h) are on the imaginary h axis. Corollary: f (β, h) = lim Λ Z d Λ 1 log Z Λ (β, h) is analytic if Re h > 0. No Phase transition for Re h > 0. d 2 dh 2 f (β, h) = j [ S 0 S j (β, h) S 0 (β, h) S j (β, h)] <
19 Let Lattice Spin systems and Mean Field For Heisenberg spins: J jk = ( W 2 + 1) 1 (j, k) e j k /W, If β < 3, h = 0. The spin correlations decay exponentially fast for all W. S 0 S j (β, h = 0) e j /l(β) After duality the Gibbs weight is log concave. In 3D, if β > 3 and W is large then there is a magnetization M(β) > 0 and order S 0 S j (β, h = 0) M 2 (β) > 0 as j
20 Mean Field Conjecture for d 3 Conjecture: Let Λ be a periodic cube of side L Z Λ (β, h/ Λ ) = e Mu h dµ(u) (1 + cβ 1 L (d 2) ) Z Λ (β, 0) u =1 Theorem (Fröhlich-Sp) Holds for almost all β for X-Y model. Conjecture Same result for 3D SUSY models: Saddle manifold is U(1, 1 2)/U(1 1) U(1 1). Gives Wigner-Dyson Universality with corrections for 3D RBM.
21 Product of Characteristic Polynomials - GUE Let H denote and N N GUE matrix Define D N (E, δ) = det(h E + δ/n) det(h E δ/n) If E < 2 then as N D N (E, δ) GUE D N (E, 0) GUE = sin( ρ(e)δ)/( ρ(e)δ) Here ρ(e) is proportional to the density of states.
22 Characteristic Polynomial for Gaussian Band Matrices Let H be an N N Gaussian Band matrix of width W. Theorem (T. Shcherbina) In 1D if E < 2, and W 2 N then D N (E, δ) RBM D N (E, 0) RBM = sin( ρ(e)δ)/( ρ(e)δ) Theorem (M. and T. Shcherbina ) If W 2 N then the limit is 1. We shall see that 1D band is similar to a 1D Heisenberg spin chain of length N at with β W 2. The spins in the chain are aligned when W 2 β N.
23 Grassmann Integral Identity Let ψ j, ψ j anti-commuting: ψ k ψ j = ψ j ψ k, ψ k ψ j = ψ j ψ k, (ψ k )2 = (ψ j ) 2 = 0 Ψ = (ψ 1, ψ 2,..., ψ N ) and Ψ = (ψ1, ψ2,..., ψn ) det(h E ɛ ) = e Ψ (H E ɛ)ψ D N Ψ where D N Ψ = n j dψ j dψ j Integration Rule: N j ψ j ψ j D N Ψ 1 Integrals of lower order polynomials vanish.
24 Sketch of proof for GUE If ψ j, ψ j, χ j, χ j, 1 j N, are Grassmann variables then D N (E, δ) = e { ψ (H E)ψ+ χ (H E)χ+ δ N ( ψ ψ χ χ)} Dψ Dχ D N (E, δ) GUE = e {tr Q2 /2N+tr QE+ δ N ( ψ ψ χ χ)} Dψ Dχ ( ) ψ ψ ψ χ where Q = χ ψ χ χ Exercise: Prove this Formula
25 Let X be a 2 2 Hermitian matrix and let DX be the flat measure. e tr Q2 /2N = C N e i tr XQ e N tr X 2 /2 DX the Grassmann s are now quadratic and we can trace them out: D N (E, δ) GUE = C N det(i X Ẽ)N e N tr X 2 /2 DX where Ẽ = diag(e + δ/n, E δ/n) = E I 2 + δ/n σ 3
26 By diagonalizing X we find the saddle X s (at δ = 0) has the following form : ˇX s = {ie/2 ± ρ(e) } I 2 or ˆX s = U {ie/2 I 2 + ρ(e) σ 3 } U where σ 3 = diag(1, 1), U SU(2) and ρ(e) = 2πρ(E) = 1 (E/2) 2. Since det(ix E + δ/nσ 3 ) det(ix E) = e tr(ix E) 1 δσ 3 /N Integration over the saddle manifold ˆX c is e iδ tr (X ie) 1 σ 3 dµ(u) = e iδ ρ tr U σ 3 Uσ 3 dµ(u) = sin( ρ(e)δ)/( ρ(e)δ)
27 ˆX s is Dominant Saddle Manifold The contribution of ˇX s and ˆX s has the same modulus. However at ˇX s, the Jacobian in DX = (λ 1 λ 2 ) 2 dλ 1 dλ 2 dµ(u) vanishes since the eigenvalues λ 1, λ 2 coincide.
28 Spectral information via Green s Function The Green s function for H provides spectral information near E: Let N or box Λ be fixed. Let ε > 0 tr Im (H E iε) 1 ε = tr (H E) 2 + ε 2 π tr δ ɛ(h E) Counts eigenvalues in ɛ - neighborhood of E. tr (H E iε) 1 = d de det(h E iɛ) det(h E iɛ) E=E
29 GUE Average Green s Function ρ N (E, ε) Im 1 N tr(h E iɛ) 1 GUE = Im s 1 SUSY N 2π s 1 e N(s2 1 +s2 2 )/2 (i s 2 E ɛ ) N (s 1 E ɛ ) N R(s 1, s 2 )ds 1 ds 2 where R 1 (s 1 E ɛ ) 1 (i s 2 E ɛ ) 1 Note 1 SUSY = 1. Deform the contour of integration. Analysis about saddle point: s 1 = E/2 i 1 (E/2) 2 There is another sub-dominant saddle point at s 1.
30 Block GUE Matrix Let H 1 and H 2 be independent N N GUE matrices. ( ) H1 c I H N c I N H 2 where c > 0. ρ Λ (E, ε) = 1 2πN Im tr(h E iɛ) 1 GUE Integral in 4 variables. Saddle points solve cubic equation. Universality: local eigenvalue statistics and correlations should be the same as for GUE.
31 Density of States ρ for RBM Let S = (S 1 (j), S 2 (j)) R 2, j Λ Z d, ρ Λ (E, ε) 1 Λ tr(h E iɛ) 1 RBM = S 1 (0) SUSY = C N S 1 (0)e j [W2 ( S)(j) 2 +S(j) 2 ]/2 R j (i S 2 (j) E ɛ ) (S 1 (j) E ɛ ) ds j W = Band Width fixed but Λ Z d - Statistical Mechanics R = det{ W δ ij (S 1 (j) E ɛ ) 1 (i S 2 (j) E ɛ ) 1 }
32 Theorem (Disertori, Pinson, Sp) For RBM with W large and fixed, and E 1.8, ρ Λ (E, ε) is smooth and uniformly bounded as ε 0, Λ Z 3. Remarks: Constantinescu, Felder, Gawedzki and Kupiainen Earlier work for N-orbital model. Theorem gives sharp estimates on density of states for narrow energy windows: ε 1/ Λ. Perturbative methods restricted to ε 1/W.
Why Hyperbolic Symmetry?
 Why Hyperbolic Symmetry? Consider the very trivial case when N = 1 and H = h is a real Gaussian variable of unit variance. To simplify notation set E ɛ = 0 iɛ and z, w C = G(E ɛ ) 2 h = [(h iɛ)(h + iɛ)]
Why Hyperbolic Symmetry? Consider the very trivial case when N = 1 and H = h is a real Gaussian variable of unit variance. To simplify notation set E ɛ = 0 iɛ and z, w C = G(E ɛ ) 2 h = [(h iɛ)(h + iɛ)]
Quasi-Diffusion in a SUSY Hyperbolic Sigma Model
 Quasi-Diffusion in a SUSY Hyperbolic Sigma Model Joint work with: M. Disertori and M. Zirnbauer December 15, 2008 Outline of Talk A) Motivation: Study time evolution of quantum particle in a random environment
Quasi-Diffusion in a SUSY Hyperbolic Sigma Model Joint work with: M. Disertori and M. Zirnbauer December 15, 2008 Outline of Talk A) Motivation: Study time evolution of quantum particle in a random environment
Universality for random matrices and log-gases
 Universality for random matrices and log-gases László Erdős IST, Austria Ludwig-Maximilians-Universität, Munich, Germany Encounters Between Discrete and Continuous Mathematics Eötvös Loránd University,
Universality for random matrices and log-gases László Erdős IST, Austria Ludwig-Maximilians-Universität, Munich, Germany Encounters Between Discrete and Continuous Mathematics Eötvös Loránd University,
Random Matrix: From Wigner to Quantum Chaos
 Random Matrix: From Wigner to Quantum Chaos Horng-Tzer Yau Harvard University Joint work with P. Bourgade, L. Erdős, B. Schlein and J. Yin 1 Perhaps I am now too courageous when I try to guess the distribution
Random Matrix: From Wigner to Quantum Chaos Horng-Tzer Yau Harvard University Joint work with P. Bourgade, L. Erdős, B. Schlein and J. Yin 1 Perhaps I am now too courageous when I try to guess the distribution
Universality of local spectral statistics of random matrices
 Universality of local spectral statistics of random matrices László Erdős Ludwig-Maximilians-Universität, Munich, Germany CRM, Montreal, Mar 19, 2012 Joint with P. Bourgade, B. Schlein, H.T. Yau, and J.
Universality of local spectral statistics of random matrices László Erdős Ludwig-Maximilians-Universität, Munich, Germany CRM, Montreal, Mar 19, 2012 Joint with P. Bourgade, B. Schlein, H.T. Yau, and J.
Density of States for Random Band Matrices in d = 2
 Density of States for Random Band Matrices in d = 2 via the supersymmetric approach Mareike Lager Institute for applied mathematics University of Bonn Joint work with Margherita Disertori ZiF Summer School
Density of States for Random Band Matrices in d = 2 via the supersymmetric approach Mareike Lager Institute for applied mathematics University of Bonn Joint work with Margherita Disertori ZiF Summer School
Quantum Diffusion and Delocalization for Random Band Matrices
 Quantum Diffusion and Delocalization for Random Band Matrices László Erdős Ludwig-Maximilians-Universität, Munich, Germany Montreal, Mar 22, 2012 Joint with Antti Knowles (Harvard University) 1 INTRODUCTION
Quantum Diffusion and Delocalization for Random Band Matrices László Erdős Ludwig-Maximilians-Universität, Munich, Germany Montreal, Mar 22, 2012 Joint with Antti Knowles (Harvard University) 1 INTRODUCTION
Local semicircle law, Wegner estimate and level repulsion for Wigner random matrices
 Local semicircle law, Wegner estimate and level repulsion for Wigner random matrices László Erdős University of Munich Oberwolfach, 2008 Dec Joint work with H.T. Yau (Harvard), B. Schlein (Cambrigde) Goal:
Local semicircle law, Wegner estimate and level repulsion for Wigner random matrices László Erdős University of Munich Oberwolfach, 2008 Dec Joint work with H.T. Yau (Harvard), B. Schlein (Cambrigde) Goal:
Multifractality in simple systems. Eugene Bogomolny
 Multifractality in simple systems Eugene Bogomolny Univ. Paris-Sud, Laboratoire de Physique Théorique et Modèles Statistiques, Orsay, France In collaboration with Yasar Atas Outlook 1 Multifractality Critical
Multifractality in simple systems Eugene Bogomolny Univ. Paris-Sud, Laboratoire de Physique Théorique et Modèles Statistiques, Orsay, France In collaboration with Yasar Atas Outlook 1 Multifractality Critical
The Matrix Dyson Equation in random matrix theory
 The Matrix Dyson Equation in random matrix theory László Erdős IST, Austria Mathematical Physics seminar University of Bristol, Feb 3, 207 Joint work with O. Ajanki, T. Krüger Partially supported by ERC
The Matrix Dyson Equation in random matrix theory László Erdős IST, Austria Mathematical Physics seminar University of Bristol, Feb 3, 207 Joint work with O. Ajanki, T. Krüger Partially supported by ERC
Two Classical models of Quantum Dynamics
 Two Classical models of Quantum Dynamics Tom Spencer Institute for Advanced Study Princeton, NJ May 1, 2018 Outline: Review of dynamics and localization for Random Schrödinger H on l 2 (Z d ) H = + λv
Two Classical models of Quantum Dynamics Tom Spencer Institute for Advanced Study Princeton, NJ May 1, 2018 Outline: Review of dynamics and localization for Random Schrödinger H on l 2 (Z d ) H = + λv
From the mesoscopic to microscopic scale in random matrix theory
 From the mesoscopic to microscopic scale in random matrix theory (fixed energy universality for random spectra) With L. Erdős, H.-T. Yau, J. Yin Introduction A spacially confined quantum mechanical system
From the mesoscopic to microscopic scale in random matrix theory (fixed energy universality for random spectra) With L. Erdős, H.-T. Yau, J. Yin Introduction A spacially confined quantum mechanical system
RANDOM MATRIX THEORY AND TOEPLITZ DETERMINANTS
 RANDOM MATRIX THEORY AND TOEPLITZ DETERMINANTS David García-García May 13, 2016 Faculdade de Ciências da Universidade de Lisboa OVERVIEW Random Matrix Theory Introduction Matrix ensembles A sample computation:
RANDOM MATRIX THEORY AND TOEPLITZ DETERMINANTS David García-García May 13, 2016 Faculdade de Ciências da Universidade de Lisboa OVERVIEW Random Matrix Theory Introduction Matrix ensembles A sample computation:
Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium
 Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium SEA 06@MIT, Workshop on Stochastic Eigen-Analysis and its Applications, MIT, Cambridge,
Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium SEA 06@MIT, Workshop on Stochastic Eigen-Analysis and its Applications, MIT, Cambridge,
Spectral Universality of Random Matrices
 Spectral Universality of Random Matrices László Erdős IST Austria (supported by ERC Advanced Grant) Szilárd Leó Colloquium Technical University of Budapest February 27, 2018 László Erdős Spectral Universality
Spectral Universality of Random Matrices László Erdős IST Austria (supported by ERC Advanced Grant) Szilárd Leó Colloquium Technical University of Budapest February 27, 2018 László Erdős Spectral Universality
Exponential tail inequalities for eigenvalues of random matrices
 Exponential tail inequalities for eigenvalues of random matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify
Exponential tail inequalities for eigenvalues of random matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify
Semicircle law on short scales and delocalization for Wigner random matrices
 Semicircle law on short scales and delocalization for Wigner random matrices László Erdős University of Munich Weizmann Institute, December 2007 Joint work with H.T. Yau (Harvard), B. Schlein (Munich)
Semicircle law on short scales and delocalization for Wigner random matrices László Erdős University of Munich Weizmann Institute, December 2007 Joint work with H.T. Yau (Harvard), B. Schlein (Munich)
Homogenization of the Dyson Brownian Motion
 Homogenization of the Dyson Brownian Motion P. Bourgade, joint work with L. Erdős, J. Yin, H.-T. Yau Cincinnati symposium on probability theory and applications, September 2014 Introduction...........
Homogenization of the Dyson Brownian Motion P. Bourgade, joint work with L. Erdős, J. Yin, H.-T. Yau Cincinnati symposium on probability theory and applications, September 2014 Introduction...........
Universality of Random Matrices and Dyson Brownian Motion
 Universality of Random Matrices and Dyson Brownian Motion Horng-Tzer Yau Harvard University Joint work with L. Erdős, and B. Schlein, J. Yin 1 Lecture 1: History of Universality and Main Results Basic
Universality of Random Matrices and Dyson Brownian Motion Horng-Tzer Yau Harvard University Joint work with L. Erdős, and B. Schlein, J. Yin 1 Lecture 1: History of Universality and Main Results Basic
Markov operators, classical orthogonal polynomial ensembles, and random matrices
 Markov operators, classical orthogonal polynomial ensembles, and random matrices M. Ledoux, Institut de Mathématiques de Toulouse, France 5ecm Amsterdam, July 2008 recent study of random matrix and random
Markov operators, classical orthogonal polynomial ensembles, and random matrices M. Ledoux, Institut de Mathématiques de Toulouse, France 5ecm Amsterdam, July 2008 recent study of random matrix and random
Differential Equations for Dyson Processes
 Differential Equations for Dyson Processes Joint work with Harold Widom I. Overview We call Dyson process any invariant process on ensembles of matrices in which the entries undergo diffusion. Dyson Brownian
Differential Equations for Dyson Processes Joint work with Harold Widom I. Overview We call Dyson process any invariant process on ensembles of matrices in which the entries undergo diffusion. Dyson Brownian
Random Matrix Theory for the Wilson-Dirac operator
 Random Matrix Theory for the Wilson-Dirac operator Mario Kieburg Department of Physics and Astronomy SUNY Stony Brook (NY, USA) Bielefeld, December 14th, 2011 Outline Introduction in Lattice QCD and in
Random Matrix Theory for the Wilson-Dirac operator Mario Kieburg Department of Physics and Astronomy SUNY Stony Brook (NY, USA) Bielefeld, December 14th, 2011 Outline Introduction in Lattice QCD and in
Introduction to Theory of Mesoscopic Systems
 Introduction to Theory of Mesoscopic Systems Boris Altshuler Princeton University, Columbia University & NEC Laboratories America Lecture 3 Beforehand Weak Localization and Mesoscopic Fluctuations Today
Introduction to Theory of Mesoscopic Systems Boris Altshuler Princeton University, Columbia University & NEC Laboratories America Lecture 3 Beforehand Weak Localization and Mesoscopic Fluctuations Today
Extreme eigenvalue fluctutations for GUE
 Extreme eigenvalue fluctutations for GUE C. Donati-Martin 204 Program Women and Mathematics, IAS Introduction andom matrices were introduced in multivariate statistics, in the thirties by Wishart [Wis]
Extreme eigenvalue fluctutations for GUE C. Donati-Martin 204 Program Women and Mathematics, IAS Introduction andom matrices were introduced in multivariate statistics, in the thirties by Wishart [Wis]
Rigidity of the 3D hierarchical Coulomb gas. Sourav Chatterjee
 Rigidity of point processes Let P be a Poisson point process of intensity n in R d, and let A R d be a set of nonzero volume. Let N(A) := A P. Then E(N(A)) = Var(N(A)) = vol(a)n. Thus, N(A) has fluctuations
Rigidity of point processes Let P be a Poisson point process of intensity n in R d, and let A R d be a set of nonzero volume. Let N(A) := A P. Then E(N(A)) = Var(N(A)) = vol(a)n. Thus, N(A) has fluctuations
DLR equations for the Sineβ process and applications
 DLR equations for the Sineβ process and applications Thomas Leble (Courant Institute - NYU) Columbia University - 09/28/2018 Joint work with D. Dereudre, A. Hardy, M. Maı da (Universite Lille 1) Log-gases
DLR equations for the Sineβ process and applications Thomas Leble (Courant Institute - NYU) Columbia University - 09/28/2018 Joint work with D. Dereudre, A. Hardy, M. Maı da (Universite Lille 1) Log-gases
Bulk scaling limits, open questions
 Bulk scaling limits, open questions Based on: Continuum limits of random matrices and the Brownian carousel B. Valkó, B. Virág. Inventiones (2009). Eigenvalue statistics for CMV matrices: from Poisson
Bulk scaling limits, open questions Based on: Continuum limits of random matrices and the Brownian carousel B. Valkó, B. Virág. Inventiones (2009). Eigenvalue statistics for CMV matrices: from Poisson
Fluctuations of the free energy of spherical spin glass
 Fluctuations of the free energy of spherical spin glass Jinho Baik University of Michigan 2015 May, IMS, Singapore Joint work with Ji Oon Lee (KAIST, Korea) Random matrix theory Real N N Wigner matrix
Fluctuations of the free energy of spherical spin glass Jinho Baik University of Michigan 2015 May, IMS, Singapore Joint work with Ji Oon Lee (KAIST, Korea) Random matrix theory Real N N Wigner matrix
Fluctuations of random tilings and discrete Beta-ensembles
 Fluctuations of random tilings and discrete Beta-ensembles Alice Guionnet CRS (E S Lyon) Workshop in geometric functional analysis, MSRI, nov. 13 2017 Joint work with A. Borodin, G. Borot, V. Gorin, J.Huang
Fluctuations of random tilings and discrete Beta-ensembles Alice Guionnet CRS (E S Lyon) Workshop in geometric functional analysis, MSRI, nov. 13 2017 Joint work with A. Borodin, G. Borot, V. Gorin, J.Huang
Random matrix pencils and level crossings
 Albeverio Fest October 1, 2018 Topics to discuss Basic level crossing problem 1 Basic level crossing problem 2 3 Main references Basic level crossing problem (i) B. Shapiro, M. Tater, On spectral asymptotics
Albeverio Fest October 1, 2018 Topics to discuss Basic level crossing problem 1 Basic level crossing problem 2 3 Main references Basic level crossing problem (i) B. Shapiro, M. Tater, On spectral asymptotics
Fluctuations of random tilings and discrete Beta-ensembles
 Fluctuations of random tilings and discrete Beta-ensembles Alice Guionnet CRS (E S Lyon) Advances in Mathematics and Theoretical Physics, Roma, 2017 Joint work with A. Borodin, G. Borot, V. Gorin, J.Huang
Fluctuations of random tilings and discrete Beta-ensembles Alice Guionnet CRS (E S Lyon) Advances in Mathematics and Theoretical Physics, Roma, 2017 Joint work with A. Borodin, G. Borot, V. Gorin, J.Huang
Comparison Method in Random Matrix Theory
 Comparison Method in Random Matrix Theory Jun Yin UW-Madison Valparaíso, Chile, July - 2015 Joint work with A. Knowles. 1 Some random matrices Wigner Matrix: H is N N square matrix, H : H ij = H ji, EH
Comparison Method in Random Matrix Theory Jun Yin UW-Madison Valparaíso, Chile, July - 2015 Joint work with A. Knowles. 1 Some random matrices Wigner Matrix: H is N N square matrix, H : H ij = H ji, EH
Concentration Inequalities for Random Matrices
 Concentration Inequalities for Random Matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify the asymptotic
Concentration Inequalities for Random Matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify the asymptotic
ORIGINS. E.P. Wigner, Conference on Neutron Physics by Time of Flight, November 1956
 ORIGINS E.P. Wigner, Conference on Neutron Physics by Time of Flight, November 1956 P.W. Anderson, Absence of Diffusion in Certain Random Lattices ; Phys.Rev., 1958, v.109, p.1492 L.D. Landau, Fermi-Liquid
ORIGINS E.P. Wigner, Conference on Neutron Physics by Time of Flight, November 1956 P.W. Anderson, Absence of Diffusion in Certain Random Lattices ; Phys.Rev., 1958, v.109, p.1492 L.D. Landau, Fermi-Liquid
III. Quantum ergodicity on graphs, perspectives
 III. Quantum ergodicity on graphs, perspectives Nalini Anantharaman Université de Strasbourg 24 août 2016 Yesterday we focussed on the case of large regular (discrete) graphs. Let G = (V, E) be a (q +
III. Quantum ergodicity on graphs, perspectives Nalini Anantharaman Université de Strasbourg 24 août 2016 Yesterday we focussed on the case of large regular (discrete) graphs. Let G = (V, E) be a (q +
Think Globally, Act Locally
 Think Globally, Act Locally Nathan Seiberg Institute for Advanced Study Quantum Fields beyond Perturbation Theory, KITP 2014 Ofer Aharony, NS, Yuji Tachikawa, arxiv:1305.0318 Anton Kapustin, Ryan Thorngren,
Think Globally, Act Locally Nathan Seiberg Institute for Advanced Study Quantum Fields beyond Perturbation Theory, KITP 2014 Ofer Aharony, NS, Yuji Tachikawa, arxiv:1305.0318 Anton Kapustin, Ryan Thorngren,
Free Probability and Random Matrices: from isomorphisms to universality
 Free Probability and Random Matrices: from isomorphisms to universality Alice Guionnet MIT TexAMP, November 21, 2014 Joint works with F. Bekerman, Y. Dabrowski, A.Figalli, E. Maurel-Segala, J. Novak, D.
Free Probability and Random Matrices: from isomorphisms to universality Alice Guionnet MIT TexAMP, November 21, 2014 Joint works with F. Bekerman, Y. Dabrowski, A.Figalli, E. Maurel-Segala, J. Novak, D.
1 Intro to RMT (Gene)
 M705 Spring 2013 Summary for Week 2 1 Intro to RMT (Gene) (Also see the Anderson - Guionnet - Zeitouni book, pp.6-11(?) ) We start with two independent families of R.V.s, {Z i,j } 1 i
M705 Spring 2013 Summary for Week 2 1 Intro to RMT (Gene) (Also see the Anderson - Guionnet - Zeitouni book, pp.6-11(?) ) We start with two independent families of R.V.s, {Z i,j } 1 i
LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations. Craig A. Tracy UC Davis
 LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations Craig A. Tracy UC Davis Bielefeld, August 2013 ASEP on Integer Lattice q p suppressed both suppressed
LECTURE III Asymmetric Simple Exclusion Process: Bethe Ansatz Approach to the Kolmogorov Equations Craig A. Tracy UC Davis Bielefeld, August 2013 ASEP on Integer Lattice q p suppressed both suppressed
Isotropic local laws for random matrices
 Isotropic local laws for random matrices Antti Knowles University of Geneva With Y. He and R. Rosenthal Random matrices Let H C N N be a large Hermitian random matrix, normalized so that H. Some motivations:
Isotropic local laws for random matrices Antti Knowles University of Geneva With Y. He and R. Rosenthal Random matrices Let H C N N be a large Hermitian random matrix, normalized so that H. Some motivations:
Universality. Why? (Bohigas, Giannoni, Schmit 84; see also Casati, Vals-Gris, Guarneri; Berry, Tabor)
 Universality Many quantum properties of chaotic systems are universal and agree with predictions from random matrix theory, in particular the statistics of energy levels. (Bohigas, Giannoni, Schmit 84;
Universality Many quantum properties of chaotic systems are universal and agree with predictions from random matrix theory, in particular the statistics of energy levels. (Bohigas, Giannoni, Schmit 84;
Modification of the Porter-Thomas distribution by rank-one interaction. Eugene Bogomolny
 Modification of the Porter-Thomas distribution by rank-one interaction Eugene Bogomolny University Paris-Sud, CNRS Laboratoire de Physique Théorique et Modèles Statistiques, Orsay France XII Brunel-Bielefeld
Modification of the Porter-Thomas distribution by rank-one interaction Eugene Bogomolny University Paris-Sud, CNRS Laboratoire de Physique Théorique et Modèles Statistiques, Orsay France XII Brunel-Bielefeld
Baby Skyrmions in AdS 3 and Extensions to (3 + 1) Dimensions
 Baby Skyrmions in AdS 3 and Extensions to (3 + 1) Dimensions Durham University Work in collaboration with Matthew Elliot-Ripley June 26, 2015 Introduction to baby Skyrmions in flat space and AdS 3 Discuss
Baby Skyrmions in AdS 3 and Extensions to (3 + 1) Dimensions Durham University Work in collaboration with Matthew Elliot-Ripley June 26, 2015 Introduction to baby Skyrmions in flat space and AdS 3 Discuss
8.334: Statistical Mechanics II Problem Set # 4 Due: 4/9/14 Transfer Matrices & Position space renormalization
 8.334: Statistical Mechanics II Problem Set # 4 Due: 4/9/14 Transfer Matrices & Position space renormalization This problem set is partly intended to introduce the transfer matrix method, which is used
8.334: Statistical Mechanics II Problem Set # 4 Due: 4/9/14 Transfer Matrices & Position space renormalization This problem set is partly intended to introduce the transfer matrix method, which is used
September 29, Gaussian integrals. Happy birthday Costas
 September 29, 202 Gaussian integrals Happy birthday Costas Of course only non-gaussian problems are of interest! Matrix models of 2D-gravity Z = dme NTrV (M) in which M = M is an N N matrix and V (M) =
September 29, 202 Gaussian integrals Happy birthday Costas Of course only non-gaussian problems are of interest! Matrix models of 2D-gravity Z = dme NTrV (M) in which M = M is an N N matrix and V (M) =
Unitary rotations. October 28, 2014
 Unitary rotations October 8, 04 The special unitary group in dimensions It turns out that all orthogonal groups SO n), rotations in n real dimensions) may be written as special cases of rotations in a
Unitary rotations October 8, 04 The special unitary group in dimensions It turns out that all orthogonal groups SO n), rotations in n real dimensions) may be written as special cases of rotations in a
Anderson Localization Looking Forward
 Anderson Localization Looking Forward Boris Altshuler Physics Department, Columbia University Collaborations: Also Igor Aleiner Denis Basko, Gora Shlyapnikov, Vincent Michal, Vladimir Kravtsov, Lecture2
Anderson Localization Looking Forward Boris Altshuler Physics Department, Columbia University Collaborations: Also Igor Aleiner Denis Basko, Gora Shlyapnikov, Vincent Michal, Vladimir Kravtsov, Lecture2
Chapter 29. Quantum Chaos
 Chapter 29 Quantum Chaos What happens to a Hamiltonian system that for classical mechanics is chaotic when we include a nonzero h? There is no problem in principle to answering this question: given a classical
Chapter 29 Quantum Chaos What happens to a Hamiltonian system that for classical mechanics is chaotic when we include a nonzero h? There is no problem in principle to answering this question: given a classical
PhD in Theoretical Particle Physics Academic Year 2017/2018
 July 10, 017 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 017/018 S olve two among the four problems presented. Problem I Consider a quantum harmonic oscillator in one spatial
July 10, 017 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 017/018 S olve two among the four problems presented. Problem I Consider a quantum harmonic oscillator in one spatial
Random Matrix Theory
 Random Matrix Theory Gernot Akemann Faculty of Physics, Bielefeld University STRONGnet summer school, ZiF Bielefeld, 14-25 June 2011 Content What is RMT about? Nuclear Physics, Number Theory, Quantum Chaos,...
Random Matrix Theory Gernot Akemann Faculty of Physics, Bielefeld University STRONGnet summer school, ZiF Bielefeld, 14-25 June 2011 Content What is RMT about? Nuclear Physics, Number Theory, Quantum Chaos,...
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Determinantal point processes and random matrix theory in a nutshell
 Determinantal point processes and random matrix theory in a nutshell part II Manuela Girotti based on M. Girotti s PhD thesis, A. Kuijlaars notes from Les Houches Winter School 202 and B. Eynard s notes
Determinantal point processes and random matrix theory in a nutshell part II Manuela Girotti based on M. Girotti s PhD thesis, A. Kuijlaars notes from Les Houches Winter School 202 and B. Eynard s notes
Airy and Pearcey Processes
 Airy and Pearcey Processes Craig A. Tracy UC Davis Probability, Geometry and Integrable Systems MSRI December 2005 1 Probability Space: (Ω, Pr, F): Random Matrix Models Gaussian Orthogonal Ensemble (GOE,
Airy and Pearcey Processes Craig A. Tracy UC Davis Probability, Geometry and Integrable Systems MSRI December 2005 1 Probability Space: (Ω, Pr, F): Random Matrix Models Gaussian Orthogonal Ensemble (GOE,
Decay of correlations in 2d quantum systems
 Decay of correlations in 2d quantum systems Costanza Benassi University of Warwick Quantissima in the Serenissima II, 25th August 2017 Costanza Benassi (University of Warwick) Decay of correlations in
Decay of correlations in 2d quantum systems Costanza Benassi University of Warwick Quantissima in the Serenissima II, 25th August 2017 Costanza Benassi (University of Warwick) Decay of correlations in
The phase diagram of polar condensates
 The phase diagram of polar condensates Taking the square root of a vortex Austen Lamacraft [with Andrew James] arxiv:1009.0043 University of Virginia September 23, 2010 KITP, UCSB Austen Lamacraft (University
The phase diagram of polar condensates Taking the square root of a vortex Austen Lamacraft [with Andrew James] arxiv:1009.0043 University of Virginia September 23, 2010 KITP, UCSB Austen Lamacraft (University
Beyond the Gaussian universality class
 Beyond the Gaussian universality class MSRI/Evans Talk Ivan Corwin (Courant Institute, NYU) September 13, 2010 Outline Part 1: Random growth models Random deposition, ballistic deposition, corner growth
Beyond the Gaussian universality class MSRI/Evans Talk Ivan Corwin (Courant Institute, NYU) September 13, 2010 Outline Part 1: Random growth models Random deposition, ballistic deposition, corner growth
Potentially useful reading Sakurai and Napolitano, sections 1.5 (Rotation), Schumacher & Westmoreland chapter 2
 Problem Set 2: Interferometers & Random Matrices Graduate Quantum I Physics 6572 James Sethna Due Friday Sept. 5 Last correction at August 28, 2014, 8:32 pm Potentially useful reading Sakurai and Napolitano,
Problem Set 2: Interferometers & Random Matrices Graduate Quantum I Physics 6572 James Sethna Due Friday Sept. 5 Last correction at August 28, 2014, 8:32 pm Potentially useful reading Sakurai and Napolitano,
Central Limit Theorems for linear statistics for Biorthogonal Ensembles
 Central Limit Theorems for linear statistics for Biorthogonal Ensembles Maurice Duits, Stockholm University Based on joint work with Jonathan Breuer (HUJI) Princeton, April 2, 2014 M. Duits (SU) CLT s
Central Limit Theorems for linear statistics for Biorthogonal Ensembles Maurice Duits, Stockholm University Based on joint work with Jonathan Breuer (HUJI) Princeton, April 2, 2014 M. Duits (SU) CLT s
Critical exponents for two-dimensional statistical
 California State University Department of Mathematics Outline Two different type of Statistical Mechanics models in 2D: Spin Systems Coulomb Gas Spin Systems Ising Model Configuration: Place +1 or 1 at
California State University Department of Mathematics Outline Two different type of Statistical Mechanics models in 2D: Spin Systems Coulomb Gas Spin Systems Ising Model Configuration: Place +1 or 1 at
Local Kesten McKay law for random regular graphs
 Local Kesten McKay law for random regular graphs Roland Bauerschmidt (with Jiaoyang Huang and Horng-Tzer Yau) University of Cambridge Weizmann Institute, January 2017 Random regular graph G N,d is the
Local Kesten McKay law for random regular graphs Roland Bauerschmidt (with Jiaoyang Huang and Horng-Tzer Yau) University of Cambridge Weizmann Institute, January 2017 Random regular graph G N,d is the
5 Topological defects and textures in ordered media
 5 Topological defects and textures in ordered media In this chapter we consider how to classify topological defects and textures in ordered media. We give here only a very short account of the method following
5 Topological defects and textures in ordered media In this chapter we consider how to classify topological defects and textures in ordered media. We give here only a very short account of the method following
4.3 Classical model at low temperature: an example Continuum limit and path integral The two-point function: perturbative
 Contents Gaussian integrals.......................... Generating function.......................2 Gaussian expectation values. Wick s theorem........... 2.3 Perturbed gaussian measure. Connected contributions.......
Contents Gaussian integrals.......................... Generating function.......................2 Gaussian expectation values. Wick s theorem........... 2.3 Perturbed gaussian measure. Connected contributions.......
Lecture Notes on the Matrix Dyson Equation and its Applications for Random Matrices
 Lecture otes on the Matrix Dyson Equation and its Applications for Random Matrices László Erdős Institute of Science and Technology, Austria June 9, 207 Abstract These lecture notes are a concise introduction
Lecture otes on the Matrix Dyson Equation and its Applications for Random Matrices László Erdős Institute of Science and Technology, Austria June 9, 207 Abstract These lecture notes are a concise introduction
Quantum chaos on graphs
 Baylor University Graduate seminar 6th November 07 Outline 1 What is quantum? 2 Everything you always wanted to know about quantum but were afraid to ask. 3 The trace formula. 4 The of Bohigas, Giannoni
Baylor University Graduate seminar 6th November 07 Outline 1 What is quantum? 2 Everything you always wanted to know about quantum but were afraid to ask. 3 The trace formula. 4 The of Bohigas, Giannoni
Lectures 6 7 : Marchenko-Pastur Law
 Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
Asymptotics of generalized eigenfunctions on manifold with Euclidean and/or hyperbolic ends
 Asymptotics of generalized eigenfunctions on manifold with Euclidean and/or hyperbolic ends Kenichi ITO (University of Tokyo) joint work with Erik SKIBSTED (Aarhus University) 3 July 2018 Example: Free
Asymptotics of generalized eigenfunctions on manifold with Euclidean and/or hyperbolic ends Kenichi ITO (University of Tokyo) joint work with Erik SKIBSTED (Aarhus University) 3 July 2018 Example: Free
LECTURE 5: THE METHOD OF STATIONARY PHASE
 LECTURE 5: THE METHOD OF STATIONARY PHASE Some notions.. A crash course on Fourier transform For j =,, n, j = x j. D j = i j. For any multi-index α = (α,, α n ) N n. α = α + + α n. α! = α! α n!. x α =
LECTURE 5: THE METHOD OF STATIONARY PHASE Some notions.. A crash course on Fourier transform For j =,, n, j = x j. D j = i j. For any multi-index α = (α,, α n ) N n. α = α + + α n. α! = α! α n!. x α =
Susceptibility of the Two-Dimensional Ising Model
 Susceptibility of the Two-Dimensional Ising Model Craig A. Tracy UC Davis September 2014 1. Definition of 2D Ising Model Outline Outline 1. Definition of 2D Ising Model 2. Why is the nearest neighbor zero-field
Susceptibility of the Two-Dimensional Ising Model Craig A. Tracy UC Davis September 2014 1. Definition of 2D Ising Model Outline Outline 1. Definition of 2D Ising Model 2. Why is the nearest neighbor zero-field
Concentration inequalities: basics and some new challenges
 Concentration inequalities: basics and some new challenges M. Ledoux University of Toulouse, France & Institut Universitaire de France Measure concentration geometric functional analysis, probability theory,
Concentration inequalities: basics and some new challenges M. Ledoux University of Toulouse, France & Institut Universitaire de France Measure concentration geometric functional analysis, probability theory,
Operator norm convergence for sequence of matrices and application to QIT
 Operator norm convergence for sequence of matrices and application to QIT Benoît Collins University of Ottawa & AIMR, Tohoku University Cambridge, INI, October 15, 2013 Overview Overview Plan: 1. Norm
Operator norm convergence for sequence of matrices and application to QIT Benoît Collins University of Ottawa & AIMR, Tohoku University Cambridge, INI, October 15, 2013 Overview Overview Plan: 1. Norm
Statistical Thermodynamics Solution Exercise 8 HS Solution Exercise 8
 Statistical Thermodynamics Solution Exercise 8 HS 05 Solution Exercise 8 Problem : Paramagnetism - Brillouin function a According to the equation for the energy of a magnetic dipole in an external magnetic
Statistical Thermodynamics Solution Exercise 8 HS 05 Solution Exercise 8 Problem : Paramagnetism - Brillouin function a According to the equation for the energy of a magnetic dipole in an external magnetic
FRG Workshop in Cambridge MA, May
 FRG Workshop in Cambridge MA, May 18-19 2011 Programme Wednesday May 18 09:00 09:10 (welcoming) 09:10 09:50 Bachmann 09:55 10:35 Sims 10:55 11:35 Borovyk 11:40 12:20 Bravyi 14:10 14:50 Datta 14:55 15:35
FRG Workshop in Cambridge MA, May 18-19 2011 Programme Wednesday May 18 09:00 09:10 (welcoming) 09:10 09:50 Bachmann 09:55 10:35 Sims 10:55 11:35 Borovyk 11:40 12:20 Bravyi 14:10 14:50 Datta 14:55 15:35
Random Fermionic Systems
 Random Fermionic Systems Fabio Cunden Anna Maltsev Francesco Mezzadri University of Bristol December 9, 2016 Maltsev (University of Bristol) Random Fermionic Systems December 9, 2016 1 / 27 Background
Random Fermionic Systems Fabio Cunden Anna Maltsev Francesco Mezzadri University of Bristol December 9, 2016 Maltsev (University of Bristol) Random Fermionic Systems December 9, 2016 1 / 27 Background
Painlevé Representations for Distribution Functions for Next-Largest, Next-Next-Largest, etc., Eigenvalues of GOE, GUE and GSE
 Painlevé Representations for Distribution Functions for Next-Largest, Next-Next-Largest, etc., Eigenvalues of GOE, GUE and GSE Craig A. Tracy UC Davis RHPIA 2005 SISSA, Trieste 1 Figure 1: Paul Painlevé,
Painlevé Representations for Distribution Functions for Next-Largest, Next-Next-Largest, etc., Eigenvalues of GOE, GUE and GSE Craig A. Tracy UC Davis RHPIA 2005 SISSA, Trieste 1 Figure 1: Paul Painlevé,
2D CFT and the Ising Model
 2D CFT and the Ising Model Alex Atanasov December 27, 207 Abstract In this lecture, we review the results of Appendix E from the seminal paper by Belavin, Polyakov, and Zamolodchikov on the critical scaling
2D CFT and the Ising Model Alex Atanasov December 27, 207 Abstract In this lecture, we review the results of Appendix E from the seminal paper by Belavin, Polyakov, and Zamolodchikov on the critical scaling
Einstein-Hilbert action on Connes-Landi noncommutative manifolds
 Einstein-Hilbert action on Connes-Landi noncommutative manifolds Yang Liu MPIM, Bonn Analysis, Noncommutative Geometry, Operator Algebras Workshop June 2017 Motivations and History Motivation: Explore
Einstein-Hilbert action on Connes-Landi noncommutative manifolds Yang Liu MPIM, Bonn Analysis, Noncommutative Geometry, Operator Algebras Workshop June 2017 Motivations and History Motivation: Explore
A determinantal formula for the GOE Tracy-Widom distribution
 A determinantal formula for the GOE Tracy-Widom distribution Patrik L. Ferrari and Herbert Spohn Technische Universität München Zentrum Mathematik and Physik Department e-mails: ferrari@ma.tum.de, spohn@ma.tum.de
A determinantal formula for the GOE Tracy-Widom distribution Patrik L. Ferrari and Herbert Spohn Technische Universität München Zentrum Mathematik and Physik Department e-mails: ferrari@ma.tum.de, spohn@ma.tum.de
Free probabilities and the large N limit, IV. Loop equations and all-order asymptotic expansions... Gaëtan Borot
 Free probabilities and the large N limit, IV March 27th 2014 Loop equations and all-order asymptotic expansions... Gaëtan Borot MPIM Bonn & MIT based on joint works with Alice Guionnet, MIT Karol Kozlowski,
Free probabilities and the large N limit, IV March 27th 2014 Loop equations and all-order asymptotic expansions... Gaëtan Borot MPIM Bonn & MIT based on joint works with Alice Guionnet, MIT Karol Kozlowski,
Eigenvalue PDFs. Peter Forrester, M&S, University of Melbourne
 Outline Eigenvalue PDFs Peter Forrester, M&S, University of Melbourne Hermitian matrices with real, complex or real quaternion elements Circular ensembles and classical groups Products of random matrices
Outline Eigenvalue PDFs Peter Forrester, M&S, University of Melbourne Hermitian matrices with real, complex or real quaternion elements Circular ensembles and classical groups Products of random matrices
ARBITRARY ROTATION INVARIANT RANDOM MATRIX ENSEMBLES HUBBARD-STRATONOVITCH TRANSFORMATION VERSUS SUPERBOSONIZATION. Mario Kieburg.
 ARBITRARY ROTATION INVARIANT RANDOM MATRIX ENSEMBLES: HUBBARD-STRATONOVITCH TRANSFORMATION VERSUS SUPERBOSONIZATION Mario Kieburg Universität Duisburg-Essen Mexico, Cuernavaca, March 2009 supported by
ARBITRARY ROTATION INVARIANT RANDOM MATRIX ENSEMBLES: HUBBARD-STRATONOVITCH TRANSFORMATION VERSUS SUPERBOSONIZATION Mario Kieburg Universität Duisburg-Essen Mexico, Cuernavaca, March 2009 supported by
Random band matrices
 Random band matrices P. Bourgade Courant Institute, ew York University bourgade@cims.nyu.edu We survey recent mathematical results about the spectrum of random band matrices. We start by exposing the Erdős-Schlein-Yau
Random band matrices P. Bourgade Courant Institute, ew York University bourgade@cims.nyu.edu We survey recent mathematical results about the spectrum of random band matrices. We start by exposing the Erdős-Schlein-Yau
1 Superfluidity and Bose Einstein Condensate
 Physics 223b Lecture 4 Caltech, 04/11/18 1 Superfluidity and Bose Einstein Condensate 1.6 Superfluid phase: topological defect Besides such smooth gapless excitations, superfluid can also support a very
Physics 223b Lecture 4 Caltech, 04/11/18 1 Superfluidity and Bose Einstein Condensate 1.6 Superfluid phase: topological defect Besides such smooth gapless excitations, superfluid can also support a very
Triangular matrices and biorthogonal ensembles
 /26 Triangular matrices and biorthogonal ensembles Dimitris Cheliotis Department of Mathematics University of Athens UK Easter Probability Meeting April 8, 206 2/26 Special densities on R n Example. n
/26 Triangular matrices and biorthogonal ensembles Dimitris Cheliotis Department of Mathematics University of Athens UK Easter Probability Meeting April 8, 206 2/26 Special densities on R n Example. n
Lecture I: Asymptotics for large GUE random matrices
 Lecture I: Asymptotics for large GUE random matrices Steen Thorbjørnsen, University of Aarhus andom Matrices Definition. Let (Ω, F, P) be a probability space and let n be a positive integer. Then a random
Lecture I: Asymptotics for large GUE random matrices Steen Thorbjørnsen, University of Aarhus andom Matrices Definition. Let (Ω, F, P) be a probability space and let n be a positive integer. Then a random
1 Tridiagonal matrices
 Lecture Notes: β-ensembles Bálint Virág Notes with Diane Holcomb 1 Tridiagonal matrices Definition 1. Suppose you have a symmetric matrix A, we can define its spectral measure (at the first coordinate
Lecture Notes: β-ensembles Bálint Virág Notes with Diane Holcomb 1 Tridiagonal matrices Definition 1. Suppose you have a symmetric matrix A, we can define its spectral measure (at the first coordinate
Kosterlitz-Thouless Transition
 Heidelberg University Seminar-Lecture 5 SS 16 Menelaos Zikidis Kosterlitz-Thouless Transition 1 Motivation Back in the 70 s, the concept of a phase transition in condensed matter physics was associated
Heidelberg University Seminar-Lecture 5 SS 16 Menelaos Zikidis Kosterlitz-Thouless Transition 1 Motivation Back in the 70 s, the concept of a phase transition in condensed matter physics was associated
H ψ = E ψ. Introduction to Exact Diagonalization. Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden
 H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml laeuchli@comp-phys.org Simulations of
H ψ = E ψ Introduction to Exact Diagonalization Andreas Läuchli, New states of quantum matter MPI für Physik komplexer Systeme - Dresden http://www.pks.mpg.de/~aml laeuchli@comp-phys.org Simulations of
Eigenvalue variance bounds for Wigner and covariance random matrices
 Eigenvalue variance bounds for Wigner and covariance random matrices S. Dallaporta University of Toulouse, France Abstract. This work is concerned with finite range bounds on the variance of individual
Eigenvalue variance bounds for Wigner and covariance random matrices S. Dallaporta University of Toulouse, France Abstract. This work is concerned with finite range bounds on the variance of individual
Types of Real Integrals
 Math B: Complex Variables Types of Real Integrals p(x) I. Integrals of the form P.V. dx where p(x) and q(x) are polynomials and q(x) q(x) has no eros (for < x < ) and evaluate its integral along the fol-
Math B: Complex Variables Types of Real Integrals p(x) I. Integrals of the form P.V. dx where p(x) and q(x) are polynomials and q(x) q(x) has no eros (for < x < ) and evaluate its integral along the fol-
XY model: particle-vortex duality. Abstract
 XY model: particle-vortex duality Subir Sachdev Department of Physics, Harvard University, Cambridge, Massachusetts, 02138, USA Dated: February 7, 2018) Abstract We consider the classical XY model in D
XY model: particle-vortex duality Subir Sachdev Department of Physics, Harvard University, Cambridge, Massachusetts, 02138, USA Dated: February 7, 2018) Abstract We consider the classical XY model in D
Is Quantum Mechanics Chaotic? Steven Anlage
 Is Quantum Mechanics Chaotic? Steven Anlage Physics 40 0.5 Simple Chaos 1-Dimensional Iterated Maps The Logistic Map: x = 4 x (1 x ) n+ 1 μ n n Parameter: μ Initial condition: 0 = 0.5 μ 0.8 x 0 = 0.100
Is Quantum Mechanics Chaotic? Steven Anlage Physics 40 0.5 Simple Chaos 1-Dimensional Iterated Maps The Logistic Map: x = 4 x (1 x ) n+ 1 μ n n Parameter: μ Initial condition: 0 = 0.5 μ 0.8 x 0 = 0.100
INTRODUCTION TO STATISTICAL MECHANICS Exercises
 École d hiver de Probabilités Semaine 1 : Mécanique statistique de l équilibre CIRM - Marseille 4-8 Février 2012 INTRODUCTION TO STATISTICAL MECHANICS Exercises Course : Yvan Velenik, Exercises : Loren
École d hiver de Probabilités Semaine 1 : Mécanique statistique de l équilibre CIRM - Marseille 4-8 Février 2012 INTRODUCTION TO STATISTICAL MECHANICS Exercises Course : Yvan Velenik, Exercises : Loren
On level crossing in deterministic and random matrix pencils
 On level crossing in deterministic and random matrix pencils May 3, 2018 Topics to discuss 1 Basic level crossing problem 2 3 4 Main references (i) B. Shapiro, M. Tater, On spectral asymptotics of quasi-exactly
On level crossing in deterministic and random matrix pencils May 3, 2018 Topics to discuss 1 Basic level crossing problem 2 3 4 Main references (i) B. Shapiro, M. Tater, On spectral asymptotics of quasi-exactly
Physics 212: Statistical mechanics II Lecture XI
 Physics 212: Statistical mechanics II Lecture XI The main result of the last lecture was a calculation of the averaged magnetization in mean-field theory in Fourier space when the spin at the origin is
Physics 212: Statistical mechanics II Lecture XI The main result of the last lecture was a calculation of the averaged magnetization in mean-field theory in Fourier space when the spin at the origin is
Non-perturbative effects in ABJM theory
 October 9, 2015 Non-perturbative effects in ABJM theory 1 / 43 Outline 1. Non-perturbative effects 1.1 General aspects 1.2 Non-perturbative aspects of string theory 1.3 Non-perturbative effects in M-theory
October 9, 2015 Non-perturbative effects in ABJM theory 1 / 43 Outline 1. Non-perturbative effects 1.1 General aspects 1.2 Non-perturbative aspects of string theory 1.3 Non-perturbative effects in M-theory
440-3 Geometry/Topology: Cohomology Northwestern University Solution of Homework 5
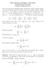 440-3 Geometry/Topology: Cohomology Northwestern University Solution of Homework 5 You can use freely the following simple results from complex analysis (which can be proved in the same way as the case
440-3 Geometry/Topology: Cohomology Northwestern University Solution of Homework 5 You can use freely the following simple results from complex analysis (which can be proved in the same way as the case
Floquet Topological Insulator:
 Floquet Topological Insulator: Understanding Floquet topological insulator in semiconductor quantum wells by Lindner et al. Condensed Matter Journal Club Caltech February 12 2014 Motivation Motivation
Floquet Topological Insulator: Understanding Floquet topological insulator in semiconductor quantum wells by Lindner et al. Condensed Matter Journal Club Caltech February 12 2014 Motivation Motivation
VI.D Self Duality in the Two Dimensional Ising Model
 VI.D Self Duality in the Two Dimensional Ising Model Kramers and Wannier discovered a hidden symmetry that relates the properties of the Ising model on the square lattice at low and high temperatures.
VI.D Self Duality in the Two Dimensional Ising Model Kramers and Wannier discovered a hidden symmetry that relates the properties of the Ising model on the square lattice at low and high temperatures.
Hyperbolic Hubbard-Stratonovich transformations
 Hyperbolic Hubbard-Stratonovich transformations J. Müller-Hill 1 and M.R. Zirnbauer 1 1 Department of Physics, University of Cologne August 21, 2008 1 / 20 Outline Motivation Hubbard-Stratonovich transformation
Hyperbolic Hubbard-Stratonovich transformations J. Müller-Hill 1 and M.R. Zirnbauer 1 1 Department of Physics, University of Cologne August 21, 2008 1 / 20 Outline Motivation Hubbard-Stratonovich transformation
Finite temperature form factors in the free Majorana theory
 Finite temperature form factors in the free Majorana theory Benjamin Doyon Rudolf Peierls Centre for Theoretical Physics, Oxford University, UK supported by EPSRC postdoctoral fellowship hep-th/0506105
Finite temperature form factors in the free Majorana theory Benjamin Doyon Rudolf Peierls Centre for Theoretical Physics, Oxford University, UK supported by EPSRC postdoctoral fellowship hep-th/0506105
