Operator norm convergence for sequence of matrices and application to QIT
|
|
|
- Brent Chase
- 5 years ago
- Views:
Transcription
1 Operator norm convergence for sequence of matrices and application to QIT Benoît Collins University of Ottawa & AIMR, Tohoku University Cambridge, INI, October 15, 2013
2 Overview
3 Overview Plan: 1. Norm convergence for simple random matrices. 2. Application: threshold for for the appt property. 3. Norm convergence for multiple random matrices. 4. Application: converse threshold for PPT. 5. Application: convergence of the collection of output states.
4 Random matrices
5 Random matrices Random matrix theory: probability theory with matrix valued random variables, study of its properties as d.
6 Random matrices Random matrix theory: probability theory with matrix valued random variables, study of its properties as d. Notation: let X d M d (C) be a (self-adjoint or normal) (random) matrix. Let λ (d) i be its eigenvalues, and µ d = d 1 λ (d) i is the eigenvalue counting measure (histogram of eigenvalues).
7 Random matrices Random matrix theory: probability theory with matrix valued random variables, study of its properties as d. Notation: let X d M d (C) be a (self-adjoint or normal) (random) matrix. Let λ (d) i be its eigenvalues, and µ d = d 1 λ (d) i is the eigenvalue counting measure (histogram of eigenvalues). Classical RMT question: When does the (random) probability measure µ d have an interesting behaviour at d? More recent RMT question: how about the (random) set supp(µ d )? (largest eigenvalue)
8 Single random matrix: Wishart matrices Let G M d s (C) be a Ginibre random matrix
9 Single random matrix: Wishart matrices Let G M d s (C) be a Ginibre random matrix ({G ij } are i.i.d. standard complex Gaussian random variables)
10 Single random matrix: Wishart matrices Let G M d s (C) be a Ginibre random matrix ({G ij } are i.i.d. standard complex Gaussian random variables) Let W = W d = GG be the corresponding Wishart matrix of parameters (d, s) (G denotes the Hermitian adjoint of G).
11 Single random matrix: Wishart matrices Let G M d s (C) be a Ginibre random matrix ({G ij } are i.i.d. standard complex Gaussian random variables) Let W = W d = GG be the corresponding Wishart matrix of parameters (d, s) (G denotes the Hermitian adjoint of G). One has E[W ij ] = sδ ij and E[Tr(W )] = ds.
12 Single random matrix: Wishart matrices The Marchenko-Pastur (or free Poisson) probability distributions, π c, (c > 0), is defined as follows (x a)(b x) π c = max(1 c, 0)δ πx [a,b] (x) dx, (1) (a = ( c 1) 2 and b = ( c + 1) 2 ).
13 Single random matrix: Wishart matrices The Marchenko-Pastur (or free Poisson) probability distributions, π c, (c > 0), is defined as follows (x a)(b x) π c = max(1 c, 0)δ πx [a,b] (x) dx, (1) (a = ( c 1) 2 and b = ( c + 1) 2 ).
14 Ginibre and Wishart ensembles Notation: Let γ be the full cycle γ = (1 2 k). For any permutation α, let α be its length on the Cayley graph of S k generated by transpositions. The geodesic inequality α + α 1 γ γ = k 1 holds. We define g(α), the genus of a permutation α on I, as g(α) = α + α 1 γ γ. (2) 2
15 Ginibre and Wishart ensembles Let W d be a d d Wishart matrix of parameter (d, s) and let Z d = ( Wd ds ds Id ) d be its centered and renormalized version. Theorem The moments of Z d are given by [ 1 E d Tr( Z p ) ] d = ( ) d α p/2 d 2g(α), (3) s α Sp o
16 Ginibre and Wishart ensembles The previous theorem implies that x k µ d (dx) x k π c (dx) (only genus zero terms survive):
17 Ginibre and Wishart ensembles The previous theorem implies that x k µ d (dx) x k π c (dx) (only genus zero terms survive): Theorem Assuming s/d c, with the renormalization W d / sd, µ d π c.
18 Ginibre and Wishart ensembles The previous theorem implies that x k µ d (dx) x k π c (dx) (only genus zero terms survive): Theorem Assuming s/d c, with the renormalization W d / sd, µ d π c. However the only thing we can say about supp(µ d ) at this point is lim d d d dsupp(µ d ) supp(π c ). The converse inclusion is not clear.
19 Ginibre and Wishart ensembles In general, convergence of µ d to something, is ensured by convergence of moments (under reasonable boundedness assumption).
20 Ginibre and Wishart ensembles In general, convergence of µ d to something, is ensured by convergence of moments (under reasonable boundedness assumption). In order to ensure the convergence of supp(µ d ), we need to look at moments k that grow as d grows.
21 Ginibre and Wishart ensembles In general, convergence of µ d to something, is ensured by convergence of moments (under reasonable boundedness assumption). In order to ensure the convergence of supp(µ d ), we need to look at moments k that grow as d grows. [for example, d 1 Tr diag(1 + ε, 1,..., 1) k ) behaves like d 1 Tr diag(1 + ε, 1,..., 1) k ) at k fixed, d. The situation starts to change when k >> log d this is the minimal growth of k needed to understand supp(µ d ).]
22 Ginibre and Wishart ensembles Theorem In the situation where s/d converges, and d, then the extremal eigenvalues of W d /d converge almost surely to a, b.
23 Ginibre and Wishart ensembles Theorem In the situation where s/d converges, and d, then the extremal eigenvalues of W d /d converge almost surely to a, b. And almost surely, when 1 d s, the extremal eigenvalues of ds(wd /ds 1/d) converge to ±2.
24 Application: APPT A quantum state ρ D(C d 1 C d 2 ) is absolutely PPT (or APPT) if for any unitary matrix U U(d), UρU PPT. APPT = U U(d) U(PPT )U PPT.
25 Application: APPT A quantum state ρ D(C d 1 C d 2 ) is absolutely PPT (or APPT) if for any unitary matrix U U(d), UρU PPT. APPT = U U(d) U(PPT )U PPT. APPT is a convex body, a convex compact set with non-empty interior. Known fact: ɛd + (1 ɛ) I d S PPT for some ɛ < 1 d 1.
26 Application: APPT A quantum state ρ D(C d 1 C d 2 ) is absolutely PPT (or APPT) if for any unitary matrix U U(d), UρU PPT. APPT = U U(d) U(PPT )U PPT. APPT is a convex body, a convex compact set with non-empty interior. Known fact: ɛd + (1 ɛ) I d S PPT for some ɛ < 1 d 1. There exists an explicit algebraic characterization.
27 Application: APPT Setup: d = d 1 d 2, we pick a Wishart matrix of parameter d, s and try to check the APPT property for s, d Let p = min(d 1, d 2 ).
28 Application: APPT When p = min(d 1, d 2 ), we have the following (almost sharp) threshold estimate
29 Application: APPT When p = min(d 1, d 2 ), we have the following (almost sharp) threshold estimate Theorem (C, Nechita, Ye) Let ρ be a random state according to the parameters d, s. (i) almost surely, when d and s > (4 + ε)p 2 d, the quantum state ρ is APPT; (ii) when 1 p 2 d and s < (4 ε)p 2 d, ρ is not APPT almost surely; (iii) when p 2 τd for a constant τ (0, 1], there exists a constant C τ such that whenever s < 4(C τ ε)p 2 d, ρ is not APPT almost surely.
30 Application: APPT When p = min(d 1, d 2 ) is fixed and s/d c for a constant c > 0 as d, sharp estimate on the threshold for APPT. Theorem (C, Nechita, Ye) Let ρ be a random induced state distributed according to the measure µ d,s. Almost surely, when d and s cd, one has: (i) ρ APPT, if c > (p + p 2 1) 2 ; (ii) ρ / APPT, if c < (p + p 2 1) 2.
31 Multimatrices So far we only dealt with one matrix. What if we take a bunch of i.i.d random matrices and take NC polynomials in them?
32 Multimatrices So far we only dealt with one matrix. What if we take a bunch of i.i.d random matrices and take NC polynomials in them? [E.g. understand the behaviour of W (1) d W (2) d + W (2) d W (1) d, if W (1) d, W (2) d are independent copies]
33 Multimatrices So far we only dealt with one matrix. What if we take a bunch of i.i.d random matrices and take NC polynomials in them? [E.g. understand the behaviour of W (1) d W (2) d + W (2) d W (1) d, if W (1) d, W (2) d are independent copies] In principle, the method of moments allows us to understand the limiting behaviour of µ d. But the limiting behaviour of supp(µ d ) is much more difficult to understand.
34 Multimatrices So far we only dealt with one matrix. What if we take a bunch of i.i.d random matrices and take NC polynomials in them? [E.g. understand the behaviour of W (1) d W (2) d + W (2) d W (1) d, if W (1) d, W (2) d are independent copies] In principle, the method of moments allows us to understand the limiting behaviour of µ d. But the limiting behaviour of supp(µ d ) is much more difficult to understand. C*-algebra vs von Neumann algebra.
35 Multimatrices So far we only dealt with one matrix. What if we take a bunch of i.i.d random matrices and take NC polynomials in them? [E.g. understand the behaviour of W (1) d W (2) d + W (2) d W (1) d, if W (1) d, W (2) d are independent copies] In principle, the method of moments allows us to understand the limiting behaviour of µ d. But the limiting behaviour of supp(µ d ) is much more difficult to understand. C*-algebra vs von Neumann algebra. In practice, we can t understand directly the behaviour of moments where k grows together with d for multi matrices.
36 Linearization trick
37 Linearization trick Roughly speaking:
38 Linearization trick Roughly speaking: Understanding supp(µ d ) for all non-commutative polynomials in W (1) d, W (2) d [W (1) d W (2) d + W (2) d W (1) d and all the others] is equivalent to
39 Linearization trick Roughly speaking: Understanding supp(µ d ) for all non-commutative polynomials in W (1) d, W (2) d [W (1) d W (2) d + W (2) d W (1) d and all the others] is equivalent to Understanding supp(µ d ) for all a 0 1 d + a 1 W (1) d + a 2 W (2) d for all a 0, a 1, a 2 M k (C) selfadjoint matrices, all k.
40 Linearization trick Advantage: no non-commutative multiplication ( linearization ).
41 Linearization trick Advantage: no non-commutative multiplication ( linearization ). Price to pay: (1) allow matrix coefficients (2) give up speed of convergence (global equivalence).
42 Linearization trick Advantage: no non-commutative multiplication ( linearization ). Price to pay: (1) allow matrix coefficients (2) give up speed of convergence (global equivalence). Extra bonus: we obtain for free the understanding of non-commutative polynomials with matrix coefficients [e.g. a 1 W (1) d W (2) d + a 2 W (2) d W (1) d.]
43 Linearization trick Advantage: no non-commutative multiplication ( linearization ). Price to pay: (1) allow matrix coefficients (2) give up speed of convergence (global equivalence). Extra bonus: we obtain for free the understanding of non-commutative polynomials with matrix coefficients [e.g. a 1 W (1) d W (2) d + a 2 W (2) d W (1) d.] (the bonus matters in the applications)
44 Free probability and random matrices A non-commutative probability space : unital algebra A with tracial state ϕ (Elements therein: NCRV). E.g. random matrices (M d (L (Ω, P)), E[d 1 Tr( )])
45 Free probability and random matrices A non-commutative probability space : unital algebra A with tracial state ϕ (Elements therein: NCRV). E.g. random matrices (M d (L (Ω, P)), E[d 1 Tr( )]) Let A 1,..., A k be subalgebras of A. They are free if for all a i A ji (i = 1,..., k) such that ϕ(a i ) = 0, one has ϕ(a 1 a p ) = 0 as soon as j 1 j 2, j 2 j 3,..., j p 1 j p.
46 Free probability and random matrices A non-commutative probability space : unital algebra A with tracial state ϕ (Elements therein: NCRV). E.g. random matrices (M d (L (Ω, P)), E[d 1 Tr( )]) Let A 1,..., A k be subalgebras of A. They are free if for all a i A ji (i = 1,..., k) such that ϕ(a i ) = 0, one has ϕ(a 1 a p ) = 0 as soon as j 1 j 2, j 2 j 3,..., j p 1 j p. The joint distribution of a k-tuple (a 1,..., a k ) of selfadjoint random variables is the collection of its NC moments.
47 Free probability and random matrices Convergence in distribution = pointwise convergence of moments.
48 Free probability and random matrices Convergence in distribution = pointwise convergence of moments. Sequences of random variables (a (d) 1 ) n,..., (a (d) k ) n are called asymptotically free as n iff the k-tuple (a (d) 1,..., a(d) k ) n converges in distribution towards a family of free random variables.
49 Free probability and random matrices Theorem (Voiculescu) Let U 1,..., U k,... be a collection of independent Haar distributed random matrices of M d (C) and (Wi d ) i I be a set of constant matrices of M d (C) admitting a joint limit distribution for large n with respect to the state d 1 Tr.
50 Free probability and random matrices Theorem (Voiculescu) Let U 1,..., U k,... be a collection of independent Haar distributed random matrices of M d (C) and (Wi d ) i I be a set of constant matrices of M d (C) admitting a joint limit distribution for large n with respect to the state d 1 Tr. Then, the family ((U 1, U1 ),..., (U k, Uk ),..., (W i)) admits a limit distribution, and is asymptotically free with respect to E(d 1 Tr).
51 Free probability and random matrices Strong convergence = in addition, convergence of the set of singular values towards the limiting set in the Hausdorff distance sense.
52 Free probability and random matrices Theorem (C, Male) Let U 1,..., U k,... be a collection of independent Haar distributed random matrices of M n (C) and (Wi d ) i I be a set of constant matrices of M d (C) admitting a STRONG joint limit distribution for large d with respect to the state d 1 Tr.
53 Free probability and random matrices Theorem (C, Male) Let U 1,..., U k,... be a collection of independent Haar distributed random matrices of M n (C) and (Wi d ) i I be a set of constant matrices of M d (C) admitting a STRONG joint limit distribution for large d with respect to the state d 1 Tr. Then the family ((U 1, U1 ),..., (U k, Uk ),..., (W i)) admits a STRONG limit distribution, and is STRONGLY asymptotically free with respect to E(d 1 Tr).
54 Application: treshold for asymetric PPT In M d M n, Banica and Nechita (arxiv ) consider the partial transpose of Wishart matrices of parameter dn, dm and prove that as d (m, n fixed), µ d converges to a free difference of Marchenko Pastur distributions of parameter m(n ± 1)/2.
55 Application: treshold for asymetric PPT In M d M n, Banica and Nechita (arxiv ) consider the partial transpose of Wishart matrices of parameter dn, dm and prove that as d (m, n fixed), µ d converges to a free difference of Marchenko Pastur distributions of parameter m(n ± 1)/2. They prove that the spectrum of this distribution is positive iff n m/4 + 1/m and m 2.
56 Application: treshold for asymetric PPT In M d M n, Banica and Nechita (arxiv ) consider the partial transpose of Wishart matrices of parameter dn, dm and prove that as d (m, n fixed), µ d converges to a free difference of Marchenko Pastur distributions of parameter m(n ± 1)/2. They prove that the spectrum of this distribution is positive iff n m/4 + 1/m and m 2. This proves that PPT does not hold with high probability if one of these conditions is violated.
57 Application: treshold for asymetric PPT In M d M n, Banica and Nechita (arxiv ) consider the partial transpose of Wishart matrices of parameter dn, dm and prove that as d (m, n fixed), µ d converges to a free difference of Marchenko Pastur distributions of parameter m(n ± 1)/2. They prove that the spectrum of this distribution is positive iff n m/4 + 1/m and m 2. This proves that PPT does not hold with high probability if one of these conditions is violated. Conversely, our result proves that PPT does hold with high probability if these conditions are satisfied.
58 Application: simultaneous behaviour of quantum channels Let π d be a (random projection) in M k M d having the following property: A M k, the pair of matrices (π d, A 1 d ) converge strongly.
59 Application: simultaneous behaviour of quantum channels Let π d be a (random projection) in M k M d having the following property: A M k, the pair of matrices (π d, A 1 d ) converge strongly. Let Φ d be the channel End(Im(π d )) M k obtained by taking the partial trace over M d. Let χ be any other quantum channel M p M q.
60 Application: simultaneous behaviour of quantum channels Let π d be a (random projection) in M k M d having the following property: A M k, the pair of matrices (π d, A 1 d ) converge strongly. Let Φ d be the channel End(Im(π d )) M k obtained by taking the partial trace over M d. Let χ be any other quantum channel M p M q. Theorem (C, Fukuda, Nechita) The collection Φ d (pure states) converges strongly to a convex body (the dual of {A, lim π d A 1 d π d 1}).
61 Application: simultaneous behaviour of quantum channels Let π d be a (random projection) in M k M d having the following property: A M k, the pair of matrices (π d, A 1 d ) converge strongly. Let Φ d be the channel End(Im(π d )) M k obtained by taking the partial trace over M d. Let χ be any other quantum channel M p M q. Theorem (C, Fukuda, Nechita) The collection Φ d (pure states) converges strongly to a convex body (the dual of {A, lim π d A 1 d π d 1}). The same holds true for for Φ d χ!
62 Application: simultaneous behaviour of quantum channels Example 1: π d is a random projection of rank tkd, t [0, 1] (allows us to obtain violation of MOE additivity as large as log 2)
63 Application: simultaneous behaviour of quantum channels Example 1: π d is a random projection of rank tkd, t [0, 1] (allows us to obtain violation of MOE additivity as large as log 2) Example 2: π d = k 1 (U (d) i U (d) j ) (complementary channel of Φ d : X k 1 U i XUi ). This allows us to prove that Φ d S1 S = 4(k 1)/k 2, k 2.
64 Application: simultaneous behaviour of quantum channels Example 1: π d is a random projection of rank tkd, t [0, 1] (allows us to obtain violation of MOE additivity as large as log 2) Example 2: π d = k 1 (U (d) i U (d) j ) (complementary channel of Φ d : X k 1 U i XUi ). This allows us to prove that Φ d S1 S = 4(k 1)/k 2, k 2. Some other applications to new example of k-positive maps...
65 Selected References (1) The strong asymptotic freeness of Haar and deterministic matrices math/arxiv: With C. Male. To appear in Annales Scientifiques de l ENS (2) Laws of large numbers for eigenvectors and eigenvalues associated to random subspaces in a tensor product math/arxiv: With S. Belinschi and I. Nechita. Inventiones Mathematicae December 2012, Volume 190, Issue 3, pp (3) Almost one bit violation for the additivity of the minimum output entropy, arxiv: with S. Belinschi and I. Nechita. (4) The absolute positive partial transpose property for random induced states. math/arxiv: With I. Nechita and D. Ye, to appear in RMTA (5) In preparation, with M. Fukuda and I. Nechita (6) In preparation, with P. Hayden and I. Nechita
Free probability and quantum information
 Free probability and quantum information Benoît Collins WPI-AIMR, Tohoku University & University of Ottawa Tokyo, Nov 8, 2013 Overview Overview Plan: 1. Quantum Information theory: the additivity problem
Free probability and quantum information Benoît Collins WPI-AIMR, Tohoku University & University of Ottawa Tokyo, Nov 8, 2013 Overview Overview Plan: 1. Quantum Information theory: the additivity problem
The norm of polynomials in large random matrices
 The norm of polynomials in large random matrices Camille Mâle, École Normale Supérieure de Lyon, Ph.D. Student under the direction of Alice Guionnet. with a significant contribution by Dimitri Shlyakhtenko.
The norm of polynomials in large random matrices Camille Mâle, École Normale Supérieure de Lyon, Ph.D. Student under the direction of Alice Guionnet. with a significant contribution by Dimitri Shlyakhtenko.
Output entropy of tensor products of random quantum channels 1
 Output entropy of tensor products of random quantum channels 1 Motohisa Fukuda 1 [Collins, Fukuda and Nechita], [Collins, Fukuda and Nechita] 1 / 13 1 Introduction Aim and background Existence of one large
Output entropy of tensor products of random quantum channels 1 Motohisa Fukuda 1 [Collins, Fukuda and Nechita], [Collins, Fukuda and Nechita] 1 / 13 1 Introduction Aim and background Existence of one large
ASYMPTOTIC EIGENVALUE DISTRIBUTIONS OF BLOCK-TRANSPOSED WISHART MATRICES
 ASYMPTOTIC EIGENVALUE DISTRIBUTIONS OF BLOCK-TRANSPOSED WISHART MATRICES TEODOR BANICA AND ION NECHITA Abstract. We study the partial transposition W Γ = (id t)w M dn (C) of a Wishart matrix W M dn (C)
ASYMPTOTIC EIGENVALUE DISTRIBUTIONS OF BLOCK-TRANSPOSED WISHART MATRICES TEODOR BANICA AND ION NECHITA Abstract. We study the partial transposition W Γ = (id t)w M dn (C) of a Wishart matrix W M dn (C)
um random g. channel & computation of / v QIT output min entropy free prob quantum groups
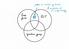 @ i e output free prob. µ @ um random g. channel / v QIT & computation of min. entropy ) quantum groups QIT LINK FP - : Belinski Collins Nechita 201282016 Invent math (2012) 190:647 697 DOI 10.1007/s00222-012-0386-3
@ i e output free prob. µ @ um random g. channel / v QIT & computation of min. entropy ) quantum groups QIT LINK FP - : Belinski Collins Nechita 201282016 Invent math (2012) 190:647 697 DOI 10.1007/s00222-012-0386-3
Selfadjoint Polynomials in Independent Random Matrices. Roland Speicher Universität des Saarlandes Saarbrücken
 Selfadjoint Polynomials in Independent Random Matrices Roland Speicher Universität des Saarlandes Saarbrücken We are interested in the limiting eigenvalue distribution of an N N random matrix for N. Typical
Selfadjoint Polynomials in Independent Random Matrices Roland Speicher Universität des Saarlandes Saarbrücken We are interested in the limiting eigenvalue distribution of an N N random matrix for N. Typical
Random Matrix Theory in Quantum Information
 Random Matrix Theory in Quantum Information Some generic aspects of entanglement Université Claude Bernard Lyon 1 & Universitat Autònoma de Barcelona Cécilia Lancien BMC & BAMC 2015 - Cambridge Cécilia
Random Matrix Theory in Quantum Information Some generic aspects of entanglement Université Claude Bernard Lyon 1 & Universitat Autònoma de Barcelona Cécilia Lancien BMC & BAMC 2015 - Cambridge Cécilia
Free Probability Theory and Random Matrices. Roland Speicher Queen s University Kingston, Canada
 Free Probability Theory and Random Matrices Roland Speicher Queen s University Kingston, Canada We are interested in the limiting eigenvalue distribution of N N random matrices for N. Usually, large N
Free Probability Theory and Random Matrices Roland Speicher Queen s University Kingston, Canada We are interested in the limiting eigenvalue distribution of N N random matrices for N. Usually, large N
Polynomials in Free Variables
 Polynomials in Free Variables Roland Speicher Universität des Saarlandes Saarbrücken joint work with Serban Belinschi, Tobias Mai, and Piotr Sniady Goal: Calculation of Distribution or Brown Measure of
Polynomials in Free Variables Roland Speicher Universität des Saarlandes Saarbrücken joint work with Serban Belinschi, Tobias Mai, and Piotr Sniady Goal: Calculation of Distribution or Brown Measure of
Second Order Freeness and Random Orthogonal Matrices
 Second Order Freeness and Random Orthogonal Matrices Jamie Mingo (Queen s University) (joint work with Mihai Popa and Emily Redelmeier) AMS San Diego Meeting, January 11, 2013 1 / 15 Random Matrices X
Second Order Freeness and Random Orthogonal Matrices Jamie Mingo (Queen s University) (joint work with Mihai Popa and Emily Redelmeier) AMS San Diego Meeting, January 11, 2013 1 / 15 Random Matrices X
Lecture III: Applications of Voiculescu s random matrix model to operator algebras
 Lecture III: Applications of Voiculescu s random matrix model to operator algebras Steen Thorbjørnsen, University of Aarhus Voiculescu s Random Matrix Model Theorem [Voiculescu]. For each n in N, let X
Lecture III: Applications of Voiculescu s random matrix model to operator algebras Steen Thorbjørnsen, University of Aarhus Voiculescu s Random Matrix Model Theorem [Voiculescu]. For each n in N, let X
Non white sample covariance matrices.
 Non white sample covariance matrices. S. Péché, Université Grenoble 1, joint work with O. Ledoit, Uni. Zurich 17-21/05/2010, Université Marne la Vallée Workshop Probability and Geometry in High Dimensions
Non white sample covariance matrices. S. Péché, Université Grenoble 1, joint work with O. Ledoit, Uni. Zurich 17-21/05/2010, Université Marne la Vallée Workshop Probability and Geometry in High Dimensions
Valerio Cappellini. References
 CETER FOR THEORETICAL PHYSICS OF THE POLISH ACADEMY OF SCIECES WARSAW, POLAD RADOM DESITY MATRICES AD THEIR DETERMIATS 4 30 SEPTEMBER 5 TH SFB TR 1 MEETIG OF 006 I PRZEGORZAłY KRAKÓW Valerio Cappellini
CETER FOR THEORETICAL PHYSICS OF THE POLISH ACADEMY OF SCIECES WARSAW, POLAD RADOM DESITY MATRICES AD THEIR DETERMIATS 4 30 SEPTEMBER 5 TH SFB TR 1 MEETIG OF 006 I PRZEGORZAłY KRAKÓW Valerio Cappellini
Limit Laws for Random Matrices from Traffic Probability
 Limit Laws for Random Matrices from Traffic Probability arxiv:1601.02188 Slides available at math.berkeley.edu/ bensonau Benson Au UC Berkeley May 9th, 2016 Benson Au (UC Berkeley) Random Matrices from
Limit Laws for Random Matrices from Traffic Probability arxiv:1601.02188 Slides available at math.berkeley.edu/ bensonau Benson Au UC Berkeley May 9th, 2016 Benson Au (UC Berkeley) Random Matrices from
GAUSSIANIZATION AND EIGENVALUE STATISTICS FOR RANDOM QUANTUM CHANNELS (III) BY BENOÎT COLLINS 1,2 AND ION NECHITA 2 University of Ottawa
 The Annals of Applied Probability 2011, Vol. 21, No. 3, 1136 1179 DOI: 10.1214/10-AAP722 Institute of Mathematical Statistics, 2011 GAUSSIANIZATION AND EIGENVALUE STATISTICS FOR RANDOM QUANTUM CHANNELS
The Annals of Applied Probability 2011, Vol. 21, No. 3, 1136 1179 DOI: 10.1214/10-AAP722 Institute of Mathematical Statistics, 2011 GAUSSIANIZATION AND EIGENVALUE STATISTICS FOR RANDOM QUANTUM CHANNELS
Induced Ginibre Ensemble and random operations
 Induced Ginibre Ensemble and random operations Karol Życzkowski in collaboration with Wojciech Bruzda, Marek Smaczyński, Wojciech Roga Jonith Fischmann, Boris Khoruzhenko (London), Ion Nechita (Touluse),
Induced Ginibre Ensemble and random operations Karol Życzkowski in collaboration with Wojciech Bruzda, Marek Smaczyński, Wojciech Roga Jonith Fischmann, Boris Khoruzhenko (London), Ion Nechita (Touluse),
Ensembles and incomplete information
 p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
Applications and fundamental results on random Vandermon
 Applications and fundamental results on random Vandermonde matrices May 2008 Some important concepts from classical probability Random variables are functions (i.e. they commute w.r.t. multiplication)
Applications and fundamental results on random Vandermonde matrices May 2008 Some important concepts from classical probability Random variables are functions (i.e. they commute w.r.t. multiplication)
Free Probability Theory and Non-crossing Partitions. Roland Speicher Queen s University Kingston, Canada
 Free Probability Theory and Non-crossing Partitions Roland Speicher Queen s University Kingston, Canada Freeness Definition [Voiculescu 1985]: Let (A, ϕ) be a non-commutative probability space, i.e. A
Free Probability Theory and Non-crossing Partitions Roland Speicher Queen s University Kingston, Canada Freeness Definition [Voiculescu 1985]: Let (A, ϕ) be a non-commutative probability space, i.e. A
Dual Temperley Lieb basis, Quantum Weingarten and a conjecture of Jones
 Dual Temperley Lieb basis, Quantum Weingarten and a conjecture of Jones Benoît Collins Kyoto University Sendai, August 2016 Overview Joint work with Mike Brannan (TAMU) (trailer... cf next Monday s arxiv)
Dual Temperley Lieb basis, Quantum Weingarten and a conjecture of Jones Benoît Collins Kyoto University Sendai, August 2016 Overview Joint work with Mike Brannan (TAMU) (trailer... cf next Monday s arxiv)
Channel capacity estimation using free probability theory
 Channel capacity estimation using free probability theory January 008 Problem at hand The capacity per receiving antenna of a channel with n m channel matrix H and signal to noise ratio ρ = 1 σ is given
Channel capacity estimation using free probability theory January 008 Problem at hand The capacity per receiving antenna of a channel with n m channel matrix H and signal to noise ratio ρ = 1 σ is given
From random matrices to free groups, through non-crossing partitions. Michael Anshelevich
 From random matrices to free groups, through non-crossing partitions Michael Anshelevich March 4, 22 RANDOM MATRICES For each N, A (N), B (N) = independent N N symmetric Gaussian random matrices, i.e.
From random matrices to free groups, through non-crossing partitions Michael Anshelevich March 4, 22 RANDOM MATRICES For each N, A (N), B (N) = independent N N symmetric Gaussian random matrices, i.e.
FREE PROBABILITY THEORY
 FREE PROBABILITY THEORY ROLAND SPEICHER Lecture 4 Applications of Freeness to Operator Algebras Now we want to see what kind of information the idea can yield that free group factors can be realized by
FREE PROBABILITY THEORY ROLAND SPEICHER Lecture 4 Applications of Freeness to Operator Algebras Now we want to see what kind of information the idea can yield that free group factors can be realized by
On the distinguishability of random quantum states
 1 1 Department of Computer Science University of Bristol Bristol, UK quant-ph/0607011 Distinguishing quantum states Distinguishing quantum states This talk Question Consider a known ensemble E of n quantum
1 1 Department of Computer Science University of Bristol Bristol, UK quant-ph/0607011 Distinguishing quantum states Distinguishing quantum states This talk Question Consider a known ensemble E of n quantum
Freeness and the Transpose
 Freeness and the Transpose Jamie Mingo (Queen s University) (joint work with Mihai Popa and Roland Speicher) ICM Satellite Conference on Operator Algebras and Applications Cheongpung, August 8, 04 / 6
Freeness and the Transpose Jamie Mingo (Queen s University) (joint work with Mihai Popa and Roland Speicher) ICM Satellite Conference on Operator Algebras and Applications Cheongpung, August 8, 04 / 6
Convergence of spectral measures and eigenvalue rigidity
 Convergence of spectral measures and eigenvalue rigidity Elizabeth Meckes Case Western Reserve University ICERM, March 1, 2018 Macroscopic scale: the empirical spectral measure Macroscopic scale: the empirical
Convergence of spectral measures and eigenvalue rigidity Elizabeth Meckes Case Western Reserve University ICERM, March 1, 2018 Macroscopic scale: the empirical spectral measure Macroscopic scale: the empirical
Lectures 6 7 : Marchenko-Pastur Law
 Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
RECTANGULAR RANDOM MATRICES, ENTROPY, AND FISHER S INFORMATION
 J. OPERATOR THEORY 00:0(XXXX), 00 00 Copyright by THETA, XXXX RECTANGULAR RANDOM MATRICES, ENTROPY, AND FISHER S INFORMATION FLORENT BENAYCH-GEORGES Communicated by Serban Stratila ABSTRACT. We prove that
J. OPERATOR THEORY 00:0(XXXX), 00 00 Copyright by THETA, XXXX RECTANGULAR RANDOM MATRICES, ENTROPY, AND FISHER S INFORMATION FLORENT BENAYCH-GEORGES Communicated by Serban Stratila ABSTRACT. We prove that
Numerical Range of non-hermitian random Ginibre matrices and the Dvoretzky theorem
 Numerical Range of non-hermitian random Ginibre matrices and the Dvoretzky theorem Karol Życzkowski Institute of Physics, Jagiellonian University, Cracow and Center for Theoretical Physics, PAS, Warsaw
Numerical Range of non-hermitian random Ginibre matrices and the Dvoretzky theorem Karol Życzkowski Institute of Physics, Jagiellonian University, Cracow and Center for Theoretical Physics, PAS, Warsaw
Concentration Inequalities for Random Matrices
 Concentration Inequalities for Random Matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify the asymptotic
Concentration Inequalities for Random Matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify the asymptotic
Free Probability Theory
 Noname manuscript No. (will be inserted by the editor) Free Probability Theory and its avatars in representation theory, random matrices, and operator algebras; also featuring: non-commutative distributions
Noname manuscript No. (will be inserted by the editor) Free Probability Theory and its avatars in representation theory, random matrices, and operator algebras; also featuring: non-commutative distributions
Preface to the Second Edition...vii Preface to the First Edition... ix
 Contents Preface to the Second Edition...vii Preface to the First Edition........... ix 1 Introduction.............................................. 1 1.1 Large Dimensional Data Analysis.........................
Contents Preface to the Second Edition...vii Preface to the First Edition........... ix 1 Introduction.............................................. 1 1.1 Large Dimensional Data Analysis.........................
Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium
 Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium SEA 06@MIT, Workshop on Stochastic Eigen-Analysis and its Applications, MIT, Cambridge,
Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium SEA 06@MIT, Workshop on Stochastic Eigen-Analysis and its Applications, MIT, Cambridge,
Comparison Method in Random Matrix Theory
 Comparison Method in Random Matrix Theory Jun Yin UW-Madison Valparaíso, Chile, July - 2015 Joint work with A. Knowles. 1 Some random matrices Wigner Matrix: H is N N square matrix, H : H ij = H ji, EH
Comparison Method in Random Matrix Theory Jun Yin UW-Madison Valparaíso, Chile, July - 2015 Joint work with A. Knowles. 1 Some random matrices Wigner Matrix: H is N N square matrix, H : H ij = H ji, EH
Triangular matrices and biorthogonal ensembles
 /26 Triangular matrices and biorthogonal ensembles Dimitris Cheliotis Department of Mathematics University of Athens UK Easter Probability Meeting April 8, 206 2/26 Special densities on R n Example. n
/26 Triangular matrices and biorthogonal ensembles Dimitris Cheliotis Department of Mathematics University of Athens UK Easter Probability Meeting April 8, 206 2/26 Special densities on R n Example. n
Factorizable completely positive maps and quantum information theory. Magdalena Musat. Sym Lecture Copenhagen, May 9, 2012
 Factorizable completely positive maps and quantum information theory Magdalena Musat Sym Lecture Copenhagen, May 9, 2012 Joint work with Uffe Haagerup based on: U. Haagerup, M. Musat: Factorization and
Factorizable completely positive maps and quantum information theory Magdalena Musat Sym Lecture Copenhagen, May 9, 2012 Joint work with Uffe Haagerup based on: U. Haagerup, M. Musat: Factorization and
FREE PROBABILITY THEORY AND RANDOM MATRICES
 FREE PROBABILITY THEORY AND RANDOM MATRICES ROLAND SPEICHER Abstract. Free probability theory originated in the context of operator algebras, however, one of the main features of that theory is its connection
FREE PROBABILITY THEORY AND RANDOM MATRICES ROLAND SPEICHER Abstract. Free probability theory originated in the context of operator algebras, however, one of the main features of that theory is its connection
Quantum Computing Lecture 2. Review of Linear Algebra
 Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture. Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev
 Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev The Superposition Principle (Physicists): If a quantum
Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev The Superposition Principle (Physicists): If a quantum
Random Matrix Theory Lecture 3 Free Probability Theory. Symeon Chatzinotas March 4, 2013 Luxembourg
 Random Matrix Theory Lecture 3 Free Probability Theory Symeon Chatzinotas March 4, 2013 Luxembourg Outline 1. Free Probability Theory 1. Definitions 2. Asymptotically free matrices 3. R-transform 4. Additive
Random Matrix Theory Lecture 3 Free Probability Theory Symeon Chatzinotas March 4, 2013 Luxembourg Outline 1. Free Probability Theory 1. Definitions 2. Asymptotically free matrices 3. R-transform 4. Additive
Free Probability, Sample Covariance Matrices and Stochastic Eigen-Inference
 Free Probability, Sample Covariance Matrices and Stochastic Eigen-Inference Alan Edelman Department of Mathematics, Computer Science and AI Laboratories. E-mail: edelman@math.mit.edu N. Raj Rao Deparment
Free Probability, Sample Covariance Matrices and Stochastic Eigen-Inference Alan Edelman Department of Mathematics, Computer Science and AI Laboratories. E-mail: edelman@math.mit.edu N. Raj Rao Deparment
Free Probability and Random Matrices: from isomorphisms to universality
 Free Probability and Random Matrices: from isomorphisms to universality Alice Guionnet MIT TexAMP, November 21, 2014 Joint works with F. Bekerman, Y. Dabrowski, A.Figalli, E. Maurel-Segala, J. Novak, D.
Free Probability and Random Matrices: from isomorphisms to universality Alice Guionnet MIT TexAMP, November 21, 2014 Joint works with F. Bekerman, Y. Dabrowski, A.Figalli, E. Maurel-Segala, J. Novak, D.
Spectral Continuity Properties of Graph Laplacians
 Spectral Continuity Properties of Graph Laplacians David Jekel May 24, 2017 Overview Spectral invariants of the graph Laplacian depend continuously on the graph. We consider triples (G, x, T ), where G
Spectral Continuity Properties of Graph Laplacians David Jekel May 24, 2017 Overview Spectral invariants of the graph Laplacian depend continuously on the graph. We consider triples (G, x, T ), where G
Algebraic Theory of Entanglement
 Algebraic Theory of (arxiv: 1205.2882) 1 (in collaboration with T.R. Govindarajan, A. Queiroz and A.F. Reyes-Lega) 1 Physics Department, Syracuse University, Syracuse, N.Y. and The Institute of Mathematical
Algebraic Theory of (arxiv: 1205.2882) 1 (in collaboration with T.R. Govindarajan, A. Queiroz and A.F. Reyes-Lega) 1 Physics Department, Syracuse University, Syracuse, N.Y. and The Institute of Mathematical
Quantum Entanglement- Fundamental Aspects
 Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Operator-Valued Free Probability Theory and Block Random Matrices. Roland Speicher Queen s University Kingston
 Operator-Valued Free Probability Theory and Block Random Matrices Roland Speicher Queen s University Kingston I. Operator-valued semicircular elements and block random matrices II. General operator-valued
Operator-Valued Free Probability Theory and Block Random Matrices Roland Speicher Queen s University Kingston I. Operator-valued semicircular elements and block random matrices II. General operator-valued
Eigenvalues and Singular Values of Random Matrices: A Tutorial Introduction
 Random Matrix Theory and its applications to Statistics and Wireless Communications Eigenvalues and Singular Values of Random Matrices: A Tutorial Introduction Sergio Verdú Princeton University National
Random Matrix Theory and its applications to Statistics and Wireless Communications Eigenvalues and Singular Values of Random Matrices: A Tutorial Introduction Sergio Verdú Princeton University National
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Quantum Statistics -First Steps
 Quantum Statistics -First Steps Michael Nussbaum 1 November 30, 2007 Abstract We will try an elementary introduction to quantum probability and statistics, bypassing the physics in a rapid first glance.
Quantum Statistics -First Steps Michael Nussbaum 1 November 30, 2007 Abstract We will try an elementary introduction to quantum probability and statistics, bypassing the physics in a rapid first glance.
Free Entropy for Free Gibbs Laws Given by Convex Potentials
 Free Entropy for Free Gibbs Laws Given by Convex Potentials David A. Jekel University of California, Los Angeles Young Mathematicians in C -algebras, August 2018 David A. Jekel (UCLA) Free Entropy YMC
Free Entropy for Free Gibbs Laws Given by Convex Potentials David A. Jekel University of California, Los Angeles Young Mathematicians in C -algebras, August 2018 David A. Jekel (UCLA) Free Entropy YMC
Random matrices: Distribution of the least singular value (via Property Testing)
 Random matrices: Distribution of the least singular value (via Property Testing) Van H. Vu Department of Mathematics Rutgers vanvu@math.rutgers.edu (joint work with T. Tao, UCLA) 1 Let ξ be a real or complex-valued
Random matrices: Distribution of the least singular value (via Property Testing) Van H. Vu Department of Mathematics Rutgers vanvu@math.rutgers.edu (joint work with T. Tao, UCLA) 1 Let ξ be a real or complex-valued
LUCK S THEOREM ALEX WRIGHT
 LUCK S THEOREM ALEX WRIGHT Warning: These are the authors personal notes for a talk in a learning seminar (October 2015). There may be incorrect or misleading statements. Corrections welcome. 1. Convergence
LUCK S THEOREM ALEX WRIGHT Warning: These are the authors personal notes for a talk in a learning seminar (October 2015). There may be incorrect or misleading statements. Corrections welcome. 1. Convergence
Mathematical Methods for Quantum Information Theory. Part I: Matrix Analysis. Koenraad Audenaert (RHUL, UK)
 Mathematical Methods for Quantum Information Theory Part I: Matrix Analysis Koenraad Audenaert (RHUL, UK) September 14, 2008 Preface Books on Matrix Analysis: R. Bhatia, Matrix Analysis, Springer, 1997.
Mathematical Methods for Quantum Information Theory Part I: Matrix Analysis Koenraad Audenaert (RHUL, UK) September 14, 2008 Preface Books on Matrix Analysis: R. Bhatia, Matrix Analysis, Springer, 1997.
Grothendieck Inequalities, XOR games, and Communication Complexity
 Grothendieck Inequalities, XOR games, and Communication Complexity Troy Lee Rutgers University Joint work with: Jop Briët, Harry Buhrman, and Thomas Vidick Overview Introduce XOR games, Grothendieck s
Grothendieck Inequalities, XOR games, and Communication Complexity Troy Lee Rutgers University Joint work with: Jop Briët, Harry Buhrman, and Thomas Vidick Overview Introduce XOR games, Grothendieck s
Maximal vectors in Hilbert space and quantum entanglement
 Maximal vectors in Hilbert space and quantum entanglement William Arveson arveson@math.berkeley.edu UC Berkeley Summer 2008 arxiv:0712.4163 arxiv:0801.2531 arxiv:0804.1140 Overview Quantum Information
Maximal vectors in Hilbert space and quantum entanglement William Arveson arveson@math.berkeley.edu UC Berkeley Summer 2008 arxiv:0712.4163 arxiv:0801.2531 arxiv:0804.1140 Overview Quantum Information
Spectral Theorem for Self-adjoint Linear Operators
 Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
SEA s workshop- MIT - July 10-14
 Matrix-valued Stochastic Processes- Eigenvalues Processes and Free Probability SEA s workshop- MIT - July 10-14 July 13, 2006 Outline Matrix-valued stochastic processes. 1- definition and examples. 2-
Matrix-valued Stochastic Processes- Eigenvalues Processes and Free Probability SEA s workshop- MIT - July 10-14 July 13, 2006 Outline Matrix-valued stochastic processes. 1- definition and examples. 2-
Math 554 Qualifying Exam. You may use any theorems from the textbook. Any other claims must be proved in details.
 Math 554 Qualifying Exam January, 2019 You may use any theorems from the textbook. Any other claims must be proved in details. 1. Let F be a field and m and n be positive integers. Prove the following.
Math 554 Qualifying Exam January, 2019 You may use any theorems from the textbook. Any other claims must be proved in details. 1. Let F be a field and m and n be positive integers. Prove the following.
2. Introduction to quantum mechanics
 2. Introduction to quantum mechanics 2.1 Linear algebra Dirac notation Complex conjugate Vector/ket Dual vector/bra Inner product/bracket Tensor product Complex conj. matrix Transpose of matrix Hermitian
2. Introduction to quantum mechanics 2.1 Linear algebra Dirac notation Complex conjugate Vector/ket Dual vector/bra Inner product/bracket Tensor product Complex conj. matrix Transpose of matrix Hermitian
The Solovay-Kitaev theorem
 The Solovay-Kitaev theorem Maris Ozols December 10, 009 1 Introduction There are several accounts of the Solovay-Kitaev theorem available [K97, NC00, KSV0, DN05]. I chose to base my report on [NC00], since
The Solovay-Kitaev theorem Maris Ozols December 10, 009 1 Introduction There are several accounts of the Solovay-Kitaev theorem available [K97, NC00, KSV0, DN05]. I chose to base my report on [NC00], since
MATHEMATICS. Course Syllabus. Section A: Linear Algebra. Subject Code: MA. Course Structure. Ordinary Differential Equations
 MATHEMATICS Subject Code: MA Course Structure Sections/Units Section A Section B Section C Linear Algebra Complex Analysis Real Analysis Topics Section D Section E Section F Section G Section H Section
MATHEMATICS Subject Code: MA Course Structure Sections/Units Section A Section B Section C Linear Algebra Complex Analysis Real Analysis Topics Section D Section E Section F Section G Section H Section
Fluctuations of Random Matrices and Second Order Freeness
 Fluctuations of Random Matrices and Second Order Freeness james mingo with b. collins p. śniady r. speicher SEA 06 Workshop Massachusetts Institute of Technology July 9-14, 2006 1 0.4 0.2 0-2 -1 0 1 2-2
Fluctuations of Random Matrices and Second Order Freeness james mingo with b. collins p. śniady r. speicher SEA 06 Workshop Massachusetts Institute of Technology July 9-14, 2006 1 0.4 0.2 0-2 -1 0 1 2-2
Quantum Symmetries in Free Probability Theory. Roland Speicher Queen s University Kingston, Canada
 Quantum Symmetries in Free Probability Theory Roland Speicher Queen s University Kingston, Canada Quantum Groups are generalizations of groups G (actually, of C(G)) are supposed to describe non-classical
Quantum Symmetries in Free Probability Theory Roland Speicher Queen s University Kingston, Canada Quantum Groups are generalizations of groups G (actually, of C(G)) are supposed to describe non-classical
Part III Symmetries, Fields and Particles
 Part III Symmetries, Fields and Particles Theorems Based on lectures by N. Dorey Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often
Part III Symmetries, Fields and Particles Theorems Based on lectures by N. Dorey Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often
The circular law. Lewis Memorial Lecture / DIMACS minicourse March 19, Terence Tao (UCLA)
 The circular law Lewis Memorial Lecture / DIMACS minicourse March 19, 2008 Terence Tao (UCLA) 1 Eigenvalue distributions Let M = (a ij ) 1 i n;1 j n be a square matrix. Then one has n (generalised) eigenvalues
The circular law Lewis Memorial Lecture / DIMACS minicourse March 19, 2008 Terence Tao (UCLA) 1 Eigenvalue distributions Let M = (a ij ) 1 i n;1 j n be a square matrix. Then one has n (generalised) eigenvalues
Paradigms of Probabilistic Modelling
 Paradigms of Probabilistic Modelling Hermann G. Matthies Brunswick, Germany wire@tu-bs.de http://www.wire.tu-bs.de abstract RV-measure.tex,v 4.5 2017/07/06 01:56:46 hgm Exp Overview 2 1. Motivation challenges
Paradigms of Probabilistic Modelling Hermann G. Matthies Brunswick, Germany wire@tu-bs.de http://www.wire.tu-bs.de abstract RV-measure.tex,v 4.5 2017/07/06 01:56:46 hgm Exp Overview 2 1. Motivation challenges
Quantum Stochastic Maps and Frobenius Perron Theorem
 Quantum Stochastic Maps and Frobenius Perron Theorem Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Institute of Physics, Jagiellonian University, Cracow,
Quantum Stochastic Maps and Frobenius Perron Theorem Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Institute of Physics, Jagiellonian University, Cracow,
COUNTEREXAMPLES TO THE COARSE BAUM-CONNES CONJECTURE. Nigel Higson. Unpublished Note, 1999
 COUNTEREXAMPLES TO THE COARSE BAUM-CONNES CONJECTURE Nigel Higson Unpublished Note, 1999 1. Introduction Let X be a discrete, bounded geometry metric space. 1 Associated to X is a C -algebra C (X) which
COUNTEREXAMPLES TO THE COARSE BAUM-CONNES CONJECTURE Nigel Higson Unpublished Note, 1999 1. Introduction Let X be a discrete, bounded geometry metric space. 1 Associated to X is a C -algebra C (X) which
Throughout these notes we assume V, W are finite dimensional inner product spaces over C.
 Math 342 - Linear Algebra II Notes Throughout these notes we assume V, W are finite dimensional inner product spaces over C 1 Upper Triangular Representation Proposition: Let T L(V ) There exists an orthonormal
Math 342 - Linear Algebra II Notes Throughout these notes we assume V, W are finite dimensional inner product spaces over C 1 Upper Triangular Representation Proposition: Let T L(V ) There exists an orthonormal
On positive maps in quantum information.
 On positive maps in quantum information. Wladyslaw Adam Majewski Instytut Fizyki Teoretycznej i Astrofizyki, UG ul. Wita Stwosza 57, 80-952 Gdańsk, Poland e-mail: fizwam@univ.gda.pl IFTiA Gdańsk University
On positive maps in quantum information. Wladyslaw Adam Majewski Instytut Fizyki Teoretycznej i Astrofizyki, UG ul. Wita Stwosza 57, 80-952 Gdańsk, Poland e-mail: fizwam@univ.gda.pl IFTiA Gdańsk University
Exponential tail inequalities for eigenvalues of random matrices
 Exponential tail inequalities for eigenvalues of random matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify
Exponential tail inequalities for eigenvalues of random matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify
Estimation of large dimensional sparse covariance matrices
 Estimation of large dimensional sparse covariance matrices Department of Statistics UC, Berkeley May 5, 2009 Sample covariance matrix and its eigenvalues Data: n p matrix X n (independent identically distributed)
Estimation of large dimensional sparse covariance matrices Department of Statistics UC, Berkeley May 5, 2009 Sample covariance matrix and its eigenvalues Data: n p matrix X n (independent identically distributed)
Sudoku and Matrices. Merciadri Luca. June 28, 2011
 Sudoku and Matrices Merciadri Luca June 28, 2 Outline Introduction 2 onventions 3 Determinant 4 Erroneous Sudoku 5 Eigenvalues Example 6 Transpose Determinant Trace 7 Antisymmetricity 8 Non-Normality 9
Sudoku and Matrices Merciadri Luca June 28, 2 Outline Introduction 2 onventions 3 Determinant 4 Erroneous Sudoku 5 Eigenvalues Example 6 Transpose Determinant Trace 7 Antisymmetricity 8 Non-Normality 9
The following definition is fundamental.
 1. Some Basics from Linear Algebra With these notes, I will try and clarify certain topics that I only quickly mention in class. First and foremost, I will assume that you are familiar with many basic
1. Some Basics from Linear Algebra With these notes, I will try and clarify certain topics that I only quickly mention in class. First and foremost, I will assume that you are familiar with many basic
Quantum Symmetric States on Free Product C -Algebras
 Quantum Symmetric States on Free Product C -Algebras School of Mathematical Sciences University College Cork Joint work with Ken Dykema & John Williams arxiv:1305.7293 WIMCS-LMS Conference Classifying
Quantum Symmetric States on Free Product C -Algebras School of Mathematical Sciences University College Cork Joint work with Ken Dykema & John Williams arxiv:1305.7293 WIMCS-LMS Conference Classifying
Free Probability Theory and Random Matrices
 Free Probability Theory and Random Matrices R. Speicher Department of Mathematics and Statistics Queen s University, Kingston ON K7L 3N6, Canada speicher@mast.queensu.ca Summary. Free probability theory
Free Probability Theory and Random Matrices R. Speicher Department of Mathematics and Statistics Queen s University, Kingston ON K7L 3N6, Canada speicher@mast.queensu.ca Summary. Free probability theory
arxiv: v3 [quant-ph] 9 Nov 2012
![arxiv: v3 [quant-ph] 9 Nov 2012 arxiv: v3 [quant-ph] 9 Nov 2012](/thumbs/74/69943064.jpg) The Annals of Applied Probability 2011, Vol. 21, No. 3, 1136 1179 DOI: 10.1214/10-AAP722 c Institute of Mathematical Statistics, 2011 arxiv:0910.1768v3 [quant-ph] 9 Nov 2012 GAUSSIANIZATION AND EIGENVALUE
The Annals of Applied Probability 2011, Vol. 21, No. 3, 1136 1179 DOI: 10.1214/10-AAP722 c Institute of Mathematical Statistics, 2011 arxiv:0910.1768v3 [quant-ph] 9 Nov 2012 GAUSSIANIZATION AND EIGENVALUE
Review (Probability & Linear Algebra)
 Review (Probability & Linear Algebra) CE-725 : Statistical Pattern Recognition Sharif University of Technology Spring 2013 M. Soleymani Outline Axioms of probability theory Conditional probability, Joint
Review (Probability & Linear Algebra) CE-725 : Statistical Pattern Recognition Sharif University of Technology Spring 2013 M. Soleymani Outline Axioms of probability theory Conditional probability, Joint
Free Probability Theory and Random Matrices
 Free Probability Theory and Random Matrices Roland Speicher Motivation of Freeness via Random Matrices In this chapter we want to motivate the definition of freeness on the basis of random matrices.. Asymptotic
Free Probability Theory and Random Matrices Roland Speicher Motivation of Freeness via Random Matrices In this chapter we want to motivate the definition of freeness on the basis of random matrices.. Asymptotic
Fourier analysis of boolean functions in quantum computation
 Fourier analysis of boolean functions in quantum computation Ashley Montanaro Centre for Quantum Information and Foundations, Department of Applied Mathematics and Theoretical Physics, University of Cambridge
Fourier analysis of boolean functions in quantum computation Ashley Montanaro Centre for Quantum Information and Foundations, Department of Applied Mathematics and Theoretical Physics, University of Cambridge
Linear and Multilinear Algebra. Linear maps preserving rank of tensor products of matrices
 Linear maps preserving rank of tensor products of matrices Journal: Manuscript ID: GLMA-0-0 Manuscript Type: Original Article Date Submitted by the Author: -Aug-0 Complete List of Authors: Zheng, Baodong;
Linear maps preserving rank of tensor products of matrices Journal: Manuscript ID: GLMA-0-0 Manuscript Type: Original Article Date Submitted by the Author: -Aug-0 Complete List of Authors: Zheng, Baodong;
Rectangular Young tableaux and the Jacobi ensemble
 Rectangular Young tableaux and the Jacobi ensemble Philippe Marchal October 20, 2015 Abstract It has been shown by Pittel and Romik that the random surface associated with a large rectangular Young tableau
Rectangular Young tableaux and the Jacobi ensemble Philippe Marchal October 20, 2015 Abstract It has been shown by Pittel and Romik that the random surface associated with a large rectangular Young tableau
Dirac Operator. Göttingen Mathematical Institute. Paul Baum Penn State 6 February, 2017
 Dirac Operator Göttingen Mathematical Institute Paul Baum Penn State 6 February, 2017 Five lectures: 1. Dirac operator 2. Atiyah-Singer revisited 3. What is K-homology? 4. The Riemann-Roch theorem 5. K-theory
Dirac Operator Göttingen Mathematical Institute Paul Baum Penn State 6 February, 2017 Five lectures: 1. Dirac operator 2. Atiyah-Singer revisited 3. What is K-homology? 4. The Riemann-Roch theorem 5. K-theory
1 Math 241A-B Homework Problem List for F2015 and W2016
 1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
1 Math 241A-B Homework Problem List for F2015 W2016 1.1 Homework 1. Due Wednesday, October 7, 2015 Notation 1.1 Let U be any set, g be a positive function on U, Y be a normed space. For any f : U Y let
A Brief Introduction to Functional Analysis
 A Brief Introduction to Functional Analysis Sungwook Lee Department of Mathematics University of Southern Mississippi sunglee@usm.edu July 5, 2007 Definition 1. An algebra A is a vector space over C with
A Brief Introduction to Functional Analysis Sungwook Lee Department of Mathematics University of Southern Mississippi sunglee@usm.edu July 5, 2007 Definition 1. An algebra A is a vector space over C with
CUT-OFF FOR QUANTUM RANDOM WALKS. 1. Convergence of quantum random walks
 CUT-OFF FOR QUANTUM RANDOM WALKS AMAURY FRESLON Abstract. We give an introduction to the cut-off phenomenon for random walks on classical and quantum compact groups. We give an example involving random
CUT-OFF FOR QUANTUM RANDOM WALKS AMAURY FRESLON Abstract. We give an introduction to the cut-off phenomenon for random walks on classical and quantum compact groups. We give an example involving random
Algebraic reformulation of Connes embedding problem and the free group algebra.
 Algebraic reformulation of Connes embedding problem and the free group algebra. Kate Juschenko, Stanislav Popovych Abstract We give a modification of I. Klep and M. Schweighofer algebraic reformulation
Algebraic reformulation of Connes embedding problem and the free group algebra. Kate Juschenko, Stanislav Popovych Abstract We give a modification of I. Klep and M. Schweighofer algebraic reformulation
An LMI description for the cone of Lorentz-positive maps II
 An LMI description for the cone of Lorentz-positive maps II Roland Hildebrand October 6, 2008 Abstract Let L n be the n-dimensional second order cone. A linear map from R m to R n is called positive if
An LMI description for the cone of Lorentz-positive maps II Roland Hildebrand October 6, 2008 Abstract Let L n be the n-dimensional second order cone. A linear map from R m to R n is called positive if
Topics in random matrices: Theory and applications to probability and statistics
 Topics in random matrices: Theory and applications to probability and statistics Termeh Kousha Thesis submitted to the Faculty of Graduate and Postdoctoral Studies in partial fulfillment of the requirements
Topics in random matrices: Theory and applications to probability and statistics Termeh Kousha Thesis submitted to the Faculty of Graduate and Postdoctoral Studies in partial fulfillment of the requirements
Random Matrix Theory Lecture 1 Introduction, Ensembles and Basic Laws. Symeon Chatzinotas February 11, 2013 Luxembourg
 Random Matrix Theory Lecture 1 Introduction, Ensembles and Basic Laws Symeon Chatzinotas February 11, 2013 Luxembourg Outline 1. Random Matrix Theory 1. Definition 2. Applications 3. Asymptotics 2. Ensembles
Random Matrix Theory Lecture 1 Introduction, Ensembles and Basic Laws Symeon Chatzinotas February 11, 2013 Luxembourg Outline 1. Random Matrix Theory 1. Definition 2. Applications 3. Asymptotics 2. Ensembles
Singular Value Decomposition (SVD) and Polar Form
 Chapter 2 Singular Value Decomposition (SVD) and Polar Form 2.1 Polar Form In this chapter, we assume that we are dealing with a real Euclidean space E. Let f: E E be any linear map. In general, it may
Chapter 2 Singular Value Decomposition (SVD) and Polar Form 2.1 Polar Form In this chapter, we assume that we are dealing with a real Euclidean space E. Let f: E E be any linear map. In general, it may
Hadamard matrices and Compact Quantum Groups
 Hadamard matrices and Compact Quantum Groups Uwe Franz 18 février 2014 3ème journée FEMTO-LMB based in part on joint work with: Teodor Banica, Franz Lehner, Adam Skalski Uwe Franz (LMB) Hadamard & CQG
Hadamard matrices and Compact Quantum Groups Uwe Franz 18 février 2014 3ème journée FEMTO-LMB based in part on joint work with: Teodor Banica, Franz Lehner, Adam Skalski Uwe Franz (LMB) Hadamard & CQG
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
Preliminaries on von Neumann algebras and operator spaces. Magdalena Musat University of Copenhagen. Copenhagen, January 25, 2010
 Preliminaries on von Neumann algebras and operator spaces Magdalena Musat University of Copenhagen Copenhagen, January 25, 2010 1 Von Neumann algebras were introduced by John von Neumann in 1929-1930 as
Preliminaries on von Neumann algebras and operator spaces Magdalena Musat University of Copenhagen Copenhagen, January 25, 2010 1 Von Neumann algebras were introduced by John von Neumann in 1929-1930 as
Random Matrix: From Wigner to Quantum Chaos
 Random Matrix: From Wigner to Quantum Chaos Horng-Tzer Yau Harvard University Joint work with P. Bourgade, L. Erdős, B. Schlein and J. Yin 1 Perhaps I am now too courageous when I try to guess the distribution
Random Matrix: From Wigner to Quantum Chaos Horng-Tzer Yau Harvard University Joint work with P. Bourgade, L. Erdős, B. Schlein and J. Yin 1 Perhaps I am now too courageous when I try to guess the distribution
Introduction to Quantum Spin Systems
 1 Introduction to Quantum Spin Systems Lecture 2 Sven Bachmann (standing in for Bruno Nachtergaele) Mathematics, UC Davis MAT290-25, CRN 30216, Winter 2011, 01/10/11 2 Basic Setup For concreteness, consider
1 Introduction to Quantum Spin Systems Lecture 2 Sven Bachmann (standing in for Bruno Nachtergaele) Mathematics, UC Davis MAT290-25, CRN 30216, Winter 2011, 01/10/11 2 Basic Setup For concreteness, consider
Shunlong Luo. Academy of Mathematics and Systems Science Chinese Academy of Sciences
 Superadditivity of Fisher Information: Classical vs. Quantum Shunlong Luo Academy of Mathematics and Systems Science Chinese Academy of Sciences luosl@amt.ac.cn Information Geometry and its Applications
Superadditivity of Fisher Information: Classical vs. Quantum Shunlong Luo Academy of Mathematics and Systems Science Chinese Academy of Sciences luosl@amt.ac.cn Information Geometry and its Applications
Supelec Randomness in Wireless Networks: how to deal with it?
 Supelec Randomness in Wireless Networks: how to deal with it? Mérouane Debbah Alcatel-Lucent Chair on Flexible Radio merouane.debbah@supelec.fr The performance dilemma... La théorie, c est quand on sait
Supelec Randomness in Wireless Networks: how to deal with it? Mérouane Debbah Alcatel-Lucent Chair on Flexible Radio merouane.debbah@supelec.fr The performance dilemma... La théorie, c est quand on sait
Functional Analysis Review
 Outline 9.520: Statistical Learning Theory and Applications February 8, 2010 Outline 1 2 3 4 Vector Space Outline A vector space is a set V with binary operations +: V V V and : R V V such that for all
Outline 9.520: Statistical Learning Theory and Applications February 8, 2010 Outline 1 2 3 4 Vector Space Outline A vector space is a set V with binary operations +: V V V and : R V V such that for all
Lecture 7. Econ August 18
 Lecture 7 Econ 2001 2015 August 18 Lecture 7 Outline First, the theorem of the maximum, an amazing result about continuity in optimization problems. Then, we start linear algebra, mostly looking at familiar
Lecture 7 Econ 2001 2015 August 18 Lecture 7 Outline First, the theorem of the maximum, an amazing result about continuity in optimization problems. Then, we start linear algebra, mostly looking at familiar
