SOBOLEV GAN ABSTRACT 1 INTRODUCTION. Published as a conference paper at ICLR 2018
|
|
|
- Violet May
- 5 years ago
- Views:
Transcription
1 Published as a conference paper at ICLR 8 SOBOLEV GAN Youssef Mroueh, Chun-Liang Li,?, Tom Sercu,?, Anant Raj,? & Yu Cheng IBM Research AI Carnegie Mellon University Max Planck Institute for Intelligent Systems? denotes Equal Contribution {mroueh,chengyu}@us.ibm.com, chunlial@cs.cmu.edu, tom.sercu@ibm.com,anant.raj@tuebingen.mpg.de ABSTRACT We propose a new Integral Probability Metric (IPM) between distributions: the Sobolev IPM. The Sobolev IPM compares the mean discrepancy of two distributions for functions (critic) restricted to a Sobolev ball defined with respect to a dominant measure µ. We show that the Sobolev IPM compares two distributions in high dimensions based on weighted conditional Cumulative Distribution Functions (CDF) of each coordinate on a leave one out basis. The Dominant measure µ plays a crucial role as it defines the support on which conditional CDFs are compared. Sobolev IPM can be seen as an extension of the one dimensional Von- Mises Cramér statistics to high dimensional distributions. We show how Sobolev IPM can be used to train Generative Adversarial Networks (GANs). We then exploit the intrinsic conditioning implied by Sobolev IPM in text generation. Finally we show that a variant of Sobolev GAN achieves competitive results in semisupervised learning on CIFAR-, thanks to the smoothness enforced on the critic by Sobolev GAN which relates to Laplacian regularization. INTRODUCTION In order to learn Generative Adversarial Networks (Goodfellow et al., 4), it is now well established that the generator should mimic the distribution of real data, in the sense of a certain discrepancy measure. Discrepancies between distributions that measure the goodness of the fit of the neural generator to the real data distribution has been the subject of many recent studies (Arjovsky & Bottou, 7; Nowozin et al., 6; Kaae Sønderby et al., 7; Mao et al., 7; Arjovsky et al., 7; Gulrajani et al., 7; Mroueh et al., 7; Mroueh & Sercu, 7; Li et al., 7), most of which focus on training stability. In terms of data modalities, most success was booked in plausible natural image generation after the introduction of Deep Convolutional Generative Adversarial Networks (DCGAN) (Radford et al., 5). This success is not only due to advances in training generative adversarial networks in terms of loss functions (Arjovsky et al., 7) and stable algorithms, but also to the representation power of convolutional neural networks in modeling images and in finding sufficient statistics that capture the continuous density function of natural images. When moving to neural generators of discrete sequences generative adversarial networks theory and practice are still not very well understood. Maximum likelihood pre-training or augmentation, in conjunction with the use of reinforcement learning techniques were proposed in many recent works for training GAN for discrete sequences generation (Yu et al., 6; Che et al., 7; Hjelm et al., 7; Rajeswar et al., 7). Other methods included using the Gumbel Softmax trick (Kusner & Hernández-Lobato, 6) and the use of auto-encoders to generate adversarially discrete sequences from a continuous space (Zhao et al., 7). End to end training of GANs for discrete sequence generation is still an open problem (Press et al., 7). Empirical successes of end to end training have been reported within the framework of WGAN-GP (Gulrajani et al., 7), using a proxy for the Wasserstein distance via a Code for semi-supervised learning experiments is available on SobolevGAN-SSL
2 Published as a conference paper at ICLR 8 pointwise gradient penalty on the critic. Inspired by this success, we propose in this paper a new Integral Probability Metric (IPM) between distributions that we coin Sobolev IPM. Intuitively an IPM (Müller, 997) between two probability distributions looks for a witness function f, called critic, that maximally discriminates between samples coming from the two distributions: sup E x P f(x) ff E x Q f(x). Traditionally, the function f is defined over a function class F that is independent to the distributions at hand (Sriperumbudur et al., ). The Wasserstein- distance corresponds for instance to an IPM where the witness functions are defined over the space of Lipschitz functions; The MMD distance (Gretton et al., ) corresponds to witness functions defined over a ball in a Reproducing Kernel Hilbert Space (RKHS). We will revisit in this paper Fisher IPM defined in (Mroueh & Sercu, 7), which extends the IPM definition to function classes defined with norms that depend on the distributions. Fisher IPM can be seen as restricting the critic to a Lebsegue ball defined with respect to a dominant measure µ. The Lebsegue norm is defined as follows: f (x)dx. where µ is a dominant measure of P and Q. In this paper we extend the IPM framework to critics bounded in the Sobolev norm: kr x f(x)k dx, In contrast to Fisher IPM, which compares joint probability density functions of all coordinates between two distributions, we will show that Sobolev IPM compares weighted (coordinate-wise) conditional Cumulative Distribution Functions for all coordinates on a leave on out basis. Matching conditional dependencies between coordinates is crucial for sequence modeling. Our analysis and empirical verification show that the modeling of the conditional dependencies can be built in to the metric used to learn GANs as in Sobolev IPM. For instance, this gives an advantage to Sobolev IPM in comparing sequences over Fisher IPM. Nevertheless, in sequence modeling when we parametrize the critic and the generator with a neural network, we find an interesting tradeoff between the metric used and the architectures used to parametrize the critic and the generator as well as the conditioning used in the generator. The burden of modeling the conditional long term dependencies can be handled by the IPM loss function as in Sobolev IPM (more accurately the choice of the data dependent function class of the critic) or by a simpler metric such as Fisher IPM together with a powerful architecture for the critic that models conditional long term dependencies such as LSTM or GRUs in conjunction with a curriculum conditioning of the generator as done in (Press et al., 7). Highlighting those interesting tradeoffs between metrics, data dependent functions classes for the critic (Fisher or Sobolev) and architectures is crucial to advance sequence modeling and more broadly structured data generation using GANs. On the other hand, Sobolev norms have been widely used in manifold regularization in the so called Laplacian framework for semi-supervised learning (SSL) (Belkin et al., 6). GANs have shown success in semi-supervised learning (Salimans et al., 6; Dumoulin et al., 7; Dai et al., 7; Kumar et al., 7). Nevertheless, many normalizations and additional tricks were needed. We show in this paper that a variant of Sobolev GAN achieves strong results in semi-supervised learning on CIFAR-, without the need of any activation normalization in the critic. The main contributions of this paper can be summarized as follows:. We overview in Section different metrics between distribution used in the GAN literature. We then generalize Fisher IPM in Section 3 with a general dominant measure µ and show how it compares distributions based on their PDFs.. We introduce Sobolev IPM in Section 4 by restricting the critic of an IPM to a Sobolev ball defined with respect to a dominant measure µ. We then show that Sobolev IPM defines a discrepancy between weighted (coordinate-wise) conditional CDFs of distributions.
3 Published as a conference paper at ICLR 8 3. The intrinsic conditioning and the CDF matching make Sobolev IPM suitable for discrete sequence matching and explain the success of the gradient pernalty in WGAN-GP and Sobolev GAN in discrete sequence generation. 4. We give in Section 5 an ALM (Augmented Lagrangian Multiplier) algorithm for training Sobolev GAN. Similar to Fisher GAN, this algorithm is stable and does not compromise the capacity of the critic. 5. We show in Appendix A that the critic of Sobolev IPM satisfies an elliptic Partial Differential Equation (PDE). We relate this diffusion to the Fokker-Planck equation and show the behavior of the gradient of the optimal Sobolev critic as a transportation plan between distributions. 6. We empirically study Sobolev GAN in character level text generation (Section 6.). We validate that the conditioning implied by Sobolev GAN is crucial for the success and stability of GAN in text generation. As a take home message from this study, we see that text generation succeeds either by implicit conditioning i.e using Sobolev GAN (or WGAN- GP) together with convolutional critics and generators, or by explicit conditioning i.e using Fisher IPM together with recurrent critic and generator and curriculum learning. 7. We finally show in Section 6. that a variant of Sobolev GAN achieves competitive semisupervised learning results on CIFAR-, thanks to the smoothness implied by the Sobolev regularizer. OVERVIEW OF METRICS BETWEEN DISTRIBUTIONS In this Section, we review different representations of probability distributions and metrics for comparing distributions that use those representations. Those metrics are at the core of training GAN. In what follows, we consider probability measures with a positive weakly differentiable probability density functions (PDF). Let P and Q be two probability measures with PDFs P(x) and Q(x) defined on R d. Let F P and F Q be the Cumulative Distribution Functions (CDF) of P and Q respectively. For x =(x,...,x d ), we have: F P (x) = x... xd P(u,...u d )du...du d. The score function of a density function is defined as: s P (x) =r x log(p(x)) R d. In this work, we are interested in metrics between distributions that have a variational form and can be written as a suprema of mean discrepancies of functions defined on a specific function class. This type of metrics include '-divergences as well as Integral Probability Metrics (Sriperumbudur et al., 9) and have the following form: d F (P, Q) = sup (f; P, Q), ff where F is a function class defined on and is a mean discrepancy, :F! R. The variational form given above leads in certain cases to closed form expressions in terms of the PDFs P, Q or in terms of the CDFs F P,F Q or the score functions s P,s Q. In Table, we give a comparison of different discrepancies and function spaces F used in the literature for GAN training together with our proposed Sobolev IPM. We see from Table that Sobolev IPM, compared to Wasserstein Distance, imposes a tractable smoothness constraint on the critic on points sampled from a distribution µ, rather then imposing a Lipschitz constraint on all points in the space. We also see that Sobolev IPM is the natural generalization of the Cramér Von-Mises Distance from one dimension to high dimensions. We note that the Energy Distance, a form of Maximum Mean Discrepancy for a special kernel, was used in (Bellemare et al., 7b) as a generalization of the Cramér distance in GAN training but still needed a gradient penalty in its algorithmic counterpart leading to a mis-specified distance between distributions. Finally it is worth noting that when comparing Fisher IPM and Sobolev IPM we see that while Fisher IPM compares joint PDF of the distributions, Sobolev IPM compares weighted (coordinate-wise) conditional CDFs. As we will see later, this conditioning nature of the metric makes Sobolev IPM suitable for comparing sequences. Note that the Stein metric (Liu et al., 6; Liu, 7) uses the score function to match distributions. We will show later how Sobolev IPM relates to the Stein discrepancy (Appendix A). 3
4 Published as a conference paper at ICLR 8 '-Divergence E x P f(x) E x Q ' (f(x)) (Goodfellow et al., 4) (Nowozin et al., 6) (f; P, Q) F d F (P, Q) Function class Closed Form ' Fenchel Conjugate Wasserstein - E x P f(x) E x Q f(x) n o f :! R,f dom ' n o f :! R, kfk lip apple h i E x Q '( P(x) Q(x) ) inf (P,Q) kx yk d (x, y) Sinkhorn Divergence (Arjovsky et al., 7) (Gulrajani et al., 7) (Genevay et al., 7) MMD E x P f(x) E x Q f(x) (Li et al., 7) (Li et al., 5) (Dziugaite et al., 5) Stein E x Q [T (P)f(x)] n o f :! R, kfk Hk apple n f :! R d ke x P k x NA in general E x Q k x k Hk Discrepancy T (P) =(r x log(p(x)) > + r x. f smooth with zero o has a closed form (Wang & Liu, 6) boundary condition in RKHS n r df (x) Cramér E x P f(x) E x Q f(x) f :! R, E x P ( dx ) apple, E FP(x) x P for d = f smooth with zeroo x R (Bellemare et al., 7a) boundary condition n µ-fisher E x P f(x) E x Q f(x) f :! R,f L (,µ), o IPM E x µ f (x) apple (Mroueh & Sercu, 7) µ-sobolev E x P f(x) E x Q f(x) r E x µ P(x) n r f :! R,f W, P ( d,µ), d E x µ i= IPM E x µ kr x f(x)k apple, o (This work) with zero boundary condition FQ(x) P(x) Q(x) where i (P) = i(p) i(q) P i(x i )F P[i i =x i ] (x i) x i =(x,...x i,x i+,...x d ) Table : Comparison of different metrics between distributions used for GAN training. References are for papers using those metrics for GAN training. 3 GENERALIZING FISHER IPM: PDF COMPARISON Imposing data-independent constraints on the function class in the IPM framework, such as the Lipschitz constraint in the Wasserstein distance is computationally challenging and intractable for the general case. In this Section, we generalize the Fisher IPM introduced in (Mroueh & Sercu, 7), where the function class is relaxed to a tractable data dependent constraint on the second order moment of the critic, in other words the critic is constrained to be in a Lebsegue ball. Fisher IPM. Let R d and P( ) be the space of distributions defined on. Let P, Q P( ), and µ be a dominant measure of P and Q, in the sense that = =) P(x) =and Q(x) =. We assume µ to be also a distribution in P( ), and assume >, 8x. Let L (,µ) be the space of µ-measurable functions. For f,g L (,µ), we define the following dot product and its corresponding norm: hf,gi L(,µ) = f(x)g(x)dx, kfk L(,µ) = s Note that L (,µ), can be formally defined as follows: L (,µ)={f :! R s.t kfk L(,µ) < }. f (x)dx. 4
5 Published as a conference paper at ICLR 8 We define the unit Lebesgue ball as follows: B (, µ) = {f L (, µ), kf kl (,µ) }. Fisher IPM defined in (Mroueh & Sercu, 7), searches for the critic function in the Lebesgue Ball B (, µ) that maximizes the mean discrepancy between P and Q. Fisher GAN (Mroueh & Sercu, 7) was originally formulated specifically for µ = (P + Q). We consider here a general µ as long as it dominates P and Q. We define Generalized Fisher IPM as follows: Fµ (P, Q) = sup Ex P f (x) Ex Q f (x) () f B (,µ) Note that: Ex P f (x) Ex Q f (x) = Hence Fisher IPM can be written as follows: Fµ (P, Q) = sup f B (,µ) f, f, P Q. µ P L (,µ) Q µ () L (,µ) We have the following result: Theorem (Generalized Fisher IPM). The Fisher distance and the optimal critic are as follows:. The Fisher distance is given by: Fµ (P, Q) = P Q µ = L (,µ) s Ex µ P(x) Q(x).. The optimal f achieving the Fisher distance Fµ (P, Q) is: P Q f =, µ almost surely. F (P, Q) µ P Proof of Theorem. From Equation (), the optimal f belong to the intersection of the hyperplane that has normal n = P µq, and the ball B (, µ), hence f = knk n. Hence F (P, Q) = knkl (,µ). Q µ f kf kl (,µ) = L (,µ) We see from Theorem the role of the dominant measure µ: the optimal critic is defined with respect to this measure and the overall Fisher distance can be seen as an average weighted distance between probability density functions, where the average is taken on points sampled from µ. We give here some choices of µ:. For µ = (P + Q), we obtain the symmetric chi-squared distance as defined in (Mroueh & Sercu, 7).. µgp, the implicit distribution defined by the interpolation lines between Pr and Q as in (Gulrajani et al., 7). 3. When µ does not dominate P, and Q, we obtain a non symmetric divergence. For example Q(x)) for µ = P, FP (P, Q) = (P(x)P(x) dx. We see here that for this particular choice we obtain the Pearson divergence. 4 S OBOLEV IPM In this Section, we introduce the Sobolev IPM. In a nutshell, the Sobolev IPM constrains the critic function to belong to a ball in the restricted Sobolev Space. In other words we constrain the norm of the gradient of the critic rx f (x). We will show that by moving from a Lebesgue constraint as in Fisher IPM to a Sobolev constraint as in Sobolev IPM, the metric changes from a joint PDF matching to weighted (ccordinate-wise) conditional CDFs matching. The intrinsic conditioning built in to the Sobolev IPM and the comparison of cumulative distributions makes Sobolev IPM suitable for comparing discrete sequences. 5
6 Published as a conference paper at ICLR 8 4. DEFINITION AND EPRESSION OF SOBOLEV IPM IN TERMS OF COORDINATE CONDITIONAL CDFS We will start by recalling some definitions on Sobolev Spaces. We assume in the following that is compact and consider functions in the Sobolev space W, (,µ): W, (,µ)= f :! R, kr x f(x)k dx <, We restrict ourselves to functions in W, (,µ) vanishing at the boundary, and note this space W, (,µ). Note that in this case: s kfk W, (,µ) = kr x f(x)k dx defines a semi-norm. We can similarly define a dot product in W, (,µ), for f,g W, (,µ): hf,gi W, (,µ) = hr x f(x), r x g(x)i R d dx. Hence we define the following Sobolev IPM, by restricting the critic of the mean discrepancy to the Sobolev unit ball : n o S µ (P, Q) = sup E x P f(x) E x Q f(x). (3) fw,,kfk, apple W (,µ) When compared to the Wasserstein distance, the Sobolev IPM given in Equation (3) uses a data dependent gradient constraint (depends on µ) rather than a data independent Lipchitz constraint. Let F P and F Q be the cumulative distribution functions of P and Q respectively. We have: and we define P(x) d F P (x), d D i =, for i i+...@x d D i computes the (d ) high-order partial derivative excluding the variable i. Our main result is presented in Theorem. Additional theoretical results are given in Appendix A. All proofs are given in Appendix B. Theorem (Sobolev IPM). Assume that F P, and F Q and its d derivatives exist and are continuous: F P and F Q C d ( ). Define the differential operator D : D =(D,...D d ). For x =(x,...x i,x i,x i+,...x d ), let x i =(x,...x i,x i+,...x d ). The Sobolev IPM given in Equation (3) has the following equivalent forms:. Sobolev IPM as comparison of high order partial derivatives of CDFs. The Sobolev IPM has the following form: s S µ (P, Q) = P d i= (D i F P (x) D i F Q (x)) dx. d. Sobolev IPM as comparison of weighted (coordinate-wise) conditional CDFs. The Sobolev IPM can be written in the following equivalent form: Sµ(P, Q) = d d E P i(x i )F (x P[i i =x i ] i) Q i(x i )F (x! Q[i i =x i ] i) x µ. i= (5) 6
7 Published as a conference paper at ICLR 8 3. The optimal critic f satisfies the following identity: r x f (x) = ds µ (P, Q) D F Q (x) D F P (x), µ almost surely. (6) Sobolev IPM Approximation. Learning in the whole Sobolev space W, is challenging hence we need to restrict our function class to a hypothesis class H, such as neural networks. We assume in the following that functions in H vanish on the boundary of, and restrict the optimization to the function space H. H can be a Reproducing Kernel Hilbert Space as in the MMD case or parametrized by a neural network. Define the Sobolev IPM approximation in H : S H,µ (P, Q) = sup fh,kfk W, apple n E x P f(x) o E x Q f(x) The following Lemma shows that the Sobolev IPM approximation in H is proportional to Sobolev IPM. The tightness of the approximation of the Sobolev IPM is governed by the tightness of the approximation of the optimal Sobolev Critic f in H. This approximation is measured in the Sobolev sense, using the Sobolev dot product. (7) Lemma (Sobolev IPM Approximation in a Hypothesis Class). Let H be a function space with functions vanishing at the boundary. For any f H and for f the optimal critic in W,, we have: S H,µ (P, Q) =S µ (P, Q) sup hr x f(x), r x f (x)i R d dx. fh,kfk, apple W (,µ) Note that this Lemma means that the Sobolev IPM is well approximated if the space H has an enough representation power to express r x f (x). This is parallel to the Fisher IPM approximation (Mroueh & Sercu, 7) where it is shown that the Fisher IPM approximation error is proportional to the critic approximation in the Lebesgue sense. Having in mind that the gradient of the critic is the information that is passed on to the generator, we see that this convergence in the Sobolev sense to the optimal critic is an important property for GAN training. Relation to Fokker-Planck Diffusion. We show in Appendix A that the optimal Sobolev critic is the solution of the following elliptic PDE (with zero boundary conditions): P Q S µ (P, Q) = div(r xf(x)). (8) We further link the elliptic PDE given in Equation (8) and the Fokker-Planck diffusion. As we illustrate in Figure (b) the gradient of the critic defines a transportation plan for moving the distribution mass from Q to P. Discussion of Theorem. We make the following remarks on Theorem :. From Theorem, we see that the Sobolev IPM compares d higher order partial derivatives of the cumulative distributions F P and F Q, while Fisher IPM compares the probability density functions.. The dominant measure µ plays a similar role to Fisher: S µ(p, Q) = d d D i F P (x) D i F Q (x) E x µ, i= the average distance is defined with respect to points sampled from µ. 7
8 Published as a conference paper at ICLR 8 3. Comparison of coordinate-wise Conditional CDFs. We note in the following x i = (x,...x i,x i+,...x d ). Note that we have: D d x xd F P (x) =... P(u...u d )du...du i+...@x d = xi P(x,...,x i,u,x i+,...,x d )du = P i(x,...,x i,x i+,...x d ) (Using Bayes rule) = P i(x i )F P[i i =x i ] (x i), xi P [i i =x i ](u x,...,x i,x i+,...x d )du Note that for each i, D i F P (x) is the cumulative distribution of the variable i given the other variables i = x i, weighted by the density function of i at x i. This leads us to the form given in Equation 5. We see that the Sobolev IPM compares for each dimension i the conditional cumulative distribution of each variable given the other variables, weighted by their density function. We refer to this as comparison of coordinate-wise CDFs on a leave one out basis. From this we see that we are comparing CDFs, which are better behaved on discrete distributions. Moreover, the conditioning built in to this metric will play a crucial role in comparing sequences as the conditioning is important in this context (See section 6.). 4. ILLUSTRATIVE EAMPLES Sobolev IPM / Cramér Distance and Wasserstein- in one Dimension. In one dimension, Sobolev IPM is the Cramér Distance (for µ uniform on, we note this µ := ). While Sobolev IPM in one dimension measures the discrepancy between CDFs, the one dimensional Wasserstein-p distance measures the discrepancy between inverse CDFs: Sµ:=(P, Q) = (F P (x) F Q (x)) dx versus Wp p (P, Q) = F P (u) F Q (u) p du, Recall also that the Fisher IPM for uniform µ is given by : Fµ:=(P, Q) = (P(x) Q(x)) dx. Consider for instance two point masses P = a and Q = a with a,a R. The rationale behind using Wasserstein distance for GAN training is that since it is a weak metric, for far distributions Wasserstein distance provides some signal (Arjovsky et al., 7). In this case, it is easy to see that W (P, Q) =Sµ:= = a a, while Fµ:=(P, Q) =. As we see from this simple example, CDF comparison is more suitable than PDF for comparing distributions on discrete spaces. See Figure, for a further discussion of this effect in the GAN context. Sobolev IPM between two D Gaussians. We consider P and Q to be two dimensional Gaussians with means µ and µ and covariances and. Let (x, y) be the coordinates in D. We note F P and F Q the CDFs of P and Q respectively. We consider in this example µ = P+Q. We know from Theorem that the gradient of the Sobolev optimal critic is proportional to the following vector field: apple (x, (F Q(x, y) F P (x, µ(x, (F (9) Q(x, y) F P (x, y)) apple apple In Figure we consider µ =[, ], =.8.3 µ =[, ], =..8.3 In Figure (a) we plot the numerical solution of the PDE satisfied by the optimal Sobolev critic given in Equation (8), using MATLAB solver for elliptic PDEs (more accurately we solve div(r x f(x)) = P(x) Q(x), hence we obtain the solution of Equation (8) up to a normalization constant ( S µ(p,q) )). We numerically solve the PDE on a rectangle with zero boundary 8
9 Published as a conference paper at ICLR 8 (a) Smoothed discrete densities: PDF versus CDF of smoothed discrete densities with non overlapping supports. (b) Smoothed Discrete and Continuous densities: PDF versus CDF of a smoothed discrete density and a continuous density with non overlapping supports. Figure : In the GAN context for example in text generation, we have to match a (smoothed) discrete real distribution and a continuous generator. In this case, the CDF matching enabled by Sobolev IPM gives non zero discrepancy between a (smoothed) discrete and a continuous density even if the densities have disjoint supports. This ensures non vanishing gradients of the critic. conditions. We see that the optimal Sobolev critic separates the two distributions well. In Figure (b) we then numerically compute the gradient of the optimal Sobolev critic on a D grid as given in Equation 9 (using numerical evaluation of the CDF and finite difference for the evaluation of the partial derivatives). We plot in Figure (b) the density functions of P and Q as well as the vector field of the gradient of the optimal Sobolev critic. As discussed in Section A., we see that the gradient of the critic (wrt to the input), defines on the support of µ = P+Q a transportation plan for moving the distribution mass from Q to P. 5 SOBOLEV GAN Now we turn to the problem of learning GANs with Sobolev IPM. Given the real distribution P r P( ), our goal is to learn a generator g : Z R nz!, such that for z p z, the distribution of g (z) is close to the real data distribution P r, where p z is a fixed distribution on Z (for instance z N (,I nz )). We note Q for the fake distribution of g (z),z p z. Consider {x i,i =...N} P r, {z i,i =...N} N (,I nz ), and { x i,i =...N} µ. We consider these choices for µ:. µ = Pr+Q i.e x P r or x = g (z),z p z with equal probability.. µ GP is the implicit distribution defined by the interpolation lines between P r and Q as in (Gulrajani et al., 7) i.e : x = ux +( u)y, x P r,y = g (z),z p z and u Unif[, ]. Sobolev GAN can be written as follows: min g sup Ê (f f p, P p,g )= N N i= krxfp( xi)k = N N f p (x i ) i= N N f p (g (z i )) For any choice of the parametric function class H p, note the constraint by S (f p,g ) = P N N i= kr xf p ( x i )k. For example if µ = Pr+Q, S (f p,g ) = P N N i= kr xf p (x i )k + 9 i=
10 Published as a conference paper at ICLR 8 (a) Numerical solution of the PDE satisfied by the optimal Sobolev critic. (b) Optimal Sobolev Transport Vector Field r xf (x) (arrows are the vector field r xf (x) evaluated on the D grid. Magnitude of arrows was rescaled for visualization.) Figure : Numerical solution of the PDE satisfied by the optimal Sobolev critic and the transportation Plan induced by the gradient of Sobolev critic. The gradient of the critic (wrt to the input), defines on the support of µ = P+Q a transportation plan for moving the distribution mass from Q to P. For a theoretical analysis of this transportation plan and its relation to Fokker-Planck diffusion the reader is invited to check Appendix A. N P N i= kr xf p (g (z i ))k. Note that, since the optimal theoretical critic is achieved on the sphere, we impose a sphere constraint rather than a ball constraint. Similar to (Mroueh & Sercu, 7) we define the Augmented Lagrangian corresponding to Sobolev GAN objective and constraint L S (p,, )=Ê (f p,g )+ ( S (f p,g )) ( S (f p,g ) ) () where is the Lagrange multiplier and >is the quadratic penalty weight. We alternate between optimizing the critic and the generator. We impose the constraint when training the critic only. Given, we solve max p min L S (p,, ), for training the critic. Then given the critic parameters p we optimize the generator weights to minimize the objective min Ê (f p,g ). See Algorithm. Algorithm Sobolev GAN Input: penalty weight, Learning rate, n c number of iterations for training the critic, N batch size Initialize p,, = repeat for j =to n c do Sample a minibatch x i,i=...n,x i P r Sample a minibatch z i,i=...n,z i p z (g p,g ) (r p L S, r L S )(p,, ) p p + ADAM (p, g p ) g {SGD rule on with learning rate } end for Sample z i,i=...n,z i p z P N d r Ê (f p,g )= r N i= f p(g (z i )) ADAM (, d ) until converges Remark. Note that in Algorithm, we obtain a biased estimate since we are using same samples for the cost function and the constraint, but the incurred bias can be shown to be small and vanishing as the number of samples increases as shown and justified in (Shivaswamy & Jebara, ).
11 Published as a conference paper at ICLR 8 Relation to WGAN-GP. WGAN-GP can be written as follows: min sup Ê (f p,g )= N f p (x i ) g N f,kr xf p( x i)k=, x i µ GP i= N N f p (g (z i )) The main difference between WGAN-GP and our setting, is that WGAN-GP enforces pointwise constraints on points drawn from µ = µ GP via a point-wise quadratic penalty (Ê (f P N p,g ) i= ( kr x f( x i )k) ) while we enforce that constraint on average as a Sobolev norm, allowing us the coordinate weighted conditional CDF interpretation of the IPM. 6 APPLICATIONS OF SOBOLEV GAN Sobolev IPM has two important properties; The first stems from the conditioning built in to the metric through the weighted conditional CDF interpretation. The second stems from the diffusion properties that the critic of Sobolev IPM satisfies (Appendix A) that has theoretical and practical ties to the Laplacian regularizer and diffusion on manifolds used in semi-supervised learning (Belkin et al., 6). In this Section, we exploit those two important properties in two applications of Sobolev GAN: Text generation and semi-supervised learning. First in text generation, which can be seen as a discrete sequence generation, Sobolev GAN (and WGAN-GP) enable training GANs without need to do explicit brute-force conditioning. We attribute this to the built-in conditioning in Sobolev IPM (for the sequence aspect) and to the CDF matching (for the discrete aspect). Secondly using GANs in semi-supervised learning is a promising avenue for learning using unlabeled data. We show that a variant of Sobolev GAN can achieve strong SSL results on the CIFAR- dataset, without the need of any form of activation normalization in the networks or any extra ad hoc tricks. 6. TET GENERATION WITH SOBOLEV GAN In this Section, we present an empirical study of Sobolev GAN in character level text generation. Our empirical study on end to end training of character-level GAN for text generation is articulated on four dimensions (loss, critic, generator, µ). () the loss used (GP: WGAN-GP (Gulrajani et al., 7), S: Sobolev or F: Fisher) () the architecture of the critic (Resnets or RNN) (3) the architecture of the generator (Resnets or RNN or RNN with curriculum learning) (4) the sampling distribution µ in the constraint. Text Generation Experiments. We train a character-level GAN on Google Billion Word dataset and follow the same experimental setup used in (Gulrajani et al., 7). The generated sequence length is 3 and the evaluation is based on Jensen-Shannon divergence on empirical 4-gram probabilities (JS-4) of validation data and generated data. JS-4 may not be an ideal evaluation criteria, but it is a reasonable metric for current character-level GAN results, which is still far from generating meaningful sentences. Annealed Smoothing of discrete P r in the constraint µ. Since the generator distribution will always be defined on a continuous space, we can replace the discrete real distribution P r with a smoothed version (Gaussian kernel smoothing) P r? N (, I d ). This corresponds to doing the following sampling for P r : x +,x P r, and N (, I d ). Note that we only inject noise to the real distribution with the goal of smoothing the support of the discrete distribution, as opposed to instance noise on both real and fake to stabilize the training, as introduced in (Kaae Sønderby et al., 7; Arjovsky & Bottou, 7). As it is common in optimization by continuation (Mobahi & III, 5), we also anneal the noise level as the training progresses on a linear schedule. Sobolev GAN versus WGAN-GP with Resnets. In this setting, we compare (WGAN- GP,G=Resnet,D=Resnet,µ = µ GP ) to (Sobolev,G=Resnet,D=Resnet,µ) where µ is one of: () µ GP, () the noise smoothed µ s ( ) = Pr?N (, I d )+Q or (3) noise smoothed with annealing µ a s( ) with the initial noise level. We use the same architectures of Resnet with D convolution for the critic and the generator as in (Gulrajani et al., 7) (4 resnet blocks with hidden layer size of 5). In order to implement the noise smoothing we transform the data into one-hot vectors. Each one hot vector x is transformed to a probability vector p with.9 replacing the one and./(dict size ) replacing the zero. We then sample from a Gaussian distribution N (, ), and i=
12 Published as a conference paper at ICLR 8 (a) Comparing Sobolev with µ GP and WGAN-GP. The JS-4 are.3363 and.33 respectively. (b) Comparing Sobolev with different µ dominant measures and WGAN-GP. The JS- 4 of µ a s( =.5) is.368. Figure 3: Result of Sobolev GAN for various dominating measure µ, for resnets as architectures of the critic and the generator. use softmax to normalize log p +. We use algorithm for Sobolev GAN and fix the learning rate to 4 and to 5. The noise level was annealed following a linear schedule starting from an i initial noise level (at iteration i, i = ( Maxiter ), Maxiter=3K). For WGAN-GP we used the open source implementation with the penalty = as in (Gulrajani et al., 7). Results are given in Figure 3(a) for the JS-4 evaluation of both WGAN-GP and Sobolev GAN for µ = µ GP. In Figure 3(b) we show the JS-4 evaluation of Sobolev GAN with the annealed noise smoothing µ a s( ), for various values of the initial noise level. We see that the training succeeds in both cases. Sobolev GAN achieves slightly better results than WGAN-GP for the annealing that starts with high noise level =.5. We note that without smoothing and annealing i.e using µ = Pr+Q, Sobolev GAN is behind. Annealed smoothing of P r, helps the training as the real distribution is slowly going from a continuous distribution to a discrete distribution. See Appendix C (Figure 6) for a comparison between annealed and non annealed smoothing. We give in Appendix C a comparison of WGAN-GP and Sobolev GAN for a Resnet generator architecture and an RNN critic. The RNN has degraded performance due to optimization difficulties. Fisher GAN Curriculum Conditioning versus Sobolev GAN: Explicit versus Implicit conditioning. We analyze how Fisher GAN behaves under different architectures of generators and critics. We first fix the generator to be ResNet. We study 3 different architectures of critics: ResNet, GRU (we follow the experimental setup from (Press et al., 7)), and hybrid ResNet+GRU (Reed et al., 6). We notice that RNN is unstable, we need to clip the gradient values of critics in [.5,.5], and the gradient of the Lagrange multiplier F to [ 4, 4 ]. We fix F = 7 and we use µ = µ GP. We search the value for the learning rate in [ 5, 4 ]. We see that for µ = µ GP and G = Resnet for various critic architectures, Fisher GAN fails at the task of text generation (Figure 4 a-c). Nevertheless, when using RNN critics (Fig 4 b, c) a marginal improvement happens over the fully collapsed state when using a resnet critic (Fig 4 a). We hypothesize that RNN critics enable some conditioning and factoring of the distribution, which is lacking in Fisher IPM. Finally Figure 4 (d) shows the result of training with recurrent generator and critic. We follow (Press et al., 7) in terms of GRU architecture, but differ by using Fisher GAN rather than WGAN-GP. We use µ = Pr+Q i.e. without annealed noise smoothing. We train (F, D=RNN,G=RNN, Pr+Q ) using curriculum conditioning of the generator for all lengths ` as done in (Press et al., 7): the generator is conditioned on 3 ` characters and predicts the ` remaining characters. We increment ` =to 3 on a regular schedule (every 5k updates). JS-4 is only computed when `>4. We see in Figure 4 that under curriculum conditioning with recurrent critics and generators, the training of Fisher GAN succeeds and reaches similar levels of Sobolev GAN (and WGAN-GP). Note that the need of this explicit brute force conditioning for Fisher GAN, highlights the implicit conditioning induced by Sobolev GAN via the gradient regularizer, without the need for curriculum conditioning.
13 Published as a conference paper at ICLR 8 Figure 4: Fisher GAN with different architectures for critics: (a-c) We see that for µ = µ GP and G = Resnet for various critic architectures, Fisher GAN fails at the task of text generation. We notice small improvements for RNN critics (b-c) due to the conditioning and factoring of the distribution. (d) Fisher GAN with recurrent generator and critic, trained on a curriculum conditioning for increasing lengths `, increments indicated by gridlines. In this curriculum conditioning setup, with recurrent critics and generators, the training of Fisher GAN succeeds and reaches similar levels of Sobolev GAN (and WGAN-GP). It is important to note that by doing this explicit curriculum conditioning for Fisher GAN, we highlight the implicit conditioning induced by Sobolev GAN, via the gradient regularizer. 6. SEMI-SUPERVISED LEARNING WITH SOBOLEV GAN A proper and promising framework for evaluating GANs consists in using it as a regularizer in the semi-supervised learning setting (Salimans et al., 6; Dumoulin et al., 7; Kumar et al., 7). As mentioned before, the Sobolev norm as a regularizer for the Sobolev IPM draws connections with the Laplacian regularization in manifold learning (Belkin et al., 6). In the Laplacian framework of semi-supervised learning, the classifier satisfies a smoothness constraint imposed by controlling its Sobolev norm: kr xf(x)k µ (x)dx (Alaoui et al., 6). In this Section, we present a variant of Sobolev GAN that achieves competitive performance in semi-supervised learning on the CIFAR- dataset Krizhevsky & Hinton (9) without using any internal activation normalization in the critic, such as batch normalization (BN) (Ioffe & Szegedy, 5), layer normalization (LN) (Ba et al., 6), or weight normalization (Salimans & Kingma, 6). In this setting, a convolutional neural network! :! R m is shared between the cross entropy (CE) training of a K-class classifier (S R K m ) and the critic of GAN (See Figure 5). We have the following training equations for the (critic + classifer) and the generator: Critic + Classifier: max L D = L GAN alm (f,g ) CE CE(p(y x),y) () S,!,f (x,y)lab Generator: max L G = Ê (f,g ) () P where the main IPM objective with N samples: Ê (f,g )= N xunl f(x) P z p z f(g (z)). Following (Mroueh & Sercu, 7) we use the following K +parametrization for the critic (See Figure 5): K f(x) = p(y x) hs y,!(x)i hv,!(x)i {z } y= {z } f : fake critic f + : real critic Note that p(y x) = Softmax(hS,!(x)i) y appears both in the critic formulation and in the Cross- Entropy term in Equation (). Intuitively this critic uses the K class directions of the classifier S y to define the real direction, which competes with another K+ th direction v that indicates fake samples. This parametrization adapts the idea of (Salimans et al., 6), which was formulated specifically for the classic KL / JSD based GANs, to IPM-based GANs. We saw consistently better results with the K +formulation over the regular formulation where the classification layer S 3
14 Published as a conference paper at ICLR 8 doesn t interact with the critic direction v. We also note that when applying a gradient penalty based constraint (either WGAN-GP or Sobolev) on the full critic f = f+ f, it is impossible for the network to fit even the small labeled training set (underfitting), causing bad SSL performance. This leads us to the formulation below, where we apply the Sobolev constraint only on f. Throughout this Section we fix µ = Pr +Q. We propose the following two schemes for constraining the K+ critic f (x) = f+ (x) f (x): ) Fisher constraint on the critic: We restrict the critic to the following set: (! ) F (f, g ) = f f = f+ f, f (x) + f (g (z)) =. N z p xunl z This constraint translates to the following ALM objective in Equation (): F (f, g )) F ( F (f, g ) LGAN alm (f, g ) = E (f, g ) + F ( ), where the Fisher constraint ensures the stability of the training through an implicit whitened mean matching (Mroueh & Sercu, 7). ) Fisher+Sobolev constraint: We impose constraints on the critic: Fisher on f & Sobolev on f n o F (f, g ) = and S (f, g ) =, f f = f+ f, P S (f, g ) = P where kr f (x)k + kr f (g (z))k. x x xunl z pz N This constraint translates to the following ALM in Equation (): F (f, g )) + S ( S (f, g )) LGAN alm (f, g ) = E (f, g ) + F ( F S S (f, g ) ). ( F (f, g ) ) ( Note that the fisher constraint on f ensures the stability of the training, and the Sobolev constraints on the fake critic f enforces smoothness of the fake critic and thus the shared CNN! (x). This is related to the classic Laplacian regularization in semi-supervised learning (Belkin et al., 6). Table shows results of SSL on CIFAR- comparing the two proposed formulations. Similar to the standard procedure in other GAN papers, we do hyperparameter and model selection on the validation set. We present baselines with a similar model architecture and leave out results with significantly larger convnets. G and D architectures and hyperparameters are in Appendix D.! is similar to (Salimans et al., 6; Dumoulin et al., 7; Mroueh & Sercu, 7) in architecture, but note that we do not use any batch, layer, or weight normalization yet obtain strong competitive accuracies. We hypothesize that we don t need any normalization in the critic, because of the implicit whitening of the feature maps introduced by the Fisher and Sobolev constraints as explained in (Mroueh & Sercu, 7). p(y x) = Softmax(hS,! (x)i)y real critic K f+ (x) = x PK y= p(y x) hsy,! (x)i f (x) = f+ (x)! CNN fake critic f (x) = hv, hv, f (x) GAN critic! (x)i! (x)i Figure 5: K+ parametrization of the critic for semi-supervised learning. 4
15 Published as a conference paper at ICLR 8 Table : CIFAR- error rates for varying number of labeled samples in the training set. Mean and standard deviation computed over 5 runs. We only use the K +formulation of the critic. Note that we achieve strong SSL performance without any additional tricks, and even though the critic does not have any batch, layer or weight normalization. Baselines with * use either additional models like PixelCNN, or do data augmentation (translations and flips), or use a much larger model, either of which gives an advantage over our plain simple training method. is the result we achieved in our experimental setup under the same conditions but without K+ critic (see Appendix D), since (Gulrajani et al., 7) does not have SSL results. Number of labeled examples 4 8 Model Misclassification rate CatGAN (Springenberg, 5) 9.58 FM (Salimans et al., 6).83 ±. 9.6 ± ± ±.8 ALI (Dumoulin et al., 7) 9.98 ± ± ± ±.5 Tangents Reg (Kumar et al., 7).6 ± ±.6 -model (Laine & Aila, 6) * 6.55 ±.9 VAT (Miyato et al., 7) 4.87 Bad Gan (Dai et al., 7) * 4.4 ±.3 VAT+EntMin+Large (Miyato et al., 7)* 3.5 Sajjadi (Sajjadi et al., 6) *.9 WGAN-GP (Gulrajani et al., 7) ± ± ± ±. Fisher, layer norm (Mroueh & Sercu, 7) 9.74 ± ± ± ±.6 Fisher, no norm (Mroueh & Sercu, 7).49 ±.8 9. ± ± ±.33 Sobolev + Fisher, no norm (This Work).4 ± ± ±.9 4. ±.8 7 CONCLUSION We introduced the Sobolev IPM and showed that it amounts to a comparison between weighted (coordinate-wise) CDFs. We presented an ALM algorithm for training Sobolev GAN. The intrinsic conditioning implied by the Sobolev IPM explains the success of gradient regularization in Sobolev GAN and WGAN-GP on discrete sequence data, and particularly in text generation. We highlighted the important tradeoffs between the implicit conditioning introduced by the gradient regularizer in Sobolev IPM, and the explicit conditioning of Fisher IPM via recurrent critics and generators in conjunction with the curriculum conditioning. Both approaches succeed in text generation. We showed that Sobolev GAN achieves competitive semi-supervised learning results without the need of any normalization, thanks to the smoothness induced by the gradient regularizer. We think the Sobolev IPM point of view will open the door for designing new regularizers that induce different types of conditioning for general structured/discrete/graph data beyond sequences. REFERENCES Ahmed El Alaoui, iang Cheng, Aaditya Ramdas, Martin J. Wainwright, and Michael I. Jordan. Asymptotic behavior of p-based laplacian regularization in semi-supervised learning. CoRR, abs/63.564, 6. Martin Arjovsky and Léon Bottou. Towards principled methods for training generative adversarial networks. In ICLR, 7. Martin Arjovsky, Soumith Chintala, and Léon Bottou. Wasserstein gan. ICML, 7. Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization. ariv:67.645, 6. Mikhail Belkin, Partha Niyogi, and Vikas Sindhwani. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. JMLR, 6. Marc G. Bellemare, Ivo Danihelka, Will Dabney, Shakir Mohamed, Balaji Lakshminarayanan, Stephan Hoyer, and Rémi Munos. The cramer distance as a solution to biased wasserstein gradients. CoRR, abs/75.743, 7a. 5
16 Published as a conference paper at ICLR 8 Marc G Bellemare, Ivo Danihelka, Will Dabney, Shakir Mohamed, Balaji Lakshminarayanan, Stephan Hoyer, and Rémi Munos. The cramer distance as a solution to biased wasserstein gradients. ariv:75.743, 7b. Tong Che, Yanran Li, Ruixiang Zhang, Devon R Hjelm, Wenjie Li, Yangqiu Song, and Yoshua Bengio. Maximum-likelihood augmented discrete generative adversarial networks. ariv:7.7983, 7. Kacper Chwialkowski, Heiko Strathmann, and Arthur Gretton. A kernel test of goodness of fit. In ICML 6, 6. Zihang Dai, Zhilin Yang, Fan Yang, William W Cohen, and Ruslan Salakhutdinov. Good semisupervised learning that requires a bad gan. ariv: , 7. Vincent Dumoulin, Ishmael Belghazi, Ben Poole, Alex Lamb, Martin Arjovsky, Olivier Mastropietro, and Aaron Courville. Adversarially learned inference. ICLR, 7. Gintare Karolina Dziugaite, Daniel M. Roy, and Zoubin Ghahramani. Training generative neural networks via maximum mean discrepancy optimization. In UAI, 5. I. Ekeland and T. Turnbull. Infinite-dimensional Optimization and Convexity. The University of Chicago Press, 983. A. Genevay, G. Peyré, and M. Cuturi. Learning generative models with sinkhorn divergences. Preprint 76.9, Arxiv, 7. URL Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing u, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial nets. In NIPS, 4. Jackson Gorham and Lester W. Mackey. Measuring sample quality with stein s method. In NIPS, pp. 6 34, 5. Arthur Gretton, Karsten M Borgwardt, Malte J Rasch, Bernhard Schölkopf, and Alexander Smola. A kernel two-sample test. JMLR,. Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron Courville. Improved training of wasserstein gans. ariv:74.8, 7. R. Devon Hjelm, Athul Paul Jacob, Tong Che, Kyunghyun Cho, and Yoshua Bengio. Boundaryseeking generative adversarial networks. ariv:7.843, 7. Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proc. ICML, 5. Casper Kaae Sønderby, Jose Caballero, Lucas Theis, Wenzhe Shi, and Ferenc Huszár. Amortised map inference for image super-resolution. ICLR, 7. A. Krizhevsky and G. Hinton. Learning multiple layers of features from tiny images. Master s thesis, 9. Abhishek Kumar, Prasanna Sattigeri, and P Thomas Fletcher. Improved semi-supervised learning with gans using manifold invariances. NIPS, 7. Matt J. Kusner and José Miguel Hernández-Lobato. Gans for sequences of discrete elements with the gumbel-softmax distribution. ariv:6.45, 6. Samuli Laine and Timo Aila. Temporal ensembling for semi-supervised learning. ariv:6.4, 6. Chun-Liang Li, Wei-Cheng Chang, Yu Cheng, Yiming Yang, and Barnabás Póczos. MMD GAN: towards deeper understanding of moment matching network. NIPS, abs/ , 7. Yujia Li, Kevin Swersky, and Richard Zemel. Generative moment matching networks. In ICML, 5. 6
17 Published as a conference paper at ICLR 8 Qiang Liu. Stein variational descent as a gradient flow. NIPS, 7. Qiang Liu and Dilin Wang. Stein variational gradient descent: A general purpose bayesian inference algorithm. In Advances in Neural Information Processing Systems Qiang Liu, Jason D. Lee, and Michael I. Jordan. A kernelized stein discrepancy for goodness-of-fit tests. In Proceedings of the 33nd International Conference on Machine Learning, ICML 6, New York City, NY, USA, June 9-4, 6, 6. udong Mao, Qing Li, Haoran ie, Raymond YK Lau, and Zhen Wang. Least squares generative adversarial networks. ariv:6.476 ICCV, 7. Takeru Miyato, Shin-ichi Maeda, Masanori Koyama, and Shin Ishii. Virtual adversarial training: a regularization method for supervised and semi-supervised learning. ariv: , 7. Hossein Mobahi and John W. Fisher III. A Theoretical Analysis of Optimization by Gaussian Continuation. In Proc. of 9th Conf. Artificial Intelligence (AAAI 5), 5. Youssef Mroueh and Tom Sercu. Fisher gan. ariv: NIPS, 7. Youssef Mroueh, Tom Sercu, and Vaibhava Goel. Mcgan: Mean and covariance feature matching gan. ariv: ICML, 7. Alfred Müller. Integral probability metrics and their generating classes of functions. Advances in Applied Probability, 997. Sebastian Nowozin, Botond Cseke, and Ryota Tomioka. f-gan: Training generative neural samplers using variational divergence minimization. In NIPS, 6. Chris J. Oates, Mark Girolami, and Nicolas Chopin. Control functionals for monte carlo integration. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 7. Ofir Press, Amir Bar, Ben Bogin, Jonathan Berant, and Lior Wolf. Language generation with recurrent generative adversarial networks without pre-training. ariv:76.399, 7. Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. ariv:5.6434, 5. Sai Rajeswar, Sandeep Subramanian, Francis Dutil, Christopher Pal, and Aaron Courville. Adversarial generation of natural language. ariv:75.99, 7. Scott E Reed, Zeynep Akata, Santosh Mohan, Samuel Tenka, Bernt Schiele, and Honglak Lee. Learning what and where to draw. In Advances In Neural Information Processing Systems, pp. 7 5, 6. Mehdi Sajjadi, Mehran Javanmardi, and Tolga Tasdizen. Regularization with stochastic transformations and perturbations for deep semi-supervised learning. In Advances in Neural Information Processing Systems, pp. 63 7, 6. Tim Salimans and Diederik P Kingma. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. In Advances in Neural Information Processing Systems, pp. 9 9, 6. Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and i Chen. Improved techniques for training gans. NIPS, 6. Pannagadatta K. Shivaswamy and Tony Jebara. Maximum relative margin and data-dependent regularization. Journal of Machine Learning Research, : ,. doi:.45/ URL Jost Tobias Springenberg. Unsupervised and semi-supervised learning with categorical generative adversarial networks. ariv:5.639, 5. Bharath K. Sriperumbudur, Kenji Fukumizu, Arthur Gretton, Bernhard Scholkopf, and Gert R. G. Lanckriet. On integral probability metrics, -divergences and binary classification. 9. 7
MMD GAN 1 Fisher GAN 2
 MMD GAN 1 Fisher GAN 1 Chun-Liang Li, Wei-Cheng Chang, Yu Cheng, Yiming Yang, and Barnabás Póczos (CMU, IBM Research) Youssef Mroueh, and Tom Sercu (IBM Research) Presented by Rui-Yi(Roy) Zhang Decemeber
MMD GAN 1 Fisher GAN 1 Chun-Liang Li, Wei-Cheng Chang, Yu Cheng, Yiming Yang, and Barnabás Póczos (CMU, IBM Research) Youssef Mroueh, and Tom Sercu (IBM Research) Presented by Rui-Yi(Roy) Zhang Decemeber
arxiv: v1 [cs.lg] 20 Apr 2017
![arxiv: v1 [cs.lg] 20 Apr 2017 arxiv: v1 [cs.lg] 20 Apr 2017](/thumbs/78/78348074.jpg) Softmax GAN Min Lin Qihoo 360 Technology co. ltd Beijing, China, 0087 mavenlin@gmail.com arxiv:704.069v [cs.lg] 0 Apr 07 Abstract Softmax GAN is a novel variant of Generative Adversarial Network (GAN).
Softmax GAN Min Lin Qihoo 360 Technology co. ltd Beijing, China, 0087 mavenlin@gmail.com arxiv:704.069v [cs.lg] 0 Apr 07 Abstract Softmax GAN is a novel variant of Generative Adversarial Network (GAN).
GENERATIVE ADVERSARIAL LEARNING
 GENERATIVE ADVERSARIAL LEARNING OF MARKOV CHAINS Jiaming Song, Shengjia Zhao & Stefano Ermon Computer Science Department Stanford University {tsong,zhaosj12,ermon}@cs.stanford.edu ABSTRACT We investigate
GENERATIVE ADVERSARIAL LEARNING OF MARKOV CHAINS Jiaming Song, Shengjia Zhao & Stefano Ermon Computer Science Department Stanford University {tsong,zhaosj12,ermon}@cs.stanford.edu ABSTRACT We investigate
Fisher GAN. Abstract. 1 Introduction
 Fisher GAN Youssef Mroueh, Tom Sercu mroueh@us.ibm.com, tom.sercu@ibm.com Equal Contribution AI Foundations, IBM Research AI IBM T.J Watson Research Center Abstract Generative Adversarial Networks (GANs)
Fisher GAN Youssef Mroueh, Tom Sercu mroueh@us.ibm.com, tom.sercu@ibm.com Equal Contribution AI Foundations, IBM Research AI IBM T.J Watson Research Center Abstract Generative Adversarial Networks (GANs)
Training Generative Adversarial Networks Via Turing Test
 raining enerative Adversarial Networks Via uring est Jianlin Su School of Mathematics Sun Yat-sen University uangdong, China bojone@spaces.ac.cn Abstract In this article, we introduce a new mode for training
raining enerative Adversarial Networks Via uring est Jianlin Su School of Mathematics Sun Yat-sen University uangdong, China bojone@spaces.ac.cn Abstract In this article, we introduce a new mode for training
A QUANTITATIVE MEASURE OF GENERATIVE ADVERSARIAL NETWORK DISTRIBUTIONS
 A QUANTITATIVE MEASURE OF GENERATIVE ADVERSARIAL NETWORK DISTRIBUTIONS Dan Hendrycks University of Chicago dan@ttic.edu Steven Basart University of Chicago xksteven@uchicago.edu ABSTRACT We introduce a
A QUANTITATIVE MEASURE OF GENERATIVE ADVERSARIAL NETWORK DISTRIBUTIONS Dan Hendrycks University of Chicago dan@ttic.edu Steven Basart University of Chicago xksteven@uchicago.edu ABSTRACT We introduce a
arxiv: v1 [cs.lg] 8 Dec 2016
![arxiv: v1 [cs.lg] 8 Dec 2016 arxiv: v1 [cs.lg] 8 Dec 2016](/thumbs/87/96766608.jpg) Improved generator objectives for GANs Ben Poole Stanford University poole@cs.stanford.edu Alexander A. Alemi, Jascha Sohl-Dickstein, Anelia Angelova Google Brain {alemi, jaschasd, anelia}@google.com arxiv:1612.02780v1
Improved generator objectives for GANs Ben Poole Stanford University poole@cs.stanford.edu Alexander A. Alemi, Jascha Sohl-Dickstein, Anelia Angelova Google Brain {alemi, jaschasd, anelia}@google.com arxiv:1612.02780v1
arxiv: v3 [stat.ml] 20 Feb 2018
![arxiv: v3 [stat.ml] 20 Feb 2018 arxiv: v3 [stat.ml] 20 Feb 2018](/thumbs/96/127732243.jpg) MANY PATHS TO EQUILIBRIUM: GANS DO NOT NEED TO DECREASE A DIVERGENCE AT EVERY STEP William Fedus 1, Mihaela Rosca 2, Balaji Lakshminarayanan 2, Andrew M. Dai 1, Shakir Mohamed 2 and Ian Goodfellow 1 1
MANY PATHS TO EQUILIBRIUM: GANS DO NOT NEED TO DECREASE A DIVERGENCE AT EVERY STEP William Fedus 1, Mihaela Rosca 2, Balaji Lakshminarayanan 2, Andrew M. Dai 1, Shakir Mohamed 2 and Ian Goodfellow 1 1
Importance Reweighting Using Adversarial-Collaborative Training
 Importance Reweighting Using Adversarial-Collaborative Training Yifan Wu yw4@andrew.cmu.edu Tianshu Ren tren@andrew.cmu.edu Lidan Mu lmu@andrew.cmu.edu Abstract We consider the problem of reweighting a
Importance Reweighting Using Adversarial-Collaborative Training Yifan Wu yw4@andrew.cmu.edu Tianshu Ren tren@andrew.cmu.edu Lidan Mu lmu@andrew.cmu.edu Abstract We consider the problem of reweighting a
MMD GAN: Towards Deeper Understanding of Moment Matching Network
 MMD GAN: Towards Deeper Understanding of Moment Matching Network Chun-Liang Li 1, Wei-Cheng Chang 1, Yu Cheng 2 Yiming Yang 1 Barnabás Póczos 1 1 Carnegie Mellon University, 2 AI Foundations, IBM Research
MMD GAN: Towards Deeper Understanding of Moment Matching Network Chun-Liang Li 1, Wei-Cheng Chang 1, Yu Cheng 2 Yiming Yang 1 Barnabás Póczos 1 1 Carnegie Mellon University, 2 AI Foundations, IBM Research
MMD GAN: Towards Deeper Understanding of Moment Matching Network
 MMD GAN: Towards Deeper Understanding of Moment Matching Network Chun-Liang Li 1, Wei-Cheng Chang 1, Yu Cheng 2 Yiming Yang 1 Barnabás Póczos 1 1 Carnegie Mellon University, 2 AI Foundations, IBM Research
MMD GAN: Towards Deeper Understanding of Moment Matching Network Chun-Liang Li 1, Wei-Cheng Chang 1, Yu Cheng 2 Yiming Yang 1 Barnabás Póczos 1 1 Carnegie Mellon University, 2 AI Foundations, IBM Research
Lecture 14: Deep Generative Learning
 Generative Modeling CSED703R: Deep Learning for Visual Recognition (2017F) Lecture 14: Deep Generative Learning Density estimation Reconstructing probability density function using samples Bohyung Han
Generative Modeling CSED703R: Deep Learning for Visual Recognition (2017F) Lecture 14: Deep Generative Learning Density estimation Reconstructing probability density function using samples Bohyung Han
Learning features to compare distributions
 Learning features to compare distributions Arthur Gretton Gatsby Computational Neuroscience Unit, University College London NIPS 2016 Workshop on Adversarial Learning, Barcelona Spain 1/28 Goal of this
Learning features to compare distributions Arthur Gretton Gatsby Computational Neuroscience Unit, University College London NIPS 2016 Workshop on Adversarial Learning, Barcelona Spain 1/28 Goal of this
arxiv: v2 [cs.lg] 21 Aug 2018
![arxiv: v2 [cs.lg] 21 Aug 2018 arxiv: v2 [cs.lg] 21 Aug 2018](/thumbs/87/96459185.jpg) CoT: Cooperative Training for Generative Modeling of Discrete Data arxiv:1804.03782v2 [cs.lg] 21 Aug 2018 Sidi Lu Shanghai Jiao Tong University steve_lu@apex.sjtu.edu.cn Weinan Zhang Shanghai Jiao Tong
CoT: Cooperative Training for Generative Modeling of Discrete Data arxiv:1804.03782v2 [cs.lg] 21 Aug 2018 Sidi Lu Shanghai Jiao Tong University steve_lu@apex.sjtu.edu.cn Weinan Zhang Shanghai Jiao Tong
Wasserstein GAN. Juho Lee. Jan 23, 2017
 Wasserstein GAN Juho Lee Jan 23, 2017 Wasserstein GAN (WGAN) Arxiv submission Martin Arjovsky, Soumith Chintala, and Léon Bottou A new GAN model minimizing the Earth-Mover s distance (Wasserstein-1 distance)
Wasserstein GAN Juho Lee Jan 23, 2017 Wasserstein GAN (WGAN) Arxiv submission Martin Arjovsky, Soumith Chintala, and Léon Bottou A new GAN model minimizing the Earth-Mover s distance (Wasserstein-1 distance)
Normalization Techniques
 Normalization Techniques Devansh Arpit Normalization Techniques 1 / 39 Table of Contents 1 Introduction 2 Motivation 3 Batch Normalization 4 Normalization Propagation 5 Weight Normalization 6 Layer Normalization
Normalization Techniques Devansh Arpit Normalization Techniques 1 / 39 Table of Contents 1 Introduction 2 Motivation 3 Batch Normalization 4 Normalization Propagation 5 Weight Normalization 6 Layer Normalization
arxiv: v1 [cs.lg] 17 Jun 2017
![arxiv: v1 [cs.lg] 17 Jun 2017 arxiv: v1 [cs.lg] 17 Jun 2017](/thumbs/80/80865410.jpg) Bayesian Conditional Generative Adverserial Networks M. Ehsan Abbasnejad The University of Adelaide ehsan.abbasnejad@adelaide.edu.au Qinfeng (Javen) Shi The University of Adelaide javen.shi@adelaide.edu.au
Bayesian Conditional Generative Adverserial Networks M. Ehsan Abbasnejad The University of Adelaide ehsan.abbasnejad@adelaide.edu.au Qinfeng (Javen) Shi The University of Adelaide javen.shi@adelaide.edu.au
arxiv: v1 [cs.lg] 11 Jul 2018
![arxiv: v1 [cs.lg] 11 Jul 2018 arxiv: v1 [cs.lg] 11 Jul 2018](/thumbs/82/85441092.jpg) Manifold regularization with GANs for semi-supervised learning Bruno Lecouat, Institute for Infocomm Research, A*STAR bruno_lecouat@i2r.a-star.edu.sg Chuan-Sheng Foo Institute for Infocomm Research, A*STAR
Manifold regularization with GANs for semi-supervised learning Bruno Lecouat, Institute for Infocomm Research, A*STAR bruno_lecouat@i2r.a-star.edu.sg Chuan-Sheng Foo Institute for Infocomm Research, A*STAR
Some theoretical properties of GANs. Gérard Biau Toulouse, September 2018
 Some theoretical properties of GANs Gérard Biau Toulouse, September 2018 Coauthors Benoît Cadre (ENS Rennes) Maxime Sangnier (Sorbonne University) Ugo Tanielian (Sorbonne University & Criteo) 1 video Source:
Some theoretical properties of GANs Gérard Biau Toulouse, September 2018 Coauthors Benoît Cadre (ENS Rennes) Maxime Sangnier (Sorbonne University) Ugo Tanielian (Sorbonne University & Criteo) 1 video Source:
Learning features to compare distributions
 Learning features to compare distributions Arthur Gretton Gatsby Computational Neuroscience Unit, University College London NIPS 2016 Workshop on Adversarial Learning, Barcelona Spain 1/28 Goal of this
Learning features to compare distributions Arthur Gretton Gatsby Computational Neuroscience Unit, University College London NIPS 2016 Workshop on Adversarial Learning, Barcelona Spain 1/28 Goal of this
Deep learning / Ian Goodfellow, Yoshua Bengio and Aaron Courville. - Cambridge, MA ; London, Spis treści
 Deep learning / Ian Goodfellow, Yoshua Bengio and Aaron Courville. - Cambridge, MA ; London, 2017 Spis treści Website Acknowledgments Notation xiii xv xix 1 Introduction 1 1.1 Who Should Read This Book?
Deep learning / Ian Goodfellow, Yoshua Bengio and Aaron Courville. - Cambridge, MA ; London, 2017 Spis treści Website Acknowledgments Notation xiii xv xix 1 Introduction 1 1.1 Who Should Read This Book?
First Order Generative Adversarial Networks
 Calvin Seward 1 2 Thomas Unterthiner 2 Urs Bergmann 1 Nikolay Jetchev 1 Sepp Hochreiter 2 Abstract GANs excel at learning high dimensional distributions, but they can update generator parameters in directions
Calvin Seward 1 2 Thomas Unterthiner 2 Urs Bergmann 1 Nikolay Jetchev 1 Sepp Hochreiter 2 Abstract GANs excel at learning high dimensional distributions, but they can update generator parameters in directions
arxiv: v3 [cs.lg] 3 Nov 2017
![arxiv: v3 [cs.lg] 3 Nov 2017 arxiv: v3 [cs.lg] 3 Nov 2017](/thumbs/82/84970819.jpg) Good Semi-supervised Learning That Requires a Bad GAN arxiv:1705.09783v3 [cs.lg] 3 Nov 2017 Zihang Dai, Zhilin Yang, Fan Yang, William W. Cohen, Ruslan Salakhutdinov School of Computer Science Carnegie
Good Semi-supervised Learning That Requires a Bad GAN arxiv:1705.09783v3 [cs.lg] 3 Nov 2017 Zihang Dai, Zhilin Yang, Fan Yang, William W. Cohen, Ruslan Salakhutdinov School of Computer Science Carnegie
Wasserstein Generative Adversarial Networks
 Martin Arjovsky 1 Soumith Chintala 2 Léon Bottou 1 2 Abstract We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability
Martin Arjovsky 1 Soumith Chintala 2 Léon Bottou 1 2 Abstract We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability
Generative Adversarial Networks
 Generative Adversarial Networks SIBGRAPI 2017 Tutorial Everything you wanted to know about Deep Learning for Computer Vision but were afraid to ask Presentation content inspired by Ian Goodfellow s tutorial
Generative Adversarial Networks SIBGRAPI 2017 Tutorial Everything you wanted to know about Deep Learning for Computer Vision but were afraid to ask Presentation content inspired by Ian Goodfellow s tutorial
Learning Interpretable Features to Compare Distributions
 Learning Interpretable Features to Compare Distributions Arthur Gretton Gatsby Computational Neuroscience Unit, University College London Theory of Big Data, 2017 1/41 Goal of this talk Given: Two collections
Learning Interpretable Features to Compare Distributions Arthur Gretton Gatsby Computational Neuroscience Unit, University College London Theory of Big Data, 2017 1/41 Goal of this talk Given: Two collections
arxiv: v2 [cs.lg] 8 Jun 2017
![arxiv: v2 [cs.lg] 8 Jun 2017 arxiv: v2 [cs.lg] 8 Jun 2017](/thumbs/74/70483782.jpg) Youssef Mroueh * 1 2 Tom Sercu * 1 2 Vaibhava Goel 2 arxiv:1702.08398v2 [cs.lg] 8 Jun 2017 Abstract We introduce new families of Integral Probability Metrics (IPM) for training Generative Adversarial Networks
Youssef Mroueh * 1 2 Tom Sercu * 1 2 Vaibhava Goel 2 arxiv:1702.08398v2 [cs.lg] 8 Jun 2017 Abstract We introduce new families of Integral Probability Metrics (IPM) for training Generative Adversarial Networks
arxiv: v1 [cs.lg] 6 Dec 2018
![arxiv: v1 [cs.lg] 6 Dec 2018 arxiv: v1 [cs.lg] 6 Dec 2018](/thumbs/91/107120580.jpg) Embedding-reparameterization procedure for manifold-valued latent variables in generative models arxiv:1812.02769v1 [cs.lg] 6 Dec 2018 Eugene Golikov Neural Networks and Deep Learning Lab Moscow Institute
Embedding-reparameterization procedure for manifold-valued latent variables in generative models arxiv:1812.02769v1 [cs.lg] 6 Dec 2018 Eugene Golikov Neural Networks and Deep Learning Lab Moscow Institute
Singing Voice Separation using Generative Adversarial Networks
 Singing Voice Separation using Generative Adversarial Networks Hyeong-seok Choi, Kyogu Lee Music and Audio Research Group Graduate School of Convergence Science and Technology Seoul National University
Singing Voice Separation using Generative Adversarial Networks Hyeong-seok Choi, Kyogu Lee Music and Audio Research Group Graduate School of Convergence Science and Technology Seoul National University
Learning to Sample Using Stein Discrepancy
 Learning to Sample Using Stein Discrepancy Dilin Wang Yihao Feng Qiang Liu Department of Computer Science Dartmouth College Hanover, NH 03755 {dilin.wang.gr, yihao.feng.gr, qiang.liu}@dartmouth.edu Abstract
Learning to Sample Using Stein Discrepancy Dilin Wang Yihao Feng Qiang Liu Department of Computer Science Dartmouth College Hanover, NH 03755 {dilin.wang.gr, yihao.feng.gr, qiang.liu}@dartmouth.edu Abstract
Deep Generative Models. (Unsupervised Learning)
 Deep Generative Models (Unsupervised Learning) CEng 783 Deep Learning Fall 2017 Emre Akbaş Reminders Next week: project progress demos in class Describe your problem/goal What you have done so far What
Deep Generative Models (Unsupervised Learning) CEng 783 Deep Learning Fall 2017 Emre Akbaş Reminders Next week: project progress demos in class Describe your problem/goal What you have done so far What
f-gan: Training Generative Neural Samplers using Variational Divergence Minimization
 f-gan: Training Generative Neural Samplers using Variational Divergence Minimization Sebastian Nowozin, Botond Cseke, Ryota Tomioka Machine Intelligence and Perception Group Microsoft Research {Sebastian.Nowozin,
f-gan: Training Generative Neural Samplers using Variational Divergence Minimization Sebastian Nowozin, Botond Cseke, Ryota Tomioka Machine Intelligence and Perception Group Microsoft Research {Sebastian.Nowozin,
Searching for the Principles of Reasoning and Intelligence
 Searching for the Principles of Reasoning and Intelligence Shakir Mohamed shakir@deepmind.com DALI 2018 @shakir_a Statistical Operations Estimation and Learning Inference Hypothesis Testing Summarisation
Searching for the Principles of Reasoning and Intelligence Shakir Mohamed shakir@deepmind.com DALI 2018 @shakir_a Statistical Operations Estimation and Learning Inference Hypothesis Testing Summarisation
Large-Scale Feature Learning with Spike-and-Slab Sparse Coding
 Large-Scale Feature Learning with Spike-and-Slab Sparse Coding Ian J. Goodfellow, Aaron Courville, Yoshua Bengio ICML 2012 Presented by Xin Yuan January 17, 2013 1 Outline Contributions Spike-and-Slab
Large-Scale Feature Learning with Spike-and-Slab Sparse Coding Ian J. Goodfellow, Aaron Courville, Yoshua Bengio ICML 2012 Presented by Xin Yuan January 17, 2013 1 Outline Contributions Spike-and-Slab
Summary of A Few Recent Papers about Discrete Generative models
 Summary of A Few Recent Papers about Discrete Generative models Presenter: Ji Gao Department of Computer Science, University of Virginia https://qdata.github.io/deep2read/ Outline SeqGAN BGAN: Boundary
Summary of A Few Recent Papers about Discrete Generative models Presenter: Ji Gao Department of Computer Science, University of Virginia https://qdata.github.io/deep2read/ Outline SeqGAN BGAN: Boundary
CLOSE-TO-CLEAN REGULARIZATION RELATES
 Worshop trac - ICLR 016 CLOSE-TO-CLEAN REGULARIZATION RELATES VIRTUAL ADVERSARIAL TRAINING, LADDER NETWORKS AND OTHERS Mudassar Abbas, Jyri Kivinen, Tapani Raio Department of Computer Science, School of
Worshop trac - ICLR 016 CLOSE-TO-CLEAN REGULARIZATION RELATES VIRTUAL ADVERSARIAL TRAINING, LADDER NETWORKS AND OTHERS Mudassar Abbas, Jyri Kivinen, Tapani Raio Department of Computer Science, School of
Black-box α-divergence Minimization
 Black-box α-divergence Minimization José Miguel Hernández-Lobato, Yingzhen Li, Daniel Hernández-Lobato, Thang Bui, Richard Turner, Harvard University, University of Cambridge, Universidad Autónoma de Madrid.
Black-box α-divergence Minimization José Miguel Hernández-Lobato, Yingzhen Li, Daniel Hernández-Lobato, Thang Bui, Richard Turner, Harvard University, University of Cambridge, Universidad Autónoma de Madrid.
The Success of Deep Generative Models
 The Success of Deep Generative Models Jakub Tomczak AMLAB, University of Amsterdam CERN, 2018 What is AI about? What is AI about? Decision making: What is AI about? Decision making: new data High probability
The Success of Deep Generative Models Jakub Tomczak AMLAB, University of Amsterdam CERN, 2018 What is AI about? What is AI about? Decision making: What is AI about? Decision making: new data High probability
Stochastic Gradient Estimate Variance in Contrastive Divergence and Persistent Contrastive Divergence
 ESANN 0 proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges (Belgium), 7-9 April 0, idoc.com publ., ISBN 97-7707-. Stochastic Gradient
ESANN 0 proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges (Belgium), 7-9 April 0, idoc.com publ., ISBN 97-7707-. Stochastic Gradient
Nishant Gurnani. GAN Reading Group. April 14th, / 107
 Nishant Gurnani GAN Reading Group April 14th, 2017 1 / 107 Why are these Papers Important? 2 / 107 Why are these Papers Important? Recently a large number of GAN frameworks have been proposed - BGAN, LSGAN,
Nishant Gurnani GAN Reading Group April 14th, 2017 1 / 107 Why are these Papers Important? 2 / 107 Why are these Papers Important? Recently a large number of GAN frameworks have been proposed - BGAN, LSGAN,
Convergence Rates of Kernel Quadrature Rules
 Convergence Rates of Kernel Quadrature Rules Francis Bach INRIA - Ecole Normale Supérieure, Paris, France ÉCOLE NORMALE SUPÉRIEURE NIPS workshop on probabilistic integration - Dec. 2015 Outline Introduction
Convergence Rates of Kernel Quadrature Rules Francis Bach INRIA - Ecole Normale Supérieure, Paris, France ÉCOLE NORMALE SUPÉRIEURE NIPS workshop on probabilistic integration - Dec. 2015 Outline Introduction
Supplementary Materials for: f-gan: Training Generative Neural Samplers using Variational Divergence Minimization
 Supplementary Materials for: f-gan: Training Generative Neural Samplers using Variational Divergence Minimization Sebastian Nowozin, Botond Cseke, Ryota Tomioka Machine Intelligence and Perception Group
Supplementary Materials for: f-gan: Training Generative Neural Samplers using Variational Divergence Minimization Sebastian Nowozin, Botond Cseke, Ryota Tomioka Machine Intelligence and Perception Group
Improving Visual Semantic Embedding By Adversarial Contrastive Estimation
 Improving Visual Semantic Embedding By Adversarial Contrastive Estimation Huan Ling Department of Computer Science University of Toronto huan.ling@mail.utoronto.ca Avishek Bose Department of Electrical
Improving Visual Semantic Embedding By Adversarial Contrastive Estimation Huan Ling Department of Computer Science University of Toronto huan.ling@mail.utoronto.ca Avishek Bose Department of Electrical
arxiv: v3 [cs.lg] 10 Sep 2018
![arxiv: v3 [cs.lg] 10 Sep 2018 arxiv: v3 [cs.lg] 10 Sep 2018](/thumbs/89/99070531.jpg) The relativistic discriminator: a key element missing from standard GAN arxiv:1807.00734v3 [cs.lg] 10 Sep 2018 Alexia Jolicoeur-Martineau Lady Davis Institute Montreal, Canada alexia.jolicoeur-martineau@mail.mcgill.ca
The relativistic discriminator: a key element missing from standard GAN arxiv:1807.00734v3 [cs.lg] 10 Sep 2018 Alexia Jolicoeur-Martineau Lady Davis Institute Montreal, Canada alexia.jolicoeur-martineau@mail.mcgill.ca
Understanding GANs: Back to the basics
 Understanding GANs: Back to the basics David Tse Stanford University Princeton University May 15, 2018 Joint work with Soheil Feizi, Farzan Farnia, Tony Ginart, Changho Suh and Fei Xia. GANs at NIPS 2017
Understanding GANs: Back to the basics David Tse Stanford University Princeton University May 15, 2018 Joint work with Soheil Feizi, Farzan Farnia, Tony Ginart, Changho Suh and Fei Xia. GANs at NIPS 2017
arxiv: v4 [cs.cv] 5 Sep 2018
![arxiv: v4 [cs.cv] 5 Sep 2018 arxiv: v4 [cs.cv] 5 Sep 2018](/thumbs/87/97408354.jpg) Wasserstein Divergence for GANs Jiqing Wu 1, Zhiwu Huang 1, Janine Thoma 1, Dinesh Acharya 1, and Luc Van Gool 1,2 arxiv:1712.01026v4 [cs.cv] 5 Sep 2018 1 Computer Vision Lab, ETH Zurich, Switzerland {jwu,zhiwu.huang,jthoma,vangool}@vision.ee.ethz.ch,
Wasserstein Divergence for GANs Jiqing Wu 1, Zhiwu Huang 1, Janine Thoma 1, Dinesh Acharya 1, and Luc Van Gool 1,2 arxiv:1712.01026v4 [cs.cv] 5 Sep 2018 1 Computer Vision Lab, ETH Zurich, Switzerland {jwu,zhiwu.huang,jthoma,vangool}@vision.ee.ethz.ch,
Nonparametric Inference for Auto-Encoding Variational Bayes
 Nonparametric Inference for Auto-Encoding Variational Bayes Erik Bodin * Iman Malik * Carl Henrik Ek * Neill D. F. Campbell * University of Bristol University of Bath Variational approximations are an
Nonparametric Inference for Auto-Encoding Variational Bayes Erik Bodin * Iman Malik * Carl Henrik Ek * Neill D. F. Campbell * University of Bristol University of Bath Variational approximations are an
arxiv: v1 [cs.lg] 22 Mar 2016
![arxiv: v1 [cs.lg] 22 Mar 2016 arxiv: v1 [cs.lg] 22 Mar 2016](/thumbs/72/67041268.jpg) Information Theoretic-Learning Auto-Encoder arxiv:1603.06653v1 [cs.lg] 22 Mar 2016 Eder Santana University of Florida Jose C. Principe University of Florida Abstract Matthew Emigh University of Florida
Information Theoretic-Learning Auto-Encoder arxiv:1603.06653v1 [cs.lg] 22 Mar 2016 Eder Santana University of Florida Jose C. Principe University of Florida Abstract Matthew Emigh University of Florida
A Unified View of Deep Generative Models
 SAILING LAB Laboratory for Statistical Artificial InteLigence & INtegreative Genomics A Unified View of Deep Generative Models Zhiting Hu and Eric Xing Petuum Inc. Carnegie Mellon University 1 Deep generative
SAILING LAB Laboratory for Statistical Artificial InteLigence & INtegreative Genomics A Unified View of Deep Generative Models Zhiting Hu and Eric Xing Petuum Inc. Carnegie Mellon University 1 Deep generative
Normalization Techniques in Training of Deep Neural Networks
 Normalization Techniques in Training of Deep Neural Networks Lei Huang ( 黄雷 ) State Key Laboratory of Software Development Environment, Beihang University Mail:huanglei@nlsde.buaa.edu.cn August 17 th,
Normalization Techniques in Training of Deep Neural Networks Lei Huang ( 黄雷 ) State Key Laboratory of Software Development Environment, Beihang University Mail:huanglei@nlsde.buaa.edu.cn August 17 th,
Negative Momentum for Improved Game Dynamics
 Negative Momentum for Improved Game Dynamics Gauthier Gidel Reyhane Askari Hemmat Mohammad Pezeshki Gabriel Huang Rémi Lepriol Simon Lacoste-Julien Ioannis Mitliagkas Mila & DIRO, Université de Montréal
Negative Momentum for Improved Game Dynamics Gauthier Gidel Reyhane Askari Hemmat Mohammad Pezeshki Gabriel Huang Rémi Lepriol Simon Lacoste-Julien Ioannis Mitliagkas Mila & DIRO, Université de Montréal
Adversarial Sequential Monte Carlo
 Adversarial Sequential Monte Carlo Kira Kempinska Department of Security and Crime Science University College London London, WC1E 6BT kira.kowalska.13@ucl.ac.uk John Shawe-Taylor Department of Computer
Adversarial Sequential Monte Carlo Kira Kempinska Department of Security and Crime Science University College London London, WC1E 6BT kira.kowalska.13@ucl.ac.uk John Shawe-Taylor Department of Computer
arxiv: v2 [cs.lg] 7 Jun 2018
![arxiv: v2 [cs.lg] 7 Jun 2018 arxiv: v2 [cs.lg] 7 Jun 2018](/thumbs/93/111471429.jpg) Calvin Seward 2 Thomas Unterthiner 2 Urs Bergmann Nikolay Jetchev Sepp Hochreiter 2 arxiv:802.0459v2 cs.lg 7 Jun 208 Abstract GANs excel at learning high dimensional distributions, but they can update
Calvin Seward 2 Thomas Unterthiner 2 Urs Bergmann Nikolay Jetchev Sepp Hochreiter 2 arxiv:802.0459v2 cs.lg 7 Jun 208 Abstract GANs excel at learning high dimensional distributions, but they can update
Introduction to Deep Neural Networks
 Introduction to Deep Neural Networks Presenter: Chunyuan Li Pattern Classification and Recognition (ECE 681.01) Duke University April, 2016 Outline 1 Background and Preliminaries Why DNNs? Model: Logistic
Introduction to Deep Neural Networks Presenter: Chunyuan Li Pattern Classification and Recognition (ECE 681.01) Duke University April, 2016 Outline 1 Background and Preliminaries Why DNNs? Model: Logistic
LEARNING TO SAMPLE WITH ADVERSARIALLY LEARNED LIKELIHOOD-RATIO
 LEARNING TO SAMPLE WITH ADVERSARIALLY LEARNED LIKELIHOOD-RATIO Chunyuan Li, Jianqiao Li, Guoyin Wang & Lawrence Carin Duke University {chunyuan.li,jianqiao.li,guoyin.wang,lcarin}@duke.edu ABSTRACT We link
LEARNING TO SAMPLE WITH ADVERSARIALLY LEARNED LIKELIHOOD-RATIO Chunyuan Li, Jianqiao Li, Guoyin Wang & Lawrence Carin Duke University {chunyuan.li,jianqiao.li,guoyin.wang,lcarin}@duke.edu ABSTRACT We link
Need for Deep Networks Perceptron. Can only model linear functions. Kernel Machines. Non-linearity provided by kernels
 Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Natural Gradients via the Variational Predictive Distribution
 Natural Gradients via the Variational Predictive Distribution Da Tang Columbia University datang@cs.columbia.edu Rajesh Ranganath New York University rajeshr@cims.nyu.edu Abstract Variational inference
Natural Gradients via the Variational Predictive Distribution Da Tang Columbia University datang@cs.columbia.edu Rajesh Ranganath New York University rajeshr@cims.nyu.edu Abstract Variational inference
Variational Autoencoders (VAEs)
 September 26 & October 3, 2017 Section 1 Preliminaries Kullback-Leibler divergence KL divergence (continuous case) p(x) andq(x) are two density distributions. Then the KL-divergence is defined as Z KL(p
September 26 & October 3, 2017 Section 1 Preliminaries Kullback-Leibler divergence KL divergence (continuous case) p(x) andq(x) are two density distributions. Then the KL-divergence is defined as Z KL(p
Deep Learning Year in Review 2016: Computer Vision Perspective
 Deep Learning Year in Review 2016: Computer Vision Perspective Alex Kalinin, PhD Candidate Bioinformatics @ UMich alxndrkalinin@gmail.com @alxndrkalinin Architectures Summary of CNN architecture development
Deep Learning Year in Review 2016: Computer Vision Perspective Alex Kalinin, PhD Candidate Bioinformatics @ UMich alxndrkalinin@gmail.com @alxndrkalinin Architectures Summary of CNN architecture development
arxiv: v3 [stat.ml] 6 Dec 2017
![arxiv: v3 [stat.ml] 6 Dec 2017 arxiv: v3 [stat.ml] 6 Dec 2017](/thumbs/84/89568555.jpg) Wasserstein GAN arxiv:1701.07875v3 [stat.ml] 6 Dec 2017 Martin Arjovsky 1, Soumith Chintala 2, and Léon Bottou 1,2 1 Introduction 1 Courant Institute of Mathematical Sciences 2 Facebook AI Research The
Wasserstein GAN arxiv:1701.07875v3 [stat.ml] 6 Dec 2017 Martin Arjovsky 1, Soumith Chintala 2, and Léon Bottou 1,2 1 Introduction 1 Courant Institute of Mathematical Sciences 2 Facebook AI Research The
Advances in kernel exponential families
 Advances in kernel exponential families Arthur Gretton Gatsby Computational Neuroscience Unit, University College London NIPS, 2017 1/39 Outline Motivating application: Fast estimation of complex multivariate
Advances in kernel exponential families Arthur Gretton Gatsby Computational Neuroscience Unit, University College London NIPS, 2017 1/39 Outline Motivating application: Fast estimation of complex multivariate
Generative Adversarial Networks (GANs) Ian Goodfellow, OpenAI Research Scientist Presentation at Berkeley Artificial Intelligence Lab,
 Generative Adversarial Networks (GANs) Ian Goodfellow, OpenAI Research Scientist Presentation at Berkeley Artificial Intelligence Lab, 2016-08-31 Generative Modeling Density estimation Sample generation
Generative Adversarial Networks (GANs) Ian Goodfellow, OpenAI Research Scientist Presentation at Berkeley Artificial Intelligence Lab, 2016-08-31 Generative Modeling Density estimation Sample generation
A Linear-Time Kernel Goodness-of-Fit Test
 A Linear-Time Kernel Goodness-of-Fit Test Wittawat Jitkrittum 1; Wenkai Xu 1 Zoltán Szabó 2 NIPS 2017 Best paper! Kenji Fukumizu 3 Arthur Gretton 1 wittawatj@gmail.com 1 Gatsby Unit, University College
A Linear-Time Kernel Goodness-of-Fit Test Wittawat Jitkrittum 1; Wenkai Xu 1 Zoltán Szabó 2 NIPS 2017 Best paper! Kenji Fukumizu 3 Arthur Gretton 1 wittawatj@gmail.com 1 Gatsby Unit, University College
Need for Deep Networks Perceptron. Can only model linear functions. Kernel Machines. Non-linearity provided by kernels
 Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Need for Deep Networks Perceptron Can only model linear functions Kernel Machines Non-linearity provided by kernels Need to design appropriate kernels (possibly selecting from a set, i.e. kernel learning)
Bayesian Semi-supervised Learning with Deep Generative Models
 Bayesian Semi-supervised Learning with Deep Generative Models Jonathan Gordon Department of Engineering Cambridge University jg801@cam.ac.uk José Miguel Hernández-Lobato Department of Engineering Cambridge
Bayesian Semi-supervised Learning with Deep Generative Models Jonathan Gordon Department of Engineering Cambridge University jg801@cam.ac.uk José Miguel Hernández-Lobato Department of Engineering Cambridge
Auto-Encoding Variational Bayes
 Auto-Encoding Variational Bayes Diederik P Kingma, Max Welling June 18, 2018 Diederik P Kingma, Max Welling Auto-Encoding Variational Bayes June 18, 2018 1 / 39 Outline 1 Introduction 2 Variational Lower
Auto-Encoding Variational Bayes Diederik P Kingma, Max Welling June 18, 2018 Diederik P Kingma, Max Welling Auto-Encoding Variational Bayes June 18, 2018 1 / 39 Outline 1 Introduction 2 Variational Lower
Multiplicative Noise Channel in Generative Adversarial Networks
 Multiplicative Noise Channel in Generative Adversarial Networks Xinhan Di Deepearthgo Deepearthgo@gmail.com Pengqian Yu National University of Singapore yupengqian@u.nus.edu Abstract Additive Gaussian
Multiplicative Noise Channel in Generative Adversarial Networks Xinhan Di Deepearthgo Deepearthgo@gmail.com Pengqian Yu National University of Singapore yupengqian@u.nus.edu Abstract Additive Gaussian
AdaGAN: Boosting Generative Models
 AdaGAN: Boosting Generative Models Ilya Tolstikhin ilya@tuebingen.mpg.de joint work with Gelly 2, Bousquet 2, Simon-Gabriel 1, Schölkopf 1 1 MPI for Intelligent Systems 2 Google Brain Radford et al., 2015)
AdaGAN: Boosting Generative Models Ilya Tolstikhin ilya@tuebingen.mpg.de joint work with Gelly 2, Bousquet 2, Simon-Gabriel 1, Schölkopf 1 1 MPI for Intelligent Systems 2 Google Brain Radford et al., 2015)
Generative adversarial networks
 14-1: Generative adversarial networks Prof. J.C. Kao, UCLA Generative adversarial networks Why GANs? GAN intuition GAN equilibrium GAN implementation Practical considerations Much of these notes are based
14-1: Generative adversarial networks Prof. J.C. Kao, UCLA Generative adversarial networks Why GANs? GAN intuition GAN equilibrium GAN implementation Practical considerations Much of these notes are based
Variational AutoEncoder: An Introduction and Recent Perspectives
 Metode de optimizare Riemanniene pentru învățare profundă Proiect cofinanțat din Fondul European de Dezvoltare Regională prin Programul Operațional Competitivitate 2014-2020 Variational AutoEncoder: An
Metode de optimizare Riemanniene pentru învățare profundă Proiect cofinanțat din Fondul European de Dezvoltare Regională prin Programul Operațional Competitivitate 2014-2020 Variational AutoEncoder: An
Provable Non-Convex Min-Max Optimization
 Provable Non-Convex Min-Max Optimization Mingrui Liu, Hassan Rafique, Qihang Lin, Tianbao Yang Department of Computer Science, The University of Iowa, Iowa City, IA, 52242 Department of Mathematics, The
Provable Non-Convex Min-Max Optimization Mingrui Liu, Hassan Rafique, Qihang Lin, Tianbao Yang Department of Computer Science, The University of Iowa, Iowa City, IA, 52242 Department of Mathematics, The
Imitation Learning via Kernel Mean Embedding
 Imitation Learning via Kernel Mean Embedding Kee-Eung Kim School of Computer Science KAIST kekim@cs.kaist.ac.kr Hyun Soo Park Department of Computer Science and Engineering University of Minnesota hspark@umn.edu
Imitation Learning via Kernel Mean Embedding Kee-Eung Kim School of Computer Science KAIST kekim@cs.kaist.ac.kr Hyun Soo Park Department of Computer Science and Engineering University of Minnesota hspark@umn.edu
Unsupervised Learning
 CS 3750 Advanced Machine Learning hkc6@pitt.edu Unsupervised Learning Data: Just data, no labels Goal: Learn some underlying hidden structure of the data P(, ) P( ) Principle Component Analysis (Dimensionality
CS 3750 Advanced Machine Learning hkc6@pitt.edu Unsupervised Learning Data: Just data, no labels Goal: Learn some underlying hidden structure of the data P(, ) P( ) Principle Component Analysis (Dimensionality
Learning Deep Architectures
 Learning Deep Architectures Yoshua Bengio, U. Montreal Microsoft Cambridge, U.K. July 7th, 2009, Montreal Thanks to: Aaron Courville, Pascal Vincent, Dumitru Erhan, Olivier Delalleau, Olivier Breuleux,
Learning Deep Architectures Yoshua Bengio, U. Montreal Microsoft Cambridge, U.K. July 7th, 2009, Montreal Thanks to: Aaron Courville, Pascal Vincent, Dumitru Erhan, Olivier Delalleau, Olivier Breuleux,
GANS for Sequences of Discrete Elements with the Gumbel-softmax Distribution
 GANS for Sequences of Discrete Elements with the Gumbel-softmax Distribution Matt Kusner, Jose Miguel Hernandez-Lobato Satya Krishna Gorti University of Toronto Satya Krishna Gorti CSC2547 1 / 16 Introduction
GANS for Sequences of Discrete Elements with the Gumbel-softmax Distribution Matt Kusner, Jose Miguel Hernandez-Lobato Satya Krishna Gorti University of Toronto Satya Krishna Gorti CSC2547 1 / 16 Introduction
Variational Dropout via Empirical Bayes
 Variational Dropout via Empirical Bayes Valery Kharitonov 1 kharvd@gmail.com Dmitry Molchanov 1, dmolch111@gmail.com Dmitry Vetrov 1, vetrovd@yandex.ru 1 National Research University Higher School of Economics,
Variational Dropout via Empirical Bayes Valery Kharitonov 1 kharvd@gmail.com Dmitry Molchanov 1, dmolch111@gmail.com Dmitry Vetrov 1, vetrovd@yandex.ru 1 National Research University Higher School of Economics,
Analysis of Spectral Kernel Design based Semi-supervised Learning
 Analysis of Spectral Kernel Design based Semi-supervised Learning Tong Zhang IBM T. J. Watson Research Center Yorktown Heights, NY 10598 Rie Kubota Ando IBM T. J. Watson Research Center Yorktown Heights,
Analysis of Spectral Kernel Design based Semi-supervised Learning Tong Zhang IBM T. J. Watson Research Center Yorktown Heights, NY 10598 Rie Kubota Ando IBM T. J. Watson Research Center Yorktown Heights,
Variational Autoencoders
 Variational Autoencoders Recap: Story so far A classification MLP actually comprises two components A feature extraction network that converts the inputs into linearly separable features Or nearly linearly
Variational Autoencoders Recap: Story so far A classification MLP actually comprises two components A feature extraction network that converts the inputs into linearly separable features Or nearly linearly
arxiv: v1 [stat.ml] 24 May 2018
![arxiv: v1 [stat.ml] 24 May 2018 arxiv: v1 [stat.ml] 24 May 2018](/thumbs/89/99416797.jpg) Primal-Dual Wasserstein GAN Mevlana Gemici arxiv:805.09575v [stat.ml] 24 May 208 mevlana.gemici@gmail.com Zeynep Akata Max Welling zeynepakata@gmail.com welling.max@gmail.com Abstract We introduce Primal-Dual
Primal-Dual Wasserstein GAN Mevlana Gemici arxiv:805.09575v [stat.ml] 24 May 208 mevlana.gemici@gmail.com Zeynep Akata Max Welling zeynepakata@gmail.com welling.max@gmail.com Abstract We introduce Primal-Dual
Eve: A Gradient Based Optimization Method with Locally and Globally Adaptive Learning Rates
 Eve: A Gradient Based Optimization Method with Locally and Globally Adaptive Learning Rates Hiroaki Hayashi 1,* Jayanth Koushik 1,* Graham Neubig 1 arxiv:1611.01505v3 [cs.lg] 11 Jun 2018 Abstract Adaptive
Eve: A Gradient Based Optimization Method with Locally and Globally Adaptive Learning Rates Hiroaki Hayashi 1,* Jayanth Koushik 1,* Graham Neubig 1 arxiv:1611.01505v3 [cs.lg] 11 Jun 2018 Abstract Adaptive
what can deep learning learn from linear regression? Benjamin Recht University of California, Berkeley
 what can deep learning learn from linear regression? Benjamin Recht University of California, Berkeley Collaborators Joint work with Samy Bengio, Moritz Hardt, Michael Jordan, Jason Lee, Max Simchowitz,
what can deep learning learn from linear regression? Benjamin Recht University of California, Berkeley Collaborators Joint work with Samy Bengio, Moritz Hardt, Michael Jordan, Jason Lee, Max Simchowitz,
arxiv: v1 [cs.lg] 28 Dec 2017
![arxiv: v1 [cs.lg] 28 Dec 2017 arxiv: v1 [cs.lg] 28 Dec 2017](/thumbs/80/82263025.jpg) PixelSNAIL: An Improved Autoregressive Generative Model arxiv:1712.09763v1 [cs.lg] 28 Dec 2017 Xi Chen, Nikhil Mishra, Mostafa Rohaninejad, Pieter Abbeel Embodied Intelligence UC Berkeley, Department of
PixelSNAIL: An Improved Autoregressive Generative Model arxiv:1712.09763v1 [cs.lg] 28 Dec 2017 Xi Chen, Nikhil Mishra, Mostafa Rohaninejad, Pieter Abbeel Embodied Intelligence UC Berkeley, Department of
Based on the original slides of Hung-yi Lee
 Based on the original slides of Hung-yi Lee New Activation Function Rectified Linear Unit (ReLU) σ z a a = z Reason: 1. Fast to compute 2. Biological reason a = 0 [Xavier Glorot, AISTATS 11] [Andrew L.
Based on the original slides of Hung-yi Lee New Activation Function Rectified Linear Unit (ReLU) σ z a a = z Reason: 1. Fast to compute 2. Biological reason a = 0 [Xavier Glorot, AISTATS 11] [Andrew L.
arxiv: v3 [stat.ml] 12 Mar 2018
![arxiv: v3 [stat.ml] 12 Mar 2018 arxiv: v3 [stat.ml] 12 Mar 2018](/thumbs/81/83158661.jpg) Wasserstein Auto-Encoders Ilya Tolstikhin 1, Olivier Bousquet 2, Sylvain Gelly 2, and Bernhard Schölkopf 1 1 Max Planck Institute for Intelligent Systems 2 Google Brain arxiv:1711.01558v3 [stat.ml] 12
Wasserstein Auto-Encoders Ilya Tolstikhin 1, Olivier Bousquet 2, Sylvain Gelly 2, and Bernhard Schölkopf 1 1 Max Planck Institute for Intelligent Systems 2 Google Brain arxiv:1711.01558v3 [stat.ml] 12
Deep Neural Networks as Gaussian Processes
 Deep Neural Networks as Gaussian Processes Jaehoon Lee, Yasaman Bahri, Roman Novak, Samuel S. Schoenholz, Jeffrey Pennington, Jascha Sohl-Dickstein Google Brain {jaehlee, yasamanb, romann, schsam, jpennin,
Deep Neural Networks as Gaussian Processes Jaehoon Lee, Yasaman Bahri, Roman Novak, Samuel S. Schoenholz, Jeffrey Pennington, Jascha Sohl-Dickstein Google Brain {jaehlee, yasamanb, romann, schsam, jpennin,
arxiv: v3 [stat.ml] 15 Oct 2017
![arxiv: v3 [stat.ml] 15 Oct 2017 arxiv: v3 [stat.ml] 15 Oct 2017](/thumbs/86/94792275.jpg) Non-parametric estimation of Jensen-Shannon Divergence in Generative Adversarial Network training arxiv:1705.09199v3 [stat.ml] 15 Oct 2017 Mathieu Sinn IBM Research Ireland Mulhuddart, Dublin 15, Ireland
Non-parametric estimation of Jensen-Shannon Divergence in Generative Adversarial Network training arxiv:1705.09199v3 [stat.ml] 15 Oct 2017 Mathieu Sinn IBM Research Ireland Mulhuddart, Dublin 15, Ireland
High Order LSTM/GRU. Wenjie Luo. January 19, 2016
 High Order LSTM/GRU Wenjie Luo January 19, 2016 1 Introduction RNN is a powerful model for sequence data but suffers from gradient vanishing and explosion, thus difficult to be trained to capture long
High Order LSTM/GRU Wenjie Luo January 19, 2016 1 Introduction RNN is a powerful model for sequence data but suffers from gradient vanishing and explosion, thus difficult to be trained to capture long
arxiv: v7 [cs.lg] 27 Jul 2018
![arxiv: v7 [cs.lg] 27 Jul 2018 arxiv: v7 [cs.lg] 27 Jul 2018](/thumbs/86/94137155.jpg) How Generative Adversarial Networks and Their Variants Work: An Overview of GAN Yongjun Hong, Uiwon Hwang, Jaeyoon Yoo and Sungroh Yoon Department of Electrical & Computer Engineering Seoul National University,
How Generative Adversarial Networks and Their Variants Work: An Overview of GAN Yongjun Hong, Uiwon Hwang, Jaeyoon Yoo and Sungroh Yoon Department of Electrical & Computer Engineering Seoul National University,
The Numerics of GANs
 The Numerics of GANs Lars Mescheder Autonomous Vision Group MPI Tübingen lars.mescheder@tuebingen.mpg.de Sebastian Nowozin Machine Intelligence and Perception Group Microsoft Research sebastian.nowozin@microsoft.com
The Numerics of GANs Lars Mescheder Autonomous Vision Group MPI Tübingen lars.mescheder@tuebingen.mpg.de Sebastian Nowozin Machine Intelligence and Perception Group Microsoft Research sebastian.nowozin@microsoft.com
Introduction to Convolutional Neural Networks (CNNs)
 Introduction to Convolutional Neural Networks (CNNs) nojunk@snu.ac.kr http://mipal.snu.ac.kr Department of Transdisciplinary Studies Seoul National University, Korea Jan. 2016 Many slides are from Fei-Fei
Introduction to Convolutional Neural Networks (CNNs) nojunk@snu.ac.kr http://mipal.snu.ac.kr Department of Transdisciplinary Studies Seoul National University, Korea Jan. 2016 Many slides are from Fei-Fei
EE613 Machine Learning for Engineers. Kernel methods Support Vector Machines. jean-marc odobez 2015
 EE613 Machine Learning for Engineers Kernel methods Support Vector Machines jean-marc odobez 2015 overview Kernel methods introductions and main elements defining kernels Kernelization of k-nn, K-Means,
EE613 Machine Learning for Engineers Kernel methods Support Vector Machines jean-marc odobez 2015 overview Kernel methods introductions and main elements defining kernels Kernelization of k-nn, K-Means,
GANs, GANs everywhere
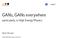 GANs, GANs everywhere particularly, in High Energy Physics Maxim Borisyak Yandex, NRU Higher School of Economics Generative Generative models Given samples of a random variable X find X such as: P X P
GANs, GANs everywhere particularly, in High Energy Physics Maxim Borisyak Yandex, NRU Higher School of Economics Generative Generative models Given samples of a random variable X find X such as: P X P
Two at Once: Enhancing Learning and Generalization Capacities via IBN-Net
 Two at Once: Enhancing Learning and Generalization Capacities via IBN-Net Supplementary Material Xingang Pan 1, Ping Luo 1, Jianping Shi 2, and Xiaoou Tang 1 1 CUHK-SenseTime Joint Lab, The Chinese University
Two at Once: Enhancing Learning and Generalization Capacities via IBN-Net Supplementary Material Xingang Pan 1, Ping Luo 1, Jianping Shi 2, and Xiaoou Tang 1 1 CUHK-SenseTime Joint Lab, The Chinese University
Lecture 17: Neural Networks and Deep Learning
 UVA CS 6316 / CS 4501-004 Machine Learning Fall 2016 Lecture 17: Neural Networks and Deep Learning Jack Lanchantin Dr. Yanjun Qi 1 Neurons 1-Layer Neural Network Multi-layer Neural Network Loss Functions
UVA CS 6316 / CS 4501-004 Machine Learning Fall 2016 Lecture 17: Neural Networks and Deep Learning Jack Lanchantin Dr. Yanjun Qi 1 Neurons 1-Layer Neural Network Multi-layer Neural Network Loss Functions
Generative Adversarial Networks, and Applications
 Generative Adversarial Networks, and Applications Ali Mirzaei Nimish Srivastava Kwonjoon Lee Songting Xu CSE 252C 4/12/17 2/44 Outline: Generative Models vs Discriminative Models (Background) Generative
Generative Adversarial Networks, and Applications Ali Mirzaei Nimish Srivastava Kwonjoon Lee Songting Xu CSE 252C 4/12/17 2/44 Outline: Generative Models vs Discriminative Models (Background) Generative
COMPARING FIXED AND ADAPTIVE COMPUTATION TIME FOR RE-
 Workshop track - ICLR COMPARING FIXED AND ADAPTIVE COMPUTATION TIME FOR RE- CURRENT NEURAL NETWORKS Daniel Fojo, Víctor Campos, Xavier Giró-i-Nieto Universitat Politècnica de Catalunya, Barcelona Supercomputing
Workshop track - ICLR COMPARING FIXED AND ADAPTIVE COMPUTATION TIME FOR RE- CURRENT NEURAL NETWORKS Daniel Fojo, Víctor Campos, Xavier Giró-i-Nieto Universitat Politècnica de Catalunya, Barcelona Supercomputing
Improved Bayesian Compression
 Improved Bayesian Compression Marco Federici University of Amsterdam marco.federici@student.uva.nl Karen Ullrich University of Amsterdam karen.ullrich@uva.nl Max Welling University of Amsterdam Canadian
Improved Bayesian Compression Marco Federici University of Amsterdam marco.federici@student.uva.nl Karen Ullrich University of Amsterdam karen.ullrich@uva.nl Max Welling University of Amsterdam Canadian
CONTINUOUS-TIME FLOWS FOR EFFICIENT INFER-
 CONTINUOUS-TIME FLOWS FOR EFFICIENT INFER- ENCE AND DENSITY ESTIMATION Anonymous authors Paper under double-blind review ABSTRACT Two fundamental problems in unsupervised learning are efficient inference
CONTINUOUS-TIME FLOWS FOR EFFICIENT INFER- ENCE AND DENSITY ESTIMATION Anonymous authors Paper under double-blind review ABSTRACT Two fundamental problems in unsupervised learning are efficient inference
Deep learning with differential Gaussian process flows
 Deep learning with differential Gaussian process flows Pashupati Hegde Markus Heinonen Harri Lähdesmäki Samuel Kaski Helsinki Institute for Information Technology HIIT Department of Computer Science, Aalto
Deep learning with differential Gaussian process flows Pashupati Hegde Markus Heinonen Harri Lähdesmäki Samuel Kaski Helsinki Institute for Information Technology HIIT Department of Computer Science, Aalto
Tutorial on: Optimization I. (from a deep learning perspective) Jimmy Ba
 Tutorial on: Optimization I (from a deep learning perspective) Jimmy Ba Outline Random search v.s. gradient descent Finding better search directions Design white-box optimization methods to improve computation
Tutorial on: Optimization I (from a deep learning perspective) Jimmy Ba Outline Random search v.s. gradient descent Finding better search directions Design white-box optimization methods to improve computation
