A New Achievability Scheme for the Relay Channel

Transcription

1 A New Achievability Scheme for the Relay Chael Wei Kag Seur Ulukus Departmet of Electrical ad Computer Egieerig Uiversity of Marylad, College Park, MD October 4, 2007 Abstract I this paper, we propose a ew codig scheme for the geeral relay chael. This codig scheme is i the form of a block Markov code. The trasmitter uses a superpositio Markov code. The relay compresses the received sigal ad maps the compressed versio of the received sigal ito a codeword coditioed o the codeword of the previous block. The receiver performs joit decodig after it has received all of the B blocks. We show that this codig scheme ca be viewed as a geeralizatio of the well-kow Compress-Ad-Forward (CAF scheme proposed by Cover ad El Gamal. Our codig scheme provides optios for preservig the correlatio betwee the chael iputs of the trasmitter ad the relay, which is ot possible i the CAF scheme. Thus, our proposed scheme may potetially yield a larger achievable rate tha the CAF scheme. This work was supported by NSF Grats CCR 03-3, CCF ad CCF , ad was preseted i part at IEEE Iformatio Theory Workshop, Lake Tahoe, CA, September 2007.

2 Itroductio As the simplest model for cooperative commuicatios, relay chael has attracted plety of attetio sice 97, whe it was first itroduced by va der Meule []. I 979, Cover ad El Gamal proposed two major codig schemes for the relay chael [2]. These two schemes are widely kow as Decode-Ad-Forward (DAF ad Compress-Ad-Forward (CAF today; see [3] for a recet review. These two codig schemes represet two differet types of cooperatio. I DAF, the cooperatio is relatively obvious, where the relay decodes the message from the trasmitter, ad the trasmitter ad the relay cooperatively trasmit the costructed commo iformatio to the receiver i the ext block. I CAF, the cooperatio spirit is less easy to recogize, as the message is set by the trasmitter oly oce. However, the relay cooperates with the trasmitter by compressig ad sedig its sigal to the receiver. The rate gais i these achievable schemes are due to the fact that, through the chael from the trasmitter to the relay, correlatio is created betwee the trasmitter ad the relay, ad this correlatio is utilized to improve the rates. I the DAF scheme, correlatio is created ad the utilized i a block Markov codig structure. More specifically, a full correlatio is created by decodig the message fully at the relay, which eables the trasmitter ad the relay to create ay kid of joit distributio for the chael iputs i the ext block. The shortcomig of the DAF scheme is that by forcig the relay to decode the message i its etirety, it limits the overall achievable rate by the rate from the trasmitter to the relay. I cotrast, by ot forcig a full decodig at the relay, the CAF scheme does ot limit the overall rate by the rate from the trasmitter to the relay, ad may yield higher overall rates. The shortcomig of the CAF scheme, o the other had, is that the correlatio offered by the block codig structure is ot utilized effectively, sice i each block the chael iputs X ad X from the trasmitter ad the relay are idepedet, as the trasmitter seds the message oly oce. However, the essece of good codig schemes i multi-user systems with correlated sources (e.g., [4, 5] is to preserve the correlatio of the sources i the chael iputs. Motivated by this basic observatio, i this paper, we propose a ew codig scheme for the relay chael, that is based o the idea of preservig the correlatio i the chael iputs from the trasmitter ad the relay. We will show that our ew codig scheme may be viewed as a more geeral versio of the CAF scheme, ad therefore, our ew codig scheme may potetially yield larger rates tha the CAF scheme. Our proposed scheme ca be further combied with the DAF scheme to yield rates that are potetially larger tha those offered by both DAF ad CAF schemes, similar i spirit to [2, Theorem 7]. Our ew achievability scheme for the relay chael may be viewed as a variatio of the codig scheme of Ahlswede ad Ha [5] for the multiple access chael with a correlated helper. I our work, we view the relay as the helper because the receiver does ot eed to decode the iformatio set by the relay. Also, we ote that the relay is a correlated helper as the commuicatio chael from the trasmitter to the relay provides relay for free a 2

3 correlated versio of the sigal set by the trasmitter. The key aspects of the Ahlswede- Ha [5] scheme are: to preserve the correlatio betwee the chael iputs of the trasmitter ad the helper (relay, ad for the receiver to decode a virtual source, a compressed versio of the helper, but ot the etire sigal of the helper. Our ew codig scheme is i the form of block Markov codig. The trasmitter uses a superpositio Markov code, similar to the oe used i the DAF scheme [2], except i the radom codebook geeratio stage, a method similar to the oe i [4] is used i order to preserve the correlatio betwee the blocks. Thus, i each block, the fresh iformatio message is mapped ito a codeword coditioed o the codeword of the previous block. Therefore, the overall codebook at the trasmitter has a tree structure, where the codewords i block l emaate from the codewords i block l. The depth of the tree is. A similar strategy is applied at the relay side where the compressed versio of the received sigal is mapped ito a two-block-log codeword coditioed o the codeword of the previous block. Therefore, the overall codebook at the relay has a tree structure as well. As a result of this codig strategy, we successfully preserve the correlatio betwee the chael iputs of the trasmitter ad the relay. However, ulike the DAF scheme where a full correlatio is acquired through decodig at the relay, our scheme provides oly a partially correlated helper at the relay by ot tryig to decode the trasmitter s sigal fully. From [4,5], we ote that the chael iputs are correlated through the virtual sources i our case, ad therefore, the chael iputs betwee the cosecutive blocks are correlated. This correlatio betwee the blocks will surely hurt the achievable rate. The correlatio betwee the blocks is the price we pay for preservig the correlatio betwee the chael iputs of the trasmitter ad the relay withi ay give block. At the decodig stage, we perform joit decodig for the etire B blocks after all of the B blocks have bee received, which is differet compared with the DAF ad CAF schemes. The reaso for performig joit decodig at the receiver is that due to the correlatio betwee the blocks, decodig at ay time before the ed of all the B blocks would decrease the achievable rate. We ote that joit decodig icreases the decodig complexity ad the delay as compared to DAF ad CAF, though either of these is a major cocer i a iformatio theoretic cotext. The oly problem with the joit decodig strategy is that it makes the aalysis difficult as it requires the evaluatio of some mutual iformatio expressios ivolvig the joit probability distributios of up to B blocks of codes, where B is very large. The aalysis of the error evets provides us three coditios cotaiig mutual iformatio expressios ivolvig ifiite letters of the uderlyig radom process. Evaluatio of these mutual iformatio expressios is very difficult, if ot impossible. To obtai a computable result, we lower boud these mutual iformatios by otig some Markov structure i the uderlyig radom process. This operatio gives us three coditios to be satisfied by the achievable rates. These coditios ivolve eleve variables, the two chael iputs from the trasmitter ad the relay, the two chael outputs at the relay ad the receiver 3

4 ad the compressed versio of the chael output at the relay, i two cosecutive blocks, ad the chael iput from the trasmitter i the previous block. We fiish our aalysis by revisitig the CAF scheme. We develop a equivalet represetatio for the achievable rates give i [2] for the CAF scheme. We the show that this equivalet represetatio for the achievable rates for the CAF scheme is a special case of the achievable rates i our ew codig scheme, which is obtaied by a special selectio of the eleve variables metioed above. We therefore coclude that our proposed codig scheme yields potetially larger rates tha the CAF scheme. More importatly, our ew codig scheme creates more possibilities, ad therefore a spectrum of ew achievable schemes for the relay chael through the selectio of the uderlyig probability distributio, ad yields the well-kow CAF scheme as a special case, correspodig to a particular selectio of the uderlyig probability distributio. 2 The Relay Chael Cosider a relay chael with fiite iput alphabets X, X ad fiite output alphabets Y, Y, characterized by the trasitio probability p(y, y x, x. A -legth block code for the relay chael p(y, y x, x cosists of ecoders f, f i, i =,..., ad a decoder g f : M X f i : Y i X, i =,..., g : Y M where the ecoder at the trasmitter seds x = f(m ito the chael, where m M {, 2,..., M}; the ecoder at the relay at the ith chael istace seds x i = f i (y i ito the chael; the decoder outputs ˆm = g(y. The average probability of error is defied as P e = M m M P r( ˆm m m is trasmitted ( A rate R is achievable for the relay chael p(y, y x, x if for every 0 < ǫ <, η > 0, ad every sufficietly large, there exists a -legth block code (f, f i, g with P e ǫ ad l M R η. 3 A New Achievability Scheme for the Relay Chael We adopt a block Markov codig scheme, similar to the DAF ad CAF schemes. We have overall B blocks. I each block, we trasmit codewords of legth. We deote the variables i the lth block with a subscript of [l]. We deote -letter codewords trasmitted i each block with a superscript of. Followig the stadard relay chael literature, we deote 4

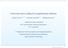
5 the (radom sigals trasmitted by the trasmitter ad the relay by X ad X, the sigals received at the receiver ad the relay by Y ad Y, ad the compressed versio of Y at the relay by Ŷ. The realizatios of these radom sigals will be deoted by lower-case letters. For example, the -letter sigals trasmitted by the trasmitter ad the relay i the lth block will be represeted by x [l] ad x [l]. Cosider the followig discrete time statioary Markov process G [l] (X, Ŷ, X, y, Y [l] for l = 0,,..., B, with the trasitio probability distributio p ( (x, ŷ, x, y, y [l] (x, ŷ, x, y, y [l ] = p(x [l] x [l ] p(y [l], y [l] x [l], x [l] p(x [l] ŷ [l ] p(ŷ [l] y [l], x [l] (2 The codebook geeratio ad the ecodig scheme for the lth block, l =,...,B, are as follows. Radom codebook geeratio: Let (x [l ] (m [l ], x [l ], y [l ], y [l ] deote the trasmitted ad the received sigals i the (l st block, where m [l ] is the message set by the trasmitter i the (l st block. A illustratio of the codebook structure is show i Figure.. For each x [l ] (m [l ] sequece, geerate M sequeces, where x [l] (m [l], the m [l] th sequece, is geerated idepedetly accordig to i= p(x i[l] x i[l ]. Here, every codeword i the (l st block expads ito a codebook i the lth block. This expasio is idicated by a directed coe from x [l ] to x [l] i Figure. 2. For each x [l ] sequece, geerate L Ŷ [l ] sequeces idepedetly uiformly distributed i the coditioal strog typical set T δ (x [l ] with respect to the distributio p(ŷ [l ] x [l ]. If l L > I(Y [l ]; Ŷ[l ] X [l ], for ay give y[l ] sequece, there exists oe ŷ[l ] sequece with high probability whe is sufficietly large such that (y[l ], ŷ [l ], x [l ] are joitly typical accordig to the probability distributio p(y [l ], ŷ [l ], x [l ]. Deote this ŷ[l ] as ŷ [l ] (y [l ], x [l ]. Here, the quatizatio from y[l ] to ŷ [l ], parameterized by x [l ], is idicated i Figure by a directed coe from y[l ] to ŷ [l ], with a straight lie from x [l ] for the parameterizatio. 3. For each ŷ[l ], geerate oe x [l] sequece accordig to i= p(x i[l] ŷ i[l ]. This oe-to-oe mappig is idicated by a straight lie betwee ŷ[l ] ad x [l] i Figure. Ecodig: Let m [l] be the message to be set i this block. If (x [l ] (m [l ], x [l ] are set ad y[l ] is received i the previous block, we choose (x [l] (m [l], ŷ[l ] (y [l ], x [l ], x [l] accordig to the code geeratio method described above ad trasmit (x [l] (m [l], x [l]. I Strog typical set ad coditioal strog typical set are defied i [6, Defiitio.2.8,.2.9]. For the sake of simplicity, we omit the subscript which is used to idicate the uderlyig distributio i [6]. 5

6 trasmitter block [] block [2] block [ l] block [B] x[] x [2] x [ l] x[b] relay x [] y y [] [] x [2] y y [2] [2] x [3] y [ l ] x y [ l] [ l] [ l+] y [ l] x y [] x y [B] [B] y [B] Figure : Codebook structure. the first block, we assume a virtual 0th block, where (x [0], x [0], ŷ [0], as well as x [], are kow by the trasmitter, the relay ad the receiver. I the Bth block, the trasmitter radomly geerates oe x [B] sequece accordig to i= p(x i[b] x i[] ad seds it ito the chael. The relay, after receivig y[b], radomly geerates oe ŷ [B] sequece accordig to i= p(ŷ i[b] y i[b], x i[b]. We assume that the trasmitter ad the relay reliably trasmit x [B] ad ŷ [B] to the receiver usig the ext b blocks, where b is some fiite positive iteger. We ote that B + b blocks are used i our scheme, while oly the first B blocks carry the message. Thus, the fial achievable rate is l M which coverges to lm for B+b sufficietly large B sice b is fiite. Decodig: After receivig B blocks of y sequeces, i.e., y [],...,y [B], ad assumig x [], x [B] ad ŷ [B] are kow at the receiver, we seek x [],...,x [], ŷ [],...,ŷ [], x [2],...,x [B], such that ( x [],...,x [B], ŷ[],...,ŷ[b], x [],...,x [B], y[],...,y[b] Tδ accordig to the statioary distributio of the Markov process G [l] i (2. The differeces betwee our scheme ad the CAF scheme are as follows. At the trasmitter side, i our scheme, the fresh message m [l] is mapped ito the codeword x [l] coditioed o the codeword of the previous block x [l ], while i the CAF scheme, m [l] is mapped ito x [l], which is geerated idepedet of x [l ]. At the relay side, i our scheme, the compressed received sigal ŷ[l ] is mapped ito the codeword x [l], which is geerated accordig to p(x [l] ŷ [l ], while i the CAF scheme, x [l] is geerated idepedet of ŷ[l ]. The aim of our desig is to preserve the correlatio built i the (l st block i the chael iputs of the lth block. At the decodig stage, we perform joit decodig for the etire B blocks after all of the B blocks have bee received, while i the CAF scheme, the decodig of the message of the (l st block is performed at the ed of the lth block. Probability of error: Whe is sufficietly large, the probability of error ca be made arbitrarily small whe the followig coditios are satisfied. 6

7 . For all j such that j B, (B j lm + (B ji(ŷ[l]; Y [l] X [l], X [l] < I(X [] 2. For all j, k such that j < k B, (B jl M + (B ki(ŷ[l]; Y [l] X [l], X [l] < I(X [] [k+] ; Y [B] 3. For all j, k such that k < j B, [j+] ; Y [B], Ŷ[B] X [j ], X (3, Ŷ[B], X [B], Ŷ [k ], X [j+] X [j ], X (4 (j ki(ŷ[l]; Y [l] X [l], X [l] + (B j lm + (B ji(ŷ[l]; Y [l] X [l], X [l] < I(X [] [k+] ; Y [B], Ŷ[B] X [j ], X (5 where the subscript [l] o the left had sides of (3, (4 ad (5 idicates that the correspodig radom variables belog to a geeric sample g [l] of the uderlyig radom process i (2. The details of the calculatio of the probability of error where these coditios are obtaied ca be foud i Appedix A.. The derivatio uses stadard techiques from iformatio theory, such as coutig error evets, etc. I the above coditios, we used the otatio A [B] as a shorthad to deote the sequece of radom variables A, A [j+],..., A [B]. Cosequetly, we ote that the mutual iformatios o the right had sides of (3, (4 ad (5 cotai vectors of radom variables whose legths go up to B, where B is very large. I order to simplify the coditios i (3, (4 ad (5, we lower boud the mutual iformatio expressios o the right had sides of (3, (4 ad (5 by those that ivolve radom variables that belog to up to three blocks. The detailed derivatio of the followig lower boudig operatio ca be foud i Appedix A.2. The derivatio uses stadard techiques from iformatio theory, such as the chai rule of mutual iformatio, ad exploitig the Markov structure of the ivolved radom variables.. For all j such that j B, ( (B j l M + I(Ŷ[l]; Y [l] X [l], X [l] < (B ji(y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (6 7

8 2. For all j, k such that j < k B, (k j ( l M + (B k l M + I(Ŷ[l]; Y [l] X [l], X [l] < (k ji(x [l] ; Y [l], Ŷ[l] X [l], Y [l ], Ŷ[l ], X [l ], X [l 2] + (B ki(y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (7 3. For all j, k such that k < j B, ( (j ki(ŷ[l];y [l] X [l], X [l] + (B j l M + I(Ŷ[l]; Y [l] X [l], X [l] < (j ki(y [l] ; Ŷ[l], X [l] X [l], X [l ], X [l ], Y [l ] + (B ji(y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (8 We ca further derive sufficiet coditios for the above three coditios i (6, (7 ad (8 as follows. We defie the followig quatities: C l M + I(Ŷ[l]; Y [l] X [l], X [l] (9 C 2 l M (0 C 3 I(Ŷ[l]; Y [l] X [l], X [l] ( D I(Y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (2 D 2 I(X [l] ; Y [l], Ŷ[l] X [l], Y [l ], Ŷ[l ], X [l ], X [l 2] (3 D 3 I(Y [l] ; Ŷ[l], X [l] X [l], X [l ], X [l ], Y [l ] (4 The, the sufficiet coditios i (6, (7 ad (8 ca also be writte as,. For all j such that j B, (B jc < (B jd (5 2. For all j, k such that j < k B, (k jc 2 + (B kc < (k jd 2 + (B kd (6 3. For all j, k such that k < j B, (j kc 3 + (B jc < (j kd 3 + (B jd (7 8

9 We ote that the above coditios are implied by the followig three coditios, C < D (8 C 2 < D 2 (9 C 3 < D 3 (20 or i other words, by, R η l M < I(X [l]; Y [l], Ŷ[l] X [l], Y [l ], Ŷ[l ], X [l ], X [l 2] (2 I(Ŷ[l]; Y [l] X [l], X [l] < I(Y [l] ; Ŷ[l], X [l] X [l], X [l ], X [l ], Y [l ] (22 R η + I(Ŷ[l]; Y [l] X [l], X [l] < I(Y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (23 The expressios i (2, (22 ad (23 give sufficiet coditios to be satisfied by the rate i order for the probability of error to become arbitrarily close to zero. We ote that these coditios deped o variables used i three cosecutive blocks, l, l ad l 2. With this developmet, we obtai the mai result of our paper which is stated i the followig theorem. Theorem The rate R is achievable for the relay chael, if the followig coditios are satisfied R I(Y, Ŷ; X X, Ŷ, Ỹ, X, X (24 I(Ŷ; Y X, X <I(Y ; Ŷ, X X, Ỹ, X, X (25 R + I(Ŷ; Y X, X I(Y ; Ŷ, X, X Ỹ, X, X (26 where X ( X, Ŷ, X, Ỹ, Ỹ (X, Ŷ, X, Y, Y (27 p(x, ŷ, x, y, y, x = p( x, ŷ, x, ỹ, ỹ, x (28 p(x, ŷ, x, y, y x, ŷ, x, ỹ, ỹ = p(x xp(x ŷ p(y, y x, x p(ŷ y, x (29 I the above theorem, the otatios ad are used to deote the sigals belogig to the previous block ad the block before the previous block, respectively, with respect to a referece block. Therefore, we see that the achievable rate i the relay chael, usig our proposed codig scheme, eeds to satisfy three coditios that ivolve mutual iformatio expressios calculated usig eleve variables which satisfy the Markov chai costrait i (27, the margial distributio costrait i (28, ad the additioal iter-block probability distributio costrait i (29. I the ext sectio, we will revisit the well-kow CAF scheme proposed i [2]. First, we 9

10 will develop a equivalet represetatio for the well-kow represetatio of the achievable rate i the CAF scheme. We will the show that the rates achievable by the CAF scheme ca be achieved with our proposed scheme by choosig a certai special structure for the joit probability distributio of the eleve radom variables i Theorem while still satisfyig the three coditios i (27, (28 ad (29. 4 Revisitig the Compress-Ad-Forward (CAF Scheme I [2], the achievable rates for the CAF are characterized as i the followig theorem. Theorem 2 ( [2] The rate R is achievable for the relay chael, if the followig coditios are satisfied R I(X; Y, Ŷ X (30 I(Y ; Ŷ X, Y < I(X ; Y (3 where p(x, x, y, y, ŷ = p(xp(x p(y, y x, x p(ŷ y, x (32 I the followig theorem, we preset three equivalet forms for the rate achievable by the CAF scheme. Theorem 3 The followig three coditios are equivalet.. For some p(x, x, y, y, ŷ = p(xp(x p(y, y x, x p(ŷ y, x R I(X; Ŷ X I(X; Y Ŷ, X (33 I(Y ; Ŷ X < I(Ŷ; Y X + I(X ; Y (34 2. For some p(x, x, y, y, ŷ = p(xp(x p(y, y x, x p(ŷ y, x R I(X; Ŷ X I(X; Y Ŷ, X (35 R I(X; Ŷ X + I(Y ; Ŷ X I(X, Ŷ; Y X + I(X ; Y (36 3. For some p(x, x, y, y, ŷ = p(xp(x p(y, y x, x p(ŷ y, x R I(X; Ŷ X I(X; Y Ŷ, X (37 I(Ŷ; Y X, X < I(Ŷ; Y X, X + I(X ; Y X (38 R I(X; Ŷ X + I(Y ; Ŷ X I(X, Ŷ; Y X + I(X ; Y (39 0

11 The proof of the above theorem is give i Appedix A.3. We rewrite the fial equivalet represetatio i (37, (38 ad (39 i the followig more compact form i order to compare the rates achievable with our proposed scheme ad the rates achievable with the CAF scheme i the ext sectio. R I(X; Y, Ŷ X (40 I(Ŷ; Y X, X < I(Ŷ, X ; Y X (4 R + I(Y ; Ŷ X, X I(X, Ŷ, X ; Y (42 5 Compariso of the Achievable Rates with Our Scheme ad with the CAF Scheme We ote that the coditios o the achievable rates with our scheme give i Theorem, i.e., (24, (25, (26, are very similar to the fial equivalet form for the coditios o the achievable rates with the CAF scheme, i.e., (40, (4, (42, except for two differeces. First, the chael iputs of the trasmitter ad the relay, i.e., X ad X, i our proposed scheme ca be correlated, while i the CAF scheme they are idepedet, ad secod, i our scheme there are some extra radom variables, which mutual iformatio expressios are coditioed o, e.g., X, X, Ỹ, Ŷ, X. These two differeces come from our codig scheme where we itroduced correlatio betwee the chael iputs of the trasmitter ad the relay i a block, ad betwee the variables across the blocks. The correlatio betwee the chael iputs from the trasmitter ad the relay i ay block is a advatage, as for chaels which favor correlatio, this traslates ito higher rates. However, the correlatio across the blocks is a disadvatage as it decreases the efficiecy of trasmissio, ad therefore the achievable rates. I fact, the price we pay for the correlatio betwee the chael iputs i ay give block is precisely the correlatio we have created across the blocks. For a give correlatio structure, it is ot clear which of these two opposite effects will overcome the other. That is, the rate of our scheme for a certai correlated distributio may be lower or higher tha the rate of the CAF scheme. However, we ote that the CAF scheme ca be viewed as a special case of our proposed scheme by choosig a idepedet distributio, i.e., by choosig the followig coditioal distributio i (29 p(x, ŷ, x, y, y x, ŷ, x, ỹ, ỹ = p(xp(x p(y, y x, x p(ŷ x, y (43 I this case, the expressios i Theorem, i.e., (24, (25, (26, degeerate ito the third equivalet form for the CAF scheme i Theorem 3, i.e., (40, (4, (42. The above observatio implies that the maximum achievable rate with our proposed scheme over all possible distributios is ot less tha the achievable rate of the CAF scheme. Thus, we ca claim that this paper offers more choices i the achievability scheme tha the CAF scheme, ad

12 that these choices may potetially yield larger achievable rates tha those offered by the CAF scheme. A Appedix A. Probability of Error Calculatio The average probability of decodig error ca be expressed as follows, where P e = Pr(E E 2 = Pr(E + Pr(E 2 E c (44 E ( x [,...,B], ŷ [,...,B], x [,...,B], [,...,B] y / Tδ (45 E 2 ( x [,...,B], ŷ [,...,B], x [,...,B], y [,...,B] Tδ (46 x [,...,B], ŷ [,...,] x [,...,B],ŷ [,...,] where ( x [,...,B], ŷ [,...,], x [2,...,B] is aother codeword that is geerated accordig to the rules of our scheme. From (2, we ote the followig Markov properties:. coditioed o (Ŷ[l], X [l], X [l], Y [l] is idepedet of G [...,l ] ad G [l,...] ; 2. coditioed o (X [l ], Ŷ[l ], G [l,...] is idepedet of G [...,l ]. Here, ad i the sequel, subscript [l] refers to a geeric block withi overall B blocks. Pr(E ca be upper bouded as follows: Pr(E B ( ( Pr (x [l], x [l], y [l], y [l], g [...,l ] / T δ g[...,l ] T δ l= + Pr ( (ŷ [l], x [l], x [l], y [l], y [l], g [...,l ] / T δ (x [l], x [l], y [l], y [l], g [...,l ] T δ (47 From the way the code is geerated, we have Pr ( (x [l], x [l], y [l], y [l], g [...,l ] / T δ g [...,l ] T δ ǫ (48 The compressio from y [l] to ŷ [l] is a coditioal versio of a rate-distortio code. If R > I(Y ; Ŷ X, the, whe is sufficietly large, we have Pr ( (ŷ [l], x [l], x [l], y [l], y [l], g [...,l ] / T δ (x [l], x [l], y [l], y [l], g [...,l ] T δ ǫ (49 Thus, Pr(E 2Bǫ (50 2

13 Now we switch to the error evet E 2. Pr(E 2 E c = p(x [,...,B], ŷ [,...,B], x [,...,B], y [,...,B] x [,...,B],ŷ [,...,B],x [,...,B],y T [,...,B] δ max x [,...,B],ŷ [,...,B],x [,...,B],y [,...,B] Pr ( E 2 (x [,...,B], ŷ [,...,B], x [,...,B], y [,...,B] set T δ Pr ( E 2 (x [,...,B], ŷ [,...,B], x [,...,B], y [,...,B] set (5 From our proposed codig scheme, we ote that the codebooks at both trasmitter ad relay have tree structures with B stages. A correct codeword x [,...,] ca be viewed as a path i the tree-structured codebook at the trasmitter. Similarly, for the codeword ŷ [,...,] at the relay. A error occurs whe we diverge from the correct path at a certai stage i the tree. Thus, the error evet E 2 ca be decomposed as E 2 = j=2,..., k=2,..., ( x [],..., x [j ], ŷ [],..., ŷ [k ]=(x [],...,x [j ],ŷ [],...,ŷ [k ] ( x, ŷ (x,ŷ ( x [],..., x [B], ŷ [],..., ŷ [B], x [],..., x [B], y [],...,y [B] Tδ (52 where each term i the uio i the above equatio represets the error evet that results whe we diverge from the correct paths at the jth stage at the trasmitter ad at the kth stage at the relay. Let us defie F to be the set cosistig of all feasible codeword pairs (x, ŷ for the jth block for a give x [j ] ad x. The, we have L F F M exp((h(ŷ X, X + 2ǫ ( ǫ exp((h(ŷ X 2ǫ exp((i(ŷ; Y X + ǫ M exp((h(ŷ X, X + 2ǫ ( ǫ exp((h(ŷ X 2ǫ M exp((i(ŷ; Y X, X + 6ǫ (53 We also defie F 2 to be the set cosistig of all feasible codewords x a give x [j ]. The, for the jth block for F 2 F 2 = M (54 Similarly, we defie F 3 to be the set cosistig of all feasible codewords ŷ for the jth block 3

14 for a give x ad x. The, F 3 F 3 L exp((h(ŷ X, X + 2ǫ ( ǫ exp((h(ŷ X 2ǫ exp((i(ŷ; Y X, X + 6ǫ (55 We defie the error evet E 2jk E 2jk ( x [],..., x [j ], ŷ [],..., ŷ [k ]=(x [],...,x [j ],ŷ [],...,ŷ [k ] ( x, ŷ (x,ŷ ( x [],..., x [B], ŷ [],..., ŷ [B], x [],..., x [B], y [],...,y [B] Tδ (56 The, we have ad Pr(E 2 E c Pr(E 2jk E c (57 j=2 k=2 Pr(E 2jk E c A jk where max ( x [],..., x [], ŷ [],..., ŷ [] A jk A jk codeword ( x ( [],..., x [], ŷ [],..., ŷ [] : x [],..., x [j ], ŷ [],..., ŷ [k ] ( x, ŷ P ( x [],..., x [], ŷ [],..., ŷ [] P ( x [],..., x [], ŷ [],..., ŷ [] (58 = ( x [],..., x [j ], ŷ [],..., ŷ [k ] ( x, ŷ Pr(( x [],..., x [B], ŷ [],..., ŷ [B], x [],..., x [B], y [],...,y [B] T δ (60 ( give x [],...,x [B], ŷ [],...,ŷ [B], x [],..., x [B], y [],..., y [B] T δ. I order to have the probability of such error evets go to zero, we eed the followig coditios to hold. Whe j = k, from the structure of the block Markov code ad (53, we have (59 A jk = F B j M B j exp((b j(i(ŷ[l]; Y [l] X [l], X [l] + 6ǫ (6 4

15 ad ad ad P ( x [],..., x [], ŷ [],..., ŷ [] exp((h(x [] exp( (H(X [] = exp(( I(X [] Whe j < k, we have [B] [j+] Y, Ŷ[B], X [j ], X + 2ǫ [j+] X [j ], X 2ǫ [j+] ; Y [B], Ŷ[B] X [j ], X + 4ǫ (62 A jk = F k j 2 F B k M B j exp((b k(i(ŷ[l]; Y [l] X [l], X [l] + 6ǫ (63 P ( x [],..., x [], ŷ [],..., ŷ [] exp((h(x [] exp( (H(X [] = exp(( I(X [] Whe j > k, we have [B] [k+] Y, Ŷ[B], Ŷ [k ], X [j ], X + 2ǫ [k+] X [j ], X 2ǫ [k+] ; Y [B], Ŷ[B], Ŷ [k ], X [j+] X [j ], X + 4ǫ (64 A jk = F j k 3 F B j exp((j k(i(ŷ; Y X, X + 6ǫ P ( x [],..., x [], ŷ [],..., ŷ [] exp((h(x [] exp( (H(X [] = exp(( I(X [] M B k l exp((b k(i(ŷ[l]; Y [l] X [l], X [l] + 6ǫ (65 [B] [k+] Y, Ŷ[B], X [j k], X + 2ǫ [k+] X[j ], X 2ǫ [k+] ; Y [B], Ŷ[B] X [j ], X + 4ǫ (66 Thus, whe is sufficietly large, usig (58 ad (6 through (66, we have if the followig coditios are satisfied: Pr(E 2jk E c ǫ, j, k = 2,...,B (67 5

16 . For all j such that j B, (B j lm + (B ji(ŷ[l]; Y [l] X [l], X [l] < I(X [] [j+] ; Y [B], Ŷ[B] X [j ], X (68 2. For all j, k such that j < k B, (B j l M + (B ki(ŷ[l]; Y [l] X [l], X [l] < I(X [] [k+] ; Y [B], Ŷ[B], X [B], Ŷ [k ], X [j+] X [j ], X (69 3. For all j, k such that k < j B, (j ki(ŷ[l]; Y [l] X [l], X [l] + (B j lm + (B ji(ŷ[l]; Y [l] X [l], X [l] < I(X [] [k+] ; Y [B], Ŷ[B] X [j ], X (70 Therefore, we have P e = Pr(E + Pr(E 2 E c (2B + B2 ǫ (7 Whe is sufficietly large, (2B + B 2 ǫ ca be made arbitrarily small. 6

17 A.2 Lower Boudig the Mutual Iformatios i (3, (4, (5 For the right had side of (3, we have I(X [] = l=j [j+] ; Y [B], Ŷ[B] X [j ], X I(X [] + I(X [] 2 = I(Y ; X, Ŷ X, X [j ] + 3 = 4 = 5 = [j+] ; Y [l] X [j ], X, Y [l ] [j+] ; Y [B], Ŷ[B] X [j ], X, Y [] l=j+ + I(Y [B], Ŷ[B] ; X [B], X [] X [j ], X, Y [] l=j+ I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] + I(Y [B] ; X [B], Ŷ[B] X [B], X [] + I(Y [B], Ŷ[B] ; X [B], X [] X [j ], X, Y [] l=j+ I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] + I(Y [B] ; X [B], Ŷ[B] X [B], X [], X [j ], X, Y [] + I(Y [B] ; X [B], X [] X [j ], X, Y [] l=j+ l=j+ I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] + I(Y [B] ; X [B], Ŷ[B], X [B], X [] X [j ], X, Y [] B I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] 6 (B ji(y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (72 where. follows from the chai rule; 2. because of Markov properties ad 2; 3. because of the statioarity of the radom process ad the property that coditioig reduces etropy; 4. because of Markov property 2; 5. because of Markov property ; 6. because of Markov property 2 ad the statioarity of the radom process. 7

18 For the right had side of (4, we have I(X [] [k+] ; Y [B], Ŷ[B], Ŷ [k ], X [j+] X [j ], X = I(X [] [k+] ; Y, Ŷ X [j ], X + k l=j+ + I(X [] + l=k+ + I(X [] I(X [] I(X [] [k+] ; Y [l], Ŷ[l], X [l] X [j ], Y [l ], Ŷ [l ], X [l ] [k+] ; Y, X X [j ], Y [k ], Ŷ [k ], X [k ] 2 I(X ; Y, Ŷ X [j ], X + 3 = 4 + I(X, Ŷ; Y X [j ], Y [k ] + l=k+ [k+] ; Y [l] X [j ], Y [l ], Ŷ [k ], X [k+] ; Y [B], Ŷ[B] X [j ], Y [] k l=j+, Ŷ [k ], X I(X [l] ; Y [l], Ŷ[l] X [j ], Y [l ], Ŷ [l ], X [l], Ŷ [k ], X I(X [l], Ŷ[l], X [l] ; Y [l] X [j ], Y [l ], Ŷ [k ], X + I(X [], X [B] ; Y [B], Ŷ[B] X [j ], Y [] k l=j+ + l=k+ I(X [l] ; Y [l], Ŷ[l] X [j ], Y [l ], Ŷ [l ], X [l] I(X [l], Ŷ[l], X [l] ; Y [l] X [j ], Y [l ] + I(X [B] ; Y [B], Ŷ[B] X [], X [B], Ŷ [k ], X, Ŷ [k ], X + I(X [B], Ŷ[B]; Y [B] X [j +B k], Y [] [j+b k] [j+b k], X[B] [j+b k] + I(X [], X [B] ; Y [B], Ŷ[B] X [j ], Y [] k l=j+ + l=k+ I(X [l] ; Y [l], Ŷ[l] X [j ], Y [l ], Ŷ [l ], X [l] I(X [l], Ŷ[l], X [l] ; Y [l] X [j ], Y [l ], Ŷ [k ], X, Ŷ [k ], X + I(X [B] ; Y [B], Ŷ[B] X [B], S + I(X [B], Ŷ[B], X [B] ; Y [B] S 5 (k ji(x [l] ; Y [l], Ŷ[l] X [l], Y [l ], Ŷ[l ], X [l ], X [l 2] + (B ki(y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (73 8

19 where S (X [j +B k], Y [] [j+b k] [j+b k], X[] [j+b k], X [j ], Y [], Ŷ [k ], X (74 ad. follows from the chai rule; 2. because of Markov properties ad 2; 3. because of the statioarity of the radom process; 4. because of the followig derivatio I(X [B] ; Y [B], Ŷ[B] X [], X [B] + I(X [B], Ŷ[B]; Y [B] X [j +B k], Y [] [j+b k] [j+b k], X[B] [j+b k] + I(X [], X [B] ; Y [B], Ŷ[B] X [j ], Y [], Ŷ [k ], X I(X [B] ; Y [B], Ŷ[B] X [], X [B], S + I(X [B], Ŷ[B]; Y [B] X [B], S + I(X [], X [B] ; Y [B], Ŷ[B] S I(X [B] ; Y [B], Ŷ[B] X [], X [B], S + I(X [B], Ŷ[B]; Y [B] X [B], S + I(X [] ; Y [B], Ŷ[B] X [B], S + I(X [B] ; Y [B] S = I(X [B] ; Y [B], Ŷ[B] X [B], S + I(X [B], Ŷ[B], X [B] ; Y [B] S (75 5. because of Markov property ad 2 ad the statioarity of the radom process. 9

20 For the right had side of (5, we have I(X [] = l=k [k+] ; Y [B], Ŷ[B] X [j ], X I(X [] + I(X [] [k+] ; Y [l] X [j ], X, Y [l ] [k+] ; Y [B], Ŷ[B] X [j ], X, Y [] 2 I(Y ; Ŷ X, X + 3 = 4 j l=k+ + I(Y ; X, Ŷ, X X [j ], X, Y [j ] + l=j+ I(Y [l] ; Ŷ[l], X [l] X [l], X, Y [l ] I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] + I(Y [B], Ŷ[B] ; X [] j l=k+ + l=j+ I(Y [l] ; Ŷ[l], X [l] X [l], X, Y [l ], X [B] X [j ], X, Y [] I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] + I(Y [B] ; Ŷ[B] X [B], X [B] + I(Y [B] ; X [B], Ŷ[B], X [B] X [] [k+b j], X [k+b j], Y [] [k+b j] + I(Y [B], Ŷ[B] ; X [] j l=k+ + l=j+ I(Y [l] ; Ŷ[l], X [l] X [l], X, Y [l ], X [B] X [j ], X, Y [] I(Y [l] ; X [l], Ŷ[l], X [l] X [j ], X, Y [l ] + I(Y [B] ; Ŷ[B], X [B] X [B], S + I(Y [B] ; X [B], Ŷ[B], X [B] S 5 (j ki(y [l] ; Ŷ[l], X [l] X [l], X [l ], X [l ], Y [l ] + (B ji(y [l] ; X [l], Ŷ[l], X [l] X [l 2], X [l ], Y [l ] (76 where S (X [k+b j], Y [], X [j ], X (77 ad. follows from the chai rule; 2. because of Markov properties ad 2; 3. because of the statioarity of the radom process; 20

21 4. because of the followig derivatio I(Y [B] ; Ŷ[B] X [B], X [B] + I(Y [B] ; X [B], Ŷ[B], X [B] X [] [k+b j], X [k+b j], Y [] [k+b j] + I(Y [B], Ŷ[B] ; X [], X [B] X [j ], X, Y [] I(Y [B] ; Ŷ[B] X [B], X [B], S + I(Y [B] ; X [B], Ŷ[B], X [B] X [], S + I(Y [B], Ŷ[B] ; X [], X [B] S = I(Y [B] ; Ŷ[B] X [B], X [B], S + I(Y [B] ; X [B], Ŷ[B], X [B] X [], S + I(Y [B], Ŷ[B] ; X [B] X [], S + I(Y [B], Ŷ[B] ; X [] S I(Y [B] ; Ŷ[B] X [B], X [B], X [], S + I(Y [B] ; X [B], Ŷ[B], X [B] X [], S + I(Y [B] ; X [B] X [B], X [], S + I(Y [B] ; X [] S = I(Y [B] ; Ŷ[B], X [B] X [B], S + I(Y [B] ; X [B], Ŷ[B], X [B] S (78 5. because of Markov property ad 2 ad the statioarity of the radom process. A.3 Proof of Theorem 3 First, we ote that coditio is equivalet to the expressio i Theorem 2. We also ote that coditio 2 is seemigly weaker tha coditio because (36 is implied by (33 ad (34, ad coditio 3 is seemigly stroger tha coditio 2 because coditio 3 cosists of every elemet i coditio 2 plus (38. Eve though they seem differet, these three coditios are ideed equivalet. The equivalece of coditios 2 ad 3 is show i [5]. Here, we use a similar proof techique to show the equivalece of coditios ad 2 as follows 2. For a give distributio p(x, x, y, y, ŷ, coditio is stroger tha coditio 2, which meas that a arbitrary rate R satisfyig coditio will also satisfy coditio 2. Coversely, for a rate R satisfyig coditio 2, if (34 is satisfied, the coditio is satisfied. If (34 is ot satisfied, i.e., I(Y ; Ŷ X I(Ŷ; Y X + I(X ; Y (79 we kow that R [0, R ], where R I(X; Ŷ X I(X; Y Ŷ, X (80 R I(X; Ŷ X + I(Y ; Ŷ X = I(X, Ŷ; Y X + I(X ; Y (8 2 A similar result is give i [7] by meas of time-sharig. 2

22 That is, R is defied such that (36 is satisfied with equality. We may rewrite (80 ad (8 as R I(X; Y X + I(X; Ŷ Y, X (82 R = I(X, X ; Y I(Y ; Ŷ X, X, Y (83 We defie a ew radom variable Ŷ such that Ŷ has the same margial distributio as Ŷ ad Ŷ Ŷ (Y, X, X, Y. Due to the cotiuity of mutual iformatio, there exists a choice of Ŷ such that I(X; Ŷ Y, X = A for ay A [0, I(X; Ŷ Y, X ]. If R I(X; Y X > 0, we choose Ŷ such that R = I(X; Y X + I(X; Ŷ that, i this case, I(Y ; Ŷ X, X, Y I(Y ; Ŷ X, X, Y. Thus, Y, X. We ote R = I(X; Y X + I(X; Ŷ Y, X (84 R I(X, X ; Y I(Y ; Ŷ X, X, Y (85 which meas that R satisfies coditio with joit distributio p(x, x, y, y, ŷ ad so does ay R R. If R I(X; Y X 0, we choose Ŷ idepedet of (Ŷ, X, X, Y, Y. I this case, R I(X; Y X + I(X; Ŷ Y, X = I(X; Y X (86 0 = I(Y ; Ŷ X I(Ŷ ; Y X + I(X ; Y (87 Therefore, i this case, R satisfies coditio with joit distributio p(x, x, y, y, ŷ ad so does ay R R. As we metioed above the equivalece betwee coditio 2 ad 3 is show i [5]. For completeess, we restate their proof here as follows. For a give distributio p(x, x, y, y, ŷ, coditio 3 is stroger tha coditio 2, which meas that a arbitrary rate R satisfyig coditio 3 will also satisfy coditio 2. Coversely, for a rate R satisfyig coditio 2, if (38 is satisfied, the coditio 3 is satisfied. If (38 is ot satisfied, i.e., the followig iequalities are satisfied R I(X; Ŷ X I(X; Y Ŷ, X (88 I(Ŷ; Y X, X I(Ŷ; Y X, X + I(X ; Y X (89 R I(X; Ŷ X + I(Y ; Ŷ X I(X, Ŷ; Y X + I(X ; Y (90 the the followig iequalities are satisfied also, sice we simply drop the first iequality, I(Ŷ; Y X, X I(Ŷ; Y X, X + I(X ; Y X (9 R I(X; Ŷ X + I(Y ; Ŷ X I(X, Ŷ; Y X + I(X ; Y (92 22

23 By combiig (9 ad (92, we have R I(X; Ŷ X I(Y ; Ŷ X + I(Ŷ; Y X, X + I(X, Ŷ; Y X + I(X ; Y I(Ŷ; Y X, X I(X ; Y X I(X; Y X (I(X ; Y X I(X ; Y I(X; Y X (93 which implies coditio 3, i.e., (37, (38 ad (39, with Ŷ set to be a costat. Refereces [] E. C. va der Meule. Three-termial commuicatio chaels. Adv. App. Prob., 3:20 54, 97. [2] T. M. Cover ad A. El Gamal. Capacity theorems for the relay chael. IEEE Tras. Iform. Theory, 25: , Sep [3] G. Kramer, M. Gastpar, ad P. Gupta. Cooperative strategies ad capacity theorems for relay etworks. IEEE Tras. Iform. Theory, 5(9: , September [4] T. M. Cover, A. El Gamal, ad M. Salehi. Multiple access chael with arbitrarily correlated sources. IEEE Tras. Iform. Theory, 26: , Nov [5] R. Ahlswede ad T. S. Ha. O source codig with side iformatio via a multiple-access chael ad related problems i multi-user iformatio theory. IEEE Tras. Iform. Theory, 29(3:396 42, 983. [6] I. Csiszar ad J. Korer. Iformatio Theory: Codig Theorems for Discrete Memoryless Systems. Academic Press, 98. [7] R. Dabora ad S. Servetto. O the role of estimate-ad-forward with time-sharig i cooperative commuicatios. Submitted to IEEE Trasactios o Iformatio Theory, 2006, 23