Distortion Bounds for Source Broadcast. Problem

Transcription

1 Distortio Bouds for Source Broadcast 1 Problem Lei Yu, Houqiag Li, Seior Member, IEEE, ad Weipig Li, Fellow, IEEE Abstract This paper ivestigates the joit source-chael codig problem of sedig a memoryless source over a memoryless broadcast chael. A ier boud ad a outer boud o the achievable distortio regio are derived, which respectively geeralize ad uify several existig bouds. As a cosequece, we also obtai a ier boud ad a outer boud for degraded broadcast chael case. Whe specialized to Gaussia source broadcast or biary source broadcast, the ier boud ad outer boud ot oly ca recover the best kow ier boud ad outer boud i the literature, but also ca be used to geerate some ew results. Besides, we also exted the ier boud ad outer boud to Wyer-Ziv source broadcast problem, i.e., source broadcast with side iformatio available at decoders. Some ew bouds are obtaied whe specialized to Wyer-Ziv Gaussia case ad Wyer-Ziv biary case. I additio, whe specialized to lossless trasmissio of a source with idepedet compoets, the bouds for source broadcast problem without side iformatio is also used to achieve a ier boud ad a outer boud o capacity regio of geeral broadcast chael with commo messages, which respectively geeralize Marto s ier boud ad Nair-El Gamal outer boud to K-user broadcast chael case. Idex Terms Joit source-chael codig JSCC, hybrid codig, hybrid digital-aalog HDA, broadcast, Wyer-Ziv, side iformatio, multivariate coverig/packig, etwork iformatio theory. I. INTRODUCTION As stated i Shao s source-chael separatio theorem [2], cascadig source codig ad chael codig does ot lose the optimality for the poit-to-poit commuicatio systems. This separatio theorem does ot oly suggest a simple system architecture i which source codig ad chael codig are separated by a uiversal digital iterface, but also guaratees that such architecture does ot icur ay asymptotic performace loss. Cosequetly, it forms the basis of the architecture of today s commuicatio systems. However, for may multi-user commuicatio systems, the optimality of such a separatio does ot hold ay more [3], [4]. Therefore, a icreasig amout of literature focus o joit source-chael codig JSCC i multi-user settig. The authors are all with the Departmet of Electroic Egieerig ad Iformatio Sciece, Uiversity of Sciece ad Techology of Chia, Hefei , Chia yulei@ustc.edu.c, lihq@ustc.edu.c, wpli@ustc.edu.c. The material i this paper will be preseted i part at IEEE ISIT 2016 [1].

2 2 Oe of the most classical problems i this area is JSCC of trasmittig a Gaussia source over average power costraied K-user Gaussia broadcast chael. Goblick [3] observed that whe the source badwidth ad the chael badwidth are matched i.e., oe chael use per source sample liear ucoded trasmissio symbol-bysymbol mappig is optimal. However, the optimality of such a simple liear scheme caot be exteded to the case of the badwidth mismatch. Oe way to approximately characterize the achievable distortio regio is fidig its ier boud ad outer boud. For ier boud, aalog codig schemes or hybrid codig schemes have bee studied i a vast body of literature [4], [5], [6], [7]. For 2-user Gaussia broadcast commuicatio, Prabhakara et al. [7] gave the tightest ier boud so far, which is achieved by hybrid digital-aalog HDA scheme. O the other had, Rezic et al. [8] derived a otrivial outer boud for 2-user Gaussia broadcast problem with badwidth expasio i.e., more tha oe chael uses per source sample by itroducig a auxiliary radom variable or remote source. Tia et al. [9] exteded this outer boud to K-user case by itroducig more tha oe auxiliary radom variables. Similar to the results of Rezic et al., the outer boud give by Tia et al. is also otrivial oly for badwidth expasio case [10]. Beyod broadcast commuicatio, Miero et al. [15] cosidered sedig memoryless correlated source trasmitted over memoryless multi-access chael ad derived a ier boud usig a uified framework of hybrid codig, ad also Lee et al. [20] derived a uified achievability result for memoryless etwork commuicatio. Besides, i [6], [17], [18] Wyer-Ziv source commuicatio problem was ivestigated, i which side iformatio of the source is available at decoders. Shamai et al. [6] studied the problem of sedig Wyer-Ziv source over poit-to-poit chael, ad proved that for such commuicatio system separate codig which combies Wyer-Ziv codig with chael codig does ot icur ay loss of optimality. Nayak et al. [17] ad Gao et al. [18] ivestigated Wyer-Ziv source broadcast problem, ad obtaied a outer boud by simply applyig cut-set boud the miimum distortio achieved i poit-to-poit settig for each receiver. I this paper, we cosider JSCC of trasmittig a memoryless source over K-user memoryless broadcast chael, ad give a ier boud ad a outer boud o the achievable distortio regio. The ier boud is derived by a uified framework of hybrid codig ispired by [15], ad the outer boud is derived by itroducig auxiliary radom variables or remote sources as i [8] ad [9]. Both these two bouds are geeralizatios ad uificatios of several existig bouds i the literature. Besides, as a cosequece, we also obtai a ier boud ad a outer boud for degraded broadcast chael case. Owig to the geeralizatio of our results, whe specialized to Gaussia source broadcast ad biary source broadcast, our ier boud could recover best kow performace achieved by hybrid codig, ad our outer boud could recover the best kow outer bouds give by Tia et al. [9] ad Khezeli et al. [11]. Moreover, for these cases, our bouds ca also be used to geerate some ew results. Besides, we also exted the ier boud ad outer boud to Wyer-Ziv source broadcast problem, i.e., source broadcast with side iformatio at decoders. Whe specialized to Wyer-Ziv Gaussia case ad Wyer-Ziv biary case, our bouds reduce to some ew bouds. I additio, whe specialized to lossless trasmissio of a source with idepedet compoets, the bouds for source broadcast problem without side iformatio is also used to achieve a ier boud ad a outer boud o capacity regio of geeral broadcast chael with commo messages,

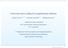
3 3 Y1 S ˆ 1 Decoder 1 S Ecoder X p Y 1 Y 2 Y K X Y K Decoder K ˆ S K Fig. 1. Source broadcast system. which respectively geeralize Marto s ier boud ad Nair-El Gamal outer boud to K-user broadcast chael case. The rest of this paper is orgaized as follows. Sectio II summarizes basic otatios, defiitios ad prelimiaries, ad formulates the problem. Sectio III gives the mai results for source broadcast problem, icludig geeral, degraded, Gaussia ad biary cases. Sectio IV exteds the results to Wyer-Ziv source broadcast problem. Fially, Sectio V gives the cocludig remarks. A. Notatio II. PROBLEM FORMULATION AND PRELIMINARIES Throughout this paper, we follow the otatio i [16]. For example, for discrete radom variable X p X o alphabet X ad ɛ 0, 1, the set of ɛ-typical -sequeces x or the typical set i short is defied as T ɛ X = {x : {i : x i = x / p X x ɛp X x for all x X. Whe it is clear from the cotext, we will use T ɛ istead of T ɛ X. I additio, we use X A to deote the vector X j : j A, use [i : j] to deote the set { i, i + 1,, j, ad use 1 to deote a all-oe vector similarly, use 2 to deote a all-2 vector. We say vector m [1:N] is smaller tha vector m [1:N] if m j = m j, k < j K ad m k < m k for some k. For two vectors m I ad m I, we say m I is compoet-wise uequal to m I, if m i m i for all i I, ad deote it as m I m I. Besides, we use 1 {A to deote idicator fuctio of evet A, i.e., 1, if A is true; 1 {A = 0, if A is false. B. Problem Formulatio Cosider the source broadcast system show i Fig. 1. The discrete memoryless source DMS S is first coded ito X usig a source-chael code, the trasmitted to K receivers through a discrete memoryless broadcast chael DM-BC p Y[1:K] X, ad fially, the receiver k produces source recostructio Ŝ k Y k. from the received sigal

4 4 Defiitio 1 Source. A discrete memoryless source DMS is specified by a probability mass fuctio pmf p S o a fiite alphabet S. The DMS p S geerates a i.i.d. radom process {S i with S i p S. Defiitio 2 Broadcast Chael. A K-user discrete memoryless broadcast chael DM-BC is specified by a collectio of coditioal pmfs p Y[1:K] X o fiite output alphabet Y 1 Y K for each x i fiite iput alphabet X. Defiitio 3 Degraded Broadcast Chael. A DM-BC p Y[1:K] X is stochastically degraded or simply degraded if there exist a radom vector Ỹ[1:K] such that Ỹk {X = x p Yk Xỹ k x, 1 k K, i.e., Ỹ [1:K] has the same coditioal margial pmfs as Y [1:K] give X, ad X ỸK ỸK 1 Ỹ1 1 form a Markov chai. I additio, as a special case, if X Y K Y K 1 Y 1, i.e., Ỹ k = Y k, 1 k K, the p Y[1:K] X is physically degraded. Defiitio 4. A -legth source-chael code is defied by the ecodig fuctio x : S X ad a sequece of decodig fuctios ŝ k : Y k ˆ S k, 1 k K, where Ŝk is the alphabet of source recostructio at receiver k. For ay -legth source-chael code, the iduced distortio is defied as Ed k S, Ŝ k = 1 Ed k S t, Ŝk,t, 1 for 1 k K, where d k s, ŝ k : S Ŝk [0, + ] is a distortio measure fuctio for receiver k. Defiitio 5. For trasmittig source S over chael p Y[1:K] X, if there exists a sequece of source-chael codes such that the we say that the distortio tuple D [1:K] is achievable. t=1 lim sup Ed k S, Ŝ k D k, 2 Defiitio 6. For trasmittig source S over chael p Y[1:K] X, the admissible distortio regio is defied as R { D [1:K] : D [1:K] is achievable. 3 The admissible distortio regio R oly depeds o the margial distributios of p Y[1:K] X, hece for source broadcast over stochastically degraded chael it suffices to oly cosider the broadcast over physically degraded chael. I additio, Shao s source-chael separatio theorem shows that the miimum distortio for trasmittig source over poit-to-poit chael satisfies R k D k = C k, 4 1 To simplify otatio, the Markov chai is assumed i this directio. Note that this differs from that i the coferece versio [1].

5 5 where R k is the rate-distortio fuctio of the source with distortio measure d k, ad C k is the capacity of the chael of the receiver k. Therefore, the optimal distortio Shao limit is D k = R 1 k C k. 5 Obviously, R R { D [1:K] : D k D k, 1 k K, 6 where R is amed trivial outer boud. I the system above, source badwidth ad chael badwidth are matched. I this paper, we also cosider the commuicatio system with badwidth mismatch, whereby m samples of a DMS are trasmitted through uses of a DM-BC. For this case, badwidth mismatch factor is defied as b = m. C. Multivariate Coverig/Packig Lemma Two importat results we eed to prove the achievability part i this work are the followig lemmas, both of which are geeralized versios of the existig coverig/packig lemmas. Let U, V [0:k] p U,V[0:k], ad let U, V 0 p U,V 0 be a radom vector sequece. For each j [1 : k], let A j [1 : j 1]. Assume A j satisfies if i A j, the A i A j. For each j [1 : k] ad each m Aj i A j [1 : 2 ri ], let V j m A j, m j, m j [1 : 2 rj ], be pairwise coditioally idepedet radom sequeces, each distributed accordig to p V j V Aj,V 0 v j,i v Aj,im Aj, v 0,i. Hece for each j [1 : k], A j {0 deotes the idex set of the radom variables o which the codeword V j is superposed. Based o the otatios above, we have the followig geeralized Multivariate Coverig Lemma ad geeralized Multivariate Packig Lemma. Lemma 1 Multivariate Coverig Lemma. Let ɛ < ɛ. If lim P U, V0 T ɛ = 1, the there exists δɛ that teds to zero as ɛ 0 such that lim P U, V0, V [1:k] m [1:k] T ɛ for some m [1:k] = 1, 7 if j J r j > j J H V j V Aj V 0 H VJ V 0 U + δɛ for all J [1 : k] such that J = ad if j J, the A j J. Lemma 2 Multivariate Packig Lemma. There exists δɛ that teds to zero as ɛ 0 such that lim P U, V0, V [1:k] m [1:k] T ɛ for some m [1:k] = 0, 8 if j J r j < j J H V j V Aj V 0 H VJ V 0 U δɛ for some J [1 : k] such that J = ad if j J, the A j J. Note that all the existig coverig ad packig lemmas such as [16, Lem. 8.2] ad [19, Lem. 4], oly ivolve sigle-layer codebook. Our Multivariate Coverig ad Packig Lemmas geeralize them to the case of multilayer codebook, ad certaily our Coverig/Packig Lemmas could recover all of them.

6 6 III. SOURCE BROADCAST A. Source Broadcast Now, we boud the distortio regio for source broadcast commuicatio. To write the ier boud, we first itroduce a auxiliary radom variable V j, 1 j N 2 K 1 for each of the 2 K 1 oempty subsets G j [1 : K], ad let V j deote a commo message trasmitted from seder to all the receivers i G j. The V j correspods to a subset G j by the followig oe-to-oe mappig. Sort all the oempty subsets G [1 : K] i the decreasig order 2. Map the jth subset i the resultig sequece to j. Obviously this mappig is oe-to-oe correspodig. For example, if K = 3, the G 1 = {1, 2, 3, G 2 = {2, 3, G 3 = {1, 3, G 4 = {1, 2, G 5 = {3, G 6 = {2, G 7 = {1. Besides, let A j {i [1 : N] : G j G i, 1 j N, 9 D k {i [1 : N] : k G i, 1 k K. 10 Later we will show that they respectively correspod to the idex set of the radom variables o which the codeword V j is superposed, ad the idex set of decodable codewords Vj s for receiver k i the proposed hybrid codig scheme; see Appedix C-A. Decoder k is able to recover correctly the Vj, desigated by the ecoder with probability approachig 1 as if j D k. I additio, it is easy to verify that if j D k, the A j D k. It meas that the proposed codebook satisfies that if iformatio V j ca be recovered correctly by receiver k, the V A j ca also be recovered correctly by it. Based o the otatios above, we defie distortio regio { R i = D [1:K] : There exist some pmf p V[1:N] S, vector r [1:N], ad fuctios x v [1:N], s, ŝ k v Dk, y k, 1 k K such that Ed k S, Ŝk D k, 1 k K, r j > H V j V Aj H VJ S j J j J for all J [1 : N] such that J = ad if j J, the A j J, r j < H Vj V Aj H VJ c Y k V J j J c j J c for all 1 k K ad for all J D k such that J c D k \J = ad if j J, the A j J We say a set G is larger tha aother H if G > H, or G = H ad there exists some 1 i G such that G [i] > H [i] ad G [l] = H [l] for all 1 l i 1, where G [i] or H [i] deotes the ith largest elemet i G or H.

7 7 S Source Ecoder V M [1: N] [1: N] x v, [1: N ] s X p Y 1 Y 2 Y K X Y1 Y K ˆ 1 V M Chael 1 1 ˆ Decoder 1 1, 1 1 ˆ ˆ S1 s v y K V M Chael K K sˆ Decoder K K v, y K K ˆ S K Fig. 2. A uified hybrid codig used to prove the ier boud i Theorem 1. Besides, defie aother distortio regio { R o = D [1:K] : There exists some pmf pŝ[1:k] S Ed k S, Ŝk D k, 1 k K, such that ad for ay pmf p U[1:L] S, oe ca fid p X, Ũ [1:L],W [1:K],W satisfyig [1:K] m m I ŜAi ; U Bi U i 1 j=0 Bj I Y Ai ; ŨB WAi+1 i Ũ i 1 WAi WAi 1, j=0 Bj for ay m 1, A i [1 : K], B i [1 : L], 0 i m, A 0, A m+1, ad W Ai W Ai, if i is odd; W A i, otherwise, or W Ai W A i, if i is odd; W Ai, otherwise. 12 The we have the followig theorem. The proof is give i Appedix C. Theorem 1. For trasmittig source S over geeral broadcast chael p Y[1:K] X, R i R R o. 13 Remark 1. The ier boud i Theorem 1 ca be easily exteded to Gaussia or ay other well-behaved cotiuousalphabet source-chael pair by stadard discretizatio method [16, Thm. 3.3], ad moreover for this case the outer boud still holds. Theorem 1 ca be also exteded to the case of source-chael badwidth mismatch, where m samples of a DMS are trasmitted through uses of a DM-BC. This ca be accomplished by replacig the source ad chael symbols i Theorem 1 by supersymbols of legths m ad, respectively. Besides, Theorem 1 could be also exteded to the problem of broadcastig correlated sources by modifyig the distortio measure or source broadcast with chael iput cost by addig chael iput costrait. The ier boud R i i Theorem 1 is achieved by a uified hybrid codig scheme depicted i Fig. 2. I this scheme, the codebook has a layered or superpositio structure, ad cosists of radomly ad idepedetly geerated codewords V [1:N] m [1:N], m [1:N] N [1 : 2ri ], where r [1:N] satisfies 11. At ecoder side, upo source sequece S, the ecoder produces digital messages M [1:N] with M i meat for all the receivers k satisfyig

8 8 i D k. The, the codeword V [1:N] M [1:N] ad the source sequece S are used to geerate chael iput X by symbol-by-symbol mappig xv [1:N], s. At decoder sides, upo received sigal Yk, decoder k could recostruct M Dk ad also V D k M Dk losslessly, ad the Ŝ k is produced by symbol-by-symbol mappig ŝ kv Dk, y k. Such a scheme could achieve ay D [1:K] i the ier boud R i. To reveal essece of such hybrid codig, the digital trasmissio part of this hybrid codig ca be roughly uderstood as cascade of a K-user Gray-Wyer source-codig ad a K-user Marto s broadcast chael-codig, which share a commo codebook. Accordig to [16, Thm. 13.3], the ecodig operatio of Gray-Wyer source-codig with rates r [1:N] is successful if j J r j > j J H V j V Aj H VJ S for all J [1 : N] such that J = ad if j J, the A j J, ad accordig to [16, Thm 5.2] the decodig operatio of Marto s broadcast chael-codig with rates r [1:N] is successful if j J c r j < j J c H V j V Aj H VJ c Y k V J for all 1 k K ad for all J D k such that J c ad if j J, the A j J. Note that i Marto s broadcast chaelcodig, r [1:N] does ot correspod to the regular broadcast-rates i.e., the rates of subcodebooks i multicodig, but is the rates of the whole codebook. Sice the proposed hybrid codig satisfies the two sufficiet coditios above, V D k M Dk could be losslessly trasmitted to receiver k. Note that such iformal uderstadig is iaccurate owig to the use of symbol-by-symbol mappig, but it provides the ratioale for our scheme. Besides, the desig of such uified hybrid codig is ispired by the hybrid codig scheme for sedig correlated sources over multi-access chael i [15]. The outer boud R o i Theorem 1 are derived by itroducig auxiliary radom variables or remote sources U[1:L]. This proof method could also be foud i [9], [11, Thm. 2] ad [12, Lem. 1]. I [9] it is used to derive the outer boud for Gaussia source broadcast, ad i [11, Thm. 2] ad [12, Lem. 1] it is used to derive the outer bouds for sedig source over 2-user geeral broadcast chael. A deeper uderstadig of this proof method has bee give by Khezeli et al. i [12]. pŝ[1:k] S ca be cosidered as a virtual broadcast chael realized over physical broadcast chael p Y[1:K] X, ad hece certai measuremets based o pŝ[1:k] S are less tha or equal to those based o p Y[1:K] X. This leads to the ecessary coditios o the commuicatio. Note that this proof method geeralizes the oe used to derive trivial outer boud, but it does ot always result i a tighter outer boud tha the trivial oe [10]. For 2-user broadcast case, the ier boud i Theorem 1 reduces to { R i = D 1, D 2 : There exist some pmf p V0,V 1,V 2 S, ad fuctios x v 0, v 1, v 2, s, ŝ k v 0, v k, y k, k = 1, 2, such that Ed k S, Ŝk D k, IV 0 V k ; S < IV 0 V k ; Y k, j = 1, 2, IV 0 V 1 V 2 ; S + IV 1 ; V 2 V 0 < mi {IV 0 ; Y 1, IV 0 ; Y 2 + IV 1 ; Y 1 V 0 + IV 2 ; Y 2 V 0, IV 0 V 1 ; S + IV 0 V 2 ; S + IV 1 ; V 2 V 0 S < IV 0 V 1 ; Y 1 + IV 0 V 2 ; Y This ier boud was first give i by Yassaee et. al [21]. O the other had, for 2-user broadcast case, lettig

9 9 L = 3, the outer boud i Theorem 1 reduces to { R o = D 1, D 2 : There exists some pmf pŝ1,ŝ2 S such that Ed k S, Ŝk D k, k = 1, 2, ad for ay pmf p U1,U 2,U 3 S, oe ca fid p X, Ũ 1,Ũ2,Ũ3,W1,W2,W 1,W 2satisfyig I ŜA1 ; U B1 U B0 I Y A1 ; ŨB 1 ŨB 0 WA1, I ŜA1 ; U B1 U B0 + I ŜA2 ; U B2 U B0 U B1 I Y A1 ; ŨB 1 WA2 ŨB 0 WA1 + I Y A2 ; ŨB 2 ŨB 0 Ũ B1 WA1 WA2, I ŜA1 ; U B1 U B0 + I ŜA2 ; U B2 U B0 U B1 + I ŜA3 ; U B3 U B0 U B1 U B2 I Y A1 ; ŨB 1 WA2 ŨB 0 WA1 + I Y A2 ; ŨB WA3 2 ŨB 0 Ũ B1 WA1 WA2 + I Y A3 ; ŨB 3 ŨB 0 Ũ B1 Ũ B2 WA2 WA3, for ay A i [1 : 2], B i [1 : 3], 0 i 3, ad W Ai W Ai, if i is odd; W A i, otherwise, or W Ai W A i, if i is odd; W Ai, otherwise. 15 This outer boud is as tight as if ot tighter tha that give by Khezeli et al. i [12, Thm. 1]. This is because the outer boud i [12, Lem 1] is just R o with A i restricted to be a elemet ot a subset of [1 : 2]. Whe cosider lossless trasmissio of idepedet source, Theorem 1 ca be used to achieve bouds o capacity regio of geeral broadcast chael with commo messages. I this case, S = M j : 1 j N ad all M j s are idepedet with each other. For each 1 j N, let R j deote the rate of the commo message M j that is to be trasmitted losslessly from seder to all the receivers i G j [1 : K]. The correspodece betwee M j ad G j is kept same to that betwee V j ad G j ; see the begiig of this sectio. The such achievable rates R [1:N] costitute the capacity regio C. Now, defie rate regio { C i = R [1:N] : There exist some pmf p V[1:N] S, vector r [1:N] ad fuctio x v [1:N] such that r j > R j + H V j V Aj H VJ S j J j J j J for all J [1 : N] such that J = ad if j J, the A j J, r j < H Vj V Aj H VJ c Y k V J j J c j J c for all 1 k K ad for all J D k such that J c D k \J ad if j J, the A j J, 16

10 10 ad aother rate regio { C o = R [1:N] : There exists some pmf m j k A D k i B i R j m I N pũi p W[1:K],W [1:K] Ũ[1:N] ad fuctio x ũ [1:N] such that Y Ai ; ŨB WAi+1 i Ũ i 1 WAi WAi 1, j=0 Bj for ay m 1, A i [1 : K], B i [1 : N], 0 i m, A 0, A m+1, ad W Ai W Ai, if i is odd; W A i, otherwise, or W Ai W A i, if i is odd; W Ai, otherwise. 17 The as a cosequece of Theorem 1, we ca establish the followig bouds o the capacity regio of geeral broadcast chael. The proof is omitted. Theorem 2. For geeral broadcast chael p Y[1:K] X, the capacity regio C with commo messages satisfies C i C C o. 18 Remark 2. The ier boud ad the outer boud i Theorem 2 respectively geeralize Marto s ier boud ad Nair-El Gamal outer boud to the case of K-user broadcast chael. B. Source Broadcast over Degraded Chael If the chael is degraded, defie R i DBC = {D [1:K] : There exist some pmf p VK Sp VK 1 V K p V1 V 2, ad ad fuctios x v K, s, ŝ k v k, y k, 1 k K such that Ed k S, Ŝk D k, I S; V k k j=1 I Y j ; V j V j 1, 1 k K, where V 0, 19 R o DBC {D = [1:K] : There exists some pmf pŝ[1:k] S such that Ed k S, Ŝk D k, 1 k K, I Ŝ[1:k] ; S : k [1 : K] C DBC p Y[1:K] X, ad for ay pmf p UK 1 Sp UK 2 U K 1 p U1 U 2, U 0, U K S, I Ŝ[1:k] ; U k U k 1 : k [1 : K] C DBC holds, 20 p Y[1:K] X where C DBC p Y[1:K] X = {R [1:K] : 0 R k I X; Y k, 1 k K for some pmf p X 21

11 11 ad { C DBC p Y[1:K] X = R [1:K] : There exists some pmf p X p VK 1 Xp VK 2 V K 1 p V1 V 2 such that 0 R k I Y k ; V k V k 1, 1 k K, where V 0, V K X. 22 Note that C DBC p Y[1:K] X is the capacity of degraded broadcast chael p Y[1:K] X, ad by rate-splittig argumet, it ca be also expressed as { C DBC p Y[1:K] X = R [1:K] : There exists some pmf p X p VK 1 Xp VK 2 V K 1 p V1 V 2 such that R k 0, k R j j=1 k j=1 I Y j ; V j V j 1, 1 k K, where V 0, V K X. 23 The as a cosequece of Theorem 1, the followig theorem holds. The proof is give i Appedix D. Theorem 3. For trasmittig source S over degraded broadcast chael p Y[1:K] X, R i DBC R Ro DBC. 24 C. Quadratic Gaussia Source Broadcast Cosider sedig Gaussia source S N 0, N S with quadratic distortio measure d k s, ŝ = ds, ŝ s ŝ 2 over Gaussia broadcast chael Y k = X +W k, 1 k K with W k N 0, N k, N 1 N 2 N K. Assume badwidth mismatch factor is b. The the ier boud R i DBC i Theorem 3 could recover the best kow ier boud so far [7, Thm. 5] by settig suitable radom variables ad symbol-by-symbol mappigs. Corollary 1. [7, Thm. 5] For trasmittig Gaussia source S with quadratic distortio measure over 2-user Gaussia broadcast chael with badwidth mismatch factor b, R i DBC R. For b < 1 badwidth compressio where R i DBC = {D 1λ, γ, D 2 λ, γ : 0 λ 1, 0 γ 1, 25 D 1 λ, γ = bn S λp +N bn S b 1 b λγp +N 1 P +N 1 λp +N 1, 26 For b > 1 badwidth expasio D 2 λ, γ = bn S λp +N 1 + λγp +N 1 1 bn S P +N 1 λp +N 1 λγp +N 2 N 2 b b R i DBC = {D 1λ, γ, D 2 λ, γ : 0 λ 1, 0 γ 1, 28

12 12 where Y k D 1 λ, γ = D 2 λ, γ = b1 γ b 1 P +N1 λ b1 γ b 1 P +N1 b1 γ b 1 P +N1 λ b1 γ b 1 P +N1 N S b 1 bγp +N1, 29 N 1 N S b 1 bγp +N2 N 2 λ b1 γ b 1 P +N2. b 1 30 N 2 Proof: For b = m < 1 badwidth compressio, the source Sm = S, S+1 m is trasmitted over chael = X + Wk, k = 1, 2. Defie a set of radom variables U1 m, E1 m, U2 m, E2 m, X1, X 2, X 2, V 1, V 2 such that S m +1 = U m 1 + E m 1, 31 E m 1 = U m 2 + E m 2, 32 X 2 = X 2 + βαs, 33 V 1 = U m 1, X 1, 34 V 2 = V 1, U m 2, X 2, 35 where U m 1, U m 2, E m 2 are mutually idepedet Gaussia variables, X 2 ad X 1 are Gaussia variables idepedet of all the other variables, VarX 2 = λγp, VarX 1 = 1 λ P, VarE 1 = VarE 1 λ1 γp b, ad α = λγp +N2 N 1 b S, β = λγp λγp +N 2. Defie a set of fuctios N 2 N S b P +N1 1 b λp +N 1, VarE 2 = x v 2, s m = x 1 + αs + x 2 βαs = x 1 + αs + x 2, 36 ŝ m 1 v 1, y1 αn S = α 2 y1 x 1, u m 1, 37 N S + N 1 ŝ m 2 v 2, y2 αn S = α 2 y2 x 1, u m 1 + u m N S + N 2 Substitute these variables ad fuctios ito the ier boud R i DBC i Theorem 3, the the b < 1 case i Corollary 1 is recovered. For b = m > 1 badwidth expasio, the source S is trasmitted over chael Wk m, W k,m+1 where U m 1, U m 2, E m 2 Y m k, Y k,m+1 = X m, Xm+1 +, k = 1, 2. Defie a set of radom variables U m 1, E m 1, U m 2, E m 2, X m 1, X m 2, V 1, V 2 such that S m = U m 1 + E m 1, 39 E m 1 = U m 2 + E m 2, 40 V 1 = U m 1, X m 1, 41 V 2 = V 1, U m 2, X m 2, 42 are mutually idepedet Gaussia variables, X m 1 ad X m 2 are two Gaussia variables idepedet of all the other radom variables, VarX 1 = 1 λ1 γbp b 1, VarX 2 = λ1 γbp b 1, VarE 1 =

13 13 b1 γ N S b 1 P +N 1 λ b1 γ b 1 P +N 1 where α = b 1 ad VarE 2 = bγp +N2 VarE 1 λ b1 γ b 1 P +N 2 N 2 N 2 b 1. Defie a set of fuctios bγp N 2 x v 2, s m = α s m u m 1, x m 1 + x m 2 = αe m 1, x m 1 + x m 2, 43 ŝ m 1 v 1, y1 = u m αvare α 2 y1 m, 44 VarE 1 + N 1 ŝ m 2 v 2, y2 = u m N α 2 u m αvare VarE 2 + N 2 α 2 y2 m, 45 VarE 2 + N 2 γbp VarE 1. Substitute these variables ad fuctios ito the ier boud Ri DBC i Theorem 3, the the b > 1 case i Corollary 1 is also recovered. O the other had, settig U [1:K 1] to be joitly Gaussia with S, the outer boud R o DBC i Theorem 3 could recover the best kow outer boud [9, Thm. 2]. Theorem 4. [9, Thm. 2] For trasmittig Gaussia source S with quadratic distortio measure over K-user Gaussia broadcast chael with badwidth mismatch factor b, R R o DBC {D [1:K] : For ay variables + = τ 0 τ 1 τ K = 0, 1 1 b 2 log N S + τ k D k + τ k 1 : k [1 : K] C GBC, 46 D k + τ k N S + τ k 1 where C GBC deotes the capacity of Gaussia broadcast chael give by { K C GBC = R [1:K] : R k 0, 1 k K, N K+1 = 0, N k N k+1 exp 2 k=1 k j=1 R j P + N To compare R o DBC with the trivial distortio boud, we cosider a set of Gaussia test chaels p Ŝ k S, 1 k K that achieves the optimal poit-to-poit distortio for each receiver. Assume pŝ S is the backward Gaussia [1:K] broadcast chael cosistig of subchaels pŝ k S, 1 k K. Sice ay backward Gaussia chael ca be trasformed ito a forward Gaussia chael with the same probability distributio, assume p V[1:K] U is the forward Gaussia broadcast chael of pŝ S. The for Gaussia source broadcast, the outer boud is i form of the [1:K] compariso of capacity regios for two Gaussia broadcast chaels p V[1:K] U ad p Y[1:K] X. Note that p Y[1:K] X ad p V[1:K] U have differet badwidth the badwidth ratio is b but the same poit-to-poit capacity for each receiver. It ca be proved that the Gaussia broadcast capacity regio shriks as the badwidth icreases. Additioally, C DBC p V[1:K] U = C DBC p Y[1:K] X whe badwidth matched. Hece C DBC p V[1:K] U C DBC p Y[1:K] X always holds for badwidth compressio case. This is the reaso why the outer boud i [9] is otrivial oly for badwidth expasio. The details ca be foud i [10]. The bouds i Corollary 1 ad Theorem 4 are illustrated i Fig. 3. D. Hammig Biary Source Broadcast Cosider sedig biary source S Ber 1 2 with Hammig distortio measure dk s, ŝ = ds, ŝ 0, if s = ŝ; 1, otherwise, over biary broadcast chael Y k = X W k, 1 k K with W k Ber p k, 1 2 p 1 p 2 p K 0. Assume badwidth mismatch factor is b.

14 x Ier Boud Outer Boud 2 D2 Ier Boud 1 1 Outer Boud 1 Trivial Outer Boud D 1 Fig. 3. Distortio bouds for sedig Gaussia source over Gaussia broadcast chael with b = 2, N S = 1, P = 50, N 1 = 10, N 2 = 1. Outer Bouds 1 ad 2 ad Ier Bouds 1 ad 2 respectively correspod to the outer boud i Theorem 4, the outer boud i Theorem 8, the ier boud i Corollary 1, ad the ier boud achieved by Wyer-Ziv separate codig ucoded systematic code [17, Lem. 3]. Trivial Outer Boud correspods to the trivial outer boud 6. Besides, Outer Boud 2 ad Ier Boud 2 could be cosidered as the outer boud ad ier boud for Wyer-Ziv source broadcast problem with b = 1, β 1 = N S N 1 P +N 1, β 2 = N S N 2 P +N 2, ad i this case Trivial Outer Boud correspods to the Wyer-Ziv outer boud 55. We first cosider the ier boud. For badwidth expasio b > 1, as a special case of hybrid codig systematic source-chael codig Ucoded Systematic Codig has bee first ivestigated i [6]. For ay poit-to-poit lossless commuicatio system, such systematic codig does ot loss the optimality; however, for some lossy cases such as Hammig biary source commuicatio, it is ot optimal ay more. To retai the optimality, we ca first quatize the source S, ad the trasmit the quatized sigal usig Ucoded Systematic Codig. The performace of this code could be obtaied directly from Theorem 3. Specifically, let U 2 = S E 2, U 1 = U 2 E 1 with E 2 BerD 2, E 1 Berd 1. Let V 2 = U 2, X b 1, V 1 = U1, X1 b 1, X b 1 1 = X b 1 B b 1, where X1 b 1 ad X b 1 are idepedet of U 2 ad U 1, ad X b 1 ad B b 1 follow b 1 dimesioal Ber 1 2 ad Berθ, respectively. Let xb v 2, s = u 2, x b 1, ŝ 2 v2, y2 b = u2 ad ŝ 1 v1, y1 b = u1, if d 1 < p 1 ; y 1, otherwise. Substitute these variables ad fuctios ito the ier boud R i Theorem 3, the we get the followig corollary. DBC i Corollary 2 Coded Systematic Codig. For trasmittig biary source S with Hammig distortio measure over

15 15 2-user biary broadcast chael with badwidth mismatch factor b, R R i CSC covexhull {D 1, D 2 : 0 θ, d 1 1 2, where deotes the biary covolutio, i.e., ad H 2 deotes the biary etropy fuctio, i.e., D 1 mi {d 1 D 2, p 1 D 2, r 1 = 1 H 2 d 1 p 1 + b 1 [1 H 2 θ p 1 ], r 2 = H 2 d 1 p 2 H 2 p 2 + b 1 [H 2 θ p 2 H 2 p 2 ], 1 H 2 d 1 D 2 r 1, 1 H 2 D 2 r 1 + r 2, 48 x y = 1 xy + x1 y, 49 H 2 p = p log p 1 p log1 p. 50 Remark 3. Coded Systematic Codig without timesharig does ot always lead to a covex distortio regio, hece a timesharig mechaism is eeded to improve performace ad achieve R i CSC. It is equivalet to addig a timesharig variable Q ito V 2 ad V 1, before substitute them ito the ier boud R i DBC. Besides, ote that ulike Ucoded Systematic Codig, the Coded Systematic Codig could always achieve the optimal distortio for at least oe of the receivers. Moreover, ulike separate codig the Coded Systematic Codig could weake the cliff effect, ad result i slope-cliff effect. I additio, the outer boud i Theorem 3 reduces to the followig outer boud for Hammig biary source broadcast problem. This outer boud was first give i [11, Equatio 41] for 2-user case. The proof is similar to that of [11, Equatio 41], hece it is omitted here. Theorem 5. For trasmittig biary source S with Hammig distortio measure over K-user biary broadcast chael with badwidth mismatch factor b, R R o DBC {D [1:K] : For ay variables 1 2 = τ 0 τ 1 τ 2 τ K = 0, 1 b H 2 τ k 1 D k H 2 τ k D k : k [1 : K] C BBC, 51 where C BBC deotes the capacity of biary broadcast chael give by { C BBC = R [1:K] : There exist some variables 1 2 = θ 0 θ 1 θ 2 θ K = 0 such that 0 R k H 2 θ k 1 p k H 2 θ k p k, 1 k K. 52 The bouds i Corollary 2 ad Theorem 5 are illustrated i Fig. 4.

16 Trivial Outer Boud Outer Boud 2 Separate Codig Ucoded Systematic Codig Wyer Ziv Broadcast Codig D Outer Boud 1 Coded Systematic Codig Trivial Outer Boud D2 Fig. 4. Distortio bouds for sedig biary source over biary broadcast chael with b = 2, p 1 = 0.18, p 2 = Outer Bouds 1 ad 2 respectively correspod to the outer boud i Theorem 5 ad the outer boud i Theorem 9. Separate Codig, Ucoded Systematic Codig ad Coded Systematic Codig respectively correspod to the separate scheme combiig successive-refiemet code [16, Example 13.3] with superpositio code [16, Example 5.3], the ier boud i Corollary 3, ad the ier boud i Corollary 2. Trivial Outer Bouds 1 ad 2 correspod to the trivial outer boud 6 ad the Wyer-Ziv outer boud 55, respectively. Besides, Trivial Outer Boud 2, Outer Boud 2 ad Ucoded Systematic Codig could be cosidered as the outer bouds ad ier boud for Wyer-Ziv source broadcast problem with b = 1, β 1 = p 1, β 2 = p 2. Y1 S ˆ 1 Decoder 1 S Ecoder X p Y 1 Y 2 Y K X Z1 Y K Decoder K ˆ S K Z K Fig. 5. Wyer-Ziv source broadcast system: broadcast commuicatio system with side iformatio at decoders. IV. WYNER-ZIV SOURCE BROADCAST: SOURCE BROADCAST WITH SIDE INFORMATION We ow exted the problem by allowig decoders to access side iformatio correlated with the source. As depicted i Fig. 5, receiver k observes memoryless side iformatio Z k, ad it produces source recostructio Ŝ k from received sigal Y k ad side iformatio Z k. Defiitio 7. A -legth Wyer-Ziv source-chael code is defied by the ecodig fuctio x : S X ad a sequece of decodig fuctios ŝ k : Y k Z k Ŝ k, 1 k K.

17 17 Defiitio 8. If there exists a sequece of Wyer-Ziv source-chael codes satisfyig lim sup Ed k S, Ŝ k D k, 53 the we say that the distortio tuple D [1:K] is achievable. Defiitio 9. The admissible distortio regio for Wyer-Ziv broadcast problem is defied as R SI { D [1:K] : D [1:K] is achievable. 54 I additio, Shamai et al. [6, Thm. 2.1] showed that for trasmittig source over poit-to-poit chael p Yk X with side iformatio Z k available at decoder, the miimum achievable distortio satisfies R S Zk D k = C k, where R S Zk is the Wyer-Ziv rate-distortio fuctio of the source S give that the decoder observes Z k [16]. Therefore, the optimal distortio is D SI,k = R 1 S Z k C k. Obviously, where R SI is amed Wyer-Ziv outer boud. R SI R SI { D [1:K] : D k D SI,k, 1 k K, 55 Besides, we also cosider the commuicatio system with badwidth mismatch, whereby m samples of a DMS are trasmitted through uses of a DM-BC with l samples of side iformatio available at each decoder. For simplicity, we let m = l, ad for this case, badwidth mismatch factor is defied as b = m. A. Wyer-Ziv Source Broadcast If cosider Z [1:K] to be trasmitted from seder to the receivers over a virtual broadcast chael p Z[1:K] S, ad defie X = S, X ad Y k = Z k, Y k, 1 k K, the the Wyer-Ziv source broadcast problem is equivalet to the problem of sedig p S over p Y with S restricted to be the iput of subchael p [1:K] X Z [1:K] S. Hece Wyer-Ziv source broadcast problem could be cosidered as the problem of ucoded systematic source-chael codig. If set x v [1:N], s = s, x v [1:N], s, the from Theorem 1, we obtai the followig ier boud for such systematic source-chael codig problem. It is therefore also a ier boud for the Wyer-Ziv source broadcast problem. { R i SI = D [1:K] : There exist some pmf p V[1:N] S, vector r [1:N], ad fuctios x v [1:N], s, ŝ k v Dk, y k, z k, 1 k K such that Ed k S, Ŝk D k, 1 k K, r j > H V j V Aj H VJ S j J j J for all J [1 : N] such that J ad if j J, the A j J, r j < Vj V Aj H VJ c Y k Z k V J j J c j J c H for all 1 k K ad for all J D k such that J c D k \J = ad if j J, the A j J. 56

18 18 O the other had, the distortio regio of systematic source-chael codig problem belogs to that of the source broadcast problem without iput costrait for subchael p Z[1:K] S. Hece R SI R p S, p Y, [1:K] X where R p S, p Y deotes the admissible distortio regio for sedig S over broadcast chael p [1:K] X Y X. [1:K] The from Theorem 1, we obtai the followig outer boud o R p S, p Y, which therefore is also a outer [1:K] X boud o R SI. R o SI,1 {D = [1:K] : There exists some pmf p V[1:K] S ad fuctios ŝ k v k, z k, 1 k K such that Ed k S, Ŝk D k, 1 k K, ad for ay pmf p U[1:L] S, oe ca fid p S,X, Ũ [1:L],W [1:K],W satisfyig [1:K] m m I V Ai Z Ai ; U Bi U i 1 j=0 Bj I Y Ai Z Ai ; ŨB WAi+1 i Ũ i 1 WAi WAi 1, j=0 Bj for ay m 1, A i [1 : K], B i [1 : L], 0 i m, A 0, A m+1, ad W Ai W Ai, if i is odd; W A i, otherwise, or W Ai W A i, if i is odd; W Ai, otherwise. 57 I additio, regard U [1:L], Z [1:K] as auxiliary radom variables followig pu[1:l] Sp Z[1:K] S, the followig a similar proof to that of the outer boud i Theorem 1, we ca achieve aother outer boud o R SI. R o SI,2 {D = [1:K] : There exists some pmf p V[1:K] S ad fuctios ŝ k v k, z k, 1 k K such that Ed k S, Ŝk D k, 1 k K, ad for ay pmf p U[1:L] S, oe ca fid p X, Ũ [1:L], Z [1:K],W [1:K],W satisfyig [1:K] m m I V Ai ; U Bi Z Ai+1 U i 1 Z j=0 Bj i j=1 Aj I Y Ai ; ŨB i ZAi+1 WAi+1 Ũ i 1 Z j=0 Bj i j=1 A WAi WAi 1 j, for ay m 1, A i [1 : K], B i [1 : L], 0 i m, A 0, A m+1, ad W Ai W Ai, if i is odd; W A i, otherwise, or W Ai W A i, if i is odd; W Ai, otherwise. 58 Therefore, the followig theorem holds. The proof is omitted. Theorem 6. For trasmittig source S over broadcast chael p Y[1:K] X with side iformatio Z k at decoder k, R i SI R SI R o SI,1 Ro SI,2. 59 Remark 4. Similar to Theorem 1, Theorem 6 could also be exteded to Gaussia or ay other well-behaved cotiuous-alphabet source-chael pair, the problem of broadcastig Wyer-Ziv correlated sources, or Wyer-Ziv source broadcast with chael iput cost.

19 19 B. Wyer-Ziv Source Broadcast over Degraded Chael with Degraded Side Iformatio Theorem 6 ca be used to derive the ier boud ad outer boud for the case of degraded chael ad degraded side iformatio. Defie R i SI-D = {D [1:K] : There exists some pmf p VK Sp VK 1 V K p V1 V 2, ad ad fuctios x v K, s, ŝ k v k, y k, z k, 1 k K such that Ed k S, Ŝk D k, I S; V k k j=1 I Y j Z j ; V j V j 1, 1 k K, where V 0, 60 R o SI-D = {D [1:K] : There exists some pmf p VK Sp VK 1 V K p V1 V 2 ad fuctios ŝ k v k, z k, 1 k K such that Ed k S, Ŝk D k, I V k ; S Z k : k [1 : K] C DBC p Y[1:K] X, ad for ay pmf p UK 1 Sp UK 2 U K 1 p U1 U 2, U 0, U K S, I V k ; U k U k 1 Z k : k [1 : K] C DBC p Y[1:K] X holds, 61 where C DBC p Y[1:K] X ad C DBC p Y[1:K] X are give i 21 ad 22, respectively. The we have the followig theorem. The proof is aalogous to that of Theorem 3, ad is therefore omitted. Theorem 7. For trasmittig source S over degraded broadcast chael p Y[1:K] X X Y K Y K 1 Y 1 with degraded side iformatio Z k S Z K Z K 1 Z 1 at decoder k, R i SI-D R SI R o SI-D. 62 C. Wyer-Ziv Gaussia Source Broadcast Cosider sedig Gaussia source S N 0, N S with quadratic distortio measure d k s, ŝ = ds, ŝ s ŝ 2 over Gaussia broadcast chael Y k = X + W k, 1 k K with W k N 0, N k, N 1 N 2 N K. Assume the side iformatio Z k observed by receiver k satisfies S = Z k +B k with idepedet Gaussia variables Z k N 0, N S β k ad B k N 0, β k. Assume badwidth mismatch factor is b. The the ier boud i Theorem 7 could recover the existig results i the literature [17], [18], ad the outer boud i Theorem 7 could be used to prove the followig outer boud for Wyer-Ziv Gaussia source broadcast problem. The proof is give i Appedix E.

20 20 Theorem 8. For trasmittig Gaussia source S over Gaussia broadcast chael with degraded side iformatio Z k β 1 β 2 β K at decoder k, R SI R o SI-D {D [1:K] : For ay variables + = τ 0 τ 1 τ K = 0, 1 1 b 2 log β k + τ k D k + τ k 1 : k [1 : K] C GBC, 63 D k + τ k β k + τ k 1 where C GBC deotes the capacity regio of the Gaussia broadcast chael give i 47. The boud i Theorem 8 is show i Fig. 3. D. Wyer-Ziv Biary Source Broadcast Cosider sedig biary source S Ber 1 2 with Hammig distortio measure dk s, ŝ = ds, ŝ 0, if s = ŝ; 1, otherwise, over biary broadcast chael Y k = X W k, 1 k K with W k Ber p k, 1 2 p 1 p 2 p K 0. Assume the side iformatio Z k observed by receiver k satisfies S = Z k B k with idepedet variables Z k Ber 1 2 ad Bk Ber β k. Assume badwidth mismatch factor is b. Let V 1 = U 1, X b 1, V2 = U 2, X b, V 3 =, ad U 1 ad U 2 are idepedet of X b 1 ad X b. S, U 2 ad U 1 satisfy the distributio p U2 Sp U1 U 2, where p U2 S = q 2ᾱ 2 q 2 α 2 q 2 q 2 α 2 q 2 ᾱ 2 q 2, 64 p U1 U 2 = q 1ᾱ 1 q 1α 1 q 1 q 1α 1 q 1ᾱ 1 q with 0 q 2, q 1 1, 0 α 2, α Xb ad X1 b satisfy X1 b = X b B b, X b b dimesioal Ber 1 2, ad B b b dimesioal Berθ with 0 θ 1 2. Deote α 1 = α 2 α 1, q 1 = q 2 q 1, ad set x b v 2, s = x b ad for i = 1, 2, Substitute these radom variables ad fuctios ito R i SI ŝ i vi, yi b z i, if α i β i or α i < β i, u i = 2;, z i = u i, if α i < β i, u i = 0, i Theorem 6, the we get the followig performace the hybrid codig reduces to a layered digital codig, which is tighter tha that of the Layered Descriptio Scheme LDS [17, Lem. 4]. Corollary 3 Layered Digital Codig. For trasmittig biary source S with Hammig distortio measure over

21 21 2-user biary broadcast chael with side iformatio Z k at decoder k, R SI R i LDC {D 1, D 2 : 0 q 1 q 2 1, 0 α 2 α 1 1 2, 0 θ 1 2, q 1 rα 1, β 1 b 1 H 2 θ p 1, q 1 rα 1, β 2 b 1 H 2 θ p 2, q 2 rα 2, β 2 b 1 H 2 p 2, q 1 rα 1, β 1 + q 2 rα 2, β 2 q 1 rα 1, β 2 b 1 H 2 θ p 1 + b H 2 θ p 2 H 2 p 2, D i q i mi {α i, β i + 1 q i β i, i = 1, 2, 67 where rα, β = H 2 α β H 2 α, 68 deotes the biary covolutio give i 49, ad H 2 deotes the biary etropy fuctio give i 50. I additio, the outer boud i Theorem 7 reduces to the followig oe for Wyer-Ziv biary case. The proof is give i Appedix F. Theorem 9. For trasmittig biary source S with Hammig distortio measure over K-user biary broadcast chael with degraded side iformatio Z k 1 2 β 1 β 2 β K 0 at decoder k, R SI R o SI-D {D [1:K] : There exists some variables 0 α 1, α 2,, α K 1 2 such that α k D k mi {D k, β k, 1 k K, ad for ay variables 1 2 = τ 0 τ 1 τ 2 τ K = 0, 1 η k H 2 β k τ k H 2 β k τ k 1 H 4 α k, β k, τ k H 4 α k, β k, τ k 1 : k [1 : K] C BBC, b where C BBC deotes the capacity regio of the biary broadcast chael give i 52, β k D k β η k k α k, if α k < β k, 0, otherwise, H 4 x, y, z xyz + xyz log xyz + xyz xyz + xyz log xyz + xyz xyz + xyz log xyz + xyz xyz + xyz log xyz + xyz, 71 ad x 1 x.. The bouds i Corollary 3 ad Theorem 9 are show i Fig. 4.

22 22 V. CONCLUDING REMARKS I this paper, we focused o the joit source-chael codig problem of sedig a memoryless source over memoryless broadcast chael, ad developed a outer boud ad a ier boud for this problem. The ier boud is achieved by a uified hybrid codig scheme, ad it ca recover the best kow performace of existig hybrid codig. Similarly, our outer boud ca also recover the best kow outer boud i the literature. Besides, we also exted the results to Wyer-Ziv source broadcast problem. All these bouds are also used to geerate some ew results, icludig the bouds o capacity regio of geeral broadcast chael with commo messages which respectively geeralize Marto s ier boud ad Nair-El Gamal outer boud. The ier boud achieved by proposed hybrid codig is established by usig geeralized Multivariate Coverig Lemma ad geeralized Multivariate Packig Lemma, ad the outer boud is derived by itroducig auxiliary radom variables or remote sources ad exploitig Csiszár sum idetity as i [12]. These lemmas ad tools are expected to be exploited to derive more ad stroger achievability ad coverse results for etwork iformatio theory. APPENDIX A PROOF OF LEMMA 1 We follow similar steps to the proof of mutual coverig lemma [15]. Let { k B = m [1:k] [1 : 2 ri ] : U, V0, V[1:k] m [1:k] T ɛ. 72 The we oly eed to show lim P B = 0 = 0. O the other had, lim P B = 0 = lim lim = lim u,v 0 p U,V 0 u, v 0 P B = 0 u, v 0 73 u,v0 T ɛ u,v0 T ɛ p U,V u, v 0 0 P B = 0 u, v0 + lim P u, v0 / T ɛ 74 p U,V 0 u, v 0 P B = 0 u, v 0 75 To prove lim P B = 0 = 0, it is sufficiet to show lim P B = 0 u, v 0 = 0 for ay u, v 0 T ɛ. Utilizig Chebyshev lemma [16, App. B], we ca boud the probability as P B = 0 u, v0 P B E B 2 E B 2 u, v0 Var B u, v 0 E B u, v Next we prove the upper boud Var B u,v 0 E B u,v teds to zero as. Defie 0 2 E 1, if u, v0, V[1:k] m m [1:k] T [1:k] 0, otherwise, ɛ ; 77

23 23 for each m [1:k] k [1 : 2ri ], the B ca be expressed as Deote p 0 = P p I = P B = m [1:k] k [1:2r i ] u, v 0, V [1:k] m [1:k] T ɛ u, v 0 u, v 0, V [1:k] m [1:k] T ɛ E m [1:k]. 78, 79, 80, u, v0, V[1:k] m I, m Ic T ɛ u, v0 for m [1:k] = 1, ad m [1:k] = 2. Obviously, p [1:k] = p 0. The E B u, v0 = P u, v0, V[1:k] m [1:k] T ɛ u, v0 = 2 k j=1 rj p 0, 81 m [1:k] ad E B 2 u, v0 = I [1:k] m [1:k] m I c :m I c m I c = 2 k j=1 rj p 0 + Defie P u, v0, V I [1:k] m [1:k] m I c :m I c m I c [1:k] m [1:k] T ɛ P u, v0, V, u, v0, V[1:k] m I, m Ic T ɛ u, v0 [1:k] m [1:k] T ɛ 82, u, v0, V[1:k] m I, m Ic T ɛ u, v0. 83 J {J [1 : k] : if j J, the A j J. 84 The ay set I [1 : k] ca trasform ito a J I J by removig all the elemets j s such that A j I. Accordig to geeratio of radom codebook, we ca observe that p I = p J I. Therefore, P u, v0, V[1:k] m [1:k] T ɛ, u, v0, V[1:k] m I, m Ic T ɛ u, v0 I [1:k] m [1:k] m I c :m I c m I c = I [1:k] m [1:k] m I c :m I c m I c I [1:k] I [1:k] J J p J I 85 2 k j=1 rj+ j I c rj p J I 86 2 k j=1 rj+ j J I c rj p J I 87 2 k J 2 k j=1 rj+ j J c rj p J 88 J J 2 k j=1 rj+ j J c rj+o1 p J, 89

24 24 where 87 follows from J I I, 88 follows from that for each J J, there are at most 2 k J of I s that could trasform ito J, ad o1 deotes a term that vaishes as. Hece Var B u, v 0 E B 2 u, v k j=1 rj p k j=1 rj+ rj+o1 j J c p J. 91 J J Furthermore we have Var B u, v0 2 E B u, v0 2 k j=1 rj p 0 + J J 2 k j=1 rj+ j J c rj+o1 p J 2 k j=1 rj p = 2 k 1 j=1 rj + 2 rj+o1 p J j J p 0 p J J 0 Accordig to geeratio process of radom codebook, we ca observe that p 0 = P V[1:k] m [1:k] = v[1:k] u, v0 v [1:k] :u,v0,v T [1:k] ɛ 94 2 k j=1 HVj V A j V 0 HV [1:k] UV 0+2δɛ, 95 where 95 follows from that for ay u, v 0, v [1:k] T ad for ay u, v 0 T Similarly, we also ca get ɛ, P V[1:k] m [1:k] = v[1:k] u, v0 2 k j=1 HVj V A j V 0+δɛ, 96 ɛ, { v[1:k] : u, v0, v[1:k] T ɛ 2 HV [1:k] UV 0+δɛ. 97 p J 2 k j=1 HVj V A j V 0+ j J c HVj V A j V 0 HV [1:k] UV 0 HV J c UV 0V J 4δɛ. 98 Substitute 95 ad 98 ito 93, the we have Var B u, v0 E B u, v0 2 k j=1 rj k j=1 HVj V A j V 0 HV [1:k] UV 0+2δɛ 2 + J J 2 j J rj j J HVj V A j V 0 HV J UV 0+6δɛ+o teds to zero if k k r j > H V j V Aj V 0 H V[1:k] UV 0 + 2δ ɛ 100 j=1 j=1 r j > H V j V Aj V 0 H VJ UV 0 + 6δ ɛ + o1, 101 j J j J i.e., j J r j > j J H V j V Aj V 0 H VJ UV 0 + δ ɛ for some δ ɛ that teds to zero as ɛ 0. This completes the proof.

25 25 u,v 0 APPENDIX B PROOF OF LEMMA 2 For ay J such that J = ad if j J the A j J, P U, V0, V[1:k] m [1:k] T ɛ for some m [1:k] P U, V0, VJ m J T ɛ for some m J = p U,V0 u, v0 P u, v0, VJ m J T ɛ for some m J u, v0 u,v p U,V0 u, v0 P u, v0, VJ m J T ɛ u, v m J Similar to 95, we ca obtai that P u, v0, VJ m J T ɛ u, v0 2 j J HVj V A j V 0 HV J UV 0 2δɛ. 105 Substitute it ito 104, the we have P U, V0, V[1:k] m [1:k] T ɛ for some m [1:k] 2 j J rj j J HVj V A j V 0 HV J UV 0 2δɛ teds to zero if This completes the proof. r j < H V j V Aj V 0 H VJ UV 0 2δ ɛ. 107 j J j J APPENDIX C PROOF OF THEOREM 1 A. Ier Boud Actually the ier boud ca be see as a corollary to [20, Thm. 1] by choosig proper etwork topology, trasit probability ad symbol-by-symbol fuctios. I the followig, we provide a direct descriptio of the proposed hybrid codig scheme ad a direct proof for it. Codebook Geeratio: Fix coditioal pmf p V[1:N] S, vector r [1:N], ecodig fuctio x v [1:N], s ad decodig

26 26 fuctios ŝ k v Dk, y k that satisfy Ed k S, Ŝk D k, 1 k K, r j > H V j V Aj H VJ S j J j J 108 for all J [1 : N] such that J = ad if j J, the A j J, 109 r j < H Vj V Aj H VJ c Y k V J j J c j J c for all 1 k K ad for all J D k such that J c D k \J ad if j J, the A j J. For each j [1 : N] ad each m Aj 110 i A j [1 : 2 ri ], radomly ad idepedetly geerate a set of sequeces vj m A j, m j, m j [1 : 2 rj ], with each distributed accordig to p V j V Aj v j,i v Aj,im Aj. The codebook { C = m[1:n] : m[1:n] N [1 : ] ri v [1:N] is revealed to the ecoder ad all the decoders. Ecodig: We use joit typicality ecodig. Give s, ecoder fids the smallest idex vector m [1:N] such that s, v[1:n] m[1:n] T ɛ. If there is o such idex vector, let m [1:N] = 1. The the ecoder trasmits the sigal x i = x v [1:N],i m[1:n], si, 1 i. 112 Decodig: We use joit typicality decodig. Let ɛ > ɛ. Upo receivig sigal yk, the decoder of the receiver k fids the smallest idex vector ˆm k D k such that v D k ˆm k D k, y k T ɛ. 113 If there is o such idex vector, let ˆm k D k = 1. The decoder recostructs the source as ŝ k,i = ŝ k v Dk,i ˆm k D k, y k,i, 1 i. 114 Aalysis of Expected Distortio: We boud the distortio averaged over S, ad the radom choice of the codebook C. Defie the error evet where for 1 k K. Usig uio boud, we have E = E 1 E 2,k E 3,k, 115 k k { E 1 = S, V[1:N] m[1:n] / T ɛ for all m [1:N], 116 { E 2,k = S, V[1:N] m[1:n], Y k / T ɛ, 117 { V E 3,k = m, Y Dk Dk k T ɛ for some m D k, m D k M Dk, 118

27 27 P E P E 1 + K k=1 P E1 c E2,k + K P E 3,k. 119 Now we claim that if 109 ad 110 hold, the P E teds to zero as. Before provig it, we show that this claim implies the ier boud of Theorem 1. Defie E 4,k = k=1 { S, VD k k ˆM D k, Yk / T ɛ. 120 the we have E c E c 4,k, i.e., E 4,k E. This implies that P E 4,k P E 0 as. The utilizig typical average lemma [16], we have lim sup Ed k S, Ŝ k = lim sup = lim sup E ] P E 4,k E [d k S, Ŝ k E 4,k + P E4,k c ] E [d k S, Ŝ k E4,k c 1 + ɛ Ed k S, Ŝk ] [d k S, Ŝ k E4,k c ɛ D k. 124 Therefore, the desired distortios are achieved for sufficietly small ɛ. Next we tur back to prove the claim above. Followig from Multivariate Coverig Lemma Lemma 1, the first term of 119, P E 1, vaishes as, ad accordig to coditioal typicality lemma [16, Sec. 3.7], the secod item teds to zero as. Now we focus o the third term of 119. E 3,k ca be write as where E I 3,k = with I c D k \I. Usig uio boud we have Each D k E 3,k = I D k E I 3,k, 125 { V M Dk I, m I c, Y k T ɛ for some m I c, m I M c I, c 126 P E 3,k I D k P E I 3,k. 127 has fiite umber of subsets, hece we oly eed to show for each I D k, P. To show this, it is eeded to aalyze the correlatio betwee codig idex M [1:N] E I 3,k vaishes as ad ochose codewords. Specifically, M [1:N] depeds o source sequece ad the etire codebook, ad hece stadard packig lemma caot be applied directly. This problem has bee resolved by the techique developed i [15], [20].