Proof In the CR proof. and
|
|
|
- Catherine Banks
- 5 years ago
- Views:
Transcription
1 Question Under what conditions will we be able to attain the Cramér-Rao bound and find a MVUE? Lecture 4 - Consequences of the Cramér-Rao Lower Bound. Searching for a MVUE. Rao-Blackwell Theorem, Lehmann-Scheffé Theorem. Corollary 1 There exists an unbiased estimator which attains the CR lower bound (under regularity conditions) if and only if Proof In the CR proof = I ( ) Cov[U, V ] 2 Var[U]Var[V ] and the lower bound is attained if and only equality is achieved. If U =, V =, the equality occurs when = c + d, where c, d are constants. E[V ] = 0 so c = d and = d( ). Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20 Multiply by / and take expectations. E [ ( ) ] 2 The LHS is I so we have d = I and [ ] [ ] = de de = d 1 0 = I ( ) Question What is the relationship between the CRLB and exponential families? Corollary 2 If there exists an unbiased estimator (X) which attains the CR lower bound (under regularity conditions) it follows that X must be in an exponential family Proof Taking n = 1 and log f (x; ) = = I ( ) log f (x; ) = A() + D() + C(x) which is an exponential family form. The constant of integration C(x) is a function of x. Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20
2 Question What is the relationship between the CRLB and MLEs? Corollary 3 Suppose (X) is an unbiased estimator that attains the CRLB, and so is a MVUE. Suppose that the MLE is a solution to / = 0 (so, not on boundary). Then =. i.e. if the CRLB is attained then it is generally the MLE that attains it. Proof must satisfy = I ( ). Setting = 0 and solving will give the MLE. Since I > 0 (in all but exceptional circumstances), this gives =. Question Do all MLEs attain the CRLB? No, because not all MLEs are unbiased. Example 11 Let X 1,..., X n be a random sample from N(µ, σ 2 ). Then we know the MLEs are µ = X, σ 2 = 1 n X 2 i X 2. Exercise µ is unbiased, but σ 2 is biased. CRLBs are 1/I µ = σ 2 and 1/I σ 2 = 2σ 4 /n. Var( µ) = σ 2 /n which equals the CRLB so is MVUE. Var( σ 2 ) = 2(n 1)σ 4 /n 2 is less than the CRLB. But σ 2 is biased. The sample variance S 2 = 1 n 1 (X i X) 2 is unbiased and has variance 2σ 4 /(n 1) which is larger than the CRLB. Question Is S 2 a MVUE? Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20 Efficiency Asymptotic normality of MLE Definition 13 The (Bahadur) efficiency of an estimator is defined as a comparison of the variance of with the CR bound I 1. That is Efficiency of = I 1 Var[ ] = 1 I Var[ ] The asymptotic efficiency is the limit as n. There are similar definitions for the relative efficiency of two estimators. Revision from Part A Statistics As the sample size n, the MLE N(, I 1 ). This is a powerful and general result. Assuming the usual regularity conditions hold then it tells us that the MLE has the following properties 1 it is asymptotically unbiased 2 it is asymptotically efficient i.e. it attains the CRLB asymptotically. 3 it has a normal distribution asymptotically. Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20
3 Extensions to the Cramér-Rao inequality 1. If is an estimator with bias b() = bias( ), then Var[ ] ( 1 + b ) 2 I 1 2. If ĝ(x) is an unbiased estimator for g(), then Var[ĝ(X)] ( ) g 2 I 1. Proof Begin with E ( (X)) = + b() (in 1.) and E (ĝ(x)) = g() (in 2.). Differentiate both sides and proceed as above to find Cov[U, V ] = (1 + b/) (in 1.) and Cov[U, V ] = g/ (in 2., with U = ĝ). The bound is against Cov[U, V ] 2 which leads to the results above. Fisher Information for a d-dimensional parameter Information matrix: [ ] [ 2 ] l I ij = E = E i j i j under regularity conditions. The CR inequality is Var( i ) [I 1 ] ii, i = 1,..., d. Exercise: verify that we have already proved Var( i ) [I ii ] 1. Note that [I 1 ] ii [I ii ] 1 (GJJ) so bound above is stronger. Exercise For an Exponential family in canonical form, 2 I ij = nd(φ). φ i φ j Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20 The CRLB may not be achievable but will still wish to search for an MVUE. Sufficiency plays an important role in the search for a MVUE. Theorem 3 : Rao-Blackwell Theorem (RBT) (GJJ 2.5.2) Let X 1,..., X n be a random sample of observations from f (x; ). Suppose that T is a sufficient statistic for and that is any unbiased estimator for. Define a new estimator T = E[ˆ T ]. Then 1. T is a function of T alone; 2. E[ T ] = ; 3. Var( T ) Var( ). Comment This says that estimators maybe be improved if we take advantage of sufficient statistics. Proof 1. T = E X [ˆ T = t] = = ˆ(x)f (x t, )dx χ χ ˆ(x)f (x t)dx 2. E[ T ] = E T [E[ˆ T ]] = E[ˆ] = (by law of total expectation) 3. Using the law of total variance Var( ) = Var(E[ˆ T ]) + E T [Var(ˆ T )] = Var( T ) + E T [Var(ˆ T )] Var( ) Var( T ) Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20
4 Example 12 Suppose X 1,..., X n be a random sample from Bernoulli(). It is easy to see that = X 1 is unbiased for. Also, we have seen before that T = N X i is sufficient for. We can use RBT to construct an estimator with smaller variance E[X 1 T = t] = P(X 1 = 1 T = t) = P(X 1 = 1, N X i = t) P( N X i = t) = P(X 1 = 1, N i=2 X i = t 1) N C t t (1 ) N t =.N 1 C t 1 t 1 (1 ) N t N C t t (1 ) n t Corollary 4 If an MVUE for exists, then there is a function T of the minimal sufficient statistic T for which is an MVUE. Proof If is a MVUE and T is minimal sufficient then by RBT we can construct T. Which implies T is a function of T alone, is unbiased and variance no larger than. Hence is also a MVUE. Comment This says that we can restrict our search for a MVUE to those based on minimal sufficient statistics. = t N Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20 Completeness Definition 14 : Complete Sufficient Statistics Let T (X 1,..., X n ) be a sufficient statistic for. The statistic T is complete if, whenever h(t ) is a function of T for which E[h(T )] = 0 for all, then h(t ) 0 almost everywhere. Lemma 4 Suppose T is a complete sufficient statistic for, and g(t ) unbiased for, so E[g(T )] =. Then g(t ) is the unique function of T which is an unbiased estimator of. Proof If there were two such unbiased estimators g 1 (T ), g 2 (T ), then E[g 1 (T ) g 2 (T )] = = 0 for all, so g 1 (T ) = g 2 (T ) almost everywhere. Question If we have an unbiased estimator what are the sufficient conditions for it to be MVUE? Lemma 5 If an MVUE for exists and T is a complete and minimal sufficient statistic for, and suppose h = h(t ) is unbiased for, then h(t ) is a MVUE. This Lemma combines the results of Corollary 4 and Lemma 4. Proof If an MVUE exists then there is a function of T which is an MVUE, by the RB Corollary 4. But h(t ) is the only function of T which is unbiased for (from Lemma 4). So h must be the function of T which an MVUE. Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20
5 Question Finally, how can we construct a MVUE? Theorem 4 : Lehmann-Scheffé theorem Let T be a complete sufficient statistic for, and let be an unbiased estimator for, then the unbiased estimator T = E[ˆ T ] has the smallest variance among all unbiased estimators of. That is, for all unbiased estimators. Var( T ) Var( ) Comment This theorem says that if we can find any unbiased estimator and a complete sufficient statistic T then we can construct a MVUE. Proof Suppose exists with Var( ) < Var( T ). Then by RBT we can construct T = E[ T ] such that Var( T ) Var( ) < Var( T ) But T and T are both unbiased and T is complete, so by Lemma 4 we have T = T and Var( T ) = Var( T ) which is a contradiction. Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20 Lemma 6 : Complete Sufficiency in EFs If the rv X has a distribution belonging to a k-parameter exponential family, then under the usual regularity conditions, the statistic ( n B 1 (X i ), n B 2 (X i ),..., n ) B k (X i ) which we already know is minimal sufficient, is complete. Comment We showed before that MLEs for exponential families were functions of this same statistic. Therefore, for a member of an exponential family if the MLE is unbiased (note : not all MLEs are unbiased), then by Lemma 5, the MLE will be MVUE. If there is an unbiased estimator that attains the CRLB then, by Corollary 3, the MLE will attain the CRLB. Example 13 Let X 1,..., X n be a random sample from N(µ, σ 2 ). Then we know the MLEs are µ = X, σ 2 = 1 n X 2 i X 2. µ is unbiased, but σ 2 is biased. Exercise ( The minimal sufficient complete statistic is n X i, ) n X i 2. So µ is MVUE and attains the CRLB with variance σ 2 /n. The sample variance S 2 = 1 n 1 (X i X) 2 is unbiased and is a function of the minimal sufficient complete statistic so is MVUE with variance 2σ 4 /(n 1) which is larger than the CRLB of 2σ 4 /n. Jonathan Marchini (University of Oxford) BS2a MT / 20 Jonathan Marchini (University of Oxford) BS2a MT / 20
Course arrangements. Foundations of Statistical Inference
 Course arrangements Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 013 Lectures M. and Th.10 SPR1 weeks 1-8 Classes Weeks 3-8 Friday 1-1, 4-5, 5-6
Course arrangements Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 013 Lectures M. and Th.10 SPR1 weeks 1-8 Classes Weeks 3-8 Friday 1-1, 4-5, 5-6
Foundations of Statistical Inference
 Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Foundations of Statistical Inference Jonathan Marchini Department of Statistics University of Oxford MT 2013 Jonathan Marchini (University of Oxford) BS2a MT 2013 1 / 27 Course arrangements Lectures M.2
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
Variations. ECE 6540, Lecture 10 Maximum Likelihood Estimation
 Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Estimation and Detection
 stimation and Detection Lecture 2: Cramér-Rao Lower Bound Dr. ir. Richard C. Hendriks & Dr. Sundeep P. Chepuri 7//207 Remember: Introductory xample Given a process (DC in noise): x[n]=a + w[n], n=0,,n,
stimation and Detection Lecture 2: Cramér-Rao Lower Bound Dr. ir. Richard C. Hendriks & Dr. Sundeep P. Chepuri 7//207 Remember: Introductory xample Given a process (DC in noise): x[n]=a + w[n], n=0,,n,
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM
 c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
c 2007-2016 by Armand M. Makowski 1 ENEE 621 SPRING 2016 DETECTION AND ESTIMATION THEORY THE PARAMETER ESTIMATION PROBLEM 1 The basic setting Throughout, p, q and k are positive integers. The setup With
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE
 557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
Chapters 9. Properties of Point Estimators
 Chapters 9. Properties of Point Estimators Recap Target parameter, or population parameter θ. Population distribution f(x; θ). { probability function, discrete case f(x; θ) = density, continuous case The
Chapters 9. Properties of Point Estimators Recap Target parameter, or population parameter θ. Population distribution f(x; θ). { probability function, discrete case f(x; θ) = density, continuous case The
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE)
 1 ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE) Jingxian Wu Department of Electrical Engineering University of Arkansas Outline Minimum Variance Unbiased Estimators (MVUE)
1 ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE) Jingxian Wu Department of Electrical Engineering University of Arkansas Outline Minimum Variance Unbiased Estimators (MVUE)
Review Quiz. 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the
 Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
A Few Notes on Fisher Information (WIP)
 A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
Theory of Statistics.
 Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
Theory of Statistics. Homework V February 5, 00. MT 8.7.c When σ is known, ˆµ = X is an unbiased estimator for µ. If you can show that its variance attains the Cramer-Rao lower bound, then no other unbiased
10-704: Information Processing and Learning Fall Lecture 24: Dec 7
 0-704: Information Processing and Learning Fall 206 Lecturer: Aarti Singh Lecture 24: Dec 7 Note: These notes are based on scribed notes from Spring5 offering of this course. LaTeX template courtesy of
0-704: Information Processing and Learning Fall 206 Lecturer: Aarti Singh Lecture 24: Dec 7 Note: These notes are based on scribed notes from Spring5 offering of this course. LaTeX template courtesy of
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Detection & Estimation Lecture 1
 Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
ECON 4130 Supplementary Exercises 1-4
 HG Set. 0 ECON 430 Sulementary Exercises - 4 Exercise Quantiles (ercentiles). Let X be a continuous random variable (rv.) with df f( x ) and cdf F( x ). For 0< < we define -th quantile (or 00-th ercentile),
HG Set. 0 ECON 430 Sulementary Exercises - 4 Exercise Quantiles (ercentiles). Let X be a continuous random variable (rv.) with df f( x ) and cdf F( x ). For 0< < we define -th quantile (or 00-th ercentile),
Inferring from data. Theory of estimators
 Inferring from data Theory of estimators 1 Estimators Estimator is any function of the data e(x) used to provide an estimate ( a measurement ) of an unknown parameter. Because estimators are functions
Inferring from data Theory of estimators 1 Estimators Estimator is any function of the data e(x) used to provide an estimate ( a measurement ) of an unknown parameter. Because estimators are functions
Classical Estimation Topics
 Classical Estimation Topics Namrata Vaswani, Iowa State University February 25, 2014 This note fills in the gaps in the notes already provided (l0.pdf, l1.pdf, l2.pdf, l3.pdf, LeastSquares.pdf). 1 Min
Classical Estimation Topics Namrata Vaswani, Iowa State University February 25, 2014 This note fills in the gaps in the notes already provided (l0.pdf, l1.pdf, l2.pdf, l3.pdf, LeastSquares.pdf). 1 Min
Statistics. Lecture 2 August 7, 2000 Frank Porter Caltech. The Fundamentals; Point Estimation. Maximum Likelihood, Least Squares and All That
 Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Estimators as Random Variables
 Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maimum likelihood Consistency Confidence intervals Properties of the mean estimator Introduction Up until
Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maimum likelihood Consistency Confidence intervals Properties of the mean estimator Introduction Up until
DA Freedman Notes on the MLE Fall 2003
 DA Freedman Notes on the MLE Fall 2003 The object here is to provide a sketch of the theory of the MLE. Rigorous presentations can be found in the references cited below. Calculus. Let f be a smooth, scalar
DA Freedman Notes on the MLE Fall 2003 The object here is to provide a sketch of the theory of the MLE. Rigorous presentations can be found in the references cited below. Calculus. Let f be a smooth, scalar
6.1 Variational representation of f-divergences
 ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016 Lecture 6: Variational representation, HCR and CR lower bounds Lecturer: Yihong Wu Scribe: Georgios Rovatsos, Feb 11, 2016
ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016 Lecture 6: Variational representation, HCR and CR lower bounds Lecturer: Yihong Wu Scribe: Georgios Rovatsos, Feb 11, 2016
Evaluating the Performance of Estimators (Section 7.3)
 Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Detection & Estimation Lecture 1
 Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Mathematical statistics
 October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
2.2.2 Comparing estimators
 2.2. POINT ESTIMATION 87 2.2.2 Comparing estimators Estimators can be compared through their mean square errors. If they are unbiased, this is equivalent to comparing their variances. In many applications,
2.2. POINT ESTIMATION 87 2.2.2 Comparing estimators Estimators can be compared through their mean square errors. If they are unbiased, this is equivalent to comparing their variances. In many applications,
Chapter 8.8.1: A factorization theorem
 LECTURE 14 Chapter 8.8.1: A factorization theorem The characterization of a sufficient statistic in terms of the conditional distribution of the data given the statistic can be difficult to work with.
LECTURE 14 Chapter 8.8.1: A factorization theorem The characterization of a sufficient statistic in terms of the conditional distribution of the data given the statistic can be difficult to work with.
March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS
 March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS Abstract. We will introduce a class of distributions that will contain many of the discrete and continuous we are familiar with. This class will help
March 10, 2017 THE EXPONENTIAL CLASS OF DISTRIBUTIONS Abstract. We will introduce a class of distributions that will contain many of the discrete and continuous we are familiar with. This class will help
Last Lecture. Biostatistics Statistical Inference Lecture 14 Obtaining Best Unbiased Estimator. Related Theorems. Rao-Blackwell Theorem
 Last Lecture Biostatistics 62 - Statistical Inference Lecture 14 Obtaining Best Unbiased Estimator Hyun Min Kang February 28th, 213 For single-parameter exponential family, is Cramer-Rao bound always attainable?
Last Lecture Biostatistics 62 - Statistical Inference Lecture 14 Obtaining Best Unbiased Estimator Hyun Min Kang February 28th, 213 For single-parameter exponential family, is Cramer-Rao bound always attainable?
Tutorial: Statistical distance and Fisher information
 Tutorial: Statistical distance and Fisher information Pieter Kok Department of Materials, Oxford University, Parks Road, Oxford OX1 3PH, UK Statistical distance We wish to construct a space of probability
Tutorial: Statistical distance and Fisher information Pieter Kok Department of Materials, Oxford University, Parks Road, Oxford OX1 3PH, UK Statistical distance We wish to construct a space of probability
Economics 620, Lecture 9: Asymptotics III: Maximum Likelihood Estimation
 Economics 620, Lecture 9: Asymptotics III: Maximum Likelihood Estimation Nicholas M. Kiefer Cornell University Professor N. M. Kiefer (Cornell University) Lecture 9: Asymptotics III(MLE) 1 / 20 Jensen
Economics 620, Lecture 9: Asymptotics III: Maximum Likelihood Estimation Nicholas M. Kiefer Cornell University Professor N. M. Kiefer (Cornell University) Lecture 9: Asymptotics III(MLE) 1 / 20 Jensen
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER. 21 June :45 11:45
 Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Two hours MATH20802 To be supplied by the Examinations Office: Mathematical Formula Tables THE UNIVERSITY OF MANCHESTER STATISTICAL METHODS 21 June 2010 9:45 11:45 Answer any FOUR of the questions. University-approved
Central Limit Theorem ( 5.3)
 Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Central Limit Theorem ( 5.3) Let X 1, X 2,... be a sequence of independent random variables, each having n mean µ and variance σ 2. Then the distribution of the partial sum S n = X i i=1 becomes approximately
Final Exam. 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given.
 1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
1. (6 points) True/False. Please read the statements carefully, as no partial credit will be given. (a) If X and Y are independent, Corr(X, Y ) = 0. (b) (c) (d) (e) A consistent estimator must be asymptotically
6 The normal distribution, the central limit theorem and random samples
 6 The normal distribution, the central limit theorem and random samples 6.1 The normal distribution We mentioned the normal (or Gaussian) distribution in Chapter 4. It has density f X (x) = 1 σ 1 2π e
6 The normal distribution, the central limit theorem and random samples 6.1 The normal distribution We mentioned the normal (or Gaussian) distribution in Chapter 4. It has density f X (x) = 1 σ 1 2π e
EIE6207: Estimation Theory
 EIE6207: Estimation Theory Man-Wai MAK Dept. of Electronic and Information Engineering, The Hong Kong Polytechnic University enmwmak@polyu.edu.hk http://www.eie.polyu.edu.hk/ mwmak References: Steven M.
EIE6207: Estimation Theory Man-Wai MAK Dept. of Electronic and Information Engineering, The Hong Kong Polytechnic University enmwmak@polyu.edu.hk http://www.eie.polyu.edu.hk/ mwmak References: Steven M.
Graduate Econometrics I: Unbiased Estimation
 Graduate Econometrics I: Unbiased Estimation Yves Dominicy Université libre de Bruxelles Solvay Brussels School of Economics and Management ECARES Yves Dominicy Graduate Econometrics I: Unbiased Estimation
Graduate Econometrics I: Unbiased Estimation Yves Dominicy Université libre de Bruxelles Solvay Brussels School of Economics and Management ECARES Yves Dominicy Graduate Econometrics I: Unbiased Estimation
2 Statistical Estimation: Basic Concepts
 Technion Israel Institute of Technology, Department of Electrical Engineering Estimation and Identification in Dynamical Systems (048825) Lecture Notes, Fall 2009, Prof. N. Shimkin 2 Statistical Estimation:
Technion Israel Institute of Technology, Department of Electrical Engineering Estimation and Identification in Dynamical Systems (048825) Lecture Notes, Fall 2009, Prof. N. Shimkin 2 Statistical Estimation:
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM
 February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
Example: An experiment can either result in success or failure with probability θ and (1 θ) respectively. The experiment is performed independently
 Chapter 3 Sufficient statistics and variance reduction Let X 1,X 2,...,X n be a random sample from a certain distribution with p.m/d.f fx θ. A function T X 1,X 2,...,X n = T X of these observations is
Chapter 3 Sufficient statistics and variance reduction Let X 1,X 2,...,X n be a random sample from a certain distribution with p.m/d.f fx θ. A function T X 1,X 2,...,X n = T X of these observations is
Lecture 7 Introduction to Statistical Decision Theory
 Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Elements of statistics (MATH0487-1)
 Elements of statistics (MATH0487-1) Prof. Dr. Dr. K. Van Steen University of Liège, Belgium November 12, 2012 Introduction to Statistics Basic Probability Revisited Sampling Exploratory Data Analysis -
Elements of statistics (MATH0487-1) Prof. Dr. Dr. K. Van Steen University of Liège, Belgium November 12, 2012 Introduction to Statistics Basic Probability Revisited Sampling Exploratory Data Analysis -
All other items including (and especially) CELL PHONES must be left at the front of the room.
 TEST #2 / STA 5327 (Inference) / Spring 2017 (April 24, 2017) Name: Directions This exam is closed book and closed notes. You will be supplied with scratch paper, and a copy of the Table of Common Distributions
TEST #2 / STA 5327 (Inference) / Spring 2017 (April 24, 2017) Name: Directions This exam is closed book and closed notes. You will be supplied with scratch paper, and a copy of the Table of Common Distributions
Chapter 8: Least squares (beginning of chapter)
 Chapter 8: Least squares (beginning of chapter) Least Squares So far, we have been trying to determine an estimator which was unbiased and had minimum variance. Next we ll consider a class of estimators
Chapter 8: Least squares (beginning of chapter) Least Squares So far, we have been trying to determine an estimator which was unbiased and had minimum variance. Next we ll consider a class of estimators
ECE534, Spring 2018: Solutions for Problem Set #3
 ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
Limiting Distributions
 Limiting Distributions We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the
Limiting Distributions We introduce the mode of convergence for a sequence of random variables, and discuss the convergence in probability and in distribution. The concept of convergence leads us to the
ECE531 Lecture 10b: Maximum Likelihood Estimation
 ECE531 Lecture 10b: Maximum Likelihood Estimation D. Richard Brown III Worcester Polytechnic Institute 05-Apr-2011 Worcester Polytechnic Institute D. Richard Brown III 05-Apr-2011 1 / 23 Introduction So
ECE531 Lecture 10b: Maximum Likelihood Estimation D. Richard Brown III Worcester Polytechnic Institute 05-Apr-2011 Worcester Polytechnic Institute D. Richard Brown III 05-Apr-2011 1 / 23 Introduction So
Estimation Theory Fredrik Rusek. Chapters
 Estimation Theory Fredrik Rusek Chapters 3.5-3.10 Recap We deal with unbiased estimators of deterministic parameters Performance of an estimator is measured by the variance of the estimate (due to the
Estimation Theory Fredrik Rusek Chapters 3.5-3.10 Recap We deal with unbiased estimators of deterministic parameters Performance of an estimator is measured by the variance of the estimate (due to the
Parameter estimation! and! forecasting! Cristiano Porciani! AIfA, Uni-Bonn!
 Parameter estimation! and! forecasting! Cristiano Porciani! AIfA, Uni-Bonn! Questions?! C. Porciani! Estimation & forecasting! 2! Cosmological parameters! A branch of modern cosmological research focuses
Parameter estimation! and! forecasting! Cristiano Porciani! AIfA, Uni-Bonn! Questions?! C. Porciani! Estimation & forecasting! 2! Cosmological parameters! A branch of modern cosmological research focuses
A General Overview of Parametric Estimation and Inference Techniques.
 A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Basic concepts in estimation
 Basic concepts in estimation Random and nonrandom parameters Definitions of estimates ML Maimum Lielihood MAP Maimum A Posteriori LS Least Squares MMS Minimum Mean square rror Measures of quality of estimates
Basic concepts in estimation Random and nonrandom parameters Definitions of estimates ML Maimum Lielihood MAP Maimum A Posteriori LS Least Squares MMS Minimum Mean square rror Measures of quality of estimates
Advanced Signal Processing Introduction to Estimation Theory
 Advanced Signal Processing Introduction to Estimation Theory Danilo Mandic, room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Advanced Signal Processing Introduction to Estimation Theory Danilo Mandic, room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
ECE 275A Homework 6 Solutions
 ECE 275A Homework 6 Solutions. The notation used in the solutions for the concentration (hyper) ellipsoid problems is defined in the lecture supplement on concentration ellipsoids. Note that θ T Σ θ =
ECE 275A Homework 6 Solutions. The notation used in the solutions for the concentration (hyper) ellipsoid problems is defined in the lecture supplement on concentration ellipsoids. Note that θ T Σ θ =
M(t) = 1 t. (1 t), 6 M (0) = 20 P (95. X i 110) i=1
 Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Hypothesis Testing. 1 Definitions of test statistics. CB: chapter 8; section 10.3
 Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Hypothesis Testing CB: chapter 8; section 0.3 Hypothesis: statement about an unknown population parameter Examples: The average age of males in Sweden is 7. (statement about population mean) The lowest
Lecture 8: Information Theory and Statistics
 Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
McGill University. Faculty of Science. Department of Mathematics and Statistics. Part A Examination. Statistics: Theory Paper
 McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
McGill University Faculty of Science Department of Mathematics and Statistics Part A Examination Statistics: Theory Paper Date: 10th May 2015 Instructions Time: 1pm-5pm Answer only two questions from Section
STATISTICS SYLLABUS UNIT I
 STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics
 Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics Data from one or a series of random experiments are collected. Planning experiments and collecting data (not discussed here). Analysis:
Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics Data from one or a series of random experiments are collected. Planning experiments and collecting data (not discussed here). Analysis:
Lecture 4: UMVUE and unbiased estimators of 0
 Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
STA 260: Statistics and Probability II
 Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Practice Problems Section Problems
 Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
MAS113 Introduction to Probability and Statistics
 MAS113 Introduction to Probability and Statistics School of Mathematics and Statistics, University of Sheffield 2018 19 Identically distributed Suppose we have n random variables X 1, X 2,..., X n. Identically
MAS113 Introduction to Probability and Statistics School of Mathematics and Statistics, University of Sheffield 2018 19 Identically distributed Suppose we have n random variables X 1, X 2,..., X n. Identically
Lecture 7: Chapter 7. Sums of Random Variables and Long-Term Averages
 Lecture 7: Chapter 7. Sums of Random Variables and Long-Term Averages ELEC206 Probability and Random Processes, Fall 2014 Gil-Jin Jang gjang@knu.ac.kr School of EE, KNU page 1 / 15 Chapter 7. Sums of Random
Lecture 7: Chapter 7. Sums of Random Variables and Long-Term Averages ELEC206 Probability and Random Processes, Fall 2014 Gil-Jin Jang gjang@knu.ac.kr School of EE, KNU page 1 / 15 Chapter 7. Sums of Random
1 Complete Statistics
 Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Complete Statistics February 4, 2016 Debdeep Pati 1 Complete Statistics Suppose X P θ, θ Θ. Let (X (1),..., X (n) ) denote the order statistics. Definition 1. A statistic T = T (X) is complete if E θ g(t
Module 2. Random Processes. Version 2, ECE IIT, Kharagpur
 Module Random Processes Version, ECE IIT, Kharagpur Lesson 9 Introduction to Statistical Signal Processing Version, ECE IIT, Kharagpur After reading this lesson, you will learn about Hypotheses testing
Module Random Processes Version, ECE IIT, Kharagpur Lesson 9 Introduction to Statistical Signal Processing Version, ECE IIT, Kharagpur After reading this lesson, you will learn about Hypotheses testing
f(y θ) = g(t (y) θ)h(y)
 EXAM3, FINAL REVIEW (and a review for some of the QUAL problems): No notes will be allowed, but you may bring a calculator. Memorize the pmf or pdf f, E(Y ) and V(Y ) for the following RVs: 1) beta(δ,
EXAM3, FINAL REVIEW (and a review for some of the QUAL problems): No notes will be allowed, but you may bring a calculator. Memorize the pmf or pdf f, E(Y ) and V(Y ) for the following RVs: 1) beta(δ,
STAT 200C: High-dimensional Statistics
 STAT 200C: High-dimensional Statistics Arash A. Amini May 30, 2018 1 / 59 Classical case: n d. Asymptotic assumption: d is fixed and n. Basic tools: LLN and CLT. High-dimensional setting: n d, e.g. n/d
STAT 200C: High-dimensional Statistics Arash A. Amini May 30, 2018 1 / 59 Classical case: n d. Asymptotic assumption: d is fixed and n. Basic tools: LLN and CLT. High-dimensional setting: n d, e.g. n/d
Nuisance parameters and their treatment
 BS2 Statistical Inference, Lecture 2, Hilary Term 2008 April 2, 2008 Ancillarity Inference principles Completeness A statistic A = a(x ) is said to be ancillary if (i) The distribution of A does not depend
BS2 Statistical Inference, Lecture 2, Hilary Term 2008 April 2, 2008 Ancillarity Inference principles Completeness A statistic A = a(x ) is said to be ancillary if (i) The distribution of A does not depend
Brief Review on Estimation Theory
 Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Module 1 - Signal estimation
 , Arraial do Cabo, 2009 Module 1 - Signal estimation Sérgio M. Jesus (sjesus@ualg.pt) Universidade do Algarve, PT-8005-139 Faro, Portugal www.siplab.fct.ualg.pt February 2009 Outline of Module 1 Parameter
, Arraial do Cabo, 2009 Module 1 - Signal estimation Sérgio M. Jesus (sjesus@ualg.pt) Universidade do Algarve, PT-8005-139 Faro, Portugal www.siplab.fct.ualg.pt February 2009 Outline of Module 1 Parameter
7 Likelihood and Maximum Likelihood Estimation
 7 Likelihood and Maximum Likelihood Estimation Exercice 7.1. Let X be a random variable admitting the following probability density : x +1 I x 1 where > 0. It is in fact a particular Pareto law. Consider
7 Likelihood and Maximum Likelihood Estimation Exercice 7.1. Let X be a random variable admitting the following probability density : x +1 I x 1 where > 0. It is in fact a particular Pareto law. Consider
MAS223 Statistical Inference and Modelling Exercises
 MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
STAT 512 sp 2018 Summary Sheet
 STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
STAT 5 sp 08 Summary Sheet Karl B. Gregory Spring 08. Transformations of a random variable Let X be a rv with support X and let g be a function mapping X to Y with inverse mapping g (A = {x X : g(x A}
MTH 215: Introduction to Linear Algebra
 MTH 215: Introduction to Linear Algebra Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 20, 2017 1 LU Factorization 2 3 4 Triangular Matrices Definition
MTH 215: Introduction to Linear Algebra Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 20, 2017 1 LU Factorization 2 3 4 Triangular Matrices Definition
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
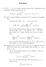 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Lecture 2: CDF and EDF
 STAT 425: Introduction to Nonparametric Statistics Winter 2018 Instructor: Yen-Chi Chen Lecture 2: CDF and EDF 2.1 CDF: Cumulative Distribution Function For a random variable X, its CDF F () contains all
STAT 425: Introduction to Nonparametric Statistics Winter 2018 Instructor: Yen-Chi Chen Lecture 2: CDF and EDF 2.1 CDF: Cumulative Distribution Function For a random variable X, its CDF F () contains all
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Probability Models. 4. What is the definition of the expectation of a discrete random variable?
 1 Probability Models The list of questions below is provided in order to help you to prepare for the test and exam. It reflects only the theoretical part of the course. You should expect the questions
1 Probability Models The list of questions below is provided in order to help you to prepare for the test and exam. It reflects only the theoretical part of the course. You should expect the questions
MA8109 Stochastic Processes in Systems Theory Autumn 2013
 Norwegian University of Science and Technology Department of Mathematical Sciences MA819 Stochastic Processes in Systems Theory Autumn 213 1 MA819 Exam 23, problem 3b This is a linear equation of the form
Norwegian University of Science and Technology Department of Mathematical Sciences MA819 Stochastic Processes in Systems Theory Autumn 213 1 MA819 Exam 23, problem 3b This is a linear equation of the form
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Foundations of Statistical Inference. Sufficient statistics. Definition (Sufficiency) Definition (Sufficiency)
 Foundaions of Saisical Inference Julien Beresycki Lecure 2 - Sufficiency, Facorizaion, Minimal sufficiency Deparmen of Saisics Universiy of Oxford MT 2016 Julien Beresycki (Universiy of Oxford BS2a MT
Foundaions of Saisical Inference Julien Beresycki Lecure 2 - Sufficiency, Facorizaion, Minimal sufficiency Deparmen of Saisics Universiy of Oxford MT 2016 Julien Beresycki (Universiy of Oxford BS2a MT
IEOR 165 Lecture 7 1 Bias-Variance Tradeoff
 IEOR 165 Lecture 7 Bias-Variance Tradeoff 1 Bias-Variance Tradeoff Consider the case of parametric regression with β R, and suppose we would like to analyze the error of the estimate ˆβ in comparison to
IEOR 165 Lecture 7 Bias-Variance Tradeoff 1 Bias-Variance Tradeoff Consider the case of parametric regression with β R, and suppose we would like to analyze the error of the estimate ˆβ in comparison to
Parametric Inference Maximum Likelihood Inference Exponential Families Expectation Maximization (EM) Bayesian Inference Statistical Decison Theory
 Statistical Inference Parametric Inference Maximum Likelihood Inference Exponential Families Expectation Maximization (EM) Bayesian Inference Statistical Decison Theory IP, José Bioucas Dias, IST, 2007
Statistical Inference Parametric Inference Maximum Likelihood Inference Exponential Families Expectation Maximization (EM) Bayesian Inference Statistical Decison Theory IP, José Bioucas Dias, IST, 2007
2.3 Methods of Estimation
 96 CHAPTER 2. ELEMENTS OF STATISTICAL INFERENCE 2.3 Methods of Estimation 2.3. Method of Moments The Method of Moments is a simple technique based on the idea that the sample moments are natural estimators
96 CHAPTER 2. ELEMENTS OF STATISTICAL INFERENCE 2.3 Methods of Estimation 2.3. Method of Moments The Method of Moments is a simple technique based on the idea that the sample moments are natural estimators
Probability Lecture III (August, 2006)
 robability Lecture III (August, 2006) 1 Some roperties of Random Vectors and Matrices We generalize univariate notions in this section. Definition 1 Let U = U ij k l, a matrix of random variables. Suppose
robability Lecture III (August, 2006) 1 Some roperties of Random Vectors and Matrices We generalize univariate notions in this section. Definition 1 Let U = U ij k l, a matrix of random variables. Suppose
5.2 Fisher information and the Cramer-Rao bound
 Stat 200: Introduction to Statistical Inference Autumn 208/9 Lecture 5: Maximum likelihood theory Lecturer: Art B. Owen October 9 Disclaimer: These notes have not been subjected to the usual scrutiny reserved
Stat 200: Introduction to Statistical Inference Autumn 208/9 Lecture 5: Maximum likelihood theory Lecturer: Art B. Owen October 9 Disclaimer: These notes have not been subjected to the usual scrutiny reserved
BEST TESTS. Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized.
 BEST TESTS Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized. 1. Most powerful test Let {f θ } θ Θ be a family of pdfs. We will consider
BEST TESTS Abstract. We will discuss the Neymann-Pearson theorem and certain best test where the power function is optimized. 1. Most powerful test Let {f θ } θ Θ be a family of pdfs. We will consider
