Estimation and Detection
|
|
|
- Lee Johnson
- 5 years ago
- Views:
Transcription
1 stimation and Detection Lecture 2: Cramér-Rao Lower Bound Dr. ir. Richard C. Hendriks & Dr. Sundeep P. Chepuri 7//207
2 Remember: Introductory xample Given a process (DC in noise): x[n]=a + w[n], n=0,,n, w[n] zero mean noise How can we estimate A? Some candidates:. Â = x[0] Consider the case A =. Which estimate is better? Â = x[0] = Â 2 = N P N n=0 x[n] Â2 = N P N n=0 x[n]=0.9 Can the performance of an estimator be based on a single realisation? No! The data is random. As a result, the estimator is a random variable too!
3 Introductory xample Use statistical descriptors: xpected value and variance of the estimator. (Â)=A (Â2)= N P N n=0 x[n] = N Both estimators are unbiased. P N n=0 (x[n]) = A Look at the variance, define 2 = var(w[n]): var(â)= 2 var(â2) = var N P N n=0 x[n] = P N N 2 n=0 var(x[n]) = 2 N Â 2 has smaller variance. Also, var(â2)! 0 as N!: the estimator is consistent. Conclusion: stimators are random variables. Question: What are good (or optimal) estimators?
4 Minimum Variance Criterion A natural criterion is the Mean Square rror (MS): h h mse(ˆ )= (ˆ ) 2i i 2 = (ˆ (ˆ )) + ((ˆ ) ) The MS consist of errors due to h = (ˆ (ˆ )) 2i +((ˆ ) ) 2 = var(ˆ ) {z } variance +((ˆ ) {z } bias ) 2 bias of the estimator variance of the estimator.
5 Minimum Variance Criterion h mse(ˆ )= (ˆ (ˆ )) 2i +((ˆ ) ) 2 = var(ˆ ) {z } variance +((ˆ ) {z } bias ) 2 Consider the (biased) estimator: Â 3 = a N P N n=0 x[n], with constant a. [Â3]=aA var[â3]= a2 2 N MS(Â3)= a2 2 N +(a )2 A 2. Find the optimal estimator requires finding the optimal a: a opt = A 2 A /N. The optimal estimator: Â 3 = P A2 N NA n=0 x[n]. ) This estimator depends on A and is therefore unrealisable!!
6 Minimum Variance Unbiased stimator The optimal estimator depends on A (and thus unrealisable), because the bias term in the MS depends on A: MS(Â3)= a2 2 N +(a )2 A 2. {z } We therefore abandon the MS and constrain the bias to be zero. Hence, if (ˆ )=, then bias h mse(ˆ )= (ˆ (ˆ )) 2i h +((ˆ ) ) 2 = (ˆ (ˆ )) 2i. This is what we call: the minimum variance unbiased estimator (MVU).
7 Minimum Variance Unbiased stimator Remark: The MVU does not always exist and is generally difficult to find. var(ˆ ) ˆ var(ˆ ) ˆ ˆ 2 ˆ 3 ˆ 2 ˆ 3 If ˆ, ˆ 2 and ˆ 3 are all unbiased estimators, then ˆ 3 is the MVU. MVU does not exist!
8 Finding the MVU How to find the MVU?!? ven if the MVU exists, there is no standard "recipe" to find it.. Determine Cramer-Rao-Bound (Today, Ch. 3) 2. Apply Rao-Blackwell-Lehmann-Scheffe theorem (will not be discussed) 3. Restrict estimators to be both unbiased AND linear (Next week, Ch. 6)
9 Today s Agenda. Stating the "The Cramer-Rao Lower Bound" 2. xample 3. Derivation of the CRLB 4. xamples
10 Cramér-Rao Lower Bound Theorem () CRLB: bound on the variance of any unbiased estimator Assume the pdf p(x; ) satisfies the regularity condition: lnp(x; ) =0 for all The variance of any unbiased estimator ˆ then satisfies var(ˆ ) 2 lnp(x; ) 2 = # 2 lnp(x; )
11 Cramér-Rao Lower Bound Theorem (2) CRLB: Can be used in some cases to find the MVU An unbiased estimator may be found that attains the bound for all lnp(x; ) = I( )(g(x) ) for some functions g and I. The estimator then is ˆ = g(x) with mean (ˆ ) = and variance var(ˆ )= I( ). An estimator is called efficient if it meets the CRLB with equality. In that case it is the MVU (the converse is not necessarily true).
12 xample CRLB () Given a process (DC in noise): x[n]=a + w[n], n=0,,n, w[n] zero mean white Gaussian noise NY " p exp 2 2 " 2 2 N # (x[n] A) 2 = 2 2 # X (x[n] A) 2 = 2 n=0 " PN # n=0 (x[n] A)2 exp (2 2 ) N/2 2 2 X (x[n] A) N 2 ln 2 = N 2, which is data independent in this case.
13 xample CRLB (2) From the CRLB we know: var(ˆ ) 2 lnp(x; ) 2 = # 2 lnp(x; ) and thus var(â) 2 @A " 2 2 # X (x[n] A) 2 = 2 N n=0 X (x[n] A)= N 2 N n=0 {z} I( ) 0 N NX n=0 x[n] {z } g(x) {z} A C A In this case, our estimator attains the bound and is thus efficient (var(â)= 2 N ).
14 The Cramér-Rao Lower Bound The CRLB is a lower bound on the variance of any unbiased estimator. Notice that a biased estimator could have a lower variance. We consider the pdf p(x; ) for a particular realisation x, as a function of the unknown parameter : the likelihood function. If p(x; ) is very "peaky" with respect to changes in it is easy to determine the correct value of from data x.
15 The Cramér-Rao Lower Bound The CRLB is a lower bound on the variance of any unbiased estimator. Notice that a biased estimator could have a lower variance. Given again a process (DC in noise): x[n]=a + w[n], n=0,,n, w[n] zero mean white Gaussian noise xample of a biased estimator: Â = c N P N n=0 x[n] with 0 apple c apple [Â]=cA (thus biased) Var[Â]=[Â2 ] [Â]2 = c 2 2, which is lower than the CRLB! N
16 The Cramér-Rao Lower Bound - Curvature p(x[0] = 3; A; < 2 = =3]) Likelihood function: p(x[0]; A) as function of A. Consider the two cases 2 =and 2 =/ A 0.5 p(x[0] = 3; A; < 2 = ]) The "sharpness" (curvature) of the likelihood function determines how accurately the unknown parameter can be estimated How to measure sharpness/curvature? A
17 The Cramér-Rao Lower Bound - Curvature easure curvature p(x[0] = 3; A; < = ]) p(x[0]; A) A ln [p(x[0]; ln[p(x[0];a)] A
18 The Cramér-Rao Lower Bound Score function The CRLB is based on the gradient of the log-likelihood function: s(x; lnp(x; ) s(x; ) is also called the score function and is a measure of the sensitivity of p(x; ) to changes in. (It scores values of.) Scores near zero are good scores" as we search for stationary points (maximum) in p(x; ). The log-likelihood function and score function, which depend on the data, is itself a random variable (so it is of interest to calculate [s(x; )] and Var[s(x; )]).
19 The xpected Value and Variance of Score Function First and second order moment of the score function are central to the CRLB theorem. An important condition when deriving the CRLB is that the first order moment of the score function is zero: lnp(x; ) =0 This is known as the regularity condition. Most pdfs are regular. First order moment nonzero when the domain of the pdf for which it is nonzero depends on the unknown parameter.
20 The xpected Value and Variance of Score Function When does the regularity condition hold? lnp(x; ) = lnp(x; ) p(x; )dx = p(x; ) p(x; ) p(x; )dx = p(x; )dx Z p(x; )dx =0 Consider p(x; )=U[0, ] Z dx Z 0 dx 6=0 The regularity condition does not hold in this case. This step assumes we can switch gradient and integral. This is only allowed in specific cases (when integral boundary, i.e., domain of the p depends on ) 2
21 The xpected Value and Variance of Score Function The 2nd moment of the score function is called the Fisher information # 2 apple lnp(x; 2 lnp(x; ) = 2 = I( ) The Fisher information is a way of measuring the amount of information that an observable random variable x carries about an unknown parameter. Fisher information is. Nonnegative. 2. Additive for independent observations lnp(x; )= NX n=0 2 N lnp(x; ) X ln p(x[n]; ) ) 2 = n=0 2 lnp(x[n]; ) 2 2
22 The xpected Value and Variance of Score Function Let us now prove that 2 lnp(x; ) 2 = Proof: From the regularity condition, we obtain # 2 lnp(x; lnp(x; ) =0 lnp(x; ) p(x; )dx =0 Z 2 lnp(x; ) ) 2 p(x; lnp(x; ) dx =0 2 Z 2 lnp(x; lnp(x; ) ) 2 p(x; )dx = p(x; )dx 2 # 2 lnp(x; ) lnp(x; ) ) 2 = 2
23 2 Proof of the Cramér-Rao Lower Bound () Starting from the unbiased assumption: Z (ˆ )p(x; )dx =0 Z (ˆ )p(x; )dx =0 Z Z ) p(x; )dx + (ˆ ) dx =0 Z ) (ˆ lnp(x; ) p(x; )dx = Z ) (ˆ ) p p(x; lnp(x; ) p p(x; )dx =
24 2 Proof of the Cramér-Rao Lower Bound (2) Let us now use the Cauchy-Schwarz inequality Z Z (ˆ ) p p(x; lnp(x; ) p p(x; )dx = Z f 2 (x)dx g 2 (x)dx Z 2 f(x)g(x)dx Then we obtain Z (ˆ ) var(ˆ ) Z lnp(x; ) ) 2 p(x; )dx p(x; )dx # 2 lnp(x; )
25 2 Proof of the Cramér-Rao Lower Bound (3) CRLB: Can be used in some cases to find the MVU An unbiased estimator may be found that attains the bound for all lnp(x; ) = I( )(g(x) ) for some functions g and I. The estimator then is ˆ = g(x) with mean (ˆ ) = and variance var(ˆ )= I( ). An estimator is called efficient if it meets the CRLB with equality. In that case it is the MVU (the converse is not necessarily true).
26 2 Proof of the Cramér-Rao Lower Bound (4) lnp(x; ) = I( )(ˆ (x) ), it follows that (ˆ )=, var(ˆ )= I( ) Proof for (ˆ )= From the regularity condition: lnp(x; ) h i h i = I( )(ˆ (x) ) = I( ) (ˆ (x) ) =0 i So, hˆ (x) =
27 2 Proof of the Cramér-Rao Lower Bound (5) lnp(x; ) = I( )(ˆ (x) ), it follows that (ˆ )=, var(ˆ )= I( ) Proof for var(ˆ )= I( ) # 2 lnp(x; ) h = I 2 ( )(ˆ (x) ) 2i h = I 2 ( ) (ˆ (x) ) 2i i = I 2 ( )var hˆ (x) i So, var hˆ (x) = 20 lnp(x; I 2 ( ) A2 3 5
28 2 Proof of the Cramér-Rao Lower Bound (5) Further it follows lnp(x; ) = I( )(ˆ (x) ) 2 lnp(x; ) 2 = I( ) (ˆ (x) ) Taking expectations: 2 lnp(x; ) 2 = I( )+ We obtain 2 lnp(x; ) 2 = I( ) ) (ˆ (x) ) = I( ) h i (ˆ (x) ) {z } =0 because unbiased
29 2 Proof of the Cramér-Rao Lower Bound (6) We already know that: 2 lnp(x; ) 2 = # 2 lnp(x; ) We just obtained I( )= 2 lnp(x; ) 2 # 2 lnp(x; ) and thus I( )= i var hˆ (x) = # 2 lnp(x; ) I 2 ( ) = # 2 lnp(x; )
30 CRLB for General Gaussian model Let us assume a Gaussian distribution for the noise: w N (0,C w ), p(w)= Then the Gaussian model is defined as (2 ) N 2 det(c w ) 2 apple exp 2 wt Cw w x = h( )+w, x N (h( ),C w ) ) p(x)= (2 ) N 2 det(c w ) 2 apple exp 2 (x h( ))T Cw (x h( ) Let us derive the CRLB for this lnp(x; ) ( ) Cw x h( ) lnp(x; ) 2 h T ( ) 2 Cw x h( ) 2 lnp(x; ) ) 2 ( ) T ( ) ) w ) var(ˆ T ( ) ) w 3
31 CRLB for Linear Gaussian model & MVU Assume the model is a linear Gaussian model: x = h + w, w N (0,C w ) From CRLB for a General Gaussian model, we obtain var(ˆ ) h T C w h. lnp(x; ) = h T Cw (x h )=h T Cw h[(h T Cw h) h T Cw x ] As a result, the MVU exists and its solution reaches the CRLB: ˆ =(h T Cw h) h T Cw x. Properties: (ˆ )= var(ˆ )=(h T C w h) ; it is equal to the CRLB: in this case the MVU is efficient. ˆ is a linear transformation of x and thus Gaussian: ˆ N [,(h T C w h) ] 3
32 3 xample Poisson Distribution Let X,...,X N be iid measurements from a Poisson ( ) distribution with marginal pmf p(x i ; )=e x i x i!, with expected value [x i ]=. Calculate the CRLB for parameter and try to find the MVU estimator for.
33 3 Summary () CRLB: bound on the variance of any unbiased estimator Assume the pdf p(x; ) satisfies the regularity condition: lnp(x; ) =0 for all The variance of any unbiased estimator ˆ then satisfies var(ˆ ) 2 lnp(x; ) 2 = # 2 lnp(x; )
34 3 Summary (2) CRLB: Can be used in some cases to find the MVU An unbiased estimator may be found that attains the bound for all lnp(x; ) = I( )(g(x) ) for some functions g and I. The estimator then is ˆ = g(x) with mean (ˆ ) = and variance var(ˆ )= I( ). An estimator is called efficient if it meets the CRLB with equality. In that case it is the MVU (the converse is not necessarily true).
Advanced Signal Processing Introduction to Estimation Theory
 Advanced Signal Processing Introduction to Estimation Theory Danilo Mandic, room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Advanced Signal Processing Introduction to Estimation Theory Danilo Mandic, room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Variations. ECE 6540, Lecture 10 Maximum Likelihood Estimation
 Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
Variations ECE 6540, Lecture 10 Last Time BLUE (Best Linear Unbiased Estimator) Formulation Advantages Disadvantages 2 The BLUE A simplification Assume the estimator is a linear system For a single parameter
EIE6207: Estimation Theory
 EIE6207: Estimation Theory Man-Wai MAK Dept. of Electronic and Information Engineering, The Hong Kong Polytechnic University enmwmak@polyu.edu.hk http://www.eie.polyu.edu.hk/ mwmak References: Steven M.
EIE6207: Estimation Theory Man-Wai MAK Dept. of Electronic and Information Engineering, The Hong Kong Polytechnic University enmwmak@polyu.edu.hk http://www.eie.polyu.edu.hk/ mwmak References: Steven M.
A Few Notes on Fisher Information (WIP)
 A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
Detection & Estimation Lecture 1
 Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Detection & Estimation Lecture 1
 Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Detection & Estimation Lecture 1 Intro, MVUE, CRLB Xiliang Luo General Course Information Textbooks & References Fundamentals of Statistical Signal Processing: Estimation Theory/Detection Theory, Steven
Chapter 8: Least squares (beginning of chapter)
 Chapter 8: Least squares (beginning of chapter) Least Squares So far, we have been trying to determine an estimator which was unbiased and had minimum variance. Next we ll consider a class of estimators
Chapter 8: Least squares (beginning of chapter) Least Squares So far, we have been trying to determine an estimator which was unbiased and had minimum variance. Next we ll consider a class of estimators
ECE531 Lecture 10b: Maximum Likelihood Estimation
 ECE531 Lecture 10b: Maximum Likelihood Estimation D. Richard Brown III Worcester Polytechnic Institute 05-Apr-2011 Worcester Polytechnic Institute D. Richard Brown III 05-Apr-2011 1 / 23 Introduction So
ECE531 Lecture 10b: Maximum Likelihood Estimation D. Richard Brown III Worcester Polytechnic Institute 05-Apr-2011 Worcester Polytechnic Institute D. Richard Brown III 05-Apr-2011 1 / 23 Introduction So
Proof In the CR proof. and
 Question Under what conditions will we be able to attain the Cramér-Rao bound and find a MVUE? Lecture 4 - Consequences of the Cramér-Rao Lower Bound. Searching for a MVUE. Rao-Blackwell Theorem, Lehmann-Scheffé
Question Under what conditions will we be able to attain the Cramér-Rao bound and find a MVUE? Lecture 4 - Consequences of the Cramér-Rao Lower Bound. Searching for a MVUE. Rao-Blackwell Theorem, Lehmann-Scheffé
PATTERN RECOGNITION AND MACHINE LEARNING
 PATTERN RECOGNITION AND MACHINE LEARNING Slide Set 2: Estimation Theory January 2018 Heikki Huttunen heikki.huttunen@tut.fi Department of Signal Processing Tampere University of Technology Classical Estimation
PATTERN RECOGNITION AND MACHINE LEARNING Slide Set 2: Estimation Theory January 2018 Heikki Huttunen heikki.huttunen@tut.fi Department of Signal Processing Tampere University of Technology Classical Estimation
Advanced Signal Processing Minimum Variance Unbiased Estimation (MVU)
 Advanced Signal Processing Minimum Variance Unbiased Estimation (MVU) Danilo Mandic room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Advanced Signal Processing Minimum Variance Unbiased Estimation (MVU) Danilo Mandic room 813, ext: 46271 Department of Electrical and Electronic Engineering Imperial College London, UK d.mandic@imperial.ac.uk,
Estimators as Random Variables
 Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maimum likelihood Consistency Confidence intervals Properties of the mean estimator Introduction Up until
Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maimum likelihood Consistency Confidence intervals Properties of the mean estimator Introduction Up until
ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE)
 1 ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE) Jingxian Wu Department of Electrical Engineering University of Arkansas Outline Minimum Variance Unbiased Estimators (MVUE)
1 ELEG 5633 Detection and Estimation Minimum Variance Unbiased Estimators (MVUE) Jingxian Wu Department of Electrical Engineering University of Arkansas Outline Minimum Variance Unbiased Estimators (MVUE)
Basic concepts in estimation
 Basic concepts in estimation Random and nonrandom parameters Definitions of estimates ML Maimum Lielihood MAP Maimum A Posteriori LS Least Squares MMS Minimum Mean square rror Measures of quality of estimates
Basic concepts in estimation Random and nonrandom parameters Definitions of estimates ML Maimum Lielihood MAP Maimum A Posteriori LS Least Squares MMS Minimum Mean square rror Measures of quality of estimates
Estimation Theory Fredrik Rusek. Chapters
 Estimation Theory Fredrik Rusek Chapters 3.5-3.10 Recap We deal with unbiased estimators of deterministic parameters Performance of an estimator is measured by the variance of the estimate (due to the
Estimation Theory Fredrik Rusek Chapters 3.5-3.10 Recap We deal with unbiased estimators of deterministic parameters Performance of an estimator is measured by the variance of the estimate (due to the
Rowan University Department of Electrical and Computer Engineering
 Rowan University Department of Electrical and Computer Engineering Estimation and Detection Theory Fall 2013 to Practice Exam II This is a closed book exam. There are 8 problems in the exam. The problems
Rowan University Department of Electrical and Computer Engineering Estimation and Detection Theory Fall 2013 to Practice Exam II This is a closed book exam. There are 8 problems in the exam. The problems
Module 2. Random Processes. Version 2, ECE IIT, Kharagpur
 Module Random Processes Version, ECE IIT, Kharagpur Lesson 9 Introduction to Statistical Signal Processing Version, ECE IIT, Kharagpur After reading this lesson, you will learn about Hypotheses testing
Module Random Processes Version, ECE IIT, Kharagpur Lesson 9 Introduction to Statistical Signal Processing Version, ECE IIT, Kharagpur After reading this lesson, you will learn about Hypotheses testing
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Terminology Suppose we have N observations {x(n)} N 1. Estimators as Random Variables. {x(n)} N 1
 Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maximum likelihood Consistency Confidence intervals Properties of the mean estimator Properties of the
Estimation Theory Overview Properties Bias, Variance, and Mean Square Error Cramér-Rao lower bound Maximum likelihood Consistency Confidence intervals Properties of the mean estimator Properties of the
STAT 730 Chapter 4: Estimation
 STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
STAT 730 Chapter 4: Estimation Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 23 The likelihood We have iid data, at least initially. Each datum
Mathematical statistics
 October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
October 18 th, 2018 Lecture 16: Midterm review Countdown to mid-term exam: 7 days Week 1 Chapter 1: Probability review Week 2 Week 4 Week 7 Chapter 6: Statistics Chapter 7: Point Estimation Chapter 8:
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Inferring from data. Theory of estimators
 Inferring from data Theory of estimators 1 Estimators Estimator is any function of the data e(x) used to provide an estimate ( a measurement ) of an unknown parameter. Because estimators are functions
Inferring from data Theory of estimators 1 Estimators Estimator is any function of the data e(x) used to provide an estimate ( a measurement ) of an unknown parameter. Because estimators are functions
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Estimation and Detection
 Estimation and Detection Lecture : Detection Theory Unknown Parameters Dr. ir. Richard C. Hendriks //05 Previous Lecture H 0 : T (x) < H : T (x) > Using detection theory, rules can be derived on how to
Estimation and Detection Lecture : Detection Theory Unknown Parameters Dr. ir. Richard C. Hendriks //05 Previous Lecture H 0 : T (x) < H : T (x) > Using detection theory, rules can be derived on how to
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275A Homework 6 Solutions
 ECE 275A Homework 6 Solutions. The notation used in the solutions for the concentration (hyper) ellipsoid problems is defined in the lecture supplement on concentration ellipsoids. Note that θ T Σ θ =
ECE 275A Homework 6 Solutions. The notation used in the solutions for the concentration (hyper) ellipsoid problems is defined in the lecture supplement on concentration ellipsoids. Note that θ T Σ θ =
EIE6207: Maximum-Likelihood and Bayesian Estimation
 EIE6207: Maximum-Likelihood and Bayesian Estimation Man-Wai MAK Dept. of Electronic and Information Engineering, The Hong Kong Polytechnic University enmwmak@polyu.edu.hk http://www.eie.polyu.edu.hk/ mwmak
EIE6207: Maximum-Likelihood and Bayesian Estimation Man-Wai MAK Dept. of Electronic and Information Engineering, The Hong Kong Polytechnic University enmwmak@polyu.edu.hk http://www.eie.polyu.edu.hk/ mwmak
Estimation, Detection, and Identification
 Estimation, Detection, and Identification Graduate Course on the CMU/Portugal ECE PhD Program Spring 2008/2009 Chapter 5 Best Linear Unbiased Estimators Instructor: Prof. Paulo Jorge Oliveira pjcro @ isr.ist.utl.pt
Estimation, Detection, and Identification Graduate Course on the CMU/Portugal ECE PhD Program Spring 2008/2009 Chapter 5 Best Linear Unbiased Estimators Instructor: Prof. Paulo Jorge Oliveira pjcro @ isr.ist.utl.pt
Lecture 4: UMVUE and unbiased estimators of 0
 Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
ECE 275A Homework 7 Solutions
 ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
ECE 275A Homework 7 Solutions Solutions 1. For the same specification as in Homework Problem 6.11 we want to determine an estimator for θ using the Method of Moments (MOM). In general, the MOM estimator
2 Statistical Estimation: Basic Concepts
 Technion Israel Institute of Technology, Department of Electrical Engineering Estimation and Identification in Dynamical Systems (048825) Lecture Notes, Fall 2009, Prof. N. Shimkin 2 Statistical Estimation:
Technion Israel Institute of Technology, Department of Electrical Engineering Estimation and Identification in Dynamical Systems (048825) Lecture Notes, Fall 2009, Prof. N. Shimkin 2 Statistical Estimation:
Module 1 - Signal estimation
 , Arraial do Cabo, 2009 Module 1 - Signal estimation Sérgio M. Jesus (sjesus@ualg.pt) Universidade do Algarve, PT-8005-139 Faro, Portugal www.siplab.fct.ualg.pt February 2009 Outline of Module 1 Parameter
, Arraial do Cabo, 2009 Module 1 - Signal estimation Sérgio M. Jesus (sjesus@ualg.pt) Universidade do Algarve, PT-8005-139 Faro, Portugal www.siplab.fct.ualg.pt February 2009 Outline of Module 1 Parameter
Linear models. x = Hθ + w, where w N(0, σ 2 I) and H R n p. The matrix H is called the observation matrix or design matrix 1.
 Linear models As the first approach to estimator design, we consider the class of problems that can be represented by a linear model. In general, finding the MVUE is difficult. But if the linear model
Linear models As the first approach to estimator design, we consider the class of problems that can be represented by a linear model. In general, finding the MVUE is difficult. But if the linear model
1. (Regular) Exponential Family
 1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
1. (Regular) Exponential Family The density function of a regular exponential family is: [ ] Example. Poisson(θ) [ ] Example. Normal. (both unknown). ) [ ] [ ] [ ] [ ] 2. Theorem (Exponential family &
Classical Estimation Topics
 Classical Estimation Topics Namrata Vaswani, Iowa State University February 25, 2014 This note fills in the gaps in the notes already provided (l0.pdf, l1.pdf, l2.pdf, l3.pdf, LeastSquares.pdf). 1 Min
Classical Estimation Topics Namrata Vaswani, Iowa State University February 25, 2014 This note fills in the gaps in the notes already provided (l0.pdf, l1.pdf, l2.pdf, l3.pdf, LeastSquares.pdf). 1 Min
Maximum Likelihood Estimation
 Connexions module: m11446 1 Maximum Likelihood Estimation Clayton Scott Robert Nowak This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License Abstract
Connexions module: m11446 1 Maximum Likelihood Estimation Clayton Scott Robert Nowak This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License Abstract
7 Likelihood and Maximum Likelihood Estimation
 7 Likelihood and Maximum Likelihood Estimation Exercice 7.1. Let X be a random variable admitting the following probability density : x +1 I x 1 where > 0. It is in fact a particular Pareto law. Consider
7 Likelihood and Maximum Likelihood Estimation Exercice 7.1. Let X be a random variable admitting the following probability density : x +1 I x 1 where > 0. It is in fact a particular Pareto law. Consider
Expectation. DS GA 1002 Probability and Statistics for Data Science. Carlos Fernandez-Granda
 Expectation DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean,
Expectation DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean,
ECE531 Lecture 8: Non-Random Parameter Estimation
 ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
10-704: Information Processing and Learning Fall Lecture 24: Dec 7
 0-704: Information Processing and Learning Fall 206 Lecturer: Aarti Singh Lecture 24: Dec 7 Note: These notes are based on scribed notes from Spring5 offering of this course. LaTeX template courtesy of
0-704: Information Processing and Learning Fall 206 Lecturer: Aarti Singh Lecture 24: Dec 7 Note: These notes are based on scribed notes from Spring5 offering of this course. LaTeX template courtesy of
Expectation. DS GA 1002 Statistical and Mathematical Models. Carlos Fernandez-Granda
 Expectation DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean, variance,
Expectation DS GA 1002 Statistical and Mathematical Models http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall16 Carlos Fernandez-Granda Aim Describe random variables with a few numbers: mean, variance,
Lecture 8: Information Theory and Statistics
 Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
Lecture 8: Information Theory and Statistics Part II: Hypothesis Testing and I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 23, 2015 1 / 50 I-Hsiang
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Part 4: Multi-parameter and normal models
 Part 4: Multi-parameter and normal models 1 The normal model Perhaps the most useful (or utilized) probability model for data analysis is the normal distribution There are several reasons for this, e.g.,
Part 4: Multi-parameter and normal models 1 The normal model Perhaps the most useful (or utilized) probability model for data analysis is the normal distribution There are several reasons for this, e.g.,
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
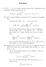 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Practice Problems Section Problems
 Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE
 557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
Brief Review on Estimation Theory
 Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Brief Review on Estimation Theory K. Abed-Meraim ENST PARIS, Signal and Image Processing Dept. abed@tsi.enst.fr This presentation is essentially based on the course BASTA by E. Moulines Brief review on
Data, Estimation and Inference
 Data, Estimation and Inference Pedro Piniés ppinies@robots.ox.ac.uk Michaelmas 2016 1 2 p(x) ( = ) = δ 0 ( < < + δ ) δ ( ) =1. x x+dx (, ) = ( ) ( ) = ( ) ( ) 3 ( ) ( ) 0 ( ) =1 ( = ) = ( ) ( < < ) = (
Data, Estimation and Inference Pedro Piniés ppinies@robots.ox.ac.uk Michaelmas 2016 1 2 p(x) ( = ) = δ 0 ( < < + δ ) δ ( ) =1. x x+dx (, ) = ( ) ( ) = ( ) ( ) 3 ( ) ( ) 0 ( ) =1 ( = ) = ( ) ( < < ) = (
ECE 6540, Lecture 06 Sufficient Statistics & Complete Statistics Variations
 ECE 6540, Lecture 06 Sufficient Statistics & Complete Statistics Variations Last Time Minimum Variance Unbiased Estimators Sufficient Statistics Proving t = T(x) is sufficient Neyman-Fischer Factorization
ECE 6540, Lecture 06 Sufficient Statistics & Complete Statistics Variations Last Time Minimum Variance Unbiased Estimators Sufficient Statistics Proving t = T(x) is sufficient Neyman-Fischer Factorization
Estimation Theory Fredrik Rusek. Chapters 6-7
 Estimation Theory Fredrik Rusek Chapters 6-7 All estimation problems Summary All estimation problems Summary Efficient estimator exists All estimation problems Summary MVU estimator exists Efficient estimator
Estimation Theory Fredrik Rusek Chapters 6-7 All estimation problems Summary All estimation problems Summary Efficient estimator exists All estimation problems Summary MVU estimator exists Efficient estimator
p(z)
 Chapter Statistics. Introduction This lecture is a quick review of basic statistical concepts; probabilities, mean, variance, covariance, correlation, linear regression, probability density functions and
Chapter Statistics. Introduction This lecture is a quick review of basic statistical concepts; probabilities, mean, variance, covariance, correlation, linear regression, probability density functions and
Lecture 7 Introduction to Statistical Decision Theory
 Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
Lecture 7 Introduction to Statistical Decision Theory I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw December 20, 2016 1 / 55 I-Hsiang Wang IT Lecture 7
LINEAR MODELS IN STATISTICAL SIGNAL PROCESSING
 TERM PAPER REPORT ON LINEAR MODELS IN STATISTICAL SIGNAL PROCESSING ANIMA MISHRA SHARMA, Y8104001 BISHWAJIT SHARMA, Y8104015 Course Instructor DR. RAJESH HEDGE Electrical Engineering Department IIT Kanpur
TERM PAPER REPORT ON LINEAR MODELS IN STATISTICAL SIGNAL PROCESSING ANIMA MISHRA SHARMA, Y8104001 BISHWAJIT SHARMA, Y8104015 Course Instructor DR. RAJESH HEDGE Electrical Engineering Department IIT Kanpur
Estimation Tasks. Short Course on Image Quality. Matthew A. Kupinski. Introduction
 Estimation Tasks Short Course on Image Quality Matthew A. Kupinski Introduction Section 13.3 in B&M Keep in mind the similarities between estimation and classification Image-quality is a statistical concept
Estimation Tasks Short Course on Image Quality Matthew A. Kupinski Introduction Section 13.3 in B&M Keep in mind the similarities between estimation and classification Image-quality is a statistical concept
STA 260: Statistics and Probability II
 Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Al Nosedal. University of Toronto. Winter 2017 1 Properties of Point Estimators and Methods of Estimation 2 3 If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition
Multivariate distributions
 CHAPTER Multivariate distributions.. Introduction We want to discuss collections of random variables (X, X,..., X n ), which are known as random vectors. In the discrete case, we can define the density
CHAPTER Multivariate distributions.. Introduction We want to discuss collections of random variables (X, X,..., X n ), which are known as random vectors. In the discrete case, we can define the density
Chapter 3. Point Estimation. 3.1 Introduction
 Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
Chapter 3 Point Estimation Let (Ω, A, P θ ), P θ P = {P θ θ Θ}be probability space, X 1, X 2,..., X n : (Ω, A) (IR k, B k ) random variables (X, B X ) sample space γ : Θ IR k measurable function, i.e.
SGN Advanced Signal Processing: Lecture 8 Parameter estimation for AR and MA models. Model order selection
 SG 21006 Advanced Signal Processing: Lecture 8 Parameter estimation for AR and MA models. Model order selection Ioan Tabus Department of Signal Processing Tampere University of Technology Finland 1 / 28
SG 21006 Advanced Signal Processing: Lecture 8 Parameter estimation for AR and MA models. Model order selection Ioan Tabus Department of Signal Processing Tampere University of Technology Finland 1 / 28
ECE534, Spring 2018: Solutions for Problem Set #3
 ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
ECE534, Spring 08: Solutions for Problem Set #3 Jointly Gaussian Random Variables and MMSE Estimation Suppose that X, Y are jointly Gaussian random variables with µ X = µ Y = 0 and σ X = σ Y = Let their
t x 1 e t dt, and simplify the answer when possible (for example, when r is a positive even number). In particular, confirm that EX 4 = 3.
 Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
Mathematical Statistics: Homewor problems General guideline. While woring outside the classroom, use any help you want, including people, computer algebra systems, Internet, and solution manuals, but mae
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2012 F, FRI Uppsala University, Information Technology 30 Januari 2012 SI-2012 K. Pelckmans
System Identification, Lecture 4
 System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
System Identification, Lecture 4 Kristiaan Pelckmans (IT/UU, 2338) Course code: 1RT880, Report code: 61800 - Spring 2016 F, FRI Uppsala University, Information Technology 13 April 2016 SI-2016 K. Pelckmans
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
Statistics. Lecture 2 August 7, 2000 Frank Porter Caltech. The Fundamentals; Point Estimation. Maximum Likelihood, Least Squares and All That
 Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Statistics Lecture 2 August 7, 2000 Frank Porter Caltech The plan for these lectures: The Fundamentals; Point Estimation Maximum Likelihood, Least Squares and All That What is a Confidence Interval? Interval
Motivation CRLB and Regularity Conditions CRLLB A New Bound Examples Conclusions
 A Survey of Some Recent Results on the CRLB for Parameter Estimation and its Extension Yaakov 1 1 Electrical and Computer Engineering Department University of Connecticut, Storrs, CT A Survey of Some Recent
A Survey of Some Recent Results on the CRLB for Parameter Estimation and its Extension Yaakov 1 1 Electrical and Computer Engineering Department University of Connecticut, Storrs, CT A Survey of Some Recent
Perhaps the simplest way of modeling two (discrete) random variables is by means of a joint PMF, defined as follows.
 Chapter 5 Two Random Variables In a practical engineering problem, there is almost always causal relationship between different events. Some relationships are determined by physical laws, e.g., voltage
Chapter 5 Two Random Variables In a practical engineering problem, there is almost always causal relationship between different events. Some relationships are determined by physical laws, e.g., voltage
Chapter 6. Convergence. Probability Theory. Four different convergence concepts. Four different convergence concepts. Convergence in probability
 Probability Theory Chapter 6 Convergence Four different convergence concepts Let X 1, X 2, be a sequence of (usually dependent) random variables Definition 1.1. X n converges almost surely (a.s.), or with
Probability Theory Chapter 6 Convergence Four different convergence concepts Let X 1, X 2, be a sequence of (usually dependent) random variables Definition 1.1. X n converges almost surely (a.s.), or with
Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee
 Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Stochastic Processes Methods of evaluating estimators and best unbiased estimators Hamid R. Rabiee 1 Outline Methods of Mean Squared Error Bias and Unbiasedness Best Unbiased Estimators CR-Bound for variance
Lecture Notes 7 Stationary Random Processes. Strict-Sense and Wide-Sense Stationarity. Autocorrelation Function of a Stationary Process
 Lecture Notes 7 Stationary Random Processes Strict-Sense and Wide-Sense Stationarity Autocorrelation Function of a Stationary Process Power Spectral Density Continuity and Integration of Random Processes
Lecture Notes 7 Stationary Random Processes Strict-Sense and Wide-Sense Stationarity Autocorrelation Function of a Stationary Process Power Spectral Density Continuity and Integration of Random Processes
Week 9 The Central Limit Theorem and Estimation Concepts
 Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Week 9 and Estimation Concepts Week 9 and Estimation Concepts Week 9 Objectives 1 The Law of Large Numbers and the concept of consistency of averages are introduced. The condition of existence of the population
Gaussian, Markov and stationary processes
 Gaussian, Markov and stationary processes Gonzalo Mateos Dept. of ECE and Goergen Institute for Data Science University of Rochester gmateosb@ece.rochester.edu http://www.ece.rochester.edu/~gmateosb/ November
Gaussian, Markov and stationary processes Gonzalo Mateos Dept. of ECE and Goergen Institute for Data Science University of Rochester gmateosb@ece.rochester.edu http://www.ece.rochester.edu/~gmateosb/ November
Technique for Numerical Computation of Cramér-Rao Bound using MATLAB
 Technique for Numerical Computation of Cramér-Rao Bound using MATLAB Hing Cheung So http://www.ee.cityu.edu.hk/~hcso Department of Electronic Engineering City University of Hong Kong H. C. So Page 1 The
Technique for Numerical Computation of Cramér-Rao Bound using MATLAB Hing Cheung So http://www.ee.cityu.edu.hk/~hcso Department of Electronic Engineering City University of Hong Kong H. C. So Page 1 The
Bias. Definition. One of the foremost expectations of an estimator is that it gives accurate estimates.
 Bias One of the foremost expectations of an estimator is that it gives accurate estimates. Definition An estimator ˆ is said to be accurate or unbiased if and only if µˆ = E(ˆ ) = 0 (19) In plain language,
Bias One of the foremost expectations of an estimator is that it gives accurate estimates. Definition An estimator ˆ is said to be accurate or unbiased if and only if µˆ = E(ˆ ) = 0 (19) In plain language,
Parameter Estimation
 Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parameter Estimation Consider a sample of observations on a random variable Y. his generates random variables: (y 1, y 2,, y ). A random sample is a sample (y 1, y 2,, y ) where the random variables y
Parametric Inference Maximum Likelihood Inference Exponential Families Expectation Maximization (EM) Bayesian Inference Statistical Decison Theory
 Statistical Inference Parametric Inference Maximum Likelihood Inference Exponential Families Expectation Maximization (EM) Bayesian Inference Statistical Decison Theory IP, José Bioucas Dias, IST, 2007
Statistical Inference Parametric Inference Maximum Likelihood Inference Exponential Families Expectation Maximization (EM) Bayesian Inference Statistical Decison Theory IP, José Bioucas Dias, IST, 2007
Probability and Statistical Decision Theory
 Tufts COMP 135: Introduction to Machine Learning https://www.cs.tufts.edu/comp/135/2019s/ Probability and Statistical Decision Theory Many slides attributable to: Erik Sudderth (UCI) Prof. Mike Hughes
Tufts COMP 135: Introduction to Machine Learning https://www.cs.tufts.edu/comp/135/2019s/ Probability and Statistical Decision Theory Many slides attributable to: Erik Sudderth (UCI) Prof. Mike Hughes
Part IB Statistics. Theorems with proof. Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua. Lent 2015
 Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part IB Statistics Theorems with proof Based on lectures by D. Spiegelhalter Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
STATISTICS/ECONOMETRICS PREP COURSE PROF. MASSIMO GUIDOLIN
 Massimo Guidolin Massimo.Guidolin@unibocconi.it Dept. of Finance STATISTICS/ECONOMETRICS PREP COURSE PROF. MASSIMO GUIDOLIN SECOND PART, LECTURE 2: MODES OF CONVERGENCE AND POINT ESTIMATION Lecture 2:
Massimo Guidolin Massimo.Guidolin@unibocconi.it Dept. of Finance STATISTICS/ECONOMETRICS PREP COURSE PROF. MASSIMO GUIDOLIN SECOND PART, LECTURE 2: MODES OF CONVERGENCE AND POINT ESTIMATION Lecture 2:
Three hours. To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER.
 Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
Three hours To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer QUESTION 1, QUESTION
APPM/MATH 4/5520 Solutions to Exam I Review Problems. f X 1,X 2. 2e x 1 x 2. = x 2
 APPM/MATH 4/5520 Solutions to Exam I Review Problems. (a) f X (x ) f X,X 2 (x,x 2 )dx 2 x 2e x x 2 dx 2 2e 2x x was below x 2, but when marginalizing out x 2, we ran it over all values from 0 to and so
APPM/MATH 4/5520 Solutions to Exam I Review Problems. (a) f X (x ) f X,X 2 (x,x 2 )dx 2 x 2e x x 2 dx 2 2e 2x x was below x 2, but when marginalizing out x 2, we ran it over all values from 0 to and so
Review Quiz. 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the
 Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
5 Operations on Multiple Random Variables
 EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
EE360 Random Signal analysis Chapter 5: Operations on Multiple Random Variables 5 Operations on Multiple Random Variables Expected value of a function of r.v. s Two r.v. s: ḡ = E[g(X, Y )] = g(x, y)f X,Y
STAT 100C: Linear models
 STAT 100C: Linear models Arash A. Amini June 9, 2018 1 / 56 Table of Contents Multiple linear regression Linear model setup Estimation of β Geometric interpretation Estimation of σ 2 Hat matrix Gram matrix
STAT 100C: Linear models Arash A. Amini June 9, 2018 1 / 56 Table of Contents Multiple linear regression Linear model setup Estimation of β Geometric interpretation Estimation of σ 2 Hat matrix Gram matrix
Parameter estimation! and! forecasting! Cristiano Porciani! AIfA, Uni-Bonn!
 Parameter estimation! and! forecasting! Cristiano Porciani! AIfA, Uni-Bonn! Questions?! C. Porciani! Estimation & forecasting! 2! Cosmological parameters! A branch of modern cosmological research focuses
Parameter estimation! and! forecasting! Cristiano Porciani! AIfA, Uni-Bonn! Questions?! C. Porciani! Estimation & forecasting! 2! Cosmological parameters! A branch of modern cosmological research focuses
P (x). all other X j =x j. If X is a continuous random vector (see p.172), then the marginal distributions of X i are: f(x)dx 1 dx n
 JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
JOINT DENSITIES - RANDOM VECTORS - REVIEW Joint densities describe probability distributions of a random vector X: an n-dimensional vector of random variables, ie, X = (X 1,, X n ), where all X is are
Some slides from Carlos Guestrin, Luke Zettlemoyer & K Gajos 2
 Logistics CSE 446: Point Estimation Winter 2012 PS2 out shortly Dan Weld Some slides from Carlos Guestrin, Luke Zettlemoyer & K Gajos 2 Last Time Random variables, distributions Marginal, joint & conditional
Logistics CSE 446: Point Estimation Winter 2012 PS2 out shortly Dan Weld Some slides from Carlos Guestrin, Luke Zettlemoyer & K Gajos 2 Last Time Random variables, distributions Marginal, joint & conditional
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM
 February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
February 26, 2017 COMPLETENESS AND THE LEHMANN-SCHEFFE THEOREM Abstract. The Rao-Blacwell theorem told us how to improve an estimator. We will discuss conditions on when the Rao-Blacwellization of an estimator
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Tutorial: Statistical distance and Fisher information
 Tutorial: Statistical distance and Fisher information Pieter Kok Department of Materials, Oxford University, Parks Road, Oxford OX1 3PH, UK Statistical distance We wish to construct a space of probability
Tutorial: Statistical distance and Fisher information Pieter Kok Department of Materials, Oxford University, Parks Road, Oxford OX1 3PH, UK Statistical distance We wish to construct a space of probability
Multiple Random Variables
 Multiple Random Variables Joint Probability Density Let X and Y be two random variables. Their joint distribution function is F ( XY x, y) P X x Y y. F XY ( ) 1, < x
Multiple Random Variables Joint Probability Density Let X and Y be two random variables. Their joint distribution function is F ( XY x, y) P X x Y y. F XY ( ) 1, < x
Probability and Statistics for Final Year Engineering Students
 Probability and Statistics for Final Year Engineering Students By Yoni Nazarathy, Last Updated: May 24, 2011. Lecture 6p: Spectral Density, Passing Random Processes through LTI Systems, Filtering Terms
Probability and Statistics for Final Year Engineering Students By Yoni Nazarathy, Last Updated: May 24, 2011. Lecture 6p: Spectral Density, Passing Random Processes through LTI Systems, Filtering Terms
Introduction to Maximum Likelihood Estimation
 Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Introduction to Maximum Likelihood Estimation Eric Zivot July 26, 2012 The Likelihood Function Let 1 be an iid sample with pdf ( ; ) where is a ( 1) vector of parameters that characterize ( ; ) Example:
Lecture 1: Introduction
 Principles of Statistics Part II - Michaelmas 208 Lecturer: Quentin Berthet Lecture : Introduction This course is concerned with presenting some of the mathematical principles of statistical theory. One
Principles of Statistics Part II - Michaelmas 208 Lecturer: Quentin Berthet Lecture : Introduction This course is concerned with presenting some of the mathematical principles of statistical theory. One
Winter 2019 Math 106 Topics in Applied Mathematics. Lecture 8: Importance Sampling
 Winter 2019 Math 106 Topics in Applied Mathematics Data-driven Uncertainty Quantification Yoonsang Lee (yoonsang.lee@dartmouth.edu) Lecture 8: Importance Sampling 8.1 Importance Sampling Importance sampling
Winter 2019 Math 106 Topics in Applied Mathematics Data-driven Uncertainty Quantification Yoonsang Lee (yoonsang.lee@dartmouth.edu) Lecture 8: Importance Sampling 8.1 Importance Sampling Importance sampling
