Series with Central Binomial Coefficients, Catalan Numbers, and Harmonic Numbers
|
|
|
- Austen Webster
- 5 years ago
- Views:
Transcription
1 Joural of Iteger Sequeces, Vol. 5 (0), Article..7 Series with Cetral Biomial Coefficiets, Catala Numbers, ad Harmoic Numbers Khristo N. Boyadzhiev Departmet of Mathematics ad Statistics Ohio Norther Uiversity Ada, Ohio 4580 USA -boyadzhiev@ou.edu Abstract We preset several geeratig fuctios for sequeces ivolvig the cetral biomial coefficiets ad the harmoic umbers. I particular, we obtai the geeratig fuctios for the sequeces ( ) H, ( ) H, ( ) + H, ad ( ) m. The techique is based o a special Euler-type series trasformatio formula. Itroductio ad mai results The cetral biomial coefficiets are defied by ( ) = ()! (!) ( = 0,,...,) ad are closely related to the Catala umbers C = ( ) + May facts about these coefficiets ad Catala umbers ca be foud i the recet boo of Koshy [9]. Hery Gould has collected umerous idetities ivolvig cetral biomial coefficiets i [5] ad a large list of refereces o Catala umbers i [6]. Riorda s boo [3] is also a good referece. Our focus here will be o power series ivolvig these umbers. Several iterestig powers series with cetral biomial coefficiets were obtaied ad discussed by Lehmer [0]
2 (see also some correctios by Mathar []). Other examples were give by Weizierl [4] ad Zucer [5]. Hase s Table [8] cotais such series too, for istace, etries (5.9.3), (5.8.9), (5.4.5), (5.4.30), (5.5.7), (5.7.9), (5.7.), (5.7.7). The geeratig fuctios of the umbers ( ) ad C are well-ow, [8, (5.4.5)], [0], =0 =0 ( ) x = C x = 4x, () + 4x. () For both series we eed 4x <. The series () follows easily from () by itegratio. I this ote we preset a method of geeratig power series ivolvig cetral biomial coefficiets by usig appropriate biomial trasforms. Our results iclude several iterestig power series where the coefficiets are products of cetral biomial coefficiets ad harmoic umbers H, ad also products of Catala umbers ad harmoic umbers. As usual, for ad H 0 = 0. H = , Theorem. For every x < 4, or, =0 ( ) H ( ) x = =0 ( ) H x = where the first series, (3), coverges also for x = 4. log + 4x + 4x + + 4x log + 4x 4x 4x (3) (4) With x = 4 i (3) we fid =0 ( ) ( ) H 4 = log +. With x = 8 i (4) we have =0 ( ) H 8 = log +. Itegratig the power series (4) (usig the substitutio 4x = y for the RHS) we obtai the followig corollary ivolvig the Catala umbers.
3 Corollary. For every x 4, C H x + = 4x log( 4x) ( + 4x) log( + 4x) + log (5) =0 I particular, with x = 4, ad whe x = 4, =0 =0 C H 4 = 4 log, ( ) C H = ( + 3 ) log ( + ) log( + ). 4 + Some umerical series ivolvig cetral biomial coefficiets ad harmoic umbers have bee computed by a differet method i the papers [, 3, 4]. Two coectios of our results with certai series i [] are specified i Sectio 3. Next we tur to series with coefficiets of the form ( ) m. Applyig the operator ( ) x d dx to () Lehmer [0] computed ad repeatig the procedure, =0 =0 ( ) x = ( ) x = x ( 4x) 4x, (6) x(x + ) ( 4x) 4x. (7) Cotiuig lie this is upleasat, but fortuately a geeral formula ca be obtaied by a differet method. Theorem 3. For every positive iteger m ad every x < 4 =0 ( ) m x = m S(m, ) 4x where S(m,) are the Stirlig umbers of the secod id. we have ( ) ( ) x!, (8) 4x Remarably, the cetral biomial coefficiets appear o both sides of this equatio! Iformatio about S(m,) ca be foud i the classical boo [7]. Whe m = 0, S(0, 0) = ad (8) turs ito (). Whe m =, S(, 0) = 0,S(, ) = ad the RHS i (8) becomes which is the RHS i (6). ( )( ) x = 4x 4x 3 x ( 4x) 4x,
4 Whe m =, S(, 0) = 0, S(, ) = S(, ) = ad the RHS i (8) becomes ( )( ) ( ) ( ) x 4 x + = 4x 4x 4x 4x + x ( 4x) 4x. Thus (8) turs ito (7). Whe m = 3, S(3, 0) = 0, S(3, ) = S(3, 3) =, S(3, ) = 3, ad simple computatio gives ( ) 3 x = x(4x + 0x + ) ( 4x) 3 4x. =0 From (8) we have the immediate corollary: Corollary 4. Let P q (z) = a q z q + a q z q a 0 be a polyomial. The =0 ( ) P q ()x = = q 4x m=0 m ( a m S(m, ) )! q ( ) ( ) x q! a m S(m,) 4x 4x m= ( x ) 4x The proofs of these theorems are give i Sectio. I Sectio 3 we preset some more corollaries ad some ew series, icludig the geeratig fuctio for the sequece ( ) H. Proofs of the theorems Let f(z) = a z (9) be a fuctio aalytical i a eighborhood of the origi. The proof of Theorem is based o the followig Euler-type series trasformatio formula. Propositio 5. For ay complex umber α ad z small eough to provide covergece we have ( ) α ( ) ( ) { ( } z α ( ) a z = (z + ) α ( ) )a. (0) z + =0 =0 (cf. [, p. 94, (.0)]). The proof is give i the Appedix. This formula ad several other series trasformatio formulas of the same type ca be foud i []. Proof. Settig α = i (0) ad usig the simple fact that ( ) ( / ( ) = ) 4 we obtai =0 ( z )a 4 = + z =0 ( ) ( z z ) { ( } )a.
5 With z = 4x this becomes ( ) a x = =0 + 4x =0 ( x + 4x ) ( ) { Now we set a = ( ) H ad use the well-ow biomial formula ( ) ( ) H = ( =,,...) to obtai from () ( ) ( ) H x = + 4x = =0 = ( x + 4x ( } )a. () ) ( ). () Next we tur to the represetatio (see, for istace [9, p. 87] or [0, (6)]). ( ) ( ) ( ) 4z z = log = log z +. (3) 4z Usig this i the RHS of () with z = x +4x we obtai (6). Thus Theorem is proved. We ca state ow the followig observatio. Method for obtaiig ew geeratig fuctios from old oes. Suppose we ow the fuctio g(z) = =0 ( ) b z (4) i explicit compact form ad suppose also that we ca compute the sequece a, = 0,,..., explicitly from ( ) a = ( ) b, = 0,,..., (5) (biomial trasform). The we have from () the ew geeratig fuctio f(x) = =0 ( ) a t = ( ) t g. (6) + 4t + 4t Note that (5) ca be iverted i the followig maer (see [, 3]), ( ) b = a. (7) Usig this method we shall prove also Theorem 3. The theorem follows from the well-ow biomial trasform ( )!S(m,) = ( ) m (8) 5
6 for ay o-egative iteger m. This is, i fact, the classical represetatio of the Stirlig umbers of the secod id (see [7]). The iverse of (8) is ( )!S(m,) = m. We set ow a =!S(m,), b = m, = 0,,..., ad apply the above method. Note that the sequece a is fiite, as S(m,) = 0 whe > m. From (6), m =0 which after the substitutio ( )!S(m,)t = + 4t =0 ( t + 4t ) ( ) m (9) becomes (8). t + 4t = x 3 Several more series I this sectio we preset some more power series related to those above. We start with the geeratig fuctio for the Catala umbers. =0 =0 ( ) x + = + 4x. (0) Itegratig both sides yields the represetatio (substitutio 4x = y for the RHS) ( ) x + ( + ) = x+ ( ) 3 ( ) ( ) + 4x + 4x +log + 4x + log. 4 or, startig from =, ( ) x + ( + ) = ( ) 3 ( ) ( ) + 4x + 4x + log + 4x + log. 4 () Also, we ca write (0) i the form (startig the summatio from = ) = = ( ) x + = + 4x = 4x ( ) + 4x ad subtractig this from (3) we obtai (cf. []) = ( ) x ( + ) = + 4x + log + 4x. () 6
7 Next, sice we ca write = H + = H + +, H + + = H + + ( + ), ( ) H+ + x+ = = ( ) H + x+ + = ad from (5) ad () we obtai after addig ad simplifyig = ( ) ( + ) x+ ( ) H+ + x+ = x + ( 4x log ) 4x + 4x, (3) or, by addig x to both sides ad startig the summatio from = 0, With x = 4 =0 ( ) H+ + x+ = + ( 4x log ) 4x + 4x. we have from (3), = which cofirms [, (3.3)]. With x = 4 ( ) ( ) H + = ( + ) = ( ) H+ 4 ( + ) = 3 i (3), ( log + ). = Some of the above geeratig fuctios are quite simple. They are possibly just lucy exceptios. The ext series is somewhat similar to () ad (), but the geeratig fuctio is more ivolved. Propositio 6. We have = ( ) x = Li ( ) 4x where the first fuctio o the RHS is the dilogarithm log ( + 4x ) log log 4x +3(log ). x (4) Li (z) = = z. 7
8 Proof. Startig from (3), = ( ) ( ) x = log + 4x we divide both sides by x ad the itegrate to fid = = log log ( + 4x ), ( ) x log( + 4x) = log log x x With the substitutio y = 4x ad by usig partial fractios log( + 4x) x dx. dx = log ( + 4x ) log( + y) + y Further, settig y = u (so that ow u = 4x), log( + y) log( u) log + log( u/) dy = du = du y u u = log log ( 4x ) + (u/) = = log log ( 4x ) + Li ( 4x Brigig all pieces together ad computig the costat of itegratio (for x = 0), we obtai (4). ). dy. Settig x = 4 i (4) yields = ( ) 4 = Li ( ) (log ) = π 6 (log ). Now we shall derive from Theorem the geeratig fuctio for the umbers ( which are close to C H ad to the coefficiets i (3). The geeratig fuctio, however, is ot so simple as the oe i (5). Corollary 7. For every x /4 ad with y = 4x we have = ( ) H x = log y log + y y + log log( + y) log ( + y) (5) ( ) y + Li ( y) Li (y) Li (log ) + π. ) H 8
9 Proof. For the proof we first write (4) i the form = ( )H x = log ( + 4x ) log log 4x, 4x 4x 4x the divide both sides by x ad itegrate. The itegrals are solved with the same techiques as those i the previous proof. Details are left to the reader. To evaluate the costat of itegratio we set x = 0 ad use the fact that Li () = π 3, Li ( ) = π 6, Li ( ) = π 6 (log ). Settig x = /4 i (5) yields = i accordace with [, (3.8)]. We fiish with a geeralizatio of (0). ( ) H 4 = π 3, Propositio 8. For every m = 0,,..., =0 ( ) x + m + = m+ x m+ m ( ) m ( ) + [ ( 4x) 4x ]. (6) I particular, for m = 0 this reduces to (0). For m = ad after simplificatio (6) becomes ( ) x + = ( ) + 4x 3 ( + 4x ). =0 Proof. Let f(x) be the LHS i (6). The ad therefore, x m+ f(x) = d ( x m+ f(x) ) = dx x 0 =0 ( ) x +m = t m dt = 4t m+ 4x x m 4x ( y ) m dy with the substitutio y = 4t. The ext step is to expad the biomial iside the itegral ad itegrate termwise. Details are left to the reader. 9
10 4 Appedix Here we prove the formula =0 ( ) α ( z ( ) a z = (z + ) α z + =0 ) ( ) { α ( ) ( } )a. (7) Proof. Let L be a circle cetered at origi ad iside a dis where the fuctio (9) is holomorphic. For the coefficiets a from (9) we have a = f(λ) dλ. (8) πi λ λ Multiplyig both sides by ( ) ad summig for we fid ( ) a = πi L { ( ) } λ L f(λ) λ dλ = ( + ) f(λ) dλ. (9) πi L λ λ Let z be a complex umber iside the circle L with z small eough to assure covergece i the followig expasios. Multiplyig i (9) by ( z ( α z+) ) ad summig for we arrive at the represetatio ( ) ( ) { z α ( } )a = { ( ) ( ) } z( + λ) α f(λ) dλ (30) z + πi L λ(z + ) λ =0 {( = z ) α } f(λ) ( + z) α πi L λ λ dλ. Expadig ow the biomial iside the itegral, itegratig termwise, ad usig (8) agai we obtai =0 {( z ) α } f(λ) πi L λ λ dλ = ( ) α ( z) a. (3) =0 Thus (7) follows from (30) ad (3). Refereces [] Horst Alzer, Dimitri Karayaais, ad H. M. Srivastava, Series represetatios for some mathematical costats, J. Math. Aal. Appl. 30 (006), [] Khristo N. Boyadzhiev, Series trasformatios formulas of Euler type, Hadamard product of series, ad harmoic umber idetities, [3] Wechag Chu ad Deyi Zheg, Ifiite series with harmoic umbers ad cetral biomial coefficiets, It. J. Number Theory 5 (009),
11 [4] Maria Gechev, Biomial sums ivolvig harmoic umbers, Math. Slovaca 6 (0), 5 6. [5] Hery W. Gould, Combiatorial Idetities, Published by the author, revised editio, 97. [6] Hery W. Gould, Catala ad Bell Numbers: Research Bibliography of Two Special Number Sequeces, Published by the author, fifth editio, 979. [7] Roald L. Graham, Doald E. Kuth, ad Ore Patashi, Cocrete Mathematics, Addiso-Wesley, 994. [8] Eldo R. Hase, A Table of Series ad Products, Pretice-Hall, 975. [9] Thomas Koshy, Catala Numbers with Applicatios, Oxford Uiversity Press, 008. [0] Derric Hery Lehmer, Iterestig series ivolvig the cetral biomial coefficiet, Amer. Math. Mothly 9 (985), [] Richard J. Mathar, Corrigeda to Iterestig Series Ivolvig the Cetral Biomial Coefficiet [Amer. Math. Mothly 9 (985)], [] N. E. Norlud, Hypergeometric Fuctios, Acta Math 94 (955), [3] Joh Riorda, Combiatorial Idetities, Robert E. Krieger Publishig Compay, Hutigto, New Yor, 979. [4] S. Weizierl, Expasios aroud half-iteger values, biomial sums ad iverse biomial sums, J. Math. Phys. 45 (004), [5] I. J. Zucer, O the series (formula) ad related sums, J. Number Theory 0 (985), Mathematics Subject Classificatio: Primary B83; Secodary 05A0. Keywords: cetral biomial coefficiet, Catala umber, harmoic umber, geeratig fuctios, Euler series trasformatio, biomial trasform. Received Jue 3 0; revised versio received December 6 0. Published i Joural of Iteger Sequeces, December 7 0. Retur to Joural of Iteger Sequeces home page.
Harmonic Number Identities Via Euler s Transform
 1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 12 2009), Article 09.6.1 Harmoic Number Idetities Via Euler s Trasform Khristo N. Boyadzhiev Departmet of Mathematics Ohio Norther Uiversity Ada, Ohio 45810
1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 12 2009), Article 09.6.1 Harmoic Number Idetities Via Euler s Trasform Khristo N. Boyadzhiev Departmet of Mathematics Ohio Norther Uiversity Ada, Ohio 45810
Binomial transform of products
 Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
Jauary 02 207 Bioial trasfor of products Khristo N Boyadzhiev Departet of Matheatics ad Statistics Ohio Norther Uiversity Ada OH 4580 USA -boyadzhiev@ouedu Abstract Give the bioial trasfors { b } ad {
Interesting Series Associated with Central Binomial Coefficients, Catalan Numbers and Harmonic Numbers
 3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
3 47 6 3 Joural of Iteger Sequeces Vol. 9 06 Article 6.. Iterestig Series Associated with Cetral Biomial Coefficiets Catala Numbers ad Harmoic Numbers Hogwei Che Departmet of Mathematics Christopher Newport
Sequences of Definite Integrals, Factorials and Double Factorials
 47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
47 6 Joural of Iteger Sequeces, Vol. 8 (5), Article 5.4.6 Sequeces of Defiite Itegrals, Factorials ad Double Factorials Thierry Daa-Picard Departmet of Applied Mathematics Jerusalem College of Techology
Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers
 Quadratic Trasformatios of Hypergeometric Fuctio ad Series with Harmoic Numbers Marti Nicholso I this brief ote, we show how to apply Kummer s ad other quadratic trasformatio formulas for Gauss ad geeralized
Quadratic Trasformatios of Hypergeometric Fuctio ad Series with Harmoic Numbers Marti Nicholso I this brief ote, we show how to apply Kummer s ad other quadratic trasformatio formulas for Gauss ad geeralized
Some integrals related to the Basel problem
 November, 6 Some itegrals related to the Basel problem Khristo N Boyadzhiev Departmet of Mathematics ad Statistics, Ohio Norther Uiversity, Ada, OH 458, USA k-boyadzhiev@ouedu Abstract We evaluate several
November, 6 Some itegrals related to the Basel problem Khristo N Boyadzhiev Departmet of Mathematics ad Statistics, Ohio Norther Uiversity, Ada, OH 458, USA k-boyadzhiev@ouedu Abstract We evaluate several
Integral Representations and Binomial Coefficients
 2 3 47 6 23 Joural of Iteger Sequeces, Vol. 3 (2, Article.6.4 Itegral Represetatios ad Biomial Coefficiets Xiaoxia Wag Departmet of Mathematics Shaghai Uiversity Shaghai, Chia xiaoxiawag@shu.edu.c Abstract
2 3 47 6 23 Joural of Iteger Sequeces, Vol. 3 (2, Article.6.4 Itegral Represetatios ad Biomial Coefficiets Xiaoxia Wag Departmet of Mathematics Shaghai Uiversity Shaghai, Chia xiaoxiawag@shu.edu.c Abstract
A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS. Mircea Merca
 Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
Idia J Pure Appl Math 45): 75-89 February 204 c Idia Natioal Sciece Academy A GENERALIZATION OF THE SYMMETRY BETWEEN COMPLETE AND ELEMENTARY SYMMETRIC FUNCTIONS Mircea Merca Departmet of Mathematics Uiversity
Sums Involving Moments of Reciprocals of Binomial Coefficients
 1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 14 (2011, Article 11.6.6 Sums Ivolvig Momets of Reciprocals of Biomial Coefficiets Hacèe Belbachir ad Mourad Rahmai Uiversity of Scieces ad Techology Houari
1 2 3 47 6 23 11 Joural of Iteger Sequeces, Vol. 14 (2011, Article 11.6.6 Sums Ivolvig Momets of Reciprocals of Biomial Coefficiets Hacèe Belbachir ad Mourad Rahmai Uiversity of Scieces ad Techology Houari
On the Inverse of a Certain Matrix Involving Binomial Coefficients
 It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
It. J. Cotemp. Math. Scieces, Vol. 3, 008, o. 3, 5-56 O the Iverse of a Certai Matrix Ivolvig Biomial Coefficiets Yoshiari Iaba Kitakuwada Seior High School Keihokushimoyuge, Ukyo-ku, Kyoto, 60-0534, Japa
GENERALIZED HARMONIC NUMBER IDENTITIES AND A RELATED MATRIX REPRESENTATION
 J Korea Math Soc 44 (2007), No 2, pp 487 498 GENERALIZED HARMONIC NUMBER IDENTITIES AND A RELATED MATRIX REPRESENTATION Gi-Sag Cheo ad Moawwad E A El-Miawy Reprited from the Joural of the Korea Mathematical
J Korea Math Soc 44 (2007), No 2, pp 487 498 GENERALIZED HARMONIC NUMBER IDENTITIES AND A RELATED MATRIX REPRESENTATION Gi-Sag Cheo ad Moawwad E A El-Miawy Reprited from the Joural of the Korea Mathematical
On a general q-identity
 O a geeral -idetity Aimi Xu Istitute of Mathematics Zheiag Wali Uiversity Nigbo 3500, Chia xuaimi009@hotmailcom; xuaimi@zwueduc Submitted: Dec 2, 203; Accepted: Apr 24, 204; Published: May 9, 204 Mathematics
O a geeral -idetity Aimi Xu Istitute of Mathematics Zheiag Wali Uiversity Nigbo 3500, Chia xuaimi009@hotmailcom; xuaimi@zwueduc Submitted: Dec 2, 203; Accepted: Apr 24, 204; Published: May 9, 204 Mathematics
ON RUEHR S IDENTITIES
 ON RUEHR S IDENTITIES HORST ALZER AND HELMUT PRODINGER Abstract We apply completely elemetary tools to achieve recursio formulas for four polyomials with biomial coefficiets I particular, we obtai simple
ON RUEHR S IDENTITIES HORST ALZER AND HELMUT PRODINGER Abstract We apply completely elemetary tools to achieve recursio formulas for four polyomials with biomial coefficiets I particular, we obtai simple
FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS. H. W. Gould Department of Mathematics, West Virginia University, Morgantown, WV 26506, USA
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007), #A58 FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS H. W. Gould Departmet of Mathematics, West Virgiia Uiversity, Morgatow, WV
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007), #A58 FLOOR AND ROOF FUNCTION ANALOGS OF THE BELL NUMBERS H. W. Gould Departmet of Mathematics, West Virgiia Uiversity, Morgatow, WV
General Properties Involving Reciprocals of Binomial Coefficients
 3 47 6 3 Joural of Iteger Sequeces, Vol. 9 006, Article 06.4.5 Geeral Properties Ivolvig Reciprocals of Biomial Coefficiets Athoy Sofo School of Computer Sciece ad Mathematics Victoria Uiversity P. O.
3 47 6 3 Joural of Iteger Sequeces, Vol. 9 006, Article 06.4.5 Geeral Properties Ivolvig Reciprocals of Biomial Coefficiets Athoy Sofo School of Computer Sciece ad Mathematics Victoria Uiversity P. O.
AMS Mathematics Subject Classification : 40A05, 40A99, 42A10. Key words and phrases : Harmonic series, Fourier series. 1.
 J. Appl. Math. & Computig Vol. x 00y), No. z, pp. A RECURSION FOR ALERNAING HARMONIC SERIES ÁRPÁD BÉNYI Abstract. We preset a coveiet recursive formula for the sums of alteratig harmoic series of odd order.
J. Appl. Math. & Computig Vol. x 00y), No. z, pp. A RECURSION FOR ALERNAING HARMONIC SERIES ÁRPÁD BÉNYI Abstract. We preset a coveiet recursive formula for the sums of alteratig harmoic series of odd order.
COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS
 COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS GONÇALO MORAIS Abstract. We preted to give a broad overview of the algorithms used to compute the Euler s costat. Four type
COMPUTING THE EULER S CONSTANT: A HISTORICAL OVERVIEW OF ALGORITHMS AND RESULTS GONÇALO MORAIS Abstract. We preted to give a broad overview of the algorithms used to compute the Euler s costat. Four type
CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS
 CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS J. W. LAYMAN Virgiia Polytechic Istitute State Uiversity, Blacksburg, Virgiia Numerous writers appear to have bee fasciated by the may iterestig summatio idetitites
CERTAIN GENERAL BINOMIAL-FIBONACCI SUMS J. W. LAYMAN Virgiia Polytechic Istitute State Uiversity, Blacksburg, Virgiia Numerous writers appear to have bee fasciated by the may iterestig summatio idetitites
1 6 = 1 6 = + Factorials and Euler s Gamma function
 Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
Royal Holloway Uiversity of Lodo Departmet of Physics Factorials ad Euler s Gamma fuctio Itroductio The is a self-cotaied part of the course dealig, essetially, with the factorial fuctio ad its geeralizatio
The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j
![The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j The z-transform. 7.1 Introduction. 7.2 The z-transform Derivation of the z-transform: x[n] = z n LTI system, h[n] z = re j](/thumbs/82/85448534.jpg) The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
The -Trasform 7. Itroductio Geeralie the complex siusoidal represetatio offered by DTFT to a represetatio of complex expoetial sigals. Obtai more geeral characteristics for discrete-time LTI systems. 7.
De la Vallée Poussin Summability, the Combinatorial Sum 2n 1
 J o u r a l of Mathematics ad Applicatios JMA No 40, pp 5-20 (2017 De la Vallée Poussi Summability, the Combiatorial Sum 1 ( 2 ad the de la Vallée Poussi Meas Expasio Ziad S. Ali Abstract: I this paper
J o u r a l of Mathematics ad Applicatios JMA No 40, pp 5-20 (2017 De la Vallée Poussi Summability, the Combiatorial Sum 1 ( 2 ad the de la Vallée Poussi Meas Expasio Ziad S. Ali Abstract: I this paper
A symmetrical Eulerian identity
 Joural of Combiatorics Volume 17, Number 1, 29 38, 2010 A symmetrical Euleria idetity Fa Chug, Ro Graham ad Do Kuth We give three proofs for the followig symmetrical idetity ivolvig biomial coefficiets
Joural of Combiatorics Volume 17, Number 1, 29 38, 2010 A symmetrical Euleria idetity Fa Chug, Ro Graham ad Do Kuth We give three proofs for the followig symmetrical idetity ivolvig biomial coefficiets
Fibonacci numbers and orthogonal polynomials
 Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
Fiboacci umbers ad orthogoal polyomials Christia Berg April 10, 2006 Abstract We prove that the sequece (1/F +2 0 of reciprocals of the Fiboacci umbers is a momet sequece of a certai discrete probability,
The Gamma function Michael Taylor. Abstract. This material is excerpted from 18 and Appendix J of [T].
![The Gamma function Michael Taylor. Abstract. This material is excerpted from 18 and Appendix J of [T]. The Gamma function Michael Taylor. Abstract. This material is excerpted from 18 and Appendix J of [T].](/thumbs/74/70221891.jpg) The Gamma fuctio Michael Taylor Abstract. This material is excerpted from 8 ad Appedix J of [T]. The Gamma fuctio has bee previewed i 5.7 5.8, arisig i the computatio of a atural Laplace trasform: 8. ft
The Gamma fuctio Michael Taylor Abstract. This material is excerpted from 8 ad Appedix J of [T]. The Gamma fuctio has bee previewed i 5.7 5.8, arisig i the computatio of a atural Laplace trasform: 8. ft
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
THE TRANSFORMATION MATRIX OF CHEBYSHEV IV BERNSTEIN POLYNOMIAL BASES
 Joural of Mathematical Aalysis ISSN: 17-341, URL: http://iliriascom/ma Volume 7 Issue 4(16, Pages 13-19 THE TRANSFORMATION MATRIX OF CHEBYSHEV IV BERNSTEIN POLYNOMIAL BASES ABEDALLAH RABABAH, AYMAN AL
Joural of Mathematical Aalysis ISSN: 17-341, URL: http://iliriascom/ma Volume 7 Issue 4(16, Pages 13-19 THE TRANSFORMATION MATRIX OF CHEBYSHEV IV BERNSTEIN POLYNOMIAL BASES ABEDALLAH RABABAH, AYMAN AL
Proc. Amer. Math. Soc. 139(2011), no. 5, BINOMIAL COEFFICIENTS AND THE RING OF p-adic INTEGERS
 Proc. Amer. Math. Soc. 139(2011, o. 5, 1569 1577. BINOMIAL COEFFICIENTS AND THE RING OF p-adic INTEGERS Zhi-Wei Su* ad Wei Zhag Departmet of Mathematics, Naig Uiversity Naig 210093, People s Republic of
Proc. Amer. Math. Soc. 139(2011, o. 5, 1569 1577. BINOMIAL COEFFICIENTS AND THE RING OF p-adic INTEGERS Zhi-Wei Su* ad Wei Zhag Departmet of Mathematics, Naig Uiversity Naig 210093, People s Republic of
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
EVALUATION OF SUMS INVOLVING PRODUCTS OF GAUSSIAN q-binomial COEFFICIENTS WITH APPLICATIONS
 EALATION OF SMS INOLING PRODCTS OF GASSIAN -BINOMIAL COEFFICIENTS WITH APPLICATIONS EMRAH KILIÇ* AND HELMT PRODINGER** Abstract Sums of products of two Gaussia -biomial coefficiets are ivestigated oe of
EALATION OF SMS INOLING PRODCTS OF GASSIAN -BINOMIAL COEFFICIENTS WITH APPLICATIONS EMRAH KILIÇ* AND HELMT PRODINGER** Abstract Sums of products of two Gaussia -biomial coefficiets are ivestigated oe of
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
#A51 INTEGERS 14 (2014) MULTI-POLY-BERNOULLI-STAR NUMBERS AND FINITE MULTIPLE ZETA-STAR VALUES
 #A5 INTEGERS 4 (24) MULTI-POLY-BERNOULLI-STAR NUMBERS AND FINITE MULTIPLE ZETA-STAR VALUES Kohtaro Imatomi Graduate School of Mathematics, Kyushu Uiversity, Nishi-ku, Fukuoka, Japa k-imatomi@math.kyushu-u.ac.p
#A5 INTEGERS 4 (24) MULTI-POLY-BERNOULLI-STAR NUMBERS AND FINITE MULTIPLE ZETA-STAR VALUES Kohtaro Imatomi Graduate School of Mathematics, Kyushu Uiversity, Nishi-ku, Fukuoka, Japa k-imatomi@math.kyushu-u.ac.p
SOME DOUBLE BINOMIAL SUMS RELATED WITH THE FIBONACCI, PELL AND GENERALIZED ORDER-k FIBONACCI NUMBERS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 43 Number 3 013 SOME DOUBLE BINOMIAL SUMS RELATED WITH THE FIBONACCI PELL AND GENERALIZED ORDER-k FIBONACCI NUMBERS EMRAH KILIÇ AND HELMUT PRODINGER ABSTRACT
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 43 Number 3 013 SOME DOUBLE BINOMIAL SUMS RELATED WITH THE FIBONACCI PELL AND GENERALIZED ORDER-k FIBONACCI NUMBERS EMRAH KILIÇ AND HELMUT PRODINGER ABSTRACT
arxiv: v1 [math.nt] 28 Apr 2014
![arxiv: v1 [math.nt] 28 Apr 2014 arxiv: v1 [math.nt] 28 Apr 2014](/thumbs/88/114694424.jpg) Proof of a supercogruece cojectured by Z.-H. Su Victor J. W. Guo Departmet of Mathematics, Shaghai Key Laboratory of PMMP, East Chia Normal Uiversity, 500 Dogchua Rd., Shaghai 0041, People s Republic of
Proof of a supercogruece cojectured by Z.-H. Su Victor J. W. Guo Departmet of Mathematics, Shaghai Key Laboratory of PMMP, East Chia Normal Uiversity, 500 Dogchua Rd., Shaghai 0041, People s Republic of
MAT 271 Project: Partial Fractions for certain rational functions
 MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
MAT 7 Project: Partial Fractios for certai ratioal fuctios Prerequisite kowledge: partial fractios from MAT 7, a very good commad of factorig ad complex umbers from Precalculus. To complete this project,
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Bernoulli numbers and the Euler-Maclaurin summation formula
 Physics 6A Witer 006 Beroulli umbers ad the Euler-Maclauri summatio formula I this ote, I shall motivate the origi of the Euler-Maclauri summatio formula. I will also explai why the coefficiets o the right
Physics 6A Witer 006 Beroulli umbers ad the Euler-Maclauri summatio formula I this ote, I shall motivate the origi of the Euler-Maclauri summatio formula. I will also explai why the coefficiets o the right
The Arakawa-Kaneko Zeta Function
 The Arakawa-Kaeko Zeta Fuctio Marc-Atoie Coppo ad Berard Cadelpergher Nice Sophia Atipolis Uiversity Laboratoire Jea Alexadre Dieudoé Parc Valrose F-0608 Nice Cedex 2 FRANCE Marc-Atoie.COPPO@uice.fr Berard.CANDELPERGHER@uice.fr
The Arakawa-Kaeko Zeta Fuctio Marc-Atoie Coppo ad Berard Cadelpergher Nice Sophia Atipolis Uiversity Laboratoire Jea Alexadre Dieudoé Parc Valrose F-0608 Nice Cedex 2 FRANCE Marc-Atoie.COPPO@uice.fr Berard.CANDELPERGHER@uice.fr
ON SOME TRIGONOMETRIC POWER SUMS
 IJMMS 0: 2002 185 191 PII. S016117120200771 http://ijmms.hidawi.com Hidawi Publishig Corp. ON SOME TRIGONOMETRIC POWER SUMS HONGWEI CHEN Received 17 Jue 2001 Usig the geeratig fuctio method, the closed
IJMMS 0: 2002 185 191 PII. S016117120200771 http://ijmms.hidawi.com Hidawi Publishig Corp. ON SOME TRIGONOMETRIC POWER SUMS HONGWEI CHEN Received 17 Jue 2001 Usig the geeratig fuctio method, the closed
arxiv: v1 [math.co] 23 Mar 2016
![arxiv: v1 [math.co] 23 Mar 2016 arxiv: v1 [math.co] 23 Mar 2016](/thumbs/92/108877827.jpg) The umber of direct-sum decompositios of a fiite vector space arxiv:603.0769v [math.co] 23 Mar 206 David Ellerma Uiversity of Califoria at Riverside August 3, 208 Abstract The theory of q-aalogs develops
The umber of direct-sum decompositios of a fiite vector space arxiv:603.0769v [math.co] 23 Mar 206 David Ellerma Uiversity of Califoria at Riverside August 3, 208 Abstract The theory of q-aalogs develops
The Riemann Zeta Function
 Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
Physics 6A Witer 6 The Riema Zeta Fuctio I this ote, I will sketch some of the mai properties of the Riema zeta fuctio, ζ(x). For x >, we defie ζ(x) =, x >. () x = For x, this sum diverges. However, we
WHAT ARE THE BERNOULLI NUMBERS? 1. Introduction
 WHAT ARE THE BERNOULLI NUMBERS? C. D. BUENGER Abstract. For the "What is?" semiar today we will be ivestigatig the Beroulli umbers. This surprisig sequece of umbers has may applicatios icludig summig powers
WHAT ARE THE BERNOULLI NUMBERS? C. D. BUENGER Abstract. For the "What is?" semiar today we will be ivestigatig the Beroulli umbers. This surprisig sequece of umbers has may applicatios icludig summig powers
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
Applicable Analysis and Discrete Mathematics available online at ON JENSEN S AND RELATED COMBINATORIAL IDENTITIES
 Applicable Aalysis ad Discrete Mathematics available olie at http://pefmathetfrs Appl Aal Discrete Math 5 2011, 201 211 doi:102298/aadm110717017g ON JENSEN S AND RELATED COMBINATORIAL IDENTITIES Victor
Applicable Aalysis ad Discrete Mathematics available olie at http://pefmathetfrs Appl Aal Discrete Math 5 2011, 201 211 doi:102298/aadm110717017g ON JENSEN S AND RELATED COMBINATORIAL IDENTITIES Victor
The log-behavior of n p(n) and n p(n)/n
 Ramauja J. 44 017, 81-99 The log-behavior of p ad p/ William Y.C. Che 1 ad Ke Y. Zheg 1 Ceter for Applied Mathematics Tiaji Uiversity Tiaji 0007, P. R. Chia Ceter for Combiatorics, LPMC Nakai Uivercity
Ramauja J. 44 017, 81-99 The log-behavior of p ad p/ William Y.C. Che 1 ad Ke Y. Zheg 1 Ceter for Applied Mathematics Tiaji Uiversity Tiaji 0007, P. R. Chia Ceter for Combiatorics, LPMC Nakai Uivercity
PAijpam.eu ON TENSOR PRODUCT DECOMPOSITION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 103 No 3 2015, 537-545 ISSN: 1311-8080 (prited versio); ISSN: 1314-3395 (o-lie versio) url: http://wwwijpameu doi: http://dxdoiorg/1012732/ijpamv103i314
Iteratioal Joural of Pure ad Applied Mathematics Volume 103 No 3 2015, 537-545 ISSN: 1311-8080 (prited versio); ISSN: 1314-3395 (o-lie versio) url: http://wwwijpameu doi: http://dxdoiorg/1012732/ijpamv103i314
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Fourier series and the Lubkin W-transform
 Fourier series ad the Lubki W-trasform Jaso Boggess, Departmet of Mathematics, Iowa State Uiversity Eric Buch, Departmet of Mathematics, Baylor Uiversity Charles N. Moore, Departmet of Mathematics, Kasas
Fourier series ad the Lubki W-trasform Jaso Boggess, Departmet of Mathematics, Iowa State Uiversity Eric Buch, Departmet of Mathematics, Baylor Uiversity Charles N. Moore, Departmet of Mathematics, Kasas
MATH 31B: MIDTERM 2 REVIEW
 MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate x (x ) (x 3).. Partial Fractios Solutio: The umerator has degree less tha the deomiator, so we ca use partial fractios. Write x (x ) (x 3) = A x + A (x ) +
MATH 3B: MIDTERM REVIEW JOE HUGHES. Evaluate x (x ) (x 3).. Partial Fractios Solutio: The umerator has degree less tha the deomiator, so we ca use partial fractios. Write x (x ) (x 3) = A x + A (x ) +
SOME TRIGONOMETRIC IDENTITIES RELATED TO POWERS OF COSINE AND SINE FUNCTIONS
 Folia Mathematica Vol. 5, No., pp. 4 6 Acta Uiversitatis Lodziesis c 008 for Uiversity of Lódź Press SOME TRIGONOMETRIC IDENTITIES RELATED TO POWERS OF COSINE AND SINE FUNCTIONS ROMAN WITU LA, DAMIAN S
Folia Mathematica Vol. 5, No., pp. 4 6 Acta Uiversitatis Lodziesis c 008 for Uiversity of Lódź Press SOME TRIGONOMETRIC IDENTITIES RELATED TO POWERS OF COSINE AND SINE FUNCTIONS ROMAN WITU LA, DAMIAN S
Shivley s Polynomials of Two Variables
 It. Joural of Math. Aalysis, Vol. 6, 01, o. 36, 1757-176 Shivley s Polyomials of Two Variables R. K. Jaa, I. A. Salehbhai ad A. K. Shukla Departmet of Mathematics Sardar Vallabhbhai Natioal Istitute of
It. Joural of Math. Aalysis, Vol. 6, 01, o. 36, 1757-176 Shivley s Polyomials of Two Variables R. K. Jaa, I. A. Salehbhai ad A. K. Shukla Departmet of Mathematics Sardar Vallabhbhai Natioal Istitute of
HARMONIC SERIES WITH POLYGAMMA FUNCTIONS OVIDIU FURDUI. 1. Introduction and the main results
 Joural of Classical Aalysis Volume 8, Number 06, 3 30 doi:0.753/jca-08- HARMONIC SERIES WITH POLYGAMMA FUNCTIONS OVIDIU FURDUI Abstract. The paper is about evaluatig i closed form the followig classes
Joural of Classical Aalysis Volume 8, Number 06, 3 30 doi:0.753/jca-08- HARMONIC SERIES WITH POLYGAMMA FUNCTIONS OVIDIU FURDUI Abstract. The paper is about evaluatig i closed form the followig classes
Evaluation of Some Non-trivial Integrals from Finite Products and Sums
 Turkish Joural of Aalysis umber Theory 6 Vol. o. 6 7-76 Available olie at http://pubs.sciepub.com/tjat//6/5 Sciece Educatio Publishig DOI:.69/tjat--6-5 Evaluatio of Some o-trivial Itegrals from Fiite Products
Turkish Joural of Aalysis umber Theory 6 Vol. o. 6 7-76 Available olie at http://pubs.sciepub.com/tjat//6/5 Sciece Educatio Publishig DOI:.69/tjat--6-5 Evaluatio of Some o-trivial Itegrals from Fiite Products
TWO INEQUALITIES ON THE AREAL MAHLER MEASURE
 Illiois Joural of Mathematics Volume 56, Number 3, Fall 0, Pages 85 834 S 009-08 TWO INEQUALITIES ON THE AREAL MAHLER MEASURE KWOK-KWONG STEPHEN CHOI AND CHARLES L. SAMUELS Abstract. Recet wor of Pritser
Illiois Joural of Mathematics Volume 56, Number 3, Fall 0, Pages 85 834 S 009-08 TWO INEQUALITIES ON THE AREAL MAHLER MEASURE KWOK-KWONG STEPHEN CHOI AND CHARLES L. SAMUELS Abstract. Recet wor of Pritser
NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE
 UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
UPB Sci Bull, Series A, Vol 79, Iss, 207 ISSN 22-7027 NEW FAST CONVERGENT SEQUENCES OF EULER-MASCHERONI TYPE Gabriel Bercu We itroduce two ew sequeces of Euler-Mascheroi type which have fast covergece
1 Generating functions for balls in boxes
 Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Math 566 Fall 05 Some otes o geeratig fuctios Give a sequece a 0, a, a,..., a,..., a geeratig fuctio some way of represetig the sequece as a fuctio. There are may ways to do this, with the most commo ways
Topics in Probability Theory and Stochastic Processes Steven R. Dunbar. Stirling s Formula Derived from the Gamma Function
 Steve R. Dubar Departmet of Mathematics 23 Avery Hall Uiversity of Nebraska-Licol Licol, NE 68588-3 http://www.math.ul.edu Voice: 42-472-373 Fax: 42-472-8466 Topics i Probability Theory ad Stochastic Processes
Steve R. Dubar Departmet of Mathematics 23 Avery Hall Uiversity of Nebraska-Licol Licol, NE 68588-3 http://www.math.ul.edu Voice: 42-472-373 Fax: 42-472-8466 Topics i Probability Theory ad Stochastic Processes
SOME NEW IDENTITIES INVOLVING π,
 SOME NEW IDENTITIES INVOLVING π, HENG HUAT CHAN π AND π. Itroductio The umber π, as we all ow, is defied to be the legth of a circle of diameter. The first few estimates of π were 3 Egypt aroud 9 B.C.,
SOME NEW IDENTITIES INVOLVING π, HENG HUAT CHAN π AND π. Itroductio The umber π, as we all ow, is defied to be the legth of a circle of diameter. The first few estimates of π were 3 Egypt aroud 9 B.C.,
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Q-BINOMIALS AND THE GREATEST COMMON DIVISOR. Keith R. Slavin 8474 SW Chevy Place, Beaverton, Oregon 97008, USA.
 INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 2008, #A05 Q-BINOMIALS AND THE GREATEST COMMON DIVISOR Keith R. Slavi 8474 SW Chevy Place, Beaverto, Orego 97008, USA slavi@dsl-oly.et Received:
INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 8 2008, #A05 Q-BINOMIALS AND THE GREATEST COMMON DIVISOR Keith R. Slavi 8474 SW Chevy Place, Beaverto, Orego 97008, USA slavi@dsl-oly.et Received:
Math 120 Answers for Homework 23
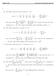 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
An Asymptotic Expansion for the Number of Permutations with a Certain Number of Inversions
 A Asymptotic Expasio for the Number of Permutatios with a Certai Number of Iversios Lae Clark Departmet of Mathematics Souther Illiois Uiversity Carbodale Carbodale, IL 691-448 USA lclark@math.siu.edu
A Asymptotic Expasio for the Number of Permutatios with a Certai Number of Iversios Lae Clark Departmet of Mathematics Souther Illiois Uiversity Carbodale Carbodale, IL 691-448 USA lclark@math.siu.edu
Mathematics review for CSCI 303 Spring Department of Computer Science College of William & Mary Robert Michael Lewis
 Mathematics review for CSCI 303 Sprig 019 Departmet of Computer Sciece College of William & Mary Robert Michael Lewis Copyright 018 019 Robert Michael Lewis Versio geerated: 13 : 00 Jauary 17, 019 Cotets
Mathematics review for CSCI 303 Sprig 019 Departmet of Computer Sciece College of William & Mary Robert Michael Lewis Copyright 018 019 Robert Michael Lewis Versio geerated: 13 : 00 Jauary 17, 019 Cotets
A Mean Paradox. John Konvalina, Jack Heidel, and Jim Rogers. Department of Mathematics University of Nebraska at Omaha Omaha, NE USA
 A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
MT5821 Advanced Combinatorics
 MT5821 Advaced Combiatorics 9 Set partitios ad permutatios It could be said that the mai objects of iterest i combiatorics are subsets, partitios ad permutatios of a fiite set. We have spet some time coutig
MT5821 Advaced Combiatorics 9 Set partitios ad permutatios It could be said that the mai objects of iterest i combiatorics are subsets, partitios ad permutatios of a fiite set. We have spet some time coutig
ON MONOTONICITY OF SOME COMBINATORIAL SEQUENCES
 Publ. Math. Debrece 8504, o. 3-4, 85 95. ON MONOTONICITY OF SOME COMBINATORIAL SEQUENCES QING-HU HOU*, ZHI-WEI SUN** AND HAOMIN WEN Abstract. We cofirm Su s cojecture that F / F 4 is strictly decreasig
Publ. Math. Debrece 8504, o. 3-4, 85 95. ON MONOTONICITY OF SOME COMBINATORIAL SEQUENCES QING-HU HOU*, ZHI-WEI SUN** AND HAOMIN WEN Abstract. We cofirm Su s cojecture that F / F 4 is strictly decreasig
The Ratio Test. THEOREM 9.17 Ratio Test Let a n be a series with nonzero terms. 1. a. n converges absolutely if lim. n 1
 460_0906.qxd //04 :8 PM Page 69 SECTION 9.6 The Ratio ad Root Tests 69 Sectio 9.6 EXPLORATION Writig a Series Oe of the followig coditios guaratees that a series will diverge, two coditios guaratee that
460_0906.qxd //04 :8 PM Page 69 SECTION 9.6 The Ratio ad Root Tests 69 Sectio 9.6 EXPLORATION Writig a Series Oe of the followig coditios guaratees that a series will diverge, two coditios guaratee that
On Infinite Series Involving Fibonacci Numbers
 Iteratioal Joural of Cotemporary Mathematical Scieces Vol. 10, 015, o. 8, 363-379 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ijcms.015.594 O Ifiite Series Ivolvig Fiboacci Numbers Robert Frotczak
Iteratioal Joural of Cotemporary Mathematical Scieces Vol. 10, 015, o. 8, 363-379 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.1988/ijcms.015.594 O Ifiite Series Ivolvig Fiboacci Numbers Robert Frotczak
REGULARIZATION OF CERTAIN DIVERGENT SERIES OF POLYNOMIALS
 REGULARIZATION OF CERTAIN DIVERGENT SERIES OF POLYNOMIALS LIVIU I. NICOLAESCU ABSTRACT. We ivestigate the geeralized covergece ad sums of series of the form P at P (x, where P R[x], a R,, ad T : R[x] R[x]
REGULARIZATION OF CERTAIN DIVERGENT SERIES OF POLYNOMIALS LIVIU I. NICOLAESCU ABSTRACT. We ivestigate the geeralized covergece ad sums of series of the form P at P (x, where P R[x], a R,, ad T : R[x] R[x]
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Partial Bell Polynomials and Inverse Relations
 1 2 3 47 6 23 11 Joural of Iteger Seueces, Vol. 13 (2010, Article 10.4.5 Partial Bell Polyomials ad Iverse Relatios Miloud Mihoubi 1 USTHB Faculty of Mathematics P.B. 32 El Alia 16111 Algiers Algeria miloudmihoubi@hotmail.com
1 2 3 47 6 23 11 Joural of Iteger Seueces, Vol. 13 (2010, Article 10.4.5 Partial Bell Polyomials ad Iverse Relatios Miloud Mihoubi 1 USTHB Faculty of Mathematics P.B. 32 El Alia 16111 Algiers Algeria miloudmihoubi@hotmail.com
arxiv: v1 [math.fa] 3 Apr 2016
![arxiv: v1 [math.fa] 3 Apr 2016 arxiv: v1 [math.fa] 3 Apr 2016](/thumbs/75/72845465.jpg) Aticommutator Norm Formula for Proectio Operators arxiv:164.699v1 math.fa] 3 Apr 16 Sam Walters Uiversity of Norther British Columbia ABSTRACT. We prove that for ay two proectio operators f, g o Hilbert
Aticommutator Norm Formula for Proectio Operators arxiv:164.699v1 math.fa] 3 Apr 16 Sam Walters Uiversity of Norther British Columbia ABSTRACT. We prove that for ay two proectio operators f, g o Hilbert
Simultaneous Generation of Koecher and Almkvist-Granville s Apéry-Like Formulae
 Simultaeous Geeratio of Koecher ad Almvist-Graville s Apéry-Lie Formulae T. Rivoal CONTENTS. Itroductio. First Step 3. Secod Step 4. Third Step 5. The Fial Step Acowledgmets Refereces We prove a very geeral
Simultaeous Geeratio of Koecher ad Almvist-Graville s Apéry-Lie Formulae T. Rivoal CONTENTS. Itroductio. First Step 3. Secod Step 4. Third Step 5. The Fial Step Acowledgmets Refereces We prove a very geeral
Factors of sums and alternating sums involving binomial coefficients and powers of integers
 Factors of sums ad alteratig sums ivolvig biomial coefficiets ad powers of itegers Victor J. W. Guo 1 ad Jiag Zeg 2 1 Departmet of Mathematics East Chia Normal Uiversity Shaghai 200062 People s Republic
Factors of sums ad alteratig sums ivolvig biomial coefficiets ad powers of itegers Victor J. W. Guo 1 ad Jiag Zeg 2 1 Departmet of Mathematics East Chia Normal Uiversity Shaghai 200062 People s Republic
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
CALCULATING FIBONACCI VECTORS
 THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
THE GENERALIZED BINET FORMULA FOR CALCULATING FIBONACCI VECTORS Stuart D Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithacaedu ad Dai Novak Departmet
A note on the p-adic gamma function and q-changhee polynomials
 Available olie at wwwisr-publicatioscom/jmcs J Math Computer Sci, 18 (2018, 11 17 Research Article Joural Homepage: wwwtjmcscom - wwwisr-publicatioscom/jmcs A ote o the p-adic gamma fuctio ad q-chaghee
Available olie at wwwisr-publicatioscom/jmcs J Math Computer Sci, 18 (2018, 11 17 Research Article Joural Homepage: wwwtjmcscom - wwwisr-publicatioscom/jmcs A ote o the p-adic gamma fuctio ad q-chaghee
5. Recurrences. The recursive denition of the Fibonacci numbers is well-known: if F n is the n th Fibonacci number, then
 5. Recurreces The recursive deitio of the Fiboacci umbers is well-kow: if F is the th Fiboacci umber, the F 0 = 0, F 1 = 1, F + = F +1 + F, if 0. We are iterested i a explicit form of the umbers F for
5. Recurreces The recursive deitio of the Fiboacci umbers is well-kow: if F is the th Fiboacci umber, the F 0 = 0, F 1 = 1, F + = F +1 + F, if 0. We are iterested i a explicit form of the umbers F for
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
arxiv: v2 [math.nt] 9 May 2017
![arxiv: v2 [math.nt] 9 May 2017 arxiv: v2 [math.nt] 9 May 2017](/thumbs/92/110806480.jpg) arxiv:6.42v2 [math.nt] 9 May 27 Itegral Represetatios of Equally Positive Iteger-Idexed Harmoic Sums at Ifiity Li Jiu Research Istitute for Symbolic Computatio Johaes Kepler Uiversity 44 Liz, Austria ljiu@risc.ui-liz.ac.at
arxiv:6.42v2 [math.nt] 9 May 27 Itegral Represetatios of Equally Positive Iteger-Idexed Harmoic Sums at Ifiity Li Jiu Research Istitute for Symbolic Computatio Johaes Kepler Uiversity 44 Liz, Austria ljiu@risc.ui-liz.ac.at
On some properties of digamma and polygamma functions
 J. Math. Aal. Appl. 328 2007 452 465 www.elsevier.com/locate/jmaa O some properties of digamma ad polygamma fuctios Necdet Batir Departmet of Mathematics, Faculty of Arts ad Scieces, Yuzucu Yil Uiversity,
J. Math. Aal. Appl. 328 2007 452 465 www.elsevier.com/locate/jmaa O some properties of digamma ad polygamma fuctios Necdet Batir Departmet of Mathematics, Faculty of Arts ad Scieces, Yuzucu Yil Uiversity,
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Physics 116A Solutions to Homework Set #9 Winter 2012
 Physics 116A Solutios to Homework Set #9 Witer 1 1. Boas, problem 11.3 5. Simplify Γ( 1 )Γ(4)/Γ( 9 ). Usig xγ(x) Γ(x + 1) repeatedly, oe obtais Γ( 9) 7 Γ( 7) 7 5 Γ( 5 ), etc. util fially obtaiig Γ( 9)
Physics 116A Solutios to Homework Set #9 Witer 1 1. Boas, problem 11.3 5. Simplify Γ( 1 )Γ(4)/Γ( 9 ). Usig xγ(x) Γ(x + 1) repeatedly, oe obtais Γ( 9) 7 Γ( 7) 7 5 Γ( 5 ), etc. util fially obtaiig Γ( 9)
arxiv: v1 [cs.sc] 2 Jan 2018
![arxiv: v1 [cs.sc] 2 Jan 2018 arxiv: v1 [cs.sc] 2 Jan 2018](/thumbs/93/111430524.jpg) Computig the Iverse Melli Trasform of Holoomic Sequeces usig Kovacic s Algorithm arxiv:8.9v [cs.sc] 2 Ja 28 Research Istitute for Symbolic Computatio RISC) Johaes Kepler Uiversity Liz, Alteberger Straße
Computig the Iverse Melli Trasform of Holoomic Sequeces usig Kovacic s Algorithm arxiv:8.9v [cs.sc] 2 Ja 28 Research Istitute for Symbolic Computatio RISC) Johaes Kepler Uiversity Liz, Alteberger Straße
Removing magic from the normal distribution and the Stirling and Wallis formulas.
 Removig magic from the ormal distributio ad the Stirlig ad Wallis formulas. Mikhail Kovalyov, email: mkovalyo@ualberta.ca Published i Mathematical Itelligecer, 0, Volume 33, Number 4. The Wallis formula
Removig magic from the ormal distributio ad the Stirlig ad Wallis formulas. Mikhail Kovalyov, email: mkovalyo@ualberta.ca Published i Mathematical Itelligecer, 0, Volume 33, Number 4. The Wallis formula
Euler-type formulas. Badih Ghusayni. Department of Mathematics Faculty of Science-1 Lebanese University Hadath, Lebanon
 Iteratioal Joural of Mathematics ad Computer Sciece, 7(), o., 85 9 M CS Euler-type formulas Badih Ghusayi Departmet of Mathematics Faculty of Sciece- Lebaese Uiversity Hadath, Lebao email: badih@future-i-tech.et
Iteratioal Joural of Mathematics ad Computer Sciece, 7(), o., 85 9 M CS Euler-type formulas Badih Ghusayi Departmet of Mathematics Faculty of Sciece- Lebaese Uiversity Hadath, Lebao email: badih@future-i-tech.et
Carleton College, Winter 2017 Math 121, Practice Final Prof. Jones. Note: the exam will have a section of true-false questions, like the one below.
 Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
Infinite Series and Improper Integrals
 8 Special Fuctios Ifiite Series ad Improper Itegrals Ifiite series are importat i almost all areas of mathematics ad egieerig I additio to umerous other uses, they are used to defie certai fuctios ad to
8 Special Fuctios Ifiite Series ad Improper Itegrals Ifiite series are importat i almost all areas of mathematics ad egieerig I additio to umerous other uses, they are used to defie certai fuctios ad to
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
arxiv: v3 [math.nt] 24 Dec 2017
![arxiv: v3 [math.nt] 24 Dec 2017 arxiv: v3 [math.nt] 24 Dec 2017](/thumbs/85/92905221.jpg) DOUGALL S 5 F SUM AND THE WZ-ALGORITHM Abstract. We show how to prove the examples of a paper by Chu ad Zhag usig the WZ-algorithm. arxiv:6.085v [math.nt] Dec 07 Keywords. Geeralized hypergeometric series;
DOUGALL S 5 F SUM AND THE WZ-ALGORITHM Abstract. We show how to prove the examples of a paper by Chu ad Zhag usig the WZ-algorithm. arxiv:6.085v [math.nt] Dec 07 Keywords. Geeralized hypergeometric series;
... and realizing that as n goes to infinity the two integrals should be equal. This yields the Wallis result-
 INFINITE PRODUTS Oe defies a ifiite product as- F F F... F x [ F ] Takig the atural logarithm of each side oe has- l[ F x] l F l F l F l F... So that the iitial ifiite product will coverge oly if the sum
INFINITE PRODUTS Oe defies a ifiite product as- F F F... F x [ F ] Takig the atural logarithm of each side oe has- l[ F x] l F l F l F l F... So that the iitial ifiite product will coverge oly if the sum
f(w) w z =R z a 0 a n a nz n Liouville s theorem, we see that Q is constant, which implies that P is constant, which is a contradiction.
 Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Factors of alternating sums of products of binomial and q-binomial coefficients
 ACTA ARITHMETICA 1271 (2007 Factors of alteratig sums of products of biomial ad q-biomial coefficiets by Victor J W Guo (Shaghai Frédéric Jouhet (Lyo ad Jiag Zeg (Lyo 1 Itroductio I 1998 Cali [4 proved
ACTA ARITHMETICA 1271 (2007 Factors of alteratig sums of products of biomial ad q-biomial coefficiets by Victor J W Guo (Shaghai Frédéric Jouhet (Lyo ad Jiag Zeg (Lyo 1 Itroductio I 1998 Cali [4 proved
The natural exponential function
 The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
The atural expoetial fuctio Attila Máté Brookly College of the City Uiversity of New York December, 205 Cotets The atural expoetial fuctio for real x. Beroulli s iequality.....................................2
PRELIM PROBLEM SOLUTIONS
 PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
