VECTORS AND THE GEOMETRY OF SPACE
|
|
|
- Todd Merritt
- 6 years ago
- Views:
Transcription
1 VECTORS AND THE GEOMETRY OF SPACE
2 VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given. The equation of the line can then be written using the point-slope form.
3 VECTORS AND THE GEOMETRY OF SPACE 1.3 Equations of Lines and Planes In this section, we will learn how to: Define three-dimensional lines and planes using vectors.
4 EQUATIONS OF LINES A line L in three-dimensional (3-D) space is determined when we know: A point P 0 (x 0, y 0, z 0 ) on L The direction of L
5 EQUATIONS OF LINES In three dimensions, the direction of a line is conveniently described by a vector.
6 EQUATIONS OF LINES So, we let v be a vector parallel to L. OP 0 Let P(x, y, z) be an arbitrary point on L. OP Let r 0 and r be the position vectors of P 0 and P. That is, they have representations and.
7 EQUATIONS OF LINES If a is the vector with representation, then the Triangle Law for vector addition gives: r = r 0 + a P P 0
8 EQUATIONS OF LINES However, since a and v are parallel vectors, there is a scalar t such that a = tv
9 VECTOR EQUATION OF A LINE Equation 1 Thus, r = r 0 + t v This is a vector equation of L.
10 VECTOR EQUATION Each value of the parameter t gives the position vector r of a point on L. That is, as t varies, the line is traced out by the tip of the vector r.
11 VECTOR EQUATION Positive values of t correspond to points on L that lie on one side of P 0. Negative values correspond to points that lie on the other side.
12 VECTOR EQUATION If the vector v that gives the direction of the line L is written in component form as v = <a, b, c>, then we have: tv = <ta, tb, tc>
13 VECTOR EQUATION We can also write: r = <x, y, z> and r 0 = <x 0, y 0, z 0 > So, vector Equation 1 becomes: <x, y, z> = <x 0 + ta, y 0 + tb, z 0 + tc>
14 VECTOR EQUATION Equations 2 Two vectors are equal if and only if corresponding components are equal. Hence, we have the following three scalar equations.
15 SCALAR EQUATIONS OF A LINE Equations 2 x = x 0 + at y = y 0 + bt z = z 0 + ct Where, t
16 PARAMETRIC EQUATIONS These equations are called parametric equations of the line L through the point P 0 (x 0, y 0, z 0 ) and parallel to the vector v = <a, b, c>. Each value of the parameter t gives a point (x, y, z) on L.
17 EQUATIONS OF LINES Example 1 a. Find a vector equation and parametric equations for the line that passes through the point (5, 1, 3) and is parallel to the vector i + 4 j 2 k. b. Find two other points on the line.
18 EQUATIONS OF LINES Example 1 a Here, and r 0 = <5, 1, 3> = 5 i + j + 3 k v = i + 4 j 2 k So, vector Equation 1 becomes: or r = (5 i + j + 3 k) + t(i + 4 j 2 k) r = (5 + t) i + (1 + 4t) j + (3 2t) k
19 EQUATIONS OF LINES Example 1 a Parametric equations are: x = 5 + t y = 1 + 4t z = 3 2t
20 EQUATIONS OF LINES Example 1 b Choosing the parameter value t = 1 gives x = 6, y = 5, and z = 1. So, (6, 5, 1) is a point on the line. Similarly, t = 1 gives the point (4, 3, 5).
21 EQUATIONS OF LINES The vector equation and parametric equations of a line are not unique. If we change the point or the parameter or choose a different parallel vector, then the equations change.
22 EQUATIONS OF LINES For instance, if, instead of (5, 1, 3), we choose the point (6, 5, 1) in Example 1, the parametric equations of the line become: x = 6 + t y = 5 + 4t z = 1 2t
23 EQUATIONS OF LINES Alternatively, if we stay with the point (5, 1, 3) but choose the parallel vector 2 i + 8 j 4 k, we arrive at: x = 5 + 2t y = 1 + 8t z = 3 4t
24 DIRECTION NUMBERS In general, if a vector v = <a, b, c> is used to describe the direction of a line L, then the numbers a, b, and c are called direction numbers of L.
25 DIRECTION NUMBERS Any vector parallel to v could also be used. Thus, we see that any three numbers proportional to a, b, and c could also be used as a set of direction numbers for L.
26 EQUATIONS OF LINES Equations 3 Another way of describing a line L is to eliminate the parameter t from Equations 2. If none of a, b, or c is 0, we can solve each of these equations for t, equate the results, and obtain the following equations.
27 SYMMETRIC EQUATIONS Equations 3 x x y y z z a b c These equations are called symmetric equations of L.
28 SYMMETRIC EQUATIONS Notice that the numbers a, b, and c that appear in the denominators of Equations 3 are direction numbers of L. That is, they are components of a vector parallel to L.
29 SYMMETRIC EQUATIONS If one of a, b, or c is 0, we can still eliminate t. For instance, if a = 0, we could write the equations of L as: x x This means that L lies in the vertical plane x = x 0. 0 y y z z b c 0 0
30 EQUATIONS OF LINES Example 2 a. Find parametric equations and symmetric equations of the line that passes through the points A(2, 4, 3) and B(3, 1, 1). b. At what point does this line intersect the xy-plane?
31 EQUATIONS OF LINES Example 2 a We are not explicitly given a vector parallel to the line. However, observe that the vector v with representation and AB is parallel to the line v = <3 2, 1 4, 1 ( 3)> = <1, 5, 4>
32 EQUATIONS OF LINES Example 2 a Thus, direction numbers are: a = 1, b = 5, c = 4
33 EQUATIONS OF LINES Example 2 a Taking the point (2, 4, 3) as P 0, we see that: Parametric Equations 2 are: x = 2 + t y = 4 5t z = 3 + 4t Symmetric Equations 3 are: x 2 y 4 z
34 EQUATIONS OF LINES Example 2 b The line intersects the xy-plane when z = 0. So, we put z = 0 in the symmetric equations and obtain: x 2 y This gives x = and y =.
35 EQUATIONS OF LINES The line intersects the xy-plane at the point 11 1,,0 4 4 Example 2 b
36 EQUATIONS OF LINES In general, the procedure of Example 2 shows that direction numbers of the line L through the points P 0 (x 0, y 0, z 0 ) and P 1 (x 1, y 1, z 1 ) are: x 1 x 0 y 1 y 0 z 1 z 0 So, symmetric equations of L are: x x y y z z x x y y z z
37 EQUATIONS OF LINE SEGMENTS Often, we need a description, not of an entire line, but of just a line segment. How, for instance, could we describe the line segment AB in Example 2?
38 EQUATIONS OF LINE SEGMENTS If we put t = 0 in the parametric equations in Example 2 a, we get the point (2, 4, 3). If we put t = 1, we get (3, 1, 1).
39 EQUATIONS OF LINE SEGMENTS So, the line segment AB is described by either: The parametric equations x = 2 + t y = 4 5t z = 3 + 4t where 0 t 1 The corresponding vector equation r(t) = <2 + t, 4 5t, 3 + 4t> where 0 t 1
40 EQUATIONS OF LINE SEGMENTS In general, we know from Equation 1 that the vector equation of a line through the (tip of the) vector r 0 in the direction of a vector v is: r = r 0 + t v
41 EQUATIONS OF LINE SEGMENTS If the line also passes through (the tip of) r 1, then we can take v = r 1 r 0. So, its vector equation is: r = r 0 + t(r 1 r 0 ) = (1 t)r 0 + t r 1 The line segment from r 0 to r 1 is given by the parameter interval 0 t 1.
42 EQUATIONS OF LINE SEGMENTS Equation 4 The line segment from r 0 to r 1 is given by the vector equation r(t) = (1 t)r 0 + t r 1 where 0 t 1
43 EQUATIONS OF LINE SEGMENTS Example 3 Show that the lines L 1 and L 2 with parametric equations x = 1 + t 1 y = 2 + 3t 1 z = 4 t 1 x = 2t 2 y = 3 + t 2 z = 3 + 4t 2 are skew lines. That is, they do not intersect and are not parallel, and therefore do not lie in the same plane.
44 EQUATIONS OF LINE SEGMENTS Example 3 The lines are not parallel because the corresponding vectors <1, 3, 1> and <2, 1, 4> are not parallel. Their components are not proportional.
45 EQUATIONS OF LINE SEGMENTS Example 3 If L 1 and L 2 had a point of intersection, there would be values of t and s such that 1 + t 1 = 2t t 1 = 3 + t 2 4 t 1 = 3 + 4s
46 EQUATIONS OF LINE SEGMENTS Example 3 However, if we solve the first two equations, we get: 11 t 1 = and t 2 = These values don t satisfy the third equation.
47 EQUATIONS OF LINE SEGMENTS Example 3 Thus, there are no values of t 1 and t 2 that satisfy the three equations. So, L 1 and L 2 do not intersect.
48 EQUATIONS OF LINE SEGMENTS Example 3 Hence, L 1 and L 2 are skew lines.
49 PLANES Although a line in space is determined by a point and a direction, a plane in space is more difficult to describe. A single vector parallel to a plane is not enough to convey the direction of the plane.
50 PLANES However, a vector perpendicular to the plane does completely specify its direction.
51 PLANES Thus, a plane in space is determined by: A point P 0 (x 0, y 0, z 0 ) in the plane A vector n that is orthogonal to the plane
52 NORMAL VECTOR This orthogonal vector n is called a normal vector.
53 PLANES Let P(x, y, z) be an arbitrary point in the plane. Let r 0 and r 1 be the position vectors of P 0 and P. Then, the vector r r 0 is represented by P 0 P
54 PLANES The normal vector n is orthogonal to every vector in the given plane. In particular, n is orthogonal to r r 0.
55 EQUATIONS OF PLANES Equation 5 Thus, we have: n. (r r 0 ) = 0
56 EQUATIONS OF PLANES Equation 6 That can also be written as: n. r = n. r 0
57 VECTOR EQUATION Either Equation 5 or Equation 6 is called a vector equation of the plane.
58 EQUATIONS OF PLANES To obtain a scalar equation for the plane, we write: n = <a, b, c> r = <x, y, z> r 0 = <x 0, y 0, z 0 >
59 EQUATIONS OF PLANES Then, the vector Equation 5 becomes: <a, b, c>. <x x 0, y y 0, z z 0 > = 0
60 SCALAR EQUATION That can also be written as: Equation 7 a(x x 0 ) + b(y y 0 ) + c(z z 0 ) = 0 This equation is the scalar equation of the plane through P 0 (x 0, y 0, z 0 ) with normal vector n = <a, b, c>.
61 EQUATIONS OF PLANES Example 4 Find an equation of the plane through the point (2, 4, 1) with normal vector n = <2, 3, 4>. Find the intercepts and sketch the plane.
62 EQUATIONS OF PLANES In Equation 7, putting Example 4 a = 2, b = 3, c = 4, x 0 = 2, y 0 = 4, z 0 = 1, we see that an equation of the plane is: 2(x 2) + 3(y 4) + 4(z + 1) = 0 or 2x + 3y + 4z = 12
63 EQUATIONS OF PLANES Example 4 To find the x-intercept, we set y = z = 0 in the equation, and obtain x = 6. Similarly, the y-intercept is 4 and the z-intercept is 3.
64 EQUATIONS OF PLANES Example 4 This enables us to sketch the portion of the plane that lies in the first octant.
65 EQUATIONS OF PLANES By collecting terms in Equation 7 as we did in Example 4, we can rewrite the equation of a plane as follows.
66 LINEAR EQUATION ax + by + cz + d = 0 Equation 8 where d = (ax 0 + by 0 + cz 0 ) This is called a linear equation in x, y, and z.
67 LINEAR EQUATION Conversely, it can be shown that, if a, b, and c are not all 0, then the linear Equation 8 represents a plane with normal vector <a, b, c>. See Exercise 77.
68 EQUATIONS OF PLANES Example 5 Find an equation of the plane that passes through the points P(1, 3, 2), Q(3, 1, 6), R(5, 2, 0)
69 EQUATIONS OF PLANES Example 5 The vectors a and b corresponding to and PR are: PQ a = <2, 4, 4> b = <4, 1, 2>
70 EQUATIONS OF PLANES Example 5 Since both a and b lie in the plane, their cross product a x b is orthogonal to the plane and can be taken as the normal vector.
71 EQUATIONS OF PLANES Example 5 Thus, n a b i j k i 20 j 14k
72 EQUATIONS OF PLANES Example 5 With the point P(1, 2, 3) and the normal vector n, an equation of the plane is: 12(x 1) + 20(y 3) + 14(z 2) = 0 or 6x + 10y + 7z = 50
73 EQUATIONS OF PLANES Example 6 Find the point at which the line with parametric equations x = 2 + 3t y = 4t z = 5 + t intersects the plane 4x + 5y 2z = 18
74 EQUATIONS OF PLANES Example 6 We substitute the expressions for x, y, and z from the parametric equations into the equation of the plane: 4(2 + 3t) + 5( 4t) 2(5 + t) = 18
75 EQUATIONS OF PLANES Example 6 That simplifies to 10t = 20. Hence, t = 2. Therefore, the point of intersection occurs when the parameter value is t = 2.
76 EQUATIONS OF PLANES Then, Example 6 x = 2 + 3( 2) = 4 y = 4( 2) = 8 z = 5 2 = 3 So, the point of intersection is ( 4, 8, 3).
77 PARALLEL PLANES Two planes are parallel if their normal vectors are parallel.
78 PARALLEL PLANES For instance, the planes x + 2y 3z = 4 and 2x + 4y 6z = 3 are parallel because: Their normal vectors are and n 2 = 2n 1. n 1 = <1, 2, 3> and n 2 = <2, 4, 6>
79 NONPARALLEL PLANES If two planes are not parallel, then They intersect in a straight line. The angle between the two planes is defined as the acute angle between their normal vectors.
80 EQUATIONS OF PLANES Example 7 a. Find the angle between the planes x + y + z = 1 and x 2y + 3z = 1 b. Find symmetric equations for the line of intersection L of these two planes.
81 EQUATIONS OF PLANES Example 7 a The normal vectors of these planes are: n 1 = <1, 1, 1> n 2 = <1, 2, 3>
82 EQUATIONS OF PLANES Example 7 a So, if θ is the angle between the planes, Corollary 6 in Section 12.3 gives: cos n n n 1(1) 1( 2) 1(3) 2 n cos 72 42
83 EQUATIONS OF PLANES Example 7 b We first need to find a point on L. For instance, we can find the point where the line intersects the xy-plane by setting z = 0 in the equations of both planes. This gives the equations x + y = 1 and x 2y = 1 whose solution is x = 1, y = 0. So, the point (1, 0, 0) lies on L.
84 EQUATIONS OF PLANES Example 7 b As L lies in both planes, it is perpendicular to both the normal vectors. Thus, a vector v parallel to L is given by the cross product i j k v n1 n i 2 j 3k 1 2 3
85 EQUATIONS OF PLANES Example 7 b So, the symmetric equations of L can be written as: x 1 y z 5 2 3
86 NOTE A linear equation in x, y, and z represents a plane. Also, two nonparallel planes intersect in a line. It follows that two linear equations can represent a line.
87 NOTE The points (x, y, z) that satisfy both a 1 x + b 1 y + c 1 z + d 1 = 0 and a 2 x + b 2 y + c 2 z + d 2 = 0 lie on both of these planes. So, the pair of linear equations represents the line of intersection of the planes (if they are not parallel).
88 NOTE For instance, in Example 7, the line L was given as the line of intersection of the planes x + y + z = 1 and x 2y + 3z = 1
89 NOTE The symmetric equations that we found for L could be written as: x 1 y y z and This is again a pair of linear equations.
90 NOTE They exhibit L as the line of intersection of the planes (x 1)/5 = y/( 2) and y/( 2) = z/( 3)
91 NOTE In general, when we write the equations of a line in the symmetric form we can regard the line as the line of intersection of the two planes x x y y 0 0 and a b x x y y z z a b c y y z z b c 0 0
92 EQUATIONS OF PLANES Example 8 Find a formula for the distance D from a point P 1 (x 1, y 1, z 1 ) to the plane ax + by + cz + d = 0.
93 EQUATIONS OF PLANES Example 8 Let P 0 (x 0, y 0, z 0 ) be any point in the plane. Let b be the vector corresponding to P P. 0 1 Then, b = <x 1 x 0, y 1 y 0, z 1 z 0 >
94 EQUATIONS OF PLANES Example 8 You can see that the distance D from P 1 to the plane is equal to the absolute value of the scalar projection of b onto the normal vector n = <a, b, c>.
95 EQUATIONS OF PLANES Thus, Example 8 D comp n b n n b a()()() x x b y y c z z a b c ()() ax by cz ax by cz a b c 2 2 2
96 EQUATIONS OF PLANES Example 8 Since P 0 lies in the plane, its coordinates satisfy the equation of the plane. Thus, we have ax 0 + by 0 + cz 0 + d = 0.
97 EQUATIONS OF PLANES E. g. 8 Formula 9 Hence, the formula for D can be written as: D ax by cz d a b c
98 EQUATIONS OF PLANES Example 9 Find the distance between the parallel planes 10x + 2y 2z = 5 and 5x + y z = 1
99 EQUATIONS OF PLANES Example 9 First, we note that the planes are parallel because their normal vectors <10, 2, 2> and <5, 1, 1> are parallel.
100 EQUATIONS OF PLANES Example 9 To find the distance D between the planes, we choose any point on one plane and calculate its distance to the other plane. In particular, if we put y = z =0 in the equation of the first plane, we get 10x = 5. So, (½, 0, 0) is a point in this plane.
101 EQUATIONS OF PLANES Example 9 By Formula 9, the distance between (½, 0, 0) and the plane 5x + y z 1 = 0 is: D 1 3 5() 2 1(0) 1(0) ( 1) So, the distance between the planes is 3 / 6.
102 EQUATIONS OF PLANES Example 10 In Example 3, we showed that the lines L 1 : x = 1 + t 1 y = 2 + 3t 1 z = 4 t 1 L 2 : x = 2t 2 y = 3 + t 2 z = 3 + 4t 2 are skew. Find the distance between them.
103 EQUATIONS OF PLANES Example 10 Since the two lines L 1 and L 2 are skew, they can be viewed as lying on two parallel planes P 1 and P 2. The distance between L 1 and L 2 is the same as the distance between P 1 and P 2. This can be computed as in Example 9.
104 EQUATIONS OF PLANES Example 10 The common normal vector to both planes must be orthogonal to both v 1 = <1, 3, 1> (direction of L 1 ) v 2 = <2, 1, 4> (direction of L 2 )
105 EQUATIONS OF PLANES So, a normal vector is: Example 10 n v v 1 2 i j k i 6 j 5k
106 EQUATIONS OF PLANES Example 10 If we put t 2 = 0 in the equations of L 2, we get the point (0, 3, 3) on L 2. So, an equation for P 2 is: 13(x 0) 6(y 3) 5(z + 3) = 0 or 13x 6y 5z + 3 = 0
107 EQUATIONS OF PLANES Example 10 If we now set t 1 = 0 in the equations for L 1, we get the point (1, 2, 4) on P 1.
108 EQUATIONS OF PLANES Example 10 So, the distance between L 1 and L 2 is the same as the distance from (1, 2, 4) to 13x 6y 5z + 3 = 0.
109 EQUATIONS OF PLANES By Formula 9, this distance is: Example 10 D 13(1) 6( 2) 5(4) ( 6)( 5)
12.5 Equations of Lines and Planes
 12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
12.5 Equations of Lines and Planes Equation of Lines Vector Equation of Lines Parametric Equation of Lines Symmetric Equation of Lines Relation Between Two Lines Equations of Planes Vector Equation of
What you will learn today
 What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
What you will learn today The Dot Product Equations of Vectors and the Geometry of Space 1/29 Direction angles and Direction cosines Projections Definitions: 1. a : a 1, a 2, a 3, b : b 1, b 2, b 3, a
Kevin James. MTHSC 206 Section 12.5 Equations of Lines and Planes
 MTHSC 206 Section 12.5 Equations of Lines and Planes Definition A line in R 3 can be described by a point and a direction vector. Given the point r 0 and the direction vector v. Any point r on the line
MTHSC 206 Section 12.5 Equations of Lines and Planes Definition A line in R 3 can be described by a point and a direction vector. Given the point r 0 and the direction vector v. Any point r on the line
Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems. Three-Dimensional Coordinate Systems
 To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
How can we find the distance between a point and a plane in R 3? Between two lines in R 3? Between two planes? Between a plane and a line?
 Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Overview Yesterday we introduced equations to describe lines and planes in R 3 : r = r 0 + tv The vector equation for a line describes arbitrary points r in terms of a specific point r 0 and the direction
Vector equations of lines in the plane and 3-space (uses vector addition & scalar multiplication).
 Boise State Math 275 (Ultman) Worksheet 1.6: Lines and Planes From the Toolbox (what you need from previous classes) Plotting points, sketching vectors. Be able to find the component form a vector given
Boise State Math 275 (Ultman) Worksheet 1.6: Lines and Planes From the Toolbox (what you need from previous classes) Plotting points, sketching vectors. Be able to find the component form a vector given
1 Vectors. c Kun Wang. Math 151, Fall Vector Supplement
 Vector Supplement 1 Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude of a vector
Vector Supplement 1 Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude of a vector
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Spring 2018, WEEK 1 JoungDong Kim Week 1 Vectors, The Dot Product, Vector Functions and Parametric Curves. Section 1.1 Vectors Definition. A Vector is a quantity that
MATH 151 Engineering Mathematics I Spring 2018, WEEK 1 JoungDong Kim Week 1 Vectors, The Dot Product, Vector Functions and Parametric Curves. Section 1.1 Vectors Definition. A Vector is a quantity that
6.1.1 Angle between Two Lines Intersection of Two lines Shortest Distance from a Point to a Line
 CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
MATH 12 CLASS 4 NOTES, SEP
 MATH 12 CLASS 4 NOTES, SEP 28 2011 Contents 1. Lines in R 3 1 2. Intersections of lines in R 3 2 3. The equation of a plane 4 4. Various problems with planes 5 4.1. Intersection of planes with planes or
MATH 12 CLASS 4 NOTES, SEP 28 2011 Contents 1. Lines in R 3 1 2. Intersections of lines in R 3 2 3. The equation of a plane 4 4. Various problems with planes 5 4.1. Intersection of planes with planes or
Math 241, Exam 1 Information.
 Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Math 241, Exam 1 Information. 2/13/13, LC 310, 11:15-12:05. Exam 1 will be based on: Sections 12.1-12.5, 14.2. The corresponding assigned homework problems (see http://www.math.sc.edu/ boylan/sccourses/241sp13/241.html)
Exam 1 Review SOLUTIONS
 1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
1. True or False (and give a short reason): Exam 1 Review SOLUTIONS (a) If the parametric curve x = f(t), y = g(t) satisfies g (1) = 0, then it has a horizontal tangent line when t = 1. FALSE: To make
Vector Supplement Part 1: Vectors
 Vector Supplement Part 1: Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude
Vector Supplement Part 1: Vectors A vector is a quantity that has both magnitude and direction. Vectors are drawn as directed line segments and are denoted by boldface letters a or by a. The magnitude
MAT 1339-S14 Class 10 & 11
 MAT 1339-S14 Class 10 & 11 August 7 & 11, 2014 Contents 8 Lines and Planes 1 8.1 Equations of Lines in Two-Space and Three-Space............ 1 8.2 Equations of Planes........................... 5 8.3 Properties
MAT 1339-S14 Class 10 & 11 August 7 & 11, 2014 Contents 8 Lines and Planes 1 8.1 Equations of Lines in Two-Space and Three-Space............ 1 8.2 Equations of Planes........................... 5 8.3 Properties
9.5. Lines and Planes. Introduction. Prerequisites. Learning Outcomes
 Lines and Planes 9.5 Introduction Vectors are very convenient tools for analysing lines and planes in three dimensions. In this Section you will learn about direction ratios and direction cosines and then
Lines and Planes 9.5 Introduction Vectors are very convenient tools for analysing lines and planes in three dimensions. In this Section you will learn about direction ratios and direction cosines and then
12.1. Cartesian Space
 12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
12.1. Cartesian Space In most of your previous math classes, we worked with functions on the xy-plane only meaning we were working only in 2D. Now we will be working in space, or rather 3D. Now we will
Math 3c Solutions: Exam 1 Fall Graph by eliiminating the parameter; be sure to write the equation you get when you eliminate the parameter.
 Math c Solutions: Exam 1 Fall 16 1. Graph by eliiminating the parameter; be sure to write the equation you get when you eliminate the parameter. x tan t x tan t y sec t y sec t t π 4 To eliminate the parameter,
Math c Solutions: Exam 1 Fall 16 1. Graph by eliiminating the parameter; be sure to write the equation you get when you eliminate the parameter. x tan t x tan t y sec t y sec t t π 4 To eliminate the parameter,
MAT1035 Analytic Geometry
 MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
MAT1035 Analytic Geometry Lecture Notes R.A. Sabri Kaan Gürbüzer Dokuz Eylül University 2016 2 Contents 1 Review of Trigonometry 5 2 Polar Coordinates 7 3 Vectors in R n 9 3.1 Located Vectors..............................................
MATH 1020 WORKSHEET 12.1 & 12.2 Vectors in the Plane
 MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
MATH 100 WORKSHEET 1.1 & 1. Vectors in the Plane Find the vector v where u =, 1 and w = 1, given the equation v = u w. Solution. v = u w =, 1 1, =, 1 +, 4 =, 1 4 = 0, 5 Find the magnitude of v = 4, 3 Solution.
mathematical objects can be described via equations, functions, graphs, parameterization in R, R, and R.
 Multivariable Calculus Lecture # Notes This lecture completes the discussion of the cross product in R and addresses the variety of different ways that n mathematical objects can be described via equations,
Multivariable Calculus Lecture # Notes This lecture completes the discussion of the cross product in R and addresses the variety of different ways that n mathematical objects can be described via equations,
Distance Formula in 3-D Given any two points P 1 (x 1, y 1, z 1 ) and P 2 (x 2, y 2, z 2 ) the distance between them is ( ) ( ) ( )
 Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Vectors and the Geometry of Space Vector Space The 3-D coordinate system (rectangular coordinates ) is the intersection of three perpendicular (orthogonal) lines called coordinate axis: x, y, and z. Their
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Calculus Vector Principia Mathematica. Lynne Ryan Associate Professor Mathematics Blue Ridge Community College
 Calculus Vector Principia Mathematica Lynne Ryan Associate Professor Mathematics Blue Ridge Community College Defining a vector Vectors in the plane A scalar is a quantity that can be represented by a
Calculus Vector Principia Mathematica Lynne Ryan Associate Professor Mathematics Blue Ridge Community College Defining a vector Vectors in the plane A scalar is a quantity that can be represented by a
CHAPTER 3 : VECTORS. Definition 3.1 A vector is a quantity that has both magnitude and direction.
 EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
SUPPLEMENT I. Example. Graph the vector 4, 3. Definition. Given two points A(x 1, y 1 ) and B(x 2, y 2 ), the vector represented by # AB is # AB =,
 SUPPLEMENT I 1. Vectors Definition. A vector is a quantity that has both a magnitude and a direction. A twodimensional vector is an ordered pair a = a 1, a 2 of real numbers. The numbers a 1 and a 2 are
SUPPLEMENT I 1. Vectors Definition. A vector is a quantity that has both a magnitude and a direction. A twodimensional vector is an ordered pair a = a 1, a 2 of real numbers. The numbers a 1 and a 2 are
1.1 Single Variable Calculus versus Multivariable Calculus Rectangular Coordinate Systems... 4
 MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
Section 8.1 Vector and Parametric Equations of a Line in
 Section 8.1 Vector and Parametric Equations of a Line in R 2 In this section, we begin with a discussion about how to find the vector and parametric equations of a line in R 2. To find the vector and parametric
Section 8.1 Vector and Parametric Equations of a Line in R 2 In this section, we begin with a discussion about how to find the vector and parametric equations of a line in R 2. To find the vector and parametric
Department of Mathematical and Statistical Sciences University of Alberta
 MATH 214 (R1) Winter 2008 Intermediate Calculus I Solutions to Problem Set #8 Completion Date: Friday March 14, 2008 Department of Mathematical and Statistical Sciences University of Alberta Question 1.
MATH 214 (R1) Winter 2008 Intermediate Calculus I Solutions to Problem Set #8 Completion Date: Friday March 14, 2008 Department of Mathematical and Statistical Sciences University of Alberta Question 1.
Mathematics 2203, Test 1 - Solutions
 Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space
 Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
Chapter 13: Vectors and the Geometry of Space 13.1 3-Dimensional Coordinate System 13.2 Vectors 13.3 The Dot Product 13.4 The Cross Product 13.5 Equations of Lines and Planes 13.6 Cylinders and Quadratic
VECTORS IN A STRAIGHT LINE
 A. The Equation of a Straight Line VECTORS P3 VECTORS IN A STRAIGHT LINE A particular line is uniquely located in space if : I. It has a known direction, d, and passed through a known fixed point, or II.
A. The Equation of a Straight Line VECTORS P3 VECTORS IN A STRAIGHT LINE A particular line is uniquely located in space if : I. It has a known direction, d, and passed through a known fixed point, or II.
OHSx XM521 Multivariable Differential Calculus: Homework Solutions 13.1
 OHSx XM521 Multivariable Differential Calculus: Homework Solutions 13.1 (37) If a bug walks on the sphere x 2 + y 2 + z 2 + 2x 2y 4z 3 = 0 how close and how far can it get from the origin? Solution: Complete
OHSx XM521 Multivariable Differential Calculus: Homework Solutions 13.1 (37) If a bug walks on the sphere x 2 + y 2 + z 2 + 2x 2y 4z 3 = 0 how close and how far can it get from the origin? Solution: Complete
- parametric equations for the line, z z 0 td 3 or if d 1 0, d 2 0andd 3 0, - symmetric equations of the line.
 Lines and Planes in Space -(105) Questions: What do we need to know to determine a line in space? What are the fms of a line? If two lines are not parallel in space, must they be intersect as two lines
Lines and Planes in Space -(105) Questions: What do we need to know to determine a line in space? What are the fms of a line? If two lines are not parallel in space, must they be intersect as two lines
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
MATH H53 : Mid-Term-1
 MATH H53 : Mid-Term-1 22nd September, 215 Name: You have 8 minutes to answer the questions. Use of calculators or study materials including textbooks, notes etc. is not permitted. Answer the questions
MATH H53 : Mid-Term-1 22nd September, 215 Name: You have 8 minutes to answer the questions. Use of calculators or study materials including textbooks, notes etc. is not permitted. Answer the questions
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF MASSACHUSETTS. MATH 233 SOME SOLUTIONS TO EXAM 1 Fall 2018
 DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF MASSACHUSETTS MATH SOME SOLUTIONS TO EXAM 1 Fall 018 Version A refers to the regular exam and Version B to the make-up 1. Version A. Find the center
DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF MASSACHUSETTS MATH SOME SOLUTIONS TO EXAM 1 Fall 018 Version A refers to the regular exam and Version B to the make-up 1. Version A. Find the center
Contents. 1 Vectors, Lines and Planes 1. 2 Gaussian Elimination Matrices Vector Spaces and Subspaces 124
 Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
1.2 LECTURE 2. Scalar Product
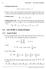 6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
Culminating Review for Vectors
 Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Culminating Review for Vectors 0011 0010 1010 1101 0001 0100 1011 An Introduction to Vectors Applications of Vectors Equations of Lines and Planes 4 12 Relationships between Points, Lines and Planes An
Lecture 5. Equations of Lines and Planes. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 5 Equations of Lines and Planes Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 Universit of Massachusetts Februar 6, 2018 (2) Upcoming midterm eam First midterm: Wednesda Feb. 21, 7:00-9:00
Lecture 5 Equations of Lines and Planes Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 Universit of Massachusetts Februar 6, 2018 (2) Upcoming midterm eam First midterm: Wednesda Feb. 21, 7:00-9:00
- parametric equations for the line, z z 0 td 3 or if d 1 0, d 2 0andd 3 0, - symmetric equations of the line.
 Lines and Planes in Space -(105) Questions: 1 What is the equation of a line if we know (1) two points P x 1,y 1,z 1 and Q x 2,y 2,z 2 on the line; (2) a point P x 1,y 1,z 1 on the line and the line is
Lines and Planes in Space -(105) Questions: 1 What is the equation of a line if we know (1) two points P x 1,y 1,z 1 and Q x 2,y 2,z 2 on the line; (2) a point P x 1,y 1,z 1 on the line and the line is
MAC Module 5 Vectors in 2-Space and 3-Space II
 MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
MAC 2103 Module 5 Vectors in 2-Space and 3-Space II 1 Learning Objectives Upon completing this module, you should be able to: 1. Determine the cross product of a vector in R 3. 2. Determine a scalar triple
(arrows denote positive direction)
 12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
12 Chapter 12 12.1 3-dimensional Coordinate System The 3-dimensional coordinate system we use are coordinates on R 3. The coordinate is presented as a triple of numbers: (a,b,c). In the Cartesian coordinate
Distances in R 3. Last time we figured out the (parametric) equation of a line and the (scalar) equation of a plane:
 Distances in R 3 Last time we figured out the (parametric) equation of a line and the (scalar) equation of a plane: Definition: The equation of a line through point P(x 0, y 0, z 0 ) with directional vector
Distances in R 3 Last time we figured out the (parametric) equation of a line and the (scalar) equation of a plane: Definition: The equation of a line through point P(x 0, y 0, z 0 ) with directional vector
1. Vectors and Matrices
 E. 8.02 Exercises. Vectors and Matrices A. Vectors Definition. A direction is just a unit vector. The direction of A is defined by dir A = A, (A 0); A it is the unit vector lying along A and pointed like
E. 8.02 Exercises. Vectors and Matrices A. Vectors Definition. A direction is just a unit vector. The direction of A is defined by dir A = A, (A 0); A it is the unit vector lying along A and pointed like
Course Notes Math 275 Boise State University. Shari Ultman
 Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
Course Notes Math 275 Boise State University Shari Ultman Fall 2017 Contents 1 Vectors 1 1.1 Introduction to 3-Space & Vectors.............. 3 1.2 Working With Vectors.................... 7 1.3 Introduction
(iii) converting between scalar product and parametric forms. (ii) vector perpendicular to two given (3D) vectors
 Vector Theory (15/3/2014) www.alevelmathsng.co.uk Contents (1) Equation of a line (i) parametric form (ii) relation to Cartesian form (iii) vector product form (2) Equation of a plane (i) scalar product
Vector Theory (15/3/2014) www.alevelmathsng.co.uk Contents (1) Equation of a line (i) parametric form (ii) relation to Cartesian form (iii) vector product form (2) Equation of a plane (i) scalar product
8. Find r a! r b. a) r a = [3, 2, 7], r b = [ 1, 4, 5] b) r a = [ 5, 6, 7], r b = [2, 7, 4]
![8. Find r a! r b. a) r a = [3, 2, 7], r b = [ 1, 4, 5] b) r a = [ 5, 6, 7], r b = [2, 7, 4] 8. Find r a! r b. a) r a = [3, 2, 7], r b = [ 1, 4, 5] b) r a = [ 5, 6, 7], r b = [2, 7, 4]](/thumbs/95/122742655.jpg) Chapter 8 Prerequisite Skills BLM 8-1.. Linear Relations 1. Make a table of values and graph each linear function a) y = 2x b) y = x + 5 c) 2x + 6y = 12 d) x + 7y = 21 2. Find the x- and y-intercepts of
Chapter 8 Prerequisite Skills BLM 8-1.. Linear Relations 1. Make a table of values and graph each linear function a) y = 2x b) y = x + 5 c) 2x + 6y = 12 d) x + 7y = 21 2. Find the x- and y-intercepts of
VECTORS IN COMPONENT FORM
 VECTORS IN COMPONENT FORM In Cartesian coordinates any D vector a can be written as a = a x i + a y j + a z k a x a y a x a y a z a z where i, j and k are unit vectors in x, y and z directions. i = j =
VECTORS IN COMPONENT FORM In Cartesian coordinates any D vector a can be written as a = a x i + a y j + a z k a x a y a x a y a z a z where i, j and k are unit vectors in x, y and z directions. i = j =
Overview. Distances in R 3. Distance from a point to a plane. Question
 Overview Yesterda we introduced equations to describe lines and planes in R 3 : r + tv The vector equation for a line describes arbitrar points r in terms of a specific point and the direction vector v.
Overview Yesterda we introduced equations to describe lines and planes in R 3 : r + tv The vector equation for a line describes arbitrar points r in terms of a specific point and the direction vector v.
Created by T. Madas VECTOR PRACTICE Part B Created by T. Madas
 VECTOR PRACTICE Part B THE CROSS PRODUCT Question 1 Find in each of the following cases a) a = 2i + 5j + k and b = 3i j b) a = i + 2j + k and b = 3i j k c) a = 3i j 2k and b = i + 3j + k d) a = 7i + j
VECTOR PRACTICE Part B THE CROSS PRODUCT Question 1 Find in each of the following cases a) a = 2i + 5j + k and b = 3i j b) a = i + 2j + k and b = 3i j k c) a = 3i j 2k and b = i + 3j + k d) a = 7i + j
Existence Postulate: The collection of all points forms a nonempty set. There is more than one point in that set.
 Undefined Terms: Point Line Distance Half-plane Angle measure Area (later) Axioms: Existence Postulate: The collection of all points forms a nonempty set. There is more than one point in that set. Incidence
Undefined Terms: Point Line Distance Half-plane Angle measure Area (later) Axioms: Existence Postulate: The collection of all points forms a nonempty set. There is more than one point in that set. Incidence
Unit 8. ANALYTIC GEOMETRY.
 Unit 8. ANALYTIC GEOMETRY. 1. VECTORS IN THE PLANE A vector is a line segment running from point A (tail) to point B (head). 1.1 DIRECTION OF A VECTOR The direction of a vector is the direction of the
Unit 8. ANALYTIC GEOMETRY. 1. VECTORS IN THE PLANE A vector is a line segment running from point A (tail) to point B (head). 1.1 DIRECTION OF A VECTOR The direction of a vector is the direction of the
Midterm 1 Review. Distance = (x 1 x 0 ) 2 + (y 1 y 0 ) 2.
 Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
Midterm 1 Review Comments about the midterm The midterm will consist of five questions and will test on material from the first seven lectures the material given below. No calculus either single variable
CALCULUS III. prepared by
 EXAMINATION 1 CALCULUS III REVIEW PROBLEMS prepared by Antony Foster Department of Mathematics (office: NAC 6-73) The City College of The City University of New York Convent Avenue At 138th Street New
EXAMINATION 1 CALCULUS III REVIEW PROBLEMS prepared by Antony Foster Department of Mathematics (office: NAC 6-73) The City College of The City University of New York Convent Avenue At 138th Street New
MTAEA Vectors in Euclidean Spaces
 School of Economics, Australian National University January 25, 2010 Vectors. Economists usually work in the vector space R n. A point in this space is called a vector, and is typically defined by its
School of Economics, Australian National University January 25, 2010 Vectors. Economists usually work in the vector space R n. A point in this space is called a vector, and is typically defined by its
SOLUTIONS TO SECOND PRACTICE EXAM Math 21a, Spring 2003
 SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
Workbook. MAT 397: Calculus III
 Workbook MAT 397: Calculus III Instructor: Caleb McWhorter Name: Summer 217 Contents Preface..................................................... 2 1 Spatial Geometry & Vectors 3 1.1 Basic n Euclidean
Workbook MAT 397: Calculus III Instructor: Caleb McWhorter Name: Summer 217 Contents Preface..................................................... 2 1 Spatial Geometry & Vectors 3 1.1 Basic n Euclidean
Basic Surveying Week 3, Lesson 2 Semester 2017/18/2 Vectors, equation of line, circle, ellipse
 Basic Surveying Week 3, Lesson Semester 017/18/ Vectors, equation of line, circle, ellipse 1. Introduction In surveying calculations, we use the two or three dimensional coordinates of points or objects
Basic Surveying Week 3, Lesson Semester 017/18/ Vectors, equation of line, circle, ellipse 1. Introduction In surveying calculations, we use the two or three dimensional coordinates of points or objects
Vectors. Section 3: Using the vector product
 Vectors Section 3: Using the vector product Notes and Examples These notes contain subsections on Using the vector product in finding the equation of a plane The intersection of two planes The distance
Vectors Section 3: Using the vector product Notes and Examples These notes contain subsections on Using the vector product in finding the equation of a plane The intersection of two planes The distance
Matrices. A matrix is a method of writing a set of numbers using rows and columns. Cells in a matrix can be referenced in the form.
 Matrices A matrix is a method of writing a set of numbers using rows and columns. 1 2 3 4 3 2 1 5 7 2 5 4 2 0 5 10 12 8 4 9 25 30 1 1 Reading Information from a Matrix Cells in a matrix can be referenced
Matrices A matrix is a method of writing a set of numbers using rows and columns. 1 2 3 4 3 2 1 5 7 2 5 4 2 0 5 10 12 8 4 9 25 30 1 1 Reading Information from a Matrix Cells in a matrix can be referenced
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication.
 This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
Linear Algebra Homework and Study Guide
 Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
Linear Algebra Homework and Study Guide Phil R. Smith, Ph.D. February 28, 20 Homework Problem Sets Organized by Learning Outcomes Test I: Systems of Linear Equations; Matrices Lesson. Give examples of
MTH MTH Lecture 6. Yevgeniy Kovchegov Oregon State University
 MTH 306 0 MTH 306 - Lecture 6 Yevgeniy Kovchegov Oregon State University MTH 306 1 Topics Lines and planes. Systems of linear equations. Systematic elimination of unknowns. Coe cient matrix. Augmented
MTH 306 0 MTH 306 - Lecture 6 Yevgeniy Kovchegov Oregon State University MTH 306 1 Topics Lines and planes. Systems of linear equations. Systematic elimination of unknowns. Coe cient matrix. Augmented
Edexcel New GCE A Level Maths workbook
 Edexcel New GCE A Level Maths workbook Straight line graphs Parallel and Perpendicular lines. Edited by: K V Kumaran kumarmaths.weebly.com Straight line graphs A LEVEL LINKS Scheme of work: a. Straight-line
Edexcel New GCE A Level Maths workbook Straight line graphs Parallel and Perpendicular lines. Edited by: K V Kumaran kumarmaths.weebly.com Straight line graphs A LEVEL LINKS Scheme of work: a. Straight-line
1.1 Bound and Free Vectors. 1.2 Vector Operations
 1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
1 Vectors Vectors are used when both the magnitude and the direction of some physical quantity are required. Examples of such quantities are velocity, acceleration, force, electric and magnetic fields.
1. Vectors in the Plane
 CHAPTER 10 Vectors and the Geometry of Space 1. Vectors in the Plane We denote the directed line segment from the point P (initial point) to the!! point Q (terminal point) as P Q. The length of P Q is
CHAPTER 10 Vectors and the Geometry of Space 1. Vectors in the Plane We denote the directed line segment from the point P (initial point) to the!! point Q (terminal point) as P Q. The length of P Q is
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Section 8.4 Vector and Parametric Equations of a Plane
 Section 8.4 Vector and Parametric Equations of a Plane In the previous section, the vector, parametric, and symmetric equations of lines in R 3 were developed. In this section, we will develop vector and
Section 8.4 Vector and Parametric Equations of a Plane In the previous section, the vector, parametric, and symmetric equations of lines in R 3 were developed. In this section, we will develop vector and
Math 233. Directional Derivatives and Gradients Basics
 Math 233. Directional Derivatives and Gradients Basics Given a function f(x, y) and a unit vector u = a, b we define the directional derivative of f at (x 0, y 0 ) in the direction u by f(x 0 + ta, y 0
Math 233. Directional Derivatives and Gradients Basics Given a function f(x, y) and a unit vector u = a, b we define the directional derivative of f at (x 0, y 0 ) in the direction u by f(x 0 + ta, y 0
ANALYTICAL GEOMETRY Revision of Grade 10 Analytical Geometry
 ANALYTICAL GEOMETRY Revision of Grade 10 Analtical Geometr Let s quickl have a look at the analtical geometr ou learnt in Grade 10. 8 LESSON Midpoint formula (_ + 1 ;_ + 1 The midpoint formula is used
ANALYTICAL GEOMETRY Revision of Grade 10 Analtical Geometr Let s quickl have a look at the analtical geometr ou learnt in Grade 10. 8 LESSON Midpoint formula (_ + 1 ;_ + 1 The midpoint formula is used
MATH 12 CLASS 2 NOTES, SEP Contents. 2. Dot product: determining the angle between two vectors 2
 MATH 12 CLASS 2 NOTES, SEP 23 2011 Contents 1. Dot product: definition, basic properties 1 2. Dot product: determining the angle between two vectors 2 Quick links to definitions/theorems Dot product definition
MATH 12 CLASS 2 NOTES, SEP 23 2011 Contents 1. Dot product: definition, basic properties 1 2. Dot product: determining the angle between two vectors 2 Quick links to definitions/theorems Dot product definition
3. Interpret the graph of x = 1 in the contexts of (a) a number line (b) 2-space (c) 3-space
 MA2: Prepared by Dr. Archara Pacheenburawana Exercise Chapter 3 Exercise 3.. A cube of side 4 has its geometric center at the origin and its faces parallel to the coordinate planes. Sketch the cube and
MA2: Prepared by Dr. Archara Pacheenburawana Exercise Chapter 3 Exercise 3.. A cube of side 4 has its geometric center at the origin and its faces parallel to the coordinate planes. Sketch the cube and
4.3 Equations in 3-space
 4.3 Equations in 3-space istance can be used to define functions from a 3-space R 3 to the line R. Let P be a fixed point in the 3-space R 3 (say, with coordinates P (2, 5, 7)). Consider a function f :
4.3 Equations in 3-space istance can be used to define functions from a 3-space R 3 to the line R. Let P be a fixed point in the 3-space R 3 (say, with coordinates P (2, 5, 7)). Consider a function f :
LB 220 Homework 2 (due Tuesday, 01/22/13)
 LB 220 Homework 2 (due Tuesday, 01/22/13) Directions. Please solve the problems below. Your solutions must begin with a clear statement (or re-statement in your own words) of the problem. You solutions
LB 220 Homework 2 (due Tuesday, 01/22/13) Directions. Please solve the problems below. Your solutions must begin with a clear statement (or re-statement in your own words) of the problem. You solutions
Review of Coordinate Systems
 Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
Vector in 2 R and 3 R Review of Coordinate Systems Used to describe the position of a point in space Common coordinate systems are: Cartesian Polar Cartesian Coordinate System Also called rectangular coordinate
11.1 Three-Dimensional Coordinate System
 11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
11.1 Three-Dimensional Coordinate System In three dimensions, a point has three coordinates: (x,y,z). The normal orientation of the x, y, and z-axes is shown below. The three axes divide the region into
Worksheet A VECTORS 1 G H I D E F A B C
 Worksheet A G H I D E F A B C The diagram shows three sets of equally-spaced parallel lines. Given that AC = p that AD = q, express the following vectors in terms of p q. a CA b AG c AB d DF e HE f AF
Worksheet A G H I D E F A B C The diagram shows three sets of equally-spaced parallel lines. Given that AC = p that AD = q, express the following vectors in terms of p q. a CA b AG c AB d DF e HE f AF
Analytic Geometry MAT 1035
 Analytic Geometry MAT 035 5.09.04 WEEKLY PROGRAM - The first week of the semester, we will introduce the course and given a brief outline. We continue with vectors in R n and some operations including
Analytic Geometry MAT 035 5.09.04 WEEKLY PROGRAM - The first week of the semester, we will introduce the course and given a brief outline. We continue with vectors in R n and some operations including
4.1 Distance and Length
 Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Chapter Vector Geometry In this chapter we will look more closely at certain geometric aspects of vectors in R n. We will first develop an intuitive understanding of some basic concepts by looking at vectors
Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017
 Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017 Since we didn t get a chance to discuss parametrized lines last week, we may spend some time discussing those before moving on to the dot
Math 32A Discussion Session Week 2 Notes October 10 and 12, 2017 Since we didn t get a chance to discuss parametrized lines last week, we may spend some time discussing those before moving on to the dot
Math 114, Section 003 Fall 2011 Practice Exam 1 with Solutions
 Math 11, Section 003 Fall 2011 Practice Exam 1 with Solutions Contents 1 Problems 2 2 Solution key 8 3 Solutions 9 1 1 Problems Question 1: Let L be the line tangent to the curve r (t) t 2 + 3t + 2, e
Math 11, Section 003 Fall 2011 Practice Exam 1 with Solutions Contents 1 Problems 2 2 Solution key 8 3 Solutions 9 1 1 Problems Question 1: Let L be the line tangent to the curve r (t) t 2 + 3t + 2, e
VCE. VCE Maths Methods 1 and 2 Pocket Study Guide
 VCE VCE Maths Methods 1 and 2 Pocket Study Guide Contents Introduction iv 1 Linear functions 1 2 Quadratic functions 10 3 Cubic functions 16 4 Advanced functions and relations 24 5 Probability and simulation
VCE VCE Maths Methods 1 and 2 Pocket Study Guide Contents Introduction iv 1 Linear functions 1 2 Quadratic functions 10 3 Cubic functions 16 4 Advanced functions and relations 24 5 Probability and simulation
Math 2433 Notes Week The Dot Product. The angle between two vectors is found with this formula: cosθ = a b
 Math 2433 Notes Week 2 11.3 The Dot Product The angle between two vectors is found with this formula: cosθ = a b a b 3) Given, a = 4i + 4j, b = i - 2j + 3k, c = 2i + 2k Find the angle between a and c Projection
Math 2433 Notes Week 2 11.3 The Dot Product The angle between two vectors is found with this formula: cosθ = a b a b 3) Given, a = 4i + 4j, b = i - 2j + 3k, c = 2i + 2k Find the angle between a and c Projection
Analytic Geometry MAT 1035
 Analytic Geometry MAT 035 5.09.04 WEEKLY PROGRAM - The first week of the semester, we will introduce the course and given a brief outline. We continue with vectors in R n and some operations including
Analytic Geometry MAT 035 5.09.04 WEEKLY PROGRAM - The first week of the semester, we will introduce the course and given a brief outline. We continue with vectors in R n and some operations including
Math 20C Homework 2 Partial Solutions
 Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Math 51, Homework-2 Solutions
 SSEA Summer 27 Math 5, Homework-2 Solutions Write the parametric equation of the plane that contains the following point and line: 3 2, 4 2 + t 3 t R 5 4 By substituting t = and t =, we get two points
SSEA Summer 27 Math 5, Homework-2 Solutions Write the parametric equation of the plane that contains the following point and line: 3 2, 4 2 + t 3 t R 5 4 By substituting t = and t =, we get two points
MTHE 227 Problem Set 2 Solutions
 MTHE 7 Problem Set Solutions 1 (Great Circles). The intersection of a sphere with a plane passing through its center is called a great circle. Let Γ be the great circle that is the intersection of the
MTHE 7 Problem Set Solutions 1 (Great Circles). The intersection of a sphere with a plane passing through its center is called a great circle. Let Γ be the great circle that is the intersection of the
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2012/2013, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: TA sessions for tutorial 1 start today Tutorial 2 will go online after lecture 3 Practicals: Make sure to find a team partner very soon
Lecture 2, curves, and surfaces Organizational remarks Tutorials: TA sessions for tutorial 1 start today Tutorial 2 will go online after lecture 3 Practicals: Make sure to find a team partner very soon
FINDING THE INTERSECTION OF TWO LINES
 FINDING THE INTERSECTION OF TWO LINES REALTIONSHIP BETWEEN LINES 2 D: D: the lines are coplanar (they lie in the same plane). They could be: intersecting parallel coincident the lines are not coplanar
FINDING THE INTERSECTION OF TWO LINES REALTIONSHIP BETWEEN LINES 2 D: D: the lines are coplanar (they lie in the same plane). They could be: intersecting parallel coincident the lines are not coplanar
Later in this chapter, we are going to use vector functions to describe the motion of planets and other objects through space.
 10 VECTOR FUNCTIONS VECTOR FUNCTIONS Later in this chapter, we are going to use vector functions to describe the motion of planets and other objects through space. Here, we prepare the way by developing
10 VECTOR FUNCTIONS VECTOR FUNCTIONS Later in this chapter, we are going to use vector functions to describe the motion of planets and other objects through space. Here, we prepare the way by developing
CALCULUS III. Paul Dawkins
 CALCULUS III Paul Dawkins Table of Contents Preface... iii Outline... iv Three Dimensional Space... Introduction... The -D Coordinate System... Equations of Lines... 9 Equations of Planes... 5 Quadric
CALCULUS III Paul Dawkins Table of Contents Preface... iii Outline... iv Three Dimensional Space... Introduction... The -D Coordinate System... Equations of Lines... 9 Equations of Planes... 5 Quadric
Intro Vectors 2D implicit curves 2D parametric curves. Graphics 2011/2012, 4th quarter. Lecture 2: vectors, curves, and surfaces
 Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
Lecture 2, curves, and surfaces Organizational remarks Tutorials: Tutorial 1 will be online later today TA sessions for questions start next week Practicals: Exams: Make sure to find a team partner very
Lesson 26: Characterization of Parallel Lines
 Student Outcomes Students know that when a system of linear equations has no solution, i.e., no point of intersection of the lines, then the lines are parallel. Lesson Notes The discussion that begins
Student Outcomes Students know that when a system of linear equations has no solution, i.e., no point of intersection of the lines, then the lines are parallel. Lesson Notes The discussion that begins
Chapter 12 Review Vector. MATH 126 (Section 9.5) Vector and Scalar The University of Kansas 1 / 30
 Chapter 12 Review Vector MATH 126 (Section 9.5) Vector and Scalar The University of Kansas 1 / 30 iclicker 1: Let v = PQ where P = ( 2, 5) and Q = (1, 2). Which of the following vectors with the given
Chapter 12 Review Vector MATH 126 (Section 9.5) Vector and Scalar The University of Kansas 1 / 30 iclicker 1: Let v = PQ where P = ( 2, 5) and Q = (1, 2). Which of the following vectors with the given
Lecture 1: Systems of linear equations and their solutions
 Lecture 1: Systems of linear equations and their solutions Course overview Topics to be covered this semester: Systems of linear equations and Gaussian elimination: Solving linear equations and applications
Lecture 1: Systems of linear equations and their solutions Course overview Topics to be covered this semester: Systems of linear equations and Gaussian elimination: Solving linear equations and applications
Math 234. What you should know on day one. August 28, You should be able to use general principles like. x = cos t, y = sin t, 0 t π.
 Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
n=0 ( 1)n /(n + 1) converges, but not
 Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
Math 07H Topics for the third exam (and beyond) (Technically, everything covered on the first two exams plus...) Absolute convergence and alternating series A series a n converges absolutely if a n converges.
VECTORS TEST. 1. Show that the vectors a and b given by a = i + j + k and b = 2i + j 3k are perpendicular. [3]
![VECTORS TEST. 1. Show that the vectors a and b given by a = i + j + k and b = 2i + j 3k are perpendicular. [3] VECTORS TEST. 1. Show that the vectors a and b given by a = i + j + k and b = 2i + j 3k are perpendicular. [3]](/thumbs/71/65586409.jpg) VECTORS TEST Show that the vectors a and b given by a = i + j + k and b = i + j k are perpendicular [] Find a unit vector which is parallel to the vector a [] Find an equation for the line through the
VECTORS TEST Show that the vectors a and b given by a = i + j + k and b = i + j k are perpendicular [] Find a unit vector which is parallel to the vector a [] Find an equation for the line through the
