Taylor Series and Asymptotic Expansions
|
|
|
- Shanon Black
- 6 years ago
- Views:
Transcription
1 Taylor Series and Asymptotic Epansions The importance of power series as a convenient representation, as an approimation tool, as a tool for solving differential equations and so on, is pretty obvious. What may not be so obvious is that power series can be very useful even when they diverge! Let us start by considering Taylor series. If f : [ a,a] has infinitely many continuous derivatives, Taylor s theorem says that for each n IN {}, f( P n (+R n ( n with P n ( m m! f(m ( m R n ( (n+! f(n+ ( n+ for some between and Since f (n+ is continuous, there eists a constant M n such that R n ( M n n+ for all [ a,a]. This says that as gets smaller and smaller, the polynomial P n ( becomes a better and better approimation to f(. The rate at which P n ( tends to f( as tends to zero is, at worst, proportional to n+. Thus the Taylor series m m! f(m ( m is an asymptotic epansion for f( where Definition. m a m m is said to be an asymptotic epansion for f(, denoted f( m a m m if, for each n IN {}, lim n [f( n a m m] m There are several important observations to make about this definition. (i The definition says that, for each fied n, n m a m m becomes a better and better approimation to f( as gets smaller. As, n m a m m approaches f( faster than n tends to zero. (ii The definition says nothing about what happens as n. There is no guarantee that for each fied, n m a m m tends to f( as n. (iii In particular, the series m a m m may have radius of convergence zero. In this case, m a m m is just a formal symbol. It does not have any meaning as a series. (iv We have seen that every infinitely differentiable function has an asymptotic epansion, regardless of whether its Taylor series converges or not. Now back to our Taylor series. There are three possibilities. (i The series m m! f(m ( m has radius of convergence zero. (ii The series m m! f(m ( m has radius of convergence r > and lim R n( for all r < < r. n In this case the Taylor series converges to f( for all ( r,r. Then f( is said to be analytic on ( r,r. (iii The series m m! f(m ( m has radius of convergence r > and the Taylor series converges to something other than f(. Here is an eample of each of these three types of behaviour. Eample (i For this eample, f( e t + t dt. Our work on interchanging the order of differentiation and integration yields that f( is infinitely differentiable and that the derivatives are given by d n d n f( n n ( e t + t dt c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions
2 Instead of evaluating the derivative directly, we will use a little trick to generate the Taylor series for f(. Recall that r n r rn+ r We just substitute r t to give and f( n n N + t n ( t n + ( t N+ + t ( t n e t ( dt+ t N+ + t e t dt ( n n t n e t dt+( N+ (N+ n ( n n +( N+ (N+ n t N+ + t e t dt t N+ + t e t dt since ( t n e t dt. To compute the m th derivative, f (m (, we choose N such that (N + > m and apply { d m d n if m n m ( if m n Applying dm d with m < (N + to ( N+ (N+ t N+ m + t e t dt gives a finite sum with every term containing a factor p with p >. When is set to, every such term is zero. So { d m d f( if m is odd m ( m!m! if m is even So the Taylor series epansion of f is m m! f(m ( m m m even ( m ( m! ( m m!m! m mn ( n n The high growth rate of makes the radius of convergence of this series zero. For eample, one formula for the radius of convergence of [ n a ]. [ ] n n is lim an+ n When an ( n, lim an+ n [ lim (n + ]. Replacing by gives that n n ( n n converges if and only if. Nonetheless, the error estimates N f( ( n n (N+ t N+ + t e t dt (N+ t N+ e t dt (N +! N+ n shows that if we fi N and make smaller and smaller, N n ( n n becomes a better and better approimation to f(. On the other hand, if we fi and let N grow, we see that the error grows dramatically for large N. Here is a graph of y (N+! N+ against N, for several different (fied values of. ( Denote γ n t n e t dt. Then γ e t dt and, by integration by parts with u t n, dv e t dt, du nt n dt and v e t, γ n nγ n for all n IN. So, by induction, γ n. c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions n
3 (N +! N N Eample (ii For this eample, f( e. By Taylor s theorem, f( n m m m! +R n( with R n ( e (n+! n+ for some between and. In this case, m m m! has radius of convergence infinity and the error Rn ( (n+! e n+ tends to zero both (a when n is fied and tends to zero and (b when is fied and n tends to infinity. Use R n ( (n+! e n+ to denote our bound on the error introduced by truncating the series at n. Then R n+ ( R n+ n (. So if, for eample, n, then increasing the inde n of R n ( by one reduces the value of R n ( by a factor of at least two. Eample (iii For this eample, f( { e / if if Of course by the usual differentiation rules, f( is infinitely differentiable, ecept possibly at. I shall show below that f is also infinitely differentiable at and f (n ( for every n IN {}. So in this case, the Taylor series is n n and has infinite radius of convergence. When we approimate f( by the Taylor polynomial, n m m, of degree n, the error, R n ( f(, is independent of n. The function f( agrees with its Taylor series only for. Similarly, the function { g( e / if > if agrees with its Taylor series if and only if. Here is the argument that f is infinitely differentiable at and f (n ( for every n IN {}. First note that, by the usual differentiation rules, when, every derivattive f (n ( is some polynomial in times e /. For any and any integer n e / + +! ( + + ( n ( + n Consequently, for any polynomial P(y, say of degree p, there is a constant C such that ( P e / P ( e C p / (p+!c +p (p+! (p+ c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions
4 for all. Hence, for any polynomial P(y, Applying ( with P(y y, we have lim P( e /. ( f f( f( ( lim lim e / f ( Applying ( with P(y y 4, we have f f ( lim ( f ( lim ( e / f ( { if e / if { if ( e / if 6 ( Indeed, for any n, if f (n ( P n e / for all, then applying ( with P(y yp n (y gives f (n f ( lim (n ( f (n ( lim P n ( e / and hence { if f (n ( [ P ( n ( + P n ] e / if Eample (iv Stirling formula ln ( n+ lnn n+ln π actually consists of the first few terms of an asymptotic epansion ln ( n+ lnn n+ln π+ n 6 n + If n >, the approimation ln ( n+ lnn n+ln π is accurate to within.6% and the eponentiated form n n+ πe n+ n is accurate to one part in,. But fiing n and taking many more terms in the epansion will in fact give you a much worse approimation to ln. Laplace s Method Stirling s formula may be generated by Laplace s method one of the more common ways of generating asymptotic epansions. Laplace s method provides good approimations to integrals of the form I(s e sf( d when s is very large and the function f is reasonably smooth and takes its minimum value at a unique point, m. The method is based on the following three observations. (i When s is verylargeand m, e sf( e sf(m e s[f( f(m] e sf(m, since f( f( m >. So, for large s, the integral will be dominated by values of near m. (ii For near m f( f( m + f ( m ( m since f ( m. (iii Integrals of the form e a( m d, or more generally e a( m ( m n d, can be computed eactly. Let s implement this strategy for the Γ function, defined in the lemma below. This will give Stirling s formula, because of part (d of the lemma. c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions 4
5 Lemma. Define, for s >, the Gamma function Γ(s t s e t dt (a Γ( (b Γ ( π. (c For any s >, Γ(s+ sγ(s. (d For any n IN, Γ(n+. Proof: (a is a trivial integration. (b Make the change of variables t, dt d td. This gives Γ ( t e t dt We compute the square of this integral by switching e d e d Γ ( ( ( e d e y dy e ( +y ddy IR to polar coordinates. This standard trick gives Γ ( π dθ dr re r π dθ [ e r] π dθ π (c By by integration by parts with u t s, dv e t dt, du st s dt and v e t Γ(s+ t s e t dt t s ( e t ( e t st s dt s t s e t dt sγ(s (d is obvious by induction, using parts (a and (c. To derive Stirling s formula, using Laplace s method, We first manipulate Γ(s + into the form e sf( d. Γ(s+ t s e t dt s s+ s e s d s s+ e s e s( ln d where t s So f( ln and f (. Consequently f ( < for < and f ( > for >, so that f has a unique minimum at and increases monotonically as gets farther from. The minimum value of f is f(. (We multiplied and divided by e s in the last line above in order to arrange that the minimum value of f be eactly zero. c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions 5
6 If ε > is any fied positive number, e sf( d +ε ε e sf( d will be agoodapproimationfor anysufficiently larges, because, when, f( > and lim s e sf(. We will derive, in an appendi, eplicit bounds on the error introduced by this approimation as well as by the other approimations we make in the course of this development. The remaining couple of steps in the procedure are motivated by the fact that integrals of the form e a( m ( m n d can be computed eactly. If we have chosen ε pretty small, Taylor s formula f( f(+f (( + f( (( +! f( (( + 4! f(4 (( 4 [ [ [ ] ( +! ] ( + ] 4! 4 ( 4 ( ( + 4 ( 4 will give a good approimation for all < ε, so that e sf( d +ε ε e s[ ( ( + 4 ( 4] d +ε ε e s ( e [s ( s 4 ( 4] d (We shall find the first two terms an epansion for Γ(s+. If we wanted to find more terms, we would keep more terms in the Taylor epansion of f(. The net step is to Taylor epand e [s ( s 4 ( 4] about, in order to give integrands of the form e s ( ( n. We could apply Taylor s formula directly, but it is easier to use the known epansion of the eponential. e sf( d +ε ε +ε ε e s ( { + [ s ( s 4 ( 4] + [ s ( s 4 ( 4] } d e s ( { + s ( s 4 ( 4 + s 8 ( 6} d e s ( { + s ( s 4 ( 4 + s 8 ( 6} d e s ( { s 4 ( 4 + s 8 ( 6} d since ( e s ( is odd about and hence integrates to zero. For n an even natural number e s ( ( n d ( s n+ ( s n+ ( s n+ ( s n+ Γ ( n+ e y y n dy where y e y y n dy e t t n dt s ( where t y, dt ydy tdy ( By the lemma at the beginning of this section, Γ ( ( π Γ Γ( ( π Γ 5 Γ( π Γ ( 7 5 Γ( 5 5 c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions 6 π
7 so that e s( ln d ( s Γ ( ( π s s 5 4( Γ ( 5 s s 8 85 s s π ( + 4s + 5 6s + s 8( s 7 Γ ( and Γ(s+ s ( + s+ e s π + s So we have the first two terms in the asymptotic epansion for Γ. We can obviously get as many as we like by taking more and more terms in the Taylor epansion for f( and e y. So far, we have not attempted to keep track of the errors introduced by the various approimations. It is not hard to do so, but it is messy. So we have relegated the error estimates to the appendi. Summability We have now seen one way in which divergent epansions may be of some use. There is another possibility. Even if we cannot take the sum of the series n in the conventional sense, there may be some more general sense in which the series is summable. We will just briefly take a look at two such generalizations. Suppose that n is a (possibly divergent series. Let S N denote the series partial sum. Then the series is said to converge in the sense of Cesàro if the limit n S S C lim +S + +S N N N+ eists. That is, if the limit of the average of the partial sums eists. The series is said to converge in the sense of Borel if the power series g(t has radius of convergence and the integral S B n t n e t g(t dt converges. As the following theorem shows, these two definitions each etends our usual definition of series convergence. Theorem. If the series n converges, then S C and S B both eist and S C S B n Proof that S C n. Write S n and σ N S+S+ +SN N+ and observe that S σ N (S S +(S S + +(S S N N + c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions 7
8 Pick any ε >. Since S lim S n there is an M such that S S m < ε n for all m M. Also since S lim S n, the sequence { } S n is bounded. That is, there is a K such that Sn K for all n. So if n N > ma { MK ε/,m} S σn S S + S S + + S S N N + S S + S S + + S S M + S S M + S S M+ + + S S N N + N + ε ε ε K + K + + K < + N + N + ε + ε ε MK N + Hence lim N σ N S and S C S. Proof that S B n. Write S n n The last step, namely the echange n + n n e t t n dt N M + N + g(t ε {}}{ t n e t dt n can be justified rigorously. If the radius of convergence of the series n α n is strictly greater than one, the justification is not very hard. But in general it is too involved to give here. That s why Proof is in quotation marks. The converse of this theorem is false of course. Consider, for eample, n ( rn with r. Then, as n, n S n ( r m ( rn+ converges to +r σ N N+ m if r < and diverges if r. But S n n +r + N+ +r r N+ (r+ + N+ As N, this converges to +r g(t n n +r [ N ( r n+] ( r N+ (r+ n N+ +r if r, r, and diverges if r >. And ( r n t n e rt e t g(t dt ] [N + ( r ( rn+ +r e (+rt dt +r if r > and diverges otherwise. Collecting together these three results, in the conventional sense if r (, ( r n +r in the sense of Cesàro if r (,] n in the sense of Borel if r (, c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions 8
9 By way of conclusion, let me remark that these generalized modes of summation are not just mathematician s toys. The Fourier series of any continuous function converges in the sense of Cesàro. To get conventional convergence, one needs a certain amount of smoothness in addition of continuity. Also the calculation of the Lamb shift of the hydrogen atom spectrum, which provided (in addition to a Nobel prize spectacular numerical agreement with one of the most accurate measurements in science, consisted of adding up the first few terms of a series. The rigorous status of this series is not known. But umber of similar series (arising in other quantum field theories are known to diverge in the conventional sense but to converge in the sense of Borel. Appendi - Error Terms for Stirling s Formula In this appendi, we will treat the error terms arising in our development of Stirling s formula. A precise statement of that development is Step. Recall that f( ln. Write e sf( d and discard the last two terms. Step. Write +ε ε +ε ε e sf( d e sf( d+ +ε ε ε e sf( d+ e sf( d +ε e s( e s[f( ( ] d Apply e t +t+ t +e c! t with t s [ f( ( ] to give e s[f( ( ] s [ f( ( ] + s[ f( ( ] e c! s[ f( ( ] where c is between and s [ f( ( ]. Discard the last term. Step. Taylor epand f( ( ( + 4 ( 4 5 ( 5 + f(6 (c 6! ( 6 for some c [ ε,+ε], substitute this into s [ f( ( ] + s[ f( ( ] and discard any terms that contain f (6 (c and any terms of the form s m ( n with m n+ 5. (You ll see the reason for this condition shortly. This leaves +ε ε because the terms with n odd integrate to zero. Step 4. Replace +ε ε by The errors introduced in each step are as follows: Step. ε e sf( d and +ε e sf( d e s( { s 4 ( 4 + s 8 ( 6} d Step. +ε ε e s( e c! s[ f( ( ] d Step. A finite number of terms, each of the form umerical constant times an integral +ε ε e s( s m ( n d with m n+ 5. Here we have used that, since c [ ε,+ε], there is a constant M such that f (6 (c M. c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions 9
10 Step 4. A finite number of terms, each of the form umerical constant times an integral ε e s( s m ( n d. To treat these error terms, we use the following information about f( ln. (F f increases monotonically as increases. (F We have fied some small ε >. There is a δ > such that f( δ( for all +ε. To see that this is the case, we first observe that if δ ( d d f( δ( δ. So it suffices to pick δ sufficiently small that +ε δ The latter is always possible just because f(+ε >. (F For each [ ε,+ε] there is a c [ ε,+ε] such that Hence, there is a constant M such that f( (! f( (c ( f( ( M for all [ ε,+ε]. (F4 If [ ε,+ε] with ε small enough that εm 4, f( ( M 4 ( We can now get upper bounds on each of the error terms. For step, we have ε e sf( d F e sf( ε ε d e sf( ε and that f(+ε δε. and For step, we have +ε e sf( d F +ε e sδ( d δs e δεs +ε ε For step, we have e s( e c! s f( ( d F4 +ε ε e s ( s m n d! s +ε ε e s ( e s 4 ( f( ( d F +ε! M s e s 4 ( 9 d ε! M s e s 4 ( 9 d! M s ( s 4 5Γ(5 M s as in ( e s ( s m n d n+ s m( s M s 5 Γ ( n+ as in ( c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions
11 if m n+ 5. For step 4, we have e s ( s m n d ε ε e 4 ε s e 4 ε s e s 4 ( e s 4 ( s m n d ε e 4 εs s m( s 4 n+ M s m n+ e 4 ε s e s 4 ( s m n d e s 4 ( s m n d Γ ( n+ as in ( As promised these error terms all decay faster than πs ( + s as s. In particular, error terms introduced in Steps and 4, by ignoring contributions for ε, decay eponentially as s. Error terms introduced in Steps and, by dropping part of the Taylor series approimation, decay like s p for some p, depending on how much of the Taylor series we discarded. In particular, error terms introduced in Step decay like s 5, because of the condition m n+ 5. c Joel Feldman. 6. All rights reserved. December, 6 Taylor Series and Asymptotic Epansions
= 1 2 x (x 1) + 1 {x} (1 {x}). [t] dt = 1 x (x 1) + O (1), [t] dt = 1 2 x2 + O (x), (where the error is not now zero when x is an integer.
![= 1 2 x (x 1) + 1 {x} (1 {x}). [t] dt = 1 x (x 1) + O (1), [t] dt = 1 2 x2 + O (x), (where the error is not now zero when x is an integer. = 1 2 x (x 1) + 1 {x} (1 {x}). [t] dt = 1 x (x 1) + O (1), [t] dt = 1 2 x2 + O (x), (where the error is not now zero when x is an integer.](/thumbs/94/118301392.jpg) Problem Sheet,. i) Draw the graphs for [] and {}. ii) Show that for α R, α+ α [t] dt = α and α+ α {t} dt =. Hint Split these integrals at the integer which must lie in any interval of length, such as [α,
Problem Sheet,. i) Draw the graphs for [] and {}. ii) Show that for α R, α+ α [t] dt = α and α+ α {t} dt =. Hint Split these integrals at the integer which must lie in any interval of length, such as [α,
Euler-Maclaurin summation formula
 Physics 4 Spring 6 Euler-Maclaurin summation formula Lecture notes by M. G. Rozman Last modified: March 9, 6 Euler-Maclaurin summation formula gives an estimation of the sum N in f i) in terms of the integral
Physics 4 Spring 6 Euler-Maclaurin summation formula Lecture notes by M. G. Rozman Last modified: March 9, 6 Euler-Maclaurin summation formula gives an estimation of the sum N in f i) in terms of the integral
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
1969 AP Calculus BC: Section I
 969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
969 AP Calculus BC: Section I 9 Minutes No Calculator Note: In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e).. t The asymptotes of the graph of the parametric
Example 1: What do you know about the graph of the function
 Section 1.5 Analyzing of Functions In this section, we ll look briefly at four types of functions: polynomial functions, rational functions, eponential functions and logarithmic functions. Eample 1: What
Section 1.5 Analyzing of Functions In this section, we ll look briefly at four types of functions: polynomial functions, rational functions, eponential functions and logarithmic functions. Eample 1: What
Taylor Series and Series Convergence (Online)
 7in 0in Felder c02_online.te V3 - February 9, 205 9:5 A.M. Page CHAPTER 2 Taylor Series and Series Convergence (Online) 2.8 Asymptotic Epansions In introductory calculus classes the statement this series
7in 0in Felder c02_online.te V3 - February 9, 205 9:5 A.M. Page CHAPTER 2 Taylor Series and Series Convergence (Online) 2.8 Asymptotic Epansions In introductory calculus classes the statement this series
Divergent Series: why = 1/12. Bryden Cais
 Divergent Series: why + + 3 + = /. Bryden Cais Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.. H. Abel. Introduction The notion of convergence
Divergent Series: why + + 3 + = /. Bryden Cais Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.. H. Abel. Introduction The notion of convergence
Fourier transform of tempered distributions
 Fourier transform of tempered distributions 1 Test functions and distributions As we have seen before, many functions are not classical in the sense that they cannot be evaluated at any point. For eample,
Fourier transform of tempered distributions 1 Test functions and distributions As we have seen before, many functions are not classical in the sense that they cannot be evaluated at any point. For eample,
1 Exponential Functions Limit Derivative Integral... 5
 Contents Eponential Functions 3. Limit................................................. 3. Derivative.............................................. 4.3 Integral................................................
Contents Eponential Functions 3. Limit................................................. 3. Derivative.............................................. 4.3 Integral................................................
FOURIER INVERSION. an additive character in each of its arguments. The Fourier transform of f is
 FOURIER INVERSION 1. The Fourier Transform and the Inverse Fourier Transform Consider functions f, g : R n C, and consider the bilinear, symmetric function ψ : R n R n C, ψ(, ) = ep(2πi ), an additive
FOURIER INVERSION 1. The Fourier Transform and the Inverse Fourier Transform Consider functions f, g : R n C, and consider the bilinear, symmetric function ψ : R n R n C, ψ(, ) = ep(2πi ), an additive
Lecture 12 Reactions as Rare Events 3/02/2009 Notes by MIT Student (and MZB)
 Lecture 1 Reactions as Rare Events 3/0/009 Notes by MIT Student (and MZB) 1. Introduction In this lecture, we ll tackle the general problem of reaction rates involving particles jumping over barriers in
Lecture 1 Reactions as Rare Events 3/0/009 Notes by MIT Student (and MZB) 1. Introduction In this lecture, we ll tackle the general problem of reaction rates involving particles jumping over barriers in
Math 1B Final Exam, Solution. Prof. Mina Aganagic Lecture 2, Spring (6 points) Use substitution and integration by parts to find:
 Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Chapter 11 - Sequences and Series
 Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
MATH39001 Generating functions. 1 Ordinary power series generating functions
 MATH3900 Generating functions The reference for this part of the course is generatingfunctionology by Herbert Wilf. The 2nd edition is downloadable free from http://www.math.upenn. edu/~wilf/downldgf.html,
MATH3900 Generating functions The reference for this part of the course is generatingfunctionology by Herbert Wilf. The 2nd edition is downloadable free from http://www.math.upenn. edu/~wilf/downldgf.html,
Mat104 Fall 2002, Improper Integrals From Old Exams
 Mat4 Fall 22, Improper Integrals From Old Eams For the following integrals, state whether they are convergent or divergent, and give your reasons. () (2) (3) (4) (5) converges. Break it up as 3 + 2 3 +
Mat4 Fall 22, Improper Integrals From Old Eams For the following integrals, state whether they are convergent or divergent, and give your reasons. () (2) (3) (4) (5) converges. Break it up as 3 + 2 3 +
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods. Section 1: Separable DEs
 Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
Math 123, Week 9: Separable, First-Order Linear, and Substitution Methods Section 1: Separable DEs We are finally to the point in the course where we can consider how to find solutions to differential
New asymptotic expansion for the Γ (x) function
 New asymptotic epansion for the Γ function Gergő Nemes December 7, 2008 http://d.doi.org/0.3247/sl2math08.005 Abstract Using a series transformation, Stirling-De Moivre asymptotic series approimation to
New asymptotic epansion for the Γ function Gergő Nemes December 7, 2008 http://d.doi.org/0.3247/sl2math08.005 Abstract Using a series transformation, Stirling-De Moivre asymptotic series approimation to
About the Gamma Function
 About the Gamma Function Notes for Honors Calculus II, Originally Prepared in Spring 995 Basic Facts about the Gamma Function The Gamma function is defined by the improper integral Γ) = The integral is
About the Gamma Function Notes for Honors Calculus II, Originally Prepared in Spring 995 Basic Facts about the Gamma Function The Gamma function is defined by the improper integral Γ) = The integral is
10.4: WORKING WITH TAYLOR SERIES
 04: WORKING WITH TAYLOR SERIES Contributed by OpenSta Mathematics at OpenSta CNX In the preceding section we defined Taylor series and showed how to find the Taylor series for several common functions
04: WORKING WITH TAYLOR SERIES Contributed by OpenSta Mathematics at OpenSta CNX In the preceding section we defined Taylor series and showed how to find the Taylor series for several common functions
Fourier Analysis Fourier Series C H A P T E R 1 1
 C H A P T E R Fourier Analysis 474 This chapter on Fourier analysis covers three broad areas: Fourier series in Secs...4, more general orthonormal series called Sturm iouville epansions in Secs..5 and.6
C H A P T E R Fourier Analysis 474 This chapter on Fourier analysis covers three broad areas: Fourier series in Secs...4, more general orthonormal series called Sturm iouville epansions in Secs..5 and.6
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
Solutions to Math 41 Final Exam December 9, 2013
 Solutions to Math 4 Final Eam December 9,. points In each part below, use the method of your choice, but show the steps in your computations. a Find f if: f = arctane csc 5 + log 5 points Using the Chain
Solutions to Math 4 Final Eam December 9,. points In each part below, use the method of your choice, but show the steps in your computations. a Find f if: f = arctane csc 5 + log 5 points Using the Chain
Tail Approximation of the Skew-Normal by the Skew-Normal Laplace: Application to Owen s T Function and the Bivariate Normal Distribution
 Journal of Statistical and Econometric ethods vol. no. 3 - ISS: 5-557 print version 5-565online Scienpress Ltd 3 Tail Approimation of the Skew-ormal by the Skew-ormal Laplace: Application to Owen s T Function
Journal of Statistical and Econometric ethods vol. no. 3 - ISS: 5-557 print version 5-565online Scienpress Ltd 3 Tail Approimation of the Skew-ormal by the Skew-ormal Laplace: Application to Owen s T Function
First Variation of a Functional
 First Variation of a Functional The derivative of a function being zero is a necessary condition for the etremum of that function in ordinary calculus. Let us now consider the equivalent of a derivative
First Variation of a Functional The derivative of a function being zero is a necessary condition for the etremum of that function in ordinary calculus. Let us now consider the equivalent of a derivative
Economics 205 Exercises
 Economics 05 Eercises Prof. Watson, Fall 006 (Includes eaminations through Fall 003) Part 1: Basic Analysis 1. Using ε and δ, write in formal terms the meaning of lim a f() = c, where f : R R.. Write the
Economics 05 Eercises Prof. Watson, Fall 006 (Includes eaminations through Fall 003) Part 1: Basic Analysis 1. Using ε and δ, write in formal terms the meaning of lim a f() = c, where f : R R.. Write the
Numerical Methods. Root Finding
 Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
Numerical Methods Solving Non Linear 1-Dimensional Equations Root Finding Given a real valued function f of one variable (say ), the idea is to find an such that: f() 0 1 Root Finding Eamples Find real
This ODE arises in many physical systems that we shall investigate. + ( + 1)u = 0. (λ + s)x λ + s + ( + 1) a λ. (s + 1)(s + 2) a 0
 Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
STEP Support Programme. Pure STEP 3 Solutions
 STEP Support Programme Pure STEP 3 Solutions S3 Q6 Preparation Completing the square on gives + + y, so the centre is at, and the radius is. First draw a sketch of y 4 3. This has roots at and, and you
STEP Support Programme Pure STEP 3 Solutions S3 Q6 Preparation Completing the square on gives + + y, so the centre is at, and the radius is. First draw a sketch of y 4 3. This has roots at and, and you
APPM 1360 Final Exam Spring 2016
 APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
Lecture 4b. Bessel functions. Introduction. Generalized factorial function. 4b.1. Using integration by parts it is easy to show that
 4b. Lecture 4b Using integration by parts it is easy to show that Bessel functions Introduction In the previous lecture the separation of variables method led to Bessel's equation y' ' y ' 2 y= () 2 Here
4b. Lecture 4b Using integration by parts it is easy to show that Bessel functions Introduction In the previous lecture the separation of variables method led to Bessel's equation y' ' y ' 2 y= () 2 Here
The incomplete gamma functions. Notes by G.J.O. Jameson. These notes incorporate the Math. Gazette article [Jam1], with some extra material.
![The incomplete gamma functions. Notes by G.J.O. Jameson. These notes incorporate the Math. Gazette article [Jam1], with some extra material. The incomplete gamma functions. Notes by G.J.O. Jameson. These notes incorporate the Math. Gazette article [Jam1], with some extra material.](/thumbs/85/92277860.jpg) The incomplete gamma functions Notes by G.J.O. Jameson These notes incorporate the Math. Gazette article [Jam], with some etra material. Definitions and elementary properties functions: Recall the integral
The incomplete gamma functions Notes by G.J.O. Jameson These notes incorporate the Math. Gazette article [Jam], with some etra material. Definitions and elementary properties functions: Recall the integral
The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. sin
 Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Introduction to Series and Sequences Math 121 Calculus II Spring 2015
 Introduction to Series and Sequences Math Calculus II Spring 05 The goal. The main purpose of our study of series and sequences is to understand power series. A power series is like a polynomial of infinite
Introduction to Series and Sequences Math Calculus II Spring 05 The goal. The main purpose of our study of series and sequences is to understand power series. A power series is like a polynomial of infinite
DIFFERENTIATING UNDER THE INTEGRAL SIGN
 DIFFEENTIATING UNDE THE INTEGAL SIGN KEITH CONAD I had learned to do integrals by various methods shown in a book that my high school physics teacher Mr. Bader had given me. [It] showed how to differentiate
DIFFEENTIATING UNDE THE INTEGAL SIGN KEITH CONAD I had learned to do integrals by various methods shown in a book that my high school physics teacher Mr. Bader had given me. [It] showed how to differentiate
Exact and Approximate Numbers:
 Eact and Approimate Numbers: The numbers that arise in technical applications are better described as eact numbers because there is not the sort of uncertainty in their values that was described above.
Eact and Approimate Numbers: The numbers that arise in technical applications are better described as eact numbers because there is not the sort of uncertainty in their values that was described above.
Mathematics 132 Calculus for Physical and Life Sciences 2 Exam 3 Review Sheet April 15, 2008
 Mathematics 32 Calculus for Physical and Life Sciences 2 Eam 3 Review Sheet April 5, 2008 Sample Eam Questions - Solutions This list is much longer than the actual eam will be (to give you some idea of
Mathematics 32 Calculus for Physical and Life Sciences 2 Eam 3 Review Sheet April 5, 2008 Sample Eam Questions - Solutions This list is much longer than the actual eam will be (to give you some idea of
3.5 Continuity of a Function One Sided Continuity Intermediate Value Theorem... 23
 Chapter 3 Limit and Continuity Contents 3. Definition of Limit 3 3.2 Basic Limit Theorems 8 3.3 One sided Limit 4 3.4 Infinite Limit, Limit at infinity and Asymptotes 5 3.4. Infinite Limit and Vertical
Chapter 3 Limit and Continuity Contents 3. Definition of Limit 3 3.2 Basic Limit Theorems 8 3.3 One sided Limit 4 3.4 Infinite Limit, Limit at infinity and Asymptotes 5 3.4. Infinite Limit and Vertical
Poisson summation and convergence of Fourier series. 1. Poisson summation
 (August 29, 213) Poisson summation and convergence of Fourier series Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/mfms/notes
(August 29, 213) Poisson summation and convergence of Fourier series Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/mfms/notes
Integration. 5.1 Antiderivatives and Indefinite Integration. Suppose that f(x) = 5x 4. Can we find a function F (x) whose derivative is f(x)?
 5 Integration 5. Antiderivatives and Indefinite Integration Suppose that f() = 5 4. Can we find a function F () whose derivative is f()? Definition. A function F is an antiderivative of f on an interval
5 Integration 5. Antiderivatives and Indefinite Integration Suppose that f() = 5 4. Can we find a function F () whose derivative is f()? Definition. A function F is an antiderivative of f on an interval
211 Real Analysis. f (x) = x2 1. x 1. x 2 1
 Part. Limits of functions. Introduction 2 Real Analysis Eample. What happens to f : R \ {} R, given by f () = 2,, as gets close to? If we substitute = we get f () = 0 which is undefined. Instead we 0 might
Part. Limits of functions. Introduction 2 Real Analysis Eample. What happens to f : R \ {} R, given by f () = 2,, as gets close to? If we substitute = we get f () = 0 which is undefined. Instead we 0 might
Harmonic Analysis Homework 5
 Harmonic Analysis Homework 5 Bruno Poggi Department of Mathematics, University of Minnesota November 4, 6 Notation Throughout, B, r is the ball of radius r with center in the understood metric space usually
Harmonic Analysis Homework 5 Bruno Poggi Department of Mathematics, University of Minnesota November 4, 6 Notation Throughout, B, r is the ball of radius r with center in the understood metric space usually
CHAPTER 8: EXPLORING R
 CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
CHAPTER 8: EXPLORING R LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN In the previous chapter we discussed the need for a complete ordered field. The field Q is not complete, so we constructed
Chapter 5: Limits, Continuity, and Differentiability
 Chapter 5: Limits, Continuity, and Differentiability 63 Chapter 5 Overview: Limits, Continuity and Differentiability Derivatives and Integrals are the core practical aspects of Calculus. They were the
Chapter 5: Limits, Continuity, and Differentiability 63 Chapter 5 Overview: Limits, Continuity and Differentiability Derivatives and Integrals are the core practical aspects of Calculus. They were the
A Symbolic Operator Approach to Several Summation Formulas for Power Series
 A Symbolic Operator Approach to Several Summation Formulas for Power Series T. X. He, L. C. Hsu 2, P. J.-S. Shiue 3, and D. C. Torney 4 Department of Mathematics and Computer Science Illinois Wesleyan
A Symbolic Operator Approach to Several Summation Formulas for Power Series T. X. He, L. C. Hsu 2, P. J.-S. Shiue 3, and D. C. Torney 4 Department of Mathematics and Computer Science Illinois Wesleyan
Course. Print and use this sheet in conjunction with MathinSite s Maclaurin Series applet and worksheet.
 Maclaurin Series Learning Outcomes After reading this theory sheet, you should recognise the difference between a function and its polynomial epansion (if it eists!) understand what is meant by a series
Maclaurin Series Learning Outcomes After reading this theory sheet, you should recognise the difference between a function and its polynomial epansion (if it eists!) understand what is meant by a series
Gaussian integrals. Calvin W. Johnson. September 9, The basic Gaussian and its normalization
 Gaussian integrals Calvin W. Johnson September 9, 24 The basic Gaussian and its normalization The Gaussian function or the normal distribution, ep ( α 2), () is a widely used function in physics and mathematical
Gaussian integrals Calvin W. Johnson September 9, 24 The basic Gaussian and its normalization The Gaussian function or the normal distribution, ep ( α 2), () is a widely used function in physics and mathematical
An Introduction to the Gamma Function
 UNIVERSITY OF WARWICK Second Year Essay An Introduction to the Gamma Function Tutor: Dr. Stefan Adams April 4, 29 Contents 1 Introduction 2 2 Conve Functions 3 3 The Gamma Function 7 4 The Bohr-Möllerup
UNIVERSITY OF WARWICK Second Year Essay An Introduction to the Gamma Function Tutor: Dr. Stefan Adams April 4, 29 Contents 1 Introduction 2 2 Conve Functions 3 3 The Gamma Function 7 4 The Bohr-Möllerup
Quantum Dynamics. March 10, 2017
 Quantum Dynamics March 0, 07 As in classical mechanics, time is a parameter in quantum mechanics. It is distinct from space in the sense that, while we have Hermitian operators, X, for position and therefore
Quantum Dynamics March 0, 07 As in classical mechanics, time is a parameter in quantum mechanics. It is distinct from space in the sense that, while we have Hermitian operators, X, for position and therefore
C.7. Numerical series. Pag. 147 Proof of the converging criteria for series. Theorem 5.29 (Comparison test) Let a k and b k be positive-term series
 C.7 Numerical series Pag. 147 Proof of the converging criteria for series Theorem 5.29 (Comparison test) Let and be positive-term series such that 0, for any k 0. i) If the series converges, then also
C.7 Numerical series Pag. 147 Proof of the converging criteria for series Theorem 5.29 (Comparison test) Let and be positive-term series such that 0, for any k 0. i) If the series converges, then also
CHAPTER 6 bis. Distributions
 CHAPTER 6 bis Distributions The Dirac function has proved extremely useful and convenient to physicists, even though many a mathematician was truly horrified when the Dirac function was described to him:
CHAPTER 6 bis Distributions The Dirac function has proved extremely useful and convenient to physicists, even though many a mathematician was truly horrified when the Dirac function was described to him:
1993 AP Calculus AB: Section I
 99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
221A Lecture Notes Steepest Descent Method
 Gamma Function A Lecture Notes Steepest Descent Method The best way to introduce the steepest descent method is to see an example. The Stirling s formula for the behavior of the factorial n! for large
Gamma Function A Lecture Notes Steepest Descent Method The best way to introduce the steepest descent method is to see an example. The Stirling s formula for the behavior of the factorial n! for large
3.8 Limits At Infinity
 3.8. LIMITS AT INFINITY 53 Figure 3.5: Partial graph of f = /. We see here that f 0 as and as. 3.8 Limits At Infinity The its we introduce here differ from previous its in that here we are interested in
3.8. LIMITS AT INFINITY 53 Figure 3.5: Partial graph of f = /. We see here that f 0 as and as. 3.8 Limits At Infinity The its we introduce here differ from previous its in that here we are interested in
LECTURE 10: REVIEW OF POWER SERIES. 1. Motivation
 LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
CONTINUITY AND DIFFERENTIABILITY
 5. Introduction The whole of science is nothing more than a refinement of everyday thinking. ALBERT EINSTEIN This chapter is essentially a continuation of our stu of differentiation of functions in Class
5. Introduction The whole of science is nothing more than a refinement of everyday thinking. ALBERT EINSTEIN This chapter is essentially a continuation of our stu of differentiation of functions in Class
MATH 117 LECTURE NOTES
 MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
MATH 117 LECTURE NOTES XIN ZHOU Abstract. This is the set of lecture notes for Math 117 during Fall quarter of 2017 at UC Santa Barbara. The lectures follow closely the textbook [1]. Contents 1. The set
THS Step By Step Calculus Chapter 1
 Name: Class Period: Throughout this packet there will be blanks you are epected to fill in prior to coming to class. This packet follows your Larson Tetbook. Do NOT throw away! Keep in 3 ring binder until
Name: Class Period: Throughout this packet there will be blanks you are epected to fill in prior to coming to class. This packet follows your Larson Tetbook. Do NOT throw away! Keep in 3 ring binder until
Math 261 Final Exam - Practice Problem Solutions. 1. A function f is graphed below.
 Math Final Eam - Practice Problem Solutions. A function f is graphed below. f() 8 7 7 8 (a) Find f(), f( ), f(), and f() f() = ;f( ).;f() is undefined; f() = (b) Find the domain and range of f Domain:
Math Final Eam - Practice Problem Solutions. A function f is graphed below. f() 8 7 7 8 (a) Find f(), f( ), f(), and f() f() = ;f( ).;f() is undefined; f() = (b) Find the domain and range of f Domain:
Properties of Derivatives
 6 CHAPTER Properties of Derivatives To investigate derivatives using first principles, we will look at the slope of f ( ) = at the point P (,9 ). Let Q1, Q, Q, Q4, be a sequence of points on the curve
6 CHAPTER Properties of Derivatives To investigate derivatives using first principles, we will look at the slope of f ( ) = at the point P (,9 ). Let Q1, Q, Q, Q4, be a sequence of points on the curve
CHAPTER 4. Series. 1. What is a Series?
 CHAPTER 4 Series Given a sequence, in many contexts it is natural to ask about the sum of all the numbers in the sequence. If only a finite number of the are nonzero, this is trivial and not very interesting.
CHAPTER 4 Series Given a sequence, in many contexts it is natural to ask about the sum of all the numbers in the sequence. If only a finite number of the are nonzero, this is trivial and not very interesting.
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions In this section, we: use implicit differentiation to find the derivatives of the logarithmic functions and, in particular,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions In this section, we: use implicit differentiation to find the derivatives of the logarithmic functions and, in particular,
5.9 Representations of Functions as a Power Series
 5.9 Representations of Functions as a Power Series Example 5.58. The following geometric series x n + x + x 2 + x 3 + x 4 +... will converge when < x
5.9 Representations of Functions as a Power Series Example 5.58. The following geometric series x n + x + x 2 + x 3 + x 4 +... will converge when < x
+ y = 1 : the polynomial
 Notes on Basic Ideas of Spherical Harmonics In the representation of wavefields (solutions of the wave equation) one of the natural considerations that arise along the lines of Huygens Principle is the
Notes on Basic Ideas of Spherical Harmonics In the representation of wavefields (solutions of the wave equation) one of the natural considerations that arise along the lines of Huygens Principle is the
Chapter 8. Infinite Series
 8.4 Series of Nonnegative Terms Chapter 8. Infinite Series 8.4 Series of Nonnegative Terms Note. Given a series we have two questions:. Does the series converge? 2. If it converges, what is its sum? Corollary
8.4 Series of Nonnegative Terms Chapter 8. Infinite Series 8.4 Series of Nonnegative Terms Note. Given a series we have two questions:. Does the series converge? 2. If it converges, what is its sum? Corollary
Some Fun with Divergent Series
 Some Fun with Divergent Series 1. Preliminary Results We begin by examining the (divergent) infinite series S 1 = 1 + 2 + 3 + 4 + 5 + 6 + = k=1 k S 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + = k=1 k 2 (i)
Some Fun with Divergent Series 1. Preliminary Results We begin by examining the (divergent) infinite series S 1 = 1 + 2 + 3 + 4 + 5 + 6 + = k=1 k S 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + = k=1 k 2 (i)
E = {x 0 < x < 1}. Z f(x) dx <.
 Chapter Devastating Eamples Students of calculus develop an intuition for the subject typically based on geometric considerations. This intuition works adequately for problems in physics and engineering.
Chapter Devastating Eamples Students of calculus develop an intuition for the subject typically based on geometric considerations. This intuition works adequately for problems in physics and engineering.
Chapter 9. Derivatives. Josef Leydold Mathematical Methods WS 2018/19 9 Derivatives 1 / 51. f x. (x 0, f (x 0 ))
 Chapter 9 Derivatives Josef Leydold Mathematical Methods WS 208/9 9 Derivatives / 5 Difference Quotient Let f : R R be some function. The the ratio f = f ( 0 + ) f ( 0 ) = f ( 0) 0 is called difference
Chapter 9 Derivatives Josef Leydold Mathematical Methods WS 208/9 9 Derivatives / 5 Difference Quotient Let f : R R be some function. The the ratio f = f ( 0 + ) f ( 0 ) = f ( 0) 0 is called difference
Answer Key. ( 1) n (2x+3) n. n n=1. (2x+3) n. = lim. < 1 or 2x+3 < 4. ( 1) ( 1) 2n n
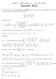 Math Midterm Eam #3 December, 3 Answer Key. [5 Points] Find the Interval and Radius of Convergence for the following power series. Analyze carefully and with full justification. Use Ratio Test. L lim a
Math Midterm Eam #3 December, 3 Answer Key. [5 Points] Find the Interval and Radius of Convergence for the following power series. Analyze carefully and with full justification. Use Ratio Test. L lim a
MATH 116, LECTURES 10 & 11: Limits
 MATH 6, LECTURES 0 & : Limits Limits In application, we often deal with quantities which are close to other quantities but which cannot be defined eactly. Consider the problem of how a car s speedometer
MATH 6, LECTURES 0 & : Limits Limits In application, we often deal with quantities which are close to other quantities but which cannot be defined eactly. Consider the problem of how a car s speedometer
February 13, Option 9 Overview. Mind Map
 Option 9 Overview Mind Map Return tests - will discuss Wed..1.1 J.1: #1def,2,3,6,7 (Sequences) 1. Develop and understand basic ideas about sequences. J.2: #1,3,4,6 (Monotonic convergence) A quick review:
Option 9 Overview Mind Map Return tests - will discuss Wed..1.1 J.1: #1def,2,3,6,7 (Sequences) 1. Develop and understand basic ideas about sequences. J.2: #1,3,4,6 (Monotonic convergence) A quick review:
A Propagating Wave Packet The Group Velocity
 Lecture 7 A Propagating Wave Pacet The Group Velocity Phys 375 Overview and Motivation: Last time we looed at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Lecture 7 A Propagating Wave Pacet The Group Velocity Phys 375 Overview and Motivation: Last time we looed at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Limit and Continuity
 Limit and Continuity Table of contents. Limit of Sequences............................................ 2.. Definitions and properties...................................... 2... Definitions............................................
Limit and Continuity Table of contents. Limit of Sequences............................................ 2.. Definitions and properties...................................... 2... Definitions............................................
Continuous functions. Limits of non-rational functions. Squeeze Theorem. Calculator issues. Applications of limits
 Calculus Lia Vas Continuous functions. Limits of non-rational functions. Squeeze Theorem. Calculator issues. Applications of limits Continuous Functions. Recall that we referred to a function f() as a
Calculus Lia Vas Continuous functions. Limits of non-rational functions. Squeeze Theorem. Calculator issues. Applications of limits Continuous Functions. Recall that we referred to a function f() as a
10.1 Sequences. Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1.
 10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
Review of elements of Calculus (functions in one variable)
 Review of elements of Calculus (functions in one variable) Mainly adapted from the lectures of prof Greg Kelly Hanford High School, Richland Washington http://online.math.uh.edu/houstonact/ https://sites.google.com/site/gkellymath/home/calculuspowerpoints
Review of elements of Calculus (functions in one variable) Mainly adapted from the lectures of prof Greg Kelly Hanford High School, Richland Washington http://online.math.uh.edu/houstonact/ https://sites.google.com/site/gkellymath/home/calculuspowerpoints
A dash of derivatives
 Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.2016-2017 Mathematics (Curriculum Economics, Markets and Finance) A dash of derivatives Luciano Battaia October 6, 2016 1 Tangents to curves
Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.2016-2017 Mathematics (Curriculum Economics, Markets and Finance) A dash of derivatives Luciano Battaia October 6, 2016 1 Tangents to curves
C) 2 D) 4 E) 6. ? A) 0 B) 1 C) 1 D) The limit does not exist.
 . The asymptotes of the graph of the parametric equations = t, y = t t + are A) =, y = B) = only C) =, y = D) = only E) =, y =. What are the coordinates of the inflection point on the graph of y = ( +
. The asymptotes of the graph of the parametric equations = t, y = t t + are A) =, y = B) = only C) =, y = D) = only E) =, y =. What are the coordinates of the inflection point on the graph of y = ( +
Review of Power Series
 Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
8 Autonomous first order ODE
 8 Autonomous first order ODE There are different ways to approach differential equations. Prior to this lecture we mostly dealt with analytical methods, i.e., with methods that require a formula as a final
8 Autonomous first order ODE There are different ways to approach differential equations. Prior to this lecture we mostly dealt with analytical methods, i.e., with methods that require a formula as a final
Last Update: March 1 2, 201 0
 M ath 2 0 1 E S 1 W inter 2 0 1 0 Last Update: March 1 2, 201 0 S eries S olutions of Differential Equations Disclaimer: This lecture note tries to provide an alternative approach to the material in Sections
M ath 2 0 1 E S 1 W inter 2 0 1 0 Last Update: March 1 2, 201 0 S eries S olutions of Differential Equations Disclaimer: This lecture note tries to provide an alternative approach to the material in Sections
Spring 2011 solutions. We solve this via integration by parts with u = x 2 du = 2xdx. This is another integration by parts with u = x du = dx and
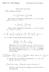 Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Lecture 5: Rules of Differentiation. First Order Derivatives
 Lecture 5: Rules of Differentiation First order derivatives Higher order derivatives Partial differentiation Higher order partials Differentials Derivatives of implicit functions Generalized implicit function
Lecture 5: Rules of Differentiation First order derivatives Higher order derivatives Partial differentiation Higher order partials Differentials Derivatives of implicit functions Generalized implicit function
APPROXIMATIONS FOR SOME FUNCTIONS OF PRIMES
 APPROXIMATIONS FOR SOME FUNCTIONS OF PRIMES Fataneh Esteki B. Sc., University of Isfahan, 2002 A Thesis Submitted to the School of Graduate Studies of the University of Lethbridge in Partial Fulfillment
APPROXIMATIONS FOR SOME FUNCTIONS OF PRIMES Fataneh Esteki B. Sc., University of Isfahan, 2002 A Thesis Submitted to the School of Graduate Studies of the University of Lethbridge in Partial Fulfillment
Limits and Continuity
 Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
Limits and Continuity Philippe B. Laval Kennesaw State University January 2, 2005 Contents Abstract Notes and practice problems on its and continuity. Limits 2. Introduction... 2.2 Theory:... 2.2. GraphicalMethod...
A Propagating Wave Packet The Group Velocity
 Lecture 7 A Propagating Wave Packet The Group Velocity Phys 375 Overview and Motivation: Last time we looked at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Lecture 7 A Propagating Wave Packet The Group Velocity Phys 375 Overview and Motivation: Last time we looked at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Classnotes - MA Series and Matrices
 Classnotes - MA-2 Series and Matrices Department of Mathematics Indian Institute of Technology Madras This classnote is only meant for academic use. It is not to be used for commercial purposes. For suggestions
Classnotes - MA-2 Series and Matrices Department of Mathematics Indian Institute of Technology Madras This classnote is only meant for academic use. It is not to be used for commercial purposes. For suggestions
Math 2300 Calculus II University of Colorado
 Math 3 Calculus II University of Colorado Spring Final eam review problems: ANSWER KEY. Find f (, ) for f(, y) = esin( y) ( + y ) 3/.. Consider the solid region W situated above the region apple apple,
Math 3 Calculus II University of Colorado Spring Final eam review problems: ANSWER KEY. Find f (, ) for f(, y) = esin( y) ( + y ) 3/.. Consider the solid region W situated above the region apple apple,
NEW ASYMPTOTIC EXPANSION AND ERROR BOUND FOR STIRLING FORMULA OF RECIPROCAL GAMMA FUNCTION
 M athematical Inequalities & Applications Volume, Number 4 8), 957 965 doi:.753/mia-8--65 NEW ASYMPTOTIC EXPANSION AND ERROR BOUND FOR STIRLING FORMULA OF RECIPROCAL GAMMA FUNCTION PEDRO J. PAGOLA Communicated
M athematical Inequalities & Applications Volume, Number 4 8), 957 965 doi:.753/mia-8--65 NEW ASYMPTOTIC EXPANSION AND ERROR BOUND FOR STIRLING FORMULA OF RECIPROCAL GAMMA FUNCTION PEDRO J. PAGOLA Communicated
MATH 6337: Homework 8 Solutions
 6.1. MATH 6337: Homework 8 Solutions (a) Let be a measurable subset of 2 such that for almost every x, {y : (x, y) } has -measure zero. Show that has measure zero and that for almost every y, {x : (x,
6.1. MATH 6337: Homework 8 Solutions (a) Let be a measurable subset of 2 such that for almost every x, {y : (x, y) } has -measure zero. Show that has measure zero and that for almost every y, {x : (x,
Pólya s Random Walk Theorem arxiv: v2 [math.pr] 18 Apr 2013
![Pólya s Random Walk Theorem arxiv: v2 [math.pr] 18 Apr 2013 Pólya s Random Walk Theorem arxiv: v2 [math.pr] 18 Apr 2013](/thumbs/74/70045711.jpg) Pólya s Random Wal Theorem arxiv:131.3916v2 [math.pr] 18 Apr 213 Jonathan ova Abstract This note presents a proof of Pólya s random wal theorem using classical methods from special function theory and
Pólya s Random Wal Theorem arxiv:131.3916v2 [math.pr] 18 Apr 213 Jonathan ova Abstract This note presents a proof of Pólya s random wal theorem using classical methods from special function theory and
NONLINEAR FUNCTIONS A. Absolute Value Exercises: 2. We need to scale the graph of Qx ( )
 NONLINEAR FUNCTIONS A. Absolute Value Eercises:. We need to scale the graph of Q ( ) f ( ) =. The graph is given below. = by the factor of to get the graph of 9 - - - - -. We need to scale the graph of
NONLINEAR FUNCTIONS A. Absolute Value Eercises:. We need to scale the graph of Q ( ) f ( ) =. The graph is given below. = by the factor of to get the graph of 9 - - - - -. We need to scale the graph of
Calculus - Chapter 2 Solutions
 Calculus - Chapter Solutions. a. See graph at right. b. The velocity is decreasing over the entire interval. It is changing fastest at the beginning and slowest at the end. c. A = (95 + 85)(5) = 450 feet
Calculus - Chapter Solutions. a. See graph at right. b. The velocity is decreasing over the entire interval. It is changing fastest at the beginning and slowest at the end. c. A = (95 + 85)(5) = 450 feet
Basic methods to solve equations
 Roberto s Notes on Prerequisites for Calculus Chapter 1: Algebra Section 1 Basic methods to solve equations What you need to know already: How to factor an algebraic epression. What you can learn here:
Roberto s Notes on Prerequisites for Calculus Chapter 1: Algebra Section 1 Basic methods to solve equations What you need to know already: How to factor an algebraic epression. What you can learn here:
0.1. Linear transformations
 Suggestions for midterm review #3 The repetitoria are usually not complete; I am merely bringing up the points that many people didn t now on the recitations Linear transformations The following mostly
Suggestions for midterm review #3 The repetitoria are usually not complete; I am merely bringing up the points that many people didn t now on the recitations Linear transformations The following mostly
We start with a simple result from Fourier analysis. Given a function f : [0, 1] C, we define the Fourier coefficients of f by
![We start with a simple result from Fourier analysis. Given a function f : [0, 1] C, we define the Fourier coefficients of f by We start with a simple result from Fourier analysis. Given a function f : [0, 1] C, we define the Fourier coefficients of f by](/thumbs/74/71304729.jpg) Chapter 9 The functional equation for the Riemann zeta function We will eventually deduce a functional equation, relating ζ(s to ζ( s. There are various methods to derive this functional equation, see
Chapter 9 The functional equation for the Riemann zeta function We will eventually deduce a functional equation, relating ζ(s to ζ( s. There are various methods to derive this functional equation, see
Solutions to Math 41 First Exam October 12, 2010
 Solutions to Math 41 First Eam October 12, 2010 1. 13 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it
Solutions to Math 41 First Eam October 12, 2010 1. 13 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it
MATH 1325 Business Calculus Guided Notes
 MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
Notes for Expansions/Series and Differential Equations
 Notes for Expansions/Series and Differential Equations In the last discussion, we considered perturbation methods for constructing solutions/roots of algebraic equations. Three types of problems were illustrated
Notes for Expansions/Series and Differential Equations In the last discussion, we considered perturbation methods for constructing solutions/roots of algebraic equations. Three types of problems were illustrated
CHAPTER 1 : BASIC SKILLS
 Mathematics with Symbols Dr Roger Ni (Queen Mary, University of London) -. CHAPTER : BASIC SKILLS Physical quantities are often represented by symbols - these may be the normal Latin characters ( a, b,
Mathematics with Symbols Dr Roger Ni (Queen Mary, University of London) -. CHAPTER : BASIC SKILLS Physical quantities are often represented by symbols - these may be the normal Latin characters ( a, b,
