arxiv: v1 [math.ap] 22 Jan 2018
|
|
|
- Maximillian Harrison
- 6 years ago
- Views:
Transcription
1 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES arxiv: v [math.ap] 22 Jan 208 CRISTIAN E. GUTIÉRREZ AND AHMAD SABRA Abstract. Due to dispersion, light with different wavelengths, or colors, is refracted at different angles. Our purpose is to determine when is it possible to design a lens made of a single homogeneous material so that it refracts light superposition of two colors into a desired fixed final direction. Two problems are considered: one is when light emanates in a parallel beam and the other is when light emanates from a point source. For the first problem, and when the direction of the parallel beam is different from the final desired direction, we show that such a lens does not exist; otherwise we prove the solution is trivial, i.e., the lens is confined between two parallel planes. For the second problem we prove that is impossible to design such a lens when the desired final direction is not among the set of incident directions. Otherwise, solving an appropriate system of functional equations we show that a local solution exists. Contents. Introduction 2 2. Preliminaries 5 3. The collimated case: Problem A Estimates of the upper surfaces for two colors 0. First order functional differential equations 3.. Uniqueness of solutions One point source case: Problem B Two dimensional case, w Ω Derivation of a system of functional equations from the solvability of Problem B in the plane Solutions of 5.) yield local solutions to the optical problem On the solvability of the algebraic system.3) Existence of local solutions to 5.) 8 Acknowledgements 55 References 55 January 23, 208.
2 2 C. E. GUTIÉRREZ AND A. SABRA. Introduction We showed in [GS6] that given a function u in Ω R 2 and a unit direction w S 2 there exists a surface parametrized by a function f such that the lens sandwiched by u and f, made of an homogeneous material and denoted by u, f ), refracts monochromatic light emanating vertically from Ω into the direction w. In the earlier paper [Gut3], a similar result is proved when light emanates from a point source. The purpose of this paper is to study if it is possible to design simple lenses doing similar refracting jobs for non monochromatic light. By a simple or single element) lens we mean a domain in R 3 bounded by two smooth surfaces that is filled with an homogeneous material. To do this we need to deal with dispersion: since the index of refraction of a material depends on the wavelength of the radiation, a non monochromatic light ray after passing through a lens splits into several rays having different refraction angles and wavelengths. Therefore, when white light is refracted by a single lens each color comes to a focus at a different distance from the objective. This is called chromatic aberration and plays a vital role in lens design, see [KJ0, Chapter 5]. Materials have various degrees of dispersion, and low dispersion ones are used in the manufacturing of photographic lenses, see [Can]. A way to correct chromatic aberration is to build lenses composed of various simple lenses made of different materials. Also chromatic aberration has recently being handled numerically using demosaicing algorithms, see [ima]. The way in which the refractive index depends of the wavelength is given by a formula for the dispersion of light due to A. Cauchy: the refractive index n in terms of the wavelength λ is given by nλ) = A + A 2 λ + A 2 λ +, where A i are constants depending on the material [Cau36]. The validity of this formula is in the visible wavelength range, see [BW59, pp ] for its accurateness in various materials. A more accurate formula was derived by Sellmeier, see [JW0, Section 23.5]. A first result related to our question is that there is no single lens bounded by two spherical surfaces that refracts non monochromatic radiation from a point into a fixed direction; this was originally stated by K. Schwarzschild [Sch05]. The question of designing a single lens, non spherical, that focuses one point into a fixed direction for light containing only two colors, i.e., for two refractive indices n n, is considered in [Sch83] in the plane; but no mathematically rigorous proof is given. In fact, by tracing back and forth rays of both colors, the author describes how a finite number of points should be located on the faces of the desired lens and he claims, without proof, that the desired surfaces can
3 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 3 be completed by interpolating adjacent points with third degree polynomials. Such an interpolation will give an undesired refracting behavior outside the fixed number of points considered. For the existence of rotationally symmetric lenses capable of focusing one point into two points for two different refractive indices see [vbo92], [vb9]. The results of all these authors require size conditions on n, n. The monochromatic case is due to Friedman and MacLeod [FM87] and Rogers [Rog88]. The solutions obtained are analytic functions. These results are all two dimensional and therefore concern only to rotationally symmetric lenses. In view of all this, we now state precisely the problems that are considered and solved in this paper. Problem A: is there a single lens sandwiched by a surface L given by the graph of a function u in Ω, the lower surface of the lens, and a surface S, the top part of the lens, such that each ray of dichromatic light superposition of two colors) emanating in the vertical direction e from x, 0) for x Ω is refracted by the lens into the direction w? We denote such a lens by the pair L, S). Notice that when a dichromatic ray enters the lens, due to chromatic dispersion, it splits into two rays having different directions and colors, say red and blue, that they both travel inside the lens until they exit it at points on the surface S and then both continue traveling in the direction w; see Figure a). w w w w w S w S x L L e e e O a) b) Figure. Problems A and B
4 C. E. GUTIÉRREZ AND A. SABRA Problem B: a similar question is when the rays emanate from a point source O and we ask if a a single lens L, S) exists such that all rays are refracted into a fixed given direction w. Now L is given parametrically by ρx)x for x Ω S 2 ; see Figure b). We will show in Section 3 using Brouwer fixed point theorem that Problem A has no solution if w e. In case w = e, the unique solution to Problem A is the trivial solution: L and S are contained in two horizontal planes. This is the contents of Theorem 3.. On the other hand, since Problem A is solvable for monochromatic light and for each given lower surface L, we obtain two single lenses, one for each color. We then show in Section 3. that the difference between the upper surfaces of these two lenses can be estimated by the difference between the refractive indices for each color. Concerning Problem B, we prove in Theorem 5.2, also using Brouwer fixed point theorem, that if w Ω then Problem B has no solution. The case when w Ω requires a more elaborate and long approach. In fact we show in Sections 5.2 and 5.3, in dimension two, that the solvability of Problem B is equivalent to solve a system of first order functional differential equations. For this we need an existence theorem for these type of equations that was introduced by Rogers in [Rog88]. We provide in Section a simpler proof of this existence and uniqueness result of local solutions using the Banach fixed point theorem, Theorems. and.7. Section is self contained and has independent interest. The existence of local solutions to Problem B in the plane is then proved in Section 5.5 by application of Theorem.. For this it is necessary to assume conditions on the ratio between the thickness of the lens and its distance to the point source, Theorem 5.3. We also derive a necessary condition for the solvability of Problem B, see Corollary 5.0. To sum up our result: for w = e Ω and fixing two points P and Q on the positive y-axis, with Q > P and letting k = P / Q P, we show that if k is small then there exists a unique lens L, S) local solution to Problem B such that L passes through the point P and S through Q; otherwise, for k large no solution exists. For intermediate values of k see Remark 5.. The analogue of Problem B for more than two colors has no solution, i.e., if rays emitted from the origin are superposition of three or more colors, there is no simple lens refracting these rays into a unique direction w, see Remark 5.2.
5 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 5 We close this introduction mentioning that a number of results have been recently obtained for refraction of monochromatic light, these include the papers [GH09], [GH], [Gut], [Kar6], [LGM7], and [GS7]. 2. Preliminaries In this section we mention some consequences from the Snell law that will be used later. In an homogeneous and isotropic medium, the index of refraction depends on the wavelength of light. Suppose Γ is a surface in R 3 separating two media I and II that are homogeneous and isotropic. If a ray of monochromatic light having unit direction x and traveling through the medium I hits Γ at the point P, then this ray is refracted in the unit direction m through medium II according with the Snell law in vector form, [Lun6], 2.) n x ν) = n 2 m ν), where ν is the unit normal to the surface to Γ at P going towards the medium II, and n, n 2 are the refractive indices for the corresponding monochromatic light. This has several consequences: a) the vectors x, m, ν are all on the same plane, called plane of incidence; b) the well known Snell law in scalar form n sin θ = n 2 sin θ 2, where θ is the angle between x and ν the angle of incidence), θ 2 the angle between m and ν the angle of refraction). From 2.), with κ = n 2 /n, 2.2) x n 2 /n ) m = λν, with 2.3) λ = x ν κ 2 + x ν) 2 = Φ κ x ν). Notice that λ > 0 when κ <, and λ < 0 if κ >. When κ < total reflection occurs, unless x ν κ 2, see [BW59] and [Gut, Sec. 2]. The following lemmas will be used in the remaining sections of the paper. Lemma 2.. Assume we have monochromatic light. Let Γ and Γ 2 be two surfaces enclosing a lens with refractive index n 2, and the outside of the lens is a medium with refractive index n with n n 2.
6 6 C. E. GUTIÉRREZ AND A. SABRA Suppose an incident ray with unit direction x strikes Γ at P, the ray propagates inside the lens and is refracted at Q Γ 2 into the unit direction w. Then w = x if and only if the unit normals ν P) = ν 2 Q). Proof. From the Snell law applied at P and Q x n 2 /n ) m = λ ν P), m n /n 2 ) w = λ 2 ν 2 Q), then 2.) x w = λ ν P) + n 2 /n ) λ 2 ν 2 Q). If x = w, since λ and n 2 /n ) λ 2 have the same sign and the normals are unit vectors, we conclude ν P) = ν 2 Q). Conversely, if ν P) = ν 2 Q) := ν, then from 2.) x w = λ + n /n 2 ) λ 2 ) ν. Notice that m ν = n /n 2 ) x ν λ ) = n /n 2 ) n 2 /n ) 2 + x ν) 2. Hence from 2.3) λ + n 2 /n ) λ 2 = x ν n 2 /n ) m ν + n 2 /n ) m ν n /n 2 ) 2 + m ν) 2 ) = 0. Let us now consider the case of dichromatic light, i.e., a mix of two colors b and r. That is, if a ray with direction x in vacuum strikes a surface Γ at P separating two media, then the ray splits into two rays one with color b and direction m b, and another with color r and direction m r. Here m r satisfies 2.) with n = and n 2 = n r the refractive index for the color r) and m b satisfies 2.) with n = and n 2 = n b the refractive index for the color b). Notice m b, m r are both in the plane of incidence containing P, the vector x, and νp) the normal to Γ at P. Assuming n b > n r, i.e., rays with color r travel faster than rays with color b, then for a given incidence angle θ by the Snell law the angles of refraction satisfy θ b θ r. In fact obtaining the following Lemma. sin θ = n b sin θ b = n r sin θ r, Lemma 2.2. Suppose a dichromatic ray with unit direction x strikes a surface Γ at a point P having normal ν. Then m b = m r if and only if x = ν.
7 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 7 3. The collimated case: Problem A In this section we consider the following set up. We are given Ω R 2 a compact and convex set with nonempty interior, and w a unit vector in R 3. Dichromatic rays with colors b and r are emitted from t, 0), with t Ω, into the vertical direction e = 0, 0, ). By application of the results from [GS6] with n = n 3 = and n 2 = n r, we have the following. Given u C 2, there exist surfaces parametrized by f r t) = t, ut)) + d r t)m r t), with m r t) = n r e λ r ν u t)) where λ r = Φ nr e ν u t)) from 2.3), ν u t) = ut), ) + ut) 2 the unit normal at t, ut)), and 3.) d r t) = C r e w) t, ut)) n r w m r t) from [GS6, Formula 3.)], such that lens bounded between u and f r refracts the rays with color r into w. Here the constant C r is chosen so that d r t) > 0 and f r has a normal vector at every point. This choice is possible from [GS7, Theorem 3.2 and Corollary 3.3]. Likewise there exist surfaces parametrized by f b t) = t, ut)) + d b t)m b t), with similar quantities as before with r replaced by b, such that lens bounded between u and f b refracts the rays with color b into w. We assume that n b > n r >, where n b, n r are the refractive indices of the material of the lens corresponding to monochromatic light having colors b or r, and the medium surrounding the lens is vacuum. To avoid total reflection compatibility conditions between u and w are needed, see [GS6, condition 3.)] which in our case reads λ r ν u t) w e w, and λ b ν u t) w e w. If w = e, these two conditions are automatically satisfied because λ r, λ b are both negative and ν u t) e = > 0. + ut) 2 The problem we consider in this section is to determine if there exist u and corresponding surfaces f r and f b for each color such that f r can be obtained by a reparametrization of f b. That is, if there exist a positive function u C 2 Ω), real numbers C r and C b, and a continuous map ϕ : Ω Ω such that the surfaces f r and f b, corresponding to u, C r, C b, have normals at each point and 3.2) f r t) = f b ϕt)) t Ω,
8 8 C. E. GUTIÉRREZ AND A. SABRA we refer to this as Problem A. Notice that if a solution exists then f r Ω) f b Ω). From an optical point of view, this means that the lens sandwiched between u and f b refracts both colors into w. Notice that there could be points in f b Ω) that are not reached by red rays. The answer to Problem A is given in the following theorem. Theorem 3.. If w e, then Problem A has no solution, and if w = e the only solutions to Problem A are lenses enclosed by two horizontal planes. To prove this theorem we need the following lemma. Lemma 3.2. Given a surface described by u C 2 Ω) and the unit direction w, let f r and f b be the surfaces parametrized as above. If f r t) = f b t) for some t Ω, then ν u t) = e, the unit normal vector to u at t, ut)). Proof. Since f b t) = t, ut)) + d b t) m b t) = f r t) = t, ut)) + d r t) m r t) we get d b t) m b t) = d r t) m r t), and since m r, m b are unit, d b t) = d r t). Therefore m b t) = m r t) which from Lemma 2.2 implies that ν u t) = e. Proof of Theorem 3.. To show the first part of the theorem, suppose by contradiction that Problem A has a solution with w e. Since Ω is compact and convex, by Brouwer fixed point theorem [Dug78, Sect. 2, Chap. XVI] there is t 0 Ω such that ϕt 0 ) = t 0, and so from 3.2) f r t 0 ) = f b t 0 ). Hence from Lemma 3.2 ν u t 0 ) = e. By Snell s law at t 0, ut 0 )), m b t 0 ) = m r t 0 ) = e. Since n r n b, and both colors with direction e are refracted at f b t 0 ) = f r t 0 ) into the direction w, it follows again from the Snell s law that w = e, a contradiction. To show the second part of the Theorem, assume there exist u and ϕ : Ω Ω such that problem A has a solution. Let t Ω, and Q = f r t) = f b ϕt)). Since the ray emitted from t, 0) with direction e and color r is refracted by u, f r ) into e at Q, then by Lemma 2. ν u t) = νq), where νq) denotes the normal to the upper face of the lens at Q. Similarly, applying Lemma 2. to the color b we have ν u ϕt)) = νq). We conclude that for every t Ω 3.3) ν u t) = ν u ϕt)). We will show that u is constant, i.e., ut) = 0, for all t Ω connected. Suppose by contradiction that there exists t 0 Ω, with ut 0 ) 0. If t = ϕt 0 ), then t t 0. Otherwise, from Lemma 3.2 ν u t 0 ) = ut 0), ) + ut 0 ) 2 = e, so ut 0 ) = 0.
9 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 9 Also from 3.3), ν u t 0 ) = ν u t ). Let L r t 0 ) be the red ray from t 0, ut 0 )) to f r t 0 ), and let L b t ) be the blue ray from t, ut )) to f b t ). We have that L r t 0 ) and L b t ) intersect at Q 0 := f r t 0 ) = f b t ). If Π r denotes the plane of incidence passing through t 0, ut 0 )) containing the directions e and ν u t 0 ), and Π b denotes the plane of incidence through t, ut )) containing the directions e and ν u t ), then Π r and Π b are parallel since ν u t 0 ) = ν u t ). Also by Snell s law L r t 0 ) Π r and L b t ) Π b, so Q 0 Π r Π b. We then obtain Π r = Π b := Π. Let l denote the segment Ω Π. We deduce from the above that t 0, t l. Next, let t 2 = ϕt ). As before, since ut ) = ut 0 ) 0, by Lemma 3.2 t 2 t ; and by 3.3) ν u t ) = ν u t 2 ). Let Π 2 be the plane through t 2, ut 2 )) and containing the vectors e and ν u t 2 ). We have L b t 2 ) Π 2, f r t ) = f b t 2 ), and f r t ) Π. Therefore Π 2 = Π, in particular, t 2 l. Let l denote the half line starting from t and containing t 0. We claim that t 2 l. In fact, we first have that L r t 0 ) and L b t ) intersect at Q 0. Since ν u t 0 ) = ν u t ) := ν, L r t 0 ) is parallel to L r t ), and L b t 0 ) is parallel to L b t ). And since n b > n r, it follows from the Snell law that the angle of refraction θ b for the blue ray L b t 0 ) and the angle of refraction θ r of the red ray L r t ) satisfy θ b < θ r. Hence L b t 0 ) and L r t ) diverge. Moreover, notice that all rays are on the plane Π, and L b t 2 ) is parallel to L b t ). Then, if t 2 l, we have L b t 2 ) and L r t ) diverge and cannot intersect, a contradiction since f b t 2 ) = f r t ) and the claim is proved; see Figure 2 illustrating that t 2 cannot be on l. Continuing in this way we construct the sequence t k = ϕt k ). By 3.3) ν u t k ) = ν u t k ) = = ν u t 0 ) 0, and again by Lemma 3.2 t k t k. By Snell s law {L b t k )} are all parallel, {L r t k )} are all parallel and arguing as before they are all contained in Π, and then t k l. In addition, the angles between L r t k ) and L b t k ) are the same for all k. Also, for k, if l k is the half line with origin t k and passing through t k, then as above t k+ l k. Hence the sequence {t k } is decreasing or increasing on the line l. Therefore t k converges to some ˆt l so by continuity ϕˆt) = ˆt. Hence by Lemma 3.2 uˆt) = 0, but since ut k ) = ut 0 ) 0 for all k, and u is C 2 we obtain a contradiction. Thus u is constant in Ω. Since the lower face is then contained in a horizontal plane, m r t) = m b t) = e = 0, 0, ). Hence from the form of the parameterizations of f b and f r, and since from 3.) d r and d b are constants, the upper face of the lens is also contained in a horizontal plane.
10 0 C. E. GUTIÉRREZ AND A. SABRA Q L r t 0 ) L b t ) L r t ) L b t 2 ) L b t 0 ) ν ν ν t 0 t2 t Figure 2. t 2 l 3.. Estimates of the upper surfaces for two colors. The purpose of this section is to measure how far the surfaces f r and f b can be when w = e. We shall prove the following. Proposition 3.3. Suppose f r t 0 ) = f b t 0 ) at some point t 0, and w = e. Then f r t) f b t) C n b n r for all t with a constant C depending only t 0 and n r, n b. Proof. We begin showing an upper estimate of the difference between m r t) and m b t). To simplify the notation write ν = ν u. We have m b t) = e λ b νt)) ; λ b = e ν n 2 n + e b ν)2 ; b m r t) = e λ r νt)) ; λ r = e ν n 2 r + e ν) n 2. r
11 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES So m b t) m r t) = ) e + nb n r λr λ ) b νt) := A + B. n r n b Notice A = n b n r. Next write n b n r λr λ ) b = n b λ r n r λ b ) n r n b n b n r = } {n b n r ) e νt)) + n r n 2b n b n + e ν)2 n b n 2r + e ν) 2. r Now n r n 2 b + e ν)2 n b n 2 r + e ν) 2 = n 2 b n2 r) e ν) 2 ) n r n 2 + e. b ν)2 + n b n 2 r + e ν) 2 Hence B n b n r n b n r + n b n r n 2 b n2 r n r n 2 + n b b n 2 r and therefore 3.) m b t) m r t) n b n r n b n r 2 + n b + n r n r n 2 + n b b n 2 r. We next estimate d r t) d b t), where d r t) = C r n r m r t) e, d bt) = C b n b m b t) e, by 3.). From Lemma 3.2, since f r t 0 ) = f b t 0 ), νt 0 ) = e = 0, 0, ). Then by the Snell law m r t 0 ) = m b t 0 ) = e, and from the parametrization of f r and f b, d r t 0 ) = d b t 0 ) := d 0. Hence We then obtain C b n b = C r n r = d 0. d r t) d b t) = = d 0 n r m r t) e)n b m b t) e) n b m b t) e)n r ) n r m r t) e)n b )) d 0 n r m r t) e)n b m b t) e).
12 2 C. E. GUTIÉRREZ AND A. SABRA Now = n r n b + m b t) m r t)) e + n b m r t) e n r m b t) e so from 3.) = n r n b + m b t) m r t)) e + n b n r ) m r t) e + n r m r t) m b t)) e, Cn r, n b ) n r n b. Since n r m r t) e)n b m b t) e) n r )n b ), we obtain 3.5) d r t) d b t) C n r n b, with C depending on d 0, n r, n b. Finally write f r t) f b t) = d r t)m r t) d b t)m b t) = d r t) m r t) m b t)) d b t) d r t)) m b t). Since d r t) C r /n r ) = d 0, then the desired estimate follows from 3.) and 3.5). We conclude this section analyzing the intersection of the upper surfaces of the single lenses u, f r ) and u, f b ). Proposition 3.. Let w = e. If ν u t) e for all t Ω, and u is injective in Ω, then S r S b =, where S r = f r Ω) and S b = f b Ω). This means that, the upper surfaces of the single lenses u, f r ) and u, f b ) are disjoint. Proof. Suppose P S r S b, i.e. there exists t 0, t Ω such that f r t 0 ) = f b t ), then as in the proof of 3.3) we get ν u t 0 ) = ν u t ), and therefore ut 0 ) = ut ). Since u is injective, then t 0 = t and so f r t 0 ) = f b t 0 ). Therefore from the proof of Lemma 3.2 we conclude that ν u t 0 ) = e. Remark 3.5. When u is not injective the upper surfaces of the single lenses u, f r ) and u, f b ) may or may not be disjoint. We illustrate this with lenses bounded by parallel planes. In fact, by Lemma 2. such a lens refracts all rays blue and red into the vertical direction e. Notice that if the planes are sufficiently far apart, depending on the refractive indices, then f r Ω) f b Ω) =. This is illustrated in Figure 3: if the lens in between the planes A and B, then f r Ω) f b Ω) ; and if the lens is between the planes A and C, then f r Ω) f b Ω) =.
13 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 3 C B A Ω Figure 3. The lens is between A and B or between A and C.. First order functional differential equations In this section we give a new and simpler proof of an existence theorem for functional differential equations originally due to J. Rogers [Rog88, Sec. 2]. It will be used in Section 5 to show the existence of a dichromatic lens when rays emanate from one point source. Developing an extension of Picard s iteration method for functional equations, Van-Brunt and Ockendon gave another proof of that theorem, [vbo92]. We present a topological proof that we believe has independent interest and uses the Banach fixed point theorem.
14 C. E. GUTIÉRREZ AND A. SABRA Let H be a continuous map defined in an open domain in R n+ with values in R n given by.) H := HX) = h X), h 2 X),, h n X)), with X := t; ζ 0, ζ ; ξ 0, ξ ), t R; ζ 0, ζ, ξ 0, ξ R n. We are interested in solving the following system of functional differential equations.2) Z t) = H t; Zt), Zz t)); Z t), Z z t))) Z0) = 0, with Zt) = z t),, z n t)). Theorem.. Let be a norm in R n. Assume that the system.3) P = H 0; 0, 0; P, P), has a solution P = p, p 2,, p n ) such that.) p. Let P = 0; 0, 0; P, P) R n+, and let N ε P) = { t; ζ 0, ζ ; ξ 0, ξ ) : t + ζ 0 + ζ + ξ 0 P + ξ P ε } be a neighborhood of P such that i) H is uniformly Lipschitz in the variable t, i.e., there exists Λ > 0 such that.5) H t; ζ 0, ζ ; ξ 0, ξ ) H t; ζ 0, ζ ; ξ 0, ξ ) Λ t t. for all t; ζ 0, ζ ; ξ 0, ξ ), t; ζ 0, ζ ; ξ 0, ξ ) N ε P); ii) H is uniformly Lipschitz in the variables ζ 0 and ζ, i.e., there exist positive constants L 0 and L such that.6) H t; ζ 0, ζ ; ξ 0, ξ ) H t; ζ 0, ζ ; ξ 0, ξ ) L 0 ζ 0 ζ 0 + L ζ ζ, for all t; ζ 0, ζ ; ξ 0, ξ ), t; ζ 0, ζ ; ξ 0, ξ ) N ε P); iii) H is a uniform contraction in the variables ξ 0 and ξ, i.e., there exists constants C 0 and C such that.7) H t; ζ 0, ζ ; ξ 0, ξ ) H t; ζ 0, ζ ; ξ 0, ξ ) C 0 ξ 0 ξ 0 + C ξ ξ, for all t; ζ 0, ζ ; ξ 0, ξ ), t; ζ 0, ζ ; ξ 0, ξ ) N ε P), with.8) C 0 + C < ;
15 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 5 iv) For all X N ε P).9) h X). Under these assumptions, there exists δ > 0 and Z C [ δ, δ] with t; Zt), Zz t)); Z t), Z z t))) N ε P) and Z solving the system Z t) = H t; Zt), Zz t)); Z t), Z z t))).0) Z0) = 0, for t δ and satisfying in addition that Z 0) = P. Proof. Since H is continuous, let.) α = max{ HX) : X N ε P)}. From.3).2) P = HP) α. Let µ be a constant such that.3) µ Λ + L 0 + L ) α C 0 C. For any map Z : R R n, we define the vector V Z t) = t; Zt), Z z t)) ; Z) t), Z) z t)) ). Definition.2. Let C [ δ, δ] denote the class of all functions Z : [ δ, δ] R n that are C equipped with the norm Z C [ δ,δ] = max [ δ,δ] Zt) + max [ δ,δ] Z t). We define the set C = Cδ) as follows: Z C if and only if ) Z C [ δ, δ], 2) Z0) = 0, Z 0) = P, 3) z t) t, ) Zt) Z t) α t t, 5) z t) z t) t t, 6) Z t) Z t) µ t t, 7) V Z t) N ε P), for all t δ. Define a map T on C as follows: T Zt) = t 0 Hs; Zs), Zz s)); Z s), Z z s))) ds.
16 6 C. E. GUTIÉRREZ AND A. SABRA Our goal is to show that T : C C, for δ sufficiently small, and therefore from Banach s fixed point theorem, T has a unique fixed point Z C and so Z solves.2). We will prove the theorem in a series of steps. Step. There exists δ 0 > 0 such that Cδ) is non empty for δ δ 0 ; in fact, the function Z 0 t) = tp C. Proof. Obviously, Z 0 0) = 0, Z 0) = P, and from.) z 0 t) = p t t. Also from.3) and.) Z 0 t) Z 0 t) P t t = HP) t t α t t, z 0 t) z0 t) = p t t t t, and Z 0) t) Z 0) t) = 0 µ t t. It remains to show that V Z 0t) N ε P). By definition V Z 0t) = t; t P, t p P; P, P ), and so V Z 0t) N ε P) if and only if t + t P + t p P ε, which is equivalent to ε.) t + P + p P := δ 0. Step 2. Cδ) is complete for every δ > 0. Proof. Let Z k be a Cauchy sequence in C. Since C [ δ, δ] is complete, Z k converges uniformly to a function Z C [ δ, δ], and Z k) converges uniformly to Z. Since Z k satisfy properties )-7) in Definition.2, then Step 2 follows by uniform convergence. Step 3. If Z C and W = TZ = w,, w n ), then w t) t. Proof. From.9) and since V Z t) N ε P) for t δ, it follows that t w t) = h V Z s)) ds t. 0 Step. If Z C and W = TZ, then Wt) W t) α t t,
17 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 7 and for every t, t [ δ, δ]. w t) w t) t t Proof. Since V Z t) N ε P), by.) for all t δ t Wt) W t) = HV Z s)) ds α t t, t and from.9), we get similarly the desired estimate for w t) w t). Step 5. If Z Cδ) and W = TZ, then for every t, t [ δ, δ]. W t) W t) µ t t, Proof. From the Lipschitz estimates for H W t) W t) = HV Z t)) HV Z t)) Λ t t + L 0 Zt) Z t) + L Zz t)) Zz t)) + C 0 Z t) Z t) + C Z z t)) Z z t)). Since z t) t δ and z t) t δ, we get from the Lipschitz properties of Z, z, and Z W t) W t) Λ t t + L 0 α t t + L α z t) z t) + C 0 µ t t + C µ z t) z t) Λ + L 0 + L )α + C 0 + C )µ ) t t. From.3), Λ + L 0 + L )α C 0 C )µ, then Step 5 follows. Step 6. For δ sufficiently small, W = TZ C for each Z C. Proof. From the previous steps, it remains to show that V W t) N ε P). Define S Z t) = t + Zt) + Zz t)) + Z t) P + Z z t)) P S W t) = t + Wt) + Ww t)) + W t) P + W w t)) P. Since V Z t) N ε P), we have S Z t) ε. We shall prove that S W t) ε by choosing δ sufficiently small. In fact, from.) for every t δ t.5) Wt) = HV Z s)) ds α t α δ, 0
18 8 C. E. GUTIÉRREZ AND A. SABRA and from.9) w t) = t 0 h V Z s)) ds t δ. Hence Ww t)) α δ. We next estimate W t) P. properties of H we write Using the Lipschitz W t) P = HV Z t)) HP) Λ t + L 0 Zt) + L Zz t)) + C 0 Z t) P + C Z z t)) P. Notice that Zt) = Zt) Z0) α t αδ, and since z t) t δ then Zz t)) αδ. Also Z t) P = Z t) Z 0) µ t µδ. and Therefore, for t δ Z z t)) P µδ. and since w t) δ, we also get We conclude that so choosing δ W t) P [ Λ + αl 0 + L )δ + µc 0 + C ) ] δ, W w t)) P [ Λ + αl 0 + L )δ + µc 0 + C ) ] δ. S W t) δ + 2Λ + 2α + L 0 + L ) + 2µC 0 + C ) ), ε Step 6 follows. + 2Λ + 2α + L 0 + L ) + 2µC 0 + C ) It remains to show that T is a contraction. Step 7. If Z, Z 2 Cδ) with δ small enough from the previous steps, then TZ TZ 2 C q Z Z 2 C, [ δ,δ] [ δ,δ] for some q <. Proof. Let W t) = TZ t), W 2 t) = TZ 2 t). By the fundamental theorem of calculus we have for every t δ W t) W 2 t) t ) ) W s) W 2 s) ds δ sup ) ) W t) W 2 t) 0 δ W W 2 C [ δ,δ], t δ
19 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 9 and similarly Z t) Z 2 t) δ Z Z 2 C [ δ,δ]. From the Lipschitz properties of H, for every t δ, ) ) W t) W 2 t) H V Z t)) H V Z 2t)) L 0 Z t) Z 2 t) + L Z z t)) Z 2 z 2 t)) + C 0 Z ) t) Z 2 ) t) + C Z ) z t)) Z 2) z 2 t)). We have Z t) Z 2 t) δ Z Z 2 C [ δ,δ] Z z t)) Z2 z 2 t)) Z z t)) Z2 z t)) Z + 2 z t)) Z2 z 2 t)) δ Z Z 2 C [ δ,δ] + α z t) z2 t) δ Z Z 2 C [ δ,δ] + αc Z t) Z 2 t) δ αc + ) Z Z 2 C [δ,δ] ) ) Z t) Z 2 t) Z Z 2 C [ δ,δ] ) Z z t)) Z 2) z 2 t)) ) Z z t)) Z 2) z t)) + ) Z 2 z t)) Z 2) z 2 t)) Z Z 2 C + [ δ,δ] µ z t) z2 t) Z Z 2 C + µc [ δ,δ] Z t) Z 2 t) µ C δ + ) Z Z 2 C [ δ,δ] ; here C is a constant larger than, depending only on the choice of the norm in R n, since all norms in R n are equivalent such constant exists. Combining the above inequalities, we obtain ) ) W t) W 2 t) L 0 δ + L δ αc + ) + C 0 + C µc δ + )) Z Z C := M δ + C 0 + C ) Z Z 2 C, and from the fundamental theorem of calculus W t) W 2 t) δ sup ) ) W t) W 2 t) δ M δ + C 0 + C ) Z Z 2 C. t δ We conclude that W W 2 C + δ) M δ + C [ δ,δ] 0 + C ) Z Z 2 C [ δ,δ] Since C 0 + C <, then choosing δ sufficiently small Step 7 follows.
20 20 C. E. GUTIÉRREZ AND A. SABRA We conclude that there exists δ > 0 small such that for 0 < δ δ, the map T : Cδ) Cδ) is a contraction and hence by the Banach fixed point theorem there is a unique Z Cδ) such that Zt) = TZt) = t 0 HV Z s)) ds. Differentiating with respect to t, we get that Z solves.0) for t δ. We make the following observations about the assumptions in Theorem.. Remark.3. We show that even for H smooth, satisfying.3) with.), and.9), the system.2) might not have any real solutions in a neighborhood of t = 0. In fact, consider for example the following ode:.6) z t) = z t) 2 + t, z0) = 0. In this case n = and H : R 5 R with H t; ζ 0, ζ ; ξ 0, ξ ) = ξ 0) 2 + t analytic. The system P = H0; 0, 0; P, P) has a unique solution P = /2, and so.3) and.) hold. Let P = 0; 0, 0; /2, /2). Since HP) <,.9) holds in a small neighborhood of P. On the other hand,.6) cannot have real solutions for t < 0 and so in any neighborhood of t = 0. This shows that there cannot exist a norm in R so that the contraction condition.8) is satisfied. In particular, this shows that the conclusion of [vbo92, Lemma 2.2] is in error. Remark.. Let H be a map from a domain in R n+ with values in R n, and let P be a solution to the system P = H0; 0, 0; P, P) satisfying.). Assume H is C in a neighborhood of P = 0; 0, 0; P, P). Given a norm in R n, let be the induced norm on the space of n n matrices, i.e., for a n n matrix A A = max{ Av : v R n, v = }, see [HJ85, Section 5.6]. Since H is C then there exists a neighborhood N ε P) as defined in Theorem. such that.5),.6),.7) are satisfied. The following proposition shows estimates for C 0 + C in.7). Proposition.5. We define the n n matrices h i h i ξ 0H = ξ 0, ξ H = ξ. j i,j n j i,j n
21 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 2 If.7) holds for some C 0, C, then.7) C 0 ξ 0HP), and C ξ 0HP). In addition,.7) holds with C 0 = max Nε P) ξ 0H and C = max Nε P) ξ H. Proof. We first prove.7). Let v R n with v = ; for s > 0 small, the vector 0; 0, 0; P + s v, P) N ε P). From.7), we get H0; 0, 0; P + s v, P) H0; 0, 0; P, P) C 0 s. Dividing by s and letting s 0 we obtain, by application of the mean value theorem on each component, that for every v R n with v = C 0 ξ 0HP) v t. Taking the supremum over all v R n we obtain C 0 ξ 0HP). Similarly we get C ξ HP). To show the second part of the proposition, by the fundamental theorem of calculus, we have for t; ζ 0, ζ ; ξ 0, ξ ), t; ζ 0, ζ ; ξ 0, ξ ) N ε P) that H t; ζ 0, ζ ; ξ 0, ξ ) H t; ζ 0, ζ ; ξ 0, ξ ) = = DH s) t; ζ 0, ζ ; ξ 0, ξ ) + s t; ζ 0, ζ ; ξ 0, ξ )) 0; 0, 0; ξ 0 ξ 0, ξ ξ ) t ds ξ 0H s) t; ζ 0, ζ ; ξ 0, ξ ) + s t; ζ 0, ζ ; ξ 0, ξ )) ξ 0 ξ 0) t ds 0 ξ H s) t; ζ 0, ζ ; ξ 0, ξ ) + s t; ζ 0, ζ ; ξ 0, ξ )) ξ ξ ) t ds, where DH is the n + ) n matrix of the first derivatives of H with respect to all variables. Then H t; ζ 0, ζ ; ξ 0, ξ ) H t; ζ 0, ζ ; ξ 0, ξ ) ξ 0H s) t; ζ 0, ζ ; ξ 0, ξ ) + s t; ζ 0, ζ ; ξ 0, ξ )) ξ 0 ξ 0 ds 0 + ξ H s) t; ζ 0, ζ ; ξ 0, ξ ) + s t; ζ 0, ζ ; ξ 0, ξ )) ξ ξ ds 0 max ξ 0H ξ 0 ξ 0 + max ξ H ξ ξ. N ε P) N ε P) The proof is then complete.
22 22 C. E. GUTIÉRREZ AND A. SABRA Given an n n matrix A, let R A be its spectral radius, i.e., R A is the largest absolute value of the eigenvalues of A. From [HJ85, Theorem 5.6.9] we have R A A for any matrix norm. Then from.7) we get the following corollary that shows that the possibility of choosing a norm in R n for which the contraction property.8) holds depends on the spectral radii of the matrices ξ 0HP), ξ HP). Corollary.6. Let H be as above. Denote by R ξ 0 and R ξ the spectral radii of the matrices ξ 0HP), and ξ HP) respectively. Then for any norm in R n and any C 0, C satisfying.7) we have C 0 + C R ξ 0 + R ξ. To apply Theorem., we need H to satisfy.7) together with the contraction condition.8) for some norm in R n. It might not be possible to find such a norm. In fact, if an n n matrix A has spectral radius R A, then for each norm in R n the induced matrix norm satisfies A ; see [Theorem and Lemma 5.6.0][HJ85]. So if the sum of the spectral radii of the Jacobian matrices ξ 0HP), ξ HP) is bigger than one, then from Corollary.6 it is not possible to find a norm in R n for which.8) holds... Uniqueness of solutions. In this section we show the following uniqueness theorem. Theorem.7. Under the assumptions of Theorem., the local solution to.0) with Z 0) = P is unique. The theorem is a consequence of the following lemma. Lemma.8. Let Cδ) be the set in Definition.2. If there exists δ > 0 such that W solves.0) for t δ, with W 0) = P, and V W t) N ε P) for t δ, then W Cδ). Proof. Since w t) = h V W t)), then.9) implies t.8) w t) = h V W s)) ds t. Also for t, t δ since W is a solution to.0) then from.) t.9) Wt) W t) = HV W s)) ds α t t and by.9).20) w t) w t) = 0 t t t h V W s)) ds t t.
23 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 23 It remains to show the Lipschitz estimate on W. Let t, t δ, then by the Lipschitz properties of H W t) W t) = HV W t)) HV W t)) Λ t t + L 0 Wt) W t) + L Ww t)) Ww t)) + C 0 W t) W t) + C W w t)) W w t)). Using.9),.8), and.20), we get that for every t, t δ.2) W t) W t) Λ+L 0 +L )α) t t +C 0 W t) W t) +C W w t)) W w t)). Fix t and t and let r = t t. Let τ, and τ be such that τ, τ δ and τ τ r, then by.20) w τ) w τ) τ τ r. Hence applying.2) for τ and τ we get for τ, τ δ, τ τ r that W τ) W τ) Λ + L 0 + L ) α) τ τ + C 0 W τ) W τ) + C W w τ)) W w τ)) Λ + L 0 + L ) α) r + C 0 + C ) sup τ, τ δ, τ τ r W τ) W τ). Hence taking the supremum on the left hand side of the inequality, and using.3) we get so for every t, t δ sup W τ) W τ) Λ + L 0 + L ) α r µ r τ, τ δ, τ τ r C 0 C W t) W t) and the lemma follows. sup W τ) W τ) µ t t, τ, τ δ, τ τ t t Proof ) of Theorem.7. Let δ, δ 2 δ and let W i solving.0) for t δ i, with W i 0) = P, and VW it) N ε P) for t δ i for i =, 2. From Lemma.8 W i Cδ i ), and since they solve.0) we have TW i t) = W i t) for t δ i, i =, 2. Let δ = min{δ, δ 2 }. We have Cδ i ) Cδ), i =, 2. Since δ δ, from the proof of the existence theorem T has a unique fixed point in Cδ). But, TW i = W i for t δ and so W = W 2 for t δ. Remark.9. If the vector P solution to the system.3) does not satisfy.), then the system.0) may have infinitely many solutions. This goes back to the paper by Kato and McLeod [KM7, Thm. 2] about single functional differential
24 2 C. E. GUTIÉRREZ AND A. SABRA equations. We refer to [FMOT7, Equation.7)] for representation formulas for infinitely many solutions. Remark.0. Theorem. has an extension to more variables and the proof is basically the same. In fact, the set up in this case and the result are as follows. We set Zt) = z t),, z n t)) where z i t) are real valued functions of one variable, and Z t) = z t),, z nt) ). Let H = h,, h n ) where h i = h i t; ζ 0, ζ,, ζ m ; ξ 0, ξ,, ξ m) are real valued functions with ζ j, ξ j R n for j m, so each h i has +2 m+) n variables. Let X = t; ζ 0, ζ,, ζ m ; ξ 0, ξ,, ξ m). We assume m n. Set Zz k t)) = z z k t)),, z n z k t))) for k m. We want to find Zt) as above satisfying the following functional differential equation Z t) = H t; Zt), Zz t)),, Zz m t)); Z t), Z z t)),, Z z m t))) Z0) = 0,, 0) R n, for t in a neighborhood of 0. We assume that there exists P = p,, p n ) R n with p i for i m solving P = H 0; 0,, 0; P,, P) where dots mean m + times. Let P = 0; 0,, 0; P,, P) R 2m+)n+, and let be a norm in R n with N ε P) = { t; ζ 0,, ζ m ; ξ 0,, ξ m) ; t + ζ ζ m + ξ 0 P + + ξ m P ε } a neighborhood of P such that i) H is uniformly Lipschitz in the variable t, i.e., there exists Λ > 0 such that H t; ζ 0,, ζ m ; ξ 0,, ξ m) H t; ζ 0,, ζ m ; ξ 0,, ξ m) Λ t t. for all t; ζ 0,, ζ m ; ξ 0,, ξ m), t; ζ 0,, ζ m ; ξ 0,, ξ m) N ε P); ii) H is uniformly Lipschitz in the variables ζ 0,, ζ m i.e., there exist positive constants L 0,, L m such that H t; ζ 0,, ζ m ; ξ 0,, ξ m) H t; ζ 0,, ζ m ; ξ 0,, ξ m) L 0 ζ 0 ζ 0 + +Lm ζ m ζ m, for all t; ζ 0,, ζ m ; ξ 0,, ξ m), t; ζ 0,, ζ m ; ξ 0,, ξ m) N ε P);
25 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 25 iii) H is a uniform contraction in the variables ξ 0,, ξ m, i.e., there exists constants C 0,, C m such that H t; ζ 0,, ζ m ; ξ 0,, ξ m) H t; ζ 0,, ζ m ; ξ 0,, ξ m) C 0 ξ 0 ξ 0 + +Cm ξ m ξ m, for all t; ζ 0,, ζ m ; ξ 0,, ξ m), t; ζ 0,, ζ m ; ξ 0,, ξ m) N ε P), with C C m < ; iv) For all X N ε P) h X). Under these assumptions, there exists δ > 0, such that the system Z t) = H t; Zt), Zz t)),, Zz m t)); Z t), Z z t)),, Z z m t))) Z0) = 0, has a unique solution defined for t δ satisfying Z 0) = P. 5. One point source case: Problem B The setup in this section is the following. We are given a unit vector w R 3, and a compact domain Ω contained in the upper unit sphere S 2, such that Ω = xd), where D is a convex and compact domain in R 2 with nonempty interior. Here xt) are for example spherical coordinates, t D. Dichromatic rays with colors b and r are now emitted from the origin with unit direction xt), t D. From the results from [Gut3, Section 3] with n = n 3 =, n 2 = n r, and e = w we have the following. Consider a C 2 surface with a given polar parametrization ρt)xt) for t D, and the surface parametrized by f r t) = ρt)xt) + d r t)m r t), with m r t) = n r xt) λr ν ρ t) ), λ r t) = Φ nr xt) νρ t) ) from 2.3), ν ρ t) the outer unit normal at ρt)xt), and with 5.) d r t) = C r ρt) w xt)), n r w m r t) for some constant C r. Then the lens bounded between ρ and f r refracts the rays with color r into the direction w provided that C r is chosen so that d r t) > 0 and f r has a normal at each point. Likewise and for the color b the surface f b t) = ρt)xt) + d b t)m b t), with similar quantities as before with r replaced by b, does a similar refracting job for rays with color b.
26 26 C. E. GUTIÉRREZ AND A. SABRA As before, we assume n b > n r >, and the medium surrounding the lens is vacuum. To avoid total reflection for each color, compatibility conditions between ρ and w are needed, see [Gut3, condition 3.8)] which in our case reads λ r ν ρ t) w xt) w, and λ b ν ρ t) w xt) w. The problem we consider in this section is to determine if there exist ρ and corresponding surfaces f r and f b for each color such that f r can be obtained by a re-parametrization of f b. That is, if there exist a positive function ρ C 2 D), real numbers C r and C b, and a C map ϕ : D D such that the surfaces f r and f b, corresponding to ρ, C r, C b, have normals at each point and 5.2) f r t) = f b ϕt)) t D. We refer to this as Problem B. As in the collimated case, if a solution exists f r D) f b D). Again, from an optical point of view, this means that the lens sandwiched between ρ and f b refracts both colors into w; however, there could be points in f b D) that are not reached by red rays. If w Ω, we will show in Theorem 5.2 that Problem B is not solvable. On the other hand, when w Ω we shall prove, in dimension two, that problem B is locally solvable, Theorem 5.3. Notice that by rotating the coordinates we may assume without loss of generality that w = e. Theorem 5.3 will follow from Theorem. on functional differential equations, assuming an initial size condition on the ratio between the thickness of the lens and its distance to the origin. By local solution we mean that there exists an interval [ δ, δ] D, a positive function ρ C 2 [ δ, δ], real numbers C r and C b, and ϕ : [ δ, δ] [ δ, δ] C such that the corresponding surfaces f r and f b have normals at every point and f r t) = f b ϕt)) t [ δ, δ]. We will also show a necessary condition for solvability of Problem B, Corollary 5.0. We first state the following lemma whose proof is the same as that of Lemma 3.2. Lemma 5.. Given a surface ρt)xt), t D, and w a unit vector in R 3, let f r and f b be the surfaces parametrized as above. If f r t) = f b t) for some t D, then ν ρ t) = xt). In addition d b t) = d r t). We next show nonexistence of solutions to Problem B for w Ω.
27 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 27 Theorem 5.2. Let w be a unit vector in R 3. If Problem B is solvable, then xt) = w for some t D. Therefore, since xd) = Ω, Problem B has no solutions for w Ω. Proof. Suppose there exist ρ and ϕ : D D satisfying 5.2). Since D is a compact and convex domain, by Brouwer fixed point theorem ϕ has a fixed point t 0, and from 5.2) f r t 0 ) = f b t 0 ). Therefore, by Lemma 5. ν ρ t 0 ) = xt 0 ), and by the Snell s law at ρt 0 )xt 0 ) we have m b t 0 ) = m r t 0 ) = xt 0 ). Using Snell s law again at f r t 0 ) = f b t 0 ), since n r n b and both colors with direction xt 0 ) are refracted at f r t 0 ) = f b t 0 ) into w, we obtain xt 0 ) = w. From now on our objective is to show that problem B is locally solvable in dimension two when w Ω, Theorem Two dimensional case, w Ω. Let w be a unit vector in R 2, by rotating the coordinates we will assume that w = e = 0, ). Let Ω be a compact domain of the upper circle, such that Ω = xd) where D is a closed interval in π/2, π/2), and xt) = sin t, cos t). We will use the following expression for the normal to a parametric curve. Lemma 5.3. If a curve is given by the polar parametrization ρt)xt) = ρt) sin t, cos t), with ρ C, then the unit outer normal is νt) = ρ2 t) + ρ t) 2 ρt) sin t ρ t) cos t, ρ t) sin t + ρt) cos t ). Proof. The tangent vector to the curve at the point ρt) xt), with xt) = sin t, cos t), equals Thus ρt) xt)) = ρ t)xt) + ρt)x t) = ρ t) sin t + ρt) cos t, ρ t) cos t ρt) sin t ). ρt) xt)) 2 = ρt) 2 + ρ t) 2. Hence the normal νt) = ± ρt) sin t ρ t) cos t, ρ t) sin t + ρt) cos t ). ρ2 t) + ρ t) 2 Since νt) is outer, i.e. xt) νt) 0, so we take the positive sign above and the lemma follows. As a consequence, we obtain the following important lemma. Lemma 5.. Assume Problem B is solvable in the plane when w = e. Then 0 D, ϕ0) = 0, d b 0) = d r 0), and ρ 0) = 0.
28 28 C. E. GUTIÉRREZ AND A. SABRA Proof. Using the proof of Theorem 5.2, there exists t 0 D such that ϕt 0 ) = t 0 and xt 0 ) = e = 0, ), then sin t 0, cos t 0 ) = 0, ), and t 0 = 0. By Lemma 5., we get d b 0) = d r 0), and ν ρ 0) = e. Therefore, Lemma 5.3 yields 0, ) = ρ2 0) + ρ 0) 2 ρ 0), ρ0)) Derivation of a system of functional equations from the solvability of Problem B in the plane. Assume Problem B has a solution refracting rays of both colors b and r into the direction e, and recall Lemma 5.. We set ρ0) = ρ 0 and d b 0) = d r 0) = d 0, and prove the following theorem. Theorem 5.5. Suppose there exist ρ and ϕ solving Problem B in an interval D. Let Zt) = z t), z 2 t), z 3 t), z t), z 5 t)) R 5 with 5.3) z t) = ϕt), z 2 t) = v t) + ρ 0, z 3 t) = v 2 t), z t) = v t), z 5t) = v 2 t) ρ 0, where v t) = ρt) cos t, and v 2 t) = ρt) sin t. Let Z = 0; 0, 0;Z 0), Z 0)) R 2. 2 There exists a neighborhood of Z and a map H defined and smooth in that neighborhood with H := Ht; ζ 0, ζ ; ξ 0, ξ ) = h,, h 5 ) where ζ 0, ζ, ξ 0, ξ R 5, ζ i = ζ i, ζi 2,, ζi 5), ξ i = ξ i, ξi 2,, ξi 5), and with the functions h,, h 5 given by 5.2), 5.26), 5.28), 5.30), and 5.32), respectively, such that Z is a solution to the system of functional differential equations 5.) Z t) = H t; Zt), Zz t)); Z t), Z z t))) Z0) = 0 for t in a neighborhood of 0. The map H depends on the values ρ 0 and d 0. Proof. From Lemma 5., Z0) = 0. We will derive the expressions for h i t; ζ 0, ζ ; ξ 0, ξ ), i 5, so that z i t) = h i t; Zt), Zz t)), Z t), Z z t))). The first step is to express the quantities involved as functions of t; Zt), Zz t)); Z t), Z z t))). We are assuming that 0 is an interior point of D. Otherwise, in our statements the interval [ δ, δ] has to be replaced by either [ δ, 0] or [0, δ]. 2 Z 0) = ϕ 0), 0, ρ 0, ρ 0) + ρ 0, 0 ).
29 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 29 From the Snell law, a ray emitted from the origin with color r and direction xt) = sin t, cos t) refracts by a curve ρt)xt) into a medium with refractive index n r into the direction m r t) such that xt) n r m r t) = Φ nr x νt)) νt), where νt) is the outward unit normal to ρ at ρt)xt). From 2.3) Φ nr s) = s n 2 r + s 2 = n 2 r s + n 2 r + s 2, and from Lemma 5.3 νt) = v t) v t), and xt) νt) = ρt) ρ2 t) + ρ t) 2 vt) = v t), v 2 t)). So Φ nr xt) νt)) = Hence vt) v t) + n 2 r n 2 r + vt) 2 v t) 2 = = vt) v t), with n 2 r) v t) vt) + vt) 2 + n 2 r ) v t) ) m r t) = n r [ xt) Φnr xt) νt))νt) ] = n r [xt) A r vt), v t)) v t)] := m r t), m 2r t)) with 5.6) A r vt), v t)) = n 2 r vt) + vt) 2 + n 2 r ) v t) 2. Rewriting the last expressions in terms of the variables z i t) introduced in 5.3), and omitting the dependance in t to simplify the notation, we obtain 5.7) A r vt), v n 2 r t)) = z 2 ρ 0, z 3 ) z2 + ρ 0, z 3 ) 2 + n 2 r ) z, z 5 + ρ 0 ) := A r Zt)), 2 5.8) 5.9) m r t) = n r [sin t A r Z) z ] := µ r t, Zt)), m 2r t) = n r [ cos t Ar Z) z 5 + ρ 0 ) ] := τ r t, Zt)). Notice that τ r 0, Z0)) = τ r 0, 0) =. If for each t, the ray with direction m r t) is refracted by the upper face of the lens into the direction e = 0, ), then the upper face is parametrized by the vector f r t) = ρt)xt) + d r t)m r t) := f r t), f 2r t) ).
30 30 C. E. GUTIÉRREZ AND A. SABRA From 5.), and 5.9) 5.0) d r t) = C r ρt) cos t) n r m 2r t) = C r vt) v t) n r τ r t, Zt)) = C r z2 ρ 0, z 3 ) z2 + ρ 0 n r τ r t, Zt)) := D r t, Zt)), with C r a constant. Since ρ and ϕ solve Problem B, from Lemma 5. we have ρ 0) = 0, and ν0) = 0, ). So m r 0) = 0, ) and from 5.) we get C r = n r ) d 0. Hence 5.) 5.2) f r t) = z 3 + D r t, Z) µ r t, Z) := F r t, Zt)) f 2r t) = z 2 + ρ 0 + D r t, Z) τ r t, Z) := F 2r t, Zt)). In addition, by the Snell law at f r t), m r t) n r e = λ 2,r t) ν r t), where ν r is the normal to the upper surface at the point f r t) we are using here that the normal to f r exists since we are assuming Problem B is solvable). Since n r >, then λ 2,r > 0 and so taking absolute values in the last expression yields 5.3) λ 2,r t) = m rt) e n r = + 2 m n 2 2r t) = + 2 τ r n r n 2 r t, Z) := Λ 2,r t, Zt)). r n r For t R and ζ = ζ,, ζ 5 ) R 5 we let n 2 r A r ζ) = ζ 2 ρ 0, ζ 3 ) ζ2 + ρ 0, ζ 3 ) 2 + n 2 r ) ζ, ζ 5 + ρ 0 ) 2 5.) µ r t, ζ) = n r [sin t A r ζ) ζ ], τ r t, ζ) = n r [ cos t Ar ζ) ζ 5 + ρ 0 ) ] D r t, ζ) = C r ζ2 ρ 0, ζ 3 ) ζ2 + ρ 0, with C r = n r ) d 0 n r τ r t, ζ) F r t, ζ) = ζ 3 + D r t, ζ) µ r t, ζ), F 2r t, ζ) = ζ 2 + ρ 0 + D r t, ζ) τ r t, ζ) Λ 2,r t, ζ) = + n 2 r 2 n r τ r t, ζ). The functions A r, µ r, τ r are well defined and smooth for all t R and for all ζ = ζ, ζ 2, ζ 3, ζ, ζ 5 ) with ζ 2, ζ 3 ) ρ 0, 0). Since τ r 0, 0) =, then all functions in 5.) are well defined and smooth in a neighborhood of t = 0 and ζ = 0. Notice that the definitions of A r ζ), µ r t, ζ), τ r t, ζ) and Λ 2,r t, ζ) depend on the value of ρ 0, and the definitions of D r t, ζ), F r t, ζ) and F 2r t, ζ) depend on the values of ρ 0 and d 0.
31 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 3 To determine later the functions h i we next calculate the derivatives of A r, m r, m 2r, d r, F r, F 2r, and λ 2,r with respect to t. Differentiating 5.7), 5.8), 5.9), 5.0), 5.), and 5.2) with respect to t yields 5.5) d d t A rvt), v t)) = 5.6) 5.7) 5.8) d d t d rt) = n 2 r z2 ρ 0, z 3 ) z2 + ρ 0, z 3 ) 2 + n 2 r ) z, z 5 + ρ 0 ) 2 = A rz) 2 n 2 r z 2 ρ 0, z 3 ) z 2, z 3 ) z 2 ρ 0, z 3 ) z 2 ρ 0, z 3 ) z 2, z 3 ) z 2 ρ 0, z 3 ) := ÃrZt), Z t)), + z 2 ρ 0, z 3 ) z 2, z 3 ) + n2 r )z, z 5 + ρ 0 ) z, z 5 ) z2 ρ 0, z 3 ) 2 + n 2 r ) z, z 5 + ρ 0 ) 2 d d t m rt) = n r [ cos t Ar Z) z ÃrZ, Z ) z ] := µr t, Zt), Z t)), + z 2 ρ 0, z 3 ) z 2, z 3 ) + n2 r )z, z 5 + ρ 0 ) z, z 5 ) ) 2 z2 ρ 0, z 3 ) 2 + n 2 r ) z, z 5 + ρ 0 ) 2 d d t m 2rt) = n r [ sin t Ar Z) z 5 ÃrZ, Z ) z 5 + ρ 0 ) ] := τ r t, Zt), Z t)), ) z2 ρ 0, z 3 z 2, z 3 ) ) z 2 z 2 ρ 0, z n r τ r t, Z)) + τ r t, Z, Z ) C r ) ) z2 ρ 0, z 3 z2 + ρ 0 3 n r τ r t, Z)) 2 z 2 ρ 0, z 3 ) z 2, z 3 ) z 2 ρ 0, z 3 ) z 2 + τ rt, Z, Z ) D r t, Z) = := D r t, Zt), Z t)) n r τ r t, Z) 5.9) 5.20) 5.2) d d t f rt) = z 3 + D rt, Z) µ r t, Z, Z ) + D r t, Z, Z ) µ r t, Z) := F r t, Zt), Z t)) d d t f 2rt) = z 2 + D rt, Z) τ r t, Z, Z ) + D r t, Z, Z ) τ r t, Z) := F 2r t, Zt), Z t)) d r t, Z, Z d t λ n 2,rt) = r τ ) := Λ 2,r t, Z) Λ 2,r t, Zt), Z t)).
32 32 C. E. GUTIÉRREZ AND A. SABRA For t R and ζ, ξ R 5 we let 5.22) Ã r ζ, ξ) = A rζ) 2 ζ 2 ρ 0, ζ 3 ) ξ 2, ξ 3 ) n 2 r ζ 2 ρ 0, ζ 3 ) + ζ 2 ρ 0, ζ 3 ) ξ 2, ξ 3 ) + n 2 r )ζ, ζ 5 + ρ 0 ) ξ, ξ 5 ) ζ2 ρ 0, ζ 3 ) 2 + n 2 r ) ζ, ζ 5 + ρ 0 ) 2 µ r t, ζ, ξ) = [ cos t Ar ζ)ξ n Ãrζ, ] ξ)ζ r τ r t, ζ, ξ) = n r [ sin t Ar ζ)ξ 5 Ãrζ, ξ)ζ 5 + ρ 0 ) ] ζ 2 ρ 0, ζ 3 ) ξ 2, ξ 3 ) ζ 2 ρ 0, ζ 3 ) ξ 2 + τ r t, ζ, ξ) D r t, ζ) D r t, ζ, ξ) = n r τ r t, ζ) F r t, ζ, ξ) = ξ 3 + D r t, ζ) µ r t, ζ, ξ) + D r t, ζ, ξ)µ r t, ζ) F 2r t, ζ, ξ) = ξ 2 + D r t, ζ) τ r t, ζ, ξ) + D r t, ζ, ξ)τ r t, ζ) r t, ζ, ξ) n Λ 2,r t, ζ, ξ) = r τ. Λ 2,r t, ζ) As for 5.), all functions in 5.22) are well defined and smooth in a neighborhood of t = 0 and ζ = 0, and for any ξ. We mention the following remark that will be used later. Remark 5.6. Using the formulas in 5.) and 5.22), notice that for any differentiable map U : V R 5 with V a neighborhood of t = 0 and with U0) = 0, we have the following formulas valid for t in a neighborhood V of t = 0 possibly smaller than V): d dt [A rut))] = ÃrUt), U t)), d dt [µ rt, Ut))] = µ r t, Ut), U t)), d dt [τ rt, Ut))] = τ r t, Ut), U t)), d dt [D rt, Ut))] = D r t, Ut), U t)), d dt [F rt, Ut))] = F r t, Ut), U t)), d dt [F 2rt, Ut))] = F 2r t, Ut), U t)), d dt [Λ 2,rt, Ut))] = Λ 2,r t, Ut), U t)). We also obtain the same formulas for the color b with n r replaced by n b. We are now ready to calculate h i, one by one, for i =,, 5 to obtain the system of functional differential equations satisfied by Zt) = ϕt), v t) + ρ 0, v 2 t), v t), v 2 t) ρ 0). Recall h i := h i t; ζ 0, ζ ; ξ 0, ξ ), with ζ 0, ζ, ξ 0, ξ R 5,
33 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 33 ζ i = ζ i,, ζi 5), ξ i = ξ i,, ξi 5), i = 0,. Calculation of h. Since z = ϕ satisfies f r t) = f b ϕt)), taking the first components and differentiating with respect to t yields 5.23) f r t) = ϕ t) f b ϕt)). We claim that f ϕt)) 0 in a neighborhood of t = 0. b Proof of the claim. By continuity of f ϕ and since ϕ0) = 0 by Lemma 5., it is b equivalent to show that f 0) 0. b Recall that f r t) = ρt) sin t + d r t)m r t), ρ0) = ρ 0, d r 0) = d 0, and m r 0) = 0, ). Then Also from 5.6), since Z0) = 0 f r 0) = ρ 0 + d 0 m r 0). m r 0) = n r Ar 0)z 0)). Notice that z t) = v t) = ρt) cos t ρ t) cos t + 2ρ t) sin t, then z 0) = ρ 0 ρ 0). Also from 5.7) A r 0) = n2 r = n r. + n r )ρ 0 ρ 0 We conclude that m r 0) = + n ) r ρ 0 ρ 0)) = n r ρ 0). n r ρ 0 n r ρ 0 Similarly, f b t) = ρt) sin t + d b t)m b t), d b 0) = d 0, m b 0) = 0, ), and we get f 0) = ρ b 0 + d 0 m 0), with b m b 0) = n b n b ρ 0) ρ 0. Suppose by contradiction that f 0) = 0. Then by 5.23) f 0) = 0. Hence from b r the calculations above m 0) = b m 0) = ρ r 0/d 0. Since n r n b, m 0) = b m 0) r implies ρ 0) = 0. So m b 0) = m r 0) = = ρ 0/d 0 < 0, a contradiction. Since z = ϕ we then conclude that f b z t)) 0 in a neighborhood of t = 0, and z t) = ϕ t) = f r t) f b z t)).
34 3 C. E. GUTIÉRREZ AND A. SABRA Applying formula 5.9) for both b and r yields with z t) = ϕ t) = F r t, Zt), Z t)) F b z t), Zz t)), Z z t))) := h t; Zt), Zz t)); Z t), Z z t))) 5.2) h t; ζ 0, ζ ; ξ 0, ξ ) = F r t, ζ 0, ξ 0 ) F b ζ 0, ζ, ξ ) ; F r is defined explicitly in 5.22), and F b has a similar expression with n r replaced by n b. We next verify that h is smooth in a neighborhood of Z = 0; 0, 0; Z 0), Z 0)); Z 0) = ϕ 0), 0, ρ 0, ρ 0) + ρ 0, 0 ). From 5.), A r is smooth in a neighborhood of 0 R 5, µ r, τ r, D r, F r, F 2r, Λ 2,r are smooth in a neighborhood of 0, 0) R 6. Also, from 5.22), Ãr is smooth in a neighborhood of 0, Z 0)) R 0, and µ r, τ r, D r, F r, F 2r, Λ 2,r are smooth in a neighborhood of 0, 0, Z 0)) R. Similarly, we have the same smoothness for the functions corresponding to n b. Therefore, from 5.2), to show that h is smooth in a neighborhood of Z, it is enough to prove that F b 0, 0, Z 0)) 0. In fact, since Z0) = 0 we obtain from 5.9) for n b and the claim above that F b 0, 0, Z 0)) = F b 0, Z0), Z 0)) = f b 0) 0. Calculation of h 2 and h 3. We have 5.25) z 2 t) = v t) = z t) := h 2 t; Zt), Zz t)); Z t), Z z t))) with, 5.26) h 2 t; ζ 0, ζ ; ξ 0, ξ ) = ζ 0. Similarly, 5.27) z 3 t) = v 2 t) = z 5t) + ρ 0 := h 3 t; Zt), Zz t)); Z t), Z z t))) with 5.28) h 3 t; ζ 0, ζ ; ξ 0, ξ ) = ζ ρ 0. Trivially, h 2 and h 3 are smooth everywhere.
35 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 35 Calculation of h. The rays m r t) and m b ϕt)) are both refracted into e = 0, ) at f r t) since Problem B is solvable f r has a normal vector), then by the Snell law m r t) n r e = λ 2,r t)ν S t) m b ϕt)) n b e = λ 2,b ϕt))ν S t) with ν S the outer unit normal to S = { f r D)}. If α S denotes the first component of ν S, then m r t) = λ 2,r t)α S t), m b ϕt)) = λ 2,b ϕt))α S t). Solving in α S t) and using 5.8) and 5.3) yields µ r t, Zt)) Λ 2,b z t), Zz t))) = µ b z t), Zz t))) Λ 2,r t, Zt)). Differentiating the last expression with respect to t, Remark 5.6 yields µ r t, Z, Z ) Λ 2,b z, Zz )) + z Λ 2,b z, Zz ), Z z )) µ r t, Z) = z µ bz, Zz ), Z z )) Λ 2,r t, Z) + µ b z, Zz )) Λ 2,r t, Z, Z ). Replacing 5.6) in the above expression cos t Ar Z) z n ÃrZ, ) Z ) z Λ2,b z, Zz )) r = z [ µb z, Zz ), Z z ))Λ 2,r t, Z) Λ 2,b z, Zz ), Z z ))µ r t, Z) ] + µ b z, Zz )) Λ 2,r t, Z, Z ). From 5.7) and 5.3), A r Z)Λ 2,b z, Zz )) < 0. Then solving the last equation in z yields 5.29) z = z [ µb z, Zz ), Z z ))Λ 2,r t, Z) Λ 2,b z, Zz ), Z z ))µ r t, Z) ] + µ b z, Zz )) Λ 2,r t, Z, Z ) n r cos t à r Z, Z ) z ) Λ2,b z, Zz )) := h t; Zt), Zz t)); Z t), Z z t))), so n r A r Z)Λ 2,b z, Zz )) 5.30) ξ 0 [ µb ζ 0 h t; ζ 0, ζ ; ξ 0, ξ, ζ, ξ )Λ 2,r t, ζ 0 ) Λ 2,b ζ 0, ζ, ξ )µ r t, ζ 0 ) ] + µ b ζ 0, ζ ) Λ 2,r t, ζ 0, ξ 0 ) ) cos t à r ζ 0, ξ 0 )ζ 0 Λ2,b ζ 0 n, ζ ) ) = r. A r ζ n 0 )Λ 2,b ζ 0, ζ ) r h is smooth in a neighborhood of Z, since A r 0)Λ 2,b 0, 0) < 0, and as shown before all the functions appearing in the expression for h are smooth in a neighborhood of Z from the comments after 5.) and 5.22).
36 36 C. E. GUTIÉRREZ AND A. SABRA Calculation of h 5. We have v 2 t) = tan t) v t). Differentiating twice we get Then 5.3) v 2 t) = tan t) v t) 2 v t) cos 2 t 2 sin t cos 3 t v t). z 5 t) = tan t) z t) 2 cos 2 t z t) 2 sin t cos 3 t z 2t) ρ 0 ) := h 5 t; Zt), Zz t)); Z t), Z z t))), and so 5.32) h 5 t; ζ 0, ζ ; ξ 0, ξ ) = tan t) ξ 0 2 cos 2 t ζ0 2 sin t cos 3 t ζ0 2 ρ 0). Since t D π/2, π/2), then h 5 is smooth in D R 20. The proof of Theorem 5.5 is then complete Solutions of 5.) yield local solutions to the optical problem. In this section, we show how to obtain a local solution to Problem B by solving the system of functional differential equations 5.). Theorem 5.7. Let ρ 0, d 0 > 0 be given, and suppose that H is the corresponding map defined in Theorem 5.5. Assume P = p,, p n ) is a solution to the system P = H0; 0, 0; P, P), such that H is smooth in a neighborhood of P := 0; 0, 0; P, P), and 5.33) 0 < p. Let Zt) = z t),, z 5 t)) be a C solution to the system 5.) in some open interval I containing 0, with Z 0) = P and 5.3) z t) t. Define 5.35) ρt) = z 2t) ρ 0, cos t and ϕt) = z t). Then there is δ > 0 sufficiently small, so that ϕ : [ δ, δ] [ δ, δ] and f r t) = f b ϕt)). Here, f r t) = ρt)xt) + d r t)m r t), and f b t) = ρt)xt) + d b t)m b t) where d r t) = C r ρt) cos t), d b t) = C b ρt) cos t) n r e m r t) n b e m b t)
37 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 37 with C r = n r ) d 0, C b = n b ) d 0 ; m r t) and m b t) are the refracted directions of the rays xt) by the curve ρt)xt) corresponding to each color r and b. In addition, for t [ δ, δ], f r and f b have normal vectors for every t and 5.36) ρt) > 0, d r t), d b t) > 0, m r t) e /n r, m b t) e /n b. Notice that 5.36) implies the lens defined with ρt)xt), f r and f b is well defined, and moreover total internal reflection is avoided. Proof. We obtain the theorem by proving a series of steps. Step. If ρ is from 5.35), then 5.37) z 3 t) = ρt) sin t. Proof. Since z 2 0) = 0, from 5.35) 5.38) ρ0) = ρ 0. Since Z is a solution to 5.), z 2 t) = z t) by the definition of h 2 in 5.26). Hence and from the definition of h 5 in 5.32), z 5 t) = tan t) z t) 2 cos 2 t z t) 2 sin t cos 3 t z 2t) ρ 0 ) = tan t) z 2 t) 2 2 sin t cos 2 t z 2 t) cos 3 t z 2t) ρ 0 ). By 5.35), we have z 2 t) = ρt) cos t + ρ 0, then z 2 t) = ρ t) cos t + ρt) sin t Replacing in the formula for z 5 we get z 2 t) = ρ t) cos t + 2ρ t) sin t + ρt) cos t. z 5 t) = tan t)ρ t) cos t 2ρ t) sin t ρt) cos t) + 2 cos 2 t ρ t) cos t ρt) sin t) + 2 sin t ρt) cos t cos 3 t = ρ t) sin t + 2ρ t) cos t ρt) sin t = d2 dt 2 [ ρt) sin t ]. Hence z 5 t) = d [ ] ρt) sin t + c = ρ t) sin t + ρt) cos t + c. Since z 5 0) = 0, then by dt 5.38) c = ρ 0, and therefore 5.39) z 5 t) = ρ t) sin t + ρt) cos t ρ 0.
38 38 C. E. GUTIÉRREZ AND A. SABRA By the definition of h 3 in 5.28), we have z 3 t) = z 5t) + ρ 0 = ρ t) sin t + ρt) cos t = d [ ] ρt) sin t, dt and since z 3 0) = 0, we conclude 5.37). Step 2. For each t I F r t, Zt)) = F b z t), Zz t))), with F r, F b from 5.). Proof. From the definition of h in 5.2) F r t, Zt), Z t)) = z t) F b z t), Zz t)), Z z t))). Hence by Remark 5.6, integrating the above equality yields F r t, Zt)) = F b z t), Zz t))) + c. Since Z0) = 0, then from the formulas of F r and µ r in 5.) we get F r 0, 0) = F b 0, 0) = 0. Hence c = 0 and Step 2 follows. Step 3. There is δ > 0 small so that 5.36) holds. Proof. Since ρ0) = ρ 0 > 0, by continuity there is δ > 0 with [ δ, δ] I so that ρt) given by 5.35) is positive for t [ δ, δ]. Rays with colors r and b emitted from the origin with direction xt) = sin t, cos t) are refracted at ρt)xt) into the directions m r t), and m b t). For the upper faces f r and f b to be able to refract the rays m r and m b into e, they need to have a normal vector for each t, d r t) and d b t) must be positive for t [ δ, δ], and m r and m b must satisfy the conditions m r t) e n r, m b t) e n b to avoid total reflection. Notice that from 5.35) ρ t) = z 2 t) cos t + z 2t) ρ 0 ) sin t. cos 2 t From the definition of h 2 in 5.26), and since z 0) = 0 we conclude that ρ 0) = 0. Hence from Lemma 5.3, the normal to ρ at ρ0)0, ) is ν0) = 0, ). Since x0) = ν0) = 0, ) we obtain from Snell s law that 5.0) m r 0) = m b 0) = 0, ). Thus, e m r 0) = e m b 0) =, and so 5.) d r 0) = C r n r = d 0 = C b n b = d b0) > 0.
39 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 39 So choosing δ small we get d r t), d b t) > 0, e m r t) n r and e m b t) n b in [ δ, δ]. Therefore, 5.36) holds for δ > 0 sufficiently small. The fact that f r and f b have a normals for every t will be proved in Step 5. Step. For each t [ δ, δ] f r t) = F r t, Zt)), F 2r t, Zt))), and similarly f b t) = F b t, Zt)), F 2b t, Zt))). Proof. We first show that 5.2) m r t) = µ r t, Zt)), τ r t, Zt)) ), and similarly for m b. Since the direction xt) = sin t, cos t) is refracted by ρ into the unit direction m r t), by 5.5) m r t) = n r [xt) A r vt), v t)) v t)] with A r given in 5.6) and vt) = ρt) cos t, ρt) sin t). From 5.35) and 5.37), vt) = z 2 t) ρ 0, z 3 t) ), v t) = z 2 t), z 3 t)). However, by the definition of h 2 in 5.26) and the definition of h 3 in 5.28), we have z 2 = z and z 3 = z 5 + ρ 0, then v t) = z, z 5 + ρ 0 ). Hence 5.6) becomes A r vt), v n 2 r t)) = z 2 t) ρ 0, z 3 t)) z2 + t) ρ 0, z 3 t)) 2 + n 2 r ) z t), z 5 t) + ρ 0 ), 2 and so by 5.), A r vt), v t)) = A r Zt)). We conclude that m r t) = n r [ sin t, cos t) Ar Zt)) z t), z 5 t) + ρ 0 )], and hence once again from 5.), the identity 5.2) follows. We now show that d r t) = D r t, Zt)). In fact, by definition of v we have ρt) = vt) = z2 t) ρ 0, z 3 t) ). Then by 5.2), 5.35) and the formula for D r in 5.) we get d r t) = C r ρt) + ρt) cos t n r m 2r t) = C r z2 t) ρ 0, z 3 t)) z2 t) + ρ 0 n r τ r t, Zt)) = D r t, Zt)).
40 0 C. E. GUTIÉRREZ AND A. SABRA Hence from 5.35), 5.37), 5.2), and the formulas of F r, F 2r in 5.), we conclude f r t) = ρt)sin t, cos t) + d r t)m r t) = z 3 t), z 2 t) + ρ 0 ) + Dr t, Zt)) µ r t, Zt)), τ r t, Zt)) ) = F r t, Zt)), F 2r t, Zt))). A similar result holds for f b. By assumption z t) t for t I, then z t) [ δ, δ] for every t [ δ, δ]. Step 5. For δ small, f r t) 0 and f b t) 0, and hence f r and f b have normal vectors for each t [ δ, δ]. Proof. By continuity of f and f, it is enough to show that f 0) 0 and f 0) 0. r b r b Since H is well defined at P, then from the definition of h in 5.2), F b 0, 0, P) 0. We have Z 0) = P, then from Remark 5.6 and Step f b 0) = F b 0, 0, Z 0)) = F b 0, 0, P) 0. We next prove that f r 0) 0. From Steps 2 and, f rt) = f b z t)). Differentiating and letting t = 0 yields f r 0) = z 0) f b 0). Since f 0) 0 and from 5.33) b z 0) = p 0, we obtain f 0) 0. r Step 6. The vectors m r t) n r e and m b z t)) n b e are colinear for every t [ δ, δ]. Proof. Since z t) = h t; Zt), Zz t)); Z t), Z z t))), from 5.30) it follows that n r cos t Ar Zt))z t) ÃrZt), Z t))z t) ) Λ 2,b z t), Zz t))) = z t) [ µ b z t), Zz t)), Z z t)))λ 2,r t, Zt)) Λ 2,b z t), Zz t)), Z z t)))µ r t, Zt)) ] + µ b z t), Zz t))) Λ 2,r t, Zt), Z t)). Hence from the formula of µ r in 5.22), we obtain µ r t, Zt), Z t)) Λ 2,b z t), Zz t))) + z t) Λ 2,b z t), Zz t))) µ r t, Zt)) = z t) µ bz t), Zz t))) Λ 2,r t, Zt)) + µ b z t), Zz t))) Λ 2,r t, Zt), Z t)). Integrating the resulting identity using Remark 5.6, and that µ r 0, 0) = µ b 0, 0) = 0 from 5.), we obtain 5.3) µ r t, Zt)) Λ 2,b z t), Zz t))) = µ b z t), Zz t))) Λ 2,r t, Zt)).
41 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES On the other hand, from 5.2) 5.) µ r t, Zt)) 2 + τ r t, Zt)) 2 =, then from 5.), Λ 2,r can be written as follows Λ 2,r t, Zt)) = + n 2 2 τ r t, Zt)) = τ r t, Zt)) r n 2 + r nr 2 = µ r t, Zt)) 2 + τ r t, Zt))), nr ) 2 τ r t, Zt)) and similarly for Λ 2,b. Squaring 5.3) and using the above identity for n r and n b we get ) 2 ] µ r t, Zt)) [µ 2 b z t), Zz t))) 2 + τ b z t), Zz t)) nb ) 2 ] = µ b z t), Zz t))) [µ 2 r t, Zt)) 2 + τ r t, Zt)). nr Hence ) 2 µ r t, Zt)) 2 τ b z t), Zz t))) = µ b z t), Zz t))) 2 n b nr τ r t, Zt))) 2, and taking square roots µ rt, Zt)) τ b z t), Zz t)))) = nb µ bz t), Zz t))) τ r t, Zt))). nr From 5.2), since δ is chosen so that 5.36) holds in [ δ, δ], and z t) [ δ, δ], we have that /n b τ b z t), Zz t))) = /n b e m b z t)) 0, and /n r τ r t, Zt)) = /n r e m r t) 0. Moreover, since the functions Λ 2,b and Λ 2,r are both positive, then by 5.3) µ r t, Zt)) and µ b z t), Zz t))) have the same sign obtaining µ r t, Zt)) τ b z t), Zz t))) ) = µ b z t), Zz t))) τ r t, Zt)) ). nb nr We conclude that the vectors µ r t, Zt)), τ r t, Zt)) nr ), µ b z t), Zz t))), τ b z t), Zz t))) nb ) are colinear and the claim follows from 5.2). By Steps 2 and, we obtain that f r t) = f b z t)), so to conclude the proof of Theorem 5.7, it remains to show the following. Step 7. We have for t δ that f 2r t) = f 2b z t)).
42 2 C. E. GUTIÉRREZ AND A. SABRA Proof. From Step 5, for t δ, f r and f b have normals at every point. From 5.36) and the definitions of f r and f b, m r t) and m b t) are refracted into the direction e at f r t) and f b t), for each t, respectively. So the Snell law at f r t) and f b t) implies that m r t) n r e is orthogonal to the tangent vector f r t), and m b z t)) n b e is orthogonal to f z b t)). Hence by Step 6, f r t) and f z b t)) are parallel. From Remark 5.6 and Steps 2 and we also obtain that f t) = r z t) f z b t)). From Step 5 and assumption 5.3), f t) 0 and f z r b t)) 0 for all t [ δ, δ], then f 2r t) = z t) f 2b z t)). Integrating the last identity, we obtain f 2r t) = f 2b z t)) + c. On the other hand, z 0) = 0, f 2r 0) = ρ0) + d r 0)m 2r 0), and f 2b 0) = ρ0) + d b 0)m 2b 0). Hence from 5.0) and 5.), f 2r 0) = f 2b 0) and so c = 0, and Step 7 follows. This completes the proof Theorem 5.7. Remark 5.8. Notice that f b has no self intersections in the interval [ δ, δ]. Because if there would exist t, t 2 [ δ, δ] such that f b t ) = f b t 2 ), then by Rolle s theorem applied to f b we would get f b t 0) = 0 for some t 0 [t, t 2 ], a contradiction with Step 5. The issue of self-intersections in the monochromatic case is discussed in detail in [GS7]. This implies that f b is injective, and similarly f r is injective. We also deduce that ϕ is injective: in fact, if ϕt ) = ϕt 2 ) then f r t ) = f b ϕt )) = f b ϕt 2 )) = f r t 2 ) and so t = t On the solvability of the algebraic system.3). In this section, we analyze for what values of ρ 0, d 0 the algebraic system P = H0; 0, 0; P, P) has a solution, where H is given in Theorem 5.5. This analysis will be used to apply Theorem., and to decide when Problem B has a local solution. Denote k 0 = ρ 0 d 0, r = n r n r, b = n b n b. Theorem 5.9. The algebraic system P = H0; 0, 0; P, P) has a solution if and only if k 0 r b ) 2 r b 3. In case of equality, the system has only one solution P with p =, and in case of strict inequality the system has two solutions P and P with 0 < p < and p >. 3 This expression is equal to r b )2 b r.
43 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 3 Proof. Recall that H = H t; ζ 0, ζ ; ξ 0, ξ ). Suppose P = p,, p 5 ) solves P = H 0; 0, 0; P, P). Then from the definitions of h 2 in 5.26), of h 3 in 5.28), and of h 5 in 5.32) we get 5.5) p 2 = h 2 0; 0, 0; P, P) = 0, p 3 = h 3 0; 0, 0;P, P) = ρ 0, p 5 = h 5 0; 0, 0;P, P) = 0. Then, from 5.) and 5.22) A r 0) = n r, r ρ 0 µ r 0, 0) = µ b 0, 0) = 0 τ r 0, 0) = τ b 0, 0) = D r 0, 0) = D b 0, 0) = d 0 A b 0) = n b b ρ 0 F r 0, 0) = F b 0, 0) = 0, F 2r 0, 0) = F 2b 0, 0) = ρ 0 + d 0 5.6) Λ 2,r 0, 0) =, Λ 2,b 0, 0) = r b à r 0, P) = Ãb 0, P) = 0 µ r 0, 0, P) = r + p ), µ b 0, 0, P) = b + p ) r n r ρ 0 b n b ρ 0 τ r 0, 0, P) = τ nr 0, 0, P) = 0 D r 0, 0, P) = D b 0, 0, P) = 0 F r 0, 0, P) = ρ 0 + d 0 r + p ), F b 0, 0, P) = ρ 0 + d 0 b + p ) r n r ρ 0 b n b ρ 0 F 2r 0, 0, P) = F 2b 0, 0, P) = 0 Λ 2,r 0, 0, P) = Λ 2,b 0, 0, P) = 0. Hence by the definition of h in 5.2), and since h 0; 0, 0; P, P) is well defined, we get that F b 0, 0, P) 0. That is, from 5.6), ρ 0 + d 0 b + p ) 0 and we have b n b ρ 0 5.7) p = h 0; 0, 0; P, P) = F ρ 0 + d 0 r + p ) r 0, 0, P) F b 0, 0, P) = r n r ρ 0 ). From the definition of h in 5.30) 5.8) p = h 0; 0, 0; P, P) = p b r ρ 0 + d 0 b b + p ) n b ρ 0 n r b r b ρ 0 = [ b n b + p ρ 0 b p + p ) n b ρ 0 ] r ρ 0. n r
44 C. E. GUTIÉRREZ AND A. SABRA To solve 5.8) in p, first notice that b n b + p ρ 0 0. Otherwise, from 5.8) we would obtain p = r, and so r ρ 0 n r n r Then 5.8) yields 5.9) p = Hence from 5.7) and 5.9) we get that Then 5.50) Simplifying, Notice that 5.5) r = b n b, hence n r = n b, a contradiction since n b > n r. + p n r ρ 0 b + p = n b ρ 0 r + p n r ρ 0 b + p. n b ρ 0 ρ 0 + d 0 r ρ 0 + d 0 b r + p ) n r ρ 0 b + p ) n b ρ 0 r + p ) ρ 0 + d 0 b + p )) b = + p ) ρ 0 + d 0 r + p )). n r ρ 0 b n b ρ 0 n b ρ 0 r n r ρ 0 r ρ 0 ) b r = + p ) b + p ) ) d 0. n r n b n r ρ 0 n b ρ 0 r b r n r b n b = n r n b = + r + b = r b. Then dividing by r b, and using the notation k 0 = ρ 0 yields d 0 b 5.52) k 0 r b + + p ) r + p ) = 0. n b ρ 0 n r ρ 0 Expanding we obtain that p /ρ 0 satisfies the following quadratic equation: ) 2 p r 5.53) + + ) b p + k 0 r b + r b = 0. n r n b ρ 0 n r n b ρ 0 The discriminant of 5.53) is 5.5) δ = r b = r n r + b n b ) 2 r b n r n b k 0 r b = n b n r n r )n b ) > 0 r n r b n b ) 2 k 0 r b,
45 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 5 then 5.5) yields 5.55) δ = r b ) 2 k 0 r b. Hence 5.53) has a real solutions if and only if k 0 r b ) 2. Therefore we have r b proved the necessity part in Theorem 5.9, and if P solves the algebraic system, then r + ) b r δ + ) b + δ n p = r n b ρ 0, p 2 = n r n b ρ 0 2 and by 5.9) and 5.5), the corresponding p and p are p = r b δ b r δ, p = r b + δ b r + δ. Therefore if P = H0; 0, 0; P, P), then the solutions are r b r + ) b δ δ P = b r δ, 0, ρ n r n 5.56) b 0, ρ 0, ) with δ given in 5.55). P r b + δ = b r + δ, 0, ρ 0, r + ) b n r n b 2 + δ ρ 0, 0 Let us now prove that if k 0 r b ) 2, then the system P = H0; 0, 0; P, P) is r b solvable. In fact, from the assumption on k 0 there is p solving 5.53). We claim that this implies ρ 0 + d 0 b + p ) 0. Assume otherwise, since 5.53) is equivalent b n b ρ 0 to 5.50) and ρ 0 > 0 then p solves the system ρ 0 + d 0 b + p ) = 0 b n b ρ 0 ρ 0 + d 0 r + p ) = 0 r n r ρ 0 Subtracting both identities we get d 0 n b n r ) + p d 0 ρ 0 b r ) = 0.
46 6 C. E. GUTIÉRREZ AND A. SABRA Since = and n r n b, dividing by d 0 ) we get p = 0, and b r n r n b n b n r ρ 0 then p = ρ 0. Replacing in the first equation of the system yields ρ 0 = d ) 0 b +, b n b and since ρ 0, d 0 > 0, we get a contradiction. Now let p be the corresponding value to this p given by 5.7), and p 2, p 3, p 5 from 5.5); and P be the point with these coordinates. Hence by the formula for F b 0, 0, P) in 5.6), we get that F b 0, 0, P) 0, and therefore h 0; 0, 0; P, P) is well defined, and P solves the algebraic system. Then the possible values of P solving the algebraic system are P and P given by 5.56) and 5.57). We now prove the last part of the theorem. If k 0 = r b ) 2 P = P =, 0, ρ 0, r + ) b n r n b 2 r b then δ = 0 and ρ 0, 0. If k 0 < r b ) 2 then the solutions P P. r b Moreover, since r > b, and from 5.55) 0 < δ < r b, Therefore 0 < r p b δ = b r δ = r b δ r b + δ < p r b + δ = b r + δ = r b + δ r b δ >. The following corollary gives a necessary condition on k 0 for the existence of solutions to Problem B. Corollary 5.0. If k 0 > r b ) 2 r b then Problem B has no local solutions. Proof. If Problem B has a solution then by Theorem 5.5, the vector Zt) = ϕt), v t)+ ρ 0, v 2 t), v t), v 2 t) ρ 0) solves the functional system 5.) for t in a neighborhood of 0. Plugging t = 0 in 5.) yields 0; 0, 0; Z 0), Z 0)) = H0; 0, 0; Z 0), Z 0)). Hence Z 0) is a solution to the algebraic system P = H0; 0, 0; P, P), and from Theorem 5.9 we have k 0 r b ) 2 r b.
47 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 7 Corollary 5.. If k 0 r b ) ) r b and a solution ρ and ϕ to Problem B exists, then ρ 0) ρ 0 b, r ) In fact, 5.59) ρ 0) ρ 0 = 2 + r + ) b n r n b 2 ± δ, with δ given in 5.55). Proof. If ρ and ϕ solve Problem B, then from the proof of Corollary 5.0, Z 0) solves the algebraic system, with Zt) = ϕt), v t) + ρ 0, v 2 t), v t), v 2 t) ρ 0). Using the proof of Theorem 5.9, it follows that z 0) satisfies 5.52) then r + z 0) ) b + z 0) ) = k 0 r b < 0, n r ρ 0 n b ρ 0 and therefore z 0) r, ) b. ρ 0 n r n b On the other hand, z t) = v t) = ρt) sin t ρ t) cos t, obtaining z 0) = ρ 0 ρ 0), so 5.60) ρ 0) ρ 0 = z 0) ρ 0. We conclude that ρ 0) ρ 0 + b, + ) r = b, r ). n b n r Finally, from 5.56), 5.57), and 5.60), we obtain 5.59). Remark 5.2. The analogue of Problem B for three or more colors has no solution. In fact, if rays, superposition of three colors, are emitted from O and n r < n j < n b are the refractive indices inside the lens for each color, then 5.58) must be satisfied for the pairs n r, n j and n j, n b. Hence ρ 0) ρ0) j, r ) b, j ), which is impossible since the last intersection is empty.
48 8 C. E. GUTIÉRREZ AND A. SABRA 5.5. Existence of local solutions to 5.). In order to prove existence of solutions to the system 5.), we will apply Theorem.. From Theorem 5.9, we must assume that k 0 r b ) 2. In this case, the algebraic system P = H0; 0, 0; P, P) r b has a solution given by 5.56) with p, and therefore.) holds. Let P = 0; 0, 0; P, P). To show that H satisfies all the hypotheses of Theorem., it remains to show there is a norm in R 5 so that H satisfies conditions i)-iv) with respect to this norm in a neighborhood N ε P). Our result is as follows. Theorem 5.3. There exists a positive constant Cr, b) < r b ) 2, depending only on r b n r and n b, such that for 0 < k 0 < Cr, b), the system 5.) has a unique local solution Zt) = z t),, z 5 t)) with Z 0) = P, and z t) t, with P given in 5.56). Hence from Theorem 5.7 and for those values of k 0, there exist unique ρ and ϕ solving Problem B. Proof. Since by construction h i are all smooth in a small neighborhood of P, H is Lipschitz in that neighborhood for any norm. To apply Theorem., we need to find a norm in R 5 and a neighborhood N ε P) so that h, and H satisfies the contraction condition.8). To prove the contraction property of H, we first calculate the following matrices h i h i ξ 0H = ξ 0, and ξ H = ξ j i,j 5 j h i Calculation of ξ 0HP) = P) ξ 0 j at the point P. i,j 5 i,j 5 From 5.26) and 5.28), h 2 and h 3 do not depend on ξ 0, then ξ 0 j Also from the definition of h 5 in 5.32). h 2 P) = ξ 0h 3 P) = 0, j 5. j ξ 0h 5 P) = δ 5 j j tan t) P = 0, j 5. We next calculate ξ 0h P). From 5.2), Recall from 5.6) ξ 0h P) = F b 0, 0, P) = ρ 0 + d 0 b F b 0, 0, P) ξ 0 F r 0, 0, P). b + p ), µ r 0, 0) = 0, D r 0, 0) = d 0. n b ρ 0
49 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 9 Differentiating F r given in 5.22) with respect to ξ 0, we then get j F r ξ 0 j 0, 0, P) = δ 3 j + d µ r 0 0, 0, P), j 5. ξ 0 j From 5.6), A r 0) = n r r ρ 0, then differentiating µ r in 5.22) with respect to ξ 0 j at 0, 0, P) yields 5.6) µ r ξ 0 j 0, 0, P) = r ρ 0 δ j. Therefore 5.62) ξ 0 F r 0, 0, P) = ) 0, 0,,, 0. k 0 r We conclude that 5.63) ξ 0h P) = ρ 0 + d 0 b + p ) b n b ρ 0 0, 0,, ), 0. k 0 r We next calculate ξ 0h P). Recall from 5.6) that µ b 0, 0) = µ r 0, 0) = 0, µ b 0, 0, P) = b + p ), Λ 2,r 0, 0) =, Λ 2,b 0, 0) =, A r 0) = n r. b n b ρ 0 r b r ρ 0 Then from 5.30) it follows that h ξ 0 j = b b + p ) n b ρ 0 r r ρ 0 b δ b j = ρ 0 + p ) δ j n b ρ, j 5. 0 Hence b 5.6) ξ 0h P) = ρ 0 + p ), 0, 0, 0, 0. n b ρ 0
50 50 C. E. GUTIÉRREZ AND A. SABRA We then conclude that k 0 0 ρ 0 + d 0 b + p ) 0 r ρ 0 + d 0 b + p ) 0 b n b ρ 0 b n b ρ ) ξ 0HP) = b ρ 0 + p ) n b ρ To calculate the spectral radius of the matrix ξ 0HP), set b 5.66) a = ρ 0 + d 0 b + p ), c = ρ 0 + p ). n b ρ 0 b n b ρ 0 ac The eigenvalues of ξ 0HP) are 0 with multiplicity 3), and ±. Notice that k 0 r from 5.56), and 5.5) 5.67) r n r + p ρ 0 = r b r b ) 2 k 0 r b 2 = 2k 0 r b r b + r b ) 2 k 0 r b > 0, then by 5.7) and 5.9) 5.68) ac k 0 r = ρ 0 b + p ) k 0 r n b ρ 0 ρ 0 + d 0 b + p ) = b n b ρ 0 ρ 0 r + p ) k 0 r n r ρ 0 ρ 0 + d 0 r + p ) > 0. r n r ρ 0 Therefore all the eigenvalues of ξ 0HP) are real and the spectral radius of ξ 0HP) ac is R ξ 0 =. We estimate R ξ 0. k 0 r From 5.55), 5.67), and 5.68) 5.69) ac k 0 r = 2 b r b + δ 2 b + r b + δ = 2 b r + b + δ 2 b r + b := δ 0 <.
51 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 5 Since δ < r b, we conclude that b 2 b 5.70) < R ξ 0 = r r + b + δ h i Calculation of ξ HP) = P) ξ j i,j 5 that h 2, h 3 and h 5 do not depend on ξ then ξ h 2 P) = ξ h 3 P) = ξ h 5 P) = 0. 2 b b + r = δ 0 <.. Notice from 5.26), 5.28) and 5.32) We calculate ξ h P). From 5.2), and the fact that p = h P) = F r 0, 0, P) F b 0, 0, P) we get ξ h P) = F r 0, 0, P) F b 0, 0, P) 2 ξ F b 0, 0, P) = F b 0, 0, P) ξ F b 0, 0, P). Recall from 5.6) Similarly as in 5.62) Hence ξ h P) = p F b 0, 0, P) = ρ 0 + d 0 b + p ). b n b ρ 0 ξ F b P) = ) 0, 0,,, 0. k 0 b p ρ 0 + d 0 b + p ) b n b ρ 0 We next calculate ξ h P). Recall from 5.6) 0, 0,, ), 0. k 0 b A b 0) = n b b ρ 0, Λ 2,b 0, 0) = b, Λ 2,r 0, 0) = r, µ r 0, 0) = µ b 0, 0) = 0, and as in 5.6) ξ µ b 0, 0, P) = b ρ 0 0, 0, 0,, 0), then from 5.30) ξ h P) = p r r ρ 0 b b ρ 0 0, 0, 0,, 0) = p 0, 0, 0,, 0)
52 52 C. E. GUTIÉRREZ AND A. SABRA We conclude that p k 0 0 ρ 0 + d 0 b + p ) 0 b ρ 0 + d 0 b + p ) 0 b n b ρ 0 b n b ρ 0 5.7) ξ HP) = p Notice that ξ HP) is an upper triangular matrix with eigenvalues 0 with multiplicity ) and p, the spectral radius of ξ HP) is 5.72) R ξ = p. Choice of the norm. We are now ready to construct a norm for which H is a contraction in the last two variables. In fact, we will construct a norm denoted by k0 in R 5 depending on k 0 such that for small k ) ξ 0HP) k0 + ξ HP) k0 < where k0 is the matrix norm in R 5 5 induced by k0. Recall that k 0 = ρ 0 /d 0. We will show that for each 0 < k 0 r b ) 2, there exist λ,, λ 5 positive r b depending on k 0 such that the norm in R 5 having the form p x k0 = max λ x, λ 2 x 2, λ 3 x 3, λ x, λ 5 x 5 ), satisfies ξ 0HP) k0 <. We first choose λ = λ 2 = λ 5 =. Assume x R 5 with x k0 x i λ i. Then from 5.65), and 5.69) ξ 0HP)x k0 = max a x 3 + a max a + λ3 λ with a and c defined in 5.66). Hence ξ 0HP) k0 = max x k0 = ) x k 0 r, λ c x ) a, λ c max k 0 r ξ 0HP)x k0 max =, which implies a + δ ) 0 λ 3 λ c, λ c { a + δ } 0 λ 3 λ c, λ c.
53 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 53 We will choose λ 3 and λ so that the last maximum is less than one. Let δ 0 < δ < δ 2 <, with δ 0 defined in 5.69), λ = δ 2 / c and λ 3 = N λ, with N to be determined depending only on n r and n b. Then max { a λ 3 + δ 0 λ c, λ c } { ) } a c = max λ c N + δ 0, λ c, r b ) 2 notice that ac > 0 from 5.68). From 5.69), a c k 0 r r := Br, b), we r b obtain { a max + δ } { ) } 0 Br, b) λ 3 λ c, λ c max δ 2 N + δ 0, δ 2. Br, b) Now pick N, large depending only on n r and n b, so that N +δ 0 < δ. Therefore, ξ 0HP) { } k0 δ max, δ 2 := s 0 <, δ 2 for all 0 < k 0 r b ) 2. r b It remains to show that with the above norm k0 we also have 5.73). To do this we need to choose k 0 sufficiently small. In fact, from 5.7) and for x k0 = we have since λ 3 = N λ, λ = δ 2 / c, and ac < k 0 r Br, b)) ξ HP)x k0 = p max a x 3 + ) a x k 0 b, λ x a p max + ) a, λ 3 λ k 0 b a c = p max δ2 N + a c ) ), k 0 b Br, b) p max δ 2 N + ) ) r, := p s, b for all 0 < k 0 r b ) 2 Therefore r b with s depending only on n r and n b s > ). Hence ξ HP) k0 p s. ξ 0HP) k0 + ξ HP) k0 s 0 + p s. From 5.55) and 5.56), p 0 as k 0 0, and therefore we obtain 5.73) for k 0 close to 0. Verification of.8). Let us now show that H satisfies the Lipschitz condition.7) with constants satisfying.8) in a sufficiently small neighborhood of P and
54 5 C. E. GUTIÉRREZ AND A. SABRA with respect to the norm chosen. In fact, for k 0 sufficiently small, from 5.73), there is 0 < c 0 < so that ξ 0HP) k0 + ξ HP) k0 c 0 <. Since H is C, there exists a norm-neighborhood N ε P) of P as in Theorem., so that max ξ 0H t; ζ 0, ζ ; ξ 0, ξ ) 5.7) t;ζ 0,ζ ;ξ 0,ξ ) N ε P) k0 + max ξ H ˆt; ˆζ 0, ˆζ ; ˆξ 0, ˆξ ) c, k0 ˆt; ˆζ 0, ˆζ ; ˆξ 0, ˆξ ) N ε P) for some c 0 < c <. Then by Proposition.5, the inequalities.7) and.8) hold with C 0 = max Nε P) ξ 0H and C = max Nε P) ξ H. Verification of.9). If k 0 < r b ) 2, then from Theorem 5.9 p <, and r b so h P) <. Hence by continuity there exists a neighborhood of P so that h t; ζ 0, ζ ; ξ 0, ξ ) < for all t; ζ 0, ζ ; ξ 0, ξ ) in that neighborhood. Therefore, condition.9) in Theorem. is satisfied. We conclude that for small values of k 0 Theorem. is applicable and therefore there exists a unique local solution to the system 5.) with Z 0) = P and P given in 5.56). Notice also that for such a solution Z, we have z 0) = 0, and z 0) = h P) = p <, then by reducing the neighborhood of zero, if necessary, we have that the solution satisfies z t) t. Since we also showed in Theorem 5.9 that p 0, Theorem 5.7 is applicable and the proof of Theorem 5.3 is then complete. Summarizing the question of solvability of Problem B in the plane in a neighborhood of zero, we have: ) If k 0 > r b ) 2 r b then Problem B is not locally solvable. 2) Let A = 0, ρ 0 ), B = 0, ρ 0 + d 0 ), and 0 < k 0 < Cr, b) < r b ) 2. Then there r b exists δ > 0 and a unique lens L, S) with lower face L = {ρt)xt)} t [ δ,δ], xt) = sin t, cos t), and upper face S = { f b t)} t [ δ,δ], f b defined in Theorem 5.7, such that L passes through A, S passes through B, and so that L, S) refracts all rays emitted from O with colors r and b and direction xt), t [ δ, δ] into the vertical direction e = 0, ).
55 ON THE EXISTENCE OF DICHROMATIC SINGLE ELEMENT LENSES 55 Remark 5.. In this final remark, we point out that Theorem. is not applicable to find solutions to the system 5.) when k 0 r b ) 2 and k 0 is away from 0. In r b this case we claim that there is no norm in R 5 for which we can obtain.7) with C 0 and C satisfying.8). In fact, from 5.55), 5.56), 5.70), and 5.72) 2 b R ξ 0 + R ξ = r + b + δ + p 2 b + >, r + b as k 0 r b ) 2 from below. Hence for k 0 close to r b ) 2, we have R ξ 0 +R r b r ξ > b, and hence by Corollary.6 the claim follows. Acknowledgements C. E. G. was partially supported by NSF grant DMS , and A. S. was partially supported by Research Grant 205/9/P/ST/0268 from the National Science Centre, Poland, entitled Variational Problems in Optical Engineering and Free Material Design. This project has received funding from the European Union s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No References [BW59] M. Born and E. Wolf. Principles of Optics, Electromagnetic theory, propagation, interference and diffraction of light. Cambridge University Press, seventh expanded), 2006 edition, 959. [Can] Cannon. Lenses: Fluorite, aspherical and UD lenses, content/education/infobank/lenses/fluorite_aspherical_and_ud_lenses.do. [Cau36] A. L. Cauchy. Mémoire sur la dispersion de la lumière mmoiresurladisp0caucgoog. J. C. Calve, Prague, 836. [Dug78] J. Dugundji. Topology. Allyn and Bacon, twelve printing, 978. [FM87] A. Friedman and B. McLeod. Optimal design of an optical lens. Arch. Rational Mech. Anal., 992):7 6, 987. [FMOT7] L. Fox, D. F. Mayers, J. R. Ockendon, and A. B. Tayler. On a functional differential equation. J. Inst. Maths Applics, 8:27 307, 97. [GH09] C. E. Gutiérrez and Qingbo Huang. The refractor problem in reshaping light beams. Arch. Rational Mech. Anal., 932):23 3, 2009.
ON THE NUMERICAL SOLUTION OF THE FAR FIELD REFRACTOR PROBLEM
 ON THE NUMERICAL SOLUTION OF THE FAR FIELD REFRACTOR PROBLEM ROBERTO DE LEO, CRISTIAN E. GUTIÉRREZ AND HENOK MAWI Abstract. The far field refractor problem with a discrete target is solved with a numerical
ON THE NUMERICAL SOLUTION OF THE FAR FIELD REFRACTOR PROBLEM ROBERTO DE LEO, CRISTIAN E. GUTIÉRREZ AND HENOK MAWI Abstract. The far field refractor problem with a discrete target is solved with a numerical
Existence and Uniqueness
 Chapter 3 Existence and Uniqueness An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect
Chapter 3 Existence and Uniqueness An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
arxiv: v1 [math.ap] 1 Jun 2018
![arxiv: v1 [math.ap] 1 Jun 2018 arxiv: v1 [math.ap] 1 Jun 2018](/thumbs/86/93625132.jpg) REFRACTORS IN ANISOTROPIC MEDIA ASSOCIATED WITH NORMS arxiv:806.0037v [math.ap] Jun 208 CRISTIAN E. GUTIÉRREZ, QINGBO HUANG AND HENOK MAWI Abstract. We show existence of interfaces between two anisotropic
REFRACTORS IN ANISOTROPIC MEDIA ASSOCIATED WITH NORMS arxiv:806.0037v [math.ap] Jun 208 CRISTIAN E. GUTIÉRREZ, QINGBO HUANG AND HENOK MAWI Abstract. We show existence of interfaces between two anisotropic
NORMS ON SPACE OF MATRICES
 NORMS ON SPACE OF MATRICES. Operator Norms on Space of linear maps Let A be an n n real matrix and x 0 be a vector in R n. We would like to use the Picard iteration method to solve for the following system
NORMS ON SPACE OF MATRICES. Operator Norms on Space of linear maps Let A be an n n real matrix and x 0 be a vector in R n. We would like to use the Picard iteration method to solve for the following system
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5
 MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
MATH 722, COMPLEX ANALYSIS, SPRING 2009 PART 5.. The Arzela-Ascoli Theorem.. The Riemann mapping theorem Let X be a metric space, and let F be a family of continuous complex-valued functions on X. We have
An introduction to Mathematical Theory of Control
 An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
Half of Final Exam Name: Practice Problems October 28, 2014
 Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
at time t, in dimension d. The index i varies in a countable set I. We call configuration the family, denoted generically by Φ: U (x i (t) x j (t))
 Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
The continuity method
 The continuity method The method of continuity is used in conjunction with a priori estimates to prove the existence of suitably regular solutions to elliptic partial differential equations. One crucial
The continuity method The method of continuity is used in conjunction with a priori estimates to prove the existence of suitably regular solutions to elliptic partial differential equations. One crucial
- 1 - θ 1. n 1. θ 2. mirror. object. image
 TEST 5 (PHY 50) 1. a) How will the ray indicated in the figure on the following page be reflected by the mirror? (Be accurate!) b) Explain the symbols in the thin lens equation. c) Recall the laws governing
TEST 5 (PHY 50) 1. a) How will the ray indicated in the figure on the following page be reflected by the mirror? (Be accurate!) b) Explain the symbols in the thin lens equation. c) Recall the laws governing
LECTURE 23: LIGHT. Propagation of Light Huygen s Principle
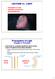 LECTURE 23: LIGHT Propagation of Light Reflection & Refraction Internal Reflection Propagation of Light Huygen s Principle Each point on a primary wavefront serves as the source of spherical secondary
LECTURE 23: LIGHT Propagation of Light Reflection & Refraction Internal Reflection Propagation of Light Huygen s Principle Each point on a primary wavefront serves as the source of spherical secondary
A Brunn Minkowski theory for coconvex sets of finite volume
 A Brunn Minkowski theory for coconvex sets of finite volume Rolf Schneider Abstract Let C be a closed convex cone in R n, pointed and with interior points. We consider sets of the form A = C \ K, where
A Brunn Minkowski theory for coconvex sets of finite volume Rolf Schneider Abstract Let C be a closed convex cone in R n, pointed and with interior points. We consider sets of the form A = C \ K, where
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
2 Sequences, Continuity, and Limits
 2 Sequences, Continuity, and Limits In this chapter, we introduce the fundamental notions of continuity and limit of a real-valued function of two variables. As in ACICARA, the definitions as well as proofs
2 Sequences, Continuity, and Limits In this chapter, we introduce the fundamental notions of continuity and limit of a real-valued function of two variables. As in ACICARA, the definitions as well as proofs
Speed of Light in Glass
 Experiment (1) Speed of Light in Glass Objective:- This experiment is used to determine the speed of propagation of light waves in glass. Apparatus:- Prism, spectrometer, Halogen lamp source. Theory:-
Experiment (1) Speed of Light in Glass Objective:- This experiment is used to determine the speed of propagation of light waves in glass. Apparatus:- Prism, spectrometer, Halogen lamp source. Theory:-
Geometry and topology of continuous best and near best approximations
 Journal of Approximation Theory 105: 252 262, Geometry and topology of continuous best and near best approximations Paul C. Kainen Dept. of Mathematics Georgetown University Washington, D.C. 20057 Věra
Journal of Approximation Theory 105: 252 262, Geometry and topology of continuous best and near best approximations Paul C. Kainen Dept. of Mathematics Georgetown University Washington, D.C. 20057 Věra
16 1 Basic Facts from Functional Analysis and Banach Lattices
 16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
16 1 Basic Facts from Functional Analysis and Banach Lattices 1.2.3 Banach Steinhaus Theorem Another fundamental theorem of functional analysis is the Banach Steinhaus theorem, or the Uniform Boundedness
Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games
 Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games Alberto Bressan ) and Khai T. Nguyen ) *) Department of Mathematics, Penn State University **) Department of Mathematics,
Stability of Feedback Solutions for Infinite Horizon Noncooperative Differential Games Alberto Bressan ) and Khai T. Nguyen ) *) Department of Mathematics, Penn State University **) Department of Mathematics,
An introduction to Birkhoff normal form
 An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
An introduction to Birkhoff normal form Dario Bambusi Dipartimento di Matematica, Universitá di Milano via Saldini 50, 0133 Milano (Italy) 19.11.14 1 Introduction The aim of this note is to present an
In essence, Dynamical Systems is a science which studies differential equations. A differential equation here is the equation
 Lecture I In essence, Dynamical Systems is a science which studies differential equations. A differential equation here is the equation ẋ(t) = f(x(t), t) where f is a given function, and x(t) is an unknown
Lecture I In essence, Dynamical Systems is a science which studies differential equations. A differential equation here is the equation ẋ(t) = f(x(t), t) where f is a given function, and x(t) is an unknown
LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES. Sergey Korotov,
 LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES Sergey Korotov, Institute of Mathematics Helsinki University of Technology, Finland Academy of Finland 1 Main Problem in Mathematical
LECTURE 1: SOURCES OF ERRORS MATHEMATICAL TOOLS A PRIORI ERROR ESTIMATES Sergey Korotov, Institute of Mathematics Helsinki University of Technology, Finland Academy of Finland 1 Main Problem in Mathematical
Notes on Complex Analysis
 Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
ON WEAKLY NONLINEAR BACKWARD PARABOLIC PROBLEM
 ON WEAKLY NONLINEAR BACKWARD PARABOLIC PROBLEM OLEG ZUBELEVICH DEPARTMENT OF MATHEMATICS THE BUDGET AND TREASURY ACADEMY OF THE MINISTRY OF FINANCE OF THE RUSSIAN FEDERATION 7, ZLATOUSTINSKY MALIY PER.,
ON WEAKLY NONLINEAR BACKWARD PARABOLIC PROBLEM OLEG ZUBELEVICH DEPARTMENT OF MATHEMATICS THE BUDGET AND TREASURY ACADEMY OF THE MINISTRY OF FINANCE OF THE RUSSIAN FEDERATION 7, ZLATOUSTINSKY MALIY PER.,
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Piecewise Smooth Solutions to the Burgers-Hilbert Equation
 Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
CONSTRAINED PERCOLATION ON Z 2
 CONSTRAINED PERCOLATION ON Z 2 ZHONGYANG LI Abstract. We study a constrained percolation process on Z 2, and prove the almost sure nonexistence of infinite clusters and contours for a large class of probability
CONSTRAINED PERCOLATION ON Z 2 ZHONGYANG LI Abstract. We study a constrained percolation process on Z 2, and prove the almost sure nonexistence of infinite clusters and contours for a large class of probability
ẋ = f(x, y), ẏ = g(x, y), (x, y) D, can only have periodic solutions if (f,g) changes sign in D or if (f,g)=0in D.
 4 Periodic Solutions We have shown that in the case of an autonomous equation the periodic solutions correspond with closed orbits in phase-space. Autonomous two-dimensional systems with phase-space R
4 Periodic Solutions We have shown that in the case of an autonomous equation the periodic solutions correspond with closed orbits in phase-space. Autonomous two-dimensional systems with phase-space R
2. The Concept of Convergence: Ultrafilters and Nets
 2. The Concept of Convergence: Ultrafilters and Nets NOTE: AS OF 2008, SOME OF THIS STUFF IS A BIT OUT- DATED AND HAS A FEW TYPOS. I WILL REVISE THIS MATE- RIAL SOMETIME. In this lecture we discuss two
2. The Concept of Convergence: Ultrafilters and Nets NOTE: AS OF 2008, SOME OF THIS STUFF IS A BIT OUT- DATED AND HAS A FEW TYPOS. I WILL REVISE THIS MATE- RIAL SOMETIME. In this lecture we discuss two
Def. A topological space X is disconnected if it admits a non-trivial splitting: (We ll abbreviate disjoint union of two subsets A and B meaning A B =
 CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
CONNECTEDNESS-Notes Def. A topological space X is disconnected if it admits a non-trivial splitting: X = A B, A B =, A, B open in X, and non-empty. (We ll abbreviate disjoint union of two subsets A and
Complex Analysis Qualifying Exam Solutions
 Complex Analysis Qualifying Exam Solutions May, 04 Part.. Let log z be the principal branch of the logarithm defined on G = {z C z (, 0]}. Show that if t > 0, then the equation log z = t has exactly one
Complex Analysis Qualifying Exam Solutions May, 04 Part.. Let log z be the principal branch of the logarithm defined on G = {z C z (, 0]}. Show that if t > 0, then the equation log z = t has exactly one
WORKSHEET #13 MATH 1260 FALL 2014
 WORKSHEET #3 MATH 26 FALL 24 NOT DUE. Short answer: (a) Find the equation of the tangent plane to z = x 2 + y 2 at the point,, 2. z x (, ) = 2x = 2, z y (, ) = 2y = 2. So then the tangent plane equation
WORKSHEET #3 MATH 26 FALL 24 NOT DUE. Short answer: (a) Find the equation of the tangent plane to z = x 2 + y 2 at the point,, 2. z x (, ) = 2x = 2, z y (, ) = 2y = 2. So then the tangent plane equation
On linear and non-linear equations. (Sect. 1.6).
 On linear and non-linear equations. (Sect. 1.6). Review: Linear differential equations. Non-linear differential equations. The Picard-Lindelöf Theorem. Properties of solutions to non-linear ODE. The Proof
On linear and non-linear equations. (Sect. 1.6). Review: Linear differential equations. Non-linear differential equations. The Picard-Lindelöf Theorem. Properties of solutions to non-linear ODE. The Proof
MATH Final Project Mean Curvature Flows
 MATH 581 - Final Project Mean Curvature Flows Olivier Mercier April 30, 2012 1 Introduction The mean curvature flow is part of the bigger family of geometric flows, which are flows on a manifold associated
MATH 581 - Final Project Mean Curvature Flows Olivier Mercier April 30, 2012 1 Introduction The mean curvature flow is part of the bigger family of geometric flows, which are flows on a manifold associated
Chapter 6: The metric space M(G) and normal families
 Chapter 6: The metric space MG) and normal families Course 414, 003 04 March 9, 004 Remark 6.1 For G C open, we recall the notation MG) for the set algebra) of all meromorphic functions on G. We now consider
Chapter 6: The metric space MG) and normal families Course 414, 003 04 March 9, 004 Remark 6.1 For G C open, we recall the notation MG) for the set algebra) of all meromorphic functions on G. We now consider
THE JORDAN-BROUWER SEPARATION THEOREM
 THE JORDAN-BROUWER SEPARATION THEOREM WOLFGANG SCHMALTZ Abstract. The Classical Jordan Curve Theorem says that every simple closed curve in R 2 divides the plane into two pieces, an inside and an outside
THE JORDAN-BROUWER SEPARATION THEOREM WOLFGANG SCHMALTZ Abstract. The Classical Jordan Curve Theorem says that every simple closed curve in R 2 divides the plane into two pieces, an inside and an outside
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
1 Lyapunov theory of stability
 M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
LECTURE 23: LIGHT. Propagation of Light Huygen s Principle
 LECTURE 23: LIGHT Propagation of Light Reflection & Refraction Internal Reflection Propagation of Light Huygen s Principle Each point on a primary wavefront serves as the source of spherical secondary
LECTURE 23: LIGHT Propagation of Light Reflection & Refraction Internal Reflection Propagation of Light Huygen s Principle Each point on a primary wavefront serves as the source of spherical secondary
(x 1, y 1 ) = (x 2, y 2 ) if and only if x 1 = x 2 and y 1 = y 2.
 1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
Chapter 33. Electromagnetic Waves
 Chapter 33 Electromagnetic Waves Today s information age is based almost entirely on the physics of electromagnetic waves. The connection between electric and magnetic fields to produce light is own of
Chapter 33 Electromagnetic Waves Today s information age is based almost entirely on the physics of electromagnetic waves. The connection between electric and magnetic fields to produce light is own of
Preliminary Exam 2018 Solutions to Morning Exam
 Preliminary Exam 28 Solutions to Morning Exam Part I. Solve four of the following five problems. Problem. Consider the series n 2 (n log n) and n 2 (n(log n)2 ). Show that one converges and one diverges
Preliminary Exam 28 Solutions to Morning Exam Part I. Solve four of the following five problems. Problem. Consider the series n 2 (n log n) and n 2 (n(log n)2 ). Show that one converges and one diverges
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
SEAFLOOR MAPPING MODELLING UNDERWATER PROPAGATION RAY ACOUSTICS
 3 Underwater propagation 3. Ray acoustics 3.. Relevant mathematics We first consider a plane wave as depicted in figure. As shown in the figure wave fronts are planes. The arrow perpendicular to the wave
3 Underwater propagation 3. Ray acoustics 3.. Relevant mathematics We first consider a plane wave as depicted in figure. As shown in the figure wave fronts are planes. The arrow perpendicular to the wave
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Introduction to Algebraic and Geometric Topology Week 14
 Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
Topological properties of Z p and Q p and Euclidean models
 Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
F (z) =f(z). f(z) = a n (z z 0 ) n. F (z) = a n (z z 0 ) n
 6 Chapter 2. CAUCHY S THEOREM AND ITS APPLICATIONS Theorem 5.6 (Schwarz reflection principle) Suppose that f is a holomorphic function in Ω + that extends continuously to I and such that f is real-valued
6 Chapter 2. CAUCHY S THEOREM AND ITS APPLICATIONS Theorem 5.6 (Schwarz reflection principle) Suppose that f is a holomorphic function in Ω + that extends continuously to I and such that f is real-valued
MURI teleconference 28 May Optical Antimatter. John Pendry and Sebastien Guenneau Imperial College London. 24 May 2004 page 1
 24 May 2004 page 1 MURI teleconference 28 May 2004 Optical Antimatter John Pendry and Sebastien Guenneau Imperial College London 05 March 2004 page 2 A Conventional Lens Contributions of the far field
24 May 2004 page 1 MURI teleconference 28 May 2004 Optical Antimatter John Pendry and Sebastien Guenneau Imperial College London 05 March 2004 page 2 A Conventional Lens Contributions of the far field
Convergence Rate of Nonlinear Switched Systems
 Convergence Rate of Nonlinear Switched Systems Philippe JOUAN and Saïd NACIRI arxiv:1511.01737v1 [math.oc] 5 Nov 2015 January 23, 2018 Abstract This paper is concerned with the convergence rate of the
Convergence Rate of Nonlinear Switched Systems Philippe JOUAN and Saïd NACIRI arxiv:1511.01737v1 [math.oc] 5 Nov 2015 January 23, 2018 Abstract This paper is concerned with the convergence rate of the
1. Bounded linear maps. A linear map T : E F of real Banach
 DIFFERENTIABLE MAPS 1. Bounded linear maps. A linear map T : E F of real Banach spaces E, F is bounded if M > 0 so that for all v E: T v M v. If v r T v C for some positive constants r, C, then T is bounded:
DIFFERENTIABLE MAPS 1. Bounded linear maps. A linear map T : E F of real Banach spaces E, F is bounded if M > 0 so that for all v E: T v M v. If v r T v C for some positive constants r, C, then T is bounded:
SHARP BOUNDARY TRACE INEQUALITIES. 1. Introduction
 SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
SHARP BOUNDARY TRACE INEQUALITIES GILES AUCHMUTY Abstract. This paper describes sharp inequalities for the trace of Sobolev functions on the boundary of a bounded region R N. The inequalities bound (semi-)norms
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Krein-Rutman Theorem and the Principal Eigenvalue
 Chapter 1 Krein-Rutman Theorem and the Principal Eigenvalue The Krein-Rutman theorem plays a very important role in nonlinear partial differential equations, as it provides the abstract basis for the proof
Chapter 1 Krein-Rutman Theorem and the Principal Eigenvalue The Krein-Rutman theorem plays a very important role in nonlinear partial differential equations, as it provides the abstract basis for the proof
8 8 THE RIEMANN MAPPING THEOREM. 8.1 Simply Connected Surfaces
 8 8 THE RIEMANN MAPPING THEOREM 8.1 Simply Connected Surfaces Our aim is to prove the Riemann Mapping Theorem which states that every simply connected Riemann surface R is conformally equivalent to D,
8 8 THE RIEMANN MAPPING THEOREM 8.1 Simply Connected Surfaces Our aim is to prove the Riemann Mapping Theorem which states that every simply connected Riemann surface R is conformally equivalent to D,
Generalized metric properties of spheres and renorming of Banach spaces
 arxiv:1605.08175v2 [math.fa] 5 Nov 2018 Generalized metric properties of spheres and renorming of Banach spaces 1 Introduction S. Ferrari, J. Orihuela, M. Raja November 6, 2018 Throughout this paper X
arxiv:1605.08175v2 [math.fa] 5 Nov 2018 Generalized metric properties of spheres and renorming of Banach spaces 1 Introduction S. Ferrari, J. Orihuela, M. Raja November 6, 2018 Throughout this paper X
Observer design for a general class of triangular systems
 1st International Symposium on Mathematical Theory of Networks and Systems July 7-11, 014. Observer design for a general class of triangular systems Dimitris Boskos 1 John Tsinias Abstract The paper deals
1st International Symposium on Mathematical Theory of Networks and Systems July 7-11, 014. Observer design for a general class of triangular systems Dimitris Boskos 1 John Tsinias Abstract The paper deals
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
MATH 12 CLASS 5 NOTES, SEP
 MATH 12 CLASS 5 NOTES, SEP 30 2011 Contents 1. Vector-valued functions 1 2. Differentiating and integrating vector-valued functions 3 3. Velocity and Acceleration 4 Over the past two weeks we have developed
MATH 12 CLASS 5 NOTES, SEP 30 2011 Contents 1. Vector-valued functions 1 2. Differentiating and integrating vector-valued functions 3 3. Velocity and Acceleration 4 Over the past two weeks we have developed
An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010
 An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010 John P. D Angelo, Univ. of Illinois, Urbana IL 61801.
An Introduction to Complex Analysis and Geometry John P. D Angelo, Pure and Applied Undergraduate Texts Volume 12, American Mathematical Society, 2010 John P. D Angelo, Univ. of Illinois, Urbana IL 61801.
INVERSE FUNCTION THEOREM and SURFACES IN R n
 INVERSE FUNCTION THEOREM and SURFACES IN R n Let f C k (U; R n ), with U R n open. Assume df(a) GL(R n ), where a U. The Inverse Function Theorem says there is an open neighborhood V U of a in R n so that
INVERSE FUNCTION THEOREM and SURFACES IN R n Let f C k (U; R n ), with U R n open. Assume df(a) GL(R n ), where a U. The Inverse Function Theorem says there is an open neighborhood V U of a in R n so that
CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS. W. Erwin Diewert January 31, 2008.
 1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
1 ECONOMICS 594: LECTURE NOTES CHAPTER 2: CONVEX SETS AND CONCAVE FUNCTIONS W. Erwin Diewert January 31, 2008. 1. Introduction Many economic problems have the following structure: (i) a linear function
Chapter 0 of Calculus ++, Differential calculus with several variables
 Chapter of Calculus ++, Differential calculus with several variables Background material by Eric A Carlen Professor of Mathematics Georgia Tech Spring 6 c 6 by the author, all rights reserved - Table of
Chapter of Calculus ++, Differential calculus with several variables Background material by Eric A Carlen Professor of Mathematics Georgia Tech Spring 6 c 6 by the author, all rights reserved - Table of
Dynamic Blocking Problems for a Model of Fire Propagation
 Dynamic Blocking Problems for a Model of Fire Propagation Alberto Bressan Department of Mathematics, Penn State University, University Park, Pa 16802, USA bressan@mathpsuedu February 6, 2012 Abstract This
Dynamic Blocking Problems for a Model of Fire Propagation Alberto Bressan Department of Mathematics, Penn State University, University Park, Pa 16802, USA bressan@mathpsuedu February 6, 2012 Abstract This
Controllability of linear PDEs (I): The wave equation
 Controllability of linear PDEs (I): The wave equation M. González-Burgos IMUS, Universidad de Sevilla Doc Course, Course 2, Sevilla, 2018 Contents 1 Introduction. Statement of the problem 2 Distributed
Controllability of linear PDEs (I): The wave equation M. González-Burgos IMUS, Universidad de Sevilla Doc Course, Course 2, Sevilla, 2018 Contents 1 Introduction. Statement of the problem 2 Distributed
Linear Ordinary Differential Equations
 MTH.B402; Sect. 1 20180703) 2 Linear Ordinary Differential Equations Preliminaries: Matrix Norms. Denote by M n R) the set of n n matrix with real components, which can be identified the vector space R
MTH.B402; Sect. 1 20180703) 2 Linear Ordinary Differential Equations Preliminaries: Matrix Norms. Denote by M n R) the set of n n matrix with real components, which can be identified the vector space R
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
ON NEARLY SEMIFREE CIRCLE ACTIONS
 ON NEARLY SEMIFREE CIRCLE ACTIONS DUSA MCDUFF AND SUSAN TOLMAN Abstract. Recall that an effective circle action is semifree if the stabilizer subgroup of each point is connected. We show that if (M, ω)
ON NEARLY SEMIFREE CIRCLE ACTIONS DUSA MCDUFF AND SUSAN TOLMAN Abstract. Recall that an effective circle action is semifree if the stabilizer subgroup of each point is connected. We show that if (M, ω)
Continuous Functions on Metric Spaces
 Continuous Functions on Metric Spaces Math 201A, Fall 2016 1 Continuous functions Definition 1. Let (X, d X ) and (Y, d Y ) be metric spaces. A function f : X Y is continuous at a X if for every ɛ > 0
Continuous Functions on Metric Spaces Math 201A, Fall 2016 1 Continuous functions Definition 1. Let (X, d X ) and (Y, d Y ) be metric spaces. A function f : X Y is continuous at a X if for every ɛ > 0
MORE CONSEQUENCES OF CAUCHY S THEOREM
 MOE CONSEQUENCES OF CAUCHY S THEOEM Contents. The Mean Value Property and the Maximum-Modulus Principle 2. Morera s Theorem and some applications 3 3. The Schwarz eflection Principle 6 We have stated Cauchy
MOE CONSEQUENCES OF CAUCHY S THEOEM Contents. The Mean Value Property and the Maximum-Modulus Principle 2. Morera s Theorem and some applications 3 3. The Schwarz eflection Principle 6 We have stated Cauchy
(convex combination!). Use convexity of f and multiply by the common denominator to get. Interchanging the role of x and y, we obtain that f is ( 2M ε
 1. Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
1. Continuity of convex functions in normed spaces In this chapter, we consider continuity properties of real-valued convex functions defined on open convex sets in normed spaces. Recall that every infinitedimensional
Chapter 9. Reflection, Refraction and Polarization
 Reflection, Refraction and Polarization Introduction When you solved Problem 5.2 using the standing-wave approach, you found a rather curious behavior as the wave propagates and meets the boundary. A new
Reflection, Refraction and Polarization Introduction When you solved Problem 5.2 using the standing-wave approach, you found a rather curious behavior as the wave propagates and meets the boundary. A new
arxiv: v1 [math.oc] 22 Sep 2016
![arxiv: v1 [math.oc] 22 Sep 2016 arxiv: v1 [math.oc] 22 Sep 2016](/thumbs/83/88751971.jpg) EUIVALENCE BETWEEN MINIMAL TIME AND MINIMAL NORM CONTROL PROBLEMS FOR THE HEAT EUATION SHULIN IN AND GENGSHENG WANG arxiv:1609.06860v1 [math.oc] 22 Sep 2016 Abstract. This paper presents the equivalence
EUIVALENCE BETWEEN MINIMAL TIME AND MINIMAL NORM CONTROL PROBLEMS FOR THE HEAT EUATION SHULIN IN AND GENGSHENG WANG arxiv:1609.06860v1 [math.oc] 22 Sep 2016 Abstract. This paper presents the equivalence
Chapter 1 - The Nature of Light
 David J. Starling Penn State Hazleton PHYS 214 Electromagnetic radiation comes in many forms, differing only in wavelength, frequency or energy. Electromagnetic radiation comes in many forms, differing
David J. Starling Penn State Hazleton PHYS 214 Electromagnetic radiation comes in many forms, differing only in wavelength, frequency or energy. Electromagnetic radiation comes in many forms, differing
arxiv: v1 [math.fa] 14 Jul 2018
![arxiv: v1 [math.fa] 14 Jul 2018 arxiv: v1 [math.fa] 14 Jul 2018](/thumbs/82/85634312.jpg) Construction of Regular Non-Atomic arxiv:180705437v1 [mathfa] 14 Jul 2018 Strictly-Positive Measures in Second-Countable Locally Compact Non-Atomic Hausdorff Spaces Abstract Jason Bentley Department of
Construction of Regular Non-Atomic arxiv:180705437v1 [mathfa] 14 Jul 2018 Strictly-Positive Measures in Second-Countable Locally Compact Non-Atomic Hausdorff Spaces Abstract Jason Bentley Department of
S chauder Theory. x 2. = log( x 1 + x 2 ) + 1 ( x 1 + x 2 ) 2. ( 5) x 1 + x 2 x 1 + x 2. 2 = 2 x 1. x 1 x 2. 1 x 1.
 Sep. 1 9 Intuitively, the solution u to the Poisson equation S chauder Theory u = f 1 should have better regularity than the right hand side f. In particular one expects u to be twice more differentiable
Sep. 1 9 Intuitively, the solution u to the Poisson equation S chauder Theory u = f 1 should have better regularity than the right hand side f. In particular one expects u to be twice more differentiable
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES. 1. Compact Sets
 FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
Best approximations in normed vector spaces
 Best approximations in normed vector spaces Mike de Vries 5699703 a thesis submitted to the Department of Mathematics at Utrecht University in partial fulfillment of the requirements for the degree of
Best approximations in normed vector spaces Mike de Vries 5699703 a thesis submitted to the Department of Mathematics at Utrecht University in partial fulfillment of the requirements for the degree of
in Electromagnetics Numerical Method Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD
 2141418 Numerical Method in Electromagnetics Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD ISE, Chulalongkorn University, 2 nd /2018 Email: charusluk.v@chula.ac.th Website: Light
2141418 Numerical Method in Electromagnetics Introduction to Electromagnetics I Lecturer: Charusluk Viphavakit, PhD ISE, Chulalongkorn University, 2 nd /2018 Email: charusluk.v@chula.ac.th Website: Light
REPRESENTATION THEORY WEEK 7
 REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
THE WAVE EQUATION. d = 1: D Alembert s formula We begin with the initial value problem in 1 space dimension { u = utt u xx = 0, in (0, ) R, (2)
 THE WAVE EQUATION () The free wave equation takes the form u := ( t x )u = 0, u : R t R d x R In the literature, the operator := t x is called the D Alembertian on R +d. Later we shall also consider the
THE WAVE EQUATION () The free wave equation takes the form u := ( t x )u = 0, u : R t R d x R In the literature, the operator := t x is called the D Alembertian on R +d. Later we shall also consider the
Open Questions in Quantum Information Geometry
 Open Questions in Quantum Information Geometry M. R. Grasselli Department of Mathematics and Statistics McMaster University Imperial College, June 15, 2005 1. Classical Parametric Information Geometry
Open Questions in Quantum Information Geometry M. R. Grasselli Department of Mathematics and Statistics McMaster University Imperial College, June 15, 2005 1. Classical Parametric Information Geometry
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
FUNDAMENTAL GROUPS AND THE VAN KAMPEN S THEOREM. Contents
 FUNDAMENTAL GROUPS AND THE VAN KAMPEN S THEOREM SAMUEL BLOOM Abstract. In this paper, we define the fundamental group of a topological space and explore its structure, and we proceed to prove Van-Kampen
FUNDAMENTAL GROUPS AND THE VAN KAMPEN S THEOREM SAMUEL BLOOM Abstract. In this paper, we define the fundamental group of a topological space and explore its structure, and we proceed to prove Van-Kampen
Centre for Mathematics and Its Applications The Australian National University Canberra, ACT 0200 Australia. 1. Introduction
 ON LOCALLY CONVEX HYPERSURFACES WITH BOUNDARY Neil S. Trudinger Xu-Jia Wang Centre for Mathematics and Its Applications The Australian National University Canberra, ACT 0200 Australia Abstract. In this
ON LOCALLY CONVEX HYPERSURFACES WITH BOUNDARY Neil S. Trudinger Xu-Jia Wang Centre for Mathematics and Its Applications The Australian National University Canberra, ACT 0200 Australia Abstract. In this
Analysis in weighted spaces : preliminary version
 Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
Notation. General. Notation Description See. Sets, Functions, and Spaces. a b & a b The minimum and the maximum of a and b
 Notation General Notation Description See a b & a b The minimum and the maximum of a and b a + & a f S u The non-negative part, a 0, and non-positive part, (a 0) of a R The restriction of the function
Notation General Notation Description See a b & a b The minimum and the maximum of a and b a + & a f S u The non-negative part, a 0, and non-positive part, (a 0) of a R The restriction of the function
1. Waves and Particles 2. Interference of Waves 3. Wave Nature of Light
 1. Waves and Particles 2. Interference of Waves 3. Wave Nature of Light 1. Double-Slit Eperiment reading: Chapter 22 2. Single-Slit Diffraction reading: Chapter 22 3. Diffraction Grating reading: Chapter
1. Waves and Particles 2. Interference of Waves 3. Wave Nature of Light 1. Double-Slit Eperiment reading: Chapter 22 2. Single-Slit Diffraction reading: Chapter 22 3. Diffraction Grating reading: Chapter
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
2. Dual space is essential for the concept of gradient which, in turn, leads to the variational analysis of Lagrange multipliers.
 Chapter 3 Duality in Banach Space Modern optimization theory largely centers around the interplay of a normed vector space and its corresponding dual. The notion of duality is important for the following
Chapter 3 Duality in Banach Space Modern optimization theory largely centers around the interplay of a normed vector space and its corresponding dual. The notion of duality is important for the following
The Minimum Speed for a Blocking Problem on the Half Plane
 The Minimum Speed for a Blocking Problem on the Half Plane Alberto Bressan and Tao Wang Department of Mathematics, Penn State University University Park, Pa 16802, USA e-mails: bressan@mathpsuedu, wang
The Minimum Speed for a Blocking Problem on the Half Plane Alberto Bressan and Tao Wang Department of Mathematics, Penn State University University Park, Pa 16802, USA e-mails: bressan@mathpsuedu, wang
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
Introduction and Preliminaries
 Chapter 1 Introduction and Preliminaries This chapter serves two purposes. The first purpose is to prepare the readers for the more systematic development in later chapters of methods of real analysis
Chapter 1 Introduction and Preliminaries This chapter serves two purposes. The first purpose is to prepare the readers for the more systematic development in later chapters of methods of real analysis
Implications of the Constant Rank Constraint Qualification
 Mathematical Programming manuscript No. (will be inserted by the editor) Implications of the Constant Rank Constraint Qualification Shu Lu Received: date / Accepted: date Abstract This paper investigates
Mathematical Programming manuscript No. (will be inserted by the editor) Implications of the Constant Rank Constraint Qualification Shu Lu Received: date / Accepted: date Abstract This paper investigates
5 Measure theory II. (or. lim. Prove the proposition. 5. For fixed F A and φ M define the restriction of φ on F by writing.
 5 Measure theory II 1. Charges (signed measures). Let (Ω, A) be a σ -algebra. A map φ: A R is called a charge, (or signed measure or σ -additive set function) if φ = φ(a j ) (5.1) A j for any disjoint
5 Measure theory II 1. Charges (signed measures). Let (Ω, A) be a σ -algebra. A map φ: A R is called a charge, (or signed measure or σ -additive set function) if φ = φ(a j ) (5.1) A j for any disjoint
The Minimal Element Theorem
 The Minimal Element Theorem The CMC Dynamics Theorem deals with describing all of the periodic or repeated geometric behavior of a properly embedded CMC surface with bounded second fundamental form in
The Minimal Element Theorem The CMC Dynamics Theorem deals with describing all of the periodic or repeated geometric behavior of a properly embedded CMC surface with bounded second fundamental form in
GALERKIN TIME STEPPING METHODS FOR NONLINEAR PARABOLIC EQUATIONS
 GALERKIN TIME STEPPING METHODS FOR NONLINEAR PARABOLIC EQUATIONS GEORGIOS AKRIVIS AND CHARALAMBOS MAKRIDAKIS Abstract. We consider discontinuous as well as continuous Galerkin methods for the time discretization
GALERKIN TIME STEPPING METHODS FOR NONLINEAR PARABOLIC EQUATIONS GEORGIOS AKRIVIS AND CHARALAMBOS MAKRIDAKIS Abstract. We consider discontinuous as well as continuous Galerkin methods for the time discretization
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Electromagnetic Waves. Chapter 33 (Halliday/Resnick/Walker, Fundamentals of Physics 8 th edition)
 PH 222-3A Spring 2007 Electromagnetic Waves Lecture 22 Chapter 33 (Halliday/Resnick/Walker, Fundamentals of Physics 8 th edition) 1 Chapter 33 Electromagnetic Waves Today s information age is based almost
PH 222-3A Spring 2007 Electromagnetic Waves Lecture 22 Chapter 33 (Halliday/Resnick/Walker, Fundamentals of Physics 8 th edition) 1 Chapter 33 Electromagnetic Waves Today s information age is based almost
