Quantum trajectories and quantum measurement theory in solid-state mesoscopics
|
|
|
- Dylan Gray
- 6 years ago
- Views:
Transcription
1 Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis HsiSng Gon Cntr or Quntum Computr nology, Univrsity o Nw Sout ls, Sydny, NS 202 Austrli Abstrt. Strting rom t ull Srödingr qution or systm nd n nvironmnt ( dttor), w prsnt uristi drivtion o t stosti Srödingr (mstr) qution or msosopi msurmnt modl to illustrt t ssntil pysis o t quntum trjtory tory. is msosopi modl dsribs twostt quntum systm, n ltron orntly tunnling btwn two oupld quntum dots, intrting wit n nvironmnt ( dttor), low trnsprny point ontt or tunnl juntion. n w provid onntion nd uniid pitur or t quntum trjtory ppro nd t mstr qution ppro. sow tt t mstr qution or t rdud or prtilly rdud dnsity mtrix n b simply obtind wn n vrg or prtil vrg is tkn on t onditionl, stosti dnsity mtrix (or quntum trjtoris) ovr t possibl outoms o t msurmnts.. Introdution tory o quntum trjtoris or stosti Sr ödingr qutions s bn dvlopd in lst tn yrs minly in t quntum optis ommunity to dsrib opn quntum systm subjt to ontinuous quntum msurmnts. But it ws introdud to t ontxt o solidstt msosopis only rntly [, 2, 3, 4. Dirnt utors, owvr, gv somwt dirnt drivtions or t stosti qutions. In s. [, 2 t prsriptions or t quntum trjtoris (or sltiv, onditionl, stosti stt volution) wr drivd bsd on t Bysin ormlism, wil ty wr drivd in s. [3, 4 strting rom unonditionl mstr qution. In ddition, t intrprttions long wit t drivtions do not sm trnsprnt noug. Hn, mny spts o t tory r still poorly undrstood in t ondnsd mttr pysis ommunity. min purposs o tis ppr r (i) to prsnt simpl, uristi drivtion or t sm msosopi modl to illustrt t ssntil pysis o t quntum trjtoris. (ii) to provid uniid pitur or t quntum trjtory ppro nd t mstr qution ppro o rdud or prtilly rdud dnsity mtrix. Hr w rr to t mstr qution ppro o t prtilly rdud dnsity mtrix s t ppro rntly dvlopd in s. [, 6, 7, minly or t purpos o rding out n initil stt o quntum bit (qubit). sow tt t mstr qution o t rdud or prtilly rdud dnsity mtrix n b obtind s rsult o nsmbl vrg or prtil vrg on t onditionl, stosti mstr qution o t dnsity mtrix (onstrutd rom t onditionl systm stt vtor) ovr ll possibl dttion rords. 2. Msosopi msurmnt modl nd quntum trjtoris 2.. Coupldquntumdot nd pointontt modl msosopi msurmnt modl onsidrd in s. [, 2, 3, 4, dsribs quntum systm, n ltron orntly tunnling btwn two oupld quntum dots (CQD s),
2 ; D ; ; ; D F Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 2 intrting wit n nvironmnt ( dttor), low trnsprny point ontt (PC) or tunnl juntion. Hmiltonin dsribing t wol systm n b writtn s [, 2, 3, 4, () wr! # $ &' # ( *), # ( # $.0/& <; BA D; : > 3#C DE6!F4G D ; $; D0 ; D ; AK H 3#CD # $ 6!I G I rprsnts t tiv tunnling Hmiltonin or t msurd twostt CQD systm (msosopi L rg qubit). 'M M tunnling N?M Hmiltonin or t PC bt (dttor) is rprsntd by. Hr ( ) nd rprsnt t ltron nniiltion (rtion) oprtor nd nrgy or singl ) ltron stt in dot N rsptivly. N oupling btwn t two dots is givn by. Similrly,, nd, r rsptivly t ltron nniiltion oprtors L nd nrgis or t lt nd rigt rsrvoir stts t wv numbr O. Eqution (4),, dsribs t intrtion btwn t bt (dttor) nd t CQD qubit systm, dpnding on wi dot is oupid. n t ltron in t CQD s is lotd in dot P F D:Q D D I, t tiv tunnling mplitud o t PC dttor ngs rom Continuous msurmnts nd quntum trjtory will driv, strting rom t ull Sr ödingr qution or t systm nd nvironmnt (bt), t stosti Sr ödingr qution wi modls t volution o t CQD systm onditiond on ontinuous in tim msurmnts o t PC bt by dttion dvi. ollow losly t drivtion [8,, 0 o t stosti Sr ödingr qution or n tom, drivn by lssil rdition ilds nd intrting wit t vuum rdition ild, or t CQD/PC modl. bsi id is s ollows. Suppos tt t ombind stt S, o t systm nd t bt is initilly disntngld, S VU VU X U. Hr t initil vuum stt UZ o t PC bt is t stt wr t nrgy lvls in t sour (t lt PC rsrvoir) nd drin (t rigt PC rsrvoir) r illd up to t Frmi nrgis (mil potntil) [ wit ltron numbr ^, nd [ wit ltron numbr ^, rsptivly. rprsnt t Hilbrt sp o t PC bt stts s t numbr or $; Fok stts $; o t lt nd rigt PC rsrvoirs. Sin t oprtor _, ommuts wit t totl Hmiltonin UZ Eq. (), t totl ltron numbr o t PC is onsrvd. n tus writ ` X ` nd `L bx ` b, bing t stts simultnously ving ddition ltrons in t drin ontinuum, nd ols in t sour ontinuum. t o mks t stt o t CQD qubit systm nd t stt o t PC rsrvoirs bom ntngld so tt t totl stt S, no longr torizs s it did t du. For t CQD/PC msosopi modl, t obsrvd quntity or pysil obsrvbl is t numbr o ltrons tunnling troug PC. Hn w n xpnd t totl stt on t ortonorml Fok (numbr) stt bsis o t PC bt s S 38g X Hr w v osn t CQD qubit systm stt to b normlizd, but ty r, in gnrl, not ortonorml. is is rltd to t t tt t indirt msurmnt on t CQD qubit systm, disussd ltr, is not projtiv. onsidr t s tt t msurmnt is prormd nd rptd witin tim intrvl Z mu smllr tn t B; F D0 ; D'; BA (2) (3) (4) ()
3 P Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 3 typil systm volution or rspons tim. Hn, t systm is tivly ontinuously monitord. Aording to t ortodox quntum tory o msurmnts, t possibl dttor outoms r t intgr ignvlus o t ltron numbr oprtor in t rigt rsrvoir o t PC t tim Z. Morovr, subsqunt to t dttion, t bt prt o t totl wv untion S Z ollpss to t orrsponding ignstt. t is to sy wn t msurmnt idntiis t stt o t PC bt to b in t prtiulr ignstt, t CQD systm is in t orrsponding pur stt Z Z. probbility or tis to ppn is qul to Z. normlizd systm stt, onditiond on t msurmnt rsult just obtind, tn srvs s t initil stt or t nxt volution nd msurmnt tim intrvl Z. us, ording to t msurmnt rord o xprimnt run, w obtin on prtiulr volution o systm stt s rsult o ontinuous projtion o t totl stt S on on o t ignstts. Su n volution is lld quntum trjtory nd its ntur is gnrlly stosti. stosti lmnt in t quntum trjtory orrsponds xtly to t onsqun o t rndom outoms o t msurmnt rord. It is importnt to rliz tt t xprimntr nvr mks dirt msurmnt on t systm o intrst. tr, t xprimntr obsrvs t numbr o ltrons tunnling troug t PC. In t msosopi modl, t CQD qubit systm intrts wit t PC rsrvoirs nd tir quntum stts r ntngld. projtiv msurmnt md on t PC bt, owvr, nbls us to disntngl t systm nd t bt stts. my tink t t on t qubit systm stt is n indirt rsult o t projtiv msurmnt on t PC bt, nd w my modl it in trms o msurmnt oprtors Z ting on t qubit systm stt lon. Howvr, su n tiv msurmnt on t qubit systm stt is, in prinipl, not projtiv. I t initil normlizd stt o t systm is immditly bor t msurmnt, t unnormlizd stt o t msurd rsult bing t t nd o t tim intrvl Z o t msurmnt n b writtn s Z Z. orrsponding probbility nd t normlizd inl stt o t systm r rsptivly (6) Z Z Z Z Z Z Z _ Hr t msurmnt oprtor stisis t ompltnss ondition wi is simply sttmnt o onsrvtion o probbility. Z or t msurmnt oprtors Z is known t tim umpr volution VU VU X U (7) Z Z P, qustion now is to ind or t CQD/PC modl givn tt First, lt us onsidr t s tt S, nd t msurmnt outom tt no ltron tunnling troug PC is dttd up to tim. trt t sum o t tunnling Hmiltonin prts in nd s t intrtion Hmiltonin. n t dynmis o t ntir systm in t intrtion pitur, is dtrmind by t timdpndnt Hmiltonin [3 D 3#C D 6!F4G D I G A ; $ B; D M! $#& (' wr H.. stnds or Hrmitin onjugt o t ntir prvious trm. totl wv untion o t ntir systm in t intrtion pitur stisis Z S * X S VU X, X Z/. /. S /. () ) (8)
4 Q F P D F Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 4 ltron troug PC is dttd: Z * P G $ G s rom Eq. (3) tt wn t msurmnt rsult is null (no ltron dttd), t systm ngs ininitsimlly, but not unitrily. nonunitry ntur o t volution xprsss t t tt t projtiv msurmnt on t bt wit rsults o no ltrons dttd still v ts on t systm. In ddition, Eq. (3) is nonlinr bus o t prsn o t xpttion vlu trm, wi nsurs tt t systm stt rmins normlizd.. $ Eqution () is xt nd n b drivd rom t Sr ödingr qution. onsidr t msurmnt sm o ounting t numbr o ltrons troug t PC. totl wv untion in t intrtion pitur n b xpndd in trms o t Fok stts o t bt s in Eq. () wit. t o zroount msurmnt rsults is tt t totl stt vtor S is rptdly projtd into U nd is rnormlizd. Hn during t zroount intrvl, t stt vtor o t systm will b in. Using Eq. () nd rrying out t projtion onto U, w ind or t volution o t unnormlizd stt s ollows: Z, D0 D0 D D 3#CD F G I?G F I. Z/. M [ N: N> [! #! #. (0) wr $, nd P or U nd 7U or U. irst trm in Eq. () dos not ontribut bus U X UZ U d. Undr t ssumption tt t orrltion tim o t bt, [ [, is mu sortr tn t typil tim onstnt xptd rom t systm, nd providd tt, w n rpl. by in t intgrnd o Eq. (0) nd xtnd t lowr limit o t tim intgrtion to ininity tr t ng o vribl.. is ssumption nd rsulting simpliitions to t intgrnd o Eq. (0) r known s t BornMrkov pproximtion. Crrying out t intgrtion nd going bk to t S ödingr pitur, w ind tt Eq. (0) boms Z * P G G. () wr t prmtrs nd r givn by, nd. I. Hr nd. r vrg ltron tunnling rts troug t PC brrir witout nd wit t prsn o t ltron in dot rsptivly, nd [ [ is t xtrnl bis pplid ross F t PC. o rriv t Eq. (), nrgyindpndnt tunnling mplituds rprsntd by nd I, nd nrgyindpndnt dnsity o stts o t rsrvoirs rprsntd by nd r ssumd. quiring tt t stt rmins normlizd so tt Z U, nd wit t lp o Eq. () nd t rltion, w obtin Z 8 (2) G G. wr nd t xpttion vlu!#!#! is tkn wit rspt to t normlizd stt. is tn yilds, rom Eq. (), t ollowing volution qution or t normlizd stt o t CQD qubit systm undr t ondition tt no. HP (3)
5 * Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 2.4. Quntum jumps Nxt w onsidr t s tt ltrons pssing troug t PC r dttd. probbility tt dttion o ltron ours in tim intrvl [, Z ) is qul to t dirn btwn t probbility tt no ltron ws dttd up to tim nd tt up to tim Z. is n b dirtly ound rom Eq. (2) wit t rsult: Z Z (4) wr t rltion s bn usd. I t dttion intrvls Z r osn to b suiintly sort or t dttion probbility to b smll, t probbility o two nd mor ltrons ould v bn dttd my b ngltd. Hn in ininitsiml tim intrvl Z, itr msurmnt rsult is null (no ltron dttd) or tr is dttion o n ltron troug t PC brrir. At rndomly dtrmind tims (onditionlly Poisson distributd), wn tr is dttion o n ltron, t systm undrgos init volution (or suddn jump du to ollps), lld quntum jump. Givn tt S X UZ t tim nd dttion rsult o n ltron t tim Z, t totl stt vtor S Z ollpss to t stt Z X P. know tt t probbility or t dttion to our is ` Z P Z Z () is is obtind rom Eq. (4) by stting P sin t initil stt X UZ t tim, s rsult o prvious msurmnt, sould b normlizd. qustion now is simply to ind t normlizd stt Z X P o t systm. It is suiint to obtin tis stt to Z U Z < t irst ordr in intrtion Hmiltonin. ind 7. Eqution (6) n lso b obtind by mns o tiv msurmnt oprtors. In tis s, only two o tm, Z or P, r ndd in quntumjump msurmnt intrvl. Using t rltions, ^ nd Z Z, w ind rom Eq. () tt P G G. Z (7) msurmnt oprtor Z Z P Z Z in Z n b obtind using Eqs. () nd (6) s Z (8) pprn o nsurs tt only init numbr o dttions n our in init tim intrvl, sin t probbility o dttion rsult is proportionl to Z. n rom Eq. (7), t normlizd stt tr dttion Eq. (6) _ rsults. On n k tt t msurmnt oprtors stisy t ompltnss ondition Z Z P, to irst ordr in tim Z. igt tr t dttion, t PC rsrvoirs r immditly rst bk to its vuum stt. t is, t dttd ltron wi s tunnld into t rigt rsrvoir is dstroyd in t ltri iruit o t dttion dvi, nd n ltron rom t outr iruit immditly lows to t lt rsrvoir to ill up t ol in t msurmnt pross. So nrgy lvls in t sour nd drin r gin illd up to t Frmi nrgis (mil potntil) [ nd [, rsptivly. In otr words, t nw stt S Z tr dttion tror boms Z X UZ. is stt tn srvs s t initil stt or nxt volution nd msurmnt intrvl. n t wol squn n b rptd to dtrmin t rndom tim volution o t CQD qubit systm stt. (6)
6 Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 6 n ombin t volution o t systm stt or t two possibl outoms o t msurmnt s # Z P # Z! # Z ( Z Hr nd rom wt ollows w xpliitly us t subsript to indit tt t quntity to wi it is ttd is onditiond on prvious msurmnt rsults, t ourrns (dttion rords) o t ltrons tunnling troug t PC brrir in t pst. n tink o ( # _ s t inrmnt in t numbr o ltrons ( pssing troug PC brrir in tim Z. In t quntumjump s, ( is qul to itr zro or on, nd n # (. In ddition, sin t ntur o ltrons tunnling troug t PC is stosti, # tus rprsnts lssil rndom pross. Formlly, t urrnt troug t PC n b writtn s # ( Z. It is t vribl, t umultd ltron numbr trnsmittd troug t PC, wi is usd in s. [, 6, 7. Intuitivly, t nsmbl vrg ( o t lssil stosti pross # quls ` ( Z, t probbility (quntum vrg) o dtting ltrons tunnling troug t PC brrir in tim Z. Hn rom Eq. (), w v ( # Z. # Z (20) wr xpttion vlu ( is tkn wit rspt to t normlizd onditionl stt # t tim. Eqution (20) simply stts tt t vrg urrnt is wn dot is mpty, nd is. wn dot is oupid. Using Eqs. (3) nd (6) [or Eqs. (7), (7) nd (8), nd xpnding nd kping t trms o irst ordr in Z, w obtin rom Eq. () t quntumjump stosti Sr ödingr qution, onditiond on t obsrvd vnt in tim Z : # ^ Not tt ( ( Z * # P G G Z r ignord in Eq. (2). o ommodt initil nonpur or mixd stts, w xprss t stosti Sr ödingr qutions s stosti mstr qutions o t CQD qubit systm dnsity mtrix. From Eq. (), t onditionl, stosti dnsity mtrix # Z # ( Z stisis #. is o ordr Z. Hn trms proportionl to ( Z wr t rltion # P ( Z! # ( Z # # Z Z ( ( s bn usd. Using Eqs. (3) nd (6) [or Eqs. (7), (7) nd (8), nd kping trms up to ordr Z, w obtin t stosti mstr qutions, onditiond on t obsrvd vnt in tim Z : ( ( Z # P # # wr!!!, nd!!!!! # Z # Z Z # B Z * #. On n lso driv, wit t lp o Eq. (2), t stosti mstr qution (23) using t stosti Itô lulus [3 # ( # ^ ( ( # ( ^ # '. Equtions (2) nd (23) r t sm s Eqs. (3) nd (33) o. [3. But t drivtion prsntd r, strting rom t Sr ödingr qution or t ombind wol systm nd illustrting t ssntil pysis o t quntum trjtoris, is mor trnsprnt nd uristi. # () (2) (22) (23)
7 S Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 7 3. Conntions to mstr qution ppro sow nxt tt t mstr qution or t rdud or prtilly rdud dnsity mtrix simply rsults wn n vrg or prtil vrg is tkn on t onditionl, stosti dnsity mtrix (onstrutd rom t onditionl, stosti CQD qubit systm stt vtor) ovr t possibl outoms o t msurmnts on t PC bt. is rsult provids uniid pitur or ts smingly dirnt ppros. trditionl, unonditionl mstr qution ppro is to din totl dnsity mtrix Z S Z Z, nd tn tr out t stt o t bt. is lds to t rdud dnsity mtrix ' Z Z 3 Z Z Z (24) or t CQD qubit systm lon. t o intgrting or tring out t nvironmntl (dttor) dgrs o t rdom to obtin t rdud dnsity mtrix is quivlnt to tt o ompltly ignoring or vrging ovr t rsults o ll msurmnt rords #. is n b sn by tking nsmbl vrg on t onditionl, stosti dnsity mtrix Eq. (22), idntiying Z # Z # Z, nd stting ( qul to its xptd vlu Eq. (20). n t rsultnt qution lds to Eq. (24) wit Z Z nd Z P Z or t quntumjump s. Furtrmor, wit t lp o Eqs. (3) nd (6) [or Eqs. (7), (7) nd (8), w ind t unonditionl mstr qution: (2) * Not tt t trm originting rom t onditionl stt Eq. (6) or (8) rprsnts t t, du to dttion o n ltron tunnling troug t PC, on t CQD dnsity mtrix. is is wy somtims is lld jump suproprtor. Eqution (2) n lso b obtind s in. [3 by tking t nsmbl vrg ovr t obsrvd stosti pross on Eq. (23) by stting ( qul to its xptd vlu Eq. (20). In tis ppro o mstr qution o t rdud dnsity mtrix, t inlun o t PC bt, dorn t or xmpl, on t CQD systm n b nlyzd [3. But tis ppro or Eq. (2) dos not tll us nyting bout t xprimntl obsrvd quntity, nmly t ltron ounts or urrnt troug PC. Hn, t PC dttor in tis ppro is trtd s pur nvironmnt or t systm, rtr tn msurmnt dvi, wi n provid inormtion bout t ng o t stt o t systm. An ltrntiv ppro rntly dvlopd in s. [, 6, 7 is to tk tr ovr nvironmntl (dttor) mirosopi dgrs o t rdom but kp trk o t numbr o ltrons,, tt v tunnld troug t PC brrir during tim in t prtilly rdud dnsity mtrix. is llows on to xtrt inormtion bout t quntum stt o t qubit, by msuring t tim vrg urrnt X troug t PC. mstr (rt) qution or tis prtilly rdud dnsity mtrix or t CQD qubit systm is drivd in. [ rom t solld mnybody Sr ödingr qution. il it is drivd in s. [6, 7, by mns o t digrmmti tniqu in t Kldys orwrd nd bkwrd in tim ontour, or Cooprpir rg qubit oupld pitivly to singlltron trnsistor. Hr w sow tt it n b obtind or t CQD/PC modl by tking prtil vrg on t onditionl, stosti CQD qubit systm dnsity mtrix ovr t possibl outoms o t msurmnt on t PC bt. produr to tk t prtil vrg n b dsribd s ollows. First, tking t nsmbl vrg on Eq. (23), w obtin Eq. (2). n to kp trk o t numbr o ltrons tt v tunnld, w nd to idntiy t t o t jump suproprtor trm in Eq. (2). I ltrons v tunnld troug t PC t tim Z, tn t umultd numbr o ltrons in t drin t t rlir tim, du to t
8 Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis 8 ontribution o t jump trm, sould b P or P mtrix s: *. Atr writing out t numbr dpndn xpliitly, w obtin t mstr qution or t prtilly rdud dnsity P Evluting Eq. (26) in t logil qubit rg stt (i.., prt loliztion stt o t rg in dot nd dot 2, rsptivly), w obtin t rt qutions, t sm s Eq. (3.3) o. [. I t sum ovr ll possibl vlus o is tkn [i.. tring out t dttor stts ompltly, _, Eq. (26) tn rdus to Eq. (2). is produr o rduing Eq. (23) or (2) to Eq. (26) nd tn to Eq. (2) by vrging ovr (tring out) mor nd mor vilbl dttor inormtion provids uniid pitur or ts smingly dirnt ppros rportd in t litrtur. is produr is prtiulrly simpl using our ormlism. t is i t (stosti) mstr qution is xprssd in orm in trms o suproprtors nd, nd t t o t jump suproprtor trm is idntiid. o summriz, w v prsntd uristi drivtion o t quntum trjtory (stosti Sr ödingr or mstr) qution strting rom t ull Sr ödingr qution o t systm nd nvironmnt. ous on t msurmnt intrprttions to t quntum trjtoris. n t onpt o quntum trjtoris riss quit nturlly rom n xpnsion o t totl stt vtor in ign bsis o t oprtor tt rprsnts t pysil quntity or obsrvbl o t nvironmnt tt is msurd. In t CQD/PC modl, t obsrvd quntity o t PC nvironmnt is t numbr o ltrons tunnling troug t PC brrir. stostiity in t quntum trjtory n b viw s bing du to t rndomnss in t possibl outoms o t msurmnt rord. v sown tt t quntum trjtory or stosti Sr ödingr qution ppro provids us wit t most (ll) inormtion s r s t systm stt volution is onrnd. In tis ppro, w r propgting in prlll t inormtion o onditiond (stosti) stt volution # nd dttion rord # rsrvoirs is rovrd nd ontind by t msurmnt rords # in ontinuous msurmnt pross. All t inormtion rrid wy rom t systm to t o prt dttion or iint msurmnt. is is wy t systm n b ontinuously dsribd by stt vtor rtr tn rdud or prtilly rdud dnsity mtrix. v lso sown tt t mstr qutions o t rdud or prtilly rdud dnsity mtrix n b obtind s rsult o tking n nsmbl vrg or prtil vrg ovr t possibl msurmnt rords in t quntum trjtory ppro. is provids uniid pitur or ts smingly dirnt ppros. produr to iv tis uniid viw is prtiulrly sy to undrstnd using our ormlism. E quntum trjtory nd orrsponding dttion rord mimis possibl singl run o t ontinuous in tim msurmnt xprimnt. will prsnt lswr t simultion rsults or n initil qubit stt rdout xprimnt using bot o t quntum trjtory nd prtilly rdud dnsity mtrix ppros. rns [ Korotkov A N Pys. v. B [2 Korotkov A N 200 Pys. v. B [3 Gon HS,Milburn G, ismn H M, nd Sun H B 200 Pys. v. B [4 Gon HS nd Milburn G 200 Pys. v. B [ Gurvitz S A 7 Pys. v. B 6 2; quntp/ [6 Snirmn A nd Sön G 8 Pys. v. B [7 Mklin, Sön G nd Snirmn A 200 v. Mod. Pys [8 Dlibrd, Cstin nd Molmr K 2 Pys. v. Ltt [ Hgrldt G C nd Sondrmnn D G 6 Quntum Smilss. Opt [0 vn Dorsslr F E nd Ninuis G Opt. B: Quntum Smilss. Opt. 2, 2. (26)
Problem 1. Solution: = show that for a constant number of particles: c and V. a) Using the definitions of P
 rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
HIGHER ORDER DIFFERENTIAL EQUATIONS
 Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
Study Of Superconductivity And Antiferromagnetism In Rare Earth Nickel Borocarbides (RNi 2 B 2 C)
 IOSR Journl o Applid Pysis IOSR-JAP -ISS: 78-86.olum 9 Issu r. II y - Jun 7 PP 7-8 www.iosrjournls.org Study O Suprondutivity And Antirromgntism In Rr Ert il ororids Ri C r. Slil s nd Prti Sumn s prtmnt
IOSR Journl o Applid Pysis IOSR-JAP -ISS: 78-86.olum 9 Issu r. II y - Jun 7 PP 7-8 www.iosrjournls.org Study O Suprondutivity And Antirromgntism In Rr Ert il ororids Ri C r. Slil s nd Prti Sumn s prtmnt
b. How many ternary words of length 23 with eight 0 s, nine 1 s and six 2 s?
 MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
OpenMx Matrices and Operators
 OpnMx Mtris n Oprtors Sr Mln Mtris: t uilin loks Mny typs? Dnots r lmnt mxmtrix( typ= Zro", nrow=, nol=, nm="" ) mxmtrix( typ= Unit", nrow=, nol=, nm="" ) mxmtrix( typ= Int", nrow=, nol=, nm="" ) mxmtrix(
OpnMx Mtris n Oprtors Sr Mln Mtris: t uilin loks Mny typs? Dnots r lmnt mxmtrix( typ= Zro", nrow=, nol=, nm="" ) mxmtrix( typ= Unit", nrow=, nol=, nm="" ) mxmtrix( typ= Int", nrow=, nol=, nm="" ) mxmtrix(
MAT3707. Tutorial letter 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS. Semester 1. Department of Mathematical Sciences MAT3707/201/1/2017
 MAT3707/201/1/2017 Tutoril lttr 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS MAT3707 Smstr 1 Dprtmnt o Mtmtil Sins SOLUTIONS TO ASSIGNMENT 01 BARCODE Din tomorrow. univrsity o sout ri SOLUTIONS TO ASSIGNMENT
MAT3707/201/1/2017 Tutoril lttr 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS MAT3707 Smstr 1 Dprtmnt o Mtmtil Sins SOLUTIONS TO ASSIGNMENT 01 BARCODE Din tomorrow. univrsity o sout ri SOLUTIONS TO ASSIGNMENT
# 1 ' 10 ' 100. Decimal point = 4 hundred. = 6 tens (or sixty) = 5 ones (or five) = 2 tenths. = 7 hundredths.
 How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Tangram Fractions Overview: Students will analyze standard and nonstandard
 ACTIVITY 1 Mtrils: Stunt opis o tnrm mstrs trnsprnis o tnrm mstrs sissors PROCEDURE Skills: Dsriin n nmin polyons Stuyin onrun Comprin rtions Tnrm Frtions Ovrviw: Stunts will nlyz stnr n nonstnr tnrms
ACTIVITY 1 Mtrils: Stunt opis o tnrm mstrs trnsprnis o tnrm mstrs sissors PROCEDURE Skills: Dsriin n nmin polyons Stuyin onrun Comprin rtions Tnrm Frtions Ovrviw: Stunts will nlyz stnr n nonstnr tnrms
Physics 222 Midterm, Form: A
 Pysis 222 Mitrm, Form: A Nm: Dt: Hr r som usul onstnts. 1 4πɛ 0 = 9 10 9 Nm 2 /C 2 µ0 4π = 1 10 7 tsl s/c = 1.6 10 19 C Qustions 1 5: A ipol onsistin o two r point-lik prtils wit q = 1 µc, sprt y istn
Pysis 222 Mitrm, Form: A Nm: Dt: Hr r som usul onstnts. 1 4πɛ 0 = 9 10 9 Nm 2 /C 2 µ0 4π = 1 10 7 tsl s/c = 1.6 10 19 C Qustions 1 5: A ipol onsistin o two r point-lik prtils wit q = 1 µc, sprt y istn
1 Introduction to Modulo 7 Arithmetic
 1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
CS 103 BFS Alorithm. Mark Redekopp
 CS 3 BFS Aloritm Mrk Rkopp Brt-First Sr (BFS) HIGHLIGHTED ALGORITHM 3 Pt Plnnin W'v sn BFS in t ontxt o inin t sortst pt trou mz? S?? 4 Pt Plnnin W xplor t 4 niors s on irtion 3 3 3 S 3 3 3 3 3 F I you
CS 3 BFS Aloritm Mrk Rkopp Brt-First Sr (BFS) HIGHLIGHTED ALGORITHM 3 Pt Plnnin W'v sn BFS in t ontxt o inin t sortst pt trou mz? S?? 4 Pt Plnnin W xplor t 4 niors s on irtion 3 3 3 S 3 3 3 3 3 F I you
Cycles and Simple Cycles. Paths and Simple Paths. Trees. Problem: There is No Completely Standard Terminology!
 Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
d e c b a d c b a d e c b a a c a d c c e b
 FLAT PEYOTE STITCH Bin y mkin stoppr -- sw trou n pull it lon t tr until it is out 6 rom t n. Sw trou t in witout splittin t tr. You soul l to sli it up n own t tr ut it will sty in pl wn lt lon. Evn-Count
FLAT PEYOTE STITCH Bin y mkin stoppr -- sw trou n pull it lon t tr until it is out 6 rom t n. Sw trou t in witout splittin t tr. You soul l to sli it up n own t tr ut it will sty in pl wn lt lon. Evn-Count
Lecture 6 Thermionic Engines
 Ltur 6 hrmioni ngins Rviw Rihrdson formul hrmioni ngins Shotty brrir nd diod pn juntion nd diod disussion.997 Copyright Gng Chn, MI For.997 Dirt Solr/hrml to ltril nrgy Convrsion WARR M. ROHSOW HA AD MASS
Ltur 6 hrmioni ngins Rviw Rihrdson formul hrmioni ngins Shotty brrir nd diod pn juntion nd diod disussion.997 Copyright Gng Chn, MI For.997 Dirt Solr/hrml to ltril nrgy Convrsion WARR M. ROHSOW HA AD MASS
5/1/2018. Huffman Coding Trees. Huffman Coding Trees. Huffman Coding Trees. Huffman Coding Trees. Huffman Coding Trees. Huffman Coding Trees
 /1/018 W usully no strns y ssnn -lnt os to ll rtrs n t lpt (or mpl, 8-t on n ASCII). Howvr, rnt rtrs our wt rnt rquns, w n sv mmory n ru trnsmttl tm y usn vrl-lnt non. T s to ssn sortr os to rtrs tt our
/1/018 W usully no strns y ssnn -lnt os to ll rtrs n t lpt (or mpl, 8-t on n ASCII). Howvr, rnt rtrs our wt rnt rquns, w n sv mmory n ru trnsmttl tm y usn vrl-lnt non. T s to ssn sortr os to rtrs tt our
Functions and Graphs 1. (a) (b) (c) (f) (e) (d) 2. (a) (b) (c) (d)
 Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
CS September 2018
 Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
Grade 7/8 Math Circles March 4/5, Graph Theory I- Solutions
 ulty o Mtmtis Wtrloo, Ontrio N ntr or ution in Mtmtis n omputin r / Mt irls Mr /, 0 rp Tory - Solutions * inits lln qustion. Tr t ollowin wlks on t rp low. or on, stt wtr it is pt? ow o you know? () n
ulty o Mtmtis Wtrloo, Ontrio N ntr or ution in Mtmtis n omputin r / Mt irls Mr /, 0 rp Tory - Solutions * inits lln qustion. Tr t ollowin wlks on t rp low. or on, stt wtr it is pt? ow o you know? () n
, each of which is a tree, and whose roots r 1. , respectively, are children of r. Data Structures & File Management
 nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
Formal Concept Analysis
 Forml Conpt Anlysis Conpt intnts s losd sts Closur Systms nd Implitions 4 Closur Systms 0.06.005 Nxt-Closur ws dvlopd y B. Gntr (984). Lt M = {,..., n}. A M is ltilly smllr thn B M, if B A if th smllst
Forml Conpt Anlysis Conpt intnts s losd sts Closur Systms nd Implitions 4 Closur Systms 0.06.005 Nxt-Closur ws dvlopd y B. Gntr (984). Lt M = {,..., n}. A M is ltilly smllr thn B M, if B A if th smllst
Module 2 Motion Instructions
 Moul 2 Motion Instrutions CAUTION: Bor you strt this xprimnt, unrstn tht you r xpt to ollow irtions EXPLICITLY! Tk your tim n r th irtions or h stp n or h prt o th xprimnt. You will rquir to ntr t in prtiulr
Moul 2 Motion Instrutions CAUTION: Bor you strt this xprimnt, unrstn tht you r xpt to ollow irtions EXPLICITLY! Tk your tim n r th irtions or h stp n or h prt o th xprimnt. You will rquir to ntr t in prtiulr
Designing A Concrete Arch Bridge
 This is th mous Shwnh ri in Switzrln, sin y Rort Millrt in 1933. It spns 37.4 mtrs (122 t) n ws sin usin th sm rphil mths tht will monstrt in this lsson. To pro with this lsson, lik on th Nxt utton hr
This is th mous Shwnh ri in Switzrln, sin y Rort Millrt in 1933. It spns 37.4 mtrs (122 t) n ws sin usin th sm rphil mths tht will monstrt in this lsson. To pro with this lsson, lik on th Nxt utton hr
16.unified Introduction to Computers and Programming. SOLUTIONS to Examination 4/30/04 9:05am - 10:00am
 16.unii Introution to Computrs n Prormmin SOLUTIONS to Exmintion /30/0 9:05m - 10:00m Pro. I. Kristin Lunqvist Sprin 00 Grin Stion: Qustion 1 (5) Qustion (15) Qustion 3 (10) Qustion (35) Qustion 5 (10)
16.unii Introution to Computrs n Prormmin SOLUTIONS to Exmintion /30/0 9:05m - 10:00m Pro. I. Kristin Lunqvist Sprin 00 Grin Stion: Qustion 1 (5) Qustion (15) Qustion 3 (10) Qustion (35) Qustion 5 (10)
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
 rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
0.1. Exercise 1: the distances between four points in a graph
 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 pg 1 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 u: W, 3 My 2017, in lss or y mil (grinr@umn.u) or lss S th wsit or rlvnt mtril. Rsults provn in th nots, or in
Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 pg 1 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 u: W, 3 My 2017, in lss or y mil (grinr@umn.u) or lss S th wsit or rlvnt mtril. Rsults provn in th nots, or in
Math 166 Week in Review 2 Sections 1.1b, 1.2, 1.3, & 1.4
 Mt 166 WIR, Sprin 2012, Bnjmin urisp Mt 166 Wk in Rviw 2 Stions 1.1, 1.2, 1.3, & 1.4 1. S t pproprit rions in Vnn irm tt orrspon to o t ollowin sts. () (B ) B () ( ) B B () (B ) B 1 Mt 166 WIR, Sprin 2012,
Mt 166 WIR, Sprin 2012, Bnjmin urisp Mt 166 Wk in Rviw 2 Stions 1.1, 1.2, 1.3, & 1.4 1. S t pproprit rions in Vnn irm tt orrspon to o t ollowin sts. () (B ) B () ( ) B B () (B ) B 1 Mt 166 WIR, Sprin 2012,
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
QUESTIONS BEGIN HERE!
 Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt o Computr n Inormtion Sins CSCI 2710 (Trno) Disrt Struturs TEST or Sprin Smstr, 2005 R this or strtin! This tst is los ook
Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt o Computr n Inormtion Sins CSCI 2710 (Trno) Disrt Struturs TEST or Sprin Smstr, 2005 R this or strtin! This tst is los ook
The University of Sydney MATH 2009
 T Unvrsty o Syny MATH 2009 APH THEOY Tutorl 7 Solutons 2004 1. Lt t sonnt plnr rp sown. Drw ts ul, n t ul o t ul ( ). Sow tt s sonnt plnr rp, tn s onnt. Du tt ( ) s not somorp to. ( ) A onnt rp s on n
T Unvrsty o Syny MATH 2009 APH THEOY Tutorl 7 Solutons 2004 1. Lt t sonnt plnr rp sown. Drw ts ul, n t ul o t ul ( ). Sow tt s sonnt plnr rp, tn s onnt. Du tt ( ) s not somorp to. ( ) A onnt rp s on n
learning objectives learn what graphs are in mathematical terms learn how to represent graphs in computers learn about typical graph algorithms
 rp loritms lrnin ojtivs loritms your sotwr systm sotwr rwr lrn wt rps r in mtmtil trms lrn ow to rprsnt rps in omputrs lrn out typil rp loritms wy rps? intuitivly, rp is orm y vrtis n s twn vrtis rps r
rp loritms lrnin ojtivs loritms your sotwr systm sotwr rwr lrn wt rps r in mtmtil trms lrn ow to rprsnt rps in omputrs lrn out typil rp loritms wy rps? intuitivly, rp is orm y vrtis n s twn vrtis rps r
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
 Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Divided. diamonds. Mimic the look of facets in a bracelet that s deceptively deep RIGHT-ANGLE WEAVE. designed by Peggy Brinkman Matteliano
 RIGHT-ANGLE WEAVE Dv mons Mm t look o ts n rlt tt s ptvly p sn y Py Brnkmn Mttlno Dv your mons nto trnls o two or our olors. FCT-SCON0216_BNB66 2012 Klm Pulsn Co. Ts mtrl my not rprou n ny orm wtout prmsson
RIGHT-ANGLE WEAVE Dv mons Mm t look o ts n rlt tt s ptvly p sn y Py Brnkmn Mttlno Dv your mons nto trnls o two or our olors. FCT-SCON0216_BNB66 2012 Klm Pulsn Co. Ts mtrl my not rprou n ny orm wtout prmsson
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
THE SPINOR FIELD THEORY OF THE PHOTON
 Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Weighted Graphs. Weighted graphs may be either directed or undirected.
 1 In mny ppltons, o rp s n ssot numrl vlu, ll wt. Usully, t wts r nonntv ntrs. Wt rps my tr rt or unrt. T wt o n s otn rrr to s t "ost" o t. In ppltons, t wt my msur o t lnt o rout, t pty o ln, t nry rqur
1 In mny ppltons, o rp s n ssot numrl vlu, ll wt. Usully, t wts r nonntv ntrs. Wt rps my tr rt or unrt. T wt o n s otn rrr to s t "ost" o t. In ppltons, t wt my msur o t lnt o rout, t pty o ln, t nry rqur
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 8: Effect of a Vertical Field on Tokamak Equilibrium
 .65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
.65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
EE1000 Project 4 Digital Volt Meter
 Ovrviw EE1000 Projt 4 Diitl Volt Mtr In this projt, w mk vi tht n msur volts in th rn o 0 to 4 Volts with on iit o ury. Th input is n nlo volt n th output is sinl 7-smnt iit tht tlls us wht tht input s
Ovrviw EE1000 Projt 4 Diitl Volt Mtr In this projt, w mk vi tht n msur volts in th rn o 0 to 4 Volts with on iit o ury. Th input is n nlo volt n th output is sinl 7-smnt iit tht tlls us wht tht input s
Majorana Neutrino Oscillations in Vacuum
 Journl of odrn Pysis 0 80-84 tt://dx.doi.org/0.46/jm.0.805 Publisd Onlin August 0 (tt://www.sip.org/journl/jm) jorn Nutrino Osilltions in Vuum Yubr Frny Prz Crlos Jos Quimby Esul d Físi Univrsidd Pdgógi
Journl of odrn Pysis 0 80-84 tt://dx.doi.org/0.46/jm.0.805 Publisd Onlin August 0 (tt://www.sip.org/journl/jm) jorn Nutrino Osilltions in Vuum Yubr Frny Prz Crlos Jos Quimby Esul d Físi Univrsidd Pdgógi
CSCI Compiler Design
 CSCI 565 - Compilr Dsign Spring 2013 Sond Tst - Solution My 1, 2013 t 3.30 PM in Room RTH 115 Durtion: 2h 30 min. Pls ll ll pgs you turn in with your nm nd studnt numr. Nm: Numr: Grd: Prolm 1 [20 points]:
CSCI 565 - Compilr Dsign Spring 2013 Sond Tst - Solution My 1, 2013 t 3.30 PM in Room RTH 115 Durtion: 2h 30 min. Pls ll ll pgs you turn in with your nm nd studnt numr. Nm: Numr: Grd: Prolm 1 [20 points]:
I. The Connection between Spectroscopy and Quantum Mechanics
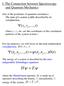 I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
ECE COMBINATIONAL BUILDING BLOCKS - INVEST 13 DECODERS AND ENCODERS
 C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
 CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
16.512, Rocket Propulsion Prof. Manuel Martinez-Sanchez Lecture 3: Ideal Nozzle Fluid Mechanics
 6.5, Rok ropulsion rof. nul rinz-snhz Lur 3: Idl Nozzl luid hnis Idl Nozzl low wih No Sprion (-D) - Qusi -D (slndr) pproximion - Idl gs ssumd ( ) mu + Opimum xpnsion: - or lss, >, ould driv mor forwrd
6.5, Rok ropulsion rof. nul rinz-snhz Lur 3: Idl Nozzl luid hnis Idl Nozzl low wih No Sprion (-D) - Qusi -D (slndr) pproximion - Idl gs ssumd ( ) mu + Opimum xpnsion: - or lss, >, ould driv mor forwrd
Outline. Computer Science 331. Computation of Min-Cost Spanning Trees. Costs of Spanning Trees in Weighted Graphs
 Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim s Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #34 Introution Min-Cost Spnnin Trs 3 Gnrl Constrution 4 5 Trmintion n Eiiny 6 Aitionl
Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim s Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #34 Introution Min-Cost Spnnin Trs 3 Gnrl Constrution 4 5 Trmintion n Eiiny 6 Aitionl
Present state Next state Q + M N
 Qustion 1. An M-N lip-lop works s ollows: I MN=00, th nxt stt o th lip lop is 0. I MN=01, th nxt stt o th lip-lop is th sm s th prsnt stt I MN=10, th nxt stt o th lip-lop is th omplmnt o th prsnt stt I
Qustion 1. An M-N lip-lop works s ollows: I MN=00, th nxt stt o th lip lop is 0. I MN=01, th nxt stt o th lip-lop is th sm s th prsnt stt I MN=10, th nxt stt o th lip-lop is th omplmnt o th prsnt stt I
In which direction do compass needles always align? Why?
 AQA Trloy Unt 6.7 Mntsm n Eltromntsm - Hr 1 Complt t p ll: Mnt or s typ o or n t s stronst t t o t mnt. Tr r two typs o mnt pol: n. Wrt wt woul ppn twn t pols n o t mnt ntrtons low: Drw t mnt l lns on
AQA Trloy Unt 6.7 Mntsm n Eltromntsm - Hr 1 Complt t p ll: Mnt or s typ o or n t s stronst t t o t mnt. Tr r two typs o mnt pol: n. Wrt wt woul ppn twn t pols n o t mnt ntrtons low: Drw t mnt l lns on
CSE 373: More on graphs; DFS and BFS. Michael Lee Wednesday, Feb 14, 2018
 CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
Improving Union. Implementation. Union-by-size Code. Union-by-Size Find Analysis. Path Compression! Improving Find find(e)
 POW CSE 36: Dt Struturs Top #10 T Dynm (Equvln) Duo: Unon-y-Sz & Pt Comprsson Wk!! Luk MDowll Summr Qurtr 003 M! ZING Wt s Goo Mz? Mz Construton lortm Gvn: ollton o rooms V Conntons twn t rooms (ntlly
POW CSE 36: Dt Struturs Top #10 T Dynm (Equvln) Duo: Unon-y-Sz & Pt Comprsson Wk!! Luk MDowll Summr Qurtr 003 M! ZING Wt s Goo Mz? Mz Construton lortm Gvn: ollton o rooms V Conntons twn t rooms (ntlly
CMPS 2200 Fall Graphs. Carola Wenk. Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk
 CMPS 2200 Fll 2017 Grps Crol Wnk Sls ourtsy o Crls Lsrson wt ns n tons y Crol Wnk 10/23/17 CMPS 2200 Intro. to Alortms 1 Grps Dnton. A rt rp (rp) G = (V, E) s n orr pr onsstn o st V o vrts (snulr: vrtx),
CMPS 2200 Fll 2017 Grps Crol Wnk Sls ourtsy o Crls Lsrson wt ns n tons y Crol Wnk 10/23/17 CMPS 2200 Intro. to Alortms 1 Grps Dnton. A rt rp (rp) G = (V, E) s n orr pr onsstn o st V o vrts (snulr: vrtx),
3-2-1 ANN Architecture
 ARTIFICIAL NEURAL NETWORKS (ANNs) Profssor Tom Fomby Dpartmnt of Economics Soutrn Mtodist Univrsity Marc 008 Artificial Nural Ntworks (raftr ANNs) can b usd for itr prdiction or classification problms.
ARTIFICIAL NEURAL NETWORKS (ANNs) Profssor Tom Fomby Dpartmnt of Economics Soutrn Mtodist Univrsity Marc 008 Artificial Nural Ntworks (raftr ANNs) can b usd for itr prdiction or classification problms.
Outline. 1 Introduction. 2 Min-Cost Spanning Trees. 4 Example
 Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim's Alorithm Introution Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #33 3 Alorithm Gnrl Constrution Mik Joson (Univrsity o Clry)
Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim's Alorithm Introution Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #33 3 Alorithm Gnrl Constrution Mik Joson (Univrsity o Clry)
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Edge-Triggered D Flip-flop. Formal Analysis. Fundamental-Mode Sequential Circuits. D latch: How do flip-flops work?
 E-Trir D Flip-Flop Funamntal-Mo Squntial Ciruits PR A How o lip-lops work? How to analys aviour o lip-lops? R How to sin unamntal-mo iruits? Funamntal mo rstrition - only on input an an at a tim; iruit
E-Trir D Flip-Flop Funamntal-Mo Squntial Ciruits PR A How o lip-lops work? How to analys aviour o lip-lops? R How to sin unamntal-mo iruits? Funamntal mo rstrition - only on input an an at a tim; iruit
Lecture 20: Minimum Spanning Trees (CLRS 23)
 Ltur 0: Mnmum Spnnn Trs (CLRS 3) Jun, 00 Grps Lst tm w n (wt) rps (unrt/rt) n ntrou s rp voulry (vrtx,, r, pt, onnt omponnts,... ) W lso suss jny lst n jny mtrx rprsntton W wll us jny lst rprsntton unlss
Ltur 0: Mnmum Spnnn Trs (CLRS 3) Jun, 00 Grps Lst tm w n (wt) rps (unrt/rt) n ntrou s rp voulry (vrtx,, r, pt, onnt omponnts,... ) W lso suss jny lst n jny mtrx rprsntton W wll us jny lst rprsntton unlss
4.1 Interval Scheduling. Chapter 4. Greedy Algorithms. Interval Scheduling: Greedy Algorithms. Interval Scheduling. Interval scheduling.
 Cptr 4 4 Intrvl Suln Gry Alortms Sls y Kvn Wyn Copyrt 005 Prson-Ason Wsly All rts rsrv Intrvl Suln Intrvl Suln: Gry Alortms Intrvl suln! Jo strts t s n nss t! Two os omptl ty on't ovrlp! Gol: n mxmum sust
Cptr 4 4 Intrvl Suln Gry Alortms Sls y Kvn Wyn Copyrt 005 Prson-Ason Wsly All rts rsrv Intrvl Suln Intrvl Suln: Gry Alortms Intrvl suln! Jo strts t s n nss t! Two os omptl ty on't ovrlp! Gol: n mxmum sust
MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS
 VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
COMP108 Algorithmic Foundations
 Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Lecture 14 (Oct. 30, 2017)
 Ltur 14 8.31 Quantum Thory I, Fall 017 69 Ltur 14 (Ot. 30, 017) 14.1 Magnti Monopols Last tim, w onsidrd a magnti fild with a magnti monopol onfiguration, and bgan to approah dsribing th quantum mhanis
Ltur 14 8.31 Quantum Thory I, Fall 017 69 Ltur 14 (Ot. 30, 017) 14.1 Magnti Monopols Last tim, w onsidrd a magnti fild with a magnti monopol onfiguration, and bgan to approah dsribing th quantum mhanis
Limits Indeterminate Forms and L Hospital s Rule
 Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
Last time: introduced our first computational model the DFA.
 Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Utilizing exact and Monte Carlo methods to investigate properties of the Blume Capel Model applied to a nine site lattice.
 Utilizing xat and Mont Carlo mthods to invstigat proprtis of th Blum Capl Modl applid to a nin sit latti Nik Franios Writing various xat and Mont Carlo omputr algorithms in C languag, I usd th Blum Capl
Utilizing xat and Mont Carlo mthods to invstigat proprtis of th Blum Capl Modl applid to a nin sit latti Nik Franios Writing various xat and Mont Carlo omputr algorithms in C languag, I usd th Blum Capl
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Depth First Search. Yufei Tao. Department of Computer Science and Engineering Chinese University of Hong Kong
 Dprtmnt o Computr Sn n Ennrn Cns Unvrsty o Hon Kon W v lry lrn rt rst sr (BFS). Toy, w wll suss ts sstr vrson : t pt rst sr (DFS) lortm. Our susson wll on n ous on rt rps, us t xtnson to unrt rps s strtorwr.
Dprtmnt o Computr Sn n Ennrn Cns Unvrsty o Hon Kon W v lry lrn rt rst sr (BFS). Toy, w wll suss ts sstr vrson : t pt rst sr (DFS) lortm. Our susson wll on n ous on rt rps, us t xtnson to unrt rps s strtorwr.
DISTORTION OF PROBABILITY MODELS
 ISTORTION OF PROBABILITY MOELS VÁVRA Frntišk (ČR), NOVÝ Pvl (ČR), MAŠKOVÁ Hn (ČR), NETRVALOVÁ Arnoštk (ČR) Abstrct. Th proposd ppr dls with on o possibl mthods or modlling th rltion o two probbility modls
ISTORTION OF PROBABILITY MOELS VÁVRA Frntišk (ČR), NOVÝ Pvl (ČR), MAŠKOVÁ Hn (ČR), NETRVALOVÁ Arnoštk (ČR) Abstrct. Th proposd ppr dls with on o possibl mthods or modlling th rltion o two probbility modls
Module graph.py. 1 Introduction. 2 Graph basics. 3 Module graph.py. 3.1 Objects. CS 231 Naomi Nishimura
 Moul grph.py CS 231 Nomi Nishimur 1 Introution Just lik th Python list n th Python itionry provi wys of storing, ssing, n moifying t, grph n viw s wy of storing, ssing, n moifying t. Bus Python os not
Moul grph.py CS 231 Nomi Nishimur 1 Introution Just lik th Python list n th Python itionry provi wys of storing, ssing, n moifying t, grph n viw s wy of storing, ssing, n moifying t. Bus Python os not
Why the Junction Tree Algorithm? The Junction Tree Algorithm. Clique Potential Representation. Overview. Chris Williams 1.
 Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
Ch 1.2: Solutions of Some Differential Equations
 Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
QUESTIONS BEGIN HERE!
 Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt of Computr n Informtion Sins CSCI 710 (Trnoff) Disrt Struturs TEST for Fll Smstr, 00 R this for strtin! This tst is los ook
Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt of Computr n Informtion Sins CSCI 710 (Trnoff) Disrt Struturs TEST for Fll Smstr, 00 R this for strtin! This tst is los ook
Having a glimpse of some of the possibilities for solutions of linear systems, we move to methods of finding these solutions. The basic idea we shall
 Hvn lps o so o t posslts or solutons o lnr systs, w ov to tos o nn ts solutons. T s w sll us s to try to sply t syst y lntn so o t vrls n so ts qutons. Tus, w rr to t to s lnton. T prry oprton nvolv s
Hvn lps o so o t posslts or solutons o lnr systs, w ov to tos o nn ts solutons. T s w sll us s to try to sply t syst y lntn so o t vrls n so ts qutons. Tus, w rr to t to s lnton. T prry oprton nvolv s
First derivative analysis
 Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
Robrto s Nots on Dirntial Calculus Chaptr 8: Graphical analysis Sction First drivativ analysis What you nd to know alrady: How to us drivativs to idntiy th critical valus o a unction and its trm points
fiziks Forum for CSIR-UGC JRF/NET, GATE, IIT-JAM, GRE in PHYSICAL SCIENCES
 fizis /o Annd Institut of mthmtis, 8-B/6 Ji Sri Nr IIT, Huz Khs, Nw Dlhi, PIN- 6 (INDIA) Phon: -78565, +9-98745498 Wbsit: http://www.physisbyfizis.om GATE-8 (PHYSICS).. rry on mr h.. For rbitrry mtris
fizis /o Annd Institut of mthmtis, 8-B/6 Ji Sri Nr IIT, Huz Khs, Nw Dlhi, PIN- 6 (INDIA) Phon: -78565, +9-98745498 Wbsit: http://www.physisbyfizis.om GATE-8 (PHYSICS).. rry on mr h.. For rbitrry mtris
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
 ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
An undirected graph G = (V, E) V a set of vertices E a set of unordered edges (v,w) where v, w in V
 Unirt Grphs An unirt grph G = (V, E) V st o vrtis E st o unorr gs (v,w) whr v, w in V USE: to mol symmtri rltionships twn ntitis vrtis v n w r jnt i thr is n g (v,w) [or (w,v)] th g (v,w) is inint upon
Unirt Grphs An unirt grph G = (V, E) V st o vrtis E st o unorr gs (v,w) whr v, w in V USE: to mol symmtri rltionships twn ntitis vrtis v n w r jnt i thr is n g (v,w) [or (w,v)] th g (v,w) is inint upon
Complete Solutions for MATH 3012 Quiz 2, October 25, 2011, WTT
 Complt Solutions or MATH 012 Quiz 2, Otor 25, 2011, WTT Not. T nswrs ivn r r mor omplt tn is xpt on n tul xm. It is intn tt t mor omprnsiv solutions prsnt r will vlul to stunts in stuyin or t inl xm. In
Complt Solutions or MATH 012 Quiz 2, Otor 25, 2011, WTT Not. T nswrs ivn r r mor omplt tn is xpt on n tul xm. It is intn tt t mor omprnsiv solutions prsnt r will vlul to stunts in stuyin or t inl xm. In
Paths. Connectivity. Euler and Hamilton Paths. Planar graphs.
 Pths.. Eulr n Hmilton Pths.. Pth D. A pth rom s to t is squn o gs {x 0, x 1 }, {x 1, x 2 },... {x n 1, x n }, whr x 0 = s, n x n = t. D. Th lngth o pth is th numr o gs in it. {, } {, } {, } {, } {, } {,
Pths.. Eulr n Hmilton Pths.. Pth D. A pth rom s to t is squn o gs {x 0, x 1 }, {x 1, x 2 },... {x n 1, x n }, whr x 0 = s, n x n = t. D. Th lngth o pth is th numr o gs in it. {, } {, } {, } {, } {, } {,
S i m p l i f y i n g A l g e b r a SIMPLIFYING ALGEBRA.
 S i m p l i y i n g A l g r SIMPLIFYING ALGEBRA www.mthltis.o.nz Simpliying SIMPLIFYING Algr ALGEBRA Algr is mthmtis with mor thn just numrs. Numrs hv ix vlu, ut lgr introus vrils whos vlus n hng. Ths
S i m p l i y i n g A l g r SIMPLIFYING ALGEBRA www.mthltis.o.nz Simpliying SIMPLIFYING Algr ALGEBRA Algr is mthmtis with mor thn just numrs. Numrs hv ix vlu, ut lgr introus vrils whos vlus n hng. Ths
Knowledge-Based Systems. Outline 1. Outline 2. Expert System. Page 1. Development of KB Systems. CI = Computational Intelligence.
 Knowldg-Bsd Systms Andrw Kusik, Profssor 9 Smns Cntr Iow City, Iow - 7 ndrw-kusik@uiow.du http://www.in.uiow.du/~nkusik Tl: 9-9 Fx: 9-9 Outlin INTRODUCTION KNOWLEDGE REPRESENTATION - First-Ordr Logi -
Knowldg-Bsd Systms Andrw Kusik, Profssor 9 Smns Cntr Iow City, Iow - 7 ndrw-kusik@uiow.du http://www.in.uiow.du/~nkusik Tl: 9-9 Fx: 9-9 Outlin INTRODUCTION KNOWLEDGE REPRESENTATION - First-Ordr Logi -
Hardy Spaces, Hyperfunctions, Pseudo-Differential Operators and Wavelets
 Hrdy Sps, Hyprfuntions, Psudo-Diffrntil Oprtors nd Wvlts Colltions from lrtur Th Hrdy Sp nd Hilbrt Sls Lt : s /, t thn th Rimnn Hypothsis is th sttmnt tht / ( s is nlyti on th hlf-pln Th ppropr Hilbrt
Hrdy Sps, Hyprfuntions, Psudo-Diffrntil Oprtors nd Wvlts Colltions from lrtur Th Hrdy Sp nd Hilbrt Sls Lt : s /, t thn th Rimnn Hypothsis is th sttmnt tht / ( s is nlyti on th hlf-pln Th ppropr Hilbrt
ENGR 323 BHW 15 Van Bonn 1/7
 ENGR 33 BHW 5 Van Bonn /7 4.4 In Eriss and 3 as wll as man othr situations on has th PDF o X and wishs th PDF o Yh. Assum that h is an invrtibl untion so that h an b solvd or to ild. Thn it an b shown
ENGR 33 BHW 5 Van Bonn /7 4.4 In Eriss and 3 as wll as man othr situations on has th PDF o X and wishs th PDF o Yh. Assum that h is an invrtibl untion so that h an b solvd or to ild. Thn it an b shown
Carriers Concentration in Semiconductors - VI. Prof.P. Ravindran, Department of Physics, Central University of Tamil Nadu, India
 Carrirs Conntration in Smionutors - VI 1 Prof.P. Ravinran, Dpartmnt of Pysis, Cntral Univrsity of Tamil au, Inia ttp://folk.uio.no/ravi/smi01 P.Ravinran, PHY0 Smionutor Pysis, 17 January 014 : Carrirs
Carrirs Conntration in Smionutors - VI 1 Prof.P. Ravinran, Dpartmnt of Pysis, Cntral Univrsity of Tamil au, Inia ttp://folk.uio.no/ravi/smi01 P.Ravinran, PHY0 Smionutor Pysis, 17 January 014 : Carrirs
VLSI Testing Assignment 2
 1. 5-vlu D-clculus trut tbl or t XOR unction: XOR 0 1 X D ~D 0 0 1 X D ~D 1 1 0 X ~D D X X X X X X D D ~D X 0 1 ~D ~D D X 1 0 Tbl 1: 5-vlu D-clculus Trut Tbl or t XOR Function Sinc 2-input XOR t wors s
1. 5-vlu D-clculus trut tbl or t XOR unction: XOR 0 1 X D ~D 0 0 1 X D ~D 1 1 0 X ~D D X X X X X X D D ~D X 0 1 ~D ~D D X 1 0 Tbl 1: 5-vlu D-clculus Trut Tbl or t XOR Function Sinc 2-input XOR t wors s
Bioconductor Expression Assessment Tool for Affymetrix Oligonucleotide Arrays (affycomp)
 Bioondutor Exprssion Assssmnt Tool or Aymtrix Oligonulotid Arrys (yomp) Rl Irizrry nd Lsli Cop Otobr, Contnts Introdution Introdution Wht s nw in vrsion.? Th Img Rport. Bsi Plots...................................
Bioondutor Exprssion Assssmnt Tool or Aymtrix Oligonulotid Arrys (yomp) Rl Irizrry nd Lsli Cop Otobr, Contnts Introdution Introdution Wht s nw in vrsion.? Th Img Rport. Bsi Plots...................................
APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS
 Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
CONTINUITY AND DIFFERENTIABILITY
 MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
Errata for Second Edition, First Printing
 Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
KOHN LUTTINGER SUPERCONDUCTIVITY IN GRAPHENE
 KOHN LUTTINGER SUPERCONDUCTIITY IN GRAPHENE J. Gonzálz Instituto d Estructur d l Mtri, CSIC, Spin Is it possibl to hv suprconducting instbility in grphn (by suitbl doping)? Thr hv bn lrdy svrl proposls
KOHN LUTTINGER SUPERCONDUCTIITY IN GRAPHENE J. Gonzálz Instituto d Estructur d l Mtri, CSIC, Spin Is it possibl to hv suprconducting instbility in grphn (by suitbl doping)? Thr hv bn lrdy svrl proposls
On-Line PI Controller Tuning Using Closed-Loop Setpoint Responses for Stable and Integrating Processes*
 On-Lin PI Controllr Tuning Using Closd-Loop Stpoint Rsponss for Stabl and Intgrating Prosss* Mohammad Shamsuzzoha a, Sigurd Skogstad a, Ivar J. Halvorsn b a Norwgian Univrsity of Sin and Thnology (NTNU),
On-Lin PI Controllr Tuning Using Closd-Loop Stpoint Rsponss for Stabl and Intgrating Prosss* Mohammad Shamsuzzoha a, Sigurd Skogstad a, Ivar J. Halvorsn b a Norwgian Univrsity of Sin and Thnology (NTNU),
Outline. Binary Tree
 Outlin Similrity Srh Th Binry Brnh Distn Nikolus Austn nikolus.ustn@s..t Dpt. o Computr Sins Univrsity o Slzur http://rsrh.uni-slzur.t 1 Binry Brnh Distn Binry Rprsnttion o Tr Binry Brnhs Lowr Boun or
Outlin Similrity Srh Th Binry Brnh Distn Nikolus Austn nikolus.ustn@s..t Dpt. o Computr Sins Univrsity o Slzur http://rsrh.uni-slzur.t 1 Binry Brnh Distn Binry Rprsnttion o Tr Binry Brnhs Lowr Boun or
Fractional Topological Insulators A Bosonization Approach
 Journl of Modrn Physis 06 7 8-8 Publishd Onlin Jnury 06 in Sis. http://www.sirp.or/journl/jmp http://d.doi.or/0.46/jmp.06.70 rtionl Topoloil Insultors A Boniztion Approh D. Shmltzr Physis Dprtmnt City
Journl of Modrn Physis 06 7 8-8 Publishd Onlin Jnury 06 in Sis. http://www.sirp.or/journl/jmp http://d.doi.or/0.46/jmp.06.70 rtionl Topoloil Insultors A Boniztion Approh D. Shmltzr Physis Dprtmnt City
Problem solving by search
 Prolm solving y srh Tomáš voo Dprtmnt o Cyrntis, Vision or Roots n Autonomous ystms Mrh 5, 208 / 3 Outlin rh prolm. tt sp grphs. rh trs. trtgis, whih tr rnhs to hoos? trtgy/algorithm proprtis? Progrmming
Prolm solving y srh Tomáš voo Dprtmnt o Cyrntis, Vision or Roots n Autonomous ystms Mrh 5, 208 / 3 Outlin rh prolm. tt sp grphs. rh trs. trtgis, whih tr rnhs to hoos? trtgy/algorithm proprtis? Progrmming
DEVELOPING COMPUTER PROGRAM FOR COMPUTING EIGENPAIRS OF 2 2 MATRICES AND 3 3 UPPER TRIANGULAR MATRICES USING THE SIMPLE ALGORITHM
 Fr Est Journl o Mthtil Sins (FJMS) Volu 6 Nur Pgs 8- Pulish Onlin: Sptr This ppr is vill onlin t http://pphjo/journls/jsht Pushp Pulishing Hous DEVELOPING COMPUTER PROGRAM FOR COMPUTING EIGENPAIRS OF MATRICES
Fr Est Journl o Mthtil Sins (FJMS) Volu 6 Nur Pgs 8- Pulish Onlin: Sptr This ppr is vill onlin t http://pphjo/journls/jsht Pushp Pulishing Hous DEVELOPING COMPUTER PROGRAM FOR COMPUTING EIGENPAIRS OF MATRICES
Theoretical Study on the While Drilling Electromagnetic Signal Transmission of Horizontal Well
 7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
PH427/PH527: Periodic systems Spring Overview of the PH427 website (syllabus, assignments etc.) 2. Coupled oscillations.
 Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
SAMPLE CSc 340 EXAM QUESTIONS WITH SOLUTIONS: part 2
 AMPLE C EXAM UETION WITH OLUTION: prt. It n sown tt l / wr.7888l. I Φ nots orul or pprotng t vlu o tn t n sown tt t trunton rror o ts pproton s o t or or so onstnts ; tt s Not tt / L Φ L.. Φ.. /. /.. Φ..787.
AMPLE C EXAM UETION WITH OLUTION: prt. It n sown tt l / wr.7888l. I Φ nots orul or pprotng t vlu o tn t n sown tt t trunton rror o ts pproton s o t or or so onstnts ; tt s Not tt / L Φ L.. Φ.. /. /.. Φ..787.
Handout 28. Ballistic Quantum Transport in Semiconductor Nanostructures
 Hanout 8 Ballisti Quantum Transport in Smionutor Nanostruturs In this ltur you will larn: ltron transport without sattring (ballisti transport) Th quantum o onutan an th quantum o rsistan Quanti onutan
Hanout 8 Ballisti Quantum Transport in Smionutor Nanostruturs In this ltur you will larn: ltron transport without sattring (ballisti transport) Th quantum o onutan an th quantum o rsistan Quanti onutan
