Majorana Neutrino Oscillations in Vacuum
|
|
|
- Megan Elliott
- 5 years ago
- Views:
Transcription
1 Journl of odrn Pysis tt://dx.doi.org/0.46/jm Publisd Onlin August 0 (tt:// jorn Nutrino Osilltions in Vuum Yubr Frny Prz Crlos Jos Quimby Esul d Físi Univrsidd Pdgógi y nológi d Colombi unj Colombi Drtmnto d Fsi Univrsidd Nionl d Colombi Ciudd Univrsitri Bogotá D.C. Colombi Emil: yubr.rz@ut.du.o jquimby@unl.du.o ivd y 0; rvisd Jun 9 0; td July 0 ABSAC In t ontxt of ty I ssw snrio wi lds to gt ligt lft-ndd nd vy rigt-ndd jorn nutrinos w obtin xrssions for t trnsition robbility dnsitis btwn two flvor nutrinos in t ss of lftndd nd rigt-ndd nutrinos. W obtin ts xrssions in t ontxt of n ro dvlod in t nonil formlism of Quntum Fild ory for nutrinos wi r onsidrd s surositions of mss-ignstt ln wvs wit sifi momnt. xrssions obtind for t lft-ndd nutrino s ftr t ultr-rltivisti limit is tking ld to t stndrd robbility dnsitis wi dsrib ligt nutrino osilltions. For t rigt-ndd nutrino s t xrssions dsribing vy nutrino osilltions in t non-rltivisti limit r diffrnt rst to t ons of t stndrd nutrino osilltions. Howvr t rigt-ndd nutrino osilltions r nomnologilly rstritd s is sown wn t rogtion of vy nutrinos is onsidrd s surositions of mss-ignstt wv kts. Kywords: jorn Frmions; jorn Nutrino Osilltions; rnsition Probbility; Non-ltivisti nd Ultr-ltivisti Aroximtions. Introdution Nutrino ysis is vry tiv r of rsr wi involvs som of t most intriguing roblms in rtil ysis. ntur of nutrinos nd t origin of t smll mss of nutrinos r two xmls of ts kinds of roblms. Sin nutrinos r ltrilly nutrl t ntur of ts lmntry rtils n b jorn or Dir frmions. first ossibility i.. nutrinos bing jorn frmions ws introdud by Etor jorn [] wn suggstd tt mssiv nutrl frmions wit sifi momnt v ssoitd only two liity stts imlying tt nutrinos nd nti-nutrinos r t sm rtils. sond ossibility imlis tt Dir nutrinos r dsribd by four-omonnt sinoril filds wi r diffrnt from sinoril filds dsribing ntinutrinos. In tis work w will onsidr nutrinos s jorn frmions wi is fvord by simliity bus ty v only two dgrs of frdom []. Dirt nd indirt xrimntl vidns sow tt nutrinos r mssiv frmions wit msss smllr tn V [4]. most td wy to gnrt nutrino msss is by mn of t ssw mnism [5]. ss for nutrinos is nssry ingrdint to undrstnd t osilltions btwn nutrino flvor stts wi v bn obsrvd xrimntlly [4]. Nutrino osilltions r origintd by t intrfrn btwn mss stts wos mixing gnrts flvor stts. is nomnon mns tt nutrino rtd in wk intrtion ross wit sifi flvor n b dttd wit diffrnt flvor. Nutrino osilltions wr first dsribd by Pontorvo [6] s n xtnsion for t ltoni stor of t strng osilltions obsrvd in t nutrl Kon systm. Nutrino osilltions n b dsribd in ontxt of Quntum nis [7-] s n lition of t two lvl systm []. Dsrition of nutrino osilltions in t ontxt of Quntum Fild ory (QF) is vry wll studid toi [-0]. In t litrtur it is ossibl to find two kinds of QF modls dsribing nutrino osilltions: intrmdit modls nd xtrnl modls [7]. In t frmwork of intrmdit modls Sssroli dvlod modl bsd in n intrting grngin dnsity wi inluds t ouling btwn two flvor filds [-]. is modl ws frmd by But s ybrid modl owing to it gos lf--wy to QF [7]. Sssroli modl ws first dvlod for ould systm of two Dir qutions [ ] nd tn it ws xtndd for ould systm of two jorn ons []. robbility mlitud of trnsition btwn two nutrino flvor stts for ts two systms [-] ws obtind strting from flvor stts wi r usd on t stndrd trtmnt of nutrino osilltions. stndrd dfinition of flvor stts n origint som ossibl limittions in t dsrition of nutrino
2 804 osilltions s ws obsrvd by Giunti t l. [4]. Sifilly in rfrn [4] it ws sown tt flvor stts n dfin n roximt Fok s of wk stts in t following two ss: ) In t xtrmly rltivisti limit i.. if nutrino momntum is mu lrgr tn t mximum mss ignvlu of nutrino mss stt; ) for lmost dgnrtd nutrino mss ignvlus i.. if t diffrns btwn nutrino mss ignvlus r mu smllr tn t nutrino momntum. first s lds to t stndrd dfinition of flvor stts. sond s s ssoitd rl mixing mtrix wi is rstritd to sifi intrtion ross. Additionlly ts utors v roosd tt osilltions n b dsribd roritly for ultr-rltivisti nd non-rltivisti nutrinos by dfining rorit flvor stts wi r surositions of mss stts wigtd by tir trnsitions mlituds in t ross undr onsidrtion [4]. By onsidring t limittions mntiond in t lst rgr it ws st down by But in [7] tt Sssroli ybrid modl n only b lid onsistntly if lton flvor wv funtions r onsidrd s obsrvbl nd t ultr-rltivisti limit is tkn into ount. On t otr nd t Sssroli modl dsribing jorn nutrino osilltions [] ws dvlod witout onsidring t four-momntum onsrvtion for nutrinos wi imlis t xistn of sifi momntum for vry nutrino mss stt. min gol of tis work is to study nutrino osilltions in vuum btwn two flvor stts onsidring nutrinos s jorn frmions nd to obtin t robbility dnsitis of trnsition for lft-ndd nutrinos (ultr-rltivisti limit) nd for rigt-ndd nutrinos (non-rltivisti limit). is work is dvlod in t ontxt of ty I ssw snrio wi lds to gt ligt lft-ndd nd vy rigt-ndd jorn nutrinos. In tis ontxt w rform n xtnsion of t modl dvlod by Sssroli in wi t jorn nutrino osilltions r obtind for t s of flvor stts onstrutd s surositions of mss stts [ ]. Our xtnsion onsists in onsidring nutrino mss stts s ln wvs wit sifi momnt. modl tt w onsidr in tis work wi is dvlod in t nonil formlism of Quntum Fild ory s t dvntg tt in t sm tortil trtmnt it is ossibl to study nutrino osilltions for ligt nutrinos nd for vy nutrinos. o do tis w first rform t nonil quntiztion rodur for jorn nutrino filds of dfinit msss nd tn w writ t nutrino flvor stts s surositions of mss stts using quntum fild ortors. Nxt w lult t robbility mlitud of trnsition btwn two diffrnt nutrino flvor stts for t ligt nd vy nutrino ss nd w stblis normliztion nd boundry onditions for t robbility dnsity. s robbility dnsitis for t lft-ndd nutrino s ftr t ultr-rltivisti limit is tking ld to t stndrd robbility dnsitis wi dsrib ligt nutrino osilltions. For t rigtndd nutrino s t xrssions dsribing vy nutrino osilltions in t non-rltivisti limit r diffrnt rst to t ons of t stndrd nutrino osilltions. Howvr t rigt-ndd nutrino osilltions r nomnologilly rstritd s is sown wn t rogtion of vy nutrinos is onsidrd s surositions of mss-ignstt wv kts [5]. osilltions do not tk l in tis s bus t orn is not rsrvd: in otr words t osilltion lngt is omrbl or lrgr tn t orn lngt of t nutrino systm [5]. ontnt of tis work s bn orgnizd s follows: In Stion ftr stblising t jorn ondition w obtin nd solv t two-omonnt jorn qution for fr frmion; in Stion w onsidr ty I ssw snrio wi lds to gt ligt lft-ndd nutrinos nd vy rigt-ndd nutrinos; in Stion 4 w obtin t jorn nutrino filds wit dfinit msss tn w rry out t nonil quntiztion rodur of ts jorn nutrino filds nd w obtin rltion btwn nutrino flvor stts nd nutrino mss stts using ortor filds; in Stion 5 w dtrmin t robbility dnsity of trnsition btwn two lft-ndd nutrino flvor stts dditionlly w stblis normliztion nd boundry onditions nd tn w obtin lft-ndd nutrino osilltions for ultr-rltivisti ligt nutrinos; in Stion 6 w study t rigt-ndd nutrino osilltions for non-rltivisti vy nutrinos; finlly in Stion 7 w rsnt som onlusions.. wo-comonnt jorn Eqution In 97 Ettor jorn roosd symmtri tory for ltron nd ositron troug gnrliztion of vritionl rinil for filds wi oby Frmi-Dir sttistis []. Wn tis tory is lid to nutrl frmion wi s sifi momntum tn tr xist only two liity stts. jorn tory imlis tt it dos not xist ntirtils ssoitd to ts frmions i.. jorn frmions r tir own ntirtils. For onvnin w study t qution of motion for nutrl frmions but using t two-omonnt tory dvlod by Cs in [6]. In ontrst wit Dir frmion jorn frmion n only b dsribd by two-omonnt sinor. o sow it w onsidr fr rltivisti frmioni fild of mss m dsribd by t Dir qution i m 0 wr Dir mtrixs oby t ntionmuttion rltions g nd mtri tnsor stisfis g g dig. Using
3 805 t irlity mtrix givn by 5 i 0 t lftnd rigt-ndd irl rojtions of t frmion fild ψ 5 r rstivly. If w writ t Dir mtrixs rojtd on t irl subs s 5 w obtin tt t ould qutions for t irl omonnts of t frmioni fild r givn by i m () i m (). W introdu t rg onjugtion ortion tt will llow us to dsrib jorn frmions. rgd onjugtd fild (or onjugtd fild) is dfind s ˆ wr t rg onjugtion ortor stisfis t ˆ rortis ˆ ˆ ˆ ˆ ˆ []. Using ts rortis w find tt t onjugtd fild obys t Dir qution i m 0. As dsribs frmion wit sifi rg its onjugtd fild rrsnts frmion wit n oosit rg nd wit t sm mss i.. dsribs t ntifrmion of. Dir qution for sould b rojtd on t irl subs nd for tis rson it 5 is nssry to rmmbr tt ˆ 5 ˆ []. So t ould qutions for t irl omonnts of t onjugtd fild r () i m (4) i m. (5) W obsrv tt t irl omonnts of t frmioni fild undr rg onjugtion nd t irl omonnts of t onjugtd fild r rltd by sowing ow t rg-onjugtion ortion ngs t irlity of filds. W dfin t jorn ondition by tking t frmioni fild s roortionl to t onjugtd fild wr t roortionl onstnt is omlx s ftor of t form wi lys n imortnt rol on i litions of jorn tory. Equlity (6) imlis tt jorn frmions r tir own ntirtils. Now t irl omonnts of t jorn fild stisfy ˆ ˆ. (7) (6) So w n writ Equtions () nd () in t form ˆ i m (8) ˆ i m. (9) If w ly t jorn ondition (7) into t Equtions (4) nd (5) w obtin Equtions (8) nd (9). Additionlly w n obsrv tt Equtions (8) nd (9) r rltd to tmslvs by mns of omlx onjugtion. In tis wy w v gon from four ould qutions dsribing frmion nd its ntifrmion to two dould qutions dsribing lft-ndd irl fild nd rigt-ndd irl fild. Du to t ft tt t rigt-ndd irl fild n b onstrutd from t lft-ndd irl fild [6] s it is sown in (7) now w v only n indndnt fild givn by. For t lst ft w will b bl to dsrib jorn frmion by mns of fild wi now s two omonnts. o vrify tis sntn w rwrit Eqution (8) s ˆ 0 i m. (0) If w dfin ˆ 0 () nd if w tk tn Eqution (0) n b writtn s i m () wi is known s t jorn qution. is qution in wi rtil is indistinguisbl from its ntirtil s two omonnts bus t mtrixs r rojtd on t irl subss of two omonnts. mtrixs r lld jorn mtrixs nd ts sould not b onfusd wit t Dir mtrixs writtn in jorn rrsnttion. Now w r intrstd in knowing t kind of rltions tt jorn mtrixs oby. So w first ly dfinition () into Eqution (9) nd w obtin 0 i m wit ˆ. n w ly i into () nd w v m 0 or its quivlnt m 0 wr w v usd. Aordingly jorn mtrixs sould stisfy rltions g nd tn t fild is stisfying t Klin-Gordon qution givn by m 0. In tis work w v tkn rtiulr rrsnttion of mtrixs wi s rmittd us to writ t twoomonnt jorn qution in t form givn by (). Now w n onsidr mtrix A wi stisfis t following rltions [6] i i A A A A A A i wr rrsnts Puli mtrixs in givn rrsnttion. W tk i wr σ () bing t unit mtrix nd σ Puli mtrixs. Sin stisfis rortis () w
4 806 Wit t uros of studying t nonil quntiztion for t jorn fild w will obtin t fr-rtil solution of Eqution (4). On t outst w onsidr bisinors wi oby t following rltions σ (5) i (6) wr ts bi-sinors orrsond to liity ignstts. If w tk t momntum in sril oordints sin os sinsin os tn t liity ortor s t form i σ os sin. i sin os (7) W oos t following rrsnttion for ts bisinors i os sin. (8) i sin os W n rov tt t following solution stisfis t two-omonnt jorn Eqution (4) E E ix x ix E E (9) wit x x Et x. W obsrv tt jorn fild n b writtn s surosition of ositiv nd ngtiv nrgy stts. grngin dnsity wi dsribs fr twoomonnt jorn fild is givn by m i i i (0) wr t two-omonnt jorn fild nd its onjugtd fild bv s Grssmnn vribls. It is vry sy to rov tt t two-omonnt jorn v tkn A. So t Eqution () n b writtn s Eqution (4) n b obtind from t grngin dn- sity (0) using t Eulr-grng qution. Additionlly i im 0. (4) w n obtin t following nrgy-momntum tnsor is qution is t wll known two-omonnt jorn qution [78] wi will b solvd in nxt from (0) substion. m i g i i i. Cnonil Quntiztion for jorn Fild Following t stndrd nonil quntiztion rodur w now onsidr t jorn fild nd its onjugtd fild s ortors wi stisfy t usul nonil ntionmuttion rltions givn by ˆ ˆ ˆ ˆ r t r' t r t r' t ˆ ˆ r t r' t r r' 0 wr. Using t Hisnbrg qution for t jorn fild i ˆ ˆ ˆ t r t ' t H r w n obtin its orrsonding jorn Eqution (4). By mns of t nrgy-momntum tnsor it is ossibl to rov tt t Hmiltonin ortor n b writtn s ˆ ˆ ˆ m ˆ H ˆ ˆ ˆ x i i i σ. xnsion in Fourir sris for t jorn fild ortor is [4-6] (s Eqution ()). wr w v usd t fr-rtil solution (9) nd ortors ˆ ˆ wi stisfy t ntionmuttion rltions ˆ ˆ ' '. ˆ ˆ ' ˆ ˆ ' 0 n w n idntify ˆ s t nniiltion ortor nd ˆ s t rtion ortor of jo- rn frmion wit momntum nd liity.. sss for jorn Nutrino Filds most td wy to gnrt nutrino msss is troug t ssw mnism. In tis stion w onsidr ty I ssw snrio wi lds to gt ligt lft-ndd nutrinos nd vy rigt-ndd nutrinos. For t s of two nutrino gnrtions Dir-jorn mss trm is givn by [9] D ˆ D Y N N H.. () wr H.. rrsnts t rmiti onjugt trm is t vtor of flvor nutrino filds writtn s N ˆ d ix ix x E ˆ E ˆ () π E
5 807 N ˆ () wr rrsnts doublt of lft-ndd nutrino filds tiv undr t wk intrtion nd rrsnts doublt of rigt-ndd jorn nutrino filds non tiv (stril) undr t wk intrtion. s doublts r givn by ;. (4) D In t Dir-jorn trm () is 4 4 non-digonl mtrix of t form ' D D (5) ' D wr nd D r mtrixs. vtor of nutrino filds wit dfinit msss n n b writtn by mn of unitry mtrix U s follows N U n (6) wr n s t form n n. (7) n 4 unitry mtrix U is osn in su wy tt D t non-digonl mtrix n b digonlizd troug t similrity trnsformtion U D U (8) wr is digonl mtrix wi is dfind by m b b wr b 4. msss of t nutrino filds of dfinit msss r m wit 4. ssw snrio is stblisd imosing t following onditions into t mtrix (5): ' ' D 0 D kj tus t mtrix kj is digonlizd s D U U l 0 0 (9) wr l is t ligt nutrino mss mtrix nd is t vy nutrino mss mtrix. If t unitry mtrix U is xnding onsidring trms until of t ordr ' D t ligt nd vy nutrino mss mtrixs n b writtn s l m 0 m 0 ;. (0) 0 m 0 m4 Dir-jorn mss trm () n b writtn in trms of t nutrino filds of dfinit msss s D ˆ ˆ Y nln n n H.. () wr t mtrixs l nd r givn by (0) nd t doublts nd n r writtn s n n ; n. 4 () nutrino filds of dfinit msss nd v ssoit rstivly t ligt msss nd m m f v m m f v nd t nutrino filds of dfinit msss nd 4 v ssoit rstivly t vy msss m f v nd 4 44v v f m f wr b r Yukw oulings m is t ltron mss nd m is t muon mss. As it will b sown in t nxt stion strting from t Dir-jorn mss trm D ˆ ˆ Y H.. () wr nd r t flvor doublts of non-dfinit msss givn by (4) wil nd r non-digonl mtrixs it will b ossibl to obtin t Dir-jorn mss trm () ftr t digonliztion of t mtrixs nd. 4. ss nd Flvor Nutrino Stts In t nxt w suos tt t jorn filds nd dsrib t tiv ligt lft-ndd nutrinos tt r rodud nd dttd in t lbortory wil t jorn filds nd dsrib t stril vy rigt-ndd nutrinos wi tr xist in ty I ssw snrio. In t Stion () w v rsntd lgrngin dnsity (0) wi dsribs fr jorn frmion. is lgrngin dnsity n b xtndd to dsrib systm of two flvor lft-ndd nutrinos nd two flvor rigtndd nutrinos wit non-dfinit msss. Using t Dir-jorn mss trm givn by () t lgrngin dnsity dsribing tis systm is givn by i i i (4) i H.. wr t non-digonl mss mtrixs nd r writtn s i i m m (5) i i m m
6 808 i i 4 m m (6) i4 i4 m m W obsrv tt t form of t mtrixs nd is t sm. In t nxt w will rstrit to t lftndd jorn nutrinos but t rsults r dirtly xt ndd to t rigt-ndd jorn nutrinos. From t Eulr-grng qutions w obtin tt t ould qution of motion for t flvor lft-ndd nutrino filds nd r i i i im im (7) i i im i im (8) rstivly. W obsrv tt flvor nutrino filds r ould by mns of t rmtr m. Wit t uros of douling t qutions of motion for t flvor lft-ndd nutrino filds now w onsidr t most gnrl unitry mtrix U givn by U i i i i (9) i wr t ss nd i r s onsqun of t jorn ondition (7). dfinit-mss nutrino fild doublt n givn by () is rltd to t flvor lft-ndd nutrino doublt givn by (4) by mn of U n. (40) Witout lost of gnrlity w n ng t ss of t flvor lft-ndd nutrino filds by mns of i i x nd x. us i tr is just s x tt n not b limi- ntd. So t mtrix U n b rwrittn s U i i. (4) Now t digonliztion of t mss mtrix (5) givn by is vlid for wit U U dig m m (4) D m m m m m 4 m (4) nd tus t nutrino filds wit dfinit msss nd v rstivly t following msss m m m (44) i m m m. ( 45) W obsrv tt in t xrssion for m rs t ftor x i wi suggst tt tis mss ould b omlx. Howvr t digonliztion givn by (4) is not omltly rigt bus is symmtri mtrix. So from (4) t digonliztion sould b of t form D U U (46) wr w v onsidrd tt tis mtrix is rmiti i... So t vlus m nd m r t qudrti roots of t ignvlus of. is lst rsult imlis tt ts ignvlus n b multilid by omlx s. xrssion (40) givs t mixing of t flvor nutrino filds in trms of t nutrino filds wit dfinit msss. nutrino filds wit dfinit msss nd oby jorn fild qutions of t form i im (47) i im. (48) i wit t uros of liminting t s from t lst qution of motion w n mk t following i s trnsformtion x. Now t unitry mtrix n b writtn s U. i i (49) W obsrv tt t s x i ws limintd from t lst qution of motion but not from t unitrin mtrix U l. So it rovs tt tis s is ysil nd sould b involvd in som rosss. is s ould ly n imortnt rol in t s of doublt bt dy ross. Following similr rodur for t rigt-ndd jorn nutrinos w find tt t dfinit-mss nutrino fild doublt n givn by () is rltd to t flvor rigt-ndd nutrino doublt givn by (4) by mn of wr t unitry mtrix U n (50) U is givn by
7 809 wr U i. i is givn by m m m wit m m 4 m. (5) (5) Nxt w onsidr t nonil quntiztion of t nutrino filds wit dfinit mss by stting t ntionmuttion rltions givn by ˆ ˆ r b r' b r r ' ˆ ˆ r br ' 0 nd ˆ ˆ b r r ' 0 wr b 4 rrsnt nutrino mss stts. E on of t dfinit-mss nutrino fild ortors ˆ x obys jorn qution. It is ossibl to x on of ts fild ortors on ln-wv nd bsis st s ws sown in () (s Eqution (5)). wr E m is t nrgy of t nutrino fild wit dfinit mss wi is tggd by 4. flvor nutrino fild ortors tggd by ˆ r dfind s surosition of t dfinit-mss nutrino fild ortors ˆ givn by (5) troug t xrssion ˆ x U ˆ x (54) wr U is t unitrin mtrix dfind by (49) for lft-ndd nutrinos nd by (5) for rigt-ndd nutrinos mnwil nutrino flvor stts r dfind in trms of t nutrino mss stts s U. (55) us w v found rltion btwn nutrino flvor stts nd nutrino mss stts using ortor filds. As flvor stts r ysil stts sin ty ould b dttd in intrtion rosss flvor stts r non-sttionry. So tir tmorl volution givs t robbility of trnsition btwn tm. rfor tis robbility dsribs jorn nutrino osilltions studid s follows. 5. ft-hndd Nutrino Osilltions Now w will fouss our intrst in t dsrition of lft- ndd nutrino osilltions in vuum from inmtil oint of viw. For tis rson w will not onsidr in dtil t wk intrtion rosss involvd in t rtion nd dttion of lft-ndd nutrinos. Howvr ts rosss r mnifstd wn boundry onditions r imosd in t robbility mlitud of trnsition btwn two nutrino flvor stts. W suos tt nutrino wit sifi flvor is rtd in oint of s-tim x0 t0 r0 s rsult of rtin wk intrtion ross. W will dtrmin t robbility mlitud to find out t nutrino wit notr flvor in diffrnt oint of s-tim x t r. W ssum tt nutrinos r rtd undr t sm rodution ross wit diffrnt vlus of nrgy nd momntum. s dynmil quntitis r rltd mong tmslvs undr t sifi rodution ross. initil lft-ndd nutrino flvor stt in t rodution tim ( t 0 ) orrsonds to t following surosition of nutrino mss stts t 0 A B. (56) wr A B. E of ts nutrino mss stts s ssoitd sifi four-momntum. W ssum tt in t rodution oint it ws rtd lft-ndd ltroni nutrino wit mssiv fild ving four-momntum givn by E wit. initil lft-ndd ltroni nutrino stt stisfying t ondition A B is writtn s i t0 (57) wr t sum ovr liitis is tkn ovr t nutrino mss stts. is sum ovr liitis must b onsidrd to dsrib roritly t initil lft-ndd nutrino flvor stt bus t liity is rorty wi is not dirtly msurd in t xrimnts. mnnr s t ltroni lft-ndd nutrino stt s bn built in t rodution oint is in grmnt wit t xrimntl ft tt lft-ndd nutrinos r ultr-rltivisti. nutrino mss stts involv in t surosition givn by (57) r obtind from t vuum stt s ˆ 0 i x 0 wr w v inludd ts ftor x i x 0. is s ftor givs us informtion bout t fours tim wr t lft-ndd nutrino ws rtd. robbility mlituds for trnsitions to ltroni nd muoni lft-ndd nutrinos r rstivly givn by d i x i ˆ ˆ x E ˆ x E (5) π E
8 80 E E i X ix ˆ X 0 0 (58) x t π E E E E 0 ˆ X x t (59) i X ix 0 π E E wr w v usd som xnsions ovr t jorn filds nd w v tkn X x x0 wi orrsonds to four-vt or ssoitd to t distn nd tim of nutrino rogtion. robbility dnsitis rstivly r X π 4 X X E E EE sin X π EE E E X EE EE sin X E E E E (60) (6) ount tt sinors wr w v tkn into nd r t sm bus vtors nd r o-linr. robbility dnsitis (60) nd (6) tt w v found rsnt sr ious roblm. If w fix X 0 into (60) nd (6) w find tt X 0 π 4 E E EE (6) π X 0 (6) E E EE nd w obsrv tt t robbility dnsity (6) n b diffrnt from zro i.. it n xist muoni nutrino in t rodution oint wi disgrs wit t initil onditions. origin of tis roblm is rltd to t wk stt dfinition (55) tt w v usd bfor. As it ws rviously mntiond into t introdution t flvor dfinition (55) is not omltly onsistnt nd it is nssry to dfin rorit flvor stts [4]. Ultr-ltivisti imit: ft-hndd Nutrino Osilltions is roblm n b solvd by tking n roximtion in t robbility dnsitis (60) nd (6) bsd on t ft tt lft-ndd nutrinos r ultr-rltivisti rtils bus tir msss r vry smll. Hr w onsidr nrgy nd momntum diffrnt for vry mss stt. In gnrl w n writ 4 E m m (64) 4 E E m m (65) wr t rmtrs nd r dtrmind in t rodution ross nd E is t nrgy for t s in wi nutrinos wr msslss. For instn for t ion dy ross w v E m mπ m π m m π 4mπ (66) (67) wr m is t muon mss nd m π is t ion mss. Bus for t ultr-rltivisti limit m 0 w n roximt t xrssions (64) nd (65) to m E (68) E
9 8 m E E. (69) E Now it is ossibl to rov tt t rigt sid of t rltion E E m m EE 8E (70) n b roximtd to t unit bus m E 0 wr m m m. On t otr nd nutrino rogtion tim is not msurd in nutrino xri- mnts [97]. In tis kind of xrimnts is msurd t distn btwn t nutrino sour nd t d- btwn ttor. By tis rson it n b ossibl to find n- tt stbliss rltion lytil xrssion nd t rogtion distn. In our ro using ln wvs for t ultr-rltivisti limit w n writ. (7) is rltion imlis tt t rogtion distn nd t rogtion tim for nutrinos r roximtly qul bus in t ultr-rltivisti limit nutrino mss stt s mss too smll nd its vloity of rogtion v k is roximtly qul to sd vloity i.. vk. Howvr most ris rltion btwn nd must b dsribd by n xrssion tt sould inlud xliitly t vloitis of t two nutrino mss stts involvd in su wy tt tis xrssion for t ultr-rltivisti limit sould ld to (7). So for t ultr-rltivisti limit t robbility dnsitis (60) nd (6) n b writtn s m sin (7) π 4E m sin π 4E (7) wr w v usd nd m m m. Undr tis roximtion it is lr tt ts robbility dnsity dos not dnd from t rodution ross du to tt tr is no dndn from. us ts robbility dnsitis stisfy t boundry onditions tt w v imosd. In t nxt w will rov tt t robbility dnsitis (7) nd (7) v t form of t stndrd robbility dnsitis for nutrino osilltions. In t ontxt of t stndrd formlism of nutrino osilltions (ssuming CP onsrvtion) for t two gnrtion s onsidring r t rrsnttion of t unitry mtrix U tt rs into t xrssion (40) is givn b y [0] os sin U (74) sin os wr is t mixing ngl. If w omr t unitry mtrix givn by (49) wit t on givn by (74) w obsrv tt os nd tn it is vry sy to obtin tt sin. (75) Substituting (75) into (7) nd (7) w obtin t xrssions sin sin π π m 4E m 4E sin sin (76) (77) wi r t stndrd robbility dnsitis for lftndd nutrino osilltions in t two flvor s [0]. 6. igt-hndd Nutrino Osilltions initil rigt-ndd nutrino flvor stt in t rodution tim ( t 0 ) orrsonds to t following surosition of nutrino mss stts t C D. (78) 0 4 wr C D. E of ts nutrino mss stts s ssoitd sifi four-momntum. W ssum tt in t rodution oint it ws rtd rigt-ndd ltroni nutrino wit mssiv fild ving four-momntum givn by E wit 4. initil rigt-ndd ltroni nutrino stt stisfying t ondition C D is writtn s i t0 4 (79) wr t sum ovr liitis is tkn ovr t nutrino mss stts. robbility mlituds for trnsitions to ltroni nd muoni rigt-ndd nutrinos r rstivly givn by X 0 ˆ x t 0 E E 4 i X 4 i4 X 4 π E E4 (80)
10 8 X 0 ˆ x t π robbility dnsitis X 0 E E 4 4 i X i X 4 4. E E4 X X rstivly r 4 π EE 4 4 E E4 E E4 X EE sin (8) (8) X π EE wr w v tkn into oun nor nd 4 r t sm bus vtors nd r o-linr. robbility dnsitis (8) nd (8) 4 t tt si s 4 4 E E4 4 E EE 4 EE 4 4 E 4 sin X (8) tt w v found rsnt srious roblm. If w fix X 0 into (8) nd (8) w find tt 4 X 0 E E4 4 (84) π X 0 4 E E 4 (85) π EE 4 nd w obsrv tt t robbility dnsity (85) n b diffrnt from zro. Non-ltivisti imit: igt-hndd Nutrino Osilltions is roblm n b solvd by tking n roximtion in t robbility dnsitis (8) nd (8) bsd on t ft tt rigt-ndd nutrinos r non-rltivisti rtils bus tir msss r vry lrg. By tis rson w tk t non-rltivisti roximtion i.. m. So w v E m. (86) m rfor w suos tt vy rigt-ndd jorn nutrinos oby simly t rltivisti disrsion rltio n. So w obtin t following roximtion E E 4 4 EE 4 vv 4 v v4v v4 8 wr t non-rltivisti vloity of t nutrino is i vi 0 mnwil t s is roximtd to m i E E m (88) wit m4 m m4. So t robbility dnsitis of trnsition r givn by m4 sin π m4 sin π (86) (87) wr is givn by (5). lst robbility dnsitis stisfy t normliztion nd boundry onditions. Unlikly to t s of lft-ndd nutrino osilltions dsribd by (60) nd (6) t rgumnt of t riodi funtion for t rigt-ndd nutrino osilltions dnds on t linr mss diffrn m4 nd t rogtion tim. dsrition of vy rigt-ndd nutrino osilltions tt w rsnt r ould b of
11 8 intrst in osmologil roblms []. As it s bn roosd in t litrtur vy-vy nutrino osilltions ould b rsonsibl for t bryon symmtry of t univrs troug ltognsis mnism [-4]. But it sould b notd tt if t rogtion of vy rigt-ndd nutrinos is onsidrd s surositions of mss-ignstt wv kts [5] tn t osilltions do not tk l bus t orn is not rsrvd: in otr words t osilltion lngt is omrbl or lrgr tn t orn lngt of t rigt-ndd nutrino systm [5]. 7. Conlusions In tis work w v studid nutrino osilltions in vuum btwn two flvor stts onsidring nutrinos s jorn frmions. W v rformd tis study for t s of flvor stts onstrutd s surositions of mss stts xtnding t Sssroli modl wi dsribs jorn nutrino osilltions by onsidring nutrino mss stts s ln wvs wit sifi momnt. In t ontxt of ty I ssw snrio wi lds to gt ligt lft-ndd nd vy rigt-ndd jorn nutrinos t min ontribution of tis work s bn to obtin in sm formlism t robbility dnsitis wi dsrib t osilltions for ligt lftndd nutrinos (ultrrltivisti limit) nd for vy rigt-ndd nutrinos (non-rltivisti limit). In tis work w v rformd t nonil quntiztion rodur for jorn nutrino filds of dfinit msss nd tn w v writtn t nutrino flvor stts s surositions of mss stts using quntum fild ortrnsition btwn two diffrnt nutrino flvor stts for t ligt nd vy nutrino ss nd w v stb- lisd normliztion nd boundry onditions for t tors. W v lultd t robbility mlitud of robbility dnsity. Aftr t ultr-rltivisti limit ws tkn in t robbility dnsitis for t lft-ndd nutrino s ld to t stndrd robbility dnsitis wi dsrib ligt nutrino osilltions. For t rigt-ndd nutrino s t xrssions dsribing vy nutrino osilltions in t non-rltivisti limit wr diffrnt rst to t ons of t stndrd nutrino osilltions. Howvr t rigt-ndd nutrino osilltions r nomnologilly rstritd s is sown wn t ro- of mss-ignstt wv kts [5]. gtion of vy nutrinos is onsidrd s surositions is work stblis frmwork to study jorn nutrino osilltions for t s wr mss stts r dsribd by Gussin wv kts s will b rsntd in fortoming work [5]. wv kt trtmnt is nssry owing to t nutrinos r rodud in wk intrtion rosss witout sifi momnt. Additionlly t ln wv trtmnt n not dsrib rodution nd dttion lolizd rosss s our in nutrino osilltions. 8. Aknowldgmnts C. J. Quimby tnks DIB by t finnil suort rivd troug t rsr rojt Proidds ltromgnétis y d osilión d nutrinos d jorn y d Dir. C. J. Quimby tnks lso Virrtorí d Invstigions of Univrsidd Nionl d Colombi by t finnil suort rivd troug t rsr grnt orí d Cmos Cuántios lid sistms d l Físi d Prtíuls d l Físi d l tri Condnsd y l dsriión d roidds dl grfno. EFEENCES [] E. jorn ori simmtri dll lttron dl ositron Nuovo Cimnto Vol [] P. B. Pl nd. N. otr siv Nutrinos in Pysis nd Astroysis World Sintifi Publising Singor 004. [] C. Giunti nd C. Kim Fundmntl of Nutrinos in Pysis nd Astroysis Oxford Univrsity Prss Nw York 007. [4] K. Nkmur t l. Prtil Dt Grou t viw of Prtil Pysis Journl of Pysis G Vol Artil ID: [5] A. Bottino C. W. Kim H. Nisiur nd W. K. Sz odl for ton ixing Angls nd jorn Nutrino sss Pysil viw D Vol. 4 No doi:0.0/pysvd.4.86 [6] B. Pontorvo Nutrino Exrimnts nd t Problm of Consrvtion of toni Crg Sovit Pysis JEP Vol [7] S.. Bilnky nd B. Pontorvo ton ixing nd Nutrino Osilltions Pysis orts Vol. 4 No doi:0.06/070-57(78) [8] B. Kysr On t Quntum nis of Nutrino Osilltion Pysil viw D Vol. 4 No doi:0.0/pysvd.4.0 [9] C. Giunti C. W. Kim nd U. W. Wn Do Nutrinos lly Osillt? Quntum nis of Nutrino Osilltions Pysil viw D Vol. 44 No doi:0.0/pysvd [0] J. i Quntum nis of Nutrino Osilltions Pysil viw D Vol. 48 No doi:0.0/pysvd []. Zrl From Kons to Nutrinos: Quntum nis of Prtil Osilltions At Pysi Poloni B Vol [] E. Sssrolli Nutrino Osilltions: A ltivisti Exml of wo-vl Systm Amrin Journl of Pysis Vol. 67 No doi:0.9/.940 []. Blson nd G. Vitillo Quntum Fild ory of Frmion ixing Annls of Pysis Vol. 44 No doi:0.006/y.995.5
12 84 [4] E. Alfinito. Blson A. Iorio nd G. Vitillo Squzd Nutrino Osilltions in Quntum Fild ory Pysis ttrs B Vol. 6 No doi:0.06/070-69(95)07- [5] C. Y. Crdll Corn of Nutrino Flvor ixing in Quntum Fild ory Pysil viw D Vol. 6 No Artil ID: doi:0.0/pysvd [6] A. D. Dolgov Nutrinos in Cosmology Pysis orts Vol. 70 No doi:0.06/s070-57(0)009-4 [7]. But Osilltions of Nutrinos nd sons in Quntum Fild ory Pysis orts Vol. 75 No doi:0.06/s070-57(0) [8] Y. F. i nd Q. Y. iu A Prdox on Quntum Fild ory of Nutrino ixing nd Osilltions Journl of Hig Enrgy Pysis Vol Artil ID: 048. doi:0.088/6-6708/006/0/048 [9]. Dvornikov nd J. lmi Osilltions of Dir nd jorn nutrinos in ttr nd gnti Fild Pysil viw D Vol. 79 No. 009 Artil ID: 05. doi:0.0/pysvd [0] E. K. Akmdov nd J. Ko Nutrino Osilltions: Quntum nis vs. Quntum Fild ory Journl of Hig Enrg y Pysis Vol. 00 No doi:0.007/jhep04(00)008 [] E. Sssroli Flvor Osilltions in Fild ory tt://rxiv.org/bs/-/ v [] E. Sssroli Nutrino Flvor ixing nd Osilltions in Fild ory tt://rxiv.org/bs/-/ [] E. Sssroli wo Comonnt ory of Nutrino Flvor ixing tt://rxiv.org/bs/-/9709v [4] C. Giunti C. W. Kim nd U. W. mrks on t Wk Stts of Nutrinos Pysil viw D Vol. 45 No doi:0.0/pysv D [5] C. W. Kim C. Giunti nd U. W. Osilltions of Non-ltivisti Nutrinos Nulr Pysis B Prodings Sulmnts Vol. 8 No doi:0.06/090-56(9)906 7-Q [6] K.. Cs formultion of t jorn ory of Nutrino Pysil viw Vol. 07 No doi:0.0/pysv [7] P. B. Pl Dir jorn nd Wyl Frmions Amrin Journl of Pysis Vol. 79 No doi:0.9/ [8] E. rs wo-comonnt jorn Eqution- Novl Drivtions nd Known Symmtris J. od. Pys Vol. No doi:0.46/jm.0.07 [9] S.. Bilnky nd S.. Ptov ssiv Nutrinos nd Nutrino Osilltions viws of odrn Pysis Vol. 59 No doi:0.0/vodpys [0] C. W. Kim nd A. Pvsnr Nutrinos in Pysis nd Astroysis Hrwood Admi Publisrs Bsl 99. [] S. S. Grstin E. P. Kuzntsov nd V. A. ybov formultion of t jorn ory of Nutrino Pysis-Uski Vol. 40 No doi:0.070/pu997v040n 08ABEH0007 [] E. K. Akmdov V. A. ubkov nd A. Yu. Smirnov Bryognsis vi Nutrino Osilltions Pysil viw ttrs Vol. 8 No doi:0.0/pysvtt.8.59 [].. Volks Nutrinos in Cosmology wit Som Signifint Digrssions Prtil Pysis nd Cosmology: ird roil Workso on Prtil Pysis nd Cosmology Nutrinos Brns nd Cosmology Sn Jun 9- August doi:0.06 /.5450 [4] A. D. Dolgov CP Violtion in Cosmology. tt://rxiv.org/bs/-/05v [5] Y. F. Pérz nd C. J. Quimby morl Disrsion Effts of jorn s Wv Pkts for Nutrino Osilltions in Vuum rintd in Prrtion.
Problem 1. Solution: = show that for a constant number of particles: c and V. a) Using the definitions of P
 rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
The Angular Momenta Dipole Moments and Gyromagnetic Ratios of the Electron and the Proton
 Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
HIGHER ORDER DIFFERENTIAL EQUATIONS
 Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Equilibrium Composition and Thermodynamic Properties of Hydrogen Plasma
 Chatr- Equilibrium Comosition and Thrmodynami Prortis of ydrogn Plasma It is wll known that th thrmodynami and transort rortis dnd dirtly on th lasma omosition, whih furthr dnds uon th inlusion of ltronially
Chatr- Equilibrium Comosition and Thrmodynami Prortis of ydrogn Plasma It is wll known that th thrmodynami and transort rortis dnd dirtly on th lasma omosition, whih furthr dnds uon th inlusion of ltronially
Elliptical motion, gravity, etc
 FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
Lecture 12 Quantum chromodynamics (QCD) WS2010/11: Introduction to Nuclear and Particle Physics
 Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
Page 1. Question 19.1b Electric Charge II Question 19.2a Conductors I. ConcepTest Clicker Questions Chapter 19. Physics, 4 th Edition James S.
 ConTst Clikr ustions Chtr 19 Physis, 4 th Eition Jms S. Wlkr ustion 19.1 Two hrg blls r rlling h othr s thy hng from th iling. Wht n you sy bout thir hrgs? Eltri Chrg I on is ositiv, th othr is ngtiv both
ConTst Clikr ustions Chtr 19 Physis, 4 th Eition Jms S. Wlkr ustion 19.1 Two hrg blls r rlling h othr s thy hng from th iling. Wht n you sy bout thir hrgs? Eltri Chrg I on is ositiv, th othr is ngtiv both
Quantum trajectories and quantum measurement theory in solid-state mesoscopics
 Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis HsiSng Gon Cntr or Quntum Computr nology, Univrsity o Nw Sout ls, Sydny, NS 202 Austrli Abstrt. Strting rom t ull Srödingr qution or systm nd
Quntum trjtoris nd quntum msurmnt tory in solidstt msosopis HsiSng Gon Cntr or Quntum Computr nology, Univrsity o Nw Sout ls, Sydny, NS 202 Austrli Abstrt. Strting rom t ull Srödingr qution or systm nd
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 8: Effect of a Vertical Field on Tokamak Equilibrium
 .65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
.65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
Chapter 11 Calculation of
 Chtr 11 Clcultion of th Flow Fild OUTLINE 11-1 Nd for Scil Procdur 11-2 Som Rltd Difficultis 11-3 A Rmdy : Th stggrd Grid 11-4 Th Momntum Equtions 11-5 Th Prssur nd Vlocity Corrctions 11-6 Th Prssur-Corrction
Chtr 11 Clcultion of th Flow Fild OUTLINE 11-1 Nd for Scil Procdur 11-2 Som Rltd Difficultis 11-3 A Rmdy : Th stggrd Grid 11-4 Th Momntum Equtions 11-5 Th Prssur nd Vlocity Corrctions 11-6 Th Prssur-Corrction
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
1.60± ± ±0.07 S 1.60± ± ±0.30 X
 02M557-01B - Pg 1 of 7 Produt Fmily: Prt Numbr Sris: Multilyr rmi itors Flxibl Trmintion ST Sris onstrution: Flxibl Trmintions NPO, X7R, X5R nd Y5V diltri mtrils Wr round ltrods 100% mtt tin ovr Ni trmintions
02M557-01B - Pg 1 of 7 Produt Fmily: Prt Numbr Sris: Multilyr rmi itors Flxibl Trmintion ST Sris onstrution: Flxibl Trmintions NPO, X7R, X5R nd Y5V diltri mtrils Wr round ltrods 100% mtt tin ovr Ni trmintions
A NEW MIXED HEXAHEDRAL FINITE ELEMENT IN HEAT TRANSFER ANALYSIS
 A NEW MIXED HEXAHEDRA FINIE EEMEN IN HEA RANSFER ANAYSIS Dubrvk MIJUCA, An ŽIBERNA & Bojn MEDJO Fulty of Mthmtis, Univrsity of Blgrd, P.O.Box 55, Srbi nd Montngro -orrsondn: dmiju@mtf.bg..yu Abstrt. A
A NEW MIXED HEXAHEDRA FINIE EEMEN IN HEA RANSFER ANAYSIS Dubrvk MIJUCA, An ŽIBERNA & Bojn MEDJO Fulty of Mthmtis, Univrsity of Blgrd, P.O.Box 55, Srbi nd Montngro -orrsondn: dmiju@mtf.bg..yu Abstrt. A
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Tangram Fractions Overview: Students will analyze standard and nonstandard
 ACTIVITY 1 Mtrils: Stunt opis o tnrm mstrs trnsprnis o tnrm mstrs sissors PROCEDURE Skills: Dsriin n nmin polyons Stuyin onrun Comprin rtions Tnrm Frtions Ovrviw: Stunts will nlyz stnr n nonstnr tnrms
ACTIVITY 1 Mtrils: Stunt opis o tnrm mstrs trnsprnis o tnrm mstrs sissors PROCEDURE Skills: Dsriin n nmin polyons Stuyin onrun Comprin rtions Tnrm Frtions Ovrviw: Stunts will nlyz stnr n nonstnr tnrms
Utilizing exact and Monte Carlo methods to investigate properties of the Blume Capel Model applied to a nine site lattice.
 Utilizing xat and Mont Carlo mthods to invstigat proprtis of th Blum Capl Modl applid to a nin sit latti Nik Franios Writing various xat and Mont Carlo omputr algorithms in C languag, I usd th Blum Capl
Utilizing xat and Mont Carlo mthods to invstigat proprtis of th Blum Capl Modl applid to a nin sit latti Nik Franios Writing various xat and Mont Carlo omputr algorithms in C languag, I usd th Blum Capl
Formal Concept Analysis
 Forml Conpt Anlysis Conpt intnts s losd sts Closur Systms nd Implitions 4 Closur Systms 0.06.005 Nxt-Closur ws dvlopd y B. Gntr (984). Lt M = {,..., n}. A M is ltilly smllr thn B M, if B A if th smllst
Forml Conpt Anlysis Conpt intnts s losd sts Closur Systms nd Implitions 4 Closur Systms 0.06.005 Nxt-Closur ws dvlopd y B. Gntr (984). Lt M = {,..., n}. A M is ltilly smllr thn B M, if B A if th smllst
Floating Point Number System -(1.3)
 Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igits in th bs xnsion
Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igits in th bs xnsion
Floating Point Number System -(1.3)
 Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igts in th bs xnsion
Floting Point Numbr Sstm -(.3). Floting Point Numbr Sstm: Comutrs rrsnt rl numbrs in loting oint numbr sstm: F,k,m,M 0. 3... k ;0, 0 i, i,...,k, m M. Nottions: th bs 0, k th numbr o igts in th bs xnsion
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
Lecture 6 Thermionic Engines
 Ltur 6 hrmioni ngins Rviw Rihrdson formul hrmioni ngins Shotty brrir nd diod pn juntion nd diod disussion.997 Copyright Gng Chn, MI For.997 Dirt Solr/hrml to ltril nrgy Convrsion WARR M. ROHSOW HA AD MASS
Ltur 6 hrmioni ngins Rviw Rihrdson formul hrmioni ngins Shotty brrir nd diod pn juntion nd diod disussion.997 Copyright Gng Chn, MI For.997 Dirt Solr/hrml to ltril nrgy Convrsion WARR M. ROHSOW HA AD MASS
Ch 1.2: Solutions of Some Differential Equations
 Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
I. The Connection between Spectroscopy and Quantum Mechanics
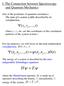 I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
A Study of the Solutions of the Lotka Volterra. Prey Predator System Using Perturbation. Technique
 Inrnionl hmil orum no. 667-67 Sud of h Soluions of h o Volrr r rdor Ssm Using rurion Thniqu D.Vnu ol Ro * D. of lid hmis IT Collg of Sin IT Univrsi Vishnm.. Indi Y... Thorni D. of lid hmis IT Collg of
Inrnionl hmil orum no. 667-67 Sud of h Soluions of h o Volrr r rdor Ssm Using rurion Thniqu D.Vnu ol Ro * D. of lid hmis IT Collg of Sin IT Univrsi Vishnm.. Indi Y... Thorni D. of lid hmis IT Collg of
Study Of Superconductivity And Antiferromagnetism In Rare Earth Nickel Borocarbides (RNi 2 B 2 C)
 IOSR Journl o Applid Pysis IOSR-JAP -ISS: 78-86.olum 9 Issu r. II y - Jun 7 PP 7-8 www.iosrjournls.org Study O Suprondutivity And Antirromgntism In Rr Ert il ororids Ri C r. Slil s nd Prti Sumn s prtmnt
IOSR Journl o Applid Pysis IOSR-JAP -ISS: 78-86.olum 9 Issu r. II y - Jun 7 PP 7-8 www.iosrjournls.org Study O Suprondutivity And Antirromgntism In Rr Ert il ororids Ri C r. Slil s nd Prti Sumn s prtmnt
Fractional Topological Insulators A Bosonization Approach
 Journl of Modrn Physis 06 7 8-8 Publishd Onlin Jnury 06 in Sis. http://www.sirp.or/journl/jmp http://d.doi.or/0.46/jmp.06.70 rtionl Topoloil Insultors A Boniztion Approh D. Shmltzr Physis Dprtmnt City
Journl of Modrn Physis 06 7 8-8 Publishd Onlin Jnury 06 in Sis. http://www.sirp.or/journl/jmp http://d.doi.or/0.46/jmp.06.70 rtionl Topoloil Insultors A Boniztion Approh D. Shmltzr Physis Dprtmnt City
OpenMx Matrices and Operators
 OpnMx Mtris n Oprtors Sr Mln Mtris: t uilin loks Mny typs? Dnots r lmnt mxmtrix( typ= Zro", nrow=, nol=, nm="" ) mxmtrix( typ= Unit", nrow=, nol=, nm="" ) mxmtrix( typ= Int", nrow=, nol=, nm="" ) mxmtrix(
OpnMx Mtris n Oprtors Sr Mln Mtris: t uilin loks Mny typs? Dnots r lmnt mxmtrix( typ= Zro", nrow=, nol=, nm="" ) mxmtrix( typ= Unit", nrow=, nol=, nm="" ) mxmtrix( typ= Int", nrow=, nol=, nm="" ) mxmtrix(
Physics 43 HW #9 Chapter 40 Key
 Pysics 43 HW #9 Captr 4 Ky Captr 4 1 Aftr many ours of dilignt rsarc, you obtain t following data on t potolctric ffct for a crtain matrial: Wavlngt of Ligt (nm) Stopping Potntial (V) 36 3 4 14 31 a) Plot
Pysics 43 HW #9 Captr 4 Ky Captr 4 1 Aftr many ours of dilignt rsarc, you obtain t following data on t potolctric ffct for a crtain matrial: Wavlngt of Ligt (nm) Stopping Potntial (V) 36 3 4 14 31 a) Plot
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Math 166 Week in Review 2 Sections 1.1b, 1.2, 1.3, & 1.4
 Mt 166 WIR, Sprin 2012, Bnjmin urisp Mt 166 Wk in Rviw 2 Stions 1.1, 1.2, 1.3, & 1.4 1. S t pproprit rions in Vnn irm tt orrspon to o t ollowin sts. () (B ) B () ( ) B B () (B ) B 1 Mt 166 WIR, Sprin 2012,
Mt 166 WIR, Sprin 2012, Bnjmin urisp Mt 166 Wk in Rviw 2 Stions 1.1, 1.2, 1.3, & 1.4 1. S t pproprit rions in Vnn irm tt orrspon to o t ollowin sts. () (B ) B () ( ) B B () (B ) B 1 Mt 166 WIR, Sprin 2012,
Functions and Graphs 1. (a) (b) (c) (f) (e) (d) 2. (a) (b) (c) (d)
 Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
 Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
d e c b a d c b a d e c b a a c a d c c e b
 FLAT PEYOTE STITCH Bin y mkin stoppr -- sw trou n pull it lon t tr until it is out 6 rom t n. Sw trou t in witout splittin t tr. You soul l to sli it up n own t tr ut it will sty in pl wn lt lon. Evn-Count
FLAT PEYOTE STITCH Bin y mkin stoppr -- sw trou n pull it lon t tr until it is out 6 rom t n. Sw trou t in witout splittin t tr. You soul l to sli it up n own t tr ut it will sty in pl wn lt lon. Evn-Count
k m The reason that his is very useful can be seen by examining the Taylor series expansion of some potential V(x) about a minimum point:
 roic Oscilltor Pottil W r ow goig to stuy solutios to t TIS for vry usful ottil tt of t roic oscilltor. I clssicl cics tis is quivlt to t block srig robl or tt of t ulu (for sll oscilltios bot of wic r
roic Oscilltor Pottil W r ow goig to stuy solutios to t TIS for vry usful ottil tt of t roic oscilltor. I clssicl cics tis is quivlt to t block srig robl or tt of t ulu (for sll oscilltios bot of wic r
MAT3707. Tutorial letter 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS. Semester 1. Department of Mathematical Sciences MAT3707/201/1/2017
 MAT3707/201/1/2017 Tutoril lttr 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS MAT3707 Smstr 1 Dprtmnt o Mtmtil Sins SOLUTIONS TO ASSIGNMENT 01 BARCODE Din tomorrow. univrsity o sout ri SOLUTIONS TO ASSIGNMENT
MAT3707/201/1/2017 Tutoril lttr 201/1/2017 DISCRETE MATHEMATICS: COMBINATORICS MAT3707 Smstr 1 Dprtmnt o Mtmtil Sins SOLUTIONS TO ASSIGNMENT 01 BARCODE Din tomorrow. univrsity o sout ri SOLUTIONS TO ASSIGNMENT
C-Curves. An alternative to the use of hyperbolic decline curves S E R A F I M. Prepared by: Serafim Ltd. P. +44 (0)
 An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
 ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
Last time: introduced our first computational model the DFA.
 Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
MASTER CLASS PROGRAM UNIT 4 SPECIALIST MATHEMATICS SEMESTER TWO 2014 WEEK 11 WRITTEN EXAMINATION 1 SOLUTIONS
 MASTER CLASS PROGRAM UNIT SPECIALIST MATHEMATICS SEMESTER TWO WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES QUESTION () Lt p ( z) z z z If z i z ( is
MASTER CLASS PROGRAM UNIT SPECIALIST MATHEMATICS SEMESTER TWO WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES QUESTION () Lt p ( z) z z z If z i z ( is
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Trigonometric functions
 Robrto s Nots on Diffrntial Calculus Captr 5: Drivativs of transcndntal functions Sction 5 Drivativs of Trigonomtric functions Wat you nd to know alrady: Basic trigonomtric limits, t dfinition of drivativ,
Robrto s Nots on Diffrntial Calculus Captr 5: Drivativs of transcndntal functions Sction 5 Drivativs of Trigonomtric functions Wat you nd to know alrady: Basic trigonomtric limits, t dfinition of drivativ,
Lecture 4. Conic section
 Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Lecture 14 (Oct. 30, 2017)
 Ltur 14 8.31 Quantum Thory I, Fall 017 69 Ltur 14 (Ot. 30, 017) 14.1 Magnti Monopols Last tim, w onsidrd a magnti fild with a magnti monopol onfiguration, and bgan to approah dsribing th quantum mhanis
Ltur 14 8.31 Quantum Thory I, Fall 017 69 Ltur 14 (Ot. 30, 017) 14.1 Magnti Monopols Last tim, w onsidrd a magnti fild with a magnti monopol onfiguration, and bgan to approah dsribing th quantum mhanis
1 General boundary conditions in diffusion
 Gnral boundary conditions in diffusion Πρόβλημα 4.8 : Δίνεται μονοδιάτατη πλάκα πάχους, που το ένα άκρο της κρατιέται ε θερμοκραία T t και το άλλο ε θερμοκραία T 2 t. Αν η αρχική θερμοκραία της πλάκας
Gnral boundary conditions in diffusion Πρόβλημα 4.8 : Δίνεται μονοδιάτατη πλάκα πάχους, που το ένα άκρο της κρατιέται ε θερμοκραία T t και το άλλο ε θερμοκραία T 2 t. Αν η αρχική θερμοκραία της πλάκας
A New Semi-Symmetric Unified Field Theory of the Classical Fields of Gravity and Electromagnetism
 Otobr, 2007 PROGRESS IN PHYSICS Volum 4 SPECIAL REPORT A Nw Smi-Symmtri Unifid Fild Thory of th Clssil Filds of Grvity nd Eltromntism Indrnu Suhndro Drtmnt of Physis, Krlstd Univrsity, Krlstd 65 88, Swdn
Otobr, 2007 PROGRESS IN PHYSICS Volum 4 SPECIAL REPORT A Nw Smi-Symmtri Unifid Fild Thory of th Clssil Filds of Grvity nd Eltromntism Indrnu Suhndro Drtmnt of Physis, Krlstd Univrsity, Krlstd 65 88, Swdn
CS 103 BFS Alorithm. Mark Redekopp
 CS 3 BFS Aloritm Mrk Rkopp Brt-First Sr (BFS) HIGHLIGHTED ALGORITHM 3 Pt Plnnin W'v sn BFS in t ontxt o inin t sortst pt trou mz? S?? 4 Pt Plnnin W xplor t 4 niors s on irtion 3 3 3 S 3 3 3 3 3 F I you
CS 3 BFS Aloritm Mrk Rkopp Brt-First Sr (BFS) HIGHLIGHTED ALGORITHM 3 Pt Plnnin W'v sn BFS in t ontxt o inin t sortst pt trou mz? S?? 4 Pt Plnnin W xplor t 4 niors s on irtion 3 3 3 S 3 3 3 3 3 F I you
The van der Waals interaction 1 D. E. Soper 2 University of Oregon 20 April 2012
 Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
 CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Elements of Statistical Thermodynamics
 24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
PH427/PH527: Periodic systems Spring Overview of the PH427 website (syllabus, assignments etc.) 2. Coupled oscillations.
 Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Case Study 1 PHA 5127 Fall 2006 Revised 9/19/06
 Cas Study Qustion. A 3 yar old, 5 kg patint was brougt in for surgry and was givn a /kg iv bolus injction of a muscl rlaxant. T plasma concntrations wr masurd post injction and notd in t tabl blow: Tim
Cas Study Qustion. A 3 yar old, 5 kg patint was brougt in for surgry and was givn a /kg iv bolus injction of a muscl rlaxant. T plasma concntrations wr masurd post injction and notd in t tabl blow: Tim
Chapter 40 Introduction to Quantum
 Catr 0 Introdution to Quantu Pysis 900-90 A nw tory alld quantu anis was igly sussful in xlaining t bavior of artils of irosoi siz. Baus sintists larn t wav and artil naturs of ligt in 9 t ntury, ty roos
Catr 0 Introdution to Quantu Pysis 900-90 A nw tory alld quantu anis was igly sussful in xlaining t bavior of artils of irosoi siz. Baus sintists larn t wav and artil naturs of ligt in 9 t ntury, ty roos
AP Calculus BC Problem Drill 16: Indeterminate Forms, L Hopital s Rule, & Improper Intergals
 AP Calulus BC Problm Drill 6: Indtrminat Forms, L Hopital s Rul, & Impropr Intrgals Qustion No. of Instrutions: () Rad th problm and answr hois arfully () Work th problms on papr as ndd () Pik th answr
AP Calulus BC Problm Drill 6: Indtrminat Forms, L Hopital s Rul, & Impropr Intrgals Qustion No. of Instrutions: () Rad th problm and answr hois arfully () Work th problms on papr as ndd () Pik th answr
THE SPINOR FIELD THEORY OF THE PHOTON
 Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Planar Upward Drawings
 C.S. 252 Pro. Rorto Tmssi Computtionl Gomtry Sm. II, 1992 1993 Dt: My 3, 1993 Sri: Shmsi Moussvi Plnr Upwr Drwings 1 Thorm: G is yli i n only i it hs upwr rwing. Proo: 1. An upwr rwing is yli. Follow th
C.S. 252 Pro. Rorto Tmssi Computtionl Gomtry Sm. II, 1992 1993 Dt: My 3, 1993 Sri: Shmsi Moussvi Plnr Upwr Drwings 1 Thorm: G is yli i n only i it hs upwr rwing. Proo: 1. An upwr rwing is yli. Follow th
SCHUR S THEOREM REU SUMMER 2005
 SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Compton Scattering. There are three related processes. Thomson scattering (classical) Rayleigh scattering (coherent)
 Comton Scattring Tr ar tr rlatd rocsss Tomson scattring (classical) Poton-lctron Comton scattring (QED) Poton-lctron Raylig scattring (cornt) Poton-atom Tomson and Raylig scattring ar lasticonly t dirction
Comton Scattring Tr ar tr rlatd rocsss Tomson scattring (classical) Poton-lctron Comton scattring (QED) Poton-lctron Raylig scattring (cornt) Poton-atom Tomson and Raylig scattring ar lasticonly t dirction
INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS. xy 1 (mod p), (x, y) I (j)
 INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS T D BROWNING AND A HAYNES Abstract W invstigat th solubility of th congrunc xy (mod ), whr is a rim and x, y ar rstrictd to li
INCOMPLETE KLOOSTERMAN SUMS AND MULTIPLICATIVE INVERSES IN SHORT INTERVALS T D BROWNING AND A HAYNES Abstract W invstigat th solubility of th congrunc xy (mod ), whr is a rim and x, y ar rstrictd to li
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
 rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
Atomic Physics. Final Mon. May 12, 12:25-2:25, Ingraham B10 Get prepared for the Final!
 # SCORES 50 40 30 0 10 MTE 3 Rsults P08 Exam 3 0 30 40 50 60 70 80 90 100 SCORE Avrag 79.75/100 std 1.30/100 A 19.9% AB 0.8% B 6.3% BC 17.4% C 13.1% D.1% F 0.4% Final Mon. Ma 1, 1:5-:5, Ingraam B10 Gt
# SCORES 50 40 30 0 10 MTE 3 Rsults P08 Exam 3 0 30 40 50 60 70 80 90 100 SCORE Avrag 79.75/100 std 1.30/100 A 19.9% AB 0.8% B 6.3% BC 17.4% C 13.1% D.1% F 0.4% Final Mon. Ma 1, 1:5-:5, Ingraam B10 Gt
Fundamental Algorithms for System Modeling, Analysis, and Optimization
 Fundmntl Algorithms for Sstm Modling, Anlsis, nd Optimiztion Edwrd A. L, Jijt Rohowdhur, Snjit A. Sshi UC Brkl EECS 144/244 Fll 2011 Copright 2010-11, E. A. L, J. Rohowdhur, S. A. Sshi, All rights rsrvd
Fundmntl Algorithms for Sstm Modling, Anlsis, nd Optimiztion Edwrd A. L, Jijt Rohowdhur, Snjit A. Sshi UC Brkl EECS 144/244 Fll 2011 Copright 2010-11, E. A. L, J. Rohowdhur, S. A. Sshi, All rights rsrvd
COMP108 Algorithmic Foundations
 Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
FINITE ELEMENT ANALYSIS OF CONSOLIDATION PROBLEM IN SEVERAL TYPES OF COHESIVE SOILS USING THE BOUNDING SURFACE MODEL
 ARPN Journl of Enginring nd Alid Sins 006-008 Asin Rsrh Publishing Ntwork (ARPN). All rights rsrvd. www.rnjournls.om FINITE ELEMENT ANALYSIS OF CONSOLIDATION PROBLEM IN SEVERAL TYPES OF COHESIVE SOILS
ARPN Journl of Enginring nd Alid Sins 006-008 Asin Rsrh Publishing Ntwork (ARPN). All rights rsrvd. www.rnjournls.om FINITE ELEMENT ANALYSIS OF CONSOLIDATION PROBLEM IN SEVERAL TYPES OF COHESIVE SOILS
Improving Union. Implementation. Union-by-size Code. Union-by-Size Find Analysis. Path Compression! Improving Find find(e)
 POW CSE 36: Dt Struturs Top #10 T Dynm (Equvln) Duo: Unon-y-Sz & Pt Comprsson Wk!! Luk MDowll Summr Qurtr 003 M! ZING Wt s Goo Mz? Mz Construton lortm Gvn: ollton o rooms V Conntons twn t rooms (ntlly
POW CSE 36: Dt Struturs Top #10 T Dynm (Equvln) Duo: Unon-y-Sz & Pt Comprsson Wk!! Luk MDowll Summr Qurtr 003 M! ZING Wt s Goo Mz? Mz Construton lortm Gvn: ollton o rooms V Conntons twn t rooms (ntlly
CHEM 333 QUANTUM THEORY AND SPECTROSCOPY PROBLEM SET I SOLUTION KEY
 CHEM QUANTUM THEORY AND SPECTROSCOPY PROLEM SET I SOLUTION KEY. T for onstant of O is N. -. Assuing a aroni osillator odl for t vibrational otion of O, wat is t diatoi vibrational frquny in - units? v
CHEM QUANTUM THEORY AND SPECTROSCOPY PROLEM SET I SOLUTION KEY. T for onstant of O is N. -. Assuing a aroni osillator odl for t vibrational otion of O, wat is t diatoi vibrational frquny in - units? v
DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P
 DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P Tsz Ho Chan Dartmnt of Mathmatics, Cas Wstrn Rsrv Univrsity, Clvland, OH 4406, USA txc50@cwru.du Rcivd: /9/03, Rvisd: /9/04,
DISTRIBUTION OF DIFFERENCE BETWEEN INVERSES OF CONSECUTIVE INTEGERS MODULO P Tsz Ho Chan Dartmnt of Mathmatics, Cas Wstrn Rsrv Univrsity, Clvland, OH 4406, USA txc50@cwru.du Rcivd: /9/03, Rvisd: /9/04,
learning objectives learn what graphs are in mathematical terms learn how to represent graphs in computers learn about typical graph algorithms
 rp loritms lrnin ojtivs loritms your sotwr systm sotwr rwr lrn wt rps r in mtmtil trms lrn ow to rprsnt rps in omputrs lrn out typil rp loritms wy rps? intuitivly, rp is orm y vrtis n s twn vrtis rps r
rp loritms lrnin ojtivs loritms your sotwr systm sotwr rwr lrn wt rps r in mtmtil trms lrn ow to rprsnt rps in omputrs lrn out typil rp loritms wy rps? intuitivly, rp is orm y vrtis n s twn vrtis rps r
Integral Calculus What is integral calculus?
 Intgral Calulus What is intgral alulus? In diffrntial alulus w diffrntiat a funtion to obtain anothr funtion alld drivativ. Intgral alulus is onrnd with th opposit pross. Rvrsing th pross of diffrntiation
Intgral Calulus What is intgral alulus? In diffrntial alulus w diffrntiat a funtion to obtain anothr funtion alld drivativ. Intgral alulus is onrnd with th opposit pross. Rvrsing th pross of diffrntiation
MAT 270 Test 3 Review (Spring 2012) Test on April 11 in PSA 21 Section 3.7 Implicit Derivative
 MAT 7 Tst Rviw (Spring ) Tst on April in PSA Sction.7 Implicit Drivativ Rmmbr: Equation of t tangnt lin troug t point ( ab, ) aving slop m is y b m( a ). dy Find t drivativ y d. y y. y y y. y 4. y sin(
MAT 7 Tst Rviw (Spring ) Tst on April in PSA Sction.7 Implicit Drivativ Rmmbr: Equation of t tangnt lin troug t point ( ab, ) aving slop m is y b m( a ). dy Find t drivativ y d. y y. y y y. y 4. y sin(
fiziks Forum for CSIR-UGC JRF/NET, GATE, IIT-JAM, GRE in PHYSICAL SCIENCES
 fizis /o Annd Institut of mthmtis, 8-B/6 Ji Sri Nr IIT, Huz Khs, Nw Dlhi, PIN- 6 (INDIA) Phon: -78565, +9-98745498 Wbsit: http://www.physisbyfizis.om GATE-8 (PHYSICS).. rry on mr h.. For rbitrry mtris
fizis /o Annd Institut of mthmtis, 8-B/6 Ji Sri Nr IIT, Huz Khs, Nw Dlhi, PIN- 6 (INDIA) Phon: -78565, +9-98745498 Wbsit: http://www.physisbyfizis.om GATE-8 (PHYSICS).. rry on mr h.. For rbitrry mtris
The University of Sydney MATH 2009
 T Unvrsty o Syny MATH 2009 APH THEOY Tutorl 7 Solutons 2004 1. Lt t sonnt plnr rp sown. Drw ts ul, n t ul o t ul ( ). Sow tt s sonnt plnr rp, tn s onnt. Du tt ( ) s not somorp to. ( ) A onnt rp s on n
T Unvrsty o Syny MATH 2009 APH THEOY Tutorl 7 Solutons 2004 1. Lt t sonnt plnr rp sown. Drw ts ul, n t ul o t ul ( ). Sow tt s sonnt plnr rp, tn s onnt. Du tt ( ) s not somorp to. ( ) A onnt rp s on n
The first practical supersonic wind tunnel, built by A. Busemann in Germany in the mid-1930s.
 Introduction Th first rcticl sursonic wind tunnl, built by. Busmnn in Grmny in th mid-93s. lrg hyrsonic wind tunnl t th U.S. ir Forc Wright ronuticl Lbortory, Dyton, Ohio. Comrssibl Chnnl Flow Qusi--D
Introduction Th first rcticl sursonic wind tunnl, built by. Busmnn in Grmny in th mid-93s. lrg hyrsonic wind tunnl t th U.S. ir Forc Wright ronuticl Lbortory, Dyton, Ohio. Comrssibl Chnnl Flow Qusi--D
1 Input-Output Stability
 Inut-Outut Stability Inut-outut stability analysis allows us to analyz th stability of a givn syst without knowing th intrnal stat x of th syst. Bfor going forward, w hav to introduc so inut-outut athatical
Inut-Outut Stability Inut-outut stability analysis allows us to analyz th stability of a givn syst without knowing th intrnal stat x of th syst. Bfor going forward, w hav to introduc so inut-outut athatical
Q39.2 An ellipsoid. The dimension in the direction of motion would be measured to be scrunched in.
 9 Rltiity CHAPTER UTNE 9 Th Prinil o Gliln Rltiity 9 Th Mihlson-Morly Exrimnt 9 Einstin s Prinil o Rltiity 94 Consquns o th Sil Thory o Rltiity 95 Th orntz Trnsormtion Equtions 96 Th orntz Vloity Trnsormtion
9 Rltiity CHAPTER UTNE 9 Th Prinil o Gliln Rltiity 9 Th Mihlson-Morly Exrimnt 9 Einstin s Prinil o Rltiity 94 Consquns o th Sil Thory o Rltiity 95 Th orntz Trnsormtion Equtions 96 Th orntz Vloity Trnsormtion
[ ] [ ] DFT: Discrete Fourier Transform ( ) ( ) ( ) ( ) Congruence (Integer modulo m) N-point signal
![[ ] [ ] DFT: Discrete Fourier Transform ( ) ( ) ( ) ( ) Congruence (Integer modulo m) N-point signal [ ] [ ] DFT: Discrete Fourier Transform ( ) ( ) ( ) ( ) Congruence (Integer modulo m) N-point signal](/thumbs/83/87440381.jpg) Congrunc (Intgr modulo m) : Discrt Fourir Transform In this sction, all lttrs stand for intgrs. gcd ( nm, ) th gratst common divisor of n and m Lt d gcd(n,m) All th linar combinations r n+ s m of n and
Congrunc (Intgr modulo m) : Discrt Fourir Transform In this sction, all lttrs stand for intgrs. gcd ( nm, ) th gratst common divisor of n and m Lt d gcd(n,m) All th linar combinations r n+ s m of n and
CONTINUITY AND DIFFERENTIABILITY
 MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
is an appropriate single phase forced convection heat transfer coefficient (e.g. Weisman), and h
 For t BWR oprating paramtrs givn blow, comput and plot: a) T clad surfac tmpratur assuming t Jns-Lotts Corrlation b) T clad surfac tmpratur assuming t Tom Corrlation c) T clad surfac tmpratur assuming
For t BWR oprating paramtrs givn blow, comput and plot: a) T clad surfac tmpratur assuming t Jns-Lotts Corrlation b) T clad surfac tmpratur assuming t Tom Corrlation c) T clad surfac tmpratur assuming
cycle that does not cross any edges (including its own), then it has at least
 W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
Brief Introduction to Statistical Mechanics
 Brif Introduction to Statistical Mchanics. Purpos: Ths nots ar intndd to provid a vry quick introduction to Statistical Mchanics. Th fild is of cours far mor vast than could b containd in ths fw pags.
Brif Introduction to Statistical Mchanics. Purpos: Ths nots ar intndd to provid a vry quick introduction to Statistical Mchanics. Th fild is of cours far mor vast than could b containd in ths fw pags.
Case Study VI Answers PHA 5127 Fall 2006
 Qustion. A ptint is givn 250 mg immit-rls thophyllin tblt (Tblt A). A wk ltr, th sm ptint is givn 250 mg sustin-rls thophyllin tblt (Tblt B). Th tblts follow on-comprtmntl mol n hv first-orr bsorption
Qustion. A ptint is givn 250 mg immit-rls thophyllin tblt (Tblt A). A wk ltr, th sm ptint is givn 250 mg sustin-rls thophyllin tblt (Tblt B). Th tblts follow on-comprtmntl mol n hv first-orr bsorption
UNCORRECTED SAMPLE PAGES 4-1. Naming fractions KEY IDEAS. 1 Each shape represents ONE whole. a i ii. b i ii
 - Nming frtions Chptr Frtions Eh shp rprsnts ONE whol. i ii Wht frtion is shdd? Writ s frtion nd in words. Wht frtion is not shdd? Writ s frtion nd in words. i ii i ii Writ s mny diffrnt frtions s you
- Nming frtions Chptr Frtions Eh shp rprsnts ONE whol. i ii Wht frtion is shdd? Writ s frtion nd in words. Wht frtion is not shdd? Writ s frtion nd in words. i ii i ii Writ s mny diffrnt frtions s you
Fr Carrir : Carrir onntrations as a funtion of tmpratur in intrinsi S/C s. o n = f(t) o p = f(t) W will find that: n = NN i v g W want to dtrmin how m
 MS 0-C 40 Intrinsi Smiondutors Bill Knowlton Fr Carrir find n and p for intrinsi (undopd) S/Cs Plots: o g() o f() o n( g ) & p() Arrhnius Bhavior Fr Carrir : Carrir onntrations as a funtion of tmpratur
MS 0-C 40 Intrinsi Smiondutors Bill Knowlton Fr Carrir find n and p for intrinsi (undopd) S/Cs Plots: o g() o f() o n( g ) & p() Arrhnius Bhavior Fr Carrir : Carrir onntrations as a funtion of tmpratur
Physics 506 Winter 2006 Homework Assignment #12 Solutions. Textbook problems: Ch. 14: 14.2, 14.4, 14.6, 14.12
 Physis 56 Wintr 6 Homwork Assignmnt # Solutions Ttbook problms: Ch. 4: 4., 4.4, 4.6, 4. 4. A partil of harg is moving in narly uniform nonrlativisti motion. For tims nar t = t, its vtorial position an
Physis 56 Wintr 6 Homwork Assignmnt # Solutions Ttbook problms: Ch. 4: 4., 4.4, 4.6, 4. 4. A partil of harg is moving in narly uniform nonrlativisti motion. For tims nar t = t, its vtorial position an
A physical solution for solving the zero-flow singularity in static thermal-hydraulics
 A ysicl solution for solving t zro-flow singulrity in sttic trml-ydrulics miing modls Dnil Bouskl Blig El Hfni EDF R&D 6, qui Wtir F-784 Ctou Cd, Frnc dnil.ouskl@df.fr lig.l-fni@df.fr Astrct For t D-D
A ysicl solution for solving t zro-flow singulrity in sttic trml-ydrulics miing modls Dnil Bouskl Blig El Hfni EDF R&D 6, qui Wtir F-784 Ctou Cd, Frnc dnil.ouskl@df.fr lig.l-fni@df.fr Astrct For t D-D
16.unified Introduction to Computers and Programming. SOLUTIONS to Examination 4/30/04 9:05am - 10:00am
 16.unii Introution to Computrs n Prormmin SOLUTIONS to Exmintion /30/0 9:05m - 10:00m Pro. I. Kristin Lunqvist Sprin 00 Grin Stion: Qustion 1 (5) Qustion (15) Qustion 3 (10) Qustion (35) Qustion 5 (10)
16.unii Introution to Computrs n Prormmin SOLUTIONS to Exmintion /30/0 9:05m - 10:00m Pro. I. Kristin Lunqvist Sprin 00 Grin Stion: Qustion 1 (5) Qustion (15) Qustion 3 (10) Qustion (35) Qustion 5 (10)
Time Dependent Quadratic Demand Inventory Models when Delay in Payments is Acceptable
 Intrntionl OPEN ACCESS Journl Of odrn Enginring Rsr IJER im Dndnt Qudrti Dmnd Invntory odls wn Dly in Pymnts is Atl R. Vnktswrlu,. S. Rddy GIA Sool of Intrntionl Businss, GIA Univrsity, Visktnm 0 0, Indi
Intrntionl OPEN ACCESS Journl Of odrn Enginring Rsr IJER im Dndnt Qudrti Dmnd Invntory odls wn Dly in Pymnts is Atl R. Vnktswrlu,. S. Rddy GIA Sool of Intrntionl Businss, GIA Univrsity, Visktnm 0 0, Indi
Similarity Search. The Binary Branch Distance. Nikolaus Augsten.
 Similrity Srh Th Binry Brnh Distn Nikolus Augstn nikolus.ugstn@sg..t Dpt. of Computr Sins Univrsity of Slzurg http://rsrh.uni-slzurg.t Vrsion Jnury 11, 2017 Wintrsmstr 2016/2017 Augstn (Univ. Slzurg) Similrity
Similrity Srh Th Binry Brnh Distn Nikolus Augstn nikolus.ugstn@sg..t Dpt. of Computr Sins Univrsity of Slzurg http://rsrh.uni-slzurg.t Vrsion Jnury 11, 2017 Wintrsmstr 2016/2017 Augstn (Univ. Slzurg) Similrity
Pion condensation with neutrinos
 Pion condnsation with nutrinos Or how dos QCD bhav undr high dnsitis of lctron/muon nutrinos Harmn Warringa, Goth Univrsität, Frankfurt Basd on work don with Hiroaki Abuki and Tomas Braunr arxiv:0901.2477
Pion condnsation with nutrinos Or how dos QCD bhav undr high dnsitis of lctron/muon nutrinos Harmn Warringa, Goth Univrsität, Frankfurt Basd on work don with Hiroaki Abuki and Tomas Braunr arxiv:0901.2477
Garnir Polynomial and their Properties
 Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
RUTH. land_of_israel: the *country *which God gave to his people in the *Old_Testament. [*map # 2]
![RUTH. land_of_israel: the *country *which God gave to his people in the *Old_Testament. [*map # 2] RUTH. land_of_israel: the *country *which God gave to his people in the *Old_Testament. [*map # 2]](/thumbs/84/89116644.jpg) RUTH 1 Elimlk g ln M 1-2 I in im n ln Irl i n *king. Tr r lr rul ln. Ty r ug. Tr n r l in Ju u r g min. Elimlk mn y in n Blm in Ju. H i nm Nmi. S n Elimlk 2 *n. Tir nm r Mln n Kilin. Ty r ll rm Er mily.
RUTH 1 Elimlk g ln M 1-2 I in im n ln Irl i n *king. Tr r lr rul ln. Ty r ug. Tr n r l in Ju u r g min. Elimlk mn y in n Blm in Ju. H i nm Nmi. S n Elimlk 2 *n. Tir nm r Mln n Kilin. Ty r ll rm Er mily.
