arxiv: v2 [quant-ph] 18 Mar 2011
|
|
|
- Oswald West
- 6 years ago
- Views:
Transcription
1 Generating random density matrices arxiv: v2 [quant-ph] 18 Mar 2011 Karol Życzkowski 1,2, Karol A. Penson 3, Ion Nechita 4,5 and Benoît Collins 4,6 1 Institute of Physics, Jagiellonian University, ul. Reymonta 4, Kraków, Poland 2 Centrum Fizyki Teoretycznej, Polska Akademia Nauk, Al. Lotników 32/44, Warszawa, Poland 3 Université Paris VI, Laboratoire de Physique de la Matière Condensée (LPTMC), CNRS UMR 7600, t.13, 5ème ét. BC.121, 4, pl. Jussieu, F Paris Cedex 05, France 4 Department of Mathematics and Statistics, University of Ottawa, ON K1N6N5, Canada 5 Laboratoire de Physique Théorique du CNRS, IRSAMC, Université de Toulouse, UPS, F Toulouse, France 6 CNRS, Institut Camille Jordan Université Lyon 1, 43 Bd du 11 Novembre 1918, Villeurbanne, France (Dated: March 18, 2011) We study various methods to generate ensembles of random density matrices of a fixed size N, obtained by partial trace of pure states on composite systems. Structured ensembles of random pure states, invariant with respect to local unitary transformations are introduced. To analyze statistical properties of quantum entanglement in bi-partite systems we analyze the distribution of Schmidt coefficients of random pure states. Such a distribution is derived in the case of a superposition of k random maximally entangled states. For another ensemble, obtained by performing selective measurements in a maximally entangled basis on a multi partite system, we show that this distribution is given by the Fuss-Catalan law and find the average entanglement entropy. A more general class of structured ensembles proposed, containing also the case of Bures, forms an extension of the standard ensemble of structureless random pure states, described asymptotically, as N, by the Marchenko-Pastur distribution. I. INTRODUCTION In this work we are going to analyze structured ensembles of random states on a composite systems, in which such a tensor product structure plays a crucial role. For Random states are often used in various problems in instance, in the case of an N K system, it is natural quantum mechanics and the theory of quantum information. On one hand, to describe properties of a quantum spect to local unitary transformations, described by the to consider ensembles of random states invariant with re- state affected by noise present in the system, one may product unitary group, U(N) U(K). Well known constructions of random product states and random maxi- assume that a given state is subjected to random interaction. On the other hand, random quantum states emerge mally entangled states can thus serve as simplest examples of the structured ensembles of random states. Other in a natural way due to time evolution of arbitraryinitial states of quantum analogues of classically chaotic systems examples of structured ensembles of random pure states, [1]. Furthermore, not knowing much about a given physical state one can ask about their generic properties, char- in [5]. which correspond to certain graphs were recently studied acteristic of a typical state. For instance, a key conjecture in the theory of quantum information concerning the motivated ensembles of structured random states and to The main aim of this paper is to introduce physically additivity of minimal output entropy was recently shown characterize the quantum entanglement of such states. to be false by investigating properties of random states For this purpose we analyze the spectral density P(x) of obtained by random operations applied to the maximally the reduced density matrix of size N, where x denotes entangled state of a composed system [2]. the rescaled eigenvalue, x = Nλ. In some cases we evaluate also the average entanglement entropy, defined as A standard ensemble of random pure states of size N is induced by the Haar measure over the unitary group the Shannon entropy of the vector λ of the Schmidt coefficients. U(N). The same construction works for quantum composite systems. For instance, random pure states of We treat in detail two cases of a direct importance an N K quantum system corresponds to the natural in the theory of quantum information. The first ensemble is obtained by taking a coherent superposition of a Fubini-Study measure, invariant with respect to the unitarygroupu(nk). Thussuchensemblesofrandompure given number of k independent, random maximally entangled states of an N N system. We derive explicit states are structureless, as the probability measure is determined by the total dimension of the Hilbert space and formulae for the asymptotic spectral density P k (x) of the is does not depend on the tensor product structure [3, 4]. reduced state and show that in the limit of large k, the density converges to the Marchenko-Pastur distribution (MP) [6, 7]. This feature is characteristic to the case of the structureless ensemble of random pure states, which Electronicaddress: karol@tatry.if.uj.edu.pl; penson@lptl.jussieu.fr; inechita@uottawa.ca; induces probability bcollins@uottawa.ca measures the set of mixed quantum
2 2 states [4, 8, 9]. To introduce the second example of a structured ensemble we need to consider a four partite system. We start with an arbitrary product state and by allowing for a generic bi-partite interaction we create two random states on subsystems AB and CD. The key step is now to perform an orthogonal selective measurement in the maximally entangled basis on subsystems B and C. Even though the resulting pure state on the remaining subsystems A and D does depend on the outcome of the measurement, its statistical properties do not, and we show that the corresponding level density is given by the Fuss-Catalan distribution. Note that the above two constructions could be experimentally accessible, at least in the two-qubit case for k = 2. The second construction can be easily generalized for a system consisting of 2s subsystems. An initially product state is then transformed by a sequence of bipartite interactions into a product of s bi-partite random states. Performing an orthogonal projection into a product of (s 1) maximally entangled bases we arrive with a random bipartite state of the structured ensemble defined in this way. The distribution of its Schmidt coefficients is shown to be asymptotically described by the Fuss- Catalan distribution of order s, since its moments are given by the generalized Fuss-Catalan numbers [10 12]. This distribution can be considered as a generalization of the MP distribution which is obtained for s = 1. We conclude this paper proposing a generalized, two-parameter ensemble of structured random states, which contains, as particular cases, all the ensembles analyzed earlier in this work. This paper is organized as follows. In section II we recall necessary definitions and describe a general scheme of generating mixed states by taking random pure states on a composite system of a given ensemble and taking an average over selected subsystems. In Section III we use 2 independent random unitary operators to construct the arcsine ensemble obtained by superposition of two random maximally entangled states. More general structured ensembles are obtained by superposing k random maximally entangled states. Other ensembles of random pure states are discussed in section IV. For completeness we review here some older results on ensembles which lead to the Hilbert-Schmidt and the Bures measures in the space of density matrices. In section V we present a scheme to generate random states by considering a state defined on a 2s partite system and performing measurement onto the product of (s 1) maximally entangled states. The distribution of the Schmidt coefficients of the resulting random pure state is then given by the Fuss-Catalan distribution of order s. An explicit form ofthis distribution is presented in Sec. VI for any s. In Sec. VII we list various ensembles of random states, characterize their statistical properties and introduce a generalized ensemble of structured states (42, 43). Details concerning the properties of the sum of k independent random unitary matrices are presented in Appendix A. Brief discussion of real random pure states and real density matrices is provided in Appendix B, in which we state that the distribution of singular values of a product of s real random Ginibre matrices can be asymptotically described by the Fuss Catalan distribution. II. ENSEMBLES OF RANDOM STATES To construct an ensemble of random states of a given size N one needs to specify a probability measure in the set of all density operators of this size. Interestingly, there is no single, distinguished probability measure in this set, so various ensembles of random density operators are used. A possible way to define such an ensemble is to take random pure states of a given ensemble on bi-partite system and to average over a chosen subsystem. The structureless ensemble of random pure states on N N system distributed according to unitarily invariant measure leads then to the Hilbert-Schmidt measure [3, 4]. A similar construction to generate random states according to the Bures measure [9, 13, 14] was recently proposed in [15]. These algorithms to generate random quantum states are already implemented in a recent Mathematica package devoted to Quantum Information [16, 17]. Let us recall here the necessary notions and definitions. Consider the set of quantum states M N which contains all Hermitian, positive operators ρ = ρ 0 of size N normalized by the trace condition Trρ = 1. Any hermitian matrix can be diagonalized, ρ = VΛV. Here V is a unitary matrix consisting of eigenvectors of ρ, while Λ is the diagonal matrix containing the eigenvalues {λ 1,...,λ N }. In order to describe an ensemble of random density matrices, one needs to specify a concrete probability distribution in the set M N of quantum states. In this work we are going to analyze ensembles of random states, for which the probability measure has a product form and may be factorized [4, 13], dµ ρ = dν(λ 1,λ 2,...,λ N ) dµ V, (1) so the distribution of eigenvalues and eigenvectors are independent. It is natural to assume that the eigenvectors are distributed according to the unique, unitarily invariant,haarmeasuredµ V onu(n). Takingthisassumption as granted, the measure in the space of density matrices will be determined by the first factor dν describing the joint distribution of eigenvalues P(λ 1,...,λ N ). In quantum theory mixed states arise due to an interaction of the system investigated with an external environment. One may then make certain assumptions concerning the distribution of pure states describing the extended system. The desired mixed state ρ on the principal system A of size N can be then obtained by partial trace over the subsystem B of an arbitrary size K.
3 3 Consider an arbitrary orthonormal product basis i j H N H K, with i = 1,...,N and j = 1,...,K. Any pure state ψ of the bi partite system (not necessarily normalized) can be expanded in this base, ψ = N i=1 j=1 K X ij i j, (2) where X is a given complex rectangular matrix of size N K. Let us then consider an arbitrary complex matrix X. It leads to a (weakly) positive matrix XX. Thus normalizing it one obtains a legitimate quantum state, which corresponds to the partial trace of the initial pure state ψ over the subsystem B, ρ = Tr B ψ ψ ψ ψ = XX TrXX. (3) For instance, taking X from the Ginibre ensemble[18, 19] of complex square matrices we get the Hilbert Schmidt ensemble of quantum states, while a more general family of induced measures corresponds [20] to the ensemble of rectangular Ginibre matrices. The spectrum of a density matrix ρ is thus equivalent to the set of Schmidt coefficient of the initially pure state ψ, which are equal to squared singular values of a matrix X, normalized in such a way that Trρ = 1. The degree of mixing of the reduced matrix ρ can be characterized by its von Neumann entropy, S(ρ) = Trρlnρ, equal to the Shannon entropy of the Schmidt vector, E( ψ ) = i λ ilnλ i. This quantity is also called entropy of entanglement of the pure state ψ, as it is equal to zero iff the state has a tensor product structure and is separable. We are also going to use the Chebyshev entropy, which depends only on the largest eigenvalue S (ρ) = lnλ max, and determines the geometric measure of entanglement of the pure state ψ. Different assumptions concerning the distributions of pure states of the bi-partite system lead to different ensembles of mixed states on the system A. A natural assumption that ψ belongs to the standard, structureless ensemble of random pure state distributed with respect to the unitarily invariant measure leads to the induced measures [4] in the space of mixed states. In the subsequent section we are going to present simple examples of structured ensembles of random states, in which the tensor structure plays a key role. For instance, we discuss first ensembles of random states of a bi-partite systems, which are invariant with respect to local unitary operations. III. TWO PARTITE SYSTEMS A. Random separable and maximally entangled pure states For completeness we shall start the discussion with the somewhat trivial case of generating random separable states. Consider an arbitrary product state on a bi-partite system, 0,0 = 0 A 0 B. A local unitary operation, U = U A U B, cannot produce quantum entanglement, so the state defined by two random unitary matrices, ψ AB = U 0,0 = U A 0 A U B 0 B is also separable. Hence a random separable state is just a product of two random states, ψ AB = ψ A ψ B Consider now a generalized Bell state defined on an N N system A,B, Ψ + = 1 N i A i B. (4) N i=1 As the entanglement entropy of this state is maximal, E( Ψ + ) = lnn, thisstateiscalledmaximallyentangled. Any local unitary operation, U A U B, preserves quantum entanglement, so the locally transformed state φ ent := (U A U B ) Ψ + remains maximally entangled. Hence taking random unitary matrices U A,U B U(N) according to the Haar measure we obtain an ensemble of random entangled states, such that their partial trace is equal to the maximally mixed state, ρ = Tr B φ ent φ ent = 1 N ½ N =: ρ. (5) ThisDiracdistributionwillbedenotedbyπ (0) (ρ) = δ(ρ ρ ) and a scheme of generating it by averaging over an auxiliary subsystem is shown in Fig. 1. FIG. 1: Generating mixed states according to π (0) : step i) a local operation U A U B on Ψ + AB creates a random entangled state φ ent, while the partial trace over an auxiliary subsystem B leads in step ii) to the maximally mixed state on the system A. B. Arcsine ensemble Consider now a more general case of a coherent superposition of two maximally entangled states. To be precise we fix a given maximally entangled state ψ 1, and use such a local basis that it is represented by (4). Taking a local random unitary matrix U A U(N) we generate another maximally entangled state ψ 2 = U A ½ ψ 1.
4 4 As shown in Fig. 2 we construct their symmetric superposition, φ = ( ψ 1 + ψ 2 ) = [½ N 2 +(U ½ N )] Ψ +. (6) Note that this ensemble is invariant with respect to local unitary operations, U(N) U(N). Let us specify a subsystem B and average over it to obtain the reduced state ρ = Tr B φ φ φ φ = 2½+U +U 2N +Tr(U +U ). (7) If the matrix U is generated according to the Haar measure on U(N) its eigenphases are distributed according to the uniform distribution [19], P(α) = 1/2π for α [0,2π). Thus the term Tr(U + U ) present in the normalization constant becomes negligible for large N. Therefore eigenvalues of a random density matrix ρ by (7) have the form λ i = (1+cosα i )/N, for i = 1,...,N. Making use of the rescaled variable x = λn we arrive at a conclusion that the spectral level density of random density matrices (7) is asymptotically described by the arcsine distribution [21] 1 P arc (x) = π x(2 x) (8) defined on the compact support [0,2]. This is a particular case of the beta distribution (with parameters α = β = 1/2) and the Dirichlet distribution. It describes the Jeffreys prior of a Bernoulli trial [22] and is related to the statistical distance between classical probability distributions [9]. The name arcsine is due to the fact that the corresponding cumulative distribution is proportional to sin 1 x/2. Thus the ensemble of random density matrices constructed according to the procedure shown in Fig. 2 will be called arcsine ensemble. The average entropy for the arcsine distribution reads 2 0 xlnxp arc(x) = ln , so the average entropy of entanglement of a random pure state on the N N system generated form this ensemble reads E ψ lnn 1+ln2. FIG. 2: To generate states from the arcsine ensemble described by (8) one has to i) construct a superposition of a maximally entangled state Ψ + AB with another maximally entangledstate(u A ½) Ψ + AB, andii)perform partialtraceover an auxiliary subsystem B. It is clear that one may define a family of interpolating ensembles by taking a convex combination of the mixed states defined by (5) and (7). In other words, one can take a family of random matrices parametrized by a real numbera [0,1]andwriteW a = a½+(1 a)u. Plugging this expression in place of X into (3) we construct a family of ensembles of density matrices which gives the Dirac mass for a = 0 and a = 1, while the arcsine ensemble is obtained for a = 1/2. C. Superposition of k maximally entangled states The arcsine ensemble introduced above can be obtained by superimposing k = 2 random maximally entangled states. It is straightforward to generalize this construction for an arbitrary number of k maximally entangled states. Each of them can be written by an action of a local unitary on the fixed maximally entangled state Ψ +. More precisely we set ψ i = (U i ½) Ψ + for i = 1,...,k and construct their equi-probable superposition φ = k i=1 ψ i = [ ( k i=1 U ] i) ½ N Ψ +. As before this ensemble is invariant with respect to local transformations. The random mixed state is obtained by taking the partial trace over the subsystem B and normalizing the outcome ρ = Tr B φ φ / φ φ as in eq. (7). This procedure leads now to the following expression for a mixed state, generated by k independent random unitaries, ρ = (U 1 + +U k )(U 1 + +U k ) Tr(U 1 + +U k )(U (9) 1 + +U k ). As shown in Appendix A the spectral density of random states defined above converges, for large system size N to the following distribution ν k (x) defined for x [0,4 k 1 k ], ν k (x) = 1 4k(k 1)x k2 x 2 2π kx x 2 (10) The shape of these distributions is presented for some valuesofk infig. 3. Itiseasytoseethatforalargenumber k the above measures converge weakly to the limit ν = π (1) = 4x x 2 2πx which is the Marchenko-Pastur distribution π (1). In other words, the superposition of a large number of random maximally entangled states destroys the structure of the ensemble, as the resulting state becomes typical of the structureless ensemble. The measure(10) canbe connected tothe free Meixner measures of [23]: ν k is the free Meixner measure of parameters a = 0 and b = 1/k. The measure ν k (x) can be characterized by its second moment, which gives the asymptotic average purity of random mixed states obtained by a superposition of k maximally entangled states, Trρ 2 νk (2 1/k) 1 N.
5 5 FIG. 4: Taking i) a random pure state U AB 0,0 on a bipartite system AB and performing ii) the partial trace over subsystem B leads random state distributed according to an induced measure, with spectral density described by the Marchenko-Pastur distribution. FIG. 3: Family of spectral distributions ν k (x) plotted for k = 2,3,5,10 and k. The support of the measures is an increasing function of the parameter k. They describe level density of mixed states generated by superposition of k random maximally entangled states and performing the partial trace. The case k = 2 corresponds to the arcsine ensemble, while in the case k the sum of k random unitaries has properties of a random Ginibre matrix, so the spectral distribution converges to the Marchenko-Pastur law. D. Induced measures Consider a quantum system composed of two subsystems. Let N denote the dimension of the principal system, which interacts with a K dimensional environment. Assume first that the state ψ H N H K is taken from the structureless ensemble, so it is distributed uniformly according to the Fubini Study measure on the complex projective space. In other words, the random pure state can be represented by ψ = U 0,0, where U is a global random unitary matrix distributed according to the Haar measure see Fig. 4. The initial state is arbitrary, so for concreteness we may choose it as a given product state 0,0 in H N H K. The mixed state ρ obtained by the partial trace over the K dimensional environment ρ = Tr K ψ ψ, with ψ H N H K, (11) is distributed accordingto the measureµ N,K in the space of density matrices of size N, induced by the Haar measure on the unitary group U(NK). This procedure yields the following probability distribution dµ(ρ) Θ(ρ) δ(trρ 1)detρ K N. (12) The Θ step function and the Dirac δ reflect key properties of density matrices: positivity, ρ 0 and normalization, Trρ = 1. If ψ is a random pure state distributed uniformly according to the unitarily invariant Fubini Study measure in the space of pure states all elements of G are independent complex Gaussian variables with the same variance, so this matrix belongs to the Ginibre ensemble [18]. Hence the reduced state (11) obtained by partial trace has the form (3) with X = G. The eigenvalues of a random matrix ρ generated with respect to the measure µ N,K are thus equal to the squared singular eigenvalues of a normalized rectangular N K complex random matrix G from the Ginibre ensemble. Any density matrix is Hermitian and can be diagonalized by a unitary rotation. Integrating out the eigenvectorsofarandomstateρdefined by(12) onereducesdµto the measure on the simplex of eigenvalues {λ 1,...,λ N } of the density operator [24], P N,K (λ 1,...λ N ) = C N,K i λ K N i 1...N i<j (λ i λ j ) 2. (13) In this expression all eigenvalues are assumed to be nonnegative, λ i 0 and they sum to unity, i λ i = 1. The normalization constant can be expressed [4] by the Gamma function Γ(KN) C N,K = N 1 (14) j=0 Γ(K j)γ(n j +1). Induced measures are stable with respect to the partial trace, what can be formulated as follows. Proposition 1. Consider a random state ρ generated according to the induced measures µ M,K. Assume that the dimension is composed, M = N L, and define the partial trace over the L dimensional subsystem, σ = Tr L (ρ). Then the reduced matrix σ is generated according to the measure µ N,KL. Proof. The state ρ can be considered as a random pure state ψ H M H K averaged over K dimensional environment. Averaging the projector ψ ψ over a composed subsystem of size KL we arrive at state σ of size N, which shows [25] that it is distributed according to the induced measure µ N,KL. IV. MEASURES DEFINED BY A METRIC Let d denote any distance in the space of the normalized density operators of a fixed size N. With respect to this distance one can define unit spheres and unit balls.
6 6 Attributing the same weight to any ball of radius equal to unity one defines the measure corresponding to a given distance. Consider, for instance, the Hilbert-Schmidt distance between any two mixed states D HS (ρ,σ) = [Tr(ρ σ) 2 ] 1/2. This distance induces in the space of density operators an Euclidean geometry: the space of one qubit mixed states has a form of the three-ball bounded by the Bloch sphere. Astherescaledeigenvalueisx = Nλ, thisresultisconsistent with the fact that the averageentropy of the asymptoticdistribution (17) reads 4 0 xlnxp HS(x)dx = 1/2. Note that the mean entropy of a random mixed state is close to the maximal entropy in the N dimensional system, which equals ln N for the maximally mixed state ρ = ½/N. The asymptotic average purity Trρ 2 HS 2/N which is consistent with the second moment of the MP distribution, 4 0 x2 P HS (x) = 2. A. Hilbert Schmidt ensemble The Hilbert Schmidt measure defined in this way belongs to the class of induced measures [4] and can be obtained by a reduction of random pure states defined on a bi partite quantum system. Looking at expression (13) we see that in the special case K = N the term with the determinant in is equal to unity, so measure reduces to the Hilbert-Schmidt measure [4]. This observation leads to a simple algorithm to generate a Hilbert-Schmidt random matrix [4]: i) Take a square complex random matrix A of size N pertaining to the Ginibre ensemble [18, 19] (with real and imaginary parts of each element being independent normal random variables); ii) Write down the random matrix ρ HS = GG TrGG, (15) which is by construction Hermitian, positive definite and normalized, so it forms a legitimate density matrix. To characterize spectral properties of random density matrices one considers the joint distribution of eigenvalues (13), integrates out N 1 variables λ 1...λ N to obtain the level density denoted by P(λ). This problem was discussed by Page [8], who found the asymptotic distribution for the rescaled variable x = Nλ. The result depends on the ratio of both dimensions c = K/N and is given by the Marchenko Pastur distribution [6], π (1) c (x) = max(1 c,0)δ(0)+ 4c (x c 1) 2. (16) 2πx This expression is valid for x [x,x + ], where x ± = 1 + c ± 2 c. In the case c = 1 corresponding to the Hilbert Schmidt ensemble this distribution reads P HS (x) = 1 2π 4 1 for x [0,4] (17) x It diverges as x 1/2 for x 0 and in the rescaled variable, y = x it becomes a quarter circle law, P(y) = 1 π 4 y2. The average von Neumann entropy of random states distributed with respect to the HS measure reads [8, 20] S(ρ) HS = lnn 1 ( ) lnn 2 +O. (18) N B. Bures ensemble Another distinguished measure in the space Ω of quantum mixed states, is induced by the Bures distance [26, 27], D B (ρ,σ) = 2 2Tr( ρσ ρ) 1/2. (19) The Bures distance plays an important role in the investigationofthe setofquantum states[9]. The Buresmetric, related to quantum distinguishability [22], is known to be the minimal monotone metric [28] and applied to any two diagonal matrices it gives their statistical distance. These special features support the claim that without any prior knowledge on a certain state acting on H N, the optimal way to mimic it is to generate a random density operator with respect to the Bures measure. The Bures measure is characterized by the following joint probability of eigenvalues [13] P B (λ 1,...λ N ) = C B N i 1...N λ 1/2 (λ i λ j ) 2 i, (20) λ i<j i +λ j where all eigenvalues are non-negative, λ i 0 and they sum to unity, i λ i = 1. The normalization constant for this measure C B N = 2N2 N Γ(N 2 /2) π N/2 N j=1 Γ(j +1) (21) was obtained in [13, 14] for small N and in [29] in the general case. To generate random states with respect to the Bures ensemble one can proceed according to the following algorithm [15]: i) Take a complex random matrix G of size N pertaining to the Ginibre ensemble and a random unitary matrix U distributed according to the Haar measure on U(N) [30]. ii) Write down the random matrix ρ B = (½+U)GG (½+U ) Tr[(½+U)GG (½+U )] (22) which is distributed according to the Bures measure. In the analogy to the Hilbert-Schmidt ensemble we can
7 7 write this state as reduction of a pure state on the composed system, ρ B = Tr N φ φ where φ := [(½+V A ) ½] ψ 1. φ φ (23) Here ψ 1 = U AB 0,0 is a random state on the bipartite system used in Eq. (11) and V A U(N). FIG. 5: To generate states according to the Bures distribution one i) constructs a superposition of a random bi-partite state ψ 1 = U AB 0,0 with a locally transformed random state ψ 2 = (V A ½) ψ 1, and ii) perform partial trace over an auxiliary subsystem B. V. PROJECTION ONTO MAXIMALLY ENTANGLED STATES A. Four-partite systems and measurements in a maximally entangled basis Consider a system consisting of four subsystems, labeled as A,B,C and D. For simplicity assume here that the dimensions of all subsystems are equal, N 1 = N 2 = N 3 = N 4 = N. Consider an arbitrary four-partite productstate,say ψ 0 = 0 A 0 B 0 C 0 D =: 0,0,0,0. Taking two independent random unitary matrices U AB and U CD of size N 2, which act on the first and the second pair of subsystems, respectively, we define a random state ψ = U AB U CD ψ 0. By construction, it is a product state with respect to the partition into two parties: (A,B) and (C,D). In the analogy to (2) it can be expanded in the product basis, ψ = N i,j=1 k,l=1 N G ij E kl i A j B k C l D (26) Consider now a maximally entangled state on the second and the third subsystem, The asymptotic probability distribution for the rescaled eigenvalue x = Nλ of a random density matrix generated according to the Bures ensemble reads [20] ( P B (x) = C a x + ) (a ) 2/3 2 1 x ( a x ) (a ) 2/3 2 1 x (24) where C = 1/4π 3 and a = 3 3. This distribution is defined on a support larger than the standard MP distribution, x [0,a] and it diverges for x 0 as x 2/3. The average entropy of a random state form the Bures ensemble reads [20] S(ρ) B = lnn ln2+o ( ) lnn. (25) N Ψ + BC = 1 N µ B µ C, (27) N µ=1 and the corresponding projector P BC := Ψ + BC Ψ+ BC. One can extend it into a four-partite operator and define ( 1 ) P := ½ A µ,µ BC ν,ν ½ D (28) N µ,ν Let us assume that the random pure state ψ defined in (26) is subjected to a projective measurement performed onto the second and third subsystem, and that the result is post-selected to be associated to the projector P. This leads to a non-normalized pure state φ describing the remaining two subsystems, φ = P ψ = 1 N N N i=1 l=1 k=1 N G ik E kl i A l D. (29) This value is smaller than the average entropy(18), which shows that the Bures states are typically less mixed that the states from the Hilbert Schmidt ensemble. A similar conclusion follows from the comparison of average purity for the Bures ensemble, Trρ 2 B 5/2N [20], with the average purity for the HS measure. By considering random matrices of the form W = (a½ +(1 a)u)g one may construct a continuous family of measures interpolating between the Bures and the Hilbert Schmidt ensembles [15] and labeled by a real parameter a [0, 1/2]. A more general class of interpolating ensembles is proposed in Sec. VII. Note that the projection on the entangled state Ψ + BC introduces a coupling between the subsystems B and C. A similar idea was used in analysis of entanglement swapping [34]. and in studies of matrix product states [31] and projected entangled pair states [32, 33]. Constructingthe matrixproduct statesan N N entangledstateis projected down into a subspace of an arbitrary dimension d, while in our approach a projection onto the maximally entangled state of BC takes place, (which formally corresponds to d = 1), and only two edge systems labeled by A and D survive the projection. Normalizing the resulting state φ and performing the partial trace over the fourth subsystem D we arrive at a
8 8 compact expression for the resulting mixed state on the first subsystem A, ρ = Tr D φ φ φ φ = GEE G Tr GEE G. (30) ForanymatricesGandE thisexpressionprovidesavalid quantum state, normalized and positive. If initial pure states are random, then the matrices G and E belong to the Ginibre ensemble and the spectrum of a random state ρ consists of squared singular values of the product GE of two random Ginibre matrices. Random states with the same statistical properties were recently found in ensembles associated with certain graphs [5]. BC. However, these results are equivalent up to a unitary transformation, which again can be absorbed into the definition of the Ginibre ensemble. Thus the statistical properties of the random state (30) on subsystem A obtained in consequence of the measurement in the maximally entangled basis in BC followed by the partial trace over subsystem D do not dependent on the outcome of the measurement. Furthermore, the same construction holds in a more general setup in which some dimensions of four subsystems are different. To use the maximally entangled state Ψ + BC we set N B = N C, but the dimensions N = N A and N D can be different. This leads to two rectangular random Ginibre matrices, G of size N N B and E of size N B N D. As in the previous case formula (30) provides a density matrix ρ of size N, but now the model is a function of two parameters: dimensions N B and N D. It is sometimes convenient to use two ratios, c 1 = N B /N and c 2 = N D /N, so the standard version of the model corresponds to putting c 1 = c 2 = 1. B. Multi partite systems FIG. 6: To generate a random mixed state with spectral density π (2) one has to i) take a product random pure state ψ AB ψ CD on a four particle system A,B,C,D, ii) measure subsystems B,C by a projection onto the maximally entangled state Ψ + BC, iii) average over the subsystem D. Observe that the statistical properties of the ensemble defined will change if the projection is performed with respect to an arbitrary maximally entangled state, Ψ + BC = (U B U C ) Ψ + BC, as the local unitaries U B and U C can be absorbed in the definition of random Ginibre matrices, G and E, respectively. Furthermore, one may chose N 2 unitary matrices U i U(N), which are orthogonal in sense of the Hilbert Schmidt scalarproduct, Tr U i U j = Nδ ij. Thenthe setof N 2 maximally entangled states, Ψ + i = (U i ½) Ψ + BC, forms a maximally entangled basis, which are known to exist in any dimension [35]. Thus one may consider another set up in which a selective measurement on subsystems B and C is performed in the maximally entangled basis. The outcome state on subsystems AD depends on the result of the quantum measurement of subsystems Another possibility to generalize the model is to consider a larger system consisting of an even number 2s of subsystems. For simplicity assume first that their dimensions are set to N. In analogy to (26) we use s independent unitaries of size N 2 to generate a random pure state ψ. To work with an arbitrary even number of subsystems it is convenient to modify the notation and label the subsystems by integers 1,2,...,2s. Consider an arbitrary product state of a 2s particle system, ψ 0 = s =: 0,...,0. Taking s independent Haar random unitary matrices U 1,2,U 3,4,...U 2s 1,2s of size N 2, we define a random state ψ = U 1,2...U 2s 1,2s ψ 0. Expanding this state in the product basis one obtains ψ = ( U 1,2 U 2s 1,2s ) 0,...,0 (31) = i 1,...i 2s (G 1 ) i1,i 2 (G s ) i2s 1,i 2s i 1,...,i 2s Performing a projection onto a product of s 1 maximally entangled states, P s := ½ 1 Ψ + 2,3 Ψ+ 2,3 Ψ+ 2s 2,2s 1 Ψ+ 2s 2,2s 1 ½ 2s (32) we obtain a pure state φ describing the remaining two subsystems, φ = P ψ = N 1 s ) (G 1 G 2 G s i 1 j 2s. (33) ij i,j Normalizing this state and performing the partial trace over the last subsystem we obtain an explicit expression for the resulting mixed state on the first subsystem ρ = Tr 2s φ φ φ φ = G 1G 2 G s (G 1 G 2 G s ) Tr [G 1 G 2 G s (G 1 G 2 G s ) ] (34)
9 9 Alternatively, one may assume that this state is obtained as a results of an orthogonal measurement into the product of s 1 maximally entangled bases. The first entangled basis correlates subsystem 2 with subsystem 3, the next one couples subsystem 4 with 5, while due to the last one the subsystem 2s 2 is correlated with 2s 1. Thus eigenvalues of a random state generated in this way coincide with squared singular values of the product of s independent random Ginibre matrices. Their statistical properties will be analyzed in the following section. In general the Ginibre matrices need not to have the same dimension so the model can be generalized. Assuming that a rectangular matrix G i has dimensions N i M i one has to put M i = N i+1 for i = 1,...,s 1, so that the product (34) is well defined. Setting N 1 = N and defining the ratios c i = M i /N for i = 1,...,s one obtains ensemble of random states parametrized by the vector of coefficients, c := {c 1,...c s }. on (0,b(s)), and bounded at x = b(s), with asymptotic behavior 1/(πx s/(s+1) ) at x 0. This distribution arises in random matrix theory as one studies the product of s independent random square Ginibre matrices, W = s j=1 G j. In this case squared singular values of W (i.e. eigenvalues of WW ) have asymptotic distribution π (s). The same Fuss Catalan distribution describes asymptotically the statistics of singular values of s-th powerofasingle randomginibre matrix[36]. In terms of free probability theory, it is the free multiplicative convolution product of s copies of the Marchenko-Pastur distribution [11, 37], which is written as π (s) = [π (1) ] s. FIG. 8: Fuss Catalan distributions π (s) (x) plotted for s = 1,2,3,4 supported on the interval [0,(s + 1) s+1 /s s ]. To demonstrate the behavior at the right edge of the support the figure is depicted for x 1. FIG. 7: To obtain a random mixed state with spectral density π (s) use a system consisting of 2s subsystems, 1,...,2s of size N: i) take the product of s bi-partite random pure states generated by random unitary matrices U 1,2,U 3,4,...U 2s 1,2s U(N 2 ), ii) measure subsystems 2,...,2s 1 by a projection onto the product of s 1 maximally entangled states, P 23 P 4,5 P 2s 2,2s 1 where P i,j = Ψ + i,j Ψ+ i,j, iii) perform partial trace average over the subsystem 2s. VI. PRODUCT OF GINIBRE MATRICES AND FUSS-CATALAN DISTRIBUTION For any integer number s, there exists a probability measure π (s), called the Fuss-Catalan distribution of order s, whose moments are the generalized Fuss-Catalan numbers [10, 12] given in terms of the binomial symbol, b(s) x m π (s) (x)dx = 1 sm+1 ( ) sm+m =: FC (s) m. 0 m (35) The measure π (s) has no atoms, it is supported on [0,b(s)] where b(s) = (s+1) s+1 /s s, its density is analytic An explicit expressionof the spectral density for s = 2, π (2) (x) = π [ 3 2 ( x ) x ] x 2 3 ( x )1 3 (36) where x [0,27/4], was derived first in [38] in context of construction of generalized coherent states from combinatorial sequences. More recently it was applied in [5] to describe random quantum states associated with certain graphs. The spectral distribution of a product of an arbitrary number of s random Ginibre matrices was recently analyzed by Burda et al. [39] also in the general case of rectangular matrices. The distribution was expressed as a result of a polynomial equation and it was conjectured that the finite size effects can be described by a simple multiplicative correction. Another recent work of Liu et al.[40] provides an integral representation of the distribution π (s) derived in the case of s square matrices of size N, which is assumed to be large. Making use of the inverse Mellin transform and the Meijer G function one may find a more explicit form of this distribution. It can be represented [41] as a super-,
10 10 position of s hypergeometric functions of the type s F s 1, π (s) (x) = s n=1 Λ n,s x n s+1 1 sf s 1 ([{ 1 1+j s where the coefficients Λ n,s read for n = 1,2,...,s Λ n,s := s 3/2 s+1 2π + n } s ] [{ ; s+1 j=1 [ n 1 ( s s/(s+1) ) n s+1 1+ n j s+1 j=1 Γ( j n s+1 } n 1 j=1, { 1+ n j s+1 } s ) ][ s j=n+1 Γ( ) ] j n s j=1 Γ( j+1 s n s+1 s+1 j=n+1 ] s s ) ; (s+1) s+1x (37) ). (38) ([ Here p F q {aj } p [ j=1] ; {bj } q ) j=1] ;x stands for the hypergeometric function [42] of the type p F q with p upper parameters a j and q lower parameters b j of the argument x. The symbol {a i } r i=1 represents the list of r elements, a 1,...a r. The above distribution is exact and it describes the density of squared singular values of s square Ginibre matrices in the limit of large matrix size N. Observe that in the simplest case s = 1 the above form reduces to the Marchenko Pastur distribution, π (1) (x) = 1 ( π x 1 F 0 [ 1 2 ];[ ]; 1 ) 1 x/4 4 x = π, (39) x while the case s = 2 π (2) (x) = 3 2πx 2/3 2 F 1 ( [ 1 6, 1 3 ];[2 3 is equivalent to the form (36) obtained in [38]. 4x ) ]; πx 1/3 2 F 1 ( [ 1 6, 2 3 ];[4 3 4x ) ]; 27 (40) The distributions (37) are thus directly applicable to describe the level density of random mixed states obtained from a 2s partite pure states by projection onto maximally entangled states and partial trace as described in previous section. This result becomes exact in the asymptotic limit, it the dimension N of a single subsystem tends to infinity. However, basing on recent results of Burda et al. [39] one can conjecture that the finite N effects can be described by a multiplicative correction. Notethattheupperedgeb(s) = (s+1) s+1 /s s ofthefc distribution π (s) (x) forlargematrices determines the size of the largest eigenvalue λ max of the reduced density matrix ρ of size N. In the case of the structureless ensemble ofrandompurestatesonn N system, correspondingto s = 1, one has b(1) = 4 so that λ max 4/N. For states obtained by projection of a 2s partite system on maximally entangled states, as described in the previous section, the largest component behaves as λ max b(s)/n. The number λ max, equal to the largest component of the Schmidt vector of a random pure state on the bi partite system, can be used to measure the degree of quantum entanglement. For instance, for a bi-partite system, the geometric measure of entanglement, related to the distance to the closest separable state (in sense of the natural Fubini-Study distance) reads [43], E g ( φ ) = lnλ max. This quantity can also be considered as the Chebyshev entropy S - the generalized Renyi entropy S q = 1 1 q lntrρq in the limit q [9]. Thus the right edge b(s) of the support of the spectral density for the reduced state ρ = Tr B φ φ determines the geometric measure of entanglement of the corresponding random pure states. In the case of structureless random pure states, related to the Marchenko Pastur distribution one becomes an asymptotic expression E g ( φ ) = ln(4/n). In thegeneralcaseofrandom state corresponding the the FC distribution π (s) (x) the typical value of the entropy reads S s = lnn lnb(s) = lnn +slns (s+1)ln(s+1). (41) The larger value of s, the smaller the Chebyshev entropy S, and the less entangled a typical random state obtained by the projection of the 2s partite system. The average von Neumann entropy, S 1 = Trρlnρ, of mixed states of size N generated according to the FC distribution reads S(ρ) s = lnn s+1 j=2 1 j [5]. The second moment of the FC distribution given in (35) implies the asymptotic average purity Trρ 2 s (s+1)/n the larger number s, the more pure the typical mixed state generated by a projection onto s 1 maximally entangled states.
11 11 VII. CONCLUDING REMARKS In this work we analyzed structured ensembles of random pure states on composite systems. They are defined with respect to a given decomposition of the entire system into its subsystems, what induces a concrete tensor product structure in the Hilbert space. The structured ensembles are thus invariant with respect to the group of local unitary transformations. Performing a partial trace over selected subsystems one obtains an ensemble of random mixed states defined on the remaining subsystems. The particular ensemble depends thus on the number of systems traced out and on the way the initial random pure states are prepared. Quantum states obtained by the partial trace of a superposition of k maximally entangled pure states of the bi-partite system involve the sum of k random unitary matrices. To generate states which involve a product of an arbitrary number of s matrices one needs to consider a system consisting of 2s subsystems, in which an orthogonal measurement is performed in the product of s 1 maximally entangled bases. Selected ensembles of random states, recipe to generate numerically the corresponding density matrices and some properties of the distribution of the Schmidt coefficients are collected in Table 1. We are going to conclude this work by writing down a more general class of structured random states, which contains all particular cases discussed in the paper and listed in Table 1. Consider the following ensemble of nonhermitian random matrices parametrized by an arbitrary k dimensional probability vector p = {p 1,...,p k } and a non-negative integer s, W k,s := [ p 1 U 1 +p 2 U 2 + +p k U k ] G1 G s. (42) Here U 1,...U k denote k independent random unitary matrix distributed according to the Haar measure on U(N), while G 1,...G s are independent square random matrices of size N from the complex Ginibre ensemble. Random density matrix is obtained as a normalized Wishart like matrix, ρ k,s := W k,sw k,s Tr(W k,s W (43) k,s ). Note that any particular ensemble from the above class can be physically realized by taking a superposition of k random pure states weighted by the vector p. Each pure state is defined on the system containing 2s subsystems. Performingameasurement in the product of (s 1) maximally entangled bases one gets a random pure state of the desired structured ensemble. Eventually, averaging over the last subsystem one arrives at the mixed state (43). k s matrix W distribution P(x) singularity at x 0 support [a,b] M 2 mean entropy 1 0 U 1 δ(1) = π (0) {1} U 1 +U 2 arcsine x 1/2 [0,2] 3/2 ln U 1 +U 2 +U 3 3 entangled states x 1/2 [0,2 2 ] 5/ U 1 +U 2 +U 3 +U 4 4 entangled states x 1/2 [0,3] 7/ G UG Marchenko Pastur π (1) x 1/2 [0,4] 2 1/2 = (U 1 +U 2)G Bures x 2/3 [0,3 3] 5/2 ln G 1G 2 Fuss Catalan π (2) x 2/3 [0,6 3 ] 3 5/ s G 1 G s Fuss Catalan π (s) x s/(s+1) [0,(s+1) s+1 /s s ] s+1 s+1 1 j=2 j TABLE I: Reduction of pure states from structured ensembles leads to random mixed states of the form ρ = WW /TrWW. Random matrix W is constructed out of random unitary matrices U i distributed according to the Haar measure and/or (independent) random Ginibre matrices G j of a given size N. Asymptotic distribution P(x) of the density of a rescaled eigenvalue x = Nλ of ρ for N is characterized by the singularity at 0, its support [a,b], the second moment M 2 determining the average purity Trρ 2 = M 2/N and the mean entropy, b xlnxp(x)dx, according to which the table is a ordered. Consider first the case of a uniform probability vector, p i = 1/k for i = 1,...,k. For k = 1 one obtains ensemblesleadingtothefuss Catalandistributionsπ (s), which in the cases = 1 reducestothe Marchenko Pasturdistribution. Taking k = 2 and s = 0 one obtains the arcsine ensemble (7), while for larger k one obtains the distributions (10), which converge to π (1) in the limit k. Moreover, the case k = 2 and s = 1 corresponds to the Bures ensemble (23). Thus the case k = 2 and arbitrary s can be called higher order Bures ensemble. In a more general case, taking an arbitrary probability vector p and varying the weights in a continuous man-
12 12 ner one can study transition between given structured ensembles. For instance, by fixing the parameter s, setting k = 2 and varying the weight p 2 = 1 p 1 one defines a continuous interpolation between the higher order Bures ensemble and the Fuss Catalan ensemble. We have shown therefore that having in our disposal simple algorithms to generate random unitary and random Ginibre matrices we can construct a wide class of ensembles of random quantum states. Furthermore, we provide constructive physical recipe to generate such states by means of generic two-particle interaction, superposition of states, selective measurements in maximally entangled basis and performing averages over certain subsystems. As discussed in Appendix B it is also possible to introduce analogous ensembles of real random density matrices. Physically this corresponds to imposing restrictions on the class of the interactions used to generate random pure states. In contrast with the complex case, the ensemble based on square real Ginibre matrices does not lead to the Bures measure in the space of real states. To achieve such a measure one needs to generalize the ensemble even further to allow also rectangular Ginibre matrices [15]. In physical terms this implies that the dimension of the principal system and the auxiliary system have to be different in this case. The notion of random quantum states is closely related with the concept of random quantum maps. Due to the Jamio lkowski isomorphism any quantum operation Φ acting on density matrices ofsize N can be represented by a state on the extended Hilbert space [9], σ = ( Φ ½ ) ψ + φ +. (44) Here ψ + = 1 N N j=1 j,j denotes the maximally entangled state from the bipartite Hilbert space H = H N H N. Any state σ on the composed Hilbert space H = H A H B defines a completely positive, trace preserving map provided the following partial trace condition is satisfied, Tr A σ(φ) = ½/N. It is possible to impose this partial trace condition on an arbitrary state ω acting on H. To this end one finds the reduced state Y := Tr A ω which is positive and allows one to take its its square root Y, and writes the normalized cognate state [44], σ = 1 N ( 1 1 ( )ω 1 1 ) ; (45) Y Y The required property, Tr A σ = ½/N, is satisfied by construction, so the state σ represents a quantum operation. As the matrix elements of the corresponding superoperatorφcanreadilybe obtainedbyreshuffling[9]the entries of the density matrix σ, any random state ω determines by (45) and (44) a quantum operation. Therefore any ensemble of random states introduced in this paper, applied for bi-partite, N N systems determines the corresponding ensemble of random operations. For instance, the induced measure with K = N 2 corresponds to the flat measure in the space of quantum operations [44, 45], but other ensembles of random states can be also applied to generate random quantum operations [9]. The present study on ensembles of random states should be concluded with a remark that apart of the methods developed in this paper several other approaches are advocated in the literature. In very recent papers [46, 47] the authors follow a statistical approach introducing a partition function which leads to a generalization of the Hilbert-Schmidt measure. Varying the parameter of the model, which corresponds to the inverse temperature, they demonstrate a phase transition during an interpolation between Marchenko-Pastur and semicircle distribution of spectral density. In another recent approach Garnerone et al. study statistical properties of random matrix product states [48], which are obtained out of products of truncated random unitary matrices. Although these models of random states do differ from the one presented in this work, a possible links and relations between results obtained in these approaches is currently under investigation. Acknowledgments. It is a pleasure to thank M. Bożejko, Z. Burda, K.J. Dykema, P. Garbaczewski, V.A. Osipov, W. M lotkowski, H.-J. Sommers, F. Verstraete, W. WasilewskiandM. Żukowskiforseveralfruitful discussions and to T. Pattard for a helpful correspondence. We are thankful to F. Benatti, J.A. Miszczak and to an anonymous referee, whose remarks helped us to improve the paper considerably. Financial support by the Transregio-12 project der Deutschen Forschungsgemeinschaft and the grant number N N of Polish Ministry of Science and Higher Education is gratefully acknowledged. KAP acknowledges support from Agence Nationale de la Recherche (Paris, France) under program No. ANR-08-BLAN BC and IN were supported by BC s NSERC discovery grants, BC acknowledges partial support from the ANRs GRANMA and GALOISINT, IN was supported by BC s Ontario s Early Research Award. KŻ acknowledges the support of the PI workshop Random Matrix Techniques in Quantum Information Theory, during which BC, IN and KŻ worked together on this paper. Appendix A: Sum of k random unitaries and the distribution ν k We compute, in the limit of large matrix size N, the asymptotic eigenvalue distribution of the random matrix V k = 1 k (U 1+U 2 + +U k )(U1 +U 2 + +U k ), (A1) where U 1,...,U k are N N random independent Haar unitary matrices. Obviously, this is equivalent to computing the singular value distribution of k 1/2 k i=1 U i. For now, we forget about the normalization pre-factor and we put W k = kv k. It is a well known result in free
Induced Ginibre Ensemble and random operations
 Induced Ginibre Ensemble and random operations Karol Życzkowski in collaboration with Wojciech Bruzda, Marek Smaczyński, Wojciech Roga Jonith Fischmann, Boris Khoruzhenko (London), Ion Nechita (Touluse),
Induced Ginibre Ensemble and random operations Karol Życzkowski in collaboration with Wojciech Bruzda, Marek Smaczyński, Wojciech Roga Jonith Fischmann, Boris Khoruzhenko (London), Ion Nechita (Touluse),
Numerical Range of non-hermitian random Ginibre matrices and the Dvoretzky theorem
 Numerical Range of non-hermitian random Ginibre matrices and the Dvoretzky theorem Karol Życzkowski Institute of Physics, Jagiellonian University, Cracow and Center for Theoretical Physics, PAS, Warsaw
Numerical Range of non-hermitian random Ginibre matrices and the Dvoretzky theorem Karol Życzkowski Institute of Physics, Jagiellonian University, Cracow and Center for Theoretical Physics, PAS, Warsaw
Valerio Cappellini. References
 CETER FOR THEORETICAL PHYSICS OF THE POLISH ACADEMY OF SCIECES WARSAW, POLAD RADOM DESITY MATRICES AD THEIR DETERMIATS 4 30 SEPTEMBER 5 TH SFB TR 1 MEETIG OF 006 I PRZEGORZAłY KRAKÓW Valerio Cappellini
CETER FOR THEORETICAL PHYSICS OF THE POLISH ACADEMY OF SCIECES WARSAW, POLAD RADOM DESITY MATRICES AD THEIR DETERMIATS 4 30 SEPTEMBER 5 TH SFB TR 1 MEETIG OF 006 I PRZEGORZAłY KRAKÓW Valerio Cappellini
MP 472 Quantum Information and Computation
 MP 472 Quantum Information and Computation http://www.thphys.may.ie/staff/jvala/mp472.htm Outline Open quantum systems The density operator ensemble of quantum states general properties the reduced density
MP 472 Quantum Information and Computation http://www.thphys.may.ie/staff/jvala/mp472.htm Outline Open quantum systems The density operator ensemble of quantum states general properties the reduced density
Quantum Chaos and Nonunitary Dynamics
 Quantum Chaos and Nonunitary Dynamics Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Phys. Lett. A 373, 320 (2009) Institute of Physics, Jagiellonian University,
Quantum Chaos and Nonunitary Dynamics Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Phys. Lett. A 373, 320 (2009) Institute of Physics, Jagiellonian University,
Quantum Stochastic Maps and Frobenius Perron Theorem
 Quantum Stochastic Maps and Frobenius Perron Theorem Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Institute of Physics, Jagiellonian University, Cracow,
Quantum Stochastic Maps and Frobenius Perron Theorem Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Institute of Physics, Jagiellonian University, Cracow,
Free probability and quantum information
 Free probability and quantum information Benoît Collins WPI-AIMR, Tohoku University & University of Ottawa Tokyo, Nov 8, 2013 Overview Overview Plan: 1. Quantum Information theory: the additivity problem
Free probability and quantum information Benoît Collins WPI-AIMR, Tohoku University & University of Ottawa Tokyo, Nov 8, 2013 Overview Overview Plan: 1. Quantum Information theory: the additivity problem
Chapter 2 The Density Matrix
 Chapter 2 The Density Matrix We are going to require a more general description of a quantum state than that given by a state vector. The density matrix provides such a description. Its use is required
Chapter 2 The Density Matrix We are going to require a more general description of a quantum state than that given by a state vector. The density matrix provides such a description. Its use is required
Ensembles and incomplete information
 p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
Distribution of Bipartite Entanglement of a Random Pure State
 Distribution of Bipartite Entanglement of a Random Pure State Satya N. Majumdar Laboratoire de Physique Théorique et Modèles Statistiques,CNRS, Université Paris-Sud, France Collaborators: C. Nadal (Oxford
Distribution of Bipartite Entanglement of a Random Pure State Satya N. Majumdar Laboratoire de Physique Théorique et Modèles Statistiques,CNRS, Université Paris-Sud, France Collaborators: C. Nadal (Oxford
Structured Hadamard matrices and quantum information
 Structured Hadamard matrices and quantum information Karol Życzkowski in collaboration with Adam G asiorowski, Grzegorz Rajchel (Warsaw) Dardo Goyeneche (Concepcion/ Cracow/ Gdansk) Daniel Alsina, José
Structured Hadamard matrices and quantum information Karol Życzkowski in collaboration with Adam G asiorowski, Grzegorz Rajchel (Warsaw) Dardo Goyeneche (Concepcion/ Cracow/ Gdansk) Daniel Alsina, José
Restricted Numerical Range and some its applications
 Restricted Numerical Range and some its applications Karol Życzkowski in collaboration with P. Gawron, J. Miszczak, Z. Pucha la (Gliwice), L. Skowronek (Kraków), M.D. Choi (Toronto), C. Dunkl (Virginia)
Restricted Numerical Range and some its applications Karol Życzkowski in collaboration with P. Gawron, J. Miszczak, Z. Pucha la (Gliwice), L. Skowronek (Kraków), M.D. Choi (Toronto), C. Dunkl (Virginia)
Quantum chaos in composite systems
 Quantum chaos in composite systems Karol Życzkowski in collaboration with Lukasz Pawela and Zbigniew Pucha la (Gliwice) Smoluchowski Institute of Physics, Jagiellonian University, Cracow and Center for
Quantum chaos in composite systems Karol Życzkowski in collaboration with Lukasz Pawela and Zbigniew Pucha la (Gliwice) Smoluchowski Institute of Physics, Jagiellonian University, Cracow and Center for
Quantum Entanglement- Fundamental Aspects
 Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Chapter 5. Density matrix formalism
 Chapter 5 Density matrix formalism In chap we formulated quantum mechanics for isolated systems. In practice systems interect with their environnement and we need a description that takes this feature
Chapter 5 Density matrix formalism In chap we formulated quantum mechanics for isolated systems. In practice systems interect with their environnement and we need a description that takes this feature
Uncertainty Relations, Unbiased bases and Quantification of Quantum Entanglement
 Uncertainty Relations, Unbiased bases and Quantification of Quantum Entanglement Karol Życzkowski in collaboration with Lukasz Rudnicki (Warsaw) Pawe l Horodecki (Gdańsk) Jagiellonian University, Cracow,
Uncertainty Relations, Unbiased bases and Quantification of Quantum Entanglement Karol Życzkowski in collaboration with Lukasz Rudnicki (Warsaw) Pawe l Horodecki (Gdańsk) Jagiellonian University, Cracow,
Numerical range and random matrices
 Numerical range and random matrices Karol Życzkowski in collaboration with P. Gawron, J. Miszczak, Z. Pucha la (Gliwice), C. Dunkl (Virginia), J. Holbrook (Guelph), B. Collins (Ottawa) and A. Litvak (Edmonton)
Numerical range and random matrices Karol Życzkowski in collaboration with P. Gawron, J. Miszczak, Z. Pucha la (Gliwice), C. Dunkl (Virginia), J. Holbrook (Guelph), B. Collins (Ottawa) and A. Litvak (Edmonton)
Multiplicativity of Maximal p Norms in Werner Holevo Channels for 1 < p 2
 Multiplicativity of Maximal p Norms in Werner Holevo Channels for 1 < p 2 arxiv:quant-ph/0410063v1 8 Oct 2004 Nilanjana Datta Statistical Laboratory Centre for Mathematical Sciences University of Cambridge
Multiplicativity of Maximal p Norms in Werner Holevo Channels for 1 < p 2 arxiv:quant-ph/0410063v1 8 Oct 2004 Nilanjana Datta Statistical Laboratory Centre for Mathematical Sciences University of Cambridge
Maximally entangled states and combinatorial designes
 Maximally entangled states and combinatorial designes Karol Życzkowski in collaboration with Dardo Goyeneche (Concepcion/ Cracow/ Warsaw) Jagiellonian University (Cracow) & Polish Academy of Sciences (Warsaw)
Maximally entangled states and combinatorial designes Karol Życzkowski in collaboration with Dardo Goyeneche (Concepcion/ Cracow/ Warsaw) Jagiellonian University (Cracow) & Polish Academy of Sciences (Warsaw)
arxiv: v2 [nlin.si] 15 Oct 2008
![arxiv: v2 [nlin.si] 15 Oct 2008 arxiv: v2 [nlin.si] 15 Oct 2008](/thumbs/93/118025177.jpg) Random Quantum Operations Wojciech Bruzda 1, Valerio Cappellini 1, Hans-Jürgen Sommers 2, and Karol Życzkowski1,3 1 Mark Kac Complex Systems Research Centre, Institute of Physics, Jagiellonian University,
Random Quantum Operations Wojciech Bruzda 1, Valerio Cappellini 1, Hans-Jürgen Sommers 2, and Karol Życzkowski1,3 1 Mark Kac Complex Systems Research Centre, Institute of Physics, Jagiellonian University,
Compression and entanglement, entanglement transformations
 PHYSICS 491: Symmetry and Quantum Information April 27, 2017 Compression and entanglement, entanglement transformations Lecture 8 Michael Walter, Stanford University These lecture notes are not proof-read
PHYSICS 491: Symmetry and Quantum Information April 27, 2017 Compression and entanglement, entanglement transformations Lecture 8 Michael Walter, Stanford University These lecture notes are not proof-read
PHY305: Notes on Entanglement and the Density Matrix
 PHY305: Notes on Entanglement and the Density Matrix Here follows a short summary of the definitions of qubits, EPR states, entanglement, the density matrix, pure states, mixed states, measurement, and
PHY305: Notes on Entanglement and the Density Matrix Here follows a short summary of the definitions of qubits, EPR states, entanglement, the density matrix, pure states, mixed states, measurement, and
Entropic Uncertainty Relations, Unbiased bases and Quantification of Quantum Entanglement
 Entropic Uncertainty Relations, Unbiased bases and Quantification of Quantum Entanglement Karol Życzkowski in collaboration with Lukasz Rudnicki (Warsaw) Pawe l Horodecki (Gdańsk) Phys. Rev. Lett. 107,
Entropic Uncertainty Relations, Unbiased bases and Quantification of Quantum Entanglement Karol Życzkowski in collaboration with Lukasz Rudnicki (Warsaw) Pawe l Horodecki (Gdańsk) Phys. Rev. Lett. 107,
FREE PROBABILITY THEORY
 FREE PROBABILITY THEORY ROLAND SPEICHER Lecture 4 Applications of Freeness to Operator Algebras Now we want to see what kind of information the idea can yield that free group factors can be realized by
FREE PROBABILITY THEORY ROLAND SPEICHER Lecture 4 Applications of Freeness to Operator Algebras Now we want to see what kind of information the idea can yield that free group factors can be realized by
Introduction to Quantum Information Hermann Kampermann
 Introduction to Quantum Information Hermann Kampermann Heinrich-Heine-Universität Düsseldorf Theoretische Physik III Summer school Bleubeuren July 014 Contents 1 Quantum Mechanics...........................
Introduction to Quantum Information Hermann Kampermann Heinrich-Heine-Universität Düsseldorf Theoretische Physik III Summer school Bleubeuren July 014 Contents 1 Quantum Mechanics...........................
Entropic characterization of quantum operations
 Entropic characterization of quantum operations W. Roga 1, M. Fannes 2 and K. Życzkowski1,3 arxiv:1101.4105v1 [quant-ph] 21 Jan 2011 1 Instytut Fizyki im. Smoluchowskiego, Uniwersytet Jagielloński, PL-30-059
Entropic characterization of quantum operations W. Roga 1, M. Fannes 2 and K. Życzkowski1,3 arxiv:1101.4105v1 [quant-ph] 21 Jan 2011 1 Instytut Fizyki im. Smoluchowskiego, Uniwersytet Jagielloński, PL-30-059
Operator norm convergence for sequence of matrices and application to QIT
 Operator norm convergence for sequence of matrices and application to QIT Benoît Collins University of Ottawa & AIMR, Tohoku University Cambridge, INI, October 15, 2013 Overview Overview Plan: 1. Norm
Operator norm convergence for sequence of matrices and application to QIT Benoît Collins University of Ottawa & AIMR, Tohoku University Cambridge, INI, October 15, 2013 Overview Overview Plan: 1. Norm
Entanglement Measures and Monotones Pt. 2
 Entanglement Measures and Monotones Pt. 2 PHYS 500 - Southern Illinois University April 8, 2017 PHYS 500 - Southern Illinois University Entanglement Measures and Monotones Pt. 2 April 8, 2017 1 / 13 Entanglement
Entanglement Measures and Monotones Pt. 2 PHYS 500 - Southern Illinois University April 8, 2017 PHYS 500 - Southern Illinois University Entanglement Measures and Monotones Pt. 2 April 8, 2017 1 / 13 Entanglement
Physics 239/139 Spring 2018 Assignment 6
 University of California at San Diego Department of Physics Prof. John McGreevy Physics 239/139 Spring 2018 Assignment 6 Due 12:30pm Monday, May 14, 2018 1. Brainwarmers on Kraus operators. (a) Check that
University of California at San Diego Department of Physics Prof. John McGreevy Physics 239/139 Spring 2018 Assignment 6 Due 12:30pm Monday, May 14, 2018 1. Brainwarmers on Kraus operators. (a) Check that
Asymptotic Pure State Transformations
 Asymptotic Pure State Transformations PHYS 500 - Southern Illinois University April 18, 2017 PHYS 500 - Southern Illinois University Asymptotic Pure State Transformations April 18, 2017 1 / 15 Entanglement
Asymptotic Pure State Transformations PHYS 500 - Southern Illinois University April 18, 2017 PHYS 500 - Southern Illinois University Asymptotic Pure State Transformations April 18, 2017 1 / 15 Entanglement
arxiv: v3 [quant-ph] 17 Nov 2014
![arxiv: v3 [quant-ph] 17 Nov 2014 arxiv: v3 [quant-ph] 17 Nov 2014](/thumbs/90/102194701.jpg) REE From EOF Eylee Jung 1 and DaeKil Park 1, 1 Department of Electronic Engineering, Kyungnam University, Changwon 631-701, Korea Department of Physics, Kyungnam University, Changwon 631-701, Korea arxiv:1404.7708v3
REE From EOF Eylee Jung 1 and DaeKil Park 1, 1 Department of Electronic Engineering, Kyungnam University, Changwon 631-701, Korea Department of Physics, Kyungnam University, Changwon 631-701, Korea arxiv:1404.7708v3
Quantum control of dissipative systems. 1 Density operators and mixed quantum states
 Quantum control of dissipative systems S. G. Schirmer and A. I. Solomon Quantum Processes Group, The Open University Milton Keynes, MK7 6AA, United Kingdom S.G.Schirmer@open.ac.uk, A.I.Solomon@open.ac.uk
Quantum control of dissipative systems S. G. Schirmer and A. I. Solomon Quantum Processes Group, The Open University Milton Keynes, MK7 6AA, United Kingdom S.G.Schirmer@open.ac.uk, A.I.Solomon@open.ac.uk
arxiv: v2 [quant-ph] 18 Jul 2014
![arxiv: v2 [quant-ph] 18 Jul 2014 arxiv: v2 [quant-ph] 18 Jul 2014](/thumbs/93/114207530.jpg) Genuinely multipartite entangled states and orthogonal arrays Dardo Goyeneche Departamento de Fisíca, Universidad de Concepción, Casilla 160-C, Concepción, Chile Center for Optics and Photonics, Universidad
Genuinely multipartite entangled states and orthogonal arrays Dardo Goyeneche Departamento de Fisíca, Universidad de Concepción, Casilla 160-C, Concepción, Chile Center for Optics and Photonics, Universidad
NON-GAUSSIANITY AND PURITY IN FINITE DIMENSION
 International Journal of Quantum Information Vol. 7, Supplement (9) 97 13 c World Scientific Publishing Company NON-GAUSSIANITY AND PURITY IN FINITE DIMENSION MARCO G. GENONI, and MATTEO G. A. PARIS,,
International Journal of Quantum Information Vol. 7, Supplement (9) 97 13 c World Scientific Publishing Company NON-GAUSSIANITY AND PURITY IN FINITE DIMENSION MARCO G. GENONI, and MATTEO G. A. PARIS,,
Entanglement and Symmetry in Multiple-Qubit States: a geometrical approach
 Entanglement and Symmetry in Multiple-Qubit States: a geometrical approach Gregg Jaeger Quantum Imaging Laboratory and College of General Studies Boston University, Boston MA 015 U. S. A. Abstract. The
Entanglement and Symmetry in Multiple-Qubit States: a geometrical approach Gregg Jaeger Quantum Imaging Laboratory and College of General Studies Boston University, Boston MA 015 U. S. A. Abstract. The
Applications and fundamental results on random Vandermon
 Applications and fundamental results on random Vandermonde matrices May 2008 Some important concepts from classical probability Random variables are functions (i.e. they commute w.r.t. multiplication)
Applications and fundamental results on random Vandermonde matrices May 2008 Some important concepts from classical probability Random variables are functions (i.e. they commute w.r.t. multiplication)
arxiv:quant-ph/ v3 7 Jun 2001
 Induced measures in the space of mixed quantum states Karol Życzkowski1 and Hans-Jürgen Sommers 2 1 Centrum Fizyki Teoretycznej, Polska Akademia Nauk, Al. Lotników 32/44, 2-668 Warszawa, Poland 2 Fachbereich
Induced measures in the space of mixed quantum states Karol Życzkowski1 and Hans-Jürgen Sommers 2 1 Centrum Fizyki Teoretycznej, Polska Akademia Nauk, Al. Lotników 32/44, 2-668 Warszawa, Poland 2 Fachbereich
Quantum Entanglement and Measurement
 Quantum Entanglement and Measurement Haye Hinrichsen in collaboration with Theresa Christ University of Würzburg, Germany 2nd Workhop on Quantum Information and Thermodynamics Korea Institute for Advanced
Quantum Entanglement and Measurement Haye Hinrichsen in collaboration with Theresa Christ University of Würzburg, Germany 2nd Workhop on Quantum Information and Thermodynamics Korea Institute for Advanced
arxiv: v2 [quant-ph] 16 Nov 2018
![arxiv: v2 [quant-ph] 16 Nov 2018 arxiv: v2 [quant-ph] 16 Nov 2018](/thumbs/90/104093222.jpg) aaacxicdvhlsgmxfe3hv62vvswncwelkrmikdlgi7cqc1yfwyro+mthmasibkjlgg+wk3u/s2/wn8wfsxs1qsjh3nuosckjhcuhb8fry5+yxfpejyawv1bx2jxnm8tto1hftcs23ui7aohciwcjnxieojjf/xphvrdcxortlqhqykdgj6u6ako5kjmwo5gtsc0fi/qtgbvtaxmolcnxuap7gqihlspyhdblqgbicil5q1atid3qkfhfqqo+1ki6e5f+cyrt/txh1f/oj9+skd2npbhlnngojzmpd8k9tyjdw0kykioniem9jfmxflvtjmjlaseio9n9llpk/ahkfldycthdga3aj3t58/gwfolthsqx2olgidl87cdyigsjusbud182x0/7nbjs9utoacgfz/g1uj2phuaubx9u6fyy7kljdts8owchowj1dsarmc6qvbi39l78ta8bw9nvoovjv1tsanx9rbsmy8zw==
aaacxicdvhlsgmxfe3hv62vvswncwelkrmikdlgi7cqc1yfwyro+mthmasibkjlgg+wk3u/s2/wn8wfsxs1qsjh3nuosckjhcuhb8fry5+yxfpejyawv1bx2jxnm8tto1hftcs23ui7aohciwcjnxieojjf/xphvrdcxortlqhqykdgj6u6ako5kjmwo5gtsc0fi/qtgbvtaxmolcnxuap7gqihlspyhdblqgbicil5q1atid3qkfhfqqo+1ki6e5f+cyrt/txh1f/oj9+skd2npbhlnngojzmpd8k9tyjdw0kykioniem9jfmxflvtjmjlaseio9n9llpk/ahkfldycthdga3aj3t58/gwfolthsqx2olgidl87cdyigsjusbud182x0/7nbjs9utoacgfz/g1uj2phuaubx9u6fyy7kljdts8owchowj1dsarmc6qvbi39l78ta8bw9nvoovjv1tsanx9rbsmy8zw==
A Holevo-type bound for a Hilbert Schmidt distance measure
 Journal of Quantum Information Science, 205, *,** Published Online **** 204 in SciRes. http://www.scirp.org/journal/**** http://dx.doi.org/0.4236/****.204.***** A Holevo-type bound for a Hilbert Schmidt
Journal of Quantum Information Science, 205, *,** Published Online **** 204 in SciRes. http://www.scirp.org/journal/**** http://dx.doi.org/0.4236/****.204.***** A Holevo-type bound for a Hilbert Schmidt
Linear Algebra and Dirac Notation, Pt. 3
 Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Linear Algebra and Dirac Notation, Pt. 3 PHYS 500 - Southern Illinois University February 1, 2017 PHYS 500 - Southern Illinois University Linear Algebra and Dirac Notation, Pt. 3 February 1, 2017 1 / 16
Meixner matrix ensembles
 Meixner matrix ensembles W lodek Bryc 1 Cincinnati April 12, 2011 1 Based on joint work with Gerard Letac W lodek Bryc (Cincinnati) Meixner matrix ensembles April 12, 2011 1 / 29 Outline of talk Random
Meixner matrix ensembles W lodek Bryc 1 Cincinnati April 12, 2011 1 Based on joint work with Gerard Letac W lodek Bryc (Cincinnati) Meixner matrix ensembles April 12, 2011 1 / 29 Outline of talk Random
1 Traces, Traces Everywhere (5 points)
 Ph15c Spring 017 Prof. Sean Carroll seancarroll@gmail.com Homework - Solutions Assigned TA: Ashmeet Singh ashmeet@caltech.edu 1 Traces, Traces Everywhere (5 points) (a.) Okay, so the time evolved state
Ph15c Spring 017 Prof. Sean Carroll seancarroll@gmail.com Homework - Solutions Assigned TA: Ashmeet Singh ashmeet@caltech.edu 1 Traces, Traces Everywhere (5 points) (a.) Okay, so the time evolved state
Is the world more classical or more quantum?
 Is the world more classical or more quantum? A. Lovas, A. Andai BUTE, Department of Analysis XXVI International Fall Workshop on Geometry and Physics Braga, 4-7 September 2017 A. Lovas, A. Andai Is the
Is the world more classical or more quantum? A. Lovas, A. Andai BUTE, Department of Analysis XXVI International Fall Workshop on Geometry and Physics Braga, 4-7 September 2017 A. Lovas, A. Andai Is the
Entropy in Classical and Quantum Information Theory
 Entropy in Classical and Quantum Information Theory William Fedus Physics Department, University of California, San Diego. Entropy is a central concept in both classical and quantum information theory,
Entropy in Classical and Quantum Information Theory William Fedus Physics Department, University of California, San Diego. Entropy is a central concept in both classical and quantum information theory,
Multipartite entangled states, orthogonal arrays & Hadamard matrices. Karol Życzkowski in collaboration with Dardo Goyeneche (Concepcion - Chile)
 Multipartite entangled states, orthogonal arrays & Hadamard matrices Karol Życzkowski in collaboration with Dardo Goyeneche (Concepcion - Chile) Institute of Physics, Jagiellonian University, Cracow, Poland
Multipartite entangled states, orthogonal arrays & Hadamard matrices Karol Życzkowski in collaboration with Dardo Goyeneche (Concepcion - Chile) Institute of Physics, Jagiellonian University, Cracow, Poland
The query register and working memory together form the accessible memory, denoted H A. Thus the state of the algorithm is described by a vector
 1 Query model In the quantum query model we wish to compute some function f and we access the input through queries. The complexity of f is the number of queries needed to compute f on a worst-case input
1 Query model In the quantum query model we wish to compute some function f and we access the input through queries. The complexity of f is the number of queries needed to compute f on a worst-case input
The Framework of Quantum Mechanics
 The Framework of Quantum Mechanics We now use the mathematical formalism covered in the last lecture to describe the theory of quantum mechanics. In the first section we outline four axioms that lie at
The Framework of Quantum Mechanics We now use the mathematical formalism covered in the last lecture to describe the theory of quantum mechanics. In the first section we outline four axioms that lie at
Algebraic Theory of Entanglement
 Algebraic Theory of (arxiv: 1205.2882) 1 (in collaboration with T.R. Govindarajan, A. Queiroz and A.F. Reyes-Lega) 1 Physics Department, Syracuse University, Syracuse, N.Y. and The Institute of Mathematical
Algebraic Theory of (arxiv: 1205.2882) 1 (in collaboration with T.R. Govindarajan, A. Queiroz and A.F. Reyes-Lega) 1 Physics Department, Syracuse University, Syracuse, N.Y. and The Institute of Mathematical
arxiv:quant-ph/ v2 7 Jun 1999
 Volume of the set of mixed entangled states II Karol Życzkowski Instytut Fizyki im. Mariana Smoluchowskiego, Uniwersytet Jagielloński, ul. Reymonta 4, 30-059 Kraków, Poland (October 15, 2018) arxiv:quant-ph/9902050v2
Volume of the set of mixed entangled states II Karol Życzkowski Instytut Fizyki im. Mariana Smoluchowskiego, Uniwersytet Jagielloński, ul. Reymonta 4, 30-059 Kraków, Poland (October 15, 2018) arxiv:quant-ph/9902050v2
Homework 3 - Solutions
 Homework 3 - Solutions The Transpose an Partial Transpose. 1 Let { 1, 2,, } be an orthonormal basis for C. The transpose map efine with respect to this basis is a superoperator Γ that acts on an operator
Homework 3 - Solutions The Transpose an Partial Transpose. 1 Let { 1, 2,, } be an orthonormal basis for C. The transpose map efine with respect to this basis is a superoperator Γ that acts on an operator
The Principles of Quantum Mechanics: Pt. 1
 The Principles of Quantum Mechanics: Pt. 1 PHYS 476Q - Southern Illinois University February 15, 2018 PHYS 476Q - Southern Illinois University The Principles of Quantum Mechanics: Pt. 1 February 15, 2018
The Principles of Quantum Mechanics: Pt. 1 PHYS 476Q - Southern Illinois University February 15, 2018 PHYS 476Q - Southern Illinois University The Principles of Quantum Mechanics: Pt. 1 February 15, 2018
Random Matrix Theory Lecture 1 Introduction, Ensembles and Basic Laws. Symeon Chatzinotas February 11, 2013 Luxembourg
 Random Matrix Theory Lecture 1 Introduction, Ensembles and Basic Laws Symeon Chatzinotas February 11, 2013 Luxembourg Outline 1. Random Matrix Theory 1. Definition 2. Applications 3. Asymptotics 2. Ensembles
Random Matrix Theory Lecture 1 Introduction, Ensembles and Basic Laws Symeon Chatzinotas February 11, 2013 Luxembourg Outline 1. Random Matrix Theory 1. Definition 2. Applications 3. Asymptotics 2. Ensembles
Composition of quantum operations and products of random matrices
 Composition of quantum operations and products of random matrices Wojciech Roga 1, Marek Smaczyński 1 and Karol Życzkowski1,2 arxiv:1105.3830v1 [quant-ph] 19 May 2011 1 InstytutFizykiim.Smoluchowskiego,UniwersytetJagielloński,PL-30-059Kraków,
Composition of quantum operations and products of random matrices Wojciech Roga 1, Marek Smaczyński 1 and Karol Życzkowski1,2 arxiv:1105.3830v1 [quant-ph] 19 May 2011 1 InstytutFizykiim.Smoluchowskiego,UniwersytetJagielloński,PL-30-059Kraków,
arxiv:math-ph/ v1 28 Jul 2006
 Invariant integration over the orthogonal group Daniel Braun Laboratoire de Physique Théorique, IRSAMC, UMR 515 du CNRS, Université Paul Sabatier, 118, route de Narbonne, 3106 Toulouse, FRANCE arxiv:math-ph/0607064v1
Invariant integration over the orthogonal group Daniel Braun Laboratoire de Physique Théorique, IRSAMC, UMR 515 du CNRS, Université Paul Sabatier, 118, route de Narbonne, 3106 Toulouse, FRANCE arxiv:math-ph/0607064v1
INSTITUT FOURIER. Quantum correlations and Geometry. Dominique Spehner
 i f INSTITUT FOURIER Quantum correlations and Geometry Dominique Spehner Institut Fourier et Laboratoire de Physique et Modélisation des Milieux Condensés, Grenoble Outlines Entangled and non-classical
i f INSTITUT FOURIER Quantum correlations and Geometry Dominique Spehner Institut Fourier et Laboratoire de Physique et Modélisation des Milieux Condensés, Grenoble Outlines Entangled and non-classical
Introduction to Quantum Information Processing QIC 710 / CS 768 / PH 767 / CO 681 / AM 871
 Introduction to Quantum Information Processing QIC 710 / CS 768 / PH 767 / CO 681 / AM 871 Lecture 9 (2017) Jon Yard QNC 3126 jyard@uwaterloo.ca http://math.uwaterloo.ca/~jyard/qic710 1 More state distinguishing
Introduction to Quantum Information Processing QIC 710 / CS 768 / PH 767 / CO 681 / AM 871 Lecture 9 (2017) Jon Yard QNC 3126 jyard@uwaterloo.ca http://math.uwaterloo.ca/~jyard/qic710 1 More state distinguishing
Composition of quantum states and dynamical subadditivity
 IOP PUBLISHIG JOURAL OF PHYSICS A: MATHEMATICAL AD THEORETICAL J. Phys. A: Math. Theor. 41 (2008) 035305 (15pp) doi:10.1088/1751-8113/41/3/035305 Composition of quantum states and dynamical subadditivity
IOP PUBLISHIG JOURAL OF PHYSICS A: MATHEMATICAL AD THEORETICAL J. Phys. A: Math. Theor. 41 (2008) 035305 (15pp) doi:10.1088/1751-8113/41/3/035305 Composition of quantum states and dynamical subadditivity
DECAY OF SINGLET CONVERSION PROBABILITY IN ONE DIMENSIONAL QUANTUM NETWORKS
 DECAY OF SINGLET CONVERSION PROBABILITY IN ONE DIMENSIONAL QUANTUM NETWORKS SCOTT HOTTOVY Abstract. Quantum networks are used to transmit and process information by using the phenomena of quantum mechanics.
DECAY OF SINGLET CONVERSION PROBABILITY IN ONE DIMENSIONAL QUANTUM NETWORKS SCOTT HOTTOVY Abstract. Quantum networks are used to transmit and process information by using the phenomena of quantum mechanics.
Volume of the set of separable states
 PHYSICAL REVIEW A VOLUME 58, NUMBER 2 AUGUST 998 Volume of the set of separable states Karol Życzkowski* Institute for Plasma Research, University of Maryland, College Park, Maryland 2742 Paweł Horodecki
PHYSICAL REVIEW A VOLUME 58, NUMBER 2 AUGUST 998 Volume of the set of separable states Karol Życzkowski* Institute for Plasma Research, University of Maryland, College Park, Maryland 2742 Paweł Horodecki
Output entropy of tensor products of random quantum channels 1
 Output entropy of tensor products of random quantum channels 1 Motohisa Fukuda 1 [Collins, Fukuda and Nechita], [Collins, Fukuda and Nechita] 1 / 13 1 Introduction Aim and background Existence of one large
Output entropy of tensor products of random quantum channels 1 Motohisa Fukuda 1 [Collins, Fukuda and Nechita], [Collins, Fukuda and Nechita] 1 / 13 1 Introduction Aim and background Existence of one large
An Introduction to Quantum Computation and Quantum Information
 An to and Graduate Group in Applied Math University of California, Davis March 13, 009 A bit of history Benioff 198 : First paper published mentioning quantum computing Feynman 198 : Use a quantum computer
An to and Graduate Group in Applied Math University of California, Davis March 13, 009 A bit of history Benioff 198 : First paper published mentioning quantum computing Feynman 198 : Use a quantum computer
6.1 Main properties of Shannon entropy. Let X be a random variable taking values x in some alphabet with probabilities.
 Chapter 6 Quantum entropy There is a notion of entropy which quantifies the amount of uncertainty contained in an ensemble of Qbits. This is the von Neumann entropy that we introduce in this chapter. In
Chapter 6 Quantum entropy There is a notion of entropy which quantifies the amount of uncertainty contained in an ensemble of Qbits. This is the von Neumann entropy that we introduce in this chapter. In
A Concise Guide to Complex Hadamard Matrices
 Open Sys. & Information Dyn. 2006 13: 133 177 DOI: 10.1007/s11080-006-8220-2 In a 1867 paper on simultaneous sign-successions, tessellated pavements in two or more colors, and ornamental tile-work Sylvester
Open Sys. & Information Dyn. 2006 13: 133 177 DOI: 10.1007/s11080-006-8220-2 In a 1867 paper on simultaneous sign-successions, tessellated pavements in two or more colors, and ornamental tile-work Sylvester
Quantum Information Types
 qitd181 Quantum Information Types Robert B. Griffiths Version of 6 February 2012 References: R. B. Griffiths, Types of Quantum Information, Phys. Rev. A 76 (2007) 062320; arxiv:0707.3752 Contents 1 Introduction
qitd181 Quantum Information Types Robert B. Griffiths Version of 6 February 2012 References: R. B. Griffiths, Types of Quantum Information, Phys. Rev. A 76 (2007) 062320; arxiv:0707.3752 Contents 1 Introduction
On positive maps in quantum information.
 On positive maps in quantum information. Wladyslaw Adam Majewski Instytut Fizyki Teoretycznej i Astrofizyki, UG ul. Wita Stwosza 57, 80-952 Gdańsk, Poland e-mail: fizwam@univ.gda.pl IFTiA Gdańsk University
On positive maps in quantum information. Wladyslaw Adam Majewski Instytut Fizyki Teoretycznej i Astrofizyki, UG ul. Wita Stwosza 57, 80-952 Gdańsk, Poland e-mail: fizwam@univ.gda.pl IFTiA Gdańsk University
Lecture: Quantum Information
 Lecture: Quantum Information Transcribed by: Crystal Noel and Da An (Chi Chi) November 10, 016 1 Final Proect Information Find an issue related to class you are interested in and either: read some papers
Lecture: Quantum Information Transcribed by: Crystal Noel and Da An (Chi Chi) November 10, 016 1 Final Proect Information Find an issue related to class you are interested in and either: read some papers
arxiv:quant-ph/ v2 25 May 2006
 A concise guide to complex Hadamard matrices arxiv:quant-ph/0512154v2 25 May 2006 Wojciech Tadej 1 and Karol Życzkowski2,3 1 Faculty of Mathematics and Natural Sciences, College of Sciences, Cardinal Stefan
A concise guide to complex Hadamard matrices arxiv:quant-ph/0512154v2 25 May 2006 Wojciech Tadej 1 and Karol Życzkowski2,3 1 Faculty of Mathematics and Natural Sciences, College of Sciences, Cardinal Stefan
1 Tridiagonal matrices
 Lecture Notes: β-ensembles Bálint Virág Notes with Diane Holcomb 1 Tridiagonal matrices Definition 1. Suppose you have a symmetric matrix A, we can define its spectral measure (at the first coordinate
Lecture Notes: β-ensembles Bálint Virág Notes with Diane Holcomb 1 Tridiagonal matrices Definition 1. Suppose you have a symmetric matrix A, we can define its spectral measure (at the first coordinate
Some Bipartite States Do Not Arise from Channels
 Some Bipartite States Do Not Arise from Channels arxiv:quant-ph/0303141v3 16 Apr 003 Mary Beth Ruskai Department of Mathematics, Tufts University Medford, Massachusetts 0155 USA marybeth.ruskai@tufts.edu
Some Bipartite States Do Not Arise from Channels arxiv:quant-ph/0303141v3 16 Apr 003 Mary Beth Ruskai Department of Mathematics, Tufts University Medford, Massachusetts 0155 USA marybeth.ruskai@tufts.edu
Quantum Entanglement and the Bell Matrix
 Quantum Entanglement and the Bell Matrix Marco Pedicini (Roma Tre University) in collaboration with Anna Chiara Lai and Silvia Rognone (La Sapienza University of Rome) SIMAI2018 - MS27: Discrete Mathematics,
Quantum Entanglement and the Bell Matrix Marco Pedicini (Roma Tre University) in collaboration with Anna Chiara Lai and Silvia Rognone (La Sapienza University of Rome) SIMAI2018 - MS27: Discrete Mathematics,
Entanglement in Topological Phases
 Entanglement in Topological Phases Dylan Liu August 31, 2012 Abstract In this report, the research conducted on entanglement in topological phases is detailed and summarized. This includes background developed
Entanglement in Topological Phases Dylan Liu August 31, 2012 Abstract In this report, the research conducted on entanglement in topological phases is detailed and summarized. This includes background developed
Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture. Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev
 Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev The Superposition Principle (Physicists): If a quantum
Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev The Superposition Principle (Physicists): If a quantum
Non white sample covariance matrices.
 Non white sample covariance matrices. S. Péché, Université Grenoble 1, joint work with O. Ledoit, Uni. Zurich 17-21/05/2010, Université Marne la Vallée Workshop Probability and Geometry in High Dimensions
Non white sample covariance matrices. S. Péché, Université Grenoble 1, joint work with O. Ledoit, Uni. Zurich 17-21/05/2010, Université Marne la Vallée Workshop Probability and Geometry in High Dimensions
CS286.2 Lecture 13: Quantum de Finetti Theorems
 CS86. Lecture 13: Quantum de Finetti Theorems Scribe: Thom Bohdanowicz Before stating a quantum de Finetti theorem for density operators, we should define permutation invariance for quantum states. Let
CS86. Lecture 13: Quantum de Finetti Theorems Scribe: Thom Bohdanowicz Before stating a quantum de Finetti theorem for density operators, we should define permutation invariance for quantum states. Let
Quantum Computing Lecture 2. Review of Linear Algebra
 Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
arxiv:quant-ph/ v1 20 Jan 2004
 On duality between quantum maps and quantum states Karol Życzkowski 1,2 and Ingemar Bengtsson 3 1 Instytut Fizyki im. Smoluchowskiego, Uniwersytet Jagielloński, ul. Reymonta 4, 30-059 Kraków, Poland 2
On duality between quantum maps and quantum states Karol Życzkowski 1,2 and Ingemar Bengtsson 3 1 Instytut Fizyki im. Smoluchowskiego, Uniwersytet Jagielloński, ul. Reymonta 4, 30-059 Kraków, Poland 2
Entanglement Measures and Monotones
 Entanglement Measures and Monotones PHYS 500 - Southern Illinois University March 30, 2017 PHYS 500 - Southern Illinois University Entanglement Measures and Monotones March 30, 2017 1 / 11 Quantifying
Entanglement Measures and Monotones PHYS 500 - Southern Illinois University March 30, 2017 PHYS 500 - Southern Illinois University Entanglement Measures and Monotones March 30, 2017 1 / 11 Quantifying
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
FREE PROBABILITY THEORY AND RANDOM MATRICES
 FREE PROBABILITY THEORY AND RANDOM MATRICES ROLAND SPEICHER Abstract. Free probability theory originated in the context of operator algebras, however, one of the main features of that theory is its connection
FREE PROBABILITY THEORY AND RANDOM MATRICES ROLAND SPEICHER Abstract. Free probability theory originated in the context of operator algebras, however, one of the main features of that theory is its connection
Probabilistic exact cloning and probabilistic no-signalling. Abstract
 Probabilistic exact cloning and probabilistic no-signalling Arun Kumar Pati Quantum Optics and Information Group, SEECS, Dean Street, University of Wales, Bangor LL 57 IUT, UK (August 5, 999) Abstract
Probabilistic exact cloning and probabilistic no-signalling Arun Kumar Pati Quantum Optics and Information Group, SEECS, Dean Street, University of Wales, Bangor LL 57 IUT, UK (August 5, 999) Abstract
ASYMPTOTIC EIGENVALUE DISTRIBUTIONS OF BLOCK-TRANSPOSED WISHART MATRICES
 ASYMPTOTIC EIGENVALUE DISTRIBUTIONS OF BLOCK-TRANSPOSED WISHART MATRICES TEODOR BANICA AND ION NECHITA Abstract. We study the partial transposition W Γ = (id t)w M dn (C) of a Wishart matrix W M dn (C)
ASYMPTOTIC EIGENVALUE DISTRIBUTIONS OF BLOCK-TRANSPOSED WISHART MATRICES TEODOR BANICA AND ION NECHITA Abstract. We study the partial transposition W Γ = (id t)w M dn (C) of a Wishart matrix W M dn (C)
SPECTRAL THEOREM FOR COMPACT SELF-ADJOINT OPERATORS
 SPECTRAL THEOREM FOR COMPACT SELF-ADJOINT OPERATORS G. RAMESH Contents Introduction 1 1. Bounded Operators 1 1.3. Examples 3 2. Compact Operators 5 2.1. Properties 6 3. The Spectral Theorem 9 3.3. Self-adjoint
SPECTRAL THEOREM FOR COMPACT SELF-ADJOINT OPERATORS G. RAMESH Contents Introduction 1 1. Bounded Operators 1 1.3. Examples 3 2. Compact Operators 5 2.1. Properties 6 3. The Spectral Theorem 9 3.3. Self-adjoint
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
2-Dimensional Density Matrices
 A Transformational Property of -Dimensional Density Matrices Nicholas Wheeler January 03 Introduction. This note derives from recent work related to decoherence models described by Zurek and Albrecht.
A Transformational Property of -Dimensional Density Matrices Nicholas Wheeler January 03 Introduction. This note derives from recent work related to decoherence models described by Zurek and Albrecht.
Random Matrix Theory in Quantum Information
 Random Matrix Theory in Quantum Information Some generic aspects of entanglement Université Claude Bernard Lyon 1 & Universitat Autònoma de Barcelona Cécilia Lancien BMC & BAMC 2015 - Cambridge Cécilia
Random Matrix Theory in Quantum Information Some generic aspects of entanglement Université Claude Bernard Lyon 1 & Universitat Autònoma de Barcelona Cécilia Lancien BMC & BAMC 2015 - Cambridge Cécilia
Quantum Information & Quantum Computing
 Math 478, Phys 478, CS4803, February 9, 006 1 Georgia Tech Math, Physics & Computing Math 478, Phys 478, CS4803 Quantum Information & Quantum Computing Problems Set 1 Due February 9, 006 Part I : 1. Read
Math 478, Phys 478, CS4803, February 9, 006 1 Georgia Tech Math, Physics & Computing Math 478, Phys 478, CS4803 Quantum Information & Quantum Computing Problems Set 1 Due February 9, 006 Part I : 1. Read
Ph 219/CS 219. Exercises Due: Friday 20 October 2006
 1 Ph 219/CS 219 Exercises Due: Friday 20 October 2006 1.1 How far apart are two quantum states? Consider two quantum states described by density operators ρ and ρ in an N-dimensional Hilbert space, and
1 Ph 219/CS 219 Exercises Due: Friday 20 October 2006 1.1 How far apart are two quantum states? Consider two quantum states described by density operators ρ and ρ in an N-dimensional Hilbert space, and
um random g. channel & computation of / v QIT output min entropy free prob quantum groups
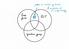 @ i e output free prob. µ @ um random g. channel / v QIT & computation of min. entropy ) quantum groups QIT LINK FP - : Belinski Collins Nechita 201282016 Invent math (2012) 190:647 697 DOI 10.1007/s00222-012-0386-3
@ i e output free prob. µ @ um random g. channel / v QIT & computation of min. entropy ) quantum groups QIT LINK FP - : Belinski Collins Nechita 201282016 Invent math (2012) 190:647 697 DOI 10.1007/s00222-012-0386-3
Principles of Quantum Mechanics Pt. 2
 Principles of Quantum Mechanics Pt. 2 PHYS 500 - Southern Illinois University February 9, 2017 PHYS 500 - Southern Illinois University Principles of Quantum Mechanics Pt. 2 February 9, 2017 1 / 13 The
Principles of Quantum Mechanics Pt. 2 PHYS 500 - Southern Illinois University February 9, 2017 PHYS 500 - Southern Illinois University Principles of Quantum Mechanics Pt. 2 February 9, 2017 1 / 13 The
Random matrices: Distribution of the least singular value (via Property Testing)
 Random matrices: Distribution of the least singular value (via Property Testing) Van H. Vu Department of Mathematics Rutgers vanvu@math.rutgers.edu (joint work with T. Tao, UCLA) 1 Let ξ be a real or complex-valued
Random matrices: Distribution of the least singular value (via Property Testing) Van H. Vu Department of Mathematics Rutgers vanvu@math.rutgers.edu (joint work with T. Tao, UCLA) 1 Let ξ be a real or complex-valued
Introduction to quantum information processing
 Introduction to quantum information processing Measurements and quantum probability Brad Lackey 25 October 2016 MEASUREMENTS AND QUANTUM PROBABILITY 1 of 22 OUTLINE 1 Probability 2 Density Operators 3
Introduction to quantum information processing Measurements and quantum probability Brad Lackey 25 October 2016 MEASUREMENTS AND QUANTUM PROBABILITY 1 of 22 OUTLINE 1 Probability 2 Density Operators 3
arxiv: v1 [quant-ph] 24 May 2011
![arxiv: v1 [quant-ph] 24 May 2011 arxiv: v1 [quant-ph] 24 May 2011](/thumbs/73/68666928.jpg) Geometry of entanglement witnesses for two qutrits Dariusz Chruściński and Filip A. Wudarski Institute of Physics, Nicolaus Copernicus University, Grudzi adzka 5/7, 87 100 Toruń, Poland May 25, 2011 arxiv:1105.4821v1
Geometry of entanglement witnesses for two qutrits Dariusz Chruściński and Filip A. Wudarski Institute of Physics, Nicolaus Copernicus University, Grudzi adzka 5/7, 87 100 Toruń, Poland May 25, 2011 arxiv:1105.4821v1
Entanglement: concept, measures and open problems
 Entanglement: concept, measures and open problems Division of Mathematical Physics Lund University June 2013 Project in Quantum information. Supervisor: Peter Samuelsson Outline 1 Motivation for study
Entanglement: concept, measures and open problems Division of Mathematical Physics Lund University June 2013 Project in Quantum information. Supervisor: Peter Samuelsson Outline 1 Motivation for study
Quantum entanglement and symmetry
 Journal of Physics: Conference Series Quantum entanglement and symmetry To cite this article: D Chrucisi and A Kossaowsi 2007 J. Phys.: Conf. Ser. 87 012008 View the article online for updates and enhancements.
Journal of Physics: Conference Series Quantum entanglement and symmetry To cite this article: D Chrucisi and A Kossaowsi 2007 J. Phys.: Conf. Ser. 87 012008 View the article online for updates and enhancements.
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
Free Probability Theory and Random Matrices. Roland Speicher Queen s University Kingston, Canada
 Free Probability Theory and Random Matrices Roland Speicher Queen s University Kingston, Canada We are interested in the limiting eigenvalue distribution of N N random matrices for N. Usually, large N
Free Probability Theory and Random Matrices Roland Speicher Queen s University Kingston, Canada We are interested in the limiting eigenvalue distribution of N N random matrices for N. Usually, large N
1 More on the Bloch Sphere (10 points)
 Ph15c Spring 017 Prof. Sean Carroll seancarroll@gmail.com Homework - 1 Solutions Assigned TA: Ashmeet Singh ashmeet@caltech.edu 1 More on the Bloch Sphere 10 points a. The state Ψ is parametrized on the
Ph15c Spring 017 Prof. Sean Carroll seancarroll@gmail.com Homework - 1 Solutions Assigned TA: Ashmeet Singh ashmeet@caltech.edu 1 More on the Bloch Sphere 10 points a. The state Ψ is parametrized on the
arxiv: v3 [quant-ph] 5 Jun 2015
![arxiv: v3 [quant-ph] 5 Jun 2015 arxiv: v3 [quant-ph] 5 Jun 2015](/thumbs/88/117676319.jpg) Entanglement and swap of quantum states in two qubits Takaya Ikuto and Satoshi Ishizaka Graduate School of Integrated Arts and Sciences, Hiroshima University, Higashihiroshima, 739-8521, Japan (Dated:
Entanglement and swap of quantum states in two qubits Takaya Ikuto and Satoshi Ishizaka Graduate School of Integrated Arts and Sciences, Hiroshima University, Higashihiroshima, 739-8521, Japan (Dated:
BOGOLIUBOV TRANSFORMATIONS AND ENTANGLEMENT OF TWO FERMIONS
 BOGOLIUBOV TRANSFORMATIONS AND ENTANGLEMENT OF TWO FERMIONS P. Caban, K. Podlaski, J. Rembieliński, K. A. Smoliński and Z. Walczak Department of Theoretical Physics, University of Lodz Pomorska 149/153,
BOGOLIUBOV TRANSFORMATIONS AND ENTANGLEMENT OF TWO FERMIONS P. Caban, K. Podlaski, J. Rembieliński, K. A. Smoliński and Z. Walczak Department of Theoretical Physics, University of Lodz Pomorska 149/153,
