A C 0 INTERIOR PENALTY METHOD FOR A FOURTH ORDER ELLIPTIC SINGULAR PERTURBATION PROBLEM
|
|
|
- Helena Hudson
- 5 years ago
- Views:
Transcription
1 A C 0 INERIOR PENALY MEHOD FOR A FOURH ORDER ELLIPIC SINGULAR PERURBAION PROBLEM SUSANNE C. BRENNER AND MICHAEL NEILAN Abstract. In tis papr, w dvlop a C 0 intrior pnalty mtod for a fourt ordr singular prturbation lliptic problm in two dimnsions on polygonal domains. Using som a postriori rror analysis tcniqus, w ar abl to sow tat t mtod convrgs in t nrgy norm uniformly wit rspct to t prturbation paramtr undr minimal rgularity assumptions. In addition, w analyz t convrgnc of t numrical solution to t unprturbd scond ordr problm. Finally, w prform som numrical xprimnts tat back up t tortical rsults. Ky words. Intrior pnalty mtod, singular prturbation problms, fourt ordr AMS subjct classifications. 65N30, 65N1, 35B5 1. Introduction. In tis papr, w construct and analyz a C 0 intrior pnalty IP mtod for t following fourt ordr problm: ε v ε A v ε = ϕ in Ω, 1.1a v ε = v ε = 0 on Ω. 1.1b Hr, Ω R is a convx polygonal domain, ε is a small, positiv paramtr, ϕ L Ω, and A = Ax [W 1, Ω]. Furtrmor, A is symmtric and positiv dfinit in t sns tat tr xist constants Λ, λ > 0 suc tat Λ w H 1 Ω A w w dx λ w H 1 Ω w H0 1 Ω. 1. Ω Problm 1.1 modls a simply supportd plat problm wit v ε rprsnting t displacmnt of t plat and ε bing t ratio of bnding rigidity to tnsil stiffnss in t plat [17]. Additionally, suc problms aris wn studying t linarization of a fourt ordr prturbation of t fully nonlinar Mong-Ampèr quation [8]. W not tat t corrsponding problm for t clampd plat was invstigatd in [17, 18, 16, 1,, ]. In ordr to avoid ig ordr conforming finit lmnt mtods [17, 9], nonconforming finit lmnt mtods ar an attractiv option. Sinc t lading trm in 1.1a is t biarmonic oprator, t Morly lmnt is appaling sinc it as t last numbr of dgrs of frdom on ac lmnt for fourt ordr problms, as its basis functions consist of only quadratic polynomials [15, 19]. Unfortunatly, t Morly lmnt is not convrgnt for gnral scond ordr lliptic problms [3], and trfor, t rror dtriorats as ε 0 + as was sown in [16]. As a rsult, svral variants of t Morly lmnt mtod av bn proposd for 1.1a wit A = I, wic itr nric t Morly finit lmnt spac [16] or modify t finit lmnt formulation [1, ]. Dpartmnt of Matmatics and Cntr for Computation and cnology, Louisiana Stat Univrsity, Baton Roug, LA work of tis autor was supportd by t National Scinc Foundation undr Grant No. DMS brnnr@mat.lsu.du work of tis autor was supportd by t National Scinc Foundation undr Grant No. DMS nilan@mat.lsu.du 1
2 S. C. BRENNER AND M. NEILAN In tis papr, w tak a diffrnt approac, and formulat and study a symmtric C 0 IP mtod [10, 6] for 1.1. Similar to t Morly lmnt, w us picwis quadratic polynomials to construct our finit lmnt spac. Howvr, unlik any of t aformntiond mtods, w do not nd to modify t spac or modify t finit lmnt formulation. Furtrmor, t finit lmnts w us com in a natural irarcy, ar simpl to implmnt, and radily availabl on commrcial softwar. Finally, as ε 0 +, t mtod convrgs to t standard finit lmnt mtod for t unprturbd problm 1.3 blow. Du to t inqualitis 1., problm 1.1 is boundd and corciv on H Ω H0 1 Ω, and trfor, tr xists a uniqu wak solution v ε H Ω H0 1 Ω. Howvr unlik t cas of t clampd plat, vn on a convx domain, t bst tat can b said about t rgularity of v ε is tat v ε H +γ Ω for som γ 0, 1 wic dpnds on t angls of t cornrs of Ω [11, 4]. at is, v ε dos not ncssarily blong to H 3 Ω. W sall rfr to γ as t indx of lliptic rgularity. W discuss tis issu in furtr dtail as wll as dvlop a priori bounds in t subsqunt sctions cf. orms On of t main goals of tis papr is to rigorously prov tat t C 0 IP mtod is robust wit rspct to ε, tat is, to driv rror stimats tat ar indpndnt of ε. Anotr focal point of tis papr is t convrgnc of v ε v and v v ε, wr vε is t solution to t C 0 IP mtod, and v is t solution to t scond ordr problm A v = ϕ in Ω, 1.3a v = 0 on Ω. 1.3b Du to 1., v is uniquly dfind. Furtrmor, sinc ϕ L Ω, A [W 1, Ω], and Ω is convx, tr olds v H Ω wit [11] v H Ω C ϕ L Ω. 1.4 papr is organizd as follows. In Sction, w provid gnral notation tat will b usd in t subsqunt sctions and dfin t finit lmnt mtod for 1.1. In Sction 3, w us a postriori tcniqus to stablis som tcnical lmmas, wic w latr us to driv abstract a priori rror stimats in t nrgy norm. In Sction 4, w driv a priori stimats of t solution v ε and dtrmin t rats of convrgnc of v ε v in various norms. Sction 5 contains t main rsults of t papr. Hr, w combin t rsults of Sctions 3 and 4 to prov stimats of v ε v ε in t nrgy norm tat ar indpndnt of t paramtr ε, as wll as driv stimats of t rror v v ε wit rspct to bot ε and. Finally in Sction 6, w provid numrical xprimnts wic confirm t tortical rsults. A tcnical proof concrning t construction of a macro bubbl function is found in t Appndix.. Notation and t C 0 Intrior Pnalty Mtod. rougout t papr, w us H k Ω k 0 to dnot t st of all L Ω functions wos distributional drivativs up to ordr k ar in L Ω, and H k 0 Ω to dnot t st of H k Ω functions wos tracs vanis up to ordr k 1 on Ω. In ordr to dfin t wak solution to 1.1, w st av, w := D v, D w, bv, w := A v, w,.1
3 A C 0 IP mtod for a fourt ordr singular prturbation problm 3 wr, dnots t L innr product ovr Ω and D v, D w = Ω D v : D w dx = i,j=1 Ω v x i x j w x i x j dx. W tn dfin a function v ε V 0 := H Ω H 1 0 Ω to b a solution to 1.1 if εav ε, w + bv ε, w = ϕ, w w V 0.. Nxt, w lt b a rgular simplical triangulation [9, 5] of t domain Ω wit = diam. Lt E i dnot t st of intrior dgs in, E b t st of boundary dgs in, and st E = E i E b. For any E i tr ar two triangls + and suc tat = +. St ω = +, }, and lt n b t unit normal of pointing from + to. For any w H + H, dfin t avrag and jump of t normal drivativ of w on as follows: n w }} = 1 n w + + n w, [[ n w ]] = n w + n w. Hr, n w := w n and w ± = w ±. Similarly, w dfin t jump of t gradint of w across by [[ w ]] = w + w. Nxt, for w H 3 + H 3, dfin t avrag and jump of t scond ordr normal drivativ of w on, and t jump of t Laplacian of w on by nn w }} = 1 nn w + + n n w [[, nn w ]] = n n w + n n w, [[ ]] w = w + w, wr n n w := D wn n. For E b, w dfin [[ nn w ]] = n n w. W dnot by V t Lagrang finit lmnt spac consisting of globally continuous picwis quadratic polynomials and lt V 0 = V H 1 0 Ω. For a positiv ral numbr σ, w dfin t following bilinar form on H 3 : a w, z : = D w, D z nn w }}, [[ n z ]].3 E i + [[ n w ]], nnz }} σ 1 [[ n w ]], [[ n z ]] }, wr = diam and, rsp., dnots t L innr product ovr rsp.. C 0 IP mtod for 1.1 is to find v ε V 0 suc tat εa v ε, w + bv ε, w = ϕ, w w V 0..4
4 4 S. C. BRENNER AND M. NEILAN W dfin t discrt norms,, a,, and ε, as follows: w, : = w H, w a, : = w, + E i 1 w ε, : = ε w a, + w H 1 Ω. [[ n w ]] L, Rmark.1. r xists σ a > 0 dpnding only on t sap rgularity of suc tat for σ σ a [6] rfor by.5 and 1., tr olds 1 w a, a w, w w V 0..5 C w ε, ε w a, + λ w H 1 Ω εa w, w + bw, w w V 0..6 It tn follows tat tr xists a uniqu solution to.4 providd σ σ a. Rmark.. It can radily b cckd tat t numrical mtod.4 is consistnt. at is, if v ε H 3 Ω H 1 0 Ω is t solution to 1.1 tn v ε satisfis.4 wit v ε rplacd by vε. Howvr, as alrady mntiond in t Introduction, v ε dos not ncssarily blong to t spac H 3 Ω. As a rsult, standard finit lmnt analysis tcniqus for driving rror stimats i.. Ca s Lmma cannot b applid dirctly. Rmark.3. Intrior pnalty mtods for t corrsponding clampd plat problm wit ε = 1 wr proposd and studid in.g. [3, 13, 14, 7]. As t solution as H 3 Ω rgularity in tis cas, t analysis is rlativly simplr tan t simply supportd plat problm 1.1, and it is straigt-foward to sow tat t rsults of orm 3.1 blow old for t clampd plat problm. 3. Convrgnc Analysis. As mntiond in t prvious sction, w cannot us Ca s Lmma to driv rror stimats of t C 0 IP mtod.4 du to t low rgularity of v ε. o ovrcom tis difficulty, w us som of t main idas of [1] to driv our main rsult of tis sction, orm 3.1, assuming only v ε H Ω H0 1 Ω. As a first stp, w us som a postriori tcniqus [1, 0] to stablis t following tcnical lmma. Lmma 3.1. Suppos tat ϕ H m Ω and A [W m+1, Ω] for som m 0. n for any w V0 tr olds ϕ + A w L C ε 4 vε w H + vε w H m ϕ Hm + w H 1, [[ nnw ]] L C ω 1 vε w H + ε v ε w H ε m+3 ϕ H m + w H 1 } E, [[ ]] A w n C ε 3 L vε w H + 1 vε w H ω
5 A C 0 IP mtod for a fourt ordr singular prturbation problm 5 + m+1 ϕ Hm + } w H 1 E. i Proof. For, coos ϕ P m 1 if m = 0, w tak ϕ = 0 and Ā [P m ] suc tat ϕ ϕ L C m ϕ H m, A Ā L + A Ā W 1, C m A W m+1,. 3.5 Lt b P 6 H0 b t bubbl function dfind on suc tat b quals on at t barycntr of, tat is b = 7λ 1, λ λ3 i wr λ }3 i=1 dnot t barycntric coordinats of. Nxt, dfin r H0 Ω suc tat r = b ϕ + Ā w, and xtnd r to b zro outsid of. First, w not tat sinc ϕ + Ā w is a polynomial, tr xists a constant C > 0 indpndnt of suc tat C ϕ + Ā w ϕ + Ā w, r L. 3.6 Nxt, using standard invrs stimats [9, 5], 3.6,., and , w av for any w V 0 C ϕ + Ā w L ϕ + Ā w, r = ϕ ε w + Ā w, r = ϕ ϕ, r + Ā A w, r + ε D v ε w, D r + A v ε w, r C ϕ ϕ L + A Ā L w H + A Ā W 1, w H1 + ε vε w H + 1 vε w H1 r L C m ϕ Hm + w H1 + ε vε w H + 1 vε w H1 ϕ + Ā w. L Hr, w av usd t fact 0 b 1 to driv t last inquality. Dividing t last xprssion by ϕ + Ā w L, and using , and t triangl and invrs inqualitis, w gt ϕ + A w L ϕ + Ā w L + A Ā w L C ϕ + Ā w L + A Ā W 1, + 1 A Ā L w H1 C m ϕ Hm + w H1 + ε vε w H + 1 vε w H 1. stimat 3.1 follows from tis last inquality.
6 6 S. C. BRENNER AND M. NEILAN Nxt lt E b an arbitray dg. If E i wit = +, w construct ζ 1 P 1 + and ζ P 8 + suc tat [1]: ζ 1 = 0, n ζ 1 = [[ nnw ]], ζ ds, ζ + \ = 0, ζ + \ = 0, + ζ dx = + +. Otrwis if E b wit = + Ω, w construct ζ 1 P 1 + and ζ P 4 + suc tat ζ 1 = 0, n ζ 1 = [[ nnw ]], ζ ds, ζ + \ = 0, ζ + \ = 0, + ζ dx = +. Intgrating by parts, w av by. Cε [[ nnw ]] ε [[ L nnw ]], n ζ 1 ζ = ε [[ nnw ]], n ζ1 ζ + A [[ w ]] n, ζ 1 ζ = ε D w, D ζ 1 ζ ω + A w, ζ 1 ζ + A w, ζ 1 ζ = ε D w v ε, D ζ 1 ζ + A w v ε, ζ 1 ζ C ω } + ϕ + A w, ζ 1 ζ ε v ε w H ζ 1 ζ H + v ε w H 1 ζ 1 ζ H 1 ω By scaling, w av [1] and by t Poincaré inquality + ϕ + A w L ζ 1ζ L ζ 1 ζ H 1 ± C 1 [[ nn w ]] L, ζ 1 ζ L ± C ζ 1 ζ H1 ±. us, by t invrs inquality and 3.1, w av ε [[ nnw ]] L C ε 1 vε w H + v ε w H 1 ω + ϕ + A w L }. } } ζ 1 ζ H 1 ±
7 A C 0 IP mtod for a fourt ordr singular prturbation problm 7 C C It tn follows tat [[ nnw ]] L C ω ε 1 vε w H + v ε w H1 + m+1 } ϕ H m + w H 1 1 [[ nn w ]] L ε 1 vε w H + 1 v ε w H1 ω + m+ 3 ω } [[ ϕ H m + w H 1 nn w ]] L. 1 vε w H + ε v ε w H 1 + ε m+3 ϕ Hm + } w H 1. W now prov 3.3. o aciv tis, for givn = + E i, w construct χ 1 P m+1 + suc tat χ 1 = Ā[[ w ]] n, and xtnd χ 1 to + by constants along t normal dirctions of. Nxt, w lt χ b t macro bubbl function wit t following proprtis cf. Appndix A: χ = 0, χ + \ = 0, + \ n χ = 0, χ ds, χ L + 1. W tn av by. and by intgration by parts, C [[ Ā w ]] n Ā [[ w ]] n L, χ 1 χ = ε [[ nnw ]], n χ 1 χ + Ā [[ w ]] n, χ 1 χ = ε D w, D χ 1 χ + Ā w, χ 1 χ + Ā w, χ 1χ ω = ω ε D w v ε, D χ 1 χ + A w v ε, χ 1 χ + Ā A w, χ 1χ + ϕ + Ā w, χ 1χ us, by t invrs and Poincaré inqualitis, 3.1, and 3.5, [[ Ā w ]] n L C ε vε w H + 1 vε w H 1 By scaling, w av ω + 1 A Ā L w H 1 + ϕ + Ā w } L χ 1 χ L C ε vε w H + 1 vε w H 1 ω + m } ϕ Hm + w H 1 χ 1 χ L. χ 1 χ L χ 1 L χ L C 1 Ā [[ w ]] n L. }. }
8 8 S. C. BRENNER AND M. NEILAN It tn follows tat Ā [[ w ]] n L C and trfor, ω + m+1 ε 3 vε w H + 1 vε w H 1 ϕ H m + } w H 1, [[ ]] A w n L [[ Ā w ]] n L + A Ā [[ w ]] n L C ε 3 vε w H + 1 vε w H 1 ω + m+1 ϕ H m + w H 1 C ω + m+1 ε 3 vε w H + 1 vε w H 1 ϕ H m + } w H 1. } + A Ā L ω [[ w ]] L Bfor continuing, w discuss som proprtis of t nricing oprator, E : V V c, wr V c H Ω H 1 0 Ω is t Hsi-Cloug-ocr finit lmnt spac [9, 5] associatd wit. W sktc som of t main proprtis of tis linar oprator and rfr t radr to t paprs [6, 7] for a mor dtaild xposition. construction of E is don by avraging. o dscrib tis procss, w lt N b a global dgr of frdom of V c, tat is, N is itr t valuation of t sap function at a vrtx in, t valuation of t first ordr drivativs of a sap function at an intrior vrtx in, t valuation of t normal drivativ of a sap function at t midpoint of an dg in E, or t valuation of t normal drivativ of a sap function at any vrtx on t boundary Ω. n for any w V, w construct E w V c so tat NE w = 1 N Nw, N wr N dnots t st of triangls tat sar t dgr of frdom, and N is t cardinality of tis st. For any, t map E satisfis t stimat [7] w E w L C4 = C 4 1 p V E i p 1 E i [[ n w ]] L 3.7 [[ n w ]] L, wr V dnots t st of vrtics of, E i p is t st of all intrior dgs in E saring t ndpoint p, and cf. Figur 3.1 E i = p V E i p.
9 A C 0 IP mtod for a fourt ordr singular prturbation problm 9 Fig triangls in t st and t dgs in t st E i dasd lins. Using a trac and invrs inquality, it follows from 3.7 tat w E w L C4 [[ n w ]] 3.8 L C 4 E i 1 E i ω w H 1 C w H 1, wr cf. Figur 3.1 = E i ω. Nxt, using t trac and invrs inqualitis again, w conclud tat ε 1 n w E w }} C ε 4 L w E w L 3.9 E E ω C ε 1 [[ n w ]] L E ω E i C w ε,, and by 3.8 and 3.7 n w E w }} C L E E C E ω C w ε,, ε nnw E w }} C L E E C E E i C w ε,. w E w L 3.10 ω ω w H 1 ε 4 w E w L 3.11 ε 1 ω E i [[ n w ]] L Using similar argumnts, w conclud tat by 3.8 w av 1 w E w L C w E w L 3.1 E i C E i and by 3.7, w av ε 3 w E w L E i E i ω ω ω w H 1 w ε,, ε 4 w E w L 3.13
10 10 S. C. BRENNER AND M. NEILAN E i ω w ε,. ε 1 [[ n w ]] L E i Finally, from 3.7 and t trac and invrs inqualitis, w av E w ε, C w ε, w V Lmma 3.. For all q H Ω, z V c, and w V, tr olds εaq, z εa w, z + bq w, z C q w ε, z ε, Proof. For any z V c and q H Ω, tr olds [[ n z ]] = [[ n q ]] = 0 E i. rfor by.1,.3, t Caucy-Scwarz inquality and trac/invrs inqualitis, w av εaq, z εa w, z + bq w, z = ε D q w, D z ε [[ n q w ]], nnz }} + bq w, z E i ε q w, z, + A L Ω q w H 1 Ω z H 1 Ω + ε 1 [[ n q w ]] 1/ L nn z }} L E i E i C q w ε, z ε,. 1/ Wit ts rsults stablisd, and wit t lp of Lmma 3.1, w can sow t following rsult. tru powr of Lmma 3.3 will b xposd in orm 3.1. Lmma 3.3. Lt v ε dnot t solution to 1.1, and lt v ε dnot t solution to.4, and suppos tat ϕ H m Ω, A [W m+1, Ω] for som m 0. W tn av [ v ε v ε ε, C1 + σ inf ε v ε w H 3.16 w V 0 + ε v ε w H 1 + m+1 w H1 + ϕ H m + E i ε 1 [[ n v ε w ]] L [ v ε v ε ε, C1 + σ inf w V 0 + v ε w H 1 + m+1 + E i ε 1 [[ n v ε w ]] L ] 1, }, ε + ε v ε w H 3.17 w H 1 + ϕ H m } ] 1.
11 A C 0 IP mtod for a fourt ordr singular prturbation problm 11 Proof. Lt w V0 suc tat w v ε, and to as notation st z = vε w. n using similar argumnts as in [1, Lmma.1], w av by.6,.4,., 3.15, and 3.14 C v ε w ε, εa v ε w, z + bv ε w, z = ϕ, z εa w, z bw, z = εav ε, E z εa w, E z + bv ε w, E z + ϕ, z E z εa w, z E z bw, z E z C v ε w ε, E z ε, + ϕ, z E z εa w, z E z bw, z E z C v ε w ε, v ε w ε, + ϕ, z E z εa w, z E z bw, z E z. It tn follows from tis xprssion and t triangl inquality tat [ ] v ε v ε ε, C inf v ε G w, z w ε, + sup, 3.18 w V0 z V0 \0} z ε, wr G w, z := ϕ, z E z εa w, z E z bw, z E z. Nxt, to as notation, st s = z E z, so tat Intgrating by parts, w av D w, D s = G w, z = ϕ, s εa w, s bw, s = D w, s + n w, s } nn w, n s + nτ w, τ s }, wr τ dnots t unit tangnt vctor of. Sinc E zp = zp for any vrtx p in, it follows tat D w, D s = nn w }}, [[ n s ]] + [[ nn w ]], n s }}. 3.0 E i By t dfinitions of t bilinar forms a, and b, and by 3.0, w av εa w, s + bw, s = A w, s + ε [[ n D w, D s ε w ]], nns }} E i + nnw }}, [[ n s ]] [[ σ 1 n w ]], [[ n s ]] } = A w, s ε [[ n w ]], nns }} E i εσ 1 [[ n w ]], [[ n s ]] A [[ w ]] n, s } E
12 1 S. C. BRENNER AND M. NEILAN + E ε [[ nnw ]], n s }}, and trfor by 3.19 and 3.11, G w, z = ϕ + A w, s + ε [[ n w v ε ]], nns }} 3.1 εσ 1 E i [[ n w v ε ]], [[ n s ]] A [[ w ]] n, s } E ε [[ nnw ]], n s }} 1 + σ v ε w ε, z ε, + + ε [[ nnw ]] L n s }} L E ϕ + A w L s L + E i A [[ w ]] n L s L. Hr, w av usd t fact v ε H Ω so tat [[ n v ε]] = 0, E i. W now bound t last tr xprssions in t rigt-and sid of 3.1. Combining 3.1 and , w av ϕ + A w L s L 3. C m+1 C m+1 ϕ Hm + w H1 + v ε w H1 z H ε v ε w H 1 [[ n z ]] 1 } L E i ϕ Hm + 1 w H 1 + v ε w ε, z ε,. Nxt, applying 3. and 3.9, w gt [[ nn w ]], n s }} 3.3 E ε ε [[ nnw ]] L E C ε [[ nnw ]] L E [ C 1 ε 1 E 1 z ε, ε v ε w H + ε 1 v ε w H 1 + ε 1 m+ n s }} L ϕ H m + w H 1 }] 1 z ε,. 1
13 A C 0 IP mtod for a fourt ordr singular prturbation problm 13 W also av by 3.10 and 3. [[ nn w ]], n s }} 3.4 E ε 1 ε [[ nnw ]] 1 L E C [ C 1 ε [[ nnw ]] L E + m+1 E 1 z H 1 Ω ε vε w H + vε w H 1 ϕ Hm + w H 1 }] 1 z ε,. n s }} L Continuing, w us 3.3 and 3.1 to conclud [[ ]] A w n, s E i [[ ]] A w n E i L C A [[ w ]] n E i C + m+1 1 L E i 1 s L 1 z H 1 ε vε w H + vε w H 1 ϕ H m + } w H 1 z ε,, and by 3.13, w av [[ ]] A w n, s E i E i ε 1 3 A [[ w ]] n L 1 E i ε 3 C ε 1 3 [[ ]] A w n z L ε, E i C ε v ε w H + ε 1 v ε w H 1 + ε 1 m+ 1 ϕ H m + } w H 1 z ε,. s L Finally, t stimat 3.16 is obtaind by combining 3.18, 3.1, and t stimats 3., 3.3, and 3.6. Similarly, t stimat 3.17 is obtaind by combining 3.18, 3.1, and t stimats 3., 3.4, and
14 14 S. C. BRENNER AND M. NEILAN orm 3.1. Suppos tat ϕ H m Ω, A [W m+1, Ω] and t ms is quasiuniform wit. n tr olds v ε v ε ε, C1 + σ inf w V0 v ε w ε, + m+1 w H 1 Ω + ϕ H Ω m. 3.7 Proof. If ε 1, tn by 3.17, w av [ ε v ε v ε ε, C1 + σ inf 1 + ε 1 v ε w, w V0 + v ε w H 1 Ω + m+1 w H 1 Ω + ϕ H m + ε 1 [[ n v ε w ]] 1 ] L E i C1 + σ inf v ε w ε, + m+1 w H1 Ω + ϕ H m. w V0 On t otr and, if ε 1, tn by 3.16 w av [ v ε v ε ε, C1 + σ inf ε 1 v ε w, w V0 + ε v ε w H1 Ω + m+1 w H1 Ω + ϕ H m + E i ε 1 [[ n v ε w ]] L 1 ] C1 + σ inf v ε w ε, + m+1 w H 1 Ω + ϕ H m. w V0 4. A Priori Estimats and Convrgnc as ε 0 +. Sinc t rror stimat 3.1 will vntually dpnd on t norms of v ε, w must driv a priori bounds of ts quantitis in ordr to obtain uniform convrgnc of t finit lmnt mtod wit rspct to ε. orm 4.1 A Priori Estimats I. Lt v ε b t solution to 1.1 and lt v dnot t solution to 1.3. n t following old: v ε H Ω C ϕ L Ω, 4.1 v ε v L Ω Cε ϕ L Ω, 4. v ε v H 1 Ω Cε 1 ϕ L Ω. 4.3 Morovr, v ε H +γ Ω for som γ 0, 1 and v ε H +γ Ω Cε γ ϕ L Ω. 4.4 Proof. Sinc v H Ω, w av for any w V 0 ε D v ε v, D w + A v ε v, w = εd v, D w.
15 A C 0 IP mtod for a fourt ordr singular prturbation problm 15 Stting w = v ε v in t xprssion abov, w us 1. to conclud ε v ε v H Ω + λ vε v H 1 Ω ε v H Ω v ε v H Ω. Assuming λ ε, w av by 1.4 v ε v H Ω C v H Ω C ϕ L Ω, v ε v H 1 Ω Cε 1 v H Ω Cε 1 ϕ L Ω, and trfor, v ε H Ω C ϕ L Ω. 4.5 o obtain t stimat 4., w lt φ H Ω H0 1 Ω b t solution to ε φ A φ = v ε v in Ω, 4.6 φ = φ = 0 on Ω. W tn av by 4.1 φ H Ω C v ε v L Ω. 4.7 W also av by 4.6, 1.1, 1.3, and 4.7 v ε v L Ω = εd v, D φ ε v H Ω φ H Ω Cε v H Ω v ε v L Ω Cε ϕ L Ω v ε v L Ω. Dividing t last xprssion by v ε v L Ω, w obtain 4.. W now sow 4.4. o tis nd, w not tat v ε = ε 1 A v ε v. Sinc A [W 1, Ω] and v ε, v H Ω, tr olds A v ε v L Ω. us by lliptic tory for t simply supportd plat, tr xists a γ 0, 1 wic w call t indx of lliptic rgularity, suc tat v ε H +γ Ω and By , w av v ε H +γ Ω Cε 1 A v ε v H +γ Ω 4.8 Cε 1 v ε v Hγ Ω. v ε v L Ω Cε ϕ L Ω, v ε v H 1 Ω Cε 1 ϕ L Ω, and trfor, by intrpolation btwn Sobolv spacs, It tn follows from tat v ε v H γ Ω Cε γ ϕ L Ω. 4.9 v ε H +γ Ω Cε γ ϕ L Ω.
16 16 S. C. BRENNER AND M. NEILAN Nxt, undr assumption tat t solution to t unprturbd scond ordr problm as igr rgularity, w ar abl to improv som of t stimats of orm 4.1. orm 4. A Priori Estimats II.. Suppos tat v H 3 Ω. n tr olds v ε v H 1 Ω Cε 3 4 v H 3 Ω, 4.10 v ε v H Ω Cε 1 4 v H 3 Ω, 4.11 v ε H +γ Ω Cε γ 4 ϕ L Ω + v H 3 Ω. 4.1 Proof. Intgrating by parts, w av ε D v ε v, D w + A v ε v, w = εd v, D w = ε v, w ε v, n w Ω. Stting w = v ε v and using trac inqualitis givs us ε v ε v H Ω + λ vε v H 1 Ω ε v L Ω v ε v L Ω + v L Ω n v ε v L Ω Cε v ε v H1 Ω + v ε v 1 H 1 Ω vε v 1 H Ω v H 3 Ω. us by Young s inquality, w av ε v ε v H Ω + λ vε v H 1 Ω C ε + ε 3 v H3 Ω Cε 3 v H3 Ω. stimats follow from tis last inquality. Nxt, by intrpolation btwn Sobolv spacs, v ε v H γ Ω Cε 4 γ 4 ϕ L Ω + v H Ω 3 γ 0, 1. It tn follows from 4.8 tat v ε H +γ Ω Cε γ 4 ϕ L Ω + v H 3 Ω. Rmark 4.1. As Ω is a polygonal domain, w cannot xpct tat v H 3 Ω in gnral. Howvr, t rsults of orm 4. xplain som of t numrical xprimnts in Sction Convrgnc Analysis Rvisitd. In tis sction, w combin t rror analysis drivd in orm 3.1 wit t a priori bounds dvlopd in t prvious sction. First, w driv stimats of t rror v ε v ε, wic w summariz in t following torm. orm 5.1. Lt γ 0, 1 dnot t indx of lliptic rgularity. n tr olds v ε v ε ε, C1 + σ γ ϕ L Ω. 5.1
17 A C 0 IP mtod for a fourt ordr singular prturbation problm 17 Proof. Lt I v ε dnot t standard finit lmnt intrpolant of v ε. By 3.7, 4.1 and 4.4, w av v ε v ε ε, C1 + σ ε 1 v ε I v ε a, + v ε I v ε H 1 Ω + I v ε H 1 Ω + ϕ L Ω C1 + σ ε 1 γ v ε H +γ Ω + v ε H Ω + ϕ L Ω C1 + σ ε 1 γ γ + ϕ L Ω C1 + σ γ ϕ L Ω. Nxt, w turn our attntion to dvloping stimats of v v ε. Of cours, t most natural approac is to combin t stimats drivd in orm 5.1 wit t convrgnc rats drivd in orms and us t triangl inquality. Howvr, a bttr stratgy is to us t stimat 3.7 dirctly and avoid t lliptic rgularity of v ε. Furtrmor, by considring t discrt vrsion of 1.3, and wit t lp of t invrs inquality, w ar also abl to trad-in powrs of for powrs of ε. orm 5.. r olds v v ε ε, C1 + σε 1 + ϕ L Ω, 5. v v ε H 1 Ω C + ε σ ϕ L Ω. 5.3 Morovr, if v H 3 Ω, ϕ H 1 Ω, and A [W, Ω], tn v v ε ε, C1 + σ ε ϕ H1 Ω + v H3 Ω, 5.4 v v ε H 1 Ω C v H 3 Ω + ε σ ϕ L Ω, 5.5 v v ε a, C v H 3 Ω + ε 1 + σ ϕ L Ω. 5.6 Proof. Lt I v dnot t finit lmnt intrpolant of v. By 3.7, 1.4, and t triangl inquality, w av v ε v ε ε, 5.7 C1 + σ v ε I v ε, + I v H1 Ω + ϕ L Ω C1 + σ v ε I v ε, + v I v H1 Ω + v H1 Ω + ϕ L Ω C1 + σ v ε v ε, + v I v ε, + ϕ L Ω. By standard intrpolation stimats and 1.4, w av v I v ε, Cε 1 + v H Ω Cε 1 + ϕ L Ω. 5.8 Morovr, by 4.1, 1.4, and 4.3, v ε v ε, Cε 1 ϕ L Ω. 5.9
18 18 S. C. BRENNER AND M. NEILAN Applying t bounds to t inquality 5.7, and using t triangl inquality, w obtain v v ε ε, v ε v ε, + v ε v ε ε, C1 + σε 1 + ϕ L Ω. In a similar fasion, if v H 3 Ω, ϕ H 1 Ω, and A [ W, Ω ], tn by 3.7 w av v ε v ε ε, C1 + σ v ε I v ε, + I v H 1 Ω + ϕ H Ω C1 + σ v ε v ε, + v I v ε, + ϕ H 1 Ω. W also av by and standard intrpolation stimats and trfor, v I v ε, C ε 1 + v H3 Ω, v ε v ε, Cε 3 4 v H 3 Ω, v v ε ε, v ε v ε, + v ε v ε ε, C1 + σ ε ε + ϕ H1 Ω + v H3 Ω Nxt, w lt v dnot t solution to C1 + σ ε ϕ H 1 Ω + v H 3 Ω. b v, w = ϕ, w By standard finit lmnt analysis tcniqus, w av and trfor, v I v H 1 Ω C v I v H 1 Ω, w V v v H1 Ω C v H Ω C ϕ L Ω. 5.1 Also, by t invrs inquality tr olds v a, C 1 v I v H1 Ω + I v a, C v H Ω C ϕ L Ω Furtrmor, if v H 3 Ω, tn v v H 1 Ω C v H 3 Ω, 5.14 v v a, C 1 v I v H1 Ω + v I v a, 5.15 C 1 v I v H 1 Ω + v v H 1 Ω + v I v a, C v H3 Ω. From t dfinition of v ε and v and by Rmark.1, w av C v ε v ε, εa v ε v, v ε v + bv ε v, v ε v = εa v, v ε v Cε1 + σ v a, v ε v a,.
19 A C 0 IP mtod for a fourt ordr singular prturbation problm 19 us by t invrs inquality, w obtain v ε v ε, Cε1 + σ v a, v ε v a, Cε σ v a, v ε v H 1 Ω Cε σ v a, v ε v ε,. rfor, dividing by v ε v ε, and using 5.13, w av and nc, v ε v ε, Cε σ v a, Cε σ ϕ L Ω, v ε v H1 Ω Cε σ ϕ L Ω, v ε v a, Cε σ ϕ L Ω. rfor, by t triangl inquality and 5.1 v v ε H1 Ω v v H1 Ω + v ε v H1 Ω C + ε σ ϕ L Ω, and if v H 3 Ω, by 5.14 w av v v ε H1 Ω C v H3 Ω + ε σ ϕ L Ω. Also, if v H 3 Ω, tn by t invrs inquality and 5.15 v v ε a, C 1 v v ε H1 Ω + v v a, C v H 3 Ω + ε 1 + σ ϕ L Ω. Rmark 5.1. By t proof of orm 5., v ε v ε ε, C1 + σ ε 1 + ϕ L Ω, 5.16 and if ϕ H 1 Ω, v H 3 Ω, and A [ W, Ω ], tn v ε v ε ε, C1 + σ ε ϕ H1 Ω + v H3 Ω Corollary 5.1. Suppos tat = ε α for som α > 0. n tr olds v v ε ε, C1 + σ ϕ L Ω ε α α 1 ε 1 α 1, 5.18 and if v H 3 Ω, ϕ H 1 Ω, and A W, Ω, tn v v ε H1 Ω C1 + σ ϕ H1 Ω + v H3 Ω ε α α 3 8 ε 3 4 α 3 8, 5.19 v v ε a, C1 + σ ε α α 1 3 ϕ H1 Ω + v H3 Ω ε 1 α 1 3 α ε 1 4 α 3 8
20 0 S. C. BRENNER AND M. NEILAN Proof. stimat 5.18 is a dirct consqunc of t rror stimat 5.. If v H 3 Ω, ϕ H 1 Ω, and A [ W, Ω ] tn by v v ε H 1 Ω C1 + σ min ε ε α, ε α + ε 1 α} ϕ H 1 Ω + v H 3 Ω } C1 + σ ε α + min ε 3 4, ε 1 α ϕ H 1 Ω + v H Ω 3. If α 1 4, tn v v ε H1 Ω C1 + σ ε α + ε 1 α ϕ H1 Ω + v H3 Ω Otrwis, if 1 4 α 3 8, tn and if α 3 8, tn v v ε H1 Ω C1 + σ v v ε H1 Ω C1 + σ C1 + σε α ϕ H 1 Ω + v H 3 Ω. ε α + ε 3 ϕ H1 4 Ω + v H3 Ω C1 + σε α ϕ H 1 Ω + v H 3 Ω, ε α + ε 3 ϕ H1 4 Ω + v H3 Ω C1 + σε 3 4 ϕ H1 Ω + v H3 Ω, wic stabliss Nxt, by 5.4 and 5.6, w av v v ε a, C1 + σ min ε ε α 1, ε α + ε 1 α} ϕ H 1 Ω + v H Ω 3. If α 1 3, tn min ε ε α 1, ε α + ε 1 α} } min ε α 1, ε α = ε α. If 1 3 α 3 8, tn min ε ε α 1, ε α + ε 1 α} } min ε α 1, ε 1 α = ε 1 α, and if α 3 8, tn min ε ε α 1, ε α + ε 1 α} } min ε 1 4, ε 1 α = ε 1 4. stimat 5.0 follows from ts last tr inqualitis. 6. Numrical Exprimnts. In tis sction, w provid svral numrical xprimnts tat back up t tortical findings in t prcding sctions. All of t tsts prsntd blow ar on t domain Ω = 0, 1 and w st A = I so tat 1.1a and 1.3a rad, rspctivly ε v ε v ε = ϕ in Ω, v = ϕ in Ω. Furtrmor, w rplac t omognous Diriclt boundary conditions 1.1b, 1.3b wit v ε Ω = g, v Ω = g.
21 A C 0 IP mtod for a fourt ordr singular prturbation problm st 1. For tis tst, w calculat t rror v v ε for fixd =6E-3, wil varying ε. W coos our data so tat t xact solution is v = x + y. W solv.4 wit =6E-3, and list t rrors and rats of convrgnc in abl 6.1. Not tat by 5.4, for ε E-6, w av v v ε ε, C1 + σ ε ϕ H 1 Ω + v H 3 Ω C1 + σε 3 4 ϕ H1 Ω + v H3 Ω. is bavior is rflctd in abl 6.1, wr t scond column sows tat v v ε H 1 Ω = Oε 3 4 and t tird column sows tat v v ε, = Oε 1 4. Also, sinc v H3 Ω = 0, t stimats rad v v ε H1 Ω Cε σ ϕ L Ω, v v ε a, Cε 1 + σ ϕ L Ω. rfor, as ε 0 + and for fixd, w xpct to s linar convrgnc wit rspct to ε in all norms. Again, tis bavior is sn in t scond and tird columns of abl 6.1. abl 6.1 st 1. Error v v ε wit rspct to ε. =6E-3, σ = 0. ε v v ε L Ω rat v v ε H 1 Ω rat v v ε, rat 1.00E E E-01.85E E E E E E E E E E-04.93E E E E E E E E E E E E-06.55E E E E E E E E E E E E-08.05E E E E E E E E-09 8.E E E E E E E st. For tis tst, w fix a rlation = 4ε α wit α = 1, α = 1 3, and α = 1 4 and stimat t rat of convrgnc of t rror v vε wit rspct to ε. W st y x = 0, ϕ = 3x + y + x y + x 3 x x, g = x y = 0, 1 + y x = 1, 1 + x x y = 1, so tat t xact solution to t scond ordr problm 1.3 is v = x + y x.
22 S. C. BRENNER AND M. NEILAN By , w av v v ε H 1 Ω C1 + σ ε 1 α = 1 4 ϕ H 1 Ω + v H 3 Ω ε 3 α = 1 3 ε 3 4 α = 1, v v ε, C1 + σ ε 1 4 α = 1 4 ϕ H 1 Ω + v H 3 Ω ε 1 3 α = 1 3 ε 1 4 α = 1 All of ts xpctd rats of convrgnc ar obsrvd in abls abl 6. st a. Error v v ε wit rspct to ε. = 4ε 1, σ = 0. ε v v ε L Ω rat v v ε H 1 Ω rat v v ε, rat 1.00E E E E E+00.00E E-01.06E E E E E E E E E E E E E E E-0.11E E E abl 6.3 st b. Error v v ε wit rspct to ε. = 4ε 1 3, σ = 0. ε v v ε L Ω rat v v ε H 1 Ω rat v v ε, rat 1.00E E E E E E-04.3E E E E E E E E E E E-0.05E E E E-07.3E-0.06E E E abl 6.4 st c. Error v v ε wit rspct to ε. = 4ε 1 4, σ = 0. ε v v ε L Ω rat v v ε H 1 Ω rat v v ε, rat 1.00E-05.5E E E-0.06E E E-01.4E E E E E-0 4.5E E E E E E E E E-09.5E E E E
23 A C 0 IP mtod for a fourt ordr singular prturbation problm 3 REFERENCES [1] M. Ainswort and J.. Odn, A Postriori Error Estimation in Finit Elmnt Analysis, Wily-Intrscinc Jon Wily & Sons, 000. [] G. Awanou, Robustnss of a splin lmnt mtod wit constraints, J. Sci. Comput., , pp [3] G.A. Bakr, Finit lmnt mtods for lliptic quations using nonconforming lmnts, Mat. Comp., , pp [4] H. Blum and R. Rannacr, On t boundary valu problm of t biarmonic oprator on domains wit angular cornrs, Mat. Mtods Appl. Sci., 1980, pp [5] S.C. Brnnr and L.R. Scott, Matmatical ory of Finit Elmnt Mtods, tird dition, Springr, 008. [6] S.C. Brnnr and L.-Y. Sung, C 0 intrior pnalty mtods for fourt ordr lliptic boundary valu problms on polygonal domains, J. Sci. Comput., /3 005, pp [7] S.C. Brnnr,. Gudi, and L.-Y. Sung, An a postriori rror stimator for a quadratic C 0 intrior pnalty mtod for t biarmonic problm, IMA J. Numr. Anal., , pp [8] S.C. Brnnr,. Gudi, M. Nilan, and L.-Y. Sung, C 0 pnalty mtods for t fully nonlinar Mong-Ampèr quation, Mat. Comp., to appar. [9] P.G. Ciarlt, Finit Elmnt Mtod for Elliptic Problms. Nort-Holland, Amstrdam, [10] G. Engl, K. Garikipati,.J.R. Hugs, M.G. Larson, L. Mazzi, and R.L. aylor, Continuous/discontinuous finit lmnt approximations of fourt ordr lliptic problms in structural and continuum mcanics wit applications to tin bams and plats, and strain gradint lasticity, Comput. Mt. Appl. Mc. Eng., , pp [11] P. Grisvard, Elliptic Problms on Nonsmoot Domains, Pitman Publising Inc., [1]. Gudi, A nw rror analysis for discontinuous finit lmnt mtods for linar lliptic problms, Mat. Comp., , pp [13] I. Mozolvski and E. Süli, A priori rror analysis for t p-vrsion of t discontinuous Galrkin finit lmnt mtod for t biarmonic quation, Comput. Mtods Appl. Mat., 3 003, pp [14] I. Mozolvski, E. Süli, and P.R. Bösing, p-vrsion a priori rror analysis of intrior pnalty discontinuous Galrkin finit lmnt approximations to t biarmonic quation, J. Sci. Comput., , pp [15] L.S.D. Morly, triangular quilibrium lmnt in t solution of plat bnding problms, Aro. Quart., , pp [16].K. Nilssn, X.C. ai, and R. Wintr, A robust nonconforming H -lmnt, Mat Comp., , pp [17] B. Smpr, Conforming finit lmnt approximations for a fourt-ordr singular prturbation problm, SIAM J. Numr. Anal., 9 199, pp [18] B. Smpr, Locking in finit-lmnt approximations to long tin xtnsibl bams, IMA J. Numr. Anal., , pp [19] Z. Si, Error stimats of Morly lmnt, Mat. Numr. Sinica, , pp [0] R. Vrfürt A Postriori Error Estimation and Adaptiv Ms-Rfinmnt cniqus, Wily-ubnr, Cicstr, [1] M. Wang, J. Xu, and Y. Hu, Modifid Morly lmnt mtod for a fourt ordr lliptic singular prturbation problm, J. Comput. Mat., 4 006, pp [] M. Wang and Y. Hu, A robust finit lmnt mtod for 3-D lliptic singular prturbation problm, J. Comput. Mat., 5 007, pp [3] M. Wang, ncssity and sufficincy of t patc tst for t convrgnc of nonconforming finit lmnts, SIAM J. Numr. Anal., , pp Appndix A. Construction of Macro Bubbl Function. Lmma A.1. For any E i wit = +, tr xists a macro bubbl function χ suc tat χ + \ = 0, χ + \ = 0, n χ = 0, χ L + 1, χ ds.
24 4 S. C. BRENNER AND M. NEILAN Proof. Witout loss of gnrality, w may assum tat t dg is orizontal. First, w considr t cas wr + is t triangl wit vrtics 0, 0, 0.5, a, 1, 0, and is t triangl wit vrtics 0, 0, 0.5, a, 1, 0, wr a is som fixd positiv numbr. Hnc, is t lin sgmnt wit vrtics 0, 0 and 1, 0. W tn dfin χ P 8 + to b χ = y + ax y ax + a y + ax a y ax. A.1 It is asy to vrify tat χ vaniss up to t first ordr on + \ and tat n χ = 0, χ 0, χ L + = a 8. Nxt, w considr t gnral cas wr + = ABC, = ACD, and is t lin sgmnt AC s Figur A.1. Lt M b t midpoint of dg, and lt E rsp. F b t point on BC rsp. AD suc tat EM rsp. F M is prpndicular to AC. Witout loss of gnrality, w may assum tat EM F M. W tn st G to b t midpoint of EM and st H to b t point on t sgmnt F M suc tat HM = GM. On ACG ACH, w tak χ to b t scald vrsion of χ dfind by A.1. W not tat by construction χ vaniss up to t first ordr on AG, CG, CH, AH, and n χ = 0. On ac of t triangls AF H, CDH, BCG, and ABG, w tak χ to b t polynomial of dgr six so tat χ vaniss up to t first ordr on AF, F H, AH, CD, DH, CH, BC, CG, and BG, and χ quals on at t cntr of ac of t triangls. It follows from tis construction tat χ C 1 +, χ vaniss up to first ordr on + \, n χ = 0, and χ 0. Furtrmor, by scaling χ L + 1 and χ ds. Fig. A.1. Partition of macro bubbl function
UNIFIED ERROR ANALYSIS
 UNIFIED ERROR ANALYSIS LONG CHEN CONTENTS 1. Lax Equivalnc Torm 1 2. Abstract Error Analysis 2 3. Application: Finit Diffrnc Mtods 4 4. Application: Finit Elmnt Mtods 4 5. Application: Conforming Discrtization
UNIFIED ERROR ANALYSIS LONG CHEN CONTENTS 1. Lax Equivalnc Torm 1 2. Abstract Error Analysis 2 3. Application: Finit Diffrnc Mtods 4 4. Application: Finit Elmnt Mtods 4 5. Application: Conforming Discrtization
Journal of Computational and Applied Mathematics. An adaptive discontinuous finite volume method for elliptic problems
 Journal of Computational and Applid Matmatics 235 (2011) 5422 5431 Contnts lists availabl at ScincDirct Journal of Computational and Applid Matmatics journal ompag: www.lsvir.com/locat/cam An adaptiv discontinuous
Journal of Computational and Applid Matmatics 235 (2011) 5422 5431 Contnts lists availabl at ScincDirct Journal of Computational and Applid Matmatics journal ompag: www.lsvir.com/locat/cam An adaptiv discontinuous
A Weakly Over-Penalized Non-Symmetric Interior Penalty Method
 Europan Socity of Computational Mthods in Scincs and Enginring (ESCMSE Journal of Numrical Analysis, Industrial and Applid Mathmatics (JNAIAM vol.?, no.?, 2007, pp.?-? ISSN 1790 8140 A Wakly Ovr-Pnalizd
Europan Socity of Computational Mthods in Scincs and Enginring (ESCMSE Journal of Numrical Analysis, Industrial and Applid Mathmatics (JNAIAM vol.?, no.?, 2007, pp.?-? ISSN 1790 8140 A Wakly Ovr-Pnalizd
Another view for a posteriori error estimates for variational inequalities of the second kind
 Accptd by Applid Numrical Mathmatics in July 2013 Anothr viw for a postriori rror stimats for variational inqualitis of th scond kind Fi Wang 1 and Wimin Han 2 Abstract. In this papr, w giv anothr viw
Accptd by Applid Numrical Mathmatics in July 2013 Anothr viw for a postriori rror stimats for variational inqualitis of th scond kind Fi Wang 1 and Wimin Han 2 Abstract. In this papr, w giv anothr viw
A UNIFIED A POSTERIORI ERROR ESTIMATOR FOR FINITE VOLUME METHODS FOR THE STOKES EQUATIONS
 A UNIFIED A POSTERIORI ERROR ESTIMATOR FOR FINITE VOLUME METHODS FOR THE STOKES EQUATIONS JUNPING WANG, YANQIU WANG, AND XIU YE Abstract. In tis papr, t autors stablisd a unifid framwork for driving and
A UNIFIED A POSTERIORI ERROR ESTIMATOR FOR FINITE VOLUME METHODS FOR THE STOKES EQUATIONS JUNPING WANG, YANQIU WANG, AND XIU YE Abstract. In tis papr, t autors stablisd a unifid framwork for driving and
arxiv: v1 [math.na] 22 Oct 2010
![arxiv: v1 [math.na] 22 Oct 2010 arxiv: v1 [math.na] 22 Oct 2010](/thumbs/93/111835118.jpg) arxiv:10104563v1 [matna] 22 Oct 2010 ABSOLUTELY STABLE LOCAL DSCONTNUOUS GALERKN METHODS FOR THE HELMHOLTZ EQUATON WTH LARGE WAVE NUMBER XAOBNG FENG AND YULONG XNG Abstract Two local discontinuous Galrkin
arxiv:10104563v1 [matna] 22 Oct 2010 ABSOLUTELY STABLE LOCAL DSCONTNUOUS GALERKN METHODS FOR THE HELMHOLTZ EQUATON WTH LARGE WAVE NUMBER XAOBNG FENG AND YULONG XNG Abstract Two local discontinuous Galrkin
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Convergence analysis of a discontinuous Galerkin method with plane waves and Lagrange multipliers for the solution of Helmholtz problems
 Convrgnc analysis of a discontinuous Galrkin mtod wit plan wavs and Lagrang multiplirs for t solution of Hlmoltz problms Moamd Amara Laboratoir d Matématiqus Appliqués Univrsité d Pau t ds Pays d l Adour
Convrgnc analysis of a discontinuous Galrkin mtod wit plan wavs and Lagrang multiplirs for t solution of Hlmoltz problms Moamd Amara Laboratoir d Matématiqus Appliqués Univrsité d Pau t ds Pays d l Adour
ETNA Kent State University
 Elctronic Transactions on Numrical Analysis Volum 41, pp 262-288, 2014 Copyrigt 2014, Knt Stat Univrsity ISSN 1068-9613 ETNA Knt Stat Univrsity ttp://tnamatkntdu A UNIFIED ANALYSIS OF THREE FINITE ELEMENT
Elctronic Transactions on Numrical Analysis Volum 41, pp 262-288, 2014 Copyrigt 2014, Knt Stat Univrsity ISSN 1068-9613 ETNA Knt Stat Univrsity ttp://tnamatkntdu A UNIFIED ANALYSIS OF THREE FINITE ELEMENT
A ROBUST NONCONFORMING H 2 -ELEMENT
 MAHEMAICS OF COMPUAION Volum 70, Numbr 234, Pags 489 505 S 0025-5718(00)01230-8 Articl lctronically publishd on Fbruary 23, 2000 A ROBUS NONCONFORMING H 2 -ELEMEN RYGVE K. NILSSEN, XUE-CHENG AI, AND RAGNAR
MAHEMAICS OF COMPUAION Volum 70, Numbr 234, Pags 489 505 S 0025-5718(00)01230-8 Articl lctronically publishd on Fbruary 23, 2000 A ROBUS NONCONFORMING H 2 -ELEMEN RYGVE K. NILSSEN, XUE-CHENG AI, AND RAGNAR
3-2-1 ANN Architecture
 ARTIFICIAL NEURAL NETWORKS (ANNs) Profssor Tom Fomby Dpartmnt of Economics Soutrn Mtodist Univrsity Marc 008 Artificial Nural Ntworks (raftr ANNs) can b usd for itr prdiction or classification problms.
ARTIFICIAL NEURAL NETWORKS (ANNs) Profssor Tom Fomby Dpartmnt of Economics Soutrn Mtodist Univrsity Marc 008 Artificial Nural Ntworks (raftr ANNs) can b usd for itr prdiction or classification problms.
Symmetric Interior penalty discontinuous Galerkin methods for elliptic problems in polygons
 Symmtric Intrior pnalty discontinuous Galrkin mthods for lliptic problms in polygons F. Müllr and D. Schötzau and Ch. Schwab Rsarch Rport No. 2017-15 March 2017 Sminar für Angwandt Mathmatik Eidgnössisch
Symmtric Intrior pnalty discontinuous Galrkin mthods for lliptic problms in polygons F. Müllr and D. Schötzau and Ch. Schwab Rsarch Rport No. 2017-15 March 2017 Sminar für Angwandt Mathmatik Eidgnössisch
Symmetric Interior Penalty Galerkin Method for Elliptic Problems
 Symmtric Intrior Pnalty Galrkin Mthod for Elliptic Problms Ykatrina Epshtyn and Béatric Rivièr Dpartmnt of Mathmatics, Univrsity of Pittsburgh, 3 Thackray, Pittsburgh, PA 56, U.S.A. Abstract This papr
Symmtric Intrior Pnalty Galrkin Mthod for Elliptic Problms Ykatrina Epshtyn and Béatric Rivièr Dpartmnt of Mathmatics, Univrsity of Pittsburgh, 3 Thackray, Pittsburgh, PA 56, U.S.A. Abstract This papr
Introduction to Arithmetic Geometry Fall 2013 Lecture #20 11/14/2013
 18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
An interior penalty method for a two dimensional curl-curl and grad-div problem
 ANZIAM J. 50 (CTAC2008) pp.c947 C975, 2009 C947 An intrior pnalty mthod for a two dimnsional curl-curl and grad-div problm S. C. Brnnr 1 J. Cui 2 L.-Y. Sung 3 (Rcivd 30 Octobr 2008; rvisd 30 April 2009)
ANZIAM J. 50 (CTAC2008) pp.c947 C975, 2009 C947 An intrior pnalty mthod for a two dimnsional curl-curl and grad-div problm S. C. Brnnr 1 J. Cui 2 L.-Y. Sung 3 (Rcivd 30 Octobr 2008; rvisd 30 April 2009)
NONCONFORMING FINITE ELEMENTS FOR REISSNER-MINDLIN PLATES
 NONCONFORMING FINITE ELEMENTS FOR REISSNER-MINDLIN PLATES C. CHINOSI Dipartimnto di Scinz Tcnologi Avanzat, Univrsità dl Pimont Orintal, Via Bllini 5/G, 5 Alssandria, Italy E-mail: chinosi@mfn.unipmn.it
NONCONFORMING FINITE ELEMENTS FOR REISSNER-MINDLIN PLATES C. CHINOSI Dipartimnto di Scinz Tcnologi Avanzat, Univrsità dl Pimont Orintal, Via Bllini 5/G, 5 Alssandria, Italy E-mail: chinosi@mfn.unipmn.it
Discontinuous Galerkin Approximations for Elliptic Problems
 Discontinuous Galrkin Approximations for lliptic Problms F. Brzzi, 1,2 G. Manzini, 2 D. Marini, 1,2 P. Pitra, 2 A. Russo 2 1 Dipartimnto di Matmatica Univrsità di Pavia via Frrata 1 27100 Pavia, Italy
Discontinuous Galrkin Approximations for lliptic Problms F. Brzzi, 1,2 G. Manzini, 2 D. Marini, 1,2 P. Pitra, 2 A. Russo 2 1 Dipartimnto di Matmatica Univrsità di Pavia via Frrata 1 27100 Pavia, Italy
AS 5850 Finite Element Analysis
 AS 5850 Finit Elmnt Analysis Two-Dimnsional Linar Elasticity Instructor Prof. IIT Madras Equations of Plan Elasticity - 1 displacmnt fild strain- displacmnt rlations (infinitsimal strain) in matrix form
AS 5850 Finit Elmnt Analysis Two-Dimnsional Linar Elasticity Instructor Prof. IIT Madras Equations of Plan Elasticity - 1 displacmnt fild strain- displacmnt rlations (infinitsimal strain) in matrix form
arxiv: v1 [math.na] 8 Oct 2008
![arxiv: v1 [math.na] 8 Oct 2008 arxiv: v1 [math.na] 8 Oct 2008](/thumbs/92/110210656.jpg) DISCONTINUOUS GALERKIN METHODS FOR THE HELMHOLTZ EQUATION WITH LARGE WAVE NUMBER XIAOBING FENG AND HAIJUN WU arxiv:080.475v [mat.na] 8 Oct 008 Abstract. Tis papr dvlops and analyzs som intrior pnalty discontinuous
DISCONTINUOUS GALERKIN METHODS FOR THE HELMHOLTZ EQUATION WITH LARGE WAVE NUMBER XIAOBING FENG AND HAIJUN WU arxiv:080.475v [mat.na] 8 Oct 008 Abstract. Tis papr dvlops and analyzs som intrior pnalty discontinuous
Finite element approximation of Dirichlet boundary control for elliptic PDEs on two- and three-dimensional curved domains
 Finit lmnt approximation of Diriclt boundary control for lliptic PDEs on two- and tr-dimnsional curvd domains Klaus Dcklnick, Andras Güntr & Mical Hinz Abstract: W considr t variational discrtization of
Finit lmnt approximation of Diriclt boundary control for lliptic PDEs on two- and tr-dimnsional curvd domains Klaus Dcklnick, Andras Güntr & Mical Hinz Abstract: W considr t variational discrtization of
arxiv: v1 [math.na] 11 Dec 2014
![arxiv: v1 [math.na] 11 Dec 2014 arxiv: v1 [math.na] 11 Dec 2014](/thumbs/81/82945957.jpg) DISCRETE KORN S INEQUALITY FOR SHELLS SHENG ZHANG arxiv:14123654v1 [matna] 11 Dc 2014 Abstract W prov Korn s inqualitis for Nagdi and Koitr sll modls dfind on spacs of discontinuous picwis functions Ty
DISCRETE KORN S INEQUALITY FOR SHELLS SHENG ZHANG arxiv:14123654v1 [matna] 11 Dc 2014 Abstract W prov Korn s inqualitis for Nagdi and Koitr sll modls dfind on spacs of discontinuous picwis functions Ty
A Family of Discontinuous Galerkin Finite Elements for the Reissner Mindlin plate
 A Family of Discontinuous Galrkin Finit Elmnts for th Rissnr Mindlin plat Douglas N. Arnold Franco Brzzi L. Donatlla Marini Sptmbr 28, 2003 Abstract W dvlop a family of locking-fr lmnts for th Rissnr Mindlin
A Family of Discontinuous Galrkin Finit Elmnts for th Rissnr Mindlin plat Douglas N. Arnold Franco Brzzi L. Donatlla Marini Sptmbr 28, 2003 Abstract W dvlop a family of locking-fr lmnts for th Rissnr Mindlin
arxiv: v1 [math.na] 3 Mar 2016
![arxiv: v1 [math.na] 3 Mar 2016 arxiv: v1 [math.na] 3 Mar 2016](/thumbs/81/83440133.jpg) MATHEMATICS OF COMPUTATION Volum 00, Numbr 0, Pags 000 000 S 0025-5718(XX)0000-0 arxiv:1603.01024v1 [math.na] 3 Mar 2016 RESIDUAL-BASED A POSTERIORI ERROR ESTIMATE FOR INTERFACE PROBLEMS: NONCONFORMING
MATHEMATICS OF COMPUTATION Volum 00, Numbr 0, Pags 000 000 S 0025-5718(XX)0000-0 arxiv:1603.01024v1 [math.na] 3 Mar 2016 RESIDUAL-BASED A POSTERIORI ERROR ESTIMATE FOR INTERFACE PROBLEMS: NONCONFORMING
1 Isoparametric Concept
 UNIVERSITY OF CALIFORNIA BERKELEY Dpartmnt of Civil Enginring Spring 06 Structural Enginring, Mchanics and Matrials Profssor: S. Govindj Nots on D isoparamtric lmnts Isoparamtric Concpt Th isoparamtric
UNIVERSITY OF CALIFORNIA BERKELEY Dpartmnt of Civil Enginring Spring 06 Structural Enginring, Mchanics and Matrials Profssor: S. Govindj Nots on D isoparamtric lmnts Isoparamtric Concpt Th isoparamtric
Uniformly stable discontinuous Galerkin discretization and robust iterative solution methods for the Brinkman problem
 www.oaw.ac.at Uniformly stabl discontinuous Galrin discrtization and robust itrativ solution mtods for t Brinman problm Q. Hong, J. Kraus RICAM-Rport 2014-36 www.ricam.oaw.ac.at UNIFORMLY STABLE DISCONTINUOUS
www.oaw.ac.at Uniformly stabl discontinuous Galrin discrtization and robust itrativ solution mtods for t Brinman problm Q. Hong, J. Kraus RICAM-Rport 2014-36 www.ricam.oaw.ac.at UNIFORMLY STABLE DISCONTINUOUS
A Family of Discontinuous Galerkin Finite Elements for the Reissner Mindlin Plate
 Journal of Scintific Computing, Volums 22 and 23, Jun 2005 ( 2005) DOI: 10.1007/s10915-004-4134-8 A Family of Discontinuous Galrkin Finit Elmnts for th Rissnr Mindlin Plat Douglas N. Arnold, 1 Franco Brzzi,
Journal of Scintific Computing, Volums 22 and 23, Jun 2005 ( 2005) DOI: 10.1007/s10915-004-4134-8 A Family of Discontinuous Galrkin Finit Elmnts for th Rissnr Mindlin Plat Douglas N. Arnold, 1 Franco Brzzi,
Christine Bernardi 1, Tomás Chacón Rebollo 1, 2,Frédéric Hecht 1 and Zoubida Mghazli 3
 ESAIM: MAN 4 008) 375 410 DOI: 10.1051/man:008009 ESAIM: Matmatical Modlling and Numrical Analysis www.saim-man.org MORTAR FINITE ELEMENT DISCRETIZATION OF A MODEL COUPLING DARCY AND STOES EQUATIONS Cristin
ESAIM: MAN 4 008) 375 410 DOI: 10.1051/man:008009 ESAIM: Matmatical Modlling and Numrical Analysis www.saim-man.org MORTAR FINITE ELEMENT DISCRETIZATION OF A MODEL COUPLING DARCY AND STOES EQUATIONS Cristin
H(curl; Ω) : n v = n
 A LOCALLY DIVERGENCE-FREE INTERIOR PENALTY METHOD FOR TWO-DIMENSIONAL CURL-CURL PROBLEMS SUSANNE C. BRENNER, FENGYAN LI, AND LI-YENG SUNG Abstract. An intrior pnalty mthod for crtain two-dimnsional curl-curl
A LOCALLY DIVERGENCE-FREE INTERIOR PENALTY METHOD FOR TWO-DIMENSIONAL CURL-CURL PROBLEMS SUSANNE C. BRENNER, FENGYAN LI, AND LI-YENG SUNG Abstract. An intrior pnalty mthod for crtain two-dimnsional curl-curl
APPROXIMATION THEORY, II ACADEMIC PRfSS. INC. New York San Francioco London. J. T. aden
 Rprintd trom; APPROXIMATION THORY, II 1976 ACADMIC PRfSS. INC. Nw York San Francioco London \st. I IITBRID FINIT L}ffiNT }ffithods J. T. adn Som nw tchniqus for dtrmining rror stimats for so-calld hybrid
Rprintd trom; APPROXIMATION THORY, II 1976 ACADMIC PRfSS. INC. Nw York San Francioco London \st. I IITBRID FINIT L}ffiNT }ffithods J. T. adn Som nw tchniqus for dtrmining rror stimats for so-calld hybrid
Construction of asymmetric orthogonal arrays of strength three via a replacement method
 isid/ms/26/2 Fbruary, 26 http://www.isid.ac.in/ statmath/indx.php?modul=prprint Construction of asymmtric orthogonal arrays of strngth thr via a rplacmnt mthod Tian-fang Zhang, Qiaoling Dng and Alok Dy
isid/ms/26/2 Fbruary, 26 http://www.isid.ac.in/ statmath/indx.php?modul=prprint Construction of asymmtric orthogonal arrays of strngth thr via a rplacmnt mthod Tian-fang Zhang, Qiaoling Dng and Alok Dy
A LOCALLY CONSERVATIVE LDG METHOD FOR THE INCOMPRESSIBLE NAVIER-STOKES EQUATIONS
 A LOCALLY CONSERVATIVE LDG METHOD FOR THE INCOMPRESSIBLE NAVIER-STOES EQUATIONS BERNARDO COCBURN, GUIDO ANSCHAT, AND DOMINI SCHÖTZAU Abstract. In this papr, a nw local discontinuous Galrkin mthod for th
A LOCALLY CONSERVATIVE LDG METHOD FOR THE INCOMPRESSIBLE NAVIER-STOES EQUATIONS BERNARDO COCBURN, GUIDO ANSCHAT, AND DOMINI SCHÖTZAU Abstract. In this papr, a nw local discontinuous Galrkin mthod for th
UNIFIED A POSTERIORI ERROR ESTIMATOR FOR FINITE ELEMENT METHODS FOR THE STOKES EQUATIONS
 UNIFIED A POSTERIORI ERROR ESTIMATOR FOR FINITE ELEMENT METHODS FOR THE STOKES EQUATIONS JUNPING WANG, YANQIU WANG, AND XIU YE Abstract. This papr is concrnd with rsidual typ a postriori rror stimators
UNIFIED A POSTERIORI ERROR ESTIMATOR FOR FINITE ELEMENT METHODS FOR THE STOKES EQUATIONS JUNPING WANG, YANQIU WANG, AND XIU YE Abstract. This papr is concrnd with rsidual typ a postriori rror stimators
A LOCALLY DIVERGENCE-FREE INTERIOR PENALTY METHOD FOR TWO-DIMENSIONAL CURL-CURL PROBLEMS
 A LOCALLY DIVERGENCE-FREE INTERIOR PENALTY METHOD FOR TWO-DIMENSIONAL CURL-CURL PROBLEMS SUSANNE C. BRENNER, FENGYAN LI, AND LI-YENG SUNG Abstract. An intrior pnalty mthod for crtain two-dimnsional curl-curl
A LOCALLY DIVERGENCE-FREE INTERIOR PENALTY METHOD FOR TWO-DIMENSIONAL CURL-CURL PROBLEMS SUSANNE C. BRENNER, FENGYAN LI, AND LI-YENG SUNG Abstract. An intrior pnalty mthod for crtain two-dimnsional curl-curl
Rational Approximation for the one-dimensional Bratu Equation
 Intrnational Journal of Enginring & Tchnology IJET-IJES Vol:3 o:05 5 Rational Approximation for th on-dimnsional Bratu Equation Moustafa Aly Soliman Chmical Enginring Dpartmnt, Th British Univrsity in
Intrnational Journal of Enginring & Tchnology IJET-IJES Vol:3 o:05 5 Rational Approximation for th on-dimnsional Bratu Equation Moustafa Aly Soliman Chmical Enginring Dpartmnt, Th British Univrsity in
A POSTERIORI ERROR ESTIMATE FOR THE H(div) CONFORMING MIXED FINITE ELEMENT FOR THE COUPLED DARCY-STOKES SYSTEM
 A POSTERIORI ERROR ESTIMATE FOR THE Hdiv CONFORMING MIXED FINITE ELEMENT FOR THE COUPLED DARCY-STOKES SYSTEM WENBIN CHEN AND YANQIU WANG Abstract An Hdiv conforming mixd finit lmnt mtod as bn proposd for
A POSTERIORI ERROR ESTIMATE FOR THE Hdiv CONFORMING MIXED FINITE ELEMENT FOR THE COUPLED DARCY-STOKES SYSTEM WENBIN CHEN AND YANQIU WANG Abstract An Hdiv conforming mixd finit lmnt mtod as bn proposd for
Trigonometric functions
 Robrto s Nots on Diffrntial Calculus Captr 5: Drivativs of transcndntal functions Sction 5 Drivativs of Trigonomtric functions Wat you nd to know alrady: Basic trigonomtric limits, t dfinition of drivativ,
Robrto s Nots on Diffrntial Calculus Captr 5: Drivativs of transcndntal functions Sction 5 Drivativs of Trigonomtric functions Wat you nd to know alrady: Basic trigonomtric limits, t dfinition of drivativ,
dy 1. If fx ( ) is continuous at x = 3, then 13. If y x ) for x 0, then f (g(x)) = g (f (x)) when x = a. ½ b. ½ c. 1 b. 4x a. 3 b. 3 c.
 AP CALCULUS BC SUMMER ASSIGNMENT DO NOT SHOW YOUR WORK ON THIS! Complt ts problms during t last two wks of August. SHOW ALL WORK. Know ow to do ALL of ts problms, so do tm wll. Itms markd wit a * dnot
AP CALCULUS BC SUMMER ASSIGNMENT DO NOT SHOW YOUR WORK ON THIS! Complt ts problms during t last two wks of August. SHOW ALL WORK. Know ow to do ALL of ts problms, so do tm wll. Itms markd wit a * dnot
Direct Discontinuous Galerkin Method and Its Variations for Second Order Elliptic Equations
 DOI 10.1007/s10915-016-0264-z Dirct Discontinuous Galrkin Mthod and Its Variations for Scond Ordr Elliptic Equations Hongying Huang 1,2 Zhng Chn 3 Jin Li 4 Ju Yan 3 Rcivd: 15 Dcmbr 2015 / Rvisd: 10 Jun
DOI 10.1007/s10915-016-0264-z Dirct Discontinuous Galrkin Mthod and Its Variations for Scond Ordr Elliptic Equations Hongying Huang 1,2 Zhng Chn 3 Jin Li 4 Ju Yan 3 Rcivd: 15 Dcmbr 2015 / Rvisd: 10 Jun
On spanning trees and cycles of multicolored point sets with few intersections
 On spanning trs and cycls of multicolord point sts with fw intrsctions M. Kano, C. Mrino, and J. Urrutia April, 00 Abstract Lt P 1,..., P k b a collction of disjoint point sts in R in gnral position. W
On spanning trs and cycls of multicolord point sts with fw intrsctions M. Kano, C. Mrino, and J. Urrutia April, 00 Abstract Lt P 1,..., P k b a collction of disjoint point sts in R in gnral position. W
A robust multigrid method for discontinuous Galerkin discretizations of Stokes and linear elasticity equations
 www.oaw.ac.at A robust multigrid mtod for discontinuous Galrin discrtizations of Stos and linar lasticity quations Q. Hong, J. Kraus, J. Xu, L. Ziatanov RICAM-Rport 2013-19 www.ricam.oaw.ac.at A ROBUST
www.oaw.ac.at A robust multigrid mtod for discontinuous Galrin discrtizations of Stos and linar lasticity quations Q. Hong, J. Kraus, J. Xu, L. Ziatanov RICAM-Rport 2013-19 www.ricam.oaw.ac.at A ROBUST
Analysis of a Discontinuous Finite Element Method for the Coupled Stokes and Darcy Problems
 Journal of Scintific Computing, Volums and 3, Jun 005 ( 005) DOI: 0.007/s095-004-447-3 Analysis of a Discontinuous Finit Elmnt Mthod for th Coupld Stoks and Darcy Problms Béatric Rivièr Rcivd July 8, 003;
Journal of Scintific Computing, Volums and 3, Jun 005 ( 005) DOI: 0.007/s095-004-447-3 Analysis of a Discontinuous Finit Elmnt Mthod for th Coupld Stoks and Darcy Problms Béatric Rivièr Rcivd July 8, 003;
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Bifurcation Theory. , a stationary point, depends on the value of α. At certain values
 Dnamic Macroconomic Thor Prof. Thomas Lux Bifurcation Thor Bifurcation: qualitativ chang in th natur of th solution occurs if a paramtr passs through a critical point bifurcation or branch valu. Local
Dnamic Macroconomic Thor Prof. Thomas Lux Bifurcation Thor Bifurcation: qualitativ chang in th natur of th solution occurs if a paramtr passs through a critical point bifurcation or branch valu. Local
VSMN30 FINITA ELEMENTMETODEN - DUGGA
 VSMN3 FINITA ELEMENTMETODEN - DUGGA 1-11-6 kl. 8.-1. Maximum points: 4, Rquird points to pass: Assistanc: CALFEM manual and calculator Problm 1 ( 8p ) 8 7 6 5 y 4 1. m x 1 3 1. m Th isotropic two-dimnsional
VSMN3 FINITA ELEMENTMETODEN - DUGGA 1-11-6 kl. 8.-1. Maximum points: 4, Rquird points to pass: Assistanc: CALFEM manual and calculator Problm 1 ( 8p ) 8 7 6 5 y 4 1. m x 1 3 1. m Th isotropic two-dimnsional
Mathematics. Complex Number rectangular form. Quadratic equation. Quadratic equation. Complex number Functions: sinusoids. Differentiation Integration
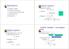 Mathmatics Compl numbr Functions: sinusoids Sin function, cosin function Diffrntiation Intgration Quadratic quation Quadratic quations: a b c 0 Solution: b b 4ac a Eampl: 1 0 a= b=- c=1 4 1 1or 1 1 Quadratic
Mathmatics Compl numbr Functions: sinusoids Sin function, cosin function Diffrntiation Intgration Quadratic quation Quadratic quations: a b c 0 Solution: b b 4ac a Eampl: 1 0 a= b=- c=1 4 1 1or 1 1 Quadratic
Discontinuous Galerkin and Mimetic Finite Difference Methods for Coupled Stokes-Darcy Flows on Polygonal and Polyhedral Grids
 Discontinuous Galrkin and Mimtic Finit Diffrnc Mthods for Coupld Stoks-Darcy Flows on Polygonal and Polyhdral Grids Konstantin Lipnikov Danail Vassilv Ivan Yotov Abstract W study locally mass consrvativ
Discontinuous Galrkin and Mimtic Finit Diffrnc Mthods for Coupld Stoks-Darcy Flows on Polygonal and Polyhdral Grids Konstantin Lipnikov Danail Vassilv Ivan Yotov Abstract W study locally mass consrvativ
Homotopy perturbation technique
 Comput. Mthods Appl. Mch. Engrg. 178 (1999) 257±262 www.lsvir.com/locat/cma Homotopy prturbation tchniqu Ji-Huan H 1 Shanghai Univrsity, Shanghai Institut of Applid Mathmatics and Mchanics, Shanghai 272,
Comput. Mthods Appl. Mch. Engrg. 178 (1999) 257±262 www.lsvir.com/locat/cma Homotopy prturbation tchniqu Ji-Huan H 1 Shanghai Univrsity, Shanghai Institut of Applid Mathmatics and Mchanics, Shanghai 272,
A POSTERIORI ERROR ESTIMATION FOR AN INTERIOR PENALTY TYPE METHOD EMPLOYING H(DIV) ELEMENTS FOR THE STOKES EQUATIONS
 A POSTERIORI ERROR ESTIMATION FOR AN INTERIOR PENALTY TYPE METHOD EMPLOYING H(DIV) ELEMENTS FOR THE STOKES EQUATIONS JUNPING WANG, YANQIU WANG, AND XIU YE Abstract. This papr stablishs a postriori rror
A POSTERIORI ERROR ESTIMATION FOR AN INTERIOR PENALTY TYPE METHOD EMPLOYING H(DIV) ELEMENTS FOR THE STOKES EQUATIONS JUNPING WANG, YANQIU WANG, AND XIU YE Abstract. This papr stablishs a postriori rror
Addition of angular momentum
 Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
SECTION where P (cos θ, sin θ) and Q(cos θ, sin θ) are polynomials in cos θ and sin θ, provided Q is never equal to zero.
 SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
3 Finite Element Parametric Geometry
 3 Finit Elmnt Paramtric Gomtry 3. Introduction Th intgral of a matrix is th matrix containing th intgral of ach and vry on of its original componnts. Practical finit lmnt analysis rquirs intgrating matrics,
3 Finit Elmnt Paramtric Gomtry 3. Introduction Th intgral of a matrix is th matrix containing th intgral of ach and vry on of its original componnts. Practical finit lmnt analysis rquirs intgrating matrics,
MAE4700/5700 Finite Element Analysis for Mechanical and Aerospace Design
 MAE4700/5700 Finit Elmnt Analysis for Mchanical and Arospac Dsign Cornll Univrsity, Fall 2009 Nicholas Zabaras Matrials Procss Dsign and Control Laboratory Sibly School of Mchanical and Arospac Enginring
MAE4700/5700 Finit Elmnt Analysis for Mchanical and Arospac Dsign Cornll Univrsity, Fall 2009 Nicholas Zabaras Matrials Procss Dsign and Control Laboratory Sibly School of Mchanical and Arospac Enginring
c 2007 Society for Industrial and Applied Mathematics
 SIAM J. NUMER. ANAL. Vol. 45, No. 3, pp. 1269 1286 c 2007 Socity for Industrial and Applid Mathmatics NEW FINITE ELEMENT METHODS IN COMPUTATIONAL FLUID DYNAMICS BY H (DIV) ELEMENTS JUNPING WANG AND XIU
SIAM J. NUMER. ANAL. Vol. 45, No. 3, pp. 1269 1286 c 2007 Socity for Industrial and Applid Mathmatics NEW FINITE ELEMENT METHODS IN COMPUTATIONAL FLUID DYNAMICS BY H (DIV) ELEMENTS JUNPING WANG AND XIU
Introduction to Condensed Matter Physics
 Introduction to Condnsd Mattr Physics pcific hat M.P. Vaughan Ovrviw Ovrviw of spcific hat Hat capacity Dulong-Ptit Law Einstin modl Dby modl h Hat Capacity Hat capacity h hat capacity of a systm hld at
Introduction to Condnsd Mattr Physics pcific hat M.P. Vaughan Ovrviw Ovrviw of spcific hat Hat capacity Dulong-Ptit Law Einstin modl Dby modl h Hat Capacity Hat capacity h hat capacity of a systm hld at
1973 AP Calculus AB: Section I
 97 AP Calculus AB: Sction I 9 Minuts No Calculator Not: In this amination, ln dnots th natural logarithm of (that is, logarithm to th bas ).. ( ) d= + C 6 + C + C + C + C. If f ( ) = + + + and ( ), g=
97 AP Calculus AB: Sction I 9 Minuts No Calculator Not: In this amination, ln dnots th natural logarithm of (that is, logarithm to th bas ).. ( ) d= + C 6 + C + C + C + C. If f ( ) = + + + and ( ), g=
Numerische Mathematik
 Numr. Math. 04 6:3 360 DOI 0.007/s00-03-0563-3 Numrisch Mathmatik Discontinuous Galrkin and mimtic finit diffrnc mthods for coupld Stoks Darcy flows on polygonal and polyhdral grids Konstantin Lipnikov
Numr. Math. 04 6:3 360 DOI 0.007/s00-03-0563-3 Numrisch Mathmatik Discontinuous Galrkin and mimtic finit diffrnc mthods for coupld Stoks Darcy flows on polygonal and polyhdral grids Konstantin Lipnikov
Supplementary Materials
 6 Supplmntary Matrials APPENDIX A PHYSICAL INTERPRETATION OF FUEL-RATE-SPEED FUNCTION A truck running on a road with grad/slop θ positiv if moving up and ngativ if moving down facs thr rsistancs: arodynamic
6 Supplmntary Matrials APPENDIX A PHYSICAL INTERPRETATION OF FUEL-RATE-SPEED FUNCTION A truck running on a road with grad/slop θ positiv if moving up and ngativ if moving down facs thr rsistancs: arodynamic
Space-Time Discontinuous Galerkin Method for Maxwell s Equations
 Commun. Comput. Pys. doi: 0.4208/cicp.23042.2722a Vol. 4, No. 4, pp. 96-939 Octobr 203 Spac-Tim Discontinuous Galrkin Mtod for Maxwll s Equations Ziqing Xi,2, Bo Wang 3,4, and Zimin Zang 5,6 Scool of Matmatics
Commun. Comput. Pys. doi: 0.4208/cicp.23042.2722a Vol. 4, No. 4, pp. 96-939 Octobr 203 Spac-Tim Discontinuous Galrkin Mtod for Maxwll s Equations Ziqing Xi,2, Bo Wang 3,4, and Zimin Zang 5,6 Scool of Matmatics
A SIMPLE FINITE ELEMENT METHOD OF THE CAUCHY PROBLEM FOR POISSON EQUATION. We consider the Cauchy problem for Poisson equation
 INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volum 14, Numbr 4-5, Pags 591 603 c 2017 Institut for Scintific Computing and Information A SIMPLE FINITE ELEMENT METHOD OF THE CAUCHY PROBLEM FOR
INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volum 14, Numbr 4-5, Pags 591 603 c 2017 Institut for Scintific Computing and Information A SIMPLE FINITE ELEMENT METHOD OF THE CAUCHY PROBLEM FOR
CPSC 665 : An Algorithmist s Toolkit Lecture 4 : 21 Jan Linear Programming
 CPSC 665 : An Algorithmist s Toolkit Lctur 4 : 21 Jan 2015 Lcturr: Sushant Sachdva Linar Programming Scrib: Rasmus Kyng 1. Introduction An optimization problm rquirs us to find th minimum or maximum) of
CPSC 665 : An Algorithmist s Toolkit Lctur 4 : 21 Jan 2015 Lcturr: Sushant Sachdva Linar Programming Scrib: Rasmus Kyng 1. Introduction An optimization problm rquirs us to find th minimum or maximum) of
Cramér-Rao Inequality: Let f(x; θ) be a probability density function with continuous parameter
 WHEN THE CRAMÉR-RAO INEQUALITY PROVIDES NO INFORMATION STEVEN J. MILLER Abstract. W invstigat a on-paramtr family of probability dnsitis (rlatd to th Parto distribution, which dscribs many natural phnomna)
WHEN THE CRAMÉR-RAO INEQUALITY PROVIDES NO INFORMATION STEVEN J. MILLER Abstract. W invstigat a on-paramtr family of probability dnsitis (rlatd to th Parto distribution, which dscribs many natural phnomna)
RELIABLE AND EFFICIENT A POSTERIORI ERROR ESTIMATES OF DG METHODS FOR A SIMPLIFIED FRICTIONAL CONTACT PROBLEM
 INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volum 16, Numbr 1, Pags 49 62 c 2019 Institut for Scintific Computing and Information RELIABLE AND EFFICIENT A POSTERIORI ERROR ESTIMATES OF DG
INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volum 16, Numbr 1, Pags 49 62 c 2019 Institut for Scintific Computing and Information RELIABLE AND EFFICIENT A POSTERIORI ERROR ESTIMATES OF DG
(Upside-Down o Direct Rotation) β - Numbers
 Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
2008 AP Calculus BC Multiple Choice Exam
 008 AP Multipl Choic Eam Nam 008 AP Calculus BC Multipl Choic Eam Sction No Calculator Activ AP Calculus 008 BC Multipl Choic. At tim t 0, a particl moving in th -plan is th acclration vctor of th particl
008 AP Multipl Choic Eam Nam 008 AP Calculus BC Multipl Choic Eam Sction No Calculator Activ AP Calculus 008 BC Multipl Choic. At tim t 0, a particl moving in th -plan is th acclration vctor of th particl
SCHUR S THEOREM REU SUMMER 2005
 SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
SCHUR S THEOREM REU SUMMER 2005 1. Combinatorial aroach Prhas th first rsult in th subjct blongs to I. Schur and dats back to 1916. On of his motivation was to study th local vrsion of th famous quation
10. The Discrete-Time Fourier Transform (DTFT)
 Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Case Study 1 PHA 5127 Fall 2006 Revised 9/19/06
 Cas Study Qustion. A 3 yar old, 5 kg patint was brougt in for surgry and was givn a /kg iv bolus injction of a muscl rlaxant. T plasma concntrations wr masurd post injction and notd in t tabl blow: Tim
Cas Study Qustion. A 3 yar old, 5 kg patint was brougt in for surgry and was givn a /kg iv bolus injction of a muscl rlaxant. T plasma concntrations wr masurd post injction and notd in t tabl blow: Tim
Elements of Statistical Thermodynamics
 24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
24 Elmnts of Statistical Thrmodynamics Statistical thrmodynamics is a branch of knowldg that has its own postulats and tchniqus. W do not attmpt to giv hr vn an introduction to th fild. In this chaptr,
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES
 BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim (implicit in notation and n a positiv intgr, lt ν(n dnot th xponnt of p in n, and U(n n/p ν(n, th unit
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim (implicit in notation and n a positiv intgr, lt ν(n dnot th xponnt of p in n, and U(n n/p ν(n, th unit
COHORT MBA. Exponential function. MATH review (part2) by Lucian Mitroiu. The LOG and EXP functions. Properties: e e. lim.
 MTH rviw part b Lucian Mitroiu Th LOG and EXP functions Th ponntial function p : R, dfind as Proprtis: lim > lim p Eponntial function Y 8 6 - -8-6 - - X Th natural logarithm function ln in US- log: function
MTH rviw part b Lucian Mitroiu Th LOG and EXP functions Th ponntial function p : R, dfind as Proprtis: lim > lim p Eponntial function Y 8 6 - -8-6 - - X Th natural logarithm function ln in US- log: function
COUNTING TAMELY RAMIFIED EXTENSIONS OF LOCAL FIELDS UP TO ISOMORPHISM
 COUNTING TAMELY RAMIFIED EXTENSIONS OF LOCAL FIELDS UP TO ISOMORPHISM Jim Brown Dpartmnt of Mathmatical Scincs, Clmson Univrsity, Clmson, SC 9634, USA jimlb@g.clmson.du Robrt Cass Dpartmnt of Mathmatics,
COUNTING TAMELY RAMIFIED EXTENSIONS OF LOCAL FIELDS UP TO ISOMORPHISM Jim Brown Dpartmnt of Mathmatical Scincs, Clmson Univrsity, Clmson, SC 9634, USA jimlb@g.clmson.du Robrt Cass Dpartmnt of Mathmatics,
A SPLITTING METHOD USING DISCONTINUOUS GALERKIN FOR THE TRANSIENT INCOMPRESSIBLE NAVIER-STOKES EQUATIONS
 ESAIM: MAN Vol. 39, N o 6, 005, pp. 5 47 DOI: 0.05/man:005048 ESAIM: Mathmatical Modlling and Numrical Analysis A SPLITTING METHOD USING DISCONTINUOUS GALERKIN FOR THE TRANSIENT INCOMPRESSIBLE NAVIER-STOKES
ESAIM: MAN Vol. 39, N o 6, 005, pp. 5 47 DOI: 0.05/man:005048 ESAIM: Mathmatical Modlling and Numrical Analysis A SPLITTING METHOD USING DISCONTINUOUS GALERKIN FOR THE TRANSIENT INCOMPRESSIBLE NAVIER-STOKES
Chapter 10. The singular integral Introducing S(n) and J(n)
 Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Difference -Analytical Method of The One-Dimensional Convection-Diffusion Equation
 Diffrnc -Analytical Mthod of Th On-Dimnsional Convction-Diffusion Equation Dalabav Umurdin Dpartmnt mathmatic modlling, Univrsity of orld Economy and Diplomacy, Uzbistan Abstract. An analytical diffrncing
Diffrnc -Analytical Mthod of Th On-Dimnsional Convction-Diffusion Equation Dalabav Umurdin Dpartmnt mathmatic modlling, Univrsity of orld Economy and Diplomacy, Uzbistan Abstract. An analytical diffrncing
Addition of angular momentum
 Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
NEW APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA
 NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
A Propagating Wave Packet Group Velocity Dispersion
 Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Lctur 8 Phys 375 A Propagating Wav Packt Group Vlocity Disprsion Ovrviw and Motivation: In th last lctur w lookd at a localizd solution t) to th 1D fr-particl Schrödingr quation (SE) that corrsponds to
Middle East Technical University Department of Mechanical Engineering ME 413 Introduction to Finite Element Analysis
 Middl East Tchnical Univrsity Dpartmnt of Mchanical Enginring ME 43 Introduction to Finit Elmnt Analysis Chaptr 3 Computr Implmntation of D FEM Ths nots ar prpard by Dr. Cünyt Srt http://www.m.mtu.du.tr/popl/cunyt
Middl East Tchnical Univrsity Dpartmnt of Mchanical Enginring ME 43 Introduction to Finit Elmnt Analysis Chaptr 3 Computr Implmntation of D FEM Ths nots ar prpard by Dr. Cünyt Srt http://www.m.mtu.du.tr/popl/cunyt
Finite element discretization of Laplace and Poisson equations
 Finit lmnt discrtization of Laplac and Poisson quations Yashwanth Tummala Tutor: Prof S.Mittal 1 Outlin Finit Elmnt Mthod for 1D Introduction to Poisson s and Laplac s Equations Finit Elmnt Mthod for 2D-Discrtization
Finit lmnt discrtization of Laplac and Poisson quations Yashwanth Tummala Tutor: Prof S.Mittal 1 Outlin Finit Elmnt Mthod for 1D Introduction to Poisson s and Laplac s Equations Finit Elmnt Mthod for 2D-Discrtization
DG Methods for Elliptic Equations
 DG Mthods for Elliptic Equations Part I: Introduction A Prsntation in Profssor C-W Shu s DG Sminar Andras löcknr Tabl of contnts Tabl of contnts 1 Sourcs 1 1 Elliptic Equations 1 11
DG Mthods for Elliptic Equations Part I: Introduction A Prsntation in Profssor C-W Shu s DG Sminar Andras löcknr Tabl of contnts Tabl of contnts 1 Sourcs 1 1 Elliptic Equations 1 11
1 Minimum Cut Problem
 CS 6 Lctur 6 Min Cut and argr s Algorithm Scribs: Png Hui How (05), Virginia Dat: May 4, 06 Minimum Cut Problm Today, w introduc th minimum cut problm. This problm has many motivations, on of which coms
CS 6 Lctur 6 Min Cut and argr s Algorithm Scribs: Png Hui How (05), Virginia Dat: May 4, 06 Minimum Cut Problm Today, w introduc th minimum cut problm. This problm has many motivations, on of which coms
COMPUTER GENERATED HOLOGRAMS Optical Sciences 627 W.J. Dallas (Monday, April 04, 2005, 8:35 AM) PART I: CHAPTER TWO COMB MATH.
 C:\Dallas\0_Courss\03A_OpSci_67\0 Cgh_Book\0_athmaticalPrliminaris\0_0 Combath.doc of 8 COPUTER GENERATED HOLOGRAS Optical Scincs 67 W.J. Dallas (onday, April 04, 005, 8:35 A) PART I: CHAPTER TWO COB ATH
C:\Dallas\0_Courss\03A_OpSci_67\0 Cgh_Book\0_athmaticalPrliminaris\0_0 Combath.doc of 8 COPUTER GENERATED HOLOGRAS Optical Scincs 67 W.J. Dallas (onday, April 04, 005, 8:35 A) PART I: CHAPTER TWO COB ATH
LINEAR DELAY DIFFERENTIAL EQUATION WITH A POSITIVE AND A NEGATIVE TERM
 Elctronic Journal of Diffrntial Equations, Vol. 2003(2003), No. 92, pp. 1 6. ISSN: 1072-6691. URL: http://jd.math.swt.du or http://jd.math.unt.du ftp jd.math.swt.du (login: ftp) LINEAR DELAY DIFFERENTIAL
Elctronic Journal of Diffrntial Equations, Vol. 2003(2003), No. 92, pp. 1 6. ISSN: 1072-6691. URL: http://jd.math.swt.du or http://jd.math.unt.du ftp jd.math.swt.du (login: ftp) LINEAR DELAY DIFFERENTIAL
AP Calculus BC AP Exam Problems Chapters 1 3
 AP Eam Problms Captrs Prcalculus Rviw. If f is a continuous function dfind for all ral numbrs and if t maimum valu of f() is 5 and t minimum valu of f() is 7, tn wic of t following must b tru? I. T maimum
AP Eam Problms Captrs Prcalculus Rviw. If f is a continuous function dfind for all ral numbrs and if t maimum valu of f() is 5 and t minimum valu of f() is 7, tn wic of t following must b tru? I. T maimum
Online Supplement: Advance Selling in a Supply Chain under Uncertain Supply and Demand
 Onlin Supplmnt Avanc Slling in a Supply Cain unr Uncrtain Supply an Dman. Proos o Analytical sults Proo o Lmma. Using a = minl 0 ; x g; w can rwrit () as ollows (x ; w ; x ; w ) = a +(m0 w )a +( +" x w
Onlin Supplmnt Avanc Slling in a Supply Cain unr Uncrtain Supply an Dman. Proos o Analytical sults Proo o Lmma. Using a = minl 0 ; x g; w can rwrit () as ollows (x ; w ; x ; w ) = a +(m0 w )a +( +" x w
Adrian Lew, Patrizio Neff, Deborah Sulsky, and Michael Ortiz
 AMRX Applid Mathmatics Rsarch Xprss 004, No. 3 Optimal V stimats for a Discontinuous Galrkin Mthod for Linar lasticity Adrian Lw, Patrizio Nff, Dborah Sulsky, and Michal Ortiz 1 Introduction Discontinuous
AMRX Applid Mathmatics Rsarch Xprss 004, No. 3 Optimal V stimats for a Discontinuous Galrkin Mthod for Linar lasticity Adrian Lw, Patrizio Nff, Dborah Sulsky, and Michal Ortiz 1 Introduction Discontinuous
16. Electromagnetics and vector elements (draft, under construction)
 16. Elctromagntics (draft)... 1 16.1 Introduction... 1 16.2 Paramtric coordinats... 2 16.3 Edg Basd (Vctor) Finit Elmnts... 4 16.4 Whitny vctor lmnts... 5 16.5 Wak Form... 8 16.6 Vctor lmnt matrics...
16. Elctromagntics (draft)... 1 16.1 Introduction... 1 16.2 Paramtric coordinats... 2 16.3 Edg Basd (Vctor) Finit Elmnts... 4 16.4 Whitny vctor lmnts... 5 16.5 Wak Form... 8 16.6 Vctor lmnt matrics...
2.3 Matrix Formulation
 23 Matrix Formulation 43 A mor complicatd xampl ariss for a nonlinar systm of diffrntial quations Considr th following xampl Exampl 23 x y + x( x 2 y 2 y x + y( x 2 y 2 (233 Transforming to polar coordinats,
23 Matrix Formulation 43 A mor complicatd xampl ariss for a nonlinar systm of diffrntial quations Considr th following xampl Exampl 23 x y + x( x 2 y 2 y x + y( x 2 y 2 (233 Transforming to polar coordinats,
perm4 A cnt 0 for for if A i 1 A i cnt cnt 1 cnt i j. j k. k l. i k. j l. i l
 h 4D, 4th Rank, Antisytric nsor and th 4D Equivalnt to th Cross Product or Mor Fun with nsors!!! Richard R Shiffan Digital Graphics Assoc 8 Dunkirk Av LA, Ca 95 rrs@isidu his docunt dscribs th four dinsional
h 4D, 4th Rank, Antisytric nsor and th 4D Equivalnt to th Cross Product or Mor Fun with nsors!!! Richard R Shiffan Digital Graphics Assoc 8 Dunkirk Av LA, Ca 95 rrs@isidu his docunt dscribs th four dinsional
Abstract Interpretation: concrete and abstract semantics
 Abstract Intrprtation: concrt and abstract smantics Concrt smantics W considr a vry tiny languag that manags arithmtic oprations on intgrs valus. Th (concrt) smantics of th languags cab b dfind by th funzcion
Abstract Intrprtation: concrt and abstract smantics Concrt smantics W considr a vry tiny languag that manags arithmtic oprations on intgrs valus. Th (concrt) smantics of th languags cab b dfind by th funzcion
Derangements and Applications
 2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
Calculus II (MAC )
 Calculus II (MAC232-2) Tst 2 (25/6/25) Nam (PRINT): Plas show your work. An answr with no work rcivs no crdit. You may us th back of a pag if you nd mor spac for a problm. You may not us any calculators.
Calculus II (MAC232-2) Tst 2 (25/6/25) Nam (PRINT): Plas show your work. An answr with no work rcivs no crdit. You may us th back of a pag if you nd mor spac for a problm. You may not us any calculators.
Recall that by Theorems 10.3 and 10.4 together provide us the estimate o(n2 ), S(q) q 9, q=1
 Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Division of Mechanics Lund University MULTIBODY DYNAMICS. Examination Name (write in block letters):.
 Division of Mchanics Lund Univrsity MULTIBODY DYNMICS Examination 7033 Nam (writ in block lttrs):. Id.-numbr: Writtn xamination with fiv tasks. Plas chck that all tasks ar includd. clan copy of th solutions
Division of Mchanics Lund Univrsity MULTIBODY DYNMICS Examination 7033 Nam (writ in block lttrs):. Id.-numbr: Writtn xamination with fiv tasks. Plas chck that all tasks ar includd. clan copy of th solutions
University of Washington Department of Chemistry Chemistry 453 Winter Quarter 2014 Lecture 20: Transition State Theory. ERD: 25.14
 Univrsity of Wasinton Dpartmnt of Cmistry Cmistry 453 Wintr Quartr 04 Lctur 0: Transition Stat Tory. ERD: 5.4. Transition Stat Tory Transition Stat Tory (TST) or ctivatd Complx Tory (CT) is a raction mcanism
Univrsity of Wasinton Dpartmnt of Cmistry Cmistry 453 Wintr Quartr 04 Lctur 0: Transition Stat Tory. ERD: 5.4. Transition Stat Tory Transition Stat Tory (TST) or ctivatd Complx Tory (CT) is a raction mcanism
A MULTI-DOMAIN SPECTRAL IPDG METHOD FOR HELMHOLTZ EQUATION WITH HIGH WAVE NUMBER. 1. Introduction
 A MULTI-DOMAI SPECTRAL IPDG METHOD FOR HELMHOLTZ EQUATIO WITH HIGH WAVE UMBER Lunji Song Scool of Matmatics and Statistics, Lanzou Univrsity, Lanzou 730000, Cina Email: song@lzu.du.cn Jing Zang Scool of
A MULTI-DOMAI SPECTRAL IPDG METHOD FOR HELMHOLTZ EQUATIO WITH HIGH WAVE UMBER Lunji Song Scool of Matmatics and Statistics, Lanzou Univrsity, Lanzou 730000, Cina Email: song@lzu.du.cn Jing Zang Scool of
is an appropriate single phase forced convection heat transfer coefficient (e.g. Weisman), and h
 For t BWR oprating paramtrs givn blow, comput and plot: a) T clad surfac tmpratur assuming t Jns-Lotts Corrlation b) T clad surfac tmpratur assuming t Tom Corrlation c) T clad surfac tmpratur assuming
For t BWR oprating paramtrs givn blow, comput and plot: a) T clad surfac tmpratur assuming t Jns-Lotts Corrlation b) T clad surfac tmpratur assuming t Tom Corrlation c) T clad surfac tmpratur assuming
Section 11.6: Directional Derivatives and the Gradient Vector
 Sction.6: Dirctional Drivativs and th Gradint Vctor Practic HW rom Stwart Ttbook not to hand in p. 778 # -4 p. 799 # 4-5 7 9 9 35 37 odd Th Dirctional Drivativ Rcall that a b Slop o th tangnt lin to th
Sction.6: Dirctional Drivativs and th Gradint Vctor Practic HW rom Stwart Ttbook not to hand in p. 778 # -4 p. 799 # 4-5 7 9 9 35 37 odd Th Dirctional Drivativ Rcall that a b Slop o th tangnt lin to th
L ubomír Baňas 1 and Robert Nürnberg Introduction A POSTERIORI ESTIMATES FOR THE CAHN HILLIARD EQUATION WITH OBSTACLE FREE ENERGY
 ESAIM: MAN 43 (009) 1003 106 DOI: 10.1051/man/009015 ESAIM: Mathmatical Modlling and Numrical Analysis www.saim-man.org A POSERIORI ESIMAES FOR HE CAHN HILLIARD EQUAION WIH OBSACLE FREE ENERGY L ubomír
ESAIM: MAN 43 (009) 1003 106 DOI: 10.1051/man/009015 ESAIM: Mathmatical Modlling and Numrical Analysis www.saim-man.org A POSERIORI ESIMAES FOR HE CAHN HILLIARD EQUAION WIH OBSACLE FREE ENERGY L ubomír
