NOTE ON CURVE AND SURFACE ENERGIES
|
|
|
- Beverly Fleming
- 5 years ago
- Views:
Transcription
1 NOTE ON CURVE AND SURFACE ENERGIES JOHANNES WALLNER ASTRACT. Energies of curves and surfaces together with their discrete variants play a prominent role as fairness functionals in geometric modeling and computer aided geometric design. This paper deals with a particular discrete surface energy which is expressible in terms of curve energies, and which occurs naturally in the problem of smoothing digital elevation data with tolerance zone constraints. We also discuss geometrically meaningful surface energies in general from the viewpoint of invariant theory, and the role of the Gauss-onnet theorem. 1. A FAIRING PROLEM WITH HARD CONSTRAINTS For a the polyline p with vertices p i we consider the discrete linearized bending energy (1) E 2 (p) = 2 p i 2, where the forward difference operator is defined by p i = p i+1 p i, which implies 2 p i = p i+2 2p i+1 + p i. This energy functional occurs e.g. in the context of energy-minimizing curves and curve networks (cf. Hofer and Pottmann (2004) and Wallner et al. (2005)). Hofer et al. (2005) apply energy-minimizing curve networks to the problem of smoothing digital elevation data, as described below. Suppose that a terrain is modeled by a rectangular grid of points p i j = (x i j,y i j,z i j ), with i = 0,...,N and = 0,...,M. The x and y coordinates have the form (2) x i j = i δ x, y i j = j δ y (δ x,δ y > 0). So in fact the shape of the terrain is given only by the height field z i j. Terrain smoothing according to Hofer et al. (2005) starts with digital terrain data, i.e., a height field. Each vertex p i j is the center of its tolerance cylinder i j whose axis is parallel to the z-axis, and whose diameter and height typically is of the same magnitude as distances between vertices (see Fig. 1a). The problem dealt with in that paper is to compute a new height field z i j which is smoother than the original and describes a surface which passes through each tolerance cylinder. The latter condition is certainly fulfilled if p i j = (x i j,y i j,z i j ) i j, as visualized by Fig. 1b. ut there is a weaker condition which still implies the required property of the new height field: It is sufficient each cylinder is met either by a horizontal or a vertical grid lines. In other words, it is sufficient that for all i, j, the cylinder i j must intersect at least one of the four line segments p i j p i 1, j, p i j p i+1, j, p i j p i, j 1, p i j p i, j+1. It is easy to check if this condition is met. It is illustrated in Fig. 1c. Starting from a given terrain (Fig. 2a), a fairness functional is minimized such that the constraints described above are respected. An example of the result of such a process is shown by Fig. 2. 1
2 2 JOHANNES WALLNER (a) (b) FIGURE 1. (a) Initial state before smoothing. (b) Result of smoothing with one type of constraint. (c) Result of smoothing with relaxed constraint. (c) p r [ ] p s [ ] (a) p s [ ] p rs p s [ ] (b) FIGURE 2. (a) Contour lines visualizing a digital terrain, represented by grid of data points. The horizontal, vertical, and diagonal grid polylines which meet in some vertex p rs are shown. (b) The same model after smoothing (images taken from Hofer et al. (2005)). The particular nature of the problem studied in Hofer et al. (2005), especially the fact that the constraints are formulated in terms of polylines, leads to fairness functionals formulated in terms of polylines lying on the discrete digital terrain model. As above, assume that vertices p i j = (x i j,y i j,z i j ) with x i j and y i j as in (2) describe the terrain. We consider the horizontal grid polylines p α [ ], whose vertices are defined by (pα [ ] ) i = p iα. For each α, there is such a grid polyline, which lives inside a previously defined are of interest. The total sum of energies of the horizonal grid lines is denoted by E [ ]. In a similar way we define polylines p α [ ], pα [ ], and pα [ ] : (3) (p α [ ] ) i = p i,α, (p α [ ] ) i = p α,i, (p α [ ] ) i = p α+i,i, (p α [ ] ) i = p α i,i. The total sums of energies of the vertical and the two types of diagonal grid polylines are denoted by they symbols E [ ], E [ ], and E [ ], respectively. It is one of the purposes of this paper to show why (4) E = E [ ] + E [ ] (E [ ]E [ ] ) is a geometrically meaningful discrete surface energy.
3 NOTE ON CURVE AND SURFACE ENERGIES 3 2. DIFFERENTIAL GEOMETRY FACTS Here we summarize some facts of Differential Geometry, whose proofs can be found in do Carmo (1976). Suppose a surface in Euclidean space contains a domain with piecwise C 2 boundary curve c of length L. An arc length parametrization of c is indicated by writing c(s). Each point p of the surface has a unit normal vector n(p). The mapping p n(p) is smooth, if the surface is C 2. Rotation by 90 degrees in the tangent plane of p is effected by X X = n(p) X. The two principal curvatures, Gaussian curvature, and mean curvatures in a point p of the surface under consideration are denoted by κ 1 (p),κ 2 (p), K(p) and H(p), respectively Angular velocities. Recall that the angular velocity of a time-dependent unit vector X(t) in the Euclidean plane is given by X(t) = Ẋ,X, where u,v denotes the scalar product of the vectors u,v, and the dot indicates differentiation. If c(t) is a curve in a given surface and X(t) is a unit vector tangent to the that surface in the point c(t), then this vector field s angular velocity and total turning angle in the interval t [a,b] are defined by (5) X := Ẋ,X = det(x,ẋ,n c), b a X(t) = b a X(t) dt. The geometric interpretation of is as follows: If Y (t) is a unit vector field along the same curve obtained by geodesic parallel transport, such that X = cosφ Y + sinφ Y, then φ = X. The usage of the symbol X(t) implies knowledge of of the surface s normal vector in the point which X(t) it is attached to. It is elementary that the total turning angle is invariant in the following sense: If t = f (t) is a transformation of the curve parameter and X (t ) := X( f (t)) is the transformed vector field, then b a X = b a X Geodesic curvature. The geodesic curvature κ g (s) of the curve c(s) is the angular velocity of ċ(s) when c is parametrized by arc length: κ g (s) = ċ(s) = det(ċ(s), c(s),n(c(s))). There are only finitely many parameter values s = s 1,s 2,... where the curve c is not twice differentiable, and where the tangent vector ċ possibly jumps. The angle of this jump, measured with respect to the orientation provided by the surface s normal vector n(c(s)), is denoted by s s ċ. We assume that arc length parametrization of c is such that the vector n(c(s)) ċ(s) points towards the inside of. Suppose a unit vector field Y is defined globally in and even a bit outside (i.e., in a neighbourhood of ). Then the following equation holds: I I (6) L 0 Y (s) = Y (s) = κ g (s)ds + s [0,L) s s(ċ) 2π. c c Here the H c sign means that we integrate along the entire closed curve c, e.g. from s = 0 to s = L. It is important that both the geodesic curvature and the turning angles use only first derivatives of the surface, viz., the normal vectors Willmore energy and the Gauss-onnet formula. For the domain, its boundary curve c =, and any globally defined vector field Y as above, we have the famous integral formula of Gauss-onnet, which relates the surface integral of Gaussian curvature with a curve integral. (7) K = L 0(Y ).
4 4 JOHANNES WALLNER The form which is usually given is retrieved from (7) via (6). The symbol means the surface area integral. As is well known, (7) can be used for identifying a boundary component in quadratic energy functionals involving the principal curvatures. An example of this is the Willmore energy (see e.g. Clarenz et al. (2004)): (8) W() = ( 1 2 (κ 1 κ 2 )) 2 = (H 2 K) = H 2 + L 0(Y ). Here Y is an arbitrary globally defined vector field, as in (7). If the curve c is considered fixed, while the surface is subject to variation, this splitting identifies a part of the Willmore energy which depends on the actual second derivates of the surface (the H 2 part), and a part which solely depends on the surface s normal vectors along (the K part). 3. GRAPH SURFACES We now consider a surface which is the graph of a C 3 function f defined in an open subset of R 2. This means that the surface is parametrized by g(u,v) = (u,v, f (u,v)). It is easy to compute normal vector n, Gaussian curvature K, and mean curvature H for such graph surfaces. The result is given below, after some notation has been introduced. Differentiation with respect to u and v is indicated by subscripts. D := 1 + f,u 2 + f,v, 2 n(u,v) = D 1/2 [ f,u, f,v,1], Hess( f ) := [ f,uu f ] (9),uv f,uv f,,vv K = D 2 dethess( f ), H = 1 ( (10) 2 D 3/2 f + f,uu f,v 2 2 f,u f,v f,uv + f,vv f,u) 2. Later we use the vector field Y = g,u / g,u, which expands to Y = (1 + f 2,u) 1 2 [1,0, f,u ] First order approximation for almost flat surfaces. In view of the applications considered below, we are mainly interested in the case the first derivatives of f are small: (11) f,u 1, f,v 1 = f 2,u 0, f,u f,v 0, f 2,v 0; but we don t require the same of the second derivatives. The reason why we consider that particular type of surface is that we are going to use graph surfaces as mathematical description of a piece of topography, which for large parts of the earth is rather flat. The exact meaning of the symbol is that of equality up to an additive constant of magnitude o( f,u 2 + f,v), 2 or more precisely, O( f,u 2 + f,v) 2 as f,u, f,v 0. In order to compute the angular velocity of Y along the curve c, we evaluate Ẏ = uy,u + vy,v and compute det(y,ẏ,n): (12) Y,u [ f,u f,uu,0, f,uu ], Y,v [ f,u f,uv,0, f,uv ], (Y ) u f,v f,uu + v f,v f,uv. According to (10), Gaussian and mean curvature are approximated by (13) K K = f,uu f,vv f 2,uv = dethess( f ), H H = 1 2 ( f,uu + f,vv ) = 1 2 f. We use the surface parametrization g to define the domain and its boundary c in R 2 by = g() and c(s) = g(c(s)), and rewrite the surface integral of the Gaussian curvature in a form which allows
5 to apply Green s theorem: dethess( f ) (14) K = 3/2 dudv NOTE ON CURVE AND SURFACE ENERGIES 5 This expression can now be converted into a curve integral: I I (15) K dudv = f,uu f,v du + f,uv f,v dv = c K dudv = (( f,uu f,v ),v ( f,uv f,v ),u )dudv. c f,v d( f,u c). This is exactly the first order approximant of the Gauss-onnet formula (7), if we adopt the first order approximants of K and (Y ) from above. Y was rather arbitrary, except that for different Y s Green s theorem may yield different approximations for the turning angle. In case the support of f is contained in, we have f,u = f,v = 0 for all boundary points. This results in R K = 0, W() = R H2, R K dudv = Curve energies. The curve c : I R 3 has the linearized bending energy (16) E 2 (c) = c(t) 2 dt. I It is well known that minimizers of E 2 under interpolation conditions are the cubic -spline curves. We are interested in the energies of special curves contained in a graph surface with parametrization g(u,v) = (u,v, f (u,v)): Assume that c(t) = g(u 0 + at,v 0 + bt). It follows that the energy of such a curve can be written as (17) E 2 (c) = [a,b] Hess( f ) I u=u0 +at v=v 0 +bt [ a ] b dt. Later we establish a connection between curve energies and surface energies, where curves of that special form occur Invariants of the Hessian. A different choice of a Cartesian coordinate system in the parameter domain causes a change of coordinates (u,v) (u,v ) and consequently f transforms to f (u,v ) := f (u(u,v ),v(u,v )): [ u ] [ u ] [ u0 ] [ cosφ sinφ ] (18) v =M v + v, M = 0 sinφ cosφ. The Hessian changes as follows: (19) Hess( f )(u,v ) = M T Hess( f )(u,v)m. It is well known that trace and determinant (or equivalently, the unordered pair of eigenvalues) constitute a complete system of invariants with respect to the planar rotation group when acting in this way on symmetric 2 2 matrices. Moreover it is easy to show that {tr 2,det} is a basis of the linear space of quadratic homogeneous invariant polynomials in the three indeterminates f,uu, f,uv, f,vv. In view of (Equ. 13), also the approximate curvatures can be used to give a basis {H 2,K} of that space. This is summarized by the following theorem, whose proof, for the convenience of the reader, is repeated in section 5.
6 6 JOHANNES WALLNER Theorem 1. A polynomial p defined in the space of symmetric n by n matrices with the property that p(g T xg) = p(x) for all orthogonal matrices g is expressible as a polynomial in the coefficients of the characteristic polynomial of x. It follows that for 2 by 2 matrices, any such invariant polynomial is expressible in terms of determinant and trace Combined curve energies. The following theorem expresses surface energies in terms of curve energies. ecause the surface energy itself is an area integral, we cannot expect that a finite number of curves defines a surface energy. Rather, we consider families of curves which cover the surface under consideration, and integrate over the energies computed from each of them. Th. 2 is the basis of a discretization discussed in Section 4. Theorem 2. Assume that is a planar domain and f is a C 2 function as above. Consider the surface parametrization g(u,v) = (u,v, f (u,v)), and its approximate curvatures K(u,v) and H(u,v) according to (13). For each α R, there are curves c 1,α (t) = g(t,α), c 2,α (t) = g(α,t), c 3,α (t) = g(α + t,t), and c 4,α (t) = g(α + t, t). These curves comprise the mesh of the u and v parameter lines, together with the diagonals of that mesh. Then (20) 8 (3H 2 K)dudv = (4E 2 (c 1,α ) + 4E 2 (c 2,α ) + E 2 (c 3,α ) + E 2 (c 4,α ))dα. α Each curve energy is computed by integration over that part of the real axis which corresponds to the points contained in. Up to a common factor, this is the only linear combination of the energies of curves c i,α which results in an invariant surface energy. Proof. We expand the right hand side of (20) according to (17) and make the following changes of variables in the four respective integrals: (t,α) = (u,v), (α,t) = (u,v), (α + t,t) = (u,v), (α + t, t) = (u,v). We get r.h.s. = 4 ( f,uu (t,α) 2 dt)dα + 4 α t + ( ( f,uu + 2 f,uv + f,vv ) α t α 2 (u,v)= (α+t,t) ( t f,vv (α,t) 2 dt)dα dt)dα + ( ( f,uu 2 f,uv + f,vv ) = (4 f,uu f,vv 2 + ( f,uu + 2 f,uv + f,vv ) 2 + ( f,uu 2 f,uv + f,vv ) 2 )dudv = (24H 2 8K)dudv. α t 2 (u,v)= (α+t,t) dt)dα The last equality follows from the definition of H and K. Now we consider the uniqueness question. We ask which linear combations of the form λ i E 2 (c i,α ) yield a meaningful surface energy, i.e., one whose definition is invariant under rotation of the coordinate system. In view of Th. 1, this boils down to the question which linear combinations of the form λ i c i 2 are also linear combinations of K and H 2. We express the norms of second derivatives of curves in terms of the Hessian: (21) c 1 2 = f 2,uu, c 2 2 = f 2,vv, c 3,4 2 = ( f,uu ± 2 f,uv + f,vv ) 2.
7 NOTE ON CURVE AND SURFACE ENERGIES 7 Then we solve the equation (22) 4 i=1 λ i c i 2 = σh 2 + τk λ 1 f 2,uu + λ 2 f 2,vv + λ 3 ( f,uu + 2 f,uv + f,vv ) 2 + λ 3 ( f,uu 2 f,uv + f,vv ) 2 = σ( f,uu + f,vv ) 2 /4 + τ( f,uu f,vv f 2,uv). Its solution, as stated in the theorem, is given by [λ 1,...,λ 4,σ,τ] = t[4,4,1,1, 24,8] (t R). 4. DISCRETIATION Th. 2 shows that a certain integral of curve energies yields a geometrically meaningful surface energy. It is easy to discretize that integral: A discretization of the linearized bending energy of (16) is given by (1). Integrating over dα in (20) is discretized by taking polylines which correspond to equidistant values of α. For a regular height field as described in the beginning, this results in summing up the curve energies of horizontal, vertical, and diagonal grid lines as already written down in (4). In explicit form, the discrete fairness functional reads (23) E = i, j ( (zi, j+1 2z i j + z i, j 1 ) 2 + (z i+1, j 2z i j + z i 1, j ) (z i+1, j+1 2z i j + z i 1, j 1 ) (z i+1, j 1 2z i j + z i 1, j+1 ) 2), Here an index pair i, j occurs only if all index pairs which contribute to the sum are within range. 5. APPENDIX: QUADRATIC INVARIANTS OF SYMMETRIC MATRICES In this paper we use properties of the Hessian of a C 2 function which are invariant with respect to a change of the Cartesian coordinate system in use. We are especially interested in polynomials of the Hesse matrix which have this property. The well known result of Th. 1 gives the required answers. Its proof on the basis of properties of elementary symmetric functions is shown below. Proof. (of Th. 1) We generally use the notation R[V ] for the ring of real polynomials defined in the vector space V, and R[X 1,...,X n ] if X i denote coordinates in such a space. The latter notation is used if we want to explicitly write p(x 1,...,X n ) for a polynomial contained in that polynomial ring. The characteristic polynomial of a symmetric matrix x reads det(x te n ) = n j=0 a j(x)t j, which defines the coefficient polynomials a j R[M symm ]. For instance, we have a 0 (x) = detx. For a diagonal matrix x = diag(t 1,..., t n ), it is elementary that a j (x) = ( 1) j s n j (t 1,..., t n ), where s i R[t 1,...,t n ] is the i-th elementary symmetric function of n variables: s 0 (t 1,...,t n ) = 1, s 1 (t 1,...,t n ) = t 1 + +t n, s 2 (t 1,...,t n ) = t i t j,... s n (t 1,...,t n ) = t 1 t n. i< j We know that for any x,y M symm there exists an orthogonal matrix g with y = g T xg if and only if the characteristic polynomials of x and y agree. It follows that a 0,...,a n are invariant polynomials. Now assume that p R[M symm ] is invariant. We define q R[t 1...,t n ] by q(t 1,..., t n ) = p(diag(t 1,..., t n )). For any permutation σ = (σ(1),...,σ(n)) of the numbers (1,...,n), there is an orthogonal matrix s such that for all vectors (t 1,..., t n ) T, we have (t σ(1),..., t σ(n) ) T = s (t 1,..., t n ) T. Then,
8 8 JOHANNES WALLNER s T diag(t 1,..., t n )s = diag(t σ(1),..., t σ(n) ). We see that permuting the diagonal elements by σ is effected by the action of an orthogonal matrix. As p was assumed invariant, q is invariant with respect to permutations of the variables t 1,...,t n. Sturmfels (1993) gives an algorithm to rewrite q as a polynomial in the elementary symmetry functions, i.e., there is r R[R n+1 ] such that (24) q(t 1,...,t n ) = r(s 0 (t 1,...,t n ),...,s n (t 1,...,t n )). We define the polynomial p R[M symm ] by (25) p (x) = r(a n (x), a n 1 (x),...,( 1) n a 0 (x)), which is invariant by construction, and it is chosen such that in case x is a diagonal matrix, p(x) = p (x). For every x M symm there is an orthogonal matrix g such that g T xg is a diagonal matrix. It follows that p(x) = p(g T xg) = p (g T xg) = p (x). These equalities follow, in turn, from invariance of p, the previous observation, and invariance of p. This concludes the proof of Th. 1. ACKNOWLEDGMENTS This research was supported by the Austrian Science Foundation (FWF) under grant number P REFERENCES Clarenz, U., Diewald, U., Dziuk, G., Rumpf, M., Rusu, R., A finite element method for surface restoration with smooth boundary conditions. Comput. Aided Geom. Design 21, do Carmo, M. P., Differential Geometry of Curves and Surfaces. Prentice-Hall, New York. Hofer, M., Pottmann, H., Energy-minimizing splines in manifolds. ACM Trans. Graphics 23 (3), , Proc. ACM SIGGRAPH Hofer, M., Sapiro, G., Wallner, J., August Fair polyline networks for constrained smoothing of digital terrain elevation data. IMA Preprint 2058, Univ. Minnesota. URL Sturmfels,., Algorithms in invariant theory. Texts and Monographs in Symbolic Computation. Springer-Verlag, Vienna. Wallner, J., Pottmann, H., Hofer, M., January Fair webs. Tech. Rep. 134, Geometry Preprint Series, Vienna Univ. of Technology. URL VIENNA UNIVERSITY OF TECHNOLOGY, INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY. WALLNER@GEOMETRIE.TUWIEN.AC.AT.
EXISTENCE OF SET-INTERPOLATING AND ENERGY- MINIMIZING CURVES
 EXISTENCE OF SET-INTERPOLATING AND ENERGY- MINIMIZING CURVES JOHANNES WALLNER Abstract. We consider existence of curves c : [0, 1] R n which minimize an energy of the form c (k) p (k = 1, 2,..., 1 < p
EXISTENCE OF SET-INTERPOLATING AND ENERGY- MINIMIZING CURVES JOHANNES WALLNER Abstract. We consider existence of curves c : [0, 1] R n which minimize an energy of the form c (k) p (k = 1, 2,..., 1 < p
1 The Differential Geometry of Surfaces
 1 The Differential Geometry of Surfaces Three-dimensional objects are bounded by surfaces. This section reviews some of the basic definitions and concepts relating to the geometry of smooth surfaces. 1.1
1 The Differential Geometry of Surfaces Three-dimensional objects are bounded by surfaces. This section reviews some of the basic definitions and concepts relating to the geometry of smooth surfaces. 1.1
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). Math 4140/5530: Differential Geometry
 Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Rational Bézier Patch Differentiation using the Rational Forward Difference Operator
 Rational Bézier Patch Differentiation using the Rational Forward Difference Operator Xianming Chen, Richard F. Riesenfeld, Elaine Cohen School of Computing, University of Utah Abstract This paper introduces
Rational Bézier Patch Differentiation using the Rational Forward Difference Operator Xianming Chen, Richard F. Riesenfeld, Elaine Cohen School of Computing, University of Utah Abstract This paper introduces
VARIATIONAL INTERPOLATION OF SUBSETS
 VARIATIONAL INTERPOLATION OF SUBSETS JOHANNES WALLNER, HELMUT POTTMANN Abstract. We consider the problem of variational interpolation of subsets of Euclidean spaces by curves such that the L 2 norm of
VARIATIONAL INTERPOLATION OF SUBSETS JOHANNES WALLNER, HELMUT POTTMANN Abstract. We consider the problem of variational interpolation of subsets of Euclidean spaces by curves such that the L 2 norm of
Final Exam - Take Home Portion Math 211, Summer 2017
 Final Exam - Take Home Portion Math 2, Summer 207 Name: Directions: Complete a total of 5 problems. Problem must be completed. The remaining problems are categorized in four groups. Select one problem
Final Exam - Take Home Portion Math 2, Summer 207 Name: Directions: Complete a total of 5 problems. Problem must be completed. The remaining problems are categorized in four groups. Select one problem
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
Lecture 13 The Fundamental Forms of a Surface
 Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
CALCULUS ON MANIFOLDS. 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M =
 CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
( sin(t), cos(t), 1) dt =
 Differential Geometry MT451 Problems/Homework Recommended Reading: Morgan F. Riemannian geometry, a beginner s guide Klingenberg W. A Course in Differential Geometry do Carmo M.P. Differential geometry
Differential Geometry MT451 Problems/Homework Recommended Reading: Morgan F. Riemannian geometry, a beginner s guide Klingenberg W. A Course in Differential Geometry do Carmo M.P. Differential geometry
Chapter 14. Basics of The Differential Geometry of Surfaces. Introduction. Parameterized Surfaces. The First... Home Page. Title Page.
 Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
HILBERT S THEOREM ON THE HYPERBOLIC PLANE
 HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
HILBET S THEOEM ON THE HYPEBOLIC PLANE MATTHEW D. BOWN Abstract. We recount a proof of Hilbert s result that a complete geometric surface of constant negative Gaussian curvature cannot be isometrically
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
GEOMETRY HW Consider the parametrized surface (Enneper s surface)
 GEOMETRY HW 4 CLAY SHONKWILER 3.3.5 Consider the parametrized surface (Enneper s surface φ(u, v (x u3 3 + uv2, v v3 3 + vu2, u 2 v 2 show that (a The coefficients of the first fundamental form are E G
GEOMETRY HW 4 CLAY SHONKWILER 3.3.5 Consider the parametrized surface (Enneper s surface φ(u, v (x u3 3 + uv2, v v3 3 + vu2, u 2 v 2 show that (a The coefficients of the first fundamental form are E G
A PROOF OF THE GAUSS-BONNET THEOREM. Contents. 1. Introduction. 2. Regular Surfaces
 A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
Exercises for Multivariable Differential Calculus XM521
 This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
This document lists all the exercises for XM521. The Type I (True/False) exercises will be given, and should be answered, online immediately following each lecture. The Type III exercises are to be done
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
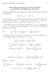 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
CMSC427 Parametric curves: Hermite, Catmull-Rom, Bezier
 CMSC427 Parametric curves: Hermite, Catmull-Rom, Bezier Modeling Creating 3D objects How to construct complicated surfaces? Goal Specify objects with few control points Resulting object should be visually
CMSC427 Parametric curves: Hermite, Catmull-Rom, Bezier Modeling Creating 3D objects How to construct complicated surfaces? Goal Specify objects with few control points Resulting object should be visually
9.1 Mean and Gaussian Curvatures of Surfaces
 Chapter 9 Gauss Map II 9.1 Mean and Gaussian Curvatures of Surfaces in R 3 We ll assume that the curves are in R 3 unless otherwise noted. We start off by quoting the following useful theorem about self
Chapter 9 Gauss Map II 9.1 Mean and Gaussian Curvatures of Surfaces in R 3 We ll assume that the curves are in R 3 unless otherwise noted. We start off by quoting the following useful theorem about self
Introduction to Algebraic and Geometric Topology Week 14
 Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
5.2 The Levi-Civita Connection on Surfaces. 1 Parallel transport of vector fields on a surface M
 5.2 The Levi-Civita Connection on Surfaces In this section, we define the parallel transport of vector fields on a surface M, and then we introduce the concept of the Levi-Civita connection, which is also
5.2 The Levi-Civita Connection on Surfaces In this section, we define the parallel transport of vector fields on a surface M, and then we introduce the concept of the Levi-Civita connection, which is also
Hyperbolic Geometry on Geometric Surfaces
 Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Sample Exam 1 KEY NAME: 1. CS 557 Sample Exam 1 KEY. These are some sample problems taken from exams in previous years. roughly ten questions.
 Sample Exam 1 KEY NAME: 1 CS 557 Sample Exam 1 KEY These are some sample problems taken from exams in previous years. roughly ten questions. Your exam will have 1. (0 points) Circle T or T T Any curve
Sample Exam 1 KEY NAME: 1 CS 557 Sample Exam 1 KEY These are some sample problems taken from exams in previous years. roughly ten questions. Your exam will have 1. (0 points) Circle T or T T Any curve
Final Exam Topic Outline
 Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
HOMEWORK 3 - GEOMETRY OF CURVES AND SURFACES. where ν is the unit normal consistent with the orientation of α (right hand rule).
 HOMEWORK 3 - GEOMETRY OF CURVES AND SURFACES ANDRÉ NEVES ) If α : I R 2 is a curve on the plane parametrized by arc length and θ is the angle that α makes with the x-axis, show that α t) = dθ dt ν, where
HOMEWORK 3 - GEOMETRY OF CURVES AND SURFACES ANDRÉ NEVES ) If α : I R 2 is a curve on the plane parametrized by arc length and θ is the angle that α makes with the x-axis, show that α t) = dθ dt ν, where
MA 323 Geometric Modelling Course Notes: Day 11 Barycentric Coordinates and de Casteljau s algorithm
 MA 323 Geometric Modelling Course Notes: Day 11 Barycentric Coordinates and de Casteljau s algorithm David L. Finn December 16th, 2004 Today, we introduce barycentric coordinates as an alternate to using
MA 323 Geometric Modelling Course Notes: Day 11 Barycentric Coordinates and de Casteljau s algorithm David L. Finn December 16th, 2004 Today, we introduce barycentric coordinates as an alternate to using
4.2. ORTHOGONALITY 161
 4.2. ORTHOGONALITY 161 Definition 4.2.9 An affine space (E, E ) is a Euclidean affine space iff its underlying vector space E is a Euclidean vector space. Given any two points a, b E, we define the distance
4.2. ORTHOGONALITY 161 Definition 4.2.9 An affine space (E, E ) is a Euclidean affine space iff its underlying vector space E is a Euclidean vector space. Given any two points a, b E, we define the distance
Gaussian and Mean Curvatures
 Gaussian and Mean Curvatures (Com S 477/577 Notes) Yan-Bin Jia Oct 31, 2017 We have learned that the two principal curvatures (and vectors) determine the local shape of a point on a surface. One characterizes
Gaussian and Mean Curvatures (Com S 477/577 Notes) Yan-Bin Jia Oct 31, 2017 We have learned that the two principal curvatures (and vectors) determine the local shape of a point on a surface. One characterizes
3.1 Classic Differential Geometry
 Spring 2015 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry Hao Li http://cs599.hao-li.com 1 Spring 2014 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry
Spring 2015 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry Hao Li http://cs599.hao-li.com 1 Spring 2014 CSCI 599: Digital Geometry Processing 3.1 Classic Differential Geometry
VECTORS AND THE GEOMETRY OF SPACE
 VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
VECTORS AND THE GEOMETRY OF SPACE VECTORS AND THE GEOMETRY OF SPACE A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given.
Inner Product Spaces 6.1 Length and Dot Product in R n
 Inner Product Spaces 6.1 Length and Dot Product in R n Summer 2017 Goals We imitate the concept of length and angle between two vectors in R 2, R 3 to define the same in the n space R n. Main topics are:
Inner Product Spaces 6.1 Length and Dot Product in R n Summer 2017 Goals We imitate the concept of length and angle between two vectors in R 2, R 3 to define the same in the n space R n. Main topics are:
THE DARBOUX TRIHEDRONS OF REGULAR CURVES ON A REGULAR SURFACE
 International lectronic Journal of eometry Volume 7 No 2 pp 61-71 (2014) c IJ TH DARBOUX TRIHDRONS OF RULAR CURVS ON A RULAR SURFAC MRAH TUNÇ AND MİN OZYILMAZ (Communicated by Levent KULA) Abstract In
International lectronic Journal of eometry Volume 7 No 2 pp 61-71 (2014) c IJ TH DARBOUX TRIHDRONS OF RULAR CURVS ON A RULAR SURFAC MRAH TUNÇ AND MİN OZYILMAZ (Communicated by Levent KULA) Abstract In
Geodesics. (Com S 477/577 Notes) Yan-Bin Jia. Nov 2, 2017
 Geodesics (om S 477/577 Notes Yan-Bin Jia Nov 2, 2017 Geodesics are the curves in a surface that make turns just to stay on the surface and never move sideways. A bug living in the surface and following
Geodesics (om S 477/577 Notes Yan-Bin Jia Nov 2, 2017 Geodesics are the curves in a surface that make turns just to stay on the surface and never move sideways. A bug living in the surface and following
The First Fundamental Form
 The First Fundamental Form Outline 1. Bilinear Forms Let V be a vector space. A bilinear form on V is a function V V R that is linear in each variable separately. That is,, is bilinear if αu + β v, w αu,
The First Fundamental Form Outline 1. Bilinear Forms Let V be a vector space. A bilinear form on V is a function V V R that is linear in each variable separately. That is,, is bilinear if αu + β v, w αu,
Math 497C Mar 3, Curves and Surfaces Fall 2004, PSU
 Math 497C Mar 3, 2004 1 Curves and Surfaces Fall 2004, PSU Lecture Notes 10 2.3 Meaning of Gaussian Curvature In the previous lecture we gave a formal definition for Gaussian curvature K in terms of the
Math 497C Mar 3, 2004 1 Curves and Surfaces Fall 2004, PSU Lecture Notes 10 2.3 Meaning of Gaussian Curvature In the previous lecture we gave a formal definition for Gaussian curvature K in terms of the
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 5. The Second Fundamental Form of a Surface
 DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 5. The Second Fundamental Form of a Surface The main idea of this chapter is to try to measure to which extent a surface S is different from a plane, in other
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 5. The Second Fundamental Form of a Surface The main idea of this chapter is to try to measure to which extent a surface S is different from a plane, in other
Two-Step Nilpotent Lie Algebras Attached to Graphs
 International Mathematical Forum, 4, 2009, no. 43, 2143-2148 Two-Step Nilpotent Lie Algebras Attached to Graphs Hamid-Reza Fanaï Department of Mathematical Sciences Sharif University of Technology P.O.
International Mathematical Forum, 4, 2009, no. 43, 2143-2148 Two-Step Nilpotent Lie Algebras Attached to Graphs Hamid-Reza Fanaï Department of Mathematical Sciences Sharif University of Technology P.O.
d F = (df E 3 ) E 3. (4.1)
 4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
Extrapolation Methods for Approximating Arc Length and Surface Area
 Extrapolation Methods for Approximating Arc Length and Surface Area Michael S. Floater, Atgeirr F. Rasmussen and Ulrich Reif March 2, 27 Abstract A well-known method of estimating the length of a parametric
Extrapolation Methods for Approximating Arc Length and Surface Area Michael S. Floater, Atgeirr F. Rasmussen and Ulrich Reif March 2, 27 Abstract A well-known method of estimating the length of a parametric
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
 Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Self-Influencing Interpolation in Groundwater Flow
 Self-Influencing Interpolation in Groundwater Flow Carolyn Atwood Whitman College Walla Walla, WA Robert Hildebrand University of Puget Sound Tacoma, WA Andrew Homan Ohio Northern University Ada, OH July
Self-Influencing Interpolation in Groundwater Flow Carolyn Atwood Whitman College Walla Walla, WA Robert Hildebrand University of Puget Sound Tacoma, WA Andrew Homan Ohio Northern University Ada, OH July
Image Analysis. Feature extraction: corners and blobs
 Image Analysis Feature extraction: corners and blobs Christophoros Nikou cnikou@cs.uoi.gr Images taken from: Computer Vision course by Svetlana Lazebnik, University of North Carolina at Chapel Hill (http://www.cs.unc.edu/~lazebnik/spring10/).
Image Analysis Feature extraction: corners and blobs Christophoros Nikou cnikou@cs.uoi.gr Images taken from: Computer Vision course by Svetlana Lazebnik, University of North Carolina at Chapel Hill (http://www.cs.unc.edu/~lazebnik/spring10/).
ON A PROBLEM OF ELEMENTARY DIFFERENTIAL GEOMETRY AND THE NUMBER OF ITS SOLUTIONS
 ON A PROBLEM OF ELEMENTARY DIFFERENTIAL GEOMETRY AND THE NUMBER OF ITS SOLUTIONS JOHANNES WALLNER Abstract. If M and N are submanifolds of R k, and a, b are points in R k, we may ask for points x M and
ON A PROBLEM OF ELEMENTARY DIFFERENTIAL GEOMETRY AND THE NUMBER OF ITS SOLUTIONS JOHANNES WALLNER Abstract. If M and N are submanifolds of R k, and a, b are points in R k, we may ask for points x M and
Notes on Cellwise Data Interpolation for Visualization Xavier Tricoche
 Notes on Cellwise Data Interpolation for Visualization Xavier Tricoche urdue University While the data (computed or measured) used in visualization is only available in discrete form, it typically corresponds
Notes on Cellwise Data Interpolation for Visualization Xavier Tricoche urdue University While the data (computed or measured) used in visualization is only available in discrete form, it typically corresponds
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
Distances, volumes, and integration
 Distances, volumes, and integration Scribe: Aric Bartle 1 Local Shape of a Surface A question that we may ask ourselves is what significance does the second fundamental form play in the geometric characteristics
Distances, volumes, and integration Scribe: Aric Bartle 1 Local Shape of a Surface A question that we may ask ourselves is what significance does the second fundamental form play in the geometric characteristics
Math 433 Outline for Final Examination
 Math 433 Outline for Final Examination Richard Koch May 3, 5 Curves From the chapter on curves, you should know. the formula for arc length of a curve;. the definition of T (s), N(s), B(s), and κ(s) for
Math 433 Outline for Final Examination Richard Koch May 3, 5 Curves From the chapter on curves, you should know. the formula for arc length of a curve;. the definition of T (s), N(s), B(s), and κ(s) for
ON JACK PHILLIP'S SPATIAL INVOLUTE GEARING
 The th International Conference on Geometry and Graphics, -5 August, 004, Guangzhou, China ON JACK PHILLIP'S SPATIAL INVOLUTE GEARING Hellmuth STACHEL Vienna University of Technology, Vienna, AUSTRIA ABSTRACT
The th International Conference on Geometry and Graphics, -5 August, 004, Guangzhou, China ON JACK PHILLIP'S SPATIAL INVOLUTE GEARING Hellmuth STACHEL Vienna University of Technology, Vienna, AUSTRIA ABSTRACT
arxiv: v1 [math.dg] 10 Dec 2015
![arxiv: v1 [math.dg] 10 Dec 2015 arxiv: v1 [math.dg] 10 Dec 2015](/thumbs/75/72687395.jpg) Preprint Curvature corrected estimates for geodesic arc-length. arxiv:1512.03461v1 [math.dg] 10 Dec 2015 Leo Brewin School of Mathematical Sciences Monash University, 3800 Australia 19-Oct-2015 Abstract
Preprint Curvature corrected estimates for geodesic arc-length. arxiv:1512.03461v1 [math.dg] 10 Dec 2015 Leo Brewin School of Mathematical Sciences Monash University, 3800 Australia 19-Oct-2015 Abstract
1.1 Single Variable Calculus versus Multivariable Calculus Rectangular Coordinate Systems... 4
 MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
MATH2202 Notebook 1 Fall 2015/2016 prepared by Professor Jenny Baglivo Contents 1 MATH2202 Notebook 1 3 1.1 Single Variable Calculus versus Multivariable Calculus................... 3 1.2 Rectangular Coordinate
Lecture 11: Differential Geometry
 Lecture 11: Differential Geometry c Bryan S. Morse, Brigham Young University, 1998 2000 Last modified on February 28, 2000 at 8:45 PM Contents 11.1 Introduction..............................................
Lecture 11: Differential Geometry c Bryan S. Morse, Brigham Young University, 1998 2000 Last modified on February 28, 2000 at 8:45 PM Contents 11.1 Introduction..............................................
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Unit Speed Curves. Recall that a curve Α is said to be a unit speed curve if
 Unit Speed Curves Recall that a curve Α is said to be a unit speed curve if The reason that we like unit speed curves that the parameter t is equal to arc length; i.e. the value of t tells us how far along
Unit Speed Curves Recall that a curve Α is said to be a unit speed curve if The reason that we like unit speed curves that the parameter t is equal to arc length; i.e. the value of t tells us how far along
Curvature variation minimizing cubic Hermite interpolants
 Curvature variation minimizing cubic Hermite interpolants Gašper Jaklič a,b, Emil Žagar,a a FMF and IMFM, University of Ljubljana, Jadranska 19, Ljubljana, Slovenia b PINT, University of Primorska, Muzejski
Curvature variation minimizing cubic Hermite interpolants Gašper Jaklič a,b, Emil Žagar,a a FMF and IMFM, University of Ljubljana, Jadranska 19, Ljubljana, Slovenia b PINT, University of Primorska, Muzejski
Lecture 2: Linear Algebra Review
 EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
Math 5378, Differential Geometry Solutions to practice questions for Test 2
 Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
Intuitive Exposition of Third Order Surface Behavior
 Intuitive Exposition of Third Order Surface Behavior Pushkar Prakash Joshi Carlo H. Séquin Electrical Engineering and Computer Sciences University of California at Berkeley Technical Report No. UCB/EECS-2008-125
Intuitive Exposition of Third Order Surface Behavior Pushkar Prakash Joshi Carlo H. Séquin Electrical Engineering and Computer Sciences University of California at Berkeley Technical Report No. UCB/EECS-2008-125
Course Summary Math 211
 Course Summary Math 211 table of contents I. Functions of several variables. II. R n. III. Derivatives. IV. Taylor s Theorem. V. Differential Geometry. VI. Applications. 1. Best affine approximations.
Course Summary Math 211 table of contents I. Functions of several variables. II. R n. III. Derivatives. IV. Taylor s Theorem. V. Differential Geometry. VI. Applications. 1. Best affine approximations.
Math 350 Fall 2011 Notes about inner product spaces. In this notes we state and prove some important properties of inner product spaces.
 Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
Math 350 Fall 2011 Notes about inner product spaces In this notes we state and prove some important properties of inner product spaces. First, recall the dot product on R n : if x, y R n, say x = (x 1,...,
SOLUTIONS TO SECOND PRACTICE EXAM Math 21a, Spring 2003
 SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
SOLUTIONS TO SECOND PRACTICE EXAM Math a, Spring 3 Problem ) ( points) Circle for each of the questions the correct letter. No justifications are needed. Your score will be C W where C is the number of
Upon successful completion of MATH 220, the student will be able to:
 MATH 220 Matrices Upon successful completion of MATH 220, the student will be able to: 1. Identify a system of linear equations (or linear system) and describe its solution set 2. Write down the coefficient
MATH 220 Matrices Upon successful completion of MATH 220, the student will be able to: 1. Identify a system of linear equations (or linear system) and describe its solution set 2. Write down the coefficient
Stable shock formation near plane-symmetry for nonlinear wave equations
 Stable shock formation near plane-symmetry for nonlinear wave equations Willie WY Wong wongwwy@member.ams.org Michigan State University University of Minnesota 9 March 2016 1 Based on: arxiv:1601.01303,
Stable shock formation near plane-symmetry for nonlinear wave equations Willie WY Wong wongwwy@member.ams.org Michigan State University University of Minnesota 9 March 2016 1 Based on: arxiv:1601.01303,
Geodesics: Minimizing Distance on a Surface
 Geodesics: Minimizing Distance on a Surface Seth Donahue 5/13/13 Abstract Geodesics use the principles of differential geometry. The system of differential equations and the analysis of these will be done
Geodesics: Minimizing Distance on a Surface Seth Donahue 5/13/13 Abstract Geodesics use the principles of differential geometry. The system of differential equations and the analysis of these will be done
L. Vandenberghe EE236C (Spring 2016) 18. Symmetric cones. definition. spectral decomposition. quadratic representation. log-det barrier 18-1
 L. Vandenberghe EE236C (Spring 2016) 18. Symmetric cones definition spectral decomposition quadratic representation log-det barrier 18-1 Introduction This lecture: theoretical properties of the following
L. Vandenberghe EE236C (Spring 2016) 18. Symmetric cones definition spectral decomposition quadratic representation log-det barrier 18-1 Introduction This lecture: theoretical properties of the following
Tangent spaces, normals and extrema
 Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE. 1. Introduction
 International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
Numerical Analysis of Electromagnetic Fields
 Pei-bai Zhou Numerical Analysis of Electromagnetic Fields With 157 Figures Springer-Verlag Berlin Heidelberg New York London Paris Tokyo Hong Kong Barcelona Budapest Contents Part 1 Universal Concepts
Pei-bai Zhou Numerical Analysis of Electromagnetic Fields With 157 Figures Springer-Verlag Berlin Heidelberg New York London Paris Tokyo Hong Kong Barcelona Budapest Contents Part 1 Universal Concepts
DIFFERENTIAL GEOMETRY HW 4. Show that a catenoid and helicoid are locally isometric.
 DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
DIFFERENTIAL GEOMETRY HW 4 CLAY SHONKWILER Show that a catenoid and helicoid are locally isometric. 3 Proof. Let X(u, v) = (a cosh v cos u, a cosh v sin u, av) be the parametrization of the catenoid and
Lectures in Discrete Differential Geometry 2 Surfaces
 Lectures in Discrete Differential Geometry 2 Surfaces Etienne Vouga February 4, 24 Smooth Surfaces in R 3 In this section we will review some properties of smooth surfaces R 3. We will assume that is parameterized
Lectures in Discrete Differential Geometry 2 Surfaces Etienne Vouga February 4, 24 Smooth Surfaces in R 3 In this section we will review some properties of smooth surfaces R 3. We will assume that is parameterized
Multidimensional Geometry and its Applications
 PARALLEL COORDINATES : VISUAL Multidimensional Geometry and its Applications Alfred Inselberg( c 99, ) Senior Fellow San Diego SuperComputing Center, CA, USA Computer Science and Applied Mathematics Departments
PARALLEL COORDINATES : VISUAL Multidimensional Geometry and its Applications Alfred Inselberg( c 99, ) Senior Fellow San Diego SuperComputing Center, CA, USA Computer Science and Applied Mathematics Departments
Exact Solutions of the Einstein Equations
 Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
II. Unit Speed Curves
 The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
The Geometry of Curves, Part I Rob Donnelly From Murray State University s Calculus III, Fall 2001 note: This material supplements Sections 13.3 and 13.4 of the text Calculus with Early Transcendentals,
GENERALIZED NULL SCROLLS IN THE n-dimensional LORENTZIAN SPACE. 1. Introduction
 ACTA MATHEMATICA VIETNAMICA 205 Volume 29, Number 2, 2004, pp. 205-216 GENERALIZED NULL SCROLLS IN THE n-dimensional LORENTZIAN SPACE HANDAN BALGETIR AND MAHMUT ERGÜT Abstract. In this paper, we define
ACTA MATHEMATICA VIETNAMICA 205 Volume 29, Number 2, 2004, pp. 205-216 GENERALIZED NULL SCROLLS IN THE n-dimensional LORENTZIAN SPACE HANDAN BALGETIR AND MAHMUT ERGÜT Abstract. In this paper, we define
Spiral spline interpolation to a planar spiral
 Spiral spline interpolation to a planar spiral Zulfiqar Habib Department of Mathematics and Computer Science, Graduate School of Science and Engineering, Kagoshima University Manabu Sakai Department of
Spiral spline interpolation to a planar spiral Zulfiqar Habib Department of Mathematics and Computer Science, Graduate School of Science and Engineering, Kagoshima University Manabu Sakai Department of
SPLIT QUATERNIONS and CANAL SURFACES. in MINKOWSKI 3-SPACE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
Problems in Linear Algebra and Representation Theory
 Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Bernstein polynomials of degree N are defined by
 SEC. 5.5 BÉZIER CURVES 309 5.5 Bézier Curves Pierre Bézier at Renault and Paul de Casteljau at Citroën independently developed the Bézier curve for CAD/CAM operations, in the 1970s. These parametrically
SEC. 5.5 BÉZIER CURVES 309 5.5 Bézier Curves Pierre Bézier at Renault and Paul de Casteljau at Citroën independently developed the Bézier curve for CAD/CAM operations, in the 1970s. These parametrically
13 Path Planning Cubic Path P 2 P 1. θ 2
 13 Path Planning Path planning includes three tasks: 1 Defining a geometric curve for the end-effector between two points. 2 Defining a rotational motion between two orientations. 3 Defining a time function
13 Path Planning Path planning includes three tasks: 1 Defining a geometric curve for the end-effector between two points. 2 Defining a rotational motion between two orientations. 3 Defining a time function
Notes on Cartan s Method of Moving Frames
 Math 553 σιι June 4, 996 Notes on Cartan s Method of Moving Frames Andrejs Treibergs The method of moving frames is a very efficient way to carry out computations on surfaces Chern s Notes give an elementary
Math 553 σιι June 4, 996 Notes on Cartan s Method of Moving Frames Andrejs Treibergs The method of moving frames is a very efficient way to carry out computations on surfaces Chern s Notes give an elementary
1. Geometry of the unit tangent bundle
 1 1. Geometry of the unit tangent bundle The main reference for this section is [8]. In the following, we consider (M, g) an n-dimensional smooth manifold endowed with a Riemannian metric g. 1.1. Notations
1 1. Geometry of the unit tangent bundle The main reference for this section is [8]. In the following, we consider (M, g) an n-dimensional smooth manifold endowed with a Riemannian metric g. 1.1. Notations
Solutions for Math 348 Assignment #4 1
 Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2
Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2
The Symmetric Space for SL n (R)
 The Symmetric Space for SL n (R) Rich Schwartz November 27, 2013 The purpose of these notes is to discuss the symmetric space X on which SL n (R) acts. Here, as usual, SL n (R) denotes the group of n n
The Symmetric Space for SL n (R) Rich Schwartz November 27, 2013 The purpose of these notes is to discuss the symmetric space X on which SL n (R) acts. Here, as usual, SL n (R) denotes the group of n n
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication.
 This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
This pre-publication material is for review purposes only. Any typographical or technical errors will be corrected prior to publication. Copyright Pearson Canada Inc. All rights reserved. Copyright Pearson
Computer Aided Geometric Design
 Computer Aided Geometric Design 27 (2010) 150 161 Contents lists available at ScienceDirect Computer Aided Geometric Design www.elsevier.com/locate/cagd An intuitive explanation of third-order surface
Computer Aided Geometric Design 27 (2010) 150 161 Contents lists available at ScienceDirect Computer Aided Geometric Design www.elsevier.com/locate/cagd An intuitive explanation of third-order surface
MA 323 Geometric Modelling Course Notes: Day 07 Parabolic Arcs
 MA 323 Geometric Modelling Course Notes: Day 07 Parabolic Arcs David L. Finn December 9th, 2004 We now start considering the basic curve elements to be used throughout this course; polynomial curves and
MA 323 Geometric Modelling Course Notes: Day 07 Parabolic Arcs David L. Finn December 9th, 2004 We now start considering the basic curve elements to be used throughout this course; polynomial curves and
Lectures 18: Gauss's Remarkable Theorem II. Table of contents
 Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
THE DIFFERENTIAL GEOMETRY OF PARAMETRIC PRIMITIVES
 THE DIFFERENTIAL GEOMETRY OF PARAMETRIC PRIMITIVES Ken Turkowski Media Technologies: Graphics Software Advanced Technology Group Apple Computer, Inc. (Draft Friday, May 18, 1990) Abstract: We derive the
THE DIFFERENTIAL GEOMETRY OF PARAMETRIC PRIMITIVES Ken Turkowski Media Technologies: Graphics Software Advanced Technology Group Apple Computer, Inc. (Draft Friday, May 18, 1990) Abstract: We derive the
Chapter 3. Riemannian Manifolds - I. The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves
 Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
Chapter 3 Riemannian Manifolds - I The subject of this thesis is to extend the combinatorial curve reconstruction approach to curves embedded in Riemannian manifolds. A Riemannian manifold is an abstraction
HOMEWORK 3 MA1132: ADVANCED CALCULUS, HILARY 2017
 HOMEWORK MA112: ADVANCED CALCULUS, HILARY 2017 (1) A particle moves along a curve in R with position function given by r(t) = (e t, t 2 + 1, t). Find the velocity v(t), the acceleration a(t), the speed
HOMEWORK MA112: ADVANCED CALCULUS, HILARY 2017 (1) A particle moves along a curve in R with position function given by r(t) = (e t, t 2 + 1, t). Find the velocity v(t), the acceleration a(t), the speed
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
 SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
Cubic Helices in Minkowski Space
 Cubic Helices in Minkowski Space Jiří Kosinka and Bert Jüttler Johannes Kepler University, Institute of Applied Geometry, Altenberger Str. 69, A 4040 Linz, Austria Abstract We discuss space like and light
Cubic Helices in Minkowski Space Jiří Kosinka and Bert Jüttler Johannes Kepler University, Institute of Applied Geometry, Altenberger Str. 69, A 4040 Linz, Austria Abstract We discuss space like and light
Math 461 Homework 8. Paul Hacking. November 27, 2018
 Math 461 Homework 8 Paul Hacking November 27, 2018 (1) Let S 2 = {(x, y, z) x 2 + y 2 + z 2 = 1} R 3 be the sphere with center the origin and radius 1. Let N = (0, 0, 1) S 2 be the north pole. Let F :
Math 461 Homework 8 Paul Hacking November 27, 2018 (1) Let S 2 = {(x, y, z) x 2 + y 2 + z 2 = 1} R 3 be the sphere with center the origin and radius 1. Let N = (0, 0, 1) S 2 be the north pole. Let F :
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Part IB GEOMETRY (Lent 2016): Example Sheet 1
 Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Vector Spaces and Subspaces
 Vector Spaces and Subspaces Our investigation of solutions to systems of linear equations has illustrated the importance of the concept of a vector in a Euclidean space. We take time now to explore the
Vector Spaces and Subspaces Our investigation of solutions to systems of linear equations has illustrated the importance of the concept of a vector in a Euclidean space. We take time now to explore the
There is a function, the arc length function s(t) defined by s(t) = It follows that r(t) = p ( s(t) )
 MATH 20550 Acceleration, Curvature and Related Topics Fall 2016 The goal of these notes is to show how to compute curvature and torsion from a more or less arbitrary parametrization of a curve. We will
MATH 20550 Acceleration, Curvature and Related Topics Fall 2016 The goal of these notes is to show how to compute curvature and torsion from a more or less arbitrary parametrization of a curve. We will
Chapter 5 Eigenvalues and Eigenvectors
 Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Gauss Theorem Egregium, Gauss-Bonnet etc. We know that for a simple closed curve in the plane. kds = 2π.
 Gauss Theorem Egregium, Gauss-Bonnet etc. We know that for a simple closed curve in the plane kds = 2π. Now we want to consider a simple closed curve C in a surface S R 3. We suppose C is the boundary
Gauss Theorem Egregium, Gauss-Bonnet etc. We know that for a simple closed curve in the plane kds = 2π. Now we want to consider a simple closed curve C in a surface S R 3. We suppose C is the boundary
Math 461 Homework 8 Paul Hacking November 27, 2018
 (1) Let Math 461 Homework 8 Paul Hacking November 27, 2018 S 2 = {(x, y, z) x 2 +y 2 +z 2 = 1} R 3 be the sphere with center the origin and radius 1. Let N = (0, 0, 1) S 2 be the north pole. Let F : S
(1) Let Math 461 Homework 8 Paul Hacking November 27, 2018 S 2 = {(x, y, z) x 2 +y 2 +z 2 = 1} R 3 be the sphere with center the origin and radius 1. Let N = (0, 0, 1) S 2 be the north pole. Let F : S
Math 118, Fall 2014 Final Exam
 Math 8, Fall 4 Final Exam True or false Please circle your choice; no explanation is necessary True There is a linear transformation T such that T e ) = e and T e ) = e Solution Since T is linear, if T
Math 8, Fall 4 Final Exam True or false Please circle your choice; no explanation is necessary True There is a linear transformation T such that T e ) = e and T e ) = e Solution Since T is linear, if T
