Integration Exercises - Part 3 (Sol'ns) (Hyperbolic Functions) (12 pages; 6/2/18) (The constant of integration has been omitted throughout.
|
|
|
- Domenic Barber
- 5 years ago
- Views:
Transcription
1 Integration Eercises - Part (Sol'ns) (Hyperbolic Functions) ( pages; 6//8) (The constant of integration has been omitted throughout.) () cosech Given that d tanh = sech, we could investigate d coth = d cosh = sinh.sinh cosh.cosh sinh sinh so that cosech = coth + c = sinh = cosech () tanh (from st principles) tanh = sinh cosh As sinh = cosh, let u = cosh Then du = sinh, and sinh = du = ln u + c cosh u = ln(cosh) + c [No moduli signs are needed, as cosh > 0 for all ] () sechtanh sechtanh = sinh cosh As sinh = cosh, let u = cosh Then du = sinh, and sinh cosh = u du = u + c
2 = sech + c (4) tanh tanh = sech = tanh + c (from differentiation table) (5) sech tanh As sech = tanh, let u = tanh, so that du = sech, and sech tanh = u du = u + c = tanh + c (6) sech tanh As we have a power of sech, consider d sech = sechtanh, from (i). Then let u = sech, so that du = sechtanh and sech tanh = u du = = u + c = sech + c
3 (7) cosh cosh sinh = & cosh + sinh = cosh, so that cosh = ( + cosh), and cosh = + cosh = + sinh + c 4 (8) cosh cosh = cosh( sinh ) Let u = sinh, so that du = cosh, and cosh( sinh ) = u du = u u + c = sinh sinh + c (9) sech Method sech = cosh = cosh cosh +sinh Let u = sinh, so that du = cosh Then cosh = du +sinh +u = arctan(sinh) + c Method sech = (e +e ) = Let u = e, so that du = e e e +
4 and e = du e + u + = arctan(e ) + c To show that arctan(sinh) + c = arctan(e ) + c : Let θ = arctan (sinh) and φ = arctan (e ) We need to show that θ & φ differ by a constant. tanθ = sinh & tan ( φ ) = e Let t = tan ( φ ) Then sinh = (e e ) = (t t ) = t [We can now use the standard right-angled triangle with sides t, t & + t : tanφ = t t & the hypotenuse follows from Pythagoras.] So sinh = tan ( π φ ) = tan (φ π ) Thus tan ( φ π ) = tanθ, and so φ π & φ differ by a multiple of π; ie θ & φ differ by a constant, as required. t (0) 4 9 = 4 9 ( ) = arcosh ( ( )) + C = arcosh ( ) + C 4
5 () (a) cosh (b) sinh (c) tanh (a) By Parts, cosh = cosh = cosh = cosh ( ) ( ) = cosh (b) By Parts, sinh = sinh = sinh + = sinh ( ) + ( ) = sinh + + (c) By Parts, tanh = tanh = tanh + = tanh + ln ( ) () ( 9) Let = coshu, so that = sinhu du Then I = sinhu 7sinh u du = 9 cosech u du 5
6 As d du tanhu = sech u, we can investigate d coshu du sinhu = sinhusinhu coshucoshu sinh u d du cothu: = sinh u = cosech u coshu Thus I = cothu = = 9 9 cosh u 9 9 = 9 9 Alternative method Let = secu, so that = secutanu Then I = secutanu 7tan u = 9 du = /cosu du = cosu du 9 ( sinu cosu ) 9 sin u ( ) = = = sinu 9 cos u 9 (/) 9 9 () 4 + Let = sinhu, so that = coshu du and I = + sinh u (coshu)du = 4 cosh u du = + cosh(u) du = (u + sinh(u)) = sinh ( ) + sinhucoshu = sinh ( ) + ( ) + = sinh ( ) + ( ) + = sinh ( )
7 [Note: The alternative substitution = tanu, leads to a much more complicated epression.] (4) + Let = sinh u, so that = sinhucoshu du and I = sinhu coshu ( sinhucoshu) du = sinh u du = (cosh(u) ) du = sinh(u) u = sinhu coshu u = ( + ) sinh ( ) (5) 4 Let = coshu, so that = sinhu du and I = sinhu. sinhu du = cosh(u) du 4 = sinh(u) u = sinhucoshu cosh () = 4 4 cosh () (6) + Let = sinhu, so that = coshu du and I = sinh u coshu coshu du 7
8 = sinh u(sinh u + )du [A reduction formula could be found for sinh 4 u du at this point, as an alternative to the following.] = [cosh(u) ] { [cosh(u) ] + } du = 4 [cosh(u) ][cosh(u) + ]du = 4 cosh (u) du = [(cosh(4u) + ] du 4 = sinh(4u) u 8 = 6 sinh(u) cosh(u) u 8 = 8 sinhucoshu(cosh u + sinh u) u 8 = 8 + ( + ) 8 sinh (7) (+) ( + ) = + = ( + ) 4 So I = (+ ) 4 = cosh ( + ) = cosh ( + ) 8
9 (8) 6 Noting that =, and that 6 = ( ), let u =, so that du = and I = u du = cosh ( ) (9) 4+ I = [arsinh ( )] = [ +9 ] + arsinh( 4 ) ( ) 0 = 4(5 ) + ln ( 4 + ( 4 ) + ) = 8 + ln ( (4 + 5)) = 8 + ln (0) Let 4 = sinhu, so that 4 = coshu du I = coshu. coshu du 0 4 = 9 ( + coshu)du 4 0 [since cosh u sinh u = & cosh u + sinh u = coshu] 9
10 = 9 8 [u + sinhu] 0 = 9 8 ( + 4 (e e )) = (e e ) () + Let = sinh y [so that + = cosh y] Then = sinhycoshy dy and I = coshy sinhy = cosh y dy = + coshy dy = y + sinhy. sinhycoshy dy = arsinh( ) + sinhycoshy = arsinh( ) + ( + ) () Method ( +) Let = sinh y, so that 4 = 6sinhycoshy dy Then I = (sinh y+) 6sinhycoshy dy 4 0
11 = sinhycoshy cosh ysinhy dy = sech y dy = tanhy = tanhy As = sinh y, cosh y = +, so that sech y = + = + and tanh y = sech y [applying Osborn's rule] so that tanhy = + = + = + Method Let = tan θ, so that 4 = 6tanθsec θ dθ Then I = (tan θ+) 6tanθsec θ 4 dθ = sec θ tanθsec θ tanθ dθ = cosθ dθ = sinθ As = tan θ, sec θ = +,
12 so that cos θ = + = + and sinθ = + = + = + () cosech()coth() Note that d (cosec) = cosec cot So suppose that the solution is of the form Acosech(). Then d (Acosech()) = A d ((sinh()) ) = A( )(sinh()) (cosh()) = Acoth()cosech() So we require A = and I = cosech()
( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C.
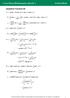 Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
Hyperbolic Functions: Exercises - Sol'ns (9 pages; 13/5/17)
 Hyperbolic Functions: Exercises - Sol'ns (9 pages; 3/5/7) () (i) Prove, using exponential functions, that (a) cosh x sinh x = (b) sinhx = sinhxcoshx (ii) By differentiating the result from (i)(b), obtain
Hyperbolic Functions: Exercises - Sol'ns (9 pages; 3/5/7) () (i) Prove, using exponential functions, that (a) cosh x sinh x = (b) sinhx = sinhxcoshx (ii) By differentiating the result from (i)(b), obtain
Hyperbolic Functions 6D
 Hyperbolic Functions 6D a (sinh cosh b (cosh 5 5sinh 5 c (tanh sech (sinh cosh e f (coth cosech (sech sinh (cosh sinh cosh cosh tanh sech g (e sinh e sinh e + cosh e (cosh sinh h ( cosh cosh + sinh sinh
Hyperbolic Functions 6D a (sinh cosh b (cosh 5 5sinh 5 c (tanh sech (sinh cosh e f (coth cosech (sech sinh (cosh sinh cosh cosh tanh sech g (e sinh e sinh e + cosh e (cosh sinh h ( cosh cosh + sinh sinh
We define hyperbolic functions cosech, sech and coth in a similar way to the definitions of trigonometric functions cosec, sec and cot respectively:
 3 Chapter 5 SECTION F Hyperbolic properties By the end of this section you will be able to: evaluate other hyperbolic functions show hyperbolic identities understand inverse hyperbolic functions F Other
3 Chapter 5 SECTION F Hyperbolic properties By the end of this section you will be able to: evaluate other hyperbolic functions show hyperbolic identities understand inverse hyperbolic functions F Other
Hyperbolics. Scott Morgan. Further Mathematics Support Programme - WJEC A-Level Further Mathematics 31st March scott3142.
 Hyperbolics Scott Morgan Further Mathematics Support Programme - WJEC A-Level Further Mathematics 3st March 208 scott342.com @Scott342 Topics Hyperbolic Identities Calculus with Hyperbolics - Differentiation
Hyperbolics Scott Morgan Further Mathematics Support Programme - WJEC A-Level Further Mathematics 3st March 208 scott342.com @Scott342 Topics Hyperbolic Identities Calculus with Hyperbolics - Differentiation
Mark Scheme (Results) Summer 2008
 (Results) Summer 8 GCE GCE Mathematics (75/) Edecel Limited. Registered in England and Wales No. 975 Registered Office: One9 High Holborn, London WCV 7BH Further Pure Mathematics FP d. ( ln( tanh ) ) sech
(Results) Summer 8 GCE GCE Mathematics (75/) Edecel Limited. Registered in England and Wales No. 975 Registered Office: One9 High Holborn, London WCV 7BH Further Pure Mathematics FP d. ( ln( tanh ) ) sech
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 3 (Elementary techniques of differentiation) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 10.3 DIFFERENTIATION 3 (Elementary techniques of differentiation) by A.J.Hobson 10.3.1 Standard derivatives 10.3.2 Rules of differentiation 10.3.3 Exercises 10.3.4 Answers to
JUST THE MATHS UNIT NUMBER 10.3 DIFFERENTIATION 3 (Elementary techniques of differentiation) by A.J.Hobson 10.3.1 Standard derivatives 10.3.2 Rules of differentiation 10.3.3 Exercises 10.3.4 Answers to
Trigonometric substitutions (8.3).
 Review for Eam 2. 5 or 6 problems. No multiple choice questions. No notes, no books, no calculators. Problems similar to homeworks. Eam covers: 7.4, 7.6, 7.7, 8-IT, 8., 8.2. Solving differential equations
Review for Eam 2. 5 or 6 problems. No multiple choice questions. No notes, no books, no calculators. Problems similar to homeworks. Eam covers: 7.4, 7.6, 7.7, 8-IT, 8., 8.2. Solving differential equations
90 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions. Name Class. (a) (b) ln x (c) (a) (b) (c) 1 x. y e (a) 0 (b) y.
 90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
Chapter 3 Differentiation Rules (continued)
 Chapter 3 Differentiation Rules (continued) Sec 3.5: Implicit Differentiation (continued) Implicit Differentiation What if you want to find the slope of the tangent line to a curve that is not the graph
Chapter 3 Differentiation Rules (continued) Sec 3.5: Implicit Differentiation (continued) Implicit Differentiation What if you want to find the slope of the tangent line to a curve that is not the graph
1. Evaluate the integrals. a. (9 pts) x e x/2 dx. Solution: Using integration by parts, let u = x du = dx and dv = e x/2 dx v = 2e x/2.
 MATH 8 Test -SOLUTIONS Spring 4. Evaluate the integrals. a. (9 pts) e / Solution: Using integration y parts, let u = du = and dv = e / v = e /. Then e / = e / e / e / = e / + e / = e / 4e / + c MATH 8
MATH 8 Test -SOLUTIONS Spring 4. Evaluate the integrals. a. (9 pts) e / Solution: Using integration y parts, let u = du = and dv = e / v = e /. Then e / = e / e / e / = e / + e / = e / 4e / + c MATH 8
Math Calculus II Homework # Due Date Solutions
 Math 35 - Calculus II Homework # - 007.08.3 Due Date - 007.09.07 Solutions Part : Problems from sections 7.3 and 7.4. Section 7.3: 9. + d We will use the substitution cot(θ, d csc (θ. This gives + + cot
Math 35 - Calculus II Homework # - 007.08.3 Due Date - 007.09.07 Solutions Part : Problems from sections 7.3 and 7.4. Section 7.3: 9. + d We will use the substitution cot(θ, d csc (θ. This gives + + cot
FP3 mark schemes from old P4, P5, P6 and FP1, FP2, FP3 papers (back to June 2002)
 FP mark schemes from old P, P5, P6 and FP, FP, FP papers (back to June ) Please note that the following pages contain mark schemes for questions from past papers. Where a question reference is marked with
FP mark schemes from old P, P5, P6 and FP, FP, FP papers (back to June ) Please note that the following pages contain mark schemes for questions from past papers. Where a question reference is marked with
CHAPTER 1. DIFFERENTIATION 18. As x 1, f(x). At last! We are now in a position to sketch the curve; see Figure 1.4.
 CHAPTER. DIFFERENTIATION 8 and similarly for x, As x +, fx), As x, fx). At last! We are now in a position to sketch the curve; see Figure.4. Figure.4: A sketch of the function y = fx) =/x ). Observe the
CHAPTER. DIFFERENTIATION 8 and similarly for x, As x +, fx), As x, fx). At last! We are now in a position to sketch the curve; see Figure.4. Figure.4: A sketch of the function y = fx) =/x ). Observe the
Differential Equations DIRECT INTEGRATION. Graham S McDonald
 Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
1 Functions and Inverses
 October, 08 MAT86 Week Justin Ko Functions and Inverses Definition. A function f : D R is a rule that assigns each element in a set D to eactly one element f() in R. The set D is called the domain of f.
October, 08 MAT86 Week Justin Ko Functions and Inverses Definition. A function f : D R is a rule that assigns each element in a set D to eactly one element f() in R. The set D is called the domain of f.
Odd Answers: Chapter Eight Contemporary Calculus 1 { ( 3+2 } = lim { 1. { 2. arctan(a) 2. arctan(3) } = 2( π 2 ) 2. arctan(3)
 Odd Answers: Chapter Eight Contemporary Calculus PROBLEM ANSWERS Chapter Eight Section 8.. lim { A 0 } lim { ( A ) ( 00 ) } lim { 00 A } 00.. lim {. arctan() A } lim {. arctan(a). arctan() } ( π ). arctan()
Odd Answers: Chapter Eight Contemporary Calculus PROBLEM ANSWERS Chapter Eight Section 8.. lim { A 0 } lim { ( A ) ( 00 ) } lim { 00 A } 00.. lim {. arctan() A } lim {. arctan(a). arctan() } ( π ). arctan()
Precalculus Review. Functions to KNOW! 1. Polynomial Functions. Types: General form Generic Graph and unique properties. Constants. Linear.
 Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
2 Recollection of elementary functions. II
 Recollection of elementary functions. II Last updated: October 5, 08. In this section we continue recollection of elementary functions. In particular, we consider exponential, trigonometric and hyperbolic
Recollection of elementary functions. II Last updated: October 5, 08. In this section we continue recollection of elementary functions. In particular, we consider exponential, trigonometric and hyperbolic
cosh x sinh x So writing t = tan(x/2) we have 6.4 Integration using tan(x/2) 2t 1 + t 2 cos x = 1 t2 sin x =
 6.4 Integration using tan/ We will revisit the ouble angle ientities: sin = sin/ cos/ = tan/ sec / = tan/ + tan / cos = cos / sin / tan = = tan / sec / tan/ tan /. = tan / + tan / So writing t = tan/ we
6.4 Integration using tan/ We will revisit the ouble angle ientities: sin = sin/ cos/ = tan/ sec / = tan/ + tan / cos = cos / sin / tan = = tan / sec / tan/ tan /. = tan / + tan / So writing t = tan/ we
JUST THE MATHS UNIT NUMBER INTEGRATION 1 (Elementary indefinite integrals) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 2. INTEGRATION (Elementary indefinite integrals) by A.J.Hobson 2.. The definition of an integral 2..2 Elementary techniques of integration 2..3 Exercises 2..4 Answers to exercises
JUST THE MATHS UNIT NUMBER 2. INTEGRATION (Elementary indefinite integrals) by A.J.Hobson 2.. The definition of an integral 2..2 Elementary techniques of integration 2..3 Exercises 2..4 Answers to exercises
6675/01 Edexcel GCE Pure Mathematics P5 Further Mathematics FP2 Advanced/Advanced Subsidiary
 6675/1 Edecel GCE Pure Mathematics P5 Further Mathematics FP Advanced/Advanced Subsidiary Monday June 5 Morning Time: 1 hour 3 minutes 1 1. (a) Find d. (1 4 ) (b) Find, to 3 decimal places, the value of.3
6675/1 Edecel GCE Pure Mathematics P5 Further Mathematics FP Advanced/Advanced Subsidiary Monday June 5 Morning Time: 1 hour 3 minutes 1 1. (a) Find d. (1 4 ) (b) Find, to 3 decimal places, the value of.3
Hyperbolic Functions Mixed Exercise 6
 Hyprbolic Functions Mid Ercis 6 a b c ln ln sinh(ln ) ln ln + cosh(ln ) + ln tanh ln ln + ( 6 ) ( + ) 6 7 ln ln ln,and ln ln ln,and ln ln 6 artanh artanhy + + y ln ln y + y ln + y + y y ln + y y + y y
Hyprbolic Functions Mid Ercis 6 a b c ln ln sinh(ln ) ln ln + cosh(ln ) + ln tanh ln ln + ( 6 ) ( + ) 6 7 ln ln ln,and ln ln ln,and ln ln 6 artanh artanhy + + y ln ln y + y ln + y + y y ln + y y + y y
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
THE COMPOUND ANGLE IDENTITIES
 TRIGONOMETRY THE COMPOUND ANGLE IDENTITIES Question 1 Prove the validity of each of the following trigonometric identities. a) sin x + cos x 4 4 b) cos x + + 3 sin x + 2cos x 3 3 c) cos 2x + + cos 2x cos
TRIGONOMETRY THE COMPOUND ANGLE IDENTITIES Question 1 Prove the validity of each of the following trigonometric identities. a) sin x + cos x 4 4 b) cos x + + 3 sin x + 2cos x 3 3 c) cos 2x + + cos 2x cos
FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS
 Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
Taylor Series 6B. lim s x. 1 a We can evaluate the limit directly since there are no singularities: b Again, there are no singularities, so:
 Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters
 Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters α( alpha), β ( beta), θ ( theta) as well as upper case letters A,B,
Trigonometry Trigonometry comes from the Greek word meaning measurement of triangles Angles are typically labeled with Greek letters α( alpha), β ( beta), θ ( theta) as well as upper case letters A,B,
PRELIM 2 REVIEW QUESTIONS Math 1910 Section 205/209
 PRELIM 2 REVIEW QUESTIONS Math 9 Section 25/29 () Calculate the following integrals. (a) (b) x 2 dx SOLUTION: This is just the area under a semicircle of radius, so π/2. sin 2 (x) cos (x) dx SOLUTION:
PRELIM 2 REVIEW QUESTIONS Math 9 Section 25/29 () Calculate the following integrals. (a) (b) x 2 dx SOLUTION: This is just the area under a semicircle of radius, so π/2. sin 2 (x) cos (x) dx SOLUTION:
2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2
![2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2 2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2](/thumbs/96/127235785.jpg) 6 FAMAT Convention Mu Integration. A. 3 3 7 6 6 3 ] 3 6 6 3. B. For quadratic functions, Simpson s Rule is eact. Thus, 3. D.. B. lim 5 3 + ) 3 + ] 5 8 8 cot θ) dθ csc θ ) dθ cot θ θ + C n k n + k n lim
6 FAMAT Convention Mu Integration. A. 3 3 7 6 6 3 ] 3 6 6 3. B. For quadratic functions, Simpson s Rule is eact. Thus, 3. D.. B. lim 5 3 + ) 3 + ] 5 8 8 cot θ) dθ csc θ ) dθ cot θ θ + C n k n + k n lim
cosh x sinh x So writing t = tan(x/2) we have 6.4 Integration using tan(x/2) = 2 2t 1 + t 2 cos x = 1 t2 We will revisit the double angle identities:
 6.4 Integration using tanx/) We will revisit the ouble angle ientities: sin x = sinx/) cosx/) = tanx/) sec x/) = tanx/) + tan x/) cos x = cos x/) sin x/) tan x = = tan x/) sec x/) tanx/) tan x/). = tan
6.4 Integration using tanx/) We will revisit the ouble angle ientities: sin x = sinx/) cosx/) = tanx/) sec x/) = tanx/) + tan x/) cos x = cos x/) sin x/) tan x = = tan x/) sec x/) tanx/) tan x/). = tan
6.7 Hyperbolic Functions
 6.7 6.7 Hyperbolic Functions Even and Odd Parts of an Exponential Function We recall that a function f is called even if f( x) = f(x). f is called odd if f( x) = f(x). The sine function is odd while the
6.7 6.7 Hyperbolic Functions Even and Odd Parts of an Exponential Function We recall that a function f is called even if f( x) = f(x). f is called odd if f( x) = f(x). The sine function is odd while the
11.4. Differentiating ProductsandQuotients. Introduction. Prerequisites. Learning Outcomes
 Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how
Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how
Pure Further Mathematics 3. Revision Notes
 Pure Further Mathematics Revision Notes June 6 FP JUNE 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Pure Further Mathematics Revision Notes June 6 FP JUNE 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Extra FP3 past paper - A
 Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
( ) = 1 t + t. ( ) = 1 cos x + x ( sin x). Evaluate y. MTH 111 Test 1 Spring Name Calculus I
 MTH Test Spring 209 Name Calculus I Justify all answers by showing your work or by proviing a coherent eplanation. Please circle your answers.. 4 z z + 6 z 3 ez 2 = 4 z + 2 2 z2 2ez Rewrite as 4 z + 6
MTH Test Spring 209 Name Calculus I Justify all answers by showing your work or by proviing a coherent eplanation. Please circle your answers.. 4 z z + 6 z 3 ez 2 = 4 z + 2 2 z2 2ez Rewrite as 4 z + 6
Pure Further Mathematics 3. Revision Notes
 Pure Further Mathematics Revision Notes February 6 FP FEB 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Pure Further Mathematics Revision Notes February 6 FP FEB 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Some functions and their derivatives
 Chapter Some functions an their erivatives. Derivative of x n for integer n Recall, from eqn (.6), for y = f (x), Also recall that, for integer n, Hence, if y = x n then y x = lim δx 0 (a + b) n = a n
Chapter Some functions an their erivatives. Derivative of x n for integer n Recall, from eqn (.6), for y = f (x), Also recall that, for integer n, Hence, if y = x n then y x = lim δx 0 (a + b) n = a n
Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics
 Pearson Edecel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics Mathematical formulae and statistical tables First certification from 08 Advanced Subsidiary GCE in Mathematics
Pearson Edecel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics Mathematical formulae and statistical tables First certification from 08 Advanced Subsidiary GCE in Mathematics
1. The following problems are not related: (a) (15 pts, 5 pts ea.) Find the following limits or show that they do not exist: arcsin(x)
 APPM 5 Final Eam (5 pts) Fall. The following problems are not related: (a) (5 pts, 5 pts ea.) Find the following limits or show that they do not eist: (i) lim e (ii) lim arcsin() (b) (5 pts) Find and classify
APPM 5 Final Eam (5 pts) Fall. The following problems are not related: (a) (5 pts, 5 pts ea.) Find the following limits or show that they do not eist: (i) lim e (ii) lim arcsin() (b) (5 pts) Find and classify
Math Analysis Chapter 5 Notes: Analytic Trigonometric
 Math Analysis Chapter 5 Notes: Analytic Trigonometric Day 9: Section 5.1-Verifying Trigonometric Identities Fundamental Trig Identities Reciprocal Identities: 1 1 1 sin u = cos u = tan u = cscu secu cot
Math Analysis Chapter 5 Notes: Analytic Trigonometric Day 9: Section 5.1-Verifying Trigonometric Identities Fundamental Trig Identities Reciprocal Identities: 1 1 1 sin u = cos u = tan u = cscu secu cot
Chapter 9: Complex Numbers
 Chapter 9: Comple Numbers 9.1 Imaginary Number 9. Comple Number - definition - argand diagram - equality of comple number 9.3 Algebraic operations on comple number - addition and subtraction - multiplication
Chapter 9: Comple Numbers 9.1 Imaginary Number 9. Comple Number - definition - argand diagram - equality of comple number 9.3 Algebraic operations on comple number - addition and subtraction - multiplication
Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions
 Chapter 5 Logarithmic, Exponential, an Other Transcenental Functions 5.1 The Natural Logarithmic Function: Differentiation 5.2 The Natural Logarithmic Function: Integration 5.3 Inverse Functions 5.4 Exponential
Chapter 5 Logarithmic, Exponential, an Other Transcenental Functions 5.1 The Natural Logarithmic Function: Differentiation 5.2 The Natural Logarithmic Function: Integration 5.3 Inverse Functions 5.4 Exponential
Analytic Trigonometry
 Chapter 5 Analytic Trigonometry Course Number Section 5.1 Using Fundamental Identities Objective: In this lesson you learned how to use fundamental trigonometric identities to evaluate trigonometric functions
Chapter 5 Analytic Trigonometry Course Number Section 5.1 Using Fundamental Identities Objective: In this lesson you learned how to use fundamental trigonometric identities to evaluate trigonometric functions
Today: 5.6 Hyperbolic functions
 Toay: 5.6 Hyerbolic functions Warm u: Let f() = (e ) an g() = (e + ) Verify the following ientities: () f 0 () =g() () g 0 () =f() (3) f() is an o function (i.e. f(-) = -f()) (4) g() is an even function
Toay: 5.6 Hyerbolic functions Warm u: Let f() = (e ) an g() = (e + ) Verify the following ientities: () f 0 () =g() () g 0 () =f() (3) f() is an o function (i.e. f(-) = -f()) (4) g() is an even function
Differential and Integral Calculus
 School of science an engineering El Akhawayn University Monay, March 31 st, 2008 Outline 1 Definition of hyperbolic functions: The hyperbolic cosine an the hyperbolic sine of the real number x are enote
School of science an engineering El Akhawayn University Monay, March 31 st, 2008 Outline 1 Definition of hyperbolic functions: The hyperbolic cosine an the hyperbolic sine of the real number x are enote
6.2. The Hyperbolic Functions. Introduction. Prerequisites. Learning Outcomes
 The Hyperbolic Functions 6. Introduction The hyperbolic functions cosh x, sinh x, tanh x etc are certain combinations of the exponential functions e x and e x. The notation implies a close relationship
The Hyperbolic Functions 6. Introduction The hyperbolic functions cosh x, sinh x, tanh x etc are certain combinations of the exponential functions e x and e x. The notation implies a close relationship
REVISION SHEET FP2 (MEI) CALCULUS. x x 0.5. x x 1.5. π π. Standard Calculus of Inverse Trig and Hyperbolic Trig Functions = + = + arcsin x = +
 the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET FP (MEI) CALCULUS The main ideas are: Calculus using inverse trig functions & hperbolic trig functions and their inverses. Maclaurin
the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET FP (MEI) CALCULUS The main ideas are: Calculus using inverse trig functions & hperbolic trig functions and their inverses. Maclaurin
C3 Exam Workshop 2. Workbook. 1. (a) Express 7 cos x 24 sin x in the form R cos (x + α) where R > 0 and 0 < α < 2
 C3 Exam Workshop 2 Workbook 1. (a) Express 7 cos x 24 sin x in the form R cos (x + α) where R > 0 and 0 < α < 2 π. Give the value of α to 3 decimal places. (b) Hence write down the minimum value of 7 cos
C3 Exam Workshop 2 Workbook 1. (a) Express 7 cos x 24 sin x in the form R cos (x + α) where R > 0 and 0 < α < 2 π. Give the value of α to 3 decimal places. (b) Hence write down the minimum value of 7 cos
Solution Sheet 1.4 Questions 26-31
 Solution Sheet 1.4 Questions 26-31 26. Using the Limit Rules evaluate i) ii) iii) 3 2 +4+1 0 2 +4+3, 3 2 +4+1 2 +4+3, 3 2 +4+1 1 2 +4+3. Note When using a Limit Rule you must write down which Rule you
Solution Sheet 1.4 Questions 26-31 26. Using the Limit Rules evaluate i) ii) iii) 3 2 +4+1 0 2 +4+3, 3 2 +4+1 2 +4+3, 3 2 +4+1 1 2 +4+3. Note When using a Limit Rule you must write down which Rule you
2 nd ORDER O.D.E.s SUBSTITUTIONS
 nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
Throughout this module we use x to denote the positive square root of x; for example, 4 = 2.
 Throughout this module we use x to denote the positive square root of x; for example, 4 = 2. You may often see (although not in FLAP) the notation sin 1 used in place of arcsin. sinh and cosh are pronounced
Throughout this module we use x to denote the positive square root of x; for example, 4 = 2. You may often see (although not in FLAP) the notation sin 1 used in place of arcsin. sinh and cosh are pronounced
FUNDAMENTAL TRIGONOMETRIC INDENTITIES 1 = cos. sec θ 1 = sec. = cosθ. Odd Functions sin( t) = sint. csc( t) = csct tan( t) = tant
 NOTES 8: ANALYTIC TRIGONOMETRY Name: Date: Period: Mrs. Nguyen s Initial: LESSON 8.1 TRIGONOMETRIC IDENTITIES FUNDAMENTAL TRIGONOMETRIC INDENTITIES Reciprocal Identities sinθ 1 cscθ cosθ 1 secθ tanθ 1
NOTES 8: ANALYTIC TRIGONOMETRY Name: Date: Period: Mrs. Nguyen s Initial: LESSON 8.1 TRIGONOMETRIC IDENTITIES FUNDAMENTAL TRIGONOMETRIC INDENTITIES Reciprocal Identities sinθ 1 cscθ cosθ 1 secθ tanθ 1
Differentials and Integrals
 Differentials and Integrals UBC Math 3 Lecture Notes by Yue-Xian Li (Feb, ). Differentials Definition: The differential, df, of any differentiable function F is an infinitely small increment or change
Differentials and Integrals UBC Math 3 Lecture Notes by Yue-Xian Li (Feb, ). Differentials Definition: The differential, df, of any differentiable function F is an infinitely small increment or change
A1. Let r > 0 be constant. In this problem you will evaluate the following integral in two different ways: r r 2 x 2 dx
 Math 6 Summer 05 Homework 5 Solutions Drew Armstrong Book Problems: Chap.5 Eercises, 8, Chap 5. Eercises 6, 0, 56 Chap 5. Eercises,, 6 Chap 5.6 Eercises 8, 6 Chap 6. Eercises,, 30 Additional Problems:
Math 6 Summer 05 Homework 5 Solutions Drew Armstrong Book Problems: Chap.5 Eercises, 8, Chap 5. Eercises 6, 0, 56 Chap 5. Eercises,, 6 Chap 5.6 Eercises 8, 6 Chap 6. Eercises,, 30 Additional Problems:
Hyperbolic Functions. Notice: this material must not be used as a substitute for attending. the lectures
 Hyperbolic Functions Notice: this material must not be use as a substitute for attening the lectures 0. Hyperbolic functions sinh an cosh The hyperbolic functions sinh (pronounce shine ) an cosh are efine
Hyperbolic Functions Notice: this material must not be use as a substitute for attening the lectures 0. Hyperbolic functions sinh an cosh The hyperbolic functions sinh (pronounce shine ) an cosh are efine
D sin x. (By Product Rule of Diff n.) ( ) D 2x ( ) 2. 10x4, or 24x 2 4x 7 ( ) ln x. ln x. , or. ( by Gen.
 SOLUTIONS TO THE FINAL - PART MATH 50 SPRING 07 KUNIYUKI PART : 35 POINTS, PART : 5 POINTS, TOTAL: 50 POINTS No notes, books, or calculators allowed. 35 points: 45 problems, 3 pts. each. You do not have
SOLUTIONS TO THE FINAL - PART MATH 50 SPRING 07 KUNIYUKI PART : 35 POINTS, PART : 5 POINTS, TOTAL: 50 POINTS No notes, books, or calculators allowed. 35 points: 45 problems, 3 pts. each. You do not have
4.1 Exponential and Logarithmic Functions
 . Exponential and Logarithmic Functions Joseph Heavner Honors Complex Analysis Continued) Chapter July, 05 3.) Find the derivative of f ) e i e i. d d e i e i) d d ei ) d d e i ) e i d d i) e i d d i)
. Exponential and Logarithmic Functions Joseph Heavner Honors Complex Analysis Continued) Chapter July, 05 3.) Find the derivative of f ) e i e i. d d e i e i) d d ei ) d d e i ) e i d d i) e i d d i)
Math 181, Exam 2, Fall 2014 Problem 1 Solution. sin 3 (x) cos(x) dx.
 Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
MAS153/MAS159. MAS153/MAS159 1 Turn Over SCHOOL OF MATHEMATICS AND STATISTICS hours. Mathematics (Materials) Mathematics For Chemists
 Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
THE INVERSE TRIGONOMETRIC FUNCTIONS
 THE INVERSE TRIGONOMETRIC FUNCTIONS Question 1 (**+) Solve the following trigonometric equation ( x ) π + 3arccos + 1 = 0. 1 x = Question (***) It is given that arcsin x = arccos y. Show, by a clear method,
THE INVERSE TRIGONOMETRIC FUNCTIONS Question 1 (**+) Solve the following trigonometric equation ( x ) π + 3arccos + 1 = 0. 1 x = Question (***) It is given that arcsin x = arccos y. Show, by a clear method,
Chapter two Functions
 Chaptr two Functions -- Eponntial Logarithm functions Eponntial functions If a is a positiv numbr is an numbr, w dfin th ponntial function as = a with domain - < < ang > Th proprtis of th ponntial functions
Chaptr two Functions -- Eponntial Logarithm functions Eponntial functions If a is a positiv numbr is an numbr, w dfin th ponntial function as = a with domain - < < ang > Th proprtis of th ponntial functions
EXAM. Practice for Second Exam. Math , Fall Nov 4, 2003 ANSWERS
 EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
FINAL - PART 1 MATH 150 SPRING 2017 KUNIYUKI PART 1: 135 POINTS, PART 2: 115 POINTS, TOTAL: 250 POINTS No notes, books, or calculators allowed.
 Math 150 Name: FINAL - PART 1 MATH 150 SPRING 2017 KUNIYUKI PART 1: 135 POINTS, PART 2: 115 POINTS, TOTAL: 250 POINTS No notes, books, or calculators allowed. 135 points: 45 problems, 3 pts. each. You
Math 150 Name: FINAL - PART 1 MATH 150 SPRING 2017 KUNIYUKI PART 1: 135 POINTS, PART 2: 115 POINTS, TOTAL: 250 POINTS No notes, books, or calculators allowed. 135 points: 45 problems, 3 pts. each. You
Calculus II. George Voutsadakis 1. LSSU Math 152. Lake Superior State University. 1 Mathematics and Computer Science
 Calculus II George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 52 George Voutsadakis (LSSU) Calculus II February 205 / 88 Outline Techniques of Integration Integration
Calculus II George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 52 George Voutsadakis (LSSU) Calculus II February 205 / 88 Outline Techniques of Integration Integration
Math 102 Spring 2008: Solutions: HW #3 Instructor: Fei Xu
 Math Spring 8: Solutions: HW #3 Instructor: Fei Xu. section 7., #8 Evaluate + 3 d. + We ll solve using partial fractions. If we assume 3 A + B + C, clearing denominators gives us A A + B B + C +. Then
Math Spring 8: Solutions: HW #3 Instructor: Fei Xu. section 7., #8 Evaluate + 3 d. + We ll solve using partial fractions. If we assume 3 A + B + C, clearing denominators gives us A A + B B + C +. Then
MA 242 Review Exponential and Log Functions Notes for today s class can be found at
 MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function
MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
UNIVERSITI TEKNOLOGI MALAYSIA FACULTY OF SCIENCE... FINAL EXAMINATION SEMESTER I SESSION 2015/2016 COURSE NAME : ENGINEERING MATHEMATICS I
 UNIVERSITI TEKNOLOGI MALAYSIA FACULTY OF SCIENCE... FINAL EXAMINATION SEMESTER I SESSION 05/06 COURSE CODE : SSCE 693 COURSE NAME : ENGINEERING MATHEMATICS I PROGRAMME : SKAW/SKEE/SKEL/SKEM/SKMM/SKMV/
UNIVERSITI TEKNOLOGI MALAYSIA FACULTY OF SCIENCE... FINAL EXAMINATION SEMESTER I SESSION 05/06 COURSE CODE : SSCE 693 COURSE NAME : ENGINEERING MATHEMATICS I PROGRAMME : SKAW/SKEE/SKEL/SKEM/SKMM/SKMV/
Practice Differentiation Math 120 Calculus I Fall 2015
 . x. Hint.. (4x 9) 4x + 9. Hint. Practice Differentiation Math 0 Calculus I Fall 0 The rules of differentiation are straightforward, but knowing when to use them and in what order takes practice. Although
. x. Hint.. (4x 9) 4x + 9. Hint. Practice Differentiation Math 0 Calculus I Fall 0 The rules of differentiation are straightforward, but knowing when to use them and in what order takes practice. Although
CHAPTER 1: FURTHER TRANSCENDENTAL FUNCTIONS
 SSCE1693 ENGINEERING MATHEMATICS CHAPTER 1: FURTHER TRANSCENDENTAL FUNCTIONS WAN RUKAIDA BT WAN ABDULLAH YUDARIAH BT MOHAMMAD YUSOF SHAZIRAWATI BT MOHD PUZI NUR ARINA BAZILAH BT AZIZ ZUHAILA BT ISMAIL
SSCE1693 ENGINEERING MATHEMATICS CHAPTER 1: FURTHER TRANSCENDENTAL FUNCTIONS WAN RUKAIDA BT WAN ABDULLAH YUDARIAH BT MOHAMMAD YUSOF SHAZIRAWATI BT MOHD PUZI NUR ARINA BAZILAH BT AZIZ ZUHAILA BT ISMAIL
School of Distance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION. B Sc Mathematics. (2011 Admission Onwards) IV Semester.
 School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
Chapter 5 Notes. 5.1 Using Fundamental Identities
 Chapter 5 Notes 5.1 Using Fundamental Identities 1. Simplify each expression to its lowest terms. Write the answer to part as the product of factors. (a) sin x csc x cot x ( 1+ sinσ + cosσ ) (c) 1 tanx
Chapter 5 Notes 5.1 Using Fundamental Identities 1. Simplify each expression to its lowest terms. Write the answer to part as the product of factors. (a) sin x csc x cot x ( 1+ sinσ + cosσ ) (c) 1 tanx
Hyperbolic Discrete Ricci Curvature Flows
 Hyperbolic Discrete Ricci Curvature Flows 1 1 Mathematics Science Center Tsinghua University Tsinghua University 010 Unified Framework of Discrete Curvature Flow Unified framework for both Discrete Ricci
Hyperbolic Discrete Ricci Curvature Flows 1 1 Mathematics Science Center Tsinghua University Tsinghua University 010 Unified Framework of Discrete Curvature Flow Unified framework for both Discrete Ricci
Revision Checklist. Unit FP3: Further Pure Mathematics 3. Assessment information
 Revision Checklist Unit FP3: Further Pure Mathematics 3 Unit description Further matrix algebra; vectors, hyperbolic functions; differentiation; integration, further coordinate systems Assessment information
Revision Checklist Unit FP3: Further Pure Mathematics 3 Unit description Further matrix algebra; vectors, hyperbolic functions; differentiation; integration, further coordinate systems Assessment information
Math F15 Rahman
 Math - 9 F5 Rahman Week3 7.3 Hyperbolic Functions Hyperbolic functions are similar to trigonometric functions, and have the following definitions: sinh x = (ex e x ) cosh x = (ex + e x ) tanh x = sinh
Math - 9 F5 Rahman Week3 7.3 Hyperbolic Functions Hyperbolic functions are similar to trigonometric functions, and have the following definitions: sinh x = (ex e x ) cosh x = (ex + e x ) tanh x = sinh
Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A2 optional unit
 Unit FP3 Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A optional unit FP3.1 Unit description Further matrix algebra; vectors, hyperbolic
Unit FP3 Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A optional unit FP3.1 Unit description Further matrix algebra; vectors, hyperbolic
Chapter 5 Analytic Trigonometry
 Chapter 5 Analytic Trigonometry Section 1 Section 2 Section 3 Section 4 Section 5 Using Fundamental Identities Verifying Trigonometric Identities Solving Trigonometric Equations Sum and Difference Formulas
Chapter 5 Analytic Trigonometry Section 1 Section 2 Section 3 Section 4 Section 5 Using Fundamental Identities Verifying Trigonometric Identities Solving Trigonometric Equations Sum and Difference Formulas
Solutions to Math 152 Review Problems for Exam 1
 Soltions to Math 5 Review Problems for Eam () If A() is the area of the rectangle formed when the solid is sliced at perpendiclar to the -ais, then A() = ( ), becase the height of the rectangle is and
Soltions to Math 5 Review Problems for Eam () If A() is the area of the rectangle formed when the solid is sliced at perpendiclar to the -ais, then A() = ( ), becase the height of the rectangle is and
Crash Course in Trigonometry
 Crash Course in Trigonometry Dr. Don Spickler September 5, 003 Contents 1 Trigonometric Functions 1 1.1 Introduction.................................... 1 1. Right Triangle Trigonometry...........................
Crash Course in Trigonometry Dr. Don Spickler September 5, 003 Contents 1 Trigonometric Functions 1 1.1 Introduction.................................... 1 1. Right Triangle Trigonometry...........................
9.1. Click here for answers. Click here for solutions. PARAMETRIC CURVES
 SECTION 9. PARAMETRIC CURVES 9. PARAMETRIC CURVES A Click here for answers. S Click here for solutions. 5 (a) Sketch the curve b using the parametric equations to plot points. Indicate with an arrow the
SECTION 9. PARAMETRIC CURVES 9. PARAMETRIC CURVES A Click here for answers. S Click here for solutions. 5 (a) Sketch the curve b using the parametric equations to plot points. Indicate with an arrow the
2 Trigonometric functions
 Theodore Voronov. Mathematics 1G1. Autumn 014 Trigonometric functions Trigonometry provides methods to relate angles and lengths but the functions we define have many other applications in mathematics..1
Theodore Voronov. Mathematics 1G1. Autumn 014 Trigonometric functions Trigonometry provides methods to relate angles and lengths but the functions we define have many other applications in mathematics..1
Test one Review Cal 2
 Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
Name: Class: Date: ID: A Test one Review Cal 2 Short Answer. Write the following expression as a logarithm of a single quantity. lnx 2ln x 2 ˆ 6 2. Write the following expression as a logarithm of a single
8. Hyperbolic triangles
 8. Hyperbolic triangles Note: This year, I m not doing this material, apart from Pythagoras theorem, in the lectures (and, as such, the remainder isn t examinable). I ve left the material as Lecture 8
8. Hyperbolic triangles Note: This year, I m not doing this material, apart from Pythagoras theorem, in the lectures (and, as such, the remainder isn t examinable). I ve left the material as Lecture 8
First Midterm Examination
 Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
MATH Section 210
 MATH 101 - Section 10 Instructor: Avner Segal (avners@math.ubc.ca) January 31 st 017 Common course page: http://www.math.ubc.ca/~gerg/teaching/101-winter017/ Individual section page: http://www.math.ubc.ca/~avners/courses/math101-017.html
MATH 101 - Section 10 Instructor: Avner Segal (avners@math.ubc.ca) January 31 st 017 Common course page: http://www.math.ubc.ca/~gerg/teaching/101-winter017/ Individual section page: http://www.math.ubc.ca/~avners/courses/math101-017.html
Section 6.2 Trigonometric Functions: Unit Circle Approach
 Section. Trigonometric Functions: Unit Circle Approach The unit circle is a circle of radius centered at the origin. If we have an angle in standard position superimposed on the unit circle, the terminal
Section. Trigonometric Functions: Unit Circle Approach The unit circle is a circle of radius centered at the origin. If we have an angle in standard position superimposed on the unit circle, the terminal
AMB121F Trigonometry Notes
 AMB11F Trigonometry Notes Trigonometry is a study of measurements of sides of triangles linked to the angles, and the application of this theory. Let ABC be right-angled so that angles A and B are acute
AMB11F Trigonometry Notes Trigonometry is a study of measurements of sides of triangles linked to the angles, and the application of this theory. Let ABC be right-angled so that angles A and B are acute
MATH 162. Midterm Exam 1 - Solutions February 22, 2007
 MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
MATH 62 Midterm Exam - Solutions February 22, 27. (8 points) Evaluate the following integrals: (a) x sin(x 4 + 7) dx Solution: Let u = x 4 + 7, then du = 4x dx and x sin(x 4 + 7) dx = 4 sin(u) du = 4 [
The number of marks is given in brackets [ ] at the end of each question or part question. The total number of marks for this paper is 72.
![The number of marks is given in brackets [ ] at the end of each question or part question. The total number of marks for this paper is 72. The number of marks is given in brackets [ ] at the end of each question or part question. The total number of marks for this paper is 72.](/thumbs/95/124097068.jpg) ADVANCED GCE UNIT / MATHEMATICS (MEI Further Methods for Advanced Mathematics (FP THURSDAY JUNE Additional materials: Answer booklet (8 pages Graph paper MEI Eamination Formulae and Tables (MF Morning
ADVANCED GCE UNIT / MATHEMATICS (MEI Further Methods for Advanced Mathematics (FP THURSDAY JUNE Additional materials: Answer booklet (8 pages Graph paper MEI Eamination Formulae and Tables (MF Morning
APPROVAL CRITERIA FOR GCE AS AND A LEVEL FURTHER MATHEMATICS
 APPROVAL CRITERIA FOR GCE AS AND A LEVEL FURTHER MATHEMATICS JULY 2016 Contents Page number Introduction 1 Subject aims and objectives 2 Overarching themes 2 Subject content 4 Assessment objectives 5 Scheme
APPROVAL CRITERIA FOR GCE AS AND A LEVEL FURTHER MATHEMATICS JULY 2016 Contents Page number Introduction 1 Subject aims and objectives 2 Overarching themes 2 Subject content 4 Assessment objectives 5 Scheme
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
MATH 162. FINAL EXAM ANSWERS December 17, 2006
 MATH 6 FINAL EXAM ANSWERS December 7, 6 Part A. ( points) Find the volume of the solid obtained by rotating about the y-axis the region under the curve y x, for / x. Using the shell method, the radius
MATH 6 FINAL EXAM ANSWERS December 7, 6 Part A. ( points) Find the volume of the solid obtained by rotating about the y-axis the region under the curve y x, for / x. Using the shell method, the radius
SET 1. (1) Solve for x: (a) e 2x = 5 3x
 () Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
() Solve for x: (a) e x = 5 3x SET We take natural log on both sides: ln(e x ) = ln(5 3x ) x = 3 x ln(5) Now we take log base on both sides: log ( x ) = log (3 x ln 5) x = log (3 x ) + log (ln(5)) x x
L Hôpital s Rule was discovered by Bernoulli but written for the first time in a text by L Hôpital.
 7.5. Ineterminate Forms an L Hôpital s Rule L Hôpital s Rule was iscovere by Bernoulli but written for the first time in a text by L Hôpital. Ineterminate Forms 0/0 an / f(x) If f(x 0 ) = g(x 0 ) = 0,
7.5. Ineterminate Forms an L Hôpital s Rule L Hôpital s Rule was iscovere by Bernoulli but written for the first time in a text by L Hôpital. Ineterminate Forms 0/0 an / f(x) If f(x 0 ) = g(x 0 ) = 0,
Department of Mathematical Sciences. Math 226 Calculus Spring 2016 Exam 2V2 DO NOT TURN OVER THIS PAGE UNTIL INSTRUCTED TO DO SO
 Department of Mathematical Sciences Math 6 Calculus Spring 6 Eam V DO NOT TURN OVER THIS PAGE UNTIL INSTRUCTED TO DO SO NAME (Printed): INSTRUCTOR: SECTION NO.: When instructed, turn over this cover page
Department of Mathematical Sciences Math 6 Calculus Spring 6 Eam V DO NOT TURN OVER THIS PAGE UNTIL INSTRUCTED TO DO SO NAME (Printed): INSTRUCTOR: SECTION NO.: When instructed, turn over this cover page
MATH QUIZ 3 1/2. sin 1 xdx. π/2. cos 2 (x)dx. x 3 4x 10 x 2 x 6 dx.
 NAME: I.D.: MATH 56 - QUIZ 3 Instruction: Each problem is worth of point in this take home project. Circle your answers and show all your work CLEARLY. Use additional paper if needed. Solutions with answer
NAME: I.D.: MATH 56 - QUIZ 3 Instruction: Each problem is worth of point in this take home project. Circle your answers and show all your work CLEARLY. Use additional paper if needed. Solutions with answer
Hyperbolic functions
 Roberto s Notes on Differential Calculus Chapter 5: Derivatives of transcendental functions Section Derivatives of Hyperbolic functions What you need to know already: Basic rules of differentiation, including
Roberto s Notes on Differential Calculus Chapter 5: Derivatives of transcendental functions Section Derivatives of Hyperbolic functions What you need to know already: Basic rules of differentiation, including
Math Section 4.3 Unit Circle Trigonometry
 Math 10 - Section 4. Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis. Positive angles are measured counterclockwise
Math 10 - Section 4. Unit Circle Trigonometry An angle is in standard position if its vertex is at the origin and its initial side is along the positive x axis. Positive angles are measured counterclockwise
Mathematical Techniques: Revision Notes
 Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
