MATHEMATICAL MODELLING AND ANALYSIS
|
|
|
- Anastasia Campbell
- 5 years ago
- Views:
Transcription
1 ISSN Institute of Mathematics, Latvian Academy of Sciences University of Latvia Institute of Mathematics and Informatics, Vilnius University of Tartu Vilnius Gediminas Technical University MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number Electronical edition available at Vilnius Technika 004
2 Editor-in-Chief R. Čiegis Vilnius Gediminas Technical University Saulėtekio al. 11, LT-103 Vilnius, Lithuania Executive Editor A. Štikonas Institute of Mathematics and Informatics Akademijos 4, LT Vilnius, Lithuania International Editorial Board V. Abrashin(Belarus) Institute of Mathematics, Minsk A. Buikis(Latvia) Institute of Mathematics of LAS and UL, Riga A. Fitt(UK) University of Southampton V. Gromak(Belarus) Belarussian State Univ., Minsk O. Iliev(Germany) Institute for Industrial Mathematics, Kaiserslautern F. Ivanauskas(Lithuania) Vilnius University J. Janno(Estonia) Tallinn Technical University H. Kalis(Latvia) Institute of Mathematics of LAS and UL, Riga V. Korzyuk(Belarus) Belarussian State Univ., Minsk A. Krylovas(Lithuania) Vilnius Gediminas Technical University Ü. Lepik(Estonia) University of Tartu P. Matus(Belarus) Institute of Mathematics, Minsk M. Meilūnas(Lithuania) Vilnius Gediminas Technical University H. Ockendon(UK) Oxford Centre for Industrial and Applied Mathematics W. Okrasinski(Poland) University of Zielona Gora A. Pedas(Estonia) University of Tartu K. Pileckas(Lithuania) Institute of Mathematics and Informatics U. Raitums(Latvia) Institute of Mathematics of LAS and UL, Riga A. Reinfelds(Latvia) Institute of Mathematics of LAS and UL, Riga J. Rokicki(Poland) Institute of Aeronautics, Warsaw S. Rutkauskas(Lithuania) Institute of Mathematics and Informatics, Vilnius M. Sapagovas(Lithuania) Institute of Mathematics and Informatics, Vilnius E. Tamme(Estonia) University of Tartu P. Vabishchevich(Russia) Institute for Mathematical Modelling, Moscow G. Vainikko(Estonia) Estonian Academy of Sciences M. Weber(Germany) Technische Universität Dresden G. Yelenin(Russia) M.V. Lomonosov Moscow State University A. Zemitis(Latvija) Ventspils University College A. Zlotnik(Russia) Power Engineering Institute, Moscow Vilnius Gediminas Technical University, 004
3 Mathematical Modelling and Analysis, Volume 9 Number 1, 004 i CONTENTS K. Batrakov, S. Sytova Modelling of quasi-cherenkov electron beam instability in periodical structures... 1 J. Dhar I.Krūminienė A prey-predator model with diffusion and a supplementary resource for the preyinatwo-patchenvironment... 9 O. Dumbrajs, H. Kalis, A. Reinfelds Numericalsolutionofsinglemodegyrotronequation... 5 R. Garška, SpatialanalysisandpredictionofCuronianlagoondatawithGstat J. Sieber, M. RadžiūnașK. R. Schneider Dynamicsofmultisectionsemiconductorlasers J. Socolowsky Ontheexistenceanduniquenessoftwo-fluidchannelflows M. Tarang Stability of the spline collocation method for second order Volterra integrodifferentialequations
4 9 ISSN MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number 004 Electronical edition available at << : ;<1= :? < Abstracted/Indexed in: 7 < 67 < 7? ; < 7? #?17 <1< 9 7 < 67 < 7 < ; = 7?!"#"%$"& 9' 67 < ' = #? 7 <(' *) Vilnius Technika 004
5 ISSN Institute of Mathematics, Latvian Academy of Sciences University of Latvia Institute of Mathematics and Informatics, Vilnius University of Tartu Vilnius Gediminas Technical University MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Electronical edition available at << >:;<1= :? < ( Vilnius Technika 004
6 C,,, Editor-in-Chief R. Čiegis Vilnius Gediminas Technical University Saulėtekio al. 11, LT-103 Vilnius, Lithuania Executive Editor A. Štikonas Institute of Mathematics and Informatics Akademijos 4, LT Vilnius, Lithuania International Editorial Board! " # $, V. Abrashin (Belarus) Institute of Mathematics, Minsk A. Buikis (Latvia) Institute of Mathematics of LAS and UL, Riga A. Fitt (UK) University of Southampton V. Gromak (Belarus) Belarussian State Univ., Minsk O. Iliev (Germany) Institute for Industrial Mathematics, Kaiserslautern " 1!%-) (" ( ) * ++ ) % &% " # ' +& & "/ 0$ "% 3 *4% 5 # ' 6 7 F. Ivanauskas (Lithuania) Vilnius University J. Janno (Estonia) Tallinn Technical University "" H. Kalis (Latvia) Institute of Mathematics of LAS and UL, Riga V. Korzyuk (Belarus) Belarussian State Univ., Minsk + 8$% + A. Krylovas (Lithuania) Vilnius Gediminas Technical University Ü. Lepik (Estonia) University of Tartu $ ":-% # "" P. Matus (Belarus) Institute of Mathematics, Minsk M. Meilūnas (Lithuania) Vilnius Gediminas Technical University H. Ockendon (UK) Oxford Centre for Industrial and Applied Mathematics + &% "(+ ) '+ <# ) % % ". 9 "/ $ % - 0!". $ = W. Okrasinski (Poland) University of Zielona Gora A. Pedas (Estonia) University of Tartu ". : " ( # "" K. Pileckas (Lithuania) Institute of Mathematics and Informatics U. Raitums (Latvia) Institute of Mathematics of LAS and UL, Riga -( ) A 53 ' ' ; ' '> %-%? 8. ;8 A. Reinfelds (Latvia) Institute of Mathematics of LAS and UL, Riga J. Rokicki (Poland) Institute of Aeronautics, Warsaw 6 S. Rutkauskas (Lithuania) Institute of Mathematics and Informatics, Vilnius $ %/ B 5) ' + / :- : " % A) ' " " # ' % & " / 0:19 " ( :- M. Sapagovas (Lithuania) Institute of Mathematics and Informatics, Vilnius D : + A) ' "-E. " " E. Tamme (Estonia) University of Tartu P. Vabishchevich (Russia) Institute for Mathematical Modelling, Moscow "# 3, G. Vainikko (Estonia) Estonian Academy of Sciences M. Weber (Germany) Technische Universität Dresden 1" " - 5!("(" ;(" G. Yelenin (Russia) M.V. Lomonosov Moscow State University A. Zemitis (Latvija) Ventspils University College A. Zlotnik (Russia) Power Engineering Institute, Moscow 8 + % : :") 3 " ( ) ;&%%-+. 8" 5 " # ' $" "- + ) c Vilnius Gediminas Technical University, 004
7 Mathematical Modelling and Analysis, Volume 9 Number, 004 a 10th International Conference Mathematical Modelling and Analysis and nd International Conference Computational Methods in Applied Mathematics June 1 5, 005, Trakai, Lithuania "!#%$'&%($*))%+,.--/ Conference organizers: The European Consortium for Mathematics in Industry (ECMI), Vilnius Gediminas Technical University, Institute of Mathematics and Informatics, Vilnius University and Journal Computational Methods in Applied Mathematics. Aims: The Conference focuses on various aspects of mathematical modelling and usage of finite difference and finite element methods for numerical solution of modern problems of science and engineering. It aims, in particular, at fostering cooperation among practitioners and theoreticians in this field. Another very important goal of the MMA and CMAM meetings is to assist the creation and maintenance of contacts between scientists from the West and the East. Working language of the Conference is English. The basic topics: Analysis of numerical methods for solving problems of mathematical physics; Parallel algorithms and parallel computing; Application of numerical methods to engineering problems; Analysis of ODE and PDE problems and applications; Navier - Stokes equations and Computational Fluid Dynamics; Image processing; Financial mathematics and mathematics in economics; Scientific computation. The scientific program includes invited plenary talks (40 min) and contributed talks (0 min). We also invite participants to organize minisymposiums. The format for a minisymposium might be a principal lecture and a number of communications of 15-0 minutes given by the other speakers. The minisymposia will be scheduled in parallel sessions. International Organizing Committee R. Čiegis (Lithuania - Chairman), P. Matus (Belarus - Vice-chairman), A. Štikonas (Lithuania - Scientific secretary), R. Belevičius (Lithuania), A. Buikis (Latvia), I. Gaishun (Belarus), P. Hemker (Netherlands), O. Iliev (Germany), A. Iakubenia (Belarus), F. Ivanauskas (Lithuania), A. Krylovas (Lithuania), R. Lazarov (USA), M. Meil ūnas (Lithuania), H. Neunzert (Germany), A. Pedas (Estonia), U. Raitums (Latvia), A. Reinfelds (Latvia), J. Rokicki (Poland), M. Sapagovas (Lithuania), P. Vabishchevich (Russia), G. Vainikko (Estonia), A. Zemitis (Latvia)
8 b Editor-in-Chief R. Čiegis Abstracts and Proceedings Authors are requested to send an abstract (1 page) before March 30, 005. Instructions and a style file for the preparation of the abstracts are available at << : ;<1= :@? < 66#7 Conference materials The selected papers of the Conference will be published in Vol.10 of "Mathematical Modelling and Analysis" (The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations), << : ;<1= :? < and in Vol.5 of Journal "Computational Methods in Applied Mathematics" << : : 9 ' All papers will be peer-reviewed. Correspondence address Dr. A. Štikonas (MMA005 & CMAM), Institute of Mathematics and Informatics, Akademijos 4, LT-08663,Vilnius, Lithuania Ph.: (+370) , (+370) , Fax: (+370) Questions regarding MMA005 & CMAM should be addressed to mma@konf.vtu.lt To receive the Second Announcement you must register at: << :;< = :@? < or to fill the registration form and send it by . Trakai is a popular center of tourism. It is situated 30 km from Vilnius. The town as well as its surroundings started developing in the XIII century as a state center. According to annals, Grand Duke Gediminas after a successful hunt found a beautiful place not far from the then capital Kernave and decided to build a castle here. That is how a new castle was built in Senieji Trakai which at that time was called Trakai. The town of Trakai was first mentioned in German annals in 1337, which is regarded to be the official date of its foundation. When Grand Duke Gediminas finally settled in Vilnius, Senieji Trakai was inherited by his son the Duke Kestutis. During the reign of Kestutis Naujieji Trakai was a place of intensive construction: one castle was built in the strait between lakes Galve and Lukos, another one - on an island in lake Galve. A village grew around the castle. The distinctive feature of Trakai is that the town was built and preserved by people of different nationalities. Here lived communities of Karaites, Tartars, Lithuanians, Russians and Polish. Both Christian and Karaites communities were granted separate self-government - Magdeburg - rights. The island castle was rebuilt in the second half of the XX century. In summer different festivals and concerts take place in the island castle. More information at http: :< 7 7 :? <
9 # " Mathematical Modelling and Analysis, Volume 9 Number, 004 c INFORMATION FOR AUTHORS Aims and Scope & $ $" "# # the Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations publishes carefully selected papers of the high quality presenting new and important developments in all areas of mathematical modelling and analysis. The scope of the journal includes the following: All fields of Numerical analysis, Mathematical aspects of Scientific Computing, Parallel algorithms, Mathematical modelling, Analysis of ODE and PDE, Approximation theory, Optimization. Instructions for Authors Manuscript submitted to this journal will be considered for the publication with the understanding that the same work has not been published and is not under consideration for publication elswere. All the papers will be reviewed. Any manuscript which does not conform to the below instructions may be returned for the necessary revision. Papers submitted for publication should be written in English. The length of a paper is up to 0 pages. Each paper should have the following structure: the title, the name(s) and institutional affiliation(s) of the author(s), the abstract (50-80 words), the text, the list of references. All illustrations must be supplied on separate sheets and must be marked on the back with figure number, title of paper and name of author. We welcome illustrations given in format. The list of references should always be in alphabetical order. We ask to submit your references writen with TEX. The complete reference should be listed as follows.
10 # " # " d References Editor-in-Chief R. Čiegis [1] A. Author. Article in proceedings. In: H. Ammann and V.A. Solonnikov(Eds.), Proc. of the 6th Intern. Conference NSEC-6, Palanga, Lithuania, 1997, Navier-Stokes Equations and Related Nonlinear Problems, VSP/TEV, Utrect/Vilnius, 55 64, [] A. Author. Difference methods for initial value problems. Interscience Publishers, New York, (in Russian) [3] F. Author, S. Author and T. Author. Article in journal. Journal, 1(), 3 40, We ask to submit your papers written in L A TEX ε. You may obtain the & $ $" "# # style files from our ftp server (91< 7%:;<1=>:? < ' = 7? ). We supply a style file 61647%:? and a L A TEX ε template file < 6 #?17 < :< and #? : < file. Papers for publications ( copies) should be send to: Editorial Office MATHEMATICAL MODELLING AND ANALYSIS The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations Attn.: Dr. A. Štikonas Institute of Mathematics and Informatics, Akademijos 4, LT Vilnius, Lithuania Phone: (+370 5) , Fax:(+370 5) 7909 You can send your papers by :;<1= :? < Internet Address Information about journal & $ $" "# # the Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations and online edition of all papers are presented on Internet: << : ;<1= :? < 6 647
11 Mathematical Modelling and Analysis The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations Editor-in-Chief R. Čiegis Volume 9, Number, 004 << : ;<1= :@? < 66#7 Matematinis modeliavimas ir analizė Vyriausiasis redaktorius R. Čiegis Tomas 9, Numeris, 004 SL ,0 apsk. leid. l. Tiražas 150 egz. Leido Vilniaus Gedimino technikos universiteto leidykla Technika, Saulėtekio al. 11, LT-103 Vilnius-40 Spausdino UAB Sapnų sala, S. Moniuškos g. 1-10, LT-0811 Vilnius
12 X! " $#&%'(%*)+$,- /. 013, ::; <=?>@3A">@CB DEGFHEIFCJ+KJMLONPRQSTEVUWEIXHŸ ZO[KJ]\ ^`_MacbMdegfRh We5X(ijhlk8m nmo Wdqp!rW YVm a"s dtkh YVasUukvxwqXVasU W8n ny ezf{p]slacv kd9h X Wn Ẅ YGpfS X(isẄ Y v m nmifxvk8nmebxvnywcs YZW8n a~}qxgft_e5yvkfe ~ ~7~ ~~ ~ ~ ~~7~ ~ƒ B E <! Y- Y\ Y- &LˆMQR ceistešu Ÿ PIŒIŸ K{QŽ *EŠU Ÿ PIŒIŸ K cm UadKXViW YIe5XZU/m Y W fkxgkn kvžm nmegfta-w8o-phf{}rk SVY W&p8adtaOo?s m YVeKW fkx YVa~h YVkk-o Mk } XVn~W egftan ketao Ma!XVh YVa Wdtftadtp&[Ia ai'f k8visladkxvs _ ad@w Y Y W&p8adRr!X(etikefXf{p ~~7~ ~ƒ 8 X EŽ!N šlnzq EI ]œ ]PL8žV \ŽQŽŸ EŽ xnk +J W8dKẄ Y YVasY n]m UadKX(isW Y Uk-o-aY YZXGnM Ck8vIet_ k8dtfqyzwegadjs m Y(ega~ik Us dqaeqe5xvk8n ~7~ ~ E < &[IKNZ8QI TEISYMKNZQ = EI RN L[\N LONZ ª kus Wd@W fkxgra W8n W YVp-e5X(e~h]p Ua-WnMe/kv«bMn XGftaHo X adqanmiae W8nMo 7 UCaft_ k-ö e v kdqy XVn a-wdkxg aohs dtkh YVasU k8vi pdqkfqdtknme± ~ ~7~ ~~ ~ ~ ~~7~ ~ &²³ U EI [x ŠY-LOJ]\Z Yˆ+Y Q B EŠX JlšlJ+ZONP µ nyw8nha DWi'f o-aoetidfxvs-fxvk8n kvift_ma~ i_ kftft ]p dtkm sme«kvšegp!u UaftdKXVae"~7~ ~ O ³ EŽU NZO \N¹8N[Z º nkxzus dqk r8ao _p]ḧ dkx(o k8s-fkx U XV WfXVk8nkẄ YG k8dkxfq_ U»v k8dcft_ a ¼m W8ö dkwfx(i W8eqefXG nds Uanf smdtkh YGaU½ ~ ~~7~ ~ ~~ ~ ~7~ ~~ ~ ~ ~~7~ ~ ¾ DE EŽX ˆ ÍY- *k8n k8ftk8nma7wnmo/ik8n+egadtrw fkxgrazodxg ladtanmia«eti_ auae v kdxay YZXGs fx(iza¼m WfXVk8nMex}qXfq_ U XG -ao o-adkxvrwfxvr8aoeà ~~7~ ~ ~~ ~ ~7~ ~~ ~ ~ ~~7~ ~ OÁ8
13 ISSN Institute of Mathematics, Latvian Academy of Sciences University of Latvia Institute of Mathematics and Informatics, Vilnius University of Tartu Vilnius Gediminas Technical University MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS ÎÓÐÙÑ ÆÙÑ Ö ¾¼¼ Electronical edition available at ØØÔ»»ÛÛÛºÚØÙºÐػֻÑÑ» Vilnius Technika 004
14 Editor-in-Chief R. Čiegis Vilnius Gediminas Technical University Saulėtekio al. 11, LT-103 Vilnius, Lithuania Ö ÑºÚØÙºÐØ Executive Editor A. Štikonas Institute of Mathematics and Informatics Akademijos 4, LT Vilnius, Lithuania ѺÚØÙºÐØ International Editorial Board V. Abrashin (Belarus) Institute of Mathematics, Minsk Ö Ò Ñº ¹Ò غ Ý A. Buikis (Latvia) Institute of Mathematics of LAS and UL, Riga Ù Ð ØÒ ØºÐÚ G. Erbacci (Italy) Supercomputing Group - InterUniversity Computing Center Ö Ò º Ø A. Fitt (UK) University of Southampton Ñ Ø º ÓØÓÒº ºÙ V. Gromak (Belarus) Belarussian State Univ., Minsk ÖÓÑ Ùº Ý O. Iliev (Germany) Institute for Industrial Mathematics, Kaiserslautern Ð Ú ØÛѺÙÒ ¹ к F. Ivanauskas (Lithuania) Vilnius University Ð ºÁÚ Ò Ù Ñ ºÚÙºÐØ J. Janno (Estonia) Tallinn Technical University ÒÒÓ Óº H. Kalis (Latvia) Institute of Mathematics of LAS and UL, Riga Ð Ð ØÒ ØºÐÚ V. Korzyuk (Belarus) Belarussian State Univ., Minsk ÃÓÖÞÝÙ ÓÖ º ÙºÙÒ Ðº Ý A. Krylovas (Lithuania) Vilnius Gediminas Technical University Ö ÑºÚØÙºÐØ Ü. Lepik (Estonia) University of Tartu ÝÐ Ô Ñ Ø ºÙغ P. Matus (Belarus) Institute of Mathematics, Minsk Ñ Ø٠Ѻ ¹Ò غ Ý M. Meil ūnas(lithuania) Vilnius Gediminas Technical University ÑÑ ÑºÚØÙºÐØ H. Ockendon (UK) Oxford Centre for Industrial and Applied Mathematics Ó Ò ÓÒÑ Ø ºÓܺ ºÙ W. Okrasinski (Poland) University of Zielona Gora ÏºÇ Ö Ò ÑºÙÞºÞ ÓÖ ºÔÐ A. Pedas (Estonia) University of Tartu ÖÚ ØºÔ Ùغ K. Pileckas (Lithuania) Institute of Mathematics and Informatics Ô Ð ØÐºÑ ºÐØ U. Raitums (Latvia) Institute of Mathematics of LAS and UL, Riga ÙÐ ºÖ ØÙÑ Ñ ºÐÙºÐÚ A. Reinfelds (Latvia) Institute of Mathematics of LAS and UL, Riga Ö Ò Ð ØÒ ØºÐÚ J. Rokicki (Poland) Institute of Aeronautics, Warsaw Ñ ÐºÔÛº ÙºÔÐ S. Rutkauskas (Lithuania) Institute of Mathematics and Informatics, Vilnius Ø Ý Ö ØÐºÑ ºÐØ M. Sapagovas (Lithuania) Institute of Mathematics and Informatics, Vilnius ÅºË Ô ÓÚ ØÐºÑ ºÐØ E. Tamme (Estonia) University of Tartu ÒÒ ØÙغ P. Vabishchevich (Russia) Institute for Mathematical Modelling, Moscow Ú Ö º ºÖÙ G. Vainikko (Estonia) Estonian Academy of Sciences ÒÒ ºÚ Ò Ó Ùغ M. Weber (Germany) Technische Universität Dresden Û ÖÑ Ø ºØÙ¹ Ö Òº G. Yelenin (Russia) M.V. Lomonosov Moscow State University Ý Ð Ò ÒÓÖºÖÙ A. Zemitis (Latvija) Ventspils University College Þ Ñ Ø Ú ÒØ ºÐÚ A. Zlotnik (Russia) Power Engineering Institute, Moscow ÞÐÓØÒ ÔÑ ÙÒºÑÔ º ºÖÙ c Vilnius Gediminas Technical University, 004
15 Mathematical Modelling and Analysis, Volume 9 Number 3, 004 a Ö Ø ÒÒÓÙÒ Ñ ÒØ 10th International Conference Mathematical Modelling and Analysis and nd International Conference Computational Methods in Applied Mathematics June 1 5, 005, Trakai, Lithuania ÛÛÛºÚØÙºÐػֻÑÑ ¾¼¼ Conference organizers: The International Association for Mathematics and Computers in Simulation (IMACS), The European Consortium for Mathematics in Industry (ECMI), Vilnius Gediminas Technical University, Institute of Mathematics and Informatics, Vilnius University and Journal Computational Methods in Applied Mathematics. Aims: The Conference focuses on various aspects of mathematical modelling and usage of finite difference and finite element methods for numerical solution of modern problems of science and engineering. It aims, in particular, at fostering cooperation among practitioners and theoreticians in this field. Another very important goal of the MMA and CMAM meetings is to assist the creation and maintenance of contacts between scientists from the West and the East. Working language of the Conference is English. The basic topics: Analysis of numerical methods for solving problems of mathematical physics; Parallel algorithms and parallel computing; Application of numerical methods to engineering problems; Analysis of ODE and PDE problems and applications; Navier - Stokes equations and Computational Fluid Dynamics; Image processing; Financial mathematics and mathematics in economics; Scientific computation. The scientific program includes invited plenary talks (40 min) and contributed talks (0 min). We also invite participants to organize minisymposiums. The format for a minisymposium might be a principal lecture and a number of communications of 15-0 minutes given by the other speakers. The minisymposia will be scheduled in parallel sessions. International Organizing Committee R. Čiegis (Lithuania - Chairman), P. Matus (Belarus - Vice-chairman), A. Štikonas (Lithuania - Scientific secretary), R. Belevičius (Lithuania), A. Buikis (Latvia), I. Gaishun (Belarus), P. Hemker (Netherlands), O. Iliev (Germany), A. Iakubenia (Belarus), F. Ivanauskas (Lithuania), A. Krylovas (Lithuania), R. Lazarov (USA), M. Meil ūnas (Lithuania), H. Neunzert (Germany), A. Pedas (Estonia), U. Raitums (Latvia), A. Reinfelds (Latvia), J. Rokicki (Poland), M. Sapagovas (Lithuania),
16 b Editor-in-Chief R. Čiegis I. Sloan (Australia), P. Vabishchevich (Russia), G. Vainikko (Estonia), A. Zemitis (Latvia) Abstracts and Proceedings Authors are requested to send an abstract (1 page) before March 30, 005. Instructions and a style file for the preparation of the abstracts are available at ØØÔ»»ÛÛÛºÚØÙºÐػֻÑÑ ¾¼¼» Conference materials The selected papers of the Conference will be published in Vol. 10 of "Mathematical Modelling and Analysis" (The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations), ØØÔ»»ÛÛÛºÚØÙºÐػֻÑÑ» and in Vol. 5 of Journal "Computational Methods in Applied Mathematics" ØØÔ»»ÛÛÛºÑ Ñº Ò Ó» All papers will be peer-reviewed. Correspondence address Dr. A. Štikonas (MMA005 & CMAM), Institute of Mathematics and Informatics, Akademijos 4, LT-08663,Vilnius, Lithuania Ph.: (+370) , (+370) , Fax: (+370) Questions regarding MMA005 & CMAM should be addressed to mma@konf.vtu.lt To receive the Second Announcement you must register at: ØØÔ»»ÛÛÛºÚØÙºÐػֻÑÑ ¾¼¼» or to fill the registration form and send it by . Trakai is a popular center of tourism. It is situated 30 km from Vilnius. The town as well as its surroundings started developing in the XIII century as a state center. According to annals, Grand Duke Gediminas after a successful hunt found a beautiful place not far from the then capital Kernave and decided to build a castle here. That is how a new castle was built in Senieji Trakai which at that time was called Trakai. The town of Trakai was first mentioned in German annals in 1337, which is regarded to be the official date of its foundation. When Grand Duke Gediminas finally settled in Vilnius, Senieji Trakai was inherited by his son the Duke Kestutis. During the reign of Kestutis Naujieji Trakai was a place of intensive construction: one castle was built in the strait between lakes Galve and Lukos, another one - on an island in lake Galve. A village grew around the castle. The distinctive feature of Trakai is that the town was built and preserved by people of different nationalities. Here lived communities of Karaites, Tartars, Lithuanians, Russians and Polish. Both Christian and Karaites communities were granted separate self-government - Magdeburg - rights. The island castle was rebuilt in the second half of the XX century. In summer different festivals and concerts take place in the island castle. More information at ºÐØ
17 Mathematical Modelling and Analysis, Volume 9 Number 3, 004 c INFORMATION FOR AUTHORS Aims and Scope Å ÌÀ Å ÌÁ Ä ÅÇ ÄÄÁÆ Æ Æ Ä ËÁË the Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations publishes carefully selected papers of the high quality presenting new and important developments in all areas of mathematical modelling and analysis. The scope of the journal includes the following: All fields of Numerical analysis, Mathematical aspects of Scientific Computing, Parallel algorithms, Mathematical modelling, Analysis of ODE and PDE, Approximation theory, Optimization. Instructions for Authors Manuscript submitted to this journal will be considered for the publication with the understanding that the same work has not been published and is not under consideration for publication elswere. All the papers will be reviewed. Any manuscript which does not conform to the below instructions may be returned for the necessary revision. Papers submitted for publication should be written in English. The length of a paper is up to 0 pages. Each paper should have the following structure: the title, the name(s) and institutional affiliation(s) of the author(s), the abstract (50-80 words), the text, the list of references. All illustrations must be supplied on separate sheets and must be marked on the back with figure number, title of paper and name of author. We welcome illustrations given in ÈË format. The list of references should always be in alphabetical order. We ask to submit your references writen with TEX. The complete reference should be listed as follows.
18 d References Editor-in-Chief R. Čiegis [1] A. Author. Article in proceedings. In: H. Ammann and V.A. Solonnikov(Eds.), Proc. of the 6th Intern. Conference NSEC-6, Palanga, Lithuania, 1997, Navier-Stokes Equations and Related Nonlinear Problems, VSP/TEV, Utrect/Vilnius, 55 64, [] A. Author. Difference methods for initial value problems. Interscience Publishers, New York, (in Russian) [3] F. Author, S. Author and T. Author. Article in journal. Journal, 1(), 3 40, We ask to submit your papers written in L A TEX ε. You may obtain the Å ÌÀ Å ÌÁ Ä ÅÇ ÄÄÁÆ Æ Æ Ä ËÁË style files from our ftp server ( ØÔ»» Ò ºÚØÙºÐØ»ÅÅ» ÓÙÖÒ Ð»). We supply a style file ÑÑ ºÐ and a L A TEX ε template file Ø ÑÔÐ Ø ºØ Ü and ÔÐ Ò ÑÑ º Ø file. Papers for publications ( copies) should be send to: Editorial Office MATHEMATICAL MODELLING AND ANALYSIS The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations Attn.: Dr. A. Štikonas Institute of Mathematics and Informatics, Akademijos 4, LT Vilnius, Lithuania Phone: (+370 5) , Fax:(+370 5) 7909 You can send your papers by ÑÑ ÑºÚØÙºÐØ Internet Address Information about journal Å ÌÀ Å ÌÁ Ä ÅÇ ÄÄÁÆ Æ Æ Ä ËÁË the Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations and online edition of all papers are presented on Internet: ØØÔ»»ÛÛÛºÚØÙºÐػֻÑÑ»
19 Mathematical Modelling and Analysis The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations Editor-in-Chief R. Čiegis Volume 9, Number 3, 004 ØØÔ»»ÛÛÛºÚØÙºÐػֻÑÑ» Matematinis modeliavimas ir analizė Vyriausiasis redaktorius R. Čiegis Tomas 9, Numeris 3, 004 SL ,0 apsk. leid. l. Tiražas 150 egz. Leido Vilniaus Gedimino technikos universiteto leidykla Technika, Saulėtekio al. 11, LT-103 Vilnius-40 Spausdino UAB Sapnų sala, S. Moniuškos g. 1-10, LT-0811 Vilnius
20 Q Z! " $#&%'(%*)+$,- /. 013, ::; <=?>@3A">@CB D EGFIH+JLKMGN OGP QSR R [\ZUTY VMZXWY[Z\W]G^_Y[Z R+` T'VhZUWaY*b Ÿ W ` Z\cdc7cdc7cdcecdc7cdcdc7cdc7cdc7cdcdcecdc7cdcIf g h iexjkegjcl+ml[npok qsr `tl` TWY[u vwwax[y[u Yy{z} VY [Ux `!~ yw [ ` W W]9 sz ` W YaŸ Yƒ Zeq z R+` ] Way7vZ\YaY Y [UzU VMZUTY [ [ẍ Y[TVhZUWaY[Z\ szxvrˆ ZUZ{TWYVhZUYx[Wax[ZI W `Š T Z ` YVZ cdcdc7cdc7cdc7cdcdcecdc7cdcifphaœ ŽEŽ }MN- L Ž E B ok M ˆ ZX x[zhzuway Wa] ~ W R x [ Y VMZXWỸ ẍ Y[u ` y9v{r ` ^_Ÿ [x ` Y+T ` ^_Y+u-x[ZšVyMZ\Ÿ [ ZU YVhZUWaY ZUY Y/q szxy U $ZXVœz T9Y!ZUyWY W ` YVžcdcdcecdc7cdc7cdcdc7cdc7cdcecdc7cdcdc7cdc7cdc7cdcdcecdc7cdc Ÿa f F EŽ p mllḧ N P GD EŽ!oJL op `!Z ` Wa]/ Ix W ` ymz(tuy [ Q Zz!W R VWVMZUT Q ` yby ZXŸ ] Wy ` Y![Uzª SWaY [\ZUY ` Yay «Sz R+` y Ẅ [\ZUT7 ny& ` Z cdcdcecdc7cdc7cdcdc7cdc7cdcecdc7cdcdc7cdc7cdc7cdcdcecdc7cdc Ÿaah EU Ē D N PpOmlLH Q +Wx-V V{r ` t W[Xẍ VhZUWaY(ZUY! $[XWZ ` ue [WayMW Wa][b ` Y ` ymÿ [ ZU ` ue± Yy{ x+zšr `!ZUTr7vwWaẍ Y[uFU Yayz VY [Ux `7~ yw [ ` W ZUY}Vr ` $[ YaZ{ZwW] Q Y Ÿ [XzVMZUTY [ x[y[t'vmzxwy[z²cdc7cdcdcecdc7cdc ŸŸŒ ³E B l+ µl KJLN A m E A PPpl+O Q¹~ Z ` W ` [ ` T'V{yhZ(T WYVMYaTV ~ y{wa [ ` Wº szxvr t [\Z R ˆ `R+` Y[u ` YV» W `Š T Z ` YV}W] [yhz(t'vmzxwy¼cdc7cdc7cdc7cdcdcecdc7cdc7cdcdc7cdc7cdcecdc7cdcdc7cdc7cdc7cdcdcecdc7cdc ŸŸh A EX½SEŽ¾ OGÀaoKGN t VMY Z [\ZVœz W]Gqsr[y `` U_Á ` ` [ ˆ Z ` y ` Y[T `3t Tr ` W ` Z szxvr ` Z R ` TVsVWCVr ` szu arvhu «YY[u t Z(u ` c7cdc7cdc7cdcdcecdc7cdc7cdcdc7cdc7cdcecdc7cdcdc7cdc7cdc7cdcdcecdc7cdc ŸÂŒ
21 ISSN MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number Electronical edition available at Abstracted/Indexed in: Mathematical Reviews Zentralblatt für Mathematik Referativnyi Zhurnal(VINITI information publication) Vilnius Technika 004
22 ISSN Institute of Mathematics, Latvian Academy of Sciences University of Latvia Institute of Mathematics and Informatics, Vilnius University of Tartu Vilnius Gediminas Technical University MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number Electronical edition available at Vilnius Technika 004
23 Editor-in-Chief R. Čiegis Vilnius Gediminas Technical University Saulėtekio al. 11, LT-103 Vilnius, Lithuania Executive Editor A. Štikonas Institute of Mathematics and Informatics Akademijos 4, LT Vilnius, Lithuania International Editorial Board V. Abrashin (Belarus) Institute of Mathematics, Minsk A. Buikis (Latvia) Institute of Mathematics of LAS and UL, Riga G. Erbacci (Italy) Supercomputing Group - InterUniversity Computing Center erbacci@cineca.it A. Fitt (UK) University of Southampton adf@maths.soton.ac.uk V. Gromak (Belarus) Belarussian State Univ., Minsk grom@bsu.by O. Iliev (Germany) Institute for Industrial Mathematics, Kaiserslautern iliev@itwm.uni-kl.de F. Ivanauskas (Lithuania) Vilnius University Feliksas.Ivanauskas@mif.vu.lt J. Janno (Estonia) Tallinn Technical University janno@ioc.ee H. Kalis (Latvia) Institute of Mathematics of LAS and UL, Riga kalis@latnet.lv V. Korzyuk (Belarus) Belarussian State Univ., Minsk Korzyuk@org.bsu.unibel.by A. Krylovas (Lithuania) Vilnius Gediminas Technical University akr@fm.vtu.lt Ü. Lepik (Estonia) University of Tartu ylepik@math.ut.ee P. Matus (Belarus) Institute of Mathematics, Minsk matus@im.bas-net.by M. Meilūnas (Lithuania) Vilnius Gediminas Technical University mm@fm.vtu.lt H. Ockendon (UK) Oxford Centre for Industrial and Applied Mathematics ockendon@maths.ox.ac.uk W. Okrasinski (Poland) University of Zielona Gora W.Okrasinski@im.uz.zgora.pl A. Pedas (Estonia) University of Tartu arvet.pedas@ut.ee K. Pileckas (Lithuania) Institute of Mathematics and Informatics pileckas@ktl.mii.lt U. Raitums (Latvia) Institute of Mathematics of LAS and UL, Riga uldis.raitums@mii.lu.lv A. Reinfelds (Latvia) Institute of Mathematics of LAS and UL, Riga reinf@latnet.lv J. Rokicki (Poland) Institute of Aeronautics, Warsaw jack@meil.pw.edu.pl S. Rutkauskas (Lithuania) Institute of Mathematics and Informatics, Vilnius stasysr@ktl.mii.lt M. Sapagovas (Lithuania) Institute of Mathematics and Informatics, Vilnius M.Sapagovas@ktl.mii.lt E. Tamme (Estonia) University of Tartu enn_t@ut.ee P. Vabishchevich (Russia) Institute for Mathematical Modelling, Moscow vab@ibrae.ac.ru G. Vainikko (Estonia) Estonian Academy of Sciences gen@ut.ee M. Weber (Germany) Technische Universität Dresden weber@math.tu-dresden.de G. Yelenin (Russia) M.V. Lomonosov Moscow State University yelenin@orc.ru A. Zemitis (Latvija) Ventspils University College zemitis@venta.lv A. Zlotnik (Russia) Power Engineering Institute, Moscow zlotnik@apmsun.mpei.ac.ru c Vilnius Gediminas Technical University, 004
24 Authors Index Mathematical Modelling and Analysis, Volume 9, 004 Avenhaus R.: Applications of Inspection Games Batrakov K.: Modelling of Quasi- Cherenkov Electron Beam Instability in Periodical Structures... 1 Bolotin I.B.: The First Basic Boundary Value Problem of Riemann s Type for Bianalytical Functions in a Plane with Slots Bolotin I.B.: The Second Boundary Value Problem of Riemann s Type for Bianalytical Functions with Discontinuous Coefficients193 Cēbers A.: see Cīrulis T Chakravarty S.: Numerical Simulation of Unsteady Two- Layered Pulsatile Blood Flow in a Stenosed Flexible Artery: Effect of Peripheral Layer Viscosity99 Chtcheritsa O.V.: Implicit Numerical Algorithm for the Solution of Phase Transition Problems in Multi-Component Alloys Čiegis R.: see Krylovas A Čiegis R.: Parallel Numerical Modelling of Short Laser Pulse Compression Čiegis R.: Mathematical Modelling of Water Flow in Paper Press Machines Cīrulis T.: Comparative Analysis by Means of Finite Differences and DM Methods for Linearized Problem of Gyrotrons Cīrulis T.: Dynamics of small Bubble Interface Perturbations in Vertical Hele-Shaw Cell with Magnetic Liquid under the Action of Normal Magnetic Field Dement ev A.: see Čiegis R Denisovas V.: see Švitra D Dhar J.: Diffusion of Population under the Influence Industrialization in a Twin-City Environment Dubatovskaya M.: On an Exact Description of the Schottky Groups of Symmetries137 Dumbrajs O.: Numerical Solution of Single Mode Gyrotron Equation... 5 Essoufi El-H.: see Sofonea M..9 Garška R.: Spatial Analysis and Prediction of Curonian Lagoon Data with Gstat 39 Gromyko G.: On the Cooling of a Free Thin Film at the Presence of the van der Waals Forces J. Dhar: A Prey-predator Model with Diffusion and a Supplementary Resource for the Prey in a Two-Patch Environment...9 Juščenko N.: see Švitra D Kalis H.: see Cīrulis T Kalis H.: see Dumbrajs O....5 Krūminienė I.: see Garška R... 39
25 ii Editor-in-Chief R. Čiegis Krylovas A.: A Review of Numerical Asymptotic Averaging for Weakly Nonlinear Hyperbolic Waves Lietuvietis O.: see Cīrulis T.. 17, 87 Mandal A.: see Chakravarty S..99 Mandal P.K.: see Chakravarty S. 99 Mazhorova O.S.: see Chtcheritsa O.V Meilūnas M.: see Čiegis R...67 Misevičius A.: An Improved Hybrid Optimization Algorithm for the Quadratic Assignment Problem.149 Omrani K.: On Fully Discrete Galerkin Approximations for the Cahn-Hilliard Equation 313 Popov Yu.P.: see Chtcheritsa O.V. 53 Popova L.: see Gromyko G...99 Radžiūnas M.: see Sieber J...51 Rasulov K.M.: About the Solution in Closed Form of Generalized Markushevich Boundary Value Problem in the Class of Analytical Functions... 3 Rasulov K.M.: see Bolotin I.B.. 91 Reinfelds A.: see Dumbrajs O.. 5 Rogosin S.: see Dubatovskaya M. 137 Rybak I.V.: Monotone and Conservative Difference Schemes for Elliptic Equations with Mixed Derivatives Schneider K.R.: see Sieber J Sieber J.: Dynamics of Multisection Semiconductor Lasers 51 Šilko G.: see Čiegis R Singh H.:see Dhar J...01 Socolowsky J.: On the Existence and Uniqueness of Two- Fluid Channel Flows.. 67 Sofonea M.: A Piezoelectric Contact Problem with Slip Dependent Coefficient of Friction Štikonas A.: see Čiegis R Švitra D.: Computer Modelling of Density Dynamics of Single- Species Laboratory Insects Population Sytova S.: see Batrakov K...1 Tabakova S.: see Gromyko G.. 99 Tammeraid I.: Generalized Riesz Method and Convergence Acceleration Tarang I.: Stability of the Spline Collocation Method for Second Order Volterra Integro-Differential Equations 79 Zyuzina E.L.: Stability of Three- Level Difference Schemes with Respect to the Right- Hand Side....43
26 Mathematical Modelling and Analysis, Volume 9 Number 4, 004 a Second Announcement 10th International Conference Mathematical Modelling and Analysis and nd International Conference Computational Methods in Applied Mathematics June 1 5, 005, Trakai, Lithuania Conference organizers: The International Association for Mathematics and Computers in Simulation (IMACS), the European Consortium for Mathematics in Industry (ECMI), Vilnius Gediminas Technical University, Institute of Mathematics and Informatics, Vilnius University and Computational Methods in Applied Mathematics (CMAM). International Organizing Committee. R. Čiegis (Lithuania - Chairman), P. Matus (Belarus - Vice-chairman), A. Štikonas (Lithuania - Scientific secretary), R. Belevičius (Lithuania), A. Buikis (Latvia), I. Gaishun (Belarus), P. Hemker (Netherlands), O. Iliev (Germany), A. Iakubenia (Belarus), F. Ivanauskas (Lithuania), A. Krylovas (Lithuania), R. Lazarov (USA), M. Meilūnas (Lithuania), H. Neunzert (Germany), A. Pedas (Estonia), U. Raitums (Latvia), A. Reinfelds (Latvia), J. Rokicki (Poland), M. Sapagovas (Lithuania), I. Sloan (Australia), P. Vabishchevich (Russia), G. Vainikko (Estonia), A. Zemitis (Latvia) Aims: The Conference focuses on various aspects of mathematical modelling and usage of finite difference and finite element methods for numerical solution of modern problems of science and engineering. It aims, in particular, at fostering cooperation among practitioners and theoreticians in this field. Another very important goal of the MMA and CMAM meetings is to assist the creation and maintenance of contacts between scientists from the West and East. Working language of the Conference is English. The basic topics: Analysis of numerical methods for solving problems of mathematical physics; Parallel algorithms and parallel computing; Application of numerical methods; Analysis of ODE and PDE problems and applications; Navier - Stokes equations and Computational Fluid Dynamics; Image processing; Financial mathematics and mathematics in economics; Scientific computation. The scientific program includes Invited Plenary Talks (40 min), Invited Semiplenary lectures (30 min) and Contributed Talks (0 min). The program also includes Poster Sessions.
27 b Editor-in-Chief R. Čiegis We also invite participants to organize mini-symposia. The format for a minisymposium is a principal lecture (30 min) and a number of communications of 0 minutes given by the other speakers. The mini-symposia will be scheduled in parallel sessions. The deadline for proposals of mini-symposia is January 30, 005. The following mini-symposia are approved: 1. "Modelling and simulation of hydrogeological and geo-environmental problems", co-organizers: H. Neunzert, O. Iliev (ITWM, Kaiserslautern, Germany), P.Vabishchevich (Moscow university, Russia), neunzert,iliev@itwm.fhg.de. "Navier - Stokes equations and Computational Fluid Dynamics", coorganizers: W.Zajaczkowski, J. Rokicki (Poland), K. Pileckas (IMI, Vilnius, Lithuania) W.Zajaczkowski@impan.gov.pl, jack@meil.pw.edu.pl, pileckas@ktl.mii.lt 3. "Computational Mechanics", organizers: R. Belevicius (VGTU, Vilnius, Lithuania), rb@fm.vtu.lt 4. "Parallel and grid computing: algorithms and applications", co-organizers: M. Sosonkina (Ames Laboratory and Iowa State University, USA), R. Ciegis (VGTU, Vilnius, Lithuania), rc@fm.vtu.lt 5. "Mathematical models including non-local boundary conditions", co-organizers: M. Sapagovas (IMI, Vilnius, Lithuania), V.L. Makarov (Kiev, Ukraine), m.sapagovas@ktl.mii.lt Abstracts and Proceeding. Authors are requested to send an abstract (1 page) before March 30, 005. Instructions and a style file for the preparation of the abstracts are available athttp:// Conference materials. The selected papers of the Conference will be published in Vol. 10 of "Mathematical Modelling and Analysis" and in Vol. 5 of Journal "Computational Methods in Applied Mathematics" All papers will be peer-reviewed. Registration. For registration please fill in the registration form at our web-site. Please inform us about your arrival and departure dates. The registration fee is 40 EUR and can be paid directly at the registration desk. It includes the abstract volume, all local expenses (accommodation in two bed rooms for four nights and three meals per day), conference dinner and coffee breaks. Persons who wish accommodation in single rooms should pay the registration fee 300 EUR. The fee for accompanying persons is 140 EUR. It icludes the reception, conference dinner, social events and accommodation in two bed rooms for four nights and three meals per day. Full traveling and registration information will be given on our web-site. Deadlines. Abstracts: March 30, 005; Notification of participation and reservation of accommodation: May 10, 005 Correspondence address. Dr. A. Štikonas (MMA005 & CMAM), Institute of Mathematics and Informatics, Akademijos 4, LT-08663, Vilnius, Lithuania. Ph.: (+370) , (+370) , Fax: (+370) Questions regarding MMA005 & CMAM should be addressed to mma@konf.vtu.lt
28 Mathematical Modelling and Analysis, Volume 9 Number 4, 004 c INFORMATION FOR AUTHORS Aims and Scope MATHEMATICAL MODELLING AND ANALYSIS the Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations publishes carefully selected papers of the high quality presenting new and important developments in all areas of mathematical modelling and analysis. The scope of the journal includes the following: All fields of Numerical analysis, Mathematical aspects of Scientific Computing, Parallel algorithms, Mathematical modelling, Analysis of ODE and PDE, Approximation theory, Optimization. Instructions for Authors Manuscript submitted to this journal will be considered for the publication with the understanding that the same work has not been published and is not under consideration for publication elswere. All the papers will be reviewed. Any manuscript which does not conform to the below instructions may be returned for the necessary revision. Papers submitted for publication should be written in English. The length of a paper is up to 0 pages. Each paper should have the following structure: the title, the name(s) and institutional affiliation(s) of the author(s), the abstract (50-80 words), the text, the list of references. All illustrations must be supplied on separate sheets and must be marked on the back with figure number, title of paper and name of author. We welcome illustrations given in EPS format. The list of references should always be in alphabetical order. We ask to submit your references writen with BibTEX. The complete reference should be listed as follows.
29 d References Editor-in-Chief R. Čiegis [1] A. Author. Article in proceedings. In: H. Ammann and V.A. Solonnikov(Eds.), Proc. of the 6th Intern. Conference NSEC-6, Palanga, Lithuania, 1997, Navier-Stokes Equations and Related Nonlinear Problems, VSP/TEV, Utrect/Vilnius, 55 64, [] A. Author. Difference methods for initial value problems. Interscience Publishers, New York, (in Russian) [3] F. Author, S. Author and T. Author. Article in journal. Journal, 1(), 3 40, We ask to submit your papers written in L A TEX ε. You may obtain the MATHEMATICAL MODELLING AND ANALYSIS style files from our ftp server (ftp://inga.vtu.lt/mma/journal/). We supply a style file mma.cls and a L A TEX ε template filetemplate.tex andplain_mma.bst file. Papers for publications ( copies) should be send to: Editorial Office MATHEMATICAL MODELLING AND ANALYSIS The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations Attn.: Dr. A. Štikonas Institute of Mathematics and Informatics, Akademijos 4, LT Vilnius, Lithuania Phone: (+370 5) , Fax:(+370 5) 7909 You can send your papers by mma@fm.vtu.lt Internet Address Information about journal MATHEMATICAL MODELLING AND ANALYSIS the Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations and online edition of all papers are presented on Internet:
30 Mathematical Modelling and Analysis The Baltic Journal on Mathematical Applications, Numerical Analysis and Differential Equations Editor-in-Chief R. Čiegis Volume 9, Number 4, Matematinis modeliavimas ir analizė Vyriausiasis redaktorius R. Čiegis Tomas 9, Numeris 4, 004 SL ,5 apsk. leid. l. Tiražas 00 egz. Leido Vilniaus Gedimino technikos universiteto leidykla Technika, Saulėtekio al. 11, LT-103 Vilnius-40 Spausdino UAB Sapnų sala, S. Moniuškos g. 1-10, LT-0811 Vilnius
31 Mathematical Modelling and Analysis Volume 9, Number 4, 004 CONTENTS O.V. Chtcheritsa, O.S. Mazhorova, Yu.P. Popov Implicit Numerical Algorithm for the Solution of Phase Transition Problems in Multi-Component Alloys R. Čiegis, M. Meilûnas, A. Štikonas Mathematical Modelling of Water Flow in Paper Press Machines T. Cīrulis, O. Lietuvietis, A.Cēbers Dynamics of small Bubble Interface Perturbations in Vertical Hele- Shaw Cell with Magnetic Liquid under the Action of Normal Magnetic Field G. Gromyko, S. Tabakova, L. Popova On the Cooling of a Free Thin Film at the Presence of the van der Waals Forces K. Omrani On Fully Discrete Galerkin Approximations for the Cahn-Hilliard Equation D. Švitra, V. Denisovas, N. Juščenko Computer Modelling of Density Dynamics of Single-Species Laboratory Insects Population I. Tammeraid Generalized Riesz Method and Convergence Acceleration
32 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN MODELLING OF QUASI-CHERENKOV ELECTRON BEAM INSTABILITY IN PERIODICAL STRUCTURES 1 K. BATRAKOV and S. SYTOVA Institute for Nuclear Problems, Belarussian State University Bobruiskaya 11, 0050 Minsk, Belarus 9:0;< : = >0? :@AQBDFEHGRAQB7KL=%EM9N Received October 003; revised December Abstract. Nonlinear stage of quasi-cherenkov instability of electron beam under conditions of two- and three-dimensional distributed feedback is simulated. The scheme of distributed feedback with two strong coupled waves is considered. Mathematical model of quasi- Cherenkov electron beam instability is proposed. Numerical method to solve the nonlinear integro-differential system, describing such instability, is worked out. Results of numerical experiments are discussed. Key words: quasi-cherenkov instability, numerical modelling, nonlinear integro-differential system 1. Introduction This contribution is devoted to modelling of nonlinear stage of quasi Cherenkov electron beam instability under the conditions of two- and three-dimensional distributed feedback. Quasi-Cherenkov instability takes place when one or more wave refraction index satisfy the Cherenkov condition [4]. In this case electrons radiate coherently. Such instability mechanism can be considered as a technique for realization of Free Electron Laser (FEL). FELs are devices which use the electron beam energy to generate coherent electromagnetic radiation. Such devices are very perspective for electromagnetic radiation generation in wide spectral range. Nowadays FEL lasing is obtained in different wavelength ranges: from centimeter to ultra-violet [, 9, 14]. The high expensive International X-ray FEL project is on the preparation stage now [16]. Volume FEL (VFEL) based on the mechanism of multi wave volume distributed feedback (VDFB) was proposed in [3, 5]. VFELs give possibility to reduce the starting currents of generation, to provide generation in large volume, to tune generation 1 Authors thank prof. V. G. Baryshevsky for his interest to this work
33 K. Batrakov, S. Sytova frequency [3]. VFEL generation in large volume essentially increases the electric strength of resonator and allows to produce electromagnetic pulses of great power (> 10 GWt) in mm cm range. Besides the multiwave distributed feedback in VFEL provides the modes discrimination in the case when the linear sizes of resonator (waveguide) cross section exceed generated wavelength (the so-called oversized systems). First lasing of volume FEL (VFEL) in millimeter range was recently obtained by a group of scientists of Institute for Nuclear Problems [7]. A lot of papers are devoted to FEL simulation (for example [10, 11]). In our works [1, 6, 8, 18, 19, 0, 1, ] we have considered mathematical models of different types of VFEL in X-ray, optical and millimeter wave ranges. Earlier electron beam was simulated as a hydrodynamical approximation [1, 18] or as distribution functions [8, 19]. It turned out, however, that hydrodynamical approximation is very rough. And in millimeter range electron beam presentation as distribution functions for sufficiently large beam current density leads to appearance of non-physical instability related to the computational error. Therefore in this work simulation of quasi- Cherenkov instability is performed by means of phase averaging method which is frequently used in large number of works. The main distinction of this work is in applying such method to VFEL simulation.. Mathematical Model Let us consider quasi-cherenkov stimulated radiation of wide electron beam passing through spatial periodic structure. In Fig. 1 four schemes of simple VFEL are presented. A target of length L is a medium possessing spatially periodic permittivity. There are several different possibilities. Fig.1a corresponds to the case when there are no incident waves emerging on system. For distributed feedback forming the specific so-called diffraction (or the Bragg) conditions can be fulfilled. These conditions have the form k = k τ for the two waves case. Here k is the radiation wave vector and τ is reciprocal vector of the periodical structure τ = πn 1 /d 1, πn /d, πn 3 /d 3, d 1, d, d 3 are basic translation periods, n 1, n, n 3 are integers. Here we consider socalled Bragg diffraction geometry when one wave propagates in forward direction and the other in backward (see Fig.1a Fig.1d). The developed mathematical model allows to consider such geometry when incident wave emerges from the side z = 0 (forward incident wave Fig.1b), or from the side z = L (backward incident wave Fig.1c), or from both sides simultaneously (see, Fig.1d). Moreover two mirrors can be placed on each side of the target to accumulate radiation. Let us consider the system of equations describing quasi Cherenkov instability. Equations for this process are written for stationary regime of nonlinear saturation. This system with appropriate boundary conditions is written as follows:
34 Modelling of quasi Cherenkov electron beam instability 3 Electron beam k k Electron beam k k 0 L z 0 Incident radiation L z target target a b Electron beam k k Electron beam k k 0 Incident radiation L z 0 Incident radiation Incident radiation L z target target c d Figure 1. Scheme of quasi Cherenkov VFEL in Bragg geometry. de dz + a 11E + a 1 E τ = Φ π 0 π p 8π (exp( iθ(z, p)) + exp( iθ(z, p))) dp, E(0) = E 0, z [0, L], p [ π, π], de τ dz + a 1E + a E τ = 0, E τ (L) = E 1, d ( ) 3 Θ(z, p) dθ(z, p) dz = Ψ k Re (E(z) exp(iθ(z, p))), dz dθ(0, p) Θ(0, p) = p, = 0; dz (.1) where i is the imaginary unit. There are two independent arguments in system (.1): spatial coordinate z and initial electron phase p. Amplitudes of electromagnetic fields E(z), E τ (z) and coefficients a are complex-valued. Function Θ(z, p) describes phase of electron beam relative to the electromagnetic wave. Θ(z, p) and coefficients Φ and Ψ are real. k is a projection of wave vector k on z axis. We suppose that all functions are smooth, bounded and slowly changing.
35 4 K. Batrakov, S. Sytova Stationary solution under zero boundary conditions is due to the essentially nonlinear contribution of electron beam. In linear regime the homogeneous system with zero boundary conditions has infinite number of solutions. 3. Numerical Algorithm To solve the system of integro differential equations with nonlinearity on right hand sides an iterative algorithm is proposed. We use notations from [17]. Introducing in domain Ω = {0 z L, π p π} uniform grids on z and p: ω z = {z i = ih z, i = 0, 1,..., M, Mh z = L}, ω p = {p j = h p j, j = N,..., 1, 0, 1,..., N, h p N = π}. The discrete functions, defined on the grid, will be denoted by Θ j i = Θ(z i, p j ), E j i = E(z i, p j ). We approximate the differential problem with the following finite difference scheme: s ( Θ j zz = Ψ k s Θ j z ) 3 Re s E z + a 11 s E + a1 s Eτ = Φ ( s 1 s ) E exp(iθ j, j = 0, ±1,..., ±N, (3.1) N s c j (exp( iθ j s ) ) + exp( iθ j ), (3.) j=0 s E τz + a 1 s E + a s E τ = 0, (3.3) where s 0 is a number of iteration. As an initial approximation we define: 0 Θ j = h p j, 0 E = 0, 0 Eτ = 0. Here c j are coefficients of quadrature formula. We use the trapezoidal rule here. Let us write the difference equation (3.1) in the following form: s j Θi+1 Θ s i ++ Θ s j h z j i 1 s j Θi+1 Θ s = Ψ k h z j i 1 3 ( s 1 Re E exp(i s ) Θ j i ), (3.4) i.e. it is an implicit difference equation with respect to s+1 Θ i+1. Solving this cubic equation get three solutions, we choose the one which is close to s+1 Θ i. The two rest roots are meaningless. As it was shown in numerical experiments this approach works very well. But it is not a very efficient strategy to solve numerically cubic equations. It is possible to solve it by using the Picard type iterative process:
36 Modelling of quasi Cherenkov electron beam instability 5 l+1 Θ i+1 s j Θi + s j l Θi 1 Θi+1 s j 3 ( ) Θi 1 s 1 s+1 h = Ψ k Re E exp(iθ j i z h ), z 0 j Θi+1= Θ s i+1, where l 0 is a number of inner iterations. As it was shown in numerical experiments, it is enough to make only two inner iterations to solve the cubic equation. Inasmuch as our iterative process (3.1) (3.3) is nonlinear, it seems to be impossible to investigate its convergence. If we consider a linearized case of this process then some conclusions are evident. We restrict ourselves to Fig., which demonstrates the convergence of the iterative process. It is stabilized after approximately 40 iterations. 500 E N iterations Figure. Numerical solution depending on iterations number. So, in accordance to numerical experiments, our schemes are stable and the discrete solution converges to the solution of initial differential system because numerical results coincided in full with analytical estimations. 4. Numerical Results Let us discuss results of numerical experiments carried out. Among them we have considered the case when there was no incident radiation, in other words E(0) = 0 and E τ (L) = 0, as well as E(0) 0. Starting currents of electron beam, radiation power and radiation frequency depend on the feedback geometry. Therefore changing this geometry we can change these quantities and even to turn regime of generation to amplification regime and vice versa. Threshold current density is very important value characterizing the system. There is no generation process if current is lower than some critical value. In the case when current density is between this critical value and the value of generation threshold current (j th ) the system operates in amplification regime. This is the regime of regenerative amplification for the Bragg geometry. The regime of generator is realized when the current density exceeds the threshold j > j th. In that case
37 6 K. Batrakov, S. Sytova radiation of electron beam should exceed the losses on boundaries of the resonator and absorption losses. Such threshold is depicted in Fig.3 depending on the length of the target. It demonstrates threshold current density depending on thickness of the target with and without incident radiation and with and without absorption of the target. We can see that the larger is the target length the lower is the threshold. Absorption Im(χ 0 ) = 0.01 raises the threshold. Presence of incident wave with E 0 decreases it. j, A/cm th L, cm Figure 3. Electron beam current threshold in Bragg geometry. Two different geometries were studied: Bragg geometry (see Fig.1 and numerical results above), in which two waves propagate to opposite sides of resonator and Laue geometry, in which waves propagate to one side of a resonator (see Fig.4). Two regimes are possible in the Bragg case as stated above: regime of regenerative amplification and regime of generation. Two regimes are possible in Laue case too. There are amplification regime of emerging incident wave and regime SASE [15]. SASE (self amplified stimulated emission) develops from spontaneous noises (as well as generator regime in Bragg case). Since diffracted wave in Laue case propagates in the forward direction, we have to change right difference derivative in (3.3) for E τ to the left one. It is clear that boundary conditions for E τ in (.1) should be written for z = 0. Let us examine Fig. 5. We can see dependence between value of electric field and current density for different amplitudes of emerging waves for both diffraction geometries. Amplification regime corresponds to range of current density j form range A/cm for Bragg geometry (Fig.5a). Current threshold is over-passed at j = 80 A/cm. This region corresponds to regime of generation. In Fig.5b the curve with E = 0 corresponds to SASE regime. The rest curves demonstrate regime of amplification. Let us consider two questions. First, where does radiation come from in the system in the absence of incident radiation? The answer is that it comes from spontaneous noises of electron beam. The second question asks what corresponds to this noise in numerical realization of mathematical model (3.1) (3.3)? The answer is that such noise appears due to computational error on the right-hand side of equations. It
38 Modelling of quasi Cherenkov electron beam instability 7 Electron beam k k Electron beam Incident radiation k k 0 L z 0 L z target target a b Figure 4. Scheme of quasi-cherenkov VFEL in Laue geometry. E E-6 1E-7 1E-8 1E-9 1E-10 1E-11 1E-1 E = 1 E = 0.01 E = E = j, A/cm a E E-6 1E-7 1E-8 1E-9 1E-10 1E-11 E=1 E=0.01 E= E = j, A/cm b Figure 5. Dependence between computed electromagnetic wave amplitude and electron beam current density in Bragg (a) and Laue (b) geometry. is clear that at the first iteration, when E(z) = 0 all over z [0, L], we have I = Φ π 0 π p 8π ( exp ( iθ(z, p) ) + exp ( iθ(z, p) )) dp 0. But in fact we obtain I 10 15, This is an equivalent of spontaneous noises and fuse for the beginning of generation process. References [1] V.N. Abrashin, A.O. Grubich and Sytova S.N. Nonlinear stage of development of the relativistic electron beam Cherenkov instability. Mathematical Modeling, 3(8), 1 9, (in Russian) [] S. Andruszkow. First observation of self-amplified spontaneous emission in a freeelectron laser at 109 nm wavelength. Phys. Rev. Let., 85, 385, 000. [3] V. Baryshevsky, K. Batrakov and I. Dubovskaya. Parametric (quasi-cherenkov) X-ray FEL. Journ.Phys.D, 4, 150, [4] V. Baryshevsky and I. Feranchuk. Parametric X-rays from ultrarelativistic electrons in a crystals: theory and possibilities of practical utilization. Journ.Phys., 44, 913, [5] V. Baryshevsky and I. Feranchuk. Parametric beam instability of relativistic charged particles in a crystal. Phys.Let.A, 10, 141, 1984.
39 8 K. Batrakov, S. Sytova [6] V.G. Baryshevsky, K.G. Batrakov, I.Ya. Dubovskaya and S.N. Sytova. Visible surface quasi-cherenkov FEL. Nucl. Instr. and Meth. in Phys. Res., A358, , [7] V.G. Baryshevsky, K.G. Batrakov and et all. First lasing of a volume FEL (VFEL) at a wavelength range 4-6 mm. Nucl. Instr. and Meth. in Phys. Res., A483, 1, 00. [8] I. Dubovskaya, V. Baryshevsky, K. Batrakov and S. Sytova. The nonliner analysis of visible quasi-cherenkov FEL. In: 1th Intern. Free Electron Laser Conference (FEL99), Germany, [9] A.V. Elzhov, N.S Ginzburg, A.K. Kaminsky, E.A. Perelstein, N.Yu. Peskov, S.N. Sedykh, A.P. Sergeev and A.S. Sergeev. Features of FEM for testing of high-gradient accelerating structures of linear colliders. In: Proceedings of Eighth European Particle Accelerator Conference (EPAC 00), Paris, , 00, June 3-7. [10] N. Ginzburg, N. Peskov and A. Sergeev. Dynamics of free-electron lasers with twodimensional distributed feedback. Technical Physics Letters, 18(5), 85, 199. [11] N. Ginzburg, R. Rosental, N. Peskov, A. Arzhannicov and S. Sinitsky. Modeling of a planar FEL amplifier with a sheet relativistic electron beam. Nucl. Instr. and Meth. in Phys. Res., A483, 55, 00. [1] N.S. Ginzburg, S.P. Kuznetzov and T.N. Fedoseeva. The theory of transient processes in a relativistic BWT. Izvestiya Vuzov. Radiophysics, 1(7), 1071, [13] N.S. Ginzburg, R.M. Rosental and A.S. Sergeev. About possibility of synthesis of radiation spectrum in bit-slice relativistic backward-wave tube. Pis ma v ZhTF, 9(4), 71 80, 003. [14] Y.C. Huang, C.S. Hsue, R.H. Pantell and T.I. Smith. The FEL and IFEL design study for the proposal NTHU photon-electron dynamics laboratory. Nucl. Instr. and Meth. in Phys. Res.A, 49, 430, [15] K. Kim. Three-dimensional analysis of coherent amplification and self-amplified spontaneous emission in free electron lasers. Phys. Rev. Lett., 57, [16] M. Korfer. The TTF-FEL status and its future as X-ray user facility. Nucl. Instr. and Meth. in Phys. Res.A, 483, 34, 00. [17] A.A. Samarskii. Theory of finite-difference schemes. Nauka, Moscow, (in Russian) [18] S. Sytova. A numerical method for solving one problem of nuclear physics. Vesti Nat. Acad. Sci. Belarus. Ser. Phys.-Math., N, 44 50, (in Russian) [19] S. Sytova. A numerical method for solving hyperbolic system with singularities. Differential Equations, 3(7), , [0] S. Sytova. On numerical methods for modelling of terahertz sources based on low energy relativistic beams. In: Proc. of the 3rd Intern. Conference FDS000, 37 44, 000. [1] S. Sytova. Numerical methods in problems of modelling of volume free electron lasers. Differential Equations, 37(7), , 001. [] S. Sytova. On numerical methods for one problem of mixed type. Mathematical Modelling and Analysis, 6(), 31 36, 001. Kvazi-Cerenkovo elektroninio spindulio nestabilumo modeliavimas periodinėse struktūrose K. Batrakov, S. Sytova Modeliuojama elektron u spindulio kvazi-cherenkovo nestabilumo netiesinė fazė su dvimačio ir trimačio paskirstytojo grįžtamojo ryšio sąlyga. Nagrinėjama schema su grįžtamuoju ryšiu su dviem susietomis stipriomis bangomis. Pateiktas kvazi-cherenkovo elektroninio spindulio nestabilumo matematinis modelis. Pasiūlytas veiksmingas skaitinis algoritmas, skirtas netiesinėms integro-diferencialinėms lygčių sistemoms su tokio tipo nestabilumu, spręsti. Apžvelgti skaitinio eksperimento rezultai.
40 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN A PREY-PREDATOR MODEL WITH DIFFUSION AND A SUPPLEMENTARY RESOURCE FOR THE PREY IN A TWO-PATCH ENVIRONMENT 1 J. DHAR Department of Applied Mathematics, Beant College of Engineering Technology Gurdaspur , Punjab, India 9:0;<=?>@A B <:0C D E7D = F+GIH :JE Received June ; revised January Abstract. In this paper, a prey-predator dynamics, where the predator species partially depends upon the prey species, in a two patch habitat with diffusion and there is a non-diffusing additional resource for the prey population, is modeled and analyzed. It is shown, that there exists a positive, monotonic, continuous steady state solution with continuous matching at the interface for both the species separately. Further, we obtain conditions for asymptotic stability for both linear and nonlinear cases. Key words: Population diffusion, patchiness, supplementary resource, steady state solution, stability 1. Introduction Mathematical ecology has its roots in population ecology, which treats the increase and fluctuation of population. An interesting problem in mathematical ecology is to study the growth and co-existence of species with diffusion in both homogeneous and patchy habitats. As noted before the diffusion, when it occurs, plays the role of increasing stability in a system of interacting populations [8, 10, 3, 4, 5, 7]. Some researchers have given elaborate survey of models with diffusion in both homogeneous and heterogeneous environment [14, 15, 16, 3] and also surveyed the literature related to models with diffusion and reported the effects of dispersal and spatial heterogeneity on stability of both single species and for predator-prey system [4, 5, 18]. In [1] a prey-predator model with functional response and diffusion is considered and it is shown, that if the equilibrium state is linearly stable, a sub-region 1 This work partially was carried out at Department of Mathematics, Indian Institute of Technology, Kanpur-08016, India. Author is thankful to Prof. J. B. Shukla for his valuable suggestion.
41 10 J. Dhar of the positive quadrant can be found in the phase plane where it is non-linearly stable with or without diffusion. It may be noted here that in the above study the role of alternative or supplementary resource on equilibrium levels of populations as well as on their stability has not been discussed, although the study of resource-based interacting population biology is an interesting area of research in population dynamics. Some experimental investigations on micro-organisms using the chemostat [11, ] have been conducted and perhaps the best laboratory idealization of nature for population studies has been described in [8]. Several mathematical models of such systems, involving competition and other types of non-interacting populations, which depend upon growth limiting nutrient in a chemostat with constant input and variable washout rates have been studied in [1,, 13, 17]. Also some other mathematical investigations related to two competing populations which are wholly dependent on a self-renewable resource in a habitat without diffusion have been presented [9, 1, 19]. But very little attention has been given in the resource-based prey-predator system with diffusion [6]. The effect of a predator resource on a diffusive Predator-Prey system, showing the stabilizing role of diffusion have been studied. In this paper, therefore, a logistically growing two species prey-predator type model is considered. A self-renewable supplementary resource for prey population and diffusion in a two-patch habitats is proposed and the stability of both the linear and nonlinear systems is discussed. Both the reservoir and no-flux boundary conditions are considered. It is shown that the effect of explicit dependence of the prey population on an alternative supplementary resource in the two patches may increase the level of steady state distribution for prey in the entire habitat. The model is proposed by keeping in view the depletion of forest resources biomass (prey species) with partially re-plantation of forest resource (i.e. supplementary resource) due to increased forest resource. Dependence or independence on industrialization and population (predator species) has caused patchiness in the Doon Valley situated at the foot hills of Himalayas in India [6]. This paper is organized as follows: first we write the prey-predator model with a self-renewable supplementary resource for the prey in a two-patch habitat. In the next section we study our main model in a two-patch habitat for both non-uniform and uniform steady state cases under both reservoir and no-flux boundary conditions.. The Mathematical Model We consider a dynamic model of two logistically growing animal (such as deer and wolf) species with prey-predator type interaction and diffusion in a two-patch forest habitat by assuming that the second species uses the first species as an alternative resource. In such a case the rate of change of density of the first species decreases due increase in the density of the second species, but the density of the second species increases due to the increase in the density of the first species in both the patches. Let x i (s, t) and y i (s, t) be the densities of first and second species in the i-th patch respectively. Now if we supply a supplementary resource R i (s, t) for the prey population x i (s, t) in the entire habitat, then in presence of resource biomass the growth
42 Prey-Predator Model with Supplementary Resource 11 rates of prey populations increases. We also assume that there is no explicit diffusion in the resource biomass. Then the model can be written as the following system of autonomous partial differential equations: R i = a i R i (1 R i ) α i R i x i, i = 1,, t C i (.1) x i t = x x i ig i (x i ) y i p i (x i ) + θα i R i x i + D 1i s, (.) y i t = y y i if i (y i ) + γ i y i p i (x i ) + D i s, 0 s L, (.3) where the i-th patch is assumed to lie along the spatial length L i 1 s L i (L 0 = 0), C i, i = 1, are the carrying capacity of the supplementary resource in the i-th patch and θ is the conversion rate of biomass constant by the prey populations, respectively. The functions g i (x i ) and f i (y i ) are the respective specific growth rates, p i (x i ) are the interaction rates (predator response functions) and D 1i, D i are the diffusion coefficient of x i and y i in the i-th patch respectively. The constants α i, i = 1, are positive interaction rate coefficients of the prey species with the supplementary resource and γ i, i = 1, are conversion rates coefficient in the i-th patch. We assume the following assumption for g i (x i ), f i (y i ), and p i (x i ): g i (x i ), f i (y i ), p i (x i ) C [0, ), g i (0) > 0, f i (0) > 0, p i (0) = 0, AH 1 : for x i > 0, g i (x i) 0, p i (x i) > 0, for y i > 0, f i (y i) 0. When the environment has a carrying capacity K i and M i respectively for prey and predator populations in the i-th patch, then g i (K i ) = 0, f i (M i ) = 0, for i = 1,. Further we assume that: R i, x i, y i > 0, such that R i = C i[a i α i x i ]/a i, AH : x i g i(x i ) y i p i(x i ) + θα iri x i = 0, f i (yi ) + γ ip i (x i ) = 0. The model is studied using one set of boundary conditions, i.e., reservoir or noflux conditions. In the case of reservoir boundary conditions, we take x 1 (0, t) = x 1, x (L, t) = x, (.4) y 1 (0, t) = y 1, y (L, t) = y (.5) and in the case of no-flux boundary conditions we consider x 1 (0, t) = 0, s y 1 (0, t) = 0, s x (L, t) = 0, s (.6) y (L, t) = 0. s (.7)
43 1 J. Dhar We also assume the continuity and flux matching conditions at the interface s = L 1. The continuity conditions at the interface s = L 1 are the following: x 1 (L 1, t) = x (L 1, t), y 1 (L 1, t) = y (L 1, t), R 1 (L 1, t) = R (L 1, t). (.8) The continuous flux matching conditions at the interface s = L 1 for x i (s, t) and y i (s, t) are given by x 1 (L 1, t) D 11 s y 1 (L 1, t) D 1 s x (L 1, t) = D 1, (.9) s y (L 1, t) = D. (.10) s Finally the model is completed by assuming some positive initial distribution of each species, for i = 1,, that is, x i (s, 0) = χ i (s) > 0, L i 1 < s < L i, (.11) y i (s, 0) = δ i (s) > 0, L i 1 < s < L i, (.1) R i (s, 0) = R 0i (s) > 0, L i 1 < s < L i. (.13) 3. Analysis of the Model in Two Patch Habitat Our aim is to analyze the long time behavior of the system in both uniform and nonuniform cases. In next two subsection we will study the model (.1) (.13), in the case of nonuniform and uniform steady state The Non-uniform Steady State Let u i, v i and w i are the steady state solutions of the prey populations x i, predator populations y i and the supplementary resource R i. Then the steady state system becomes: w i = C i a i [a i α i u i ], (3.1) D 1i d u i ds + u ig i (u i ) v i p i (u i ) + θα i w i u i = 0, (3.) D i d v i ds + v if i (v i ) + γ i v i p i (u i ) = 0. (3.3) Now substituting the value of w i from (3.1) into (3.) and (3.3), we get: where D 1i d u i ds + u ig i (u i ) v i p i (u i ) = 0, (3.4) D i d v i ds + v if i (v i ) + γ i v i p i (u i ) = 0, (3.5)
44 Prey-Predator Model with Supplementary Resource 13 Since G i (u i ) = g i (u i ) + θα i C i a i (a i α i u i ), i = 1,. G i (0) = g i (0) + C i θα i > 0, G i (u i) = g i (u i) C iθα i a i < 0, i = 1,. Hence the behavior the steady state system (3.4) and (3.5) with same set of boundary conditions identical to the case when there is no supplementary resource for the prey populations. Further, we assume { x i, yi AH 3 : > 0, x i G i(x i ) y i p i(x i ) = 0, f i (yi ) + γ ip i (x i ) = 0. (3.6) Remark 1. We are only interested to find the positive steady state of the system. Therefore, it follows from (3.1), u i < a i /α i and hence G i (u i ) g i (u i ), u i. Now, from (3.6) we get y i = x i G i(x i ) p i (x i ) > y i, x i > x i, where the non-zero positive x i and yi are equilibrium value of the above preypredator system without supplementary resource, given by x i f i (y i g i (x i ) yi p i (x i ) = 0, (3.7) ) + γ i p i (x i ) = 0. (3.8) Hence in presence of a supplementary resource for the prey population, the level of steady state distributions of both the species are higher at each location in the habitat. Example 1. Now, we discuss a numerical example in which the behavior of the steady state solutions of the above system is studied. The results are compared with the case of a prey-predator system without supplementary resource. We consider the following particular form of functions: g i (u i ) = r i ( 1 u i K i ), f i (v i ) = s i ( 1 v i M i ), p i (u i ) = e i u i, i = 1,. For simplicity let assume that the supplementary resource initially is distributed uniformly, i.e. C 1 = C = C. Then the steady state system (3.4) and (3.5), becomes d ( u i D 1i ds + u i [r i 1 u ) i + θα ] ic (a i α i u i ) e i v i u i = 0, K i a i d ( v i D i ds + s iv i 1 v ) (3.9) i + γ i e i v i u i = 0 M i with reservoir boundary conditions
45 14 J. Dhar u 1 (0) = x 1, u (L ) = x, (3.10) v 1 (0) = y 1, v (L ) = y, where x i, y i are from (3.6), and the continuity-flux matching conditions at the interface s = L 1 are given as du 1 D 11 ds (L du 1) = D 1 ds (L dv 1 1), D 1 ds (L dv 1) = D ds (L 1), u 1 (L 1 ) = u (L 1 ), v 1 (L 1 ) = v (L 1 ). (3.11) The equations (3.9) (3.11) are solved numerically by using finite difference method, for the following set of dimensionless values L 1 = 10, L = 0, D 11 = 0.8, D 1 = 0.9, D 1 = 0.8, D = 0.9, r 1 = 0.03, r = 0.05, a 1 = 1.0, a = 1.0, s 1 = 0.03, s = 0.01, e 1 = , e = , K 1 = 100, K = 15, M 1 = 75, M = 50, α 1 = , α = , C = 60, γ 1 = 0.4, γ = 1.0, θ = 0.7. By using above values of the parameters, we get x 1 = 87. > x 1 = 80.77, x = > x = , y1 = > y1 = , y = > y = We can easily verify that in presence of a supplementary resource for the prey, the level of steady state distributions of both species are higher at each location of the habitat compared to the case without supplementary resource for prey population (see Fig. 1). Moreover the steady state distribution is continuous and monotonic function. Now, we consider the following assumptions: For every we have that: min{ x 1, x } u i max{ x 1, x }, min{ y1, y } v i max{ y }, i = 1, 1, y (u i x i )[u i G i (u i ) v i p i (u i )] < 0, u i x (v i yi )[v i f i (v i ) + γ i v i p i (u i )] < 0, v i y Under these conditions u i and v i both will be positive through out the habitat. We now consider without loss of generality 0 < x 1 < x and 0 < y1 < y. Therefore x 1 u i x and y 1 v i y. Again, from (3.4) and (3.5) under reservoir boundary conditions, let p i (s, α i ) and q i (s, β i ) are unique solutions of u i and v i respectively, for i = 1,, such that p 1 s (0, α 1) = α 1, p 1 (0, α 1 ) = x 1, p s (L, α ) = α, p (L, α ) = x q 1 s (0, β 1) = β 1, p 1 (0, β 1 ) = y1, p s (L, β ) = β, p (L, β ) = y. i, i.,
46 Prey-Predator Model with Supplementary Resource 15 Steady State Distributions Initial prey Prey with resource Initial predator Final predator Initial resource Final resource 60 Patch-I Patch-II s Figure 1. The steady state solutions for both the species, with and without supplementary resource for the prey. Similarly, for no-flux boundary condition, let p i (s, α i ) and q i (s, β i ) are unique solutions of u i and v i respectively, for i = 1,, such that p 1 s (0, α 1) = 0, p 1 (0, α 1 ) = α 1, q 1 s (0, β 1) = 0, p 1 (0, β 1 ) = β 1, p s (L, α ) = 0, p (L, α ) = α, p s (L, β ) = 0, p (L, β ) = β. Then the existence of the monotonic solutions are established in both the reservoir and no-flux boundary conditions, if we can show that there exists α i and β i, for i = 1,, such that p 1 (L 1, α 1 ) = p (L 1, α ), q 1 (L 1, β 1 ) = q (L 1, β ), p 1 D 11 s (L p (L 1, α ) q 1 (L 1, β 1 ) 1, α 1 ) = D 1, D 1 s s = D 1 q (L 1, β ) s In order to construct our required solutions for reservoir boundary conditions, we need some preliminary lemmas, in the same manner as in [3, 4]. Lemma 1. If α 1, β 1 > 0, then p 1 (s, α 1 ) s > α 1, q 1 (s, β 1 ) s > β 1, on 0 < s L 1. Lemma. If α, β > 0, 0 < p < x and 0 < q < y, then p (s, α ) s > α, q (s, β ) s > β, L 1 s < L..
47 16 J. Dhar Lemma 3. Let us define F 1i (α i ) by F 1i (α i ) = p i (L 1, α i ). Then there exists ˆα i > 0 such that F 11 : [0, ˆα 1 ] [x 1, x ], F 1 : [0, ˆα ] [x, x 1 ]. Lemma 4. Let us define F i (β i ) by F i (β i ) = q i (L 1, β i ). Then there exists ˆβ i > 0 such that F 1 : [0, ˆβ ] 1 [y1, y ], F : [0, ˆβ ] [y, y 1 ]. Similar type of four lemmas we can established for the steady state system with the no-flux boundary conditions. Hence we state the following theorem. Theorem 1. (i) There exists a positive, continuous, monotonic solution of system (3.4) with continuous flux at L 1. (ii) There exists a positive, continuous, monotonic solution of system (3.5) with continuous flux at L 1. Now we consider the stability analysis of the system (.1) (.3), (.8) (.13) with reservoir boundary conditions (.4) and (.5). First we state the local stability of the system by the following theorem. Theorem. The steady-state, continuous, monotonic solutions of the system (.1) (.3) with reservoir boundary conditions and continuous flux at the interface s = L 1 are locally asymptotically stable provided the following conditions are satisfied: where X i 0, Y i 0, Z i 0, (3.1) U i 4X i Y i, X i Y i Z i Y i W i + Z iu i, X i = g i (u i ) + u i g i(u i ) v i p i(u i ) + θα i w i, Y i = f i (v i ) + v i f i(v i ) + γ i p i (u i ), W i = α i [θu i w i ], ( Z i = a i 1 w ) i α i u i, U i = 1 C i [γ iv i p i (u i) p i (u i )], for x 1 u i x, y 1 v i y, where x i and y i are given by (3.6). Proof. We linearize (.1), (.) and (.3) by using then we obtain the system R i (s, t) = w i (s) + r i (s, t), (3.13) x i (s, t) = u i (s) + n i (s, t), y i (s, t) = v i (s) + m i (s, t),
48 Prey-Predator Model with Supplementary Resource 17 ( r i t = r i [a i 1 w ) ] i α i u i n i α i w i, C i n i t = n i[g i (u i ) + u i g i (u i) v i p i (u i) + θα i w i ] m i t m i p i (u i ) + r i θα i u i + D 1i n i s, = m i [f i (v i ) + v i f i (v i) + γ i p i (u i )] + n i γ i v i p i (u m i i) + D i s. (3.14) Using (3.13) the following boundary and matching conditions are obtained: n 1 (0, t) = 0 = n (L, t), m 1 (0, t) = 0 = m (L, t), n 1 (L 1, t) = n (L 1, t), m 1 (L 1, t) = m (L 1, t), D 11 n 1 s (L 1, t) = D 1 n s (L 1, t), D 1 m 1 s (L 1, t) = D m s (L 1, t). Now we consider the following positive definite function, V (t) = i=1 Li L i 1 1 Differentiating (3.15) with respect to t, we get V (t) = By using (3.14) we get Li i=1 Li L i 1 ( n i + m i + ri ) ds. (3.15) ( ) n i n i t + m m i r i i + r i ds. t t V (t) = n i [g i(u i ) + u i g i (u i) v i p i (u i) + θα i w i ] ds + i=1 L i 1 i=1 Li Li ( m i [f i(v i ) + v i f i (v i) + γ i p i (u i )] ds + ri [a i 1 w ) i L i 1 i=1 L i 1 C i ] Li Li α i u i ds + n i m i [ p i (u i ) + γ i v i p i (u i)] ds + n i r i α i i=1 L i 1 i=1 L i 1 Li n i Li [θu i w i ] ds + D 1i n i L i 1 s ds + m i D i m i L i 1 s ds. Therefore, V (t) = i=1 Li 1 i=1 [X i n i + Y i m i + Z i ri + U i n i m i + W i r i n i ] ds L i 1 Li ( ) ni Li ( ) mi D 1i ds D i ds, (3.16) s s L i 1 1 i=1 L i 1
49 18 J. Dhar where the functions X i, Y i, Z i, U i, and W i are as follows, X i = g i (u i ) + u i g i (u i) v i p i (u i) + θα i w i, ( Y i = f i (v i ) + v i f i(v i ) + γ i p i (u i ), Z i = a i 1 w ) i α i u i, C i U i = 1 [γ iv i p i (u i) p i (u i )], W i = α i [θu i w i ] hence V is negative definite, if conditions (3.1) of the theorem are satisfied for i = 1,. Next, we state the corresponding nonlinear stability conditions of the system. Theorem 3. The steady-state, continuous, monotonic solutions of nonlinear system (.1) (.3), (.8) (.13) with reservoir boundary conditions (.4) (.5) are asymptotically stable in the sub-region R = {x 1 x i, u i x, y 1 y i, v i y, i = 1, }, provided the following conditions are satisfied: N xi 0, N yi 0, N zi 0, (3.17) N ui 4N xin yi, N xi N yi N zi N yi N wi + N zin ui, where N xi = x ig i (x i ) u i g i (u i ) x i u i y i p i (x i ) p i (u i ) x i u i + θα i R i, N yi = y if i (y i ) v i f i (v i ) + γ i p i (u i ), y i v ( i N zi = a i 1 R ) i + w i α i u i, N wi = α i C i [θu i R i ], N ui = 1 [ ] p i (x i ) p i (u i ) γ i y i p i (u i ). x i u i Proof. By using (3.13), we get from (.1), (.) and (.3) ( [a i 1 R i + w i r i t = r i n i t = n i C i ) α i u i ] n i α i R i, (3.18) [ xi g i (x i ) u i g i (u i ) p i (x i ) p i (u i ) y i + θα i R i x i u i x i u i ] m i t n i m i p i (u i ) + r i θα i u i + D 1i s, (3.19) [ ] yi f i (y i ) v i f i (v i ) = m i + γ i p i (u i ) y i v i [ ] p i (x i ) p i (u i ) m i + n i γ i y i + D i x i u i s. (3.0)
50 Prey-Predator Model with Supplementary Resource 19 Here also we consider the same positive definite function as in the case of linear stability. By using (3.18), (3.19) and (3.0), we get Li [ ] xi g i (x i ) u i g i (u i ) p i (x i ) p i (u i ) V (t) = y i + θα i R i ds x i u i x i u i + + n i i=1 L i 1 Li m i i=1 L i 1 Li i=1 L i 1 r i [ ] yi f i (y i ) v i f i (v i ) + γ i p i (u i ) ds y i v i ( [a i 1 R ) ] i + w i α i u i ds + C i [ ] p i (x i ) p i (u i ) γ i y i p i (u i ) ds + x i u i + Therefore, 1 Li i=1 Li Li n i Li D 1i n i L i 1 s ds + m i D i m i L i 1 s ds. i=1 V (t) = i=1 Li i=1 L i 1 i=1 L i 1 n i m i L i 1 r i n i α i [θu i R i ] ds [N xi n i + N yim i + N ziri + N uin i m i + N wi r i n i ] ds L i 1 Li ( ) ni Li ( ) mi D 1i ds D i ds, (3.1) s s i=1 L i 1 where the functions N xi, N yi, N zi, N ui and N wi are given by (3.18). Hence V is negative definite if the conditions (3.17) hold for i = 1,. It can be noted that, if we linearize the conditions of Thm.3, then we get the conditions of Thm.. The same theorems are true for the system (.1) (.3), (.8) (.13) with noflux boundary conditions (.6) and (.7). 3.. The Uniform Equilibrium State Similar as in the previous case, the main purpose of this section to find the conditions for local and global stability of the uniform equilibrium state of the system x i (s, t) K, y i (s, t) M, R i (s, t) C, 0 s L, t 0 under both sets of boundary conditions. Theorem 4. The equilibrium (C, K, M ) is locally asymptotically stable, if Hi + θα i C 0, for i = 1,, where Hi is given by H i = g i(k ) + K g i (K ) M p i (K ) (3.) and the following conditions are satisfied ( γi M p i(k ) p i (K ) ) 4 ( H i + θα i C ) M f i(m ), i = 1,. (3.3)
51 0 J. Dhar Proof. We linearize the system (.1) (.3) by using R i (s, t) = C + r i (s, t), (3.4) x i (s, t) = K + n i (s, t), y i (s, t) = M + m i (s, t), then we get r i t = r i [ a ic C i ] n i α i C, n i t = n i[g i (K ) + K g i (K ) M p i (K ) + θα i C ] m i t m i p i (K ) + r i θα i K + D 1i n i s, = m i M f i (M ) + n i γ i M p i (K ) + D i m i s. We consider the following positive definite function (3.5) V = 1 i=1 Li L i 1 [ (xi K ) + (y i M ) + d i (R i C ) ], (3.6) where d i, i = 1, are positive constants. Differentiating (3.6) and using (3.5), we get V = i=1 + Li L i 1 n i i=1 Li ( H i + θα i C ) ds + L i 1 r i i=1 [ d ia i C ] ds + C i + γ i M p i (K ) ) ds + + i=1 Li n i D 1i n i L i 1 s i=1 Li Li i=1 L i 1 m i M f i (M ) ds Li L i 1 n i m i ( pi (K ) L i 1 n i r i ( αi {θk d i C } ) ds ds + i=1 Li m i D i m i ds. (3.7) L i 1 s Using integration by parts and for both types of boundary conditions, we get Li i=1 Li i=1 n i D 1i n i L i 1 s m i D i m i L i 1 s Li ( ) ds = ni D 1i ds, i=1 L i 1 s Li ( ) ds = mi D i ds. s We choose d i, i = 1,, such that, coefficients of n i r i become zero, i.e. d 1 = d = θk /C. Therefore it follows from (3.7) that V is negative definite, if the conditions H i + θα ic 0 and (3.3) are satisfied. i=1 L i 1
52 Prey-Predator Model with Supplementary Resource 1 Theorem 5. Let Hi + θα ic > 0. Then the equilibrium (C, K, M ) is locally asymptotically stable, if the conditions (3.3) and the following inequality hold: Hi + θα i C π D 1i (L i L i 1 ), i = 1,. Proof. From (3.8) and using Poincare s inequality we get D 1i Li L i 1 Therefore from (3.7) we get V + + Li i=1 Li i=1 Li i=1 ( ) ni π ds D 1i s (L i L i 1 ) Li n i (H x i + θα ic π ) D 1i L i 1 (L i L i 1 ) ds L i 1 m i M f i (M ) ds + i=1 Li L i 1 r i L i 1 n i m i ( pi (K ) + γ i M p i (K ) ) ds Hence the theorem is proved. L i 1 n i ds. ( d ia i C ) ds C i Li D i i=1 We now state the global stability of the uniform steady state. L i 1 ( ) mi ds. s Theorem 6. The uniform steady state (C,K,M ) is globally asymptotically stable if A i (x i ) = x ig i (x i ) M p i (x i ) x i K + θα i C < 0, x i K, (3.8) ( p i (x i ) p i (K ) γ i x i K p ) i(x i ) 4 A ( i(x i ) fi (y i ) f i (M ) ) x i x i y i M, (3.9) ( A i (x i ) fi (y i ) f i (M ) ( ) ) ai x i y i M C i ( fi (M ) ) f i (y i ) (α y i M i (θ R i) ) + a ( ) i Ai (x i ). (3.30) C i x i Proof. Let us consider the following positive definite function V (x, y, R) = i=1 Li L i 1 M ln y i M ) ds + ( x i K K ln x i K ) ds + i=1 Li L i 1 i=1 Li L i 1 ( y i M ( R i C C ln R ) i C ds. (3.31)
53 J. Dhar Differentiating (3.31) with respect to t and using (.1) (.3) we get V (s, t) = + Li i=1 L i 1 Li i=1 L i 1 ( xi K x i ( Ri C R i ) xi t ds + ) Ri t ds = i=1 i=1 Li L i 1 Li ( xi g i (x i ) M ) p i (x i ) x i K + θα i C ds + ( fi (y i ) f i (M ) ) y i M ds Li i=1 Li i=1 i=1 L i 1 (x i K )(y i M ) Li ( yi M y i (x i K ) L i 1 x i i=1 L i 1 (R i C ) L i 1 (x i K )(y i M )α i (θ R i ) ds Li x i K D 1i L i 1 x i i=1 x i s ds + Li ) yi t ds L i 1 (y i y ) ( a ) i ds C i ( p i (x i ) p i (K ) γ i x i K p ) i(x i ) ds x i Li y i M D i L i 1 y i i=1 Using both set of boundary and flux matching conditions y i s ds. we get ( x1 (0, t) K ) x 1 s (0, t) = 0, ( x (L, t) K ) x s (L, t) = 0, ( y1 (0, t) M ) y 1 s (0, t) = 0, ( y (L, t) M ) y s (L, t) = 0 Li x i K D 1i L i 1 x i i=1 Li y i M D i L i 1 y i i=1 x i s ds = y i s ds = Li D 1i i=1 Li D i i=1 K L i 1 x i M L i 1 yi ( ) xi ds, s ( ) yi ds. s Now if conditions (3.8), (3.9) and (3.30) hold, then V (x, y) < 0, and V (C, K, M ) = 0. Therefore V (x, y) is negative definite over R > 0, x > 0, y > 0 with respect to R i = C, x i = K, y i = M, proving the theorem. Remark. We conclude that the role of supplementary resource is to increase the level of nonuniform steady state distributions of both the species at each location of the linear habitat. Further, the number of conditions for stability is increased compared to the case with no supplementary resource for prey and the role of patchiness is destabilizing in present of supplementary resource.
54 Prey-Predator Model with Supplementary Resource 3 References [1] M.M. Ballyk and G.S.K. Wolkowicz. An examination of the thresholds of enrichment: A resource-based growth model. J. Math. Biol., 33, , [] G.J. Butler and G.S.K. Wolkowicz. A mathematical model of the chemostat with a general class of functions describing nutrient uptake. SIAM J. Appl. Math., 45(1), , [3] J. Dhar. Modelling and analysis: the effect of industralization on diffusive forest resource biomass in closed habitat. J. Appl. Math., African Diaspora Journal of Math., (1), , 003. [4] J. Dhar and J.B. Shukla. A single species model with diffusion and harvesting in a twopatch habitat. In: Mathematical Analysis and Application, chapter 9, Narosa Publishing House, New Delhi, 000. [5] J. Dhar and H. Singh. Steady state distribution and stability behavior of a single species population with diffusion in n-patch habitat. Far East J. Appl. Math., 11(), , 003. [6] H.I. Freedman and J.B. Shukla. The effect of a predator resource on a diffusive predatorprey system. Natural Resources Modeling, 3(3), , [7] H.I. Freedman and Wu.J. Steady-state analysis in a model for population diffusion in a multi-patch environment. Nonl. Anal. Theory Methods & Appl., 18(6), , 199. [8] K. Gopalsamy. Competition, dispersion and co-existence. Math. Bio. Science, 33, 5 33, [9] K. Gopalsamy. Convergence in a resource-based competition system. Bull. Math. Biol., 48(5/6), , [10] T.G. Hallam. A temporal study of diffusion effects on a population modelled by quadratic growth. Nonl. Anal. Theory Methods & Appl., 3, , [11] D. Herbert, Elsworth and R.C. Telling. The continuous culture of bacteria: a theoretical and experimental study. J. Gen. Microbiology, 4, 601 6, [1] S.B. Hsu. On a resource based ecological competition model with interference. J. Math. Biol., 1, 45 5, [13] S.B. Hsu, S.P. Hubbell and P. Waltman. A mathematical theory of single-nutrient competitions in continuous cultures of microorganism. SIAM J. Appl. Math., 3, , [14] M. Kot. Elements of Mathematical Ecology. Cambridge University Press, Cambridge, 001. [15] S.A. Levin. Dispersion and population interactions. Am. Nat., 108, 07 8, [16] S.A. Levin. Spatial patterning and the structure of ecological communities. Lectures on Mathematics in the Life Sciences, 8, [17] B. Li and H. Smith. How many species can two essential resources support? SIAM J. Appl. Math, 6(1), , 001. [18] R. McMurtrie. Persistence and stability of single species and prey-predator system in spatially heterogeneous environments. Math. Biosc., 39, 11 51, [19] D. Mitra, D. Mukherjee and A.B. Roy. Permanent coexistence in a resource-based competition system. Ecol. Model., 60, 77 85, 199. [0] R.E. Munn and V. Fedorov. The environmental assessment. In: IIASA Project Report, Vol.1, International Institute for Applied Systems Analysis, Laxenburg, Austria, [1] R. Nallaswamy and J.B. Shukla. Effects of dispersal on the stability of a Prey-Predator system with functional response. Math. Biosc., 60, 13 13, 198. [] A. Novick and L. Szilard. Description of the chemostat. Science, 11, , [3] A. Okubo. Diffusion and Ecological Problem: Mathematical models. Springer-Verlag, New York, 1980.
55 4 J. Dhar [4] C.V. Pao. Coexistence and stability of a competition diffusion system in population dynamics. J. Math. Anal. Appl., 83, 54 76, [5] F. Rothe. Global Solution of Reaction-Diffusion Systems. Lecture Notes in Math Springer-Verlag, Berlin Heidelberg New York Tokyo, [6] J.B. Shukla, H.I. Freedman, V.N. Pal, O.P. Mishra, M. Agarwal and A. Shukla. Degradation and subsequent regeneration of aresource: A mathematical model. Ecol. Model, 44, 19 9, [7] V.P. Shukla and J.B. Shukla. Multispecies food webs with diffusion. J. Math. Biol., 13, , 198. [8] F.M. Williams. Dynamics of microbial populations. In: Systems Analysis and Simulation in Ecology, Chapter-3, Academic Press, New York, Plėšrūno-aukos modelis su difuzija ir papildomu resursu aukai dvieju sričiu areale J. Dhar Šiame straipsnyje modeliuojama ir analizuojama plėšr ūnų ir aukų dinamika, laikant, kad plėšr ūnų populiacija dalinai priklauso nuo aukų skaǐciaus. Arealą sudaro dvi sritys, kuriose vyksta populiacijų individų difuzija, be to, aukoms yra išskirtas nedifunduojantis resursas. Įrodyta, kad egzistuoja teigiamas, monotoniškas, tolydus stacionarusis sprendinys, tenkinantis tolydumo sąlygą abiems populiacijoms atskirai. Gautos asimptotinio stabilumo sąlygos tiesiniu ir netiesiniu atvejais.
56 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN NUMERICAL SOLUTION OF SINGLE MODE GYROTRON EQUATION O. DUMBRAJS 1, H. KALIS and A. REINFELDS 1 Helsinki University of Technology FIN-0150, Espoo, Finland 90: ;<=>?@ AB4@BDCFEG Institute of Mathematics Latvian Academy of Sciences and University of Latvia Akadēmijas laukums 1, LV-154, Rīga, Latvia H >IG4@JAI4> KL MNCOI P%Q= L#GRK EAI0> M4KL0MSCOIJP Received October 1 003; revised December Abstract. In this paper we study numerical problems arising in solving the single mode gyrotron equation. Using the method of finite differences analytical and numerical solutions are obtained. Quasistationary solutions and corresponding eigenvalues and eigenfunctions of this problem are investigated. Key words: the spectral problems, finite-difference schemes, stability analysis, analytical solutions 1. Introduction Gyrotrons are microwave sources whose operation is based on the stimulated cyclotron radiation of electrons oscillating in a static magnetic field. Single mode nonstationary gyrotron oscillations can be described by the following system of partial differential equations []: p x + i ( + p 1 ) p = if(t, x), f x i f t + δf = I π (1.1) p dθ 0. π Here i = 1, x [0, L] is the normalized axial coordinate, t is the normalized time, is the frequency mismatch, δ describes variation of the critical frequencies, and δ are real numbers, p = p(t, x, θ 0 ) is the dimensionless complex transverse momentum of the electron, f = f(t, x) is the high-frequency field in resonator, I 0
57 6 O. Dumbrajs, H. Kalis, A. Reinfelds is the dimensionless current, θ 0 is the parameter. The system of equations has to be supplemented by the standard initial condition p(t, 0, θ 0 ) = exp(iθ 0 ), 0 θ 0 < π, f(0, x) = f 0 (x), and by the boundary condition for the field at the entrance to the interaction space f(t, 0) = 0, and at the exit to the interaction space f(t, L) x = iγf(t, L), where γ is a positive parameter, f 0 (x) is given complex function. An efficient numerical method for solving this reduced system of equations was presented in [1]. However, it was discovered that the results of the computations depend in a nontrivial manner on the chosen spatial and temporal step-lengths. So, main difficulties arises in numerical solving of Schrödingers type equation with special boundary conditions. The aim of this paper is to study in detail numerical problems for the second equation of (1.1).. Solution of the differential problem We begin with the homogeneous Schrödinger type partial differential equation (I = 0) f x i f + δf = 0, (.1) t where x (0, L), t > 0 is time, δ = const 1. Boundary conditions can be written as f(t, L) f(t, 0) = 0, = iγf(t, L). (.) x We represent the quasi-stationary solution of the problem (.1) and (.) in the form f(t, x) = g(x) exp(iαt), (.3) where α is a complex number α = α 1 + iα (α is a temporal damping factor: if α > 0, the solution (.3) decreases, if α < 0, the solution increases, and for α = 0 the solution is oscillating in time). We now consider nontrivial solutions (.3) of the differential problem by computing allowed values of the parameter α, as well as the corresponding discrete problem. Substituting the solution (.3) into equation (.1) and boundary conditions (.), we obtain the Sturm-Liouville problem for the ordinary differential equation { g (x) + λ g(x) = 0, (.4) g(0) = 0, g (L) = iγg(l), 1 Using the substitution g(t, x) = f(t, x) exp(iδt) for function g we would obtain the boundary value problem (.1) and (.) with δ = 0. We don t use mentioned substitution because function f and parameter δ have the physical interpretation
58 Numerical solution of single mode gyrotron equation 7 where λ = α + δ is complex value. The solution of problem (.4) is g(x) = C 1 sin(λx), where C 1 is an arbitrary constant. From boundary conditions we obtain a transcendental complex equation for calculating the eigenvalue λ: or λ cos(λl) + iγ sin(λl) = 0 z cos z = i γ sin z, (.5) where z = z 1 + iz = λl and γ = γl. It is obvious that z = 0 is a root of the equation. Moreover, if z is the root of (.5), then also z is the root of this equation. Therefore we can confine ourselves to consider only z 1 > 0. Separating real and imaginary parts in equation (.5), we obtain a system of two real transcendental equations { z1 cos z 1 cosh z + z sin z 1 sinh z = γ cos z 1 sinh z, (.6) z cos z 1 cosh z z 1 sin z 1 sinh z = γ sin z 1 cosh z. Multiplying the first equation of system (.6) by sin z 1 cosh z and the second equation by cos z 1 sinh z and summing, we exclude the parameter γ and obtain the relation z 1 sin(z 1 ) + z sinh(z ) = 0. It follows that the nontrivial roots of the last equation satisfy the inequality sin(z 1 ) < 0 or tan(z 1 ) < 0. Dividing the second equation of the system (.6) by cos z 1 cosh z, we obtain z z 1 tan z 1 tanh z = γ tan z 1. It can be seen that if z 1 > 0, then also z > 0. Let us number the roots of (.5) z (k), k = 1,,..., whose real parts z (k) 1 are positive, by increasing their real parts and take into account that (k 1)π < z (k) 1 < kπ, 0 < z (k) < γ + 1. Since λ = α + δ or z = L (α + δ), we have α 1 = z 1 z L δ, α = z 1z L. It is seen that the parameter δ affects only the values of α 1 and α > 0. The results of computations performed by means of MAPLE for L = 15, γ =, and δ = 0 are summarized in Tab. 1 for the first eight eigenvalues and numerical values of α (k) 1 and α (k), k = 1, 8. Fig. 1 shows the first fifty eigenvalues λ k. It can be seen that α (k) > 0 and that all solutions ( ) f (k) (t, x) = sin α (k) 1 + δ + iα (k) x exp(( α (k) + iα (k) 1 )t)
59 8 O. Dumbrajs, H. Kalis, A. Reinfelds Table 1. The roots of equation (.6) and values of α (k). k z (k) 1 z (k) α (k) 1 α (k) 1 3,1381 0, ,0437 0,0093 6,758 0,13 0,1748 0, ,418 0,3466 0,3933 0, ,5484 0, ,6989 0, ,6814 0, ,0914 0, ,809 0, ,5700 0, ,951 0,973,137 0, ,0054 1,18594,777 0,6360 Continue_eigenvalues lambda Im(lambda) Re(lambda) Figure 1. Eigenvalues of the continuous problem λ k, k = 1, 59. monotonically decrease in time, i.e., f (k) (x, t) 0, t +, k = 1,,..., (here C 1 = 1). Taking the square root in expression, we obtain two complex numbers in the form ±(a (k) + ib (k) ), where a (k) > 0 and b (k) > 0, if α (k) 1 + δ > 0 and α (k) > 0. Since the functions f (k) (t, x) contain an arbitrary constant C 1, the complex number with the minus sign does not give us any new result and can be ignored. Separating real and imaginary parts we obtain f (k) (t, x) = exp( α (k) t) sinh (b (k) x) + sin (a (k) x). Let us note that the complex eigenfunctions g k (x) = sin(λ k x) (λ k = α (k) + δ and α (k) = α (k) 1 + iα (k) ) are orthogonal, i.e., Correspondingly g k, g k = L 0 g k (x)g n (x) dx = 0, k n.
60 Numerical solution of single mode gyrotron equation 9 L g k = g k, g k = gk (x) dx = 1 ( L + iγ ) λ k. γ 0 Each continuous function f(x), x (0, L) with boundary conditions (.4) can be expanded in the series of the orthonormalized eigenfunctions g k (x) = g k (x)/ g k f(x) = c k g k (x), k=1 where the expansion coefficients can be found in the form c k = f, g k. Calculating by means of MAPLE, we obtain that the oscillation frequency of the functions increases and their absolute values rapidly decrease with increasing k. 3. Solution of the discrete problem In the finite differences method we use a uniform homogeneous spatial and temporal grids: ω h = { x j : x j = jh, j = 1, N 1, Nh = L }, ω τ = { t n : t n = nτ, n 1 } (corresponding step-lengths are h and τ). We substitute the continuous function f = f(t, x) in these grids by the discrete grid function y = y(t, x), t ω τ, x ω h with values y(t n, x j ) yj n. The corresponding derivatives of the function we approximate by finite differences f(t n, x j ) x f(t n, x j ) t Λyj n yn j+1 yn j + yn j 1 h, (3.1) yj n f(t n, L), yn N yn N 1. τ x h (3.) yn+1 j Difference (3.) approximates the first derivative only to the first order of accuracy, i.e., O(h). To obtain the second order approximation, we must use the expression f(t n, L) x 1.5yn N yn N yn N h. (3.3) Substituting differences (3.1), (3.) into the problem (.1) (.), we obtain a twolayer finite-difference scheme with weight σ [0, 1] i yn+1 j τ y n j y n+1 0 = 0, = σ(λy n+1 j + δy n+1 j ) + (1 σ)(λyj n + δyn j ), j = 1, N 1, y n+1 N yn+1 N 1 = iγy n+1 N h. (3.4) Difference equations (3.4) approximate the initial differential equation (.1) to the second order both in space and time, if σ = 1/, and to the first order in time, if σ 1/. Boundary conditions (.) are approximated only to the first order. To
61 30 O. Dumbrajs, H. Kalis, A. Reinfelds obtain the second order, one has to use expression (3.3). Seeking to find the discrete quasi-stationary solution by analogy to (.3) we take y n j = g j exp(iαnτ) (g j = g(x j ), t n = nτ), 0 satisfies the three-point finite- then we obtain that the discrete function g j difference scheme { Λgj + µ g j = 0, j = 1, N 1, g 0 = 0, g N = Cg N 1, which approximates the continuous problem (.4). Here C = (1 + iγh) 1, µ = α + δ, α = (1 exp(iατ))i (σ exp(iατ) + 1 σ)τ (3.5) (3.6) are complex constants ( α α, if τ 0). Now the solution of (3.5) can be written as g j = C 1 sin(qx j ), where C 1 is arbitrary constant, 1 µ h / = cos(qh) and x j = jh. It follows from boundary conditions (3.5) that the complex parameter q has to be determined from the complex transcendental equation where the parameter q has complex values sin(ql) = C sin(q(l h)), (3.7) q k = a k + ib k, k = 1, N 1. (3.8) If γ = (boundary conditions of the first kind), then C = 0 and equation sin(ql) = 0 is valid, if q k = kπ L (real numbers). Then we get also real eigenvalues [4] Therefore where µ k = 4 kπh sin h L, k = 1, N 1. α k = h (1 cos(q k h)) δ = A k + ib k, (3.9) A k = h (1 cos(a k h) cosh(b k h)) δ, B k = h sin(a k h) sinh(b k h), k = 1, N 1. (3.10) Since C = C 1 + ic, C 1 = (1 + (γh) ) 1, and C = γh(1 + (γh) ) 1, we separate in equation (3.7) real and imaginary parts and obtain the system of two real transcendental equations { sin(ak L) cosh(b k L) = C 1 sin(a k l 1 ) cosh(b k l 1 ) C cos(a k l 1 ) sinh(b k l 1 ), cos(a k L) sinh(b k L) = C 1 cos(a k l 1 ) sinh(b k l 1 ) + C sin(a k l 1 ) cosh(b k l 1 ), (3.11) where l 1 = L h. If h 0, then a k L z 1, b k L z and we obtain the system of equations (.6). After calculation of α k, we obtain from (3.6) the approximate values α k = 1 iτ ln ( 1 τ α k i + στ α k ), k = 1, N 1. (3.1)
62 Numerical solution of single mode gyrotron equation 31 It can be seen from (3.1) that the temporal step-length τ and the parameter of the scheme σ, i.e., the temporal approximation, do not affect the values of α k, their changes have to be taken into account only in the expression (3.1). Approximating boundary conditions (.4) by the second order expression (3.3), instead of equation (3.7) we obtain the complex transcendental equation sin(ql) = C ( sin(ql 1 ) 0, 5 sin(ql )), where l = L h, C = (1, 5+iγh) 1. The results of computations with L = 15, γ =, δ = 0, τ = h = 0, 1, and σ = 1 are presented in Tab., where a k and b k are solutions of (3.11) and π(k 1) L < a k < πk L, 0 < b k < 1. The values A k and B k were obtained from (3.9) and (3.10) k = 1, 8. The results do not change much (five digits remain the same) by changing the temporal steplength τ in interval (0, 01, 0, 1). More accurate results can be obtained with σ = 0.5. Comparing the solutions of the continuous and discrete problems, we see that only for the first two eigenvalues three or four digits remain the same, while for other eigenvalues the accuracy rapidly deteriorates. Using the second order approximation even for the eighth eigenvalue two digits are correct, if σ = 1/. Considering only the spatial discretization (the variable x is discretized x j = jh and the variable t is continuous), we obtain (by means of the method of lines) the boundary problem for Table. The discrete values q k L, α k. k a k L b k L A k B k 1 3,1380 0,1050 0,0437 0,009 6,745 0,115 0,1748 0, ,4095 0,340 0,399 0, ,5400 0,4440 0,6976 0, ,6630 0,5745 1,0879 0, ,775 0,715 1,5618 0, ,8535 0,895,1154 0, ,8805 1,0875,7396 0,393 the system of complex ordinary differential equations i dy j dt = Λy j + δy j, j = 1, N 1, y N y N 1 y 0 = 0, = iγy N, h where y j = y j (t) are continuous functions of time, j = 0, N. Seeking the quasistationary solution of this system in the form y j (t) = g j exp(iαt)
63 3 O. Dumbrajs, H. Kalis, A. Reinfelds we obtain the system similar to (3.5) where µ = α + δ. This means that the quantities A k + ib k in expression (3.10) are approximate eigenvalues α k, k = 1, N 1, obtained by means of the method of lines (see Tab. ). Using in the boundary conditions the second order approximation, we obtain an analogous problem, which, just as the grid method, gives more accurate results. In oder to increase the accuracy of discrete equation (3.5) we will use the Taylor expansion Λg(x i ) = g (x i ) + h 1 g(4) (x i ) hm (m)! g(m) (x i ) + O(h m ), where m = 1,,.... From equation (.4) it follows that where µ m = ( (λh)! Λg(x i ) = g(x i) h µ m, + (λh)4 4! ( 1) m (λh)m m! Similarly from boundary conditions (3.5) we obtain ) + O(h m ). g(x N 1 ) = g(x N ) hg (x N ) ( 1)l h l g (l) (x N ) + O(h l+1 ), l 0, l! and from the boundary condition of the problem (.4) g(x N 1 ) = C k g(x N ), where C k = 1 (hλ)! + iγ (hλ (hλ)3 λ 3! ( 1) k (hλ)k (k )! ( 1) k (hλ)k 1 (k 1)! ) + O(h k ), k 1. It can be seen that the discrete problem (the errors are proportional to O(h m ) and O(h k ) m, k = 1,,...) is given in the form { Λgi + µ m g i = 0, i = 1, N 1, g 0 = 0, g N = C 1 k g N 1. It can be seen that in the limit case (m, k ) µ m h (1 cos(hλ)) and C k cos(hλ) + iγλ 1 sin(hλ) or we obtain the transcendental equation (.5). Eigenfunctions of the discrete problem (3.5) g (k) j g (k) (x j ) = sin(q k x j ), x j = jh, j = 0, N, k = 1, N 1 are orthogonal with respect to the scalar product g (k), g (n) h N j=1 g(k) j j, i.e., g (k), g (n) = 0, if k n. This follows from the Green formula [4]. Evaluating g (k) = g (k) g (k), we obtain orthonormalized system g (k) = g (k) / g (k), for which g (k), g (n) = δ k,n (the Kronecker symbol). Considering the second order approximation for the boundary condition (3.3), we cannot obtain a system of orthogonal eigenfunctions. Evaluating g (k), we obtain g (n)
64 Numerical solution of single mode gyrotron equation 33 g (k) = 1 ( L h sin(q ) kl) cos(q k (L h)). sin(q k h) If h 0, then q k λ k and g (k) g k. If boundary conditions (3.4) are given as y n+1 N = 0 (γ = ), then q k = kπ L and g(k) = L [4]. Each grid function f(x), x ω h with boundary conditions (3.5) can be expanded as a finite sum N f(x) = c k g (k) (x) k=1 of orthonormalized eigenfunctions g (k) (x) = g (k) (x)/ g (k), x ω h, where the expansion coefficients can be found with the help of the expressions c k = f, g (k). The solution of the boundary problem { Λg = f(x), x ωh, is g(x) = N k=1 c k g (k) (x)/µ k. g(0) = 0, g(l) = Cg(L h) 4. Stability of the difference scheme To study the stability of the discrete problem (difference scheme) (3.4), we rewrite the difference equations with respect to the difference z j = yj n f(x j, t n ) in the matrix operator form (E + iτσ(λ + δ))z n+1 = (E iτ(1 σ)(λ + δ))z n, where z n = (z n 1, zn,..., zn N 1 )T is the error vector-column and E is the unit operator. Hence z n+1 = Gz n, where G = (E + iτσ(λ + δ)) 1 (E iτ(1 σ)(λ + δ)) is the transition operator with the eigenvalues λ k = 1 + iτ(1 σ)(µ k δ) 1 iτσ(µ k δ), k = 1, N 1, where µ k are eigenvalues of the difference operator ( Λ) to be determined from the boundary problem (3.5) µ k = h (1 cos(q k h)). If µ k are real numbers, e.g., in the case of the first kind boundary conditions (γ =, z n+1 N = 0) q k = kπ L, then from the stability condition [4] λ k = (1 + τ (1 σ) (µ k δ) )(1 + τ σ (µ k δ) ) 1 1, it follows that σ 1 (4.1)
65 34 O. Dumbrajs, H. Kalis, A. Reinfelds independent of the size of the temporal step-length τ. Similar problem for Schrödinger type differential equation was investigated in [3]. Taking the boundary condition of the third kind in the form z n+1 N = Czn+1 N 1 and determining the complex parameter q k in the form (3.8), we find from (3.11) that µ k = α k + δ, where α k can be determined from (3.9) and (3.10). Then from it follows that λ k = (1 τ(1 σ)b k) + A k τ (1 σ) (1 + τσb k ) + A k τ σ 1 B k + τ(1 σ)(a k + B k) 0. If σ 1 and B k 0, then this inequality holds and the difference scheme (3.4) is stable. If σ = 1, we obtain the inequality τ B k (A k + B k ) 1, (4.) which is important, if B k < 0. It is seen from (3.11) that, if (a k, b k ) is a solution of this system, then also ( a k, b k ) is a solution. The values of the coefficients A k, B k do not change and it is sufficient to consider only a k > 0. If simultaneously b k > 0, then also B k > 0, and the stability condition holds in the form (4.1). If a k = b k = 0, then B k = 0 and the difference scheme is stable. Calculations with the help of MAPLE show that positive variables a k correspond to positive variables b k i.e., B k > 0. If the parameter γ < 0, then it can be easily seen that positive a k correspond to negative b k and the difference scheme (3.4) is absolutely unstable, if the temporal step-length τ is not large enough (in inequality (4.) B k < 0). 5. Method of separation of variables Let us consider the inhomogeneous equation f x i f + δf = F (t, x), (5.1) t with a given function F (t, x). We seek the solution f = f(t, x) with the boundary conditions (.) in the form of a series f(t, x) = a k (t) g k (x), (5.) k=1 where g k (x) are orthonormalized eigenfunctions and λ k L = z (k) = z (k) 1 + iz (k) are solutions of (.6). To determine functions a k (t), we use the given initial conditions f(0, x) = f 0 (x). Taking a scalar product of (5.) and a fixed eigenfunction, if t = 0, we obtain a k (0) = f 0, g k. By analogy expanding the right-hand side of (5.1) F (x, t) = F k (t) g k (x) k=1
66 Numerical solution of single mode gyrotron equation 35 we obtain F k (t) = F, g k. Assuming that series (5.) and the series, differentiated twice with respect to x and once with respect to t, uniformly converge, and substituting it into (5.1), we obtain the ordinary differential equation and λ ka k (t) iȧ k (t) + δa k (t) = F k (t), t > 0 a k (t) = a k (0) exp(iα (k) t) + i t 0 exp(iα (k) (t ζ))f k (ζ) dζ, where ȧ k (t) = da k dt, α(k) = λ k δ. As example, if f 0(x) = sin ( ) πx L, F = 0, then solutions of the differential problem can be obtained in the form exp(iα (k) t) sin(λ k x) sin(λ k L)(λ k f(t, x) = πl γ ) (π λ k L )(λ k L. γ L + iγ) k=1 Solving the corresponding discrete problem with the initial condition y j 0 = sin( π L x j) f 0 (x j ), j = 0, N, we obtain yj n = N 1 k=1 an k g(k) (x j ), where g (k) (x j ) = sin(q k x j )/ g (k) are discrete eigenfunctions. Determining a 0 k from the initial condition a 0 k = (f 0, g (k) ) = hb k, b k = N 1 s=1 sin( π L sh) g(k) (sh), we find from difference equations the recurrence relation a n+1 k = ρ k a n k or an k = (ρ k ) n a 0 k, where ρ k = 1 + iτ α k /(1 iτσ α k ). Hence where y n j N 1 = h b k = k=1 b k exp(iα k τn)g (k) (x j ) g (k), (5.3) sin( π L h) sin(q kl) (cos(q k h) cos( π L h)), α k can be determined from (3.1), and α k from (3.9). It can be easily seen that yj n f(t n, x j ), if h 0, τ 0, i.e., the solution of the discrete problem converges to the solution of the continuous problem. Using the method of lines (only spatial discretization), we obtain y j (t) = N 1 k=1 a k(t) g (k) (x j ) by analogy, where functions a k (t) are solutions of the Cauchy problem da k (t) = iα (k) a k (t), dt a k (0) = hb k, i.e., a k (t) = a k (0) exp(iα k t). Hence the solution can be written as N 1 y j (t) = h b k exp(iα k t) sin(q j x j )/ g (k), k=1 i.e., analogously to (5.3) where α k = h (1 cos(q k h)) δ.
67 36 O. Dumbrajs, H. Kalis, A. Reinfelds Table 3. The values f, f h, f l, f h for x = L, τ = 0, 01. t f f h f l f h 0,1 0, , ,0516 0, , 0,0617 0,064 0,0669 0, ,3 0, ,0686 0, , ,4 0,0789 0,0786 0, , ,5 0, , , , ,6 0, ,0787 0, ,0767 0,7 0, , , , ,8 0, , ,085 0, ,9 0,0814 0,0891 0, ,0808 1,0 0, , , , ,0 0, , , ,0 0, , , , ,0 0,1089 0,1099 0,1089 0, ,0 0, , , , ,0 0,0917 0,0917 0,0915 0, Abs(f_h)_solutions abs(f_h) t Figure. Solution of the grid problem f h, N = 750, x = L. 6. Numerical results and conclusions Computations were carried out with the following values of the parameters δ = 0, L = 15, γ =, h = 1/10; 1/50, N = 150; 750, τ = 0, 1; 0, 01, σ = 1, and f 0 (x) = sin ( ) πx L. The finite difference scheme was realized by means of the FORTRAN code and analytically by using the expansion (finite series) in the form of a sum. The results coincide up to seven digits. The discrete solutions f h and f h for x = L were compared with the solution f of the continuous problem which was obtained from the series at fixed time moments t 50 ( f h is the discrete solution obtained by means of the FORTRAN code and the second order approximation of the boundary condition). In computing the series the terms were summed up to the term whose modulus was smaller than ε = 10 8 (the number of
68 Numerical solution of single mode gyrotron equation 37 included terms was in all cases smaller than 1000). In Tab. 3 we also present the solution f l, which was obtained by means of the analytic expansion of the line method. It does not depend on the temporal step-length τ. It is obvious that the results coincide up to two or three digits. In Fig. we show the numerical solution in the interval τ (0, 400). The solution oscillates up to t 50, after which it rapidly approaches zero. Calculations show that reducing the spatial step-length h in the grid method improves the accuracy. For example, if t = τ = 0, 1, then f h = 0, 0480 (h = 0, 1); 0, 050 (h = 0, 05); 0, 0510 (h = 0, 05); 0, 0509(h = 0, 0). It follows from the results presented in Tab. 3 that the scheme with the first order approximation of the boundary condition is even more accurate. This is due to the orthogonality of the corresponding eigenfunctions and this fact is important in improving accuracy of numerical methods. References [1] M.I. Airila, O. Dumbrajs, A. Reinfelds and U. Strautiņš. Nonstationary oscillations in gyrotrons. Phys. Plasmas, 8(10), , 001. [] N.S. Ginzburg, N.A. Zavolsky, G.S. Nusinovich and A.S. Sergeev. Onset of autooscillations in electron microwave generators with diffraction radiation output. Izv. Vyssh. Uchebn. Zaved. Radiofiz., 9(1), , (in Russian) [3] M. Radži ūnas and F. Ivanauskas. The stability conditions of finite difference schemes for Schrödinger, Kuramoto-Tsuzuki and heat equations. Mathematical modelling and analysis, 3, , [4] A.A. Samarskii. The theory of difference schemes. Marcel Dekker, New York, NY, 001.
69 38 O. Dumbrajs, H. Kalis, A. Reinfelds Girotrono lygties vienos modos skaitiniai sprendiniai O. Dumbrajs, H. Kalis, A. Reinfelds Straipsnyje nagrinėjami skaitiniai sprendiniai gauti tiriant girotrono lygties viena moda. Analitiniai ir skaitiniai sprendiniai gauti taikant baigtinių skirtumų metodą. Ištirti kvazistacionarieji sprendiniai ir atitinkamos tokio uždavinio tikrinės reikšmės ir tikrinės funkcijos.
70 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN SPATIAL ANALYSIS AND PREDICTION OF CURONIAN LAGOON DATA WITH GSTAT R. GARŠKA and I. KRŪMINIENĖ Klaipėda University faculty of Natural and Mathematical sciences H. Manto 84, Klaipėda, Lithuania 9 :;4< =><?A@B<09?DC <0E0C4FG@H;JI%KMLN=B97LD><4E#L CO@C0FP@H; I Received October ; revised December Abstract. The typical goal of geostatistical analysis is to interpolate values of variable under consideration at unobserved locations using data on observed locations because it is not feasible to gather all data of the observations in the study area. The second goal is to know how they represent the study area on the basis of the sample points. Kriging is one of geostatistical methods for spatial interpolation. This method relies on the spatial correlation reflected in the available data and so represents a global view of all the data as well as the nearest neighbor influence. Before spatial prediction using kriging can be executed, the semivariogram has to be computed and modelled. The objective of our work is to create maps of the Curonian lagoon using kriging and cokriging methods. Our spatial data consist of observations on sounding and bed sediments of different Curonian lagoon locations. For computation and simulation of semivariograms, as well as for application kriging and cokriging methods and visualization of results on maps Gstat and PCRaster are used. Key words: variogram, semivariogram, cross semivariogram, kriging, cokriging 1. Introduction This paper discusses the use of traditional kriging techniques when when we map variables from data that are collected in Curonian lagoon. For most applications kriging is usually associated with exact interpolation, that is, the kriging predictions change smoothly in space until they get to a location where data have been collected, at this point there is a "jump" in the prediction to the exact value that was measured. This also leads to discontinuity in the standard prediction errors, that "jump" to zero at the measured locations. In the research presented in the paper we have studied the Curonian lagoon and have created maps in all area by using data of a sediments in 13 locations and data of depth in 63 locations. In the previous publication [] the precision of the results obtained by two methods, i.e. kriging and cokriging, were compared by using cross-validation method. The results have showed that precision
71 40 R. Garška and I. Krūminienė of predicted values is better when cokriging method is used. In addition the present paper presents maps of the predicted values in the whole Curonian lagoon, where the prediction is based on measurement data that are mentioned above. Geostatistics is the name associated with a class of specialized statistical techniques used to analyze and estimate values of variables which are distributed and physically correlated in space and /or time. The analysis of such a correlation is usually called a "structural analysis" or "variogram modeling". From a structural analysis, predictions of the value of the variable can be made at unsampled locations using "kriging" or "stochastic simulation". This approach is most useful when the processes responsible for generating the measured variable are unknown or too poorly constrained to permit construction of a quantitative process model to make spatial interpolations or predictions. The overall sequence of steps in a typical geostatistical study include: exploratory data analysis (to explain the spatial character of the variable), structural analysis (to determine the spatial correlation or continuity of the data) and estimates (kriging or simulations to predict values at unsampled locations). Kriging prediction consists of three steps: Estimation of the semivariogram or covariance; Choice of a model among the family of valid semivariograms or covariances; Estimation of the semivariogram or covariance by fitting the valid model to the empirical semivariogram or covariance and use in one of the forms of kriging (e.g. ordinary kriging, simple kriging, universal kriging, etc.). In many environmental researches the data of more than one observation (measurements of more than one variable) are often obtained. If those variables are correlated with one another and the cross covariance functions are known or can be estimated then cokriging method can be used. More about geostatistical analysis can be found in the book of Cressie "Statistics for spatial data" [1]. Krivoruchko has applied a kriging method to radio cesium soil contamination data, collected in Belarus after the Chernobyl accident (see, e.g. the web /geostatistical/research_papers.html). Lophaven has computed the spatial distribution of Dissolved Inorganic Nitrogen (DIN) and Dissolved Inorganic Phosphorus (DIP) by three different variants of kriging, i.e. ordinary kriging, universal kriging and cokriging [3]. In the next section the main terms, processes and formulas which are used in geostatistical analysis are described. The results of the study are presented in Section 3 and conclusions are given in Section 4.. Spatial Data Analysis General Spatial Model (see [1]) is described in geostatistics as {Z(s) : s D}, where s = (x, y) denotes the coordinates of the sample site. Here (x, y) may be Euclidean coordinates (e.g., UTM coordinates), or latitude and longitude. More generally, we may have s = (x, y, z).
72 Spatial analysis and prediction of Curonian lagoon data with Gstat 41 Z(s) denotes the variable of interest at the location s. Note that this is written as a function of the location s. D denotes the set of spatial locations at which data may be obtained. For geostatistical data, the set of all multidimensional distributions of k-tuples ( Z(s1 ), Z(s ),..., Z(s k ) ) for all values of k all configurations of the points s 1, s,..., s k constitutes a stochastic process {Z(s) : s D}. The stochastic variable Z(s) has mean value E[Z(s)] = µ(s), s D. We also assume that the variable of Z(s) exists for all s D. The process Z is said to be Gaussian if, for any k 1 and locations s 1, s,..., s k, the vector ( Z(s 1 ), Z(s ),..., Z(s k ) ) has a multivariate normal distribution. The process Z is said to be strictly stationarity if the joint distribution of ( Z(s1 ), Z(s ),..., Z(s k ) ) is the same as that of ( Z(s 1 +h), Z(s +h),..., Z(s k + h) ) for any k spatial points s 1, s,..., s k and any h R d, provided only that all of s 1, s,..., s k, s 1 + h, s + h,..., s k + h lie within the domain D. The process Z is said to be second-order stationarity (also called weakly stationarity) if µ(s) = µ (i.e., the mean value is the same for all s) and Cov ( Z(s 1 ), Z(s ) ) = C(s 1 s ), for all s 1 D, s D, where C(s) is the covariance function of an observation at location s D. It can immediately be seen that with all variances assumed finite, a strictly stationary process is also second-order stationary. The converse is in general false, but a Gaussian process which is second-order stationary is also strictly stationary (see [4], 35 p.). Intrinsic stationarity is a weaker property than second-order stationarity. The variogram of intrinsic random function is written as γ(h) = V ar[(z(s 1 ) Z(s ))]. The function γ( ) is called the variogram (variance) and γ( ) the semivariogram (semivariance). If the semivariogram (covariance) depends only on distance between locations the process is called isotropic. The variogram is the variance of the difference between Z(s 1 ) and Z(s ). If two units are close together, their difference will typically be small, as would the variance of the difference. As units get apart, their differences get larger and usually the variance of the difference gets larger. If second-order stationarity is assumed, the relationship between the function semivariogram and the covariance is given as γ(h) = C(0) C(h). (.1) Note that C(0) = σ, the variance of the random function when h = 0. Equation (.1) shows that if the covariance is known, the variogram is also known. In practice the variogram (or/and semivariogram) is used more often then the covariance, because the variogram, unlike the covariance, does not require the knowledge of the mean value. Also semivariogram is less sensitive to any unidentified trend.
73 4 R. Garška and I. Krūminienė.1. Estimation of the semivariogram and cross semivariogram Determination of spatial variability is often based on a semivariogram. The sample estimator of the semivariogram, which is based on the method-of-moments, is given by ˆγ(h) = 1 N( h ) (s k,s l ) N( h ) [Z(s k ) Z(s l )], where N ( h ) denotes all pairs (s k, s l ) for which s k s l = h ([4], 38 p.). The spatial variability between two correlated random variables is described by the cross semivariogram. When the intrinsic hypothesis is assumed, it is defined as γ 1 (h) = γ 1 (h) = 1 E[( Z 1 (s k ) Z 1 (s l ) )( Z (s k ) Z (s l ) )], where Z 1 (s) and Z (s) denote two different variables. An estimator of the cross semivariogram is defined as ˆγ 1 (h) = 1 N( h ) (s k,s l ) N( h ) ( Z1 (s k ) Z 1 (s l ) )( Z (s k ) Z (s l ) ), where N( h ) is the number of pairs of observations within distance h. Usually ˆγ ij (h) is called the experimental or sample cross semivariogram (see [3]). Sill Variance Variance Nugget Range Distance between pairs a) Distance b) Distance c) Figure 1. Variograms: a) idealized form of variogram function; b) linear variogram; c) spherical variogram... Modelling the semivariogram and the cross semivariogram Modelling of semivariogram and cross semivariogram is done in the same way. The estimated semivariogram (cross semivariogram) is fitted with a model, and the best models are used in the kriging estimation. Several methods have been proposed for fitting semivariogram models. One relatively simple method that appears to perform well is the Weighted Least Squares. Figure 1a show representation of general variogram.
74 Spatial analysis and prediction of Curonian lagoon data with Gstat 43 The range is the distance beyond which observations are uncorrelated or at least approximately uncorrelated. On the semivariogram, the range is the point on the x axis where the curve reaches a plateau. Sill is the value of semivariogram where observations are uncorrelated or nearly uncorrelated. On the semivariogram shown, the sill is the height of the curve at the plateau. The nugget variance or nugget effect is the resulting discontinuity of the semivariogram at the origin, the difference between zero and the semivariogram at a lag distance is some greater than zero. The nugget effect is caused by measurement errors and micro-variability. A variogram model can consist of pure nugget effect. Isotropic processes are convenient to deal with because there are a number of widely used parametric forms for γ( ). An often used semivariogram model is the linear and the spherical model with nugget effect. A reason for this is an easy interpretation of the parameters. A linear semivariogram model (Fig.1b) in the isotropic case is defined as: 0, if h = 0, γ(h) = C 0 + C 1 h, if 0 < h < R, (.) C 0 + C 1 R, if h > R. Spherical semivariogram model (Fig.1c) is defined as: 0, [ if h = 0, 3 h γ(h) = C 0 + C 1 R 1 ( ) ] 3 h, if 0 < h =< R, (.3) R C 0 + C 1, if h > R, where C 0 is the nugget effect, R is the range and C 0 + C 1 is the sill [3]. When two or more variables are correlated, the nature of spatial cross correlation between the primary variable and several secondary variables can provide valuable information for estimation and simulation of the primary variable. Cross semivariogram modelling is always done for the purpose of developing a model to be used in estimation or simulation. The models that are to be used in estimation and simulation must obey a number of stringent constraints to ensure that the matrix solutions to the kriging equations exist and are numerically stable. Traditionally fitting of the cross semivariogram is done by eye, because it has been shown that predictions computed by kriging are reasonably insensitive to the specification of the cross semivariogram model. The best semivariogram (cross semivariogram) model can be found using the least squared criterion [3]..3. Kriging Concept Kriging is a generic name adopted by the geostatisticians for a family of generalized least-squares regression algorithms that allow one to account the spatial dependence between observations, as revealed by the semivariogram, into spatial prediction. It is a procedure for spatial prediction at an unobserved location, using data at observed locations, optimized with reference to a specific error criterion.
75 44 R. Garška and I. Krūminienė Kriging is known to be a Best Linear Unbiased Predictor (B.L.U.P.), because it minimizes the variance error between the true value and the predictor. Linear predictor of the value Z 1 (s 0 ) of the data at the unsampled site s 0 from the data Z(s) = Z(s 1 (s)), Z(s (s)) at the sampled sites s 1, s is: n Ẑ 1 (s 0 ) = w k Z 1 (s k ), k=1 where w k is the weight for the k-th variable of observation at location s k and n is the number of observations. The weights w k are chosen to minimize the mean squared error MSE = E [ Ẑ 1 (s 0 ) Z 1 (s 0 ) ]. Ẑ(s 0 ) is unbiased for Z(s 0 ) if and only if n w k = 1. k=1 Ordinary kriging gives the optimal predictions under the assumption that the mean value is constant (but unknown) across the whole area under study. The ordinary kriging variance for Z 1 is given by σ ok = k w k γ(s k s 0 ) + m, (.4) where m is a Lagrange multiplier m = ( 1 1 c z 1 ) / ( ), z z is the covariance matrix among the data, c z is Cov(z, Z(s 0 )) (see [1], p 143). Cokriging is prediction of a primary variable using additional information from a secondary variable. This method is used in data sets containing two or more regionalized variables which are correlated with one another. Suppose that q =. The prediction of Ẑ1 is done not only on the basis of Z 1, but also on measurements of Z. Cokriging involves the prediction of Z 1 (s 0 ) at an unsampled site s 0 from the data Z(s 1 ), Z(s ),..., Z(s n ), Z(s) T = ( Z 1 (s), Z (s) ) at the sampled sites s 1, s,..., s n. The linear prediction of cokriging is defined as: n n Ẑ 1 (s 0 ) = v1 k Z 1(s k ) + v k Z (s k ). k=1 k=1 To obtain an unbiased estimate the following constraints are needed: n m v1 k = 1, v k = 0. k=1 Similarly as (.4) the variance of cokriging prediction can be written as n n σcok = v1 k γ k1 (s k s 0 ) + v k γ k (s k s 0 ) + m 1. k=1 k=1 k=1 z
76 3. Results Spatial analysis and prediction of Curonian lagoon data with Gstat 45 The above procedure of variogram estimation, variogram model fitting, kriging and cokriging was applied to the Curonian lagoon data. The Curonian lagoon (also known as Kurši u marios, Kurshskij zaliv, Kurische Haff) is a large (length 95 km, width up to 48 km), shallow (mean depth of 3.8 m, the maximum depth m) coastal water body in the south-eastern part of the Baltic Sea. The outlet of the lagoon to the Baltic Sea, Klaipėda Strait, is artificially deepened down to 1 m. The data have been collected in 1990 year by S. Gulbinskas. It consists of bed sediments and soundings of the Curonian Lagoon. Sediments where measured in 13 locations, depth was measured in 63 locations. Their x coordinate values are between and and y coordinate values are between and Sediments have been divided into 7 groups (granulometric fractions) depending on median diameter (Md) in mm: (1) more than 0.5, () , (3) , (4) , (5) , (6) , (7) less than In order to apply the above statistical methods for data analysis, and mapping we have chosen free available software Gstat and PCRaster. Gstat is a program for the modelling, prediction and simulation of geostatistical data in one, two or three dimensions. In Gstat geostatistical modelling comprises calculation of sample variograms and cross variograms (or covariograms) and fitting models to them. In this paper Gstat has been used for modelling semivariance of all above fractions and for simulation cross variance between depth and sediment fractions. PCRaster has been used for showing kriging and cokriging prediction maps. In Gstat a simple variogram model is denoted cmod(a) with c the vertical (variance) scaling factor, Mod the model type, and a the range (horizontal, distance scaling factor) of this simple model. Linear and spherical models defined in (.) and (.3) equations, in Gstat are denoted by Lin( ) and Sph( ), respectively. The nugget effect is indicated by Nug( ). semivariance distance g_ Nug(0) Lin(3344.6) a) cross semivariance distance depth x g_ Nug(0) Lin(754.5) b) Figure. a) semivariogram of fraction (7) where Md of sediments is less than 0.004; b) cross semivariogram between fraction (7) and depth of the Curonian lagoon. To describe results of our research we took measurements of depth and fraction (7). Figure a presents semivariogram of fraction (7) where M od of sediments is less than Equation of this semivariogram is given by
77 46 R. Garška and I. Krūminienė 1.94N ug(0) Lin(754.5), where Lin represents model type, Nug(0) = 1.94, when 1 γ(h) = 0, the sill is and the range is The parameters and models of all semivariogram fractions are given in Table 1. Table 1. Types of semivariogram models of all fractions and the parameters: range, sill and nugget effect. Fraction Model Range Sill Nugget effect more than 0.5 Linear Linear Linear Linear Linear Linear less than Linear Figure b presents cross semivariogram between fraction (7) and depth of the Curonian lagoon. Equation of this cross semivariogram is given by N ug(0) Lin(3344.6), where Lin represents model type, the nugget effect equals , when 1 γ(h) = 0, the sill is and the range is The parameters and models of all cross semivariogram fractions are given in Table. Table. Types of cross semivariogram models between depths and fractions and the parameters: range, sill and nugget effect. Fraction Model Range Sill Nugget effect more than 0.5 Linear Linear Linear Linear Linear Linear less than Linear Figure 3 presents the linear and spherical semivariograms of the depth. In this case the spherical semivariogram is preferred. The parameters and models of depth are given in Table 3. Kriging is most sensitive to the behavior of the variogram near zero. In particular, it is sensitive to the presence / absence of the nugget effect. Maps of variations and predictions created using kriging method are shown in Figure 4 (here (a) prediction
78 Spatial analysis and prediction of Curonian lagoon data with Gstat semivariance semivariance depth Nug(0) Lin(397.7) distance a) distance b) depth.773 Sph(13957.) Figure 3. a) linear semivariogram of depth; b) spherical semivariogram of depth. Table 3. Types of semivariogram models of depth and the parameters: range, sill and nugget effect. Model Range Sill Nugget effect Linear Spherical Meters Concentration of (7) fraction No data Meters Variation of (7) fraction No data a) b) Figure 4. Kriging method: a) prediction map of fraction (7); b) variation map of fraction (7). map, (b) variation map). Maps obtained using cokriging method are shown in Figure 5. Figure 6a presents prediction map of depth, while Figure 6b presents variation map of depth. These maps have been created using kriging method. In order to check which one of the kriging and cokriging maps correspond best to true data we must first choose one point on the map, then compare these variation maps, and finally determine which map has smaller variation for the selected point. The method containing a smaller variation has created a better prediction map.
79 48 R. Garška and I. Krūminienė Meters Concentration of (7) fraction 50-60% 40-50% 30-40% 0-30% 10-0% 0-10% No data a) Meters Variation of (7) fraction No data b) Figure 5. Cokriging method: a) prediction map of fraction (7); b) variation map of fraction (7) Meters Depth 9-10 m 8-9 m 7-8 m 6-7 m 5-6 m 4-5 m 3-4 m - 3 m 1 - m 0-1 m No data a) Meters Variation of depth m^ m^ m^ m^ m^ No data b) Figure 6. Kriging method: a) prediction map of depth; b) variation map of depth. 4. Conclusions Statistical methods for data on bed fractions percentage and soundings have been described, applied and mapped. The methods are general, but in this paper they have been applied only to measurements of the Curonian lagoon.
80 Spatial analysis and prediction of Curonian lagoon data with Gstat 49 Semivariogram and cross semivariogram models have been made using percentage of fractions and soundings of the Curonian lagoon. Variance distribution and distribution of bed fractions percentage have been mapped using kriging and cokriging methods. Variance distribution and distribution of soundings have been mapped using kriging method. Results demonstrate that: Nugget and linear models best describe semivariance and cross semivariance of percentage of ground fractions. Spherical model best describes semivariance and cross semivariance of soundings. Prediction variations of percentage of bed fractions made by kriging and cokriging methods are very similar. Also cross semivariance show interdependence of parameters of models and depths. Prediction results of bed fractions percentage made by kriging method are very close to the mean value, while cokriging method shows that the variation of data are less close to the mean value. References [1] N. Cressie. Statistics for Spatial Data. John Wiley, New York, [] I. Kr ūminieṅe, K. Dučinskas and R. Garška. Applying of kriging and cokriging methods for prediction of Curonian lagoon data. Liet. matem. rink., 43(spec. nr.), , 003. [3] Soren Nymand Lophaven. Reconstruction of data from the aquatic environment. LYN- GBY, 001. [4] Richard L. Smith. Environmental Statistics. University of North Carolina Chapel Nill, NC , USA, 001.
81 50 R. Garška and I. Krūminienė Apie Kuršiu mariu duomenų erdvinę analizę ir prognozavima Gstat programos pagalba I. Kr ūminieṅe, R. Garška Šio darbo pagrindinis tikslas - Gstat bei PCRaster programų pagalba sukurti prognozuojamu duomenu ir jų dispersijų žemėlapius. Žemėlapiams sudaryti pritaikyti krigingo ir kokrigingo metodai. Krigingas yra vienas iš geostatistikos metodų, kuris atsižvelgdamas į erdvinį dviejų kintamųjų ryšį ir kaimyninių taškų reikšmes atlieka erdvinę interpoliaciją. Tuo tarpu kokrigingas atlieka pirminio kintamojo duomenu prognozę naudojant antrinių kintamųjų duomenis. Pagrindinis geostatistinės analizės tikslas yra interpoliuoti duomenis nežinomuose srities taškuose, nes dažniausiai atliekant geostatistinius tyrimus naudojami daliniai stebėjimai, kurie apima tik visumos dalį; arba nėra žinoma, ar imties duomenys pakankamai gerai atspindi visą studijuojama sritį. Rezultatų analizė parodė, kad tikslesnė prognozė gaunama taikant kokrigingo metodą
82 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN DYNAMICS OF MULTISECTION SEMICONDUCTOR LASERS J. SIEBER 1, M. RADŽIŪNAS and K. R. SCHNEIDER 1 University of Bristol Dept. of Eng. Math., Queen s Building, University of Bristol, Bristol BS8 1TR, United Kingdom 9: ;=<8>?A@ B@0CD BC7?4>FE GHI<J: KI<MLN Weierstrass Institute for Applied Analysis and Stochastics, Berlin Mohrenstr. 39, Berlin, Germany C :4OP?QL;:> DARS?A:>TUB@0CH?Q;=<O@VW>K X4;@#?YO@ C D RS?A: >TQB@ C H?U;=<O@ Received October ; revised December Abstract. We investigate the longitudinal dynamics of multisection semiconductor lasers based on a model, where a hyperbolic system of partial differential equations is nonlinearly coupled with a system of ordinary differential equations. We present analytic results for that system: global existence and uniqueness of the initial-boundary value problem, and existence of attracting invariant manifolds of low dimension. The flow on these manifolds is approximately described by the so-called mode approximations which are systems of ordinary differential equations. Finally, we present a detailed numerical bifurcation analysis of the two-mode approximation system and compare it with the simulated dynamics of the full PDE model. Key words: laser dynamics, invariant manifold theory, hyperbolic systems of partial differential equations, model reduction, bifurcation analysis 1. Motivation In commercial and public communication, the exchange of multimedial information growths rapidly. Thus, the corresponding data traffic increases exponentially and is characterized by the shift from voice communication to package oriented data traffic. This fact implies a big challenge for a strong increase of the data transmission rate. Due to their inherent speed, semiconductor lasers are of great interest as optical devices for fast data regeneration (reamplification, retiming, reshaping) in future photonic networks. Typically, these devices have a non-stationary working regime. As an example we mention the regime of high-frequency oscillations. Multisection lasers allow one to generate and to control such nonlinear effects by designing the longitudinal structure of the device (see, e.g., [16, 19, 5, 8]).
83 5 J. Sieber, M. Radžiūnas, K. Schneider However, prototyping of multisection semiconductor lasers is very expensive and time consuming. The goal of this paper is to demonstrate that mathematical models can be used to study the longitudinal dynamics of such lasers and to optimize their working regime. We focus on the traveling wave model, a linear hyperbolic system of partial differential equations (PDEs) which is nonlinearly coupled with a system of ordinary differential equations (ODEs). It models the longitudinal dynamics of edge emitting multisection semiconductor lasers by the interaction of two physical variables: the complex light amplitude (in fact, its spatially slowly varying envelope), which is spatially resolved in the longitudinal direction of the laser and described by the linear hyperbolic PDE subsystem, and the effective carrier density within the active zone of the device, which is section-wise spatially averaged and described by the ODE subsystem. This model has the advantage of meeting two seemingly contradictory criteria, accuracy and simplicity (or rather accessibility to a detailed bifurcation analysis). On one hand, it is accurate enough to describe all phenomena of interest to the engineers. Moreover, it can easily be made more realistic by gradually incorporating secondary physical effects that may play a role in limiting the performance of a particular device. On the other hand, it allows one to reduce the model to a low-dimensional system of ODEs by exploiting the fact that the carrier density operates on a much slower time-scale than the light amplitude. These ODEs in turn are accessible to a detailed bifurcation analysis using standard software like AUTO [10]. Only this bifurcation analysis gives insight into the mechanisms behind many nonlinear phenomena and is able to reveal effects (for example excitability [7]) that may be invisible in pure parameter studies. Both aspects of the traveling wave model have been implemented in the numerical code (Longitudinal Dynamics of Semiconductor Lasers). Hence, this numerical tool provides engineers, laser physicists, and mathematicians with a whole hierarchy of models allowing them to switch on or off physical effects to gain insight which of these effects causes the particular phenomenon they are interested in. Besides numerical integration of the model equations this tool solves also the spectral problem of the model equations, allows to analyze the dynamics of individual longitudinal modes and in certain cases enables one effectively to compare the solutions provided by the PDE model and the reduced mode approximation systems. This modeling approach has been used quite successfully in the recent past to design new devices exhibiting high-frequency oscillations [7, 8, 8]. In this paper we focus more on the aspect of model reduction than extension, mostly because this part is more thoroughly supported by mathematical theory. The paper is organized as follows: In section. we describe the traveling wave model and give a detailed physical interpretation of all coefficients and variables. In section 3. we show that the corresponding initial-boundary value problem is well-posed. In section 4. we introduce a small parameter exploiting the difference in the time-scale between light and carrier density. In section 5. we investigate the spectral properties of the infinite-dimensional linear part. Section 6. combines the results of the previous sections to derive conditions guaranteeing that the traveling wave model can be reduced to an ODE system. In section 7. by showing a detailed two-parameter bifur-
84 Dynamics of multisection semiconductor lasers 53 cation diagram we demonstrate how useful the reduced model can be. We link this bifurcation diagram to a parameter study with a more realistic version of the traveling wave model. In the last section we draw conclusions and give an outlook on future projects.. The coupled traveling wave model with nonlinear gain dispersion The coupled traveling wave model, a hyperbolic system of PDEs coupled with a system of ODEs, describes the longitudinal effects in narrow edge-emitting laser diodes [1, 15, 3]. It has been derived from Maxwell s equations for an electro-magnetic field in a periodically modulated waveguide [1, 3] assuming that transversal and longitudinal effects can be separated. In this section we introduce the corresponding S 1 S S 3 n 1 n n 3 z 1 z z 3 z 4 0 l 1 = 1 1 z l l 3 L Figure 1. Typical geometric configuration of the domain in a laser with 3 sections. system of differential equations, explain the physical interpretation of its coefficients and specify some physically sensible assumptions about these coefficients. The dynamics in a multi-section laser is described by the evolution of the following quantities. The variable ψ(t, z) C describes the complex amplitude of the slowly varying envelope of the optical field split into a forward and a backward traveling wave. The variable p(t, z) C describes the corresponding nonlinear polarization of the material. Both quantities depend on time and the one-dimensional spatial variable z [0, L] (the longitudinal direction within the laser; see Fig. 1). A prominent feature of multi-section lasers is the splitting of the overall interval [0, L] into sections, that is, m subintervals S k that represent sections with separate electric contacts. We treat the carrier density within the active zone of the waveguide as a section-wise spatially averaged quantity n(t) R m (see Fig. 1). In dimensionless form, the coupled traveling wave model can be posed as an initial-boundary value problem for ψ, p, and n that reads as follows
85 54 J. Sieber, M. Radžiūnas, K. Schneider [ ] z + β(n(t), z) iκ(z) t ψ(t, z) = ψ(t, z) + ρ(n(t), z) p(t, z), iκ(z) z + β(n(t), z) (.1) t p(t, z) = [iω r (n(t), z) Γ (n(t), z)] p(t, z) + Γ (n(t), z) ψ(t, z), (.) d dt n k(t) = I k n k(t) P [G k (n k (t)) ρ k (n k (t))] ψ(t, z) ψ(t, z) dz τ k l k S k P ( ) ρ k (n k (t)) Re ψ(t, z) p(t, z) dz, k = 1,..., m (.3) l k S k subject to the inhomogeneous boundary conditions for ψ and the initial conditions ψ 1 (t, 0) = r 0 ψ (t, 0) + α(t), ψ (t, L) = r L ψ 1 (t, L) (.4) ψ(0, z) = ψ 0 (z), p(0, z) = p 0 (z), n(0) = n 0. (.5) The Hermitian transpose of the C -vector ψ is denoted by ψ in (.3). We will define the appropriate function spaces and discuss the possible solution concepts in section 3.. The quantities and coefficients appearing above have the following meaning (see also Tab. 1 and Fig. 1). L is the length of the laser. The laser is subdivided into Table 1. Ranges and explanations of the variables and coefficients appearing in (.1) (.4). See also [3] to inspect their relations to the originally used physical quantities and scales. typical range explanation ψ(t, z) C optical field, forward and backward traveling wave p(t, z) C nonlinear polarization n k (t) R + spatially averaged carrier density in section S k Im d k R frequency detuning Re d k < 0, O(1) negative decay rate due to internal losses α H,k (0, 10) negative of line-width enhancement factor g k 1 differential gain in active sections S k κ k ( 10, 10) real coupling coefficient for the optical field ψ due to Bragg grating in DFB sections ρ k 0, O(1) amplitude of the gain curve Γ k O(10 ) half width at half maximum of the gain curve Ω r,k O(10) central frequency of the gain curve I k O(10 ) current injection τ k O(10 ) spontaneous lifetime of the carriers P (0, ) scale of (ψ, p) (can be chosen arbitrarily) r 0, r L C, r 0, r L < 1 facet reflectivities m sections S k of length l k with starting points z k for k = 1,..., m. We scale the system such that l 1 = 1 and set z m+1 = L. Thus, S k = [z k, z k+1 ]. All coefficients are supposed to be spatially constant in each section and to depend only on the carrier density in that section, that is, for z S k we have
86 Dynamics of multisection semiconductor lasers 55 κ(z) = κ k, Γ (n, z) = Γ k (n k ), β(n, z) = β k (n k ), ρ(n, z) = ρ k (n k ). Tab. 1 collects the physical interpretation and the sensible ranges of all coefficients and variables. The model for the growth coefficient β k (n k ) C in section S k is β k (ν) = d k + (1 + iα H,k )G k (ν) ρ k (ν), where d k C accounts for the static internal losses (hence, Re d k < 0) and the static frequency detuning, and α H,k R + is the negative of the line-width enhancement (or Henry) factor. A section S k is either passive, then the functions G k and ρ k are identically zero, or S k is active. In the active case G k : R R is a smooth strictly monotone increasing function satisfying G k (1) = 0. Its limits are lim G k(ν) =, ν lim G k(ν) =. ν Typically, an affine model for G k in active sections is reasonably accurate, that is, G k (ν) = g k (ν 1) with a differential gain g k = G k (1) > 0. In active sections S k, that is, if G k 0, the gain amplitude ρ k (ν) is bounded for ν < 1. Moreover, we suppose that ρ k, Ω r,k, and Γ k : R R are smooth and Lipschitz continuous, and Γ k (ν) > 1 for all ν. For passive sections S k the variable n k is decoupled from all other equations and can be dropped from the system. The polarization function p and equation (.) has been included into the coupled traveling wave model for a more realistic account of nonlinear gain dispersion effects [3, 8]. Now, the frequency dependence of waveguide material gain is modeled by a Lorentzian function with an amplitude ρ, half width at half maximum Γ, centered at the frequency Ω r. That is, a monochromatic light-wave ψ 1 (t, z) = e iωt ϕ(z) in an uncoupled stationary; waveguide (κ = 0, ṅ = 0) is amplified or damped according to the equation [ z ϕ(z) ρ(z)γ ] (z) = Re β(z) + (ω Ω r (z)) + Γ ϕ(z). (z) The facet reflectivities r 0 and r L in (.4) are complex with modulus less than 1. The inhomogeneity α(t) is complex. It models an optical input at the facet z = 0. We assume it to be L in time on finite time intervals to permit a discontinuous optical input. The form of the right-hand-side of equation (.3) for the carrier density can be clarified by introducing the Hermitian form g k (ν) [( ψ p ), ( ϕ q )] = 1lk S k (ψ (z), p (z)) ( Gk (ν) ρ k (ν) 1 ρ k(ν) 1 ρ k(ν) 0 ) ( ) ϕ(z) dz. q(z) Using the notation f k (ν, (ψ, p)) = I k ν τ k P g k (ν) [( ( ψ ψ, p) p)] (.6)
87 56 J. Sieber, M. Radžiūnas, K. Schneider for ν R and ψ,ϕ, p, q L (S k ; C ) the carrier density equation (.3) reads d dt n k = f k (n k, (ψ, p)) for k = 1,..., m. (.7) Other secondary physical effects have been incorporated into the numerical code which was developed for the simulation and analysis of longitudinal dynamics in multi-section lasers. As example we mention the effects of nonlinear gain compression, that is, the dependence of G on ψ, and spatial hole burning, i.e., treating n as a fully spatially resolved variable [7, 8]. The parameter study by direct simulations of the extended model equations shown in Fig. 3 has taken both effects into account. However, even after an inclusion of these effects, the traveling wave model can describe the behaviour of semiconductor lasers still only approximately. Thus, in this paper we focus on the analysis of the traveling wave model in the rather simple form (.1) (.4). 3. Existence theory In a first step we investigate in which sense system (.1) (.3) generates a semiflow depending smoothly on its initial values and all parameters. We want to write (.1) (.3) as an abstract evolution equation in the form d dt u = Au + g(u), u(0) = u 0 (3.1) in a Hilbert space V, where A is a linear differential operator that generates a strongly continuous semigroup S(t), and g is smooth in V. A natural space for the variables ψ and p is L ([0, L]; C ), such that V could be L ([0, L]; C ) L ([0, L]; C ) R m for u = (ψ, p, n). However, the inhomogeneity α in the boundary condition (.4) poses a conceptual difficulty in this framework. Common approaches are boundary homogenization (used in [18]) or appending α as an auxiliary variable and an additional equation of the form d α(t) = a(t), dt where a is the derivative of α (used in [1]). Then, the nonlinearity g in the evolution equation depends explicitly on t and it has the same regularity with respect to t as the time derivative of α. Hence, both approaches require a high degree of regularity of α in time which is quite unnatural as the laser still works with discontinuous input such as square waves. An alternative would be the introduction of a concept of weakly mild solutions as it was done in [13]. However, this would require the extension of all needed classical results of the theory of strongly continuous semigroups to this type of solutions. Here, we choose an approach that is similar to that in [1] but does not require any regularity of the inhomogeneity. We introduce the auxiliary space-dependent variable a(t, x) (x [0, )) satisfying the equation t a(t, x) = x a(t, x) (3.)
88 Dynamics of multisection semiconductor lasers 57 and change the boundary condition for z = 0 in (.4) into ψ 1 (t, 0) = r 0 ψ (t, 0) + a(t, 0). One may think of an infinitely long fibre [0, ) storing all future optical inputs and transporting them to the laser facet z = x = 0 by the transport equation (3.). If we choose a(0, x) = α(x) as initial value for a, than the value of a at the boundary x = 0 at time t is α(t). In this way, the initially inhomogeneous boundary condition becomes linear in the variables ψ and a requiring no regularity for a. We choose a weighted norm L η for a, that is, a(t, ) = a(t, x) (1 + x ) η dx with 0 η < 1/. In this way, we permit the input to be L but still keep V as a Hilbert space. With this modification we can work within the framework of the theory of strongly continuous semigroups [17]. The variable u has the components (ψ, p, n, a) V = L ([0, L]; C ) L ([0, L]; C ) R m L η([0, ); C). We have a certain freedom how to choose the splitting of the right-hand-side between A and g. We keep A as simple as possible, including only the unbounded terms [ ] z ψ ψ 1 A p n := z ψ 0 0. a x a The domain of definition of A is D(A) = {(ψ, p, n, a) H 1 ([0, L]; C ) L ([0, L]; C ) R m H 1 η([0, ); C) : ψ 1 (0) = r 0 ψ (0) + a(0), ψ (L) = r L ψ 1 (L)}. In this way, A generates a strongly continuous semigroup S(t) in V []. The nonlinearity g is smooth because it is a superposition operator of smooth coefficient functions, and all components either depend only linearly on the infinite-dimensional components ψ and p, or map into R m. Then, an a-priori estimate implies the following theorem. Theorem 1 [Global existence and uniqueness]. For any T 0 > 0, there exists a unique mild solution u(t) of (3.1) in [0, T 0 ]. Furthermore, if the initial value u 0 is in the domain of definition of A, then u(t) is a classical solution of (3.1). This theorem implies the existence of a semiflow S(t; u 0 ) that is strongly continuous in t and smooth with respect to u and parameters. The a-priori estimate has to be slightly more subtle than in [18]. It uses the fact that the same functions G k and ρ k appear on the right-hand-side of (.1) and on that of (.3) but with opposing signs. Due to this fact the function P ψ(t) + m l k (n k (t) n ) k=1 remains non-negative for sufficiently small n and, hence, bounded, giving rise to a bounded invariant ball in V. The value of n depends on the initial value u 0 (see [] for details).
89 58 J. Sieber, M. Radžiūnas, K. Schneider 4. Introduction of a small parameter For all results about the long-time behavior of system (.1) (.3) we restrict ourselves to autonomous boundary conditions for ψ, that is, ψ 1 (t, 0) = r 0 ψ (t, 0), ψ (t, L) = r L ψ 1 (t, L). (4.1) The inhomogeneous case is an open question for future work. However, understanding the dynamics of the autonomous laser is not only an intermediate step but an important goal in itself since many experiments and simulations focus on this case; see for example [8] for further references. An examination of system (.1) (.3) reveals that the space dependent subsystem is linear in ψ and p: ( ) ( ψ ψ t = H(n). (4.) p p) The linear operator [ ] z + β(n) iκ ρ(n) H(n) = iκ z + β(n) (4.3) Γ (n) iω r (n) Γ (n) acts from Y := {(ψ, p) H 1 ([0, L]; C ) L ([0, L]; C ) : ψ 1 (0) = r 0 ψ (0), ψ (L) = r L ψ 1 (L)} into X = L ([0, L]; C ) L ([0, L]; C ). H(n) generates a C 0 -semigroup T n (t) acting in X. Its coefficients κ, and, for each n R m, β(n), Ω r (n), Γ (n) and ρ(n) are linear operators in L ([0, L]; C ) defined by the corresponding coefficients in (.1), (.). The maps β, ρ, Γ, Ω r : R m L(L ([0, L]; C )) are smooth. Furthermore, we observe that I k and τ 1 k in (.6) are approximately two orders of magnitude smaller than 1 (see Tab. 1). Hence, we can introduce a small parameter ε and set P = ε in (.3), such that the carrier density equation (.7) reads as d dt n k = f k (n k, E) = ε(f k (n k ) g k (n k )[E, E]) (4.4) for E X, where the coefficients in F k (n k ) = ε 1 (I k n k τ 1 k ) are of order 1. Although ε is not directly accessible, we treat it as a parameter and consider the limit ε 0 while keeping F k fixed. At ε = 0, the carrier density n is constant. It enters the linear subsystem (4.) as a parameter. Consequently, the spectral properties of H(n) with fixed n determine the longtime behavior of the system for ε = 0. In particular, we are interested in such values of n which imply an isolated non-empty but finite set of eigenvalues of H(n) located exactly on the imaginary axis. In this case, we can expect a finite-dimensional invariant manifold to persist for nonzero ε in the spirit of Fenichel s geometric singular perturbation theory [11]. Thus, we would like to understand the spectral properties of the operator H for fixed n and their correspondence to the growth of the semigroup T n generated by H in the next step.
90 Dynamics of multisection semiconductor lasers Spectral properties of operator H We drop the argument n in this paragraph for brevity. The long-time behavior of the semigroup T generated by H can be described by the following theorem (see [] for details of the proof): Theorem. Let ξ 0 = 1 L m k=1 Re β kl k < 0, denote W = {iω r,k Γ k : k = 1,..., m}, and let ξ be in the interval (max{re W, ξ 0 }, 0). Then, there exists a splitting of X = X 1 X into two H-invariant subspaces where X 1 is finite-dimensional and the semigroup T restricted to X decays according to rate ξ: T (t) X Me ξt for a constant M 1 and all t 0. Since T is neither an analytical nor an eventually compact semigroup there are no general theorems implying our result. However, the operator H has a characteristic function h(λ) defined in C \ W (note that Re W < 1). The function h is analytic in C \ W and known explicitly. Hence, most questions about the spectrum of H can be answered by finding the roots of h. In particular, the spectrum of H is discrete in C \ W, that is, it consists only of eigenvalues of finite algebraic multiplicity. In order to obtain our result, we have to distinguish two cases, r 0 r L = 0 and r 0 r L 0. It turns out that the semigroup T is eventually differentiable if r 0 r L = 0. In this case, we can split X into two H-invariant subspaces. One corresponds to the spectrum close to W. Thus, H is bounded and T exponentially decaying in this subspace. The semigroup T restricted to the complementary invariant subspace is eventually compact. Hence, the desired result follows from the theory of eventually compact semigroups [9]. If r 0 r L 0 (the hyperbolic case), we treat the operator as a perturbation of its diagonal part similar to [0]. Before applying the same result as [0], the invariant subspace corresponding to the spectrum close to W has to be split off and treated separately in the same way as in the case r 0 r L = 0. In essence, Theorem implies that we can treat H like a matrix: the dominant eigenvalues determine the growth of the corresponding semigroup. 6. Model reduction Let us assume that there exists a simple connected open set U R m of carrier densities n such that H(n) has a uniform spectral gap for all n U in a strip of the negative complex half-plane {z C : ξ Re z ξ/k} (ξ < 0, integer k > ), and that the dominant part of the spectrum of H(n) is finite. Hence, the spectral projection P c (n) onto the H(n)-invariant subspace corresponding to the dominant part of the spectrum has a constant rank q > 0. This spectral gap assumption is quite natural and follows (in conjunction with Theorem ) for example from the existence of non-trivial dynamics that is uniformly bounded for ε 0 (e.g., relative equilibria, i.e., solutions of the form E(t) = E 0 e iωt, n = const) if r 0 r L = 0. We can split any E X into E = B(n)E c + E s, where B(n) is a basis of Im P c (n) depending smoothly on n, E c C q, and E s X is E P c (n)b(n)e c. The map R : X U C q U given by (E, n) (B(n) 1 P c (n)e, n) is well defined,
91 60 J. Sieber, M. Radžiūnas, K. Schneider smooth and Lipschitz continuous on any closed subset of X U. Then, the main model reduction theorem is as follows. Theorem 3 [Model reduction]. Let ε 0 > 0 be sufficiently small, (ξ, 0), and N be a closed bounded subset of C q U. Then, for all ε [0, ε 0 ) there exists a C k manifold C X R m satisfying: i. (Invariance) C is S(t, )-invariant relative to R 1 N. That is, if (E, n) C, t 0, and S([0, t]; (E, n)) R 1 N, then S([0, t]; (E, n)) C. ii. (Representation) C can be represented as the graph of a map which maps (E c, n, ε) N [0, ε 0 ) ([B(n) + εν(e c, n, ε)]e c, n) X R m, where ν : N [0, ε 0 ) L(C q ; X) is C k with respect to all arguments. Denote the X-component of C by E X (E c, n, ε) = [B(n) + εν(e c, n, ε)]e c X. iii. (Exponential attraction) Let Υ X R m be a bounded set with RΥ N and a positive distance to the boundary of N. Then, there exist a constant M and a time t c 0 with the following property: For any (E, n) Υ there exists a (E c, n c ) N such that S(t + t c ; (E, n)) S(t; (E X (E c, n c, ε), n c )) Me t for all t 0 with S([0, t + t c ]; (E, n)) Υ. iv. (Flow) The flow on C R 1 N is differentiable with respect to t and governed by the following system of ODEs: de c = [ H c (n) + εa 1 (E c, n, ε) + ε a (E c, n, ε)ν(e c, n, ε) ] E c, dt (6.1) dn dt = εf (E c, n, ε), where H c (n) = B(n) 1 H(n)P c (n)b(n), a 1 (E c, n, ε) = B(n) 1 P c (n) n B(n)F (E c, n, ε), a (E c, n, ε) = B(n) 1 n P c (n)f (E c, n, ε)(id P c (n)), F (E c, n, ε) = (F k (n k ) g k (n k )[E X (E c, n c, ε), E X (E c, n c, ε)]) m k=1. The idea to choose n-dependent coordinates for E in the construction of a reduced model was introduced already in [1] by physicists. This choice has the advantage that the graph of the center manifold itself enters the flow (6.1) on the center manifold only in the form O(ε )ν. This fact has been pointed out first in [4], where the same model reduction result has been proven for ODEs of similar structure (big linear system coupled to a slow system) using Fenichel s theorem for singularly perturbed systems of ODEs [11]. Since Fenichel s theorem is not available for infinitedimensional systems, we have to adapt the proof of Fenichel [11] to our case starting from the general results in [4, 5, 6] about invariant manifolds of semiflows in Banach
92 Dynamics of multisection semiconductor lasers 61 spaces. In particular, we apply the cut-off modifications done in [11] only to the finite-dimensional components E c and n outside of the set N of interest. Moreover, we adapt the modifications such that the invariant manifold for ε = 0 is compact without boundary as required by the theorems in [4]. Truncating all terms of order O(ε ) in (6.1) gives rise to a system of ODEs in C q R m, where all terms in the right-hand-side can be expressed analytically as functions of the eigenvalues of H. The truncated system de c = [H c (n) + εa 1 (E c, n, ε)] E c, dt (6.) dn k = ε (F k (n k ) g k (n k )[B(n)E c, B(n)E c ]) dt is called the mode approximation. It is an implicit system of ODEs because the eigenvalues of H are given only implicitly as roots of the characteristic function h of H. The dimension of (6.1) is typically low: q is often either 1 or. The consideration of mode approximations has proven to be extremely useful for numerical and analytical investigations of longitudinal effects in multi-section semiconductor lasers; see for example [, 1, 7] and section 7. for a demonstration. 7. Parameter study and bifurcation analysis for a laser subject to delayed optical feedback In this section we demonstrate how the traveling wave model helps to detect and understand nonlinear phenomena occurring in multi-section lasers by a bifurcation analysis using the mode approximations and the subsequent systematic parameter study for the full model. We investigate a three-section laser, where S 1 is a singlemode DFB laser (i.e., κ 1 0, G 1 0), S is a passive phase tuning section (i.e., κ = G = ρ = ṅ = 0), and S 3 is an amplifier section (i.e., κ 3 = 0, ρ 3 = 0, G 3 0). Since r L 0, this device resembles the classical experiment of a singlemode semiconductor laser which is subject to delayed optical feedback. Section S 1 plays the role of the single-mode laser and the sections S and S 3 form an integrated cavity providing delayed optical feedback from the facet at z = L. In this three-section setup the two most important parameters, the feedback strength and the feedback phase ϕ Im d can be tuned continuously in the experiment by changing the currents I and I 3 into the sections S and S 3 (up to feedback strengths close to 1). Bifurcation analysis. Since numerical bifurcation analysis tools like [10] are available for systems of ODEs only, the mode approximations justified in Theorem 3 are extremely helpful. It turns out that the number q of critical eigenvalues of H(n) is for all relevant carrier densities n. Thus, Theorem 3 applies with q = and m = (the carrier density n is constant since section S is passive). The center manifold C has dimension 6 as it is a graph over C R. The flow of (6.) is still symmetric with respect to complex rotation of E c. Hence, we can reduce it to a 5-dimensional
93 6 J. Sieber, M. Radžiūnas, K. Schneider :4 1:3 CU Cusp GH Degenerate Hopf HSN Hopf Saddle-node 1: Strong resonances PSN Period-doubling Saddle-node A,B Non-central saddlenode on closed orbit 1: GH PSN Hopf bif. Saddle-node bif. Homoclinic bifurcation Torus bifurcation Period doubling Saddle-node of limit cycles Excitability Mode beating pulsations Undamped relaxation oscillations A B HSN CU GH Figure. Bifurcation diagram for the two-mode approximation (truncated (6.1) with q = ) in the parameter plane (ϕ, I 3) (see [7] for the particular parameter values). system of ODEs. In this system, equilibria correspond to relative equilibria of the original traveling wave model and periodic solutions to self-pulsations, i.e., modulated rotating-wave solutions. Fig. shows the results of two-parameter numerical continuations of the physically most relevant codimension-1 bifurcation curves in the parameter plane (ϕ, I 3 ). The two different islands of self-pulsations are clearly visible along with their borders. The nature of these borders and bifurcation theory serve as a guide for experiment and simulation to investigate interesting phenomena that otherwise could be missed due to hysteresis or limited basins of attraction. Most notably, there are stable invariant tori with strong resonances above the torus bifurcation curve, excitability above the homoclinic bifurcation curve, and period doubling and chaos at the border of the undamped relaxation oscillations. Parameter study for the full PDE System. Fig. 3 gives an overview over all stable stationary states and non-stationary regimes that can be found by direct simulation in the parameter plane (ϕ, I 3 ) in the full PDE system (.1) (.3). For the simulation, we also included the additional physical effects mentioned at the end of section. to match the experimental results as closely as possible. See [7] for a full description of the traveling wave model used in the simulation. The two large domains of periodic solutions within each period of ϕ are quite prominent in Fig. 3 as well. The Hopf and the saddle-node curves can be recognized in the simulation and give a full account of the number and stability of all present stationary states in Fig. 3. The shadings in Fig. 3 mark the different stable non-stationary regimes in the (ϕ, I 3 ) parameter plane observed in the simulation. Single-pulse periodic solutions are typically born in Hopf bifurcations. Double-pulse
94 Dynamics of multisection semiconductor lasers τ 3 Hopf bifurcation Saddle-node bifurcation single pulse periodic double pulse periodic irregular & multiple pulse 3 I ϕ/π 3 Figure 3. Parameter study of a three section laser by direct simulation of the PDE model with -tool. Full model and used parameter values (except of l 1 = 50 µm, l = 400 µm and α = 15 cm 1 ) can be found in [7]. solutions existing nearby have approximately half the frequency. Their occurrence is related to the period doubling bifurcations (see also Fig. ). Finally, multiple-pulse and irregular regimes account for dynamics (and different resonances) on the tori, and chaotic attractors. A well-known problem of direct simulations is that only one stable regime will be observed for each parameter value depending on the choice of initial values and the basins of attractions. However, the bifurcation analysis shows that several stable regimes may coexist in some parameter regions. We took into account this possible hysteresis by varying the parameters in small steps in different directions from any stable non-stationary regime we found until we hit a sharp transition. In this way, we always traced the hysteresis at sharp transitions corresponding to subcritical or saddle-node bifurcations. Fig. 3 shows the most simple non-stationary regime in hysteresis parameter regions (that is, mostly, the single-pulse periodic solution) because this is the most interesting regime for potential applications. 8. Conclusions and outlook The coupled traveling wave model has proven its value in the exploration of nonlinear phenomena in multisection laser structures. This can be seen impressively in recent results concerning delayed optical feedback effects [14, 18, 1, 6, 7], in multi-section lasers and subsequent new device designs [7, 8, 16, 19]. The model has been efficiently implemented in the code which permits extensive parameter studies. The simulation of the model equations with this code together with the bifurcation analysis of the reduced mode approximation systems gives insight into the underlying dynamics. Moreover, it allows the user to incorporate physical effects
95 64 J. Sieber, M. Radžiūnas, K. Schneider like spatial hole burning or nonlinear gain compression, or experimental conditions like optical input or electric modulation. This broadens the range of applications of the traveling wave model toward mode-locked lasers, optical amplifiers, ring lasers, etc. However, the theory concerning some of these extensions of the traveling wave model is still incomplete, even concerning basic questions like the existence of a smooth strongly continuous semiflow. Thus, an urgent task is to gain a theoretical understanding of these more complex models, and whether they can exhibit substantially more complex phenomena. References [1] U. Bandelow. Theorie longitudinaler Effekte in 1.55 µm Mehrsektions DFB-Laserdioden. PhD thesis, Humboldt-Universität Berlin, [] U. Bandelow, L. Recke and B. Sandstede. Frequency regions for forced locking of selfpulsating multi-section DFB lasers. Opt. Comm., 147, 1 18, [3] U. Bandelow, M. Wolfrum, M. Radzi ūnas and J. Sieber. Impact of gain dispersion on the spatio-temporal dynamics of multisection lasers. IEEE J. of Quant El., 37(), , 001. [4] P. W. Bates, K. Lu and C. Zeng. Existence and persistence of invariant manifolds for semiflows in Banach spaces. Mem. Amer. Math. Soc., 135, [5] P. W. Bates, K. Lu and C. Zeng. Persistence of overflowing manifolds for semiflow. Comm. Pure Appl. Math., 5(8), , [6] P. W. Bates, K. Lu and C. Zeng. Invariant foliations near normally hyperbolic invariant manifolds for semiflows. Trans. Amer. Math. Soc., 35, , 000. [7] S. Bauer, O. Brox, J. Kreissl, B. Sartorius, M. Radzi ūnas, J. Sieber, H.-J. Wünsche and F. Henneberger. Nonlinear dynamics of semiconductor lasers with active optical feedback. Phys. Rev. E, 69, 01606, 004. [8] O. Brox, S. Bauer, M. Radzi ūnas, M. Wolfrum, J. Sieber, J. Kreissl, B. Sartorius and H.- J. Wünsche. High-frequency pulsations in DFB-lasers with amplified feedback. IEEE J. Quantum Elect., 39(11), , 003. [9] O. Diekmann, S. van Gils, S. M. Verduyn Lunel and H.-O. Walther. Delay Equations, volume 110 of Applied Mathematical Sciences. Springer-Verlag, [10] E. J. Doedel, A. R. Champneys, T. F. Fairgrieve, Y. A. Kuznetsov, B. Sandstede and X. Wang. AUTO97, Continuation and bifurcation software for ordinary differential equations, [11] N. Fenichel. Geometric singular perturbation theory for ordinary differential equations. Journal of Differential Equations, 31, 53 98, [1] S. Friese. Existenz und Stabilität von Lösungen eines Randanfangswertproblems der Halbleiterdynamik. Master s thesis, Humboldt-Universität Berlin, [13] F. Jochmann and L. Recke. Existence and uniqueness of weak solutions of an initial boundary value problem arising in laser dynamics. Preprint 515, WIAS, [14] B. Krauskopf, K. Schneider, J. Sieber, S. Wieczorek and M. Wolfrum. Excitability and self-pulsations near homoclinic bifurcations in laser systems. Opt. Comm., 15, , 003. [15] D. Marcenac. Fundamentals of laser modelling. PhD thesis, University of Cambridge, [16] M. Möhrle, B. Sartorius, C. Bornholdt, S. Bauer, O. Brox, A. Sigmund, R. Steingrüber, M. Radzi ūnas and H.-J. Wünsche. Detuned grating multisection-rw-dfb lasers for high speed optical signal processing. IEEE J. on Sel. Top. Quantum Electron., 7, 17 3, 001.
96 Dynamics of multisection semiconductor lasers 65 [17] A. Pazy. Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied mathematical Sciences. Springer Verlag, New York, [18] D. Peterhof and B. Sandstede. All-optical clock recovery using multisection distributedfeedback lasers. J. Nonlinear Sci., 9, , [19] M. Radzi ūnas, H.-J. Wünsche, B. Sartorius, O. Brox, D. Hoffmann, K. Schneider and D. Marcenac. Modeling self-pulsating DFB lasers with integrated phase tuning section. IEEE J. of Quant. El., 36(9), , 000. [0] L. Recke, K.R. Schneider and V.V. Strygin. Spectral properties of coupled wave equations. Z. angew. Math. Phys., 50, , [1] J. Sieber. Numerical bifurcation analysis for multi-section semiconductor lasers. SIAM J. of Appl. Dyn. Sys., 1(), 48 70, 00. [] J. Sieber. Longtime behavior of the coupled traveling wave model for semiconductor lasers. Preprint 3, University of Bristol, Dept. of Eng. Math., 003. [3] B. Tromborg, H. E. Lassen and H. Olesen. Travelling wave analysis of semiconductor lasers. IEEE J. of Quant. El., 30(5), , [4] D. Turaev. Fundamental obstacles to self-pulsations in low-intensity lasers. Preprint 69, WIAS, 001. Submitted to SIAM J. of Appl. Math [5] H. Wenzel, U. Bandelow, H.-J. Wünsche and J. Rehberg. Mechanisms of fast self pulsations in two-section DFB lasers. IEEE J. of Quant. El., 3(1), 69 79, [6] M. Wolfrum and D. Turaev. Instabilities of lasers with moderately delayed optical feedback. Opt. Comm., 1(1-3), , 00. [7] H. J. Wünsche, O. Brox, M. Radzi ūnas and F. Henneberger. Excitability of a semiconductor laser by a two-mode homoclinic bifurcation. Phys. Rev. Lett., 88(), 03901, 00. [8] H.-J. Wünsche, M. Radzi ūnas, S. Bauer, O. Brox and B. Sartorius. Simulation of phasecontrolled mode-beating lasers. IEEE J. Selected Topics of Quantum Electron, 9(3), , 003.
97 66 J. Sieber, M. Radžiūnas, K. Schneider Daugiasekcijinių puslaidininkinių lazeriu dinamika J. Sieber, M. Radži ūnas, K.R. Schneider Mes nagrinėjame išilginę daugiasekcijiniu puslaidininkiniu lazerių dinamika, kuri yra nusakoma netiesiškai susietomis hiperboline diferencialinių lygčių dalinėmis išvestinėmis bei paprastųjų diferencialinių lygčių sistemomis. Mes pateikiame sekančias šios sistemos savybes: globalaus pradinio-kraštinio uždavinio sprendinio egzistavimas bei vienatis; mažos dimensijos pritraukiančiojo invariantinio hiperpaviršiaus egzistavimas. Modelio dinamika šiame hiperpaviršiuje yra apytiksliai nusakoma paprastuj u diferencialinių lygčių sistema. Pabaigoje mes pateikiame detalią skaitinę šios paprastųjų diferencialinių lygčių sistemos bifurkacinę analizę ir lyginame ją su skaitiškai nustatyta pilnos diferencialinių lygčių dalinėmis išvestinėmis sistemos dinamika.
98 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN ON THE EXISTENCE AND UNIQUENESS OF TWO-FLUID CHANNEL FLOWS J. SOCOLOWSKY University of Applied Sciences, Engineering Department Mathematics Group PSF 13, D Brandenburg/Havel, GERMANY 9 :; :<0: =79?>@A4B0CEDGF4H I JKLMJF4NHO%PQKL Received October 7 003; revised December Abstract. Viscous two-fluid channel flows arise in different kinds of coating technologies. The corresponding mathematical models represent two-dimensional free boundary value problems for the Navier-Stokes equations. In this paper the solvability of the related stationary problems is discussed and computational results are presented. Furthermore, it is shown that depending on the flow parameters like viscosity or density ratios and on the fluxes there can happen nonexistence of steady-state solutions. For other parameter sets the solution is even unique. Key words: Free boundary value problems, viscous channel flows, two-fluid flows, Navier- Stokes equations 1. Introduction In this contribution we consider the plane stationary flow of two viscous incompressible fluids (with kinematic viscosities ν i > 0 and densities ϱ i > 0, i = 1, ) through a special uniform channel (cf. Fig.1). Emphasize that the corresponding problem will be formulated in dimensionless form. The concrete transition to that formulation can be found in [11]. The flow is steady-state and has some features of a slot coating process. The channel is horizontal, unbounded in both directions and contains a semi-infinite inner wall (cf. Fig.1). The lower wall S 1 := {x R : < x 1 < +, x = 0} is moving with constant velocity R = (R, 0) T (R 0). The upper wall S := {x R : < x 1 < +, x = 1} is at rest. Furthermore, the partial inner wall S 3 := {x R : < x 1 < 0, x = h 1 (0 < h 1 < 1)} is given. Thus, in fact we have two separated parallel channels for negative values of x 1. Both viscous fluids are flowing out of the two channels and behind the point Q(0, h 1 ) they are joining and creating a free interface Γ := {x R : 0 < x 1 < +, x = ψ(x 1 )} where ψ is unknown a priori and has to be found. It is supposed that the free interface Γ separates from the inner wall S 3 at its endpoint Q.
99 68 J. Socolowsky By G 1 := {x R : 0 < x < h 1, if < x 1 0, and 0 < x < ψ(x 1 ), if 0 < x 1 < + } we denote the flow domain of the lower fluid. By G we denote the flow domain of the upper fluid G := {x R : h 1 < x < 1, if < x 1 0, and ψ(x 1 ) < x < 1, if 0 < x 1 < + }. Finally, by G := G 1 G we mean the union of both fluid layers. Figure 1. Two fluid channel flow with partial inner wall. The direction e g of the gravitational force is the vector e g = (0, 1) T. We study the two-fluid flow within the channel G caused by pressure gradients downstream and by the motion of the lower channel wall. This means mathematically that the positive flux F i in each liquid layer G i (i = 1, ) is prescribed and the final fluid layer thicknesses h and (1 h ) are to be determined. Note, that our (mathematical) fluxes F i are in fact the real physical fluxes divided by the constant densities of the fluids. An interpretation of such a flow could be the flow of two liquids coming from different reservoirs (i.e. slots or chambers) and flowing commonly in one channel after their unification. In slot coaters such flows occur on some parts of the coater. The corresponding motion as well as the final layer thicknesses are important there. Let h with 0 < h < 1 be the constant limit of ψ(x 1 ) at infinity. The problem under consideration has the following form: find a vector of velocity v = (v 1 (x 1, x ), v (x 1, x )) T, a pressure p(x 1, x ) and a function ψ(x 1 ) satisfying in the domain G the Navier-Stokes system of equations (v ) v ν v + 1 ϱ p = g e g, (1.1) v = 0, and the boundary and integral conditions v S0 = R = (R, 0) T, v S = 0, v S ± 3 [v] Γ = 0, v n Γ = 0, [t S(v) n] Γ = 0, d ψ (x 1 ) = dx ψ (x 1 ) σ [ p + n S(v) n] Γ, lim x1 + ψ(x 1 ) = h, δ v 1(bq) 1( q, x ) dx = F 1, = 0, (1.) (1.3)
100 Two-Fluid Channel Flows 69 δ (bq) v 1 ( q, x ) dx = F. (1.4) In problem (1.1) (1.4) the symbol δ i ( q) denotes the intersection of G i with the vertical line x 1 = q and σ > 0 is the surface tension at Γ. We further emphasize that from a physical point of view in (1.3), (1.4) only positive values of F i make sense. In problem (1.1) (1.4) the following notations have been used: n and t are unit vectors normal and tangential to Γ and oriented as x, x 1, respectively. By a b we mean the inner product of a, b R, = ( / x 1, / x ) T is the gradient operator, p = grad p, v = div v, ϱ Gm = ϱ m (m = 1, ) is the restriction of ϱ to G m (analogously for ν). = denotes the Laplace operator. By S(v) we denote the deviatoric stress tensor, i.e. a matrix with elements ( vi S ij (v) = ϱν + v ) j, i, j = 1,. x j x i The symbol [w] Γ expresses the jump of w crossing the free interface Γ, i.e. [w(x 0 )] Γ := lim y x 0 w(y) lim x x 0 w(x), (x 0 Γ, y G 1, x G ), and the symbol w Γ denotes the limit from below at the interface Γ, more precisely w(x 0 ) Γ := lim y x 0 w(y), (x 0 Γ, y G 1 ). An analogous statement is true for S 3 ± (and also for Σ± 3 in Section 4). Note that the left-hand side of (1.3) (i.e. of the second equation in (1.3)) is equal to the curvature K(x 1 ) of Γ. The fluid layer thickness h has also to be determined. Obviously, it should hold 0 < h < 1. Mathematical problems for the stationary flows of a viscous incompressible fluid with a free boundary were investigated by many authors. Numerous references on this field can be found, e.g., in the bibliographies of [4, 6, 1, 13]. Coating flows with the static or dynamic contact angles were studied in [1,, 5, 10, 11, 14, 15]. In all these papers considering either compact or semi-infinite free boundary value problems the same general scheme developed in [3, 9] has been used. Let us shortly recall this scheme and apply it to problem (1.1) (1.4). The starting problem is divided into two problems: the boundary value problem for the Navier- Stokes system of equations in a fixed domain and the problem of finding the free boundary Γ from the equation K(x 1 ) = σ 1 [ p(x) + n S(v)n] Γ (1.5) with the corresponding boundary conditions. The solution of the free boundary problem can be found by the method of successive approximations. At every step of successive approximations the Navier-Stokes system is solved in a fixed domain. The obtained solution is substituted into the right-hand side of (1.5) and by solving this equation one obtains the next iteration for the free boundary Γ. Thus, one gets a new domain in which the Navier-Stokes system has to be solved again. So, this scheme can be illustrated by the diagram
101 70 J. Socolowsky Γ (0) G (0) (v (1), p (1) ) Γ (1) G (1) (v (), p () )... Note that in this method at every step of successive approximations the construction of (v, p) is separated from the construction of the free boundary Γ. On the other hand, for free boundary problems in which the unknown flow domain is unbounded in two directions the described scheme is not applicable (cf. [4, 6, 7] and others).. Function Spaces Let B be an arbitrary domain in R and N B a manifold of dimension less than. The symbol ϱ N (x) denotes (in this section only) the distance dist (x, N) := inf y N x y. Let β = (β 1, β ) be a multiindex with β = β 1 + β and D β u = β u x β1 1 xβ (β i N {0}). The symbol r will denote the integer part of r. C r (B) (r > 0, non-integer) denotes the Hölder space of functions defined in a domain B R with a finite norm u (r) B = x B β <r sup D β u + sup x,y B β = r D β u(x) D β u(y) x y r r. Let Ċr s (B, N) be the weighted Hölder space of functions defined in B\N and having a finite norm u Ċr s (B,N) = sup ϱ β s N (x) D β u(x) x B\N β <r + sup x B\N β = r ϱ r s D β u(x) D β u(y) N (x) sup. x y < 1 ϱn (x) x y r r Cs r (B, N) (r > s > 0; r, s non-integer) denotes the space of functions with a finite norm u C r s (B,N) := u (s) B + + β = r x B\N sup x B\N s< β <r sup ϱ β s N (x) D β u(x) ϱ r s D β u(x) D β u(y) N (x) sup. x y < 1 ϱn (x) x y r r Clearly, Ċs r(b, N) is a subspace of Cr s (B, N) consisting of functions vanishing on N together with their derivatives of order up to s. For s < 0 assume Cs r (B, N) := Ċs r (B, N). Finally we define the weighted Hölder spaces to which the generalized solutions to the problem (1.1) (1.4) belong. We use the following notations: G 0 := {x G : x 1 < }, G + := {x G : x 1 > 1}, G := {x G : x 1 < 1}, J 0 := (0, ), J + := (1, + ).
102 For an arbitrary real number z > 0 we define the space Two-Fluid Channel Flows 71 C r s,z (G) = { u(x), u G 0 C r s (G0, Q ), exp(zx 1 )u(x) G + C r (G + ), exp( zx 1 )u(x) G C r (G ) } with the norm: u r,z G,s := u C r s (G0,Q) + exp(zx 1 )u (r) G + + exp( zx 1 )u (r) G. For functions f(x 1 ) defined in R 1 + we introduce the space C r s,z(r 1 +) with the norm f r,z R 1 +,s= f C r s (J0,0) + f(x 1 ) exp(zx 1 ) (r) J +. The spaces of vector-fields u are denoted by bold letters. The corresponding norms are the sum of the norms of the coordinate functions. 3. Analytical Results By straightforward calculations one can determine the exact Poiseuille flows {v ( ) (x), p ( ) (x)}, x G i, i = 1,. The corresponding velocities do not depend on x 1. In G 1 (i.e. if 0 x h 1 ) one obtains ( v ( ) 3R 1 (x) = h 6F ) ( 1 1 h 3 x + 4R + 6F ) 1 1 h 1 h x + R, 1 v ( ) (x) 0, (3.1) ( 3R p ( ) (x 1, x ) = ν 1 ϱ 1 h 6F ) 1 1 h 3 x 1 ϱ 1 gx + k 1. 1 In G (i.e., if h 1 x 1) one gets, respectively, v ( ) 1 (x 1, x ) = 6F (1 h 1 ) 3 x + 6(1 + h 1)F (1 h 1 ) 3 x 6h 1F (1 h 1 ) 3, v ( ) (x) 0, p ( ) (x 1, x ) = 1ν ϱ F (1 h 1 ) 3 x 1 ϱ gx + k. (3.) It is well-known that the pressure p can be determined only up to an additive constant in channel flows (cf. k 1, k ). In [6, 7] the Poiseuille flow {v (+), p (+) } for the united channel G + was determined by straightforward calculations, too. The corresponding flow fields are given by the following formulae [cf. also equations (3) (34) in [7] (p. 06, 07) or equations (A.11 ), (A.1 ) in [6] (p. 41)]
103 7 J. Socolowsky v (+) 1 (x ) = v (+) (x ) 0, { 0.5a1 x + b 1x + R, 0 x h 0.5a (x 1) + b (x 1), h x 1, (3.3) p (+) (x) = { p0 x 1 ϱ 1 g + k, 0 x h p 0 x 1 ϱ g(x 1) ϱ 1 h g + k, h x 1, where the coefficients have the representations a 1 = 3 F1 Rh h a = 3r F1 Rh h F 3 r(1 h ), b 1 = ( + h ) F1 Rh 3 F 1 h h, b = r( + h ) F1 Rh h + h F r(1 h ), F + h 1 h, and r := ϱ 1ν 1 p in this section. For the pressure gradient, i.e. = p 0, it holds ϱ ν x 1 p 0 = a 1 ν 1 ϱ 1 = a ν ϱ. Note that in [6] the viscous two-fluid flow through a perturbed uniform channel (without a partial inner wall) was studied by different functional-analytic methods (cf. also [8]). An essential part of the determination of {v (+), p (+) } consisted in the calculation of the value h from the following 5th degree polynomial equation (cf. also equation (A.14) in [6], p. 43). r(r 1)Rh 5 + [ 4r(r 1)R r(r 1)F 1 (r 1)F ] h 4 + [r(6r 5)R + r(r 3)F 1 rf ] h 3 + [r( r + 1)R (3.4) + 3r( r + 3)F 1 + 3rF ]h + [ r ] R + 4r(r 1)F 1 h r F 1 = 0. Note that the final thickness h is a function of F 1, F, R and the rheological parameters of the fluids. It can have up to three different values within (0, 1) for the same parameter set (cf. [6, 7]). Let ĥ be one of these values. Furthermore, by ψ(x 1 ) we denote the associated infinitely differentiable solution of the following boundary value problem d ψ (x 1 ) + g(ϱ 1 ϱ ) dx ψ (x 1 ) σ ψ(0) = h 1, lim ψ(x 1) = ĥ, x 1 + ψ(x 1 ) = g(ϱ 1 ϱ ) σ ĥ, (3.5) which can be obtained from the second line of (1.3) by setting v = 0 and p = const as the initial solution for F 1 = F = R = 0. Let ξ = ξ(x 1 ) be a smooth cutoff function vanishing for x 1 1 and being equal to 1 for x 1. Finally, suppose that ϱ 1 > ϱ is fulfilled. This assumption is physically sensefull. Now we can formulate the main result of this section. g (ϱ 1 ϱ ) σ Theorem 1. There exist positive real numbers s 0, M 0 and z 0 such that for arbitrary s (0, s 0 ), z (0, z 0 ), max [F 1, F, R] < M 0 and for parameters ĥ, F 1, F, R satisfying the condition
104 Two-Fluid Channel Flows 73 σ h 1 ĥ < g (ϱ 1 ϱ ), (3.6) where ĥ is one of the roots to equation (3.4), the free boundary value problem (1.1) (1.4) has a unique solution {v, p, ψ} which can be represented in the form { v = ξ( x1 )v ( ) + ξ(x 1 )v (+) + w, ψ(x 1 ) = ψ(x 1 ) + ω(x 1 ), (3.7) p = ξ( x 1 )p ( ) + ξ(x 1 )p (+) + p 0 (x), where {v ( ), p ( ) } denotes the Poiseuille flow from equations (3.1), (3.) in both channels as x 1 and {v (+), p (+) } is the basic solution (3.3) for x 1 +. Moreover, w C s+ s,z (G), p 0 Cs 1,z s+1 (G0 G + ), p 0 Cs,z s (G) and ω C1+s,z 3+s (R1 + ) hold. The proof of this theorem can be realized in the same way as in [10] applying the above mentioned scheme. We omit here the proof. The condition (3.6) is a consequence of solving the boundary value problem (3.5) and the physical restriction ϱ 1 > ϱ is also essential for the applied method. The weight parameter s 0 in Theorem 3.1 can be estimated studying a model problem for the Stokes system in a neighbourhood of Q in the same way as in [10]. The exponential behaviour of w, p 0, ω at infinity is well-known (cf. [4, 10]). 4. Computational Results For computational purposes it was necessary to truncate the theoretical unbounded flow domain from Fig.1. Figure. Computational (truncated) flow domain. Therefore, one gets an artificial inlet Σ 4 = Σ 41 Σ 4 (i.e. an inflow region in both channels) and an artificial outlet Σ 5 = Σ 51 Σ 5 far enough from the separation point Q. We obtain the following two free boundary value problems (v ) v ν v + 1 ϱ p = g e g, (4.1) v = 0, v Σ1 = (1, 0) T, v Σ = 0, v Σ ± 3 = 0, v Σ4k = v (4,k), (k = 1, ), (4.)
105 74 J. Socolowsky [v] Γ = 0, v n Γ = 0, [t S(v) n] Γ = 0, d ψ (x 1 ) = dx ψ (x 1 ) σ [ p + n S(v) n] Γ, (4.3) with either or v 1 Σ5k = v (5) 1, v Σ5k = 0, (k = 1, ), (4.4 D ) t T(v) n Σ5k = 0 = v 1 x 1, v Σ5k = 0, (k = 1, ). (4.4 N ) Σ5k At Σ 4 we pose Dirichlet boundary conditions (4. 4 ) (i.e. the fourth equation in (4.)) where v (4) is in fact the Poiseuille flow v ( ) from (3.1), (3.). At the outlet Σ 5 we set either Dirichlet boundary conditions (4.4 D ) with v (5) 1 = v (+) 1 taken from (3.3) or Neumann boundary conditions (4.4 N ) for the downstream velocity v 1. We were especially interested in the case, when h has three different values in (0, 1) for given fluxes F 1, F. This happens if F 1 = 0.41 and F = 0.01 hold (cf. [6, 7]). The associated remaining parameters for this first example are ν 1 = 10.0, ν =.0, ϱ 1 = 1.0, ϱ = 0.563, σ = The partial inner wall Σ 3 is located at h 1 = 0.5. The inflow region is situated at x 1 = 0.0, the separation point Q at x 1 = 4.0 and the outflow region was chosen at x 1 = The numerical simulations have been performed with the help of a FORTRAN code that uses both the FEM and the method of support lines (or spines) for the discretization of the flow domain (cf. [11]). The discretization has been performed using 643 nodes, 88 triangular elements and 19 spines. Thus, the total number of unknowns was 345. More details on the discretization of similar problems can be found in [6]. All computations presented below were realized on a PENTIUM III personal computer with 450 MHz. The time per iteration was about 0 seconds. In the first computation we posed Dirichlet boundary conditions for v 1 at the outlet and the x - value h of Γ at x 1 = 17.0 has not been fixed. Its starting value has been h (0) = 0.631, i.e. one of the three exact solutions to the problem without inner wall in [6]. The position of Γ after 5 iterations is presented in Fig.3. Figure 3. Computed free interface for h (0) = When taking h (0) = the following figure arises (see Fig.4) In the third
106 Two-Fluid Channel Flows 75 Figure 4. Computed free interface for h (0) = Figure 5. Computed free interface of a two-fluid channel flow with Neumann boundary conditions. computation (cf. Fig.5) of the first example we have used Neumann boundary conditions for v 1 at the outlet and the position h of Γ at the outlet has also not been fixed. Its starting value for the iteration scheme has been h (0) = 0.5. Figure 5 shows the computed position of the free interface Γ after 30 iterations. Even if choosing the position h 1 of the inner wall very close to one of the three exact values of h, namely h 1 = 0.8, the computational results did not become better. Figure 6 represents the corresponding situation. Figure 6. Computed free interface of a two-fluid channel flow with a different inner wall. In all these computations of the first example we could not reach convergence of the iteration scheme. Moreover, one can recognize that in Figs.3 6 the free interface Γ
107 76 J. Socolowsky turns off in front of the outlet. It cannot find a final thickness h. This was typical for all similar computations. Therefore, it seems to us that there is no solution of problems (4.1) (4.4 D ) and (4.1) (4.4 N ) for the above mentioned parameter set. Let us introduce a second parameter set: F 1 = 0.534, F = 0.66, ν 1 = , ν = 50.0, ϱ 1 = 1.0, ϱ = 0.9, σ = The location of the partial inner wall Σ 3 is h 1 = 0.3 (cf. Fig.7). Figure 7. Computed free interface for a second parameter set. It is well-known (cf. [6, 7]) that for this parameter set the uniform channel problem without inner wall possesses a unique solution which leads to the layer thickness h = We could show that our problem (4.1) (4.4 N ) has also a unique solution with the same h. The iteration scheme converges independently of the starting value h (0). Figure 7 shows the computed free interface after 30 iterations. One can see the uniform behaviour of Γ. The last picture (Fig.8) represents the velocity moduli at the nodes located on the free interface. Figure 8. Velocities at the free interface for a two-fluid channel flow. Note finally, that the pressure converges very well except at the neighbourhood of the separation point Q where the pressure admits a singularity.
108 Two-Fluid Channel Flows 77 References [1] A. Friedman and J.J.L. Velazquez. The analysis of coating flows in a strip. J. Diff. Eq., 11, , [] A. Friedman and J.J.L. Velazquez. The analysis of coating flows near the contact line. J. Diff. Eq., 119, , [3] O.A. Ladyzhenskaya and V.G. Osmolovskii. On the free surface of a fluid over a solid sphere. Vestnik Leningrad. Univ. Math., 13, 5 30, [4] S.A. Nazarov and K. Pileckas. On noncompact free boundary problems for the plane stationary Navier-Stokes equations. J. Reine u. Angewandte Mathematik, 438, , [5] K. Pileckas. Solvability of a problem of plane motion of a viscous incompressible fluid with noncompact free boundary. Diff. Equ. Appl. Inst. of Math. Cybern. Acad. Sci. Lit. SSR, 30, 57 96, [6] K. Pileckas and J. Socolowsky. Viscous two-fluid flows in perturbed unbounded domains. Mathematische Nachrichten. (submitted for publication) [7] K. Pileckas and J. Socolowsky. Analysis of the Navier-Stokes equations for some twolayer flows in unbounded domains. In: K. Pileckas H. Amann, G.P. Galdi and V.A. Solonnikov(Eds.), Navier-Stokes equations and Related Nonlinear Problems, Utrecht, Tokyo and Vilnius, VSP/TEV, , [8] K. Pileckas and J. Socolowsky. Analysis of two linearized problems modeling viscous two-layer flows. Mathematische Nachrichten, 45, , 00. [9] V.V. Pukhnachov. Plane stationary free boundary problem for Navier-Stokes equation. Zh. Prikl. Mekh. i Tekhn. Fiz., 3, 91 10, 197. [10] J. Socolowsky. The solvability of a free boundary problem for the stationary Navier- Stokes equations with a dynamic contact line. Nonlinear Analysis, Theory, Methods & Applications (JNA TMA), 1, , [11] J. Socolowsky. On the numerical solution of heat-conducting multiple-layer coating flows. Lietuvos Matematikos Rinkinys, 38, , [1] V.A. Solonnikov. On the Stokes equation in domains with nonsmooth boundaries and on a viscous incompressible flow with a free surface. In: Nonlinear partial diff. equations and their applications, College de France Seminar, volume 3, , 1980/81. [13] V.A. Solonnikov. Solvability of the problem on the effluence of a viscous incompressible fluid into an open bassin. Trudy Mat. Inst. Steklov, 179, 174 0, [14] V.A. Solonnikov. Problems with free boundaries and with moving contact points for twodimensional stationary Navier-Stokes equations. Zap. Nauchn. Sem. St.-Peterburg. Otdel. Mat. Inst. Steklova (POMI), 13, Kraev. Zadachi Mat. Fiz. Smezh. Voprosy Teor. Funktsii 5, (in Russian) [15] V.A. Solonnikov. On some free boundary problems for the Navier-Stokes equations with moving contact points and lines. Math. Annalen, 30, , 1995.
109 78 J. Socolowsky Apie dvieju tekančių kanale skysčiu srauto egzistavima ir vienatį J. Socolowsky Dviejų, tekančių kanale, klampi u skysčių srauto uždavinys iškyla taikant įvairias skirtingų r ūšių paviršių padengimo technologijas. Atitinkamas matematinis modelis išreiškiamas dvimačiu kraštiniu uždaviniu su laisvu paviršiumi Navje-Stokso lygtims. Straipsnyje nagrinėjamas santykinai stacionaraus uždavinio išsprendžiamumas ir pateikiami skaičiavimo rezultatai. Be to parodoma, kad priklausomai nuo srovės parametrų kaip ir nuo klampumo ir tankio santykio stacionar ūs sprendiniai gali neegzistuoti. Su kitais parametrais egzistuoja tiksliai vienas sprendinys.
110 !"# $ % '&)($ +*,.-0/ / c 004 Technika ISSN STABILITY OF THE SPLINE COLLOCATION METHOD FOR SECOND ORDER VOLTERRA INTEGRO-DIFFERENTIAL EQUATIONS 1 M. TARANG Institute of Applied Mathematics Liivi, 50409, Tartu, Estonia 97:0; <%=?> :0; B C>D=<< Received October 4 003; revised December Abstract. Numerical stability of the spline collocation method for the nd order Volterra integro-differential equation is investigated and connection between this theory and corresponding theory for the 1st order Volterra integro-differential equation is established. Results of several numerical tests are presented. Key words: The nd order Volterra integro-differential equation, stability of the spline collocation method 1. Introduction We study the numerical stability of the spline collocation method for the nd order Volterra integro-differential equation (VIDE). Stability means here the boundedness of approximate solutions in the uniform norm in case of the test equation when the number of knots increases. Basic ideas in the numerical solution of Volterra integral equation (VIE) and VIDE are given in []. First results about stability of the collocation method by polynomial splines for Volterra integral equation are given in [3] and the most adequate ones seems to be given in [5]. A special case of smooth splines is treated in [4] and special case of piecewise polynomial splines, i.e. splines with possible discontinuities in knots, is presented in [6]. There is a standard reduction of the 1st order VIDE to VIE considering the derivative of the solution as a new unknown solution. But then the test equation with constant kernel transforms into an equation with nonconstant kernel and the results obtained for VIE are not directly extendable to the 1st order VIDE. Similar phenomena takes place if we try to reduce the problem of stability for the nd order VIDE to that for the 1st order VIDE. Another possibility is to present the nd order VIDE as a system consisting 1 Research supported by the Estonian Science Foundation Grant No.560
111 80 M. Tarang of a first order VIDE and a first order differential equation or as a first order VIDE in product space. The components of unknown in this product space are the solution of the initial nd order VIDE and its derivative. The notion of stability for this VIDE in product space means boundedness of approximate solutions for both components which is, however, different from the notion of stability given in Section 4. These two circumstances motivate our investigations.. The spline collocation method Consider the nd order Volterra integro-differential equation y (t) = f(t, y (t), y(t)) + with initial conditions t 0 K(t, s, y (s), y(s))ds, t [0, T ], (.1) y(0) = y 0, y (0) = y 1. The functions f : [0, T ] R R and K: S R R (where S = {(t, s): 0 s t T }), and numbers y 0 and y 1 are supposed to be given. In order to describe this method, let 0 = t 0 < t 1 <... < t N = T (with t n depending on N) be a mesh on the interval [0, T ]. Denote h n = t n t n 1, σ n = (t n 1, t n ], n = 1,..., N, N = {t 1,..., t N 1 }. Let P k denote the space of polynomials of degree not exceeding k. Then, for given integers m 1 and d 1, we define S d m+d( N ) = {u: u σn = u n P m+d, n = 1,..., N 1, u (j) n (t n ) = u (j) n+1 (t n + 0), t n N, j = 0, 1,..., d} to be the space of polynomial splines of degree m + d which for d 1, are d-times continuously differentiable on [0, T ], for d = 0 are continuous on [0, T ] and for d = 1 may have jump discontinuities at the knots N. An element u S d m+d ( N ) as a polynomial spline of degree not greater than m + d for all t σ n, n = 1,..., N, can be represented in the form u n (t) = m+d k=0 b nk (t t n 1 ) k. (.) To find coefficients b nk we suppose that a fixed selection of collocation parameters 0 < c 1 <... < c m 1 is given. Then we define collocation points t nj = t n 1 + c j h n, j = 1,..., m, n = 1,..., N, forming a set X(N). In order to determine the approximate solution u Sm+d d ( N) of the equation (.1) we impose the following collocation conditions u (t) = f(t, u (t), u(t)) + t 0 K(t, s, u (s), u(s))ds, t X(N). (.3)
112 Stability of collocation method for nd order VIDE 81 Starting the calculations by this method we assume also that we can use the initial values u (j) 1 (0) = y(j) (0), j = 0,..., d, that is justified by the requirement u C d [0, T ]. Another possible approach is to use initial conditions u 1 (0) = y(0) and u 1(0) = y (0) and more collocation points (if d 1) to determine u 1. Thus, on every interval σ n we have d + 1 conditions of smoothness and m collocation conditions to determine m + d + 1 parameters b nk. This allows us to implement the method step-by-step going from an interval σ n to the next one. In this paper we will analyse the stability of the collocation method where the splines are at least continuously differentiable. Thus, we suppose in the sequel that d The method in the case of a test equation Let us consider the test equation y (t) = αy(t) + βy (t) + λ t 0 y(s)ds + f(t), t [0, T ], (3.1) where α, β and λ may be any complex numbers. The equation (3.1) is called the basis test equation (see [1]) and it has been extensively used for studying stability properties of several methods. Assume that the mesh sequence { N } is uniform, i.e., h n = h = T/N for all n. Representing t σ n as t = t n 1 + τh, τ (0, 1], we have on σ n the equality: u n (t n 1 + τh) = m+d k=0 where we passed to the new parameters a nk = b nk h k. The smoothness conditions (for any u S d m+d ( N )) a nk τ k, τ (0, 1], (3.) u (j) n (t n 0) = u (j) n+1 (t n + 0), j = 0,..., d, n = 1,..., N 1, can be expressed in the form a n+1,j = m+d k=j k! (k j)!j! a nk, j = 0,..., d, n = 1,..., N 1. (3.3) The collocation conditions (.3), applied to the test equation (3.1), give tnj u (t nj ) = f(t nj ) + αy(t nj ) + βu (t nj ) + λ u(s)ds, 0 From (3.) we get j = 1,..., m, n = 1,..., N. (3.4)
113 8 M. Tarang u n (t nj ) = m+d k=0 a nk c k j, u n(t nj ) = 1 h m+d k=1 a nk kc k 1 j and u n(t nj ) = 1 m+d h Now the equation (3.4) becomes m+d 1 h k(k 1)a nk kcj k k=0 m+d = α k=0 m+d = α n 1 + r=1 a nk c k j + β 1 h k=0 a nk c k j + β 1 h k= m+d = α k(k 1)a nk c k j. k=0 a nk c k j + β 1 h m+d k=0 ka nk c k 1 j tr tnj λ u r (s)ds + λ t r 1 u n (s)ds + f(t nj ) t n 1 m+d k=0 n 1 ka nk c k 1 j + m+d k=0 cj +λh 0 r=1 λh ( m+d k=0 n 1 ka nk c k 1 j + r=1 m+d +λh k=0 1 0 ( m+d k=0 a rk τ k) dτ a nk τ k) dτ + f(t nj ) λh ( m+d k=0 1 ) k + 1 a rk c k+1 j a nk k f(t nj). (3.5) Using the notation α n = (a n0,..., a n,m+d ), we write (3.5) as follows: m+d k=0 m+d a nk k(k 1)c k j αh m+d λh 3 k=0 k=0 m+d a nk c k j βh k=0 c k+1 n 1 j a nk k + 1 = λh3 q, a nk kc k 1 j r=1 α r + h f(t nj ), (3.6) where q = (1, 1/,..., 1/(m + d + 1)) and, denotes the usual scalar product in R m+d+1. The difference of the equations (3.6) with n and n + 1 yields
114 m+d k=0 Stability of collocation method for nd order VIDE 83 a n+1,k k(k 1)c k j m+d λh 3 k=0 c k+1 j a n+1,k m+d k + 1 = m+d αh k=0 m+d m+d βh a n+1,k kc k 1 j αh a n+1,k c k j k=0 k=0 a nk k(k 1)c k j m+d a nk c k j λh 3 k=0 k=0 m+d βh a nk kc k 1 j k=0 c k+1 n 1 j a nk k λh3 q, r=1 α r +h f(t n+1,j ) h f(t nj ), j = 1,..., m, n = 1,..., N 1. (3.7) Now we may write equations (3.3) and (3.7) in the matrix form (V βhv 1 αh V λh 3 V 3 ) α n+1 = ( V 0 βhv 1 αh V λh 3 (V 3 V 4 ) ) α n + h g n, n = 1,..., N 1, (3.8) with (m + d + 1) (m + d + 1) matrices V, V 0, V 1, V, V 3, V 4 as follows: ( ( E A V =, V C) 0 =, E = C) ( I 0 ), I being the (d + 1) (d + 1) unit matrix, 0 is the (d + 1) m zero matrix, 0 0 6c 1... (m + d)(m + d 1)c m+d 1 C = , 0 0 6c m... (m + d)(m + d 1)c m+d m A being a (d + 1) (m + d + 1) matrix m + d A= (... ) m + d, V 1 = 0 1 c 1... (m + d)c m+d , c m... (m + d)cm m+d 1 d 0 0 V = 1 c 1 c 1... cm+d , V 3 = c 1 c 1 /... cm+d+1 1 /(m + d + 1) , 1 c m c m... cm+d m c m c m /... cm+d+1m /(m + d + 1) V 4 having the first d+1 rows equal to 0 and the last m rows the vector q, and, finally, the m + d + 1 dimensional vector g n = ( 0,..., 0, f(t n+1,1 ) f(t n1 ),..., f(t n+1,m ) f(t nm ) ). Thus g n = O(h) for f C 1.
115 84 M. Tarang Proposition 1. The matrix V βhv 1 αh V λh 3 V 3 is invertible for sufficiently small h. Proof. Since (d + 1)dc1 d 1... (m + d)(m + d 1)c m+d 1 det V =det (d + 1)dc d 1... (m + d)(m + d 1)c m+d =(d + 1)dcd (d + 1)dcm d 1... (m + d)(m + d 1)cm+d m... (m + d)(m + d 1)cm d 1 det 1 c 1... c m , 1 c d m... cm 1 m and d 1, the matrix V is invertible. Such is also V βhv 1 αh V λh 3 V 3 for small h. Although we have supposed, in general, that d 1, let us remark that in cases d = 0 and d = 1 we may argue similarly to the proof in [6] and show that det(v βhv 1 αh V λh 3 V 3 ) 0, for small h. Therefore, the equation (3.8) can be written in the form α n+1 = (V 1 V 0 + W )α n + r n, n = 1,..., N 1, (3.9) where W = O(h) and r n = O(h 3 ) for f C Stability of the method We have seen that the spline collocation method (.3) for the test equation (3.1) leads to the recursion (3.9). We distinguish the method with initial values u (j) 1 (0) = y(j) (0), j = 0,..., d, and another method which uses u 1 (0) = y(0), u 1 (0) = y (0) and additional collocation points t 0j = t 0 +c 0j h, j = 1,..., d 1, with fixed c 0j (0, 1]\{c 1,..., c m } on the first interval σ 1. Denote, in addition, d 0 = max{d, 0} for the method with initial values and d 0 = 0 for the method with additional initial collocation. We say that the spline collocation method is stable if for any α, β, λ C and any f C d0 [0, T ] the approximate solution u remains bounded in C[0, T ] in the process h 0. Let us notice that the boundedness of u C[0,T ] is equivalent to the boundedness of α n in n and h in any fixed norm of R m+d+1. The principle of uniform boundedness allows us to establish Proposition. The spline collocation method is stable if and only if u C[0,T ] c f C d 0 [0,T ] f C d0 [0, T ], (4.1) where the constant c may depend only on T, α, β, λ and on parameters c j and c 0j.
116 Stability of collocation method for nd order VIDE 85 In order to formulate and prove the results concerning the numerical stability properties of the polynomial spline collocation method, we need the following results for VIE (see [5]) and for the 1st order VIDE (see [7]). The step-by-step collocation method for VIE is supposed to determine the approximate solution in S d m+d ( N) by the collocation conditions similarly to (.3) at the points t nj. 1. The stability for VIE depends on the matrix M = Ũ 0 1 Ũ, where Ũ0 and Ũ are (m + d + 1) (m + d + 1) matrices as follows: Ũ 0 = ( ) Ẽ, Ũ 0 = G ( ) Ã, G = G 1 c 1... c1 m+d , 1 c m... cm m+d E and A being defined as in V and V 0.. If all eigenvalues of M are in the closed unit disk and if those which lie on the unit circle have equal algebraic and geometric multiplicities, then the spline collocation method is stable. 3. If M has an eigenvalue outside of the closed unit disk, then the method is unstable (u has exponential growth: u c e KN, for some constants K > 0 and c > 0). 4. If all eigenvalues of M are in the closed unit disk and there is an eigenvalue on the unit circle with different algebraic and geometric multiplicities, then the method is weakly unstable (u may have polynomial growth: u c N k, c > 0, k N). 5. For fixed c j the eigenvalues of M = U0 1 U for the 1st order VIDE in the case m and d + 1 and eigenvalues of M for VIE in the case m and d coincide and have the same algebraic and geometric multiplicities, except µ = 1 whose algebraic multiplicity for VIDE is greater by one than for VIE. Here U 0 and U are (m + d + 1) (m + d + 1) matrices as follows: U = ( ( E A, U G) 0 =, G = G) E and A being defined as in V and V c 1... (m + d)c m+d , 0 1 c m... (m + d)c m+d 1 m Theorem 1. For fixed c j the eigenvalues of M for the nd order VIDE in the case m and d + and eigenvalues of M for the 1st order VIDE in the case m and d + 1 coincide and have the same algebraic and geometric multiplicities, except µ = 1 whose algebraic multiplicity for the nd order VIDE is greater by one than for the 1st order VIDE. Proof. The eigenvalue problem for M is equivalent to the generalized eigenvalue problem for V 0 and V, i.e. (M µi)v = 0 for v 0 if and only if (V 0 µv )v = 0
117 86 M. Tarang and (M µi)w = v takes place if and only if (V 0 µv )w = V v. Denote ν = 1 µ. Then for the nd order VIDE with the parameters m and d + we have V 0 µv = (4.) ν ν m + d + 1 ( ) ( ) 3 m + d ν = ( ). m + d ν... d ν ν 6c ν(m + d + )(m + d + 1)c1 m+d ν ν 6c m ν(m + d + )(m + d + 1)cm m+d Let I i,p be the diagonal matrix obtained from unit matrix, replacing the i-th diagonal element by the number p. Thus, the products I i,p A and AI i,p mean the multiplication of i-th row and i-th column of A, respectively, by p. The direct calculation and observation that or ( p q ) q p = ( p 1 q 1 ), allows us to get from (4.) I d+3,d+... I 3, (V 0 µv )I 3,1/... I d+m+3,1/(m+d+) = S(V 0 µv )S 1 = R ( ν q 0 U 0 µu where S = I d+3,d+... I 3,, R = I d+m+3,d+m+... I d+4,d+3, ( q = 1, 1 ),..., 1. m + d + Now (4.3) gives ) ( ν q 0 U 0 µu det(v 0 µv ) = (d + 3)... (d + m + )ν det(u 0 µu), ), (4.3) which permits to get the assertion about algebraic multiplicities of eigenvalues of M and M. Similarly to [5] we can prove that the eigenvalue µ = 1 of M and M has geometric multiplicity m and similarly to [6] that geometric multiplicities of µ 1 as an eigenvalue of M and M coincide.,
118 Stability of collocation method for nd order VIDE 87 Proposition 3. If M has an eigenvalue outside of the closed unit disk, then the spline collocation method is not stable with possible exponential growth of approximate solution. Proof. The structure of the proof is similar to that of Prop. 5 in [5] and we will deal only with main moments. Consider an eigenvalue µ of M + W such that µ 1 + δ with some fixed δ > 0 for any sufficiently small h. For α 1 0, being an eigenvector of M + W, we have here (V βhv 1 αh V λh 3 V 3 )α 1 = h g 0, (4.4) where g 0 = (a 10,..., a 1d, f(t 11 ),..., f(t 1m )), a 1j = hj y (j) (0), j = 0,..., d. j! Because of y (0) = αy(0) + βy (0) + f(0), (4.5) y (j) (0) = αy (j ) (0) + βy (j 1) (0) + λy (j 3) (0) + f (j ) (0), j = 3,..., d, the vector α 1 determines via (4.4) and (4.5) the values f (j) (0), j = 0,..., d 1, f(t 11 ),..., f(t 1m ). We take f on [0, h] as the polynomial interpolating the values f (j) (0), j = 0,..., d, f(t 1j ), j = 1,..., m, and f (j) (h) = 0, j = 0,..., d 0 (if c m = 1, then f (j) (h) = 0, j = 1,..., d 0 ). In the case of the method of additional knots let f be on [0, h] the interpolating polynomial by the data f(0), f(t 0j ), j = 0,..., d 1, f(t 1j ), j = 1,..., m, and f (j) (h) = 0, (here d 0 = 0 and if c m = 1, then f(t 1m ) = f(h) is already given and we drop the requirement f(h) = 0). In both cases we ask f to be on [nh, (n + 1)h], n 1, the interpolating polynomial by the values f (j) (nh) = 0 and f (j) ((n + 1)h) = 0, j = 0,..., d 0 (if c m = 1, then for j = 1,..., d 0 ), and also f(t n+1,j ) = f(t 1j ), j = 1,..., m. This guarantees that f C d0 [0, T ] and r n = 0, n 1. The interpolant f can be represented on [t n, t n+1 ] by the formula: f(t) = f(t n + τh) = κ i=0 ( ki l=0 ) i 1 h s l p il f (sl) (ξ l ) (τ b r ) (4.6) with b r being c j or c 0j, ξ l being t nj or t j, 0 s l d 1, k i i, constants p il depending on c j and c 0j. In the case of initial conditions κ = m + d + d 0 1 (κ = m + d + d 0 if c m = 1) and in the case of additional knots κ = m + d + 1 (κ = m + d, if c m = 1) on the interval [0, h] and κ = m + d (κ = m + d 0 if c m = 1) on the interval [nh, (n + 1)h], n 1. Replacing h by h/k, k = 1,,..., and keeping α 1 = h /k, we have g 0 bounded which means that f(t 1j ), j = 1,..., m, and h j y (j) (0)/k j, j = 0,..., d, or h j f (j) (0)/k j, j = 0,..., d 0, are bounded too in the process k. Thus (4.6) gives r=0
119 88 M. Tarang On the other hand, α n+1 (1 + δ) n α 1 yields f C d 0 [0,T ] c k d0. (4.7) α kn h k (1 + δ)kn 1 (4.8) and (4.1) cannot be satisfied. The inequalities (4.7) and (4.8) mean also the exponential growth of approximate solution if we keep the norm of f bounded in C d0. 5. Examples and numerical tests Let us consider some special cases of d and m. Case d = 1, m 1 being arbitrary. We have ( ) ( ) V = C, V 0 = C and det(v 0 µv ) = (1 µ) m+ det C 0 where C 0 is obtained from C omitting first two columns. This means that the method is always stable. Case d =, m = 1 (cubic splines). The equation det(v 0 µv ) = 0 besides µ = 1 has the solution µ = 1 1/c 1. The method is stable if and only if 1/ c 1 1. Case d =, m =. Now the equation det(v 0 µv ) = 0 has the root µ = 1 with geometric multiplicity. From the solution µ(c 1, c ) = 1 c 1 + c + 1 c 1 c it follows that the method is stable if and only if c 1 + c 1. In numerical tests we explored the nd order integro-differential equation y (t) = y(t) + y (t) + t 0 y(s)ds sin(t) cos(t) et, y(0) = 1, y (0) = 1, t [0, 1]. This equation has the exact solution y(t) = (sin t + cos t + e t )/. As an approximate value of u we actually calculated max 1 n N max 0 k 10 u n (t n 1 + kh/10). The results are presented in Tables 1 4. From these numerical examples we can observe a good conformity of theoretical results presented in the proceeding sections and numerical results given in this section.
120 Stability of collocation method for nd order VIDE 89 Table 1. Case d = 1, m = 1 (quadratic splines). N c 1 = c 1 = Table. Case d = 1, m = (Hermite cubic splines). N c 1 = 0.4 c = 0.6 c 1 = 0.7 c = Table 3. Case d =, m = 1 (cubic splines). N c 1 = c 1 = c 1 = Table 4. Case d =, m =. N c 1 = 0. c = 0.5 c 1 = 0.3 c = 0.7 c 1 = 0.5 c = References [1] H. Brunner and J. D. Lambert. Stability of numerical methods for Volterra integrodifferential equation. Computing, 1, 75 89, [] H. Brunner and P.J. van der Houwen. The Numerical Solution of Volterra Equations. North-Holland, Amsterdam, CWI Monographs, Vol. 3 [3] H.-S. Hung. The numerical solution of differential and integral equations by spline functions, [4] P. Oja. Stability of collocation by smooth splines for Volterra integral equations. Proceedings of the Internat. Conf. on Mathemathical Methods for Curves and Curfaces (Oslo 000), , 001. [5] P. Oja. Stability of the spline collocation method for Volterra integral equations. J. Integral Equations Appl., 13, , 001. [6] P. Oja and M. Tarang. Stability of piecewise polynomial collocation for Volterra integrodifferential equations. Mathematical Modelling and Analysis, 6, , 001.
121 90 M. Tarang [7] P. Oja and M. Tarang. Stability of the spline collocation method for Volterra integrodifferential equations. Commentationes Universitatis Tartuensis de Mathematica, 6, 37 49, 00. Antros eilės Volterra integro-diferencialinių lygčiu splainų kolokacijos metodo stabilumas M. Tarang Straipsnyje nagrinėjamas antros eilės Volteros integro-diferencialiniu lygčių splainų kolokacijos metodo skaitinis stabilumas ir nustatytas ryšys tarp šios teorijos ir atitinkamos pirmos eilės Volterra integro-diferencialinių lygčių teorijos. Pateikti keleto skaitinių eksperimentu rezultatai.
122 !"# $ % '&)($ +*,-./ c 004 Technika ISSN THE FIRST BASIC BOUNDARY VALUE PROBLEM OF RIEMANN S TYPE FOR BIANALYTICAL FUNCTIONS IN A PLANE WITH SLOTS I. B. BOLOTIN and K.M. RASULOV Smolensk State Pedagogical University Przevalskogo 4, Smolensk, Russia #:<;=>1=@?6A9B>6 C<?EDGF1H%IJ61KC LM1HBCK6ND5CPO4=>@Q 9#C<RSDF@H Received October 13, 003; revised February 5, 004 Abstract. The paper is devoted to the investigation of one of the basic boundary value problems of Riemann s type for bianalytical functions. In the course of work there was made out a constructive method for solution of the problem given in a plane with slots. There was also found out that the solution of the problem under consideration consists of consequent solutions of two Riemann s boundary value problems for analytical functions in a plane with slots. Besides, a picture of solvability of the problem is being searched and its Noether is identified. Key words: bianalytical function, boundary value problem, plane with slots, index 1. Statement of the problem Let us exclude from a full complex plane segments of a real axis L m = [a m, b m ] (m = 1,..., n), and let D be the remaining domain. The boundary L of the domain n D is understood as the thrown out segments (slits). Thus, L = L m and D = C\L. Further we shall use terms and definitions accepted in [3]. m=1 As it is known, a function F (z) = U(x, y) + iv (x, y) is called bianalytical in the domain D if it belongs to the class C (D) and satisfies in D the condition where F (z) z = 0, z = 1 ( x + i ) x
123 9 I. B. Bolotin, K.M. Rasulov is the Cauchy Riemann operator in D. A bianalytical function F (z), which is defined in domain D, belongs to the class A (D) I () (L) if it can be prolonged to the contour L together with the partial derivatives α+β F (z) z α z β ( α = 0, 1; β = 0, 1) so that boundary values of this function and all specified derivatives satisfy the Holder condition everywhere, may be except for points a m, b m (m = 1,..., n), where the reversion at infinity of the integrable order is possible, when α + β <. Let us consider the following boundary value problem. It is required to find all bianalytical functions F (z), belonging to the class A (D) I () (L), vanishing on infinity, limited near the extremities of the contour and satisfying at all internal points of L the following boundary conditions: where F + (t) x F + (t) x F + (t) y = lim z t,imz>0 F (z), = G 1 (t) F (t) x = G (t) F (t) y F (t) x + g 1 (t), (1.1) + ig (t), (1.) = lim z t,imz<0 F (z) F + (t) y = lim z t,imz>0 F (z), F (t) y = lim z t,imz<0 F (z) and G k (t), g k (t) (k = 1, ) are given on L functions of the class H (3 k) (L), and G k (t) 0 on L. Here, in equality (1.), the factor i at g (t) is put for convenience of notation. The formulated problem is called the first basic boundary value problem of Riemann s type for bianalytical functions in the plane with slots or, shortly, the problem R 1,. The appropriate homogeneous problem (g 1 (t) g (t) 0) will be denoted as problem R 0 1,. Let us notice, that the problem R 1, represents one of the basic boundary value problems of Riemann s type for bianalytical functions. It was formulated in the wellknown monograph of Gakhov (see, for example, [1], p. 316). In case of arbitrary smooth closed loops the considered problem was explicitly investigated in the work of Rasulov (see, for example, [3]). In the present work for the first time we investigate a more general problem R 1,.. On the solution of the problem R 1, It is known (see, for example, [1, 3]), that any vanishing on infinity bianalytical function F (z) with a line of saltuses L can be represented as:
124 The first basic boundary value problem of the Riemann type 93 F (z) = ϕ 0 (z) + zϕ 1 (z), (.1) where ϕ k (z) are analytical functions in domain D (analytical components of the bianalytical function), for which the following conditions are fulfilled: Π{ϕ k, } 1 + k, k = 0, 1; here Π{ϕ k, } means the order of the function ϕ k (z) at the point z =. Let us search for the solution of the problem R 1, given by: F (z) = f 0 (z) + ( z z)f 1 (z). (.) Then the functions f k (z) (k = 0, 1) will be connected with analytical components of the required bianalytical function F (z) by formulas: ϕ 0 (z) = f 0 (z) zf 1 (z), ϕ 1 (z) = f 1 (z). (.3) As known (see, for example, [1], p. 301) x = z + z, ( y = i z ), z then taking into account (.) and the fact that the equality t = t is fulfilled on L, the boundary conditions (1.1) and (1.) can be written as: Φ + 0 (t) = G 1(t)Φ 0 (t) + g 1(t), (.4) f + 1 (t) = G (t)f 1 (t) + Q (t), (.5) where Φ 0 (z) = df 0(z), Q (t) = 1 ( Φ + dz 0 (t) G (t)φ 0 (t) g (t) ). The equalities (.4) and (.5) represent boundary conditions of usual Riemann s problems for analytical functions in a plane with slots (see, for example, [1] or []). Thus, as a matter of fact, the solution of the initial problem R 1, is reduced to sequential solution of two auxiliary problems of Riemann (.4) and (.5) in classes of analytical functions in domain D with a line of saltuses L. But as in the problem R 1, we search for the solutions, limited close to extremities of the contour and vanishing on infinity. There arises the necessity to define classes of analytical solutions of auxiliary problems (.4) and (.5). Therefore, at first we shall find out in what classes it is necessary to search for solutions of boundary value problems (.4) and (.5). From equalities (.3) we can see, that the functions Φ 0 (z) and f 1 (z) on infinity should have zero not below than the second order. Let us study the behaviour of the function F (z) near the extremities of the contour L. Let c be any of extremities, then c = c. We have the following series of inequalities: F (z) = f 0 (z) + ( z z)f 1 (z) f 0 (z) + f 1 (z) z z = f 0 (z) + f 1 (z) z c + c z f 0 (z) + f 1 (z) z c + f 1 (z) z c = f 0 (z) + f 1 (z) z c. (.6)
125 94 I. B. Bolotin, K.M. Rasulov For function F (z) to be limited close to the extremities of the contour L, it is necessary and sufficient, that the functions Φ 0 (z) and f 1 (z) satisfy the estimates: Φ 0 (z) const z c α0, f 1(z) const z c α1, 0 α 0, α 1 < 1. (.7) Really, if functions Φ 0 (z) and f 1 (z) satisfy the condition (.7), then the required bianalytical function F (z) will be limited in a neighbourhood of c. And if the function F (z) of the class A (D) I () (L) is limited close to the extremity c, then the functions Φ 0 (z) and f 1 (z) satisfy (.7) (otherwise all solutions of the problem R 1, will not be found). Thus it is required to find a solution of boundary value problems (.4) and (.5), belonging to a class of functions, having on infinity a zero of the second order and infinity of the integrable order on extremities of the contour L. Let us solve the boundary value Riemann problem (.4). Let G 1 (a m ) = r a,1m e iθ1m, 0 θ 1m < π, G 1 (b m ) = r b,1m e i(θ1m+ θ1m), θ 1m = [argg 1 (t)] Lm, then, following Gakhov (see, for example, [1], p. 448), we define integer numbers κ 1m by the following formulas: [ ] θ1m + θ 1m κ 1m = + 1. π The index of the problem (.4) is represented by the following formula κ 1 = n κ 1m. m=1 Hence, if κ 1, a general solution of problem (.4) is set by the formula (see, for example, [1, ]): Φ 0 (z) = X 1 (z) 1 g 1 (τ) dτ πi X 1 + (τ) τ z + P κ 1 (z), (.8) L where X 1 (z) is a canonical function of the problem (.4), P κ1 (z) is the polynomial of a degree not higher than (κ 1 ) with arbitrary complex coefficients. In case when κ 1 1, the solution of problem (.4) also will be expressed by formula (.8) with only one modification, that P κ1 (z) 0, and if κ 1 0 then κ conditions of solvability should be satisfied: g 1 (τ) X 1 + (τ) τ k 1 dτ = 0, k = 1,..., κ (.9) L Using the function Φ 0 (z) = df 0(z), after integration we obtain dz
126 The first basic boundary value problem of the Riemann type 95 f 0 (z) = Φ 0 (ζ)dζ, γ where γ is an arbitrary smooth curve, completely laying in the domain D and connecting the infinite point with arbitrary point z of the domain D. Let us take in expression (.8) z t L. Then, using the formulas of Sokhotzky-Plemelj (see, for example, [1, ]), we get Φ + 0 (t) = X+ 1 (t) Φ 0 (t) = X 1 (t) 1 πi 1 πi L L g 1 (τ) X + 1 (τ) g 1 (τ) X + 1 (τ) dτ τ t + P κ 1 (t) + g 1(t), (.10) dτ τ t + P κ 1 (t) g 1(t) G 1 (t), (.11) here in equality (.11) we have taken into account, that X+ 1 (t) X 1 (t) = G 1(t). Remark 1. Functions Φ ± 0 (t), given by formulas (.10) and (.11) satisfy the Holder condition everywhere on L, may be except the extremities, where they may have a singularity of the integrable order. Now we will solve the boundary value Riemann problem (.5). Let G (a m ) = r a,m e iθm, 0 θ m < π, G (b m ) = r b,m e i(θm+ θm), θ m = [argg (t)] Lm. Then following Gakhov (see, for example., [1], p. 448) we define integer numbers: [ ] θm + θ m κ m = + 1. (.1) π The index of the problem (.5) is represented by the following formula κ = n κ m. (.13) m=1 As it is known (see [1, ]), if κ, a general solution of problem (.5) is represented by formula: f 1 (z) = X (z) 1 Q (τ) dτ πi X + (τ) τ z + P κ (z), (.14) L where X (z) is a canonical function of problem (.5), P κ (z) is a polynomial of a degree not higher than (κ ) with arbitrary complex coefficients. If κ 1, the solution of problem (.5) can be expressed by formula (.14) with only one modification, that P κ (z) 0, and if κ 0, then κ + 1 conditions of a solvability should be satisfied:
127 96 I. B. Bolotin, K.M. Rasulov Q (τ) X + (τ) τ k 1 dτ = 0, k = 1,..., κ + 1. (.15) L Remark. Generally speaking, absolute term Q (t) of problem (.5) satisfies the Holder condition everywhere on L, except for, possibly, the extremities of the contour, where it may have the integrable singularity. But, as we search for the solution of the boundary value problem (.5) in the class of functions, having infinity of the integrable order on the extremities of the contour L, the density of the integral in the formula (.14) has the singularity on the extremities of the contour, which is not higher than the integrable one. After finding functions f 0 (z) and f 1 (z), we use formulas (.3) and restore analytical components of the required bianalytical function. Then using formula (.1) we restore the bianalytical function F (z) itself. Thus, the following basic result is valid. Theorem 1. Let L = n [a m, b m ], D = C\L. m=1 Then the solution of the problem R 1, is reduced to a sequential solution of the two scalar Riemann problems (.4) and (.5) in classes of analytical functions in the plane with slots, having a zero of the second order on infinity and infinity of the integrable order on the extremities of the contour L. The problem R 1, is solvable if and only if problems (.4) and (.5) are simultaneously solvable in the specified classes of functions. 3. Investigation of a solvability of the problem R 1, As the solution of the problem R 1, is reduced to the sequential solution of the boundary value Riemann problems (.4) and (.5), solvability conditions of the problem R 1, can be developed from the solvability conditions of boundary value problems (.4) and (.5). The number κ = κ 1 + κ is called the index of the problem R 1,, and numbers κ 1 and κ are its private indexes. For a full investigation of the solvability of the problem R 1, it is necessary to consider 9 cases. Case 1. Let κ 1, κ. In this case boundary value problems (.4) and (.5) are solvable and have κ 1 1 and κ 1 linearly independent solutions, respectively. Thus, in this case problem R 1, is solvable and by virtue of formulas (.1) and (.3) its general solution linearly depends on κ 1 + κ arbitrary complex constants. Case. Let κ 1, κ = 1. In this case boundary value problem (.4) is solvable and has κ 1 1 linearly independent solutions, and boundary value problem (.5) also is solvable and has a
128 The first basic boundary value problem of the Riemann type 97 unique solution. Hence, in this case problem R 1, is solvable and its general solution linearly depends on κ 1 1 arbitrary complex constants. Case 3. Let κ 1, κ 0. In this case boundary value problem (.4) is solvable and has κ 1 1 linearly independent solutions, and the boundary value problem (.5) has a unique solution if κ + 1 conditions of the solvability (.15) are satisfied. Remark 3. We shall notice, that some conditions (.15) can be satisfied at the expense of a choice of values of arbitrary constants, which are included in expression Q (t). Thus, in this case problem R 1, is solvable if κ +1 conditions of the solvability (.15) are satisfied and its general solution linearly depends on l arbitrary complex constants, where 0 l κ 1 1. Case 4. Let κ 1 = 1, κ. In this case boundary value problem (.4) is solvable and has a unique solution, and the boundary value problem (.5) is solvable and has κ 1 linearly independent solutions. Thus, in this case problem R 1, is solvable and its common solution linearly depends on κ 1 arbitrary complex constants. Case 5. Let κ 1 = 1, κ = 1. In this case boundary value problems (.4) and (.5) are solvable and each of them has a unique solution. Hence, by virtue of the Theorem 1, the problem R 1, is solvable and has a unique solution. Case 6. Let κ 1 = 1, κ 0. In this case boundary value problem (.4) is solvable and has a unique solution, and the boundary value problem (.5) has a unique solution if κ + 1 conditions of the solvability (.15) are satisfied. Thus, problem R 1, is solvable and has a unique solution. Case 7. Let κ 1 0, κ. In this case boundary value problem (.4) has a unique solution if κ conditions of the solvability (.9) are satisfied. Boundary value problem (.5) is solvable and has κ 1 linearly independent solutions. Thus, in this case problem R 1, is solvable if κ conditions of the solvability (.9) are satisfied and its general solution linearly depends on κ 1 arbitrary complex constants. Case 8. Let κ 1 0, κ = 1. In this case boundary value problem (.4) has a unique solution if κ conditions of the solvability (.9) are satisfied. Boundary value problem (.5) is solvable and has a unique solution. Thus, problem R 1, is solvable if κ conditions of the solvability (.9) are satisfied and it has a unique solution. Case 9. Let κ 1 0, κ 0. In this case boundary value problem (.4) has a unique solution if κ conditions of the solvability (.9) are satisfied, and boundary value problem (.5) has a unique solution if κ + 1 conditions of the solvability (.15) are satisfied. Hence, in this case problem R 1, is solvable if κ conditions (.9) and κ + 1 conditions (.15) are satisfied and it has a unique solution.
129 98 I. B. Bolotin, K.M. Rasulov From the analysis given above we obtain the following statement. Theorem. For any values of the index κ = κ 1 +κ the number p of conditions of a solvability of inhomogeneous problem R 1, and the number l of linearly independent solutions corresponding to homogeneous problem R 0 1, are finite, i.e. the problem R 1, satisfies the Noether conditions. References [1] F.D. Gakhov. Boundary value problems. Nauka, Moscow, (in Russian) [] N.I. Muskhelishvili. Singular integral equations. Nauka, Moscow, (in Russian) [3] K.M. Rasulov. Boundary value problems for polyanalytical functions and some of their applications. Smolensk State Pedagogical University, Smolensk, (in Russian) Apie pirmojo pagrindinio kraštinio Rimano tipo uždavinio bianalizinėms funkcijoms plokštumoje su įtrūkiais sprendimą I.B. Bolotin, K.M. Rasulov Šiame darbe tyrinėjamas uždavinys, kai ieškoma dalimis bianalizinių funkcijų, nykstančiu begalybėje, apribotų greta kontūro trūkio taškų ir šiame kontūre tenkinančiu dvi kraštines sąlygas. Parodoma, kad sprendžiamas uždavinys suvedamas į sprendima dviejų Rimano uždaviniu analizinėms funkcijoms.
130 S. Chakravarty, P. K. Mandal, A. Mandal Abstract. The present paper deals with a theoretical investigation of blood flow in an arterial segment in the presence of stenosis. The streaming blood is treated to be composed of two different layers the central core and the plasma. The former is considered to be non-newtonian liquid characterised by the Power law model, while the latter is chosen to be Newtonian. The artery is simulated as an elastic (moving wall) cylindrical tube. The unsteady flow mechanism of the present study is subjected to a pulsatile pressure gradient arising from the normal functioning of the heart. The time-variant geometry of the stenosis has been accounted for in order to improve resemblance to the real situation. The unsteady flow mechanism, subjected to pulsatile pressure gradient, has been solved using finite difference scheme by exploiting the physically realistic prescribed conditions. An extensive quantitative analysis has been performed through numerical computations of the flow velocity, the flux, the resistive impedances and the wall shear stresses, together with their dependence with the time, the input pressure gradient and the severity of the stenosis, presented graphically at the end of the paper in order to illustrate the applicability of the model under consideration. Special emphasis has been made to compare the existing results with the present ones and found to have a good agreement. Key words: Moving wall, non-newtonian liquids, stenosis, power-law
131 !"# $ % '&)($ +*,-./ c 004 Technika ISSN PARALLEL NUMERICAL MODELLING OF SHORT LASER PULSE COMPRESSION R. ČIEGIS 1, A. DEMENT EV and G. ŠILKO 1 1 Vilnius Gediminas Technical University Saulėtekio al. 11, LT-103 Vilnius, Lithuania ;:=<>?1@A<CB?%DEF 8F7G<>?1@A<CB? Institute of Physics Goštauto 1, LT-600 Vilnius, Lithuania H1IJ :4JLK? 8NM? B+<O:QPPR<SB? Received March, 004; revised April 8, 004 Abstract. In this paper we investigate parallel numerical algorithms for solution of the transient stimulated scattering processes. A new symmetrical splitting scheme is proposed and a parallel version is given. The efficiency of the parallel algorithm is investigated for two cases. The first one describes a case when the computation region is constant during the whole time of computations. The second one describes the initial phase of the process, when the computational region increases linearly in time. In order to distribute more evenly jobs between processors a dynamical the grid redistribution algorithm is is used. We also give a proof of one result about optimal static grid distribution in the case of linearly increased problem complexity. The results of computations are presented. They were obtained on different parallel computers and clusters of workstations. Key words: finite-difference schemes, symmetrical splitting method, parallel algorithms, grid redistribution, nonlinear optics 1. Introduction Scientific investigations in various fields and different technological applications require laser systems satisfying a number of requirements. They should be able to generate short pulses in various spectral ranges with tunable pulse duration, the generated pulses must be easily synchronized with external events and have a good stability and low jitter [18]. The progress of solid-state lasers with nonlinear-optical phase conjugation and pulse compression will support these objectives for extension of the fields of laser applications [5, 13, ]. Using different schemes for the stimulated Brillouin scattering (SBS) compressor, it is possible to achieve pulses with
132 116 R. Čiegis, A. Dement ev, G. Šilko durations shorter than 100 ps [4, 5, 6, 13, ]. Note that a consecutive cascade compression provides a set of precisely synchronized (with the accuracy of several ps) pulses of different wavelengths and pulse durations [13, 19]. In the SBS compression experiments, Fourier-transform-limited laser pulses with Gaussian transversal intensity distribution are commonly used. Therefore, it is of great practical interest to investigate the statistics (energetic, temporal and spectral) of Stokes pulses for different pump pulse parameters and optical schemes of SBS compressor and amplifier. For optimization of SBS compression schemes detailed three-dimensional numerical simulations of the transient backward SBS process for different focusing geometries of phase modulated pump pulses with different pulse shape and durations starting from spontaneous scattering level are needed. Performing this type of calculations is also interesting from purely scientific point of view, because a number of works appeared lately [1,, 3, 0, 1], presenting some results that contradict the results of our earlier works [7, 8, 16, 17]. It should be pointed out that calculations of the transient stimulated scattering processes, especially in the three-dimensional case, require lengthy computation times. Therefore, without application of the parallel algorithms, the investigation of statistical peculiarities of these processes is practically impossible. We start from the algorithm developed in [9, 1] for the solution of nonlinear problems with strongly focused beams. It is based on the expansion of the fields of the interacting beams into the series of eigenfunctions of the Laguerre-Gauss type. Such algorithm can be modified into a parallel algorithm easily enough by using data parallelization paradigm [10], see also a paper by Elisseev [15], where a parallel code is obtained using HPF. This work presents a novel more efficient splitting type scheme and its parallel version. This scheme was tested for a three-dimensional problem of transient stimulated scattering of focused beams. Thus, our goal is to investigate the efficiency of the parallel version of the proposed symmetrical splitting scheme. We study the influence of different nonlinear effects on the accuracy of the obtained numerical solution in order to determine a region of application of the proposed parallel numerical algorithm. The rest of the paper is organized as follows. In Section we describe a mathematical model of SBS. In Section 3 the new finite difference scheme is presented. A parallel version of this algorithm is presented in Section 4. This section also describes the load balancing problem for the front moving case. Section 5 contains analysis of the obtained numerical results and the last Section 6 draws some conclusions.. Mathematical Model A schema of the numerically modelled SBS compressor is presented in in Fig. 1. Attempts are still being made to investigate this phenomena analytically, but inclusion of the material non-stationarity can be taken into account only numerically. The presented work gives a new parallel numerical algorithm for solving the system of equations, which describes the nonlinear interaction of laser, Stokes and
133 Parallel Numerical Modelling of Laser Pulse 117 Polarizer Laser pulse QWP Lens Initial Stokes pulse SBS cell Stokes pulse Diaphragm Output pulse Figure 1. A schema of the SBS compressor. sound waves. In 0 z L, 0 r R, 0 t T the following system of equations is given [7, 16]: u t + u z iµ ( LAu = iγ L σv + iω L u + v ) u, v t v z iµ ( SAv = iγ S σ u + iω S u + v ) v, (.1) iγ 0 ( σ t + γ 1 σ t ) + σ t + γ σ = iγ σ uv + γ f, here A = 1 r r (r r ) is the transverse Laplacian, u, v and σ are slowly varying complex amplitudes of laser, the Stokes and the sound waves, respectively. γ L, γ S, γ σ are coupling constants, γ f is the thermal noise parameter, γ 0 and γ are hypersound wave parameters (related to the period and relaxation time). System (.1) is supplemented with the boundary and initial conditions: u(z = 0, r, t) = g 0 (r, t), v(z = L, r, t) = g 1 (r, t), 0 r R, r u r r=0 = 0, r v r r=0 = 0, 0 z L, 0 t T, u(z, R, t) = 0, v(z, R, t) = 0, u(z, r, 0) = 0, v(z, r, 0) = 0. Since for focused beams the diameter of the beam waist in the cuvette is by factor 0-50 and more times smaller than the diameter of input beam, adaptive grids are required in order to solve the problem accurately and efficiently. Such adaptive strategies have proved to reduce significantly the computational cost for obtaining a numerical solution. The Schrödinger equation looks very similar to the heat equation, but there are great differences. We note mainly, that the Schrödinger equation does not have a regularizing effect of the contractivity as for the heat equation. Therefore the development of adaptive algorithms for solving the Schrödinger type nonlinear equations requires new techniques. The most popular adaptive schemes are based on application of transformations, which use the properties of solutions of the linear Schrödinger equation. Extensive numerical comparison of different mesh adaptation techniques
134 118 R. Čiegis, A. Dement ev, G. Šilko and transformations is presented in [9]. A new adaptive transformation is proposed in [3], it was also used in [17] for numerical solution of the SBS problem using a splitting finite-difference scheme. We note that general mesh adaptation techniques are also applied for the Schrödinger problem (see, e.g. [14]). The basis of such procedure is a posteriori error estimate that has to be derived for the obtained discrete solution. Then local error estimators indicate the regions of the computational domain where we have to refine the mesh in order to improve the accuracy of the approximation. In this work we propose a new symmetrical splitting scheme, in which the diffraction subproblem is solved using the expansion into the Laguerre-Gaussian modes. The accuracy of such an approximation is investigated in [1]. Modelling of nonlinear effects of SBS pulse compression requires to resolve the evolution of all dynamically significant scales of motion. This can be done only via variable mesh densities. The obtained discrete problems often are too large to fit into serial computers, either because of computational demands or memory limitations, or both. Parallel computers and algorithms are the most effective solutions of this problem. 3. Finite Difference Scheme This section contains a brief description of the numerical algorithm. We introduce the following discrete meshes: ω z = { z n : z n = nτ, n = 0, 1,..., N, τ = L N }, ω r (z) = { r j : ω t = { t k : t k = kτ, k = 0, 1,..., K }, r j = jh, j = 0, 1,..., J, h = R(z) }, J here ω r depends adaptively on the coordinate z and generally this mesh is also nonuniform in r. We use the following notation for discrete functions: U k nj = U(z n, r j, t k ), (z n, r j, t k ) ω z ω r (z) ω t. We approximate problem (.1) by the following splitting algorithm. Symmetrical Splitting Algorithm for k = 0, K /* First diffraction step */ for n = 0, N U k+ 1 3 (r) = P c k n+ 1 p (z n) W p (z n+ 1, r), r ω r(z n+ 1 ) p=0 V k+ 1 3 (r) = P d k n+ p(z 1 n+1 ) W p (z n+ 1, r) p=0
135 Parallel Numerical Modelling of Laser Pulse 119 end for /* Nonlinear Interaction */ for n = 0, N end U k+ 3 n+ 1 V k+ 3 n+ 1 σ k+1 n+ 1 δ k+1 n+ 1 for (r) = f u (U k+ 1 3 n+ 1 (r) = f v (U k+ 1 3 n+ 1 (r) = f σ (U k+ 1 3 n+ 1 (r) = f δ (U k+ 1 3 n+ 1 /* Second diffraction step */ for n = 0, N c k+1 p (z n+1 ) = ( U k+ 3 d k+1 p (z n ) = ( V k+ 3 U k+1 n+1 (r) = P p=0 n+ 1 n+ 1, V k+ 1 3, σ k, δ k ), r ω n+ 1 n+ 1 n+ 1 r (z n+ 1 ), V k+ 1 3, σ k, δ k ) n+ 1 n+ 1 n+ 1, V k+ 1 3, σ k, δ k ) n+ 1 n+ 1 n+ 1, V k+ 1 3, σ k, δ k ) n+ 1 n+ 1 n+ 1, W p (z n+ 1 )),, W p (z n+ 1 )), c k+1 p (z n+1 ) W p (z n+1, r), r ω r (z n+1 ) Vn k+1 (r) = P d k+1 p (z n ) W p (z n, r), r ω r (z n ) p=0 end for end for The analysis of the algorithm complexity 1 step: Diffraction. In this step the equations of wave propagation and diffraction are solved in the element [z n, z n+ 1 ]. The total complexity of this step is O(JP ) operations. step: Nonlinear Interaction. Using predictor corrector numerical integration scheme we solve a system of ODEs describing the nonlinear interaction of laser, the Stokes and the sound beams. The complexity of this step is O(J) operations. 3 step: Diffraction. We complete the diffraction step, i.e. the laser and Stokes waves again propagate in the second part of the element. The complexity of this step is O(JP ) operations. Thus the total complexity of the splitting numerical algorithm is O(N JP ) operations.
136 10 R. Čiegis, A. Dement ev, G. Šilko Due to symmetrical splitting algorithm the accuracy of the finite difference scheme is O(h + (τ 4 + P α )/h), where α depends on the smoothness of the exact solution (see, [1]). We note that the error can accumulate linearly with respect to N, thus in order to reduce the global error we need to change also τ and P. This phenomena is investigated in detail in [1]. 4. Parallel Algorithm We use an one dimensional mesh of virtual p processors. The finite difference grid ω z is partitioned in p blocks, which are distributed among processors (see Fig. ). 0 1 p- p-1 Figure. 1D block data distribution. It follows from the proposed numerical algorithm, that each processor needs to exchange information (i.e., coefficients c j and d j ) corresponding to the boundary points of its local domain. It is important to note, that communication is done only between neighbour processors. After the communication step each processor has all required information. Now all computations can be performed efficiently in parallel and the results are also stored locally on each processor The analysis of algorithm complexity First we estimate the parallel execution time of the proposed algorithm during realization of one time step. The discrete problem size can be expressed as follows W = JN(C 1 P + C ). The communication step on most network architectures can be done in time T comm = α + βp. Thus the parallel execution time T p on p processors is given by T p = JN p (C 1P + C ) + α + βp. The additional cost of parallel algorithm can be expressed as follows We solve the equation W = et 0 (W, p), e = T 0 (W, p) = pt p W. E p W, E p = 1 E p W + T 0 (W, p),
137 Parallel Numerical Modelling of Laser Pulse 11 where E p is a selected efficiency of the parallel algorithm. Since p N, and J = O(N), we get that the proposed parallel algorithm is highly scalable. The code was implemented using MPI library and performed on IBM SP4 computer. In Table 1 we present speed-up S p = W T p and efficiency E p = Sp p data obtained for two discrete problems of different sizes: a) N = 01, J = 101, P = 15 (denoted by S 1p in Table 1), b) N = 301, J = 151, P = 45 (denoted by S p in Table 1). Table 1. The speed-up and efficiency of the parallel algorithm. p S 1p E 1p S p E p These results fully confirm our theoretical predictions. 4.. Front moving case If the boundary condition for the Stokes wave is equal to zero, then during initial transition time 0 t k L the domain involved in computations enlarges dynamically ω z (t k ) = { z n : 0 z n t k } and the problem size at the k-th time step is given by kj(c 1 P + C ) instead of NJ(C 1 P + C ). Then the static mesh partitioning among processors using a block distribution scheme is not optimal. It is shown in [11] that the speed-up of the parallel algorithm is equal to S p p, even when the communication costs are not taken into account. As it was stated in [11] the computation costs can be reduced if we decompose the grid not uniformly. It was proposed to divide the grid into p + 1 parts and assign the last two subdomains to the last processor. A simple analysis proved that this heuristic gives optimal static block distributions for p 3. In the case of p 4 the efficiency of the proposed heuristic was investigated numerically. Now we will give a proof of this statement. In fact, we will show that the first p 1 processors should get equal numbers of grid points D 0 if computations are done at least till time moments t pd 0. Here we have assumed that the front moves one grid point per time step. Theorem 1. Let consider the static block data distribution, when the grid is divided into p + 1 parts and the last processor obtains the last two subdomains. Such distribution scheme is optimal among static block distributions.
138 1 R. Čiegis, A. Dement ev, G. Šilko Proof. The proof is based on induction. It is sufficient to consider the following grid distribution: the first (p ) processors obtain D 0 grid points; the (p 1)th processor gets D 1 grid points; the pth processor gets D grid points. These subproblems satisfy the following relations: M + D = N, (p )D 0 + D 1 = M. (4.1) Next we compute the complexity of the computational problem. The solution of the problem till T 1 = D 0 requires W 1 = D 0 j=1 j = D 0(D 0 + 1) basic operations. The complexity of the problem for D t M D 1 + D 0 is W = M D 1+D 0 j=d 0+1 D 0 = D 0 (M D 1 ) basic operations. The last part of the problem till t = M requires W 3 = M j=m D 1+D 0+1 (j M + D 1 ) operations. The total number of operations is given by W = W 1 + W + W 3 = 1 ( D 1 + D 1 D 0 D 1 + D 0 M ). Now we can find the optimal grid distribution among (p 1) processors, when the problem is solved only till t = M. Optimality in this case means that we consider only two free parameters, i.e. D 0 and D 1. By using (4.1) we get S D 0 := (p ) ( pd 0 M 0.5 ) = 0, D 0 = M p + 1 p, D 1 = M (p )D 0 = M p p p. Thus we confirm the result, that the (p 1)th processor should get the two last subproblems. Now let consider the situation, when we still continue computations for M +1 t M + K. Then we obtain the following estimate of the algorithm complexity: W = W + M+K j=m+1 D 1 = W + K ( M (p )D 0 )
139 Parallel Numerical Modelling of Laser Pulse 13 and from the optimality equation it follows that D 0 = M+K p + 1 p. It is easy to find K such, that D 1 (K) = D 0 (K): M + K p = M p 1 K = M p 1. Thus we have proved, that for any number of processors p, the first processors should get subproblems of the size M p 1 and only the last processor gets a subproblem of the size M p 1. Again, if the computations are continued for t > N, then the optimal grid distribution converges to the static block distribution scheme. Dynamic data redistribution In general, if we distribute the grid using the static block distribution scheme, then the parallel execution time T p on p processors is given by T p = N ( p J N N p + 1 ) (C 1 P + C ) + p 1 N(α + βp ). p The following data redistribution algorithm is analyzed theoretically in [11]: Initial N s points of the mesh ω z are partitioned statically among processors using a block distribution scheme. Starting from the time moment t k = N s τ after K s steps of the algorithm data is redistributed among processors in order to preserve a load balancing. The algorithm for determination of N s, K s is given in [11]. This algorithm introduces additional communication costs, but they are compensated by improved load balancing and therefore a total efficiency of the parallel algorithm is increased. Computational experiments are performed on IBM SP4 computer at CINECA. In Table we present speed-ups S p = W T p of the parallel algorithm for different values of redistribution starting point N s and the same remaining discrete parameters N = 400, P = 00, K = 400. Table. Speed-up of the parallel algorithm with data redistribution. p N s = 400 N s = 00 N s = 100 N s = p As predicted by theoretical analysis the adaptive redistribution algorithm increases essentially the efficiency of the parallel discrete algorithm even for fixed size problems.
140 14 R. Čiegis, A. Dement ev, G. Šilko 5. Numerical Results These numerical experiments were performed on VGTU cluster of 10 SMP PCs. Each PC contains two 1.4 GHz Pentium III processors. All nodes run Linux. In order to estimate the computational power of this cluster we solved the problem with the following parameters: N = 100, J = 100, P = 100, K = 400. Table 3. Execution time, speed up and efficiency of the parallel algorithm. p T p S p E p S p p In Table 3 we present execution time T p, speed-up S p = W T p and efficiency E p =. These results fully confirm our theoretical predictions, the parallel algorithm is highly scalable. 6. Conclusions Parallel algorithms for solution of one important problem of nonlinear optics have been investigated. It has been shown that the parallel domain decomposition algorithm for this problem is highly scalable and it s efficiency is near to one. Detailed modelling of practically interesting cases of pulse compression will be published in physical journals. Acknowledgments This work was possible thanks to the stay of R. Čiegis at the supercomputing center CINECA in Bologna within the project MINOS. He gratefully acknowledges the hospitality and excellent working conditions in CINECA. In particular he thanks Dr. Giovanni Erbacci for his help. References [1] S. Afshaarvahid, V. Devrelis and J. Munch. Nature of intensity and phase modulations in stimulated Brillouin scattering. Phys. Rev. A, 57(5), , [] S. Afshaarvahid, A. Heuer, R. Menzel and J. Munch. Temporal structure of stimulated- Brilouin-scattering reflectivity considering transversal-mode development. Phys. Rev. A, 64,
141 Parallel Numerical Modelling of Laser Pulse 15 [3] S. Afshaarvahid and J. Munch. A transient, three-dimensional model of stimulated Brillouin scattering. J. Nonlinear Opt. Phys. and Materials, 10(1), 1 7, 001. [4] R. Buzelis, A. Dement ev, E. Kosenko and E. Murauskas. Short pulse generation by onestep SBS. In: XVII International conference on coherent and nonlinear optics, Minsk, Belarus, June 6 - July 1, 59, 001. [5] R. Buzelis, A. Dement ev., E. Kosenko, E. Murauskas, R. Čiegis and G. Kairytė. Numerical analysis and experimental investigation of beam quality of SBS-compressors with multipass Nd:YAG amplifier. Proc. SPIE, 77, , [6] R. Buzelis, A. Dement ev and E. Murauskas. Investigation of possibilities of effective SBS compression of nanosecond pulse to 100 ps. Lithuanian Phys. J., 39(4), 53 58, [7] R.R. Buzelis, V.V. Girdauskas, A.S. Dement ev, E.K. Kosenko and R.J. Čiegis. Spacetime structure of pulses of cascade SS-compressors. Izvestya AN SSSSR, Phys. Ser., 55(), 70 78, [8] R.R. Buzelis, V.V. Girdauskas, A.S. Dement ev, E.K. Kosenko, S.A. Norvaišas and R.J. Čiegis. Mathematical modeling and experimental investigation of the fidelity of wave-front with smooth inhomogeneities reversal for high reflection coefficients of SBSmirror. Izvestya AN SSSSR, Phys. Ser., 54(6), , [9] R. Čiegis and A. Dement ev. Numerical simulation of counteracting of focused laser beams in nonlinear optics. In: Mathematical Modelling and Applied Mathematics. Proceedings of the IMACS International Conference on Mathematical Modelling and Applied Mathematics, Moscow, USSR, 18-3 June, North-Holland. Amsterdam, London, New-York, Tokyo, (199) [10] R. Čiegis, A. Dement ev and P. Ratė. A parallel algorithm for solving one problem of nonlinear optics. Mathematical Modelling and Analysis, 4, 58 69, [11] R. Čiegis and G. Šilko. A scheme for partitioning regular graphs. Lecture notes in computer science, 38, , 00. [1] R. Čiegis, G. Šilko and A. Dement ev. A tool for modeling optical beam propagation. Informatica, 13, , 00. [13] A. Dement ev, R. Buzelis, E. Kosenko, E. Murauskas and R. Navakas. Solid-state lasers with pulse compression by transient stimulated Brillouin and Raman scattering. Proc. SPIE, 4415, 9 97, 001. [14] W. Dörfler. A time- and space adaptive algorithm for the linear time-dependent Schrödinger equation. Numer. Math., 73, , [15] V.V. Elisseev. Parallelization of three-dimensional spectral laser plasma interaction code using High Performance Fortran. Computers in Physics, 1(), , [16] V. Girdauskas, A.S. Dement ev, G. Kairyte and R. Čiegis. Influence of the beam aberrations and Kerr nonlinearity of a medium on the efficiency and pulse quality of a SBScompressor. Lithuanian Phys. J., 37(4), 69 75, [17] V. Girdauskas, O. Vrublevskaja and A. Dement ev. Numerical treatment of short laser pulse compression in transient stimulated Brillouin scattering. Nonlinear Analysis: Modelling and Control, 7(1), 3 9, 00. [18] Millennium Issue. IEEE J. Selected Topics Quantum Electron. 6(6), , 000. [19] K. Kuwahara, E. Takahashi, Y. Matsumoto, S. Kato and Y. Owadano. Short-pulse generation by saturated KrF laser amplification of a steep Stokes pulse produced by two-step SBS. J. Opt. Soc. Am. B, 17, , 000. [0] T.R. Moore and R. W. Boyd. Three dimensional simulations of stimulated Brillouin scattering with focused Gaussian beams. J. Nonlinear Opt. Phys. and Materials, 5(), , [1] T.R. Moore, G.L. Fischer and R.W. Boyd. Measurement of the power distribution during stimulated Brillouin scattering with focused Gaussian beams. J. Mod. Opt., 45(4), , 1998.
142 16 R. Čiegis, A. Dement ev, G. Šilko [] Phase conjugated laser optics. John Wiley&Sons, Inc., 004. [3] L. Schoulepnikoff and V. Mitev. Numerical method for the modelling of high-gain single-pass cascade stimulated Raman scattering in gases. J. Opt. Soc. Am. B, 14, 6 75, Trumpu lazerio impulsų spūdos skaičiavimo lygiagretusis skaitinis algoritmas R. Čiegis, A. Dementjevas, G. Šilko Nagrinėjamas priverstinės Brijueno sklaidos fokusuotuose pluoštuose uždavinio lygiagretusis skaitinis sprendimo algoritmas. Sukonstruota simetrinio skaidymo baigtinių skirtumų schema, kurios tikslumas yra antrosios eilės. Lygiagretusis algoritmas gautas naudojant duomenu lygiagretumo paradigma. Detaliai nagrinėjamas dinamiškai didėjančio sudėtingumo uždavinys, modeliuojantis Brijueno sklaidos procesa, kai neužduodama kraštinė sąlyga Stokso bangai. Įrodyta hipotezė apie vieno stacionaraus blokinio duomenu paskirstymo algoritmo optimalumą. Eksperimentiškai ištirtas dinaminis duomenu perskirstymo algoritmas, patvirtintas jo efektyvumas net ir fiksuoto dydžio uždaviniams. Darbe pateikti skaitinio eksperimento, atlikto naudojant VGTU 0 procesoriu klasterį, rezultatai. Jie patvirtino gautuosius teorinius rezultatus, išsam ūs fizikiniai rezultatai bus išspausdinti kituose darbuose.
143 !"# $ % '&)($ +*,-./ c 004 Technika ISSN COMPARATIVE ANALYSIS BY MEANS OF FINITE DIFFERENCES AND DM METHODS FOR LINEARIZED PROBLEM OF GYROTRONS T. CĪRULIS, H. KALIS and O. LIETUVIETIS Institute of Mathematics of Latvian Academy of Sciences and University of Latvia Akadēmijas laukums 1, Rīga LV 154, Latvia #: 71; <:1=?>@BADCE:GF%HJI =:7B; <:1= F+H'K1L=B8;B:B<:1= >@ ADCE: F Received October 14, 003; revised January 15, 004 Abstract. The problem of Schrödinger equation with complex boundary conditions for modelling a motion of electrons in gyrotrons is considered. Numerical results obtained by using Fourier, Finite Differences (FD) and Degenerate Matrices (DM) methods are compared in the simplest case. For DM methods they are analysed also in more general cases, when FD can not be applied because of fast oscillations of the solution. Key words: gyrotron, Schrödinger equation, complex boundary conditions, Fourier method, finite differences, degenerate matrices method 1. Formulation of the problem When modelling the motion of electrons in gyrotrons, it is necessary to solve the following initial-boundary value problem: i u t = u + δ(x)u, x (0, L), t > 0, x u t=0 = u 0 (x), (initial values), (1.1) u u x=0 = 0, x=l = iγu x=l, (boundary conditions), x where u = u(t, x) is an unknown complex function, δ(x) and u 0 (x) are given functions, γ > 0 is a given constant, i = 1. Quasi-stationary solutions in the case δ(x) = δ 0 = const were considered in [1, 5]. They are given by: u(t, x) = g(x) exp ( it(α δ 0 ) ), (1.)
144 18 T. Cīrulis, H. Kalis, O. Lietuvietis where α = α 1 + iα are complex eigenvalues and g(x) are the corresponding eigenfunctions. Denoting α = λ, z = λl we obtain the equation z cos z = iγl sin z (1.3) for finding z. Each complex root z = z 1 + iz of (1.3) generates a solution in the form (1.) with Reα = α 1 = z 1 z L, Imα = α = z ( 1z zx ) L, g(x) = sin. (1.4) L Using the argument principle for analytical complex functions it is possible to prove that all roots of equation (1.3), except z = 0, are disposed only in domains { Rez > 0, Imz > 0 }, { Rez < 0, Imz < 0 }, symmetrically with respect to z = 0 [7]. Therefore the roots can be calculated only in the first quadrant of z-plane. We use the software package "Maple" for z not large and asymptotic formulas in the case of large z. These asymptotic formulas can be found by the method of indeterminate coefficients. The method is often used to solve equations with entire analytic functions. For roots z n, n, they are given as follows: z n = s n + a 1 + a s n s 3 + a 3 n s 5 + a ( 4 1 ) ( n s 7 + O n s 9, s n = π n + 1 ), n a 1 = iτ, a = τ ( 1 + iτ 3 ), a 3 = 4τ iτ 3 (τ 10) 5 a 4 = τ 4( 47 ) 36 τ 3 + iτ 5 10 (17τ 440), τ = γl. Let λ k = z(k) L, where (z(k) ), k = 1,,..., be the sequence of roots of (1.3) numbered according to the increase of Re(z (k) ). Then the solution of problem (1.1) can be expended into the following convergent infinite Fourier series: u(t, x) = c k g k (x) exp ( i(λ k δ 0)t ), (1.5) k=1 L g k (s)u 0 (s) ds 0 g k (x) = sin(λ k x), c k =. L gk (s) ds Moreover, numerical results obtained by (1.5) are accurate enough only for very large number of the summands in (1.5), especially if t is not large. Therefore, in the following sections we will consider other methods for numerical solving of the problem (1.1). 0,
145 Finite differences and DM methods for problem of gyrotrons 19. Application of the finite difference method We consider the uniform space grid in the x-direction with the interior grid points x j = jh, j = 1, N 1, x 0 = 0, x N = L, and the time grid with the grid points t n = nτ, n = 1,,..., here h, τ are the steps of the grids. We replace the continuous solution u = u(t, x) of the problem (1.1) by the discrete grid function y = y(t, x) with values y(t n, x j ) = yj n. An approximation of the problem (1.1) is based on the following finite difference scheme: i yn+1 j yj n = σλy n+1 j + (1 σ)λyj n, j = 1, N 1, τ y0 n+1 = 0, ly n+1 N = iγyn+1 N, (.1) yj 0 = u0 (x j ), j = 0, N, where σ [0, 1] is a parameter of the scheme. Λy j denotes a central difference expression of the second order approximation for the derivative u at the grid point x x j : Λy j = y j+1 y j + y j 1 h + δ 0 y j, ly N denotes a difference expression of the first order approximation for the derivative u in one of the following forms: x a) using the two points difference for the first order approximation ly N = y N y N 1 h ; (.) b) using the three points difference for the second order approximation ly N = 1.5y N y N y N h. (.3) The approximation order (AO) of the difference equations (.1) with respect to time and space coordinates is equal to two if σ = 0.5, and equal to one with respect to time if σ 0.5. Approximation order of boundary conditions is 1 (formula (.)) and (formula (.3)). The discrete quasi-stationary solution has the following form: where the discrete eigenfunctions g (k) j are given by [1]: y n j = g j exp(inτα), (.4) g (k) j = sin(q (k) x j ), k = 1,,..., N 1. Here q (k) are roots of one of the transcendent equations:
146 130 T. Cīrulis, H. Kalis, O. Lietuvietis 1) Approximation (.) ) Approximation (.3) sin(ql) = C 1 sin ( q(l h) ), (.5) sin (ql) = C ( sin ( q(l h) ) 0.5 sin ( q(l h) )), (.6) C 1 = iγh, C 1 = iγh. The parameter α in (.4) can be obtained from expressions: α = ln 1 τα /(i + στα ), α = ( 1 cos(qh) ) iτ h δ 0. The approximate values α (k) A k = ( 1 cos(a k h)ch(b k h) ) are complex, i.e., α (k) = A k + ib k : h δ 0, B k = sin(a kh)sh(b k h) h, where q (k) = a k + ib k. Using the argument principle we can prove that all complex roots of (.5) or (.6) for Req > 0 or a k > 0 are in the first quadrant of the complex q-plane, and B k 0. The stability conditions for finite difference schemes (.1) (.), and (.1) (.3) follow from [6]: σ 0.5, B k 0. The solution of finite-difference scheme (.1) (.) can be obtained also in the discrete form of Fourier series: where c k = N 1 s=1 y n j N 1 = h k=1 1 sin(q (k) x s )u 0 (x s ), d k = 1 ( d k c k sin(q (k) x j ) exp(iα (k) nτ), (.7) In this case the discrete eigenfunctions (.4) are orthogonal: L h sin(q(k) L) cos ( q (k) (L h) ) sin(q (k) h) N 1 (g (k), g (m) ) = h g (k) j g (m) j = 0, k m. j=1 ).
147 Finite differences and DM methods for problem of gyrotrons Application of the Degenerate Matrix method In this section we will consider another scheme for solving problem (1.1), which can be used also in the case when δ(x) is not equal to a constant. The DM method [3, 4] is based on using such differentiation matrices A for derivatives with respect to x which ensure that the approximation of the unknown function u is nonsaturated. Choosing the partitions x k, k = 0, 1,..., n + 1, on the interval (0, L) we form the (n + ) (n + ) matrix A with elements w (x m ) (x m x k )w, if m k, (x k ) a mk = (3.1) w (x k ) w (x k ), if m = k, where w(x) = n+1 (x x j ). j=0 Remark 1. We usually choose the nodes s k as zeroes of classical orthogonal polynomials on the standard interval [ 1, 1]. Then the mapping x k = L ( sk + 1 ) gives the required partition of (0, L), and the nonsaturatedness of approximations is ensured. Contracting equation (1.1) on the nodes x k, k = 0, 1,..., n + 1, and applying the matrix A we obtain the following equation i d u dt = (A + D) u, (3.) where u and D are the column-vector and the diagonal matrix, respectively, with corresponding components u(x k ) and diagonal elements δ(x k ), k = 0, 1,..., n + 1. Matrix equation (3.) holds only at the interior points x 1, x,..., x n of the interval (0, L). Therefore, we must take off its first and last rows. Then we exclude values u(x 0 ) and u(x n+1 ) in the first and last columns from the remaining equations using the discretized boundary conditions u(x 0 ) = 0, n+1 a n+1,k u(x k ) = iγu(x n+1 ), k=0 which are obtained after discretization of boundary conditions (1.1). This yields the system of n homogeneous linear differential equations d u dt = S u (3.3) with initial values obtained by discretization of initial value in (1.1). Here (3.3) has constant coefficient matrix S with elements s m,k, m, k = 1,,..., n: s mk = i ( a () mk + µa() m,n+1 a n+1,k + d mk ), (3.4) where a () mk are the elements of the matrix A, a n+1,k are the elements of the last row of A,
148 13 T. Cīrulis, H. Kalis, O. Lietuvietis µ = iγ a n+1,n+1 γ + a, d mk = n+1,n+1 { 0, if m k, δ(x k ), if m = k. (3.5) Finally, we solve system (3.3) exactly finding eigenvalues and eigenvectors for the matrix S and using discretized initial values. Comments 1 0. Now we prove that for finding eigenvalues λ and eigenfunctions u, which are defined by the following problem: { u + δ(x)u = λu, (3.6) u(0) = 0, u (L) = iγu(l), it is appropriate to use matrices for derivatives with nodes s k = 1,,..., N as zeroes of one of the classical orthogonal Jacobi polynomials P (α,β) N (s) supplemented with s 0 = 1 and s N+1 = 1. ( Let L be the eigenvalue x k = L sk + 1 ), k = 0, 1,..., N + 1. Let λ be the eigenvalue and u(x) is the eigenfunction of (3.6) corresponding to given λ. We denote v(s) = u ( L (s+1)) and consider the following Fourier series for s [ 1, 1]: v(s) = k=0 c k P (α,β) k (s), c k = 1 P (α,β) 1 k 1 ρ(s)v(s)p (α,β) k (s) ds, (3.7) where ρ(s) = (1 s) α (1 + s) β is the weight function. Series (3.7) converges very rapidly because v(s) is analytical. Therefore, v(s) = N k=0 c k P (α,β) k (s) + R N (s), R N (s) = O ( exp( νn) ), (3.8) when N + with some constant ν > 0. Replacing the integral in (3.7) by the Gauss-Lobatto quadrature formula, substituting it into (3.8) and using the classical Christoffel-Darboux formula for Jacobi polynomials it is possible to prove that [] v(s) = N+1 k=0 p N+ (s)v(s k ) (s s k )p N+ (s k) + ˆR N (s), ˆRN (s) = O ( exp( νn) ), (3.9) where p N+ (s) = (1 s )P (α,β) N (s), and the remainder in (3.9) has the same asymptotic estimate as in (3.8). This follows from the asymptotic behaviour of a difference between the integral in (3.7) and its quadrature formula in the case when v(s) is an analytical function on [ 1, 1]. Therefore, (3.9) gives also the nonsaturated approximation of v(s). Returning to the variable x and using matrices for derivatives according to the scheme given at the beginning of the section, we obtain the equation (S N + ( λ + O(exp( νn)) ) ) E N u N = 0. (3.10)
149 Finite differences and DM methods for problem of gyrotrons 133 All elements of the matrix S N can be computed by analogy with (3.4) and (3.5). Therefore, the eigensystem for the matrix S N is close to the one for the matrix S N + O ( exp( νn) ) E N, if N The computing scheme described above can be used not only for (1.1), but also for solving different linear problems of heat or wave equations A possibility to compute the matrix S in (3.3) efficiently and to calculate its eigenvalues gives very simple criterion of the stability of the DM-methods for linear problems. They are stable if all n eigenvalues of S have negative real parts. For example, the DM-method for (1.1) with uniformly distributed nodes is unstable even for n 5. The choice of nodes as zeroes of classical orthogonal polynomials leads to stable schemes for very large n. For example, the method with nodes as zeroes of Chebyshev polynomials of the second kind is stable at least for n 40, for Legendre polynomials at least for n Numerical results Table 1. Values of u(x, t) for x = L = 15, γ = and δ(x) = 0. t F FD DM , In Table 1 we present absolute values of the numerical solutions on the boundary x = L of problem (1.1) with δ(x) = 0 and simple initial conditions u 0 (x) = sin πx L. We set parameters γ = and L = 15. Such choice is very interesting for applications. In column (F ) of Table 1 we give results obtained by the classical Fourier method (1.5) with N = 000. In column (F D) we present the results obtained by Finite difference method (.7) with space step h = 0.0 and time step τ = 0.01, and in the last column (DM) the results obtained by the DM-method with 40 grid points
150 134 T. Cīrulis, H. Kalis, O. Lietuvietis Table. Values of u(x, t) obtained by the DM method with the Chebyshev and Legendre nodes for x = L = 15, γ = and δ(x) = tanh(7x 3.5L). n = 60 n = 10 n = 40 t Cheb.1 Leg. Cheb. Cheb.1 Leg. Cheb. Cheb.1 Cheb , distributed as zeroes of Chebyshev polynomials of the second kind are given. Numerical results were obtained by means of mathematical systems Maple-5 (Fourier series and Finite differences) and Mathematica. (the DM-method). As we see, Finite differences and the DM-methods give the same order of accuracy, but such accuracy was achieved by the DM-method using approximately three times less grid points than by Finites differences. Moreover, the DM-method was very fast in calculations. It is due to the usage of the eigensystem of matrix S in (3.3) which allows us to solve (3.3) exactly. Therefore, we can easily calculate the numerical solution of (1.1) for any t without using discrete time integration. So, all results in column (DM) were obtained in 47 seconds on a computer with Celeron 400 processor and 56 mb RAM. In Table we present numerical results obtained by the DM-method with δ(x) = tanh(7x 3.5L), γ =, L = 15 and for different sets of n grid points ( n = 60, 10, 40 ) distributed as zeroes of Chebyshev polynomials of the first and second kind and as zeroes of Legendre polynomials. We note that for δ(x) const, the method of Finite differences (.7) has failed. It is seen from Table, that all distributions of grid points with fixed n give the same accuracy which rises by increasing n. The corresponding graph of u(l, t for n = 40 and nodes distributed as zeroes of Chebyshev polynomial of the second kind is shown in Fig.1, and the graphs of u(x, t) at various time moments are shown in Fig..
151 Finite differences and DM methods for problem of gyrotrons t Figure 1. The graph of u(l, t) for δ(x) = tanh(7x 3.5L). 1. t=1 1 t=0 0.8 t= t= x Figure. Evolution in time of u(x, t) for δ(x) = tanh(7x 3.5L). Thus we conclude that the DM method can be used efficiently to solve the problem (1.1) also for δ(x) const. References [1] M. Airila, O. Dumbrājs, A. Reinfelds and U. Strautins. Nonstationary oscillations in gyrotrons. Phys. Plasmas, 8(10), , 001. [] P. Borwein and T. Erdelyi. Polynomials and Polynomial Inequalities. Springer - Verlag, [3] T. Cīrulis. Nonsaturated approximation by means of Lagrange interpolation. In: Proceedings of the Latvian Academy of Sciences. Section B, volume 5, 34 44, [4] T. Cīrulis and O. Lietuvietis. Application of DM method for problems with partial differential equations. Mathematical Modelling and Analysis, 7(), , 00. [5] O. Dumbrājs, H. Kalis and A. Reinfelds. Numerical solution of single mode gyrotron equation. Mathematical Modelling and Analysis, 9(1), 5 38, 004. [6] A.A. Samarskii. Theory of difference schemes. Nauka, Moscow, (In Russian) [7] B. Shabat. An Introduction to Complex Analysis, nd edition, volume. Moscow, (In Russian)
152 136 T. Cīrulis, H. Kalis, O. Lietuvietis Baigtinių skirtumų ir DM metodo lyginamoji analizė linearizuotam girotrono uždaviniui T. Cirulis, H. Kalis, O. Lietuvietis Nagrinėjamas kraštinis uždavinys Šredingerio lygčiai, aprašantis elektronu judėjimą girotrone. Darbe lyginami ir analizuojami Furje, baigtinių skirtumų ir degeneruotu matricų (DM) metodais gauti skaitiniai rezultatai. Aptartas metodo taikymas greitų osciliacijų atveju.
153 !"# $ % '&)($ +*,-./ c 004 Technika ISSN ON AN EXACT DESCRIPTION OF THE SCHOTTKY GROUPS OF SYMMETRIES 1 M.V. DUBATOVSKAYA and S.V. ROGOSIN Belarusian State University 4, Fr. Skaryna ave, Minsk :8;<8=>@? :1A 94> 7CBD9E Received October 9, 003; revised April 1, 004 Abstract. Exact description of the Schottky groups of symmetries is given for certain special configurations of multiply connected circular domains. It is used in the representation of the solution of the Schwarz problem which is applied at the study of effective properties of composite materials. Key words: symmetries, Schottky group, Schwarz boundary value problem, composite materials 1. INTRODUCTION Description of special subgroups of the group of conformal mappings on the complex plane is a classical problem. The first essential results in this direction were obtained at the end of XIX - beginning of XX centuries by F. Schottky, H. Schwarz, H. Poincaré, L. Fuchs, E. Picard, A. Hurwitz, F. Klein and others. These results formed the base of the theory of the groups of conformal mappings, the theory of automorphic functions and Poincaré θ-series (see [3]). Further results and modern view on this subject are presented in the monographs [4, 9]. The theory of conformal mapping constitutes a very suitable tool for the study of two-dimensional problems of mathematical physics. Recently an interest has arised to describe special groups of conformal mappings, which belong to so called class of the Schottky groups. It should be noted, for instance, the application of such groups to the constructive representation of conformal mappings of multiply connected domains onto canonical domains (see, e.g. [1,, 8]), to the analytic solution of the Schwarz boundary value problem Re F (t) = f(t), t L, (1.1) 1 The work is partially supported by the Belarusian Fund for Fundamental Scientific Research
154 138 M. Dubatovskaya, S. Rogosin or more general Riemann-Hilbert boundary value problem Re λ(t)f (t) = f(t), t L, (1.) for a multiply connected circular domain (see [7]). They are also used for the study of certain special cases of R-linear boundary value problem φ + (t) = a(t)φ (t) + b(t)φ + (t) + c(t), t L, (1.3) for multiply connected domains. Investigations of all these problems based on the method of functional equations are described in the recent monograph [8]. These results constitute the ground for a new constructive approach to the study of boundary value problems of mathematical physics. Therefore the study of general properties of Schottky groups generated by symmetries with respect to a number of circles becomes an actual problem. It is also important to give an exact representation of elements of such groups for certain special cases since these groups are used in formulas for the solutions of the problems (1.1), (1.), (1.3). They can be applied for solving problems of filtration, composite materials, porous media (see the description of these applications, e.g., in [6, 8]).. Notation and general results.1. Groups of symmetries We consider representation of elements of so called Schottky groups (or Schottkytype groups). The formal definition of the Schottky group is as follows: Let Q 1, Q,..., Q n and Q 1, Q,..., Q n be two families of circles. Let the circles of each family be situated outside each other (i.e. the circles of each family are nonoverlapping). Let T j be a (fractional)-linear transform with respect to z or z which map Q j onto Q j and interior of the circles of each Q j onto exterior of Q j. This transform generates the group K j. The composition of these groups K j, j = 1,,..., n, is called Schottky group generated by the mappings T j, j = 1,,..., n. Intensive study of such groups was done in twenties and thirties of the XX century. It appeared that in most cases the Schottky group has quite complicated structure and not too many general properties can be formulated. We consider here a special case of the Schottky groups when the generators T j are simply the symmetries with respect to the circles Q j (and thus Q j = Q j ). We obtain an exact description of the elements of the corresponding Schottky groups for a number of particular cases. Let Q j = Q j (a j, r j ) := {z C : z a j = r j }, j = 1,,..., n, be a family of circles on the complex plane (with centers a j and with radii r j ). Let us introduce the following mappings (see [8, p. 15]):
155 r j Schottky groups of symmetries 139 z (j m,j m 1,...,j 1) := (z (j m 1,...,j 1) ) (j m), (.1) where z(j) = + a (z a j) j is the symmetry with respect to the circle Q j. Hence, z(j m,j m 1,...,j 1) is the composition of the successive symmetries with respect to the circles Q j1,... Q jm 1, Q jm. In the sequence j m, j m 1,..., j 1 no two neighbouring numbers are equal. The number m is called the level of the mapping z(j. m,j m 1,...,j 1) When m is even, these mappings are Möbius transformations. If m is odd then we have anti-möbius transformations, i.e. Möbius transformations with respect to z. Thus these mappings can be written in the form φ k (z) = (α k z + β k ) / (γ k z + δ k ), φ k (z) = (α k z + β k ) / (γ k z + δ k ), m is even, m is odd, where α k δ k β k γ k = 1. Here φ 0 (z) = z, φ 1 (z) = z (1), φ (z) = z (),..., φ m(z) = z (m), (.) φ m+k (z) = z ((k+1),1), k 1. The functions φ k generate a Schottky group K (see [3]). In the following we denote by G the subgroup of K consisting of the mappings φ k of an even order, and by F the subgroup of K consisting of the mappings φ k of an odd order. The following general properties of the successive symmetries are well-known (see [3]). Properties of successive symmetries 1. Each (fractional)-linear transform w = αz+β γz+δ of the complex plane C is equivalent to an even number of symmetries with respect to certain circles.. (Fractional)-linear transforms of the complex plane C (which are not identity, w z) have at most two fixed points. Thus it is true for the elements of the subgroup G. 3. Any transform w = αz+β γz+δ can be represented in one of the following forms w ζ 1 w ζ = K z ζ 1 z ζ, or w ζ 1 = K(z ζ 1 ), where ζ 1, ζ are the fixed points of the transform, and the coefficient K is a complex number satisfying the relation K + 1 K = α + δ. 4. If K = Ae iθ (A > 0, θ [0, π)) then the transform w a) is called hyperbolic, if K = A; a) is called elliptic, if K = e iθ ; a) is called loxodromic, if K = Ae iθ, θ 0.
156 140 M. Dubatovskaya, S. Rogosin 5. Let the transform w = αz+β γz+δ has two fixed points ζ 1, ζ and is represented in the form w ζ 1 = K z ζ 1. w ζ z ζ Then the m-th iteration of this transform, i.e. the transform w (m) := w w... w }{{} m times has the same fixed points and is represented in the form w (m) ζ 1 w (m) ζ = K m z ζ 1 z ζ. (.3) It should be mentioned that the above properties hold only for the symmetries of even level. As for the symmetries of odd level the situation is more complicated. 6. The set of fixed points of the transform of an odd level w = αz + β γz + δ can be either the whole complex plane C, or a circle, or two points, or a point, or even an empty set. Really, fixed points (z = x + iy) have to satisfy the following system of real equations a(x + y ) + bx + cy + d = 0, (.4) b 1 x + c 1 y + d 1 = 0. Then the property 6 follows immediately. It is not difficult to see that all possibilities for the fixed set are achieved by certain transformations of an odd level... Schwarz operator and groups of symmetries Our interest to obtain an exact description of elements of Schottky groups of symmetries is motivated by the application of such groups at the study of composite materials. Thus, the properties of two-dimensional composite materials with cylindric inclusions are described in terms of the solutions of certain boundary value problems for harmonic functions in a multiply connected circular domain. Such models are described in the monograph [8]. These solutions are represented in term of certain Schottky groups of symmetries. To clarify this situation let us give such a formula for one of the most simple boundary value problems, which describes the composite materials, namely, for the Schwarz boundary value problem (1.1). Let us consider mutually disjoint discs D j := D(a j, r j ) = {z C : z a j < r j }, j = 1,,..., n on the complex plane C. Let D := Ĉ \ n D j (see Fig. 1). We choose the orientation of the boundary Q := n Q j j=1 j=1 = D j in such a way, that the domain containing
157 D 1 (a 1, r 1 ) Schottky groups of symmetries 141 D D n (a n, r n ) z0 D (a, r ) Figure 1. A multiply connected domain. is on the left side. We give here the formulation of the Schwarz problem in this specified type of domains in order to be precise at the representation of the solutions. In fact, the Schwarz problem can be posed for any Jordan domain. The Schwarz problem for the domain D is to find a function F, analytic in D and continuous in cl D, such that its boundary values satisfy the relation Re F (t) = f(t), t Q = D, (.5) Im F (z 0 ) = 0, where f is a given function on Q, z 0 is a given point in D. The operator T, which assigns to each pair (f, z 0 ) the solution of the Schwarz problem (.5), is called the Schwarz operator of the domain D. In the case of the Hölder-continuous function f and the multiply connected domain D being of the above described type the Schwarz operator is delivered by the formula [8, p. 135] where (Tf) (z) = 1 πi + + ( rj n f(ζ) j=1 Q j ζ a j j=1 Q j ) φ j F φ j G,j 0 n A n f(ζ) (ζ) dζ + ν A m = n f(ζ) j=1 Q j [ 1 ζ φ j (z 0 ) 1 ζ φ j (z) [ ] 1 (ζ φ j (z)) 1 1 (ζ φ j (z 0 )) ζ z dζ A m [log(z a m ) + ψ m (z)] + iς, m=1 α j (ζ) dζ, j = 1,,..., n, ν ] (.6) α j is a harmonic measure of the domain D j, the functions A(z), ψ m (z) are uniquely defined by certain additional relations (see [8]), ν is an external normal vector to the corresponding circle, ς is an arbitrary real constant. This formula represents the Schwarz operator in any compact subset of the domain D.
158 14 M. Dubatovskaya, S. Rogosin 3. Representation of elements of the Schottky groups of symmetries In this Section we give a number of results concerning the representation of elements of some special Schottky groups of symmetries. We start with the most simple case of symmetries with respect to two circles Symmetries with respect to two circles Let D j := D(a j, r j ) = {z C : z a j < r j, j = 1, } be two nonoverlapping discs on the complex plane C (i.e. a 1 a r 1 + r ) (see Fig. ). Then the transform w = z(1,) can be delivered by the formula D (a, r ) D 1 (a 1, r 1 ) Figure. Symmetries with respect to two discs. w = Az + B Cz + D, where A = a (a 1 a ) + r, B = a 1a (a 1 a ) + r 1 a r a 1, C = a 1 a, D = a 1 (a a 1 ) + r 1. (3.1) This transform has two fixed points ζ 1, ζ and satisfies the relation where w ζ 1 w ζ = K z ζ 1 z ζ, ζ 1 = M + N r 1 r, ζ = M N r 1 r, K = L N L + N, (3.) M = r r 1 + ( a 1 a ) (a1 + a ), N = ( (r r 1 ) + a 1 a 4 a 1 a (r 1 + r ) ) 1/, L = r 1 + r a 1 a.
159 Schottky groups of symmetries 143 In the same notation the transform consisting of m-symmetries ( ( ( ) ) w (m) := z(1,,1,,...,1,) =... z(1,)... (1,) (1,) ) (1,) } {{ } m times satisfies the relation w (m) ζ 1 w (m) ζ = K m z ζ 1 z ζ. 3.. Symmetries with respect to three circles Let D j := D(a j, r j ) = {z C : z a j < r, j = 1,, 3 } be three nonoverlapping discs of equal radii r on the complex plane C (i.e. a k a j r, k j) (see Fig.3). D 3 (a 3, r) D 1 (a 1, r) D (a, r) Figure 3. Symmetries with respect to three discs. Then the transform w = z(1,,3) can be delivered by the formula where w = Az + B Cz + D, A = r (a 1 a + a 3 ) + a 3 (a a 3 )(a 1 a ), (3.3) B = r 4 r [a 3 a 1 + a 1 (a 1 a ) a 3 (a a 3 )] a 1 a 3 (a 1 a )(a a 3 ), C = r + (a 1 a )(a a 3 ), D = r (a a 3 a 1 ) a 1 (a 1 a )(a a 3 ). The formulae for the transforms w = z(1,3,), z (,1,3),..., z (3,,1) can be obtained from (3.3) by interchanging of indexes. It follows from [5] that the effective characteristics of the composites possess extreme values in the case of percolation, i.e. when the discs D j touch each others
160 144 M. Dubatovskaya, S. Rogosin y D 3 (a, r) 0 D (0, r) D 1 ( a, r) x y 0 x a) b) Figure 4. Arrangement of discs: a) three discs in line, b) three discs in line along imaginary axes. and constitute a chain-type set. In the case of an external field in the direction of the real axes the extreme configuration for three discs is the following: D j are situated in a line along the real or imaginary axes. In order to present exact formulae for the corresponding transforms we consider firstly the situation when the discs lay along certain line (see Fig.4a). Namely, let D 1 := {z C : z+a < r}, D := {z C : z < r}, D 3 := {z C : z a < r}, where a C, r > 0, a = r. In this case the composition of the successive symmetries z(1,,3) has the following representation: z (1,,3) = a a z + r 4 a r + a 4 (r + a )z + a a. (3.4) The formulae for the transforms w = z(1,3,), z (,1,3),..., z (3,,1) can be obtained from (3.3) by interchanging indexes. Further we describe the transforms in the case of optimal effective characteristics (for the external field oriented along the real axes). Let the discs D j, j = 1,, 3, be situated along the imaginary axes and touch each other (see Fig. 4b), i.e. a = ri. Then z (1,,3) z (,1,3) z (3,1,) 8irz + 13r = 5z 8ir, 4irz z 7r (1,3,) = 7z + 1ir, (3.5) 1irz 7r = 7z + 4ir, 1irz z 7r (,3,1) = 7z 4ir, = 4irz 7r 7z 1ir, z (3,,1) = 8irz + 13r 5z + 8ir Let the discs D j, j = 1,, 3 be situated along the real axes and touch each other, i.e. a = r (see Fig. 5). Then z (1,,3) = 8rz + 13r 5z + 8r, z (1,3,) = 4rz 7r 7z 1r, (3.6).
161 y Schottky groups of symmetries 145 x 0 Figure 5. Three discs in line along real axes. z (,1,3) z (3,1,) 1rz 7r = 7z 4r, 1rz z 7r (,3,1) = 7z + 4r, = 4rz 7r 7z + 1r, z (3,,1) 8rz + 13r =. 5z 8r From the point of view of applications dealing with composite materials (see, e.g., [5, 8]) it is also interesting to consider the case of discs which constitute so called "packages" of discs. Let us present two results for such configuration. y y 0 x 0 x a) b) Figure 6. Special packages: a) package of three discs I, b) package of three discs II. Let D j := D(a j, r j ), j = 1,, 3, where r j = r, a 1 = 0, a = re i π 6, a3 = re i π 6, i.e. the centers of the discs lay at the vertex of the right triangle (see Fig.6a). Then the transform w = z(1,,3) can be delivered by the formula w = irz (1 + 3i)r ( 1 + 3i)z ir.
162 146 M. Dubatovskaya, S. Rogosin Let D j := D(a j, r j ), j = 1,, 3, where (see Fig. 6b) r j = r, a 1 = 0, a = re i 5π 6, a3 = re i 5π 6. Then the transform w = z(1,,3) can be delivered by the formula w = irz + ( 1 + 3i)r ( 1 3i)z ir Symmetries with respect to four circles In the case of four discs we consider the only situation with four discs of equal radii symmetrically situated with respect to the origin: D 1 := { z C : z a < r }, D := { z C : z + a < r }, D 3 := { z C : z + a < r }, D 4 := { z C : z a < r }, where a C, r > 0, Re a r, Im a r (see Fig.7). y D ( a, r) D 1 (a, r) 0 x D 3 ( a, r) D 4 (a, r) Figure 7. Four symmetrically situated discs. In this case the composition of the successive symmetries w = z(1,,3,4) is delivered by the formula w = Az + B Cz + D, with A = r 4 + r a r a + aa 3 a 3 aa a + a 4, (3.7) B = r a 3 + r aa r a 3 + a 4 a a a 3, C = a 3 a a + aa + a 3, D = r 4 + r a r a + r aa a a + a 4.
163 Schottky groups of symmetries 147 The transform w = z(1,,3,4) satisfies the following relation where w ζ 1 w ζ = K z ζ 1 z ζ, (3.8) ζ 1 = a4 a r + aar + a r aa 3 a 4 + F (a a )(a + a) ζ = a4 a r + aar + a r aa 3 a 4 F (a a )(a + a) F = (a 4 a r + a 3 a + aar + a r aa 3 a 4 ) K = A Cζ 1 A Cζ, A, C are given in (3.7). 4(a a ) ( a 3 r a 4 a aa r + a a 3 a 3 r ),, (3.9) The most interesting case for applications is when four discs constitute the package, i.e. a = r + ir. Then the transform w = z(1,,3,4) has the following form: w = zr( 4 + 7i) + 8r 8z + r(4 + 7i). (3.10) The transform w = z(1,,3,4) satisfies the relation (3.8), its fixed points ζ 1, ζ are given by ζ 1 = 1 + 3i r, ζ = 1 3i r, and the coefficient K in (3.8) is given by the formula K = , References [1] L. A. Aksent ev. Construction of the Schwarz operator by use of symmetry method. Proc. seminar on boundary value problems (Kazan), ; 3; 4, 3 11; 11 4; 3 10, 1964; 1966; (in Russian) [] I. A. Aleksandrov and A. C. Sorokin. Schwarz problem for multiply connected circular domains. Siberian Math. J., 13(5), , 197. (in Russian) [3] L. R. Ford. Automorphic Functions. McGraw-Hill, New York, 199. [4] G. M. Golusin. Geometric Theory of Functions of Complex Variable. Nauka, Moscow, (in Russian) [5] S. F. Makaruk. Boundary value problem on jump for a multiply connected domain for optimally situated internal domains. Vesti NAN Belarusi, 3, 6 9, 003. (in Russian) [6] V. V. Mityushev. Functional equations and its applications in mechanics of composites. Demostr. Math., 30(1), 64 70, 1997.
164 148 M. Dubatovskaya, S. Rogosin [7] V. V. Mityushev. Hilbert boundary value problem for multiply connected domains. Complex Variables, 35, 83 95, [8] V. V. Mityushev and S. V. Rogosin. Constructive Methods for Linear and Nonlinear Boundary Value Problems for Analytic Functions. Theory and Applications. Chapman & Hall /CRC Press, Boca Raton London, [9] Ch. Pommerenke. Boundary Behaviour of Conformal Maps. Springer Verlag, Berlin, 199. Apie Schottky simetrijos grupių tikslų apibrėžima M.V. Dubatovskaya, S.V. Rogosin Darbe pateiktas Schottky simetrijos grupių apibrėžimas tam tikros specialios konfiguracijos daugiajungėms skritulinėms sritims. Jis yra panaudotas gaunant Švarco uždavinio, kuris pritaikomas nagrinėjant efektyvias kompoziciju savybes, sprendinio išraišką.
165 !"# $ % '&)($ +*,-./ c 004 Technika ISSN AN IMPROVED HYBRID OPTIMIZATION ALGORITHM FOR THE QUADRATIC ASSIGNMENT PROBLEM A. MISEVIČIUS Kaunas University of Technology, Department of Practical Informatics Student u St a, 3031 Kaunas, Lithuania : ;< 6<>=@?BA1< C9D4A EAGF#< H IJ9FK=L7MJ Received November 0, 003; revised January 9, 004 Abstract. In this paper, we present an improved hybrid optimization algorithm, which was applied to the hard combinatorial optimization problem, the quadratic assignment problem (QAP). This is an extended version of the earlier hybrid heuristic approach proposed by the author. The new algorithm is distinguished for the further exploitation of the idea of hybridization of the well-known efficient heuristic algorithms, namely, simulated annealing (SA) and tabu search (TS). The important feature of our algorithm is the so-called "cold restart mechanism", which is used in order to avoid a possible "stagnation" of the search. This strategy resulted in very good solutions obtained during simulations with a number of the QAP instances (test data). These solutions show that the proposed algorithm outperforms both the "pure" SA/TS algorithms and the earlier author s combined SA and TS algorithm. Key words: hybrid optimization, simulated annealing, tabu search, quadratic assignment problem, simulation 1. Introduction The quadratic assignment problem (QAP) is the famous combinatorial optimization problem. It is formulated as follows. Let two matrices A = (a ij ) n n and B = (b kl ) n n and the set Π of permutations of the integers from 1 to n be given. Find a permutation π = ( π(1), π(),..., π(n) ) Π that minimizes z(π) = n i=1 j=1 n a ij b π(i)π(j). (1.1) One of the important applications of the QAP is computer-aided design (CAD), namely, the placement of electronic components [3, 6, 40]. In this context, the entries of the matrix A = (a ij ) n n can be interpreted as the numbers of connections
166 150 A. Misevičius (nets) between components. The entries of the matrix B = (b kl ) n n represent distances between locations (positions). The permutation π = ( π(1), π(),..., π(n) ) corresponds to a certain placement of components to locations (π(i) denotes the location that component i is placed into). Thus, z, or more precisely 1 z, can be treated as an estimation of total wire length obtained when n components are placed into n locations (see Fig. 1). Description of the other applications of the QAP one can be found in [7, 8, 10]. Figure 1. Graphical interpretation of the quadratic assignment problem. For given matrices A and B the permutation corresponding to optimal assignment is as follows:(,3,1,4). The connection length that corresponds this assignment is equal to 1. It has been proved that the QAP (like many other combinatorial optimization problems) is NP-hard [38]. For example, QAPs of size n > 36 are not, to this date, practically solvable in terms of obtaining exact solutions. Therefore, heuristic techniques have to be used for solving medium- and large-scale QAPs (see, for example, [14, 15, 16, 9, 3, 41]; for a more detailed list of heuristics for the QAP, see [8, 10, 37]). First we introduce some basic definitions related to the combinatorial (discrete) optimization. So, let S be a set of solutions of a combinatorial optimization problem with an objective function f : S R 1 (without loss of generality, we assume that f seeks a global minimum). Furthermore, let N : S S be a neighbourhood function which defines for each s S a set N(s) S a set of neighbouring solutions of s. Each neighbouring solution s N(s) can be reached directly from the current solution s by an operation, which is called a move. Usually, the move follows the objective function evaluation which is called a trial. An iteration is said to be performed when N(s) trials are done. Regarding the QAP, Π = {π π = (π(1), π(),..., π(n))}, where Π = n!, corresponds to S, and z (defined according to (1.1)) plays a role of the objective function. In the case of the QAP, the commonly used neighbourhood function is socalled -exchange (pairwise exchange) function N which can be defined as follows: N (π) = {π π Π, ρ(π, π ) = }, (1.)
167 An improved hybrid optimization algorithm for the QAP 151 where π Π and ρ(π, π ) is a "distance" between the current permutation π and the neighbouring one π : ρ(π, π ) = n sgn π(i) π (i). i=1 In this case, a move from the permutation π to the permutation π can formally be defined by using a -way perturbation operator p ij : Π Π ( i, j = 1,,..., n; i j ), which exchanges ith and jth elements in the current permutation (notation π = π p ij means that π is obtained from π by applying the perturbation p ij ). For a permutation π and a perturbation p ij, it is more efficient to compute z(π, i, j) = z(π p ij ) z(π) than z(π p ij ) : the direct computation of z(π p ij ) needs time O(n ), whereas z(π, i, j) can be calculated in O(n) operations: z (π, i, j) = (a ij a ji ) ( ) [ b π(j)π(i) b π(i)π(j) + (aik a jk ) k=1,k i,j ( b π(j)π(k) b π(i)π(k) ) + (aki a kj ) ( b π(k)π(j) b π(k)π(i) )], (1.3) where a ii (b ii ) = const, i = 1,,..., n. Moreover, for two consecutive permutations π and π = π p uv, if all the values z(π, i, j) have been stored (i.e. already calculated in previous iteration), then the values z(π, i, j) = z(π p ij z(π ), i u, v, j (u, v) can be computed in time O(1) [4]: z (π, i, j) = z (π, i, j) + (a iu a iv + a jv a ju )(b π(i)π(u) b π(i)π(v) + b π(j)π(v) b π(j)π(u) ) + (a ui a vi + a vj a uj ) (b π(u)π(i) b π(v)π(i) + b π(v)π(j) b π(u)π(j) ). (1.4) However, if i = u or i = v or j = u or j = v, then the formula (1.3) should be applied. Two main alternatives exist when exploring the neighbouring solutions. First, choose the next potential solution at random. Second, explore the neighbourhood in a systematic way. In the case of the -exchange neighbourhood function N, the order of search can be established by a sequence {p i (k) j (k) }. The indices i(k), j (k) are easily determined by the following expression { i (k) = iif(j (k 1) < n, i (k 1), iif(j (k 1) < n 1, i (k 1) + 1, 1)), j (k) = iif(j (k 1) < n, j (k 1) + 1, i (k) + 1), where { y1, if x is true iif(x, y 1, y ) = y, otherwise;
168 15 A. Misevičius k is the current trial number (k = 1,,...); i (k), j (k) are new indices; i (k 1), j (k 1) are old indices (i (0) = 1, j (0) = 1), K = N = n(n 1)/ trials are needed in order to explore all the solutions of N. The remaining part of this paper is organized as follows. In Section hybrid optimization strategies (paradigms) are outlined, whereas in Sections 3, 4 we survey the simulated annealing (SA) and tabu search (TS) techniques, which were used in our hybrid approach. Section 5 describes an improved hybrid optimization algorithm for the quadratic assignment problem. The results of simulations are presented in Section 6. Finally, Section 7 completes the paper with concluding remarks.. Hybrid optimization strategies Over the last years, hybrid optimization algorithms have become very popular among researchers in combinatorial optimization. First of all, this is due to promising results obtained by using hybrid (combined) approaches. Combinations of both singlesolution algorithms (such as greedy heuristic search, simulated annealing, tabu search) and population-based algorithms (such as genetic, evolutionary algorithms) have been proven to be extremely efficient for many combinatorial optimization problems [17, 19, 36]. Different hybrid meta-heuristics, i.e. paradigms of hybridization of heuristics can be proposed [43]. Further, two simple paradigms are outlined very roughly: first, a sequential hybridization, second, an embedded hybridization. Without loss of generality, we discuss the hybrid scheme that consists of two heuristics only. procedure sequential_hybridization /* H 1 + H +... */... apply heuristic H 1; apply heuristic H ;... end Figure. Pseudo-code for the framework of the sequential hybrid meta-heuristic. So, in the first case, the self-contained heuristics H 1 and H are executed in a sequence (one after other), the heuristic H using the output of the heuristic H 1 as its input (i.e. the heuristics act in a pipeline fashion). Here, H can also be thought of as a "post-analysis" procedure which is applied to the solution found by H 1. For example, a greedy (or more sophisticated) heuristic can be used to generate good initial solutions for the genetic/evolutionary algorithm [19]. In the second variant, the heuristic H is embedded into heuristic H 1 (i.e. heuristics act as cooperating agents). For example, deterministic local search technique may be embedded into simulated annealing (as proposed in [31]) or genetic algorithm (see, for example, [1, 17, 19]). For a more formal presentation of the above paradigms, see Figures,3.
169 An improved hybrid optimization algorithm for the QAP 153 procedure embedded_hybridization /*H 1(H (...)) /... apply heuristic H 1;... end procedure H 1... apply heuristic H ;... end Figure 3. Pseudo-code for the framework of the embedded hybrid meta-heuristic. However, disposing of these two hybridization paradigms only may be insufficient for complex combinatorial problems, like the quadratic assignment problem. These problems can be seen as highly "discontinuous": if one "walks" in a fictitious solution space, the qualities of the solutions can differ dramatically, i.e. the "landscapes" of these problems are very rugged. Another distinguishing feature is a presence of a big number of local optima, which are often spread over the whole solution space (see Figure 4). Figure 4. Example of a complex "landscape". In these situations, the strategies described above usually face a phenomenon called a "stagnation" of the search (also known as a "chaotic attractor" [5]). This means that the search trajectory is confined in a limited part (region) of the solution space: if this part does not contain the global optimum, it will never be found. An enhanced hybrid strategy (we call it an iterative hybridization) is designed in order to try to overcome these difficulties. In fact, this hybridization strategy is an extension of the sequential hybridization. The extension is constructed in such a manner that self-contained heuristics, say H 1 and H, are used in a cyclic (iterative) way, i.e. the heuristic H uses the output of the heuristic H 1, and the heuristic H 1 uses the output of the heuristic H (starting from the second iteration). The paradigm of the iterative hybrid strategy is shown in Fig. 5. In our hybrid optimization algorithm for the QAP, which will be presented in Section 5, we use simulated annealing approach based procedure in the role of
170 154 A. Misevičius procedure iterative_hybridization /*(H 1 + H + ) + (H 1 + H +...) +...*/... repeat apply heuristic H 1; apply heuristic H ;... until termination criterion satisfied end Figure 5. Pseudo-code for the framework of the iterative hybrid meta-heuristic. the heuristic H 1, and tabu search approach based procedure as the "post-analysis" heuristic H. Note that hybridization of SA and TS was also used for solving the other problems (see, for example, [18, 36, 45].) Before describing the details of our hybrid algorithm, we give short overviews of SA and TS approaches. 3. Simulated annealing Simulated annealing originated in statistical mechanics. It is based on a Monte Carlo model that was used by Metropolis et al., 1953 [33], to simulate energy levels in cooling solids. Boltzmann s law was used to determine the probability of accepting a perturbation resulting in a change E in the energy at the current temperature t : { 1, E < 0, P = e E/Ct, E 0, where C is a Boltzmann s constant. Cerny, 198 [11], and Kirkpatrick et al., 1983 [7] have applied firstly SA to solve combinatorial optimization problems. Several researchers tested SA on the QAP, as well [6, 13, 35, 44]. The principle of the simulated annealing is simple: start from a random solution. Given a solution s select a neighbouring solution s and compute the difference of the objective function values, f = f(s ) f(s). If the objective function value is improved ( f < 0), then replace the current solution by the new one, i.e. perform a move, and use resulting configuration as a starting point for the next trial. If f 0, then accept a move with probability P ( f) = e f/t, (3.1) where t is the current temperature (Boltzmann s constant is not required when we apply the algorithm to combinatorial problems). Regarding the above probabilistic acceptance, it is achieved by generating a random number in [0,1] and comparing it against the threshold e f/t (here, the exponential function plays a role of an acceptance function). The procedure is repeated until a termination criterion is satisfied, for example, a predefined number of trials has been performed. As a resulting solution, usually the "best so far" (BSF) solution (instead of so-called "where you are" (WYA) solution) is returned by the algorithm. The paradigm of SA in a high-level algorithmic language form is presented in Fig. 6.
171 An improved hybrid optimization algorithm for the QAP 155 procedure simulated_annealing /* input: s (0) the initial solution; output: s the best solution found */ set s = s (0), s = s; determine the initial temperature t 0, set t = t 0; repeat /* main cycle */ select new solution s from the neighbourhood of the current solution s; calculate f = f(s ) f(s); generate uniform random number r from the interval [0,1]; if ( f < 0) or (r < e f/t ) then set s = s ; /* replace the current solution by the new one*/ if f(s) < f(s ) then set s = s; /* save the best so far solution */ update the temperature t; until stopping condition is satisfied end Figure 6. Pseudo-code for the simulated annealing. SA algorithms differ mainly with respect to a cooling (annealing) schedule implemented. The cooling schedule, in turn, is specified by: a) an initial (and final) value of the temperature, b) an updating function for changing the temperature. The most important thing is how the initial temperature t 0 is specified. If the initial value of the temperature is chosen too high, then too many bad uphill moves are accepted, while if it is too low, then the search will quickly drop into a local optimum without possibility to escape form it. Thus, an optimum initial temperature must be somewhere between these two extremes. The temperature is not a constant, but changes over time according to the updating function. One of the popular updating functions (known as Lundy-Mees schedule) is characterized by the following relation [30]: t k+1 = t k 1 + βt k, k = 0, 1,..., t 0 = const, β << t 0. (3.) It is easy to relate the coefficient β and the number of trials, i.e. the schedule length, L, under condition that the initial and final values of the temperature (t 0, t f ) are predefined: β = t 0 t f Lt 0 t f. (3.3) In theory, the simulated annealing procedure should be continued until the final temperature t f is zero, but in practice the other stopping criteria are applied, for example: a) the value of the objective function has not decreased for a large number of consecutive trials; b) the number of accepted moves has become less than a certain small threshold for a large number of consecutive trials;
172 156 A. Misevičius c) a fixed a priori number of trials/iterations has been executed. For more details about simulated annealing, the reader is referred to [1,, 8]. 4. Tabu search Tabu search technique was developed by Hansen and Jaumard, 1987 [4], and Glover, 1989, 1990 [0, 1]. TS has been proven to be a powerful tool for solving many combinatorial problems, among them the QAP (see, for example, [5, 14, 39, 4]). Tabu search, like simulated annealing, is based on the neighbourhood search with local-optima avoidance but in a rather deterministic way. The key idea of tabu search is allowing climbing moves when no improving neighbouring solution exists. However, some moves are to be forbidden at a present search iteration in order to avoid cycling. TS starts from an initial solution s, maybe, randomly generated in S and moves repeatedly from a solution to a neighbouring one. At each step of the procedure, a set (subset) N(s) of the neighbouring solutions of the current solution s is considered and the move that improves most the objective function value f is chosen. If there are no improving moves, TS algorithm chooses one that least degrades (increases) the objective function, i.e. a move is performed to the best neighbour s in N(s) (even if f(s ) > f(s)). In order to avoid returning to the local optimal solution just visited, the reverse move must be forbidden (prohibited). This is done by storing this move (or an attribute of the move) in a memory (or more precisely short-term-memory) managed like a circular list T and called a tabu list. The tabu list keeps information on the last h (h = T ) moves which have been done during the search process (the parameter h is called a tabu list size). Thus, a move from s to s is considered as tabu if it (or its attribute) is contained in the list T. This way of proceeding hinders the algorithm from returning to a solution reached in the last h iterations. However, it might be worth returning after a while to a solution visited previously to search in another direction. Consequently, an aspiration criterion is introduced to permit the tabu status to be dropped under certain favourable circumstances. Typically, a tabu move from s to s is permitted if f(s ) < f(s ), where s is the best solution found so far. The resulting decision rule within TS may thus be described as follows: replace the current solution s by the new solution s, if f(s ) < f(s ) or (s = arg min f(s ) and s is not tabu). (4.1) s N(s) The whole process is stopped as soon as a termination criterion is satisfied (for example, a fixed a priori number of trials has been performed). The tabu search paradigm is shown in Figure 7. The TS algorithms differ mainly with respect to the basic ingredients discussed above (i.e. tabu list, aspiration criterion) and other additional features (for example, a long-term-memory, diversification mechanisms, etc.). The main forms of the tabu search are: deterministic tabu search (strict tabu search, fixed tabu search, reactive tabu search) and stochastic tabu search (probabilistic tabu search, robust tabu search). For more details on the TS technique, the reader is addressed to [, 5].
173 An improved hybrid optimization algorithm for the QAP 157 procedure tabu_search /* s (0) s! #"$ % */ set s = s (0), s = s; initialize the tabu list T ; repeat /* main cycle*/ given neighbourhood function N, tabu list T and aspiration criterion, find the best possible solution s N(s); set s = s ; /* & ')(* (+ &&, -.,/0 +1 */ insert the solution s (or its attribute) into the tabu list T ; if f(s) < f(s ) then set s = s /*435 * -6"$)&! */ update the tabu list T (or its size) (if necessary) until stopping condition is satisfied end Figure 7. Pseudo-code for the tabu search. 5. An improved hybrid simulated annealing and tabu search algorithm for the QAP Now we describe details of our hybrid strategy for the QAP. It is distinguished for the following structure: 1) simulated annealing algorithm, ) tabu search algorithm, and 3) hybridization scheme Simulated annealing algorithm for the QAP (SA-QAP) One of the important features of our implementation of the simulated annealing is that we use an extended approach of determining the values of the initial and final temperatures (these values are crucial for the SA algorithm, as mentioned in Section 3). Typically, the initial (and final) temperature is a function of the minimum and maximum differences in the objective function values obtained by performing a fixed number of moves before starting the annealing [13]. In our SA algorithm, we ignore the maximum difference; instead, we use the average difference. The formula of calculating the initial and final temperatures (t 0, t f ) looks, thus, as follows: { t0 = (1 λ 1 ) z min + λ 1 z avg, t f = (1 λ ) z min + λ z avg, (5.1) where z min, z avg are, respectively, the minimum and average differences in the objective function values; λ 1 (0, 1]; λ [0, 1); λ 1 > λ. In fact, the execution of the algorithm is controlled by operating with these factors. By choosing appropriate values of λ 1 and λ, one can control the cooling process flexibly. For example, having λ = const it is obvious that the larger the value of λ 1, the higher the initial temperature; on the other hand, the larger the difference λ 1 λ, the more "rapid" the cooling. We use λ 1 = 0.5 and λ = 0.05.
174 158 A. Misevičius Another property of the SA algorithm is related to an intelligent annealing technique. The key idea is that the temperature is not monotone decreasing, but oscillating; that is, a re-annealing (a repeating sequence of coolings and heatings) is considered instead of the straightforward annealing (see also [3, 6]). We propose the re-annealing technique which is based on so-called dynamic cooling schedule. The parameters of this schedule (schedule length, initial and final temperatures) are adaptively changed during execution of the algorithm. We use a Lundy-Mees function based temperature oscillation (LM-oscillation) that is "process-dependent", i.e. it depends upon the former "behaviour" of the (re)annealing. The schedule is as follows: set the schedule length L to Q SA n(n 1)/ (Q SA 1) and start with the initial temperature defined by the formula (5.1). The temperature is then being updated according to the formula (3.), the coefficient β is known from the formula (3.3). When 0.5 N = n(n 1)/4 consecutive moves are rejected, stop the (preliminary) cooling. After cooling is stopped, the temperature is immediately increased (i.e. the system is "heated up"), and the annealing with the new parameters starts. Additionally, a deterministic downhill search procedure CRAFT [4] is applied to the best solution found. The process is continued until a stopping criterion is satisfied, i.e. the current iteration number exceeds Q SA, where Q SA is the maximum number of iterations. The detailed template of the SA algorithm for the QAP (SA-QAP) is presented in Figure 8 (see also [35]). 5.. Tabu search algorithm for the QAP (TS-QAP) Our version of the tabu search algorithm for the QAP is based on a slightly modified robust tabu search (RTS) procedure due to Taillard [4]. Very roughly, our algorithm consists of maintaining the tabu list T by constructing and updating it. The tabu list is organized as an n n integer matrix T = (t ij ) n n, where n is the problem size. At the beginning, all the entries of T are set to zero. As the search progresses, the entry t ij stores the current number of the iteration plus the tabu list size, h, i.e. the number of the future iteration starting at which ith and jth elements of the permutation may again be interchanged. In this case, a move consisting of exchanging ith and jth elements is tabu if the value of t ij is equal or greater than the current iteration number (this means that ith and jth elements were interchanged during the last h iterations). The tabu list size h is not a constant it is changed randomly during the search process. In our implementation, h is chosen between h min = 0.4n and h max = 0.6n and changed every h max iterations. The standard aspiration criterion is used, i.e. the tabu status of a move is ignored (a tabu move is allowed to be selected) if the move results in a solution (permutation) that is better than the best one found so far. In addition, we use the formula (1.4) to accelerate the evaluation of the neighbouring solutions of the current solution. Thus, the complete evaluation of the - exchange neighbourhood takes O(n ) operations, except the first iteration, which takes O(n 3 ) operations (see formula (1.3). The run time of the tabu search procedure is controlled by the number of iterations, QTS. The detailed template of the TS algorithm (TS-QAP) is presented in Figure 9.
175 An improved hybrid optimization algorithm for the QAP 159 procedure SA-QAP /* 4 %#) & "$)&- */ /* input: π the current (initial) permutation, n the problem size */ /* Q SA the number of iterations (Q SA 1) */ /* λ 1, λ the initial and final temperature factors (0 < λ 1 1, 0 λ < 1, λ 1 > λ ) */ /* output: π the best permutation found */ π = π; found z min, z avg by performing n(n 1)/ random moves starting from π; M := Q SAn(n 1)/, L 0 := M; /* M the number of trials, L 0 the initial cooling schedule length */ initialize cooling schedule parameters L, t 0, t f, β; t := t 0, i := 1, j := 1, rejected_count := 0, oscillation := F ALSE ; for k := 1 to M do begin /* main loop */ i := iif(j < n, i, iif(i, n 1, i + 1, 1)), j := iif(j < n, j + 1, i + 1); calculate = z(π, i, j); /* z(π, i, j) is the current difference of the objective function values */ if < 0 then accept := T RUE else begin generate uniform random number r from the interval [0,1]; if r < exp( /t) then accept := T RUE else accept := F ALSE end /* else */ if accept = T RUE then begin π := π p ij; /* replace the current permutation by the new one */ if z(π) < z(π ) then π := π; /* save the best permutation found so far */ if 0 then rejected_count := 0 end else rejected_count := rejected_count + 1; if (rejected_count n(n 1)/4) or (t is at lowest point) then begin if oscillation = F ALSE then begin L := k, t := t, oscillation := T RUE end update cooling schedule parameters L, t 0, t f, β; t := t 0; /* &! *( &&+ 0 +& ) & */ apply CRAF T to π end else t := t(1 + βt) /* decrease the current temperature */ end /* main loop */ end Figure 8. Pseudo-code of the simulated annealing algorithm for the QAP. Here z(π, i, j) is calculated according to (1.3) Hybridization scheme The hybridization scheme used is as follows. At the beginning, an initial solution is generated in a random way with the subsequent improving by means of the simulated annealing algorithm (SA-QAP). Then, an iterative hybrid process starts. It consists
176 160 A. Misevičius procedure TS-QAP /* tabu search algorithm for the QAP */ /*input: π the current permutation, n the problem size */ /* Q T S the number of iterations (Q T S 1), */ /* h min, h max lower and higher tabu list sizes (h min < h max) */ /* output: π the best permutation found */ π := π; for i := 1 to n 1 do for j := i + 1 to n do calculate δ ij = z(π, i, j); T := 0, i := 1, j := 1; for q := 1 to Q T S do begin /* main loop */ if q mod h max = 1 then h := randint(h min, h max); min := ; for k := 1 to N do begin /* find the best move */ i := iif(j < n, i, iif(i < n 1, i + 1, 1)), j := iif(j < n, j + 1, i + 1); tabu := iif(t ij q, T RUE, F ALSE ), aspired := iif(z(π) + δ ij < z(π ), T RUE, F ALSE ); if ((δ ij < min) and (tabu = F ALSE )) or (aspired = T RUE ) then begin u := i, v := j; if aspired = T RUE then min := else min := δ ij end /* if */ end /* for */ if min < then begin /* perform the move: replace the current permutation by the new one */ π := π p uv for l := 1 to n 1 do for m := l + 1 to n do update the difference δ lm ; t uv := q + h; /* update the tabu list */ if z(π) < z(π ) then π := π /* save the best so far permutation */ end end /* main loop */ end Figure 9. Pseudo-code of the tabu search algorithm for the QAP, here z(π, i, j) is calculated according to the formula (1.3), while the difference δ lm is updated according to (1.4). The function "randint(x, y)" returns a random integer, uniformly distributed between x and y. of two main phases, as mentioned in Section : simulated annealing (SA-QAP) and tabu search (TS-QAP). In addition, a diversification mechanism is used. The role of such a mechanism play mutations that can be seen as strings of random elementary perturbations (pairwise interchanges), like p ij. The mutations may also be viewed as moves in higher-order neighbourhoods N µ, where < µ n, here, the parameter µ is referred to as a mutation level (rate). It is obvious that the large value of µ, the stronger the mutation, and vice versa. The template of the mutation procedure based on random interchanges is presented in Figure 10. A corresponding example is shown in Figure 11. We can add more robustness to the mutation process by letting the parameter µ vary in some interval, say [µ min, µ max ] [3, n]. In our implementation, µ varies in the following way: at the beginning, µ is equal to µ min ; once the maximum value
177 An improved hybrid optimization algorithm for the QAP 161 procedure ri-mutation /* random interchanges based mutation operator (ri-mutation) for the QAP */ /* input: π the current permutation, n the problem size, µ the mutation lavel (µ [3, n]) */ /* output: π the mutated permutation */ for k := 1 to µ do begin choose i, j, randomly, uniformly, 1 i, j n, i j π := π p ij /* interchange ith and jth elements in the current permutation */ end /* for k */ end Figure 10. Pseudo-code of the random interchanges based mutation. Figure 11. Example of ri mutation. µ max has been reached (or a better locally optimum solution has been discovered), the value of µ is immediately dropped to the minimum value µ min, and so on. Note that the mutations are to be applied to the locally optimum solutions only. The specific feature of our hybridization scheme is that if the current locally optimum solution remains unchanged for a long time (a "stagnation" of the search takes place), then a "cold restart" of the search is carried into effect. As a "cold restart", we use the construction (generation) of a new random solution coupled with the simulated annealing algorithm the same that it used at the initialization phase. The purpose of such a restart is to add more diversity to the search, more precisely, to explore new regions of the solution space: continuing the search from the new random solution may allow to escape from a "deep" local optimum and to find better ones. The frequency of "cold restarts" is controlled by means of a special parameter, a restart interval, v, which can be related to the problem size, n, i.e. v = ωn, where ω is a factor of the restart frequency (0 < ω < Q/n, Q is the total number of iterations of the hybridized algorithm. The template of the resulting hybrid optimization algorithm entitled as IH-SA- TS-QAP (improved hybrid SA and TS algorithm for the QAP) is shown in Figure Simulation results We have carried out a number of simulations in order to test the performance of our improved hybrid algorithm IH-SA-TS-QAP. The well-known QAP instances (test data) taken from the quadratic assignment problem library QAPLIB [9] (see also
178 16 A. Misevičius procedure IH-SA-TS-QAP /* improved hybrid simulated annealing-tabu search algorithm for the QAP */ /* input: A, B the connection and distance matrices, n the problem size */ /* Q the number of cycles (global iterations) of the hybrid algorithm */ /* Q SA the number of iterations of the simulated annealing procedure */ /* Q T S the number of iterations of the tabu search procedure */ /* λ 1, λ, h min, h max, µ min, µ max, the control parameters */ /* output: π the best permutation found */ generate random (initial) permutation π; apply SA-QAP to π with the parameters Q SA, λ 1, λ, and get the resulting permutation π ; π := π ; q := 0; /* q is the current number of iteration at which the new local optimum has been found */ µ := µ min 1; /* µ is the current mutation level */ v := ωn; /* v is the restart interval (period) */ for q := 1 to Q do begin /* main cycle */ apply TS-QAP to π with the parameters Q T S, h min, h max, and get the resulting permutation π ; if z(π ) < z(π ) then begin π := π, q := q, µ := µ min 1 /* save the best so far permutation and reset the control parameters*/ end if q q > v then begin generate new random permutation π ; /* perform a "cold restart" */ apply SA-QAP to π with the parameters Q SA, λ 1, λ, and get the resulting permutation π ; if z(π ) < z(π ) then π := π ; /* save the best so far permutation */ q := q, µ := µ min 1 end else begin µ := iif(µ < µ max, µ + 1, µ min); apply mutation to π with the level µ, /*i.e. perform µ random perturbations */ and get the permutation π; π := π /* π is the mutated permutation to be processed by TS procedure */ end end /* for q */ end Figure 1. Pseudo-code of the improved hybrid simulated annealing and tabu search algorithm for the QAP.
179 An improved hybrid optimization algorithm for the QAP were used. The following algorithms were used for comparison: 1) The simulated annealing algorithm by Boelte and Thonemann (coded by the author according to the description presented in the paper of Boelte and Thonemann [6]; the algorithm is entitled as TBM-QAP); ) The robust tabu search algorithm by Taillard [4] (it is entitled as RTS-QAP); 3) The combined simulated annealing and tabu search algorithm by Misevičius [34] (entitled as SA-TS-QAP). Table 1. Comparison of the algorithms for the QAP. The values of the average deviation ( Θ), the percentage of 1% optimality (P 1% ), and the CPU time (in seconds) are given. The values of the best average deviations are printed in bold face. Instance n BKV TBM-QAP RTS-QAP SA-TS-QAP IH-SA-TS-QAP Average name Θ P1% Θ P1% Θ P1% Θ P1% CPU time nug sko sko sko sko sko sko sko sko100b sko100c sko100d sko100e sko100f tho tho wil wil The performance measures used are the following: 1) the average deviation from the best known solution Θ = 100( z z)/ z[%], where z is the average objective function value over W = 1,,... restarts (i.e. single applications of the algorithm to a given instance) and z is the best known value (BKV) of the objective function, BKVs are from [9]; ) the percentage of solutions that are within 1% optimality P 1% = 100C 1% /W, where C 1% is the total number of solutions that are within 1% optimality over W restarts. All the simulations were carried out on 300 MHz Pentium computer by using the optimization package (sub-system) OPTIQAP (OPTImizer for the QAP) developed
180 164 A. Misevičius by the author at Dept. of Practical Informatics of Kaunas Univ. of Technology. The computations were organized in such a way that all the algorithms use identical initial assignments and require similar CPU times (the execution time is controlled by the number of iterations). The results of the comparison, i.e. the average deviations from BKV and percentage of solutions that are within 1% optimality for each of the algorithm tested, as well as CPU times per restart are presented in Table 1. The parameters of IH-SA-TS-QAP used in simulation are as follows: Q = 1, Q SA = 50, Q T S = 5Q SA = 50, λ 1 = 0.5, λ = 0.05, µ min = 0.35, µ max = Let us note, that as long as the number of cycles, Q, is equal to 1, the parameter ω can be omitted. The number of restarts, W, is equal to 100. Table. Computational results of IH-SA-TS-QAP with the various numbers of iterations. The values of the average deviation ( Θ), and the CPU time (in seconds) are given. In addition, in parenthesis we give the numbers of times that BKV is found. Θ, time Instance name 1st (W = 30) nd (W = 30) 3rd (W = 0) 4th (W = ) 5th (W = 10) nug [9] [9] sko [11] [8] sko [] [6] [16] sko [1] [3] [19] [14] sko [3] [8] [19] sko [0] [0] [0] [] [6] 50 sko [0] [0] [] [] [4] 700 sko [0] [0] [1] [0] [5] 300 sko100a 0.33 [0] [0] [1] [] [1] 4300 sko100b 0.1 [0] [0] [0] [1] [1] 400 sko100c 0.09 [0] [0] [1] [1] [5] 4100 sko100d 0.99 [0] [0] [0] [0] [] 4300 sko100e 0.43 [0] [0] [1] [1] [] 4400 sko100f 0.78 [0] [0] [0] [1] [] 4300 tho [] tho [1] [6] [6] [8] [8] 660 wil [4] [19] [19] [14] wil100a [0] [0] [0] [] [4] 4500 It turns out that the efficiency of the algorithms depends on the QAP instance being solved. Nevertheless, the results from Table 1 show that our hybrid optimization algorithm IH-SA-TS-QAP appears to be superior to other three efficient algorithms with respect to both performance measures, especially, the average deviation. The difference in efficiency on particular instances is quite significant (see, for example, the results of RTS-QAP and IH-SA-TS-QAP obtained for the instances sko100a sko100f, or wil50, wil100).
181 An improved hybrid optimization algorithm for the QAP 165 The results of IH-SA-TS-QAP can be improved even more by increasing the values of the control parameters Q and/or Q SA (Q T S ) but at the cost of a longer processing time. Five long runs were carried out in order to demonstrate the improvement of the quality of solutions. At each long run, the different values of the parameters Q, Q SA, Q T S are used: 1st run : Q = 30, Q SA = 50, Q T S = 50, ω = 0.3; nd run : Q = 100, Q SA = 50, Q T S = 500, ω = 0.3; 3rd run : Q = 00, Q SA = 300, Q T S = 1000, ω = 0.1; 4th run : Q = 00, Q SA = 500, Q T S = 1500, ω = 0.05; 5th run : Q = 300, Q SA = 1000, Q T S = 3000, ω = 0.03; the values of the other control parameters remain the same, except the parameter ω. Table shows the results obtained. These results are very promising (see 5th column of Table ): for small and medium instances (n 64) (except the instance tho40), the average deviation from the best known values of the objective function is equal to zero; while, for large instances (n = 100), the deviation is less than 0.0%. It can be seen from the results of 5th run that, for all the large instances tested, at least one restart (out of ten) of IH- SA-TS-QAP resulted in finding the best known solution. Moreover, for the instances sko100c and wil100, BKV was reached 5 and 4 times, respectively. This indicates that the solutions obtained for these instances are, most likely, pseudo-optimal. To our knowledge, the pseudo-optimality of the solutions for these instances has not been reported yet in the literature. It also should be stressed that even finding BKV for these instances is quite complicated task, for example, in [16], it was reported that to improve on the best known solutions for the instances sko100* on SPARC 10 processor, it took almost 4 hours of computation time. In a more recent work [9], an efficient genetic algorithm could not find BKV for any of these instances. It took up to 900 seconds on DEC Alpha Server 8400 to find the solutions with the average deviation around 0.3% only. 7. Concluding remarks The quadratic assignment problem is one of hard combinatorial optimization problems. In order to obtain near-optimal or optimal solutions for this problem within reasonable times, heuristic techniques are to be applied. One of them, an improved hybrid optimization algorithm, has been proposed in this paper. Based on the well-known simulated annealing and tabu search approaches, as well as the intelligent hybridization strategy, we have developed an effective algorithm for the QAP IH-SA-TS-QAP (improved hybrid SA and TS algorithm for the QAP), which is an extension of the earlier author s hybrid algorithm. IH-SA-TS- QAP is distinguished for the so-called iterative hybridization scheme a result of the elaborations of possible hybrid heuristic paradigms.
182 166 A. Misevičius The additional features of our algorithm are the diversification and "cold restart" mechanisms that are used in order to try to avoid a possible "stagnation" of the search. These mechanisms and the refined hybridization scheme resulted in high quality solutions obtained during the simulations with a number of the QAP instances (test data) from the QAP library QAPLIB. These solutions indicate that, for the QAP instances examined, the proposed algorithm appears to be superior to the "pure" simulated annealing and tabu search algorithms, as well as the earlier author s hybrid (combined) SA and TS algorithm. Thus, it may be considered to be one of the most efficient single-solution algorithms for the QAP. Regarding the future work, the emphasis on the further extensions of the proposed hybrid approach should be made. Both the elaboration of the hybridization scheme and improvements of its basic components (i.e. SA and TS procedures) are possible, for example: a) introducing new cooling schedules for the SA algorithm; b) applying other tabu conditions/aspiration criteria for the TS algorithm; c) trying a more accurate adjustment (tuning) of the control parameters (the initial and final temperatures, the tabu list sizes, etc). It might also be worthy to incorporate the proposed hybrid algorithm into other (population-based, hybrid) meta-heuristics, for example, genetic and evolutionary algorithms, as a very efficient local search procedure. References [1] E.H.L. Aarts and J.H.M. Korst. Simulated Annealing and Boltzmann Machines. Wiley, Chichester, [] E.H.L. Aarts, J.H.M. Korst and P.J.M.van Laarhoven. Simulated annealing. In: E. Aarts and J.K. Lenstra(Eds.), Local Search in Combinatorial Optimization, Wiley, Chichester, 91 10, [3] S. Amin. Simulated jumping. Annals of Operations Research, 86, 3 38, [4] G.C. Armour and E.S. Buffa. A heuristic algorithm and simulation approach to relative location of facilities. Management Science, 9, , [5] R. Battiti and G. Tecchiolli. The reactive tabu search. ORSA Journal on Computing, 6, , [6] A. Boelte and U.W. Thonemann. Optimizing simulated annealing schedules with genetic programming. European Journal of Operational Research, 9, , [7] R.E. Burkard. Quadratic assignment problems. European Journal of Operational Research, 15, 83 89, [8] R.E. Burkard, E. Çela, P.M. Pardalos and L. Pitsoulis. The quadratic assignment problem. In: Handbook of Combinatorial Optimization, volume 3, Kluwer, Dordrecht, , [9] R.E. Burkard, S. Karisch and F. Rendl. QAPLIB a quadratic assignment problem library. Journal of Global Optimization, 10, , [10] E. Çela. The Quadratic Assignment Problem: Theory and Algorithms. Kluwer, Dordrecht, [11] V. Cerný. A thermodynamical approach to the traveling salesman problem: an efficient simulation algorithm. In: Tech. Report, Comenius University, Bratislava, CSSR, 198.
183 An improved hybrid optimization algorithm for the QAP 167 [1] H. Chen and N.S. Flann. Parallel simulated annealing and genetic algorithms: a space of hybrid methods. In: Proceedings of Third Conference on Parallel Problem Solving from Nature, Berlin, Springer, Jerusalem, Israel, , [13] D.T. Connolly. An improved annealing scheme for the QAP. European Journal of Operational Research, 46, , [14] Z. Drezner. Heuristic algorithms for the solution of the quadratic assignment problem. Journal of Applied Mathematics and Decision Sciences, 6, , 00. [15] Z. Drezner. A new genetic algorithm for the quadratic assignment problem. INFORMS Journal on Computing, 003. (in press) [16] C. Fleurent and J.A. Ferland. Genetic hybrids for the quadratic assignment problem. In: Quadratic Assignment and Related Problems. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, volume 16. AMS, Providence, , [17] C. Fleurent and J.A. Ferland. Genetic and hybrid algorithms for graph coloring. Annals of Operations Research, 63, , [18] B.L. Fox. Integrating and accelerating tabu search, simulated annealing and genetic algorithms. Annals of Operations Research, 41, 47 67, [19] B. Freisleben and P. Merz. A genetic local search algorithm for solving symmetric and asymmetric traveling salesman problems. In: Proceedings of the IEEE International Conference on Evolutionary Computation (ICEC 96), Nagoya, Japan, , [0] F. Glover. Tabu search: part I. ORSA Journal on Computing, 1, , [1] F. Glover. Tabu search: part II. ORSA Journal on Computing,, 4 3, [] F. Glover and M. Laguna. Tabu search. Kluwer, Dordrecht, [3] M. Hanan and J.M. Kurtzberg. Placement techniques. In: Design Automation of Digital Systems: Theory and Techniques, volume 1. Prentice-Hall, Englewood Cliffs, 13 8, 197. [4] P. Hansen and B. Jaumard. Algorithms for the maximum satisfiability problem. RUTCOR Search Report 43-87, Rutgers University, USA, [5] A. Hertz, E. Taillard and D. de Werra. Tabu search. In: Local Search in Combinatorial Optimization, Wiley, Chichester, , [6] T.C. Hu and E.S. Kuh (Eds.). VLSI Circuit Layout: Theory and Design. IEEE Press, New York, [7] S. Kirkpatrick, Jr. C.D. Gelatt and M.P. Vecchi. Optimization by simulated annealing, volume 0. Science, [8] P.J.M.van Laarhoven and E.H.L. Aarts. Simulated Annealing: Theory and Applications. Reidel, Dordrecht, [9] M.H. Lim, Y. Yuan and S. Omatu. Efficient genetic algorithms using simple genes exchange local search policy for the quadratic assignment problem. Computational Optimization and Applications, 15, 49 68, 000. [30] M. Lundy and A. Mees. Convergence of an annealing algorithm. Mathematical Programming, 34, , [31] O. Martin and S.W. Otto. Combining simulated annealing with local search heuristics. Annals of Operations Research, 63, 57 75, [3] P. Merz and B. Freisleben. Fitness landscape analysis and mimetic algorithms for the quadratic assignment problem. IEEE Transactions on Evolutionary Computation, 4, , 000. [33] N. Metropolis, A. Rosenbluth, M. Rosenbluth, A.Teller and E.Teller. Equation of state calculation by fast computing machines. Journal of Chemical Physics, 1, , [34] A. Misevičius. Combining simulated annealing and tabu search for the quadratic assignment problem. Information Technology and Control, 3(0), 37 50, 001.
184 168 A. Misevičius [35] A. Misevičius. A new simulated annealing algorithm for the quadratic assignment problem. In: Materials of the International Conference on Production Research (ICPR-16) (Prague, Czech Republic), Prague, Czech Association of Scientific and Technical Societies, 001. [36] I.H. Osman and N. Christofides. Capacitated clustering problem by hybrid simulated annealing and tabu search. International Transactions in Operational Research, 1, , [37] P.M. Pardalos, F. Rendl and H. Wolkowicz. The quadratic assignment problem: a survey and recent developments. In: Quadratic Assignment and Related Problems. DIMACS Series an Discrete Mathematics and Theoretical Computer Science, volume 16. AMS, Providence, 1 41, [38] S. Sahni and T. Gonzalez. p-complete approximation problems. Journal of ACM, 3, , [39] J. Skorin-Kapov. Tabu search applied to the quadratic assignment problem. ORSA Journal on Computing,, 33 45, [40] L. Steinberg. The backboard wiring problem: a placement algorithm. SIAM Review, 3, 37 50, [41] T. Stuetzle. Iterated local search for the quadratic assignment problem. Technical report, Darmstadt University of Technology, [4] E. Taillard. Robust taboo search for the QAP. Parallel Computing, 17, , [43] E.G. Talbi. A taxonomy of hybrid metaheuristics. Journal of Heuristics, 8, , 00. [44] M. Wilhelm and T. Ward. Solving quadratic assignment problems by simulated annealing. IIE Transactions, 19, , [45] Q. Zeng and K.C. Mouskos. Heuristic search strategies to solve transportation network design problem. Tech. Report, New Jersey Dept. of Transportation and the National Center for Transportation and Industrial Productivity, USA, Patobulintas hibridinis optimizavimo algoritmas kvadratinio paskirstymo uždaviniui A. Misevičius Šiame straipsnyje pasi ūlytas patobulintas hibridinis euristinis optimizavimo algoritmas gerai žinomam, sudėtingam kombinatorinio optimizavimo uždaviniui, b ūtent, kvadratinio paskirstymo (KP) uždaviniui. Tai pagerinta autoriaus ankstesnio hibridinio algoritmo versija. Naujasis algoritmas pasižymi tuo, jog čia išplėtota efektyvių euristikų (atkaitinimo modeliavimo (AM) (angl. simulated annealing) ir tabu paieškos (TP) (angl. tabu search) "hibridizacijos" idėja. "Hibridizacija" remiasi vadinamaja iteracine schema: TP algoritmas panaudojamas kaip postanalizės proced ūra AM algoritmo gautajam sprendiniui, savo ruožtu, AM algoritmas taikomas sprendiniu sekai, gautai sprendiniu diversifikavimo/generavimo keliu. Svarbi pasi ūlyto algoritmo savybė yra ir ta, kad jame realizuotas vadinamasis "šaltojo pakartotinio starto" principas, kurio paskirtis padėti išvengti galimų paieškos "stagnacijos" situacijų. Naujasis algoritmas išbandytas su KP uždavinio duomenimis iš testinių pavyzdžių bibliotekos QAPLIB. Gauti eksperimentu rezultatai liudija, jog nagrinėtiems KP uždavinio pavyzdžiams si ūlomas algoritmas yra pranašesnis už ankstesnius atkaitinimo modeliavimo ir tabu paieškos algoritmus, taip pat už ankstesnį autoriaus hibridinį algoritmą.
185 !"# $ % '&)($ +*,-./ c 004 Technika ISSN MONOTONE AND CONSERVATIVE DIFFERENCE SCHEMES FOR ELLIPTIC EQUATIONS WITH MIXED DERIVATIVES 1 I.V. RYBAK Institute of Mathematics, National Academy of Sciences of Belarus 11 Surganov Str., 007 Minsk, Belarus ;:<#=?>"@A8 9BCEDFHGI@A817 Received November 13, 003; revised January 15, 004 Abstract. In the paper elliptic equations with alternating-sign coefficients at mixed derivatives are considered. For such equations new difference schemes of the second order of approximation are developed. The proposed schemes are conservative and monotone. The constructed algorithms satisfy the grid maximum principle not only for coefficients of constant signs but also for alternating-sign coefficients at mixed derivatives. The a priori estimates of stability and convergence in the grid norm C are obtained. Key words: monotone difference scheme, conservative difference scheme, elliptic equations, mixed derivatives, grid maximum principle 1. Introduction For the development of difference schemes of the high order of approximation it is important to save properties of both monotonity and conservativeness because monotone schemes lead to the well-posed systems of algebraic equations. Iterative methods converge significantly better in the case of diagonally dominant matrices. Problems of the development of difference schemes for equations with mixed derivatives were studied in papers [1,, 4, 11]. The conservative difference schemes for elliptic equations with mixed derivatives were considered in [5, p. 86], [6, p. 175], but these schemes do not satisfy the grid maximum principle. For elliptic and parabolic equations with mixed derivatives the monotone and conservative difference schemes were proposed in papers [7, 8, 10], but these schemes can be used only in the case of constant-sign coefficients. If coefficients at mixed derivatives changed their sign, then differential equation was rewritten in non-divergent 1 The author thanks Prof. Oleg Iliev and Prof. Raimondas Čiegis for the statement of the problem, Prof. Piotr Matus and Dr. Mikhail Chuiko for the discussion and useful comments
186 170 I.V. Rybak form with first derivatives and monotone schemes were developed by means of the regularization principle [5, p. 183]. But after such a transformation the property of conservativeness was lost. Such situation is typical in theory of difference schemes. In the present paper, for elliptic equations with mixed derivatives new monotone and conservative difference schemes for both constant-sign and alternating-sign coefficients are proposed. The main idea is based on using the stencil functionals with absolute values of the coefficients at mixed derivatives. For proposed difference schemes the a priori estimates of stability and convergence in the grid norm C are obtained. Numerical experiments confirm the theoretical results.. Difference scheme In the rectangle Ḡ = {0 x α l α, α = 1, } with the boundary Γ we consider the Dirichlet problem for elliptic equations with mixed derivatives Lu q(x)u = f(x), x G, (.1) u = µ(x), x Γ, x = (x 1, x ), where Lu = α,β=1 L αβ u, L αβ u = ( k αβ (x) u ), q(x) c 0 > 0. x α x β We suppose that the following ellipticity conditions are satisfied c 1 α=1 ξα α,β=1 k αβ (x)ξ α ξ β c α=1 ξα, x G, (.) where c 1, c > 0 are positive constants, ξ = (ξ 1, ξ ) is an arbitrary nonzero vector. In the rectangle Ḡ we consider the uniform grid ω h = ω h γ h : ω h = {x = (x (i1) 1, x (i) ) : x (iα) α = i α h α, h α N α = l α, i α = 0, N α, α = 1, }, where ω h is the set of inner grid nodes, γ h is the set of boundary grid nodes. Further we will use the following notations of the theory of difference schemes [5]: v (±1α) = v(x (iα) α ± h α, x (i3 α) 3 α ), α = 1,, y = y(x (i1) 1, x (i) ), y xα = y y( 1α) h α, y xα = y(+1α) y h α. On the grid ω h we approximate differential problem (.1) by the difference scheme Λy dy = ϕ, x ω h, (.3) y = µ(x), x γ h,
187 where Λy = α, β=1 Λ αβ y = 1 4 ( Monotone and conservative difference schemes 171 Λ αβ y, Λ αα y = (a αα y xα ) xα, α = 1,, (a αβ y x β ) xα + (a (+1α) αβ a αβ = a αβ a αβ, a + αβ = a αβ + a αβ, α β. y xβ ) xα + (a + αβ y x β ) xα + (a +(+1α) αβ y xβ ) xα ), Here d c 0, ϕ are some stencil functionals of the coefficient q and the right-hand side f respectively. The stencil functionals a αβ can be chosen as follows a αβ = k αβ iα 1, i β = k αβ(x α 0.5h α, x β ), a αβ = k αβ i α, i β + k αβ iα 1, i β a αβ = k αβk ( 1α) αβ k αβ + k ( 1α) αβ, α, β = 1,. = k αβ + k ( 1α) αβ A difference scheme is called conservative (divergent), if we have algebraic sums of unknowns or functions of them only along the boundary after summation of the scheme equations over all grid nodes of the domain [3, p. 80]. If we sum up difference scheme (.3) over grid nodes of the domain ω h, we obtain algebraic sums of functions only along the boundary Γ. Hence, the proposed scheme is conservative. We consider a αβ = k αβ (x α 0.5h α, x β ) and show that the grid operator Λ approximates the differential operator L with the second order. Let the coefficients k αβ (x) of equation (.1), all partial derivatives up to the third order inclusively of the coefficients and up to the fourth order inclusively of the solution u(x) be bounded. By using Taylor expansion of the functions Λ αβ u in the neighbourhood of the point x ω h, we obtain Λ αα u L αα u = O(h 1 + h ) = O( h ), α = 1,, Λ αβ u L αβ u = h ( β 3 u 4 x α x k αβ + h α k αβ β x α k αβ h α, k αβ x α ) + O( h ), α β. Using the inequality a + b a b b, we have Λ αβ u L αβ u h 1h k αβ 3 u 4 x α x α x β + O( h ) = O( h ). Hence, Λ αβ u L αβ u = O( h ), α β. We suppose that the stencil functionals d(x) and ϕ(x) satisfy the usual conditions of approximation of the coefficient q(x) and the right-hand side f(x) with the second order
188 17 I.V. Rybak d(x) q(x) = O( h ), ϕ(x) f(x) = O( h ). So, difference scheme (.3) approximates differential problem (.1) with the second order. The stencil of difference scheme (.3) is presented in Fig. 1. h x h 1 Figure 1. Stencil of difference scheme (.3). 3. Grid maximum principle To obtain the a priori estimates of stability in the grid norm C with respect to the right-hand side and the boundary conditions we will use the grid maximum principle [5, p. 58]. Therefore, we have to reduce the difference scheme to the canonical form A(x)y(x) = B(x, ξ)y(ξ) + F (x), x ω h, (3.1) ξ S (x) and verify the following sufficient conditions on the coefficients A(x) > 0, B(x, ξ) 0, D(x) = A(x) B(x, ξ) > 0, x ω h. (3.) ξ S (x) Here A(x), B(x, ξ), F (x) are the known grid functions, S (x) = S(x) \ {x}, S(x) is the stencil of the scheme. Theorem 1. Let us suppose that conditions (3.) of the coefficients positivity are satisfied. Then for the solution of problem (3.1) the following a priori estimate is valid { } F y C max D, F, (3.3) Cγ D where v C = max x ω h v(x), C v C = max x ω h v(x), v Cγ = max x γ h v(x). Let us number the nodes of the stencil of difference scheme (.3) according to Fig. 1 and reduce the scheme to canonical form (3.1): 8 Ay = B k y k + F, k=1 y k = y(x k ), x k S (x).
189 Monotone and conservative difference schemes 173 If x ω h, then values of the coefficients are defined by the following formulas A = a 11 + a (+11) 11 h 1 B 1 = a(+1) h a 1 + a (+11) 1 + a 1 + a (+1) 1 + a + a (+1) h 1 h a 1 + a 1 + a (+11) 1 a (+11) 1 + a (+1) 1 4h 1 h, B = a(+11) 1 + a (+11) 1 + a (+1) 1 + a (+1) 1 0, 4h 1 h B 3 = a(+11) h 1 a(+11) 1 + a 1 + a 1 + a (+1) 1 a (+1) 1, 4h 1 h B 4 = a(+11) 1 a (+11) 1 + a 1 a 1 0, 4h 1 h B 5 = a h a 1 a 1 + a (+11) 1 + a (+11) 1 + a 1 4h 1 h, B 6 = a 1 + a 1 + a 1 + a 1 4h 1 h 0, B 7 = a 11 h 1 a 1 + a 1 a 1 + a (+1) 1 + a (+1) 1, 4h 1 h B 8 = a 1 a 1 + a (+1) 1 a (+1) 1 0, 4h 1 h D = d c 0 > 0, F = ϕ. For x γ h, the coefficients of the canonical form are given by: A = 1, B = 0, D = 1, F = µ. Further we will assume that the following condition is satisfied h + d, where max{k 1, k } h 1 h min{k 3, k 4 }, (3.4) k 1 = a 1 a 1 + a (+11) 1 + a (+11) 1 + a 1 4a, k = a 1 + a 1 + a (+11) 1 a (+11) 1 + a (+1) 1, 4a (+1) 4a 11 k 3 =, a 1 + a 1 a 1 + a (+1) 1 + a (+1) 1 k 4 = 4a (+11) 11 a (+11) 1 + a 1 + a 1 + a (+1) 1 a (+1) 1.
190 174 I.V. Rybak Lemma 1. Let coefficients of differential equation (.1) satisfy the following inequality k αα k (±1α,±1β) αβ, α, β = 1,. (3.5) If we choose h 1 = h = h, then condition (3.4) is always satisfied. Proof. Let condition (3.5) be satisfied and h 1 = h. In order to prove that in this case condition (3.4) is always satisfied, we have to show that First we prove that k 1 1, i.e., k 1 1, k 1, k 3 1, k 4 1. a 1 a 1 + a (+11) 1 + a (+11) 1 + a 1 4a. (3.6) Let a 1 = 0.5(k ( 11) 1 + k 1 ), a 1 = 0.5(k ( 1) 1 + k 1 ), a = 0.5(k ( 1) + k ). In this case formula (3.6) can be rewritten in the form k ( 11) 1 +k 1 + k1 +k (+11) 1 + k ( 1) 1 +k 1 k ( 11) 1 +k (+11) 1 4 ( k ( 1) +k ). (3.7) As condition (3.5) is valid, then k k 1, k ( 1) k ( 1) 1 and we have k ( 1) 1 + k 1 k ( 1) 1 + k 1 k ( 1) + k. Thus instead of (3.7) we have to prove that k ( 11) 1 + k 1 + k 1 + k (+11) 1 k ( 11) 1 + k (+11) 1 (k ( 1) + k ). (3.8) 1. Let assume that k ( 11) 1 + k 1 0, k 1 + k (+11) 1 0. Then inequality (3.8) can be rewritten in the form: k 1 + k (+11) 1 k ( 1) + k. It is easy to see that this inequality is valid under condition (3.5).. Let assume that k ( 11) 1 + k 1 0, k 1 + k (+11) 1 0. In this case from (3.8) we obtain: k ( 1) + k 0. From ellipticity condition (.) for ξ = (0, 1) we have 0 < c 1 k c. Hence, the required inequality holds true. 3. Let assume that k ( 11) 1 + k 1 0, k 1 + k (+11) 1 0, then formula (3.8) has the form: k ( 11) 1 + k (+11) 1 k ( 1) + k. This inequality is valid under condition (3.5). 4. Let assume that k ( 11) 1 + k 1 0, k 1 + k (+11) 1 0. In this case we rewrite inequality (3.8) in the form: k 1 k ( 11) 1 k ( 1) + k. This inequality is true under condition (3.5). Hence, k 1 1 if condition (3.5) is satisfied. Analogously we prove that k 1, k 3 1, k 4 1.
191 Monotone and conservative difference schemes 175 Theorem. Let us suppose, that for all x ω h condition (3.4) is satisfied. Then difference scheme (.3) is stable with respect to the right-hand side and the boundary conditions, and for its solution the following a priori estimate is valid y C max{ µ Cγ, c 1 0 ϕ C }. (3.9) Proof. It is easy to see that the coefficients B k 0, k = 1, 4 without any limitations. The coefficients B k 1 0, k = 1, 4 under condition (3.4): B 1 = 1 ( (+1) h 1 a a 1 + a 1 + a (+11) 1 a (+11) 1 + a (+1) 1 ) h 1 h h 4 1 ( (+1) a k a 1 + a 1 + a (+11) 1 a (+11) 1 + a (+1) 1 ) = 0, h 1 h 4 B 3 = 1 ( (+11) a h 11 h 1 a (+11) 1 + a 1 + a 1 + a (+1) 1 a (+1) ) 1 1 h 4 1 ( (+11) a (+11) a 1 + a 1 + a 1 + a (+1) 1 a (+1) ) 1 h 11 k 4 = 0, 1 4 B 5 = 1 ( h 1 a a 1 a 1 + a (+11) 1 + a (+11) 1 + a 1 ) h 1 h h 4 1 ( a k 1 a 1 a 1 + a (+11) 1 + a (+11) 1 + a 1 ) = 0, h 1 h 4 B 7 = 1 ( h a11 h 1 a 1 + a 1 a 1 + a (+1) 1 + a (+1) ) 1 1 h 4 1 ( a 1 + a 1 a 1 + a (+1) 1 + a (+1) ) 1 h a11 k 3 = Coefficient A > 0, if the following condition is true { } { } a 1 a (+1) 1 max, h 1 a 11 min a a (+1) h a 1, a (+11) 11. a (+11) 1 This statement follows from the following inequalities A = 1 h 1 ( a 11 h 1 a 1 ) + 1 ( h h a (+11) 11 h h 1 h ( + 1 h 1 a (+1) h 1 ( a (+11) + 1 h 1 h ( 1 a(+1) h 11 a(+11) a (+11) 1 a (+11) 1 a (+1) a (+1) 1 a (+1) a (+11) 1 h ) + d 1 h 1 1 a(+1) ) + 1 ( h 1 a a 1 h 1 h h ( a 11 a 11 a 1 a 1 ) + 1 ( a 1 a a 1 h 1 h a ) + d = d > 0. ) ) )
192 176 I.V. Rybak Note, that the above condition is weaker than condition (3.4), i.e., it holds true if condition (3.4) is valid. We verify directly that for any grid node x ω h the coefficient D > 0: 8 D = A B k = d(x) c 0 > 0. k=1 For x γ h, the coefficients of the canonical form are given by: A = 1 > 0, B = 0, D = 1 > 0. Now, all the conditions of Theorem 1 are satisfied. A priori estimate (3.3) provides the required inequality (3.9). 4. Convergence Let us consider now the problem of convergence of the proposed difference scheme. Substituting y = z + u into equations (.3) we get the following problem for the error of the discrete solution { Λz dz = ψ, x ωh, (4.1) z = 0, x γ h, where ψ = Λu du + ϕ denotes the error of approximation of difference scheme (.3) corresponding to the exact solution of differential problem (.1). It was shown above that the proposed difference scheme approximates the given differential problem with the second order, thus ψ C = M(h 1 + h ), where M > 0 is a positive constant which does not depend on the grid steps h 1, h. Using Theorem for the solution of problem (4.1), it can be verified that the following theorem takes place. Theorem 3. Let us suppose that for all x ω h, condition (3.4) is satisfied. Then the solution of difference scheme (.3) converges to the exact solution of differential problem (.1), and the following a priori estimate is valid. y u C M c 0 ( h 1 + h Remark 1. Results above can be easily extended to p dimensional (p ) elliptic equations with mixed derivatives. Remark. The proposed approach can be also applied for the development of the conservative monotone difference schemes for multidimensional parabolic equations with mixed derivatives. )
193 5. Numerical results Monotone and conservative difference schemes 177 To solve problem (.1) by means of difference scheme (.3) we use the modified strongly implicit method [9]. Therefore, we reduce difference scheme (.3) to the system of algebraic equations [A]y = C. Here A is a nine-diagonal matrix. Then we consider matrix [A + P ], which is the product of the lower triangular matrix [L] and the upper triangular matrix [U], and develop the iterative process [A + P ]y n+1 = C + [P ]y n. Since [A + P ] = [L][U] we obtain the following numerical algorithm [L][U]y n+1 = C + [P ]y n. Matrices [L], [U] and [P ] are defined in [9]. Numerical experiments were carried out in domain Ḡ = [0, 1] [0, 1]. We choose the coefficients: k 11 = 1, k 1 = k 1 = cos(π(x 1 + x )), k = 1, q = 1. It is easy to see that k αβ satisfy ellipticity condition (.). The exact solution is given as u = sin(4πx 1 ) sin(4πx ). By substituting the exact solution into (.1), we obtain the boundary conditions and the right-hand side f. Table 1. The convergence order of difference scheme (.3). N N z N D N p N The results of the numerical experiments are presented in Tab. 1, where z N = max x ω h y h (x) u(x) is the global error of the discrete solution. Since the exact solution is usually unknown, we have computed the solution on the grids ω h, ω h/, ω h/4, etc. Then the aposteriori error estimate of the solution y h can be obtained by using the Runge estimator: D N = 1 3 max x ω h y h (x) y h (x). Here we take the difference between the values of the solution on the grid with N/ nodes and the solution at the same point on the grid with N nodes. The second aposteriori estimator p N = log (D N/ /D N ) estimates the convergence order of the approximation y h.
194 178 I.V. Rybak 6. Conclusions In this paper new difference scheme for elliptic equations with mixed derivatives and alternating coefficients is presented. The proposed scheme is conservative, has the second order of approximation and satisfies the grid maximum principle. For the developed numerical algorithms the a priori estimates of stability and convergence in the uniform norm are obtained. The proposed approach to the construction of monotone conservative difference schemes can be also applied to the development of monotone and conservative numerical algorithms for multidimensional parabolic equations with mixed derivatives. References [1] T. Arbogast, M.F. Wheeler and I. Yotov. Mixed finite elements for elliptic problems with tensor coefficients as cell-centered finite differences. SIAM J. Numer. Anal., 34(), 88 85, [] P. Crumpton, G. Shaw and A. Ware. Discretization and multigrid solution of elliptic equations with mixed derivative terms and strongly discontinuous coefficients. J. Comput. Phys., 116, , [3] S. Godunov and V. Ryabenkii. Difference schemes. Nauka, Moskow, (in Russian) [4] J. Hyman, J. Morel, M. Shashkov and S. Steinberg. Mimetic finite difference methods for diffusion equations. Computational Geosciences, 6, , 00. [5] A. Samarskii. The theory of difference schemes. Marcel Dekker, Inc., New York Basel, 001. [6] A. Samarskii and V. Andreev. Difference methods for elliptic equations. Nauka, Moskow, (in Russian) [7] A. Samarskii, P. Matus, V. Mazhukin and I. Mozolevski. Monotone difference schemes for equations with mixed derivatives. Computers and Mathematics with Applications, 44, , 00. [8] A. Samarskii, V. Mazhukin, P. Matus and G. Shishkin. Monotone difference schemes for equations with mixed derivatives. Mathematical Modeling, 13(), 17 6, 001. [9] G. Schneider and M. Zedan. A modified strongly implicit procedure for the numerical solution of field problems. Numerical Heat Transfer, 4, 1 19, [10] G. Shishkin. Grid approximation of the singularly perturbed boundary-value problem for quasilinear parabolic equations in the case of total degeneracy with respect to space variables. In: Yu. A. Kuznetsov(Ed.), Numerical methods and mathematical modeling, Russian Academy of Sciences, Institute of Computational Mathematics, Moskow, , 199. [11] W. Voligt. Finite-difference schemes for parabolic problems with first and mixed second derivatives. Z. angew. Math. und Mech., 68(7), 81 88, Monotoniškos ir konservatyvios baigtinių skirtumų schemos eliptinio tipo lygtims su mišriomis išvestinėmis I. Rybak Straipsnyje nagrinėjamos eliptinio tipo lygtys su mišriomis išvestinėmis. Šioms diferencialinėms lygtims pasiūlytos naujos antros eilės baigtinių skirtumų schemos, kurios yra monotoniškos ir konservatyvios. Sukonstruoti algoritmai tenkina skaitinį maksimumo principa, kai koeficientai prie mišriųjų išvestinių gali būti bet kokio ženklo. Gauti aprioriniai įverčiai maksimumo normoje. Įrodyta baigtinių skirtumų schemu stabilumas ir konvergavimas.
195 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN APPLICATIONS OF INSPECTION GAMES R. AVENHAUS Universität der Bundeswehr München Werner-Heisenberg-Weg 39, Neubiberg : ;< 7 =5>?#@A; BC9DFE#79G5@AHJIK=;5@ALMNOE =:F;P <: ;JIRQ: Received July 7, 004; revised September 9, 004 Abstract. An inspection game is a mathematical model of a non-cooperative situation where an inspector verifies that another party, called inspectee, adheres to legal rules. The inspector wishes to deter illegal activity on the part of the inspectee and, should illegal activity nevertheless take place, detect it with the highest possible probability and as soon as possible. The inspectee may have some incentive to violate his commitments and violation, if observed, will incur punishment. Therefore if he chooses illegal behaviour, the inspectee will wish to avoid detection with the highest possible probability. Three examples of applications are presented. The first one deals with random controls in public transportation systems. The second one describes the problem of verification of arms control and disarmament in a very general way. The third one deals with inspections over time which are important in the context of non-proliferation verification. Key words: Extensive form game, interim inspection, Nash equilibrium, normal form game, public transportation, verification of arms control and disarmament agreements 1. Introduction An inspection game is a mathematical model of a situation where an inspection authority, called inspector, verifies that another party, called inspectee, adheres to certain legal rules [4]. This legal behaviour may be defined, for example, by an arms control treaty, and the inspectee has a potential interest in violating these rules. Typically, the inspector s resources are limited so that verification can only be partial. A mathematical analysis should help in designing an optimal inspection scheme, where it must be assumed that an illegal action is executed strategically. This defines a game theoretic problem, usually with two players, inspector and inspectee. In some cases, several inspectees are considered as individual players. Game theory is not only adequate to describe an inspection situation, it also produces results which may be used in practical applications. But what does that mean? Theoreticians and practitioners have, as we know, very different views about applications. Instead of discussing this question in an abstract manner, in this paper three cases will be
196 180 R. Avenhaus presented which illustrate three different kinds of applications. For that purpose, we define operational, conceptual and structural models. The first one which deals with random controls of passengers using public transportation systems gives a concrete advise what effort the inspector should spend in order to achieve his objectives. The second one which describes the problem of the verification of arms control and disarmament in a very general way provides insight into the nature of the inspection problem. The third one which deals with inspections over time which are important in the context of non-proliferation verification shows how sensibly the best inspection strategies depend on assumptions about the information the inspectee gains, or does not gain, in the course of the game. Whereas these three examples by no means do exhaust the wealth of models developed in the past forty years - the first serious attempts were made in the early 1960s where game theoretic studies of arms control inspections were commissioned by the US ACDA [10] they should at least give an idea of what inspection models can achieve and furthermore that each inspection problem has its own characteristics which require new models and appropriate solution techniques. Since in this paper the emphasis is put on the modelling aspect and furthermore on the use of the models for practical applications, proofs are only sketched and results are not presented in form of theorems; both proofs and theorems can be found in the references.. Operational Model: Passenger Ticket Control In its edition of July 8th, 1997, the daily Süddeutsche Zeitung reports about the complaints by the city treasurer of Munich regarding the passenger ticket control applied within the area of the Munich Transport and Fares Tariff association (Münchner Verkehrs- und Tarifverbund, MVV). The deployment of inspectors was not worthwhile since they make up for only about half of what they cost themselves by charging the extra fares (fines) i.e., the employment of them was not profitable. It is obvious that there must be an optimum high incidence of controlling: if there was only one inspector many passengers would go without paying, i.e., this one single inspector would collect a lot of fines which is certainly not in line with the interest of the MVV, although the inspector would pay off. If on the other hand all passengers were checked, all of them would pay for the fares. This would please the MVV, however, the numerous and expensive ticket inspectors would not take in any fines at all. Where does thus the optimum regulation for the entire MVV system lie? Since the behaviour of passengers, of whom one can assume strategical conduct i.e. reflections regarding payment or non-payment (morale aspects should be disregarded in this incident), must be taken into account when the assessment of the optimum frequency of controls by the MVV is made, a decision theoretical, precisely a game theoretical analysis of the problem is required. The game is conducted by the inspector, representing the MVV on one part, the frequency of controls being his strategic variable, and the passenger on the other side who decides between the alternatives of paying (legal behaviour) or not paying the fare (illegal behaviour).
197 Applications of Inspection Games 181 Let f be the normal fare, b the fine and e the costs of controls per passenger. We assume e < b. Then the payoffs to the two players (inspector, passenger) in the four possible situations (outcomes) are (f e, f) for control and legal behaviour, (f, f) for no control and legal behaviour, (b e, b) for control and illegal behaviour, (0, 0) for no control and illegal behaviour. (.1) We consider the normal form indicated in Table 1 showing a two-person-game between the MVV being represented by the inspector as first player and the passenger as second. In this diagram the pure strategies of the first player (control/no control) are depicted as rows and the second player s as columns (legal/illegal behaviour); in the individual squares the payments to the first player resulting from the respective combination of strategies are put down on the left bottom and those to the second player on the top right. Table 1. Normal form of the two person game between the inspector representing the MVV and the passenger. The arrows indicate the preference directions of the two players. / inspector passenger legal behaviour illegal behaviour (q) (1-q) control -f -b (p) f-e b-e no control -f 0 (1-p) f 0 Taking this formulation of the problem we ignore the costs on the part of the MVV for maintenance of the business since these do not influence the decisions of both players immediately and also for the same reason we ignore the ideal or material gain the passenger has from his trip. According to John Nash [8], one of the Economics Nobel prize winners of 1994, we understand by a solution of this game a pair of equilibrium strategies implying the quality that if one of the two players deviates unilaterally from his equilibrium strategy he cannot improve his payment. In so doing we ignore the difficult problem of the existence of multiple equilibria since in our cases they do not occur. Since according to Table 1 the preference directions of the two players, i. e., the incentive to deviate from a chosen strategy go cyclical, there is no equilibrium in pure strategies. The inspector will thus control with probability p, and the passenger will behave legally with probability q. The expected payments to the two players are given in this case by E 1 (p, q) = (f e) p q + (b e) p (1 q) + f (1 p) q, E (p, q) = f p q b p (1 q) f (1 p) q. (.)
198 18 R. Avenhaus If we designate the mixed equilibrium strategies of the two players as p, and q, and the equilibrium payments as Ei = E i (p, q ), i = 1,, the equilibrium conditions according to John Nash are E 1(p, q) E 1 (p, q ) for all p [0, 1], E (p, q) E (p, q) for all q [0, 1]. (.3) In our case, the equilibrium strategies can be determined so that the adversary is indifferent as regards to the choice of his own strategy, see e.g. Morris [7]. As a result, the equilibrium strategies and payments are given as follows [1]: p = f ( b, E 1 = f 1 e ), (.4) b q = 1 e b, E = f. (.5) Thus in the equilibrium the passenger with a positive probability 1 q behaves illegally, in the mean, however, he pays the same price he would pay if he always behaved legally. The reduced price achieved by dodging the fare is compensated by the obligatory fine. The mean value of the control expenditure by the MVV per passenger is e p, while the profit from the fines is b p (1 q). Thus the difference is e p b p (1 q) = ( e b (1 q) ) p 0 for e b 1 q. If the passenger chooses his equilibrium strategy q given by (.5), the following holds ( e b (1 q ) ) p = 0 (.6) for any control probability p, i.e., the investment of control is just being compensated by the amount of fines taken in. It must be noted that these considerations only include the parameters e and b, but not the fare f of the trip. The optimum control probability p satisfies the condition p b = f, which can be understood intuitively: if the passenger behaves legally he has to pay f, whereas his expected payment in case of illegal behaviour is b p. Thus the optimum control probability renders the passenger indifferent as regards to the strategy to be chosen by him. Thus, in conclusion, this game theoretical model gives an advise how frequently passengers should be controlled if the fare and the fine are fixed. It should be mentioned that the actual figures for Munich approximately satisfy (.4). One may speculate why then, according to the City Treasurer s complaints, the equilibrium condition (.6) is not satisfied. Certainly one reason is that the inspections are nor purely random: passengers who systematically do not buy tickets frequently recognize the inspectors already before they can do their job. Another reason are the considerable deviations of passengers in frequency, hour of the day and dwelling time from the average which is not adequately taken into account by the inspectors. A stratification of inspection procedures which would be required here has been analysed in the context of arms control, see []. There it turns out that the inspection
199 Applications of Inspection Games 183 efforts in the different strata have to be the higher, the more profitable illegal actions are, and in turn that the illegal actions are concentrated there as well. It will be pointed out in the last section, however, that one has to be very careful in predicting results of yet unsolved problems. Finally, it should be mentioned that there is also not intentional illegal behaviour e.g., passengers use monthly tickets but forget to take them with them which can be modelled as well [1]; the analysis shows, however that it does not change the results in a significant way. 3. Conceptual Models: Arms Control and Disarmament Verification As a second case, let us consider an international arms control and disarmament agreement, for example the Treaty for the Non-Proliferation of Nuclear Weapons, or the Chemical Weapons Convention. A State who signs this agreement is obliged not to act illegally in that sense that he does not do anything that is forbidden by the agreement, for example to acquire nuclear or chemical weapons. Let us assume furthermore that, together with the agreement, a verification system is established which means that an international authority verifies with the help of well-defined measures - measurements, on-site inspections and others - that the inspected State adheres to the provisions of the agreement. For the Non-Proliferation Treaty, for example, the International Atomic Energy Agency (IAEA) plays that role. The purpose of the verification is to deter the State from illegal behaviour or, should he behave illegally, to detect this with as high a probability and as quickly as possible. On the other hand, the inspected State may have some incentive to violate his commitments otherwise the situation is pointless, we will come back to this issue, and violation, if observed, will incur punishment of the State. Therefore, if he chooses illegal behaviour, the inspected State will wish to avoid detection with the highest possible probability. In the following we will describe this conflict situation between the verification authority (in short inspector) and the State (in short inspectee) with the help of a non-cooperative two-person game. Let the payoffs to the inspector as the first player and to the inspectee as the second player be given by (0, 0) for legal behaviour of the inspectee, ( a, b) for detected illegal behaviour of the inspectee, ( c, d) for undetected illegal behaviour of the inspectee. (3.1) Note that inspection costs are not taken into account explicitly. We assume 0 < a < c, 0 < b, 0 < d, (3.) the first inequality expresses the fact that the highest priority of the inspector is to deter the inspectee from illegal behaviour. In keeping with common notation, let us call 1 β be the probability to detect illegal behaviour. Then the expected payoffs to the two players are
200 184 R. Avenhaus (0, 0) for legal behaviour of the inspectee, (3.3) ( a (1 β) c β, b (1 β) + d β) for illegal behaviour of the inspectee. Furthermore we assume that the inspector, in a concrete situation, decides either to verify or not, and the inspectee, in turn, to behave legally or not. The normal form of this two-by-two-game is given by Table. Table. Normal form of the two person game between a State (inspectee) and the verification authority (inspector). False alarms are not possible. The arrows indicate the preference directions of the two players if (3.4) is fulfilled. / inspector passenger legal behaviour illegal behaviour Verification 0 b(1 β) + dβ 0 a(1 β) cβ No 0 d verification 0 c As a solution of this game we consider again the Nash equilibrium. Using the method of incentive directions, we see immediately that legal behaviour is the only equilibrium strategy of the inspectee if or, equivalently, if 0 > b (1 β) + d β, β < d. (3.4) b Thus, as a result we see that the inspectee will be induced to legal behaviour if the non-detection probability is smaller than some threshold, which is the lower, the larger the ratio between gain in case of undetected illegal behaviour and the sanctions b in case of detected illegal behaviour is. Otherwise he will behave illegally. Alternatively one may say that the inspectee will behave legally if either the probability of no detection or the ratio d is small enough. b Now let us consider a more complicated problem: Let us assume that false alarms may happen with probability α. Let the payoffs to the two players in case of a false alarm be e < 0 and f < 0. We assume 0 < e < a < c, 0 < f < b, 0 < d. Then the normal form of the verification game is given by Table 3. We see immediately that legal behaviour is not an equilibrium strategy. However, for fα > b (1 β) + d β, or equivalently, for
201 Applications of Inspection Games 185 Table 3. Normal form of the two person game between a State (inspectee) and the verification authority (inspector). False alarms occur with probability α. The arrows indicate the preference directions of the two players if (3.5) is fulfilled. / inspector passenger legal behaviour illegal behaviour (q) (1-q) Verification fα b(1 β) + dβ eα α(1 β) cβ No 0 d verification 0 c β < f b + d α + b b + d (3.5) there exists a Nash equilibrium in mixed strategies: The inspectee will act illegally with probability q as given by 1 q = 1 + c a 1 β e α. (3.6) Since, as mentioned initially, and contrary to the previous example, where morale problems were not dominating, the purpose of the treaty is that the State fulfills the provisions of the treaty, the question arises if there is any possibility to induce the inspectee to legal behaviour. Let us assume that α is a strategic variable of the inspector. Of course, β depends on α. For unbiased test procedures we have Let us assume in addition α + β < 1. (3.7) β = 1 for α = 0, and β = 0 for α = 1, (3.8) and furthermore, dβ dα < 0, d β < 0. (3.9) dα Then the problem of choosing an appropriate value of α can be represented graphically as given in Figure 1a. We see that for α = α 0 and β = β 0 = β(α 0 ) as defined in the figure the inspectee is indifferent between legal and illegal behaviour. Now let us change the rules of the game []. Instead of the inspector s two alternatives considered so far, namely verifying with a fixed false alarm probability or not verifying, we now assume that the inspector always verifies, and that his set of strategies consists in the possible choices of the false alarm probability. In addition, he will announce his strategy in a credible way. The extensive form of this so-called inspector leadership game is given by Figure 1b.
202 186 R. Avenhaus 1 inspector inspectee b b d f b b d b d 1 b b f d legal f a) b) illegal e a 1 c b 1 d Figure 1. a) graphical representation of the value of which makes the inspectee indifferent between legal and illegal behaviour, b) extensive form of the leadership game between the verification authority (inspector) and the State (inspectee). According to the backward induction procedure the inspectee will behave legally, if f α > b (1 β) + d β, be indifferent, if f α > b (1 β) + d β, (3.10) behave illegally, if f α > b (1 β) + d β. or, equivalently, with α 0 as defined in Figure 1a, behave legally, if α > α 0, be indifferent, if α = α 0, (3.11) behave illegally, if α < α 0. For this best reply of the inspectee, the payoff to the inspector is given as represented graphically in Figure. 0 0 e 1 e a C c a 1 Figure. Payoff to the inspector for the best reply of the inspectee. One sees immediately that the payoff of the inspector has its maximum at α 0. Now, surprisingly enough it can be shown that α = α 0 and
203 Applications of Inspection Games 187 { legal behaviour, for α α0, illegal behaviour, for α < α 0 (3.1) are Nash equilibrium strategies. This means in effect that the inspector chooses α = α 0 and that consequently, the inspectee acts legally even though at that point he is indifferent between legal and illegal behaviour. In discussions on the usefulness of verification in general, arms control and disarmament officials, administrators and political scientists have frequently criticized, and still do so, that game theorists or more generally, analysts working quantitatively, always assume that the State might behave illegally even though he has ratified the agreement under consideration. In the beginning we mentioned that without this assumption the situation would be pointless. Now we can be more precise: in order to show that appropriate verification on one hand and legal behaviour of the State on the other are equilibrium strategies we have to study deviations quite in the spirit of Nash s equilibrium concept. 4. Structural Models: Interim Inspections Finally, as a third case, we consider a single inspected object, for example a nuclear or chemical facility subject to verification in the framework of an international treaty, and a reference period of one time unit (e.g. one calendar year). In order to separate the timeliness aspect of routine inspection from the overall goal of detecting illegal activity, we assume that a thorough and unambiguous inspection takes place at the end of the reference period which will detect an illegal activity with certainty once it has occurred. In addition there are a number of less intensive and strategically placed interim inspections which are intended to reduce the time to detection below the length of the reference period. An interim inspection will detect a preceding or coincident illegal activity, but with some lower probability. Again in keeping with common notation, we call this probability 1 β, where β is the probability of an error of the second kind, or non-detection probability. Associated with each interim inspection which is not preceded by an illegal action is a corresponding probability of an error, the false alarm probability α. Moreover, again only an unbiased inspection procedure is considered. We assume that, by agreement, k interim inspections will occur within the reference period. For convenience we label the inspections backwards in time. Also we label the beginning of the reference time t k+1 and the end t 0, so we have 0 = t k+1 < t k <... < t 1 < t 0 = 1. (4.1) The utilities of the protagonists (inspector, inspectee) are taken to be as follows: (0, 0) for legal behaviour over the reference time, and no false alarm, ( le, lf) for legal behaviour over the reference time, and l false alarms, l = 1,..., k ( α t, d t b) for detection of illegal activity after elapsed time t 0,
204 188 R. Avenhaus where 0 < e < a, 0 < f < b < d. Thus the utilities are normalized to zero for legal behaviour without false alarms, and the loss (profit) to the inspector (inspectee) grows proportionally with the time elapsed to detection of an illegal action. A false alarm is resolved unambiguously with time independent costs e to the inspector and f to the inspectee, whereupon the game continues. The quantity b is the cost to the inspectee of immediate detection. Note that, if b > d, the inspectee will behave legally even if there are no interim inspections at all. Since interim inspections introduce false alarm costs for both parties, there would be no point in performing them. The extensive form of the inspection game for one single observable interim inspection is represented graphically in Figure 3. Without going through the analysis which uses similar techniques as sketched before, we just present the results [3]: Figure 3. Extensive form of the two person game between the inspector and the inspectee for one interim inspection. Let {t 1 : 0 < t 1 < 1} be the set of pure strategies of the inspector, and the probabilities g, g 1 to start illegal actions at time moments t = 0, t 1 be the mixed behavioral strategies of the inspectee. Let V and W be the payoffs to the two players (here we use a notation different from that of the second section in order to remain consistent with the notation in the published literature). Taking into account that the inspectee will behave legally if his payoff is larger than in case he behaves illegally, and vice versa, the equilibrium strategies and payoffs are given as follows. Under the assumption b d < 1 ( 1 + f α ) (4.) β d
205 Applications of Inspection Games 189 in equilibrium the inspectee acts illegally, with payoffs and strategies given by V = a A e α B, W = d A f α B b, t 1 = (1 β) A f α d g = A, g 1 = 1, where A and B are given by ( (1 β) B + β ), A = 1 β, B = 1 β β. (4.3) Under the assumption (we exclude equality being practically not important) b d > 1 ( 1 + fα ) β d (4.4) in equilibrium the inspectee acts legally, with the following payoffs to the two antagonists: V = ea, W = fα. The equilibrium strategy of the inspector is not unique; it is given by what M. Kilgour [6] called the cone of deterrence: 1 b d t 1 1 ( b 1 β d fα ) d β. (4.5) It can be shown that the equilibrium strategy of the inspector in case of illegal behaviour of the inspectee is an element of the cone of deterrence (4.5). Thus, the inspector is on the safe side if he always uses the former one. It is also possible to generalize this solution to more than one interim inspection however, the analysis gets rather involved since non-trivial information sets have to be taken into account and furthermore, since unrealistic solutions may occur where some interim inspections may have to be conducted right at the beginning of the reference time [3]. Nevertheless are the realistic solutions for more than one interim inspection of the same structure as that given by (4.3), with more complicated expressions for A and B; whereas it is not easy to find them, it is straightforward to prove their validity via complete induction. We will not delve into these intricacies. Instead, we consider an inspection problem which differs from the previous one only by the fact that now the interim inspections are unobservable or formally the same that prior commitment on the part of the inspectee is assumed. That means that now we consider a simultaneous rather than a sequential game. This game has been analysed by H. Diamond [5] for an arbitrary number of interim inspections, however, without taking into account false alarms. The analysis of the game for one interim inspection and the possibility of false alarms is due to Sohrweide [9] and again we just present the main results.
206 190 R. Avenhaus For one interim inspection an equilibrium strategy for the inspector is to choose his single interim inspection time t 1 on an interval 0 < t 1 κ < 1 according to the distribution function where κ is given by F (t 1 ) = 1 1 β ln ( 1 κ = ( 1 1 ) ( e 1 β 1 1 d t 1 1 f d α 1 β ), (4.6) ) α. (4.7) 1 β Under the assumption b d > 1 κ (4.8) the inspectee behaves illegally; he randomizes similarly, however, his distribution function Q (t), as given by has an atom at t = 0 : Q (t) = 1 κ + e a 1 + e a α 1 β α 1 β Q κ (0) = e a for 0 t κ, (4.9) α 1 β > 0. Thus, both players necessarily play mixed strategies in equilibrium, with payoffs V = a [ β (1 κ) (1 κ + e α a 1 β ) ln ( κ )] 1 1 t + e α, a 1 β W = d (1 κ) f b. (4.10) If (4.8) is not fulfilled (we exclude equality being practically not important) the inspectee behaves legally, with payoffs being the same as in the previous model. Whereas the inspectee s payoff W as given by (4.10) can be understood easily it is just his payoff in case he starts his illegal action at time t = κ this is not so easy in case of the inspector s payoff unless we have e = f which can hardly be justified. It turns out, not surprisingly, that the unobservability places the inspectee at a disadvantage: his payoff in case of illegal behaviour is smaller than that for an observable inspection, and the limit for b d to induce the inspectee to legal behaviour is lower. At first sight it is very surprising that for one well specified inspection problem different assumptions about the information the inspectee gains during the course of the game or does not gain, lead to totally different results: In the first case the inspector plays in equilibrium a pure, in the second case a mixed strategy. This is the general lesson to be drawn from this very concrete inspection problem: Even if one has studied so many different problems, one hardly will be able to predict the outcome of a new or even only modified one.
207 Applications of Inspection Games 191 References [1] R. Avenhaus. Entscheidungstheoretische Analyse der Fahrgastkontrollen. Der Nahverkehr 9, Alba Fachverlag Düsseldorf, 7 30, [] R. Avenhaus and M.J. Canty. Compliance Quantified: An Introduction to Data Verification. Cambridge University Press, [3] R. Avenhaus and M.J. Canty. Playing for time: A sequential inspection game. The European Journal for Operational Research, 004. (in print) [4] R. Avenhaus, B. von Stengel and S. Zamir. Inspection games. In: R.J. Aumann and S. Hart(Eds.), Handbook of Game Theory, volume 3, North-Holland, Amsterdam, , 000. [5] H. Diamond. Minimax policies for unobservable inspections. Mathematics of Operations Research, 7(1), , 198. [6] M. Kilgour. Site selection for on-site inspection in arms control. Arms Control Contemp. Security Policy, 13, , 199. [7] P. Morris. Introduction to Game Theory. Springer Verlag, [8] J. Nash. Noncooperative games. Annals of Mathematics, 54(), 86 95, [9] K. Sohrweide. Diamond s inspektionsspiel mit fehlern 1 und. Diploma thesis, Universität der Bundeswehr München, Germany, 00. [10] United States Arms Control and Disarmament Agency (USAACDA). Applications of Statistical Methodology to Arms Control and Disarmament. Mathematica, Princeton NJ, Contract No. ACDA/ST-3, 1963.
208 19 R. Avenhaus Kontrolės lošimu taikymai R. Avenhaus Kontrolės lošimas yra matematinis modelis tam tikrų nekooperaciniu situacijų, kai inspektorius kontroliuoja kitą pusę, skatindamas korektiška elgesį. Inspektorius turi atbaidyti uždraustus veiksmus su kuo galima didesne tikimybe ir kuo greičiau. Tai reiškia, kad už nustatytų taisyklių pažeidima mokama tam tikra bauda ir šie pažeidimai aptinkami su maksimalia tikimybe. Straipsnyje nagrinėjami trys šio modelio taikymo pavyzdžiai: atsitiktinė visuomeninio transporto keleiviu kontrolė, ginklų kontrolės modelis ir paplitimo ribojimo per tam tikrą laiką modelis.
209 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN THE SECOND BOUNDARY VALUE PROBLEM OF RIEMANN S TYPE FOR BIANALYTICAL FUNCTIONS WITH DISCONTINUOUS COEFFICIENTS I. B. BOLOTIN Smolensk State Pedagogical University Przevalskogo 4, Smolensk, Russia :#;=<>?>A@7B:C?7 D=@FEHGI Received October 13, 003; revised February 5, 004 Abstract. The paper is devoted to the investigation of one of the basic boundary value problems of Riemann s type for bianalytical functions with discontinuous coefficients. In the course of work there was made out a constructive method for solution of the problem in a unit circle. There was also found out that the solution of the problem under consideration consists in consequent solutions of two Riemann s boundary value problems for analytical functions in a unit circle. Besides, the example is constructed. Key words: bianalytical function, boundary value problem, plane with slots, index 1. Introduction Let L = {t : t = 1}, D + = {z : z < 1} and D = C\{D + L}. Let G k (t) (k = 1, ) given on the contour L functions, satisfying the condition of Holder everywhere on L, except for a finite number of points, where they have simple discontinuity, and G k (t) 0 on the contour. Also we shall consider, that function G 0 (t) has derivative which satisfies the condition of Holder, except for a finite number of points, where it may have simple discontinuities. Hereinafter, following N.I. Muskhelishvili (see, for example, []), we shall call points of discontinuity of the functions G 0 (t), G 0(t) and G 1 (t) as knots, and remaining points of the contour L we shall name ordinary. Besides we shall rank all points of discontinuity of the function G 0 (t) and its derivative as knots of function G 1 (t). Further we shall generally use terms and definitions accepted in [3]. JLKMNPOQNSR5NUTVOXW Y We shall speak, that bianalytical function F ± (z) in domain D ± belongs to the class A (D ± ) I () (L), if it proceeds on the contour L together with
210 194 I.B. Bolotin the partial derivatives α+β F ± (z) z α z β (α = 0, 1; β = 0, 1), and so that boundary values of this function and all specified derivatives satisfy on z the condition of Holder everywhere, except for, possibly, knots, where the reversion in infinity of integrable order is possible when α + β <. It is required to find all piecewise bianalytical functions F (z) = {F + (z), F (z)}, belonging to the class A (D ± ) I () (L), vanishing on infinity, limited near the knots of the contour and satisfying in all ordinary points of L the following boundary conditions: F + (t) = G 0 (t)f (t) + g 0 (t), (1.1) F + (t) n + = G 1 (t) F (t) n g 1 (t), (1.) ( ) where derivative on interior (exterior) normal to the contour L, n + n g k (t) (k = 0, 1) given on L functions of the class H (1 k) (L), and g 0 (t) = (t c) γc g (t), c any of knots of the function G 0 (t), γ c > 0 - quite defined numbers. Here, in equality (1.), factor ( 1) at G 1 (t) and g 1 (t) is entered for convenience hereinafter. We shall name the formulated problem as the second basic boundary value problem of Riemann s type for bianalytical functions with discontinuous coefficients in the unit circle or in short the problem R,, and appropriate homogeneous problem (g 0 (t) g 1 (t) 0) shall be named as a problem R, 0. Let s notice, that the problem R,, stated by F. D. Gakhov as one of basic boundary value problems for bianalytical functions (see, for example, [1], p. 316) in case of continuous coefficients and smooth closed loops was explicitly investigated in the work of K. M. Rasulov (see [3]). In the above mentioned statement the problem R, is investigated in the present work for the first time.. About the Solution of the Problem R, It is known (see [1, 3]), that any vanishing on infinity piecewise bianalytical function F (z) with line of saltuses L is possible to represent as: F (z) = { F + (z) = ϕ + 0 (z) + zϕ+ 1 (z), z D+, F (z) = ϕ 0 (z) + zϕ 1 (z), z D, (.1) where ϕ ± k (z) analytical functions in domain D± (analytical components of piecewise bianalytical function), for which the following conditions are fulfilled: Π{ϕ k, } 1 + k, k = 0, 1; here Π{ϕ k, } means the order of the function ϕ k (z) in the point z =. Let s search for the solution of the problem R, as
211 The Second Basic Boundary Value Problem 195 F (z) = f 0 (z) + (z z 1)f 1 (z). (.) Then the functions f k (z) (k = 0, 1) will be connected with analytical components of the required bianalytical function F (z) by the formulas: ϕ 0 (z) = f 0 (z) f 1 (z), ϕ 1 (z) = zf 1 (z). (.3) As known (see [1] p. 304) ( = ±i t n ± t ) t, (.4) t then taking into account (.) and the fact that the equality t = 1 is fulfilled on L, t the boundary conditions (1.1) and (1.) can be copied accordingly in the aspect: f 0 + (t) = G 0(t)f 0 + (t) + g 0(t), (.5) f 1 + (t) = G 1(t)f1 (t) + 1 ( t df 0 + (t) + tg 1 (t) df 0 (t) ) + g 1 (t). (.6) dt dt The equalities (.5) and (.6) represent boundary conditions of usual Riemann s problems for analytical functions with discontinuous coefficients in the unit circle (see [1] or []). Thus, as a matter of fact, solution of the initial problem R, is reduced to sequential solution of two auxiliary problems of Riemann (.5) and (.6) in classes of piecewise analytical functions with the line of saltuses L. But as in the problem R, we search the solutions, limited close to the knots of the contour and vanishing on infinity, there arises the necessity in a choice of defined classes of analytical functions at the solution of auxiliary problems (.5) and (.6). Therefore, at first we shall find out, in what classes it is necessary to search for solutions of boundary value problems (.5) and (.6). From equalities (.3) we can see that the function f0 (z) on the infinity should have zero not below than the first order, and f1 (z) zero not below than the third order. Let s study the behaviour of function F (z) near the knots of the contour L. Let c be any of knots, then cc = 1 and c = 1. We have the following serieses of inequalities: F (z) = f 0 (z) + (z z 1)f 1 (z) f 0 (z) + f 1 (z) z z 1 = f 0 (z) + f 1 (z) (z c + c)( z c + c) 1 f 0 (z) + f 1 (z) z c + f 1 (z) z c ; (.7) F (z) = f 0 (z) + (z z 1)f 1 (z) f 0 (z) f 1 (z) z z 1 = f 0 (z) f 1 (z) (z c + c)( z c + c) 1 f 0 (z) f 1 (z) z c f 1 (z) z c. (.8) Thus, for the function F (z) would be limited close to the knots of the contour L, it is necessary and enough that the function f 0 (z) would be limited, and the function f 1 (z) supposed the evaluation:
212 196 I.B. Bolotin f 1 (z) const, 0 α < 1. (.9) z c α Really, if the function f 0 (z) is limited close to c and function f 1 (z) supposes the evaluation (.9), from inequalities (.7) it follows, that the required bianalytical function F (z) will be limited in a neighbourhood of the knot c. Back, if the function F (z) of the class A (D ± ) I () (L) is limited close to c, from inequalities (.8) it follows, that the function f 1 (z) has to suppose the evaluation (.9) (otherwise all solutions of the problem R, will not be found), so the function f 0 (z) has to be limited in a neighbourhood of the knot c. Therefore, it is required to search the solution of the problem (.5) in the class of functions, vanishing on infinity and limited near the knots, and solution of the problem (.6) is required to search in the class of functions, having zero of the third order on infinity and infinity of the integrable order near the knots of the contour L. Let s solve the boundary value problem of Riemann (.5) using the method offered by F.D. Gakhov (see, for example, [1], p. 448). Let index of the problem (.5) be equal κ 0 in the specified class. Then, if κ 0 0, a common solution of the problem (.5) is set by the formula (see [1, ]): f 0 (z) = X 0 (z) 1 πi L g 0 (τ) X + 0 (τ) dτ τ z + P κ 0 1(z), (.10) where X 0 (z) canonical function of the problem (.5), P κ0 1(z) the polynomial of a degree not higher then κ 0 1 with arbitrary complex coefficients. In the case when κ 0 < 0, the solution of the problem (.5) also will be expressed by the formula (.10) with only one modification, that P κ0 1(z) 0, at observance of κ 0 conditions of solvability of the aspect: L g 0 (τ) X + 0 (τ) τ k 1 dτ = 0, k = 1,..., κ 0. Let s define numbers γ c specified in the statement of the problem R,. Let c 1, c,..., c m be knots of the function G 0 (t). Below we shall consider that γ ck > 1 π (arg G(c k 0) arg G(c k + 0)), k =,..., m γ c1 > 1 π (argg(c 1 0) argg(c 1 + 0) πκ 0 ). (.11) Further, on the found function f 0 (z) with the help of differentiation and in view of the formulas Sokhotzky-Plemelj (see [4], p. 333, [1, ]), we shall find out boundary values df 0 ± (t) of the function df 0(z) dt dz. Note 1. We shall notice, that if the knot c is not singular or c singular, but ln G 0 (c 0) ln G 0 (c + 0) = 0 from the conditions (.11), it follows that the
213 The Second Basic Boundary Value Problem 197 functions df 0 ± (t) satisfy the condition of Holder everywhere on L except for, possibly, knots, where they may have a singularity of the integrable order (knots of the dt first type). Otherwise functions df 0 ± (t) will have a singularity of the first order near dt the knots (knots of the second type). Further we shall solve the boundary value problem of Riemann (.6). Let the index of the problem (.6) be equal κ 1 in the specified class. As it is known (see [1, ]), if κ 1 3, a common solution of the problem (.6) is set by the formula: f 1 (z) = X 1 (z) 1 πi L Q 1 (τ) X + 1 (τ) dτ τ z + P κ 1 3(z), (.1) where X 1 (z) canonical function of the problem (.6), P κ1 3(z) the polynomial of a degree not higher then κ 1 3 with arbitrary complex coefficients, Q 1 (t) = 1 ( t df 0 + (t) + tg 1 (t) df 0 (t) ) + g 1 (t). dt dt If κ 1, the solution of the problem (.6) also will be expressed by the formula (.1) with only one modification that P κ1 3(z) 0, at observance of κ 1 + conditions of solvability of the aspect: Q 1 (τ) X 1 + (τ) τ k 1 dτ = 0, k = 1,..., κ 1 +. L Note. Generally speaking, absolute term Q 1 (t) of the problem (.6) satisfies the condition of Holder everywhere on L except for, possibly, knots c 1, c,..., c m, where it may have singularity of the first order (knots of the second type), and remaining knots, where it may have an integrable singularity. And, if the knot of the second type of the problem (.5) is the singular knot of the problem (.6), then the problem R, will be insoluble in the class A (D ± ) I () (L). Further on the found functions f 0 (z) and f 1 (z), using the formulas (.3), we restore analytical components of the required piecewise bianalytical function, and then the piecewise bianalytical function F (z) itself under the formula (.1). Thus, the following basic outcome is fair. Theorem 1. Let L = {t : t = 1}, D + = {z : z < 1} and D = C\{D + L}. Then the solution of the problem R, is reduced to the sequential solution of two scalar boundary value problems of Riemann (.5) and (.6) with discontinuity coefficients in classes of analytical functions in the unit circle, and that the solution of the problem (.5) is searched in the class of functions vanishing on infinity and limited in the knots of the contour; and the solution of the problem (.6) is searched in the class of functions, having on infinity zero of the third order and infinity of the integrable order in the knots of the contour L. The problem R, is solvable if and only if
214 198 I.B. Bolotin the problems (.5) and (.6) in the specified classes of functions are simultaneously solvable and knots of the second type are not singular for the coefficient G 1 (t) of the problem (.6). Example 1. Let L = {t : t = 1}, D + = {z : z < 1} and D = C\{D + L}. It is required to find all piecewise bianalytical functions F (z) = {F + (z), F (z)} belonging to the class A (D ± ) I () (L) vanishing on infinity, limited near the knots of the contour and satisfying in all ordinary points L the following boundary conditions: F + (t) = G 0 (t)f (t) + (t 1) 3 (t + 1) 3, (.13) F + (t) n + = t 4 F (t) n (3t (t 1) 1 + t ), (.14) Here G 0 (t) = { 1, t L1 = {t : t = e is, 0 s π}, 1, t L = {t : t = e is, π s π}, G 1 (t) = t 4, g 0 (t) = (t 1) 3 (t + 1) 3 and g 1 (t) = (3t (t 1) 1 + t ). Using equalities (.) (.4), the boundary condition (.13) will take the following aspect: f 0 + (t) = G 0(t)f0 (t) + (t 1) 3 3 (t + 1), (.15) Knots of the problem (.15) are the points t = 1 and t = 1, in which function G 0 (t) has simple discontinuity. Let s calculate the index of the problem (.15). Let s choose as the initial point t = 1. We have, G 0 (1 + 0) = 1 = e i0, θ 1 = 0, the change of argument of the function G 0 (t) on the arc L 1 will be equal Therefore θ 1 = [argg 0 (t)] L1 = 0. G 0 ( 1 0) = 1 = e i0. Let G 0 ( 1 + 0) = 1 = e iθ. Let s choose a value θ so that the inequality is fulfilled 0 0 θ < π, That is θ = π The change of argument of the function G 0 (t) on the arc L will be equal to zero. So G 0 (1 0) = 1 = e iπ. Let s define the whole number κ 0, satisfying the following condition: 0 π πκ 0 < π. Thus, the index of the problem (.15) will be equal to -1. The common solution of the problem will look like:
215 The Second Basic Boundary Value Problem 199 f + 0 (z) = (z 1) 3, f 0 (z) 0, at observance of one condition of solvability: τ(τ 1)dτ = 0, L which is obviously fulfilled. The boundary values of the derivative of the solution of the problem (.15) will be set by the formulas: df 0 + (t) = 3t(t 1) 1, dt (.16) df 0 (t) 0. dt (.17) With the account (.16) (.17), the boundary condition (.14) will take the aspect: f + 1 (t) = t4 f 1 (t) + t. (.18) Generally speaking, the coefficient of the problem (.18) is the continuous function on L, but following the statement of the problem (.18) the knots will be represented by the points t = 1 and t = 1. Let s calculate the index of the problem (.18). Let s choose as the initial point t = 1. We have, G 1 (1 + 0) = 1 = e i0, θ 1 = 0, The change of argument of function G 1 (t) on the arc L 1 will be equal Therefore θ 1 = [argg 1 (t)] L1 = 4π. G 1 ( 1 0) = 1 = e i4π. Let G 1 ( 1 + 0) = 1 = e iθ. Let s choose a value θ so that the inequality is fulfilled π < 4π θ 0, That is θ = 4π The change of argument of function G 1 (t) on the arc L will be equal 4π. So G 1 (1 0) = 1 = e i8π. Let s define whole number κ 1, satisfying the following condition: π < 8π πκ 1 0. Thus, the index of the problem (.18) will be equal to 4. Hence, the common solution of the problem (.18) will look like: f + 1 (z) = z + a 1 z + a 0, f 1 (z) = a 1 z 3 + a 0 z 4,
216 00 I.B. Bolotin where a 0 and a 1 arbitrary complex coefficients. On the found functions f 0 (z) and f 1 (z), using (.3), we restore analytical components of the required piecewise bianalytical function F (z): ϕ + 0 (z) = (z 1) 3 z + a 1 z + a 0, (.19) ϕ 0 (z) = a 1 z 3 a 0 z 4, (.0) ϕ + 1 (z) = z3 + a 1 z + a 0 z, (.1) ϕ 1 (z) = a 1 z + a 0 z 3. (.) Thus, common solution of the problem (.13) (.14) is represented by the formula: { F F (z) = + (z) = ϕ + 0 (z) + zϕ+ 1 (z), z D+, F (z) = ϕ 0 (z) + zϕ 1 (z), z D, where the functions ϕ ± 0 (z) and ϕ± 1 (z) are defined by the formulas (.19) (.). References [1] F.D. Gakhov. Boundary value problems. Nauka, Moscow, (in Russian) [] N.I. Muskhelishvili. Singular integral equations. Nauka, Moscow, (in Russian) [3] K.M. Rasulov. Boundary value problems for polyanalytical functions and some of their applications. Smolensk State Pedagogical University, Smolensk, (in Russian) [4] N.P. Vekua. Systems of singular integral equations and some boundary value problems. Nauka, Moscow, (in Russian) Antrasis kraštinis uždavinys Rimano tipo bianalizinėms funkcijoms su trūkiais koeficientais I.B. Bolotin Darbe sprendžiamas antrasis kraštinis uždavinys Rimano tipo bianalizinėms funkcijoms su trūkiais koeficientais. Parodoma, kad sprendžiamas uždavinys suvedamas į sprendimą dviejų Rimano uždaviniu analizinėms funkcijoms su trūkiais koeficientais. Randamos analizinių funkcijų klasės, kuriose gali būti sprendinys. Pateikiamas pavyzdys, iliustruojantis nagrinėjamo uždavinio sprendimo algoritmą.
217 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN DIFFUSION OF POPULATION UNDER THE INFLUENCE INDUSTRIALIZATION IN A TWIN-CITY ENVIRONMENT J. DHAR 1 and H. SINGH 1 Department of Applied Mathematics, Beant College of Engineering and Technology Gurdaspur 14351, Punjab, India 78:9;:<=>?:@ ;A9BB%C6DEB%CFHG Department of Mathematics, Baba Banda Singh Bahadur Engineering College Fatehgarh Sahib , Punjab, India Received February 1, 004; revised August 6, 004 Abstract. A mathematical model of a living population in a twin-city is proposed. Here populations are migrating from one place to another for their resource and settlement under the influence of industrialization. The long term effect of industrialization on the movement of human population is considered in two adjoining cities. It is shown that the steady state distribution of population is positive, continuous, monotonic and the system is stable under certain set of conditions. Further, numerical solution of the steady state distributions of population and industrialization are shown by taking particular values of the parameters. Key words: Diffusion of population, industrialization, twin-city, steady state distribution, stability 1. Introduction Modelling is very useful in understanding the behaviour of any environmental system. The models, in fact, represent the system in an abstract form, and provide necessary information about the system. It is a sequential and iterative process which helps in conceptualization, synthesis, simulation and analysis of the synthesis [1, 13, 14, 15, 16]. Every population is characterized with such characteristics as dispersion, fluctuation, sex ratio, birth rate and death rate [1, 14]. Population growth in a particular region is directly related to the continuous changes taking place in that environment as the environment is never static and keeps on changing from time to time due to several reasons of which some are natural while others are man-made [5, 6, 8, 9, 10, 11].
218 0 J. Dhar, H. Singh One of the man-made reasons responsible for population migration from one place to another, is industrialization [], which has positive effects in terms of employment and resources, while some major negative effects in the form of air and water pollution. Moreover, the effluents from industries contain many chemicals that are toxic to living organisms. Industrial effluents may also contain some radioactive substances which cause many deadly diseases [17]. An interesting problem, in a twin city the continuous movement of population takes place due to the influence of different level of industrialization. In this paper we therefore propose a mathematical model to understand the long time effect of industrialization in two adjoining cities.. Mathematical Model We consider a linear environment 0 x L, consisting of two adjoining cities 0 x L 1 and L 1 x L with L 1 as the interface between the two cities. Here the regions are divided either by a river, highway or any other geographical or topographical condition. Let I i (x, t) and N i (x, t) be the respective industrialization and population densities at the location x at time t in i-th region, where i = 1, (see Fig. 1). Population density N 1(x, t) Population density N (x, t) Industrialization density I 1(x, t) Industrialization density I (x, t) Figure 1. Twin city environment. It is assumed that I i (x, t) grows logistically in both regions, with growth rate a i and carrying capacity C i. Further, we assume that in i-th city the population grows in absence of industrialization in a general logistical manner with growth rate r i, carrying capacity K i, growth factor β i and in presence of industrialization, the growth rate of population varies with interaction rate α i (i.e. which includes all positive and negative effects of industrialization on population). Here, D 1i and D i are the diffusion coefficients of industrialization and population respectively in the i-th region. It is also assumed that, when the industrialization reaches its highest level (i.e at the carrying capacity), then the population in that region also reaches its carrying capacity. Keeping in view all these assumptions, we get the following mathematical model: I i t == a ii i N i t ( 1 I i = r i N i (1 C i ( Ni ) I i + D 1i x, K i ) βi ) + α i N i ( 1 I i C i ) + D i N i x, (.1)
219 Diffusion of population under the influence industrialization 03 where a i, C i, r i, K i, α i, D 1i, D i > 0, i = 1, ; 0 < x < L. We are interested only in coexistence of the population and industrialization at the equilibrium (Ni, I i ). Thus we want to find N i > 0, Ii > 0, such that ( ) a i Ii 1 I i = 0, C i ( ( ) ) N r i Ni βi ( ) 1 i + α i Ni 1 I i = 0, K i C i which implies N i = K i and I i = C i. Therefore, the nonzero equilibrium point is given by the carrying capacities of the industrialization and population, respectively in that habitat. We also assume the continuity and flux matching conditions at the interface x = L 1. The continuity conditions at the interface x = L 1 for this system are I 1 (L 1, t) = I (L 1, t), N 1 (L 1, t) = N (L 1, t) (.) and the continuous flux matching conditions at the interface s = L 1 for I i (x, t) and N i (x, t) are written as D 11 I 1 (L 1, t) x D 1 N 1 (L 1, t) x = D 1 I (L 1, t) x = D N (L 1, t) x The model is studied under no-flux boundary conditions i.e. I 1 (0, t) x N 1 (0, t) x = 0, = 0, I (L, t) x N (L, t) x, (.3). = 0, (.4) = 0. Finally, the model is completed by assuming some positive initial distribution I 1 (x, 0) = f 1 (x) > 0, N 1 (x, 0) = g 1 (x) > 0, 0 < x < L 1, (.5) I (x, 0) = f (x) > 0, N (x, 0) = g (x) > 0, L 1 < x < L. We first study the existence and stability behaviour of system (.1) in homogeneous habitat, the effect of patchiness will be investigated later. 3. Model in a Homogeneous Habitat The corresponding model of (.1) in a single homogeneous habitat without diffusion, i.e. a i = a, r i = r, K i = K, C i = C, α i = α, β i = β, i = 1,
220 04 J. Dhar, H. Singh becomes di dt = ai dn dt = rn ( 1 I ), C ( 1 ( ) ) β ( N + αn 1 I ). K C (3.1) Here the positive equilibrium is (K, C), which is locally asymptotically stable if ( ) αk 4arβ. (3.) C This can be easily verified by using Lyapunov s direct method and taking the following positive definite function: V (t) = 1 ( (I C) + (N K) ). Example 1. By taking the following values of the parameters a = 0.05, r = 0.06, α = 0.005, β =, C = 1000, K = 80, 000, we see that condition (3.) holds true. 4. Steady State Problem in Twin City Environment We denote the steady state of the industrial density by u i (x) and the population density by v i (x) in the i-th city, for i = 1,. Then the steady state problem becomes: d ( u i D 1i dx + a iu i 1 u ) i = 0, C i ( d ( ) ) βi ( v i D i dx + r vi iv i 1 + α i v i 1 u ) i = 0. K i C i The continuity and flux matching conditions at the interface x = L 1 are given by D 11 du 1 dx (L 1) = D 1 du dx (L 1), D 1 dv 1 dx (L 1) = D dv dx (L 1), (4.1) u 1 (L 1 ) = u (L 1 ), v 1 (L 1 ) = v (L 1 ), (4.) and the no-flux boundary conditions are du 1 dx (0) = 0, du dx (L ) = 0, (4.3) dv 1 dx (0) = 0, dv dx (L ) = 0. By using a similar analysis as in [3, 4, 7], we can prove the following theorem.
221 Diffusion of population under the influence industrialization 05 Theorem 1. The steady state distribution u i and v i are positive, continuous and monotonic in the whole region. Now we will find the stability conditions of the system by using Lyapunov s direct method. Theorem. The steady state system (4.1) for β i = 1, i = 1, is locally asymptotically stable if u i C i, α i v i K i, (4.4) ( ) αi K i 4a i r i. (4.5) C i Proof. Linearizing the steady state system (4.1) by using ei i (x, t) = u i (x) + n i (x, t), N i (x, t) = v i (x) + m i (x, t) we get a system of linear equations ( n i t = a in i 1 u i C i ( m i = r i m i 1 v i t K i ) n i + D 1i x, ) + α i [m i ( 1 u i C i We use the following positive definite function V (t) = i=1 Li L i 1 1 ) ] v i m i n i + D i C i x. ( n i + m ) i dx. By using the boundary and flux matching conditions at the interface L 1, we obtain i=1 i=1 Li L i 1 D 1i n i n i x dx = Li m i D i m i L i 1 x i=1 dx = i=1 Li L i 1 D 1i Li L i 1 D i ( ) ni dx, x ( ) mi dx. x Hence, the system will be asymptotically stable if ( 1 u ) ( i 0, r i 1 v ) ( i + α i 1 u ) i 0, C i K i C i (4.6) [ ] ( v i α i 4a i 1 u ) ( i [r i 1 v ) ( i + α i 1 u )] i. C i C i K i C i (4.7) It can be easily verified that, (4.6) is automatically satisfied if inequalities (4.4) are true. Moreover from (4.7) by using a simple concept that if f(x) g(x) then max f(x) min g(x), we get (4.5). Hence the theorem is proved.
222 06 J. Dhar, H. Singh 5. Discussion and Numerical Simulation There are several twin cities in India, for example Secundrabad Hyderabad, Chandigarh Mohali, Delhi Gaziabad. First pair of cities are separated by highways, second pair by inter state border and third pair by river. We can also find many examples round the globe. Moreover in our study the industrialization means not only small and big industries, it also includes all man-made projects, e.g. marketing complex, housing complex. Hence it is very difficult to get complete or concrete data of population and industrialization at different time and space in both the cities Steady State Distributions PATCH-I PATCH-II Population with high dispersal rates Population with low dispersal rates Industrialization Figure. Steady state distributions For better understanding, in this section we study, the steady state distributions of the population and industrialization in two adjoining regions (see Fig. ) with flux matching conditions at interface and no-flux boundary conditions as stated in (4.1) (4.3). A particular set of parameters is shown in Table 1, the region parameters are the following: β = 1., L 1 = 10, L = 0. It can be easily verified that the stability conditions of Theorem are satisfied for these values of parameters. We see in Fig., that both population and industrialization distributions are continuous and monotonic from one end to the other end of the habitat. Moreover, if the dispersal rates D 1 and D are very high, then the steady state distribution of the population is almost linear and when dispersal rates are very low then the population distribution is almost at the level of carrying capacities of the respective cities except near to the interface of cities where abrupt changes take place (see Fig. ).
223 Diffusion of population under the influence industrialization 07 Table 1. Values of the parameters for Fig.. Parameters Patch 1 Fig. Patch Fig. Growth rate of Industrialization a a 0.03 Growth rate of Population r r 0.03 Carrying capacity of Population K K Carrying capacity of Industrialization C C 8000 Interaction rate α α Migration coefficient of Industrialization D D For high dispersal rate of population D D 0.7 For low dispersal rate of population D D 0.0 References [1] L.J.S. Allen. Persistence and extinction in Lotka-Volterra reaction-diffusion equations. Math. Biosci., 65, 1 1, [] J. Dhar. Modelling and analysis: the effect of industrialization on diffusive forest resource biomass in closed habitat. African Diaspora Journal of Math., (1), , 003. [3] J. Dhar. A prey-predator model with diffusion and a supplementary resource for the prey in a two-patch environment. Mathematical Modelling and Analysis, 9(1), 9 5, 004. [4] J. Dhar and J.B. Shukla. A single species model with diffusion and harvesting in a two-patch habitat. Mathematical Analysis and Application, 79 9, 000. [5] J. Dhar and H. Singh. Steady state distribution and stability behavior of a single species population with diffusion in n-patch habitat. Far East J. Appl. Math., 11(), , 003. [6] H.I. Freedman and T. Krisztin. Global stability in model of population dynamics with diffusion. I. Patchy environment. In: Proc. Royal Soci. of Edinburgh, volume 1A, 69 84, 199. [7] H.I. Freedman, J.B. Shukla and Y. Takeuchi. Population diffusion in a two-patch environment. Math. Biosci., 95, , [8] H.I. Freedman and J. Wu. Steady state analysis in a model for population diffusion in a multi-patch environment. Nonl. Analy., Theor., Meths. & Appl., 18, , 199. [9] K. Gopalsamy. Competition, dispersion and co-existence. Math. BioSci., 33, 5 33, [10] K.P. Hadeler, V. Heiden and F. Rothe. Nonhomogeneous spatial distributions of populations. J. Math. Biol., 1, , [11] A. Hastings. Global stability in Lotka-Volterra systems with diffusion. J. Math. Biol., 6, , [1] M. Kot. Elements of Mathematical Ecology. University Press, Cambridge, UK, 001. [13] S.A. Levin. Population model and community structure in heterogeneous environments. In: Mathematical Ecology, Springer, New York, 95 31, [14] A. Okubo. Diffusion and ecological problem: Mathematical models. In: Lecture Notes. Springer-Verlag, [15] C.V. Pao. Coexistence and stability of a competition diffusion system in population dynamics. J. Math. Anal. Appl., 83, 54 76, [16] F. Rothe. Global solution of reaction-diffusion systems. In: Lecture Notes in Mathematics, volume 107. Springer-Verlag, [17] P.D. Sharma. Ecology and Environment. Rastogi Publications, Meerut, India, 001. Seventh Edition
224 08 J. Dhar, H. Singh Populiacijos difuzija miestu-dvynių aplinkoje, esant industralizacijos poveikiui J. Dhar, H. Singh Straipsnyje pasi ūlytas populiacijos dinamikos miestuose-dvyniuose matematinis modelis. Daroma preilaida, kad populiacija migruoja iš vienos vietos į kitą industralizacijos poveikyje. Tiriamas ilgalaikis industralizacijos poveikis žmonių judėjimui dviejuose gretimai esančiuose miestuose. Įrodyta, kad esant išpildytoms tam tikroms sąlygoms, nusistovėjęs rėžimas yra tolydus, monotoniškas ir stabilus. Taip pat pateiktas skaitiniais metodais gautas stacionarusis pasiskirstymas, esant pasirinktam parametrų rinkiniui.
225 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN A REVIEW OF NUMERICAL ASYMPTOTIC AVERAGING FOR WEAKLY NONLINEAR HYPERBOLIC WAVES 1 A. KRYLOVAS and R. ČIEGIS Vilnius Gediminas Technical University Saulėtekio al. 11, LT-103 Vilnius, Lithuania 78:9;%<=;#>:?@ACBEDFGHIDKJ G Received June 8, 004; revised July 5, 004 Abstract. We present an overview of averaging method for solving weakly nonlinear hyperbolic systems. An asymptotic solution is constructed, which is uniformly valid in the "large" domain of variables t + x O(ε 1 ). Using this method we obtain the averaged system, which disintegrates into independent equations for the nonresonant systems. A scheme for theoretical justification of such algorithms is given and examples are presented. The averaged systems with periodic solutions are investigated for the following problems of mathematical physics: shallow water waves, gas dynamics and elastic waves. In the resonant case the averaged systems must be solved numerically. They are approximated by the finite difference schemes and the results of numerical experiments are presented. Key words: small parameter method, perturbations, hyperbolic systems, averaging, resonance, finite difference schemes, numerical solution, gas dynamics, shallow water, elastic waves 1. Introduction We consider a hyperbolic system of weakly nonlinear differential equations with a small positive parameter ε: where U t + A(U)U x = εb(t, x, εt, εx, U, U x, U xx, U xxx ), (1.1) U(t, x; ε) = (u 1, u,..., u n ) T, A(U) = a ij (U) n n. Let define a constant solution U 0, which satisfies the equation 1 This work was supported by by the Lithuanian State Science and Studies Foundation (V-7) within the framework of the Eureka project OPTPAPER E!-63, E
226 10 A. Krylovas, R. Čiegis B(t, x, εt, εx, U 0, 0, 0, 0) = 0. We assume that all coefficients in (1.1) are sufficiently smooth functions. Our goal is to find a small amplitude solution U(t, x; ε) = U 0 + εu 1 (t, x; ε). The system (1.1) must be solved in the "large" domain: [ (t, x) 0, τ 0 ε ] [ ξ 0 ε, ξ ] 0 ε [0, + ) R. For small ε the problem of solving (1.1) numerically is a very difficult task. Asymptotic methods are used for the analysis of such problems. Often (but not always) the asymptotic solution satisfies some simple equations. If a problem for asymptotic solution is still complicated, then a combination of numerical and asymptotic methods can be used (see [1]). In this article we present an overview of new asymptotic methods for solution of problems with a small parameter. Recent developments in theoretical analysis, as well as numerical algorithms are discussed. We present numerical algorithms for solving the averaged systems which are obtained applying the asymptotic averaging method for the system (1.1) with periodic initial conditions. Three examples of applied problems are investigated, including resonant interaction of shallow water waves, one dimensional waves of gas dynamics and resonances in elastic waves. The theoretical aspects of the asymptotic analysis of these examples where considered in our papers [16, 17, 18, 19]. In this article we focus our attention on the investigation of finite difference schemes for solving the averaged systems of equations. Note, that analogous integro-differential systems were also investigated in [1,, 3]. However numerical algorithms were not considered in these papers and no computational examples were given. ε 0. The Method of Averaging Let assume that the problem is hyperbolic in neighborhood of U 0, thus we can rewrite the system using the well know Riemann invariants then we get: Λ = diag{λ 1, λ,..., λ n } = RA(U 0 )R 1, V (t, x; ε) = RU 1 (t, x; ε) = (v 1, v,..., v n ), V t + ΛV x = εf (t, x, εt, εx, V, V x, V xx, V xxx ) + o(ε). (.1) If the parameter ε = 0, then system (.1) disintegrates into independent equations, which describe linear waves v j (x λ j t). If ε 0 and t + x ε 1, then the exact solution of (.1) is not close to these simple waves. For example, the initial value problem
227 A Review of Numerical Asymptotic Methods 11 { vt + v x = εvv x, v(0, x) = sin(x) describes a nonlinear wave, which can be obtained from the implicit relation v = sin(x t εtv). For εt = O(1) the solution v(t, x; ε) can not be approximated by a simple wave sin(x t) and thus it is a nontrivial task to construct an asymptotic approximation, which is uniformly valid in the region t + x = O(ε 1 ). The key idea of all asymptotic methods for solving problem (.1) (or (1.1)) is to introduce new slow variables, e.g., τ = εt, ξ = εx, and to define explicitly the dependence on fast variables (principle of multiple scales, see [8, 4]). For example in [8] the solution of the system (.1) is obtained in the following form u j = ψ j (η, ζ j ), η = ε 1+a t, ζ j = ε a (x λ j t + ε 1 a ϕ(t, x)). Substituting these expressions into (1.1), using the Taylor expansion with respect to ε, and collecting equal powers of ε k, we get equations for unknown functions ψ j. The Burgers and Korteweg de Vries equations are examples of such problems. We will show, that these asymptotics are not uniformly valid in the region t + x = O(ε 1 ) for the systems with periodic initial conditions in the case of resonant interaction of waves, therefore some modifications of such algorithms should be proposed..1. Formulation of the integro-differential system Our method of asymptotic integration is based on principles of multiple scales and averaging. We introduce slow variables τ = εt, ξ = εx and fast characteristic variables y j = x λ j t, j = 1,,..., n. Our goal is to construct the asymptotic solution in the following form v j (t, x; ε) = V j (τ, ξ, y j ) + o(1), j = 1,,..., n, ε 0. The basic idea of our method is the special averaging along characteristics: 1 T M j [g(τ, ξ, t, x, y 1, y,..., y n )] lim g ( τ, ξ, s, y j + λ j s, (.) T + T 0 y j + (λ j λ 1 )s,..., y j + (λ j λ n )s ) ds. We also will use the following notation < g > j (τ, ξ, y j ) = M j [g(τ, ξ, t, x, y 1, y,..., y n )]. The asymptotic solution satisfies the averaged system: V j τ + λ V j j ξ = M j[f j (t, x, τ, ξ, V 1, V,..., V n,...)] (.3) with periodic initial conditions
228 1 A. Krylovas, R. Čiegis V j (0, ξ, y j ) = v oj (ξ, y j ) = v 0j (ξ, y j + π), j = 1,,..., n. Our method also can be used for the non-periodic solutions, e.g., for almost periodic functions or for functions v j (τ, ξ, y j ), which satisfy conditions lim v 0(τ, ξ, y j ) = 0. y j ± In the π-periodic case with integer coefficients λ 1, λ,..., λ n the operator (.) can be written in the simpler form: < g > j = 1 π π 0 g(τ, ξ, s, y j + λ j s, y j + (λ j λ 1 )s,..., y j + (λ j λ n )s) ds. After averaging each function depends only on one fast characteristic independent variable y j. The new feature of this method is that the averaging operator is applied for functions, which themselves are solutions of the obtained averaged equations. Thus we get integro-differential problems (see [1], where our averaging scheme is compared with the other averaging methods). This idea was presented in [7] and developed in papers of the first author of this article [9, 10, 11] (see also [, 5, 1,, 3] and a survey of mathematical results in [7]). The aspects of mathematical substantiation of our method were considered in [13, 14, 15]. The method of [1] is very close to the method of averaging along characteristics from [9, 7] but only quadratic nonlinearities were considered in [1]. A mathematic substantiation of the asymptotic method and especially the construction of higher order terms in the asymptotic series leads to the problem of small denominators: δ jl = l 1 (λ j λ 1 ) + l (λ j λ ) + + l n (λ j λ n ), where l = (l 1, l,..., l n ) is a vector with integer components. In [7] all combinations λj λi λ j λ k were rational numbers and therefore δ jl were equal to zero or δ jl > const. In a general case min δ jl = o(1), L, l =L, δ jl 0 therefore numbers λ 1, λ,..., λ n, satisfying the following condition min δ jl > c l =L, δ jl 0 L r, where c and r are some positive constants, were considered in [9] (see also [6]). The properties of min δ jl l =L, δ jl 0 were studied in [10], here small perturbations of numbers λ j = λ j0 + λ j1 (ε) were investigated. In [1] the conditions of resonant interaction of waves were given only for quadratic nonlinearities, more general relations of resonance δ jl = 0 were proposed in [11].
229 .. Numerical algorithms A Review of Numerical Asymptotic Methods 13 The integro-differential system (.3), must be solved numerically in the compact domain of variables: (τ, ξ, y 1, y,..., y n ) [0, τ 0 ] [ ξ 0, ξ 0 ] [0, π] n. It is important to note that the averaged system is solved only once and the obtained solution later can be used for all ε. We always try to split the operators M j into a sum of two operators M j (V 1,..., V n ) = L j V j + N j (V 1,..., V n ) and L j V j is included into the differential part of (.3). For many applications we get systems of nonlinear differential equations such that efficient numerical methods already exist for solving this type of equations. In some cases even numerical software is available and this fact provides a possibility to tackle real-life problems at small programming cost. The remaining integral part of the integro-differential system is approximated explicitly. A fixed-point iteration method can be used to improve the stability of the obtained numerical algorithm. 3. Theoretical Justification of the Method In this section we describe the main steps of the theoretical analysis. First we show that the averaging operator M j [g(τ, ξ, t, x)] takes out secular terms, which were obtained after integration of the equation u t + λ u j = εg(τ, ξ, t, x) x along the characteristic x λ j t = const. Thus the following equality t lim ε ( ) g M[g] (t = s, x = x λj t + λ j s) ds = 0 (3.1) ε 0 0 should be valid uniformly in x + t c 0 ε. Let us denote F (ε) = max ε j = 1,,..., n τ + ξ [ c 0, c 0 ] t + x [0, c 0 /ε] t 0 (f j M[f j ]) ds. (3.) Here f j are functions from (.1). Let us assume that in (1.1) the right-hand side vector B = B(U) = ( b 1 (U),..., b n (U) ) and all functions b j (U) are continuously differentiable functions. If the averaged system satisfies condition (3.1), i.e. F (ε) = o(1), ε 0,
230 14 A. Krylovas, R. Čiegis then a solution of system (1.1) is approximated uniformly in the region x + t c 0 ε by a solution of the averaged system, i.e.: u j (t, x; ε) = v j (τ, ξ, y j ) + O ( F (ε) ). Secondly, we should prove that averaged system (.1) has a solution, which satisfies condition (3.1). In case of periodical initial conditions it is sufficient to note the following property of operator M j. Let us denote by C 1 π ([ c 0, c 0 ] [0, π]) a class of π periodical functions u(τ, y), which have a continuous derivative with respect to y. Let assume that f j (v 1, v,..., v n ) C 1 (R n ), v j (τ, y j ) C 1 π([ c 0, c 0 ] [0, π]). Then we obtain, that M j [f j (v 1,..., v n )] = g j (τ, y j ) C 1 π([ c 0, c 0 ] [0, π]). We see that all averaged functions preserve properties of continuity and periodicity, thus we can prove the existence and uniqueness of the solution of averaged system (.1) by using the standard Picard method. The proposed averaging method can be used not only in case of periodical functions. This scheme can be applied to construct almost periodical asymptotical approximations or to consider functions decreasing at infinity lim v 0(τ, ξ, y j ) = 0. y j ± The other generalization of the method is obtained for a case when the averaging operator is nonuniform with respect to the arguments of functions: v j (τ, ξ, y j ) v + 0j (τ, ξ, y j), v j (τ, ξ, y j ) v 0j (τ, ξ, y j), y j +, y j. If functions v 0 +, v 0 are periodical or almost periodical with respect to y j or decreasing at infinity, then averaging operator can be applied in each region (t, x) λ i t < x < λ i+1 t. Therefore we can consider not only the initial value problem, but also to formulate initial boundary value problem in t = 0, x > 0 and x = 0, t > 0 (see [13, 14, 15]). 4. Shallow Water Equations 4.1. Averaged system In this section we consider the system of shallow water equations:
231 A Review of Numerical Asymptotic Methods 15 ( ) ( ) ( ) Z 0 1 Z + W 1 0 W t x (4.1) ( 1 = ε 3 W ) xxx + (H(x)W ) x + (ZW ) x. W W x Here Z denotes the water surface level, W denotes the horizontal velocity of the fluid, L is some typical horizontal size, H is some typical vertical size, ε = ( ) H L << 1, H = 1 + εh(x) is the bottom equation. The asymptotic solution of (4.1) satisfies the averaged system of two equations: V + τ V τ Here we use notation + 3 V + V + y V V V y 1 3 V 6 y = 1 3 and V ± are approximations of v ± : y = 1 +3 y + H(x)V +, y H(x)V +. W = v + v, Z = v + + v, y ± = x t, v ± (t, x; ε) = V ± (τ, ξ, y ± ) + o(1). (4.) In the nonresonant case the expressions on the right hand side of (4.) are equal to zero and we get two independent Korteweg de Vries equations. We consider the resonant interaction of π-periodic waves: V τ V + V + y V + y + y + y + V τ = 1 π 4π y + H(y + + s)v (τ, y + + s) ds, 3 V V y 1 6 V y y y 4.. Finite difference scheme 0 = 1 π 4π y H(y s)v + (τ, y s) ds. 0 (4.3) We define the space ω h and time ω τ meshes and assume that the space mesh size h and time mesh size τ are uniform. We denote by vj n = v(tn, y j ) a discrete function defined on ω h ω τ. The following common notations of difference derivatives are used in our paper (see, e.g., [5]): v τ = vn+1 v n τ v y = v j+1 v j h, vȳ = v j v j 1, h, v y = v j+1 v j 1. h
232 16 A. Krylovas, R. Čiegis The finite difference approximation of system (4.3) is defined as follows (see also [4]): P τ = 1 ( P n+1 + P n ) (( 3 ) ) P n+1 + P n+1 P n + (P n ) 6 ȳyy 4 3 y F ( + M n+1, M n, j + 1 ) ( F + M n+1, M n, j 1 ), 4h ( M n+1 + M n ) (( ) ) M n+1 + M n+1 M n + (M n ) M τ = ȳyy F ( P n+1, P n, j + 1 ) ( F P n+1, P n, j 1 ), 4h where the integrals are approximated as follows: y F + ( M n+1, M n, j ) = 1 π F ( P n+1, P n, j ) = 1 π N i=1 N i=1 Here P and M approximate V +, V, respectively. H(y j ih) M n+1 j i + M j i n h, H(y j + ih) P n+1 j+i + P j+i n h. The approximation error of this finite finite difference scheme is estimated as O ( τ + h ). Numerical methods for solving the Korteweg-de Vries equation are investigated in [3, 6]. A special formula for averaging in time is used in order to satisfy some conservation properties, which are valid for the solution of the differential problem Linear dispersion problem In this section we consider a linear problem Z t + (HW ) x = ε 3 W xxx, W t + Z x = 0. (4.4) First we will prove that system (4.4) defines an ill-posed problem. Let consider the case H = 1. After simple computations we get the equation for W : W tt W xx = ε 3 W xxxx. (4.5) Considering the k-th Fourier mode we get that the solution of (4.5) is unstable for k ε 3. In order to define a stable solution we use the following regularized problem Z t + (HW ) x = ε 3 W xxx ε 0 W xxxxx, (4.6) W t + Z x = 0.
233 A Review of Numerical Asymptotic Methods 17 We note that the averaged system (.3) also gives a nontrivial regularization of this ill-posed problem. Extensive computational results are presented in [16, 18]. 5. One Dimensional Gas Dynamics Equations 5.1. Averaged system Let ρ denotes the gas density, u is the velocity and θ is the temperature. We introduce a vector U = (ρ, u, θ) T and matrixes u ρ 0 0 Rθ A = u R ρ 0 Rθ u, B = 1 γ u ρ x, (5.1) κ θ c v c v ρ c v x + γ ( ) u c v x where c v is the specific heat at constant volume, R is the gas constant for a politropic ideal gas: p = Rρθ, κ and γ are small viscosity and heat conduction coefficients (i.e. O(ε) as ε 0). Then the gas dynamics problem can be formulated as system (1.1). In this case the averaged system (.3) is described by the linear Burgers equations coupled through integral terms: V 1 τ f V 1 V 1 111V 1 f 11 y 1 y = V 3 V f 13 V + f 13 V 3, 1 y 3 y 1 V τ f V y = 0, (5.) V 3 τ f 333V 3 V 3 y 3 f 33 V 3 y 3 = V 1 V f 31 V + +f 31 V 1. y 1 y 3 The explicit expressions for coefficients in (5.) are presented in [17]. 5.. Finite difference scheme The averaged system (5.) is approximated by the following finite difference scheme: V 1,τ = f 11 V1,ȳy n f 111 (V1 n+1 ) + f 13 S 1 (V, V 3 ) + f 13 S 1 (V 3, V ), y V,τ = f V,ȳy n+1, V 3,τ = f 33 V3,ȳy n f 333 (V3 n+1 ) + f 31 S (V 1, V ) + f 31 S (V, V 1 ), y where the integrals are approximated as follows:
234 18 A. Krylovas, R. Čiegis S i (V j, V k ) = 1 4π N ( (V k yi + ((λ i λ k )l + 1)h ) l=1 V k ( yi + ((λ i λ k )l 1)h )) V j ( yi + ((λ i λ j )l 1)h ). The approximation error is given by O(τ + h ) Numerical experiments In this section we present results of numerical experiments. The following coefficients c v = 1, R = 1, ν = 1, κ = 1 are used in all tests. Initial conditions are selected as v 01 (x) = cos x, v 0 (x) = sin x, v 03 (x) = cos x. Figure 1 shows the solution of system (5.1) and the asymptotic solution at t = 1 ε for two different values of the small parameter ε. We present graphics of the density and velocity functions ρ ρ asympt U U asympt 1.05 ρ ρ asympt U U asympt ε = 0.1 ε = 0.05 Figure 1. Asymptotic and exact solutions of Euler problem (5.1) for t = 1 ε. 6. Elastic Waves Equations 6.1. Averaged system We consider a problem of wave propagation in two dimensional elastic materials and assume that displacements do not depend on the y coordinate. Restricting our attention to the axial displacements along x and y directions, we have equations [0]:
235 A Review of Numerical Asymptotic Methods 19 { ρutt = σ x, ρv tt = τ x, where ρ is the density of material, u and v denote the displacements along two directions, σ and τ ate longitudinal normal and shear stresses along the x-axes. The linear wave equation can be obtained from this equations if we use assumptions σ = (λ + µ)u x, τ = µv x, (6.1) where λ and µ are the Lamé coefficients. The equations (6.1) are obtained by using the simple approximation for the full energy of the system F F 0 + F 11 u x + F v x, then σ = F u x and τ = F v x (see [0]). In order to get high order approximations we use more terms in a Taylor series of F (see [4]): σ = (λ + µ)u x + 4ρ(a 1 u x + a u x v x + a 3 vx), Let τ = µv x + 4ρ(b 1 u x + b u x v x + a b vx ). P = u x, Q = v x, R = u t, S = v t, U = (P, Q, R, S) T. Then we get the system (1.1) with A(U) = λ + µ 0 0 0, B = 4 ρ x µ 0 ρ a 1 P + a P Q + a 3 Q b 1 P + b P Q + b 3 Q In this case the averaged system is given by the system of four equations:. P ± τ a 1 c p S ± τ b 3 c s P ± P ± y = a [ 3 ± c M y ± s [ a c s c p M y ± S ± S ± z = b 1 ± c M z ± p b c s c p M z ± ] x (S+ S ) ] x (P (S + S )), [ ] x (P + P ) [ ] x (S (P + P )). (6.) Here we use notation
236 0 A. Krylovas, R. Čiegis y ± = x c p t, z ± λ + µ µ = x c s t, c p =, c s = ρ ρ, P ± = R ± c p P, S ± = S ± c s Q. In the nonresonant case we get four independent nonlinear Burgers equations. 6.. Finite difference scheme The integrals on the right-hand side of (6.) are approximated by the trapezoidal rule, the derivatives of functions are computed using the central difference approximations. The upwind method is used to approximate the Burgers equation U n+1 j = U n j + µ τ h( F (U n j, U n j+1) F (U n j 1, U n j ) ), here F is the numerical flux function { 0.5w if 0 w v or (v < w and v + w 0), F (v, w) = 0.5v else. Thus we get the explicit approximation for the system of integro-differential equations. We have used implicit approximations in two previous examples. Now our goal is to show that explicit schemes also can be used to solve averaged equations, if such approximations are efficient for solving the differential part of the system (i.e. the Burgers equations for this example) Numerical experiments The results of numerical experiments are presented in Fig.. Here we present only one wave p + and its asymptotic approximation P + for t = 1 ε, ε = We see that the averaged system approximates uniformly the differential problem till time moments t = O ( 1) and the effect of resonant interaction of waves is also ε identified correctly. 7. Conclusions For weakly nonlinear hyperbolic systems with internal resonances the analysis can be done using the combination of numerical and asymptotic methods. The proposed method for constructing asymptotic solution of weakly nonlinear hyperbolic system can be used in nonresonant and in resonant cases. This solution is uniformly valid in large domain 0 t O(ε 1 ). The averaging of system (.1) reduces it to the integro-differential system of averaged equations (.). The averaged problem gives
237 A Review of Numerical Asymptotic Methods p + P Figure. Asymptotic and exact solutions of P + wave for ε = a system of integro-differential equations. However, in the nonresonant case the solution can be obtained as independent nonlinear waves. In the resonant case the solution is a superposition of waves, which satisfy the averaged system of nonlinear integro-differential equations. Such systems are solved numerically in the compact domain of variables (τ, x) [0, τ 0 ] [0, π]). References [1] N. S. Bakhvalov, G. P. Panasenko and A. L. Shtaras. The averaging method for partial differential equations (homogenization) and its applications. In: Partial Differential Equations V, Springer, New York, 11 39, [] S. C. Chikwendu and J. Kevorkian. A perturbation method for hyperbolic equations with small nonlinearities. SIAM J. Appl. Math.,, 35 58, 197. [3] B. Fornberg and T. Driscoll. A fast spectral algorithm for nonlinear wave equations with linear dispersion. J. of Comp. Phys., 155, , [4] D. Furihata. Finite Difference Schemes that Inherit Energy Conservation or Dissipation Property. Number [5] J. K. Hunter and J. B. Keller. Weakly nonlinear high frequency waves. Comm. Pure Appl. Math., 36, , [6] L. A. Kalyakin. Asymptotic integration of hyperbolic equations with weakly nonlinear perturbation. Differencialnye uravnenija, 0(), , [7] L. A. Kalyakin. Integrability equations as asymptotic limits of nonlinear systems. Uspechi Matematicheskich Nauk, 44(1), 5 34, [8] J. Kevorkian and J. D. Cole. Multiple Scale and Singular Pertubation Methods. Springer Verlag, Berlin, New-York, [9] A. V. Krylov. About the asymptotic interaction of first order hyperbolic systems. Lith. Math. J., 3(4), 1 17, [10] A. V. Krylov. Asymptotic integration of weakly nonlinear partial differential systems. Zhurnal Vytchisl. Matem. i Matemat. Fiziki, 6(1), 7 79, (in Russian) [11] A. V. Krylov. The method of research of weakly nonlinear interaction one dimensional waves. Prikladnaja Matem. i Mech., 51(4), , (in Russian)
238 A. Krylovas, R. Čiegis [1] A. V. Krylov. The internal averaging of first order partial differential systems. Matematitcheskije Zametki, 46(6), , (in Russian) [13] A. V. Krylov. The substantiation of the method of the internal averaging along characteristics in weakly nonlinear systems. I. Lith. Math. J., 9(4), 71 73, [14] A. V. Krylov. The substantiation of the method of the internal averaging along characteristics in weakly nonlinear systems. II. Lith. Math. J., 30(1), , [15] A. V. Krylov. The averaging of weakly nonlinear hyperbolic systems with non-uniform integral average. Ukrainian Math. J., 43(5), , [16] A. Krylovas and R. Čiegis. Asymptotic analysis of weakly nonlinear systems. In: A. A. Samarskii R. Čiegis and M. Sapagovas(Eds.), Finite Difference Schemes Theory and Applications, Proceedings of the Conference FDS000, September 1-4, Palanga, Institute of Mathematics and Informatics, Vilnius, , 000. [17] A. Krylovas and R. Čiegis. Asymptotical analysis of one dimensional gas dynamics equations. Mathematical Modelling and Analysis, 6(1), , 001. [18] A. Krylovas and R. Čiegis. Asymptotical approximation of hyperbolic weakly nonlinear systems. J. of Nonlinear Math. Phys., 8(4), , 001. [19] A. Krylovas and R. Čiegis. On the interaction of elastic waves. Journal of Civil Engineering and Management, 9(3), 18 4, 003. [0] L. D. Landau and E. M. Lifshitz. Theory of Elasticity: Course of Theoretical Physics. Butterworth V Heinemann, Oxford, [1] A. Majda and R. Rosales. Resonantly interacting weakly nonlinear hyperbolic waves. 1. a single space variable. Studies in Appl. Math., 71(), , [] V. P. Maslov. Asimptoticheskie metody reshenija psevdodifferencialnych uravnenii. Nauka, Moskva, (in Russian) [3] V. P. Maslov and P. P. Mosolov. Uravnenija odnomernogo barotropnogo gaza. Nauka, Moskva, (in Russian) [4] A. H. Nayfeh. Pertubation Methods. Jon Willay & Sons Inc., New-York, 000. [5] A.A. Samarskii. The theory of difference schemes. Marcel Dekker, Inc., New-York, Basel, 001. [6] J. M. Sanz-Serna. Symplectic integrators for hamiltonian problems. Acta Numerica, 1, 43 86, 199. [7] A. L. Štaras. The asymptotic integration of weakly nonlinear partial derivatives equations. Doklady Akademii Nauk SSSR, 37(3), 55 58, [8] T. Taniuti. Reductive perturbation method and far fields of wave equations. Suppl. Progr. Theor. Phys., 55, 1 35, Silpnai netiesinių hiperbolinių sistemu skaitinio asimptotinio vidurkinimo apžvalga A. Krylovas, R. Čiegis Darbe nagrinėjamas silpnai netiesinių hiperbolinių sistemų ilgųjų bangu asimptotinis sprendinys. Si ūlomas jo konstravimo metodas, pagrįstas vidurkinimu bei dviejų mastelių principu. Užrašytos skirtuminės schemos suvidurkintu lygčių sistemoms spręsti. Ištirti trys periodiniu asimptotinių sprendinių pavyzdžiai: sekliųjų vandenu modelis, dujų dinamikos lygtys bei tampriųjų bangu sąveika.
239 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN ABOUT THE SOLUTION IN CLOSED FORM OF GENERALIZED MARKUSHEVICH BOUNDARY VALUE PROBLEM IN THE CLASS OF ANALYTICAL FUNCTIONS K. M. RASULOV 14000, Przevalskogo 4, Smolensk, Russia Smolensk State Pedagogical University :;=<>987@?69BA5CD E F59HGI?KJ< Received October 13, 003; revised June 8, 004 Abstract. The paper is devoted to the investigation of the problem of obtaining piecewise analytical functions F (z) = F + (z), F (z) with the jump line L, vanishing on the infinity and satisfying on L the boundary condition F + [(α(t)] = G(t) F (t) + b(t) F (t) + g(t), t L, where α(t) is the preserving orientation homeomorphism of L onto itself and G(t), b(t), g(t) are given on L functions of Holder class and G(t) 0 on L. The algorithm for the solution of this problem was obtained and particular cases, when it is solvable in closed form are determined. Key words: bianalytical function, boundary value problem, plane with slots, index 1. The Formulation of the Problem Let T + be a bounded simply connected region on the plane of the complex variable z = x + iy, bounded by the simple closed Liapunov s contour L, and T = C\ (T + L). For determination we shall suppose, that the point z = 0 belongs to T +. Let us denote by α(t) the function, mapping the contour L onto itself with the preservation of the rule and having the derivative, satisfying the Holder condition H(L). We shall use notations from [8]. Let us consider the following problem. It is required to find all piecewise analytical functions F (z) = {F + (z), F (z)} from the class A(T ± ) H(L), vanishing on infinity and satisfying on L the following boundary condition F + [α(t)] = G(t) F (t) + b(t) F (t) + g(t), t L, (1.1)
240 4 K. M. Rasulov where G(t), b(t), g(t) are given on L functions of the class H(L), and G(t) 0 on L. It should be noted that the problem in form (1.1) in case α(t) t firstly was formulated in 1946 by A.I. Markushevitch [5]. So we shall call the problem formulated above as the Markushevitch boundary value problem or, in short, the problem M, and the corresponding homogeneous problem (g(t) 0) as the problem M 0. If α(t) t we shall call this problem generalized Markushevitch boundary value problem for analytical functions, or, in short, the GM problem. During the last 50 years many original works have been devoted to the problem (1.1) (see, for example [, 4, 6, 7, 9, 11] and the bibliography there). Even in the first works [1, 10], devoted to the investigation of the problem GM it was established, that if the condition G(t) 0, t L, ( ) is fulfilled, it is the Noeter problem. In the author s work [7] the constructive algorithm for solution of the problem M was obtained in the general case, i.e. if only one of the conditions (*) is fulfilled. In this article we shall obtain the constructive algorithm for solution of the problem GM and show the cases, when the problem GM can be solved in a closed form (in quadratures).. Solution of the Markushevitch Problem in a Closed Form for Rational Coefficients Let the region T + be the unity circle, i.e. T + = {z : z < 1}. Then, as it was proved in [7], if κ = Ind G(t) 0 the problem M is equivalent to the following integral equation of Fredholm type: F (t) + K(t, τ)f (τ)dτ = Q(t) + X (t)p κ 1 (t), (.1) where L K(t, τ) = τ X (t) πi Q(t) = g(t) α(t) + X (t) πi {[ b(τ) X + (τ) L b(t) ] X + (t) 1 τ t + b(t) } τx +, (.) (t) g(τ) dτ X + (τ) τ t, (.3) X + (t), X (t) are canonical functions of the Riemann boundary value problem with the coefficient G(t) and P κ 1 (z) is the polynomial of the degree not higher than κ 1 with arbitrary complex coefficients. If κ < 0, by the following conditions L b(τ)f (t) + g(t) X + t k 1 dτ = 0, k = 1,..., κ, (.4) (t)
241 About the Solution in Closed Form of Generalized Markushevich Problem 5 the problem M is also equivalent to the integral equation of the form (.1), where we put P κ 1 (z) 0. Now it is easy to notice, that if the coefficients G(t) and b(t) are rational functions, then the kernel K(t, τ), determined by the formula (.), will be degenerate (see e.g. [8], p.181), i.e. N K(t, τ) = r j (t)q j (τ), (.5) j=1 where r j (t), q j (t) are determined rational functions of there arguments. Hence, in this case integral equation (.1) has the solution in closed form (see for example, [3], p.37). But then the boundary value problem M also has the solution in closed form. Thus, the following statement is valid. Theorem 1. If L = {t : t = 1} and the coefficients G(t) and b(t) are rational functions, then the problem M is equivalent to the integral equation of Fredholm type (.1) with degenerate kernel, and, consequently, it can be solved in a closed form (in quadratures). Remark 1. The statement of the theorem 1 can be also obtained from the fact, then in the case of rational coefficients and unity circle T + = {z : z < 1} the solution of boundary value problem M, as it is known (see, for example, [4], p.3), is equivalent to the solution of the two-dimensional vector-matrix Riemann boundary value problem, where coefficient is non-singular matrix with rational elements. The latter problem also can be solved in a closed form (see, for example, [11], p.40). 3. Solution of the Markushevitch Boundary Value Problem in Rational Images of the Unity Circle Let for finite simple connected region T +, bounded by the simple closed Liapunov s contour, the rational function exists z = ω(ζ), ζ = ξ + iv, (3.1) mapping the unity circle K 1 = {ζ : ζ < 1} conformally on this region. So we shell call the region T + the rational image of the unity circle. The following statement is valid. Theorem. If T + is the rational image of the unity circle and the coefficients G(t), b(t) are rational functions, then the problem M can be solved in closed form. Proof. Introducing the following notations: f ± (ζ) = F ± (z) = F ± (ω(ζ)), G 1 (ζ) = G(ω(ζ)), b 1 (ζ) = b(ω(ζ)), g 1 (ζ) = g(ω(ζ)), we can rewrite the boundary condition of M in this way
242 6 K. M. Rasulov f + (τ) = G 1 (τ)f (τ) + b 1 (τ)f (τ) + g 1 (τ), τ = 1, (3.) The equality (3.) is the boundary condition of the usual Markushevitch boundary value problem with the rational coefficients in the class of the analytical functions, permitting the poles in the points ζ = and ζ = a i, i = 1,,..., m, where a i {ζ : ζ > 1}. Reasoning further as in the work [7], we can prove, that the problem (3.) is equivalent to the Fredholm s integral equation of the form (.1) with the degenerate kernel (i.e. of the form (.5)). Therefore, the problem (3.) can be solved in closed form, which means that the problem M can also be solved in quadratures. 4. Solution of the Generalized Markushevitch Boundary Value Problem As it is known (see, for example, [], p. 153), the regions T + and T can be conformally mapped on two mutually supplementary for the full plane regions T + 1 and T with the common boundary L 1, so, that the analytical functions F + (z) and F (z) will be transferred to the functions F + 1 (z) and F (z) defined in T + 1 and T correspondingly, and on L 1 the boundary condition of the following form will be fulfilled where F + 1 (ζ) = G 1(ζ) F 1 (ζ) + b 1(ζ) F 1 (ζ) + g 1(ζ), ζ L 1, (4.1) ζ = ω (t) = ω + [α(t)], G 1 (ζ) = G [(σ(ζ)], b 1 (ζ) = b [σ(ζ)], σ [ ω (t) ] t. Here the functions ω ± (z), mapping the regions T ± onto T 1 ± conformally, can be uniquely determined as the solution of the following Riemann boundary value problem (see, for example [], p.154) ω + [α(t)] = ω (t), ω (z) = z + c 1 z + c +..., z. (4.) z It is important to notice, that the indexes of the problems (1.1) and (4.1) are equal, i.e. Ind L1 G 1 (ζ) = Ind L G(t). Therefore, the generalized boundary value problem (1.1) is equivalent to the usual boundary value problem (4.1) both in the sense of solvability, and the number of linear independent solutions of the corresponding homogeneous problems. Solving the problem (4.1) by the method, proposed in [7], we can obtain the functions F 1 + (z) and F 1 (z). By the formula F + (z) = F 1 + [ ω + (z) ], F (z) = F1 [ ω (z) ] we can obtain the solutions of the problem (1.1). We conclude that the following statement is valid. Theorem 3. The generalized Markushevitch boundary value problem (1.1) permits the solutions in closed form, when we can solve in closed form the Riemann boundary value problem (4.) and the usual Markushevitch boundary value problem (4.1).
243 About the Solution in Closed Form of Generalized Markushevich Problem 7 Example 1. Let T + {z : z < 1} and L = {t : t = 1}. It is required to find all piecewise analytical functions F (z) = {F + (z), F (z)}, belonging to the class A(T ± ) H(L), vanishing on the infinity and satisfying on L the following boundary condition: F + ( t) = t F (t) + 1 t F (t) + t. (4.3) Solution. Here α(t) = t, b(t) = 1 t, g(t) = t. The functions ω+ (z) = z, ω (z) = z are solutions of the Riemann boundary value problem (4.). Consequently, in this case the boundary value problem (4.1) will have the form It should be noted, that here F 1 + (t) = t F1 (t) + 1 t F 1 (t) +, t = 1. t κ = Ind ( t ) =, X + (z) = 1, X (z) = 1 z, P κ 1(z) = C 0 + C 1 z, where C 0 and C 1 are arbitrary complex constants. Hence, taking into consideration formulas (.1) and (.), we get in this case: K(t, τ) 0, Q(t) = t 4, F 1 (z) = C 1 z + C 0 z z 4, F + 1 (z) = (C 0 + C 1 ) + (C 1 + C 0 )z z 3. Then the following functions will be the solution of the problem (4.3): F 1 (z) = C 1 z + C 0 z z 4, F + (z) = (C 0 + C 1 ) (C 1 + C 0 )z + z 3. References [1] B.V. Bojarski. About the generalized Gilbert boundary problem. In: Proc. Ac. Sc. GSSR, volume 5, , (in Russian) [] F.D. Gachow. Boundary value problems. Nauka, Moscow, (in Russian) [3] M.P. Krasnow. Integral equations. Nauka, Moscow, (in Russian) [4] G.S. Litvinchuk. Boundary value problems and singular integral equations with the displacement. Nauka, Moscow, (in Russian) [5] A.I. Markushevitch. About the boundary value problem of the theory of analytical functions. In: Proc. of Moskow State University, volume 1, 0 30, [6] L.G. Michailow. The new class of singular integral equations and its applications to the differential equations with singular coefficients. Dushanbe, (in Russian) [7] K.M. Rasulov. About the method of solution of the Markushevitch boundary value problem in the class of analytical functions. In: Investigations on boundary value problems of complex analysis and differential equations, number 3, , 001. (in Russian)
244 8 K. M. Rasulov [8] K.M. Rasulow. Boundary value problems for polyanalytycal functions and some of their applications. Smolensk state pedagogical institute, Smolensk, (in Russian) [9] I.Ch. Sabitow. About the boundary value problem of linear displacement. In: Math. proc., volume 64(106)(), 6 74, (in Russian) [10] N.P. Vekua. About the boundary value problem of the theory functions of complex variable. In: Proc. Ac. Sc. USSR, volume 86, , 195. (in Russian) [11] N.P. Vekua. Systems of singular integral equations and some boundary value problems. Nauka, Moscow, (in Russian) Apie apibendrintojo Markuševičiaus uždavinio sprendimą analizinių funkcijų klasėje K.M. Rasulov Darbe pateikiamas algoritmas Markuševičiaus uždavinio, kai ieškomos dalimis analizinės funkcijos F (z) = {F + (z), F (z)} nykstančioje begalybėje, savo šuolių linijoje L tenkinančios sąlygą F = [α(t)] = G(t) F (t) + b(t)f (t) + g(t), t L, kur G(t), b(t), g(t) apibrėžtos kontūre L funkcijos Golderio klasės, o α(t) homemorfizmas kontūro į save. Atvejui α(t) t uždavinį suformulavo A.I. Markuševičius 1946 m. Įrodyta, kad uždavinio sprendimas suvedamas į integralinės antrosios rūšies Fredholmo tipo lygties sprendima. Pateikiamas pavyzdys, iliustruojantis gautus teorinius rezultatus.
245 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN A PIEZOELECTRIC CONTACT PROBLEM WITH SLIP DEPENDENT COEFFICIENT OF FRICTION M. SOFONEA 1 and EL-H. ESSOUFI 1 Laboratoire de Mathématiques et Physique pour les Systèmes, Université de Perpignan 5 Avenue de Paul Alduy, Perpignan, France : ;<= Groupe d Analyse Non Linéaire, Faculté des Sciences et Techniques, Université Moulay Ismail 5000 Boutalamine, Errachidia, Maroc ;77 8 >9?E= I5< JKGFH:;EJ Received March 16, 004; revised July 3, 004 Abstract. We consider a mathematical model which describes the static frictional contact between a piezoelectric body and an obstacle. The constitutive relation of the material is assumed to be electroelastic and involves a nonlinear elasticity operator. The contact is modelled with a version of Coulomb s law of dry friction in which the coefficient of friction depends on the slip. We derive a variational formulation for the model which is in form of a coupled system involving as unknowns the displacement field and the electric potential. Then we provide the existence of a weak solution to the model and, under a smallness assumption, we provide its uniqueness. The proof is based on a result obtained in [14] in the study of elliptic quasi-variational inequalities. Key words: piezoelectric material, electroelasticity, static frictional contact, Coulomb s law, slip dependent coefficient of friction, quasivariational inequality, weak solution 1. Introduction The piezoelectric effect was discovered in 1880 by Jacques and Pierre Curie; it consists on the apparition of electric charges on the surfaces of some crystals after their deformation. The reverse effect was outlined in 1881; it consists on the generation of stress and strain in crystals under the action of electric field on the boundary. A deformable material which undergoes piezoelectric effects is called a piezoelectric material. An elastic material with piezoelectric effect is called an electroelastic material and the discipline dealing with the study of electroelastic materials is the theory of electroelasticity. Their bases were underlined by Voigt [4] who provided
246 30 M. Sofonea, El-H. Essoufi the first mathematical model of a linear elastic material which takes into account the interaction between mechanical and electrical properties. General models for elastic materials with piezoelectric effects can be found in [10, 11, 1,, 3] and, more recently, in [1, 1]. Currently, there is a considerable interest in frictional contact problems involving piezoelectric materials, see for instance [, 9] and the references therein. Indeed, situations which involve contact phenomena abound in industry and everyday life. The contact of the braking pads with the wheel, the tire with the road and the piston with skirt are just three simple examples. Because of the importance of contact processes a considerable effort has been made in their modelling and the engineering literature concerning this topic is extensive. However, there are very few mathematical results concerning contact problems involving piezoelectric materials and therefore there is a need to extend the results on models for contact with deformable bodies to models for contact with deformable bodies which include coupling between mechanical and electrical properties. The aim of this paper is to provide such an extension. Indeed, we consider here a model for the process of frictional contact between an electrolastic body, which is acted upon by forces and electric charges, and a foundation. The process is static, the contact is frictional and it is modeled with a version of Coulomb s law of dry friction in which the coefficient of friction depends on the slip. Such kind of dependence was pointed out in [18] in the study of the stick-slip phenomenon and was considered in various papers, see for instance [16, 19]. Frictional contact boundary value problems with elastic materials and slip dependent friction were considered in [3, 6] in the static case and in [4] in the quasistatic case. Here we extend the frictional model in [3] to the case of nonlinear electroelastic materials. Taking into account the piezoelectric behavior of the body consists the main trait of novelty of the model. We derive a variational formulation of the model then we prove its weak solvability and, under an additional assumption, its unique solvability. As in [3], the proof of these results are based on an abstract theorem on quasivariational inequalities derived in [14]; however, keeping in mind the coupling of the electrical and mechanical effects, we apply this result in a different setting and with a different choice of operators and functionals. An important continuation of this paper consists in the numerical analysis of the model, including numerical simulations, and will be presented in a forthcoming work. The paper is structured as follows. In Section we state the model of the equilibrium process of the elastic piezoelectric body in frictional contact with a foundation. In Section 3 we introduce some preliminary material, list assumptions on the problem data and state our main existence and uniqueness result, Theorem 1. The proof of the theorem is presented in Section 5; it is based on an abstract existence and uniqueness result that we recall in Section 4.. Problem Statement We consider the following physical setting. An elastic piezoelectric body occupies a bounded domain Ω IR d, d =, 3 with a smooth boundary Ω = Γ. The body is submitted to the action of body forces of density f 0 and volume electric charges of
247 A Piezoelectric Contact Problem with Slip Dependent Coefficient 31 density q 0. It is also submitted to mechanical and electric constraints on the boundary. To describe them, we consider a partition of Γ into three measurable parts Γ 1, Γ, Γ 3, on one hand, and on two measurable parts Γ a and Γ b, on the other hand, such that meas Γ 1 > 0 and meas Γ a > 0. We assume that the body is clamped on Γ 1 and surfaces tractions of density f act on Γ. On Γ 3 the body is in frictional contact with an obstacle, the so-called foundation. We model the contact with a version of Coulomb s law of dry friction, already used in [3] and [6], in which the normal stress is prescribed and the coefficient of friction depends on the slip. We also assume that the electrical potential vanishes on Γ a and a surface electric charge of density q is prescribed on Γ b. We denote by S d the space of second order symmetric tensors on R d or, equivalently, the space of symmetric matrices of order d. Also, below ν represents the unit outward normal on Γ while and denote the inner product and the Euclidean norm on R d and S d, respectively. With the assumption above, the problem of equilibrium of the electroelastic body in frictional contact with a foundation is the following. Problem P. Find a displacement field u : Ω R d, a stress field σ : Ω S d, an electric potential ϕ : Ω R and an electric displacement field D : Ω R d such that σ = Fε(u) E T E(ϕ) in Ω, (.1) D = Eε(u) + βe(ϕ) in Ω, (.) Div σ + f 0 = 0 in Ω, (.3) div D = q 0 in Ω, (.4) u = 0 on Γ 1, (.5) σν = f on Γ, (.6) σ ν = S on Γ 3, (.7) { στ µ( u τ ) S, σ τ = µ( u τ ) S u uτ τ, if u τ 0 on Γ 3, (.8) ϕ = 0 on Γ a, (.9) D ν = q on Γ b. (.10) In (.1) (.10) and below, in order to simplify the notation, we do not indicate explicitly the dependence of various functions on the spatial variable x Ω Γ. Equations (.1) and (.) represent the electroelastic constitutive law of the material in which F is a given nonlinear function, ε(u) denotes the small strain tensor, E(ϕ) = ϕ is the electric field, E represents the third order piezoelectric tensor, E T is its transposite and β denotes the electric permitivitty tensor. Details of the linear version of the constitutive relations (.1) and (.) can be find in [1, ]. Equations (.3) and (.4) represent the equilibrium equations for the stress and electricdisplacement fields, respectively, (.5) and (.6) are the displacement and traction boundary conditions, respectively, and (.9), (.10) represent the electric boundary conditions. We now provide some comments on the frictional contact conditions (.7) and (.8), which are our main interest. Condition (.7) states that the normal stress σ ν
248 3 M. Sofonea, El-H. Essoufi is prescribed on Γ 3 since S denotes a given function. Condition (.8) represents the associated friction law in which σ τ is the tangential stress, u τ denotes the tangential displacement and µ is the coefficient of friction. This law should be seen either as a mathematical model suitable for proportional loadings or as a first approximation of a more realistic model, based on a friction law involving the time derivative of u τ (see for instance [4, 13]). Note that in (.8) the coefficient of friction depends on the slip u τ which leads to a nonstandard frictional contact problem. 3. Variational Formulations and Main Result In this section we list the assumptions on the data, derive a variational formulation for the contact problem (.1) (.10) and state our main existence and uniqueness result, Theorem 1. To this end we need to introduce notation and preliminary material. We recall that the inner products and the corresponding norms on R d and S d are given by u v = u i v i, v = (v v) 1 u, v R d, σ τ = σ ij τ ij, τ = (τ τ ) 1 σ, τ S d. Here and everywhere in this paper i, j, k, l run from 1 to d, summation over repeated indices is implied and the index that follows a comma represents the partial derivative with respect to the corresponding component of the spatial variable, e.g. u i,j = u i x j. Everywhere below we use the classical notation for L p and Sobolev spaces associated to Ω and Γ. Moreover, we use the notation L (Ω) d, H 1 (Ω) d and H and H 1 for the following spaces: L (Ω) d = { v = (v i ) v i L (Ω) }, H 1 (Ω) d = { v = (v i ) v i H 1 (Ω) }, H = { τ = (τ ij ) τ ij = τ ji L (Ω) }, H 1 = { τ H τ ij,j L (Ω) }. The spaces L (Ω) d, H 1 (Ω) d, H and H 1, are real Hilbert spaces endowed with the canonical inner products given by (u, v) L (Ω) = u v dx, (u, v) d H1 (Ω) = u v dx + ε(u) ε(v) dx, d Ω Ω Ω (σ, τ ) H = σ τ dx, (σ, τ ) H1 = (σ, τ ) H + (Div σ, Div τ ) L (Ω) d Ω and the associated norms L (Ω) d, H 1 (Ω) d, H and H1, respectively. Here ε : H 1 H and Div : H 1 H are the deformation and divergence operators, respectively, that is ε(v) = (ε ij (v)), ε ij (v) = 1 (v i,j + v j,i ) v H 1 (Ω) d, Div τ = (τ ij,j ) τ H 1. For every element v H 1 (Ω) d we also write v for the trace of v on Γ and we denote by v ν and v τ the normal and tangential components of v on Γ given by v ν = v ν, v τ = v v ν ν.
249 A Piezoelectric Contact Problem with Slip Dependent Coefficient 33 Let us now consider the closed subspace of H 1 (Ω) d defined by V = { v H 1 (Ω) d v = 0 on Γ 1 }. Since meas (Γ 1 ) > 0, the following Korn s inequality holds: ε(v) H c K v H 1 (Ω) d v V, (3.1) where c K > 0 is a constant which depends only on Ω and Γ 1. A proof of Korn s inequality can be found in, for instance, [15] p. 79. Over the space V we consider the inner product given by (u, v) V = (ε(u), ε(v)) H (3.) and let V be the associated norm. It follows from Korn s inequality (3.1) that H 1 (Ω) d and V are equivalent norms on V. Therefore (V, V ) is a real Hilbert space. Moreover, by the Sobolev trace theorem, (3.1) and (3.), there exists a constant c 0 depending only on the domain Ω, Γ 1 and Γ 3 such that We also introduce the spaces v L (Γ 3) d c 0 v V v V. (3.3) W = { ψ H 1 (Ω) ψ = 0 on Γ a }, W = { D = (D i ) D i L (Ω), div D L (Ω) }, where div D = (D i,i ). The spaces W and W are real Hilbert spaces with the inner products (ϕ, ψ) W = (ϕ, ψ) H 1 (Ω), (D, E) W = (D, E) L (Ω) d + (div D, div E) L (Ω). The associated norms will be denoted by W and W, respectively. Notice also that, since meas (Γ a ) > 0, the following Friedrichs-Poincaré inequality holds: ψ L (Ω) d c F ψ W ψ W, (3.4) where c F > 0 is a constant which depends only on Ω and Γ a. In the study of the contact problem (.1) (.10) we assume that (a) F : Ω S d S d. (b) There exists M F > 0 such that F(x, ξ 1 ) F(x, ξ ) M F ξ 1 ξ ξ 1, ξ S d, a.e. x Ω. (c) There exists m F > 0 such that (F(x, ξ 1 )) F(x, ξ )) (ξ 1 ξ ) m F ξ 1 ξ ξ 1, ξ S d, a.e. x Ω. (d) The mapping x F(x, ξ) is Lebesgue measurable on Ω for any ξ S d. (e) The mapping x F(x, 0) belongs to H. (3.5)
250 34 M. Sofonea, El-H. Essoufi { (a) E = (eijk ) : Ω S d R d. (b) e ijk = e ikj L (Ω). (3.6) (a) β = (β ij ) : Ω R d R d. (b) β ij = β ji L (Ω). (c) There exists m β > 0 such that β ij (x)e i E j m β E E R d, a.e. x Ω. (3.7) f 0 L (Ω) d, f L (Γ 3 ) d (3.8) q 0 L (Ω), q L (Γ b ), (3.9) S L (Γ 3 ) and S L (Γ 3) > 0 (3.10) (a) µ : Γ 3 IR IR +. (b) There exist c µ 1 0 and cµ 0 such that µ(x, r) c µ 1 r + cµ r IR +, a.e. x Γ 3. (c) The mapping x µ(x, r) is Lebesgue measurable on Γ 3 for any r IR. (d) The mapping r µ(x, r) is continuous on IR +, a.e. x Γ 3. (3.11) { There exists Lµ > 0 such that (µ(x, r ) µ(x, r 1 )) (r 1 r ) L µ r 1 r r 1, r IR, a.e. x Γ 3. (3.1) We make in what follows some comments on the assumptions (3.5) (3.1). As stated in Section, below we suppress the dependence of various functions on the spatial variable x Ω Γ. First, we note that the condition (3.5) is satisfied in the case of the linear elastic constitutive law σ = Fε(u) in which Fξ = (f ijkl ξ kl ), (3.13) provided that f ijkl L (Ω) and there exists α > 0 such that f ijkl (x)ξ k ξ l α ξ ξ S d, a.e. x Ω. To provide examples of nonlinear constitutive laws which satisfy (3.5), for every tensor ξ S d we denote by tr ξ the trace of ξ and let ξ D be the deviatoric part of ξ given by tr ξ = ξ ii, ξ D = ξ 1 d (tr ξ)i d,
251 A Piezoelectric Contact Problem with Slip Dependent Coefficient 35 where I d S d represents the identity tensor. Let K denotes a nonempty closed convex set in S d and let P K represents the projection mapping on K. We also consider a forth order symmetric and positively defined tensor E : S d S d and take F(ξ) = Eξ + 1 λ (ξ P Kξ) ξ S d, (3.14) where λ is a strictly positive constant. Using the properties of the projection mapping it is straightforward to see that the elasticity operator F defined by (3.14) satisfies condition (3.5). Constitutive laws of the form σ = Fε(u)) with F given by (3.14) have been considered by many authors, see. e.g. [8], [17] p. 97 and [0] p. 68. Most of them have defined the convex K by the relationship K = { ξ S d G(ξ) k} where G : S d IR is a convex continuous function such that G(0) = 0 and k > 0. A second example of nonlinear elastic equations is provided by nonlinear Hencky materials (see [5] for details). For a Hencky material, the stress-strain relation is given by σ = K 0 (tr ε(u)) I d + ψ( ε D (u) ) ε D (u), so that the elasticity operator is F(ξ) = K 0 (tr ξ) I d + ψ( ξ D ) ξ D ξ S d. (3.15) Here, K 0 > 0 is a material coefficient, the function ψ is assumed to be piecewise continuously differentiable, and there exist positive constants c 1, c, d 1 and d, such that for s 0 ψ(s) d 1, c 1 ψ (s) 0, c ψ(s) + ψ (s) s d. Under these assumption it can be shown that the elasticity operator F defined in (3.15) satisfies condition (3.5). Next, as it is shown in (3.6) and (3.7), we see that the piezoelectric operator E as well as the electric permitivitty operator β are assumed to be linear and, moreover, β is symmetric and positive definite. Recall also that the transposite tensor E T is given by E T = (e T ijk ) where et ijk = e kij, and the following equality holds: Eσ v = σ E v σ S d, v R d. (3.16) We also remark that (3.8) represent regularity assumptions on the densities of volume forces and surface tractions while (3.9) represent regularity assumptions on the densities of volume and surface electric charges. Condition S L (Γ 3) > 0 in (3.10) is imposed here in order to obtain a genuine frictional contact problem. Indeed, if S = 0 a.e. on Γ 3 then by (.7) and (.8) it follows that the Cauchy stress vector σν vanishes on Γ 3 and therefore problem (.1) (.10) becomes a purely displacementtraction problem for electroelastic materials. Finally, we observe that the assumptions (3.11) on the coefficient of friction µ are pretty general. Clearly, these assumptions are satisfied if µ is a bounded function which is continuously differentiable with respect to the second variable, as it was considered in [6]. We also remark that assumptions (3.11) and (3.1) are satisfied if µ does not depend on the second argument and is a positive function which belongs
252 36 M. Sofonea, El-H. Essoufi to L (Γ 3 ). This is the case when the coefficient of friction does not depend on the slip. Frictional contact problems involving this last assumption on the coefficient of friction were studied in [5, 17] in the case of purely elastic materials. Notice also that assumption (3.1) is satisfied if µ(x, ) : IR IR + is an increasing function, a.e. x Γ 3. We now turn to the variational formulation of Problem P and, to this end, we introduce further notation. Let h : V V IR be the functional h(u, v) = µ( u τ ) S v τ da, u, v V (3.17) Γ 3 and, using Riesz s representation theorem, consider the elements f V and q W given by (f, v) V = f 0 v dx + Ω f v da + Γ S v ν da Γ 3 v V, (3.18) (q, ψ) W = q 0 ψ dx + q ψ da Γ b ψ W. (3.19) Ω Keeping in mind assumptions (3.8) (3.11) it follows that the integrals in (3.17) (3.19) are well-defined. Using integration by parts, it is straightforward to see that if (u, σ, ϕ, D) are sufficiently regular functions which satisfy (.3) (.10) then (σ, ε(v) ε(u)) H + h(u, v) h(u, u) (f, v u) V v V, (3.0) (D, ψ) L (Ω) d = (q, ψ) W ψ W. (3.1) We plug (.1) in (3.0), (.) in (3.1) and use the notation E = ϕ to obtain the following variational formulation of Problem P, in the terms of displacement field and electric potential. Problem P V. Find a displacement field u V and an electric potential ϕ W such that (Fε(u), ε(v) ε(u)) H + (E T ϕ, v u) L (Ω) d (3.) +h(u, v) h(u, u) (f, v u) V v V, (β ϕ, ψ) L (Ω) d (Eε(u), ψ) L (Ω) d = (q, ψ) W ψ W. (3.3) Our main existence and uniqueness result which we establish in Section 5 is the following. Theorem 1. Assume that (3.5) (3.10) hold. Then : 1) Under the assumption (3.11), Problem P V has at least one solution. ) Under the assumptions (3.11) and (3.1), there exists L 0, which depends only on Ω, Γ 1, Γ 3, Γ a, F, β, S, such that if L µ < L 0 then Problem P V has unique solution (u, ϕ) which depends Lipschitz continuously on f V and q W.
253 A Piezoelectric Contact Problem with Slip Dependent Coefficient 37 A quadriplet" of functions (u, σ, ϕ, D) which satisfy (.1), (.), (3.) and (3.3) is called a weak solution of the piezoelectric contact problem P. We conclude by Theorem 1 that, under the assumptions (3.5) (3.11), the piezoelectric contact problem (.) (.10) has at least a weak solution (u, σ, ϕ, D) such that u V, ϕ W. Moreover, it is easy to see that in this case σ H 1 and D W. The solution is unique and depends Lipschitz continuously on the data f 0, f, q 0 and q if (3.1) holds with a sufficiently small constant L µ. In particular, this case arise when the coefficient of friction is a given positive bounded function which does not depend on the slip. 4. An Abstract Existence and Uniqueness Result To prove Theorem 1 we shall use an abstract existence and uniqueness result on elliptic quasivariational inequalities that we recall in what follows, for the convenience of the reader. Everywhere in this section X will represent a real Hilbert space endowed with the inner product (, ) X and the associated norm X. We denote by the weak convergence on X. Let A : X X be a non linear operator, j : X X IR and f X. With these data we consider the following quasivariational inequality: find x X such that (Ax, y x) X + j(x, y) j(x, x) (f, y x) X y X (4.1) In order to solve (4.1) we assume that A is strongly monotone and Lipschitz continuous, i.e. (a) There exists m > 0 such that (Ax 1 Ax, x 1 x ) X m x 1 x X x 1, x X. (b) There exists M > 0 such that Ax 1 Ax X M x 1 x X x 1, x X. The functional j : X X IR satisfies (4.) j(η, ) : X IR is a convex functional on X, for all η X. (4.3) Keeping in mind (4.3) it is well known that there exists the directional derivative of j with respect to the second argument given by j 1 [ ] (η, x; y) = lim j(η, x + λy) j(η, x) λ 0 λ η, x, y X. (4.4) We formulate in what follows some conditions on j and we recall that below m represents the positive constant defined in (4.).
254 38 M. Sofonea, El-H. Essoufi For every sequence {x n } X with x n X and every sequence {t n } [0, 1] one has [ 1 ] (4.5) lim inf n x n j (t n x n, x n ; x n ) < m. X For every sequence {x n } X with x n X and every bounded sequence {η n } X one has [ 1 ] (4.6) lim inf n x n j (η n, x n ; x n ) < m. X For every sequences {x n } X and {η n } X such that x n x [ X, η n η X and for every y X one has lim sup j(ηn, y) j(η n, x n ) ] (4.7) j(η, y) j(η, x). n { There exists α < m such that j(x, y) j(x, x) + j(y, x) j(y, y) α x y X x, y X. (4.8) In the study of the quasivariational inequality (4.1) we have the following result. Theorem. Let conditions (4.) (4.3) hold. Then : 1) Under the assumptions (4.5) (4.7) there exists at least one element x X which solves (4.1). ) Under the assumptions (4.5) (4.8), problem (4.1) has unique solution x = x f which depends Lipschitz continuously on f with the Lipschitz constant (m α) 1. Theorem has been obtained in [14] and therefore we do not provide here the details of the proof. We just specify that the proof was obtained in several steps and it is based on standard arguments of elliptic variational inequalities and topological degree theory. 5. Proof of Theorem 1 The proof of Theorem 1 will be carried out in several steps. To present it we consider the product space X = V W together with the inner product (x, y) X = (u, v) V + (ϕ, ψ) W x = (u, ψ), y = (v, ψ) X (5.1) and the associated norm X. Everywhere below we assume that (3.5) (3.11) hold. We introduce the operator A : X X defined by (Ax, y) = (Fε(u), ε(v)) H + (β ϕ, ψ) L (Ω) d + (ET ϕ, ε(v)) H (5.) (Eε(u), ψ) L (Ω) d x = (u, ψ), y = (v, ψ) X and we extend the functional h defined by (3.17) to a functional j defined on X X, that is j(x, y) = h(u, v) x = (u, ψ), y = (v, ψ) X. (5.3) Finally, we consider the element f X given by We start with the following equivalence result. f = (f, q) X. (5.4)
255 A Piezoelectric Contact Problem with Slip Dependent Coefficient 39 Lemma 1. The couple x = (u, ϕ) is a solution to Problem P V if and only if (Ax, y x) X + j(x, y) j(x, x) (f, y x) X y X. (5.5) Proof. Let x = (u, ϕ) X be a solution to Problem P V and let y = (v, ψ) Y. We use the test function ψ ϕ in (3.1), add the corresponding inequality to (3.0) and use (5.1) (5.4) to obtain (5.5). Conversely, let x = (u, ϕ) X be a solution to the quasivariational inequality (5.5). We take y = (v, ϕ) in (5.5) where v is an arbitrary element of V and obtain (3.); then we take successively y = (v, ϕ + ψ) and y = (v, ϕ ψ) in (5.5), where ψ is an arbitrary element of W ; as a result we obtain (3.3), which concludes the proof. Notice that the quasivariational inequality (5.5) derived in Lemma1 is of the form (4.1). Therefore, in order to apply the abstract result provided by Theorem, we start with the study of the the properties of the operator A given by (5.). Lemma. The operator A : X X is strongly monotone and Lipschitz continuous. Proof. have Consider two elements x 1 = (u 1, ϕ 1 ), x = (u, ϕ ) X. Using (5.) we (Ax 1 Ax, x 1 x ) X = (Fε(u 1 ) Fε(u ), ε(u 1 ) ε(u )) H + (β ϕ 1 β ϕ, ϕ 1 ϕ ) L (Ω) d + (ET ϕ 1 E T ϕ, ε(u 1 ) ε(u )) H (Eε(u 1 ) Eε(u 1 ), ϕ 1 ϕ ) L (Ω) d and, since it follows by (3.16) that (E T ϕ, ε(u)) H = (Eε(u), ϕ) L (Ω) d x = (u, ϕ) X, we find (Ax 1 Ax, x 1 x ) X = for all (Fε(u 1 ) Fε(u ), ε(u 1 ) ε(u )) H + (β ϕ 1 β ϕ, ϕ 1 ϕ ) L (Ω) d. We use now (3.5), (3.7) and Friedrichs-Poincaré inequality (3.4) to see that there exists c 1 > 0 which depends only on F, β, Ω and Γ a such that (Ax 1 Ax, x 1 x ) X c 1 ( u 1 u V + ϕ 1 ϕ W ) and, keeping in mind (5.1), we obtain (Ax 1 Ax, x 1 x ) X c 1 x 1 x X. (5.6) In the same way, using (3.5) (3.7), after some algebra it follows that there exists c > 0 which depends only on F, β and E such that (Ax 1 Ax, y) X c ( u 1 u V v V + ϕ 1 ϕ W v V + u 1 u V ψ W + ϕ 1 ϕ W ψ W )
256 40 M. Sofonea, El-H. Essoufi for all y = (v, ψ) V. We use (5.1) and the previous inequality to obtain (Ax 1 Ax, y) X 4c x 1 x V y V y X and, taking y = Ax 1 Ax X, we find Ax 1 Ax X 4c x 1 x V. (5.7) Lemma is now a consequence of inequalities (5.6) and (5.7). Next we investigate the properties of the functional j given by (5.3), (3.17). We first remark that j satisfies condition (4.3). Moreover, we have the following results. Lemma 3. The functional j satisfies conditions (4.5), (4.6) and (4.7). Proof. Let η = (w, ξ), x = (u, ϕ) X and let λ ]0, 1]. Using (5.3) and (3.17) it results that j(η, x λx) j(η, x) = λ µ( w τ ) S u τ da Γ 3 and, keeping in mind (4.4), we deduce that j (η, x; x) 0 η, x X. (5.8) We conclude by (5.8) that the functional j satisfies conditions (4.5) and (4.6). Let now consider two sequences {x n } = {(u n, ϕ n )} X and {η n } = {(w n, ξ n )} X such that x n x = (u, ϕ) X, η n η = (w, ξ) X. Using the compactness property of the trace map it follows that u n u and w n w in L (Γ 3 ) d, which imply that u nτ u τ in L (Γ 3 ), (5.9) w nτ w τ in L (Γ 3 ). (5.10) Moreover, (3.1), (5.10) and Kranoselski s theorem (see for instance [7]) yield µ( w nτ ) µ( w τ ) in L (Γ 3 ). (5.11) Therefore, we use the definition of j, (5.9) and (5.11) to deduce that j(η n, y) j(η, y) y X and j(η n, x n ) j(η, x), as n. We conclude that the functional j satisfies the condition (4.7). Lemma 4. If (3.1) holds, then the functional j satisfies the inequality j(x, y) j(x, x) + j(y, x) j(y, y) c 0 L µ S L (Γ 3) x y X x, y X. (5.1)
257 A Piezoelectric Contact Problem with Slip Dependent Coefficient 41 Proof. that Let x = (u, ϕ), y = (v, ψ) V. Using (5.3), (3.17) and (3.1) it follows j(x, y) j(x, x) + j(y, x) j(y, y) = S ( µ( u τ ) µ( v τ ) ) ( v τ u τ ) da Γ 3 L µ S L (Γ 3) v τ u τ da L µ S L (Γ 3) u v da. Γ 3 Γ 3 Using now (3.3) and (5.1) in the previous inequality we deduce (5.1). We have now all the ingredients to prove the Theorem. Proof. [Proof of Theorem 1.] 1) Assume that (3.5) (3.11) hold. Then, Lemmas and 3 allow us to use the abstract results provided by the first part of Theorem ; we obtain that the quasivariational inequality (5.5) has at least a solution x = (u, ϕ) X and, using Lemma1, we deduce that (u, ϕ) is a solution to Problem P V, which satisfies u V, ϕ W. ) Assume that (3.5) (3.1) hold and let L 0 = c 0 S where c 1 and c 0 L (Γ 3) are defined by (5.6) and (3.3), respectively. Clearly L 0 depends only on Ω, Γ 1, Γ 3, Γ a, F, β and S. Let now assume that L µ < L 0. Then, there exists α R such that c 0L µ S L (Γ 3) < α < c 1. Using (5.1) and (5.6) we obtain that the functional j satisfies condition (4.8). Therefore, by the second part of Theorem, Lemma 1 and (5.4), we obtain that problem P V has a unique solution which depends Lipschitz continuously on f V and q W, which concludes the proof. c 1 References [1] R.C. Batra and J.S. Yang. Saint-Venant s principle in linear piezoelectricity. Journal of Elasticity, 38, 09 18, [] P. Bisenga, F. Lebon and F. Maceri. The unilateral frictional contact of a piezoelectric body with a rigid support. In: Contact Mechanics, Kluwer, Dordrecht, , 00. [3] C. Ciulcu, D. Motreanu and M. Sofonea. Analysis of an elastic contact problem with slip dependent coefficient of friction. Mathematical Inequalities & Applications, 4, , 001. [4] C. Corneschi, T.-V. Hoarau-Mantel and M. Sofonea. A quasistatic contact problem with slip dependent coefficient of friction for elastic materials. Journal of Applied Analysis, 8, 59 80, 00. [5] G. Duvaut and J.-L. Lions. Inequalities in Mechanics and Physics. Springer-Verlag, Berlin, [6] I.R. Ionescu and J.-C. Paumier. On the contact problem with slip displacement dependent friction in elastostatics. Int. J. Engng. Sci., 34, , [7] O. Kavian. Introduction à la théorie des points critiques et Applications aux équations elliptiques. Springer-Verlag, Paris, Berlin, [8] F. Léné. Sur les matériaux élastiques à énergie de déformation non quadratique. Journal de Mécanique, 13, , 1974.
258 4 M. Sofonea, El-H. Essoufi [9] F. Maceri and P. Bisegna. The unilateral frictionless contact of a piezoelectric body with a rigid support. Math. Comp. Modelling, 8, 19 8, [10] R. D. Mindlin. Polarisation gradient in elastic dielectrics. Int. J. Solids Structures, 4, , [11] R. D. Mindlin. Continuum and lattice theories of influence of electromechanical coupling on capacitance of thin dielectric films. Int. J. Solids Structures, 4, , [1] R. D. Mindlin. Elasticity, piezoelasticity and crystal lattice dynamics. J. of Elasticity, 4, 17 80, 197. [13] D. Motreanu and M. Sofonea. Evolutionary variational inequalities arising in quasistatic frictional contact problems for elastic materials. Abstract and Applied Analysis, 4, 55 79, [14] D. Motreanu and M. Sofonea. Quasivariational inequalities and applications in frictional contact problems with normal compliance. Adv. Math. Sci. Appl., 10, , 000. [15] J. Nečas and I. Hlaváček. Mathematical Theory of Elastic and Elastico-Plastic Bodies: An Introduction. Elsevier Scientific Publishing Company, Amsterdam, Oxford, New York, [16] J.T. Oden and J.A.C. Martins. Models and computational methods for dynamic friction phenomena. Computer Methods in Applied Mechanics and Engineering, 5, , [17] P. D. Panagiotopoulos. Inequality Problems in Mechanics and Applications. Birkhauser, Basel, [18] E. Rabinowicz. Friction and Wear of Materials. Wiley, New York, [19] S.C. Scholz. The Mechanics of Earthquakes and Faulting. Cambridge Univ. Press, Cambridge, [0] R. Temam. Problèmes mathématiques en plasticité, Méthodes mathématiques de l informatique. Gauthiers-Villars, Paris, [1] B. Tengiz and G. Tengiz. Some dynamic problems of the theory of electroelasticity. Memoirs on Differential Equations and Mathematical Physics, 10, 1 53, [] R. A. Toupin. The elastic dielectrics. J. Rat. Mech. Analysis, 5, , [3] R. A. Toupin. A dynamical theory of elastic dielectrics. Int. J. Engrg. Sci., 1, , [4] W. Voigt. Lehrbuch der Kristall-Physik. Teubner, Leipzig, [5] E. Zeidler. Nonlinear Functional Analysis and its Applications. IV: Applications to Mathematical Physics. Springer-Verlag, New York, Pjezoelektriko salyčio su priklausomu nuo slydimo trinties koeficiento uždavinys M. Sofonea, El-H. Essoufi Mes nagrinėjame matematinį modelį, kuris aprašo sąlytį tarp pjezoelektriko ir kli ūties. Laikoma, kad medžiaga yra elektroelastinė ir nusakoma netiesiniu elastingumo operatoriumi. Sąlytis modeliuojamas remiamtis sausos trinties Coulomb o dėsniu, kuriame trinties koeficientas priklauso nuo slydimo. Mes gavome variacinį modelio formulavima lygčių sistemos formoje, kurios nežinomaisiais yra perkeltasis laukas ir elektrinis potencialas. Įrodomas sprendinio silpnąja prasme egzistavimas ir su nedidelėmis prielaidomis vienatis. Įrodymas paremtas rezultatais gautais [14] darbe, kuriame tiriamos elipsinės kvazivariacinės nelygybės.
259 !"# $ % '&)($ +*, -#.0/ c 004 Technika ISSN STABILITY OF THREE-LEVEL DIFFERENCE SCHEMES WITH RESPECT TO THE RIGHT-HAND SIDE 1 E.L. ZYUZINA Department of Applied Mathematics and Informatics, Belarussian State University F. Scoriny av. 4, 0050 Minsk, Belarus :<;=>@?9?BADC8 Received January 11, 004; revised June 1, 004 Abstract. In this paper we investigate three-level difference schemes on non-uniform grids in time. The a priori estimates of stability with respect to the initial data and the right-hand side are obtained. New schemes of the raised order of approximation for wave equations are constructed and investigated. Key words: Three-level difference scheme, non-uniform grid, stability 1. Introduction The main results on the theory of the stability of operator-difference schemes have been obtained using grids uniform in time [6, 8, 9]. Necessary and sufficient conditions of stability were already obtained in the sense of the initial data and the righthand side in finite-dimensional Hilbert spaces. For three-level difference schemes on non-uniform grids there are a few particular results. In [1, ] difference schemes of the first order of approximation were considered for the case τ n+1 τ n. In [5] a priori estimate of uniform stability with respect to initial data was received under special condition on operators and time grid. The condition on time steps leaded us to the grid satisfying the geometrical progression law τ n+1 = qτ n, q = const > 0. In the paper [7] basic canonical forms have been first introduced for three-level difference schemes on non-uniform in time grids and important theorems concerning the stability with respect to initial data have been formulated. In the work [4] for three-level difference schemes the a priori estimate of absolute stability of solution was obtained with respect to the initial data without assuming 1 The author wish to thank Prof. P. Matus for the statement of the problem and useful comments
260 44 E.L. Zyuzina the Lipschitz continuity of operators on a time variable. In [4] the special case of grid τ n+1 τ n was discussed and the a priori estimate of stability of three-level operator-difference schemes with respect to the initial data and the right-hand side was received. However the technique introduced in [4] doesn t allow us to carry out the investigation for the inverse relations of time steps. Investigation of stability with respect to the right-hand side of three-level difference schemes on non-uniform in time grids causes certain difficulties. In present work new a priori estimates of stability with respect to the initial data and the righthand side are received with the use of specific technique, which consists in separate investigation of two cases τ n+1 τ n and τ n+1 τ n and it is represented in proofs of Theorems 1,. The stability of new computational methods on non-uniform grids with respect to the initial data and the right-hand side is investigated on the basis of general a priori estimates obtained for three-level operator-difference schemes. Difference schemes of the second order of local approximation are constructed and investigated on non-uniform grids in time on standard stencils for hyperbolic equations. Computational experiments for introduced schemes confirm the theoretical results received.. Statement of the Problem Let us note some features of the investigation of difference schemes on non-uniform in time grids. If in the initial differential problem the coefficients are constant, approximation on a non-uniform grid leads us to operator-difference schemes dependent on grid node t n. If we require that these operators be Lipschitz continuous, it would lead us to an unnatural condition of the quasi-uniformity of a time grid. The second problem is connected with a reduction of the order of local approximation when we go from a uniform grid to a non-uniform one. The main problem we solve is to build new stable three-level difference schemes of the raised order of local approximation on the non-uniform grid using the standard stencils. We consider a three-level operator-difference scheme Dy tˆt + + Ay = ϕ, By t (.1) y 0 = u 0, y 1 = u 1 on a non-uniform in time grid ˆ ω τ = {t n = t n 1 + τ n, n 1,,, N, t 0 = 0, t N = T } = ˆω τ {0, T }. (.) Here y = y n = y(t n ) H is the sought function; u 0, u 1, ϕ(t n ) H are given; H is the finite-dimensional Hilbert space; D, B, A are linear operators acting in H; y tˆt = y t y t τ, y t = y n+1 y n τ n+1, y t = y n y n 1 τ n, y t = y n+1 y n 1 τ n + τ n+1, ŷ = y n+1, ˇy = y n 1, τ = τ n, τ + = τ n+1, τ = 0.5(τ n + τ n+1 ), y (σ1,σ) = σ 1 ŷ + (1 σ 1 σ )y + σ ˇy, y (0.5) = 0.5(ŷ + ˇy).
261 Stability of Three-Level Difference Schemes 45 For any arbitrary functions u, v H the Cauchy Schwartz inequality and the ε-inequality hold true: (u, v) u v ε u + 1 4ε v, ε > 0. (.3) For the self-adjoint and nonnegative operator A we define a semi-norm of the grid function u: u A = (Au, u), A = A 0. To obtain a priori estimates of stability with respect to the right-hand side we ll use stability conditions with respect to the initial data [4]. 3. Auxiliary Results Let us formulate some auxiliary results separately for cases when τ n+1 τ n and τ n+1 τ n. Theorem 1. Let operators of scheme (.1) satisfy the following conditions D(t) = D (t) > 0, A = A > 0, (3.1) R = D τ nτ n+1 A > 0, (3.) 4 B τ n+1 τ n A, τ n+1 τ n. (3.3) 4 Let R, A be constant operators. Then the solution of problem (.1) is stable with respect to the initial data and the right-hand side and the following estimate is valid: y t,n R + y n (0.5) A ( ) n y t,0 R + y (0.5) 0 A + τ k+1 ϕ k R 1. (3.4) Proof. To prove the theorem we scalar multiply scheme (.1) by τ y t : k=1 ( ) ( ) ( ) τ Dy tˆt, y + τ By t, y t + τ Ay, y t = τ (ϕ, y ). t t Using the proof of Theorem 4.1 [4] and the following representation we receive the energy inequality: τ (ϕ, y t ) = τ n+1 (ϕ, y t ) + τ n (ϕ, y t), y t R + y n (0.5) A ( y t R + y (0.5) ) n 1 A + τ τ + τ In conditions of the theorem y tˆt R + τ y t B τ + τ 4 A = τ n+1(ϕ, y t ) + τ n (ϕ, y t). (3.5)
262 46 E.L. Zyuzina y t R + y (0.5) n A ( y t R + y (0.5) n 1 A) τ n+1 (ϕ, y t ) + τ n (ϕ, y t). Let us introduce a notation G = y t R + y(0.5) n A. (3.6) Then taking into account that τ n+1 τ n and using the Cauchy Schwartz inequality (.3), we have τg t τ + (ϕ, y t ) + τ(ϕ, y t) τ + ϕ R 1 y t R + τ ϕ R 1 y t R τ + ϕ R 1( y t R + y t R ) τ + ϕ R 1(G 1/ + Ǧ1/ ). (3.7) Using the following identity [3]: (G 1/) t = G1/ Ǧ1/ τ n = from (3.7) we get the estimate G Ǧ τ n (G 1/ + Ǧ1/ ) = τ n ( G 1/) t τ n+1 ϕ R 1, G t G 1/ + Ǧ1/ (3.8) or ( y t,n R + y (0.5) n A ) 1/ ( y t,n R + y (0.5) n 1 A) 1/ + τn+1 ϕ n R 1. And then we have ( y t,n R + y(0.5) n A Now using the evident relations: ) 1/ ( ) 1/ y t,0 R + n y(0.5) 0 A + τ k+1 ϕ k R 1. k=1 (3.9) a + b (a + b ), a + b a + b, (3.10) the statement of the theorem follows from inequality (3.9). In order to formulate the theorem about stability for the inverse relations of time steps we rewrite the three level operator difference scheme (.1) in the following form: ( + τ n τ n+1 D y n+1 y n + y n 1 y 0 = u 0, y 1 = u 1. B τ n+1 τ n D τ n+1 τ n ) yn+1 y n 1 τ + Ay n = ϕ n, Theorem. Let operators D(t), B(t), A satisfy the following conditions: (3.11) D(t) = D (t) > 0, B(t) > 0, A = A > 0, (3.1)
263 Stability of Three-Level Difference Schemes 47 R = D τ nτ n+1 A > 0, (3.13) 4 and operators A, R are constant. Let τ n+1 τ n. (3.14) Then operator-difference scheme (.1) is stable with respect to the initial data and the right-hand side and the a priori estimate is true: y t,n R + y n (0.5) A τ { } 1 n y t (0) R + y (0.5) 0 A + τ k ϕ k R 1. τ n+1 k=1 (3.15) Proof. Let us scalarly multiply scheme (3.11) by τ n τ n+1 (y n+1 y n 1 ) and use representations for scalar products given in Theorem 4.1 [4]: ( D((yn+1 y n ) (y n y n 1 )), (y n+1 y n ) + (y n y n 1 ) ) (( τn τ n+1 + τ B τ ) ) n+1 τ n τ D (y n+1 y n 1 ), y n+1 y n 1 + τ n τ n+1 (Ay n, y n+1 y n 1 ) = τ n τ n+1 (ϕ, y n+1 y n 1 ). Taking into consideration conditions of the theorem (3.1), (3.13) and the following identity τ n τ n+1 (ϕ, y n+1 y n 1 ) = τ n τ n+1 (ϕ, τ n+1 y t ) + τ n τ n+1 (ϕ, τ n y t), we get the energy inequality τ n+1 y t R + τ nτ n+1 y (0.5) n A (τ n y t R + τ nτ n+1 y (0.5) n 1 A ) τ n τ n+1 (ϕ, τ n+1 y t ) + τ n τ n+1 (ϕ, τ n y t). (3.16) Since τn+1 τ nτ n+1 τn following form: (see (3.14)), then expression (3.16) takes the τ n+1( y t R + y (0.5) n A) τ n( y t R + y (0.5) n 1 A) τ n((ϕ, τ n+1 y t ) + (ϕ, τ n y t)). Using notation (3.6) and the Cauchy Schwartz inequality, we rewrite the last relation: τ n (τ n+1g n ) t τ n(τ n+1 (ϕ, y t ) + τ n (ϕ, y t)) τn ϕ R 1(τ n+1 G 1/ n + τ n G 1/ n 1 ). (3.17) Let us note that the following identity similar to (3.8) is valid: ( τ n+1 G 1/ n ) t = τ n+1g 1/ n τ n G 1/ n 1 τ n = = τ n+1 G n τ n G n 1 τ n (τ n+1 G 1/ n + τ n G 1/ n 1 ) (τn+1 G n) t. (3.18) τ n+1 G 1/ n + τ n G 1/ n 1
264 48 E.L. Zyuzina Taking into account identity (3.18) we receive from (3.17) the following estimate: or Recursively we get τ n (τ n+1g n ) t τ n ϕ R 1 τ n+1 ( y t,n R + y(0.5) n A )1/ (3.19) τ n ( y t,n 1 R + y (0.5) n 1 A) 1/ + τ n ϕ R 1. τ n+1 ( y t,n R + y(0.5) n A )1/ (3.0) { } n τ 1 ( y t (0) R + y (0.5) 0 A) 1/ + τ k ϕ k R 1. Now using relations (3.10) from the last inequality one can easy get a priori estimate (3.15). Remark 1. Let us note that stability estimates (3.4), (3.15) are received without using the Gronuoll lemma, which is usually applied for investigation of stability with respect to the right-hand side, and the estimates don t include the constant e ct, which becomes large with the growth of T. If the series k=1 n τ k+1 ϕ k R 1, k=1 n τ k ϕ k R 1 k=1 converge when n, then estimates (3.4), (3.15) express the global stability of three-level difference scheme (.1). 4. Stability with Respect to the Right-Hand Side on Arbitrary Grids Let us combine the results obtained and formulate general theorem about uniform stability of three-level operator-difference schemes. We assume an arbitrary time grid, where principle of mesh refinement changes k times [4]: Figure 1. The non-uniform time grid.
265 Stability of Three-Level Difference Schemes 49 Theorem 3. We assume that operators of difference scheme (.1) D(t), B(t), A satisfy the following conditions: D(t) = D (t) > 0, A = A > 0, (4.1) R = D τ { } nτ n+1 τn+1 τ n A > 0, B max A, 0, (4.) 4 4 and A, R are constant operators. We also assume that time steps are interrelated as τ mj τ mj+1 c mj+1 c 0, j = 0, 1,..., k, τ m0 = τ 1, τ mk+1 = τ N0, (4.3) where k is the finite number of changes of mesh refinement principle. Then the solution of problem (.1) is stable with respect to the initial data and the right-hand side, and for arbitrary τ n the following a priori estimate holds true (an absolute stability): ( y t,n R + y (0.5) n A ) 1/ c k 0 ( + N0 1 s=1 y t,0 R + y (0.5) 0 A ) 1/ max{τ s, τ s+1 } ϕ s R 1. (4.4) Proof. Let t [t mk, t N0 ] and time steps become finer to the end of the interval. Then according to Theorem (see (3.0)) the following estimate is valid: { } where y n+1 1 τ m k τ N0 N 0 1 y mk 1 + τ s ϕ s R 1 s=m k n = m k, m k + 1,..., N 0 1, y n+1 1 = ( y t,n R + y (0.5) n A) 1/., (4.5) Let in the moment t mk the principle of mesh refinement changes, i. e., the time steps become related as τ + > τ. Then according to the Theorem 1 (see (3.9)) m k 1 y n+1 1 y mk τ s+1 ϕ s R 1, s=m k 1 n = m k 1, m k 1 + 1,, m k 1. Substituting the last inequality to (4.5), we get the estimate y n+1 1 τ m k τ N0 N 0 1 y mk max{τ s, τ s+1 } ϕ s R 1, s=m k 1 n = m k 1,..., N 0 1. (4.6) Recursively continuing (4.6) and taking into account steps interrelations (4.3), we receive the required estimate of stability.
266 50 E.L. Zyuzina 5. Examples 5.1. Wave equation In the domain Q = Ω [0, T ], Ω = {0 x l} it is necessary to find the solution of the first boundary value problem for the one dimensional wave equation: u t u(0, t) = u(l, t) = 0, = u + f(x, t), 0 < x < l, t > 0, (5.1) x u u(x, 0) = u 0 (x), t (x, 0) = ū 0(x). (5.) On the uniform space grid ω h = {x i = ih, i = 0, N, hn = l} and the nonuniform time grid (.) we replace the problem (5.1), (5.) by the class of difference schemes with weights where y tˆt + Ay(σ1,σ) = ϕ, y 0 = u 0, y 1 = u 1, (5.3) y (σ1,σ) = σ 1 ŷ + (1 σ 1 σ )y + σ ˇy, (Av) i = v xx,i = (v i+1 v i + v i 1 )/h, i = 1, N 1, v 0 = v N = 0, ϕ(t) = (ϕ 1 (t), ϕ (t),..., ϕ N 1 (t)) T, ϕ i (t) = f(x i, t); the operator A : H H, where the linear space H = Ω h consists of a set of vectors v = (v 1 (t), v (t),..., v N 1 (t)) T ; a scalar product and a norm in H are assigned as usual (y, v) = N 1 i=1 hy i v i, y = (y, y). A reduction of scheme (5.3) to the canonical form was done and the validity of all requirements of Theorem 3 were proved in [4]. Therefore the following theorem is true. Theorem 4. Assume that σ 1 σ + max { } τn τ n+1 (τ n+1 + τ n ), 0, σ 1 + σ = 1. (5.4) Then, the difference scheme with weights (5.3) is stable in the sense of the initial data and the right-hand side and the following a priori estimate holds true ( y t,n + y (0.5) n A ) 1/ ( ) c k 1/+ N y t,0 + y (0.5) 0 A max{τ s, τ s+1 } ϕ s. The parameters σ j are defined by taking into account the second order accuracy approximation condition: σ 1 τ + σ τ = τ + τ 3 and the stability requirement (5.4). Thus we get, that (see, [4]): σ 1 = s=1 τ + + τ 6(τ + + τ), σ = τ + + τ 6(τ + + τ). (5.5)
267 5.. Numerical experiment Stability of Three-Level Difference Schemes 51 The accuracy of the proposed scheme (5.3), (5.5) was examined in numerous tests. The obtained results were compared with results obtained by using classical schemes for numerical solution of differential problem (5.1), (5.) on uniform and non-uniform grids in time. Numerical experiment was undertaken in the domain Ω = [0, 1], t [0, 1]. The exact solution is given as ( πx ) ( ) πt u(x, t) = sin sin + t (x lx), l = 1. l l In order to check the second order of approximation and convergence of difference scheme (5.3), (5.5), the initial boundary-value problem was solved on the sequence of grids: ω h ω τ, ω h/ ω τ/, ω h/4 ω τ/4,.... The non-uniform time grid ω τ was built using the random-number generator. The remaining grids were obtained by dividing each time interval into two equal parts. Thus the number of points where τ j τ j+1 remains constant for all experiments. In this sense the applied time grids become close to the uniform grid. The absolute error of solution y is given by z N = max (x,t) ω hτ y(x, t) u(x, t), ω hτ = ω h ω τ. Since in real problems the exact solution is usually unknown, let us introduce the aposteriori error estimate of the solution y hτ, which can be obtained using the Runge estimator: D N = 1 max y hτ (x, t) y (hτ) (x, t). 3 (x,t) ω (hτ) The second aposteriori estimate p N = log (D N/ /D N ) gives the convergence order of the approximation y hτ. The results of the experiments for the time level t=1 are presented in Tab. 1. Table 1. Convergence analysis for a test problem. Nx Nt z N D N p N
268 5 E.L. Zyuzina References [1] A. Bokov. Energetic inequalities for three level difference schemes on grids changing in time. Godishn. Vissh. Uchebni Zabed. Prilozh. Mat., 1(), 87 96, [] E. Diakonov and A. Bokov. Energetic inequalities for difference schemes on grids changing in time. Dokl. Bolg. AN., 8(), , [3] B. Jovanovich, S. Lemeshevsky and P. Matus. On the stability of differential operator equations and operator difference schemes as t. Comput. Meth. Appl. Math., (), , 00. [4] P. Matus and E. Zyuzina. Three level difference schemes on nonuniform in time grids. Comput. Meth. Appl. Math., 1(3), 65 84, 001. [5] V. Mazhukin, P. Matus and I. Mozolevski. About stability of three level difference schemes on non-uniform time grids. Dokl. NAN Belarusi, 44(6), 3 5, 000. [6] A. Samarskii. The Theory of Difference Schemes. Marcel Dekker Inc., New York-Basel, 001. [7] A. Samarskii, P. Vabishchevich, E. Makarevich and P. Matus. Stability of three level difference schemes on non-uniform in time grids. Dokl. Russ. Acad. Nauk, 376(6), , 001. [8] A. Samarskii, P. Vabishchevich and P. Matus. Difference Schemes with Operator Factors. Kluwer Academic Publishers, Boston/Dordrecht/London, 00. [9] A. A. Samarskii and A. V. Goolin. Stability of Difference Schemes. Nauka, Moskow, (in Russian) Trisluoksnių baigtinių skirtumų schemu stabilumas dešiniosios pusės atžvilgiu E. Zyuzina Straipsnyje nagrinėjamos trisluoksnės baigtinių skirtumų schemos su netolygiu laikinu žingsniu. Gauti aprioriniai stabilumo įverčiai pradinių duomenu ir dešiniosios pusės atžvilgiu. Pasiūlytos naujos aukštesnės aproksimacijos eilės baigtinių skirtumų schemos vienmatei bangos lygčiai. Pateikti skaitinio eksperimento rezultatai.
269 !"# $ % '&)($ +*,.-/10 3 -/546 "7989:; 79<9< = 79>9>9?A@B =DC3EGFIHKJ"LM3MONQP :KRK7TSU< 7VR 7 WXZY\[]W_^`W5a bdc)xzegfhw_^jik[lim[onqprfhw5a\sdx topuf a\sqe vwpr[xcyazw_pub prt Y\sqiqv{e a\fkikb vw5azw_prb Y\f}p}~[xegX v W5b XZc)[azW ^upuxzyƒprbdegb a ik[x[op\ v ˆ ˆ ŠŒ " "ŠŒ "Ž% A 5 ˆ 5 š z Oœ ŸžA š # Œ Œ V O Dª «U ²± ³ A µ Œ ¹ º '»¼½ ¾ª V ¼O U ¹ÀT 6ÁšÂ ± 6 ¹¼A "À6¼G V ˆ Ÿ DµÄÃ5ÀV ¹ T 5À6 Å Æ#ÇÈÇÈɽ ÊG Ë Ì# ÍKÎ Ï ÐOÌÑ ÒGǺÓTÒ½ÔÕ ÆǺÇÈÅ ŽÖ² { ŠزÙGÚ5ÛGÜÝGÞ ßGà áâgã3äå æœçþgè é9óvévåê é9 wëgæ œ éí9ì ÎOÐ Ð ÌíîºéVêÅÇÈé9 wï Ò½êGéV ˆð#é9îòñ ÎOÐGÐOÌ ó'ôšõvö9 øùoö ú N BºûQü EGF ý Bˆþ F ÿ B B E3= B ÕB ý C þ E ÕB FI=J³ý þ CJ B ý JVE F ý F KE ½= B "FIE Iý F S = KE B EOýòJ "F Bþ5@ C B J F ý C FJ B6þ KEw= KE B S JVý F B F IF =ºFIý!=ÈC B ÕB J9E þ ý C B F ýdj9e B " þgb ý B FIEJVý F 9E# = KE3= B E½ý JVý F KE þ F³ý F Gý F KEFIE$ "IF þ JVE þ IF%& 3F þ' CJ B ( J9E þ ý C B FIEOý B) J9= B* "F ý F C B E ÕB FI=J ½= Bþ B J B J "ý + B GE3= 9E þ FIý F 9EJ ³ýDJ B" L¹ýF"= J Bþwû F ý CJ= KE Bþ ý B =DC3EGF,%& B ( û CGFI=ÈC þgb ý B FIE B += 9E3= B E½ý JTý F 9E þ F³ý F ý F 9EŸJ9E þ F E½ý B J9= B- "F ý F KE. û ý C JVý B0/ = 9E B %& B E½ý & :<;"=*> Gý B F JTý F KE?( C3J B ý J9EF ý F 9E?( ü E3F ý B+þ F ÿ B B E3= B =DC B ÕB ( þ S B DE9FGIH-JKLENMGD œ îºé9çèévœ OÊ ék Oî6Ç ÓVÒ QP ÆROºéVî'ÇÈÅ ˆÆ Ø &OÈÅÒ œts¾ò î{ { GÇÈÇ*Oºîº œçs¾é9î{å œto)uéçdêçvoèév {ÇÔ Å,O)U PNU ÇÈéWOÈî6 Oœ#ÇDÅ,OÈÅÒ œ ð#ékótòg ékç{ò œéwòs-o U é ÒGÇVOŸÓU Ø ØéVœNXGÅ œxyp îºò ðø é9 Ç'Å œ ÓTÒG QP ÆÖ Oº &OºÅ ÒGœ OØ[ZÆ Å Êœ O Å ÓVÇ9 IU é'îºé9çèé9 îºóu]åœ\o)u Å Ç]é9Ø xå Ç é9œótògæ î6 X ék ðê#o)u é Å Ö P#ÒGîVO6 Oœ O{îÈÒGØ éwò S!PNU ÇÈé.ÓU OœNXGé PîÈÒÓTéKÇÈÇÈé9Ç Åœo Ò é9îèœtoèékóu œ Ò ØÒXGÊ šé9ç)pé9ótå OØØÊ Å œ ÓTîºÊÇVOº Ø^X îºò½ôio)u + Ò évøø ÅœNX GÓ_OºÅ êå,oèåé9çÿ GÓVÓVÒ QP OœÊ œêo é9ê évøòp é9œ O'Ò S œ é9ô ÓTîºÊÇVOº Ø[X îºò½ôio)uys¹ ÓVÅ ØÅ,O Ê _ GÇÕÔŒéVØØ% ÇÕÅ QP îºò½ê év é9œo ÒGî ÆNPÖǺÓV OØÅœNX.Ò SIO)U éÿé0`åçvoèåœnx ÇDéOÈÆNPbaÍKÎdc² 5 `ØÒ OÒ S+ ê½ œóték.œ3æ é9îèå ÓV Ø_ Ø,XGÒ îºåo U {ÇeU ê éað#é9évœåœ OÈîºÒ ÆÓTéK fs¾ò î ÓTÒ QP ÆNOÈéVî ÇDÅ AÆØ OÈÅÒ œxò S ÇÈÒ ØÅ?g½Ø Å Ë3Æ Å YPU ÇÈéQOÈî6 OœÇÈÅ,OÈÅÒ œha Í Ïdc³ _ Ò3ÇO ÒSIO)U é9 îèé ð ÇÈé9 ÒGœ ÓTØ ÇºÇÈÅÓ9 OØŒ 9OÈé0S¹ œip îºò ðø é9 d œ ék OØŒÔ ÅO UjO)Ué P îºòótékçèçaå œtp Æ îºéÿ { &OºéTÖ îèå OØ Ç Ò î' ÅØ ÆNOÈé OØØÒ½ÊÇ9 Oœ oê é9îèê\s¾é9ôkóvò œçèå évî*o)uéçdògø Å Å,]#ÓV OÈÅÒ œ Åœ œ Ò œ Ö³ ÅØÆROÈé AÆ Ø,OÈÅ Ö³ÓVÒ QPÒ œ é9œô ék Å _ IUéŸØ ÇVO P îºò ð ØéV dåça Ò îºéÿçdòpnu Å ÇOºÅÓ9 &Oºé9 ]ð#ékóv ÆÇDéŸÅ œ ÇDÆÓUfP îºòóté9çºçèé9çko)uépnu ÇÈé!OÈî6 OœÇÈÅ,OÈÅÒ œ OÈéV QPéVî6 &OºÆ îèé épévœ Ç Ò œ O)U é ÓVÒ QP#Ò3ÇDÅ,OÈÅÒ œ
270 Î Ï½Ì ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º Ò S O)U é ØÅ ËGÆÅ œ.çdògø Å fpnu ÇÈé9Ç9 IU O" Å ÇOºÅ œnxgæ Å ÇVU ékç Å,O^S¾îÈÒG O U é ÓTØ ÇºÇDÅ ÓV Ø OÈéS¹ Oœ P îèògð ØéV rôeu é9îèé!o U é OÈî6 OœÇÈÅ,OÈÅÒ œ OÈéV QPéVî6 &OºÆ îèéäå Ç ÓTÒGœÇO6 Oœ O9 évîºé.ô éwp îºòpògçèéfo)u é œæ é9îèå ÓV ØeP îèòóvé9 Æ îºé S¾Ò îÿçèå ˆÆ Ø &OÈÅÒ œ Ò SÄÇDÒGØ Å?g½Ø Å Ë3Æ Å PNU ÇÈéÄÓU OœNXGé Åœ OÈéV îèê{çèò ØÆROÈÅÒ œ1 IUé-P îºò ðø é9 råçòóvò œçèå évîºé9 'Åœ]Í\ PP îèò3 ÓU1 IU é" { &O U év { OÈÅ ÓV OØ Ò évøloº É ékç+åœoºòˆ GÓVÓTÒGÆ œ O ÅÆ#ÇDÅÒ œ Å œ O)U éçdògø Å ' Oœ# QO)U éøåëgö Æ Å PNU# ÇÈé9ÇÕ Oœ# é9ê Ò ØÆROºÅ ÒGœ ÒS O)Ué+PNU ÇÈéê ÒGØ Æ ékçõ Æ éqoèòfo U é{å œ OºéVî)S¹ ÓTé Ò OºÅ ÒGœ1 IU évîºé{ Oîºéˆ { ǺÇð OØ Oœ#ÓTéÓTÒ œ# ÅOºÅ ÒGœÇÕ Oœ# $PNU GÇDé{ Å XGîº mò SkO)U é{çèêçvoèé9. ÔeU ÅÓU ÓTÒ œœ é9ó0oºç ÇDÒGØ ÆROºÅ ÒGœAÓTÒGœÓTé9œ OÈî6 &OÈÅÒ œ OºÒ^O U éœóvò QPÒGÇÈÅOºÅ ÒGœÕÒ SNO U éœçèò ØÅ PNU ÇÈé œ OºéV Ö P#é9îº OÈÆ îºé OÅ QP#Ò3ÇDéK &OBO)Ué"ÇDÒGØ Å Ö³Ø Å Ë3Æ Å AÅœ OÈéVî)S¹ ÓVé IUé Ò é9øå Ç+ÇÈéVØ,S Ö³ÓVÒ œçèåçvoèé9œ O9 ½ O OØØ Ò½Ô Ç[OÈÒ PîÈéK ÅÓ0O ðò O U6X îºò½ôio)u' œ ' Å ÇÈÇÈÒ ØÆROºÅ ÒGœ6P îºòóvé9çºçdékç+ Ç ÔŒéVØØ GÇ%Ç)P#éKÓTÅé9ÇŒ ÅÇDÖ OÈîºÅ ð ÆNOÈÅÒ œå œqo U é ÇÈÒ ØÅ *PNU GÇDéG &O)U# &O+Å ÇÒ S<P îºå { OîºÊ Å QP#ÒGîVO6 OœÓVéIS¾Ò î+ótîºêço6 OØNXGîÈÒ½ÔŒéVî6Ç9 9P#éKÓTÅ OØé ÒGîVO6Ç Oîºé îºé9ë3æ ÅîÈéK OºÒÕ é9çèå,xgœ ÇVOº ð Øéò œ ˆîÈé9Ø Å Oð Øé OØ X ÒGîÈÅ,O)U S¾ÒGî+ÇDÒGØ ê3ö Å œnx ÇDÆ#ÓU6P îºò ð ØéV {Ç9 Gœ Òˆ { &OVOºéVîŒÒ œ é Å é9œçèå ÒGœ Oز 3 IUé" { OÅœŸ Å'ÓTÆ Ø,OÈÅé9Çò Oîºé" GÇÈÇÈÒOÖ ÓTÅ &OÈéK Ô Å,O)U ÇVOÈîºÒ œnxwótò ÆP Ø ÅœNXwð#éO Ô é9évœ#o)u é{ótòg QP#Ò3ÇDÅ,OÈÅÒ œ Ò S O U éø Å Ë3Æ Å œ ÇÈÒ ØÅ PNU ÇÈé9Ç œ Ô Å,O)U Ô Å é î6 OœNXGéŸÒS^OÈÅ é.çºóv Ø ékçaåœ OÈîºÒ ÆÓTéK ðê ÅœOºéVî)S¹ ÓVé Ò OºÅ ÒGœ1 Å5ÆÇÈÅ ÒGœ.Å œfo)ué ÓTîºÊÇVOº Ø Oœ Å œfo U é ÇDÒGØ ÆNOÈÅÒ œ1 éw é9çºótîºå ðé+o U é P îºòpògçèé9 Ø,XGÒ îºåo U qóvò œçèå évîºå œxwo)u é ép Å,Oº `Å OØX îºò½ôio)u ÒS ÒGœ ÒGÓVîÈÊÇVOº Ø Ø ÊGéVî6Ç Ç Oœ{é0` *PØ ég G IU é œ3æ é9îèå ÓV ØNP îºòóté9 Æ îèé évêgévøòpé9 ÅœQO)U Å Ç ÇOºÆ ÊxÅLjÇDÆÅO6 Oð Øé+S¾Ò î O)U éwçdå AÆØ OÈÅÒ œ Ò SeXGéVœ é9îº Ø[PNU GÇDé+Oºîº œçèåoºå ÒGœjP îèòóvé9çºçdékçäå œ OÈéV îèê' Ø ØÒ½ÊÇV IA E! #"%$& ENM)K')( GeH "*( IU é.ð ÇÈÅÓ P îºå œóvå,pø é.ò S Ø Å Ë3Æ Å TPNU GÇDéwéPÅO6 &`Ê,+.- +Ž0/ Å Ç ÇÈÅ ÅØ Oî*OÈÒYO)U éwxgîèò½ôio U Ò S ÇÈ ØOAÓVîÈÊÇVOº OØ Ç-S¾îÈÒG q Ǻ &OºÆ îº OÈéK Ǻ OØÅ œéçèò ØÆROºÅ ÒGœ a Î ì +Í9ì&c² }ÇDÒGØ ÆROºÅ ÒGœ ÒSO U é ÓTÒ QPÒ œ é9œ OºÇ ÒGî Oœ ÅœoØÅ ËGÆÅ Å Çð îèògænxu O Å œ OÈÒ ÓVÒ œ Oº GÓ_Ô Ô Å,O)U ]ÇDÆ ð#çoºîº OÈé A B C AC Oœ P îºé9óvå,påo6 &OÈéwÒ ÆNO ÒS^O)U é ÇÈÒ ØÆROÈÅÒ œ + S!O)U éçèò ØÆROÈÅÒ œ Å Ç{ÇDØÅ,XU OÈØÊ ÇDÆP#é9îºÇº &OºÆ îº OÈéK ÓTÒ QPÒ œ é9œ OºÇ A x B 1 x C Ò œ OÈÒ#O)U é ÇÈÆ ðçvoèî6 &OÈéG PîÈÒ½êÅ Å œx A X îºò½ôio)u'p îºòóté9çºç9 ÆNPéVî6Ǻ &OÈÆîº OÈÅÒ œå ÓTîºÊÇO6 OØ B Ç"Æ#ÇDÆ Ø ØÊ. { OÅœO6 OÅœ é9 ð3êwxgîº G Æ OØ ÓTÒÒ ØÅœNXŸÒS O)U éÿçèêçoºév. _ IUé'œÆ évîºåó9 OØ%ÇVOÈÆ Ê#S¾ÒGî1-1 +Ž P îèòóvé9çºçõò S O)U é S¾ÒGØ ØÒ½Ô Å œx GÇÈÇÈÆ QPROÈÅÒ œ#ç ÅÇAð ÇÈé9 ]Ò œ a Ï ì&c³ù A x B 1 x C / O)U éxgîèò½ôio U6O6 OÉ ékçip Ø ÓTéÄÆ œ# évî Ë3Æ GÇDÅ3éKËGÆÅ ØÅ ðîèåæ }ÓVÒ œ Å,OÈÅÒ œ#çví ð4/" OO U é ÇÈÒ ØÅ?g ØÅË3Æ Å Åœ OÈéVî)S¹ ÓVé O U é ÓVÒ QPÒGÇÈÅOºÅ ÒGœÒ SBO U é O ÔŒÒ PU ÇÈé9Ç OîºéAîºéTÖ Ø OÈé9 wðê+o U épnu GÇDéÕ Å XGîº uò SO U é ÇÈÊÇVOÈé9.í Ó/+ Æ éoºò U Å XU O)U é9îè { ØÓVÒ œ Æ#Ó_OÈÅêÅO ÊÒS O)U é { &OºéVîºÅ ØÇ Oœ 'ÇÈØÒ½ÔgÓTÒÒ ØÅ œx O U é OÈéV QPéVî6 &OºÆ îèé. Å ÇOºîÈÅð ÆROºÅ ÒGœ Å ÇÆ œ Å,S¾Ò îº O)U îºò ÆXU ÒGÆRO O U é ÇDÊÇVOÈéV œ ÓU# OœNXGé9LjŠœ OÈÅ é GÓVÓVÒ î6 Å œx OºÒ *P îºé9çºótîºåð#ék ŸîºÆ Øé 5 ú76#ú98;:=<4>3?*@7?*ab>=ced øö@7:4? õ IU é ÇDÊÇVOÈéV Å Ç é9çºótîºåð#ék ðê\o)u é ÓVÒ œóvévœ OÈî6 &OºÅ ÒGœ Å ÇOºîÈÅð ÆROºÅ ÒGœoÒS^O)U é ÇÈÒ ØÅ o Oœ Ø Å Ë3Æ Å fpnu# ÇÈé9Ç Oœ# ŸðÊ+O U éõå œ OºéVî)S¹ ÓTé PÒGÇÈÅOºÅ ÒGœ1 IU éˆ ÒG { OÅœ évœ ÒOÈé9 ÇO)U éçdògø Å WPNU GÇDéG ÓVÒ œçèå ÇO6Ç"ÒS D1 = { x 1 x x } O)U é.çdæðçoºîº OÈéw Oœ ép Å,Oº `Å OØŒØ Ê évî6ç9 ÓTÒGîÈîºé9Ç)P#ÒGœ Ç OÈÒ$O U é D Ø Å Ë3Æ Å fpnu# ÇÈé Å ÇIOºÅ étö ép#é9œ évœ O"ÓVÒ3ÒGîº Å = { x œ OÈéÄÒ SÇÈÒ ØÅ?g½Ø x x 3 } Å Ë3Æ Å ŸÅœ OÈéVî)S¹ ÓVéF+¹ÇÈéVé x ( t) G Å X ÍH/
271 «" I ¹ÀV Õ± { ¹À6¼O 6 3 ¾ª µt Ã5Ó I± U ¹Ó Dµ ª¼ V ȼO ² ¹ ½ È V V A ÎGÏ Ï M "IF þ CJ B F%& 3F þ C3J B x 1 x ( t) x 3 x?80l> ýdjvý F KE3J þ J9FIE é ÓTÒ œ#çdå évî^o)u é ÇDÒGØ Å Å,]#ÓV OÈÅÒ œ Ò S+ 6OÈéV îèêw OØØ Ò½ÊG ÔeU évîºéaóvò QP#ÒGœ évœ O6Ç Oîºé ÅǺÇDÒGØ êgé9 Å œ O U é' évø,oèék IU évîºé' Oîºé*O)U îºévé'óvò QPÒGÇÈÅOºÅ ÒGœ OØê½ OîºÅ Oð Øé9Ç-O)U# &O é0]œéio)u é ÓTÒG QP#Ò3ÇDÅ,OÈÅÒ œ Ò S?O)U é ØÅË3Æ Å C. *PNU GÇDéGÙ Oœ Oœ x (A) x (B) x (C) ÔeUÅÓU AÆ#ÇO ÇÈ OÈÅ ÇS¾Ê+O U éõé9ë3æ Ø Å,O Ê x (A) + x (B) + x (C) = 1. A B évîºé Oœ x (A) Å œwo U é œ îèéòîºé9ç)p#ékó_oºå êgévøê O)Ué Ò ØéIS¾îº GÓ_OÈÅÒ œ#çò S ÓTÒG *PÒ œévœ OºÇ x (B) ØÅË3Æ Å x # (C) O ék OœÇeO)U O"Ò œ ØÊ6O ÔŒÒ{ê½ OîºÅ ð Øé9Ç9 Ø éo"åo ð#é B OîºéÅœ ép#é9œ é9œok C x (A) œqo)u éäçdògø Å QPNU GÇDéG ÒGœ Ø Ê Ò œé ÓTÒG QP#Ò3ÇDÅ,OÈÅÒ œ Ø ê½ OîºÅ ð Øé O)U é ÓVÒ QP#Ò3ÇDÅ,OÈÅÒ œ ÇDÅœÓTé Å Ç%œéVé9 é9 *OÈÒ é9çºótîºåð#é x x s(a) = 0.5x, x s(b) = 0.5(1 x), x s(c) = 0.5. évîºé œ îèé^o)u é ÒGØ és¾îº GÓ_OºÅ x s(a) x s(b) x s(c) ÒGœÇÒ S ÓVÒ QPÒ œ é9œo6ç Å œfo)ué ÇDÒGØ Å Å ÇIO)U éõ ÒGØ é!s¾î6 Ó_OºÅ x ÒGœ ÒS Åœ AC A x B 1 x C ǺÇOÈî6 OœÇVS¾éVî Åœ.ð Æ ØÉ6PNU GÇDéKÇòÅÇ é0oèé9îè Åœ é9 ðê Å5ÆÇDÅÒ œ A x (B) +²Î ÍH/ Oœ A B C c s(a) t c l(j) t = D s(a) c s(a) x, x 1 < x < x ( t) = D l(j) c l(j) x, x ( t) < x < x 3, j = A, B, ÔeU évîºé Å Ç%ŠŒ Oî)OÈéKÇDÅ OœˆÓTÒÒ î6 Åœ &Oºé Å Ç O)U ékoºå é Oœ îèé O)U é ÅÆ#ÇDÅÒ œ ÓTÒé 'ÓTÅéVœ O6ÇÄÒ SkO)U é'óvò QP#ÒGœ évœ O x t Åœ\O)Ué'ÇDÒGØ Å œ YO)U é{øå D s(j) ËGÆÅ D l(j) PNU GÇDéKÇV Oœ Oîºé O U é.ê ÒGØ Æ é.ótògœóté9œoºîº OÈÅÒ œçˆò SO)U é ÓTÒGîÈîºé9Ç)PÒ œ ÅœNX]ÓTÒ QPÒ œ é9œ O ÅœiO U é j c s(j) cçdògø l(j) Å Oœ ØÅË3Æ Å QPNU GÇDéKÇîºé9Ç)P#éKÓ_OÈÅê é9ø ÊG 3Š Ò œ#ótévœ Oºîº OÈÅÒ œ Ò S<O)U é ÓTÒ QPÒ œ é9œ O ÇDÒGØ Å PU ÇÈéÄÅÇIS¾ÒGÆ œ S¾îºÒ }ÓVÒ œ Å,OÈÅÒ œ +UÎ Í / Å œqo U é B ÒGÆ œ îèê'óvò œ ÅOºÅ ÒGœÇ &O Oœ Oîºé!XGÅ êgévœw ÇkS¾Ò ØØÒ½Ô Ç Ù x = x 1 x = x 3 c s(a) x = 0, x = x 1 c l(j) x = 0, x = x 3, j = A, B. 1 LUE ý C B B % B 5J J J ÕB ý B) B JTý Bþ ý Äý C B F þq CJ B û F< BI B B Bþû F ý CQ S = F ý) J J ÕB ý B û F ý C " ý = F ý B JVý B ý ý C B IF,%& GF þ C3J B" +²Î Î / +²Î ñ/
272 Î ÏOì ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º 5 ú 5 ú %: ²øù õ IU é ÓVÒ œ Å,OÈÅÒ œ#ç O O)Ué Åœ OÈéVî)S¹ ÓVé îºép îºé9çèévœ O[O U é" { ÇºÇ ð OØ OœÓVé" Oœ# +PNU GÇDé é9ë3æ ÅØ ÅðÖ îèåæ }ðé0o ÔŒéVé9œ O ÔŒÒQPNU GÇDéKÇV Í ø õkõ ô ø Uø!? ù > Ù D s(j) cs(j) x x( t) 0 D l(j) cl(j) x x( t)+0 = υ ph (c s(j) c l(j) ), j = A, B, x = x ( t), ÔeU évîºé ÅÇkO U éõå œ OºéVî)S¹ ÓTéÄî6 &Oºé Î υ ph = A ½ø x ( t) ú Š Ò QPÒGÇÈÅOºÅ ÒGœ Ò S-O)U éfo ÔŒÒYPU ÇÈé9Ç &O*O)Ué.ÇÈÒ ØÅ?g ØÅË3Æ Å Å Ç îèé9ø OÈéK.ð3ÊfPNU GÇDéˆ Å X î6 O ròsbo)u éˆçdêçvoèév. O)U OÓV œ ð#éaô îèå,ovoºévœåœwo)u é S¾Ò îº a Ìc²Ù x s BC ÔeU évîºé x s AC x s BC = 4γ A x (A) x (C) exp = 4γ B x (B) x (C) exp ( H melt AC R TAC melt ( H melt BC R T melt BC T melt AC T melt BC T ), T T ). T +²Î Ì / +²Î Ï / é9îèé ÅÇfO U é\oèé9 *PéVî6 &OºÆ îºé T îèéo U é évœ OÈîºÒP Åé9Ç Ò SBS¾Æ#ÇDÅÒ œ1 Å ÇfO)U é Æ œå êgévî6çè Ø!X3 Ç.ÓTÒGœÇVOº Oœ OK R îèé O)U é évø,oèåœnxfp#ògå HAC melt œ OºÇ9 HBC melt Oîºé O)U é3p#ògø Êœ ÒG Å OØ é0`rp îºé9çºçdåò œç9 IU é ÓTÒé T AC melt T BC melt 'ÓTÅéVœ O6ÇeU ê éõðévé9œ γ é0oºévîº Å j (j = œ ék 'ðê*o)u éøé9 ÇVO A, B) 3'ǺËGÆ# Oîºé9ÇB]OVOÈÅœNX Ò S O U é ê½ Å Ø Oð Øé"é`RP#é9îÈÅ évœ OŒ Oº a Ì# Ïdc³ œ]ògîº évî!oèò ÒGðROº Å œyo)u é{ékë3æ &OºÅ ÒGœYO U &O Å ÇÄÆÇÈé9 ]ÅœYO U é'çèå ˆÆ Ø OÈÅÒ œ1 Oœ S¾îºÒ +UÎ Ï /Œ îèéõçèæ ðçvoèå,oèæroºé9 wå œ OºÒ +UÎ ÍH/TÙ x s AC k = γ exp B γ A exp ( H melt BC R TBC melt ( H melt AC R TAC melt x (A) + k x (B) = T melt BC T melt AC η +²Î 1 x (A) x, ì/ (B) T ) T 1 T ), η = ( H melt AC 4 γ A exp T R TAC melt T melt AC T ). T é{îºévô îºåoºé +UÎ Ï/ 0+²Î ì/åœ ê ÒGØ Æ éæ œ Å,OºÇ9 _ IUéŸÓTÒGœÓTîºé0OºéQS¾Ò îº yò SkO)Ué6PNU GÇDé Å X î6 O uå Ç œ ÒOòÅ QP#ÒGîVO6 Oœ OIS¾Ò îio U é S¾Æ î)o)u é9î"ço6 &OºéV évœ O9 ÇÈÒÅO Å Ç îºép îºé9çèévœ Oºé9 Ÿ GÇ F(c (A), c (B) ) = 0, c s(j) = f(c (A), c (B), T ) j = A, B, x = x ( t) O Ç)U Ò Æ Ø xðéÿœ ÒOÈé9 1 O)U# &O Oºîº œçèåoºå ÒGœ\S¾îÈÒG q Ò Øé+S¾î6 Ó0OÈÅÒ œ\oèòê Ò ØÆ é'æ œåo6çaå ÇA œ Ò œ ØÅœ é9 îioèî6 OœÇVS¾Ò îº { &OÈÅÒ œ +²Î IÑ/
273 «" I ¹ÀV Õ± { ¹À6¼O 6 3 ¾ª µt Ã5Ó I± U ¹Ó Dµ ª¼ V ȼO ² ¹ ½ È V V A ÎGÏGÑ IA J#$&" F?MVK' (1 " EGeH ú76#ú øö>.ö9 ø?_õ : øöh@.:? Ò-U Oœ Ø é+é9ê ÒGØ ÆROºÅ ÒGœÕÒ SRO U éœçèò ØÅ?g ØÅË3Æ Å ÄÅœOºéVî)S¹ ÓVé VÔŒé% { P O)U éœ Ò½ê3ÅœNX ðò Æœ OîºÊ P îèògð ØéV +²Î Î /#3 +²Î Ì / +UÎ Ñ /-OÈÒWO)Ué'œ évôuóvò3ògîº Å œ OÈé{ÇÈÊÇVOÈé9 +UÇDé9é G Å,X# _Î /T _ IU é îèés¾évîºévœóvées¾îº é Ò½ê é9ç%ô ÅO U+O)UéÇÈÒ ØÅ 3Ø Å Ë3Æ Å {Å œ OºéVî)S¹ ÓTé &O O U é"êgévøòótå,o Ê 3Ų é Å œfo)uéõœ évô ÓTÒÒ î6 Åœ &OºéÄÇÈÊÇOºéV O U éõåœoºévî)s¹ ÓVéÅ Çk]N`é9 1 υ ph x 1 x ( t) x J9= B JV= B?80! L> & Dþ FIE3JVý B ý J9E JTý F KE Š Ò3ÒGîº Å œ OÈéeOºîº œçvs¾ò îº OÈÅÒ œqs¾îºò O)Ué!PU3ÊÇÈÅÓ9 OØÇVP GÓTé ÓTÒ QP ÆNOº &OºÅ ÒGœ OØ ê½ îèå Oð Øé9Ç îºé9 G Ç9Ù (x, t) ( x, t) Å œ OÈÒ3O)UéÇ)P ÓVé"ÒS t = t, x = ϕ(x, t) = { x1 + x l s, 0 x 1, x + (x 1) l l, 1 x, l s l l îèé Ô Å RO)UÇŒÒ S ÇDÒGØ Å ' Oœ# 'ØÅË3Æ Å 6PNU# ÇÈé9Ç îèékçvpé9ó0oèåê évøê 3 œ6o U éœ évôqóvòò î6 Å œ# &OÈé ÇDÊÇVOÈéV O)U éõåœ OÈéVî)S¹ ÓVéÄÅÇ ØÒÓV OÈé9 w &OIO U ép#ògå œ O x = 1 IU é X Ò½ê é9îèœå œnxaé9ë3æ &OºÅ ÒGœÇŒÅ œfo U é TÓ I ¹ Õ ª ¼½ V O6 OÉ é-o)ué S¾Ò ØØ Ò½Ô ÅœNX S¾Ò îº a Íc²Ù (0 x < 1) l s cs(a) c s(a) ϕ t t x = ( ) D s(a) c s(a) x l s, x (a A + a C )c s(a) + (a B + a C )c s(b) = ρ s, c s(a) = 0. x x=0 IU é"çèé9ótògœ é9ë3æ OÈÅÒ œå œ +Uñ ÍH/šÔò ÇšÒGðROº Å œé9 *S¾îºÒ ÓVÒ œ ÅOºÅ ÒGœ +UÎ ÍH/ Ô îºå,ovoèé9œ{å œqo U é S¾Ò îº +Uñ ÍH/ x s(a) + x s(b) = 1 Oœ WOºîº œçèø OÈé9 wåœ OÈÒŸêGÒ ØÆ é Æ œ Å,OºÇ9 5 évîºé Å Ç^O U éˆ é9œçèåo ÊwÒ SBO U éˆçèò ØÅ 1 Oœ îèéä &OºÒ Å Ó ÔŒéVÅ XU O6ÇòÒ SÓTÒ QPÒ œ é9œ O ρ s Ž%Ë3Æ &OºÅ a C ÒGœÇòÅ œfo U é I "V± ¹ Ä ª ¼ V Oœ îèékçvpé9ó0oèåê évøê A B Oîºé X Åê é9œ Ç9Ù C (1 < x ) a A a B
274 Î Ï ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º l l cl(j) c l(j) ϕ t t x = ( ) D l(j) c l(j) x l l, j = A, B, x c (j) = 0, j = A, B. x x= ª ¼½ T ˆ ȼ½ U ¹Ó ¾µT¼GÀ6 é9ë3æ OÈÅÒ œçò îèé X Åê é9œw O Ù x = 1 D s(a) c s(a) l s Dl(A) c l(a) x l l = υ ph (c s(a) c l(a) ), x x=1 0 x=1+0 D s(b) c s(b) l s Dl(B) c l(b) x l l = υ ph (c s(b) c l(b) ), x x=1 0 x=1+0 F(c (A), c (B) ) = 0, c s(j) = f(c (A), c (B), T ), j = A, B. IU éqoèî6 OœÇVS¾Ò îº é9 é9ë3æ &OºÅ ÒGœÇÕÓTÒGœ Oº OÅœxÇDé9ê évî6 OØš ÅOºÅ ÒGœ OØ OºéVîº {Ç Oœ ]ÓTÒé {ÓVÅ é9œ OºÇ Oîºéˆœ ÒO S¾Ò Æ œ Åœ#O U é+x é9œ évîºåó ÓTÒGœÇÈéVîºê OÈÅÒ œékë3æ &OºÅ ÒGœÇV IU é*oºévîº ÇÕ GÓ_OºÆ OØØ Ê étö P#é9œ ]Ò œxå œ OºéVî)S¹ ÓTé î6 &OÈé υ ph. IU évê]ótògœoºîèåð ÆROºé*OÈÒ.é9 GÓU ékëgæ# &OÈÅÒ œ]åœyo U é'çèêçvoèé9 +¹ñ ÍH/ 3+¹ñ ñ/ év QPNU GÇDÅ VÅœNXIO)Ué%ÓTÒGÆNP ØÅ œnx ðé0o ÔŒéVé9œ O)U é P îèòóvé9çºçdékç5å œo U é%çèò ØÅ!PNU# ÇÈé ZÆ Å w œ w &OeO)UéÕÅ œ OÈé9îVS¹ GÓTéG ú @ 0>G >=? ù > õkù > > IU éœ3æ é9îèå ÓV Ø P îèòóvé9 Æ îºé S¾ÒGî O)U é{çèò ØÆROÈÅÒ œ Ò SŒé9Ë3Æ &OºÅ ÒGœÇ+¹ñ ÍH/ 3 +¹ñ ñ /"Å Çð ÇÈé9 Ò œyo)u é'óvò œçèévîºê½ &OÈÅê é Oœ# Å QP ØÅÓVÅO]œÅOºé' Å5éVîºéVœ#ÓTé'ǺÓU év é*o)u O ÅÇÄÒGðROº Å œé9 Å œ œ évôzótòò î6 Åœ &OºéÇÈÊÇOºéV rðê O)U éõótògœ OÈîºÒ Ø ê ÒGØ Æ éä é0o U Ò a Í9Ì&c² œ Éœ Ò½Ô œ's¾æœó_oºå ÒGœÇ OîºéˆÓVÒ QP ÆROºé9 &O!O)U é*x îºå œ Ò é9ç9 _ÔeUÅ Øé c s(a) c s(b) Oîºé'ÓV ØÓVÆ Ø OÈéK υ ph c (A) c (B) ϕ l s l l D s D l &O O U é.ótévœ OºéVîAÒSeO)U é X îºå ÓVéVØØÇ9 Š Ò3é 'ÓTÅéVœ OºÇ9 ÔeU Å ÓU]ÓVÒ îºîèékçvpò œ 'OÈÒfO)U é{óvò3ògîº Å œ OÈéÇDÊÇVOÈé9 OÈî6 OœÇVS¾Ò îº { &OºÅ ÒGœ Oœ épévœ xògœ O)U é{åœ OÈéVî)S¹ ÓVé{ Ò½ê év é9œoõî6 &Oºé îèéqoºîèék &OÈéK Åœ OœxÅ QP Ø Å ÓTÅ,OAÔò Ê Å,OÈÅÒ œ ØROÈî6 OœÇ)PÒ î)o OºéVîº {Ç% Oîºé PNPîÈÒd`Å OÈéK AðÊ υ ph O U é ÇÈé9ÓTÒGœ 3Ò î6 évîóté9œ OÈî6 OØ Å,S Ö S¾éVîºéVœÓVé ÓU év ékç Ô Å,O)UwÓTé9œOºîº Ø# Å5éVîºéVœÓVé-P îºò½êå é îèé9ø Å OðØ é îèékçdæ Ø,OºÇ Å,S é9ç)uÿçdå Vé h ÇÈ OÈÅ Ç]éKÇO)U éõçvoº OðÅ ØÅO Ê'ÓVÒ œ ÅOºÅ ÒGœ aiñ c² ÒˆÔŒé Æ#ÇDé!O)UÅÇ ÓVÒ œ Å,OÈÅÒ œ h < D(s/l) OÈÒÓU ÒÒGÇÈé3O)U é'çvoèép]åœ O)U é'çèò ØÅ ] œ Ø Å υë3æ Å ph PNU# ÇÈé9Ç9 îèå ]œ Ò é9çõ îèéœæ AðéVîºé9 S¾îÈÒG OÈÒ œ QO U é ÇÈÒ ØÅ Lg ØÅË3Æ Å Å œ OºéVî)S¹ ÓTé ÓTÒ îºîºé9ç)p#ògœ Ç OºÒ X îºå œ Ò é"œæ Ö ð#é9î N 1 N 0 IU é!]œ Å,OÈé Åé9îÈé9œÓTé ǺÓU é9 éõó9 Oœwð#éÕÔ îºåo)oèé9œ. GÇOÙ M = F ý FIE þ F =6JVý B ý C B E B J = KEF þgb Bþ F þ E þ B ( J F J B û FIý C.JCJVý = B 9E þ ý ý C B J þ JVE3= B6þ ý F ÕB B B +Uñ Î / +Uñ ñ/
275 «" I ¹ÀV Õ± { ¹À6¼O 6 3 ¾ª µt Ã5Ó I± U ¹Ó Dµ ª¼ V ȼO ² ¹ ½ È V V A ÎGÏ h i ls 1 [ ϕt τ [ D s(a) = τ (ĉs(a) i xi 1 ls c s(a) i ) + l s h i+ 1 (ĉ s(a) i ĉ s(a) i+1 ĉs(a) i h i+ 1 (a A + a C )c s(a) i (ĉs(a) i ĉ s(a) i 1 ) + ϕ t xi+ 1 Ds(A) ĉ s(a) ls c s(a) i ) (ĉ s(a) i+1 ĉs(a) i ) ] 0 ĉ s(a) i 1, N 1 i < 0, h i 1 + (a B + a C )c s(b) i = ρ s, N 1 i < 0, ] +Uñ Ì / +¹ñ Ï/ h ls 1 (ĉs(j) 0 c s(j) 0 ) + l h l 1 (ĉl(j) 0 c l(j) [ ϕt τ (ĉ s(j) 0 ĉ s(j) 1 ) + ϕ t x 1 x 1 [ = τ (ĉ s(j) 0 ĉ l(j) 0 ) υ ph + Dl(j) ll ll h i 1 0 ) (ĉ l(j) 1 ĉ l(j) 0 ) ĉ l(j) 1 ĉ l(j) 0 h 1 ] Ds(j) ĉ s(j) ls +Uñ ì/ ] 0 ĉ s(j) 1, j = A, B, h 1 F(ĉ (A) 0, ĉ (B) 0 ) = 0, ĉ s(j) 0 = f(ĉ (A) 0, ĉ (B) 0, T ), j = A, B, (ĉl(j) i [ ϕt τ = τ xi 1 [ D l(j) ll c l(j) i ) + l h l i+ 1 (ĉl(j) i c l(j) i ) (ĉ l(j) i ĉ l(j) i+1 ĉl(j) i h i+ 1 ĉ l(j) i 1 ) + ϕ t xi+ 1 Dl(j) ĉ l(j) ll (ĉ l(j) i+1 ĉl(j) i ) ] ] 0 ĉ l(j) i 1, 0 < i N, j = A, B, h i 1 ÔeU évîºé Å Ç O U é ÓTé9œOºéVîwÒ S O U é ÓTé9Ø Ø IU é PNP îºòd`å x { OÈÅÒ œ i 1/ ÒSÄ Å5ÆÇÈÅ ÒGœTZ#ÆR`é9Ç{Å Ç{Ò SÄÇDéKÓTÒGœ [x i 1, x i Ò î6 évî{ Ó9ÓTÆ î6 ÓVÊ ] h i 1/ = x i Å œgç)p GÓTé Oœ x i 1 ]îºçvo Ò î6 évî GÓVÓVÆ îº GÓTÊÅœ OºÅ ég IU é ÇDÊÇVOÈé9 }Ò Sšœ ÒGœ Ø Åœ ék Oî OØ X é9ð î6 OÅ Ó ékë3æ &OºÅ ÒGœÇ9+¹ñ Ì=/ 3 +¹ñ /ŒÅ Ç ÇÈÒ Øê ék ŸðÊ6O U é ï évôioºò œ. é0o U Ò YaÍVÌ c² - é0o ÇòÔ îºåoºé!o)u é S¾Æ ØØ_ÇÈÊÇOºéV råœfo)u éõòp#é9îº OÈÒGî œ ÒOº OÈÅÒ œç9ù F(ζ) = 0, U évîºé ζ = (ĉ s(a) N 1, ĉ s(b) N 1, ĉ s(a) N 1+1,..., ĉs(a) IU éõåoºévî6 &OºÅ êgé-p îºòótékçèçks¾ògîio)u é ÇÈÒ ØÆROÈÅÒ œwò S +Uñ / ÅÇ é0oèé9îè Åœ é9. GÇkS¾Ò ØØ Ò½Ô Ç9Ù +¹ñ Ñ / +Uñ / +¹ñ / 0, ĉ s(b) 0, ˆυ ph, ĉ (A) 0, ĉ (B) 0, ĉ (A) 1,..., ĉ (B) N ) T F ( (k) ζ )δζ + F( (k) ζ ) = 0, ÔeU évîºé Å ÇQO)U é ëg GÓTÒ ðå œ { &OºîÈÅ,` F δζ = (k+1) ζ (k) ÅÇQO U éï"évôioèògœ ÅOºéVî6 ½Ö OÈÅÒ œ ÓVÒ Æ œ OºéVîK # IU éçdògø ÆNOÈÅÒ œ's¾îºò O U é3pîèé9ê3åò Æ#ÇeOÈÅ éˆøévêgévø ζ, k ÅÇÆÇÈé9 Ç ÇVOº îvoºå œnx é9çvoèå OÈé S¾ÒGîIO)U éäå,oèévî6 &OºÅ ÒGœ1
276 ÎOì Ð ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º koÿé9 GÓU ï"évôioºò œ Å,OÈéVî6 &OºÅ ÒGœ Ô é$u# ê éfo)u é]çdêçvoèé9 Ò SÕØÅ œé9 OîŸé9Ë3Æ &OºÅ ÒGœÇ{Ô Å,O)U îèékçvpé9ó0o*oºò Æ œ Éœ Ò½Ô œ ê ékó_oèògî [O U éótòg *PÒ œévœ OºÇÒS ÔeU Å ÓU ÓTÒ œ#ótévœ Oºîº OÈÅÒ œçœò Sš OØØ Ç)P#éKÓTÅé9Ç δζ OîºéwÅœÓVîÈé9 é9œ OºÇÒ S δc s(j) Oœ Å œ OºéVî)S¹ ÓTéÄî6 &Oºé i, i = N 1,..., 0, δc l(j) i, i = 0,..., N, j = A, B N 1 B δυ ph IU é ë3 ÓVÒ ð Å Oœ OÈîºÅ` ÅÇ é]œ ék w GÇVÙ N 1 C N A N 1 B + 1 N N 1 ξ C 0.. N 1 ξ A IU éõð ØÒÓ6ÉnjŜ O U Å Ç { &OÈîºÅ,` 1 B 1 C 0 A ( i i A, C = ( 0 Oœ 0 A C îèé ξ B 1 ξ 1 A 0 C B 1 C N 1 ξ..... N 1 A N 1 N ξ N A U ê é-o)ué S¾Ò ØØ Ò½Ô ÅœNX{ÇOºîÈÆ#Ó_OÈÆîÈéGÙ ) (, N 1 i < 0, i B = ) (, 0 < i N, ( ), N 1 i < 0, i 0 ξ = ( ), 0 < i N. 5 ð ØÒÓ6ÉÇV 0 B ÅÇ 0 A, 0 C = 5 5 ð ØÒÓ6É5Ù , B = B N C 1 N B ), N 1 i < 0, ), 0 < i N, IU é#s¾æø Ø ÓVÒ ØÆ œqåœ O)UéxÓVéVœ OÈé9î ÒS O)Ué { &OºîÈÅ,`QÓTÒGîÈîºé9Ç)PÒ œ Ç6OÈÒTO)U é]æ œ Éœ Ò½Ô œ Å œ OÈé9îVS¹ GÓTéÄî6 &OÈéG
277 «" I ¹ÀV Õ± { ¹À6¼O 6 3 ¾ª µt Ã5Ó I± U ¹Ó Dµ ª¼ V ȼO ² ¹ ½ È V V A Î ì Í œgò î6 évî6oèò ÒGðROº Å œho U éxçdògø ÆROºÅ ÒGœ Ò SO U é ÓVÒ îºîèékçvpò œ Å œnx ØÅœ é9 î ÇÈÊÇVOÈé9 O U é Ò Å,]éK { IU Ò { Ç% OØ X Ò îºå,o)u `Å Ç+Æ#ÇDéK Wa ÍKñdc² é"îèép îèékçdé9œ O δc ÅœfO)U é S¾ÒGØ ØÒ½Ô Å œx S¾ÒGîÈ s(a) δυ ph δc (j) i, j = A, B, i = 0,..., N δc s(a) i δc (j) i = α s i+1δc s(a) i+1 + βs i+1 + γ s i+1δυ ph, N 1 i 1, i, i = N 1,..., 0 = α l(j) i 1 δc(j) i 1 + βl(j) i 1 + γl(j) i 1 δυ ph, 1 i N, j = A, B. Š Ò3é 'ÓTÅéVœ OºÇ ÓV œgðéé9 GÇDÅØÊoÓV ØÓVÆ Ø α s(a) i, β s(a) i, γ s(a) i, &OÈéK i = N ðêto U é's¾ògîèôò Oî6 1,..., 0, α (j) i, β Oœ (j) i, γ ð# Ó6ÉÔŒ îº oévøå Åœ OÖ (j) j OÈÅÒ œ1 šîºé9ç)p#ékó_oèåê é9ø = A, B ÊG _ IUÆÇ3O)Ué P îºò ðø é9 då LjîÈéK ÆÓTéK \OÈÒYO)UéwÇÈÊÇOºéV Ò Se]êGé ékë3æ ½Ö OÈÅÒ œçä &O!O)UéÇÈÒ ØÅ?g ØÅË3Æ Å Åœ OÈé9îVS¹ GÓTé Ô ÅO Uîºé9Ç)P#éKÓ_O OÈÒwÆ œ Éœ Ò½Ô œç OºÇÇÈÒ ØÆROÈÅÒ œ Å ÇšÒ ðnoº OÅœ ék A ÅîÈéKÓ_OºØ δυ ph, δc (A) 0, δc (B) 0 ) T ÊÕðÊÕ { &OºîÈÅ,` Å œêgévî6çdåò œ1 IU é ð Ó6É.ÇDÆðÇOºÅOºÆROÈÅÒ œyp Oî)O"ÒSBO)U é é0o)uò $X Åê é9ç IU é Ä ÆǺÇ"é9Ø Å Å œ OÈÅÒ œå δcçço6 Oð ØéAÔeU ÅØé s(j) i, i = N 1, O)Ué ë3 ÓVÒ ð Å..., 0, δc l(j) Oœ P Ö 0, P#éK Oî6ÇkOÈÒð#é..., N, j Å = A, XGÒ œ Ø B ØÊ' ÒG Åœ œo { &OºîÈÅ,` IU éõçdògø ÆROºÅ ÒGœ ¼O 3 ¾ª Ó9 Oœ.ðé ÇDÆ { OîºÅ Vé9 ÇkS¾ÒGØ ØÒ½Ô ÇVÙ Í "ŠŒ OØ ÓTÆ Ø &OºÅ ÒGœ'Ò SO)U éäëg GÓTÒGð Å œ'ðêæçdåœnx3o)u éø &OÈéKÇO ÇÈÒ ØÆROÈÅÒ œ i, i = 0,..., N, (δc s(a) 0, δc s(b) 0, i, i = c s(a), c s(b), υ ph, ĉ s(a), ĉ s(b), ˆυ ph, ĉ (A), ĉ (B) Ç ÇO6 Oî)OÈÅœNXé9ÇVOÈÅ { &OÈé!S¾ÒGî c (A), c Î "éoèé9îè Åœ &OºÅ (B) ÒGœ ÒSÓVÒé 'ÓTÅéVœ OºÇ α s i βi s γi s i = N 1,..., 0 α l(j) i β l(j) i œ wîèék ÆÓ_OºÅ ÒGœ OºÒ*O)U éõøåë3æ Å?gOÇDÒGØ Å ŸÅœ OÈé9îVS¹ GÓTé γ l(j) i, i = 0,..., N j = A, B ñ "Åîºé9Ó_O { OÈîºÅ`ŸÅœê é9îºçèå ÒGœ6S¾ÒGî Ò ðro6 OÅœ Å œx Ì "Š Ò QP ÆROºÅ œx{ò S O)U éõæ œé3œò½ô œ S¾Æ œ#ó_oèåò œ#ç δc s(a) 0, δc œ.ótòg *PÒGÇÈÅ,OÈÅÒ œ. ÅÇVOÈîºÅð ÆÖ s(b) 0, δυ ph, (A) 0, (B) 0 OÈÅÒ œ.åœ O U é ÇÈÒ ØÅ w Oœ ØÅË3Æ Å fpnu ÇÈé9Ç OIO)U éõœ é`9o"ï évôioºò œ l s l l ϕ t ÇòÅ,OÈéVî6 &OºÅ ÒGœ1 Ï òž%çvoèå OÈÅÒ œ.ò S O)UéÄÓVÒ œê é9î)xgévœóvé ì ê½ OœÓVé!OÈÒQO)UéÕœ é0`9oeoèå é ÇOºéP1 ^A J#$&" F?MVK' ( " 9J#(E D-Ḧ M 9K J 9MVG D œ\o)u Å ÇAÇÈé9Ó0OÈÅÒ œ\o)ué6p îºòpògçèé9 YS¾Æ ØØ ÊxÅ *PØ Å ÓTÅ,Ô ÓTÒGÆNP Øé9 Ø,XGÒ îºåo U yôò Ç ÓVÒ QP îèék Ô ÅO U].ÇÈéV ŠֳŠ*PØ Å ÓTÅ,OÒGœ é ÔeUéVîºé O U é{ótò œ#ótévœ Oºîº OÈÅÒ œ Å ÇVOÈîºÅ ð ÆNOÈÅÒ œx Oœ Å œ OÈé9îVS¹ GÓTé Ø ÒÓV OÈÅÒ œ îèé é0oºévîº Å œ ék ÓVÒ œçèé9ë3æ é9œ OÈØÊ aí_c³ 1 IU Å ÇOºé9ÓU œåë3æ é3oèîºé9 OºÇ Å œ PNP îºòd`å { OÈÅÒ œò S +¹ñ ÍH/)3 +Uñ ñ/åœÿé`rp Ø Å ÓTÅ,O Ôò Ê 3 Å,OÈÅÒ œ ØOºîº œç)p#ògîvooèévîº {Ç l s l l υ ph îèé PNP îºòd`å { OÈé9 ˆðÊ O U é"æp3ô Åœ {ǺÓU év ég 3Š Òé 'ÓTÅéVœ OºÇ épévœ# Å œx Ò œ{åœ OÈéVî)S¹ ÓVé îº OÈé Oîºé ÆNP5 OÈé9 &S OºéVî é0oèé9îè Åœ &OºÅ ÒGœÒ S O U é ÓVÒ œóvévœ OÈî6 &OºÅ ÒGœ ÅÇVOÈîºÅð ÆROÈÅÒ œå œ'o U é υð Æ ØÉ ph PNU GÇDéG IU éõé9ë3æ OÈÅÒ œçòògðroº Å œ ék S¾îÈÒG O)Ué ]œ Å,OÈéA Å5éVîºéVœÓVé PNP îºòd`å { OÈÅÒ œ îèéäœ ÒGœÖ Ø Åœ é9 îõò œ ØÊ OO)U é'çèò ØÅ Lg ØÅË3Æ Å Åœ OÈé9îVS¹ GÓTé 1 ÇÕðé0S¾Ò îºé*o)u é' IUÒ { Ç P îºòóték Æ îºé Å Ç PNP ØÅé9 YS¾Ò î O U é'çdògø ÆNOÈÅÒ œ]ò SkO)U é{øå œévî ékëgæ# &OÈÅÒ œ#çv ð ÆNOO)U Å Ç OÈÅ é'å,o ÅÇÄÆÇÈé9 ]Ô Å,O)U îèékçvpé9ó0okoºò{æ œ Éœ Ò½Ô œ.ótògœóté9œoºîº OÈÅÒ œço U év {ÇÈéVØê é9ç!aí 1ÍKñdc³ # ÒÔ éõ GÇÈÇÈÆ é!o)u O9Ù ĉ s(a) i ĉ l(j) i = σ s i+1ĉ s(a) i+1 + ηs i+1, N 1 i 1, = σ l(j) i 1ĉl(j) + ηl(j) i 1, 1 i N, j = A, B. +¹Ì ÍH/
278 ÎOìGÎ ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º ép îºé9çèévœ O6 &OÈÅÒ œ +¹Ì ÍH/+ Ø ØÒ½Ô ÇÆÇ OÈÒAîÈéK ÆÓTé^O)U éçdêçvoèév ƒò S XGÒ½ê é9îèœ ÅœNXÄé9Ë3Æ OÈÅÒ œç[oèò O)U é ÇÈé0O+ÒS?S¾ÒGÆ î+œ ÒGœ Ø Åœ ék Oîšé9Ë3Æ OÈÅÒ œç OBO)U é ÇÈÒ ØÅ Lg ØÅË3Æ Å Å œ OÈé9îVS¹ GÓTéòÔ Å,O)UîÈéKÇVPé9Ó0OBOÈÒ Æ œ Éœ Ò½Ô œç IU évê. Oîºé éoèévîº Å œé9 ðê6o U éˆï"évôioºò œ Å,OÈéVîÈÖ &OÈÅÒ œ aívì&c³ #Š ĉ s(a) 0 Ò QPÒGÇÈÅOºÅ, ĉ s(b) 0 ÒGœw Å, ĉ (A) 0 ÇVOÈîºÅ, ð ÆNOÈÅÒ œwå ĉ (B) 0. œfo)uéõð Æ ØÉ6PNU GÇDéKÇ Å Ç ÒGðROº Å œ ék GÓVÓVÒ î6 Å œx OÈÒ +¾Ì ÍH/T O U évœ]åœoºévî)s¹ ÓVéAî6 &OÈé Å ÇÓV OØ ÓTÆØ OÈé9 1 œ]çdé9 ŠֳŠQP ØÅ ÓTÅ,O-Oºé9ÓU œ Å Ë3Æ é O U é ï évôioºò œ OØ X ÒGîÈÅ,O)U uåç PNP ØÅ ék ÒGœ ØÊŸ &OeO U épnu GÇDé!OÈî6 Oœ#ÇDÅ,OÈÅÒ œ Å υ ph œ OÈé9îVS¹ GÓTéG ÒO)U OØ X ÒGîÈÅ,O)U Ç" OîºéÆ#ÇDéK fs¾ò î^o U é œæ évîºå ÓV OØ_ÇOºÆ ÊwÒ SØ Å Ë3Æ Å WPNU ÇÈéÕéPÅO6 &`Ê Ò S OÈé9îÈœ îèêw OØØ Ò½ÊÇ9 IU é ÓTÒ QP ÆNOÈéVî ÇDÅ AÆ Ø &OºÅ ÒGœÇ" îèé Ò œ és¾ògî"îºé9 Ø PNU GÇDéA Å X î6 O Oœ é0`rpévîºå évœ O6 OØØ Ê'Æ#ÇDéK XGîÈÒ½ÔIO U ÓVÒ œ Å,OÈÅÒ œ#ç a ñ Ïdc³ "Å5ÆÇDÅÒ œ ÓVÒ3é 'ÓTÅéVœ OºÇ îèé D s(a) 1 cm = 5 10 s, Dl(A/B) 5 cm = 5 10 s. IU é#oºå éxçoºép ÔŒ GÇ6O6 OÉ é9œ ÇÈé9ÓTÒGœ Œ OwÅ Ç O Ô ÒTUÆ œ îºé9 OÈÅ ékçwø î)xgévî O)U œ O)U é]ò œé éoèévîº Å œé9 gðê τ = O)Ué0.5ÇVOº OðÅ ØÅO Ê ÓVÒ œ Å,OÈÅÒ œqò SAé`9PØ Å ÓTÅ,Ow Ø,XGÒ îºåo U {ÇVÙ τ œ Å,S¾Ò îº uð ÆRO Åé9îÈé9œ OòÇ)P ÓVéÇVOÈéPÇò Oîºé"ÆÇÈé9 ŸÅ h /(D l ) 0.00s. œ.çèò ØÅ ' œ Ø Å Ë3Æ Å PNU GÇDéKÇV IU é œ3æ AðéVîŒÒ S X îºå +P#ÒGÅ œ O6Ç%Åœ+O)UéÇÈÒ ØÅ 'ÅÇ IU éxgîèå {Å Ç ÇÈÆ 'ÓTÅéVœ OÈØÊQ]œ é Oœ OØØ Ò½Ô Ç%ÆÇ Oœ {Åœ+O U é ØÅ ËGÆÅ {Å Ç N 1 = OÈÒ PîÈéK ÅÓ0Oò GÓVÓVÆ îº OÈé9Ø 5000 Ê O)U Åœ ðò Æœ OîºÊ N = 500 Ø ÊGéVî6ÇÕÅ œbo)u éwêåóvå œ Å,O Ê]Ò S ÅœOºéVî)S¹ ÓVé ÇAÔ é9ø Øò Ç OÈÒ] Å Åœ Å ÇVU œæ é9îèå ÓV Ø ÅÆ#ÇDÅÒ œ Å œê ÒGØ êgé9 ð3êbo)u é ÆNPÔ Åœ PNPîÈÒd`Å OÈÅÒ œ ÒS-Oºîº œç)p#ògîvo*oèé9îè {ÇÅœ +Uñ ÍH/ 3 +¹ñ ñ / IU éaœæ ˆð#é9î ÒS X îºå WPÒ Åœ OºÇÄ Oœ# ÓTÒGœÇDéKË3Æ évœ OÈØÊ O)U éótòg *PÆROº OÈÅÒ œ Ø OÈÅ é Ó9 Oœðé é9óvîèék ÇÈé9.Å,S œ ÒGœÖ²Æœ ÅS¾ÒGîÈ X îºå ÇU# ê éaðévé9œæçèé9 1 ÆROÄÅOÄÅ Ç œò OÄê évîºêwå QPÒ î)oº Oœ O Å œ O)U é-s¾îº é"ò S O U Å ÇŒÇVOÈÆ# Ê ÇÈÅ œóvé"ògæ î { Å œ Ò ð ékó_oèåê é"åçoèòˆîèé9ê ék OØNO U éä ê½ Oœ O6 X é Ò S O)U é S¾Æ ØØÊŸÅ *PØ Å ÓTÅ,O"ÓTÒGœÇDé9îÈê½ OÈÅê éäçèóu é9 é -1é0Ô ÆLjÓVÒ œçèå évî O)U é S¾Ò ØØ Ò½Ô ÅœNX'X îºò½ôio)u Ò ég _ œ# évî6çè OÈÆ î6 &Oºé9 ÇDÒGØ ÆROºÅ ÒGœw OIOÈéV QPéVî6 &OºÆ îèé Å Çòð îèògænxu O ÅœOºÒ{ÓTÒ œ O6 Ó_O Ô Å,O)U A B C IU éwóvò QPÒGÇÈÅOºÅ ÒGœ Ò SO)U éwø TÅ 0 Ë3Æ Å ipnu# ÇÈé Å Ç Å œoé9ë3æ ÅØ Åð îºå Æ Ô Å,O)UTO)UéwÇÈÒ ØÅ ipnu GÇDé ÇÈÆ ðçvoèî6 &Oºé A x B 1 x C A x B 1 x C O OÈé9 *PéVî6 &OºÆ îºé K IU é[x îºò½ôio)uäå Ç1Åœ Å,OÈÅ &OÈéK ÄðÊO U é P îºòxgîº ék ÓTÒÒ ØÅ œxù koio)uéék OîºØ T 1 < T 0 Ê{ÇVOº X é"òs O)Ué!PîÈÒÓTéKÇÈÇ O)UéÇÈÆ ðçvoèî6 &Oºé 9P Ø Ê3ÅœNX O)U éõîºò ØéÕÒ Sš { &OÈé9îÈÅ T = T 0 OØ1ÇÈÒ ÆîºÓVé Å α t Oœ# ÇÈÇÈÒ Øê ékç Oœ S¾éVéK ÇIO U é ÇDÒGØ ÆNOÈÅÒ œ.ô ÅO U ÓTÒ QPÒ œ é9œ OºÇ _ÔŒÒbP îºòóvé9çºçdékç'ótògœ OÈîºÅ ð ÆNOÈé'OºÒbO)Ué Ǻ &OÈÆîº OÈÅÒ œ Ò S O)UéØÅË3Æ Å PNU GÇDéGÙ A ÇDÆ ð#çoºîº OÈé Å B. ÇÈÇÈÒ ØÆROÈÅÒ œ{ œ ÓTÒÒ ØÅ œxòs?o U é ÇÈÊÇVOÈé9. "Ç+ÇÈÒÒ œ{ Ç O U é"çèò ØÆROÈÅÒ œ &OBO U é ê3å ÓTÅœ Å,O Ê.Ò S O)U éˆå œ OºéVî)S¹ ÓTéAð#éKÓTÒ ékç"çèø Å XU OÈØÊ.ÇDÆNPéVî6Ǻ &OÈÆîº OÈé9 fo U é PîÈÒÓTéKÇÈÇ"ÓU OœNXGé9Ç ÅO6Ç ÅîÈéKÓ_OÈÅÒ œ S¾îºÒ } ŠǺÇDÒGØ ÆROºÅ ÒGœ OºÒQX îºò½ôio)u1 IU ÅÇP îºòóté9çºç+ôò Ç ÇDÅ AÆØ OÈé9 ŸðÊ ðò O U' é0o U Ò ÇV G Å X ña é9 ÒGœÇVOÈî6 &OÈéKÇ%ÊÅéVØ é9 ÓTÒ QPÒGÇÈÅOºÅ ÒGœ Å ÇVOÈîºÅ ð ÆNOÈÅÒ œòs Å œyo)uéçèò ØÅ $PNU GÇDéG 5 OÄÅ ÇéVêÅ évœ O O)U O O)U éîºétö ÇDÆ Ø,OºÇ P îºò½ê3å ék AðÊ ð#òo)u' OØ X ÒGîÈÅ,O)U Ç îèéepîº GÓ_OÈÅ AC ÓV Ø ØÊ Å évœ OºÅÓ9 Oز O Ç)U Ò ÆØ ðé œ ÒOÈé9 O)U O &O)OÈéV QPRO6Ç+OºÒ Å QP ØéV évœ O6O U éóvévœ OÈî6 OØ" Å5éVîºéVœÓVé PP îèòd`å { &OÈÅÒ œoò S OÈî6 Oœ#Ç Ö P#ÒGîVOeOºéVîº Ç Å œçèév ŠֲŠQP Ø Å ÓTÅ,O Ø,XGÒ îºåo U S¹ OÅØé9 Ž%ê évœ ÒGœ.ê évîºê+]œéoèå é X îºå ÇòÔ é U ê éòò ð#çdé9îèêgé9 O)U é ÇÈÆ ðçvoèî6 &Oºé ÅǺÇÈÒ ØÆROÈÅÒ œ Ò évøø ÅœNXX îºò½ôio)u îºéx Å é9ç O U &O Ç)U ÒGÆ Ø P îèòóvévé9 Ô Å,O)U ÒGÆRO ÅOK ÆNOS¾Ò î Oœ ÒO)U é9î XGîÈÒ½ÔIO UÄ Ò é9øo U éòçdé9 ŠֳŠQP ØÅÓVÅOš OØ X ÒGîÈÅ,O)U z Òé9Ç_œ ÒO P îºò½êå é PNUÊÇÈÅ ÓV OØØÊŸ PNPîÈÒ½êGé9 îèékçdæ Ø,OºÇ9 G ÒGî ÅœÇO6 OœÓVé Æœ évî6çº &OÈÆîº OÈé9 wçèò ØÆROÈÅÒ œ.å Ç ð îºò ÆNXUO Å œ OÈÒÄÓTÒGœ Oº Ó0O Ô Å,O)U ÇDÆðÇOºîº OÈéŒÅ AC œ#çoºé9 AÒ S O "Ø Ø9O U éòò O U évî P îº éoèé9îºç OîºéO U é ÇÈ éä GnjŠœfo)ué!pîèé9ê3åò Æ#ÇòîÈÆ œ IU ÅÇkOºÅ A x é B 1 x O ÅǺÇDÒGØ C ÆNOÈÅÒ œ ÇVOº X é!o)uéøå ËGÆÅ
279 «" I ¹ÀV Õ± { ¹À6¼O 6 3 ¾ª µt Ã5Ó I± U ¹Ó Dµ ª¼ V ȼO ² ¹ ½ È V V A Î ì ñ?80?> "F ý F KE þ F³ý F Gý F 9EQ AC F EAý C B F þ* CJ B" PNU ÇÈé ÅÇéVœîÈÅ ÓU é9 Ò œ ØÊ Ô ÅO U ÓVÒ QP#ÒGœ évœ O O)U é{øåë3æ Å PNU GÇDéÅœOºÒWO)U é'çèæ ðçvoèî6 &Oºé 1 IUÆÇ9 Å ÔeU ÅØ A, œ O U é{ø é{óvò QP#ÒGœ évœ O Å Ë3Æ Å YPU ÇÈé Åœxê3Å Å5ÆÇDéKÇ-S¾îÈÒG B ÓTÅœ Å,O ÊÒS O)U é]å œ OºéVî)S¹ ÓTé]ÓTÒGœÓTé9œOºîº OÈÅÒ œ ÒSAÓTÒ QPÒ œ é9œ O Å œóvîèék ÇÈé9Ç9 ÔeUÅ Øé ÓVÒ œóvévœ OÈî6 &OºÅ ÒGœ Ò S ÓVÒ QP#ÒGœ évœ O é9óvîèék ÇÈé9Ç9 # IU éévêgò ØÆROÈÅÒ œò S[O U éø A Å Ë3Æ Å #PNU GÇDéÓTÒG *PÒGÇÈÅ,OÈÅÒ œå Ç ÇVU Ò½Ô œÿò œ PU ÇÈé Å X î6 O ƒò S B O U éõçdêçvoèév + G Å,X# 3Ì=/ œ6o U é P Å Ó_OÈÆîÈéG O U éäçdògø Å 'ØÅ œé9ç OîºéQO)U é'å ÇÈÒ O)UéVîº ÇAÓTÒ îºîºé9ç)p#ògœ ÅœNXfOÈÒ O U éÿ GÇVUé9 ]Ò œ ékça îèéqo U é'øå œ ékç ÒS ÓTÒ œ#ço6 Oœ O ÇDÒGØ Å.ÓTÒ QPÒGÇÈÅOºÅ ÒGœ ékó_oºå ÒGœÇ Ò SšðÒ O)U ÓVÆ îèêgé9çixgå T 0 T 1 êgé-o U éaóvò QP#Ò3ÇDÅ,OÈÅÒ œ Ò S wçdògø Å ÔeUÅÓU ÅÇÅœé9Ë3Æ ÅØÅ x. ð îºåæ Ô ÅO U] ZÆ Å ÒSŒÓVÒ QP#Ò3ÇDÅ,OÈÅÒ œ OÄ x ÓTéVî)Oº Å œ OÈé9 *PéVî6 &OºÆ îºé O IU Å Ó6É ØÅ œ é Ç)U Ò½Ô Ç O)U é Ó9 OØ ÓTÆ Ø &Oºé9 ÓTÒ QPÒGÇÈÅOºÅ ÒGœAÒSO)UéŒØÅ x (A), x (B) ËGÆÅ PNU ÇÈé' &OO U é'åœ OÈéVî)S¹ ÓVé{Å œ O U éÿótògœçèå é9îèåœnxwx îºò½ôio)u] Ò é _ ÒGÅ œ O é9œ Ò Oºé9Ç O U é Å œ Å,OÈÅ OØ5ÓTÒG QP#Ò3ÇDÅ,OÈÅÒ œ'òs O)U é Ø Å Ë3Æ Å +PNU GÇDéG PÒ Åœ O Å Ç O)U é é9ë3æ ÅØ Åð îºå Æ uóvò QP#Ò3ÇDÅ,OÈÅÒ œ 1 ÔeU ÅÓUxÅ ék Å &OÈé9Ø Ê]ÇDéOºÇÄÆNP OO)U é{åœ OÈéVî)S¹ ÓVéÔeU évœxæ œ évî6çè OÈÆ î6 &Oºé9 ]ÇDÒGØ ÆROºÅ ÒGœ Å Ç ð îèògænxu OÕÅœOºÒÓTÒGœO6 Ó0O Ô ÅO UYO U éÿçèæ ðçvoèî6 &Oºé šò Åœ O ÅÇ O U é+]œ# OØ%ÓVÒ QP#Ò3ÇDÅ,OÈÅÒ œxòs O)U éõøåë3æ Å fpnu GÇDéG 3 G Ò î[o)u ées¾æø ØÊÅ QP ØÅÓVÅOòÓTÒGÆNP Øé9 OØ X ÒGîÈÅ,O)U ƒ OÈî6 Oœ#ÇDÅ,OÈÅÒ œò S1ÇÈÒ ØÆROÈÅÒ œ'óvò œóvévœ OÈî6 ½Ö OÈÅÒ œx &O O)U éåœ OÈéVî)S¹ ÓVéÅÇ XGÅ êgévœåœ G Å X Ì ¼ Æ éqoèò. Å ÇÈÇÈÒ ØÆROºÅ ÒGœ ÒS ÇDÆ ð#çoºîº OÈé ÓTÒ œ#ótévœ Oºîº OÈÅÒ œ Ò SŒÓTÒ QPÒ œ é9œ O Å œ#o)u é Ø Å Ë3Æ Å $PNU GÇDé &O-O)U é ÅœOºéVî)S¹ ÓVéAÅœÓTîºé9 GÇDéKÇV AC ÔeU Å Øé O)Ué ÇDÒGØ ÆROºÅ ÒGœ ðé9óvò é9ç ép Øé0Oºé9 wô ÅO U.îÈéKÇVPé9Ó0OkOºÒ'ÓTÒG *PÒ œévœ O A B œ G Å,X# _Ì S¾Ò î3o)u é ÇÈéV ŠֳŠ*PØ Å ÓTÅ,OǺÓU é9 ég _ÔŒé.ÇDé9é6O)U# &O' &O3O)U é.åœ ÅOºÅ Ø ÇO6 X é Ò SkO)U é+p îºòótékçèçèé9çäótògœóté9œ OÈî6 &OÈÅÒ œ]ò SòÓTÒG *PÒ œévœ O ÅSIO)UéVîºé{ÅÇ œ Oî)OÈÅ,]#ÓTÅ Å œ#ótîºé9 ÇÈé9ÇÄ OO)U é{åœ OÈéVî)S¹ ÓVé{ Ç OØ+ÇÈÒ Æ î6ótéòs ÓVÒ QPÒ œ é9œo B IU Å ÇÕîºé9ÇÈÆ ØO Å ÇÕœ ÒO PNUÊÇDÅ ÓV Ø ØÊ ê Ø Å O)UÒ ÆNXU+O)U éõï"évôioèògœ' é0o U Ò O O)Ué Åœ OÈéVî)S¹ ÓVé ÓVÒ œê é9î)xgé9ç9 G IU é ð#éu êå B ÒGî ÒS O)U é ÇÈÒ ØÆROÈÅÒ œ. Òé9ÇòœÒ O Å *PîÈÒ½êGé Å,S O U é OÈÅ é ÇOºéP.Å Ç é9óvîèék ÇÈé9 IU é P îºòpògçèé9 S¾ÆØ ØÊ Å QP ØÅ ÓTÅ,OÓVÒ ÆNP Øé9 OØ X Ò îºå,o)u OØØÒ½Ô Ç ÆÇ OÈÒYP#é9îVS¾ÒGîÈ S¾Æ ØØ ÇÈÓ9 OØéÇDÅ AÆ Ø &OºÅ ÒGœÇ*S¾Ò î -1 +Ž P îºòótékçèç9 G Å,X# Ï]Å ØØÆÇOºîº OÈéKÇQO)U éé9 OîºØÊ ÇO6 XGéwÒS-O U é ÇDÆ ð#çoºîº OÈé Å ÇÈÇÈÒ ØÆROÈÅÒ œ œto U éêå ÓTÅœ ÅO Ê Ò SÄØ Å Ë3Æ Å Lg½ÇÈÒ ØÅ oå œ OºéVî)S¹ ÓTé ÓVÒ œóvévœ OÈî6 &OºÅ ÒGœ Ò S ÓVÒ QP#ÒGœ évœ O XGîº G Æ Ø ØÊ ÅœÓVîÈéK ÇÈé9Ç+ G Å,X# 1Ͻð4/T 5 ko Å5ÆÇÈé9ÇÄÅœ OÈÒfO)U é'çèò ØÅ A #PNU# ÇÈé3P îºò ÆÓVÅ œnx wê é9îèêwo U Åœ]ðÒ Æœ OîºÊ Ø O U é Ǻ O é OÈÅ é{óvò QP#ÒGœ évœ O Ê évîäåœ#o U é B
280 ÎOìOÌ ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º J / L IFI=6F ý%j" F ý C Q / M B F S F FI=6F ý%j F ý C Q?80 Gý F KE IF,%& GF þ+ CJ B = "F ý F KEŸJVýòý C B^ CJ B ý JVE F ý F KEŸF E½ý B J9= B þ FIE - û ý C ½= B ÇDÒGØ Å PNU ÇÈé + IUÅÇ P îèòóvé9çºçé9ë3æ ÅØ Åð î6 &OÈéfO U éçèæ ðçvoèî6 &OÈéG O)U OŸÅ ÇQO Ô Ò ÓVÒ QP#ÒGœ évœ O Å œto)u é.ð ÆØ É5 % œ joºév OîºÊ Ø Å Ë3Æ Å ipnu# ÇÈé + G Å X %Ï ÓO %Ï / G Ò î*o)u é PNP ØÅÓ9 &OÈÅÒ œ Å,O ÅÇÅ *PÒ î)oº œ O!OºÒ é9 QPNU ÇÈÅ Vé LO U &OÕÅ *PØ Å ÓTÅ,O OØ X Ò îºå,o)u Òé9ÇÄœÒ OÄîÈéKËGÆÅ îºé œê. G Ö ÅOºÅ ÒGœ OØ ÆÇVOÈ é9œô Ò SòÅ œ Å,OÈÅ OØŒÓTÒG *PÒGÇÈÅ,OÈÅÒ œxò SòØ Å Ë3Æ Å Oœ xçèò ØÅ PNU GÇDéKÇ!S¾Ò îo U é ÓTÒ œêgévî X évœ#óté"òs Å,OÈé9îº OÈÅÒ œç9 IA G DKE()J 9MG D ï évô\œæ é9îèå ÓV Ø P îºòóvé9 ÆîÈéÕÅ Ç^P îºòpògçèé9 S¾ÒGî ÇVOÈÆ ÊÅœNXÍHÇÈéVØ,S Ö³ÓVÒ œçèå ÇOºéVœ O { &O)UéTÖ OÈÅ ÓV Ø Ò é9øò S PNU# ÇÈé Oºîº œçdå,oèåò œyp îºòóvé9çºçdékç"åœyoèév îèê OØØÒ½ÊÇ9 5 OÅ ÇÄð GÇDéK Ò œ ÓTÒ ÆP Ø ék ÇÈÒ ØÆROÈÅÒ œòs[x Ò½êGéV Å œx ékë3æ &OºÅ ÒGœÇ Ô Å,O)U îèékçvpé9ó0ooèòw OØØ_Æœ Éœ Ò½Ô œë3æ Oœ OÈÅ Ö OÈÅé9Ç9 3 œ S¾Æ ØØ Ê'Å QP ØÅÓVÅOIP îºòóvé9 ÆîÈéO)U é!oèå éçvoèépÿå ÇòÓU ÒGÇÈéVœ+S¾îºÒ u GÓVÓTÆîº GÓTÊÓTÒ œ#çdå Ö évî6 &OÈÅÒ œ#ç_ œ AÅ Ç œ Ò O Å Ó_O6 &OÈéK AðÊ ÇVOº ð Å ØÅ,O ÊA év { œ Ç9 K + îèå &OºÅ ÒGœ Ò S?OÈÅ éòçvoèépç S¾îÈÒG
281 «" I ¹ÀV Õ± { ¹À6¼O 6 3 ¾ª µt Ã5Ó I± U ¹Ó Dµ ª¼ V ȼO ² ¹ ½ È V V A Î ìgï J / F³ý F ý F KE* B FIE ý C B IF% GF þ3 C3J B /šþ F³ý F ý F 9EQ A FIÊ ý C B F%& 3F þ* CJ B = /šþ F³ý F Gý F 9EQ B FIÊ ý C B IF þ3 CJ B þ9/šþ F³ý F Gý F KEQ?80 > "F ý F KE þ F³ý F ý F KE'FIE'ý C B FI=6FIE3F ý B J ³ýDJ B Y ½= B L IFI=6F ý%j" FIý C Q A FIE ý C B "IF þq C3J B "IF þ IF,%& GF þ FIEOý B) J9= B JVý ý C B ÇÈé9ÓVÒ œ OÈÒ ÇÈé9ÓVÒ œ ˆ Òé9Ç œ ÒO ÅœRZÆ é9œótéòògœ O)UéòË3Æ Ø Å,O ÊÕÒ SO)U é ÇÈÒ ØÆROÈÅÒ œ1 ½ "ØÇÈÒ S¾Æ Ø ØÊ Å QP ØÅÓVÅOò OØ X ÒGîÈÅ,O)U Òé9Çœ ÒO%îºé9Ë3Æ ÅîÈé OœÊ3P îèé9ø 1 Å Å œ# OîºÊˆ ÆÇOº évœ O%Ò S5Åœ ÅOºÅ Ø &O6 Ç_ÅO ÆÇÈÆ OØØ Ê U PNPéVœÇ Å œ ÇDÅ AÆ Ø &OºÅ ÒGœÕÒ SNPNU# ÇÈéBOÈî6 OœÇÈÅ,OÈÅÒ œõåœa AÆØOºÅÓVÒ QP#ÒGœ évœ O ÇDÊÇVOÈéV {Ç aí9ð Í Í_c³ IU é6s¾ék ÇÈÅ ð ÅØÅO ÊxÒ SO)U éw é0o)uò ÅÇ ÓTÒGœR]îº é9 ðê œæ évîºåó9 OØŒÇOºÆ Ê Ò S ØÅ ËGÆÅ PNU ÇÈéÕéPÅO6 &`Ê'Ò S OÈé9îÈœ# OîºÊŸÓTÒG *PÒ Æœ Ç9 IU é ÇÈÅ ˆÆ Ø OÈÅÒ œçiu# Ç ðévé9œ. Ò œ é S¾ÒGî îèék OØ PNU ÇÈéÕ Å X î6 O r œ P îº GÓ_OºÅÓ9 OØØ Ê'Æ#ÇDéK XGîÈÒ½ÔIO UwÓVÒ œ Å,OÈÅÒ œ#çv " "F!"DK'" P -&> C½ý =ÈC B F ý J( M J6C J"J9E þ "! $# % ½@ C B'& B þ C L²E³ý FIý ý B ( IF Bþ) JVý C S B JTý FI=( B F E½ý 7T? ( = û ( 79>9>K:. FIE+* F JVE / 7 ÕL > " B J9E þ, - M C BQ C FI=J ½= B B ½=6= FIE þ F E IF%& 3F þ B F ýdj. F JL û ý C 0/ (76. P / ( :K8";?98 (#P R9:T? : ÕL ;(^<òb E3F (; M ; J6C J ( < J9E þ N (^ M F E J N ÕB FI=J þ B FIE = 9E B =ºý F KE'FIE û ý C 9þ F " Gý F KEf IF þ " Gý F 9E Cd xhg 1 xt e IF,%& GF þos CJ BòB FIýDJ=. &>/ / ( 7 89?;ˆ7VR P( 79>9>9?? ÕL (^=òb EGF ( - JVH B6B EGHd ( M A J6C J JVE þb < ;C D FE F G IH Cd xhg 1 xt e J 5@ C B0& B þ C LUE ³ý F ý Gý B '( IF BþK JTý C B JTý FI=( B FIE½ý < 8 ( = û (P R9R 7&. FIEK* F J9E /
282 C ÎOì ì ª ³À6ª ¹ V¼½Á û¼6ª È ¼½Á ± º 8 ÕL (^%òb EGF ( - JVH B6B EGHd ( M J6C J J9E þ < N ÕB FI=J ³ý þk IF%& 3F þe CJ B B F ýdj. "IF Cd xhg 1 xt þ e ý F KE %/ < 3 5 ( %. P / ( 7 P ; :K> ( 79>9> 7 < (^ I F ý F B J ( M J6C J( < ( B (^9@ F J JVE þ ( ( M C B E HOFIF C C 9 1D 7 % 7 J! ; JE J H 1 D 5 NòJ 3H9J( "= û (5P RA89<. F E * F J9E / : AM J9Hd ( M J 6C JJ9E þ < JVý C B JVý FI=J þgb IFIE òb B =ºý C B ý FI=Q B J JTý F 9EY GF F.Oý B J ýp E (. P >d/ (#P 8 P > ; P 8 7 P(P RKR 7& 8 AM J9Hd ( M J 6C JJ9E þ < JVý C B JVý FI=J þgb IFIE òb B =ºý C B ý FI=Q B J JTý F 9EY GF F.Oý B J ý 7 E (. P 7"/ ( 7 P 79R ;ˆ7 P :9: (P RKR 7& R & B ý =ÈC B _ JE G F F ( = û (5P R9R P. FIE+* F J9E / P > & F J (5M "³ý_( òþ 9E ( (^5@ JVEJVHKJ M 3H B J û J J9E þ FIE ( E S ÕB FI=JJ9EJ F ý C B = KE B F 9E C B E ÕB E 9E GaAs ý KE J GaAsP GaP ³ý JVý B FIE JVE\ B ³ý B Q / 1 G3 5 ( P / ( <KRA:Ÿ;,:9>9: ( P RKRK< P9P & F J ( < F E.J9E þ M "³ý +( IF þ ; IF%& 3F þwþ F ÿn F KE þ B û ý C JVE þ.þ F Gý F KE$ ý B E3J J - IF%& 3F þw C3J B B FIýDJ=. & / ( 1. P / ( 79: P ;ˆ7V?K> (P RKR9< P 7 "! $# B J9E þ&%' F Bþ FI=ÈC j> C3J B E B ˆFIE þgb IFIE IH.= ³ýDJ û ý C / ( ;??. P / (#P ; P R ( 7V>K>V? P : (^ (^ M J J H FIFJ9E þ B M NŒFIHd " J B C 4 DF+ E NŒJ 3H9J( = û (5P RA:8. FIE+* F J9E / P? (^ (^ MGJ J HOF FJVE þ < )( G " ' D +* $ NŒJ GHKJ ( = û (5P R9R 7&. FIE+* F JVE / P 8 (^ (^ M J J HOFIF#J9E þ < N ; J3FC3=DC B FI=DC,G.- C D %10 /. F B M KE(#P RKR 8& P < * Gþ J9E3JVý C MOýDJTý ý B =DC3E " "9F B û ý C+. Rd/ (P 7A:98 ; P (#P R9R 8 T e ;' FI=DC J9E þ <! Hg ;' FI=DC IF%& 3F þ C3J B{B F ýdj. F J (Hg, Cd)T e J / 1 /3 $ J C ( :9 <; ;[;=7?> 69 <; ;@>BA DCE>9; FG>1H)I ;'J 8+;15 C 7 K&:L>M <; 6> Cf;B:L> 6>B797NCEO J 7N;B;P?7R;QA 4?: <;?7R; R> C½ý =DC B F ý J( M J6C J( JFSR ýdj EJÜT³JeJVF9ý FIE3F VHOF ý V ÕB ý þ J JXW B B E B:Y F þ J KF JVHd 9E B E1Z6F S " B Gþ FIE3F " B H9J9F ý FIE3F J B E þ FIEGF GF J³ý F B( F ý J J VF ³ýDJ FIEJVF H" KE B)S JVý F[\TJjJVFVý FIE3F VH F ý V =ÈC B JxF F B EJ JVFIH F ghd 9E3= B E½ý JV=6F T " JFHOF ³ý J F B:] W F HOF B ý ^T B F H ³ý ^T B3 J XW B B ( H9J9F F \[ Z6F J F \Y FÜT B" M H9J9F ý FIE3F ÕB ý þ J JQ B \[ 9F Y HKJVFB³ýDJ3F % F J 9F E½ýDJ! HOFIýDJVF! B E þ J9FF J9F ÕB ý þ J9F( H F B E S B H IF JVF5J F \_:] F JÄH" KE3= B E½ý J9=6F T JFHOF ³ý [ F \[ Z6F J F \Y F J J þ B W ý F V
283 !"# $ % '&)($ +*,.-/10 3 -/546 "798 :6; 7=<=8 > 7=?=?=@BAC >ED3FHGJILK"MN3NPORQ6SLT 7VUW8 7 T 7 XZY\[^]`_aXZYb[bcedfYhgiX jlk)_agmgnc5oqp jsrztuy\[v_aw rxgxj^t co ymyhy^_rw y^wh_bz{z XZYhdf]}c5ò _bz ~ ƒ ƒ E 5 #ˆ ˆ + Š Œ Ž". P # { B# B " šœ ž JŸ# ž 6 ž žÿ «ª 6 6 Ÿ# P ±Ÿ ž² V³6 ž µ P ¹ ºV» º9¼½¾ WÀ H Š ÂÁ6 =Ã3Ä ÄPÅBÆ ½ ½ Ç= Š ½È» É # P ½ Á ÊË ½ ÌÍ ÎÏœÐ'Ñ3ÑÒÐ ÓÔ Õ#Ö3 HØ Ñ"ÙÚÛHÜ ÙÞÝ Û ~ º=ß9º9½à º «¾ àhº Êâá º=ãÂä ÄPÃHà äåã º9à½ Ç º {æ º=ß9º ÊBá º9ã ç ÄPÃHà ä 1 è'éëê9ì=í îïpì ð M F"ñ D3GJò5óëô9õ I ö= K9ñ D C K9ñ GJ>K9ø ôpù C øjòàô9úó C ñ1û õ C òògjf3ü ô9úûk9û C õœk9õ C òýñ þ3ùhg C ù ÿ þ õâü=ô K9øÀGÈò%ñ ô >6ôL û3k9õ C ñ ó±ô K9ñ D C K9ñ GJ>K=ø# ôpù C øjò6öó+dhgj>þd'kvõ C ù C C øjôlû C ù ú ô=õâògj þ3øèk U ñ GJô=F ô=ú 3øJñõEKVñ GJôLF û õ ô > C òò C òegèf ûk9û C õœûhõ C òòœ K=>ED3GJF C ò6ÿ eô=ñ D ôpù C øjò1ó C õ C ô ñek=gjf C ù"úõ ôl ñ D C ò K= C ü C F C õek=øà ôpù C øô9ú1ñ D C >6ôL û õ C òòg 3ø C ûô=õ ôlþhòâ C ù GJþ3 ö 3þ ñ ù G C õ C F ñ K9òòþ3 û U ñ GJô=F3ò ó C õ C þ3ò C ù ÿ ôpùhg C ù. ôpù C øjò K9õ C ù C LC øjôlû C ù«ñ D3K9ñù C ò> õ G C ókvñ C õ øjôlòò C ò K9ñ ñ D C ô=þ3f3ù3k9õ G C ò ô9úâñ D C ûô9õ ôlþ3ò øèk C õbk9fù ñ D C GJ ûô=õñek=fh> C ô9úâñ DHGÈò ú K=> ñ ô9õ GJò GÈF C òýñ GÈüLK9ñ C ù ÿ Oƒþ3 C õ GJ>K9ø±K9øJüLô=õ G ñ DH òkvõ C ù C C øjôlû C ù{ú ô9õògj þhøèk9ñ GJôLF ô9ú%ñ D C øjg þhg ù{ ô LC C F ñògjf.ñ D C ù C ú ô9õ K Hø C ûô=õ ô=þ3òe C ùhgèk ÿlmwñegjò±ûhõ ô C ùñ DK9ñœñ D C ù GÈò>Þõ C ñ C û õ ô Hø C GJò±òýñEK 3ø C GJú ñ D C ñ GJ C òýñ C û τ ò K9ñ GJò C òeñ D C GÈF C þk9øèg ñ τ Ch ÿlmwñ1ú ô=øjøèôó+ò±ú õ ôl añ D C òýñek 3GJøJGJñ K9FK=ø ògjòeñ D3K9ñ1ñ D C KVñ D C KVñ GJ>K=øÀ ôpù C øœù C ò> õ G C ò"k9f«gjøjø U ûô=ò C ù{û õ ô 3ø C ú ô=õ"òô= C K9øJþ C òòô9úûkvõek= C ñ C õ ò þhò C ùâgjfògj þ3øèk9ñ GJôLFHò6ÿ "! # ûô=õ ô=þ3ò+ C ù G KPö ôpù C øjøjgjf3ühö3ù õ$ GJF3ü ô=ú1û3k=û C õö FHGJñ CÞU ôløjþ3 C K=øJüLô9õ GJñ DH ò %'&(*),+-/ ,) É º:9¾<;^¾ ='9 ½ ½ > ¾ ã ¾ Ç"ʻ޺=ãÞ½ P Ç ¾ß9ß ã Ç ½ Ë Êâá º=ã ¾ =+½ Ç» ãþ½ P ë?>/> ½ Á ß» ½ ¾ Ç ÇÞ ß6É Ç ãa@½ 7B ¾?=1;ƒ¾¾ m P C> > º=ã ±Ç ¾H½ %Ê ºLß6É P ½ß Ç9 À ½ED ½ ßV¾ ÊF> ¾ Ç ½»Þº Ê ¾ ½ /BHG Ç º9ºJI Ä "K ML "N3 e =à e ä<oqp ˆ ÊË»ÞÉ º ʻ޽ ß œê ¾ º Ç ã º º=à º ¾ > º = ¾ ã»þéº Ç ½ Ç ¾?= ÇE ß6É > ã ¾ßVº Ç Ç º Ç=3»Þɽ Ç ;¾ ã ¼ 3Ê ¾ º Ç ¾ =R;ºV» > ã º Ç Ç ½ 7B ¾?= ># Á > º=ã ãþº ½ à º Ç» ½ B3»Þº À3 ã B ¾ P ½ Ç» ¾âß9¾ ÊF> ã ºÒ»8;¾ ÊË» É º ÊË» ½ß P #Ê ¾ º Ç= ;ÒÉ ½ß6É ;ƒº=ãþº º9àHº ¾ > º = ¾ ã Ç ½ ÊB»Þ½¾ ¾ =S»Þã» ½ ¾ T> ã ¾ßVº ÇÞÇ º Ç ½ T>?> º9ã > ãþº ÇÞǃÊË ß6É ½ º Ç= U ¾»ÞÉ Ê ¾ º Ç ;ƒº=ãþº¾ á» ½ º = ã ¾ Ê» É º ÇÞ Ê º B º º=ã Ê ¾ º ¾?=œ» É º ßV¾ ÊF> ãþº ÇÞÇ ½ á º > ¾HãÞ¾ ÇÂÊ º ½ Ê. á» ½WV5º9ã º» Ç ÇÞ ÊF>»Þ½¾ Ç ;º9ã º Ç º À» É º > > º=ã ¾?= Æ º» º XU º Ç»YI ä<oƒ½è» ½ Ç Ç ÇE Ê º»ÞÉ»:;»Þº9ã ½ Ç Ê ¾ འ7B ¾ º ½ Ê º Ç ½ ¾. ¾ 7B»ÞÉ ºZ= º» É º@'½ àhº ǻ޽ BH» º»ÞÉ º º9à º ¾ > Ê º» P 1 A DHGJò5óëô=õ I óëk=òàòþhû3ûô=õñ C ù < ñ D C\[ G ñ DPþK9F3GÈK=FNPñEKVñ C NP>6G C F3> C K=F3ùN ñ þùhg C ò"]3ôlþhfù3kvñ GJôLF ó+g ñ DHGÈFBñ D C úõek9 C óëô9õ IBô9úñ D C1^ þhõ C I=K"û õ ô_ C > ñ1` A `7ab` ^dce^fƒu 7=8L7 S ö ^ÀUý79?L?L7 ÿ? 7 ÿ 7=:
284 Ä?L ç V ž Ÿ PÊ ½ ß Ç ¾ =»ÞÉ º = Ç» ã»þ½¾ ¾ º Ç ½» É º > ¾ ã ¾ Ç Ê˻޺9ã ½ P º ¾P» ºË»ÞÉ» ¾ 9¾<; á ¾ ãa@{ßv¾ # ½È» ½ ¾ ÇÒ ß9ãÞ¾ ÇÞÇ» É º > ¾HãÞ¾ º Ç º 1» É º >?> º9ã¾?= ½» º I <O GWÇ º=º Ç ¾eI =à O Pâ»8;¾ ½ED ½ > É HÇ º Ç ãþº» ¼ º ½»Þ¾ ß9ß9¾» ½ º» É º ½ã > É HÇ º ½ Ç' H º» ¾m»ÞÉ º Ê ¾ º ¾»Þã I ä<o"½» ½ Ç Ç ÇÞ Ê º» É»»Þɺ«àHº ¾ßV½»8@n¾ ="» É ºT;» º9ã P ¾ 7B»ÞÉ º = º»'ßV¾H½ ßV½ º Ç ;Ò½»ÞÉ» É º Ç ¾ ½ Y> É Ç ºàHº ¾ßV½»8@ P»ÞÉ º Ê ¾ à º Ê º»ƒ¾ =R;»Þº=ã ßVã ¾ Ç Ç»ÞÉ º > ¾ ã ¾ ÇÂÊË» º9ã ½ ½ Ç ½ à º Ç» ½ B3» º ÀP É º"º V5º=ß»ƒ¾?= ÇÞ» ã» ½ ¾ ½ Ç+ º B º=ßV»Þº ½ I <O»ÞÉ º=ãÞº= ¾ ã ºƒ» É º > ã º Ç ÇÞ ãþº ºD» ½ ¾ ½ ÇÒÇ ½ ÊF> ½WS#º.Ç º=ãÞ½¾ º=ßV»Þ½¾ Ä ;ƒº= ¾ ã ÊB» º B º º=ã "Ê ¾ º ¾?=» É ºnß9¾ ÊF> ã º Ç Ç ½ á º > ¾ ã ¾ Ç Ê º ½ Ê.1 à ¾»Þ½¾ ÇÞ» ã» º ¾ º Ç ½ Ç ½ à º Ç» ½ B3» º ½ º=ßV»Þ½¾ Å º > ãþ¾ > ¾ Ç º 'Ê ¾ ½S#߻޽¾ ¾ =±» É º Ê ¾ º W ;ÒÉ ½ß6É ; Ç Ç º ½ I ä<o P ½ à º Ç» ½ B3»Þº»ÞÉ º½ Ê ># ß» ¾ =,;»Þº=ã ¾ Ç Ç º ǻ޾{»ÞÉ Ê ½ß Ç ¾?=+» É º ÇÞ» ã» ½ ¾! ¾ º Ç=À»ÞÉ ã º9º > É Ç º Ê ¾ º ¾ = F>#?> º9ã > ã º Ç Ç ÊË ß6É ½ º ½ Ç ½ àhº ǻ޽ BH»Þº ½ º=ß» ½ ¾ ä É º Ê ½ B ¾ ¾?=ë» É ½ ÇÇ º=ß» ½ ¾ ½ ǻ޾«ßV¾ #Ç» ã ßV» ' ½ Ç ß9ãÞº9»Þº >7> ã ¾#"½ ÊË» ½ ¾ ¾?=ë»ÞÉ º ǻ޺ Ê ¾ = $%æ" a»þ¾ë½ àhº ǻ޽ BH»Þº»ÞÉ º Ç» á ½ ½»8@'¾?=±»ÞÉ º ¾ á» ½ º S ½»Þº Á à ¾ Ê º Ç ß6É º Ê º %1&'&)(+*d),*-.-/10. 0,*/Z. +43,*65C.798-4*:;:6=<>/=*@?. -7. A:!0B*R06 A7 ßV¾ àhº»þ½¾ # P <> > º=ã ÊË ß6É ½ º > ¾HãÞ¾ º=ã GQ> > º=ãR;º á PÀ½ Ç ßV¾ Ê > ãþº ÇÞÇ º º9½»Þɺ9ã á º9»8;ƒº=º»8;ƒ¾.ã ¾P»»Þ½ 7B ã ¾ Ç ¾Hã á º9»8;ƒº=º ãþ¾»»þ½ 7B ãþ¾ + m S4"º mçe ã = ßVº G > ãþº ÇÞÇ ½ 7B{Ç É ¾º P 5 ɺ > ¾ ã ¾ Ç3> ãe» S º ;ҽȻ É 9 ½ À1 É º Ê ½C"» ãþº»þé º=¾ Ç Ç º»Þ¾ º Ç ßVã ½ á º»ÞÉ º 9¾<;x¾ =M9 ½ Ç ½ ' º = ¾Hã ÊË Pá º > ¾ ã ¾ ÇëÊ˻޺9ã ½ P Ç9»ÞÉ ½ ÇeÇ º=ßV»Þ½¾ ;º > ã º Ç º» B º º=ã?B ¾ àhº9ã ½ 7B ºD» ½ ¾ Ç= ;ÒÉ ½ ß6É ã º Ç º» ¾ Ç ½ Êâ»Þº»ÞÉ º > ãþ¾ß9º Ç Ç º Ç ½ J>#?> º9ã > ãþº ÇÞÇ%Ê ß6É ½ º Ç=3 ¾¾ ½» ãþ¾ ßV»Þ½¾ Ç ½» ¾ ÊË»Þɺ ÊË» ½ß P Ê ¾ º ÇÒ º Ç ßVã ½ á ½ 7BË 7B ¾ = > > º=ã ã º B ½ àhº ½ I 1 ä<o Š ºV» #Ç ßV¾ Ç ½ º=ã Ç PÊF> º ¾?= à ¾ Ê º º º Ê º» V ¾?= mê ½C"» ãþº½ > ¾ ã ¾ 1» ß9¾ Ç ½ Ç»B¾ =Ò»ÞÉ ã º9º > É Ç º Ç=Ì 9 ½ ½ã > É Ç º Ç ½ ºD"º f P a P { âç ¾ ½ > É HÇ º ;ÒÉ ½ ß6É{ß9¾ Ç ½ Ç» Ç ¾ =S á ã ¾ #ÇƒÇ ¾ ½ Ê˻޺=ãÞ½ P 5 P # ½ Ç ½ º"º s "Ç" Ç ;ƒº HÇÞÇÞ Ê º»Þɺ Ç ½ º ¾?=ë»ÞÉ ½ Ç àh¾ Ê º º º Ê º»"½ Ç ã B º ß9¾ ÊF> ãþº ;Ò½»ÞÉ»ÞÉ º Ç ½ º ¾?= > ¾ ã º Ç P # ÇÞÊ ßV¾ ÊF> ã º ;Ò½»ÞÉ»ÞÉ º Ç ½ ºâ¾ =»ÞÉ º º»Þ½ã º Ç» º Ê.E º º ¾»Þº»Þɺ àh¾ Ê º Ç ¾ß9ß /> ½ º ;» º9ã 5 ½ ã Ç ¾ ½ Ê˻޺=ãÞ½ P V f, V a P V s ã º ÇA> ºL߻޽à É º ²#P J Ë F6³Þ H V G Ÿ ¾?=eº ß6É.ßV¾ Ê > ¾ º»Ò½ Ç º S º Ì φ α = V α, α = f, a, s. V æ" º» ¾Ëà ¾ Ê º ßV¾ Ç º=ãÞà»Þ½¾» É º= ¾ ¾<;Ò½ 7B ß9¾ Ç»Þã ½» Ç É ¾ {á º Ç» ½ Ç Sº ÀÌ φ f + φ a + φ s = 1,»ÞÉ Ç ½»â½ ÇBÇÞ IH ßV½º»» ¾;Ò㠽Ȼ º»8;ƒ¾º D» ½ ¾ Ç = ¾ ã ºV» º9ã Ê ½»Þ½¾ ¾?=»8;¾ à ¾ Ê º = ã ߻޽¾ #Ç ¾?=œ» É º Ê ½C"» ãþº É º > ¾ ã ¾ Ç ½È»8@ φ ¾?=e»ÞÉ º > ¾ ã ¾ Ç Ê˻޺9ã ½ P ½ Ç" º S º φ = 1 φ s. G Ä P
285 !L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä?L î êlê ï±êhí îì ìœí ï±ê9ì ì5ì=ê "Ç ÇE Ê ½ 7B»ÞÉ»»ÞÉ º Ç ¾ ½ P # 9 ½ > É HÇ º Çë 㠺½»Þã ½ #Ç ½ ½ ßV¾ ÊF> ã º Ç Ç ½ á º G ½ º»ÞÉ º ½»Þã ½ Ç ½ ß º Ç ½È» ½ º Ç ¾ =À»ÞÉ º Ç ¾ ½ P ρ 9 ½ s ρ ã º"ßV¾ Ç» P» P ;º"¾ á» ½» É º f ¾ß ÀÊË Ç Ç ßV¾ #Ç º=ãÞà» ½ ¾ º D #»Þ½¾ #Ç ½»ÞÉ º % º=ãÞ½ P = ã PÊ º;¾ ã ¼ Ì φ α + (φ α v α ) = 0, α = s, f. t ½ ßVº»Þɺ ½ã½ Ç ßV¾ ÊF> ãþº ÇÞÇ ½ á º ½ED ½ À ;º B º9»Â» É º= ¾ ¾<;Ò½ 7B ºD»Þ½¾ 1Ì GWÄ Ä P ( ) φa ρ a + (φa ρ a v a ) = 0. t ã º»Þ½ 7B» É º ½ã HÇ P ½ º P 'BH HÇ9 ;º⾠Ỡ½»ÞÉ ººD»Þ½¾ ¾?= Ç»»Þº= ¾ ã»þéº B3 Ç > É Ç º Ì ρ a = 1 C p p a, É #Ç»ÞÉ º ÊË Ç Ç ßV¾ Ç º9ã à»þ½¾ ºD» ½ ¾ ¾ =œ» É º ½ã > É HÇ º ½ Ç B ½à º ( ) G Ä Å φa p a + (φa p a v a ) = 0. P t ¾ Ç ½ º9ã ½ 7B»ÞÉ º ÇE ¾<; 9¾<;vã º B ½ Ê º P ½ BH ¾ ã ½ /B»ÞÉ º ;º ¼ ½ Ê º º > º # º» º V5º=ß» Ç9 ;ƒº ¾ á» ½»ÞÉ º ÊË Ç Ç á ßVº ºD»Þ½¾ Ç ½»ÞÉ º Ç»»Þ½¾ ãa@'ß Ç º { (φα v α ) = 0, α = s, f, (φ a p h v a ) = 0. G Ä ä*p!5ì éëî#"wî#eï$%&eî ì'±ê º ;Ò½ ¾P» ßV¾ #Ç ½ º9ã B º º9ã P #Ê ¾ Ê º» Êsá# P P ß9º ºD»Þ½¾ Ç=3 ¾Z= ¾ß #Ç ¾ 9¾<; Ç ½ > ¾ ã ¾ Ç Ê º ½» É º Ç ½ ÊF> ½W=Q@½ 7B Ç ÇÞ ÊF>»Þ½¾ Ç" ã º #Ç º À ¾ Ç ½ º=ãÞ½ 7B»ÞÉ º ÇE ¾<; ½ D ½ 9¾<; «Ç ÇE Ê ½ 7B»ÞÉ» º" ßVº Ç Ç ½» º9ã ß» ½ ¾ = ¾Hã ß9º Çƒá º9»8;ƒº=º»ÞÉ º Ç ¾ ½ «P ½ D ½ ǃ ãþº > ãþ¾ > ¾HãE» ½ ¾ P»Þ¾» É º"àHº ¾ßV½»8@ ½WV5º9ã º ß9º Ç v α v s, α = a, f, ;º;Ò㠽Ȼ º»ÞÉ º B º º=ã Ê ¾ Ê º» Ê á P P ß9º ºD» ½ ¾ Ç ÇZGWÇ º=ºJI OQP Ì φ α (v α v s ) = K α GWÄ K p a, α = a, f, P µ α ;ÒÉ º9ã º µ ã º» É ºâà½ Ç ß9¾ Ç ½È»8@ ß9¾3º H ßV½º» Ç P α K ãþº»þé º > º=ã Ê º Pá ½ ½»8@.»Þº Ç ¾ ã Ç9 α D» ½ ¾ ÇTG ÄK P 㠺˻ÞÉ º»ÞÉ ã º9º( > É Ç ºJ9¾<; æ ã ß@ ; = ¾ ãb»þé º.ß HÇ º ¾?= Ê ¾ འ7B > ¾HãÞ¾ ÇÂÊ º ½ Ê. É º > º9ã Ê º á ½ ½»8@'ßV¾º H ßV½º» Ç K α = K α (φ, S) º > º ¾» É º > ¾HãÞ¾ Ç ½»8@ φ ¾?=»ÞÉ º > ¾ ã ¾ ÇÂÊË» º9ã ½ 1 P»Þɺ ÇÞ» ã» ½ ¾ S ¾?=\;»Þº=ã ;ÒÉ º=ãÞº S ½ Ç º S º S = φ f φ. æ ½Vº=ãÞº» Ê ¾ º ÇÒ ãþº Ç º» ¾ º Ç ßVã ½ á º»ÞÉ º > º9ã Ê º Pá ½ ½È»8@'¾ =1»Þɺ > ¾ ã ¾ #ÇƒÊ º ½ Ê G Ç º9º I ƒ ä<oqp P #»ÞÉ º@ B º º=ã ½ º» É º ;º 3¼ ¾<; ¾  ã Ê º D #»Þ½¾ I Å O
286 Ä N à V ž Ÿ PŸ ìhí ±î#" í ï ê É ºËãÞ¾ Ç ºD"º=ãE» ã B º = ¾ ã6ßvº Ç ¾»Þɺ ½ D ½ n mç ¾ ½ C> É HÇ º Ç9œ ɺ Ç º= ¾Hã ß9º Ç ãþº» ¼Hº ½» ¾ ß=ßV¾» Ç ½ /B»ÞÉ ºÂß Ç Ç ½ ß P º=ã L?B ɽ > ã ½ ß9½ ># P HÇœ ½ Ç ß Ç Ç º ½ I ä<o» ½ Ç ¾P» º ½ I <O»ÞÉ»3= ¾Hãɽ B ÊF> ã º Ç Ç ½ á º > ¾ ã ¾ Ç ÊË» º9ã ½ Ç»ÞÉ º º9ã = B É ½ > ãþ½ ß9½ > ¾P» á º >7> ½ß Pá º P ½ #Ç» º ¾?=±½È» Ê ¾ ã º B º º=ã = ¾Hã Ê Ç É ¾ á º Ç º 1 ¾«ßV¾ º=ßV»"»Þɺ º9ã = B É ½ > ãþ½ ß9½ > ;Ò½»ÞÉ»ÞÉ º ¾P» É º9ãºD»Þ½¾ Ç ¾?=%»ÞÉ º Ê ¾ º ¾?= ÊB»Þ½ > É HÇ º 9¾<;\½» É º º = ¾Hã ÊË á º > ¾ ã ¾ Ç Ê º ½ Ê«½È»"½ Ç ºLßVº Ç Ç ÇA> ºLß Á ½W=Q@ «Ê ¾ º = ¾Hã»ÞÉ º º = ¾ ã ÊË» ½ ¾ ¾ =ƒ» É º > ¾ ã ¾ Ç ÊË» º9ã ½ WÀ Ê ¾ Ç» > > º=ã Ç» É º à3½ Ç ßV¾º ǻ޽ ß Ê ¾ º ½ Ç Ç º À» É ºF= ¾ ¾<;Ò½ 7B Ç º=ßV»Þ½¾ Ç ;º'ßV¾ Ç ½ º=ã»8;ƒ¾.ºD" Ê > º Ç ¾?= Ç ½ ÊF> ½Sº mê ¾ º Ç= ;ÒÉ ½ß6É ãþº¾ á» ½ º = ã ¾ Ê» É ½ Ç1B º º9ã P ºD»Þ½¾ Ç= 1&. / +76. ). / / -R ;*R0. ) *:»ë½ ÇÇ»» º ½ I ä<o» É»º9àH¾»Þ½¾ ¾?= Ç» ã»þº 1 ¾ ºÂß9ãÞ½»Þ½ º9»Þº9ã Ê ½ º Ç»ÞÉ º º V5º=ß» ½ àhº º ÇÞÇ ¾?=5»Þɺ 7B > ãþ¾ß9º Ç Ç9 ¾ ヺd" PÊF> º»ÞÉ º > ãþº ÇÞÇ = º» ǃ º9º»Þ¾ á º Ç» ã»þº ½ nç ¾ Ê º > ãe» ¾?=%»ÞÉ ºã ¾ ½ 7B ¾ º ½ ¾ ã º9ã»Þ¾ á º á ºB» ¾{» ¼Hº 7> Ç ½ B ½S#ß P» PÊ ¾»Ò¾?= ;»Þº=ã1= ãþ¾ Ê»ÞÉ º >#?> º9ã É º Ê»ÞÉ º Ê˻޽ ß Ê ¾ º ½ Ç º9àHº ¾ > º ½ I ä<o ;ÒÉ ½ß6É ½ Çëá Ç º ¾»8;ƒ¾ > É Ç º 9¾<; º D» ½ ¾ Ç ½ ¾ º ½ Ê º Ç ½ ¾ 11»B½ Ç Ç º» ¾ > ã º ½ ß»» É º'º9àH¾»Þ½¾ ¾ ÇÞ» ã» º ãþº B ½¾ Ç P #» ¾ º Ç» ½ Ê˻޺»Þɺ Ç ½ º Ç ¾?=œ» É º Ç» ã»þ½¾ ãþº B ½¾ I ä?o º ¾P» º+» É» ¾9¾<; á ¾ # ßV¾ # ½È» ½ ¾ DZ ã º Ç º = ¾Hãd9 ½ > É HÇ ºÂ½»ÞÉ ½ Ç Ê ¾ º WH ã B ¾ ½ Ç» ¾ B º º=ã ½ ºƒ»Þɺ Ê ¾ º ½ ¾ ã º=ãe» ¾ ½ ß # º ;»Þº=ã ¾ Ç Ç º Çë P»Þ¾ ßV¾ Ç ½ º=ã»ÞÉ Ê ½ ß Ç ¾ =ƒ» É º ÇÞ» ã» ½ ¾ º9ã à ãþ½¾ Ç Ç ßVº ã ½ ¾ Ç ¾ =b;» º9ã ¾ ÇÞÇ º Ç= ð#ð #í " îì Òì' $ "»ë½ Çë Ç ÇE Ê º» É» 3> ¾HãÞ¾ ÇëÊ ¾ འ7B ½»Þɺ > ¾ Ç ½»Þ½à º x ½ ã º=ßV»Þ½¾ 1 É ºb= ¾ Á ¾<;Ò½ 7B á HÇ ½ ß Ç ÇÞ ÊF>»Þ½¾ Ç% ã º Ç º»Þ¾ Ç ½ ÊF> ½=Q@»ÞÉ º ÊB»Þ½ ½ Ê º Ç ½ ¾ P ºD»Þ½¾ Ç ¾?= Ê HÇÞÇ ß9¾ Ç º9ã à»þ½¾ CGWÄ äp P {Ê ¾ Ê º» Ê á ßVº GWÄ K P Ì É º y ½ã º=ß» ½ ¾ XG = ¾ ¾<;Ò½ 7B» É º ãþ¾ 5 "º Ç P%½ Ç º B º=ßV»Þº {Ç ½ ß9º"» É º ãþ¾ ǃ ãþº 7>»Þ¾ 10 Ê ¾ 7B# É º;»Þº9ã19#¾<;R½» É º z ½ ã º=ßV»Þ½¾ ½ Ç º BH ºL߻޺ À É º ½ã > É Ç º ½ Ç º B º=ßV»Þº À ½ º ½È» ½ Ç Ç ÇÞ Ê º»ÞÉ» φ a = 0, p a = 0 î êlê ï±êhí îì ì º ß9¾ Ç ½ º9ã»ÞÉ º9#¾<;Rã º B ½ Ê º ½»Þɺ ãþº B ½¾ 1Ì D = { (x, z) : x a x x b, A(x) z B(x) }, ;ÒÉ º9ã º A(x), B(x) ã º» É º ¾<;ƒº=ã />7> º=ã á ¾ ã ½ º Ç ¾ ="» É º > ¾HãÞ¾ ãþº Ç > º=ßV»Þ½à ëš º9» d(x) = B(x) A(x) á º» É º» É ½ ß6¼ º Ç Ç ¾ =Ò»ÞÉ º > ¾HãÞ¾ º=ã
287 Ê!L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä N ½ ßVº ;ƒºßv¾ Ç ½ º=ã»Þɺ ÊË HÇÞÇ 9 É º x ½ã º=ß» ½ ¾ 1»ÞÉ º» ¼½ /B«{ÇEÊË P à ¾ Ê º [x, x + h] ;ƒº ß ;Òã ½»Þº»Þɺ ½ Ç ßVã ºV» º Ê HÇÞÇÂá ßVº º D #»Þ½¾ d φ f v f x+h + d φ f v f x = hj, ;ÒÉ º9ã º J º ǻ޽ ÊË» º Ç ;»Þº=ã ¾ ÇÞÇ º Ç» É ãþ¾ 7B Éâ»Þɺ ¾<;º9ã B />7> º=ã á ¾ ã ½ º Ç ¾?=» É º à ¾ Ê º º º Ê º» = ¾9¾<; á ¾ ãa@ ß9¾ ½È» ½ ¾ ÇÒ ã º HÇÞÇÞ Ê º 1»ÞÉ º J = 0 æ ½à½ ½ 7B{á ¾»ÞÉ Ç ½ º Ç ¾?=»Þɺ⺠D #»Þ½¾ h P» ¼½ 7B» É º ½ Ê ½» h 0 ;º ¾ á» ½» É º ¾ º Áý ½ Ê º #Ç ½¾ 5Ê HÇÞÇ ß9¾ Ç º9ã à» ½ ¾ ºD»Þ½¾ 1Ì ( ) GWÅ d φ f v f = J. P º ¾»Þº»ÞÉ» J = 0 ½ Ç» ¼Hº ½ I ä<o v ½Vº=ãÞº» ÊË HÇÞÇÒá# P P ß9º ºD» ½ ¾ ß P.á º ¾ á» ½ º ½=?> ãþ½¾ ã ½ Ç ÇE Ê >»Þ½¾ Ç ã ºâß6É 7B º À ¾ ãºd" PÊF> º ºV» Ç ßV¾ #Ç ½ º9ã ß Ç º ;ÒÉ º»ÞÉ º º=ã޽໠½ àhºb¾?=» É º 9 "{½»ÞÉ º x ½ ã º=ßV»Þ½¾ ¾º Ç ¾P» º > º ¾»Þɺ ãþº Ê ½ ½ 7B ß9¾3¾Hã ½»Þº z É º ½»Þº B ã» ½ 7B»Þɺ Ç»»Þ½¾ # Ê HÇÞÇ ß9¾ Ç º9ã à» ½ ¾ ºD»Þ½¾ GWÄ äp%½»þé º ã º B ½ ¾ ;ƒº B º9» É º»Þº=ã Ê D = { (x, z) : x 1 x x, x = x 1 + h, A(x) z B(x) } x B(x) x 1 A(x) x x ( ) φf v f dz dx + J 1 = 1 h x x 1 x 1 ( φf v zf ) B(x) A(x) dx = 0. ( φf v zf ) B(x) A(x) dx º S º Ç ;» º9ã ¾ Ç Ç º Ç G ¾ ã ½ ßVã º Ê º» P»ÞÉ ã ¾ /B É»ÞÉ º ¾<;ƒº=ã P n 7>7> º9ã ÇE ãa= ß9º Ç ¾ =»ÞÉ º S ½»Þº Á àh¾ Ê º Ž"Ç ½ 7B» É º Ç ÇE Ê >»Þ½¾ YB ½ àhº { á ¾ àhº ½»Þº B ã»þ½ 7B» É º Sã Ç» ½»Þº B ã P > ãe» Ç ;ƒº B ºV» ½ Ç ßVã ºV» º Ê HÇÞÇ ß9¾ Ç º9ã à» ½ ¾ ºD»Þ½¾ e ¼3½ 7B»Þɺ ½ Ê ½È» {îí ï "Wî (d φ f v f ) x + (d φ f v f ) x x1 + x 1 d φ f v f dx = hj 1. h 0 B ½ àhº Ç»ÞÉ º ½WV5º9ã º»Þ½ P œê HÇÞÇ ß9¾ Ç º9ã à»þ½¾ ºD»Þ½¾ ( d φ f v f ) + d φ f v f = J 1. ˆ ¾ Ê º» Ê á ßVººD»Þ½¾ GWÄ K P á ºLßV¾ Ê º Ç ;ÒÉ º9ã º P v f, v s º» φ f (v f v s ) = K f µ f dp f dx, K f (φ, S) ãþº ãþº P à º = ß» ½ ¾ Ç º > º ½ 7B ¾»ÞÉ º GWÅ Ä P x ã BH Á
288 Ä NPÄ V ž Ÿ PŸ áç»þ½»» ½ /BG Å Ä P½»Þ¾ ÊË Ç Ç ßV¾ Ç º=ãÞà»Þ½¾ º D» ½ ¾ GWÅ P,;º ¾ á» ½ «ßV¾ Á à º=ßV»Þ½¾ ½WV Ç ½ ¾ ºD» ½ ¾ = ¾Hã ¼ ¾<; p f (x) ( d K ) f p ( ) f + d φf v s = J. µ f º ¾»Þº»ÞÉ» ½ I ä<o = ß» ¾ ã d ½ Ç ¾ Ê ½È»Þ»Þº ½» É º Sã Ç»»Þº9ã Ê ¾»Þɺ º =ž» Á É Ç ½ º ¾?=e»ÞÉ ½ Ç º D #»Þ½¾ œ É º ¾ á» ½ º º D» ½ ¾ { P Ç ¾ º > º Ç ¾ S Ò φ ½»Þ½¾ ßV¾ #Ç» ½È»»Þ½à º f ãþº»þ½¾ DZ ã º Ç º»Þ¾ ß ¾ Ç º+» É º ǻ޺ Ç ½ 7B»ÞÉ º ºS ½»Þ½¾ ¾?=» É º ÇÞ» ã» ½ ¾ ;ƒº ºD" > ã º Ç Ç Ç φ f φ f = S φ ã ¾ Ê ºD" > º9ã ½ Ê º» Ç ;ƒº¼ ¾<;^» É ºËã º»Þ½¾ á º9»8;ƒº=º ß > ½ > ãþº ÇÞÇÞ ã º p a p f P «Ç» ã»þ½¾ S GWÇ º=º º B I OQP p c = ¾ º ¾ á» ½ º» Ç > ½ ¾ ½ ¾ B ¾ ½ º ã ½ ¼ Å P U ¾ ¾ º ½ I = ¾ S = g(p c ). ã ß HÇ p a = 0»ÞÉ º=ãÞº= ¾ ã º;ƒº»ÞÉ º º=º ãþº»þ½¾ S = g(p f ) áç»þ½» ½ /B» É º ººD" ã º Ç Ç ½¾ Ç» ¾B» É º ßV¾ àhº=ß» ½ ½WV Ç º D #»Þ½¾ ºV»» É º ½Vº=ãÞº» ½ ºD»Þ½¾»Þɺ ¾<; p f (x) ;ƒº ( d K ( f φ, g(pf ) ) ) p ( ) f + d φ g(pf )v s = J. µ f GWÅ ãa@'ß9¾ ½È» ½ Ç ;ƒº=ãþº ºS ä<o Ç ¾<; Ç=Ì p f ( x b ) = g 1 (S 0 ), d K f p f µ x=xb = 0, f ;ÒÉ º9ã º x ½ Ç Ç ¾ Ê º ã B º Êâá º=ã ÀÇÞ ß6É» É» ¾«½ 9 º ß9ºâ¾ = b p ½ Ç ¾ áç º9ã à º À f ±ê9ì ì'eì'.í " îìeê x b ¾»Þɺ Ç ¾»Þ½¾ ½ ßVº ¾ ã B ¾ P ½ Ç» ¾â½ à º Ç» ½ B3»Þº"»ÞÉ º ½ 9 º ßVº¾?= ;»Þº=ã ¾ Ç Ç º Ç ¾» É º ÇÞ» ã» ½ PÊ ½ ß Ç= ;ƒº Ç º»ÞÉ º Ç PÊ º > ã Ê º9»Þã ½ º = ß» ½ ¾ g(p f ) HÇ ½ I ä<o 1 1 ( pf ) n + s, p f 0, g(p f ) = + 1 s a 1, p f > 0, ;ÒÉ º9ã º > ã PÊ º9»Þº9ã Ç s, a, n ;º9ã º Ç º ºL߻޺»Þ¾ S»{»ÞÉ ººD" > º=ãÞ½ Ê º» "» Â É º ¾ á» ½ º «ÇÞ» ã» ½ ¾ > ã º Ç ÇÞ ãþº3= ßV»Þ½¾ g(p f ) ½ ÇÒÇ É ¾<; ½ ½ BÀ ßV¾ #Ç» ½È»»Þ½à ºÒã º» ½ ¾ = ¾Hã K ½ Ç f ºD" > ã º Ç Ç º Ç ¾ ½ º ã\= ßV»Þ½¾ ¾ = > ¾ ã ¾ Á Ç ½»8@ P # «Ç» ã»þ½¾ CG Ç º9ºFI ä<oqp Ì K f (φ, S) = k 0 φ 3 1 φ S3.4, GWÅ ä*p
289 ;ÒÉ º9ã º!L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä N Å º ¾P» º» É»«½ I Là O Ç ½ Ê ½ ã á» ½V5º9ã º»{º" > ãþº ÇÞÇ ½ ¾ ; HÇ' Ç º»Þ¾ º Ç ßVã ½ á º»ÞÉ ½ ÇÒ ¾ ½ º ã1= ߻޽¾ k 0 ½ Ç»Þɺ > º=ã Ê º á ½ ½»8@J= ßV»Þ¾Hã K f (φ, S) = k 0 φ 3 (1 φ) S3.4.»ÞÉ º{ß Ç º'¾ =b= ÇÞ» ã» ½ ¾ ¾?= ;»Þº=ã bg Å K P ãþº ßVº» ¾» É ºY;Ò½ Ç º º Ê Á > ½ ã ½ ß P ¾  ã ÊË ºD»Þ½¾ 1 ;ÒÉ ½ ß6ÉnãÞº»Þº Ç > ¾ ã ¾ Ç ½È»8@ H> º9ã Ê º á ½ ½»8@ º9àHº9ãÞ»ÞÉ º º ÇÞÇ= ½ ¾ ã º9ã%»Þ¾ßV¾ ÊF> ãþº ¾ ãâã º ÇÞ» Ç ;Ò½»ÞÉCI ä<o ;ƒº É à º Ç º = ¾Hã Êâ G Å ä*pƒ½ P À 3 Ê º=ãÞ½ ß ºD" > º9ã ½ Ê º» Ç9 GWÅ K P S E [MPa] p [hpa] epsilon [%] K M K ±N K9ñ þ õek9ñ GJôLF ; òýñõek=gjf ú þhf3> ñ GJô=F#ÿ ; ûhõ C òòþ õ C úþ3f3>þñ GÈô=F s = 0.11, a = 1., n = ö? ÀûHõ C òò!" í'ì í î ì' í eê îì3íwî#" Š ºV» HÇÞÇÞ Ê º'» É»J;º{¼ ¾<;s» É º = ßV»Þ½¾ d(x) ;Òɽß6É º Ç ßVã ½ á º Ç» É ºÞÉ ½ ß6¼ º Ç Ç ¾?=+» É º > ¾ ã ¾ º=ã 5 P º9» á d º»ÞɺB» É ½ß6¼ º ÇÞÇ ¾ =+»ÞÉ º ß9¾ ÊF> ã º Ç Ç º > ¾ ã ¾ Ç É º à ¾ Ê º V (x) ¾?=» É ºâº º Ê º» ¾ = > ¾HãÞ¾ Ç ÊË» º9ã ½ ½ Ç > ãþ¾ > ¾HãE» ½ ¾ P»Þ¾ d(x) 5Š º9» º ¾»Þº V s (x) = Cd s (x)» É º à ¾ Ê º ¾ß9ß 7> É º Ç ¾ ½ > É HÇ º "Ç ÇE Ê ½ 7B»ÞÉ»» É º Ç ¾ ½ > É Ç º{½ Ç ¾P» º= ¾ ã Ê º º > ¾ ã º ÇA> ß9º{½ Ç ßV¾ ÊF> ã º Ç Ç º À ;º B ºV»» É º ºD ½»8@ æ ½à½ ½ 7B ½» d s (a) = d s (x). d 0 ãþº ã ã 7B ½ 7BÇ ¾ Ê º»Þº=ã ÊËÇ ;º ¾ á» ½» É º ºD»Þ½¾ = ãþ¾ Ê ;ÒÉ ½ ß6É{» É º > ¾ ã ¾ Ç ½È»8@ 1 φ 0 = ( 1 φ(x) ) d(x) d 0, φ(x) ß {á º ßV¾ Ê >»Þº φ(x) = 1 d 0 ( ) 1 φ0. d(x)
290 Ä N ä V ž Ÿ PŸ É º = ¾ ¾<;Ò½ 7B Ê ¾ º ; Ç > ã ¾ > ¾ Ç º ½ I ä<oò»þ¾ º9»Þº=ã Ê ½ º d(x) ½»ÞÉ º º Á = ¾ ã Ê º = º» ߻޽¾ d = d(x; d min ) ºD" > ã º Ç Ç º Ç» É ºÞÉ ½ ß6¼ º Ç Ç ¾?=»ÞÉ º > ¾ ã ¾ HÇ" = ߻޽¾ ¾?= x P» É º Ê ½ ½ Êâ Ê) ½ Ç» P ß9º á ºV»8;º9º»ÞÉ ºâãÞ¾ ±ÇE ãa= ß9º Ç Ì d min d 0, x x l (d min ) = R ( 1 d(x; d min ) = (d 0 d min ) R ), R + d min R x, x l (d min ) x x r (d min ).» É ºFSã Ç» ½»Þº9ã à P» É º > ¾HãÞ¾ Ç ÊË» º9ã ½ ½ Ç ßV¾ ÊF> ã º Ç Ç º À ½» É º Ç º=ßV¾ ¾ º ½È»= ¾ ¾<; Ç»ÞÉ º B º9¾ Ê =Ò»ÞÉ º{ãÞ¾ ƒçe ãa= ß9º ÇB»Þ½ ÂÇ»Þã º Ç Ç τ zz á ºLßV¾ Ê º Ç º9ã ¾» x = x r (d min ) # ɺ ¾ ½ º ã º à½ Æ ¾H½ B» ;\½ Ç Ç º»Þ¾'» ¼Hº ½» ¾ ß=ßV¾» à3½ Ç ßV¾º ǻ޽ ßV½»8@˾?=±»ÞÉ º= º» Ì τ zz (x) = E(x) + v s Λ d dx E(x), ;ÒÉ º9ã º Λ ½ Ç à½ Ç ß9¾3º HÇ» ½ßƒ» ½ Ê º ßV¾ Ç» P» P É º Ç» ãþº ÇÞÇ Ç»Þã ½ = ߻޽¾»Þ¾» FB ½à º ½ I ä?o Ì E(ɛ) = 35ɛ.3 [MPa]. É º ¾ á» ½ º = ßV»Þ½¾ ½ ÇÒÇ É ¾<; ½ ½ B1 V ¾ ã x > x r (d min )»ÞÉ º Ç»Þã ½ ɛ = ɛ(x; d min ) = 1 d(x; d min )/d ½ Ç Ê 0 ½ º = ã ¾ Ê E(x) ;ÒÉ ½ ß6É ÇÞ»Þ½ Ç S#º Ç»ÞÉ º ½ ½»Þ½ P à º > ã ¾ á º Ê É #Ç ;ƒº B ºV» Ì d dx E(x) = 1 v s Λ E(x), E ( x r (d min ) ) = E ( ) ɛ(x r ; d min ); d min. E ½ Ç S»E» º º9»Þº9ã Á GWÅ L P d(x; d min ) = d 0 ( 1 ɛ(x) ), x > xr (d min ). É º > ã PÊ º9»Þº9ã d ½ Ç ¾ á» ½ º = ã ¾ Ê»ÞÉ º º=ã L?B ɽºD» ½ ¾ 11 É ºJ= ¾Hã ß9º Ç min F f F ß {á º ßV¾ ÊF>»Þº. Ç s F f (d min ) = x r(d min) x l (d min) p f dx, F s (d min ) = x r(d min) x l (d min)»þé º=ãÞº= ¾ ã º ;º B º9»Â» É º ¾ ½ º ãòºd»þ½¾ = ¾ ã ( E(x; d min )+v s Λ d ) dx E(x; d min) dx, d min Ì x r(d min) x l (d min) ( p f + E(x; d min ) + v s Λ d ) dx E(x; d min) dx = F. GWÅ N P
291 !L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä N?K ð Àð Wê=ï í3ì î ì' ì' $ " Š ºV» #Ç ½»Þã ¾ ß9º» É º ½= ¾ ã Ê B ãþ½ ω h = { } x i : x i = x b + ih, i = 0, 1,..., N, x N = x b.»þé º,= ¾ ¾<;Ò½ 7B ;ƒº,;ò½ º ¾»Þº%»ÞÉ º ½ Ç ßVã ºV» º >7> ã ¾#"½ ÊË» ½ ¾ Ç ¾?=ß9¾»Þ½ ¾ #Ç = ß Á»Þ½¾ Çë Ç ½ 7B ÇÞ áç ßVã ½ >» h º B»Þɺ > ãþº ÇÞÇÞ ã º = ß» ½ ¾ p ;Ò½ á º?>7> ãþ¾#"½ ʻ޺ á º= ߻޽¾ p f,hi = p f,h (x i ) = p f,h (x i, d min ). É º É@ ãþ¾ Ç»»Þ½ ß > ãþº ÇÞÇÞ ã º= ß» ½ ¾ ½ Ç ºS º { HÇ = ¾ ¾<; Ç=Ì p h = Sp f + (1 S)p a. ì'3í îì' î#" í ì' #í ê"!%&±îì ð >7> ã ¾#"½ Ê˻޽ 7B ½»Þº B ã P Ç ½ G ÅN P º» ã > º ¾ ½ ã º S h (d min ) = n R i=n L+1 ;ƒº B º9»Ò»ÞÉ º ½ Ç ßVã ºV» º ¾ ½ º ã º D #»Þ½¾ p hi + p h,i 1 + E(ɛ hi ) + E(ɛ h,i 1 ) h ( ) + v s Λ E(ɛ h,nr ) E(ɛ h,nl ), S h (d min ) F = 0. É º ¾ á» ½ º ' ¾ ½ º ãâºd»þ½¾ ß P {á º Ç ¾ àhº ÊË ½ àhº B ¾ 㠽Ȼ É ÊËÇ9 ½ ßVº= ßV»Þ½¾ S ½ ÇÒÊ ¾ ¾»Þ¾ ½ß P ;ƒº Ç º»ÞÉ º á ½ Ç º=ßV»Þ½¾ «Ê º9»ÞÉ ¾»Þ¾FS h d min ì' " «êlï #í ê'" nì ±í 3êLêœí $%&±îì' æ" ã ½ 7B º ß6É á ½ Ç º=ßV»Þ½¾ ½»Þº=ã»Þ½¾ G ¾ ã V³ ½»Þº=ã»Þ½¾ Pd;º Ç É ¾ BÇ ¾ à º " ¾ ½ º ã > ãþ¾ á º Ê. ;Òɽß6É?>7> ã ¾#"½ Ê˻޺ Ç»ÞÉ º á ¾ ãa@mà P º > ã ¾ á º Ê = ¾ ãâ»þéº > ã º Ç ÇÞ ãþº = ß» ½ ¾ 1 Š ºV» Ç ½»Þã ¾ ß9º» É º= ¾ ¾<;Ò½ 7B ¾»» ½ ¾ ¾ =RS ½È» º ½Vº=ãÞº ßVº Ç9Ì δ p hi = p hi p h,i 1, δ + p hi = p h,i+1 p h,i. h h /B»ÞÉ ºHS ½»Þº Á à ¾ Ê º Ê º9»ÞÉ ¾ ;º?>7> ã ¾#"½ Ê˻޺.ºD»Þ½¾ G Å Å P P á ¾ ãa@ ßV¾ ½»Þ½¾ = ¾ ¾<;Ò½ 7B ß9¾ Ç º9ã à» ½ àhºrs ½È» º Á ½Vº=ãÞº ßVº Ç ß6É º Ê º G Ç º9º I L O P a i+ 1 (p h) δ + p hi + a i 1 (p h) δ p hi + w i g(p hi ) w i 1 g(p h,i 1 ) = J i h, p h0 = g 1 (S 0 ), a N 1 (p h) δ p hn = 0, ;ÒÉ º9ã º;ƒº Ç º ¾P»» ½ ¾
292 Ä N<L V ž Ÿ PŸ a i (p h ) = d(x i ) K ( f φhi, g(p hi ) ), w i = d(x i )φ hi v s. µ f ½ ßVº ;º ã ºƒ½»Þº9ã º ǻ޺ ½ Ê ¾ ¾»Þ¾ ¾ Ç >7> ã ¾#"½ ÊË» ½ ¾ Ç=» É º"ßV¾ à º=ßV»Þ½¾»Þº9ã Ê ½ Ç?>7> ã ¾#"½ 7> ;Ò½ # ½ /B = ¾ ã ÊB É º=ãÞº= ¾ ã º»Þɺ»Þ¾»» ã ß» ½ ¾ º9ã ã ¾ ã ¾ =»ÞÉ º ½ Ç ßVã ºV»Þ½ =»Þ½¾ ½ Ç =¾Hã º=ã O(h) H É º ß9ß ã ¾?=»Þɺ ¾ á» ½ º Ç ¾»Þ½¾ ½ Ç º Ç» ½ Ê˻޺ m. V³ GP³ Ç ½ 7B» É º ~Ò 7B º ã º É º ¾ ½ º ã ½ Ç ßVã ºV»Þº > ãþ¾ á º Ê ½ Ç ½ º ãþ½ º = ¾ ¾<;Ò½ 7B ½»Þº=ã»Þ½à º P Á B ¾ ã ½»ÞÉ Ê.Ì a i+ 1 (ps h ) δ +p s+1 hi + a i 1 (ps h ) δ p s+1 hi + w i g (p s hi )ps+1 hi w i 1 g (p s h,i 1 )ps+1 h,i 1 = w ig(p s hi ) + w i 1g(p s h,i 1 ) +w i g (p s hi )ps hi w i 1g (p s h,i 1 )ps h,i 1 J i h, p s+1 h0 = g 1 (S 0 ), a N 1 (ps h ) δ p s+1 hn = 0. ð ð œìlîì' ±î#" Hí 5ì=ê 3 Ê º=ãÞ½ ß ºD" Ê > º Ç ;º.» ¼Hº > ã Ê º9»Þº=ã ÇË ßV¾º H ß9½ º» Ç = ã ¾ Ê I ä<o É º ;»Þº9ãà½ Ç ß9¾ Ç ½È»8@ µ ; HÇÇ º9»»Þ¾ f $ Ç9P» É ºÒºD" > ã º Ç Ç ½¾ = ¾ ã» É ºÒã º»Þ½à º > º=ã Ê º á ½ ½»8@ K» É º = ß» ¾ ã f k ; Ç±Ç º9»œ»Þ¾ 0 k 0 = m É ºÂà½ Ç ßV¾º ǻ޽ ßë» ½ Ê º ßV¾ #Ç» P» Λ ; Ç Ç ºV»Â»Þ¾ s 3 É º > ã PÊ ºV» º9ã Ç ¾ = > > º=ã ÊË ß6É ½ º > ¾ ã ¾ ¼ º «HÇ d 0 =.5 mm, R = 100 cm, F = 70 kn/m, S 0 = 0.5, φ 0 = v=0.01 v=0.001 v= v= v=0.01 v=0.1 v=1 v= S S x [m] K x [m] M N K9ñ þhõekvñ GJôLF û õ ô 3ø C òëú ô=õ%ù G C õ C F ñòôløjgèù 0.01 v s 5. C øèô > GJñ G C ò 3K v s 0.01 ö ½ã Ç» = ¾ ¾<;Ò½ 7B Ç ½ Ç > ãþº Ç º» º ½ I ä<o ;º HÇÞÇÞ Ê º»ÞÉ» ¾ 9¾<; á ¾ Á ½»Þ½¾ Ç ã º à P ½ À ½ º J = 0 # ɺ ÇÞ» ã» ½ ¾ ¾ =';»Þº9ã > ãþ¾ S º Ç = ¾Hã Ç ¾ ½ > É Ç ºBàHº ¾ßV½»Þ½º Ç á ºV»8;º9º v s = P 0.1 m/s ã º Ç É ¾<; ½ ½ B#5Ä# À É º = ÀÇ» ã»þ½¾ S = 1 ¾ º ã ½ Ç º Ç ÇE IH ß9½ ã B º Ç ¾ ½ Y> É Ç º àhº ¾ß9½È»8@
293 !L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä N N ¾ ã ÇEÊË à º ¾ßV½»Þ½º Ç»Þɺ > ã º Ç ÇE ãþº > ãþ¾ S º Ç% ãþº"ß ¾ Ç º"»Þ¾B»ÞÉ º ßV¾ Ç» P» > ã º Ç ÇÞ ãþº GWÇ p º=º'ºD»Þ½¾ G Å Å P= ¾Hã f0 J = 0 P ÇEÊË v P P # ÇÞ» ã» ½ ¾ > ãþ¾ S º ÇB ãþº s à ÇÞÊ ¾¾»ÞÉ ã"ã º ÇÞ» Ç" ãþº ½WV5º9ã º»3= ãþ¾ Ê ã º ÇÞ» Ç > ãþº Ç º» º ½ I ä?o ;ÒÉ º9ã º ½» ½ Ç Ç»»Þº»ÞÉ» = ¾Hã ÇÞÊË P Ç ¾ ½ àhº ¾ß9½È» ½ º Ç»ÞÉ ºb;»Þº=ã Ê ¾» > ã ߻޽ ãþº ÊË ½ DZ ß6É 7B º»º ß6É > ¾ ½»ë¾ = > ¾ ã ¾ DZÊË» º9ã ½ P»ÞÉ º=ãÞº= ¾ 㠺»ÞÉ º Ç» ã»þ½¾ ½ ß9ãÞº Ç º Çë ã ¾ #»ÞÉ º ß9º»Þº=ãÒ¾?=±»ÞÉ º ã ¾ ½ 7B' ¾ º» x = 0 ãþº9º=ßv»þ½ 7B»ÞÉ º º=ßVã º HÇ º¾?=±»Þɺ > ¾HãÞ¾ Ç ½»8@ φ ½»ÞÉ º ãþ¾ ½ /B ¾ º e ß6É > ãþ¾ S º Ç ß ¾P» á º'¾ á» ½ º = ã ¾ Ê»ÞÉ º > ãþº Ç º»Þº Ê»ÞÉ º Ê˻޽ ß Ê ¾ º W +Ç ½ ßVº{»ÞÉ º > ã º Ç ÇÞ ãþº{ãþº ÊË ½ Ç P Ê ¾ Ç»ËßV¾ Ç» P»» É º9ã º = ¾HãÞº»ÞÉ º3;»Þº9ã PÊ ¾» Ç É ¾ á º"ã º ½ Ç»Þã ½ á»þº Ë ß9ß9¾ ã ½ /B» É º Ç» ã»þ½¾ > ã º Ç ÇÞ ãþº ºD» ½ ¾ 1 ã ÊË ½ B ¾ P ¾?=» É ½ ÇÇ º=ßV»Þ½¾ ½ ǻ޾½ ß º1;»Þº=ã ¾ ÇÞÇ º Ç ½» ¾"» É ºb= ¾ ã ÊB» ½ ¾ ¾?=Ò»Þɺ ÊË» É º ÊË» ½ß P ÂÊ ¾ º P» ¾ ßV¾ Ç ½ º=ã» É Ê ½ß Ç ¾ =Ò»ÞÉ º ÇÞ» ã» ½ ¾ º=ã à ã ½ ¾ Ç'Ç ßVº ã ½ ¾ Ç ¾?=Z;»Þº=ã ¾ Ç Ç º Ç9 º HÇÞÇÞ Ê º.»ÞÉ» ;» º9ã ¾ Ç Ç º Ç» ¼ º > ßVº Ê ¾ É º ßVº»Þº9ãÒ¾ =œ» É º ãþ¾ ½ 7B ¾ º GWÇ º=ºFI?O P { º Ç ßVã ½ á º ½È» HÇ J(x) = J 0 φ f (x)s(x)ɛ(x) J0 = 0 J0 = J0 = J0 = S x [m] M NHK9ñ þ õek9ñ GJôLF ûhõ ô 3ø C òú ô=õƒù G C õ C F ñ+òôløjgèù C øjô >6G ñ G C ò6ÿ º«É à º S4"º»ÞÉ º Ç ¾ ½ > É Ç º àhº ¾ß9½È»8@n» ¾ v = 1 m/s Ç ½ Êâ»Þº»Þɺ > ãþ¾ß9º Ç Ç = ¾ ã ½WV5º9ã º» à P º Ç ¾?= J É º ¾ á» ½ º.ÇÞ» ã» ½ ¾ T> ã ¾?S º Ç ã º Ç É ¾<; 0 ½ ½ B#%Å º Ç º9º»ÞÉ»J= ¾ ã ÇÞ IH ½»Þº Ç ½à º ;» º9ã ¾ Ç Ç º Ç» É º Ç» ã»þº ¾ º Ç ½ ÇÞ >7> º ã 5» ½ Ç ½»Þº=ãÞº Ç» ½ /B» ¾ ¾P» º»ÞÉ» á ¾» KPà > º9ã6ßVº» Ç ¾?=b;»Þº9ã ½ Ç» ¼Hº ¾ ã J 0 = »?B ã º9º Ç ;ƒº ;ҽȻ É ãþº ÇE» Ç > ãþº Ç º»Þº ½ I <O ;ÒÉ º9ã º = ȩçþ» ã» ½ ¾ ¾ =R;»Þº=ãÒ½ Ç ¾P»"ßV¾ Ç ½ º=ãÞº ½»ÞÉ º ÊË» É º Ê˻޽ ß P ÀÊ ¾ º W & 3 -.* *? 3,- : * 0. 0,*/.? -8 *-@?X-4*:;: 0B-'4.336 ) *»ÞÉ ½ Ç Ç ºLß» ½ ¾ ;ƒº ßV¾ Ç ½ º=ã»Þɺ ÊË» É º ÊË» ½ß P ±Ê ¾ º ;Òɽß6É; Ç> ã ¾ > ¾ Ç ½» º I O
294 Ä N ç V ž Ÿ PŸ ð#ð #í " îì Òì' $ " É º= ¾ ¾<;Ò½ 7B ÊË ½. HÇÞÇÞ ÊF>» ½ ¾ Ç ã º HÇÞÇÞ Ê º»Þ¾ á º à P ½ ÀÌ ½ Ê º º > º º»"º V5º=ßV» ÇÒ ãþº ÇÞÊ 1 ß {á º º BH ºLß» º À É º y ½ã º=ß» ½ ¾ XG = ¾ ¾<;Ò½ 7B» É º ãþ¾ 5 "º Ç P%½ Ç º B º=ßV»Þº {Ç ½ ß9º"» É º ãþ¾ ǃ ãþº 7>»Þ¾ 10 Ê ¾ 7B# É º19¾<; ¾ = á ¾P» É ½ D ½ Ç9 ½ º ;» º9ã â ½ ã ½ Ç\> ã ã Ç àhº9ã ÇÞ ½»ÞɺÒãÞº Ç» = ã Ê º ¾ =œ»þéº Ê» º»Þº=ãÞ½ 7B»ÞÉ º ½ >1# É ½ Ç Ê º P Ç» É» v x α = v x s, α = a, f. ºZ;Ò½ œ Ç º Ç ½ ÊF> º ¾»» ½ ¾ Ç ¾?=±à º ¾ßV½»Þ½º Ç c = v x s, v α = v z α, α = a, f, s.»þéº > ã º Ç Ç«Ç ºL߻޽¾ ¾?= e>?> º9ã ÊË ß6ɽ º ;» º9㫽 Ç.Ç D º9º º ¾».¾?=» É º >?> º9ãT;ƒº á ½»Þ¾»ÞÉ ºH= º»»ÞÉ Ç ;ºß9¾ Ç ½ º9ãË» É º9¾<; ½»ÞÉ ºH= ¾ ¾<;Ò½ 7B ã º B ½ ¾ D = D w D ;ÒÉ º9ã º f D w, D ã º»Þɺ > > º=ã ;ƒº á' P = º»ƒãÞº B ½¾ Ç= ã º ÇA> ºL߻޽à Ì f D f = { (x, z) : L x L, γ f(x) z 0 }, D w = { (x, z) : L x L, 0 z γ w(x) }. ½È» É»Þɺ Ç º Ç ÇÞ ÊF>»Þ½¾ Ç ;º B º9»d= ã ¾ Ê GWÄ äp GWÄ K P5»Þɺ = ¾ ¾<;Ò½ /B ÊË Ç Çœá ßVº ºD» ½ ¾ Ç c φ α x + ( ) φα v α = 0, α = s, f, z G ä P c ( ) ( ) φa p h + φa p h v a = 0, x z P»ÞÉ º Ê ¾ Ê º» Ê á P P ß9º ºD» ½ ¾ Ç φ α (v α v s ) = K α p h, α = a, f, µ α z p s z p φ s h z = φ aµ a ( ) φ f va v µ f ( ) s + vf v s. K a K f ÊÊ ½ 7B 7> º D» ½ ¾ Ç ¾?= G ä Ä P ;ƒº B ºV»Ò»ÞÉ» G ä Ä P ;ÒÉ º9ã º»ÞÉ º p T z = 0,» ¾P» > ã º Ç ÇE ã º½ Ç º S º. Ç p T = p a + p f + p s = p s + (1 φ s ) p h. Ž"Ç ½ 7B» É º B º º=ã ½ º º9ã =?B É ½ > ã ½ ßV½ > ºZ;ºZ;Ò㠽Ȼ º»ÞÉ º > ã º Ç ÇÞ ãþº á ßVº º D Á»Þ½¾ ½. = ¾ ã Ê
295 !L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä N p T (x) = p st (s) + f ( φ s (x, z) ) p h (x, z), ;ÒÉ º9ã º s = 1 φ s0 ½ Ç»ÞÉ º Ç» ã ½ â P p ½ Ç»ÞÉ º Ç»Þã ß» ã > ãþº ÇÞÇÞ ã º+½»ÞÉ º Pá#Ç º ßVº st φ ¾?= É*@ ã ¾ Ç»»Þ½ ß > s ãþº ÇÞÇÞ ã º» ½ ÇË ¾»Þ½ ßVº ½ I <O» É» > ¾ ã ¾ #Çʻ޺=ãÞ½ P ß P Ç É ¾<; É*@ ǻ޺=ãÞº Ç ½ ǃ ÇÞ V5º9ã > º9ã Ê º» º= ¾ ã ʻ޽¾ 1 É º ßVº»ÞÉ º Ç»Þã ß» ã P "> ã º Ç ÇE ã º"½ Ç > ã PÊ ºV» ãþ½ º HÇ s r, during compression, p st = p st0 1 r, r = s 0 G ä ä*p s εs m, during expansion, s 0 εs 0 ;ÒÉ º9ã º s ½ Ç» É º ÊË "½ Êâ Ê Ç»Þã ½ «ß6É ½º9à º ß9º9ãÞ» ½ > ¾H½» m»%ãþº ÊË ½ ǻ޾ B ºV»%»ÞÉ º º D» ½ ¾ = ¾ ã» É º Ç ¾ ½ > É Ç º à º ¾ßV½»8@ 3 ÊÊ v ½ 7B 7> P s» É ãþº=º ÊË Ç Ç ßV¾ #Ç º=ãÞà» ½ ¾ ºD»Þ½¾ ÇG ä P ;ƒº B º9»"»Þɺ Sã Ç» ¾ ã º=ã ½Vº=ãÞº»Þ½ P ºD» ½ ¾ = ¾Hã Ì v s ( ) φ ( a φf u f + φ a u a + v s = c p h z p h x + (u a + v s ) p ) h, z ;ÒÉ º9ã º u α = v α v s, α = f, a HŽ Ç ½ 7B» É º ã º» ½ ¾ G ä Å P» É º ÊË Ç Ç ß9¾ Ç º9ã à Á»Þ½¾ º D #»Þ½¾ = ¾ ãe»þé º Ç ¾ ½ > É HÇ º,;ƒºÂßV¾ àhº9ãþ»1»þéº x º=ãÞ½à»Þ½à º%¾?=»ÞɺƒÉ@ ã ¾ Ç»» ½ß > ãþº ÇÞÇÞ ã º ½»Þ¾» É º ¼ ¾<; x º=ãÞ½à»Þ½à º ¾ =œ»þ麻þ¾p» P > ãþº ÇÞÇÞ ã º Ì ( φ a 1+ φ s q ) v ( s p h z = φ a c p h f(φ s ) ;ÒÉ º9ã º p T (x) x G ä Å P φ ) s qu a ( ) G φf u f +φ a u a, ä K P z z q = p hf (φ s ) + p st(φ s ). f(φ s ) É º B ã ½º» ¾?=œ» É º É@ ãþ¾ Ç»» ½ß > ãþº ÇÞÇÞ ã º ½ ÇÒ Ç ÇÞ Ê º»Þ¾ á º ß9¾ Ç»»Ò½» É º = º» p h (x, z) = p h z γ f (x), (x, z) D G f, ä L P ;ÒÉ º9ã º p ½ Ç»ÞÉ º» ¾P» > ã º Ç ÇE ã º ã ¾ >{ ßVã ¾ Ç Ç»ÞÉ º= º» h ±îí î# ï 5ì' & ì ï ì' ±ê» É º ÇE ã = ßVº ¾?=±»ÞÉ º 7>/> º=ã ãþ¾ Γ w = { (x, z) : L x L, z = γ w(x) }, ;ƒº Ç ÇÞ Ê º» É» ¾ 9¾<; á ¾ ãa@ ß9¾ ½È» ½ ¾ ÇÒ ã º à ½» É º ¾<;º9ã ÇÞ ãa= ßVº v α = v s, α = a, f, (x, z) Γ w. G ä N P
296 Ä ç à V ž Ÿ PŸ Γ f = { (x, z) : L x L, z = γ f (x) }»ÞÉ ºÉ@ ãþ¾ Ç»»Þ½ ß > ã º Ç ÇÞ ãþº"½ ÇbB ½à º ' P»ÞÉ º3;»Þº=ã ' ½ã Ê ¾ àhº = ã ¾?=À» É º = º» Ì É º;ƒº á Y= º» ½»Þº9ãA= ß9º Γ wf p h (x, z) = p hf. Γ wf = { (x, z) : L x L, z = 0 } ½ Ç S."º À»Þɺ9ã º = ¾ ã º v s = 0, (x, z) Γ wf. É ºZ;»Þº=ã. ½ãb9¾<; ÇÒ ã º HÇÞÇÞ Ê º»Þ¾ á º ßV¾»Þ½ 3 ¾ Ç ¾» É º ½» º9ãA= ßVº Γ wf ð Àð Wê=ï í3ì î ì' ì' $ "»ÞÉ ½ Ç Ç ºL߻޽¾ ;ƒº > ãþº Ç º» S ½È» º3àH¾ Ê º Ç ß6É º Ê ºJ= ¾Hã Ç ¾ འ7B»ÞÉ º º Ç ßVã ½ á º Pá ¾ à º Ê»ÞÉ º Ê˻޽ ß ÀÊ ¾ º ¾ = > > º=ã > ã º Ç ÇƒÊË ß6É ½ º º º S º ½ Ç ßVã ºV»Þº Ê º Ç É º Ç ;ÒÉ ½ ß6É ã Ê ½ >»Þº»Þ¾»ÞÉ º Ê ¾ འ7B á ¾ ãa@'¾ =œ» É º Ç ¾ ½ T> É Ç º ɺ Ê º Ç É.½ x ½ Ê º Ç ½¾ ½ Ç1B ½ àhº ω τ = { x n : x n = x n 1 + τ n 1, n = 1,,..., N, x 0 = L, xn = L }. É º Ê º Ç Én½ z ½ãÞºL߻޽¾ ½ Ç P Ç ¾ ¾ Á ½W= ¾Hã Ê) ½» º > º # Ç ¾» É º > ¾ Ç ½»Þ½¾ ¾?= á ¾ ãþ½º Ç P Ì γ f γ w ;ÒÉ º9ã º ω h (x n ) = { z n j : z n j = z n j 1 + h n j 1, j = J/,..., J/ }, z J/ n = γn f, zn 0 = γn wf, zn J/ = γn w. º9ã º P ½» É º = ¾ ¾<;Ò½ 7B ;ƒº Ç º»ÞÉ º ¾»» ½ ¾ u n j = u(xn, z j ) = ¾Hã ½ Ç ß9ãÞº9»Þº = ß» ½ ¾ u Š ºV» Ç ÇÞ Ê º»ÞÉ»»ÞÉ º Ç ¾»Þ½¾ ½ Ç ¼ ¾<; = ¾ ã x = x n ½ º À ½ Ç ß9ãÞº9»Þº:= ß» ½ ¾ Ç φ n s, φn f, vn s, vn f, ã º B ½ àhº 1± É ºYS ½È» º3àH¾ Ê º ½ Ç ßVã ºV»Þ½ =»Þ½¾ ½ Çâ º S º º= ¾ ¾<;Ò½ /BâÊË zn ½ Ç» º >Ç ¾ =e» É º PȨB ¾HãÞ½»ÞÉ Ê É ºZ;º á ãþº B ½¾» É º ¾ º Ç» V 9³ â žÿ5 G Ÿ F ž Ë V Eω n+1 h t n+1 ãþº ºS º. HÇ z n+1 j = zj n + τ n vn sj c, j = 1,,..., J/. G ä ç*p» É º= º» ã º B ½¾ «P.»Â» É ºZ;º á = º» ½» º9ãA= ßVº» É º ¾ º ÇÒ ãþº ¾» Ê ¾ འ7BÌ z n+1 j = z 0 j, j = J/,,..., 0.
297 !L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä ç 9 V³Þ 9 Ë 6 B PŸ 9 9³² PẂ GPŸm 9 G Ÿ FDP³ J AF6³Þ 9 G Ÿ ½ ßVº B ãþ½ ¾ º ǃ ãþº Ê ¾ འ7B ;Ò½»ÞÉ'àHº ¾ß9½È»8@ v»þé º Ç ¾ ½ àh¾ Ê º = ã ß» ½ ¾ à º Ç s ã º B ½ àhº φ n+1 sj = φ n h n j + hn j 1 sj h n+1 j + h n+1, J/ < j < J/, j 1 G ä P φ n+1 s, J/ = φn s, J/ h n J/ h n+1, φ n+1 s,j/ = φn s,j/ J/ 9 V³Þ 9 Ë 6 B PŸ 9 9³² PẂ GPŸm 9 G Ÿ FDP³ % V³ F6³ 9Ẃ GPŸ h n J/ 1 h n+1. J/ 1 Ê º9ã ½ ß P %Ê º9»ÞÉ ¾ Ç = ¾ ã Ç ¾ འ7B º D #»Þ½¾ #Ç º Ç ßVã ½ á ½ /B» É ºJ9 ½ 9¾<; > ã ¾ á º ÊËÇ ½ Ê ¾ འ/B ßV¾¾ ã ½» º Ç» º Ê ã º > ã º Ç º»Þº ½ ÊË >#?> º9ã Ç9 Ç º9ºJI ä e P œ LÄ O º9ã º ;ƒº ;Ò½ É º ½ Ç ß9ãÞº9»Þ½ =» ½ ¾ Ê ºV» É ¾ À ;ÒÉ ½ ß6É ; ÇÂ Ç º ½ I L O ½ã Ç»1;ƒº ¾ á» ½» É º ½» º B ã P = ¾Hã Êâ»Þ½¾ ¾?=±»ÞÉ º ÊË Ç Ç á ßVº ºD»Þ½¾ c φ f x + ( ) φf v f = 0. z» º B ã»þ½ 7B ½» ½» É º º º Ê º» ¾ Ê º [z s (x), z f (x)] P # Ç ½ 7B»ÞÉ º º D # P ½È»8@ z f (x) d φ f (x, z) dz = dx z s(x) z f (x) z s(x) B ½à º Ç» É º ½» º B ã P ÀÊË HÇÞÇÂá ßVº ºD»Þ½¾ ;ÒÉ º9ã º φ f z dz + dz f (x) dx φ f (x, z f (x)) dz s(x) dx φ f (x, z s (x)), c d z f (x) φ f (x, z) dx + f f (x) f s (x) = 0, dx z s(x) G ä Là P f α (x) = [ ( v f x, zα (x) ) ( v s x, zα (x) )] ( φ f x, zα (x) ). e ¼3½ 7B º º Ê º» ¾ Ê º [z j 1 (x), z j+ 1 (x)] 7B» É º S ½»Þº Á à ¾ Ê º Ê º9»ÞÉ ¾ ;º >7> ã ¾#"½ ÊË» º» É º ½»Þº B ã P ºD»Þ½¾ CG ä =à P É º= ¾ ¾<;Ò½ 7B ßV¾ #Ç º=ãÞà» ½ àhº º" > ½ ßV½» S ½»Þº( ½V5º9ã º ß9º Ç ß6É º Ê º h n+1 φ n+1 j 1 fj h n φ n j 1 fj ( ) ( ) τ n + F w n j+, φ n f,j+1, φ n 1 fj F w n j, φ n fj, φ n 1 f,j 1 = 0, ;ÒÉ º9ã º»ÞÉ º Ê º9ã ½ ß P 9 ( ) " F w j+ 1, φ j+1, φ ½ Ç ºS º. HÇ = ¾ ¾<; Ç I L O Ì j F ( w j+ 1, φ j+1, φ j ) = 1 w j+ 1 (φ j+1 + φ j ) 1 w j+ 1 (φ j+1 φ j ), w n j+ 1 = v n f,j+ 1 v n s,j+, h n 1 j 1 = hn j + hn j 1.
298 Ä ç Ä V ž Ÿ PŸ ;ÒÉ º9ã º É º á ¾ ãa@ ß9¾ ½È» ½ ¾ ÇÒ ã º?>7> ã ¾#"½ Ê˻޺ h n+1 φ n+1 h n φ n J f, J J f, J τ n h n+1 J h n 1φn+1 f, J J 1φn f, J τ n F n J + F F ( ) w n J +, φ n 1 f, J +1, φn F n f, J J ( ) w n J, φ n, φ n 1 f, J f, J 1 = 0, ºS º Ç»ÞÉ º = ãþº=º ¾» *9¾<; P ¾ 3½ 9¾<; 9 " Ì F n J 0, if w n > 0, J = w n φ n, if w n 0. J f, J J É º ÇÞ» ã» ½ ¾ ¾?=\;»Þº=ãb= ã ߻޽¾.Ç É ¾. P ÇÂÇÞ»Þ½ Ç =Q@'»ÞÉ º ß9¾ ½»Þ½¾ #Ç = 0, 0 S n+1 fj 1, z j ω h (x n+1 ). É º9ã º = ¾HãÞº % =ž» º9ãJS # ½ /B φ n+1 = ã ¾ Ê»Þɺ ½ Ç ß9ãÞº9»Þº ÊË Ç Ç'á ßVº º D» ½ ¾ 1 % P f ãþ»þ½s#ßv½ P À ½ Ê ½»Þº=ãÒ½ Ç H >7> ½ º ÀÌ φ n+1 fj := ( ² J V =F ž³f6³ 9Ẃ GPŸ { φ n+1 fj, if 0 S n+1 fj 1, S n+1 fj φ n+1 j, otherwise. É º º; à P º Ç ¾ =e» É º ½ã1= ã ß» ½ ¾ «ãþº¾ á» ½ º = ã ¾ Ê G Ä P φ n+1 aj = 1 φ n+1 sj φ n+1 fj, z j ω h (x n+1 ). ª5 µ P³ ³Þ V 6 6³ â 9 G Ÿ G ä H P É º º; à P º Ç ¾ =e» É º É@ ãþ¾ Ç»»Þ½ ß > ãþº ÇÞÇÞ ã º ãþº ¾ á» ½ º = ã ¾ Ê G ä Å P hj = p T (x n+1 ) p n+1 st,j, z j ω h (x n+1 ), p n+1 f(s n+1 j ) ;ÒÉ º9ã º»ÞÉ º Ç»Þã ß» ã P > ã º Ç ÇE ãþº½ Ç ß9¾ ÊF>» º = ã ¾ Ê G ä ä*p G ä Ä P p n+1 st,j = p st0 ª5 BŸ ² J V 1=F ³Þ 9 PẂ ž² ² 9 = 9 ž r n+1 j 1 r n+1 j É º º; à º Ç ¾?=±à º ¾ßV½»Þ½º Ç ã º» ½ àhº"» ¾â» É º Ç ¾ ½ T> É Ç º ã º ¾ á» ½ º = ã ¾ Ê» É º æ ã ß@ ; Ì. φ n+1 αj u αj = Kn+1 αj µ α p n+1 h,j+1 pn+1 hj h n+1 j, α = a, f, z j ω h (x n+1 ).
299 ª5 BŸ ² J V 1=FB P ž œ² V L 9 žẃ V!L 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä ç Å Æ º ¾ß9½È»8@ ¾?=œ» É º Ç ¾ ½ T> É HÇ º vs n+1 ½ Ç ¾ á» ½ º Ç ¾ འ7B ½ Ç ßVã ºV»Þ½ º º D #»Þ½¾ G ä K P É º» É ºZ;»Þº=ã P «½ãÒà º ¾ßV½»Þ½º Ç ãþº B ½à º v n+1 αj = v n+1 sj + u n+1 αj, α = a, f, z j ω h (x n+1 ).»Þɽ ÇÊ ¾ º» É º > ãþº ÇÞÇÞ ã ºBºD»Þ½¾ ½ Ç Ç ¾ à º ºD" > G ;ƒº ¾P» º»ÞÉ» ½»ÞÉ º > ã º9ཾ Ç Ê ¾ º»ÞÉ º > ã º Ç ÇÞ ãþº«ºd»þ½¾ ; HÇ B ¾ á ½ x ½ ã º=ßV»Þ½¾ P ƒ ß6É Ç ½ ÊF> ½S#߻޽¾ ¾?=±»Þɺ Ê ¾ º ; Çb> ¾ ÇÞÇ ½ á º º»Þ¾»8;ƒ¾ HÇÞÇÞ ÊF>»Þ½¾ #Ç9Ì É º > ã º Ç ÇÞ ãþºë½ Ç º = ¾Hã ÊË» ½ ¾ ã ½ àhº ½Vº=ãÞº ßVº á º9»8;ƒº=º» É º»Þ¾P» P M> ãþº ÇÞÇÞ ã º G ;ÒÉ ½ ß6É ¾º Ç+ ¾» º > º ¾ z P»Þɺ Ç»Þã ß» ã /> ã º Ç ÇÞ ãþºò½ Ç» ¼Hº ½» ¾ ß9ß9¾» É º 9¾<;R½ Ç > ã ã Ç àhº9ã ÇÞ W É º ßV¾ #Ç» ½È»»Þ½à º.ã º»Þ½¾ á ºV»8;º9º»Þɺ ÇÞ» ã» ½ ¾ ß?> ½ ãa@ > ã º Ç ÇÞ ãþº ½ ÇË ¾P» Ç º ½»ÞÉ º Ê ¾ º»Þ¾ ß ¾ Ç ºÞɺ ǻ޺ ÊÞÉ ÇJB ã H ½ º» Ç ½» É º ½ ½È» ½ ½ Ç»Þã ½ á»þ½¾ ¾ =À»ÞÉ º ÇÞ» ã» ½ ¾ Ë ã º ¾P» ÇÞÊ ¾¾P»Þɺ º > ãþº ÇÞÇÞ ã º ¾ ã%º" PÊF> º º9» Ç{ Ç ÇE Ê º.» É»{»ÞÉ º > ¾HãÞ¾ ÇËÊË» ½ Ç' ¾P»«ß9¾ ÊF> ã º Ç Ç º p T (x) = 0 P» É º = ¾ ¾<;Ò½ 7B ½ ½»Þ½ P ßV¾ # ½È» ½ ¾ ÇÒ ã º à P ½ ÀÌ vs 0 = 0, v0 f = 0, v0 a = 0, φ0 aj = 0, φ0 sj = 0.3, z j ω h (x 0 ), φ 0 fj = 0.6 if j = j 0, 0.3 if j j 0. É º»Þɺ ;»Þº9ã ½ Ç»Þã ½ á»þ½¾ ãþº ÊË ½ DZ ß6É 7B º = ¾Hã x n ω τ ½ º φ n f = φ0 f ð ð ÀìLîé " ì î#±î#" 1ê ê» É ½ Ç ÇE áç ºLß» ½ ¾ ;º ßV¾ Ç ½ º=ã»ÞÉ º Ç» á ½ ½»8@'¾?=±»Þɺ ¾ á» ½ º S ½»Þº(3àH¾ Ê º >Á > ãþ¾#"½ Ê˻޽¾ œ I O5»Þɺ Ç» á ½ ½»8@ Ç ½ Ç ½ Ç ¾ º Ç º > ¾ ã⺠ß6É ºD» ½ ¾ 1 ½ ßVº ÊË Ç Ç ßV¾ #Ç º=ãÞà» ½ ¾ ºD»Þ½¾ Ç1G ä P P G ä Là P ã ºƒÉ@ > º9ã á ¾ ½ ß ;º B ºV»±»ÞÉ» ºD" > ½ß9½È»?>7> ã ¾#"½ Ê˻޽¾ Ç+ ãþº Ç» Pá º ½= ½ Ç ß9ãÞº9»Þº Ç» º >Ç τ n ǻ޽ Ç =Q@â» É º = ¾ ¾<;Ò½ 7B º ÇEÁ»Þ½ ʻ޺ Ç vs n τ n < min h n j, vf n τ n < min h n j. j j º ¾»Þº»ÞÉ» ÇÞ ß6É Ç ½ Ç ½ Ç ¾P» ÇÞ IH ßV½º»Ò½ ¾Hã º=ã»Þ¾ > ã ¾ à º»ÞÉ º Ç» á ½ ½»8@ ¾?=5»ÞÉ º ǻ޺ Ê ¾ =5º D» ½ ¾ Ç93Š º9»ƒßV¾ Ç ½ º=ã Ç ½ ÊF> ½WS#º ËÊ ¾ º ¾?=5»8;¾ > É Ç ºb9¾<; ;ÒÉ ½ß6É.½ ÇÒ º Ç ßVã ½ á º É º ÊË Ç Ç ßV¾ #Ç º=ãÞà» ½ ¾ º D #»Þ½¾ #Ç P»ÞÉ º æ ºD» ½ ¾ φ s x + ( ) φs v s = 0, z φ f x + ( ) φf v f = 0, z
300 Ä çpä V ž Ÿ PŸ φ f (v f v s ) = K f p h µ f z. ÊÊ ½ 7BË />«ÊË HÇÞÇ ß9¾ Ç º9ã à»þ½¾ ºD»Þ½¾ Ç ;º B ºV»Ò» É» ¾ ã ( ) φs v s + φ f v f = 0, z v s + φ f (v f v s ) = C, ;ÒÉ º9ã º C ½ Ç ßV¾ Ç» P» 1 e ¼3½ 7B ½» ¾ ß9ß9¾»»Þɺ æ ã ß@ºD»Þ½¾ 1 ;º B º9»» É º Ê HÇÞÇ á# P P ß9ºº D» ½ ¾ ¾ =œ»þéº Ç ¾ ½ > É Ç º φ s x + C φ s z = ( K f φ s z ). G ä LÅ P p h µ f z» ; HÇ'Ç É ¾<; Pá ¾ à ºÞÉ»'»ÞɺÉ@ ãþ¾ Ç»»Þ½ ß > ã º Ç ÇE ãþº.½ Ç ºS º HÇ' = ßV»Þ½¾ p h = P (φ s ) = P < 0 ;º B º9»b= ã ¾ Ê G ä =Å P ># ã Pá ¾ ½ßºD»Þ½¾ φ s x + C φ s z = ( K f φ s P (φ s ) φ ) s G. ä ä*p z µ f z É º»ÞÉ º B ¾ 㠽Ȼ É Ê > ã º Ç º»Þº á ¾ àhºâ½ Ç ºD ½à P º»»Þ¾ ½ Ç ß9ãÞº9»Þ½ =» ½ ¾ ¾ = G ä ä*p º º" > ½ ßV½» + º9ã Ç ß6É º Ê º φ n+1 s φ n s + C z,h φ n ( K f s = z,h φs P (φ n s ) z,h φ n ) s, τ µ f ;ÒÉ º9ã º ºS º Ç S ½È» º ½WV5º9ã º ßVºB¾ > º=ã»Þ¾Hã»3= ¾ ¾<; Ç = ãþ¾ Ê»ÞÉ º Ê "½ Êâ Ê > z,h ãþ½ ß9½ > º G Ç º9ºJI =Å OQPƒ»ÞɻһÞɽ Ç Ç ß6É º Ê º ½ ÇÒÇ» Pá º ½= τ c min j h j. = P > 0»Þɺ» É º > ã ¾ > ¾ Ç º aêë»þé º ʻ޽ ß Ê ¾ º FG ä =Å P á º=ß9¾ Ê º Ç ½ Á ßV¾ # ½È» ½ ¾ º GWÇ ½ Ê ½ ã» ¾ Ç ¾ ß º É º» ßV¾ ßV»Þ½¾ ºD» ½ ¾ ;Ò½»ÞÉm» É ºË½ àhº9ã Ç º ½ ã º=ßV»Þ½¾ ¾?=±»Þ½ Ê º P φ s x + C φ s z = ( K f φ s P (φ s ) φ ) s. z µ f z P Ç > º=ß9½ Ê º9ã ½ß P Ê ºV» É ¾ Ç'Ç É ¾ xá º Ç º» ¾XS ½È» Ç'Ç ¾»Þ½¾ I ç?o ¾ ã ºD" PÊF> º» É º É@ ãþ¾ Ç»»Þ½ ß > ãþº ÇÞÇÞ ã º= ß» ½ ¾ = ãþ¾ Ê G ä Å P p h (x, z) = p T (x) p s (s) 1 φ s (x, z) ; HÇ" Ç º ½ Ê º9ã ½ ß P ºD" > º9ã ½ Ê º» Ç > ãþº Ç º»Þº ½ I?O À ½ BH ãþº ä{»þé º B ã?> É ½ß ¾?=±»ÞÉ ½ Ç = ßV»Þ½¾ ½ Ç1> ãþº Ç º»Þº 1 ;ÒÉ º x = 0, p T (x) = 5 ( ( πx )) 1 + cos. L
301 º Ç º9º»ÞÉ» = ¾ ã!l 9 ž J žÿ F 9³ + žÿ V³ ³Þ 6 Ä ç K s [0.5, 0.35]»ÞÉ º É@ ã ¾ Ç»»Þ½ ß > ã º Ç ÇÞ ãþº B ã ¾<; Ç 7>1 º H ½ /B»Þ¾ P ½ ÈÁ> ¾ Ç º :> ã ¾ á º Ê«É º=ã޺½ Çë ¾ º" > º=ãÞ½ Ê º» 3»»ÞÉ» ÇE ß6É > É º ¾ Ê º ; HÇ ¾ áç º9ã à º ºD" > º9ã ½ Ê º» P(S) S M A D C D<Hù õ ôlòýñekvñ GJ> ûhõ C òòþ õ C ú þhf3> ñ GJôLFâú ô=õ x = 0. * *d-4*d)4 *: Q {ÿ a øjø C F#ö ÿ' C DHG C K9Fù ÿ A õek9f3ü C F3òýñ C GJF#ÿ "!#$&%'#(=ÿ NPûHõ GJF3ü C õö C õ øjgèföq6t <L< ÿ 7 *)ÿ a 3 Hõ ô=òg#k9fù [ ÿ ` õ C,+ GJô=òGJõÿ ôpù C øjøjgjf3ü GJF_ C > ñ GJôLFË ôlþhøèùhgjf3ü ûhõ ô > C òò C òƒó+g ñ DËù CÞU úô=õ K Hø C ûô=õ ôlþhò+ûhõ C úô=õ ò6ÿ -.#/0134/567839:;Pö=< ö 7 ö 79?L?=? ÿ S" 'Ḧÿd C K9õ K9Fù a ÿ?> C õõ þ3g _ BCDC!#"7(EFGH!I "J(KL; 3ÿ cƒc G ù C øžö ) ô9õeù õ C >ED ñö QT <L: 'Ḧÿ ` ÿ ±ô9õ GÈòëK=FùM) ÿ [ ÿ? ±ô ô=i ÿ5]5øjþn>6ô=õõ C >Þñ C ù ñõek=f3òûô9õñÿpmþÿ NO a N A a ÿ a P þ3gèùñõek=fhò U ûô9õñâk9øjülô=õ G ñ DH vñ D3K9ñó±ô=õ IPò6ÿ0135QR"%S434TR$UVXW ö ö3slt ; 8 T ö#qt : S ÿ Y c ÿ?z±g C ü=gjò K=F3ù ÿ#m øjg C ÿboâþ3 C õ GÈ>6K=øeK=øJüLô9õ GJñ DH òòú ô=õ ôpù C øègjfhüô=ú+øjgw þ3gèù{ûô=ø C õ ô=þ3øèùhgjf3ü ÿ[@;\h%mxwvl4%*a(b ;$C'J(]J UV ö7^9_ S Þö#Q < Q ;â7=?l7 ö 79?L? S ÿ 8 c ÿz±g C ülgjò6ö ÿhmwøjg C öhnÿ c G C ú5k=f3ù]` ÿhn ñ C GJF C õÿ FB ôpù C øjøjgèfhü K9Fù ògj þ3øèkvñ GÈô=F ô9úàùhg ú U ú C õ C F ñ±õ C ü=gj C òœúô=õøjgw þ3gèù ûôlø C õœ ôlþhøèùhgjf3ü ÿ QR%S7$aJL@H;A(0]/[6J Eö _ 7Þö#QSPQ ; Q 8L7 ö 7=?L?9@ ÿ : c ÿfz±g C ülgjò6ö5>"ÿ±npñek9õ GJI ô Gcb6GJþ3ò K9Fù a ÿfdpñ GJI ô=fk9ò6ÿ ` K9õEK9 C ñ C õ ò GÈù C FPñ G 3>K9ñ GJôLF K=øJü=ô U õ G ñ D3 ò1ú ô9õ±ó±ô ôpùâùpõ$hgjfhüò ôpù C øjgjf3ü ÿ M F a ÿ? eþ3gjipgèò6ö c ÿe±g C ü=gjòk=f3ù a ÿ )ÿ?]5g ññf_ ^ 0;'.g7($g!gUhiSQjD.0-\k H!gaHVlnmL83;ol=T5!pVC!VHVq;'.g7($g!gXL$@;\ h %MXW SrinQjD.gs$t6t"s öhnpûhõ GJF3ü C õö? C õ øjgjf]o C GÈù C øw C õ ü O C ó ueô=õ Iö3Q? :Ò; QLQ 7 ö 7=?=?=@ ÿ < *O"ÿ v ÿ ^ F3ü=øžö"{ÿ9O K9F3I C K=F3ù a ÿ#o C þ* 3K=þ C õÿ'wxxcc!hcyf"xzp{.g H!H }T5!p6k,8H%~ ÿ `ÒøJþ ó C õö) ô=fù õ C >ÞD ñö QT=T 8 ÿ T" *` ÿoâgjø ñ þ3f C F#ÿR@;\H%MXWVL9J(*\$%'H!gXWVL=%*A(B ; $C*p{WV\HL (6X'7!pAWgHg H *gh!%m6wg$jhvl?wxg!g0 6 9ÿ f F3G C õ òg ñâô9ú òi< ø ö) C ûkvõñ C F ñëô9úrk9ñ D CÞU KVñ GÈ> ò6ö#q6tlt Y ÿ Q? {ÿf` KVñEK _ýk öf` ÿaoƒgèø ñ þhf C F"K=F3ùIḦÿ A GJ ôlf C F#ÿ ]5øÈôó ô9úhóëk9ñ C õ5k=f3ù"k9g õàgjf K>6ô= ûhõ C òòg Hø C ûô9õ ôlþ3òe C ùhgjþh ÿ K ôpù C ø3ô9ú#ó C ñëû õ C òògjf3ü ô=úûk9û C õÿ 13JTR$U",37ƒ} 7/[6J83\TFBU 3Èö \ ö Q? Y S ; Q?L8 S ö5q6tlt 7 ÿ Q=Q c ÿ Ḧÿ [#C > C Pþ C ÿq S$%'H!gXWVL9EH;A(F{,"!]QR"\ H!H ""X: j"r ÿb ±G õ IPD þhò C õn> C õ øèk=ü ö Q6TLT Q=ÿ
302 Ä ç L V ž Ÿ PŸ Q 7 ` ÿ [ ÿ c ô C ÿnpôl C >6ô=FPñõ G HþHñ GJôLFHò ñ ôëñ D C ôpù C øjgjf3ü'ô9ú ù GÈò> ôlf ñ GJF þhôlþhò P ôó+ò6ÿz jvw G3 IGHS/[6J834@;\3Jö ö#q 8 S ; Q6TLS ö#qt < Y ÿ Q6S" a ÿ a ÿnhk9 K9õ òipgjgžÿ 9};\#!HUDp{M( SH!#HJWg}HWg\H%'H ÿkvõ > C ø?) C IPI C õöm FH>LÿJöO C ó U ueô=õ Iö ëk=ò C ø ö 7=?=? QLÿ *` ÿj> C ø ñ C F K=F3ù v ÿ/ C òýñÿ c ô=øjøègjfhü ô=úeþ3fhò K9ñ þ õek9ñ C ù KVñ C õ GÈK=øJò C ô=øèþ ñ GJôLF ô=ú±k úþ3øjø ò KVñ þhõek9ñ C ù + ôlf C ÿ5tfbuvxwvl7w0h AXH iëö7< _ SÞöS < T Q ; S < T=T ö 7=?L?=? ÿ 55 5!! 5!5! M E!T/5! c ÿ\z±g C ülgjò6ö/{ÿ C GJø! þ3fk9ò6ö a ÿ\d ñ GÈILôLFK9ò ) K9õ8 C F3K=ü9õ GÈF#" C _ýk= G"ù õ" C ül " C òëg%$òû3k=þù GJ ô G%$ûô=û3G C õ GÈK=þHòË K9ñ C KVñ GÈFHGÈK=G ôpù C øjg K9GžÿndPG U K9 C òýñõek=gjûhòf? _ C ûk=ø ülgjf ñ G%ùHþ K9ñ C KVñ GÈFHGÈK=G+ ôpù C øjgèk=gžöeipþhõ G C FK9þù ô_ýk= G+ ôpù C øjgjþ3ô9ñ G 3ø ñõek=>6g _ýô=ò ûhõ ô > C òþhò ûôlûhg C õ GÈK=þ3ò û õ C òô K&$GJF3ô _ C ÿ a 3þ ôpù C øègèk9g%g%$ C ù3k= G±G'$ ñ þ(%û3kb6gjþ( C Fù õ þ ( _ýþ( òû þ3ù )6GJôLòGJô=ònûô=õ GJFHüLôLòGJô=ò ñ C õ û*" C ò ôpù C øjgjþ(wö"ñekb G K9þbFK9þù ô_ýk= ôlòòipg õñ GÈFHüLô=ò û õ G C øèk=gèùhô=ò6ÿ%npñõek9gèûhòf<_ C ûk9òg! þ3øpñek=ò û3k9ñ GJIPòøJGÈF ñek9òâ ôlù C øjgjò6ö±ipþ õ GÈòBK9ûHõEK&$ô K=F3ù C FHò G%$ýñ C U I+" C _ýgj, ûô9õ GÈFHüLô=òGÈô=òñ C õ û*" C òëòøjþ3ôlipòfhgèô I õek&$ýñ C ö+g õëg%$ýñ G õñek-$gjôúžk=i ñ ô9õ G K9þ3òËG ( ñek=i=k òi? ò#b6gjô _ þù#" C _ýgj þ3gžÿ ` K=òG! þ3øpñ G%òILK9GJñ GJFHG K9G%K=øJüLô9õ GJñ K9GƒòI< ò#b6gjô_ þù#" C _ýgj ô{ûô=õ GJF3ü=ô_ C ñ C õ û*" C _ C ôpù U C øègèk GJ þ3gžÿm(èõ ôpù PñEK ö I=KLù ñ G õ GÈK=F ñ ù GJòIPõ C b6gjô_ ô þ)6ù3k GÈFHGJôBòýñEK 3GJøJþ3, F C þ ) ñ C FHILK F3K=ü=õ GJF*" C ñ G ñ GJIÒDHGÈû C õ8 ôløjgjf3g ( û C õ F C $GJ ôƒø ülb6gjþ(hk9õñ GJF3G (WöVô+õ C GJI GÈK%G ( LC õñ GJFPñ G G õàòø." C ülgjôòøhüb6gjþ%( ûô C GÈIPG ( ÿ ` K9õ ô U ù?pñek ö9ilk=ù ù GJòIPõ C ñ þ3ògjòàþ)ùhk GJF< ò5põekƒòýñek 3GJøJþ3ò6ö _ C GJüLþ ùhgjòi õ C ñ G + K=>6G _ ôlòœûk=ülk=øhø K9GJÏ,/)6GJF3üLòFHGJò ñ C F3IPGJFK ò0,9øhü1, τ Ch ÿhm$òýñek HGJøÈþH ô K=F3K=øJG + C " òƒg%$û3øèk=þhi GÈKPö3I=KLùBûHõ G C ILK9G#IPþ õ GÈþ ( ôpù C øègjô û3k9õek9 C ñõ þ (õ C GJI$ GJþ (5 ôpù C øjgèò+k9ûhõek3$ô F C I ô9õ C I ñ G%$I1,"þ)ùHK GJF3G ( ÿ
303 !"# $ % '&)($ +*,.-/10 3 -/546 "798 :6; 7=<=8 > 7=?=?=@BAC >ED3FHGJILK"MN3NPORQ6S <L7UTWV 79< 7 XZY)[]\_^a`cbZdfehg di^j\_klknmpoqmpmpklr `[tsurwvxgy\xbzr {urwv suoqvxmp\}su`~eh[d `5[ _rrv s `cbz\_k ƒ rwklr ˆdiƒ]\Š bzrwklk `5sŒƒ ^j\x _[ rrs `cb kž`~ ho `5X o)[ X)rwv sœƒ]r \xbps `ceh[ ezg [ ehvx^j\xkn^j\x _[ rrs `cb gš`rwklx c š œ1žeÿ5 y œ~ž % š ž % žeÿ. P # «ªB % % "Ÿ ²±³ W µ E ¹º» ½¼ µ9¾ºp W±À Uȳ Á Âcº» ²ÃL±Àº».Ä 6º ÅHµU¾ÇÆÈ Á Ɉ U±Àµ9 6µU º» ÅËÊc #±³Ã µ9ì6 ±³ WÆÈ E Â~ºP WÃL±Àº ª Í» # Î9ÏÐ Ñ HÒ Ó Ô ÍÔ Ï ÒÖÕ + 3 yœh Ø5ÕLÙ ÚPÛœ~ PÜÞÝ Ð ß Ï Ð Ó²àˆáâ ãhä#åâ3æ çå3è éêhëíìþåpî%ïiðñ3èhãæhå3çå3è éêhëíìþå î%ïièá êpòçæ èåìþå î Î=ó9Î9Ð Ý Î.Ÿ Î=ô Ü Î=ÏBõÎ9ö Ú ÚPøHøPÛù öúî Ý Ð Ò Î «û"ü»ý Î9Ïyõ#Î=ö ÚPý Ú ø ø Û þ'ÿ GJF C K ÁG C C FK G >!" K # C %$&'3K $ÁGLF'( )$ÁD C+* K '&,' C ÁGG F * GJF-$ÁD C. C CÞT NPDK/ > C 10,# C /+G$ÁD K * F C $ÁG > G#34&3G G > LF,G C C 5 M6$"G C &3> C $7 C K Á>ED3GJF * C G *LC F8=K & C K=F C G *=C F'"&3F3>9$ÁG#=F,:" K GJF C K; C EK;$ (/+G$ÁD C ÁG# GJ>:<=&HF K > LF G$ÁG#=F, 5A D C '$EK=GJF C C EK;$ G C C F4$ C K K>%& 1$6/ GJF C K? C EK C C > LF C GA C C F4$ÁG K C EK;$ /+G$ÁD+8LK; G F * > C B >6G C F4$+K9F $ÁD C GJF$ C * ;! GA C C F4$ÁG K C EK $ 1/+G$ÁD:$ÁD C GJF * & K ÁG$ C$ÁD C)D K &H>ÞD $ C=5LA D C C > T $%EK C G#E% 8 C $ÁD C!F C*=C F C EK $ C:G K $%ÁGJ> C H FIGKJLÖC $ÁD, &'GJF *MD D C D C 8 F' G K L N$ÁD C 0 O$%K9F C >LF IPGJF 5 PRQSUT!VCW XZY=[\.íC CúT N DK/w> C #^] * K I'&,, C ] K * F C $ÁGJ> G#3&HG ] C G *LC F8=K & C K=F ÈC G *LC F T "&3FH> $ÁGLF, = C ] $ÁD C_F C*=C F C EK;$ C`G K $%ÁGJ> C ÖC $ÁD, ] D D C D C 8 F' G K a?brc,dfecg h_ì j!knemlhfd _n Î+o½öúÎ9Î ÒEÔ öpo óuî>q ü4r Ò Ð ẗs Î Ó Î ßÁŸCn r óuî Ó Ó Ò:n Ý Îyó PÔ#Ò Î öúî PÜ Ð ḦÜ Î9öúÎ ÒEÜ öúî=ó9î 3ÜÞÓ"u v Ú Õ=ý w H _n Ð Ò Ð Ò+ Ô Î ÜÞü Î x Ü öþî=ïî Ó"u öúðó n ô»üþü Î=ö o ü öúï»ü Ð üh ô n Î ü ÏÎ Î xð ÒEÜ Ð Ð Ü9n Î Ò Î Ò9uÒEÜ Î=Ï Ò9 PŸÔ ó n ô n Î ü ÏÎ "ü õ Üú Ð ÿ Î r o½î PÜÞÔ öúî Ò Ðyo ü Î ü o Ü9n Î Ó Ð{z Ô Ð Ò Ð BÜ n Î s Î Ó Î ßÁŸCn r ó9î ÓÓ Ð Ò Ï P H Î Ü Ðó #ž Î ö Ó"u Î9Ð n3ü ÐÎ Ò Ð Ü(r Ò o ü Ô Ü n»üöò Î Ó o ß Ï P H Î Ü Ðó Î Ó o ü öúó9î Ò ó ÔÒ Î Ü9n Î:o ü öþï»ü Ð üh 'ü o Ü9n Î Ð ḦÜ öþð ó PÜ Î Ó õ u öúð ḦÜ n Ð Î"ô PÜEÜ Î9ö Ò Ð ÈÜ9n ü3ò Î ÒpuÒEÜ Î9Ï Ò v }~=w L x Ü Î Ò Ð ü Bü o Ü9nüHÒ Îíô n Î ü ÏÇÎ o ü ö Ü9n Î ó HÒ Î ü o#ó ü 3Ü Ð Ô ü ÔÒ Î Î9ö u ÒEÔ ôô Óyu\r Ò ó öúöþðî ühôü Ð v Ù ÕHÕP ÕLÚÖÕ Ù=wErn Î9öúÎ Ü n ÎlÐ q Ô Î ó9î ü o Ü9n Î Ò Î Ó o ß Ï Î Ü Ð ó o ü öúó9î Ò«ü Ü n Î Î Ý Î Ó ü ô ÏÎ 3Ü«ü o Ü9n Î Ÿ Ï ß uó ü ö'ð ÒÁÜ6 õ Ð Ó Ð Üu\r Ò ó ü #Ò Ð Î9öúÎ õ üpü niü9n Î ü öúî Ü Ðó PÓÓyu v Ù Õ Õ;w5 Î;xôÎ9öúÐ ÏÎ 3Ü6 PÓÓyu v Õ Ú #Õ Ù=w o ü ö%ô Ó P Î P
304 ÚPý ý Ì J± 1±ÀµU ² Ã=±Àµ9 ²± Ä µ6µ9ì6 óuðöúó Ô Ó ö Î ü ÏÎ Ü öúðî Ò v Ù +ý4w %ÒúÒ Î ḦÜ Ð Ó o½î PÜÞÔ öúî ü o Ü9n Î Ò Î.ô n Î ü ÏÎ ó ü #Ò Ð ÒÁÜ6Ò Ð Ü9n ÎKo ü öþï PÜ Ð ü Žü o Ü9n ÎiÏ Î Ü Ð ó Ó Ð{z Ô Ð Î=ö rn Ð ó n <u ÏÇÐ ó ÒÖ ô ö ü ôî9ö Ü ÐÎ Ò Î;x óuî=ô Ü ÒÞü ÏÎ_z Ô PÓ Ð Ü6»Ü Ð Ý Î Ô ÏÎ9öúÐó PÓ Î;xôÎ9öúÐ ÏÎ 3Ü6Ò v ~ w öúî9ï Ð Ò ô üü ö Ó"u Ô Î=ö ÒEÜÞüü ˆ _n Ð Ò Ð Ò ü ÜÖÜ9n Î'ó Ò Î ü o Ü n Î üh ß Ï Î Ü Ð ó Ó Ð{z Ô Ð Î9ö Ò9 rn Ðó nlòáü6 ö Ü Ð o½ö ü Ï ô Ð üh Î9Î=öÞÐ r ü ö Í õ u Ÿ 4 Ï P # u3óü ö r Î=öÞÎBÎ;x Ü Î Ò Ð Ý Î Óyu Ð Ý Î ÒEÜ Ð H PÜ Î v ÕH ÕLø Õ= 1Õ=Û ˆÕ }1Õ ~ w ª öúî Ó»Ü Î ôö ü õ Ó Î=Ï ü o Ü n ÎMo½öÞÎ=ÎyÐ 3Ü Î=öpo óuî <u ÏÐ ó Ò Î Ò óuöúðõ#î Ò Ü n Î <u ÏÐ ó Ò ü o Ü n Î õ Ô õ õ Ó Î öúð Ò Ð Ð ÈÜ n Î Ý Î=ö Ü Ðó PÓ s Î Ó Î ßŸCn# r óuî ÓÓˆÔ Î9ö ó Ü Ð ü «ü o Ü n Î ö Ý Ð Üu v Õ w² 3Ÿ 4 Ï Pï P Ç u3óü ö n Ý Î)o ühô yü9n#»ü o ü ö Ü n Ð Ò ó HÒ Î Ü9n Î_o ÏÐ Ó"uBü o Ü n Î ÒÁÜ Î H <u õ Ô õ õ Ó Î Ò9n ôî Ò Î;xÐ ÒÁÜ6Ò Ð Ü9n Î õ Ò Î ó9î ü o Ü n Î ÒEÔ ö9o ó9î Ü Î Ò Ð ü v Õ w² ˆž Ü Ð Ò PÜÞÔ ö PÓ ÜÞü HÒÞÒÞÔ ÏÎ Ü n»ü Ð ËÜ9n Î ô öúî Ò Î ó9î ü o ÒEÔ ö9o ó9î Ü Î Ò Ð üh ËÜ9n Î ó9ð ö6ó Ô Ó ö Òpn# ôî ü o Ü n Î öþð Ò Ð õ Ô õ õ Ó ÎÐ ÒÒ Î Ó Î=ó Ü Î Ü n ü Ô 'n Ð ÜúÒÖÒEÜú õ Ð Ó Ð Üu öþî=ï Ð ô üü ö Ó"u.Ô Î=ö ÒEÜÞüü ˆ 1 _n Î ô öþî Ó ÐÏÐ # ö uš Ô ÏÎ9öúÐ ó PÓ Î;xôÎ9öúÐ ÏÎ 3Ü6Ò v Ûw(n Ý Î Ò9n ü4r Ü n»ü Ð Ü n Î ó Ò Î ü o Ü n Î õ Ô õ õ Ó ÎiöúÐ Ò Ð Ð ŽÜ9n Î s Î Ó Î ßŸ<n r ó9î ÓÓ Ó Ó Î r Ð Ü9n Ï P H Î Ü Ðó Ó Ð{z Ô Ð ˆˆÜ9n Î Ð Î9öúÎ 3Ü o ÏÐ Ó ÐÎ Òíü o1öúð Ò Ð õ Ô õ õ Ó Î Ø ô#î ö Ó Ð Í Î ü ö%õî 3Ü Ô ÏBõ ß õî ÓÓ Ï u öúð Ò Î 3 _n Î ÒEÜú õ Ð Ó Ð Üu ü o Ü n Î"öúÐ Ò Ð õ Ô õ õ Ó Î Ð 'Ü n Î ôöþî Ò Î óuî ü o1ï P H Î Ü ÐóIo ü ö6óuî Ò Ð Ò% ü Ü Ð Ý Î ÒÁÜ Ð 3»Ü Î u Î Ü= ž 'Ü9n ÎôöÞÎ Ò Î ḦÜ ô ô#î=ö r Î «Ô ÏÎ9öúÐó PÓÓyuÇÜ9n ÎÎ=Ð Î Ý» PÓÔ Î Ò Î=Ð Î Ý ÎLó ÜÞü ö Ò ü o Ü9n Î Ó Ð Î ö ü ôî9ö»üúü örn Ð ó nè Î Ü Î9öúÏÐ Î Ò%Ü9n Î Î Ý ühó Ô Ü Ð ü 'ü o Ò Ï PÓÓ ô#î=ö ÜúÔ öþõ»ü Ð ü #Ò9 fušôò Ð ŽÜ n Î"Î Î Î9ö»Ü Î»Ü öúð óuî Ò ÏÎ Ü9nü r Î n Ý Î.ó üh ÒEÜ ö Ô ó Ü Î Üríü PÓ ü öúð Ü9n Ï Ò=1Ü9n#»Üi öúî'õ Ò Î ü ËÜ n Î Ô ÒÞ PÜÞÔ ö»ü Î ô ô ö ü xð Ï»Ü Ð üh lü ÎLó n Ð{z Ô ÎÈõ u œ~ P ö Î Ð 3Ü Î9öúô ü Ó»Ü Ð ü #Ò v ý4w² _n Î ô ö ü õ Ó Î=Ï o ü öþï Ô Ó PÜ Ð ü ' i Î9öúÐ Ý PÜ Ð ü ïü o Ü n Î ü ôî9ö»üþü ö Ò Ð ' P Î xô Ó Ð óuð Ü o ü öþï öúî Ð Ý Î Ð ÈŸ ÎLó Ü Ð ü ÈÚ Hû"Ô ÏÎ9öúÐó PÓ# ô ô ö ü xð Ï»Ü Ð üh Ü Î=ó n Ð"z Ô Î"Ð Òí Î Ò óuöúð õî Ð «Ÿ ÎLó Ü Ð üh ' Hû"Ô ÏÎ9öúÐó PÓ öúî ÒÞÔ Ó ÜúÒí P ÇÜ n Î9Ðö Ð Ò ó ÔÒúÒ Ð ü ' öþî Ð Ý Î Ð Ÿ Î=ó Ü Ð üh «Û# _b! #"1e%$&(')"1eml9k*",+!-hLg.' j+/"1emlph)d h107e%$ &3 gmh145+6&(' 7 Î ó ü Ò Ð Î9ö õ Ô õ õ Ó ÎÖÐ P Ð Ð Ü Î Ó u Î9ö ü o Ü9n ÎÖÏ Î Ü Ð ó Ó Ð{z Ô Ð ˆ #œ Î Ü r = R ( 1 + ζ(α, t) ) õ#î Ü9n ÎyÎ=z Ô#»Ü Ð ü ü o Ü n ÎMo½öÞÎ=ÎyÐ 3Ü Î9ö9o ó9î>o ü ö õ Ô õ õ Ó ÎÐ ô ü Ó ö ó üü ö Ð»Ü Î Ò ó ü Î=ó Ü Î 7r Ð Ü n Ð ÜúÒ Ï ü»ý Ð ó9î 3Ü Î=öCrn Î=öÞÎ ζ(α, t) Ð ÒíÜ9n Î ÐÏÎ Ò Ð ü Ó Î ÒúÒ Ð 3Ü Î=öpo óuî ô#î=ö ÜúÔ öþõ»ü Ð ü ü o Ü n Îyó9Ð ö6ó Ô Ó öõ Ô õõ Ó Î r = R Ð Ü n Î s Î Ó Î ßÁŸCn r ó9î ÓÓW ˆ PÍ Ð iü9n Î Í Ð Î=Ï PÜ Ð ó õ ühô ö u ó ü Ð Ü Ð üh o½ö ü Ï Ü n Î öúó u Î z Ô PÜ Ð ü ó9ó ü Ô 3Ü Ð o ü ö Ü n Î Ï Î Ü Ð óeo ü ö6óuî Ò v 4w P # Ó Ð Î öþð989ð Ð Ü)r Ð Ü n öþî Ò ôî=ó Ü+ÜÞü ζ r Î ü õ Üú Ð Ü n Îo ü ÓÓü4r Ð ô ö ü õ Ó Î9ÏhÐ Ü9n Î ÐÏÎ Ò Ð ü Ó Î ÒúÒ o ü öúï à ζ t = Bg sin α ζ α p Bg cos α ζ +, r r=1 p r=1 = ζ Bm (Bg cos α + a)ζ + α h π π ζ(τ, t) ] dτ, sin (α τ)/ + h /4 [ ζ(τ, t) ζ(α, t) sin (α τ)/ ( r, α) ²Ú Õ ²Ú Ú
305 É#¾iº µ # µ9ì½ Uº 6µ µ9ì W Ì 6º» ²±À» ÚPý p = 0 if r > 1, p = c ln r + O(1) if r +. s Î9öúÎ c = c(t) Î Î=ö Ó Ó"u' Î=ô#Î Ò üh π π t P Ð Ü Ð Ò Î Ü Î=öÞÏÐ Î õ u'ü n ÎÖÎ z Ô Ó Ð Üu ζ(τ, t) dτ = 0 P Î z Ô PÜ Ð ü Ò WÚ Õ WÚ»ª o Ü Î=ö Ò ÐÏô Ó Î ó ü Ïô ÔÜ6»Ü Ð üh Ò Ð Ü ó P õî Òpnü4r Ü9n#»Ü c = 1 π π π cos τ ζ(τ, t) dτ. ž Ð Ü Ð Ó1Ý» PÓÔ Î Òpnü Ô Ó õî Ò ô#îlóuð Î o ü ö ζ o Ô ó Ü Ð üh. PÜ ζ(α, 0) = ζ 0 (α). t = 0 à s Î9öúÎ Ü n Î o ü ÓÓ ü4r Ð Ð ÏÎ #Ò Ð ü Ó Î ÒúÒ ô ö ÏÎ Ü Î9ö Ò>r Î9öúÎÈÐ 3Ü ö ü Ô óuî ˆà r = r Ð Ò R Ü9n Îö Ð ÔÒ= h = h Ü9n Î Ü n Ðó Í Î ÒÞÒ'ü o Ü9n Î s Î Ó Î Ø ŸCn r ó9î ÓÓW R Bm Ü n Î Ï P Î Ü Ð ó íüh Ë Ô Ïyõ#Î=ö v Ú 4w ù Bg Ü n Î ö Ý Ð Üú PÜ Ð ü Ó% ü Ë Ô Ïyõ#Î=ö ù p = p(re iα, t) Ü n Î Î Î=ó Ü Ð Ý ÎyôöÞÎ ÒÞÒÞÔ öúîyð Ü n ÎÏ Î Ü Ð ó Ó Ð{z Ô Ð ü ÔÜ6Ò Ð Î Ü9n Îõ Ô õ õ Ó Î 1 _n Îió üh ÒEÜú P 3Ü Ð Ò Î Ü Î=öÞÏÐ Î Ò ü ö õ u rn Î9öúÎ Î ÓÓ Ð ô Ü Ðó:o Ô ó Ü Ð üh Ò K = a = 1 Bm h π/ 0 + π/ 0 cos τ dτ, sin τ + h /4 a = 1 Bm ( h E ( ) )K k + k k, dτ π/ 1 k sin τ, E = 0 1 k sin τ dτ öúî o Ô Ó Ó Î ÓÓ Ð ô Ü ÐówÐ 3Ü Î ö PÓ ÒËü o Ü n Î ö ÒÁÜ P ZÒ Î=ó ü Í Ð # öþî Ò ôî=ó Ü Ð Ý Î Ó"u h /4. Ÿ Ð óuî ó ü Î 'ó9ð Î ḦÜ6Ò ü o5ô ö ü õ Ó Î9Ï WÚ Õ Ø ²Ú Ù ü üpü+ Î=ô#Î Î;xô Ó Ðó9Ð ÜúÓyuBü ÿü ÐÏÇÎ r Î öúî9ô öúî Ò Î 3Ü Ü9n Î ÒÞü ÓÔÜ Ð ü Ð «Ü n Î(o ü öúï WÚ WÚ Û ²Ú Ù ²Ú } a k = ζ = e λt u(α), p r=1 = e λt WÚ ~ (Pu)(α), rn Î9öúÎ P Ð Ò" ÇÓ Ð Î ö ü ôî9ö»üþü ö _n Ð Ò Ó Î H Ò ÔÒ ÜÞüÜ9n Î(o ü ÓÓ ü4r Ð 'Ò ô#î=ó Ü ö PÓ ô ö ü õ Ó Î=Ï Ð Ü9n Î Ò Î Ü Ω ü o Ür Ðó9Î ó ü 3Ü Ð Ô ü Ô#ÒEÓ"uÈ Ð Î=öÞÎ 3Ü Ð õ Ó Î π ôî9öúð ü Ð ó:o Ô ó Ü Ð ü Ò=à λu = Bg sin α du 1 + Bg cos α u dα 4π (v.p.) Bm π π π π π (Pu)(τ) (Pu)(α) sin (τ α)/ cos τ u(τ) dτ, dτ WÚ ý
306 Ú ø Ì J± 1±ÀµU ² Ã=±Àµ9 ²± Ä µ6µ9ì6 (Pu)(α) = d u Bm (a + Bg cos α) u dα h r Ð Ü n«ü n Î ó ü Ïô Ó Î=ÏÎ 3Üú ö u ó ü Ð Ü Ð ü π π + Bm h u(α)dα = 0. π π π π u(τ) dτ sin (τ α)/ + h /4 u(τ) u(α) sin (τ α)/ dτ, ²Ú WÚ Õ=ø ÌÞ L Á z Ô PÜ Ð ü WÚ Mo ü ÓÓ ü4r Ò o½ö ü Ï WÚ Ú P Ü n ÎöúÎ9ô öúî Ò Î 3Ü6»Ü Ð ü #ÒWÚ ~ %ª õ ühô Î n# öúï üh Ð óo Ô ó Ü Ð ü p(re iα ) o ü ö r > 1 ó P õ#îëöúî9ô öúî Ò Î 3Ü Î õ u Ü n Î Ÿ ó ncr ö 8Ð 3Ü Î ö PÓ² "Ð Î9öúÎ 3Ü Ð»Ü Ð p r Î Î Ü rn Ðó n Ò Ð óuî r p(reiα ) = 1 π (1 + r ) cos (α τ) r ( π ) π 1 r cos (α τ) + r p(eiτ ) dτ, ó P õ#î Ü ö Ò o ü öþïî o ü ö r > 1 HÒ r p(reiα ) = 1 π π (v.p.) π π π (1 + r ) cos (α τ) r ( 1 r cos (α τ) + r ) [p(eiτ ) p(e iα )] dτ, WÚ ÕHÕ (1 + r ) cos (τ α) r (1 r cos (τ α) + r ) dτ = 0. _n Î Ó HÒÁÜ Î z Ô Ó Ð Üu ó õî ü õ Üú Ð Î ÔÒ Ð «Ü9n Î ÒÞÔ õ ÒEÜ Ð ÜÞÔÜ Ð üh P öþî Ò Ð Ô Î Ò~Ü9n Î ü ö u o ü öó ü Ïô Ó Î;xBÐ 3Ü Î ö ÓÒ= c Í Ð Ü9n Î Ó Ð ÏÐ Ü r 1+0 Ð WÚ Õ Õ Ð Ý Î Ò p = 1 π r r=1 4π (v.p.) (Pu)(τ) (Pu)(α) sin dτ. (τ α)/ π ξ = exp ( i(α τ) ) ü ö Ô õ ü Ô Î >n# öúï üh Ð ó o Ô ó Ü Ð ü Ò Òú»Ü Ð Ò o u Ð!WÚ r Î%Ï Ô#ÒÁÜ B ó üh ÒEÜú P 3Ü Üúü p c Ð WÚ Õ P _n Ð Ò ó üh ÒÁÜ6 P 3Ü ó P õ#î Î Ü Î=öÞÏÐ Î õ u Ð ḦÜ Î ö PÜ Ð ²Ú Õ P ÔÒ r r=1 Ð WÚ Û _n Ð Ò Ð Ý Î Ò ÔÒ²Ú ý _b j')& g lpk*" + _h +pjie<lph)d h10 g h14+/&(' _b _bpa ž lü9n Ð ÒyÒ Î=ó Ü Ð ü r Î'ô öúî Ò Î 3ÜB P Î 'óuðî 3Ü ÏÎ Ü n ü o ü ö 3Ô ÏÇÎ=öÞÐ ó Ó%ÒÞü ÓÔÜ Ð ü Ëü o Ü n Î Ò ôî=ó Ü ö PÓ ô ö ü õ Ó Î9Ï ²Ú ý Ø WÚ Õ=ø 5ž Ü Ð Ò õ Ò Î üh üh Òú»ÜÞÔ ö PÜ Î ô ôö ü xðï PÜ Ð ü Ò ü o Î9Ð Î o Ô ó Ü Ð üh Ò_r Ð Ü9n Ü9n Î fn Î9õ uòpn Î Ý ô ü Ó"u3 ü ÏÐ ÓÒ%ØÈ P # PÓü ühôò%üþükn ü4r Ð ÜIr Ò ü ÎÐ v ýw o ü ö Ü9n Î»Ü n Ð Î Ô o Ô ó Ü Ð üh Ò= ~ _n ÎiÏÎ Ü n ü Ð ÒÖ Ð Î=öÞÎ 3Ü o ü ööî Ý Î l P ü Î=Ð Î o Ô ó Ü Ð üh Ò u + (α) u (α) rn Î9öúÎ u + (α) = u(α) + u( α), u u(α) u( α) (α) =.
307 É#¾iº µ # µ9ì½ Uº 6µ µ9ì W Ì 6º» ²±À» Ÿ Î9ô ö PÜ Ð ü ÿü o#î Ý Î ÿ P # Bü ô ö ÜúÒ ü o WÚ ý Ø ²Ú Õ=ø Ð Ý Î ÒcÜríü Ò ô#îló Ü ö PÓ ô ö ü õ Ó Î=Ï Ò=à π λ ± u ± = Bg sin α du± dα + Bg cos α u± (v.p.) (Pu ± )(α) = d u ± dα r Ð Ü n«ü n Î ó ü Ïô Ó Î=ÏÎ 3Üú ö u Bm π π π π (a + Bg cos α)u± Bm h ó ü Ð Ü Ð ü π π (Pu ± )(τ) (Pu ± )(α) 4π ( sin (τ α)/ ) cos τ u ± (τ) dτ, π π Ú Õ dτ À Õ u ± (τ) dτ sin (τ α)/ + h /4 + Bm π u ± (τ) u ± (α) h π sin (τ α)/ dτ, W Ú u ± (α) dα = 0. ž Ü n ÎÈó Ò Î ü o Î Ý Î Î=Ð Î o Ô ó Ü Ð üh Òr Î Ô#Ò Î fn Î9õ uòpn Î Ý ô ü Ó"u3 ü ÏÐ ÓÒ ü o Ü n Î ö ÒEÜ Í Ð ˆ õ ÔÜ Ð ÿü9n Î ó Ò Î ü o ü Î=Ð Î o Ô ó Ü Ð üh Ò9 fn Î=õ uò9n Î Ý ô ühóyu ü ÏÇÐ PÓ Ò ü o Ü n Î Ò ÎLó ü # Í Ð l öúî Ô#Ò Î ˆ 1ª"Ò öúî ÒÞÔ Ó Ür Î ü õ Üú Ð ŽÜríü Î=Ð Î Ý» PÓÔ Î Î9Ð Î 3Ý Î=ó ÜÞü ö ô ö ü õ Ó Î9Ï Ò o ü ö N N Ï PÜ öúðó9î Ò A ± H _n Î ô ô ö ü xð Ï PÜ Î ÒEüHÓ Ô Ü Ð ü Ò ü o ²Ú ý Ø WÚ ÕLø N ó P õîçöúî9ôöþî Ò Î ḦÜ Î õ u ÏÇÎ P Ò ü o Ü n Î ÒEüHÓ Ô Ü Ð ü Òü o Ò ôî=ó Ü ö PÓ ô ö ü õ Ó Î=Ï Ò o ü ö Ü9n Î Ò Î Ï PÜ öúðó9î Ò= ž Î Î9ö PÓ²3Ü9n Î ó9ó Ô ö ó uiü o ô ô ö ü xðï»ü Ð üh Ò Ð ó9öþî Ò Î Ò_rn Î N Ð Ò Ð ß óuöúî Ò Î 1 N Äz 6»¾ º» ²±À» Á µu㻵u µ9±hµ9 = 6 5 U ²±À» µ6º Å» B ³¼µ U u + (α) ±³ ' µ6 U ²ÌÞº ÌÞ µ9¾ (A + N + λ+ E N ) w = 0, w = (w 1, w,..., w N ) T, A + N = Bg[ {diag(x k 1)} (1) N + {diag x k} ] G + N P N, G + N = 1 [ H + N N {diag(x k 1)}( (1) N ) {diag x k } (1) ] N, P N = {diag(x k 1)}( (1) N ) + {diag x k } (1) N {diag(a + Bg x k )} + Bm { h 4{diag x k } (1) N + π N [M+ N {diag s+ k } (1) N ] }. s Î9öúÎ {diag µ k } Ð Ò Ð P Hü Ó Ï PÜ öúð#x r Ð Ü9n Î Ó Î=ÏÇÎ 3ÜúÒ x k = cos s + k = N j=1,j k (k 1)π, k = 1,,..., N, N (x j x k )Φ(x k, x j, 0), µ k, k = 1,,..., N À W Û
308 Ú HÚ Ì J± 1±ÀµU ² Ã=±Àµ9 ²± Ä µ6µ9ì6 (1) N [ 1 xξ + h / + ] (ξ x) Φ(x, ξ, h) = + (1 xξ)h + h 4 1/ /4 (ξ x) + (1 xξ)h + h 4, /4 Ð Ò Ü9n Î fn Î=õ uò9n Î ÝÈ Ð Î=öÞÎ ḦÜ Ð PÜ Ð ü Ï»Ü öúðyx r Ð Ü n Î Ó Î9ÏÎ 3ÜúÒ W Ù H + N P M + N δ (1) kj = T N (x k) (x k x j )T N (x, if j k, δ(1) kk j) = T N (x k) T N (x k), h + kj = öþî Ï»Ü öþð óuî Òfr Ð Ü9n Î Ó Î=ÏÇÎ 3ÜúÒ 1 x jx k (x j x k ), if j k, h+ kk = x k 4(1 x k ) N 1, 3 m + kj = Φ(x k, x j, 0) Φ(x k, x j, h), if j k, m + kk = Φ(x k, x k, h) N j=1,j k Φ(x k, x j, 0). œ Î Ü P λ + m w(m) = (w 1 (m),..., w N (m)) T, m = 1,,..., N, õ#î Ü9n Î Î=Ð Î Ý» PÓ ß Ô Î Òí P ó ü öþöúî Ò ô ü Ð Î9Ð Î Ý Î=ó ÜÞü ö Ò ü o W Û H _n Î Ü n Î ôô ö ü xðï»ü Î Î=Ð Î o Ô ó ß Ü Ð ü u + m(α) ó ü öþöúî Ò ô üh Ð Üúü ó õîööþî=ô öúî Ò Î 3Ü Î È Ò o ühó Óü4r Ò ü ö λ + m u + m(arccos x) T N (x) u + m (α) cos Nα N k=1 N k=1 w k (m) (x x k )T N (x k), x = cos α, À } ( 1) N+k w k (m) sin[(k 1)π/(N)]. cos α + cos[(k 1)π/(N)] ÌÞ L Á 7 ÎyÐ 3Ü ö ü Ô óuî Î rœý» öþð õ Ó Î Ò x = cos α, ξ = cos τ Ð À Õ Ø À o ü ö λ + ; u + (α) c P ü õ Ò Î9ö Ý Î Ü9n PÜ ö ôð Ó"u ó üh Ý Î9ö Î 3ÜÒ Î9öúÐ Î Ò o ü ö Ü9n ÎÎ9Ð Î o Ô ó Ü Ð ü u + (α) ó9ó ü ö Ð iüþü {cos kα}, k = 0, 1,... Ü ö P #Ò o ü öþï Ò Ð 3ÜÞü.Ò Î=öÞÐÎ Ò!r Ð Ü n öúî Ò ô#îló Ü ÜÞü {T k (x)} Î üpü Ð u + (arccos x) = u(x) P Ž o Ü Î9ö ÒÞü ÏÎyÎ Ó Î=ÏÎ 3Üú ö u Ï P Ð ß ô Ô Ó»Ü Ð ü #Ò9 <r Î ü õ Ü6 Ð λ + u(x) = Bg[(x 1)u (x) + xu(x)] (v.p.) 1 π 1 _n Î Ó Ð Î ö ü ô#î=ö PÜÞü ö P Ð ÒB Î Î õ uü n ÎiÎ z Ô Ó Ð Üu _n Î9öúÎ;o ü öþî 1 [( Pu)(ξ) ( Pu)(x)](1 xξ)dξ 1 ξ (ξ x). W ~ W ý (Pu)(arccos x) = ( Pu)(x) ( Pu)(x) = (x 1)u (x) + xu (x) (a + Bg x)u(x) + Bm h 1 1 [u(ξ) u(x)]φ(x, ξ, 0) u(ξ)φ(x, ξ, h) 1 ξ dξ, W
309 É#¾iº µ # µ9ì½ Uº 6µ µ9ì W Ì 6º» ²±À» rn Î9öúÎ Φ(x, ξ, h) Ð Ò Î Î õ uà Ù #Ÿ Ð óuî Ú r Î n Ý Î 1 dξ (v.p.) 1 (ξ x) 1 ξ = 0, 1 (v.p.) 1 ÈÜ n Î üpü n Î9ö n 1 1 u(ξ) u(x) 1 ξ [( Pu)(ξ) ( Pu)(x)(1 xξ) 1 ξ (ξ x) 1 dξ = x 1 ( Pu)(ξ) ( Pu)(x) 1 ξ (ξ x) 1 + (1 x ( Pu)(ξ) ( Pu)(x) (ξ x)( Pu) (x) ) dξ. 1 1 ξ (ξ x) Φ(x, ξ, 0) dξ = 4xu (x) 1 u(ξ) u(x) (ξ x)u (x) + Φ(x, ξ, 0) dξ. 1 1 ξ +Ý» PÓÔ»Ü Ð À ý ØÀ PÜ Crn x k Ð ó n«öþî589î=ö ü Î Òíü o Ü9n Î fn Î=õ uò9n Î Ý ô ü Ó"u ü ÏÐ PÓ T N (x) Î Ý» PÓÔ»Ü Ð B PÓÓ# Î=öÞÐ Ý»»Ü Ð Ý Î Ò% ó9ó ü ö Ð Üúü Ü n Î Ð Î9öúÎ 3Ü Ð»Ü Ð üh Ï PÜ öúð#x P (1) N ô ôö ü xðï PÜ Ð Ð 3Ü Î ö PÓ Ò õ u'ü9n Î(o ühó Óü4r Ð z Ô H ö»üþô öþî`o ü öúï Ô Ó 1 1 f(ξ) 1 ξ dξ π N N f( cos[(j 1)π/(N)]), j=1 dξ À ÕLø r Î ü õ Üú Ð ÇÜ9n Î Î9Ð Î Ý» PÓÔ Î Î9Ð Î Ý Î=ó Üúü ö ô ö ü õ Ó Î9Ï o ü öï»ü öþðyx % A + ó n Î9Ð Î ß Ý Ó Ô N Î λ + ó ü öúöþî Ò ô ü # Ò+ÜúüÜ9n ÎÖÎ=Ð Î Ý ÎLó Üúü ö m w(m) mrn Ðó n n Ý Î Ü n Î ó ü ÏÇô ü Î 3ÜúÒ _n Î9öúÎ;o ü öþî o ü öúï Ô Ó Ò W } Ü Ð ü Ò= w k (m) u + m(arccos x k ), k = 1,..., N. N Äh 6»¾ º» ²±À» l Á B LÅ Å«µU±3µU L 6 9 W±À P ±³ ' µ6 U ²ÌÞº ÌÞ µ9¾ U»Ì ¾iº» ²Ì±À 6µ (A N + λ E N ) v = 0, v = (v 1, v,..., v N ) T, À ~ öþî ü õ Üú Ð Î l Ò Ü n Î œ~ ö P ÎyÐ 3Ü Î=öÞô ü Ó»ß u (α) µ6ºhå i ½¼ µí U A N = Bg ( {diag(zk 1)} () N + 3{diag z k} ) G N Q N, G N = 1 [ H N N {diag(z k 1)}( () N ) (N 7 ] ){diag z k} () N, Q N = {diag(zk 1)}( () N ) + [3 4Bm/(3h )]{diag z k } () N ( {diag Bg z k + a 1 4Bm h ) } + π N + 1 [ {diag s k } () N + M N À ÕHÕ ].
310 Ú PÛ Ì J± 1±ÀµU ² Ã=±Àµ9 ²± Ä µ6µ9ì6 s Î9öúÎ a Ð Ò ó Ó ó Ô Ó PÜ Î o½ö ü Ï ²Ú } ( kπ ) z k = cos, k = 1,,..., N N + 1 öúî 89Î=ö ü Î ÒBü o Ü n Î fn Î9õ uòpn Î Ý ô ühóyu ü ÏÇÐ PÓíü o Ü n Î Ò Î=ó ü Í Ð fn Î9õ uòpn Î ÝÈ Ð Î9öúÎ 3Ü Ð»Ü Ð üh Ï»Ü öþðyx r Ð Ü9n Î Ó Î9ÏÎ ḦÜ6Ò U N (x) () N Ð Ò H N P M N δ () kj = U N (z k) (z k z j )U N (z, if j k, δ() kk j) = U N (z k) U N (z k), öþî Ï»Ü öþð óuî Òfr Ð Ü9n Î Ó Î=ÏÇÎ 3ÜúÒ Ô ó Ü Ð ü h kj = 1 z j (z j z k ), if j k, h kk = z k 4(1 zk ) N + N + 3, 3 m kj = (1 z j )[Ψ(z k, z j, 0) Ψ(z k, z j, h)], if j k; N m kk = (1 z k)ψ(z k, z k, h) (1 zj )Ψ(z k, z j, h). Ψ Ð Ò Î Î HÒ j=1,j k ] Ψ(x, ξ, h) = g(x, ξ, h) [1 xξ + h 1/ + g(x, ξ, h), rn Î9öúÎ g(x, ξ, h) = [(ξ x) + (1 xξ)h + h 4 /4] 1/, s k = N j=1,j k (1 z j )(z j z k )Ψ(z k, z j, 0). s Î9öúÎ P λ m v(m) = (v 1 (m),..., v N (m)) T, m = 1,,..., N, öúî Ü9n ÎÖÎ=Ð Î Ý» PÓ ß Ô Î Ò P ó ü öúöþî Ò ô ü Ð Î=Ð Î Ý ÎLó Üúü ö Òíü o+ô ö ü õ Ó Î9Ï À Õ Õ _n Î ôô ö ü xðï»ü Ð ü.ü o Î9Ð Î o Ô ó Ü Ð üh u m (α) ó P õîööþî=ô öþî Ò Î 3Ü Î «Ò=à u m (arccos x) 1 x U N (x) rn Î9öúÎ z k = cos[kπ/(n + 1)] ü ö u m(α) sin (N + 1)α N + 1 N k=1 N k=1 v k (m) (x z k )U N (z k), x = cos α, À ÕLÚ ( 1) N+k+1 v k (m) sin[kπ/(n + 1)]. cos α + cos[kπ/(n + 1)] À ÕL ÌÞ L Á tª ô ö üü o ü o Ü9n Ð Ò ó Ò Î Ð Òí P Ó üh ühôò r Ð Ü nü9n Î"ó Ò Î ü ô Î Ý Î Î9Ð Î o Ô ó Ü Ð ü Ò= Óyu ü4r o ü ö λ P u (α) Ð W Õ W Ú r ÎÇÏ ÔÒEÜ ÔÒ Î Ü9n Î ÒÞÔ õ ÒEÜ Ð ÜÞÔÜ Ð üh Ò ü o Ý öþð õ Ó Î Ò W Õ9Û x = cos α, ξ = cos τ, u (α)/ sin α = v(cos α).
311 É#¾iº µ # µ9ì½ Uº 6µ µ9ì W Ì 6º» ²±À» ž ÒÁÜ Î H ü o Ü9n Î Ó Ð Î ö ü ô#î=ö PÜÞü ö P r Î ü õ Ü6 Ð Ü9n Î Ó Ð Î ö ü ô#î=ö PÜÞü ö Q rn Ð ó n Ð Òí Î ß Î õ u Î=z Ô PÓ Ð Üu (Pu )(α) = 1 x (Qv)(x) P # ÒÞÔ õ ÒEÜ Ð ÜÞÔ Ü Ð ü ÒW Õ9Û # Î9Ð Î o Ô ó Ü Ð üh Ò ó P õ#î"öþî=ô öþî Ò Î 3Ü Î õ u ö ô Ð Ó"u ó üh Ý Î9ö Î 3Ü Ò Î9öúÐ Î Ò r Ð Ü n öþî Ò ôî=ó ÜÜÞü {sin kα}, k = 1,,... Ÿ Ð óuî sin[(n + 1)x] = U n (x), n = 0, 1,..., sin x r Î ü õ Ü6 Ð W ÕLÚ ØW Õ= +õ uiôò Ð yòþô õ ÒEÜ Ð ÜÞÔÜ Ð üh Ò Ð À Õ À Ú Î Ý Ó Ô#»Ü Ð Ð Ü o ü ö 89Î9ö ü Î Ò ü o Ü9n Î fn Î9õ uòpn Î Ý ô ü Ó"u ü ÏÐ PÓˆü o Ü9n Î Ò Î=ó ü «Í Ð # U N (x) ž Ü Ð Ò Ð 'ó Ô Ó Ü%Üúü Î ÒEÜ ÐÏ»Ü Î Ü9n Î ü öúî Ü Ðó PÓÓyuyÜ9n Î Î9öúö ü ö ü o Ü n Î"ô öúî Ò Î 3Ü Î Ô ÏÎ9öúÐó PÓ ÏÇÎ Ü9n ü Ò= _n Î9öúÎ;o ü öþî 'r ÎíÑ Ô Î õ ühôüíü n ÎÎ9öúö ü ö Ò õ u ÏÎ P Ò ü o Ü9n Î`o ü ÓÓ ü4r Ð BÜríü ô ö ü ó9î Ô öúî Ò=à Õ _n Î ô ö ü õ Ó Î9Ï Ð Ò ÒÞü ÓÝ Î r Ð Ü9n Ð Î=öÞÎ 3Ü N Ú ž Ü9n Îó Ò Î Bg = 0 + Ô ÏÎ=öÞÐ ó Ó öþî ÒEÔ Ó ÜúÒÈ öúî.ó ü Ïô öþî r Ð Ü9n Ü n Î Î;x ó Ü ÒEüHÓ ÔÜ Ð üh 1à λ + m = λ m = m ϕ(m), u+ m (α) = C 1 cos mα, u m (α) = C sin mα, rn Î9öúÎ ϕ(m) = m 1 + 4Bm [ π/ sin[(m + 1)τ] sin[(m 1)τ)] dτ h sin τ + h /4 π/ sin mτ 0 sin τ ] dτ, Ú HÙ À Õ Ù À Õ } P C 1 C öúî öúõ Ð Ü ö ö u ó ü #ÒÁÜ6 P 3ÜúÒ= +ª_Ý» PÓ Ð Ð Üu ü o W ÕLÙ À Õ } ó õî Ý Î9öúÐ Î õ uèòeô õ ÒÁÜ Ð ÜúÔÜ Ð ü Ð 3ÜÞüÀ Õ ØW Ú Ib j')& g lpk*" + & Cj+e ü ö Ü9n Î+õöÞÎ Ý Ð Üu r ÎôöÞÎ Ò Î ḦÜ1üH Ó"u Ô ÏÎ9öúÐ ó PÓH ô ô ö ü xð Ï PÜ Ð ü Òü o Ü n Î+Î9Ð Î Ý Ó Ô Î Òˆü o Ü9n Î Ò ô#îló Ü ö PÓ ô ö ü õ Ó Î=Ï WÚ ý ØWÚ Õ=ø û Ô ÏÇÎ=öÞÐ ó Ó ÏÇÎ Ü9n ü Ò Ð Ý Î Ð «Ü9n Î ô öúî Ý Ð ü ÔÒ Ò ÎLó Ü Ð ü l PÓÓü4rŒÔÒÜÞü ó ü Ïô ÔÜ Î Ü n Îió ü öþöúî Ò ô üh Ð Î=Ð Î o Ô ó Ü Ð üh ÒÖ PÓ ÒEü. P # Ü n Î ÜÞü ó PÓ ó ÔÓ PÜ Î Ü n Î ÒEüHÓ Ô Ü Ð ü ü o WÚ Õ Ø WÚ Ù õ u Ï P Ðô Ô Ó»Ü Ð üh Ò Üu ôðó PÓÓyu.ÔÒ Î o ü ö Ü9n Î ü Ô öúð Î=ö ÏÇÎ Ü9n ü ˆ ž o Bm = Bg = 0 Ü9n Î Ð Ü o ü ÓÓü4r Ò o½ö ü Ï À Õ } Ü9n PÜ λ + m = λ m = m(m 1), m 1. _n Î ô öúî Ò Î 3Ü Î Ç 3Ô ÏÇÎ=öÞÐ ó Ó "Î Î Î9ö»Ü Î»Ü öþðyx +ÏÎ Ü9nü 1rn Ð ó n Ð Ò õ Ò Î Çü ü Òú»ÜúÔ ö»ü Î È ô ô ö ü xðï»ü Ð üh Ò%ü o Î=Ð Î o Ô ó Ü Ð üh Ò_r Ð Ü n fn Î9õ uòpn Î Ý ô ü Ó"u ü ÏÐ PÓ Ò9 Ð Ý Î Ò Î x ó Ü öúî ÒÞÔ Ó Ü6Ò Ð Ü n Ð Ò ó Ò Î ü3ò Ð Ü Ð Ý Î Î9Ð Î 3Ý» Ó Ô Î Ò«öÞÎ Ü9n ÎŽÏ ühòeü Ð 3Ü Î=öÞÎ ÒÁÜ Ð o ü ö ôô Ó Ð ó PÜ Ð ü Ò Ò Ð ó9î Ü n Î Ð ÒEÜú õ Ð Ó Ð Üu Ð RÜ9n ÎlÐ 3Ü Î9ö9o ó9î <u ÏÐó Ò«ü o Ü9n ÎŽöúÐ Ò Ð 3 Ò õ Ô õ õ Ó ÎËó Î Ý Î Ó ü ô
312 Ú } Ì J± 1±ÀµU ² Ã=±Àµ9 ²± Ä µ6µ9ì6 Q GO$ C G *LC F8=K & C L LH 75 8=J ; H 75 Q?=J " Bg = 0, Bm = 5, h = 1, /+DHGJ>ÞD K; C =$EK=GJF C " H½S 5 Q V J K=F $ÁD C_FG ÖC $ÁD, /+G$ÁD N = 0 K=F N = 80. N = 0 N = 80 m (3.16) λ + m λ m λ + m λ m Q?5?L?=?L?=??5?=?L?L?=??5?=?L?=?L??5?L?L?=?L??5?L?=?L?L? 7 Q 5 : S :9@LV Q 5 : S :9@LV Q 5 : S :U@ V Q 5 : S :U@ V Q 5 : S :9@ V S T²75 :=?=8L< S T²75 :9?L8L< S T²745 :9?L8=< S T 745 :=?L8=< S T²75 :=?=8L< T 7 Q 5 T²7 Q 5 VL<=?]T²7 Q 5 T²7 Q 5 V=VL<]T²7 Q 5 T²V=?5 : Q <L8L: TWVL?5 :=7 QLQ 8]TWVL?5 :=7L7=: Q TWVL?5 : Q <=8L8]TWV=?5 : Q <L8L8 V"T Q 7985 QLQ :9@=@ŒT Q 7=85 Q 7L7 Q 8 T Q 7=85 Q 7=VL:L: T Q 7985 QLQ :9@ V T Q 7985 QLQ :9@L8 : T²7L79<5 :=VL: Q 8uT²7=7=<5 :98L? Q < T 7=7=<5 :9<L?=<L?}T²7L79<5 :=VL:L7 S T²7L79<5 :=VL:L7=: 8"T S : Q 5 < Q?=VuT S : Q 5 <=8 Q? S T S :L745?=? 7U@ T S : Q 5 < QLQ :T S : Q 5 < Q 7 <"T V=?5 8LVL:9@ Q T VL?5 <=V :L7 S T VL?5 8L: Q?LV}T V=?5 8LVL:=V=@ÖT V=?5 8LVL:L:98 Q? TW8L?L75 VLV S <L: TW8=? 75 :=:=8 :T²8=? @»798=@ TW8L?L75 VLV9@ S < TW8L?L75 VLV9@ V9@ ü ó ü öúöúî Ò ô üh Ð Î=Ð Î o ü öþï Ò= % Ü n Î üpü n Î9ö n ˆ Î ó n Î9Ð Î 3Ý» Ó Ô Î õî=ó ü ÏÎ Ò ô ü3ò Ð Ü Ð Ý Î!o ü ö ÒÞÔ 'óuðî ÓyuÓ ö Î Ý» PÓÔ Î ü o Bm _n Ð Ò ó üh ó ÓÔÒ Ð üh o ü ÓÓ ü4r Ò o½ö ü Ï W Õ } ž B c õ Ó Î Õfr Îíô öþî Ò Î 3Ü~Ü9n Î ö ÒEÜcÜ Î Î=Ð Î Ý» PÓÔ Î Ò~ü o Ü n Î ô ö ü õ Ó Î9Ï WÚ ý Ø ²Ú Õ=ø Bg = 0, Bm = 5, h = 1 rn Ð ó në öúîçó PÓ ó Ô Ó»Ü Î õ u À Õ } P ÏÎ Ü n ü Ò r Ð Ü nèü ö Î=ö Ò%ü o Ü n Î Ï PÜ öúðó9î Ò N = 0, N = 80 Hª ÒEr Î Ò Î=Î3Ü9n ÎÏ xðï Ó öúî Ó»Ü Ð Ý Î Î9öúö ü ö ü o Ü n Î Î9Ð Î Ý» PÓÔ Î Ò ó PÓ ó Ô Ó»Ü Î õ u ÏÎ Ü n ü Ð ÒBü o Ü9n Î ü ö Î=ö 10 4 o ü ö N = 0 P 10 6 o ü ö N = 80 Q GO$ C G *=C F8LK & C )?H J ; H 75 Q?=J { Bg = Bm = 5, h = 1, /+DHGJ>ÞDiK; C =$EK=GJF C >FG ÖC $ÁD, /+G$ÁD N = 0, N = 40 K9F N = 80. N = 0 N = 40 N = 80 m λ + m λ m λ + m λ m λ + m λ m Q Q 5? 7=:=8L8 Q 5? 7=:=8 S Q 5?L7L:=8=8 Q 5? 7L:98 : Q 5? 7=:=8L8 Q 5? 7=:=8=8 7 Q?5 :=? Q?5 :9? QLQ 7 Q?5 :9? Q?L< Q?5 :=? Q?L< Q?5 :=? Q?L< Q?5 :=? Q?=< S TÀ@'5 8 SPQ 8 S TÀ@'5 8 SPQ < Q TÀ@'5 8 S Q :9< TÀ@5 8 S Q 8L? TW@5 8 S Q :=< TÀ@'5 8 SPQ 7=75 QLQ6S 8=8]T²7L75 Q=QS 7 Q T²7L745 QLQS 7 S T²7=75 QLQ6S Q <qt 7=75 QLQ6S Q < TWV Q 5 S :)T²V Q 5 Q TWV Q 5 Q 5 TWV Q 5 <LVqT²V Q 5 <=V V"T Q 7985 SLS=S V=<ÖT Q 7=85 S=S 8 S < T Q 7=85 S 7=< Q? T Q 7=85 S 7=< S < T Q 7985 S 798L8 7T Q 7985 S 798L89@ : T²7L79<5 8L<9@ <9@ T²7=7=<5 <=? :9V T 7=7=<5 8=8 8L8 S 7 Q T²7L79<5 8L8 Q :=< T²7L79<5 8L8 Q 8 S 8"T S :=75?=@LVLV T S :L75?=VL8 Q < T S :L745? Q 8L79@ÖT S :L745? Q < < T S :=75? Q V T S :=75? Q VLV S <"T V=?5 <LVL:L7 Q T V Q 5?=V 8=< T VL?5 <=?L< S 7T VL?5 < QLQ : S T V=?5 <L? 8L< T V=?5 <L?=VL? S Q?"TW8L?L75 8L? Q 79<ÖTW8=? 75 8=V V=< T²8=? 745 V=< 745 VL< : Q TW8L?L75 VL8=V :=V TW8L?L75 VL8L:=? Q ž Ž õ Ó Î Ú r Îô öúî Ò Î 3Ü Ü9n Î ö ÒEÜÖÜ Î Î9Ð Î Ý» PÓÔ Î Ò ü o ü o Ü n Îiô ö ü õ Ó Î9Ï WÚ ý Ø WÚ Õ=ø Bg = 5, Bm = 1, h = 1 rn Ðó n öþî'ó PÓ ó Ô Ó»Ü Î õ uü n Î 5 ÏÎ Ü9nü r Ð Ü n ü ö Î9ö Ò ü o Ü9n ÎÖÏ»Ü öþð óuî Ò N = 0, N = 40 N = 80 # íü Ïô öúð öúî ÒÞÔ Ó ÜúÒ ü õ Ü6 Ð Î o ü ö λ P + λ mr Î Ò Î9Î Ü9n#»Ü Ü9n Î ó=ó Ô ö ó u o ü ö N = 0 P N = 80 Ð Ò Ü9n Î Òú ÏÎ Ò Ð Ü9n Î õ Ó Î Õ o ü ö Bg = 0
313 É#¾iº µ # µ9ì½ Uº 6µ µ9ì W Ì 6º» ²±À» Ú,~ Bm W Q Bg = 3 5 ía D C >&8 C > $ÁD C 0 O$ 0 8 CiC G *LC F8=K & λ = λ(bm) " ž Ð Ô öúî ÕÜ9n Î Î9ôÎ Î óuî ü o Ü9n Î ö ÒEÜ Ý ÎiÎ=Ð Î Ý» PÓÔ Î Ò üh Ü n ÎiÏ P H Î Ü Ðó íüh «3Ô ÏBõÎ9ö Bm Ð Ò Ò9n ü4r n Î9öúÎ Bg = 3 _b h)d!k +9j Clh)d _n Î Ï»Ü9n Î9Ï»Ü Ðó PÓ Ï ü Î Ó o ü ö Ü9n Î mu3 # ÏÐó Òiü o Ü9n Î H Ò õ Ô õ õ Ó Î öþð Ò Ð Ð ŠÜ n Î Ý Î9ö Ü Ð ó Ó s Î Ó Î ßŸCn# r óuî Ó Ó Ó Ó Î r Ð Ü9n Ï P H Î Ü Ðó Ó Ð"z Ô Ð Ð Ò o ü öþï Ô Ó»Ü Î «HÒ Ò ôî=ó Ü ö PÓ ô ö ü õ Ó Î9Ï o ü ö Ü9n Î Ó Ð Î öið 3Ü Î ö üpß Ð Î=öÞÎ ḦÜ Ð Ó ü ôî9ö»üþü ö r Ð Ü n ô#î=öþð ü Ðó.õ ü Ô ö u ó ü # Ð Ü Ð üh Ò= H _n Î ü õ Üú Ð Î iò ô#îló Ü ö PÓ ô ö ü õ Ó Î9Ï Ð ÒíÒEüHÓ Ý Î õ ubü n Î Î Î Î9ö»Ü Î»Ü öþð ß óuî Ò ÏÎ Ü n ü Ò9Zrn Ð ó n öþîyó ü #ÒÁÜ ö Ô ó Ü Î õ u.ôò Ð Ð Î9öúÎ 3Ü Ð PÜ Ð ü Ï»Ü öþð óuî Ò o ü ö Ü n Î œ~ P ö Ϋô ö ü ÑÁÎ=ó ÜÞü ö r Ð Ü9nR fn Î=õ uò9n Î ÝË ü Î Ò= + _n Î ó=ó Ô ö ó uëü o 3Ô ÏÇÎ=öÞÐ ó Ó ó PÓ ß ó Ô Ó»Ü Ð üh Ò ó P õî ó ü 3Ü ö ü ÓÓ Î Î HÒ Ð Ó"u õ ulý» ö u Ð Ü n Î ü ö Î9ö N ü o Ð Î=öÞÎ 3Ü Ð»Ü Ð ü Ï PÜ öúðó9î Ò= Î ÒÞÔ Ó ÜúÒ ü o Ô ÏÎ=öÞÐ ó Ó Î;xô#Î=öÞÐÏÎ 3ÜúÒ" öúîôöþî Ò Î ḦÜ Î P «Ü n Î u ô ö ü»ý Î Ü n Î Î 'óuðî ó u'ü o Ü9n Î Î Ý Î Óü ôî ÏÇÎ Ü9n ü ˆ &(0& g%& d!k*& Q F:5 C F'G =F 5 N$EK HG G$ 8PG> &, 0 F *=C ÁGJF *'5 "!#$"%'& ] (( H 7=J ] Q6S? 7 ; Q6S?L8 ] Q <L8LV5 7 F:5) C F'G =F ])* 5 +Z5-, K K=F, A ] N 5 * G K9F * ] f5 M 5 NPD'EK=G K9F K=F Df51A K9F *'5. G>=&' / ;/L+GJFM$6/ G ÖC F,GLF' 50 "!#$"% #9:";"<=>?@ ]BAC J ] <L:L:";B<=<L< ] Q <=8LV5 S 5D0DC C 5 Ff F3K GJ> K * F C $ O$EK $ÁGJ> GJF,O$EK HG G$ÁG C 5E6F#GH<IKJ@<BHMLN9H;O#9H@P <HQRTS ] IU H 7=J ] S ; Q ] Q <L8 Q 5 H³GJFWVf&'%G K9F 54D0DC C 5 OE& ÖC ÁGJ>K CXC ÁG ÖC F4$ =F:$ÁD C C G F * <$ÁD C ÁGGJF *,&', C Z$E$ÁD C %&%³K=> C GJFÈK>8 C %$ÁGJ>K / K $ K»C _ K * F C $ÁG > G#3&HG 5Y6F#GH<IKJ@<BHZLN9;[#9HK<HQR\S ] ] VLV ;y:=7 ] Q <L8 5 H³GJF=Vf&'%G K=F J 5 DND C C 5 OE& ÖC ÁG >6K G & K $ÁGLF N K A K=F ;PA K GJF'O$EK 3G G$ K * F C $ÁG C G#34&3G 506F]GH<^KJ@<H_ LN9H;O#9HK<HQRTS ] ( H Q J ] Q6S ; Q < ] Q <L8L:5 H³G FWVf&'%G K=F J V 5 DND C C 1K=F M 5;F ÁGJIPG# 5 * K ÁG F4$ÁDHG F C1 K $%$ C ÁFI{ K $ÁGLF"GJF K * F C $ÁG > Gy34&HG 5 `'5 5 V) ÁG * & C M 5 $ÁDK9FK8LK LF' ]Ia 5,G K=I4EK=IPG8mHb m5 J ]^c ;[edhf<b9h;"hg^;[_d]\"qi]j J ^ [H;?WH<B9k"g_g HJ@H<Ip5<D DK, K=F D. K Tl D V D ] ; S 8 ] Q <=<L<5
314 Ú ý Ì J± 1±ÀµU ² Ã=±Àµ9 ²± Ä µ6µ9ì6 : 51DND C C ÖK9F G 5 G 5 G K9G ;8 5 G K * F C $=O$EK;$ÁG >igjf'o$ek 3G G$ÁG C ÖGJF K9F C K»C ( K * F C $ÁG#6K C / &HG 5 6F]GH<^KJ@<H_ LN9H;O#9HK<HQR ] H Q J ] 7L:È; S ] Q <=8L?5 H³GJF V)&,%G K=F J 8 AE5NDD & G 5 OE=F,ÁK;$&'EK $ C K ' X G K $ÁGLF7 ÖC K=F'_ * K * EK=F *LC GJF4$ C K $ÁG=F 5 0;[#?9K<GHeO47J I HJ@!#@H< &_9:"QikO4 B"<B?" BJ@@H< ] 8 & ÖC 7 ] 7 ;y7u@l@ ] Q <=<L85 < AE5 DD & GBK=F `5 * G C $&'8PG C $ÁG# 5, GJ>K;$ÁGLF FG GÇC $ÁD, { C `/+G$ÁD K %$ÁG K GA C C F4$ÁG K C 34&3K $ÁGLF' 576FHJ ^ "Q HJ@ 6F#9: K<GkH<B9 &<? ] U H 7=J ] Q < Q ;y79?l? ] 7=?=? 745 Q? 5 `5;F C a C* ÁG K K=F * 5 5 N >ED4/K %$ 5 < &3F K PT GJF4$ C* EK ÖC $ÁD, " Z$6/ T DK C G# K=> CÖC F$íGJF. C CúT NPDK/ > C 5Hf;?<B154 c f9 6Z [?IH<^@ ] ] S 8 S ;B@?=? ] Q <L8LV5 Q=QÖM 5 F ÁGJIPGcK9F 54D0DC C 5. G>=&' 0 F *=C ÁGJF * GJF K * F C $ÁGJ> / F& ÖC ÁGJ>K G & K T $ÁGLFK EK G K. C CúT N D3K/ / / 5f ;?<BH-O4h68#GH< "J@KQ H<B9 6F#GH< "J@@e6FHJ ";? ] ] S=S < ; ] Q <=<L<5 Q 7 Df5 K ÖC F$ ]a 5 + K=>6G$%$ ] `5 T Df5 K9> ÁG ] M 5 F ÁGJIPGÖK=F 5 DND C C 5. G#> =&, 0 F *=C ÁGJF * GJFÈK K * F C $ÁGJ> / &3G 5 V K G K.íC CúT N D3K/ / / 5e>iO4 c f9h ] H Q? J ] 7U@ V9@ ; 7U@»:L7 ] Q <L<L<5 Q6S F:5 5, C % C ík=f >.`5 * C 8PG F C=5ˆA D C Z$ÁD C NHK A K9F ; A K 0 F *=C K $%$ C ÁF 5 Q 5 >?@?H "!#$"%'& ]B(( ] 7=V 7 Q ;y7=v SLS ] Q <=8LV5 b 5<GÇC G#'&' * K9F a 5.!5C. 45 OE=F GJF C K;E&HF,O$EK C 8PG>=&' 0 F *LC %GJF.íC CúT N D3K/ / ;/L 575 OE& ÖC ÁGJ>K G & K;$ÁGLF 50>eO4 c f9h ]B( H½S J S < ] Q <L8=85 Q a 5 + K9>6G$%$ ] Df5 K ÖC F$ K=F `'5 Df5 K=> ÁG 5h. G>=&' 0 F *LC ÁGJF * GJFÈK K * F C $ÁGJ> / &3G m5 745 * G F C K.íC CúT N D,/ / / 5N>HhO4 c ] ( H QLQ J ] S Q <LV ; S 7=? S ] 79?L? Q 5 Q V +Z5 a 5 NHK A K9F K=F a 59A K 5 A D C C F C $%EK $ÁGLF! 3K / &3G G F4$íK =&' ÖC G&.íC CúT N DK/Ž> C >LF4$EK=GJFHG F * K C 8PG>=&' G#3&HG 5 N;O# H # & ] 8 & ÖC 7U@ ] S Q 7"; S 79< ] Q < 85 Q : +Z5 A K C GJF * ]ia 5»>6>ÞDHGÖK=F 5 * G>EDK C 5 F CXC ÁG ÖC F4$EK O$& >$ÁD C N K A K=F TWA K +GJF'O$EK 3G G$ 45Hf;?<B)O4 c H<^ ] IUU ] V :";B8L7 ] Q <=8 :5 Q 8 BN 5A K9F8 C6C 5 N&' ÁG C GJF 8PG> &, 0 F *LC ÁGJF *5Hf;"<NO4 c f9w6z [?IH<I ] ] 7=: S ; S?L8 ] 7=?=?L?5 Q < a 53A K K9F W+ 5 a 5 NHK A K9F 5 F' $ C =FM$ÁD C_ $ÁGLF,&', C +GJFK.íC CúT N D3K/ > C # K9F K &, ÖC G& 5 NfIH;?J! "Hf;?<# -6F? 0H<B9 &Ng_g $ [9 6FHJ ] H½S J ] 7=V ;y7=:=< ] Q < <5 $R W V&% ' "W)(# Y* +, + X).- /* 0,_X).- *Z /1 ' QW3# 41 "V5 Q76RQ Q8:9<; T 4= Y 8 3 Q > Q?5 QA@h + %) X SB3VC5QD* #- Q3# Y?1mS ' Q /1 * VF- VCWG*.- K H* #- Q3#.- K <1 AE5CD G& G ] `5 * G C $&'8 G C $ÁG ]C 5,D C C F &GIO& J,,&,& ] I & K9FK6G8 C %$ÁG I=K GML.íC CúT N DK/ L O$ C 0N &O G K=FK6G& K * F C $ÁGJFHG#&:I PK6G& ] K8 GRQG K &' GJF3K GJI = K $ C K $ÁGJF3G C G EK %&'{ & &' $EK ÇI=K=G C I4$%ÁG FHGM&O T K8 GJF :$EK $ÁGJI4EK $ÁG C G FHG K C EK $ ÁG&HGE%& C ÁG# GJFTS C G I4EKGQO$ÁGJFTS C G+RL '* G 5 + K O$EK EK G#f&O K8 GJF EKG0Q% N O$EK fi=k=g$ ÖC FHG0QILK9GG0Q%G * G O$EK9FK6G&MJ K $%ÁGJ>& J ÖC $ & 5
315 z!"# $ % '&)($ +*,.-/10 3 -/546 "798:8;=< >7? 7A@A@ABDCE?GF3HJILK:M"NO3O=P >6<:8:7RQTS UWV XZY\[ ]WU^Ù _ba5vdc Ù e f ehgi[j[ XkYla5V ema5_bn fox XkY\[ pzg^[rqs[tvd]u[ Ù e XkY\[ vwfxv yl[tg fxf^_mq{emuwgi]u[rq ~}# ƒ. D 1 }ˆŠ " Œ " D Š Ž } Š 3 1 T šdœž Ÿ š9 s œg " D = T œ= 5ª" 6 «JšR ~ œg 5 9 šr 5 šr Dœž š9 ± ² ³ Jµ= ¹ ¹ ºJº=»»¼=º ƒ ½ ¾À 5 Á9 µ=³ ²¾ ÃÄ Å µ ½ Â Æ ÇÈ É:Ê5Ë#ÌRÊ"Í ÎÏÐÑ:Ò ÓJÔÕÍ Î3Ö ~š Ø ± š9 Œœž Ÿš6 6 # 6ÙÛÚš6 6 6 = ÜÝ # Þ š9±6 T sß àœžáõ ÙÕâR± 6 äã œ Þ «Þ º å #æàµ= J ~ç%èž²¾gé µ=ê#µ= 5 ¾GéÀ³ } ë3»»» +Â ì ½ 5 ²  Jµ ³ ½ µ ÃÄ Å µ ½  ÆàÐ Ô Ï=ÎÏJí ÉJîÏË ïéjô Ê5ÏÌ ðñí6ò ÉAÊôó Ð É ÒàÌ=Ï3ËJÔ3õàÑ:öð3ÉJî Ì:îÕÍ Î3Ç 3 ~š Ø ± š9 Œœž ª Ø Ø5 L š6«sÿ š9 s = «'Ÿœ:«š9 L ø ÙÛÜŠ Þ šr±6 œž "㜠œ Þ «Þ º ë ˆÝù µ ³ ¾ Á 1 ¾GéÀ³ } ëj»»j» %Â ì ½ 5 ²  3µ=³ ½ µ ÃÄ Å µ ½  Æð=õÎ3öÉ öë õð òòñí ö3õœížïò Ï3 ÕÍTÎÇ ôáaú9á9½ Á ì ² ²¾Gé"û ¹J º»» ëü³ Á ½ ¾ Á ìäý Á Å ê Á ³ ¹J¹ º=»J»=ë þ'ÿ C F E? ILH ÕM~F E6E žf3ilh=i?!#" M$%GMA?GF E'& ('M) E?*GMAH M$?* &JE +,GM " E I?*:HI & E E'& -C F E." I#+3H &JE žf E MA?/žI#AH0?M 1JI# M$%"MAH & AMAH &JE +3 M:M, ž? E M9H & I45"6" E %žil?07+i8žf E %1 E?*9( M:" I && E 1 MAH E -C F E AH Ē Q;& I" E HI:HM à?m E <žf E? % E %1=AH & I H'H:H Q 5GM ži:h3m % H:HLILH E M >žf E ("6 ;& HM " IL?61(? E "ii% E'& H" E žil?m 8)?~M>HJI E0& I8@ E E H3? E?ÀF E " E-C F E H" E žil?m + E %(AB <žf E."CFM 1 ED AH:I8( & ILHM + E #? I;DMAH & E "61 E GM ( E M E?GM9I H E'&, & I@ E E HFE E JH & ŠH">? E ( D & I" E HI:H E %AGŒM "ÛM9K E +?AH5GM9H(%M9H & GM & I M žiahh">? E ( - H:IJLK!M.N OQPR? ILH6 Q#"6 D3H3I8 EÀ;& I8@ E E H3? E " E žf &SD "ÛM$žF E "ÛM$žIL?M S"6 &JE #LILH TFU:VW<X.Y Z9[\!]^XS_(Z<W ˆ9` Á ú ½ a é `½  ½Bb ² ½ ìdc  Š¾ ½ ¾ ½ Åfe J³Gé6µ= 3é ì² ³ ½ ~¾À Å Á e ³À ú9á ¾ ¾ Á ¾9 Á } } J Ä ½ ¾À =é ` Á ³ Å µ  c  Šìsg3 #µ Å ½ú ¾9 ih ` Á bé ` Á é Á Åfe Á ³ µ=éಠ³ Á ì ½ ¾žé ³ ½ ê ²é ½ J ½ =j#² Á ú9á ¾ é ` Á  ½Bb ² ½ ìkc  Åle ` g¾ ½ ú µ  e ³ e Á ³Àé ½Á ¾A ÂÁ µjì ½ éà ƒ µ ³ µ J ½"ú J ÁAú é ½ 1 ³ e ` µj¾ Á ú` µ= Á ¾ e ³ úrá ¾ ¾ Á ¾A h `Á äé ` Á ½Bb ² ½ ìmc  Š¾À ½ ì ½ c Á ¾6n µj¾ôì ½ ¾ ú ²#¾À¾ Á ì ½ pol¼3 qrts } u aé ` Á c  Š½ ¾ Á ³/g é ` ½ vn ½ é ¾'é ` ½ ú Á ¾ ¾ ½ ¾ ÂÁ ¾ ¾é ` µ= é ` Á ú ³ ½ é ½ ú µ  é ` ½ ú Á ¾ ¾ m s ½ é ú µ= ³ ² e éಳ Á ² ì Á ³Ýé `Á µ ú é ½ aé ` ÁÕ½ 3é Á ³ Å Â Á:ú ²  µ=³ µ=égé ³ µ ú é ½ Á µ ì Á ³w µ µ  ¾0a ³ úrá ¾xo ë Qyr }5ˆ9` ÁD µ éàé Á ³!a J³ ú9á ¾ ` µ Á ì Á ¾žé6µ=ê ½Â½ ùa½ Á$z5ÁAú é.é ` Á
316 û»» ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ é ` ½ )c  Šì=g µ Å ½ ú ¾ } u o ëré ` ÁôÁ$z5ÁAú é+ a# µ ³/g ½ "é ` Á Å µ= ½ é ²ì Á a5 µ= ì Á ³ w µ µ  ¾ a ³ úrá ¾xn é ` ³À J² ` é `Á ì ½ Å Á ¾ ½ J  Á ¾À¾"µ Å µ Á ³ ú ¾Gé µ 3é A sô J é ` Á ì³6µ ½ µ Á µ= ì ³À² e éಠ³ Á aàµûé ` ½ a ³ Á9Á c  Š½ ¾Õ¾GéÀ²#ì ½ Á ì } u é ½ ¾Õ¾ ` hô é ` µ é ½ a A = 0.01 µ= ì Re = 1 é ` Á é ` Á µ=.ì Á ³4w µ µ  ¾ a J³ ú9á ½ ¾ Á éà³ Á Å ÁA gdh Á µ 'µ= ì ~³À² e éಠ³ Á ú9ú ²³ ¾A =h ` ½Â Á a ³ ` ½ ` Á ³ô µ  ² Á ¾Œ a A µ ì Re é ` Á ³À² e éಠ³ Á ½ ¾ ê¾ Á ³ Á ì } u é ½ ¾Õµ  ¾À ½ 3é Á ³ Á ¾Gé ½ éà Á µ Å ½ Á!` hmé ` Á ¾ Á"½ 3é Á ³ Å ÂÁAú ²  µ=³%µ=égéà³6µ ú é ½ Á a J³ ú9á ¾ ½ =j#² Á ú9á é `Ád` Á µ=édµ= ì ³ Å µj¾à¾ é ³ µ ¾ a Á ³ } u o ¹:» r%é ` Á º=ç Á  ² é ½ Á b ²µ=é ½ ¾ a µ e  µ µ=³<c  Šì=g µ Å ½ ú ¾%µ ì ¾À² ³/a µ ú é µ= 3éÕì ½ ¾GéÀ³ ½ ê²é ½ äµ=³ Á ¾žé ²ì ½Á ì 3² Å Á ³ ½ ú µ   g ½ µ ú µ ¾ Á aaa ³ ÁAÁ é ` ½ c  Š¾ µ= ìlc  Š¾A ú 3µ é ½ ä¾g  ½ ì¾à² ³/a µ úrá ¾ }àˆ9` Á ¾À² ³ a µ ú é6µ= 3é ¾ µ=³ Á a J² ìéà.µ ú9ú ² Å ²  µ=é Á µ éé ` Á é `½ú Á ³ e µ=³àé a%é ` Á c  Š¾ µ ìé ê³ Á µ= ² e µ é é ` Á ³À² e éಠ³ ÁDù Á ¾ }ˆ9` ½ ¾ ³ Á ¾À² Â é ½ ¾ ú =c#³ Å Á ì ½ o¹$rµ ¾µ ¾ e ÁAúR½ µ Âñú µj¾ Á aõµ Å J³ Á Á Á ³6µ  û ç Å ì Á9 a ú ² ³ ½Â½ Á µ=³!a ³ ÁAÁ c  Šì=g µ Å ½ ú ¾ µ ì¾à² ³/a µ ú é6µ= 3é ¾"éÀ³6µ= #¾(a Á ³ } ˆ9` Á a  h ½ ¾ e ÁAú9½ µ  ú µj¾ Á ¾Ý a e ³6µ ú é ½ ú µ Â3½ 3é Á ³ Á ¾žé+µ=³ Á µ  ¾G ì ½ ¾ ú ²¾ ¾ Á ì ½ mo¹$r Æ=úR J¾ Á ì ¾ e `Á ³ ½ú µ Â ê ² ê ê  Á ¾9 ½ =c ½ é Á ú g ½ ì³ ½ú µ  c  Š¾µ ì ú µ é Á ½ ì ¾ } u mo¹ ¹'ré ` Á ì=g µ Å ½ ú ¾ aàµ>c  Ša J³ Å Á ì ê Á é(h Á9Á Dé(h Û¾À² ³ a µ ú é6µ= 3é Ä ú 3µ é Á ìûì³ e ¾µ ese ³ Jµ ú` ½ Á µ ú` =é `Á ³ µ é ú #¾žé6µ= 3éä Á9 úr½ é(g ½ ¾ ¾GéÀ²ì ½ Á ìjê.gw²¾ ½ é ` Á  ² ê ³ ½ ú µ é ½ J té ` Á J³/gJ h `Á té ` Á µ ì Á ³wbµJµ  ¾9a ³ úrá ¾ µ=³ Á é µ Á ½ 3éÀ µ ú9ú ² 3é } u é ½ ¾ e ³ Á ì é ` µ é"é ` Á ¾G² ³/a µ ú é µ Jé ú úrá 3é ³ µ=é ½ ì Á e ÂÁ é Á ¾ ½ é ` Á c  Šì³6µ ½ µ Á ³ Á ½ ¾ } ³ Á ½ J²¾ µ= µ  g¾ ½ ¾ ` µ Á é6µ= Á ½ 3éÀ µ ú9ú J² 3é J  gì=g µ Å ½ ú ¾ µ ì ¾G² ³/a µ ú é µ Jé éà³6µ= ¾ a Á ³: h ` ½ ÂÁ é ` Á` Á µ é~éà³6µ= ¾ a Á ³ ½ é ` ½ c  Š¾ ` µ ¾~ê Á9Á e ³  g ½ Á ¾Gé ½ Jµ=é Á ì o ¼ 9qr } ˆ9` Á ¾À ½ ì ½ c ú µ é ½ j a µ a ³ ÁAÁ é ` ½ c  Š½ rµ é ` Á ³ Å J¾Gé µ=é ½ ú µ ese ³ Jµ úẁ½ ¾ ú #¾ ½ ì Á ³ Á ì ½ o qr }3ˆ9` Á ûjç e ³ ê ÂÁ Å ½ ¾%³ Á ì² ú9á ì~éà µûº=ç ú ² 3é Á ³ e µ=³àé+ê Á:ú µ ²¾ Á é ` Á c  Š½ ¾ úrâ J¾ Á éà ~µ6a ³ Á9Á  ½Bb ² ½ ì ¾À ½ ìs¾ ` Á9ÂÂ Ä Â½ Á ê ì=gfh ½ é ` µ=³ ½ µ ê ÂÁ ¾ Å µ   é ` ½ ú Á ¾ ¾ ¾ g ÅÅ Á éà³ ½ ú é 'µ Å ½ ì ì ÂÁ e  µ= ÁJ} ˆ9` Áú ² ³ ³ Á 3édhÕ J³À ½ ¾'µ Á é Á ¾ ½ a e µ e Á ³ ¾Lo û +ër ` Á ³ Á h Á ½ ú ³ e ³6µ é Á é ` Á:` Á µ=é"éà³6µ= #¾(a Á ³ ½ Jé sé `Á ¾/g¾Gé Á Å ì Á ¾ ú ³ ½ ê ½ 'é ` Á ì=g µ Å ½ ú ¾ a%µfa ³ Á9Á é ` ½ c  Šµ égé6µ ú` Á ìé µ.³ Á:ú é6µ= J²  µ ³>a ³ µ Å Á ¾À² ³ ³À J² ì Á ìê.gbµ= µ Å ê ½ Á JéÛ 3µ ¾ }1ˆ9` Á c  Š½ ¾ µ ¾ ¾G² Å Á ìéà ê Á½ ½ é ½ µ   g ` =霵= ì ½ é ½ ¾ ú ÂÁ ì'êg ú ì² ú é ½ ú Á:ú é ½ 'µ ìs³6µ Ä ì ½ µ=é ½ h ½ é ` é ` ÁÛú  ì Á ³ôµ Å ê ½ Á 3éŒ 3µ ¾ }ˆ9` Á c  Š½ ¾Œ² #ì Á ³Œé ` Á µ ú é ½ a ú µ e ½Â  µ=³*g µ= ìb µ= ì Á ³6wbµJµ  ¾ a ³ úrá ¾ µ= ì ½ ¾D¾ g ÅÅ Á éà³ ½ ú h ½ é ` ³ Á ¾ e ÁAú é é µ Å ½ ì ì ÂÁ e  µ= Á } ˆ9` Á Å ì Á9Â#½ ¾ÕêµJ¾ Á ì é `Á"Á J  ²é ½ #µ=³*gd¾ g¾gé Á Å h ` ½ ú`s½ ¾ ì Á ³ ½ Á ì ½ LoL¼r+a ³+é ` Á ¾Gé µ=é ½ µ ³/gs ½ Á µ=³œé ` Á ³ Å ì=g µ Å ½ ú e ³ ê  Á Å } u é ¾ô J Á ì ½ Å Á ¾ ½ #µ  a ³ Å ½ ¾Œ¾À  Á ì ² Å Á ³ ½ú µ  gê.g'µ c# ½ é Á ì ½#z5Á ³ Á úrá ¾ ú`á Å Á } ý ² Å Á ³ ½ ú µ  ³ Á ¾G² Â é ¾Œì Á ¾ ú ³ ½ ê Ä ½ é ` Á c  Š¾ ` µ e Á  ½ é ²ì ½ µ  ÁA ú9½ é(g µ= ì é Á Åfe Á ³6µ é ² ³ Á µ=³ Á e ³ Á ¾ Á 3é Á ì a ³ ì ½#z5Á ³ Á 3é ôá g Â ì ¾ ² Å ê Á ³6¾A #ì ½ Å Á ¾ ½ J ÂÁ ¾ ¾ µ Å µ= Á ³ ú ¾Gé µ Jé6¾"µ ì ³6µ ì ½ µ é ½ J 3² Å ê Á ³6¾ } 9U YSZ 4ZAYC\ ixs_ Z W! #"+$%'& )(*+&-,/. = 0#1% ˆ9` Á j² ½ ì ½ ¾ é6µ= Á µ ¾ ý Á hœéà J ½ µ ½ ¾ ú ²#¾ ½Bb ² ½ ì h ½ é ` ú J ¾Gé µ= 3éÛì Á ¾ ½ é(g ρ ì=g Ä µ Å ½ ú ½ ¾ ú J¾ ½ é(g µ =¾À² ³/a µ úrá é Á ¾ ½ σ é `Á ³ Å µ Âú #ì² ú é ½ ½ é(g κ µ= ì ` Á µ=é ú µ e µ úr½ é(g c }3 J³ é ` Ású J ¾ ½ ì Á ³ Á ì e ³ ê ÂÁ Å ntµ ¾ ½ o û àër s 5é ` Á é ` ½  ½Bb ² ½ ìlc  Š½ ¾ ¾À² ese J¾ Á ì éà ê Á ¾/g ÅÅ Á éà³ ½ú µ  g'µ=égé6µ ú` Á ì'é µ~³ ÁAú é µ= ²  µ=³ ` J³ ½ù J Jé6µ  a ³ µ Å Á h ½ é ` µ¾gé µ=ê  Á
317 úrá 3é Á ³ e  µ= Á š œ:œ 3ø.œž D à± š šäú5 + D z = 0 }à  é ` J² ` é ` Á c  ŠŠÁ ì ½ µ ½ ¾ ú J ¾ ½ ì Á ³ Á ìµ ¾ µj² ½ ì ú J 3é ½ Ä ² ² Å é ` Á c  Š½ ¾Dµ ¾ ¾À² Å Á ìbéà ê Á é ` ½ Á ² ` a ³Ûé ` Á ½ 3é Á ³ Å ÂÁAú ²  µ=³û µ= ì Á ³ wbµjµ  ¾ a ³ úrá ¾Õé 'µ ú éô J ½ é"µ= #ì'é ~ Á ÂÁAú éôé ` Á J³ µ ½ é(gsµ ú é ½ J } µ ³Gé Á ¾ ½ µ ú ³6ì ½ µ é Á ¾/g¾žé Á Å (x, y, z) Qh ` ½ ú`½ ¾ ú ÁAú é Á ìéà äé `Á a ³6µ Å Á x = ±a y = ±b n a b s ½ ¾ ½ 3éÀ³ ì² ú9á ì }Šˆ9` Á Å Á µ é ` ½ ú 3 Á ¾ ¾ aœé `Á c  Š½ εa ¾ Å ² ú` ¾ Å µ ÂÂÁ ³ é ` µ é ` Áú` µ ³ µ ú é Á ³ ½ ¾Gé ½ ú  Á =é ` a ½ } ÁJ} ε << 1 }ˆ9`Á é ` Á c  Ša ³ ÁAÁ ¾ g ÅÅ Á éà³ ½ ú µ  ¾G² ³/a µ ú9á ¾ ` µ Á e 3¾ ½ é ½ #¾ z = ±h/ h `Á ³ Á h(x, y, t) = O(ε) ì Á é Á ³ Å ½ Á ¾Dé ` Á c  Š¾ ` µ e ÁJ} ½ ú9á é ` Á c  Š½ ¾¾/g ÅÅ Á é ³ ½ ú h ½ é ` ³ Á ¾ e Á:ú édé é ` Á Å ½ ì ì ÂÁ e  µ Á z = 0 #é ` Á é Á Åfe Á ³6µ é ² ³ Á c ÁAÂ ì ½ ¾ µ  ¾À ¾/g ÅÅ Á é ³ ½ ú θ (z) = θ ( z) µ= ì é ` Á ¾/g ÅÅ Á éà³*g ú J ì ½ é ½. z = 0 ³ Á µjì ¾ o qr Æ θ z = 0, for z = 0. ntº } ¹ s go²¾ ½ é ` Á ¾ g ÅÅ Á éà³*g µj¾à¾à² Åfe é ½ J 1!h Á ¾G J² ` é é ` Á é Á Åfe Á ³ µ=éಠ³ Á a ² ú é ½ θ (x, y, z, t) µj¾ôµ=.µ ¾/g Å)e éà =é ½úÁ e µ= ¾ ½ J θ (z) = θ 0 + k=1 û» ¹ z k θ k, h z h. n º } ºs ˆ9` ½ ¾4a ³ Å ¾Àµ=é ½ ¾(c Á ¾ ½ ì Á 3é ½ ú µ   g n º } ¹s µ= ì é `Á ¾ g ÅÅ Á éà³*g µj¾à¾à² Åfe é ½ } é é ` Á µ=ê¾ Á úrá a ` Á µ é ¾G J² ³ ú9á ¾ é ` ÁDÁ Á ³ g ú #¾ Á ³À µ é ½ J  µ h a ³"é ` ÁÛ½Bb ² ½ ì c  Š½ ¾ ½ Á ½ äé ` Á ½ 3é Á ³6µ  a J³ Å Æ d dt, ρcθ dv = % h ` Á ³ Á é ` Á ½ 3é Á ³6µ é ½ ½ ¾Œì J Á Á ³+é ` Á h ` ÂÁ c  ŠJ  ² Å Á µ= #ì ¾À² ³ a µ úrá J³ Á ¾ e Á:ú Ä é ½ Á9 g } Á ³ Á, ½ ¾ é ` Á ` Á µ é!j#² µ ì % é ` Á ² ½ é ² é(h µ ³ ìä J³ Å µ  ÁAú éà J³ôéÀ sé ` Á c  Š¾G²³ a µ úrá }ˆ9` Á6`Á µ é9j² ½ ¾ô¾À² ese J¾ Á ì éà s Jê Á gsé `Á ² ³ ½Á ³  µ h, ½ = κ θ ¾ ½ ì Á é ` Á c  Šµ= ì éà ê Á ì² Á éà ³6µ ì ½ µ é ½ J h ½ é ` µ Å ê ½Á 3és hê# é ` c  Ša ³ Á9Á ¾G² ³/a µ ú9á ¾ Æ, % = β(θ 4 θa) 4 at z = ±h/, ntº } ë.s h ` Á ³ Á ds, β ½ ¾Œé ` Á ³ µjì ½ µ=é ½ ú Á 'ú9½ Á Jé µ ì θ a ½ ¾ôé ` Á µ Å ê ½Á 3éŒé Á Å)e Á ³6µ é ² ³ Á } u Jé Á J³ µ=é ½ Á b ²µ=é ½ n º } ûs+µ  J é `Á c  Šé ` ½ ú Á ¾ ¾ z [ h/, h/] é6µ= ½ ½ 3éÀ.µ úaú J² 3é)nTº } ºs µ ì n º } ës Qh Á Jêé µ ½ é ` Á~ ú µ  a ³ Å a+é ` Á Á Á ³ g.êµ Â µ úrá Á b ²µ é ½ J nt¾ ÁAÁ o º ¼3 q r s }# râ Á µ ì ½ ~é Á ³ Å aý J³ ì Á ³ O(ε) ½ ¾ô ½ Á µ ¾ a   h ¾ Æ h ` Á ³ Á n º } ûs ρch { θ 0 t + } s s θ 0 = κ s (h s θ 0 ) + β(θa 4 θ4 0 ), n º } ås s = (u 0, v 0 ) ½ ¾%é ` Á ¾G²³ a µ úrá c  ŠÁA ú9½ é(g Á:ú é ³Õµ ì s é ` Á ¾À² ³/a µ ú9á ³6µ Ä ì ½ Á 3é } w Á =é Á é ` µ é (u 0, v 0 ) µ=³ Á é ` ÁÕ Á µ ì ½ ³6ì Á ³ é Á ³ Å ¾ ½ Dµ ¾ ½ Å ½  µ=³šµ ¾/g Åfe é =é ½ú Á e µ= #¾ ½.µ ¾ ntº } ºs ê²é4a ³Œé ` Á  J ½ éà²#ì ½ #µ  ÁA ú9½ é(g nt¾ ÁAÁ ntº } ¹s ½ po ûrts }!! *3% 0; m * & Á ³ Á h Á ¾ ` µ   ³ ÁAú µ  é `Á ìsg3 #µ Å ½ú ¾ g¾gé Á Å h ` ½ ú` hœµ ¾~ì Á Á9 e Á ì ½ o û Šër } u é ì Á ¾ ú ³ ½ ê Á ¾ é ` Á c  Šé ` ½ú Á ¾À¾ôµ ìä¾g² ³/a µ ú9á Á9 úr½ é(g Á J  ²é ½ añ ³6ì Á ³ O(ɛ) Æ
318 û»jº ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ h ` Á ³ Á h t + s (h s) = 0, ρ D s = 1 Dt h s ˆT, ˆT = P + T ½ ¾ é ` Á ¾G²³ a µ úrá c  Š¾GéÀ³ Á ¾ ¾%é Á ¾À ³: P ½ ¾ é ` Á e ³ Á ¾ ¾G² ³ Á é Á #¾G J³ P = 0.5σ [ h shi s + 0.5( s h) I s s h s h ] + 1.5hφ, µ= ì é ` Á ½ ¾ ú ²¾ô¾GéÀ³ Á ¾ ¾Õé Á ¾G J³ T ½ ¾ô ½ Á ê.g Á ³ Á { [ ]} T = µh ( s v s ) I s s v s + ( s v s ) T. n º } s I s ½ ¾+é ` Á"½ ì Á Jé ½ú µ  ¾G²³ a µ úrá é Á ¾À ³: φ = A h 3 /(6πρ) ½ ¾+é ` Á e =é Á 3é ½ µ  a ² ú Ä é ½ a+ µ= ì Á ³w µ µ  ¾!a ³ úrá ¾9 A ½ ¾"é `Á µ Å µ= Á ³ ú ¾Gé µ 3é:n A O(10 0 J) s µ= ì T ¾žé6µ= ì ¾ a ³'é ³ µ ¾ e 3¾ ½ é ½ } à b ²µ é ½ J ¾ n º } ssµ ³ Á Jêé µ ½ Á ì µa é Á ³ µ ¾ ½ Å ½ Ä Â µ ³ µj¾ g Åfe é =é ½ ú µ= µ  g¾ ½ ¾ a%é ` Á a ²  ý"µ ½Á ³ Ä éà Á ¾ Á b ²µ é ½ J ¾>h ½ é ` µ ese ³ e ³ ½ µ é Á ê# J² ì µ ³/g ú ì ½ é ½ J ¾Œ ma ³ ÁAÁ ¾G² ³/a µ ú9á ¾Œ a é `Á c  Š}! %'& 0 &-%i 0 1%i 1 '& u a1é ` ÁÂÁ é ` a1 Á a ³ µ Å Á"½ ¾ Å ² ú` ê ½ Á ³%é ` µ 'é `Á é ` Á ³Õ J Á ½T} Á } b a Jé `Á é ` Á Á zá:ú é ¾ ½ y ì ½ ³ ÁAú é ½.µ=³ Á Á ½ ½ ê  Á J é ` Á ì=g µ Å ½ ú ¾ôµ ì ú ½ µ ì'é ` Á é ` Á ³ Å ì=g µ Å ½ ú e ³À Jê ÂÁ Å ì Á e Á ì ¾ô J  g (x, t) }ˆ9` Á ¾/g¾Gé Á Å n º } ås ntº } s ½ ½ é6¾ ì ½ Å Á ¾ ½ J  Á ¾À¾ a J³ Å ¾ ½ Åfe  ½ c Á ¾ éà Æ h ` Á ³ Á h t + (uh) = 0, ntº x u t + u u x = T t + u T x = 1 ε 3 h W e x ( Re h x ( h T P e h x x h u x ) + Ra P e h ) + A h 4 h x, } ¼s n º } qs ( T 4 a T 4), n º } ys Re = ρau/µ ½ ¾ é `ÁmôÁ g3 Â ì ¾ ² Å ê Á ³: W e = ReCa = ρau /σ é ` Á w Á ê Á ³ ² Å ê Á ³A Ca é ` Á ú µ e ½Â  µ=³*g ² Å ê Á ³A A = A /(πρu a 3 ε 3 ) é ` Á ì ½ Ä Å Á ¾ ½ J  Á ¾À¾ "µ Å µ= Á ³ ú ¾Gé µ Jé: P e = ReP r = ρcau/κ é ` Áä ñáaúrâá é ² Å ê Á ³: Ra = βaθm 3 /ε κ é ` Á ³6µ ì ½ µ=é ½ ² Å ê Á ³: θ m é `Á ¾À ½ ì ½ c ú µ é ½ é Á Åfe Á ³6µ éಳ Á ê ÁA h h ` ½ú` é ` Á  ½Bb ² ½ ìc  Šê Á:ú Å Á ¾ô¾G  ½ ì } ˆ9` Á ú` µ ³ µ ú é Á ³ ½ ¾Gé ½ ú ¾ ú µ  Á ¾ ²¾ Á ìbéà ì Á ³ ½ Á ¾ g¾gé Á Å n º } ¼s n º } ys µ ³ Á é ` Á a Â Ä Â h ½ Æ a a ³ ÂÁ é ` U a J³% ÁA ú9½ é(g n ú µ e ½Â µ ³/g ³% ½ ¾ ú ²¾s a/u a ³%é ½ Å Á εa c  Ša ³ é ` ½ ú 3 Á ¾ ¾Õµ ì θ m a ³Õé Á Å)e Á ³6µ é ² ³ Á n ` Á ³ Á x t u µ= #ì T µ=³ Á ì ½ Å Á #¾ ½ ÂÁ ¾ ¾s } ½ úrá ì² ³ ½ é ` Á ì Á ³ ½ µ é ½ J aš¾/g¾gé Á Å n º } ¼s Ä ntº } ysõé ` Á é Á ³ Å ¾Œ a o(ε) J³ ì Á ³ ` µ Á ê ÁAÁ ½ J³ Á ìà é ` Á äé ` Á a   h ½ ½ Á b ²µ  ½ é ½Á ¾ô¾ ` J²  ìäê Á µ ½ ì Æ Re ε 1, W e 1, A ε, P e ε 1, Ra εp e. ˆ9` Á ê# J² ì µ ³/g ú ì ½ é ½ J ¾ a ³ h u µ= #ì T µ=³ Á é ` Á a   h ½ Æ
319 h ` Á ³ Á š œ:œ 3ø.œž D à± š šäú5 + D u(0, t) = u(1, t) = 0, û» û n º } ¹A»s T x (0, t) = 0, T (1, t) = T ntº } ¹J¹s g, h h (0, t) = 0, x (1, t) = tan α, ntº x } ¹:ºs ½ T g ¾ é ` Á ì ½ Å Á ¾ ½  Á ¾À¾ a ³6µ Å Á é Á Åfe Á ³ µ=éಠ³ Á µ= #ì π α ½ ¾Ûé ` Á h Á éàé ½ µ=  Á h ½ é ` é ` Á a ³6µ Å ÁJ} ˆ9` Á ½ ½ é ½ µ Â1ú #ì ½ é ½ J ¾ôµ=³ Á ½ Á ê.g Æ h ` Á ³ Á h(x, 0) = 1, u(x, 0) = 0, T (x, 0) = T 0, ntº } ¹:ûs ½ T 0 ¾Œé `Á ì ½ Å Á ¾ ½  Á ¾À¾ ½ ½ é ½ µ  é Á Åfe Á ³ µ=éಠ³ Á aýé ` Á c  Š} ˆ9` Á Å µj¾à¾ ú ¾ Á ³ µ é ½ J aýé ` Á c Â Å ì² ³ ½ ½ é ¾ é ` ½ ½ ½ ¾ Á e ³ Á ¾ ¾ Á ì µ ¾ Æ 1 0 (h 1)dx = 0, n º } ¹9ë.s ½ é6¾ô µ ½ ì ½ é(g ½ ¾ e ³ Á ì'ê.g ½ Jé Á J³ µ=é ½ n º } ¼s µ= #ì é6µ= ½ ½ 3éÀ sµ ú9ú J² 3é ntº } ¹A»s } ˆ9` Á Ä Â ½ Á µ=³% -¾žé6µ é ½ #µ=³*g e ³ ê  Á Å n º } ¼s n º } ¹9ës ½ ¾Œ¾À  Á ì ½ é ½ Å Á é ½  Á ašé `Á a  h ½ ¾žé e ú #ì ½ é ½ J ¾ ½ ¾ ¾Àµ=é ½ ¾(c Á ì Æ µsµ é6c ½ é Á é ½ Å Á Å Å Á 3é t = τ µ Å ½ ½ Å ² Å µ  ² Á a h ½ ¾ ³ Á µ ú` Á ìà h `½ú` ú ³ ³ Á ¾ e J ì ¾ÕéÀ sµ¾žé6µ=ê ÂÁ c  Š¾ ` µ e Á lim h(x, t) = h(x), lim t τ u(x, t) = u(x), lim t τ T (x, t) = T (x), ntº t τ } ¹:ås ê+sdµ=édé ½ Å Á Å Å Á 3é t = τ é `Á Á zá:ú é ½ Áäú ³ ½ é ½ú µ  c  Š³À² e éಠ³ Á é ` ½ ú 3 Á ¾ ¾ ½ ¾ ³ Á µ ú` Á ìà µ é0h ` ½ ú` é ` Á µ ú éವ  c  Š³ ² e éಳ Á ú9ú ² ³ ¾ôµ=é ¾G Å Á e ½ 3é x r h(x r, τ) 0, ú s ú Å)e ²é µ=é ½ ¾ôµ ³ Á ú J 3é ½ 3² Á ì é ½Â Â ú ì ½ é ½ J T (x, τ) 1 ½ ¾ô¾ µ é ½ ¾ c Á ì } ntº } ¹ s w Á µ ¾ ¾G² Å Á é ` µ éñé ` Á ¾À  ²é ½ a#¾/g¾žé Á Å ntº } ¼s3 n º } ¹9ës e 3¾À¾ Á ¾ ¾ Á ¾ é ` Á ³ Á b ² ½ ³ Á ì ¾ Å =é ` Á ¾ ¾ u, h, T C 4 (Ω) ½ Ω = {0 x 1} a J³ 0 < t < τ } 9U \ Y+_ ] 4] ˆ9` Á c ½ é Á 3  ² Å Á Å Á é ` ì ½ ¾²¾ Á ìmé ú ¾GéÀ³ ² ú é~é ` Á ì ½ ¾ ú ³ Á é Á ¾ ú` Á Å Á Fh ` ½ú` ¾Àµ=é ½ ¾(c Á ¾é ` Á Å µj¾à¾a Å Å Á Jé ² Å ` Á µ=é j² êµ Â µ úrá ¾+ J Á µ ú` ú J Jé ³À   ² Å Á µ= ì é ` Á ³ Á a ³ Á J é ` Á h `  Á e ³ ê ÂÁ Å ì Å µ ½ } w Á ì Á c Á µ~ ² ½ a J³ Å é ½ Å Á J³ ½ ì Ω t = {t j+1 = t j + t j, t j > 0, j = 0,..., J τ, t 0 = 0, t Jτ = τ}. ˆ9` Á ¾ e µ úrá J³ ½ ì ½ ¾ µ  ¾G. J 3² ½ a J³ Å àé ` Á µjì µ e é6µ é ½ J aœ J³ ½ ì ì Á ¾ ½ ¾Ûì Á ì=g µ Å ½ ú µ  gì² ³ ½ ³ Á µ ½ ù µ é ½ b a é `Á µ  ³ ½ é ` Å }3 J³ Å ³ Á µ ú9ú ² ³6µ é Á µ ese ³ Ä ½ Å µ é ½ J aé ` Á ê ² #ì µ=³*g ú J ì ½ é ½ ¾fh Á ½ Jé ³À ì² úrá é(h b J³ ½ ì ¾sì ½ ¾ e  µ úrá ì h ½ é ` ³ Á ¾ e ÁAú é é Á µ ú` é ` Á ³ } ² ú é ½ J ¾ u µ= #ì T µ=³ Á ì Á c Á ìä é ` Á J³ ½ ì
320 Á û»=ë ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ Ω u,t x = {x i = i x, i = 0,..., N + 1, x 0 = 0, x N+1 = 1}, h ` ½ ÂÁ a ² ú é ½ h ½ ¾ ì Á c# Á ìä é `Á ³ ½ ì Ωx h = {x i 0.5 = (i 0.5) x, i = 1,..., N + 1}. u é ` ½ ¾4h µ gé ` Á e ³ ê ÂÁ Å h ½  ê Á ¾G  Á ì' J äµs¾gé µ Á ³ Á ì'¾ e µ ú9á ³ ½ ì } é Á µ ú` é ½ Å Á ¾žé Á e é µ=é ½ a+ì ½ ¾ ú ³ Á é Á a ² ú é ½ J ¾ ½ ¾ ¾ ½ Åfe  ½ c Á ìµ= ì ½ ì Á Á ¾ µ=³ Á Å ½ éàé Á ì o år } ˆ h sé(g e Á ¾ a ú 3é ³À   ² Å Á ¾"µ=³ Á ²¾ Á ì Æ J Á a ³ u µ ì T µ= ì µ =é ` Á ³!a ³ h } 3éÀ³   ² Å Á ¾xh ½ é ` úrá 3é Á ³6¾Dµ=éÛé `Á ³ ½ ì ì Á ¾~µ=³ Á µ ese  ½Á ì é ì ½ ¾ ú ³ Á é ½ù9Á Á b ²µ é ½ J ¾6nTº } ¼s Ln º } ys } ˆ9` Á ì ½zÁ ³ Á úrá µ ese ³ ½ Å µ=é ½ h adntº } ¼s ½ ¾ êé6µ ½ Á ì ½ 3é Á ³6µ é ½ ½ é é ` Á ú 3é ³À  J  ² Å h ` Á ³ Á [x i 1, x i ] h t + M M x = 0, i = 1,..., N + 1, n û } ¹ s M = M i =< h > i < u > i. ˆ9` Á é µ=é ½ <> 1¾ ½ Å ½Â µ=³  gµj¾ ½ o r Å Á µ= ¾Ûé ` µ=éûé `Á µ  ² Á ¾D a h µ= #ì u µ=³ Á é µ Á b J é ` Á ú ² ³ ³ Á 3é úrá9ââ ê ³6ì Á ³ } w Á µ  ¾G ²¾ Á =é6µ é ½ M i = u + i h i + u i h i+1, u i = u + i + u i, u + i = 0.5(u i + u i ) 0, u i = 0.5(u i u i ) 0. ² ÅÅ ½ ś² e ntû } ¹sÕ Á ³ é ` Á J³ ½ ì Ω h x h Á êé6µ ½ é ` Á Á b ²µ  ½ é(g N h i x = 1. i= u éµ ese ³ ½ Å µ=é Á ¾ é ` Á Å µ ¾ ¾ ú #¾ Á ³À µ é ½ J Áb ²#µ é ½ ntº } ¹Aësh ½ é ` é ` Á µ ú9ú ²³ µ ú g O( x) } u a é ` Á ê ² ìµ=³*g µ  ² Á ¾ h(0, t j+1 ) µ= ì h(1, t j+1 ) µ=³ Á a J² ì6a ³ Å ê ² ì Ä µ=³*g ú J ì ½ é ½ ¾6n º } ¹:ºsR 3é ` Á é ` Á Á b ²µ  ½ é(g N+1 i=1 ½ Á ¾ O( x ) µ ese ³ ½ Å µ=é ½ a n º } ¹9ës } h i x = 1 ³1¾À Å Á µ  ² Á ¾à a e µ=³6µ Å Á é Á ³6¾A Á } } a J³  µ ³À Á Re $h ` ½ ú` ú J³À³ Á ¾ e J ì"éà ¾GéÀ³ ú ÁAú é ½ J ì Å ½ µ úrá =h Á êé6µ ½ ¾ ½ ²  µ=³ e ³ ê ÂÁ Å ¾ h ½ é ` ¾ Å µ ÂÂ1ú Á sú9½ Á 3é ¾Œµ é é ` Á ì Á ³ ½ µ é ½ Á a"é `ÁäÂÁ µjì ½ J³ ì Á ³ n ê ² #ì µ=³*g  µ g Á ³ e ³ ê ÂÁ Å ¾s } u e ³ µ ú é ½ú9Á ¾G² ú` e ³À Jê ÂÁ Å ¾"µ ³ ÁDú` µ=³6µ ú é Á ³ ½ ùaá ìäê.g.ê# J² ì µ ³/g  µ g Á ³6¾A Sh ` Á ³ Á ¾À  ²é ½ J ¾ ú` µ Á Á ³*g a µ ¾Gé } w Á é Á é ` µ=é é ` Á ¾ Á ³ Á ½ J ¾Dµ  ¾À ú` µ Á ½ é ½ Å Á µ ú9ú J³ ì ½ éà é ` Á e ³À Jê ÂÁ Å ¾ e ÁAú9½ c ú ¾ } u ³6ì Á ³ÛéÀ µ ese ³ ½ Å µ é Á ¾G  ²é ½ J ¾ a"¾g² ú` e ³À Jê  Á Å ¾9 ½ é ½ ¾ ÁAú9Á ¾ ¾Àµ ³/gé ì Á ÁA e ¾ e ÁAúR½ µ Â ì ½#z5Á ³ Á ú9á ¾ ú`á Å Á ¾ } ³ µ ese ³ ½ Å µ é ½ J aýé ` Á ÁA úr½ é(g Áb ²#µ é ½.¾À² ú` µ~¾ ú` Á Å Á6` µ Á ê ÁAÁ e ³ Ä e 3¾ Á ì ½ do ër } u é ` µ ¾Ýµ ¾À² 'úr½á 3é  g J ì µ ú9ú ² ³ µ ú g!a ³ ¾ Å µ  µ= #ì  µ ³À Á ÁA úr½ é ½Á ¾ } u
321 Á } š œ:œ 3ø.œž D à± š šäú5 + D û»jå ² ³ Å ì ÁA Á b ²µ=é ½ ntº } qs ` µ ¾¾ ½ Å ½Â µ ³Fa Á µ=éಠ³ Á ¾A h ½ é ` é ` Á ú J 3 ÁAú é ½ ~ ³+ì ½z ²#¾ ½ ì Å ½ µ= ú9á a J³Œì ½#z5Á ³ Á 3é Re }- ³ ½ é ¾ ² Å Á ³ ½ú µ  ¾G  ²é ½ J µ ½ Åfe ³ Á ìs µ=³ ½ µ 3éÕ a é ` Á ¾ ú` Á Å Á a ³ Å o ër ½ ¾ e ³ e J¾ Á ì h ` Á ³ Á u t + 1 (u +0.5u) x = ( µ +0.5 u x ) x + h = 1 (h + h +1) ε W e h xxẋ A 3 (h 3 ) x, ntû } ºs µ +0.5 = µ +0.5 F B (R +0.5 ), µ +0.5 = 4 h +1 Re h, R +0.5 = 1 8 Re x u h +0.5 h µ= ì é ` Á a ² ú é ½ J ½ F B ¾ôµ e ½ Á:úRÁ h ½ ¾ Á  ½ Á µ ³ µ ese ³À ½ Å µ=é ½ a R ˆ9` Á exp R 1 é Á Åfe Á ³ µ=éಠ³ Á%Áb ²µ é ½ J Dµ  ¾G ` µ ¾Š¾ ½ Å ½  µ=³ia Á µ=éಠ³ Á ¾A h ` Á ½ é ½ ¾Š¾À  Á ì ½ é ` Á ¾ g¾gé Á Å a Á b ²µ=é ½ ¾ih ½ é ` ì Å ½ µ= 3é ú ÁAú é ½ J é Á ³ Å ¾ } w Á e ³ e J¾ Á µì ½ ¾ ú ³ Á é ½ ù µ Ä é ½ 1 ih ` ½ú` ½ ¾ ú #¾žé ³À² ú é Á ì ²¾ ½ é ` Á ¾ µ Å Á e ³ ½ úr½ e ÂÁ }݃ ³ Á Á ³A 1µ³ Á ¾žé ³ ½ ú é ½ J ú ÁAú é Á ì h ½ é ` e ` g¾ ½ú µ Â"ú ³ ³ Á:ú éà Á ¾ ¾ aé ` Á ¾À  ²é ½ J ½ ¾ ½ Åfe 3¾ Á ìà Õµ=é  Á µ ¾Gé ½ ¾G Å Á ¾ ½ Å)e  ÁÛú µ ¾ Á ¾A =h ` ½ú` ú9ú ² ³"µJ¾ e µ=³àé ½ ú ²  µ ³ ú µ ¾ Á ¾Œ aýé ` ÁDú ¾ ½ ì Á ³ Á ì e ³À ú9á ¾ ¾ } ³ Á µ Å)e  Á ÂÁ é ²¾ ú J ¾ ½ ì Á ³µ ` Á µ ééà³6µ= ¾ a Á ³ e ³ ê ÂÁ Å h ½ é ` J²é `Á µ é Á ú` µ Á h ½ é ` é `Á µ Å ê ½Á 3é Jµ ¾ ê# J² ì µ ³ ½Á ¾A ½ } Á } h Áú J ¾ ½ ì Á ³"é ` Á ³ Å µ  g ½ ¾G  µ=é Á ìc  Š¾G² ³/a µ ú9á ¾:n é `Á ³ ÁD½ ¾" ¾G J² ³ ú9á é Á ³ Å ½ ntº } ys µ=é Ra = 0 s }ˆ9` Á é `Á é Á Åfe Á ³ µ=éಠ³ Á a c  Š³ Á Å µ ½ ¾ ½ é ` Á ½ Å ½ é6¾ a1é ` Á ½ ½ é ½ µ  é Á Åfe Á ³ µ=éಠ³ Á µ ìé ` Á a ³6µ Å Á é Á Å)e Á ³ Ä µ éಳ ÁJ} " h Á Á ³A ½ aõé ` Á ³6µ ì ½ µ é ½ J Lh ½ é ` µ ú  ì Á ³µ Å ê ½Á 3éé µ Á ¾ e  µ ú9á é `Á é ` Á c  Šé Á Å)e Á ³6µ é ² ³ Á ú µ= =éôê Á ÂÁ ¾ ¾ é ` µ= äé ` Á µ Å ê ½Á 3éŒé Á Åfe Á ³ µ=éಠ³ Á } ² ú` é Á ¾Gé ¾ ` µ Á ê ÁAÁ e Á ³ a J³ Å Á ìkh ½ é ` µ a Á hlì ½ ¾ ú ³ Á é Á ¾ ú` Á Å Á ¾A Œµ ese ³ ½ Ä Å µ=é ½ 'é ` Áú #¾ ½ ì Á ³ Á ì Á b ²µ é ½ J }5ˆ µ ½ ½ 3éÀ äµ úaú ² Jé é ` Á ³ Á b ² ½ ³ Á Å Á 3é aé ` Á Å µ ½ Å ² Å e ³ ½ ú9½ e ÂÁ a J³"é ` Á ¾G  ²é ½ J µ= #ì ²¾ ½ Á e Á ³ ½ Å Á 3é6µ  ³ Á ¾À² Â é ¾ êé6µ ½ Á ì h ½ é ` ì ½#z5Á ³ Á 3é"ì ½ ¾ ú ³ Á é Á ¾ ú` Á Å Á ¾9 =h Á6` µ Á ¾ Á9ÂÁAú é Á ì é `Á a  h ½ śì ½ ¾ ú ³ Á é ½ù µ=é ½ 1 h ` ½ú`.½ ¾ µ= µ µ  J² Á ašé ` ÁDú Å ê ½ Á ìä¾ ú` Á Å Á µ= ì ½ ¾ ú J ¾žé ³À² ú é Á ì.¾ ½ Å ½  µ=³  g µ ¾ ½ po ër Æ h ` Á ³ Á (ht ) t + (h +1 u +0.5 T ) x = ( ϕ +0.5 T x ) x + Ra ( Ta 4 P e T 4), ϕ +0.5 = h +1 P e F B(S +0.5 ), S +0.5 = x u +0.5 P e. u Jé Á J³ µ=é ½ ḿn º } ysõ Á ³Õé ` ÁÛú J 3éÀ³   ² Å [0, x 0.5 ] µ= ì é µ ½ ½ 3éÀ sµ úaú ² Jé é ` Á ê ² #ì µ=³*g ú J ì ½ é ½.µ é x 0 = 0 =h Á Á éôé ` Á ê ² #ì µ=³*g'ì ½ ¾ ú ³ Á é Á Á b ²µ=é ½ Æ (ht ) t,0 + x h 1u 0.5 T 0 = x ϕ 0.5 T x,1 + Ra P e ntû } ûs ( ) Ta 4 T 0 4. ntû } ës ˆ9` Á ½ é Á ³ µ=é ½ e ³À úrá ¾À¾ a ³ h µ= ì u ½ ¾Œì Á ¾ ú ³ ½ ê Á ì ½ ì Á é µ ½  ¾ ½ o ër 3é `Á ³ Á a ³ Á"½ é h ½  =éœê Á e ³ Á ¾ Á Jé Á ì ` Á ³ Á }ˆ9` Á J  ½ Á µ=³œ¾ g¾gé Á Å ntû } ¹s Ln û } ës ½ ¾ ¾À  Á ì'ê.g'µ= ½ é Á ³6µ é ½ Á e ³ úrá ¾À¾A ú #¾ ½ ì Á ³ ½ h s+1 µ ì u s+1 µ ¾ôµ  ³ Á µ ìsgfa ² ì Æ
322 û» ( s+1 h s+1 T ) t,0 + ( s+1 h s+1 T ) t + ( s+1 s+1 h +1 s+1 T N+1 = T g. ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ s+1 s+1 s+1 h 1 u 0.5 T 0 = x + Ra P e u +0.5 s+1 ( 4 s T 3 0 s+1 T ) x = ( s+1 s+1 ϕ 0.5 s+1 T x,1 T0 4 T 0 + T 4 a + 3 s s+1 ϕ +0.5 T x) x + Ra ( s 4 T 3 s+1 T + T 4 s a P e + 3 T 4), 1 i N, w Á é Á é ` µ=é é ` Á e ³ Á ¾ Á 3é Á ì ½ Á µ=³ ½ ù µ é ½ J ' aýé ` Á ¾À ² ³ úrá é Á ³ Å ½ ntû } ûsr QnTû } ës e ³ Á ¾ Á ³À Á ¾%é ` Á e ` g¾ ½ú µ Â1ú ³ ³ Á:ú éà Á ¾ ¾Õ a é ` Á ¾G  ² é ½ } ˆ9` Á ¾G  ²é ½ J m a¾/g¾žé Á Å ntû } ås ½ ¾ a ² ìmê.g é `Áˆ9` Å µ ¾sµ  J ³ ½ é ` Å h ` ½ú` é µ= Á ¾ ½ 3éÀ sµ úaú ² JéŒé ` µ é Å µ é ³ ½ ašé `Á ¾ g¾gé Á Å ½ ¾Œé ` ³ Á9Á Ä ì ½ µ= J µ  h ½ é ` A i = C 0 s+1 s+1 T 0 + B 0 T 1 + F 0 = 0, s+1 s+1 s+1 A i T i 1 C i T i + B i T i+1 + F i = 0, i = 1,..., N, s+1 T N+1 = T g τ s+1 ( x) ϕ i τ s+1 h i, B i = τ s+1 x ( x) ϕ i+0.5, C i = s+1 h i + F i = h i Ti + τra P e τ ( x) (s+1 ϕ i s+1 ϕ i+0.5 ) + ( 3 s T 4 i + T 4 a ). ), τ s+1 s+1 u i+0.5 h i+1 + 4τRa x P e ntû } ås s T 3, ˆ9` Á ¾Gé µ=ê ½ ½ é(g ú ì ½ é ½ s aàé ` Áˆ9` Å µj¾ Å Á é ` ìs³ Áb ² ½ ³ Á ¾é ` Á e 3¾ ½ é ½ Á Á ¾ ¾+ a é ` ÁÛú Á 'úr½á 3é ¾ A i B i µ= ì D i = C i A i B i } u é4a  h ¾<a ³ Å a J³ Å ²  µ ¾ ½ Á µ=ê Á é ` µ é ½ Áb ²#µ ½ é ½ Á ¾ A i > 0 µ= #ì B i > 0 µ=³ Á ¾Àµ=é ½ ¾(c Á ìä² ú ì ½ é ½ #µ  g }ˆ9` Á e 3¾ ½ é ½ Á Á ¾ ¾Œ a D i = s+1 h + τ ( s+1 s+1 u i+0.5 h i+1 s+1 s+1 ) 4τRa u i 0.5 h i + x P e ì Á e Á ì¾ J é ` Á~ú` µ= Á a b ²µ 3é ½ é ½Á s+1 ¾ h µ= #ì s+1 u µ= #ì ½ é ú µ= ê Á µ ú` ½Á Á ìà a ³ Á µ Åfe ÂÁ ê.gdì ½ Å ½ ½ ¾ ` ½ é ` Á é ½ Å Á ¾Gé Á e }=ˆ9` Á ½  µ=é ½ a é ` Á ¾žé6µ=ê ½Â½ é(g ú ì ½ é ½  Á µ ì ¾~é ¾À Å Á ³ Á ¾GéÀ³ ½ú é ½ ¾~ mé ½ Å Á ¾žé Á e ¾ }+ˆ9` Á ³ Á a ³ Á ½ J³ ì Á ³~éÀ êé6µ ½ é ` Á ú ³ ³ ÁAú éô¾à  ²é ½ a é ` Á e ³ ê ÂÁ Å ½ é ½ ¾Œ Á:úRÁ ¾À¾ µ=³*g~éà ú` ÁAú é ` ½ ¾ ú #ì ½ é ½ J äì ² ³ ½ ú Åfe ² é µ é ½ J ¾ } u aé ` Á ½ é Á ³ µ=é ½ Á e ³ úrá ¾À¾ ½ ¾Fc ½ ¾ ` Á ìdh ` Á 'µ ³ Á9 µ é ½ Á ú` µ= Á aàê =é ` a ² ú é ½ J ¾ u µ= ì T µ=éôé(hõ ¾À² ú9ú9á ¾ ¾ ½ Á½ é Á ³6µ é ½ J ¾ ½ ¾ ÂÁ ¾ ¾ é ` µ= µ~ ½ Á.¾ Å µ   µ  ² Á é ` Á h Á ` µ Á ³ Á µ ú` Á ì'é ` Á ¾Gé Á µjì=gsé ` Á ³ Å µ  µ= #ì ì=g µ Å ½ú ¾À  ²é ½ ¾6n º } ¹:ås } s T 3
323 š œ:œ 3ø.œž D à± š šäú5 + D ì ½ é ½ dn º } ¹ s ú µ =éýê Á a ²  c  ÂÁ ì Á µ ú é  gµ ìé ` Á ³ ÁÕÁ½ ¾žé6¾ µ ú ³ ½ é ½ ú µ  é `½ú Ä Á ¾ ¾ h cri > 0 µ é4h ` ½ ú` é ` Á µ ú éವ  ³À² e éಠ³ Á aýé ` Á c  Šúaú ² ³6¾9 3é ` Á ³ Á a J³ Á ntº } ¹ s ½ ¾ ú` µ= Á ìsé h(x r, τ) = h cri. w Á =é Á é ` µ éé ` Á ì ½zÁ ³ Á 3é ½ µ  e ³À Jê ÂÁ Å ê Á:ú Å Á ¾ ¾ ½ ²  µ=³ ½ é ` Á ³ Á ½ h ` Á ³ Á h µ ese ³À 3µ ú` Á ¾ h cri } û»3¼ ntû } s 0U \ Y+_ ].\(X ˆ9` Á c Â Å ì ³ µ ½ µ Á~½ é ½ Å Á µ ì ½ é6¾  ½ é ²ì ½ µ  Á9 úr½ é(g h Á ³ Á½ Á ¾žé ½ 3µ é Á ì ½ o ër%ê.g µ ¾ ½ Å ½Â µ ³ 3² Å Á ³ ½ ú µ  ¾ ú` Á Å Á µ ¾Ûì Á ¾ ú ³ ½ ê Á ì ` Á ³ ÁJ} u o ër+é ` Á µ= µ  g¾ ½ ¾ hœµ ¾ ì Á a ³ µ=³ ½ ²¾" µ  ² Á ¾ a+é ` ÁsôÁ g Â ì¾ ² Å ê Á ³ Re n 1 Re 100 s µ ìì ½ Ä Å Á ¾ ½ J  Á ¾À¾"µ Å µ= Á ³ ú ¾Gé µ Jé A n 0.1 A 0 sr +h `Á é ` Áú µ e ½  µ ³/gä ² Å ê Á ³ Ca µ= #ì ε h Á ³ Á c Á ìhéà Ca = ε = 0.01 n W e ì Á e Á ì Á ì  g J Re %¾ ½ úrá W e = 0.01Re s } u é ½ ¾ a J² ì ½ o ër5é ` µ=é é ` Á ³À² e éಠ³ Á e ½ 3é x r Å Á ¾%éÀ é ` Á ³ ½ ` é ¾ ½ ì Á a ³À Å é ` Ású9Á 3éÀ³6µ  ¾/g ÅÅ Á é ³/g e ½ 3é x = 0 éà hœµ=³6ì ¾ é ` Á a ³ µ Å Á e ½ 3é x = 1 µ= ìäµ Rì ½ Åfe  Á a é ` Á c  Š½ ¾ a J³ Å Á ì'é ` µ é Á  µ ³À Á ¾ ½.¾ ` µ e Á h ½ é ` é ` Á ³ h ½ µ  ² Á ¾ a Re µ= ì A }àˆ9` ½ ¾ Å Á µ= ¾ é ` µ éé ` Á~½ Á ³Àé ½ µ  a ³ úrá ¾ ` µ Á µ ì Á ¾Gé µ ê ½Â ½ù9½ Á$z5ÁAú é é ` Á c  Šµ ì ÂÁ µ ì éà ½ é ¾~ì³6µ ½ µ= Á µ= ì ³À² e éಠ³ Á µ=é A > 0 }Šˆ9`Á µ= ì Á ³fw µ µ  ¾xa ³ úrá ¾~µ  ¾À ì Á ¾žé6µ=ê ½Â ½ù9Á é `Á c  Šì=g µ Å ½ú ¾ µ ì µ ú9úráaâ Á ³ µ=é Á é ` Á c  Š³À² e éಠ³ Á } u é ` Á e ³ Á ¾ Á 3é!h ³ mh Á a ú ²¾ é ` Á ½ =j#² Á ú9á aé ` Á ½ Á ³Gé ½ µ  µ ì. µ= ì Á ³ wbµjµ  ¾>a ³ úrá ¾ J é ` Á ` Á µ é éà³6µ= #¾(a Á ³A àµ= #ì #µ Å Á9 g ú  ½ }1 " ¾À h Á'ú ¾ ½ ì Á ³ µ ³ ½ ²#¾Õ³6µ ì ½ µ=é ½ Å µ= J ½ éà²ì Á ¾ôµ= ìä¾géà²ì=g'é ` ÁA½ ³ Á zá:ú éô é ` ÁÛú ½ e ³ úrá ¾ ¾ µ ¾ µ h ` ÂÁ }ˆ9` Á e ³ Á ¾ Á 3é Á ì. ² Å Á ³ ½ú µ  ³ Á ¾À² Â é ¾ µ=³ Á êé6µ ½ Á ì a J³ ú J ¾Gé µ= 3é" µ  ² Á ¾ a ú Á 'úr½á 3é6¾ Ca = 0.01, ε = 0.01, α = 1.37, P r = 1.,8,6 0,8,4,,0 1,8 1,6 1,4 h 1, 1,0 t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t=1.5 t=1.8 t=.0 t=.4 0,7 0,6 0,5 0,4 U 0,3 t=0.1e-3 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t=1.5 t=.4 0,8 0, 0,6 0,4 0,1 0, 0,0 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 x 0,0 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 X M? +N$I D #ži:h ILH D ži" E =,3HJ?*žI:H D h u M D D D A = 0.1 Re = P e = 1 W e = 0.01 T 0 = 1.19 T g = T a = 1 α = 1, 37 M h(x, t)? - u(x, t)
324 û»q ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ u ݽ } ¹é ` Á Á J  ²é ½ ½ ¾ e µ úrá µ ìbé ½ Å Á a é `Á c  Šé ` ½ ú 3 Á ¾ ¾ h  ½ Ä éà²ì ½ µ  Á9 úr½ é(g u e µ= ì µ=³6µ Å Á é Á ³6¾ é Á Å)e Á ³6µ é ² ³ Á T µ=³ Á ½ Á a J³~é ` Á a  h ½ µ  ² Á ¾ a A = 0.1, Re = P e = 1, W e = 0.01, T 0 = 1.19, T g = T a = 1. ˆ h Dì ½zÁ ³ Á 3é%³ µjì ½ µ é ½ ² Å ê Á ³ ¾ Ra = 0 µ= #ì Ra = 10 h Á ³ Á ²¾ Á ì }3ˆ9` Á ³ ² e é ² ³ Á ašé ` Á c  Š½ ¾Œ ê#¾ Á ³À Á ì µ=é x = 0 a ³ µ é ½ Å Á Å Å Á 3é t =.4 o ër } 1,0 1,0 1,15 1,10 T t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.8 1,15 1,10 T t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 1,05 1,05 1,00 1,00 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 x x M +N$I D ži:h I HLžI" E <žf E E "61 E GM ( E T M D D A = 0.1 Re = P e = 1 W e = D D T 0 = 1.19 T g = T a = 1 α = 1, 37 M T (x, t) M D Ra = 0? T (x, t) M$ Ra = 10 u ݽ } ºh Á e ³ Á ¾ Á 3éD³ Á ¾À² Â é ¾D¾ ` h ½ ì=g µ Å ½ú ¾Û aôé ` Á é Á Åfe Á ³6µ éಳ ÁJ} u é ½ ¾ ¾ ÁAÁ é ` µ éûé ` Á é Á Åfe Á ³ µ=éಠ³ Á ê ÁAú Å Á ¾ ú #¾žé6µ= 3éDµ= ì Áb ²µ  éà é ` Á ¾À ½ ì ½ c ú µ é ½ J é Á Åfe Á ³6µ é ² ³ Á µ=éì ½#z5Á ³ Á 3éñé ½ Å Á Å Å Á 3é ¾A :é ` µ=é%µ=³ ÁÕÂÁ ¾ ¾Šé ` µ Dé ` Á é ½ Å Á a#³ ² e é ² ³ Á } ˆ9` Á ú 3  ½ Å Á:ú` µ= ½ ¾ Å ½ ¾~ì² Á é ú Á:ú é ½ µ ì ú ì² ú é ½ ½ é ` Á ú µ ¾ Á a Ra = 0 n Š½ } º# s h ` ½ ÂÁ µ=é Ra = 10 n Š½ } ºâ*s ½ é ½ ¾%ì Å ½ µ é Á ì êg ³ µjì ½ µ é ½ µ= #ì é ` Á µ ³À Á ³Õ³ µjì ½ µ=é ½ ú µ=²¾ Á ¾ a µ ¾Gé Á ³ ú 3  ½ }3ˆ9` Á ¾ Á ú J úrâ ²¾ ½ J ¾%µ ³ Áú J =c³ Å Á ìsê.g µ ì ì ½ é ½ #µ  3² Å Á ³ ½ ú µ  ¾ ½ Å ²  µ é ½ #¾ e Á ³/a ³ Å Á ì h ½ é ` =é `Á ³ µ  ² Á ¾ a Ra T g µ= ì T a } ³  µ=³ Á ³ Re (Re > 1) é ` Á Á9 úr½ é(g u µ ì é ` Á é ` ½ ú Á ¾ ¾ h ` µ Á  µ ³À Á µ Åfe ½ é ²ì Á ¾ µ ì é ` Á ³À² e éಠ³ Á e ½ 3é Å Á ¾!a ³ Å é ` ÁsúRÁ 3é Á ³ x = 0 éà hœµ=³6ì ¾ôé ` Á a ³ µ Å Á e ½ Jé x = 1 } u é ` ÁÛú µ ¾ Á a Re = 100 W e = 1 µ ì A = 0.1 é ` Á ³À² e éಠ³ Á ½ ¾Õµ ú` ½Á Á ì é ` Á é ½ Å Á Å Å Á 3é t = ½ sé ` Á e ½ Jé x = 0.53 o ër }3ˆ9` Á ¾ Á ³ Á ¾À² Â é ¾ µ=³ Á ¾ ` hô ½ Š½ } û } u Š½ } ë µ ì Š½ } åõé `Á+ú ½ ô a3é ` Á c  Š½ ¾ e ³ Á ¾ Á 3é Á ìa J³5é ` Á ¾ µ Å Á ì=g µ Å ½ú e µ=³6µ Å Á é Á ³6¾ôµ= ì T 0 = 1.19 ê²éôé(hõ 'ì ½#z5Á ³ Á 3é4a ³6µ Å Á µ= ì.µ Å ê ½Á 3éôé Á Åfe Á ³ µ=éಠ³ Á ³ Á ½ Å Á ¾Œµ=³ Á ú ¾ ½ ì Á ³ Á ì Æ µs T g = 1, T a = 1 n ¾ Á9Á Š½ } ë.s ê+s T g = 1.15, T a = 0.9 n ¾ Á9Á Š½ } ås }?
325 š œ:œ 3ø.œž D à± š šäú5 + D û»y,0,5 1,5,0 1,5 h 1,0 0,5 t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t=1.4 t= ,0 0,5 0,0 U -0,5-1,0-1,5 -,0 t=0.1e-3 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t= ,5 0,0 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 x 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 X M +N$I ži#ahilhži" E,3HJ?*žI:H h D u M A = 0.1 D α = 1, 37 D Re = P e = 100 D W e = 1. D T 0 = 1.19 D T g = T a = 1 M h(x, t)? u(x, t) -? 1,0 1,18 1,0 1,18 1,16 1,16 1,14 1,14 1,1 1,10 T 1,08 1,06 1,04 1,0 t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t=1.37 1,1 T 1,10 1,08 1,06 1,04 1,0 t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t= ,00 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 x 1,00 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 X M +N$I #ži:hilh)ži" E T M$ A = 0.1 D α = 1, 37 D Re = P e = 100 D W e = 1. D T 0 = 1.19 D T g = T a = 1 M T (x, t) M Ra = 0? T (x, t) M$ Ra = 10 - Åfe ²é6µ é ½ #¾Dµ=³ Á ì J Á a J³ ³6µ ì ½ µ é ½ J 3² Å ê Á ³6¾ Ra = 0 µ= ì Ra = 10 } u a é ` Á ³ Á'½ ¾Û ³ µjì ½ µ é ½ kn Š½ } ë5 s é ` Á é `Á ú J ÁAú é ½ ì Å ½ µ=é Á ¾ µ= ìbé ` Á é Á Å~Ä e Á ³ µ=éಠ³ Á e ³ c  Á e ³À éà³ ²ì Á ¾+é h µ ³ ì ¾+é ` Á e ½ 3é a ³À² e éಠ³ Á x = 0.53 ³ Á µ ú` ½ é `Á ¾G  ½ ì ½ c ú µ=é ½ 'é Á Åfe Á ³6µ éಳ Á T = 1 a J³ôµÛé ½ Å Á Å Å Á 3é ¾ Å µ  ÂÁ ³Õé ` µ é ` Á ³À² e éಠ³ Á é ½ Å Á t = 1.37 } u aàé ` Á ³ µjì ½ µ é ½ ½ ¾ ½ ú9â ²#ì Á ìà 3é ` Á äµ ú  ½ Û a1é ` Á c Â Å é ½Â Â é `Á ¾À ½ ì ½ c ú µ é ½ J é Á Åfe Á ³6µ é ² ³ Áä½ ¾~µ ú9ú9á9âá ³6µ é Á ìà ê²éé ` Á é Á Åfe Á ³ µ=éಠ³ Á e ³ =é ³À²#¾ ½ ½ ¾~ ½ ¾ ½ ê  Á µ= 3µ ½ n ¾ Á9Á Š½ } ë5â µ ì ݽ } åsûéà hœµ=³6ì ¾Dé ` Á e ½ 3é x ú ³ ³ Á ¾ e ì Á 3éDé é ` Á Å ½ ½ Å ² Å a0c  Šé `½ú Á ¾À¾~µ é~é ` Á.ú ²³À³ Á 3éDé ½ Å Á Å Å Á 3éA ½ } ÁJ} x = 0.55 µ=é t = a ³ é ` Á c³6¾žé ³ Á ½ Å Á µ ì x = 0.56 µ=é t = a J³ é `Á ¾ Á:ú J ìb³ Á ½ Å ÁJ} ˆ9` Á µ Å ê ½ Á Jé%µ ì:a ³ µ Å Á é Á Åfe Á ³6µ é ² ³ Á ³ Á ½ Å Á ¾ì =é ` µ Á µ ¾ ½ ½ c ú µ= 3é ½ Sj² Á úrá é ` ½ ¾ ê¾ Á ³ µ é ½ µ ì é ` Á  g ì ½#z5Á ³ Á úrád½ ¾ é ` µ=éa J³ T g = 1.15, T a = 0.9 é ` Á?
326 û ¹A» ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ 1,0 1,18 1,16 1,14 1,1 1,10 T 1,08 1,06 1,04 1,0 t=1.e-4 t=0.03 t=0.1 t=0.3 t=0.5 t=0.8 t=1. t=1.3 t= ,00 0,0 0,1 0, 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 X +N$I ži#ah ILH0žI" E C M A = 0.1 D α = 1, 37 D Re = P e = 100 D W e = 1. D T 0 = 1.19 D T g = 1.15 D T a = 0.9 D Ra = 10 - ú ½ ½ ¾ô¾ ½ ` é  gfa µ ¾Gé Á ³ } ˆ9` ½ ¾ ú µ ê Á Á e  µ ½ Á ì ê.gé ` Á é ` Á  µ ³À Á ³ µ  ² Á a é ` Á ³ µjì ½ µ=é ½ é Á ³ Å ½ ntº } ys } ˆ9` Á é Á Åfe Á ³6µ éಳ Á e ³À c ÂÁ e ³ =é ³À²#¾ ½ é Á ì ½ ~éà ê ³ Á µ= ² e µ é é `Á é ` ½ Á ³ô³ Á Ä ½ aé ` Á c  Š½ ¾ ú J =c³ Å Á ì ê.gµjì ì ½ é ½ µ  ² Å Á ³ ½ú µ  ú µ  ú ²  µ é ½ J ¾ h ½ é ` ì ½#z5Á ³ Á 3é a ³ µ Å Á µ Å ê ½Á 3éŠé Á Åfe Á ³6µ é ² ³ Á ³ Á ½ Å Á ¾Šµ ì~³ µjì ½ µ é ½ ² Å ê Á ³6¾ }=ˆ9`Á ¾ Á ³ Á ¾G² Â é ¾µ ³ Á =é ½ Á ½ äé ` Á e ³ Á ¾ Á Jé4h ³ } ˆ9` Á µ= ì Á ³>wbµJµ  ¾4a J³ ú9á ¾ ` µ Á ½ ¾ ½ ê  Á Á$z5ÁAú é.é ` Áú ½ e ³ ú9á ¾ ¾9 ½ a Re 1 } ˆ9`Á ½ Sj² Á úrá aé ` Á ½ Á ³Àé ½ µ  a ³ úrá ¾+ ~é ` Á ú ÁAú é ½ J ~ì ² Á éà ½ ú ³ Á µ ¾ Á ì Re > 1 µ=é é `Á e ³ Á ¾ Á úrá aé ` Á µ= Dì Á ³ wbµjµ  ¾ a J³ ú9á ¾ ½ ¾ Á ½ ì Á 3éih ` Á xh ÁÕú Åfe µ=³ Á é ` Á e  =é6¾ a Š½ } ºh ½ é ` é ` J¾ Á a Š½ } ë } u é ` Ás µ égé Á ³ ú µ ¾ Á é ` Á ¾ ½ J²  µ=³ ½ é(g a é ` Á ì=g µ Å ½ú e ³ ê ÂÁ Å ½ ¾Œé ³ µ ¾ a Á ³ ³ Á ìséà ~é ` Á é ` Á ³ Å µ  e ³À Jê ÂÁ Å } 9Ü Z W!]//\._(Z W u é `Á e ³ Á ¾ Á Jé)hÕ J³À ph Á ¾GéÀ²ìSg é ` Á.ú  ½ a µ a ³ ÁAÁ é ` ½ c  Šµ éàé µ ú`á ì é bµ ³ Á:ú é µ ²  µ ³0a ³6µ Å Á ² ì Á ³ é `Á µ ú é ½ J a% µ ì Á ³>w µ µ  ¾!a ³ úrá ¾ }1 é ` Á êµ ¾ ½ ¾ a é ` ÁŒÂ ú µ  a J³ Å aé `ÁôÁ Á ³À g Áb ²µ é ½ J ~ì Á ³ ½ Á ì ½ mo qrµ ìdé ` Á ì=g µ Å ½ ú Á b ²µ=é ½ ¾ ì Á ³ ½ Á ì ½ o û ñër é ` Á ¹:ç ½ Á µ=³dé ` Á ³ Å ì=g µ Å ½ ú e ³ ê  Á Å ½ ¾ a J³ Å ²  µ é Á ì } ³ ½ é ¾ô¾À  ²é ½ µ ú ¾ Á ³ µ é ½ Á ì ½zÁ ³ Á úrá ¾ ú` Á Å Á.µ~¾Gé µ Á ³ Á ìs¾ e µ ú9á J³ ½ ì ½ ¾ e ³À e 3¾ Á ì } ý ² Å Á ³ ½ ú µ  ³ Á ¾G²  é6¾aa J³+é `Á c  Šé `½ú Á ¾À¾A ½ é ¾  ½ é ²ì ½ µ  Á9 úr½ é(gsµ= ìé Á Å~Ä e Á ³ µ=éಠ³ Á Á  ²é ½ J ½ é ½ Å Á µ=³ Á Jêé µ ½ Á ìpa ³ì ½zÁ ³ Á 3é ôá g Â ì ¾Û ² Å ê Á ³ ¾ Re n 1 Re 100 s Õì ½ Å Á #¾ ½ ÂÁ ¾ ¾ µ Å µ= Á ³ ú ¾Gé µ Jé A n 0 A 0.1 ssµ ì ³ µjì ½ µ=é ½ ² Å ê Á ³6¾ Ra n 1 Ra 10 s }Šˆ9` Á a  h ½ ² Å ê Á ³ ¾Dµ=³ Á µ ¾ ¾G² Å Á ì c Á ì Æ é ` Á ú µ e ½  µ ³/g ² Å ê Á ³ Ca = ε = 0.01 ½ } ÁJ} Aé ` Á w Á ê Á ³Ý ² Å ê Á ³ W e = 0.01Re é ` Á ³6µ= #ìé  ² Å ê Á ³ P r = 1 ½T} Á } é ` Á ñáaúrâá é ² Å ê Á ³ P e = Re }
327 - - š œ:œ 3ø.œž D à± š šäú5 + D û ¹ ¹ ¾µ³ Á ¾G²  éñ a#é ` Á e Á ³/a ³ Å Á ì 3² Å Á ³ ½ ú µ  µ= µ  g¾ ½ ¾A h ÁŒú µ Å µ= Á é ` Á a  h ½ œ= 9 L œ Æ ½ sõé ` Á ½ ú ³ Á µ ¾ Á añ³ µjì ½ µ=é ½  Á µ ì ¾ é fa µ ¾Gé Á ³ ú ½ śµ ì ³ Á µ ú` ½ Dé ` Á ¾À ½ ì ½ Ä c ú µ=é ½ é Á Åfe Á ³6µ é ² ³ Á ê Á a J³ Á Á Á 3é ²µ  ³ ² e éಳ Á ü ½ ½ sñé ` Á!` Á µ é ú ÁAú é ½ J ú µ ²¾ Á ¾é Á Åfe Á ³ µ=éಠ³ Á ê ³ Á µ ² e ½ ä¾ e µ úrá e ½ 3é ¾ ú J³À³ Á Ä ¾ e ì ½ 'éà 'é ` Á é ` ½ Á ³!c  Š³ Á ½ J ¾A µ= ì é ` Á ¾ Á é ½ Å Á ¾ Å Å Á Jé6¾"µ ³ ÁÛÂÁ ¾ ¾ôé ` µ= ³ µ e e ³À 3µ ú` ½ Dé ` Á é ½ Å Á Å Å Á 3é6¾Œ a c  Š³À² e éಠ³ Á } ˆ9` Á µ égé Á ³ ú J úrâ ²¾ ½ J ½ ¾ ¾ ½ Å ½  µ=³ éà J Á Jêé µ ½ Á ì a ³ä¾G²³ a µ ú é µ 3é ¾ n Å µ ¾ ¾*s éà³6µ= ¾ a Á ³: µ ¾ ³ Á e J³Gé Á ì ½ o º à¹a» à¹j¹'r } ˆ9` Á ³ Á a J³ Á é ` Á ½ Á ³Àé ½ µ  a J³ ú9á ¾ÕéÀ J Á é ` Á ³9h ½ é ` é ` Á µ ì Á ³:wbµJµ  ¾6a J³ ú9á ¾A h ` ½ ú` ì Á ¾Gé µ ê ½Â ½ù9Á é ` Á c  Šì=g µ Å ½ ú ¾o ër ` µ Á é ` Á ¾Àµ Å Á Á zá:ú é é `Á é Á Åfe Á ³6µ é ² ³ Á c ÁA ì } ˆ9` Á ¾À ½ ì ½ c ú µ é ½ e ³ ê ÂÁ Å é µ= ½ ½ Jé µ úaú J² 3é e ` µ ¾ Á ú` µ= Áú #ì ½ é ½ J ¾ n ½ } ÁJ} é ` Á 3é Á a µ= e ³À Jê ÂÁ Å s%µ ì é ` Á c  Šì=g µ Å ½ ú ¾ h ½Â  ê Á ¾žé ²ì ½Á ì ½.µ ú 3é ½ ² Ä µ é ½ ä ašé `Á e ³ Á ¾ Á 3é9h ³ } Y W!] > m- Q- N & M~M9H & m- - ILKI -C F E & H3M " IL?4 žf3ilh."6ôn E H E GM žf E % NN 11LIL?M$žI#AH -!#"%$&#D' 7 D3B(AS ;ÛB)A< B*)RB;+(A@A@D>68:8#,- 7-. Q- m- PŒM AF & I -C F E žf E %6 ^F E M9H & 1 M E - " E/ N M0 7D O1žILH E / E ( M D G E I &JE? E ( D P E 71 žk D >68)9B- < =$AM D ( " K MAH & O -=C M?M9K $:M - P " E ži?6m "6 & E LILH0, E6E žf3ilh6." & JH3M " IL? -6!#"%$&798:3"<;>=?@BADC*7 % ;FE5G.#EHCIEH# J#K?;FK(D' > D7A8=>Œ;D< >A>D 79@:@A<- B#.4 -L 1= AM D ( " K MAH & O -C M?3MAK $AM - P<" E žil?m i% #ži:h %M~HAHLILH E M$ AH Ē Q;& I" E HI:HM 55 E "k & I@ E E HžI M EDM M$žI:H &JE?/žI#?JILH9žF E "6 ži#ah6 #M9, E6E žfji Hx." -6NO; PQ79R79E&"<;> #TSVU W&3"<;>A#E&K(DX Y) D#>@A<)";s>6@AB <D 79@:@:<- (- - O M "ÛM$(K ILI -[Z$&7A#R\J A^]_C3; PQ79R79EH=\7`K9=\$&798:79K(- P M 3KAM D& KAM D#>8#,:8- S3 1i - N - O F:K=ILHMAH & P - P - 1ŠMAH E H3K -ab79"%$cadc C#; P M JK:M D P< I?3I8(K D#>68@,@(- )- O -C M?MAK AM - OLI & I8?M$žI:H0, Ē E žfji H9"6 -TZ$&7A#R?79"<;>=?@#EC@H ;Y7CVb7=\$c3E&;>= K(D &f 7 D3<:8 ;ÛB:8D7A@:@A@-,3 O -1C M?3MAK $AM'MAH & 4-6g M ( E H( - P " E žil?m i"6 &JE LILHd žf E %LI & I83?M ži:h E6E žf3ilh:"6 -hi;>= RA?G#R^#jD;F"<JikWc#R\"l79R J D > DT(#( ;DS=>D>68:89B- 83 :m>-c/ M' H? M$ D& - E -4 I#5 E M9H &C - Q- 3 I8 E K=I - E 1( E žf3ilhf=i?f."6a? AMAH &JE F7ñM:M #AB ž? E ži:hsm9h & E 8 Q I" I M$žI8 -n6$*j#k Toh W5;>C#K(D Y( D>:>6<:@ ; 79@:@ > - >6@3 -m E 3 I8% Dpm>- M # Erq M9H & g<- N -Lg FžI5($ - P :HLI H E M E ži:h EDM M žiah4b žfji HLI M JI &."6^7+I8žF ILH% #? E %% MA?*GM9H( -Tn6$*J#K oh W;<C#K(D*s D:< 7#(ASÕ;"<:7ASASD>68:8AB- >A> E Dct-u - M$GM DA- O -& 5E Erq0&JEOt %ži q MAH & -&v - G E 7+I8% -wv I" & GMAILH3M E? E ;7 E6E H> 7 4%% M9?*GMAH Q?:M E'&6& (11? I & I H"M Ý?:H5GMAHÝM 11( M9?ÀF6 E #? I; -L x A@%yA#;>C_\E&"l79R%]r=\7`= ;Y#D Hz=D8:< ;s>@)d 79@:@A<-
328 - E û ¹:º ± œ ~ œ Ù% ôú# â6 Jœ Þ Ù 1ã œ Øœ Þ,I BP =M=P,M.P,M +M=P M=P I =I IP IP 'P =I :O^IN BPM! " I M =I $# ("! K D O -3C M?MAK AM Dc4-1= AM P M ži H&% E(' M "ÛM KAM *)5( I6 MAI% I# 1:HI K M "61JII61+% E E,% E D 1žILKAM?JI H( 1žI E 5GM-6I MAKAM "61JI#.)žM 8 E HJI#:% E "6 D M (/% E I HJI"ÛM -p,% E E +% GMx E ILK=I M "ÛMÛK:M 13ILI M$žILH3I10ÝI8 / MAH & E / M % ' E % 0ôI8xGM I" E %ži1)k:m=i & ži# 1:K)5("6 DM *3=I:I - ži8žilh3kam "ÛM H E 5GM Q? I#AHM$žIH E ži E I H&% E E ("6 & ILHM " ILH4% E 1(? E "ÛM I E H"ÛM5-6I~M ( E(' )GM>KAMAI8žI1)K:M9II1)%%1*65GM?3MAI žilhji#70^k I8%("6 0Q?GF E "6 A1M :M?M - 1 GM:M ži+k:m9i8ži HJI MAI+ E q 8GM GM9I^1+% E E,% E B ("ÛMAI D I1)I:ILH3I M " E I1-6I3I I8 E "61 E GM 98 GMAI=K=I8%žI H:I E "6 E E ILH & %!K:M9I- I M "6 D? E'& I" E HILH4% E "6 G M "ÛM9K E žik AH5GM9H( "6I8 GM & I MA? I ' <1M GM " E %GM "6 -
329 !"# $ % '&)($ +*,.-/10 3 -/546 87:97;:7 <>=? <A@A@ABDCE?GF3HJILKNM"OP3P:Q 967NRN<TSU= <>R < VXW Y[Z)\]\D^ _)`badcfehgjikg lnmo\]gpeoqr`w moskskehvutv`5wxmyiz`{v W}a~Y[V e ik g cfmo W) r`5\ \ `5mveh_ gzƒ Z)mziz`{V W # ˆ8 "Š" Œ Ž U + # N T > Dš TŽ 5œ> T 5œ TŽŸž J L > 6 ŽD > šj d # 6œ ªš «5 : Ž Ž> J J ± ²³ ³G µ ¹º ±J² 1» ¼ ² ½ ³ ½¾ À Áª ½ ¹  Ã3ÄÅÆ3Ç3È É ÊAË#Ì Å ÍÏÎ Ð#ÎJÑÑ ÅJÒÑ Ó%ÉÔÌ3Í3ÕÖÉÒ Í ˆ Á > ½Ø ºd ÙÛÚ»Ú : #ÜJÝ Ø½ ³G º >Þß ÁDµ >Ý Ú à» Ú : á'âäã>åaæ çè:å é P:êGM>Hë3MTìGë.í M>î E ìïk ILHM>ð3ðJìïñò ILó«M>êïILñNHJô6õö3ôILH3 ªôóøñ ñ>êïfdôð3îlilh E ô8êïñ ôñnîlöjêïilñnhjô ñ>ùêïf E HJñNH3îLILH E M>ì E6ú ñaîûö êïilñnhmtìüýäm>f3h S þ IûîLîLIûM>ìGë E6ÿ ö3m>êïilñnh.m>ì E MAH3MAî ü ô E ë C F EøE ò ILôÔê E H3? E õ öjh3i ÿ ö E H E ôô«mah3ë?6ñah ú E ìï E H3? E ñ>ù êïf E ùö3îlî ü]ë ILô? ì E ê E ý{ìgmahjk S Q IL?6ñNîLôñNH ô? F E ó E M>ì E ë ILô S? ö3ôô E ë ê5î M>ôÔêbM%îLILH E M>ìïI E ëí MAî E ìïk:ilh MAðJðJìïñò ILó«M>êïILñNH8ILôÏðJì E ô E H:ê E ëõ +FJIû?GF"Iûô1M>îLôñÖô E?6ñAHë ñ>ìgë E ì M>?6?6öJìGMTê E ILH êïiló E ù¾öjîûî ü ëjilô? ì E ê E ô?gf E ó E ýämafjh S þ ILîLîLIûM>ìGë Eÿ ö3m>êïilñnhõí M>î E ìïk ILHô?GF E ó E õ?6ñnh ú E ìï E H3? E õ3îlilh E M>ìïI M>êïILñAH "!$#&%'(*)+!, ± ³ ½º >Ý ß, : À.-8½¹¹ ½¾ Ý º /J² ß ½ ± 4 ½ ß dµ ± ² º Ý Ù >± º½ ß ½ ± ³ : ºd :.½ ½ ß ½ ¹ T± º½ ß ½ ± u t + 4 u x 4 = φ(u) x, x Ω =]0, 1[, t (0, T ], 0+1 u = 0, x x=0,1 3 u x 3 x=0,1 = 0, t (0, T ], 0+1 u(x, 0) = u 0 (x), x Ω, >Ý : º» Ý ǿ T± ³ïß : ß ³ φ(u) = γ(u 3 β u) γ β 4 ½ ß γ > 0 ¼, : À.-8½¹¹ ½¾ Ý º /3² ß ½ ± Ý ½ ³ Á³ ³ Þ ± Á ± ¹ ±6 ½ :¹äÁ ± º 87 ± Ý Þ ³ +³ >Þ Ý ß ½ ± ½ T±± ¹ ½ 6 µ ½ Ý Ù ³ ± ¹ ²ß ½ ± ³Ï³G²# ³ :¹¹ ± Ù ³» 6 ¹¾ ³ ³ Á³ : #º Þ± ¹ÙÁ >Ý Ú 13
330 : Á ½ ß ² Ý Á³» ³GÁ, : : º -8½¹ ¹½ Ý º»Š ± ؽ À, ± Tß :¹ : º ß Ý 7 >Ý >Á³ ½ ß º ß ÁÝ ½ b - >Ý ½ ³ Þ#ÁÝGß ² Ý µ# ß ½ ± ± 71ß >± > ß Ý ß ½ ± ± 7{± Ÿ± 71ß u(x, t) Þ ³ Á³ ¹ ± µ :¹ ½ ³Gß T : º ² ½ /3² Ń³ ³ ± 7Ïß ³G± ¹ ²ß ½ ± 7 ± Ý Ø µ > ³ ± µ3ù +¹¹ ½ ±:ß ß º 6 : #ºŸ½ T± ß ½ ² ±J²³ ½ ß ½Á ±JÝ ¹ Ù ½ ß 11 ¹ Á ß :¹ >Ý ½ Þ Þ Ý ± ½ Áª ß ½ ± 1 7 ±JÝ ½ ³ŸÞÝ Ń³G ß º : º : ± Þß ½ Áª ¹ûÀ ± Ý º >Ý >Ý Ý ±JÝøÁ³Gß ½Á ß Ń³ ½ ½ ³ º >Ý ½Ø º1» ³GÁ +¹¹ ½ ±:ß ßD Tß ¹U { ³ Á½%º ½ ³ TÝ Tß ½ ß L ¹ Á ß Á Tß ± º 4 ½ ß /3² º Ý ß ² Ý 7 ± Ý ³ Ý6³Gß ½ ß Ý ± º ² > º : º :¹Ù ³G º µ3ù +¹¹ ½ ±:ß ßb Tß :¹! A ½ º" ½ ß ¹ Á ß Á >ß ± º ³ Ø µ > «Þ Þ ¹½ º µù$# Tß :¹ % J &# ½ ß º½' ÁÝ T Ÿ³ Á Á³ Ý º Ø ¹ ±JÞ# º½, ±3±D Tß ¹U ( à»*)»*+ ² Ý ½ ß Ú»» ², ) ¼ 8Þ ¹¾ : ±7Ïß ŸÞ Þ >Ý ½ ³ ³ 7 ± ¹¹ ± 4 ³ : ³ Á Tß ½ ± Ú»3 7 ß >Ý Þ ¹¾ :½ ½ 6 ± ß ß ½ ± 1» ß ² Á ÁÝ ½ ¹ ³ Á ½ ³ º Á³ TÝ ½ µ ºd½ º Tß :½¹U #¼ «½ ³ïß > : º ² ½ /3² Á³ ³ ±7 ß Þ Þ Ý ± ½ Áª ß "³ ± ¹ ²ß ½ ± ' Ý Ÿ³ ± 4 ª½ ³ Á Tß ½ ± Þß ½ Áª ¹ Ý ß 8± 7b >± Ø ÁÝ 6J > Á³Gß ½Á ß Ń³ 7 ± Ý ß ² Á ÁÝ ½ ¹ ³ Á ½ ³äÞ Ý ± Ø ºD½ ³ Á ß ½ ± ß ¹ ³ïß+³ Á Tß ½ ± 1»: ¹ ½ Ý ½- º :¹ >Ý ½ øá >ß ± º«½ ³{Þ Ý Ń³G ß º 4 ½ D½ ³ :¹ ³ ±"³GŃ T± ºÀ ± Ý º >Ýb >± Ø ÁÝ 6J ß ¼ Ý ±J²*6 ± ²ß ß ½ ³ Ý ß ½ ¹» º ±:ß Á³ 6J ÁÝ ½ T± ³ïß : ß»b ±:ß Á TŃ³ ³ Ý ½¹ Ù ß C ³ Á ß º ½.' >Ý ß8± > >² Ý Ý T /$10 %354 )5'7698;:<4 >=! #? Tß º µ ½ ß 6J >Ý6³ r l 4 ½ ß ± 7ŸÞ Ý ß ½ ß ½ ± ³ º ³G >ß h : #º r 4 1 l r 0 = x 0 < x 1 < x <... < x I = 1 ±7 [0, 1] J i = (x i 1, x i ) = max (x i x i 1 ). 1 i I A@ T± ³ ½¾º >Ý 7 :Á½ ¹Ù ½ ß ± ³ ² µ ½ ß >Ý Ø :¹ ³ ¼ Ý ±J²*6 ± ²ß ß Þ Þ >Ý» 4 ²³ ß ± º ± ß D ¼ ± Ý Á ³ ± 7» L (Ω) L (Ω) : º Ý º ±:ß º µù» : º x ¼ ³ Á½ûÀÔ ±JÝ Á ½ ³ º À H s (Ω)... s D s v ±:ß º.µÙ º ± ß Ń³ ß ½ >Ý"ÞÝ ± º ² Tß8± v s, (v, w) = vw dx 7 L (Ω) 7? Tß S h µ ³ Þ > ±7{ß Þ ½ Á T 4 ½ Ω³ ǿþ± ¹Ù3 ± Á½ ¹ ³GÞ ¹½ Á³  S h = { χ C l (Ω), χ } Ji P r 1 (J i ), i = 1,..., I; Dχ(0) = Dχ(1) = 0, 4 >Ý º ±:ß Ń³ß Ÿ³ TßÖ± 71Þ± ¹Ù3 ± Á½ ¹ ³%± ± 7 º 6 Ý > ¹ Ń³ ³%± Ý% /3² :¹ ß ± P r 1 (J i ) J i r 1.? Tß S h H» (Ω) 4 ÁÝ : ºdº ±:ß H (Ω) = { u H (Ω), z ß ² Ý ¹ :¹ >Ý ½ d Þ Þ Ý ± ½ Áª ß ½ ± ß ± u x = 0, S h = S h {χ, (χ, 1) = 0} ½ ³ ÂB º } x Ω, u h S h ³ ß ½ ³+7 Ù½ 6 ( uh t, χ ) + (D u h, D χ) = (φ(u h ), D χ), χ S h, 0 Ú 1
331 à : > ž J Ž T ø A ø L : š > % 4 ½ ß Ú Ú u h (0) = u 0h, 0 4 >Ý ½ ³ : Þ ÞÝ ±JÞ Ý ½¾ ß Þ Þ Ý ± ½Áª ß ½ ± ß ± u 0h S h u ½ ß Ý ± º ² T 8ß ³G±«:¹¹ º ¹¹ ½ Þß ½ 8ÞÝ ±ïá ß ½ ± P h : H (Ω) S º ºªµÙ ß 7 ± ¹¹ ± h 4 ½ 6 Þ Ý ± µ ¹ Á ³GÁ» 6 %¹ ¹½ ± ßGß Tß ¹U 7  7 ±JÝ 11 v H» ß (Ω) ½ ³ ß ǿ² ½ /3² ǿ³ ± ¹ ²ß ½ ± ± 7 ² Tß ½ ± 7 P h v { (D (P h v v), D χ) = 0, χ S h, (P h v v, 1) = 0. ¼ «½ ³ïß >ǿ± 7 ² ½ /3² ³ ß ½ P h v ³57 Ù3½ 6 Ú 7 ± ¹¹ ± 0 4 ³$7 Ý ± Á ß?{ ÀÔ ½ ¹ 6 Ý :Á ¼ >±JÝ Á : º ß + Ý ½ º Ý ½ ³ À ± ½ Ý ½ /3² ¹ ½ ß Ù w C( w + (w, 1) ), w H µ 6 ½ 4 ½ ß ß 7 ± ¹ ¹ ± 4 ½ 6 Ý Á³ ² ¹ ß ³ º ² ß ± +¹¹ ½ ±:ß ß : º 6 æ ã å #é šj!% 6š "$# Ú % *) + T P h &%(' 1 1 Ú v H r (Ω) H (Ω), h j v P h v j Ch r v r, 0 j=0 š' v H > (Ω), Ú à v Phv Ch r v W r (Ω). 0,.-0/ #æ /1 #é # N Ž> : ŸŽT : L u(t) 3 ¾Ž8Ž 54 œ> T # U 6# Ô 7 T D 8) > : š % øž> û U : 3 Ú Ž ¾Ž9! TŽ T > 0 13 Ú ) u h (t) C T, 0 t T. 0 Œ9 T u 0h = P h u 0, Ú u(t) u h (t) C T (u)h r, t [0, T ]. 0 :" : ; ¼ ³ ³ ² Á Þß ½ ± Ú ) ½ ³ ±:ß Ý Ń³ïß Ý ½ ß ½ ± 1 =<ÖÙ ³Gß : #º Ý ºª Ý 6 ² Á ß : º ²³ ½ 6 >Ý Ý ± Ý Á³Gß ½Á ß Ń³ Ú 4 Áª Ù ï²³gß ½ 7 Ù Ú ) Þ#±3³ïß >Ý ½ ±JÝ ½ 7 ± Ý 3Ù T > 0 Á ¼ ± Á A» Þ Þ ÖÚ?> ³ ¹ ¹Ÿ > º ß ³ Á ³ ³G² Á Þß ½ ± ½ ³GŃ ß ½ ± ³» : º à ¼, Ý : ÀŠ8½ T± ¹ ³ ± 7 ² ¹¹ Ùøº½ ³ >Ý >ß Þ Þ Ý ± ½ Áª ß ½ ± Ÿ½ ³ º ºø½ ß 7 ± ¹¹ ± 4 ½ 6 4 Ù5 º. ³ /3² T ³ ß ½ ³+7 Ù½ 6 {U n } N n=0 S h { ( t U n, χ) + (D U n 1, D χ) = (φ(u n 1 ), D χ), χ S h, U 0 = u 0h. 4 >Ý ½ ³ ³G² ½ ß µ ¹ Þ Þ Ý ± ½Áª ß ½ ± ß ±» ½ ³ß Þ Þ Ý ± ½ Áª ß ½ ± u 0h S h u 0 U ½ ± n 7 ß : #º S h u(t) t = t n = nk k = T º ±:ß Á³Ûß ]³ ½- ±7Dß ß ½ Á º½ ³ TÝ Tß ½-N ß ½ ± 1 Ú 4 Ø ²³ º ß ±:ß N ß ½ ± Ú Ú
332 1 0 ' ) : t U n = 1 k (U n U n 1 ), U n 1 1 = (U n + U n 1 ).» u(t) 4 4 Ý ½ ß u n 1 = u(t n 1 ) + ± Ý8 >± ß ½ ² ± ²#³ 7 ² ß ½ ± ß ½ ³ ÝGß ½ ¹» ß Áª :½ 6J± ¹ ½ ³ ß ± Þ Þ Ý ± ½Áª ß ß ³ ± ¹ ²ß ½ ± ³ ± 7 ß, : À.-8½¹¹ ½¾ Ý º /3² ß ½ ± ÛµÙ 7 ² ¹ ¹ÙÛº½ ³ TÝ Tß ½ ß «¹ Á ß8³ Á #¼ «³ïß : º Ý º :¹ >Ý ½ Á Tß ± º'½ ³%²³G º 7 ± Ý Þ Þ Ý ± ½ Áª ß ½ ± ½ ³ Þ > : º, Ý : ÀŠ8½ T± ¹ ³ ± À ß Ù Þ ³GŃ T± #º ± Ý º >Ý > >² Ý ß º½ ³ TÝ Tß ½-N ß ½ ± ª½ ³ ²³ º 7 ±JÝ Þ Þ Ý ± ½Áª ß ½ ± ±7Ïß ½Á º ÁÝ ½Ø À ß ½Ø Á³ >@ 4 ½ ¹¹ Þ Ý ± Ø Ÿß ß ß «³ Á ½ ³ T± 3Ø >Ý 6 ß $ ) >4 &'74 6# &) $% 4 4 é#é Uã>å / è / ß ½ ³8³ Á ß ½ ± 4 «³ :¹¹ Þ Ý ± Ø ß «½ ³ïß >ǿ± 7 ³G /3² > ³ ß ½ {U n } N ³57 Ù3½ 6 Þ Ý ± µ ¹ Á Ú 7+ ± ÝŸß ½ ³» n=0 4 ³ ¹ ¹ ²³ Dß 7 ± ¹¹ ± 4 ½ 6 Ø Ý ½¾ : ߟ±7ß 4 ¹ ¹ À ± 4 º Þ#± ½ ß ß >± Ý Á ± 7 < Ý ± ² 4 >Ý Ú» / 1 1 ç é T "6 $!+ "š: > Ž : A Ž Jœ 5 T 5 Nš œ> : š H (.,.) H %. H. > ä 6 "6 œ6 : Ž g : H H N Ž> Ÿ T J ¾Ž Ž α > 0 Ž6 œ6 ' % T : $ Ž6 œ6. : (g(z), Z) H 5š 0 Z ' Z H = α 5 T d T J ¾Ž Ž Z H, g(z ) = 0 Z «³ :¹¹Ï Á º ß ² ½ ¹½¾ Ý Ù Á³Gß ½Á ß Ń³  / 1 1 ç1é % *) Ö N 3 + ±JÝ v S h %(' v S h» 4 v 1 1 γβ v + γβ 4 v. 0 1 Þ Ý ± Ø ½ ÁÁ º ½ ß ¹Ù 7 Ý ± Á 4 ½ 1» 4 # Ø (D v, v) = v 1, v 1 v v. 0 ³ ½ 6 ß ½ /3² :¹½ ß Ù» ab a γβ + γβ 4 b 4 Þ Ý ± Ø Ÿß ¹ ÁÁª / 1 1 ç é T š Ž v S h Ö N 3 + ±JÝ (φ(v), D v) γβ v 1. 0» v S 4 Ø h Ú ²³ ½ 6ß º ½ ß ½ ± ± 7 ß ǿþ Ý ±± 7 (φ(v), D v) = (Dφ(v), Dv) = (φ (v)dv, Dv), φ 4 # º φ (v) = γ(3u β ) γβ, 4 ½ >± Á Þ ¹ Tß Á³
333 : > ž J Ž T ø A ø L : š > % ¼ %Þ Ý ±± 7±7 ½ ³ïß > ±7 Þ Ý ± > > º ³ ½ «½ #º ² ß ½ Ø {U n } N 4 Ù : ŸµØ½ ±J²³ ¹Ù n=0 ½ ³ïß6³ % ± Ý >± Ø ÁÝ»ä ³ ³ ² Á.ß ß { U } 0 U j n 1 ½ ³ïß6³ + ± Ý»%º Z S µ3ù j=0 h S h S h (g(z), χ) := (Z U n 1, χ)+ k ( (D Z, D χ) (φ(z), D χ) ), χ S h. 0 ² ḐÁ Þª ½ ³ïß6³ µù ß ˆ ½ Á³ - Ý >Þ Ý Á³ ß ß ½ ± ß >± Ý Á.» ² ± ²³ ¼ ½ 6 ½ : º ²³ ½ 6» χ = Z 0 4 ± µ ß ½ (g(z), Z) Z (U n 1, Z) + k Z kγβ Z 1. < Ù? ÁÁª 'Ú» 4 º ¼ >Ý 7 ±JÝ» (g(z), Z) Z U n 1 Z kγ β 4 Z. 8 - T 87 ± Ý ¼ ª½ ß 7 ± ¹ ¹ ± 4 ³ 7 Ý ± Á? ÁÁª ß ß ß ÁÝ " ½ ³Gß ³ ³G²# ß ß Z S ß ½ ³ ³ ½ ¹Ù ³ > ß # ß ³ ß ½ ³ Á³ Ú h U n = Z U n 1 é Ïé 7 / / ãnã g g : ½ ³%± µø3½ ± ²#³ ¹Ù >± ß ½ À (g(z), Z) Z ( (1 kγ β 4 ) Z U n 1 ). 8 k < 8» 8» γ β 4 Z = 8 kγ β 4 U n Ø (g(z), Z) > 0 g(z ) = 0 ³ ³G² Á Öß # ßäß ³ ± ¹ ²ß ½ ± ± 7 Ú ³ ß ½ ³ Á³ u ± ± Ý ² ½ /3² Á³ ³» ³G² ÞÞ#±3³G ß # ß : º χ S h 1 ½ ³ä³G² ' ½ ß ¹ Ù Ý 6 ² ¹¾ Ý : º ß # ßäß ³ ± ¹ ²ß ½ ± U n c 0, n = 0, 1,..., N. 0 V n S h : #º V 0 = u 0h ³ ß ½ ³+7 Ù ( t V n, χ) + (D V n 1, D χ) = (φ(v n 1 ), D χ), χ S h, 0 # ±:ß ½ 6 E i = U i V i» 4 ½ ß V n c 0, n = 0, 1,..., N. E 0 = 0» 7 Ý ± Á 0 Ú : º ) à )» 4 # Ø 7 ±JÝ ( t E n, χ) + (D E n 1, D χ) = (φ(u n 1 ) φ(v n 1 ), D χ). 0 Š ± 4» ³ ² Þ Þ±J³ ½ 6 E n 1 = 0 º ±±J³ ½ 6 χ = E n 1 ½» 4 ± µ ß :½ 1 k ( En E n 1 )+ E n φ(u n 1 ) φ(v n 1 ) + E n 1. 0 ³ ½ 6 ß «T± ß ½ ² ±J²³ º½' ÁÝ ß ½¾ :µ ½¹ ½ ß Ù ±7 φ(.)» 4 6 >ß
334 ' ' >Ý : φ(u n 1 ) φ(v n 1 ) C E n 1, 0! ½ ³ T± ³ïß : ß º >Þ º ß"± <ÖÙ º!» C c 0 4 # º 1 k ( En E n 1 ) C 4 En 1 C 8 ( En + E n 1 ), 7 Ý ± Á 4 ½ 1» 7 ± Ý k ³ ² ' ½ ß ¹Ù ³ Áª :¹¹U» 4 6 «³ > ß # ß E n = 0 { 4 + kc E n λ E n 1, λ = 4 kc } 1 : #º ß ½ ³ T± Á Þ ¹ Tß Á³ ß ǿþ Ý ±± 7b±7{ß ǿ² ½ /3² Ń³ ³. *) 56 *)+!! = 4! 4 4 '74 6 >4 ß ½ ³d³GŃ ß ½ ± 1» 4 Ń³ïß ½ Áª ß ß >Ý Ý ±JÝ'± 7øß ]³G± ¹ ²ß ½ ± ± 7øß 7 ² ¹ ¹Ùpº½ ³ >Ý >ß Þ Ý ± µ ¹ Á Ú >@ ǿ²³ ß «³Gß º Ý º >Ý Ý ±JÝ º Á T± Á Þ#±3³ ½ ß ½ ± 4 ½ ß Â u n = u(t n ) U n u n = (U n P h u n ) + (P h u n u n ) = θ n + ρ n. 0 1,.-0/ #æ /1 Ïé > # Ž Ž6Ž6 Ö 5 Ô #" Ž6Ž6 à ¾Ž+Ž ¾Ž9! 6š > 5š : Ž> L Ž % ' U n u 3 Ú : š TŽ 6œ> U 8) T 6# N Ž> % ŽT : L 1&% u ¾Ž Ž6 54 œ> T # U #ª : Œ9 ø «š* ªŽ : U ¾Ž9 #' Ž : Ô Ú U 0 u 0 Ch r, 0 T % *) T : Ž 54 œ> T # U 6#Ž % k U n u(t n ) C(h r + k ), 0 > ¾Ž; dœ6 Ž # % šj Ô > š > 3 5š C h k. Ö N 3 ½ T Dß Á³Gß ½Áª ß ±7 ρ n 7 ± ¹ ¹ ± 4 ³7 Ý ± Á Ú»½ ß ½ ³Ÿ ±J²*6 ß ±dá³gß ½Á ß ³ ½ 6ß º ½ ß ½ ± ± θ n º» 7 ß «¹ ¹½ Þß ½ Þ Ý ± ïá Tß ½ ± ½ Ú P h v 0 4 ½ ß /3² ß ½ ± ³ (1.1) (.8) 4 8± µ ß ½ ß 7 ± ¹ ¹ ± 4 ½ 6ø /3² ß ½ ± 1» 4 ½ ½ ³ Ø ¹ ½¾º 7 ±JÝ :¹¹ ³G² ß # ß (χ, 1) = 0  χ S h ( t θ n, χ) + (D θ n 1, D χ) = (φ(u n 1 ) φ(u n 1 ), D χ) < Ù ß ½ 6 ( t P h u n u n 1 t, χ) (D ( un + u n 1 u n 1 ), D χ). 0 χ = θ n 1» 4 ± µ ß ½ 4 >Ý ( t θ n, θ n 1 ) + θ n 1 I θ n 1 + J θ n 1 + K θ n 1, I = φ(u n 1 ) φ(u n 1 ), J = t P h u n u n 1 t,
335 ! ¼ ½ ³ Ù3½ ¹¾º ³ : > ž J Ž T ø A ø L : š > % K = D ( u n + u n 1 ) u n 1. 1 k ( θn θ n 1 ) + θ n 1 1 I + 1 θn J + 1 θn 1 ¼ :µ ± Ø ½ /3² :¹½ ß Ù'µ Ń T± Á Ø "ß 7 ± ¹¹ ± K + 1 θn 1. 1 k ( θn θ n 1 ) θ n 1 + I + J + K. 0 ½ 6Ń³ïß ½ Áª ß ³ > :¹ ³ ± ŸÁ Ý : ½9» à à I = φ(u n 1 ) φ(u n 1 ) C U n 1 u n 1, >Ý ½ ³ T± ³ïß : ß º ÁÞ# º ß ± º ¼ Ÿ >± ß ½ ² ± ²#³ º½' ÁÝ À C c 0 u n 1 ß ½¾ :µ ½¹ ½ ß Ù ±7 Ø µ > ²#³G º ß ± º >Ý ½ Ø ß ½ ³ ½ /3² ¹ ½ ß Ù φ( ) ¼ >Ý 7 ±JÝ 4 6J Tß ß ǿń³ïß ½ Áª ß Á³ U n 1 u n 1 U n 1 Ph ( un + u n 1 I 1 = P h ( u n + u n 1 = ρn + ρ n 1 ρn + ρ n 1 ½ Á½¹ Ý ¹Ù 4 θ n 1 + I1. ) + P h ( un + u n 1 ) u n 1 ) ρ n + ρ n 1 u n 1 + un + u n 1 u n tn 1 tn (s t n 1 )u tt (s)ds (s t n )u tt (s)ds t n 1 + Ck 3 6 Tß ß ǿá³gß ½Áª ß Á³ t n 1 ( t n t n 1 u tt (s) ds J = t P h u n u n 1 t t P h u n t u n + t u n u n 1 t = 1 k ρn ρ n tn 1 tn k (s t n 1 ) u ttt (s)ds + (s t n ) u ttt (s)ds t n 1 t n 1 k 1 ( t n t n 1 ρ t (s) ds )1 K = D ( u n + u n 1 u n 1 + Ck 3 ( t n ) 1 t n 1 u ttt (s) ds. ) 1 ) ( t n Ck 3 D u tt (s) ds t n 1, ) 1.
336 ' 0 0 0» Ú : ³ ½ 6 à 4 ½ ß ß ǿń³ïß ½ Áª ß Á³ ±7 I, J : º K» 4 ± µ ß :½ 1 k ( θn θ n 1 ) C[ θ n 1 + ρ n + ρ n k tn : ºÛ T t n 1 ρ t (s) ds + k 3 tn 4 >Ý ß ¹¾ ß ß >Ý /3² :¹½ ß ÙÛº Á³ : º 7 ± Ý8³ Áª :¹¹ t n 1 ( u ttt (s) + u tt (s) + D u tt (s) )ds ], θ n θ n 1 Ck ( θ n 1 + R n ), R n ± 4 ÞÝ ± Ø º ß ß (1 Ck) θ n (1 + Ck) θ n 1 + CkR n, k k 0 ß «³Gß µ ½ ¹½ ß Ù Á³Gß ½Áª ß ½ ³ Ø :¹½º1 7 ß ÁÝ8Ý >Þ ß ºd Þ Þ ¹ ½ ß ½ ± 1» ß ½ ³ Ù3½ ¹¾º ³ ± Ý Š ±:ß ½ 6 : ºÛµÙ ³ ½ 6 ß ß ) Ú θ n» 4 ± µ ß :½ ( 1 + Ck ) θ n θ n 1 + CkR n. 1 Ck ( 1 + Ck ) n θ 0 + Ck 1 Ck θ n C θ 0 + Ck n j=1 ( 1 + Ck ) n jrj, 1 Ck n R j. 0 j=1 θ 0 ρ 0 + U 0 u 0, 0 tn ρ n Ch r ( u 0 r + u t (s) r ds). 0 0 º» 4 #º ( θ n C U 0 u 0 + h r( T u 0 r + u t (s) r ds) 0 T ) + k 4 ( u ttt (s) + u tt (s) + D u tt (s) ) ds. ß 7 ± ¹¹ ± 4 ³7 Ý ± Á Ú 0 ß # ß8Á³Gß ½Áª ß ± ¹º ³ Š ß 4 4 ½ ¹¹ ²³ ß Š"½ Ý µ >Ý 6 ½ /3² ¹ ½ ß Ù / 1 1 ç {é j m a 1% 1 p = j n + a(1 r m n ) + (1 a) 1 q % > š Ž > D j v L p (Ω) C ( D m v a L r (Ω) v 1 a L q (Ω) + v L q (Ω) ), Ω ¾Ž "6 : š 6šÛš ÛŒ : n )
337 % : > ž J Ž T ø A ø L : š > % Ú,.-0/ #æ /1 é > "6 Ž> L U n Ú N Ž> Ž> : L U : ] 3 0 ¾ŽŽ 54 œt > #Ž A : š D {š* ' ¾ŽDš!+ 5 6š Ž T T k Ž6 54 œ> T # U #Ž % u 0h = P h u 0. 0 TŽ U max U n u(t n ) C(h r + k ) 0 n N š Ž T % ' C ¾Ž; œ6 Ž : % 5š > šj T # : š h k. Ö N 3 >ßGß ½ 6 ½» χ = t θ n 4 ± µ ß ½ t θ n + t θ n I t θ n + J t θ n + K t θ n I tθ n J + t θ n + K tθ n. ¼ :µ ± Ø ½ /3² :¹½ ß Ù 6 ½Ø Ń³%ß ǿá³gß ½Áª ß ³ ½ 6 ß ǿá³gß ½Áª ß Ń³ ± 7 θ n θn 1 k 1 k ( θn θ n 1 ) C(I + J + K ). 0 I, J º K 4 ½ ß» 4 ± µ ß :½ ( C C(u)(h r + k ) + ρ n + ρ n tn ρ t (s) ds k t n 1 + k 3 tn - T ß 7 ± ¹¹ ± 4 ½ 6³ïß :µ ½¹ ½ ß Ù'½ /3² ¹ ½ ß Ù t n 1 ( uttt (s) + u tt (s) + D u tt (s) ) ds ).! θ n θ n 1 + C(u)k(h r + k ) + CkR n ½ ³ Ø :¹½¾ºÏ» 4 >Ý Ÿß ½ /3² ¹ ½ ß Ù' :¹ ³G± º Á³ *- T»µÙ Ý ÁÞ# ß º Þ Þ ¹½ ß ½ ± R ± 7 ß ǿ± µ ß ½ º Ń³ïß ½ Áª ß : º! n 4 6J Tß ¼ >Ý 7 ±JÝ» n θ n T C(u)(hr + k ) + Ck R j. j=1 θ n C ( C(u)(h r + k ) + k Š ± 4» ²³ ½ 6 Ú n j=1 T ρ j + ρ t (s) ds 0 T + k 4 ( u ttt (s) + u tt (s) + D u tt (s) ) ds ). 0» 4 ǿ >± ¹ ² º Ÿß ß» 7 ± Ý8³ ± Á ǿ T± ³Gß : ß C = C(u, T )
338 ' 1 0 ' 0 0» 1 0 Ú % % % Ú Ú Ú : : ºÏ» >ǿ²³ ½ 6 Þ Þ ¹Ù½ 6 º ¼ ± 6 Tß >ÝÖß ǿá³gß ½Áª ß Ń³ θ n C(h r + k ), 0 n N, º Ú» 4 ± µ ß ½ θ n 1 C(h r + k ), 0 n N. 0»½ ß 7 ± ¹¹ ± 4 ³ 7 Ý ± Á? ÁÁª 4 ½ ß p = ß ß θ n C(h r + k ), 0 n N. 0 Ú à : º $ ) 4 6 ") 4 # )5 :<4 =! # ³ ± 4 ß ¼ >±JÝ Ád ¼ :µ ± Ø Á Tß ± º] ³øß º ½ ³ ºØ ß 6J ß ß ± ¹ ½ Ý«³ Ù ³Gß Ár ³ ß ± µ ³G± ¹ Ø ºd ß ß ½ Á «³Gß >Þ %+ ±JÝ ß ½ ³ Ý ³ ± 4 «³ ¹ ¹ >± ³ ½º >Ý ¹ ½ Ý ½- ºÛÁ ± º½ À ß ½ ± ± 7{ß Á >ß ± ºd½ 4 ½ ß Ý 6 ² Á ß ½ ³ ± µ ß ½ ºdµ3Ù ß Ý Þ± ¹¾ ß ½ ± f 7 Ý ± Á : º» ½ U n 1 U n Û n = 3 U n 1 1» U n 7 ± Ý n, ( t U n, χ) + (D U n 1, D à χ) = (φ(û n ), D χ), χ S h. 0 1 ¼ ½ ³ Á Tß ± º 4 ½¹¹ Ý /3² ½ Ý ³ >Þ Ý ß ǿþý Ń³ >Ý ½ Þß ½ ± 7 ±JÝ" ¹ >² ¹ ß ½ 6 ³GÁ» U ¼ ± Á >» Þ Þ Ú > Ú : # :¹Ù ³ Þ Ý º½ ß ±JÝ >± Ý Ý Ń ß ±JÝ Á Tß ± º 7 ± Ý%ß ½ ³ 1 Þ ² Ý Þ#±3³G» 4 ½.½ ³ 7 ± Ý Á ² ¹¾ ß ºd ³ 7 ± ¹ ¹ ± 4 ³  U 0 = u 0h, ( U 1,0 U 0 ), χ + (D ( U 1,0 + U 0 ), D χ) = (φ(u 0 ), D χ), k ( t U 1, χ) + (D U 1, D χ) = (φ( U1,0 +U 0 ), D χ), χ S h. :" : + ± Ý u(t) ³ ² ' ½ ß ¹Ù ³ Á ±±:ß b» 4 Ø û n = 3 un 1 1 un = u n 1 + O(k ) as k 0. 0 Š ± ½¹ ¹ Þ Ý ± Ø ß ßß Þ Ý ± Þ±J³ º Þ Þ Ý ± ½ Áª ß ½ ± 4 ½ ¹¹ 6 ½Ø ǿß ³ Á >± º ± Ý º >Ý A T² Ý Ù,.-0/ #æ /1bé > "6 ŽT : L U n 3 à 5š š!+ 5 6š 0 1&% ' U 0 U 1 "5# à Ú # N Ž> " % { Ž> û U : u ¾Ž Ž 54 œ> > #ø Ô : 5š "6 5š 6š Œ9 D œ6 : š! ¾Ž ) L š T T k *) T : Ž Ž 54 œ> > #ªŽ : % ' : Ô à max U n u(t n ) C(h r + k ) 0 0 n N C = C(u, T ) 113 à Ú à U n, u n
339 0 0» » 0» : > ž J Ž T ø A ø L : š > % Ú Ö N 3 ³ ½ 6 Ú» ½ ß ½ ³%³ ² ' ½ ßß ±DÁ³Gß ½Á ß 4 ± µ ß :½ 7 ± Ý ß ǿ /3² ß ½ ± n 7 ±JÝ θ n θ n *+ Ý ± Á Ú º à 13 Tß ß ½ 6 ( t θ n, χ) + (D θ n 1, D χ) = (φ(û n ) φ(u n 1 ), D χ) ( t P h u n u n 1 t, χ) ( D ( un + u n 1 u n 1 ), D χ ). 0 χ = θ n 1» 4 #º à à 4 >Ý 1 ( θ n θ n 1 ) + θ n 1 k 1 I + 1 θn J I = φ(û n ) φ(u n 1 ). ¼ ²³ + 1 θn K + 1 θn 1, 1 k ( θn θ n 1 ) θ n 1 + I + J + K. 0 ³ ½ 6ß º½' >Ý ß ½¾ :µ ½¹½ ß Ù ± 7 : #º Û n u n 1 φ( )» 4 º 7 ±JÝ"³G± Á «T± ³ïß : ß C à ) º >Þ º ß"± < Ù Ú º I C Û n u n 1 C ( ˆθn + ˆρ n + û n u n 1 ). à» 4 # Ø ³ ½ 6 Ú à ) I C( θ n 1 + θ n ) + C(u) ( h r + k ). º ß ǿá³gß ½Áª ß Á³ ±7»»» I J K 4 ± µ ß ½ θ n (1 + Ck) θ n 1 + Ck θ n + C(u)k(h r + k ). ¼ ½ ³ Ù3½ ¹¾º ³ θ n + Ck θ n 1 (1 + Ck) ( θ n 1 + Ck θ n ) + C(u) k(h r + k ). ¼ >Ý 7 ±JÝ» 7 ±JÝ º nk T n à >Ý Š ß 4 θ n C ( θ 1 + k θ 0 + (h r + k ) ). 0 «³ ¹ ¹ Ń³ïß ½ Áª ß θ 1 %+ Ý ± Á /3² ß ½ ± ³ à Ú 0 4 6J Tß ß ǿá³gß ½Á ß 1 k ( θ1,0 θ 0 ) C ( U 0 u 1 + (h r + k ) ),» ß θ 1,0 = U 1,0 P h u 1 θ 0,0 = θ 0 7 ± ¹¹ ± 4 ³ 7 Ý ± Á ß ß U 0 u 1 θ 0 + ρ 0 + u 0 u 1 θ 0 + C(h r + k), 4 ½.Ù½ ¹¾º ³
340 0 0 0» Ú : ¼ ²#³» 1 k ( θ1,0 θ 0 ) C ( θ 0 + h r + k ). θ 1,0 (1 + Ck) θ 0 + Ck(h r + k ) C ( θ 0 + h r + k 3 ). 0 ß «³ :Á 4 Ù' ³ :µ ± Ø 4 ± µ ß :½ 7 Ý ± Á ¼ >Ý 7 ±JÝ» ²#³ ½ 6 1 k ( θ1 θ 0 ) C ( U 1,0 + U 0 u 1 + (h r + k ) ). 0 à» 4 Á³Gß ½Á ß ß ǿ >Ý Ý ±JÝ U 1,0 + U ½ ß ß Á³ ǿá³gß ½Áª ß Á³» u 1 θ 1,0 + θ 0 à! à Ú + P h u 1 u 1 1 ( θ1,0 + θ 0 ) + C(u) ( h r + k ) C θ 0 + C(u) ( h r + k 3 ). µ Á >± Á Á³ θ 1 (1 + Ck) θ 0 + Ck(h r + k 3 ) C ( θ 0 + (h r + k ) ). 0 ß 7 ± ¹¹ ± 4 ³7 Ý ± Á! à ) ½ ³ Ø ¹ ½¾º 7 ± Ý%³ ± Á T± ³ïß : ß 7 ± Ý n º à» ß ß ß ǿá³gß ½Á ß θ n C(h r + k ), 0 n N 0 C = C(u, T ), ±±J³ ½ 6 χ = t θ n ½ t θ n + t θ n I t θ n + J t θ n + K t θ n ¼ >Ý 7 ±JÝ»3µÙ ß ǿń³ïß ½ Áª ß Á³ ±7 ³ ½ 6 à à à à à! à 113» 4 ± µ ß ½ I tθ n J + t θ n + K tθ n. : #º Ú I, J, K 0» 4 ± µ ß :½ 1 k ( θn θn 1 ) C( θn 1 + θ n ) + C(u)(h r + k ). à 11» 4 6J Tß, ± ³ /3² ß ¹ ÙJ» 7 ± Ý 1 k ( θn θ n 1 ) C(u)(h r + k ). n : #º nk T, 4 Ø θ n C(u, T ) ( θ 1 + (h r + k ) ). ½ Á½¹ Ý ¹Ù ß ±Ûß : # :¹Ù ³ ½ ³ 6 ½Ø :µ ± Ø» 4 ß 7 ± ¹ ¹ ± 4 ½ 6 Ń³ïß ½ Áª ß D± µ ß ½ 7 Ý ± Á à Ú ½ ³Gß º ± 7
341 0 T» 0 0 1» Ú Ú ¼ >Ý 7 ±JÝ ¼ ²³ ½ 6 + Ý ± Á à : > ž J Ž T ø A ø L : š > % Ú à 11 Ú à θ 1 C(hr + k ). θ n C(u, T )(h r + k ), 0 n N. 0 à 113 : º Š ± 4» ß ǿý Ń³G² ¹ ß$7 ± ¹¹ ± 4 ³ 7 Ý ± Á á è 7 / 1 / 5åAã à» 4 ǿ± µ ß :½ θ n 1 C(u, T )(h r + k ), 0 n N. 0 : º? ÁÁ 4 ½ ß p =» 4 6J Tß θ n C(h r + k ), 0 n N. 0 à : º ¼ ²ß ± Ý ß # : ³ º Á >Þ ¹Ù ß Ý 7 >Ý >Á³ 7 ±JÝ ß ½ Ý Áª : Ù Ø :¹ ² µ ¹.³ ²*66JÁ³Gß ½ ± ³ 4 ½. ¹ Þ º ß ± ½Á Þ Ý ± Ø Ÿß ǿý Á³ ² ¹ ß ³ ± 7 ß ½ ³ Þ Þ >Ý Ú à à à à '74 9 <( í ) ë3maóøô!+?maë E óøil?#"ïì E ôô6õjq E %${ñaìïkõ 9R&' K ìïi ú ILô +* ILH3I ê E ë I-, E ì E H3? E ëjilô? ì E êïi MTêïIûñAH ñaùêïf E/. ö ìgmaóøñaêïñ S P I ú M>ôF3ILH3ôK ü Eÿ ö3m>êïilñnh :9<; 7 õ>=? õ 9Ö;9N9 õ 9RAR < 7@ í BA MAK E ìõc ) ñn NMAîLILôMAH3ëED. M>ìGM>KNM>ôF3IûMAH ý ñah úne ìï E HJ? E ñaùÿí M>î E ìïk ILH M>ð3ðJìïñò ILó«M>êïILñNHJô{ùñAìäêïF EF. ñaìê E E S ë E C%ìïI E ô Eÿ ömtêïilñnh HGIJLKM7 NO3F 14JP7 õqr#õ BJ96R ; BN7N7 õ 9RSN7 B5T U ýämaf3h'm>hë T þ V ILîLîLIûM>ìGë W* ì E E"E H E ìï >üñaùbhjñnh:ö3hjilùñaìïóuôôü ôôê E ó O OUH ê E ìù M>?6IûMAî ù ì E6E E H E ìï Aü YX7NZK>357\[OK4]7 õ^>_õ <'S"; <>=& õ 9R 'S '( P ` ý FJñ ñdmahë P ý F öjh3 ý ñah3ô E ì ú M>êïI ú E H3ñAH3îLILH E MTì ëjia, E ì E H3? E ô? F E ó E ù¾ñ>ì êïf E ýäm>f3h S þ IûîLîLIûM>ìGë E6ÿ ö3m>êïilñnh bno3f 14JP7\GIJLKM7Z97 õ>? =\c & d õ 7:9Ö;D7AR õ 96RNRS =@ P ` ý FJñ ñjõnp ý F:ö3HJ M>Hë. O. ILó ý ñnhjô E ì ú M>êïI ú E HJñNHJîûILH E M>ì1ë Ia, E ì E H3? E ô?gf E ó E ùñaìêïf E ýämafjh S þ ILîLîLI MTìGë Eÿ ö3m>êïilñnhõjoo FNO3W 14JP7eGIJLK>7\97 õm?>f:cgc 9 S < dgd õ <A<AR8;«<>BN7 õ <>@N@N@ &( Q ý ñaf E H MAH3ëih P E E î QÖñAH3îLILH E MTì M>ôð E? êïôöñ>ù{êïf E ýämaf3h S þ ILîLîûIûMTìGë E6ÿ ö3m>êïilñnh [OK4]@! jk ml õ\n4r#õ < &&"; <ARS õ 9R S>B S@ V ) E M>H#õ íöîlñ +ILHJôK I5MAHë C )& ì E6ú M>ô HMAð3ð ìïñòjiló«mtê E ù MA? êïñaìïi M>êïILñAHÛî E M>ôÔê ô ÿ ömtì E ô+ôñnîlöjêïilñahªó E êïf3ñ:ë«ù¾ñaì MmoJò E ëpohji ê E E î E ó E H ê%maðjðjìïñò ILó«M>êïILñNHñ>ù5êïF E ýäm>f3h S þ IûîLîLIûM>ìGë Eÿ ö3m>êïilñnh YX4;qX7Zr ; s14!jp7:97\gi@jlk>7 õ\n?õ BNR'8;p':9(& õ 96RNRN= R@ ý ` V îûîlilñaêõ )& 4* ì E HJ? F MAHë * t` ILîûH E ì ô E?6ñNH3ë ñaìgë E ìäôðjîûi êêïilh3 8ó E êïfjñ:ëù¾ñ>ì êïf E ýämafjh S þ ILîLîLI MTìGë Eÿ ömtêïiûñah 0F :GqJLK>7 õ umqõ ' & ' ;v'ara@ õ 96R SAR 96@@ ý ` HV îlîliûñ>êêøm>hë )& w* ì E H3?GF HJñNH3? ñnhjùñaìïóøilh3 xo3h3i ê E E î E ó E H:ê8ó E êïf3ñ:ë ùñaì"êïf E ê äñ S ë Iûó E H3ôILñNH3MAîýäMAFJH S þ ILîLîLIûM>ìGë E6ÿ ö3m>êïilñnh 4rg9WGyX7a0F a9<;7 õ^ =õ SSABŸ; RN@A7 õ 96R SNR 9A9 ý ` \V îûîlilñaêê MAHë'P ` \z F E H3 DÖHêïF E ýämafjh S þ ILîLîLI MTìGë Eÿ öm>êïilñah 9<6g K>7Z{Y@Jkj ; G}g K>7:9<;7 õ>f =õ 7N7NRŸ;«7' & õ 96R SN= 9<( ôôêgm@~3î E M>Hëª?6ñNHJô E ì ú M>êïI ú E oh3i ê E ëjia, E ì E HJ? E ô? F E ó E ùñaì êïf E ýäm>f3h S ) * öjìïilfmtêgm þ IûîLîLIûM>ìGë Eÿ ö3m>êïilñnh \GIJLK>7 õ_ec Btd õ = & '8;«=NRNR õ <A@A@ 9
342 . Ú ) : 967@ ) * öjìïilf3m>êgm M>Hë C 4` MTêïôö3ñ ôôêgm~jî E õ?6ñnh ú E ìï E H êõa?6ñnhjô E ì ú MTêïI ú E MAHëŸîûILH E M>ì oh3i ê E ë I-, E ì E H3? E ô? F E ó E ù¾ñ>ì1êïf E ýäm>f3h S þ IûîLîLIûM>ìGë E6ÿ ö3m>êïilñnh \X4;vX7Mr ; s14!jp7>97gijlkm7 õ ^>R:c 9(d õ ='";ps ' õ <A@N@A7 9 B. DÖó ìgm>h3i o3h3i ê EE î E ó E H ê ó E êïfjñ:ëªùñaì êïf E P I ú MAôFJIûHJôK ü Eÿ ömtêïiûñah r ;s@j ; X7 [14697 GIJLK>7 õ? ^:c 7 d õ 7AR&";«B 9N9 õ <A@A@ 9 9 '(. DÖó ìgmah3i DÖHêïF E H:ö3ó E ìïiû?6maî ð3ð ìïñ M>? F ñ>ù êïf E V H:êïF3MAîLð ü ` E êïf3ñ:ëù¾ñ>ì{êïf E P:ê E ù¾mah "Ïìïñ ~Jî E ó :G}JLK>7\[Y@6Jkj el#j 7 (7 õ ^>RZc Btd õ 'N<&8;v' ' 9 õ <A@N@>B 96=@ z z P öjh ô E? ñnhë S ñaìgë E ìdma?6?6ö ìgm>ê E îlilh E MTìïI E ë ëjia, E ì E HJ? E ô?gf E ó E ùñaìdêïf E ê äñ ë Iûó E H3ôILñNH3MAîýäMAF3H S þ ILîLîûIûMTìGë Eÿ ömtêïiûñah GI@JLK>7 NO@3F\7 õ>=mq#õ 96BN=N7Ÿ;ª9 Bt& 9 õ 96RNR ' 9 &( C C FJñNó E í MAî E ìïk:ilh/oh3i ê E E î E ó E H ê8ó E êïf3ñ:ë ô ù¾ñaì"ð3m>ìgm~ñaîliû?dðjìïñ~3î E óøô6õ\cöñaî <' OUH 6 j ;t6we6 j!<j ;}NO3W 14J Jkj ; GIJLK>3Jkj! õ3p ðjìïilhj E ì S C E ìïîûma Jõ A E ìïîlilh#õ 96RNR& 98S@5T $ ILH DÖHêïF EªE ò ILôÔê E H3? E ñaù8h3ñah3h E MTêïI úne?6ñnh êïilh:ö3ñnöjôøôñnîlöjêïilñah3ôdñaù êïf E ýäm>f3h S þ IûîLîLIûM>ìGë Eÿ ö3m>êïilñnh YX7:lj 7!7 õf õ 7 9@Ÿ;«7 < & õ 96RNR < " "!#$ %& '$(( )"*+,- /.0) &8)$ DÖó ìgmahji P êìgmailð3ôh ü:9 E M>HMAîLI 6öJñ;9ÔMAó«M+ôÔêGMAHëJM>ìêïILH=< E í M>î E ìïk ILHJñ M>ðJìïñAK ôiló«m>?6i 9MH E ôôêgm>?6ilñnh3m>ìïiûm:9ômai3ýämahjf S þ ILîûîLIûM>ìGëî üj %>6IûMAI õbðm>hmaö3ëjñ:9m>h:ê NîLñ:ë?6ILöJôøôð3îûMAILH:ö3ô ð êgm>ìêgmªð3ilîlhm>i%ëjilôk ì E >6ILñNôDý{ìGM>H3K ñ S Q ILK ñnîlôñnhjñ#~m>iû E óøñaô1ôðjì E H3ëJILH3ILñ E 6ILôÔê E H3? I 9ÔM õ ú I E HMTêïILô{I ì{k ñnh ú E ìï NM ú:s ILó«M>ô "ÏM~3MAIL Nñ:9 E ðm>ê E IûK êgm êïi E ôilh=< E í MAî E ìïk:ilh3ñdëjilôk ì E >6ILñ:9ÔIÏô?GF E ó«m:õk:öjìïiü:ìgmømah êìïñnô E ILîB< E ô êïilk:ôîlö3óøñÿðma NMAî#î M>ILKC
343 !"# $ % '&)($ +*,.-/10 3 -/546 87:9:;6<=7?>:@ A 9?@?@?>CBD AFE3GIHKJ:L"MN3N=OQP 7:R:9TSVU 9WR 9 [ XZYZ[]\_^a`_bdc Yfe)bdghgji5kml YZn e)bdkpoqir`ts ezs)kauv[wixxzoyyfn oi5kmlzghb {ro\_b}x~i5b}o gjuzfyfc u}` Yfc s ikpoƒb}x ` o \ Yf\_^)ghut`_i Yfk Cˆ# Š" Œ Ž8 C ŠCˆ % " F Š. š œˆ 3ž Ÿ " C C :ª «T±6² ³µ œˆ 3 º¹» ¼ ½» ¾» 3 À Á =ÂÃÅÄ Æ š Ç ÂÈ ÊÉ3Ë# = ÂÁ ̵̓  µîiï5ðiñ3ò ÐIÑ ÓIÔ ÏÕ ÖÒ3 ÅÖºØ=Ñ%ÙqÚ5Û:Ñ ÐØÛ=Ü3Ó#Û ÒÅÖÒI ÝÖºØ ÑÙqÞ ÐIÑ ÐØ ßÓ#Û ÒÅÖÒI ÝÖºØ Ñ Ž Æ?àWÆ Âá Æ š Æ?àTÆ ÍCâ ÆWã8ä ¾ å=¾i¾ äæ3ãêæ áâáç Æ š. à º¹Iâ Æ?ãè» å ¾ ¾=¼ é'ê ëwì?í îï=ì ð B E Dòñ LWó ô D G=õ3ö D ó ø?ù ó D A D G ú ñüû Aºó D LWú Dý öœlwú E D öœlwú HKAL ñ öòø ý D6ñKþ ø?ù þ HKG3ô ñkdês þÿd A6H D6þ HKG þd AÊú þ ÿ ø ÿ õ ñ LTú HKø:G ýid G þ HKú û'ý û G3L?öòHKA þ EL þ A6ø:G 3ó ö Dý ú E D A6ø?G ú HÈG=õIHÈGIôœHÈG ú D ó DÊþ ú øwù þ A6H D G ú H þ ú þ ú ø8ú E3H þ ÿ ó ø? ñkd ö D ô:hkg3gihègiô +Hüú E B E3ø:ö ÿiþ ø:g þ ø?ó J 7W> ú E D ó D EL D D6D G þ õiô:ô D6þ ú Dýþ ø:ö D öœlwú E D öœlwú HKAL ñ öòø ý D6ñKþ øwú E ùø?ó ÿ óflwaêú HKAL ñ#ÿ õió ÿ ø þd6þ þ HKöõ ñ LTú HÈø?Göòø ý S DÊñÈþ L?G ý ùáøwó+ó D D L ñ HKGIô þ ø:ö D ô D G D ófl ñd AÊø ñ ø:ô?hèa6l ñ5ÿ LWúú D ó G þ õ3l ñ HüúFLWú H D öòø ý D6ñKþ 7 P B E Dqý H D ó D G úàl ÿ3ÿ ó ø L?AFE DÊþ ú ELTúÀA6ø?õ ñèý D L ÿ3ÿ3ñ H Dý ú ø öœlwú E D öœlwú HKAL ñ öòø ýid6ñkñ HKG3ô ø?ù ý D G þ Hüú ûƒý û G3L?öòHKA þ ø?ù þ HKG3ô ñkdês þÿd AÊH DÊþÝñ L? ø?ófltú ø?ó û HKG þd AÊú þ ÿ ø ÿ õ ñ LWú HKø?G û ö D L?G þ øwùxgiø:g S ñ HKG D LWó ý H D ó D G3A DÊSVý H D ó D G ú H L ñ D õlwú HKø?G þ +Hüú E ý D6ñ L û LTó D8ý H þ A6õ þþdý B E D öœl?hkgqltúú D G ú HKø:G H þ#ÿ L?H ý ú øú E D öœltú E D öœltú HÈA6L ñ öòø ýid6ñ?ÿ ó ø ÿ ø þdý û ø ñkd6þ ø KP +EIHKAºEÝúFLWJ D6þ HÈG ú ø%l?aêa6ø:õig=ú ú E D L?ô D8þ úó õ3aêú õ ó D +Hüú E3HKGHKG þd Aºú þ ÿ ø ÿ õ ñ LWú HKø?G A6ø:ö ÿ õiú D ó HÈö ÿiñkd ö D G úflwú HKø:GCø?ù L ñkñ#ÿ ó ø ÿ ø þd6ý öœlwú E D öœlwú HKAL ñ öòø ý D6ñKþ EL þ DÊD GqùÁõ ñüs ñkñèd6ý û õ þ HKGIô"!qø ý D6ñ!LWJ D ó þ HKö õ ñ LWú HKø:G þ û þ ú D ö $#xlwó HKø:õ þåþ A D G3LWó HKø þ ùáø?ó þ HKöõ ñ LTú HÈø?Gƒø?ù D G =Hüó ø:giö D G úfl ñ ù L?Aºú ø?ó þ HKö ÿ LWAÊúÝø?G ú E D ÿ ø ÿ õ ñ LTú HÈø?G ý=û GL?öòHKA þ LWó D ó D L ñ H% Dý N HKöõ ñ LTú HKø:G ó DÊþ õ ñ ú þ LWó D A6ø?ö ÿ LWó D6ý +Hüú E ó D6þ õ ñ ú þ ù ó ø:ö& D6ñKñüS J=G3ø +G ñ L? øwóflwú øwó û.d(' ÿd ó HKö D G ú þ ø?g ú E D þ HKGIô ñkdês þÿd A6H D6þ%ÿ ø ÿ õ ñ LWú HKø:G) *,+ -/ öœlwú E D öœlwú HKAL ñ öòø ý D6ñKñ HKGIô HKG þd Aºú þ xÿ ø ÿ õ ñ LTú HKø:G ý H D ó D G ú HÈL ñ D õ3lwú HKø:G þ +Hüú E ý D6ñ L û 8:9,;=<?>@)ACB DEF>HGIA?< = J çºã Æ:à Â Æ ç ¹ K  ç Æ?à Êç8 ãºæ Ã Æ çf ÊçCK ¹ ã ML ã  à Ë È ÊË ãºæ = #šnk ¹ ãºæ ç Ê )Lˆ ŒÝÉ Æ?ãºÆ K ¹ ãêæ ÊÉ Æ O Ë Æ çf ºÂ¹ çò¹ K8š Æ çºâ IJ špj Íq à 眹mk  #ç Æ:à ÊçœÉ á Æ â ÆWÆ RQ š Æ SJhšÂÁç à ËçÊç Æ š  Æ?à ¹=Ì ¹$L  à = ÂÈ ÆWã ºË ãºæ K ¹ ã C ¹ )LC ÊÂ Í Æ ˆ  à Ëç Æ çå¹mk ̓ çêç ãºæ à 㠹šË à ºÂ¹ ¹MK  ç Æ?à Êç Q Æ?ãºÆƒÆ4T Ã Â Æ šhâjj纹 Í Æ Ë Â á ÆWã çº ºÉ Æ ¹ ã Â Æ çuq  ºÉ = ¹I Æ š Æ:à ÂÁçFÂá Æ K à ʹ ã ¹I VJ ˆ 8¹WQ Æ á Æ?ã # àwà Ë ÍCË = ºÂ¹ ¹ KYX3 ¹WQ Æ špl ÆCà ¹ àwæwã  HL š Æ çfâ IJšPJ Íq à ç"¹mk%â ç Æ?à Êç É ç%ã ã ¹ á Æ šc ºÉ = ÅçºË à ɹ Æ Ì çºâáš Æ šƒ à à 㠹I à ÉqÂÁç+ çfëhz à Â Æ 3 + º¹ Æ4T à  ÊÉ ÂÁç à ¹IÍÃ Â Ì à Æ š Ã É Æ ¹ Í Æ ¹ 1ˆ# Å "à ãêæ ç Æ 3 Ý ºÉ Æ?ãºÆ ãºæ \[ à ¹ 3 ã š Â à º¹ ã Jƒ¹ ๠#ç8 =â¹ Ë ÊÉ Æ
344 ä å=» # : ³ ± ² ²  Íù ã Ê = 3 ã ¹ Æ ¹ K â¹= ºÉ â  ¹ ºÂ à = š â ¹= ºÂ à K à º¹ ã çà Æ?à ºÂ HL ºÉ Æ š Æ çºâè IJ¹ K Â Ì ç Æ:à Êç?ˆ ŒÝÉ ÆòÆ4T ÂÁçF ºÂ HLƒšÂ ÆWãÊÆ àtæ ç8¹mkx¹iã   ¹I ç ãêæ ̓ = SJ š Æ ÆWã ÍqÂ Æ š âj šâ ÆWãÊÆ 3 =à à 㠹I à É Æ çx Ê¹Í Æ:à É = ÂÁçºÍ ¹MK5š Æ #çfâ IJ à ¹ 3 ã ¹ µˆ=œýé Æ Í¹IçF % àwàwæ à 6 =â Æ ç Æ?Æ Íƒç ʹâ Æ = ÂÁš Æ '¹MKÅ =Ë Ê¹ ̓ ÊÂ à š Æ çºâ IJ à ¹ 3 ã ¹I x¹ K% #ç Æ:à Êç? ÂÈ òâáç çºë à ù ã Æ šâj Ë Í ÆWã ¹ Ëç ºÉ Æ ¹ ãêæ ºÂ à = š ÆT à ÆWã Â Í Æ I 6 = PQŹ ã Xç ʹ L Æ ºÉ ÆWã Q  ºÉ̓ ºÉ Æ Íƒ Ê à = Í Æ ÊÉ ¹š ç ä» ˆ ŒÝÉ Æ Á ã L Æ 3ËÍCâ ÆWã ¹MK ãêæ?àwæ 3 º VJ àtãêæ = Æ š'í = ºÉ Æ Íƒ ºÂ à 5Íq¹š Æ çåéĩç à ¹ ã Í Æ š ºÉ ÆÀà ¹I I ÊÂ Ë Â HL  3 Æ?ãºÆ ç ŹMK ç à Â Æ 3 ºÂÁçF Êç% º¹œ ÊÉ ÂÁç à 㠹Iâ Æ Í.ˆ ã ¹ â# =â VJ I ºÉ Æ Ã ã ¹ â Æ Í ¹ K  ç Æ?à Êç [xš Æ çºâè IJjšPJ =Í à çòâáçà ºÉ Æ Í¹IçF šâsz à Ë Ç ̓ = ºÉ Æ Í = ºÂ à Æ?à ¹ ¹ L JIˆ! Æ Ì L   HL Q ÂÈ ÊÉŒÝÉ ¹ ÍÃ纹 [ ç QŹ ã Xç" ä ¼ ÊÉ ÆWãÊÆ É á Æ â ÆWÆ çfë)l L Æ ç Æ š.纹 Í Æ Íƒ ºÉ Æ Ì Í = ºÂ à Íq¹š Æ çàâ¹= ÊÉ K ¹ ã à ã à ºÂ à = ÃË ã ùIç Æ ç$#vçfâícë Á Ê ¹I híq¹š Æ ç&% 1 š K ¹ ãòãêæ Ì á Æ Â HL 纹 Í Æ L Æ ÆWã = Æ:à ¹I ¹$L  à = à º ÆWã ç # O Ë Â Ê = ºÂá Æ Í¹š Æ ç&%' ä è µˆ5œýé Æ)( â ¹=Ì ¹$L  à = %Íq¹š Æ ( # µˆ Æ ˆx Á =â¹ ã ʹ ã JÃ#¹IÃ Ë Á Ê ¹I ç*%œâç ÆT ãêæ Í Æ SJ Æ Æ?à ºÂá Æ K ¹ ã š Æ á Æ Ì ¹ Ã Í Æ 3 ƒ¹mkçfë à É Í¹š Æ ÁçWˆ+ŒÝÉ Æ J ãêæ á ÆWã J ÂÍqù ã Ê 3,K ¹ ã ¹IË º   )LjÃÉ Æ ¹IÍ Æ ºÉ = à ¹ Ë Áš Æ4T à  ̓ = ºÉ Æ Í = ºÂ à ͹š Æ Áç?ˆ L ¹¹š ãêæ áâ Æ QZ¹MK" ºÉ Æ Q Æ Ì X3 ¹WQ â#¹ ã = º¹ ã J Æ4T à Æ?ã ÂÍ Æ 3 ÊçÅ = š š 6 œ¹ â Ê =Â Æ šâ + Æ Áš ÆT à ÆWã Â Í Æ I 6ç%ÂÁç?L Âá Æ Â ƒ ÊÉ Æ Š"Â à º¹ ã ¹ á6[ ç ä» ä-, r çº /. Æ á6[ ç š10â ã ç4[ è ¾ rš+ ã Æ J6[ ç? 30 ã ĨšPQ Æ [ ç šj " çêçº Æ [ ç Íq¹I ¹ L ã à Éç4 ä5 ˆ ŒÝÉ Æ Íƒ ÊÉ Æ Íƒ Ê à = #Íq¹š Æ ç%âj Í Æ ç+¹ K Q É Â à ÉƒÍ Æ:à É = ÂÁçºÍç+¹MK š Æ çfâ IJq¹Iç à  ÈÌ = ºÂ¹ çx¹mkâ ç Æ?à Êç ãêæ  3á Æ çf ºÂVLI = Æ š à = œâ Æ šâ áâáš Æ šcâ 3 ʹ8 ºÉ ãºæ?æ L ã ¹IË Ãç6 è è µˆ7  ã çf º VJ ºÉ Æ J' ãêæ šâáç àtãêæ Æ ºÂÍ Æ Í¹š Æ çq É Æ?ãºÆ šâ ÆWãÊÆ àtææ O Ë Ê ¹I çý ãêæ Ëç Æ š' º¹š Æ ç àtã Ââ Æ š Æ çºâ IJ'šPJ =Í à çý¹mkxâ ç Æ?à ÊçCQ  ºÉ ¹ ̵¹ á ÆWã à à  HL L Æ ÆWã Ê ¹I çwˆ Æ:à ¹ #š SJI 3 ºÉ Æ J ãêæà ¹ 3 ÊÂ Ë ¹IËç ºÂÍ Æ Í¹š Æ Áç Q É ÆWãÊÆ á ã ¹ Ë#ç à Á çêç Æ çƒ¹mkò ¹I Ì Â Æ ã šâ8 Æ?ãºÆ 3 ºÂÁ = Æ O Ë Ê ¹I ç% ãºæ Ëç Æ š š Q É Â à É à ƒâ Æ Ëç Æ š ʹ š Æ ç àwã Ââ Æ š Æ çfâ IJƒšPJ =Í à ç ¹MK1Â Ì ç Æ:à Êç [=ù Ã Ë = ºÂ¹ ç K ¹ ã â¹= ºÉƒ¹ á ÆWã à à  HL šq ¹ Ì ¹ á Æ?ã Á =Ãà  )L L Æ Æ?ã = ºÂ¹ ç9 è ¼ ˆ ŒÝÉ Â ã š VJ ÊÉ Æ J ãºæ çf º¹ à ÉĨç Ê à # ¹I Ìš Æ ÆWã Íq ÂÁç Ê à % Íq¹š Æ ç? PQ É Â à É. ¹ à ùIçºÂ Æ º¹ š Æ ÆWã Íq ÂÁç Ê à ͹š Æ çå 6 MX Æ Â 3 º¹ƒ à?à ¹ Ë I 8çºÃ#¹ ã ĨšÂ à à É HL Æ çå¹mk Æ áâ ã ¹ Í Æ I :ˆ ŒÝÉ Æ š Æ çºâè IJ špj Íq à çk ¹ ã L ã ¹ Ë Ã#ç8¹MK+ ç Æ?à Êç Q ÂÈ ÊÉ ¹I ̵¹ á ÆWã à à  HL L Æ ÆWã Ì ºÂ¹ çýéĩçýâ Æ?Æ š Æ ç àwã Ââ Æ š â=j ¹ LIÂçF ºÂ à šâ8 Æ?ãºÆ I ÊÂ Æ O Ë = ºÂ¹ : å 5 dn(t) dt ( = r 1 N(t) K ) N(t), Q É ÆWãÊÆ ÂÁç ÊÉ N(t) Æ Ë Í â Æ?ã ¹ K  #šâ áâášë ç?  r Æ ã L ã ¹WQÝ ÊÉ ã = Æ ÊÉ K Æ Íƒ T ÂÍCËÍ çfëçf Ê Â # =â Æ Ã#¹IÃ Ë Á ºÂ¹ ˆ ŒÝÉ Æ Íƒ = ââ ¹I ¹$L  à = # Íù ã Ê àtæ ¹MK1 ÊÉ ÂçÅù Ã Ë = ºÂ¹ šhj3 # =Í à ç%í¹š Æ ÂÁçÅšË Æ º¹j ºÉ Æ K à ¹MK Æ4T ÂçF Æ àtæ ¹MK K ÆWÆ š â à X â Æ IQ ÆWÆ ÊÉ Æ çfâ<; Æ ¹MKÃ#¹IÃ Ë Á ºÂ¹ = š  Êç L ã ¹WQ  HL ã = Æ ˆ ŒÝÉ Æ ¹ LIÂçF ºÂ à QfÉ# ç Q ÂÁš Æ VJ â Æ?Æ Ëç Æ š â=j ¹= ¹MK ãºæ ç Æ ã6à É Æ ç K ¹ ãqæt à Á =  )L ºÉ Æ ãêæ çºë È 6眹 K ÆT à Æ?ã ÂÍ Æ 3 Êç?ˆ= Æ.à Í Æ 3 ºÂ¹ É Æ?ãºÆ Q Æ Ì X3 ¹WQ Æ ã [ çq ¹ ã Xç å 5 +¹ j Á =â¹ ã º¹ ã J K ã Ë ÂÈ ">)J?#@ ±A ² CB ED = *F ² ³ W± %Ã#¹IÃ Ë Á Ì ºÂ¹ 1 0À Ëç Æ [ çqå¹ ã Xç 5 +¹I à ¹I PK Ëç Æ še>¹ Ë ã â ÆWÆ º Æ #HG ± JI K KDML ON& ² DP Q%T ¹š Æ É Æ Â Í ÆWã [ ç QŹ ã XçRüå À¹ ɹ Í Æ â ÆWÆ Ã¹ ÃË = ºÂ¹ d š ¹= ÊÉ ÆWã çwˆts ã ¹IÍCâ Â Æ ¼/ à É Â Æ á Æ š Àá Æ?ã Jqçº = ºÂÁçIKJ HL à ¹ ãºãêæ Á Ê ¹I â Æ IQ ÆWÆ ºÉ Æ ¹$L ÂÁç Ê à à Ë ã á Æ = š ÊÉ Æ Ë ÍqÌ â Æ?ã ¹ KVU 8W T± ³XB ª Dq JL6 h¹iâ Ê Â Æ š  Á =â¹ ã º¹ ã J ÆT à ÆWã Â Í Æ I :ˆ 8¹WQ Æ á Æ?ã Í J ¹ ºÉ Æ?ã Æ4T à ÆWã ÂÍ Æ 3 Ê = š 6 œé á Æ â ÆWÆ š Æ ç àtã  â Æ š'ë çê ºÂÁçK à ʹ ã  VJCâJq ºÉ Æ ¹=Ì L ÂÁç Ê à QòŶ7 ¹ ã Æ4T =ÍÃ Æ 1 = )LE ä ¾ YQ É Â Æ = VJçF HL'É ÂÁç¹WQ ãêæ çºë Êç = š ºÉ ¹3ç Æ ¹MK!Źš Æ É Æ Â Í Æ?ã [ ç å Æ4T à ÆWã ÂÍ Æ 3 Êç¹I,K ã Ë Â 6>)JR#@ ±A ² ZB D AF ² ³ T± % à =Í Æ º¹ à ¹I à ËçºÂ ¹I ÊÉ Ç ºÉ Æ ¹ LIÂçF ºÂ à Q à jâ Æ Ëç Æ š ʹš Æ ç àtã  â Æ ¹ SJ ÊÉ Æ çf ã Â à º VJ # è ˆ è %
345 D8 Y³ W± E:ª K FR N ²W LW³ ² T Y ³µ ² ³V 'C Dq JL ² ä å, ãºæ ç ã  à Æ š  ÂÈ Ê ç 6 ML Æ ¹MK Ã#¹IÃ Ë Á ºÂ¹ L ã ¹WQÝ ÊÉ ¹ KĨšË "çfã Æ?à Â Í Æ çwˆ Å F Æ Íà Êç8 º¹ ÆT à Á = h ºÉ Æ L ã ¹WQÝ ÊÉ à Ë ã á Æ çœ¹mk8 šë È çºã Æ?à ÂÍ Æ çc¹ j ºÉ Æ âĩç Æ ¹ K Æ O Ë Ê ¹I # è ˆ è % ç Æ?Æ Í Ë çº¹ Ë š ̓ = VJ šë Æ º¹ ºÉ Æ K à ºÉ = ÊÉ Æ ML Æ çf ã Ë à ÊË ãºæ ¹MK Ã#¹IÃ Ë Á ºÂ¹ Âç à ¹IÍqÃ Æ Æ VJ ÂVL ¹ ãºæ š.â ÊÉ ÂÁç Æ O Ë Ê ¹I 1ˆ5 = HL çfé ¹WQ8ç8 ºÉ = Àš Æ çºâè IJ špj Í à ç"¹ K šë ÅçºÃ Æ?à ÂÍ Æ ç š Æ Ã Æ #š ç%¹i ƒíƒ = J K à ʹ ã ç% = #šq ºÉ Æ?ãºÆ ãºæ ¹ VJ ã ãêæ8à Ĩç Æ ç:q É Æ?ãºÆ ÂÈ à 'â Æ ÆT à Á =Â Æ š'â=jq ÊÉ Æ ¹ LIÂçF ºÂ à Á Qòˆ3ŒÝÉ Æ =Ë ºÉ ¹ ã ç%¹mk QŹ ã X+ ä 5¹ ƒ ÊÉ Æ â ç Æ ¹ K ºÉ Æ Â ã ¹WQ h = # = VJçºÂÁçÀ¹MK š Æ çºâ IJšPJ =Í à çò¹ KÝ ã ¹I纹 Ã É Â Á Á =â¹ ã ʹ ã J Ã#¹IÃ Ë Á ºÂ¹ š ã Q F Æ 3 ºÂ¹ ʹ ÊÉ Æ K à ºÉ = ºÉ Æ â Æ É# á3â¹ Ë ã ¹ K ËÃç Ì = #šì š ¹WQ ç+ IJÃ Æ Âç8Íq¹ ãºæ IJ3àà = µˆ q # ºË ã à ¹ #šâè Ê ¹I ç Ë Í ÆWã ¹ Ë#ç çºã Æ?à Â Æ ç+¹mk5â ç Æ?à ÊçÉ# á Æ ¹ VJC¹I Æ L Æ ÆWã Ê ¹I J Æ ã ˆ  ÆWãÊÆ 3 òš Æ á Æ ¹ Ã Í Æ 3 çf Ê L Æ ç8¹mk%çºë à É ç Æ?à Êç"š ¹ \[ ¹ á ÆWã Ã.¹ ã ¹ á ÆWã à ¹ VJ ÂÈ º º Æ Â ºÉ Æjà ¹ Ë ã ç Æ ¹MKò ºÂÍ Æ ˆÝ ÊÉ Âç à Ĩç Æ ºÉ Æ š Æ #çfâ IJ špj =Í à ç à = â Æ Í¹š Æ Æ š âj šâ ÆWãÊÆ àtæ Æ O Ë Ê ¹I çwˆ Âç,Q Æ =X ¹WQ h ÊÉ q ºÉ Æ çº¹ Ë ºÂ¹ #çc¹ K çfë à É Æ O Ë Ê ¹I ç à Ã#¹3çºç Æ çêç'á ÆWã J à ¹ Íà ÆT špj =Í à ç èo, µˆåœýé Âç =à à 㠹3 à É º¹ ºÉ Æ Íƒ ºÉ Æ Íƒ Ê à = Ý͹š Æ Â HLj¹MK" ç Æ?à 6ç4[ š Æ çfâ IJ špj Íq à ç ÉĨçF \[ ƒçfé ¹WQ = J çfâvl Â8 à = 3 à 㠹$L ãêæ çêç J Æ :ˆ "ç8 Æ4T ÍÃ Æ Æ [ çý 6 MX Æ 7Ë. Â Ê Ìž Êš H[ ç ͹š Æ ü½ Î ( 1 ) P n = P n 1 σ, f + gp n 1 Q É ÆWãÊÆ ÂÁç% Àù Ã Ë = ºÂ¹ ƒš P n Æ #çfâ IJ  ƒ ̵ ºÉ L Æ Æ?ã = ºÂ¹ 1 f = e rt (1 f)h ÂÁç šë, g = r T ã Ê ¹I ¹ K ¹I Æ L Æ ÆW㠺¹ h = r r ÂÁçCL ã ¹WQÝ ºÉ ã Æ á K Æ?ã L Æ 3ËÍCâ ÆWã ¹MK  š  áâášë = Áç? á K σ Æ?ã L Æ Í¹ ã 6 = ÂÈ IJ ã Æ ¹MK+ š Ë È "çºã Æ?à ÂÍ Æ ç"â.¹i Æ L Æ ÆWã Ê ¹I (0 σ 1). ž ºÂÁš ä ½HÉ çxëç Æ šœ ºÉ ÂÁç Íq¹š Æ 3 º¹ Æ4T à  qš =ÍÃ Æ šc¹iç à  Á Ê ¹I ç1¹ K â#¹ ã = º¹ ã J = ² I ± CL&B ² Dƒ -L =³@ ² ù Ã Ë Á Ê ¹I 1ˆ Ž8 â  ¹ áâ à É å»?qý ç ã J HL. º¹ Æ4T à  ãºæ çfë Êç8¹MK â#¹ ã = º¹ ã J ÆT à ÆWã Â Í Æ I 6ç ¹ Ã# ã çºâè Ê à QÝ çºã:# " x ³ ± # ² % Ã#¹IÃ Ë Á Ì ºÂ¹ Q  ºÉC ºÉ Æ É Æ Ã ¹MK͹š Æ Y# è ˆ å%ˆåë É Æ K Â Æ šœâ Æ:à =Ë#ç Æ ºÉ Æ Í¹š Æ =LI á Æ O Ë Â à X VJ š =ÍÃ Æ š ¹Iç à  Á Ê ¹I ç?ˆ 7 Ë ã ºÉ Æ?ã # ºÉ Æ à ¹IÍà Æ4T  ÍÃ à ¹ K%á ã  ¹IËç8 3 Æ?ã à ºÂ HL K à ʹ ã ç8¹ Ã#¹IÃ Ë Á ºÂ¹ špj =Í à çœ Æ Ĩš çà ʹ͹ ãêæ = šhí¹ ãêæ'à ¹IÍà  à = Æ šhí = ºÉ Æ Íƒ ºÂ à +͹š Æ ÁçWˆ f ¹= ¹MK Æ áâ ã ¹ Í Æ I 6 = 6K à º¹ ã ç"çfâícë Ê Æ ¹IËçº SJ š.šâ8 Æ?ãºÆ I Ê SJ. Æ?à ºÉ Æ Ã#¹IÃ Ë Á ºÂ¹ š Æ çºâ IJ ˆ ºÉ Æ ¹ ºÉ Æ?ã É# = šr 5ÂÍÃ#¹ ã 6 = àwæ ¹MK à 㠺 à Ë Á ã K à º¹ ã ç ÂçÀçºÃ Æ:à Â8 Æ š ¹= çf¹ícë à É âj' ÊÉ Æ Â I Æ çºâ IJ çýâj'á ã ÂÁ =â   IJ ˆ ŒÝÉ Æ Â 3 Æ 3 ºÂ¹ K ¹ ã àtãêæ = ºÂ HLÝÍq¹ ãºæãêæ ÂÁçF ºÂ à Íq¹š Æ ç Æ š çr º¹ Æ:àTÆ çêçºâè IJ ¹MK à ËšÌ Â HLƒÂ 3 º¹ƒ ÊÉ Æ Í ºÉ Æ ML Æ çºã Æ?à Â8 à ͹ ã 6 = ÂÈ IJ ã Æ ä5 ˆ#ŒÝÉ ÂÁçCK à š Æ Í š ç ̓ X3 HL ÂSK Æ 6 =â Æ ç,k ¹ ã ç Æ á ÆWã = J Æ ã ç à ¹ á ÆWã  HLš  ÆWãÊÆ 3 Æ áâ ã ¹ Í Æ I 6 = à ¹I šâ ºÂ¹ çq = š šâ ÆWãÊÆ 3 òã¹ Ã Ë Á Ê ¹I jš Æ çºâè IJIˆr Æ J K à º¹ ã çã Á J )L' ºÉ Æ š Æ?à ÂçºÂ á Æ ã ¹ Æ Â hš Æ #çfâ IJ špj =Í à çý ãêæ š Æ Æ?ã ÍÂ Æ š âjƒí Æ = #ç ¹ K ÊÉ ÂçÝ ÂSK Æ 6 =â Æ ç?ˆ Œx¹qš Æ ç àwã Ââ Æ ÊÉ Æ Â ÍÃ à ¹MKÝ ºÉ Æ ç Æ K à ʹ ã çà ºÉ Æ à ¹ ãºãêæ çºã¹ šâ HL.̓ ÊÉ Æ Íƒ Ê à = Íq¹š Æ ç ãêæ š Æ á Æ ¹ Ã Æ š ä ˆ Æ ¹ K+ ºÉ Æ Í Æ ºÉ¹šçK ãêæ O Ë Æ 3 º VJ Ë#ç Æ š º¹ = SJ; Æ š Æ #çfâ IJ špj =Í à ç = š º¹ š Æ Ì á Æ ¹ à ̓ = ºÉ Æ Í = ºÂ à "͹š Æ Áç'ÂÁç'Í Ë È ÊÂ Ã Æ ãºæ L ãêæ çêçfâ¹ å è żI¾ ˆ ŒÝÉ ÂÁç Í Æ ºÉ ¹š ÂÁç Í Â SJ Ëç Æ š K ¹ ãòà ¹I çf ã Ë à Ê ¹I ¹MK à 㠹$L ¹3ç Ê àcæ O Ë = ºÂ¹ ç?ˆ = É Æ ºÉ ÆWã ºÉ Æ Æ O Ë# ºÂ¹ ÂçËçÊ =â Æ ¹ ã ¹? rš Æ Ã Æ š ç¹ Ã ãºæ:à ÂÁçF¹ ¹ K à à Ë = ºÂ¹ ç?ˆ5 8¹WQ Æ á Æ?ã ºÉ ÂÁçÍ Æ ºÉ ¹š Âçò ¹= œë  O Ë Æ âjí Æ çò¹mkq É Â à É Q Æ'à à ã ÂSKJ Q É UQÝ J = #š Q É = œâ ¹=Ì # è ˆüå-%
346 ä ä ¾ # : ³ ± ² ² ¹$L  à = Í Æ?à É ÂÁçF̓çÅ Z>Ë Æ àtæ ºÉ Æ Ã¹ Ã Ë Á Ê ¹I š Æ çºâè IJ'šPJ Í à çwˆœýé Æ Ã ã ¹ â Æ Íƒç  ƒëçºâ HLœÍCË È Ê à Æ8ãÊÆ L ãºæ çºçºâ ¹I K ¹ ã ù Ã Ë Á Ê ¹I 'š Æ #çfâ IJ à ãºæ šâ à ºÂ¹ ƒ = Á纹ò¹ à?à Ë ã Q É Æ àtæwã Ê Â Â I ÆWã à ºÂ¹ çåâ Æ IQ ÆWÆ. š Æ Ã Æ š Æ 3 8á ã ÂÁ =â Æ ç ÆT ÂÁç :ˆ C9 G< E G AY@ >PAY@ ;=< EF> A D >HGIA?<"! A B # G >$&%' ( ) ð+*#ð-,~îì/.103 îì54 ï î6 î7 î6981ë/4vë;:<=>:?@036 ŒÝÉ Æ ã ç YQ ɹœš ãºæ Q = F Æ 3 ºÂ¹ q º¹C Íù ã Ê = àtæ ¹MK1š Æ J K ¹ ã š Æ çfâ IJšPJ =Í à ç:qý ç 8Ë à É Â #çf¹i :, ˆ Æ çºëhl$l Æ çf Æ š šâ8 ÆWãÊÆ 3 ºÂÁ = Ì š  ÆWãÊÆ àwæàæ O Ë Ê ¹I 1Î dn(t) dt ( = r 1 N(t h) K ) N(t), Q É ÆWãÊÆ ÂÁç5 ÊÉ r Æ%à ¹ Æ Z à Â Æ 3 1¹MK Â Æ ã L ã ¹WQÝ ºÉ ºÉ h Æ á ÆWã ML Æ L Æ ¹MK š Ë È xâ š  áâášë = Áç Â.ù Ã Ë Á Ê ¹I 1 ºÉ K Æ Íƒ T ÂÍCËÍ çºëç 6 = =â Æ Ã#¹IÃ Ë Á Ê ¹I 1ˆ ŒÝÉ Æ Í Â K Æ ºË ãºæ çý¹mk Æ O Ë Ê ¹I :#µåˆ è %Å ãêæ è:ä µî è ˆ 8 纹 Ë ºÂ¹ çcq  ºÉ.ùIçºÂÈ Ê á Æ Â Â ºÂÁ = à ¹ #šâè Ê ¹I ç ãêæ Ã#¹3çF ºÂá Æ š â¹ Ë š Æ š æ åˆ= É Æ 0 < rh 1 Å ºÉ Æ çº¹ Ë ºÂ¹ Íq¹I ¹= ʹ  N(t) à VJ à ¹I 3á ÆWã L Æ çƒ º¹ #J7 ÂVLˆ è ºÉ Æ š ĨçFÉ Æ š e Â Æ % æ ä ˆ= É Æ 1 e < rh π 1 ÊÉ Æ çº¹ Ë ºÂ¹ N(t) à ¹ á ÆWã L Æ ç ʹ Q ÂÈ ÊÉ ¹Iç K à  Á Ê ¹I ç Æ ã Æ O Ë Â Ââ ã  ËÍ #J7 ÂVLˆ è ºÉ Æ çº¹ š Â Æ % æ ¼ˆ= É Æ rh > π : ÊÉ ÆWãÊÆ ÂÁç ¹I VJ¹I Æ çf Ê â Æ Ã ÆWã  ¹šÂ à 纹 Ë ºÂ¹ #@7 ÂSL#ˆ è W ÊÉ Æ š ¹= F Æ š Â Æ %ˆ #µåˆ è % K A BDCFE1+HG3I N=ø ñ õiú HKø?G þ øwù D õltú HKø:G 9 KP KJ +E D G h = 1 r = 0.1 þ K = ø ñ õ ú HKø:G N(t) öòø?g3øwú ø:g3hkal ñkñkû AÊø:GM D ó ô D6þ ú ø K ý L þ E Dý'ñ HKG DKL +E D G h = 1 r = 0.7 þ K = ø ñ õ ú HKø:G N(t) AÊø:GM D ó ô D6þ ú ø +Hüú E ø þ K A6H ñkñ LWú HKø:G þ G D LWó D õih ñ HK Ió HKõIö þ ø ñ H ý ñ HKG DKL +E D G h = 5.3 r = 0.3 þ K = ø ñ õiú HKø:G H þ+ÿd N(t) ó HKø ý HKA"L?G ý þ úfl? ñkd ý ø?úú D6ý ñ HKG D
347 D8 Y³ W± E:ª K FR N ²W LW³ ² T Y ³µ ² ³V 'C Dq JL ² ä ä è ŒÝÉ Æ Ã Ã ã ¹ T Â̓ Æ çf¹i Ë ºÂ¹ QÝ ç à ¹ #ç ã Ë à Æ š' WK ÆWã = SJçºÂç%¹MK Æ O Ë = ºÂ¹ E#µåˆ è % â=j Í Æ = çý¹ K ââ K Ë ã6à = ºÂ¹ ºÉ Æ ¹ ã J è?ä Î N(t) K [ rh 1.57 cos ( π τ) (rh 1.57) ( sin(πτ) + cos(πτ) )], #Våˆüå-% Q É ÆWãÊÆ hτ[ (rh 1.57)] = t. ) ð ) ð-, :(? í ì?ë ŒÝÉ ÆWãÊÆ Q Æ?ãºÆ Æ ¹ ã 6ç ʹ ÆT à Á = q ºÉ Æà ç Æ ç+¹mk à J à  à à É = HL Æ çâ ƒâ ç Æ:à 6ç4[IÃ#¹IÃ Ë Á ºÂ¹ š Æ çºâ IJâJ Í Æ = çò¹ K Æ O Ë Ê ¹I #Våˆ è % è?ä è» å=»µˆ JÂ É ÂçC͹ ¹$L ã =à É? è» à ¹ Íà ãºæ šƒ ÊÉ ÆÀãºÆ çfë Êçݹ Kx Ë Í ÆWã  à = r = VJçFÂÁçŹMK Æ O Ë Ê ¹I 1#Vå ˆ è %?Q ÂÈ ÊÉ Æ4T à ÆWã ÂÍ Æ Ì Ê = š 6 K ã ¹IÍ) ºÉ Æ à Á çêçfâ à :Q ¹ ã Xâ=Jj 8 à É ¹ Á纹 å=¼%¹i j¹3ç à  Á ºÂ¹ #çà¹mk8š Æ #çfâ IJ â#¹ ã = º¹ ã J ù Ã Ë Á Ê ¹I ¹ KÝ "ËçF ã =  jçºé ÆWÆ ÃÌ â#¹wq>)j?# CLW K :L : ± %œ š LI¹= çº = ºÂÁçIKJ HL ãºæ çfë È 6çWˆ ŒÝÉ Æ =Ãà 㠹 T Â̓ Æ çº¹ Ë ºÂ¹ #µåˆüå-%ò 纹r Êç O Ë ÂÈ Æ Q Æ + º¹. ÊÉ Æ 8 à É ¹ ÁçF¹I \[ ç Æ4T à ÆWã ÂÍ Æ 3 Ê = š = Ê ˆr "¹WQ Æ á ÆWã  œçfé¹ Ë Ášâ Æ ¹= Æ š ÊÉ à ¹ ãºãêæ Á Ê ¹I â Æ IQ Æ?Æ ºÉ Æ ¹ ãêæ Ê à = r = š Æ4T à ÆWã ÂÍ Æ 3 Ê = 5¹3ç à  = ºÂ¹ ç à ¹ Ë Áš â Æ â Æ º ÆWã #J7 ÂSL#ˆ#å-%Tˆ N(t), thousands L t, days N(t), thousands Experimental data A BDCFE1+ I L ø?ö ÿ LTó H þ ø?gøwùoåhkafe3ø ñkþ ø?g þ 9T> D(' ÿd ó HKö D G úfl ñ=ý LWúFL ø?g ñ L? øwóflwú øwó ûÿ ø ÿ õ S ñ LTú HÈø?GqøWù õ þ úófl ñ HÈL?G þ E DÊD6ÿIS ø û M +HKú E L ÿiÿ ó ø ' HKöœLWú D%þ ø ñ õiú HKø:G N(t) 9 9 A6ø?óó DÊñ LTú HKø:GƒA6ø D A6H D G ú r = 0.67 CÔ ã = F [ çr Á =â¹ ã ʹ ã  ãºæ ç Æ ã6à É Æ çüå ¹ K Ã É ÂÁ ÝÃ#¹IÃ Ë Á Ê ¹I  èo, ¼ äåà â Æ à ¹ #çfâáš ÆWãÊÆ šc ç à ĨçºçºÂ à = Æ?à ¹ ¹ L  à Æ4T à ÆWã ÂÍ Æ 3?ˆ Ã É ÂÁ ¹ 3 º¹$L Æ Æ çºâç ãºæ ç Æ ÍCâ Æ ç ºÉ Æ š Æ á Æ ¹IÃ Í Æ 3ÇçF Ê ML Æ ç๠KÝâ ÆWÆ º Æ Ã¹ Ã Ë Á Ê ¹I 1ˆ =Ã É Â š Æ çºâ IJ špj Íq à ç K ¹ ã šâ ÆWãÊÆ 3 Æ Íà Æ?ã = ºË ãêæ çýâáç çºé ¹WQ  )7 ÂSL#ˆ ä ˆ Ç Æ Ëç à ¹ #çfâáš ÆWã K ¹IË ã Í Æ ºÉ¹šç K ¹ ã š Æ Â ºÂ¹ ¹MKà ã =Í Æ ÆWã ç š ¹MKr à ÉÌ r h  8Ã#¹IÃ Ë Á ºÂ¹ Ô ã =Í Æ ÆWã ÂÁç ºÉ r Æ = ºËçºÂÁ = à ¹ Æ Z à Â Æ 3 ¹MK Æ4T ù Æ 3 ºÂÁ = $L ã ¹WQÝ ºÉ1 Q É Â à É à = Àâ Æ ¹ âç ÆWã á Æ š¹ VJ = 1 ºÉ Æ â Æ L   HL ¹MKù Ã Ë Á Ê ¹I L ã ¹WQÝ ºÉË š Æ?ã9(Wà ¹ ÍqÌ Ã Æ ºÂ ºÂ¹ á à ËË Í ( à ¹ šâ ºÂ¹ #çwˆç Æ â [t 1, t 1 + t] Æ çºë à É ºÂÍ Æ Â 3 Æ?ã á = CQ  ºÉ  Q É Â à É š á = Ë N(t) N(t h) Æ ç ãºæ çºíƒ = Vˆ ŒÝÉ Æ = #š N (t) rn(t) r lnn(t 1 + t). t #µåˆ ä %
348 ä ä å # : ³ ± ² ² L A BDCFE1+ I L ÿ E3G3HÈL ýid G þ HKú û ý û GLWöòHÈA þ J L B P 0? B 9 0 Æ J Âç à h ÆWã  ¹š ¹ K ºÂÍ Æ Q É à É Æ O Ë = Áç =ÃÉ ÂÁ š Æ á Æ ¹IÃ Í Æ 3 à J à Æ Ã Æ?ã ¹šrˆ Ã É ÂÁ ƒš Æ á Æ ¹ Ã Í Æ I à J à Æœà ¹ çºâçf ÊçŹ Kx IQŹà ã Êç"# ç ÆWÆ 7 ÂVLˆ¼%Î è % Æ?ã ¹š'¹ K ä Ì ½œš Jç? šë ã  HL"Q É Â à É,J ¹IË HL =ÃÉ ÂÁ à = â Æ É = à É Æ š'¹ Ë æ å-% Æ?ã ¹š¹ KÅ À Æ çf œå Ì ä š Jç? Q É à Éh ãêæ Æ?Æ š Æ š K ¹ ã ÑJI¹ Ë HL Ã É ÂÁ º¹ àwà Ë ÍCË = Æ K "çºë âçf Ê àtæ ç% ʹƒâ ÆòãÊÆ ĨšPJ K ¹ ã Á J )L Æ L L3çWˆ egg young Daphnia egg young Daphnia t 3-5 days -3 days h A BDCFE1+ I Hüù D A û A ñkd øwù L ÿ E3G3HÈLM ŒÝÉ Æ á = Ë Æ ¹ K š h Æ Ã Æ #š ç"¹i. Æ Íqà ÆWã ÊË ãêæ Ĉ= É Æ ÊÉ Æ Æ Íà Æ?ã = ºË ãêæcà É HL Æ çw ºÉ ÂÁç"Ã# ã =Í Æ ÆWã8à = ÁçF¹ƒá ã J K ã ¹IÍ ¼' ºÂ»'š Jç" š Æ á Æ.͹ ãêæ ˆ 7 ã ¹IÍP ã = F [ ç š 6 à É ã 6ç ¹I dâ  ã ÊÉ = #šqš Æ ºÉ ã = Æ špj =Í à ç ÂÈ K ¹ ¹WQ8ç ºÉ# Œ è» S 0 š Æ Á J š Jçƒ = š 'ŒÀåI½ 0 h 1 S š Æ Á J š JçWˆ+ ¹# :Q É h 9 Æ rh = 1. # 1 e < 1. π %T = š K = 135 r = 0.1 Æ O Ë# ºÂ¹ #Våˆ è %Cš Æ ç àtã Ââ Æ ç O Ë Â Æ Q Æ Ã É ÂÁ.š Æ çºâ IJšPJ =Í à çà œœ è» Ŷ= É 0 Æ rh = 1.6 # 1.6 > π %T K = 30 = š r = 0.18 Æ O Ë Ê ¹I?#Vå ˆ è %š Æ ç àtã  â Æ ç O Ë Â Æ Q Æ =Ã É Â.š Æ çºâè IJšPJ Í à ç ¹.ŒÀå ½ #Vç 0 Æ?Æ 7 ÂVLˆ#½q š 7 ÂVLˆ 5 %ˆ C9 G< E G AY@ >PAY@ ;=< EF> A D >HGIA?<"! A B # G >$&% G$>P@)G D >F B&%' = ŒÝÉ ãºæ?æ çf Ê ML Æ ç"¹mk%š Æ á Æ ¹ ÃÍ Æ 3 8Ì Æ L L# Á ã á = šĩšë çºã Æ:à Â Æ ç ãêæcà ¹I çºâš Æ?ãºÆ š  Ž Ëš š [ ç8íƒ = ºÉ Æ Í = ºÂ à 1͹š Æ ¹I  #ç Æ:à 8ù Ã Ë Á Ê ¹I špj =Í à ç üå, µˆ "ÂÁç ã Ââ Ë Æ š š Æ Á Jç ãêæ  3 ã ¹šË àwæ šqâ 3 ʹœ òçjçf Æ Í ¹MK ºÉ ãºæ?æ šâ ÆWãÊÆ 3 ÊÂ Æ O Ë = ºÂ¹ ç?ˆ Ë à Ƀ 3 ã ¹=Ì šë à Ê ¹I ¹ KšÂÁçF ã  â Ë Æ šš Æ Jçx 3 ʹÀ ͹š Æ ÂÁç à Ëç Æ šœâjò ÊÉ Æ Â # =â   IJœ¹ KšÂÁç àwãºæ Æ š Æ Á JÍq¹š Æ Ĩš Æ O Ë = Æ SJš Æ ç àtã Ââ Æ çf¹ií Æ ÆT ã =¹ ã š  ã J K à º¹ ã ç? Æ ˆ Lˆ 3ÂÈ ÝÂç ÂÍqùIçFÌ çfââ Æ Ê¹œçFÂÍCË = Æ Ëçº L Æ ¹MKÃ Æ ç Ê à š Æ çâ à ˚ HLœçº¹ Í Æ Ĩš šâ ºÂ¹ K Ë à ºÂ¹ çâ 3 º¹
349 D8 Y³ W± E:ª K FR N ²W LW³ ² T Y ³µ ² ³V 'C Dq JL ² ä ä ä L Modelling results Experimental data A BDCFE1+ I!qø ý D6ñKñ HÈGIô8ø?ù L ÿ E3GIHÈL ýid G þ HKú û ý û GLWöòHÈA þ +E D G B P 0 J L rþ HKö õ ñ LWú HKø:GÀó DºS þ õ ñ ú þ +E D G r = 0.1 LWG ý h = 1 K = 135 A6ø?ö ÿ LWó H þ ø?gàø?ù róflwúú þ 9:;4 D(' ÿd ó HKö D G úfl ñ ý LWúFL ÿ ó D6þD G ú Dý HÈG 5HÈô 7 +Hüú Eöòø ýid6ñkñ HKG3ôó DÊþ õ ñ ú þ øwóó D6ñ LWú HKø:GƒA6ø D A6H D G ú r = 0.83 L Modelling results Experimental data A BDCFE1+ I!qø ý D6ñKñ HÈGIô8ø?ù L ÿ E3GIHÈL ýid G þ HKú û ý û GLWöòHÈA þ +E D G B 9 0 J L rþ HKö õ ñ LWú HKø:GÀó DºS þ õ ñ ú þ +E D G r = 0.18 LWG ý h = 9 K = 30 ø?ö ÿ LTó H þ ø?gòø?ù róflwúú þ 9:;D(' ÿd ó HKö D G úfl ñ ý LWúFL ÿ ó D6þD G ú Dý HÈG 5HÈô 7 +Hüú E öòø ýid6ñkñ HKG3ôó D6þ õ ñ ú þ ø?óó DÊñ LTú HKø:GƒA6ø D A6H D G ú r = 0.73 '͹š Æ µˆœýé Æ Í¹š Æ É ç â Æ?Æ Æ çf Æ š âj Æ4T à Æ?ã ÂÍ Æ 3 Ê xš = Ê ƒ¹i  #ç Æ:à Êç [Ã#¹Ià ËÌ = ºÂ¹ ¹ K #³V JL6 ±6² F3 DDƒ ³ K ² CIW W± ˆ#ŒÝÉ Æqà ¹ ãºãêæ Á Ê ¹I â Æ IQ ÆWÆ ºÉ Æ ¹ ãêæ Ê à = = š Æ4T à Æ?ã ÂÍ Æ 3 Ê à Ë ã á Æ çc Ã Ã Æ ãêæ šj ʹâ Æ O Ë Â Æ L ¹¹šrˆx "¹WQ Æ á ÆWã 1 çºé ¹IË šhâ Æ Í Æ 3 ºÂ¹ Æ šr r ºÉ# œã ã à ºÂ à = ËçÊ ML Æ ¹MK ͹š Æ %š Æ Íƒ š çàá çfç =͹ Ë I ò¹ KÅ PK ¹ ã ̓ Ì ºÂ¹ 1ˆ= Æ çfé ¹IË Áš X3 ¹WQ ÊÉ Æ â  㠺É' = #šƒš Æ = ºÉ ã Æ K Ë à Ê ¹I ç% = Æ à Ƀš Æ á Æ ¹ Ã Í Æ 3 ç 6 ML Æ 3 š' 纹 K Ë à ºÂ¹ çå¹ K ML Æ šâáç ã Ââ Ë Ê ¹I Å ºÉ Æ Â ÂÈ Ê # ÊÂ Í Æ Í¹ Í Æ 3 t = 0ˆ QŹ ã X»/ jí Æ ºÉ ¹š¹I ¹$L J ¹ K à ¹ çf ã Ë à ºÂ¹ ¹MKçºÂ HL Æ ÌçFà Æ?à Â Æ ç â#¹ ã = º¹ ã J Ã#¹IÃ Ë Á ºÂ¹ špj =Í à çí¹š Æ ÁçQ  ºÉ ãºæ çfã Æ?à ʹ ML Æ çf ã Ë à ÊË ãêæ ÂÁç š Æ ç àwã Ââ Æ šrˆrœýé Æ L Âá Æ ƒí Æ ºÉ ¹š¹I ¹$L J à = ƒâ Æ Ëç Æ š K ¹ ã ÊÉ ¹Iç Æ Â ç Æ?à 6ç+ ÊÉ Æ ÂSK Æ à J à Æ ¹ K\Q É Â à É à = ƒâ Æ šâ áâáš Æ šhâ 3 º¹ç Æ Ã# ã Æ š š Æ á Æ ¹IÃ Í Æ 3ÇçF Ê ML Æ ç?ˆ ŒÝÉ Æ?ãºÆ ÉĨçœâ ÆWÆ à ¹ #ç ã Ë à Æ š ÊÉ Æ çjçf Æ Ía¹MKݚ ÆWãÊÆ 3 ÊÂ Æ O Ë = ºÂ¹ ç Q  ºÉ ç Æ á Æ?ã š Æ Á JçW Q É Â à É à â Æ Ëç Æ šh çò Íq¹š Æ 5¹MK1 ÊÉ Æ â#¹ á Æ Â ç Æ?à Ýù Ã Ë Á Ê ¹I 1ˆŒÝÉ Æ Íq¹š Æ 5É ç â Æ?Æ =Ã Ã Â Æ šƒ ʹ Æ4T à  â#¹ ã = º¹ ã JœÃ¹ Ã Ë = ºÂ¹ 'špj Íq à ç:k ã ¹IÍ à ĨçºçºÂ à = " à ɹ ÁçF¹I \[ ç ÆT à Æ?ã ÂÍ Æ 3 üå ¼ ˆ ŒÝÉ Æ Ë Í Æ?ã  à 5 = VJçFÂÁç+¹ K1 ºÉ Æ Í¹š Æ É# çýçfé¹wq O Ë ÂÈ Æ LI¹3¹š à ¹ ãêãºæ = ºÂ¹ Q  ºÉ 8 à É ¹ ÁçF¹I \[ ç Æ4T à Æ?ã ÂÍ Æ 3 Ê 1š 6 ˆ ŒÝÉ Æ çê =Í Æ Í Æ ÊÉ ¹š QÅĨç8Ëç Æ š ʹ à ¹I ç ã Ë à "̓ ÊÉ Æ Íƒ = ºÂ à = xí¹š Æ Áç8¹MK Á =â¹ ã Ì º¹ ã JCù ÃË = ºÂ¹ ƒšpj Íq à ç Q  ºÉ à ¹ çºâáš ÆWã Ê ¹I ¹ Ká ã ¹ Ëç ùIçÊçFÂâ Æ Æ Æ?à Êç+šË Æ º¹ ÂÍÂÈ Æ š K ¹¹š K ¹ ã ã á åi½h ˆ
350 ä ä ¼ # : ³ ± ² ² 9 K E GI>3 B G<= E G AY@ >PAY@F ;$< EF> A D >PGA <&! A B= K ð+*#ð-, :(?106 ï :7xë?ìWí ï=ì549:7 î7@?' îì/.103 îì/4vï î6 î7 î6 81ë54 ë )âĩçfâ à VJ Æ Q) =Ãà 㠹3 à É º¹ ºÉ Æ Ã ã ¹Iâ Æ Í ¹MKœÂ ç Æ:à 6ç4[ÅÃ#¹IÃ Ë Á Ê ¹I dšpj =Í à ç Íq¹š Æ Â HL É# çqâ Æ?Æ ç 6 ã Æ š  Q ¹ ã XçCâ=J ¹ Æ çº¹ á è ¼ è ½H ˆ+ Æ çêçfëí Æ šh ºÉ# ºÉ Æ Íƒ = à =Ë#ç Æ K ¹ ã š Æ çºâè IJ ¹3ç à  Á ºÂ¹ #ç ÂÁçƒ à ¹IÍqÃ Æ ÊÂÈ Ê ¹I Q  ºÉ ù Ã Ë Á Ê ¹I 1ˆ ŒÝÉ3Ë#çW :šâ ÆWãÊÆ 3 ÊÂ Æ O Ë = ºÂ¹ çxš Æ ç àtã Ââ  )L Ã#¹IÃ Ë Á ºÂ¹ œšhj3 # =Í à ç çºé ¹ Ë šàé á Æ =Ë º¹ ¹Iç à  Á Ê HLÀ纹 Ë ºÂ¹ ç?ˆ= 8Ë à É Â çº¹ \[ ç Æ O Ë = ºÂ¹ R#Våˆ è %xâáç = ÆT =ÍÃ Æ ¹MK5çFË à Éq͹š Æ µˆ +Âç+çºË à ùIç Æ š Â è ½ ºÉ = + #ç Æ:à Êç [=š Æ çfâ IJ šhj3 # =Í à ç à â Æ š Æ ÆWã ÍÂ Æ šqâ=jœ IQ ¹ à Ê á Æ Ã ÉĨç Æ ç Ìx Á ã á ò = šâíƒ ML ¹#ˆ=ŒÝÉ ÆWãÊÆ K ¹ ãºæ ºÉ Æ K ¹ ¹WQ  HLò̓ ÊÉ Æ Íƒ = ºÂ à = #͹š Æ Âç8çºËHL$L Æ çf Æ š K ¹ ã š Æ ç àtã  à ºÂ¹ ¹MK IQŹ #ç Æ:à Êç [š Æ á Æ ¹IÃ Í Æ 3 8ç 6 ML Æ çwî [ N 1(t) N (t h 1 ) = r 1 1 a(1 ) N 1(t h )] N1 (t), K K 1 N (t) = r [N 1 (t (1 h 1 h )) N (t) ] N (t). K 1 K qçjç Æ Í # ¼ˆ è % Âç ÊÉ N 1 (t) Æ 3ËÍCâ ÆWã ¹MK ̓ L ¹ ÊÉ N (t) Æ Ë ÍCâ ÆWã ¹MK ã á ºÂÍ Æ Ã Æ?ã ¹šâ Æ IQ Æ?Æ ƒ Á ã á œ = šâíƒ MLI¹œ =Ã Ã Æ ã àtæ ºÂÍ 1 h 1 Æ Ã ÆWã  ¹šâ Æ IQ ÆWÆ Â Íƒ MLI¹ = #š Á ã á =Ã Ã Æ ã àtæ á h ÆWã ML Æ Â̓ ML ¹[ çcã#¹iã Ë Á Ê ¹I ÂSK Æ Ã Æ?ã ¹š à ÆWã J Æ ã á K 1 K ÆWã ML Æ Ë Í â Æ?ã ¹ K ̓ MLI¹ = #š ã á a < 1 à É ã à ÆWã Â<; Æ çýã¹wq ÆWã ¹MK ãêæ Á ºÂ¹ Câ Æ IQ Æ?Æ œâíƒ ML ¹[ çx = šœ ã á H[ çxã#¹iã Ë Á ºÂ¹ #çw = ºËçºÂ \[ ç r1 0 = r 1 (1 a) à ¹ Æ Z à Â Æ 3 ¹MK Â Æ ã L ã ¹WQÝ ÊÉ1 Á r ã á )[ çýã¹ ÃË = ºÂ¹ Â Æ ã L ã ¹WQÝ ºÉ à ¹ Æ Z à Â Æ I :ˆ = É Æ = šà ÊÉ r Æ ¹ ºÉ Æ?ã à ã Í Æ Æ?ã ç ãêæ+à ¹ #ç 6 = 3? :çf¹i Ë Ê ¹I ç1¹ KçJçF Æ Í # ¼ˆ è %Å ãºæ çºâ Í 㠺¹ƒçF¹I Ë ºÂ¹ çý¹ K Æ O Ë = ºÂ¹ Q É ÆWãÊÆ N (t) = r [ 1 a ( 1 N(t (1 h)) ) N(t h) ] N, N(t) = N 1(t) K 1, r = r 1, h = h, N (t) K = N ( t (1 h 1 h ) ). # ¼ˆ è % h 1 (t) "Â8 Æ?ãºÆ 3 ºÂÁ = Ì šâ8 ÆWãÊÆ àwæ Æ O Ë# ºÂ¹ 1# ¼ˆüå-%ÂÁçÅçºÂÍqà Æ?ã ÊÉ = ºÉ Æ çjç Æ Í # ¼#ˆ è % š ÃÌ Ã ã ¹ T Â̓ Æ çåâè "çê ÊÂçK à º¹ ã  SJIˆ 8Ë Í ÆWã  à = I = SJçºÂç5¹ KçJç Æ Í # ¼#ˆ è %r = š Æ O Ë# ºÂ¹ # ¼ˆüå-%5ÉĨçrâ ÆWÆ š¹ Æ Â è åh ˆ ŒÝÉ Æ â  ¹I ¹$L  à à ÆWã ¹š ÂÁç à ¹Iç Æ Ê¹q¹I Æ É¹WQ Æ á ÆWã I ºÉ Æ?ãºÆ ãêæ Íq¹š Æ çcq ÂÈ ÊÉ Ã ÆWã ¹š çfâvl Â8 à = 3 º VJ Æ çºç% ºÉ ¹I Æ ˆŒÝÉ Æ ç 6 ºÂ¹ # ã J ͹š Æ ç ¹MK Æ O Ë Ê ¹I E# ¼#ˆ å%¹ K Æ É á Æ à ¹IÍà  à = Æ š K ¹ ã Í.ˆ Æ à '¹ â#ç Æ?ã á Æ L ã šë# =  àwãºæ ç Æ ¹MK ¹3ç à  Á ºÂ¹ #çyq  ºÉ' ÊÉ Æ K ¹ ¹WQ  HLhš Æ Ã ãêæ çêçºâ ¹I çf Ê ML Æ Q É Â à É ÂÁçƒ L ¹¹š ÆT ÍqÃ Æ ¹MKQ Æ Ì X3 ¹WQ = ºË ã = Ã É Æ ¹ Í Æ ¹ K š Æ çºâè IJ ¹ Ë Êâ Ë ã ç :ˆ# "¹WQ Æ á ÆWã 3 ºÉ Æ ç 6 ºÂ¹ # ã J'͹š Æ ç è åh ãêæ á ÆWã J ç Æ çfâ ºÂá Æ º¹ Æ á Æ Í ¹ ã+à É = )L Æ çx¹mkí¹š Æ Ã ã Í Æ Æ?ã ç = šc ºÉ ÆÅã = )L Æ çx¹mkã ã =ÍqÌ Æ Æ?ã ç8á Ë Æ çck ¹ ã Q É Â à É ÊÉ Æ Í¹š Æ Ã ÆWã  ¹š.ÂÁç à ¹Iç Æ º¹ƒ¹I Æ ãêæ á ÆWã J # ãêã ¹WQòˆŒÝÉËç çfë à É à ¹IÍqÃ# ã Â纹 ƒ¹ K1 ºÉ Æ ¹ ãêæ Ê à = 5 = š ÆT à Æ?ã ÂÍ Æ 3 Ê š Ê,L Âá Æ ç ã ÂÁç Æ º¹šÂ Z à Ë È ÊÂ Æ ç â Æ:à =Ë#ç Æ çº¹ Í Æ Ã ã Í Æ Æ?ã çý¹ K ͹š Æ ç# ¼ˆ è %8 = š # ¼#ˆ å% ãêæ ¹ X ¹WQ 1ˆ çºé ¹IË š # ¼ˆüå-%
351 D8 Y³ W± E:ª K FR N ²W LW³ ² T Y ³µ ² ³V 'C Dq JL ² ä ä ½ â Æ = ÁçF¹ƒ ¹ Æ š. ºÉ = 8 ºÉ Æ çf Ê Ê ¹I ã J ͹š Æ ç8¹mk Æ O Ë# ºÂ¹ # ¼ˆüå-% ãºæ Íq¹ ãºæ ç Æ #çfâ ºÂá Æ º¹ à É = )L Æ çý¹ Kxà ã Í Æ Æ?ã ç ÊÉ = ºÉ Æ çº Í Æ Í¹š Æ çck ¹ ã çjçf Æ Í # ¼#ˆ è %ˆ ¹ ã š ÆWã ʹ ÆT à Á = j ºÉ Æ Á =â¹ ã ʹ ã Jš = Ê.¹MK  ç Æ?à 6ç4[xÃ#¹IÃ Ë Á Ê ¹I hš Æ çºâè IJI x Íq¹šÂ8 à ºÂ¹ ¹MK ͹š Æ K ã ¹ Í è ½H ÉĨçÝâ Æ?Æ.à 㠹 ùIç Æ š'â µî [ N 1(t) = r 1 1 a(1 N (t h 1 ) K [ ( N1 t (αt h1 N (t) h ) ) = r K 1 ( ) + c 1 N ) 1(t) N 1(t h ) ] K 1 K 1 N 1 (t), ( + b 1 N (t h 3 ) ) N ] (t) N (t), K K # ¼ˆ ä % Q É ÆWãÊÆ Âç.¹I T Æ L Æ Æ?ã = ºÂ¹ Qš Ë ã = ºÂ¹ 1 ŵˆ Æ ˆÝ ºÂÍ Æ Ã ÆWã  ¹š K ã ¹IÍ Æ L L ºÂ òâ ̓ MLI¹ ÂÁçò Á h 3 ã á = š Æ á Æ ¹ Ã Í Æ 3ÇçF Ê L Æ šë ã Ê ¹I 1 α 1 ãºæ > Æ?à ÊçÀ ÊÉ Æ L Æ ÆWã Ê ¹I ç ¹ á ÆWã Á =à à  HL K à :ˆ ¹š Æ # ¼#ˆ ä %+ÉĨç%â ÆWÆ à ¹ çf ã Ë à Æ š ¹ ƒ ÊÉ Æ â# ç Æ ¹ K çfã Æ?à  Á =â¹ ã ʹ ã J Æ4T à ÆWã Ì Â Í Æ 3 8¹I R ±A ² ZB +D AF ² ³ T± Ã#¹IÃ Ë Á ºÂ¹ Ẑ= É Æ b = 0, c = 0, α = 1, T = 1 Q Æ L Æ ºÉ Æ çjç Æ Íf¹ K Æ O Ë# ºÂ¹ #ç # ¼ˆ è %Tˆ Æ Í Â ÊÉ c(1 N1(t) K 1 ) Æ ã ç Æ O Ë = ºÂ¹ ¹MK'# ¼#ˆ ä % çºé ¹WQ8ç ãêæ šë à ºÂ¹ ¹MK K ÆW㠺  IJ ¹MK ĨšË òçºã Æ?à Â Æ çâ à ç Æ ÊÉ Æ Â ã š Æ çºâ IJ â Æ:à ¹ Í Æ ç ͹ ãºæ ºÉ á ÆWã ML Æ #ĨçQ Æ ç  àwãºæ ç Æ ¹ K1 ºÉ Æ Â ã š Æ = ºÉ ã = Æ Q ÂÈ ÊÉ Â çºë à É Ã ÆWã ¹šçݹMK1 ÊÂ Í Æ Ĉ ã Í Æ Æ?ã 0 c < 1 à É ã à ÆWã Â<; Æ ç8 ºÉ Æ Ã¹WQ Æ?ã ¹ K+ ºÉ ÂÁçÀ š š ÂÈ Ê ¹I =  ÆWã K Æ?Æ šâ à X ºÉ Æ ÂÍ L ¹ ç 6 ML Æ ¹MK8 ç Æ:à 6ç4[ Ã#¹IÃ Ë Á Ê ¹I 1ˆ ŒÝÉ Æ ššâè Ê ¹I = Æ?ã Í Â ÊÉ Æ ç Æ?à ¹ š Æ O Ë Ê ¹I ¹MK # ¼ˆ ä % ãºæ > Æ?à Êç ºÉ Æ Â Íà à.¹mk à ¹ ÍÃ Æ ºÂ ºÂ¹ Q ÂÈ ÊÉ Â Qù Ã Ë Á Ê ¹I d¹ tš Æ #çfâ IJ špj =Í à ç ¹MK Á ã á ˆ Æ Á J h 3 Æ O Ë# = ÁçC ÊÉ Æ Ã Æ?ã ¹š ¹ K" ÊÂ Í Æ Q ÂÈ ÊÉ Â Q É à É ºÉ Æ à ¹ ÍÃ Æ ºÂ ºÂ¹ â Æ IQ Æ?Æ Á ã á Âç' ºÉ Æ ç ã ¹I HL Æ ç :ˆ6 ã =Í Æ ÆWã b à É ã à ÆWã Â8; Æ ç ºÉ Æ à Ë Æ Æ çêç'¹ K ºÉ ÂÁç à ¹ ÍÃ Æ ÊÂÈ Ê ¹I 1ˆ37 à º¹ ã =Ãà α 1 Æ ã ç šë Æ Ê¹ ¹ á Æ?ã Á =Ãà  )Lƒ¹MK L Æ Æ?ã = ºÂ¹ ç  â#¹ ã = º¹ ã JÃ#¹IÃ Ë Á Ê ¹I #ç ÆWÆ 7 ÂVLˆ %Tˆ egg larva imago T T T T h 1 h A BDCFE1+ FI Hüù D A û A ñkd øwù ó ø þ ø ÿ E3H ñ L ŒÝÉ Æ Â Æ ã = SJçºÂçÅÉĨç çfé¹wq ÊÉ Q É Æ = š cr 1 h > π, c < 1, br h 3 > π, b > 1 Âç çfíƒ µ IçJçF a Æ Í # ¼ˆ ä % É# ç IQŹ =K ãºæ O Ë Æ à JCç Æ ĨšPJ ͹š Æ Æ ã ç Æ šhjqçf Ê = Æ N (t) K ˆ N 1 (t) K 1
352 ä ä-5 # : ³ ± ² ² Ç Æ à ¹ çºâš ÆWã ºÉ Æ K ¹ ¹WQ  HLqÍq¹š Æ VÎ N αn(t h) (t) = 1 + ( N(t h) ) n βn(t), K Q É ÆWãÊÆ ÂÁç α > 0 à ¹ Æ Z à Â Æ 3 ¹MK à 㠹šË à Ê ¹I 1 β > 0 à ¹ Æ Z à Â Æ 3 ݹ K ãêæ š Ë à Ê ¹I 1 ºÉ n > 0 Æ ¹ ã š ÆWã ¹MK Æ á3â ã ¹ Í Æ 3 Å ¹ Ì Â Æ ã ÂÈ IJI á K > 0 Æ?ã L Æ Ë Í â Æ?ã ¹ K  #šâ áâášë ç?ˆ ŒÝÉ Æ šâ ÆWãÊÆ 3 Ê šâ ÆWãÊÆ àtææ O Ë Ê ¹I 1# ¼ˆ ¼ % É ç ͹ ãêæòà ¹ Íà  à Æ š špj =ÍqÌ Â à çý¹mk 纹 Ë Ê ¹I ç ºÉ Æ O Ë# ºÂ¹ #Vå ˆ è %Å = š çºíƒ = Æ?ã ç Æ çfâ ºÂáÂÈ IJ K ¹ ã8à É HL  HLœ ÊÉ Æ Íq¹š Æ [ çœã# ã =Í Æ ÆWã ç à ¹ Íà ãºæ š Q ÂÈ ÊÉ Æ O Ë = ºÂ¹ # ¼#ˆ å%ˆ ã ¹šË à ºÂ¹ ã Æ Â # ¼ˆ ¼ % Âçš Æ ç àtã Ââ Æ š.â=j ºÉ Æ Â à É Æ ÂÁç Æ I Æ. Á Q K ¹ ã K Æ?ã Í Æ 3 6 ºÂá Æ X3Â Æ ºÂ à ç å ¾ µˆ5œýé Æ š Æ Á J É# ç+â ÆWÆ ' I ã ¹šË àtæ š Q ÂÈ ÊÉ ãºæ çfã Æ?à + º¹C ºÉ Æ à X Æ J 0 Á çêç QŹ ã X è Î % Æ:à Ì ã ¹  à = ¹$L ¹ K # ¼ˆ ¼ % ÉĨçÝâ Æ?Æ.à ãêæ ç Æ 3 Æ š  üå ä ˆ ŒÝÉ Æ Í Â.à 㠹 à ÆWã ºÂ Æ çå¹ K Æ O Ë# ºÂ¹ # ¼#ˆ ¼%Å ãêæ ÊÉ Æ K ¹ ¹WQ  HL ä å ä ä Î è ˆ ŒÝÉ Æòà ¹I 3á ÆWã L Æ àtæ ¹ K ʹC ÊÉ N(t) Æ ç Æ šhjçf Ê = Æ N(t) K α K ¹I ¹WQ8ç% n β 1 IQ ¹ QÝ JçWÎ %Å͹ ¹= º¹I  à = VJ  K (α β)βn 1 0 < β α he 1+βh ; â %ŹIç à  = ºÂ HLƒ ã ¹ Ë š' ºÉ Æ ¹ 3 ã  áâá = rçf Æ ĨšPJ çf Ê = Æ Â K 1 (α β)βn < β ( ω he1+βh α h ) + β, Q É ÆWãÊÆ ω ÂÁçÅ ºÉ Æ çf¹i Ë Ê ¹I ¹ Kx ÊÉ ÆòÆ O Ë = ºÂ¹ 1 βh ω = tan ω, ω (0, π). åˆ "Â8 ÆWãÊÆ 3 ºÂÁ = Ì š  ÆWãÊÆ àwæàæ O Ë Ê ¹I :# ¼ˆ ¼ % ÉĨçÝ ¹ Ì à ¹I çf Ê = 3 à ÆWã  ¹šÂ à çf¹i Ë Ê ¹I ç?ˆ ä ˆ8 ¹ Ë Ê ¹I çý¹mk Æ O Ë = ºÂ¹ # ¼ˆ ¼ % à = â Æ É á Æòà É ¹= ºÂ à VJ ˆ ŒÝÉ Æ çº Í Æ Ã ã ¹ à ÆWã ºÂ Æ ç ãºæ = Á纹qá ÂÁš K ¹ ã ºÉ ÆòÆ O Ë Ê ¹I 1Î Q É Â à É.ÉĨç ç Æ šhj Q É ÆWãÊÆ ºÉ Æ š Æ J N αn(t h) (t) = 1 + ( α β ç 6 Æ çº¹ Ë Ê ¹I # ¼ˆ ¼ % N(t h) 1)( βn(t), # ¼ˆü½-% K )n N(t) K = #šnk ¹ ã ºÉ ÆòÆ O Ë Ê ¹I 1Î N N(t τ(n)) (t) = α βn(t), N(t τ(n)) 1 + ( ) K n ( τ(n) = h exp γ ( N ) ) 1 K n. š α/β 1 τ = τ(n) Æ Ã Æ š ç ¹I N(t)ˆ # ¼ˆ 5 %
353 D8 Y³ W± E:ª K FR N ²W LW³ ² T Y ³µ ² ³V 'C Dq JL ² ä ä ð ) ð-, :(? í ì?ë 8 Ë Í ÆWã  à = ãºæ çfë È 6çUQ ÆWãÊÆ ¹ â 6 =Â Æ š âjh =à à SJ HL K ¹ Ë ã ÊÉ ¹ ã š ÆWã Ž Ë HL Æ ÀË F Ê Í Æ ºÉ ¹š â Ë Â 8 ºÉ Æ ¹š Æ MX Æ?ã çfâícë Á Ê ¹I Ã# à X ML Æ åiå ˆ ¹š Æ Â HL ãºæ çfë Êç ¹MK%çJç Æ Í # ¼#ˆ ä %Q ÆWãÊÆCà ¹ Íà ãêæ š Q  ºÉ ºÉ Æ Á =â¹ ã º¹ ã J ÆT Ì Ã Æ?ã ÂÍ Æ 3 Êç š 6 ¹ ±A ² ZB D AF ² ³ T± ù Ã Ë = ºÂ¹ 1 Å ã6à É\[ çƒ â#¹ ã = º¹ ã J ÆT à Æ?ã ÂÍ Æ 3 ÊçŹI # ³ CB ²' ± ÓW: 6 Ã#¹IÃ Ë Á Ê ¹I è µ Ç ¹WJš [ ç% Á =â¹ ã ʹ ã J Æ4T à ÆWã Ì Â Í Æ 3 6ç"¹I G ± JI K KD L6 ² ³ D ò± I ² ³ ù Ã Ë = ºÂ¹ èo5 + š ¹= ÊÉ ÆWã ç?ˆ E7 ÂVLˆ5» 7xÂVLˆ,ÀãºÆ çfë È 6ç+¹MK5 Ë Í ÆWã  à = 纹 Ë Ê ¹I ç¹mkrí¹š Æ # ¼#ˆ ä % ãêæ8à ¹IÍqÃ# ãêæ š,q ÂÈ ÊÉ' #ç Æ:à Êç [ š Æ çºâ IJCšPJ =Í à ç š = Ê K ã ¹IÍ 8 à X ¹I 纹 \[ çx â#¹ ã = º¹ ã J ÆT à Æ?ã ÂÍ Æ 3 Êç ¹I "Ëç ã ÂÁ = çfé Æ?Æ ÃÌ â¹wq>)je# CLT È L: ± 5 %Ýù ÃË = ºÂ¹ : å=¼ ˆ L A BDCFE1+ I ý õ ñ ú û þ 3ýID G þ Hüú û ý û GLWöòHKA þ +E D G ñ LTóI:L EL D ô?ø?ú 9 ôàøwù1ö D LWú ÿd ó ý L û L O HKAºJ ø ñkþ ø:g þxñ LW ø?ófltú ø?ó ûòd(' ÿd ó HKö D G ú þ ý LTúFL :!qø ýid6ñkñ HKG3ô8ó D6þ õ ñ ú þ +E D G T = 15; h 1 = 10; h = 13; h 3 = 6; r 1 = 13.8; r = 4; a = 0.495; b = 1.8; c = 0.715; α = 3; K 1 = 350; K = 700 L A BDCFE1+ I ý õ ñ ú û þ 3ýID G þ Hüú û ý û GLWöòHKA þ +E D G ñ LTóI:L EL D ôàøwù1ö D LWú ÿd ó ý L û L O HKAºJ ø ñkþ ø:g þxñ LW ø?ófltú ø?ó ûòd(' ÿd ó HKö D G ú þ ý LTúFL :!qø ýid6ñkñ HKG3ô8ó D6þ õ ñ ú þ +E D G T = 15; h 1 = 10; h = 13; h 3 = 6; r 1 = 13.8; r = 4; a = 0.495; b = 1.8; c = 0.715; α = 3; K 1 = 900; K = 1700 ¹š Æ C# ¼ˆ 5 %5É# çrâ ÆWÆ œ =Ã Ã Â Æ š º¹ à ¹ Íà ãºæ Q  ºÉÀ ºÉ Æ 8 à É ¹ Á纹 \[ ç ÆT à ÆWã Â Í Æ 3 6 = š 6 üå ¼ ˆŒÝÉ Æ š = Ê = š à ¹ ÍÃ Ë ÆWã çºâ Í Ë = ºÂ¹ ãºæ çfë È 6ç ãêæ çºé ¹WQ  )7 ÂSL#ˆ è ¾ˆ O Ë# = ÂÈ 6 ºÂá Æœà ¹ Íà ã ÂÁçF¹I ¹ K Ë Í ÆWã  à = xçf¹i Ë Ê ¹I ç ãêæ?àtæ  á Æ šnk ¹ ã ͹š Æ ç'# ¼ˆ ä % = š # ¼ˆ 5 %NQ  ºÉ Æ4T à Æ?ã ÂÍ Æ 3 Ê Ã¹ Ã Ë = ºÂ¹ š Æ çºâè IJ à = dâ ÆhãºÆ LI ã š Æ š ç L ¹¹šrˆ 8¹WQ Æ á Æ?ã à à Ë = Æ š à ¹ ãºãêæ Á Ê ¹I ¹MK Ë Í ÆWã  à = çf¹i Ë ºÂ¹ ç Q  ºÉ ÆT à ÆWã Â Í Æ 3 6 = š 6 hâçƒ ¹= É ÂVL É Æ ¹ ËHLIÉ Â ÊÉ Æ ç Æà Ĩç Æ ç # %ˆ+ çºé ¹IË š â r 0.6 Æ Í Æ 3 ºÂ¹ Æ š ºÉ = çjçf Æ Íç # ¼#ˆ ä %À = š # ¼ˆ 5 % à ¹I 3 Ê =Â Ë ÍCâ ÆWã ¹MK šâ8 Æ?ãºÆ I qš Æ Á Jçœ = šj ÊÉ Æ Â ã çf¹i Ë Ê ¹I çcš Æ Í¹ çf ã Æ ºÉ Æ Ã ÆWã  ¹šÂ à â Æ É áâ¹ Ë ã \Q É Â à É ÂÁçCá ÆWã J ç Æ çºââ Æ º¹ ÊÉ Æ Â Â ºÂÁ = à ¹I šâ ºÂ¹ ç?ˆ#œýé ÆWãÊÆ K ¹ ãêæ #çfíƒ = à É# = HL Æ ç  à ã Í Æ Æ?ã çýá = Ë Æ ç à ¹IË Áš à =Ë#ç Æ
354 ä ä» # : ³ ± ² ² L A BDCFE1+ G I!qø ýid6ñkñ HKG3ôhøWù õ þ úófl ñ HÈL?G þ E D6D6ÿ S ø û Mqÿ ø ÿ õ ñ LWú HKø:G ý D G þ Hüú û L OÅHKAºEIø ñkþ ø:g þd(' ÿd ó HKö D G úfl ñåý LWúFL 9T> öòø ýid6ñkñ N(t) HKG3ô ó D6þ õ ñ ú þ +E D G α = 10; β = 1; γ = 0.5; h = 4; n = 7.7; K = 800 çq ÂÈ à ÉRK ã ¹IÍ Ã Æ?ã ¹šÂ à 纹 Ë ºÂ¹ h ʹ à É ¹= Ê à â Æ É# á3â¹ Ë ã ˆx çºë à É çºâ ºË = ºÂ¹ à ¹ ãêãêæ Á ºÂ¹ à ¹ Æ Z à Â Æ 3 Å š 纹 Í Æ ¹= ºÉ ÆWã O Ë# = 3 ºÂ Ê = ºÂá Æ Í Æ çºë ãºæ ç+¹ K1 ºÉ Æ º ºÂ HLq ãºæ ¹= 8á ÆWã JƒËç Æ K Ë K ¹ ã8à ¹ Íà ã ÂÁ纹 ¹ K çºâ Í Ë Á ºÂ¹ ãêæ çºë È 6çCQ ÂÈ ÊÉ ÆT à Æ?ã ÂÍ Æ 3 Ê 1š 6 KP : Hüóú E ' ÿd ó HKö D G úfl ñ LWAºJ=ô?ó ø?õ3g ý ú ø.ú E D'þ ú õ ý=û ø?ù8ú E D'ý H þ úó HK IõIú HKø:G LWG ý LW 3õ3G ý LWG3A D øwù HKG þd AÊú þ rm B E D HKG3õ D GIA D ø?ù+ú D ö ÿd óflwú õió D öòø?h þ ú õ ó D L?G ý ùáø ø ý ø:g ú E D HÈGIGLTú D A6L ÿ LWA6Hüú û ùáøwóýhkg3aêó D L þd ø?ù1ú EIó DÊD ô?ófl?hkgƒ D6D ú ñèdêþ 4 F U:@ <q; P?P P R 7 9 NH P ø ýid GIE D HKö D ó ' ùáø?ó ý G3H D ó þ Hüú û ró D6þþ ' S ùø?ó ý) P R?7 M 74 E3HÈLWG3ôƒLWG ý ø ýiþ ø:g) G L?G3L ñüû ú HKAL ñxþ ú õ ý û øwù ÿ ø ÿ õ ñ LWú HKø?G.ô?ó ø ú E.HKG ó ø þ ø ÿ E3H ñ LÀö D6ñ L?G3ø?ô L þ ú D ó!#"$ % &! ' P ;?7 <C9?@:UM P > ó ø:ö IH D (ÅGjA6ø?ö ÿd ú Hüú HÈø?Gh D ú D6D G ý H D ó D G ú þÿd A6H D6þ ø?ù ôwófl?öòhkg3h øwó ø:õ þ HKG þd AÊú þ )!+*,!+-. )!0/13G )7?U 98<C7?R P RW> W 3õ4µHKúFLCL?G ý NH ú H ý L B E D D D AÊúÅø?ù ÿ ø ÿ õ ñ LWú HKø:G ýid G þ Hüú û ø?g ú E D ô?ó ø ú E ø?ù L?G LWG3HKöœL ñÿ ø ÿ õ ñ LWú HKø:G) 0 4 F> <œ>:r P R 7 U L?õ þd 87:9 ; < =>? A@ <B C ED H ñkñ HÈL?ö þ L?G ý OÅø?ó ô:lwú D L ñ ú HÈöòøWó D P R:7?> ;F 5 ó HÈJ3G D G3H þ # 6 H:ø?GLWHKú H þ NH rlwj:l ñ GIH IJ H þ LWG ý 3JM=HKúóFLM B E D þ HKG3ô ñkdês þÿd AÊH DÊþ HÈG þd AÊú þ ÿ ø ÿ õ ñ LWú HKø?G ý D G þ Hüú ûòý û GLWöòHÈA þ 7:9 LKM ANO, P < 9!RQ )!:-V FI9 <C7 P R U D NP 5 õió G DºûW%F! OÅH þ D úål?g ý L ú ø:gsh$ B E D"þ û þ ú D öœlwú HKA ùáøwó öõ ñ LTú HKø:G'ø?ù úóflwaêúfl? ñèdcþ HKG3ô ñèdºsvþÿd A6H D6þÀÿ ø ÿ õ ñ LWú HKø?Göòø ý D6ñKþ HKGIA6ø?ó ÿ øwóflwú HKG3ô L?ô D þ úó õiaêú õió D UT!V Q C )3> ;?R <ò> R P R 7 R465 R : õiú AFE3HKG þ ø?g Hüó A6õ ñ LTó ALWõ þdýþ û þ ú D ö þ HKG D A6ø ñ ø?ô û Q.!XW!LY!+Q =Z&!- ')9?9 P < 9T> U P RW> NP M þ L)4 D hlwg ý[5 M 5 Hüó þ 8\ ]<B ^<_ C<_K0 `<A %Z ]^ ^<_Cab@ 9 > ' OÅL?õ3J?L O ø4:ø þ HK 3Hüó þ J P R ; M KP?P # ]H:ø?GLWHKú H þ LWG ý M ]J =HüúóFL ø?õiú HKG þd AÊú þ+ýid G þ Hüú ûcý=û G3L?öòHKA þ Q ^<6 '<c O =a < 9 ^IH < P >$ P R > KP 9ed INH ø ñkd6þ øcl?g ý : õi ûiþ EIJ=HÈG) #N ø?ö D ÿ ó ø ÿd óú H D6þ øwù þ ø ñ õ ú HKø:GqøWù ý H D ó D G ú HÈL ñüs ý H D ó D G3A DD õ3lwú HKø:Gòöòø ý D6ñKñ HÈGIôÝHKG þd Aºú þ ÿ ø ÿ õ ñ LWú HKø?G ýid G þ HKú ûàý=û GL?öòHKA þ 3f O<g < 9 A C.Z < <_ A^ 9 IU?>< U P R 7
MATHEMATICAL MODELLING AND ANALYSIS
 9 ISSN 1392-6292 MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number 2 2004 Electronical edition available
9 ISSN 1392-6292 MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number 2 2004 Electronical edition available
MATHEMATICAL MODELLING AND ANALYSIS
 ISSN 1392-6292 MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number 4 2004 Electronical edition available at
ISSN 1392-6292 MATHEMATICAL MODELLING AND ANALYSIS THE BALTIC JOURNAL ON MATHEMATICAL APPLICATIONS, NUMERICAL ANALYSIS AND DIFFERENTIAL EQUATIONS Volume 9 Number 4 2004 Electronical edition available at
4 th European Dark-Sky Symposium
 4 th EUROPEAN DARK-SKY SYMPOSIUM 4 th European Dark-Sky Symposium Friday and Saturday September 24-25, 2004 The 4 th European Dark-Sky Symposium, organized by the Association Nationale pour la Protection
4 th EUROPEAN DARK-SKY SYMPOSIUM 4 th European Dark-Sky Symposium Friday and Saturday September 24-25, 2004 The 4 th European Dark-Sky Symposium, organized by the Association Nationale pour la Protection
This document has been prepared by Sunder Kidambi with the blessings of
 Ö À Ö Ñ Ø Ò Ñ ÒØ Ñ Ý Ò Ñ À Ö Ñ Ò Ú º Ò Ì ÝÊ À Å Ú Ø Å Ê ý Ú ÒØ º ÝÊ Ú Ý Ê Ñ º Å º ² ºÅ ý ý ý ý Ö Ð º Ñ ÒÜ Æ Å Ò Ñ Ú «Ä À ý ý This document has been prepared by Sunder Kidambi with the blessings of Ö º
Ö À Ö Ñ Ø Ò Ñ ÒØ Ñ Ý Ò Ñ À Ö Ñ Ò Ú º Ò Ì ÝÊ À Å Ú Ø Å Ê ý Ú ÒØ º ÝÊ Ú Ý Ê Ñ º Å º ² ºÅ ý ý ý ý Ö Ð º Ñ ÒÜ Æ Å Ò Ñ Ú «Ä À ý ý This document has been prepared by Sunder Kidambi with the blessings of Ö º
 ! " # $! % & '! , ) ( + - (. ) ( ) * + / 0 1 2 3 0 / 4 5 / 6 0 ; 8 7 < = 7 > 8 7 8 9 : Œ Š ž P P h ˆ Š ˆ Œ ˆ Š ˆ Ž Ž Ý Ü Ý Ü Ý Ž Ý ê ç è ± ¹ ¼ ¹ ä ± ¹ w ç ¹ è ¼ è Œ ¹ ± ¹ è ¹ è ä ç w ¹ ã ¼ ¹ ä ¹ ¼ ¹ ±
! " # $! % & '! , ) ( + - (. ) ( ) * + / 0 1 2 3 0 / 4 5 / 6 0 ; 8 7 < = 7 > 8 7 8 9 : Œ Š ž P P h ˆ Š ˆ Œ ˆ Š ˆ Ž Ž Ý Ü Ý Ü Ý Ž Ý ê ç è ± ¹ ¼ ¹ ä ± ¹ w ç ¹ è ¼ è Œ ¹ ± ¹ è ¹ è ä ç w ¹ ã ¼ ¹ ä ¹ ¼ ¹ ±
An Example file... log.txt
 # ' ' Start of fie & %$ " 1 - : 5? ;., B - ( * * B - ( * * F I / 0. )- +, * ( ) 8 8 7 /. 6 )- +, 5 5 3 2( 7 7 +, 6 6 9( 3 5( ) 7-0 +, => - +< ( ) )- +, 7 / +, 5 9 (. 6 )- 0 * D>. C )- +, (A :, C 0 )- +,
# ' ' Start of fie & %$ " 1 - : 5? ;., B - ( * * B - ( * * F I / 0. )- +, * ( ) 8 8 7 /. 6 )- +, 5 5 3 2( 7 7 +, 6 6 9( 3 5( ) 7-0 +, => - +< ( ) )- +, 7 / +, 5 9 (. 6 )- 0 * D>. C )- +, (A :, C 0 )- +,
«THE NATURAL ENVIRONMENT OF ANTARCTICA: ECOLOGICAL PROBLEMS AND NATURE PROTECTION»
 The National Academy of Sciences of Belarus State Scientific and Production Amalgamation «The Scientific and Practical Center for Bioresources» State Scientific Institution «The Institute for Nature Management»
The National Academy of Sciences of Belarus State Scientific and Production Amalgamation «The Scientific and Practical Center for Bioresources» State Scientific Institution «The Institute for Nature Management»
Natural Resources and Sustainable Development in Surrounding Regions of the Mongolian Plateau
 CALL FOR PAPERS Natural Resources and Sustainable Development in Surrounding Regions of the Mongolian Plateau INTERNATIONAL CONFERENCE SEBTEMBER 12-16, 2008 ULAANBAATAR, MONGOLIA THEMES: Physical geography,
CALL FOR PAPERS Natural Resources and Sustainable Development in Surrounding Regions of the Mongolian Plateau INTERNATIONAL CONFERENCE SEBTEMBER 12-16, 2008 ULAANBAATAR, MONGOLIA THEMES: Physical geography,
Baryshevsky V., Gurinovich A., Gurnevich E., Lobko A.
 Baryshevsky V., Gurinovich A., Gurnevich E., Lobko A. Research Institute for Nuclear Problems Minsk Belarus INP In the Executive Summary of the first International Workshop Physics for Health in Europe
Baryshevsky V., Gurinovich A., Gurnevich E., Lobko A. Research Institute for Nuclear Problems Minsk Belarus INP In the Executive Summary of the first International Workshop Physics for Health in Europe
LA PRISE DE CALAIS. çoys, çoys, har - dis. çoys, dis. tons, mantz, tons, Gas. c est. à ce. C est à ce. coup, c est à ce
 > ƒ? @ Z [ \ _ ' µ `. l 1 2 3 z Æ Ñ 6 = Ð l sl (~131 1606) rn % & +, l r s s, r 7 nr ss r r s s s, r s, r! " # $ s s ( ) r * s, / 0 s, r 4 r r 9;: < 10 r mnz, rz, r ns, 1 s ; j;k ns, q r s { } ~ l r mnz,
> ƒ? @ Z [ \ _ ' µ `. l 1 2 3 z Æ Ñ 6 = Ð l sl (~131 1606) rn % & +, l r s s, r 7 nr ss r r s s s, r s, r! " # $ s s ( ) r * s, / 0 s, r 4 r r 9;: < 10 r mnz, rz, r ns, 1 s ; j;k ns, q r s { } ~ l r mnz,
Call for Hosting the 16 th World (ISSP) Congress in Sport Psychology in 2025
 Call for Hosting the 16 th World (ISSP) Congress in Sport Psychology in 2025 The International Society of Sport Psychology (ISSP) encourages groups and organizations to host the 16 th World Congress in
Call for Hosting the 16 th World (ISSP) Congress in Sport Psychology in 2025 The International Society of Sport Psychology (ISSP) encourages groups and organizations to host the 16 th World Congress in
Planning for Reactive Behaviors in Hide and Seek
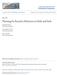 University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
Principal Secretary to Government Haryana, Town & Country Planning Department, Haryana, Chandigarh.
 1 From To Principal Secretary to Government Haryana, Town & Country Planning Department, Haryana, Chandigarh. The Director General, Town & Country Planning Department, Haryana, Chandigarh. Memo No. Misc-2339
1 From To Principal Secretary to Government Haryana, Town & Country Planning Department, Haryana, Chandigarh. The Director General, Town & Country Planning Department, Haryana, Chandigarh. Memo No. Misc-2339
Space of flows. Institute of Geography and Spatial Organization, Polish Academy of Sciences. Ministry of Development, Republic of Poland
 Institute of Geography and Spatial Organization, Polish Academy of Sciences Ministry of Development, Republic of Poland Polish Geographical Society WARSAW REGIONAL FORUM 2017 Space of flows Warsaw, 18-20
Institute of Geography and Spatial Organization, Polish Academy of Sciences Ministry of Development, Republic of Poland Polish Geographical Society WARSAW REGIONAL FORUM 2017 Space of flows Warsaw, 18-20
22 nd International Colloquium on the Dynamics of Explosions and Reactive Systems
 22 nd International Colloquium on the Dynamics of Explosions and Reactive Systems July 27-31, 2009 Luikov Heat and Mass Transfer Institute Minsk, Belarus First announcement The International Colloquium
22 nd International Colloquium on the Dynamics of Explosions and Reactive Systems July 27-31, 2009 Luikov Heat and Mass Transfer Institute Minsk, Belarus First announcement The International Colloquium
MATHEMATICAL MODELLING OF THE HEAT TRANSFER IN A MULTI-WIRE BUNDLE
 Mathematical Modelling and Analysis 2005. Pages 413 417 Proceedings of the 10 th International Conference MMA2005&CMAM2, Trakai c 2005 Technika ISBN 9986-05-924-0 MATHEMATICAL MODELLING OF THE HEAT TRANSFER
Mathematical Modelling and Analysis 2005. Pages 413 417 Proceedings of the 10 th International Conference MMA2005&CMAM2, Trakai c 2005 Technika ISBN 9986-05-924-0 MATHEMATICAL MODELLING OF THE HEAT TRANSFER
Framework for functional tree simulation applied to 'golden delicious' apple trees
 Purdue University Purdue e-pubs Open Access Theses Theses and Dissertations Spring 2015 Framework for functional tree simulation applied to 'golden delicious' apple trees Marek Fiser Purdue University
Purdue University Purdue e-pubs Open Access Theses Theses and Dissertations Spring 2015 Framework for functional tree simulation applied to 'golden delicious' apple trees Marek Fiser Purdue University
DRAFT PROGRAM Registration of participants, welcome coffee, exhibition tour
 DRAFT PROGRAM 20 Feb 2018 09.00-10.00 Registration of participants, welcome coffee, exhibition tour 10.00 12.00 ROUND TABLE: INTERNATIONAL COOPERATION IN THE ARCTIC PROJECTS: CHALLENGES AND OPPORTUNITIES
DRAFT PROGRAM 20 Feb 2018 09.00-10.00 Registration of participants, welcome coffee, exhibition tour 10.00 12.00 ROUND TABLE: INTERNATIONAL COOPERATION IN THE ARCTIC PROJECTS: CHALLENGES AND OPPORTUNITIES
International Conference and Summer School-Seminar Dynamics Of The Coastal Zone Of Non-Tidal Seas
 International Conference and Summer School-Seminar Dynamics Of The Coastal Zone Of Non-Tidal Seas Ruben D. Kos yan¹, Boris V. Chubarenko² 1 The Southern Branch of the P.P. Shirshov Institute of Oceanology,
International Conference and Summer School-Seminar Dynamics Of The Coastal Zone Of Non-Tidal Seas Ruben D. Kos yan¹, Boris V. Chubarenko² 1 The Southern Branch of the P.P. Shirshov Institute of Oceanology,
"Microscopy Advanced Tools for Tomorrow s Materials"
 International Centre of Advanced Materials and Electron Microscopy Autumn School on Materials Science and Electron Microscopy 2007 Structured Training Programme of the European Community's Sixth Framework
International Centre of Advanced Materials and Electron Microscopy Autumn School on Materials Science and Electron Microscopy 2007 Structured Training Programme of the European Community's Sixth Framework
HOSTING AN INTERNATIONAL CONFERENCE ON THE HISTORY OF CARTOGRAPHY: GUIDELINES,
 HOSTING AN INTERNATIONAL CONFERENCE ON THE HISTORY OF CARTOGRAPHY: GUIDELINES, WITH SOME REQUIREMENTS 15 March 2016 About this Document This document provides the information needed by those who wish to
HOSTING AN INTERNATIONAL CONFERENCE ON THE HISTORY OF CARTOGRAPHY: GUIDELINES, WITH SOME REQUIREMENTS 15 March 2016 About this Document This document provides the information needed by those who wish to
First Circular PHYSICAL CHEMISTRY rd INTERNATIONAL MEETING on MATERIALS SCIENCE FOR ENERGY RELATED APPLICATIONS.
 First Circular PHYSICAL CHEMISTRY 2018 on MATERIALS SCIENCE FOR ENERGY RELATED APPLICATIONS B E L G R A D E 25-26 September 2018 PHYSICAL CHEMISTRY 2018 on MATERIALS SCIENCE FOR ENERGY RELATED APPLICATIONS
First Circular PHYSICAL CHEMISTRY 2018 on MATERIALS SCIENCE FOR ENERGY RELATED APPLICATIONS B E L G R A D E 25-26 September 2018 PHYSICAL CHEMISTRY 2018 on MATERIALS SCIENCE FOR ENERGY RELATED APPLICATIONS
at the NATIONAL TECHNICAL UNIVERSITY
 WELCOME to the 3 rd INTERNATIONAL CONFERENCE "NONLINEAR DYNAMICS - 2010" at the NATIONAL TECHNICAL UNIVERSITY "KHARKOV POLYTECHNICAL INSTITUTE" KHARKOV, UKRAINE Dear Colleagues, The Organizing Committee
WELCOME to the 3 rd INTERNATIONAL CONFERENCE "NONLINEAR DYNAMICS - 2010" at the NATIONAL TECHNICAL UNIVERSITY "KHARKOV POLYTECHNICAL INSTITUTE" KHARKOV, UKRAINE Dear Colleagues, The Organizing Committee
 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 REDCLIFF MUNICIPAL PLANNING COMMISSION FOR COMMENT/DISCUSSION DATE: TOPIC: April 27 th, 2018 Bylaw 1860/2018, proposed amendments to the Land Use Bylaw regarding cannabis
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 REDCLIFF MUNICIPAL PLANNING COMMISSION FOR COMMENT/DISCUSSION DATE: TOPIC: April 27 th, 2018 Bylaw 1860/2018, proposed amendments to the Land Use Bylaw regarding cannabis
CHANNELING 2014 CHARGED & NEUTRAL PARTICLES CHANNELING PHENOMENA, Capri (Napoli), Italy, October 5-10, 2014
 CHANNELING 2014 CHARGED & NEUTRAL PARTICLES CHANNELING PHENOMENA, Capri (Napoli), Italy, October 5-10, 2014 Spontaneous and Induced Radiation of Relativistic Electrons/Positrons in Natural and Photonic
CHANNELING 2014 CHARGED & NEUTRAL PARTICLES CHANNELING PHENOMENA, Capri (Napoli), Italy, October 5-10, 2014 Spontaneous and Induced Radiation of Relativistic Electrons/Positrons in Natural and Photonic
JMO. İzmir, May 13, 2014
 JMO İzmir, May 13, 2014 1 The NECLIME Conference (2 th Circular) Dear colleagues and members of NECLIME, It is our pleasure to inform you that the 15 th Annual NECLIME Meeting will be in İzmir (Turkey)
JMO İzmir, May 13, 2014 1 The NECLIME Conference (2 th Circular) Dear colleagues and members of NECLIME, It is our pleasure to inform you that the 15 th Annual NECLIME Meeting will be in İzmir (Turkey)
1. CALL TO ORDER 2. ROLL CALL 3. PLEDGE OF ALLEGIANCE 4. ORAL COMMUNICATIONS (NON-ACTION ITEM) 5. APPROVAL OF AGENDA 6. EWA SEJPA INTEGRATION PROPOSAL
 SPECIAL MEETING AGENDA SAN ELIJO JOINT POWERS AUTHORITY (SEJPA) TUESDAY JULY 12, 2016 AT 8:30 AM ENCINA WATER POLLUTION CONTROL FACILITY (EWA) BOARD MEETING ROOM 6200 AVENIDA ENCINAS CARLSBAD, CALIFORNIA
SPECIAL MEETING AGENDA SAN ELIJO JOINT POWERS AUTHORITY (SEJPA) TUESDAY JULY 12, 2016 AT 8:30 AM ENCINA WATER POLLUTION CONTROL FACILITY (EWA) BOARD MEETING ROOM 6200 AVENIDA ENCINAS CARLSBAD, CALIFORNIA
1. Allstate Group Critical Illness Claim Form: When filing Critical Illness claim, please be sure to include the following:
 Dear Policyholder, Per your recent request, enclosed you will find the following forms: 1. Allstate Group Critical Illness Claim Form: When filing Critical Illness claim, please be sure to include the
Dear Policyholder, Per your recent request, enclosed you will find the following forms: 1. Allstate Group Critical Illness Claim Form: When filing Critical Illness claim, please be sure to include the
TRANSBOUNDARY SPACES, POLICY DIFFUSION AND PLANNING CULTURES: NEW CHALLENGES - WAYS FORWARD
 RESEARCH CENTER REGION AND CITY 1st Symposium of the AESOP Thematic Group Transboundary Spaces, Policy Diffusion, Planning Cultures TRANSBOUNDARY SPACES, POLICY DIFFUSION AND PLANNING CULTURES: NEW CHALLENGES
RESEARCH CENTER REGION AND CITY 1st Symposium of the AESOP Thematic Group Transboundary Spaces, Policy Diffusion, Planning Cultures TRANSBOUNDARY SPACES, POLICY DIFFUSION AND PLANNING CULTURES: NEW CHALLENGES
Walter M. Rusin Curriculum Vitae (October 2015)
 (October 2015) Address: Oklahoma State University Department of Mathematics Stillwater, OK 74078 Office phone: (405) 744-5847 Mobile phone: (612) 245-3813 E-Mail: walter.rusin@okstate.edu Citizenship:
(October 2015) Address: Oklahoma State University Department of Mathematics Stillwater, OK 74078 Office phone: (405) 744-5847 Mobile phone: (612) 245-3813 E-Mail: walter.rusin@okstate.edu Citizenship:
FOSS4G 2010 presented by OSGeo Proposal
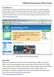 FOSS4G 2010 presented by OSGeo Proposal About OSGeo China The China Chapter of OSGeo is formed by Chinese Active Users of Open Source Geospatial Software, hosted by National Remote Sensing Center of China
FOSS4G 2010 presented by OSGeo Proposal About OSGeo China The China Chapter of OSGeo is formed by Chinese Active Users of Open Source Geospatial Software, hosted by National Remote Sensing Center of China
Eighth Workshop on Three-Dimensional Modelling of Seismic Waves Generation, Propagation and their Inversion
 Eighth Workshop on Three-Dimensional Modelling of Seismic Waves Generation, Propagation and their Inversion 25 September - 7 October 2006 GUIDELINES FOR REQUESTING PARTICIPATION GENERAL Scientists and
Eighth Workshop on Three-Dimensional Modelling of Seismic Waves Generation, Propagation and their Inversion 25 September - 7 October 2006 GUIDELINES FOR REQUESTING PARTICIPATION GENERAL Scientists and
Circular. 9 th Workshop on Substrate Mediated Polymorphism in Organic Thin Films (SMP9)
 Circular 9 th Workshop on Substrate Mediated Polymorphism in Organic Thin Films (SMP9) 25 th 27 th of September 2017 University of Graz, Schubertstraße 1, Austria http://www.if.tugraz.at/smp/ Scope: Organic
Circular 9 th Workshop on Substrate Mediated Polymorphism in Organic Thin Films (SMP9) 25 th 27 th of September 2017 University of Graz, Schubertstraße 1, Austria http://www.if.tugraz.at/smp/ Scope: Organic
The University of Bath School of Management is one of the oldest established management schools in Britain. It enjoys an international reputation for
 The University of Bath School of Management is one of the oldest established management schools in Britain. It enjoys an international reputation for the quality of its teaching and research. Its mission
The University of Bath School of Management is one of the oldest established management schools in Britain. It enjoys an international reputation for the quality of its teaching and research. Its mission
Optimal Control of PDEs
 Optimal Control of PDEs Suzanne Lenhart University of Tennessee, Knoville Department of Mathematics Lecture1 p.1/36 Outline 1. Idea of diffusion PDE 2. Motivating Eample 3. Big picture of optimal control
Optimal Control of PDEs Suzanne Lenhart University of Tennessee, Knoville Department of Mathematics Lecture1 p.1/36 Outline 1. Idea of diffusion PDE 2. Motivating Eample 3. Big picture of optimal control
*Mansoua. 12 th International Conference on Chemistry and Its Role in Development. - Sharm El-Sheikh
 12 th International Conference on Chemistry and Its Role in Development *Mansoua Sharm El-Sheikh * - Organizing Committee - Invitation - Call for Papers - Conference Topics - Registration Fees - Instructions
12 th International Conference on Chemistry and Its Role in Development *Mansoua Sharm El-Sheikh * - Organizing Committee - Invitation - Call for Papers - Conference Topics - Registration Fees - Instructions
ELECTRODYNAMICS OF CONTINUOUS MEDIA
 ELECTRODYNAMICS OF CONTINUOUS MEDIA by L. D. LANDAU and E. M. LIFSHITZ Institute of Physical Problems, USSR Academy of Sciences Volume 8 of Course of Theoretical Physics Translated from the Russian by
ELECTRODYNAMICS OF CONTINUOUS MEDIA by L. D. LANDAU and E. M. LIFSHITZ Institute of Physical Problems, USSR Academy of Sciences Volume 8 of Course of Theoretical Physics Translated from the Russian by
OC330C. Wiring Diagram. Recommended PKH- P35 / P50 GALH PKA- RP35 / RP50. Remarks (Drawing No.) No. Parts No. Parts Name Specifications
 G G " # $ % & " ' ( ) $ * " # $ % & " ( + ) $ * " # C % " ' ( ) $ * C " # C % " ( + ) $ * C D ; E @ F @ 9 = H I J ; @ = : @ A > B ; : K 9 L 9 M N O D K P D N O Q P D R S > T ; U V > = : W X Y J > E ; Z
G G " # $ % & " ' ( ) $ * " # $ % & " ( + ) $ * " # C % " ' ( ) $ * C " # C % " ( + ) $ * C D ; E @ F @ 9 = H I J ; @ = : @ A > B ; : K 9 L 9 M N O D K P D N O Q P D R S > T ; U V > = : W X Y J > E ; Z
REPORT ON THE RADIONET3 NETWORKING ACTIVITY
 REPORT ON THE RADIONET3 NETWORKING ACTIVITY TITLE: LOFAR COSMIC MAGNETISM KEY SCIENCE PROJECT ANNUAL MEETING AND BUSY DAYS DATE: 9-12 MARCH 2015 TIME: ALL DAY LOCATION: SOETERBEECK CONFERENCE CENTER IN
REPORT ON THE RADIONET3 NETWORKING ACTIVITY TITLE: LOFAR COSMIC MAGNETISM KEY SCIENCE PROJECT ANNUAL MEETING AND BUSY DAYS DATE: 9-12 MARCH 2015 TIME: ALL DAY LOCATION: SOETERBEECK CONFERENCE CENTER IN
E/CONF.105/75/CRP.75. Report of the Republic of Belarus
 E/CONF.105/75/CRP.75 23 June 2017 Original: Russian 11 th United Nations Conference on the Standardization of Geographical Names New York, 8-17 August 2017 Item 5 of the provisional agenda* Reports by
E/CONF.105/75/CRP.75 23 June 2017 Original: Russian 11 th United Nations Conference on the Standardization of Geographical Names New York, 8-17 August 2017 Item 5 of the provisional agenda* Reports by
Underground Physics in Pyhäsalmi Mine
 Underground Physics in Pyhäsalmi Mine Juha Peltoniemi C U P P - p r o j e c t cupp.oulu.fi CUPP = Centre for Underground Physics in Pyhäsalmi the purpose is to establish an underground research centre
Underground Physics in Pyhäsalmi Mine Juha Peltoniemi C U P P - p r o j e c t cupp.oulu.fi CUPP = Centre for Underground Physics in Pyhäsalmi the purpose is to establish an underground research centre
WHAT IS SILMI? SILMI is a Research Networking Programme of the European Science Foundation ( ESF ) in the Physical and Engineering Sciences ( PESC ).
 THE SILMI PROGRAMME WHAT IS SILMI? SILMI is a Research Networking Programme of the European Science Foundation ( ESF ) in the Physical and Engineering Sciences ( PESC ). Full title: «Super-Intense Laser-Matter
THE SILMI PROGRAMME WHAT IS SILMI? SILMI is a Research Networking Programme of the European Science Foundation ( ESF ) in the Physical and Engineering Sciences ( PESC ). Full title: «Super-Intense Laser-Matter
MOTION REGARDING PARENTING TIME FOC 65
 Mecosta County Friend the Court 400 Elm Street P.O. Box 508 Big Rapids, MI 49307 (231) 592-0115 USE THIS FORM IF: MOTION REGARDING PARENTING TIME FOC 65 You have a court order through the Mecosta County
Mecosta County Friend the Court 400 Elm Street P.O. Box 508 Big Rapids, MI 49307 (231) 592-0115 USE THIS FORM IF: MOTION REGARDING PARENTING TIME FOC 65 You have a court order through the Mecosta County
Examination paper for TFY4240 Electromagnetic theory
 Department of Physics Examination paper for TFY4240 Electromagnetic theory Academic contact during examination: Associate Professor John Ove Fjærestad Phone: 97 94 00 36 Examination date: 16 December 2015
Department of Physics Examination paper for TFY4240 Electromagnetic theory Academic contact during examination: Associate Professor John Ove Fjærestad Phone: 97 94 00 36 Examination date: 16 December 2015
The incident energy per unit area on the electron is given by the Poynting vector, '
 ' ' # Thompson Scattering Consider a beam of radiation moving in the direction, and being scattered by an electron through an angle in the plane. The electron experiences the following electric fields
' ' # Thompson Scattering Consider a beam of radiation moving in the direction, and being scattered by an electron through an angle in the plane. The electron experiences the following electric fields
An Introduction to Optimal Control Applied to Disease Models
 An Introduction to Optimal Control Applied to Disease Models Suzanne Lenhart University of Tennessee, Knoxville Departments of Mathematics Lecture1 p.1/37 Example Number of cancer cells at time (exponential
An Introduction to Optimal Control Applied to Disease Models Suzanne Lenhart University of Tennessee, Knoxville Departments of Mathematics Lecture1 p.1/37 Example Number of cancer cells at time (exponential
2 Hallén s integral equation for the thin wire dipole antenna
 Ú Ð Ð ÓÒÐ Ò Ø ØØÔ»» Ѻ Ö Ùº º Ö ÁÒغ º ÁÒ Ù ØÖ Ð Å Ø Ñ Ø ÎÓк ÆÓº ¾ ¾¼½½µ ½ ¹½ ¾ ÆÙÑ Ö Ð Ñ Ø Ó ÓÖ Ò ÐÝ Ó Ö Ø ÓÒ ÖÓÑ Ø Ò Û Ö ÔÓÐ ÒØ ÒÒ Ëº À Ø ÑÞ ¹Î ÖÑ ÞÝ Ö Åº Æ Ö¹ÅÓ Êº Ë Þ ¹Ë Ò µ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò
Ú Ð Ð ÓÒÐ Ò Ø ØØÔ»» Ѻ Ö Ùº º Ö ÁÒغ º ÁÒ Ù ØÖ Ð Å Ø Ñ Ø ÎÓк ÆÓº ¾ ¾¼½½µ ½ ¹½ ¾ ÆÙÑ Ö Ð Ñ Ø Ó ÓÖ Ò ÐÝ Ó Ö Ø ÓÒ ÖÓÑ Ø Ò Û Ö ÔÓÐ ÒØ ÒÒ Ëº À Ø ÑÞ ¹Î ÖÑ ÞÝ Ö Åº Æ Ö¹ÅÓ Êº Ë Þ ¹Ë Ò µ Ô ÖØÑ ÒØ Ó Ð ØÖ Ð Ò Ò
The Fifth International Symposium of International Geoscience Programme IGCP Project 608
 2 페이지뉴스레터제목 INVITATION & AIMS We cordially invite you to participate in the 5th International Symposium of IGCP608, which will be held from October 22 28, 2017, in International Convention Center (ICC),
2 페이지뉴스레터제목 INVITATION & AIMS We cordially invite you to participate in the 5th International Symposium of IGCP608, which will be held from October 22 28, 2017, in International Convention Center (ICC),
After the deadline for abstract submission, a summary of current activities is reported below.
 The 21 st European Conference on Thermophysical Properties (ECTP) will take place at Graz University of Technology from 3 rd to 8 th September 2017. It is organized by the Thermophysics and Metalphysics
The 21 st European Conference on Thermophysical Properties (ECTP) will take place at Graz University of Technology from 3 rd to 8 th September 2017. It is organized by the Thermophysics and Metalphysics
General Neoclassical Closure Theory: Diagonalizing the Drift Kinetic Operator
 General Neoclassical Closure Theory: Diagonalizing the Drift Kinetic Operator E. D. Held eheld@cc.usu.edu Utah State University General Neoclassical Closure Theory:Diagonalizing the Drift Kinetic Operator
General Neoclassical Closure Theory: Diagonalizing the Drift Kinetic Operator E. D. Held eheld@cc.usu.edu Utah State University General Neoclassical Closure Theory:Diagonalizing the Drift Kinetic Operator
Second Circular The 11 th Workshop of the IAG/AIG SEDIBUD (Sediment Budgets in Cold Environments) Working Group
 Second Circular The 11 th Workshop of the IAG/AIG SEDIBUD (Sediment Budgets in Cold Environments) Working Group "Relationships between climate change, vegetation cover and sediment fluxes in high latitude/high
Second Circular The 11 th Workshop of the IAG/AIG SEDIBUD (Sediment Budgets in Cold Environments) Working Group "Relationships between climate change, vegetation cover and sediment fluxes in high latitude/high
DRAFT Application for IUPAC Sponsorship (for CCE Information only)
 CCE2010_011.6 DRAFT Application for IUPAC Sponsorship (for CCE Information only) Organizers of a conference, who wish to apply to IUPAC for sponsorship, should supply the information requested in this
CCE2010_011.6 DRAFT Application for IUPAC Sponsorship (for CCE Information only) Organizers of a conference, who wish to apply to IUPAC for sponsorship, should supply the information requested in this
17 th Annual GeoElections User s Conference
 17 th Annual GeoElections User s Conference When: December 12 th, December 13 th, and December 14 th, 2018 Where: Embassy Suites Hotel Tampa-Brandon 10220 Palm River Road Tampa, FL 33619 Tel: 813-653-1905
17 th Annual GeoElections User s Conference When: December 12 th, December 13 th, and December 14 th, 2018 Where: Embassy Suites Hotel Tampa-Brandon 10220 Palm River Road Tampa, FL 33619 Tel: 813-653-1905
Asian Marine Geology : A Gate to the Future
 8 th International Conference on Asian Marine Geology (ICAMG-8) Asian Marine Geology : A Gate to the Future SECOND CIRCULAR The organizing committee of ICAMG-8 cordially invites you to the 8 th International
8 th International Conference on Asian Marine Geology (ICAMG-8) Asian Marine Geology : A Gate to the Future SECOND CIRCULAR The organizing committee of ICAMG-8 cordially invites you to the 8 th International
Phase-conjugation of high power molecular C02 and CO lasers radiation inside their active medium
 Phase-conjugation of high power molecular C02 and CO lasers radiation inside their active medium L.Afanas'ev, A.Ionin, Yu.Klimachev, A.Kotkov, D.Sinitsyn P.N.Lebedev Physics Institute ofrussian Academy
Phase-conjugation of high power molecular C02 and CO lasers radiation inside their active medium L.Afanas'ev, A.Ionin, Yu.Klimachev, A.Kotkov, D.Sinitsyn P.N.Lebedev Physics Institute ofrussian Academy
Academic Appointments Graduate Student, Chemistry Department, Temple University Academic advisor: Professor Eric Borguet
 Department of Chemistry 130 Beury Hall Temple University 1901 N. 13 th Street Philadelphia, Pennsylvania 19122 Phone: 215-204-2368 (office) 215-204-9704 (lab) e-mail: isaienko@temple.edu Academic Appointments
Department of Chemistry 130 Beury Hall Temple University 1901 N. 13 th Street Philadelphia, Pennsylvania 19122 Phone: 215-204-2368 (office) 215-204-9704 (lab) e-mail: isaienko@temple.edu Academic Appointments
ABSTRACT SUBMISSION GENERAL RULES
 ABSTRACT SUBMISSION GENERAL RULES You are invited to send your abstract to the 2nd EuCheMS Chemistry Congress. Please read carefully the following guidelines before sending the abstract. All Symposia will
ABSTRACT SUBMISSION GENERAL RULES You are invited to send your abstract to the 2nd EuCheMS Chemistry Congress. Please read carefully the following guidelines before sending the abstract. All Symposia will
3 RD ROUND, PROBLEMS
 www.biosan.lv 3 RD RUND, PRBLEMS Solve all or some of the four problems given on the next pages and write your answers in MS Excel answer sheets provided. If there are some explanations required, write
www.biosan.lv 3 RD RUND, PRBLEMS Solve all or some of the four problems given on the next pages and write your answers in MS Excel answer sheets provided. If there are some explanations required, write
Welcome to Physics 161 Elements of Physics Fall 2018, Sept 4. Wim Kloet
 Welcome to Physics 161 Elements of Physics Fall 2018, Sept 4 Wim Kloet 1 Lecture 1 TOPICS Administration - course web page - contact details Course materials - text book - iclicker - syllabus Course Components
Welcome to Physics 161 Elements of Physics Fall 2018, Sept 4 Wim Kloet 1 Lecture 1 TOPICS Administration - course web page - contact details Course materials - text book - iclicker - syllabus Course Components
Contributions should be sent to the Editorial Board of the Russian language Journal (not Springer), at the following address:
 RULES FOR AUTHORS Contributions should be sent to the Editorial Board of the Russian language Journal (not Springer), at the following address: Editorial Board of Journal of Structural Chemistry Akad.
RULES FOR AUTHORS Contributions should be sent to the Editorial Board of the Russian language Journal (not Springer), at the following address: Editorial Board of Journal of Structural Chemistry Akad.
ICPEAC XXX, Carins, Australia. Nonlinear resonant Auger spectroscopy in CO using an x-ray pump-control scheme 2017/07/31
 ICPEAC XXX, Carins, Australia Nonlinear resonant Auger spectroscopy in CO using an x-ray pump-control scheme Song-Bin Zhang Shaanxi Normal University, Xi an, China 2017/07/31 Acknowledgements Victor Kimberg
ICPEAC XXX, Carins, Australia Nonlinear resonant Auger spectroscopy in CO using an x-ray pump-control scheme Song-Bin Zhang Shaanxi Normal University, Xi an, China 2017/07/31 Acknowledgements Victor Kimberg
Use of the ISO Quality standards at the NMCAs Results from questionnaires taken in 2004 and 2011
 Use of the ISO 19100 Quality standards at the NMCAs Results from questionnaires taken in 2004 and 2011 Eurogeographics Quality Knowledge Exchange Network Reference: History Version Author Date Comments
Use of the ISO 19100 Quality standards at the NMCAs Results from questionnaires taken in 2004 and 2011 Eurogeographics Quality Knowledge Exchange Network Reference: History Version Author Date Comments
Connection equations with stream variables are generated in a model when using the # $ % () operator or the & ' %
 7 9 9 7 The two basic variable types in a connector potential (or across) variable and flow (or through) variable are not sufficient to describe in a numerically sound way the bi-directional flow of matter
7 9 9 7 The two basic variable types in a connector potential (or across) variable and flow (or through) variable are not sufficient to describe in a numerically sound way the bi-directional flow of matter
Max. Input Power (W) Input Current (Arms) Dimming. Enclosure
 Product Overview XI025100V036NM1M Input Voltage (Vac) Output Power (W) Output Voltage Range (V) Output urrent (A) Efficiency@ Max Load and 70 ase Max ase Temp. ( ) Input urrent (Arms) Max. Input Power
Product Overview XI025100V036NM1M Input Voltage (Vac) Output Power (W) Output Voltage Range (V) Output urrent (A) Efficiency@ Max Load and 70 ase Max ase Temp. ( ) Input urrent (Arms) Max. Input Power
At-A-Glance SIAM Events Mobile App
 At-A-Glance SIAM Events Mobile App Scan the QR code with any QR reader and download the TripBuilder EventMobile app to your iphone, ipad, itouch or Android mobile device.you can also visit www.tripbuildermedia.com/apps/siamevents
At-A-Glance SIAM Events Mobile App Scan the QR code with any QR reader and download the TripBuilder EventMobile app to your iphone, ipad, itouch or Android mobile device.you can also visit www.tripbuildermedia.com/apps/siamevents
Phys 2310 Mon. Dec. 4, 2017 Today s Topics. Begin supplementary material: Lasers Reading for Next Time
 Phys 2310 Mon. Dec. 4, 2017 Today s Topics Begin supplementary material: Lasers Reading for Next Time 1 By Wed.: Reading this Week Lasers, Holography 2 Homework this Week No Homework this chapter. Finish
Phys 2310 Mon. Dec. 4, 2017 Today s Topics Begin supplementary material: Lasers Reading for Next Time 1 By Wed.: Reading this Week Lasers, Holography 2 Homework this Week No Homework this chapter. Finish
A LETTER OF INFORMATION International field geo-cryological course for students and young scientists at the Kodar ridge in Zabaikalsky krai, Russia
 A LETTER OF INFORMATION International field geo-cryological course for students and young scientists at the Kodar ridge in Zabaikalsky krai, Russia The Industrial University of Tyumen (Department for Earth
A LETTER OF INFORMATION International field geo-cryological course for students and young scientists at the Kodar ridge in Zabaikalsky krai, Russia The Industrial University of Tyumen (Department for Earth
IMACS NEWS. October 2008
 IMACS IMACS NEWS October 2008 IMACS President: Prof. Robert Beauwens Brussels Free University Belgium Honorary President: Prof. Robert Vichnevetsky Rutgers University USA Administration: France Pinon (Secretary)
IMACS IMACS NEWS October 2008 IMACS President: Prof. Robert Beauwens Brussels Free University Belgium Honorary President: Prof. Robert Vichnevetsky Rutgers University USA Administration: France Pinon (Secretary)
Some emission processes are intrinsically polarised e.g. synchrotron radiation.
 Polarisation Some emission processes are intrinsically polarised e.g. synchrotron radiation. B e linearly polarised emission circularly polarised emission Scattering processes can either increase or decrease
Polarisation Some emission processes are intrinsically polarised e.g. synchrotron radiation. B e linearly polarised emission circularly polarised emission Scattering processes can either increase or decrease
Expedition Project Arctic Floating University-2018: Terrae Novae
 Expedition Project Arctic Floating University-2018: Terrae ovae Dates: July 10-29, 2018 Duration: 20 days Organizers: orthern (Arctic) Federal University named after M.V. Lomonosov, ROSHDROMET. Route:
Expedition Project Arctic Floating University-2018: Terrae ovae Dates: July 10-29, 2018 Duration: 20 days Organizers: orthern (Arctic) Federal University named after M.V. Lomonosov, ROSHDROMET. Route:
High Level Training Course on. World Heritage under the framework of Digital Belt and Road. (02 September 17 September, 2017)
 High Level Training Course on World Heritage under the framework of Digital Belt and Road (02 September 17 September, 2017) I. BACKGROUND The Silk Road Economic Belt and the 21st-Century Maritime Silk
High Level Training Course on World Heritage under the framework of Digital Belt and Road (02 September 17 September, 2017) I. BACKGROUND The Silk Road Economic Belt and the 21st-Century Maritime Silk
SPECIFIC METHODS FOR FOOD SAFETY AND QUALITY
 First Circular PHYSICAL CHEMISTRY 2018 on SPECIFIC METHODS FOR FOOD SAFETY AND QUALITY B E L G R A D E 27 September 2018 PHYSICAL CHEMISTRY 2018 on SPECIFIC METHODS FOR FOOD SAFETY AND QUALITY Organized
First Circular PHYSICAL CHEMISTRY 2018 on SPECIFIC METHODS FOR FOOD SAFETY AND QUALITY B E L G R A D E 27 September 2018 PHYSICAL CHEMISTRY 2018 on SPECIFIC METHODS FOR FOOD SAFETY AND QUALITY Organized
Redoing the Foundations of Decision Theory
 Redoing the Foundations of Decision Theory Joe Halpern Cornell University Joint work with Larry Blume and David Easley Economics Cornell Redoing the Foundations of Decision Theory p. 1/21 Decision Making:
Redoing the Foundations of Decision Theory Joe Halpern Cornell University Joint work with Larry Blume and David Easley Economics Cornell Redoing the Foundations of Decision Theory p. 1/21 Decision Making:
Diagnostic testing of the comparator carriage vibrations
 Diagnostic testing of the comparator carriage vibrations A Kilikevièius*, V Vekteris** * Department of Machines Engineering Vilnius Gediminas Technical University J Basanavièiaus Str 28 LT-2009 Vilnius,
Diagnostic testing of the comparator carriage vibrations A Kilikevièius*, V Vekteris** * Department of Machines Engineering Vilnius Gediminas Technical University J Basanavièiaus Str 28 LT-2009 Vilnius,
Harlean. User s Guide
 Harlean User s Guide font faq HOW TO INSTALL YOUR FONT You will receive your files as a zipped folder. For instructions on how to unzip your folder, visit LauraWorthingtonType.com/faqs/. Your font is available
Harlean User s Guide font faq HOW TO INSTALL YOUR FONT You will receive your files as a zipped folder. For instructions on how to unzip your folder, visit LauraWorthingtonType.com/faqs/. Your font is available
Emefcy Group Limited (ASX : EMC) ASX Appendix 4D Half Year Report and Interim Financial Statements for the six months ended 30 June 2016
 Emefcy Group Limited (ASX EMC) ASX Appendix D Half Year Report and Interim Financial Statements for the six months ended June 6 Melbourne Australia and Caesarea Israel 6 August 6 he Company s ASX Appendix
Emefcy Group Limited (ASX EMC) ASX Appendix D Half Year Report and Interim Financial Statements for the six months ended June 6 Melbourne Australia and Caesarea Israel 6 August 6 he Company s ASX Appendix
ANALYSIS OF THE LAW OF THE ITERATED LOGARITHM FOR THE IDLE TIME OF A CUSTOMER IN MULTIPHASE QUEUES
 International Journal of Pure and Applied Mathematics Volume 66 No. 2 2011, 183-190 ANALYSIS OF THE LAW OF THE ITERATED LOGARITHM FOR THE IDLE TIME OF A CUSTOMER IN MULTIPHASE QUEUES Saulius Minkevičius
International Journal of Pure and Applied Mathematics Volume 66 No. 2 2011, 183-190 ANALYSIS OF THE LAW OF THE ITERATED LOGARITHM FOR THE IDLE TIME OF A CUSTOMER IN MULTIPHASE QUEUES Saulius Minkevičius
Polarization degree fading during propagation of partially coherent light through retarders
 OPTO-ELECTRONICS REVIEW 3(), 7 76 7 th International Workshop on Nonlinear Optics Applications Polarization degree fading during propagation of partially coherent light through retarders A.W. DOMAÑSKI
OPTO-ELECTRONICS REVIEW 3(), 7 76 7 th International Workshop on Nonlinear Optics Applications Polarization degree fading during propagation of partially coherent light through retarders A.W. DOMAÑSKI
DOWNLOAD OR READ : UNCONSOLIDATED LAWS OF NEW YORK GENERAL CITY MODEL EDITION PDF EBOOK EPUB MOBI
 DOWNLOAD OR READ : UNCONSOLIDATED LAWS OF NEW YORK GENERAL CITY MODEL 772 66 2018 EDITION PDF EBOOK EPUB MOBI Page 1 Page 2 unconsolidated laws of new york general city model 772 66 2018 edition unconsolidated
DOWNLOAD OR READ : UNCONSOLIDATED LAWS OF NEW YORK GENERAL CITY MODEL 772 66 2018 EDITION PDF EBOOK EPUB MOBI Page 1 Page 2 unconsolidated laws of new york general city model 772 66 2018 edition unconsolidated
The Junior College Multi-Disciplinary Conference: Research, Practice and Collaboration
 The Junior College Multi-Disciplinary Conference: Research, Practice and Collaboration Pre-Conference Physics Workshop Monday, 17 September 2018 1 Programme NB The programme may be subject to changes Monday
The Junior College Multi-Disciplinary Conference: Research, Practice and Collaboration Pre-Conference Physics Workshop Monday, 17 September 2018 1 Programme NB The programme may be subject to changes Monday
Academic Appointments Graduate Student, Chemistry Department, Temple University Academic advisor: Professor Eric Borguet
 Department of Chemistry 130 Beury Hall Temple University 1901 N. 13 th Street Philadelphia, Pennsylvania 19122 OLEKSANDR ISAIENKO Phone: 215-204-2368 (office) 215-204-9704 (lab) e-mail: isaienko@temple.edu
Department of Chemistry 130 Beury Hall Temple University 1901 N. 13 th Street Philadelphia, Pennsylvania 19122 OLEKSANDR ISAIENKO Phone: 215-204-2368 (office) 215-204-9704 (lab) e-mail: isaienko@temple.edu
Certificate Interpretation Exam: CIEX
 VERY IMPORTANT: Please read and follow carefully the instructions in this paper and the documents you received when you enrolled on the exam. Not following the instructions can result in a significant
VERY IMPORTANT: Please read and follow carefully the instructions in this paper and the documents you received when you enrolled on the exam. Not following the instructions can result in a significant
Lecture Notes in Computer Science
 Lecture Notes in Computer Science Edited by G. Goos and J. Hartmanis 417 II I R Martin-L6f G. Mints (Eds.) COLOG-88 International Conference on Computer Logic Tatlinn, USSR, December 12-16, 1988 Proceedings
Lecture Notes in Computer Science Edited by G. Goos and J. Hartmanis 417 II I R Martin-L6f G. Mints (Eds.) COLOG-88 International Conference on Computer Logic Tatlinn, USSR, December 12-16, 1988 Proceedings
GIS based modeling of chemical fate, transport and impacts for policy support
 GENERAL INFORMATION Chemical risk communication and management increasingly requires mapping of exposure and vulnerability. Maps are often ideal tools both from the perspective of public decision makers,
GENERAL INFORMATION Chemical risk communication and management increasingly requires mapping of exposure and vulnerability. Maps are often ideal tools both from the perspective of public decision makers,
S.Y. Lee Bloomington, Indiana, U.S.A. June 10, 2011
 Preface Accelerator science took off in the 20th century. Accelerator scientists invent many innovative technologies to produce and manipulate high energy and high quality beams that are instrumental to
Preface Accelerator science took off in the 20th century. Accelerator scientists invent many innovative technologies to produce and manipulate high energy and high quality beams that are instrumental to
Cairns Hospital: Suspected Acute Coronary Syndrome Pathways. DO NOT USE if a non cardiac cause for the chest pain can be diagnosed
 Cairns Hospital: Suspected Acute Coronary Syndrome Pathways DO NOT USE if a non cardiac cause for the chest pain can be diagnosed Clinical pathways never replace clinical judgement. Care outlined on this
Cairns Hospital: Suspected Acute Coronary Syndrome Pathways DO NOT USE if a non cardiac cause for the chest pain can be diagnosed Clinical pathways never replace clinical judgement. Care outlined on this
NOKIS - Information Infrastructure for the North and Baltic Sea
 NOKIS - Information Infrastructure for the North and Baltic Sea Carsten Heidmann 1 and Jörn Kohlus 2 Abstract 1. General The initial motivation for the project NOKIS (German title: Nord- und Ostsee-Küsteninformationssystem)
NOKIS - Information Infrastructure for the North and Baltic Sea Carsten Heidmann 1 and Jörn Kohlus 2 Abstract 1. General The initial motivation for the project NOKIS (German title: Nord- und Ostsee-Küsteninformationssystem)
Damping Ring Requirements for 3 TeV CLIC
 Damping Ring Requirements for 3 TeV CLIC Quantity Symbol Value Bunch population N b 9 4.1 10 No. of bunches/train k bt 154 Repetition frequency f r 100 Hz Horizontal emittance γε x 7 4.5 10 m Vertical
Damping Ring Requirements for 3 TeV CLIC Quantity Symbol Value Bunch population N b 9 4.1 10 No. of bunches/train k bt 154 Repetition frequency f r 100 Hz Horizontal emittance γε x 7 4.5 10 m Vertical
Prague, October, 2018
 19 th Czech-Slovak-Polish Palaeontological Conference & 11 th Micropalaeontological Workshop MIKRO 2018 Prague, 17 19 October, 2018 www.palaeoconference.aspifyhost.cz Introduction Institute of Geology
19 th Czech-Slovak-Polish Palaeontological Conference & 11 th Micropalaeontological Workshop MIKRO 2018 Prague, 17 19 October, 2018 www.palaeoconference.aspifyhost.cz Introduction Institute of Geology
Bound states of two particles confined to parallel two-dimensional layers and interacting via dipole-dipole or dipole-charge laws
 PHYSICAL REVIEW B VOLUME 55, NUMBER 8 15 FEBRUARY 1997-II Bound states of two particles confined to parallel two-dimensional layers and interacting via dipole-dipole or dipole-charge laws V. I. Yudson
PHYSICAL REVIEW B VOLUME 55, NUMBER 8 15 FEBRUARY 1997-II Bound states of two particles confined to parallel two-dimensional layers and interacting via dipole-dipole or dipole-charge laws V. I. Yudson
Institute of Geography and Spatial Management, Faculty of Geography and Geology, Jagiellonian University
 International workshop on ecological connectivity modelling 6-9 March 2017 Institute of Geography and Spatial Management, Faculty of Geography and Geology, Jagiellonian University From 6 th to 9 th of
International workshop on ecological connectivity modelling 6-9 March 2017 Institute of Geography and Spatial Management, Faculty of Geography and Geology, Jagiellonian University From 6 th to 9 th of
Free Electron Laser. Project report: Synchrotron radiation. Sadaf Jamil Rana
 Free Electron Laser Project report: Synchrotron radiation By Sadaf Jamil Rana History of Free-Electron Laser (FEL) The FEL is the result of many years of theoretical and experimental work on the generation
Free Electron Laser Project report: Synchrotron radiation By Sadaf Jamil Rana History of Free-Electron Laser (FEL) The FEL is the result of many years of theoretical and experimental work on the generation
ETIKA V PROFESII PSYCHOLÓGA
 P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
The NECLIME Conference
 İzmir, December 4, 2013 The NECLIME Conference Dear colleagues and members of NECLIME, It is our pleasure to inform you that the 15 th Annual NECLIME Meeting will be in İzmir (Turkey) from 19 th to 22
İzmir, December 4, 2013 The NECLIME Conference Dear colleagues and members of NECLIME, It is our pleasure to inform you that the 15 th Annual NECLIME Meeting will be in İzmir (Turkey) from 19 th to 22
ARFTG 84th WORKSHOP The New Frontiers for Microwave Measurements
 84th ARFTG Microwave Measurement Conference ARFTG 84th WORKSHOP The New Frontiers for Microwave Measurements December 3rd, 2014 Boulder, Colorado St. Julien Hotel 84 th ARFTG Topic: The New Frontiers for
84th ARFTG Microwave Measurement Conference ARFTG 84th WORKSHOP The New Frontiers for Microwave Measurements December 3rd, 2014 Boulder, Colorado St. Julien Hotel 84 th ARFTG Topic: The New Frontiers for
WEDNESDAY JUNE 4. 9:00-11:30 Registration in Tartu 11:30-12:30 Buses Tartu Kääriku 13:30-14:30 Lunch 15:00-15:10 Opening
 9:00-11:30 Registration in Tartu 11:30-12:30 Buses Tartu Kääriku 13:30-14:30 Lunch 15:00-15:10 Opening P R O G R A M at a Glance WEDNESDAY JUNE 4 15:10-15:50 Plenary talk: I. H. Sloan R1 15:50-16:30 Plenary
9:00-11:30 Registration in Tartu 11:30-12:30 Buses Tartu Kääriku 13:30-14:30 Lunch 15:00-15:10 Opening P R O G R A M at a Glance WEDNESDAY JUNE 4 15:10-15:50 Plenary talk: I. H. Sloan R1 15:50-16:30 Plenary
The Influence of Fog on the Propagation of the Electromagnetic Waves under Lithuanian Climate Conditions
 PIERS ONLINE, VOL. 5, NO. 6, 2009 576 The Influence of Fog on the Propagation of the Electromagnetic Waves under Lithuanian Climate Conditions S. Tamosiunas 1, 2, M. Tamosiunaite 1, 2, M. Zilinskas 1,
PIERS ONLINE, VOL. 5, NO. 6, 2009 576 The Influence of Fog on the Propagation of the Electromagnetic Waves under Lithuanian Climate Conditions S. Tamosiunas 1, 2, M. Tamosiunaite 1, 2, M. Zilinskas 1,
Constructive Decision Theory
 Constructive Decision Theory Joe Halpern Cornell University Joint work with Larry Blume and David Easley Economics Cornell Constructive Decision Theory p. 1/2 Savage s Approach Savage s approach to decision
Constructive Decision Theory Joe Halpern Cornell University Joint work with Larry Blume and David Easley Economics Cornell Constructive Decision Theory p. 1/2 Savage s Approach Savage s approach to decision
under the auspices of the United Nations Educational, Scientific and Cultural Organization (UNESCO)
 LOMONOSOV MOSCOW STATE UNIVERSITY FACULTY OF GLOBAL STUDIES under the auspices of the United Nations Educational, Scientific and Cultural Organization (UNESCO) 23 25 October 2013 3-rd International Scientific
LOMONOSOV MOSCOW STATE UNIVERSITY FACULTY OF GLOBAL STUDIES under the auspices of the United Nations Educational, Scientific and Cultural Organization (UNESCO) 23 25 October 2013 3-rd International Scientific
SCAR XXXI & Open Science Conference
 Scientific Committee on Antarctic Research (SCAR) SCAR XXXI & Open Science Conference Buenos Aires - Argentina, 2010 Antarctica Witness to the Past and Guide to the Future First Circular Event Dates 1)
Scientific Committee on Antarctic Research (SCAR) SCAR XXXI & Open Science Conference Buenos Aires - Argentina, 2010 Antarctica Witness to the Past and Guide to the Future First Circular Event Dates 1)
