Aplikace matematiky. El Said El Shinnawy The Euclidean plane kinematics. Terms of use: Aplikace matematiky, Vol. 24 (1979), No.
|
|
|
- Sharleen Gaines
- 5 years ago
- Views:
Transcription
1 Aplikace matematiky El Said El Shinnawy The Euclidean plane kinematics Aplikace matematiky, Vol 24 (1979), No 2, Persistent URL: Terms of use: Institute of Mathematics AS CR, 1979 Institute of Mathematics of the Academy of Sciences of the Czech Republic provides access to digitized documents strictly for personal use Each copy of any part of this document must contain these Terms of use This paper has been digitized, optimized for electronic delivery and stamped with digital signature within the project DML-CZ: The Czech Digital Mathematics Library
2 SVAZEK 24 (1979) APLIKACE MATEMATIKY ČÍSLO 2 THE EUCLIDEAN PLANE KINEMATICS EL SAID EL SHINNAWY (Received April 22, 1977) In his paper [1], A Karger devoted himself to the study of the kinematic geometry in homogeneous spaces, the groups of motions of which are special 3-dimensional Lie groups In what follows, I restrict myself to the Euclidean plane, but I am going to show a method leading to the solution of the equivalence problem for all Lie groups of motions Besides this, I present all transitive one-parametric systems of motions in E 2 Let E 2 denote the Euclidean plane, let G be the Lie group of direct isometries of F 2 onto itself By a motion we will understand a mapping g : J -> G, J c U being an interval Our first problem may be formulated as follows: Let g, g : J -> G be two motions; we have to find conditions which ensure the equivalence of g y g 9 ie, the existence of a direct isometry o : E 2 -> E 2 such that a g[t) = g(t) for each t e J 0 We will solve this problem by constructing an invariant parameter and two "curvatures" on g; the desired condition will be then reduced to the equality of invariant parameters and curvatures As a by-product, we will present a complete list of motions with constant curvatures Let {M, e l9 e 2 } be an orthonormal frame in E 2 Then a general direct isometry g e G is given by (1) g(m) = M + ae 1 + be 2, g(e 1 ) = cos a e 1 sin a e 2, g(e 2 ) = sin a e x -f cos a e 2 Thus we may identify the group G with the subgroup of GL(3, IR) of matrices of the form (2) [la b \ g = 0 cos a sin a L \0 sin a cos ocj 105
3 The Lie algebra is then, as is easy to see, identified with the Lie algebra of matrices of the form (3) /0 /dt db/dt\ V= 00 -/dt ; \0 /dt 0 / let (4) be its basis Then (5) [V!, V 2 ] = 0, [V V 3 ] = - V 2, [V 2, V 3 ] = V! Now, let g : J -* G, g = g(t) be a motion Then we get a mapping v : J -> (S given by (6) <0 = *(0- ld f- Taking into consideration (1), the motion g(t) is represented by the equations (7) a = a(t), a = a(t), b = b(t) ; t e J It is easy to see that /n\ / \ / \ /db \ T7 T/ (8) v(t) = ( b V! + + a )V 2 + V 3 W V J \dt dtj \dt dtj dt With the second motion g : J -* G, we associate similarly the mapping v Let In ((E>) denote the Lie group of inner automorphisms of (5 Then it is known that g and g are equivalent if and only if there is a F 0 e In ((5) such that v(t) = F 0 {KO} f r eacn t e J Because the motion g(i) is given, up to the equivalence, by v(t), our problem reduces to the equivalence problem for two mappings v, v : J -> with respect to the group In ((5) We are now going to solve this problem even with respect to a more general group Aut ( ) of all automorphisms of Let F e Aut ( ) be given by (9) T(V 1 ) = a 1 V 1 + a 2 V 2 + a 3 V3, 106 at r^^bv, + b 2 V 2 + b 3 V 3, r(v 3 ) = c l v 1 +c 2 V 2 +c 3 V 3
4 From (10) [r(v x ), r(v 2 )] = o, [rfy), r(v 3 )] = -r(v 2 ), [r(^),r(v3)] = r(n) we see that Aut ( ) cz GL (3, (R) may be identified with the set of all matrices of the form (11) / a x a 2 0\ la x a 2 0\ and a 2 a! 0 J with a 2 + a\ =j= 0 Vi ^2 1/ Of course, the Lie algebra $tut ( ) cz (3, (R) of Aut ( ) is the set of all matrices of the form (12) It is known that the Lie algebra 3n ( ) is the set of all homomorphisms ad u: : (5 ->, u e For u = u 1^ + u 2 V 2 + u 3 V 3, we have (13) ad(u)(x 1 V 1 + x 2 V 2 + x 3 V 3 ) - x l u 3 V 2 - x 2 u 3 Vi - x\u l V 2 - u 2^), ie, we may identify 3n ( ) cz 2Iut ( ) with the set of all matrices of the form (14) / 0 u 3 0\ u u 2 -u 1 0/ From this (or by a direct calculation) we get that In ( ) cz Aut ( ) is the group of all matrices (11) with a 2 + a 2 = 1, ie, its identity component is the group of all matrices of the form (15) cos Фl sin Фl tí sin Фl cos Фi 0 Фl Фъ 1 First of all, let us study the mapping v : J > with respect to the group In ( ) acting on By a frame of (with respect to this group) we shall mean each triple {*>i> ^2> ^} such that v t = F 0 (Vi) for a F 0 e In ( ) and i = 1, 2, 3 If {v 1? v 2, v 3 } and {w l9 w 2, w 3 } are two frames, then there are (p, k, fx such that (16) w t = cos cp v! + sin (p v 2, w 2 = sin q> v x + cos <p v 2, w 3 = A v! + /1 v 2 + v 3 107
5 Let {v x (t), v 2 (t), v 3 (t)}, t 6 J be a field of frames Then there are functions a^(t) such that (17) * >-<%<)>#), df but (14) implies that (17) should have the form /io\ dv! n dv 2 dv 3 (18) 1 = ^, -^=-p v -* = y 1 v 1 +y 2 v 2 dt dt dt Consider v = v(f), t e J, and suppose of course v(t) + 0 for each t e J> With each t, let us associate a frame {v x (t), v 2 (t), v 3 (t)} such that v 3 (t) and v(t) are dependent; this can always be achieved because of (15) by a suitable choice of \j/ 2, \j/ 3 Any other field of frames {w x (t), w 2 (t), w 3 (t)} with the same property is given by (19) Wj = cos cp v l + sin cp v 2, w 2 = sin cp vi + cos cp v 2, w 3 = v 3 For {w t (t), w 2 (t), w 3 (t)}, we may write equations similar to (18): / \ dw x ~ dw 2 ~ dw 3 (20) - = fiw 2, - = -^Wi, - = y^i + y 2 w 2 dt dt dt From the equations (18) (20) we obtain (21) sin cp + p sin cp = /? sin cp, cos cp + /? cos cp cos <p, dt dr From ( ) we get 7 r cos (B y 2 sin 9 = y t, ^ sin cp + y 2 cos cp y 2 (22) yl + yl = i\ + 72, and y 1 + y 2 is thus an invariant of our system of frames We have to distinguish two cases Let us, first of all, consider the case (23) 7l = y 2 = 0 The equations (21 12 ) reduce to (24)? + *-* at 108
6 and we may choose, at least locally, cp(t) in such a way that ft = 0 Thus we may associate with v(t) a field of frames such that (25) ^ = 0, -^ = 0, ^ = 0, dt dt dt ie, v(t) reduces to a fixed line and g(t) may be parametrized in such a way that it becomes a one-parametric subgroup of G Let us suppose (26) y\ + y\ + 0 It is easy to see that we may then choose the frames restricted by the condition (27) y 2 = 0 ; from (21) we get (28) ft = p, y x = yi, /? and y! being thus the invariants of v(t) From (19) we see that the condition (27) associates with v(t) just one field of frames Let us now determine explicitly the invariants of our initial motion (7) For / \,/ \ d# i r,r \ db _, N (29) (_) = b, ftfrt = + a, C(t) =, V 7 W V/ W dt dt dt dt dt (8) takes the form (30) v(t) = A(t) V, + B(t) V 2 + C(t) V 3 It is not necessary to study the case C(t) = 0; in this case a = constant, and our motion consists just of a group of translations Thus we may suppose (31) C(t) =j= 0 for tej The general field of frames associated with v(t) is then (32) Vl(t) = cos (t) Vi + sin (t) V 2, and we get v 2 (t) = -sin (t) V! + cos (t) V 2, v 3 (t) = A(t) C(t)- 1 V! + B(t) C(t)" 1 V 2 + V 3 ( v dv! d dv 2 d (33) - = v 2, _ = - _ v!, dt dt dt dt -^1 = { (АС х ) соз I; + (ВС 1 ) зт А ^ + {- (АС^зт^ + ~ (ВС 1 ) со5 А V 2 109
7 According to our previous discussion, we may choose <J(t) in such a way that (34) (AC~ ') sin { - -i (BC~*) cos { = 0, dt dt the functions (35) ^, -(AC- 1 )cos^ + -(BC- 1 )sin^ dt dt dt being then the invariants of our motion For g(t) we may introduce a canonical parameter by the condition v(t) = v 3 (t), ie, C(t) = 1; from (29) we see that t = = a + const From now on, let us use the canonical parameter a Define Q by The case Q = 0 corresponds to (23) Therefore, let us suppose Q =1= 0 To get the invariants, we have to choose (IH\ - t _i db _! da (37) sin c = O, cos q = Q and we see that the invariants (35) take the final form day /dbyi 1/2 / \/ J Let us turn our attention to the study of motions with constant invariants First of all, let us study the case Q = J 2 = 0 Introduce the functions r, s : J > C by (39) r(a) = a(a) + i 6(a), s(a) = ^ + i r(a) Then it is easy to see that (40) J 2 = % J 2 = 0 implies the existence of x t e C such that /,,\ d r (41) + ir = ^ 110
8 The general solution of this equation is then (42) r = x 2 e~ /a - ix {, x 2 e C In F 2, introduce the coordinates (x, y) of a point X with respect to the basis {M, e u e 2 } by means of X = M + xe t + ye 2 By # e G (1), this point is mapped onto the point g(x) = g(m) + xg(e t ) + yg(e 2 ); let it have coordinates x*, y* Then (43) x* = cos a x + sin a y + a, y* = sin a x + cos a y + b, ie, (44) z* = e",a z + r; z = x + iy, z* = x* + /y* Thus our g(oc) associates with the point z the point (45) z* = e~' m (z + x 2 ) - ix t Suppose that the canonical parameter is chosen in such a way that g(0) is the identity mapping Then x 2 = \x x and the motion is given by (x = x 2 ) (46) z* = e~' m (z + x) - x Hence (47) \z* + x\ = \z + x\ and we see that the motion considered is just the rotation around the point x Let us now consider the case (48) J 2 = constant + 0 It is not difficult to see that (48) implies (49) J, = JV g First of all, let (50) J x = 0, ie, (51) s = Q tcc + Q 2 ; Q U Q 2 ec The general solution of the differential equation / x dr (52) \- ir = Q X OC + O 2 is (53) r = O 3 e~ /a - i^a + O x - /O 2 ; O 3 e C ; 111
9 and our motion is given by (44), ie, (54) z* = e~ ia (z + O 3 ) - io x a + Ql - i^2 Let us suppose O(0) to be identity Then O 3 + Ql - i^2 = o and (54) reduces to (55) z* = e~ ta (z + O) - io x a - O^ ; O = O 3 e C ; of course, J 2 = \Q X \ Let us calculate the centroids of (55) The fixed centroid is the set of points z 0 (a) such that (dz*/) = 0, ie, it is given by z 0 = -Q x e iol - O Because of \z 0 + O = [O^, we see that it is a circle with the center -O and the radius J 2 The moving centroid is then given by z* = e~ ia (z 0 + O) - io x a - O = - jo x a - O! O, and it is the straight line with the equation (56) Q t Z + Q X Z + O^O! + O^O + 2O!O! = 0 Thus our motion is produced by rolling a straight line upon a circle of radius J Let us turn our attention to the case (57) J! = constant =f= 0, J 2 = constant + 0 The function s(a) should then be the solution of the differential equations (see (49)) (58) ds = Jг, å 2 s 2 = J X J 2 From (58j) we get (59) ds d 2 s dš d 2 s 2 2 Multiplying this by ds d 2 s 2 and inserting from (58), we have (60) ІЄ, (бi) Uv + JJ > d 2 s т ás 2 ±1 The general solution of this equation is (62) s = six^; 1 e~ EiJia + x 2 > *ъ Kг ' C 112
10 From (581) we obtain (63) %i = J 2 Now, the general solution of (dr/) + ir = s (see (39)) is (64) r = %iji _1 (l - eji)- 1 e~ EiJlCC + x 3 e~ ia - ix 2 ; x 3 e C in the case (65) Ji + 1 ; the case J X = 1 will be considered later on The motion g(ot) is then (see (44)) (66) z* = (z + x 3 ) e~ ia + ^ij-^l - fiji)" 1 e~ lvia - ix 2 The condition a(0) = identity implies x 3 ix 2 + XiJi" 1 (l Ji) _1 we get = 0, and (67) z* = (z + % 3 ) e~ ia + fixijr^l - eji)" 1 (<T l/ia - l) - x 3 It is easy to see that the fixed centroid is given by (68) z + x 3 = -xi(l - ej t Y l e i{i - Eji)a, and it is a circle C F, its center S F and its radius R F being given by (69) S F =-x 3, R F = J 2 l - Ji _1 The moving centroid is then (70) z + XiJi _1 (l - sj,)- 1 + x 3 = fixijr 1 e~ EiJl0C ; it is a circle C M with (7i) S M = -xs-cx^r^i-fiji)" 1, RM^J; 1 Jiit remains to consider the case Ji = 1 Because of J ± > 0, we have (72) Ji = 1, = 1, and (62) reduces to (73) 5 = ix t e~ ia + x 2, x u x 2 e C Hence (74) r = (ix^a + x 3 ) e~ la - ix 2 and (75) z* = (z + ixia + x 3 ) e~ /a - ix 2 113
11 The condition g(0) = identity implies x 3 ix 2 = 0, ie, (76) z^ = (z + ix^ct + x 3 ) e~ ia x 3 The fixed centroid is then (77) z = \X X OL + x x % 3, ie, a straight line with the equation (see (63)) (78) ~ t z + x t z 2J 2 + x 1 x 3 + Xi^3 = 0 The moving centroid is (79) z = x x e~ ia ~ x 3, and it is a circle with S M = x 3, R M = J 2 The summary of our results is contained in the following Theorem 1 Let g(a) be a motion in E 2 with constant invariants J ±, J 2 Then it is the so-called planetary motion, ie, it is produced by rolling a circle C M upon a fixed circle C F In the case J 2 = 0 both circles degenerate to one point, and g(cc) is just the rotation around this point In the case J x =0, J 2 + 0, C M becomes a straight line; in the case J t e = 1, J 2 + 0, C F is a straight line Finally, let us study the invariants of our motion with respect to the group Aut ( ) By a frame we call now each triple {vj such that v t = F(V*), F e Aut ( ) With v(t) let us associate a frame {v^t), v 2 (f), v 3 (t)} such that v 3 (t) and v(t) are dependent Then (see (12)) / \ dv t dv 2 dv 3 0, 0 (80) i = cc i v 1 + a 2 v 2, - = -a 2 v! + a^, - = jvi + p 2 v 2, dt dt dt and the possible changes of the frames are given by (81) w x a x v t + a 2 v 2, w 2 = ~a 2 v 1 + a x v 2, w 3 = v 3 ; a Y + a For / \ dwi _ dw 2 dw 3 *» (82) - = a^i + a 2 w 2, - = -OL 2 W 1 + a x w 2, - = p 1 w 1 + p 2 w 2 dt dt dt we get (83) - + a 1 OL 1 - a 2 a 2 = a 1 ot 1 - a 2 a 2, - + a 2 a x + a x a 2 = a 2 a x + a x a 2, dt dt 114 Pi ~ a Ji - a J 2 > P 2 ~ a ih + a ipi
12 Hence (84) Pl + Pl = (al + al)(ft + Pl) and we have to distinguish two cases In the first case (85) j8 = /? 2 = 0 and v(t) is situated in a fixed straight line; we have seen that this leads to a rotation In the general case fi\ + /?_ + 0 and we may achieve (86) /? = 1, p 2 = 0 These conditions determine the frames (i\-(*)} uniquely, and a_(f)? a 2 (t) are the invariants of our motion Let us suppose (30) and (87) vi(t) = a x V x + a 2 V 2, v 2 (t) - -a 2 V 1 + a x V 2, Then v 3 (t) = AC~ l Vi + BC" 1 V 2 + V 3 (88) ^ = W + «Г'{(<,^ + aj 2 \ / 2 i\ dv 2 / 7 2\-i f/, 2 \ /, 2 + = («i + aj) 1 \(a 2 - -a 2)» + ( + a 2 _J d' (V d( d/ / \ df d* d» 3 / 2 24-, f d(ac_1 ) d^c" 1 )} -! = W +«>) {«, _ j,, w + «ir'{-«^- ) + «,^- ) }^ In the general case «(^)j +(^))%0; of course, we are going to study just this case The conditions (86) determine a u a 2 and it is easy to see that the invariants of our motion are given by, = tf_í I_L)ľ + ffi ^ dř / V dř fd U» d d^c- 1 ) d C ) 1 dt dt 2 dt dt 115
13 Let the canonical parameter be, as above, introduced by the condition v 3 (t) = v(t); we see that a + constant is the set of canonical parameters Using (39), a simple calculation yields (91) ds 1 ds, a 2 = - ř 2 2 /ds d 2^ _ dš dv I 2 2 > Let us determine the motions with constant invariants From (91 x ) we have (92) and ds ds c x e laxa ; c x > 0 (93) (91 2 ) implies (94) and we get (95) ds d 2 š dš d 2 s 2 ia + = 2c 1 a 1 c 2aia 2 2 ds d 2 s dš d 2 s 2 2 2ic x a 2 e 2axa á 2 s, v ds = (a x + ia 2 ), z ie, in the case a 2 + a 2 =f= 0, (96) of course, s = c 2 e" (ai ax + ía 2)a + c 3 ; c 2, c 3 є C ; (97) c = c 2 2 (a 2 + a 2 ) Thus we have to solve the equation (98) + ir = c 2 e (ax + ia2)a + c 3 Suppose (99) a x + i(a 2 + 1) + 0 The general solution of (98) is then (100) r = c 2 (a x + ia 2 + i) _1 e (ai + ia2)a + c 4 c~ ia - ic 3 ; c 4 e C Our motion normalized by the condition #(0) = identity is then (101) z^ = (z + c 4 ) c~ ia + c 2 (a x + ia 2 + i)' 1 (e (ax + ia2)a - 1) ~ c 4 П6
14 In the čase (102) «! = 0, a 2 = -1, the generál solution of (98) is (103) r = (c 2 a + c 4 ) e~ ia - ic 3 and the corresponding motion is (104) z* = (z + c 2 oc + c 4 ) e~ ia - c 4 It remains to deal with the čase a 1 = a 2 = 0 Then (105) 5 = c 2 a + c 3, c 2, c 3 e C ; of course, (106) c 2 2 = c x From (105), (107) r = c\e~ ia - ic 2 a + c 2 - ic 3 ; c 4 e C The corresponding motion is then (108) z* = (z + c 4 ) e~ ia - ic 2 a - c 4 Theorem 2 The motions with constant invariants a l5 a 2 are ^iven either by (101) Or (104) Or (108) Bibliography [1] A Karger: Lie groups and kinematic geometry in the plane (Czech) Čas pěst mat, 93 (1968), Souhrn KINEMATIKA V EUKLIDOVĚ ROVINĚ EL SAID EL SHINNAWY A Karger [1] studoval kinematickou geometrii v homogenním prostoru, jehož grupy pohybů jsou jisté speciální Lieovy grupy Předložený článek se omezuje na Euklidovu rovinu, ale podává metodu, vedoucí k řešení problému ekvivalence pro všechny Lieovy grupy pohybů Kromě toho jsou uvedeny všechny transitivní jednoparametrické soustavy pohybů v E 2 Authoťs address: Dr El Said El Shinnawy, Department of Geometry, MTC, Cairo 117
Linear Differential Transformations of the Second Order
 Linear Differential Transformations of the Second Order In: Otakar Borůvka (author); Felix M. Arscott (translator): Linear Differential Transformations of the Second Order. (English). London: The English
Linear Differential Transformations of the Second Order In: Otakar Borůvka (author); Felix M. Arscott (translator): Linear Differential Transformations of the Second Order. (English). London: The English
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Alois Švec Determination of a surface by its mean curvature Časopis pro pěstování matematiky, Vol. 103 (1978), No. 2, 175--180 Persistent URL: http://dml.cz/dmlcz/108617
Časopis pro pěstování matematiky Alois Švec Determination of a surface by its mean curvature Časopis pro pěstování matematiky, Vol. 103 (1978), No. 2, 175--180 Persistent URL: http://dml.cz/dmlcz/108617
Aplikace matematiky. Gene Howard Golub Numerical methods for solving linear least squares problems
 Aplikace matematiky Gene Howard Golub Numerical methods for solving linear least squares problems Aplikace matematiky, Vol. 10 (1965), No. 3, 213--216 Persistent URL: http://dml.cz/dmlcz/102951 Terms of
Aplikace matematiky Gene Howard Golub Numerical methods for solving linear least squares problems Aplikace matematiky, Vol. 10 (1965), No. 3, 213--216 Persistent URL: http://dml.cz/dmlcz/102951 Terms of
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky án Andres On stability and instability of the roots of the oscillatory function in a certain nonlinear differential equation of the third order Časopis pro pěstování matematiky,
Časopis pro pěstování matematiky án Andres On stability and instability of the roots of the oscillatory function in a certain nonlinear differential equation of the third order Časopis pro pěstování matematiky,
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Jan Ligȩza On distributional solutions of some systems of linear differential equations Časopis pro pěstování matematiky, Vol. 102 (1977), No. 1, 37--41 Persistent URL:
Časopis pro pěstování matematiky Jan Ligȩza On distributional solutions of some systems of linear differential equations Časopis pro pěstování matematiky, Vol. 102 (1977), No. 1, 37--41 Persistent URL:
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Kristína Smítalová Existence of solutions of functional-differential equations Časopis pro pěstování matematiky, Vol. 100 (1975), No. 3, 261--264 Persistent URL: http://dml.cz/dmlcz/117875
Časopis pro pěstování matematiky Kristína Smítalová Existence of solutions of functional-differential equations Časopis pro pěstování matematiky, Vol. 100 (1975), No. 3, 261--264 Persistent URL: http://dml.cz/dmlcz/117875
Aplikace matematiky. Gene Howard Golub Least squares, singular values and matrix approximations. Terms of use:
 Aplikace matematiky Gene Howard Golub Least squares, singular values and matrix approximations Aplikace matematiky, Vol. 3 (968), No., 44--5 Persistent URL: http://dml.cz/dmlcz/0338 Terms of use: Institute
Aplikace matematiky Gene Howard Golub Least squares, singular values and matrix approximations Aplikace matematiky, Vol. 3 (968), No., 44--5 Persistent URL: http://dml.cz/dmlcz/0338 Terms of use: Institute
EQUADIFF 1. Rudolf Výborný On a certain extension of the maximum principle. Terms of use:
 EQUADIFF 1 Rudolf Výborný On a certain extension of the maximum principle In: (ed.): Differential Equations and Their Applications, Proceedings of the Conference held in Prague in September 1962. Publishing
EQUADIFF 1 Rudolf Výborný On a certain extension of the maximum principle In: (ed.): Differential Equations and Their Applications, Proceedings of the Conference held in Prague in September 1962. Publishing
Matematický časopis. Bedřich Pondělíček A Note on Classes of Regularity in Semigroups. Terms of use: Persistent URL:
 Matematický časopis Bedřich Pondělíček A Note on Classes of Regularity in Semigroups Matematický časopis, Vol. 21 (1971), No. 4, 312--317 Persistent URL: http://dml.cz/dmlcz/127068 Terms of use: Mathematical
Matematický časopis Bedřich Pondělíček A Note on Classes of Regularity in Semigroups Matematický časopis, Vol. 21 (1971), No. 4, 312--317 Persistent URL: http://dml.cz/dmlcz/127068 Terms of use: Mathematical
Aplikace matematiky. Jiří Neuberg Some limit properties of the best determined terms method. Terms of use:
 Aplikace matematiky Jiří Neuberg Some limit properties of the best determined terms method Aplikace matematiky, Vol. 21 (1976), No. 3, 161--167 Persistent URL: http://dml.cz/dmlcz/103635 Terms of use:
Aplikace matematiky Jiří Neuberg Some limit properties of the best determined terms method Aplikace matematiky, Vol. 21 (1976), No. 3, 161--167 Persistent URL: http://dml.cz/dmlcz/103635 Terms of use:
e 2 = e 1 = e 3 = v 1 (v 2 v 3 ) = det(v 1, v 2, v 3 ).
 3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
Archivum Mathematicum
 Archivum Mathematicum Miloš Háčik Contribution to the monotonicity of the sequence of zero points of integrals of the differential equation y + g(t)y = 0 with regard to the basis [α, β] Archivum Mathematicum,
Archivum Mathematicum Miloš Háčik Contribution to the monotonicity of the sequence of zero points of integrals of the differential equation y + g(t)y = 0 with regard to the basis [α, β] Archivum Mathematicum,
Toposym 2. Zdeněk Hedrlín; Aleš Pultr; Věra Trnková Concerning a categorial approach to topological and algebraic theories
 Toposym 2 Zdeněk Hedrlín; Aleš Pultr; Věra Trnková Concerning a categorial approach to topological and algebraic theories In: (ed.): General Topology and its Relations to Modern Analysis and Algebra, Proceedings
Toposym 2 Zdeněk Hedrlín; Aleš Pultr; Věra Trnková Concerning a categorial approach to topological and algebraic theories In: (ed.): General Topology and its Relations to Modern Analysis and Algebra, Proceedings
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Angeline Brandt; Jakub Intrator The assignment problem with three job categories Časopis pro pěstování matematiky, Vol. 96 (1971), No. 1, 8--11 Persistent URL: http://dml.cz/dmlcz/117707
Časopis pro pěstování matematiky Angeline Brandt; Jakub Intrator The assignment problem with three job categories Časopis pro pěstování matematiky, Vol. 96 (1971), No. 1, 8--11 Persistent URL: http://dml.cz/dmlcz/117707
DIFFERENTIAL GEOMETRY HW 7
 DIFFERENTIAL GEOMETRY HW 7 CLAY SHONKWILER 1 Show that within a local coordinate system x 1,..., x n ) on M with coordinate vector fields X 1 / x 1,..., X n / x n, if we pick n 3 smooth real-valued functions
DIFFERENTIAL GEOMETRY HW 7 CLAY SHONKWILER 1 Show that within a local coordinate system x 1,..., x n ) on M with coordinate vector fields X 1 / x 1,..., X n / x n, if we pick n 3 smooth real-valued functions
Czechoslovak Mathematical Journal
 Czechoslovak Mathematical Journal Garyfalos Papaschinopoulos; John Schinas Criteria for an exponential dichotomy of difference equations Czechoslovak Mathematical Journal, Vol. 35 (1985), No. 2, 295 299
Czechoslovak Mathematical Journal Garyfalos Papaschinopoulos; John Schinas Criteria for an exponential dichotomy of difference equations Czechoslovak Mathematical Journal, Vol. 35 (1985), No. 2, 295 299
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Vlastimil Pták A modification of Newton's method Časopis pro pěstování matematiky, Vol. 101 (1976), No. 2, 188--194 Persistent URL: http://dml.cz/dmlcz/117905 Terms of
Časopis pro pěstování matematiky Vlastimil Pták A modification of Newton's method Časopis pro pěstování matematiky, Vol. 101 (1976), No. 2, 188--194 Persistent URL: http://dml.cz/dmlcz/117905 Terms of
Časopis pro pěstování matematiky
 Časopis pro pěstování matematiky Mieczysław Borowiecki Partition numbers, connectivity and Hamiltonicity Časopis pro pěstování matematiky, Vol. 112 (1987), No. 2, 173--176 Persistent URL: http://dml.cz/dmlcz/118305
Časopis pro pěstování matematiky Mieczysław Borowiecki Partition numbers, connectivity and Hamiltonicity Časopis pro pěstování matematiky, Vol. 112 (1987), No. 2, 173--176 Persistent URL: http://dml.cz/dmlcz/118305
Časopis pro pěstování matematiky
 Časopis pro pěstování ateatiky Beloslav Riečan On the lattice group valued easures Časopis pro pěstování ateatiky, Vol. 101 (1976), No. 4, 343--349 Persistent URL: http://dl.cz/dlcz/117930 Ters of use:
Časopis pro pěstování ateatiky Beloslav Riečan On the lattice group valued easures Časopis pro pěstování ateatiky, Vol. 101 (1976), No. 4, 343--349 Persistent URL: http://dl.cz/dlcz/117930 Ters of use:
THE TRANSLATION PLANES OF ORDER 49 AND THEIR AUTOMORPHISM GROUPS
 MATHEMATICS OF COMPUTATION Volume 67, Number 223, July 1998, Pages 1207 1224 S 0025-5718(98)00961-2 THE TRANSLATION PLANES OF ORDER 49 AND THEIR AUTOMORPHISM GROUPS C. CHARNES AND U. DEMPWOLFF Abstract.
MATHEMATICS OF COMPUTATION Volume 67, Number 223, July 1998, Pages 1207 1224 S 0025-5718(98)00961-2 THE TRANSLATION PLANES OF ORDER 49 AND THEIR AUTOMORPHISM GROUPS C. CHARNES AND U. DEMPWOLFF Abstract.
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
 Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Parts Manual. EPIC II Critical Care Bed REF 2031
 EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EQUADIFF 1. Milan Práger; Emil Vitásek Stability of numerical processes. Terms of use:
 EQUADIFF 1 Milan Práger; Emil Vitásek Stability of numerical processes In: (ed.): Differential Equations and Their Applications, Proceedings of the Conference held in Prague in September 1962. Publishing
EQUADIFF 1 Milan Práger; Emil Vitásek Stability of numerical processes In: (ed.): Differential Equations and Their Applications, Proceedings of the Conference held in Prague in September 1962. Publishing
Mathematica Slovaca. Pavol Šoltés Oscillatoriness of solutions of a nonlinear second order differential equation
 Mathematica Slovaca Pavol Šoltés Oscillatoriness of solutions of a nonlinear second order differential equation Mathematica Slovaca, Vol. 26 (1976), No. 4, 337--342 Persistent URL: http://dml.cz/dmlcz/136127
Mathematica Slovaca Pavol Šoltés Oscillatoriness of solutions of a nonlinear second order differential equation Mathematica Slovaca, Vol. 26 (1976), No. 4, 337--342 Persistent URL: http://dml.cz/dmlcz/136127
Toposym Kanpur. T. Soundararajan Weakly Hausdorff spaces and the cardinality of topological spaces
 Toposym Kanpur T. Soundararajan Weakly Hausdorff spaces and the cardinality of topological spaces In: Stanley P. Franklin and Zdeněk Frolík and Václav Koutník (eds.): General Topology and Its Relations
Toposym Kanpur T. Soundararajan Weakly Hausdorff spaces and the cardinality of topological spaces In: Stanley P. Franklin and Zdeněk Frolík and Václav Koutník (eds.): General Topology and Its Relations
Lecture 13 The Fundamental Forms of a Surface
 Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
DIFFERENTIAL GEOMETRY HW 5. Show that the law of cosines in spherical geometry is. cos c = cos a cos b + sin a sin b cos θ.
 DIFFEENTIAL GEOMETY HW 5 CLAY SHONKWILE Show that the law of cosines in spherical geometry is 5 cos c cos a cos b + sin a sin b cos θ. Proof. Consider the spherical triangle depicted below: Form radii
DIFFEENTIAL GEOMETY HW 5 CLAY SHONKWILE Show that the law of cosines in spherical geometry is 5 cos c cos a cos b + sin a sin b cos θ. Proof. Consider the spherical triangle depicted below: Form radii
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Antonín Špaček Note on successive cumulative sums of independent random variables Časopis pro pěstování matematiky a fysiky, Vol. 74 (1949), No. 1, 41--45 Persistent
Časopis pro pěstování matematiky a fysiky Antonín Špaček Note on successive cumulative sums of independent random variables Časopis pro pěstování matematiky a fysiky, Vol. 74 (1949), No. 1, 41--45 Persistent
Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica-Physica-Chemica
 Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica-Physica-Chemica Vladimír Janků The thermodynamical properties of an ideal gas in a periodical potential field Acta Universitatis
Acta Universitatis Palackianae Olomucensis. Facultas Rerum Naturalium. Mathematica-Physica-Chemica Vladimír Janků The thermodynamical properties of an ideal gas in a periodical potential field Acta Universitatis
Archivum Mathematicum
 Archivum Mathematicum Theodore Artikis Constructing infinitely divisible characteristic functions Archivum Mathematicum, Vol. 19 (1983), No. 2, 57--61 Persistent URL: http://dml.cz/dmlcz/107156 Terms of
Archivum Mathematicum Theodore Artikis Constructing infinitely divisible characteristic functions Archivum Mathematicum, Vol. 19 (1983), No. 2, 57--61 Persistent URL: http://dml.cz/dmlcz/107156 Terms of
Acta Universitatis Carolinae. Mathematica et Physica
 Acta Universitatis Carolinae. Mathematica et Physica Jaroslav Hora An easily computable invariant of trilinear alternating forms Acta Universitatis Carolinae. Mathematica et Physica, Vol. 51 (2010), No.
Acta Universitatis Carolinae. Mathematica et Physica Jaroslav Hora An easily computable invariant of trilinear alternating forms Acta Universitatis Carolinae. Mathematica et Physica, Vol. 51 (2010), No.
Hyperbolic Geometry on Geometric Surfaces
 Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Commentationes Mathematicae Universitatis Carolinae
 Commentationes Mathematicae Universitatis Carolinae David Preiss Gaussian measures and covering theorems Commentationes Mathematicae Universitatis Carolinae, Vol. 20 (1979), No. 1, 95--99 Persistent URL:
Commentationes Mathematicae Universitatis Carolinae David Preiss Gaussian measures and covering theorems Commentationes Mathematicae Universitatis Carolinae, Vol. 20 (1979), No. 1, 95--99 Persistent URL:
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
EQUADIFF 6. Jean-Claude Nédélec Mixed finite element in 3D in H(div) and H(curl) Terms of use:
 EQUADIFF 6 Jean-Claude Nédélec Mixed finite element in 3D in H(div) and H(curl) In: Jaromír Vosmanský and Miloš Zlámal (eds.): Equadiff 6, Proceedings of the International Conference on Differential Equations
EQUADIFF 6 Jean-Claude Nédélec Mixed finite element in 3D in H(div) and H(curl) In: Jaromír Vosmanský and Miloš Zlámal (eds.): Equadiff 6, Proceedings of the International Conference on Differential Equations
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Commentationes Mathematicae Universitatis Carolinae
 Commentationes Mathematicae Universitatis Carolinae Pavel Drábek Remarks on multiple periodic solutions of nonlinear ordinary differential equations Commentationes Mathematicae Universitatis Carolinae,
Commentationes Mathematicae Universitatis Carolinae Pavel Drábek Remarks on multiple periodic solutions of nonlinear ordinary differential equations Commentationes Mathematicae Universitatis Carolinae,
EXAM 2, MATH 132 WEDNESDAY, OCTOBER 23, 2002
 EXAM 2, MATH 132 WEDNESDAY, OCTOBER 23, 2002 This examination has 20 multiple choice questions, and two essay questions. Please check it over and if you find it to be incomplete, notify the proctor. Do
EXAM 2, MATH 132 WEDNESDAY, OCTOBER 23, 2002 This examination has 20 multiple choice questions, and two essay questions. Please check it over and if you find it to be incomplete, notify the proctor. Do
Multiple Time Analyticity of a Statistical Satisfying the Boundary Condition
 Publ. RIMS, Kyoto Univ. Ser. A Vol. 4 (1968), pp. 361-371 Multiple Time Analyticity of a Statistical Satisfying the Boundary Condition By Huzihiro ARAKI Abstract A multiple time expectation ^(ABjC^)---^^))
Publ. RIMS, Kyoto Univ. Ser. A Vol. 4 (1968), pp. 361-371 Multiple Time Analyticity of a Statistical Satisfying the Boundary Condition By Huzihiro ARAKI Abstract A multiple time expectation ^(ABjC^)---^^))
NOTES ON LINEAR ALGEBRA. 1. Determinants
 NOTES ON LINEAR ALGEBRA 1 Determinants In this section, we study determinants of matrices We study their properties, methods of computation and some applications We are familiar with the following formulas
NOTES ON LINEAR ALGEBRA 1 Determinants In this section, we study determinants of matrices We study their properties, methods of computation and some applications We are familiar with the following formulas
Kybernetika. Milan Mareš On fuzzy-quantities with real and integer values. Terms of use:
 Kybernetika Milan Mareš On fuzzy-quantities with real and integer values Kybernetika, Vol. 13 (1977), No. 1, (41)--56 Persistent URL: http://dml.cz/dmlcz/125112 Terms of use: Institute of Information Theory
Kybernetika Milan Mareš On fuzzy-quantities with real and integer values Kybernetika, Vol. 13 (1977), No. 1, (41)--56 Persistent URL: http://dml.cz/dmlcz/125112 Terms of use: Institute of Information Theory
f. D that is, F dr = c c = [2"' (-a sin t)( -a sin t) + (a cos t)(a cost) dt = f2"' dt = 2
 SECTION 16.4 GREEN'S THEOREM 1089 X with center the origin and radius a, where a is chosen to be small enough that C' lies inside C. (See Figure 11.) Let be the region bounded by C and C'. Then its positively
SECTION 16.4 GREEN'S THEOREM 1089 X with center the origin and radius a, where a is chosen to be small enough that C' lies inside C. (See Figure 11.) Let be the region bounded by C and C'. Then its positively
Sophus Lie s Approach to Differential Equations
 Sophus Lie s Approach to Differential Equations IAP lecture 2006 (S. Helgason) 1 Groups Let X be a set. A one-to-one mapping ϕ of X onto X is called a bijection. Let B(X) denote the set of all bijections
Sophus Lie s Approach to Differential Equations IAP lecture 2006 (S. Helgason) 1 Groups Let X be a set. A one-to-one mapping ϕ of X onto X is called a bijection. Let B(X) denote the set of all bijections
Kybernetika. Jan Havrda; František Charvát Quantification method of classification processes. Concept of structural a-entropy
 Kybernetika Jan Havrda; František Charvát Quantification method of classification processes. Concept of structural a-entropy Kybernetika, Vol. 3 (1967), No. 1, (30)--35 Persistent URL: http://dml.cz/dmlcz/125526
Kybernetika Jan Havrda; František Charvát Quantification method of classification processes. Concept of structural a-entropy Kybernetika, Vol. 3 (1967), No. 1, (30)--35 Persistent URL: http://dml.cz/dmlcz/125526
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
Algebra II. Paulius Drungilas and Jonas Jankauskas
 Algebra II Paulius Drungilas and Jonas Jankauskas Contents 1. Quadratic forms 3 What is quadratic form? 3 Change of variables. 3 Equivalence of quadratic forms. 4 Canonical form. 4 Normal form. 7 Positive
Algebra II Paulius Drungilas and Jonas Jankauskas Contents 1. Quadratic forms 3 What is quadratic form? 3 Change of variables. 3 Equivalence of quadratic forms. 4 Canonical form. 4 Normal form. 7 Positive
Algebra I Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 18.701 Algebra I Fall 007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.701 007 Geometry of the Special Unitary
MIT OpenCourseWare http://ocw.mit.edu 18.701 Algebra I Fall 007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.701 007 Geometry of the Special Unitary
WSAA 14. A. K. Kwaśniewski Algebraic properties of the 3-state vector Potts model. Terms of use:
 WSAA 14 A. K. Kwaśniewski Algebraic properties of the 3-state vector Potts model In: Zdeněk Frolík and Vladimír Souček and Marián J. Fabián (eds.): Proceedings of the 14th Winter School on Abstract Analysis.
WSAA 14 A. K. Kwaśniewski Algebraic properties of the 3-state vector Potts model In: Zdeněk Frolík and Vladimír Souček and Marián J. Fabián (eds.): Proceedings of the 14th Winter School on Abstract Analysis.
a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Tangent and Normal Vectors
 Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Study guide for Exam 1. by William H. Meeks III October 26, 2012
 Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Study guide for Exam 1. by William H. Meeks III October 2, 2012 1 Basics. First we cover the basic definitions and then we go over related problems. Note that the material for the actual midterm may include
Commentationes Mathematicae Universitatis Carolinae
 Commentationes Mathematicae Universitatis Carolinae Aleš Pultr An analogon of the fixed-point theorem and its application for graphs Commentationes Mathematicae Universitatis Carolinae, Vol. 4 (1963),
Commentationes Mathematicae Universitatis Carolinae Aleš Pultr An analogon of the fixed-point theorem and its application for graphs Commentationes Mathematicae Universitatis Carolinae, Vol. 4 (1963),
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
z, w = z 1 w 1 + z 2 w 2 z, w 2 z 2 w 2. d([z], [w]) = 2 φ : P(C 2 ) \ [1 : 0] C ; [z 1 : z 2 ] z 1 z 2 ψ : P(C 2 ) \ [0 : 1] C ; [z 1 : z 2 ] z 2 z 1
![z, w = z 1 w 1 + z 2 w 2 z, w 2 z 2 w 2. d([z], [w]) = 2 φ : P(C 2 ) \ [1 : 0] C ; [z 1 : z 2 ] z 1 z 2 ψ : P(C 2 ) \ [0 : 1] C ; [z 1 : z 2 ] z 2 z 1 z, w = z 1 w 1 + z 2 w 2 z, w 2 z 2 w 2. d([z], [w]) = 2 φ : P(C 2 ) \ [1 : 0] C ; [z 1 : z 2 ] z 1 z 2 ψ : P(C 2 ) \ [0 : 1] C ; [z 1 : z 2 ] z 2 z 1](/thumbs/95/123523548.jpg) 3 3 THE RIEMANN SPHERE 31 Models for the Riemann Sphere One dimensional projective complex space P(C ) is the set of all one-dimensional subspaces of C If z = (z 1, z ) C \ 0 then we will denote by [z]
3 3 THE RIEMANN SPHERE 31 Models for the Riemann Sphere One dimensional projective complex space P(C ) is the set of all one-dimensional subspaces of C If z = (z 1, z ) C \ 0 then we will denote by [z]
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Math 234. What you should know on day one. August 28, You should be able to use general principles like. x = cos t, y = sin t, 0 t π.
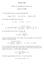 Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
Math 234 What you should know on day one August 28, 2001 1 You should be able to use general principles like Length = ds, Area = da, Volume = dv For example the length of the semi circle x = cos t, y =
WSGP 9. Peter W. Michor Knit products of graded Lie algebras and groups. Terms of use:
 WSGP 9 Peter W. Michor Knit products of graded Lie algebras and groups In: Jarolím Bureš and Vladimír Souček (eds.: Proceedings of the Winter School "Geometry and Physics". Circolo Matematico di Palermo,
WSGP 9 Peter W. Michor Knit products of graded Lie algebras and groups In: Jarolím Bureš and Vladimír Souček (eds.: Proceedings of the Winter School "Geometry and Physics". Circolo Matematico di Palermo,
Kybernetika. Šarūnas Raudys Intrinsic dimensionality and small sample properties of classifiers
 Kybernetika Šarūnas Raudys Intrinsic dimensionality and small sample properties of classifiers Kybernetika, Vol. 34 (1998), No. 4, [461]--466 Persistent URL: http://dml.cz/dmlcz/135232 Terms of use: Institute
Kybernetika Šarūnas Raudys Intrinsic dimensionality and small sample properties of classifiers Kybernetika, Vol. 34 (1998), No. 4, [461]--466 Persistent URL: http://dml.cz/dmlcz/135232 Terms of use: Institute
Two-parametric Motions in the Lobatchevski Plane
 Journal for Geometry and Graphics Volume 6 (), No., 7 35. Two-parametric Motions in the Lobatchevski Plane Marta Hlavová Department of Technical Mathematics, Faculty of Mechanical Engineering CTU Karlovo
Journal for Geometry and Graphics Volume 6 (), No., 7 35. Two-parametric Motions in the Lobatchevski Plane Marta Hlavová Department of Technical Mathematics, Faculty of Mechanical Engineering CTU Karlovo
Chapter 4. Matrices and Matrix Rings
 Chapter 4 Matrices and Matrix Rings We first consider matrices in full generality, i.e., over an arbitrary ring R. However, after the first few pages, it will be assumed that R is commutative. The topics,
Chapter 4 Matrices and Matrix Rings We first consider matrices in full generality, i.e., over an arbitrary ring R. However, after the first few pages, it will be assumed that R is commutative. The topics,
::::l<r/ L- 1-1>(=-ft\ii--r(~1J~:::: Fo. l. AG -=(0,.2,L}> M - &-c ==- < ) I) ~..-.::.1 ( \ I 0. /:rf!:,-t- f1c =- <I _,, -2...
 Math 3298 Exam 1 NAME: SCORE: l. Given three points A(I, l, 1), B(l,;2, 3), C(2, - l, 2). (a) Find vectors AD, AC, nc. (b) Find AB+ DC, AB - AC, and 2AD. -->,,. /:rf!:,-t- f1c =-
Math 3298 Exam 1 NAME: SCORE: l. Given three points A(I, l, 1), B(l,;2, 3), C(2, - l, 2). (a) Find vectors AD, AC, nc. (b) Find AB+ DC, AB - AC, and 2AD. -->,,. /:rf!:,-t- f1c =-
Mathematica Slovaca. Antonín Dvořák; David Jedelský; Juraj Kostra The fields of degree seven over rationals with a normal basis generated by a unit
 Mathematica Slovaca Antonín Dvořák; David Jedelský; Juraj Kostra The fields of degree seven over rationals with a normal basis generated by a unit Mathematica Slovaca, Vol. 49 (1999), No. 2, 143--153 Persistent
Mathematica Slovaca Antonín Dvořák; David Jedelský; Juraj Kostra The fields of degree seven over rationals with a normal basis generated by a unit Mathematica Slovaca, Vol. 49 (1999), No. 2, 143--153 Persistent
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A NOTE ON CONFIDENCE BOUNDS CONNECTED WITH ANOVA AND MANOVA FOR BALANCED AND PARTIALLY BALANCED INCOMPLETE BLOCK DESIGNS. v. P.
 ... --... I. A NOTE ON CONFIDENCE BOUNDS CONNECTED WITH ANOVA AND MANOVA FOR BALANCED AND PARTIALLY BALANCED INCOMPLETE BLOCK DESIGNS by :}I v. P. Bhapkar University of North Carolina. '".". This research
... --... I. A NOTE ON CONFIDENCE BOUNDS CONNECTED WITH ANOVA AND MANOVA FOR BALANCED AND PARTIALLY BALANCED INCOMPLETE BLOCK DESIGNS by :}I v. P. Bhapkar University of North Carolina. '".". This research
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Felix Adalbert Behrend On sequences of integers containing no arithmetic progression Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. 4, 235--239
Časopis pro pěstování matematiky a fysiky Felix Adalbert Behrend On sequences of integers containing no arithmetic progression Časopis pro pěstování matematiky a fysiky, Vol. 67 (1938), No. 4, 235--239
Mathematica Slovaca. Jaroslav Hančl; Péter Kiss On reciprocal sums of terms of linear recurrences. Terms of use:
 Mathematica Slovaca Jaroslav Hančl; Péter Kiss On reciprocal sums of terms of linear recurrences Mathematica Slovaca, Vol. 43 (1993), No. 1, 31--37 Persistent URL: http://dml.cz/dmlcz/136572 Terms of use:
Mathematica Slovaca Jaroslav Hančl; Péter Kiss On reciprocal sums of terms of linear recurrences Mathematica Slovaca, Vol. 43 (1993), No. 1, 31--37 Persistent URL: http://dml.cz/dmlcz/136572 Terms of use:
Mathematica Bohemica
 Mathematica Bohemica Radomír Halaš Remarks on commutative Hilbert algebras Mathematica Bohemica, Vol. 127 (2002), No. 4, 525--529 Persistent URL: http://dml.cz/dmlcz/133956 Terms of use: Institute of Mathematics
Mathematica Bohemica Radomír Halaš Remarks on commutative Hilbert algebras Mathematica Bohemica, Vol. 127 (2002), No. 4, 525--529 Persistent URL: http://dml.cz/dmlcz/133956 Terms of use: Institute of Mathematics
9.5 The Transfer Function
 Lecture Notes on Control Systems/D. Ghose/2012 0 9.5 The Transfer Function Consider the n-th order linear, time-invariant dynamical system. dy a 0 y + a 1 dt + a d 2 y 2 dt + + a d n y 2 n dt b du 0u +
Lecture Notes on Control Systems/D. Ghose/2012 0 9.5 The Transfer Function Consider the n-th order linear, time-invariant dynamical system. dy a 0 y + a 1 dt + a d 2 y 2 dt + + a d n y 2 n dt b du 0u +
Properties of Transformations
 6. - 6.4 Properties of Transformations P. Danziger Transformations from R n R m. General Transformations A general transformation maps vectors in R n to vectors in R m. We write T : R n R m to indicate
6. - 6.4 Properties of Transformations P. Danziger Transformations from R n R m. General Transformations A general transformation maps vectors in R n to vectors in R m. We write T : R n R m to indicate
Math 814 HW 3. October 16, p. 54: 9, 14, 18, 24, 25, 26
 Math 814 HW 3 October 16, 2007 p. 54: 9, 14, 18, 24, 25, 26 p.54, Exercise 9. If T z = az+b, find necessary and sufficient conditions for T to cz+d preserve the unit circle. T preserves the unit circle
Math 814 HW 3 October 16, 2007 p. 54: 9, 14, 18, 24, 25, 26 p.54, Exercise 9. If T z = az+b, find necessary and sufficient conditions for T to cz+d preserve the unit circle. T preserves the unit circle
EXERCISE SET 5.1. = (kx + kx + k, ky + ky + k ) = (kx + kx + 1, ky + ky + 1) = ((k + )x + 1, (k + )y + 1)
 EXERCISE SET 5. 6. The pair (, 2) is in the set but the pair ( )(, 2) = (, 2) is not because the first component is negative; hence Axiom 6 fails. Axiom 5 also fails. 8. Axioms, 2, 3, 6, 9, and are easily
EXERCISE SET 5. 6. The pair (, 2) is in the set but the pair ( )(, 2) = (, 2) is not because the first component is negative; hence Axiom 6 fails. Axiom 5 also fails. 8. Axioms, 2, 3, 6, 9, and are easily
PLANAR KINETICS OF A RIGID BODY FORCE AND ACCELERATION
 PLANAR KINETICS OF A RIGID BODY FORCE AND ACCELERATION I. Moment of Inertia: Since a body has a definite size and shape, an applied nonconcurrent force system may cause the body to both translate and rotate.
PLANAR KINETICS OF A RIGID BODY FORCE AND ACCELERATION I. Moment of Inertia: Since a body has a definite size and shape, an applied nonconcurrent force system may cause the body to both translate and rotate.
Sec. 1.1: Basics of Vectors
 Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Sec. 1.1: Basics of Vectors Notation for Euclidean space R n : all points (x 1, x 2,..., x n ) in n-dimensional space. Examples: 1. R 1 : all points on the real number line. 2. R 2 : all points (x 1, x
Exercises for Unit I I (Vector algebra and Euclidean geometry)
 Exercises for Unit I I (Vector algebra and Euclidean geometry) I I.1 : Approaches to Euclidean geometry Ryan : pp. 5 15 1. What is the minimum number of planes containing three concurrent noncoplanar lines
Exercises for Unit I I (Vector algebra and Euclidean geometry) I I.1 : Approaches to Euclidean geometry Ryan : pp. 5 15 1. What is the minimum number of planes containing three concurrent noncoplanar lines
Solutions for Chapter 3
 Solutions for Chapter Solutions for exercises in section 0 a X b x, y 6, and z 0 a Neither b Sew symmetric c Symmetric d Neither The zero matrix trivially satisfies all conditions, and it is the only possible
Solutions for Chapter Solutions for exercises in section 0 a X b x, y 6, and z 0 a Neither b Sew symmetric c Symmetric d Neither The zero matrix trivially satisfies all conditions, and it is the only possible
necessita d'interrogare il cielo
 gigi nei necessia d'inegae i cie cic pe sax span s inuie a dispiegaa fma dea uce < affeandi ves i cen dea uce isnane " sienzi dei padi sie veic dei' anima 5 J i f H 5 f AL J) i ) L '3 J J "' U J J ö'
gigi nei necessia d'inegae i cie cic pe sax span s inuie a dispiegaa fma dea uce < affeandi ves i cen dea uce isnane " sienzi dei padi sie veic dei' anima 5 J i f H 5 f AL J) i ) L '3 J J "' U J J ö'
2013/2014 SEMESTER 1 MID-TERM TEST. 1 October :30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY:
 2013/2014 SEMESTER 1 MID-TERM TEST MA1505 MATHEMATICS I 1 October 2013 8:30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY: 1. This test paper consists of TEN (10) multiple choice questions
2013/2014 SEMESTER 1 MID-TERM TEST MA1505 MATHEMATICS I 1 October 2013 8:30pm to 9:30pm PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY: 1. This test paper consists of TEN (10) multiple choice questions
c) LC=Cl+C2+C3; C1:x=dx=O; C2: y=1-x; C3:y=dy=0 1 ydx-xdy (1-x)~x-x(-dx)+ = Jdldx = 1.
 4. Line Integrals in the Plane 4A. Plane Vector Fields 4A- a) All vectors in the field are identical; continuously differentiable everywhere. b) he vector at P has its tail at P and head at the origin;
4. Line Integrals in the Plane 4A. Plane Vector Fields 4A- a) All vectors in the field are identical; continuously differentiable everywhere. b) he vector at P has its tail at P and head at the origin;
Math113: Linear Algebra. Beifang Chen
 Math3: Linear Algebra Beifang Chen Spring 26 Contents Systems of Linear Equations 3 Systems of Linear Equations 3 Linear Systems 3 2 Geometric Interpretation 3 3 Matrices of Linear Systems 4 4 Elementary
Math3: Linear Algebra Beifang Chen Spring 26 Contents Systems of Linear Equations 3 Systems of Linear Equations 3 Linear Systems 3 2 Geometric Interpretation 3 3 Matrices of Linear Systems 4 4 Elementary
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
Practice Qualifying Exam Questions, Differentiable Manifolds, Fall, 2009.
 Practice Qualifying Exam Questions, Differentiable Manifolds, Fall, 2009. Solutions (1) Let Γ be a discrete group acting on a manifold M. (a) Define what it means for Γ to act freely. Solution: Γ acts
Practice Qualifying Exam Questions, Differentiable Manifolds, Fall, 2009. Solutions (1) Let Γ be a discrete group acting on a manifold M. (a) Define what it means for Γ to act freely. Solution: Γ acts
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
APPH 4200 Physics of Fluids
 APPH 42 Physics of Fluids Problem Solving and Vorticity (Ch. 5) 1.!! Quick Review 2.! Vorticity 3.! Kelvin s Theorem 4.! Examples 1 How to solve fluid problems? (Like those in textbook) Ç"Tt=l I $T1P#(
APPH 42 Physics of Fluids Problem Solving and Vorticity (Ch. 5) 1.!! Quick Review 2.! Vorticity 3.! Kelvin s Theorem 4.! Examples 1 How to solve fluid problems? (Like those in textbook) Ç"Tt=l I $T1P#(
M.6. Rational canonical form
 book 2005/3/26 16:06 page 383 #397 M.6. RATIONAL CANONICAL FORM 383 M.6. Rational canonical form In this section we apply the theory of finitely generated modules of a principal ideal domain to study the
book 2005/3/26 16:06 page 383 #397 M.6. RATIONAL CANONICAL FORM 383 M.6. Rational canonical form In this section we apply the theory of finitely generated modules of a principal ideal domain to study the
Aktuárské vědy. D. P. Misra More Multiplicity in the Rate of Interest; Poly-party and Poly-creditor Transactions. II
 Aktuárské vědy D. P. Misra More Multiplicity in the Rate of Interest; Poly-party and Poly-creditor Transactions. II Aktuárské vědy, Vol. 7 (1938), No. 2, 60 70 Persistent URL: http://dml.cz/dmlcz/144689
Aktuárské vědy D. P. Misra More Multiplicity in the Rate of Interest; Poly-party and Poly-creditor Transactions. II Aktuárské vědy, Vol. 7 (1938), No. 2, 60 70 Persistent URL: http://dml.cz/dmlcz/144689
Algebraic structures I
 MTH5100 Assignment 1-10 Algebraic structures I For handing in on various dates January March 2011 1 FUNCTIONS. Say which of the following rules successfully define functions, giving reasons. For each one
MTH5100 Assignment 1-10 Algebraic structures I For handing in on various dates January March 2011 1 FUNCTIONS. Say which of the following rules successfully define functions, giving reasons. For each one
Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl --
 Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl -- Consider the function h(x) =IJ\ 4-8x 3-12x 2 + 24x {?\whose graph is
Using the Rational Root Theorem to Find Real and Imaginary Roots Real roots can be one of two types: ra...-\; 0 or - l (- - ONLl -- Consider the function h(x) =IJ\ 4-8x 3-12x 2 + 24x {?\whose graph is
Pullbacks, Isometries & Conformal Maps
 Pullbacks, Isometries & Conformal Maps Outline 1. Pullbacks Let V and W be vector spaces, and let T : V W be an injective linear transformation. Given an inner product, on W, the pullback of, is the inner
Pullbacks, Isometries & Conformal Maps Outline 1. Pullbacks Let V and W be vector spaces, and let T : V W be an injective linear transformation. Given an inner product, on W, the pullback of, is the inner
DIFFERENTIAL GEOMETRY HW 5
 DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 1 Check the calculations above that the Gaussian curvature of the upper half-plane and Poincaré disk models of the hyperbolic plane is 1. Proof. The calculations
DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 1 Check the calculations above that the Gaussian curvature of the upper half-plane and Poincaré disk models of the hyperbolic plane is 1. Proof. The calculations
Conformal Mapping, Möbius Transformations. Slides-13
 , Möbius Transformations Slides-13 Let γ : [a, b] C be a smooth curve in a domain D. Let f be a function defined at all points z on γ. Let C denotes the image of γ under the transformation w = f (z).
, Möbius Transformations Slides-13 Let γ : [a, b] C be a smooth curve in a domain D. Let f be a function defined at all points z on γ. Let C denotes the image of γ under the transformation w = f (z).
Problems and Solutions
 Problems and Solutions Problems and Solutions. The aim of this section is to encourage readers to participate in the intriguing process of problem solving in Mathematics. This section publishes problems
Problems and Solutions Problems and Solutions. The aim of this section is to encourage readers to participate in the intriguing process of problem solving in Mathematics. This section publishes problems
Worksheet A VECTORS 1 G H I D E F A B C
 Worksheet A G H I D E F A B C The diagram shows three sets of equally-spaced parallel lines. Given that AC = p that AD = q, express the following vectors in terms of p q. a CA b AG c AB d DF e HE f AF
Worksheet A G H I D E F A B C The diagram shows three sets of equally-spaced parallel lines. Given that AC = p that AD = q, express the following vectors in terms of p q. a CA b AG c AB d DF e HE f AF
MAT 2037 LINEAR ALGEBRA I web:
 MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
Matrix operations Linear Algebra with Computer Science Application
 Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Mathematica Bohemica
 Mathematica Bohemica Young Hee Kim; Hee Sik Kim Subtraction algebras and BCK-algebras Mathematica Bohemica, Vol. 128 (2003), No. 1, 21 24 Persistent URL: http://dml.cz/dmlcz/133931 Terms of use: Institute
Mathematica Bohemica Young Hee Kim; Hee Sik Kim Subtraction algebras and BCK-algebras Mathematica Bohemica, Vol. 128 (2003), No. 1, 21 24 Persistent URL: http://dml.cz/dmlcz/133931 Terms of use: Institute
Mathematica Slovaca. Ján Borsík Products of simply continuous and quasicontinuous functions. Terms of use: Persistent URL:
 Mathematica Slovaca Ján Borsík Products of simply continuous and quasicontinuous functions Mathematica Slovaca, Vol. 45 (1995), No. 4, 445--452 Persistent URL: http://dml.cz/dmlcz/136657 Terms of use:
Mathematica Slovaca Ján Borsík Products of simply continuous and quasicontinuous functions Mathematica Slovaca, Vol. 45 (1995), No. 4, 445--452 Persistent URL: http://dml.cz/dmlcz/136657 Terms of use:
Lines and points. Lines and points
 omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
A CONVEXITY CONDITION IN BANACH SPACES AND THE STRONG LAW OF LARGE NUMBERS1
 A CONVEXITY CONDITION IN BANACH SPACES AND THE STRONG LAW OF LARGE NUMBERS1 ANATOLE BECK Introduction. The strong law of large numbers can be shown under certain hypotheses for random variables which take
A CONVEXITY CONDITION IN BANACH SPACES AND THE STRONG LAW OF LARGE NUMBERS1 ANATOLE BECK Introduction. The strong law of large numbers can be shown under certain hypotheses for random variables which take
Exercise 2.2. Find (with proof) all rational points on the curve y = 2 x.
 Exercise 2.2. Find (with proof) all rational points on the curve y = 2 x. Exercise 2.4: Prove that for any integer n 0, e n is not a rational number. Exercise 2.5: Prove that the only rational point on
Exercise 2.2. Find (with proof) all rational points on the curve y = 2 x. Exercise 2.4: Prove that for any integer n 0, e n is not a rational number. Exercise 2.5: Prove that the only rational point on
