On the Asymptotic Normality of an Estimate of a Regression Functional
|
|
|
- Scarlett Shields
- 5 years ago
- Views:
Transcription
1 Joural of Machie Learig Research 6 205) Submitted 6/5; Published 9/5 O the Asymptotic Normality of a stimate of a Regressio Fuctioal László Györfi Departmet of Computer Sciece Iformatio Theory Budapest Uiversity of Techology coomics Magyar Tudósok körútja 2., H-7 Budapest, Hugary Harro Walk Departmet of Mathematics Uiversity of Stuttgart Pfaffewaldrig 57, D Stuttgart, Germay gyorfi@cs.bme.hu walk@mathematik.ui-stuttgart.de ditor: Alex Gammerma Vladimir Vovk Abstract A estimate of the secod momet of the regressio fuctio is itroduced. Its asymptotic ormality is proved such that the asymptotic variace depeds either o the dimesio of the observatio vector, or o the smoothess properties of the regressio fuctio. The asymptotic variace is give explicitly. Keywords: oparametric estimatio, regressio fuctioal, cetral limit theorem, partitioig estimate. Itroductio This paper cosiders a histogram-based estimate of secod momet of the regressio fuctio i multivariate problems. The iterest i the secod momet is motivated by the fact that by estimatig it oe obtais a estimate of the best possible achievable mea squared error, a quatity of obvious statistical iterest. It is show that the estimate is asymptotically ormally distributed. It is remarkable that the asymptotic variace oly depeds o momets of the regressio fuctio but either o its smoothess, or o the dimesio of the space. The proof relies o a Poissoizatio techique that has bee used successfully i related problems. Let Y be a real valued rom variable with {Y 2 } < let X = X ),..., X d) ) be a d-dimesioal rom observatioal vector. I regressio aalysis oe wishes to estimate Y give X, i.e., oe wats to fid a fuctio g defied o the rage of X so that gx) is close to Y. Assume that the mai aim of the aalysis is to miimize the mea squared error : mi g {gx) Y ) 2 }.. This research has bee partially supported by the uropea Uio Hugary co-fiaced by the uropea Social Fud through the project TMOP C-//KONV Natioal Research Ceter for Developmet Market Itroductio of Advaced Iformatio Commuicatio Techologies. c 205 László Györfi Harro Walk.
2 Györfi Walk As is well-kow, this miimum is achieved by the regressio fuctio mx), which is defied by mx) = {Y X = x}. ) For each measurable fuctio g oe has {gx) Y ) 2 } = {mx) Y ) 2 } + {mx) gx)) 2 } = {mx) Y ) 2 } + mx) gx) 2 µdx), where µ sts for the distributio of the observatio X. It is of great importace to be able to estimate the miimum mea squared error L = {mx) Y ) 2 } accurately, eve before a regressio estimate is applied: i a stard oparametric regressio desig process, oe cosiders a fiite umber of real-valued features X i), i I, evaluates whether these suffice to explai Y. I case they suffice for the give explaatory task, a estimatio method ca be applied o the basis of the features already uder cosideratio, if ot, more or differet features must be cosidered. The quality of a subvector {X i), i I} of X is measured by the miimum mea squared error ) 2 L I) := Y {Y X i), i I} that ca be achieved usig the features as explaatory variables. L I) depeds upo the ukow distributio of Y, X i) : i I). The first phase of ay regressio estimatio process therefore heavily relies o estimates of L eve before a regressio estimate is picked). Cocerig dimesio reductio the related testig problem is o the hypothesis L = L I). This testig problem ca be maaged such that we estimate both L L I), accept the hypothesis if the two estimates are close to each other. Cf. De Brabater et al. 204).) Devroye et al. 2003), vas Joes 2008), Liitiäie et al. 2008), Liitiäie et al. 2009), Liitiäie et al. 200), Ferrario Walk 202) itroduced earest eighbor based estimates of L, proved strog uiversal cosistecy calculated the fast) rate of covergece. Because of L = {Y 2 } {mx) 2 } {Y 2 } <, estimatig L is equivalet to estimatig the secod momet S of the regressio fuctio: S = {mx) 2 } = mx) 2 µdx). I this paper we itroduce a partitioig based estimator of S, show its asymptotic ormality. It turs out that the asymptotic variace depeds either o the dimesio of the observatio vector, or o the smoothess properties of the regressio fuctio. The asymptotic variace is give explicitly. 864
3 O the Asymptotic Normality of a Regressio Fuctioal stimate 2. A Splittig stimate We suppose that the regressio estimatio problem is based o a sequece X, Y ), X 2, Y 2 ),... of i.i.d. rom vectors distributed as X, Y ). Let P = {A,j, j =, 2,...} be a cubic partitio of IR d of size h > 0. The partitioig estimator of the regressio fuctio m is defied as iterpretig 0/0 = 0) with m x) = ν A,j ) µ A,j ) if x A,j, 2) ν A) = µ A) = I {Xi A}Y i I {Xi A}. Here I deotes the idicator fuctio.) If for cubic partitio h d h 0 3) as, the the partitioig regressio estimate 2) is weakly uiversally cosistet, which meas that { } lim m x) mx)) 2 µdx) = 0 4) for ay distributio of X, Y ) with {Y 2 } <, for bouded Y it holds m x) mx)) 2 µdx) = 0 5) lim a.s. Cf. Theorems i Györfi et al. 2002).) Assume splittig data Z = {X, Y ),..., X, Y )} D = {X, Y ),..., X, Y )} such that X, Y ),..., X, Y ), X, Y ),..., X, Y ) are i.i.d. The splittig data estimate of S is defied as S := Y i m X i) = I {X i A,j }Y i ν A,j ) µ A,j ). 865
4 Györfi Walk Put the S has the equivalet form ν A) = S = I {X i A}Y i, ν A,j ) ν A,j ) µ A,j ). 6) Theorem Assume 3) that µ is o-atomic has bouded support. Suppose that there is a fiite costat C such that The { Y 3 X} < C. 7) S {S }) /σ D N0, ), where σ 2 = 2 M 2 x)mx) 2 µdx) 2 mx) µdx)) 2 mx) 4 µdx), with M 2 X) = {Y 2 X}. The estimatio problem is motivated by the above metioed dimesio reductio such that oe estimates S for the origial observatio vector for the observatio vector where some compoets are left out. If the two estimates are close to each other, the we decide that the left out compoets are ieffective. Theorem is o the rom part of the estimates. Therefore there is a further eed to study the differece of the biases of the estimates. Uder 3) we have lim {S } = S for Lipschitz cotiuous m the rate of covergece ca be of order /d for suitable choice of h. Cf. Devroye et al. 203).) Similarly to De Brabater et al. 204) we cojecture that this differece of the biases has uiversally a fast rate of covergece. Obviously, there are several other possibilities for defiig partitioig based estimates provig their asymptotic ormality, for example, or m X i) 2 ν A,j ) 2 µ A,j ). Notice that both estimates have larger bias variace tha our estimate 6) has. The proof of Theorem works without ay major modificatio for cosistet k earest eighbor k -NN) estimate m if k k / 0. A delicate importat research problem is the case of o-cosistet -NN estimate m, because for -NN estimate m the bias is smaller. We cojecture that eve i this case oe has a CLT. We prove Theorem i the ext sectio. 866
5 O the Asymptotic Normality of a Regressio Fuctioal stimate 3. Proof of Theorem Itroduce the otatios the U = S {S Z }) V = {S Z } {S }), S {S }) = U + V. We prove Theorem by showig that for ay u, v IR ) ) u v P{U u, V v} Φ Φ where Φ deotes the stard ormal distributio fuctio, 2 σ 2 = M 2 x)mx) 2 µdx) mx) µdx)) 2 9) σ σ 2 8) σ2 2 = M 2 x)mx) 2 µdx) mx) 4 µdx). 0) Notice that V is measurable with respect to Z, therefore ) ) u v P{U u, V v} Φ Φ σ σ 2 ) ) = u v {I {V v}p{u u Z }} Φ Φ σ σ 2 ))} u {I {V v} P{U u Z } Φ σ )) ) + v u P{V v} Φ Φ σ 2 σ { ) } ) u P{U u Z } Φ + v P{V v} Φ. Thus, 8) is satisfied if i probability Proof of ). Let s start with the represetatio U = = σ ) u P{U u Z } Φ σ σ 2 ) ) v P{V v} Φ. 2) σ 2 Y i m X i) {Y i m X i) Z }) Y i m X i) {Y i m X i) Z }). ) 867
6 Györfi Walk Because of 7) the Jese iequality, for ay s 3, we get M s X) := { Y s X} = { Y s X} /s ) s { Y 3 X} /3 ) s C s/3, 3) especially, for s = M X) = mx) C /3 { Y 3 } C. Next we apply a Berry-ssee type cetral limit theorem see Theorem 4 i Petrov 975)). It implies that ) P{U u u Z } Φ VarY m X ) Z ) c { Y m X ) 3 Z } VarY m X ) Z ) 3 with the uiversal costat c > 0. Because of {Y m X ) Z } = we get that mx)m x)µdx), VarY m X ) Z ) = {Y 2 m X ) 2 Z } {Y m X ) Z } 2 2 = M 2 x)m x) 2 µdx) mx)m x)µdx)). Now 4), together with the boudedess of M 2 by 3), implies that VarY m X ) Z ) σ 2 i probability, where σ 2 is defied by 9). Further { Y m X ) 3 Z } C m x) 3 µdx). Put Agai, applyig the Jese iequality we get A x) = A,j if x A,j. m x) 3 I {X i A x)} Y i 3/2 I {X i A x)} the right h side of which is the square of the regressio estimate, where Y is replaced by Y 3/2. Thus, 4) together with { Y 3 } < implies that I {X i A x)} Y i 3/2 I {X i A x)} 2 µdx) {{ Y 3/2 X} 2 } < C 2, 868
7 O the Asymptotic Normality of a Regressio Fuctioal stimate i probability. These limit relatios imply ). Proof of 2). Assumig that the support S of µ is bouded, let l be such that S l A,j. Also we re-idex the partitio so that µa,j ) µa,j+ ), with µa,j ) > 0 for j l, µa,j ) = 0 otherwise. The, S = ν A,j ) ν A,j ) µ A,j ), 4) The coditio h d implies that l c h d. where Because of 4) we have that V = = l / 0. { }) {ν A ν A,j ),j ) Z } µ A,j ) ν A,j ) µ A,j ) { }) ν A,j ) νa,j ) µ A,j ) ν A,j ), µ A,j ) νa) = {ν A)}. Observe that we have to show the asymptotic ormality for a fiite sum of depedet rom variables. I order to prove 2), we follow the lies of the proof i Beirlat Györfi 998) use a Poissoizatio argumet. With this we itroduce a modificatio M of V such that := V M 0, the proof of which follows, startig from 23). Now we proceed arguig for M. Itroduce the otatio N for a Poisso) rom variable idepedet of X, Y ), X 2, Y 2 ),.... Moreover put N ν A) = N µ A) = I {Xi A}Y i I {Xi A}. The key result i this step is the followig property: 869
8 Györfi Walk Propositio 2 Beirlat Maso 995), Beirlat et al. 994).) Put M = l { }) ν A,j ) νa,j ) µ A,j ) ν A,j ), 5) µ A,j ) Assume that M = { }) ν A,j ) νa,j ) µ A,j ) ν A,j ). 6) µ A,j ) Φ t, v) = exp it M + iv N )) e t2 ρ 2 +v 2 )/2 for a costat ρ > 0, where i =. The Put M /ρ D N0, ). T = t M + v N, for which a cetral limit result is to hold: as. Remark that { VarT ) = t 2 Var M ) + 2tv T D N 0, t 2 ρ 2 + v 2) 7) M N } + v 2. For a cell A = A,j from the partitio with µa) > 0, let Y A) be a rom variable such that P{Y A) B} = P{Y B X A}, where B is a arbitrary Borel set. Itroduce the otatios q,k = P{µ A) = k} = ) µa) k µa)) k k q,k = P{ µ A) = k} = µa))k e µa). k! Cocerig the expectatio, with Y A), Y 2 A),...) a i.i.d. sequece of rom variables distributed as Y A) we fid that { } ν A) { } ν A) = µ A) µ A) µ A) = k P{ µ A) = k} k=0 { k } = Y ia) q,k k k= = {Y A)} q,0 ) = νa) µa) q,0), 8) 870
9 O the Asymptotic Normality of a Regressio Fuctioal stimate further, by 24) { } ν A) µ A) { = Moreover, { ν A) 2 } µ A) 2 = k= k q,k = = k= k= k = = Y A) + )µ A) k=0 } = νa) µa) µa)) )), 9) { ν A) 2 } µ A) 2 µ A) = k P{ µ A) = k} k 2 ia)) Y k 2 q,k k= k { Y A) 2} + kk ) {Y A)} 2 k= = Var Y A)) µa)) k k + k= e µa) k 2 k! µa)) k e µa) + k! q,k k q,k + {Y A)} 2 q,0 ), k= kk + ) µa) q 3,0) + 2 µa) 2 q,0). µa)) k The idepedece of the Poisso masses over differet cells leads to Var M l ) ) = νa,j ) 2 ν A,j ) Var µ A,j ) + νa,j ) 2 Var Y A,j )) µa,j ) e µa,j) ) 3 2 µa,j ) 2 e µa,j) ) ) k! e µa) + {Y A,j )} 2 e µa,j) ) {Y A,j )} 2 e µa,j) ) 2) + + νa,j ) 2 µa,j ) 2 Var Y A,j )) µa,j ) 3Var Y A,j )) νa,j ) 2 µa,j ) 2 νa,j ) 2 {Y A,j )} 2 e µa,j) ) 87
10 Györfi Walk such that the boudig error i these iequalities is of order Ol /). 4) together with the boudedess of M 2 m implies that νa,j ) 2 µa,j ) 2 Var Y A,j )) µa,j ) A = M x) 2z)µdz) A mz)µdz) ) 2 x) A µdx) mz)µdz) ) 4 x) µdx) µa x)) µa x)) µa x)) = σ o), where σ 2 2 is defied by 0). Moreover, l 3Var Y A,j )) νa,j ) 2 µa,j ) 2 3C4/3 l 0. The = C 4/3 νa,j ) 2 {Y A,j )} 2 e µa,j) νa,j ) 2 µa,j ) 2 {Y A,j )} 2 µa,j )e µa,j) µa,j ) µa,j ) 2 e µa,j) C 4/3 max z>0 z2 e z )l / 0. So we proved that Var M ) σ 2 2. To complete the asymptotics for VarT ), it remais to show that { } N M 0 as. Because of N = = µ A,j ) µa,j ), 872
11 O the Asymptotic Normality of a Regressio Fuctioal stimate we have that { } N M = = = = { } ν A,j ) µ A,j ) νa,j) µ A,j ) µa,j )) { } ) ν A,j ) νa,j ) { ν A,j )} µa,j )) µ A,j ) νa,j ) νa,j ) νa ),j) µa,j ) e µa,j) )µa,j )) νa,j ) 2 e µa,j) C 2/3 max z>0 z2 e z )l / 0. To fiish the proof of 7) by Lyapuov s cetral limit theorem, it suffices to prove that 3/2 { }) ν A,j ) { t µ A,j ) ν A,j ) νa,j ) + v µ A,j ) µa,j )) 3} 0 µ A,j ) or, by ivokig the c 3 iequality a + b 3 4 a 3 + b 3 ), that 3/2 { { } } ν A,j ) µ A,j ) ν A,j ) 3 νa,j) ) µ A,j ) 3/2 I view of 20), because of 3) it suffices to prove D := 3/2 For a cell A, 8) implies that { µ A,j ) µa,j ) 3} 0. 2) { { } } ν A,j ) µ A,j ) ν A,j ) 3 µa,j) ) µ A,j ) { { } } { ν A) µ A) ν A) 3 ν A) 4 µ A) µ A) νa) µa) q } 3,0)I { µa)>0} { νa) + 4 µa) q,0)i { µa)>0} νa) µa) q 3},0). 873
12 Györfi Walk O the oe h, 8), 3) 25) imply that, for a costat K, { ν A) µ A) νa) µa) q,0)i { µa)>0} { ν A) = µ A) νa) µa) q,0)i { µa)>0} k=0 k Y ia) {Y i A)}) 3 = k 3 q,k k= K k= k 3/2 q,k c 3/2 µa) 3/2, 3 } 3 µ A) = k } P{ µ A) = k} where we applied the Marcikiewicz Zygmud 937) iequality for absolute cetral momets of sums of i.i.d. rom variables. O the other h { νa) µa) q,0)i { µa)>0} νa) µa) q 3},0) C q,0. Therefore D 3/2 c 2 c 2 c 2 = c 3 0, ) 3/2 µa,j ) 3/2 + e µa,j) µa,j ) 3 µa,j ) 3/2 + ) µa,j ) 3/2 + max z>0 z3/2 e z µa x)) /2 µdx) 3/2 e µa,j) µa,j ) 3 where we used the assumptio that µ is o-atomic. Thus, 20) is proved. The proof of 2) is easier. Notice that 2) meas F := 3/2 N 3 I {Xi A,j } µa,j )
13 O the Asymptotic Normality of a Regressio Fuctioal stimate Oe has Therefore N 3 I {Xi A,j } µa,j ) N 3 { 4 I {Xi A,j } µa,j )) + 4 N )µa,j ) 3} ) { c 4 k 3/2 µa,j ) 3/2 k e k! + N 3} µa,j ) 3 k= c 5 3/2 µa,j ) 3/2 + 3/2 µa,j ) 3). F 2c 5 µa,j ) 3/2 0, so 2) is proved, too. The remaiig step i the proof of 2) is to show that := V M = /2 By 8) 9) have that = /2 = /2 C 2/3 /2 { } ν A,j ) µ A,j ) { }) ν A,j ) νa,j ) 0. 23) µ A,j ) νa,j ) µa,j ) e µa,j) µa,j )) )νa,j ) νa,j ) 2 µa,j ) 2 e µa,j) µa,j )) )µa,j ) For 0 z, usig the elemetary iequalities we have that e µa,j) µa,j )) )µa,j ). z e z z + z 2 e z z) = e z z)) e kz z) k z 2 e )z, k=0 875
14 Györfi Walk thus we get that l C 2/3 /2 e µa,j) µa,j )) )µa,j ) C 2/3 /2 C2/3 /2 C2/3 /2 0. µa,j ) 3 e )µa,j) ) µa,j ) [µa,j )] 2 e µa,j) e µa,j ) max z 0 z2 e z )e This eds the proof of 2) so the proof of Theorem is complete. Next we give two lemmas, which are used above. Lemma 3 If B, p) is a biomial rom variable with parameters, p), the { } = + B, p) p)+. 24) + )p Lemma 4 If P oλ) is a Poisso rom variable with parameter λ, the { } P oλ) 3 I {P oλ)>0} 24 λ 3. 25) Refereces J. Beirlat L. Györfi. O the asymptotic L 2 -error i partitioig regressio estimatio. Joural of Statistical Plaig Iferece, 7:93 07, 998. J. Beirlat D. Maso. O the asymptotic ormality of l p -orms of empirical fuctioals. Mathematical Methods of Statistics, 4: 9, 995. J. Beirlat, L. Györfi, G. Lugosi. O the asymptotic ormality of the l - l 2 - errors i histogram desity estimatio. Caadia J. Statistics, 22:309 38, 994. K. De Brabater, P. G. Ferrario, L. Györfi. Detectig ieffective features for oparametric regressio. I J. A. K. Suykes, M. Sigoretto, A. Argyriou, editors, Regularizatio, Optimizatio, Kerels, Support Vector Machies, pages Chapma & Hall/CRC Machie Learig Patter Recogitio Series, 204. L. Devroye, D. Schäfer, L. Györfi, H. Walk. The estimatio problem of miimum mea squared error. Statistics Decisios, 2:5 28,
15 O the Asymptotic Normality of a Regressio Fuctioal stimate L. Devroye, P. Ferrario, L. Györfi, H. Walk. Strog uiversal cosistet estimate of the miimum mea squared error. I B. Schölkopf, Z. Luo, V. Vovk, editors, mpirical Iferece - Festschrift i Hoor of Vladimir N. Vapik, pages Spriger, Heidelberg, 203. D. vas A. J. Joes. No-parametric estimatio of residual momets covariace. Proceedigs of the Royal Society, A 464: , P. G. Ferrario H. Walk. Noparametric partitioig estimatio of residual local variace based o first secod earest eighbors. Joural of Noparametric Statistics, 24:09 039, 202. L. Györfi, M. Kohler, A. Krzyżak, H. Walk. A Distributio-Free Theory of Noparametric Regressio. Spriger Verlag, New York, Liitiäie, F. Coroa, A. Ledasse. O oparametric residual variace estimatio. Neural Processig Letters, 28:55 67, Liitiäie, M. Verleyse, F. Coroa, A. Ledasse. Residual variace estimatio i machie learig. Neurocomputig, 72: , Liitiäie, F. Coroa, A. Ledasse. Residual variace estimatio usig a earest eighbor statistic. Joural of Multivariate Aalysis, 0:8 823, 200. J. Marcikiewicz A. Zygmud. Sur les foctios idépedates. Fudameta Mathematicae, 29:60 90, 937. V. V. Petrov. Sums of Idepedet Rom Variables. Spriger-Verlag, Berli,
Estimation of the essential supremum of a regression function
 Estimatio of the essetial supremum of a regressio fuctio Michael ohler, Adam rzyżak 2, ad Harro Walk 3 Fachbereich Mathematik, Techische Uiversität Darmstadt, Schlossgartestr. 7, 64289 Darmstadt, Germay,
Estimatio of the essetial supremum of a regressio fuctio Michael ohler, Adam rzyżak 2, ad Harro Walk 3 Fachbereich Mathematik, Techische Uiversität Darmstadt, Schlossgartestr. 7, 64289 Darmstadt, Germay,
Nonparametric estimation of conditional distributions
 Noparametric estimatio of coditioal distributios László Györfi 1 ad Michael Kohler 2 1 Departmet of Computer Sciece ad Iformatio Theory, udapest Uiversity of Techology ad Ecoomics, 1521 Stoczek, U.2, udapest,
Noparametric estimatio of coditioal distributios László Györfi 1 ad Michael Kohler 2 1 Departmet of Computer Sciece ad Iformatio Theory, udapest Uiversity of Techology ad Ecoomics, 1521 Stoczek, U.2, udapest,
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
January 25, 2017 INTRODUCTION TO MATHEMATICAL STATISTICS
 Jauary 25, 207 INTRODUCTION TO MATHEMATICAL STATISTICS Abstract. A basic itroductio to statistics assumig kowledge of probability theory.. Probability I a typical udergraduate problem i probability, we
Jauary 25, 207 INTRODUCTION TO MATHEMATICAL STATISTICS Abstract. A basic itroductio to statistics assumig kowledge of probability theory.. Probability I a typical udergraduate problem i probability, we
Sieve Estimators: Consistency and Rates of Convergence
 EECS 598: Statistical Learig Theory, Witer 2014 Topic 6 Sieve Estimators: Cosistecy ad Rates of Covergece Lecturer: Clayto Scott Scribe: Julia Katz-Samuels, Brado Oselio, Pi-Yu Che Disclaimer: These otes
EECS 598: Statistical Learig Theory, Witer 2014 Topic 6 Sieve Estimators: Cosistecy ad Rates of Covergece Lecturer: Clayto Scott Scribe: Julia Katz-Samuels, Brado Oselio, Pi-Yu Che Disclaimer: These otes
Lecture 7: Density Estimation: k-nearest Neighbor and Basis Approach
 STAT 425: Itroductio to Noparametric Statistics Witer 28 Lecture 7: Desity Estimatio: k-nearest Neighbor ad Basis Approach Istructor: Ye-Chi Che Referece: Sectio 8.4 of All of Noparametric Statistics.
STAT 425: Itroductio to Noparametric Statistics Witer 28 Lecture 7: Desity Estimatio: k-nearest Neighbor ad Basis Approach Istructor: Ye-Chi Che Referece: Sectio 8.4 of All of Noparametric Statistics.
7.1 Convergence of sequences of random variables
 Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit Theorems Throughout this sectio we will assume a probability space (, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
MATH 320: Probability and Statistics 9. Estimation and Testing of Parameters. Readings: Pruim, Chapter 4
 MATH 30: Probability ad Statistics 9. Estimatio ad Testig of Parameters Estimatio ad Testig of Parameters We have bee dealig situatios i which we have full kowledge of the distributio of a radom variable.
MATH 30: Probability ad Statistics 9. Estimatio ad Testig of Parameters Estimatio ad Testig of Parameters We have bee dealig situatios i which we have full kowledge of the distributio of a radom variable.
Lecture 33: Bootstrap
 Lecture 33: ootstrap Motivatio To evaluate ad compare differet estimators, we eed cosistet estimators of variaces or asymptotic variaces of estimators. This is also importat for hypothesis testig ad cofidece
Lecture 33: ootstrap Motivatio To evaluate ad compare differet estimators, we eed cosistet estimators of variaces or asymptotic variaces of estimators. This is also importat for hypothesis testig ad cofidece
Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.
![Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f. Let us give one more example of MLE. Example 3. The uniform distribution U[0, θ] on the interval [0, θ] has p.d.f.](/thumbs/91/105380228.jpg) Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
Lecture 5 Let us give oe more example of MLE. Example 3. The uiform distributio U[0, ] o the iterval [0, ] has p.d.f. { 1 f(x =, 0 x, 0, otherwise The likelihood fuctio ϕ( = f(x i = 1 I(X 1,..., X [0,
A survey on penalized empirical risk minimization Sara A. van de Geer
 A survey o pealized empirical risk miimizatio Sara A. va de Geer We address the questio how to choose the pealty i empirical risk miimizatio. Roughly speakig, this pealty should be a good boud for the
A survey o pealized empirical risk miimizatio Sara A. va de Geer We address the questio how to choose the pealty i empirical risk miimizatio. Roughly speakig, this pealty should be a good boud for the
SDS 321: Introduction to Probability and Statistics
 SDS 321: Itroductio to Probability ad Statistics Lecture 23: Cotiuous radom variables- Iequalities, CLT Puramrita Sarkar Departmet of Statistics ad Data Sciece The Uiversity of Texas at Austi www.cs.cmu.edu/
SDS 321: Itroductio to Probability ad Statistics Lecture 23: Cotiuous radom variables- Iequalities, CLT Puramrita Sarkar Departmet of Statistics ad Data Sciece The Uiversity of Texas at Austi www.cs.cmu.edu/
Parameter, Statistic and Random Samples
 Parameter, Statistic ad Radom Samples A parameter is a umber that describes the populatio. It is a fixed umber, but i practice we do ot kow its value. A statistic is a fuctio of the sample data, i.e.,
Parameter, Statistic ad Radom Samples A parameter is a umber that describes the populatio. It is a fixed umber, but i practice we do ot kow its value. A statistic is a fuctio of the sample data, i.e.,
Kernel density estimator
 Jauary, 07 NONPARAMETRIC ERNEL DENSITY ESTIMATION I this lecture, we discuss kerel estimatio of probability desity fuctios PDF Noparametric desity estimatio is oe of the cetral problems i statistics I
Jauary, 07 NONPARAMETRIC ERNEL DENSITY ESTIMATION I this lecture, we discuss kerel estimatio of probability desity fuctios PDF Noparametric desity estimatio is oe of the cetral problems i statistics I
7.1 Convergence of sequences of random variables
 Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Chapter 7 Limit theorems Throughout this sectio we will assume a probability space (Ω, F, P), i which is defied a ifiite sequece of radom variables (X ) ad a radom variable X. The fact that for every ifiite
Precise Rates in Complete Moment Convergence for Negatively Associated Sequences
 Commuicatios of the Korea Statistical Society 29, Vol. 16, No. 5, 841 849 Precise Rates i Complete Momet Covergece for Negatively Associated Sequeces Dae-Hee Ryu 1,a a Departmet of Computer Sciece, ChugWoo
Commuicatios of the Korea Statistical Society 29, Vol. 16, No. 5, 841 849 Precise Rates i Complete Momet Covergece for Negatively Associated Sequeces Dae-Hee Ryu 1,a a Departmet of Computer Sciece, ChugWoo
5.1 A mutual information bound based on metric entropy
 Chapter 5 Global Fao Method I this chapter, we exted the techiques of Chapter 2.4 o Fao s method the local Fao method) to a more global costructio. I particular, we show that, rather tha costructig a local
Chapter 5 Global Fao Method I this chapter, we exted the techiques of Chapter 2.4 o Fao s method the local Fao method) to a more global costructio. I particular, we show that, rather tha costructig a local
Dimension-free PAC-Bayesian bounds for the estimation of the mean of a random vector
 Dimesio-free PAC-Bayesia bouds for the estimatio of the mea of a radom vector Olivier Catoi CREST CNRS UMR 9194 Uiversité Paris Saclay olivier.catoi@esae.fr Ilaria Giulii Laboratoire de Probabilités et
Dimesio-free PAC-Bayesia bouds for the estimatio of the mea of a radom vector Olivier Catoi CREST CNRS UMR 9194 Uiversité Paris Saclay olivier.catoi@esae.fr Ilaria Giulii Laboratoire de Probabilités et
ECONOMETRIC THEORY. MODULE XIII Lecture - 34 Asymptotic Theory and Stochastic Regressors
 ECONOMETRIC THEORY MODULE XIII Lecture - 34 Asymptotic Theory ad Stochastic Regressors Dr. Shalabh Departmet of Mathematics ad Statistics Idia Istitute of Techology Kapur Asymptotic theory The asymptotic
ECONOMETRIC THEORY MODULE XIII Lecture - 34 Asymptotic Theory ad Stochastic Regressors Dr. Shalabh Departmet of Mathematics ad Statistics Idia Istitute of Techology Kapur Asymptotic theory The asymptotic
ECE 901 Lecture 12: Complexity Regularization and the Squared Loss
 ECE 90 Lecture : Complexity Regularizatio ad the Squared Loss R. Nowak 5/7/009 I the previous lectures we made use of the Cheroff/Hoeffdig bouds for our aalysis of classifier errors. Hoeffdig s iequality
ECE 90 Lecture : Complexity Regularizatio ad the Squared Loss R. Nowak 5/7/009 I the previous lectures we made use of the Cheroff/Hoeffdig bouds for our aalysis of classifier errors. Hoeffdig s iequality
A RANK STATISTIC FOR NON-PARAMETRIC K-SAMPLE AND CHANGE POINT PROBLEMS
 J. Japa Statist. Soc. Vol. 41 No. 1 2011 67 73 A RANK STATISTIC FOR NON-PARAMETRIC K-SAMPLE AND CHANGE POINT PROBLEMS Yoichi Nishiyama* We cosider k-sample ad chage poit problems for idepedet data i a
J. Japa Statist. Soc. Vol. 41 No. 1 2011 67 73 A RANK STATISTIC FOR NON-PARAMETRIC K-SAMPLE AND CHANGE POINT PROBLEMS Yoichi Nishiyama* We cosider k-sample ad chage poit problems for idepedet data i a
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
Estimation for Complete Data
 Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Estimatio for Complete Data complete data: there is o loss of iformatio durig study. complete idividual complete data= grouped data A complete idividual data is the oe i which the complete iformatio of
Lecture 15: Density estimation
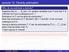 Lecture 15: Desity estimatio Why do we estimate a desity? Suppose that X 1,...,X are i.i.d. radom variables from F ad that F is ukow but has a Lebesgue p.d.f. f. Estimatio of F ca be doe by estimatig f.
Lecture 15: Desity estimatio Why do we estimate a desity? Suppose that X 1,...,X are i.i.d. radom variables from F ad that F is ukow but has a Lebesgue p.d.f. f. Estimatio of F ca be doe by estimatig f.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 21 11/27/2013
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 21 11/27/2013 Fuctioal Law of Large Numbers. Costructio of the Wieer Measure Cotet. 1. Additioal techical results o weak covergece
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 21 11/27/2013 Fuctioal Law of Large Numbers. Costructio of the Wieer Measure Cotet. 1. Additioal techical results o weak covergece
On the asymptotic properties of a nonparametric L 1 -test statistic of homogeneity
 O the asymptotic properties of a oparametric L 1 -test statistic of homogeeity Gérard Biau László Györfi Jue 28, 2005 Abstract We preset two simple ad explicit procedures for testig homogeeity of two idepedet
O the asymptotic properties of a oparametric L 1 -test statistic of homogeeity Gérard Biau László Györfi Jue 28, 2005 Abstract We preset two simple ad explicit procedures for testig homogeeity of two idepedet
ECE 901 Lecture 14: Maximum Likelihood Estimation and Complexity Regularization
 ECE 90 Lecture 4: Maximum Likelihood Estimatio ad Complexity Regularizatio R Nowak 5/7/009 Review : Maximum Likelihood Estimatio We have iid observatios draw from a ukow distributio Y i iid p θ, i,, where
ECE 90 Lecture 4: Maximum Likelihood Estimatio ad Complexity Regularizatio R Nowak 5/7/009 Review : Maximum Likelihood Estimatio We have iid observatios draw from a ukow distributio Y i iid p θ, i,, where
G. R. Pasha Department of Statistics Bahauddin Zakariya University Multan, Pakistan
 Deviatio of the Variaces of Classical Estimators ad Negative Iteger Momet Estimator from Miimum Variace Boud with Referece to Maxwell Distributio G. R. Pasha Departmet of Statistics Bahauddi Zakariya Uiversity
Deviatio of the Variaces of Classical Estimators ad Negative Iteger Momet Estimator from Miimum Variace Boud with Referece to Maxwell Distributio G. R. Pasha Departmet of Statistics Bahauddi Zakariya Uiversity
Machine Learning Theory Tübingen University, WS 2016/2017 Lecture 3
 Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture 3 Tolstikhi Ilya Abstract I this lecture we will prove the VC-boud, which provides a high-probability excess risk boud for the ERM algorithm whe
Machie Learig Theory Tübige Uiversity, WS 06/07 Lecture 3 Tolstikhi Ilya Abstract I this lecture we will prove the VC-boud, which provides a high-probability excess risk boud for the ERM algorithm whe
Statistical Inference Based on Extremum Estimators
 T. Rotheberg Fall, 2007 Statistical Iferece Based o Extremum Estimators Itroductio Suppose 0, the true value of a p-dimesioal parameter, is kow to lie i some subset S R p : Ofte we choose to estimate 0
T. Rotheberg Fall, 2007 Statistical Iferece Based o Extremum Estimators Itroductio Suppose 0, the true value of a p-dimesioal parameter, is kow to lie i some subset S R p : Ofte we choose to estimate 0
Regression with an Evaporating Logarithmic Trend
 Regressio with a Evaporatig Logarithmic Tred Peter C. B. Phillips Cowles Foudatio, Yale Uiversity, Uiversity of Aucklad & Uiversity of York ad Yixiao Su Departmet of Ecoomics Yale Uiversity October 5,
Regressio with a Evaporatig Logarithmic Tred Peter C. B. Phillips Cowles Foudatio, Yale Uiversity, Uiversity of Aucklad & Uiversity of York ad Yixiao Su Departmet of Ecoomics Yale Uiversity October 5,
First Year Quantitative Comp Exam Spring, Part I - 203A. f X (x) = 0 otherwise
 First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
First Year Quatitative Comp Exam Sprig, 2012 Istructio: There are three parts. Aswer every questio i every part. Questio I-1 Part I - 203A A radom variable X is distributed with the margial desity: >
Asymptotic Results for the Linear Regression Model
 Asymptotic Results for the Liear Regressio Model C. Fli November 29, 2000 1. Asymptotic Results uder Classical Assumptios The followig results apply to the liear regressio model y = Xβ + ε, where X is
Asymptotic Results for the Liear Regressio Model C. Fli November 29, 2000 1. Asymptotic Results uder Classical Assumptios The followig results apply to the liear regressio model y = Xβ + ε, where X is
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Berry-Esseen bounds for self-normalized martingales
 Berry-Essee bouds for self-ormalized martigales Xiequa Fa a, Qi-Ma Shao b a Ceter for Applied Mathematics, Tiaji Uiversity, Tiaji 30007, Chia b Departmet of Statistics, The Chiese Uiversity of Hog Kog,
Berry-Essee bouds for self-ormalized martigales Xiequa Fa a, Qi-Ma Shao b a Ceter for Applied Mathematics, Tiaji Uiversity, Tiaji 30007, Chia b Departmet of Statistics, The Chiese Uiversity of Hog Kog,
Bull. Korean Math. Soc. 36 (1999), No. 3, pp. 451{457 THE STRONG CONSISTENCY OF NONLINEAR REGRESSION QUANTILES ESTIMATORS Seung Hoe Choi and Hae Kyung
 Bull. Korea Math. Soc. 36 (999), No. 3, pp. 45{457 THE STRONG CONSISTENCY OF NONLINEAR REGRESSION QUANTILES ESTIMATORS Abstract. This paper provides suciet coditios which esure the strog cosistecy of regressio
Bull. Korea Math. Soc. 36 (999), No. 3, pp. 45{457 THE STRONG CONSISTENCY OF NONLINEAR REGRESSION QUANTILES ESTIMATORS Abstract. This paper provides suciet coditios which esure the strog cosistecy of regressio
MA Advanced Econometrics: Properties of Least Squares Estimators
 MA Advaced Ecoometrics: Properties of Least Squares Estimators Karl Whela School of Ecoomics, UCD February 5, 20 Karl Whela UCD Least Squares Estimators February 5, 20 / 5 Part I Least Squares: Some Fiite-Sample
MA Advaced Ecoometrics: Properties of Least Squares Estimators Karl Whela School of Ecoomics, UCD February 5, 20 Karl Whela UCD Least Squares Estimators February 5, 20 / 5 Part I Least Squares: Some Fiite-Sample
Detailed proofs of Propositions 3.1 and 3.2
 Detailed proofs of Propositios 3. ad 3. Proof of Propositio 3. NB: itegratio sets are geerally omitted for itegrals defied over a uit hypercube [0, s with ay s d. We first give four lemmas. The proof of
Detailed proofs of Propositios 3. ad 3. Proof of Propositio 3. NB: itegratio sets are geerally omitted for itegrals defied over a uit hypercube [0, s with ay s d. We first give four lemmas. The proof of
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
Distribution of Random Samples & Limit theorems
 STAT/MATH 395 A - PROBABILITY II UW Witer Quarter 2017 Néhémy Lim Distributio of Radom Samples & Limit theorems 1 Distributio of i.i.d. Samples Motivatig example. Assume that the goal of a study is to
STAT/MATH 395 A - PROBABILITY II UW Witer Quarter 2017 Néhémy Lim Distributio of Radom Samples & Limit theorems 1 Distributio of i.i.d. Samples Motivatig example. Assume that the goal of a study is to
Maximum Likelihood Estimation and Complexity Regularization
 ECE90 Sprig 004 Statistical Regularizatio ad Learig Theory Lecture: 4 Maximum Likelihood Estimatio ad Complexity Regularizatio Lecturer: Rob Nowak Scribe: Pam Limpiti Review : Maximum Likelihood Estimatio
ECE90 Sprig 004 Statistical Regularizatio ad Learig Theory Lecture: 4 Maximum Likelihood Estimatio ad Complexity Regularizatio Lecturer: Rob Nowak Scribe: Pam Limpiti Review : Maximum Likelihood Estimatio
Lecture 2: Monte Carlo Simulation
 STAT/Q SCI 43: Itroductio to Resamplig ethods Sprig 27 Istructor: Ye-Chi Che Lecture 2: ote Carlo Simulatio 2 ote Carlo Itegratio Assume we wat to evaluate the followig itegratio: e x3 dx What ca we do?
STAT/Q SCI 43: Itroductio to Resamplig ethods Sprig 27 Istructor: Ye-Chi Che Lecture 2: ote Carlo Simulatio 2 ote Carlo Itegratio Assume we wat to evaluate the followig itegratio: e x3 dx What ca we do?
Lecture 20: Multivariate convergence and the Central Limit Theorem
 Lecture 20: Multivariate covergece ad the Cetral Limit Theorem Covergece i distributio for radom vectors Let Z,Z 1,Z 2,... be radom vectors o R k. If the cdf of Z is cotiuous, the we ca defie covergece
Lecture 20: Multivariate covergece ad the Cetral Limit Theorem Covergece i distributio for radom vectors Let Z,Z 1,Z 2,... be radom vectors o R k. If the cdf of Z is cotiuous, the we ca defie covergece
Summary and Discussion on Simultaneous Analysis of Lasso and Dantzig Selector
 Summary ad Discussio o Simultaeous Aalysis of Lasso ad Datzig Selector STAT732, Sprig 28 Duzhe Wag May 4, 28 Abstract This is a discussio o the work i Bickel, Ritov ad Tsybakov (29). We begi with a short
Summary ad Discussio o Simultaeous Aalysis of Lasso ad Datzig Selector STAT732, Sprig 28 Duzhe Wag May 4, 28 Abstract This is a discussio o the work i Bickel, Ritov ad Tsybakov (29). We begi with a short
Lecture 7: October 18, 2017
 Iformatio ad Codig Theory Autum 207 Lecturer: Madhur Tulsiai Lecture 7: October 8, 207 Biary hypothesis testig I this lecture, we apply the tools developed i the past few lectures to uderstad the problem
Iformatio ad Codig Theory Autum 207 Lecturer: Madhur Tulsiai Lecture 7: October 8, 207 Biary hypothesis testig I this lecture, we apply the tools developed i the past few lectures to uderstad the problem
STA Object Data Analysis - A List of Projects. January 18, 2018
 STA 6557 Jauary 8, 208 Object Data Aalysis - A List of Projects. Schoeberg Mea glaucomatous shape chages of the Optic Nerve Head regio i aimal models 2. Aalysis of VW- Kedall ati-mea shapes with a applicatio
STA 6557 Jauary 8, 208 Object Data Aalysis - A List of Projects. Schoeberg Mea glaucomatous shape chages of the Optic Nerve Head regio i aimal models 2. Aalysis of VW- Kedall ati-mea shapes with a applicatio
Machine Learning Brett Bernstein
 Machie Learig Brett Berstei Week Lecture: Cocept Check Exercises Starred problems are optioal. Statistical Learig Theory. Suppose A = Y = R ad X is some other set. Furthermore, assume P X Y is a discrete
Machie Learig Brett Berstei Week Lecture: Cocept Check Exercises Starred problems are optioal. Statistical Learig Theory. Suppose A = Y = R ad X is some other set. Furthermore, assume P X Y is a discrete
1 = δ2 (0, ), Y Y n nδ. , T n = Y Y n n. ( U n,k + X ) ( f U n,k + Y ) n 2n f U n,k + θ Y ) 2 E X1 2 X1
 8. The cetral limit theorems 8.1. The cetral limit theorem for i.i.d. sequeces. ecall that C ( is N -separatig. Theorem 8.1. Let X 1, X,... be i.i.d. radom variables with EX 1 = ad EX 1 = σ (,. Suppose
8. The cetral limit theorems 8.1. The cetral limit theorem for i.i.d. sequeces. ecall that C ( is N -separatig. Theorem 8.1. Let X 1, X,... be i.i.d. radom variables with EX 1 = ad EX 1 = σ (,. Suppose
Study the bias (due to the nite dimensional approximation) and variance of the estimators
 2 Series Methods 2. Geeral Approach A model has parameters (; ) where is ite-dimesioal ad is oparametric. (Sometimes, there is o :) We will focus o regressio. The fuctio is approximated by a series a ite
2 Series Methods 2. Geeral Approach A model has parameters (; ) where is ite-dimesioal ad is oparametric. (Sometimes, there is o :) We will focus o regressio. The fuctio is approximated by a series a ite
18.657: Mathematics of Machine Learning
 8.657: Mathematics of Machie Learig Lecturer: Philippe Rigollet Lecture 4 Scribe: Cheg Mao Sep., 05 I this lecture, we cotiue to discuss the effect of oise o the rate of the excess risk E(h) = R(h) R(h
8.657: Mathematics of Machie Learig Lecturer: Philippe Rigollet Lecture 4 Scribe: Cheg Mao Sep., 05 I this lecture, we cotiue to discuss the effect of oise o the rate of the excess risk E(h) = R(h) R(h
Lecture 19: Convergence
 Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
Lecture 19: Covergece Asymptotic approach I statistical aalysis or iferece, a key to the success of fidig a good procedure is beig able to fid some momets ad/or distributios of various statistics. I may
A Central Limit Theorem for Spatial Observations
 AUSTRIAN JOURNAL OF STATISTICS Volume 41 (01, Number 3, 7 39 A Cetral Limit Theorem for Spatial Observatios Istvá Fazekas 1, Zsolt Karácsoy ad Reáta Vas 1 1 Faculty of Iformatics, Uiversity of Debrece,
AUSTRIAN JOURNAL OF STATISTICS Volume 41 (01, Number 3, 7 39 A Cetral Limit Theorem for Spatial Observatios Istvá Fazekas 1, Zsolt Karácsoy ad Reáta Vas 1 1 Faculty of Iformatics, Uiversity of Debrece,
Chapter 6 Principles of Data Reduction
 Chapter 6 for BST 695: Special Topics i Statistical Theory. Kui Zhag, 0 Chapter 6 Priciples of Data Reductio Sectio 6. Itroductio Goal: To summarize or reduce the data X, X,, X to get iformatio about a
Chapter 6 for BST 695: Special Topics i Statistical Theory. Kui Zhag, 0 Chapter 6 Priciples of Data Reductio Sectio 6. Itroductio Goal: To summarize or reduce the data X, X,, X to get iformatio about a
Unbiased Estimation. February 7-12, 2008
 Ubiased Estimatio February 7-2, 2008 We begi with a sample X = (X,..., X ) of radom variables chose accordig to oe of a family of probabilities P θ where θ is elemet from the parameter space Θ. For radom
Ubiased Estimatio February 7-2, 2008 We begi with a sample X = (X,..., X ) of radom variables chose accordig to oe of a family of probabilities P θ where θ is elemet from the parameter space Θ. For radom
NYU Center for Data Science: DS-GA 1003 Machine Learning and Computational Statistics (Spring 2018)
 NYU Ceter for Data Sciece: DS-GA 003 Machie Learig ad Computatioal Statistics (Sprig 208) Brett Berstei, David Roseberg, Be Jakubowski Jauary 20, 208 Istructios: Followig most lab ad lecture sectios, we
NYU Ceter for Data Sciece: DS-GA 003 Machie Learig ad Computatioal Statistics (Sprig 208) Brett Berstei, David Roseberg, Be Jakubowski Jauary 20, 208 Istructios: Followig most lab ad lecture sectios, we
Introduction to Extreme Value Theory Laurens de Haan, ISM Japan, Erasmus University Rotterdam, NL University of Lisbon, PT
 Itroductio to Extreme Value Theory Laures de Haa, ISM Japa, 202 Itroductio to Extreme Value Theory Laures de Haa Erasmus Uiversity Rotterdam, NL Uiversity of Lisbo, PT Itroductio to Extreme Value Theory
Itroductio to Extreme Value Theory Laures de Haa, ISM Japa, 202 Itroductio to Extreme Value Theory Laures de Haa Erasmus Uiversity Rotterdam, NL Uiversity of Lisbo, PT Itroductio to Extreme Value Theory
Economics 241B Relation to Method of Moments and Maximum Likelihood OLSE as a Maximum Likelihood Estimator
 Ecoomics 24B Relatio to Method of Momets ad Maximum Likelihood OLSE as a Maximum Likelihood Estimator Uder Assumptio 5 we have speci ed the distributio of the error, so we ca estimate the model parameters
Ecoomics 24B Relatio to Method of Momets ad Maximum Likelihood OLSE as a Maximum Likelihood Estimator Uder Assumptio 5 we have speci ed the distributio of the error, so we ca estimate the model parameters
Asymptotic distribution of products of sums of independent random variables
 Proc. Idia Acad. Sci. Math. Sci. Vol. 3, No., May 03, pp. 83 9. c Idia Academy of Scieces Asymptotic distributio of products of sums of idepedet radom variables YANLING WANG, SUXIA YAO ad HONGXIA DU ollege
Proc. Idia Acad. Sci. Math. Sci. Vol. 3, No., May 03, pp. 83 9. c Idia Academy of Scieces Asymptotic distributio of products of sums of idepedet radom variables YANLING WANG, SUXIA YAO ad HONGXIA DU ollege
This section is optional.
 4 Momet Geeratig Fuctios* This sectio is optioal. The momet geeratig fuctio g : R R of a radom variable X is defied as g(t) = E[e tx ]. Propositio 1. We have g () (0) = E[X ] for = 1, 2,... Proof. Therefore
4 Momet Geeratig Fuctios* This sectio is optioal. The momet geeratig fuctio g : R R of a radom variable X is defied as g(t) = E[e tx ]. Propositio 1. We have g () (0) = E[X ] for = 1, 2,... Proof. Therefore
Journal of Multivariate Analysis. Superefficient estimation of the marginals by exploiting knowledge on the copula
 Joural of Multivariate Aalysis 102 (2011) 1315 1319 Cotets lists available at ScieceDirect Joural of Multivariate Aalysis joural homepage: www.elsevier.com/locate/jmva Superefficiet estimatio of the margials
Joural of Multivariate Aalysis 102 (2011) 1315 1319 Cotets lists available at ScieceDirect Joural of Multivariate Aalysis joural homepage: www.elsevier.com/locate/jmva Superefficiet estimatio of the margials
LECTURE 8: ASYMPTOTICS I
 LECTURE 8: ASYMPTOTICS I We are iterested i the properties of estimators as. Cosider a sequece of radom variables {, X 1}. N. M. Kiefer, Corell Uiversity, Ecoomics 60 1 Defiitio: (Weak covergece) A sequece
LECTURE 8: ASYMPTOTICS I We are iterested i the properties of estimators as. Cosider a sequece of radom variables {, X 1}. N. M. Kiefer, Corell Uiversity, Ecoomics 60 1 Defiitio: (Weak covergece) A sequece
Bayesian Methods: Introduction to Multi-parameter Models
 Bayesia Methods: Itroductio to Multi-parameter Models Parameter: θ = ( θ, θ) Give Likelihood p(y θ) ad prior p(θ ), the posterior p proportioal to p(y θ) x p(θ ) Margial posterior ( θ, θ y) is Iterested
Bayesia Methods: Itroductio to Multi-parameter Models Parameter: θ = ( θ, θ) Give Likelihood p(y θ) ad prior p(θ ), the posterior p proportioal to p(y θ) x p(θ ) Margial posterior ( θ, θ y) is Iterested
MOMENT-METHOD ESTIMATION BASED ON CENSORED SAMPLE
 Vol. 8 o. Joural of Systems Sciece ad Complexity Apr., 5 MOMET-METHOD ESTIMATIO BASED O CESORED SAMPLE I Zhogxi Departmet of Mathematics, East Chia Uiversity of Sciece ad Techology, Shaghai 37, Chia. Email:
Vol. 8 o. Joural of Systems Sciece ad Complexity Apr., 5 MOMET-METHOD ESTIMATIO BASED O CESORED SAMPLE I Zhogxi Departmet of Mathematics, East Chia Uiversity of Sciece ad Techology, Shaghai 37, Chia. Email:
5. Likelihood Ratio Tests
 1 of 5 7/29/2009 3:16 PM Virtual Laboratories > 9. Hy pothesis Testig > 1 2 3 4 5 6 7 5. Likelihood Ratio Tests Prelimiaries As usual, our startig poit is a radom experimet with a uderlyig sample space,
1 of 5 7/29/2009 3:16 PM Virtual Laboratories > 9. Hy pothesis Testig > 1 2 3 4 5 6 7 5. Likelihood Ratio Tests Prelimiaries As usual, our startig poit is a radom experimet with a uderlyig sample space,
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 5
 CS434a/54a: Patter Recogitio Prof. Olga Veksler Lecture 5 Today Itroductio to parameter estimatio Two methods for parameter estimatio Maimum Likelihood Estimatio Bayesia Estimatio Itroducto Bayesia Decisio
CS434a/54a: Patter Recogitio Prof. Olga Veksler Lecture 5 Today Itroductio to parameter estimatio Two methods for parameter estimatio Maimum Likelihood Estimatio Bayesia Estimatio Itroducto Bayesia Decisio
HAJEK-RENYI-TYPE INEQUALITY FOR SOME NONMONOTONIC FUNCTIONS OF ASSOCIATED RANDOM VARIABLES
 HAJEK-RENYI-TYPE INEQUALITY FOR SOME NONMONOTONIC FUNCTIONS OF ASSOCIATED RANDOM VARIABLES ISHA DEWAN AND B. L. S. PRAKASA RAO Received 1 April 005; Revised 6 October 005; Accepted 11 December 005 Let
HAJEK-RENYI-TYPE INEQUALITY FOR SOME NONMONOTONIC FUNCTIONS OF ASSOCIATED RANDOM VARIABLES ISHA DEWAN AND B. L. S. PRAKASA RAO Received 1 April 005; Revised 6 October 005; Accepted 11 December 005 Let
J. Stat. Appl. Pro. Lett. 2, No. 1, (2015) 15
 J. Stat. Appl. Pro. Lett. 2, No. 1, 15-22 2015 15 Joural of Statistics Applicatios & Probability Letters A Iteratioal Joural http://dx.doi.org/10.12785/jsapl/020102 Martigale Method for Rui Probabilityi
J. Stat. Appl. Pro. Lett. 2, No. 1, 15-22 2015 15 Joural of Statistics Applicatios & Probability Letters A Iteratioal Joural http://dx.doi.org/10.12785/jsapl/020102 Martigale Method for Rui Probabilityi
Random Variables, Sampling and Estimation
 Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
Chapter 1 Radom Variables, Samplig ad Estimatio 1.1 Itroductio This chapter will cover the most importat basic statistical theory you eed i order to uderstad the ecoometric material that will be comig
EFFECTIVE WLLN, SLLN, AND CLT IN STATISTICAL MODELS
 EFFECTIVE WLLN, SLLN, AND CLT IN STATISTICAL MODELS Ryszard Zieliński Ist Math Polish Acad Sc POBox 21, 00-956 Warszawa 10, Polad e-mail: rziel@impagovpl ABSTRACT Weak laws of large umbers (W LLN), strog
EFFECTIVE WLLN, SLLN, AND CLT IN STATISTICAL MODELS Ryszard Zieliński Ist Math Polish Acad Sc POBox 21, 00-956 Warszawa 10, Polad e-mail: rziel@impagovpl ABSTRACT Weak laws of large umbers (W LLN), strog
Output Analysis and Run-Length Control
 IEOR E4703: Mote Carlo Simulatio Columbia Uiversity c 2017 by Marti Haugh Output Aalysis ad Ru-Legth Cotrol I these otes we describe how the Cetral Limit Theorem ca be used to costruct approximate (1 α%
IEOR E4703: Mote Carlo Simulatio Columbia Uiversity c 2017 by Marti Haugh Output Aalysis ad Ru-Legth Cotrol I these otes we describe how the Cetral Limit Theorem ca be used to costruct approximate (1 α%
1 Review and Overview
 DRAFT a fial versio will be posted shortly CS229T/STATS231: Statistical Learig Theory Lecturer: Tegyu Ma Lecture #3 Scribe: Migda Qiao October 1, 2013 1 Review ad Overview I the first half of this course,
DRAFT a fial versio will be posted shortly CS229T/STATS231: Statistical Learig Theory Lecturer: Tegyu Ma Lecture #3 Scribe: Migda Qiao October 1, 2013 1 Review ad Overview I the first half of this course,
Resampling Methods. X (1/2), i.e., Pr (X i m) = 1/2. We order the data: X (1) X (2) X (n). Define the sample median: ( n.
 Jauary 1, 2019 Resamplig Methods Motivatio We have so may estimators with the property θ θ d N 0, σ 2 We ca also write θ a N θ, σ 2 /, where a meas approximately distributed as Oce we have a cosistet estimator
Jauary 1, 2019 Resamplig Methods Motivatio We have so may estimators with the property θ θ d N 0, σ 2 We ca also write θ a N θ, σ 2 /, where a meas approximately distributed as Oce we have a cosistet estimator
Investigating the Significance of a Correlation Coefficient using Jackknife Estimates
 Iteratioal Joural of Scieces: Basic ad Applied Research (IJSBAR) ISSN 2307-4531 (Prit & Olie) http://gssrr.org/idex.php?joural=jouralofbasicadapplied ---------------------------------------------------------------------------------------------------------------------------
Iteratioal Joural of Scieces: Basic ad Applied Research (IJSBAR) ISSN 2307-4531 (Prit & Olie) http://gssrr.org/idex.php?joural=jouralofbasicadapplied ---------------------------------------------------------------------------------------------------------------------------
Statistical Pattern Recognition
 Statistical Patter Recogitio Classificatio: No-Parametric Modelig Hamid R. Rabiee Jafar Muhammadi Sprig 2014 http://ce.sharif.edu/courses/92-93/2/ce725-2/ Ageda Parametric Modelig No-Parametric Modelig
Statistical Patter Recogitio Classificatio: No-Parametric Modelig Hamid R. Rabiee Jafar Muhammadi Sprig 2014 http://ce.sharif.edu/courses/92-93/2/ce725-2/ Ageda Parametric Modelig No-Parametric Modelig
11 Correlation and Regression
 11 Correlatio Regressio 11.1 Multivariate Data Ofte we look at data where several variables are recorded for the same idividuals or samplig uits. For example, at a coastal weather statio, we might record
11 Correlatio Regressio 11.1 Multivariate Data Ofte we look at data where several variables are recorded for the same idividuals or samplig uits. For example, at a coastal weather statio, we might record
The standard deviation of the mean
 Physics 6C Fall 20 The stadard deviatio of the mea These otes provide some clarificatio o the distictio betwee the stadard deviatio ad the stadard deviatio of the mea.. The sample mea ad variace Cosider
Physics 6C Fall 20 The stadard deviatio of the mea These otes provide some clarificatio o the distictio betwee the stadard deviatio ad the stadard deviatio of the mea.. The sample mea ad variace Cosider
Supplementary Material for Fast Stochastic AUC Maximization with O(1/n)-Convergence Rate
 Supplemetary Material for Fast Stochastic AUC Maximizatio with O/-Covergece Rate Migrui Liu Xiaoxua Zhag Zaiyi Che Xiaoyu Wag 3 iabao Yag echical Lemmas ized versio of Hoeffdig s iequality, ote that We
Supplemetary Material for Fast Stochastic AUC Maximizatio with O/-Covergece Rate Migrui Liu Xiaoxua Zhag Zaiyi Che Xiaoyu Wag 3 iabao Yag echical Lemmas ized versio of Hoeffdig s iequality, ote that We
Empirical Process Theory and Oracle Inequalities
 Stat 928: Statistical Learig Theory Lecture: 10 Empirical Process Theory ad Oracle Iequalities Istructor: Sham Kakade 1 Risk vs Risk See Lecture 0 for a discussio o termiology. 2 The Uio Boud / Boferoi
Stat 928: Statistical Learig Theory Lecture: 10 Empirical Process Theory ad Oracle Iequalities Istructor: Sham Kakade 1 Risk vs Risk See Lecture 0 for a discussio o termiology. 2 The Uio Boud / Boferoi
Chapter 5. Inequalities. 5.1 The Markov and Chebyshev inequalities
 Chapter 5 Iequalities 5.1 The Markov ad Chebyshev iequalities As you have probably see o today s frot page: every perso i the upper teth percetile ears at least 1 times more tha the average salary. I other
Chapter 5 Iequalities 5.1 The Markov ad Chebyshev iequalities As you have probably see o today s frot page: every perso i the upper teth percetile ears at least 1 times more tha the average salary. I other
Quantile regression with multilayer perceptrons.
 Quatile regressio with multilayer perceptros. S.-F. Dimby ad J. Rykiewicz Uiversite Paris 1 - SAMM 90 Rue de Tolbiac, 75013 Paris - Frace Abstract. We cosider oliear quatile regressio ivolvig multilayer
Quatile regressio with multilayer perceptros. S.-F. Dimby ad J. Rykiewicz Uiversite Paris 1 - SAMM 90 Rue de Tolbiac, 75013 Paris - Frace Abstract. We cosider oliear quatile regressio ivolvig multilayer
Linear regression. Daniel Hsu (COMS 4771) (y i x T i β)2 2πσ. 2 2σ 2. 1 n. (x T i β y i ) 2. 1 ˆβ arg min. β R n d
 Liear regressio Daiel Hsu (COMS 477) Maximum likelihood estimatio Oe of the simplest liear regressio models is the followig: (X, Y ),..., (X, Y ), (X, Y ) are iid radom pairs takig values i R d R, ad Y
Liear regressio Daiel Hsu (COMS 477) Maximum likelihood estimatio Oe of the simplest liear regressio models is the followig: (X, Y ),..., (X, Y ), (X, Y ) are iid radom pairs takig values i R d R, ad Y
REGRESSION WITH QUADRATIC LOSS
 REGRESSION WITH QUADRATIC LOSS MAXIM RAGINSKY Regressio with quadratic loss is aother basic problem studied i statistical learig theory. We have a radom couple Z = X, Y ), where, as before, X is a R d
REGRESSION WITH QUADRATIC LOSS MAXIM RAGINSKY Regressio with quadratic loss is aother basic problem studied i statistical learig theory. We have a radom couple Z = X, Y ), where, as before, X is a R d
Entropy Rates and Asymptotic Equipartition
 Chapter 29 Etropy Rates ad Asymptotic Equipartitio Sectio 29. itroduces the etropy rate the asymptotic etropy per time-step of a stochastic process ad shows that it is well-defied; ad similarly for iformatio,
Chapter 29 Etropy Rates ad Asymptotic Equipartitio Sectio 29. itroduces the etropy rate the asymptotic etropy per time-step of a stochastic process ad shows that it is well-defied; ad similarly for iformatio,
Properties and Hypothesis Testing
 Chapter 3 Properties ad Hypothesis Testig 3.1 Types of data The regressio techiques developed i previous chapters ca be applied to three differet kids of data. 1. Cross-sectioal data. 2. Time series data.
Chapter 3 Properties ad Hypothesis Testig 3.1 Types of data The regressio techiques developed i previous chapters ca be applied to three differet kids of data. 1. Cross-sectioal data. 2. Time series data.
Research Article On the Strong Laws for Weighted Sums of ρ -Mixing Random Variables
 Hidawi Publishig Corporatio Joural of Iequalities ad Applicatios Volume 2011, Article ID 157816, 8 pages doi:10.1155/2011/157816 Research Article O the Strog Laws for Weighted Sums of ρ -Mixig Radom Variables
Hidawi Publishig Corporatio Joural of Iequalities ad Applicatios Volume 2011, Article ID 157816, 8 pages doi:10.1155/2011/157816 Research Article O the Strog Laws for Weighted Sums of ρ -Mixig Radom Variables
The Central Limit Theorem
 Chapter The Cetral Limit Theorem Deote by Z the stadard ormal radom variable with desity 2π e x2 /2. Lemma.. Ee itz = e t2 /2 Proof. We use the same calculatio as for the momet geeratig fuctio: exp(itx
Chapter The Cetral Limit Theorem Deote by Z the stadard ormal radom variable with desity 2π e x2 /2. Lemma.. Ee itz = e t2 /2 Proof. We use the same calculatio as for the momet geeratig fuctio: exp(itx
Notes 19 : Martingale CLT
 Notes 9 : Martigale CLT Math 733-734: Theory of Probability Lecturer: Sebastie Roch Refereces: [Bil95, Chapter 35], [Roc, Chapter 3]. Sice we have ot ecoutered weak covergece i some time, we first recall
Notes 9 : Martigale CLT Math 733-734: Theory of Probability Lecturer: Sebastie Roch Refereces: [Bil95, Chapter 35], [Roc, Chapter 3]. Sice we have ot ecoutered weak covergece i some time, we first recall
On Classification Based on Totally Bounded Classes of Functions when There are Incomplete Covariates
 Joural of Statistical Theory ad Applicatios Volume, Number 4, 0, pp. 353-369 ISSN 538-7887 O Classificatio Based o Totally Bouded Classes of Fuctios whe There are Icomplete Covariates Majid Mojirsheibai
Joural of Statistical Theory ad Applicatios Volume, Number 4, 0, pp. 353-369 ISSN 538-7887 O Classificatio Based o Totally Bouded Classes of Fuctios whe There are Icomplete Covariates Majid Mojirsheibai
BIRKHOFF ERGODIC THEOREM
 BIRKHOFF ERGODIC THEOREM Abstract. We will give a proof of the poitwise ergodic theorem, which was first proved by Birkhoff. May improvemets have bee made sice Birkhoff s orgial proof. The versio we give
BIRKHOFF ERGODIC THEOREM Abstract. We will give a proof of the poitwise ergodic theorem, which was first proved by Birkhoff. May improvemets have bee made sice Birkhoff s orgial proof. The versio we give
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
of (X n ) are available at certain points. Under assumption of weak dependency we proved the consistency of Hill s estimator of the tail
 Novi Sad J. Math. Vol. 38, No. 3, 2008, 97-104 INCOMPLETE SAMPLES AND TAIL ESTIMATION FOR STATIONARY SEQUENCES 1 Ivaa Ilić 2, Pavle Mladeović 3 Abstract. Let (X ) be a strictly statioary sequece with a
Novi Sad J. Math. Vol. 38, No. 3, 2008, 97-104 INCOMPLETE SAMPLES AND TAIL ESTIMATION FOR STATIONARY SEQUENCES 1 Ivaa Ilić 2, Pavle Mladeović 3 Abstract. Let (X ) be a strictly statioary sequece with a
Probability and Statistics
 ICME Refresher Course: robability ad Statistics Staford Uiversity robability ad Statistics Luyag Che September 20, 2016 1 Basic robability Theory 11 robability Spaces A probability space is a triple (Ω,
ICME Refresher Course: robability ad Statistics Staford Uiversity robability ad Statistics Luyag Che September 20, 2016 1 Basic robability Theory 11 robability Spaces A probability space is a triple (Ω,
It should be unbiased, or approximately unbiased. Variance of the variance estimator should be small. That is, the variance estimator is stable.
 Chapter 10 Variace Estimatio 10.1 Itroductio Variace estimatio is a importat practical problem i survey samplig. Variace estimates are used i two purposes. Oe is the aalytic purpose such as costructig
Chapter 10 Variace Estimatio 10.1 Itroductio Variace estimatio is a importat practical problem i survey samplig. Variace estimates are used i two purposes. Oe is the aalytic purpose such as costructig
Regression with quadratic loss
 Regressio with quadratic loss Maxim Ragisky October 13, 2015 Regressio with quadratic loss is aother basic problem studied i statistical learig theory. We have a radom couple Z = X,Y, where, as before,
Regressio with quadratic loss Maxim Ragisky October 13, 2015 Regressio with quadratic loss is aother basic problem studied i statistical learig theory. We have a radom couple Z = X,Y, where, as before,
ESTIMATING THE ERROR DISTRIBUTION FUNCTION IN NONPARAMETRIC REGRESSION WITH MULTIVARIATE COVARIATES
 ESTIMATING THE ERROR DISTRIBUTION FUNCTION IN NONPARAMETRIC REGRESSION WITH MULTIVARIATE COVARIATES URSULA U. MÜLLER, ANTON SCHICK AND WOLFGANG WEFELMEYER Abstract. We cosider oparametric regressio models
ESTIMATING THE ERROR DISTRIBUTION FUNCTION IN NONPARAMETRIC REGRESSION WITH MULTIVARIATE COVARIATES URSULA U. MÜLLER, ANTON SCHICK AND WOLFGANG WEFELMEYER Abstract. We cosider oparametric regressio models
CEE 522 Autumn Uncertainty Concepts for Geotechnical Engineering
 CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
CEE 5 Autum 005 Ucertaity Cocepts for Geotechical Egieerig Basic Termiology Set A set is a collectio of (mutually exclusive) objects or evets. The sample space is the (collectively exhaustive) collectio
Pattern Classification, Ch4 (Part 1)
 Patter Classificatio All materials i these slides were take from Patter Classificatio (2d ed) by R O Duda, P E Hart ad D G Stork, Joh Wiley & Sos, 2000 with the permissio of the authors ad the publisher
Patter Classificatio All materials i these slides were take from Patter Classificatio (2d ed) by R O Duda, P E Hart ad D G Stork, Joh Wiley & Sos, 2000 with the permissio of the authors ad the publisher
A Note on Box-Cox Quantile Regression Estimation of the Parameters of the Generalized Pareto Distribution
 A Note o Box-Cox Quatile Regressio Estimatio of the Parameters of the Geeralized Pareto Distributio JM va Zyl Abstract: Makig use of the quatile equatio, Box-Cox regressio ad Laplace distributed disturbaces,
A Note o Box-Cox Quatile Regressio Estimatio of the Parameters of the Geeralized Pareto Distributio JM va Zyl Abstract: Makig use of the quatile equatio, Box-Cox regressio ad Laplace distributed disturbaces,
A Weak Law of Large Numbers Under Weak Mixing
 A Weak Law of Large Numbers Uder Weak Mixig Bruce E. Hase Uiversity of Wiscosi Jauary 209 Abstract This paper presets a ew weak law of large umbers (WLLN) for heterogeous depedet processes ad arrays. The
A Weak Law of Large Numbers Uder Weak Mixig Bruce E. Hase Uiversity of Wiscosi Jauary 209 Abstract This paper presets a ew weak law of large umbers (WLLN) for heterogeous depedet processes ad arrays. The
