2D electron systems beyond the diffusive regime
|
|
|
- Oliver Wilkins
- 5 years ago
- Views:
Transcription
1 2D electron systems beyond the diffusive regime Peter Markoš FEI STU Bratislava 9. June 211 Collaboration with: K. Muttalib, L. Schweitzer Typeset by FoilTEX
2 Introduction: Spatial distribution of the electron propagating through a disordered sample Weak disorder: homogeneous: electron is everywhere Strong disorder: selected path through the sample Is it possible to describe both limits analytically? Typeset by FoilTEX 1
3 Scattering experiment: A B Conductance g. C D Transfer matrix: ( ) C = T D ( A B ) T = ( t 1 rt 1 r t 1 t r t 1 r ) (1) Conductance g ( Economou and Soukoulis) g = e2 π h Tr t t. Typeset by FoilTEX 2
4 T = ( u u u,v are N N matrices Parametrization of the Transfer matrix )( )( ) 1 + λ λ v λ 1 + λ v. (2) Orthogonal symmetry: u = u and v = v. Symplectic symmetry: u = ku k T, v = kv k T, k = Conductance (e 2 /π h = 1) ( 1 1 ). (3) g = Tr t t = Tr v 1 (1 + λ) 1 v = N a= λ a = N a=1 4 cosh 2 x a /2 (4) g does not depend on matrices u and v. Typeset by FoilTEX 3
5 Generalized DMPK Equation p L z(λ) (L z /l) = 1 J N a λ a [ λ a (1 + λ a )K aa J p ], (5) λ a l is the mean free path J N a<b λ a λ b γ ab, γ ab 2K ab K aa. (6) Original DMPK Equation: K aa 1/L, 1 orthogonal β = 2 unitary 4 symplectic γ ab β (the symmetry parameter) (7) Universal properties of weakly disordered Q1D systems. Typeset by FoilTEX 4
6 General form of the matrix K K ab k ab... represents the ensemble average. Symmetry k ab K ab in diffusive limit Orthogonal Unitary k O ab = L α=1 v αa 2 v αb 2 K O ab = 1 + δ ab L + 1 L k U ab = v αa 2 v αb 2 K U ab = 1 L Symplectic α=1 L k S ab = v αa v αb v αbv α a α=1 K S ab = 2 δ ab 2L 1 v = ( v 11 v 21 v 12 v 22 ) v = ( v 11 v 12 v 21 v 22 ) v = ( v22 v 12 v 21 v 11 ) (8) Typeset by FoilTEX 5
7 Approximation Consider only two parameters: K aa K 11 γ ab γ for all a, b (a b). K O ab = K U ab = b b b K S ab = 1. (9) Typeset by FoilTEX 6
8 Physical interpretation (Muttalib) In the localized regime, K 11 L and lim L K 12 = Therefore γ = 2K 12 K 11 in the insulating regime. The localized regime differs from the metallic regime because the wave function is not homogeneous. For the strong disorder, there is only a few possible paths through the sample: u(x) u(x) γ = β γ K aa... inverse participation ratio for the electron on the back side of the sample Typeset by FoilTEX 7
9 Motivation: Distribution of the conductance in the localized regime.1 L = 1 <ln g> = -16 var ln g = 2.6 L = 2 <ln g> = var ln g = 33.4 L = 4 <ln g> = var ln g = 1,2,15 3D L=26, W=16 ξ=5.41 <ln g>=-1.66 Eq. (83) Γ=.63, γ=γ/2, <ln g>= D L=1, W=26 ξ=1.8 <ln g>=-1.94 P (ln g) P(ln g),1.5, ln g ln g The distribution P(ln g) is not Gaussian (2D symplectic and 3D orthogonal systems) Typeset by FoilTEX 8
10 2D disordered systems Numerical estimation of the matrix K Identification of the critical point from the L- dependence of K and γ What is the role of the symmetry parameter β in the localized regime? (γ ) Typeset by FoilTEX 9
11 Diffusive regime K 11 S.55 K 11 O W = 2 K 12 S 1.7 K 12 O 1.73 W = 2 K 11 U 1.6 K 11 U 1.1 K 11 K /L /L K O ab = 1 + δ ab L + 1. KU ab = 1 L. KS ab = 2 δ ab 2L 1 (1) Typeset by FoilTEX 1
12 Critical regime - symplectic symmetry 1.5 Metal: W < W c γ S 2. W = 2 W = 3 W = 4 W = 5 W = 5.25 W = 5.5 W = W = 5.75 W = 6 W = <g> Insulator: W > W c L γ S = 2K 12 K L Metal: Critical Insulator γ S 4 γ S 2.6 γ S Typeset by FoilTEX 11
13 Absence of critical regime - orthogonal symmetry 2D orthogonal system box disorder γ O γ U W 1 1 L W = 1 W = 2 W = 3 W = 4 <g> 1 W = 1 W = 2 W = 3 W = L Typeset by FoilTEX 12
14 Random matrix theory 1 p( ).5 W = 2 W = 5.84 L = 3 W = 5.84 W = 2 W = 5 What is the form of the probability distribution of = x 2 x 1 In particular, we expect that P( ) β In the limit of strong disorder, γ What is the true - dependence pf P( )? Typeset by FoilTEX 13
15 Probability distribution P(ln ) (β = 4) p(ln ) W <ln g> P P P ln lnp(ln ) (β+1)ln Symplectic models: Numerical data for L = 14, N stat 1 8. Slope: 4.8, 3.78, 3., 3.3 Typeset by FoilTEX 14
16 Probability distribution P(ln ) (β = 1) 1 P P P 1 p(ln ) 1-6 W L <ln g> slope ln Typeset by FoilTEX 15
17 Correlation of x 1 and x 2 (symplectic model) 2 W = 3 L = 2 3 W = 8 L = x x 2.5 x 2 -x x 2 -x x x x x 1 g = λ a = a 4 cosh 2 (x a /2), λ a = [coshx a 1]/2 x 1 < x 2 <... The conductance is large when x 1 is small. However, small value of x 2 x 1 occurs only in samples with large value of x 1. The samples with small have small g and do not affect the statistical distribution of the conductance. Typeset by FoilTEX 16
18 Conclusions Generalized DMPK is suitable for the description of transport in strongly disordered systems New parameters: K 11 and γ can be used to detect critical points γ β in the diffusive regime γ = const < β at the critical point γ in the localized regime Symmetry parameter β determines the distribution P( ) β The statistical properties of the conductance can be estimated from the model with β PRB 65, 14297, PRB 72, , PRB 82, 9423, PRB 82, Typeset by FoilTEX 17
arxiv: v2 [cond-mat.dis-nn] 21 Jul 2010
![arxiv: v2 [cond-mat.dis-nn] 21 Jul 2010 arxiv: v2 [cond-mat.dis-nn] 21 Jul 2010](/thumbs/93/114269488.jpg) Two-dimensional electron systems beyond the diffusive regime P. Markoš Department of Physics FEI, lovak University of Technology, 8 9 Bratislava, lovakia arxiv:5.89v [cond-mat.dis-nn] Jul Transport properties
Two-dimensional electron systems beyond the diffusive regime P. Markoš Department of Physics FEI, lovak University of Technology, 8 9 Bratislava, lovakia arxiv:5.89v [cond-mat.dis-nn] Jul Transport properties
Numerical Analysis of the Anderson Localization
 Numerical Analysis of the Anderson Localization Peter Marko² FEI STU Bratislava FzU Praha, November 3. 23 . introduction: localized states in quantum mechanics 2. statistics and uctuations 3. metal - insulator
Numerical Analysis of the Anderson Localization Peter Marko² FEI STU Bratislava FzU Praha, November 3. 23 . introduction: localized states in quantum mechanics 2. statistics and uctuations 3. metal - insulator
Universal conductance fluctuation of mesoscopic systems in the metal-insulator crossover regime
 Universal conductance fluctuation of mesoscopic systems in the metal-insulator crossover regime Zhenhua Qiao, Yanxia Xing, and Jian Wang* Department of Physics and the Center of Theoretical and Computational
Universal conductance fluctuation of mesoscopic systems in the metal-insulator crossover regime Zhenhua Qiao, Yanxia Xing, and Jian Wang* Department of Physics and the Center of Theoretical and Computational
Intensity distribution of scalar waves propagating in random media
 PHYSICAL REVIEW B 71, 054201 2005 Intensity distribution of scalar waves propagating in random media P. Markoš 1,2, * and C. M. Soukoulis 1,3 1 Ames Laboratory and Department of Physics and Astronomy,
PHYSICAL REVIEW B 71, 054201 2005 Intensity distribution of scalar waves propagating in random media P. Markoš 1,2, * and C. M. Soukoulis 1,3 1 Ames Laboratory and Department of Physics and Astronomy,
Interpolating between Wishart and inverse-wishart distributions
 Interpolating between Wishart and inverse-wishart distributions Topological phase transitions in 1D multichannel disordered wires with a chiral symmetry Christophe Texier December 11, 2015 with Aurélien
Interpolating between Wishart and inverse-wishart distributions Topological phase transitions in 1D multichannel disordered wires with a chiral symmetry Christophe Texier December 11, 2015 with Aurélien
REPLACE ONE ROW BY ADDING THE SCALAR MULTIPLE OF ANOTHER ROW
 20 CHAPTER 1 Systems of Linear Equations REPLACE ONE ROW BY ADDING THE SCALAR MULTIPLE OF ANOTHER ROW The last type of operation is slightly more complicated. Suppose that we want to write down the elementary
20 CHAPTER 1 Systems of Linear Equations REPLACE ONE ROW BY ADDING THE SCALAR MULTIPLE OF ANOTHER ROW The last type of operation is slightly more complicated. Suppose that we want to write down the elementary
Today: 5 July 2008 ٢
 Anderson localization M. Reza Rahimi Tabar IPM 5 July 2008 ١ Today: 5 July 2008 ٢ Short History of Anderson Localization ٣ Publication 1) F. Shahbazi, etal. Phys. Rev. Lett. 94, 165505 (2005) 2) A. Esmailpour,
Anderson localization M. Reza Rahimi Tabar IPM 5 July 2008 ١ Today: 5 July 2008 ٢ Short History of Anderson Localization ٣ Publication 1) F. Shahbazi, etal. Phys. Rev. Lett. 94, 165505 (2005) 2) A. Esmailpour,
SCATTERING OF ELECTROMAGNETIC WAVES ON METAL NANOPARTICLES. Tomáš Váry, Juraj Chlpík, Peter Markoš
 SCATTERING OF ELECTROMAGNETIC WAVES ON METAL NANOPARTICLES Tomáš Váry, Juraj Chlpík, Peter Markoš ÚJFI, FEI STU, Bratislava E-mail: tomas.vary@stuba.sk Received xx April 2012; accepted xx May 2012. 1.
SCATTERING OF ELECTROMAGNETIC WAVES ON METAL NANOPARTICLES Tomáš Váry, Juraj Chlpík, Peter Markoš ÚJFI, FEI STU, Bratislava E-mail: tomas.vary@stuba.sk Received xx April 2012; accepted xx May 2012. 1.
arxiv: v1 [cond-mat.mes-hall] 23 Jun 2009
![arxiv: v1 [cond-mat.mes-hall] 23 Jun 2009 arxiv: v1 [cond-mat.mes-hall] 23 Jun 2009](/thumbs/72/66291648.jpg) EPJ manuscript No. (will be inserted by the editor) Conductance distribution in two-dimensional localized systems with and without magnetic fields J. Prior 1,2, A. M. Somoza 3 and M. Ortuño 3 arxiv:0906.4188v1
EPJ manuscript No. (will be inserted by the editor) Conductance distribution in two-dimensional localized systems with and without magnetic fields J. Prior 1,2, A. M. Somoza 3 and M. Ortuño 3 arxiv:0906.4188v1
Strauss PDEs 2e: Section Exercise 4 Page 1 of 6
 Strauss PDEs 2e: Section 5.3 - Exercise 4 Page of 6 Exercise 4 Consider the problem u t = ku xx for < x < l, with the boundary conditions u(, t) = U, u x (l, t) =, and the initial condition u(x, ) =, where
Strauss PDEs 2e: Section 5.3 - Exercise 4 Page of 6 Exercise 4 Consider the problem u t = ku xx for < x < l, with the boundary conditions u(, t) = U, u x (l, t) =, and the initial condition u(x, ) =, where
Trigonometric SOS model with DWBC and spin chains with non-diagonal boundaries
 Trigonometric SOS model with DWBC and spin chains with non-diagonal boundaries N. Kitanine IMB, Université de Bourgogne. In collaboration with: G. Filali RAQIS 21, Annecy June 15 - June 19, 21 Typeset
Trigonometric SOS model with DWBC and spin chains with non-diagonal boundaries N. Kitanine IMB, Université de Bourgogne. In collaboration with: G. Filali RAQIS 21, Annecy June 15 - June 19, 21 Typeset
Large deviations of the top eigenvalue of random matrices and applications in statistical physics
 Large deviations of the top eigenvalue of random matrices and applications in statistical physics Grégory Schehr LPTMS, CNRS-Université Paris-Sud XI Journées de Physique Statistique Paris, January 29-30,
Large deviations of the top eigenvalue of random matrices and applications in statistical physics Grégory Schehr LPTMS, CNRS-Université Paris-Sud XI Journées de Physique Statistique Paris, January 29-30,
Nonlinear σ model for disordered systems: an introduction
 Nonlinear σ model for disordered systems: an introduction Igor Lerner THE UNIVERSITY OF BIRMINGHAM School of Physics & Astronomy OUTLINE What is that & where to take it from? How to use it (1 or 2 simple
Nonlinear σ model for disordered systems: an introduction Igor Lerner THE UNIVERSITY OF BIRMINGHAM School of Physics & Astronomy OUTLINE What is that & where to take it from? How to use it (1 or 2 simple
arxiv:cond-mat/ v1 23 May 1995
 Universal Spin-Induced Magnetoresistance in the Variable-Range Hopping Regime Yigal Meir Physics Department, Ben Gurion University, Beer Sheva 84105, ISRAEL arxiv:cond-mat/9505101v1 23 May 1995 Abstract
Universal Spin-Induced Magnetoresistance in the Variable-Range Hopping Regime Yigal Meir Physics Department, Ben Gurion University, Beer Sheva 84105, ISRAEL arxiv:cond-mat/9505101v1 23 May 1995 Abstract
Numerical estimates of critical exponents of the Anderson transition. Keith Slevin (Osaka University) Tomi Ohtsuki (Sophia University)
 Numerical estimates of critical exponents of the Anderson transition Keith Slevin (Osaka University) Tomi Ohtsuki (Sophia University) Anderson Model Standard model of a disordered system H W c c c V c
Numerical estimates of critical exponents of the Anderson transition Keith Slevin (Osaka University) Tomi Ohtsuki (Sophia University) Anderson Model Standard model of a disordered system H W c c c V c
Universality for random matrices and log-gases
 Universality for random matrices and log-gases László Erdős IST, Austria Ludwig-Maximilians-Universität, Munich, Germany Encounters Between Discrete and Continuous Mathematics Eötvös Loránd University,
Universality for random matrices and log-gases László Erdős IST, Austria Ludwig-Maximilians-Universität, Munich, Germany Encounters Between Discrete and Continuous Mathematics Eötvös Loránd University,
Gap probability of a one-dimensional gas model
 Gap probability of a one-dimensional gas model arxiv:cond-mat/9605049v 9 May 1996 Y Chen 1, and S. M. Manning, 1 Department of Mathematics, Imperial College 180 Queen s Gate,London SW7 BZ UK Department
Gap probability of a one-dimensional gas model arxiv:cond-mat/9605049v 9 May 1996 Y Chen 1, and S. M. Manning, 1 Department of Mathematics, Imperial College 180 Queen s Gate,London SW7 BZ UK Department
Numerical study of localization in antidot lattices
 PHYSICAL REVIEW B VOLUME 58, NUMBER 16 Numerical study of localization in antidot lattices 15 OCTOBER 1998-II Seiji Uryu and Tsuneya Ando Institute for Solid State Physics, University of Tokyo, 7-22-1
PHYSICAL REVIEW B VOLUME 58, NUMBER 16 Numerical study of localization in antidot lattices 15 OCTOBER 1998-II Seiji Uryu and Tsuneya Ando Institute for Solid State Physics, University of Tokyo, 7-22-1
arxiv:cond-mat/ v1 [cond-mat.dis-nn] 29 Mar 2006
![arxiv:cond-mat/ v1 [cond-mat.dis-nn] 29 Mar 2006 arxiv:cond-mat/ v1 [cond-mat.dis-nn] 29 Mar 2006](/thumbs/72/66291558.jpg) Conductance fluctuations in the localized regime A. M. Somoza, J. Prior and M. Ortuño arxiv:cond-mat/0603796v1 [cond-mat.dis-nn] 29 Mar 2006 Departamento de Física, Universidad de Murcia, Murcia 30.071,
Conductance fluctuations in the localized regime A. M. Somoza, J. Prior and M. Ortuño arxiv:cond-mat/0603796v1 [cond-mat.dis-nn] 29 Mar 2006 Departamento de Física, Universidad de Murcia, Murcia 30.071,
Why Hyperbolic Symmetry?
 Why Hyperbolic Symmetry? Consider the very trivial case when N = 1 and H = h is a real Gaussian variable of unit variance. To simplify notation set E ɛ = 0 iɛ and z, w C = G(E ɛ ) 2 h = [(h iɛ)(h + iɛ)]
Why Hyperbolic Symmetry? Consider the very trivial case when N = 1 and H = h is a real Gaussian variable of unit variance. To simplify notation set E ɛ = 0 iɛ and z, w C = G(E ɛ ) 2 h = [(h iɛ)(h + iɛ)]
Where Probability Meets Combinatorics and Statistical Mechanics
 Where Probability Meets Combinatorics and Statistical Mechanics Daniel Ueltschi Department of Mathematics, University of Warwick MASDOC, 15 March 2011 Collaboration with V. Betz, N.M. Ercolani, C. Goldschmidt,
Where Probability Meets Combinatorics and Statistical Mechanics Daniel Ueltschi Department of Mathematics, University of Warwick MASDOC, 15 March 2011 Collaboration with V. Betz, N.M. Ercolani, C. Goldschmidt,
Quantum transport of 2D Dirac fermions: the case for a topological metal
 Quantum transport of 2D Dirac fermions: the case for a topological metal Christopher Mudry 1 Shinsei Ryu 2 Akira Furusaki 3 Hideaki Obuse 3,4 1 Paul Scherrer Institut, Switzerland 2 University of California
Quantum transport of 2D Dirac fermions: the case for a topological metal Christopher Mudry 1 Shinsei Ryu 2 Akira Furusaki 3 Hideaki Obuse 3,4 1 Paul Scherrer Institut, Switzerland 2 University of California
Fluctuations in the aging dynamics of structural glasses
 Fluctuations in the aging dynamics of structural glasses Horacio E. Castillo Collaborator: Azita Parsaeian Collaborators in earlier work: Claudio Chamon Leticia F. Cugliandolo José L. Iguain Malcolm P.
Fluctuations in the aging dynamics of structural glasses Horacio E. Castillo Collaborator: Azita Parsaeian Collaborators in earlier work: Claudio Chamon Leticia F. Cugliandolo José L. Iguain Malcolm P.
RANDOM MATRICES and ANDERSON LOCALIZATION
 RANDOM MATRICES and ANDERSON LOCALIZATION Luca G. Molinari Physics Department Universita' degli Studi di Milano Abstract: a particle in a lattice with random potential is subject to Anderson localization,
RANDOM MATRICES and ANDERSON LOCALIZATION Luca G. Molinari Physics Department Universita' degli Studi di Milano Abstract: a particle in a lattice with random potential is subject to Anderson localization,
HOMEWORK 4 1. P45. # 1.
 HOMEWORK 4 SHUANGLIN SHAO P45 # Proof By the maximum principle, u(x, t x kt attains the maximum at the bottom or on the two sides When t, x kt x attains the maximum at x, ie, x When x, x kt kt attains
HOMEWORK 4 SHUANGLIN SHAO P45 # Proof By the maximum principle, u(x, t x kt attains the maximum at the bottom or on the two sides When t, x kt x attains the maximum at x, ie, x When x, x kt kt attains
Universal Post-quench Dynamics at a Quantum Critical Point
 Universal Post-quench Dynamics at a Quantum Critical Point Peter P. Orth University of Minnesota, Minneapolis, USA Rutgers University, 10 March 2016 References: P. Gagel, P. P. Orth, J. Schmalian Phys.
Universal Post-quench Dynamics at a Quantum Critical Point Peter P. Orth University of Minnesota, Minneapolis, USA Rutgers University, 10 March 2016 References: P. Gagel, P. P. Orth, J. Schmalian Phys.
ɛ(k) = h2 k 2 2m, k F = (3π 2 n) 1/3
 4D-XY Quantum Criticality in Underdoped High-T c cuprates M. Franz University of British Columbia franz@physics.ubc.ca February 22, 2005 In collaboration with: A.P. Iyengar (theory) D.P. Broun, D.A. Bonn
4D-XY Quantum Criticality in Underdoped High-T c cuprates M. Franz University of British Columbia franz@physics.ubc.ca February 22, 2005 In collaboration with: A.P. Iyengar (theory) D.P. Broun, D.A. Bonn
Universality of local spectral statistics of random matrices
 Universality of local spectral statistics of random matrices László Erdős Ludwig-Maximilians-Universität, Munich, Germany CRM, Montreal, Mar 19, 2012 Joint with P. Bourgade, B. Schlein, H.T. Yau, and J.
Universality of local spectral statistics of random matrices László Erdős Ludwig-Maximilians-Universität, Munich, Germany CRM, Montreal, Mar 19, 2012 Joint with P. Bourgade, B. Schlein, H.T. Yau, and J.
arxiv: v2 [cond-mat.dis-nn] 9 Feb 2011
![arxiv: v2 [cond-mat.dis-nn] 9 Feb 2011 arxiv: v2 [cond-mat.dis-nn] 9 Feb 2011](/thumbs/90/102203677.jpg) Level density and level-spacing distributions of random, self-adjoint, non-hermitian matrices Yogesh N. Joglekar and William A. Karr Department of Physics, Indiana University Purdue University Indianapolis
Level density and level-spacing distributions of random, self-adjoint, non-hermitian matrices Yogesh N. Joglekar and William A. Karr Department of Physics, Indiana University Purdue University Indianapolis
Models for measurement of thermophysical parameters
 Models for measurement of thermophysical parameters P. Dieška Department of Physics, STU FEI Ilkovičova 3, 812 19 Bratislava, Slovakia October 16, 2008 44 Model as a image of real experiment Heat equation:
Models for measurement of thermophysical parameters P. Dieška Department of Physics, STU FEI Ilkovičova 3, 812 19 Bratislava, Slovakia October 16, 2008 44 Model as a image of real experiment Heat equation:
Charge transport in oxides and metalinsulator
 Charge transport in oxides and metalinsulator transitions M. Gabay School on modern topics in Condensed matter Singapore, 28/01 8/02 2013 Down the rabbit hole Scaling down impacts critical parameters of
Charge transport in oxides and metalinsulator transitions M. Gabay School on modern topics in Condensed matter Singapore, 28/01 8/02 2013 Down the rabbit hole Scaling down impacts critical parameters of
Progress in Gauge-Higgs Unification on the Lattice
 Progress in Gauge-Higgs Unification on the Lattice Kyoko Yoneyama (Wuppertal University) in collaboration with Francesco Knechtli(Wuppertal University) ikos Irges(ational Technical University of Athens)
Progress in Gauge-Higgs Unification on the Lattice Kyoko Yoneyama (Wuppertal University) in collaboration with Francesco Knechtli(Wuppertal University) ikos Irges(ational Technical University of Athens)
Anderson Localization Looking Forward
 Anderson Localization Looking Forward Boris Altshuler Physics Department, Columbia University Collaborations: Also Igor Aleiner Denis Basko, Gora Shlyapnikov, Vincent Michal, Vladimir Kravtsov, Lecture2
Anderson Localization Looking Forward Boris Altshuler Physics Department, Columbia University Collaborations: Also Igor Aleiner Denis Basko, Gora Shlyapnikov, Vincent Michal, Vladimir Kravtsov, Lecture2
ORIGINS. E.P. Wigner, Conference on Neutron Physics by Time of Flight, November 1956
 ORIGINS E.P. Wigner, Conference on Neutron Physics by Time of Flight, November 1956 P.W. Anderson, Absence of Diffusion in Certain Random Lattices ; Phys.Rev., 1958, v.109, p.1492 L.D. Landau, Fermi-Liquid
ORIGINS E.P. Wigner, Conference on Neutron Physics by Time of Flight, November 1956 P.W. Anderson, Absence of Diffusion in Certain Random Lattices ; Phys.Rev., 1958, v.109, p.1492 L.D. Landau, Fermi-Liquid
Introduction - Motivation. Many phenomena (physical, chemical, biological, etc.) are model by differential equations. f f(x + h) f(x) (x) = lim
 Introduction - Motivation Many phenomena (physical, chemical, biological, etc.) are model by differential equations. Recall the definition of the derivative of f(x) f f(x + h) f(x) (x) = lim. h 0 h Its
Introduction - Motivation Many phenomena (physical, chemical, biological, etc.) are model by differential equations. Recall the definition of the derivative of f(x) f f(x + h) f(x) (x) = lim. h 0 h Its
Matrix-valued stochastic processes
 Matrix-valued stochastic processes and applications Małgorzata Snarska (Cracow University of Economics) Grodek, February 2017 M. Snarska (UEK) Matrix Diffusion Grodek, February 2017 1 / 18 Outline 1 Introduction
Matrix-valued stochastic processes and applications Małgorzata Snarska (Cracow University of Economics) Grodek, February 2017 M. Snarska (UEK) Matrix Diffusion Grodek, February 2017 1 / 18 Outline 1 Introduction
1.1 A Scattering Experiment
 1 Transfer Matrix In this chapter we introduce and discuss a mathematical method for the analysis of the wave propagation in one-dimensional systems. The method uses the transfer matrix and is commonly
1 Transfer Matrix In this chapter we introduce and discuss a mathematical method for the analysis of the wave propagation in one-dimensional systems. The method uses the transfer matrix and is commonly
Calculus II Practice Test Questions for Chapter , 9.6, Page 1 of 9
 Calculus II Practice Test Questions for Chapter 9.1 9.4, 9.6, 10.1 10.4 Page 1 of 9 This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for
Calculus II Practice Test Questions for Chapter 9.1 9.4, 9.6, 10.1 10.4 Page 1 of 9 This is in no way an inclusive set of problems there can be other types of problems on the actual test. To prepare for
Schur parametrizations of stable all-pass discrete-time systems and balanced realizations. Application to rational L 2 approximation.
 Schur parametrizations of stable all-pass discrete-time systems and balanced realizations. Application to rational L 2 approximation. Martine Olivi INRIA, Sophia Antipolis 12 Mai 2004 1 Outline. Introduction
Schur parametrizations of stable all-pass discrete-time systems and balanced realizations. Application to rational L 2 approximation. Martine Olivi INRIA, Sophia Antipolis 12 Mai 2004 1 Outline. Introduction
Local semicircle law, Wegner estimate and level repulsion for Wigner random matrices
 Local semicircle law, Wegner estimate and level repulsion for Wigner random matrices László Erdős University of Munich Oberwolfach, 2008 Dec Joint work with H.T. Yau (Harvard), B. Schlein (Cambrigde) Goal:
Local semicircle law, Wegner estimate and level repulsion for Wigner random matrices László Erdős University of Munich Oberwolfach, 2008 Dec Joint work with H.T. Yau (Harvard), B. Schlein (Cambrigde) Goal:
MIT Term Project: Numerical Experiments on Circular Ensembles and Jack Polynomials with Julia
 MIT 18.338 Term Project: Numerical Experiments on Circular Ensembles and Jack Polynomials with Julia N. Kemal Ure May 15, 2013 Abstract This project studies the numerical experiments related to averages
MIT 18.338 Term Project: Numerical Experiments on Circular Ensembles and Jack Polynomials with Julia N. Kemal Ure May 15, 2013 Abstract This project studies the numerical experiments related to averages
Disordered topological insulators with time-reversal symmetry: Z 2 invariants
 Keio Topo. Science (2016/11/18) Disordered topological insulators with time-reversal symmetry: Z 2 invariants Hosho Katsura Department of Physics, UTokyo Collaborators: Yutaka Akagi (UTokyo) Tohru Koma
Keio Topo. Science (2016/11/18) Disordered topological insulators with time-reversal symmetry: Z 2 invariants Hosho Katsura Department of Physics, UTokyo Collaborators: Yutaka Akagi (UTokyo) Tohru Koma
Quantum Billiards. Martin Sieber (Bristol) Postgraduate Research Conference: Mathematical Billiard and their Applications
 Quantum Billiards Martin Sieber (Bristol) Postgraduate Research Conference: Mathematical Billiard and their Applications University of Bristol, June 21-24 2010 Most pictures are courtesy of Arnd Bäcker
Quantum Billiards Martin Sieber (Bristol) Postgraduate Research Conference: Mathematical Billiard and their Applications University of Bristol, June 21-24 2010 Most pictures are courtesy of Arnd Bäcker
Chaotic behavior of disordered nonlinear systems
 Chaotic behavior of disordered nonlinear systems Haris Skokos Department of Mathematics and Applied Mathematics, University of Cape Town Cape Town, South Africa E-mail: haris.skokos@uct.ac.za URL: http://math_research.uct.ac.za/~hskokos/
Chaotic behavior of disordered nonlinear systems Haris Skokos Department of Mathematics and Applied Mathematics, University of Cape Town Cape Town, South Africa E-mail: haris.skokos@uct.ac.za URL: http://math_research.uct.ac.za/~hskokos/
Geometric Dyson Brownian motion and May Wigner stability
 Geometric Dyson Brownian motion and May Wigner stability Jesper R. Ipsen University of Melbourne Summer school: Randomness in Physics and Mathematics 2 Bielefeld 2016 joint work with Henning Schomerus
Geometric Dyson Brownian motion and May Wigner stability Jesper R. Ipsen University of Melbourne Summer school: Randomness in Physics and Mathematics 2 Bielefeld 2016 joint work with Henning Schomerus
Interfaces with short-range correlated disorder: what we learn from the Directed Polymer
 Interfaces with short-range correlated disorder: what we learn from the Directed Polymer Elisabeth Agoritsas (1), Thierry Giamarchi (2) Vincent Démery (3), Alberto Rosso (4) Reinaldo García-García (3),
Interfaces with short-range correlated disorder: what we learn from the Directed Polymer Elisabeth Agoritsas (1), Thierry Giamarchi (2) Vincent Démery (3), Alberto Rosso (4) Reinaldo García-García (3),
Random Matrix Pencils, Branching Points, and Monodromy
 Random Matrix Pencils, Branching Points, and Monodromy Mathew Ellis, Ian Ford, Emily Heath, Christopher Linden, Mychael Sanchez, Dara Zirlin August, 5 Introduction We define complex projective n-space
Random Matrix Pencils, Branching Points, and Monodromy Mathew Ellis, Ian Ford, Emily Heath, Christopher Linden, Mychael Sanchez, Dara Zirlin August, 5 Introduction We define complex projective n-space
Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium
 Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium SEA 06@MIT, Workshop on Stochastic Eigen-Analysis and its Applications, MIT, Cambridge,
Universality of distribution functions in random matrix theory Arno Kuijlaars Katholieke Universiteit Leuven, Belgium SEA 06@MIT, Workshop on Stochastic Eigen-Analysis and its Applications, MIT, Cambridge,
Eigenvalue spectra of time-lagged covariance matrices: Possibilities for arbitrage?
 Eigenvalue spectra of time-lagged covariance matrices: Possibilities for arbitrage? Stefan Thurner www.complex-systems.meduniwien.ac.at www.santafe.edu London July 28 Foundations of theory of financial
Eigenvalue spectra of time-lagged covariance matrices: Possibilities for arbitrage? Stefan Thurner www.complex-systems.meduniwien.ac.at www.santafe.edu London July 28 Foundations of theory of financial
Valerio Cappellini. References
 CETER FOR THEORETICAL PHYSICS OF THE POLISH ACADEMY OF SCIECES WARSAW, POLAD RADOM DESITY MATRICES AD THEIR DETERMIATS 4 30 SEPTEMBER 5 TH SFB TR 1 MEETIG OF 006 I PRZEGORZAłY KRAKÓW Valerio Cappellini
CETER FOR THEORETICAL PHYSICS OF THE POLISH ACADEMY OF SCIECES WARSAW, POLAD RADOM DESITY MATRICES AD THEIR DETERMIATS 4 30 SEPTEMBER 5 TH SFB TR 1 MEETIG OF 006 I PRZEGORZAłY KRAKÓW Valerio Cappellini
ARBITRARY ROTATION INVARIANT RANDOM MATRIX ENSEMBLES HUBBARD-STRATONOVITCH TRANSFORMATION VERSUS SUPERBOSONIZATION. Mario Kieburg.
 ARBITRARY ROTATION INVARIANT RANDOM MATRIX ENSEMBLES: HUBBARD-STRATONOVITCH TRANSFORMATION VERSUS SUPERBOSONIZATION Mario Kieburg Universität Duisburg-Essen Mexico, Cuernavaca, March 2009 supported by
ARBITRARY ROTATION INVARIANT RANDOM MATRIX ENSEMBLES: HUBBARD-STRATONOVITCH TRANSFORMATION VERSUS SUPERBOSONIZATION Mario Kieburg Universität Duisburg-Essen Mexico, Cuernavaca, March 2009 supported by
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
Weak Ergodicity Breaking
 Weak Ergodicity Breaking Eli Barkai Bar-Ilan University 215 Ergodicity Ergodicity: time averages = ensemble averages. x = lim t t x(τ)dτ t. x = xp eq (x)dx. Ergodicity out of equilibrium δ 2 (, t) = t
Weak Ergodicity Breaking Eli Barkai Bar-Ilan University 215 Ergodicity Ergodicity: time averages = ensemble averages. x = lim t t x(τ)dτ t. x = xp eq (x)dx. Ergodicity out of equilibrium δ 2 (, t) = t
The effect of spin in the spectral statistics of quantum graphs
 The effect of spin in the of quantum graphs J. M. Harrison and J. Bolte Baylor University, Royal Holloway Banff 28th February 08 Outline Random matrix theory 2 Pauli op. on graphs 3 Motivation Bohigas-Gianonni-Schmit
The effect of spin in the of quantum graphs J. M. Harrison and J. Bolte Baylor University, Royal Holloway Banff 28th February 08 Outline Random matrix theory 2 Pauli op. on graphs 3 Motivation Bohigas-Gianonni-Schmit
Chaos in disordered nonlinear lattices
 Chaos in disordered nonlinear lattices Haris Skokos Physics Department, Aristotle University of Thessaloniki Thessaloniki, Greece E-mail: hskokos@auth.gr URL: http://users.auth.gr/hskokos/ Work in collaboration
Chaos in disordered nonlinear lattices Haris Skokos Physics Department, Aristotle University of Thessaloniki Thessaloniki, Greece E-mail: hskokos@auth.gr URL: http://users.auth.gr/hskokos/ Work in collaboration
Vector-Valued Functions
 Vector-Valued Functions 1 Parametric curves 8 ' 1 6 1 4 8 1 6 4 1 ' 4 6 8 Figure 1: Which curve is a graph of a function? 1 4 6 8 1 8 1 6 4 1 ' 4 6 8 Figure : A graph of a function: = f() 8 ' 1 6 4 1 1
Vector-Valued Functions 1 Parametric curves 8 ' 1 6 1 4 8 1 6 4 1 ' 4 6 8 Figure 1: Which curve is a graph of a function? 1 4 6 8 1 8 1 6 4 1 ' 4 6 8 Figure : A graph of a function: = f() 8 ' 1 6 4 1 1
PhD in Theoretical Particle Physics Academic Year 2017/2018
 July 10, 017 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 017/018 S olve two among the four problems presented. Problem I Consider a quantum harmonic oscillator in one spatial
July 10, 017 SISSA Entrance Examination PhD in Theoretical Particle Physics Academic Year 017/018 S olve two among the four problems presented. Problem I Consider a quantum harmonic oscillator in one spatial
can be moved in energy/momentum but not individually destroyed; in general: topological Fermi surfaces
 nodes protected against gapping can be moved in energy/momentum but not individually destroyed; in general: topological Fermi surfaces physical realization: stacked 2d topological insulators C=1 3d top
nodes protected against gapping can be moved in energy/momentum but not individually destroyed; in general: topological Fermi surfaces physical realization: stacked 2d topological insulators C=1 3d top
1 Intro to RMT (Gene)
 M705 Spring 2013 Summary for Week 2 1 Intro to RMT (Gene) (Also see the Anderson - Guionnet - Zeitouni book, pp.6-11(?) ) We start with two independent families of R.V.s, {Z i,j } 1 i
M705 Spring 2013 Summary for Week 2 1 Intro to RMT (Gene) (Also see the Anderson - Guionnet - Zeitouni book, pp.6-11(?) ) We start with two independent families of R.V.s, {Z i,j } 1 i
Stochastic Differential Equations Related to Soft-Edge Scaling Limit
 Stochastic Differential Equations Related to Soft-Edge Scaling Limit Hideki Tanemura Chiba univ. (Japan) joint work with Hirofumi Osada (Kyushu Unv.) 2012 March 29 Hideki Tanemura (Chiba univ.) () SDEs
Stochastic Differential Equations Related to Soft-Edge Scaling Limit Hideki Tanemura Chiba univ. (Japan) joint work with Hirofumi Osada (Kyushu Unv.) 2012 March 29 Hideki Tanemura (Chiba univ.) () SDEs
Introduction to Theory of Mesoscopic Systems
 Introduction to Theory of Mesoscopic Systems Boris Altshuler Princeton University, Columbia University & NEC Laboratories America Lecture 3 Beforehand Weak Localization and Mesoscopic Fluctuations Today
Introduction to Theory of Mesoscopic Systems Boris Altshuler Princeton University, Columbia University & NEC Laboratories America Lecture 3 Beforehand Weak Localization and Mesoscopic Fluctuations Today
PH1105 Lecture Notes on Linear Algebra.
 PH05 Lecture Notes on Linear Algebra Joe Ó hógáin E-mail: johog@mathstcdie Main Text: Calculus for the Life Sciences by Bittenger, Brand and Quintanilla Other Text: Linear Algebra by Anton and Rorres Matrices
PH05 Lecture Notes on Linear Algebra Joe Ó hógáin E-mail: johog@mathstcdie Main Text: Calculus for the Life Sciences by Bittenger, Brand and Quintanilla Other Text: Linear Algebra by Anton and Rorres Matrices
Asymptotic Behavior of the Random 3-Regular Bipartite Graph
 Asymptotic Behavior of the Random 3-Regular Bipartite Graph Tim Novikoff Courant Institute New York University, 10012 December 17,2002 Abstract In 2001, two numerical experiments were performed to observe
Asymptotic Behavior of the Random 3-Regular Bipartite Graph Tim Novikoff Courant Institute New York University, 10012 December 17,2002 Abstract In 2001, two numerical experiments were performed to observe
Various Facets of Chalker- Coddington network model
 Various Facets of Chalker- Coddington network model V. Kagalovsky Sami Shamoon College of Engineering Beer-Sheva Israel Context Integer quantum Hall effect Semiclassical picture Chalker-Coddington Coddington
Various Facets of Chalker- Coddington network model V. Kagalovsky Sami Shamoon College of Engineering Beer-Sheva Israel Context Integer quantum Hall effect Semiclassical picture Chalker-Coddington Coddington
Theory of Quantum Transport in Graphene and Nanotubes II
 CARGESE7B.OHP (August 26, 27) Theory of Quantum Transport in Graphene and Nanotubes II 1. Introduction Weyl s equation for neutrino 2. Berry s phase and topological anomaly Absence of backscattering in
CARGESE7B.OHP (August 26, 27) Theory of Quantum Transport in Graphene and Nanotubes II 1. Introduction Weyl s equation for neutrino 2. Berry s phase and topological anomaly Absence of backscattering in
Travelling waves. Chapter 8. 1 Introduction
 Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
Chapter 8 Travelling waves 1 Introduction One of the cornerstones in the study of both linear and nonlinear PDEs is the wave propagation. A wave is a recognizable signal which is transferred from one part
PH.D. PRELIMINARY EXAMINATION MATHEMATICS
 UNIVERSITY OF CALIFORNIA, BERKELEY SPRING SEMESTER 207 Dept. of Civil and Environmental Engineering Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
UNIVERSITY OF CALIFORNIA, BERKELEY SPRING SEMESTER 207 Dept. of Civil and Environmental Engineering Structural Engineering, Mechanics and Materials NAME PH.D. PRELIMINARY EXAMINATION MATHEMATICS Problem
c 2005 Society for Industrial and Applied Mathematics
 SIAM J. MATRIX ANAL. APPL. Vol. XX, No. X, pp. XX XX c 005 Society for Industrial and Applied Mathematics DISTRIBUTIONS OF THE EXTREME EIGENVALUES OF THE COMPLEX JACOBI RANDOM MATRIX ENSEMBLE PLAMEN KOEV
SIAM J. MATRIX ANAL. APPL. Vol. XX, No. X, pp. XX XX c 005 Society for Industrial and Applied Mathematics DISTRIBUTIONS OF THE EXTREME EIGENVALUES OF THE COMPLEX JACOBI RANDOM MATRIX ENSEMBLE PLAMEN KOEV
Section 9.2: Matrices. Definition: A matrix A consists of a rectangular array of numbers, or elements, arranged in m rows and n columns.
 Section 9.2: Matrices Definition: A matrix A consists of a rectangular array of numbers, or elements, arranged in m rows and n columns. That is, a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn A
Section 9.2: Matrices Definition: A matrix A consists of a rectangular array of numbers, or elements, arranged in m rows and n columns. That is, a 11 a 12 a 1n a 21 a 22 a 2n A =...... a m1 a m2 a mn A
Random Matrix Theory and Quantum Transport
 Random Matrix Theory and Quantum Transport S.M. Kravec, E.V. Calman, A.P. Kuczala 1 1 Department of Physics, University of California at San Diego, La Jolla, CA 9093 We review the basics of random matrix
Random Matrix Theory and Quantum Transport S.M. Kravec, E.V. Calman, A.P. Kuczala 1 1 Department of Physics, University of California at San Diego, La Jolla, CA 9093 We review the basics of random matrix
Chapter 29. Quantum Chaos
 Chapter 29 Quantum Chaos What happens to a Hamiltonian system that for classical mechanics is chaotic when we include a nonzero h? There is no problem in principle to answering this question: given a classical
Chapter 29 Quantum Chaos What happens to a Hamiltonian system that for classical mechanics is chaotic when we include a nonzero h? There is no problem in principle to answering this question: given a classical
Constructing a sigma model from semiclassics
 Constructing a sigma model from semiclassics In collaboration with: Alexander Altland, Petr Braun, Fritz Haake, Stefan Heusler Sebastian Müller Approaches to spectral statistics Semiclassics Approaches
Constructing a sigma model from semiclassics In collaboration with: Alexander Altland, Petr Braun, Fritz Haake, Stefan Heusler Sebastian Müller Approaches to spectral statistics Semiclassics Approaches
Eigenvalue PDFs. Peter Forrester, M&S, University of Melbourne
 Outline Eigenvalue PDFs Peter Forrester, M&S, University of Melbourne Hermitian matrices with real, complex or real quaternion elements Circular ensembles and classical groups Products of random matrices
Outline Eigenvalue PDFs Peter Forrester, M&S, University of Melbourne Hermitian matrices with real, complex or real quaternion elements Circular ensembles and classical groups Products of random matrices
2.1 Definition and general properties
 Chapter 2 Gaussian states Gaussian states are at the heart of quantum information processing with continuous variables. The basic reason is that the vacuum state of quantum electrodynamics is itself a
Chapter 2 Gaussian states Gaussian states are at the heart of quantum information processing with continuous variables. The basic reason is that the vacuum state of quantum electrodynamics is itself a
arxiv:cond-mat/ v1 [cond-mat.stat-mech] 13 Mar 2003
![arxiv:cond-mat/ v1 [cond-mat.stat-mech] 13 Mar 2003 arxiv:cond-mat/ v1 [cond-mat.stat-mech] 13 Mar 2003](/thumbs/86/94456714.jpg) arxiv:cond-mat/0303262v1 [cond-mat.stat-mech] 13 Mar 2003 Quantum fluctuations and random matrix theory Maciej M. Duras Institute of Physics, Cracow University of Technology, ulica Podchor ażych 1, PL-30084
arxiv:cond-mat/0303262v1 [cond-mat.stat-mech] 13 Mar 2003 Quantum fluctuations and random matrix theory Maciej M. Duras Institute of Physics, Cracow University of Technology, ulica Podchor ażych 1, PL-30084
Superconducting fluctuations, interactions and disorder : a subtle alchemy
 Les défis actuels de la supraconductivité Dautreppe 2011 Superconducting fluctuations, interactions and disorder : a subtle alchemy Claude Chapelier, Benjamin Sacépé, Thomas Dubouchet INAC-SPSMS-LaTEQS,
Les défis actuels de la supraconductivité Dautreppe 2011 Superconducting fluctuations, interactions and disorder : a subtle alchemy Claude Chapelier, Benjamin Sacépé, Thomas Dubouchet INAC-SPSMS-LaTEQS,
Anomalous wave transport in one-dimensional systems with. Lévy disorder
 Anomalous wave transport in one-dimensional systems with Lévy disorder Xujun Ma,2 and Azriel Z. Genack,2 Department of Physics, Queens College of the City University of New York, Flushing, NY, 367 USA
Anomalous wave transport in one-dimensional systems with Lévy disorder Xujun Ma,2 and Azriel Z. Genack,2 Department of Physics, Queens College of the City University of New York, Flushing, NY, 367 USA
Things you should have learned in Calculus II
 Things you should have learned in Calculus II 1 Vectors Given vectors v = v 1, v 2, v 3, u = u 1, u 2, u 3 1.1 Common Operations Operations Notation How is it calculated Other Notation Dot Product v u
Things you should have learned in Calculus II 1 Vectors Given vectors v = v 1, v 2, v 3, u = u 1, u 2, u 3 1.1 Common Operations Operations Notation How is it calculated Other Notation Dot Product v u
Mathematical Techniques: Revision Notes
 Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Mass Components of Mesons from Lattice QCD
 Mass Components of Mesons from Lattice QCD Ying Chen In collaborating with: Y.-B. Yang, M. Gong, K.-F. Liu, T. Draper, Z. Liu, J.-P. Ma, etc. Peking University, Nov. 28, 2013 Outline I. Motivation II.
Mass Components of Mesons from Lattice QCD Ying Chen In collaborating with: Y.-B. Yang, M. Gong, K.-F. Liu, T. Draper, Z. Liu, J.-P. Ma, etc. Peking University, Nov. 28, 2013 Outline I. Motivation II.
The Derivative of a Function Measuring Rates of Change of a function. Secant line. f(x) f(x 0 ) Average rate of change of with respect to over,
 The Derivative of a Function Measuring Rates of Change of a function y f(x) f(x 0 ) P Q Secant line x 0 x x Average rate of change of with respect to over, " " " " - Slope of secant line through, and,
The Derivative of a Function Measuring Rates of Change of a function y f(x) f(x 0 ) P Q Secant line x 0 x x Average rate of change of with respect to over, " " " " - Slope of secant line through, and,
Engg. Math. I. Unit-I. Differential Calculus
 Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Purely electronic transport in dirty boson insulators
 Purely electronic transport in dirty boson insulators Markus Müller Ann. Phys. (Berlin) 18, 849 (2009). Discussions with M. Feigel man, M.P.A. Fisher, L. Ioffe, V. Kravtsov, Abdus Salam International Center
Purely electronic transport in dirty boson insulators Markus Müller Ann. Phys. (Berlin) 18, 849 (2009). Discussions with M. Feigel man, M.P.A. Fisher, L. Ioffe, V. Kravtsov, Abdus Salam International Center
Reading: Chapter 28. 4πε r. For r > a. Gauss s Law
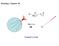 Reading: Chapter 8 Q 4πε r o k Q r e For r > a Gauss s Law 1 Chapter 8 Gauss s Law lectric Flux Definition: lectric flux is the product of the magnitude of the electric field and the surface area, A, perpendicular
Reading: Chapter 8 Q 4πε r o k Q r e For r > a Gauss s Law 1 Chapter 8 Gauss s Law lectric Flux Definition: lectric flux is the product of the magnitude of the electric field and the surface area, A, perpendicular
Spreading mechanism of wave packets in one dimensional disordered Klein-Gordon chains
 Spreading mechanism of wave packets in one dimensional disordered Klein-Gordon chains Haris Skokos Max Planck Institute for the Physics of Complex Systems Dresden, Germany E-mail: hskokos@pks.mpg.de URL:
Spreading mechanism of wave packets in one dimensional disordered Klein-Gordon chains Haris Skokos Max Planck Institute for the Physics of Complex Systems Dresden, Germany E-mail: hskokos@pks.mpg.de URL:
Lecture 8 Nature of ensemble: Role of symmetry, interactions and other system conditions: Part II
 Lecture 8 Nature of ensemble: Role of symmetry, interactions and other system conditions: Part II We continue our discussion of symmetries and their role in matrix representation in this lecture. An example
Lecture 8 Nature of ensemble: Role of symmetry, interactions and other system conditions: Part II We continue our discussion of symmetries and their role in matrix representation in this lecture. An example
The dynamics of small particles whose size is roughly 1 µmt or. smaller, in a fluid at room temperature, is extremely erratic, and is
 1 I. BROWNIAN MOTION The dynamics of small particles whose size is roughly 1 µmt or smaller, in a fluid at room temperature, is extremely erratic, and is called Brownian motion. The velocity of such particles
1 I. BROWNIAN MOTION The dynamics of small particles whose size is roughly 1 µmt or smaller, in a fluid at room temperature, is extremely erratic, and is called Brownian motion. The velocity of such particles
Important Matrix Factorizations
 LU Factorization Choleski Factorization The QR Factorization LU Factorization: Gaussian Elimination Matrices Gaussian elimination transforms vectors of the form a α, b where a R k, 0 α R, and b R n k 1,
LU Factorization Choleski Factorization The QR Factorization LU Factorization: Gaussian Elimination Matrices Gaussian elimination transforms vectors of the form a α, b where a R k, 0 α R, and b R n k 1,
Effective Actions Approach for Improving Numerical Calculation of Path Integrals
 Effective Actions Approach for Improving Numerical Calculation of Path Integrals A. Balaž, A. Bogojević, I. Vidanović, A. Belić Scientific Computing Laboratory Institute of Physics Belgrade Pregrevica
Effective Actions Approach for Improving Numerical Calculation of Path Integrals A. Balaž, A. Bogojević, I. Vidanović, A. Belić Scientific Computing Laboratory Institute of Physics Belgrade Pregrevica
Large Petermann factor in chaotic cavities with many scattering channels
 EUROPHYSICS LETTERS January 2000 Europhys. Lett., 49 (), pp. 48 54 (2000) Large Petermann factor in chaotic cavities with many scattering channels K. M. Frahm, H. Schomerus 2,M.Patra 2 and C. W. J. Beenakker
EUROPHYSICS LETTERS January 2000 Europhys. Lett., 49 (), pp. 48 54 (2000) Large Petermann factor in chaotic cavities with many scattering channels K. M. Frahm, H. Schomerus 2,M.Patra 2 and C. W. J. Beenakker
Chapter 2 Superconducting Gap Structure and Magnetic Penetration Depth
 Chapter 2 Superconducting Gap Structure and Magnetic Penetration Depth Abstract The BCS theory proposed by J. Bardeen, L. N. Cooper, and J. R. Schrieffer in 1957 is the first microscopic theory of superconductivity.
Chapter 2 Superconducting Gap Structure and Magnetic Penetration Depth Abstract The BCS theory proposed by J. Bardeen, L. N. Cooper, and J. R. Schrieffer in 1957 is the first microscopic theory of superconductivity.
Inner products and Norms. Inner product of 2 vectors. Inner product of 2 vectors x and y in R n : x 1 y 1 + x 2 y x n y n in R n
 Inner products and Norms Inner product of 2 vectors Inner product of 2 vectors x and y in R n : x 1 y 1 + x 2 y 2 + + x n y n in R n Notation: (x, y) or y T x For complex vectors (x, y) = x 1 ȳ 1 + x 2
Inner products and Norms Inner product of 2 vectors Inner product of 2 vectors x and y in R n : x 1 y 1 + x 2 y 2 + + x n y n in R n Notation: (x, y) or y T x For complex vectors (x, y) = x 1 ȳ 1 + x 2
8.513 Lecture 14. Coherent backscattering Weak localization Aharonov-Bohm effect
 8.513 Lecture 14 Coherent backscattering Weak localization Aharonov-Bohm effect Light diffusion; Speckle patterns; Speckles in coherent backscattering phase-averaged Coherent backscattering Contribution
8.513 Lecture 14 Coherent backscattering Weak localization Aharonov-Bohm effect Light diffusion; Speckle patterns; Speckles in coherent backscattering phase-averaged Coherent backscattering Contribution
Zonal Polynomials and Hypergeometric Functions of Matrix Argument. Zonal Polynomials and Hypergeometric Functions of Matrix Argument p.
 Zonal Polynomials and Hypergeometric Functions of Matrix Argument Zonal Polynomials and Hypergeometric Functions of Matrix Argument p. 1/2 Zonal Polynomials and Hypergeometric Functions of Matrix Argument
Zonal Polynomials and Hypergeometric Functions of Matrix Argument Zonal Polynomials and Hypergeometric Functions of Matrix Argument p. 1/2 Zonal Polynomials and Hypergeometric Functions of Matrix Argument
Boolean Inner-Product Spaces and Boolean Matrices
 Boolean Inner-Product Spaces and Boolean Matrices Stan Gudder Department of Mathematics, University of Denver, Denver CO 80208 Frédéric Latrémolière Department of Mathematics, University of Denver, Denver
Boolean Inner-Product Spaces and Boolean Matrices Stan Gudder Department of Mathematics, University of Denver, Denver CO 80208 Frédéric Latrémolière Department of Mathematics, University of Denver, Denver
Non-equilibrium time evolution of bosons from the functional renormalization group
 March 14, 2013, Condensed Matter Journal Club University of Florida at Gainesville Non-equilibrium time evolution of bosons from the functional renormalization group Peter Kopietz, Universität Frankfurt
March 14, 2013, Condensed Matter Journal Club University of Florida at Gainesville Non-equilibrium time evolution of bosons from the functional renormalization group Peter Kopietz, Universität Frankfurt
Lectures 6 7 : Marchenko-Pastur Law
 Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
Optical Imaging Chapter 5 Light Scattering
 Optical Imaging Chapter 5 Light Scattering Gabriel Popescu University of Illinois at Urbana-Champaign Beckman Institute Quantitative Light Imaging Laboratory http://light.ece.uiuc.edu Principles of Optical
Optical Imaging Chapter 5 Light Scattering Gabriel Popescu University of Illinois at Urbana-Champaign Beckman Institute Quantitative Light Imaging Laboratory http://light.ece.uiuc.edu Principles of Optical
Knudsen Diffusion and Random Billiards
 Knudsen Diffusion and Random Billiards R. Feres http://www.math.wustl.edu/ feres/publications.html November 11, 2004 Typeset by FoilTEX Gas flow in the Knudsen regime Random Billiards [1] Large Knudsen
Knudsen Diffusion and Random Billiards R. Feres http://www.math.wustl.edu/ feres/publications.html November 11, 2004 Typeset by FoilTEX Gas flow in the Knudsen regime Random Billiards [1] Large Knudsen
Hamiltonian Mechanics
 Chapter 3 Hamiltonian Mechanics 3.1 Convex functions As background to discuss Hamiltonian mechanics we discuss convexity and convex functions. We will also give some applications to thermodynamics. We
Chapter 3 Hamiltonian Mechanics 3.1 Convex functions As background to discuss Hamiltonian mechanics we discuss convexity and convex functions. We will also give some applications to thermodynamics. We
