Random Matrix Pencils, Branching Points, and Monodromy
|
|
|
- Cameron Day
- 5 years ago
- Views:
Transcription
1 Random Matrix Pencils, Branching Points, and Monodromy Mathew Ellis, Ian Ford, Emily Heath, Christopher Linden, Mychael Sanchez, Dara Zirlin August, 5 Introduction We define complex projective n-space CP n as C n+ \ {} under the equivalence relation (z : z :... : z n ) (cz : cz :... : cz n ) where c C \ {}. A complex projective curve is then the set of points (a : a :... : a n ) CP n such that p(a, a,..., a n ) = for a fixed complex homogeneous polynomial p(z, z,..., z n ). Such a curve is a -dimensional, real, orientable Riemannian manifold, or Riemann surface. For a non-constant holomorphic map f : X Y between compact, connected Riemann surfaces X and Y, f is locally a covering map. The preimage f (p) of a point p Y generally consists of d distinct points, where d is the degree of the map f. If the preimage f (p) consists of fewer than d distinct points, p is called a branching point of the map f. In appropriate local coordinates at each point x f (p), the map f looks like z z k for some positive integer k Z + called the ramification index of x. A branching point p is called simple if some point x f (p) has ramification index and the rest have index. Let br(f) be the set of branching points of f and fix a base point y Y which is not a branching point. Each loop in Y \ br(f) with base point y lifts to d distinct paths in X with endpoints in f (y), and thus we get a group homomorphism from the fundamental group π (Y \ br(f)) to the symmetric group S f (y) S d called the monodromy. The image of a simple branching point is a transposition, and the image of br(f) is called the monodromy group. For complex n n matrices A and B, define the characteristic polynomial χ(t, λ) = det(a + tb + λi). By considering the homogenized polynomial χ(t, λ, z) = z n χ(t/z, λ/z), let R be the zero set of χ in CP. Let f : R CP be the projection onto the t-coordinate. The branching points of this map are precisely the values of t such that A + tb has repeated eigenvalues. In this project, we studied the distribution of the branching points of this map where A and B are random matrices sampled from the Gaussian Orthogonal Ensemble GOE n or from the Gaussian Unitary Ensemble GUE n and investigate the monodromy of each.
2 Distributions of Branching Points We consider two probability spaces of random matrices, the Gaussian Orthogonal Ensemble GOE n and the Gaussian Unitary Ensemble GUE n, so named because their distributions are invariant under conjugation by orthogonal and unitary matrices, respectively. The ensemble GOE n consists of real symmetric matrices X = (X ij ) n i,j= where the diagonal elements X ii, i n are independently sampled from the normal distribution N(, ) and the above-diagonal elements X ij, i < j n are independently sampled from the standard normal distribution N(, ). Similarly, GUE n consists of complex Hermitian matrices X = (X ij ) n i,j= where the diagonal elements X ii, i n are independently sampled from the standard normal distribution N(, ) and the real and imaginary parts of the above-diagonal elements X ij, i < j n are independently sampled from the normal distribution N(, ). In this section, we first calculate the distributions of the branching points for random matrix pencils of GUE and GOE matrices. Then, we present experimental results for the distributions of branching points for these ensembles for larger values of n, Finally, we explore symmetries of the distributions of the branching points for GOE n and GUE n which restrict the possible theoretical distributions for all n. The ensemble GUE n is invariant under conjugation by unitary matrices, so for GUE matrices A and B, we can conjugate A + tb with a unitary matrix( such that) A is diagonal. λ Therefore, we will assume that A is a diagonal matrix, i.e., A =. Notice that λ since A is diagonal, λ and λ are the eigenvalues of ( A. Without ) a loss of generality, λ < λ. Then, we can shift our matrix pencil so that A =, where = λ λ. We know that the branching points of our projection are exactly the zeroes of the discriminant of our characteristic polynomial χ(λ, t) = det(a + tb + λi) = t ((b b ) + b ) + t (b b ) +. Since this is a real polynomial, our branching points come in complex conjugate pairs (τ, τ) where τ = (b b ) + i b. (b b ) + b In order to find the distribution of τ, we will first find the conditional distribution of τ, assuming a constant value for. Set X = (b b ) and Y = b so that τ =. X Y i Since b, b N(, ), then b b N(, ), and hence, X N(, ). Therefore, the conditional PDF of X is P (x) = Since Re(b ), Im(b ) N(, e x / = π π e x /. ), then / b χ. Thus, the conditional PDF of Y is P (y) = y e y /. Taking the joint distribution of X and Y gives us the conditional distribution of. Since τ b is independent from b and b, then X and Y are also independent, so the conditional PDF of is the product of the PDFs of X and Y, τ
3 P (x, y) = P (x)p (y) = 3 π ye (x +y ) /. To find the conditional distribution for τ, we will change variables in order to write τ in X Y terms of its real and imaginary components. Set U = and V = so that X +Y X +Y τ = = U + V i. Then the Jacobian is (u,v) X Y i (x,y) = = (u + v ), so the conditional (x +y ) distribution for τ in terms of U and V is P (u, v) = P (x, y) (u,v) (x,y) = v 3 e /(u +v ) π(u + v ) 3. As U = Re(τ) and V = Im(τ), the conditional distribution of τ for a given value of is P (τ) = Im(τ) 3 e / τ π τ 6. So, in order to find the distribution of τ, we need the joint distribution for the eigenvalues λ and λ of matrices belonging to GUE, P(λ, λ ) = π (λ λ ) e (λ +λ)/. Therefore, the distribution for τ is P(τ) = = λ P(λ, λ )P (τ, τ) dλ dλ 8π (λ 3/ λ ) Im(τ) τ 6 λ 3 = 8Im(τ) π( + τ ) 3. e τ (λ +λ ) dλ dλ However, since we assumed that Im(τ) >, the distribution for τ over the whole plane is P(τ) = Im(τ) π( + τ ) 3. Using the same methods as above, we calculated the distribution of the branching points of GOE matrices. As in the previous case, τ = (b b ) +i b (b b ) + b = where X = b b X Y i and Y = b. Note that X N(, ) and Y χ. Thus, P (x) = P (y) = Letting U = Therefore, π e y 8. Therefore, P (x, y) = P (x)p (y) = X and V = Y so that τ = X +Y X +Y X iy P (u, v) = P (τ) = π(u + v ) e π τ e 3 (x +y ) π e 8. = U + iv, we get (u +v )8. 8 τ. π e x 8 and
4 The distribution of the eigenvalues of a GOE matrix is where λ λ. Thus, the distribution of τ is P(τ) = = P(λ, λ ) = λ π e + λ (λ λ ), λ π e + λ (λ λ ) π τ e λ π(+ τ ) 8 τ dλ dλ Since we were assuming that the imaginary part of τ is positive, to get the real PDF of τ we must divide by, so P(τ) = π(+ τ ). These theoretical results for the distributions of branching points for GUE and GOE are further supported by the experimental results which we gathered, shown in Figure. Notice that the distribution for the branching points of GOE is clearly the uniform distribution on the sphere. This realization led us to observe that SO acts on D n H n H n CP the ste of triples A, B, [u : v] such that [u : v] is a branch point of the pair A, B. SO acts on H n H n by ( α β β α and on CP by ( α β β α ) ( A B ) = ( αa + βb βa + αb ) ) [u : v] = [αu + βv : βu + αv] Observe that if φ [, π] and α = cos(φ), β = sin(φ), then [αu + βv : βu + αv] is a branch point of the pair αa + βb, βa + αb. Indeed, (αu + βv)(αa + βb) + ( βu + αv)( βa + αb) = α ua + αβva + αβub + β B + β ua αβub αβva + α vb = ua + vb. Hence SO acts on D n, and this action commutes with the projections π : D n H n H n and ζ : D n CP. Moreover, the action on H n H n preserves the densities of the GOE n and GUE n ensembles. These densities are given by C GOEn e n tr(m ) and C GUEn e n tr(m ) respectively, so the density of the pair A, B is determined by tr(a + B ) and tr((αa + βb) + ( βa + αb) ) = tr(α A + αβab + αβba + β B + β A αβab αβba + α B) = tr(a + B ).
5 Density Density Density Density Re(=) Re(=) Im(=) Im(=) Figure : The density of branching points for GUE on the left and GOE on the right. 5
6 ZESquared Z GOE ObservationENumber ObservationENumber Figure : The ordered values of z of the branching points of GUE n on the left and the ordered values of z of the branching points of GOE n matrices on the right, for n {,..., 6}. i p f(p) -i Figure 3: The circle action on GUE n and GOE n. 6
7 H n H n CP CP π ζ H n H n The density of the branching points in CP is given by the pushforward of the pullback of the density on H n H n. That is, the measure µ of a set E CP is given by µ(π(ζ (E)). µ(g E) = µ(π(ζ (g E))) = µ(π(g ζ (E))) = µ(g π(ζ (E))) = µ(π(ζ (E))) = µ(e), so we conclude that the densty of the branching points is invariant under this action by SO. Changing to cylindrical coordinates on CP, φ(a, B, (θ, z)) = (αa + βb, βa + αb, (θ φ, z)) so the action is a rotation of the sphere about the imaginary axis. Applying this change of coordinates to our distribution of the branching points of GUE, we get the distribution P(θ, z) = z, where θ π and z. Integrating over θ gives the marginal π PDF P(z) = z, therefore the CDF for z is z. We then found, branching points for GUE n matrices for each n {,..., 6} and plotted their corresponding z values in increasing order, shown in Figure. In the same way, our change of coordinates for the distribution of the branching points of GOE yields the distribution P(θ, z) =, where π θ π and z. Then, the marginal PDF of z is P(z) =, and integrating gives that the CDF for z is z. Plotting the z values of, branching points for GOE n matrices for each n {,..., 6}, as in Figure, suggests that the branching points of GOE n are uniformly distributed on the sphere for all n. 3 Monodromy For general A and B in GOE n, the branching points are all simple and come in complex conjugate pairs, ( n ) of which lie in the upper half plane. Let τ, τ,..., τ ( n be the branching points in the upper half plane ordered by real part. Since the branching points are ) simple, let σ, σ,..., σ ( n be the associated transpositions in the monodromy group. These ) transpositions (i) generate the symmetric group S n and (... n (ii) their product σ σ...σ ( n ) is n n... For n = 3, it is easy to see that there are only 8 words of ( n ) transpositions which satisfy (i) and (ii). For n =, we wrote a program to loop through all ( ) ( ) = 6, 656 such words and checked properties (i) and (ii). There are 387 words that satisfy (ii), which is easy to verify. For S, property (i) is equivalent to the word containing at least 3 distinct transpositions and the transpositions σ, σ,..., σ ( having no common fixed points. ) This check eliminates 3 words, for a total of 38 possible words. Next, we experimentally ) 7
8 Im(6) determined the frequency of the words that arise from the monodromy for matrices sampled from GOE 3, but we lacked the computational resources for n =. We wrote a short MATLAB program to compute the transposition associated to a branching point τ of a pair of matrices (A, B). The program calculates the eigenvalues of A + (Re(τ) + ɛim(τ))b as ɛ runs from to in steps of.. A typical plot of the eigenvalues during this process is shown in Figure. At ɛ = all of the eigenvalues are real, so we number them in increasing order. For each new ɛ, the new eigenvalues are assigned the same numbers as the closest eigenvalues from the previous ɛ. Then, when two eigenvalues collide at ɛ =, the numbers assigned to the two eigenvalues give the transposition for τ. By following this procedure for each of the branching points in the upper half plane, in order of increasing real part, as shown in Figure 5, we obtain the monodromy associated to (A, B). Because errors can occur if the real parts of different branching points are very similar, we rejected matrices with this property when gathering monodromy statistics. The resulting statistics for GUE 3 and GOE 3 matrices are shown in Figure 6 and 7, respectively Re(6) Figure : The first and second eigenvalues collide as we approach the branching point, giving the transposition (). Figure 5: Path which gives the transpostion sequence. 8
9 Probability Probability ()()(3) ()(3)(3) ()(3)() (3)()() (3)(3)(3) (3)()(3) (3)(3)() (3)(3)(3) Transposition Sequence Figure 6: The statistics for the monodromy of GUE 3 matrices ()()(3) ()(3)(3) ()(3)() (3)()() (3)(3)(3) (3)()(3) (3)(3)() (3)(3)(3) Transposition Sequence Figure 7: The statistics for the monodromy of GOE 3 matrices. 9
10 Notice that the statistics for the monodromy ( of GUE n and ) GOE n are invariant under... n conjugation by the inverse transposition as well as under reversing n n... the order of the transpositions. These symmetries can be explained as consequences of the symmetries of the ensembles. If the matrix A+tB has eigenvalues λ, λ,..., λ n, then the matrix A tb has eigenvalues λ, λ,... λ n. These matrix pencils share the same branching points, and if a loop in CP permutes the eigenvalues of A + tb, then it must apply the same permutation to the eigenvalues of A tb. However, when we compute the monodromy associated to a pair of matrices in our ensembles, we order the (real) eigenvalues for real t, and the transpositions associated to each branching point are written with respect to this ordering. Since the eigenvalues of A tb will have the opposite ordering as those of A + tb, the monodromy ( associated) to the pair ( A, B) will be the mondodromy of (A, B), conjugated... n by. Since the pairs (A, B) and ( A, B) have the same density, each n n... monodromy will appear with the same frequency as its conjugate. The other symmetry of the data, invariance under reversing the order of the transpositions, can be similarly explained by the equal density of the pairs (A, B) and (A, B). If the branching points of A + tb are τ, τ,...τ m, then the branching points of A tb are τ, τ,... τ m. Branching points come in conjugate pairs, and the same transpositions are associated to these pairs, so if τ, τ,...τ n are the branching points of A + tb in the upper half plane, τ, τ,... τ n are the branching points of A tb in the upper half plane. Since we order these by their real parts, which have been inverted, it now remains to show that the transposition associated to (A, B, τ i ) is the same as that associated to (A, B, τ i ). Since the transposition associated to a branching point is the same as that associated to its conjugate, we instead consider (A, B, τ i ). Observe that the transposition associated to (A, B, τ i ) is determined by the eigenvalues of A + (Re(τ i ) + ɛim(τ i ))B for ɛ, and in the same way the transposition asociated to (A, B, τ i ) is determined by A + (Re( τ i ) + ɛim( τ i ))( B) = A + (Re(τ i ) + ɛim(τ i ))B These coincide, and we conclude that the monodromy associated to (A, B) is the reverse of that associated to (A, B).
Random matrix pencils and level crossings
 Albeverio Fest October 1, 2018 Topics to discuss Basic level crossing problem 1 Basic level crossing problem 2 3 Main references Basic level crossing problem (i) B. Shapiro, M. Tater, On spectral asymptotics
Albeverio Fest October 1, 2018 Topics to discuss Basic level crossing problem 1 Basic level crossing problem 2 3 Main references Basic level crossing problem (i) B. Shapiro, M. Tater, On spectral asymptotics
On level crossing in deterministic and random matrix pencils
 On level crossing in deterministic and random matrix pencils May 3, 2018 Topics to discuss 1 Basic level crossing problem 2 3 4 Main references (i) B. Shapiro, M. Tater, On spectral asymptotics of quasi-exactly
On level crossing in deterministic and random matrix pencils May 3, 2018 Topics to discuss 1 Basic level crossing problem 2 3 4 Main references (i) B. Shapiro, M. Tater, On spectral asymptotics of quasi-exactly
Linear Algebra Review
 Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Chapter 1 Linear Algebra Review It is assumed that you have had a course in linear algebra, and are familiar with matrix multiplication, eigenvectors, etc. I will review some of these terms here, but quite
Linear Algebra. Workbook
 Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
Math 462: Homework 2 Solutions
 Math 46: Homework Solutions Paul Hacking /6/. Consider the matrix A = (a) Check that A is orthogonal. (b) Determine whether A is a rotation or a reflection / rotary reflection. [Hint: What is the determinant
Math 46: Homework Solutions Paul Hacking /6/. Consider the matrix A = (a) Check that A is orthogonal. (b) Determine whether A is a rotation or a reflection / rotary reflection. [Hint: What is the determinant
Foundations of Matrix Analysis
 1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
THE EULER CHARACTERISTIC OF A LIE GROUP
 THE EULER CHARACTERISTIC OF A LIE GROUP JAY TAYLOR 1 Examples of Lie Groups The following is adapted from [2] We begin with the basic definition and some core examples Definition A Lie group is a smooth
THE EULER CHARACTERISTIC OF A LIE GROUP JAY TAYLOR 1 Examples of Lie Groups The following is adapted from [2] We begin with the basic definition and some core examples Definition A Lie group is a smooth
Matrix Lie groups. and their Lie algebras. Mahmood Alaghmandan. A project in fulfillment of the requirement for the Lie algebra course
 Matrix Lie groups and their Lie algebras Mahmood Alaghmandan A project in fulfillment of the requirement for the Lie algebra course Department of Mathematics and Statistics University of Saskatchewan March
Matrix Lie groups and their Lie algebras Mahmood Alaghmandan A project in fulfillment of the requirement for the Lie algebra course Department of Mathematics and Statistics University of Saskatchewan March
Further Mathematical Methods (Linear Algebra)
 Further Mathematical Methods (Linear Algebra) Solutions For The 2 Examination Question (a) For a non-empty subset W of V to be a subspace of V we require that for all vectors x y W and all scalars α R:
Further Mathematical Methods (Linear Algebra) Solutions For The 2 Examination Question (a) For a non-empty subset W of V to be a subspace of V we require that for all vectors x y W and all scalars α R:
REPRESENTATION THEORY WEEK 7
 REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators.
 MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
MATH 423 Linear Algebra II Lecture 33: Diagonalization of normal operators. Adjoint operator and adjoint matrix Given a linear operator L on an inner product space V, the adjoint of L is a transformation
Math 215B: Solutions 1
 Math 15B: Solutions 1 Due Thursday, January 18, 018 (1) Let π : X X be a covering space. Let Φ be a smooth structure on X. Prove that there is a smooth structure Φ on X so that π : ( X, Φ) (X, Φ) is an
Math 15B: Solutions 1 Due Thursday, January 18, 018 (1) Let π : X X be a covering space. Let Φ be a smooth structure on X. Prove that there is a smooth structure Φ on X so that π : ( X, Φ) (X, Φ) is an
ACM 104. Homework Set 4 Solutions February 14, 2001
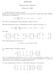 ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
Part II. Riemann Surfaces. Year
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 96 Paper 2, Section II 23F State the uniformisation theorem. List without proof the Riemann surfaces which are uniformised
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 96 Paper 2, Section II 23F State the uniformisation theorem. List without proof the Riemann surfaces which are uniformised
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial.
 MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial. Geometric properties of determinants 2 2 determinants and plane geometry
MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial. Geometric properties of determinants 2 2 determinants and plane geometry
Review of Linear Algebra Definitions, Change of Basis, Trace, Spectral Theorem
 Review of Linear Algebra Definitions, Change of Basis, Trace, Spectral Theorem Steven J. Miller June 19, 2004 Abstract Matrices can be thought of as rectangular (often square) arrays of numbers, or as
Review of Linear Algebra Definitions, Change of Basis, Trace, Spectral Theorem Steven J. Miller June 19, 2004 Abstract Matrices can be thought of as rectangular (often square) arrays of numbers, or as
Second Order Freeness and Random Orthogonal Matrices
 Second Order Freeness and Random Orthogonal Matrices Jamie Mingo (Queen s University) (joint work with Mihai Popa and Emily Redelmeier) AMS San Diego Meeting, January 11, 2013 1 / 15 Random Matrices X
Second Order Freeness and Random Orthogonal Matrices Jamie Mingo (Queen s University) (joint work with Mihai Popa and Emily Redelmeier) AMS San Diego Meeting, January 11, 2013 1 / 15 Random Matrices X
FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES
 FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES MARGARET NICHOLS 1. Introduction In this paper we study the complex structures which can occur on algebraic curves. The ideas discussed
FAMILIES OF ALGEBRAIC CURVES AS SURFACE BUNDLES OF RIEMANN SURFACES MARGARET NICHOLS 1. Introduction In this paper we study the complex structures which can occur on algebraic curves. The ideas discussed
Basic Concepts of Group Theory
 Chapter 1 Basic Concepts of Group Theory The theory of groups and vector spaces has many important applications in a number of branches of modern theoretical physics. These include the formal theory of
Chapter 1 Basic Concepts of Group Theory The theory of groups and vector spaces has many important applications in a number of branches of modern theoretical physics. These include the formal theory of
A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].
![A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3]. A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].](/thumbs/78/77913594.jpg) Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
1 Linear Algebra Problems
 Linear Algebra Problems. Let A be the conjugate transpose of the complex matrix A; i.e., A = A t : A is said to be Hermitian if A = A; real symmetric if A is real and A t = A; skew-hermitian if A = A and
Linear Algebra Problems. Let A be the conjugate transpose of the complex matrix A; i.e., A = A t : A is said to be Hermitian if A = A; real symmetric if A is real and A t = A; skew-hermitian if A = A and
DIFFERENTIAL GEOMETRY CLASS NOTES INSTRUCTOR: F. MARQUES. September 25, 2015
 DIFFERENTIAL GEOMETRY CLASS NOTES INSTRUCTOR: F. MARQUES MAGGIE MILLER September 25, 2015 1. 09/16/2015 1.1. Textbooks. Textbooks relevant to this class are Riemannian Geometry by do Carmo Riemannian Geometry
DIFFERENTIAL GEOMETRY CLASS NOTES INSTRUCTOR: F. MARQUES MAGGIE MILLER September 25, 2015 1. 09/16/2015 1.1. Textbooks. Textbooks relevant to this class are Riemannian Geometry by do Carmo Riemannian Geometry
NATIONAL BOARD FOR HIGHER MATHEMATICS. M. A. and M.Sc. Scholarship Test. September 24, Time Allowed: 150 Minutes Maximum Marks: 30
 NATIONAL BOARD FOR HIGHER MATHEMATICS M. A. and M.Sc. Scholarship Test September 24, 2011 Time Allowed: 150 Minutes Maximum Marks: 30 Please read, carefully, the instructions on the following page 1 INSTRUCTIONS
NATIONAL BOARD FOR HIGHER MATHEMATICS M. A. and M.Sc. Scholarship Test September 24, 2011 Time Allowed: 150 Minutes Maximum Marks: 30 Please read, carefully, the instructions on the following page 1 INSTRUCTIONS
6 Inner Product Spaces
 Lectures 16,17,18 6 Inner Product Spaces 6.1 Basic Definition Parallelogram law, the ability to measure angle between two vectors and in particular, the concept of perpendicularity make the euclidean space
Lectures 16,17,18 6 Inner Product Spaces 6.1 Basic Definition Parallelogram law, the ability to measure angle between two vectors and in particular, the concept of perpendicularity make the euclidean space
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 2010
 A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
RANDOM MATRIX THEORY AND TOEPLITZ DETERMINANTS
 RANDOM MATRIX THEORY AND TOEPLITZ DETERMINANTS David García-García May 13, 2016 Faculdade de Ciências da Universidade de Lisboa OVERVIEW Random Matrix Theory Introduction Matrix ensembles A sample computation:
RANDOM MATRIX THEORY AND TOEPLITZ DETERMINANTS David García-García May 13, 2016 Faculdade de Ciências da Universidade de Lisboa OVERVIEW Random Matrix Theory Introduction Matrix ensembles A sample computation:
Math Homework 8 (selected problems)
 Math 102 - Homework 8 (selected problems) David Lipshutz Problem 1. (Strang, 5.5: #14) In the list below, which classes of matrices contain A and which contain B? 1 1 1 1 A 0 0 1 0 0 0 0 1 and B 1 1 1
Math 102 - Homework 8 (selected problems) David Lipshutz Problem 1. (Strang, 5.5: #14) In the list below, which classes of matrices contain A and which contain B? 1 1 1 1 A 0 0 1 0 0 0 0 1 and B 1 1 1
Math 108b: Notes on the Spectral Theorem
 Math 108b: Notes on the Spectral Theorem From section 6.3, we know that every linear operator T on a finite dimensional inner product space V has an adjoint. (T is defined as the unique linear operator
Math 108b: Notes on the Spectral Theorem From section 6.3, we know that every linear operator T on a finite dimensional inner product space V has an adjoint. (T is defined as the unique linear operator
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Topic 1: Matrix diagonalization
 Topic : Matrix diagonalization Review of Matrices and Determinants Definition A matrix is a rectangular array of real numbers a a a m a A = a a m a n a n a nm The matrix is said to be of order n m if it
Topic : Matrix diagonalization Review of Matrices and Determinants Definition A matrix is a rectangular array of real numbers a a a m a A = a a m a n a n a nm The matrix is said to be of order n m if it
Progress in the method of Ghosts and Shadows for Beta Ensembles
 Progress in the method of Ghosts and Shadows for Beta Ensembles Alan Edelman (MIT) Alex Dubbs (MIT) and Plamen Koev (SJS) Oct 8, 2012 1/47 Wishart Matrices (arbitrary covariance) G=mxn matrix of Gaussians
Progress in the method of Ghosts and Shadows for Beta Ensembles Alan Edelman (MIT) Alex Dubbs (MIT) and Plamen Koev (SJS) Oct 8, 2012 1/47 Wishart Matrices (arbitrary covariance) G=mxn matrix of Gaussians
The following definition is fundamental.
 1. Some Basics from Linear Algebra With these notes, I will try and clarify certain topics that I only quickly mention in class. First and foremost, I will assume that you are familiar with many basic
1. Some Basics from Linear Algebra With these notes, I will try and clarify certain topics that I only quickly mention in class. First and foremost, I will assume that you are familiar with many basic
Part IA. Vectors and Matrices. Year
 Part IA Vectors and Matrices Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2018 Paper 1, Section I 1C Vectors and Matrices For z, w C define the principal value of z w. State de Moivre s
Part IA Vectors and Matrices Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2018 Paper 1, Section I 1C Vectors and Matrices For z, w C define the principal value of z w. State de Moivre s
Representations of Matrix Lie Algebras
 Representations of Matrix Lie Algebras Alex Turzillo REU Apprentice Program, University of Chicago aturzillo@uchicago.edu August 00 Abstract Building upon the concepts of the matrix Lie group and the matrix
Representations of Matrix Lie Algebras Alex Turzillo REU Apprentice Program, University of Chicago aturzillo@uchicago.edu August 00 Abstract Building upon the concepts of the matrix Lie group and the matrix
Möbius Transformation
 Möbius Transformation 1 1 June 15th, 2010 Mathematics Science Center Tsinghua University Philosophy Rigidity Conformal mappings have rigidity. The diffeomorphism group is of infinite dimension in general.
Möbius Transformation 1 1 June 15th, 2010 Mathematics Science Center Tsinghua University Philosophy Rigidity Conformal mappings have rigidity. The diffeomorphism group is of infinite dimension in general.
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane.
 Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 8 Lecture 8 8.1 Matrices July 22, 2018 We shall study
Queens College, CUNY, Department of Computer Science Numerical Methods CSCI 361 / 761 Spring 2018 Instructor: Dr. Sateesh Mane c Sateesh R. Mane 2018 8 Lecture 8 8.1 Matrices July 22, 2018 We shall study
Chapter 5 Eigenvalues and Eigenvectors
 Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Lecture 10 - Eigenvalues problem
 Lecture 10 - Eigenvalues problem Department of Computer Science University of Houston February 28, 2008 1 Lecture 10 - Eigenvalues problem Introduction Eigenvalue problems form an important class of problems
Lecture 10 - Eigenvalues problem Department of Computer Science University of Houston February 28, 2008 1 Lecture 10 - Eigenvalues problem Introduction Eigenvalue problems form an important class of problems
Clifford Algebras and Spin Groups
 Clifford Algebras and Spin Groups Math G4344, Spring 2012 We ll now turn from the general theory to examine a specific class class of groups: the orthogonal groups. Recall that O(n, R) is the group of
Clifford Algebras and Spin Groups Math G4344, Spring 2012 We ll now turn from the general theory to examine a specific class class of groups: the orthogonal groups. Recall that O(n, R) is the group of
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 213br HW 3 solutions
 Math 13br HW 3 solutions February 6, 014 Problem 1 Show that for each d 1, there exists a complex torus X = C/Λ and an analytic map f : X X of degree d. Let Λ be the lattice Z Z d. It is stable under multiplication
Math 13br HW 3 solutions February 6, 014 Problem 1 Show that for each d 1, there exists a complex torus X = C/Λ and an analytic map f : X X of degree d. Let Λ be the lattice Z Z d. It is stable under multiplication
Spectral Theorem for Self-adjoint Linear Operators
 Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Notes for the undergraduate lecture by David Adams. (These are the notes I would write if I was teaching a course on this topic. I have included more material than I will cover in the 45 minute lecture;
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
A Brief Introduction to Functional Analysis
 A Brief Introduction to Functional Analysis Sungwook Lee Department of Mathematics University of Southern Mississippi sunglee@usm.edu July 5, 2007 Definition 1. An algebra A is a vector space over C with
A Brief Introduction to Functional Analysis Sungwook Lee Department of Mathematics University of Southern Mississippi sunglee@usm.edu July 5, 2007 Definition 1. An algebra A is a vector space over C with
Real symmetric matrices/1. 1 Eigenvalues and eigenvectors
 Real symmetric matrices 1 Eigenvalues and eigenvectors We use the convention that vectors are row vectors and matrices act on the right. Let A be a square matrix with entries in a field F; suppose that
Real symmetric matrices 1 Eigenvalues and eigenvectors We use the convention that vectors are row vectors and matrices act on the right. Let A be a square matrix with entries in a field F; suppose that
GROUP THEORY PRIMER. New terms: so(2n), so(2n+1), symplectic algebra sp(2n)
 GROUP THEORY PRIMER New terms: so(2n), so(2n+1), symplectic algebra sp(2n) 1. Some examples of semi-simple Lie algebras In the previous chapter, we developed the idea of understanding semi-simple Lie algebras
GROUP THEORY PRIMER New terms: so(2n), so(2n+1), symplectic algebra sp(2n) 1. Some examples of semi-simple Lie algebras In the previous chapter, we developed the idea of understanding semi-simple Lie algebras
NPTEL web course on Complex Analysis. A. Swaminathan I.I.T. Roorkee, India. and. V.K. Katiyar I.I.T. Roorkee, India
 NPTEL web course on Complex Analysis A. Swaminathan I.I.T. Roorkee, India and V.K. Katiyar I.I.T. Roorkee, India A.Swaminathan and V.K.Katiyar (NPTEL) Complex Analysis 1 / 36 Complex Analysis Module: 7:
NPTEL web course on Complex Analysis A. Swaminathan I.I.T. Roorkee, India and V.K. Katiyar I.I.T. Roorkee, India A.Swaminathan and V.K.Katiyar (NPTEL) Complex Analysis 1 / 36 Complex Analysis Module: 7:
Mathematics 1. Part II: Linear Algebra. Exercises and problems
 Bachelor Degree in Informatics Engineering Barcelona School of Informatics Mathematics Part II: Linear Algebra Eercises and problems February 5 Departament de Matemàtica Aplicada Universitat Politècnica
Bachelor Degree in Informatics Engineering Barcelona School of Informatics Mathematics Part II: Linear Algebra Eercises and problems February 5 Departament de Matemàtica Aplicada Universitat Politècnica
Paradigms of Probabilistic Modelling
 Paradigms of Probabilistic Modelling Hermann G. Matthies Brunswick, Germany wire@tu-bs.de http://www.wire.tu-bs.de abstract RV-measure.tex,v 4.5 2017/07/06 01:56:46 hgm Exp Overview 2 1. Motivation challenges
Paradigms of Probabilistic Modelling Hermann G. Matthies Brunswick, Germany wire@tu-bs.de http://www.wire.tu-bs.de abstract RV-measure.tex,v 4.5 2017/07/06 01:56:46 hgm Exp Overview 2 1. Motivation challenges
COUNTING COVERS OF AN ELLIPTIC CURVE
 COUNTING COVERS OF AN ELLIPTIC CURVE ABSTRACT. This note is an exposition of part of Dijkgraaf s article [Dij] on counting covers of elliptic curves and their connection with modular forms. CONTENTS 0.
COUNTING COVERS OF AN ELLIPTIC CURVE ABSTRACT. This note is an exposition of part of Dijkgraaf s article [Dij] on counting covers of elliptic curves and their connection with modular forms. CONTENTS 0.
Matrix Theory, Math6304 Lecture Notes from September 27, 2012 taken by Tasadduk Chowdhury
 Matrix Theory, Math634 Lecture Notes from September 27, 212 taken by Tasadduk Chowdhury Last Time (9/25/12): QR factorization: any matrix A M n has a QR factorization: A = QR, whereq is unitary and R is
Matrix Theory, Math634 Lecture Notes from September 27, 212 taken by Tasadduk Chowdhury Last Time (9/25/12): QR factorization: any matrix A M n has a QR factorization: A = QR, whereq is unitary and R is
Algebra C Numerical Linear Algebra Sample Exam Problems
 Algebra C Numerical Linear Algebra Sample Exam Problems Notation. Denote by V a finite-dimensional Hilbert space with inner product (, ) and corresponding norm. The abbreviation SPD is used for symmetric
Algebra C Numerical Linear Algebra Sample Exam Problems Notation. Denote by V a finite-dimensional Hilbert space with inner product (, ) and corresponding norm. The abbreviation SPD is used for symmetric
z, w = z 1 w 1 + z 2 w 2 z, w 2 z 2 w 2. d([z], [w]) = 2 φ : P(C 2 ) \ [1 : 0] C ; [z 1 : z 2 ] z 1 z 2 ψ : P(C 2 ) \ [0 : 1] C ; [z 1 : z 2 ] z 2 z 1
![z, w = z 1 w 1 + z 2 w 2 z, w 2 z 2 w 2. d([z], [w]) = 2 φ : P(C 2 ) \ [1 : 0] C ; [z 1 : z 2 ] z 1 z 2 ψ : P(C 2 ) \ [0 : 1] C ; [z 1 : z 2 ] z 2 z 1 z, w = z 1 w 1 + z 2 w 2 z, w 2 z 2 w 2. d([z], [w]) = 2 φ : P(C 2 ) \ [1 : 0] C ; [z 1 : z 2 ] z 1 z 2 ψ : P(C 2 ) \ [0 : 1] C ; [z 1 : z 2 ] z 2 z 1](/thumbs/95/123523548.jpg) 3 3 THE RIEMANN SPHERE 31 Models for the Riemann Sphere One dimensional projective complex space P(C ) is the set of all one-dimensional subspaces of C If z = (z 1, z ) C \ 0 then we will denote by [z]
3 3 THE RIEMANN SPHERE 31 Models for the Riemann Sphere One dimensional projective complex space P(C ) is the set of all one-dimensional subspaces of C If z = (z 1, z ) C \ 0 then we will denote by [z]
MTH 102: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur. Problem Set
 MTH 102: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set 6 Problems marked (T) are for discussions in Tutorial sessions. 1. Find the eigenvalues
MTH 102: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set 6 Problems marked (T) are for discussions in Tutorial sessions. 1. Find the eigenvalues
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES
 MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
MATRICES ARE SIMILAR TO TRIANGULAR MATRICES 1 Complex matrices Recall that the complex numbers are given by a + ib where a and b are real and i is the imaginary unity, ie, i 2 = 1 In what we describe below,
Computational Methods CMSC/AMSC/MAPL 460. Eigenvalues and Eigenvectors. Ramani Duraiswami, Dept. of Computer Science
 Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
Quantum Chaos and Nonunitary Dynamics
 Quantum Chaos and Nonunitary Dynamics Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Phys. Lett. A 373, 320 (2009) Institute of Physics, Jagiellonian University,
Quantum Chaos and Nonunitary Dynamics Karol Życzkowski in collaboration with W. Bruzda, V. Cappellini, H.-J. Sommers, M. Smaczyński Phys. Lett. A 373, 320 (2009) Institute of Physics, Jagiellonian University,
MIMO Capacities : Eigenvalue Computation through Representation Theory
 MIMO Capacities : Eigenvalue Computation through Representation Theory Jayanta Kumar Pal, Donald Richards SAMSI Multivariate distributions working group Outline 1 Introduction 2 MIMO working model 3 Eigenvalue
MIMO Capacities : Eigenvalue Computation through Representation Theory Jayanta Kumar Pal, Donald Richards SAMSI Multivariate distributions working group Outline 1 Introduction 2 MIMO working model 3 Eigenvalue
Conformal field theory in the sense of Segal, modified for a supersymmetric context
 Conformal field theory in the sense of Segal, modified for a supersymmetric context Paul S Green January 27, 2014 1 Introduction In these notes, we will review and propose some revisions to the definition
Conformal field theory in the sense of Segal, modified for a supersymmetric context Paul S Green January 27, 2014 1 Introduction In these notes, we will review and propose some revisions to the definition
NOTES ON BILINEAR FORMS
 NOTES ON BILINEAR FORMS PARAMESWARAN SANKARAN These notes are intended as a supplement to the talk given by the author at the IMSc Outreach Programme Enriching Collegiate Education-2015. Symmetric bilinear
NOTES ON BILINEAR FORMS PARAMESWARAN SANKARAN These notes are intended as a supplement to the talk given by the author at the IMSc Outreach Programme Enriching Collegiate Education-2015. Symmetric bilinear
Physics 215 Quantum Mechanics 1 Assignment 1
 Physics 5 Quantum Mechanics Assignment Logan A. Morrison January 9, 06 Problem Prove via the dual correspondence definition that the hermitian conjugate of α β is β α. By definition, the hermitian conjugate
Physics 5 Quantum Mechanics Assignment Logan A. Morrison January 9, 06 Problem Prove via the dual correspondence definition that the hermitian conjugate of α β is β α. By definition, the hermitian conjugate
Since G is a compact Lie group, we can apply Schur orthogonality to see that G χ π (g) 2 dg =
 Problem 1 Show that if π is an irreducible representation of a compact lie group G then π is also irreducible. Give an example of a G and π such that π = π, and another for which π π. Is this true for
Problem 1 Show that if π is an irreducible representation of a compact lie group G then π is also irreducible. Give an example of a G and π such that π = π, and another for which π π. Is this true for
Lectures 6 7 : Marchenko-Pastur Law
 Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
Fall 2009 MATH 833 Random Matrices B. Valkó Lectures 6 7 : Marchenko-Pastur Law Notes prepared by: A. Ganguly We will now turn our attention to rectangular matrices. Let X = (X 1, X 2,..., X n ) R p n
AN INTRODUCTION TO THE MASLOV INDEX IN SYMPLECTIC TOPOLOGY
 1 AN INTRODUCTION TO THE MASLOV INDEX IN SYMPLECTIC TOPOLOGY Andrew Ranicki and Daniele Sepe (Edinburgh) http://www.maths.ed.ac.uk/ aar Maslov index seminar, 9 November 2009 The 1-dimensional Lagrangians
1 AN INTRODUCTION TO THE MASLOV INDEX IN SYMPLECTIC TOPOLOGY Andrew Ranicki and Daniele Sepe (Edinburgh) http://www.maths.ed.ac.uk/ aar Maslov index seminar, 9 November 2009 The 1-dimensional Lagrangians
Introduction to Matrix Algebra
 Introduction to Matrix Algebra August 18, 2010 1 Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p
Introduction to Matrix Algebra August 18, 2010 1 Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p
IIT Mumbai 2015 MA 419, Basic Algebra Tutorial Sheet-1
 IIT Mumbai 2015 MA 419, Basic Algebra Tutorial Sheet-1 Let Σ be the set of all symmetries of the plane Π. 1. Give examples of s, t Σ such that st ts. 2. If s, t Σ agree on three non-collinear points, then
IIT Mumbai 2015 MA 419, Basic Algebra Tutorial Sheet-1 Let Σ be the set of all symmetries of the plane Π. 1. Give examples of s, t Σ such that st ts. 2. If s, t Σ agree on three non-collinear points, then
EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. 1. Determinants
 EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. Determinants Ex... Let A = 0 4 4 2 0 and B = 0 3 0. (a) Compute 0 0 0 0 A. (b) Compute det(2a 2 B), det(4a + B), det(2(a 3 B 2 )). 0 t Ex..2. For
EXERCISES ON DETERMINANTS, EIGENVALUES AND EIGENVECTORS. Determinants Ex... Let A = 0 4 4 2 0 and B = 0 3 0. (a) Compute 0 0 0 0 A. (b) Compute det(2a 2 B), det(4a + B), det(2(a 3 B 2 )). 0 t Ex..2. For
A = 3 1. We conclude that the algebraic multiplicity of the eigenvalues are both one, that is,
 65 Diagonalizable Matrices It is useful to introduce few more concepts, that are common in the literature Definition 65 The characteristic polynomial of an n n matrix A is the function p(λ) det(a λi) Example
65 Diagonalizable Matrices It is useful to introduce few more concepts, that are common in the literature Definition 65 The characteristic polynomial of an n n matrix A is the function p(λ) det(a λi) Example
FFTs in Graphics and Vision. Rotational and Reflective Symmetry Detection
 FFTs in Graphics and Vision Rotational and Reflective Symmetry Detection Outline Representation Theory Symmetry Detection Rotational Symmetry Reflective Symmetry Representation Theory Recall: A group is
FFTs in Graphics and Vision Rotational and Reflective Symmetry Detection Outline Representation Theory Symmetry Detection Rotational Symmetry Reflective Symmetry Representation Theory Recall: A group is
Math 215 HW #9 Solutions
 Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Representations of su(2)
 Representations of su2 The purpose of these notes is to construct the representations of su2 using the method of weightvectors, based on the discussion of the representations of sl2, R in the notes for
Representations of su2 The purpose of these notes is to construct the representations of su2 using the method of weightvectors, based on the discussion of the representations of sl2, R in the notes for
Chapter 6. Eigenvalues. Josef Leydold Mathematical Methods WS 2018/19 6 Eigenvalues 1 / 45
 Chapter 6 Eigenvalues Josef Leydold Mathematical Methods WS 2018/19 6 Eigenvalues 1 / 45 Closed Leontief Model In a closed Leontief input-output-model consumption and production coincide, i.e. V x = x
Chapter 6 Eigenvalues Josef Leydold Mathematical Methods WS 2018/19 6 Eigenvalues 1 / 45 Closed Leontief Model In a closed Leontief input-output-model consumption and production coincide, i.e. V x = x
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 1 Introduction to Linear Algebra
 1.1. Introduction SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 1 Introduction to Linear algebra is a specific branch of mathematics dealing with the study of vectors, vector spaces with functions that
1.1. Introduction SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 1 Introduction to Linear algebra is a specific branch of mathematics dealing with the study of vectors, vector spaces with functions that
235 Final exam review questions
 5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
BASIC ALGORITHMS IN LINEAR ALGEBRA. Matrices and Applications of Gaussian Elimination. A 2 x. A T m x. A 1 x A T 1. A m x
 BASIC ALGORITHMS IN LINEAR ALGEBRA STEVEN DALE CUTKOSKY Matrices and Applications of Gaussian Elimination Systems of Equations Suppose that A is an n n matrix with coefficents in a field F, and x = (x,,
BASIC ALGORITHMS IN LINEAR ALGEBRA STEVEN DALE CUTKOSKY Matrices and Applications of Gaussian Elimination Systems of Equations Suppose that A is an n n matrix with coefficents in a field F, and x = (x,,
where m is the maximal ideal of O X,p. Note that m/m 2 is a vector space. Suppose that we are given a morphism
 8. Smoothness and the Zariski tangent space We want to give an algebraic notion of the tangent space. In differential geometry, tangent vectors are equivalence classes of maps of intervals in R into the
8. Smoothness and the Zariski tangent space We want to give an algebraic notion of the tangent space. In differential geometry, tangent vectors are equivalence classes of maps of intervals in R into the
Argument shift method and sectional operators: applications to differential geometry
 Loughborough University Institutional Repository Argument shift method and sectional operators: applications to differential geometry This item was submitted to Loughborough University's Institutional
Loughborough University Institutional Repository Argument shift method and sectional operators: applications to differential geometry This item was submitted to Loughborough University's Institutional
Algebra II. Paulius Drungilas and Jonas Jankauskas
 Algebra II Paulius Drungilas and Jonas Jankauskas Contents 1. Quadratic forms 3 What is quadratic form? 3 Change of variables. 3 Equivalence of quadratic forms. 4 Canonical form. 4 Normal form. 7 Positive
Algebra II Paulius Drungilas and Jonas Jankauskas Contents 1. Quadratic forms 3 What is quadratic form? 3 Change of variables. 3 Equivalence of quadratic forms. 4 Canonical form. 4 Normal form. 7 Positive
Mobile Robotics 1. A Compact Course on Linear Algebra. Giorgio Grisetti
 Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Introduction to Group Theory
 Chapter 10 Introduction to Group Theory Since symmetries described by groups play such an important role in modern physics, we will take a little time to introduce the basic structure (as seen by a physicist)
Chapter 10 Introduction to Group Theory Since symmetries described by groups play such an important role in modern physics, we will take a little time to introduce the basic structure (as seen by a physicist)
6 EIGENVALUES AND EIGENVECTORS
 6 EIGENVALUES AND EIGENVECTORS INTRODUCTION TO EIGENVALUES 61 Linear equations Ax = b come from steady state problems Eigenvalues have their greatest importance in dynamic problems The solution of du/dt
6 EIGENVALUES AND EIGENVECTORS INTRODUCTION TO EIGENVALUES 61 Linear equations Ax = b come from steady state problems Eigenvalues have their greatest importance in dynamic problems The solution of du/dt
A new product on 2 2 matrices
 A new product on 2 2 matrices L Kramer, P Kramer, and V Man ko October 17, 2018 arxiv:1802.03048v1 [math-ph] 8 Feb 2018 Abstract We study a bilinear multiplication rule on 2 2 matrices which is intermediate
A new product on 2 2 matrices L Kramer, P Kramer, and V Man ko October 17, 2018 arxiv:1802.03048v1 [math-ph] 8 Feb 2018 Abstract We study a bilinear multiplication rule on 2 2 matrices which is intermediate
CLASSICAL GROUPS DAVID VOGAN
 CLASSICAL GROUPS DAVID VOGAN 1. Orthogonal groups These notes are about classical groups. That term is used in various ways by various people; I ll try to say a little about that as I go along. Basically
CLASSICAL GROUPS DAVID VOGAN 1. Orthogonal groups These notes are about classical groups. That term is used in various ways by various people; I ll try to say a little about that as I go along. Basically
Combinatorial equivalence of topological polynomials and group theory
 Combinatorial equivalence of topological polynomials and group theory Volodymyr Nekrashevych (joint work with L. Bartholdi) March 11, 2006, Toronto V. Nekrashevych (Texas A&M) Topological Polynomials March
Combinatorial equivalence of topological polynomials and group theory Volodymyr Nekrashevych (joint work with L. Bartholdi) March 11, 2006, Toronto V. Nekrashevych (Texas A&M) Topological Polynomials March
CLASSIFICATION OF COMPLETELY POSITIVE MAPS 1. INTRODUCTION
 CLASSIFICATION OF COMPLETELY POSITIVE MAPS STEPHAN HOYER ABSTRACT. We define a completely positive map and classify all completely positive linear maps. We further classify all such maps that are trace-preserving
CLASSIFICATION OF COMPLETELY POSITIVE MAPS STEPHAN HOYER ABSTRACT. We define a completely positive map and classify all completely positive linear maps. We further classify all such maps that are trace-preserving
On the topology of H(2)
 On the topology of H(2) Duc-Manh Nguyen Max-Planck-Institut für Mathematik Bonn, Germany July 19, 2010 Translation surface Definition Translation surface is a flat surface with conical singularities such
On the topology of H(2) Duc-Manh Nguyen Max-Planck-Institut für Mathematik Bonn, Germany July 19, 2010 Translation surface Definition Translation surface is a flat surface with conical singularities such
Mathematical Methods for Engineers and Scientists 1
 K.T. Tang Mathematical Methods for Engineers and Scientists 1 Complex Analysis, Determinants and Matrices With 49 Figures and 2 Tables fyj Springer Part I Complex Analysis 1 Complex Numbers 3 1.1 Our Number
K.T. Tang Mathematical Methods for Engineers and Scientists 1 Complex Analysis, Determinants and Matrices With 49 Figures and 2 Tables fyj Springer Part I Complex Analysis 1 Complex Numbers 3 1.1 Our Number
ALGEBRAIC GEOMETRY AND RIEMANN SURFACES
 ALGEBRAIC GEOMETRY AND RIEMANN SURFACES DANIEL YING Abstract. In this thesis we will give a present survey of the various methods used in dealing with Riemann surfaces. Riemann surfaces are central in
ALGEBRAIC GEOMETRY AND RIEMANN SURFACES DANIEL YING Abstract. In this thesis we will give a present survey of the various methods used in dealing with Riemann surfaces. Riemann surfaces are central in
Applied Mathematics 205. Unit V: Eigenvalue Problems. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.2: Fundamentals 2 / 31 Eigenvalues and Eigenvectors Eigenvalues and eigenvectors of
Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.2: Fundamentals 2 / 31 Eigenvalues and Eigenvectors Eigenvalues and eigenvectors of
Vector Spaces, Affine Spaces, and Metric Spaces
 Vector Spaces, Affine Spaces, and Metric Spaces 2 This chapter is only meant to give a short overview of the most important concepts in linear algebra, affine spaces, and metric spaces and is not intended
Vector Spaces, Affine Spaces, and Metric Spaces 2 This chapter is only meant to give a short overview of the most important concepts in linear algebra, affine spaces, and metric spaces and is not intended
Herbert Stahl s proof of the BMV conjecture
 Herbert Stahl s proof of the BMV conjecture A. Eremenko August 25, 203 Theorem. Let A and B be two n n Hermitian matrices, where B is positive semi-definite. Then the function is absolutely monotone, that
Herbert Stahl s proof of the BMV conjecture A. Eremenko August 25, 203 Theorem. Let A and B be two n n Hermitian matrices, where B is positive semi-definite. Then the function is absolutely monotone, that
M3/4/5P12 PROBLEM SHEET 1
 M3/4/5P12 PROBLEM SHEET 1 Please send any corrections or queries to jnewton@imperialacuk Exercise 1 (1) Let G C 4 C 2 s, t : s 4 t 2 e, st ts Let V C 2 with the stard basis Consider the linear transformations
M3/4/5P12 PROBLEM SHEET 1 Please send any corrections or queries to jnewton@imperialacuk Exercise 1 (1) Let G C 4 C 2 s, t : s 4 t 2 e, st ts Let V C 2 with the stard basis Consider the linear transformations
October 4, 2017 EIGENVALUES AND EIGENVECTORS. APPLICATIONS
 October 4, 207 EIGENVALUES AND EIGENVECTORS. APPLICATIONS RODICA D. COSTIN Contents 4. Eigenvalues and Eigenvectors 3 4.. Motivation 3 4.2. Diagonal matrices 3 4.3. Example: solving linear differential
October 4, 207 EIGENVALUES AND EIGENVECTORS. APPLICATIONS RODICA D. COSTIN Contents 4. Eigenvalues and Eigenvectors 3 4.. Motivation 3 4.2. Diagonal matrices 3 4.3. Example: solving linear differential
Distance Between Ellipses in 2D
 Distance Between Ellipses in 2D David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To
Distance Between Ellipses in 2D David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To
Mathematical Foundations
 Chapter 1 Mathematical Foundations 1.1 Big-O Notations In the description of algorithmic complexity, we often have to use the order notations, often in terms of big O and small o. Loosely speaking, for
Chapter 1 Mathematical Foundations 1.1 Big-O Notations In the description of algorithmic complexity, we often have to use the order notations, often in terms of big O and small o. Loosely speaking, for
1. General Vector Spaces
 1.1. Vector space axioms. 1. General Vector Spaces Definition 1.1. Let V be a nonempty set of objects on which the operations of addition and scalar multiplication are defined. By addition we mean a rule
1.1. Vector space axioms. 1. General Vector Spaces Definition 1.1. Let V be a nonempty set of objects on which the operations of addition and scalar multiplication are defined. By addition we mean a rule
