Introduction to Matrix Algebra
|
|
|
- Christian Norman
- 6 years ago
- Views:
Transcription
1 Introduction to Matrix Algebra August 18, Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p = 2 it represents a point in a plane; when p = 3, it represents a point in the 3-d space. For general p, this represents a point in a p-dimension Euclidean space, written as R p. Alternatively, it can also be interpreted as an arrow, or vector, starting from the origin, pointing to that point. The transpose operation changes a column vector to a row vector; and is written as x ; that is x = (x 1,..., x p ). A number is also called a scalar. We can define the product between a vector x R p and a scalar, c R, as follows: x 1 cx 1 cx = c. =.. x p cx p Draw a picture here. We define addition of two vectors, y, as follows x 1 y 1 x 1 + y 1 x + y =. +. =. x p y p x p + y p Draw a picture here. 1
2 1.2 Length and angle Suppose p = 2, then by Pythagoras theorem we know that the length of x = (x 1, x 2 ) is simply x x 2 2. We can extend this concept to arbitrary p. The length of a vector x R p is the length of the arrow from origin to that point: x = x x 2 p Note that, for any scalar c R p, cx = c x. Now let us define the angle between two vectors. Again start with p = 2. Let θ be the angle between x and y. Let θ 1 be the angle between x and the horizontal axis and θ 2 be the angle between y and the horizontal axis. Then cos(θ 1 ) = x 1 x, cos(θ 2) = y 1 x, sin(θ 1) = x 2 x, sin(θ 2) = y 2 x, Now we can express the cosine of the angle θ in terms of x and y, as follows: cos(θ 2 θ 1 ) = cos(θ 2 ) cos(θ 1 ) + sin(θ 2 ) sin(θ 1 ) = x 1y 1 + x 2 y 2 x y. This formula is generalized to the p-dimensional case as cos(θ) = x 1y x p y p. x y We call x 1 y x p y p the inner product, or scalar product, between x and y, and write it as x y; that is, In this notation, The number θ: x y = x 1 y x p y p. cos(θ) = x y x y. ( ) x cos 1 y x y is defined as the angle between two vectors x and y in R p. Draw a picture here. 2
3 Example. Let x = (1, 3, 2), y = ( 2, 1, 1). 1. Find 3x, 2. Find x + y, 3. Find the lengths of x and y, 4. Find the cosine of the angle between x and y, 5. Find the angle between x and y. 6. Check that 3x = 3 x. Solution: 1. 3x = 3(1, 3, 2) = (3 1, 3 3, 3 2) = (3, 9, 6). 2. x + y = (1, 3, 2) + ( 2, 1, 1) = (1 2, 3 + 1, 2 1) = ( 1, 4, 1). 3. x = = 14 = 3.742, y = ( 2) ( 1) 2 = 6 = Let θ be the angle between x and y. Then cos(θ) = (1)( 2) + (3)(1) + (2)( 1) 14 6 = Now θ = cos 1 ( 0.109) = = x = 3 14, 3x = 3 2 (14). Obviously, they are the same. 3
4 1.3 Linear independence A set of vectors x 1,..., x k are said to be linearly dependent, if there exist scalars c 1,..., c k, not all zero, such that c 1 x 1 + c k x k = 0. Interpretation: if k = 2, then this means two vectors are proportional to each other; that is, they are on the same line. When k = 3, this means the k points are in the same plane. The set of vectors {x 1,... x k } are linearly dependent if they are not linear independent. That is, if there does not exist c 1,..., c k, not all zero, such that the above holds. In other words, whenever the above holds, c 1 = = c k = 0. Interpretation, they do not reside in any lower dimensional hyperplane. Example. Are the following groups of vectors linearly dependent? 1. x 1 = (1, 2, 3), x 2 = (1, 1, 1), x 3 = (0, 0, 1) 2. x 1 = (1, 2, 3), x 2 = (1, 1, 1), x 3 = (1, 3, 5). 3. Illustrate your conclusions by vectors in a 3-dimensional space. Solution: 1. Suppose c 1 x 1 + c 2 x 2 + c 3 x 3 = 0. (1) Then c c c 3 0 = This is equivalent to c 1 + c 2 = 0 (2) 2c 1 + c 2 = 0 (3) 3c 1 + c 2 + c 3 = 0 (4) 4
5 From equation (2) we see that c 2 = c 1. Substitute this into equation (3) to obtain 2c 1 c 1 = c 1 = 0. Substitute this into (2) to show that c 2 = 0. Substitute c 1 = c 2 = 0 into (4) to show that c 3 = 0. Thus we have shown that whenever (1) holds we have that c 1 = c 2 = c 3 = 0. That is, x 1, x 2, x 3 are linearly independent. 2. Similarly, equation (1) implies that c 1 + 2c 2 + 3c 3 =0 (5) c 1 + c 2 + c 3 =0 (6) c 2 + 2c 3 =0 (7) From (7) we see that c 2 = 2c 3. Substitute this into (6) and (5) to obtain c 1 c 3 =0 c 1 c 3 =0 Thus equation (1) will be satisfied if c 1 = c 3 and c 2 = 2c 3. For example, if (c 1, c 2, c 3 ) = (1, 2, 1) the equation (1) is satisfied. Hence x 1, x 2, x 3 are linearly dependent. 3. Draw two pictures here to illustrate whether the three points are on the lower dimensional space or not. 1.4 Projection of a vector Suppose I have two vectors, x, y R p. The vector (x y)(y y) 1 y is called the projection of x onto y. We write this as P y (x). Note that this vector is proportional to y. Then length of this projection is P y (x) = x y y y 2 = x y y = x y x = x cos(θ). x y Notice that y y is a vector with unit length, and P y (x) = x y y y = x x y y 2 x y y = x cos(θ) y y. Draw a picture here. 5
6 2 Matrices 2.1 Notations A matrix is a collection of numbers ordered by rows and columns. It is customary to enclose the elements of a matrix in parentheses, brackets, or braces. For example, the following is a matrix: ( ) X = This matrix has two rows and three columns, so it is referred to as a 2 by 3 matrix. The elements of a matrix are numbered in the following way: ( ) X11 X X = 12 X 13. X 21 X 22 X 23 The first subscript in a matrix refers to the row and the second subscript refers to the column. X ij denotes the element on the ith row and jth column of matrix X. A square matrix has as many rows as it has columns. ( ) 1 3 A =. 6 2 A symmetric matrix is a square matrix in which x ij = x ji for all possible i and j. ( ) 1 3 A =. 3 2 A diagonal matrix is a square matrix where all the off diagonal elements are 0. A diagonal matrix is always symmetric. ( ) 1 0 A =. 0 2 An identity matrix is a diagonal matrix with 1s and only 1s on the diagonal. The p p identity matrix is almost always denoted as I p I 3 =
7 2.2 Basic operations Matrix addition: to add two matrices, they both must have the same number of rows and they both must have the same number of columns. The elements of the two matrices are simply added together, element by element, to produce the results. Let A and B be two m n matrices, then (A + B) ij = A ij + B ij for 1 i m, 1 j n. ( ) ( ) ( ) = Matrix subtraction works in the same way. Scalar multiplication: each element in the product matrix is simply the scalar multiplied by the element in the matrix. Let c be a scalar and A be a m n matrix, then (ca) ij = ca ij for 1 i m, 1 j n. ( ) ( ) = Scalar multiplication is commutative, or ca = Ac. Multiplication of a row vector and a column vector: the row vector must have as many columns as the column vector has rows. The product is a scalar. Let a 1 b = ( ) b 1 b p, a =. a 1 then ba = ( ) b 1 b p. a p = p i=1 b ia i. a p, Multiplication of two matrices: multiplication of two matrices is defined only if the number of columns of the left matrix is the same as the number of rows of the right matrix. Let A be m p and B be p n, then (AB) ij = 7 p A il B lj l=1
8 Let a i be the ith row vector of A. Let b j be the jth column vector of B. Then (AB) ij = a i b j Some properties: 1. A + B = B + A (commutativity). 2. (ca)b = A(cB) (scalar associativity). 3. c(a + B) = ca + cb (scalar distributivity). 4. (AB)C = A(BC) (matrix associativity). 5. (A + B)C = AC + BC (matrix left distributivity). 6. C(A + B) = CA + CB (matrix right distributivity). 7. AI = A, IB = B. Generally, AB BA. Matrix transpose: the transpose of a matrix A is denoted by A or A T. The first row of a matrix becomes the first column of the transpose matrix, the second row of the matrix becomes the second column of the transpose, etc. A ij = A ji. The transpose of a row vector will be a column vector, and the transpose of a column vector will be a row vector. The transpose of a symmetric matrix is simply the original matrix. Matrix inverse: the inverse of a matrix A is denoted by A 1. AA 1 = A 1 A = I. A matrix must be square to have an inverse, but not all square matrices have an inverse. In some cases, the inverse does not exist. Trace of matrix: denoted as tr(a), the trace is used only for square matrices and equals the sum of the diagonal elements of the matrix. Let A be p p, then tr(a) = p i=1 A ii. Determinant: the determinant of A is denoted by det(a) or A. Some properties: 8
9 1. A matrix is invertible if and only if its determinant is nonzero. 2. The determinant of a product of square matrices equals the product of their determinants: det(ab) = det(a)det(b). 3. det(a 1 ) = [det(a)] 1, det(a ) = det(a). 4. Adding a multiple of any row to another row, or a multiple of any column to another column, does not change the determinant. 5. Interchanging two rows or two columns affects the determinant by multiplying it by -1. ( ) a b 6. The 2 2 matrix A = has determinant det(a) = ad bc. c d 7. The determinant det(a) can be viewed as the oriented area of the parallelogram with vertices at (0, 0), (a, b), (a+c, b+d), and (c, d). The oriented area is the same as the usual area, except that it is negative when the vertices are listed in clockwise order. Let A be an n p matrix. The column rank of a matrix is the maximal number of independent columns of A; the row rank of A is the maximal number of independent rows of A. Let a 1,..., a p be the columns of A. For any 1 k p, we can find ( p k) sets of k columns. If there is one set of columns are linearly independent, then we know the column rank of A is no less than k. Increase k to k + 1. There are ( p k+1) sets of k + 1 columns. If all sets are linearly independent, then we know the rank is k. The row rank is always equal to the column rank, and they are called the rank of A. A square matrix A of dimension k k is a full rank matrix if its rank is k. A square matrix is invertible if and only if it is full rank. Orthogonal matrices: only square matrices may be orthogonal matrices. An orthogonal matrix satisfies: AA = A A = I. The inverse of an orthogonal matrix is the transpose of that matrix, or A = A 1. Eigenvalues and Eigenvectors: a non-zero vector v of dimension n is an eigenvector of square (n n) matrix A if and only if it satisfies the eigenvalue equation Aq = λq, 9
10 where λ is a scalar called the eigenvalue and q is a vector called the eigenvector corresponding to λ. This yields the characteristic equation p(λ) = 0, where the characteristic polynomial is defined as p(λ) = det(a λi). Eigenvalue decomposition: If (λ 1, e 1 ),..., (λ k, e k ) are the k eigenpairs of the matrix A k k, then the following equality holds: A = λ 1 e 1 e λ k e k e k. This is called the spectral decomposition of A, or eigen decomposition of A. Let A be a k k square, symmetric matrix, and let (λ 1, e 1 ),..., (λ k, e k ) be the eigen pairs of A. Let α be a number. The following k k matrix λ α 1 e 1 e λ α k e k e k is called the αth power of A. Notice that when 0 α < 1, the above is defined only when λ 1,..., λ k are nonnegative. This is written as A α. In particular, if λ 1 0,... λ k 0 and α = 1/2, then A 1/2 is called the square root of the matrix A. The matrix A raised to the power 1 is the same as the inverse of a matrix. Definiteness: a symmetric n n matrix A is called positive definite, if for all nonzero vectors x R n, the associated quadratic form takes only positive values. Q(x) = x Ax If the quadratic form takes only non-negative values, the symmetric matrix is called semi-positive definite; if the quadratic form takes only negative values, the matrix is called negative definite. 10
Math Bootcamp An p-dimensional vector is p numbers put together. Written as. x 1 x =. x p
 Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
MATRIX ALGEBRA. or x = (x 1,..., x n ) R n. y 1 y 2. x 2. x m. y m. y = cos θ 1 = x 1 L x. sin θ 1 = x 2. cos θ 2 = y 1 L y.
 as Basics Vectors MATRIX ALGEBRA An array of n real numbers x, x,, x n is called a vector and it is written x = x x n or x = x,, x n R n prime operation=transposing a column to a row Basic vector operations
as Basics Vectors MATRIX ALGEBRA An array of n real numbers x, x,, x n is called a vector and it is written x = x x n or x = x,, x n R n prime operation=transposing a column to a row Basic vector operations
2. Matrix Algebra and Random Vectors
 2. Matrix Algebra and Random Vectors 2.1 Introduction Multivariate data can be conveniently display as array of numbers. In general, a rectangular array of numbers with, for instance, n rows and p columns
2. Matrix Algebra and Random Vectors 2.1 Introduction Multivariate data can be conveniently display as array of numbers. In general, a rectangular array of numbers with, for instance, n rows and p columns
Review of Linear Algebra
 Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
1 Matrices and matrix algebra
 1 Matrices and matrix algebra 1.1 Examples of matrices A matrix is a rectangular array of numbers and/or variables. For instance 4 2 0 3 1 A = 5 1.2 0.7 x 3 π 3 4 6 27 is a matrix with 3 rows and 5 columns
1 Matrices and matrix algebra 1.1 Examples of matrices A matrix is a rectangular array of numbers and/or variables. For instance 4 2 0 3 1 A = 5 1.2 0.7 x 3 π 3 4 6 27 is a matrix with 3 rows and 5 columns
Math Linear Algebra Final Exam Review Sheet
 Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Matrices and Linear Algebra
 Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Appendix A: Matrices
 Appendix A: Matrices A matrix is a rectangular array of numbers Such arrays have rows and columns The numbers of rows and columns are referred to as the dimensions of a matrix A matrix with, say, 5 rows
Appendix A: Matrices A matrix is a rectangular array of numbers Such arrays have rows and columns The numbers of rows and columns are referred to as the dimensions of a matrix A matrix with, say, 5 rows
3 Matrix Algebra. 3.1 Operations on matrices
 3 Matrix Algebra A matrix is a rectangular array of numbers; it is of size m n if it has m rows and n columns. A 1 n matrix is a row vector; an m 1 matrix is a column vector. For example: 1 5 3 5 3 5 8
3 Matrix Algebra A matrix is a rectangular array of numbers; it is of size m n if it has m rows and n columns. A 1 n matrix is a row vector; an m 1 matrix is a column vector. For example: 1 5 3 5 3 5 8
Basic Concepts in Matrix Algebra
 Basic Concepts in Matrix Algebra An column array of p elements is called a vector of dimension p and is written as x p 1 = x 1 x 2. x p. The transpose of the column vector x p 1 is row vector x = [x 1
Basic Concepts in Matrix Algebra An column array of p elements is called a vector of dimension p and is written as x p 1 = x 1 x 2. x p. The transpose of the column vector x p 1 is row vector x = [x 1
Phys 201. Matrices and Determinants
 Phys 201 Matrices and Determinants 1 1.1 Matrices 1.2 Operations of matrices 1.3 Types of matrices 1.4 Properties of matrices 1.5 Determinants 1.6 Inverse of a 3 3 matrix 2 1.1 Matrices A 2 3 7 =! " 1
Phys 201 Matrices and Determinants 1 1.1 Matrices 1.2 Operations of matrices 1.3 Types of matrices 1.4 Properties of matrices 1.5 Determinants 1.6 Inverse of a 3 3 matrix 2 1.1 Matrices A 2 3 7 =! " 1
Knowledge Discovery and Data Mining 1 (VO) ( )
 Knowledge Discovery and Data Mining 1 (VO) (707.003) Review of Linear Algebra Denis Helic KTI, TU Graz Oct 9, 2014 Denis Helic (KTI, TU Graz) KDDM1 Oct 9, 2014 1 / 74 Big picture: KDDM Probability Theory
Knowledge Discovery and Data Mining 1 (VO) (707.003) Review of Linear Algebra Denis Helic KTI, TU Graz Oct 9, 2014 Denis Helic (KTI, TU Graz) KDDM1 Oct 9, 2014 1 / 74 Big picture: KDDM Probability Theory
Matrix Algebra. Matrix Algebra. Chapter 8 - S&B
 Chapter 8 - S&B Algebraic operations Matrix: The size of a matrix is indicated by the number of its rows and the number of its columns. A matrix with k rows and n columns is called a k n matrix. The number
Chapter 8 - S&B Algebraic operations Matrix: The size of a matrix is indicated by the number of its rows and the number of its columns. A matrix with k rows and n columns is called a k n matrix. The number
Linear Algebra V = T = ( 4 3 ).
 Linear Algebra Vectors A column vector is a list of numbers stored vertically The dimension of a column vector is the number of values in the vector W is a -dimensional column vector and V is a 5-dimensional
Linear Algebra Vectors A column vector is a list of numbers stored vertically The dimension of a column vector is the number of values in the vector W is a -dimensional column vector and V is a 5-dimensional
Matrix Algebra: Summary
 May, 27 Appendix E Matrix Algebra: Summary ontents E. Vectors and Matrtices.......................... 2 E.. Notation.................................. 2 E..2 Special Types of Vectors.........................
May, 27 Appendix E Matrix Algebra: Summary ontents E. Vectors and Matrtices.......................... 2 E.. Notation.................................. 2 E..2 Special Types of Vectors.........................
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
MATH 240 Spring, Chapter 1: Linear Equations and Matrices
 MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
MATH 240 Spring, 2006 Chapter Summaries for Kolman / Hill, Elementary Linear Algebra, 8th Ed. Sections 1.1 1.6, 2.1 2.2, 3.2 3.8, 4.3 4.5, 5.1 5.3, 5.5, 6.1 6.5, 7.1 7.2, 7.4 DEFINITIONS Chapter 1: Linear
MATH2210 Notebook 2 Spring 2018
 MATH2210 Notebook 2 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH2210 Notebook 2 3 2.1 Matrices and Their Operations................................
MATH2210 Notebook 2 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 2 MATH2210 Notebook 2 3 2.1 Matrices and Their Operations................................
Quantum Computing Lecture 2. Review of Linear Algebra
 Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Quantum Computing Lecture 2 Review of Linear Algebra Maris Ozols Linear algebra States of a quantum system form a vector space and their transformations are described by linear operators Vector spaces
Chapter 1: Systems of linear equations and matrices. Section 1.1: Introduction to systems of linear equations
 Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1. Prof. N. Harnew University of Oxford TT 2013
 CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1 Prof. N. Harnew University of Oxford TT 2013 1 OUTLINE 1. Vector Algebra 2. Vector Geometry 3. Types of Matrices and Matrix Operations 4. Determinants
CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1 Prof. N. Harnew University of Oxford TT 2013 1 OUTLINE 1. Vector Algebra 2. Vector Geometry 3. Types of Matrices and Matrix Operations 4. Determinants
Linear Algebra Review. Vectors
 Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Linear Algebra - Part II
 Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
ELEMENTARY LINEAR ALGEBRA WITH APPLICATIONS. 1. Linear Equations and Matrices
 ELEMENTARY LINEAR ALGEBRA WITH APPLICATIONS KOLMAN & HILL NOTES BY OTTO MUTZBAUER 11 Systems of Linear Equations 1 Linear Equations and Matrices Numbers in our context are either real numbers or complex
ELEMENTARY LINEAR ALGEBRA WITH APPLICATIONS KOLMAN & HILL NOTES BY OTTO MUTZBAUER 11 Systems of Linear Equations 1 Linear Equations and Matrices Numbers in our context are either real numbers or complex
NOTES FOR LINEAR ALGEBRA 133
 NOTES FOR LINEAR ALGEBRA 33 William J Anderson McGill University These are not official notes for Math 33 identical to the notes projected in class They are intended for Anderson s section 4, and are 2
NOTES FOR LINEAR ALGEBRA 33 William J Anderson McGill University These are not official notes for Math 33 identical to the notes projected in class They are intended for Anderson s section 4, and are 2
TBP MATH33A Review Sheet. November 24, 2018
 TBP MATH33A Review Sheet November 24, 2018 General Transformation Matrices: Function Scaling by k Orthogonal projection onto line L Implementation If we want to scale I 2 by k, we use the following: [
TBP MATH33A Review Sheet November 24, 2018 General Transformation Matrices: Function Scaling by k Orthogonal projection onto line L Implementation If we want to scale I 2 by k, we use the following: [
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
Introduction. Vectors and Matrices. Vectors [1] Vectors [2]
![Introduction. Vectors and Matrices. Vectors [1] Vectors [2] Introduction. Vectors and Matrices. Vectors [1] Vectors [2]](/thumbs/77/76245607.jpg) Introduction Vectors and Matrices Dr. TGI Fernando 1 2 Data is frequently arranged in arrays, that is, sets whose elements are indexed by one or more subscripts. Vector - one dimensional array Matrix -
Introduction Vectors and Matrices Dr. TGI Fernando 1 2 Data is frequently arranged in arrays, that is, sets whose elements are indexed by one or more subscripts. Vector - one dimensional array Matrix -
Lecture 7. Econ August 18
 Lecture 7 Econ 2001 2015 August 18 Lecture 7 Outline First, the theorem of the maximum, an amazing result about continuity in optimization problems. Then, we start linear algebra, mostly looking at familiar
Lecture 7 Econ 2001 2015 August 18 Lecture 7 Outline First, the theorem of the maximum, an amazing result about continuity in optimization problems. Then, we start linear algebra, mostly looking at familiar
A matrix is a rectangular array of. objects arranged in rows and columns. The objects are called the entries. is called the size of the matrix, and
 Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Linear Algebra. Matrices Operations. Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0.
 Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
OHSx XM511 Linear Algebra: Solutions to Online True/False Exercises
 This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
IMPORTANT DEFINITIONS AND THEOREMS REFERENCE SHEET
 IMPORTANT DEFINITIONS AND THEOREMS REFERENCE SHEET This is a (not quite comprehensive) list of definitions and theorems given in Math 1553. Pay particular attention to the ones in red. Study Tip For each
IMPORTANT DEFINITIONS AND THEOREMS REFERENCE SHEET This is a (not quite comprehensive) list of definitions and theorems given in Math 1553. Pay particular attention to the ones in red. Study Tip For each
A matrix is a rectangular array of. objects arranged in rows and columns. The objects are called the entries. is called the size of the matrix, and
 Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
IMPORTANT DEFINITIONS AND THEOREMS REFERENCE SHEET
 IMPORTANT DEFINITIONS AND THEOREMS REFERENCE SHEET This is a (not quite comprehensive) list of definitions and theorems given in Math 1553. Pay particular attention to the ones in red. Study Tip For each
IMPORTANT DEFINITIONS AND THEOREMS REFERENCE SHEET This is a (not quite comprehensive) list of definitions and theorems given in Math 1553. Pay particular attention to the ones in red. Study Tip For each
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Matrix Algebra Determinant, Inverse matrix. Matrices. A. Fabretti. Mathematics 2 A.Y. 2015/2016. A. Fabretti Matrices
 Matrices A. Fabretti Mathematics 2 A.Y. 2015/2016 Table of contents Matrix Algebra Determinant Inverse Matrix Introduction A matrix is a rectangular array of numbers. The size of a matrix is indicated
Matrices A. Fabretti Mathematics 2 A.Y. 2015/2016 Table of contents Matrix Algebra Determinant Inverse Matrix Introduction A matrix is a rectangular array of numbers. The size of a matrix is indicated
MAT 2037 LINEAR ALGEBRA I web:
 MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
MAT 237 LINEAR ALGEBRA I 2625 Dokuz Eylül University, Faculty of Science, Department of Mathematics web: Instructor: Engin Mermut http://kisideuedutr/enginmermut/ HOMEWORK 2 MATRIX ALGEBRA Textbook: Linear
Matrices. Chapter Definitions and Notations
 Chapter 3 Matrices 3. Definitions and Notations Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which
Chapter 3 Matrices 3. Definitions and Notations Matrices are yet another mathematical object. Learning about matrices means learning what they are, how they are represented, the types of operations which
Matrix & Linear Algebra
 Matrix & Linear Algebra Jamie Monogan University of Georgia For more information: http://monogan.myweb.uga.edu/teaching/mm/ Jamie Monogan (UGA) Matrix & Linear Algebra 1 / 84 Vectors Vectors Vector: A
Matrix & Linear Algebra Jamie Monogan University of Georgia For more information: http://monogan.myweb.uga.edu/teaching/mm/ Jamie Monogan (UGA) Matrix & Linear Algebra 1 / 84 Vectors Vectors Vector: A
Math Camp II. Basic Linear Algebra. Yiqing Xu. Aug 26, 2014 MIT
 Math Camp II Basic Linear Algebra Yiqing Xu MIT Aug 26, 2014 1 Solving Systems of Linear Equations 2 Vectors and Vector Spaces 3 Matrices 4 Least Squares Systems of Linear Equations Definition A linear
Math Camp II Basic Linear Algebra Yiqing Xu MIT Aug 26, 2014 1 Solving Systems of Linear Equations 2 Vectors and Vector Spaces 3 Matrices 4 Least Squares Systems of Linear Equations Definition A linear
ENGI 9420 Lecture Notes 2 - Matrix Algebra Page Matrix operations can render the solution of a linear system much more efficient.
 ENGI 940 Lecture Notes - Matrix Algebra Page.0. Matrix Algebra A linear system of m equations in n unknowns, a x + a x + + a x b (where the a ij and i n n a x + a x + + a x b n n a x + a x + + a x b m
ENGI 940 Lecture Notes - Matrix Algebra Page.0. Matrix Algebra A linear system of m equations in n unknowns, a x + a x + + a x b (where the a ij and i n n a x + a x + + a x b n n a x + a x + + a x b m
Linear Algebra Highlights
 Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Online Exercises for Linear Algebra XM511
 This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
Linear Algebra: Characteristic Value Problem
 Linear Algebra: Characteristic Value Problem . The Characteristic Value Problem Let < be the set of real numbers and { be the set of complex numbers. Given an n n real matrix A; does there exist a number
Linear Algebra: Characteristic Value Problem . The Characteristic Value Problem Let < be the set of real numbers and { be the set of complex numbers. Given an n n real matrix A; does there exist a number
Chapter 2:Determinants. Section 2.1: Determinants by cofactor expansion
 Chapter 2:Determinants Section 2.1: Determinants by cofactor expansion [ ] a b Recall: The 2 2 matrix is invertible if ad bc 0. The c d ([ ]) a b function f = ad bc is called the determinant and it associates
Chapter 2:Determinants Section 2.1: Determinants by cofactor expansion [ ] a b Recall: The 2 2 matrix is invertible if ad bc 0. The c d ([ ]) a b function f = ad bc is called the determinant and it associates
Problem Set (T) If A is an m n matrix, B is an n p matrix and D is a p s matrix, then show
 MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
[ Here 21 is the dot product of (3, 1, 2, 5) with (2, 3, 1, 2), and 31 is the dot product of
 . Matrices A matrix is any rectangular array of numbers. For example 3 5 6 4 8 3 3 is 3 4 matrix, i.e. a rectangular array of numbers with three rows four columns. We usually use capital letters for matrices,
. Matrices A matrix is any rectangular array of numbers. For example 3 5 6 4 8 3 3 is 3 4 matrix, i.e. a rectangular array of numbers with three rows four columns. We usually use capital letters for matrices,
Graduate Mathematical Economics Lecture 1
 Graduate Mathematical Economics Lecture 1 Yu Ren WISE, Xiamen University September 23, 2012 Outline 1 2 Course Outline ematical techniques used in graduate level economics courses Mathematics for Economists
Graduate Mathematical Economics Lecture 1 Yu Ren WISE, Xiamen University September 23, 2012 Outline 1 2 Course Outline ematical techniques used in graduate level economics courses Mathematics for Economists
Undergraduate Mathematical Economics Lecture 1
 Undergraduate Mathematical Economics Lecture 1 Yu Ren WISE, Xiamen University September 15, 2014 Outline 1 Courses Description and Requirement 2 Course Outline ematical techniques used in economics courses
Undergraduate Mathematical Economics Lecture 1 Yu Ren WISE, Xiamen University September 15, 2014 Outline 1 Courses Description and Requirement 2 Course Outline ematical techniques used in economics courses
4. Determinants.
 4. Determinants 4.1. Determinants; Cofactor Expansion Determinants of 2 2 and 3 3 Matrices 2 2 determinant 4.1. Determinants; Cofactor Expansion Determinants of 2 2 and 3 3 Matrices 3 3 determinant 4.1.
4. Determinants 4.1. Determinants; Cofactor Expansion Determinants of 2 2 and 3 3 Matrices 2 2 determinant 4.1. Determinants; Cofactor Expansion Determinants of 2 2 and 3 3 Matrices 3 3 determinant 4.1.
MATRICES AND MATRIX OPERATIONS
 SIZE OF THE MATRIX is defined by number of rows and columns in the matrix. For the matrix that have m rows and n columns we say the size of the matrix is m x n. If matrix have the same number of rows (n)
SIZE OF THE MATRIX is defined by number of rows and columns in the matrix. For the matrix that have m rows and n columns we say the size of the matrix is m x n. If matrix have the same number of rows (n)
Introduction to Matrices
 POLS 704 Introduction to Matrices Introduction to Matrices. The Cast of Characters A matrix is a rectangular array (i.e., a table) of numbers. For example, 2 3 X 4 5 6 (4 3) 7 8 9 0 0 0 Thismatrix,with4rowsand3columns,isoforder
POLS 704 Introduction to Matrices Introduction to Matrices. The Cast of Characters A matrix is a rectangular array (i.e., a table) of numbers. For example, 2 3 X 4 5 6 (4 3) 7 8 9 0 0 0 Thismatrix,with4rowsand3columns,isoforder
Linear Algebra Primer
 Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Elementary Linear Algebra
 Matrices J MUSCAT Elementary Linear Algebra Matrices Definition Dr J Muscat 2002 A matrix is a rectangular array of numbers, arranged in rows and columns a a 2 a 3 a n a 2 a 22 a 23 a 2n A = a m a mn We
Matrices J MUSCAT Elementary Linear Algebra Matrices Definition Dr J Muscat 2002 A matrix is a rectangular array of numbers, arranged in rows and columns a a 2 a 3 a n a 2 a 22 a 23 a 2n A = a m a mn We
Econ Slides from Lecture 7
 Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
MATH Topics in Applied Mathematics Lecture 12: Evaluation of determinants. Cross product.
 MATH 311-504 Topics in Applied Mathematics Lecture 12: Evaluation of determinants. Cross product. Determinant is a scalar assigned to each square matrix. Notation. The determinant of a matrix A = (a ij
MATH 311-504 Topics in Applied Mathematics Lecture 12: Evaluation of determinants. Cross product. Determinant is a scalar assigned to each square matrix. Notation. The determinant of a matrix A = (a ij
CS123 INTRODUCTION TO COMPUTER GRAPHICS. Linear Algebra 1/33
 Linear Algebra 1/33 Vectors A vector is a magnitude and a direction Magnitude = v Direction Also known as norm, length Represented by unit vectors (vectors with a length of 1 that point along distinct
Linear Algebra 1/33 Vectors A vector is a magnitude and a direction Magnitude = v Direction Also known as norm, length Represented by unit vectors (vectors with a length of 1 that point along distinct
Topic 1: Matrix diagonalization
 Topic : Matrix diagonalization Review of Matrices and Determinants Definition A matrix is a rectangular array of real numbers a a a m a A = a a m a n a n a nm The matrix is said to be of order n m if it
Topic : Matrix diagonalization Review of Matrices and Determinants Definition A matrix is a rectangular array of real numbers a a a m a A = a a m a n a n a nm The matrix is said to be of order n m if it
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.7 LINEAR INDEPENDENCE LINEAR INDEPENDENCE Definition: An indexed set of vectors {v 1,, v p } in n is said to be linearly independent if the vector equation x x x
1 Linear Equations in Linear Algebra 1.7 LINEAR INDEPENDENCE LINEAR INDEPENDENCE Definition: An indexed set of vectors {v 1,, v p } in n is said to be linearly independent if the vector equation x x x
APPENDIX A. Background Mathematics. A.1 Linear Algebra. Vector algebra. Let x denote the n-dimensional column vector with components x 1 x 2.
 APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
APPENDIX A Background Mathematics A. Linear Algebra A.. Vector algebra Let x denote the n-dimensional column vector with components 0 x x 2 B C @. A x n Definition 6 (scalar product). The scalar product
Lecture 3: Matrix and Matrix Operations
 Lecture 3: Matrix and Matrix Operations Representation, row vector, column vector, element of a matrix. Examples of matrix representations Tables and spreadsheets Scalar-Matrix operation: Scaling a matrix
Lecture 3: Matrix and Matrix Operations Representation, row vector, column vector, element of a matrix. Examples of matrix representations Tables and spreadsheets Scalar-Matrix operation: Scaling a matrix
Computational Methods CMSC/AMSC/MAPL 460. Eigenvalues and Eigenvectors. Ramani Duraiswami, Dept. of Computer Science
 Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
Computational Methods CMSC/AMSC/MAPL 460 Eigenvalues and Eigenvectors Ramani Duraiswami, Dept. of Computer Science Eigen Values of a Matrix Recap: A N N matrix A has an eigenvector x (non-zero) with corresponding
NOTES ON LINEAR ALGEBRA CLASS HANDOUT
 NOTES ON LINEAR ALGEBRA CLASS HANDOUT ANTHONY S. MAIDA CONTENTS 1. Introduction 2 2. Basis Vectors 2 3. Linear Transformations 2 3.1. Example: Rotation Transformation 3 4. Matrix Multiplication and Function
NOTES ON LINEAR ALGEBRA CLASS HANDOUT ANTHONY S. MAIDA CONTENTS 1. Introduction 2 2. Basis Vectors 2 3. Linear Transformations 2 3.1. Example: Rotation Transformation 3 4. Matrix Multiplication and Function
EE731 Lecture Notes: Matrix Computations for Signal Processing
 EE731 Lecture Notes: Matrix Computations for Signal Processing James P. Reilly c Department of Electrical and Computer Engineering McMaster University September 22, 2005 0 Preface This collection of ten
EE731 Lecture Notes: Matrix Computations for Signal Processing James P. Reilly c Department of Electrical and Computer Engineering McMaster University September 22, 2005 0 Preface This collection of ten
a 11 a 12 a 11 a 12 a 13 a 21 a 22 a 23 . a 31 a 32 a 33 a 12 a 21 a 23 a 31 a = = = = 12
 24 8 Matrices Determinant of 2 2 matrix Given a 2 2 matrix [ ] a a A = 2 a 2 a 22 the real number a a 22 a 2 a 2 is determinant and denoted by det(a) = a a 2 a 2 a 22 Example 8 Find determinant of 2 2
24 8 Matrices Determinant of 2 2 matrix Given a 2 2 matrix [ ] a a A = 2 a 2 a 22 the real number a a 22 a 2 a 2 is determinant and denoted by det(a) = a a 2 a 2 a 22 Example 8 Find determinant of 2 2
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Review of Vectors and Matrices
 A P P E N D I X D Review of Vectors and Matrices D. VECTORS D.. Definition of a Vector Let p, p, Á, p n be any n real numbers and P an ordered set of these real numbers that is, P = p, p, Á, p n Then P
A P P E N D I X D Review of Vectors and Matrices D. VECTORS D.. Definition of a Vector Let p, p, Á, p n be any n real numbers and P an ordered set of these real numbers that is, P = p, p, Á, p n Then P
Lecture Summaries for Linear Algebra M51A
 These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
Chapter 2 Notes, Linear Algebra 5e Lay
 Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Contents.1 Operations with Matrices..................................1.1 Addition and Subtraction.............................1. Multiplication by a scalar............................ 3.1.3 Multiplication
Math Camp Lecture 4: Linear Algebra. Xiao Yu Wang. Aug 2010 MIT. Xiao Yu Wang (MIT) Math Camp /10 1 / 88
 Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections )
 c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
c Dr. Igor Zelenko, Fall 2017 1 10. Linear Systems of ODEs, Matrix multiplication, superposition principle (parts of sections 7.2-7.4) 1. When each of the functions F 1, F 2,..., F n in right-hand side
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
Foundations of Matrix Analysis
 1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
Fundamentals of Engineering Analysis (650163)
 Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
Philadelphia University Faculty of Engineering Communications and Electronics Engineering Fundamentals of Engineering Analysis (6563) Part Dr. Omar R Daoud Matrices: Introduction DEFINITION A matrix is
Math Matrix Algebra
 Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Matrix operations Linear Algebra with Computer Science Application
 Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Linear Algebra with Computer Science Application February 14, 2018 1 Matrix operations 11 Matrix operations If A is an m n matrix that is, a matrix with m rows and n columns then the scalar entry in the
Study Notes on Matrices & Determinants for GATE 2017
 Study Notes on Matrices & Determinants for GATE 2017 Matrices and Determinates are undoubtedly one of the most scoring and high yielding topics in GATE. At least 3-4 questions are always anticipated from
Study Notes on Matrices & Determinants for GATE 2017 Matrices and Determinates are undoubtedly one of the most scoring and high yielding topics in GATE. At least 3-4 questions are always anticipated from
Lecture 1 Review: Linear models have the form (in matrix notation) Y = Xβ + ε,
 2. REVIEW OF LINEAR ALGEBRA 1 Lecture 1 Review: Linear models have the form (in matrix notation) Y = Xβ + ε, where Y n 1 response vector and X n p is the model matrix (or design matrix ) with one row for
2. REVIEW OF LINEAR ALGEBRA 1 Lecture 1 Review: Linear models have the form (in matrix notation) Y = Xβ + ε, where Y n 1 response vector and X n p is the model matrix (or design matrix ) with one row for
Matrix Arithmetic. j=1
 An m n matrix is an array A = Matrix Arithmetic a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn of real numbers a ij An m n matrix has m rows and n columns a ij is the entry in the i-th row and j-th column
An m n matrix is an array A = Matrix Arithmetic a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn of real numbers a ij An m n matrix has m rows and n columns a ij is the entry in the i-th row and j-th column
88 CHAPTER 3. SYMMETRIES
 88 CHAPTER 3 SYMMETRIES 31 Linear Algebra Start with a field F (this will be the field of scalars) Definition: A vector space over F is a set V with a vector addition and scalar multiplication ( scalars
88 CHAPTER 3 SYMMETRIES 31 Linear Algebra Start with a field F (this will be the field of scalars) Definition: A vector space over F is a set V with a vector addition and scalar multiplication ( scalars
ACM 104. Homework Set 4 Solutions February 14, 2001
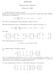 ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
Linear Algebra and Matrix Inversion
 Jim Lambers MAT 46/56 Spring Semester 29- Lecture 2 Notes These notes correspond to Section 63 in the text Linear Algebra and Matrix Inversion Vector Spaces and Linear Transformations Matrices are much
Jim Lambers MAT 46/56 Spring Semester 29- Lecture 2 Notes These notes correspond to Section 63 in the text Linear Algebra and Matrix Inversion Vector Spaces and Linear Transformations Matrices are much
Dot Products. K. Behrend. April 3, Abstract A short review of some basic facts on the dot product. Projections. The spectral theorem.
 Dot Products K. Behrend April 3, 008 Abstract A short review of some basic facts on the dot product. Projections. The spectral theorem. Contents The dot product 3. Length of a vector........................
Dot Products K. Behrend April 3, 008 Abstract A short review of some basic facts on the dot product. Projections. The spectral theorem. Contents The dot product 3. Length of a vector........................
Linear Systems and Matrices
 Department of Mathematics The Chinese University of Hong Kong 1 System of m linear equations in n unknowns (linear system) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.......
Department of Mathematics The Chinese University of Hong Kong 1 System of m linear equations in n unknowns (linear system) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.......
Math113: Linear Algebra. Beifang Chen
 Math3: Linear Algebra Beifang Chen Spring 26 Contents Systems of Linear Equations 3 Systems of Linear Equations 3 Linear Systems 3 2 Geometric Interpretation 3 3 Matrices of Linear Systems 4 4 Elementary
Math3: Linear Algebra Beifang Chen Spring 26 Contents Systems of Linear Equations 3 Systems of Linear Equations 3 Linear Systems 3 2 Geometric Interpretation 3 3 Matrices of Linear Systems 4 4 Elementary
Matrices Gaussian elimination Determinants. Graphics 2009/2010, period 1. Lecture 4: matrices
 Graphics 2009/2010, period 1 Lecture 4 Matrices m n matrices Matrices Definitions Diagonal, Identity, and zero matrices Addition Multiplication Transpose and inverse The system of m linear equations in
Graphics 2009/2010, period 1 Lecture 4 Matrices m n matrices Matrices Definitions Diagonal, Identity, and zero matrices Addition Multiplication Transpose and inverse The system of m linear equations in
CS123 INTRODUCTION TO COMPUTER GRAPHICS. Linear Algebra /34
 Linear Algebra /34 Vectors A vector is a magnitude and a direction Magnitude = v Direction Also known as norm, length Represented by unit vectors (vectors with a length of 1 that point along distinct axes)
Linear Algebra /34 Vectors A vector is a magnitude and a direction Magnitude = v Direction Also known as norm, length Represented by unit vectors (vectors with a length of 1 that point along distinct axes)
Vectors and Matrices
 Vectors and Matrices Scalars We often employ a single number to represent quantities that we use in our daily lives such as weight, height etc. The magnitude of this number depends on our age and whether
Vectors and Matrices Scalars We often employ a single number to represent quantities that we use in our daily lives such as weight, height etc. The magnitude of this number depends on our age and whether
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Chapter 3 Transformations
 Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Extra Problems for Math 2050 Linear Algebra I
 Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
Extra Problems for Math 5 Linear Algebra I Find the vector AB and illustrate with a picture if A = (,) and B = (,4) Find B, given A = (,4) and [ AB = A = (,4) and [ AB = 8 If possible, express x = 7 as
4 Linear Algebra Review
 4 Linear Algebra Review For this topic we quickly review many key aspects of linear algebra that will be necessary for the remainder of the course 41 Vectors and Matrices For the context of data analysis,
4 Linear Algebra Review For this topic we quickly review many key aspects of linear algebra that will be necessary for the remainder of the course 41 Vectors and Matrices For the context of data analysis,
Linear algebra for computational statistics
 University of Seoul May 3, 2018 Vector and Matrix Notation Denote 2-dimensional data array (n p matrix) by X. Denote the element in the ith row and the jth column of X by x ij or (X) ij. Denote by X j
University of Seoul May 3, 2018 Vector and Matrix Notation Denote 2-dimensional data array (n p matrix) by X. Denote the element in the ith row and the jth column of X by x ij or (X) ij. Denote by X j
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Linear Algebra and Matrices
 Linear Algebra and Matrices 4 Overview In this chapter we studying true matrix operations, not element operations as was done in earlier chapters. Working with MAT- LAB functions should now be fairly routine.
Linear Algebra and Matrices 4 Overview In this chapter we studying true matrix operations, not element operations as was done in earlier chapters. Working with MAT- LAB functions should now be fairly routine.
