Rational Gauss-Radau and rational Szegő-Lobatto quadrature on the interval and the unit circle respectively
|
|
|
- Lambert Harris
- 5 years ago
- Views:
Transcription
1 Rational Gauss-Radau and rational Szegő-Lobatto quadrature on the interval and the unit circle respectively Francisco Perdomo-Pio Departament of Mathematical Analysis. La Laguna University La Laguna. Tenerife. Canary Islands. Spain. Joint work with: Adhemar Bultheel and Karl Deckers
2 Aim of the talk Present relation between Rational Gauss-Radau and Rational Szegő-Lobatto quadrature formulas. Motivation interchange properties, analytic computations, reduces computational effort,...
3 Aim of the talk Present relation between Rational Gauss-Radau and Rational Szegő-Lobatto quadrature formulas. Motivation interchange properties, analytic computations, reduces computational effort,...
4 Preliminaries Interval I = [ 1, 1] C I = (C { }) \ I {α 1, α{ 2,...} C I p L n = n(x) n k=1 (1 x/α k) : p n P n }, n = 1, 2,... Unit circle T = {z C : z = 1} D = {z C : z < 1} {β 1, β 2 {,...} D p L n = n(z) : p n k=1 (1 β k z) n P n }, n = 1, 2,... Quadrature rules J µ (f) := K n f(t)dµ(t) λ j f(t j ) =: J n (f), j=1 {t j } n j=1 K where K = I or K = T, and t = x or t = z.
5 Preliminaries Interval I = [ 1, 1] C I = (C { }) \ I {α 1, α{ 2,...} C I p L n = n(x) n k=1 (1 x/α k) : p n P n }, n = 1, 2,... Unit circle T = {z C : z = 1} D = {z C : z < 1} {β 1, β 2 {,...} D p L n = n(z) : p n k=1 (1 β k z) n P n }, n = 1, 2,... Quadrature rules J µ (f) := K n f(t)dµ(t) λ j f(t j ) =: J n (f), j=1 {t j } n j=1 K where K = I or K = T, and t = x or t = z.
6 positive rational interpolatory quadrature rule on I µ a positive bounded Borel measure on I, {λ j } n j=1 R+ 0, J µ (f) = J n (f) at least for all f L n 1. Special cases Rational Gaussian quadrature formula, which has maximal domain of exactness: L n L c n 1 = {f(x) g(x) : f L n, g L n 1 }. Rational Gauss-Radau quadrature formula (i.e, one node x α fixed in advance), with domain of exactness: L n 1 L c n 1.
7 Construction quadratures Rational Gaussian quadrature nodes x k = zeros of ϕ n L n \ L n 1, where ϕ n µ L n 1 w.r.t. the inner product f, g µ = 1 1 f(x)g(x)dµ(x). λ k = { n 1 j=0 ϕ j(x k ) 2 } 1. Rational Gauss-Radau quadrature nodes x k = zeros of the quasi-orthogonal rational function (qorf) Q n,τn = ϕ n (x) + τ n 1 x/α n 1 1 x/α n ϕ n 1 (x), τ n C. λ k = { n 1 j=0 ϕ j(x k ) 2 } 1. In remainder we assume α n R I.
8 positive rational interpolatory quadrature rule on T µ a positive bounded Borel measure on T, { λ j } n j=1 R+ 0, J µ ( f) = J n ( f) for all f L p L p = {f(z) g(1/z) : f, g L p }, (n 1)/2 p n 1. Special cases Rational Szegő quadrature formula, which has maximal domain of exactness: L n 1 L (n 1). Rational Szegő-Lobatto quadrature formula (i.e., two nodes z α and z β fixed in advance) with domain of exactness: L n 2 L (n 2).
9 Construction quadratures Rational Szegő quadrature nodes z k = zeros of a para-orthogonal rational function (porf) Q n,ξn (z) = z β n 1 1 β n z φ n 1(z) + ξ n 1 β n 1 z 1 β n z φ n 1(z), where φ n µ Ln 1 w.r.t. the inner product f, g = π f(z) g(1/z)d µ(θ), µ π φ n(z) = φ n (1/z) n j=1 λk = { n 1 j=0 φ j(z k ) 2 } 1. z β k 1 β k z, and ξ n T.
10 Construction quadratures Rational Szegő-Lobatto quadrature nodes z k = zeros of a porf Q n, ξn (z) = z β n 1 φ 1 β n z n 1 (z) + ξ 1 β n 1 z n 1 β n z ( φ n 1 (z) = c z βn 2 k φ 1 β n 1 z n 2(z) + δ 1 β n 2 z n 1 δ n 1 D, and ξ n T. λk = { n 1 j=0 φ j (x k ) 2 } 1. In remainder we assume β n ( 1, 1). φ n 1 (z), where ) 1 β n 1 z φ n 2 (z),
11 Connection between I and T Joukowski transformation x = J(z) = 1 2 (z + z 1 ). {α 1, α 2,...} C I { ˆβ 1, ˆβ 2,... } D. ˆβ 2k = ˆβ 2k 1 = β k, α k = J(β k ). The measures µ on I µ on T a symmetric measure µ(e) = µ({cos θ, θ E [0, π)}) + µ({cos θ, θ E [ π, 0)}), The integrals I f(x)dµ(x) = 1 2 T f(z)d µ(z), f = f J.
12 Connection between I and T Theorem Sym {β 1,..., β n 1 } real or complex conjugate pairs, and µ positive symmetric Borel measure on T. Then, 1 zeros of Q n,ξn appear in complex conjugate pairs iff ξ n = ±1. 2 z = 1 is zero iff ξ n = 1 and z = 1 iff ξ n = ( 1) n+1. 3 Let J n ( f) be an n-point rational Szegő-Lobatto quadrature formula based on zeros of Q n,±1. Then for k = 1,..., n, the weight λ k = λ j if z j = z k. Theorem Rel µ related with µ by Joukowski transform, then ) ϕ k (x) = F (φ 2k (z), φ 2k (z) ( ) = G φ 2k 1 (z), φ 2k 1(z).
13 Relating rational Szegő-Lobatto and Gauss-Radau rules Theorem SL-GR µ and µ related by Joukowski transform. Let J 2n ( f) = λ α (z α ) f(z α ) + λ β f(zα ) + 2n 2 k=1 λ k f(zk ) be a 2n-point rational Szegő-Lobatto quadrature formula with fixed nodes {z α, z α } T \ { 1, +1} for J µ ( f). Set x α = J(z α ), λ α = λ α, x k = J(z k ) and λ k = λ k. Then the formula J n (f) = λ α f(x α ) + n 1 j=1 λ jf(x j ) coincides with the n-point rational Gauss-Radau formula based on the zeros of the qorf where τ n depends of x α Q n,τn (x) = H(z) Q2n,1 (z)
14 Relating rational Szegő-Lobatto and Gauss-Radau rules Proof From Theorem Sym it follows that Q2n,1 has 2n zeros (all different from 1 and 1), appearing in complex conjugate pairs, and λ α = λ β, λ n 1+k = λ k. If f L n 1 L c n 1 then f(z) = (f J)(z) ˆ L2n 2 ˆ L(2n 2) n 1 J n (f) = λ α f(x α ) + λ k f(x k ) = 1 2 { k=1 λα (z α ) f(z α ) + λ β f(zα ) + = 1 2 J 2n( f) = 1 2 J µ( f) = J µ (f). 2n 2 k=1 λk f(zk ) }
15 Relating rational Gauss-Radau and Szegő-Lobatto rules Theorem GR-SL Let µ and µ related by the Joukowski transformation. Let J n (f) = λ α f(x α ) + n j=1 λ kf(x k ) be an n-point rational Gauss-Radau quadrature formula with fixed node x α for J µ (f), based on the zeros of the qorf Q n,τn. Set x k = cos θ k, x α = cos θ α, and define z k = z n 1+k = e iθ k, λ k = λ n 1+k = λ k, k = 1,..., n 1. z α = e iθα, λ α = λ α. Then J 2n ( f) = λ α f(zα ) + λ 2n 2 α f(zα ) + λk f(zk ) k=1 coincides with the 2n-point rational Szegő-Lobatto quadrature formula with fixed nodes {z α, z α } for J µ ( f) based on the zeros of the porf Q2n, ξ2n with ξ 2n = 1, and with δ 2n 1 depending on τ n.
16 Relating rational Gauss-Radau and Szegő-Lobatto rules Outline of the proof It is known that the qorf is orthogonal to L n 1 w.r.t. a measure µ (not necessarily supported in I). We can express Q n,τn (x) in terms of ˆφ 2n 2 (z) and ˆφ 2n 2 (z) in two ways: by assuming that Q n,τn (x) = H(z) Q2n,1 (z), which is equivalent with assuming that the measure µ is supported on I; by making use of the definition of Q n,τn (x) together with Theorem Rel. By comparison we then obtain a relation between δ 2n 1 and τ n.
17 Relating rational Gauss-Radau and Szegő-Lobatto rules Next, we need the following lemma. Lemma {β 1,..., β n 1 } real or complex conjugate pairs, and µ positive symmetric Borel measure on T. φ c n 1(z) = b n z β n 1 z β n 1 φ n 1 (z) + a n 1 β n 1 z z β n 1 φ n 1 (1/z) a n and b n can be expressed in terms of δ n. Since φ c n 1 (z) is independent of δ n, so are a n and b n. Hence, the expressions for a n and b n remains the same when replacing δ n with δ n. As a result, we find that δ n C D, a n 0 δ n L D, a n = 0 with C a circle and L a line that depends of a n and b n.
18 Relating rational Gauss-Radau and Szegő-Lobatto rules Finally, we have the following lemma. Lemma Let τ n be such that Q n,τn (x) has all its zeros in ( 1, 1). Then the corresponding δ 2n 1 satisfies the condition given in the previous lemma.
19 Bibliography A. Bultheel, L. Daruis, P. González-Vera, A connection between quadrature formulas on the unit circle and the interval [ 1, 1] Journal of Computational and Applied Mathematics, 132 (1) (2001) A. Bultheel, P. González-Vera, E. Hendriksen, O. Njåstad, Orthogonal Rational Functions, volume 5 of Cambridge Monographs on Applied and Computational Mathematics, Cambridge University Press, Cambridge, A. Bultheel, P. González-Vera, E. Hendriksen, O. Njåstad, Computation of rational Szegő-Lobatto quadrature formulas, Applied Numerical Mathematics, (2010). Submitted. K. Deckers, A. Bultheel, R. Cruz-Barroso, F. Perdomo-Pío, Positive rational interpolatory quadrature formulas on the unit circle and the interval, Applied Numerical Mathematics, Publish online 30 March K. Deckers, A. Bultheel, J. Van Deun, A generalized eigenvalue problem for quasi-orthogonal rational functions, Numerische Mathematik, (2010). Submitted. K. Deckers, J. van Deun, A. Bultheel, An extended relation between orthogonal rational functions on the unit circle and the interval [ 1, 1], Journal of Mathematical Analysis and Applications, 334 (2) (2007) J. van Deun, A. Bultheel, Orthogonal rational functions and quadrature on an interval, Journal of Computational and Applied Mathematics, 153 (1-2) (2003)
Computation of Rational Szegő-Lobatto Quadrature Formulas
 Computation of Rational Szegő-Lobatto Quadrature Formulas Joint work with: A. Bultheel (Belgium) E. Hendriksen (The Netherlands) O. Njastad (Norway) P. GONZÁLEZ-VERA Departament of Mathematical Analysis.
Computation of Rational Szegő-Lobatto Quadrature Formulas Joint work with: A. Bultheel (Belgium) E. Hendriksen (The Netherlands) O. Njastad (Norway) P. GONZÁLEZ-VERA Departament of Mathematical Analysis.
Katholieke Universiteit Leuven Department of Computer Science
 Separation of zeros of para-orthogonal rational functions A. Bultheel, P. González-Vera, E. Hendriksen, O. Njåstad Report TW 402, September 2004 Katholieke Universiteit Leuven Department of Computer Science
Separation of zeros of para-orthogonal rational functions A. Bultheel, P. González-Vera, E. Hendriksen, O. Njåstad Report TW 402, September 2004 Katholieke Universiteit Leuven Department of Computer Science
Szegő-Lobatto quadrature rules
 Szegő-Lobatto quadrature rules Carl Jagels a,, Lothar Reichel b,1, a Department of Mathematics and Computer Science, Hanover College, Hanover, IN 47243, USA b Department of Mathematical Sciences, Kent
Szegő-Lobatto quadrature rules Carl Jagels a,, Lothar Reichel b,1, a Department of Mathematics and Computer Science, Hanover College, Hanover, IN 47243, USA b Department of Mathematical Sciences, Kent
Rational bases for system identification
 Rational bases for system identification Adhemar Bultheel, Patrick Van gucht Department Computer Science Numerical Approximation and Linear Algebra Group (NALAG) K.U.Leuven, Belgium adhemar.bultheel.cs.kuleuven.ac.be
Rational bases for system identification Adhemar Bultheel, Patrick Van gucht Department Computer Science Numerical Approximation and Linear Algebra Group (NALAG) K.U.Leuven, Belgium adhemar.bultheel.cs.kuleuven.ac.be
On Gauss-type quadrature formulas with prescribed nodes anywhere on the real line
 On Gauss-type quadrature formulas with prescribed nodes anywhere on the real line Adhemar Bultheel, Ruymán Cruz-Barroso,, Marc Van Barel Department of Computer Science, K.U.Leuven, Celestijnenlaan 2 A,
On Gauss-type quadrature formulas with prescribed nodes anywhere on the real line Adhemar Bultheel, Ruymán Cruz-Barroso,, Marc Van Barel Department of Computer Science, K.U.Leuven, Celestijnenlaan 2 A,
A matricial computation of rational quadrature formulas on the unit circle
 A matricial computation of rational quadrature formulas on the unit circle Adhemar Bultheel and Maria-José Cantero Department of Computer Science. Katholieke Universiteit Leuven. Belgium Department of
A matricial computation of rational quadrature formulas on the unit circle Adhemar Bultheel and Maria-José Cantero Department of Computer Science. Katholieke Universiteit Leuven. Belgium Department of
formulas with complex poles
 Computing rational Gauss-Chebyshev quadrature formulas with complex poles Karl Deckers Joris Van Deun Adhemar Bultheel Department of Computer Science K.U.Leuven Augustus 7, 2006 Rational Gauss-Chebyshev
Computing rational Gauss-Chebyshev quadrature formulas with complex poles Karl Deckers Joris Van Deun Adhemar Bultheel Department of Computer Science K.U.Leuven Augustus 7, 2006 Rational Gauss-Chebyshev
Matrix methods for quadrature formulas on the unit circle. A survey
 Matrix methods for quadrature formulas on the unit circle A survey Adhemar Bultheel a, María José Cantero b,1,, Ruymán Cruz-Barroso c,2 a Department of Computer Science, KU Leuven, Belgium b Department
Matrix methods for quadrature formulas on the unit circle A survey Adhemar Bultheel a, María José Cantero b,1,, Ruymán Cruz-Barroso c,2 a Department of Computer Science, KU Leuven, Belgium b Department
Orthogonal Rational Functions on the Unit Circle with Prescribed Poles not on the Unit Circle
 Symmetry, Integrability and Geometry: Methods and Applications SIGMA 13 (27), 090, 49 pages Orthogonal Rational Functions on the Unit Circle with Prescribed Poles not on the Unit Circle Adhemar BULTHEEL,
Symmetry, Integrability and Geometry: Methods and Applications SIGMA 13 (27), 090, 49 pages Orthogonal Rational Functions on the Unit Circle with Prescribed Poles not on the Unit Circle Adhemar BULTHEEL,
Orthogonal Polynomials, Quadratures & Sparse-Grid Methods for Probability Integrals
 1/31 Orthogonal Polynomials, Quadratures & Sparse-Grid Methods for Probability Integrals Dr. Abebe Geletu May, 2010 Technische Universität Ilmenau, Institut für Automatisierungs- und Systemtechnik Fachgebiet
1/31 Orthogonal Polynomials, Quadratures & Sparse-Grid Methods for Probability Integrals Dr. Abebe Geletu May, 2010 Technische Universität Ilmenau, Institut für Automatisierungs- und Systemtechnik Fachgebiet
On the remainder term of Gauss Radau quadratures for analytic functions
 Journal of Computational and Applied Mathematics 218 2008) 281 289 www.elsevier.com/locate/cam On the remainder term of Gauss Radau quadratures for analytic functions Gradimir V. Milovanović a,1, Miodrag
Journal of Computational and Applied Mathematics 218 2008) 281 289 www.elsevier.com/locate/cam On the remainder term of Gauss Radau quadratures for analytic functions Gradimir V. Milovanović a,1, Miodrag
ETNA Kent State University
 Electronic Transactions on Numerical Analysis. Volume 9, 1999, pp. 39-52. Copyright 1999,. ISSN 1068-9613. ETNA QUADRATURE FORMULAS FOR RATIONAL FUNCTIONS F. CALA RODRIGUEZ, P. GONZALEZ VERA, AND M. JIMENEZ
Electronic Transactions on Numerical Analysis. Volume 9, 1999, pp. 39-52. Copyright 1999,. ISSN 1068-9613. ETNA QUADRATURE FORMULAS FOR RATIONAL FUNCTIONS F. CALA RODRIGUEZ, P. GONZALEZ VERA, AND M. JIMENEZ
NUMERICAL CALCULATION OF RANDOM MATRIX DISTRIBUTIONS AND ORTHOGONAL POLYNOMIALS. Sheehan Olver NA Group, Oxford
 NUMERICAL CALCULATION OF RANDOM MATRIX DISTRIBUTIONS AND ORTHOGONAL POLYNOMIALS Sheehan Olver NA Group, Oxford We are interested in numerically computing eigenvalue statistics of the GUE ensembles, i.e.,
NUMERICAL CALCULATION OF RANDOM MATRIX DISTRIBUTIONS AND ORTHOGONAL POLYNOMIALS Sheehan Olver NA Group, Oxford We are interested in numerically computing eigenvalue statistics of the GUE ensembles, i.e.,
Quadrature Rules With an Even Number of Multiple Nodes and a Maximal Trigonometric Degree of Exactness
 Filomat 9:10 015), 39 55 DOI 10.98/FIL151039T Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Quadrature Rules With an Even Number
Filomat 9:10 015), 39 55 DOI 10.98/FIL151039T Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Quadrature Rules With an Even Number
PARA-ORTHOGONAL POLYNOMIALS IN FREQUENCY ANALYSIS. 1. Introduction. By a trigonometric signal we mean an expression of the form.
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 33, Number 2, Summer 2003 PARA-ORTHOGONAL POLYNOMIALS IN FREQUENCY ANALYSIS LEYLA DARUIS, OLAV NJÅSTAD AND WALTER VAN ASSCHE 1. Introduction. By a trigonometric
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 33, Number 2, Summer 2003 PARA-ORTHOGONAL POLYNOMIALS IN FREQUENCY ANALYSIS LEYLA DARUIS, OLAV NJÅSTAD AND WALTER VAN ASSCHE 1. Introduction. By a trigonometric
SPRING 2006 PRELIMINARY EXAMINATION SOLUTIONS
 SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
OSTROWSKI S THEOREM. Contents
 OSTROWSKI S THEOREM GEUNHO GIM Contents. Ostrowski s theorem for Q 2. Ostrowski s theorem for number fields 2 3. Ostrowski s theorem for F T ) 4 References 5. Ostrowski s theorem for Q Definition.. A valuation
OSTROWSKI S THEOREM GEUNHO GIM Contents. Ostrowski s theorem for Q 2. Ostrowski s theorem for number fields 2 3. Ostrowski s theorem for F T ) 4 References 5. Ostrowski s theorem for Q Definition.. A valuation
Katholieke Universiteit Leuven Department of Computer Science
 Growth properties of Nevanlinna matrices for rational moment problems Adhemar Bultheel, Pablo González-Vera, Erik Hendriksen, Olav Njåstad eport TW 56, February 200 Katholieke Universiteit Leuven Department
Growth properties of Nevanlinna matrices for rational moment problems Adhemar Bultheel, Pablo González-Vera, Erik Hendriksen, Olav Njåstad eport TW 56, February 200 Katholieke Universiteit Leuven Department
STIELTJES-TYPE POLYNOMIALS ON THE UNIT CIRCLE
 STIELTJES-TYPE POLYNOMIALS ON THE UNIT CIRCLE B. DE LA CALLE YSERN, G. LÓPEZ LAGOMASINO, AND L. REICHEL Abstract. Stieltjes-type polynomials corresponding to measures supported on the unit circle T are
STIELTJES-TYPE POLYNOMIALS ON THE UNIT CIRCLE B. DE LA CALLE YSERN, G. LÓPEZ LAGOMASINO, AND L. REICHEL Abstract. Stieltjes-type polynomials corresponding to measures supported on the unit circle T are
ETNA Kent State University
 Electronic Transactions on Numerical Analysis. Volume 35, pp. 148-163, 2009. Copyright 2009,. ISSN 1068-9613. ETNA SPHERICAL QUADRATURE FORMULAS WITH EQUALLY SPACED NODES ON LATITUDINAL CIRCLES DANIELA
Electronic Transactions on Numerical Analysis. Volume 35, pp. 148-163, 2009. Copyright 2009,. ISSN 1068-9613. ETNA SPHERICAL QUADRATURE FORMULAS WITH EQUALLY SPACED NODES ON LATITUDINAL CIRCLES DANIELA
Instructions for Matlab Routines
 Instructions for Matlab Routines August, 2011 2 A. Introduction This note is devoted to some instructions to the Matlab routines for the fundamental spectral algorithms presented in the book: Jie Shen,
Instructions for Matlab Routines August, 2011 2 A. Introduction This note is devoted to some instructions to the Matlab routines for the fundamental spectral algorithms presented in the book: Jie Shen,
You may not start to read the questions printed on the subsequent pages until instructed to do so by the Invigilator.
 MATHEMATICAL TRIPOS Part IB Thursday 7 June 2007 9 to 12 PAPER 3 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each question in Section
MATHEMATICAL TRIPOS Part IB Thursday 7 June 2007 9 to 12 PAPER 3 Before you begin read these instructions carefully. Each question in Section II carries twice the number of marks of each question in Section
COURSE Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method
 COURSE 7 3. Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method The presence of derivatives in the remainder difficulties in applicability to practical problems
COURSE 7 3. Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method The presence of derivatives in the remainder difficulties in applicability to practical problems
A numerical solution of the constrained weighted energy problem and its relation to rational Lanczos iterations
 A numerical solution of the constrained weighted energy problem and its relation to rational Lanczos iterations Karl Deckers, Andrey Chesnokov, and Marc Van Barel Department of Computer Science, Katholieke
A numerical solution of the constrained weighted energy problem and its relation to rational Lanczos iterations Karl Deckers, Andrey Chesnokov, and Marc Van Barel Department of Computer Science, Katholieke
Simultaneous Gaussian quadrature for Angelesco systems
 for Angelesco systems 1 KU Leuven, Belgium SANUM March 22, 2016 1 Joint work with Doron Lubinsky Introduced by C.F. Borges in 1994 Introduced by C.F. Borges in 1994 (goes back to Angelesco 1918). Introduced
for Angelesco systems 1 KU Leuven, Belgium SANUM March 22, 2016 1 Joint work with Doron Lubinsky Introduced by C.F. Borges in 1994 Introduced by C.F. Borges in 1994 (goes back to Angelesco 1918). Introduced
Example 9 Algebraic Evaluation for Example 1
 A Basic Principle Consider the it f(x) x a If you have a formula for the function f and direct substitution gives the indeterminate form 0, you may be able to evaluate the it algebraically. 0 Principle
A Basic Principle Consider the it f(x) x a If you have a formula for the function f and direct substitution gives the indeterminate form 0, you may be able to evaluate the it algebraically. 0 Principle
Orthogonal rational functions and modified approximants
 Numerical Algorithms 11(1996)57-69 57 Orthogonal rational functions and modified approximants A. Bultheel Department of Computer Science, K.U. Leuven, B-3001 Leuven, Belgium P. Gonzfilez-Vera Facultad
Numerical Algorithms 11(1996)57-69 57 Orthogonal rational functions and modified approximants A. Bultheel Department of Computer Science, K.U. Leuven, B-3001 Leuven, Belgium P. Gonzfilez-Vera Facultad
IV. Conformal Maps. 1. Geometric interpretation of differentiability. 2. Automorphisms of the Riemann sphere: Möbius transformations
 MTH6111 Complex Analysis 2009-10 Lecture Notes c Shaun Bullett 2009 IV. Conformal Maps 1. Geometric interpretation of differentiability We saw from the definition of complex differentiability that if f
MTH6111 Complex Analysis 2009-10 Lecture Notes c Shaun Bullett 2009 IV. Conformal Maps 1. Geometric interpretation of differentiability We saw from the definition of complex differentiability that if f
Chapter 7 Polynomial Functions. Factoring Review. We will talk about 3 Types: ALWAYS FACTOR OUT FIRST! Ex 2: Factor x x + 64
 Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Numerical Analysis Preliminary Exam 10.00am 1.00pm, January 19, 2018
 Numerical Analysis Preliminary Exam 0.00am.00pm, January 9, 208 Instructions. You have three hours to complete this exam. Submit solutions to four (and no more) of the following six problems. Please start
Numerical Analysis Preliminary Exam 0.00am.00pm, January 9, 208 Instructions. You have three hours to complete this exam. Submit solutions to four (and no more) of the following six problems. Please start
(x x 0 )(x x 1 )... (x x n ) (x x 0 ) + y 0.
 > 5. Numerical Integration Review of Interpolation Find p n (x) with p n (x j ) = y j, j = 0, 1,,..., n. Solution: p n (x) = y 0 l 0 (x) + y 1 l 1 (x) +... + y n l n (x), l k (x) = n j=1,j k Theorem Let
> 5. Numerical Integration Review of Interpolation Find p n (x) with p n (x j ) = y j, j = 0, 1,,..., n. Solution: p n (x) = y 0 l 0 (x) + y 1 l 1 (x) +... + y n l n (x), l k (x) = n j=1,j k Theorem Let
A NOTE ON RATIONAL OPERATOR MONOTONE FUNCTIONS. Masaru Nagisa. Received May 19, 2014 ; revised April 10, (Ax, x) 0 for all x C n.
 Scientiae Mathematicae Japonicae Online, e-014, 145 15 145 A NOTE ON RATIONAL OPERATOR MONOTONE FUNCTIONS Masaru Nagisa Received May 19, 014 ; revised April 10, 014 Abstract. Let f be oeprator monotone
Scientiae Mathematicae Japonicae Online, e-014, 145 15 145 A NOTE ON RATIONAL OPERATOR MONOTONE FUNCTIONS Masaru Nagisa Received May 19, 014 ; revised April 10, 014 Abstract. Let f be oeprator monotone
Numerical Analysis Preliminary Exam 10 am to 1 pm, August 20, 2018
 Numerical Analysis Preliminary Exam 1 am to 1 pm, August 2, 218 Instructions. You have three hours to complete this exam. Submit solutions to four (and no more) of the following six problems. Please start
Numerical Analysis Preliminary Exam 1 am to 1 pm, August 2, 218 Instructions. You have three hours to complete this exam. Submit solutions to four (and no more) of the following six problems. Please start
Complex Analysis, Stein and Shakarchi The Fourier Transform
 Complex Analysis, Stein and Shakarchi Chapter 4 The Fourier Transform Yung-Hsiang Huang 2017.11.05 1 Exercises 1. Suppose f L 1 (), and f 0. Show that f 0. emark 1. This proof is observed by Newmann (published
Complex Analysis, Stein and Shakarchi Chapter 4 The Fourier Transform Yung-Hsiang Huang 2017.11.05 1 Exercises 1. Suppose f L 1 (), and f 0. Show that f 0. emark 1. This proof is observed by Newmann (published
5.3 The Upper Half Plane
 Remark. Combining Schwarz Lemma with the map g α, we can obtain some inequalities of analytic maps f : D D. For example, if z D and w = f(z) D, then the composition h := g w f g z satisfies the condition
Remark. Combining Schwarz Lemma with the map g α, we can obtain some inequalities of analytic maps f : D D. For example, if z D and w = f(z) D, then the composition h := g w f g z satisfies the condition
The result above is known as the Riemann mapping theorem. We will prove it using basic theory of normal families. We start this lecture with that.
 Lecture 15 The Riemann mapping theorem Variables MATH-GA 2451.1 Complex The point of this lecture is to prove that the unit disk can be mapped conformally onto any simply connected open set in the plane,
Lecture 15 The Riemann mapping theorem Variables MATH-GA 2451.1 Complex The point of this lecture is to prove that the unit disk can be mapped conformally onto any simply connected open set in the plane,
Fourth Week: Lectures 10-12
 Fourth Week: Lectures 10-12 Lecture 10 The fact that a power series p of positive radius of convergence defines a function inside its disc of convergence via substitution is something that we cannot ignore
Fourth Week: Lectures 10-12 Lecture 10 The fact that a power series p of positive radius of convergence defines a function inside its disc of convergence via substitution is something that we cannot ignore
Method of Finite Elements I
 Method of Finite Elements I PhD Candidate - Charilaos Mylonas HIL H33.1 and Boundary Conditions, 26 March, 2018 Institute of Structural Engineering Method of Finite Elements I 1 Outline 1 2 Penalty method
Method of Finite Elements I PhD Candidate - Charilaos Mylonas HIL H33.1 and Boundary Conditions, 26 March, 2018 Institute of Structural Engineering Method of Finite Elements I 1 Outline 1 2 Penalty method
Outline. 1 Numerical Integration. 2 Numerical Differentiation. 3 Richardson Extrapolation
 Outline Numerical Integration Numerical Differentiation Numerical Integration Numerical Differentiation 3 Michael T. Heath Scientific Computing / 6 Main Ideas Quadrature based on polynomial interpolation:
Outline Numerical Integration Numerical Differentiation Numerical Integration Numerical Differentiation 3 Michael T. Heath Scientific Computing / 6 Main Ideas Quadrature based on polynomial interpolation:
Trivariate polynomial approximation on Lissajous curves 1
 Trivariate polynomial approximation on Lissajous curves 1 Stefano De Marchi DMV2015, Minisymposium on Mathematical Methods for MPI 22 September 2015 1 Joint work with Len Bos (Verona) and Marco Vianello
Trivariate polynomial approximation on Lissajous curves 1 Stefano De Marchi DMV2015, Minisymposium on Mathematical Methods for MPI 22 September 2015 1 Joint work with Len Bos (Verona) and Marco Vianello
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
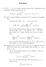 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
GENERALIZED GAUSS RADAU AND GAUSS LOBATTO FORMULAE
 BIT 0006-3835/98/3804-0101 $12.00 2000, Vol., No., pp. 1 14 c Swets & Zeitlinger GENERALIZED GAUSS RADAU AND GAUSS LOBATTO FORMULAE WALTER GAUTSCHI 1 1 Department of Computer Sciences, Purdue University,
BIT 0006-3835/98/3804-0101 $12.00 2000, Vol., No., pp. 1 14 c Swets & Zeitlinger GENERALIZED GAUSS RADAU AND GAUSS LOBATTO FORMULAE WALTER GAUTSCHI 1 1 Department of Computer Sciences, Purdue University,
The Hardy-Littlewood Function
 Hardy-Littlewood p. 1/2 The Hardy-Littlewood Function An Exercise in Slowly Convergent Series Walter Gautschi wxg@cs.purdue.edu Purdue University Hardy-Littlewood p. 2/2 OUTLINE The Hardy-Littlewood (HL)
Hardy-Littlewood p. 1/2 The Hardy-Littlewood Function An Exercise in Slowly Convergent Series Walter Gautschi wxg@cs.purdue.edu Purdue University Hardy-Littlewood p. 2/2 OUTLINE The Hardy-Littlewood (HL)
Computational Linear Algebra
 Computational Linear Algebra PD Dr. rer. nat. habil. Ralf Peter Mundani Computation in Engineering / BGU Scientific Computing in Computer Science / INF Winter Term 2017/18 Part 3: Iterative Methods PD
Computational Linear Algebra PD Dr. rer. nat. habil. Ralf Peter Mundani Computation in Engineering / BGU Scientific Computing in Computer Science / INF Winter Term 2017/18 Part 3: Iterative Methods PD
ANALYSIS QUALIFYING EXAM FALL 2017: SOLUTIONS. 1 cos(nx) lim. n 2 x 2. g n (x) = 1 cos(nx) n 2 x 2. x 2.
 ANALYSIS QUALIFYING EXAM FALL 27: SOLUTIONS Problem. Determine, with justification, the it cos(nx) n 2 x 2 dx. Solution. For an integer n >, define g n : (, ) R by Also define g : (, ) R by g(x) = g n
ANALYSIS QUALIFYING EXAM FALL 27: SOLUTIONS Problem. Determine, with justification, the it cos(nx) n 2 x 2 dx. Solution. For an integer n >, define g n : (, ) R by Also define g : (, ) R by g(x) = g n
Introduction to Estimation Methods for Time Series models Lecture 2
 Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
Introduction to Estimation Methods for Time Series models Lecture 2 Fulvio Corsi SNS Pisa Fulvio Corsi Introduction to Estimation () Methods for Time Series models Lecture 2 SNS Pisa 1 / 21 Estimators:
Numerical integration and differentiation. Unit IV. Numerical Integration and Differentiation. Plan of attack. Numerical integration.
 Unit IV Numerical Integration and Differentiation Numerical integration and differentiation quadrature classical formulas for equally spaced nodes improper integrals Gaussian quadrature and orthogonal
Unit IV Numerical Integration and Differentiation Numerical integration and differentiation quadrature classical formulas for equally spaced nodes improper integrals Gaussian quadrature and orthogonal
Part IB Geometry. Theorems. Based on lectures by A. G. Kovalev Notes taken by Dexter Chua. Lent 2016
 Part IB Geometry Theorems Based on lectures by A. G. Kovalev Notes taken by Dexter Chua Lent 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IB Geometry Theorems Based on lectures by A. G. Kovalev Notes taken by Dexter Chua Lent 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Quasi-conformal maps and Beltrami equation
 Chapter 7 Quasi-conformal maps and Beltrami equation 7. Linear distortion Assume that f(x + iy) =u(x + iy)+iv(x + iy) be a (real) linear map from C C that is orientation preserving. Let z = x + iy and
Chapter 7 Quasi-conformal maps and Beltrami equation 7. Linear distortion Assume that f(x + iy) =u(x + iy)+iv(x + iy) be a (real) linear map from C C that is orientation preserving. Let z = x + iy and
Assignment 1: From the Definition of Convexity to Helley Theorem
 Assignment 1: From the Definition of Convexity to Helley Theorem Exercise 1 Mark in the following list the sets which are convex: 1. {x R 2 : x 1 + i 2 x 2 1, i = 1,..., 10} 2. {x R 2 : x 2 1 + 2ix 1x
Assignment 1: From the Definition of Convexity to Helley Theorem Exercise 1 Mark in the following list the sets which are convex: 1. {x R 2 : x 1 + i 2 x 2 1, i = 1,..., 10} 2. {x R 2 : x 2 1 + 2ix 1x
CS 450 Numerical Analysis. Chapter 8: Numerical Integration and Differentiation
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Cyclic Vector of the Weighted Mean Matrix Operator
 Punjab University Journal of Mathematics (ISSN 1016-2526) Vol. 50(1)(2018) pp. 79-88 Cyclic Vector of the Weighted Mean Matrix Operator Ebrahim Pazouki Mazandaran Management and Planning Organization P.
Punjab University Journal of Mathematics (ISSN 1016-2526) Vol. 50(1)(2018) pp. 79-88 Cyclic Vector of the Weighted Mean Matrix Operator Ebrahim Pazouki Mazandaran Management and Planning Organization P.
Introduction. Chapter One
 Chapter One Introduction The aim of this book is to describe and explain the beautiful mathematical relationships between matrices, moments, orthogonal polynomials, quadrature rules and the Lanczos and
Chapter One Introduction The aim of this book is to describe and explain the beautiful mathematical relationships between matrices, moments, orthogonal polynomials, quadrature rules and the Lanczos and
Matrices and Moments: Least Squares Problems
 Matrices and Moments: Least Squares Problems Gene Golub, SungEun Jo, Zheng Su Comparative study (with David Gleich) Computer Science Department Stanford University Matrices and Moments: Least Squares Problems
Matrices and Moments: Least Squares Problems Gene Golub, SungEun Jo, Zheng Su Comparative study (with David Gleich) Computer Science Department Stanford University Matrices and Moments: Least Squares Problems
256 Summary. D n f(x j ) = f j+n f j n 2n x. j n=1. α m n = 2( 1) n (m!) 2 (m n)!(m + n)!. PPW = 2π k x 2 N + 1. i=0?d i,j. N/2} N + 1-dim.
 56 Summary High order FD Finite-order finite differences: Points per Wavelength: Number of passes: D n f(x j ) = f j+n f j n n x df xj = m α m dx n D n f j j n= α m n = ( ) n (m!) (m n)!(m + n)!. PPW =
56 Summary High order FD Finite-order finite differences: Points per Wavelength: Number of passes: D n f(x j ) = f j+n f j n n x df xj = m α m dx n D n f j j n= α m n = ( ) n (m!) (m n)!(m + n)!. PPW =
ON SPECTRAL METHODS FOR VOLTERRA INTEGRAL EQUATIONS AND THE CONVERGENCE ANALYSIS * 1. Introduction
 Journal of Computational Mathematics, Vol.6, No.6, 008, 85 837. ON SPECTRAL METHODS FOR VOLTERRA INTEGRAL EQUATIONS AND THE CONVERGENCE ANALYSIS * Tao Tang Department of Mathematics, Hong Kong Baptist
Journal of Computational Mathematics, Vol.6, No.6, 008, 85 837. ON SPECTRAL METHODS FOR VOLTERRA INTEGRAL EQUATIONS AND THE CONVERGENCE ANALYSIS * Tao Tang Department of Mathematics, Hong Kong Baptist
The Hardy-Littlewood Function: An Exercise in Slowly Convergent Series
 The Hardy-Littlewood Function: An Exercise in Slowly Convergent Series Walter Gautschi Department of Computer Sciences Purdue University West Lafayette, IN 4797-66 U.S.A. Dedicated to Olav Njåstad on the
The Hardy-Littlewood Function: An Exercise in Slowly Convergent Series Walter Gautschi Department of Computer Sciences Purdue University West Lafayette, IN 4797-66 U.S.A. Dedicated to Olav Njåstad on the
On rational approximation of algebraic functions. Julius Borcea. Rikard Bøgvad & Boris Shapiro
 On rational approximation of algebraic functions http://arxiv.org/abs/math.ca/0409353 Julius Borcea joint work with Rikard Bøgvad & Boris Shapiro 1. Padé approximation: short overview 2. A scheme of rational
On rational approximation of algebraic functions http://arxiv.org/abs/math.ca/0409353 Julius Borcea joint work with Rikard Bøgvad & Boris Shapiro 1. Padé approximation: short overview 2. A scheme of rational
ZERO DISTRIBUTION OF POLYNOMIALS ORTHOGONAL ON THE RADIAL RAYS IN THE COMPLEX PLANE* G. V. Milovanović, P. M. Rajković and Z. M.
 FACTA UNIVERSITATIS (NIŠ) Ser. Math. Inform. 12 (1997), 127 142 ZERO DISTRIBUTION OF POLYNOMIALS ORTHOGONAL ON THE RADIAL RAYS IN THE COMPLEX PLANE* G. V. Milovanović, P. M. Rajković and Z. M. Marjanović
FACTA UNIVERSITATIS (NIŠ) Ser. Math. Inform. 12 (1997), 127 142 ZERO DISTRIBUTION OF POLYNOMIALS ORTHOGONAL ON THE RADIAL RAYS IN THE COMPLEX PLANE* G. V. Milovanović, P. M. Rajković and Z. M. Marjanović
LECTURE 18: NONLINEAR MODELS
 LECTURE 18: NONLINEAR MODELS The basic point is that smooth nonlinear models look like linear models locally. Models linear in parameters are no problem even if they are nonlinear in variables. For example:
LECTURE 18: NONLINEAR MODELS The basic point is that smooth nonlinear models look like linear models locally. Models linear in parameters are no problem even if they are nonlinear in variables. For example:
Problem 1A. Suppose that f is a continuous real function on [0, 1]. Prove that
![Problem 1A. Suppose that f is a continuous real function on [0, 1]. Prove that Problem 1A. Suppose that f is a continuous real function on [0, 1]. Prove that](/thumbs/73/68962001.jpg) Problem 1A. Suppose that f is a continuous real function on [, 1]. Prove that lim α α + x α 1 f(x)dx = f(). Solution: This is obvious for f a constant, so by subtracting f() from both sides we can assume
Problem 1A. Suppose that f is a continuous real function on [, 1]. Prove that lim α α + x α 1 f(x)dx = f(). Solution: This is obvious for f a constant, so by subtracting f() from both sides we can assume
Math Spring 2014 Solutions to Assignment # 8 Completion Date: Friday May 30, 2014
 Math 3 - Spring 4 Solutions to Assignment # 8 ompletion Date: Friday May 3, 4 Question. [p 49, #] By finding an antiderivative, evaluate each of these integrals, where the path is any contour between the
Math 3 - Spring 4 Solutions to Assignment # 8 ompletion Date: Friday May 3, 4 Question. [p 49, #] By finding an antiderivative, evaluate each of these integrals, where the path is any contour between the
Recurrence Relations and Fast Algorithms
 Recurrence Relations and Fast Algorithms Mark Tygert Research Report YALEU/DCS/RR-343 December 29, 2005 Abstract We construct fast algorithms for decomposing into and reconstructing from linear combinations
Recurrence Relations and Fast Algorithms Mark Tygert Research Report YALEU/DCS/RR-343 December 29, 2005 Abstract We construct fast algorithms for decomposing into and reconstructing from linear combinations
Polynomial interpolation on the sphere, reproducing kernels and random matrices
 Polynomial interpolation on the sphere, reproducing kernels and random matrices Paul Leopardi Mathematical Sciences Institute, Australian National University. For presentation at MASCOS Workshop on Stochastics
Polynomial interpolation on the sphere, reproducing kernels and random matrices Paul Leopardi Mathematical Sciences Institute, Australian National University. For presentation at MASCOS Workshop on Stochastics
Lecture 14 Conformal Mapping. 1 Conformality. 1.1 Preservation of angle. 1.2 Length and area. MATH-GA Complex Variables
 Lecture 14 Conformal Mapping MATH-GA 2451.001 Complex Variables 1 Conformality 1.1 Preservation of angle The open mapping theorem tells us that an analytic function such that f (z 0 ) 0 maps a small neighborhood
Lecture 14 Conformal Mapping MATH-GA 2451.001 Complex Variables 1 Conformality 1.1 Preservation of angle The open mapping theorem tells us that an analytic function such that f (z 0 ) 0 maps a small neighborhood
A PROOF OF CARLESON S THEOREM BASED ON A NEW CHARACTERIZATION OF THE LORENTZ SPACES L(p, 1) FOR 1 < p < AND OTHER APPLICATIONS
 PROOF OF CRLESON S THEOREM BSED ON NEW CHRCTERIZTION OF THE LORENTZ SPCES L(p, ) FOR < p < ND OTHER PPLICTIONS GERLDO SORES DE SOUZ bstract. In his 95 nnals of Mathematics paper entitled Some New Functional
PROOF OF CRLESON S THEOREM BSED ON NEW CHRCTERIZTION OF THE LORENTZ SPCES L(p, ) FOR < p < ND OTHER PPLICTIONS GERLDO SORES DE SOUZ bstract. In his 95 nnals of Mathematics paper entitled Some New Functional
A MOMENT PROBLEM ASSOCIATED TO RATIONAL SZEGO FUNCTIONS
 A MOMENT PROBLEM ASSOCIATED TO RATIONAL SZEGO FUNCTIONS A. Bultheel Department of Comput.er Science, K.U. Leuven, B-3001 Leuven, Belgium. P. Gonzalez-Vera Facultad de Matematicas. Universidad de La Laguna,
A MOMENT PROBLEM ASSOCIATED TO RATIONAL SZEGO FUNCTIONS A. Bultheel Department of Comput.er Science, K.U. Leuven, B-3001 Leuven, Belgium. P. Gonzalez-Vera Facultad de Matematicas. Universidad de La Laguna,
GENERALIZED STIELTJES POLYNOMIALS AND RATIONAL GAUSS-KRONROD QUADRATURE
 GENERALIZED STIELTJES POLYNOMIALS AND RATIONAL GAUSS-KRONROD QUADRATURE M. BELLO HERNÁNDEZ, B. DE LA CALLE YSERN, AND G. LÓPEZ LAGOMASINO Abstract. Generalized Stieltjes polynomials are introduced and
GENERALIZED STIELTJES POLYNOMIALS AND RATIONAL GAUSS-KRONROD QUADRATURE M. BELLO HERNÁNDEZ, B. DE LA CALLE YSERN, AND G. LÓPEZ LAGOMASINO Abstract. Generalized Stieltjes polynomials are introduced and
8 The Gelfond-Schneider Theorem and Some Related Results
 8 The Gelfond-Schneider Theorem and Some Related Results In this section, we begin by stating some results without proofs. In 1900, David Hilbert posed a general problem which included determining whether
8 The Gelfond-Schneider Theorem and Some Related Results In this section, we begin by stating some results without proofs. In 1900, David Hilbert posed a general problem which included determining whether
Complex Analytic Functions and Differential Operators. Robert Carlson
 Complex Analytic Functions and Differential Operators Robert Carlson Some motivation Suppose L is a differential expression (formal operator) N L = p k (z)d k, k=0 D = d dz (0.1) with p k (z) = j=0 b jz
Complex Analytic Functions and Differential Operators Robert Carlson Some motivation Suppose L is a differential expression (formal operator) N L = p k (z)d k, k=0 D = d dz (0.1) with p k (z) = j=0 b jz
12.0 Properties of orthogonal polynomials
 12.0 Properties of orthogonal polynomials In this section we study orthogonal polynomials to use them for the construction of quadrature formulas investigate projections on polynomial spaces and their
12.0 Properties of orthogonal polynomials In this section we study orthogonal polynomials to use them for the construction of quadrature formulas investigate projections on polynomial spaces and their
The Szego matrix recurrence and its associated linear non-autonomous area-preserving map
 Electronic Journal of Linear Algebra Volume 24 Volume 24 2012/2013 Article 13 2012 The Szego matrix recurrence and its associated linear non-autonomous area-preserving map J Abderraman Marrero jcabderraman@upmes
Electronic Journal of Linear Algebra Volume 24 Volume 24 2012/2013 Article 13 2012 The Szego matrix recurrence and its associated linear non-autonomous area-preserving map J Abderraman Marrero jcabderraman@upmes
Generalizations of orthogonal polynomials
 WOG project J. Comput. Appl. Math., Preprint 28 June 2004 Generalizations of orthogonal polynomials A. Bultheel Dept. Computer Science (NALAG), K.U.Leuven, Celestijnenlaan 200 A, B-300 Leuven, Belgium.
WOG project J. Comput. Appl. Math., Preprint 28 June 2004 Generalizations of orthogonal polynomials A. Bultheel Dept. Computer Science (NALAG), K.U.Leuven, Celestijnenlaan 200 A, B-300 Leuven, Belgium.
B8.1 Martingales Through Measure Theory. Concept of independence
 B8.1 Martingales Through Measure Theory Concet of indeendence Motivated by the notion of indeendent events in relims robability, we have generalized the concet of indeendence to families of σ-algebras.
B8.1 Martingales Through Measure Theory Concet of indeendence Motivated by the notion of indeendent events in relims robability, we have generalized the concet of indeendence to families of σ-algebras.
Final Exam A Name. 20 i C) Solve the equation by factoring. 4) x2 = x + 30 A) {-5, 6} B) {5, 6} C) {1, 30} D) {-5, -6} -9 ± i 3 14
 Final Exam A Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 1 1) x + 3 + 5 x - 3 = 30 (x + 3)(x - 3) 1) A) x -3, 3; B) x -3, 3; {4} C) No restrictions; {3} D)
Final Exam A Name First, write the value(s) that make the denominator(s) zero. Then solve the equation. 1 1) x + 3 + 5 x - 3 = 30 (x + 3)(x - 3) 1) A) x -3, 3; B) x -3, 3; {4} C) No restrictions; {3} D)
Algebraic aspects of the Dirichlet problem
 Algebraic aspects of the Dirichlet problem P. Ebenfelt, D. Khavinson, and H. S. Shapiro. Introction Our aim in this paper is to make some remarks about certain algebraic aspects of the classical Dirichlet
Algebraic aspects of the Dirichlet problem P. Ebenfelt, D. Khavinson, and H. S. Shapiro. Introction Our aim in this paper is to make some remarks about certain algebraic aspects of the classical Dirichlet
Measures, orthogonal polynomials, and continued fractions. Michael Anshelevich
 Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. 2 MEASURES
Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. 2 MEASURES
Bounded point derivations on R p (X) and approximate derivatives
 Bounded point derivations on R p (X) and approximate derivatives arxiv:1709.02851v3 [math.cv] 21 Dec 2017 Stephen Deterding Department of Mathematics, University of Kentucky Abstract It is shown that if
Bounded point derivations on R p (X) and approximate derivatives arxiv:1709.02851v3 [math.cv] 21 Dec 2017 Stephen Deterding Department of Mathematics, University of Kentucky Abstract It is shown that if
Computational Linear Algebra
 Computational Linear Algebra PD Dr. rer. nat. habil. Ralf-Peter Mundani Computation in Engineering / BGU Scientific Computing in Computer Science / INF Winter Term 2018/19 Part 4: Iterative Methods PD
Computational Linear Algebra PD Dr. rer. nat. habil. Ralf-Peter Mundani Computation in Engineering / BGU Scientific Computing in Computer Science / INF Winter Term 2018/19 Part 4: Iterative Methods PD
On Optimal Stopping Problems with Power Function of Lévy Processes
 On Optimal Stopping Problems with Power Function of Lévy Processes Budhi Arta Surya Department of Mathematics University of Utrecht 31 August 2006 This talk is based on the joint paper with A.E. Kyprianou:
On Optimal Stopping Problems with Power Function of Lévy Processes Budhi Arta Surya Department of Mathematics University of Utrecht 31 August 2006 This talk is based on the joint paper with A.E. Kyprianou:
GAUSS-KRONROD QUADRATURE FORMULAE A SURVEY OF FIFTY YEARS OF RESEARCH
 Electronic Transactions on Numerical Analysis. Volume 45, pp. 371 404, 2016. Copyright c 2016,. ISSN 1068 9613. ETNA GAUSS-KRONROD QUADRATURE FORMULAE A SURVEY OF FIFTY YEARS OF RESEARCH SOTIRIOS E. NOTARIS
Electronic Transactions on Numerical Analysis. Volume 45, pp. 371 404, 2016. Copyright c 2016,. ISSN 1068 9613. ETNA GAUSS-KRONROD QUADRATURE FORMULAE A SURVEY OF FIFTY YEARS OF RESEARCH SOTIRIOS E. NOTARIS
CESÁRO TYPE OPERATORS ON SPACES OF ANALYTIC FUNCTIONS. S. Naik
 Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Filomat 25:4 2, 85 97 DOI:.2298/FIL485N CESÁRO TYPE OPERATORS ON SPACES OF ANALYTIC FUNCTIONS
Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Filomat 25:4 2, 85 97 DOI:.2298/FIL485N CESÁRO TYPE OPERATORS ON SPACES OF ANALYTIC FUNCTIONS
Adaptive Fourier series a variation of greedy algorithm
 Adv Comput Math (2011) 34:279 293 DOI 10.1007/s10444-010-9153-4 Adaptive Fourier series a variation of greedy algorithm Tao Qian Yan-Bo Wang Received: 5 September 2009 / Accepted: 6 April 2010 / Published
Adv Comput Math (2011) 34:279 293 DOI 10.1007/s10444-010-9153-4 Adaptive Fourier series a variation of greedy algorithm Tao Qian Yan-Bo Wang Received: 5 September 2009 / Accepted: 6 April 2010 / Published
Conformal maps. Lent 2019 COMPLEX METHODS G. Taylor. A star means optional and not necessarily harder.
 Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
AP Calculus 2004 AB (Form B) FRQ Solutions
 AP Calculus 4 AB (Form B) FRQ Solutions Louis A. Talman, Ph.D. Emeritus Professor of Mathematics Metropolitan State University of Denver July, 7 Problem. Part a The curve intersects the x-axis at x =,
AP Calculus 4 AB (Form B) FRQ Solutions Louis A. Talman, Ph.D. Emeritus Professor of Mathematics Metropolitan State University of Denver July, 7 Problem. Part a The curve intersects the x-axis at x =,
Stochastic Spectral Approaches to Bayesian Inference
 Stochastic Spectral Approaches to Bayesian Inference Prof. Nathan L. Gibson Department of Mathematics Applied Mathematics and Computation Seminar March 4, 2011 Prof. Gibson (OSU) Spectral Approaches to
Stochastic Spectral Approaches to Bayesian Inference Prof. Nathan L. Gibson Department of Mathematics Applied Mathematics and Computation Seminar March 4, 2011 Prof. Gibson (OSU) Spectral Approaches to
Preliminary draft only: please check for final version
 ARE211, Fall2012 CALCULUS4: THU, OCT 11, 2012 PRINTED: AUGUST 22, 2012 (LEC# 15) Contents 3. Univariate and Multivariate Differentiation (cont) 1 3.6. Taylor s Theorem (cont) 2 3.7. Applying Taylor theory:
ARE211, Fall2012 CALCULUS4: THU, OCT 11, 2012 PRINTED: AUGUST 22, 2012 (LEC# 15) Contents 3. Univariate and Multivariate Differentiation (cont) 1 3.6. Taylor s Theorem (cont) 2 3.7. Applying Taylor theory:
Numerische Mathematik
 Numer. Math. (1998) 80: 39 59 Numerische Mathematik c Springer-Verlag 1998 Electronic Edition Numerical integration over a disc. A new Gaussian quadrature formula Borislav Bojanov 1,, Guergana Petrova,
Numer. Math. (1998) 80: 39 59 Numerische Mathematik c Springer-Verlag 1998 Electronic Edition Numerical integration over a disc. A new Gaussian quadrature formula Borislav Bojanov 1,, Guergana Petrova,
Measures, orthogonal polynomials, and continued fractions. Michael Anshelevich
 Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. A linear functional µ[p ] = P (x) dµ(x), µ
Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. A linear functional µ[p ] = P (x) dµ(x), µ
{σ x >t}p x. (σ x >t)=e at.
 3.11. EXERCISES 121 3.11 Exercises Exercise 3.1 Consider the Ornstein Uhlenbeck process in example 3.1.7(B). Show that the defined process is a Markov process which converges in distribution to an N(0,σ
3.11. EXERCISES 121 3.11 Exercises Exercise 3.1 Consider the Ornstein Uhlenbeck process in example 3.1.7(B). Show that the defined process is a Markov process which converges in distribution to an N(0,σ
A Product Integration Approach Based on New Orthogonal Polynomials for Nonlinear Weakly Singular Integral Equations
 Acta Appl Math (21) 19: 861 873 DOI 1.17/s144-8-9351-y A Product Integration Approach Based on New Orthogonal Polynomials for Nonlinear Weakly Singular Integral Equations M. Rasty M. Hadizadeh Received:
Acta Appl Math (21) 19: 861 873 DOI 1.17/s144-8-9351-y A Product Integration Approach Based on New Orthogonal Polynomials for Nonlinear Weakly Singular Integral Equations M. Rasty M. Hadizadeh Received:
OR MSc Maths Revision Course
 OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
University of Houston, Department of Mathematics Numerical Analysis, Fall 2005
 4 Interpolation 4.1 Polynomial interpolation Problem: LetP n (I), n ln, I := [a,b] lr, be the linear space of polynomials of degree n on I, P n (I) := { p n : I lr p n (x) = n i=0 a i x i, a i lr, 0 i
4 Interpolation 4.1 Polynomial interpolation Problem: LetP n (I), n ln, I := [a,b] lr, be the linear space of polynomials of degree n on I, P n (I) := { p n : I lr p n (x) = n i=0 a i x i, a i lr, 0 i
Properties of orthogonal polynomials
 University of South Africa LMS Research School University of Kent, Canterbury Outline 1 Orthogonal polynomials 2 Properties of classical orthogonal polynomials 3 Quasi-orthogonality and semiclassical orthogonal
University of South Africa LMS Research School University of Kent, Canterbury Outline 1 Orthogonal polynomials 2 Properties of classical orthogonal polynomials 3 Quasi-orthogonality and semiclassical orthogonal
Math 489AB Exercises for Chapter 1 Fall Section 1.0
 Math 489AB Exercises for Chapter 1 Fall 2008 Section 1.0 1.0.2 We want to maximize x T Ax subject to the condition x T x = 1. We use the method of Lagrange multipliers. Let f(x) = x T Ax and g(x) = x T
Math 489AB Exercises for Chapter 1 Fall 2008 Section 1.0 1.0.2 We want to maximize x T Ax subject to the condition x T x = 1. We use the method of Lagrange multipliers. Let f(x) = x T Ax and g(x) = x T
Asymptotics of minimax stochastic programs
 Asymptotics of minimax stochastic programs Alexander Shapiro Abstract. We discuss in this paper asymptotics of the sample average approximation (SAA) of the optimal value of a minimax stochastic programming
Asymptotics of minimax stochastic programs Alexander Shapiro Abstract. We discuss in this paper asymptotics of the sample average approximation (SAA) of the optimal value of a minimax stochastic programming
SPECTRAL METHODS: ORTHOGONAL POLYNOMIALS
 SPECTRAL METHODS: ORTHOGONAL POLYNOMIALS 31 October, 2007 1 INTRODUCTION 2 ORTHOGONAL POLYNOMIALS Properties of Orthogonal Polynomials 3 GAUSS INTEGRATION Gauss- Radau Integration Gauss -Lobatto Integration
SPECTRAL METHODS: ORTHOGONAL POLYNOMIALS 31 October, 2007 1 INTRODUCTION 2 ORTHOGONAL POLYNOMIALS Properties of Orthogonal Polynomials 3 GAUSS INTEGRATION Gauss- Radau Integration Gauss -Lobatto Integration
THE CAUCHY INTEGRAL FORMULA, QUADRATURE DOMAINS, AND RIEMANN MAPPING THEOREMS
 THE CAUCHY INTEGRAL FORMULA, QUADRATURE DOMAINS, AND RIEMANN MAPPING THEOREMS STEVEN R. BELL Abstract. It is well known that a domain in the plane is a quadrature domain with respect to area measure if
THE CAUCHY INTEGRAL FORMULA, QUADRATURE DOMAINS, AND RIEMANN MAPPING THEOREMS STEVEN R. BELL Abstract. It is well known that a domain in the plane is a quadrature domain with respect to area measure if
Boundary behaviour of optimal polynomial approximants
 Boundary behaviour of optimal polynomial approximants University of South Florida Laval University, in honour of Tom Ransford, May 2018 This talk is based on some recent and upcoming papers with various
Boundary behaviour of optimal polynomial approximants University of South Florida Laval University, in honour of Tom Ransford, May 2018 This talk is based on some recent and upcoming papers with various
Largest dual ellipsoids inscribed in dual cones
 Largest dual ellipsoids inscribed in dual cones M. J. Todd June 23, 2005 Abstract Suppose x and s lie in the interiors of a cone K and its dual K respectively. We seek dual ellipsoidal norms such that
Largest dual ellipsoids inscribed in dual cones M. J. Todd June 23, 2005 Abstract Suppose x and s lie in the interiors of a cone K and its dual K respectively. We seek dual ellipsoidal norms such that
