Necklace Flower Constellations
|
|
|
- Herbert Cook
- 5 years ago
- Views:
Transcription
1 David Arnas Martínez Necklace Flower Constellations Departamento Instituto Universitario de Investigación en Matemáticas y sus Aplicaciones Director/es Eva Tresaco Vidaller Antonio Elipe Sánchez
2 Reconocimiento NoComercial SinObraDerivada (by-nc-nd): No se permite un uso comercial de la obra original ni la generación de obras derivadas. Universidad de Zaragoza Servicio de Publicaciones ISSN
3 Tesis Doctoral NECKLACE FLOWER CONSTELLATIONS Autor David Arnas Martínez Director/es Eva Tresaco Vidaller Antonio Elipe Sánchez UNIVERSIDAD DE ZARAGOZA Instituto Universitario de Investigación en Matemáticas y sus Aplicaciones 2018 Repositorio de la Universidad de Zaragoza Zaguan
4
5
6
7
8
9
10
11 G M G M L Ω L M N M L Ω L M
12 J2 n J 2
13
14
15
16
17
18
19
20 n n
21
22
23
24 n n
25
26
27 m 1 ẍ 1 = G m 1m 2 x 1 x 2 2 x 1 x 2 x 1 x 2, m 2 ẍ 2 = G m 1m 2 x 2 x 1 2 x 2 x 1 x 2 x 1,
28 G m 1 m 2 x 1 x 2 ẍ 1 ẍ 2 r = µ r r 3, µ = G(M +m 2 ) GM M r h h = r ṙ, r ṙ h ḣ = ṙ ṙ + r ṙ = r ṙ µ (r r) = 0, r3 r = r h r = 0 h v = 0 h r ṙ u x, u y u z r = ( 3µ yz ) ( r 5 3µyz r 5 u x + 3µ xz ) ( r 5 3µxz r 5 u y + 3µ xy ) r 5 3µxy r 5 u z = 0, V V = r r r r dr = µ r 3 dr = µ r.
29 ξ ξ = v2 2 µ r. d ( r ) r (ṙ r) = dt r r 3 = r h = d (ṙ ) h, µ dt µ e = eu e = ṙ h µ r r, h e h = 0,
30 u r u θ u h u r u h u h = h/ h u θ = u h u r r, θ r = ru r, ṙ = ṙu r + r θu θ, ( r = r θ ) 2 r u r + ( θr + 2 θṙ ) u θ, h = hu h = r 2 θuh θ = h r 2, θ e = ( ) θrh µ 1 u r ṙh µ u θ, e ξ ξ = (e2 1)µ 2 2h 2, Ω i z
31 x cos(i) = h u z h, cos(ω) = (u z h) u x u z h, i [0, π) Ω [0, 2π) ω u e u n = u z u h cos(ω) = (u z h) e u z h e, ω [0, 2π) Ω, i ω ν cos(ν) = r e re, r = p 1 + e cos(ν), p = h 2 /µ r 2 = x 2 p + y 2 p x p = r cos(ν) x p y p (u e, u p = (u h u e ), u h ) (1 e 2 )x 2 p + y 2 p + 2epx p p 2 = 0, e a r per r apo a = r per + r apo 2 = p 2 ( e + 1 ) = p 1 e 1 e 2.
32 ṙ = p e sin(ν) ν, (1 + e cos(ν)) 2 sin(ν) = 0 ṙ 2 = h2 r 2, ξ = 1 h 2 2 p 2 (1 + e)2 µ p (1 + e) = 1 2 µ(1 e2 ) = µ p 2a, a e i Ω ω ν E r 2 = a 2 (1 e 2 ) sin 2 (E) + (ae a cos(e)) 2, r = a(1 e cos(e)). ṙ = ae sin(e)ė. ṙ 2 + ( ) h 2 = 2µ r r µ a, ṙ ṙ 2 = µ ( 2 a r 1 (1 ) e2 ) r 2.
33 E µ = (1 e cos(e))ė, a3 M = E e sin(e) = µ a 3 t. M M n M n = µ a 3, M = 0 M = 2π a 3 T = 2π µ, T µ J 2
34 J 2 J 2, J 3, J 4
35 J 2 S m S/m = 0.001m 2 /kg S/m = 0.01m 2 /kg r = µ r r 3 + γ, γ H t H = µ R(a, e, i, ω, Ω, M, t), 2a R
36 da dt de dt di dt dω dt dω dt dm dt = 2 R na M, = 1 e2 R 1 e na 2 e M 2 R na 2 e ω, cos i R = na 2 1 e 2 sin i M 1 R na 2 1 e 2 sin i Ω, 1 e 2 R = na 2 e e cos i R na 2 1 e 2 sin i i, 1 R = na 2 1 e 2 sin i i, = n 2 na R a 1 e2 na 2 e R e. J 2 J 2 R = 3µJ 2 2r ( R r ) 2 ( sin 2 (i) sin 2 (ω + ν) 1 ), 3 R J 2 = R avg = µj 2 a ( R a ) 2 ( 3 4 sin2 (i) 1 ) ( 2 1 (1 e 2 ) 3/2 ), ȧ sec = 0, ė sec = 0, i sec = 0, ( R ω sec = 3 ) 2 4 J 2 a(1 e 2 n ( 4 5sin 2 (i) ), ) Ω sec = 3 ) 2 2( 2 J R a(1 e 2 n cos(i), ) [ µ Ṁ sec = a ( ) 2 4 J R ( 2 2 3sin 2 a(1 e 2 (i) ) 1 e 2], ) ȧ sec ė sec i sec ω sec Ωsec Ṁsec J 2 sin 2 (i) = 4/5
37 ω sec = 0 i = o u r, u θ, u h γ r γ θ γ h ȧ = 2a2 h ( e sin(ν)γ r + p ) r γ θ, ė = 1 h (p sin(ν)γ r + ((p + r) cos(ν) + re) γ θ ), i = r h cos(ω + ν)γ h, Ω = r sin(ω + ν) γ h, h sin(i) ω = 1 eh ( p cos(ν)γ r + (p + r) sin(ν)γ θ ) + r sin(ω + ν) γ h, h tan(i) 1 e 2 Ṁ = n + ((p cos(ν) 2re)γ r (p + r) sin(ν)γ θ ). eh
38 N o N so N c N c [0, N o 1] Ω, M Ω M Ω, M Ω M 2π N o 0 N c N so Ω ij M ij = 2π i 1 j 1, i = 1,, N o j = 1,, N so N c [0, N o 1] Ω ij M ij (i, j) j i a e i ω Ω 11 M N o = 5 3 N so = 3 a = 14419, 944 km i = o e = 0 N c = 3 Ω 11 = 0 M 11 = 0 (Ω, M) (Ω, M)
39 (Ω, M) Ω = 0 Ω M (Ω, M)
40 N o N w N so N c1, N c2, N c3 N c1 [0, N o 1] N c2 [0, N w 1] N c3 [0, N o 1] N o 0 0 Ω ijk i 1 N c3 N w 0 ω ijk = 2π k 1 ; N c1 N c2 N so M ijk j 1 Ω ijk ω ijk M ijk Ω 111 ω 111
41 M 111 i = 1,, N o j = 1,, N so k = 1,, N w i k j Ω ijk ω ijk M ijk [0, 2π] N o = 5 N w = 3 N so = 3 N c1 = 3 N c2 = 2 N c3 = Ω ijk ω ijk M ijk = 2π i 1 k 1 j 1 ; N o N w N so = 45 N o N ω N so = 45 N ω N so = 9 N c1, N c2, N c3 N o N so (Ω, ω, M) N c1 N c2 N c3
42 (Ω, ω, M) a = 11522, 451 km e = 0.25 i = o y = 0
43 n 1 n + 1 G Z n = {1,..., n} G = {1, 2, 4} Z 4 G 1 G 2 = G 1 = G2 s : G 1 = G 2 + s mod (n), s Z n s G = {1, 2, 4} = {1, 2, 3} = {2, 3, 4} = {1, 3, 4} ;
44 K(n) = K(n) = { Z n }/ =, G G Z n Sym(G) r Z n G + r = G Z n Sym(G) = min {1 r n : G + r = G Z n }. r G 1 = G2 Sym(G 1 ) = Sym(G 2 ) Sym : K(n) N G Sym(G). n = 6 G = {1, 3, 5} Z 6
45 Sym(G) = 2 {1, 3, 5} {3, 5, 7} mod (6) {2, 4, 6} G n k N k (n) = 1 φ(d)k n/d, n d n d n φ(d) d d d k = 2 Ω ij M ij M Ω Ω ij M ij G k {1,..., Sym(G) 1} Ω M
46 M = 2π N so k 2π N so N c N o, k N o M Sym(G) kn o N c, Sym(G) kn o N c Sym(G) N o N c G = {1, 2} N so = 4 Sym(G) = 4 N o = 6 N c = 2 k Ω = 2π 4 6k 2, k = {1, 3}
47 G + X + : G X X (g, x) g + x, g 1 + (g 2 + x) = (g 1 + g 2 ) + x 1 G + x = x g 1, g 2 G, x X (x) x + (x) = {g + x g G} X; g (g) X g (g) = {x X g + x = x}. X y = g + x y x + 1 (g), G g G Y Y
48
49
50 L Ω 0 L MΩ L M Ω ij M ij = 2π i 1 j 1, L Ω L M L MΩ i {1,..., L Ω } j {1,..., L M } Ω ij = 2π L Ω (i 1), M ij = 2π L M (j 1) 2π L M L MΩ L Ω (i 1), G M Z LM N M G M G M {1,..., L M }, G M = N M G M G M = {G M (1),..., G M (j ),..., G M (N M )}, 1 G M (1) < < G M (j ) < < G M (N M ) L M, j G M N M j + N M j G M : Z NM Z LM j G M (j ).
51 G M (j ) j {1,..., N M } (a, b) = a mod (b) G M (j ) = G M ( (j + N M, N M )), j = j + L M mod (L M ), S MΩ Z j : (Z LΩ Z NM ) (Z LΩ Z LM ) (i, j ) (i, j), j = G M (j ) + S MΩ (i 1). j 1 = G M (j ) 1 + S MΩ (i 1). j G M = G M + Sym(G M ) Z LM, j 1 = (G M (j ) 1 + S MΩ (i 1), Sym(G M )). Ω ij = 2π L Ω (i 1), M ij = 2π L M ( (G M (j ) 1 + S MΩ (i 1), Sym(G M ))) 2π L M L MΩ L Ω (i 1), G M i j
52 S MΩ S MΩ {0,..., Sym(G M ) 1} Sym(G M ) Ω ij = Ω i(j M +N M ), M ij = M i(j +N M ), Ω ij = Ω (i+lω )j Ω, M ij = M (i+lω )j, M 2π L Ω (i 1) = 2π L Ω (i 1), (G M (j ) 1 + S MΩ (i 1), Sym(G M )) = = (G M ( (j + N M, N M )) 1 + S MΩ (i 1), Sym(G M )). G M (j ) = G M ( (j + N M, N M )) 2π L Ω (i 1) = 2π L Ω (L Ω + i 1) mod (L Ω ), L M 2π M (i+l Ω )j = L M 2π M ij, (G M (j ) 1 + S MΩ (L Ω + i 1), Sym(G M )) L MΩ L Ω (L Ω + i 1) = = (G M (j ) 1 + S MΩ (i 1), Sym(G M )) L MΩ L Ω (i 1). A Z G M (j ) 1 + S MΩ (i 1) + ASym(G M ) = G M (j ) 1 + S MΩ (L Ω + i 1) L MΩ, ASym(G M ) = S MΩ L Ω L MΩ,
53 S MΩ G M L Ω L MΩ Sym(G M ) S MΩ L Ω L MΩ, Sym(G M ) (S MΩ L Ω L MΩ ) G M 14 e = 0 a = km i = o L Ω = 7 N M = 2 N c = {0,..., 6} L M = 20 L Ω L M = 140 N M = 2 70 G M = {1, 2} Z 20 L MΩ = 6 Sym(G M ) = 20 {1, 2} = {1, 2} + 20 mod (20) Sym(G M ) S MΩ L Ω L MΩ 20 7S MΩ 6, S MΩ = 18 (Ω, M) Ω 11 = M 11 = 0 Ω = 0 Ω = 2π L Ω L M (Ω, M) N M = 2
54 (Ω, M) (Ω, M) 90 o
55 G M G M S MΩ G M gcd(sym(g M ), L Ω ) L MΩ gcd(sym(g M ), L Ω ). ASym(G M ) + L Ω S MΩ = L MΩ,
56 A A S MΩ gcd(sym(g M ), L Ω ) L MΩ. (S MΩ ) λ = (S MΩ ) 0 + λ l, l = L Ω (A) λ = (A) 0 λ gcd(sym(g M ), L Ω ), Sym(G M ) gcd(sym(g M ), L Ω ), (S MΩ ) 0 (A) 0 λ Sym(G M ) {1,..., L M }, S MΩ {0,..., Sym(G M ) 1}, L MΩ {0,..., L Ω 1}, S MΩ S MΩ = (Sym(G M ) 1) λ l S MΩ SMΩ (Sym(GM ) 1) gcd(sym(g M ), L Ω ) = = l x x = Sym(G M ) gcd(sym(g M ), L Ω ) gcd(sym(g M), L Ω ) Sym(G M ), gcd(sym(g M ), L Ω ) gcd(sym(gm ), L Ω ) gcd(sym(g M ), L Ω ), Sym(G M ) x x gcd(sym(g M ), L Ω ) [1, Sym(G M )] gcd(sym(g M ), L Ω ) Sym(G M ) (0, 1], gcd(sym(g M ), L Ω ) 1.
57 S MΩ (S MΩ ) λ gcd(sym(g M ), L Ω ), L Ω L MΩ Sym(G M ) G M L Ω L M G M L Ω L M Sym(G M ) {S MΩ, L MΩ } G M L Ω L M L Ω L Ω S MΩ 1L MΩ = ASym(G M ), S MΩ L MΩ gcd(l Ω, 1) ASym(G M ), gcd(l Ω, 1) = 1 ASym(G M ) Sym(G M ) L Ω (S MΩ ) λ = (S MΩ ) 0 + λ, (L MΩ ) λ = (L MΩ ) 0 λl Ω, (S MΩ ) 0 (L MΩ ) 0 λ ASym(G M ) L MΩ {0,..., L Ω 1} A
58 ASym(G M ) min (ASym(G M )) = (L Ω 1), max (ASym(G M )) = (Sym(G M ) 1)L Ω. ASym(G M ) (ASym(G M )) = max (ASym(G M )) min (ASym(G M )) = L Ω Sym(G M ) 1. Sym(G M ) (ASym(G M )) = ASym(G M ), A A = L Ω 1 Sym(G M ). 1 A A A A = 1 L Ω Sym(G M ) = L Ω 1 Sym(G M ). Sym(G M ) 1 (0, 1] L Ω 1 L Ω A A L Ω Sym(G M ) L Ω L M L Ω L M L Ω L M d L M φ(d)2 LM /d, d L M φ(d) d {L MΩ, S MΩ } {L MΩ, S MΩ }
59 N M L Ω L M N M = G M N M L Ω L M L Ω L M L M g=1 g L M L Mg N M (g), (g) g (g) = L M g g N M g L M L M g g 1 g =1 g g N M g (g ). L M + Z LM G M Z LM G = Z LM L M ϕ ϕ : G X X (g, x) x + g mod (L M ). (g) g G (X) g = Sym(G M ) g L M L M g N M
60 g = Sym(G M ) (g) g L M /g L M N M g/l M g P C(g) P C(g) = g N M g L M. L M /g L M N M L M g L M g P C(g) = L M g g N M. g L M L M = 4 N M = 2 g = 4 g = 2 {1, 3} {2, 4} g N M g (g) g g P C(g ) = g L M (g ). g g < g P C(g) = g N M g L M L M g g 1 g =1 g g N M g L M (g ), g g g L M g N M g
61 (g) (g) = L M g g N M g L M L M g g 1 g =1 g g N M g (g ), L M g G = Z LM g N M L M 1 g g N M g L M (g ) L M g g 1 g =1 g g N M g (g ). L M L Ω g L Ω g g N M g L M L M g g 1 g =1 g g N M g (g ). L M L M g=1 g L M L Mg N M L Ω g g N M g L M L M g g 1 g =1 g g N M g (g ), L M
62 L Ω L M L M g=1 g L M L Mg N M (g), (g) G M G Ω N Ω L Ω G Ω {1,..., L Ω }, G Ω = N Ω i G Ω G Ω (i ) = G Ω ( (i + N Ω, N Ω )), i = (i + L Ω, L Ω ). i i G Ω i = G Ω (i ), Ω i j = 2π L Ω (G Ω (i ) 1), M i j = 2π ( (G M (j ) 1 + S MΩ (G Ω (i ) 1), Sym(G M ))) L M 2π L MΩ (G Ω (i ) 1), L M L Ω
63 G Ω N Ω N M G Ω G M Sym(G M ) S MΩ L Ω L MΩ L Ω L M S MΩ L MΩ a e i ω Ω i j M i j a e i ω N Ω, N M L Ω, L M S MΩ L MΩ Ω i j M i j
64
65
66 L Ω L ω L M L MΩ, L Mω, L ωω L MΩ [0, L Ω 1] L Mω [0, L w 1] L ωω [0, L Ω 1] L Ω 0 0 L ωω L ω 0 L MΩ L Mω L M Ω ijk ω ijk M ijk = 2π i 1 k 1 j 1 Ω ijk ω ijk M ijk {Ω 000, ω 000, M 000 } (i, j, k) i [1, L Ω ] k [1, L ω ] j [1, L M ] Ω ijk ω ijk M ijk [0, 2π] ; Ω ijk = 2π L Ω (i 1), ω ijk = 2π L ω (k 1) 2π L ω L ωω L Ω (i 1), M ijk = 2π (j 1) 2π L Mω (k 1) 2π L M L M L ω L M ( LMΩ L Ω L Mω L ω ) L ωω (i 1), L Ω ω ijk i = 1 i = L Ω +1 i [1, L Ω + 1] k ω ijk ω (i+lω )jk
67 M ijk M (i+lω )jk M ijk M ij(k+lω) G M N M = G M G M Z LM N M L M G M N M G M = (G M (1),, G M (j ),, G M (N M )), 1 G M (1) G M (j ) G M (N M ) L M, j N M j + N M j : Z NM Z LM j G M (j ). G M (j ) j {1,, N M } (a, b) = a mod (b) G M (j ) = G M ( (j + N M, N M )), j = j + L M mod (L M ), G ω N ω = G ω L ω G M G ω = (G ω (1),, G ω (k ),, G ω (N ω )), 1 G ω (1) G ω (k ) G M (N ω ) L ω,
68 k N ω : Z Nω Z Lω k G ω (k ), G ω (k ) k {1,, N ω } G ω (k ) = G ω ( (k + N ω, N ω )), k = k + L ω mod (L ω ), (i, j, k ) (i, j, k) : Z LΩ Z NM Z Nω Z LΩ Z LM Z Lω (i, j, k ) (i, j, k), S ωω S MΩ S Mω k j k = G ω (k ) + S ωω (i 1), j = G M (j ) + S Mω (k 1) + S MΩ (i 1). k 1 = G ω (k ) 1 + S ωω (i 1), j 1 = G M (j ) 1 + S Mω (k 1) + S MΩ (i 1). k 1 = G ω (k ) 1 + S ωω (i 1) mod Sym(G ω ), j 1 = G M (j ) 1 + S Mω (k 1) + S MΩ (i 1) mod Sym(G M ).
69 j k k k j 1 = G M (j ) 1 + S Mω (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) + + S MΩ (i 1) mod Sym(G M ), j Ω ij k = 2π (i 1), L Ω ω ij k = 2π [ (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ωω L ω M ij k = 2π L M [ ( G M (j ) 1 + S Mω ( G ω (k ) S ωω (i 1), Sym(G ω ) ) ) + S MΩ (i 1), Sym(G M ) ] (i 1) L Ω, L Mω L ( ω LMΩ (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ) ] Mω L ωω (i 1), L ω L Ω L Ω G M G ω M ij k S ωω, S Mω, S MΩ S ωω [0, Sym(G ω ) 1], S Mω [0, Sym(G M ) 1], S MΩ [0, Sym(G M ) 1],
70 Ω ij k = Ω i(j +N M )k, ω ij k = ω i(j +N M )k, M ij k = M i(j +N M )k, Ω ij k ω ij k M ij k Ω ij k = Ω ij(k +N ω), ω ij k = ω ij (k +N ω), M ij k = M ij (k +N ω), k ω ij k k + N ω ω ij k + 2π = ω ij (k +N ω), [ 2π (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ] ωω (i 1) + 2π = L ω L Ω = 2π [ (G ω (k + N ω ) 1 + S ωω (i 1), Sym(G ω )) L ] ωω (i 1), L ω L Ω
71 (G ω (k + N ω ) 1 + S ωω (i 1), Sym(G ω )) (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) = L ω, M ij k [ 2π ( G M (j ) 1 + S Mω ( G ω (k ) 1 + L M + S ωω (i 1), Sym(G ω ) ) ) + S MΩ (i 1), Sym(G M ) L Mω L ( ω LMΩ (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ) ] Mω L ωω (i 1) = L ω L Ω L Ω = 2π [ ( G M (j ) 1 + S Mω ( G ω (k + N ω ) 1 + L M + S ωω (i 1), Sym(G ω ) ) ) + S MΩ (i 1), Sym(G M ) L Mω L ( ω LMΩ (G ω (k + N ω ) 1 + S ωω (i 1), Sym(G ω )) L ) ] Mω L ωω (i 1) ; L ω L Ω L Ω ( G M (j ) 1 + S Mω (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) + ) + S MΩ (i 1), Sym(G M ) L Mω (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) = L ( ω = G M (j ) 1 + S Mω (G ω (k + N ω ) 1 + S ωω (i 1), Sym(G ω )) + ) + S MΩ (i 1), Sym(G M ) L Mω (G ω (k + N ω ) 1 + S ωω (i 1), Sym(G ω )). L ω Sym(G M ) ASym(G M ) = S Mω L ω L Mω ; A Sym(G M ) S Mω L ω L Mω, Sym(G M ) (S Mω L ω L Mω )
72 S Mω Ω ij k = Ω (i+l Ω )j k, ω ij k = ω (i+l Ω )j k, M ij k = M (i+l Ω )j k. Ω ij k = 2π L Ω (i 1) = 2π L Ω (i 1) + 2π mod (2π), L ω 2π ω ij k = L ω 2π ω (i+l Ω )j k, (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ωω L Ω (i 1) = = (G ω (k ) 1 + S ωω (i 1) + S ωω L Ω, Sym(G ω )) L ωω L Ω (i 1) L ωω, (G ω (k ) 1 + S ωω (i 1) + S ωω L Ω, Sym(G ω )) (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) = L ωω, Sym(G ω ) BSym(G ω ) = S ωω L Ω L ωω ; B Sym(G ω ) S ωω L Ω L ωω.
73 S ωω Sym(G ω ) L Ω L ωω L M 2π M ij k = L M 2π M (i+l Ω )j k, ( ) G M (j ) 1 + S Mω (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) + S MΩ (i 1), Sym(G M ) ( ) LMΩ (i 1) = L Mω (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L Mω L ωω L ω L Ω L ω L Ω ( = G M (j ) 1 + S Mω (G ω (k ) 1 + S ωω (i 1) + S ωω L Ω, Sym(G ω )) + ) + S MΩ (i 1) + S MΩ L Ω, Sym(G M ) (G ω (k ) 1 + S ωω (i 1) + S ωω L Ω, Sym(G ω )) ( LMΩ L Ω L Mω L ω L ωω L Ω ) (i 1) L Mω L ω ( L MΩ L MωL ωω L ω ), ( G M (j ) 1 + S Mω (G ω (k ) 1 + S ωω (i 1)+ ) + S ωω L Ω, Sym(G ω )) + S MΩ (i 1) + S MΩ L Ω, Sym(G M ) ( G M (j ) 1 + S Mω (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) + ) + S MΩ (i 1), Sym(G M ) = L MΩ. Sym(G ω ) CSym(G M ) = S MΩ L Ω (L MΩ S Mω L ωω ), C Sym(G M ) S MΩ L Ω (L MΩ S Mω L ωω ). S MΩ S Mω
74 G Ω ij k = 2π (i 1), L Ω ω ij k = 2π [ (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ωω L ω M ij k = 2π L M [ ( G M (j ) 1 + S Mω ( G ω (k ) S ωω (i 1), Sym(G ω ) ) ) + S MΩ (i 1), Sym(G M ) ] (i 1) L Ω, L Mω L ( ω LMΩ (G ω (k ) 1 + S ωω (i 1), Sym(G ω )) L ) ] Mω L ωω (i 1), L ω L Ω L Ω S ωω S Mω S Mω Sym(G ω ) S ωω L Ω L ωω, Sym(G M ) S Mω L ω L Mω, Sym(G M ) S MΩ L Ω (L MΩ S Mω L ωω ). Sym(G) S MΩ L Ω N c, G N c L MΩ
75 L Ω = 7 N ω = 2 N M = 3 L ω = 6 L M = 9 G M = 10 G ω = 3 G M G ω L 2 Ω L ω = 8820 L 2 Ω N ω = 98 L MΩ = 4 L Mω = 3 L ωω = 6 G M = {1, 4, 7} G ω = {1, 4} Sym(G M ) = 3 Sym(G ω ) = 3 Sym(G ω ) S ωω L Ω L ωω 3 7S ωω 6, S ωω = 0 Sym(G M ) S Mω L ω L Mω 3 6S Mω 3, S Mω = 0, 1, 2 Sym(G M ) S MΩ L Ω (L MΩ S Mω L ωω ) 3 7S MΩ (4 6S Mω ), S MΩ = 1 S Mω = 0, 1, 2 S Mω S MΩ S Mω S ωω = 0 S Mω = 2 S MΩ = 1 (Ω, ω, M)
76 (Ω, ω, M) e = 0.3 i = o a = 12, 770 km
77
78 n
79 J 2 J 2
80 a M ω Ω {V a, V Ω, V ω, V M } V a V Ω V ω V M {V a, V Ω, V ω, V M } {V a, V Ω, V ω, V M } [0, 1] {r, i, k, j} L a L Ωa L Ω 0 0 L ωa L ωω L ω 0 L Ma L MΩ L Mω L M V a ijkr V Ω ijkr V ω ijkr V M ijkr = r i k j ; L a L Ω L ω L M r = {1,..., L a } i = {1,..., L Ω } k = {1,..., L ω } j = {1,..., L M } L Ωa {0,..., L a 1} L ωa {0,..., L a 1} L ωω {0,..., L Ω 1} L Ma {0,..., L a 1} L MΩ {0,..., L Ω 1} L Mω {0,..., L ω 1}
81 V a ijkr = 1 L a r, V Ω ijkr = 1 L Ω i L Ωa L a L Ω r, Vijkr ω = 1 k L ωω i 1 L ω L ω L Ω L ω Vijkr M = 1 j L Mω k 1 L M L M L ω 1 L M ( LMa L a L MΩ L Ω L M ( Lωa L Ωa L a L a ( LMΩ L ωω L Ωa L Ω L Ω L Mω L ω L a L Mω L ω ( Lωa L a ) r, L ωω L Ω ) i L Ωa L a L ωω L Ω )) r, [ ] 1 Vijkr a = r, 1, L a [ ( 1 Vijkr Ω = i L ) ] Ωa r, 1, L Ω L a [ ( 1 Vijkr ω = k L ( ωω Lωa i L ) ) ] ωω L Ωa r, 1, L ω L ω L a L Ω L a [ ( 1 Vijkr M = j L ( Mω LMΩ k L ) Mω L ωω i L M L ω L Ω L ω L Ω ( LMa L MΩ L Ωa L ( Mω Lωa L )) ) ] Ωa L ωω r, 1, L a L Ω L a L ω L a L a L Ω [a, b] a b L a L a L Ω L a L Ω L ω L a L Ω L ωm L a Vijkr a = [r, L a ], L Ω L a Vijkr Ω = [L a i L Ωa r, L Ω L a ], L ω L Ω L a Vijkr ω = [L Ω L a k L ωω L a i (L ωa L Ω L ωω L Ωa ) r, L ω L Ω L a ], L M L ω L Ω L a Vijkr M = [L ω L Ω L a j L Mω L Ω L a k (L MΩ L ω L a L Mω L ωω L a ) i (L Ma L ω L Ω L MΩ L Ωa L ω L Mω (L ωa L Ω L Ωa L ωω )) r, L M L ω L Ω L a ]. {N a, N Ω, N ω, N M } N a ijkr = L a V a ijkr, Nijkr Ω = L Ω L a Vijkr Ω Nijkr ω = L ω L Ω L a Vijkr ω N M ijkr = L M L ω L Ω L a V M ijkr,
82 Nijkr a = [r, L a ], Nijkr Ω = [L a i L Ωa r, L Ω L a ], Nijkr ω = [L Ω L a k L ωω L a i (L ωa L Ω L ωω L Ωa ) r, L ω L Ω L a ], Nijkr M = [L ω L Ω L a j L Mω L Ω L a k (L MΩ L ω L a L Mω L ωω L a ) i (L Ma L ω L Ω L MΩ L Ωa L ω L Mω (L ωa L Ω L Ωa L ωω )) r, L M L ω L Ω L a ], {N a, N Ω, N ω, N M } N a {1,..., L a }, N Ω {1,..., L Ω L a }, N ω {1,..., L ω L Ω L a }, N M {1,..., L M L ω L Ω L a }, L a L Ω = 4 N Ω = {1, 2, 3, 4} Ω 1 = 0 o Ω 2 = 30 o Ω 3 = 90 o Ω 4 = 180 o N p N d N p N d T c = N p T = N d T d, T T d
83 T c N d N p N p J2 J 2 J 2 J 2 [ µ ȧ sec = 0; n = a ( ) 2 4 J R ( 2 2 3sin 2 a(1 e 2 (i) ) 1 e 2] ; ) ( R ) 2 n ( 5cos 2 (i) 1 ) ; ė sec = 0; ω sec = 3 4 J 2 a(1 e 2 ) i sec = 0; Ωsec = 3 ) 2 2( 2 J R a(1 e 2 n cos(i); ) µ R n Ω sec = Ω sec0 ω sec = ω sec0 T c Ω sec0 ω sec0 T c = N p 2π n = N dt d.
84 [ 2π N p µ = T d N d a ( ) 2 4 J R ( 2 2 3sin 2 a(1 e 2 (i) ) 1 e 2], ) ω sec0 = 3 ( ) 2 4 J R 2π N p ( 2 5cos 2 a(1 e 2 (i) 1 ), ) T d N d Ω sec0 = 3 ) 2 2( 2 J R 2π N p a(1 e 2 cos(i), ) T d N d N a ω sec0 Ω sec0 cos(i) = ω sec0 ± ω sec Ω 2 sec0 5 Ω, sec0 ω sec0 Ω sec0 Ω sec0 1 e 2 = R a 3 2 J 2 2π N p cos(i), Ω sec0 T d N d a 3 T d N d 2 = µ 1 Ω sec0 T d N d 2 3 sin 2 (i) R 3 J 2 2π N p cos(i), 2π N p 4π N p cos(i) a 2 Ω sec0 T d N d N a L a = 2
85 L Ω = 3 L ω = 3 L M = 3 N d = 3 i = o e = 0.1 N p = {8, 6} km km Ω ijkr = 2π N ijkr Ω ; ω ijkr = 2π N ijkr ω ; L a L Ω L a L Ω L ω N M ijkr M ijkr = 2π. L a L Ω L ω L M L ij L 21 = 0 L 32 = 2 L 31 = 1 L 43 = 0 L 42 = 2 L 41 = 1
86 N a G Ω G ω G M
87 G G Ω {1,..., L Ω }, G ω {1,..., L ω }, G M {1,..., L M }, G Ω = N Ω G Ω G ω = N ω G ω G M = N M G M G Ω = {G Ω (1),..., G Ω (i ),..., G Ω (N Ω )}, G ω = {G ω (1),..., G ω (k ),..., G ω (N ω )}, G M = {G M (1),..., G M (j ),..., G M (N M )}, 1 G Ω (1) < < G Ω (i ) < < G Ω (N Ω ) L Ω, 1 G ω (1) < < G ω (k ) < < G ω (N ω ) L ω, 1 G M (1) < < G M (j ) < < G M (N M ) L M, i k j G Ω G ω G M G : Z La Z NΩ Z Nω Z NM Z La Z LΩ Z Lω Z LM (r, i, k, j ) (r, G Ω (i ), G ω (k ), G M (j )). G i {1,..., N Ω } k {1,..., N ω } j {1,..., N M } S Ωr S ωr S ωω S Mr S MΩ S Mω i = G Ω (i ) + S Ωr r, k = G ω (k ) + S ωr r + S ωω i, j = G M (j ) + S Mr r + S MΩ i + S Mω k. Sym(G) Sym(G) = min {1 r n : G + r G}. i = [G Ω (i ) + S Ωr r, Sym(G Ω )], k = [G ω (k ) + S ωr r + S ωω i, Sym(G ω )], j = [G M (j ) + S Mr r + S MΩ i + S Mω k, Sym(G M )].
88 S Ωr {0,..., Sym(G Ω ) 1}, S ωr, S ωω {0,..., Sym(G ω ) 1}, S Mr, S MΩ, S Mω {0,..., Sym(G M ) 1}. i k j k i = [G Ω (i ) + S Ωr r, Sym(G Ω )], k = [G ω (k ) + S ωr r + S ωω [G Ω (i ) + S Ωr r, Sym(G Ω )], Sym(G ω )], j = [G M (j ) + S Mr r + S MΩ [G Ω (i ) + S Ωr r, Sym(G Ω )] + + S Mω [G ω (k ) + S ωr r+ + S ωω [G Ω (i ) + S Ωr r, Sym(G Ω )], Sym(G ω )], Sym(G M )], Ni a j k r = [r, L a ], Ni Ω j k r = [L a [G Ω (i ) + S Ωr r, Sym(G Ω )] L Ωa r, L Ω L a ], Ni ω j k r = [L Ω L a [G ω (k ) + S ωr r + S ωω [G Ω (i )+ + S Ωr r, Sym(G Ω )], Sym(G ω )] L ωω L a [G Ω (i )+ + S Ωr r, Sym(G Ω )] (L ωa L Ω L ωω L Ωa ) r, L ω L Ω L a ], Ni M j k r = [L ω L Ω L a [G M (j ) + S Mr r + S MΩ [G Ω (i )+ + S Ωr r, Sym(G Ω )] + S Mω [G ω (k ) + S ωr r+ + S ωω [G Ω (i ) + S Ωr r, Sym(G Ω )], Sym(G ω )], Sym(G M )] L Mω L Ω L a [G ω (k ) + S ωr r + S ωω [G Ω (i )+ + S Ωr r, Sym(G Ω )], Sym(G ω )] (L MΩ L ω L a L Mω L ωω L a ) [G Ω (i ) + S Ωr r, Sym(G Ω )] (L Ma L ω L Ω L MΩ L Ωa L ω L Mω (L ωa L Ω L Ωa L ωω )) r, L M L ω L Ω L a ].
89 ( ) Ni a j k (r+l, N Ω a) i j k (r+l, N ω a) i j k (r+l, N M a) i j k (r+l a) = = ( Ni a j k r, N i Ω j k r, N i ω j k r, N i M j k r), ( ) N(i a +N Ω )j k r, N (i Ω +N Ω )j k r, N (i ω +N Ω )j k r, N (i M +N Ω )j k r = = ( Ni a j k r, N i Ω j k r, N i ω j k r, N i M j k r), ( ) Ni a j (k +N, N Ω ω)r i j (k +N, N ω ω)r i j (k +N, N M ω)r i j (k +N ω)r = = ( Ni a j k r, N i Ω j k r, N i ω j k r, N i M j k r), ( ) Ni a (j +N M )k r, N i Ω (j +N M )k r, N i ω (j +N M )k r, N i M (j +N M )k r = = ( N a i j k r, N Ω i j k r, N ω i j k r, N M i j k r), Sym(G Ω ) S Ωr L r L Ωr, Sym(G ω ) S ωω L Ω L ωω, Sym(G ω ) S ωr L r (L ωr S ωω L Ωr ), Sym(G M ) S Mω L ω L Mω, Sym(G M ) S MΩ L Ω (L MΩ S Mω L ωω ), Sym(G M ) S Mr L r (L Mr S MΩ L Ωr S Mω L ωr ), a > Ω > ω > M
90 G M = {1} N M = 1 G ω = {1, 2, 3} G ω = {1, 2, 3} Sym(G M ) = 3 1 2S Ωr 0, S Ωr = 0 1 3S ωω 2, S ωω = 0 S ωr = 0 1 2S ωr (1 0), 3 3S Mω 0, S Mω = 0, 1, 2 3 3S MΩ (2 2S Mω ), S Mω = 1 S MΩ = 0, 1, 2 3 2S Mr (1 0 1), S Mr = 0 S MΩ S MΩ S MΩ = 0, 1, 2 S MΩ = 2
91 M ω M ω M Ω M r
92 x z L a = 1 L ω = 1
93 J 2 J 2
94
95 n n n (n 1) n
96 n n n n Z n R n : Z n R n k V, k V k i i Z n V i [0, 1] i = 1,..., n {V i V V i [0, 1]} i {k i k k i Z} L ii V i {k j j i} L ii i k i L ii k i {V (k)} {V (k )} {V (k)} {V (k )} {V (k )} = {V (k)}. V (k ) = V (k), V i (k ) = V i (k), i {1,..., n} V (k) V i ({1,..., k m 1, k m, k m+1,..., k n }) = = V i ({1,..., k m 1, k m + L mm, k m+1,..., k n }) i, m {1, 2,..., n}, k V i (k m ) = V i (k m + L mm ).
97 L ij n n n V i = 1 i 1 k i (L ij V j ), 1, L ii (a, b) b a L ij Z n R n j=1 : Z n R n {α 1,..., α i,..., α n } {V 1,..., V i,..., V n }, n P 1,1 P 1,2 P 1,n V 1 α 1 P 2,1 P 2,2 P 2,n V 2 α = 2, P n,1 P n,2 P n,n P i,j V i P i,j α i L 1, V 1 k 1 L 2,1 L 2,2 0 0 V 2 k 2 =, L n 1,1 L n 1,2 L n 1,n 1 0 V n 1 k n 1 L n,1 L n,2 L n,n L ij Z k i Z P ij α i i L ij V j = k i, V i V i = 1 i 1 k i L ij V j, L ii j=1 j=1 V n V n α n k n
98 n V i (k m ) = V i (k m + L mm ), m > i V i k j j i m = i 1 L ii V i (k i ) = V i (k i + L ii ) i {1, 2,..., n}, i 1 k i L ij V j = 1 i 1 k i + L ii L ij V j, L ii j=1 j=1 L ii = 0 V i = 1 i 1 k i L ij V j, L ii, L ii j=1 k i = k i + L ii mod (L ii ). k i Z Lii k i = k i + L ii mod (L ii ). m < i 1 i 1 k i L ij V j (k m ) = 1 L ii j=1 L ii i 1 k i L ij V j (k m + L mm ), j=1 V j (k m ) = V j (k m + L mm ) j, m {1, 2,..., n},
99 L ii V i = 1 i 1 k i L ij V j, 1. L ii k i = L ii i Z n j=1 L ii L ii V i {k j j i} {L ij i j} k i L ij k i k i {1, 2,..., L ii } k m k m Z k m km Z k m m 1 L mm k m m 1 j=1 L mj V j, 1 = 1 L mm k m m 1 j=1 L mj V j, 1. 1 k m L mm m 1 j=1 L mj V j + A = 1 L mm k m m 1 j=1 L mj V j, A k m + AL mm = km, k m Z Lmm = {1, 2,..., L mm } km Z k m {1, 2,..., L mm }
100 n L ij L ij {0, 1,..., L jj 1}. L L i 1 L ij = L ij + A p L pj, p=j A p n n L ij [0, L jj 1] i L ij L L L L n L ij = L ij + A p L pj, p=1 A p n i 1 L ij = L ij + A p L pj, p=j L ij = L ij + i 1 p=j+1 A p L pj + A j L jj,
101 A j L ij = L ij + i 1 p=j+1 A p L pj mod (L jj ), L ij {0, 1,..., L jj 1}, L ij {0, 1,..., L jj 1} i (L ii ) V i = 1 i 1 k i (L ij V j ), 1, L ii j=1 i (L ii ) n n i i=1 j=1 L ii n L ii L ij i j L ij i i 1 L jj j=1 n i 1 i=1 j=1 L jj
102 n n 1 n 2 n (n 1) L jj L jj L jj = L (n 1) 11 L (n 2) 22 L (1) (n 1)(n 1), j=1 j=1 n i=1 j=1 L (n i) ii = n n i L ii. i=1 j=1 n G Z m, m G 1 G 2 G 1 G 2 {G 1 } = {G 2 }. G 1 G 2 = s Z m G 1 = G2 s : G 1 G 2 + s mod (m), s m
103 G Sym(G) Sym(G) = min {1 r n : G + r G}. G {s : Sym(G) s} G G (Sym(G) 1) S S {0, 1,..., (Sym(G) 1)}. G i i G i N i N i i {k j j i} G i Z Lii G i {1,..., L ii }, G i = N i G i G i = {G i (1),..., G M (k i ),..., G i (N i )}, 1 G i (1) G i (k i ) G i (N i ) L ii, k i {1,..., N i} N i k i + N i k i G i G i : Z Ni Z Lii k i G i (k i ). G i (ki ) G i (ki ) = G i ( (ki + N i, N i )),
104 n i k i = k i + L ii mod (L ii ), i Sym(G i ) G i G i G i + ASym(G i ), A G i = G i + Sym(G i ) mod (Sym(G i )). L ii Sym (G) Sym (G) Sym (G) L ii S n n S ij Z G i j G i G j j < i V i k i n i L ij V j = k i ; j=1 i 1 k i = G i (ki ) + S ij k j, Sym (G i ), j=1 G i i k i S ij G i j k i G i (ki ) : (Z N1 Z N2 Z Nn ) (Z L11 Z L22 Z Lnn ) (k 1, k 2,..., k n) (k 1, k 2,..., k n ),
105 k i i 1 k i = G i (ki ) + S ij k j, G i (ki ) i 1 j=1 S ijk j G i i 1 k i = G i (ki ) + S ij k j, Sym(G i ), j=1 j=1 i L ij V j = k i ; j=1 i 1 k i = G i (ki ) + S ij k j, Sym (G i ). j=1 L ij S ij j > i i L ij V j = k i ; j=1 i 1 k i = G i (ki ) + S ij k j, Sym (G i ), Sym(G i ) S ijl jj L ij j=1 i 1 q=j+1 S iq L qj. i V i (k j ) = V i (k j + L jj ) i, j {1, 2,..., n},
106 n j i V i (k j ) = V i (k j + L jj ) i j, j > i j = i j < i i L ip V p (k j ) = k i (k j ) p=1 i 1 k i (k j ) = G i (ki ) + S ip k p (k j ) + A i Sym (G i ), p=1 j V p (k j ) k p (k j ) A i i L ip V p (k j + L jj ) = k i (k j + L jj ) p=1 i 1 k i (k j + L jj ) = G i (ki ) + S ip k p (k j + L jj ) + B i Sym (G i ), p=1 j V q (k j + L jj ) q j k p (k j + L jj ) k p B i j > i j k i i i i L ip V p (k j + L jj ) L ip V p (k j ) = L ip [V p (k j + L jj ) V p (k j )] = 0, p=1 p=1 p=1 k p (k j + L jj ) = k p (k j ) p < j. i 1 0 = S ip [k p (k j + L jj ) k p (k j )] + (B i A i )Sym (G i ) p=1
107 j = i j L jp [V p (k j + L jj ) V p (k j )] = L jj, p=1 L jj = k j (k j + L jj ) k j (k j ) j 1 L jj [V j (k j + L jj ) V j (k j )] + L jp [V p (k j + L jj ) V p (k j )] = L jj, p=1 V j (k j + L jj ) V j (k j ) = 1 i V i 1 V i (k i + L ii ) = V i (k i ) j 1 L jj = S jp [k p (k j + L jj ) k p (k j )] + (B j A j )Sym (G j ), p=1 L jj = (B j A j )Sym (G j ), Sym (G j ) L jj j < i i i L iq V q (k j + L jj ) L iq V q (k j ) = k i (k j + L jj ) k i (k j ), q=1 q=1 i L iq [V q (k j + L jj ) V q (k j )] = k i (k j + L jj ) k i (k j ), q=1 + j 1 L iq [V q (k j + L jj ) V q (k j )] + L ij [V j (k j + L jj ) V j (k j )] + q=1 i q=j+1 L iq [V q (k j + L jj ) V q (k j )] = k i (k j + L jj ) k i (k j ),
108 n L ij = k i (k j + L jj ) k i (k j ). i 1 k i (k j + L jj ) k i (k j ) = S ip [k p (k j + L jj ) k p (k j )] + (B j A j )Sym (G j ), p=1 i 1 L ij = S ip [k p (k j + L jj ) k p (k j )] + (B j A j )Sym (G j ). p=j L ij = S ij [k j (k j + L jj ) k j (k j )] + + i 1 p=j+1 S ip [k p (k j + L jj ) k p (k j )] + (B j A j )Sym (G j ), k j (k j + L jj ) k j (k j ) = L jj, j k p (k j + L jj ) k p (k j ) = L pj L ij = S ij L jj + i 1 p=j+1 Sym(G i ) S ij L jj L ij S ip L pj + (B j A j )Sym (G j ), i 1 q=j+1 S iq L qj, Sym(G i ) S i 1 ijl jj L ij S iq L qj. q=j+1
109 n G i i {1,..., n} G i L ii i {1,..., n} N i = G i L ii i {1,..., n} L G N G {1,..., L} G = N = N L L g=1 g L L g N 1 g g N L g g 1 g =1 g g L g N g L (g ). g = Sym(G) (g ) g (g) = L g g N L g g 1 g =1 g g L g N (g ), g L + Z L G Z L G = Z L L ϕ ϕ : G X X (g, x) x + g mod (L). (g) g G (X)
110 n g = Sym(G) g L L g N g = Sym(G) (g) g L/g L Ng/L g P C(g) P C(g) = g N L g. L/g L N L g L g P C(g) = L g g N L g. L = 6 N = 3 g = 6 g = 3 {1, 4} {2, 5} {3, 6} g N g (g) g g P C(g ) = g (g ). L g g < g P C(g) = g g 1 N g L g (g ), L g g g L g N g g =1 g g L g N
111 (g) (g) = L g g N L g g 1 g =1 g g L g N g L (g ), g G = Z L 1 L L M g=1 g L M L Mg N M L M g=1 g L M L g N 1 g g N L g (g), g 1 g =1 g g L g N g L (g ). G i i {1,..., n} G i S ij G i i {1,..., n} gcd(sym(g i ), L jj ) L ij i 1 q=j+1 S ij L qj, {i, j : i > j},
112 n n i 1 gcd(sym(g i ), L jj ), i=1 j=1 ASym(G i ) + L jj S ij = L ij i 1 q=j+1 S ij L qj, A A S ij gcd(sym(g i ), L jj ) L i 1 ij S ij L qj. q=j+1 (S ij ) λ = (S ij ) 0 + λ l, l = L jj (A) λ = (A) 0 λ gcd(sym(g i ), L jj ), Sym(G i ) gcd(sym(g i ), L jj ), (S ij ) 0 (A) 0 λ S ij S ij {0,..., Sym(G i ) 1} S ij Sym(Gi ) 1 (Sym(Gi ) 1) gcd(sym(g i ), L jj ) + 1 = + 1 = l Sym(G i ) gcd(sym(gm ), L Ω ) = gcd(sym(g i ), L jj ) + 1 = Sym(G M ) = gcd(sym(g i ), L jj ). S ij gcd(sym(g i ), L jj ) L ij i 1 q=j+1 S ij L qj, {i, j : i > j}, S ij n i 1 gcd(sym(g i ), L jj ). i=1 j=1
113 Sym(G i ) = 1 n i 1 gcd(1, L jj ) = 1. i=1 j=1 G i L ii i {1,..., n} G i L ii Sym(G i ) {S ij, L ij } G i L ii n n i L ii. i=1 j=1 i S ij L ij L jj S ij 1L ij = ASym(G M ) i 1 q=j+1 S iq L qj, S iq L qj q > j S ij L ij gcd(l jj, 1) ASym(G M) i 1 q=j+1 (S ij ) λ = (S ij ) 0 + λ, S iq L qj (L ij ) λ = (L ij ) 0 + λl jj, (S ij ) 0 (L ij ) 0 λ
114 n A L ij {0,..., L jj 1} A L ij S ij A A min = 1 i 1 Sym(G i ) S iq L qj (L jj 1), A max = 1 Sym(G i ) q=j+1 i 1 q=j+1 S iq L qj + L jj (Sym(G i ) 1), Ljj (Sym(G i ) 1) + (L jj 1) A max A min + 1 = + 1 = L jj Sym(G i ) A L jj {L ij, S ij } L ij {0,..., L jj 1} n n i L ii, i=1 j=1 G i L ii N i L ii i {1,..., n} G i N i = G i
115 L ii i {1,..., n} i n N i n i=1 L (n i) ii L ii g=1 g L ii L ii g N i 1 g g N i g L ii g 1 g =1 g g L ii g N i g (g ), L ii (g ) i g (g) = L g g N L g g 1 g =1 g g L g N (g ), i P i = L ii g=1 g L ii L ii g N i 1 g g N i g L ii g 1 g =1 g g L ii g N i g L g (g ), L ii (g) = L ii g g N i g L ii g 1 g =1 g g L ii g N i g (g ). L ii n P i. i=1 n n P i i=1 i=1 L (n i) ii.
116 n n P i L (n i) ii, n i=1 L (n i) ii L ii g=1 g L ii L ii g N i 1 g i=1 g N i g L ii g 1 g =1 g g L ii g N i g (g ), L ii N i L ii N i = L ii i V i i L ij V j = k i, i 1 p=1 L pp i j=1 j=1 i 1 L pp V j = k i L pp, L ij i 1 p=1 i 1 L pp V i + L ii i 1 p=1 j=1 L ij i 1 p=1 i 1 L pp V j = k i L pp, p=1 p=1 i i 1 i 1 j i 1 L pp V i + L pp V j = k i L pp. p=1 L ij L mm j=1 m=j+1 p=1 p=1
117 V i N i V i i N i = L pp V i. p=1 i 1 N i + L ij N j j=1 i 1 m=j+1 i 1 L mm = k i L pp, p=1 k i i 1 i 1 N i = k i L pp L ij N j p=1 j=1 i 1 m=j+1 L mm. V i N i = [ i p=1 L ppv i N i 0, ] i p=1 L pp N i = k i i 1 i 1 L pp L ij N j p=1 j=1 i 1 m=j+1 L mm, i p=1 L pp. N i Z i i 1 N i + L ij N j j=1 i 1 m=j+1 i 1 L mm = k i L pp ; p=1 i 1 k i = G i (ki ) + S ij k j, Sym (G i ), j=1 N i [ N i 1,..., ] i p=1 L pp
118 n n n n
119
120 a e i ω Ω M x = (r cos f, r sin f, 0), r r = a ( 1 e 2) 1 + e cos f,
121 f R 3 R 1 x ECI = R 3 (Ω) R 1 (i) R 3 (ω) x, x ECEF = R 3 ( ψ G0 ω t) x ECI, ψ G0 t = 0 ω r cos f x ECEF = R 3 ( ψ G0 ω t) R 3 (Ω) R 1 (i) R 3 (ω) r sin f, 0 r cos f x ECEF = R 3 (Ω ψ G0 ω t) R 1 (i) R 3 (ω) r sin f. 0 a e i ω a e i ω Ω 0 t 0 x 0 r cos f x 0 ECEF = R 3 (Ω 0 ψ G0 ω t) R 1 (i) R 3 (ω) r sin f, 0 r f t t 0 t 1 t 0
122 Ω = ω (t 1 t 0 ) x 1 t 1 r cos f x 1 ECEF = R 3 (Ω 0 ψ G0 ω (t 1 t 0 + t)) R 1 (i) R 3 (ω) r sin f, 0 r f t 1 + t x 1 ECI = R 3 (ψ G0 + ω t) x 1 ECEF, x 1 ECI = R 3 (Ω 0 ω (t 1 t 0 )) R 1 (i) R 3 (ω) r cos f r sin f 0. {a, e, i, ω, Ω 0, M 0 } {a, e, i, ω, Ω 1, M 1 } M 0 M 1 x 0 ECEF (t + (t 1 t 0 )) = x 1 ECEF (t) t R, t 1 t Ω 1 = Ω 0 ω (t 1 t 0 ). M = n(t + t 0 τ), τ t 0 n n = µ a 3, µ τ 0 τ 1 M 1 = n(t + t 1 τ),
123 t 1 1 M 1 = M 0 + n(t 1 t 0 ). M 1 Ω 1 ( M 1 = M 0 + n ) Ω 0 n Ω 1 ; ω ω M 1 (Ω 1 ) n/ω (Ω, M) (Ω, M) t q t 1 N st q [1, N st ] q ( M q = M 0 + n ) Ω 0 n Ω q ; ω ω r cos f x q ECI = R 3 (Ω 0 ω (t q t 0 )) R 1 (i) R 3 (ω) r sin f. 0 Ω q q Ω q = Ω 0 ω (t q t 0 ).
124 t q t 0 t t q ω Ω q f q t q t q x q ECI = R 3 (Ω 0 ω (t q t 0 )) R 1 (i) R 3 (ω) a ( 1 e 2) 1 + e cos f q cos f q a ( 1 e 2) 1 + e cos f q sin f q 0. t q Ω q = Ω 0 ω (t q t 0 ); M q = M 0 + n(t q t 0 ); t q Ω 0 t 0 M 0 a = km e = 0.4 i = o Ω 0 = 0 M 0 = 0 t 0 = 0 t q = 300(q 1); q [1, 5] 300 Ω q = ω t q ; M q = nt q ;
125 Ω q deg M q deg N t k [1, N t ] N s N s = N st N t, N st k0 k 00
126 r cos f x kq ECEF = R 3 (σ) R 1 (i) R 3 (ω) r sin f, 0 σ = Ω 0 + Ω k ψ G0 ω (t kq t 0 + t), Ω k t kq r f t kq t kq k q Ω k t kq f kq q k x kq ECI = R 3 (Ω kq ) R 1 (i) R 3 (ω) a ( 1 e 2) 1 + e cos f kq cos f kq a ( 1 e 2) 1 + e cos f kq sin f kq 0, Ω kq = Ω 0 + Ω k ω (t kq t 0 ), (Ω, M) Ω kq = Ω 0 + Ω k ω (t kq t 0 ), M kq = M 0 + n(t kq t 0 ), Ω kq M kq M kq = ( M 0 + n ) Ω 0 + n Ω k n Ω kq ; ω ω ω 11 k = 1, q = 1 Ω 1
127 (Ω, M) 880km a = 7260 km i = o Ω k = 2π k 1 N t, t kq = 2π q 1 N st ; N t = 3 N st = 5 Ω kq = 2π k 1 N t M kq = 2π q 1 N st, 2πω n q 1 N st, k [1, N t ] q [1, N st ] (Ω, M)
128 (Ω, M) Ω kq Ω kq
129 t kq Ω k t kq Ω k t kq t k t q t kq = t k + t q, t q t k k t k Ω k t q Ω kq = Ω 0 + Ω k ω (t k + t q t 0 ), k t k = Ω k ω, t k Ω kq = Ω 0 ω (t q t 0 ). Ω kq k t q q k f kq t q + t k (Ω, M) Ω kq = Ω 0 ω (t q t 0 ), ( ) Ωk M kq = M 0 + n + t q t 0, ω ( M kq = M 0 + n ) Ω 0 + n Ω k n Ω kq. ω ω ω t q t k
130 (Ω, M) a = km e = 0 i = 50 o Ω 0 = 0 M 0 = 0 t 0 = 0 t q Ω k k = 1 k = 2 k = 3 q = 2
131 q = 3 q = 1 t q t 1 = 0 s t 2 = 600 s t 3 = 600 s Ω k Ω 1 = 0 Ω 2 = ω t 2 Ω 3 = ω t 3 (k, q) q k (1, 1) (1, 2) (1, 3) (2, 2) (3, 3) Ω kq deg M kq deg
132 x 0 t = t q t 0, t 0 t q q [1, N st ] x q ECI ṽ q ECI x q ECEF v q ECEF x q ECEF = R 3 ( ψ G0 ω (t q t 0 )) x q ECI, v q ECEF = R 3 ( ψ G0 ω (t q t 0 )) ṽ q ECI ω x q ECEF. x q ECI v q ECI x q ECI = R 3 (ψ G0 ) x q ECEF, v q ECI = R 3 (ψ G0 ) v q ECEF + ω x q ECI.
133 t kq Ω k a 0 e 0 i 0 w 0 Ω k0 = Ω 0 + Ω k ω (t k0 t 0 ), Ω k0 k [1, N t ] t 0 t k0 t kq t k0 N t t = t kq t 0 x kq ECEF = R 3 ( ψ G0 ω (t kq t 0 )) x kq ECI, v kq ECEF = R 3 ( ψ G0 ω (t kq t 0 )) ṽ kq ECI ω x kq ECEF ; x kq ECI = R 3 (ψ G0 ) x kq ECEF, v kq ECI = R 3 (ψ G0 ) v kq ECEF + ω x kq ECI. x kq ECI v kq ECI N t N s t k t q t kq = t k + t q t k Ω k
134 t k ω ω Ω Ω t k = Ω k ω Ω k0, Ω k0 k t k N s N t N st T c T c = N p T Ω = N d T ΩG, N p N d T Ω T ΩG N st q [1, N st ] t q T c t q < T c t q = (q 1) T c N st. N t k [1, N t ]
135 Ω k = Ω 0 + (k 1) 2π N t, Ω k = Ω k Ω 0 = (k 1) 2π N t. t k t k = (k 1) 2π N t ω Ω k0, t kq = t k + t q t kq = (q 1) T c 2π + (k 1) ( N st N t ω Ω ). k0 N d N p N p = 2 N d = 3 N p = 4 N d = 6 N p N t N f N p N t Ω k = Ω 0 + (k 1) 2π, N t N f t kq = (q 1) T c 2π + (k 1) ( N st N t N f ω Ω ), k0
136 N p N d N st N t (ψ r, ϕ r ) f = π x y z v x v y v z
137 t 0 t 0 = 0 N p = 2 N d = 1 i = o e = 0.5 N t = 6 N st = 4 N s = N t N st = 24 N t = 6 N p = 2 N f = 2 ϕ r = o ψ r = o
138
139 o 705 ± 5 km a = km e = 0 i = o x y z v x v y v z 16 16
140 16 16
141
142
143
144 a e i ω Ω M ω µ R J 2 J 2 T c T c = N p T Ω = N d T ΩG, N p N d T Ω n M o ω T Ω = 2π Ṁ + ω = 2π n + M o + ω.
145 T ΩG T ΩG = 2π ω Ω, n + M o + ω = N ( p ω N Ω ), d J 2 n = M o = ω = µ a 3 ; 3J 2 nr 2 4a 2 (1 e 2 ) 2 1 e 2 ( 2 3 sin 2 i ) = 3J 2 nr 2 4a 2 (1 e 2 ) 2 ( 4 5 sin 2 i ) = 3J 2nR 2 4a 2 (1 e 2 ) 2 1 e 2 ( 3 cos 2 i 1 ) ; 3J 2nR 2 4a 2 (1 e 2 ) 2 ( 5 cos 2 i 1 ) ; Ω = 3J 2nR 2 2a 2 (1 e 2 2 cos i. ) [ µ 3J 2 R 2 [ (2 a sin 2 4a 2 (1 e 2 ) 2 i ) ] ] 1 e sin 2 i = µ = N p 3J 2 N d ω a + 3 R2 2a 2 (1 e 2 ) 2 cos i, µ [a 2 + 3J 2R 2 [ (2 3 sin 2 4 (1 e 2 ) 2 i ) 1 e sin 2 i 2 N ]] p cos i = N p ω a 7/2. N d N d k 1 k 2 k 1 = N d µ ; N p ω k 2 = k 1 3J 2 R 2 4 (1 e 2 ) 2 [ (2 3 sin 2 i ) 1 e sin 2 i 2 N ] p cos i, N d a 7/2 k 1 a 2 k 2 = 0.
146 a j+1 = a j a7/2 j k 1 a 2 j k 2, 7 2 a5/2 j 2k 1 a j a j+1 a j < tol tol a 0 [ a 3 0 µ N p = N (Nd ) ] 2 1/3 d µ = a 0 =. ω J 2 T Ω N p ω 2 J 2 i = o N p = 14 N d = 1 ϕ r = o N ψ r = o W
147 N p = 14 N d = 1 i = o T c Δψ ψ
148 2N p T c ψ a 0 N p N d ψ 0 ψ 0 a ψ 0 = ω (T c0 T c ) = ω N p (T 0 T ), N p T 0 T a 0 a ψ 0 = ω N p 2π a 3 0 µ 2π a 3. µ dψ dψ 0 = ψ 0 T c. dψ 0 ( ) dψ 0 = ω 1 a3 a 3. 0 a 0 dψ 0 a ( a = a 0 1 dψ ) 2/3 0. ω ( a i = a i 1 1 dψ ) 2/3 i 1, ω
149 a j = a (j 1) dψ (j 1) ( a(j 1) a (j 2) ) ( dψ(j 1) dψ (j 2) ), a j dψ j < ϵ ϵ N d = 1 N p = 14 N p = 14 N d = 1 e = 0.0 i = o
150 J < km km/day km km/day < x y z v x v y v z
151 N p N d 0 o 0 o w = 90 o 0 o N p N d km N p = 15 N d = km/day km km 0.55 km 1 km
152 Deviation in Equator (km/day) e = 0.00 e = 0.01 e = 0.02 e = 0.03 e = 0.04 e = Inclination (deg) N p = 15 N d = Difference in semi major axis (km) e = 0.00 e = e = 0.02 e = e = 0.04 e = Inclination (deg) N p = 15 N d = 1 N p = 3 N d = 1 8 km/day
153 Deviation in Equator (km/day) e = 0.0 e = 0.1 e = 0.2 e = 0.3 e = 0.4 e = Inclination (deg) N p = 3 N d = km Difference in semi major axis (km) e = 0.0 e = 0.1 e = 0.2 e = 0.3 e = 0.4 e = Inclination (deg) N p = 3 N d = 1
154 N p = 1 N d = 1 Deviation in Equator (km/day) e = 0.0 e = 0.1 e = 0.2 e = 0.3 e = 0.4 e = Inclination (deg) N p = 1 N d = 1 Difference in semi major axis (km) e = 0.0 e = 0.1 e = 0.2 e = 0.3 e = 0.4 e = Inclination (deg) N p = 1 N d = 1
155 Ω sec = ω yr, Ω sec yr = Ω sec = 3 2 J R 2 µ 2 a 7/2 (1 e 2 2 cos i. )
156 N p N d ( 1 e 2 ) ( 2 3 N = 2 J 2 yr R 2 7 p Nd 7 ω 4 µ 2 ) 1/3 cos i. r p = a (1 e), N p N d e max = 1 ( N 2 p ω 2 N 2 d µ ) 1/3 r p. ( e min = 3 N 1 2 J 2 yr R 2 7 p N 7 d ω 4 ) 1/3 µ 2. cos i max = 2 ( ) 1 e 2 2 ( min N 7 d 3 J 2 yr R Np 7 cos i min = 2 ( ) 1 e 2 2 ( max N 7 d 3 J 2 yr R Np 7 ω 4 µ 2 ) 1/3 ω 4 µ 2 ) 1/3.
157 J 2 J 3 J 2 J 3 ė = 3 2 [ ẇ = µ a 3 3J 3 (1 e 2 ) 2 ( R ) 3 J 3 (1 e 2 ) a µ R 2 a 3 a 2 ( 2 sin i cos ω )] [ ( sin2 i 1 5 ) 4 sin2 i, 1 + J 3 R J 2 2a sin ω 1 e 2 ( sin 2 i e 2 cos 2 i e sin i )]. ω = π/2, 3π/2 ( 1 e 2 ) e = 1 J 3 R sin 2 i e 2 cos 2 i sin ω, 2 J 2 a sin i a i
158 Ω kq = Ω 00 ω (t q t 0 ), M kq = M 00 + n (t k + t q t 0 ) ; Ω 00 M 00 t 0 t q t k k Ω kq M kq q k 2π t k = (k 1) ( N t N f ω Ω ), k0 t q = (q 1) T c N st, N t N st Ωk0 k0 N f N p N t N f = gcd(n p, N t ) k [1, N t ] q [1, N st ] N p = 59 N d = 4
159 N t = 1 N st = 4 N st /gcd(n st, N d ) x y z v x v y v z J 2
160
161
162
163
164 Ω kq = Ω k ω (t kq t 0 ), M kq = n(t kq t 0 ), (t kq t 0 ) Ω k Ω ij = 2π L Ω (i 1), M ij = 2π L M (j 1) 2π L M L MΩ L Ω (i 1), L Ω L M [( ) (i 1) Ω k = 2π (t kq t 0 ) = 2π n 1 ω n [ (j 1) L M L MΩ L M L Ω L MΩ L M (i 1) L Ω ] (j 1) L M + ω mod (2π), n ], (i 1) = G Ω 1, (j 1) = G M 1 + S MΩ (G Ω 1),
165 [( Ω k = 2π 1 ω n (t kq t 0 ) = 2π n L MΩ L M ) (GΩ 1) L Ω [ (GM 1 + S MΩ (G Ω 1)) L M + ω n ] (G M 1 + S MΩ (G Ω 1)) L MΩ L M (G Ω 1) L Ω mod (2π), ]. L M n ω N p N d n = 2π N p T c, ω = 2π N d T c, T c [( Ω k = 2π 1 N ) d L MΩ (GΩ 1) + N ] d (G M 1 + S MΩ (G Ω 1)) N p L M L Ω N p L M (t kq t 0 ) = T [ ] ( c (GM 1 + S MΩ (G Ω 1)) Tc + A N p N p L M L MΩ L M (G Ω 1) L Ω mod (2π), ), A (t kq t 0 ) = (q 1) T c = T [ c (GM 1 + S MΩ (G Ω 1)) L ] ( ) MΩ (G Ω 1) Tc + A, N st N p L M L M L Ω N p N st = L Ω L M (q 1) (q 1) = N st N p [ (GM 1 + S MΩ (G Ω 1)) L M L ] MΩ (G Ω 1) + A L M L Ω ( Nst N p ), (q 1) = 1 [ ] ( ) LΩ L M (G M 1 + S MΩ (G Ω 1))L Ω (G Ω 1)L MΩ + A. N p N p (q 1) L MΩ
166 Ω q = 2πN d (q 1) N st, M q = 2πN p (q 1) N st,
167 ±7.5 o 185 km 705 km ± 5 km 38.5 o o 32.9 o o
168 ±0.15 o 1982 kg 4 m 2.7 m 705 km ±0.1 o 530 kg 2.3 m 1.4 m 705 km 999 kg 2.3 m 2.3 m 2.8 m 1.5 km ±0.01
169 705 km N p N d N p = 233 N d = km o o
170 51.43 o 360 o / o 7 L Ω = 7 N Ω = 3 0 = 2πN d (q 1) N st mod (2π), N d L M = N d = 16 N M = 2 (Ω, M) L Ω L M L MΩ
171 L MΩ = 2 (Ω, M) G M G M = {1, 9} G M (1) = 1 G M (2) = 9 8 7S MΩ 2, S MΩ = o
172 G Ω = {1, 2, 7} G Ω (1) = 1 G Ω (2) = 2 G Ω (3) = 7 G Ω (1) G Ω (2) G Ω (3) G M (1) G M (2) G M (1) G M (2) G M (1) G M (2) Ω o o o o o o M o o o o o o (Ω, M) q {1,..., L Ω L M }
173 G Ω (1) G Ω (2) G Ω (3) G M (1) G M (2) G M (1) G M (2) G M (1) G M (2) q J 2
174 J 2 ±0.01 o ±1.5 km
175
176
177 v
178 v
179
180 v 0.02 o v = m/s
181 ±0.01 o
182
183
184
185
186 n
187
188 n
189
190 th J 2
191
192 J 2
ENGIN 211, Engineering Math. Fourier Series and Transform
 ENGIN 11, Engineering Math Fourier Series and ransform 1 Periodic Functions and Harmonics f(t) Period: a a+ t Frequency: f = 1 Angular velocity (or angular frequency): ω = ππ = π Such a periodic function
ENGIN 11, Engineering Math Fourier Series and ransform 1 Periodic Functions and Harmonics f(t) Period: a a+ t Frequency: f = 1 Angular velocity (or angular frequency): ω = ππ = π Such a periodic function
I. Relationship with previous work
 x x i t j J t = {0, 1,...J t } j t (p jt, x jt, ξ jt ) p jt R + x jt R k k ξ jt R ξ t T j = 0 t (z i, ζ i, G i ), ζ i z i R m G i G i (p j, x j ) i j U(z i, ζ i, x j, p j, ξ j ; G i ) = u(ζ i, x j,
x x i t j J t = {0, 1,...J t } j t (p jt, x jt, ξ jt ) p jt R + x jt R k k ξ jt R ξ t T j = 0 t (z i, ζ i, G i ), ζ i z i R m G i G i (p j, x j ) i j U(z i, ζ i, x j, p j, ξ j ; G i ) = u(ζ i, x j,
Easy and not so easy multifacility location problems... (In 20 minutes.)
 Easy and not so easy multifacility location problems... (In 20 minutes.) MINLP 2014 Pittsburgh, June 2014 Justo Puerto Institute of Mathematics (IMUS) Universidad de Sevilla Outline 1 Introduction (In
Easy and not so easy multifacility location problems... (In 20 minutes.) MINLP 2014 Pittsburgh, June 2014 Justo Puerto Institute of Mathematics (IMUS) Universidad de Sevilla Outline 1 Introduction (In
E.., (2) g t = e 2' g E. g t = g ij (t u k )du i du j, i j k =1 2. (u 1 0 0) u2 2 U, - v, w, g 0 (v w) = g ij (0 u k 0)v i w j = 0, (t) = g ij (t u k
 2007 10 (545) 517.929..,.. 1. g t M, d dt g t = ;2 Ric(g t ) (1) Ric(g) g.,, -, - (., [1], [2]).,,.,, f t - (M G), g t = ft G,, (1)., -, -, (, ), - (,, [3]). t - E 3, g t, t E 3, (1). t -., -. (M g) Ric
2007 10 (545) 517.929..,.. 1. g t M, d dt g t = ;2 Ric(g t ) (1) Ric(g) g.,, -, - (., [1], [2]).,,.,, f t - (M G), g t = ft G,, (1)., -, -, (, ), - (,, [3]). t - E 3, g t, t E 3, (1). t -., -. (M g) Ric
 D D = 2, 3, 4, 5, 6 D D = 2, 3, 4, 5, 6 N =(2, 0) N =(2, 0) N =(2, 0) N =2 (2) l (2) r (2) R (2) r (2) R (2) r N =2 S 4 N =2 S 4 N =2 (2) l (2) r (2) R (2) r (2) R (2) r N =2 S 4 N =2 S 4 T µν g µν T
D D = 2, 3, 4, 5, 6 D D = 2, 3, 4, 5, 6 N =(2, 0) N =(2, 0) N =(2, 0) N =2 (2) l (2) r (2) R (2) r (2) R (2) r N =2 S 4 N =2 S 4 N =2 (2) l (2) r (2) R (2) r (2) R (2) r N =2 S 4 N =2 S 4 T µν g µν T
Lecture D20-2D Rigid Body Dynamics: Impulse and Momentum
 J Peraire 1607 Dynamics Fall 004 Version 11 Lecture D0 - D Rigid Body Dynamics: Impulse and Momentum In lecture D9, we saw the principle of impulse and momentum applied to particle motion This principle
J Peraire 1607 Dynamics Fall 004 Version 11 Lecture D0 - D Rigid Body Dynamics: Impulse and Momentum In lecture D9, we saw the principle of impulse and momentum applied to particle motion This principle
does not change the dynamics of the system, i.e. that it leaves the Schrödinger equation invariant,
 FYST5 Quantum Mechanics II 9..212 1. intermediate eam (1. välikoe): 4 problems, 4 hours 1. As you remember, the Hamilton operator for a charged particle interacting with an electromagentic field can be
FYST5 Quantum Mechanics II 9..212 1. intermediate eam (1. välikoe): 4 problems, 4 hours 1. As you remember, the Hamilton operator for a charged particle interacting with an electromagentic field can be
Ossama Abdelkhalik and Daniele Mortari Department of Aerospace Engineering, Texas A&M University,College Station, TX 77843, USA
 Two-Way Orbits Ossama Abdelkhalik and Daniele Mortari Department of Aerospace Engineering, Texas A&M University,College Station, TX 77843, USA November 17, 24 Abstract. This paper introduces a new set
Two-Way Orbits Ossama Abdelkhalik and Daniele Mortari Department of Aerospace Engineering, Texas A&M University,College Station, TX 77843, USA November 17, 24 Abstract. This paper introduces a new set
 K(ζ) = 4ζ 2 x = 20 Θ = {θ i } Θ i=1 M = {m i} M i=1 A = {a i } A i=1 M A π = (π i ) n i=1 (Θ) n := Θ Θ (a, θ) u(a, θ) E γq [ E π m [u(a, θ)] ] C(π, Q) Q γ Q π m m Q m π m a Π = (π) U M A Θ
K(ζ) = 4ζ 2 x = 20 Θ = {θ i } Θ i=1 M = {m i} M i=1 A = {a i } A i=1 M A π = (π i ) n i=1 (Θ) n := Θ Θ (a, θ) u(a, θ) E γq [ E π m [u(a, θ)] ] C(π, Q) Q γ Q π m m Q m π m a Π = (π) U M A Θ
Useful Formulae ( )
 Appendix A Useful Formulae (985-989-993-) 34 Jeremić et al. A.. CHAPTER SUMMARY AND HIGHLIGHTS page: 35 of 536 A. Chapter Summary and Highlights A. Stress and Strain This section reviews small deformation
Appendix A Useful Formulae (985-989-993-) 34 Jeremić et al. A.. CHAPTER SUMMARY AND HIGHLIGHTS page: 35 of 536 A. Chapter Summary and Highlights A. Stress and Strain This section reviews small deformation
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License.
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 015 14. Oscillations Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License This wor
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 015 14. Oscillations Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License This wor
Chemistry 532 Practice Final Exam Fall 2012 Solutions
 Chemistry 53 Practice Final Exam Fall Solutions x e ax dx π a 3/ ; π sin 3 xdx 4 3 π cos nx dx π; sin θ cos θ + K x n e ax dx n! a n+ ; r r r r ˆL h r ˆL z h i φ ˆL x i hsin φ + cot θ cos φ θ φ ) ˆLy i
Chemistry 53 Practice Final Exam Fall Solutions x e ax dx π a 3/ ; π sin 3 xdx 4 3 π cos nx dx π; sin θ cos θ + K x n e ax dx n! a n+ ; r r r r ˆL h r ˆL z h i φ ˆL x i hsin φ + cot θ cos φ θ φ ) ˆLy i
Linear and Nonlinear Oscillators (Lecture 2)
 Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Phys 7221 Homework # 8
 Phys 71 Homework # 8 Gabriela González November 15, 6 Derivation 5-6: Torque free symmetric top In a torque free, symmetric top, with I x = I y = I, the angular velocity vector ω in body coordinates with
Phys 71 Homework # 8 Gabriela González November 15, 6 Derivation 5-6: Torque free symmetric top In a torque free, symmetric top, with I x = I y = I, the angular velocity vector ω in body coordinates with
X-MA2C01-1: Partial Worked Solutions
 X-MAC01-1: Partial Worked Solutions David R. Wilkins May 013 1. (a) Let A, B and C be sets. Prove that (A \ (B C)) (B \ C) = (A B) \ C. [Venn Diagrams, by themselves without an accompanying logical argument,
X-MAC01-1: Partial Worked Solutions David R. Wilkins May 013 1. (a) Let A, B and C be sets. Prove that (A \ (B C)) (B \ C) = (A B) \ C. [Venn Diagrams, by themselves without an accompanying logical argument,
THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3
 THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3 Any periodic function f(t) can be written as a Fourier Series a 0 2 + a n cos( nωt) + b n sin n
THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3 Any periodic function f(t) can be written as a Fourier Series a 0 2 + a n cos( nωt) + b n sin n
Noninertial Reference Frames
 Chapter 12 Non Reference Frames 12.1 Accelerated Coordinate Systems A reference frame which is fixed with respect to a rotating rigid is not. The parade example of this is an observer fixed on the surface
Chapter 12 Non Reference Frames 12.1 Accelerated Coordinate Systems A reference frame which is fixed with respect to a rotating rigid is not. The parade example of this is an observer fixed on the surface
Chapter 6: Vector Analysis
 Chapter 6: Vector Analysis We use derivatives and various products of vectors in all areas of physics. For example, Newton s 2nd law is F = m d2 r. In electricity dt 2 and magnetism, we need surface and
Chapter 6: Vector Analysis We use derivatives and various products of vectors in all areas of physics. For example, Newton s 2nd law is F = m d2 r. In electricity dt 2 and magnetism, we need surface and
Suggested solutions, FYS 500 Classical Mechanics and Field Theory 2015 fall
 UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mecanics and Field Teory 015 fall Set 1 for 16/17. November 015 Problem 68: Te Lagrangian for
UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mecanics and Field Teory 015 fall Set 1 for 16/17. November 015 Problem 68: Te Lagrangian for
Treball final de grau GRAU DE MATEMÀTIQUES Facultat de Matemàtiques Universitat de Barcelona MARKOV CHAINS
 Treball final de grau GRAU DE MATEMÀTIQUES Facultat de Matemàtiques Universitat de Barcelona MARKOV CHAINS Autor: Anna Areny Satorra Director: Dr. David Márquez Carreras Realitzat a: Departament de probabilitat,
Treball final de grau GRAU DE MATEMÀTIQUES Facultat de Matemàtiques Universitat de Barcelona MARKOV CHAINS Autor: Anna Areny Satorra Director: Dr. David Márquez Carreras Realitzat a: Departament de probabilitat,
[ zd z zdz dψ + 2i. 2 e i ψ 2 dz. (σ 2 ) 2 +(σ 3 ) 2 = (1+ z 2 ) 2
 2 S 2 2 2 2 2 M M 4 S 2 S 2 z, w : C S 2 z = 1/w e iψ S 1 S 2 σ 1 = 1 ( ) [ zd z zdz dψ + 2i 2 1 + z 2, σ 2 = Re 2 e i ψ 2 dz 1 + z 2 ], σ 3 = Im [ 2 e i ψ 2 dz 1 + z 2 σ 2 σ 3 (σ 2 ) 2 (σ 3 ) 2 σ 2 σ
2 S 2 2 2 2 2 M M 4 S 2 S 2 z, w : C S 2 z = 1/w e iψ S 1 S 2 σ 1 = 1 ( ) [ zd z zdz dψ + 2i 2 1 + z 2, σ 2 = Re 2 e i ψ 2 dz 1 + z 2 ], σ 3 = Im [ 2 e i ψ 2 dz 1 + z 2 σ 2 σ 3 (σ 2 ) 2 (σ 3 ) 2 σ 2 σ
Urban heat islands: An optimal control approach. Departamento de Matemática Aplicada II Universidad de Vigo Spain
 Urban heat islands: An optimal control approach L.J. Alvarez-Vázquez, F.J.Fernández, N. García-Chan, A. Martínez, M.E. Vázquez-Méndez. Departamento de Matemática Aplicada II Universidad de Vigo Spain The
Urban heat islands: An optimal control approach L.J. Alvarez-Vázquez, F.J.Fernández, N. García-Chan, A. Martínez, M.E. Vázquez-Méndez. Departamento de Matemática Aplicada II Universidad de Vigo Spain The
Lecture D10 - Angular Impulse and Momentum
 J. Peraire 6.07 Dynamics Fall 2004 Version.2 Lecture D0 - Angular Impulse and Momentum In addition to the equations of linear impulse and momentum considered in the previous lecture, there is a parallel
J. Peraire 6.07 Dynamics Fall 2004 Version.2 Lecture D0 - Angular Impulse and Momentum In addition to the equations of linear impulse and momentum considered in the previous lecture, there is a parallel
Towards a Search for Stochastic Gravitational-Wave Backgrounds from Ultra-light Bosons
 Towards a Search for Stochastic Gravitational-Wave Backgrounds from Ultra-light Bosons Leo Tsukada RESCEU, Univ. of Tokyo The first annual symposium "Gravitational Wave Physics and Astronomy: Genesis"
Towards a Search for Stochastic Gravitational-Wave Backgrounds from Ultra-light Bosons Leo Tsukada RESCEU, Univ. of Tokyo The first annual symposium "Gravitational Wave Physics and Astronomy: Genesis"
FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 2017
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II November 5, 207 Prof. Alan Guth FORMULA SHEET FOR QUIZ 2 Exam Date: November 8, 207 A few items below are marked
Spaceflight Dynamics
 Spaceflight Dynamics Prof. S. P. Bhat Department of Aerospace Engineering Indian Institute of Technology, Bombay April 21, 2006 Prof. S. P. Bhat (IITB) Spaceflight Dynamics April 21, 2006 1 / 97 Outline
Spaceflight Dynamics Prof. S. P. Bhat Department of Aerospace Engineering Indian Institute of Technology, Bombay April 21, 2006 Prof. S. P. Bhat (IITB) Spaceflight Dynamics April 21, 2006 1 / 97 Outline
Physics 443, Solutions to PS 4
 Physics, Solutions to PS. Neutrino Oscillations a Energy eigenvalues and eigenvectors The eigenvalues of H are E E + A, and E E A and the eigenvectors are ν, ν And ν ν b Similarity transformation S S ν
Physics, Solutions to PS. Neutrino Oscillations a Energy eigenvalues and eigenvectors The eigenvalues of H are E E + A, and E E A and the eigenvectors are ν, ν And ν ν b Similarity transformation S S ν
Short-Ranged Central and Tensor Correlations. Nuclear Many-Body Systems. Reaction Theory for Nuclei far from INT Seattle
 Short-Ranged Central and Tensor Correlations in Nuclear Many-Body Systems Reaction Theory for Nuclei far from Stability @ INT Seattle September 6-, Hans Feldmeier, Thomas Neff, Robert Roth Contents Motivation
Short-Ranged Central and Tensor Correlations in Nuclear Many-Body Systems Reaction Theory for Nuclei far from Stability @ INT Seattle September 6-, Hans Feldmeier, Thomas Neff, Robert Roth Contents Motivation
On Sun-Synchronous Orbits and Associated Constellations
 On Sun-Synchronous Orbits and Associated Constellations Daniele Mortari, Matthew P. Wilkins, and Christian Bruccoleri Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843,
On Sun-Synchronous Orbits and Associated Constellations Daniele Mortari, Matthew P. Wilkins, and Christian Bruccoleri Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843,
Oscillations and Waves
 Oscillations and Waves Somnath Bharadwaj and S. Pratik Khastgir Department of Physics and Meteorology IIT Kharagpur Module : Oscillations Lecture : Oscillations Oscillations are ubiquitous. It would be
Oscillations and Waves Somnath Bharadwaj and S. Pratik Khastgir Department of Physics and Meteorology IIT Kharagpur Module : Oscillations Lecture : Oscillations Oscillations are ubiquitous. It would be
Handout 6: Rotational motion and moment of inertia. Angular velocity and angular acceleration
 1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
1 Handout 6: Rotational motion and moment of inertia Angular velocity and angular acceleration In Figure 1, a particle b is rotating about an axis along a circular path with radius r. The radius sweeps
Ab initio asymptotic-expansion coefficients for pair energies in Møller-Plesset perturbation theory for atoms
 Ab initio asymptotic-expansion coefficients for pair energies in Møller-Plesset perturbation theory for atoms K. JANKOWSKI a, R. SŁUPSKI a, and J. R. FLORES b a Nicholas Copernicus University 87-100 Toruń,
Ab initio asymptotic-expansion coefficients for pair energies in Møller-Plesset perturbation theory for atoms K. JANKOWSKI a, R. SŁUPSKI a, and J. R. FLORES b a Nicholas Copernicus University 87-100 Toruń,
Rotational Kinematics. Description of attitude kinematics using reference frames, rotation matrices, Euler parameters, Euler angles, and quaternions
 Rotational Kinematics Description of attitude kinematics using reference frames, rotation matrices, Euler parameters, Euler angles, and quaternions Recall the fundamental dynamics equations ~ f = d dt
Rotational Kinematics Description of attitude kinematics using reference frames, rotation matrices, Euler parameters, Euler angles, and quaternions Recall the fundamental dynamics equations ~ f = d dt
Lecture II: Rigid-Body Physics
 Rigid-Body Motion Previously: Point dimensionless objects moving through a trajectory. Today: Objects with dimensions, moving as one piece. 2 Rigid-Body Kinematics Objects as sets of points. Relative distances
Rigid-Body Motion Previously: Point dimensionless objects moving through a trajectory. Today: Objects with dimensions, moving as one piece. 2 Rigid-Body Kinematics Objects as sets of points. Relative distances
 S i = a b i A i r i i T avg T min T max T vit e 2 e 2 (4/1.8) 2 ϕ inc ϕ diff m B λ = Λ(sin θ incident + sin θ diffracted ) m B λ Λ θ diffracted F uel ext Air Nozzle Fuel 1 Spark Vitiation Stage Second
S i = a b i A i r i i T avg T min T max T vit e 2 e 2 (4/1.8) 2 ϕ inc ϕ diff m B λ = Λ(sin θ incident + sin θ diffracted ) m B λ Λ θ diffracted F uel ext Air Nozzle Fuel 1 Spark Vitiation Stage Second
sin(y + z) sin y + sin z (y + z)sin23 = y sin 23 + z sin 23 [sin x][sinx] = [sinx] 2 = sin 2 x sin x 2 = sin ( x 2) = sin(x x) ...
![sin(y + z) sin y + sin z (y + z)sin23 = y sin 23 + z sin 23 [sin x][sinx] = [sinx] 2 = sin 2 x sin x 2 = sin ( x 2) = sin(x x) ... sin(y + z) sin y + sin z (y + z)sin23 = y sin 23 + z sin 23 [sin x][sinx] = [sinx] 2 = sin 2 x sin x 2 = sin ( x 2) = sin(x x) ...](/thumbs/92/110801024.jpg) Sec. 01 notes Some Observations Not Linear Doubling an angles does NOT usually double the ratio. Compare sin10 with sin 20, for example. generally,... sin(2x) 2 sinx sin IS NOT a number If x, y and z are
Sec. 01 notes Some Observations Not Linear Doubling an angles does NOT usually double the ratio. Compare sin10 with sin 20, for example. generally,... sin(2x) 2 sinx sin IS NOT a number If x, y and z are
Chapter 5 - Part 1. Orbit Perturbations. D.Mortari - AERO-423
 Chapter 5 - Part 1 Orbit Perturbations D.Mortari - AERO-43 Orbital Elements Orbit normal i North Orbit plane Equatorial plane ϕ P O ω Ω i Vernal equinox Ascending node D. Mortari - AERO-43 Introduction
Chapter 5 - Part 1 Orbit Perturbations D.Mortari - AERO-43 Orbital Elements Orbit normal i North Orbit plane Equatorial plane ϕ P O ω Ω i Vernal equinox Ascending node D. Mortari - AERO-43 Introduction
Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section The (DT) Fourier transform (or spectrum) of x[n] is
![Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section The (DT) Fourier transform (or spectrum) of x[n] is Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section The (DT) Fourier transform (or spectrum) of x[n] is](/thumbs/89/98498368.jpg) Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section 5. 3 The (DT) Fourier transform (or spectrum) of x[n] is X ( e jω) = n= x[n]e jωn x[n] can be reconstructed from its
Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section 5. 3 The (DT) Fourier transform (or spectrum) of x[n] is X ( e jω) = n= x[n]e jωn x[n] can be reconstructed from its
Phys 7221, Fall 2006: Homework # 5
 Phys 722, Fal006: Homewor # 5 Gabriela González October, 2006 Prob 3-: Collapse of an orbital system Consier two particles falling into each other ue to gravitational forces, starting from rest at a istance
Phys 722, Fal006: Homewor # 5 Gabriela González October, 2006 Prob 3-: Collapse of an orbital system Consier two particles falling into each other ue to gravitational forces, starting from rest at a istance
Prime Numbers and Irrational Numbers
 Chapter 4 Prime Numbers and Irrational Numbers Abstract The question of the existence of prime numbers in intervals is treated using the approximation of cardinal of the primes π(x) given by Lagrange.
Chapter 4 Prime Numbers and Irrational Numbers Abstract The question of the existence of prime numbers in intervals is treated using the approximation of cardinal of the primes π(x) given by Lagrange.
Physics 8, Fall 2011, equation sheet work in progress
 1 year 3.16 10 7 s Physics 8, Fall 2011, equation sheet work in progress circumference of earth 40 10 6 m speed of light c = 2.9979 10 8 m/s mass of proton or neutron 1 amu ( atomic mass unit ) = 1 1.66
1 year 3.16 10 7 s Physics 8, Fall 2011, equation sheet work in progress circumference of earth 40 10 6 m speed of light c = 2.9979 10 8 m/s mass of proton or neutron 1 amu ( atomic mass unit ) = 1 1.66
Continuum Theory of Liquid Crystals continued...
 Continuum Theory of Liquid Crystals continued... Iain W. Stewart 25 July 2013 Department of Mathematics and Statistics, University of Strathclyde, Glasgow, UK Raffaella De Vita, Don Leo at Virginia Tech,
Continuum Theory of Liquid Crystals continued... Iain W. Stewart 25 July 2013 Department of Mathematics and Statistics, University of Strathclyde, Glasgow, UK Raffaella De Vita, Don Leo at Virginia Tech,
Partial Derivatives of Observables with Respect to Two-Body Orbital Elements
 Partial Derivatives of Observables with Respect to Two-Body Orbital Elements Marc A. Murison U.S. Naval Observatory, Washington, DC murison@usno.vy.mil 6 November, 26 Abstract We calculate the partial
Partial Derivatives of Observables with Respect to Two-Body Orbital Elements Marc A. Murison U.S. Naval Observatory, Washington, DC murison@usno.vy.mil 6 November, 26 Abstract We calculate the partial
Reduction of Symplectic Lie Algebroids by a Lie Subalgebroid and a Symmetry Lie Group
 Symmetry, Integrability and Geometry: Methods and Applications SIGMA 3 (2007), 049, 28 pages Reduction of Symplectic Lie Algebroids by a Lie Subalgebroid and a Symmetry Lie Group David IGLESIAS, Juan Carlos
Symmetry, Integrability and Geometry: Methods and Applications SIGMA 3 (2007), 049, 28 pages Reduction of Symplectic Lie Algebroids by a Lie Subalgebroid and a Symmetry Lie Group David IGLESIAS, Juan Carlos
ANSWERS TO PROBLEM SET 1
 CHM1485: Molecular Dynamics and Chemical Dynamics in Liquids ANSWERS TO PROBLEM SET 1 1 Properties of the Liouville Operator a. Give the equations of motion in terms of the Hamiltonian. Show that they
CHM1485: Molecular Dynamics and Chemical Dynamics in Liquids ANSWERS TO PROBLEM SET 1 1 Properties of the Liouville Operator a. Give the equations of motion in terms of the Hamiltonian. Show that they
SOLUTIONS, PROBLEM SET 11
 SOLUTIONS, PROBLEM SET 11 1 In this problem we investigate the Lagrangian formulation of dynamics in a rotating frame. Consider a frame of reference which we will consider to be inertial. Suppose that
SOLUTIONS, PROBLEM SET 11 1 In this problem we investigate the Lagrangian formulation of dynamics in a rotating frame. Consider a frame of reference which we will consider to be inertial. Suppose that
Dynamics and Control of Rotorcraft
 Dynamics and Control of Rotorcraft Helicopter Aerodynamics and Dynamics Abhishek Department of Aerospace Engineering Indian Institute of Technology, Kanpur February 3, 2018 Overview Flight Dynamics Model
Dynamics and Control of Rotorcraft Helicopter Aerodynamics and Dynamics Abhishek Department of Aerospace Engineering Indian Institute of Technology, Kanpur February 3, 2018 Overview Flight Dynamics Model
Physics 8, Fall 2013, equation sheet work in progress
 (Chapter 1: foundations) 1 year 3.16 10 7 s Physics 8, Fall 2013, equation sheet work in progress circumference of earth 40 10 6 m speed of light c = 2.9979 10 8 m/s mass of proton or neutron 1 amu ( atomic
(Chapter 1: foundations) 1 year 3.16 10 7 s Physics 8, Fall 2013, equation sheet work in progress circumference of earth 40 10 6 m speed of light c = 2.9979 10 8 m/s mass of proton or neutron 1 amu ( atomic
Speed of light c = m/s. x n e a x d x = 1. 2 n+1 a n π a. He Li Ne Na Ar K Ni 58.
 Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
z 0 > 0 z = 0 h; (x, 0)
 n = (q 1,..., q n ) T (,, t) V (,, t) L(,, t) = T V d dt ( ) L q i L q i = 0, i = 1,..., n. l l 0 l l 0 l > l 0 {x} + = max(0, x) x = k{l l 0 } +ˆ, k > 0 ˆ (x, z) x z (0, z 0 ) (0, z 0 ) z 0 > 0 x z =
n = (q 1,..., q n ) T (,, t) V (,, t) L(,, t) = T V d dt ( ) L q i L q i = 0, i = 1,..., n. l l 0 l l 0 l > l 0 {x} + = max(0, x) x = k{l l 0 } +ˆ, k > 0 ˆ (x, z) x z (0, z 0 ) (0, z 0 ) z 0 > 0 x z =
Distance travelled time taken and if the particle is a distance s(t) along the x-axis, then its instantaneous speed is:
 Chapter 1 Kinematics 1.1 Basic ideas r(t) is the position of a particle; r = r is the distance to the origin. If r = x i + y j + z k = (x, y, z), then r = r = x 2 + y 2 + z 2. v(t) is the velocity; v =
Chapter 1 Kinematics 1.1 Basic ideas r(t) is the position of a particle; r = r is the distance to the origin. If r = x i + y j + z k = (x, y, z), then r = r = x 2 + y 2 + z 2. v(t) is the velocity; v =
ESM 3124 Intermediate Dynamics 2012, HW6 Solutions. (1 + f (x) 2 ) We can first write the constraint y = f(x) in the form of a constraint
 ESM 314 Intermediate Dynamics 01, HW6 Solutions Roller coaster. A bead of mass m can slide without friction, under the action of gravity, on a smooth rigid wire which has the form y = f(x). (a) Find the
ESM 314 Intermediate Dynamics 01, HW6 Solutions Roller coaster. A bead of mass m can slide without friction, under the action of gravity, on a smooth rigid wire which has the form y = f(x). (a) Find the
On complexified quantum mechanics and space-time
 On complexified quantum mechanics and space-time Dorje C. Brody Mathematical Sciences Brunel University, Uxbridge UB8 3PH dorje.brody@brunel.ac.uk Quantum Physics with Non-Hermitian Operators Dresden:
On complexified quantum mechanics and space-time Dorje C. Brody Mathematical Sciences Brunel University, Uxbridge UB8 3PH dorje.brody@brunel.ac.uk Quantum Physics with Non-Hermitian Operators Dresden:
MATH 31BH Homework 5 Solutions
 MATH 3BH Homework 5 Solutions February 4, 204 Problem.8.2 (a) Let x t f y = x 2 + y 2 + 2z 2 and g(t) = t 2. z t 3 Then by the chain rule a a a D(g f) b = Dg f b Df b c c c = [Dg(a 2 + b 2 + 2c 2 )] [
MATH 3BH Homework 5 Solutions February 4, 204 Problem.8.2 (a) Let x t f y = x 2 + y 2 + 2z 2 and g(t) = t 2. z t 3 Then by the chain rule a a a D(g f) b = Dg f b Df b c c c = [Dg(a 2 + b 2 + 2c 2 )] [
DEVELOPMENT OF A MULTIPURPOSE LOW THRUST INTERPLANETARY TRAJECTORY CALCULATION CODE
 AAS 03-667 DEVELOPMENT OF A MULTIPURPOSE LOW THRUST INTERPLANETARY TRAJECTORY CALCULATION CODE Tadashi Sakai 1 and John R. Olds 2 A multipurpose low thrust interplanetary trajectory calculation code has
AAS 03-667 DEVELOPMENT OF A MULTIPURPOSE LOW THRUST INTERPLANETARY TRAJECTORY CALCULATION CODE Tadashi Sakai 1 and John R. Olds 2 A multipurpose low thrust interplanetary trajectory calculation code has
Trade Patterns, Production networks, and Trade and employment in the Asia-US region
 Trade Patterns, Production networks, and Trade and employment in the Asia-U region atoshi Inomata Institute of Developing Economies ETRO Development of cross-national production linkages, 1985-2005 1985
Trade Patterns, Production networks, and Trade and employment in the Asia-U region atoshi Inomata Institute of Developing Economies ETRO Development of cross-national production linkages, 1985-2005 1985
Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be.
 Chapter 4 Energy and Stability 4.1 Energy in 1D Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be T = 1 2 mẋ2 and the potential energy
Chapter 4 Energy and Stability 4.1 Energy in 1D Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be T = 1 2 mẋ2 and the potential energy
Quantum chaos in ultra-strongly coupled nonlinear resonators
 Quantum chaos in ultra-strongly coupled nonlinear resonators Uta Naether MARTES CUANTICO Universidad de Zaragoza, 13.05.14 Colaborators Juan José García-Ripoll, CSIC, Madrid Juan José Mazo, UNIZAR & ICMA
Quantum chaos in ultra-strongly coupled nonlinear resonators Uta Naether MARTES CUANTICO Universidad de Zaragoza, 13.05.14 Colaborators Juan José García-Ripoll, CSIC, Madrid Juan José Mazo, UNIZAR & ICMA
Merton College Maths for Physics Prelims August 29, 2008 HT I. Multiple Integrals
 Merton College Maths for Physics Prelims August 29, 28 HT I Multiple Integrals 1. (a) For the following integrals sketch the region of integration and so write equivalent integrals with the order of integration
Merton College Maths for Physics Prelims August 29, 28 HT I Multiple Integrals 1. (a) For the following integrals sketch the region of integration and so write equivalent integrals with the order of integration
Kerr black hole and rotating wormhole
 Kerr Fest (Christchurch, August 26-28, 2004) Kerr black hole and rotating wormhole Sung-Won Kim(Ewha Womans Univ.) August 27, 2004 INTRODUCTION STATIC WORMHOLE ROTATING WORMHOLE KERR METRIC SUMMARY AND
Kerr Fest (Christchurch, August 26-28, 2004) Kerr black hole and rotating wormhole Sung-Won Kim(Ewha Womans Univ.) August 27, 2004 INTRODUCTION STATIC WORMHOLE ROTATING WORMHOLE KERR METRIC SUMMARY AND
Formulas to remember
 Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Complex numbers Let z = x + iy be a complex number The conjugate z = x iy Formulas to remember The real part Re(z) = x = z+z The imaginary part Im(z) = y = z z i The norm z = zz = x + y The reciprocal
Outline PGeneral Many body 2Pconsistent Conclusions Basics
 Ĥ = kσ ϵ(k)c kσ c kσ + iσ V i n iσ + U i n i n i { Ĥ ext = d1d2 η σ(1, 2)c σ(1)c σ (2)... σ ] + [η (1, 2)c (1)c (2) + η (1, 2)c (2)c (1)... + ] [ ξ σ(1, 2)c σ (1)c σ (2) + ξ σ(1, 2)c σ(1)c σ(2)... σ ]
Ĥ = kσ ϵ(k)c kσ c kσ + iσ V i n iσ + U i n i n i { Ĥ ext = d1d2 η σ(1, 2)c σ(1)c σ (2)... σ ] + [η (1, 2)c (1)c (2) + η (1, 2)c (2)c (1)... + ] [ ξ σ(1, 2)c σ (1)c σ (2) + ξ σ(1, 2)c σ(1)c σ(2)... σ ]
Green s function, wavefunction and Wigner function of the MIC-Kepler problem
 Green s function, wavefunction and Wigner function of the MIC-Kepler problem Tokyo University of Science Graduate School of Science, Department of Mathematics, The Akira Yoshioka Laboratory Tomoyo Kanazawa
Green s function, wavefunction and Wigner function of the MIC-Kepler problem Tokyo University of Science Graduate School of Science, Department of Mathematics, The Akira Yoshioka Laboratory Tomoyo Kanazawa
Chapter 10 Solutions
 Chapter 0 Solutions 0. (a) α ω ω i t.0 rad/s 4.00 rad/s 3.00 s θ ω i t + αt (4.00 rad/s )(3.00 s) 8.0 rad 0. (a) ω ω π rad 365 days π rad 7.3 days *0.3 ω i 000 rad/s α 80.0 rad/s day 4 h day 4 h h 3600
Chapter 0 Solutions 0. (a) α ω ω i t.0 rad/s 4.00 rad/s 3.00 s θ ω i t + αt (4.00 rad/s )(3.00 s) 8.0 rad 0. (a) ω ω π rad 365 days π rad 7.3 days *0.3 ω i 000 rad/s α 80.0 rad/s day 4 h day 4 h h 3600
MAS113 CALCULUS II SPRING 2008, QUIZ 5 SOLUTIONS. x 2 dx = 3y + y 3 = x 3 + c. It can be easily verified that the differential equation is exact, as
 MAS113 CALCULUS II SPRING 008, QUIZ 5 SOLUTIONS Quiz 5a Solutions (1) Solve the differential equation y = x 1 + y. (1 + y )y = x = (1 + y ) = x = 3y + y 3 = x 3 + c. () Solve the differential equation
MAS113 CALCULUS II SPRING 008, QUIZ 5 SOLUTIONS Quiz 5a Solutions (1) Solve the differential equation y = x 1 + y. (1 + y )y = x = (1 + y ) = x = 3y + y 3 = x 3 + c. () Solve the differential equation
Mathematical Relativity, Spring 2017/18 Instituto Superior Técnico
 Mathematical Relativity, Spring 2017/18 Instituto Superior Técnico 1. Starting from R αβµν Z ν = 2 [α β] Z µ, deduce the components of the Riemann curvature tensor in terms of the Christoffel symbols.
Mathematical Relativity, Spring 2017/18 Instituto Superior Técnico 1. Starting from R αβµν Z ν = 2 [α β] Z µ, deduce the components of the Riemann curvature tensor in terms of the Christoffel symbols.
Newman-Penrose formalism in higher dimensions
 Newman-Penrose formalism in higher dimensions V. Pravda various parts in collaboration with: A. Coley, R. Milson, M. Ortaggio and A. Pravdová Introduction - algebraic classification in four dimensions
Newman-Penrose formalism in higher dimensions V. Pravda various parts in collaboration with: A. Coley, R. Milson, M. Ortaggio and A. Pravdová Introduction - algebraic classification in four dimensions
PROPERTIES OF FLUIDS
 Unit - I Chapter - PROPERTIES OF FLUIDS Solutions of Examples for Practice Example.9 : Given data : u = y y, = 8 Poise = 0.8 Pa-s To find : Shear stress. Step - : Calculate the shear stress at various
Unit - I Chapter - PROPERTIES OF FLUIDS Solutions of Examples for Practice Example.9 : Given data : u = y y, = 8 Poise = 0.8 Pa-s To find : Shear stress. Step - : Calculate the shear stress at various
Short-time Fourier transform for quaternionic signals
 Short-time Fourier transform for quaternionic signals Joint work with Y. Fu and U. Kähler P. Cerejeiras Departamento de Matemática Universidade de Aveiro pceres@ua.pt New Trends and Directions in Harmonic
Short-time Fourier transform for quaternionic signals Joint work with Y. Fu and U. Kähler P. Cerejeiras Departamento de Matemática Universidade de Aveiro pceres@ua.pt New Trends and Directions in Harmonic
EN221 - Fall HW # 1 Solutions
 EN221 - Fall2008 - HW # 1 Solutions Prof. Vivek Shenoy 1. Let A be an arbitrary tensor. i). Show that II A = 1 2 {(tr A)2 tr A 2 } ii). Using the Cayley-Hamilton theorem, deduce that Soln. i). Method-1
EN221 - Fall2008 - HW # 1 Solutions Prof. Vivek Shenoy 1. Let A be an arbitrary tensor. i). Show that II A = 1 2 {(tr A)2 tr A 2 } ii). Using the Cayley-Hamilton theorem, deduce that Soln. i). Method-1
Solutions. Problems of Chapter 1
 Solutions Problems of Chapter 1 1.1 A real square matrix A IR n n is invertible if and only if its determinant is non zero. The determinant of A is a polynomial in the entries a ij of A, whose set of zeros
Solutions Problems of Chapter 1 1.1 A real square matrix A IR n n is invertible if and only if its determinant is non zero. The determinant of A is a polynomial in the entries a ij of A, whose set of zeros
1 r. Published on 28 January Abstract. will be discussed period Recently frequency jumps
 L R R 6 L L R R 6 R ˆ R - - ˆ 6 ˆ ˆ ˆ q q R R G P S G P S N A 4 N A D P U D C P U C B CO 89 -z 9 B CO 89 z9 U S R A q q q G q P q S U S A N A N A @ N A W W A 8 J A D 8 J P U C P 8 J P 8 J A A B CO 89 z
L R R 6 L L R R 6 R ˆ R - - ˆ 6 ˆ ˆ ˆ q q R R G P S G P S N A 4 N A D P U D C P U C B CO 89 -z 9 B CO 89 z9 U S R A q q q G q P q S U S A N A N A @ N A W W A 8 J A D 8 J P U C P 8 J P 8 J A A B CO 89 z
Lagrange s Equations of Motion with Constraint Forces
 Lagrange s Equations of Motion with Constraint Forces Kane s equations do not incorporate constraint forces 1 Ax0 A is m n of rank r MEAM 535 Review: Linear Algebra The row space, Col (A T ), dimension
Lagrange s Equations of Motion with Constraint Forces Kane s equations do not incorporate constraint forces 1 Ax0 A is m n of rank r MEAM 535 Review: Linear Algebra The row space, Col (A T ), dimension
Classical Mechanics. Luis Anchordoqui
 1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
Dynamic Asset Allocation - Identifying Regime Shifts in Financial Time Series to Build Robust Portfolios
 Downloaded from orbit.dtu.dk on: Jan 22, 2019 Dynamic Asset Allocation - Identifying Regime Shifts in Financial Time Series to Build Robust Portfolios Nystrup, Peter Publication date: 2018 Document Version
Downloaded from orbit.dtu.dk on: Jan 22, 2019 Dynamic Asset Allocation - Identifying Regime Shifts in Financial Time Series to Build Robust Portfolios Nystrup, Peter Publication date: 2018 Document Version
Fourier Series and Fourier Transforms
 Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic
Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic
EE GATE
 EE GATE-009 www.gateforum.com GATE - 009 Answer Keys 1 B C 3 A 4 D 5 B 6 D 7 A 8 A 9 B 10 D 11 D 1 B 13 A 14 C 15 B 16 C 17 C 18 D 19 B 0 C 1 D C 3 A 4 A 5 D 6 C 7 D 8 D 9 B 30 C 31 C 3 A 33 A 34 B 35
EE GATE-009 www.gateforum.com GATE - 009 Answer Keys 1 B C 3 A 4 D 5 B 6 D 7 A 8 A 9 B 10 D 11 D 1 B 13 A 14 C 15 B 16 C 17 C 18 D 19 B 0 C 1 D C 3 A 4 A 5 D 6 C 7 D 8 D 9 B 30 C 31 C 3 A 33 A 34 B 35
Diameter of the Zero Divisor Graph of Semiring of Matrices over Boolean Semiring
 International Mathematical Forum, Vol. 9, 2014, no. 29, 1369-1375 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/imf.2014.47131 Diameter of the Zero Divisor Graph of Semiring of Matrices over
International Mathematical Forum, Vol. 9, 2014, no. 29, 1369-1375 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/imf.2014.47131 Diameter of the Zero Divisor Graph of Semiring of Matrices over
MATH45061: SOLUTION SHEET 1 V
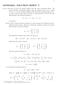 1 MATH4561: SOLUTION SHEET 1 V 1.) a.) The faces of the cube remain aligned with the same coordinate planes. We assign Cartesian coordinates aligned with the original cube (x, y, z), where x, y, z 1. The
1 MATH4561: SOLUTION SHEET 1 V 1.) a.) The faces of the cube remain aligned with the same coordinate planes. We assign Cartesian coordinates aligned with the original cube (x, y, z), where x, y, z 1. The
Half BPS solutions in type IIB and M-theory
 Half BPS solutions in type IIB and M-theory Based on work done in collaboration with Eric D Hoker, John Estes, Darya Krym (UCLA) and Paul Sorba (Annecy) E.D'Hoker, J.Estes and M.G., Exact half-bps type
Half BPS solutions in type IIB and M-theory Based on work done in collaboration with Eric D Hoker, John Estes, Darya Krym (UCLA) and Paul Sorba (Annecy) E.D'Hoker, J.Estes and M.G., Exact half-bps type
Singular Monopoles and Instantons on Curved Backgrounds
 Singular Monopoles and Instantons on Curved Backgrounds Sergey Cherkis (Berkeley, Stanford, TCD) C k U(n) U(n) U(n) Odense 2 November 2010 Outline: Classical Solutions & their Charges Relations between
Singular Monopoles and Instantons on Curved Backgrounds Sergey Cherkis (Berkeley, Stanford, TCD) C k U(n) U(n) U(n) Odense 2 November 2010 Outline: Classical Solutions & their Charges Relations between
Structures of AS-regular Algebras
 Structures of AS-regular Algebras Hiroyuki Minamoto and Izuru Mori Abstract In this paper, we define a notion of AS-Gorenstein algebra for N-graded algebras, and show that symmetric AS-regular algebras
Structures of AS-regular Algebras Hiroyuki Minamoto and Izuru Mori Abstract In this paper, we define a notion of AS-Gorenstein algebra for N-graded algebras, and show that symmetric AS-regular algebras
 Equations. A body executing simple harmonic motion has maximum acceleration ) At the mean positions ) At the two extreme position 3) At any position 4) he question is irrelevant. A particle moves on the
Equations. A body executing simple harmonic motion has maximum acceleration ) At the mean positions ) At the two extreme position 3) At any position 4) he question is irrelevant. A particle moves on the
M2A2 Problem Sheet 3 - Hamiltonian Mechanics
 MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
Mathematical Tripos Part IA Lent Term Example Sheet 1. Calculate its tangent vector dr/du at each point and hence find its total length.
 Mathematical Tripos Part IA Lent Term 205 ector Calculus Prof B C Allanach Example Sheet Sketch the curve in the plane given parametrically by r(u) = ( x(u), y(u) ) = ( a cos 3 u, a sin 3 u ) with 0 u
Mathematical Tripos Part IA Lent Term 205 ector Calculus Prof B C Allanach Example Sheet Sketch the curve in the plane given parametrically by r(u) = ( x(u), y(u) ) = ( a cos 3 u, a sin 3 u ) with 0 u
CLASSIFICATION OF MÖBIUS ISOPARAMETRIC HYPERSURFACES IN THE UNIT SIX-SPHERE
 Tohoku Math. J. 60 (008), 499 56 CLASSIFICATION OF MÖBIUS ISOPARAMETRIC HYPERSURFACES IN THE UNIT SIX-SPHERE Dedicated to Professors Udo Simon and Seiki Nishikawa on the occasion of their seventieth and
Tohoku Math. J. 60 (008), 499 56 CLASSIFICATION OF MÖBIUS ISOPARAMETRIC HYPERSURFACES IN THE UNIT SIX-SPHERE Dedicated to Professors Udo Simon and Seiki Nishikawa on the occasion of their seventieth and
Prescribed Mean Curvature Systems. Conrad Alexander Hengesbach
 Prescribed Mean Curvature Systems by Conrad Alexander Hengesbach A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Mathematics in the Graduate
Prescribed Mean Curvature Systems by Conrad Alexander Hengesbach A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Mathematics in the Graduate
LYAPUNOV-BASED ELLIPTICAL TO CIRCULAR PLANAR ORBIT TRANSFERS IN LEVI-CIVITA COORDINATES
 (Preprint) AAS 2-66 LYAPUNOV-BASED ELLIPTICAL TO CIRCULAR PLANAR ORBIT TRANSFERS IN LEVI-CIVITA COORDINATES Sonia Hernandez, Maruthi R. Akella, and Cesar A. Ocampo INTRODUCTION We consider planar orbit
(Preprint) AAS 2-66 LYAPUNOV-BASED ELLIPTICAL TO CIRCULAR PLANAR ORBIT TRANSFERS IN LEVI-CIVITA COORDINATES Sonia Hernandez, Maruthi R. Akella, and Cesar A. Ocampo INTRODUCTION We consider planar orbit
Sinc Functions. Continuous-Time Rectangular Pulse
 Sinc Functions The Cooper Union Department of Electrical Engineering ECE114 Digital Signal Processing Lecture Notes: Sinc Functions and Sampling Theory October 7, 2011 A rectangular pulse in time/frequency
Sinc Functions The Cooper Union Department of Electrical Engineering ECE114 Digital Signal Processing Lecture Notes: Sinc Functions and Sampling Theory October 7, 2011 A rectangular pulse in time/frequency
Simultaneous Linear, and Non-linear Congruences
 Simultaneous Linear, and Non-linear Congruences CIS002-2 Computational Alegrba and Number Theory David Goodwin david.goodwin@perisic.com 09:00, Friday 18 th November 2011 Outline 1 Polynomials 2 Linear
Simultaneous Linear, and Non-linear Congruences CIS002-2 Computational Alegrba and Number Theory David Goodwin david.goodwin@perisic.com 09:00, Friday 18 th November 2011 Outline 1 Polynomials 2 Linear
Course 2BA1: Hilary Term 2007 Section 8: Quaternions and Rotations
 Course BA1: Hilary Term 007 Section 8: Quaternions and Rotations David R. Wilkins Copyright c David R. Wilkins 005 Contents 8 Quaternions and Rotations 1 8.1 Quaternions............................ 1 8.
Course BA1: Hilary Term 007 Section 8: Quaternions and Rotations David R. Wilkins Copyright c David R. Wilkins 005 Contents 8 Quaternions and Rotations 1 8.1 Quaternions............................ 1 8.
Physics H7A, Fall 2011 Homework 4 Solutions
 Physics H7A, Fall 20 Homework 4 Solutions. (K&K Problem 2.) A mass m is connected to a vertical revolving axle by two strings of length l, each making an angle of 45 with the axle, as shown. Both the axle
Physics H7A, Fall 20 Homework 4 Solutions. (K&K Problem 2.) A mass m is connected to a vertical revolving axle by two strings of length l, each making an angle of 45 with the axle, as shown. Both the axle
Advanced Newtonian gravity
 Foundations of Newtonian gravity Solutions Motion of extended bodies, University of Guelph h treatment of Newtonian gravity, the book develops approximation methods to obtain weak-field solutions es the
Foundations of Newtonian gravity Solutions Motion of extended bodies, University of Guelph h treatment of Newtonian gravity, the book develops approximation methods to obtain weak-field solutions es the
Semester University of Sheffield. School of Mathematics and Statistics
 University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS152: Civil Engineering Mathematics MAS152: Essential Mathematical Skills & Techniques MAS156: Mathematics
University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS152: Civil Engineering Mathematics MAS152: Essential Mathematical Skills & Techniques MAS156: Mathematics
The distance of the object from the equilibrium position is m.
 Answers, Even-Numbered Problems, Chapter..4.6.8.0..4.6.8 (a) A = 0.0 m (b).60 s (c) 0.65 Hz Whenever the object is released from rest, its initial displacement equals the amplitude of its SHM. (a) so 0.065
Answers, Even-Numbered Problems, Chapter..4.6.8.0..4.6.8 (a) A = 0.0 m (b).60 s (c) 0.65 Hz Whenever the object is released from rest, its initial displacement equals the amplitude of its SHM. (a) so 0.065
Physics 70007, Fall 2009 Answers to Final Exam
 Physics 70007, Fall 009 Answers to Final Exam December 17, 009 1. Quantum mechanical pictures a Demonstrate that if the commutation relation [A, B] ic is valid in any of the three Schrodinger, Heisenberg,
Physics 70007, Fall 009 Answers to Final Exam December 17, 009 1. Quantum mechanical pictures a Demonstrate that if the commutation relation [A, B] ic is valid in any of the three Schrodinger, Heisenberg,
L = 1 2 a(q) q2 V (q).
 Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
Relativistic Dynamics
 Chapter 4 Relativistic Dynamics The most important example of a relativistic particle moving in a potential is a charged particle, say an electron, moving in an electromagnetic field, which might be that
Chapter 4 Relativistic Dynamics The most important example of a relativistic particle moving in a potential is a charged particle, say an electron, moving in an electromagnetic field, which might be that
Solution Set Five. 2 Problem #2: The Pendulum of Doom Equation of Motion Simple Pendulum Limit Visualization...
 : Solution Set Five Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein November 4, 2015 Contents 1 Problem #1: Coupled Mass Oscillator System. 2 1.1 Normal Modes.......................................
: Solution Set Five Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein November 4, 2015 Contents 1 Problem #1: Coupled Mass Oscillator System. 2 1.1 Normal Modes.......................................
This sample exam is longer than the actual exam will be. Many of the sample exam problems are similar to those of the actual exam. = m a. I xx.
 Phys 326 Sample Final Exam SOLUTION 8-11 am 18 December 2012 144 Loomis Closed book, no calculators, but you are permitted one two-sided 8 1/2 x 11" set of notes. This sample exam is longer than the actual
Phys 326 Sample Final Exam SOLUTION 8-11 am 18 December 2012 144 Loomis Closed book, no calculators, but you are permitted one two-sided 8 1/2 x 11" set of notes. This sample exam is longer than the actual
