Block-Göttsche invariants from wall-crossing
|
|
|
- Angel May
- 5 years ago
- Views:
Transcription
1 Block-Göttsche invariants from wall-crossing Sara Angela Filippini 6 giugno 2014
2 Outline GW theory of GPS Quiver representations GW invariants q-deformation q-deformed GW invariants
3 The GW theory of GPS Ppa, b, 1q C 3 zt0, 0, 0u{pC a,b,1q weighted projective plane Assume: gcdpa, bq 1 Toric picture: x 2l2 D 0 out D 0 2 x 22 x 21 x 11 x 12 x 1l1 D 0 1
4 Fix partitions P 1, P 2 ; P i pp ij q. Suppose gcdpp 1, P 2 q 1. Invariants: N pa,bq rpp 1, P 2 qs 7 vir $ & % rational curves with x ij prescribed singularities with multiplicities p ij and tangent to order k to D out at some point,. -
5 Examples 1 N p1,3q rp1, 1 1 1qs 1 given by pu : vq ÞÑ pu : y 1 x 1 x 2 x 3 pu x 1 vqpu x 2 vqpu x 3 vq : vq 2 N p1,1q rp1 1, 1 1qs 2 given by pu : vq ÞÑ pupu vq : pu 2vqpu 4vq : v 2 q pu : vq ÞÑ pupu 5? 3 vq : pu 2? 3vqpu 4? 3 vq : v 2 q
6 Conjectural BPS structure Define a series N Ppa,b,1q : 8 k1 N pa,bq rpkp 1, kp 2 qsτ k where gcdp P 1, P 2 q 1 (start with coprime pair of partitions). Then rewrite formally N Ppa,b,1q : 8 k1 n pa,bq rpkp 1, kp 2 qs 8 d1 1 dpk 1q 1 d 2 τ dk d 1 The n pa,bq rpkp 1, kp 2 qs are the BPS invariants underlying the GW invariants N pa,bq rpkp 1, kp 2 qs.
7 Conjecture (GPS) n pa,bq rpkp 1, kp 2 qs P Z for every a, b, k, P 1, P 2. Remark. When k 1 n pa,bq rpp 1, P 2 qs N pa,bq rpp 1, P 2 qs. Vague expectation: In great generality people expect BPS invariants to be integers because they are the Euler characteristic χ of some suitable moduli space. This is true for N pa,bq rpp 1, P 2 qs in the coprime case!
8 Reineke Weist Theorem If gcdp P 1, P 2 q 1, then N pa,bq rpp 1, P 2 qs χ pmpp loooooomoooooon 1, P 2 qq moduli space of stable representations of complete bipartite quiver l 1 l 2
9 Vague expectation: In great generality, BPS invariants should admit a natural q-deformation or quantization. In our case the Reineke Weist Theorem provides a natural candidate: pn 1 rpp 1, P 2 qs PpMpP1 p, P 2 qqpqq : q 1 2 dim MpP 1,P 2 q PpMpP 1, P 2 qqpqq, where p PpMpP1, P 2 qqpqq is the symmetrized Poincaré polynomial.
10 Tropical vertex group Fix integers a, b and a function f pa,bq P Crx, x 1, y, y 1 srrtss of the form f pa,bq 1 t x a y b gpx loooomoooon a y b, tq gpcrzsrrtss Define θ pa,bq,fpa,bq P Aut Crrtss Crx, x 1, y, y 1 srrtss by # b θpa,bq,fpa,bq pxq x f pa,bq, θ pa,bq,fpa,bq pyq y fpa,bq a.
11 Definition (KS, GS) The tropical vertex group V Aut Crrtss Crx, x 1, y, y 1 srrtss is the t-adic comletion of the subgroup generated by all θ pa,bq,fpa,bq. Remark. Elements of V are formal 1-parameter families of holomorphic symplectomorphisms of C C : they preserve the form dx x ^ dy y.
12 Example Fix l 1, l 2 P N. Then # θp1,0q,p1 txq l1 pxq x, θ p1,0q,p1 txq l 1 pyq yp1 txq l 1. # θ p0,1q,p1 tyq l 2 pxq xp1 txq l 2, θ p0,1q,p1 tyq l 2 pyq y. Basic question: compute commutators in V. More precisely, compute rθ pa,bq,f, θ pa1,b 1 q,f 1s θ 1 pa 1,b 1 q,f θ 1 pa,bq,f θ pa1,b 1 q,f 1θ 1 pa,bq,f as some expression involving the generators θ pa2,b 2 q,f 2.
13 Fundamental result: In principle, this is always possible. Suppose that a, b, a 1, b 1 0, and that µpa, bq µpa 1, b 1 q (pa, bq follows pa 1, b 1 q in clockwise order). Then D! collection of vectors pa 2, b 2 q with positive entries, and attached functions f pa2,b 2 q such that with gcdpa 2, b 2 q 1. rθ pa,bq,f, θ pa1,b 1 q,f 1s ѹ θ pa2,b 2 q,f pa 2,b 2 q pa 2,b looooooooooomooooooooooon 2 q decreasing slopes of rays (from L to R), Question: How do we compute tpa 2, b 2 q, f pa2,b 2 qu?
14 Example For l 1 l 2 2 a closed formula is known: ѹ rθ p1,0q,p1 txq 2, θ p0,1q,p1 tyq 2s k θ pk,k 1q,fpk,k 1q θ p1,1q,fp1,1q θ pk 1,kq,fpk 1,kq, where $ & % f 1,1 p1 t 2 xyq 4 f k,k 1 p1 t 2k 1 x k y k 1 q 2 f k 1,k p1 t 2k 1 x k 1 y k q 2.
15 For now we restrict to the simplest case: rθ p1,0q,p1 txq l 1, θ p0,1q,p1 tyq l 2 s ѹ pa,bq θ pa,bq,fpa,bq. Even this is already very hard: Closed formulae are not known for l 1 l 2 4. However, there are very interesting theoretical results on computing tpa, bq, f pa,bq u: Theorem (Theorem A (GPS 10)) Consider the formal power series log f pa,bq c pa,bq k ptxq ak ptyq bk. Then c pa,bq k k k 0 P a ka P b kb N pa,bq rpp a, P b qs, where P a, P b ordered partitions, and lenp a l 1, lenp b l 2.
16 Tropical significance The GPS Theorem is based on a tropical computation together with some nice correspondence results. The tropical technique is called factor{defo and leads to: Theorem (Theorem A (GPS)) c pa,bq k k 2¹ P a ka P b kb w i1 R Pi w i Autpw i q Ntrop pa,bq pwq, where w pw 1, w 2 q is a pair of weight vectors of arbitrary length parametrizing a family of tropical counts tn trop pa,bq pwqu. R Pi w i, Autpw i q are some ramification and automorphism factors.
17 Geometric meaning: rational plane tropical curves with w 1 w 2 incoming ends and a single outgoing end. Example N trop pp1, 1q, p1, 2qq Fact: These counts are well-defined, and depend only on w.
18 Refinement We can actually work over Crrs 1,..., s l1, t 1,..., t l2 ss, and consider r l 1 ¹ i1 θ p1,0q,1 si x, l 2 ¹ j1 θ p0,1q,1 tj y s. Then again r l 1 ¹ θ p1,0q,1 si x, l 2 ¹ θ p0,1q,1 tj y s ѹ i1 j1 pa,bq θ pa,bq,fpa,bq, () where log f pa,bq k P a ka P b kb N pa,bq rpp 1, P 2 qss P 1 t P 2 x ka y kb. Corollary The invariants N pa,bq rpp 1, P 2 qs are determined by the factorization pq.
19 Natural q-deformation Basic idea: Some of the factorizations admit a natural q-deformation. This can be used to q-deform the GW invariants. To see the q-deformation we need a different point of view on the θ s. Let pγ, x, yq be a lattice with antisymmetric, bilinear form. Consider the Lie algebra with ñ g becomes a Poisson algebra. g generated by e α, α P Γ, re α, e β s xα, βye α β, e α e β e α β.
20 Let R be a complete local or Artin C-algebra. Then pg g bc p R lim g b C R{m k Ñ R. Let f α P pg be an element of the form f α P 1 m R re α se α. (1.1) Then we introduce θ α,fα automorphisms of the R-algebra pg by Write: θ Ω α,f α θ α,f Ω α for Ω P Q. θ α,fα pe β q e β f xα,βy α.
21 The Wall-crossing Group Definition The wall-crossing group VΓ,R r V Γ,R is the completion of the subgroup generated by automorphisms of the form θα,1 Ω σe α for α P Γ, σ P m R and Ω P Q. Dilogarithm: Li 2 pσe α q k 1 σ k e kα k 2. Fact: θ α,1 σemα expp 1 m adpli 2p σe mα qqq.
22 q-deformed algebra We replace g with the associative, noncommutative algebra over Cpq 1 2 q: g q generated by ê α, α P Γ, with ê α ê β q 1 2 xα,βy ê α β. 1 Classical limit: lim q 1 q 1 rê α, ê β s xα, βyê α β. 2 Ñ1 Fixing a local complete or Artin C-algebra R as usual, we define pg q g q p bc R. (fundamental case: g q rrtss, where t is a central variable.)
23 q-dilogarithm: Epσê α q n 0 p q 1 2 σê α q n p1 qqp1 q 2 q p1 q n q. For Ω P Q we introduce automorphisms ˆθ Ω rσê α s of pg q acting by ˆθ Ω rσê α spê β q Ad E Ω pσê α qpê β q E Ω pσê α qê β E Ω pσê α q. Definition U Γ,R is the completion of the subgroup of Aut Cpq 12 qb C R pg q generated by automorphisms of the form ˆθ Ω rp q 1 2 q n σê α qs (where α P Γ, σ P m R, Ω P Q, n P Z), with respect to the m R -adic topology.
24 Refinement: as in the numerical case, we can work over Crrs 1,..., s l1, t 1,..., t l2 ss, and look at Lemma (Stoppa-F.) rˆθ l 1 rσ 1 ê α1 s, ˆθ l 2 rσ 2 ê α2 ss ˆθ a1 α 1 a 2 α 2 Ad exp P 1 ka 1 P 2 ka 2 w 2¹ i1 pr Pi w i Autpw i q pn trop pα 1,α 2 q pwqsp 1 t P 2 êkpa 1 α 1 a 2 α 2 q q 1 2 q 1 2. where pr Pi w i,q ¹ j p 1q w ij 1 w ij rw ij s q #ti i,, P i w i u, and N p trop pα 1,α 2 qpwq is the Block-Göttsche invariant obtained by replacing m Υ pv q with rm Υ pv qs q for every V P Υ.
25 Main theorem Corollary A natural candidate for the q-deformed GW invariant is pnrpp 1, P 2 qs w 2¹ i1 pr Pi w i Autpw i q p N trop pα 1,α 2 q pwq. Theorem (Stoppa-F.) Suppose pp 1, P 2 q is primitive. Then the two choices of quantization coincide: pn 1 rpp 1, P 2 qs p NrpP1, P 2 qs.
Outline of mini lecture course, Mainz February 2016 Jacopo Stoppa Warning: reference list is very much incomplete!
 Outline of mini lecture course, Mainz February 2016 Jacopo Stoppa jacopo.stoppa@unipv.it Warning: reference list is very much incomplete! Lecture 1 In the first lecture I will introduce the tropical vertex
Outline of mini lecture course, Mainz February 2016 Jacopo Stoppa jacopo.stoppa@unipv.it Warning: reference list is very much incomplete! Lecture 1 In the first lecture I will introduce the tropical vertex
A degeneration formula for quiver moduli and its GW equivalent
 A degeneration formula for quiver moduli and its GW equivalent CRM Bellaterra 19 June 2012 Joint work with M. Reineke and T. Weist Quivers Quiver Q: an oriented graph; vertices Q 0, arrows Q 1 (α : i j).
A degeneration formula for quiver moduli and its GW equivalent CRM Bellaterra 19 June 2012 Joint work with M. Reineke and T. Weist Quivers Quiver Q: an oriented graph; vertices Q 0, arrows Q 1 (α : i j).
q-de Rham cohomology via Λ-rings
 q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
Markov Chains. Andreas Klappenecker by Andreas Klappenecker. All rights reserved. Texas A&M University
 Markov Chains Andreas Klappenecker Texas A&M University 208 by Andreas Klappenecker. All rights reserved. / 58 Stochastic Processes A stochastic process X tx ptq: t P T u is a collection of random variables.
Markov Chains Andreas Klappenecker Texas A&M University 208 by Andreas Klappenecker. All rights reserved. / 58 Stochastic Processes A stochastic process X tx ptq: t P T u is a collection of random variables.
Stability and Wall-Crossing
 Stability and Wall-Crossing Tom Bridgeland Notes by Tony Feng 1 Hearts and tilting 1.1 Torsion pair Let A be an abelian category. A torsion pair axiomatizes the idea of torsion and torsion-free objects.
Stability and Wall-Crossing Tom Bridgeland Notes by Tony Feng 1 Hearts and tilting 1.1 Torsion pair Let A be an abelian category. A torsion pair axiomatizes the idea of torsion and torsion-free objects.
Free fermion and wall-crossing
 Free fermion and wall-crossing Jie Yang School of Mathematical Sciences, Capital Normal University yangjie@cnu.edu.cn March 4, 202 Motivation For string theorists It is called BPS states counting which
Free fermion and wall-crossing Jie Yang School of Mathematical Sciences, Capital Normal University yangjie@cnu.edu.cn March 4, 202 Motivation For string theorists It is called BPS states counting which
arxiv: v1 [math.ag] 7 Mar 2016
![arxiv: v1 [math.ag] 7 Mar 2016 arxiv: v1 [math.ag] 7 Mar 2016](/thumbs/88/117211315.jpg) HILBERT SCHEME OF POINTS ON CYCLIC QUOTIENT SINGULARITIES OF TYPE (p,1) arxiv:163.2114v1 [math.ag] 7 Mar 216 Abstract. In this note we investigate the generating series of the Euler characteristics of
HILBERT SCHEME OF POINTS ON CYCLIC QUOTIENT SINGULARITIES OF TYPE (p,1) arxiv:163.2114v1 [math.ag] 7 Mar 216 Abstract. In this note we investigate the generating series of the Euler characteristics of
Notes on p-divisible Groups
 Notes on p-divisible Groups March 24, 2006 This is a note for the talk in STAGE in MIT. The content is basically following the paper [T]. 1 Preliminaries and Notations Notation 1.1. Let R be a complete
Notes on p-divisible Groups March 24, 2006 This is a note for the talk in STAGE in MIT. The content is basically following the paper [T]. 1 Preliminaries and Notations Notation 1.1. Let R be a complete
Invariance of tautological equations
 Invariance of tautological equations Y.-P. Lee 28 June 2004, NCTS An observation: Tautological equations hold for any geometric Gromov Witten theory. Question 1. How about non-geometric GW theory? e.g.
Invariance of tautological equations Y.-P. Lee 28 June 2004, NCTS An observation: Tautological equations hold for any geometric Gromov Witten theory. Question 1. How about non-geometric GW theory? e.g.
Very quick introduction to the conformal group and cft
 CHAPTER 1 Very quick introduction to the conformal group and cft The world of Conformal field theory is big and, like many theories in physics, it can be studied in many ways which may seem very confusing
CHAPTER 1 Very quick introduction to the conformal group and cft The world of Conformal field theory is big and, like many theories in physics, it can be studied in many ways which may seem very confusing
Intermediate Jacobians and Abel-Jacobi Maps
 Intermediate Jacobians and Abel-Jacobi Maps Patrick Walls April 28, 2012 Introduction Let X be a smooth projective complex variety. Introduction Let X be a smooth projective complex variety. Intermediate
Intermediate Jacobians and Abel-Jacobi Maps Patrick Walls April 28, 2012 Introduction Let X be a smooth projective complex variety. Introduction Let X be a smooth projective complex variety. Intermediate
arxiv: v2 [math.ca] 13 May 2015
![arxiv: v2 [math.ca] 13 May 2015 arxiv: v2 [math.ca] 13 May 2015](/thumbs/88/114667751.jpg) ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
4.4 Solving Congruences using Inverses
 4.4 Solving Congruences using Inverses Solving linear congruences is analogous to solving linear equations in calculus. Our first goal is to solve the linear congruence ax b pmod mq for x. Unfortunately
4.4 Solving Congruences using Inverses Solving linear congruences is analogous to solving linear equations in calculus. Our first goal is to solve the linear congruence ax b pmod mq for x. Unfortunately
Outline. 1 Geometry and Commutative Algebra. 2 Singularities and Resolutions. 3 Noncommutative Algebra and Deformations. 4 Representation Theory
 Outline Geometry, noncommutative algebra and representations Iain Gordon http://www.maths.ed.ac.uk/ igordon/ University of Edinburgh 16th December 2006 1 2 3 4 1 Iain Gordon Geometry, noncommutative algebra
Outline Geometry, noncommutative algebra and representations Iain Gordon http://www.maths.ed.ac.uk/ igordon/ University of Edinburgh 16th December 2006 1 2 3 4 1 Iain Gordon Geometry, noncommutative algebra
arxiv: v3 [math.rt] 14 Mar 2014
![arxiv: v3 [math.rt] 14 Mar 2014 arxiv: v3 [math.rt] 14 Mar 2014](/thumbs/76/73768875.jpg) arxiv:1210.6410v3 [math.rt] 14 Mar 2014 Free resolutions of orbit closures for the representations associated to gradings on Lie algebras of type E 6, F 4 and G 2 Federico Galetto March 18, 2014 Abstract
arxiv:1210.6410v3 [math.rt] 14 Mar 2014 Free resolutions of orbit closures for the representations associated to gradings on Lie algebras of type E 6, F 4 and G 2 Federico Galetto March 18, 2014 Abstract
Realization problems in algebraic topology
 Realization problems in algebraic topology Martin Frankland Universität Osnabrück Adam Mickiewicz University in Poznań Geometry and Topology Seminar June 2, 2017 Martin Frankland (Osnabrück) Realization
Realization problems in algebraic topology Martin Frankland Universität Osnabrück Adam Mickiewicz University in Poznań Geometry and Topology Seminar June 2, 2017 Martin Frankland (Osnabrück) Realization
EKT of Some Wonderful Compactifications
 EKT of Some Wonderful Compactifications and recent results on Complete Quadrics. (Based on joint works with Soumya Banerjee and Michael Joyce) Mahir Bilen Can April 16, 2016 Mahir Bilen Can EKT of Some
EKT of Some Wonderful Compactifications and recent results on Complete Quadrics. (Based on joint works with Soumya Banerjee and Michael Joyce) Mahir Bilen Can April 16, 2016 Mahir Bilen Can EKT of Some
(1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3
 Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
Math 127 Introduction and Review (1) Recap of Differential Calculus and Integral Calculus (2) Preview of Calculus in three dimensional space (3) Tools for Calculus 3 MATH 127 Introduction to Calculus III
for counting plane curves
 for counting plane curves Hannah Markwig joint with Andreas Gathmann and Michael Kerber Georg-August-Universität Göttingen Barcelona, September 2008 General introduction to tropical geometry and curve-counting
for counting plane curves Hannah Markwig joint with Andreas Gathmann and Michael Kerber Georg-August-Universität Göttingen Barcelona, September 2008 General introduction to tropical geometry and curve-counting
Exercises for algebraic curves
 Exercises for algebraic curves Christophe Ritzenthaler February 18, 2019 1 Exercise Lecture 1 1.1 Exercise Show that V = {(x, y) C 2 s.t. y = sin x} is not an algebraic set. Solutions. Let us assume that
Exercises for algebraic curves Christophe Ritzenthaler February 18, 2019 1 Exercise Lecture 1 1.1 Exercise Show that V = {(x, y) C 2 s.t. y = sin x} is not an algebraic set. Solutions. Let us assume that
arxiv: v1 [math.ag] 15 Jul 2018
![arxiv: v1 [math.ag] 15 Jul 2018 arxiv: v1 [math.ag] 15 Jul 2018](/thumbs/89/97528851.jpg) . NOTE ON EQUIVARIANT I-FUNCTION OF LOCAL P n HYENHO LHO arxiv:1807.05501v1 [math.ag] 15 Jul 2018 Abstract. Several properties of a hyepergeometric series related to Gromov-Witten theory of some Calabi-Yau
. NOTE ON EQUIVARIANT I-FUNCTION OF LOCAL P n HYENHO LHO arxiv:1807.05501v1 [math.ag] 15 Jul 2018 Abstract. Several properties of a hyepergeometric series related to Gromov-Witten theory of some Calabi-Yau
MTH 505: Number Theory Spring 2017
 MTH 505: Number Theory Spring 017 Homework 4 Drew Armstrong 4.1. (Squares Mod 4). We say that an element ras n P Z{nZ is square if there exists an element rxs n P Z{nZ such that ras n prxs n q rx s n.
MTH 505: Number Theory Spring 017 Homework 4 Drew Armstrong 4.1. (Squares Mod 4). We say that an element ras n P Z{nZ is square if there exists an element rxs n P Z{nZ such that ras n prxs n q rx s n.
STRUCTURE THEORY OF UNIMODULAR LATTICES
 STRUCTURE THEORY OF UNIMODULAR LATTICES TONY FENG 1 Unimodular Lattices 11 Definitions Let E be a lattice, by which we mean a free abelian group equipped with a symmetric bilinear form, : E E Z Definition
STRUCTURE THEORY OF UNIMODULAR LATTICES TONY FENG 1 Unimodular Lattices 11 Definitions Let E be a lattice, by which we mean a free abelian group equipped with a symmetric bilinear form, : E E Z Definition
Poisson geometry of b-manifolds. Eva Miranda
 Poisson geometry of b-manifolds Eva Miranda UPC-Barcelona Rio de Janeiro, July 26, 2010 Eva Miranda (UPC) Poisson 2010 July 26, 2010 1 / 45 Outline 1 Motivation 2 Classification of b-poisson manifolds
Poisson geometry of b-manifolds Eva Miranda UPC-Barcelona Rio de Janeiro, July 26, 2010 Eva Miranda (UPC) Poisson 2010 July 26, 2010 1 / 45 Outline 1 Motivation 2 Classification of b-poisson manifolds
Symplectic varieties and Poisson deformations
 Symplectic varieties and Poisson deformations Yoshinori Namikawa A symplectic variety X is a normal algebraic variety (defined over C) which admits an everywhere non-degenerate d-closed 2-form ω on the
Symplectic varieties and Poisson deformations Yoshinori Namikawa A symplectic variety X is a normal algebraic variety (defined over C) which admits an everywhere non-degenerate d-closed 2-form ω on the
THE NONCOMMUTATIVE TORUS
 THE NONCOMMUTATIVE TORUS The noncommutative torus as a twisted convolution An ordinary two-torus T 2 with coordinate functions given by where x 1, x 2 [0, 1]. U 1 = e 2πix 1, U 2 = e 2πix 2, (1) By Fourier
THE NONCOMMUTATIVE TORUS The noncommutative torus as a twisted convolution An ordinary two-torus T 2 with coordinate functions given by where x 1, x 2 [0, 1]. U 1 = e 2πix 1, U 2 = e 2πix 2, (1) By Fourier
Inverse Galois Problem for C(t)
 Inverse Galois Problem for C(t) Padmavathi Srinivasan PuMaGraSS March 2, 2012 Outline 1 The problem 2 Compact Riemann Surfaces 3 Covering Spaces 4 Connection to field theory 5 Proof of the Main theorem
Inverse Galois Problem for C(t) Padmavathi Srinivasan PuMaGraSS March 2, 2012 Outline 1 The problem 2 Compact Riemann Surfaces 3 Covering Spaces 4 Connection to field theory 5 Proof of the Main theorem
The Riemann Roch theorem for metric graphs
 The Riemann Roch theorem for metric graphs R. van Dobben de Bruyn 1 Preface These are the notes of a talk I gave at the graduate student algebraic geometry seminar at Columbia University. I present a short
The Riemann Roch theorem for metric graphs R. van Dobben de Bruyn 1 Preface These are the notes of a talk I gave at the graduate student algebraic geometry seminar at Columbia University. I present a short
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
Integrable structure of various melting crystal models
 Integrable structure of various melting crystal models Kanehisa Takasaki, Kinki University Taipei, April 10 12, 2015 Contents 1. Ordinary melting crystal model 2. Modified melting crystal model 3. Orbifold
Integrable structure of various melting crystal models Kanehisa Takasaki, Kinki University Taipei, April 10 12, 2015 Contents 1. Ordinary melting crystal model 2. Modified melting crystal model 3. Orbifold
Donaldson Thomas theory of Calabi Yau 3-folds, and generalizations
 Donaldson Thomas theory of Calabi Yau 3-folds, and generalizations Lecture 1 of 3: Classical Donaldson Thomas theory Dominic Joyce, Oxford University Modern Moduli Theory graduate school, September 2017
Donaldson Thomas theory of Calabi Yau 3-folds, and generalizations Lecture 1 of 3: Classical Donaldson Thomas theory Dominic Joyce, Oxford University Modern Moduli Theory graduate school, September 2017
STEENROD OPERATIONS IN ALGEBRAIC GEOMETRY
 STEENROD OPERATIONS IN ALGEBRAIC GEOMETRY ALEXANDER MERKURJEV 1. Introduction Let p be a prime integer. For a pair of topological spaces A X we write H i (X, A; Z/pZ) for the i-th singular cohomology group
STEENROD OPERATIONS IN ALGEBRAIC GEOMETRY ALEXANDER MERKURJEV 1. Introduction Let p be a prime integer. For a pair of topological spaces A X we write H i (X, A; Z/pZ) for the i-th singular cohomology group
Donaldson-Thomas invariants
 Donaldson-Thomas invariants Maxim Kontsevich IHES Bures-sur-Yvette, France Mathematische Arbeitstagung June 22-28, 2007 Max-Planck-Institut für Mathematik, Bonn, Germany 1 Stability conditions Here I ll
Donaldson-Thomas invariants Maxim Kontsevich IHES Bures-sur-Yvette, France Mathematische Arbeitstagung June 22-28, 2007 Max-Planck-Institut für Mathematik, Bonn, Germany 1 Stability conditions Here I ll
Symbolic-Algebraic Methods for Linear Partial Differential Operators (LPDOs) RISC Research Institute for Symbolic Computation
 Symbolic-Algebraic Methods for Linear Partial Differential Operators (LPDOs) Franz Winkler joint with Ekaterina Shemyakova RISC Research Institute for Symbolic Computation Johannes Kepler Universität.
Symbolic-Algebraic Methods for Linear Partial Differential Operators (LPDOs) Franz Winkler joint with Ekaterina Shemyakova RISC Research Institute for Symbolic Computation Johannes Kepler Universität.
FMM Preconditioner for Radiative Transport
 FMM Preconditioner for Radiative Transport SIAM CSE 2017, Atlanta Yimin Zhong Department of Mathematics University of Texas at Austin In collaboration with Kui Ren (UT Austin) and Rongting Zhang (UT Austin)
FMM Preconditioner for Radiative Transport SIAM CSE 2017, Atlanta Yimin Zhong Department of Mathematics University of Texas at Austin In collaboration with Kui Ren (UT Austin) and Rongting Zhang (UT Austin)
Knots-quivers correspondence, lattice paths, and rational knots
 Knots-quivers correspondence, lattice paths, and rational knots 1 CAMGSD, Departamento de Matemática, Instituto Superior Técnico, Portugal 2 Mathematical Institute SANU, Belgrade, Serbia Warszawa, September
Knots-quivers correspondence, lattice paths, and rational knots 1 CAMGSD, Departamento de Matemática, Instituto Superior Técnico, Portugal 2 Mathematical Institute SANU, Belgrade, Serbia Warszawa, September
The L 3 (4) near octagon
 The L 3 (4) near octagon A. Bishnoi and B. De Bruyn October 8, 206 Abstract In recent work we constructed two new near octagons, one related to the finite simple group G 2 (4) and another one as a sub-near-octagon
The L 3 (4) near octagon A. Bishnoi and B. De Bruyn October 8, 206 Abstract In recent work we constructed two new near octagons, one related to the finite simple group G 2 (4) and another one as a sub-near-octagon
Black Holes and Hurwitz Class Numbers
 Black Holes and Hurwitz Class Numbers Shamit Kachru a,1, Arnav Tripathy b a Stanford Institute for Theoretical Physics Stanford University, Palo Alto, CA 94305, USA Email: skachru@stanford.edu b Department
Black Holes and Hurwitz Class Numbers Shamit Kachru a,1, Arnav Tripathy b a Stanford Institute for Theoretical Physics Stanford University, Palo Alto, CA 94305, USA Email: skachru@stanford.edu b Department
ADELIC VERSION OF MARGULIS ARITHMETICITY THEOREM. Hee Oh
 ADELIC VERSION OF MARGULIS ARITHMETICITY THEOREM Hee Oh Abstract. In this paper, we generalize Margulis s S-arithmeticity theorem to the case when S can be taken as an infinite set of primes. Let R be
ADELIC VERSION OF MARGULIS ARITHMETICITY THEOREM Hee Oh Abstract. In this paper, we generalize Margulis s S-arithmeticity theorem to the case when S can be taken as an infinite set of primes. Let R be
Degeneration of Bethe subalgebras in the Yangian
 Degeneration of Bethe subalgebras in the Yangian National Research University Higher School of Economics Faculty of Mathematics Moscow, Russia Washington, 2018 Yangian for gl n Let V C n, Rpuq 1 P u 1
Degeneration of Bethe subalgebras in the Yangian National Research University Higher School of Economics Faculty of Mathematics Moscow, Russia Washington, 2018 Yangian for gl n Let V C n, Rpuq 1 P u 1
A geometric solution of the Kervaire Invariant One problem
 A geometric solution of the Kervaire Invariant One problem Petr M. Akhmet ev 19 May 2009 Let f : M n 1 R n, n = 4k + 2, n 2 be a smooth generic immersion of a closed manifold of codimension 1. Let g :
A geometric solution of the Kervaire Invariant One problem Petr M. Akhmet ev 19 May 2009 Let f : M n 1 R n, n = 4k + 2, n 2 be a smooth generic immersion of a closed manifold of codimension 1. Let g :
Group Actions and Cohomology in the Calculus of Variations
 Group Actions and Cohomology in the Calculus of Variations JUHA POHJANPELTO Oregon State and Aalto Universities Focused Research Workshop on Exterior Differential Systems and Lie Theory Fields Institute,
Group Actions and Cohomology in the Calculus of Variations JUHA POHJANPELTO Oregon State and Aalto Universities Focused Research Workshop on Exterior Differential Systems and Lie Theory Fields Institute,
14 From modular forms to automorphic representations
 14 From modular forms to automorphic representations We fix an even integer k and N > 0 as before. Let f M k (N) be a modular form. We would like to product a function on GL 2 (A Q ) out of it. Recall
14 From modular forms to automorphic representations We fix an even integer k and N > 0 as before. Let f M k (N) be a modular form. We would like to product a function on GL 2 (A Q ) out of it. Recall
Combinatorial bases for representations. of the Lie superalgebra gl m n
 Combinatorial bases for representations of the Lie superalgebra gl m n Alexander Molev University of Sydney Gelfand Tsetlin bases for gln Gelfand Tsetlin bases for gl n Finite-dimensional irreducible representations
Combinatorial bases for representations of the Lie superalgebra gl m n Alexander Molev University of Sydney Gelfand Tsetlin bases for gln Gelfand Tsetlin bases for gl n Finite-dimensional irreducible representations
FUNDAMENTAL GROUPS OF COMPLEMENTS OF PLANE CURVES AND SYMPLECTIC INVARIANTS
 FUNDAMENTAL GROUPS OF COMPLEMENTS OF PLANE CURVES AND SYMPLECTIC INVARIANTS D. AUROUX, S. K. DONALDSON, L. KATZARKOV, AND M. YOTOV Abstract. Introducing the notion of stabilized fundamental group for the
FUNDAMENTAL GROUPS OF COMPLEMENTS OF PLANE CURVES AND SYMPLECTIC INVARIANTS D. AUROUX, S. K. DONALDSON, L. KATZARKOV, AND M. YOTOV Abstract. Introducing the notion of stabilized fundamental group for the
New Negative Latin Square Type Partial Difference Sets in Nonelementary Abelian 2-groups and 3-groups
 New Negative Latin Square Type Partial Difference Sets in Nonelementary Abelian 2-groups and 3-groups John Polhill Department of Mathematics, Computer Science, and Statistics Bloomsburg University Bloomsburg,
New Negative Latin Square Type Partial Difference Sets in Nonelementary Abelian 2-groups and 3-groups John Polhill Department of Mathematics, Computer Science, and Statistics Bloomsburg University Bloomsburg,
p-regular functions and congruences for Bernoulli and Euler numbers
 p-regular functions and congruences for Bernoulli and Euler numbers Zhi-Hong Sun( Huaiyin Normal University Huaian, Jiangsu 223001, PR China http://www.hytc.edu.cn/xsjl/szh Notation: Z the set of integers,
p-regular functions and congruences for Bernoulli and Euler numbers Zhi-Hong Sun( Huaiyin Normal University Huaian, Jiangsu 223001, PR China http://www.hytc.edu.cn/xsjl/szh Notation: Z the set of integers,
Letting be a field, e.g., of the real numbers, the complex numbers, the rational numbers, the rational functions W(s) of a complex variable s, etc.
 1 Polynomial Matrices 1.1 Polynomials Letting be a field, e.g., of the real numbers, the complex numbers, the rational numbers, the rational functions W(s) of a complex variable s, etc., n ws ( ) as a
1 Polynomial Matrices 1.1 Polynomials Letting be a field, e.g., of the real numbers, the complex numbers, the rational numbers, the rational functions W(s) of a complex variable s, etc., n ws ( ) as a
What is the Langlands program all about?
 What is the Langlands program all about? Laurent Lafforgue November 13, 2013 Hua Loo-Keng Distinguished Lecture Academy of Mathematics and Systems Science, Chinese Academy of Sciences This talk is mainly
What is the Langlands program all about? Laurent Lafforgue November 13, 2013 Hua Loo-Keng Distinguished Lecture Academy of Mathematics and Systems Science, Chinese Academy of Sciences This talk is mainly
1 Moduli spaces of polarized Hodge structures.
 1 Moduli spaces of polarized Hodge structures. First of all, we briefly summarize the classical theory of the moduli spaces of polarized Hodge structures. 1.1 The moduli space M h = Γ\D h. Let n be an
1 Moduli spaces of polarized Hodge structures. First of all, we briefly summarize the classical theory of the moduli spaces of polarized Hodge structures. 1.1 The moduli space M h = Γ\D h. Let n be an
REPRESENTATION THEORY WEEK 5. B : V V k
 REPRESENTATION THEORY WEEK 5 1. Invariant forms Recall that a bilinear form on a vector space V is a map satisfying B : V V k B (cv, dw) = cdb (v, w), B (v 1 + v, w) = B (v 1, w)+b (v, w), B (v, w 1 +
REPRESENTATION THEORY WEEK 5 1. Invariant forms Recall that a bilinear form on a vector space V is a map satisfying B : V V k B (cv, dw) = cdb (v, w), B (v 1 + v, w) = B (v 1, w)+b (v, w), B (v, w 1 +
arxiv: v1 [math.co] 23 May 2013
![arxiv: v1 [math.co] 23 May 2013 arxiv: v1 [math.co] 23 May 2013](/thumbs/88/115262721.jpg) arxiv:1305.5328v1 [math.co] 23 May 2013 Orbits of pairs in abelian groups C. P. Anilkumar and Amritanshu Prasad Abstract. We compute the number of orbits of pairs in a finitely generated torsion module
arxiv:1305.5328v1 [math.co] 23 May 2013 Orbits of pairs in abelian groups C. P. Anilkumar and Amritanshu Prasad Abstract. We compute the number of orbits of pairs in a finitely generated torsion module
FROM CLASSICAL THETA FUNCTIONS TO TOPOLOGICAL QUANTUM FIELD THEORY
 FROM CLASSICAL THETA FUNCTIONS TO TOPOLOGICAL QUANTUM FIELD THEORY Răzvan Gelca Texas Tech University Alejandro Uribe University of Michigan WE WILL CONSTRUCT THE ABELIAN CHERN-SIMONS TOPOLOGICAL QUANTUM
FROM CLASSICAL THETA FUNCTIONS TO TOPOLOGICAL QUANTUM FIELD THEORY Răzvan Gelca Texas Tech University Alejandro Uribe University of Michigan WE WILL CONSTRUCT THE ABELIAN CHERN-SIMONS TOPOLOGICAL QUANTUM
Addition sequences and numerical evaluation of modular forms
 Addition sequences and numerical evaluation of modular forms Fredrik Johansson (INRIA Bordeaux) Joint work with Andreas Enge (INRIA Bordeaux) William Hart (TU Kaiserslautern) DK Statusseminar in Strobl,
Addition sequences and numerical evaluation of modular forms Fredrik Johansson (INRIA Bordeaux) Joint work with Andreas Enge (INRIA Bordeaux) William Hart (TU Kaiserslautern) DK Statusseminar in Strobl,
Torus Knots and q, t-catalan Numbers
 Torus Knots and q, t-catalan Numbers Eugene Gorsky Stony Brook University Simons Center For Geometry and Physics April 11, 2012 Outline q, t-catalan numbers Compactified Jacobians Arc spaces on singular
Torus Knots and q, t-catalan Numbers Eugene Gorsky Stony Brook University Simons Center For Geometry and Physics April 11, 2012 Outline q, t-catalan numbers Compactified Jacobians Arc spaces on singular
Categories of noncrossing partitions
 Categories of noncrossing partitions Kiyoshi Igusa, Brandeis University KIAS, Dec 15, 214 Topology of categories The classifying space of a small category C is a union of simplices k : BC = X X 1 X k k
Categories of noncrossing partitions Kiyoshi Igusa, Brandeis University KIAS, Dec 15, 214 Topology of categories The classifying space of a small category C is a union of simplices k : BC = X X 1 X k k
Difference Painlevé equations from 5D gauge theories
 Difference Painlevé equations from 5D gauge theories M. Bershtein based on joint paper with P. Gavrylenko and A. Marshakov arxiv:.006, to appear in JHEP February 08 M. Bershtein Difference Painlevé based
Difference Painlevé equations from 5D gauge theories M. Bershtein based on joint paper with P. Gavrylenko and A. Marshakov arxiv:.006, to appear in JHEP February 08 M. Bershtein Difference Painlevé based
Random Variables. Andreas Klappenecker. Texas A&M University
 Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Generalized string equations for Hurwitz numbers
 Generalized string equations for Hurwitz numbers Kanehisa Takasaki December 17, 2010 1. Hurwitz numbers of Riemann sphere 2. Generating functions of Hurwitz numbers 3. Fermionic representation of tau functions
Generalized string equations for Hurwitz numbers Kanehisa Takasaki December 17, 2010 1. Hurwitz numbers of Riemann sphere 2. Generating functions of Hurwitz numbers 3. Fermionic representation of tau functions
Lecture 20 FUNDAMENTAL Theorem of Finitely Generated Abelian Groups (FTFGAG)
 Lecture 20 FUNDAMENTAL Theorem of Finitely Generated Abelian Groups (FTFGAG) Warm up: 1. Let n 1500. Find all sequences n 1 n 2... n s 2 satisfying n i 1 and n 1 n s n (where s can vary from sequence to
Lecture 20 FUNDAMENTAL Theorem of Finitely Generated Abelian Groups (FTFGAG) Warm up: 1. Let n 1500. Find all sequences n 1 n 2... n s 2 satisfying n i 1 and n 1 n s n (where s can vary from sequence to
p-adic families of modular forms II
 April 5, 2009 Leftovers from last time Lemma Proof. We have G k = (1 pk 1 V p )G k p d np d k 1 = p k 1 d n d k 1 So equality holds in all coefficients except possibly the constant. But then G k (1 pk
April 5, 2009 Leftovers from last time Lemma Proof. We have G k = (1 pk 1 V p )G k p d np d k 1 = p k 1 d n d k 1 So equality holds in all coefficients except possibly the constant. But then G k (1 pk
Latin Squares and Projective Planes Combinatorics Seminar, SPRING, 2010
 Latin Squares and Projective Planes Combinatorics Seminar, SPRING, 2010 1 CHAPTER 1 Finite Fields F 4 (x 2 + x + 1 is irreducable) x x + 1 x x + 1 1 x + 1 1 x 1. Examples F 4 = {(a, b) a, b Z 2 } (a,
Latin Squares and Projective Planes Combinatorics Seminar, SPRING, 2010 1 CHAPTER 1 Finite Fields F 4 (x 2 + x + 1 is irreducable) x x + 1 x x + 1 1 x + 1 1 x 1. Examples F 4 = {(a, b) a, b Z 2 } (a,
Public-key Cryptography: Theory and Practice
 Public-key Cryptography Theory and Practice Department of Computer Science and Engineering Indian Institute of Technology Kharagpur Chapter 2: Mathematical Concepts Divisibility Congruence Quadratic Residues
Public-key Cryptography Theory and Practice Department of Computer Science and Engineering Indian Institute of Technology Kharagpur Chapter 2: Mathematical Concepts Divisibility Congruence Quadratic Residues
COMPLEX NUMBERS LAURENT DEMONET
 COMPLEX NUMBERS LAURENT DEMONET Contents Introduction: numbers 1 1. Construction of complex numbers. Conjugation 4 3. Geometric representation of complex numbers 5 3.1. The unit circle 6 3.. Modulus of
COMPLEX NUMBERS LAURENT DEMONET Contents Introduction: numbers 1 1. Construction of complex numbers. Conjugation 4 3. Geometric representation of complex numbers 5 3.1. The unit circle 6 3.. Modulus of
9. Integral Ring Extensions
 80 Andreas Gathmann 9. Integral ing Extensions In this chapter we want to discuss a concept in commutative algebra that has its original motivation in algebra, but turns out to have surprisingly many applications
80 Andreas Gathmann 9. Integral ing Extensions In this chapter we want to discuss a concept in commutative algebra that has its original motivation in algebra, but turns out to have surprisingly many applications
Definitions, Theorems and Exercises. Abstract Algebra Math 332. Ethan D. Bloch
 Definitions, Theorems and Exercises Abstract Algebra Math 332 Ethan D. Bloch December 26, 2013 ii Contents 1 Binary Operations 3 1.1 Binary Operations............................... 4 1.2 Isomorphic Binary
Definitions, Theorems and Exercises Abstract Algebra Math 332 Ethan D. Bloch December 26, 2013 ii Contents 1 Binary Operations 3 1.1 Binary Operations............................... 4 1.2 Isomorphic Binary
The Real Grassmannian Gr(2, 4)
 The Real Grassmannian Gr(2, 4) We discuss the topology of the real Grassmannian Gr(2, 4) of 2-planes in R 4 and its double cover Gr + (2, 4) by the Grassmannian of oriented 2-planes They are compact four-manifolds
The Real Grassmannian Gr(2, 4) We discuss the topology of the real Grassmannian Gr(2, 4) of 2-planes in R 4 and its double cover Gr + (2, 4) by the Grassmannian of oriented 2-planes They are compact four-manifolds
Linear algebra comments. Sophie Marques
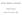 Linear algebra comments Sophie Marques Friday 9 th October, 2015 2 Of course this does not cover all the class notes and it is not enough to do the midterm. It is just a way to extract the very very important
Linear algebra comments Sophie Marques Friday 9 th October, 2015 2 Of course this does not cover all the class notes and it is not enough to do the midterm. It is just a way to extract the very very important
McGill University Department of Mathematics and Statistics. Ph.D. preliminary examination, PART A. PURE AND APPLIED MATHEMATICS Paper BETA
 McGill University Department of Mathematics and Statistics Ph.D. preliminary examination, PART A PURE AND APPLIED MATHEMATICS Paper BETA 17 August, 2018 1:00 p.m. - 5:00 p.m. INSTRUCTIONS: (i) This paper
McGill University Department of Mathematics and Statistics Ph.D. preliminary examination, PART A PURE AND APPLIED MATHEMATICS Paper BETA 17 August, 2018 1:00 p.m. - 5:00 p.m. INSTRUCTIONS: (i) This paper
VARIETIES WITHOUT EXTRA AUTOMORPHISMS II: HYPERELLIPTIC CURVES
 VARIETIES WITHOUT EXTRA AUTOMORPHISMS II: HYPERELLIPTIC CURVES BJORN POONEN Abstract. For any field k and integer g 2, we construct a hyperelliptic curve X over k of genus g such that #(Aut X) = 2. We
VARIETIES WITHOUT EXTRA AUTOMORPHISMS II: HYPERELLIPTIC CURVES BJORN POONEN Abstract. For any field k and integer g 2, we construct a hyperelliptic curve X over k of genus g such that #(Aut X) = 2. We
Convergence of Star Products and the Nuclear Weyl Algebr
 Convergence of Star Products and the Nuclear Weyl Algebra Institut für Mathematik, Universität Würzburg, Germany Bayrischzell 2013 Beiser, S., Waldmann, S.: Fréchet algebraic deformation quantization of
Convergence of Star Products and the Nuclear Weyl Algebra Institut für Mathematik, Universität Würzburg, Germany Bayrischzell 2013 Beiser, S., Waldmann, S.: Fréchet algebraic deformation quantization of
COMPLEX MULTIPLICATION: LECTURE 15
 COMPLEX MULTIPLICATION: LECTURE 15 Proposition 01 Let φ : E 1 E 2 be a non-constant isogeny, then #φ 1 (0) = deg s φ where deg s is the separable degree of φ Proof Silverman III 410 Exercise: i) Consider
COMPLEX MULTIPLICATION: LECTURE 15 Proposition 01 Let φ : E 1 E 2 be a non-constant isogeny, then #φ 1 (0) = deg s φ where deg s is the separable degree of φ Proof Silverman III 410 Exercise: i) Consider
Suppose A h is a flat family of non-commutative algebras, such that A 0 is commutative.
 Suppose A h is a flat family of non-commutative algebras, such that A 0 is commutative. Suppose A h is a flat family of non-commutative algebras, such that A 0 is commutative. Then A 0 has an additional
Suppose A h is a flat family of non-commutative algebras, such that A 0 is commutative. Suppose A h is a flat family of non-commutative algebras, such that A 0 is commutative. Then A 0 has an additional
Generalized Wentzell boundary conditions and holography
 Generalized Wentzell boundary conditions and holography Jochen Zahn Universität Leipzig based on arxiv:1512.05512 LQP38, May 2016 Introduction We study a scalar field subject to the action S 1 g 2 µ B
Generalized Wentzell boundary conditions and holography Jochen Zahn Universität Leipzig based on arxiv:1512.05512 LQP38, May 2016 Introduction We study a scalar field subject to the action S 1 g 2 µ B
Cover Page. The handle holds various files of this Leiden University dissertation
 Cover Page The handle http://hdl.handle.net/1887/25833 holds various files of this Leiden University dissertation Author: Palenstijn, Willem Jan Title: Radicals in Arithmetic Issue Date: 2014-05-22 Chapter
Cover Page The handle http://hdl.handle.net/1887/25833 holds various files of this Leiden University dissertation Author: Palenstijn, Willem Jan Title: Radicals in Arithmetic Issue Date: 2014-05-22 Chapter
Flag Varieties. Matthew Goroff November 2, 2016
 Flag Varieties Matthew Goroff November 2, 2016 1. Grassmannian Variety Definition 1.1: Let V be a k-vector space of dimension n. The Grassmannian Grpr, V q is the set of r-dimensional subspaces of V. It
Flag Varieties Matthew Goroff November 2, 2016 1. Grassmannian Variety Definition 1.1: Let V be a k-vector space of dimension n. The Grassmannian Grpr, V q is the set of r-dimensional subspaces of V. It
Generating functions and enumerative geometry
 Generating functions and enumerative geometry Ragni Piene Centre of Mathematics for Applications and Department of Mathematics, University of Oslo October 26, 2005 KTH, Stockholm Generating functions Enumerative
Generating functions and enumerative geometry Ragni Piene Centre of Mathematics for Applications and Department of Mathematics, University of Oslo October 26, 2005 KTH, Stockholm Generating functions Enumerative
General tensors. Three definitions of the term V V. q times. A j 1...j p. k 1...k q
 General tensors Three definitions of the term Definition 1: A tensor of order (p,q) [hence of rank p+q] is a multilinear function A:V V }{{ V V R. }}{{} p times q times (Multilinear means linear in each
General tensors Three definitions of the term Definition 1: A tensor of order (p,q) [hence of rank p+q] is a multilinear function A:V V }{{ V V R. }}{{} p times q times (Multilinear means linear in each
AUTOMORPHISM GROUPS AND SPECTRA OF CIRCULANT GRAPHS
 AUTOMORPHISM GROUPS AND SPECTRA OF CIRCULANT GRAPHS MAX GOLDBERG Abstract. We explore ways to concisely describe circulant graphs, highly symmetric graphs with properties that are easier to generalize
AUTOMORPHISM GROUPS AND SPECTRA OF CIRCULANT GRAPHS MAX GOLDBERG Abstract. We explore ways to concisely describe circulant graphs, highly symmetric graphs with properties that are easier to generalize
Conjugacy classes of torsion in GL_n(Z)
 Electronic Journal of Linear Algebra Volume 30 Volume 30 (2015) Article 32 2015 Conjugacy classes of torsion in GL_n(Z) Qingjie Yang Renmin University of China yangqj@ruceducn Follow this and additional
Electronic Journal of Linear Algebra Volume 30 Volume 30 (2015) Article 32 2015 Conjugacy classes of torsion in GL_n(Z) Qingjie Yang Renmin University of China yangqj@ruceducn Follow this and additional
Evgeniy V. Martyushev RESEARCH STATEMENT
 Evgeniy V. Martyushev RESEARCH STATEMENT My research interests lie in the fields of topology of manifolds, algebraic topology, representation theory, and geometry. Specifically, my work explores various
Evgeniy V. Martyushev RESEARCH STATEMENT My research interests lie in the fields of topology of manifolds, algebraic topology, representation theory, and geometry. Specifically, my work explores various
1 Vectors and Tensors
 PART 1: MATHEMATICAL PRELIMINARIES 1 Vectors and Tensors This chapter and the next are concerned with establishing some basic properties of vectors and tensors in real spaces. The first of these is specifically
PART 1: MATHEMATICAL PRELIMINARIES 1 Vectors and Tensors This chapter and the next are concerned with establishing some basic properties of vectors and tensors in real spaces. The first of these is specifically
Section 8.4: Generating functions.
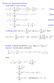 Section 8.4: Generating functions. Taylor series to know and love: nÿ ˆn ˆn p ` xq n x k ` k x ` x n n x ÿ x k ` x ` x 2 ` `x n x e x x k ` x ` x 2 ` x k {k! ` x ` x2 2 ` x3 3! Combining series: Let f
Section 8.4: Generating functions. Taylor series to know and love: nÿ ˆn ˆn p ` xq n x k ` k x ` x n n x ÿ x k ` x ` x 2 ` `x n x e x x k ` x ` x 2 ` x k {k! ` x ` x2 2 ` x3 3! Combining series: Let f
QUIVERS AND LATTICES.
 QUIVERS AND LATTICES. KEVIN MCGERTY We will discuss two classification results in quite different areas which turn out to have the same answer. This note is an slightly expanded version of the talk given
QUIVERS AND LATTICES. KEVIN MCGERTY We will discuss two classification results in quite different areas which turn out to have the same answer. This note is an slightly expanded version of the talk given
A distance space on Cayley s ruled surface
 A distance space on Cayley s ruled surface Hans Havlicek Joint work with Johannes Gmainer DIFFERENTIALGEOMETRIE UND GEOMETRISCHE STRUKTUREN Basic notions Let P 3 (K) be the 3-dimensional projective space
A distance space on Cayley s ruled surface Hans Havlicek Joint work with Johannes Gmainer DIFFERENTIALGEOMETRIE UND GEOMETRISCHE STRUKTUREN Basic notions Let P 3 (K) be the 3-dimensional projective space
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION. Contents 1. Overview Steenrod s construction
 NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
1 Notations and Statement of the Main Results
 An introduction to algebraic fundamental groups 1 Notations and Statement of the Main Results Throughout the talk, all schemes are locally Noetherian. All maps are of locally finite type. There two main
An introduction to algebraic fundamental groups 1 Notations and Statement of the Main Results Throughout the talk, all schemes are locally Noetherian. All maps are of locally finite type. There two main
LECTURE IV: PERFECT PRISMS AND PERFECTOID RINGS
 LECTURE IV: PERFECT PRISMS AND PERFECTOID RINGS In this lecture, we study the commutative algebra properties of perfect prisms. These turn out to be equivalent to perfectoid rings, and most of the lecture
LECTURE IV: PERFECT PRISMS AND PERFECTOID RINGS In this lecture, we study the commutative algebra properties of perfect prisms. These turn out to be equivalent to perfectoid rings, and most of the lecture
FINITE RESOLUTIONS DIGEST NORTHWESTERN TAF SEMINAR FEBRUARY 21, Introduction
 FINITE RESOLUTIONS DIGEST NORTHWESTERN TAF SEMINAR FEBRUARY, 04 Remark 0.. My main reference is A Resolution of the Kpq-Local Sphere at the Pme 3 by Goerss, Henn, Mahowald and Rezk, and Finite Resolutions
FINITE RESOLUTIONS DIGEST NORTHWESTERN TAF SEMINAR FEBRUARY, 04 Remark 0.. My main reference is A Resolution of the Kpq-Local Sphere at the Pme 3 by Goerss, Henn, Mahowald and Rezk, and Finite Resolutions
MATH 423/ Note that the algebraic operations on the right hand side are vector subtraction and scalar multiplication.
 MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
Symplectic Geometry versus Riemannian Geometry
 Symplectic Geometry versus Riemannian Geometry Inês Cruz, CMUP 2010/10/20 - seminar of PIUDM 1 necessarily very incomplete The aim of this talk is to give an overview of Symplectic Geometry (there is no
Symplectic Geometry versus Riemannian Geometry Inês Cruz, CMUP 2010/10/20 - seminar of PIUDM 1 necessarily very incomplete The aim of this talk is to give an overview of Symplectic Geometry (there is no
BPS states, Wall-crossing and Quivers
 Iberian Strings 2012 Bilbao BPS states, Wall-crossing and Quivers IST, Lisboa Michele Cirafici M.C.& A.Sincovics & R.J. Szabo: 0803.4188, 1012.2725, 1108.3922 and M.C. to appear BPS States in String theory
Iberian Strings 2012 Bilbao BPS states, Wall-crossing and Quivers IST, Lisboa Michele Cirafici M.C.& A.Sincovics & R.J. Szabo: 0803.4188, 1012.2725, 1108.3922 and M.C. to appear BPS States in String theory
The symplectic structure on moduli space (in memory of Andreas Floer)
 The symplectic structure on moduli space (in memory of Andreas Floer) Alan Weinstein Department of Mathematics University of California Berkeley, CA 94720 USA (alanw@math.berkeley.edu) 1 Introduction The
The symplectic structure on moduli space (in memory of Andreas Floer) Alan Weinstein Department of Mathematics University of California Berkeley, CA 94720 USA (alanw@math.berkeley.edu) 1 Introduction The
Orbit closures of quiver representations
 Orbit closures of quiver representations Kavita Sutar Chennai Mathematical Institute September 5, 2012 Outline 1 Orbit closures 2 Geometric technique 3 Calculations 4 Results Quiver Q = (Q 0, Q 1 ) is
Orbit closures of quiver representations Kavita Sutar Chennai Mathematical Institute September 5, 2012 Outline 1 Orbit closures 2 Geometric technique 3 Calculations 4 Results Quiver Q = (Q 0, Q 1 ) is
Stability data, irregular connections and tropical curves
 Stability data, irregular connections and tropical curves Mario Garcia-Fernandez Instituto de iencias Matemáticas (Madrid) Barcelona Mathematical Days 7 November 2014 Joint work with S. Filippini and J.
Stability data, irregular connections and tropical curves Mario Garcia-Fernandez Instituto de iencias Matemáticas (Madrid) Barcelona Mathematical Days 7 November 2014 Joint work with S. Filippini and J.
PERMUTATION-EQUIVARIANT QUANTUM K-THEORY IV. D q -MODULES
 PERMUTATION-EQUIVARIANT QUANTUM K-THEORY IV. D q -MODULES ALEXANDER GIVENTAL Abstract. In Part II, we saw how permutation-equivariant quantum K-theory of a manifold with isolated fixed points of a torus
PERMUTATION-EQUIVARIANT QUANTUM K-THEORY IV. D q -MODULES ALEXANDER GIVENTAL Abstract. In Part II, we saw how permutation-equivariant quantum K-theory of a manifold with isolated fixed points of a torus
Betti numbers of abelian covers
 Betti numbers of abelian covers Alex Suciu Northeastern University Geometry and Topology Seminar University of Wisconsin May 6, 2011 Alex Suciu (Northeastern University) Betti numbers of abelian covers
Betti numbers of abelian covers Alex Suciu Northeastern University Geometry and Topology Seminar University of Wisconsin May 6, 2011 Alex Suciu (Northeastern University) Betti numbers of abelian covers
1 Fields and vector spaces
 1 Fields and vector spaces In this section we revise some algebraic preliminaries and establish notation. 1.1 Division rings and fields A division ring, or skew field, is a structure F with two binary
1 Fields and vector spaces In this section we revise some algebraic preliminaries and establish notation. 1.1 Division rings and fields A division ring, or skew field, is a structure F with two binary
On Asymptotic Bounds for the Number of Irreducible Components of the Moduli Space of Surfaces of General Type II
 Documenta Math. 197 On Asymptotic Bounds for the Number of Irreducible Components of the Moduli Space of Surfaces of General Type II Michael Lönne and Matteo Penegini Received: July 29, 2015 Revised: December
Documenta Math. 197 On Asymptotic Bounds for the Number of Irreducible Components of the Moduli Space of Surfaces of General Type II Michael Lönne and Matteo Penegini Received: July 29, 2015 Revised: December
A GUIDE FOR MORTALS TO TAME CONGRUENCE THEORY
 A GUIDE FOR MORTALS TO TAME CONGRUENCE THEORY Tame congruence theory is not an easy subject and it takes a considerable amount of effort to understand it. When I started this project, I believed that this
A GUIDE FOR MORTALS TO TAME CONGRUENCE THEORY Tame congruence theory is not an easy subject and it takes a considerable amount of effort to understand it. When I started this project, I believed that this
