Lecture 22: Section 4.7
|
|
|
- Camilla Farmer
- 5 years ago
- Views:
Transcription
1 Lecture 22: Section 47 Shuanglin Shao December 2, 213
2 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n ] r 2 = [ a 21 a 22 a 2n ] r m = [ a m1 a m2 a mn ] in R n that are formed from the rows of A are called the row vectors of A,
3 and the vectors a 11 a 21 c 1 =, c 2 = a 12 a 22,, c n = a 1n a 2n a m1 a m2 a mn in R m formed from the columns of A are called the column vectors of A
4 Example Let The row vectors of A are A = [ ] r 1 = [2, 1, ], r 2 = [3, 1, 4] and the column vectors of A are [ ] [ 2 1 c 1 =, c 3 2 = 1 ] [, c 3 = 4 ]
5 Def Definition If A is an m n matrix, then the subspace of R n spanned by the row vectors of A is called the row space of A, and the subspace of R m spanned by the column vectors of A is called the column space of A The solution space of the homogeneous system of equations Ax =, which is a subspace of R n, is called the null space of A
6 Theorem A system of linear equations Ax = b is consistent if and only if b is in the column space of A Proof The linear system Ax = b is a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn x 1 x 2 x n = b 1 b 2 b n
7 This linear system can be written as a 11 a 12 a 21 x 1 + x a x n a m1 This proves the theorem a m2 a 1n a 2n a mn = b 1 b 2 b m
8 Example 2 Example 2 Let Ax = b be the linear system x x 2 = x 3 3 Solving the linear system by Gaussian elimination yields x 1 = 2, x 2 = 1, x 3 = 3 Thus from the theorem above, = 1 9 3
9 Theorem If x is any solution of a consistent linear system Ax = b, and if S = {v 1, v 2,, v k } is a basis for the null space of A, then every solution of Ax = b can be expressed in the form x = x + c 1 v 1 + c 2 v c k v k Conversely, for all choices of scalars c 1, c 2,, c k, the vector x in this formula is a solution of Ax = b
10 Bases for row spaces, column spaces, and null spaces Theorem Elementary row operations do not change the null space of a matrix Theorem Elementary row operations do not change the row space of a matrix Both proofs follow if we consider the three elementary row operations: exchange two rows, a nonzero constant multiplying a row, adding a multiple of a row to another row
11 We just learned from the elementary row operations do not change the row space of a matrix However the elementary row operations do change the column space of a matrix For instance, let A = [ ]
12 [ 1 The column space is spanned by 1 elementary row operations, we obtain [ 1 1 A = ] Applying the third [ ] 1 The column space is spanned by The spanning vectors are different, which generate different column spaces ]
13 Finding a basis for the null space of a matrix A = Solving the equation Ax =, we obtain x = r s t 2 1 These three vectors generate the null space
14 Basis for row spaces and column spaces Theorem If a matrix R is in row echelon form, then the row vectors with the leading 1 s (the nonzero row vectors ) form a basis for the row space of R, and the column vectors with the leading 1 s of the row vectors form a bassi for the column space of R Remark Only when a matrix is in the row echelon form, the columns with leading 1 s of the row vectors form a basis for the column space In general, it is not true for the original matrix since the elementary row operations will change the column space
15 Example Bases for row and column spaces The matrix A = The basis for the row space is r 1 = [ ], r 2 = [ 1 3 ], r 3 = [ 1 ]
16 The basis for the column space is c 1 = 1, c 2 = 2 1, c 3 = 1
17 Example: basis for a row space by row reduction Find a basis for the row space of a matrix A = By row reductions, we have R =
18 The basis for the row space is r 1 = [ ], r 2 = [ ], r 3 = [ 1 5 ]
19 We have talked about how to find a basis for the null space of a matrix by solving the linear system; how to find a basis for the row space by using the elementary row operations and select the rows with the leading 1 s In the remark above: only when a matrix is in the row echelon form, the columns with leading 1 s of the row vectors form a basis for the column space In general, it is not true for the original matrix since the elementary row operations will change the column space We will see how to find a basis for the column space for a matrix
20 Definition If B is obtained from A by applying elementary row operations to A, then A and B are said to be row equivalent Theorem (a) (b) If A and B are row equivalent matrices, then A given set of column vectors of A is linearly independent if and only if the corresponding column vectors are linearly independent A given set of column vectors of A forms a basis for the column space of A if and only if the corresponding column vectors of B form a basis for the column space of B
21 Example Find a basis by row reductions A = By row reductions, we have R = The 1st, 3rd, 5th columns form a basis for the matrix R By the theorem above, since A and R are row equivalent, the 1st, 3rd, 5th columns of the matrix A form a basis for A
22 Basis for a vector space using row operations Find a basis for the subspace of R 5 spanned by the vectors and v 1 = (1, 2,,, 3), v 2 = (2, 5, 3, 2, 6), v 3 = (, 5, 15, 1, ), v 4 = (2, 6, 18, 8, 6) We use the vectors form a matrix, A =
23 By using elementary row operations, it reduces to R = The 1st, 2nd, 3rd rows form a basis for the subspace spanned by v 1, v 2, v 3, v 4
24 Finding a basis for the row space of A = consisting entirely of row vectors from A
25 Basis for the row space of a matrix We know how to find a basis for the row space of a matrix by using the elementary row operations The basis vectors come from the row echelon form of the original matrix If we want to find the basis expressible by the original matrix We use A T A T =
26 By elementary row operations, So the 1st, 2nd, 4th columns of A T form a basis for the column space of A T That is to say, the 1st, 2nd, 4th rows of A form a basis for the row space of A
27 Homework and Reading Homework Ex # 1, # 2 (b) (d), # 3(b), # 4, # 5 (b), # 6(b) (c), # 7 (b), # 9, #1 (c) True or false questions on page 237 Reading Section 48
Lecture 6 & 7. Shuanglin Shao. September 16th and 18th, 2013
 Lecture 6 & 7 Shuanglin Shao September 16th and 18th, 2013 1 Elementary matrices 2 Equivalence Theorem 3 A method of inverting matrices Def An n n matrice is called an elementary matrix if it can be obtained
Lecture 6 & 7 Shuanglin Shao September 16th and 18th, 2013 1 Elementary matrices 2 Equivalence Theorem 3 A method of inverting matrices Def An n n matrice is called an elementary matrix if it can be obtained
Row Space, Column Space, and Nullspace
 Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Lecture 18: Section 4.3
 Lecture 18: Section 4.3 Shuanglin Shao November 6, 2013 Linear Independence and Linear Dependence. We will discuss linear independence of vectors in a vector space. Definition. If S = {v 1, v 2,, v r }
Lecture 18: Section 4.3 Shuanglin Shao November 6, 2013 Linear Independence and Linear Dependence. We will discuss linear independence of vectors in a vector space. Definition. If S = {v 1, v 2,, v r }
Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination
 Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination Winfried Just, Ohio University September 22, 2017 Review: The coefficient matrix Consider a system of m linear equations in n variables.
Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination Winfried Just, Ohio University September 22, 2017 Review: The coefficient matrix Consider a system of m linear equations in n variables.
Midterm 1 Review. Written by Victoria Kala SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015
 Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Lecture 17: Section 4.2
 Lecture 17: Section 4.2 Shuanglin Shao November 4, 2013 Subspaces We will discuss subspaces of vector spaces. Subspaces Definition. A subset W is a vector space V is called a subspace of V if W is itself
Lecture 17: Section 4.2 Shuanglin Shao November 4, 2013 Subspaces We will discuss subspaces of vector spaces. Subspaces Definition. A subset W is a vector space V is called a subspace of V if W is itself
MTH 362: Advanced Engineering Mathematics
 MTH 362: Advanced Engineering Mathematics Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 26, 2017 1 Linear Independence and Dependence of Vectors
MTH 362: Advanced Engineering Mathematics Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 26, 2017 1 Linear Independence and Dependence of Vectors
Determine whether the following system has a trivial solution or non-trivial solution:
 Practice Questions Lecture # 7 and 8 Question # Determine whether the following system has a trivial solution or non-trivial solution: x x + x x x x x The coefficient matrix is / R, R R R+ R The corresponding
Practice Questions Lecture # 7 and 8 Question # Determine whether the following system has a trivial solution or non-trivial solution: x x + x x x x x The coefficient matrix is / R, R R R+ R The corresponding
Math 3C Lecture 20. John Douglas Moore
 Math 3C Lecture 20 John Douglas Moore May 18, 2009 TENTATIVE FORMULA I Midterm I: 20% Midterm II: 20% Homework: 10% Quizzes: 10% Final: 40% TENTATIVE FORMULA II Higher of two midterms: 30% Homework: 10%
Math 3C Lecture 20 John Douglas Moore May 18, 2009 TENTATIVE FORMULA I Midterm I: 20% Midterm II: 20% Homework: 10% Quizzes: 10% Final: 40% TENTATIVE FORMULA II Higher of two midterms: 30% Homework: 10%
Chapter 3. Directions: For questions 1-11 mark each statement True or False. Justify each answer.
 Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
The definition of a vector space (V, +, )
 The definition of a vector space (V, +, ) 1. For any u and v in V, u + v is also in V. 2. For any u and v in V, u + v = v + u. 3. For any u, v, w in V, u + ( v + w) = ( u + v) + w. 4. There is an element
The definition of a vector space (V, +, ) 1. For any u and v in V, u + v is also in V. 2. For any u and v in V, u + v = v + u. 3. For any u, v, w in V, u + ( v + w) = ( u + v) + w. 4. There is an element
Algorithms to Compute Bases and the Rank of a Matrix
 Algorithms to Compute Bases and the Rank of a Matrix Subspaces associated to a matrix Suppose that A is an m n matrix The row space of A is the subspace of R n spanned by the rows of A The column space
Algorithms to Compute Bases and the Rank of a Matrix Subspaces associated to a matrix Suppose that A is an m n matrix The row space of A is the subspace of R n spanned by the rows of A The column space
Linear Algebra I Lecture 8
 Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
MATH 304 Linear Algebra Lecture 20: Review for Test 1.
 MATH 304 Linear Algebra Lecture 20: Review for Test 1. Topics for Test 1 Part I: Elementary linear algebra (Leon 1.1 1.4, 2.1 2.2) Systems of linear equations: elementary operations, Gaussian elimination,
MATH 304 Linear Algebra Lecture 20: Review for Test 1. Topics for Test 1 Part I: Elementary linear algebra (Leon 1.1 1.4, 2.1 2.2) Systems of linear equations: elementary operations, Gaussian elimination,
R b. x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 1 1, x h. , x p. x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9
 The full solution of Ax b x x p x h : The general solution is the sum of any particular solution of the system Ax b plus the general solution of the corresponding homogeneous system Ax. ) Reduce A b to
The full solution of Ax b x x p x h : The general solution is the sum of any particular solution of the system Ax b plus the general solution of the corresponding homogeneous system Ax. ) Reduce A b to
Lecture 18: The Rank of a Matrix and Consistency of Linear Systems
 Lecture 18: The Rank of a Matrix and Consistency of Linear Systems Winfried Just Department of Mathematics, Ohio University February 28, 218 Review: The linear span Definition Let { v 1, v 2,..., v n }
Lecture 18: The Rank of a Matrix and Consistency of Linear Systems Winfried Just Department of Mathematics, Ohio University February 28, 218 Review: The linear span Definition Let { v 1, v 2,..., v n }
YORK UNIVERSITY. Faculty of Science Department of Mathematics and Statistics MATH M Test #1. July 11, 2013 Solutions
 YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 222 3. M Test # July, 23 Solutions. For each statement indicate whether it is always TRUE or sometimes FALSE. Note: For
YORK UNIVERSITY Faculty of Science Department of Mathematics and Statistics MATH 222 3. M Test # July, 23 Solutions. For each statement indicate whether it is always TRUE or sometimes FALSE. Note: For
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix.
 MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix. Basis Definition. Let V be a vector space. A linearly independent spanning set for V is called a basis.
MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix. Basis Definition. Let V be a vector space. A linearly independent spanning set for V is called a basis.
6.4 BASIS AND DIMENSION (Review) DEF 1 Vectors v 1, v 2,, v k in a vector space V are said to form a basis for V if. (a) v 1,, v k span V and
 6.4 BASIS AND DIMENSION (Review) DEF 1 Vectors v 1, v 2,, v k in a vector space V are said to form a basis for V if (a) v 1,, v k span V and (b) v 1,, v k are linearly independent. HMHsueh 1 Natural Basis
6.4 BASIS AND DIMENSION (Review) DEF 1 Vectors v 1, v 2,, v k in a vector space V are said to form a basis for V if (a) v 1,, v k span V and (b) v 1,, v k are linearly independent. HMHsueh 1 Natural Basis
Solutions to Homework 5 - Math 3410
 Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
Chapter 1. Vectors, Matrices, and Linear Spaces
 1.6 Homogeneous Systems, Subspaces and Bases 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.6. Homogeneous Systems, Subspaces and Bases Note. In this section we explore the structure of the solution
1.6 Homogeneous Systems, Subspaces and Bases 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.6. Homogeneous Systems, Subspaces and Bases Note. In this section we explore the structure of the solution
Department of Aerospace Engineering AE602 Mathematics for Aerospace Engineers Assignment No. 4
 Department of Aerospace Engineering AE6 Mathematics for Aerospace Engineers Assignment No.. Decide whether or not the following vectors are linearly independent, by solving c v + c v + c 3 v 3 + c v :
Department of Aerospace Engineering AE6 Mathematics for Aerospace Engineers Assignment No.. Decide whether or not the following vectors are linearly independent, by solving c v + c v + c 3 v 3 + c v :
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3
 ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
We showed that adding a vector to a basis produces a linearly dependent set of vectors; more is true.
 Dimension We showed that adding a vector to a basis produces a linearly dependent set of vectors; more is true. Lemma If a vector space V has a basis B containing n vectors, then any set containing more
Dimension We showed that adding a vector to a basis produces a linearly dependent set of vectors; more is true. Lemma If a vector space V has a basis B containing n vectors, then any set containing more
Lecture 6: Spanning Set & Linear Independency
 Lecture 6: Elif Tan Ankara University Elif Tan (Ankara University) Lecture 6 / 0 Definition (Linear Combination) Let v, v 2,..., v k be vectors in (V,, ) a vector space. A vector v V is called a linear
Lecture 6: Elif Tan Ankara University Elif Tan (Ankara University) Lecture 6 / 0 Definition (Linear Combination) Let v, v 2,..., v k be vectors in (V,, ) a vector space. A vector v V is called a linear
Chapter 1: Systems of Linear Equations
 Chapter : Systems of Linear Equations February, 9 Systems of linear equations Linear systems Lecture A linear equation in variables x, x,, x n is an equation of the form a x + a x + + a n x n = b, where
Chapter : Systems of Linear Equations February, 9 Systems of linear equations Linear systems Lecture A linear equation in variables x, x,, x n is an equation of the form a x + a x + + a n x n = b, where
DEF 1 Let V be a vector space and W be a nonempty subset of V. If W is a vector space w.r.t. the operations, in V, then W is called a subspace of V.
 6.2 SUBSPACES DEF 1 Let V be a vector space and W be a nonempty subset of V. If W is a vector space w.r.t. the operations, in V, then W is called a subspace of V. HMHsueh 1 EX 1 (Ex. 1) Every vector space
6.2 SUBSPACES DEF 1 Let V be a vector space and W be a nonempty subset of V. If W is a vector space w.r.t. the operations, in V, then W is called a subspace of V. HMHsueh 1 EX 1 (Ex. 1) Every vector space
Review Notes for Linear Algebra True or False Last Updated: February 22, 2010
 Review Notes for Linear Algebra True or False Last Updated: February 22, 2010 Chapter 4 [ Vector Spaces 4.1 If {v 1,v 2,,v n } and {w 1,w 2,,w n } are linearly independent, then {v 1 +w 1,v 2 +w 2,,v n
Review Notes for Linear Algebra True or False Last Updated: February 22, 2010 Chapter 4 [ Vector Spaces 4.1 If {v 1,v 2,,v n } and {w 1,w 2,,w n } are linearly independent, then {v 1 +w 1,v 2 +w 2,,v n
REPLACE ONE ROW BY ADDING THE SCALAR MULTIPLE OF ANOTHER ROW
 20 CHAPTER 1 Systems of Linear Equations REPLACE ONE ROW BY ADDING THE SCALAR MULTIPLE OF ANOTHER ROW The last type of operation is slightly more complicated. Suppose that we want to write down the elementary
20 CHAPTER 1 Systems of Linear Equations REPLACE ONE ROW BY ADDING THE SCALAR MULTIPLE OF ANOTHER ROW The last type of operation is slightly more complicated. Suppose that we want to write down the elementary
Chapter 5. Linear Algebra. Sections A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra Sections 5.1 5.3 A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are
Chapter 5. Linear Algebra Sections 5.1 5.3 A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are
Linear Independence x
 Linear Independence A consistent system of linear equations with matrix equation Ax = b, where A is an m n matrix, has a solution set whose graph in R n is a linear object, that is, has one of only n +
Linear Independence A consistent system of linear equations with matrix equation Ax = b, where A is an m n matrix, has a solution set whose graph in R n is a linear object, that is, has one of only n +
System of Linear Equations
 Math 20F Linear Algebra Lecture 2 1 System of Linear Equations Slide 1 Definition 1 Fix a set of numbers a ij, b i, where i = 1,, m and j = 1,, n A system of m linear equations in n variables x j, is given
Math 20F Linear Algebra Lecture 2 1 System of Linear Equations Slide 1 Definition 1 Fix a set of numbers a ij, b i, where i = 1,, m and j = 1,, n A system of m linear equations in n variables x j, is given
1. TRUE or FALSE. 2. Find the complete solution set to the system:
 TRUE or FALSE (a A homogenous system with more variables than equations has a nonzero solution True (The number of pivots is going to be less than the number of columns and therefore there is a free variable
TRUE or FALSE (a A homogenous system with more variables than equations has a nonzero solution True (The number of pivots is going to be less than the number of columns and therefore there is a free variable
MATH 2331 Linear Algebra. Section 1.1 Systems of Linear Equations. Finding the solution to a set of two equations in two variables: Example 1: Solve:
 MATH 2331 Linear Algebra Section 1.1 Systems of Linear Equations Finding the solution to a set of two equations in two variables: Example 1: Solve: x x = 3 1 2 2x + 4x = 12 1 2 Geometric meaning: Do these
MATH 2331 Linear Algebra Section 1.1 Systems of Linear Equations Finding the solution to a set of two equations in two variables: Example 1: Solve: x x = 3 1 2 2x + 4x = 12 1 2 Geometric meaning: Do these
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Notes on Row Reduction
 Notes on Row Reduction Francis J. Narcowich Department of Mathematics Texas A&M University September The Row-Reduction Algorithm The row-reduced form of a matrix contains a great deal of information, both
Notes on Row Reduction Francis J. Narcowich Department of Mathematics Texas A&M University September The Row-Reduction Algorithm The row-reduced form of a matrix contains a great deal of information, both
Chapter 3. Vector spaces
 Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
Chapter 3. Vector spaces Lecture notes for MA1111 P. Karageorgis pete@maths.tcd.ie 1/22 Linear combinations Suppose that v 1,v 2,...,v n and v are vectors in R m. Definition 3.1 Linear combination We say
System of Linear Equations
 Chapter 7 - S&B Gaussian and Gauss-Jordan Elimination We will study systems of linear equations by describing techniques for solving such systems. The preferred solution technique- Gaussian elimination-
Chapter 7 - S&B Gaussian and Gauss-Jordan Elimination We will study systems of linear equations by describing techniques for solving such systems. The preferred solution technique- Gaussian elimination-
MATH 2360 REVIEW PROBLEMS
 MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
Worksheet for Lecture 23 (due December 4) Section 6.1 Inner product, length, and orthogonality
 Worksheet for Lecture (due December 4) Name: Section 6 Inner product, length, and orthogonality u Definition Let u = u n product or dot product to be and v = v v n be vectors in R n We define their inner
Worksheet for Lecture (due December 4) Name: Section 6 Inner product, length, and orthogonality u Definition Let u = u n product or dot product to be and v = v v n be vectors in R n We define their inner
This MUST hold matrix multiplication satisfies the distributive property.
 The columns of AB are combinations of the columns of A. The reason is that each column of AB equals A times the corresponding column of B. But that is a linear combination of the columns of A with coefficients
The columns of AB are combinations of the columns of A. The reason is that each column of AB equals A times the corresponding column of B. But that is a linear combination of the columns of A with coefficients
Topics. Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij
 Topics Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij or a ij lives in row i and column j Definition of a matrix
Topics Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij or a ij lives in row i and column j Definition of a matrix
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 1 Material Dr. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University January 9, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 1 Material Dr. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University January 9, 2018 Linear Algebra (MTH 464)
Chapter 5. Linear Algebra. Sections A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra Sections 5.1 5.3 A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are
Chapter 5. Linear Algebra Sections 5.1 5.3 A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are
LECTURES 14/15: LINEAR INDEPENDENCE AND BASES
 LECTURES 14/15: LINEAR INDEPENDENCE AND BASES MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1. Linear Independence We have seen in examples of span sets of vectors that sometimes adding additional vectors
LECTURES 14/15: LINEAR INDEPENDENCE AND BASES MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1. Linear Independence We have seen in examples of span sets of vectors that sometimes adding additional vectors
Systems of Linear Equations. By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University
 Systems of Linear Equations By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University Standard of Competency: Understanding the properties of systems of linear equations, matrices,
Systems of Linear Equations By: Tri Atmojo Kusmayadi and Mardiyana Mathematics Education Sebelas Maret University Standard of Competency: Understanding the properties of systems of linear equations, matrices,
Math 3C Lecture 25. John Douglas Moore
 Math 3C Lecture 25 John Douglas Moore June 1, 2009 Let V be a vector space. A basis for V is a collection of vectors {v 1,..., v k } such that 1. V = Span{v 1,..., v k }, and 2. {v 1,..., v k } are linearly
Math 3C Lecture 25 John Douglas Moore June 1, 2009 Let V be a vector space. A basis for V is a collection of vectors {v 1,..., v k } such that 1. V = Span{v 1,..., v k }, and 2. {v 1,..., v k } are linearly
Remark By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
SYMBOL EXPLANATION EXAMPLE
 MATH 4310 PRELIM I REVIEW Notation These are the symbols we have used in class, leading up to Prelim I, and which I will use on the exam SYMBOL EXPLANATION EXAMPLE {a, b, c, } The is the way to write the
MATH 4310 PRELIM I REVIEW Notation These are the symbols we have used in class, leading up to Prelim I, and which I will use on the exam SYMBOL EXPLANATION EXAMPLE {a, b, c, } The is the way to write the
Rank and Nullity. MATH 322, Linear Algebra I. J. Robert Buchanan. Spring Department of Mathematics
 Rank and Nullity MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Objectives We have defined and studied the important vector spaces associated with matrices (row space,
Rank and Nullity MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Objectives We have defined and studied the important vector spaces associated with matrices (row space,
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
5x 2 = 10. x 1 + 7(2) = 4. x 1 3x 2 = 4. 3x 1 + 9x 2 = 8
 1 To solve the system x 1 + x 2 = 4 2x 1 9x 2 = 2 we find an (easier to solve) equivalent system as follows: Replace equation 2 with (2 times equation 1 + equation 2): x 1 + x 2 = 4 Solve equation 2 for
1 To solve the system x 1 + x 2 = 4 2x 1 9x 2 = 2 we find an (easier to solve) equivalent system as follows: Replace equation 2 with (2 times equation 1 + equation 2): x 1 + x 2 = 4 Solve equation 2 for
Math 4A Notes. Written by Victoria Kala Last updated June 11, 2017
 Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
DM559 Linear and Integer Programming. Lecture 2 Systems of Linear Equations. Marco Chiarandini
 DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
Math 54 HW 4 solutions
 Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
Math 54 HW 4 solutions 2.2. Section 2.2 (a) False: Recall that performing a series of elementary row operations A is equivalent to multiplying A by a series of elementary matrices. Suppose that E,...,
SECTION 3.3. PROBLEM 22. The null space of a matrix A is: N(A) = {X : AX = 0}. Here are the calculations of AX for X = a,b,c,d, and e. =
 SECTION 3.3. PROBLEM. The null space of a matrix A is: N(A) {X : AX }. Here are the calculations of AX for X a,b,c,d, and e. Aa [ ][ ] 3 3 [ ][ ] Ac 3 3 [ ] 3 3 [ ] 4+4 6+6 Ae [ ], Ab [ ][ ] 3 3 3 [ ]
SECTION 3.3. PROBLEM. The null space of a matrix A is: N(A) {X : AX }. Here are the calculations of AX for X a,b,c,d, and e. Aa [ ][ ] 3 3 [ ][ ] Ac 3 3 [ ] 3 3 [ ] 4+4 6+6 Ae [ ], Ab [ ][ ] 3 3 3 [ ]
Math Final December 2006 C. Robinson
 Math 285-1 Final December 2006 C. Robinson 2 5 8 5 1 2 0-1 0 1. (21 Points) The matrix A = 1 2 2 3 1 8 3 2 6 has the reduced echelon form U = 0 0 1 2 0 0 0 0 0 1. 2 6 1 0 0 0 0 0 a. Find a basis for the
Math 285-1 Final December 2006 C. Robinson 2 5 8 5 1 2 0-1 0 1. (21 Points) The matrix A = 1 2 2 3 1 8 3 2 6 has the reduced echelon form U = 0 0 1 2 0 0 0 0 0 1. 2 6 1 0 0 0 0 0 a. Find a basis for the
Math 2174: Practice Midterm 1
 Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
MAT 242 CHAPTER 4: SUBSPACES OF R n
 MAT 242 CHAPTER 4: SUBSPACES OF R n JOHN QUIGG 1. Subspaces Recall that R n is the set of n 1 matrices, also called vectors, and satisfies the following properties: x + y = y + x x + (y + z) = (x + y)
MAT 242 CHAPTER 4: SUBSPACES OF R n JOHN QUIGG 1. Subspaces Recall that R n is the set of n 1 matrices, also called vectors, and satisfies the following properties: x + y = y + x x + (y + z) = (x + y)
1 Last time: inverses
 MATH Linear algebra (Fall 8) Lecture 8 Last time: inverses The following all mean the same thing for a function f : X Y : f is invertible f is one-to-one and onto 3 For each b Y there is exactly one a
MATH Linear algebra (Fall 8) Lecture 8 Last time: inverses The following all mean the same thing for a function f : X Y : f is invertible f is one-to-one and onto 3 For each b Y there is exactly one a
Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.
 Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.. Recall that P 3 denotes the vector space of polynomials of degree less
Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.. Recall that P 3 denotes the vector space of polynomials of degree less
2018 Fall 2210Q Section 013 Midterm Exam I Solution
 8 Fall Q Section 3 Midterm Exam I Solution True or False questions ( points = points) () An example of a linear combination of vectors v, v is the vector v. True. We can write v as v + v. () If two matrices
8 Fall Q Section 3 Midterm Exam I Solution True or False questions ( points = points) () An example of a linear combination of vectors v, v is the vector v. True. We can write v as v + v. () If two matrices
1 - Systems of Linear Equations
 1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
Section Gaussian Elimination
 Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Section. - Gaussian Elimination A matrix is said to be in row echelon form (REF) if it has the following properties:. The first nonzero entry in any row is a. We call this a leading one or pivot one..
Solving Linear Systems Using Gaussian Elimination
 Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Matrices and RRE Form
 Matrices and RRE Form Notation R is the real numbers, C is the complex numbers (we will only consider complex numbers towards the end of the course) is read as an element of For instance, x R means that
Matrices and RRE Form Notation R is the real numbers, C is the complex numbers (we will only consider complex numbers towards the end of the course) is read as an element of For instance, x R means that
Linear independence, span, basis, dimension - and their connection with linear systems
 Linear independence span basis dimension - and their connection with linear systems Linear independence of a set of vectors: We say the set of vectors v v..v k is linearly independent provided c v c v..c
Linear independence span basis dimension - and their connection with linear systems Linear independence of a set of vectors: We say the set of vectors v v..v k is linearly independent provided c v c v..c
MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian.
 MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian. Spanning set Let S be a subset of a vector space V. Definition. The span of the set S is the smallest subspace W V that contains S. If
MATH 304 Linear Algebra Lecture 10: Linear independence. Wronskian. Spanning set Let S be a subset of a vector space V. Definition. The span of the set S is the smallest subspace W V that contains S. If
Elementary Matrices. MATH 322, Linear Algebra I. J. Robert Buchanan. Spring Department of Mathematics
 Elementary Matrices MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Outline Today s discussion will focus on: elementary matrices and their properties, using elementary
Elementary Matrices MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Outline Today s discussion will focus on: elementary matrices and their properties, using elementary
NAME MATH 304 Examination 2 Page 1
 NAME MATH 4 Examination 2 Page. [8 points (a) Find the following determinant. However, use only properties of determinants, without calculating directly (that is without expanding along a column or row
NAME MATH 4 Examination 2 Page. [8 points (a) Find the following determinant. However, use only properties of determinants, without calculating directly (that is without expanding along a column or row
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
MATH 225 Summer 2005 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 2005
 MATH 225 Summer 25 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 25 Department of Mathematical and Statistical Sciences University of Alberta Question 1. [p 224. #2] The set of all
MATH 225 Summer 25 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 25 Department of Mathematical and Statistical Sciences University of Alberta Question 1. [p 224. #2] The set of all
Study Guide for Linear Algebra Exam 2
 Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Lecture Notes: Solving Linear Systems with Gauss Elimination
 Lecture Notes: Solving Linear Systems with Gauss Elimination Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Echelon Form and Elementary
Lecture Notes: Solving Linear Systems with Gauss Elimination Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Echelon Form and Elementary
1. Let m 1 and n 1 be two natural numbers such that m > n. Which of the following is/are true?
 . Let m and n be two natural numbers such that m > n. Which of the following is/are true? (i) A linear system of m equations in n variables is always consistent. (ii) A linear system of n equations in
. Let m and n be two natural numbers such that m > n. Which of the following is/are true? (i) A linear system of m equations in n variables is always consistent. (ii) A linear system of n equations in
Linear Algebra Exam 1 Spring 2007
 Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Methods for Solving Linear Systems Part 2
 Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
Math 1314 Week #14 Notes
 Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
1 Last time: linear systems and row operations
 1 Last time: linear systems and row operations Here s what we did last time: a system of linear equations or linear system is a list of equations a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22
1 Last time: linear systems and row operations Here s what we did last time: a system of linear equations or linear system is a list of equations a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22
Math 314H EXAM I. 1. (28 points) The row reduced echelon form of the augmented matrix for the system. is the matrix
 Math 34H EXAM I Do all of the problems below. Point values for each of the problems are adjacent to the problem number. Calculators may be used to check your answer but not to arrive at your answer. That
Math 34H EXAM I Do all of the problems below. Point values for each of the problems are adjacent to the problem number. Calculators may be used to check your answer but not to arrive at your answer. That
MATH 2050 Assignment 6 Fall 2018 Due: Thursday, November 1. x + y + 2z = 2 x + y + z = c 4x + 2z = 2
 MATH 5 Assignment 6 Fall 8 Due: Thursday, November [5]. For what value of c does have a solution? Is it unique? x + y + z = x + y + z = c 4x + z = Writing the system as an augmented matrix, we have c R
MATH 5 Assignment 6 Fall 8 Due: Thursday, November [5]. For what value of c does have a solution? Is it unique? x + y + z = x + y + z = c 4x + z = Writing the system as an augmented matrix, we have c R
Determining a span. λ + µ + ν = x 2λ + 2µ 10ν = y λ + 3µ 9ν = z.
 Determining a span Set V = R 3 and v 1 = (1, 2, 1), v 2 := (1, 2, 3), v 3 := (1 10, 9). We want to determine the span of these vectors. In other words, given (x, y, z) R 3, when is (x, y, z) span(v 1,
Determining a span Set V = R 3 and v 1 = (1, 2, 1), v 2 := (1, 2, 3), v 3 := (1 10, 9). We want to determine the span of these vectors. In other words, given (x, y, z) R 3, when is (x, y, z) span(v 1,
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T. KEMP)
 MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
MATH 20F: LINEAR ALGEBRA LECTURE B00 (T KEMP) Definition 01 If T (x) = Ax is a linear transformation from R n to R m then Nul (T ) = {x R n : T (x) = 0} = Nul (A) Ran (T ) = {Ax R m : x R n } = {b R m
18.06 Problem Set 3 Solution Due Wednesday, 25 February 2009 at 4 pm in Total: 160 points.
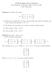 8.6 Problem Set 3 Solution Due Wednesday, 25 February 29 at 4 pm in 2-6. Total: 6 points. Problem : Consider the matrix A = 2 4 2 6 3 4 2 7 (a) Reduce A to echelon form U, find a special solution for each
8.6 Problem Set 3 Solution Due Wednesday, 25 February 29 at 4 pm in 2-6. Total: 6 points. Problem : Consider the matrix A = 2 4 2 6 3 4 2 7 (a) Reduce A to echelon form U, find a special solution for each
MODEL ANSWERS TO THE FIRST QUIZ. 1. (18pts) (i) Give the definition of a m n matrix. A m n matrix with entries in a field F is a function
 MODEL ANSWERS TO THE FIRST QUIZ 1. (18pts) (i) Give the definition of a m n matrix. A m n matrix with entries in a field F is a function A: I J F, where I is the set of integers between 1 and m and J is
MODEL ANSWERS TO THE FIRST QUIZ 1. (18pts) (i) Give the definition of a m n matrix. A m n matrix with entries in a field F is a function A: I J F, where I is the set of integers between 1 and m and J is
Kevin James. MTHSC 3110 Section 4.3 Linear Independence in Vector Sp
 MTHSC 3 Section 4.3 Linear Independence in Vector Spaces; Bases Definition Let V be a vector space and let { v. v 2,..., v p } V. If the only solution to the equation x v + x 2 v 2 + + x p v p = is the
MTHSC 3 Section 4.3 Linear Independence in Vector Spaces; Bases Definition Let V be a vector space and let { v. v 2,..., v p } V. If the only solution to the equation x v + x 2 v 2 + + x p v p = is the
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
CS6964: Notes On Linear Systems
 CS6964: Notes On Linear Systems 1 Linear Systems Systems of equations that are linear in the unknowns are said to be linear systems For instance ax 1 + bx 2 dx 1 + ex 2 = c = f gives 2 equations and 2
CS6964: Notes On Linear Systems 1 Linear Systems Systems of equations that are linear in the unknowns are said to be linear systems For instance ax 1 + bx 2 dx 1 + ex 2 = c = f gives 2 equations and 2
CSL361 Problem set 4: Basic linear algebra
 CSL361 Problem set 4: Basic linear algebra February 21, 2017 [Note:] If the numerical matrix computations turn out to be tedious, you may use the function rref in Matlab. 1 Row-reduced echelon matrices
CSL361 Problem set 4: Basic linear algebra February 21, 2017 [Note:] If the numerical matrix computations turn out to be tedious, you may use the function rref in Matlab. 1 Row-reduced echelon matrices
Lecture 4: Gaussian Elimination and Homogeneous Equations
 Lecture 4: Gaussian Elimination and Homogeneous Equations Reduced Row Echelon Form An augmented matrix associated to a system of linear equations is said to be in Reduced Row Echelon Form (RREF) if the
Lecture 4: Gaussian Elimination and Homogeneous Equations Reduced Row Echelon Form An augmented matrix associated to a system of linear equations is said to be in Reduced Row Echelon Form (RREF) if the
This lecture is a review for the exam. The majority of the exam is on what we ve learned about rectangular matrices.
 Exam review This lecture is a review for the exam. The majority of the exam is on what we ve learned about rectangular matrices. Sample question Suppose u, v and w are non-zero vectors in R 7. They span
Exam review This lecture is a review for the exam. The majority of the exam is on what we ve learned about rectangular matrices. Sample question Suppose u, v and w are non-zero vectors in R 7. They span
MAC1105-College Algebra. Chapter 5-Systems of Equations & Matrices
 MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
MA 0540 fall 2013, Row operations on matrices
 MA 0540 fall 2013, Row operations on matrices December 2, 2013 This is all about m by n matrices (of real or complex numbers). If A is such a matrix then A corresponds to a linear map F n F m, which we
MA 0540 fall 2013, Row operations on matrices December 2, 2013 This is all about m by n matrices (of real or complex numbers). If A is such a matrix then A corresponds to a linear map F n F m, which we
web: HOMEWORK 1
 MAT 207 LINEAR ALGEBRA I 2009207 Dokuz Eylül University, Faculty of Science, Department of Mathematics Instructor: Engin Mermut web: http://kisideuedutr/enginmermut/ HOMEWORK VECTORS IN THE n-dimensional
MAT 207 LINEAR ALGEBRA I 2009207 Dokuz Eylül University, Faculty of Science, Department of Mathematics Instructor: Engin Mermut web: http://kisideuedutr/enginmermut/ HOMEWORK VECTORS IN THE n-dimensional
1111: Linear Algebra I
 1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 13 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 13 1 / 8 The coordinate vector space R n We already used vectors in n dimensions
1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 13 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 13 1 / 8 The coordinate vector space R n We already used vectors in n dimensions
Math 323 Exam 2 Sample Problems Solution Guide October 31, 2013
 Math Exam Sample Problems Solution Guide October, Note that the following provides a guide to the solutions on the sample problems, but in some cases the complete solution would require more work or justification
Math Exam Sample Problems Solution Guide October, Note that the following provides a guide to the solutions on the sample problems, but in some cases the complete solution would require more work or justification
