SYMBOL EXPLANATION EXAMPLE
|
|
|
- Everett Daniels
- 5 years ago
- Views:
Transcription
1 MATH 4310 PRELIM I REVIEW Notation These are the symbols we have used in class, leading up to Prelim I, and which I will use on the exam SYMBOL EXPLANATION EXAMPLE {a, b, c, } The is the way to write the set containing the elements a, b, c, etc {1, 2} is the set whose elements are the numbers 1 and 2 or or \ N, N Z, Z Read this symbol as is an element of a A means that a is an element of the set A a, b A means that both a and b are elements of the set A In the above example, 1, 2 {1, 2} These are symbols for subset You can use If A = {1, 5} and B = {1, 5, 16}, then A B either If A and B are sets then A B if all of the elements of A are also elements of B This is the symbol for union If A and B are sets then A B is the set that consists of all of the elements in A and all of the elements in B This is the symbol for intersection If A and B are sets then A B is the set that consists of all of the elements that are in both of A and B These are symbols for set minus If A and B are sets then B A (or B \ A) is the set which consists of the elements of B which are NOT elements of A If A = {1, 2} and B = {2, 3, 4}, then A B = {1, 2, 3, 4} If A = {1, 2} and B = {2, 3, 4}, then A B = {2} If A = {1, 2} and B = {2, 3, 4}, then B A = {3, 4} This is the set of natural numbers, ie N = {0, 1, 2, } 17, 24, , N This is the set of integers, ie Z = {, 2, 1, 0, 1, 2, } 63, 24, Z Q, Q This is the set of rational numbers, ie fractions of integers If a, b Z and b 0, then a b Q We have 1 2, 2 17 Q Note that Z Q 1
2 SYMBOL EXPLANATION EXAMPLE R, R C, C F, F V S(a 1,, a n ) S + T A = (α i,j ) v w This is the set of real numbers, numbers that may be written in decimal form We did not give a more rigorous definition of the real numbers We have assumed the basic properties of arithmetic in the real number system This is the set of complex numbers, numbers that may be written in the form a + b 1 where a, b R The number a is the real part, and the number b is the imaginary part We sometimes denote i = 1 We may add complex numbers by adding the real and imaginary components individually This denotes a field or number system that has two operations + and that satisfy seven axioms If you want to refer to the axioms, you may either refer to an axiom by the number we used in class, or by a description such as commutativity or existence of multiplicative inverses We denote general field elements by Greek letters α F This denotes a vector space (over a field F) together with two operations, + : V V V and : F V V, satisfying seven axioms We denote vectors by Roman letters v V This represents the subspace of all linear combinations λi a i of a 1,, a n This denotes the sum of two subspaces S and T of a vector space V It is again a subspace of V This denotes a matrix with entries in a field F The set of m n matrices with entries in F is denoted M m n (F) This denotes the dot product of two vectors v, w F n, n defined by (α 1,, α n ) (β 1,, β n ) = α i β i i=1 3, 1, 1 2, 2, π R Note that Q R 3, 1, 1 2, 2, π, 2 3 i, 1 C Note that R C Examples include Q, R, C, and the integers modulo a prime F p You may use on the exam that these are fields Neither N nor Z is a field! F n, Pol n (F), Pol(F) = F[x], F un(x, F) are all vector spaces over the field F We have a few special examples for the field F = R: C 0 (R), C k (R), C (R) Let e 1,, e n denote the standard basis vectors in F n That is, e i is the vector with a single non-zero entry in the i th coordinate Then F n = S(e 1,, e n ) The xy-plane in R 3 is the sum of S = {(α, 0, 0} and T = {(0, β, 0)} [ 1 1 π 0 ] [ M 2 2 (R) and (1, 1, 0) (1, 1, 0) = = 2 in R 3, and (1, 1, 0) (1, 1, 0) = = 0 in (F 2 ) 3 ] M 2 3 (F 7 ) 2
3 Material we have covered This is a brief summary of the material we have covered, and that you are responsible for knowing for Prelim I The material we have covered corresponds to 1 9 in our textbook Linear Algebra, An Introductory Approach, by Charles W Curtis It is listed here in a slightly different order from how we covered it in class The axioms we assume are the ground rules we agree upon For us, we have agreed on the properties of arithmetic of the real and complex numbers We are also assuming some familiar properties of sets, as laid out in the notation tables above Methods of proof We specifically discussed direct proofs and proofs by induction A fields is a set with two operations, + and, satisfying by seven axioms We deduced a number of basic properties from the axioms A vector space over a field F is a set V of vectors, together with two operations, vector addition + : V V V and scalar multiplication : F V V, satisfying seven axioms We deduced a number of basic properties of vector spaces from the axioms A subspace of a vector space is a subset of vectors that is closed under vector addition and scalar multiplication We defined linear combinations of a set of vectors {v 1,, v n }, and showed that the set of all linear combinations of {v 1,, v n } is a subspace, denoted S(v 1,, v n ) It is the smallest subspace of V that contains the set {v 1,, v n } We defined linearly dependent and linearly independent sets of vectors For a single vector, it is linearly independent if and only if it is not zero Two vectors are linearly independent if and only if they are not scalar multiples of one another A subspace S V is generated by or spanned by a set of vectors {a 1,, a n } if it is the space of all linear combinations of {a 1,, a n }, S = S(a 1,, a n ) If S is spanned by n vectors, then for any m > n, any set of m vectors in S will necessarily be linearly dependent A set of vectors {b 1,, b k } V is called a basis for V if it is a linearly independent set and it spans V We proved that every basis has the same number of vectors, and we define the dimension of a vector space to be * 0 if V = {0} (and we declare S( ) = {0}, so is a basis); * k if there is a basis of V containing k elements; and * infinite, for all other vector spaces Every finitely generated vector space has a basis, and the basis can be chosen to be a subset of any generating set Thus, every spanning set containing exactly dim(v ) vectors must be a basis In a finite dimensional vector space, any list of linearly independent vectors may be extended to be a basis The vectors you must add can be chosen from a prescribed basis Thus, every linearly independent set containing exactly dim(v ) vectors must be a basis The sum S + T of two vector subspaces S and T of V is again a subspace of V, and its dimension satisfies dim(s + T ) = dim(s) + dim(t ) dim(s T ) A matrix is an m n array of scalars α i,j F It has m rows r 1,, r m that can be thought of as vectors in F n, and n columns c 1,, c n that can be thought of as vectors in F m The row space of A is R(A) = S(r 1,, r m ) F n, and the column space is C (A) = S(c 1,, c n ) F m We recalled some properties and algorithms that you should have seen in Math 2210/2940 (at least over R or C), and discussed how they work when the entries are in a more general field A matrix is in row echelon form if * all non-zero rows of the matrix are at the top of the matrix; * the left-most non-zero entry in a row (called the leading coefficient or pivot) is strictly to the right of the pivot in the row above; and * all entries below a pivot are zero A matrix is in reduced row echelon form if, in addition, * the pivots are all 1, and the pivot column has a single non-zero entry (the pivot) 3
4 We may use elementary row operations to transform a matrix into one that is in (reduced) row echelon form They are I Exchange two rows; II Add µ times one row to another row, for µ F; and III Multiply a row by a non-zero scalar 0 µ F Two matrices are row equivalent if there is a sequence of elementary row operations starting from one and ending at the other Row equivalent matrices have the same row space The algorithm to transform a matrix into one in (reduced) row echelon form systematically is called row reduction or Gaussian elimination A system of m linear equations in n unknowns is a system of equations α 1,1 x α 1,n x n = β 1 α m,1 x α m,n x n = β m for scalars α i,j, β k F We may represent this by putting the scalars α i,j into a matrix A M m n (F), and the variables and βs into vectors x = x 1 x n and b = β 1 β n, and writing Ax = b Alternatively, if c 1,, c n are the columns of A, this is equivalent to the vector equation x 1 c x n c n = b Finally, if the rows of A are r 1,, r m, then the system of equations may be written using the dot product as r 1 x = β 1 r m x = β m The dot product is an operation : F n F n F defined by (α 1,, α n ) (β 1,, β n ) = n α i β i A solution to the system is a vector l = (λ 1,, λ n ) F n that satisfies λ 1 c λ n c n = b; or equivalently satisfies r i l = β i for i = 1,, m We denote the set of all solutions to Ax = b by Sol(Ax = b) The rank of a matrix is the dimension of the column space C (A) We denote the rank by rank(a) Suppose that l is one solution to Ax = b Then the set of all solutions to Ax = b is the set Sol(Ax = b) = {l + m m Sol(Ax = 0)} The set Sol(Ax = 0) is a subspace of F n called the nullspace and denoted N(A) or Null(A) It has dimension dim(sol(ax = 0)) = n rank(a) The row rank of a matrix is the dimension of the row space R(A) We proved that the row rank of a matrix is equal to the rank i=1 4
5 Some sample true/false questions The first (in-class) prelim will consist of 5 6 true/false questions (where you do NOT need to give an explanation), followed by some questions that are similar to the problems in the homework You will have a choice in which questions you answer, you will probably have to do 3 of 5 problems Some sample true/false questions (HINT: five are true and seven are false) Every vector space contains a zero vector TRUE FALSE The empty set is a subspace of every vector space TRUE FALSE The intersection of any two subsets of V is a subspace of V TRUE FALSE If S is a linearly dependent set, then each element of S is a linear combination of other elements of S TRUE FALSE Any set containing the zero vector is linearly dependent TRUE FALSE Every vector space that is generated by a finite set has a basis TRUE FALSE A vector space cannot have more than one basis TRUE FALSE If a vector space has a finite basis, then the number of vectors in every basis is the same TRUE FALSE The dimension of Pol n (F) is n TRUE FALSE The dimension of M m n (F) is m + n TRUE FALSE If S = S(b 1,, b k ), then every vector in S can be written as a linear combination of b 1,, b k in only one way TRUE FALSE If V is a vector space of dimension n, then V has exactly one subspace of dimension 0 and exactly one subspace of dimension n TRUE FALSE 5
Row Space, Column Space, and Nullspace
 Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
MTH 362: Advanced Engineering Mathematics
 MTH 362: Advanced Engineering Mathematics Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 26, 2017 1 Linear Independence and Dependence of Vectors
MTH 362: Advanced Engineering Mathematics Lecture 5 Jonathan A. Chávez Casillas 1 1 University of Rhode Island Department of Mathematics September 26, 2017 1 Linear Independence and Dependence of Vectors
MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix.
 MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix. Basis Definition. Let V be a vector space. A linearly independent spanning set for V is called a basis.
MATH 323 Linear Algebra Lecture 12: Basis of a vector space (continued). Rank and nullity of a matrix. Basis Definition. Let V be a vector space. A linearly independent spanning set for V is called a basis.
Solving Linear Systems Using Gaussian Elimination
 Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Lecture 22: Section 4.7
 Lecture 22: Section 47 Shuanglin Shao December 2, 213 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n
Lecture 22: Section 47 Shuanglin Shao December 2, 213 Row Space, Column Space, and Null Space Definition For an m n, a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn, the vectors r 1 = [ a 11 a 12 a 1n
MODEL ANSWERS TO THE FIRST QUIZ. 1. (18pts) (i) Give the definition of a m n matrix. A m n matrix with entries in a field F is a function
 MODEL ANSWERS TO THE FIRST QUIZ 1. (18pts) (i) Give the definition of a m n matrix. A m n matrix with entries in a field F is a function A: I J F, where I is the set of integers between 1 and m and J is
MODEL ANSWERS TO THE FIRST QUIZ 1. (18pts) (i) Give the definition of a m n matrix. A m n matrix with entries in a field F is a function A: I J F, where I is the set of integers between 1 and m and J is
Math Linear Algebra Final Exam Review Sheet
 Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
MATH 2331 Linear Algebra. Section 2.1 Matrix Operations. Definition: A : m n, B : n p. Example: Compute AB, if possible.
 MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
MATH 2331 Linear Algebra Section 2.1 Matrix Operations Definition: A : m n, B : n p ( 1 2 p ) ( 1 2 p ) AB = A b b b = Ab Ab Ab Example: Compute AB, if possible. 1 Row-column rule: i-j-th entry of AB:
Midterm 1 Review. Written by Victoria Kala SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015
 Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Math 323 Exam 2 Sample Problems Solution Guide October 31, 2013
 Math Exam Sample Problems Solution Guide October, Note that the following provides a guide to the solutions on the sample problems, but in some cases the complete solution would require more work or justification
Math Exam Sample Problems Solution Guide October, Note that the following provides a guide to the solutions on the sample problems, but in some cases the complete solution would require more work or justification
(a) Let F be a field, and E F a subfield. Then F can be regarded as a vector space over E (with + and the field operations).
 Sample True/False To demonstrate in class (a) If f(x) is an even function, then so i Presentation Math 4310problem 1. Determine whether Prelim the following I Solutions statements (10/09/2015) are (always)
Sample True/False To demonstrate in class (a) If f(x) is an even function, then so i Presentation Math 4310problem 1. Determine whether Prelim the following I Solutions statements (10/09/2015) are (always)
Math 369 Exam #2 Practice Problem Solutions
 Math 369 Exam #2 Practice Problem Solutions 2 5. Is { 2, 3, 8 } a basis for R 3? Answer: No, it is not. To show that it is not a basis, it suffices to show that this is not a linearly independent set.
Math 369 Exam #2 Practice Problem Solutions 2 5. Is { 2, 3, 8 } a basis for R 3? Answer: No, it is not. To show that it is not a basis, it suffices to show that this is not a linearly independent set.
MATH 167: APPLIED LINEAR ALGEBRA Chapter 2
 MATH 167: APPLIED LINEAR ALGEBRA Chapter 2 Jesús De Loera, UC Davis February 1, 2012 General Linear Systems of Equations (2.2). Given a system of m equations and n unknowns. Now m n is OK! Apply elementary
MATH 167: APPLIED LINEAR ALGEBRA Chapter 2 Jesús De Loera, UC Davis February 1, 2012 General Linear Systems of Equations (2.2). Given a system of m equations and n unknowns. Now m n is OK! Apply elementary
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
Math 353, Practice Midterm 1
 Math 353, Practice Midterm Name: This exam consists of 8 pages including this front page Ground Rules No calculator is allowed 2 Show your work for every problem unless otherwise stated Score 2 2 3 5 4
Math 353, Practice Midterm Name: This exam consists of 8 pages including this front page Ground Rules No calculator is allowed 2 Show your work for every problem unless otherwise stated Score 2 2 3 5 4
MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam. Topics
 MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam This study sheet will not be allowed during the test Books and notes will not be allowed during the test Calculators and cell phones
MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam This study sheet will not be allowed during the test Books and notes will not be allowed during the test Calculators and cell phones
The definition of a vector space (V, +, )
 The definition of a vector space (V, +, ) 1. For any u and v in V, u + v is also in V. 2. For any u and v in V, u + v = v + u. 3. For any u, v, w in V, u + ( v + w) = ( u + v) + w. 4. There is an element
The definition of a vector space (V, +, ) 1. For any u and v in V, u + v is also in V. 2. For any u and v in V, u + v = v + u. 3. For any u, v, w in V, u + ( v + w) = ( u + v) + w. 4. There is an element
Math 1060 Linear Algebra Homework Exercises 1 1. Find the complete solutions (if any!) to each of the following systems of simultaneous equations:
 Homework Exercises 1 1 Find the complete solutions (if any!) to each of the following systems of simultaneous equations: (i) x 4y + 3z = 2 3x 11y + 13z = 3 2x 9y + 2z = 7 x 2y + 6z = 2 (ii) x 4y + 3z =
Homework Exercises 1 1 Find the complete solutions (if any!) to each of the following systems of simultaneous equations: (i) x 4y + 3z = 2 3x 11y + 13z = 3 2x 9y + 2z = 7 x 2y + 6z = 2 (ii) x 4y + 3z =
18.06 Problem Set 3 Solution Due Wednesday, 25 February 2009 at 4 pm in Total: 160 points.
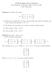 8.6 Problem Set 3 Solution Due Wednesday, 25 February 29 at 4 pm in 2-6. Total: 6 points. Problem : Consider the matrix A = 2 4 2 6 3 4 2 7 (a) Reduce A to echelon form U, find a special solution for each
8.6 Problem Set 3 Solution Due Wednesday, 25 February 29 at 4 pm in 2-6. Total: 6 points. Problem : Consider the matrix A = 2 4 2 6 3 4 2 7 (a) Reduce A to echelon form U, find a special solution for each
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
MATH 315 Linear Algebra Homework #1 Assigned: August 20, 2018
 Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Chapter 2 Subspaces of R n and Their Dimensions
 Chapter 2 Subspaces of R n and Their Dimensions Vector Space R n. R n Definition.. The vector space R n is a set of all n-tuples (called vectors) x x 2 x =., where x, x 2,, x n are real numbers, together
Chapter 2 Subspaces of R n and Their Dimensions Vector Space R n. R n Definition.. The vector space R n is a set of all n-tuples (called vectors) x x 2 x =., where x, x 2,, x n are real numbers, together
This lecture is a review for the exam. The majority of the exam is on what we ve learned about rectangular matrices.
 Exam review This lecture is a review for the exam. The majority of the exam is on what we ve learned about rectangular matrices. Sample question Suppose u, v and w are non-zero vectors in R 7. They span
Exam review This lecture is a review for the exam. The majority of the exam is on what we ve learned about rectangular matrices. Sample question Suppose u, v and w are non-zero vectors in R 7. They span
Math 4A Notes. Written by Victoria Kala Last updated June 11, 2017
 Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Chapter 1 Vector Spaces
 Chapter 1 Vector Spaces Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 110 Linear Algebra Vector Spaces Definition A vector space V over a field
Chapter 1 Vector Spaces Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 110 Linear Algebra Vector Spaces Definition A vector space V over a field
Math 1553 Introduction to Linear Algebra
 Math 1553 Introduction to Linear Algebra Lecture Notes Chapter 2 Matrix Algebra School of Mathematics The Georgia Institute of Technology Math 1553 Lecture Notes for Chapter 2 Introduction, Slide 1 Section
Math 1553 Introduction to Linear Algebra Lecture Notes Chapter 2 Matrix Algebra School of Mathematics The Georgia Institute of Technology Math 1553 Lecture Notes for Chapter 2 Introduction, Slide 1 Section
MTH 309 Supplemental Lecture Notes Based on Robert Messer, Linear Algebra Gateway to Mathematics
 MTH 309 Supplemental Lecture Notes Based on Robert Messer, Linear Algebra Gateway to Mathematics Ulrich Meierfrankenfeld Department of Mathematics Michigan State University East Lansing MI 48824 meier@math.msu.edu
MTH 309 Supplemental Lecture Notes Based on Robert Messer, Linear Algebra Gateway to Mathematics Ulrich Meierfrankenfeld Department of Mathematics Michigan State University East Lansing MI 48824 meier@math.msu.edu
Math 21b: Linear Algebra Spring 2018
 Math b: Linear Algebra Spring 08 Homework 8: Basis This homework is due on Wednesday, February 4, respectively on Thursday, February 5, 08. Which of the following sets are linear spaces? Check in each
Math b: Linear Algebra Spring 08 Homework 8: Basis This homework is due on Wednesday, February 4, respectively on Thursday, February 5, 08. Which of the following sets are linear spaces? Check in each
Linear Algebra problems
 Linear Algebra problems 1. Show that the set F = ({1, 0}, +,.) is a field where + and. are defined as 1+1=0, 0+0=0, 0+1=1+0=1, 0.0=0.1=1.0=0, 1.1=1.. Let X be a non-empty set and F be any field. Let X
Linear Algebra problems 1. Show that the set F = ({1, 0}, +,.) is a field where + and. are defined as 1+1=0, 0+0=0, 0+1=1+0=1, 0.0=0.1=1.0=0, 1.1=1.. Let X be a non-empty set and F be any field. Let X
MATH 225 Summer 2005 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 2005
 MATH 225 Summer 25 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 25 Department of Mathematical and Statistical Sciences University of Alberta Question 1. [p 224. #2] The set of all
MATH 225 Summer 25 Linear Algebra II Solutions to Assignment 1 Due: Wednesday July 13, 25 Department of Mathematical and Statistical Sciences University of Alberta Question 1. [p 224. #2] The set of all
MATH 2360 REVIEW PROBLEMS
 MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
MATH 2360 REVIEW PROBLEMS Problem 1: In (a) (d) below, either compute the matrix product or indicate why it does not exist: ( )( ) 1 2 2 1 (a) 0 1 1 2 ( ) 0 1 2 (b) 0 3 1 4 3 4 5 2 5 (c) 0 3 ) 1 4 ( 1
LINEAR ALGEBRA REVIEW
 LINEAR ALGEBRA REVIEW SPENCER BECKER-KAHN Basic Definitions Domain and Codomain. Let f : X Y be any function. This notation means that X is the domain of f and Y is the codomain of f. This means that for
LINEAR ALGEBRA REVIEW SPENCER BECKER-KAHN Basic Definitions Domain and Codomain. Let f : X Y be any function. This notation means that X is the domain of f and Y is the codomain of f. This means that for
Solutions to Homework 5 - Math 3410
 Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
Solutions to Homework 5 - Math 34 (Page 57: # 489) Determine whether the following vectors in R 4 are linearly dependent or independent: (a) (, 2, 3, ), (3, 7,, 2), (, 3, 7, 4) Solution From x(, 2, 3,
Maths for Signals and Systems Linear Algebra in Engineering
 Maths for Signals and Systems Linear Algebra in Engineering Lecture 3, Friday 4 th October 26 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Mathematics for
Maths for Signals and Systems Linear Algebra in Engineering Lecture 3, Friday 4 th October 26 DR TANIA STATHAKI READER (ASSOCIATE PROFFESOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON Mathematics for
SUMMARY OF MATH 1600
 SUMMARY OF MATH 1600 Note: The following list is intended as a study guide for the final exam. It is a continuation of the study guide for the midterm. It does not claim to be a comprehensive list. You
SUMMARY OF MATH 1600 Note: The following list is intended as a study guide for the final exam. It is a continuation of the study guide for the midterm. It does not claim to be a comprehensive list. You
The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items.
 AMS 10: Review for the Midterm Exam The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items. Complex numbers
AMS 10: Review for the Midterm Exam The scope of the midterm exam is up to and includes Section 2.1 in the textbook (homework sets 1-4). Below we highlight some of the important items. Complex numbers
Check that your exam contains 20 multiple-choice questions, numbered sequentially.
 MATH 22 MAKEUP EXAMINATION Fall 26 VERSION A NAME STUDENT NUMBER INSTRUCTOR SECTION NUMBER On your scantron, write and bubble your PSU ID, Section Number, and Test Version. Failure to correctly code these
MATH 22 MAKEUP EXAMINATION Fall 26 VERSION A NAME STUDENT NUMBER INSTRUCTOR SECTION NUMBER On your scantron, write and bubble your PSU ID, Section Number, and Test Version. Failure to correctly code these
NAME MATH 304 Examination 2 Page 1
 NAME MATH 4 Examination 2 Page. [8 points (a) Find the following determinant. However, use only properties of determinants, without calculating directly (that is without expanding along a column or row
NAME MATH 4 Examination 2 Page. [8 points (a) Find the following determinant. However, use only properties of determinants, without calculating directly (that is without expanding along a column or row
Chapter 2: Linear Independence and Bases
 MATH20300: Linear Algebra 2 (2016 Chapter 2: Linear Independence and Bases 1 Linear Combinations and Spans Example 11 Consider the vector v (1, 1 R 2 What is the smallest subspace of (the real vector space
MATH20300: Linear Algebra 2 (2016 Chapter 2: Linear Independence and Bases 1 Linear Combinations and Spans Example 11 Consider the vector v (1, 1 R 2 What is the smallest subspace of (the real vector space
Solutions to Exam I MATH 304, section 6
 Solutions to Exam I MATH 304, section 6 YOU MUST SHOW ALL WORK TO GET CREDIT. Problem 1. Let A = 1 2 5 6 1 2 5 6 3 2 0 0 1 3 1 1 2 0 1 3, B =, C =, I = I 0 0 0 1 1 3 4 = 4 4 identity matrix. 3 1 2 6 0
Solutions to Exam I MATH 304, section 6 YOU MUST SHOW ALL WORK TO GET CREDIT. Problem 1. Let A = 1 2 5 6 1 2 5 6 3 2 0 0 1 3 1 1 2 0 1 3, B =, C =, I = I 0 0 0 1 1 3 4 = 4 4 identity matrix. 3 1 2 6 0
Linear equations in linear algebra
 Linear equations in linear algebra Samy Tindel Purdue University Differential equations and linear algebra - MA 262 Taken from Differential equations and linear algebra Pearson Collections Samy T. Linear
Linear equations in linear algebra Samy Tindel Purdue University Differential equations and linear algebra - MA 262 Taken from Differential equations and linear algebra Pearson Collections Samy T. Linear
Review Notes for Linear Algebra True or False Last Updated: February 22, 2010
 Review Notes for Linear Algebra True or False Last Updated: February 22, 2010 Chapter 4 [ Vector Spaces 4.1 If {v 1,v 2,,v n } and {w 1,w 2,,w n } are linearly independent, then {v 1 +w 1,v 2 +w 2,,v n
Review Notes for Linear Algebra True or False Last Updated: February 22, 2010 Chapter 4 [ Vector Spaces 4.1 If {v 1,v 2,,v n } and {w 1,w 2,,w n } are linearly independent, then {v 1 +w 1,v 2 +w 2,,v n
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 1 Material Dr. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University January 9, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 1 Material Dr. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University January 9, 2018 Linear Algebra (MTH 464)
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Dr. Abdulla Eid. Section 4.2 Subspaces. Dr. Abdulla Eid. MATHS 211: Linear Algebra. College of Science
 Section 4.2 Subspaces College of Science MATHS 211: Linear Algebra (University of Bahrain) Subspaces 1 / 42 Goal: 1 Define subspaces. 2 Subspace test. 3 Linear Combination of elements. 4 Subspace generated
Section 4.2 Subspaces College of Science MATHS 211: Linear Algebra (University of Bahrain) Subspaces 1 / 42 Goal: 1 Define subspaces. 2 Subspace test. 3 Linear Combination of elements. 4 Subspace generated
Lecture Summaries for Linear Algebra M51A
 These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
Linear Systems. Math A Bianca Santoro. September 23, 2016
 Linear Systems Math A4600 - Bianca Santoro September 3, 06 Goal: Understand how to solve Ax = b. Toy Model: Let s study the following system There are two nice ways of thinking about this system: x + y
Linear Systems Math A4600 - Bianca Santoro September 3, 06 Goal: Understand how to solve Ax = b. Toy Model: Let s study the following system There are two nice ways of thinking about this system: x + y
Math 301 Test I. M. Randall Holmes. September 8, 2008
 Math 0 Test I M. Randall Holmes September 8, 008 This exam will begin at 9:40 am and end at 0:5 am. You may use your writing instrument, a calculator, and your test paper; books, notes and neighbors to
Math 0 Test I M. Randall Holmes September 8, 008 This exam will begin at 9:40 am and end at 0:5 am. You may use your writing instrument, a calculator, and your test paper; books, notes and neighbors to
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
Lecture 13: Row and column spaces
 Spring 2018 UW-Madison Lecture 13: Row and column spaces 1 The column space of a matrix 1.1 Definition The column space of matrix A denoted as Col(A) is the space consisting of all linear combinations
Spring 2018 UW-Madison Lecture 13: Row and column spaces 1 The column space of a matrix 1.1 Definition The column space of matrix A denoted as Col(A) is the space consisting of all linear combinations
MA 242 LINEAR ALGEBRA C1, Solutions to First Midterm Exam
 MA 242 LINEAR ALGEBRA C Solutions to First Midterm Exam Prof Nikola Popovic October 2 9:am - :am Problem ( points) Determine h and k such that the solution set of x + = k 4x + h = 8 (a) is empty (b) contains
MA 242 LINEAR ALGEBRA C Solutions to First Midterm Exam Prof Nikola Popovic October 2 9:am - :am Problem ( points) Determine h and k such that the solution set of x + = k 4x + h = 8 (a) is empty (b) contains
Test 3, Linear Algebra
 Test 3, Linear Algebra Dr. Adam Graham-Squire, Fall 2017 Name: I pledge that I have neither given nor received any unauthorized assistance on this exam. (signature) DIRECTIONS 1. Don t panic. 2. Show all
Test 3, Linear Algebra Dr. Adam Graham-Squire, Fall 2017 Name: I pledge that I have neither given nor received any unauthorized assistance on this exam. (signature) DIRECTIONS 1. Don t panic. 2. Show all
Math 2174: Practice Midterm 1
 Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
Math 74: Practice Midterm Show your work and explain your reasoning as appropriate. No calculators. One page of handwritten notes is allowed for the exam, as well as one blank page of scratch paper.. Consider
Department of Aerospace Engineering AE602 Mathematics for Aerospace Engineers Assignment No. 4
 Department of Aerospace Engineering AE6 Mathematics for Aerospace Engineers Assignment No.. Decide whether or not the following vectors are linearly independent, by solving c v + c v + c 3 v 3 + c v :
Department of Aerospace Engineering AE6 Mathematics for Aerospace Engineers Assignment No.. Decide whether or not the following vectors are linearly independent, by solving c v + c v + c 3 v 3 + c v :
Name: Handed out: 14 November Math 4310 Take-home Prelim 2 Solutions OFFICIAL USE ONLY 1. / / / / / 16 6.
 Math 43 Take-home Prelim 2 Solutions Name: Handed out: 4 November 27 INSTRUCTIONS PLEASE READ THIS NOW Please answer all the questions on this exam to the extent that you can. Some are very challenging.
Math 43 Take-home Prelim 2 Solutions Name: Handed out: 4 November 27 INSTRUCTIONS PLEASE READ THIS NOW Please answer all the questions on this exam to the extent that you can. Some are very challenging.
A Brief Outline of Math 355
 A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
MATH 1120 (LINEAR ALGEBRA 1), FINAL EXAM FALL 2011 SOLUTIONS TO PRACTICE VERSION
 MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
MATH (LINEAR ALGEBRA ) FINAL EXAM FALL SOLUTIONS TO PRACTICE VERSION Problem (a) For each matrix below (i) find a basis for its column space (ii) find a basis for its row space (iii) determine whether
Linear Algebra Exam 1 Spring 2007
 Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
Linear Algebra Exam 1 Spring 2007 March 15, 2007 Name: SOLUTION KEY (Total 55 points, plus 5 more for Pledged Assignment.) Honor Code Statement: Directions: Complete all problems. Justify all answers/solutions.
EXERCISE SET 5.1. = (kx + kx + k, ky + ky + k ) = (kx + kx + 1, ky + ky + 1) = ((k + )x + 1, (k + )y + 1)
 EXERCISE SET 5. 6. The pair (, 2) is in the set but the pair ( )(, 2) = (, 2) is not because the first component is negative; hence Axiom 6 fails. Axiom 5 also fails. 8. Axioms, 2, 3, 6, 9, and are easily
EXERCISE SET 5. 6. The pair (, 2) is in the set but the pair ( )(, 2) = (, 2) is not because the first component is negative; hence Axiom 6 fails. Axiom 5 also fails. 8. Axioms, 2, 3, 6, 9, and are easily
MATH 304 Linear Algebra Lecture 20: Review for Test 1.
 MATH 304 Linear Algebra Lecture 20: Review for Test 1. Topics for Test 1 Part I: Elementary linear algebra (Leon 1.1 1.4, 2.1 2.2) Systems of linear equations: elementary operations, Gaussian elimination,
MATH 304 Linear Algebra Lecture 20: Review for Test 1. Topics for Test 1 Part I: Elementary linear algebra (Leon 1.1 1.4, 2.1 2.2) Systems of linear equations: elementary operations, Gaussian elimination,
Math 321: Linear Algebra
 Math 32: Linear Algebra T. Kapitula Department of Mathematics and Statistics University of New Mexico September 8, 24 Textbook: Linear Algebra,by J. Hefferon E-mail: kapitula@math.unm.edu Prof. Kapitula,
Math 32: Linear Algebra T. Kapitula Department of Mathematics and Statistics University of New Mexico September 8, 24 Textbook: Linear Algebra,by J. Hefferon E-mail: kapitula@math.unm.edu Prof. Kapitula,
Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.
 Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.. Recall that P 3 denotes the vector space of polynomials of degree less
Instructions Please answer the five problems on your own paper. These are essay questions: you should write in complete sentences.. Recall that P 3 denotes the vector space of polynomials of degree less
LINEAR ALGEBRA BOOT CAMP WEEK 1: THE BASICS
 LINEAR ALGEBRA BOOT CAMP WEEK 1: THE BASICS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts (in
LINEAR ALGEBRA BOOT CAMP WEEK 1: THE BASICS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts (in
Span & Linear Independence (Pop Quiz)
 Span & Linear Independence (Pop Quiz). Consider the following vectors: v = 2, v 2 = 4 5, v 3 = 3 2, v 4 = Is the set of vectors S = {v, v 2, v 3, v 4 } linearly independent? Solution: Notice that the number
Span & Linear Independence (Pop Quiz). Consider the following vectors: v = 2, v 2 = 4 5, v 3 = 3 2, v 4 = Is the set of vectors S = {v, v 2, v 3, v 4 } linearly independent? Solution: Notice that the number
Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007
 Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007 You have 1 hour and 20 minutes. No notes, books, or other references. You are permitted to use Maple during this exam, but you must start with a blank
Math 224, Fall 2007 Exam 3 Thursday, December 6, 2007 You have 1 hour and 20 minutes. No notes, books, or other references. You are permitted to use Maple during this exam, but you must start with a blank
SSEA Math 51 Track Final Exam August 30, Problem Total Points Score
 Name: This is the final exam for the Math 5 track at SSEA. Answer as many problems as possible to the best of your ability; do not worry if you are not able to answer all of the problems. Partial credit
Name: This is the final exam for the Math 5 track at SSEA. Answer as many problems as possible to the best of your ability; do not worry if you are not able to answer all of the problems. Partial credit
Math Camp Lecture 4: Linear Algebra. Xiao Yu Wang. Aug 2010 MIT. Xiao Yu Wang (MIT) Math Camp /10 1 / 88
 Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Topics. Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij
 Topics Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij or a ij lives in row i and column j Definition of a matrix
Topics Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij or a ij lives in row i and column j Definition of a matrix
Linear Algebra Practice Problems
 Linear Algebra Practice Problems Math 24 Calculus III Summer 25, Session II. Determine whether the given set is a vector space. If not, give at least one axiom that is not satisfied. Unless otherwise stated,
Linear Algebra Practice Problems Math 24 Calculus III Summer 25, Session II. Determine whether the given set is a vector space. If not, give at least one axiom that is not satisfied. Unless otherwise stated,
OHSx XM511 Linear Algebra: Solutions to Online True/False Exercises
 This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
2.3. VECTOR SPACES 25
 2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
2.3. VECTOR SPACES 25 2.3 Vector Spaces MATH 294 FALL 982 PRELIM # 3a 2.3. Let C[, ] denote the space of continuous functions defined on the interval [,] (i.e. f(x) is a member of C[, ] if f(x) is continuous
Linear Algebra Highlights
 Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Chapter 2. General Vector Spaces. 2.1 Real Vector Spaces
 Chapter 2 General Vector Spaces Outline : Real vector spaces Subspaces Linear independence Basis and dimension Row Space, Column Space, and Nullspace 2 Real Vector Spaces 2 Example () Let u and v be vectors
Chapter 2 General Vector Spaces Outline : Real vector spaces Subspaces Linear independence Basis and dimension Row Space, Column Space, and Nullspace 2 Real Vector Spaces 2 Example () Let u and v be vectors
Vector Spaces. 9.1 Opening Remarks. Week Solvable or not solvable, that s the question. View at edx. Consider the picture
 Week9 Vector Spaces 9. Opening Remarks 9.. Solvable or not solvable, that s the question Consider the picture (,) (,) p(χ) = γ + γ χ + γ χ (, ) depicting three points in R and a quadratic polynomial (polynomial
Week9 Vector Spaces 9. Opening Remarks 9.. Solvable or not solvable, that s the question Consider the picture (,) (,) p(χ) = γ + γ χ + γ χ (, ) depicting three points in R and a quadratic polynomial (polynomial
Choose three of: Choose three of: Choose three of:
 MATH Final Exam (Version ) Solutions July 8, 8 S. F. Ellermeyer Name Instructions. Remember to include all important details of your work. You will not get full credit (or perhaps even any partial credit)
MATH Final Exam (Version ) Solutions July 8, 8 S. F. Ellermeyer Name Instructions. Remember to include all important details of your work. You will not get full credit (or perhaps even any partial credit)
Linear Algebra. Preliminary Lecture Notes
 Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date April 29, 23 2 Contents Motivation for the course 5 2 Euclidean n dimensional Space 7 2. Definition of n Dimensional Euclidean Space...........
Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date April 29, 23 2 Contents Motivation for the course 5 2 Euclidean n dimensional Space 7 2. Definition of n Dimensional Euclidean Space...........
Math 3C Lecture 20. John Douglas Moore
 Math 3C Lecture 20 John Douglas Moore May 18, 2009 TENTATIVE FORMULA I Midterm I: 20% Midterm II: 20% Homework: 10% Quizzes: 10% Final: 40% TENTATIVE FORMULA II Higher of two midterms: 30% Homework: 10%
Math 3C Lecture 20 John Douglas Moore May 18, 2009 TENTATIVE FORMULA I Midterm I: 20% Midterm II: 20% Homework: 10% Quizzes: 10% Final: 40% TENTATIVE FORMULA II Higher of two midterms: 30% Homework: 10%
Math 54 First Midterm Exam, Prof. Srivastava September 23, 2016, 4:10pm 5:00pm, 155 Dwinelle Hall.
 Math 54 First Midterm Exam, Prof Srivastava September 23, 26, 4:pm 5:pm, 55 Dwinelle Hall Name: SID: Instructions: Write all answers in the provided space This exam includes two pages of scratch paper,
Math 54 First Midterm Exam, Prof Srivastava September 23, 26, 4:pm 5:pm, 55 Dwinelle Hall Name: SID: Instructions: Write all answers in the provided space This exam includes two pages of scratch paper,
Glossary of Linear Algebra Terms. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Linear Algebra. Preliminary Lecture Notes
 Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date May 9, 29 2 Contents 1 Motivation for the course 5 2 Euclidean n dimensional Space 7 2.1 Definition of n Dimensional Euclidean Space...........
Linear Algebra Preliminary Lecture Notes Adolfo J. Rumbos c Draft date May 9, 29 2 Contents 1 Motivation for the course 5 2 Euclidean n dimensional Space 7 2.1 Definition of n Dimensional Euclidean Space...........
THE REAL NUMBERS Chapter #4
 FOUNDATIONS OF ANALYSIS FALL 2008 TRUE/FALSE QUESTIONS THE REAL NUMBERS Chapter #4 (1) Every element in a field has a multiplicative inverse. (2) In a field the additive inverse of 1 is 0. (3) In a field
FOUNDATIONS OF ANALYSIS FALL 2008 TRUE/FALSE QUESTIONS THE REAL NUMBERS Chapter #4 (1) Every element in a field has a multiplicative inverse. (2) In a field the additive inverse of 1 is 0. (3) In a field
Advanced Engineering Mathematics Prof. Pratima Panigrahi Department of Mathematics Indian Institute of Technology, Kharagpur
 Advanced Engineering Mathematics Prof. Pratima Panigrahi Department of Mathematics Indian Institute of Technology, Kharagpur Lecture No. # 02 Vector Spaces, Subspaces, linearly Dependent/Independent of
Advanced Engineering Mathematics Prof. Pratima Panigrahi Department of Mathematics Indian Institute of Technology, Kharagpur Lecture No. # 02 Vector Spaces, Subspaces, linearly Dependent/Independent of
MTH 464: Computational Linear Algebra
 MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
MTH 464: Computational Linear Algebra Lecture Outlines Exam 2 Material Prof. M. Beauregard Department of Mathematics & Statistics Stephen F. Austin State University March 2, 2018 Linear Algebra (MTH 464)
A Do It Yourself Guide to Linear Algebra
 A Do It Yourself Guide to Linear Algebra Lecture Notes based on REUs, 2001-2010 Instructor: László Babai Notes compiled by Howard Liu 6-30-2010 1 Vector Spaces 1.1 Basics Definition 1.1.1. A vector space
A Do It Yourself Guide to Linear Algebra Lecture Notes based on REUs, 2001-2010 Instructor: László Babai Notes compiled by Howard Liu 6-30-2010 1 Vector Spaces 1.1 Basics Definition 1.1.1. A vector space
Study Guide for Linear Algebra Exam 2
 Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
Study Guide for Linear Algebra Exam 2 Term Vector Space Definition A Vector Space is a nonempty set V of objects, on which are defined two operations, called addition and multiplication by scalars (real
GRE Subject test preparation Spring 2016 Topic: Abstract Algebra, Linear Algebra, Number Theory.
 GRE Subject test preparation Spring 2016 Topic: Abstract Algebra, Linear Algebra, Number Theory. Linear Algebra Standard matrix manipulation to compute the kernel, intersection of subspaces, column spaces,
GRE Subject test preparation Spring 2016 Topic: Abstract Algebra, Linear Algebra, Number Theory. Linear Algebra Standard matrix manipulation to compute the kernel, intersection of subspaces, column spaces,
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3
 ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
ANALYTICAL MATHEMATICS FOR APPLICATIONS 2018 LECTURE NOTES 3 ISSUED 24 FEBRUARY 2018 1 Gaussian elimination Let A be an (m n)-matrix Consider the following row operations on A (1) Swap the positions any
Rings. EE 387, Notes 7, Handout #10
 Rings EE 387, Notes 7, Handout #10 Definition: A ring is a set R with binary operations, + and, that satisfy the following axioms: 1. (R, +) is a commutative group (five axioms) 2. Associative law for
Rings EE 387, Notes 7, Handout #10 Definition: A ring is a set R with binary operations, + and, that satisfy the following axioms: 1. (R, +) is a commutative group (five axioms) 2. Associative law for
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
Chapter 3. Directions: For questions 1-11 mark each statement True or False. Justify each answer.
 Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
Chapter 3 Directions: For questions 1-11 mark each statement True or False. Justify each answer. 1. (True False) Asking whether the linear system corresponding to an augmented matrix [ a 1 a 2 a 3 b ]
Linear Algebra March 16, 2019
 Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Linear Algebra March 16, 2019 2 Contents 0.1 Notation................................ 4 1 Systems of linear equations, and matrices 5 1.1 Systems of linear equations..................... 5 1.2 Augmented
Online Exercises for Linear Algebra XM511
 This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
Math Final December 2006 C. Robinson
 Math 285-1 Final December 2006 C. Robinson 2 5 8 5 1 2 0-1 0 1. (21 Points) The matrix A = 1 2 2 3 1 8 3 2 6 has the reduced echelon form U = 0 0 1 2 0 0 0 0 0 1. 2 6 1 0 0 0 0 0 a. Find a basis for the
Math 285-1 Final December 2006 C. Robinson 2 5 8 5 1 2 0-1 0 1. (21 Points) The matrix A = 1 2 2 3 1 8 3 2 6 has the reduced echelon form U = 0 0 1 2 0 0 0 0 0 1. 2 6 1 0 0 0 0 0 a. Find a basis for the
POLI270 - Linear Algebra
 POLI7 - Linear Algebra Septemer 8th Basics a x + a x +... + a n x n b () is the linear form where a, b are parameters and x n are variables. For a given equation such as x +x you only need a variable and
POLI7 - Linear Algebra Septemer 8th Basics a x + a x +... + a n x n b () is the linear form where a, b are parameters and x n are variables. For a given equation such as x +x you only need a variable and
Math Linear algebra, Spring Semester Dan Abramovich
 Math 52 0 - Linear algebra, Spring Semester 2012-2013 Dan Abramovich Fields. We learned to work with fields of numbers in school: Q = fractions of integers R = all real numbers, represented by infinite
Math 52 0 - Linear algebra, Spring Semester 2012-2013 Dan Abramovich Fields. We learned to work with fields of numbers in school: Q = fractions of integers R = all real numbers, represented by infinite
Linear Algebra. Min Yan
 Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
Linear Algebra Min Yan January 2, 2018 2 Contents 1 Vector Space 7 1.1 Definition................................. 7 1.1.1 Axioms of Vector Space..................... 7 1.1.2 Consequence of Axiom......................
χ 1 χ 2 and ψ 1 ψ 2 is also in the plane: αχ 1 αχ 2 which has a zero first component and hence is in the plane. is also in the plane: ψ 1
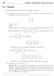 58 Chapter 5 Vector Spaces: Theory and Practice 57 s Which of the following subsets of R 3 are actually subspaces? (a The plane of vectors x =(χ,χ, T R 3 such that the first component χ = In other words,
58 Chapter 5 Vector Spaces: Theory and Practice 57 s Which of the following subsets of R 3 are actually subspaces? (a The plane of vectors x =(χ,χ, T R 3 such that the first component χ = In other words,
Contents. 1 Vectors, Lines and Planes 1. 2 Gaussian Elimination Matrices Vector Spaces and Subspaces 124
 Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
Matrices Math 220 Copyright 2016 Pinaki Das This document is freely redistributable under the terms of the GNU Free Documentation License For more information, visit http://wwwgnuorg/copyleft/fdlhtml Contents
web: HOMEWORK 1
 MAT 207 LINEAR ALGEBRA I 2009207 Dokuz Eylül University, Faculty of Science, Department of Mathematics Instructor: Engin Mermut web: http://kisideuedutr/enginmermut/ HOMEWORK VECTORS IN THE n-dimensional
MAT 207 LINEAR ALGEBRA I 2009207 Dokuz Eylül University, Faculty of Science, Department of Mathematics Instructor: Engin Mermut web: http://kisideuedutr/enginmermut/ HOMEWORK VECTORS IN THE n-dimensional
MATH2210 Notebook 3 Spring 2018
 MATH2210 Notebook 3 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 3 MATH2210 Notebook 3 3 3.1 Vector Spaces and Subspaces.................................
MATH2210 Notebook 3 Spring 2018 prepared by Professor Jenny Baglivo c Copyright 2009 2018 by Jenny A. Baglivo. All Rights Reserved. 3 MATH2210 Notebook 3 3 3.1 Vector Spaces and Subspaces.................................
