1 Lecture 1 Preliminaries
|
|
|
- Erik McKinney
- 5 years ago
- Views:
Transcription
1 1 Lecture 1 Preliminaries Textbook Sections: Chapter 1, Sections 2.1,2.2,3.1,3.2 Problems: 1.3,1.5,1.7,2.3,2.4,2.13,3.20,3.25,3.45a-d These notes are intended to simultaneously review and extend the basic concepts of STA 2023 that are used in business applications. In this section, we describe the notions of: Populations and Samples Descriptive and Inferential Statistics Variable Types Tabular and Graphical Descriptions Numerical Descriptive Measures 1.1 Populations and Samples Populations are collections of individuals or items of interest to a researcher. We are typically concerned with one or more characteristics of the elements of the population. Examples include: PO1 All firms listed on the New York Stock Exchange (NYSE) throughout year PO2 All living graduates of the University of Florida. PO3 All pairs of Levi s 550 jeans produced in January, Samples are subsets of their corresponding populations, used to describe or make inferences concerning particular characteristics of the elements of the population. Examples include: SA1 30 firms sampled at random from all firms listed on NYSE throughout SA2 100 UF graduates sampled from alumni records. SA3 A randomly selected set of 250 pairs of Levi s 550 jeans produced in January, Descriptive and Inferential Statistics Descriptive Statistics Methods used to describe a group of measurements (e.g. mean, median, standard deviation, proportion (percent) with some characteristic). Examples include (Sources: Wall Street Journal Almanac,1999, US Statistical Abstract, 1992): Average daily shares traded NYSE (millions): Median earnings for year round full time workers (1990, in $1000): Males 27.7 Females 19.8 Mean and standard deviation of heights of adults years old: Females Mean=63.5, std. dev=2.5 Males Mean=68.5, std dev=2.7
2 Percent of families in US living below poverty level: Inferential Statistics Methods used to reach conclusions (decisions) concerning a population, based on measurements from a sample. Examples include: A sample of 2007 American adults were asked if they tought there would be a recession in the next five years. Of those sampled, 66% answered Yes. Based on this sample we can be very confident that a majority of American adults feel there will be a recession in the next five years. (Source: WSJ, 6/27/97, p. R1). After determining a safe dosing regimen, drug manufacturers must demonstrate efficacy of new drugs by comparing them with a placebo or standard drug in large scale Phase III trials. In one such trial for the antidepressant Prozac (Eli Lilly & Co), researchers measured the change from baseline in Hamilton Depression (HAM D) scale. Based on a sample of 185 patients receiving Prozac, the mean change (improvement) was 11.0 points, and among 169 patients receiving placebo, the mean change was 8.2 points. Based on these samples, we can conclude that mean change from baseline in all patients receiving Prozac would be higher than the mean change from baseline in all patients receiving placebo at a very high level of confidence. 1.3 Levels of Data Measurement Nominal Variable s levels have no distinct ordering. Examples: Type of business (cyclical,non cyclical,utility,... ) Sex (female,male) Brand of beer purchased (Bud,Miller,Coors,... ) Ordinal Levels can be ordered, but distances between levels are indeterminable. Examples: Product quality (poor,fair,good,excellent) Stanard & Poor s Corporate bond rating (AAA,AA,A,BBB,BB,B,CCC,CC,C,D) Response to test drug (death,extensive deterioration,moderate/slight deterioration,no change,mod/slight improvement,extensive improvement). Placement in sales rankings (1 st, 2 nd,...,last). Interval Measurements fall along a numerical scale, such that distances between levels have meaning. Examples: Quarterly corporate profits (in dollars) Time to assemble an automobile (in minutes) Number of items sold by a salesman in one month (units) Number of defective computer keyboards produced by a worker on a given day. Ratio Same as interval, but also containing an absolute 0, so that ratios, as well as distances have meaning. All examples above, except profits (which can be negative) are ratio scale.
3 1.4 Tabular and Graphical Distribtions Frequency distributions are lists of classes of levels of a variable, and the number of observed outcomes within that range. Relative frequency distributions can be obtained for data of any level of measurement. They can be depicted in tabular or graphical form. Example Florida County Data Table 1.4 gives the population, total income (in $1000s), per capita income (in $1000s), and retail sales (in $1000s) for Florida s 67 counties in 1994 (Source: U.S. Census Bureau). The classes chosen for the frequency distribution for per capita income (in $1000s) are 5-10, 10 15, etc. If any observation fell right on a breakpoint between classes, it was assigned to the upper class. The following computer output gives the following distributions for the 67 counties in this dataset: Frequency Labelled Frequency, this gives the list of the numbers of counties falling in the various categories. Relative Frequency Labelled Percent, this gives the percentage of the counties falling in each of the categories. Cumulative Frequency Labelled Cumulative Frequency, this gives the number of counties falling in or below this category. Relative Cumulative Frequency Labelled Cumulative Percent, this gives the percent of counties falling in or below this category. Cumulative Cumulative pci94 Frequency Percent Frequency Percent Various graphs are useful in describing bodies of data, and are often given in business reporting. Histograms Vertical bar charts that identify categories for categorical variables and ranges of values for interval scale variables, with heights representing frequencies of outcomes for a single variable. Pie Charts Circular graphs where the size of each slice represents the frequency for a particular category or range of values. Scatter Plots Plots of pairs of outcomes on two variables, where each point on the graph represents a single element from a set of data. Time Series Plots Plot of a single variable that is measured over a series of points in time.
4 Total Per Capita Retail County Population Income Income Sales Alachua Baker Bay Bradford Brevard Broward Calhoun Charlotte Citrus Clay Collier Columbia Dade De Soto Dixie Duval Escambia Flagler Franklin Gadsden Gilchrist Glades Gulf Hamilton Hardee Hendry Hernando Highlands Hillsborough Holmes Indian River Jackson Jefferson Lafayette Lake Lee Leon Levy Liberty Madison Manatee Marion Martin Monroe Nassau Okaloosa Okeechobee Orange Osceola Palm Beach Pasco Pinellas Polk Putnam St. Johns St. Lucie Santa Rosa Sarasota Seminole Sumter Suwannee Taylor Union Volusia Wakulla Walton Washington
5 Data Maps Plot of a single variable that is measured over a series of points in 2-dimensional space. A histogram of per capita income is given in Figure 1. We see that most counties are in the range of $10,000 to $25,000 (the second, third, and fourth ranges of values), with one county lower than this range, and the seven most affluent counties being above this range. A pie chart of the same data is given in Figure 2. A scatter plot of retail sales (on the vertical or up/down axis) versus total income (on the horizontal or left/right axis) is given in Figure 3. A tendency for counties with higher total incomes to have higher retail sales can be seen. This is considered to be a postive association. A data map of per capita income is given in Figure 4. We can see visually where the most affluent and poorest counties are. A time series plot of monthly average airfares (per 1000 miles of domestic flights) is given in Figure?? for the period January 1980 through December 2001 (Source: Air Transport Association). We observe periodic trends (as demand shifts throughout the year) as well as longer term cycles, however, the series is showing only a very small long-term increase in trend. These prices are not adjusted for inflation and are called nominal prices (not to be confused with nominal variable types). Figure?? gives the series adjusted for inflation, showing that real prices have decreased over this period. Figure 7 gives the monthly consumer price index (CPI) over this 22 year (264 month) period (Source: US Department of Commerce). 1.5 Parameters and Statistics Parameters are numerical descriptive measures corresponding to populations. We will use the general notation θ to represent parameters. Special cases include: µ Population mean The average value of all elements in the population. It is also considered the long run average measurement in terms of conceptual populations. It can be thought of as the value each unit would receive if the total of the outcomes had been evenly distributed among the units. σ 2 Population variance Measure of spread (around µ) of the elements of the population. P Population proportion The proportion of all elements of the population that posess a particular characteristic. µ 1 µ 2 The difference between 2 population means. P 1 P 2 The difference between 2 population proportions. Examples related to previous scenarios, as well as new ones include: PA1 The proportion of all NYSE listed firms whose stock value increased in 1991 (P ). PA2 The proportion of all living UF graduates who are members of the alumni association (P ). PA3 The mean number of flaws in all pairs of Levis 550 jeans manufactured in January, 1992 (µ). PA4 The proportion of all people who have (or will have) a disease that show remission due to drug treatment (P ). PA5 The difference between mean lifetimes of two brands of automobile tires (µ 1 µ 2 ).
6 FREQUENCY pci94 MIDPOINT Figure 1: Frequency histogram of per capita incomes among Florida counties
7 FREQUENCY pci94 MIDPOINT Figure 2: Pie chart of per capita incomes among Florida counties
8 rtl inc94 Figure 3: Scatter plot of retail sales versus total income among Florida counties
9 pci pci Figure 4: Data map of per capita incomes among Florida counties
10 airfare time Figure 5: Monthly nominal (unadjusted for inflation) airfares (price per 1000 miles) on domestic flights
11 airfare time Figure 6: Monthly real (adjusted for inflation) airfares (price per 1000 miles) on domestic flights
12 cpi time Figure 7: Monthly Consumer Price Index (CPI-U) for all goods
13 PA6 The difference in the proportions of all men and women who have made credit card purchases over the internet (P 1 P 2 ). Statistics are numerical descriptive measures corresponding to samples. We will use the general notation ˆθ to represent statistics. Special cases include: Mode Outcome that occurs most often. Usually is reported for nominal or ordinal variables or simply as a peak of a continuous distribution when variable is continuous. Median Middle value (after numbers have been sorted from smallest to largest). Can be reported for ordinal or interval scale data. Let X (1) be the smallest, X (n) be the largest, and X (i) be the i th ordered observation in a sample of n items: n even: Median = M = X ( n 2 ) + X ( n 2 +1) 2 n odd: Median = M = X ( n+1 2 ) X Sample mean The average value of the elements of the sample: X = ni=1 X i n S 2 Sample variance Measure of the spread (around X) of the elements of the sample: S 2 = ni=1 (X i X) 2 n 1 ni=1 X 2 i nx2 n 1 S Sample standard deviation Measure of the spread (around X) of the elements of the sample: S = ni=1 (X i X) 2 n 1 n i=1 X 2 i nx2 n 1 ˆp Sample proportion The proportion of elements in the sample that have a particular characteristic: ˆp = X n = # of elements with characterisic (Successes) # of elements in the sample (trials) X 1 X 2 The difference between two sample means. ˆp 1 ˆp 2 The difference between two sample proportions. Examples related to previous scenarios, as well as new ones include: ST1 Among a random sample of n = 50 firms listed on the NYSE in 2001, 18 (ˆp =18/50 = 0.36) had stock prices increase during 2001.
14 ST2 Among a sample of 200 UF graduates, 44 are paying members of the alumni association (ˆp =44/200 = 0.22). ST3 A quality inspector samples 60 pairs of Levis 550 jeans, and finds a total of 66 flaws, yielding an average of X =66/60 = 1.10 flaws per pair of jeans. ST4 Of 20 patients selected with a particular disease, 12 (ˆp =12/20 =.60) show some remission after drug treatment. ST5 Samples of 20 tires from each of two manufacturers are obtained, and the number of miles run until the tread is worn to the legal limit are measured. Brand A has an average of X 1 =27, 459 miles, while Brand B has an average of X 2 =32, 671 miles. The difference between the two brands sample means is X 1 X 2 =27, , 671 = 5212 miles. ST6 Independent samples of male and female consumers find that among males, ˆp 1 =0.26 have made credit card purchases over the internet. Among females, ˆp 2 =0.44 have made credit card purchases on the internet. Statistics based on samples will be used to estimate parameters corresponding to populations, as well as test hypotheses concerning the true values of parameters. Example 1.2 Closing Prices for Stocks: 3/5/2002 A sample of n = 5 firms are obtained from the NYSE, and their closing prices are obtained in Table 1.5. We then compute the sample mean, median, variance, and standard deviation, where X i is the closing price for firm i. Firm (i) X i Rank Xi 2 X i X (X i X) 2 Coca-Cola (1) =8.1 (8.1) 2 =65.61 GE (2) =1.0 (1.0) 2 =1.0 Pfizer (3) =1.1 (1.1) 2 =1.21 Sony (4) =10.8 (10.8) 2 = Toys R Us (5) =-21.0 ( 21.0) 2 = Sum ( n i=1 ) The sample mean, X is computed as follows: ni=1 X i X = = =39.50 n 5 The median is the ((n +1)/2) th = ((5 + 1)/2) th =3 rd ordered outcome, which is Pfizer s closing price (not because i = 3, but because its rank=3), which is M = X (3) = The sample variance, S 2, and sample standard deviation, S, can be computed in two ways, the definitional form, and the short cut form. The definitional form is as follows: ni=1 S 2 (X i X) 2 = = n = S =+ S 2 = = The short cut form is as follows: n S 2 i=1 = X2 i nx (39.50) = = = = S = = n
15 2 Lecture 2 Probability Textbook Sections: Problems: 4.25,4.27,4.29,4.31,4.33,4.39,4.43 Probability is used to measure the likelihood or chances of certain events (prespecified outcomes) of an experiment. Certain rules of probability will be used in this course and are reviewed here. We first will define 2 events A and B, with probabilities P (A) and P (B), respectively. The intersection of events A and B is the event that both A and B occur, the notation being AB (sometimes written A B). The union of events A and B is the event that either A or B occur, the notation being A B. The complement of event A is the event that A does not occur, the notation being A. Some useful rules on obtaining these and other probabilities include: P (A B) =P (A)+P (B) P (AB) P (A B) =P (A occurs given B has occurred) = P (AB) P (B) (assuming P (B) > 0) P (AB) =P (A)P (B A) =P (B)P (A B) P (A) =1 P (A) A special case occurs when events A and B are said to be independent. This is when P (A B) = P (A), or equivalently P (B A) =P (B), in this situation, P (AB) =P (A)P (B). We will be using this idea later in this course. Example 2.1 Phase III Clinical Trial for Pravachol Among a population of adult males with high cholesterol, approximately half of the males were assigned to receive Pravachol (Bristol Myers Squibb), and approximately half received a placebo. The outcome observed was whether or not the patient suffered from a cardiac event within five years of beginning treatment. The counts of patients falling into each combination of treatment and outcome are given in Table 1. Cardiac Event Treatment Present (B) Absent (B) Total Pravachol (A) Placebo (A) Total Table 1: Numbers of patients falling in each treatment/cardiac outcome combination (Source: NEJM, 11/16/95, pp ) If we define the event A to be that the patient received pravachol, and the event B to be that the patient suffers from a cardiac event over the study period, we can use the table to obtain some pertinent probabilities: 1. P (A) =P (AB)+P (AB) = (174/6595) + (3128/6595) = (3302/6595) = P (A) =P (AB)+P (AB) = (248/6595) + (3045/6595) = (3293/6595) =.4993
16 3. P (B) =P (AB)+P (AB) = (174/6595) + (248/6595) = (422/6595) = P (B) = P (AB) + P (AB) = (3128/6595) + (3045/6595) = (6173/6595) = P (AB) = 174/6595 = P (AB) =248/6595 = P (A B) =P (A)+P (B) P (AB) = (174/6595) = P (B A) = P (AB) P (A) = = P (B A) = P (AB) P (A) = = Bayes Rule Sometimes we can easily obtain probabilities of the form P (A B) and P (B) and wish to obtain P (B A). This is very important in decision theory with respect to updating information. We start with a prior probability, P (B), we then observe an event A, and obtain P (A B). Then, we update our probability of B in light of knowledge that A has occurred. In the case of B only having two possible outcomes: B and B, Bayes rule can be stated as follows: P (B A) = P (AB) P (A) = P (AB) P (AB)+P (AB) P (A B)P (B) P (A B)P (B)+P (A B)P (B) In general if B has k possible (mutually exclusive and exhaustive) outcomes, the rule can be stated as follows: P (B j A) = P (AB j) P (A) = P (AB j ) ki=1 P (AB i ) P (A B j )P (B j ) ki=1 P (A B i )P (B i ) Example 2.2 Moral Hazard A manager cannot observe whether her salesperson works hard. She believes based on prior experience that the probability her salesperson works hard (H) is She believes that if the salesperson works hard, the probability a sale (S) is made is If the salesperson does not work hard, the probability the sale is made is What is the probability that the salesperson worked hard if the sale was made? If not made? Pr{Works Hard}=P (H) = 0.30 Pr{Not Works Hard}=P (H) = = 0.70 Pr{Makes Sale Works Hard}=P (S H) = 0.75 Pr{Makes Sale Not Works Hard}=P (S H) = 0.15 = P (H S) = P (HS) P (S) P (S H) P (H) = P (S H) P (H)+P(S H) P (H) 0.75(0.30) 0.75(0.30) (0.70) = = =0.68
17 0.25(0.30) P (H S) = 0.25(0.30) (0.70) = = =0.11 Note the amount of updating of the probability the salesperson worked hard, depending on whether the sale was made. This is a simplistic example of a theoretical area in information economics (See e.g. D.M. Kreps, A Course in Microeconomic Theory, Chapter 16). Example 2.3 O.J. Simpson s DNA In the O.J. Simpson murder trial, it was stated that 0.43% (proportion=.0043) of blood samples taken from all victims and suspects observed by the LA police department match the blood taken from the murder scene of Nicole Brown Simpson and Ronald Goldman. We will assume that this is representative of the fraction of people in the general population whose blood types match the blood at the crime scene. Define the following events: A A randomly selected person s blood matches that found at the crime scene B A person is innocent of the murders B A person is guilty of the murders Assume that a guilty person s blood will match with that at the crime scene with certainty. In terms of diagnostic testing, the sensitivity of this test is 100% and the specificity of the test is 99.57%. That is: P (A B) =1 P (A B) =.0043 = Suppose you had a prior (to observing blood evidence) probability that O.J. was innocent of 0.5 (P (B) =0.5). You now find out that his blood matches that at the crime scene. What is your updated probability that he is innocent (ignoring possibility of tampering)? P (B A) = 0.5(.0043) 0.5(.0043) + (1 0.5)(1) = = =.0043 Repeat for prior probabilities of 0.9 and 0.1. Source: Forst B. (1996). Evidence, Probabilities and Legal Standards for the Determination of Guilt: Beyond the O.J. Trial. In Representing O.J.: Murder, Criminal Justice, and the Mass Culture, ed. G. Barak, pp Guilderland, N.Y.: Harrow and Heston. Example 2.4 Adverse Selection (Job Market Signaling) Consider a simple model where there are two types of workers low quality and high quality. Employers are unable to determine the worker s quality type. The workers choose education levels to signal to employers their quality types. Workers can either obtain a college degree (high education level) or not obtain a college degree (low education level). The effort of obtaining a college degree is lower for high quality workers than for low quality workers. Employers pay higher wages to workers with higher education levels, since this is a (imperfect) signal for their quality types. Suppose you know that in the population of workers, half are low quality and half are high quality. Thus, prior to observing a potential employee s education level, the employer thinks the probability the worker will be high quality is 0.5. Among high quality workers, 70% will pursue a
18 college degree (30% do not pursue a degree), and among low quality workers, 20% pursue a college degree (80% do not). Let Q be the event a worker is high quality, and Q be the event the worker is low quality. Further, let E be the event the worker obtains a college degree, and E be the event that the worker does not obtain a college degree. Then we are given the following probabilities from the previous problem description: P (Q) =0.5 P (Q) =1 P (Q) =1 0.5 =0.5 P (E Q) =0.70 P (E Q) =0.20 What is the probability a worker is high quality, given (s)he has a college degree? P (Q) P (E Q) P (Q E) = P (Q) P (E Q)+P(Q) P (E Q) = 0.5(0.70) 0.5(0.70) + 0.5(0.20) = = =0.78 What is the probability a worker is high quality, given (s)he does not have a college degree? P (Q E) = P (Q) P (E Q) P (Q) P (E Q)+P (Q) P (E Q) = 0.5(0.30) 0.5(0.30) + 0.5(0.80) = = =0.27 This is a simplistic example of a theoretical area in information economics (See e.g. D.M. Kreps, A Course in Microeconomic Theory, Chapter 17). vsa Example 2.5 Cholera and London Water Companies Epidemiologist John Snow conducted a massive survey during a cholera epidemic in London during He found that water was being provided through the pipes of two companies: Southwark & Vauxhall (S&V) and Lambeth (L). Apparently, the Lambeth company was obtaining their water upstream in the Thames River from the London sewer outflow, while the S&V company got theirs near the sewer outflow. Table 2 gives the numbers (or counts) of people who died of cholera and who did not, seperately for the two firms. Outcome Lambeth S&V Row Total Cholera Death No Cholera Death Column Total Table 2: John Snow s London cholera results a) What is the probability a randomly selected person received water from the Lambeth company? From the S&V company? b) What is the probability a randomly selected person died of cholera? Did not die of cholera? c) What proportion of the Lambeth consumers died of cholera? Among the S&V consumers? Is the incidence of cholera death independent of firm? d) What is the probability a person received water from S&V, given (s)he died of cholera? Source: W.H. Frost (1936). Snow on Cholera, London, Oxford University Press.
19 3 Lecture 3 Discrete Random Variables and Probability Distributions Textbook Sections: 5.1,5.2,Notes(for bivariate r.v. s) Problems: 5.1,5.3, see lecture notes An experiment is conducted and some measurement is to be made regarding the outcome. This type of measurement can be classified as either discrete or continuous. Discrete random variables can take on only a finite (or countably infinite) possible set of outcomes. Examples include: RV1 The number of surveyed voters who favor Al Gore in the upcoming election from a survey of 722 registered voters RV2 The number of military personnel that oppose the military s ban on homosexuals from a survey of 300 current military personnel RV4 The number of patients, out of a group of 20 under study, that react positively to a new drug treatment RV5 The number of successful shuttle launches out of the first 30 shuttle missions Continuous random variables can take on any value corresponding to points on a line interval. It should be noted that while this type of variable occurs on a continuous scale, it is measured on some sort of discrete scale (a news weatherman reports the temperature as 93 F, not F ). Examples include: RV3 The gas mileage of a Ford Mustang GT convertible when run at 65 miles per hour. RV7 The number of miles a tire can travel before wearing out. RV9 The amount of time needed to housetrain a dog. These are considered random variables because we have randomly selected some subject or object from a population of such subjects (objects). The populations of these subjects (whether existing or conceptual) are said to have probability distributions. These are models of the distribution of the measurements corresponding to the elements of the population. Discrete probability distributions are a set of outcomes (denoted by x) and their corresponding probabilities. The distribution can be presented in terms of a table, graph, or formula representing each possible outcome of the random variable and its probability of occuring. Defining p(x) as the probability the random variable takes on the value x, we have the following simple rules for discrete probability distributions: 1. 0 p(x) 1 2. x p(x) =1 Thus, all probabilities must be between 0 and 1, and all probabilities must sum to 1. We consider discrete random variables in this lecture. Example 3.1 New Florida Lotto Game
20 Consider Florida s newly renovated lotto game. Before the drawing, you buy a card by choosing 6 different numbers between 1 and 53 inclusive, and giving the clerk $1. When the state chooses their 6 numbers subsequently, there will be either 0, 1, 2, 3, 4, 5 or 6 numbers that match yours. This is a discrete random variable. You do not know how many of the state s numbers will match yours, but you can obtain the probability of each possible outcome. This is a set of probabilities that can be used to set up the corresponding probability distribution. For this case, if we let X be the random variable representing how many of the state s numbers match yours, it has the probability distribution given in Table 3. The distribution used is the hypergeometric distribution, which is described in many textbooks on mathematical statistics. x p(x) Table 3: Probability distribution for number of winning digits on a Florida lotto ticket Note that all probabilities are between 0 and 1, and that they sum to 1. Of course, your ticket is worthless unless x 3, so the probability distribution corresponding to your prize amount will be different than this distribution (you will pool p(0),p(1), and p(2) to obtain the probability you win nothing ( )). For discrete probability distributions, the mean, µ is interpreted as the long run average outcome if the experiment were conducted many times. The variance, σ 2 is a measure of how variable these outcomes are. The variance is the average squared distance between the outcome of the random variable and the mean. The positive square root of the variance is the standard deviation, σ and is in the units of the original data. For a discrete random variable: µ = E(X) = x x p(x) σ 2 = V (X) =E[(X µ) 2 ]= x (x µ)2 p(x) = x x2 p(x) µ 2 σ = + σ 2 Example 3.1 continued Referring back to the new Florida lotto example, we obtain the mean and variance from calculations in Table 4. Thus, under the new game, the average number of winning digit is µ =0.6792, with a variance and standard deviation of (using 4 digits in calculations): σ 2 = (0.6792) 2 = σ =0.7379
21 x p(x) x p(x) x 2 p(x) ( ) = ( ) = Table 4: Probability distribution for number of winning digits on a Florida lotto ticket The variation in the correct numbers is relatively small as well, reflecting the fact that almost always people get either 0, 1, or 2 correct numbers. Example 3.2 Adverse Selection (Akerlof s Market for Lemons) George Akerlof shared the Nobel Prize for Economics in 2002 for an extended version of this model. There are two used car types: peaches and lemons. Sellers know the car type, having been driving it for a period of time. Buyers are unaware of a car s quality. Buyers value peaches at $3000 and lemons at $2000. Sellers value peaches at $2500 and lemons at $1000. Note that if sellers had higher valuations, no cars would be sold. Suppose that 1/3 of the cars are peaches and the remaining 2/3 are lemons. What is the expected value to a buyer, if (s)he purchases a car at random? We will let X represent the value to the buyer, which takes on the values 3000 (for peaches) and 2000 (for lemons). µ = E(X) = x p(x) = 3000(1/3) (2/3) = Thus, buyers will not pay over $ for a used car, and since the value of peaches is $2500 to sellers, only lemons will be sold, and buyers will learn that, and pay only $2000. At what fraction of the cars being peaches, will both types of cars be sold? For a theoretical treatment of this problem, see e.g. D.M. Kreps, A Course in Microeconomic Theory, Chapter Bivariate Distributions Often we are interested in the outcomes of 2 (or more) random variables. Suppose you have the opporunity to purchase shares of two firms. Your (subjective) joint probability distribution (p(x, y)) for the return on the two stocks is given in Table 5. Stock A 6% 10% Stock 0% A 16% Table 5: Joint probability distribution for stock returns Substitutable Industries
22 Thus, you have reason to believe there is little possibility that both will perform poorly or strongly. For now, denote X as the return for stock A and Y as the return for stock B. We can think of these industries as substitutes. Marginally, what is the probability distribution for stock A (this called the marginal distribution)? For stock B? These are giben in Table 6. Stock A Stock B x P(X = x) y P(Y = y) = = = =.50 Table 6: Marginal probability distributions for stock returns Hence, we can compute the mean and variance for X and Y: E(X) =µ X =0(.5) + 16(0.5) = 8.0 V (X) =σ 2 X =(0 8) 2 (0.5) + (16 8) 2 (0.5) = 64.0 E(Y )=µ Y =6(.5) + 10(0.5) = 8.0 V (Y )=σ 2 Y =(6 8) 2 (0.5) + (10 8) 2 (0.5) = 4.0 So, both stocks have the same expected return, but stock A is riskier, in the sense that its variance is much larger. How do X and Y co-vary together? For these two firms, we find that the covariance is negative, since high values of X tend to be seen with low values of Y and vice versa. We compute the Covariance of their returns, which we denote as COV (X, Y )=E(X µ X )(Y µ Y ) in Table 7. COV (X, Y )=E[(X µ X )(Y µ Y )] = σ XY = (x µ X )(y µ Y )p(x, y) =E(XY ) µ X µ Y x y x x µ X y y µ Y P (X = x, Y = y) =p(x, y) (x µ X )(y µ Y )p(x, y) ( 8)( 2)(.10) = ( 8)(2)(.40) = (8)( 2)(.40) = (8)(2)(.10) = Table 7: Covariance of stock returns Functions of Random Variables Suppose we are interested in the sum of X and Y. What will be its probability distribution (specifically its mean and variance)? E(X + Y ) = E(X)+E(Y ) = µ X + µ Y V (X + Y ) = V (X)+V (Y )+2COV (X, Y )=σ 2 X + σ2 Y +2σ XY
23 x y p(x, y) x + y Table 8: Distribution for the sum of stock returns To see this, look at the distribution of the random variable X + Y in Table 8. 1) By definition of mean and variance: E(X + Y )=6(.10) + 10(.40) + 22(.40) + 26(.10) = =16 V (X + Y )=(6 16)2(.1) + (10 16)2(.4) + (22 16)2(.4) + (26 16)2(.1) = 100(.1) + 36(.4) + 36(.4) + 100(.1) = =48.8 2) By the formula: E(X + Y )=E(X)+E(Y )=8+8=16 V (X + Y )=V (X)+V (Y )+2COV (X, Y )=64+4+2( 9.6) = 48.8 General Case (Linear Function) where a and b are any constants: E(aX + by )=ae(x)+be(y )=aµ Y + bµ Y V (ax + by )=a 2 V (X)+b 2 V (Y )+2abCOV (X, Y )=a 2 σ 2 X + b2 σ 2 Y +2abσ XY Example 3.3 Stock Purchase You can purchase either stock A, stock B, or any combination of A and B. Your two criteria for choosing are 1) highest expected return, and 2) lowest variance of return. You can choose p between 0 and 1 (inclusive), where p is the fraction of A you will purchase and 1 p is the fraction of B you will purchase. Your (random) return is: 1) Compute your expected return: 2) Compute the variance of your return: 3) What value of p should you choose? R = px +(1 p)y E(R) = V (R) =
24 Stock A 6% 10% Stock 0% A 16% Table 9: Joint probability distribution for stock returns Complementary Industries Problem 3.1 Conduct the analysis for two complementary industries, where their fortunes tend to be good/bad simultaneously. The joint probabiliy distribution is given in Table 9. A classic paper on this topic (more mathematically rigorous than this example, where each stock has only two possible outcomes) is given in: Harry M. Markowitz, Portfolio Selection, Journal of Finance, 7 (March 1952), pp
25 4 Lecture 4 Introduction to Decision Analysis Textbook Sections: 18.1,18.2(1st 2 subsections),18.3(1st 3 subsections) Problems: 18.1a,b,3,5,6,7,8,9 Often times managers must make long-term decisions without knowing what future events will occur that will effect the firm s financial outcome from their decisions. Decision analysis is a means for managers to consider their choices and help them select an optimal strategy. For instance: Financial officers must decide among certain investment strategies without knowing the state of the economy over the investment horizon. A buyer must choose a model type for the firm s fleet of cars, without knowing what gas prices will be in the future. A drug company must decide whether to aggressively develop a new drug without knowing whether the drug will be effective the patient population. The decision analysis in its simplest form include the following components: Decision Alternatives These are the actions that the decision maker has to choose from. States of Nature These are occurrences that are out of the control of the decision maker, and that occur after the decision has been made. Payoffs Benefits (or losses) that a particular decision alternative has been selected and a given state of nature has observed. Payoff Table A tabular listing of payoffs for all combinations of decision alternatives and states of nature. Case 1 - Decision Making Under Certainty In the extremely unlikely case that the manager knows which state of nature will occur, the manager will simply choose the decision alternative with the highest payoff conditional on that state of nature. Of course, this is a very unlikely situation unless you have a very accurate psychic on the company payroll. Case 2 - Decision Making Under Uncertainty When the decision maker does not know which state will occur, or even what probabilities to assign to the states of nature, several options occur. The two simplest criteria are: Maximax Look at the maximum payoff for each decision alternative. Choose the alternative with the highest maximum payoff. This is optimistic. Maximin Look at the minimum payoff for each decision alternative. with the highest minimum payoff. This is pessimistic. Choose the alternative
26 Case 3 - Decision Making Under Risk In this case, the decision maker does not know which state will occur, but does have probabilities to assign to the states. Payoff tables can be written in the form of decision trees. Note that in diagarams below, squares refer to decision alternatives and circles refer to states of nature. Expected Monetary Value (EMV) This is the expected payoff for a given decision alternative. We take each payoff times the probability of that state occuring, and sum it across states. There will be one EMV per decision alternative. One criteria commonly used is to select the alternative with the highest EMV. Expected Value of Perfect Information (EVPI) This is a measure of how valuable it would be to know what state will occur. First we obtain the expected payoff with perfect information by multiplying the probability of each state of nature and its highest payoff, then summing over states of nature. Then we subtract off the highest EMV to obtain EVPI. Example 4.1 Long-term Marketing Plan A drug manufacturer has two potential drugs for research and development. One drug targets a childhood illness, the other targets an illness among the elderly. The firm expects that both drugs will be effective and will obtain FDA approval, but it will be 10 years before either drug will be brought to market, and involve very expensive research and development. They are not sure what the size of each market will be in 10 years. The firm has four decision alternatives: Pursue neither drug Pursue only the childhood drug Pursue only the elderly drug Pursue both drugs Their are six possible states of nature: Birth rates decrease and life expectancies stay constant (B /L0) Birth rates stay constant and life expectancies stay constant (B0/L0) Birth rates increase and life expectancies stay constant (B + /L0) Birth rates decrease and life expectancies increase (B /L+) Birth rates stay constant and life expectancies increase (B0/L+) Birth rates increase and life expectancies increase (B + /L+) The payoffs (in $million) for each combination of decisions and states of nature are given in Table 10. a) What would be your decision and payoff under each state of nature, if you were certain that state were to occur? B /L0 Decision: B0/L0 Decision: B + /L0 Decision: Payoff: Payoff: Payoff:
27 Decision State of Nature Alternative B /L0 B0/L0 B + /L0 B /L+ B0/L+ B + /L+ Neither Child Elderly Both Table 10: Payoff table for drug development decision B /L+ Decision: B0/L+ Decision: B + /L+ Decision: Payoff: Payoff: Payoff: b) Give the maximax and minimax decisions and their corresponding criteria: Maximax Decision: Maximin Decision: Criteria: Criteria: c) Suppose we are given the probability distribution for the 6 states of nature in Table 11. State Probability B /L B0/L B + /L B /L B0/L B + /L Table 11: Probability distribution for states of nature for drug development decision To obtain the expected monetary value for each decision alternative, we multiply the payoffs for each state of nature and their corresponding probabilities, summing over states of nature. For the decision to develop only the childhood drug: EMV (Child) = ( 20)(0.05) + 10(0.10) + 40(0.15) + ( 20)(0.15) + 10(0.25) + 40(0.30) = Neither EMV (Neither)= Child EMV (Child)= Elderly EMV (Elderly)= Both EMV (Both)= =17.5
28 Based on the EMV criteria, which decision should the firm make? d) A firm that conducts extensive research on population dynamics can be hired and can be expected to tell your firm exactly which state of nature will occur. Give the expected payoff under perfect information, and how much you would be willing to pay for that (EVPI). Example 4.2 Merck s Decision to Build New Factory Around 1993, Merck had to decide whether to build a new plant to manufacture the AIDS drug Crixivan. The drug had not been tested at the time in clinical trials. The plant would be very specialized as the process to synthesize the drug was quite different from the process to produce other drugs. Consider the following facts that were known at the time (I obtained most numbers through newspaper reports, and company balance sheets, all numbers are approximate): Projected revenues $500M/Year Merck profit margin 25% Probability that drug will prove effective and obtain FDA approval 0.10 Cost of building new plants $300M Sunk costs $400M (Money spent in development prior to this decision) Length of time until new generation of drugs 8 years Ignoring tremendous social pressure, does Merck build the factory now, or wait two years and observe the results of clinical trials (thus, forfeiting market share to Hoffman-Laroche and Abbott, who are in fierce competition with Merck). Assume for this problem that if Merck builds now, and the drug gets approved, they will make $125M/Year (present value) for eight years (Note 125=500(0.25)). If they wait, and the drug gets approved, they will generate $62.5M/Year (present value) for six years. This is a by product of losing market share to competitors and 2 years of production. Due to the specificity of the production process, the cost of the plant will be a total loss if the drug does not obtain FDA approval. a) What are Merck s decision alternatives? b) What are the states of nature? c) Give the payoff table. d) Give the Expected Monetary Value (EMV) for each decision. Ignoring social pressure, should Merck go ahead and build the plant? e) At what probability of the drug being successful, is Merck indifferent to building early or waiting. That is, for what value are the EMV s equal for the decision alternatives?
29 Note: Merck did build the plant early, and the drug did receive FDA approval.
30 5 Lecture 5 Normal Distribution and Sampling Distributions Textbook Sections and pages: 6.2,7.2,7.3,pp ,pp ,9.1 Problems: 6.7,9,11, 7.13,21,22,23,25,27 Continuous probability distributions are smooth curves that represent the density of probability around particular values. This density is not interpreted as a probability at the point (all points will have probability of 0), but rather the probability of an outcome occuring between points a and b is measured as the area under the density function between a and b. The density function is always defined so that the total area under it is 1, and it is never negative. The continuous distribution you have seen most often is the normal distribution, but many others exist including the t-distribution, which you also have already seen. 5.1 The Normal Distribution Normal distributions are indexed by 2 parameters, the mean and variance (standard deviation). Figure 8 depicts 3 normal distributions with the same mean (µ = 100) and varying standard deviations (σ = 3, 10, and 25). Figure 9 depicts 3 normal distributions with the same standard deviation (σ = 10) and varying means (µ = 75, 100, and 125). F Figure 8: Normal distributions with common means and varying standard deviations (3, 10, 25) Standard notation for a random variable X, that follows a normal distribution with mean µ and standard deviation σ is X N(µ, σ). Since there are infinitely many normal distributions (corresponding to any µ and any σ > 0), we must standardize normal random variables to obtain probabilities corresponding to them. If X N(µ, σ), we define Z = X µ σ. Z represents the number of standard deviations above (or below, if negative) the mean that X lies. Table A.5 (p. A 14 and last page of text, not including inside back cover) gives the probability that Z lies between 0 and z for values of z between 0 and Recall that the total area under the curve is 1, that the probability that Z is larger than 0 is 0.5, and that the curve is symmetric. X Example 5.1
31 F X Figure 9: Normal distributions with common standard deviations and varying means (75, 100, 125) Scores on the Verbal Ability section of the Graduate Record Examination (GRE) between 10/01/92 and 9/30/95 had a mean of 479 and a standard deviation of 116, based on a population of N = examinations. Scores can range between 200 and 800. Scores on standardized tests tend to be approximately normally distributed. Let X be a score randomly selected from this population. That is, X N(479, 116). What is the probability that a randomly selected student scores above 700? What is the probability the student scores between 400 and 600? Above what score do the top 5% of all students score above? 1. P (X 700) = P ( X µ σ = )=P (Z 1.91) = P (Z 0) P (0 Z 1.91) = 2. P (400 X 600) = P ( σ )=P(.68 Z 1.04) = P (.68 Z 0) + P (0 Z 1.04) = P (0 Z.68) + P (0 Z 1.04) = = X µ = =.5 P (0 Z 1.645) = P (Z 1.645) = P ( X µ σ µ σ) =P (X (116)) = P (X 670) = ) = P (X Source: Interpreting Your GRE General Test and Subject Test Scores , Educational Testing Service. 5.2 Sample Statistics and Sampling Distributions We have described sample statistics previously, showing how they are calculated once a sample has been taken from a larger population. Since these samples are taken at random, the elements of the sample, and thus the sample statisics themselves are random variables. One of the most important theorems in statistics is the Central Limit Theorem, which states that when the sample size is large (n 30), the sample mean is approximately normally distributed with mean µ and variance σ 2 /n, regardless of the shape of the underlying distribution of measurements. Here, µ and σ 2 are the mean and variance of the distribution of the measurements. We can then write X N(µ, σ/ n).
32 The other sample statistics ˆp, X 1 X 2, and ˆp 1 ˆp 2 are also approximately normal in large samples. The distribution of a sample statistic is called its sampling distribution. The standard deviation of a sample statistic s sampling distribution is called its standard error. Table 12 gives each of these 4 sample statistics as well as the means and standard errors of their sampling distributions. The row involving d is a special case of the sample mean for differences among matched pairs of observations (see the paired difference experiment). Estimator (ˆθ) Parameter (θ) Std. Error (σˆθ) Estimated Std. Error (Sˆθ) Degrees of Freedom (ν) X µ n σ n S n 1 ˆp P P (1 P ) n ˆp(1 ˆp) σ 2 X 1 X 2 µ 1 µ 1 2 n 1 + σ2 2 S 2 1 n 2 n 1 + S2 2 n 2 σ d µ d d n S d ˆp 1 ˆp 2 P 1 P 2 P1(1 P 1) n 1 + P2(1 P2) n 2 ˆp1(1 ˆp 1) n 1 n n 1 + n 2 2 n n 1 + ˆp2(1 ˆp2) n 2 Table 12: Means, standard errors, and estimated standard errors of four sample statistics (estimators) To obtain probabilities of observing particular values of a sample statisic, we use the fact that the statistic is normally distributed, and work with Z = ˆθ θ. σˆθ Example 5.2 NCAA Basketball Tournament Scores The NCAA basketball tournament (often referred to as March Madness ) has been held every spring since In the 55 years of the tournament (up until 1993), there had been 1583 games played. Among these 1583 games (the population), the mean and standard deviation of the combined scores of the two combatants are µ = and σ = points, respectively. Suppose each person in this class took samples of size 1, 10, 25, and 50, respectively, from this population of games. Between what two bounds would virtually all students sample means fall between? We know that the sample mean is approximately normally distributed with mean µ = and standard error σ/ n, (the underlying distribution is very well approximated by the normal, meaning that we don t need large samples sizes for the Central Limit Theorem to hold). We also know that for any random variable that is normally distributed, the probability that the random variable falls within two standard deviations (standard errors) of the mean is approximately.95. So, for each sample size, we obtain bounds by computing µ ± 2 σ n. Table 13 gives these bounds for the sample sizes mentioned above. n µ 2 σ n µ +2 σ n = = = = = = = = Table 13: Sample sizes and upper and lower bounds for sample means (95% confidence) As the sample size increases, the sample means get closer and closer to the true mean. Thus if
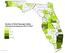
Number of Child Passenger Safety Instructors by County as of 6/2/2017
 Escambia Santa Rosa Okaloosa Walton Holmes Washington Bay Jackson Gadsden Calhoun Leon Liberty Wakulla Gulf Franklin Jefferson Hamilton Madison Suwannee Taylor Lafayette Dixie Gilchrist Columbia Baker
Escambia Santa Rosa Okaloosa Walton Holmes Washington Bay Jackson Gadsden Calhoun Leon Liberty Wakulla Gulf Franklin Jefferson Hamilton Madison Suwannee Taylor Lafayette Dixie Gilchrist Columbia Baker
Voter Registration by Party Affiliation Year to Date Report August 2015
 Page 1 of 10 Republican Party ALACHUA 44,891 44,940 45,112 45,152 45,164 45,214 44,511 44,593 44,791 0 0 0 0 BAKER 6,091 6,116 6,126 6,148 6,154 6,086 6,069 6,086 6,135 0 0 0 0 BAY 55,439 55,559 55,613
Page 1 of 10 Republican Party ALACHUA 44,891 44,940 45,112 45,152 45,164 45,214 44,511 44,593 44,791 0 0 0 0 BAKER 6,091 6,116 6,126 6,148 6,154 6,086 6,069 6,086 6,135 0 0 0 0 BAY 55,439 55,559 55,613
Page 1 of 10 Prepared by Florida Department of State - Division of Elections Voter Registration by Party Affiliation Year to Date Report February 2015
 Page 1 of 10 Republican Party ALACHUA 44,891 44,940 45,112 0 0 0 0 0 0 0 0 0 0 BAKER 6,091 6,116 6,126 0 0 0 0 0 0 0 0 0 0 BAY 55,439 55,559 55,613 0 0 0 0 0 0 0 0 0 0 BRADFORD 6,447 6,464 6,375 0 0 0
Page 1 of 10 Republican Party ALACHUA 44,891 44,940 45,112 0 0 0 0 0 0 0 0 0 0 BAKER 6,091 6,116 6,126 0 0 0 0 0 0 0 0 0 0 BAY 55,439 55,559 55,613 0 0 0 0 0 0 0 0 0 0 BRADFORD 6,447 6,464 6,375 0 0 0
Voter Registration by Party Affiliation Year to Date Report February 2016
 Page 1 of 10 Republican Party ALACHUA 45,660 45,788 46,714 0 0 0 0 0 0 0 0 0 0 BAKER 6,212 6,242 6,632 0 0 0 0 0 0 0 0 0 0 BAY 54,386 54,647 56,237 0 0 0 0 0 0 0 0 0 0 BRADFORD 6,499 6,506 6,761 0 0 0
Page 1 of 10 Republican Party ALACHUA 45,660 45,788 46,714 0 0 0 0 0 0 0 0 0 0 BAKER 6,212 6,242 6,632 0 0 0 0 0 0 0 0 0 0 BAY 54,386 54,647 56,237 0 0 0 0 0 0 0 0 0 0 BRADFORD 6,499 6,506 6,761 0 0 0
FLORIDA EDUCATION FINANCE PROGRAM GOVERNOR'S RECOMMENDED CALCULATION
 2016-17 2017-18 3rd Governor's Recommended Calculation Calculation Difference Difference STUDENT COUNT Unweighted FTE 2,800,009.16 2,828,202.04 28,192.88 1.01% Weighted FTE 3,033,279.31 3,067,030.86 33,751.55
2016-17 2017-18 3rd Governor's Recommended Calculation Calculation Difference Difference STUDENT COUNT Unweighted FTE 2,800,009.16 2,828,202.04 28,192.88 1.01% Weighted FTE 3,033,279.31 3,067,030.86 33,751.55
FLORIDA EDUCATION FINANCE PROGRAM GOVERNOR'S RECOMMENDED CALCULATION
 2017-18 2018-19 2nd Governor's Recommended Calculation Calculation Difference Difference STUDENT COUNT Unweighted FTE 2,829,107.39 2,856,291.81 27,184.42 0.96% Weighted FTE 3,077,667.93 3,106,707.31 29,039.38
2017-18 2018-19 2nd Governor's Recommended Calculation Calculation Difference Difference STUDENT COUNT Unweighted FTE 2,829,107.39 2,856,291.81 27,184.42 0.96% Weighted FTE 3,077,667.93 3,106,707.31 29,039.38
FLORIDA EDUCATION FINANCE PROGRAM GOVERNOR'S BUDGET RECOMMENDATION CALCULATION rd
 2014-15 2015-16 3rd Governor's Budget Recommendation Calculation Calculation Difference Difference STUDENT COUNT Unweighted FTE 2,733,871.84 2,751,718.00 17,846.16 0.65% Weighted FTE 2,964,193.76 2,984,383.46
2014-15 2015-16 3rd Governor's Budget Recommendation Calculation Calculation Difference Difference STUDENT COUNT Unweighted FTE 2,733,871.84 2,751,718.00 17,846.16 0.65% Weighted FTE 2,964,193.76 2,984,383.46
Voluntary Prekindergarten Estimating Conference Executive Summary December 7, Principals. Mark Armstrong, Designee
 Voluntary Prekindergarten Estimating Executive Summary December 7, 2009 Principals Office Office of Economic & Demographic Research (Chair) Executive Office of the Governor House of Representatives Senate
Voluntary Prekindergarten Estimating Executive Summary December 7, 2009 Principals Office Office of Economic & Demographic Research (Chair) Executive Office of the Governor House of Representatives Senate
Florida Department of Education FEFP Second Calculation Certified Required Local Effort Millage Rates
 7/17/2017 Attachment 1 Cert. Mills Florida Department of Education 2017-18 FEFP Second Calculation Certified Required Local Effort Millage Rates Certified Prior Potential Additional Total Certified 2017
7/17/2017 Attachment 1 Cert. Mills Florida Department of Education 2017-18 FEFP Second Calculation Certified Required Local Effort Millage Rates Certified Prior Potential Additional Total Certified 2017
CONFERENCE REPORT FOR EDUCATION ESTIMATING CONFERENCE. PreK-12 ENROLLMENT FLORIDA SCHOOL DISTRICT PROGRAMS
 CONFERENCE REPORT FOR EDUCATION ESTIMATING CONFERENCE PreK-12 ENROLLMENT FLORIDA SCHOOL DISTRICT PROGRAMS UNWEIGHTED FULL-TIME EQUIVALENT (FTE) STUDENT ENROLLMENT Tuesday, July 24, 2018 Forecasts of Student
CONFERENCE REPORT FOR EDUCATION ESTIMATING CONFERENCE PreK-12 ENROLLMENT FLORIDA SCHOOL DISTRICT PROGRAMS UNWEIGHTED FULL-TIME EQUIVALENT (FTE) STUDENT ENROLLMENT Tuesday, July 24, 2018 Forecasts of Student
CHART D-1: RESIDENT DEATHS AND RATES PER 100,000 POPULATION, BY RACE AND GENDER, FLORIDA AND UNITED STATES, CENSUS YEARS AND
 Deaths CHART D-1: RESIDENT DEATHS AND RATES PER 100,000 POPULATION, BY RACE AND GENDER, FLORIDA AND UNITED STATES, CENSUS YEARS 1970-2000 AND 2005-2015 WHITE BLACK YEAR TOTAL WHITE BLACK OTHER MALE FEMALE
Deaths CHART D-1: RESIDENT DEATHS AND RATES PER 100,000 POPULATION, BY RACE AND GENDER, FLORIDA AND UNITED STATES, CENSUS YEARS 1970-2000 AND 2005-2015 WHITE BLACK YEAR TOTAL WHITE BLACK OTHER MALE FEMALE
. In 2009, Florida resident deaths decreased to 169,854. This is a 0.4 percent decrease from 2008.
 Deaths DEATHS. In 2009, Florida resident deaths decreased to 169,854. This is a 0.4 percent decrease from 2008.. The overall resident death rate per 1,000 population decreased 1.1 percent from 9.1 per
Deaths DEATHS. In 2009, Florida resident deaths decreased to 169,854. This is a 0.4 percent decrease from 2008.. The overall resident death rate per 1,000 population decreased 1.1 percent from 9.1 per
DEATHS. In 2011, Florida resident deaths increased to 172,856. This is a 0.2 percent increase from 2010.
 Deaths DEATHS In 2011, Florida resident deaths increased to 172,856. This is a 0.2 percent increase from 2010. The overall resident death rate decreased slightly from 9.2 in 2010 to 9.1 per 1,000 population
Deaths DEATHS In 2011, Florida resident deaths increased to 172,856. This is a 0.2 percent increase from 2010. The overall resident death rate decreased slightly from 9.2 in 2010 to 9.1 per 1,000 population
A Comparison of Hurricane Loss Models (Preliminary Results)
 A Comparison of Hurricane Loss Models (Preliminary Results) presentation to the Florida House of Representatives Committee on Insurance April 16, 2007 1 Today s Briefing Overview of the Commission How
A Comparison of Hurricane Loss Models (Preliminary Results) presentation to the Florida House of Representatives Committee on Insurance April 16, 2007 1 Today s Briefing Overview of the Commission How
BOATING ACCIDENTS STATISTICAL REPORT
 BOATING ACCIDENTS STATISTICAL REPORT BOATING ACCIDENTS STATISTICAL REPORT Personal Watercraft Accidents photo detail Cover Photos: (Courtesy of FWC) NC7-438: On June 24, 207, a was traveling east on Pottsburg
BOATING ACCIDENTS STATISTICAL REPORT BOATING ACCIDENTS STATISTICAL REPORT Personal Watercraft Accidents photo detail Cover Photos: (Courtesy of FWC) NC7-438: On June 24, 207, a was traveling east on Pottsburg
Florida's Refugee Population Statistical Report
 Florida's Refugee Population Statistical Report October 1 st, 2004 September 30 th, 2005 Courtesy of the US Coast Guard Prepared By: Florida Department of Children & Families Refugee Services State of
Florida's Refugee Population Statistical Report October 1 st, 2004 September 30 th, 2005 Courtesy of the US Coast Guard Prepared By: Florida Department of Children & Families Refugee Services State of
Florida's Refugee Population Statistical Report
 Florida's Refugee Population Statistical Report October 1 st, 2002 September 30 th, 2003 Courtesy of the US Coast Guard Prepared By: Florida Department of Children & Families Refugee Services State of
Florida's Refugee Population Statistical Report October 1 st, 2002 September 30 th, 2003 Courtesy of the US Coast Guard Prepared By: Florida Department of Children & Families Refugee Services State of
Personal Watercraft Accidents photo detail
 Personal Watercraft Accidents photo detail Cover Photos: (Courtesy of FWC) On August, 06, at approximately :00 pm, a struck a pontoon boat at Stump Pass State Park. The and pontoon boat were both rental
Personal Watercraft Accidents photo detail Cover Photos: (Courtesy of FWC) On August, 06, at approximately :00 pm, a struck a pontoon boat at Stump Pass State Park. The and pontoon boat were both rental
FLORIDA DIVISION OF EMERGENCY MANAGEMENT STATE WATCH OFFICE DAILY INCIDENT REPORT
 FLORIDA DIVISION OF EMERGENCY MANAGEMENT STATE WATCH OFFICE DAILY INCIDENT REPORT Incident Number: 2018-8027 Occurred: 12/30/2018 03:35 ET Reported to SWO: 12/30/2018 03:36 ET Affecting: Broward, Collier,
FLORIDA DIVISION OF EMERGENCY MANAGEMENT STATE WATCH OFFICE DAILY INCIDENT REPORT Incident Number: 2018-8027 Occurred: 12/30/2018 03:35 ET Reported to SWO: 12/30/2018 03:36 ET Affecting: Broward, Collier,
Lecture Notes for BUSINESS STATISTICS - BMGT 571. Chapters 1 through 6. Professor Ahmadi, Ph.D. Department of Management
 Lecture Notes for BUSINESS STATISTICS - BMGT 571 Chapters 1 through 6 Professor Ahmadi, Ph.D. Department of Management Revised May 005 Glossary of Terms: Statistics Chapter 1 Data Data Set Elements Variable
Lecture Notes for BUSINESS STATISTICS - BMGT 571 Chapters 1 through 6 Professor Ahmadi, Ph.D. Department of Management Revised May 005 Glossary of Terms: Statistics Chapter 1 Data Data Set Elements Variable
Bureau of Economic and Business Research May 29, Measuring Population Density for Counties in Florida
 Bureau of Economic and Business Research May 29, 2015 Measuring Population Density for Counties in Florida By: Stefan Rayer, PhD; Ying Wang, PhD https://www.bebr.ufl.edu/content/measuring-population-density-counties-florida
Bureau of Economic and Business Research May 29, 2015 Measuring Population Density for Counties in Florida By: Stefan Rayer, PhD; Ying Wang, PhD https://www.bebr.ufl.edu/content/measuring-population-density-counties-florida
Salt Lake Community College MATH 1040 Final Exam Fall Semester 2011 Form E
 Salt Lake Community College MATH 1040 Final Exam Fall Semester 011 Form E Name Instructor Time Limit: 10 minutes Any hand-held calculator may be used. Computers, cell phones, or other communication devices
Salt Lake Community College MATH 1040 Final Exam Fall Semester 011 Form E Name Instructor Time Limit: 10 minutes Any hand-held calculator may be used. Computers, cell phones, or other communication devices
Estadística I Exercises Chapter 4 Academic year 2015/16
 Estadística I Exercises Chapter 4 Academic year 2015/16 1. An urn contains 15 balls numbered from 2 to 16. One ball is drawn at random and its number is reported. (a) Define the following events by listing
Estadística I Exercises Chapter 4 Academic year 2015/16 1. An urn contains 15 balls numbered from 2 to 16. One ball is drawn at random and its number is reported. (a) Define the following events by listing
Exam III Review Math-132 (Sections 7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.3)
 1 Exam III Review Math-132 (Sections 7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.3) On this exam, questions may come from any of the following topic areas: - Union and intersection of sets - Complement of
1 Exam III Review Math-132 (Sections 7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.3) On this exam, questions may come from any of the following topic areas: - Union and intersection of sets - Complement of
Basic Concepts of Probability. Section 3.1 Basic Concepts of Probability. Probability Experiments. Chapter 3 Probability
 Chapter 3 Probability 3.1 Basic Concepts of Probability 3.2 Conditional Probability and the Multiplication Rule 3.3 The Addition Rule 3.4 Additional Topics in Probability and Counting Section 3.1 Basic
Chapter 3 Probability 3.1 Basic Concepts of Probability 3.2 Conditional Probability and the Multiplication Rule 3.3 The Addition Rule 3.4 Additional Topics in Probability and Counting Section 3.1 Basic
Measuring Urban Form and Examining Its Impact on Traffic Congestion in Florida
 Measuring Urban Form and Examining Its Impact on Traffic Congestion in Florida By Vince Wang Chair: Ruth Steiner Co-Chair: Andres Blanco March 04, 2011 Department of Urban and Regional Planning Overview
Measuring Urban Form and Examining Its Impact on Traffic Congestion in Florida By Vince Wang Chair: Ruth Steiner Co-Chair: Andres Blanco March 04, 2011 Department of Urban and Regional Planning Overview
CIVL 7012/8012. Collection and Analysis of Information
 CIVL 7012/8012 Collection and Analysis of Information Uncertainty in Engineering Statistics deals with the collection and analysis of data to solve real-world problems. Uncertainty is inherent in all real
CIVL 7012/8012 Collection and Analysis of Information Uncertainty in Engineering Statistics deals with the collection and analysis of data to solve real-world problems. Uncertainty is inherent in all real
Introduction to Probability
 Introduction to Probability Content Experiments, Counting Rules, and Assigning Probabilities Events and Their Probability Some Basic Relationships of Probability Conditional Probability Bayes Theorem 2
Introduction to Probability Content Experiments, Counting Rules, and Assigning Probabilities Events and Their Probability Some Basic Relationships of Probability Conditional Probability Bayes Theorem 2
ANNUAL POWER POLE INTEGRITY PROGRAM MAY 2005 SUMMARY
 ANNUAL POWER POLE INTEGRITY PROGRAM MAY 2005 SUMMARY Overview In the spring of 2005, due to concern over the number of poles damaged and downed by the storms of 2004, the Commission s Electric Safety group
ANNUAL POWER POLE INTEGRITY PROGRAM MAY 2005 SUMMARY Overview In the spring of 2005, due to concern over the number of poles damaged and downed by the storms of 2004, the Commission s Electric Safety group
Marketing Research Session 10 Hypothesis Testing with Simple Random samples (Chapter 12)
 Marketing Research Session 10 Hypothesis Testing with Simple Random samples (Chapter 12) Remember: Z.05 = 1.645, Z.01 = 2.33 We will only cover one-sided hypothesis testing (cases 12.3, 12.4.2, 12.5.2,
Marketing Research Session 10 Hypothesis Testing with Simple Random samples (Chapter 12) Remember: Z.05 = 1.645, Z.01 = 2.33 We will only cover one-sided hypothesis testing (cases 12.3, 12.4.2, 12.5.2,
Probability and Probability Distributions. Dr. Mohammed Alahmed
 Probability and Probability Distributions 1 Probability and Probability Distributions Usually we want to do more with data than just describing them! We might want to test certain specific inferences about
Probability and Probability Distributions 1 Probability and Probability Distributions Usually we want to do more with data than just describing them! We might want to test certain specific inferences about
hypotheses. P-value Test for a 2 Sample z-test (Large Independent Samples) n > 30 P-value Test for a 2 Sample t-test (Small Samples) n < 30 Identify α
 Chapter 8 Notes Section 8-1 Independent and Dependent Samples Independent samples have no relation to each other. An example would be comparing the costs of vacationing in Florida to the cost of vacationing
Chapter 8 Notes Section 8-1 Independent and Dependent Samples Independent samples have no relation to each other. An example would be comparing the costs of vacationing in Florida to the cost of vacationing
7/29/2012 FLORIDA DEPARTMENT OF STATE DIVISION OF ELECTIONS Primary Election County Voter Registration By Congressional District July 16, 2012.
 Page 1 Congressional District 1 SCAMBIA 83440 70071 0 5 46 3 1 0 1 116 617 3960 333 0 1 35 4 28767 187400 HOLMS 2414 4023 0 0 2 0 0 0 0 4 5 83 5 0 0 0 0 581 7117 OKALOOSA 72644 26647 3 8 21 0 0 0 4 50
Page 1 Congressional District 1 SCAMBIA 83440 70071 0 5 46 3 1 0 1 116 617 3960 333 0 1 35 4 28767 187400 HOLMS 2414 4023 0 0 2 0 0 0 0 4 5 83 5 0 0 0 0 581 7117 OKALOOSA 72644 26647 3 8 21 0 0 0 4 50
Section 4.2 Basic Concepts of Probability
 Section 4.2 Basic Concepts of Probability 2012 Pearson Education, Inc. All rights reserved. 1 of 88 Section 4.2 Objectives Identify the sample space of a probability experiment Identify simple events Use
Section 4.2 Basic Concepts of Probability 2012 Pearson Education, Inc. All rights reserved. 1 of 88 Section 4.2 Objectives Identify the sample space of a probability experiment Identify simple events Use
Florida's Refugee Population Statistical Report
 Florida's Refugee Population Statistical Report October 1 st, 2008 September 30 th, 2009 And Federal Fiscal Year 2005-2009 Courtesy of the US Coast Guard Prepared By: Florida Department of Children & Families
Florida's Refugee Population Statistical Report October 1 st, 2008 September 30 th, 2009 And Federal Fiscal Year 2005-2009 Courtesy of the US Coast Guard Prepared By: Florida Department of Children & Families
Queen s University Faculty of Arts and Sciences Department of Economics Winter Economics 250 A and B: Introduction to Statistics
 Queen s University Faculty of Arts and Sciences Department of Economics Winter 2007 Economics 250 A and B: Introduction to Statistics Instructions: Term Test 1 February 7th, 2007 Read questions and instructions
Queen s University Faculty of Arts and Sciences Department of Economics Winter 2007 Economics 250 A and B: Introduction to Statistics Instructions: Term Test 1 February 7th, 2007 Read questions and instructions
DSST Principles of Statistics
 DSST Principles of Statistics Time 10 Minutes 98 Questions Each incomplete statement is followed by four suggested completions. Select the one that is best in each case. 1. Which of the following variables
DSST Principles of Statistics Time 10 Minutes 98 Questions Each incomplete statement is followed by four suggested completions. Select the one that is best in each case. 1. Which of the following variables
Expectations and Variance
 4. Model parameters and their estimates 4.1 Expected Value and Conditional Expected Value 4. The Variance 4.3 Population vs Sample Quantities 4.4 Mean and Variance of a Linear Combination 4.5 The Covariance
4. Model parameters and their estimates 4.1 Expected Value and Conditional Expected Value 4. The Variance 4.3 Population vs Sample Quantities 4.4 Mean and Variance of a Linear Combination 4.5 The Covariance
2.4. Conditional Probability
 2.4. Conditional Probability Objectives. Definition of conditional probability and multiplication rule Total probability Bayes Theorem Example 2.4.1. (#46 p.80 textbook) Suppose an individual is randomly
2.4. Conditional Probability Objectives. Definition of conditional probability and multiplication rule Total probability Bayes Theorem Example 2.4.1. (#46 p.80 textbook) Suppose an individual is randomly
Chapter 2 Class Notes
 Chapter 2 Class Notes Probability can be thought of in many ways, for example as a relative frequency of a long series of trials (e.g. flips of a coin or die) Another approach is to let an expert (such
Chapter 2 Class Notes Probability can be thought of in many ways, for example as a relative frequency of a long series of trials (e.g. flips of a coin or die) Another approach is to let an expert (such
Statistics for IT Managers
 Statistics for IT Managers 95-796, Fall 2012 Module 2: Hypothesis Testing and Statistical Inference (5 lectures) Reading: Statistics for Business and Economics, Ch. 5-7 Confidence intervals Given the sample
Statistics for IT Managers 95-796, Fall 2012 Module 2: Hypothesis Testing and Statistical Inference (5 lectures) Reading: Statistics for Business and Economics, Ch. 5-7 Confidence intervals Given the sample
SALES AND MARKETING Department MATHEMATICS. 2nd Semester. Bivariate statistics. Tutorials and exercises
 SALES AND MARKETING Department MATHEMATICS 2nd Semester Bivariate statistics Tutorials and exercises Online document: http://jff-dut-tc.weebly.com section DUT Maths S2. IUT de Saint-Etienne Département
SALES AND MARKETING Department MATHEMATICS 2nd Semester Bivariate statistics Tutorials and exercises Online document: http://jff-dut-tc.weebly.com section DUT Maths S2. IUT de Saint-Etienne Département
SESSION 5 Descriptive Statistics
 SESSION 5 Descriptive Statistics Descriptive statistics are used to describe the basic features of the data in a study. They provide simple summaries about the sample and the measures. Together with simple
SESSION 5 Descriptive Statistics Descriptive statistics are used to describe the basic features of the data in a study. They provide simple summaries about the sample and the measures. Together with simple
A is one of the categories into which qualitative data can be classified.
 Chapter 2 Methods for Describing Sets of Data 2.1 Describing qualitative data Recall qualitative data: non-numerical or categorical data Basic definitions: A is one of the categories into which qualitative
Chapter 2 Methods for Describing Sets of Data 2.1 Describing qualitative data Recall qualitative data: non-numerical or categorical data Basic definitions: A is one of the categories into which qualitative
The point value of each problem is in the left-hand margin. You must show your work to receive any credit, except in problem 1. Work neatly.
 Introduction to Statistics Math 1040 Sample Final Exam - Chapters 1-11 6 Problem Pages Time Limit: 1 hour and 50 minutes Open Textbook Calculator Allowed: Scientific Name: The point value of each problem
Introduction to Statistics Math 1040 Sample Final Exam - Chapters 1-11 6 Problem Pages Time Limit: 1 hour and 50 minutes Open Textbook Calculator Allowed: Scientific Name: The point value of each problem
AP Statistics Review Ch. 7
 AP Statistics Review Ch. 7 Name 1. Which of the following best describes what is meant by the term sampling variability? A. There are many different methods for selecting a sample. B. Two different samples
AP Statistics Review Ch. 7 Name 1. Which of the following best describes what is meant by the term sampling variability? A. There are many different methods for selecting a sample. B. Two different samples
TOPIC: Descriptive Statistics Single Variable
 TOPIC: Descriptive Statistics Single Variable I. Numerical data summary measurements A. Measures of Location. Measures of central tendency Mean; Median; Mode. Quantiles - measures of noncentral tendency
TOPIC: Descriptive Statistics Single Variable I. Numerical data summary measurements A. Measures of Location. Measures of central tendency Mean; Median; Mode. Quantiles - measures of noncentral tendency
Introduction to Statistics
 Why Statistics? Introduction to Statistics To develop an appreciation for variability and how it effects products and processes. Study methods that can be used to help solve problems, build knowledge and
Why Statistics? Introduction to Statistics To develop an appreciation for variability and how it effects products and processes. Study methods that can be used to help solve problems, build knowledge and
20 Hypothesis Testing, Part I
 20 Hypothesis Testing, Part I Bob has told Alice that the average hourly rate for a lawyer in Virginia is $200 with a standard deviation of $50, but Alice wants to test this claim. If Bob is right, she
20 Hypothesis Testing, Part I Bob has told Alice that the average hourly rate for a lawyer in Virginia is $200 with a standard deviation of $50, but Alice wants to test this claim. If Bob is right, she
Statistics for Managers Using Microsoft Excel/SPSS Chapter 4 Basic Probability And Discrete Probability Distributions
 Statistics for Managers Using Microsoft Excel/SPSS Chapter 4 Basic Probability And Discrete Probability Distributions 1999 Prentice-Hall, Inc. Chap. 4-1 Chapter Topics Basic Probability Concepts: Sample
Statistics for Managers Using Microsoft Excel/SPSS Chapter 4 Basic Probability And Discrete Probability Distributions 1999 Prentice-Hall, Inc. Chap. 4-1 Chapter Topics Basic Probability Concepts: Sample
Probability Experiments, Trials, Outcomes, Sample Spaces Example 1 Example 2
 Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
Probability Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application. However, probability models underlie
AP Final Review II Exploring Data (20% 30%)
 AP Final Review II Exploring Data (20% 30%) Quantitative vs Categorical Variables Quantitative variables are numerical values for which arithmetic operations such as means make sense. It is usually a measure
AP Final Review II Exploring Data (20% 30%) Quantitative vs Categorical Variables Quantitative variables are numerical values for which arithmetic operations such as means make sense. It is usually a measure
Chapter 4 - Introduction to Probability
 Chapter 4 - Introduction to Probability Probability is a numerical measure of the likelihood that an event will occur. Probability values are always assigned on a scale from 0 to 1. A probability near
Chapter 4 - Introduction to Probability Probability is a numerical measure of the likelihood that an event will occur. Probability values are always assigned on a scale from 0 to 1. A probability near
Problems Pages 1-4 Answers Page 5 Solutions Pages 6-11
 Part III Practice Problems Problems Pages 1-4 Answers Page 5 Solutions Pages 6-11 1. In estimating population mean or proportion what is the width of an interval? 2. If 25 college students out of 80 graduate
Part III Practice Problems Problems Pages 1-4 Answers Page 5 Solutions Pages 6-11 1. In estimating population mean or proportion what is the width of an interval? 2. If 25 college students out of 80 graduate
Final Exam Review. Name: Class: Date: Short Answer
 Name: Class: Date: ID: A Final Exam Review Short Answer. Use x, 2, 0,, 2 to graph the function f( x) 2 x. Then graph its inverse. Describe the domain and range of the inverse function. 2. Graph the inverse
Name: Class: Date: ID: A Final Exam Review Short Answer. Use x, 2, 0,, 2 to graph the function f( x) 2 x. Then graph its inverse. Describe the domain and range of the inverse function. 2. Graph the inverse
15. (,4)
 CHAPTER Algebra Toolbox CHAPTER Functions Graphs, and Models; Linear Functions Toolbox Exercises. {,,,,5,6,7,8} and { xx< 9, x N} Remember that x N means that x is a natural number.. (,7]. (,7 ] 5. (,)
CHAPTER Algebra Toolbox CHAPTER Functions Graphs, and Models; Linear Functions Toolbox Exercises. {,,,,5,6,7,8} and { xx< 9, x N} Remember that x N means that x is a natural number.. (,7]. (,7 ] 5. (,)
Chapter 4 Probability
 4-1 Review and Preview Chapter 4 Probability 4-2 Basic Concepts of Probability 4-3 Addition Rule 4-4 Multiplication Rule: Basics 4-5 Multiplication Rule: Complements and Conditional Probability 4-6 Counting
4-1 Review and Preview Chapter 4 Probability 4-2 Basic Concepts of Probability 4-3 Addition Rule 4-4 Multiplication Rule: Basics 4-5 Multiplication Rule: Complements and Conditional Probability 4-6 Counting
Elementary Statistics
 Elementary Statistics Q: What is data? Q: What does the data look like? Q: What conclusions can we draw from the data? Q: Where is the middle of the data? Q: Why is the spread of the data important? Q:
Elementary Statistics Q: What is data? Q: What does the data look like? Q: What conclusions can we draw from the data? Q: Where is the middle of the data? Q: Why is the spread of the data important? Q:
8.1 Frequency Distribution, Frequency Polygon, Histogram page 326
 page 35 8 Statistics are around us both seen and in ways that affect our lives without us knowing it. We have seen data organized into charts in magazines, books and newspapers. That s descriptive statistics!
page 35 8 Statistics are around us both seen and in ways that affect our lives without us knowing it. We have seen data organized into charts in magazines, books and newspapers. That s descriptive statistics!
Chapter 6. Probability
 Chapter 6 robability Suppose two six-sided die is rolled and they both land on sixes. Or a coin is flipped and it lands on heads. Or record the color of the next 20 cars to pass an intersection. These
Chapter 6 robability Suppose two six-sided die is rolled and they both land on sixes. Or a coin is flipped and it lands on heads. Or record the color of the next 20 cars to pass an intersection. These
Topic 5: Discrete Random Variables & Expectations Reference Chapter 4
 Page 1 Topic 5: Discrete Random Variables & Epectations Reference Chapter 4 In Chapter 3 we studied rules for associating a probability value with a single event or with a subset of events in an eperiment.
Page 1 Topic 5: Discrete Random Variables & Epectations Reference Chapter 4 In Chapter 3 we studied rules for associating a probability value with a single event or with a subset of events in an eperiment.
Exam: practice test 1 MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Exam: practice test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Using the information in the table on home sale prices in
Exam: practice test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. ) Using the information in the table on home sale prices in
Discrete Distributions
 Discrete Distributions STA 281 Fall 2011 1 Introduction Previously we defined a random variable to be an experiment with numerical outcomes. Often different random variables are related in that they have
Discrete Distributions STA 281 Fall 2011 1 Introduction Previously we defined a random variable to be an experiment with numerical outcomes. Often different random variables are related in that they have
Chapter 6 Continuous Probability Distributions
 Continuous Probability Distributions Learning Objectives 1. Understand the difference between how probabilities are computed for discrete and continuous random variables. 2. Know how to compute probability
Continuous Probability Distributions Learning Objectives 1. Understand the difference between how probabilities are computed for discrete and continuous random variables. 2. Know how to compute probability
CONTINUOUS RANDOM VARIABLES
 the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET STATISTICS (AQA) CONTINUOUS RANDOM VARIABLES The main ideas are: Properties of Continuous Random Variables Mean, Median and Mode
the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET STATISTICS (AQA) CONTINUOUS RANDOM VARIABLES The main ideas are: Properties of Continuous Random Variables Mean, Median and Mode
Discrete probability distributions
 Discrete probability s BSAD 30 Dave Novak Fall 08 Source: Anderson et al., 05 Quantitative Methods for Business th edition some slides are directly from J. Loucks 03 Cengage Learning Covered so far Chapter
Discrete probability s BSAD 30 Dave Novak Fall 08 Source: Anderson et al., 05 Quantitative Methods for Business th edition some slides are directly from J. Loucks 03 Cengage Learning Covered so far Chapter
Introduction to Statistics
 Introduction to Statistics Data and Statistics Data consists of information coming from observations, counts, measurements, or responses. Statistics is the science of collecting, organizing, analyzing,
Introduction to Statistics Data and Statistics Data consists of information coming from observations, counts, measurements, or responses. Statistics is the science of collecting, organizing, analyzing,
Math 10 - Compilation of Sample Exam Questions + Answers
 Math 10 - Compilation of Sample Exam Questions + Sample Exam Question 1 We have a population of size N. Let p be the independent probability of a person in the population developing a disease. Answer the
Math 10 - Compilation of Sample Exam Questions + Sample Exam Question 1 We have a population of size N. Let p be the independent probability of a person in the population developing a disease. Answer the
What is statistics? Statistics is the science of: Collecting information. Organizing and summarizing the information collected
 What is statistics? Statistics is the science of: Collecting information Organizing and summarizing the information collected Analyzing the information collected in order to draw conclusions Two types
What is statistics? Statistics is the science of: Collecting information Organizing and summarizing the information collected Analyzing the information collected in order to draw conclusions Two types
College Algebra. Word Problems
 College Algebra Word Problems Example 2 (Section P6) The table shows the numbers N (in millions) of subscribers to a cellular telecommunication service in the United States from 2001 through 2010, where
College Algebra Word Problems Example 2 (Section P6) The table shows the numbers N (in millions) of subscribers to a cellular telecommunication service in the United States from 2001 through 2010, where
Inferences Based on Two Samples
 Chapter 6 Inferences Based on Two Samples Frequently we want to use statistical techniques to compare two populations. For example, one might wish to compare the proportions of families with incomes below
Chapter 6 Inferences Based on Two Samples Frequently we want to use statistical techniques to compare two populations. For example, one might wish to compare the proportions of families with incomes below
Tropical Update 6 AM EDT Friday, October 7, 2016 Hurricane Matthew & Hurricane Nicole
 Tropical Update 6 AM EDT Friday, October 7, 2016 Hurricane Matthew & Hurricane Nicole This update is intended for government and emergency response officials, and is provided for informational and situational
Tropical Update 6 AM EDT Friday, October 7, 2016 Hurricane Matthew & Hurricane Nicole This update is intended for government and emergency response officials, and is provided for informational and situational
Statistics for Managers Using Microsoft Excel (3 rd Edition)
 Statistics for Managers Using Microsoft Excel (3 rd Edition) Chapter 4 Basic Probability and Discrete Probability Distributions 2002 Prentice-Hall, Inc. Chap 4-1 Chapter Topics Basic probability concepts
Statistics for Managers Using Microsoft Excel (3 rd Edition) Chapter 4 Basic Probability and Discrete Probability Distributions 2002 Prentice-Hall, Inc. Chap 4-1 Chapter Topics Basic probability concepts
Chapter. Probability
 Chapter 3 Probability Section 3.1 Basic Concepts of Probability Section 3.1 Objectives Identify the sample space of a probability experiment Identify simple events Use the Fundamental Counting Principle
Chapter 3 Probability Section 3.1 Basic Concepts of Probability Section 3.1 Objectives Identify the sample space of a probability experiment Identify simple events Use the Fundamental Counting Principle
Table of z values and probabilities for the standard normal distribution. z is the first column plus the top row. Each cell shows P(X z).
 Table of z values and probabilities for the standard normal distribution. z is the first column plus the top row. Each cell shows P(X z). For example P(X.04) =.8508. For z < 0 subtract the value from,
Table of z values and probabilities for the standard normal distribution. z is the first column plus the top row. Each cell shows P(X z). For example P(X.04) =.8508. For z < 0 subtract the value from,
Probability the chance that an uncertain event will occur (always between 0 and 1)
 Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
Quantitative Methods 2013 1 Probability as a Numerical Measure of the Likelihood of Occurrence Probability the chance that an uncertain event will occur (always between 0 and 1) Increasing Likelihood of
where Female = 0 for males, = 1 for females Age is measured in years (22, 23, ) GPA is measured in units on a four-point scale (0, 1.22, 3.45, etc.
 Notes on regression analysis 1. Basics in regression analysis key concepts (actual implementation is more complicated) A. Collect data B. Plot data on graph, draw a line through the middle of the scatter
Notes on regression analysis 1. Basics in regression analysis key concepts (actual implementation is more complicated) A. Collect data B. Plot data on graph, draw a line through the middle of the scatter
CHAPTER 8 INTRODUCTION TO STATISTICAL ANALYSIS
 CHAPTER 8 INTRODUCTION TO STATISTICAL ANALYSIS LEARNING OBJECTIVES: After studying this chapter, a student should understand: notation used in statistics; how to represent variables in a mathematical form
CHAPTER 8 INTRODUCTION TO STATISTICAL ANALYSIS LEARNING OBJECTIVES: After studying this chapter, a student should understand: notation used in statistics; how to represent variables in a mathematical form
ALGEBRA 1 SEMESTER 1 INSTRUCTIONAL MATERIALS Courses: Algebra 1 S1 (#2201) and Foundations in Algebra 1 S1 (#7769)
 Multiple Choice: Identify the choice that best completes the statement or answers the question. 1. Ramal goes to the grocery store and buys pounds of apples and pounds of bananas. Apples cost dollars per
Multiple Choice: Identify the choice that best completes the statement or answers the question. 1. Ramal goes to the grocery store and buys pounds of apples and pounds of bananas. Apples cost dollars per
Math 218 Supplemental Instruction Spring 2008 Final Review Part A
 Spring 2008 Final Review Part A SI leaders: Mario Panak, Jackie Hu, Christina Tasooji Chapters 3, 4, and 5 Topics Covered: General probability (probability laws, conditional, joint probabilities, independence)
Spring 2008 Final Review Part A SI leaders: Mario Panak, Jackie Hu, Christina Tasooji Chapters 3, 4, and 5 Topics Covered: General probability (probability laws, conditional, joint probabilities, independence)
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
15: CHI SQUARED TESTS
 15: CHI SQUARED ESS MULIPLE CHOICE QUESIONS In the following multiple choice questions, please circle the correct answer. 1. Which statistical technique is appropriate when we describe a single population
15: CHI SQUARED ESS MULIPLE CHOICE QUESIONS In the following multiple choice questions, please circle the correct answer. 1. Which statistical technique is appropriate when we describe a single population
Hypothesis testing for µ:
 University of California, Los Angeles Department of Statistics Statistics 10 Elements of a hypothesis test: Hypothesis testing Instructor: Nicolas Christou 1. Null hypothesis, H 0 (always =). 2. Alternative
University of California, Los Angeles Department of Statistics Statistics 10 Elements of a hypothesis test: Hypothesis testing Instructor: Nicolas Christou 1. Null hypothesis, H 0 (always =). 2. Alternative
4. Conditional Probability
 1 of 13 7/15/2009 9:25 PM Virtual Laboratories > 2. Probability Spaces > 1 2 3 4 5 6 7 4. Conditional Probability Definitions and Interpretations The Basic Definition As usual, we start with a random experiment
1 of 13 7/15/2009 9:25 PM Virtual Laboratories > 2. Probability Spaces > 1 2 3 4 5 6 7 4. Conditional Probability Definitions and Interpretations The Basic Definition As usual, we start with a random experiment
Mt. Douglas Secondary
 Foundations of Math 11 Calculator Usage 207 HOW TO USE TI-83, TI-83 PLUS, TI-84 PLUS CALCULATORS FOR STATISTICS CALCULATIONS shows it is an actual calculator key to press 1. Using LISTS to Calculate Mean,
Foundations of Math 11 Calculator Usage 207 HOW TO USE TI-83, TI-83 PLUS, TI-84 PLUS CALCULATORS FOR STATISTICS CALCULATIONS shows it is an actual calculator key to press 1. Using LISTS to Calculate Mean,
(quantitative or categorical variables) Numerical descriptions of center, variability, position (quantitative variables)
 3. Descriptive Statistics Describing data with tables and graphs (quantitative or categorical variables) Numerical descriptions of center, variability, position (quantitative variables) Bivariate descriptions
3. Descriptive Statistics Describing data with tables and graphs (quantitative or categorical variables) Numerical descriptions of center, variability, position (quantitative variables) Bivariate descriptions
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Chapter 9 Hypothesis Testing: Single Population Ch. 9-1 9.1 What is a Hypothesis? A hypothesis is a claim (assumption) about a population parameter: population
Econ 325: Introduction to Empirical Economics Chapter 9 Hypothesis Testing: Single Population Ch. 9-1 9.1 What is a Hypothesis? A hypothesis is a claim (assumption) about a population parameter: population
Point Estimation and Confidence Interval
 Chapter 8 Point Estimation and Confidence Interval 8.1 Point estimator The purpose of point estimation is to use a function of the sample data to estimate the unknown parameter. Definition 8.1 A parameter
Chapter 8 Point Estimation and Confidence Interval 8.1 Point estimator The purpose of point estimation is to use a function of the sample data to estimate the unknown parameter. Definition 8.1 A parameter
MATH 10 INTRODUCTORY STATISTICS
 MATH 10 INTRODUCTORY STATISTICS Tommy Khoo Your friendly neighbourhood graduate student. Week 1 Chapter 1 Introduction What is Statistics? Why do you need to know Statistics? Technical lingo and concepts:
MATH 10 INTRODUCTORY STATISTICS Tommy Khoo Your friendly neighbourhood graduate student. Week 1 Chapter 1 Introduction What is Statistics? Why do you need to know Statistics? Technical lingo and concepts:
FLORIDA DIVISION OF EMERGENCY MANAGEMENT STATE WATCH OFFICE DAILY INCIDENT REPORT
 FLORIDA DIVISION OF EMERGENCY MANAGEMENT STATE WATCH OFFICE DAILY INCIDENT REPORT Incident Number: 2018-7765 Incident Name: Areal Flood Watch Occurred: 12/19/2018 04:06 ET Reported to SWO: 12/19/2018 04:07
FLORIDA DIVISION OF EMERGENCY MANAGEMENT STATE WATCH OFFICE DAILY INCIDENT REPORT Incident Number: 2018-7765 Incident Name: Areal Flood Watch Occurred: 12/19/2018 04:06 ET Reported to SWO: 12/19/2018 04:07
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 7 Inferences Based on Two Samples: Confidence Intervals & Tests of Hypotheses Content 1. Identifying the Target Parameter 2. Comparing Two Population Means:
Statistics for Business and Economics Chapter 7 Inferences Based on Two Samples: Confidence Intervals & Tests of Hypotheses Content 1. Identifying the Target Parameter 2. Comparing Two Population Means:
MATH 081. Diagnostic Review Materials PART 2. Chapters 5 to 7 YOU WILL NOT BE GIVEN A DIAGNOSTIC TEST UNTIL THIS MATERIAL IS RETURNED.
 MATH 08 Diagnostic Review Materials PART Chapters 5 to 7 YOU WILL NOT BE GIVEN A DIAGNOSTIC TEST UNTIL THIS MATERIAL IS RETURNED DO NOT WRITE IN THIS MATERIAL Revised Winter 0 PRACTICE TEST: Complete as
MATH 08 Diagnostic Review Materials PART Chapters 5 to 7 YOU WILL NOT BE GIVEN A DIAGNOSTIC TEST UNTIL THIS MATERIAL IS RETURNED DO NOT WRITE IN THIS MATERIAL Revised Winter 0 PRACTICE TEST: Complete as
2.6 Tools for Counting sample points
 2.6 Tools for Counting sample points When the number of simple events in S is too large, manual enumeration of every sample point in S is tedious or even impossible. (Example) If S contains N equiprobable
2.6 Tools for Counting sample points When the number of simple events in S is too large, manual enumeration of every sample point in S is tedious or even impossible. (Example) If S contains N equiprobable
LC OL - Statistics. Types of Data
 LC OL - Statistics Types of Data Question 1 Characterise each of the following variables as numerical or categorical. In each case, list any three possible values for the variable. (i) Eye colours in a
LC OL - Statistics Types of Data Question 1 Characterise each of the following variables as numerical or categorical. In each case, list any three possible values for the variable. (i) Eye colours in a
Practice Questions for Exam 1
 Practice Questions for Exam 1 1. A used car lot evaluates their cars on a number of features as they arrive in the lot in order to determine their worth. Among the features looked at are miles per gallon
Practice Questions for Exam 1 1. A used car lot evaluates their cars on a number of features as they arrive in the lot in order to determine their worth. Among the features looked at are miles per gallon
Lesson B1 - Probability Distributions.notebook
 Learning Goals: * Define a discrete random variable * Applying a probability distribution of a discrete random variable. * Use tables, graphs, and expressions to represent the distributions. Should you
Learning Goals: * Define a discrete random variable * Applying a probability distribution of a discrete random variable. * Use tables, graphs, and expressions to represent the distributions. Should you
All the men living in Turkey can be a population. The average height of these men can be a population parameter
 CHAPTER 1: WHY STUDY STATISTICS? Why Study Statistics? Population is a large (or in nite) set of elements that are in the interest of a research question. A parameter is a speci c characteristic of a population
CHAPTER 1: WHY STUDY STATISTICS? Why Study Statistics? Population is a large (or in nite) set of elements that are in the interest of a research question. A parameter is a speci c characteristic of a population
Math 074 Final Exam Review. REVIEW FOR NO CALCULATOR PART OF THE EXAM (Questions 1-14)
 Math 074 Final Exam Review REVIEW FOR NO CALCULATOR PART OF THE EXAM (Questions -4) I. Can you add, subtract, multiply and divide fractions and mixed numbers?. Perform the indicated operations. Be sure
Math 074 Final Exam Review REVIEW FOR NO CALCULATOR PART OF THE EXAM (Questions -4) I. Can you add, subtract, multiply and divide fractions and mixed numbers?. Perform the indicated operations. Be sure
Record your answers and work on the separate answer sheet provided.
 MATH 106 FINAL EXAMINATION This is an open-book exam. You may refer to your text and other course materials as you work on the exam, and you may use a calculator. You must complete the exam individually.
MATH 106 FINAL EXAMINATION This is an open-book exam. You may refer to your text and other course materials as you work on the exam, and you may use a calculator. You must complete the exam individually.
3 PROBABILITY TOPICS
 Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
