Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules).
|
|
|
- Gyles Anthony
- 5 years ago
- Views:
Transcription
1 Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates pairs of 0s and 1s. T generates 0s or wipes out Rs. Since T can wipe out Rs, the first rule creates a 0 that can be at the beginning, end, or somewhere in the middle of the string. T guarantees that we can have as many 0s as we want, but S guarantees that we have at least one more 0 than 1.) 1b) Begin with the CFG grammar, G = ({S, S 1, S 2, S 3, R 1, R 2, R 3, A, B, C}, {a, b, c}, P, S) where P is: (S produces the union of the three cases) S S 1 S 2 S 3 (These two rules produce strings with at least 2 symbols out of order ) S 1 R 1 bar 1 R 1 car 1 R 1 cbr 1 R 1 ar 1 br 1 cr 1 ε (These two rules produce strings of form a i b j c k with i j) S 2 R 2 C R 2 R 2 ar 2 b A B (These two rules produce strings of form a i b j c k with j k) S 3 AR 3 R 3 R 3 br 3 c B C (These three rules produce a string of characters of the same symbol) A aa a B bb b C cc c Convert to CNF 0. We skip creating a new start variable since the existing start variable, S, is non-recursive. 1. Remove ε-productions. R 1 is the only nullable variable. S S 1 S 2 S 3 S 1 R 1 bar 1 R 1 car 1 R 1 cbr 1 bar 1 car 1 cbr 1 R 1 ba R 1 ca R 1 cb ba ca cb R 1 ar 1 br 1 cr 1 a b c S 2 R 2 C R 2 R 2 ar 2 b A B S 3 AR 3 R 3 R 3 br 3 c B C A aa a B bb b C cc c 2. Remove unit productions. S R 1 bar 1 R 1 car 1 R 1 cbr 1 bar 1 car 1 cbr 1 R 1 ba R 1 ca R 1 cb ba ca cb R 2 C ar 2 b aa a bb b AR 3 br 3 c cc c Page 1/8
2 S 1 R 1 bar 1 R 1 car 1 R 1 cbr 1 bar 1 car 1 cbr 1 R 1 ba R 1 ca R 1 cb ba ca cb R 1 ar 1 br 1 cr 1 a b c S 2 R 2 C ar 2 b aa a bb b R 2 ar 2 b aa a bb b S 3 AR 3 br 3 c bb b cc c R 3 br 3 c bb b cc c A aa a B bb b C cc c 3. Remove useless (nonproductive, unreachable) productions. S R 1 bar 1 R 1 car 1 R 1 cbr 1 bar 1 car 1 cbr 1 R 1 ba R 1 ca R 1 cb ba ca cb R 2 C ar 2 b aa a bb b AR 3 br 3 c cc c R 1 ar 1 br 1 cr 1 a b c R 2 ar 2 b aa a bb b R 3 br 3 c bb b cc c A aa a B bb b C cc c 4. Add variables to make RHS have exactly two variables or exactly one terminal. S R 1 V 1 R 1 V 3 R 1 V 4 V b V 2 V c V 2 V c V 5 R 1 V 6 R 1 V 7 R 1 V 8 V b V a V c V a V c V b R 2 C V a V 9 V a A a V b B b AR 3 V b V 10 V c C c R 1 V a R 1 V b R 1 V c R 1 a b c R 2 V a V 9 V a A a V b B b R 3 V b V 10 V b B b V c C c A V a A a B V b B b C V c C c V a a V b b V c c V 1 V b V 2 V 2 V a R 1 V 3 V c V 2 V 4 V cv 5 V 5 V b R 1 V 6 V b V a V 7 V c V a V 8 V c V b V 9 R 2 V b V 10 R 3 V c 1c) G = ({S}, {0, 1}, P, S) where P is: S 0S0 1S1 0 1 ε Page 2/8
3 (The first two productions make matching characters on either side of the string, working from the outside in. The next two productions allow us to wipe out the last S with either a 0 or a 1; this places that character in the center of the string and yields an odd length string. Alternately, the last production allows us to wipe out the last S with an ε, resulting in an even length string.) 1d) G = ({S, S'}, {a, b}, P, S) where P is: S asb S' S' bs'a ε (S' generates the n as and bs on the outside. S' generates the m as and bs on the inside.) 1e) If L is a finite subset of {a, b}*, we can make a CFG, G = ({S, W 1, W 2,...W n }, {a, b}, P, S), for L. Let n be the number of strings in L (n is a fixed finite number since L is a finite subset). For each string of terminals, w i, in L, add to P a production of the form W i w i, and a production S W i. We do this n times, and then we have a grammar that produces all strings in L. This grammar is context-free because there is a single non-terminal on the left-hand side of every production. (Since all productions are either of the form A Bx or A x where A, B are non-terminals and x {a, b}*, all productions are left-linear, and therefore this grammar is also regular. We know that all regular grammars are CFGs, although it is not the case that all CFGs are also regular grammars.) 2a) Informal description: match 1s to 0s in a way that ensures if you have symbols on the stack, they are of the same type (all either 0s or 1s) so the number of symbols on the stack is the surplus of that symbol, or how many more of that symbol we've seen than the other. Therefore, once we've read all of the input, accept iff there is a 0 on top of the stack. 2b) Informal description: we have three pieces to deal with. The first piece reads {a, b, c}*, followed by either ba, ca, or cb, followed by {a, b, c}*. It does not use its stack. The second piece reads and pushes as, followed by popping one a for every b read. If the number of bs exceeds as, it pushes bs. Then it reads any number of cs. It accepts iff there is either an a or at least one b on the top of the stack at the end of the input. The third piece is similar to the second piece, except it checks bs against cs. It reads but not not track as. Then it pushes bs to the stack as it reads bs. Last, it pops one b for every c Page 3/8
4 read. If the number of cs exceeds the number of bs, it pushes cs. It accepts iff there is at least one b or c on top of the stack after it has read all of the input. The three pieces are joined to the start state via ε- transitions. 2c) Informal description: since a palindrome over alphabet {0, 1} basically has the form x{0,1, ε}x R, we want a portion of the PDA that pushes x to the stack, a portion to guess the middle of the string and whether the string has even length, and therefore ε-transition to the next portion, or odd length and transition while throwing away either a 0 or a 1, and then a portion to pop x R from the stack while Page 4/8
5 matching it against x. Accept iff we read all of the input and end with an empty stack, which means x matched exactly to x R. 2d) Informal description: read and push the first n as. Read and push the m bs. Read the m as and pop one b for every a read. Read the n bs and pop an a for every b read. Accept iff all of the input is read and we finish with an empty stack. 2e) Since we don't know what L is, we can't produce a PDA, but we can describe how we would do so. Informal description: we're going to build a PDA that mimcs the grammar. For every string in L, we will build a PDA that reads the string and ends in a final state. Then, create a new start state and ε- transition to the old start state of every PDA created for a string. Constructive description: Let P = (Q, {a, b}, {}, δ, q 0, F). For every w i in L, add q i0 to Q and add δ (q 0, ε) = (q i0, ε). Then for every x j with w i = x 1 x 2...x n, add q ij to Q and add δ (q ij-1, x j ) = (q ij, ε). Add q in to F. Since every string is of finite length, and as L is a finite subset of {a, b}*, we have a finite number of strings, we will have a finite number of states and a finite number of transitions to add, so this procedure will terminate. Note that this PDA does not use its stack. 3) First, to show that R is a CFL, let's produce a CFG, G=({S, T}, {a, b, c, (, ),,, *, ε, }, P, S), for R, where P is: S (S) S S S S S* a b c ε (You need to provide some kind of justification that L(G) = R, but not necessarily using an inductive proof.) To show that L(G) = R, we can refer to the inductive definition of regular expressions to see that everything this grammar generates is a regular expression, and that it generates all regular expressions using alphabet {a, b, c}. First, let's show that R L(G). Base case: Choose r R with r = 1. Then, apply one of the rules S a b c ε to produce a derivation of r in L(G). Then, if r R, r = 1, r L(G). Inductive Hypothesis: Assume it is the case that if r R, r < k, k>1, there is a derivation of r using productions in G, so r L(G). Page 5/8
6 Inductive Step: If r = k, k> 1, it must be the case that r is of the form (R 1 ), R 1 R 2, R 1 R 2, or R 1 *. Using one of the productions S (S) S S S S S* we can generate a string in any one of these forms. In any of these cases, R 1, R 2 < k, so we know that R 1, R 2 R implies R 1, R 2 L(G) by the inductive hypothesis, and so there is a derivation of the grammar that can produce R 1 and R 2. Then, there is a derivation of the grammar that can produce r, so r L(G). This shows that R L(G). Now, let's show that L(G) R. Base case: Choose r L(G) with number of steps in a derivation of r, n = 1. Then the only productions that could have been applied to produce a string of terminals in one step are from the set S a b c ε. Then, r is an element of the set {a, b, c, ε, }. These are the primitive regular expressions, and so r R. Inductive Hypothesis: Assume it is the case that if r L(G), n<k, k>1, then r R. Inductive Step: Choose r L(G) with number of steps in a derivation of r, n = k, k>1. Since n>1, one of the productions from the set S (S) S S S S S* must have been applied. Then, r is an element from the set {(R 1 ), R 1 R 2, R 1 R 2, R 1 *}. Then, for any of these elements, there is a derivation of R 1, R 2 in less than k steps, so, R 1, R 2 R. Since all of these elements are regular expressions if their components are regular expressions, and R 1, R 2 R, then r R. This shows that R L(G). Since R L(G) and L(G) R, then R = L(G). Since G is a CFG, L(G) = R, then R is a CFL. To show that R is not regular, we must show that R cannot be pumped by applying pumping for regular languages. Let p be the pumping constant. Choose w = ( p a) p. We can produce this string by applying the production S (S) p times followed by S a, so w R. Any decomposition of w = xyz with xy < p and y > 0 is such that y is composed of one or more ( symbols. Let y = k. Then for i = 0, the pumped string is w i = ( p-k a) p. Since k > 0, p-k < p. Therefore, w i could not have been produced by a derivation of G, and is therefore not in R, and therefore, R is not regular. 4a) L={a n b m a n b m : n,m > 0} Let p be the pumping constant. Choose w = a p b 2p a p b 2p. w L and w > p. Case 1: v = 0, y = k, k>0, and y consists of just one symbol. Let i = 0. If y is as, then p-k<p, and if y is bs, then 2p-k<2p, so w 0 is not in the language. The cases where y =0, v =j, j>0, and v consists of just one symbol is symmetric. Case 2: v = 0, y = k, k>0, and y consists of two symbols. Let i = 2. If y is n as followed by m bs, then w 2 = a p b m a n b 2p a p b 2p, and w 2 is not in the language. The cases where y occurs on the other side of the string, is composed of bs followed by as, or is empty and v is nonempty and meets these conditions are similar enough to state, but not necessary to show. Case 3: v = j, y = k, j, k > 0. Since j+k<p, either vxy consists of only one symbol, or at most two symbols. If vxy consists of only one symbol, this is similar enough to case 1 to state, but not necessary to show. If vxy consists of two symbols with either v or y consisting of two symbols, this is similar enough to case 2. If vxy consists of two symbols with v consisting of all as and y consisting of all bs, then if i = 0, the pumped string w 0 is either a n-j b m-k a n b m or a n b m a n-j b m-k. Likewise, if v is all bs and y is all as, then w 0 = a n b m-j a n-k b m. In all of these cases, w 0 is not in the language. For all decompositions of w, there exists an i for which uv i xy i z is not in the language, this language is not context-free. Page 6/8
7 4b) L = {a i b j c k : i > j > k > 0} Let p be the pumping constant. Choose w= a p b p c p. p > p > p > 0 so w L and w > p. Case 1: v = 0, y = k, k>0 and y contains only one symbol. If y contains as, let i = 0. Then w 0 = a p- k b p c p. Then n a < n b, so w 0 L. If y contains bs, let i = 2. Then w2 = a p b p+k c p. Then n a < n b, so w 2 L. If y contains cs, let Ii= 3. Then w 3 = a p b p c p+2k. Then n b < n c so w 3 L. The case where y is empty and v is nonempty and contains all one symbol is symmetric. This also covers the case where both v and y are nonempty and both contain the same symbol. Case 2: v = 0, y = k, k>0, and y contains two symbols. If y contains m as followed by n bs, then let i = 2. Then w 2 = a p b n a m b p c p and w 2 L. If y contains n bs followed by m cs, then let i = 2. Then w2 = a p b p c m b n c p and w 2 L. The case where y is empty and v is nonempty and contains two symbols is symmetric. This also covers the case where both v and y are nonempty, but one of v or y contains two symbols. Case 3: v = j, y = k, j, k > 0 and v and y contain different symbols. If v contains as and y contains bs, let I = 0. Then w 0 = a p-j b p-k c p. Then n c > n b so w 0 L. If v contains bs and y contains cs, let i = 2. Then w2 = a p b p+j c p+k. Then n b > n a so w 2 L. For any decomposition of w, there exists an i such that w i L, so w cannot be pumped using pumping for context-free languages, so L is not context-free. 4c) L = {palindromes in {a, b}* that have the same number of as and bs} Let p be the pumping constant. Choose w = a p b 2p a p. Since n b =2p and n a = 2p, n b = n a, and if x=a p b p then w=xx R, so w L, and w > p. Case 1: v = 0, y = k, 0<k<p and y contains only one symbol. Then when i = 0, 2p > 2p -k, so n a n b so w 0 L. The case where y is empty and v is nonempty and contains all one symbol is symmetric. This also covers the case where both v and y are nonempty and both contain the same symbol (both v and y are all as, or v and y are all bs). Case 2: v = 0, y = k, 0<k<p and y contains two symbols. If y contains m as followed by n bs, when i=2, w 2 = a p-m a m b n a m b n b 2p-n a p = a p b n a m b 2p a p. Since vxy < p, n+m < p, and n, m > 0, then n < 2p, so this is not a palindrome, so w 2 L. Alternately, if y contains n bs followed by m as, w 2 = a p b 2p a m b n a p. Again, n<2p, so w 2 L. The case where y is empty and v is nonempty and contains two symbols is symmetric. This also covers the case where both v and y are nonempty and v or y contains two symbols. Case 3: v = j, y = k, j, k > 0, both v and y contain only one symbol, but the symbol for v is different from that for y. There are two subcases. If v contains as and y contains bs, then for i=0, w 0 = a p-j b 2p-k a p. Then p-j < p, so this is not a palindrome. Else, if v contains bs and y contains as, for i=0, w 0 = a p b 2p-j a p-k. p-k<p, so this is not a palindrome. In either case, w 0 L. For any decomposition of w, there exists an i such that w i L, so w cannot be pumped using pumping for context-free languages, so L is not context-free. 5a) No. Let's prove this by providing a counter example. Let L = {a n b n : n > 0}. Then let G = ({S}, {a, b}, P, S), be a CFG with L(G) = L, where P is: S asb ε Now make G' by adding the rule S SS ε S asb SS ε There is a string, w, in L(G') that has the derivation S asb assb aasbsb aabsb aabasbb aababb Page 7/8
8 but w L*, so L(G') L*. 5b) Yes. For this, let's consider a parse tree. The problem with the grammar from 5a is that, due to the recursive start variable, given a parse tree for a string, we could create some terminals, then later create additional copies of the start variable, and then create more terminals. Thus it is not the case that the terminals produced by a particular instance of S (as the S closest to those terminal leaves in the parse tree) must appear in a contiguous substring of the derived string. Put another way, in the grammar from 5a, we were able to make more copies of the start variable after generating other terminals and variables, and were therefore not able to guarantee that any strings produced must be composed of a string from the language concatenated with other strings from the language. Indeed, the actual result was an interleaving, where we inserted one string from L in the middle of another string from L. To guarantee this, we need to be sure that, if w = x 1 x 2...x n, and particular occurrence of S, S', is the S closest to leaves x j and x l with j < k < l, then S' is also the occurrence of S closest to x k. For example, if w = x 1 x 2 x 3 x 4 x 5 x 6 = aababb, consider this derivation with occurrences of S labeled: S 1 as 2 b as 3 S 4 b aas 5 bs 4 b aabs 4 b aabas 6 bb aababb using the derivation above, then x 1 and x 6 are produced by S 1, while x 2 and x 3 are produced by S 3 and x 4 and x 5 are produced by S 4. Grammars in CNF afford us this guarantee when we add the rule S SS ε because they have a nonrecursive start variable. Then there is no path in which a variable other than the start variable occurs between the root and an occurrence of the start variable. This ensures that we cannot insert a string produced by a derivation from S (a string in L) into another string produced by a derivation from S (another string in L). The rule does allow us to create two or more S variables side by side in a sentential form, allowing us to produce strings from L concatenated with strings from L. Alternately, we can also produce the empty string. Thus, it is the case that, given a grammar, G, in CNF, with L = L(G), if we add the rule S SS ε, we get exactly L*. To illustrate, let's look at the grammar from 5a converted to CNF. S 0 V a V 1 V a V b ε S V a V 1 V a V b V 1 SV b V a a V b b Now let's add the rule S 0 S 0 S 0 ε. Note that we're adding this instead of S SS... because S 0 is now the start variable instead of S. S 0 V a V 1 V a V b S 0 S 0 ε S V a V 1 V a V b V 1 SV b V a a V b b Since we began with a non-recursive start variable, there is no variable that can produce S 0 other than S 0 itself. If I apply any rule other than S 0 S 0 S 0, I replace S 0 with some variable that cannot produce another S 0 later in the parse tree. Then all terminals produced by this S 0 will be a string from L. I can also produce as many S 0 s as I want so I can concatenate as many strings from L together as I want, or alternately, I can immediately apply S 0 ε to produce the empty string. Page 8/8
2.1 Solution. E T F a. E E + T T + T F + T a + T a + F a + a
 . Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
. Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
CS 341 Homework 16 Languages that Are and Are Not Context-Free
 CS 341 Homework 16 Languages that Are and Are Not Context-Free 1. Show that the following languages are context-free. You can do this by writing a context free grammar or a PDA, or you can use the closure
CS 341 Homework 16 Languages that Are and Are Not Context-Free 1. Show that the following languages are context-free. You can do this by writing a context free grammar or a PDA, or you can use the closure
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Lecture 12 Simplification of Context-Free Grammars and Normal Forms
 Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Problem 2.6(d) [4 pts] Problem 2.12 [3pts] Original CFG:
![Problem 2.6(d) [4 pts] Problem 2.12 [3pts] Original CFG: Problem 2.6(d) [4 pts] Problem 2.12 [3pts] Original CFG:](/thumbs/87/95229917.jpg) Problem 2.6(d) [4 pts] S X T#X X#T T#X#T X axa bxb #T# # T at bt #T ε Problem 2.12 [3pts] Original CFG: R XRX S S atb bta T XTX X ε X a b q start ε, ε $ ε, R X ε, ε R ε, ε X ε, R S ε, T X ε, T ε ε, X a
Problem 2.6(d) [4 pts] S X T#X X#T T#X#T X axa bxb #T# # T at bt #T ε Problem 2.12 [3pts] Original CFG: R XRX S S atb bta T XTX X ε X a b q start ε, ε $ ε, R X ε, ε R ε, ε X ε, R S ε, T X ε, T ε ε, X a
Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Chap. 7 Properties of Context-free Languages
 Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating
Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition
 Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
The Pumping Lemma for Context Free Grammars
 The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
Theory of Computation - Module 3
 Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Parsing. Context-Free Grammars (CFG) Laura Kallmeyer. Winter 2017/18. Heinrich-Heine-Universität Düsseldorf 1 / 26
 Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
CS500 Homework #2 Solutions
 CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Context-Free Languages (Pre Lecture)
 Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
PUSHDOWN AUTOMATA (PDA)
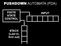 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
HW 3 Solutions. Tommy November 27, 2012
 HW 3 Solutions Tommy November 27, 2012 5.1.1 (a) Online solution: S 0S1 ɛ. (b) Similar to online solution: S AY XC A aa ɛ b ɛ C cc ɛ X axb aa b Y by c b cc (c) S X A A A V AV a V V b V a b X V V X V (d)
HW 3 Solutions Tommy November 27, 2012 5.1.1 (a) Online solution: S 0S1 ɛ. (b) Similar to online solution: S AY XC A aa ɛ b ɛ C cc ɛ X axb aa b Y by c b cc (c) S X A A A V AV a V V b V a b X V V X V (d)
Automata Theory CS F-08 Context-Free Grammars
 Automata Theory CS411-2015F-08 Context-Free Grammars David Galles Department of Computer Science University of San Francisco 08-0: Context-Free Grammars Set of Terminals (Σ) Set of Non-Terminals Set of
Automata Theory CS411-2015F-08 Context-Free Grammars David Galles Department of Computer Science University of San Francisco 08-0: Context-Free Grammars Set of Terminals (Σ) Set of Non-Terminals Set of
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
AC68 FINITE AUTOMATA & FORMULA LANGUAGES JUNE 2014
 Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u,
 1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Solutions to Problem Set 3
 V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Solution Scoring: SD Reg exp.: a(a
 MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
Notes for Comp 497 (Comp 454) Week 10 4/5/05
 Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Context Free Languages: Decidability of a CFL
 Theorem 14.1 Context Free Languages: Decidability of a CFL Statement: Given a CFL L and string w, there is a decision procedure that determines whether w L. Proof: By construction. 1. Proof using a grammar
Theorem 14.1 Context Free Languages: Decidability of a CFL Statement: Given a CFL L and string w, there is a decision procedure that determines whether w L. Proof: By construction. 1. Proof using a grammar
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
Context-Free Grammars and Languages. Reading: Chapter 5
 Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
UNIT II REGULAR LANGUAGES
 1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
This lecture covers Chapter 7 of HMU: Properties of CFLs
 This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
Theory Bridge Exam Example Questions
 Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
Theory Bridge Exam Example Questions Annotated version with some (sometimes rather sketchy) answers and notes. This is a collection of sample theory bridge exam questions. This is just to get some idea
CS375: Logic and Theory of Computing
 CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS 373: Theory of Computation. Fall 2010
 CS 373: Theory of Computation Gul Agha Mahesh Viswanathan Fall 2010 1 1 Normal Forms for CFG Normal Forms for Grammars It is typically easier to work with a context free language if given a CFG in a normal
CS 373: Theory of Computation Gul Agha Mahesh Viswanathan Fall 2010 1 1 Normal Forms for CFG Normal Forms for Grammars It is typically easier to work with a context free language if given a CFG in a normal
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
Please give details of your answer. A direct answer without explanation is not counted.
 Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Part 3 out of 5. Automata & languages. A primer on the Theory of Computation. Last week, we learned about closure and equivalence of regular languages
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Simplification of CFG and Normal Forms. Wen-Guey Tzeng Computer Science Department National Chiao Tung University
 Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Simplification of CFG and Normal Forms. Wen-Guey Tzeng Computer Science Department National Chiao Tung University
 Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
CPS 220 Theory of Computation Pushdown Automata (PDA)
 CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
Properties of context-free Languages
 Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
CpSc 421 Final Exam December 15, 2006
 CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
An automaton with a finite number of states is called a Finite Automaton (FA) or Finite State Machine (FSM).
 Automata The term "Automata" is derived from the Greek word "αὐτόματα" which means "self-acting". An automaton (Automata in plural) is an abstract self-propelled computing device which follows a predetermined
Automata The term "Automata" is derived from the Greek word "αὐτόματα" which means "self-acting". An automaton (Automata in plural) is an abstract self-propelled computing device which follows a predetermined
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
TAFL 1 (ECS-403) Unit- III. 3.1 Definition of CFG (Context Free Grammar) and problems. 3.2 Derivation. 3.3 Ambiguity in Grammar
 TAFL 1 (ECS-403) Unit- III 3.1 Definition of CFG (Context Free Grammar) and problems 3.2 Derivation 3.3 Ambiguity in Grammar 3.3.1 Inherent Ambiguity 3.3.2 Ambiguous to Unambiguous CFG 3.4 Simplification
TAFL 1 (ECS-403) Unit- III 3.1 Definition of CFG (Context Free Grammar) and problems 3.2 Derivation 3.3 Ambiguity in Grammar 3.3.1 Inherent Ambiguity 3.3.2 Ambiguous to Unambiguous CFG 3.4 Simplification
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
5 Context-Free Languages
 CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
Context-free Grammars and Languages
 Context-free Grammars and Languages COMP 455 002, Spring 2019 Jim Anderson (modified by Nathan Otterness) 1 Context-free Grammars Context-free grammars provide another way to specify languages. Example:
Context-free Grammars and Languages COMP 455 002, Spring 2019 Jim Anderson (modified by Nathan Otterness) 1 Context-free Grammars Context-free grammars provide another way to specify languages. Example:
Pushdown Automata: Introduction (2)
 Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner. Tel Aviv University. November 21, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
download instant at Assume that (w R ) R = w for all strings w Σ of length n or less.
 Chapter 2 Languages 3. We prove, by induction on the length of the string, that w = (w R ) R for every string w Σ. Basis: The basis consists of the null string. In this case, (λ R ) R = (λ) R = λ as desired.
Chapter 2 Languages 3. We prove, by induction on the length of the string, that w = (w R ) R for every string w Σ. Basis: The basis consists of the null string. In this case, (λ R ) R = (λ) R = λ as desired.
10. The GNFA method is used to show that
 CSE 355 Midterm Examination 27 February 27 Last Name Sample ASU ID First Name(s) Ima Exam # Sample Regrading of Midterms If you believe that your grade has not been recorded correctly, return the entire
CSE 355 Midterm Examination 27 February 27 Last Name Sample ASU ID First Name(s) Ima Exam # Sample Regrading of Midterms If you believe that your grade has not been recorded correctly, return the entire
Homework 4. Chapter 7. CS A Term 2009: Foundations of Computer Science. By Li Feng, Shweta Srivastava, and Carolina Ruiz
 CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 4 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 7 Problem: Chap 7.1 part a This PDA accepts the language
CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 4 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 7 Problem: Chap 7.1 part a This PDA accepts the language
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
Plan for 2 nd half. Just when you thought it was safe. Just when you thought it was safe. Theory Hall of Fame. Chomsky Normal Form
 Plan for 2 nd half Pumping Lemma for CFLs The Return of the Pumping Lemma Just when you thought it was safe Return of the Pumping Lemma Recall: With Regular Languages The Pumping Lemma showed that if a
Plan for 2 nd half Pumping Lemma for CFLs The Return of the Pumping Lemma Just when you thought it was safe Return of the Pumping Lemma Recall: With Regular Languages The Pumping Lemma showed that if a
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
Properties of Context-free Languages. Reading: Chapter 7
 Properties of Context-free Languages Reading: Chapter 7 1 Topics 1) Simplifying CFGs, Normal forms 2) Pumping lemma for CFLs 3) Closure and decision properties of CFLs 2 How to simplify CFGs? 3 Three ways
Properties of Context-free Languages Reading: Chapter 7 1 Topics 1) Simplifying CFGs, Normal forms 2) Pumping lemma for CFLs 3) Closure and decision properties of CFLs 2 How to simplify CFGs? 3 Three ways
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
Properties of Context-Free Languages. Closure Properties Decision Properties
 Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Intro to Theory of Computation
 Intro to Theory of Computation LECTURE 9 Last time: Converting a PDA to a CFG Pumping Lemma for CFLs Today: Pumping Lemma for CFLs Review of CFGs/PDAs Sofya Raskhodnikova 2/9/2016 Sofya Raskhodnikova;
Intro to Theory of Computation LECTURE 9 Last time: Converting a PDA to a CFG Pumping Lemma for CFLs Today: Pumping Lemma for CFLs Review of CFGs/PDAs Sofya Raskhodnikova 2/9/2016 Sofya Raskhodnikova;
ÖVNINGSUPPGIFTER I SAMMANHANGSFRIA SPRÅK. 17 april Classrum Edition
 ÖVNINGSUPPGIFTER I SAMMANHANGSFRIA SPRÅK 7 april 23 Classrum Edition CONTEXT FREE LANGUAGES & PUSH-DOWN AUTOMATA CONTEXT-FREE GRAMMARS, CFG Problems Sudkamp Problem. (3.2.) Which language generates the
ÖVNINGSUPPGIFTER I SAMMANHANGSFRIA SPRÅK 7 april 23 Classrum Edition CONTEXT FREE LANGUAGES & PUSH-DOWN AUTOMATA CONTEXT-FREE GRAMMARS, CFG Problems Sudkamp Problem. (3.2.) Which language generates the
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},
![(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3}, (b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},](/thumbs/81/83182922.jpg) Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Notes for Comp 497 (454) Week 10
 Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 14 SMALL REVIEW FOR FINAL SOME Y/N QUESTIONS Q1 Given Σ =, there is L over Σ Yes: = {e} and L = {e} Σ Q2 There are uncountably
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 14 SMALL REVIEW FOR FINAL SOME Y/N QUESTIONS Q1 Given Σ =, there is L over Σ Yes: = {e} and L = {e} Σ Q2 There are uncountably
Lecture 11 Context-Free Languages
 Lecture 11 Context-Free Languages COT 4420 Theory of Computation Chapter 5 Context-Free Languages n { a b : n n { ww } 0} R Regular Languages a *b* ( a + b) * Example 1 G = ({S}, {a, b}, S, P) Derivations:
Lecture 11 Context-Free Languages COT 4420 Theory of Computation Chapter 5 Context-Free Languages n { a b : n n { ww } 0} R Regular Languages a *b* ( a + b) * Example 1 G = ({S}, {a, b}, S, P) Derivations:
Finite Automata and Formal Languages TMV026/DIT321 LP Useful, Useless, Generating and Reachable Symbols
 Finite Automata and Formal Languages TMV026/DIT321 LP4 2012 Lecture 13 Ana Bove May 7th 2012 Overview of today s lecture: Normal Forms for Context-Free Languages Pumping Lemma for Context-Free Languages
Finite Automata and Formal Languages TMV026/DIT321 LP4 2012 Lecture 13 Ana Bove May 7th 2012 Overview of today s lecture: Normal Forms for Context-Free Languages Pumping Lemma for Context-Free Languages
