Chap. 7 Properties of Context-free Languages
|
|
|
- Sharyl Mills
- 5 years ago
- Views:
Transcription
1 Chap. 7 Properties of Context-free Languages 7.1 Normal Forms for Context-free Grammars Context-free grammars A where A N, (N T). 0. Chomsky Normal Form A BC or A a except S where A, B, C N, a T. 1. Eliminating useless symbols(non generating and non reachable) 2. Eliminating -productions(no A except S ) 1 3. Eliminating unit productions(no A B) A or A a where A N, (N T), 2, a T. 4. Introducing variables for each terminals(a a a, a T) A or A a where A N, N, 2, a T. 5. Reducing length of RHS to two A BC or A a except S where A, B, C N, a T. 11/8/16 Kwang-Moo Choe 1
2 7.1.1 Eliminating Useless Symbols We say X N T is useful, if S X w, X (N T), w T ; useless otherwise. 1. We say X is generating, if X w, w T. 2. We say X is reachable, if S X. 1. Eliminate non generating symbols and productions 2. Eliminate non reachable symbols and productions Theorem 7.2 Let G = (N, T, P, S) be a CGF where L(G). 1. Eliminate non generating symbols, and productions in G, G 2 = (N 2, T 2, P 2, S). 2. Eliminate non reachable symbols and productions from G 2, G 1 = (N 1, T 1, P 1, S). Then G 1 has no useless symbols, and L(G 1 ) = L(G). 11/8/16 Kwang-Moo Choe 2
3 Theorem 7.4 Finding generating symbols basis a T, a is generating. Rec. A X 1 X n P, if (1 i n: X i is generating) or (n = 0), then X is generating. Proof X w, w T. (induction on number of steps in algorithm) basis zero step. a. Rec. Consider X n-1 w, w T. X X 1 X n P. 1 i n, X i w i, w i T by IH. X X 1 X n w 1 w n = w, w. Theorem 7.6 Finding reachable symbols. Basis S is reachable. G reach = (N, E), (A, B) E, if A B P. Rec. If A N is reachable, A X 1 X n P, 1 i n, X i is reachable. Proof X (N T) is reachable, if S X.G reach = (N, E ) from S N. 11/8/16 Kwang-Moo Choe 3
4 7.1.3 Eliminating -Productions A is called -production. G is -free, if P has no -production. A is nullable, iff A. Theorem 7.7 Finding nullable symbols Basis If A P, A is nullable. Rec. B C 1 C k P: if (1 i k) C i N is nullable, then B is nullable. Proof A, if and only if, A is nullable in the above algorithm. (If) If A is nullable in the above algorithm, then A P. trivial. (Only if) induction on number the shortest derivation to. basis One step. A P, A 1. A. induction Suppose A n where n 1 derivations. Then A B 1 B k +. where 1 i k: B i n. 1 i k: B i is nullable by IH. A is nullable in the above algorithm. 11/8/16 Kwang-Moo Choe 4
5 Theorem 7.9 Let G = (N, T, P, S) be a cfg. Then G 1 = (N, T, P 1, S) is -free and L(G 1 ) = L(G) { }. P 1 : A X 1 X n P, add A Z 1 Z n to P 1. i) If X i is not nullable, Z i = X i. (no change!) ii) If X i is nullable, Z i = (X i ). iii) remove A, if any. (if m-nullable symbols, 2 m rules) (if m=n, upper bound 2 n-1 rule) Proof A G1 w if and only if A G w and w (w T + ). (If) If A G k w and w, A G1 w. basis If A G w and w, and w +, then A w P 1. A G1 w. induction A G X 1 X n G k-1 w = w 1 w n, X i G w i and w. If w i, X i G1 w i by IH(X i G k x i ). 11/8/16 Kwang-Moo Choe 5
6 If w i =, X i is nullable. A G X 1 X i-1 X i X i+1 X n G w 1 w i-1 w i+1 w n = w. A X 1 X i-1 X i+1 X n P 1 by construction of P 1. A G1 X 1 X i-1 X i+1 X n G1 w 1 w i-1 w i+1 w n = w. (Only if) If A G1 k w, A G w and w. basis If A G1 w, w (G 1 is -free). A G, G w ( -rules only, w ) induction Assume A G1 Z 1 Z n G1 k-1 w = x 1 x n, Z i G1 x i. A Z 1 Z n P 1 comes from A X 1 X m P, (m n). A G X 1 X m G Z 1 Z n ( -rules only) G x 1 x n and x i by IH(Z i G1 k x i ) = x and x. 11/8/16 Kwang-Moo Choe 6
7 7.1.4 Eliminating Unit productions A B is called a unit production, if A, B N. (A, B) is called a unit pair, if A B. Theorem 7.11 Following algorithm finds exactly unit pairs. basis (A, A) is a unit pair. induction If (A, B) is a unit pair and B C P, (A, C) is a unit pair. Proof Number of derivation steps unit pair is found. basis Zero steps. A = B, (A, A) is added in basis. induction Assume A n C. Then B, A n-1 B C. (A, C) is in unit pair(ih) and the induction rule B C P adds (A, B) in unit pair. 11/8/16 Kwang-Moo Choe 7
8 Theorem 7.13 Let G = (N,, P, S) be a cfg. Then G 1 = (N,, P 1, S) that has no unit productions and L(G 1 ) = L(G), P 1 = {A (A, B) is a unit pair, B P, N}. Proof A G w if and only if A G1 w. If A P 1, N. Non-unit productions. (If) If A P 1, A P or A G B G. If A P 1, A G. If A G1 w, A G w. (Only if) If A G w, A lm G w in G. Assume A = 0 lm 1 lm 2 lm n = w in G. 0 i n, 1) If i lm i+1 by non unit production in G, i lm G1 i+1. 2) If i lm i+1 in G by unit production, 11/8/16 Kwang-Moo Choe 8
9 i k,. i j k, j lm G j+1 by unit productions and finally k lm k+1 by non unit production i lm G1 k+1. If A lm G w, A lm G1 w Chomsky Normal Form(CNF) 1. S P or 2. A BC P where B, C N or 3. A a P where a. Theorem 7.16 Let G = (N, T, P, S) be a CFG. There is a CFG G 1 such that G 1 is CNF and L(G) = L(G 1 ). Proof 1. Eliminate useless symbols and productions. 2. Eliminate -rules. 11/8/16 Kwang-Moo Choe 9
10 3. Eliminate unit production. No -productions and no unit productions. If L(G), S P 1. A a P, CNF. A X 1 X n P where n 2, X i N T. X i, B a a(=x i ) P 1 and replace X i by B a. A C 1 C n P where n 2, C i N. If n = 2, CNF. A C 1 C n P where n 3, C i N. A C 1 D 1 P 1, D 1 C 2 D 2 P 1, D n-3 C n-2 D n-2 P 1, D n-2 C n-1 C n P 1. 11/8/16 Kwang-Moo Choe 10
11 Proof G 1 is CNF is trivail. 1) If A X 1 X k P, A G1 + X 1 X k. If A G w, A G1 w. 2) If A G1 w and consider the parse tree of w in G 1. Convert the parse tree into the parse tree of w in G. i) A C 1 D 1,, D n-3 C n-2 D n-2, D n-2 C n-1 C n into A C 1 C n-1 C n. (Fig. 7.4) ii) B a a into a L(G) = L(G 1 ). See Ex in p /8/16 Kwang-Moo Choe 11
12 Regular(type 3) grammar(normal form) A ab or b A, B N, a, b T. right linear A ab ac non-deterministic! \ A ab ac, if B C. deterministic! A Ba or b A, B N, a, b T. left linear (Extended )regular(type 3) grammar A xb or y A, B N, x, y T. extended right linear A Bx or y A, B N, x, y T. extended left linear Context-free(type 2) grammar(chomsky s normal form) A BC or a A, B, C N, a T. Context free(type 2) grammar(extended) A A N, (N T). 11/8/16 Kwang-Moo Choe 12
13 7.2 The Pumping Lemma for context-free Languages The size of parse tree Theorem 7.17 Let G = (N, T, P, S) be a Chomsky Normal Form contextfree grammar and consider a parse tree for w L(G). If n is the length(# of edges) of the longest path in the parse tree, w 2 n-1. Proof Induction on n, i) n = 1, w, w = = 1. ii) n 1, S AB is the root of the tree. Two subtrees with roots A and B, respectively, and assume A w a, B w b, and w = w a w b. By induction hypothesis, w a 2 n-2 and w b 2 n-2. w 2 n n-2 = 2 n-1. Binary(A BC) tree with unary leaf(a a). w 2 n-1. 11/8/16 Kwang-Moo Choe 13
14 7.2.2 Statement of the pumping Lemma Theorem 7.18 (The pumping lemma for context-free languages) Let L be a CFL. n N. if z L and z n, then we write z = uvwxy 1) vwx n, the first pump 2) vx, nontrivial pump 3) i 0, uv i wx i y L. pump Proof Since L is CFL, G = (N, T, P, S) where L = L(G) and G is CNF. Choose n = 2 N and suppose the longest path P of the parse tree for z L is k+1. n = 2 N z 2 (k+1)-1 = 2 k. (Def. of n, and Thm. 7.17) N k. Consider the longest path(k+1), (A 0, A 1,, A k, a) 11/8/16 Kwang-Moo Choe 14
15 A 0 = S, 0 i k: A i N, a T. (Fig. 7.5) Since N k, 1 i j k. A i = A j = A. Assume S ua i y uva j xy uvwxy. (Fig. 7.6) Note that A = A i va j x = vax or A = A j w, and S uay. (1) S uay uwy = uv 0 wx 0 y; or (2) Assume S uay uv i-1 wx i-1 y for i 1, and S uay uvaxy uvv i-1 wxx i-1 y = uv i wx i y. (Fig. 7.7) S uv i wx i y for i 0. 3) pumping(xy i z in RL s) Since G is useful and -free(cnf) v and x, vx. 2) nonempty pumping(y in RL s) We can select A i to be the closest to the bottom of the tree, k - i N, Since the length of the longest path in A i -subtree N + 1, vwx n (Thm. 7.17) 1) first pumping( xy n in RL s) 11/8/16 Kwang-Moo Choe 15
16 7.2.3 Application of the Pumping Lemma for CFL s 1. Pick L that we want to prove that L is not context-free. 2. Adversary pick n(any possible n) 3. Pick z, we may use n as a parameter 4. Adversary break z into uvwxy. vwx n, vx 5. To win the game, find i. uv i wx i y L. Context-free languages cannot match more than two groups of symbols for equality or inequality. Example 7.19 L = {0 n 1 n 2 n n 1} Let K be the adversary number, and z = 0 n 1 n 2 n, For all breaks of z into uvwxy. vwx K, vx (1) u = 0 n-i, vwx = 0 i 1 n-i, and y = 1 i 2 n. Since vx, uwy L. (2) u = 0 n 1 n-i, vwx = 1 i 2 n-i, and y = 2 i. Since vx, uwy L. 11/8/16 Kwang-Moo Choe 16
17 Two groups match cannot be interleaved. Example 7.20 L = {0 i 1 j 2 i 3 j i, j 1} Let n be the adversary number and z = 0 n 1 n 2 n 3 n. For all breaks of z into uvwxy. vwx n, vx, vwy: substring of at most two consecutive symbols Nontrivial (vx ) pumping of v and x Less than or equal to n symbols that is in vwx. CFL s cannot match two strings of arbitrary length Exercise 7.21 L ww = {ww w (0+1) } vs. L wwr = {ww R w (0+1) } Consider z = 0 n 1 n 0 n 1 n. 11/8/16 Kwang-Moo Choe 17
18 7.3 Closure properties of Context Free Languages Context-free languages are closed under 1. union, 2. concatenation, 3. closure, 4. substitution, 5. reversal Let G A = (N A, T A, P A, S A ) and G B = (N B, T B, P B, S B ) be cfg s. Then G 1 = (N A N B {S 1 }, A B, P A P B {S 1 S A S B }, S 1 ). L(G 1 ) = L(G A ) L(G B ), G 2 = (N A N B {S 2 }, T A T B, P A P B {S 2 S A S B }, S 2 ). L(G 2 ) = L(G A )L(G B ), G 3 = (N A {S 3 }, A, P A {S 3 S A S 3 }, S 3 ). L(G 3 ) = L(G A ), G 5 = (N A, A, {A R A P}, S A ). L(G 5 ) = L(G A ) R. 11/8/16 Kwang-Moo Choe 18
19 Context-free language is not closed under intersection Example 7.26 We know that L = {0 n 1 n 2 n n 1} is not cfl in Ex Consider L 1 = {0 n 1 n 2 i n 1, i 1} G 1 : S AB A 0A1 01 B 2B 2. L 2 = {0 i 1 n 2 n n 1, i 1} G 2 : S AB A 0A 0 B 1B2 12. L 1 and L 2 are context-free but L = L 1 L 2 = {0 n 1 n 2 n n 1} is not context-free counter example 11/8/16 Kwang-Moo Choe 19
20 Theorem 7.27 If L is CFL and R is regular language, then L R is context-free. Proof Let P = (Q P, T,, P, q P, Z P, F P ) be a PDA, L(P) = L, and A = (Q A,, A, q A, F A ) be a FA, L(A) = R. Then P = (Q P Q A, T,,, (q P, q A ), Z P, F P F A ) where a { } and ((q, p), a, X) = {((r, s), ) s A (p, a), (r, ) P (q, a, X)}. Induction (q P, w, Z P ) (q,, ) if and only if ((q P, q A ), w, Z P ) ((q, p),, ) and q A (q A, w). Theorem 7.29 If L, L 1, and L 2 are CFL s and R is regular language. 1. L R is context-free. 2. L is not (necessary) context-free. 3. L 1 L 2 is not (necessary) context-free. 11/8/16 Kwang-Moo Choe 20
21 7.4 Decision Properties of CFL s PDA by empty stack PDA by final state Thm 6.9, 11 O(n) CFG PDA Thm 6.13 O(n) PDA CFG Thm 6.14 O(n 3 ) CFG CNF O(n 2 ) 1. Detecting reachable and generating symbol O(n) Eliminating useless symbols and productions O(n) 2. Eliminating -production O(2 k ) where k is maximum length of RHS O(2 n ) 3. Eliminating unit productions O(n 2 ) 4. Replacing terminal symbols by nonterminal symbols O(n) 5. Breaking length of RHS O(n) 2 Eliminating -production 2 2 O(n) O(n) 11/8/16 Kwang-Moo Choe 21
22 Membership problem CYK algorithm(coke, Younger, Kasami) Given w = a 1 a n T and a cfg G in CNF, test if w L(G) or not. We can compute X ij = {A N A a i a j }, 1 i j n. If S X 1n, w L(G); otherwise w L(G). How to compute X ij.(w.l.o.g assume CNF) basis X ii = {A A a i P} induction Assume A a i a j. Since i j, and CNF( -free) A BC P where B a i a k and C a k+1 a j, i k j. if B X ik, C X k+1,j, and A BC P; A X ij. Test j i pairs (X ii, X i+1,j ), (X i,i+1, X i+2,j ),,(X i,j-1, X jj ) Since for each O(n 2 ) X ij, test at most n pairs, O(n 3 ). 11/8/16 Kwang-Moo Choe 22
23 CYK algorithm in PASCAL style for i:=1 to n do for j:=i to n do X ij := ; ( initalize O(n 2 ), i j, see Fig ) for i:=1 to n do ( basis O(n) ) if A a i P then X ii := X ii {A}; for k:=1 to n-1 do for i:=1 to n-k do ( consider X i,i+k ) for j:=i to i+k do ( recursion O(n 3 ) ) for A BC P do if (B X i,j ) and (C X j+1,i+k ) then X i,i+k := X i,i+k {A}; ( See Fig ) 11/8/16 Kwang-Moo Choe 23
24 Some undecidable problems on CFL s 1. Is a given CFG G ambiguous? 2. Is a given CFL L is inherently ambiguous? 3. Is the intersection of two CFL s are empty? 4. Are two CFL s are same? 5. Is given CFL L, L = where is the alphabet of L. 11/8/16 Kwang-Moo Choe 24
Properties of context-free Languages
 Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
Properties of context-free Languages We simplify CFL s. Greibach Normal Form Chomsky Normal Form We prove pumping lemma for CFL s. We study closure properties and decision properties. Some of them remain,
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-free Languages. Reading: Chapter 7
 Properties of Context-free Languages Reading: Chapter 7 1 Topics 1) Simplifying CFGs, Normal forms 2) Pumping lemma for CFLs 3) Closure and decision properties of CFLs 2 How to simplify CFGs? 3 Three ways
Properties of Context-free Languages Reading: Chapter 7 1 Topics 1) Simplifying CFGs, Normal forms 2) Pumping lemma for CFLs 3) Closure and decision properties of CFLs 2 How to simplify CFGs? 3 Three ways
The Pumping Lemma for Context Free Grammars
 The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
This lecture covers Chapter 7 of HMU: Properties of CFLs
 This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
NPDA, CFG equivalence
 NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
NPDA, CFG equivalence Theorem A language L is recognized by a NPDA iff L is described by a CFG. Must prove two directions: ( ) L is recognized by a NPDA implies L is described by a CFG. ( ) L is described
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
CS20a: summary (Oct 24, 2002)
 CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
CS20a: summary (Oct 24, 2002) Context-free languages Grammars G = (V, T, P, S) Pushdown automata N-PDA = CFG D-PDA < CFG Today What languages are context-free? Pumping lemma (similar to pumping lemma for
Ogden s Lemma for CFLs
 Ogden s Lemma for CFLs Theorem If L is a context-free language, then there exists an integer l such that for any u L with at least l positions marked, u can be written as u = vwxyz such that 1 x and at
Ogden s Lemma for CFLs Theorem If L is a context-free language, then there exists an integer l such that for any u L with at least l positions marked, u can be written as u = vwxyz such that 1 x and at
Properties of Context-Free Languages. Closure Properties Decision Properties
 Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Notes for Comp 497 (Comp 454) Week 10 4/5/05
 Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules).
 Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Lecture 12 Simplification of Context-Free Grammars and Normal Forms
 Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Lecture 12 Simplification of Context-Free Grammars and Normal Forms COT 4420 Theory of Computation Chapter 6 Normal Forms for CFGs 1. Chomsky Normal Form CNF Productions of form A BC A, B, C V A a a T
Fall 1999 Formal Language Theory Dr. R. Boyer. Theorem. For any context free grammar G; if there is a derivation of w 2 from the
 Fall 1999 Formal Language Theory Dr. R. Boyer Week Seven: Chomsky Normal Form; Pumping Lemma 1. Universality of Leftmost Derivations. Theorem. For any context free grammar ; if there is a derivation of
Fall 1999 Formal Language Theory Dr. R. Boyer Week Seven: Chomsky Normal Form; Pumping Lemma 1. Universality of Leftmost Derivations. Theorem. For any context free grammar ; if there is a derivation of
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition
 Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
Harvard CS 121 and CSCI E-207 Lecture 12: General Context-Free Recognition Salil Vadhan October 11, 2012 Reading: Sipser, Section 2.3 and Section 2.1 (material on Chomsky Normal Form). Pumping Lemma for
CS Pushdown Automata
 Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Context-Free Languages (Pre Lecture)
 Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context Free Language Properties
 Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Notes for Comp 497 (454) Week 10
 Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Simplification of CFG and Normal Forms. Wen-Guey Tzeng Computer Science Department National Chiao Tung University
 Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Simplification of CFG and Normal Forms. Wen-Guey Tzeng Computer Science Department National Chiao Tung University
 Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Simplification of CFG and Normal Forms Wen-Guey Tzeng Computer Science Department National Chiao Tung University Normal Forms We want a cfg with either Chomsky or Greibach normal form Chomsky normal form
Plan for 2 nd half. Just when you thought it was safe. Just when you thought it was safe. Theory Hall of Fame. Chomsky Normal Form
 Plan for 2 nd half Pumping Lemma for CFLs The Return of the Pumping Lemma Just when you thought it was safe Return of the Pumping Lemma Recall: With Regular Languages The Pumping Lemma showed that if a
Plan for 2 nd half Pumping Lemma for CFLs The Return of the Pumping Lemma Just when you thought it was safe Return of the Pumping Lemma Recall: With Regular Languages The Pumping Lemma showed that if a
CS375: Logic and Theory of Computing
 CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS311 Computational Structures More about PDAs & Context-Free Languages. Lecture 9. Andrew P. Black Andrew Tolmach
 CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
CS311 Computational Structures More about PDAs & Context-Free Languages Lecture 9 Andrew P. Black Andrew Tolmach 1 Three important results 1. Any CFG can be simulated by a PDA 2. Any PDA can be simulated
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Theory of Computation 8 Deterministic Membership Testing
 Theory of Computation 8 Deterministic Membership Testing Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Theory of Computation
Theory of Computation 8 Deterministic Membership Testing Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Theory of Computation
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Finite Automata and Formal Languages TMV026/DIT321 LP Useful, Useless, Generating and Reachable Symbols
 Finite Automata and Formal Languages TMV026/DIT321 LP4 2012 Lecture 13 Ana Bove May 7th 2012 Overview of today s lecture: Normal Forms for Context-Free Languages Pumping Lemma for Context-Free Languages
Finite Automata and Formal Languages TMV026/DIT321 LP4 2012 Lecture 13 Ana Bove May 7th 2012 Overview of today s lecture: Normal Forms for Context-Free Languages Pumping Lemma for Context-Free Languages
Parsing. Context-Free Grammars (CFG) Laura Kallmeyer. Winter 2017/18. Heinrich-Heine-Universität Düsseldorf 1 / 26
 Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
SYLLABUS. Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 3 : REGULAR EXPRESSIONS AND LANGUAGES
 Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
AC68 FINITE AUTOMATA & FORMULA LANGUAGES JUNE 2014
 Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs
 CSC4510/6510 AUTOMATA 6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs The Pumping Lemma for Context Free Languages One way to prove AnBn is not regular is to use the pumping lemma
CSC4510/6510 AUTOMATA 6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs The Pumping Lemma for Context Free Languages One way to prove AnBn is not regular is to use the pumping lemma
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
DD2371 Automata Theory
 KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
KTH CSC VT 2008 DD2371 Automata Theory Dilian Gurov Lecture Outline 1. The lecturer 2. Introduction to automata theory 3. Course syllabus 4. Course objectives 5. Course organization 6. First definitions
CYK Algorithm for Parsing General Context-Free Grammars
 CYK Algorithm for Parsing General Context-Free Grammars Why Parse General Grammars Can be difficult or impossible to make grammar unambiguous thus LL(k) and LR(k) methods cannot work, for such ambiguous
CYK Algorithm for Parsing General Context-Free Grammars Why Parse General Grammars Can be difficult or impossible to make grammar unambiguous thus LL(k) and LR(k) methods cannot work, for such ambiguous
Context Free Languages: Decidability of a CFL
 Theorem 14.1 Context Free Languages: Decidability of a CFL Statement: Given a CFL L and string w, there is a decision procedure that determines whether w L. Proof: By construction. 1. Proof using a grammar
Theorem 14.1 Context Free Languages: Decidability of a CFL Statement: Given a CFL L and string w, there is a decision procedure that determines whether w L. Proof: By construction. 1. Proof using a grammar
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CSE 105 Homework 5 Due: Monday November 13, Instructions. should be on each page of the submission.
 CSE 05 Homework 5 Due: Monday November 3, 207 Instructions Upload a single file to Gradescope for each group. should be on each page of the submission. All group members names and PIDs Your assignments
CSE 05 Homework 5 Due: Monday November 3, 207 Instructions Upload a single file to Gradescope for each group. should be on each page of the submission. All group members names and PIDs Your assignments
COMP-330 Theory of Computation. Fall Prof. Claude Crépeau. Lec. 10 : Context-Free Grammars
 COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
COMP-330 Theory of Computation Fall 2017 -- Prof. Claude Crépeau Lec. 10 : Context-Free Grammars COMP 330 Fall 2017: Lectures Schedule 1-2. Introduction 1.5. Some basic mathematics 2-3. Deterministic finite
TAFL 1 (ECS-403) Unit- III. 3.1 Definition of CFG (Context Free Grammar) and problems. 3.2 Derivation. 3.3 Ambiguity in Grammar
 TAFL 1 (ECS-403) Unit- III 3.1 Definition of CFG (Context Free Grammar) and problems 3.2 Derivation 3.3 Ambiguity in Grammar 3.3.1 Inherent Ambiguity 3.3.2 Ambiguous to Unambiguous CFG 3.4 Simplification
TAFL 1 (ECS-403) Unit- III 3.1 Definition of CFG (Context Free Grammar) and problems 3.2 Derivation 3.3 Ambiguity in Grammar 3.3.1 Inherent Ambiguity 3.3.2 Ambiguous to Unambiguous CFG 3.4 Simplification
Computability and Complexity
 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Closure Properties of Context-Free Languages. Foundations of Computer Science Theory
 Closure Properties of Context-Free Languages Foundations of Computer Science Theory Closure Properties of CFLs CFLs are closed under: Union Concatenation Kleene closure Reversal CFLs are not closed under
Closure Properties of Context-Free Languages Foundations of Computer Science Theory Closure Properties of CFLs CFLs are closed under: Union Concatenation Kleene closure Reversal CFLs are not closed under
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
Homework 4. Chapter 7. CS A Term 2009: Foundations of Computer Science. By Li Feng, Shweta Srivastava, and Carolina Ruiz
 CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 4 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 7 Problem: Chap 7.1 part a This PDA accepts the language
CS3133 - A Term 2009: Foundations of Computer Science Prof. Carolina Ruiz Homework 4 WPI By Li Feng, Shweta Srivastava, and Carolina Ruiz Chapter 7 Problem: Chap 7.1 part a This PDA accepts the language
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
6.8 The Post Correspondence Problem
 6.8. THE POST CORRESPONDENCE PROBLEM 423 6.8 The Post Correspondence Problem The Post correspondence problem (due to Emil Post) is another undecidable problem that turns out to be a very helpful tool for
6.8. THE POST CORRESPONDENCE PROBLEM 423 6.8 The Post Correspondence Problem The Post correspondence problem (due to Emil Post) is another undecidable problem that turns out to be a very helpful tool for
CS481F01 Solutions 6 PDAS
 CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
CS481F01 Solutions 6 PDAS A. Demers 2 November 2001 1. Give a NPDAs that recognize the following languages: (a) The set of all strings in {0, 1} that contain twice as many 1s as 0s. (answer a) We build
Computability Theory
 CS:4330 Theory of Computation Spring 2018 Computability Theory Decidable Problems of CFLs and beyond Haniel Barbosa Readings for this lecture Chapter 4 of [Sipser 1996], 3rd edition. Section 4.1. Decidable
CS:4330 Theory of Computation Spring 2018 Computability Theory Decidable Problems of CFLs and beyond Haniel Barbosa Readings for this lecture Chapter 4 of [Sipser 1996], 3rd edition. Section 4.1. Decidable
Context-Free Grammars (and Languages) Lecture 7
 Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Concordia University Department of Computer Science & Software Engineering
 Concordia University Department of Computer Science & Software Engineering COMP 335/4 Theoretical Computer Science Winter 2015 Assignment 3 1. In each case, what language is generated by CFG s below. Justify
Concordia University Department of Computer Science & Software Engineering COMP 335/4 Theoretical Computer Science Winter 2015 Assignment 3 1. In each case, what language is generated by CFG s below. Justify
Ogden s Lemma. and Formal Languages. Automata Theory CS 573. The proof is similar but more fussy. than the proof of the PL4CFL.
 CS 573 Automata Theory and Formal Languages Professor Leslie Lander Lecture # 24 December 4, 2000 Ogden s Lemma (6.2) Let L be a CFL, then there is a constant n such that if z is a word in L with z > n
CS 573 Automata Theory and Formal Languages Professor Leslie Lander Lecture # 24 December 4, 2000 Ogden s Lemma (6.2) Let L be a CFL, then there is a constant n such that if z is a word in L with z > n
Even More on Dynamic Programming
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Even More on Dynamic Programming Lecture 15 Thursday, October 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 26 Part I Longest Common Subsequence
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Even More on Dynamic Programming Lecture 15 Thursday, October 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 26 Part I Longest Common Subsequence
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Finite Automata Theory and Formal Languages TMV026/TMV027/DIT321 Responsible: Ana Bove
 Finite Automata Theory and Formal Languages TMV026/TMV027/DIT321 Responsible: Ana Bove Tuesday 28 of May 2013 Total: 60 points TMV027/DIT321 registration VT13 TMV026/DIT321 registration before VT13 Exam
Finite Automata Theory and Formal Languages TMV026/TMV027/DIT321 Responsible: Ana Bove Tuesday 28 of May 2013 Total: 60 points TMV027/DIT321 registration VT13 TMV026/DIT321 registration before VT13 Exam
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Solution. S ABc Ab c Bc Ac b A ABa Ba Aa a B Bbc bc.
 Section 12.4 Context-Free Language Topics Algorithm. Remove Λ-productions from grammars for langauges without Λ. 1. Find nonterminals that derive Λ. 2. For each production A w construct all productions
Section 12.4 Context-Free Language Topics Algorithm. Remove Λ-productions from grammars for langauges without Λ. 1. Find nonterminals that derive Λ. 2. For each production A w construct all productions
Context Free Languages and Grammars
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
CS 373: Theory of Computation. Fall 2010
 CS 373: Theory of Computation Gul Agha Mahesh Viswanathan Fall 2010 1 1 Normal Forms for CFG Normal Forms for Grammars It is typically easier to work with a context free language if given a CFG in a normal
CS 373: Theory of Computation Gul Agha Mahesh Viswanathan Fall 2010 1 1 Normal Forms for CFG Normal Forms for Grammars It is typically easier to work with a context free language if given a CFG in a normal
Testing Emptiness of a CFL. Testing Finiteness of a CFL. Testing Membership in a CFL. CYK Algorithm
 Testing Emptiness of a CFL As for regular languages, we really take a representation of some language and ask whether it represents φ Can use either CFG or PDA Our choice, since there are algorithms to
Testing Emptiness of a CFL As for regular languages, we really take a representation of some language and ask whether it represents φ Can use either CFG or PDA Our choice, since there are algorithms to
Grammars and Context Free Languages
 Grammars and Context Free Languages H. Geuvers and A. Kissinger Institute for Computing and Information Sciences Version: fall 2015 H. Geuvers & A. Kissinger Version: fall 2015 Talen en Automaten 1 / 23
Grammars and Context Free Languages H. Geuvers and A. Kissinger Institute for Computing and Information Sciences Version: fall 2015 H. Geuvers & A. Kissinger Version: fall 2015 Talen en Automaten 1 / 23
CSCI Compiler Construction
 CSCI 742 - Compiler Construction Lecture 12 Cocke-Younger-Kasami (CYK) Algorithm Instructor: Hossein Hojjat February 20, 2017 Recap: Chomsky Normal Form (CNF) A CFG is in Chomsky Normal Form if each rule
CSCI 742 - Compiler Construction Lecture 12 Cocke-Younger-Kasami (CYK) Algorithm Instructor: Hossein Hojjat February 20, 2017 Recap: Chomsky Normal Form (CNF) A CFG is in Chomsky Normal Form if each rule
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
PUSHDOWN AUTOMATA (PDA)
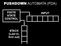 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Question Bank UNIT I
 Siddhivinayak Technical Campus School of Engineering & Research Technology Department of computer science and Engineering Session 2016-2017 Subject Name- Theory of Computation Subject Code-4KS05 Sr No.
Siddhivinayak Technical Campus School of Engineering & Research Technology Department of computer science and Engineering Session 2016-2017 Subject Name- Theory of Computation Subject Code-4KS05 Sr No.
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
The Chomsky Hierarchy(review)
 The Chomsky Hierarchy(review) Languages Machines Other Moels Recursively Enumerable Sets Turing Machines Post System Markov Algorithms, µ-recursive Functions Context-sensitive Languages Context-free Languages
The Chomsky Hierarchy(review) Languages Machines Other Moels Recursively Enumerable Sets Turing Machines Post System Markov Algorithms, µ-recursive Functions Context-sensitive Languages Context-free Languages
V Honors Theory of Computation
 V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
V22.0453-001 Honors Theory of Computation Problem Set 3 Solutions Problem 1 Solution: The class of languages recognized by these machines is the exactly the class of regular languages, thus this TM variant
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad
 St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FORMAL LANGUAGES AND AUTOMATA THEORY Class : CSE II PART A (SHORT ANSWER QUESTIONS) UNIT- I 1 Explain transition diagram, transition
St.MARTIN S ENGINEERING COLLEGE Dhulapally, Secunderabad-500 014 Subject: FORMAL LANGUAGES AND AUTOMATA THEORY Class : CSE II PART A (SHORT ANSWER QUESTIONS) UNIT- I 1 Explain transition diagram, transition
VTU QUESTION BANK. Unit 1. Introduction to Finite Automata. 1. Obtain DFAs to accept strings of a s and b s having exactly one a.
 VTU QUESTION BANK Unit 1 Introduction to Finite Automata 1. Obtain DFAs to accept strings of a s and b s having exactly one a.(5m )( Dec-2014) 2. Obtain a DFA to accept strings of a s and b s having even
VTU QUESTION BANK Unit 1 Introduction to Finite Automata 1. Obtain DFAs to accept strings of a s and b s having exactly one a.(5m )( Dec-2014) 2. Obtain a DFA to accept strings of a s and b s having even
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Theory of Computation - Module 3
 Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
Grammars and Context Free Languages
 Grammars and Context Free Languages H. Geuvers and J. Rot Institute for Computing and Information Sciences Version: fall 2016 H. Geuvers & J. Rot Version: fall 2016 Talen en Automaten 1 / 24 Outline Grammars
Grammars and Context Free Languages H. Geuvers and J. Rot Institute for Computing and Information Sciences Version: fall 2016 H. Geuvers & J. Rot Version: fall 2016 Talen en Automaten 1 / 24 Outline Grammars
Context-Free Grammars: Normal Forms
 Context-Free Grammars: Normal Forms Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Context-Free Grammars: Normal Forms Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
CDM Parsing and Decidability
 CDM Parsing and Decidability 1 Parsing Klaus Sutner Carnegie Mellon Universality 65-parsing 2017/12/15 23:17 CFGs and Decidability Pushdown Automata The Recognition Problem 3 What Could Go Wrong? 4 Problem:
CDM Parsing and Decidability 1 Parsing Klaus Sutner Carnegie Mellon Universality 65-parsing 2017/12/15 23:17 CFGs and Decidability Pushdown Automata The Recognition Problem 3 What Could Go Wrong? 4 Problem:
Context-Free Grammars and Languages. Reading: Chapter 5
 Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
