Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
|
|
|
- Alisha Waters
- 5 years ago
- Views:
Transcription
1 Automata & languages A primer on the Theory of Computation Laurent Vanbever Part 4 out of 5 ETH Zürich (D-ITET) October, Last week, we showed the equivalence of DFA, NFA and REX We also looked at nonregular languages is equivalent to Pumping lemma If A is a regular language, then there exist a number p s.t. DFA NFA REX Any string in A whose length is at least p can be divided into three pieces xyz s.t. xy i z A, for each i 0 and y > 0 and xy p
2 To prove that a language A is not regular: To prove that a language A is not regular: 1 Assume that A is regular 1 Assume that A is regular 2 Since A is regular, it must have a pumping length p 2 Since A is regular, it must have a pumping length p 3 Find one string s in A whose length is at least p 3 Find one string s in A whose length is at least p 4 For any split s=xyz, 4 For any split s=xyz, Show that you can not satisfy all three conditions Show that you can not satisfy all three conditions 5 Conclude that s cannot be pumped 5 Conclude that s cannot be pumped A is not regular CFG s: Proving Correctness This week is all about Context-Free Languages The recursive nature of CFG s means that they are especially amenable to correctness proofs. For example let s consider again our grammar G = (S ab ba asb bsa SS) We claim that L(G) = L = { x {a,b}* n a (x) = n b (x) }, where n a (x) is the number of a s in x, and n b (x) is the number of b s. a superset of Regular Languages Proof: To prove that L = L(G) is to show both inclusions: i. L L(G ): Every string in L can be generated by G. ii. L L(G ): G only generate strings of L. 2/1
3 CFG s: Proving Correctness Proving L L(G) The recursive nature of CFG s means that they are especially amenable to correctness proofs. For example let s consider again our grammar G = (S ab ba asb bsa SS) We claim that L(G) = L = { x {a,b}* n a (x) = n b (x) }, where n a (x) is the number of a s in x, and n b (x) is the number of b s. Proof: To prove that L = L(G) is to show both inclusions: i. L L(G ): Every string in L can be generated by G. ii. L L(G ): G only generate strings of L. Part ii. is easy (see why?), so we ll concentrate on part i. L L(G): Show that every string x with the same number of a s as b s is generated by G. Prove by induction on the length n = x. Base case: The empty string is derived by S Inductive hypothesis: Assume that G generates all strings of equal number of a s and b s of (even) length up to n. Consider any string of length n+2. There are essentially 4 possibilities: 1. awb 2. bwa 3. awa 4. bwb 2/2 2/3 Proving L L(G) Proving L L(G) Inductive hypothesis: Consider any string of length n+2. There are essentially 4 possibilities: 1. awb 2. bwa 3. awa 4. bwb Given S * w, awb and bwa are generated from w using the rules S asb and S bsa (induction hypothesis) Inductive hypothesis: Now, consider a string like awa. For it to be in L requires that w isn t in L as w needs to have 2 more b s than a s. Split awa as follows: a a where the subscripts after a prefix v of awa denotes n v n v Think of this as counting starting from 0. Each a adds 1. Each b subtracts 1. At the end, we should be at 0. Somewhere along the string (in w), the counter crosses 0 (more b s) 2/4 2/5
4 Proving L L(G) Designing Context-Free Grammars Inductive hypothesis: Somewhere along the string (in w), the counter crosses 0: u a x y a with x, y a, b v As for regular languages this is a creative process. However, if the grammar is the union of simpler grammars, you can design the simpler grammars (with starting symbols S 1, S 2 ), and then add a new starting symbol/production S S 1 S 2. u and v have an equal number of a s and b s and are shorter than n. Given S * u and S * v, the rule S SS generates awa = uv (induction hypothesis) The same argument applies for strings like bwb 2/6 2/7 Designing Context-Free Grammars Push-Down Automata (PDA) As for regular languages this is a creative process. However, if the grammar is the union of simpler grammars, you can design the simpler grammars (with starting symbols S 1, S 2 ), and then add a new starting symbol/production S S 1 S 2. If the CFG happens to be regular, you can first design the FA, introduce a variable/production for each state of the FA, and then add a rule x ay to the CFG if (x,a) = y is in the FA. If a state x is accepting in FA then add x to CFG. The start symbol of the CFG is the start state in the FA. There are quite a few other tricks. Try yourself Finite automata where the machine interpretation of regular languages. Push-Down Automaton are the machine interpretation for grammars. The problem of finite automata was that they couldn t handle languages that needed some sort of unbounded memory something that could be implemented easily by a single (unbounded) integer register! Example: To recognize the language L = {0 n 1 n n 0}, all you need is to count how many 0 s you have seen so far Push-Down Automata allow even more than a register: a full stack! 2/8 2/9
5 Recursive Algorithms and Stacks Recursive Algorithms and Stacks A stack allows the following basic operations Push, pushing a new element on the top of the stack. Pop, removing the top element from the stack (if there is one). Peek, checking the top element without removing it. A stack allows the following basic operations Push, pushing a new element on the top of the stack. Pop, removing the top element from the stack (if there is one). Peek, checking the top element without removing it. General Principle in Programming: Any recursive algorithm can be turned into a non-recursive one using a stack and a while-loop which exits only when stack is empty. General Principle in Programming: Any recursive algorithm can be turned into a non-recursive one using a stack and a while-loop which exits only when stack is empty. It seems that with a stack at our fingertips we can even recognize palindromes! Yoo-hoo! Palindromes are generated by the grammar S asa bsb. Let s simplify for the moment and look at S # asa bsb. 2/10 2/11 From CFG s to Stack Machines PDA s à la Sipser The CFG S # asa bsb describes palindromes containing exactly 1 #. Question: Using a stack, how can we recognize such strings? To aid analysis, theoretical stack machines restrict the allowable operations. Each text-book author has his/her own version. Sipser s machines are especially simple: Push/Pop rolled into a single operation: replace top stack symbol. In particular, replacing top by is a pop. No intrinsic way to test for empty stack. Instead often push a special symbol ( $ ) as the very first operation! Epsilon s used to increase functionality result in default nondeterministic machines. 2/12 2/13
6 Sipser s PDA Version PDA: Formal Definition p x, y z If at state p and next input is x and top stack is y, then go to state q and replace y by z on stack. x = : ignore input, don t read y = : ignore top of stack and push z z = : pop y q Definition: A pushdown automaton (PDA) is a 6-tuple M = (Q,,,, q 0, F ): Q,, and q 0, and F are defined as for an FA. is the stack alphabet. is as follows: Given a state p, an input symbol x and a stack symbol y, p,x,y returns all (q,z) where q is a target state and z a stack replacement for y. δ : Q Σ ε P ( Q ) ε ε In addition, push $ initially to detect the empty stack. 2/14 2/15 PDA Exercises Model Robustness Draw the PDA {a i b j c k i,j,k 0 and i=j or i=k} The class of regular languages was quite robust Allows multiple ways for defining languages (automaton vs. regexp) Slight perturbations of model do not change result (non-determinism) The class of context free languages is also robust: you can use either PDA s or CFG s to describe the languages in the class. Draw the PDA for L = {x {a,e}* n a (x) = 2n e (x)} However, it is less robust than regular languages when it comes to slight perturbations of the model: Smaller classes Right-linear grammars Deterministic PDA s Larger classes Context Sensitive Grammars 2/16 2/17
7 Right Linear Grammars vs. Regular Languages 0 The DFA above can be simulated by the grammar x 0x 1y y 0x 1z z 0x 1z 1 x y z 1 0 Definition: A right-linear grammar is a CFG such that every production is of the form A ub, or A u where u is a terminal string, and A,B are variables. 0 1 Right Linear Grammars vs. Regular Languages Theorem: If M = (Q,,, q 0, F ) is an NFA then there is a right-linear grammar G(M) which generates the same language as M. Proof: Variables are the states: V = Q Start symbol is start state: S = q 0 Same alphabet of terminals A transition q 1 a q 2 becomes the production q 1 aq 2 For each transition, q 1 aq 2 where q 2 is an accept state, add q 1 a to the grammar Homework: Show that the reverse holds. Right-linear grammar can be converted to a FSA. This implies that RL Right-linear CFL. 2/18 2/19 Right Linear Grammars vs. Regular Languages Chomsky Normal Form Theorem: If M = (Q,,, q 0, F ) is an NFA then there is a right-linear grammar G(M) which generates the same language as M. Proof: Variables are the states: V = Q Start symbol is start state: S = q 0 Same alphabet of terminals A transition q 1 a q 2 becomes the production q 1 aq 2 For each transition, q 1 aq 2 where q 2 is an accept state, add q 1 a to the grammar Homework: Show that the reverse holds. Right-linear grammar can be converted to a FSA. This implies that RL Right-linear CFL. Question: Can every CFG be converted into a right-linear grammar? Chomsky came up with an especially simple type of context free grammars which is able to capture all context free languages, the Chomsky normal form (CNF). Chomsky's grammatical form is particularly useful when one wants to prove certain facts about context free languages. This is because assuming a much more restrictive kind of grammar can often make it easier to prove that the generated language has whatever property you are interested in. Noam Chomsky, linguist at MIT, creator of the Chomsky hierarchy, a classification of formal languages. Chomsky is also widely known for his left-wing political views and his criticism of the foreign policy of U.S. government. 2/20 2/21
8 Chomsky Normal Form CFG CNF Definition: A CFG is said to be in Chomsky Normal Form if every rule in the grammar has one of the following forms: S ( for epsilon s sake only) A BC (dyadic variable productions) A a (unit terminal productions) where S is the start variable, A,B,C are variables and a is a terminal. Thus epsilons may only appear on the right hand side of the start symbol and other rights are either 2 variables or a single terminal. Converting a general grammar into Chomsky Normal Form works in four steps: 1. Ensure that the start variable doesn't appear on the right hand side of any rule. 2. Remove all epsilon productions, except from start variable. 3. Remove unit variable productions of the form A B where A and B are variables. 4. Add variables and dyadic variable rules to replace any longer nondyadic or non-variable productions 2/22 2/23 CFG CNF: Example CFG CNF: Example continued S ε a b asa bsb 1. No start variable on right hand side S S S ε a b asa bsb 2. Only start state is allowed to have S S ε S ε a b asa bsb aa bb 3. Remove unit variable productions of the form A B. S S ε a b asa bsb aa bb S a b asa bsb aa bb S S ε a b asa bsb aa bb S a b asa bsb aa bb 4. Add variables and dyadic variable rules to replace any longer productions. S ε a b asa bsb aa bb AB CD AA CC S a b asa bsb aa bb AB CD AA CC A a B SA C b D SC 2/24 2/25
9 CFG PDA CFG GPDA Recipe CFG s can be converted into PDA s. In NFA REX it was useful to consider GNFA s as a middle stage. Similarly, it s useful to consider Generalized PDA s here. A Generalized PDA (GPDA) is like a PDA, except it allows the top stack symbol to be replaced by a whole string, not just a single character or the empty string. It is easy to convert a GPDA s back to PDA s by changing each compound push into a sequence of simple pushes. 1. Push the marker symbol $ and the start symbol S on the stack. 2. Repeat the following steps forever a. If the top of the stack is the variable symbol A, nondeterministically select a rule of A, and substitute A by the string on the right-hand-side of the rule. b. If the top of the stack is a terminal symbol a, then read the next symbol from the input and compare it to a. If they match, continue. If they do not match reject this branch of the execution. c. If the top of the stack is the symbol $, enter the accept state. (Note that if the input was not yet empty, the PDA will still reject this branch of the execution.) 2/26 2/27 CFG GPDA PDA: Example CFG PDA: Now you try! S atb b T Ta Convert the grammar S a b asa bsb q0, S S a S b a a b b, $, S, $ q1 q2 q3 S a, a S b, b q4 q5 q6 q7, S, S 2/28 2/29
10 PDA CFG Context Sensitive Grammars To convert PDA s to CFG s we ll need to simulate the stack inside the productions. Unfortunately, in contrast to our previous transitions, this is not quite as constructive. We will therefore only state the theorem. Theorem: For each push-down automation there is a context-free grammar which accepts the same language. Corollary: PDA CFG. An even more general form of grammars exists. In general, a non-context free grammar is one in which whole mixed variable/terminal substrings are replaced at a time. For example with = {a,b,c} consider: S ASBC A a CB BC ab ab bb bb bc bc cc cc What language is generated by this noncontext-free grammar? When length of LHS always length of RHS (plus some other minor restrictions), these general grammars are called context sensitive. 2/30 2/31 Are all languages context-free? Tandem Pumping Design a CFG (or PDA) for the following languages: L = { w {0,1,2}* there are k 0 s, k 1 s, and k 2 s for k 0 } L = { w {0,1,2}* with 0 = 1 or 0 = 2 or 1 = 2 } L = { 0 k 1 k 2 k k 0 } Analogous to regular languages there is a pumping lemma for context free languages. The idea is that you can pump a context free language at two places (but not more). Theorem: Given a context free language L, there is a number p (tandem-pumping number) such that any string in L of length p is tandem-pumpable within a substring of length p. In particular, for all w L with w p we we can write: w = uvxyz vy 1 (pumpable areas are non-empty) vxy p (pumping inside length-p portion) uv i xy i z L for all i 0 (tandem-pump v and y) If there is no such p the language is not context-free. 2/32 2/33
11 Proving Non-Context Freeness: Example Proving Non-Context Freeness: You try! L ={1 n 0 n 1 n 0 n n is non-negative } Let s try w = 1 p 0 p 1 p 0 p. Clearly w L and w p. With vxy p, there are only three places where the sliding window vxy could be: I III II In all three cases, pumping up such a case would only change the number of 0s and 1s in that part and not in the other two parts; this violates the language definition. L = { x=y+z x, y, and z are binary bit-strings satisfying the equation } The hard part is to come up with a word which cannot be pumped, such as 1 p+1 =1 p +10 p Applying the tandem pumping lemma is easy I 1 p+1 =1 p +10 p II 2/34 2/35 Transducers Definition: A finite state transducer (FST) is a type of finite automaton whose output is a string and not just accept or reject. Each transition of an FST is labeled with two symbols, one designating the input symbol for that transition (as for automata), and the other designating the output symbol. We allow as output symbol if no symbol should be added to the string. The figure on the right shows an example of a FST operating on the input alphabet {0,1,2} and the output alphabet {0,1} Exercise: Can you design a transducer that produces the inverted bitstring of the input string (e.g )? 2/36
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 5 2017 Part 3 out of 5 Last week, we learned about closure and equivalence of regular
Part 3 out of 5. Automata & languages. A primer on the Theory of Computation. Last week, we learned about closure and equivalence of regular languages
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 3 out of 5 ETH Zürich (D-ITET) October, 5 2017 Last week, we learned about closure and equivalence of regular
Chapter 2 SMARTER AUTOMATA. Roger Wattenhofer. ETH Zurich Distributed Computing
 Chapter 2 SMARTER AUTOMATA Roger Wattenhofer ETH Zurich Distributed Computing www.disco.ethz.ch Overview Motivation Context free grammars (CFG) Derivations Parse trees Ambiguity Pushdown Automata Stacks
Chapter 2 SMARTER AUTOMATA Roger Wattenhofer ETH Zurich Distributed Computing www.disco.ethz.ch Overview Motivation Context free grammars (CFG) Derivations Parse trees Ambiguity Pushdown Automata Stacks
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Define push down automata Trace the computation of a push down automaton Design
CpSc 421 Final Exam December 15, 2006
 CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
CpSc 421 Final Exam December 15, 2006 Do problem zero and six of problems 1 through 9. If you write down solutions for more that six problems, clearly indicate those that you want graded. Note that problems
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) September,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) September, 24 2015 Last week was all about Deterministic Finite Automaton We saw three main
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) September, 24 2015 Last week was all about Deterministic Finite Automaton We saw three main
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) October,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 19 2017 Part 5 out of 5 Last week was all about Context-Free Languages Context-Free
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) October, 19 2017 Part 5 out of 5 Last week was all about Context-Free Languages Context-Free
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: Captured by Regular Operations a b
Automata & languages. A primer on the Theory of Computation. Laurent Vanbever. ETH Zürich (D-ITET) September,
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) September, 28 2017 Part 2 out of 5 Last week was all about Deterministic Finite Automaton
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu ETH Zürich (D-ITET) September, 28 2017 Part 2 out of 5 Last week was all about Deterministic Finite Automaton
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules).
 Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Note: In any grammar here, the meaning and usage of P (productions) is equivalent to R (rules). 1a) G = ({R, S, T}, {0,1}, P, S) where P is: S R0R R R0R1R R1R0R T T 0T ε (S generates the first 0. R generates
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation Turing Machine and Pushdown Automata
 Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
PS2 - Comments. University of Virginia - cs3102: Theory of Computation Spring 2010
 University of Virginia - cs3102: Theory of Computation Spring 2010 PS2 - Comments Average: 77.4 (full credit for each question is 100 points) Distribution (of 54 submissions): 90, 12; 80 89, 11; 70-79,
University of Virginia - cs3102: Theory of Computation Spring 2010 PS2 - Comments Average: 77.4 (full credit for each question is 100 points) Distribution (of 54 submissions): 90, 12; 80 89, 11; 70-79,
CISC 4090 Theory of Computation
 CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
CISC 4090 Theory of Computation Context-Free Languages and Push Down Automata Professor Daniel Leeds dleeds@fordham.edu JMH 332 Languages: Regular and Beyond Regular: a b c b d e a Not-regular: c n bd
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
2.1 Solution. E T F a. E E + T T + T F + T a + T a + F a + a
 . Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
. Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
Computational Models - Lecture 4 1
 Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 4 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 3/8, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Please give details of your answer. A direct answer without explanation is not counted.
 Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
Please give details of your answer. A direct answer without explanation is not counted. Your answers must be in English. Please carefully read problem statements. During the exam you are not allowed to
The Pumping Lemma for Context Free Grammars
 The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
The Pumping Lemma for Context Free Grammars Chomsky Normal Form Chomsky Normal Form (CNF) is a simple and useful form of a CFG Every rule of a CNF grammar is in the form A BC A a Where a is any terminal
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
AC68 FINITE AUTOMATA & FORMULA LANGUAGES JUNE 2014
 Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
Q.2 a. Show by using Mathematical Induction that n i= 1 i 2 n = ( n + 1) ( 2 n + 1) 6 b. Define language. Let = {0; 1} denote an alphabet. Enumerate five elements of the following languages: (i) Even binary
CPS 220 Theory of Computation Pushdown Automata (PDA)
 CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
Problem 2.6(d) [4 pts] Problem 2.12 [3pts] Original CFG:
![Problem 2.6(d) [4 pts] Problem 2.12 [3pts] Original CFG: Problem 2.6(d) [4 pts] Problem 2.12 [3pts] Original CFG:](/thumbs/87/95229917.jpg) Problem 2.6(d) [4 pts] S X T#X X#T T#X#T X axa bxb #T# # T at bt #T ε Problem 2.12 [3pts] Original CFG: R XRX S S atb bta T XTX X ε X a b q start ε, ε $ ε, R X ε, ε R ε, ε X ε, R S ε, T X ε, T ε ε, X a
Problem 2.6(d) [4 pts] S X T#X X#T T#X#T X axa bxb #T# # T at bt #T ε Problem 2.12 [3pts] Original CFG: R XRX S S atb bta T XTX X ε X a b q start ε, ε $ ε, R X ε, ε R ε, ε X ε, R S ε, T X ε, T ε ε, X a
(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},
![(b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3}, (b) If G=({S}, {a}, {S SS}, S) find the language generated by G. [8+8] 2. Convert the following grammar to Greibach Normal Form G = ({A1, A2, A3},](/thumbs/81/83182922.jpg) Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
Code No: 07A50501 R07 Set No. 2 III B.Tech I Semester Examinations,MAY 2011 FORMAL LANGUAGES AND AUTOMATA THEORY Computer Science And Engineering Time: 3 hours Max Marks: 80 Answer any FIVE Questions All
CSE 355 Test 2, Fall 2016
 CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
CSE 355 Test 2, Fall 2016 28 October 2016, 8:35-9:25 a.m., LSA 191 Last Name SAMPLE ASU ID 1357924680 First Name(s) Ima Regrading of Midterms If you believe that your grade has not been added up correctly,
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
CS500 Homework #2 Solutions
 CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
CS500 Homework #2 Solutions 1. Consider the two languages Show that L 1 is context-free but L 2 is not. L 1 = {a i b j c k d l i = j k = l} L 2 = {a i b j c k d l i = k j = l} Answer. L 1 is the concatenation
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Theory of Computation - Module 3
 Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Theory of Computation - Module 3 Syllabus Context Free Grammar Simplification of CFG- Normal forms-chomsky Normal form and Greibach Normal formpumping lemma for Context free languages- Applications of
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
I have read and understand all of the instructions below, and I will obey the University Code on Academic Integrity.
 Midterm Exam CS 341-451: Foundations of Computer Science II Fall 2016, elearning section Prof. Marvin K. Nakayama Print family (or last) name: Print given (or first) name: I have read and understand all
Midterm Exam CS 341-451: Foundations of Computer Science II Fall 2016, elearning section Prof. Marvin K. Nakayama Print family (or last) name: Print given (or first) name: I have read and understand all
PUSHDOWN AUTOMATA (PDA)
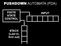 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Notes for Comp 497 (Comp 454) Week 10 4/5/05
 Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
Pushdown Automata. Reading: Chapter 6
 Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Design a PDA and a CFG for a given language Give informal description for a PDA,
CSE 105 THEORY OF COMPUTATION Spring 2016 http://cseweb.ucsd.edu/classes/sp16/cse105-ab/ Today's learning goals Sipser Ch 2 Design a PDA and a CFG for a given language Give informal description for a PDA,
CS 154. Finite Automata vs Regular Expressions, Non-Regular Languages
 CS 154 Finite Automata vs Regular Expressions, Non-Regular Languages Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and guessing
CS 154 Finite Automata vs Regular Expressions, Non-Regular Languages Deterministic Finite Automata Computation with finite memory Non-Deterministic Finite Automata Computation with finite memory and guessing
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Notes for Comp 497 (454) Week 10
 Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 14 Ana Bove May 14th 2018 Recap: Context-free Grammars Simplification of grammars: Elimination of ǫ-productions; Elimination of
CISC 4090: Theory of Computation Chapter 1 Regular Languages. Section 1.1: Finite Automata. What is a computer? Finite automata
 CISC 4090: Theory of Computation Chapter Regular Languages Xiaolan Zhang, adapted from slides by Prof. Werschulz Section.: Finite Automata Fordham University Department of Computer and Information Sciences
CISC 4090: Theory of Computation Chapter Regular Languages Xiaolan Zhang, adapted from slides by Prof. Werschulz Section.: Finite Automata Fordham University Department of Computer and Information Sciences
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
Before We Start. The Pumping Lemma. Languages. Context Free Languages. Plan for today. Now our picture looks like. Any questions?
 Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
Before We Start The Pumping Lemma Any questions? The Lemma & Decision/ Languages Future Exam Question What is a language? What is a class of languages? Context Free Languages Context Free Languages(CFL)
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
Computational Theory
 Computational Theory Finite Automata and Regular Languages Curtis Larsen Dixie State University Computing and Design Fall 2018 Adapted from notes by Russ Ross Adapted from notes by Harry Lewis Curtis Larsen
Computational Theory Finite Automata and Regular Languages Curtis Larsen Dixie State University Computing and Design Fall 2018 Adapted from notes by Russ Ross Adapted from notes by Harry Lewis Curtis Larsen
Lecture 4: More on Regexps, Non-Regular Languages
 6.045 Lecture 4: More on Regexps, Non-Regular Languages 6.045 Announcements: - Pset 1 is on piazza (as of last night) - If you don t have piazza access but are registered for 6.045, send email to TAs with
6.045 Lecture 4: More on Regexps, Non-Regular Languages 6.045 Announcements: - Pset 1 is on piazza (as of last night) - If you don t have piazza access but are registered for 6.045, send email to TAs with
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
Theory of Computation (II) Yijia Chen Fudan University
 Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
Theory of Computation (II) Yijia Chen Fudan University Review A language L is a subset of strings over an alphabet Σ. Our goal is to identify those languages that can be recognized by one of the simplest
CS 341 Homework 16 Languages that Are and Are Not Context-Free
 CS 341 Homework 16 Languages that Are and Are Not Context-Free 1. Show that the following languages are context-free. You can do this by writing a context free grammar or a PDA, or you can use the closure
CS 341 Homework 16 Languages that Are and Are Not Context-Free 1. Show that the following languages are context-free. You can do this by writing a context free grammar or a PDA, or you can use the closure
Computational Models - Lecture 3
 Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Slides modified by Benny Chor, based on original slides by Maurice Herlihy, Brown University. p. 1 Computational Models - Lecture 3 Equivalence of regular expressions and regular languages (lukewarm leftover
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Spring 27 Alexis Maciel Department of Computer Science Clarkson University Copyright c 27 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata Theory CS F-08 Context-Free Grammars
 Automata Theory CS411-2015F-08 Context-Free Grammars David Galles Department of Computer Science University of San Francisco 08-0: Context-Free Grammars Set of Terminals (Σ) Set of Non-Terminals Set of
Automata Theory CS411-2015F-08 Context-Free Grammars David Galles Department of Computer Science University of San Francisco 08-0: Context-Free Grammars Set of Terminals (Σ) Set of Non-Terminals Set of
CS 530: Theory of Computation Based on Sipser (second edition): Notes on regular languages(version 1.1)
 CS 530: Theory of Computation Based on Sipser (second edition): Notes on regular languages(version 1.1) Definition 1 (Alphabet) A alphabet is a finite set of objects called symbols. Definition 2 (String)
CS 530: Theory of Computation Based on Sipser (second edition): Notes on regular languages(version 1.1) Definition 1 (Alphabet) A alphabet is a finite set of objects called symbols. Definition 2 (String)
10. The GNFA method is used to show that
 CSE 355 Midterm Examination 27 February 27 Last Name Sample ASU ID First Name(s) Ima Exam # Sample Regrading of Midterms If you believe that your grade has not been recorded correctly, return the entire
CSE 355 Midterm Examination 27 February 27 Last Name Sample ASU ID First Name(s) Ima Exam # Sample Regrading of Midterms If you believe that your grade has not been recorded correctly, return the entire
Homework. Context Free Languages. Announcements. Before We Start. Languages. Plan for today. Final Exam Dates have been announced.
 Homework Context Free Languages PDAs and CFLs Homework #3 returned Homework #4 due today Homework #5 Pg 169 -- Exercise 4 Pg 183 -- Exercise 4c,e,i (use JFLAP) Pg 184 -- Exercise 10 Pg 184 -- Exercise
Homework Context Free Languages PDAs and CFLs Homework #3 returned Homework #4 due today Homework #5 Pg 169 -- Exercise 4 Pg 183 -- Exercise 4c,e,i (use JFLAP) Pg 184 -- Exercise 10 Pg 184 -- Exercise
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION "Winter" 2018 http://cseweb.ucsd.edu/classes/wi18/cse105-ab/ Today's learning goals Sipser Section 1.4 Explain the limits of the class of regular languages Justify why the
CSE 105 THEORY OF COMPUTATION "Winter" 2018 http://cseweb.ucsd.edu/classes/wi18/cse105-ab/ Today's learning goals Sipser Section 1.4 Explain the limits of the class of regular languages Justify why the
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
Computer Sciences Department
 1 Reference Book: INTRODUCTION TO THE THEORY OF COMPUTATION, SECOND EDITION, by: MICHAEL SIPSER 3 objectives Finite automaton Infinite automaton Formal definition State diagram Regular and Non-regular
1 Reference Book: INTRODUCTION TO THE THEORY OF COMPUTATION, SECOND EDITION, by: MICHAEL SIPSER 3 objectives Finite automaton Infinite automaton Formal definition State diagram Regular and Non-regular
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
Sri vidya college of engineering and technology
 Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
CS 301. Lecture 18 Decidable languages. Stephen Checkoway. April 2, 2018
 CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
CS 301 Lecture 18 Decidable languages Stephen Checkoway April 2, 2018 1 / 26 Decidable language Recall, a language A is decidable if there is some TM M that 1 recognizes A (i.e., L(M) = A), and 2 halts
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
The View Over The Horizon
 The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
The View Over The Horizon enumerable decidable context free regular Context-Free Grammars An example of a context free grammar, G 1 : A 0A1 A B B # Terminology: Each line is a substitution rule or production.
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
CS375: Logic and Theory of Computing
 CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
Outline. CS21 Decidability and Tractability. Machine view of FA. Machine view of FA. Machine view of FA. Machine view of FA.
 Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
September 11, Second Part of Regular Expressions Equivalence with Finite Aut
 Second Part of Regular Expressions Equivalence with Finite Automata September 11, 2013 Lemma 1.60 If a language is regular then it is specified by a regular expression Proof idea: For a given regular language
Second Part of Regular Expressions Equivalence with Finite Automata September 11, 2013 Lemma 1.60 If a language is regular then it is specified by a regular expression Proof idea: For a given regular language
Computability and Complexity
 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. The stack
 A pushdown automata (PDA) is essentially: An NFA with a stack A move of a PDA will depend upon Current state of the machine Current symbol being read in Current symbol popped off the top of the stack With
A pushdown automata (PDA) is essentially: An NFA with a stack A move of a PDA will depend upon Current state of the machine Current symbol being read in Current symbol popped off the top of the stack With
CPSC 421: Tutorial #1
 CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
CPSC 421: Tutorial #1 October 14, 2016 Set Theory. 1. Let A be an arbitrary set, and let B = {x A : x / x}. That is, B contains all sets in A that do not contain themselves: For all y, ( ) y B if and only
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Theory of Computation p.1/?? Theory of Computation p.2/?? Unknown: Implicitly a Boolean variable: true if a word is
 Abstraction of Problems Data: abstracted as a word in a given alphabet. Σ: alphabet, a finite, non-empty set of symbols. Σ : all the words of finite length built up using Σ: Conditions: abstracted as a
Abstraction of Problems Data: abstracted as a word in a given alphabet. Σ: alphabet, a finite, non-empty set of symbols. Σ : all the words of finite length built up using Σ: Conditions: abstracted as a
Context Free Languages and Grammars
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Intro to Theory of Computation
 Intro to Theory of Computation LECTURE 9 Last time: Converting a PDA to a CFG Pumping Lemma for CFLs Today: Pumping Lemma for CFLs Review of CFGs/PDAs Sofya Raskhodnikova 2/9/2016 Sofya Raskhodnikova;
Intro to Theory of Computation LECTURE 9 Last time: Converting a PDA to a CFG Pumping Lemma for CFLs Today: Pumping Lemma for CFLs Review of CFGs/PDAs Sofya Raskhodnikova 2/9/2016 Sofya Raskhodnikova;
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
5 Context-Free Languages
 CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
ÖVNINGSUPPGIFTER I SAMMANHANGSFRIA SPRÅK. 17 april Classrum Edition
 ÖVNINGSUPPGIFTER I SAMMANHANGSFRIA SPRÅK 7 april 23 Classrum Edition CONTEXT FREE LANGUAGES & PUSH-DOWN AUTOMATA CONTEXT-FREE GRAMMARS, CFG Problems Sudkamp Problem. (3.2.) Which language generates the
ÖVNINGSUPPGIFTER I SAMMANHANGSFRIA SPRÅK 7 april 23 Classrum Edition CONTEXT FREE LANGUAGES & PUSH-DOWN AUTOMATA CONTEXT-FREE GRAMMARS, CFG Problems Sudkamp Problem. (3.2.) Which language generates the
