Momentum and the Flow of Mass Challenge Problems Solutions
|
|
|
- Adam Charles
- 5 years ago
- Views:
Transcription
1 Poblem 1: Steam Bouncing off Wall Momentum and the Flow of Ma Challenge Poblem Solution A team of paticle of ma m and epaation d hit a pependicula uface with peed v. The team ebound along the oiginal line of motion with the ame peed. The ma pe unit length of the incident team i! = m / d. What i the magnitude of the foce on the uface? Solution: We begin by defining ou ytem a a tube of wate of co ectional aea A and length v!t. Ma Conevation: The ma of the wate in thi tube i given by!m i = "Av!t = #v!t (1.1) - 1 -
2 whee! = " A = m / d i the ma pe unit length. Thi mean that all the wate inide thi tube will hit the wall duing the inteval [ t, t +!t] and eflect. Note that if the colliion with the wall i elatic, the eflected wate will have the ame peed a the incident wate. Othewie to allow fo a lightly moe geneal cae, we hall aume that the eflected wate tavel backwad with peed v!. We aume that the wate i incompeible o that the denity ha not changed. The ma of the wate that ha been eflected i given by!m = "A#v#!t = $#v#!t (1.2) whee!# = " A# = m / d# i the ma pe unit length of the eflected wate. We aume that the wate i incompeible o that the denity ha not changed. We hall alo aume fo implicity that all the wate incident on the wall eflect with the peed v!. Thu Thu in the time inteval!m i =!m. (1.3) Thi implie that!m i!m =. (1.4)!t!t!v =!"v". (1.5) Note that the intantaneou ate that ma i deliveed to the uface and leave i "m dm dm dm i "m i! = lim = lim = = $v = $%v%. (1.6) "t#0 "t "t#0 "t Momentum Pinciple: The momentum pinciple tate that the impule fom the uface change the momentum of the wate. The momentum of the incident wate i given by! p = "m v i ˆ = (!v" ) ˆ =!v 2 i i t v i "t i ˆ. (1.7) The x-component of the momentum of the eflected wate i given by! p = #$ m v i ˆ = #(!"v" $ t) v" i ˆ = #!" v" 2 $t i ˆ. (1.8)!! ave ave The uface exet an aveage foce on the wate, F w, hence an impule F w!t. So the momentum pinciple become! ave! F w!t =!p. (1.9) - 2 -
3 Baed on ou analyi of the momentum incident and eflected the momentum pinciple become! ave!! 2 2 F #t = p $ p = $!"v" #t i ˆ $!v #t i ˆ = $(!"v" v " +!vv)#t i ˆ. (1.10) w i Theefoe the foce of the uface on the wate i! ave Fw = #(!"v" v " +!vv) î. (1.11) We can apply ou condition fo ma conevation, Eq. (1.5) and find that! ave Fw = #!v( v " + v) î. (1.12) By Newton Thid Law the aveage foce of the wate on the uface i!! ave ave F = #F =!v( v " + v) î. (1.13) w w In ode to poduce the maximum poible aveage foce of wate on the uface, the colliion mut be elatic ince then the eflected peed i equal to the incident peed and! ave 2 ) max = 2!v i ˆ. (1.14) (F w Note that the uing the intantaneou ate that ma aive o leave the uface, we have that So the magnitude of the foce on the uface i! ave ˆ dm (F ) = 2!vv i = 2 v i ˆ w max. (1.15)! ave (Fw ) max = 2!v 2. (1.16) - 3 -
4 Poblem 2 A ocket ha a dy ma (empty of fuel) m,0 = 2! 10 7 kg, and initially caie fuel with ma m f,0 = 5! 10 7 kg. The fuel i ejected at a peed u = 2.0! 10 3 m " -1 elative to the ocket. What i the final peed of the ocket afte all the fuel ha buned? Solution The initial ma of the ocket included the fuel i m = m + m = 2! 10 7 kg + 5! 10 7 kg = 7! 10 7 kg (2.1),i,0 f,0 The atio of the initial ma of the ocket (including the ma of the fuel) to the final dy ma of the ocket (empty of fuel) i The final peed of the ocket i then m,i 7! 10 7 kg R = = = 3.5 (2.2) m,d 2! 10 7 kg v = u ln R = (2.0! 10 3 m " -1 )ln3.5 = 2.5! 10 3 m " -1. (2.3), f - 4 -
5 Poblem 3: Coal Ca An empty coal ca of ma m 0 tat fom et unde an applied foce of magnitude F. At the ame time coal begin to un into the ca at a teady ate b fom a coal hoppe at et along the tack. Find the peed when a ma m c of coal ha been tanfeed. Solution: We hall analyze the momentum change in the hoizontal diection which we call the x-diection.. Since the coal doe not have any hoizontal velocity, the falling coal i not tanfeing any momentum to the coal ca. So we hall take a ou ytem the empty coal ca and a ma m c of coal that ha been tanfeed. Ou initial tate at t = 0 i when the coal ca i empty and at et befoe any coal ha been tanfeed. The x- component of the momentum of thi initial tate i zeo, p x (0) = 0. (3.1) Ou final tate at t = t i when all the coal of ma m = bt ha been tanfeed into the f c f ca which i now moving at peed v f. The x-component of the momentum of thi final tate i p x (t f ) = (m 0 + m c )v f = (m 0 + bt f )v f. (3.2) Thee i an extenal contant foce F x = F applied though the tanfe. The momentum pinciple applied to the x-diection i t f F = "p = p ) # p (0). (3.3)! x x x (t f x 0 Since the foce i contant, the integal i imple and the momentum pinciple become Ft f = (m 0 + bt f )v f. (3.4) So the final peed i - 5 -
6 Ft f v f =. (3.5) (m 0 + bt f ) - 6 -
7 Poblem 4: Emptying a Feight Ca A feight ca of ma m c contain a ma of and m. At t = 0 a contant hoizontal foce of magnitude F i applied in the diection of olling and at the ame time a pot in the bottom i opened to let the and flow out at the contant ate b = dm /. Find the peed of the feight ca when all the and i gone. Aume that the feight ca i at et at t = 0. Solution: Chooe the poitive-diection to point in the diection that the ca i moving. Let take a ou ytem the amount of and of ma!m that leave the feight ca duing the time inteval [ t, t +!t], and the feight ca and whateve and i in it at time t. At the beginning of the inteval the ca and and i moving with peed v o the x- component of the momentum at time t i given by p (t) = (!m + m (t))v), (4.1) x c whee m c ( t ) i the ma of the ca and and in it at time t. Denote by m c,0 = m c + m whee the m c i the ma of the ca and m i the ma of the and in the ca at t = 0, and m ( t ) = bt i the ma of the and that ha left the ca at time t ince Thu t t dm m (t) = = b = bt. (4.2)!! 0 0 m (t) = m! bt = m + m! bt. (4.3) c c,0 c Duing the inteval [ t, t +!t], the mall amount of and of ma!m leave the ca with the peed of the ca at the end of the inteval v +!v. So the x-component of the momentum at time t +!t i given by - 7 -
8 p (t +!t) = (!m + m (t))(v +!v). (4.4) x c Thoughout the inteval a contant foce F i applied to the ca o p x (t +!t) # p x ( t) F = lim. (4.5)!t"0!t Fom ou analyi above Eq. (4.5) become Eq. (4.6) implifie to (m c ( t ) +!m )( v +!v) # (m c ( t ) +!m )v F = lim. (4.6)!t"0!t!v!m!v F = lim m c ( t ) + lim. (4.7)!t"0!t! t " 0!t The econd tem vanihe when we take the!t " 0 becaue it i of econd ode in the infiniteimal quantitie (in thi cae!m!v ) and o when dividing by!t the quantity i of fit ode and hence vanihe ince both!m " 0 and!v " 0. So Eq. (4.7) become We now ue the definition of the deivative: in Eq. (4.8) to fund the diffeential equation Uing Eq. (4.3) we have!v F = lim m c ( t ). (4.8)! t " 0!t!v dv lim = (4.9)!t"0!t dv F = m c ( t ). (4.10) dv F = (m c + m! bt ). (4.11) (b) We can integate thi equation though the epaation of vaiable technique. Rewite Eq. (4.11) a - 8 -
9 F dv = (mc + m! bt ). (4.12) We can then integate both ide of Eq. (4.12) with the limit a hown v( t ) t F " dv = " m + m! bt. (4.13) v=0 0 c Integation yield the velocity of the ca a a function of time F t F! m c + m # bt " v( t ) = # ln( m c + m # bt ) %. (4.14) b 0 = # ln $ b & m c + m ' - 9 -
10 Poblem 5: Falling Chain A chain of ma m and length l i upended vetically with it lowet end touching a cale. The chain i eleaed and fall onto the cale. What i the eading of the cale when a length of chain, y, ha fallen? (Neglect the ize of the individual link.) Let g denote the gavitational contant. Solution: Suppoe the chain i eleaed at time t = 0. At time t, a length y of the chain ha fallen onto the cale and the et of the chain ha fallen a ditance y. (Note that we have choen downwad a the poitive y-diection.) We can ue ou enegy condition, applied to the potion of the chain that i feely falling (ma m( t ) ), to find that 2 (1/ 2) m( t) v y =!m( t ) g "h = m( t ) gy. (5.1) Hence at time t, the entie chain i falling with a y-component of the velocity given by v y = 2gy. (5.2) Note at the bottom of the chain, a mall incement of chain, (length!y and ma "m =!"y = (m / l )"y ), i moving with peed v y = 2gy. Afte a mall inteval of time!t ha elaped (we hall hotly conide the limit a!t " 0 ), thi mall piece of chain ha come to et on the cale. Note that we have aumed that the ma pe unit length! = m / l i unifom
11 Let take a ou ytem thi mall piece of chain. Thee i a contact foce between the!! chain and the cale, F ( t ), that act on thi piece. Thi foce F ( t ) vaie in time ince c, c, the peed of the chain inceae in time a the chain fall. It alo vaie due to the uneven colliion between the chain link and the cale. We will aveage thi foce ove the uneven colliion in ode to mooth out thee mall vaiation, and o the aveage! extenal foce on ou ytem i F ave ( t ). c, The y-component of the momentum of the ytem at time t +!t i at time i p y (t +!t) = 0. (5.3) The y-component of the momentum of the ytem at time t i at time i p ( t ) =!mv = (m / l )!y v, (5.4) y y y The change in the y-component of the momentum i theefoe!p y = p y (t +!t) " p y ( t ) = "(m / l )!y v y, (5.5) Since the extenal foce i equal to the change in momentum we have that.!!p ave y!y dy 2 F c, ( t ) = lim ĵ = #(m / l ) v y lim ĵ = #(m / l ) v y ĵ = #(m / l ) v y ĵ, (5.6)!t"0!t! t " 0!t whee we have ued the fact that dy / = v y. Note that we have choen downwad a the poitive y-diection o the foce on the chain i upwad a we expect in ode to top the 2 chain. Recall fom the enegy condition that v y = 2gy. So the magnitude of the extenal foce i given by! F ave ( t ) = 2( m / l ) gy. (5.7) c, The cale eading i equal to the magnitude of thi foce plu the weight of the chain, (m / l ) yg, that i aleady on the cale
12 ! Scale eading = F ave ( t ) + (m / l ) yg = 2( m / l ) yg + (m / l ) yg = 3( m / l ) gy. (5.8) c, Note that at time t, the amount of chain that i eted on the cale i 1 2 So the cale eading a a function of time i given by y( t ) = gt. (5.9) Scale eading = (m / l ) g t. (5.10) 2 We note that when the entie chain ha jut come to et on the cale, y = l, the cale ead Scale eading = 3mg. (5.11) Afte the colliion ha ended the cale eading dop to the weight of the chain. Scale eading = mg
13 Poblem 6 A pacecaft i launched fom an ateoid by being bombaded by a team of ock dut. The team of dut i ejected fom the dut gun at a contant ate dm e / = b at a peed u with epect to the ateoid, which we take to be tationay. Aume that the dut come momentaily to et at the pacecaft and then lip away ideway; the effect i to keep the pacecaft ma m contant. a) Deive an equation fo the acceleation dv / of the pacecaft at time t, in tem of the ate that the dut ma hit the uface of the pacecaft dm d /, the peed of the dut elative to the ateoid u, the ma of the pacecaft m, and the velocity of the pacecaft v. Show you momentum flow diagam at time t and time t +!t. Clealy identify you ytem and label all the object in you ytem. What i the teminal velocity of the pacecaft? Hint: dm d /! b. b) Uing conevation of ma, at time t, find an expeion fo the ate that the dut ma hit the pacecaft, dm d /, a a function of the peed of the pacecaft v, the ate that the dut ma i hot fom the ateoid dm e / = b, and the peed u of the dut elative to the ateoid. Hint: dm d /! b. c) Ue you eult fom pat b) in pat a) to find the peed v (t) of the pacecaft a a function of time, auming v (t = 0) = 0. (If you get an integal that you ae not ue how to integate, you can leave you anwe in integal fom.) Solution: We chooe a ou ytem, the mall amount of dut!m d that hit the pacecaft duing the inteval [t,t +!t] and the pacecaft of ma m. Becaue we aumed that the dut come momentaily to et at the pacecaft and then lip away ideway; at the end of the inteval the dut ha the ame peed a the pacecaft and the ma m of the pacecaft emain contant. We how the momentum diagam fo the ytem at time t and t +!t below
14 Becaue we ae ignoing the gavitational foce (it i vey mall), the x-component of the momentum of the ytem i contant duing the inteval [t,t +!t] and o p x (t +!t) # p x (t) 0 = lim. (6.1)!t"0!t Uing the infomation fom the figue above, Eq. (4.5) become Eq. (4.6) implifie to (m +!m d )(v +!v ) # (!m d u + m v ) 0 = lim. (6.2)!t"0!t!v!m!v d!m d!m 0 = lim m + lim v + lim # lim d u. (6.3)!t"0!t!t"0!t!t"0!t!t"0!t The thid tem vanihe when we take the!t " 0 becaue it i of econd ode in the infiniteimal quantitie (in thi cae!m d!v ) and o when dividing by!t the quantity i of fit ode and hence vanihe ince both!m d " 0 and!v " 0. So Eq. (4.7) become!v!m d!m 0 = lim m + lim v # lim d u. (6.4)!t"0!t!t"0!t!t"0!t We now ue the definition of the deivative:!v dv!m d dm d lim = ; lim =. (6.5)!t"0!t!t"0!t
15 in Eq. (4.8) to fund the diffeential equation decibing the elation between the acceleation of the pacecaft and the time ate of change of the ma of dut tiking the pacecaft dv dm 0 = m + d (v! u). (6.6) In the limit a t! ", dv /! 0, hence v (!) = u the pacecaft can go no fate than the peed of the dut. In ode to olve the above diffeential equation, we begin by obeving that dm d dm! e = b (6.7) The eaon i that b i the ate that the dut i ejected fom the ateoid. In the figue below a column of ejected dut of length!l = u!t ha ma!m ejected = "u!t whee! i the ma pe unit length and i aumed to be contant. The ate that the ma i ejected fom the ateoid i then dm!m b = e = lim e = #u. (6.8)!t"0!t In the figue below we conide a column of dut of length u!t that i jut behind a pependicula uface of the pacecaft at time t
16 Duing the time inteval [t,t +!t], the pacecaft i moving a ditance v!t o the entie column of dut doe not hit the pacecaft. Only a faction of the column hit the pacecaft with the ma of the dut that tike the pacecaft given by b = "(u # v )!t = (u # v )!t (6.9)!m d u whee we ued! = b / u. Dividing the equation though by!t and taking limit we have that dm d!m d b = lim = (u # v ). (6.10)!t"0!t u Subtituting into Eq. (4.10) and afte ome eaanging yield dv b m = (v! u) 2. (6.11) u We can integate thi equation by epaating vaiable to find an integal expeion fo the ma of the pacecaft a a function of time v! = v (t ) t!=t dv! b =!. (6.12) (v! " u) 2 um # # v! =0 t!=0 We can eaily integate both ide of the equation, yielding v" =v (t ) 1 b! = t. (6.13) (v "! u) um v" =0-16 -
17 Evaluating the endpoint of the integal yield A little algebaic eaangement yield Inveting yield So the peed of the pacecaft a a function of time i then 1 1 b t. (6.14)!! = u (v (t)! u) um u m + bt! =. (6.15) (v (t)! u) m m v (t)! u =!u. (6.16) m + bt ubt v (t) = m + bt. (6.17) Note that in the limit a t! ", v (!) = u in ageement with what expect, that the pacecaft can go no fate than the peed of the dut
18 Poblem 7 Space Junk A pacecaft of co-ectional aea A, poceeding along the poitive x-diection, ente an ateoid tom at time t = 0, in which the mean ma denity of the ateoid tom i!! and the aveage ateoid velocity i u =!u î in the negative x-diection. A the pacecaft poceed though the tom, all of the ateoid that hit the pacecaft tick to it.! a) Suppoe that at time t the velocity of the pacecaft i v = v î in the poitive x- diection, and it ma i m. Futhe, uppoe that in an inteval! t, the ma of the pacecaft inceae by an amount! m. Given that thee ae no extenal foce, uing conevation of momentum find an equation fo the change of the pacecaft velocity!v, in tem of! m, u, and v? b) When the pacecaft ente the ateoid tom, the magnitude of it velocity and ma ae v 0 and m 0, epectively. Integate you diffeential equation in pat a) to find the velocity v of the pacecaft when the ma i m. c) Find an expeion fo the ma of the ateoid! m that tick to the pacecaft within the time inteval! t? (Hint: conide the volume of ateoid wept up by the pacecaft in time! t). d) When the pacecaft ente the ateoid tom, the magnitude of it velocity and ma ae v 0 and m 0, epectively. What i the ma of the pacecaft at time t? (Ue you eult fom pat c) and b).) Solution: Let chooe a ou ytem a mall element of the ateoid cloud! m that i abobed by the ocket duing the inteval [ t, t +! t] and the ocket itelf. Chooe poitive x-diection a the diection the ocket i moving. The momentum diagam at the beginning of the inteval at time t i hown in the figue below. The momentum diagam at time t +! t i alo hown below
19 Becaue we ae auming that thee ae no extenal foce acting on ou ytem, p x (t +!t) # p x ( t) 0 = lim. (7.1)! t " 0! t Uing the infomation fom the figue above, Eq. (7.1) become (m +!m)( v +!v) # (#! mu + mv ) 0 = lim. (7.2)! t " 0!t Eq. (7.2) implifie to!v!m!m!v!m 0 = lim m + lim v + lim + lim u. (7.3)! t " 0!t! t " 0!t! t " 0!t! t " 0!t The thid tem vanihe when we take the!t " 0 becaue it i of econd ode in the infiniteimal quantitie (in thi cae!m!v ) and o when dividing by!t the quantity i of fit ode and hence vanihe ince both!m " 0 and!v " 0. So Eq. (7.3) become We now ue the definition of the deivative:!v!m!m 0 = lim m + lim v + lim u. (7.4)! t " 0!t!t"0!t! t " 0!t!v dv!m dm lim = ; lim =. (7.5)!t"0!t! t " 0!t in Eq. (7.5) to find the diffeential equation decibing the elation between the acceleation of the ocket and the time ate of change of the ma of the ocket dv dm 0 = m + (v + u). (7.6) b) We can integate thi equation though the epaation of vaiable technique. Rewite Eq. (7.6) a (cancel the common facto ) dv dm! =. (7.7) u + v m We can then integate both ide of Eq. (7.7) with the limit a hown
20 Integation yield v!=v( m ) m!=m dv! dm! " # = # (7.8) u + v! m! v!=v0 m!=m0! u + v( m ) "! m " # ln $ % = ln $ % (7.9) & u + v0 ' & m0 ' Recall that ln( a / b ) =! ln( b / a ) o Eq. (7.9) become! u + v 0 "! m " ln # $ = ln # $ (7.10) % u + v & % m 0 & Alo ecall that exp(ln( a / b )) = a / b and o exponentiating both ide of Eq. (7.10) yield u + v0 m = (7.11) u + v( m ) m 0 Afte ome eaanging, the peed v(m) of the ocket a a function of m can be expeed a m( u + v( m )) = m 0 (u + v 0 ) m u + ( ) 0 (u + v 0 ) (7.12) v m = m m v( m ) = 0 (u + v 0 )! u m In the above expeion fo the peed v( m ) of the ocket i a function of the ma of the ocket. We can detemine how the ma of the ocket behave a a function of time by conideing ma conevation. In the inteval [ t, t +! t] the ocket weep out a tube of length!l = v! t. All the ateoid inide thi tube ae collected by the ocket adding an amount of ma to the ocket "m 1 =! Av " t. In addition, becaue the ateoid ae moving towad the ocket an additional amount of ma "m 2 =! Au " t alo i collected by the ocket (ee figue below)
21 Theefoe the total amount of ma collected by the ocket duing the inteval i!m =!m 1 +!m 2 = " Av! t + " Au!t = " A(v + u)!t. (7.13) Dividing Eq. though by!t and taking limit we have that dm "m = lim =! A( v + u). (7.14) " t # 0 "t We now ubtitute the econd line in Eq. (7.12) into Eq. (7.14) and find that dm m =! A 0 (u + v0 ). (7.15) m We can integate thi equation by epaating vaiable to find an integal expeion fo the ma of the ocket a a function of time m" =m( t ) t"=t # m " dm " b = #! Am (u + v 0 0 )". (7.16) m" =m t" =0 0 We can eaily integate both ide of the equation yielding So the ma of the ocket a a function of time i then 1 (m(t) 2! m 0 2 ) = "Am 0 (u + v 0 )t. (7.17) 2 2! A( u + v 0 )t m( t ) = m (7.18) We now ubtitute Eq. (7.18) into the thid line of Eq. (7.12) yielding the peed of the ocket a a function of time m 0 v ( t ) = u + v 2! A ( u + v 0 ) t 1 + m 0 0 " u. (7.19)
22 Poblem 8 Continuou Ma Tanpot: falling aindop A aindop of initial ma m 0 tat falling fom et unde the influence of gavity. Aume that the aindop gain ma fom the cloud at a ate popotional to the momentum of the aindop, dm / = km v, whee m i the intantaneou ma of the aindop, v i the intantaneou velocity of the aindop, and k i a contant with unit [m -1 ]. You may neglect ai eitance. a) Deive a diffeential equation fo the velocity of the aindop. b) Show that the peed of the dop eventually become effectively contant and give an expeion fo the teminal peed. Solution: At time t chooe the aindop with ma m (t) and a mall ma element!m c in the cloud that will be added to the aindop duing the time inteval!t. Chooe the poitive y diection downwad. Then the momentum flow diagam i hown in the figue below. At time t, the mall ma element!m c i at et in the cloud at time t. The aindop i moving downwad with velocity! v ˆ ( t ) = v j. (8.1) So the momentum of the dop i equal to the momentum of the ytem! p ( t ) = m v ˆj (8.2) y At time t +!t, the aindop ha added ome ma!m c fom the cloud and i moving downwad with velocity! ˆ v (t +!t) = (v +!v ) j. (8.3)
23 whee!v i the infiniteimal change in the y-component of the velocity of the aindop. So the momentum of the dop i! ˆ p (t +!t) = (m +!m ) ( v +!v ) j. (8.4) y c Duing thi inteval thee i an extenal gavitational foce acting on the ytem and a buoyant foce in the cloud that i keeping the ma element!m c fom falling. Since the total foce on the ma element!m c i zeo, the total extenal foce acting on the ytem i jut the gavitational foce acting on the aindop,! F total ˆ ext = m g j. (8.5) Newton Second Law and Thid Law fo the ytem tate that he total extenal foce i equal to the deivative of the momentum!! total dp y F ext =. (8.6) Recall the definition of the deivative of the ytem momentum,!!! dpy p y (t +!t) # p y ( t) = lim. (8.7)! t " 0!t Subtitute Eq.(8.4), Eq.(8.2), and Eq.(8.5) into Eq.(8.6) yield Expanding the numeato in Eq.(8.8), (m ˆ ˆ ˆ +!m c ) ( v +!v ) j # m v j m g j = lim. (8.8)! t " 0! t (m!v +!m v +!m!v ) ˆ ˆ c c j m g j = lim. (8.9)! t " 0!t The thid tem in the numeato on the ight hand ide of Eq.(8.9) i a econd oede tem in infiniteimal and hence in the limit a!t " 0 vanihe, Thu Eq.(8.9) become!m ˆ c!v j lim " 0. (8.10)! t " 0! t
24 !v!m c dv dm m g ˆ j = m lim ˆ j + v lim ˆ j = m ˆ j + v ˆ j (8.11)! t " 0!t! t " 0!t The y-component of Eq.(8.11) ae equal, dv dm m g = m + v (8.12) Fom the tatement of the poblem, we have modeled the ate that the ate that aindop add ma i popotional to the momentum of the aindop Thu Eq.(8.12) become dm = km v. (8.13) Divide out the ma of the aindop fom Eq.(8.14) giving dv 2 m g = m + km v. (8.14) dv 2 g = + kv (8.15) Thu the acceleation of the aindop i thu non-unifom and given by dv = g! kv 2. (8.16) The aindop will each a teminal velocity when the acceleation i zeo, So the teminal velocity i 0 = g! kv,te 2. (8.17) g v =. (8.18),te k
25 Poblem 9: Rocket Poblem A ocket acend fom et in a unifom gavitational field by ejecting exhaut with contant peed u elative to the ocket. Aume that the ate at which ma i expelled i given by dm f / =! m, whee m i the intantaneou ma of the ocket and! i a contant. The ocket i etaded by ai eitance with a foce F = bm v contant and v time. popotional to the intantaneou momentum of the ocket whee b i a i the peed of the ocket. Find the peed of the ocket a a function of Solution: To find the ocket velocity a a function of time, we fit need to find how the velocity change with epect to time, the diffeential equation mentioned in the poblem tatement. Take the poitive y-diection to be upwad and aume that the ocket velocity i upwad a well. Fo pupoe of pace and claity, the poitive upwad diection i hown a being to the ight in the figue. The gavitational foce and ai eitance foce ae then in the negative diection, to the left in the figue. A uggeted by the figue above, take the ytem to be the ocket and fuel combination. The malle quae epeent the mall amount of fuel of ma!m f,out that i ejected duing the inteval [t,t +!t]. In the above figue m (t) = m + m (t) (9.1),0 f,in i the combined ma of the ocket whee m,0 i the dy ma of the ocket and m f,in ( t ) i the ma of fuel inide the ocket at time t that doe not leave the ocket duing the inteval. Note that diffeentiating the above equation yield Denote by m f,0 the fuel in the ocket at t = 0. Then dm (t) dm f,in (t) =. (9.2)
26 m f,0 = m f,in (t) + m f,out (t) (9.3) whee m f,out ( t ) i the ma of the fuel that ha been ejected duing the inteval [0,t ]. Since m f,0 i contant, we can diffeentiate the above equation yielding Thu combining equation Eq. (9.2) and Eq. (9.4) yield 0 = dm f,0 dm f,in (t) dm f,out (t) = +. (9.4) (t) dm f,out dm (t) =!. (9.5) Fom the tatement of the poblem, the bun ate of fuel i then equal to the negative of the ate that the ma of the ocket i deceaing and fom the tatement of the poblem i given by dm f,out (t) dm (t)! m (t)= = ". (9.6) Retuning to ou momentum diagam we ee that at time t, the y-component of the y momentum of the ytem p y ( t ) i given by y p y ( t ) = (m ( t ) +!m f,out ) v (9.7) Duing the inteval the fuel i ejected backwad elative to the ocket with peed u. Afte the inteval ha ended the momentum diagam of the ytem i hown below. At time t +!t, the y-component of the momentum of the ytem p y y (t +!t) i given by p y (t t)= m t v +!v ) m v +!v - u) (9.8) y +! ( )( +! f,out (
27 and o the change in y-component of the momentum of the ytem duing the inteval [t,t +!t] i y y y!p y = p y (t +!t) " p y ( t ) = m ( t )( v +!v ) +!m f,out (v +!v " u) " (m ( t ) +!m f,out ) v. (9.9) = m ( t )!v +!m f,out!v "! m f,out u The extenal foce acting on the ytem i given by The momentum pinciple F ext =!m (t)g! bm (t)v. (9.10) y!p y ext y F = lim (9.11) y!t"0!t then become We note that m ( t )!v +!m f,out!v #! m f,out u #m ( t) g # bm ( t) v = lim. (9.12)! t " 0!t!m f,out!v lim = 0. (9.13)!t"0!t Then uing the definition of the deivative, we find that the diffeential equation decibing the motion of the ytem i given by dv d m f,out!m (t)g! bm (t)v = m (t)! u (9.14) We can now ubtitute Eq. (9.6) into the above equation and find that dv!m (t)g! bm (t)v = m (t)! " m (t)u. (9.15) We can divide though by the ma of the ocket in the above equation yielding
28 dv =! u " g " bv (9.16) On to the Diffeential Equation: We ve done the phyic, but thee ae eveal inteeting apect to the calculation of the velocity a a function of time. Ou diffeential equation i epaable and o Rewite Eq. (9.16) a We can integate both ide dv =. (9.17)! u " g " bv v " =v ( t) t"=t dv " = ". (9.18)! u # g # bv " $ $ v" =0 t" =0 Integation yield $ 1 ln "! u $ g $ bv ( t ) # % & b! u $ g = t. (9.19) ' ( Afte a light eaangement, thi expeion can be exponentiated yielding! u " g " bv (t) "bt = e. (9.20)! u " g Afte ome eaangement we find that the peed of the ocket i given by 1 " bt v (t) = (! u " g)(1" e ). (9.21) b Thee ae eveal apect of the eult in Eq. (9.21) that ae woth conideing. Fit, unle! u > g, the ocket doen t get off the gound. Next, the ocket continue to acceleate, only eaching teminal peed v teminal = (! u " g )/ b in the limit t! " ; the ai eitance foce eem to have wimped out. The key point in conideing the eult of Eq. (9.21) i in the model fo the ate at which the fuel i exhauted
29 dm f,out dm = " =! m ( t ), (9.22) Solving Equation (9.22) would yield that the ma of the ocket and emaining fuel i m (t) = m 0 e!" t (9.23) whee m 0 = m,0 + m f,0 The ma being acceleated deceae exponentially, the gavitation foce and the ai eitance foce, being popotional to the ma, deceae a well, and o the ocket can continue to acceleate indefinitely. The poduct u( dm f,out / ) i ometime called the thut (ak you Coue XVI fiend); check to ee that the thut ha dimenion of foce. In the model fo thi poblem, we would have that the thut foce i dm f,out F = u =! u m, (9.24) thut an unlikely featue of ealitic ocket deign. At bet, even if Equation (9.24) wee an appoximate model, the thut would have to vanih when the fuel un out. The bottom line i that the model fo the fuel bun ate wa given in the fom it wa in ode to make olving fo the velocity a a function of time poible. Maybe a neat math poblem, but the phyic wa done once we found the ate of change of momentum
30 MIT OpenCoueWae SC Phyic I: Claical Mechanic Fo infomation about citing thee mateial o ou Tem of Ue, viit:
Chapter 19 Webassign Help Problems
 Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
Chapte 9 Webaign Help Poblem 4 5 6 7 8 9 0 Poblem 4: The pictue fo thi poblem i a bit mileading. They eally jut give you the pictue fo Pat b. So let fix that. Hee i the pictue fo Pat (a): Pat (a) imply
12.1 Introduction 12-1
 12.1 Intoduction So fa we have esticted ouselves to consideing systems consisting of discete objects o point-like objects that have fixed amounts of mass. We shall now conside systems in which mateial
12.1 Intoduction So fa we have esticted ouselves to consideing systems consisting of discete objects o point-like objects that have fixed amounts of mass. We shall now conside systems in which mateial
Solutions Practice Test PHYS 211 Exam 2
 Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Solution Pactice Tet PHYS 11 Exam 1A We can plit thi poblem up into two pat, each one dealing with a epaate axi. Fo both the x- and y- axe, we have two foce (one given, one unknown) and we get the following
Impulse and Momentum
 Impule and Momentum 1. A ca poee 20,000 unit of momentum. What would be the ca' new momentum if... A. it elocity wee doubled. B. it elocity wee tipled. C. it ma wee doubled (by adding moe paenge and a
Impule and Momentum 1. A ca poee 20,000 unit of momentum. What would be the ca' new momentum if... A. it elocity wee doubled. B. it elocity wee tipled. C. it ma wee doubled (by adding moe paenge and a
AE 245 homework #9 solutions
 AE 245 homewok #9 olution Tim Smith 13 Apil 2000 1 Poblem1 In the Apollo miion fom the Eath to the Moon, the Satun thid tage povided the tan-luna inetion bun that tanfeed the Apollo pacecaft fom a low
AE 245 homewok #9 olution Tim Smith 13 Apil 2000 1 Poblem1 In the Apollo miion fom the Eath to the Moon, the Satun thid tage povided the tan-luna inetion bun that tanfeed the Apollo pacecaft fom a low
Gravity. David Barwacz 7778 Thornapple Bayou SE, Grand Rapids, MI David Barwacz 12/03/2003
 avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
avity David Bawacz 7778 Thonapple Bayou, and Rapid, MI 495 David Bawacz /3/3 http://membe.titon.net/daveb Uing the concept dicued in the peceding pape ( http://membe.titon.net/daveb ), I will now deive
LECTURE 14. m 1 m 2 b) Based on the second law of Newton Figure 1 similarly F21 m2 c) Based on the third law of Newton F 12
 CTU 4 ] NWTON W O GVITY -The gavity law i foulated fo two point paticle with ae and at a ditance between the. Hee ae the fou tep that bing to univeal law of gavitation dicoveed by NWTON. a Baed on expeiental
CTU 4 ] NWTON W O GVITY -The gavity law i foulated fo two point paticle with ae and at a ditance between the. Hee ae the fou tep that bing to univeal law of gavitation dicoveed by NWTON. a Baed on expeiental
Section 25 Describing Rotational Motion
 Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Section 25 Decibing Rotational Motion What do object do and wh do the do it? We have a ve thoough eplanation in tem of kinematic, foce, eneg and momentum. Thi include Newton thee law of motion and two
Rotational Kinetic Energy
 Add Impotant Rotational Kinetic Enegy Page: 353 NGSS Standad: N/A Rotational Kinetic Enegy MA Cuiculum Famewok (006):.1,.,.3 AP Phyic 1 Leaning Objective: N/A, but olling poblem have appeaed on peviou
Add Impotant Rotational Kinetic Enegy Page: 353 NGSS Standad: N/A Rotational Kinetic Enegy MA Cuiculum Famewok (006):.1,.,.3 AP Phyic 1 Leaning Objective: N/A, but olling poblem have appeaed on peviou
one primary direction in which heat transfers (generally the smallest dimension) simple model good representation for solving engineering problems
 CHAPTER 3: One-Dimenional Steady-State Conduction one pimay diection in which heat tanfe (geneally the mallet dimenion) imple model good epeentation fo olving engineeing poblem 3. Plane Wall 3.. hot fluid
CHAPTER 3: One-Dimenional Steady-State Conduction one pimay diection in which heat tanfe (geneally the mallet dimenion) imple model good epeentation fo olving engineeing poblem 3. Plane Wall 3.. hot fluid
Test 2 phy a) How is the velocity of a particle defined? b) What is an inertial reference frame? c) Describe friction.
 Tet phy 40 1. a) How i the velocity of a paticle defined? b) What i an inetial efeence fae? c) Decibe fiction. phyic dealt otly with falling bodie. d) Copae the acceleation of a paticle in efeence fae
Tet phy 40 1. a) How i the velocity of a paticle defined? b) What i an inetial efeence fae? c) Decibe fiction. phyic dealt otly with falling bodie. d) Copae the acceleation of a paticle in efeence fae
RE 7.a. RE 7.b Energy Dissipation & Resonance RE 7.c EP7, HW7: Ch 7 Pr s 31, 32, 45, 62 & CP
 Wed. Lab Fi. Mon. Tue. 7.-.4 Macocopic Enegy Quiz 6 4pm, hee Math & Phy Reeach L6 Wok and Enegy 7.5-.9 Enegy Tanfe RE 7.a RE 7.b 7.0-. Enegy Diipation & Reonance RE 7.c EP7, HW7: Ch 7 P 3, 3, 45, 6 & CP
Wed. Lab Fi. Mon. Tue. 7.-.4 Macocopic Enegy Quiz 6 4pm, hee Math & Phy Reeach L6 Wok and Enegy 7.5-.9 Enegy Tanfe RE 7.a RE 7.b 7.0-. Enegy Diipation & Reonance RE 7.c EP7, HW7: Ch 7 P 3, 3, 45, 6 & CP
Honors Classical Physics I
 Hono Claical Phyic I PHY141 Lectue 9 Newton Law of Gavity Pleae et you Clicke Channel to 1 9/15/014 Lectue 9 1 Newton Law of Gavity Gavitational attaction i the foce that act between object that have a
Hono Claical Phyic I PHY141 Lectue 9 Newton Law of Gavity Pleae et you Clicke Channel to 1 9/15/014 Lectue 9 1 Newton Law of Gavity Gavitational attaction i the foce that act between object that have a
V V The circumflex (^) tells us this is a unit vector
 Vecto Vecto have Diection and Magnitude Mike ailey mjb@c.oegontate.edu Magnitude: V V V V x y z vecto.pptx Vecto Can lo e Defined a the oitional Diffeence etween Two oint 3 Unit Vecto have a Magnitude
Vecto Vecto have Diection and Magnitude Mike ailey mjb@c.oegontate.edu Magnitude: V V V V x y z vecto.pptx Vecto Can lo e Defined a the oitional Diffeence etween Two oint 3 Unit Vecto have a Magnitude
TRAVELING WAVES. Chapter Simple Wave Motion. Waves in which the disturbance is parallel to the direction of propagation are called the
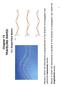 Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
Chapte 15 RAVELING WAVES 15.1 Simple Wave Motion Wave in which the ditubance i pependicula to the diection of popagation ae called the tanvee wave. Wave in which the ditubance i paallel to the diection
ASTR 3740 Relativity & Cosmology Spring Answers to Problem Set 4.
 ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
ASTR 3740 Relativity & Comology Sping 019. Anwe to Poblem Set 4. 1. Tajectoie of paticle in the Schwazchild geomety The equation of motion fo a maive paticle feely falling in the Schwazchild geomety ae
Then the number of elements of S of weight n is exactly the number of compositions of n into k parts.
 Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Geneating Function In a geneal combinatoial poblem, we have a univee S of object, and we want to count the numbe of object with a cetain popety. Fo example, if S i the et of all gaph, we might want to
Inference for A One Way Factorial Experiment. By Ed Stanek and Elaine Puleo
 Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Infeence fo A One Way Factoial Expeiment By Ed Stanek and Elaine Puleo. Intoduction We develop etimating equation fo Facto Level mean in a completely andomized one way factoial expeiment. Thi development
Potential Energy and Conservation of Energy
 Potential Enegy and Consevation of Enegy Consevative Foces Definition: Consevative Foce If the wok done by a foce in moving an object fom an initial point to a final point is independent of the path (A
Potential Enegy and Consevation of Enegy Consevative Foces Definition: Consevative Foce If the wok done by a foce in moving an object fom an initial point to a final point is independent of the path (A
Fall 2004/05 Solutions to Assignment 5: The Stationary Phase Method Provided by Mustafa Sabri Kilic. I(x) = e ixt e it5 /5 dt (1) Z J(λ) =
 8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
8.35 Fall 24/5 Solution to Aignment 5: The Stationay Phae Method Povided by Mutafa Sabi Kilic. Find the leading tem fo each of the integal below fo λ >>. (a) R eiλt3 dt (b) R e iλt2 dt (c) R eiλ co t dt
Lecture No. 6 (Waves) The Doppler Effect
 Lectue No. 6 (Wave) The Dopple Eect 1) A ound ouce i moving at 80 m/ towad a tationay litene that i tanding in till ai. (a) Find the wavelength o the ound in the egion between the ouce and the litene.
Lectue No. 6 (Wave) The Dopple Eect 1) A ound ouce i moving at 80 m/ towad a tationay litene that i tanding in till ai. (a) Find the wavelength o the ound in the egion between the ouce and the litene.
Can a watch-sized electromagnet deflect a bullet? (from James Bond movie)
 Can a peon be blown away by a bullet? et' ay a bullet of a 0.06 k i ovin at a velocity of 300 /. And let' alo ay that it ebed itelf inide a peon. Could thi peon be thut back at hih peed (i.e. blown away)?
Can a peon be blown away by a bullet? et' ay a bullet of a 0.06 k i ovin at a velocity of 300 /. And let' alo ay that it ebed itelf inide a peon. Could thi peon be thut back at hih peed (i.e. blown away)?
Physics 4A Chapter 8: Dynamics II Motion in a Plane
 Physics 4A Chapte 8: Dynamics II Motion in a Plane Conceptual Questions and Example Poblems fom Chapte 8 Conceptual Question 8.5 The figue below shows two balls of equal mass moving in vetical cicles.
Physics 4A Chapte 8: Dynamics II Motion in a Plane Conceptual Questions and Example Poblems fom Chapte 8 Conceptual Question 8.5 The figue below shows two balls of equal mass moving in vetical cicles.
Physics 107 TUTORIAL ASSIGNMENT #8
 Physics 07 TUTORIAL ASSIGNMENT #8 Cutnell & Johnson, 7 th edition Chapte 8: Poblems 5,, 3, 39, 76 Chapte 9: Poblems 9, 0, 4, 5, 6 Chapte 8 5 Inteactive Solution 8.5 povides a model fo solving this type
Physics 07 TUTORIAL ASSIGNMENT #8 Cutnell & Johnson, 7 th edition Chapte 8: Poblems 5,, 3, 39, 76 Chapte 9: Poblems 9, 0, 4, 5, 6 Chapte 8 5 Inteactive Solution 8.5 povides a model fo solving this type
Estimation and Confidence Intervals: Additional Topics
 Chapte 8 Etimation and Confidence Inteval: Additional Topic Thi chapte imply follow the method in Chapte 7 fo foming confidence inteval The text i a bit dioganized hee o hopefully we can implify Etimation:
Chapte 8 Etimation and Confidence Inteval: Additional Topic Thi chapte imply follow the method in Chapte 7 fo foming confidence inteval The text i a bit dioganized hee o hopefully we can implify Etimation:
HRW 7e Chapter 13 Page 1 of 5
 HW 7e Chapte Pae o 5 Halliday/enick/Walke 7e Chapte Gaitation The manitude o the oce o one paticle on the othe i ien by F = Gm m /, whee m and m ae the mae, i thei epaation, and G i the unieal aitational
HW 7e Chapte Pae o 5 Halliday/enick/Walke 7e Chapte Gaitation The manitude o the oce o one paticle on the othe i ien by F = Gm m /, whee m and m ae the mae, i thei epaation, and G i the unieal aitational
PHYS Summer Professor Caillault Homework Solutions. Chapter 5
 PHYS 1111 - Summe 2007 - Pofesso Caillault Homewok Solutions Chapte 5 7. Pictue the Poblem: The ball is acceleated hoizontally fom est to 98 mi/h ove a distance of 1.7 m. Stategy: Use equation 2-12 to
PHYS 1111 - Summe 2007 - Pofesso Caillault Homewok Solutions Chapte 5 7. Pictue the Poblem: The ball is acceleated hoizontally fom est to 98 mi/h ove a distance of 1.7 m. Stategy: Use equation 2-12 to
Force & Motion: Newton s Laws
 oce & otion: Newton Law ( t Law) If no net foce act on a body then the body velocity cannot change. Zeo net foce implie zeo acceleation. The ma of an object detemine how difficult it i to change the object
oce & otion: Newton Law ( t Law) If no net foce act on a body then the body velocity cannot change. Zeo net foce implie zeo acceleation. The ma of an object detemine how difficult it i to change the object
Chapter 6. NEWTON S 2nd LAW AND UNIFORM CIRCULAR MOTION
 Chapte 6 NEWTON S nd LAW AND UNIFORM CIRCULAR MOTION Phyic 1 1 3 4 ting Quetion: A ball attached to the end of a ting i whiled in a hoizontal plane. At the point indicated, the ting beak. Looking down
Chapte 6 NEWTON S nd LAW AND UNIFORM CIRCULAR MOTION Phyic 1 1 3 4 ting Quetion: A ball attached to the end of a ting i whiled in a hoizontal plane. At the point indicated, the ting beak. Looking down
Motion in Two Dimensions
 SOLUTIONS TO PROBLEMS Motion in Two Dimensions Section 3.1 The Position, Velocity, and Acceleation Vectos P3.1 x( m) 0!3 000!1 70!4 70 m y( m)!3 600 0 1 70! 330 m (a) Net displacement x + y 4.87 km at
SOLUTIONS TO PROBLEMS Motion in Two Dimensions Section 3.1 The Position, Velocity, and Acceleation Vectos P3.1 x( m) 0!3 000!1 70!4 70 m y( m)!3 600 0 1 70! 330 m (a) Net displacement x + y 4.87 km at
Perhaps the greatest success of his theory of gravity was to successfully explain the motion of the heavens planets, moons, &tc.
 AP Phyic Gavity Si Iaac Newton i cedited with the dicovey of gavity. Now, of coue we know that he didn t eally dicove the thing let face it, people knew about gavity fo a long a thee have been people.
AP Phyic Gavity Si Iaac Newton i cedited with the dicovey of gavity. Now, of coue we know that he didn t eally dicove the thing let face it, people knew about gavity fo a long a thee have been people.
Phys 201A. Homework 5 Solutions
 Phys 201A Homewok 5 Solutions 3. In each of the thee cases, you can find the changes in the velocity vectos by adding the second vecto to the additive invese of the fist and dawing the esultant, and by
Phys 201A Homewok 5 Solutions 3. In each of the thee cases, you can find the changes in the velocity vectos by adding the second vecto to the additive invese of the fist and dawing the esultant, and by
( ) Physics 1401 Homework Solutions - Walker, Chapter 9
 Phyic 40 Conceptual Quetion CQ No Fo exaple, ey likely thee will be oe peanent deoation o the ca In thi cae, oe o the kinetic enegy that the two ca had beoe the colliion goe into wok that each ca doe on
Phyic 40 Conceptual Quetion CQ No Fo exaple, ey likely thee will be oe peanent deoation o the ca In thi cae, oe o the kinetic enegy that the two ca had beoe the colliion goe into wok that each ca doe on
10.2 Parametric Calculus
 10. Paametic Calculus Let s now tun ou attention to figuing out how to do all that good calculus stuff with a paametically defined function. As a woking eample, let s conside the cuve taced out by a point
10. Paametic Calculus Let s now tun ou attention to figuing out how to do all that good calculus stuff with a paametically defined function. As a woking eample, let s conside the cuve taced out by a point
Between any two masses, there exists a mutual attractive force.
 YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
Magnetic Dipoles Challenge Problem Solutions
 Magnetic Dipoles Challenge Poblem Solutions Poblem 1: Cicle the coect answe. Conside a tiangula loop of wie with sides a and b. The loop caies a cuent I in the diection shown, and is placed in a unifom
Magnetic Dipoles Challenge Poblem Solutions Poblem 1: Cicle the coect answe. Conside a tiangula loop of wie with sides a and b. The loop caies a cuent I in the diection shown, and is placed in a unifom
F g. = G mm. m 1. = 7.0 kg m 2. = 5.5 kg r = 0.60 m G = N m 2 kg 2 = = N
 Chapte answes Heinemann Physics 4e Section. Woked example: Ty youself.. GRAVITATIONAL ATTRACTION BETWEEN SMALL OBJECTS Two bowling balls ae sitting next to each othe on a shelf so that the centes of the
Chapte answes Heinemann Physics 4e Section. Woked example: Ty youself.. GRAVITATIONAL ATTRACTION BETWEEN SMALL OBJECTS Two bowling balls ae sitting next to each othe on a shelf so that the centes of the
Physics 181. Assignment 4
 Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
Chapter 6. NEWTON S 2nd LAW AND UNIFORM CIRCULAR MOTION. string
 Chapte 6 NEWTON S nd LAW AND UNIFORM CIRCULAR MOTION 103 PHYS 1 1 L:\103 Phy LECTURES SLIDES\103Phy_Slide_T1Y3839\CH6Flah 3 4 ting Quetion: A ball attached to the end of a ting i whiled in a hoizontal
Chapte 6 NEWTON S nd LAW AND UNIFORM CIRCULAR MOTION 103 PHYS 1 1 L:\103 Phy LECTURES SLIDES\103Phy_Slide_T1Y3839\CH6Flah 3 4 ting Quetion: A ball attached to the end of a ting i whiled in a hoizontal
FI 2201 Electromagnetism
 FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
FI Electomagnetim Aleande A. Ikanda, Ph.D. Phyic of Magnetim and Photonic Reeach Goup ecto Analyi CURILINEAR COORDINAES, DIRAC DELA FUNCION AND HEORY OF ECOR FIELDS Cuvilinea Coodinate Sytem Cateian coodinate:
SPH4U Magnetism Test Name: Solutions
 SPH4U Magneti et Nae: Solution QUESION 1 [4 Mak] hi and the following two quetion petain to the diaga below howing two cuent-caying wie. wo cuent ae flowing in the ae diection (out of the page) a hown.
SPH4U Magneti et Nae: Solution QUESION 1 [4 Mak] hi and the following two quetion petain to the diaga below howing two cuent-caying wie. wo cuent ae flowing in the ae diection (out of the page) a hown.
- 5 - TEST 1R. This is the repeat version of TEST 1, which was held during Session.
 - 5 - TEST 1R This is the epeat vesion of TEST 1, which was held duing Session. This epeat test should be attempted by those students who missed Test 1, o who wish to impove thei mak in Test 1. IF YOU
- 5 - TEST 1R This is the epeat vesion of TEST 1, which was held duing Session. This epeat test should be attempted by those students who missed Test 1, o who wish to impove thei mak in Test 1. IF YOU
QUESTION 1 [25 points]
![QUESTION 1 [25 points] QUESTION 1 [25 points]](/thumbs/75/72643675.jpg) (Fist) QUESTION 1 [5 points] An object moves in 1 dimension It stats at est and unifomly acceleates at 5m/s fo s It then moves with constant velocity fo 4s It then unifomly acceleates at m/s until it comes
(Fist) QUESTION 1 [5 points] An object moves in 1 dimension It stats at est and unifomly acceleates at 5m/s fo s It then moves with constant velocity fo 4s It then unifomly acceleates at m/s until it comes
Precision Spectrophotometry
 Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Peciion Spectophotomety Pupoe The pinciple of peciion pectophotomety ae illutated in thi expeiment by the detemination of chomium (III). ppaatu Spectophotomete (B&L Spec 20 D) Cuvette (minimum 2) Pipet:
Equations of 2-body motion
 Equation of -body motion The fundamental eqn. of claical atodynamic i Newton Law of Univeal Gavitation: F g = Gm i i i ˆ i (1) We ae inteeted in atellite in obit about ingle planet, o (1) educe to the
Equation of -body motion The fundamental eqn. of claical atodynamic i Newton Law of Univeal Gavitation: F g = Gm i i i ˆ i (1) We ae inteeted in atellite in obit about ingle planet, o (1) educe to the
When a mass moves because of a force, we can define several types of problem.
 Mechanics Lectue 4 3D Foces, gadient opeato, momentum 3D Foces When a mass moves because of a foce, we can define seveal types of poblem. ) When we know the foce F as a function of time t, F=F(t). ) When
Mechanics Lectue 4 3D Foces, gadient opeato, momentum 3D Foces When a mass moves because of a foce, we can define seveal types of poblem. ) When we know the foce F as a function of time t, F=F(t). ) When
Δt The textbook chooses to say that the average velocity is
 1-D Motion Basic I Definitions: One dimensional motion (staight line) is a special case of motion whee all but one vecto component is zeo We will aange ou coodinate axis so that the x-axis lies along the
1-D Motion Basic I Definitions: One dimensional motion (staight line) is a special case of motion whee all but one vecto component is zeo We will aange ou coodinate axis so that the x-axis lies along the
Momentum is conserved if no external force
 Goals: Lectue 13 Chapte 9 v Employ consevation of momentum in 1 D & 2D v Examine foces ove time (aka Impulse) Chapte 10 v Undestand the elationship between motion and enegy Assignments: l HW5, due tomoow
Goals: Lectue 13 Chapte 9 v Employ consevation of momentum in 1 D & 2D v Examine foces ove time (aka Impulse) Chapte 10 v Undestand the elationship between motion and enegy Assignments: l HW5, due tomoow
Central Force Motion
 Cental Foce Motion Cental Foce Poblem Find the motion of two bodies inteacting via a cental foce. Examples: Gavitational foce (Keple poblem): m1m F 1, ( ) =! G ˆ Linea estoing foce: F 1, ( ) =! k ˆ Two
Cental Foce Motion Cental Foce Poblem Find the motion of two bodies inteacting via a cental foce. Examples: Gavitational foce (Keple poblem): m1m F 1, ( ) =! G ˆ Linea estoing foce: F 1, ( ) =! k ˆ Two
Kinematics in 2-D (II)
 Kinematics in 2-D (II) Unifom cicula motion Tangential and adial components of Relative velocity and acceleation a Seway and Jewett 4.4 to 4.6 Pactice Poblems: Chapte 4, Objective Questions 5, 11 Chapte
Kinematics in 2-D (II) Unifom cicula motion Tangential and adial components of Relative velocity and acceleation a Seway and Jewett 4.4 to 4.6 Pactice Poblems: Chapte 4, Objective Questions 5, 11 Chapte
( ) rad ( 2.0 s) = 168 rad
 .) α 0.450 ω o 0 and ω 8.00 ω αt + ω o o t ω ω o α HO 9 Solution 8.00 0 0.450 7.8 b.) ω ω o + αδθ o Δθ ω 8.00 0 ω o α 0.450 7. o Δθ 7. ev.3 ev π.) ω o.50, α 0.300, Δθ 3.50 ev π 7π ev ω ω o + αδθ o ω ω
.) α 0.450 ω o 0 and ω 8.00 ω αt + ω o o t ω ω o α HO 9 Solution 8.00 0 0.450 7.8 b.) ω ω o + αδθ o Δθ ω 8.00 0 ω o α 0.450 7. o Δθ 7. ev.3 ev π.) ω o.50, α 0.300, Δθ 3.50 ev π 7π ev ω ω o + αδθ o ω ω
Cartesian Coordinate System and Vectors
 Catesian Coodinate System and Vectos Coodinate System Coodinate system: used to descibe the position of a point in space and consists of 1. An oigin as the efeence point 2. A set of coodinate axes with
Catesian Coodinate System and Vectos Coodinate System Coodinate system: used to descibe the position of a point in space and consists of 1. An oigin as the efeence point 2. A set of coodinate axes with
How can you find the dimensions of a square or a circle when you are given its area? When you multiply a number by itself, you square the number.
 7. Finding Squae Root How can you find the dimenion of a quae o a cicle when you ae given it aea? When you multiply a numbe by itelf, you quae the numbe. Symbol fo quaing i the exponent. = = 6 quaed i
7. Finding Squae Root How can you find the dimenion of a quae o a cicle when you ae given it aea? When you multiply a numbe by itelf, you quae the numbe. Symbol fo quaing i the exponent. = = 6 quaed i
Sections and Chapter 10
 Cicula and Rotational Motion Sections 5.-5.5 and Chapte 10 Basic Definitions Unifom Cicula Motion Unifom cicula motion efes to the motion of a paticle in a cicula path at constant speed. The instantaneous
Cicula and Rotational Motion Sections 5.-5.5 and Chapte 10 Basic Definitions Unifom Cicula Motion Unifom cicula motion efes to the motion of a paticle in a cicula path at constant speed. The instantaneous
AE 423 Space Technology I Chapter 2 Satellite Dynamics
 AE 43 Space Technology I Chapte Satellite Dynamic.1 Intoduction In thi chapte we eview ome dynamic elevant to atellite dynamic and we etablih ome of the baic popetie of atellite dynamic.. Dynamic of a
AE 43 Space Technology I Chapte Satellite Dynamic.1 Intoduction In thi chapte we eview ome dynamic elevant to atellite dynamic and we etablih ome of the baic popetie of atellite dynamic.. Dynamic of a
1121 T Question 1
 1121 T1 2008 Question 1 ( aks) You ae cycling, on a long staight path, at a constant speed of 6.0.s 1. Anothe cyclist passes you, tavelling on the sae path in the sae diection as you, at a constant speed
1121 T1 2008 Question 1 ( aks) You ae cycling, on a long staight path, at a constant speed of 6.0.s 1. Anothe cyclist passes you, tavelling on the sae path in the sae diection as you, at a constant speed
6.4 Period and Frequency for Uniform Circular Motion
 6.4 Peiod and Fequency fo Unifom Cicula Motion If the object is constained to move in a cicle and the total tangential foce acting on the total object is zeo, F θ = 0, then (Newton s Second Law), the tangential
6.4 Peiod and Fequency fo Unifom Cicula Motion If the object is constained to move in a cicle and the total tangential foce acting on the total object is zeo, F θ = 0, then (Newton s Second Law), the tangential
Physics C Rotational Motion Name: ANSWER KEY_ AP Review Packet
 Linea and angula analogs Linea Rotation x position x displacement v velocity a T tangential acceleation Vectos in otational motion Use the ight hand ule to detemine diection of the vecto! Don t foget centipetal
Linea and angula analogs Linea Rotation x position x displacement v velocity a T tangential acceleation Vectos in otational motion Use the ight hand ule to detemine diection of the vecto! Don t foget centipetal
SPH3UW/SPH4U Unit 3.2 Forces in Cetripetal Motion Page 1 of 6. Notes Physics Tool Box
 SPH3UW/SPH4U Unit 3. Foce in Cetipetal Motion Page 1 o 6 Note Phyic Tool Box Net Foce: acting on an object in uniom cicula motion act towad the cente o the cicle. Magnitude o Net Foce: combine Newton Second
SPH3UW/SPH4U Unit 3. Foce in Cetipetal Motion Page 1 o 6 Note Phyic Tool Box Net Foce: acting on an object in uniom cicula motion act towad the cente o the cicle. Magnitude o Net Foce: combine Newton Second
Physics Fall Mechanics, Thermodynamics, Waves, Fluids. Lecture 18: System of Particles II. Slide 18-1
 Physics 1501 Fall 2008 Mechanics, Themodynamics, Waves, Fluids Lectue 18: System of Paticles II Slide 18-1 Recap: cente of mass The cente of mass of a composite object o system of paticles is the point
Physics 1501 Fall 2008 Mechanics, Themodynamics, Waves, Fluids Lectue 18: System of Paticles II Slide 18-1 Recap: cente of mass The cente of mass of a composite object o system of paticles is the point
7.2. Coulomb s Law. The Electric Force
 Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Theory. Single Soil Layer. ProShake User s Manual
 PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
PoShake Ue Manual Theoy PoShake ue a fequency domain appoach to olve the gound epone poblem. In imple tem, the input motion i epeented a the um of a eie of ine wave of diffeent amplitude, fequencie, and
Easy. r p 2 f : r p 2i. r p 1i. r p 1 f. m blood g kg. P8.2 (a) The momentum is p = mv, so v = p/m and the kinetic energy is
 Chapte 8 Homewok Solutions Easy P8. Assume the velocity of the blood is constant ove the 0.60 s. Then the patient s body and pallet will have a constant velocity of 6 0 5 m 3.75 0 4 m/ s 0.60 s in the
Chapte 8 Homewok Solutions Easy P8. Assume the velocity of the blood is constant ove the 0.60 s. Then the patient s body and pallet will have a constant velocity of 6 0 5 m 3.75 0 4 m/ s 0.60 s in the
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Phases of Matter. Since liquids and gases are able to flow, they are called fluids. Compressible? Able to Flow? shape?
 Fluids Chapte 3 Lectue Sequence. Pessue (Sections -3). Mechanical Popeties (Sections 5, and 7) 3. Gauge Pessue (Sections 4, and 6) 4. Moving Fluids (Sections 8-0) Pessue Phases of Matte Phase Retains its
Fluids Chapte 3 Lectue Sequence. Pessue (Sections -3). Mechanical Popeties (Sections 5, and 7) 3. Gauge Pessue (Sections 4, and 6) 4. Moving Fluids (Sections 8-0) Pessue Phases of Matte Phase Retains its
AP-C WEP. h. Students should be able to recognize and solve problems that call for application both of conservation of energy and Newton s Laws.
 AP-C WEP 1. Wok a. Calculate the wok done by a specified constant foce on an object that undegoes a specified displacement. b. Relate the wok done by a foce to the aea unde a gaph of foce as a function
AP-C WEP 1. Wok a. Calculate the wok done by a specified constant foce on an object that undegoes a specified displacement. b. Relate the wok done by a foce to the aea unde a gaph of foce as a function
PHYSICS 151 Notes for Online Lecture 2.6
 PHYSICS 151 Note fo Online Lectue.6 Toque: The whole eaon that we want to woy about cente of ma i that we ae limited to lookin at point mae unle we know how to deal with otation. Let eviit the metetick.
PHYSICS 151 Note fo Online Lectue.6 Toque: The whole eaon that we want to woy about cente of ma i that we ae limited to lookin at point mae unle we know how to deal with otation. Let eviit the metetick.
Chapter 5 Applications of Newton s Laws
 Chapte 5 Application of Newton Law Conceptual Poblem Detemine the Concept Becaue the object ae peeding up (acceleating), thee mut be a net foce acting on them. The foce acting on an object ae the nomal
Chapte 5 Application of Newton Law Conceptual Poblem Detemine the Concept Becaue the object ae peeding up (acceleating), thee mut be a net foce acting on them. The foce acting on an object ae the nomal
Determining the Best Linear Unbiased Predictor of PSU Means with the Data. included with the Random Variables. Ed Stanek
 Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Detemining te Bet Linea Unbiaed Pedicto of PSU ean wit te Data included wit te andom Vaiable Ed Stanek Intoduction We develop te equation fo te bet linea unbiaed pedicto of PSU mean in a two tage andom
Mon , (.12) Rotational + Translational RE 11.b Tues.
 Mon..-.3, (.) Rotational + Tanlational RE.b Tue. EP0 Mon..4-.6, (.3) Angula Momentum & Toque RE.c Tue. Wed..7 -.9, (.) Toque EP RE.d ab Fi. Rotation Coue Eval.0 Quantization, Quiz RE.e Mon. Review fo Final
Mon..-.3, (.) Rotational + Tanlational RE.b Tue. EP0 Mon..4-.6, (.3) Angula Momentum & Toque RE.c Tue. Wed..7 -.9, (.) Toque EP RE.d ab Fi. Rotation Coue Eval.0 Quantization, Quiz RE.e Mon. Review fo Final
Announcements. Description Linear Angular position x θ displacement x θ rate of change of position v x ω x = = θ average rate of change of position
 Announcement In the lectue link Look o tet 1 beakdown liting the topic o the quetion. Look o m umma o topic o the eam. We ll ue it on the eiew net Tueda. Look o a lit o baic phic act eleant o thi eam.
Announcement In the lectue link Look o tet 1 beakdown liting the topic o the quetion. Look o m umma o topic o the eam. We ll ue it on the eiew net Tueda. Look o a lit o baic phic act eleant o thi eam.
06 - ROTATIONAL MOTION Page 1 ( Answers at the end of all questions )
 06 - ROTATIONAL MOTION Page ) A body A of mass M while falling vetically downwads unde gavity beaks into two pats, a body B of mass ( / ) M and a body C of mass ( / ) M. The cente of mass of bodies B and
06 - ROTATIONAL MOTION Page ) A body A of mass M while falling vetically downwads unde gavity beaks into two pats, a body B of mass ( / ) M and a body C of mass ( / ) M. The cente of mass of bodies B and
Movie Review Part One due Tuesday (in class) please print
 Movie Review Pat One due Tuesday (in class) please pint Test in class on Fiday. You may stat at 8:30 if you want. (The topic of powe is not on test.) Chaptes 4-6 Main Ideas in Class Today Afte class, you
Movie Review Pat One due Tuesday (in class) please pint Test in class on Fiday. You may stat at 8:30 if you want. (The topic of powe is not on test.) Chaptes 4-6 Main Ideas in Class Today Afte class, you
Chapter 13 Gravitation
 Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
PS113 Chapter 5 Dynamics of Uniform Circular Motion
 PS113 Chapte 5 Dynamics of Unifom Cicula Motion 1 Unifom cicula motion Unifom cicula motion is the motion of an object taveling at a constant (unifom) speed on a cicula path. The peiod T is the time equied
PS113 Chapte 5 Dynamics of Unifom Cicula Motion 1 Unifom cicula motion Unifom cicula motion is the motion of an object taveling at a constant (unifom) speed on a cicula path. The peiod T is the time equied
Chapter 4: The laws of motion. Newton s first law
 Chapte 4: The laws of motion gavitational Electic magnetic Newton s fist law If the net foce exeted on an object is zeo, the object continues in its oiginal state of motion: - an object at est, emains
Chapte 4: The laws of motion gavitational Electic magnetic Newton s fist law If the net foce exeted on an object is zeo, the object continues in its oiginal state of motion: - an object at est, emains
The Laws of Motion ( ) N SOLUTIONS TO PROBLEMS ! F = ( 6.00) 2 + ( 15.0) 2 N = 16.2 N. Section 4.4. Newton s Second Law The Particle Under a Net Force
 SOLUTIONS TO PROBLEMS The Laws of Motion Section 4.3 Mass P4. Since the ca is moving with constant speed and in a staight line, the esultant foce on it must be zeo egadless of whethe it is moving (a) towad
SOLUTIONS TO PROBLEMS The Laws of Motion Section 4.3 Mass P4. Since the ca is moving with constant speed and in a staight line, the esultant foce on it must be zeo egadless of whethe it is moving (a) towad
Phys 201A. Homework 6 Solutions. F A and F r. B. According to Newton s second law, ( ) ( )2. j = ( 6.0 m / s 2 )ˆ i ( 10.4m / s 2 )ˆ j.
 7. We denote the two foces F A + F B = ma,sof B = ma F A. (a) In unit vecto notation F A = ( 20.0 N)ˆ i and Theefoe, Phys 201A Homewok 6 Solutions F A and F B. Accoding to Newton s second law, a = [ (
7. We denote the two foces F A + F B = ma,sof B = ma F A. (a) In unit vecto notation F A = ( 20.0 N)ˆ i and Theefoe, Phys 201A Homewok 6 Solutions F A and F B. Accoding to Newton s second law, a = [ (
21 MAGNETIC FORCES AND MAGNETIC FIELDS
 CHAPTER 1 MAGNETIC ORCES AND MAGNETIC IELDS ANSWERS TO OCUS ON CONCEPTS QUESTIONS 1. (d) Right-Hand Rule No. 1 gives the diection of the magnetic foce as x fo both dawings A and. In dawing C, the velocity
CHAPTER 1 MAGNETIC ORCES AND MAGNETIC IELDS ANSWERS TO OCUS ON CONCEPTS QUESTIONS 1. (d) Right-Hand Rule No. 1 gives the diection of the magnetic foce as x fo both dawings A and. In dawing C, the velocity
Physics 11 Chapter 4: Forces and Newton s Laws of Motion. Problem Solving
 Physics 11 Chapte 4: Foces and Newton s Laws of Motion Thee is nothing eithe good o bad, but thinking makes it so. William Shakespeae It s not what happens to you that detemines how fa you will go in life;
Physics 11 Chapte 4: Foces and Newton s Laws of Motion Thee is nothing eithe good o bad, but thinking makes it so. William Shakespeae It s not what happens to you that detemines how fa you will go in life;
OSCILLATIONS AND GRAVITATION
 1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
Electricity Revision ELECTRICITY REVISION KEY CONCEPTS TERMINOLOGY & DEFINITION. Physical Sciences X-Sheets
 Electicity Revision KEY CONCEPTS In this session we will focus on the following: Stating and apply Coulomb s Law. Defining electical field stength and applying the deived equations. Dawing electical field
Electicity Revision KEY CONCEPTS In this session we will focus on the following: Stating and apply Coulomb s Law. Defining electical field stength and applying the deived equations. Dawing electical field
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Describing Circular motion
 Unifom Cicula Motion Descibing Cicula motion In ode to undestand cicula motion, we fist need to discuss how to subtact vectos. The easiest way to explain subtacting vectos is to descibe it as adding a
Unifom Cicula Motion Descibing Cicula motion In ode to undestand cicula motion, we fist need to discuss how to subtact vectos. The easiest way to explain subtacting vectos is to descibe it as adding a
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department. Problem Set 10 Solutions. r s
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.033 Decembe 5, 003 Poblem Set 10 Solutions Poblem 1 M s y x test paticle The figue above depicts the geomety of the poblem. The position
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.033 Decembe 5, 003 Poblem Set 10 Solutions Poblem 1 M s y x test paticle The figue above depicts the geomety of the poblem. The position
Static Electric Fields. Coulomb s Law Ε = 4πε. Gauss s Law. Electric Potential. Electrical Properties of Materials. Dielectrics. Capacitance E.
 Coulomb Law Ε Gau Law Electic Potential E Electical Popetie of Mateial Conducto J σe ielectic Capacitance Rˆ V q 4πε R ρ v 2 Static Electic Field εe E.1 Intoduction Example: Electic field due to a chage
Coulomb Law Ε Gau Law Electic Potential E Electical Popetie of Mateial Conducto J σe ielectic Capacitance Rˆ V q 4πε R ρ v 2 Static Electic Field εe E.1 Intoduction Example: Electic field due to a chage
Question 1: The dipole
 Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
Septembe, 08 Conell Univesity, Depatment of Physics PHYS 337, Advance E&M, HW #, due: 9/5/08, :5 AM Question : The dipole Conside a system as discussed in class and shown in Fig.. in Heald & Maion.. Wite
KEPLER S LAWS OF PLANETARY MOTION
 EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
Physics 111 Lecture 5 Circular Motion
 Physics 111 Lectue 5 Cicula Motion D. Ali ÖVGÜN EMU Physics Depatment www.aovgun.com Multiple Objects q A block of mass m1 on a ough, hoizontal suface is connected to a ball of mass m by a lightweight
Physics 111 Lectue 5 Cicula Motion D. Ali ÖVGÜN EMU Physics Depatment www.aovgun.com Multiple Objects q A block of mass m1 on a ough, hoizontal suface is connected to a ball of mass m by a lightweight
Two-Body Problem with Varying Mass in Case. of Isotropic Mass Loss
 Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
Adv Theo Appl Mech Vol no 69-8 Two-Body Poblem with Vaying Ma in Cae of Iotopic Ma o W A Rahoma M K Ahmed and I A El-Tohamy Caio Univeity Faculty of Science Dept of Atonomy Caio 6 Egypt FA Abd El-Salam
to point uphill and to be equal to its maximum value, in which case f s, max = μsfn
 Chapte 6 16. (a) In this situation, we take f s to point uphill and to be equal to its maximum value, in which case f s, max = μsf applies, whee μ s = 0.5. pplying ewton s second law to the block of mass
Chapte 6 16. (a) In this situation, we take f s to point uphill and to be equal to its maximum value, in which case f s, max = μsf applies, whee μ s = 0.5. pplying ewton s second law to the block of mass
SAMPLE QUIZ 3 - PHYSICS For a right triangle: sin θ = a c, cos θ = b c, tan θ = a b,
 SAMPLE QUIZ 3 - PHYSICS 1301.1 his is a closed book, closed notes quiz. Calculatos ae pemitted. he ONLY fomulas that may be used ae those given below. Define all symbols and justify all mathematical expessions
SAMPLE QUIZ 3 - PHYSICS 1301.1 his is a closed book, closed notes quiz. Calculatos ae pemitted. he ONLY fomulas that may be used ae those given below. Define all symbols and justify all mathematical expessions
17.1 Electric Potential Energy. Equipotential Lines. PE = energy associated with an arrangement of objects that exert forces on each other
 Electic Potential Enegy, PE Units: Joules Electic Potential, Units: olts 17.1 Electic Potential Enegy Electic foce is a consevative foce and so we can assign an electic potential enegy (PE) to the system
Electic Potential Enegy, PE Units: Joules Electic Potential, Units: olts 17.1 Electic Potential Enegy Electic foce is a consevative foce and so we can assign an electic potential enegy (PE) to the system
Development of Model Reduction using Stability Equation and Cauer Continued Fraction Method
 Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Intenational Jounal of Electical and Compute Engineeing. ISSN 0974-90 Volume 5, Numbe (03), pp. -7 Intenational Reeach Publication Houe http://www.iphoue.com Development of Model Reduction uing Stability
Problem 1: Multiple Choice Questions
 Mathematics 102 Review Questions Poblem 1: Multiple Choice Questions 1: Conside the function y = f(x) = 3e 2x 5e 4x (a) The function has a local maximum at x = (1/2)ln(10/3) (b) The function has a local
Mathematics 102 Review Questions Poblem 1: Multiple Choice Questions 1: Conside the function y = f(x) = 3e 2x 5e 4x (a) The function has a local maximum at x = (1/2)ln(10/3) (b) The function has a local
AH Mechanics Checklist (Unit 2) AH Mechanics Checklist (Unit 2) Circular Motion
 AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
Universal Gravitation
 Add Ipotant Univeal Gavitation Pae: 7 Note/Cue Hee Unit: Dynaic (oce & Gavitation Univeal Gavitation Unit: Dynaic (oce & Gavitation NGSS Standad: HS-PS-4 MA Cuiculu aewok (00:.7 AP Phyic Leanin Objective:.B..,.B..,
Add Ipotant Univeal Gavitation Pae: 7 Note/Cue Hee Unit: Dynaic (oce & Gavitation Univeal Gavitation Unit: Dynaic (oce & Gavitation NGSS Standad: HS-PS-4 MA Cuiculu aewok (00:.7 AP Phyic Leanin Objective:.B..,.B..,
MATERIAL SPREADING AND COMPACTION IN POWDER-BASED SOLID FREEFORM FABRICATION METHODS: MATHEMATICAL MODELING
 MATERIAL SPREADING AND COMPACTION IN POWDER-BASED SOLID FREEFORM FABRICATION METHODS: MATHEMATICAL MODELING Yae Shanjani and Ehan Toyekani Depatment of Mechanical and Mechatonic Engineeing, Univeity of
MATERIAL SPREADING AND COMPACTION IN POWDER-BASED SOLID FREEFORM FABRICATION METHODS: MATHEMATICAL MODELING Yae Shanjani and Ehan Toyekani Depatment of Mechanical and Mechatonic Engineeing, Univeity of
Circular Motion & Torque Test Review. The period is the amount of time it takes for an object to travel around a circular path once.
 Honos Physics Fall, 2016 Cicula Motion & Toque Test Review Name: M. Leonad Instuctions: Complete the following woksheet. SHOW ALL OF YOUR WORK ON A SEPARATE SHEET OF PAPER. 1. Detemine whethe each statement
Honos Physics Fall, 2016 Cicula Motion & Toque Test Review Name: M. Leonad Instuctions: Complete the following woksheet. SHOW ALL OF YOUR WORK ON A SEPARATE SHEET OF PAPER. 1. Detemine whethe each statement
Translation and Rotation Kinematics
 Tanslation and Rotation Kinematics Oveview: Rotation and Tanslation of Rigid Body Thown Rigid Rod Tanslational Motion: the gavitational extenal foce acts on cente-of-mass F ext = dp sy s dt dv total cm
Tanslation and Rotation Kinematics Oveview: Rotation and Tanslation of Rigid Body Thown Rigid Rod Tanslational Motion: the gavitational extenal foce acts on cente-of-mass F ext = dp sy s dt dv total cm
