From Whittaker Functions. by Daniel Bump. to Quantum Groups. Supported in part by NSF grant
|
|
|
- Alicia Todd
- 5 years ago
- Views:
Transcription
1 From Whittaker Functions to Quantum Groups by Daniel ump Supported in part by NSF grant
2 etween Physics and Number Theory We will describe a new connection between existing topics in Mathematical Physics and Number Theory. In Physics, Solvable Lattice Models are an important example in Statistical Mechanics. The key to their secrets is the Yang-axter equation. In Number Theory Whittaker functions appear in the Fourier coefficients of automorphic forms. Particularly Metaplectic Whittaker functions are somewhat mysterious. The key to their properties are intertwining integrals which relate different principal series representations of covers of GL(r, Q p ). We will connect these topics, reviewing two papers: Metaplectic Ice (2012) by rubaker, ump, Friedberg, hinta, Gunnells Yang-axter equation for Metaplectic Ice (2016) by uciumas, rubaker, ump 2
3 Overview If H is a quantum group (quasitriangular Hopf algebra) and if U, V are modules, then there is an isomorphism U V V U making the modules into a braided category. This isomorphism is described by an R-matrix. particular quantum group is H = U q (gl ˆ(n)). For z it has an n-dimensional module V (z). If F is a nonarchimedean local field containing the group µ 2n of n-th roots of unity, there is a metaplectic n-fold cover of GL(r, F). It is a central extension: 0 µ 2n GL(r, F) GL(r, F) 0. The spherical representations are parametrized by a Langlands parameter z = (z 1,, z n ). There is a vector space W z of Whittaker functions and standard intertwining maps W z W w(z) (w W, the Weyl group). We will explain that W z V 1 ) V (z n ) and the intertwining maps are described by R-matrices. The supersymmetric quantum group U q (gl ˆ(n 1)) also plays a role. 3
4 Part I: Quantum Groups 4
5 Statistical Mechanics In Statistical Mechanics, each state s i of a system S with energy E i has probability proportional to e ke i. The exact probability is Z 1 e ke i where Z = e ke i (k=oltzmann s constant) s i S is the partition function. In this setting it is real valued, but: In 1952, Lee and Yang showed that sometimes the partition function may be extended to an analytic function of a complex parameter. Its zeros lie on the unit circle. This is like a Riemann hypothesis. We will represent p-adic Whittaker functions as complex analytic partition functions. The Langlands parameters are in. Solvable Lattice Models In some cases the partition function may be solved exactly. These examples are important for studying phase transitions. Unfortunately all known examples are two-dimensional. 5
6 Solvable Lattice Models In these examples, the state of a model is described by specifying the values of parameters associated with the vertices or edges of a planar graph. The Ising Model was solved by Onsager in The six-vertex model was solved by Lieb, Sutherland and axter in the 1960 s. The six-vertex model is a key example in the history of Quantum Groups. key principle underlying these examples is the Yang-axter equation. (This is not one equation but a class of equations.) The algebraic context for understanding Yang-axter equations is quantum groups. Once the theory of quantum groups is in place, many examples of Yang-axter equations present themselves. For us the important ones are associated with the quantum groups U q (gl(n)) and U q (gl(n 1)). 6
7 Two Dimensional Ice egin with a grid, usually (but not always) rectangular: Each exterior edge is assigned a fixed spin or. The inner edges are also assigned spins but these will vary. state of the system is an assignment of spins to the interior edges The allowed configuration of spins around a vertex has six allowed possibilities 7
8 Six Vertex Model state of the model is an assignment of spins to the inner edges. (The outer edges have preassigned spins. Every vertex is assigned a set of oltzmann weights. These depend on the spins of the four adjacent edges. For the six-vertex model there are only six nonzero oltzman weights: a 1 a 2 b 1 b 2 c 1 c 2 The oltzmann weight of the state is the product of the weights at the vertices. The partition function is the sum over the states of the system. 8
9 axter In the field-free case let S be oltzmann weights for some vertex with a = a 1 = a 2 and b = b 1 = b 2 and c = c 1 = c 2. Following Lieb and axter let S = a2 b 2 c 2. 2ab Given one row of ice with oltzmann weights S at each vertex: δ 1 δ 2 δ 2 δ 2 Here δ i, ε i are fixed. µ S S S S ν Toroidal domain: µ is considered an interior edge after gluing the left and ǫ 1 ǫ 2 ǫ 3 ǫ 4 right edges. So we sum over µ and the other interior edges. Let δ = (δ 1, δ 2, ) and ε = (ε 1, ε 2, ) be the states of the top and bottom rows. The partition function then is a row transfer matrix Θ S (δ, ε). The partition function with several rows is a product transfer matrices. Theorem 1. (axter) If S = T then Θ S and Θ T commute. (This is closely related to solvability of the model.) 9
10 The Yang-axter equation Theorem 2. (axter) Let S and T be vertices with field-free oltzmann weights. If S = T then there exists a third R with R = S = T such that the two systems have the same partition function for any spins δ 1, δ 2, δ 3, ε 1, ε 2, ε 3. ǫ 3 ǫ 3 ǫ 2 S δ 1 ǫ 2 T δ 1 R R ǫ 1 T δ 2 ǫ 1 S δ 2 δ 3 δ 3 Remember: R = a2 b 2 c 2. 2ab 10
11 ommutativity of Transfer Matrices This is used to prove the commutativity of the transfer matrices as follows. onsider the following system, whose partition function is the product of transfer matrices Θ S Θ T (φ, δ)= ε Θ S(φ, ε)θ T (ε, δ): φ 1 φ 2 φ 3 φ 4 µ S S S S 1 µ 1 µ T T T T 2 µ 2 δ 1 δ 2 δ 3 δ 4 Toroidal oundary onditions: µ 1, µ 2 are interior edges and so we sum over µ 1, µ 2. Insert R and another vertex R 1 that undoes its effect: 11
12 φ 1 φ 2 φ 3 φ 4 µ 1 R 1 R S S S S µ 1 µ 2 T T T T µ 2 δ 1 δ 2 δ 3 δ 4 Now use YE repeatedly: φ 1 φ 2 φ 3 φ 4 T T T T µ 1 R 1 µ 1 µ 2 S S S S µ2 δ 1 δ 2 δ 3 δ 4 R Due to toroidal now R, R 1 are adjacent again and they cancel. The transfer matrices have been shown to commute. 12
13 raided ategories monoidal category (Maclane) has associative operation. In symmetric monoidal category (Maclane) we assume: oherence: any two ways of going from one permutation of 1 2 to another give the same result. τ, Important generalization! 1 τ, τ, 1 Maclane assumed that τ, : and τ, : are inverses. ut... Joyal and Street proposed eliminating this assumption. This leads to the important notion of a braided monoidal category. 13
14 In a symmetric monoidal category τ, : and τ 1, : same. In a braided monoidal category they may be different. are the τ, τ, 1 Represent them as braids. The top row is The bottom row is oherence: ny two ways of going from 1 2 to itself gives the same identity provided the two ways are the same in the rtin braid group. These diagrams describe two morphisms. The morphisms are the same since the braids are the same. 14
15 Quantum Groups Hopf algebras are convenient substitutes essentially generalizations of the notion of a group. The category of modules or comodules of a Hopf algebra is a monoidal category. The group G has morphisms µ: G G G and : G G G, namely the multiplication and diagonal map. These become the multiplication and the comultiplication in the Hopf algebra. The modules over a group form a symmetric monoidal category. There are two types of Hopf algebras with an analogous property. In a cocommutative Hopf algebra, the modules form a symmetric monoidal category. In a commutative Hopf algebra, the comodules form a symmetric monoidal category. quantum group is a Hopf algebra whose modules (or comodules) form a braided monoidal category. The axioms needed for this define a quasitriangular Hopf algebra (Drinfeld). These are quantum group. 15
16 The R-matrix a a b b c c Field-free oltzmann weights From this point of view, the oltzmann weights at a field-free vertex R go into a matrix, an endomorphism of V 1 V 2, where V 1 and V 2 are two-dimensional vector spaces, each with a basis labeled v and v. ε 2 ε 1 ε 3 R ε 3 ε 4 ε 1 ε 2 ε 4 We interpret the vertex as a linear transformation R(v ε1 v ε2 ) = ε R 3 ε 4 ε1 ε 2 (v ε3 v ε4 ) If τ: V 1 V 2 V 2 V 1 is τ(x y)= y x Then τr: V 1 V 2 V 2 V 1 is a candidate for a morphism in a braided monoidal category 16
17 raid Picture Given R,S,T with R = S = T, rotate Yang-axter equation picture: U V W U V W R T S S T R W V U W V U So associating with R, S, T two dimensional vector spaces and interpreting τr: U V V U as a morphism in a suitable category, the Yang- axter equation means the category is braided. Tannakian Program: text Yang axter equation text raided category Quantum Group In the axter case, the relevant quantum group is U q (sl ˆ2). 17
18 Parametrized Yang-axter equations U V W U V W R T S S T R W V U W V U If we unravel the definitions, the Yang-axter equation means that R 12 S 13 T 23 = T 23 S 13 R 12 where R 12 is the endomorphism R I W acting on the first and third components of U V W and trivially on W, etc. parametrized YE gives an R-matrix R(γ) for every element γ of a group Γ such that R 12 (γ)r 13 (γδ)r 23 (δ) = R 23 (δ)r 13 (γδ)r 12 (γ). The axter YE discussed gives a parametrized equation with Γ =. 18
19 ffine quantum groups Where do parametrized Yang axter equations come from? Given a Lie group G with Lie algebra g we can try to build a deformation of the universal enveloping algebra U(g). This is U q (g), invented by Drinfeld and Jimbo after the example g = sl 2 was found by Kulish, Reshetikhin and Sklyanin. The quantum group U q (g) will have modules corresponding to the irreducible representations of G. The untwisted affine Lie algebra ĝ was constructed first by physicists, then appeared as a special case of the Kac-Moody Lie algebras. It is a central extension 0 c ĝ g [t, t 1 ] 0. Given a G-module V, U q (ĝ) will have one copy of V for every z. The corresponding Yang-axter equation will be a parametrized one. For the axter example, g = sl 2 and z corresponds to (a, b, c). The parameter q is chosen so = 1 2 (q q1 ). 19
20 Part II: Tokuyama s formula and the asselman-shalika formula 20
21 Whittaker models Let F be a nonarchimedean local field, G a reductive algebraic group like GL(r). Langlands associated another algebraic group Ĝ (the connected L- group) such that very roughly (some) representations of G(F) are related to the conjugacy classes of Ĝ(). Let T and Tˆ be maximal tori in G and Ĝ. If z Tˆ() there is a representation π z of G(F) called a spherical principal series. It is infinite-dimensional. If z and z are conjugate then there exists a Weyl group element such that w(z) = z. orrespondingly there is an intertwining operator w : π z π w(z) which is usually an isomorphism. The representation π z may (usually) be realized on a space W z of functions on the group called the Whittaker model. The representation π is infinitedimensional. ut let K be a (special) maximal compact subgroup. Then the space of K-fixed vectors is (usually) one-dimensional. orrespondingly there is a unique K-fixed vector in the Whittaker model. 21
22 The Weight Lattice Let G and Ĝ be a reductive group and its dual, with dual maximal tori T and Tˆ. Then there is a lattice Λ, the weight lattice which may be identified with either the group X (Tˆ) of characters of Tˆ, or the group T(F)/T(o) where o is the ring of integers in the local field F. There is a cone Λ in Λ consisting of dominant weights. If λ Λ let z z λ (z Tˆ) be λ regarded as a character of Tˆ. Let λ T(F) correspond. Example. If G = GL(r) then Ĝ = GL(r) also. T and Tˆ are the diagonal tori. The weight lattice Λ Z r and if λ (λ 1,,λ r ) then z = z 1 λ1 z λ λ = z 1 λ 1 z r r,, λ=, λr o a prime element. z r 22
23 The Weyl haracter Formula Let Ĝ() be a reductive Lie group. Irreducible characters χ λ are parametrized by dominant weights λ. The Weyl character formula is (1 z α )χ λ (z) = ( 1) l(w) z w(λρ)ρ ρ = 1 2 α Φ w W The asselman-shalika Formula α Φ α Let F be a nonarchimedean local field and o its ring of integers. Let Ĝ be the Langlands dual of the split reductive group G. Let T and Tˆ be dual maximal tori of G, Ĝ. The weight lattice Λ of Ĝ is in bijection with T(F)/ T(o). Let λ Λ be a dominant weight an t λ be a representative in T(F). The asselman-shalika formula shows that for the spherical Whittaker function W W(t λ ) = { ( ) α Φ (1 q1 z α )χ λ (z) if λ is dominant, 0 otherwise. Here q is the residue field size. The unimportant constant ( ) is a power of q. The expression is a deformation of the Weyl character formula. 23
24 The Weyl character formula The Weyl character formula can be thought of as a formula for α Φ (1 z α )χ λ (z). λ = dominant weight of some Lie group Ĝ Φ = positive roots χ λ = character of an irreducible representation with highest weight λ Tokuyama s deformation of the WF The Weyl character formula has a deformation (Tokuyama, 1988). This was stated for GL(r) but other artan types may be done similarly. It is a formula for: α Φ (1 vz α )χ λ (z). Tokuyama expressed this as a sum over strict Gelfand-Tsetlin patterns with shape λ ρ. 24
25 Tokuyama s Formula: rystal Version There are two ways of expressing Tokuyama s formula. α Φ (1 vz α )χ λ (z). s a sum over the Kashiwara crystal based λρ. s a partition function. We will not discuss the first way, except to mention that it was a milestone towards the discovery of the connection between Whittaker functions and quantum groups. rystal bases are combinatorial analogs of representations of Lie groups. In Kashiwara s development, they come from the theory of quantum groups. 25
26 Tokuyama s Formula: Six Vertex Model There is another way of writing Tokuyama s formula that was first found by Hamel and King. In this view, Tokuyama s formula represents Z(S) = α Φ (1 vz α )χ λ (z) as the partition function of a six-vertex model system Z(S). We may use the following oltzmann weights. We will label this vertex T(z i ) T(z i ) a 1 a 2 b 1 b 2 c 1 1 z i v z i (1 v)z i 1 Here if z 1,, z r are the eigenvalues of z GL(r, ), we take an ice model with r rows, and the above weights at each vertex in the r-th row. (The boundary conditions depend on λ.) These weights are free-fermionic meaning a 1 a 2 b 1 b 2 = c 1 c 2. c 2 26
27 The R-matrix The Yang-axter equation was introduced into this setting by rubaker, ump and Friedberg. Here is the R-matrix (also free-fermionic): R z1,z 2 z 2 vz 1 z 1 vz 2 v(z 1 z 2 ) z 1 z 2 (1 v)z 1 (1 v)z 2 Yang-axter equation: the following partition functions are equal. It can be used to prove Tokuyama s theorem. ǫ 3 T(z 1 ) T(z 2 ) ǫ 3 ǫ 2 δ 1 ǫ 2 δ 1 R z1,z 2 R z1,z 2 ǫ 1 δ 2 T(z 2 ) ǫ 1 T(z 1 ) δ 2 δ 3 δ 3 27
28 nother Yang-axter equation We can make a Yang-axter equation involving only the R z1,z 2. The following partition functions are equal. ε 3 ε 4 ε 3 ε 4 R z2,z 3 R z1,z 2 R z1,z 3 ε 2 ε 5 ε 2 ε 5 R z1,z 3 ε 1 R z1,z 2 R z2,z 3 ε 1 ε 6 ε 6 This is a parametrized YE with parameter group. So we expect the corresponding quantum group to be affine. It turns out to be U v (gl ˆ(1 1)). Here gl ˆ(1 1) is a Lie superalgebra. 28
29 Digression: the Free-Fermionic Quantum Group It was shown by Korepin and by rubaker-ump-friedberg that all free-fermionic oltzmann weights (a 1 a 2 b 1 b 2 = c 1 c 2 ) can be assembled into a parametrized YE with nonabelian parameter group GL(2) GL(1). Thus the weights R z1,z 2 and T(z 1 ), T(z 2 ) all fit into a single YE. This does not generalize to the metaplectic case that we consider next. The corresponding quantum group appears to be new. It has been studied by uciumas. 29
30 Part II: Metaplectic Ice 30
31 The Metaplectic Group If F contains the group µ 2n of n-th roots of unity, there is a metaplectic n- fold cover of GL(r, F). It is a central extension: 0 µ 2n GL(r, F) GL(r, F) 0. This fact may be generalized to general reductive groups. Whittaker models are no longer unique. Metaplectic Ice: the Question In 2012, rubaker, ump, hinta, Friedberg and Gunnells showed that Whittaker functions on GL(r, F) could be represented as partition functions of generalized six-vertex models. They were not able to find the R-matrix for reasons that are now finally understood. 31
32 The partition function a1 a 0 0 a1 a z i g(a) z i (1 v)z i 1 We decorate each horizontal edges spin with an integer modulo n. The spins must be decorated with 0. v = q 1 where q is the cardinality of the residue field. Here g(a) is a Gauss sum. g(a)g( a)=v if a 0 mod n, while g(0) = v. s before, λ is built into the boundary conditions. The partition function equals a metaplectic Whittaker function evaluated at λ. The decorated edges span (Z/2Z)-graded super vector space with n even-graded basis vectors and 1 odd-graded vector. 32
33 Metaplectic Ice: the nswer In very recent work of rubaker, uciumas and ump: a a a b a a 0 0 a a z 2 n vz 1 n 0 a b a b b g(a b)(z 1 n z 2 n ) (1 v)z 1 c z 2 nc a 0 a a 0 0 z 1 n vz 2 n 0 0 a 0 0 a 0 0 a a v(z n 1 z n 2 ) z n n 1 z 2 (1 v)z a 1 z na 2 (1 v)z na a 1 z 2 c a b. The representatives a and c are chosen between 0 and n. This R-matrix gives the Yang-axter equation for metaplectic ice. 33
34 Supersymmetric partition function The quantum group is U v (gl ˆ(n 1)) with v = q 1 procedure introduces Gauss sums into the R-matrix. The U v (gl ˆ(n m)) R-matrix was discovered by Perk and Schultz. It was not related to U v (gl ˆ(n m)) until later. It appears in the theory of superconductivity. Intertwining integrals The Whittaker model is no longer one-dimensional. Let W z be the finitedimensional space of spherical Whittaker functions. We recall that the standard intertwining integrals w : W z W w(z) for Weyl group elements w. Theorem 3. (rubaker, uciumas, ump) The quantum group U v (gl ˆ(n)) has one n-dimensional module V (z) for each z. We have an isomorphism W z V 1 ) V (z n ) that realizes the standard intertwining integrals as U v (gl ˆ(n))-module homomorphisms. Lie superalgebra is not involved in this statement. It is very plausible that an identical statement is true for general artan types. 34
Whittaker Functions. by Daniel Bump. and Quantum Groups. Supported in part by NSF grant
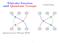 Whittaker Functions and Quantum Groups by Daniel Bump A B C A B C C B A C B A upported in part by NF grant 1001079 1 Whittaker Functions Let F =, C, Q p or F q. Let G=GL(n,F) or more generally a split
Whittaker Functions and Quantum Groups by Daniel Bump A B C A B C C B A C B A upported in part by NF grant 1001079 1 Whittaker Functions Let F =, C, Q p or F q. Let G=GL(n,F) or more generally a split
SPHERICAL UNITARY REPRESENTATIONS FOR REDUCTIVE GROUPS
 SPHERICAL UNITARY REPRESENTATIONS FOR REDUCTIVE GROUPS DAN CIUBOTARU 1. Classical motivation: spherical functions 1.1. Spherical harmonics. Let S n 1 R n be the (n 1)-dimensional sphere, C (S n 1 ) the
SPHERICAL UNITARY REPRESENTATIONS FOR REDUCTIVE GROUPS DAN CIUBOTARU 1. Classical motivation: spherical functions 1.1. Spherical harmonics. Let S n 1 R n be the (n 1)-dimensional sphere, C (S n 1 ) the
Copyrighted Material. Type A Weyl Group Multiple Dirichlet Series
 Chapter One Type A Weyl Group Multiple Dirichlet Series We begin by defining the basic shape of the class of Weyl group multiple Dirichlet series. To do so, we choose the following parameters. Φ, a reduced
Chapter One Type A Weyl Group Multiple Dirichlet Series We begin by defining the basic shape of the class of Weyl group multiple Dirichlet series. To do so, we choose the following parameters. Φ, a reduced
From Schur-Weyl duality to quantum symmetric pairs
 .. From Schur-Weyl duality to quantum symmetric pairs Chun-Ju Lai Max Planck Institute for Mathematics in Bonn cjlai@mpim-bonn.mpg.de Dec 8, 2016 Outline...1 Schur-Weyl duality.2.3.4.5 Background.. GL
.. From Schur-Weyl duality to quantum symmetric pairs Chun-Ju Lai Max Planck Institute for Mathematics in Bonn cjlai@mpim-bonn.mpg.de Dec 8, 2016 Outline...1 Schur-Weyl duality.2.3.4.5 Background.. GL
Weyl Group Multiple Dirichlet Series: Type A Combinatorial Theory
 Weyl Group Multiple Dirichlet Series: Type A Combinatorial Theory Ben Brubaker, Daniel Bump and Solomon Friedberg Department of Mathematics, MIT, Cambridge MA 02139-4307, USA Department of Mathematics,
Weyl Group Multiple Dirichlet Series: Type A Combinatorial Theory Ben Brubaker, Daniel Bump and Solomon Friedberg Department of Mathematics, MIT, Cambridge MA 02139-4307, USA Department of Mathematics,
Weyl group multiple Dirichlet series
 Weyl group multiple Dirichlet series Paul E. Gunnells UMass Amherst August 2010 Paul E. Gunnells (UMass Amherst) Weyl group multiple Dirichlet series August 2010 1 / 33 Basic problem Let Φ be an irreducible
Weyl group multiple Dirichlet series Paul E. Gunnells UMass Amherst August 2010 Paul E. Gunnells (UMass Amherst) Weyl group multiple Dirichlet series August 2010 1 / 33 Basic problem Let Φ be an irreducible
Schur Polynomials and The Yang-Baxter Equation
 Schur Polynomials and The Yang-Baxter Equation The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation As Published Publisher Brubaker,
Schur Polynomials and The Yang-Baxter Equation The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation As Published Publisher Brubaker,
Structure of Compact Quantum Groups A u (Q) and B u (Q) and their Isomorphism Classification
 Structure of Compact Quantum Groups A u (Q) and B u (Q) and their Isomorphism Classification Shuzhou Wang Department of Mathematics University of Georgia 1. The Notion of Quantum Groups G = Simple compact
Structure of Compact Quantum Groups A u (Q) and B u (Q) and their Isomorphism Classification Shuzhou Wang Department of Mathematics University of Georgia 1. The Notion of Quantum Groups G = Simple compact
Supercategories. Urs July 5, Odd flows and supercategories 4. 4 Braided monoidal supercategories 7
 Supercategories Urs July 5, 2007 ontents 1 Introduction 1 2 Flows on ategories 2 3 Odd flows and supercategories 4 4 Braided monoidal supercategories 7 1 Introduction Motivated by the desire to better
Supercategories Urs July 5, 2007 ontents 1 Introduction 1 2 Flows on ategories 2 3 Odd flows and supercategories 4 4 Braided monoidal supercategories 7 1 Introduction Motivated by the desire to better
HECKE MODULES FROM METAPLECTIC ICE
 HECKE MODULES FROM METAPLECTIC ICE BEN BRUBAKER, VALENTIN BUCIUMAS, DANIEL BUMP, AND SOLOMON FRIEDBERG Abstract. We present a new framework for a broad class of affine Hecke algebra modules, and show that
HECKE MODULES FROM METAPLECTIC ICE BEN BRUBAKER, VALENTIN BUCIUMAS, DANIEL BUMP, AND SOLOMON FRIEDBERG Abstract. We present a new framework for a broad class of affine Hecke algebra modules, and show that
Geometric Structure and the Local Langlands Conjecture
 Geometric Structure and the Local Langlands Conjecture Paul Baum Penn State Representations of Reductive Groups University of Utah, Salt Lake City July 9, 2013 Paul Baum (Penn State) Geometric Structure
Geometric Structure and the Local Langlands Conjecture Paul Baum Penn State Representations of Reductive Groups University of Utah, Salt Lake City July 9, 2013 Paul Baum (Penn State) Geometric Structure
The six vertex model is an example of a lattice model in statistical mechanics. The data are
 The six vertex model, R-matrices, and quantum groups Jethro van Ekeren. 1 The six vertex model The six vertex model is an example of a lattice model in statistical mechanics. The data are A finite rectangular
The six vertex model, R-matrices, and quantum groups Jethro van Ekeren. 1 The six vertex model The six vertex model is an example of a lattice model in statistical mechanics. The data are A finite rectangular
REPRESENTATIONS OF FINITE GROUPS OF LIE TYPE: EXERCISES. Notation. 1. GL n
 REPRESENTATIONS OF FINITE GROUPS OF LIE TYPE: EXERCISES ZHIWEI YUN Fix a prime number p and a power q of p. k = F q ; k d = F q d. ν n means ν is a partition of n. Notation Conjugacy classes 1. GL n 1.1.
REPRESENTATIONS OF FINITE GROUPS OF LIE TYPE: EXERCISES ZHIWEI YUN Fix a prime number p and a power q of p. k = F q ; k d = F q d. ν n means ν is a partition of n. Notation Conjugacy classes 1. GL n 1.1.
Coloured Kac-Moody algebras, Part I
 Coloured Kac-Moody algebras, Part I Alexandre Bouayad Abstract We introduce a parametrization of formal deformations of Verma modules of sl 2. A point in the moduli space is called a colouring. We prove
Coloured Kac-Moody algebras, Part I Alexandre Bouayad Abstract We introduce a parametrization of formal deformations of Verma modules of sl 2. A point in the moduli space is called a colouring. We prove
Weyl Group Representations and Unitarity of Spherical Representations.
 Weyl Group Representations and Unitarity of Spherical Representations. Alessandra Pantano, University of California, Irvine Windsor, October 23, 2008 β ν 1 = ν 2 S α S β ν S β ν S α ν S α S β S α S β ν
Weyl Group Representations and Unitarity of Spherical Representations. Alessandra Pantano, University of California, Irvine Windsor, October 23, 2008 β ν 1 = ν 2 S α S β ν S β ν S α ν S α S β S α S β ν
Goals of this document This document tries to explain a few algorithms from Lie theory that would be useful to implement. I tried to include explanati
 Representation Theory Issues For Sage Days 7 Goals of this document This document tries to explain a few algorithms from Lie theory that would be useful to implement. I tried to include explanations of
Representation Theory Issues For Sage Days 7 Goals of this document This document tries to explain a few algorithms from Lie theory that would be useful to implement. I tried to include explanations of
SAMPLE TEX FILE ZAJJ DAUGHERTY
 SAMPLE TEX FILE ZAJJ DAUGHERTY Contents. What is the partition algebra?.. Graphs and equivalence relations.. Diagrams and their compositions.. The partition algebra. Combinatorial representation theory:
SAMPLE TEX FILE ZAJJ DAUGHERTY Contents. What is the partition algebra?.. Graphs and equivalence relations.. Diagrams and their compositions.. The partition algebra. Combinatorial representation theory:
1. Group Theory Permutations.
 1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
LECTURE 20: KAC-MOODY ALGEBRA ACTIONS ON CATEGORIES, II
 LECTURE 20: KAC-MOODY ALGEBRA ACTIONS ON CATEGORIES, II IVAN LOSEV 1. Introduction 1.1. Recap. In the previous lecture we have considered the category C F := n 0 FS n -mod. We have equipped it with two
LECTURE 20: KAC-MOODY ALGEBRA ACTIONS ON CATEGORIES, II IVAN LOSEV 1. Introduction 1.1. Recap. In the previous lecture we have considered the category C F := n 0 FS n -mod. We have equipped it with two
SOLVABLE FUSION CATEGORIES AND A CATEGORICAL BURNSIDE S THEOREM
 SOLVABLE FUSION CATEGORIES AND A CATEGORICAL BURNSIDE S THEOREM PAVEL ETINGOF The goal of this talk is to explain the classical representation-theoretic proof of Burnside s theorem in finite group theory,
SOLVABLE FUSION CATEGORIES AND A CATEGORICAL BURNSIDE S THEOREM PAVEL ETINGOF The goal of this talk is to explain the classical representation-theoretic proof of Burnside s theorem in finite group theory,
Highest-weight Theory: Verma Modules
 Highest-weight Theory: Verma Modules Math G4344, Spring 2012 We will now turn to the problem of classifying and constructing all finitedimensional representations of a complex semi-simple Lie algebra (or,
Highest-weight Theory: Verma Modules Math G4344, Spring 2012 We will now turn to the problem of classifying and constructing all finitedimensional representations of a complex semi-simple Lie algebra (or,
Discrete Series and Characters of the Component Group
 Discrete Series and Characters of the Component Group Jeffrey Adams April 9, 2007 Suppose φ : W R L G is an L-homomorphism. There is a close relationship between the L-packet associated to φ and characters
Discrete Series and Characters of the Component Group Jeffrey Adams April 9, 2007 Suppose φ : W R L G is an L-homomorphism. There is a close relationship between the L-packet associated to φ and characters
R-matrices, affine quantum groups and applications
 R-matrices, affine quantum groups and applications From a mini-course given by David Hernandez at Erwin Schrödinger Institute in January 2017 Abstract R-matrices are solutions of the quantum Yang-Baxter
R-matrices, affine quantum groups and applications From a mini-course given by David Hernandez at Erwin Schrödinger Institute in January 2017 Abstract R-matrices are solutions of the quantum Yang-Baxter
On some conjectures on VOAs
 On some conjectures on VOAs Yuji Tachikawa February 1, 2013 In [1], a lot of mathematical conjectures on VOAs were made. Here, we ll provide a more mathematical translation, along the lines of [2]. I m
On some conjectures on VOAs Yuji Tachikawa February 1, 2013 In [1], a lot of mathematical conjectures on VOAs were made. Here, we ll provide a more mathematical translation, along the lines of [2]. I m
1 Fields and vector spaces
 1 Fields and vector spaces In this section we revise some algebraic preliminaries and establish notation. 1.1 Division rings and fields A division ring, or skew field, is a structure F with two binary
1 Fields and vector spaces In this section we revise some algebraic preliminaries and establish notation. 1.1 Division rings and fields A division ring, or skew field, is a structure F with two binary
Specialized Macdonald polynomials, quantum K-theory, and Kirillov-Reshetikhin crystals
 Specialized Macdonald polynomials, quantum K-theory, and Kirillov-Reshetikhin crystals Cristian Lenart Max-Planck-Institut für Mathematik, Bonn State University of New York at Albany Geometry Seminar,
Specialized Macdonald polynomials, quantum K-theory, and Kirillov-Reshetikhin crystals Cristian Lenart Max-Planck-Institut für Mathematik, Bonn State University of New York at Albany Geometry Seminar,
Lie Superalgebras and Sage
 1/19 Lie Superalgebras and Sage Daniel Bump July 26, 2018 With the connivance of Brubaker, Schilling and Scrimshaw. 2/19 Lie Methods in Sage Lie methods in WeylCharacter class: Compute characters of representations
1/19 Lie Superalgebras and Sage Daniel Bump July 26, 2018 With the connivance of Brubaker, Schilling and Scrimshaw. 2/19 Lie Methods in Sage Lie methods in WeylCharacter class: Compute characters of representations
Casimir elements for classical Lie algebras. and affine Kac Moody algebras
 Casimir elements for classical Lie algebras and affine Kac Moody algebras Alexander Molev University of Sydney Plan of lectures Plan of lectures Casimir elements for the classical Lie algebras from the
Casimir elements for classical Lie algebras and affine Kac Moody algebras Alexander Molev University of Sydney Plan of lectures Plan of lectures Casimir elements for the classical Lie algebras from the
H(G(Q p )//G(Z p )) = C c (SL n (Z p )\ SL n (Q p )/ SL n (Z p )).
 92 19. Perverse sheaves on the affine Grassmannian 19.1. Spherical Hecke algebra. The Hecke algebra H(G(Q p )//G(Z p )) resp. H(G(F q ((T ))//G(F q [[T ]])) etc. of locally constant compactly supported
92 19. Perverse sheaves on the affine Grassmannian 19.1. Spherical Hecke algebra. The Hecke algebra H(G(Q p )//G(Z p )) resp. H(G(F q ((T ))//G(F q [[T ]])) etc. of locally constant compactly supported
Generators of affine W-algebras
 1 Generators of affine W-algebras Alexander Molev University of Sydney 2 The W-algebras first appeared as certain symmetry algebras in conformal field theory. 2 The W-algebras first appeared as certain
1 Generators of affine W-algebras Alexander Molev University of Sydney 2 The W-algebras first appeared as certain symmetry algebras in conformal field theory. 2 The W-algebras first appeared as certain
Conference on Infinite Dimensional Lie Theory and its Applications (15-20 December, 2014) Title & Abstract
 Conference on Infinite Dimensional Lie Theory and its Applications (15-20 December, 2014) Title & Abstract S. No. Name Title Abstract 1 Yuly Billig Proof of Rao's conjecture on classification of simple
Conference on Infinite Dimensional Lie Theory and its Applications (15-20 December, 2014) Title & Abstract S. No. Name Title Abstract 1 Yuly Billig Proof of Rao's conjecture on classification of simple
Primitive Ideals and Unitarity
 Primitive Ideals and Unitarity Dan Barbasch June 2006 1 The Unitary Dual NOTATION. G is the rational points over F = R or a p-adic field, of a linear connected reductive group. A representation (π, H)
Primitive Ideals and Unitarity Dan Barbasch June 2006 1 The Unitary Dual NOTATION. G is the rational points over F = R or a p-adic field, of a linear connected reductive group. A representation (π, H)
On the geometric Langlands duality
 On the geometric Langlands duality Peter Fiebig Emmy Noether Zentrum Universität Erlangen Nürnberg Schwerpunkttagung Bad Honnef April 2010 Outline This lecture will give an overview on the following topics:
On the geometric Langlands duality Peter Fiebig Emmy Noether Zentrum Universität Erlangen Nürnberg Schwerpunkttagung Bad Honnef April 2010 Outline This lecture will give an overview on the following topics:
BRST and Dirac Cohomology
 BRST and Dirac Cohomology Peter Woit Columbia University Dartmouth Math Dept., October 23, 2008 Peter Woit (Columbia University) BRST and Dirac Cohomology October 2008 1 / 23 Outline 1 Introduction 2 Representation
BRST and Dirac Cohomology Peter Woit Columbia University Dartmouth Math Dept., October 23, 2008 Peter Woit (Columbia University) BRST and Dirac Cohomology October 2008 1 / 23 Outline 1 Introduction 2 Representation
Local Langlands correspondence and examples of ABPS conjecture
 Local Langlands correspondence and examples of ABPS conjecture Ahmed Moussaoui UPMC Paris VI - IMJ 23/08/203 Notation F non-archimedean local field : finite extension of Q p or F p ((t)) O F = {x F, v(x)
Local Langlands correspondence and examples of ABPS conjecture Ahmed Moussaoui UPMC Paris VI - IMJ 23/08/203 Notation F non-archimedean local field : finite extension of Q p or F p ((t)) O F = {x F, v(x)
FAMILIES OF IRREDUCIBLE REPRESENTATIONS OF S 2 S 3
 FAMILIES OF IRREDUCIBLE REPRESENTATIONS OF S S 3 JAY TAYLOR We would like to consider the representation theory of the Weyl group of type B 3, which is isomorphic to the wreath product S S 3 = (S S S )
FAMILIES OF IRREDUCIBLE REPRESENTATIONS OF S S 3 JAY TAYLOR We would like to consider the representation theory of the Weyl group of type B 3, which is isomorphic to the wreath product S S 3 = (S S S )
Hecke Operators for Arithmetic Groups via Cell Complexes. Mark McConnell. Center for Communications Research, Princeton
 Hecke Operators for Arithmetic Groups via Cell Complexes 1 Hecke Operators for Arithmetic Groups via Cell Complexes Mark McConnell Center for Communications Research, Princeton Hecke Operators for Arithmetic
Hecke Operators for Arithmetic Groups via Cell Complexes 1 Hecke Operators for Arithmetic Groups via Cell Complexes Mark McConnell Center for Communications Research, Princeton Hecke Operators for Arithmetic
EXERCISES IN MODULAR FORMS I (MATH 726) (2) Prove that a lattice L is integral if and only if its Gram matrix has integer coefficients.
 EXERCISES IN MODULAR FORMS I (MATH 726) EYAL GOREN, MCGILL UNIVERSITY, FALL 2007 (1) We define a (full) lattice L in R n to be a discrete subgroup of R n that contains a basis for R n. Prove that L is
EXERCISES IN MODULAR FORMS I (MATH 726) EYAL GOREN, MCGILL UNIVERSITY, FALL 2007 (1) We define a (full) lattice L in R n to be a discrete subgroup of R n that contains a basis for R n. Prove that L is
Classification of root systems
 Classification of root systems September 8, 2017 1 Introduction These notes are an approximate outline of some of the material to be covered on Thursday, April 9; Tuesday, April 14; and Thursday, April
Classification of root systems September 8, 2017 1 Introduction These notes are an approximate outline of some of the material to be covered on Thursday, April 9; Tuesday, April 14; and Thursday, April
Finite Subgroups of Gl 2 (C) and Universal Deformation Rings
 Finite Subgroups of Gl 2 (C) and Universal Deformation Rings University of Missouri Conference on Geometric Methods in Representation Theory November 21, 2016 Goal Goal : Find connections between fusion
Finite Subgroups of Gl 2 (C) and Universal Deformation Rings University of Missouri Conference on Geometric Methods in Representation Theory November 21, 2016 Goal Goal : Find connections between fusion
Borcherds proof of the moonshine conjecture
 Borcherds proof of the moonshine conjecture pjc, after V. Nikulin Abstract These CSG notes contain a condensed account of a talk by V. Nikulin in the London algebra Colloquium on 24 May 2001. None of the
Borcherds proof of the moonshine conjecture pjc, after V. Nikulin Abstract These CSG notes contain a condensed account of a talk by V. Nikulin in the London algebra Colloquium on 24 May 2001. None of the
DESCRIPTION OF SIMPLE MODULES FOR SCHUR SUPERALGEBRA S(2j2)
 DESCRIPTION OF SIMPLE MODULES FOR SCHUR SUPERALGEBRA S(22) A.N. GRISHKOV AND F. MARKO Abstract. The goal of this paper is to describe explicitly simple modules for Schur superalgebra S(22) over an algebraically
DESCRIPTION OF SIMPLE MODULES FOR SCHUR SUPERALGEBRA S(22) A.N. GRISHKOV AND F. MARKO Abstract. The goal of this paper is to describe explicitly simple modules for Schur superalgebra S(22) over an algebraically
Representations Are Everywhere
 Representations Are Everywhere Nanghua Xi Member of Chinese Academy of Sciences 1 What is Representation theory Representation is reappearance of some properties or structures of one object on another.
Representations Are Everywhere Nanghua Xi Member of Chinese Academy of Sciences 1 What is Representation theory Representation is reappearance of some properties or structures of one object on another.
REPRESENTATION THEORY OF S n
 REPRESENTATION THEORY OF S n EVAN JENKINS Abstract. These are notes from three lectures given in MATH 26700, Introduction to Representation Theory of Finite Groups, at the University of Chicago in November
REPRESENTATION THEORY OF S n EVAN JENKINS Abstract. These are notes from three lectures given in MATH 26700, Introduction to Representation Theory of Finite Groups, at the University of Chicago in November
On the Langlands Program
 On the Langlands Program John Rognes Colloquium talk, May 4th 2018 The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2018 to Robert P. Langlands of the Institute for
On the Langlands Program John Rognes Colloquium talk, May 4th 2018 The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2018 to Robert P. Langlands of the Institute for
Representation Theory
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 Paper 1, Section II 19I 93 (a) Define the derived subgroup, G, of a finite group G. Show that if χ is a linear character
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 Paper 1, Section II 19I 93 (a) Define the derived subgroup, G, of a finite group G. Show that if χ is a linear character
Reducibility of generic unipotent standard modules
 Journal of Lie Theory Volume?? (??)???? c?? Heldermann Verlag 1 Version of March 10, 011 Reducibility of generic unipotent standard modules Dan Barbasch and Dan Ciubotaru Abstract. Using Lusztig s geometric
Journal of Lie Theory Volume?? (??)???? c?? Heldermann Verlag 1 Version of March 10, 011 Reducibility of generic unipotent standard modules Dan Barbasch and Dan Ciubotaru Abstract. Using Lusztig s geometric
EKT of Some Wonderful Compactifications
 EKT of Some Wonderful Compactifications and recent results on Complete Quadrics. (Based on joint works with Soumya Banerjee and Michael Joyce) Mahir Bilen Can April 16, 2016 Mahir Bilen Can EKT of Some
EKT of Some Wonderful Compactifications and recent results on Complete Quadrics. (Based on joint works with Soumya Banerjee and Michael Joyce) Mahir Bilen Can April 16, 2016 Mahir Bilen Can EKT of Some
The Outer Automorphism of S 6
 Meena Jagadeesan 1 Karthik Karnik 2 Mentor: Akhil Mathew 1 Phillips Exeter Academy 2 Massachusetts Academy of Math and Science PRIMES Conference, May 2016 What is a Group? A group G is a set of elements
Meena Jagadeesan 1 Karthik Karnik 2 Mentor: Akhil Mathew 1 Phillips Exeter Academy 2 Massachusetts Academy of Math and Science PRIMES Conference, May 2016 What is a Group? A group G is a set of elements
ON THE CLASSIFICATION OF RANK 1 GROUPS OVER NON ARCHIMEDEAN LOCAL FIELDS
 ON THE CLASSIFICATION OF RANK 1 GROUPS OVER NON ARCHIMEDEAN LOCAL FIELDS LISA CARBONE Abstract. We outline the classification of K rank 1 groups over non archimedean local fields K up to strict isogeny,
ON THE CLASSIFICATION OF RANK 1 GROUPS OVER NON ARCHIMEDEAN LOCAL FIELDS LISA CARBONE Abstract. We outline the classification of K rank 1 groups over non archimedean local fields K up to strict isogeny,
A NOTE ON TENSOR CATEGORIES OF LIE TYPE E 9
 A NOTE ON TENSOR CATEGORIES OF LIE TYPE E 9 ERIC C. ROWELL Abstract. We consider the problem of decomposing tensor powers of the fundamental level 1 highest weight representation V of the affine Kac-Moody
A NOTE ON TENSOR CATEGORIES OF LIE TYPE E 9 ERIC C. ROWELL Abstract. We consider the problem of decomposing tensor powers of the fundamental level 1 highest weight representation V of the affine Kac-Moody
Subquotients of Minimal Principal Series
 Subquotients of Minimal Principal Series ν 1 = ν 2 Sp(4) 0 1 2 ν 2 = 0 Alessandra Pantano, UCI July 2008 1 PART 1 Introduction Preliminary Definitions and Notation 2 Langlands Quotients of Minimal Principal
Subquotients of Minimal Principal Series ν 1 = ν 2 Sp(4) 0 1 2 ν 2 = 0 Alessandra Pantano, UCI July 2008 1 PART 1 Introduction Preliminary Definitions and Notation 2 Langlands Quotients of Minimal Principal
L(C G (x) 0 ) c g (x). Proof. Recall C G (x) = {g G xgx 1 = g} and c g (x) = {X g Ad xx = X}. In general, it is obvious that
 ALGEBRAIC GROUPS 61 5. Root systems and semisimple Lie algebras 5.1. Characteristic 0 theory. Assume in this subsection that chark = 0. Let me recall a couple of definitions made earlier: G is called reductive
ALGEBRAIC GROUPS 61 5. Root systems and semisimple Lie algebras 5.1. Characteristic 0 theory. Assume in this subsection that chark = 0. Let me recall a couple of definitions made earlier: G is called reductive
arxiv: v1 [math.rt] 9 Sep 2010
![arxiv: v1 [math.rt] 9 Sep 2010 arxiv: v1 [math.rt] 9 Sep 2010](/thumbs/83/87621877.jpg) METAPLECTIC ICE BEN BRUBAKER, DANIEL BUMP, GAUTAM CHINTA, SOLOMON FRIEDBERG, AND PAUL E. GUNNELLS arxiv:009.74v [math.rt] 9 Sep 00 Abstract. We study spherical Whittaker functions on a metaplectic cover
METAPLECTIC ICE BEN BRUBAKER, DANIEL BUMP, GAUTAM CHINTA, SOLOMON FRIEDBERG, AND PAUL E. GUNNELLS arxiv:009.74v [math.rt] 9 Sep 00 Abstract. We study spherical Whittaker functions on a metaplectic cover
Nonsolvable Groups with No Prime Dividing Three Character Degrees
 Nonsolvable Groups with No Prime Dividing Three Character Degrees Mark L. Lewis and Donald L. White Department of Mathematical Sciences, Kent State University Kent, Ohio 44242 E-mail: lewis@math.kent.edu,
Nonsolvable Groups with No Prime Dividing Three Character Degrees Mark L. Lewis and Donald L. White Department of Mathematical Sciences, Kent State University Kent, Ohio 44242 E-mail: lewis@math.kent.edu,
CRYSTAL GRAPHS FOR BASIC REPRESENTATIONS OF QUANTUM AFFINE ALGEBRAS
 Trends in Mathematics Information Center for Mathematical Sciences Volume 4, Number, June, Pages 8 CRYSTAL GRAPHS FOR BASIC REPRESENTATIONS OF QUANTUM AFFINE ALGEBRAS SEOK-JIN KANG Abstract. We give a
Trends in Mathematics Information Center for Mathematical Sciences Volume 4, Number, June, Pages 8 CRYSTAL GRAPHS FOR BASIC REPRESENTATIONS OF QUANTUM AFFINE ALGEBRAS SEOK-JIN KANG Abstract. We give a
Background on Chevalley Groups Constructed from a Root System
 Background on Chevalley Groups Constructed from a Root System Paul Tokorcheck Department of Mathematics University of California, Santa Cruz 10 October 2011 Abstract In 1955, Claude Chevalley described
Background on Chevalley Groups Constructed from a Root System Paul Tokorcheck Department of Mathematics University of California, Santa Cruz 10 October 2011 Abstract In 1955, Claude Chevalley described
Combinatorial bases for representations. of the Lie superalgebra gl m n
 Combinatorial bases for representations of the Lie superalgebra gl m n Alexander Molev University of Sydney Gelfand Tsetlin bases for gln Gelfand Tsetlin bases for gl n Finite-dimensional irreducible representations
Combinatorial bases for representations of the Lie superalgebra gl m n Alexander Molev University of Sydney Gelfand Tsetlin bases for gln Gelfand Tsetlin bases for gl n Finite-dimensional irreducible representations
Operads. Spencer Liang. March 10, 2015
 Operads Spencer Liang March 10, 2015 1 Introduction The notion of an operad was created in order to have a well-defined mathematical object which encodes the idea of an abstract family of composable n-ary
Operads Spencer Liang March 10, 2015 1 Introduction The notion of an operad was created in order to have a well-defined mathematical object which encodes the idea of an abstract family of composable n-ary
`-modular Representations of Finite Reductive Groups
 `-modular Representations of Finite Reductive Groups Bhama Srinivasan University of Illinois at Chicago AIM, June 2007 Bhama Srinivasan (University of Illinois at Chicago) Modular Representations AIM,
`-modular Representations of Finite Reductive Groups Bhama Srinivasan University of Illinois at Chicago AIM, June 2007 Bhama Srinivasan (University of Illinois at Chicago) Modular Representations AIM,
A PROOF OF BURNSIDE S p a q b THEOREM
 A PROOF OF BURNSIDE S p a q b THEOREM OBOB Abstract. We prove that if p and q are prime, then any group of order p a q b is solvable. Throughout this note, denote by A the set of algebraic numbers. We
A PROOF OF BURNSIDE S p a q b THEOREM OBOB Abstract. We prove that if p and q are prime, then any group of order p a q b is solvable. Throughout this note, denote by A the set of algebraic numbers. We
1 Categorical Background
 1 Categorical Background 1.1 Categories and Functors Definition 1.1.1 A category C is given by a class of objects, often denoted by ob C, and for any two objects A, B of C a proper set of morphisms C(A,
1 Categorical Background 1.1 Categories and Functors Definition 1.1.1 A category C is given by a class of objects, often denoted by ob C, and for any two objects A, B of C a proper set of morphisms C(A,
(E.-W. Zink, with A. Silberger)
 1 Langlands classification for L-parameters A talk dedicated to Sergei Vladimirovich Vostokov on the occasion of his 70th birthday St.Petersburg im Mai 2015 (E.-W. Zink, with A. Silberger) In the representation
1 Langlands classification for L-parameters A talk dedicated to Sergei Vladimirovich Vostokov on the occasion of his 70th birthday St.Petersburg im Mai 2015 (E.-W. Zink, with A. Silberger) In the representation
The Casselman-Shalika Formula for a Distinguished Model
 The Casselman-Shalika ormula for a Distinguished Model by William D. Banks Abstract. Unramified Whittaker functions and their analogues occur naturally in number theory as terms in the ourier expansions
The Casselman-Shalika ormula for a Distinguished Model by William D. Banks Abstract. Unramified Whittaker functions and their analogues occur naturally in number theory as terms in the ourier expansions
COLOR LIE RINGS AND PBW DEFORMATIONS OF SKEW GROUP ALGEBRAS
 COLOR LIE RINGS AND PBW DEFORMATIONS OF SKEW GROUP ALGEBRAS S. FRYER, T. KANSTRUP, E. KIRKMAN, A.V. SHEPLER, AND S. WITHERSPOON Abstract. We investigate color Lie rings over finite group algebras and their
COLOR LIE RINGS AND PBW DEFORMATIONS OF SKEW GROUP ALGEBRAS S. FRYER, T. KANSTRUP, E. KIRKMAN, A.V. SHEPLER, AND S. WITHERSPOON Abstract. We investigate color Lie rings over finite group algebras and their
Dualities in Mathematics: Locally compact abelian groups
 Dualities in Mathematics: Locally compact abelian groups Part III: Pontryagin Duality Prakash Panangaden 1 1 School of Computer Science McGill University Spring School, Oxford 20-22 May 2014 Recall Gelfand
Dualities in Mathematics: Locally compact abelian groups Part III: Pontryagin Duality Prakash Panangaden 1 1 School of Computer Science McGill University Spring School, Oxford 20-22 May 2014 Recall Gelfand
Topics in Representation Theory: Roots and Weights
 Topics in Representation Theory: Roots and Weights 1 The Representation Ring Last time we defined the maximal torus T and Weyl group W (G, T ) for a compact, connected Lie group G and explained that our
Topics in Representation Theory: Roots and Weights 1 The Representation Ring Last time we defined the maximal torus T and Weyl group W (G, T ) for a compact, connected Lie group G and explained that our
A global version of the quantum duality principle
 A global version of the quantum duality principle Fabio Gavarini Università degli Studi di Roma Tor Vergata Dipartimento di Matematica Via della Ricerca Scientifica 1, I-00133 Roma ITALY Received 22 August
A global version of the quantum duality principle Fabio Gavarini Università degli Studi di Roma Tor Vergata Dipartimento di Matematica Via della Ricerca Scientifica 1, I-00133 Roma ITALY Received 22 August
Quantizations and classical non-commutative non-associative algebras
 Journal of Generalized Lie Theory and Applications Vol. (008), No., 35 44 Quantizations and classical non-commutative non-associative algebras Hilja Lisa HURU and Valentin LYCHAGIN Department of Mathematics,
Journal of Generalized Lie Theory and Applications Vol. (008), No., 35 44 Quantizations and classical non-commutative non-associative algebras Hilja Lisa HURU and Valentin LYCHAGIN Department of Mathematics,
Endoscopic character relations for the metaplectic group
 Endoscopic character relations for the metaplectic group Wen-Wei Li wwli@math.ac.cn Morningside Center of Mathematics January 17, 2012 EANTC The local case: recollections F : local field, char(f ) 2. ψ
Endoscopic character relations for the metaplectic group Wen-Wei Li wwli@math.ac.cn Morningside Center of Mathematics January 17, 2012 EANTC The local case: recollections F : local field, char(f ) 2. ψ
Raynaud on F -vector schemes and prolongation
 Raynaud on F -vector schemes and prolongation Melanie Matchett Wood November 7, 2010 1 Introduction and Motivation Given a finite, flat commutative group scheme G killed by p over R of mixed characteristic
Raynaud on F -vector schemes and prolongation Melanie Matchett Wood November 7, 2010 1 Introduction and Motivation Given a finite, flat commutative group scheme G killed by p over R of mixed characteristic
Decomposition Matrix of GL(n,q) and the Heisenberg algebra
 Decomposition Matrix of GL(n,q) and the Heisenberg algebra Bhama Srinivasan University of Illinois at Chicago mca-13, August 2013 Bhama Srinivasan (University of Illinois at Chicago) Heisenberg algebra
Decomposition Matrix of GL(n,q) and the Heisenberg algebra Bhama Srinivasan University of Illinois at Chicago mca-13, August 2013 Bhama Srinivasan (University of Illinois at Chicago) Heisenberg algebra
What is the Langlands program all about?
 What is the Langlands program all about? Laurent Lafforgue November 13, 2013 Hua Loo-Keng Distinguished Lecture Academy of Mathematics and Systems Science, Chinese Academy of Sciences This talk is mainly
What is the Langlands program all about? Laurent Lafforgue November 13, 2013 Hua Loo-Keng Distinguished Lecture Academy of Mathematics and Systems Science, Chinese Academy of Sciences This talk is mainly
Introduction to Arithmetic Geometry Fall 2013 Lecture #7 09/26/2013
 18.782 Introduction to Arithmetic Geometry Fall 2013 Lecture #7 09/26/2013 In Lecture 6 we proved (most of) Ostrowski s theorem for number fields, and we saw the product formula for absolute values on
18.782 Introduction to Arithmetic Geometry Fall 2013 Lecture #7 09/26/2013 In Lecture 6 we proved (most of) Ostrowski s theorem for number fields, and we saw the product formula for absolute values on
Lectures on Quantum Groups
 Lectures in Mathematical Physics Lectures on Quantum Groups Pavel Etingof and Olivier Schiffinann Second Edition International Press * s. c *''.. \ir.ik,!.'..... Contents Introduction ix 1 Poisson algebras
Lectures in Mathematical Physics Lectures on Quantum Groups Pavel Etingof and Olivier Schiffinann Second Edition International Press * s. c *''.. \ir.ik,!.'..... Contents Introduction ix 1 Poisson algebras
Representations and Linear Actions
 Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Topics in Representation Theory: SU(n), Weyl Chambers and the Diagram of a Group
 Topics in Representation Theory: SU(n), Weyl hambers and the Diagram of a Group 1 Another Example: G = SU(n) Last time we began analyzing how the maximal torus T of G acts on the adjoint representation,
Topics in Representation Theory: SU(n), Weyl hambers and the Diagram of a Group 1 Another Example: G = SU(n) Last time we began analyzing how the maximal torus T of G acts on the adjoint representation,
Notes on nilpotent orbits Computational Theory of Real Reductive Groups Workshop. Eric Sommers
 Notes on nilpotent orbits Computational Theory of Real Reductive Groups Workshop Eric Sommers 17 July 2009 2 Contents 1 Background 5 1.1 Linear algebra......................................... 5 1.1.1
Notes on nilpotent orbits Computational Theory of Real Reductive Groups Workshop Eric Sommers 17 July 2009 2 Contents 1 Background 5 1.1 Linear algebra......................................... 5 1.1.1
Thus we get. ρj. Nρj i = δ D(i),j.
 1.51. The distinguished invertible object. Let C be a finite tensor category with classes of simple objects labeled by a set I. Since duals to projective objects are projective, we can define a map D :
1.51. The distinguished invertible object. Let C be a finite tensor category with classes of simple objects labeled by a set I. Since duals to projective objects are projective, we can define a map D :
Three Descriptions of the Cohomology of Bun G (X) (Lecture 4)
 Three Descriptions of the Cohomology of Bun G (X) (Lecture 4) February 5, 2014 Let k be an algebraically closed field, let X be a algebraic curve over k (always assumed to be smooth and complete), and
Three Descriptions of the Cohomology of Bun G (X) (Lecture 4) February 5, 2014 Let k be an algebraically closed field, let X be a algebraic curve over k (always assumed to be smooth and complete), and
ENTRY GROUP THEORY. [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld.
![ENTRY GROUP THEORY. [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld. ENTRY GROUP THEORY. [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld.](/thumbs/90/104374286.jpg) ENTRY GROUP THEORY [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld Group theory [Group theory] is studies algebraic objects called groups.
ENTRY GROUP THEORY [ENTRY GROUP THEORY] Authors: started Mark Lezama: October 2003 Literature: Algebra by Michael Artin, Mathworld Group theory [Group theory] is studies algebraic objects called groups.
The Grothendieck-Katz Conjecture for certain locally symmetric varieties
 The Grothendieck-Katz Conjecture for certain locally symmetric varieties Benson Farb and Mark Kisin August 20, 2008 Abstract Using Margulis results on lattices in semi-simple Lie groups, we prove the Grothendieck-
The Grothendieck-Katz Conjecture for certain locally symmetric varieties Benson Farb and Mark Kisin August 20, 2008 Abstract Using Margulis results on lattices in semi-simple Lie groups, we prove the Grothendieck-
1. Let r, s, t, v be the homogeneous relations defined on the set M = {2, 3, 4, 5, 6} by
 Seminar 1 1. Which ones of the usual symbols of addition, subtraction, multiplication and division define an operation (composition law) on the numerical sets N, Z, Q, R, C? 2. Let A = {a 1, a 2, a 3 }.
Seminar 1 1. Which ones of the usual symbols of addition, subtraction, multiplication and division define an operation (composition law) on the numerical sets N, Z, Q, R, C? 2. Let A = {a 1, a 2, a 3 }.
Quantum Groups. Jesse Frohlich. September 18, 2018
 Quantum Groups Jesse Frohlich September 18, 2018 bstract Quantum groups have a rich theory. Categorically they are wellbehaved under the reversal of arrows, and algebraically they form an interesting generalization
Quantum Groups Jesse Frohlich September 18, 2018 bstract Quantum groups have a rich theory. Categorically they are wellbehaved under the reversal of arrows, and algebraically they form an interesting generalization
Representation theory and combinatorics of diagram algebras.
 Representation theory and combinatorics of diagram algebras. Zajj Daugherty May 15, 2016 Combinatorial representation theory Combinatorial representation theory Representation theory: Given an algebra
Representation theory and combinatorics of diagram algebras. Zajj Daugherty May 15, 2016 Combinatorial representation theory Combinatorial representation theory Representation theory: Given an algebra
The Contragredient. Spherical Unitary Dual for Complex Classical Groups
 The Contragredient Joint with D. Vogan Spherical Unitary Dual for Complex Classical Groups Joint with D. Barbasch The Contragredient Problem: Compute the involution φ φ of the space of L-homomorphisms
The Contragredient Joint with D. Vogan Spherical Unitary Dual for Complex Classical Groups Joint with D. Barbasch The Contragredient Problem: Compute the involution φ φ of the space of L-homomorphisms
5-VERTEX MODELS, GELFAND-TSETLIN PATTERNS AND SEMISTANDARD YOUNG TABLEAUX
 5-VERTEX MODELS, GELFAND-TSETLIN PATTERNS AND SEMISTANDARD YOUNG TABLEAUX TANTELY A. RAKOTOARISOA 1. Introduction In statistical mechanics, one studies models based on the interconnections between thermodynamic
5-VERTEX MODELS, GELFAND-TSETLIN PATTERNS AND SEMISTANDARD YOUNG TABLEAUX TANTELY A. RAKOTOARISOA 1. Introduction In statistical mechanics, one studies models based on the interconnections between thermodynamic
10 l-adic representations
 0 l-adic representations We fix a prime l. Artin representations are not enough; l-adic representations with infinite images naturally appear in geometry. Definition 0.. Let K be any field. An l-adic Galois
0 l-adic representations We fix a prime l. Artin representations are not enough; l-adic representations with infinite images naturally appear in geometry. Definition 0.. Let K be any field. An l-adic Galois
GENERALIZED BRAUER TREE ORDERS
 C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 2 GENERALIZED BRAUER TREE ORDERS BY K. W. R O G G E N K A M P (STUTTGART) Introduction. p-adic blocks of integral group rings with cyclic defect
C O L L O Q U I U M M A T H E M A T I C U M VOL. 71 1996 NO. 2 GENERALIZED BRAUER TREE ORDERS BY K. W. R O G G E N K A M P (STUTTGART) Introduction. p-adic blocks of integral group rings with cyclic defect
7+(),(/'6,167,787( ABSTRACTS 1.2 )255(6($5&+,10$7+(0$7,&$/6&,(1&(6
 YURI BAHTURIN Memorial University of Newfoundland and Moscow State University Exchange Theorem and its Applications to the Gradings of Algebras and Superalgebras In this talk we present a tool that proved
YURI BAHTURIN Memorial University of Newfoundland and Moscow State University Exchange Theorem and its Applications to the Gradings of Algebras and Superalgebras In this talk we present a tool that proved
SERRE S CONJECTURE AND BASE CHANGE FOR GL(2)
 SERRE S CONJECTURE AND BASE CHANGE OR GL(2) HARUZO HIDA 1. Quaternion class sets A quaternion algebra B over a field is a simple algebra of dimension 4 central over a field. A prototypical example is the
SERRE S CONJECTURE AND BASE CHANGE OR GL(2) HARUZO HIDA 1. Quaternion class sets A quaternion algebra B over a field is a simple algebra of dimension 4 central over a field. A prototypical example is the
e j = Ad(f i ) 1 2a ij/a ii
 A characterization of generalized Kac-Moody algebras. J. Algebra 174, 1073-1079 (1995). Richard E. Borcherds, D.P.M.M.S., 16 Mill Lane, Cambridge CB2 1SB, England. Generalized Kac-Moody algebras can be
A characterization of generalized Kac-Moody algebras. J. Algebra 174, 1073-1079 (1995). Richard E. Borcherds, D.P.M.M.S., 16 Mill Lane, Cambridge CB2 1SB, England. Generalized Kac-Moody algebras can be
Hopf Algebras. Zajj Daugherty. March 6, 2012
 Hopf Algebras Zajj Daugherty March 6, 2012 Big idea: The Hopf algebra structure is essentially what one needs in order to guarantee that tensor products of modules are also modules Definition A bialgebra
Hopf Algebras Zajj Daugherty March 6, 2012 Big idea: The Hopf algebra structure is essentially what one needs in order to guarantee that tensor products of modules are also modules Definition A bialgebra
Lie Algebras of Finite and Affine Type
 Lie Algebras of Finite and Affine Type R. W. CARTER Mathematics Institute University of Warwick CAMBRIDGE UNIVERSITY PRESS Preface page xiii Basic concepts 1 1.1 Elementary properties of Lie algebras 1
Lie Algebras of Finite and Affine Type R. W. CARTER Mathematics Institute University of Warwick CAMBRIDGE UNIVERSITY PRESS Preface page xiii Basic concepts 1 1.1 Elementary properties of Lie algebras 1
The Image of Weyl Group Translations in Hecke Algebras
 The Image of Weyl Group Translations in Hecke Algebras UROP+ Final Paper, Summer 2015 Arkadiy Frasinich Mentor: Konstantin Tolmachov Project Suggested By Roman Bezrukavnikov September 1, 2015 Abstract
The Image of Weyl Group Translations in Hecke Algebras UROP+ Final Paper, Summer 2015 Arkadiy Frasinich Mentor: Konstantin Tolmachov Project Suggested By Roman Bezrukavnikov September 1, 2015 Abstract
Half the sum of positive roots, the Coxeter element, and a theorem of Kostant
 DOI 10.1515/forum-2014-0052 Forum Math. 2014; aop Research Article Dipendra Prasad Half the sum of positive roots, the Coxeter element, and a theorem of Kostant Abstract: Interchanging the character and
DOI 10.1515/forum-2014-0052 Forum Math. 2014; aop Research Article Dipendra Prasad Half the sum of positive roots, the Coxeter element, and a theorem of Kostant Abstract: Interchanging the character and
Topics in Representation Theory: Fourier Analysis and the Peter Weyl Theorem
 Topics in Representation Theory: Fourier Analysis and the Peter Weyl Theorem 1 Fourier Analysis, a review We ll begin with a short review of simple facts about Fourier analysis, before going on to interpret
Topics in Representation Theory: Fourier Analysis and the Peter Weyl Theorem 1 Fourier Analysis, a review We ll begin with a short review of simple facts about Fourier analysis, before going on to interpret
Whittaker models and Fourier coeffi cients of automorphic forms
 Whittaker models and Fourier coeffi cients of automorphic forms Nolan R. Wallach May 2013 N. Wallach () Whittaker models 5/13 1 / 20 G be a real reductive group with compact center and let K be a maximal
Whittaker models and Fourier coeffi cients of automorphic forms Nolan R. Wallach May 2013 N. Wallach () Whittaker models 5/13 1 / 20 G be a real reductive group with compact center and let K be a maximal
Baxter Q-operators and tau-function for quantum integrable spin chains
 Baxter Q-operators and tau-function for quantum integrable spin chains Zengo Tsuboi Institut für Mathematik und Institut für Physik, Humboldt-Universität zu Berlin This is based on the following papers.
Baxter Q-operators and tau-function for quantum integrable spin chains Zengo Tsuboi Institut für Mathematik und Institut für Physik, Humboldt-Universität zu Berlin This is based on the following papers.
REPRESENTATION THEORY WEEK 7
 REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
REPRESENTATION THEORY WEEK 7 1. Characters of L k and S n A character of an irreducible representation of L k is a polynomial function constant on every conjugacy class. Since the set of diagonalizable
