Solving Systems of Polynomial Equations: Algebraic Geometry, Linear Algebra, and Tensors?
|
|
|
- Alexander Parks
- 5 years ago
- Views:
Transcription
1 Solving Systems of Polynomial Equations: Algebraic Geometry, Linear Algebra, and Tensors? Philippe Dreesen Bart De Moor Katholieke Universiteit Leuven ESAT/SCD Workshop on Tensor Decompositions and Applications (TDA2010) Monopoli, Italy, September / 27
2 Outline 1 Univariate Polynomials 2 Multivariate Polynomials 3 Applications 4 Tensors 5 Conclusions and Future Work 2/ 27
3 Outline 1 Univariate Polynomials 2 Multivariate Polynomials 3 Applications 4 Tensors 5 Conclusions and Future Work 3/ 27
4 Polynomials, Matrices and Eigenvalue Problems Characteristic Polynomial The eigenvalues of A are the roots of p(λ) = det(a λi) = 0 Companion Matrix Solving q(x) = 7x 3 2x 2 5x + 1 = 0 leads to /7 5/7 2/7 1 x x 2 = x 1 x x 2 4/ 27
5 Sylvester Matrix Sylvester Resultant Consider two polynomials f(x) and g(x): f(x) = x 2 3x + 2 g(x) = x 3 4x 2 11x + 30 Common roots iff S(f, g) = S(f,g) = det James Joseph Sylvester 5/ 27
6 Sylvester Matrix Sylvester s construction can be understood from 1 x x 2 x 3 x 4 f(x) = x f(x) = x x 2 f(x) = x 2 g(x) = x 3 = 0 x g(x) = x 4 evaluate the vector containing the powers of x at x = 2 6/ 27
7 Sylvester Matrix Find a vector in the nullspace of the Sylvester matrix, = normalize such that the first entry equals 1: = / 27
8 Conclusion: Main Ingredients Linear Algebra turns out to be suitable framework Main Ingredients: Linearize problem by separating coefficients and monomials Solutions live in the nullspace of coefficient matrix Exploit structure in monomial basis Eigenvalue problems Multivariate case? 8/ 27
9 Outline 1 Univariate Polynomials 2 Multivariate Polynomials 3 Applications 4 Tensors 5 Conclusions and Future Work 9/ 27
10 Outline of Algorithm Macaulay: multivariate Sylvester construction Linearize by separating coefficients and monomials Algorithm: 1 Build coefficient matrix M 2 Find basis for nullspace of M 3 Find solutions from eigenvalue problem Étienne Bézout James Joseph Sylvester Francis Sowerby Macaulay 10/ 27
11 Build Matrix M Consider j p(x, y) = x 2 + 3y 2 15 = 0 q(x, y) = y 3x 3 2x x 2 = 0 Construct M Write the system in matrix-vector notation: 1 x y x 2 2 xy y 2 x 3 x 2 y xy 2 y 3 3 p(x, y) q(x, y) x p(x, y) y p(x, y) / 27
12 Build Matrix M Continue to enlarge M: 1 x y x 2 xy y 2 x 3 x 2 y xy 2 y 3 x 4 x 3 yx 2 y 2 xy 3 y 4 x 5 x 4 yx 3 y 2 x 2 y 3 xy 4 y 5... p q xp yp x 2 p xyp y 2 q xq yq x 3 p x 2 yp xy 2 p y 3 p x 2 q xyq y 2 q / 27
13 Solutions in Nullspace of M Coefficient matrix M: M = " Solutions generate vectors in nullspace of M: Mv = 0 Number of solutions s follows from corank # Canonical nullspace V built from s solutions (x i, y i): x 1 x 2... x s y 1 y 2... y s x 2 1 x x 2 s x 1 y 1 x 2 y 2... x sy s y1 2 y ys 2 x 3 1 x x 3 s x 2 1 y 1 x 2 2 y 2... x 2 sy s x 1 y1 2 x 2 y x sys 2 y1 3 y ys 3 x 4 1 x x 4 4 x 3 1 y 1 x 3 2 y 2... x 3 sy s x 2 1 y2 1 x 2 2 y x 2 s y2 s x 1 y1 3 x 2 y x sys 3 y1 4 y ys / 27
14 Solutions in Nullspace of M Nullspace of M Find a basis for the nullspace of M using an SVD: [ ][ M = Σ1 0 W T ] = [ X Y ] Z T Hence, MZ = 0 14/ 27
15 Find Solutions Shift property in monomial basis [ ] x = [ ] 1 x y x 2 xy y 2 1 x y x 2 xy y 2 y = [ [ Finding the x-roots: let D = diag(x 1, x 2,..., x s ), then S 1 VD = S 2 V, where S 1 and S 2 select rows from V wrt. shift property Reminiscent of Realization Theory ] ] 1 x y x 2 xy y 2 1 x y x 2 xy y 2 15/ 27
16 Find Solutions We have S 1 VD = S 2 V However, V is not known, instead a basis Z is computed as ZT = V Which leads to or Hence, S 1 ZTD = S 2 ZT S 1 Z ( TDT 1) = S 2 Z TDT 1 = (S 1 Z) S 2 Z 16/ 27
17 Algorithm Summary Algorithm 1 Construct coefficient matrix M 2 Compute basis for nullspace of M, Z 3 Choose shift function, e.g., x 4 Write down shift relation in monomial basis v for the chosen shift function using row selection matrices S 1 and S 2 5 The construction of above gives rise to a generalized eigenvalue problem S 1 Z ( TDT 1) = S 2 Z of which the eigenvalues correspond to the, e.g., x-solutions of the system of polynomial equations. 17/ 27
18 Algorithm Summary Approach has been generalized to Multivariate Polynomials Elegant link with Linear Algebra, especially eigenvalue problems Finds all solutions (or alternatively, global solutions) (Numerical) LA: embed into well-known matrix computations Limiting computational complexity (but inherent to the problem) 18/ 27
19 Outline 1 Univariate Polynomials 2 Multivariate Polynomials 3 Applications 4 Tensors 5 Conclusions and Future Work 19/ 27
20 Relevant applications are found in Polynomial Optimization Problems Structured Total Least Squares Model order reduction Analyzing identifiability nonlinear model structures Robotics: kinematic problems Computational Biology: conformation of molecules Algebraic Statistics Signal Processing... 20/ 27
21 6 3 Hankel STLS 3 min v τ 2 = v T A T D 1 v Av s.t. v T v = 1. phi STLS Hankel cost function TLS/SVD soln STSL/RiSVD/invit steps STLS/RiSVD/invit soln STLS/RiSVD/EIG global min STLS/RiSVD/EIG extrema theta method TLS/SVD STLS inv. it. STLS eig v v v τ global solution? no no yes (eigenvalue decomposition on matrix) 21/ 27
22 Outline 1 Univariate Polynomials 2 Multivariate Polynomials 3 Applications 4 Tensors 5 Conclusions and Future Work 22/ 27
23 Links with Tensors A homogeneous polynomial of degree d is a d-mode tensor, e.g., a 0 + a T 1 x + x T A 2 x + A 3 (x,x,x) A d (x,...,x) +... where a 0 R a 1 R n A 2 R n n A 3 R n n n. 23/ 27
24 Is it useful to decouple along tensor directions? 24/ 27
25 Outline 1 Univariate Polynomials 2 Multivariate Polynomials 3 Applications 4 Tensors 5 Conclusions and Future Work 25/ 27
26 Conclusions Link polynomial system solving and linear algebra Polynomial system solving reduces to eigenvalue problems! Problem tackled using matrix computations Computational complexity Topic touches on the fundamentals of applied mathematics Will it be interesting to look at tensors? 26/ 27
27 Thank You! 27/ 27
Back to the Roots: Solving Polynomial Systems with Numerical Linear Algebra Tools
 Back to the Roots: Solving Polynomial Systems with Numerical Linear Algebra Tools Bart De Moor Katholieke Universiteit Leuven Department of Electrical Engineering ESAT/SCD 1 / 56 Outline 1 Introduction
Back to the Roots: Solving Polynomial Systems with Numerical Linear Algebra Tools Bart De Moor Katholieke Universiteit Leuven Department of Electrical Engineering ESAT/SCD 1 / 56 Outline 1 Introduction
Structured Matrices and Solving Multivariate Polynomial Equations
 Structured Matrices and Solving Multivariate Polynomial Equations Philippe Dreesen Kim Batselier Bart De Moor KU Leuven ESAT/SCD, Kasteelpark Arenberg 10, B-3001 Leuven, Belgium. Structured Matrix Days,
Structured Matrices and Solving Multivariate Polynomial Equations Philippe Dreesen Kim Batselier Bart De Moor KU Leuven ESAT/SCD, Kasteelpark Arenberg 10, B-3001 Leuven, Belgium. Structured Matrix Days,
Computing the common zeros of two bivariate functions via Bézout resultants Colorado State University, 26th September 2013
 Work supported by supported by EPSRC grant EP/P505666/1. Computing the common zeros of two bivariate functions via Bézout resultants Colorado State University, 26th September 2013 Alex Townsend PhD student
Work supported by supported by EPSRC grant EP/P505666/1. Computing the common zeros of two bivariate functions via Bézout resultants Colorado State University, 26th September 2013 Alex Townsend PhD student
BACK TO THE ROOTS POLYNOMIAL SYSTEM SOLVING USING LINEAR ALGEBRA AND SYSTEM THEORY
 BACK TO THE ROOTS POLYNOMIAL SYSTEM SOLVING USING LINEAR ALGEBRA AND SYSTEM THEORY PHILIPPE DREESEN, KIM BATSELIER, AND BART DE MOOR Abstract. We return to the algebraic roots of the problem of finding
BACK TO THE ROOTS POLYNOMIAL SYSTEM SOLVING USING LINEAR ALGEBRA AND SYSTEM THEORY PHILIPPE DREESEN, KIM BATSELIER, AND BART DE MOOR Abstract. We return to the algebraic roots of the problem of finding
Maximum Likelihood Estimation and Polynomial System Solving
 Maximum Likelihood Estimation and Polynomial System Solving Kim Batselier Philippe Dreesen Bart De Moor Department of Electrical Engineering (ESAT), SCD, Katholieke Universiteit Leuven /IBBT-KULeuven Future
Maximum Likelihood Estimation and Polynomial System Solving Kim Batselier Philippe Dreesen Bart De Moor Department of Electrical Engineering (ESAT), SCD, Katholieke Universiteit Leuven /IBBT-KULeuven Future
The Sylvester Resultant
 Lecture 10 The Sylvester Resultant We want to compute intersections of algebraic curves F and G. Let F and G be the vanishing sets of f(x,y) and g(x, y), respectively. Algebraically, we are interested
Lecture 10 The Sylvester Resultant We want to compute intersections of algebraic curves F and G. Let F and G be the vanishing sets of f(x,y) and g(x, y), respectively. Algebraically, we are interested
Linear Algebra 2 More on determinants and Evalues Exercises and Thanksgiving Activities
 Linear Algebra 2 More on determinants and Evalues Exercises and Thanksgiving Activities 2. Determinant of a linear transformation, change of basis. In the solution set of Homework 1, New Series, I included
Linear Algebra 2 More on determinants and Evalues Exercises and Thanksgiving Activities 2. Determinant of a linear transformation, change of basis. In the solution set of Homework 1, New Series, I included
Math Matrix Algebra
 Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 28, 2011
 Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Question: Given an n x n matrix A, how do we find its eigenvalues? Idea: Suppose c is an eigenvalue of A, then what is the determinant of A-cI?
 Section 5. The Characteristic Polynomial Question: Given an n x n matrix A, how do we find its eigenvalues? Idea: Suppose c is an eigenvalue of A, then what is the determinant of A-cI? Property The eigenvalues
Section 5. The Characteristic Polynomial Question: Given an n x n matrix A, how do we find its eigenvalues? Idea: Suppose c is an eigenvalue of A, then what is the determinant of A-cI? Property The eigenvalues
Linear Algebra- Final Exam Review
 Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra- Final Exam Review. Let A be invertible. Show that, if v, v, v 3 are linearly independent vectors, so are Av, Av, Av 3. NOTE: It should be clear from your answer that you know the definition.
Linear Algebra 1 Exam 2 Solutions 7/14/3
 Linear Algebra 1 Exam Solutions 7/14/3 Question 1 The line L has the symmetric equation: x 1 = y + 3 The line M has the parametric equation: = z 4. [x, y, z] = [ 4, 10, 5] + s[10, 7, ]. The line N is perpendicular
Linear Algebra 1 Exam Solutions 7/14/3 Question 1 The line L has the symmetric equation: x 1 = y + 3 The line M has the parametric equation: = z 4. [x, y, z] = [ 4, 10, 5] + s[10, 7, ]. The line N is perpendicular
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Joint Regression and Linear Combination of Time Series for Optimal Prediction
 Joint Regression and Linear Combination of Time Series for Optimal Prediction Dries Geebelen 1, Kim Batselier 1, Philippe Dreesen 1, Marco Signoretto 1, Johan Suykens 1, Bart De Moor 1, Joos Vandewalle
Joint Regression and Linear Combination of Time Series for Optimal Prediction Dries Geebelen 1, Kim Batselier 1, Philippe Dreesen 1, Marco Signoretto 1, Johan Suykens 1, Bart De Moor 1, Joos Vandewalle
MAT Linear Algebra Collection of sample exams
 MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
MAT 342 - Linear Algebra Collection of sample exams A-x. (0 pts Give the precise definition of the row echelon form. 2. ( 0 pts After performing row reductions on the augmented matrix for a certain system
and let s calculate the image of some vectors under the transformation T.
 Chapter 5 Eigenvalues and Eigenvectors 5. Eigenvalues and Eigenvectors Let T : R n R n be a linear transformation. Then T can be represented by a matrix (the standard matrix), and we can write T ( v) =
Chapter 5 Eigenvalues and Eigenvectors 5. Eigenvalues and Eigenvectors Let T : R n R n be a linear transformation. Then T can be represented by a matrix (the standard matrix), and we can write T ( v) =
A Cholesky LR algorithm for the positive definite symmetric diagonal-plus-semiseparable eigenproblem
 A Cholesky LR algorithm for the positive definite symmetric diagonal-plus-semiseparable eigenproblem Bor Plestenjak Department of Mathematics University of Ljubljana Slovenia Ellen Van Camp and Marc Van
A Cholesky LR algorithm for the positive definite symmetric diagonal-plus-semiseparable eigenproblem Bor Plestenjak Department of Mathematics University of Ljubljana Slovenia Ellen Van Camp and Marc Van
Systems of Algebraic Equations and Systems of Differential Equations
 Systems of Algebraic Equations and Systems of Differential Equations Topics: 2 by 2 systems of linear equations Matrix expression; Ax = b Solving 2 by 2 homogeneous systems Functions defined on matrices
Systems of Algebraic Equations and Systems of Differential Equations Topics: 2 by 2 systems of linear equations Matrix expression; Ax = b Solving 2 by 2 homogeneous systems Functions defined on matrices
Mathematics 206 Solutions for HWK 23 Section 6.3 p358
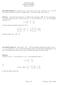 Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
OWELL WEEKLY JOURNAL
 Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
Minimum Polynomials of Linear Transformations
 Minimum Polynomials of Linear Transformations Spencer De Chenne University of Puget Sound 30 April 2014 Table of Contents Polynomial Basics Endomorphisms Minimum Polynomial Building Linear Transformations
Minimum Polynomials of Linear Transformations Spencer De Chenne University of Puget Sound 30 April 2014 Table of Contents Polynomial Basics Endomorphisms Minimum Polynomial Building Linear Transformations
A DARK GREY P O N T, with a Switch Tail, and a small Star on the Forehead. Any
 Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X»
Math 250B Final Exam Review Session Spring 2015 SOLUTIONS
 Math 5B Final Exam Review Session Spring 5 SOLUTIONS Problem Solve x x + y + 54te 3t and y x + 4y + 9e 3t λ SOLUTION: We have det(a λi) if and only if if and 4 λ only if λ 3λ This means that the eigenvalues
Math 5B Final Exam Review Session Spring 5 SOLUTIONS Problem Solve x x + y + 54te 3t and y x + 4y + 9e 3t λ SOLUTION: We have det(a λi) if and only if if and 4 λ only if λ 3λ This means that the eigenvalues
Linear Algebra problems
 Linear Algebra problems 1. Show that the set F = ({1, 0}, +,.) is a field where + and. are defined as 1+1=0, 0+0=0, 0+1=1+0=1, 0.0=0.1=1.0=0, 1.1=1.. Let X be a non-empty set and F be any field. Let X
Linear Algebra problems 1. Show that the set F = ({1, 0}, +,.) is a field where + and. are defined as 1+1=0, 0+0=0, 0+1=1+0=1, 0.0=0.1=1.0=0, 1.1=1.. Let X be a non-empty set and F be any field. Let X
Problems for M 10/26:
 Math, Lesieutre Problem set # November 4, 25 Problems for M /26: 5 Is λ 2 an eigenvalue of 2? 8 Why or why not? 2 A 2I The determinant is, which means that A 2I has 6 a nullspace, and so there is an eigenvector
Math, Lesieutre Problem set # November 4, 25 Problems for M /26: 5 Is λ 2 an eigenvalue of 2? 8 Why or why not? 2 A 2I The determinant is, which means that A 2I has 6 a nullspace, and so there is an eigenvector
CAAM 335 Matrix Analysis
 CAAM 335 Matrix Analysis Solutions to Homework 8 Problem (5+5+5=5 points The partial fraction expansion of the resolvent for the matrix B = is given by (si B = s } {{ } =P + s + } {{ } =P + (s (5 points
CAAM 335 Matrix Analysis Solutions to Homework 8 Problem (5+5+5=5 points The partial fraction expansion of the resolvent for the matrix B = is given by (si B = s } {{ } =P + s + } {{ } =P + (s (5 points
Calculus 2502A - Advanced Calculus I Fall : Local minima and maxima
 Calculus 50A - Advanced Calculus I Fall 014 14.7: Local minima and maxima Martin Frankland November 17, 014 In these notes, we discuss the problem of finding the local minima and maxima of a function.
Calculus 50A - Advanced Calculus I Fall 014 14.7: Local minima and maxima Martin Frankland November 17, 014 In these notes, we discuss the problem of finding the local minima and maxima of a function.
MATH Topics in Applied Mathematics Lecture 2-6: Isomorphism. Linear independence (revisited).
 MATH 311-504 Topics in Applied Mathematics Lecture 2-6: Isomorphism. Linear independence (revisited). Definition. A mapping f : V 1 V 2 is one-to-one if it maps different elements from V 1 to different
MATH 311-504 Topics in Applied Mathematics Lecture 2-6: Isomorphism. Linear independence (revisited). Definition. A mapping f : V 1 V 2 is one-to-one if it maps different elements from V 1 to different
CS 143 Linear Algebra Review
 CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
Announcements Wednesday, November 01
 Announcements Wednesday, November 01 WeBWorK 3.1, 3.2 are due today at 11:59pm. The quiz on Friday covers 3.1, 3.2. My office is Skiles 244. Rabinoffice hours are Monday, 1 3pm and Tuesday, 9 11am. Section
Announcements Wednesday, November 01 WeBWorK 3.1, 3.2 are due today at 11:59pm. The quiz on Friday covers 3.1, 3.2. My office is Skiles 244. Rabinoffice hours are Monday, 1 3pm and Tuesday, 9 11am. Section
Math 240 Calculus III
 Generalized Calculus III Summer 2015, Session II Thursday, July 23, 2015 Agenda 1. 2. 3. 4. Motivation Defective matrices cannot be diagonalized because they do not possess enough eigenvectors to make
Generalized Calculus III Summer 2015, Session II Thursday, July 23, 2015 Agenda 1. 2. 3. 4. Motivation Defective matrices cannot be diagonalized because they do not possess enough eigenvectors to make
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Elimination Methods: An Introduction
 Elimination Methods: An Introduction Deepak Kapur Institute for Programming and Logics Department of Computer Science State University of New York Albany, NY 12222 kapur@cs.albany.edu Lakshman Y.N. Department
Elimination Methods: An Introduction Deepak Kapur Institute for Programming and Logics Department of Computer Science State University of New York Albany, NY 12222 kapur@cs.albany.edu Lakshman Y.N. Department
Eigenvalues and Eigenvectors
 5 Eigenvalues and Eigenvectors 5.2 THE CHARACTERISTIC EQUATION DETERMINANATS nn Let A be an matrix, let U be any echelon form obtained from A by row replacements and row interchanges (without scaling),
5 Eigenvalues and Eigenvectors 5.2 THE CHARACTERISTIC EQUATION DETERMINANATS nn Let A be an matrix, let U be any echelon form obtained from A by row replacements and row interchanges (without scaling),
Math 215 HW #9 Solutions
 Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Remark By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
Sec 6 Eigenvalues and Eigenvectors Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called an eigenvalue of A if there is a nontrivial
CHAPTER 3. Matrix Eigenvalue Problems
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
Ruppert matrix as subresultant mapping
 Ruppert matrix as subresultant mapping Kosaku Nagasaka Kobe University JAPAN This presentation is powered by Mathematica 6. 09 : 29 : 35 16 Ruppert matrix as subresultant mapping Prev Next 2 CASC2007slideshow.nb
Ruppert matrix as subresultant mapping Kosaku Nagasaka Kobe University JAPAN This presentation is powered by Mathematica 6. 09 : 29 : 35 16 Ruppert matrix as subresultant mapping Prev Next 2 CASC2007slideshow.nb
Linear Algebra in Actuarial Science: Slides to the lecture
 Linear Algebra in Actuarial Science: Slides to the lecture Fall Semester 2010/2011 Linear Algebra is a Tool-Box Linear Equation Systems Discretization of differential equations: solving linear equations
Linear Algebra in Actuarial Science: Slides to the lecture Fall Semester 2010/2011 Linear Algebra is a Tool-Box Linear Equation Systems Discretization of differential equations: solving linear equations
OR MSc Maths Revision Course
 OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
A = 3 1. We conclude that the algebraic multiplicity of the eigenvalues are both one, that is,
 65 Diagonalizable Matrices It is useful to introduce few more concepts, that are common in the literature Definition 65 The characteristic polynomial of an n n matrix A is the function p(λ) det(a λi) Example
65 Diagonalizable Matrices It is useful to introduce few more concepts, that are common in the literature Definition 65 The characteristic polynomial of an n n matrix A is the function p(λ) det(a λi) Example
Matrices and Linear Algebra
 Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
MATH 304 Linear Algebra Lecture 34: Review for Test 2.
 MATH 304 Linear Algebra Lecture 34: Review for Test 2. Topics for Test 2 Linear transformations (Leon 4.1 4.3) Matrix transformations Matrix of a linear mapping Similar matrices Orthogonality (Leon 5.1
MATH 304 Linear Algebra Lecture 34: Review for Test 2. Topics for Test 2 Linear transformations (Leon 4.1 4.3) Matrix transformations Matrix of a linear mapping Similar matrices Orthogonality (Leon 5.1
The F 4 Algorithm. Dylan Peifer. 9 May Cornell University
 The F 4 Algorithm Dylan Peifer Cornell University 9 May 2017 Gröbner Bases History Gröbner bases were introduced in 1965 in the PhD thesis of Bruno Buchberger under Wolfgang Gröbner. Buchberger s algorithm
The F 4 Algorithm Dylan Peifer Cornell University 9 May 2017 Gröbner Bases History Gröbner bases were introduced in 1965 in the PhD thesis of Bruno Buchberger under Wolfgang Gröbner. Buchberger s algorithm
EE263: Introduction to Linear Dynamical Systems Review Session 5
 EE263: Introduction to Linear Dynamical Systems Review Session 5 Outline eigenvalues and eigenvectors diagonalization matrix exponential EE263 RS5 1 Eigenvalues and eigenvectors we say that λ C is an eigenvalue
EE263: Introduction to Linear Dynamical Systems Review Session 5 Outline eigenvalues and eigenvectors diagonalization matrix exponential EE263 RS5 1 Eigenvalues and eigenvectors we say that λ C is an eigenvalue
2 Eigenvectors and Eigenvalues in abstract spaces.
 MA322 Sathaye Notes on Eigenvalues Spring 27 Introduction In these notes, we start with the definition of eigenvectors in abstract vector spaces and follow with the more common definition of eigenvectors
MA322 Sathaye Notes on Eigenvalues Spring 27 Introduction In these notes, we start with the definition of eigenvectors in abstract vector spaces and follow with the more common definition of eigenvectors
Chapter 7 Polynomial Functions. Factoring Review. We will talk about 3 Types: ALWAYS FACTOR OUT FIRST! Ex 2: Factor x x + 64
 Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Chapter 7 Polynomial Functions Factoring Review We will talk about 3 Types: 1. 2. 3. ALWAYS FACTOR OUT FIRST! Ex 1: Factor x 2 + 5x + 6 Ex 2: Factor x 2 + 16x + 64 Ex 3: Factor 4x 2 + 6x 18 Ex 4: Factor
Section Properties of Rational Expressions
 88 Section. - Properties of Rational Expressions Recall that a rational number is any number that can be written as the ratio of two integers where the integer in the denominator cannot be. Rational Numbers:
88 Section. - Properties of Rational Expressions Recall that a rational number is any number that can be written as the ratio of two integers where the integer in the denominator cannot be. Rational Numbers:
Section 9.8 Higher Order Linear Equations
 Section 9.8 Higher Order Linear Equations Key Terms: Higher order linear equations Equivalent linear systems for higher order equations Companion matrix Characteristic polynomial and equation A linear
Section 9.8 Higher Order Linear Equations Key Terms: Higher order linear equations Equivalent linear systems for higher order equations Companion matrix Characteristic polynomial and equation A linear
Ph.D. Katarína Bellová Page 1 Mathematics 2 (10-PHY-BIPMA2) EXAM - Solutions, 20 July 2017, 10:00 12:00 All answers to be justified.
 PhD Katarína Bellová Page 1 Mathematics 2 (10-PHY-BIPMA2 EXAM - Solutions, 20 July 2017, 10:00 12:00 All answers to be justified Problem 1 [ points]: For which parameters λ R does the following system
PhD Katarína Bellová Page 1 Mathematics 2 (10-PHY-BIPMA2 EXAM - Solutions, 20 July 2017, 10:00 12:00 All answers to be justified Problem 1 [ points]: For which parameters λ R does the following system
Linear transformations
 Linear transformations Samy Tindel Purdue University Differential equations and linear algebra - MA 262 Taken from Differential equations and linear algebra by Goode and Annin Samy T. Linear transformations
Linear transformations Samy Tindel Purdue University Differential equations and linear algebra - MA 262 Taken from Differential equations and linear algebra by Goode and Annin Samy T. Linear transformations
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
EE5120 Linear Algebra: Tutorial 6, July-Dec Covers sec 4.2, 5.1, 5.2 of GS
 EE0 Linear Algebra: Tutorial 6, July-Dec 07-8 Covers sec 4.,.,. of GS. State True or False with proper explanation: (a) All vectors are eigenvectors of the Identity matrix. (b) Any matrix can be diagonalized.
EE0 Linear Algebra: Tutorial 6, July-Dec 07-8 Covers sec 4.,.,. of GS. State True or False with proper explanation: (a) All vectors are eigenvectors of the Identity matrix. (b) Any matrix can be diagonalized.
MATH Spring 2011 Sample problems for Test 2: Solutions
 MATH 304 505 Spring 011 Sample problems for Test : Solutions Any problem may be altered or replaced by a different one! Problem 1 (15 pts) Let M, (R) denote the vector space of matrices with real entries
MATH 304 505 Spring 011 Sample problems for Test : Solutions Any problem may be altered or replaced by a different one! Problem 1 (15 pts) Let M, (R) denote the vector space of matrices with real entries
Compatible Systems and Charpit s Method
 MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 28 Lecture 5 Compatible Systems Charpit s Method In this lecture, we shall study compatible systems of first-order PDEs the Charpit s method for solving
MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 28 Lecture 5 Compatible Systems Charpit s Method In this lecture, we shall study compatible systems of first-order PDEs the Charpit s method for solving
Math 205, Summer I, Week 4b:
 Math 205, Summer I, 2016 Week 4b: Chapter 5, Sections 6, 7 and 8 (5.5 is NOT on the syllabus) 5.6 Eigenvalues and Eigenvectors 5.7 Eigenspaces, nondefective matrices 5.8 Diagonalization [*** See next slide
Math 205, Summer I, 2016 Week 4b: Chapter 5, Sections 6, 7 and 8 (5.5 is NOT on the syllabus) 5.6 Eigenvalues and Eigenvectors 5.7 Eigenspaces, nondefective matrices 5.8 Diagonalization [*** See next slide
SOLUTIONS TO PRACTICE EXAM 3, SPRING 2004
 8034 SOLUTIONS TO PRACTICE EXAM 3, SPRING 004 Problem Let A be a real matrix and consider the linear system of first order differential equations, y y (t) Ay(t), y(t) (t) y (t) Let α be a real number,
8034 SOLUTIONS TO PRACTICE EXAM 3, SPRING 004 Problem Let A be a real matrix and consider the linear system of first order differential equations, y y (t) Ay(t), y(t) (t) y (t) Let α be a real number,
LINEAR ALGEBRA W W L CHEN
 LINEAR ALGEBRA W W L CHEN c W W L Chen, 1997, 2008. This chapter is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied,
LINEAR ALGEBRA W W L CHEN c W W L Chen, 1997, 2008. This chapter is available free to all individuals, on the understanding that it is not to be used for financial gain, and may be downloaded and/or photocopied,
MEM 355 Performance Enhancement of Dynamical Systems MIMO Introduction
 MEM 355 Performance Enhancement of Dynamical Systems MIMO Introduction Harry G. Kwatny Department of Mechanical Engineering & Mechanics Drexel University 11/2/214 Outline Solving State Equations Variation
MEM 355 Performance Enhancement of Dynamical Systems MIMO Introduction Harry G. Kwatny Department of Mechanical Engineering & Mechanics Drexel University 11/2/214 Outline Solving State Equations Variation
c c c c c c c c c c a 3x3 matrix C= has a determinant determined by
 Linear Algebra Determinants and Eigenvalues Introduction: Many important geometric and algebraic properties of square matrices are associated with a single real number revealed by what s known as the determinant.
Linear Algebra Determinants and Eigenvalues Introduction: Many important geometric and algebraic properties of square matrices are associated with a single real number revealed by what s known as the determinant.
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Linear Algebra Methods for Data Mining
 Linear Algebra Methods for Data Mining Saara Hyvönen, Saara.Hyvonen@cs.helsinki.fi Spring 2007 1. Basic Linear Algebra Linear Algebra Methods for Data Mining, Spring 2007, University of Helsinki Example
Linear Algebra Methods for Data Mining Saara Hyvönen, Saara.Hyvonen@cs.helsinki.fi Spring 2007 1. Basic Linear Algebra Linear Algebra Methods for Data Mining, Spring 2007, University of Helsinki Example
Topics in linear algebra
 Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Math 205, Summer I, Week 4b: Continued. Chapter 5, Section 8
 Math 205, Summer I, 2016 Week 4b: Continued Chapter 5, Section 8 2 5.8 Diagonalization [reprint, week04: Eigenvalues and Eigenvectors] + diagonaliization 1. 5.8 Eigenspaces, Diagonalization A vector v
Math 205, Summer I, 2016 Week 4b: Continued Chapter 5, Section 8 2 5.8 Diagonalization [reprint, week04: Eigenvalues and Eigenvectors] + diagonaliization 1. 5.8 Eigenspaces, Diagonalization A vector v
Chapter 7. Canonical Forms. 7.1 Eigenvalues and Eigenvectors
 Chapter 7 Canonical Forms 7.1 Eigenvalues and Eigenvectors Definition 7.1.1. Let V be a vector space over the field F and let T be a linear operator on V. An eigenvalue of T is a scalar λ F such that there
Chapter 7 Canonical Forms 7.1 Eigenvalues and Eigenvectors Definition 7.1.1. Let V be a vector space over the field F and let T be a linear operator on V. An eigenvalue of T is a scalar λ F such that there
8. Diagonalization.
 8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
8. Diagonalization 8.1. Matrix Representations of Linear Transformations Matrix of A Linear Operator with Respect to A Basis We know that every linear transformation T: R n R m has an associated standard
MATH 369 Linear Algebra
 Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
Ch 7 Summary - POLYNOMIAL FUNCTIONS
 Ch 7 Summary - POLYNOMIAL FUNCTIONS 1. An open-top box is to be made by cutting congruent squares of side length x from the corners of a 8.5- by 11-inch sheet of cardboard and bending up the sides. a)
Ch 7 Summary - POLYNOMIAL FUNCTIONS 1. An open-top box is to be made by cutting congruent squares of side length x from the corners of a 8.5- by 11-inch sheet of cardboard and bending up the sides. a)
MATH 315 Linear Algebra Homework #1 Assigned: August 20, 2018
 Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Homework #1 Assigned: August 20, 2018 Review the following subjects involving systems of equations and matrices from Calculus II. Linear systems of equations Converting systems to matrix form Pivot entry
Educjatipnal. L a d ie s * COBNWALILI.S H IG H SCHOOL. I F O R G IR L S A n B k i n d e r g a r t e n.
 - - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
- - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
Remark 1 By definition, an eigenvector must be a nonzero vector, but eigenvalue could be zero.
 Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
Sec 5 Eigenvectors and Eigenvalues In this chapter, vector means column vector Definition An eigenvector of an n n matrix A is a nonzero vector x such that A x λ x for some scalar λ A scalar λ is called
UNIT 6: The singular value decomposition.
 UNIT 6: The singular value decomposition. María Barbero Liñán Universidad Carlos III de Madrid Bachelor in Statistics and Business Mathematical methods II 2011-2012 A square matrix is symmetric if A T
UNIT 6: The singular value decomposition. María Barbero Liñán Universidad Carlos III de Madrid Bachelor in Statistics and Business Mathematical methods II 2011-2012 A square matrix is symmetric if A T
Review of Linear Algebra
 Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
Linear Algebra. Workbook
 Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
6.3 Partial Fractions
 6.3 Partial Fractions Mark Woodard Furman U Fall 2009 Mark Woodard (Furman U) 6.3 Partial Fractions Fall 2009 1 / 11 Outline 1 The method illustrated 2 Terminology 3 Factoring Polynomials 4 Partial fraction
6.3 Partial Fractions Mark Woodard Furman U Fall 2009 Mark Woodard (Furman U) 6.3 Partial Fractions Fall 2009 1 / 11 Outline 1 The method illustrated 2 Terminology 3 Factoring Polynomials 4 Partial fraction
A simple dynamic model of labor market
 1 A simple dynamic model of labor market Let e t be the number of employed workers, u t be the number of unemployed worker. An employed worker has probability of 0.8 to be employed in the next period,
1 A simple dynamic model of labor market Let e t be the number of employed workers, u t be the number of unemployed worker. An employed worker has probability of 0.8 to be employed in the next period,
Review 1 Math 321: Linear Algebra Spring 2010
 Department of Mathematics and Statistics University of New Mexico Review 1 Math 321: Linear Algebra Spring 2010 This is a review for Midterm 1 that will be on Thursday March 11th, 2010. The main topics
Department of Mathematics and Statistics University of New Mexico Review 1 Math 321: Linear Algebra Spring 2010 This is a review for Midterm 1 that will be on Thursday March 11th, 2010. The main topics
Vector Spaces and SubSpaces
 Vector Spaces and SubSpaces Linear Algebra MATH 2076 Linear Algebra Vector Spaces & SubSpaces Chapter 4, Section 1b 1 / 10 What is a Vector Space? A vector space is a bunch of objects that we call vectors
Vector Spaces and SubSpaces Linear Algebra MATH 2076 Linear Algebra Vector Spaces & SubSpaces Chapter 4, Section 1b 1 / 10 What is a Vector Space? A vector space is a bunch of objects that we call vectors
1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem.
 STATE EXAM MATHEMATICS Variant A ANSWERS AND SOLUTIONS 1 1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem. Definition
STATE EXAM MATHEMATICS Variant A ANSWERS AND SOLUTIONS 1 1.1 Limits and Continuity. Precise definition of a limit and limit laws. Squeeze Theorem. Intermediate Value Theorem. Extreme Value Theorem. Definition
235 Final exam review questions
 5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
LinGloss. A glossary of linear algebra
 LinGloss A glossary of linear algebra Contents: Decompositions Types of Matrices Theorems Other objects? Quasi-triangular A matrix A is quasi-triangular iff it is a triangular matrix except its diagonal
LinGloss A glossary of linear algebra Contents: Decompositions Types of Matrices Theorems Other objects? Quasi-triangular A matrix A is quasi-triangular iff it is a triangular matrix except its diagonal
DIAGONALIZATION. In order to see the implications of this definition, let us consider the following example Example 1. Consider the matrix
 DIAGONALIZATION Definition We say that a matrix A of size n n is diagonalizable if there is a basis of R n consisting of eigenvectors of A ie if there are n linearly independent vectors v v n such that
DIAGONALIZATION Definition We say that a matrix A of size n n is diagonalizable if there is a basis of R n consisting of eigenvectors of A ie if there are n linearly independent vectors v v n such that
Chapter 5. Linear Algebra. A linear (algebraic) equation in. unknowns, x 1, x 2,..., x n, is. an equation of the form
 Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
Chapter 5. Linear Algebra A linear (algebraic) equation in n unknowns, x 1, x 2,..., x n, is an equation of the form a 1 x 1 + a 2 x 2 + + a n x n = b where a 1, a 2,..., a n and b are real numbers. 1
THE GEOMETRY OF MULTIVARIATE POLYNOMIAL DIVISION AND ELIMINATION
 THE GEOMETRY OF MULTIVARIATE POLYNOMIAL DIVISION AND ELIMINATION KIM BATSELIER, PHILIPPE DREESEN, AND BART DE MOOR Abstract. Multivariate polynomials are usually discussed in the framework of algebraic
THE GEOMETRY OF MULTIVARIATE POLYNOMIAL DIVISION AND ELIMINATION KIM BATSELIER, PHILIPPE DREESEN, AND BART DE MOOR Abstract. Multivariate polynomials are usually discussed in the framework of algebraic
The characteristic equation and minimal state space realization of SISO systems in the max algebra
 KULeuven Department of Electrical Engineering (ESAT) SISTA Technical report 93-57a The characteristic equation and minimal state space realization of SISO systems in the max algebra B De Schutter and B
KULeuven Department of Electrical Engineering (ESAT) SISTA Technical report 93-57a The characteristic equation and minimal state space realization of SISO systems in the max algebra B De Schutter and B
Linear Algebra - Part II
 Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Sparse representations from moments
 Sparse representations from moments Bernard Mourrain Inria Méditerranée, Sophia Antipolis BernardMourrain@inriafr Sparse representation of signals Given a function or signal f (t): decompose it as f (t)
Sparse representations from moments Bernard Mourrain Inria Méditerranée, Sophia Antipolis BernardMourrain@inriafr Sparse representation of signals Given a function or signal f (t): decompose it as f (t)
Linear Algebra. Shan-Hung Wu. Department of Computer Science, National Tsing Hua University, Taiwan. Large-Scale ML, Fall 2016
 Linear Algebra Shan-Hung Wu shwu@cs.nthu.edu.tw Department of Computer Science, National Tsing Hua University, Taiwan Large-Scale ML, Fall 2016 Shan-Hung Wu (CS, NTHU) Linear Algebra Large-Scale ML, Fall
Linear Algebra Shan-Hung Wu shwu@cs.nthu.edu.tw Department of Computer Science, National Tsing Hua University, Taiwan Large-Scale ML, Fall 2016 Shan-Hung Wu (CS, NTHU) Linear Algebra Large-Scale ML, Fall
1. Select the unique answer (choice) for each problem. Write only the answer.
 MATH 5 Practice Problem Set Spring 7. Select the unique answer (choice) for each problem. Write only the answer. () Determine all the values of a for which the system has infinitely many solutions: x +
MATH 5 Practice Problem Set Spring 7. Select the unique answer (choice) for each problem. Write only the answer. () Determine all the values of a for which the system has infinitely many solutions: x +
Math 0312 EXAM 2 Review Questions
 Name Decide whether the ordered pair is a solution of the given system. 1. 4x + y = 2 2x + 4y = -20 ; (2, -6) Solve the system by graphing. 2. x - y = 6 x + y = 16 Solve the system by substitution. If
Name Decide whether the ordered pair is a solution of the given system. 1. 4x + y = 2 2x + 4y = -20 ; (2, -6) Solve the system by graphing. 2. x - y = 6 x + y = 16 Solve the system by substitution. If
A geometrical approach to finding multivariate approximate LCMs and GCDs
 A geometrical approach to finding multivariate approximate LCMs and GCDs Kim Batselier, Philippe Dreesen, Bart De Moor 1 Department of Electrical Engineering, ESAT-SCD, KU Leuven / IBBT Future Health Department
A geometrical approach to finding multivariate approximate LCMs and GCDs Kim Batselier, Philippe Dreesen, Bart De Moor 1 Department of Electrical Engineering, ESAT-SCD, KU Leuven / IBBT Future Health Department
Solutions to the Multivariable Calculus and Linear Algebra problems on the Comprehensive Examination of January 31, 2014
 Solutions to te Multivariable Calculus and Linear Algebra problems on te Compreensive Examination of January 3, 24 Tere are 9 problems ( points eac, totaling 9 points) on tis portion of te examination.
Solutions to te Multivariable Calculus and Linear Algebra problems on te Compreensive Examination of January 3, 24 Tere are 9 problems ( points eac, totaling 9 points) on tis portion of te examination.
Econ Slides from Lecture 7
 Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Diagonalization. Hung-yi Lee
 Diagonalization Hung-yi Lee Review If Av = λv (v is a vector, λ is a scalar) v is an eigenvector of A excluding zero vector λ is an eigenvalue of A that corresponds to v Eigenvectors corresponding to λ
Diagonalization Hung-yi Lee Review If Av = λv (v is a vector, λ is a scalar) v is an eigenvector of A excluding zero vector λ is an eigenvalue of A that corresponds to v Eigenvectors corresponding to λ
Lecture 5. 1 Goermans-Williamson Algorithm for the maxcut problem
 Math 280 Geometric and Algebraic Ideas in Optimization April 26, 2010 Lecture 5 Lecturer: Jesús A De Loera Scribe: Huy-Dung Han, Fabio Lapiccirella 1 Goermans-Williamson Algorithm for the maxcut problem
Math 280 Geometric and Algebraic Ideas in Optimization April 26, 2010 Lecture 5 Lecturer: Jesús A De Loera Scribe: Huy-Dung Han, Fabio Lapiccirella 1 Goermans-Williamson Algorithm for the maxcut problem
Chapter 5 Eigenvalues and Eigenvectors
 Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
a 11 a 12 a 11 a 12 a 13 a 21 a 22 a 23 . a 31 a 32 a 33 a 12 a 21 a 23 a 31 a = = = = 12
 24 8 Matrices Determinant of 2 2 matrix Given a 2 2 matrix [ ] a a A = 2 a 2 a 22 the real number a a 22 a 2 a 2 is determinant and denoted by det(a) = a a 2 a 2 a 22 Example 8 Find determinant of 2 2
24 8 Matrices Determinant of 2 2 matrix Given a 2 2 matrix [ ] a a A = 2 a 2 a 22 the real number a a 22 a 2 a 2 is determinant and denoted by det(a) = a a 2 a 2 a 22 Example 8 Find determinant of 2 2
Vectors and Matrices Statistics with Vectors and Matrices
 Vectors and Matrices Statistics with Vectors and Matrices Lecture 3 September 7, 005 Analysis Lecture #3-9/7/005 Slide 1 of 55 Today s Lecture Vectors and Matrices (Supplement A - augmented with SAS proc
Vectors and Matrices Statistics with Vectors and Matrices Lecture 3 September 7, 005 Analysis Lecture #3-9/7/005 Slide 1 of 55 Today s Lecture Vectors and Matrices (Supplement A - augmented with SAS proc

 Y G q G Y Y 29 8 $ 29 G 6 q )
Y G q G Y Y 29 8 $ 29 G 6 q )