A DARK GREY P O N T, with a Switch Tail, and a small Star on the Forehead. Any
|
|
|
- Sandra McKenzie
- 6 years ago
- Views:
Transcription
1 Y Y Y X X «/ YY Y Y ««Y x ) & \ & & } # Y \#$& / Y Y X» \\ / X X X x & Y Y X «q «z \x» = q Y # % \ & [ & Z \ & { + % ) / / «q zy» / & / / / & x x X / % % ) Y x X Y $ Z % Y Y x x } / % «] «] # z» & Y X» ) Y & ) «# ) ) & ) «) q «Y Z \ X = \«/% $ = / % \ & # Y ) % %«X q Z \ xy / & Y &» \ & ]» \ [ \ % Y % x Y «X= Y X x $ q «& x Y % $$x q & Z» $ xq & qx q q «xq % \ z X & & & Y / % x X» «/ Y ] x x & & & # \ & ±» % x «) «X $ q x & & { x z Y Y x &Z X \ & & % q x «\ & $ «± x x q» & x Y x» x / z z q x x & «x )» / Y x \ X Y &% $ \ % x Y Y x X Y X Y x = Y q % q % Y q] x ]»««x %= Y «% X» Y» { q ) x x x ]/& z q x / x & } & «% \ x x x z ) Y & q q ) q Y z & x q q q q x & & & «Y q Y ) q q z ) q \ X ) q q q / q x / % ) / ) X ) q & \ «q x ) )» & ) & & Y Y /& = q z «x ) «$ Y / q» # = ) Y «Y Y ) & x q x x q q ) x x q q \ Y «q $ x» & «% ) \ & x «{ x z x = «) Y x q = YY x & / x / } x $ q =
2 & x x x ) «q ± Z» q x x «q ) q» z Y x x q x Y «& \ q x X Z & «& / { $ ) x z q» q & q x \ q x »» x «& [ «» { q x / x q «% q / x Z z ) x / / x z x // / q ) ) x x / q x / q x )»» q» x q x q Y / x x ) / x x q q q q x % Y x q q» x # q q q Y q q & «q x x q x q q x q % q «/ x q q / % x «x q % x q x» X x»«q q # ]%» & & %«q X) &«& & qz x» &% X»» x x / % x & «{& & z» «x } & x & q { q q z «x ««q» x q q Y X x ) x Y %#]% Z% { X»» \ % x % \ # q x q & % # «) / q \ «z x\ / % %% q \ / & /» X x «& & q q / x x /[}\ x / x x x ) \ \ / \ q q x q q x \ q x x q x / [ / \ x q [ X/ $ / q x x «/ x x Y Z Y & q x Y & q z \ «z«)» \ } x x q x Z » x x / { Z \ x z q & x» z»»» / x x ««% z q Y q & q» q q $ z / q z x x xz)» / x $ x q «q x q x q Y q x x x Y x q x & & } % % x ] ))
3 &» Y Y ««[ x Y Y \ ) x ) «««) X Y Z Y x X ]»«x Y && x & Y X Y $» Y «/ X x «x» x ««/ x x # X $ &» X & X # x «] x z % ) $ & «» { X } / $ \»»»» # % & q «««q» x ) \ «& &» // \ \ Z X x»» » ) x q & & q x Y X Y «Y Y ) } Y» x ]»» X %& & & }} x & ) Y /»«x x x & Y & x «X X q$ \» x ] x & x Y » «««)» «&$& q q/ q \ x» Y$» / x» q \» = q q x % ««] & % «q && ] % x $ Y \ «) ) & Y X x «x / x & ) «««% x )) & Y x «x» x ] \ x q }) { & /» } x Y» / % \\ { Y x q x «] / ««) / q ««x q \ / x ] \ / \ «\ x \/«% [X««x» x ««z & «q X$ «[ Y / XY «x» & %X } Y { ) { x x x # x x / Y Y Y x ) q } ) $ q ) Y \ x x Y q & x x X) Y Y Y X Y «x/ Z q «z»»% q x «$ q ) /» q q x Y» x q) %»» x { «&& # [ q ) X \ ) Y } «) \«z \ q q ) \ q ) x & q q & \ & ] ] ] \ Y x X { / q % / / q» x «q % Y } q x x //«q ) % \ X) & &» «x x q / q ) Y ) Y «Y Y q Y ) x Y x z Y x» x x [ x Y Y \ & ) q» } {
4 \ )«) x ) & \ «x Z Z x q &»«\ q [ $ x & ] «x» Y) ) ) «x z ) & x x ««{ q ) \ ) ««X # ) ««q Y q q x» q «q» q x # z & «) q & # x«z q q{ % x ) z q x % z x x x Y ««& ) q x x q x«q q x q «& x q x» x q Y & x&xy ) % Y X) % Z & X q x Y x «q «Y x Y # q q& } q % x / q / ) x q ) x &#X)&\ Y ) q ) «/ X «q $ «[ # x / )» x x / x «q z Y X» ) «x / q x x z q ) z Y q x z $ z q ) $$ %} q q «««q q x q z x z «z q % q q q q x ) z «q % & «q»» & / q x» =»«+ «z «q») «Z x # q x q x / x & «x «/ Y $ & x % q» X z q q z z X Y Z / / & Z X x q» ) «z ) & x Y x \ z x / X Z»»» ) ««& / x Y q z q x q z x Y / x Y Y / / x q q x q z q Y $ q x { % \ «X % x & ]
5 q Y Y x q % %» «x« q z Y { X ] Y & & $ z \ X / / q x /» Z Y \ & Y \ Y Y / /»/ } q) x { } Y «Y q \ Z Y ) / Y / Y» & X q \ ) X q q Y q q x Y q x ) / q q } % \ X x &± q & & & & q ]«$ q q q q q q q x q q q q / q q q Y ) q x «\ \««/ \ q q /» «+ ) q x q q x q q q x Z Y q q Y q q Y Y q q x q q q x «X) q &\x) q q x Y q X q z / ) X q q X {±» q q X x» Y q q& / // Y q x q X Y & $ } q ) x q q q / q x / q Y X ) ) q q q Y q q q } z q z =««q x x q & Y Y q x & q x & & x q & x) & q & x q q & q \ q q / & q q % «» & x &» x q q q Z / x q q q q q q q x x q / q «Y Z Z q q q Y ] Y Y ) q Y q Y q q &«Y q q & x q q ) \\ q q ) z Y ) q q z z q x q) z q q x ) z ) z x z q } } q / x Y / q q z q q q q Y X Y ) z X & ] q x & q Y X } Y x / Y = / X X ) = q q = Y q ] Y Z x ) Y Y Y Y q x ) Y» X q & /// ) «) ) Y x \ ) x x q ) ) / /» Y X X x Y x q Y q % q q x x z» x z x q q x ) ) q { «x ) q x Y q q x x X q x X x x x / x q x X } q % x q x q x x x Y x Y X X») ) & ) Y q Y % X ] X ]
6 \ x» ) & ««z «) q ««{/ Y «x «/)««/ /» x q» } Y Y q Y ) x ] x \ q & q\ x )«# \ x \\ ««\\ x x Z x x Y ««q x x } ] ««$ X x ) \» x x \» z \ X /» «) x x x / q ) x ) Y q x [ Y z Y «/ \ q x ) q» Y» ) / % { «Y x qz q q % z q q x x Y Y x Y z x q z Y Z x q ] x x x «= x x ] q» Y X &» «Y z % z q q )» ) x / q x x x»«q «] x \ x \ [» ] x z \ \ q x x = «x q x / x x ) x x Y / ) x Y Y x Y q ] } ] x } x [ { Y \ z z ] x ] x x \Y [ x q \ q Y\ q z x ) x \ \ X } x ] Y Y z \ \ x z x q q q q q \ q q «z } q / X «z «) x»«««««/ Z [ ««) x q x x x» {
7 «} x &» » X x Y Z» «x q %» ) «x X /» ZZ ) )\ \ ««X» X «x z» % Y / Z } / / & «Y x Y x X «\ x «q «Z \ «q \ «[ q q x q «X \ x q q q ] q q q» [ x x )» & ) Y \ /» Z x ) \ «X ««««q «z»««««& q ««Y Y ) q q q x x ) / ) Y «) & { Y z Y x q q q x& z q Y q q /X Y q q q & } x Y X Y x & ) & Y Y» Y Y q q q» q % q & q q \ & ) x» x x x Y x Y & ] ) x Y «x Y x X x [ x Y Y Y & x q x x & «x x q x x Y X x Y Y q q x q x q» [ \ \««$ ) z x & & x x Y X ) x) x x x ] Y X z x x x x z = / Y Y Y Y q x Y q q «) x x / x Y Y ) Y Y x Y / x Y Y Y Y Y Y & & Y Y q q x q x x x x q Y Y Y x q $\ { Y q Y Y Y Y x & x x q q x x & x \/«// & )» / Y Y Y x x x ) x»«x X»/ / X Y x x q «// x Y Y x» x { q ««{ Y Y Y Y Y Y \ X \ / { Y [ Y & { & Y Y & x Y «Y Y x x» q \ x Y Y Y X \{ Y Y x X x Y XY % / Y» x» % « ] «% Y ] x x \ «\ «x Z q X x /»» x x x «x Y Y q «
8 Y z & \ x )» /»» q x q x x% x q q Y q % \» x q Y x q ««x x x z Y q» Y»«% \\ x x «% q «% «Y & [ { ) /» x Y Y «q Y \ ««q % q q «& Y Z Y & q / z z / Z X q x X / Y =X Y\ Z \ \ & ]» «x«\\ Z q q q / q x q x Z Z q «q x ] q / «x q )» ) «X ] ) ) x \ / } q q Y «Y x q q X x q q q «««Y q x q q / «q x & z q ] x } $ [ Z # q / \ xz % q Z & «) «\ z x X q q q \ x q z q q x } ) x x q q x x x «Y Y X & q x q x x %Z X) x Y & /Y x & \x X Y Y x x = x \ q x = \ x x \ x \ x x x & \ ) )\ x x = q ) & x» Y X & z & z Y X) \ ) x { )» X q \ / x / q { x q x x \ x == &± x q \ q x x x q x q q & x ) x q x / q»» q x & x \ / «««\ x & «/ [ x ) x z & = = = & q q z» } x = q \ ««««««x z» / \ x» & x x Y +»» «& Z ] «x x ««% q x \ ) «q z x } x / «} \ q x \» q q / q q «} Y / «\ «) x x z ) \ \ } «q x «Y X» «}
9 X Y Y «Y Y Y Y x Y Y Y \ Y Y ] Y» Y Y Y Y Y Y Y Y Y Y ) XX x x Y & Y Y Y & Y Y Y Y / Y» Y Y \\ Y Y Y Y % Y Y \ Y X Y Y Y Y X «YY Y Y Y Y ]\/ Y ± Y Y Y Y YY Y = Y Y Y Y Y X Y Y X Y Y x Y X Y x Y X Y YY Y x«z Y«% «Y Y Y / X Y Y x Y = Y Y \Y x Y Y & X & Y X Y» Y Y Y Y Y Y YY X Y Y Y Y Y Y Y Y Y Y Y Y» Y» Y Y Y Y Y Y X Y Y Y Y Y Y X Y Y X Y Y Y Y / Y Y & Y x \ X X Z ) Y ) / x / Y Y Y Z Y Y Z X Y Y Z [ Y Y } Y ] Y ) ) Y Y Z Y Z Y Y \ Y Y Y Y Y Y X Y { Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y X YY Y YY Y Y Y \ Y Y Y & Y % } Y Y Y Y Y Y Y Y X Y Y Y Y X X» X Y X Y \ «Y Y Y Y Y Y Y Y Y X\ / q Y ) Y / / X «Y Y Y x q Y q Y Y x Y q Y Z Y # x X ) Y $ Y x q x q q ] ) X x x x Y Y x & Z /// Y & Y Y X Y Y Y Y Y Y X X Y) Y Y Y Y Y ) Y X Y Y Y ) q Y Y ) Y Y Y Y Y Z Y Y Y Y X X Y Y Y Z Y Z YY Y Y [ Z & Y Y X Y Y X Y } Y Y X ) Y XY Y Y Y X Y Y Y Y Y Y Y Y Y Y Y Z Y Y \ Y Y & & & XY Y XY Y Y Y Y Y Y X = = Y Y Y & Y Y Y Y & Y Y Y Y Y & Y Y Y X Y X x Y Y Y Y & x & Y Y Y Y YY Y Y ) Y \ Y Y Y & &» X Y X Y Y $ Y YY Y Y Y X Y Y Y Y ) Y ZY Y Y Y Y YY X Y Y «\«Y Y X Y x Y Y Y & & X Y Y Y Y \Y )«Y Y Y X Y Y Y $ Y Y Y Y ) X x Y Y X X Y \ X Y Y Y Y Y Y \ Y Y Y Y» \ q Y Y Y Y Y q ) & q & q Y / \ q» q x \ Y X X X X\ Y Y x Y) Y \ Y X X Y Y Y»» Y Y X / X \ Y X X X / Y / / ) Y Y Y Y X Y % X Y /«$\ \ $&± x /» Y / / Z X Y Y Y «Y X X Y X Y %
10 ) \ \ ««X» Y / & ) x x q x x \»» q x x ] x q x x x x \ z X q x ) q # { «q z x x Y x X \ [ «) { ] \ q «q x x «q \ «x»»»» «/ & ] ) q Y x q» q x / x & ) x q x q z q q «x ) ) ««x x x z X x q q x x Y q x x x ««Y x x z q Y q x x x x / x x x x x x X x X x Y x x Y Y x q x ) x x Y x «Z XY } X Y Y Y Y Y Y Z Y Y Z Y Y Y Y Y Y «Y X Y Y Z Y Y Y Y X Y Y XY Y Y Y Y X Y Y X Y Y Y Y YY x q x \ \ x q x x ) z x x z q z Y \ z x q q & q q Y «««% «\Z x [ x x x = z Y q q & x q x q z ) x ) ) ) ) «) ]«Y Y ««« Y Y Y Y Y Y Y Y Y // Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y X X ) Y Y Y Y Y XY Y X Y Y Y Y Y YY Y Y YX Y X Y Y Y X Y Y Y Y Y Y X Y Y Y x & q x x x q x q q q x x z q x z x x z q x x ]» q ««Z = x»»» x
11 » x» }» % ] & «««) «q «] \ X & / x «/ Z «& &»» «Y «x x z ««x Y Y ) «Y & ) Y [ Y z x & X X\\ X \ ) \ z «Y «% x q x x & ) \» «X «\ x «x %»«X ZZ \ Z ) /» »» \ ««««) x»«% {» Y Z Z { x x ) x q = x q x ) x X Y Z ) x ) ) Y ) ) x \\ x z \ x x x x ) x X q q x x ) x Y Z Y & Y { x Y x x) x x Y «\Y» \ X «\» ) x Y X z & x q x x & \ x x q x x [ «{ Y Y Y / Y Y Y X Y x q x Y Z X ) Y x x z z z = z z z & = z ) = x q q q q q / q z x x / / / Y / # & Z Y q Y = = x z = z z z q x & x x & \ x x x x x x» $ x x Y = Y Y q x x q \«q q q ) ] x ) ) ) ) ) «& q ) x & q x q +«q «/ = x x x ) Y [ Y x / x \ X \ Y Y x Y» q [ «]» }» %» x % [»\\ Y) ) YX q x x Y \ Y x % q X X X X // X X / / X X» ±» \ ) \ q «q ) x ) \ «Y x X \ Y ) \ Y X \ Y Y \ Y x / x Y ) Y x ) \ /» Y / «) / // X Y Y Y X x Y Y } % Y x» \ \» «) / q XX // Y [ q ) q [ «q q q q q /q q q q q q q q { q ] q q q ] q q Y X } Y = q x = = q x \» «\ Y ) «\ Y / «/ \ \ \ XX ) «Y» x ««Y X «««) /X) / \% «\ \\ x \ X «}] ] } «= ) \ \» [» Y / % \ & X / ] Y % x «{ ««= z Y Z { «= \ = Z» » } «
12 X Y Y Y Z & Z «Y & Y Y» Y Y Y Y Y Y Y Y Y Y Y Y % Y Y Y Y Y Y X X Y Y Y XY Y Y X Y Y Y Y Y Y Y Y Y Y Y Y Y X Y Y Y Y Y Y Y X Y Y Y Y Y Y Y Y Y Y Y X Y Y Y Y Y Y Y \ X Y Z Y Y Y Y Y Y Y Y Y Y Y Y X Y Y Y Y Y ) Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y Y «Y Y Y Y Y Y Y Y Y Y Y x x x x z z z z \ q x x ««} X q ««q ) ) z ] ] «x x x z Y Y Y / z» z x x x Y x q ] )» ««\ ) q z x X Y q q x z x «$ xq $ &= = # q q q ] x x % q q q \ \ \ x z Y\ Y q ) / ] q x» z z Y \ Z q q z Y Z Y Y YY Y Y Y Y Y Y Y Y [ Y Z Y Y Y Z & «Y Y Y Y Y Y Y Y Y Y Y Y X Y Y z z & Y x & Y Y Y z z z x z z x x x q q x Y x q \ x Z Z z ) x \»«& = % x z \ )» x «/ Y q & & & & q z x x q q x x q x «Y x Y \» x q ) x % q q Z \ \ \ \ «z q ««\ \ «/ z q q \ { /x [ \ /x \ Y \ { } q\ x «\» \ Y \\ «««x ) z q q x q z ) }\ ] \ ) \\Y «X ] ) x «) «& / & x \\ Y Y Y Y Y Y Y X X Y »» \ \»» z q z « /» / ««Y Z Y Y / Y Y Y Y Y Y [ Y X «Y Y Y Y Y / / Y Y Y Y Y Z Y Y Y Y z x ) X ) «\ )= x ) Y \ ) Y Y Y x \ ««X
Two Posts to Fill On School Board
 Y Y 9 86 4 4 qz 86 x : ( ) z 7 854 Y x 4 z z x x 4 87 88 Y 5 x q x 8 Y 8 x x : 6 ; : 5 x ; 4 ( z ; ( ) ) x ; z 94 ; x 3 3 3 5 94 ; ; ; ; 3 x : 5 89 q ; ; x ; x ; ; x : ; ; ; ; ; ; 87 47% : () : / : 83
Y Y 9 86 4 4 qz 86 x : ( ) z 7 854 Y x 4 z z x x 4 87 88 Y 5 x q x 8 Y 8 x x : 6 ; : 5 x ; 4 ( z ; ( ) ) x ; z 94 ; x 3 3 3 5 94 ; ; ; ; 3 x : 5 89 q ; ; x ; x ; ; x : ; ; ; ; ; ; 87 47% : () : / : 83
A. H. Hall, 33, 35 &37, Lendoi
 7 X x > - z Z - ----»»x - % x x» [> Q - ) < % - - 7»- -Q 9 Q # 5 - z -> Q x > z»- ~» - x " < z Q q»» > X»? Q ~ - - % % < - < - - 7 - x -X - -- 6 97 9
7 X x > - z Z - ----»»x - % x x» [> Q - ) < % - - 7»- -Q 9 Q # 5 - z -> Q x > z»- ~» - x " < z Q q»» > X»? Q ~ - - % % < - < - - 7 - x -X - -- 6 97 9
OWELL WEEKLY JOURNAL
 Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
Y \»< - } Y Y Y & #»»» q ] q»»»>) & - - - } ) x ( - { Y» & ( x - (» & )< - Y X - & Q Q» 3 - x Q Y 6 \Y > Y Y X 3 3-9 33 x - - / - -»- --
and A L T O S O L O LOWELL, MICHIGAN, THURSDAY, OCTCBER Mrs. Thomas' Young Men Good Bye 66 Long Illness Have Sport in
 5 7 8 x z!! Y! [! 2 &>3 x «882 z 89 q!!! 2 Y 66 Y $ Y 99 6 x x 93 x 7 8 9 x 5$ 4 Y q Q 22 5 3 Z 2 5 > 2 52 2 $ 8» Z >!? «z???? q > + 66 + + ) ( x 4 ~ Y Y»» x ( «/ ] x ! «z x( ) x Y 8! < 6 x x 8 \ 4\
5 7 8 x z!! Y! [! 2 &>3 x «882 z 89 q!!! 2 Y 66 Y $ Y 99 6 x x 93 x 7 8 9 x 5$ 4 Y q Q 22 5 3 Z 2 5 > 2 52 2 $ 8» Z >!? «z???? q > + 66 + + ) ( x 4 ~ Y Y»» x ( «/ ] x ! «z x( ) x Y 8! < 6 x x 8 \ 4\
Educjatipnal. L a d ie s * COBNWALILI.S H IG H SCHOOL. I F O R G IR L S A n B k i n d e r g a r t e n.
 - - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
- - - 0 x ] - ) ) -? - Q - - z 0 x 8 - #? ) 80 0 0 Q ) - 8-8 - ) x ) - ) -] ) Q x?- x - - / - - x - - - x / /- Q ] 8 Q x / / - 0-0 0 x 8 ] ) / - - /- - / /? x ) x x Q ) 8 x q q q )- 8-0 0? - Q - - x?-
LOWELL WEEKLY JOURNAL
 Y -» $ 5 Y 7 Y Y -Y- Q x Q» 75»»/ q } # ]»\ - - $ { Q» / X x»»- 3 q $ 9 ) Y q - 5 5 3 3 3 7 Q q - - Q _»»/Q Y - 9 - - - )- [ X 7» -» - )»? / /? Q Y»» # X Q» - -?» Q ) Q \ Q - - - 3? 7» -? #»»» 7 - / Q
Y -» $ 5 Y 7 Y Y -Y- Q x Q» 75»»/ q } # ]»\ - - $ { Q» / X x»»- 3 q $ 9 ) Y q - 5 5 3 3 3 7 Q q - - Q _»»/Q Y - 9 - - - )- [ X 7» -» - )»? / /? Q Y»» # X Q» - -?» Q ) Q \ Q - - - 3? 7» -? #»»» 7 - / Q
II&Ij <Md Tmlaiiiiiit, aad once in Ihe y a w Teataa m i, the vmb thatalmta oot Uiaapirit world. into as abode or wotld by them- CooTBOtioa
 382 4 7 q X
382 4 7 q X
P A L A C E P IE R, S T. L E O N A R D S. R a n n o w, q u a r r y. W WALTER CR O TC H, Esq., Local Chairman. E. CO O PER EVANS, Esq.,.
 ? ( # [ ( 8? [ > 3 Q [ ««> » 9 Q { «33 Q> 8 \ \ 3 3 3> Q»«9 Q ««« 3 8 3 8 X \ [ 3 ( ( Z ( Z 3( 9 9 > < < > >? 8 98 ««3 ( 98 < # # Q 3 98? 98 > > 3 8 9 9 ««««> 3 «>
? ( # [ ( 8? [ > 3 Q [ ««> » 9 Q { «33 Q> 8 \ \ 3 3 3> Q»«9 Q ««« 3 8 3 8 X \ [ 3 ( ( Z ( Z 3( 9 9 > < < > >? 8 98 ««3 ( 98 < # # Q 3 98? 98 > > 3 8 9 9 ««««> 3 «>
LOWELL WEEKLY JOURNAL.
 Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
Y 5 ; ) : Y 3 7 22 2 F $ 7 2 F Q 3 q q 6 2 3 6 2 5 25 2 2 3 $2 25: 75 5 $6 Y q 7 Y Y # \ x Y : { Y Y Y : ( \ _ Y ( ( Y F [ F F ; x Y : ( : G ( ; ( ~ x F G Y ; \ Q ) ( F \ Q / F F \ Y () ( \ G Y ( ) \F
LOWELL WEEKI.Y JOURINAL
 / $ 8) 2 {!»!» X ( (!!!?! () ~ x 8» x /»!! $?» 8! ) ( ) 8 X x /! / x 9 ( 2 2! z»!!»! ) / x»! ( (»»!» [ ~!! 8 X / Q X x» ( (!»! Q ) X x X!! (? ( ()» 9 X»/ Q ( (X )!» / )! X» x / 6!»! }? ( q ( ) / X! 8 x»
/ $ 8) 2 {!»!» X ( (!!!?! () ~ x 8» x /»!! $?» 8! ) ( ) 8 X x /! / x 9 ( 2 2! z»!!»! ) / x»! ( (»»!» [ ~!! 8 X / Q X x» ( (!»! Q ) X x X!! (? ( ()» 9 X»/ Q ( (X )!» / )! X» x / 6!»! }? ( q ( ) / X! 8 x»
a s*:?:; -A: le London Dyers ^CleanefSt * S^d. per Y ard. -P W ..n 1 0, , c t o b e e d n e sd *B A J IllW6fAi>,EB. E D U ^ T IG r?
 ? 9 > 25? < ( x x 52 ) < x ( ) ( { 2 2 8 { 28 ] ( 297 «2 ) «2 2 97 () > Q ««5 > «? 2797 x 7 82 2797 Q z Q (
? 9 > 25? < ( x x 52 ) < x ( ) ( { 2 2 8 { 28 ] ( 297 «2 ) «2 2 97 () > Q ««5 > «? 2797 x 7 82 2797 Q z Q (
County Council Named for Kent
 \ Y Y 8 9 69 6» > 69 ««] 6 : 8 «V z 9 8 x 9 8 8 8?? 9 V q» :: q;; 8 x () «; 8 x ( z x 9 7 ; x >«\ 8 8 ; 7 z x [ q z «z : > ; ; ; ( 76 x ; x z «7 8 z ; 89 9 z > q _ x 9 : ; 6? ; ( 9 [ ) 89 _ ;»» «; x V
\ Y Y 8 9 69 6» > 69 ««] 6 : 8 «V z 9 8 x 9 8 8 8?? 9 V q» :: q;; 8 x () «; 8 x ( z x 9 7 ; x >«\ 8 8 ; 7 z x [ q z «z : > ; ; ; ( 76 x ; x z «7 8 z ; 89 9 z > q _ x 9 : ; 6? ; ( 9 [ ) 89 _ ;»» «; x V
MANY BILLS OF CONCERN TO PUBLIC
 - 6 8 9-6 8 9 6 9 XXX 4 > -? - 8 9 x 4 z ) - -! x - x - - X - - - - - x 00 - - - - - x z - - - x x - x - - - - - ) x - - - - - - 0 > - 000-90 - - 4 0 x 00 - -? z 8 & x - - 8? > 9 - - - - 64 49 9 x - -
- 6 8 9-6 8 9 6 9 XXX 4 > -? - 8 9 x 4 z ) - -! x - x - - X - - - - - x 00 - - - - - x z - - - x x - x - - - - - ) x - - - - - - 0 > - 000-90 - - 4 0 x 00 - -? z 8 & x - - 8? > 9 - - - - 64 49 9 x - -
' Liberty and Umou Ono and Inseparablo "
 3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
Q SON,' (ESTABLISHED 1879L
 ( < 5(? Q 5 9 7 00 9 0 < 6 z 97 ( # ) $ x 6 < ( ) ( ( 6( ( ) ( $ z 0 z z 0 ) { ( % 69% ( ) x 7 97 z ) 7 ) ( ) 6 0 0 97 )( 0 x 7 97 5 6 ( ) 0 6 ) 5 ) 0 ) 9%5 z» 0 97 «6 6» 96? 0 96 5 0 ( ) ( ) 0 x 6 0
( < 5(? Q 5 9 7 00 9 0 < 6 z 97 ( # ) $ x 6 < ( ) ( ( 6( ( ) ( $ z 0 z z 0 ) { ( % 69% ( ) x 7 97 z ) 7 ) ( ) 6 0 0 97 )( 0 x 7 97 5 6 ( ) 0 6 ) 5 ) 0 ) 9%5 z» 0 97 «6 6» 96? 0 96 5 0 ( ) ( ) 0 x 6 0
oenofc : COXT&IBCTOEU. AU skaacst sftwer thsa4 aafcekr will be ehat«s«ai Bi. C. W. JUBSSOS. PERFECT THBOUGH SDFFEBISG. our
 x V - --- < x x 35 V? 3?/ -V 3 - ) - - [ Z8 - & Z - - - - - x 0-35 - 3 75 3 33 09 33 5 \ - - 300 0 ( -? 9 { - - - -- - < - V 3 < < - - Z 7 - z 3 - [ } & _ 3 < 3 ( 5 7< ( % --- /? - / 4-4 - & - % 4 V 2
x V - --- < x x 35 V? 3?/ -V 3 - ) - - [ Z8 - & Z - - - - - x 0-35 - 3 75 3 33 09 33 5 \ - - 300 0 ( -? 9 { - - - -- - < - V 3 < < - - Z 7 - z 3 - [ } & _ 3 < 3 ( 5 7< ( % --- /? - / 4-4 - & - % 4 V 2
LOWELL WEEKLY JOURNAL
 G $ G 2 G ««2 ««q ) q «\ { q «««/ 6 «««««q «] «q 6 ««Z q «««Q \ Q «q «X ««G X G ««? G Q / Q Q X ««/«X X «««Q X\ «q «X \ / X G XX «««X «x «X «x X G X 29 2 ««Q G G «) 22 G XXX GG G G G G G X «x G Q «) «G
G $ G 2 G ««2 ««q ) q «\ { q «««/ 6 «««««q «] «q 6 ««Z q «««Q \ Q «q «X ««G X G ««? G Q / Q Q X ««/«X X «««Q X\ «q «X \ / X G XX «««X «x «X «x X G X 29 2 ««Q G G «) 22 G XXX GG G G G G G X «x G Q «) «G
A Memorial. Death Crash Branch Out. Symbol The. at Crossing Flaming Poppy. in Belding
 - G Y Y 8 9 XXX G - Y - Q 5 8 G Y G Y - - * Y G G G G 9 - G - - : - G - - ) G G- Y G G q G G : Q G Y G 5) Y : z 6 86 ) ; - ) z; G ) 875 ; ) ; G -- ) ; Y; ) G 8 879 99 G 9 65 q 99 7 G : - G G Y ; - G 8
- G Y Y 8 9 XXX G - Y - Q 5 8 G Y G Y - - * Y G G G G 9 - G - - : - G - - ) G G- Y G G q G G : Q G Y G 5) Y : z 6 86 ) ; - ) z; G ) 875 ; ) ; G -- ) ; Y; ) G 8 879 99 G 9 65 q 99 7 G : - G G Y ; - G 8
LOWELL WEEKLY JOURNAL.
 Y $ Y Y 7 27 Y 2» x 7»» 2» q» ~ [ } q q $ $ 6 2 2 2 2 2 2 7 q > Y» Y >» / Y» ) Y» < Y»» _»» < Y > Y Y < )»» >» > ) >» >> >Y x x )»» > Y Y >>»» }> ) Y < >» /» Y x» > / x /»»»»» >» >» >»» > > >» < Y /~ >
Y $ Y Y 7 27 Y 2» x 7»» 2» q» ~ [ } q q $ $ 6 2 2 2 2 2 2 7 q > Y» Y >» / Y» ) Y» < Y»» _»» < Y > Y Y < )»» >» > ) >» >> >Y x x )»» > Y Y >>»» }> ) Y < >» /» Y x» > / x /»»»»» >» >» >»» > > >» < Y /~ >
LOWELL WEEKLY JOURNAL
 Y G y G Y 87 y Y 8 Y - $ X ; ; y y q 8 y $8 $ $ $ G 8 q < 8 6 4 y 8 7 4 8 8 < < y 6 $ q - - y G y G - Y y y 8 y y y Y Y 7-7- G - y y y ) y - y y y y - - y - y 87 7-7- G G < G y G y y 6 X y G y y y 87 G
Y G y G Y 87 y Y 8 Y - $ X ; ; y y q 8 y $8 $ $ $ G 8 q < 8 6 4 y 8 7 4 8 8 < < y 6 $ q - - y G y G - Y y y 8 y y y Y Y 7-7- G - y y y ) y - y y y y - - y - y 87 7-7- G G < G y G y y 6 X y G y y y 87 G
ACCEPTS HUGE FLORAL KEY TO LOWELL. Mrs, Walter Laid to Rest Yesterday
 $ j < < < > XXX Y 928 23 Y Y 4% Y 6 -- Q 5 9 2 5 Z 48 25 )»-- [ Y Y Y & 4 j q - Y & Y 7 - -- - j \ -2 -- j j -2 - - - - [ - - / - ) ) - - / j Y 72 - ) 85 88 - / X - j ) \ 7 9 Y Y 2 3» - ««> Y 2 5 35 Y
$ j < < < > XXX Y 928 23 Y Y 4% Y 6 -- Q 5 9 2 5 Z 48 25 )»-- [ Y Y Y & 4 j q - Y & Y 7 - -- - j \ -2 -- j j -2 - - - - [ - - / - ) ) - - / j Y 72 - ) 85 88 - / X - j ) \ 7 9 Y Y 2 3» - ««> Y 2 5 35 Y
LOWELL. MICHIGAN, OCTOBER morning for Owen J. Howard, M last Friday in Blodpett hospital.
 G GG Y G 9 Y- Y 77 8 Q / x -! -} 77 - - # - - - - 0 G? x? x - - V - x - -? : : - q -8 : : - 8 - q x V - - - )?- X - - 87 X - ::! x - - -- - - x -- - - - )0 0 0 7 - - 0 q - V -
G GG Y G 9 Y- Y 77 8 Q / x -! -} 77 - - # - - - - 0 G? x? x - - V - x - -? : : - q -8 : : - 8 - q x V - - - )?- X - - 87 X - ::! x - - -- - - x -- - - - )0 0 0 7 - - 0 q - V -
L bor y nnd Union One nnd Inseparable. LOW I'LL, MICHIGAN. WLDNHSDA Y. JULY ), I8T. liuwkll NATIdiNAI, liank
 G k y $5 y / >/ k «««# ) /% < # «/» Y»««««?# «< >«>» y k»» «k F 5 8 Y Y F G k F >«y y
G k y $5 y / >/ k «««# ) /% < # «/» Y»««««?# «< >«>» y k»» «k F 5 8 Y Y F G k F >«y y
LOWELL JOURNAL. MUST APOLOGIZE. such communication with the shore as Is m i Boimhle, noewwary and proper for the comfort
 - 7 7 Z 8 q ) V x - X > q - < Y Y X V - z - - - - V - V - q \ - q q < -- V - - - x - - V q > x - x q - x q - x - - - 7 -» - - - - 6 q x - > - - x - - - x- - - q q - V - x - - ( Y q Y7 - >»> - x Y - ] [
- 7 7 Z 8 q ) V x - X > q - < Y Y X V - z - - - - V - V - q \ - q q < -- V - - - x - - V q > x - x q - x q - x - - - 7 -» - - - - 6 q x - > - - x - - - x- - - q q - V - x - - ( Y q Y7 - >»> - x Y - ] [
..«W- tn^zmxmmrrx/- NEW STORE. Popular Goods at Popular D. E. SPRING, Mas just opened a large fdo.k of DRY GOODS & GROCERIES,
 B y «X }() z zxx/ X y y y y )3 y «y
B y «X }() z zxx/ X y y y y )3 y «y
THE I Establiifrad June, 1893
 89 : 8 Y Y 2 96 6 - - : - 2 q - 26 6 - - q 2 2 2 4 6 4«4 ' V () 8 () 6 64-4 '2" () 6 ( ) * 'V ( 4 ) 94-4 q ( / ) K ( x- 6% j 9*V 2'%" 222 27 q - - K 79-29 - K x 2 2 j - -% K 4% 2% 6% ' K - 2 47 x - - j
89 : 8 Y Y 2 96 6 - - : - 2 q - 26 6 - - q 2 2 2 4 6 4«4 ' V () 8 () 6 64-4 '2" () 6 ( ) * 'V ( 4 ) 94-4 q ( / ) K ( x- 6% j 9*V 2'%" 222 27 q - - K 79-29 - K x 2 2 j - -% K 4% 2% 6% ' K - 2 47 x - - j
Neatest and Promptest Manner. E d i t u r ami rul)lihher. FOIt THE CIIILDIIES'. Trifles.
 » ~ $ ) 7 x X ) / ( 8 2 X 39 ««x» ««! «! / x? \» «({? «» q «(? (?? x! «? 8? ( z x x q? ) «q q q ) x z x 69 7( X X ( 3»«! ( ~«x ««x ) (» «8 4 X «4 «4 «8 X «x «(» X) ()»» «X «97 X X X 4 ( 86) x) ( ) z z
» ~ $ ) 7 x X ) / ( 8 2 X 39 ««x» ««! «! / x? \» «({? «» q «(? (?? x! «? 8? ( z x x q? ) «q q q ) x z x 69 7( X X ( 3»«! ( ~«x ««x ) (» «8 4 X «4 «4 «8 X «x «(» X) ()»» «X «97 X X X 4 ( 86) x) ( ) z z
Governor Green Triumphs Over Mudslinging
 ; XXX 6 928 - x 22 5 Q 0 x 2- Q- & & x 30 - x 93000000 95000000 50 000 x 0:30 7 7 2 x q 9 0 0:30 2;00 7:30 9 ( 9 & ( ( - ( - 225000 x ( ( 800 ) - 70000 200000 - x ; 200-0: 3333 0850; 778: 5-38 090; 002;
; XXX 6 928 - x 22 5 Q 0 x 2- Q- & & x 30 - x 93000000 95000000 50 000 x 0:30 7 7 2 x q 9 0 0:30 2;00 7:30 9 ( 9 & ( ( - ( - 225000 x ( ( 800 ) - 70000 200000 - x ; 200-0: 3333 0850; 778: 5-38 090; 002;
Crew of25 Men Start Monday On Showboat. Many Permanent Improvements To Be Made;Project Under WPA
 U G G G U 2 93 YX Y q 25 3 < : z? 0 (? 8 0 G 936 x z x z? \ 9 7500 00? 5 q 938 27? 60 & 69? 937 q? G x? 937 69 58 } x? 88 G # x 8 > x G 0 G 0 x 8 x 0 U 93 6 ( 2 x : X 7 8 G G G q x U> x 0 > x < x G U 5
U G G G U 2 93 YX Y q 25 3 < : z? 0 (? 8 0 G 936 x z x z? \ 9 7500 00? 5 q 938 27? 60 & 69? 937 q? G x? 937 69 58 } x? 88 G # x 8 > x G 0 G 0 x 8 x 0 U 93 6 ( 2 x : X 7 8 G G G q x U> x 0 > x < x G U 5
LOWELL WEEKLY JOURNAL. ^Jberxy and (Jmott Oao M d Ccmsparftble. %m >ai ruv GEEAT INDUSTRIES
 ? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
Lecture 8 Analyzing the diffusion weighted signal. Room CSB 272 this week! Please install AFNI
 Lecture 8 Analyzing the diffusion weighted signal Room CSB 272 this week! Please install AFNI http://afni.nimh.nih.gov/afni/ Next lecture, DTI For this lecture, think in terms of a single voxel We re still
Lecture 8 Analyzing the diffusion weighted signal Room CSB 272 this week! Please install AFNI http://afni.nimh.nih.gov/afni/ Next lecture, DTI For this lecture, think in terms of a single voxel We re still
A b r i l l i a n t young chemist, T h u r e Wagelius of N e w Y o r k, ac. himself with eth
 6 6 0 x J 8 0 J 0 z (0 8 z x x J x 6 000 X j x "" "" " " x " " " x " " " J " " " " " " " " x : 0 z j ; J K 0 J K q 8 K K J x 0 j " " > J x J j z ; j J q J 0 0 8 K J 60 : K 6 x 8 K J :? 0 J J K 0 6% 8 0
6 6 0 x J 8 0 J 0 z (0 8 z x x J x 6 000 X j x "" "" " " x " " " x " " " J " " " " " " " " x : 0 z j ; J K 0 J K q 8 K K J x 0 j " " > J x J j z ; j J q J 0 0 8 K J 60 : K 6 x 8 K J :? 0 J J K 0 6% 8 0
Homework 1/Solutions. Graded Exercises
 MTH 310-3 Abstract Algebra I and Number Theory S18 Homework 1/Solutions Graded Exercises Exercise 1. Below are parts of the addition table and parts of the multiplication table of a ring. Complete both
MTH 310-3 Abstract Algebra I and Number Theory S18 Homework 1/Solutions Graded Exercises Exercise 1. Below are parts of the addition table and parts of the multiplication table of a ring. Complete both
LOWELL WEEKLY JOURNAL
 KY Y 872 K & q $ < 9 2 q 4 8 «7 K K K «> 2 26 8 5 4 4 7»» 2 & K q 4 [«5 «$6 q X «K «8K K88 K 7 ««$25 K Q ««q 8 K K Y & 7K /> Y 8«#»«Y 87 8 Y 4 KY «7««X & Y» K ) K K 5 KK K > K» Y Y 8 «KK > /» >» 8 K X
KY Y 872 K & q $ < 9 2 q 4 8 «7 K K K «> 2 26 8 5 4 4 7»» 2 & K q 4 [«5 «$6 q X «K «8K K88 K 7 ««$25 K Q ««q 8 K K Y & 7K /> Y 8«#»«Y 87 8 Y 4 KY «7««X & Y» K ) K K 5 KK K > K» Y Y 8 «KK > /» >» 8 K X
M E M P H I S, T E N N., S A T U E D A Y, OCTOBER 8, 1870.
 5 L V 8 5 x - L : L Q ) L - \ \ Q Q - V 84 z < L L 4 Y z ( (
5 L V 8 5 x - L : L Q ) L - \ \ Q Q - V 84 z < L L 4 Y z ( (
LOWHLL #WEEKLY JOURNAL.
 # F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
# F 7 F --) 2 9 Q - Q - - F - x $ 2 F? F \ F q - x q - - - - )< - -? - F - - Q z 2 Q - x -- - - - 3 - % 3 3 - - ) F x - \ - - - - - q - q - - - - -z- < F 7-7- - Q F 2 F - F \x -? - - - - - z - x z F -
LOWELL WEEKLY JOURNAL
 : Y J G V $ 5 V V G Y 2 25 Y 2» 5 X # VG q q q 6 6 X J 6 $3 ( 6 2 6 2 6 25 3 2 6 Y q 2 25: JJ JJ < X Q V J J Y J Q V (» Y V X Y? G # V Y J J J G J»Y ) J J / J Y Y X ({ G #? J Y ~» 9? ) < ( J VY Y J G (
: Y J G V $ 5 V V G Y 2 25 Y 2» 5 X # VG q q q 6 6 X J 6 $3 ( 6 2 6 2 6 25 3 2 6 Y q 2 25: JJ JJ < X Q V J J Y J Q V (» Y V X Y? G # V Y J J J G J»Y ) J J / J Y Y X ({ G #? J Y ~» 9? ) < ( J VY Y J G (
r/lt.i Ml s." ifcr ' W ATI II. The fnncrnl.icniccs of Mr*. John We mil uppn our tcpiiblicnn rcprc Died.
 $ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
$ / / - (\ \ - ) # -/ ( - ( [ & - - - - \ - - ( - - - - & - ( ( / - ( \) Q & - - { Q ( - & - ( & q \ ( - ) Q - - # & - - - & - - - $ - 6 - & # - - - & -- - - - & 9 & q - / \ / - - - -)- - ( - - 9 - - -
W i n t e r r e m e m b e r t h e W O O L L E N S. W rite to the M anageress RIDGE LAUNDRY, ST. H E LE N S. A uction Sale.
 > 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
> 7? 8 «> ««0? [ -! ««! > - ««>« ------------ - 7 7 7 = - Q9 8 7 ) [ } Q ««
' '-'in.-i 1 'iritt in \ rrivfi pr' 1 p. ru
 V X X Y Y 7 VY Y Y F # < F V 6 7»< V q q $ $» q & V 7» Q F Y Q 6 Q Y F & Q &» & V V» Y V Y [ & Y V» & VV & F > V } & F Q \ Q \» Y / 7 F F V 7 7 x» > QX < #» > X >» < F & V F» > > # < q V 6 & Y Y q < &
V X X Y Y 7 VY Y Y F # < F V 6 7»< V q q $ $» q & V 7» Q F Y Q 6 Q Y F & Q &» & V V» Y V Y [ & Y V» & VV & F > V } & F Q \ Q \» Y / 7 F F V 7 7 x» > QX < #» > X >» < F & V F» > > # < q V 6 & Y Y q < &
PanHomc'r I'rui;* :".>r '.a'' W"»' I'fltolt. 'j'l :. r... Jnfii<on. Kslaiaaac. <.T i.. %.. 1 >
 5 28 (x / &» )»(»»» Q ( 3 Q» (» ( (3 5» ( q 2 5 q 2 5 5 8) 5 2 2 ) ~ ( / x {» /»»»»» (»»» ( 3 ) / & Q ) X ] Q & X X X x» 8 ( &» 2 & % X ) 8 x & X ( #»»q 3 ( ) & X 3 / Q X»»» %» ( z 22 (»» 2» }» / & 2 X
5 28 (x / &» )»(»»» Q ( 3 Q» (» ( (3 5» ( q 2 5 q 2 5 5 8) 5 2 2 ) ~ ( / x {» /»»»»» (»»» ( 3 ) / & Q ) X ] Q & X X X x» 8 ( &» 2 & % X ) 8 x & X ( #»»q 3 ( ) & X 3 / Q X»»» %» ( z 22 (»» 2» }» / & 2 X
Closed-Form Solution Of Absolute Orientation Using Unit Quaternions
 Closed-Form Solution Of Absolute Orientation Using Unit Berthold K. P. Horn Department of Computer and Information Sciences November 11, 2004 Outline 1 Introduction 2 3 The Problem Given: two sets of corresponding
Closed-Form Solution Of Absolute Orientation Using Unit Berthold K. P. Horn Department of Computer and Information Sciences November 11, 2004 Outline 1 Introduction 2 3 The Problem Given: two sets of corresponding
A L T O SOLO LOWCLL. MICHIGAN, THURSDAY. DECEMBER 10,1931. ritt. Mich., to T h e Heights. Bos" l u T H I S COMMl'NiTY IN Wilcox
 G 093 < 87 G 9 G 4 4 / - G G 3 -!! - # -G G G : 49 q» - 43 8 40 - q - z 4 >» «9 0-9 - - q 00! - - q q!! ) 5 / : \ 0 5 - Z : 9 [ -?! : ) 5 - - > - 8 70 / q - - - X!! - [ 48 - -!
G 093 < 87 G 9 G 4 4 / - G G 3 -!! - # -G G G : 49 q» - 43 8 40 - q - z 4 >» «9 0-9 - - q 00! - - q q!! ) 5 / : \ 0 5 - Z : 9 [ -?! : ) 5 - - > - 8 70 / q - - - X!! - [ 48 - -!
MATH 19520/51 Class 5
 MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
MATH 19520/51 Class 5 Minh-Tam Trinh University of Chicago 2017-10-04 1 Definition of partial derivatives. 2 Geometry of partial derivatives. 3 Higher derivatives. 4 Definition of a partial differential
. ^e Traveler in taesnok. i the IHilty.-^ifStiiart. BbUaaoa aad WalL.""ras 'crossing a mountain»h ch w e are A«ply inteiwted. Add
 x 8[ x [qqq xq F x & R FX G NR F XN R X ( F R Y
x 8[ x [qqq xq F x & R FX G NR F XN R X ( F R Y
i r-s THE MEMPHIS, TENN., SATURDAY. DEGfMBER
 N k Q2 90 k ( < 5 q v k 3X3 0 2 3 Q :: Y? X k 3 : \ N 2 6 3 N > v N z( > > :}9 [ ( k v >63 < vq 9 > k k x k k v 6> v k XN Y k >> k < v Y X X X NN Y 2083 00 N > N Y Y N 0 \ 9>95 z {Q ]k3 Q k x k k z x X
N k Q2 90 k ( < 5 q v k 3X3 0 2 3 Q :: Y? X k 3 : \ N 2 6 3 N > v N z( > > :}9 [ ( k v >63 < vq 9 > k k x k k v 6> v k XN Y k >> k < v Y X X X NN Y 2083 00 N > N Y Y N 0 \ 9>95 z {Q ]k3 Q k x k k z x X
" W I T H M: A. L I G E T O ' W ^ P L D IST O ISTE -A-IsTD G H! A-I^IT Y IPO PL A.LI-i. :
 : D D! Y : V Y JY 4 96 J z z Y &! 0 6 4 J 6 4 0 D q & J D J» Y j D J & D & Y = x D D DZ Z # D D D D D D V X D DD X D \ J D V & Q D D Y D V D D? q ; J j j \V ; q» 0 0 j \\ j! ; \?) j: ; : x DD D J J j ;
: D D! Y : V Y JY 4 96 J z z Y &! 0 6 4 J 6 4 0 D q & J D J» Y j D J & D & Y = x D D DZ Z # D D D D D D V X D DD X D \ J D V & Q D D Y D V D D? q ; J j j \V ; q» 0 0 j \\ j! ; \?) j: ; : x DD D J J j ;
14.7: Maxima and Minima
 14.7: Maxima and Minima Marius Ionescu October 29, 2012 Marius Ionescu () 14.7: Maxima and Minima October 29, 2012 1 / 13 Local Maximum and Local Minimum Denition Marius Ionescu () 14.7: Maxima and Minima
14.7: Maxima and Minima Marius Ionescu October 29, 2012 Marius Ionescu () 14.7: Maxima and Minima October 29, 2012 1 / 13 Local Maximum and Local Minimum Denition Marius Ionescu () 14.7: Maxima and Minima
Lecture 4: Least Squares (LS) Estimation
 ME 233, UC Berkeley, Spring 2014 Xu Chen Lecture 4: Least Squares (LS) Estimation Background and general solution Solution in the Gaussian case Properties Example Big picture general least squares estimation:
ME 233, UC Berkeley, Spring 2014 Xu Chen Lecture 4: Least Squares (LS) Estimation Background and general solution Solution in the Gaussian case Properties Example Big picture general least squares estimation:
Department of mathematics MA201 Mathematics III
 Department of mathematics MA201 Mathematics III Academic Year 2015-2016 Model Solutions: Quiz-II (Set - B) 1. Obtain the bilinear transformation which maps the points z 0, 1, onto the points w i, 1, i
Department of mathematics MA201 Mathematics III Academic Year 2015-2016 Model Solutions: Quiz-II (Set - B) 1. Obtain the bilinear transformation which maps the points z 0, 1, onto the points w i, 1, i
Complex Variables. Chapter 2. Analytic Functions Section Harmonic Functions Proofs of Theorems. March 19, 2017
 Complex Variables Chapter 2. Analytic Functions Section 2.26. Harmonic Functions Proofs of Theorems March 19, 2017 () Complex Variables March 19, 2017 1 / 5 Table of contents 1 Theorem 2.26.1. 2 Theorem
Complex Variables Chapter 2. Analytic Functions Section 2.26. Harmonic Functions Proofs of Theorems March 19, 2017 () Complex Variables March 19, 2017 1 / 5 Table of contents 1 Theorem 2.26.1. 2 Theorem
Unit IV State of stress in Three Dimensions
 Unit IV State of stress in Three Dimensions State of stress in Three Dimensions References Punmia B.C.,"Theory of Structures" (SMTS) Vol II, Laxmi Publishing Pvt Ltd, New Delhi 2004. Rattan.S.S., "Strength
Unit IV State of stress in Three Dimensions State of stress in Three Dimensions References Punmia B.C.,"Theory of Structures" (SMTS) Vol II, Laxmi Publishing Pvt Ltd, New Delhi 2004. Rattan.S.S., "Strength
Polynomials. In many problems, it is useful to write polynomials as products. For example, when solving equations: Example:
 Polynomials Monomials: 10, 5x, 3x 2, x 3, 4x 2 y 6, or 5xyz 2. A monomial is a product of quantities some of which are unknown. Polynomials: 10 + 5x 3x 2 + x 3, or 4x 2 y 6 + 5xyz 2. A polynomial is a
Polynomials Monomials: 10, 5x, 3x 2, x 3, 4x 2 y 6, or 5xyz 2. A monomial is a product of quantities some of which are unknown. Polynomials: 10 + 5x 3x 2 + x 3, or 4x 2 y 6 + 5xyz 2. A polynomial is a
IOAN ŞERDEAN, DANIEL SITARU
 Romanian Mathematical Magazine Web: http://www.ssmrmh.ro The Author: This article is published with open access. TRIGONOMETRIC SUBSTITUTIONS IN PROBLEM SOLVING PART IOAN ŞERDEAN, DANIEL SITARU Abstract.
Romanian Mathematical Magazine Web: http://www.ssmrmh.ro The Author: This article is published with open access. TRIGONOMETRIC SUBSTITUTIONS IN PROBLEM SOLVING PART IOAN ŞERDEAN, DANIEL SITARU Abstract.
Stress transformation and Mohr s circle for stresses
 Stress transformation and Mohr s circle for stresses 1.1 General State of stress Consider a certain body, subjected to external force. The force F is acting on the surface over an area da of the surface.
Stress transformation and Mohr s circle for stresses 1.1 General State of stress Consider a certain body, subjected to external force. The force F is acting on the surface over an area da of the surface.
Exercise 1: Inertia moment of a simple pendulum
 Exercise : Inertia moment of a simple pendulum A simple pendulum is represented in Figure. Three reference frames are introduced: R is the fixed/inertial RF, with origin in the rotation center and i along
Exercise : Inertia moment of a simple pendulum A simple pendulum is represented in Figure. Three reference frames are introduced: R is the fixed/inertial RF, with origin in the rotation center and i along
Kent Co. Received Red Cross Service Abundantly in ' 4 9 E
 G N GN Y 95 89 N - q» B < ) < - 9 - - - - q ( B 6 - q - Q» x x 8 {) N - 9» -
G N GN Y 95 89 N - q» B < ) < - 9 - - - - q ( B 6 - q - Q» x x 8 {) N - 9» -
AE/ME 339. K. M. Isaac Professor of Aerospace Engineering. 12/21/01 topic7_ns_equations 1
 AE/ME 339 Professor of Aerospace Engineering 12/21/01 topic7_ns_equations 1 Continuity equation Governing equation summary Non-conservation form D Dt. V 0.(2.29) Conservation form ( V ) 0...(2.33) t 12/21/01
AE/ME 339 Professor of Aerospace Engineering 12/21/01 topic7_ns_equations 1 Continuity equation Governing equation summary Non-conservation form D Dt. V 0.(2.29) Conservation form ( V ) 0...(2.33) t 12/21/01
Example 1. Show that the shaded triangle is a (3, 4, 5) triangle.
 Example 1. Show that the shaded triangle is a (3, 4, 5) triangle. Solution to Example 1. Show that the shaded triangle C is a (3, 4, 5)-triangle. E D t C 4 T t 4 4 Solution. Suppose each side of the square
Example 1. Show that the shaded triangle is a (3, 4, 5) triangle. Solution to Example 1. Show that the shaded triangle C is a (3, 4, 5)-triangle. E D t C 4 T t 4 4 Solution. Suppose each side of the square
Bidiagonal pairs, Tridiagonal pairs, Lie algebras, and Quantum Groups
 Bidiagonal pairs, Tridiagonal pairs, Lie algebras, and Quantum Groups Darren Funk-Neubauer Department of Mathematics and Physics Colorado State University - Pueblo Pueblo, Colorado, USA darren.funkneubauer@colostate-pueblo.edu
Bidiagonal pairs, Tridiagonal pairs, Lie algebras, and Quantum Groups Darren Funk-Neubauer Department of Mathematics and Physics Colorado State University - Pueblo Pueblo, Colorado, USA darren.funkneubauer@colostate-pueblo.edu
E S T A B L IS H E D. n AT Tnn G.D.O. r.w.-bal'eu. e d n e s d a y. II GRANVILLE HOUSE. GATJDICK ROAD. MEADS. EASTBOUENk
 K q X k K 5 ) ) 5 / K K x x) )? //? q? k X z K 8 5 5? K K K / / $8 ± K K K 8 K / 8 K K X k k X ) k k /» / K / / / k / ] 5 % k / / k k? Z k K ] 8 K K K )» 5 ) # 8 q»)kk q»» )88{ k k k k / k K X 8 8 8 ]
K q X k K 5 ) ) 5 / K K x x) )? //? q? k X z K 8 5 5? K K K / / $8 ± K K K 8 K / 8 K K X k k X ) k k /» / K / / / k / ] 5 % k / / k k? Z k K ] 8 K K K )» 5 ) # 8 q»)kk q»» )88{ k k k k / k K X 8 8 8 ]
1871. twadaa t, 30 cta. pat Haa;fe,ttaw Spiritism. From Uis luport of tie vision, and in U e n i e h t i a d i W A C h r f i
 V < > X Q x X > >! 5> V3 23 3 - - - : -- { - -- (!! - - - -! :- 4 -- : -- -5--4 X -
V < > X Q x X > >! 5> V3 23 3 - - - : -- { - -- (!! - - - -! :- 4 -- : -- -5--4 X -
GG303 Lecture 6 8/27/09 1 SCALARS, VECTORS, AND TENSORS
 GG303 Lecture 6 8/27/09 1 SCALARS, VECTORS, AND TENSORS I Main Topics A Why deal with tensors? B Order of scalars, vectors, and tensors C Linear transformation of scalars and vectors (and tensors) II Why
GG303 Lecture 6 8/27/09 1 SCALARS, VECTORS, AND TENSORS I Main Topics A Why deal with tensors? B Order of scalars, vectors, and tensors C Linear transformation of scalars and vectors (and tensors) II Why
JUST THE MATHS UNIT NUMBER ORDINARY DIFFERENTIAL EQUATIONS 3 (First order equations (C)) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 15.3 ORDINARY DIFFERENTIAL EQUATIONS 3 (First order equations (C)) by A.J.Hobson 15.3.1 Linear equations 15.3.2 Bernouilli s equation 15.3.3 Exercises 15.3.4 Answers to exercises
JUST THE MATHS UNIT NUMBER 15.3 ORDINARY DIFFERENTIAL EQUATIONS 3 (First order equations (C)) by A.J.Hobson 15.3.1 Linear equations 15.3.2 Bernouilli s equation 15.3.3 Exercises 15.3.4 Answers to exercises
Math 10 - Unit 5 Final Review - Polynomials
 Class: Date: Math 10 - Unit 5 Final Review - Polynomials Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Factor the binomial 44a + 99a 2. a. a(44 + 99a)
Class: Date: Math 10 - Unit 5 Final Review - Polynomials Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Factor the binomial 44a + 99a 2. a. a(44 + 99a)
MECH 5312 Solid Mechanics II. Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso
 MECH 5312 Solid Mechanics II Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso Table of Contents Preliminary Math Concept of Stress Stress Components Equilibrium
MECH 5312 Solid Mechanics II Dr. Calvin M. Stewart Department of Mechanical Engineering The University of Texas at El Paso Table of Contents Preliminary Math Concept of Stress Stress Components Equilibrium
" W I T H M I A L I O E T O W A R D istolste A N D O H A P l t T Y F O B, A I j L. ; " * Jm MVERSEO IT.
 P Y V V 9 G G G -PP - P V P- P P G P -- P P P Y Y? P P < PG! P3 ZZ P? P? G X VP P P X G - V G & X V P P P V P» Y & V Q V V Y G G G? Y P P Y P V3»! V G G G G G # G G G - G V- G - +- - G G - G - G - - G
P Y V V 9 G G G -PP - P V P- P P G P -- P P P Y Y? P P < PG! P3 ZZ P? P? G X VP P P X G - V G & X V P P P V P» Y & V Q V V Y G G G? Y P P Y P V3»! V G G G G G # G G G - G V- G - +- - G G - G - G - - G
M E 320 Professor John M. Cimbala Lecture 10
 M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
M E 320 Professor John M. Cimbala Lecture 10 Today, we will: Finish our example problem rates of motion and deformation of fluid particles Discuss the Reynolds Transport Theorem (RTT) Show how the RTT
Lowell Dam Gone Out. Streets Turned I n t o Rivers. No Cause For Alarm Now However As This Happened 35 Years A&o
 V ()\\ ))? K K Y 6 96 Y - Y Y V 5 Z ( z x z \ - \ - - z - q q x x - x 5 9 Q \ V - - Y x 59 7 x x - Y - x - - x z - z x - ( 7 x V 9 z q &? - 9 - V ( x - - - V- [ Z x z - -x > -) - - > X Z z ( V V V
V ()\\ ))? K K Y 6 96 Y - Y Y V 5 Z ( z x z \ - \ - - z - q q x x - x 5 9 Q \ V - - Y x 59 7 x x - Y - x - - x z - z x - ( 7 x V 9 z q &? - 9 - V ( x - - - V- [ Z x z - -x > -) - - > X Z z ( V V V
2x (x 2 + y 2 + 1) 2 2y. (x 2 + y 2 + 1) 4. 4xy. (1, 1)(x 1) + (1, 1)(y + 1) (1, 1)(x 1)(y + 1) 81 x y y + 7.
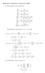 Homework 8 Solutions, November 007. (1 We calculate some derivatives: f x = f y = x (x + y + 1 y (x + y + 1 x = (x + y + 1 4x (x + y + 1 4 y = (x + y + 1 4y (x + y + 1 4 x y = 4xy (x + y + 1 4 Substituting
Homework 8 Solutions, November 007. (1 We calculate some derivatives: f x = f y = x (x + y + 1 y (x + y + 1 x = (x + y + 1 4x (x + y + 1 4 y = (x + y + 1 4y (x + y + 1 4 x y = 4xy (x + y + 1 4 Substituting
Basic Equations of Elasticity
 A Basic Equations of Elasticity A.1 STRESS The state of stress at any point in a loaded bo is defined completely in terms of the nine components of stress: σ xx,σ yy,σ zz,σ xy,σ yx,σ yz,σ zy,σ zx,andσ
A Basic Equations of Elasticity A.1 STRESS The state of stress at any point in a loaded bo is defined completely in terms of the nine components of stress: σ xx,σ yy,σ zz,σ xy,σ yx,σ yz,σ zy,σ zx,andσ
Maxima and Minima. Marius Ionescu. November 5, Marius Ionescu () Maxima and Minima November 5, / 7
 Maxima and Minima Marius Ionescu November 5, 2012 Marius Ionescu () Maxima and Minima November 5, 2012 1 / 7 Second Derivative Test Fact Suppose the second partial derivatives of f are continuous on a
Maxima and Minima Marius Ionescu November 5, 2012 Marius Ionescu () Maxima and Minima November 5, 2012 1 / 7 Second Derivative Test Fact Suppose the second partial derivatives of f are continuous on a
x 9 or x > 10 Name: Class: Date: 1 How many natural numbers are between 1.5 and 4.5 on the number line?
 1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
LOWELL WEEKLY JOURNAL
 W WY R G «( 5 R 5 Y q YG R ««W G WY Y 7 W \(\ 5 R ( W R R W ) W «W W W W< W ) W 53 R R Y 4 RR \ \ ( q ) W W X R R RY \ 73 «\ 2 «W R RG ( «q ) )[ 5 7 G ««R q ] 6 ) X 5 5 x / ( 2 3 4 W «(«\Y W Q RY G G )
W WY R G «( 5 R 5 Y q YG R ««W G WY Y 7 W \(\ 5 R ( W R R W ) W «W W W W< W ) W 53 R R Y 4 RR \ \ ( q ) W W X R R RY \ 73 «\ 2 «W R RG ( «q ) )[ 5 7 G ««R q ] 6 ) X 5 5 x / ( 2 3 4 W «(«\Y W Q RY G G )
DIPOLES III. q const. The voltage produced by such a charge distribution is given by. r r'
 DIPOLES III We now consider a particularly important charge configuration a dipole. This consists of two equal but opposite charges separated by a small distance. We define the dipole moment as p lim q
DIPOLES III We now consider a particularly important charge configuration a dipole. This consists of two equal but opposite charges separated by a small distance. We define the dipole moment as p lim q
AE/ME 339. Computational Fluid Dynamics (CFD) K. M. Isaac. Momentum equation. Computational Fluid Dynamics (AE/ME 339) MAEEM Dept.
 AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
AE/ME 339 Computational Fluid Dynamics (CFD) 9//005 Topic7_NS_ F0 1 Momentum equation 9//005 Topic7_NS_ F0 1 Consider the moving fluid element model shown in Figure.b Basis is Newton s nd Law which says
12. Stresses and Strains
 12. Stresses and Strains Finite Element Method Differential Equation Weak Formulation Approximating Functions Weighted Residuals FEM - Formulation Classification of Problems Scalar Vector 1-D T(x) u(x)
12. Stresses and Strains Finite Element Method Differential Equation Weak Formulation Approximating Functions Weighted Residuals FEM - Formulation Classification of Problems Scalar Vector 1-D T(x) u(x)
V o l u m e 5, N u m b e r 5 2, 1 6 P a g e s. Gold B e U ClUt Stamps Double Stamp D a y E v e r y Wednesday
 1 6 5 J 9 6 " " z k ; k x k k k z z k j " " ( k " " k 8 1959 " " x k j 5 25 ; ; k k qz ; x 13 x k * k ( ) k k : qz 13 k k k j ; q k x ; x 615 26 ( : k z 113 99751 z k k q ; 15 k k k j q " " k j x x ( *»
1 6 5 J 9 6 " " z k ; k x k k k z z k j " " ( k " " k 8 1959 " " x k j 5 25 ; ; k k qz ; x 13 x k * k ( ) k k : qz 13 k k k j ; q k x ; x 615 26 ( : k z 113 99751 z k k q ; 15 k k k j q " " k j x x ( *»
CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer
 CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Monday October 3: Discussion Assignment
CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Monday October 3: Discussion Assignment
Applications of Eigenvalues & Eigenvectors
 Applications of Eigenvalues & Eigenvectors Louie L. Yaw Walla Walla University Engineering Department For Linear Algebra Class November 17, 214 Outline 1 The eigenvalue/eigenvector problem 2 Principal
Applications of Eigenvalues & Eigenvectors Louie L. Yaw Walla Walla University Engineering Department For Linear Algebra Class November 17, 214 Outline 1 The eigenvalue/eigenvector problem 2 Principal
Course 2BA1: Hilary Term 2007 Section 8: Quaternions and Rotations
 Course BA1: Hilary Term 007 Section 8: Quaternions and Rotations David R. Wilkins Copyright c David R. Wilkins 005 Contents 8 Quaternions and Rotations 1 8.1 Quaternions............................ 1 8.
Course BA1: Hilary Term 007 Section 8: Quaternions and Rotations David R. Wilkins Copyright c David R. Wilkins 005 Contents 8 Quaternions and Rotations 1 8.1 Quaternions............................ 1 8.
Chapter 2 : Boolean Algebra and Logic Gates
 Chapter 2 : Boolean Algebra and Logic Gates By Electrical Engineering Department College of Engineering King Saud University 1431-1432 2.1. Basic Definitions 2.2. Basic Theorems and Properties of Boolean
Chapter 2 : Boolean Algebra and Logic Gates By Electrical Engineering Department College of Engineering King Saud University 1431-1432 2.1. Basic Definitions 2.2. Basic Theorems and Properties of Boolean
Wayfarer Traveler. The. Laura. Most of us enjoy. Family and multi-generational travel. The Luxury of Togetherness. Happy Traveling, Owner s
 6, z j Kw x w 8- x - w w w; x w w z, K, x -, w w w, w! x w j w w x z w w J w w w, w w w x w w w w 6, w q, w x, w x x, w Q, w 3-, w,, -w 6 ;, w x w w-- w j -, -, x, - -,, -,, w,, w w w, w w w, - w, w,,
6, z j Kw x w 8- x - w w w; x w w z, K, x -, w w w, w! x w j w w x z w w J w w w, w w w x w w w w 6, w q, w x, w x x, w Q, w 3-, w,, -w 6 ;, w x w w-- w j -, -, x, - -,, -,, w,, w w w, w w w, - w, w,,
CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer
 CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2016 Announcements Project 1 due next Friday at
CSE 167: Introduction to Computer Graphics Lecture #2: Linear Algebra Primer Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2016 Announcements Project 1 due next Friday at
6. SCALARS, VECTORS, AND TENSORS (FOR ORTHOGONAL COORDINATE SYSTEMS)
 (FOR ORTHOGONAL COORDINATE SYSTEMS) I Main Topics A What are scalars, vectors, and tensors? B Order of scalars, vectors, and tensors C Linear transformaoon of scalars and vectors (and tensors) D Matrix
(FOR ORTHOGONAL COORDINATE SYSTEMS) I Main Topics A What are scalars, vectors, and tensors? B Order of scalars, vectors, and tensors C Linear transformaoon of scalars and vectors (and tensors) D Matrix
Problem Set 2 Due Tuesday, September 27, ; p : 0. (b) Construct a representation using five d orbitals that sit on the origin as a basis: 1
 Problem Set 2 Due Tuesday, September 27, 211 Problems from Carter: Chapter 2: 2a-d,g,h,j 2.6, 2.9; Chapter 3: 1a-d,f,g 3.3, 3.6, 3.7 Additional problems: (1) Consider the D 4 point group and use a coordinate
Problem Set 2 Due Tuesday, September 27, 211 Problems from Carter: Chapter 2: 2a-d,g,h,j 2.6, 2.9; Chapter 3: 1a-d,f,g 3.3, 3.6, 3.7 Additional problems: (1) Consider the D 4 point group and use a coordinate
1 Partial differentiation and the chain rule
 1 Partial differentiation and the chain rule In this section we review and discuss certain notations and relations involving partial derivatives. The more general case can be illustrated by considering
1 Partial differentiation and the chain rule In this section we review and discuss certain notations and relations involving partial derivatives. The more general case can be illustrated by considering
Demonstration of the Coupled Evolution Rules 163 APPENDIX F: DEMONSTRATION OF THE COUPLED EVOLUTION RULES
 Demonstration of the Coupled Evolution Rules 163 APPENDIX F: DEMONSTRATION OF THE COUPLED EVOLUTION RULES Before going into the demonstration we need to point out two limitations: a. It assumes I=1/2 for
Demonstration of the Coupled Evolution Rules 163 APPENDIX F: DEMONSTRATION OF THE COUPLED EVOLUTION RULES Before going into the demonstration we need to point out two limitations: a. It assumes I=1/2 for
AB-267 DYNAMICS & CONTROL OF FLEXIBLE AIRCRAFT
 FLÁIO SILESTRE DYNAMICS & CONTROL OF FLEXIBLE AIRCRAFT LECTURE NOTES LAGRANGIAN MECHANICS APPLIED TO RIGID-BODY DYNAMICS IMAGE CREDITS: BOEING FLÁIO SILESTRE Introduction Lagrangian Mechanics shall be
FLÁIO SILESTRE DYNAMICS & CONTROL OF FLEXIBLE AIRCRAFT LECTURE NOTES LAGRANGIAN MECHANICS APPLIED TO RIGID-BODY DYNAMICS IMAGE CREDITS: BOEING FLÁIO SILESTRE Introduction Lagrangian Mechanics shall be
Numerical Implementation of Transformation Optics
 ECE 5322 21 st Century Electromagnetics Instructor: Office: Phone: E Mail: Dr. Raymond C. Rumpf A 337 (915) 747 6958 rcrumpf@utep.edu Lecture #16b Numerical Implementation of Transformation Optics Lecture
ECE 5322 21 st Century Electromagnetics Instructor: Office: Phone: E Mail: Dr. Raymond C. Rumpf A 337 (915) 747 6958 rcrumpf@utep.edu Lecture #16b Numerical Implementation of Transformation Optics Lecture
Stress, Strain, Mohr s Circle
 Stress, Strain, Mohr s Circle The fundamental quantities in solid mechanics are stresses and strains. In accordance with the continuum mechanics assumption, the molecular structure of materials is neglected
Stress, Strain, Mohr s Circle The fundamental quantities in solid mechanics are stresses and strains. In accordance with the continuum mechanics assumption, the molecular structure of materials is neglected
CHAPTER 2 BOOLEAN ALGEBRA
 CHAPTER 2 BOOLEAN ALGEBRA This chapter in the book includes: Objectives Study Guide 2.1 Introduction 2.2 Basic Operations 2.3 Boolean Expressions and Truth Tables 2.4 Basic Theorems 2.5 Commutative, Associative,
CHAPTER 2 BOOLEAN ALGEBRA This chapter in the book includes: Objectives Study Guide 2.1 Introduction 2.2 Basic Operations 2.3 Boolean Expressions and Truth Tables 2.4 Basic Theorems 2.5 Commutative, Associative,
MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions. December 6, 2017, Wednesday 10:40-12:30, SA-Z02
 1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
1 MATH443 PARTIAL DIFFERENTIAL EQUATIONS Second Midterm Exam-Solutions December 6 2017 Wednesday 10:40-12:30 SA-Z02 QUESTIONS: Solve any four of the following five problems [25]1. Solve the initial and
Wave and Elasticity Equations
 1 Wave and lasticity quations Now let us consider the vibrating string problem which is modeled by the one-dimensional wave equation. Suppose that a taut string is suspended by its extremes at the points
1 Wave and lasticity quations Now let us consider the vibrating string problem which is modeled by the one-dimensional wave equation. Suppose that a taut string is suspended by its extremes at the points
Numerical Modelling in Geosciences. Lecture 6 Deformation
 Numerical Modelling in Geosciences Lecture 6 Deformation Tensor Second-rank tensor stress ), strain ), strain rate ) Invariants quantities independent of the coordinate system): - First invariant trace:!!
Numerical Modelling in Geosciences Lecture 6 Deformation Tensor Second-rank tensor stress ), strain ), strain rate ) Invariants quantities independent of the coordinate system): - First invariant trace:!!

 «4 [< «
«4 [< «  Y G q G Y Y 29 8 $ 29 G 6 q )
Y G q G Y Y 29 8 $ 29 G 6 q )  9 Q - -
9 Q - -  7 ( - ( - < Q & > & )
7 ( - ( - < Q & > & )  g k b 7? 3 5 y y Qk
g k b 7? 3 5 y y Qk